| 1. |
Выразить одну переменную через другую
Сложность: лёгкое |
1 |
| 2. |
Выразить переменную a через переменную b
|
1 |
| 3. |
Система линейных уравнений
Сложность: лёгкое |
2 |
| 4. |
Вычисление одной переменной системы, если известна вторая переменная (обыкновенные дроби)
Сложность: лёгкое |
2 |
| 5. | Сложность: среднее |
3 |
| 6. |
Прямая пропорциональность и линейная функция (коэффициент — отрицательная десятичная дробь)
Сложность: среднее |
3 |
| 7. |
Система двух уравнений (число, противоположное отрицательному)
Сложность: среднее |
4 |
| 8. |
Система линейных уравнений (переменная во втором уравнении выражена)
Сложность: среднее |
5 |
| 9. | Система двух линейных уравнений (распределительный закон умножения) Сложность: среднее | 5 |
| 10. |
Система линейных уравнений, раскрытие скобок
Сложность: сложное | 8 |
| 11. |
Система дробных уравнений
Сложность: сложное |
8 |
| 12. |
Система двух дробных уравнений
Сложность: сложное |
8 |
www.yaklass.ru
План-конспект урока по алгебре (7 класс): Разработка урока «Метод подстановки» 7 класс
Конспект урока по алгебре в 7 классе на тему:
«Метод подстановки»
Учитель: Покацкая Анна Федоровна ,учитель МБОУ «Тарбагатайская СОШ»
Цель урока: формирование у учащихся умения решать системы линейных уравнений с двумя неизвестными способом подстановки.
Образовательные: обобщение и систематизация знаний и умений учащихся при решении систем линейных уравнений с двумя переменными.
Развивающие: развитие математического и общего кругозора, мышления и речи учащихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.
Воспитательные: воспитание интереса к математике, активности, общей культуры, организованности и взаимопомощи через работу в парах.
Методы: частично – поисковый, коллективный, индивидуальный.
Тип урока: урок открытия новых знаний
Оборудование: мультимедийное оборудование, проектор, экран, раздаточный материал.
Литература: Учебник Макарычев Ю.Н. Алгебра 7. Издательство «Мнемозина»
№ | Этап урока | Время | Задачи этапа |
1. | Организационный момент | 1 мин. | |
2. | Проверка домашнего задания | 3 мин. | Проверка правильности выполнения домашнего задания. |
3. | Актуализация опорных знаний учащихся | 5 мин. | Повторить основные определения; активизировать осознанность применения знаний при решении задач. |
4. | Изучение нового материала | 15 мин. | Знакомство учащихся с алгоритмом решения системы двух уравнений с двумя переменными методом подстановки (обратить внимание на оформление решений) |
6. | Закрепления изученного материала | 15 мин. | Сформировать умение решать системы уравнений методом подстановки |
7. | Домашнее задание | 2 мин. | Инструктаж по домашнему заданию |
Ход урока:
Этап №1. Организационный момент:
-Здравствуйте, ребята. Сегодня у нас на уроке присутствуют гости, поздоровайтесь, пожалуйста, садитесь.
Улыбнемся друг другу, и с хорошим настроением начинаем работать.
Один из великих философов сказал: “ ГДЕ ЕСТЬ ЖЕЛАНИЕ, НАЙДЕТСЯ ПУТЬ!”. Я думаю, что сегодня на уроке мы с большим желанием будем решать системы, и не просто решать, а определяя свой рациональный путь.
Как вы справились с домашним заданием? Есть вопросы? Давайте просто я вам скажу ответы, а вы поставите себе балл.
На прошлом уроке мы с вами познакомились с новой математической моделью.
Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными.
Ответим на несколько вопросов:
Этап №2. Теоретический опрос (устно)
Слайд3
1. что такое решение системы? (это пара значений, которая одновременно является решением всех уравнений системы)
2. что означает решить систему уравнений? (значит найти все её решения или установить, что их нет) Слайд 4
3. Является ли решением системы (Слайд 7)
пара чисел: а) х=3, у=1
б) х=2, у=2 ?
- Раскрыть скобки -2(х-3)= -2х+6
2) Выразить у через х
х+у=3 у=3-х
3) Выразить х через у
2х-у=4 х=2+0,5у
4) Решить уравнение
2х-8=1
Этап №3. Актуализация опорных знаний
-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).
Алгоритм графического способа:
- Построить графики каждого из уравнений системы.
- Найти координаты точки пересечения построенных прямых (если они пересекаются)
- Графический способ удобен, для определения количества корней ситемы уравнений.
(слайд 10,11,12,13)
Практическое задание:
Решить систему уравнений графическим способом (работаем в парах)
Задания делают на заранее приготовленных листах А4 с клетками, чтобы потом вывесить на доску, сравнить результаты и установить проблему урока.(слайд №14,15)
Вывод:
Для решения данных систем уравнений графический способ не удобен. Решением первой системы являются дробные числа, которые трудно определить по графику. Решением второй системы являются большие числа, для определения которых не достаточно тетради.
Таким образом, необходим другой способ решения систем уравнений, который нас не подведет в случае с дробными значениями координат точки.
Этим мы и займемся сегодня на уроке
Этап №4
-В тетрадях запишите, пожалуйста, число.
Тема урока: «Метод подстановки».
Как вы думаете, какова цель нашего урока?
— узнать новый метод
— получить алгоритм решения систем
— научиться применять алгоритм
Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках. Итак:
№1. Выразить переменную У через Х в следующих уравнениях: (К доске пойдет…)
(Вызвать к доске ученика, задание на доске, следить за устной речью ученика, ученик комментирует свое решение)
5х-2у=0,
3х+2у=16
Ответ: у=2,5х у=8-1,5х.
Решаем из учебника у доски и в тетрадях № 12.7(а,б)
№2. Слайд 5, 6 На слайде приведено решение системы двух линейных уравнений с двумя переменными методом подстановки.
Затем еще 2 примера и дети составляют алгоритм.
Составим алгоритм по ключевым словам:
— выразим
— подставим
— решим
— подставим
— ответ
В учебнике найдите алгоритм решения и внимательно прочитайте его.
-Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.
Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.
Попробуем решить системы, которые вы решали в начале урока, но теперь методом подстановки:
Кто может пойти к доске и выполнить это задание? (К доске…)
-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений — почему?
Работа в парах
Сейчас мы с вами будем работать в парах: Решаем №1069, а)
Странички истории.
Существует, ребята, еще один способ решения систем уравнений, который мы с вами еще не рассматривали. Это метод — метод перебора или подбора. Например, дается система:
х + у = 7,
х – у = 1
Можно легко подобрать значения х и у: х = 4, у = 3
-Попробуйте решить систему методом подбора:
х + у = 5
х2 — у = 7, х = 3, у = 2
Все эти способы решения систем уравнений знали люди давно. Точной даты неизвестно, но они имеются в книге Ньютона «Всеобщая арифметика», которая была издана в 1707 году.
Рефлексия:
Обратите внимание на доску. В начале урока мы с вами записали цели урока. Добились ли мы цели? Решили ли проблему? Чем будем заниматься на следующих уроках?
Шёл мудрец, а навстречу ему три человека, везли под горячим солнцем тележки с камнями для строительства храма. Мудрец остановился и задал каждому по вопросу. У первого спросил: — Что ты делал целый день?
И тот с ухмылкою ответил, что целый день возил проклятые камни.
У второго спросил: ” А ты что делал целый день? ”- И тот ответил: ” Я добросовестно выполнял свою работу. А третий улыбнулся, его лицо засветилось радостью и удовольствием, и он ответил: “ А я принимал участие в строительстве Храма“ .
-Ребята! Кто работал так как первый человек? (поднимаем желтые)
-Кто работал добросовестно? (зелёные )
-А кто принимал участие в строительстве Храма знаний? (красные
Этап № 9. Итог урока: Домашнее задание: знать алгоритм, № 1072 (б), № 1070(в,г),
Дополнительно в тетради.
Оценки сегодня получили… Спасибо за урок. До свидания.
nsportal.ru
Урок алгебры в 7-м классе по теме «Метод подстановки»
Цель урока:
- Повторить правила раскрытия скобок, приведения подобных и решения линейных уравнений.
- Формировать умение решать системы линейных уравнений методом подстановки.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
Устно (с использованием мультимедийной презентации).
№ 1. Раскрыть скобки:
1)
2)
3)
4)
№ 2. Привести подобные:
1)
2)
3)
4)
№ 3. Решить уравнение:
1)
2)
III. Практическая работа: решить систему уравнений графическим способом.
| I вариант | II вариант |
IV. Проверка практической работы:
Вывод: для решения данных уравнений графический способ не удобен: в варианте 1 решением являются дробные числа, определить которые по графику трудно: в варианте 2 решением являются большие числа, для определения которых не достаточно страницы тетради. Для решения данных систем необходим другой способ решения.
V. Изучение нового материала (с использованием мультимедийной презентации).
1. Решение системы уравнений.
2. Составление алгоритма решения систем уравнений методом подстановки.
- Из любого уравнения выразить x или y (например: y из 1 уравнения).
- В другое уравнение вместо выраженной переменной (y) подставить полученное буквенное выражение .
- Получилось уравнение с одной переменной (x). Решив его, найти значение переменной (x).
- Подставить найденное значение переменной (x) в выражение, определённое на первом шаге (например: y). Вычислить значение другой переменной (y).
VI. Решение систем способом подстановки:
№ 1. Решить систему
Решение: , , 4х = 2 , х = 1/2.
y = 1/2 +1 = 1,5 . Ответ: ( 1/2; 1,5 ) .
№ 2. Решить систему
Решение: , , , y = 34, x = 21.
Ответ: (21; 34).
VII. Дополнительные задания: № 1081 (а), 1082 (а), 1085 (а).
VIII. Домашнее задание: стр. 151 , выучить алгоритм. № 1081 (б), 1082 (б), 1085 (б).
urok.1sept.ru
Методическая разработка по алгебре (7 класс) на тему: Конспект урока 7 класс » «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ»
Итак, у нас есть опыт и мы убедились, что графический метод решения выручает нас не всегда. Значит, нам нужно располагать надежным алгебраическим методом, который нас не подведет в случае с большими или дробными значениями координат точки.
Этим мы и займемся сегодня на уроке.
-В тетрадях запишите, пожалуйста, число, Классная работа.
Тема урока: «Метод подстановки». Как вы думаете, какова цель нашего урока?
Попробуем решить систему, которою решал на доске ….(ученик, вызванный ранее) другим способом: (учитель начинает рассуждение, затем продолжают ученики)
какова цель ? (1. найти общее решение уравнений;
- на языке графиков : найти точку пересечения соответствующих прямых, но….
не строя графики )
— Как тогда можно сформулировать задание( обсудите в парах если необходимо) :
Найдите координаты точки пересечения графиков уравнений ) 2х-у = 8 и х-у = -13 не выполняя построения.
Кто может пойти к доске и выполнить это задание? (К доске…)
Преобразуем уравнения (выразим в каждом значение у)
у = 2х-8 и у = х+13
-Нас интересует такое значение х, при которых:
2х-8 = х+13
х=21 , тогда у=34 Ответ(21;34)
-Чем эти рассуждения отличались от тех, которые применял ….(имя ученика) при решении этой системы графическим методом?
-Откройте, пожалуйста, учебник на странице 65 и, прочитав текст, ответьте мне на этот вопрос.
-Как же мы рассуждали? — выразили
— подставили
— решили
-нашли
-записали ответ
— У меня на доске, а у вас на столах листочки с этапами алгоритма, восстановите его последовательность (напечатано на цветных листах):
- Выбрать переменнную (выбираем желательно хорошую переменную: хорошо когда перед переменной коэффициент 1 или -1) и выразить одну (любую) переменную из любого уравнения.
- Подставить полученное выражение во второе уравнение
- Решить уравнение с одной переменной.
- Найденное значение переменной подставить в первое уравнение и найти значение второй переменной.
- Записать ответ
— Проанализируйте и сопоставьте алгоритм и решение которое мы получили. Сделайте выводы…..
— Ели бы вы решали бы сейчас систему с чего бы вы начали ….
Что делали бы дальше ….
( обсуждение в парах ), выводы учащихся.
Сравните свои рассуждения с предложенными
Решить систему уравнений методом подстановки | ||
1 вариант рассуждений | 2 вариант рассуждений |
|
| ||
2у-26-у=8 у=34 | х-2х+8=-13 -х=-21 х=21 |
|
х-34=-13 х=21 | 21-у=-13 -у=-34 у=34 |
|
Ответ : (21;34) | Ответ : (21;34) |
|
Выводы учащихся……
— Давайте вернемся ко второй системе, которая осталась без ответа и решим ее способом подстановки (вызвать к доске….)
=> => =>=> =>
=> => =>
Ответ : ()
Еще раз проговорим этапы алгоритма: (проговорить этапы, слайд мультимедиа)
nsportal.ru
План-конспект урока по алгебре (7 класс) на тему: Метод подстановки. 7 класс
Тема урока: «Метод подстановки»
Цели урока:
Образовательные: – отработка умений систематизировать, обобщать теоретические знания; закрепить и усовершенствовать навыки решения систем линейных уравнений методом подстановки.
Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Развивающие: — развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала.
Тип урока: — урок закрепления по теме.
Структура урока:
1. Организационный момент.
2. Мотивация учебной деятельности через осознание учащимися практической значимости применяемых знаний и умений; сообщение темы, целей и задач урока.
3. Воспроизведение изученного и его применение в стандартных ситуациях.
4. Элементы здоровьесберегающих технологий.
5. Перенос приобретенных знаний, их первичное применение в новых или изменённых условиях, с целью формирования умений.
6. Самостоятельное выполнение учащимися заданий под контролем учителя.
7. Подведение итогов урока и постановка домашнего задания.
Ход урока.
Организационный момент,
Тех, кто готов работу начать
Улыбки свои я прошу показать!
Все ребята готовы? Тогда повторяем,
Систематизируем, обобщаем, ИТАК, НАЧИНАЕМ!
Учитель объявляет тему урока, цели, настраивает учащихся на работу.
проверка д/з.
- Повторение теоретического материала, необходимого при выполнении заданий
Выполнение в парах работы «Соотнеси термины и формулировки»
1 | Система уравнений — это | 1 | пара их |
2 | Решение уравнения с двумя переменными — это | 2 | называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. |
3 | Если графики | 3 | Уравнение вида ax + by + c = 0 , где a, b и c — некоторые числа ( a ≠ 0 , b ≠ 0 ), |
4 | Линейное уравнение — это | 4 | то система не имеет решений; |
5 | Решением системы двух уравнений с двумя неизвестными | 5 | два или несколько уравнений, для которых необходимо найти все их общие решения |
6 | Если графики | 6 | Значит, найти все ее решения или установить, что их нет |
7 | Решить систему линейных уравнений — это | 7 | то система имеет одно решение; |
8 | Если графики | 8 | то система имеет бесконечное множество решений. |
- «Найди ошибку»
На доске записана часть решения №12.4 а из домашнего задания. Ребята должны указать на ряд ошибок, допущенных при решении. ( ответ системы уравнений соответствует оригиналу)
◦(-0,5)-2у=9,
+2у=9,
.
-0,5◦9, х=-4,5.
Ответ:(-4,5;9)
Фронтальная работа с классом.
- Учащийся у доски с объяснением решает № 12.9 а. Остальные работают на месте, после чего анализируют решение одноклассника.
- Самостоятельное выполнение №12.9 по рядам: б-1 ряд, в -2 ряд и г — 3 ряд. Первый решивший ученик с ряда выходит к доске и показывает решение, учащиеся проверяют решение.
ФИЗКУЛЬТМИНУТКА
Во всех делах умеренность нужна,
Пусть будет главным правилом она.
Гимнастикой займись, коль мыслил долго,
Болезни чтоб прогнать и сохранить здоровье.
Гимнастика не изнуряет тела,
Но очищает организм всецело!
Закройте глаза, расслабьте тело,
Представьте – вы птицы, вы вдруг полетели!
Теперь в океане дельфином плывете,
Теперь в саду яблоки спелые рвете.
Налево, направо, вокруг посмотрели,
Открыли глаза, и снова за дело!
III. Формирование знаний.
- Решение системы уравнений, состоящей из трех линейных уравнений.
IV. Самостоятельное выполнение теста на определение уровня усвоения базовых знаний
I вариант
- Решением системы является пара чисел
А. (0; 3)
Б. (3; 0)
В. (1; 2)
- Найдите систему линейных уравнений с двумя переменными:
А.
Б.
- Из уравнения х+2у = 1 выразите переменную х через переменную у.
А. х=2у-1
Б. х= -2у+1
В. Х=-2у-1
- Из первого уравнения системы выразили переменную x через переменную у. Подставив во второе уравнение вместо переменной х это выражение, получили:
А. 2(5-2у)+4у=8,
Б. 2(2у+5)+4у=8,
В. 2(2у-5)+4у=8.
- При каком значении k система имеет одно решение
А. k= -5
Б. k= 5
II вариант
- Решением системы является пара чисел
А. (0; 2)
Б. (2; 0)
В. (1; 2)
- Найдите систему линейных уравнений с двумя переменными:
А.
Б.
- Из уравнения 3х+у = 3 выразите переменную у через х.
А. у= 3х-3
Б. у= -3х-3
В. у= -3х-3
- Из второго уравнения системы выразили переменную у через переменную х. Подставив в первое уравнение вместо переменной у это выражение, получили:
А. 2х+3(4х+1) =9,
Б. 2х-3(4х+1) =9,
В. 2х+3(1-4х) =9
- При каком значении k система имеет множество решений
А. k= -8
V. Подведение итогов урока
Домашняя работа: №12.2-12.3 (а,б), №12.4б
Отметьте в оценочной карточке ваше отношение к уроку:
∙ Я доволен уроком, мне очень понравилось.
∙ Мне понравилось на уроке, но в моих знаниях есть пробелы.
∙ Урок прошел для меня даром, ничего нового я на нем не узнал.
∙ Я не доволен уроком, ничего не понял и как решать примеры я не знаю.
nsportal.ru
Конспект урока по математике на тему «Метод подстановки», 7 класс
Открытый урок: «Метод подстановки» 7 класс
Цель урока: формирование у учащихся умения решать системы линейных уравнений с двумя неизвестными способами подстановки.
Образовательные: обобщение и систематизация знаний и умений учащихся при решении систем линейных уравнений с двумя переменными.
Развивающие: развитие математического и общего кругозора, мышления и речи учащихся, способствовать формированию умений применять приёмы: обобщения, сравнения, выделения главного.
Воспитательные: воспитание интереса к математике, активности, общей культуры, организованности и взаимопомощи через работу в парах.
Методы: частично – поисковый, коллективный, групповой, индивидуальный.
Тип урока: урок открытия новых знаний
Оборудование: мультимедийное оборудование, проектор, экран, жетоны, раздаточный материал.
Литература: Учебник А.Г. Мордковича Алгебра 7. Издательство «Мнемозина» 2007.
Ход урока:
№1. Организационный момент:
Приготовились к уроку, встали у своих мест.
-Здравствуйте, ребята. Сегодня у нас на уроке присутствуют гости, поздоровайтесь, пожалуйста, садитесь.
Улыбнитесь себе, друг другу и мне, мы дружно и с хорошим настроением начинаем работать.
Унынье и лень уничтожить на нуль.
№2. Проверка домашнего задания
—Пока мы будем проверять домашнее задание, у доски нам решит систему графическим методом…(вызвать ученика к доске, задание на карточке).
. Открыли тетради, взяли красную пасту, проверяем:
-У кого не было ошибок, может поставить себе «5», у кого были помарки, исправления, неточности – красной пастой пишут: Домашнее задание проверено.
№3. Актуализация опорных знаний
На прошлом уроке мы с вами познакомились с новой математической моделью.
Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными. Перед нами стояла задача найти такие пары значений (х; у), которые одновременно удовлетворяют и первому, и второму уравнению.
-Кто может мне сказать:
Что называется решением системы двух линейных уравнений с двумя переменными
—Хорошо.
-А что значит решить систему двух линейных уравнений с двумя переменными?
-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).
-Дома, я также просила поработать вас с текстом параграфа №11, и найти ответ на вопрос: Почему для нас графический способ решения системы двух линейных уравнений имеет большое значение?». Кто нашел ответ на этот вопрос?
—ученик закончил решение системы. Сейчас он прокомментирует нам ее решение.
-Спасибо, садись.
-А сейчас, внимание на экран, я хочу показать вам решение графическим методом еще одной системы:
— На чертеже: построен синим цветом график первого линейного уравнения и зеленым цветом график второго уравнения. Как видите, графики пересекаются.
Координаты точки пересечения графиков и будут являться решением данной системы. Координаты данной точки являются решением и первого и второго линейных уравнений, т.к. точка принадлежит и первому и второму графикам функций. Однако, чему конкретно равны абсцисса и ордината точки, определить очень сложно. Точка «висит» внутри определенной клеточки.
Из этого примера видно, что графический метод решения выручает нас не всегда. Значит, нам нужно располагать надежным алгебраическим методом, который нас не подведет в случае с дробными значениями координат точки.
Этим мы и займемся сегодня на уроке.
Этап №4
—В тетрадях запишите, пожалуйста, число, Классная работа.
Тема урока: «Метод подстановки». Как вы думаете, какова цель нашего урока? Молодцы, правильно.
Джордж Бернард Шоу сказал: «Деятельность – единственный путь к знаниям».
— Как вы думаете, какой смысл заложен в этом изречении? (высказывания ребят).
-Правильно, ребята. Поэтому я предлагаю вам провести наш урок под этим девизом. За активную работу предусмотрены жетоны.
Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках. И так:
№1. Выразить переменную У через Х в следующих уравнениях: (К доске пойдет…)
(Вызвать к доске ученика, задание на доске, следить за устной речью ученика, ученик комментирует свое решение)
5х-2у=0, 3х+2у-16=0
Ответ: у=2,5х у=8-1,5х.
№2. Попробуем решить систему, которою решал на доске ….(ученик, вызванный ранее) другим способом: (учитель начинает рассуждение, затем продолжают ученики)
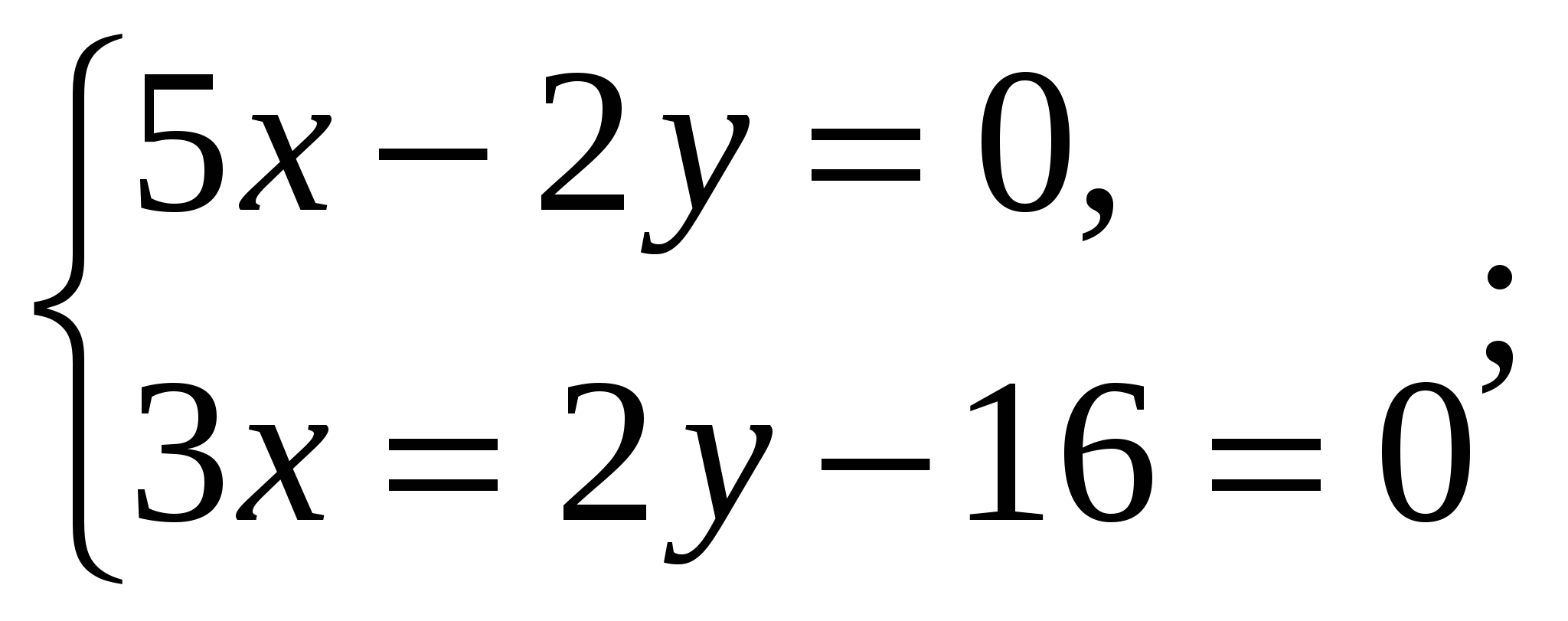Преобразуем эту систему к виду: 
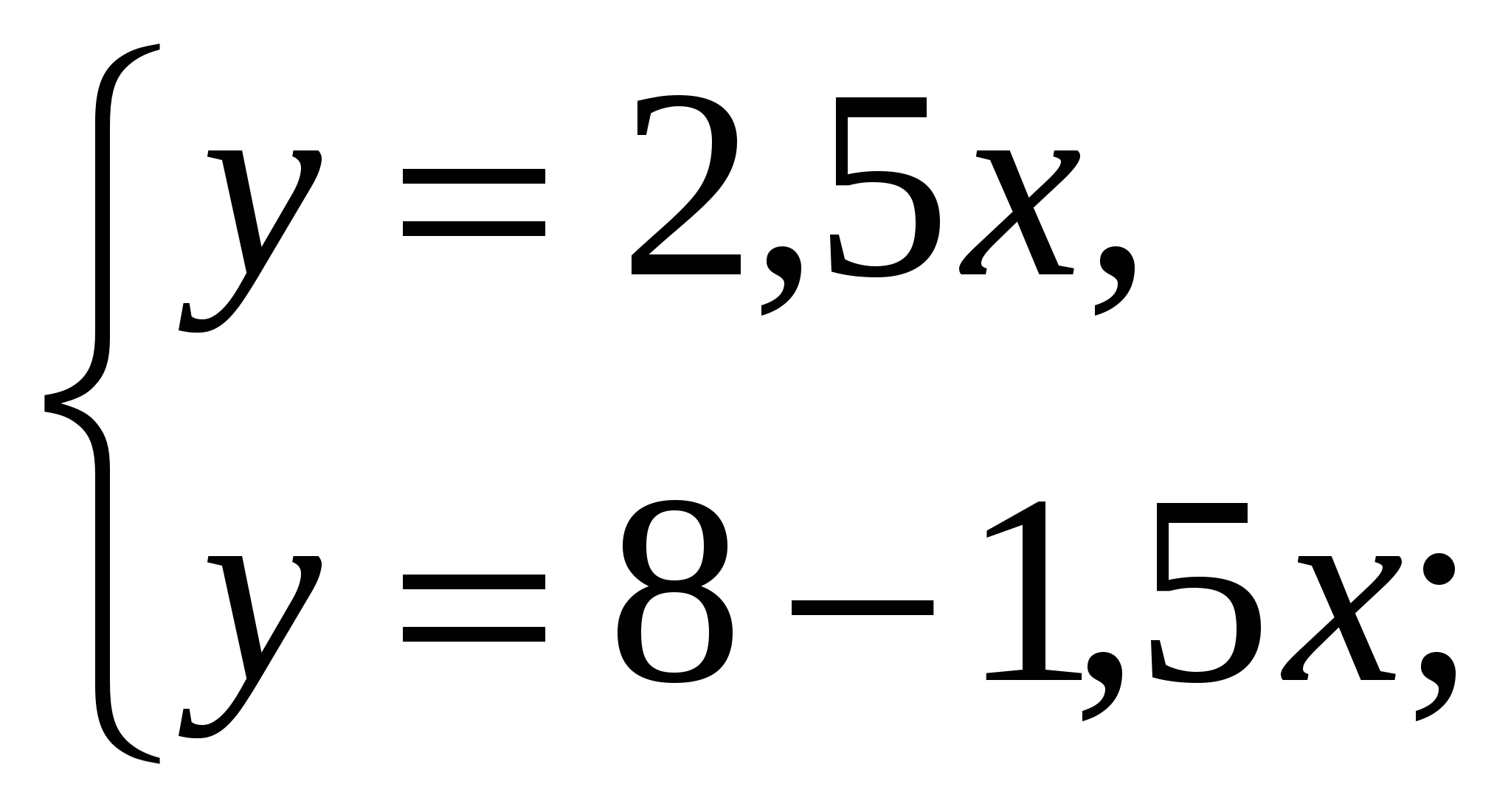
Вспомним, какие задания с такой формой записи мы решали с вами ранее? (Вопрос классу)
-Ответ: Найти точку пересечения графиков двух данных функций
Кто может пойти к доске и выполнить это задание? (К доске…)
-Нас интересует такое значение х, при которых: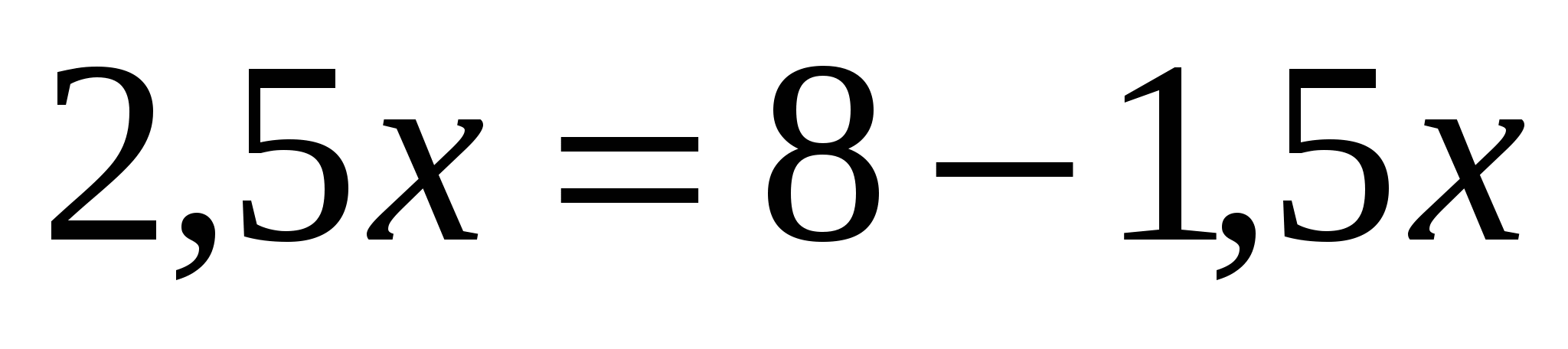 
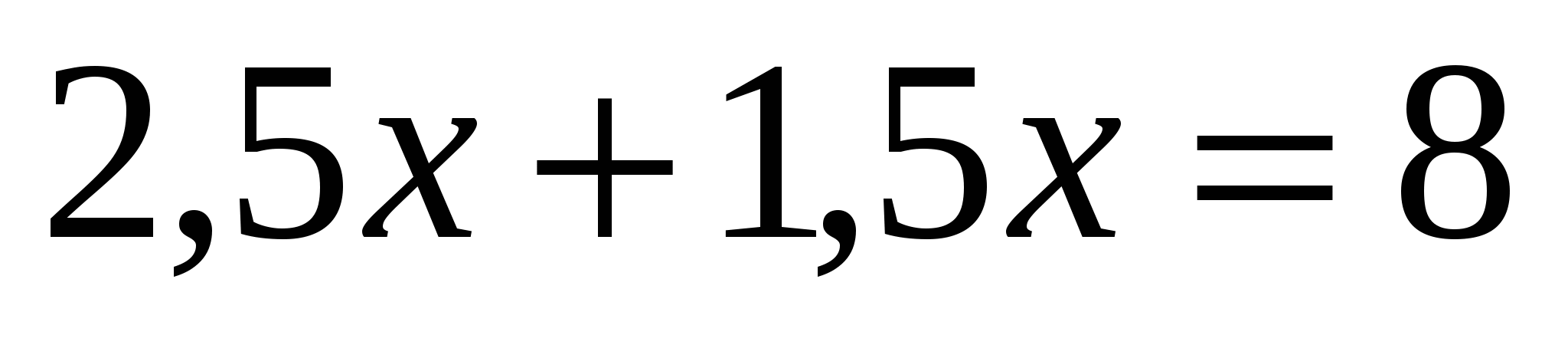
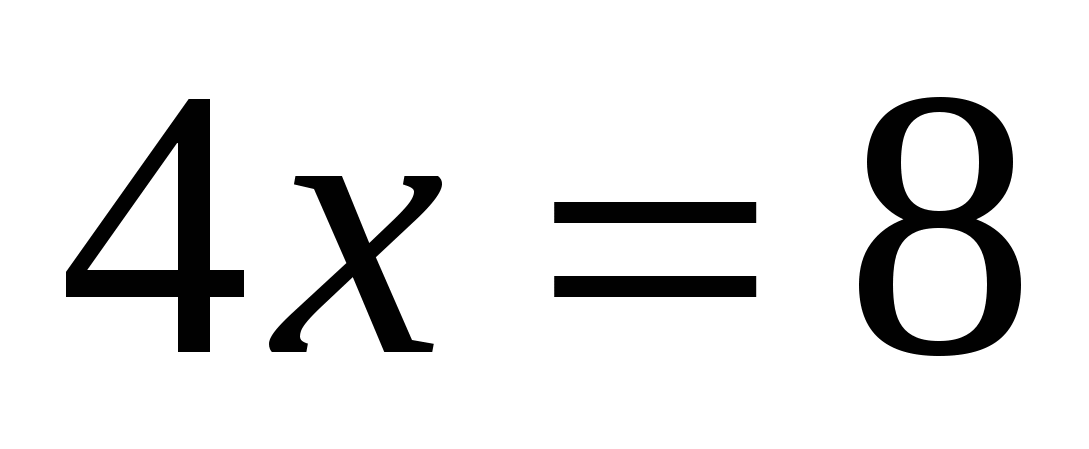
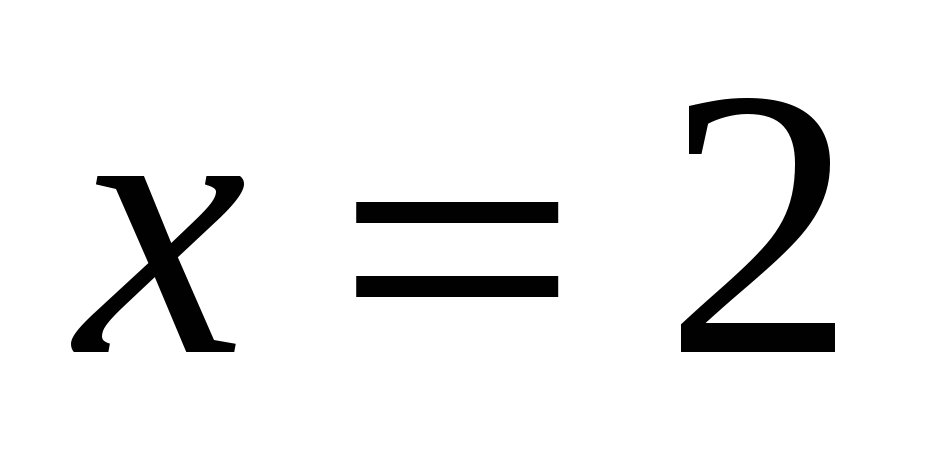Ответ(2;5)
-Чем эти рассуждения отличались от тех, которые применял ….(имя ученика) при решении этой системы графическим методом?
-Откройте, пожалуйста, учебник на странице 65 и, прочитав текст, ответьте мне на этот вопрос.
-Как же мы рассуждали? Еще раз по учебнику прочитает нам………..
-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений — почему?
Итак: — выразили
— подставили
— решили
-нашли
-записали ответ
В учебнике найдите алгоритм решения и внимательно прочитайте его.
-Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.
Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.
-Давайте вернемся к системе, которая осталась без ответа и решим ее способом подстановки (вызвать к доске….)
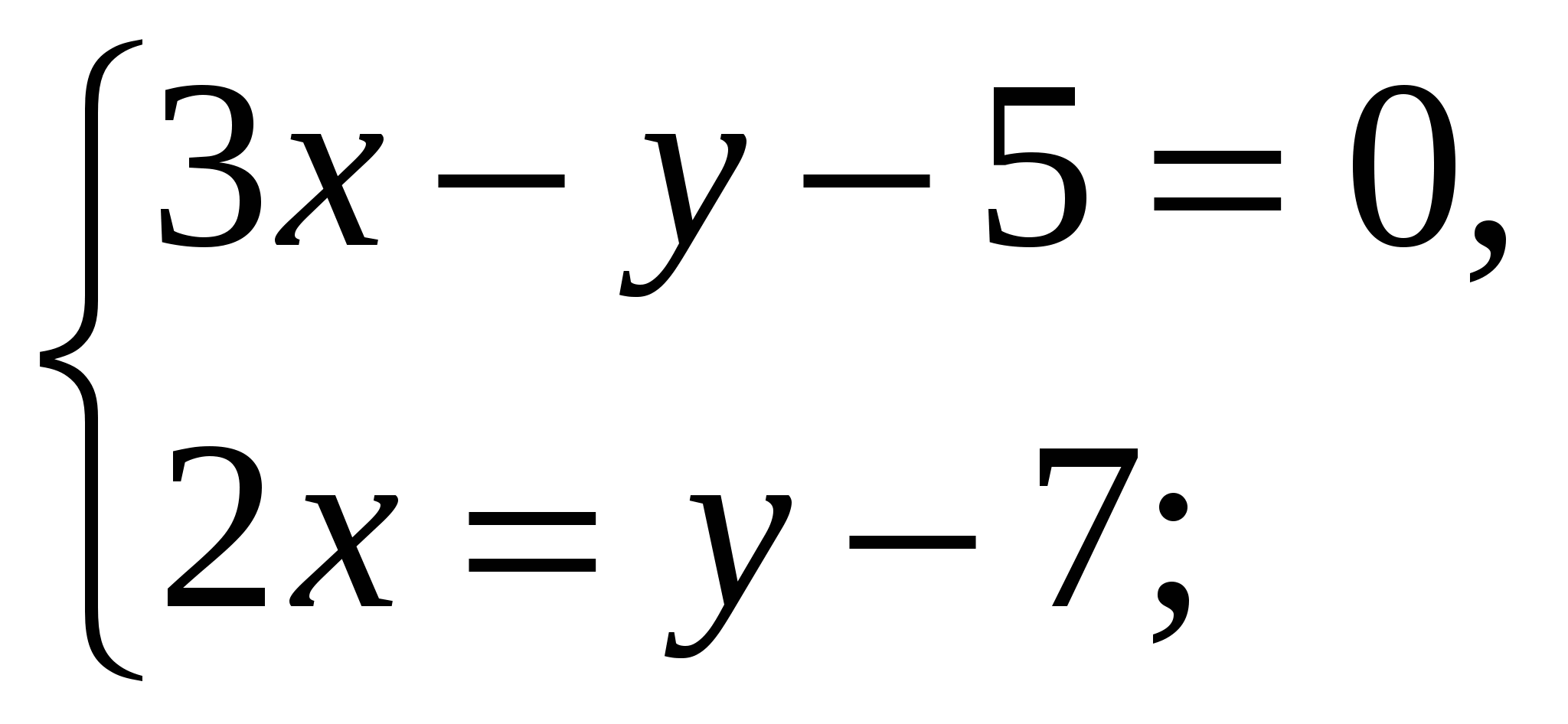
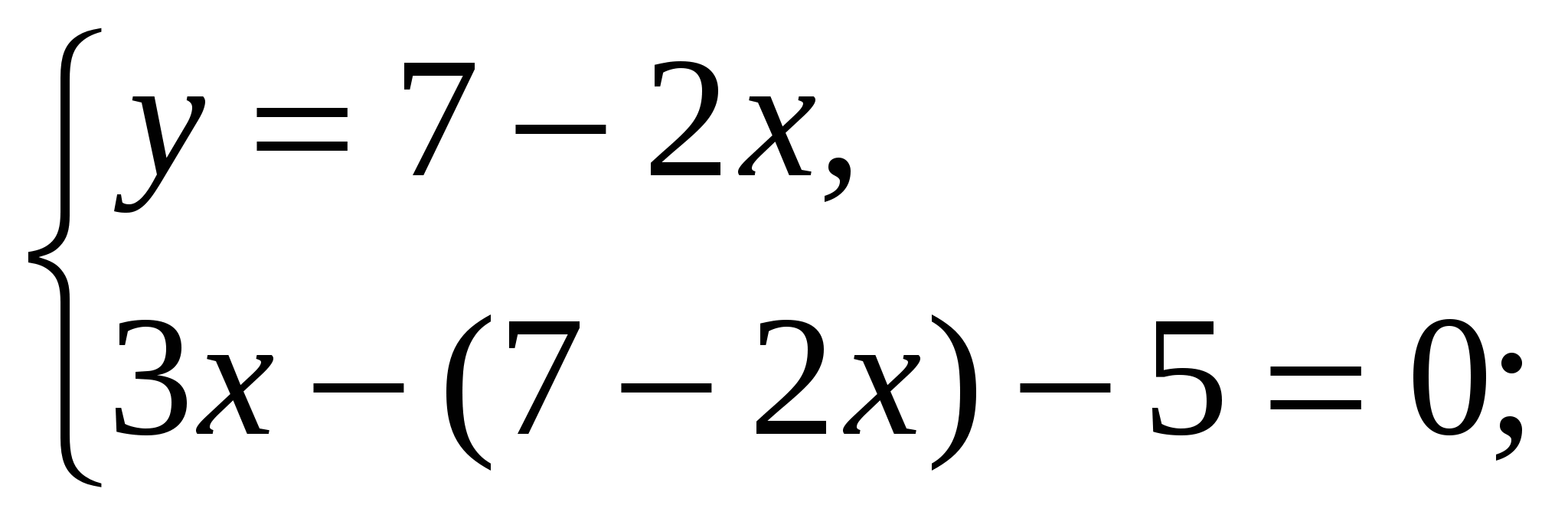
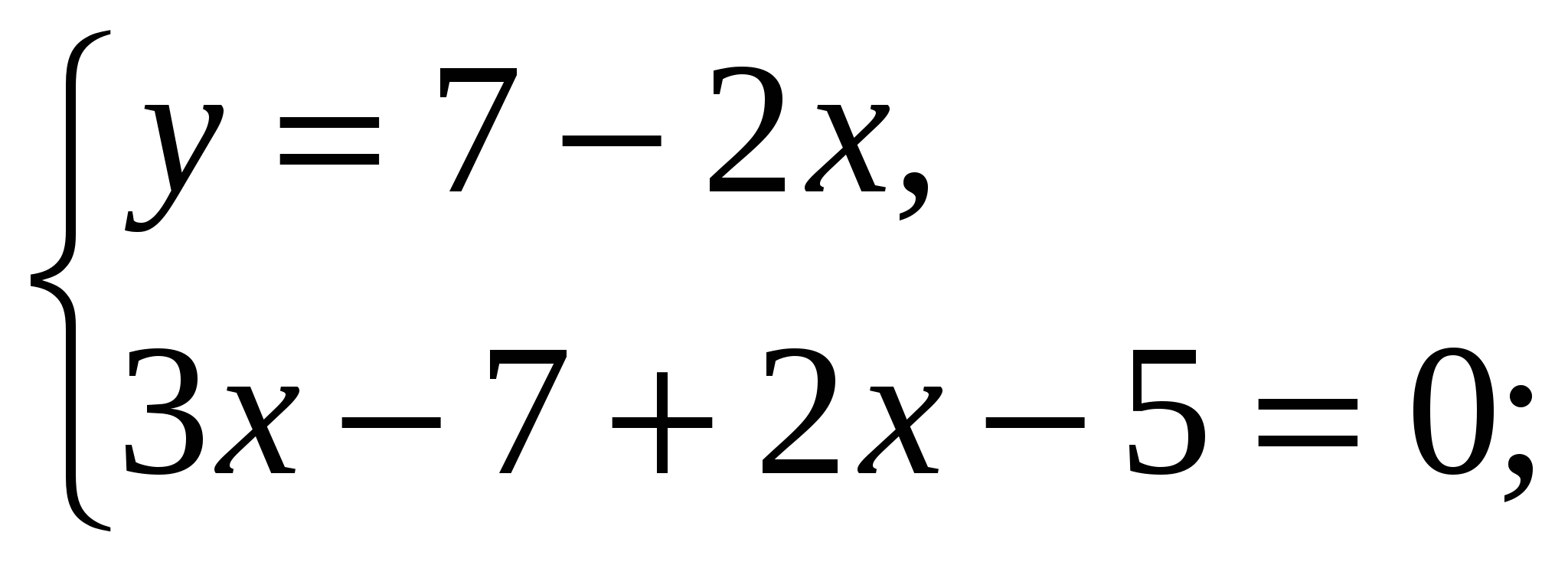
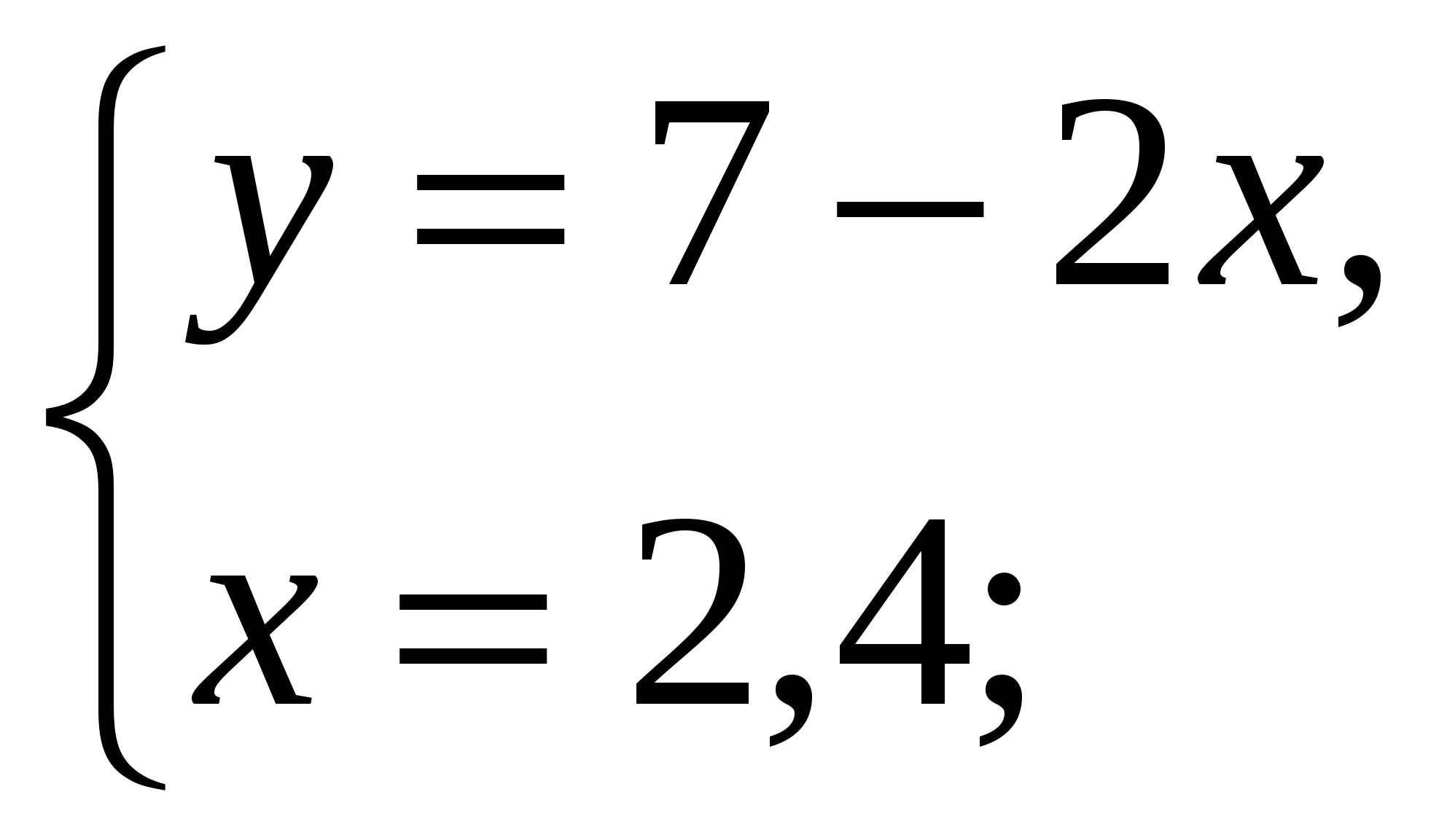
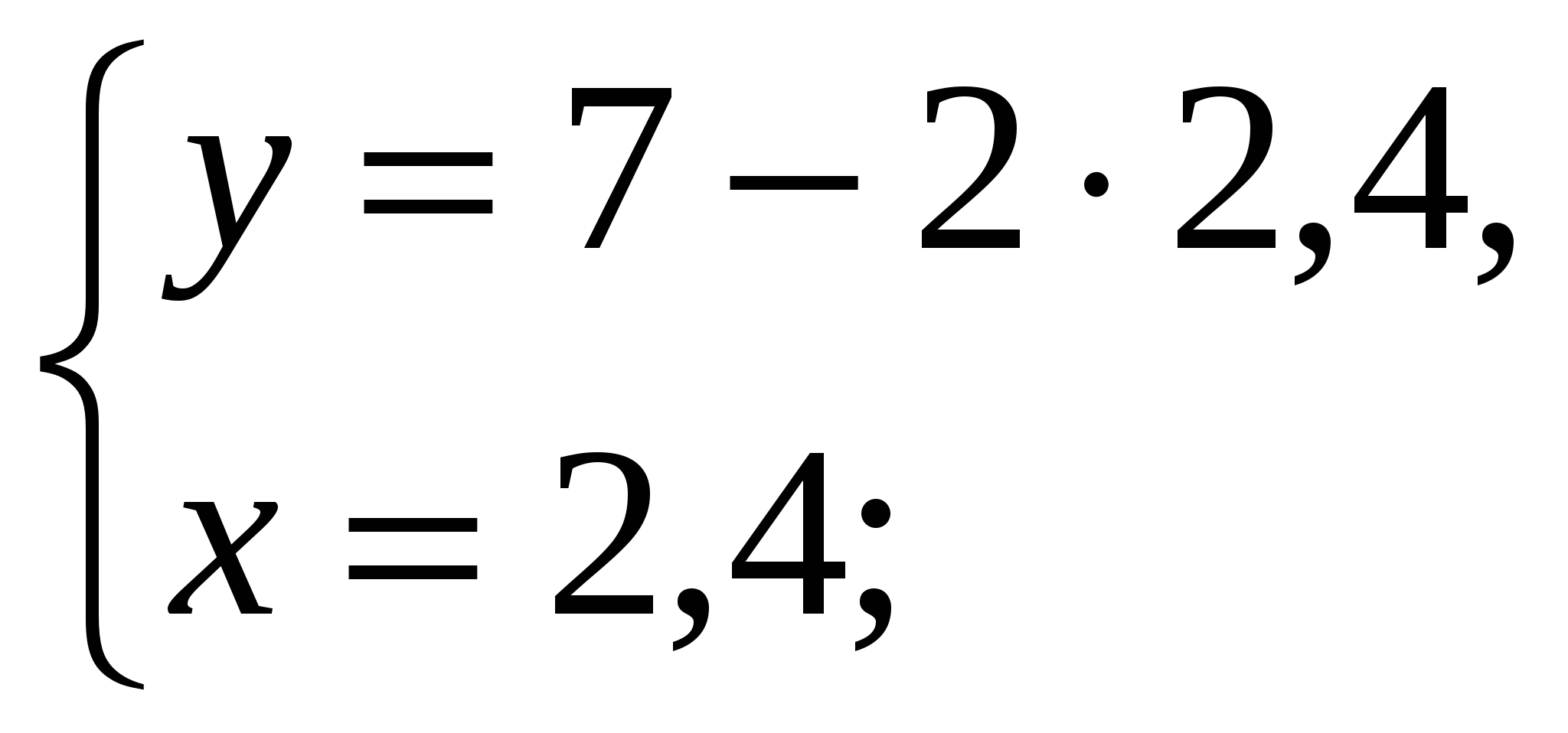
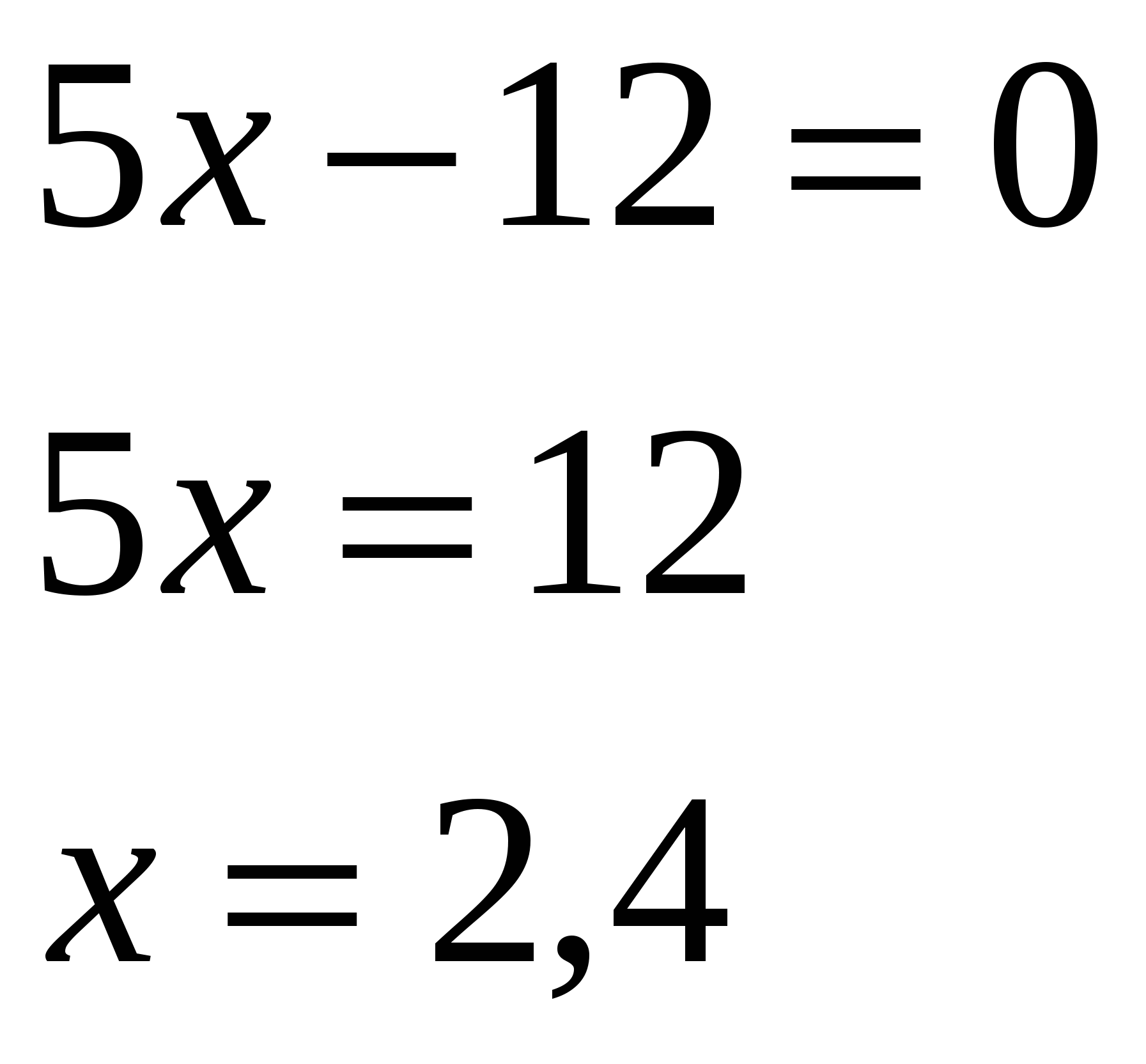
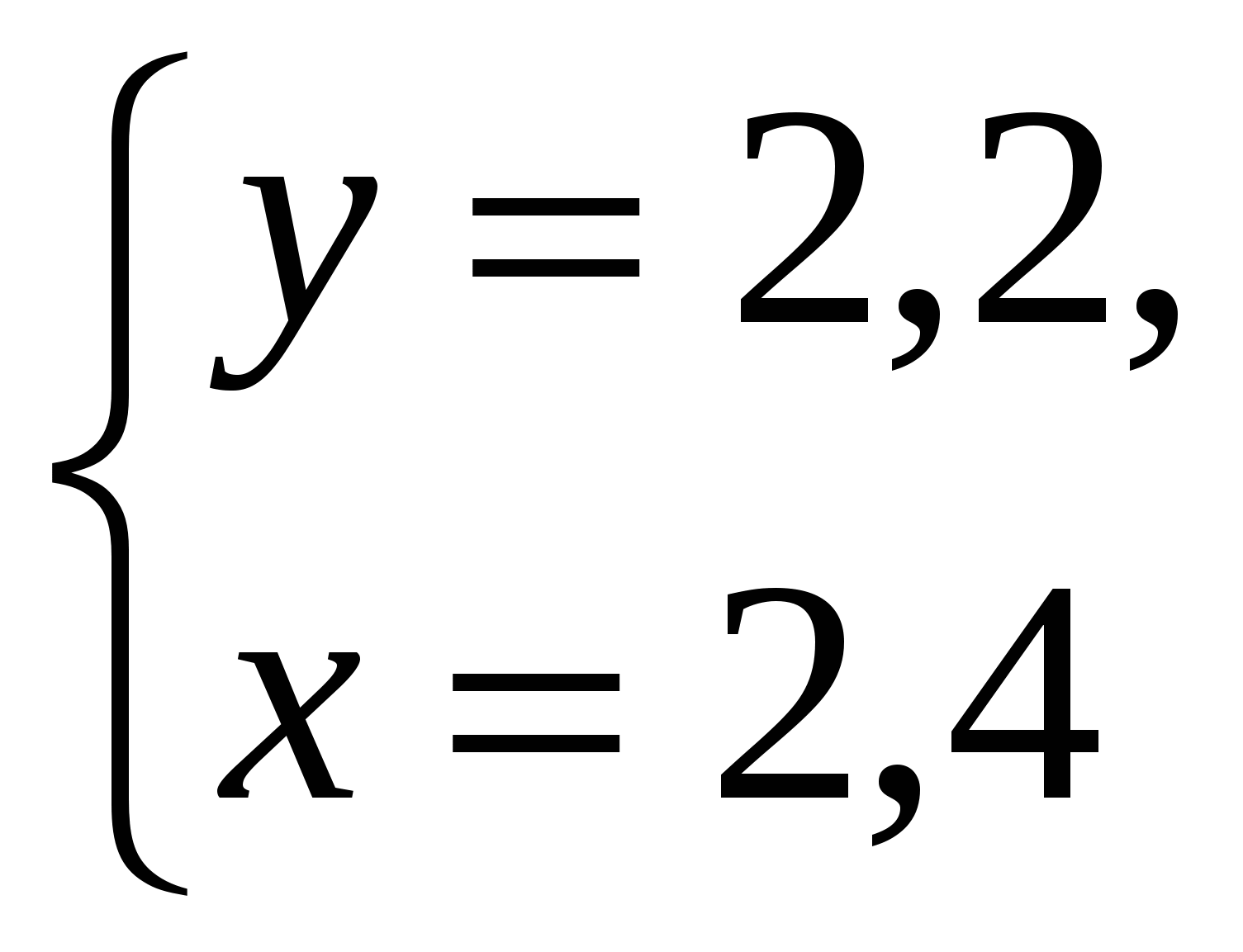Ответ: ( 2,4 ;2,2)
Еще раз проговорим этапы алгоритма: (проговорить этапы, слайд мультимедиа)
Этап№ 5. Физкультминутка
Комплекс упражнений + зарядка для глаз.
Этап № 6. Фронтальный устный опрос
1) Что называют решением системы уравнений с двумя переменными? Что значит решить систему уравнений?
2) Способы решения систем линейных уравнений с двумя переменными.
3) Назови методы решения систем линейных уравнений с двумя переменными.
4) Сформулируйте алгоритм решения по каждому способу решения в нескольких словах, назвав самое главное.
Этап № 7. Работа в парах
Сейчас мы с вами будем работать в парах: 1 вариант решает №12.4, а 2вариант решает №12.3; после того как ответы будут получены, меняемся тетрадями и проверяем ход решения соседа. Если все верно ставим +, если нет — (взаимопроверка с помощью мультимедиа)
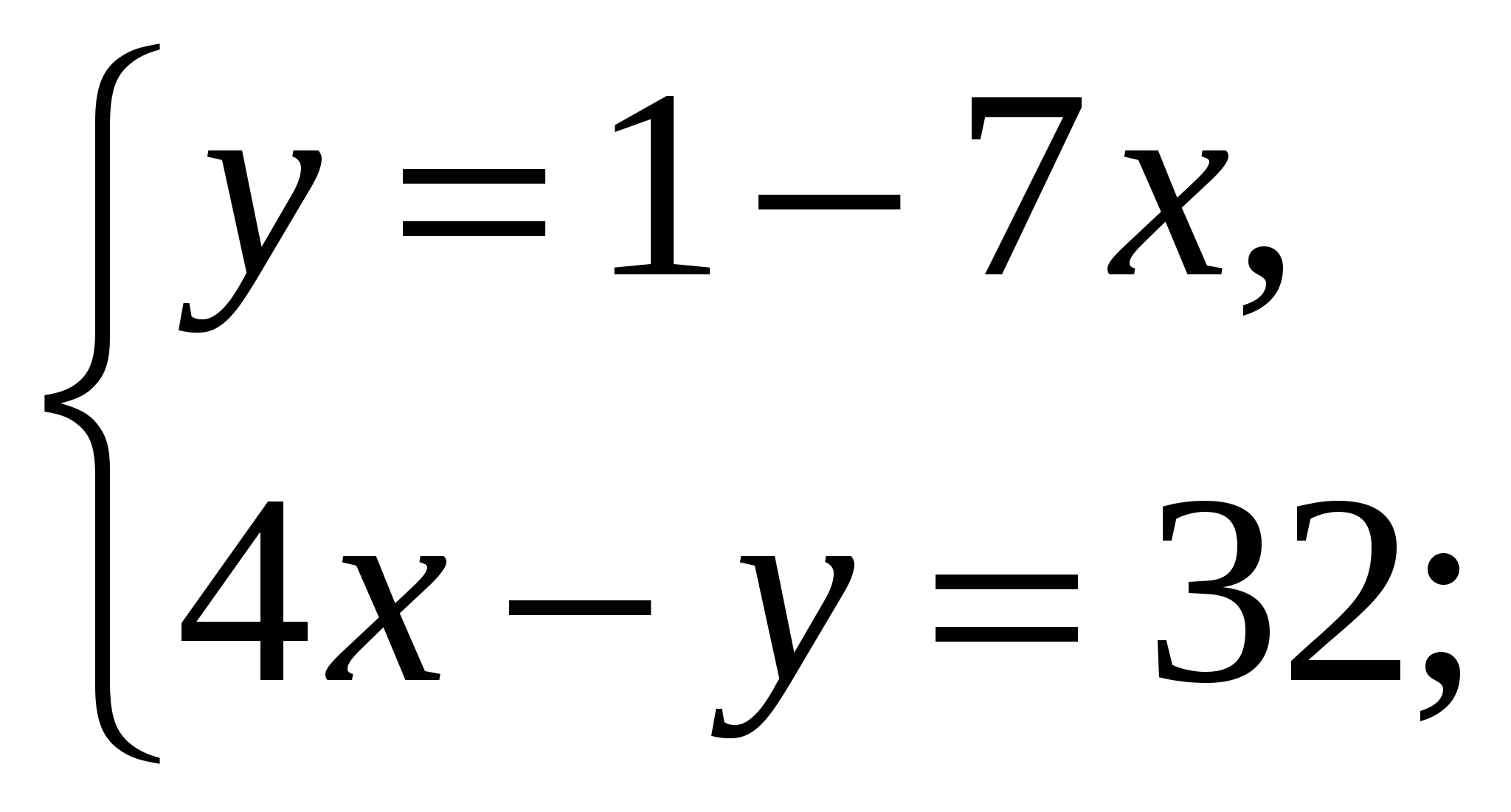
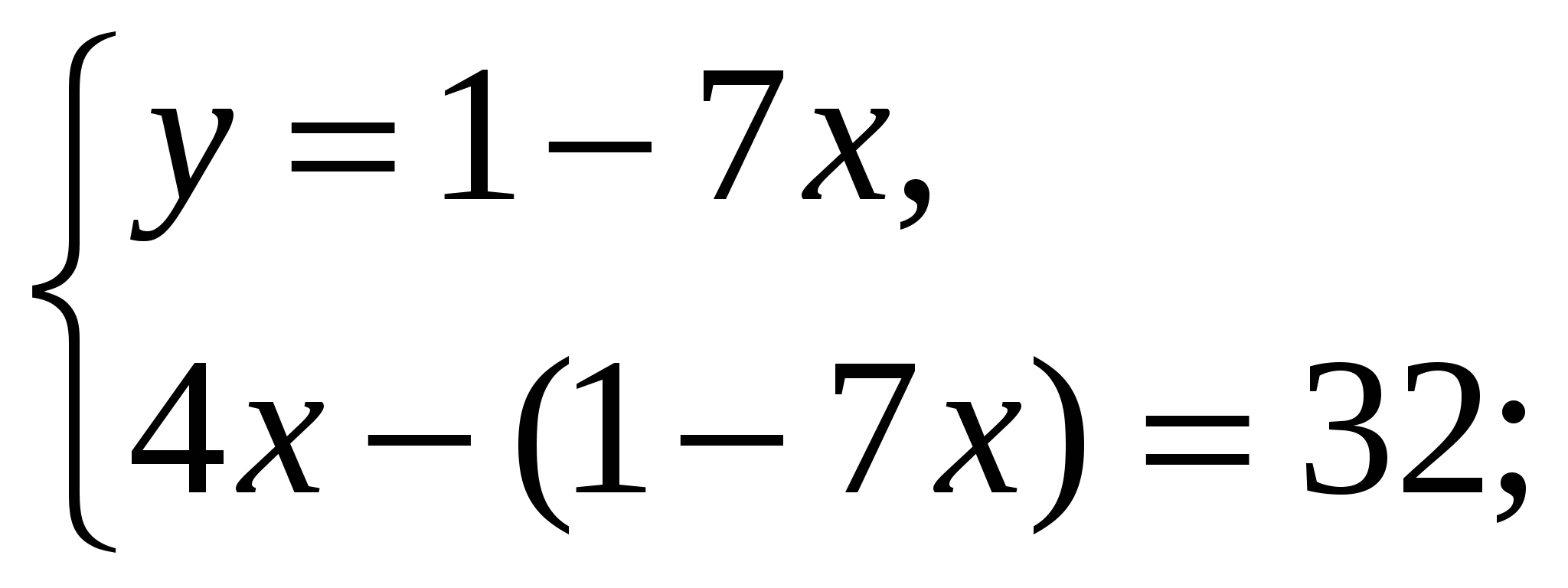
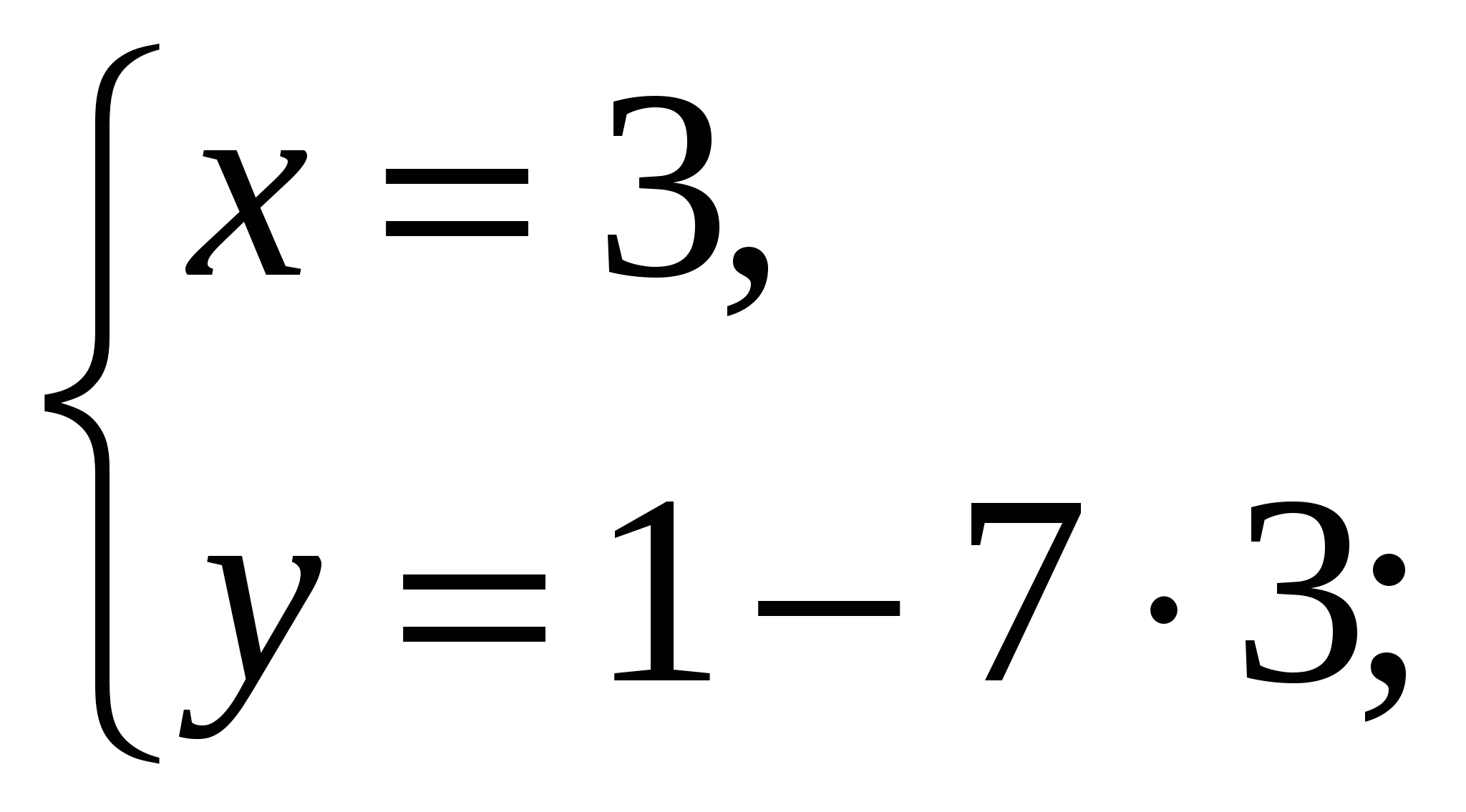
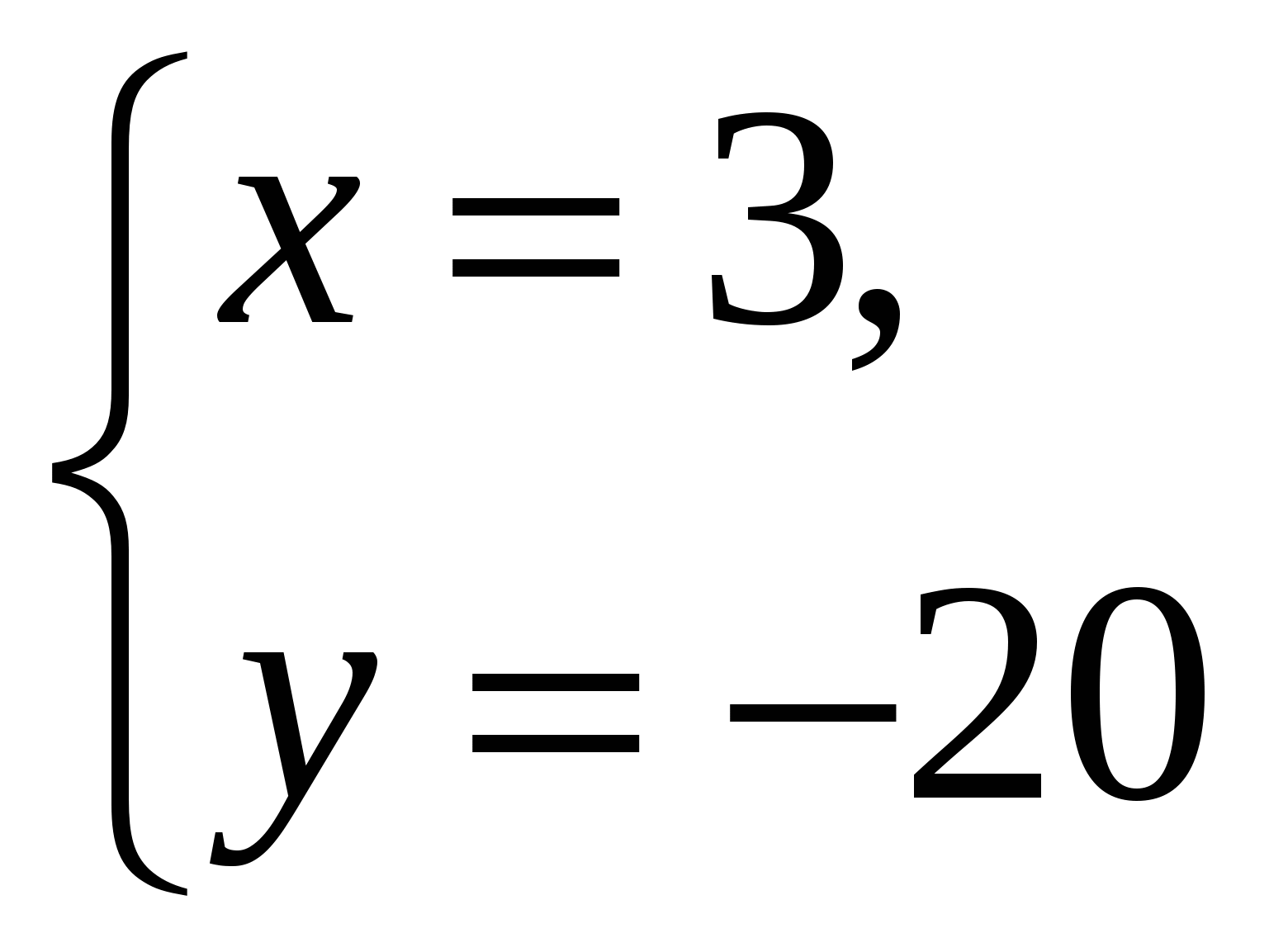Ответ: (3;-20).
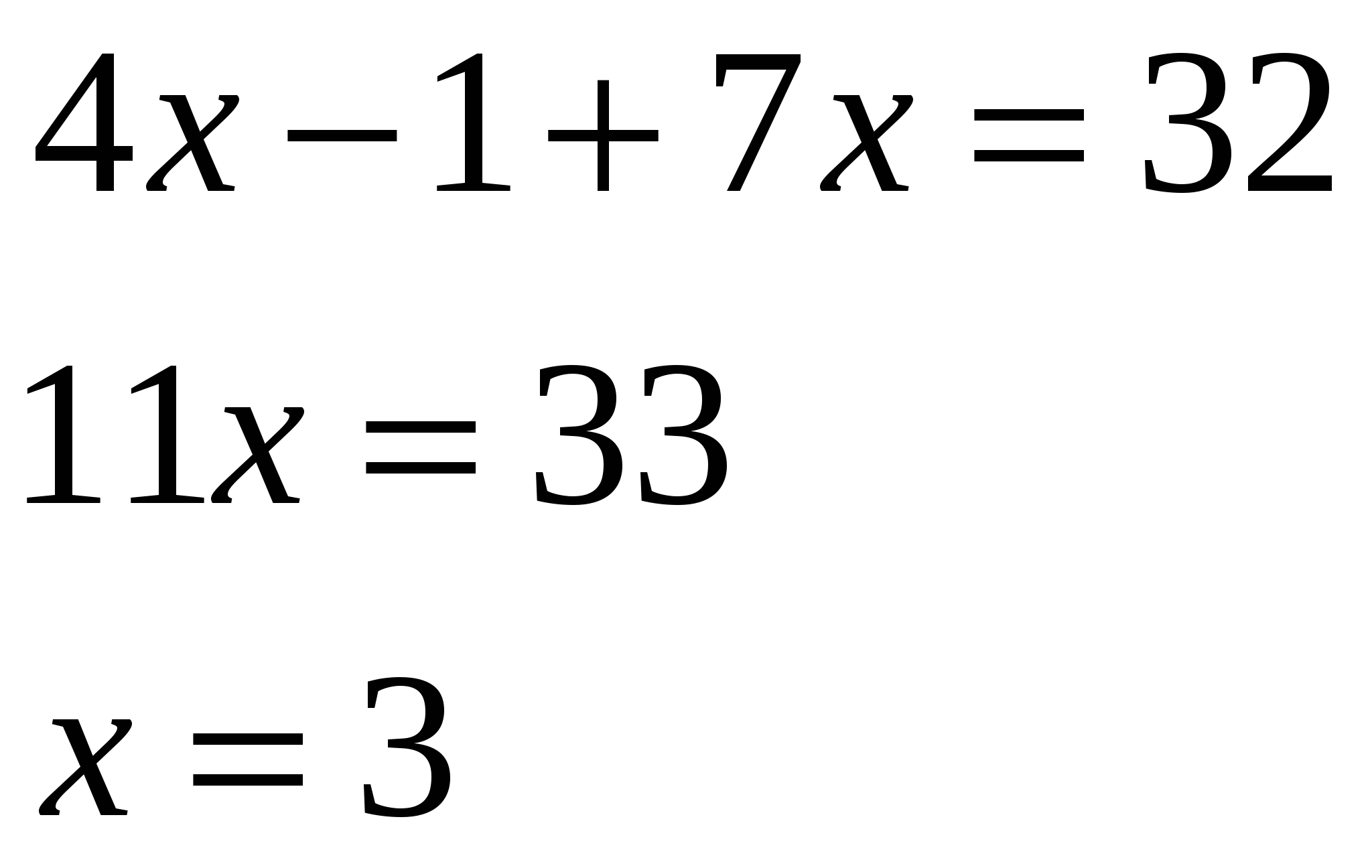
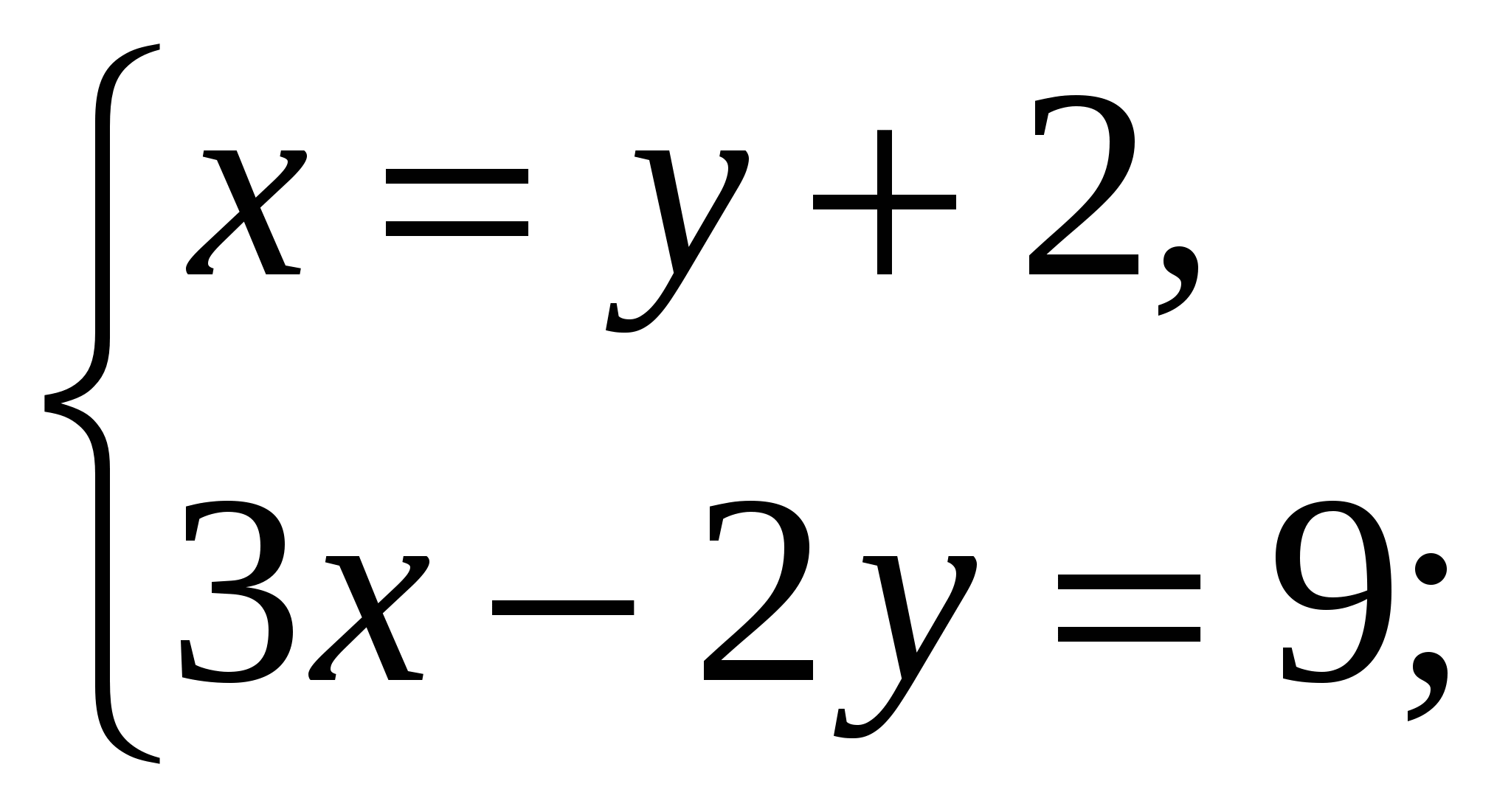
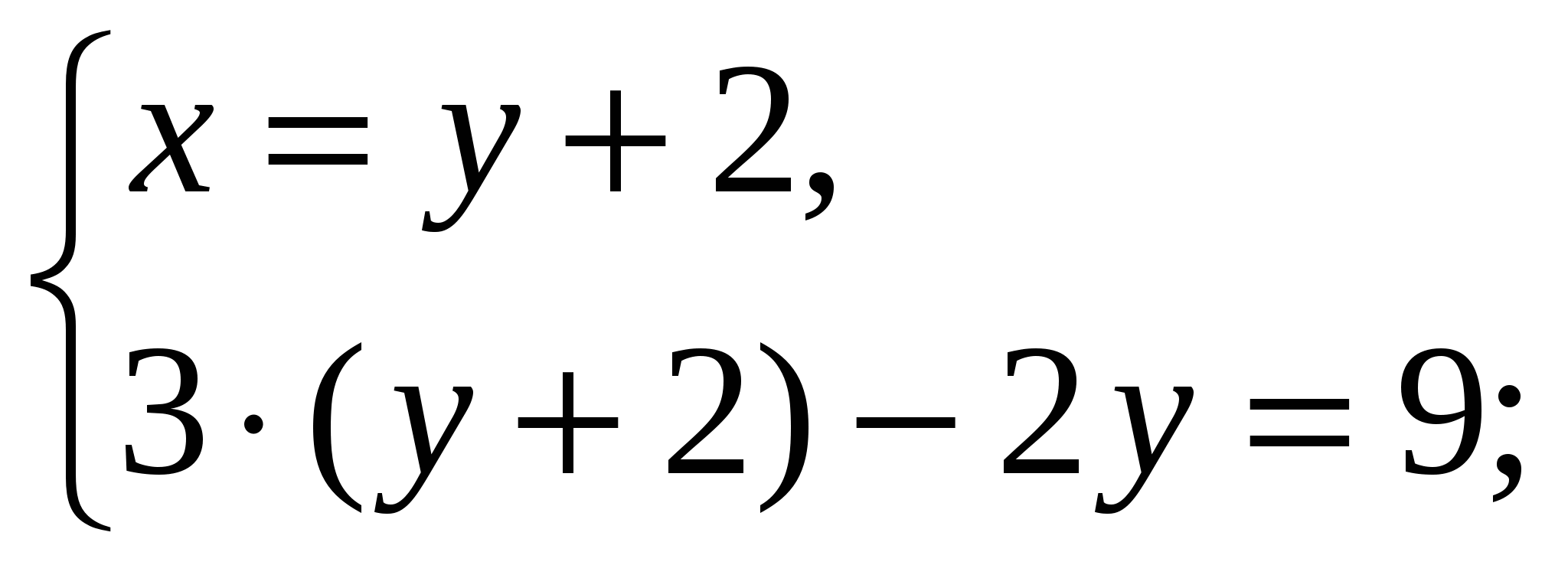
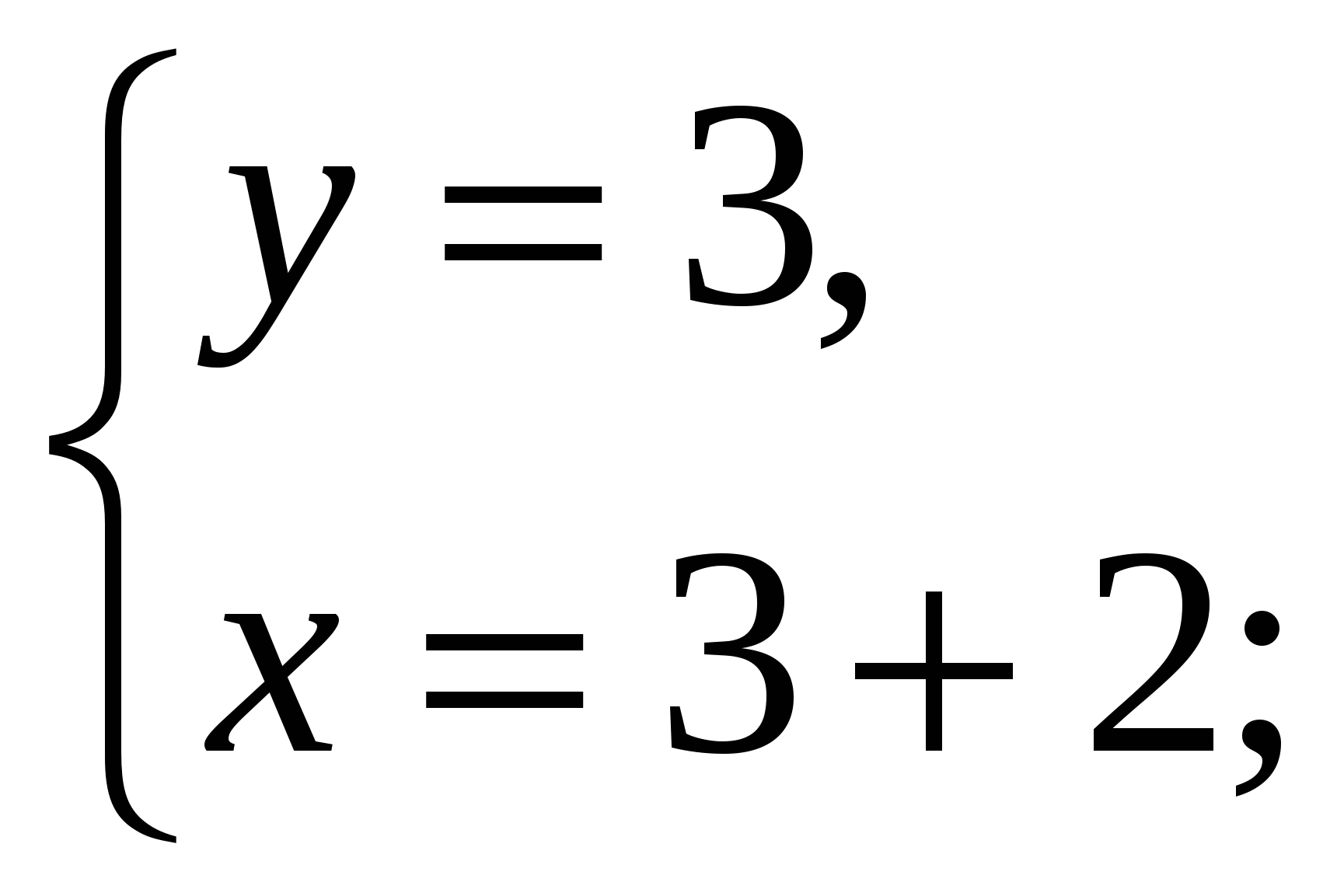
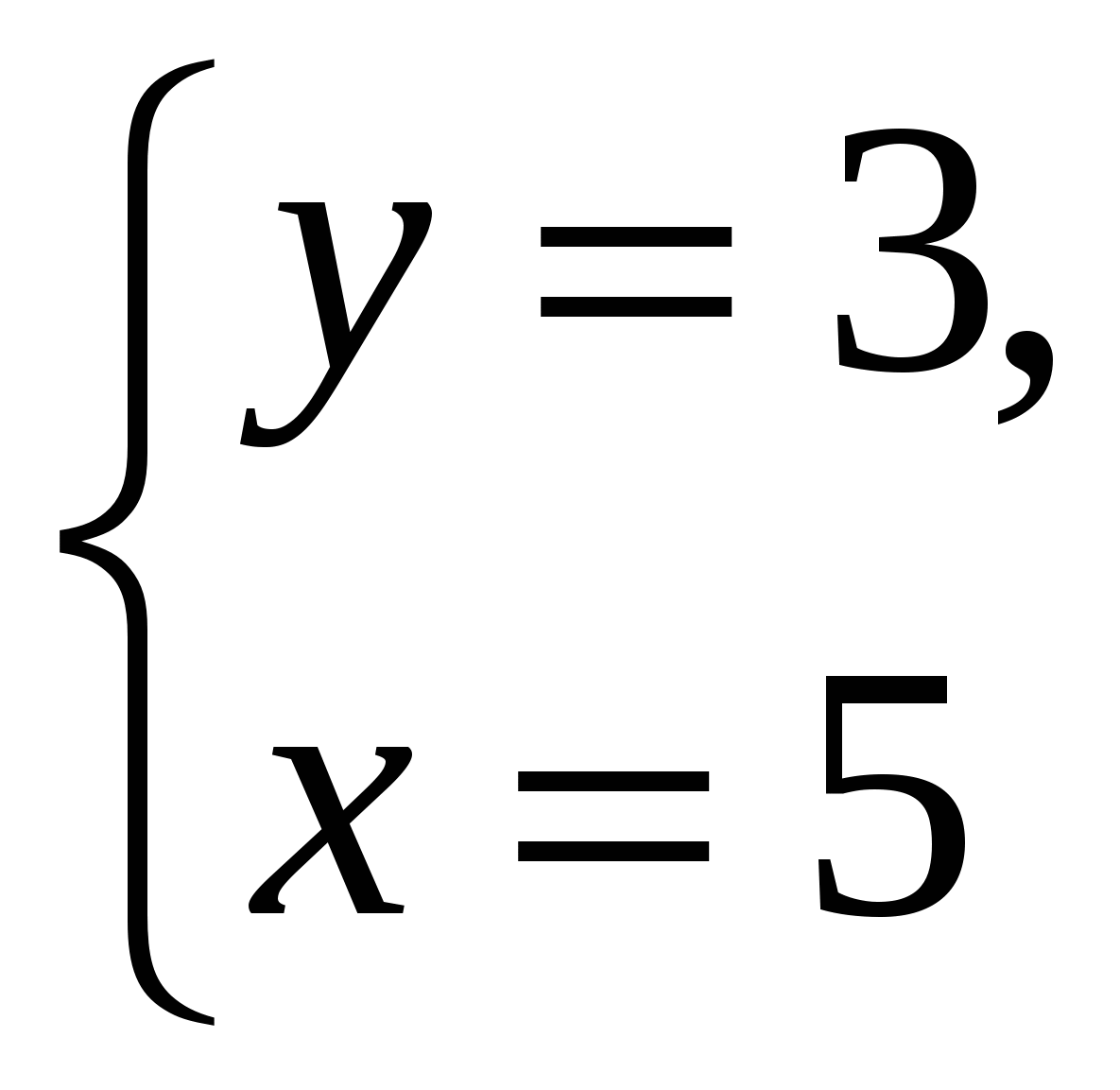Ответ: (5;2).
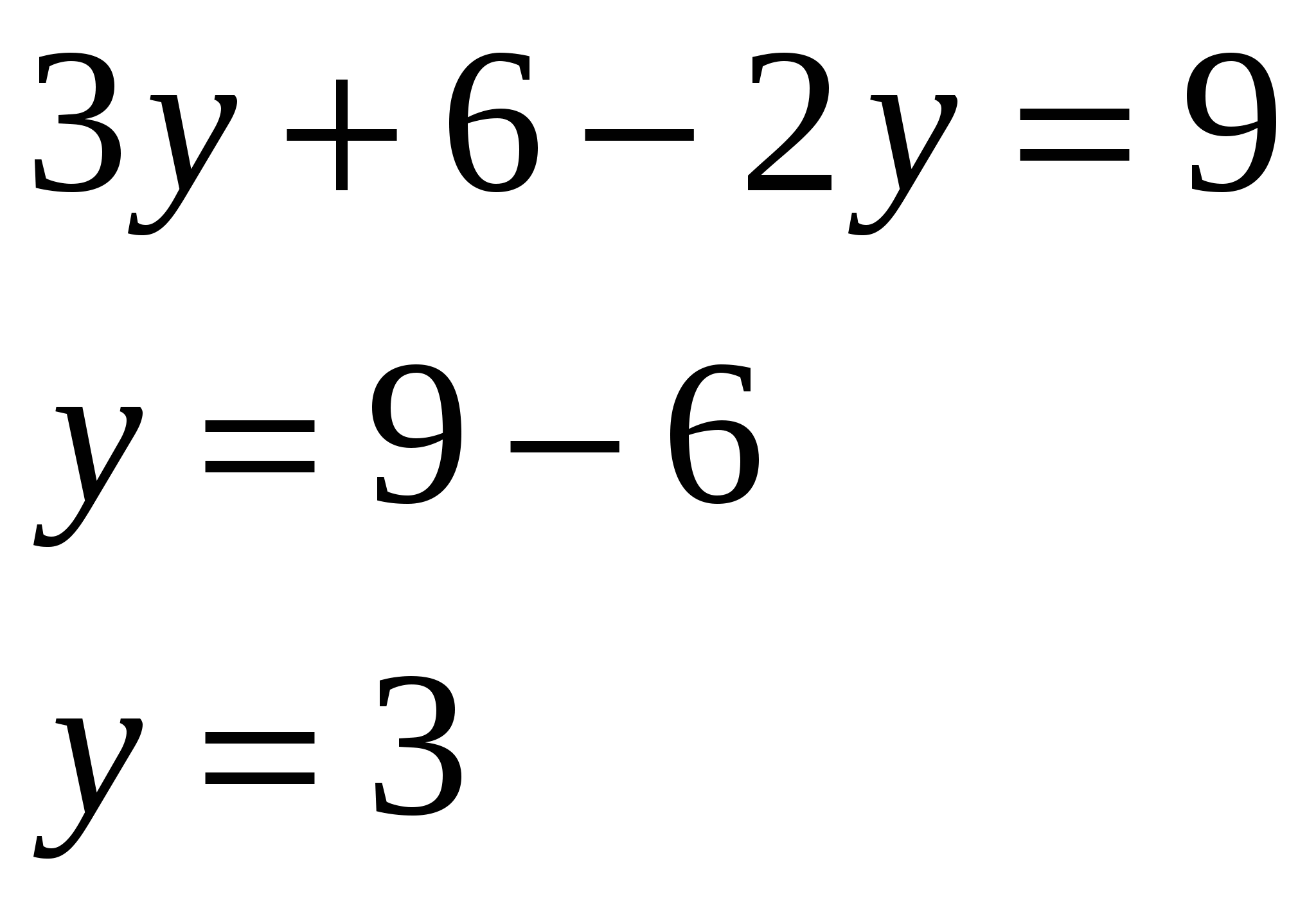
Этап № 7. Закрепление изученного материала:
Для закрепления изученного материала, давайте отгадаем крассворд.
Кроссворд
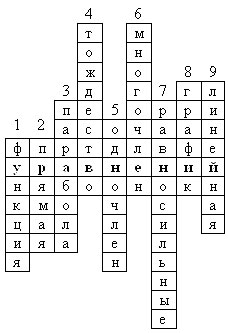
1.Зависимость, в которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называется…
Что является графиком линейного уравнения с двумя переменными?
Как называется график функции у=х2?
Равенство, верное при любых значениях переменных, называется…
Произведение нескольких сомножителей, один из которых числовой, а другие – переменные и их степени, называется…
Сумма нескольких одночленов называется…
Как называются уравнения, имеющие одни и те же корни?
Множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, называются…
Как называется функция, которую можно задать формулой у=кх+в, где х – независимая переменная, к, в – некоторые числа?
Этап № 8. Рефлексия :
Найдите своё место на горе.
Учащимся предлагается рисунок, на котором нужно отметить свое место положение для данного урока, т.е.:
Если мало чего понятного и придется разбираться ещё раз с этим материалом, то вы у подножья горы;
Если все предельно понятно, но вы не уверены в своих силах, то вы на пути к вершине;
Если нет ни каких вопросов, и вы чувствуете власть над данной темой, то вы на пике.
Этап № 9. Итог урока: Домашнее задание: параграф 12, знать алгоритм, разобрать самостоятельно примеры 1, 3, № 12.2, №12.6
-Сегодня мы познакомились с вами с еще одним способом решения систем двух линейных уравнений с двумя переменными. Сформулировали алгоритм этого метода. На следующих уроках мы отработаем этот алгоритм на более сложных системах и познакомимся с еще одним очень интересным способом решения.
Оценки сегодня получили… Спасибо за урок. До свидания.
infourok.ru
Урок №6 Системы уравнений. Способ ПОДСТАНОВКИ 7 класс
Цель урока: Решение систем уравнений с двумя неизвестными.
I этап. Вопросы по домашнему заданию и Упражнения на вычисления. (15 мин)
1. Проверка домашнего задания (диктуем точки пересечения)
2. В домашних тетрадях решаем: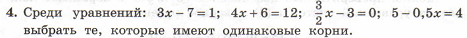 
План решения: решить все уравнения и отсортировать для ответа
3. После: Собрать тетради на проверку.
II этап. Алгебраические способы решения систем уравнений. СПОСОБ ПОДСТАНОВКИ (15 мин)
При выполнении заданий некоторые столкнулись с проблемой, что чертеж бывает неточным и из-за этого результат решения системы уравнений графическим способом будет приближенным.
Чтобы получить точный ответ, используют алгебраические способы решения.
Сегодня мы познакомимся с одним из них.
Пусть x – количество индуков, y – количество жеребят
30 ног всего, значит: и 11 хвостов:
X и y одинаковые для обоих уравнений, поэтому можем составить систему:
СПОСОБ ПОДСТАНОВКИ.
В одном из уравнений выразить одно неизвестное через другоеПОДСТАВИТЬ (заменит неизвестное выражением) в другом уравнениии. Получаем уравнение с одним неизвестным, которое мы умеем решать.
Решаем уравнение с одним неизвестным
И снова ПОДСТАВЛЯЕМ полученные данные вместо буквы в другое уравнение.
Решением является пара чисел: x и y
Записываем ответ.
III этап. Решение систем уравнений (15 мин)
Первые две решаем вместе, далее — самостоятельно
Домашнее задание: дорешать №1034
ОТВЕТЫ: №1034 1) (2;5), 2) (-20;-6), 3) (48;8) 4)(4;2)
5) (7;3) 6) (38;-6) 7) (9;3) 8) (2;3,8)
Лебединцева Е.А., Беленкова Е.Ю. Алгебра 8 класс. Задания для обучения и развития учащихся. Учебное пособие. — М.: Интеллект-Центр, 2013. – 176 с.
Изучение алгебры в 7-9 классах: Кн. Для учителя / Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева и др. – М. : Просвещение, 2002. – 287 с.: — ISBN 5-09-010414-X.
Алгебра. Дидактические материалы. 8 класс / М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин. – 2-е изд., дораб. – М.: Просвещение, 2013. – 96 с. : ил. – ISBN 978-5-09-028132-4
Мерзляк А.Г. Алгебра: 9 класс: учебник для учащихся общеобразовательных организация/ А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2014. – 304 c.: ил. ISBN 978-5-360-05308-8
Колягин Ю.М., Ткачева М.В., Федорова Н.Е., Шабунин М.И. АЛГЕБРА. Рабочая тетрадь. 8 класс. Пособие для учащихся общеобразовательных организаций в двух частях. Издательство «Просвещение», 2013 ISBN 978-5-09-032404-5(общ.) ISBN 978-5-09-032403-8(1)
Лебединцева Е.А., Беленкова Е.Ю. Алгебра 7 класс. Задания для обучения и развития учащихся. Учебное пособие.
infourok.ru