Подобные треугольники
Подобные треугольники
Простыми словами:Два треугольника называются подобными если один из них является уменьшенной копией второго
Стороны одного цвета называются сходственными
Знак \( ∾ \) означает подобие
\( \Delta ABC ∾ \Delta A_1B_1C_1 \)
\( \dfrac{A_1B_1}{AB}=\dfrac{A_1C_1}{AC}=\dfrac{B_1C_1}{BC}=k \)
\(k\) это коэффициент подобия
Первый признак подобия:
Если любые два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны
В подобных треугольниках каждый угол одного треугольника соответственно равен одному из углов другого треугольника
В подобных треугольниках против равных углов лежат сходственные стороны
1. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=2, \; A_1B_1=4 , \; BC=1,5 .
Показать ответ
Показать решение
Видеорешение
Ответ: \( B_1C_1 =3 \)
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( BC \) лежит против \(\angle A \),
\( B_1C_1 \) лежит против \(\angle A_1 \)
\( \angle A=\angle A_1, \; \) значит \( BC и B_1C_1 \) сходственные
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \angle C=\angle C_1, \; \) значит \( AB и A_1B_1 \) сходственные
\( \dfrac{A_1B_1}{AB}=\dfrac{B_1C_1}{BC} \)
\( \dfrac{4}{2}=\dfrac{B_1C_1}{1,5} \)
\( B_1C_1 =3 \)
Ответ: \( B_1C_1 =3 \)
2. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=2, \; A_1B_1=4 , \; AC=1 . \) Найти \(A_1C_1 \)
\) Найти \(A_1C_1 \)
Показать ответ
Показать решение
Видеорешение
Ответ: \( A_1C_1 =2 \)
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( AC \) лежит против \(\angle B \),
\( A_1C_1 \) лежит против \(\angle B_1 \)
\( \angle B=\angle B_1, \; \) значит \( AC и A_1C_1 \) сходственные
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \angle C=\angle C_1, \; \) значит \( AB и A_1B_1 \) сходственные
\( \dfrac{A_1B_1}{AB}=\dfrac{A_1C_1}{AC} \)
\( \dfrac{4}{2}=\dfrac{A_1C_1}{1} \)
\( A_1C_1 =2 \)
Ответ: \( A_1C_1 =2 \)
3. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=5, \; A_1B_1=15 , \; BC=4 . \) Найти \(B_1C_1 \)
\) Найти \(B_1C_1 \)
Показать ответ
Показать решение
Видеорешение
Ответ: \( B_1C_1 =12 \)
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( BC \) лежит против \(\angle A \),
\( B_1C_1 \) лежит против \(\angle A_1 \)
\( \angle A=\angle A_1, \; \) значит \( BC и B_1C_1 \) сходственные
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \dfrac{A_1B_1}{AB}=\dfrac{B_1C_1}{BC} \)
\( \dfrac{15}{5}=\dfrac{B_1C_1}{4} \)
\( B_1C_1 =12 \)
Ответ: \( B_1C_1 =12 \)
4. На рисунке \( \angle A= \angle A_1, \; \angle C= \angle C_1 , \; AB=4, \; A_1B_1=10 , \; BC=8 . \) Найти \(B_1C_1 \)
\) Найти \(B_1C_1 \)
Показать ответ
Показать решение
Видеорешение
Ответ: \( B_1C_1 =20 \)
\( \Delta ABC ∾ \Delta A_1B_1C_1 \;\; \) (по двум углам)
\( BC \) лежит против \(\angle A \),
\( B_1C_1 \) лежит против \(\angle A_1 \)
\( AB \) лежит против \(\angle C \),
\( A_1B_1 \) лежит против \(\angle C_1 \)
\( \angle C=\angle C_1, \; \) значит \( AB и A_1B_1 \) сходственные
\( \dfrac{A_1B_1}{AB}=\dfrac{B_1C_1}{BC} \)
\( \dfrac{10}{4}=\dfrac{B_1C_1}{8} \)
\( B_1C_1 =20 \)
Ответ: \( B_1C_1 =20 \)
Игро+матика: Подобные треугольники.
Что такое равные треугольники, более или менее понятно всем: если их наложить друг на друга, то они полностью совпадут. А вот что такое подобные?
А вот что такое подобные?
Давайте посмотрим на рисунки, расположенные ниже. Что у них общего? Все матрешки похожи друг на друга: все они одинаковой формы, на них насен один и тот же рисунок, а отличаются они только размерами. Тоже самое можно сказать и про треугольники — форма одинаковая, а размеры разные. Фигуры одной формы, но разных размеров в математике называют подобными.
Прослушай объяснение здесь
Итак:
ПОДОБНЫМИ НАЗЫВАЮТСЯ ТРЕУГОЛЬНИКИ, ЕСЛИ У НИХ ВСЕ УГЛЫ РАВНЫ, А СТОРОНЫ ПРОПОРЦИОНАЛЬНЫЧто значит подобие треугольников? Это значит, что подобные треугольники получаются сжатием или растяжением исходного треугольника. При этом соответствующие углы у них равны, а стороны находятся в прямой пропорциональности. Так, каждая из сторон треугольника АВС (на рисунке ниже), в два раза больше соответствующих сторон треугольника А2В2С2, а стороны треугольника А1В1С1 в три раза больше соответствующих сторон треугольника А2В2С2, значит стороны треугольников пропорциональны
Итак, на рисунке три подобных треугольника: DА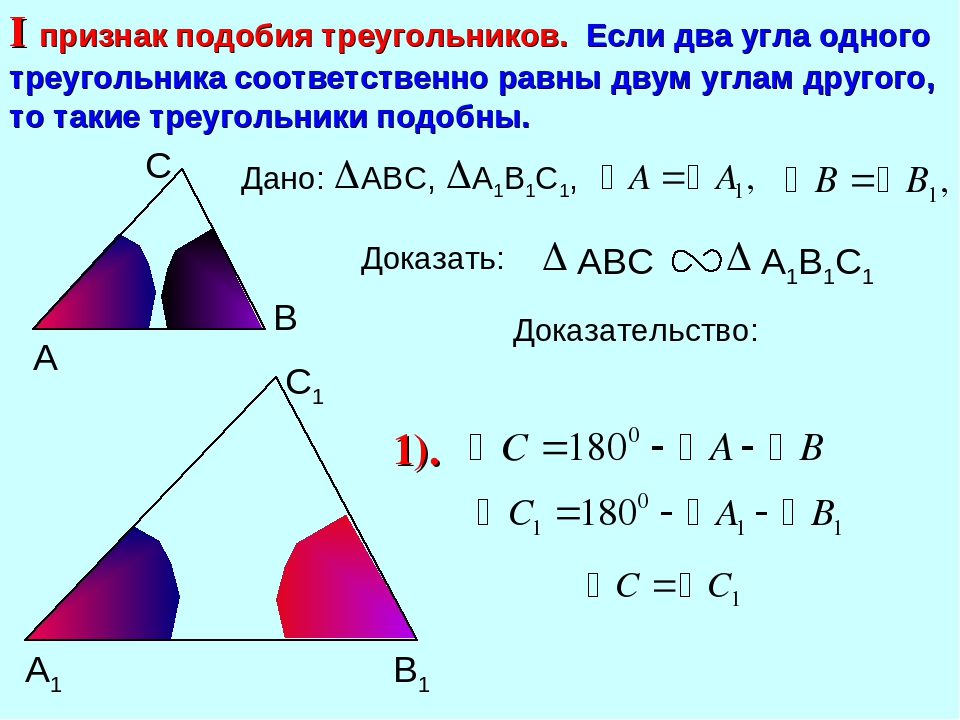 Соответствующие углы у них равны, а соответствующие стороны находятся в одном отношении друг к другу.
Соответствующие углы у них равны, а соответствующие стороны находятся в одном отношении друг к другу. То число раз, в которое отличаются стороны подобных треугольников,
называются коэффициентом подобия и, обычно, обозначается с помощью буквы k.
Стороны, лежащие против равных углов называются сходственными. Решая задачи, важно правильно определить сходственные стороны, чтобы верно записать пропорциональность сторон. При этом нужно быть очень внимательным, тем более, что треугольники, как на чертеже справа, могут быть расположены произвольным образом.
Здесь треугольники ABC и EDF — подобны, (называя подобные треугольники, следим, чтобы перечисление вершин соответствовало равным углам), поэтому стороны AC и ЕF, AB и ED, BC и FD — сходственные, и, следовательно, пропорциональные. Свойства подобных треугольников издревле широко применяются на практике для измерения расстояния до недоступных объектов, для измерения высоты предмета или ширины водоема, при проведении строительных или геодезических работ.
А сейчас, кликните по картинке ниже и попробуйте применить полученные знания при решении задач на сайте «Оценок нет!»
Определение подобных треугольников
Рассмотрим два прямоугольных треугольника с острыми углами в 60° и 30° (рис. 364).
Стороны второго треугольника по сравнению с первым уменьшены в два раза:
\(\frac{AB}{A’B’}\) = 2; \(\frac{AC}{A’C’}\) = 2; \(\frac{BC}{B’C’}\) = 2.
У этих треугольников углы попарно равны. Стороны, лежащие против равных углов, пропорциональны:
\(\frac{AB}{A’B’}\) = \(\frac{AC}{A’C’} = \frac{BC}{B’C’}\) = 2.
Такие треугольники называют подобными. Стороны, лежащие против равных углов, называются сходственными.
Таким образом, подобными называются треугольники, у которых yглы попарно равны, а сходственные стороны пропорциональны.
Подобие треугольников записывается так: \(\Delta\)ABС \(\sim\) \(\Delta\)А’В’С’.
Отношение сходственных сторон подобных фигур называется коэффициентом подобия. В данном случае коэффициентом подобия треугольников АBС и А’В’С’ будет число 2.
Если же взять отношения A’B’/AB = A’C’/AC = B’C’/BC , то коэффициент подобия будет равен 1/2.
Свойство прямой, параллельной какой-либо стороне треугольника.
Проведём в треугольнике АBС прямую DЕ параллельно стороне АС (рис. 365).
Получим треугольник DВЕ. Докажем, что \(\Delta\)ABС \(\sim\) \(\Delta\)DВЕ.
Вследствие параллельности сторон DЕ и АС ∠1 = ∠2 и ∠3 = ∠4.
Угол В является общим для этих треугольников. Следовательно, углы этих треугольников попарно равны.
Так как DЕ || АС, то \(\frac{AB}{DB} = \frac{BC}{BE}\).
Проведём через точку Е прямую, параллельную стороне AB (рис. 366).
Получим: \(\frac{BC}{BE} = \frac{AC}{AK}\), но АК = DЕ.
Поэтому
\(\frac{BC}{BE} = \frac{AC}{DE}\)
Сопоставляя полученную пропорцию с пропорцией \(\frac{AB}{DB} = \frac{BC}{BE}\) получим:
\(\frac{AB}{DB} = \frac{BC}{BE} = \frac{AC}{DE}\), т.е.
сходственные стороны треугольников AВС и DВЕ пропорциональны.
Раньше было доказано, что углы этих треугольников попарно равны.
Значит, \(\Delta\)ABС \(\sim\) \(\Delta\)DВЕ.
Следовательно, прямая, проведённая параллельно какой-либо стороне треугольника, отсекает от него треугольник, подобный данному.
Отношение площадей двух подобных треугольников
Пусть \(\triangle AВС \sim \triangle AВС\)(черт. 380). Из подобия треугольников следует, что
380). Из подобия треугольников следует, что
∠A = ∠A, ∠B = ∠B и ∠С = ∠С. Кроме того, AB/AB = BC/BC = AC/AC.
В этих треугольниках из вершин В и В проведём высоты и обозначим их через h и h. Площадь первого треугольника будет равна AC•h/2, а площадь второго треугольника AC•h/2.
Обозначив площадь первого треугольника через S, а площадь второго — через S получим: S/S = AC•h/AC•h или S/S = AC/AC • h/h
Из подобия треугольников АВО и АВО (они подобны, потому что прямоугольные, и, кроме того, имеют по равному острому углу, а именно ∠A = ∠A) следует:
h/h = AB/AB . Но AB/AB= AC/AC . 2} $$
2} $$
Итак, площади подобных треугольников относятся как квадраты сходственных сторон.
Полученную формулу можно преобразовать так: S/S = (AC/AC)2.
Значит, можно сказать, что отношение площадей двух подобных треугольников равно квадрату отношения их сходственных сторон.
Построение подобных треугольников
Мы уже знаем, что для построения треугольника, подобного данному, достаточно из какой-нибудь точки, взятой на стороне треугольника, провести прямую, параллельную стороне треугольника. Получим треугольник, подобный данному (черт. 382):
$$ \triangle AСВ \sim \triangle AСB $$Средняя линия треугольника / Подобные треугольники / Справочник по геометрии 7-9 класс
Средняя линия треугольника — отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия . На рисунке 1 изображен треугольник АВС, отрезки МЕ, МК и КЕ являются средними линиями данного треугольника, ВМЕ =АМК =СЕК =МЕК.
На рисунке 1 изображен треугольник АВС, отрезки МЕ, МК и КЕ являются средними линиями данного треугольника, ВМЕ =АМК =СЕК =МЕК.
Теорема
| Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. |
Доказательство
Дано: АВС, МЕ — средняя линия.
Доказать: МЕАС, МЕ = АС.
Доказательство:
В треугольниках МВЕ и АВС:
- В — общий;
- ВА = 2ВМ, т.
 к. МЕ — средняя линия, значит, М — середина АВ, тогда , аналогично, , т.е. .
к. МЕ — средняя линия, значит, М — середина АВ, тогда , аналогично, , т.е. .
Следовательно, треугольники МВЕ и АВС подобны (по 2 признаку подобия треугольников), поэтому 1 =2 и .
Прямые МЕ и АС пересечены секущей АВ, углы 1 и 2 — соответственные, при этом 1 =2, следовательно, МЕАС (по признаку параллельности двух прямых).
Из равенства следует, что МЕ = АС. Теорема доказана.
Задача:
Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2 : 1, считая от вершины.
Дано: АВС, АА1 и ВВ1, СС1 — медианы, АА1ВВ1 = О.
Доказать: АА1ВВ1СС1 = О, АО : ОА1 = ВО : ОВ1 = СО : ОС1 = 2 : 1.
Доказательство:
Проведем среднюю линию В1А1 треугольника АВС (В1А1 — средняя линия, т.к. по условию АА1 и ВВ1 — медианы, значит точки А1 и В1 — середины сторон АС и СВ).
А1В1АВ (по теореме, доказанной выше), АА1 и ВВ1 — секущие, 1 и 2, 3 и 4 — накрест лежащие, значит, 1 =2, 3 =4 (по теореме о накрест лежащих углах).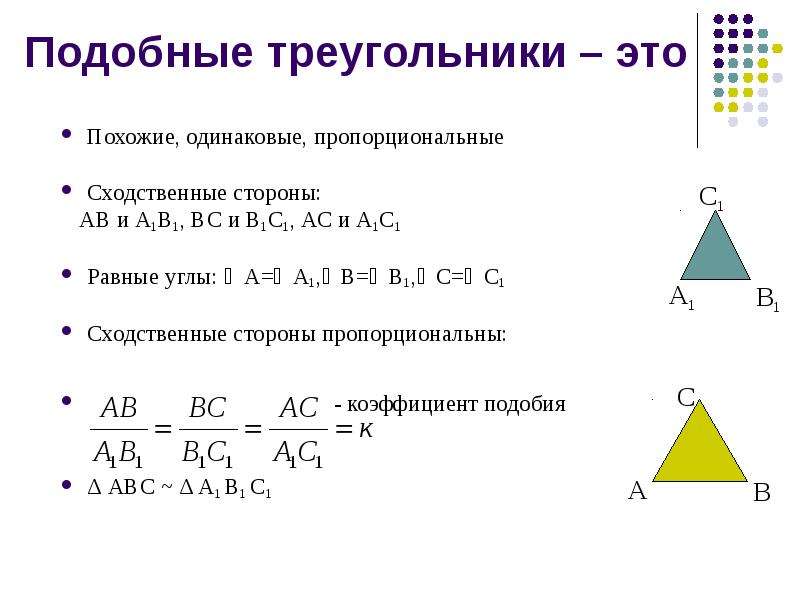 Следовательно, треугольники АОВ и А1ОВ1подобны (по 1 признаку подобия), тогда сходственные стороны данных треугольников пропорциональны:
Следовательно, треугольники АОВ и А1ОВ1подобны (по 1 признаку подобия), тогда сходственные стороны данных треугольников пропорциональны:
. (1)
Так как А1В1 — средняя линия, А1В1 = АВ, откуда АВ = 2А1В1, поэтому АО = 2А1О и ВО = 2В1О. Подставляя три последних равенства в (1), получим:
.
Следовательно, точка О, в которой пересекаются медианы АА1 и ВВ1 делит каждую из них в отношении 2 : 1, считая от вершины.
Аналогично доказывается, что точка пересечения медиан ВВ1 и СС1 делит каждую из них в отношении 2 : 1, считая от вершины, и, значит, совпадает с точкой О.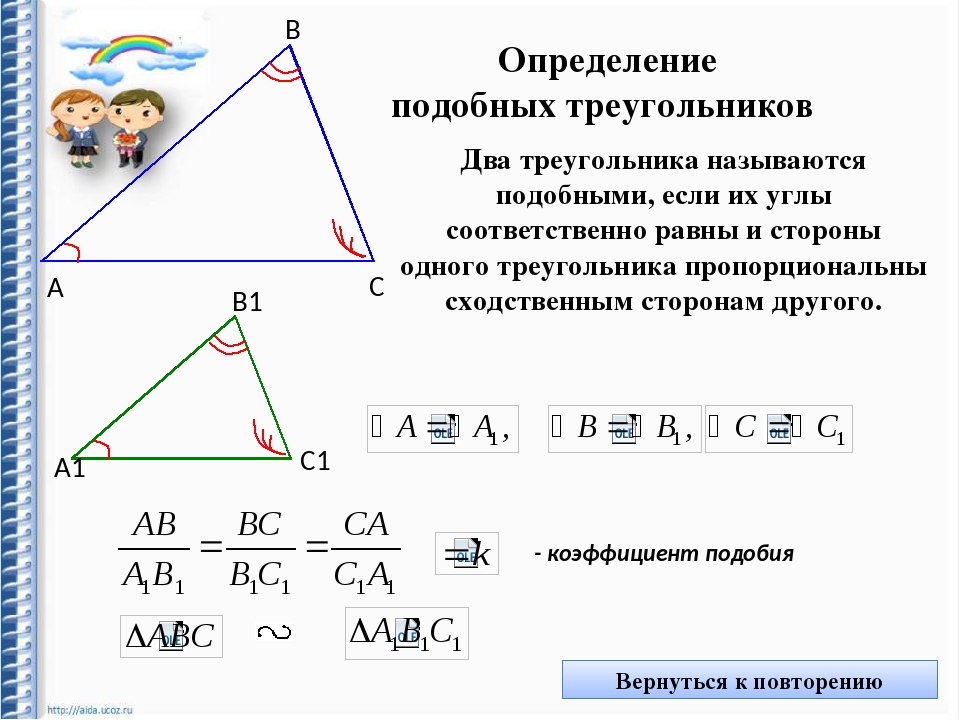
Итак, все три медианы АВС пересекаются в точке О и делятся ею в отношении 2 : 1, считая от вершины. Что и требовалось доказать.
Подобие треугольников определение презентация. Подобие прямоугольных треугольников
Геометрия
глава 7
Подготовила Намазгулова Гульназ ученица 8б класса ГБОУ РПЛИ г.Кумертау
Учитель: Баянова Г.А.
Отношением отрезков АВ и СD называется отношение их длин, т.е. АВ:CD
АВ = 8 см
СD = 11,5 см
Отрезки АВ и CD пропорциональны отрезкам А 1 В 1 и С 1 D 1 , если:
CD= 8 см
АВ= 4см
С 1 D 1 = 6 см
А1В1=3 см
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника
K- коэффициент подобия
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия
Доказательство:
Коэффициент подобия равен К
S и S 1 — площади треугольников, то
По формуле имеем
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны
Доказать:
Доказательство
1)По теореме о сумме углов треугольника
2)Докажем, что стороны треугольников пропорциональны
Аналогично и с углами
Итак, стороны
пропорциональны сходственным сторонам
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны
Доказать:
Доказательство
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны
Доказать:
Доказательство
Средней линией называется отрезок, соединяющий середины двух его сторон
Теорема:
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
Доказать:
Доказательство
Теорема:
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины
Доказать:
Доказательство
Теорема:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику
Доказать:
Доказательство
Теорема:
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой
Доказать:
Доказательство
Синус — отношение противолежащего катета к гипотенузе в прямоугольном треугольнике
Косинус — отношение прилежащего катета к гипотенузе в прямоугольном треугольнике
Тангенс- отношение противолежащего катета к прилежащему катету в прямоугольном треугольнике
0 , 45 0 , 60 0
Значение синуса, косинуса и тангенса для углов 30 0 , 45 0 , 60 0
Слайд 2 . На этом слайде показано, как представлена теорема Пифагора
в учебнике. Текст и готовый чертеж. В презентации статический чертеж из учебника
мы можем «оживить», т.е. показать последовательные шаги построения, показать
динамику дополнительных построений, необходимых для доказательства.
На этом слайде показано, как представлена теорема Пифагора
в учебнике. Текст и готовый чертеж. В презентации статический чертеж из учебника
мы можем «оживить», т.е. показать последовательные шаги построения, показать
динамику дополнительных построений, необходимых для доказательства.
Я работаю в классе с
дистанционной мышью, поэтому я могу управлять презентацией и одновременно
индивидуально работать с обучающимися. Я считаю это главным преимуществом
применения презентаций на уроке геометрии. Я не «привязана» к доске, к компьютеру, имею дополнительное время
для индивидуальной работы. Появившееся свободное время позволяет мне обойти
всех детей и проверить правильность выполнения чертежа в тетрадях. Бывает ощущение,
что в классе два учителя. Первый работает «в реале» индивидуально
– это я. Второй
виртуальный учитель, показывает шаги построения – это компьютер. У меня есть
возможность по просьбе детей повторить шаги построения, прокрутить колесико
мышки назад.
Слайд 3 . Теорема Пифагора. Алгоритм работы на уроке с модулем.
Теорема Пифагора. Алгоритм работы на уроке с модулем.
— Для доказательства нам необходимо достроить треугольник до квадрата. Учитель демонстрирует построение на слайде, работая с дистанционной мышью, и ведет индивидуальную работу с обучающимися.
-Для доказательства вычисляем площадь построенного квадрата двумя способами.
Как можно вычислить площадь квадрата? Фронтальная работа над идеей доказательства.
Первый способ. S = а². Сторона
квадрата равна (a+b), тогда S = (a+b)².
Второй способ вычисления с применением свойства
площадей: площадь квадрата равна сумме площадей четырех прямоугольных
треугольников и площади квадрата со стороной с.
Приравняем правые
части этих равенств. Вызываю к доске ученика. Преобразования оформляем мелом на
доске.
Слайд 4. Технически более сложный слайд. Использованы анимации:
вращения, пути перемещения. В этом модуле используется анимационный герой для
сопровождения объяснения.
Слайд 5. Используя презентацию можно дать значительно больший объем
информации на уроке. Например, представить другие способы доказательства
теоремы.
А сколько задач для отработки
доказанных теорем можно предложить! Вот например, какие задачи я составила для
отработки записи формулировки теоремы Пифагора.
Слайды 6, 7 для устной работы. Технически эти модули достаточно
простые.
Алгоритм работы на уроке.
Обучающиеся должны сформулировать свойство диагоналей ромба и назвать все треугольники. А затем для каждого треугольника составить запись теоремы Пифагора.
Внеся небольшие изменения на
слайдах, эти задания можно предложить на следующем уроке, как задания с
последующей проверкой.
Алгоритм организации работы на
уроке. Слайды 8, 9.
Слайд 8. Математический диктант. Записать последовательно теорему
Пифагора для каждого треугольника. Треугольники появляются по щелчку мыши в
любой части слайда (но не по
шторке). Переходим на слайд 9. Еще для четырех треугольников записываем
теорему. По кнопке возвращаемся назад на слайд 8. Щелчком по шторке открываем
ответы. Самопроверка или взаимопроверка. Переходим на слайд 9, щелчком по
шторке открываем ответы. В ходе урока можно запланировать 1 или более слайдов с
самостоятельной работой с последующей самопроверкой.
Треугольники появляются по щелчку мыши в
любой части слайда (но не по
шторке). Переходим на слайд 9. Еще для четырех треугольников записываем
теорему. По кнопке возвращаемся назад на слайд 8. Щелчком по шторке открываем
ответы. Самопроверка или взаимопроверка. Переходим на слайд 9, щелчком по
шторке открываем ответы. В ходе урока можно запланировать 1 или более слайдов с
самостоятельной работой с последующей самопроверкой.
Слайд 10. Алгоритмы организации работы на
уроке над теоремой могут быть разными. В одном классе мы отработаем с теоремой
одним способом, в другом классе организуем работу иначе. Например. Я рассмотрю
свойство углов равнобедренного треугольника.
1 способ организации
работы над теоремой.
Учитель. Выделяем условие и
заключение теоремы.
Обучающиеся формулируют, что «дано» в теореме и что надо «доказать».
Учитель. Прошу закончить мои
предложения-подсказки. Равенство углов следует обычно из … Учащиеся продолжают …
из равенства треугольников.
Учитель. Значит, нам нужны
треугольники. Чтобы треугольники появились, сделаем дополнительное построение. Придумайте,
как разбить треугольник на два равные треугольника? Построим биссектрису ВD. (На этом построении показ презентации останавливаю).
Ученики обычно сразу видят
равные треугольники. Докажем равенство треугольников.
Один ученик приглашается к доске
и мелом на доске записывает доказательство равенства треугольников. Выписывает
равные элементы. Делает вывод, о равенстве треугольников, называет признак.
Итоговый вывод, о равенстве углов при основании.
Учитель. Проверим и повторим
доказательство. (Продолжает показ
презентации).
Таким образом, доказательство
выполнено обучающимся самостоятельно, а через проектор учитель показывает его
еще раз, идет пошаговый разбор доказательства.
2 способ работы над
теоремой.
Если в классе нет учеников,
которые могут доказать теорему самостоятельно и сделать грамотные
последовательные записи шагов доказательства от начала до конца.
Просматриваем весь ход
доказательства от начала до конца. Делаем чертеж, формулируем условие и
заключение теоремы. Оформляем в тетради чертеж, дано, доказать.
Обсуждаем доказательство фронтально. Вместе ищем равные элементы появившихся на
чертеже треугольников. После устного разбора теоремы, вызываем к доске ученика,
который сможет восстановить доказательство. Так и формулируем перед ним задачу
«Восстановить доказательство». Колесиком на мышке возвращаемся на начало
доказательства (Дано, доказать, ДП – биссектриса).
Итак, в первом случае учащиеся доказывают теорему самостоятельно . После этого показываем доказательство через
проектор, обобщаем. Во втором случае сначала просматриваем доказательство через
проектор, а затем просим восстановить доказательство .
Но бывают теоремы, которые
ученикам не под силу доказать самостоятельно. Здесь учителю придет на помощь
компьютер. В презентации можно «оживить» чертеж, анимировать последовательные
шаги доказательства, используя выделение цветом фигур, сделать более доступным
для понимания доказательство.
Слайды 11 – 13.
На слайде 11 дана визуальная
подсказка компьютера – красным цветом выделены слова «Если» и «то». Не сложно
сформулировать условие и заключение теоремы.
На слайде 12 анимированное
доказательство. В подготовленном классе можно сначала просмотреть теорему, а
затем предложить восстановить доказательство мелом на доске. После просмотра
доказательства можно ПКМ выбрать Экран-Черный экран.
В другом классе можно одновременно
с показом оформлять доказательство в тетради. На слайде приведены записи,
которые должны быть оформлены в тетради.
Также можно привести и еще два
случая, которые предложим для самостоятельного доказательства (например, выполнить по желанию дома). После оформления записей в тетради, просматриваем
доказательство повторно. Учитель повторяет все шаги.
Я использовала еще такой
алгоритм. Например, одновременно с демонстрацией, ученики записали
доказательство в тетради. Т.е. одновременно смотрим, обсуждаем фронтально,
записываем в тетради доказательство. После завершения этой работы, колесиком на
мышке возвращаюсь на начало теоремы. Приглашаю к экрану ученика. С указкой в
руке он доказывает теорему. А учитель, делая клик мышкой, раскрывает каждый
верный шаг рассуждения.
После завершения этой работы, колесиком на
мышке возвращаюсь на начало теоремы. Приглашаю к экрану ученика. С указкой в
руке он доказывает теорему. А учитель, делая клик мышкой, раскрывает каждый
верный шаг рассуждения.
Этот неплохой алгоритм я
перестала использовать. Т.к. проектор в классе стоит на парте. В этом случае
луч проектора светит в глаза ребенку, он зажмуривается, испытывает дискомфорт.
Это очень вредно для глаз! Оптимальное место расположения проектора – на
потолке. Тогда луч проектора идет у нас над головой, а не светит нам в глаза.
Приглашая учеников к доске во время работы проектора, подбирайте удаленное
место от экрана. Дорогие коллеги, берегите и свои глаза! Избегайте прямого
попадания луча проектора в глаза.
На слайдах 14 -17 приведены игровые задания. Как сделать такие
модули, описано в ресурсе «Геометрия. Применение презентаций для
иллюстрирования определений». Используя время записи начала анимации с помощью
триггера, можно делать игровые модули. Эти маленькие тестовые задания удачно предложить на любом этапе урока. Главное – мера.
Эти маленькие тестовые задания удачно предложить на любом этапе урока. Главное – мера.
Авторский прием. При изучении
многих тем геометрии полезно давать «Парные задачи». Опять преимущество
презентации в том, что можно заранее подготовить слайд. На доске мелом к уроку
подготовить такие «пары» достаточно сложно, требуется время.
Цель составления «Парных задач»
— это систематизация знаний по теме.
На слайде 18 приводится пример. Задачи по теме «Свойства параллелограмма» и «Признаки параллелограмма». Как организовать работу?
Учитель. На слайде даны две задачи. В первой задаче Дано: АВСD – параллелограмм, а во второй задаче надо доказать, что АВСD – параллелограмм. В какой задаче нам потребуются свойства параллелограмма, а в какой признаки параллелограмма?Ученики. Дают ответ.
Устно решаем две задачи. Проговаривая формулировки применяемых свойств.
Слайд 19 – домашняя задача № 383.
Учитель. А вот ваша домашняя
задача.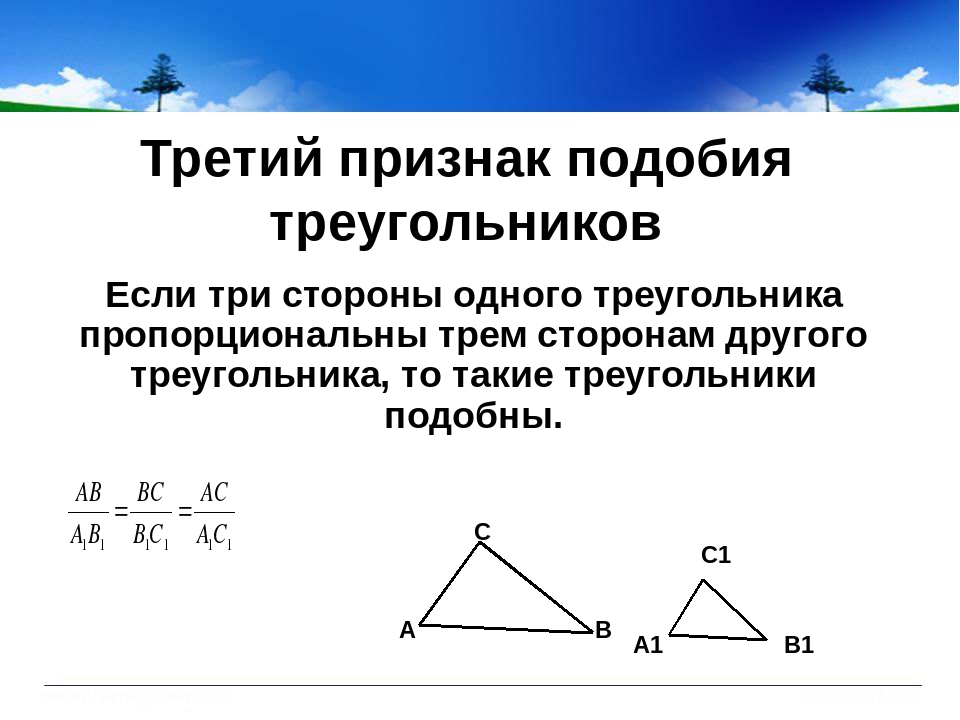 Давайте разберемся, что вам потребуется для решения этой задачи: свойства или признаки параллелограмма.
Давайте разберемся, что вам потребуется для решения этой задачи: свойства или признаки параллелограмма.
Ученики. Дан параллелограмм АВСD, значит можно применить
свойства параллелограмма. Чтобы доказать, что APCQ является параллелограммом потребуются признаки
параллелограмма.
Мои ученики сразу увидели, что
можно доказать равенство треугольников АВР и СDQ,
DQ и СВР по 1
признаку равенства треугольников. Тогда, АР=СQ, PC=AQ, а если в 4-угольнике
противолежащие стороны равны, то АРСQ параллелограмм.
А вот еще один способ, который
заложен в анимациях слайда, пришлось им показать. Тогда они догадались, что
есть и еще способ доказать, что АВСQ параллелограмм. Используя признак 3º, через
диагонали.
Мы обсудили две дороги для
решения этой задачи дома.
Слайд 20. Еще пример задач-пар. В 7 классе важно научить детей
различать, в каких задачах потребуются признаки параллельности прямых, а в
каких задачах необходимо применить обратные теоремы.
На этом слайде для парных задач дана визуальная подсказка – красным цветом на слайде выделено ключевое различие между задачами. В первой задаче цветом выделено «AB II CD», а во второй задаче «a II b». Если предложить подобные парные задачи на следующем уроке, то визуальную подсказку цветом уже можно не давать.
Учитель. Ключевое различие между
задачами выделено на слайде цветом. В первой задаче требуется доказать,
что прямые параллельны . А во второй задаче даны две параллельные прямые . В
какой задаче потребуются признаки параллельности прямых. А в какой обратные
теоремы – о пересечении двух параллельных прямых секущей?
Первую задачу решаем устно, с
комментированием. Кстати, в первой задаче можно обосновать решение иначе: по
признаку параллельности через односторонние углы.
Вторую задачу решаем в тетради.
Начинаем рассуждать устно все вместе. Если никто не вспомнит, что такие задачи
решаем алгебраическим способом, обозначив за «х» одну часть, то выводим визуальную подсказку
сопровождающего героя «Пусть х – 1 часть». Далее дети вспомнят: тогда углы соответственно
равны 5х и 4х, а сумма односторонних углов при пересечении двух параллельных
прямых третей равна 180º. Значит, можно составить уравнение.
Далее дети вспомнят: тогда углы соответственно
равны 5х и 4х, а сумма односторонних углов при пересечении двух параллельных
прямых третей равна 180º. Значит, можно составить уравнение.
Пусть (х)º – 1 часть
Составлю и решу уравнение…
Замечание. При записи решения в
тетради я часто использую аббревиатуры. Например, ОУ – односторонние углы,
аналогично, НЛУ, СУ. Теорема о трех
перпендикулярах ТТП и т.д.
Слайды 21 – 23 . На этапе подготовки к новой теореме можно создать
модули для организации повторения. Пример из курса геометрии 8 класса. Для
доказательства теоремы о площади трапеции, мне потребовалось напомнить детям о
свойстве площадей. Я решила рассмотреть задачу из учебника, чтобы доказательство
теоремы дети затем смогли бы придумать сами.
Слайд 21. Повторили свойство площадей. С помощью этого свойства
можно вычислять площади различных фигур, разбивая их на части.
Слайд 22. Рассмотрим задачу из учебника №478. На слайде показан
способ построения четырехугольника. Начать построение удобно с диагоналей! А
затем построить стороны четырехугольника. Никогда не вывожу на экран визуальных
подсказок, сначала слушаю идеи учеников. Одна ученица предложила вычислить
площадь для каждого из четырех прямоугольных треугольников, а затем их сложить.
Других идей, к сожалению, предложено не было. Я пригласила девочку к доске, она
решила задачу своим способом.
На слайде показан
способ построения четырехугольника. Начать построение удобно с диагоналей! А
затем построить стороны четырехугольника. Никогда не вывожу на экран визуальных
подсказок, сначала слушаю идеи учеников. Одна ученица предложила вычислить
площадь для каждого из четырех прямоугольных треугольников, а затем их сложить.
Других идей, к сожалению, предложено не было. Я пригласила девочку к доске, она
решила задачу своим способом.
Снова предлагаю детям подумать.
Ведь можно рассмотреть и другие треугольники и решить задачу проще. Теперь
догадались. Назвали треугольники КМB, ВРК и МВР, МКР. Второй вариант рассмотрели устно. Какой способ
более красивый? Тот, который мы записали в тетради или тот, который нам
предлагает компьютер? Сделали выбор. Выгодно разбить фигуру на меньшее число
частей. Мы начали чертеж с диагоналей, возможно, это и помешало детям мыслить. Но, тем не
менее, мы подготовились к восприятию теоремы о вычислении площади трапеции.
Слайд 23 . Итак, предложите способ, как разбить фигуру на части, для
которых мы можем найти площадь по известным нам формулам. Предложили диагональ
ВD или АС.
Итак, предложите способ, как разбить фигуру на части, для
которых мы можем найти площадь по известным нам формулам. Предложили диагональ
ВD или АС.
С комментированием просматриваем
анимации дополнительных построений, доказательства. Затем щелчок ПКМ, выбираем
«черный экран». Оформите доказательство в тетради. Один ученик приглашается к
доске.
Слайды 24 – 29. Фрагмент урока. Теорема об отношении площадей
треугольников, имеющих по равному углу. Актуальны знания: следствие 2 об
отношении площадей треугольников, имеющих равные высоты. Слайды 24, 25
актуализация знаний. Повторили, закрепили на примере. На слайде 25 обратили
внимание, что для треугольника АВС высота лежит во внутренней области
треугольника, а для треугольника FBR высота прошла во внешней области. Например, можно задать детям вопрос:
чем различается расположение высоты для каждого треугольника?
В теореме очень сложный чертеж.
Учителю сложно на доске начертить и одновременно оказать индивидуальную помощь детям. Работать
над теоремой с заготовленным заранее модулем более удобно. Учитель показывает
анимации, работая с дистанционной мышью, и одновременно работает индивидуально
с обучающимися. Строим чертеж и доказываем вместе с компьютером.
Работать
над теоремой с заготовленным заранее модулем более удобно. Учитель показывает
анимации, работая с дистанционной мышью, и одновременно работает индивидуально
с обучающимися. Строим чертеж и доказываем вместе с компьютером.
Оговариваем, что вершину А 1
будем называть А. Поэтому А 1 запишем в скобках. После каждой
анимации задаем детям вопрос. Например, вышла на экран высота СН. Для каких
треугольников эта высота является общей?…
Ответ. Как записать отношение площади треугольника АВС к площади АВ 1 С.
Ответ… Выводим на экран высоту СН 1 . Для каких треугольников эта
высота является общей?… Ответ. Как
записать отношение площади треугольника АВ 1 С к площади АВ 1 С 1 .
Ответ… Умножим равенства… и т.д.
Слайды 28, 29 для закрепления доказанной теоремы. Согласитесь, что выполнить всю эту работу мелом на доске учителю сложно. А значит, есть еще важное преимущество применения модулей: облегчить тяжелый труд учителя.
«Задачи на подобие» — Подобные треугольники. Найти x, y, z. Пример № 4. Решение задач по геометрии на готовых чертежах. Условие задачи: Дано: ?ABC ~ ?A1B1C1. Темы задач. Пример № 2. Автор: Скурлатова Г.Н. МОУ «СОШ № 62». Первый признак подобия треугольников. Завершить презентацию. Пример № 1. Второй и третий признаки подобия треугольников.
Найти x, y, z. Пример № 4. Решение задач по геометрии на готовых чертежах. Условие задачи: Дано: ?ABC ~ ?A1B1C1. Темы задач. Пример № 2. Автор: Скурлатова Г.Н. МОУ «СОШ № 62». Первый признак подобия треугольников. Завершить презентацию. Пример № 1. Второй и третий признаки подобия треугольников.
«Урок Признаки подобия треугольников» — В подобных фигурах стороны пропорциональны. А. А1. Урок геометрии «Признаки подобия треугольников». В1. Цель урока: Обобщение по теме «Признаки подобия треугольников». Когда. В. В подобных фигурах углы равны. Подобные фигуры. Задачи урока: Треугольники подобны?
«Практические приложения подобия треугольников» — Какие существуют способы для определения высоты предмета? Вопрос учебной темы: Применение подобия треугольников. Презентация-реферат, буклет, информационный бюллетень по способам определения высоты предмета. Как с помощью простых приспособлений можно измерять высоту предмета? Учебные предметы: геометрия, литература, физика.
«Признаки подобия» — A. Подобные треугольники. C. АВС и А1 В1С1 –треугольники
Подобные треугольники. C. АВС и А1 В1С1 –треугольники
«Подобие треугольников 8 класс» — 1 признак подобия треугольника. Подготовил ученик 8 «б» класса Михальченко Дмитрий. 3 признак подобия треугольника. Задача № 1. 2 признак подобия треугольника. Стороны a и d, b и c – сходственные. Применение подобия в жизни человека.
«Применение подобия треугольников» — Пропорциональные отрезки в прямоугольном треугольнике. Деление отрезка в заданном отношении. Разделить отрезок в отношении 2/3. Практическое применение подобия треугольников. В. Применение подобия треугольников при доказательстве теорем. Измерительные работы на местности. Теорема о средней линии треугольника.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Подобные треугольники
Подобные фигуры Фигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).
Подобие в жизни(карты местности)
Пропорциональные отрезки Определение: отрезки называются пропорциональными, если пропорциональны их длины. 12 6 8 4 А 1 В 1 АВ С 1 К 1 СК Говорят, что отрезки А 1 В 1 и С 1 К 1 пропорциональны отрезкам АВ и СК. Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если: а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см? б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см? в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см? да нет нет А В 6 см С К 4 см А 1 В 1 12 см С 1 8 см К 1
б Пропорциональные отрезки Тест 1. Указать верное утверждение: а) отрезки АВ и РН пропорциональны отрезкам СК и МЕ; б) отрезки МЕ и АВ пропорциональны отрезкам РН и СК; в) отрезки АВ и МЕ пропорциональны отрезкам РН и СК. А В 3 см С К 2см М Е 9 см Р Н 6 см Приложение: равенство МЕ АВ РН СК можно записать ещё тремя равенствами: РН СК МЕ АВ; МЕ РН АВ СК; АВ СК МЕ РН.
Пропорциональные отрезки 2 . Тест F Y Z R L S N 1 c м 2 см 4 см 2 см 3 см Какой отрезок нужно вписать, чтобы было верным утверждение: отрезки FY и YZ пропорциональны отрезкам LS и ……. а) RL ; б) RS ; в) SN а) RL
а) RL ; б) RS ; в) SN а) RL
Пропорциональные отрезки (нужное свойство) Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Н Дано: АВС, АК – биссектриса. Доказательство: 1 А В К С 2 Т. к. АК – биссектриса, то 1 = 2, значит, АВК и АСК имеют по равному углу, поэтому Доказать: ВК АВ КС АС S АВК S АСК АВ ∙ АК АС ∙ АК AB AC АВК и АСК имеют общую высоту АН, значит, S АВК S АСК ВК К C AB А C BK K С ВК АВ КС АС Следовательно, Проведём АН ВС.
Подобные треугольники Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого. А 1 В 1 С 1 А В С Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов. А 1 = А, В 1 = В, С 1 = С А 1 В 1 В 1 С 1 А 1 С 1 АВ ВС АС k A 1 B 1 C 1 ABC K – коэффициент подобия ~
Подобные треугольники А 1 В 1 С 1 А В С Нужное свойство: А 1 = А, В 1 = В, С 1 = С, АВ ВС АС А 1 В 1 В 1 С 1 А 1 С 1 1 k ABC ~ A 1 B 1 C 1 , – коэффициент подобия 1 k A 1 B 1 C 1 ABC , K – коэффициент подобия ~
Реши задачи 3. По данным на чертеже найти стороны АВ и В 1 С 1 подобных треугольников АВС и А 1 В 1 С 1: А В С А 1 С 1 В 1 6 3 4 2,5 ? ? Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 3 . 2. Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 1/3.
По данным на чертеже найти стороны АВ и В 1 С 1 подобных треугольников АВС и А 1 В 1 С 1: А В С А 1 С 1 В 1 6 3 4 2,5 ? ? Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 3 . 2. Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 1/3.
Теорема 1. Отношение периметров подобных треугольников равно коэффициенту подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: Р МКЕ: Р АВС = k Доказательство: K , МК АВ КЕ ВС МЕ АС Значит, МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС. Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то Р МКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ Р АВС. Значит, Р МКЕ: Р АВС = k .
Теорема 2. Отношение площадей подобных треугольников равно квадрату коэффициент a подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: S МКЕ: S АВС = k 2 Доказательство: Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то M = A, k, MK AB ME AC значит, МК = k ∙ АВ, МЕ = k ∙ АС. S MKE S ABC MK ∙ ME AB ∙ AC k ∙ АВ ∙ k ∙ АС АВ ∙ АС k 2
S MKE S ABC MK ∙ ME AB ∙ AC k ∙ АВ ∙ k ∙ АС АВ ∙ АС k 2
Реши задачи Две сходственные стороны подобных треугольников равны 8 см и 4 см. Периметр второго треугольника равен 12 см. Чему равен периметр первого треугольника? 24 см 2. Две сходственные стороны подобных треугольников равны 9 см и 3 см. Площадь второго треугольника равна 9 см 2 . Чему равна площадь первого треугольника? 81 см 2 3. Две сходственные стороны подобных треугольников равны 5 см и 10 см. Площадь второго треугольника равна 32 см 2 . Чему равна площадь первого треугольника? 8 см 2 4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 . Одна из сторон первого треугольника равна 4 см. Чему равна сходственная сторона второго треугольника? 8 см
Решение задачи Площади двух подобных треугольников равны 50 дм 2 и 32 дм 2 , сумма их периметров равна 117 дм. Найдите периметр каждого треугольника. Найти: Р АВС, Р РЕК Решение: Т. к. по условию треугольники АВС и РЕК подобны, то: Дано: АВС, РЕК подобны, S АВС = 50 дм 2 , S РЕК = 32 дм 2 , Р АВС + Р РЕК = 117дм. S АВС S РЕК 50 32 25 16 K 2 . Значит, k = 5 4 K , Р АВС Р РЕК Р АВС Р РЕК 5 4 1,25 Значит, Р АВС = 1,25 Р РЕК Пусть Р РЕК = х дм, тогда Р АВС = 1,25 х дм Т. к. по условию Р АВС + Р РЕК = 117дм, то 1,25 х + х = 117, х = 52. Значит, Р РЕК = 52 дм, Р АВС = 117 – 52 = 65 (дм). Ответ: 65 дм, 52 дм.
S АВС S РЕК 50 32 25 16 K 2 . Значит, k = 5 4 K , Р АВС Р РЕК Р АВС Р РЕК 5 4 1,25 Значит, Р АВС = 1,25 Р РЕК Пусть Р РЕК = х дм, тогда Р АВС = 1,25 х дм Т. к. по условию Р АВС + Р РЕК = 117дм, то 1,25 х + х = 117, х = 52. Значит, Р РЕК = 52 дм, Р АВС = 117 – 52 = 65 (дм). Ответ: 65 дм, 52 дм.
« Математику уже затем учить следует, что она ум в порядок приводит» М. В. Ломоносов Желаю успехов в учёбе! Михайлова Л. П. ГОУ ЦО № 173.
Слайд 2
СТРУКТУРА ИГРЫ 1 гонка 2 гонка 3 гонка 4 гонка 5 гонка УРА!!! «Дальше…,дальше…,дальше…» «Ты – мне, я – тебе» «В прошлое на машине времени» «Заморочки из горшочка» «Ты и только ты» Подведение итогов
Слайд 3
«Дальше…,дальше…,дальше…» Первая команда Вторая команда Как продолжить утверждение, чтобы оно стало верным? «Если два угла одного треугольника…» 1 Продолжите фразу так, чтобы утверждение стало верным. «Катет прямоугольного треугольника есть …» З н а й!!!
Слайд 4
Первая команда
Вторая команда
2
Подумай!!!
Дано:ABCD-параллелограмм. Найти:подобные треугольникиидоказатьих подобие.
Дальше…
Дано:DE║AC.
Найти:X.
A
B
F
C
D
K
A
B
C
D
E
X
3
6
12
Рис. 1
Рис. 2
Найти:подобные треугольникиидоказатьих подобие.
Дальше…
Дано:DE║AC.
Найти:X.
A
B
F
C
D
K
A
B
C
D
E
X
3
6
12
Рис. 1
Рис. 2
Слайд 5
Первая команда Вторая команда 3 Примени!!! Дальше… Дано: ∆ABC ∆MNK. Найти:x, y. S Дано: DC ┴ AB,AE ┴ BC. Верно ли, что ∆BAE ∆BCD ? S A A B B C C M N K 8 4 x y 4 3 D E Рис. 3 Рис. 4
Слайд 6
Первая команда Вторая команда 4 Сообрази!!! Дальше… ПустьBC║AD. Запишите пропорциональные отрезки. Дано:AB·BK = CB·BP.Найдитеравные углы,если они есть. Рис. 5 Рис. 6 A B C D A B C K P
Слайд 7
Первая команда Вторая команда 5 Напрягись!!! Дальше… Дано:MNKF-прямоугольник. Сколькообразовалось подобных треугольников? Подобны ли нарисованные треугольники? A B C M N K F 43° 73° 43° 64° Рис. 7 Рис. 8
Слайд 8
«Ты – мне, я – тебе» ! ! ! ? ? ?
Слайд 9
«В прошлое на машине времени»
Древняя Греция
Милет
Деньги
Мужской костюм
Древний Египет
Измерил высоту пирамиды, не влезая на неё. Кто он???
Жил 640-548 г. до н.э
Причислен к одному из СЕМИ
МУДРЕЦОВ СВЕТА.
Ему принадлежит афоризм:
«Познай самого себя».
Начал игру в «ДОКАЖИ».
Ввёл календарь: 1 год = 365 дней
Кто он???
Жил 640-548 г. до н.э
Причислен к одному из СЕМИ
МУДРЕЦОВ СВЕТА.
Ему принадлежит афоризм:
«Познай самого себя».
Начал игру в «ДОКАЖИ».
Ввёл календарь: 1 год = 365 дней
Слайд 10
Солнечный свет B C измерение тень K E D Θαλῆςὁ Μιλήσιος Рис. 9 A «О том, как Фалес измерил высоту пирамиды»
Слайд 11
Угол зрения шест скала Рис. 10 ? 10 15 500 «Заморочки из горшочка» Задача 1. Способ Жюля Верна (писатель-путешественник) 1828-1905
Слайд 12
Задача 2. Способ лесорубов для определения высоты деревьев, доступ к которым невозможен Приборы для построения угла зрения 2X 2X X Две дощечки 2X 2X 2X X Угол зрения Угол зрения Блокнот и карандаш 2X 2X X 2X M F h A K B D E C H N Рис. 11
Слайд 13
«Ты и только ты»
Рис. 12
A
B
C
D
E
M
O
F
Дано:BD║AE.
Назовитепарыподобных треугольников.
Сформулируйтеизвестную теорему,
при доказательстве которой используется
данная геометрическая конструкция.
Дано:
длины
отрезков
aиb . Построить
при помощи
циркуля
и линейки отрезок
X –среднее геометрическое
длин отрезков
aиb.
Подобныли
два любых равнобедренных треугольника?
3
1
2
Построить
при помощи
циркуля
и линейки отрезок
X –среднее геометрическое
длин отрезков
aиb.
Подобныли
два любых равнобедренных треугольника?
3
1
2
Слайд 14
«Ты и только ты» Даны длины отрезковa,bиc.Отрезки bи cлежат на одной прямой.Какпри помощи данной геометрической конструкции построитьX =a b/c, где Xназываютчетвертым пропорциональным? с b a Рис. 13 4 5 Можноли две стороны треугольника пересечьпрямой, не параллельной третьей стороне,так, чтобы ею отсекался треугольник,подобныйисходному? ║ ║
Слайд 15
Слайд 16
ВСЕМ ДАЛЬНЕЙШИХ ТВОРЧЕСКИХ УСПЕХОВ СПАСИБО!
Слайд 17
Интернет-источники
2. Древняя Греция
1. Звуковое сопровождение
(пение птиц, шум морского прибоя)
http://wav.wizardsound.ru/main/sounds/animals/
http://wav.wizardsound.ru/main/sounds/nature/
http://afield.org.ua/mod3/mod40_2.htmlhttp://www.vrata11.ru/gallery/turkey5.htm
http://ru.wikipedia.org/w/index.php?title=%D0%A4%
D0%B0%D0%BB%D0%B5%D1%81&redirect=no
http://pavlov-museum.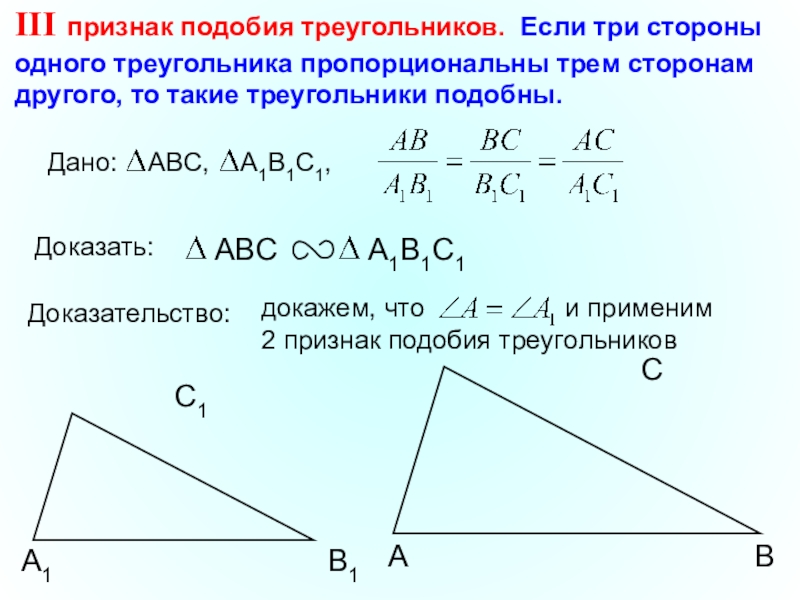 narod.ru/antiq/index.html
http://history.rin.ru/text/tree/124.html
http://history.rin.ru/cgi-bin/history.pl?num=3645
narod.ru/antiq/index.html
http://history.rin.ru/text/tree/124.html
http://history.rin.ru/cgi-bin/history.pl?num=3645
Слайд 18
http://www.3dnews.ru/editorial/it_apocalypse/ http://www.detfond.org/cover.php?izdanie=classic&id=36 http://my-shop.ru/shop/books/154411.html http://innatour.ur.ru/Izrail/o_strane/eylat_kruiz.htm 3. Древний Египет 4. Жюль Верн http://www.morev.de/wonders/classic/piramides.htmlhttp://afield.org.ua/ist/neit.html http://helen.org.ua/photo/gallery/thumbnails.php?album=10 http://www.tmn.fio.ru/works/101x/311/102.htm
Посмотреть все слайды
Первый признак подобия треугольников
Первый признак подобия треугольников
Вспомним подобные треугольники :
Определение: треугольники называются подобными, если углы
одного треугольника равны углам другого треугольника
и стороны одного треугольника пропорциональны
сходственным сторонам другого.
В 1
В
С 1
С
А
А 1
~
А 1 = А, В 1 = В, С 1 = С ,
A 1 B 1 C 1 ABC,
K – коэффициент подобия .
А 1 В 1
А 1 С 1
В 1 С 1
k.
АС
ВС
АВ
Сходственными сторонами в подобных треугольниках
называются стороны, лежащие против равных углов .
Теорема. Если два угла одного треугольника соответственно
равны двум углам другого треугольника,
то такие треугольники подобны.
(по двум углам)
B
Дано: АВС и МРК ,
Р
А = М ,
В = Р .
Доказать:
АВС МРК .
~
М
К
C
A
Доказательство:
Т. к. по условию А = М и В = Р, то С = К .
По теореме об отношении площадей треугольников, имеющих равный угол,
получаем:
S АВС
СА ∙ СВ
S АВС
АВ ∙ АС
ВА ∙ ВС
S АВС
;
;
РМ ∙ РК
МР ∙ МК
КМ ∙ КР
S МРК
S МРК
S МРК
АВ
Из этих равенств следует:
ВС
АС
МР
МК
РК
Итак, углы одного треугольника равны углам другого треугольника,
а их сходственные стороны пропорциональны, значит,
по определению треугольники АВС и МРК подобны .
Реши задачу
1.
Являются ли треугольники подобными ?
R
T
N
S
D
F
Реши задачу
2.
Являются ли треугольники подобными ?
В
Р
М
68 0
А
С
22 0
К
Реши задачу
3.
Являются ли треугольники подобными ?
А
В
М
Е
С
Реши задачу
4 .
Назови подобные треугольники и сходственные стороны в них:
FN RS
N
F
A
R
S
Реши задачу
5.
Назови подобные треугольники и сходственные стороны в них:
D
HZ CK
H
Z
K
C
Реши задачу
6 .
Назови подобные треугольники и сходственные стороны в них:
L
N
V
Q
F
FLNQ – трапеция .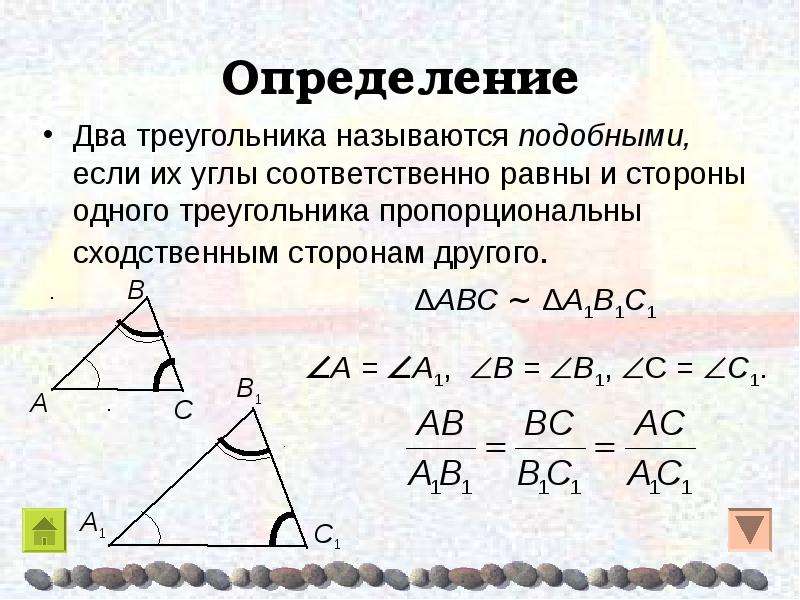
Реши задачу
7 .
Е
6
В
К
5
С
?
3
А
Реши задачу
8 .
x
7
5
14
Реши задачу
9 .
Х
М
12
?
12
4
Р
О
Н
Реши задачу
10 .
АО
3
В
СО
2
С
9
О
?
А
У
Реши задачу
11 .
В
АВ СУ
С
?
2,5
1,4
О
10
У
А
О
Решение задачи
Диагонали трапеции АВСК пересекаются в точке О. Площади треугольников ВОС и АОК относятся как 1: 9. Сумма оснований ВС и АК равна 4,8 см. Найдите основания трапеции.
В
С
Дано: АВСК – трапеция, ВС + АК = 4,8 см ,
S СОВ : S АОК = 1 : 9 .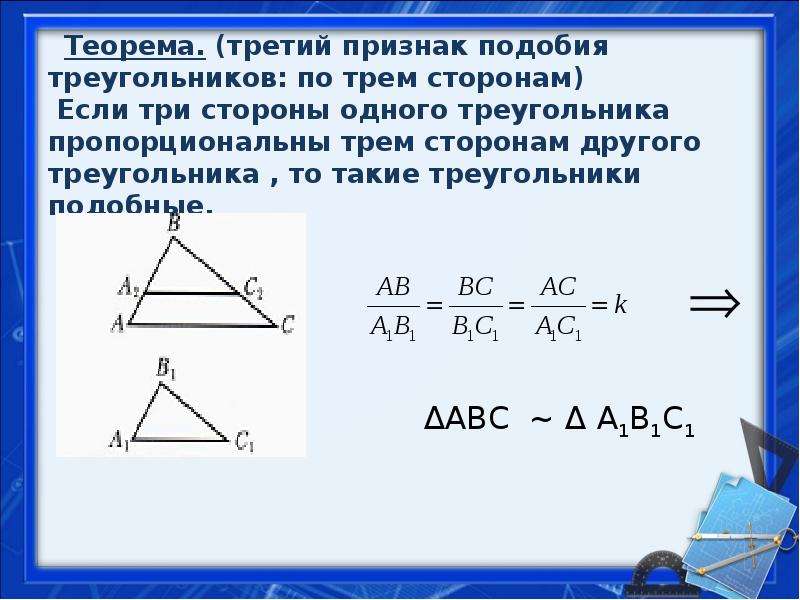
Найти: ВС, АК.
Решение:
К
А
АВСК – трапеция, значит, ВС АК, следовательно, САК = АСВ , как накрест лежащие (секущая – АС), аналогично АКВ = СВК .
Значит, по двум углам треугольники СОВ и АОК подобны, следовательно,
S СОВ : S АОК = k 2 , а по условию S СОВ : S АОК = 1 : 9, т. е. k 2 = 1/9; k = 1/3 .
По доказанному треугольники СОВ и АОК подобны, следовательно,
ВС : АК = k , т. е. ВС : АК = 1/3, значит, ВС = 1/3 АК или АК = 3 ВС .
А по условию ВС + АК = 4,8 см, значит, ВС + 3 ВС = 4,8; 4 ВС = 4,8 .
Получаем: ВС = 1,2 см, АК = 4,8 – 1,2 = 3,6(см).
Ответ: ВС = 1,2 см, АК = 3,6 см.
Нужный вывод
Дано: О, АВ СК .
Доказать:
С
АС
ОА
ВК
ОВ
3
М
Доказательство:
А
1
2
Проведём АМ ОК, значит, 1 = О.
О
В
К
Т. к. по условию АВ СК, то 2 = 3.
Значит, АОВ и САМ подобны по двум углам, следовательно,
ОА
АС
сходственные стороны пропорциональны:
ОВ
АМ
АС
ОА
ВАМК – параллелограмм, значит, АМ = ВК
ВК
ОВ
Вывод: если стороны угла пересечены параллельными прямыми,
то отрезки, образованные последовательно на одной стороне угла,
пропорциональны отрезкам, образованным последовательно
на другой стороне угла.
Реши задачу
С
5
А
6
Дано: АВ СМ .
О
М
3
В
?
Реши задачу
6
М
?
В
О
Дано: АВ СМ .
6
А
8
С
.
Подобие треугольников определение презентация. Презентация «определение подобных треугольников». Использования в жизни
Привет всем меня зовут Алеся мне 15 лет учусь в №11 школе в 8 «Г» классе. Я занимаюсь в клубе самодеятельной песни.
Мой клуб называется КСП «Вдохновение».
Люблю делать проекты. Один из которых вы видите сейчас.
Я занимаюсь в клубе самодеятельной песни.
Мой клуб называется КСП «Вдохновение».
Люблю делать проекты. Один из которых вы видите сейчас.
Сделать всё возможное для ребят чтобы они поняли где использовались подобные треугольники в древности и для чего они нужны
Я считаю подобные треугольники нужны для определения расстояния до недоступной нам точки и высоты предмета
Ну я думаю что подобные треугольники пригодились бы для определения расстояния до недоступной точки и в строительстве здания.
Слайд 8
Пропорциональные отрезки. Определение подобных треугольников Отношение площадей подобных треугольников Первый признак подобия треугольников (Доказательство) Второй признак подобия треугольников (Доказательство) Третий признак подобия треугольников (Доказательство) Практическое приложение
Слайд 9
Продолжение
Основные сведенья Измерительные работы на местности Определения высоты предмета Определение расстояния до недоступной точки Определения расстояния построением подобных треугольников (1) (2) (5) (4) (3)
Слайд 10
Пропорциональные отрезки
Отношением отрезков АВ и СD называется отношение их длин т. е АВ/СD .Говорят что отрезки АВ и CD пропорциональны отрезкам A1 B1 и C1 D1,если AB/А1В1=CD/C1D1.
Понятие пропорциональности вводится и для большого числа отрезков
е АВ/СD .Говорят что отрезки АВ и CD пропорциональны отрезкам A1 B1 и C1 D1,если AB/А1В1=CD/C1D1.
Понятие пропорциональности вводится и для большого числа отрезков
Слайд 11
Определение подобных треугольников.
Два треугольника называются подобными, Если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
Слайд 12
Отношение площадей подобных треугольников
Теорема Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия
Слайд 13
Доказательство.
Пусть треугольники АВС иА1В1С1 подобны и причем коэффициент подобия равен r. Обозначим буквами S и S1 площади этих треугольников. Так как угол А=углуА1, то S/S1=AB*AC/A1B1*A1C1(по теореме об отношение площадей отношения подобия треугольников, имеющих по равному углу). По формулам(2) имеем: АВ/А1В1=R, АС/А1С1=R, поэтому S/S=R 2
Слайд 14
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники равны А В С
Слайд 15
Второй признак подобия треугольников
Если две стороны другого треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Слайд 16
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. А В С
Слайд 17
Доказательство.(1)
Дано:АВС и А1В1С1-два треугольника, у которых угол А =углуА1, угол В= углу В1 Докажем,что треугольник АВС треугольник А!В1С1
Слайд 18
Доказательство.
По теореме о сумме углов треугольника угол С=180градусов-угол А-угол В, угол С=180градусов-уголА – угол В, и, значит, угол С= углу С. Таким образом, углы треугольника АВС соответственно равны углам треугольника А В С 1 1 1 1 1 1 1
Слайд 19
Докажем,что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С.Так как угол А= углу А и угол С= углу С,то S авс /Sa в c =АВ*АС/А В * А С S авс /Sа в с = СА*СВ/С А *С В. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Слайд 20
Из этих равенств следует, что АВ/А В =ВС/В С Аналогично используя равенства угол А= углу А
Угол В = углу В,получаем,ВС/В С = СА/С А. Итак стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С
Теорема доказана.
1
1
1
1
1
1
1
1
Итак стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С
Теорема доказана.
1
1
1
1
1
1
1
1
Слайд 21
Доказательство (2)
Дано: два треугольника АВС и А В С,у которых АВ/А В=АС/А С, угол А= углу А Доказать что треугольник АВС треугольнику А В С.Для этого, учитывая первый признак подобия треугольников, достаточно доказать, что угол В = углу В 1 1 1 1 1 1 1 1 1 1
Слайд 22
Рассмотрим треугольник АВС, у которого угол1=углуА, угол2 = углу В.Треугольники АВС А В С подобны по первому признаку подобия треугольников, поэтому АВ/А В = АС /А С. С другой стороны, по условию АВ/А В =АС /А С.Из этих двух равенств получаем АС=АС. 2 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 2
Слайд 23
Треугольники АВС и АВС равны по двум сторонам между ними (АВ — общая сторона,
АС=АС и угол А = углу 1 ,поскольку угол А= углу А и угол 1=углу А). Отсюда следует,что угол В = углу 2 ,а так как угол 2 = углу В,то угол В = углу В.
Теорема доказана. 2
2
1
1
1
1
2
2
1
1
1
1
Слайд 24
Доказательство (3)
Дано: стороны треугольников АВС и А В С пропорциональны. Докажем,что треугольник АВС треугольнику А В С 1 1 1
Слайд 25
Доказательство
Для этого,учитывая второй признак подобия треугольников достаточно доказать что угол А= углу А. Рассмотрим треугольник АВС, у которого угол 1=углу А, угол 2= углу В. Треугольники АВС и А В С подобны по первому признаку подобия треугольников,поэтому АВ/А В = ВС / В С = С А/С А.
Слайд 26
Сравнивая эти равенства с равенствами (1) получаем: ВС=ВС, СА= С А. Треугольники АВС и АВС равны по трем сторонам. Отсюда следует,что угол А = углу 1 а так как угол1 = углу А, то угол А = углу А. Теорема доказана. 2 2 2 1 1
Слайд 27
Практические приложения подобия треугольников
При решение многих задач на построение треугольников применяют так называемый метод подобия. Он состоит в том, что сначала на основании некоторых данных стоят треугольник, подобный искомому, а затем, используя остальные данные,строят искомый треугольник
Слайд 28
Задача №1
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла
Слайд 29
Решение
Сначала построим какой — нибудь треугольник,подобный искомому. Для этого начертим произвольный отрезок А В и постоим треугольник А В С, у которого углы А и В соответственно равны данным углам
Для этого начертим произвольный отрезок А В и постоим треугольник А В С, у которого углы А и В соответственно равны данным углам
Слайд 30
Продолжение
Далее построим биссектрису угла С и отложим на ней отрезок СD ,равны данному отрезку. Через точку D проведём прямую, параллельную А В. Она пересекает стороны угла С в некоторых точках А и В.треугольник АВС искомый
Слайд 31
В само деле,так как АВ параллельна А В,то угол А = углу А,угол В = углу В, и, следовательно,два угла треугольника АВС соответственно равны данным углам. По построению биссектриса CD треугольника АВС равна данному отрезку.Итак, треугольник АВС удовлетворяет всем условиям задачи.
Слайд 32
Основное сведенья(1)
1.Треугольник АВС подобен треугольнику А В С тогда и только тогда,когда выполнено одно из следующих эквивалентных условий. 1 1 1
Слайд 33
Условия
А)АВ:ВС:СА = А В: В С: С А;
В)АВ:ВС=А В:В С и угол АВС= углу А В С;
В)угол АВС= углу А В С и угол ВАС = углу В А С. 1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Слайд 34
Основное сведенья(2)
2) если параллельные прямые отсекают от угла с вершиной А треугольники АВ С и АВ С, то эти треугольники подобны и АВ:АВ = АС: АС (точки В и В лежат на одной стороне угла, С и С – на другой). 1 1 2 2 1 2 1 2 1 2 1 2
Слайд 35
Основное сведенья(3)
3) средней линией треугольника называют отрезок,соединяющий середины боковых сторон. Этот отрезок параллелен третьей стороне и равен половине её длины. Средней линией трапеции называют отрезок,соединяющий середины боковых сторон трапеции. Этот отрезок параллелен основаниям и равен полусумме их длин
Слайд 36
Основное сведенья (4)
4) отношение площадей подобных треугольников равно квадрату коэффициента подобия, т.е.квадрату отношения длин соответствующих сторон. Это следует,например,из формулы Sавс=0,5*АВ*АСsinА.
Слайд 37
Основное сведенье (5)
Многоугольники А А …А и В В …В называют подобными, если А А:А А:…:А А =В В:В В:…В В и углы при вершинах А …,А. Равны соответственно углам при вершинах А,….,А равны
Отношение соответственных диагоналей подобных многоугольников равно коэффициенту подобия; для описанных подобных многоугольников отношение радиусов вписанных окружностей также равно коэффициенту подобия
1
2
n
1
2
n
1
2
2
3
n
1
1
2
2
3
n
1
1
n
1
n
Равны соответственно углам при вершинах А,….,А равны
Отношение соответственных диагоналей подобных многоугольников равно коэффициенту подобия; для описанных подобных многоугольников отношение радиусов вписанных окружностей также равно коэффициенту подобия
1
2
n
1
2
n
1
2
2
3
n
1
1
2
2
3
n
1
1
n
1
n
Слайд 38
Измерительные работы на местности
Свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности. Мы рассмотрим две задачи: определение высоты предмета на местности и расстояние до недоступной точки.
Слайд 39
Задача №1
Определение высоты предмета
Слайд 40
Продолжение
Предположим что нам нужно определить высоту какого-нибудь предмета,например высоту телеграфного столба А С, для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку А столба.отметим на поверхности земли точку В, в которой прямая А А пересекается с поверхностью земли.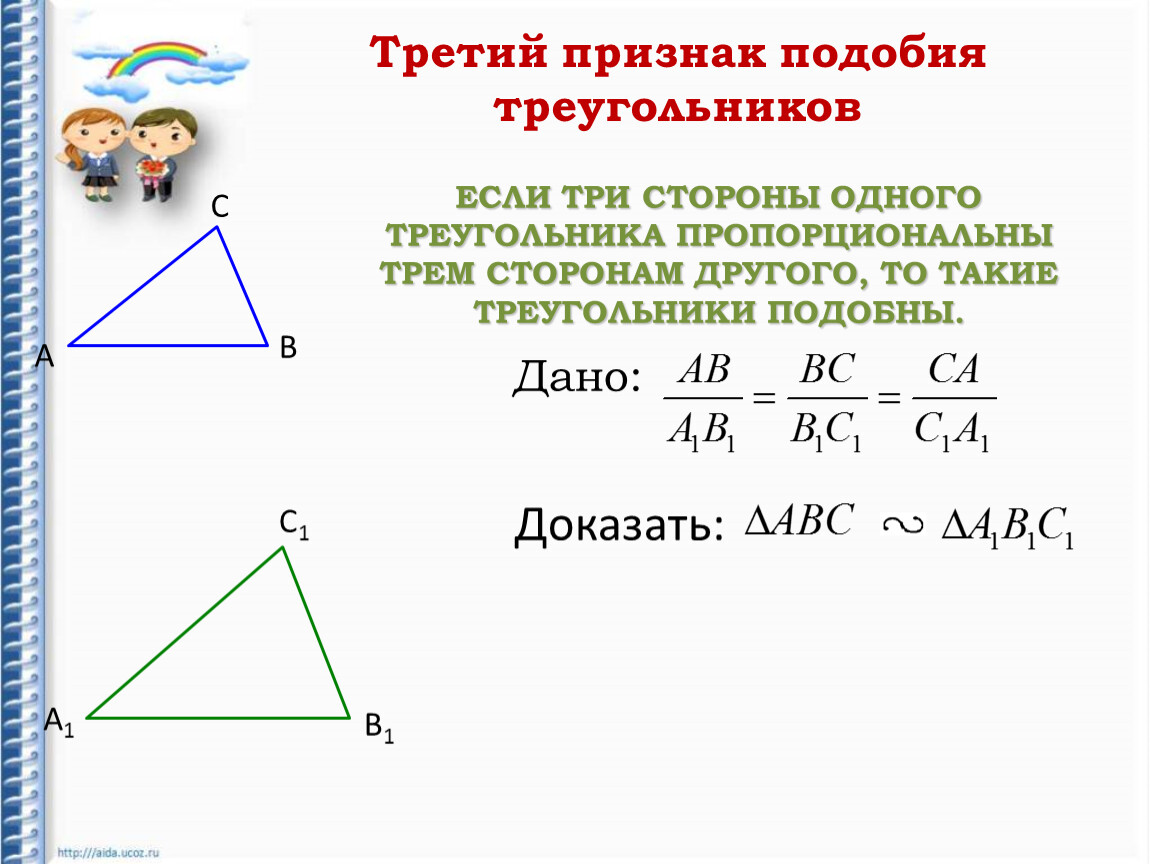 1
1
1
1
1
1
1
1
Слайд 41
Прямоугольные треугольники А С В и АСВ подобны по первому признаку треугольников (угол С = углу С = 90градусов, угол В – общий). Из подобия треугольников следует А С /АС= ВС /ВС, откуда А С =АС*ВС /ВС измерив расстояние ВС и ВС и зная длину АС шеста по полученной формуле определяем высоту А С телеграфного столба 1 1 1 1 1 1 1 1 1 1
Слайд 42
Задача (2)
Определения расстояния до недоступной точки
Слайд 43
Продолжение
Предположим,что нам нужно найти расстояние от пункта А до недоступного пункта В.для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябия измеряем углы А и С. На листе бумаги строим какой-нибудь треугольник А В С,у которого угол А = углу А, угол С = углу С,и измеряем длины сторон А В и А С этого треугольника. 1 1 1 1 1 1 1 1 1
Слайд 44
Так как треугольник АВС и А В С подобны (по первому признаку подобия треугольников), то АВ/А В =АС А С,откуда получаем АВ= АС*А В /А С. Эта формула позволяет по известным расстояниям АС, А С и А В,найти расстояние АВ.
1
1
1
1
1
1
1
1
1
1
1
1
1
Эта формула позволяет по известным расстояниям АС, А С и А В,найти расстояние АВ.
1
1
1
1
1
1
1
1
1
1
1
1
1
Слайд 45
Для упрощения вычислений удобно построить треугольник А В С таким образом,чтобы А С: АС =1:1000. например если АС=130м,то расстояние А С возьмём равным 130мм. В этом случае АВ=АС/А С * А В =1000*А В,поэтому,измерив расстояние А В в миллиметрах,мы сразу получаем расстояние АВ в метрах 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Слайд 46
Пример
Пусть АС=130м, угол А=73градусов,угол С=58градусов.на бумаге строим треугольник А В С так, чтобы угол А =73градуса,угол С =58градусов, А С =130мм,и измеряем отрезок А В. Он равен 153мм, поэтому искомое расстояние рано153м. 1 1 1 1 1
Слайд 47
Определение расстояние построением подобных треугольников
При определении расстояния до отдалённых или недоступных предметов, можно использовать следующий приём. На обычную спичку надо нанести чернилами или карандашом двухмиллиметровые деления. Также нужно знать примерную высоту предмета, до которого определяется расстояние. Так рост человека равен 1,7-1,8 м, колесо автомобиля 0,5 м, всадник-2,2м,телеграфический столб-6м,одноэтажный дом без крыши -2,5-4м.
Также нужно знать примерную высоту предмета, до которого определяется расстояние. Так рост человека равен 1,7-1,8 м, колесо автомобиля 0,5 м, всадник-2,2м,телеграфический столб-6м,одноэтажный дом без крыши -2,5-4м.
Слайд 48
Продолжение
Допустим, надо определить расстояние до столба. Направляем на него спичку на вытянутой руке, длина которой приблизительно равна 60 см.предположим, высота столба выглядит равной двум делениям спички, т.е. 4 мм. Имея такие данные составим пропорцию:0.6/х=0.004/6.0;х=(0,6*6)/0ю004=900.Таким образом до столба 900м.
Посмотреть все слайды
1.1. Пропорциональные отрезки Определение подобных треугольников 1.2. Определение подобных треугольников 1.3. Отношение площадей подобных треугольников Отношение площадей подобных треугольников Свойства подобия.
1.1 Пропорциональные отрезки. Отношением отрезков AB и CD называется отношение их длин, т. е. Говорят, что отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1, если ПРИМЕР 1. Отрезки AB и CD, длины которых равны 2 см и 1см, пропорциональны отрезкам A 1 B 1 и C 1 D 1,отрезки которых равны 3см и 1,5см. В самом деле,
Отрезки AB и CD, длины которых равны 2 см и 1см, пропорциональны отрезкам A 1 B 1 и C 1 D 1,отрезки которых равны 3см и 1,5см. В самом деле,
1.2. Определение подобных треугольников. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Так, подобными являются любые два квадрата, любые два круга. Введем понятие подобных треугольников.
1.2. Определение подобных треугольников. ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы у геометрических фигур, независимо от их размеров. Две фигуры F1 и F2 называются подобными, если между их точками можно установить взаимно однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек фигур F1 и F2 равно одной и той же постоянной k, называемой коэффициентом подобия. Углы между соответствующими линиями подобных фигур равны. Подобные фигуры F1 и F2.
Подобные фигуры F1 и F2.
Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. Другими словами, два треугольника подобны, если их можно обозначить буквами ABC и A 1 B 1 C 1 так, что A= A 1, B= B 1, C= C 1, Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
1.3. Отношение площадей подобных треугольников. Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Доказательство. Пусть треугольники ABC и A1B1C1 подобны и коэффициент подобия равен k. Обозначим буквами S и S1 площади этих треугольников. Так как A= A1, то
Свойства подобия. Задача 2. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника Решение.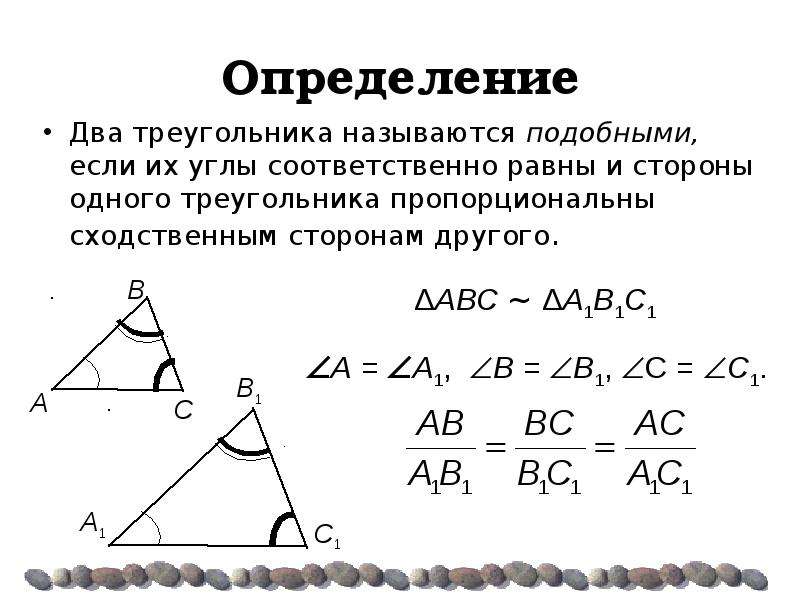 Пусть AD – биссектриса треугольника ABC. Докажем, что Треугольники ABD и ACD имеют общую высоту AH, поэтому 12 A H B D C
Пусть AD – биссектриса треугольника ABC. Докажем, что Треугольники ABD и ACD имеют общую высоту AH, поэтому 12 A H B D C
Доказательство: По теореме о сумме углов: С = А — В, а С 1 = А 1 — В 1,значит С= С 1. Так как А= А 1 и С= С 1, то и От этого следует: Получается, что сходственные стороны пропорциональны. Дано: АВС и А 1 В 1 С 1 А= А 1 В= В 1 Доказать: АВС А 1 В 1 С 1 А С В А1А1 В1В1 С1С1
АВС 2 А 1 В 1 С 1 (по первому признаку),значит, с другой стороны,из этих равенств получается АС= =АС 2. АВС= АВС 2 -по двум сторонам и углу между ними (АВ-общая сторона, АС=АС 2 и,т.к. и).Значит и, то АВС А1В1С1 Дано: АВС и А 1 В 1 С 1 Д-ть: Доказательство: Рассмотрим АВС 2, у которого и
Доказательство: А 1 В 1 – средняя линия, и А 1 В 1 //АВ, поэтому и Значит АОВ А 1 ОВ 1 (по двум углам),то Но АВ=А 1 В 1, поэтому АО=2А 1 О и ВО=2В 1 О. Значит точка О- пересечение медиан АА 1 и ВВ 1 делит каждую из них в отношении 2:1, считая от вершины. Аналогично доказывается, что точка О – пересечение медиан ВВ 1 и СС 1 делит каждую из них в отношении 2:1, считая от вершины. Значит точка О – пересечения медиан АА 1, ВВ 1 и СС 1 делит их в отношении 2:1, считая от вершины.
Значит точка О- пересечение медиан АА 1 и ВВ 1 делит каждую из них в отношении 2:1, считая от вершины. Аналогично доказывается, что точка О – пересечение медиан ВВ 1 и СС 1 делит каждую из них в отношении 2:1, считая от вершины. Значит точка О – пересечения медиан АА 1, ВВ 1 и СС 1 делит их в отношении 2:1, считая от вершины.
Презентация «Определение подобных треугольников» охватывает этап введения нового понятия на уроке геометрии в 8 классе — подобия треугольников. После уточнения понятия пропорциональности отрезков, на основе которого строится понятие подобия, ученики переходят к рассмотрению достаточно сложного для них материала — подобия. При помощи презентации учитель во время объяснения формирует четкое представление учеников об изучаемом предмете — подобии треугольников, продолжает формировать навыки использования математической речи, формирует навыки применения изученного понятия для решения практических задач.
слайды 1-2 (Тема презентации «Определение подобных треугольников», примерs)
Для объяснения свойства подобия треугольников в презентации используются следующие инструменты:
- выделение красным цветом главных понятий;
- анимированное построение графической части для уточнения определения, наглядности при объяснении материала;
- заключение в рамку основных алгебраических выражений по теме;
- использование рисунков для понимания практического смысла изучаемого понятия.

Такая демонстрация позволяет углубить понимание материала, облегчить его запоминание.
Начинается презентация с демонстрации предметов, на очертаниях которых строятся подобные геометрические фигуры. В качестве примеров приводятся футбольный и гандбольный мячи, узорчатые тарелки разных размеров. Справа от предметов изображаются очертания фигур, которые подобны между собой — большой и маленький квадрат, большой и маленький круг.
слайды 3-4 (определение подобных треугольников)
Такая демонстрация, вводящая ученика в изучение данного понятия через практическое применение, очень эффективна и помогает решить одну из важных целей урока — закрепить представление ученика об изучаемом предмете.
На следующем слайде понятие подобия раскладывается на составляющие при помощи двух построенных треугольников АВС и А1В1С1. Используя анимацию, постепенно соответствующие углы отмечаются как равные. Соответствующие углы обозначаются одинаково — А и А1 одним полукругом, В и В1 — двумя, С и С1 — тремя. При том, что данные треугольники имеют равные углы, их соответствующие стороны называют сходственными. Данное выражение в дальнейшем необходимо употреблять при решении геометрических задач, поэтому выражение выделено зеленым цветом, означая необходимость запомнить его и употреблять в дальнейшем.
При том, что данные треугольники имеют равные углы, их соответствующие стороны называют сходственными. Данное выражение в дальнейшем необходимо употреблять при решении геометрических задач, поэтому выражение выделено зеленым цветом, означая необходимость запомнить его и употреблять в дальнейшем.
слайд 5 (сайт)
Теперь можно сформулировать определение подобия треугольников при соответствующем равенстве углов и пропорциональности сходственных сторон. Далее демонстрируется алгебраическая запись условий подобия треугольников — равенство углов и пропорциональность всех трех сторон. Условие пропорциональности сторон заключено в рамку для запоминания. Результат отношения каждой пары — одно и то же число. Оно обозначается k и определяется как коэффициент подобия треугольников.
На основе изученного понятия следует изучение следующих тем курса геометрии — отношения площадей подобных треугольников, признаки подобия треугольников.
Данная презентация «Определение подобных треугольников» может быть рекомендована не только в качестве демонстрационного материала на уроке геометрии, сопровождающая объяснение учителя. Она может помочь ученику в самостоятельном изучении материала, а также поможет объяснить понятие подобия на уроке при дистанционном обучении.
Она может помочь ученику в самостоятельном изучении материала, а также поможет объяснить понятие подобия на уроке при дистанционном обучении.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Подобные треугольники
Подобные фигуры Фигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).
Подобие в жизни(карты местности)
Пропорциональные отрезки Определение: отрезки называются пропорциональными, если пропорциональны их длины. 12 6 8 4 А 1 В 1 АВ С 1 К 1 СК Говорят, что отрезки А 1 В 1 и С 1 К 1 пропорциональны отрезкам АВ и СК. Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если: а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см? б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см? в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см? да нет нет А В 6 см С К 4 см А 1 В 1 12 см С 1 8 см К 1
б Пропорциональные отрезки Тест 1. Указать верное утверждение: а) отрезки АВ и РН пропорциональны отрезкам СК и МЕ; б) отрезки МЕ и АВ пропорциональны отрезкам РН и СК; в) отрезки АВ и МЕ пропорциональны отрезкам РН и СК. А В 3 см С К 2см М Е 9 см Р Н 6 см Приложение: равенство МЕ АВ РН СК можно записать ещё тремя равенствами: РН СК МЕ АВ; МЕ РН АВ СК; АВ СК МЕ РН.
Указать верное утверждение: а) отрезки АВ и РН пропорциональны отрезкам СК и МЕ; б) отрезки МЕ и АВ пропорциональны отрезкам РН и СК; в) отрезки АВ и МЕ пропорциональны отрезкам РН и СК. А В 3 см С К 2см М Е 9 см Р Н 6 см Приложение: равенство МЕ АВ РН СК можно записать ещё тремя равенствами: РН СК МЕ АВ; МЕ РН АВ СК; АВ СК МЕ РН.
Пропорциональные отрезки 2 . Тест F Y Z R L S N 1 c м 2 см 4 см 2 см 3 см Какой отрезок нужно вписать, чтобы было верным утверждение: отрезки FY и YZ пропорциональны отрезкам LS и ……. а) RL ; б) RS ; в) SN а) RL
Пропорциональные отрезки (нужное свойство) Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Н Дано: АВС, АК – биссектриса. Доказательство: 1 А В К С 2 Т. к. АК – биссектриса, то 1 = 2, значит, АВК и АСК имеют по равному углу, поэтому Доказать: ВК АВ КС АС S АВК S АСК АВ ∙ АК АС ∙ АК AB AC АВК и АСК имеют общую высоту АН, значит, S АВК S АСК ВК К C AB А C BK K С ВК АВ КС АС Следовательно, Проведём АН ВС.
Подобные треугольники Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого. А 1 В 1 С 1 А В С Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов. А 1 = А, В 1 = В, С 1 = С А 1 В 1 В 1 С 1 А 1 С 1 АВ ВС АС k A 1 B 1 C 1 ABC K – коэффициент подобия ~
Подобные треугольники А 1 В 1 С 1 А В С Нужное свойство: А 1 = А, В 1 = В, С 1 = С, АВ ВС АС А 1 В 1 В 1 С 1 А 1 С 1 1 k ABC ~ A 1 B 1 C 1 , – коэффициент подобия 1 k A 1 B 1 C 1 ABC , K – коэффициент подобия ~
Реши задачи 3. По данным на чертеже найти стороны АВ и В 1 С 1 подобных треугольников АВС и А 1 В 1 С 1: А В С А 1 С 1 В 1 6 3 4 2,5 ? ? Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 3 . 2. Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 1/3.
Теорема 1. Отношение периметров подобных треугольников равно коэффициенту подобия.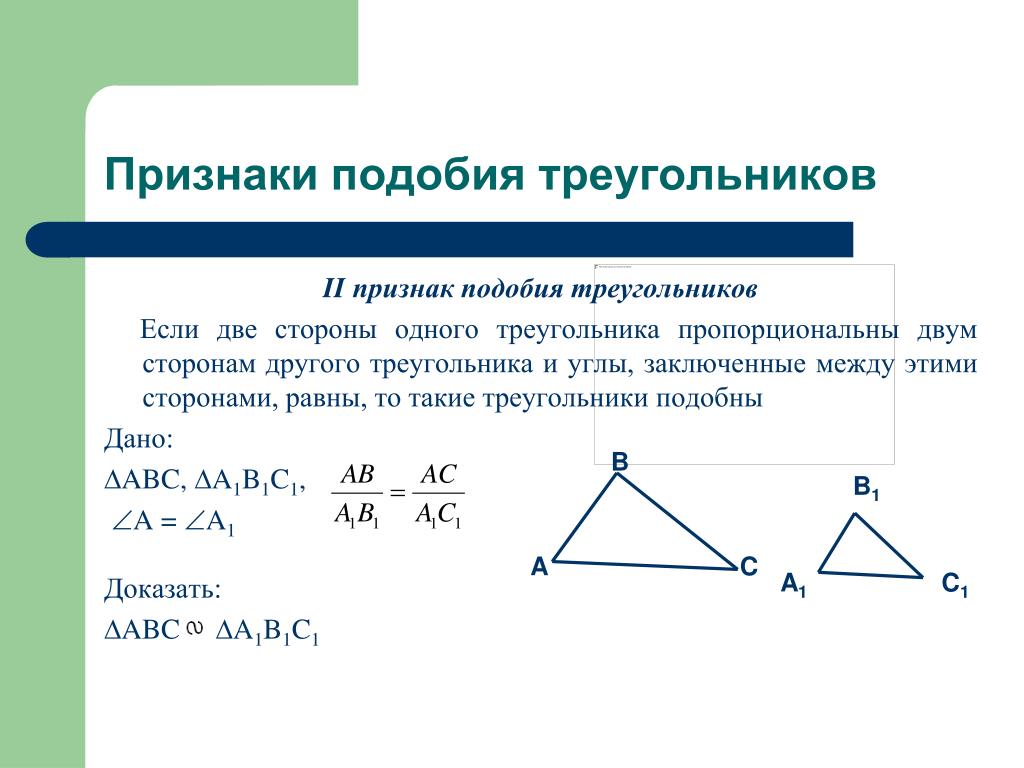 М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: Р МКЕ: Р АВС = k Доказательство: K , МК АВ КЕ ВС МЕ АС Значит, МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС. Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то Р МКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ Р АВС. Значит, Р МКЕ: Р АВС = k .
М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: Р МКЕ: Р АВС = k Доказательство: K , МК АВ КЕ ВС МЕ АС Значит, МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС. Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то Р МКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ Р АВС. Значит, Р МКЕ: Р АВС = k .
Теорема 2. Отношение площадей подобных треугольников равно квадрату коэффициент a подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: S МКЕ: S АВС = k 2 Доказательство: Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то M = A, k, MK AB ME AC значит, МК = k ∙ АВ, МЕ = k ∙ АС. S MKE S ABC MK ∙ ME AB ∙ AC k ∙ АВ ∙ k ∙ АС АВ ∙ АС k 2
Реши задачи Две сходственные стороны подобных треугольников равны 8 см и 4 см. Периметр второго треугольника равен 12 см. Чему равен периметр первого треугольника? 24 см 2. Две сходственные стороны подобных треугольников равны 9 см и 3 см. Площадь второго треугольника равна 9 см 2 . Чему равна площадь первого треугольника? 81 см 2 3. Две сходственные стороны подобных треугольников равны 5 см и 10 см. Площадь второго треугольника равна 32 см 2 . Чему равна площадь первого треугольника? 8 см 2 4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 . Одна из сторон первого треугольника равна 4 см. Чему равна сходственная сторона второго треугольника? 8 см
Две сходственные стороны подобных треугольников равны 5 см и 10 см. Площадь второго треугольника равна 32 см 2 . Чему равна площадь первого треугольника? 8 см 2 4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 . Одна из сторон первого треугольника равна 4 см. Чему равна сходственная сторона второго треугольника? 8 см
Решение задачи Площади двух подобных треугольников равны 50 дм 2 и 32 дм 2 , сумма их периметров равна 117 дм. Найдите периметр каждого треугольника. Найти: Р АВС, Р РЕК Решение: Т. к. по условию треугольники АВС и РЕК подобны, то: Дано: АВС, РЕК подобны, S АВС = 50 дм 2 , S РЕК = 32 дм 2 , Р АВС + Р РЕК = 117дм. S АВС S РЕК 50 32 25 16 K 2 . Значит, k = 5 4 K , Р АВС Р РЕК Р АВС Р РЕК 5 4 1,25 Значит, Р АВС = 1,25 Р РЕК Пусть Р РЕК = х дм, тогда Р АВС = 1,25 х дм Т. к. по условию Р АВС + Р РЕК = 117дм, то 1,25 х + х = 117, х = 52. Значит, Р РЕК = 52 дм, Р АВС = 117 – 52 = 65 (дм). Ответ: 65 дм, 52 дм.
« Математику уже затем учить следует, что она ум в порядок приводит» М.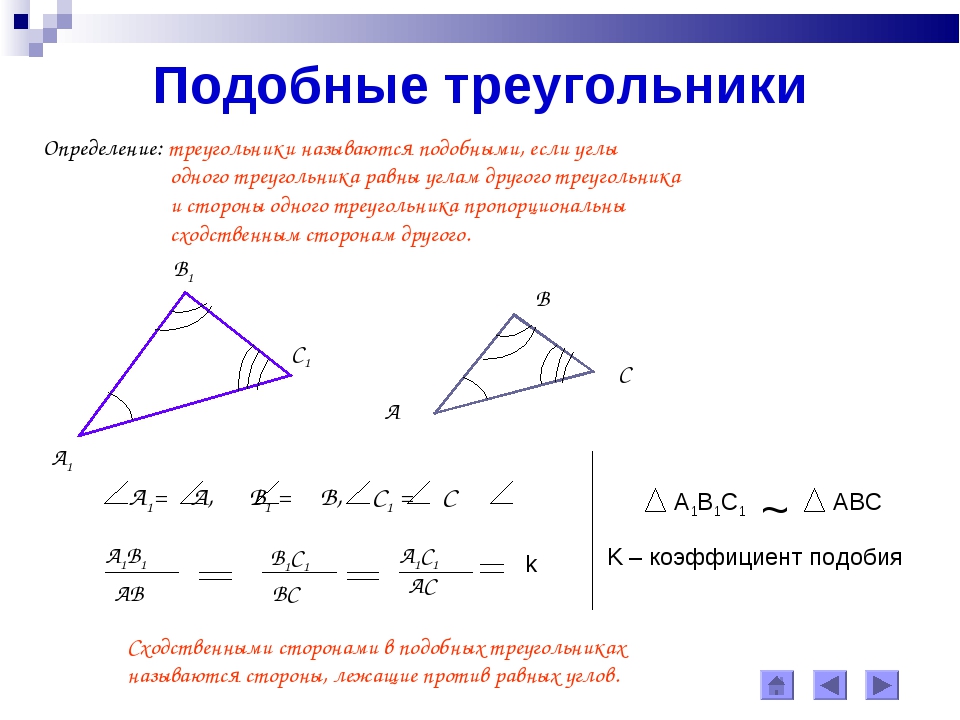 В. Ломоносов Желаю успехов в учёбе! Михайлова Л. П. ГОУ ЦО № 173.
В. Ломоносов Желаю успехов в учёбе! Михайлова Л. П. ГОУ ЦО № 173.
подобных треугольников
Два треугольника похожи, если разница только в размере (и, возможно, в необходимости повернуть или перевернуть один из них).
Все эти треугольники подобны:
(Равные углы отмечены одинаковым количеством дуг)
Некоторые из них имеют разные размеры, а некоторые перевернуты или перевернуты.
Для подобных треугольников:
Все соответствующие углы равны
и
Все соответствующие стороны имеют одинаковое соотношение
Также обратите внимание, что соответствующие стороны обращены под соответствующими углами.Например, стороны, обращенные к углам с двумя дугами, соответствуют друг другу.
Соответствующие стороны
В подобных треугольниках соответствующие стороны всегда находятся в одном и том же отношении.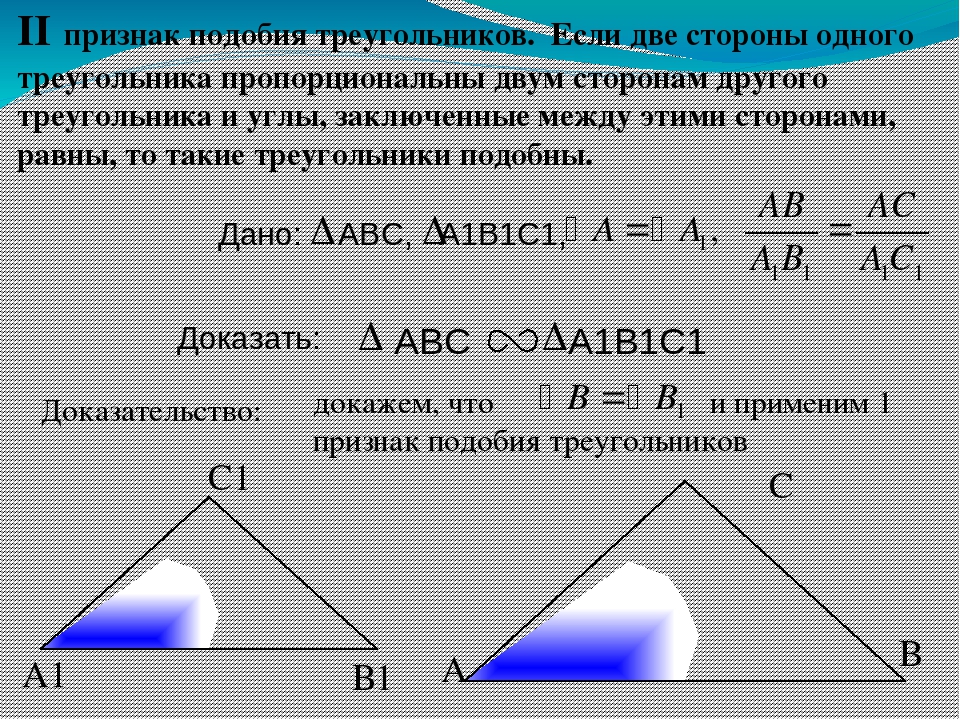
Например:
Треугольники R и S подобны. Равные углы отмечены одинаковым количеством дуг.
Каковы соответствующие длины?
- Длины 7 и a соответствуют (они смотрят на угол, отмеченный одной дугой)
- Длины 8 и 6.4 соответствуют (они обращены к углу, отмеченному двумя дугами)
- Длины 6 и b соответствуют (они смотрят на угол, отмеченный тремя дугами)
Вычисление длин соответствующих сторон
Иногда мы можем вычислить длину, которую еще не знаем.
- Шаг 1: Найти отношение соответствующих сторон
- Шаг 2: Используйте это соотношение, чтобы найти неизвестные длины
Пример: найти длины a и b треугольника S
Шаг 1: Найдите соотношение
Нам известны все стороны треугольника R , а
Нам известна сторона 6.4 в треугольнике S
Сторона 6. 4 обращена к углу, отмеченному двумя дугами, как и сторона длины 8 в треугольнике R .
4 обращена к углу, отмеченному двумя дугами, как и сторона длины 8 в треугольнике R .
Итак, мы можем сопоставить 6.4 с 8 , и поэтому отношение сторон треугольника S к треугольнику R равно:
от 6,4 до 8
Теперь мы знаем, что длины сторон треугольника S равны 6,4/8 умножить на длин сторон треугольника R .
Шаг 2: Используйте соотношение
a обращен к углу с одной дугой, как и сторона длины 7 в треугольнике R .
a = (6,4/8) × 7 = 5,6
b обращен к углу с тремя дугами, как и сторона длины 6 в треугольнике R .
б = (6,4/8) × 6 = 4,8
Готово!
подобных треугольников — объяснение и примеры
Теперь, когда мы закончили с конгруэнтными треугольниками, мы можем перейти к другому понятию, называемому подобных треугольников.
В этой статье мы узнаем о подобных треугольниках, свойствах подобных треугольников, как использовать постулаты и теоремы для определения подобных треугольников и, наконец, как решать задачи о подобных треугольниках.
Что такое подобные треугольники?
Понятие подобных треугольников и конгруэнтных треугольников — это два разных термина, тесно связанных между собой. Подобные треугольники — это два или более треугольника с одинаковой формой, равными парами соответствующих углов и одинаковым отношением соответствующих сторон.
Иллюстрация подобных треугольников:
Рассмотрим три треугольника ниже. Если:
- Отношение их соответствующих сторон равно.
AB/PQ = AC/PR= BC= QR, AB/XY= AC/XZ= BC/YZ
- ∠ A= ∠ P=∠X, ∠B = ∠Q= ∠Y, ∠C= ∠r = ∠z
Поэтому, ΔABC ~ Δpqr ~ Δxyz
Сравнение между похожими треугольниками и конгруэнтными треугольниками
| 495150 | Connoguent Trangles | Подобные треугольники | |
| Размер | Один размер и форма | и такая же форма, но разный размер | |
| символ | ≅ | ~ | |
| Соответствующая длина боковых сторон | Соотношение соответствующих сторон Congruent Trangles всегда равна постоянное число 1.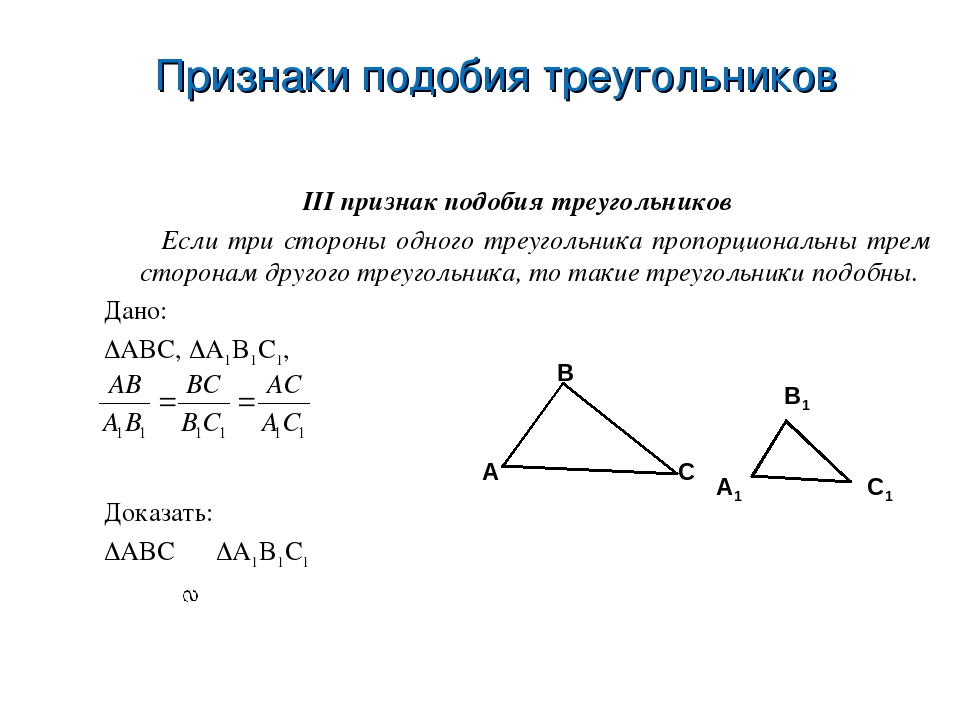 | Отношение всех соответствующих сторон в подобных треугольниках постоянно. | |
| Соответствующие углы | Все соответствующие углы равны. | Каждая пара соответствующих углов равна. |
Как определить подобные треугольники?
Сходство треугольников можно доказать, применяя теоремы о подобных треугольниках. Это постулаты или правила, используемые для проверки подобных треугольников.
Существует три правила проверки подобных треугольников: правило AA, правило SAS или правило SSS.
Правило угла-угла (AA):
Согласно правилу AA два треугольника называются подобными, если два угла в одном треугольнике равны двум углам другого треугольника.
Правило Side-Angle-Side (SAS):
Правило SAS гласит, что два треугольника подобны, если отношение их соответствующих двух сторон равно, а также угол, образованный двумя сторонами, равен.
Правило стороны-стороны-стороны (SSS):
Два треугольника подобны, если все соответствующие три стороны данных треугольников находятся в одной пропорции.
Как решать подобные треугольники?
Есть два типа подобных задач на треугольник ; это задачи, которые требуют от вас доказать, подобны ли данный набор треугольников, и те, которые требуют от вас вычисления недостающих углов и длин сторон подобных треугольников.
Давайте посмотрим на следующие примеры:
Пример 1
Проверьте, являются ли следующие треугольники похожими
81 Решение
Сумма углов внутренней части в треугольнике = 180 °
Таким образом, принимая во внимание Δ PQR
∠P + ∠Q + ∠R = 180°
60° + 70° + ∠R = 180°
130° + ∠R = 180°
вычесть обе стороны 0 на 00023 9 °.180° °
Вычесть обе стороны на 110°
∠ Y = 70°
Отсюда;
- По правилу угла-угла (AA), ΔPQR~ΔXYZ.
- ∠Q = ∠ Y = 70° и ∠Z = ∠ R= 50°
Пример 2
Решение
Учитывая, что два треугольника подобны, тогда;
WY/QR = WX/PR
30/15 = 36/x
Перемножить
30x = 15 * 36
Разделить обе стороны на 30.
x = (15 * 36)/30
x = 18
Следовательно, PR = 18
Проверим, равны ли пропорции соответствующих двух сторон треугольников.
WY/QR = WX/PR
30/15 = 36/18
2 = 2 (RHS = LHS)
Пример 3 значение к.
Решение
Согласно правилу SAS, два треугольника подобны.
Доказательство:
8/ 4 = 20/10 (левая = правая)
2 = 2
Теперь вычислите значение k
12/k = 8/4
12/k = 2
900 стороны к.
12 = 2k
Разделить обе части на 2
12/2 = 2k/2
k = 6.
Решение
Пусть треугольники ABD и ECD подобны.
Применить правило «сторона-угол-сторона» (SAS), где A = 90 градусов.
AE/EC= BD/CD
x/1,8 = (24 + 12)/12
x/1,8 = 36/12
Перемножить
12x = 36 * 1,8
x = (36 * 1,8)/12
= 5,4
Следовательно, значение x равно 5,4 мм.
Подобные треугольники: определение, формула и свойства — видео и расшифровка урока
Важная лексика и обозначения
Есть несколько ключевых терминов и обозначений, которые необходимо обсудить, прежде чем мы сможем перейти к использованию характеристик подобных треугольников для нахождения соответствующих сторон.
- Конгруэнтно: причудливый способ сказать равный.
- Пропорциональный: все соответствующие стороны имеют постоянное соотношение. Это будет объяснено далее, когда мы найдем конгруэнтные стороны.
- Соответствие: в случае подобных треугольников соответствие относится к углам и сторонам, которые находятся в одном и том же месте в обоих треугольниках. Каждому углу или стороне одного треугольника соответствует сторона или угол второго треугольника.

Дуги, начерченные на углах обоих треугольников, важны, чтобы помочь нам понять, какие углы соответствуют друг другу или находятся в одном и том же положении. Это особенно важно, когда треугольники повернуты в разные стороны. Хотя на этом изображении эти дуги имеют цветовую кодировку, чтобы сделать рисунок более четким, рисунки обычно выполняются черно-белыми, поэтому мы должны смотреть на количество дуг в каждом углу, чтобы определить соответствующий им угол.
Например, одна дуга нарисована желтым цветом.Следовательно, угол с желтой одинарной дугой в каждом подобном треугольнике соответствующий. Это также верно для углов с двойными красными дугами и тройными зелеными дугами.
Теперь вы почти всегда будете видеть каждый треугольник, помеченный заглавными буквами. Эти буквы, как правило, расположены в алфавитном порядке, где каждая буква обозначает один из углов. Возьмем, к примеру, этот треугольник.
Треугольник обозначен заглавными буквами ABC . Это позволяет нам легко устанавливать связи между конгруэнтными углами и соответствующими сторонами подобных треугольников.
Это позволяет нам легко устанавливать связи между конгруэнтными углами и соответствующими сторонами подобных треугольников.
Нахождение соответствующих сторон
Возьмем в качестве примера эти подобные треугольники.
Мы видим, что:
- Угол A и угол D соответствуют
- Уголок B и уголок E соответствуют
- Угол C и уголок F соответствуют
Нам также известны все длины сторон треугольника ABC и одна из длин сторон треугольника DEF .Это все, что нам нужно, чтобы определить длины двух других сторон треугольника DEF .
Чтобы освежить нашу память, пропорционально означает, что все соответствующие стороны подобных треугольников имеют постоянное соотношение. Это ключ к нахождению недостающих длин в треугольнике DEF . Мы уже определили соответствующие углы между двумя треугольниками, поэтому мы можем использовать их для организации соответствующих сторон.
Глядя на наши соответствующие углы, мы видим, что:
- Сторона AB и сторона DE соответствуют
- Сторона BC и сторона EF соответствуют
- Сторона AC и сторона DF соответствуют
Теперь мы можем использовать эти соответствующие стороны, чтобы установить пропорцию или долю отношения.Поскольку мы знаем только длину одной стороны в треугольнике DEF — сторона DE — мы должны использовать эту длину и длину соответствующей стороны из треугольника ABC . Из списка, который мы составили ранее, мы знаем, что сторона AB соответствует стороне DE .
Глядя на наши треугольники, мы видим, что сторона AB имеет длину 6, а сторона DE имеет длину 4.
Здесь в игру вступает наша пропорция.Давайте сначала найдем недостающую сторону EF , которая обозначена как x на треугольнике. Начнем с того, что запишем наши две известные соответствующие стороны в виде дроби отношения:
Затем мы должны установить дробь для нашей недостающей стороны. Придерживаясь структуры нашей дроби отношения, нам нужно поместить нашу сторону из треугольника ABC вверху, а нашу сторону из треугольника DEF внизу. Мы знаем, что сторона EF соответствует стороне BC .Таким образом, мы можем выписать другую дробь отношения:
Придерживаясь структуры нашей дроби отношения, нам нужно поместить нашу сторону из треугольника ABC вверху, а нашу сторону из треугольника DEF внизу. Мы знаем, что сторона EF соответствует стороне BC .Таким образом, мы можем выписать другую дробь отношения:
Теперь, когда у нас есть и наша относительная дробь, и наша неизвестная дробь, мы можем установить их равными друг другу и использовать перекрестное умножение, чтобы найти недостающую сторону.
Мы начинаем с перекрестного умножения, чтобы получить 6, умноженное на x , равно 4, умноженное на 7. Затем мы умножаем наши 4 на 7, чтобы получить 6, x равно 28.Отсюда мы делим обе стороны на 6, чтобы получить само по себе x , так как это недостающая сторона, которую мы пытаемся найти. Это дает нам решение с повторением 4,6, которое мы округляем до 4,67.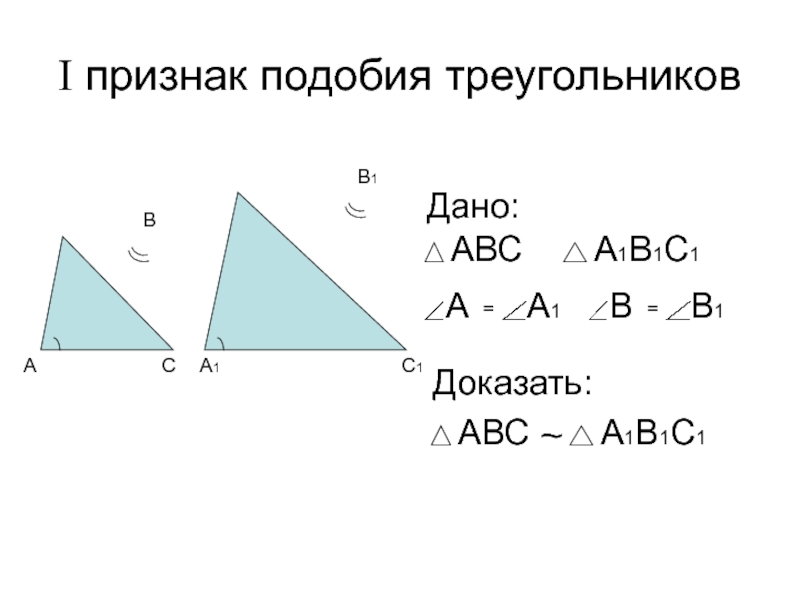 Это означает, что недостающая длина стороны EF равна 4,67.
Это означает, что недостающая длина стороны EF равна 4,67.
Мы должны повторить эти шаги, чтобы найти недостающую сторону DF . Возвращаясь к составленному нами списку соответствующих сторон, мы видим, что сторона DF , помеченная как y , соответствует стороне AC , длина которой равна 8.
Начнем с перекрестного умножения, чтобы получить 6 умножить на y равно 4 умножить на 8. Затем мы умножим наши 4 на 8, чтобы получить 6 y равно 32. Отсюда мы разделим обе части на 6, чтобы получить y сам по себе, так как это недостающая сторона, которую мы пытаемся найти. Это дает нам решение с повторением 5,3, которое мы округляем до 5,33. Это означает, что недостающая длина стороны DF равна 5,33.
Краткое содержание урока
Мы сделали это! В этом уроке вы узнали не только определение подобных треугольников, но и свойства, которые делают эти треугольники подобными. Вы знаете, что подобных треугольников — это треугольники, у которых соответствующие углы равны и пропорциональны соответствующим сторонам. Кроме того, теперь вы являетесь экспертом в использовании пропорций для нахождения недостающей стороны треугольника!
Вы знаете, что подобных треугольников — это треугольники, у которых соответствующие углы равны и пропорциональны соответствующим сторонам. Кроме того, теперь вы являетесь экспертом в использовании пропорций для нахождения недостающей стороны треугольника!
Определение подобных треугольников | StudyPug
Подобие треугольника
определить сходство
Когда вы слышите, что два треугольника подобны, что это на самом деле означает? Это означает, что их единственная разница заключается в их размере.В противном случае их углы будут одинаковыми, когда вы их сопоставите! Вы можете увидеть треугольники, которые перевернуты или повернуты, но они все равно могут быть похожими, если разница только в их размере.
Следует также отметить, что у двух подобных треугольников соответствующие стороны имеют одинаковое отношение. Так, например, один треугольник может быть 1:2 к другому треугольнику, поэтому все их соответствующие стороны будут 1:2 к другому треугольнику.
Давайте углубимся в различные способы доказательства того, что два треугольника подобны.
Теорема подобия SAS
Теорема подобия SAS означает сторону угла стороны. Если у вас есть два треугольника и отношение двух их сторон одинаково, плюс один из их углов равен, вы можете доказать, что эти два треугольника подобны. Вы только что выучили определение SAS! Но это еще не все…
Теорема подобия SSS
В теореме подобия SSS вы ищете доказательство для боковой стороны. Когда у вас есть два треугольника с тремя сторонами, которые имеют одинаковое отношение, вы еще раз можете доказать, что у вас есть два подобных треугольника SSS.
Теорема подобия AA
Теорема подобия AA названа в честь угла угла. В этом случае можно доказать, что два треугольника подобны, если два их соответствующих угла равны. Это нетрудно понять, поскольку вы знаете, что внутренние углы любого треугольника должны быть равны 180 градусам. Если вы вычислили 2 угла, то вы знаете, что значение последнего также имеет значение. По сути, это означает, что если вы знаете, что 2 угла в двух соответствующих треугольниках одинаковы, последний угол из двух треугольников также будет одинаковым.
По сути, это означает, что если вы знаете, что 2 угла в двух соответствующих треугольниках одинаковы, последний угол из двух треугольников также будет одинаковым.
Примеры проблем
Вопрос 1:
Определить, подобны ли треугольники:
Решение:
Чтобы вам было легче ответить на этот вопрос, попробуйте переориентировать треугольники так, чтобы они были одинаково ориентированы. Это поможет вам легче сравнивать стороны и углы. Когда вы это сделаете, давайте посмотрим на соотношение сторон этих двух треугольников.
Отношение соответствующих сторон:
ДЭАБ=1.80,9=2\frac{DE}{AB}=\frac{1,8}{0,9}=2ABDE=0,91,8=2 EFBC=21=2\frac{EF}{BC}=\frac{2}{1}=2BCEF=12=2Две стороны треугольников имеют одинаковое соотношение. Вы также можете видеть, что в обоих треугольниках есть угол 90 градусов. Таким образом, вы доказали, что они похожи на основе правила треугольника SAS.
Вопрос 2:
Какие треугольники подобны?
Подобный треугольник должен иметь все углы равными/конгруэнтными. Итак, о треугольнике GHI не может быть и речи.Теперь посчитаем отношения сторон. Для треугольников JKL и DEF отношение их сторон равно 2. Для треугольников DEF и ABC отношение сторон равно 1,25. Можно сделать вывод, что треугольники ABC, DEF и JKL — подобные треугольники.
Итак, о треугольнике GHI не может быть и речи.Теперь посчитаем отношения сторон. Для треугольников JKL и DEF отношение их сторон равно 2. Для треугольников DEF и ABC отношение сторон равно 1,25. Можно сделать вывод, что треугольники ABC, DEF и JKL — подобные треугольники.
Не уверены в доказательствах подобных треугольников? Посмотрите эту интерактивную онлайн-диаграмму, которая показывает, как меняются углы и отношение сторон двух подобных треугольников, когда один треугольник становится меньше или больше.
Чтобы лучше понять треугольники, не стесняйтесь просмотреть теорему Пифагора и узнать, как использовать соотношение Пифагора.Это хорошая ступенька, которая поможет вам понять стороны треугольников.
Позже вы узнаете о конгруэнтных треугольниках, как доказать конгруэнтность с помощью SSS, а также SAS и HL и, наконец, что не менее важно, ASA и AAS.
Подобные треугольники — Высшее — Конгруэнтные и подобные формы — CCEA — GCSE Maths Revision — CCEA
kpp7byzrx6.0.0.0.1:0.1.0.$0.$1.$0″> Два треугольника подобны, если углы имеют одинаковый размер или соответствующие стороны находятся в одинаковом соотношении. Любое из этих условий докажет, что два треугольника подобны.Треугольник B является увеличенным треугольником A с коэффициентом масштабирования 2. Каждая длина треугольника B в два раза больше длины треугольника A.
Эти два треугольника подобны.
Пример 1
Укажите, подобны ли два треугольника. Приведите причину, подтверждающую ваш ответ.
Да, похожи. Две длины были увеличены с коэффициентом масштабирования 2. Соответствующий угол остался прежним.
Пример 2
0.0.0.1:0.1.0.$0.$1.$9″> Укажите, подобны ли два треугольника.\circ\)Да, похожи. Три угла равны.
Пример 3
Укажите, подобны ли два треугольника. Приведите причину, подтверждающую ваш ответ.
Нет. Две стороны треугольника увеличены в 1,5 раза. Другая сторона увеличена в 2 раза.
Подобные треугольники: периметры и площади
Подобные треугольники: периметры и площади
Когда два треугольника подобны, уменьшенное отношение любых двух соответствующих сторон называется масштабным коэффициентом подобных треугольников.На рисунке 1 Δ ABC ~ Δ DEF .
Рисунок 1 Подобные треугольники с масштабным коэффициентом 2 : 1.
Соотношение соответствующих сторон 6/3, 8/4, 10/5. Все они уменьшаются до 2/1. Тогда говорят, что масштабный коэффициент этих двух подобных треугольников равен 2 : 1.
Периметр Δ ABC составляет 24 дюйма, а периметр Δ DEF — 12 дюймов. Когда вы сравниваете отношения периметров этих подобных треугольников, вы также получаете 2 : 1.Это приводит к следующей теореме.
Теорема 60: Если два подобных треугольника имеют масштабный коэффициент a : b, , то отношение их периметров равно a : b.
Пример 1: На рисунке 2 Δ ABC ∼ Δ DEF . Найдите периметр Δ DEF
Рисунок 2 Периметр подобных треугольников.
На рис. 3 показаны два подобных прямоугольных треугольника с масштабным коэффициентом 2 : 3.Поскольку GH ⊥ GI и JK ⊥ JL , их можно считать основанием и высотой для каждого треугольника. Теперь вы можете найти площадь каждого треугольника.
Теперь вы можете найти площадь каждого треугольника.
Рисунок 3 Нахождение площадей подобных прямоугольных треугольников с масштабным коэффициентом 2 : 3.
Теперь вы можете сравнить отношение площадей этих подобных треугольников.
Это приводит к следующей теореме:
Теорема 61: Если два подобных треугольника имеют масштабный коэффициент a : b , то отношение их площадей равно a 2 : b 2 1 .
Пример 2: На рисунке 4 Δ PQR ∼ Δ STU . Найдите площадь Δ СТУ .
Рисунок 4 Использование коэффициента масштабирования для определения отношения между площадями подобных треугольников.
Масштаб этих подобных треугольников составляет 5 : 8.
Пример 3: Периметры двух подобных треугольников относятся как 3 : 4.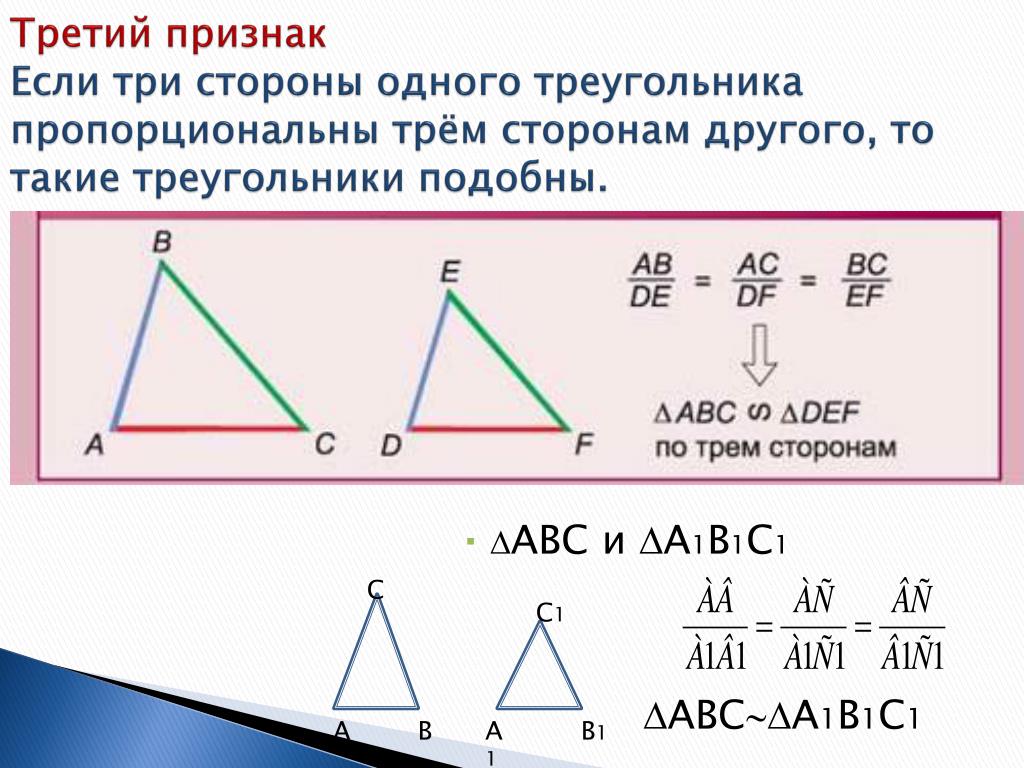 Сумма их площадей равна 75 см 2 .Найдите площадь каждого треугольника.
Сумма их площадей равна 75 см 2 .Найдите площадь каждого треугольника.
Если назвать треугольники Δ 1 и Δ 2 , то
Согласно Теореме 60, это также означает, что масштабный коэффициент этих двух подобных треугольников равен 3 : 4.
Поскольку сумма площадей равна 75 см 2 , получается
Пример 4: Площади двух подобных треугольников равны 45 см 2 и 80 см 2 .Сумма их периметров равна 35 см. Найдите периметр каждого треугольника.
Назовите два треугольника Δ 1 и Δ 2 и пусть масштабный коэффициент двух подобных треугольников будет a : b.
a : b – сокращенная форма коэффициента масштабирования. 3 : 4 является сокращенной формой сравнения периметров.
Уменьшить дробь.
Извлечение квадратных корней из обеих сторон.
Геометрия: свойства подобных треугольников
свойства подобных треугольников
Когда мы говорим о сходстве двух вещей, мы пытаемся показать, что наши два объекта во многом похожи. Они не обязательно должны быть взаимозаменяемыми или идентичными, но у них должно быть достаточно общего. Можно подумать, что все треугольники подобны, потому что у них одинаковое количество сторон и одинаковое количество углов. А подобие — это особое отношение только между определенными треугольниками.Чтобы два треугольника были объявлены подобными, они должны удовлетворять определенным критериям угла и длины.
Два треугольника подобны , если все пары соответствующих углов равны и все пары соответствующих сторон пропорциональны. Если мы посмотрим на два треугольника на рис. 13.2, то сможем определить соответствующие углы и различные пропорции, которые должны быть удовлетворены.
Рисунок 13.2 Два подобных треугольника.
Конгруэнтность углов: ?A ~= ?R , ?B ~= ?S и ?C ~= ?T.Используемые пропорции: AB / RS = BC / ST = AC / RT и все возможные перестановки с использованием различных свойств пропорций.
Я буду использовать символ ~, чтобы указать, что два треугольника подобны. Если вы пробежитесь по списку, то увидите, что ~ — это отношение эквивалентности, поэтому оно будет иметь рефлексивные, симметричные и транзитивные свойства.
Если вы знаете, что два треугольника подобны, вы можете использовать расширенные пропорции, чтобы узнать больше о треугольниках.
- Пример 5 : Если ?ABC ~ ?RST, как показано на рис. 13.3, используйте указанные меры, чтобы найти меры оставшихся сторон и углов каждого из треугольников.
Рисунок 13.3 ?ABC ~ ?RST.
- Решение : Вам нужно найти целый список вещей: меру третьего угла в ?ABC ; все три угла ?RST и длины AC и ST.
 Поскольку сумма внутренних углов треугольника равна 180, вы можете довольно легко найти m?A:
Поскольку сумма внутренних углов треугольника равна 180, вы можете довольно легко найти m?A: - m?A + m?B + m?C = 180
- m?A + 90 + 37 = 180
- m. ?A = 53
- Поскольку соответствующие углы конгруэнтны, вы знаете, что m?R = 53 , m?S = 90 и m?R = 37.Используя ваши пропорции, вы имеете
- AB / RS = BC / ST = AC / RT 5 Вы можете подставить известные значения ST в пропорциональность: 1
- 3 / 6 / 6 = 4 / ST
- 3 (ST) = 24
- ST = 8
- Чтобы определить AC, вы будете использовать другую половину пропорциональности:
- 3 / 6 = AC / 10
- 6(AC) = 30
- AC = 5
себя с аббревиатурой для этой фразы сейчас? это CPSSAT.
Выдержки из The Complete Idiot’s Guide to Geometry 2004 Denise Szecsei, Ph.
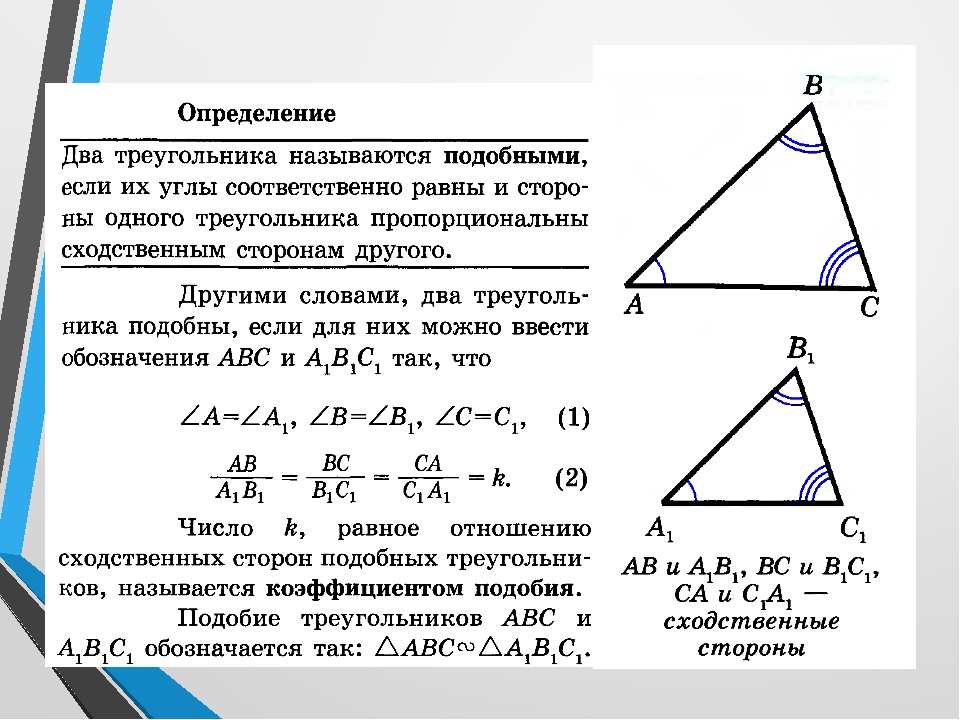 к. МЕ — средняя линия, значит, М — середина АВ, тогда , аналогично, , т.е. .
к. МЕ — средняя линия, значит, М — середина АВ, тогда , аналогично, , т.е. .

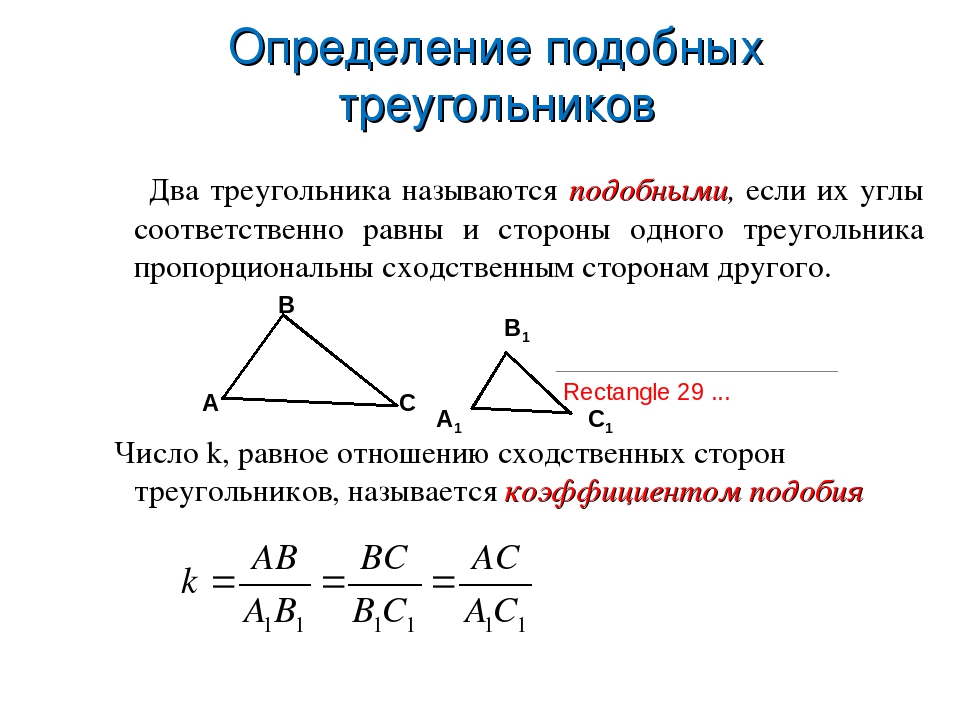 Поскольку сумма внутренних углов треугольника равна 180, вы можете довольно легко найти m?A:
Поскольку сумма внутренних углов треугольника равна 180, вы можете довольно легко найти m?A: