Простейшие тригонометрические уравнения

Простейшими тригонометрическими уравнениями называют уравнения

Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a

Уравнение cos (x) = a

Объяснение и обоснование

 

1. Корни уравнения cosx = а. При | a | > 1 уравнение не имеет корней, по­скольку | cosx | < 1 для любого x (прямая y = а при а > 1 или при а < -1 не пересекает график функцииy = cosx).

Пусть | а | < 1. Тогда прямая у = а пересекает график функции

у = cos х. На промежутке [0; п] функция y = cos x убы­вает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = а имеет на этом промежутке только один корень, который по опреде­лению арккосинуса равен: x₁ = arccos а (и для этого корня cos x = а).

Косинус — четная функция, поэтому на промежутке [-п; 0] уравнение cos x = а также имеет только один корень — число, противоположное x

1, то есть

x₂ = -arccos а.

Таким образом, на промежутке [-п; п] (длиной 2п) уравнение cos x = а при | а | < 1 имеет только корни x = ±arccos а.

Функция y = cos x периодическая с периодом 2п, поэтому все остальные корни отличаются от найденных на 2пп (n € Z). Получаем следующую фор­мулу корней уравнения cos x = а при

| а | < 1:

x = ±arccos а + 2пп, n £ Z.

2. Частные случаи решения уравнения cosx = а.

Полезно помнить специальные записи корней уравнения cos x = а при

а = 0, а = -1, а = 1, которые можно легко получить, используя как ори­ентир единичную окружность.

Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответ­ствующей точкой единичной окружности является точка A или точка B.

Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C, следовательно,

x = 2πп, k € Z.

Также cos х = —1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, х = п + 2пn,

k € Z.

Примеры

Уравнение sin (x) = a

Объяснение и обоснование

1. Корни уравнения sinx = а. При | а | > 1 уравнение не имеет корней, по­скольку | sinx | < 1 для любого x (прямая y = а на рисунке при а > 1 или при а < -1 не пересекает график функции y = sinx).

Уравнение cosx=a

Итак, уравнение, которое содержит переменную под знаком тригонометрических функций, называется тригонометрическим уравнением. Уравнения вида ,

,  и , где  – переменная, а число , называются простейшими тригонометрическими уравнениями. На этом уроке мы с вами подробно рассмотрим решение уравнений вида .

Напомним, что косинусом угла  называется абсцисса точки

, полученной поворотом точки  вокруг начала координат на угол . При этом не забудем отметить, что так как координаты  и  точек единичной окружности удовлетворяют неравенствам  и , то для  справедливо неравенство . Из этого следует, что уравнение  имеет корни только при .

Так как же решают такие уравнения? Давайте рассмотрим два уравнения:  и

. Чтобы найти х в первом уравнении, нам нужно ответить на вопрос, чему равен косинус точки . Для этого нам достаточно вспомнить таблицу значений косинуса.

Тогда . Давайте покажем это на единичной окружности. Отметим точку . У этой точки, как и у любой другой, есть свои координаты. Если мы опустим перпендикуляр из точки

 на ось абсцисс, то попадём в .

А теперь вернёмся ко второму уравнению – . Чтобы здесь найти х, нам нужно ответить на вопрос, косинус каких точек равен .

Давайте ненадолго отвлечёмся от тригонометрии. Начертим координатную плоскость. А теперь найдём все те точки, у которых абсцисса равна . Несложно догадаться, что таких точек будет бесконечное множество и все они будут лежать на вертикальной прямой, проходящей через точки с абсциссой, равной

.

А теперь вернёмся к тригонометрии. Нас будут интересовать все точки, которые лежат на единичной окружности и пересекаются вертикальной прямой, проходящей через точки, имеющие абсциссу, равную . Заметим, что наша прямая пересекает единичную окружность в двух точках –  и . Исходя из таблицы значений косинусов, точка

 получается из начальной точки  поворотом на угол , а тогда точка  – поворотом на угол . Тогда решением нашего уравнения будут два корня –  и . Но ведь в эти точки мы можем попасть не по одному разу. Если мы сделаем полный оборот по единичной окружности, то снова попадём в эти точки. Сделав ещё полный оборот, снова попадём в эти точки и так далее. Отсюда уравнение  имеет две серии решений:

.

Как правило, эти серии решений совмещают и записывают как .

Вообще при решении уравнений вида  возможны четыре случая.

Первый случай: . Раскрывая модуль, имеем . В этом случае на единичной окружности будут располагаться две точки –  и , абсциссы которых равны а. Эти точки получаются путём поворота начальной точки на угол  и  соответственно. Тогда решения уравнения  можно записать в виде: , и . Заметим, что эти точки симметричны относительно оси абсцисс. Следовательно, . Тогда все решения уравнения  можно объединить в одно: .

Например, решим следующие уравнения  и . Абсциссу, равную , имеют две точки единичной окружности. Так как , то угол , а потому угол . Следовательно, все корни уравнения  можно найти по формуле .

Перейдём к уравнению . Абсциссу, равную , имеют две точки единичной окружности. Так как , то угол , а потому угол . Следовательно, все корни уравнения  можно найти по формуле .

Заметим, что каждое из уравнений  и к имеет бесконечное множество корней. Однако на отрезке  каждое из этих уравнений имеет только один корень. Так, , – это корень уравнения , а , – это корень уравнения . Число  называют арккосинусом числа . Записывают так: . Число  называют арккосинусом числа . Записывают так: .

Кстати, «арккосинус» в переводе с латинского означает «дуга» и «косинус». Это обратная функция.

Вообще уравнение , где , на отрезке  имеет только один корень. Если , то этот корень заключён в промежутке ;

если же , то корень располагается в промежутке .

Этот корень называют арккосинусом числа а и обозначают так .

Запомните! Арккосинусом числа а, , называется такое число , косинус которого равен а.

, если  и

Например, , так как , . , так как , .

Возвращаясь к нашему уравнению , где , можно утверждать, что все корни уравнения можно найти по формуле: .

Запомните! Для любого  справедлива формула . Эта формула позволяет находить значения арккосинусов отрицательных чисел через значения арккосинусов положительных чисел.

Например, .

Второй случай: . Раскрывая модуль, имеем  и . Поскольку для  справедливо неравенство , то понятно, что в этом случае уравнение  не будет иметь корней.

Например, уравнения  и  не имеют корней.

Третий случай (частный): . В этом случае есть две точки тригонометрической окружности, которые имеют абсциссу, равную 0. Точка  получается из начальной точки  поворотом на угол , а точка  – поворотом на угол . Тогда уравнение  имеет две серии решений:

Однако эти две серии решений можно выразить одной формулой: . Полученная формула задаёт множество корней уравнения .

И последний, четвёртый случай (тоже частный): . Раскрывая модуль, имеем , и . В этом случае вертикальные прямые, проходящие через точки, имеющие абсциссы, равные –1 и 1, будут касаться единичной окружности в точках с координатами (–1;0) и (1;0). Эти точки получаются путём поворота начальной точки на угол , и . Тогда решением уравнения  будет , а решением уравнения  будет .

А теперь давайте приступим к практической части нашего урока.

Задание первое. Решите уравнение .

Решение. По формуле нахождения корней уравнения , имеем: . Значение  вычислим с помощью калькулятора. .

Задание второе. Решите уравнение .

Решение. По формуле нахождения корней уравнения , имеем: . . Перенесём  в правую часть равенства. Затем разделим обе части равенства на 2: . Отсюда .

Арккосинус и решение уравнения cos x = a. Видеоурок. Алгебра 10 Класс

На уроке по  теме «Арккосинус и решение уравнения cos x=a» рассматривается понятие арккосинуса числа с примерами. Также решается уравнение вида cos x=a.

На уроке рассматривается понятие функции арккосинус, как обратной для  функции косинус на отрезке .

По теореме о существовании обратной функции прямая функция должна быть непрерывной и монотонной.

Функция  не монотонна на всей своей области определения, а на промежутке  она непрерывна и монотонна и пробегает все значения из области значений. Значит, существует обратная функция для нее на этом промежутке, она называется арккосинус.

Построим график функции  на отрезке  (рис. 1) и будем находить значения арккосинусов чисел по этому графику.

Рис. 1.

Пример 1. (рис. 1):

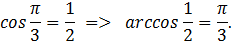
Пример 2. (рис. 1):

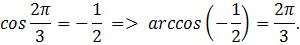
Определение:

Арккосинусом числа  называется такой угол 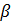 из промежутка , косинус которого равен .

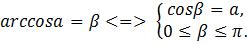
Свойство: для любого числа,  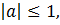выполняется равенство

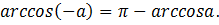
Пример 3. Найти

Решение:

1-й способ: по графику на рис. 1:

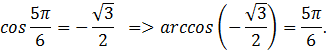
2-й способ: по свойству:

Пример 4. (рис. 1):

Построим единичную окружность и отметим на окружности точки , спроектируем на ось абсцисс (рис. 2) и запишем соответствующие значения косинусов.

Рис. 2. 

Примеры 5. (рис. 2):

Пример 6. Решить уравнение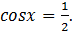

Решение: на оси косинусов отложим  и проведем перпендикуляр до пересечения с окружностью в точках  и  (рис. 3).

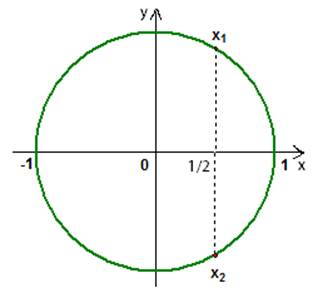
Рис. 3.

Объединяем эти решения одной формулой:

Ответ:

В общем виде решение уравнения  при :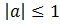

На уроке был рассмотрен график функции  на промежутке , поскольку на этом промежутке функция монотонна и пробегает все свои значения от  до  Также было рассмотрено понятие арккосинуса числа и решено уравнения вида , при .

 

Список рекомендованной литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. ЗвавичЛ.И., Шляпочник Л.Я., Чинкина Алгебра и начала анализа. 8-11 кл.: Пособие для школ и классов с углубленным изучением математики (дидактические материалы).-М.: Дрофа, 2002.

8. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

9. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

10. Глейзер Г.И. История математики в школе. 9-10 классы (пособие для учителей).-М.: Просвещение, 1983

 

Дополнительные веб-ресурсы

1. Интернет-портал Mathematics.ru (Источник). 

2. Портал Естественных Наук (Источник). 

3. Интернет-портал Exponenta.ru (Источник).

 

Сделай дома

Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

№№ 21.13, 21.17, 21.20(а).

Урок 41. уравнение cos x = a — Алгебра и начала математического анализа — 10 класс

Урок Конспект Дополнительные материалы

Уравнение cos x = a

Сколько точек пересечения с тригонометрической окружностью имеет прямая x=m в зависимости от значения m:

Подсказка

Вспомните, какой радиус имеет тригонометрическая окружность

Ни одной	Одной	Две

m=-1,2

m=3

m=1,000001

m=2,22

m=-5

m=-1,001001

m=1

m=-1

m=0

m=-0,9999999

m=0,45

m=0,91

Уравнение cos x = a

Выберите из списка решение уравнения

$cosx=\frac{1}{2}$

Подсказка

Вспомните, косинус какого аргумента равен $\frac{1}{2}$

Уравнение cos x = a

Поставьте в соответствие каждому уравнению его решение.

Подсказка

Вспомните формулы решения простейшего тригонометрического уравнения $cos x=а.$

Уравнение cos x = a

Подчеркните верное равенство

1. $arccos (-\frac{1}{2})=-\frac{2\pi}{3}$
2. $arccos (-\frac{1}{2})= \frac{2\pi}{3}$
3. $arccos (-\frac{1}{2})= -\frac{\pi}{3}$
4. $arccos (-\frac{1}{2})= \frac{\pi}{3}$
5. $arccos (-\frac{1}{2})= \frac{\pi}{3}$

Уравнение cos x = a

Сколько точек на отрезке $ [-\pi; \pi] $имеет уравнение $2 cos (2x) = \sqrt{3}$

Подсказка

Вспомните формулу решения простейшего квадратного уравнения $cos x=a$, затем разделите результат на коэффициент при х

Уравнение cos x = a

Решите уравнение $cos \alpha =-\frac{1}{2}$. Заполните пропуски в ответе

Ответ: $\alpha = \pm \frac{a \pi}{b}+c\pi k, k \epsilon Z$

Подсказка

Вспомните формулу решения простейшего квадратного уравнения $cos x=a$

Уравнение cos x = a

Расположите значения арккосинусов в порядке возрастания.

Подсказка

Подумайте, как ведет себя арккосинус при увеличении значений его аргумента

$arccos (-\frac{\sqrt{3}}{2})$

$arccos (\frac{\sqrt{3}}{2})$

$arccos (-\frac{\sqrt{2}}{2})$

Уравнение cos x = a

Выделите цветом верные равенства

Подсказка

Вспомните тождества с арккосинусом

1. cos(arccos(−0,4))=−0,4
2. arccos(cos2)=2
3. cos(arccos2)=2
4. arccos(cos(−2))=−2
5. cos(arccos(0,2))=0,2

Уравнение cos x = a

Найдите для каждого уравнения количество решений на отрезке $[0; 2π]$.

Подсказка

Вспомните решение простейшего уравнения cos x=a

Ни одного решения	Одно решение	Два решения	Больше двух решений

$cosx=1,1$

$(cos x +1)(cos x -2)=0$

$(2cosx -1)(2cosx -3)=0$

$(2cosx +1)(3cos x -2)=0$

Уравнение cos x = a

Решите уравнение $cos (2-3x) = cos (4x -5)$

В ответ запишите наименьший положительный корень.

Подсказка

Вспомните условие равенства косинусов

Уравнение cos x = a

Решите уравнение $(4cos x +1)(2 cos x +3)$

Выберите верный ответ.

Подсказка

Вспомните условие равенства произведения нулю, затем решите простейшие тригонометрические уравнения $cos x=a$

Уравнение cos x = a

Решите уравнение $cos (x^2 -4x + \frac{\pi}{4}) = \frac{1}{2}$

Определите, сколько решений имеет это уравнение при:

Подсказка

Вспомните формулу решения простейшего тригонометрического уравнения, а затем зависимость числа корней квадратного уравнения от его дискриминанта

Уравнение cos x = a

Даны числа

1) $arccos(\frac{1}{4})$

2) $arccos(0,2)$

3) $arccos(\frac{\sqrt5}{12})$

4) $arccos(−0,14)$

5) $arccos(\frac{\sqrt3}{6})$

6) $arccos(−0,4)$

7) $arccos(−\frac{\sqrt2}{3})$

Подсказка

Вспомните, как ведет себя значение арккосинуса при увеличении значения аргумента

Уравнение cos x = a

Найдите для каждого уравнения его наименьшее решение на отрезке $[0;2π]$

Подсказка

Вспомните формулу решения простейшего тригонометрического уравнения $cos x=a$

1 cos

Вы искали 1 cos? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и 1 cos 2, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «1 cos».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как 1 cos,1 cos 2,1 cos 2 3x,1 cos 2x формула,1 cos t,1 cos2x формула,1 cosx,1 кос х,1 косинус x,1 косинус х,1 минус косинус,100 формул тригонометрия,2sinx формула,cos 1 2 чему равен,cos 2 tg 2 sin 2,cos 2x x,cos x 1,cos x равен,cos x чему равен,cos альфа 1,cos в квадрате x,cos х 1,cos2x 1 формула,cos2x sin2x формула,cos2x как разложить,cos3x формула,cosx,cosx 1,cosx a формулы,ctg 2 x,sin 2 1 cos,sin 2t,sin cos tg ctg формулы,sin2,sin2x cos2x формула,sin3x формула,tg x sin x cos x,tg через cos,tg2x формула,x 1 cosx,x cosx,кос и син формулы,косинус x 1,косинус минус 1,косинус х,косинус х 1,соsx 1,ф лы тригонометрии,формула 1 cos 2x,формула 1 cos2x,формула cos 2x sin 2x,формула cos умножить на sin,формула cos3x,формула sin 2x cos 2x,формула sin2x cos2x,формула sin3x,формула tgx,формулы cosx a,формулы кос и син,чему равен cos 2 1. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и 1 cos. Просто введите задачу в окошко и нажмите «решить» здесь (например, 1 cos 2 3x).

Где можно решить любую задачу по математике, а так же 1 cos Онлайн?

Решить задачу 1 cos вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.