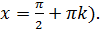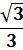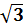Тригонометрические функции y = tg t, y = ctg t. Видеоурок. Алгебра 11 Класс
Тема: Повторение курса алгебры 10 класса
Урок: Тригонометрические функции y = tg t, y = ctg t
Функцией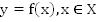 
называется закон, по которому каждому допустимому значению 
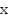ставится в соответствие единственное значение 
.
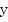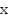– аргумент, независимая переменная
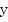– функция, зависимая переменная
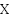– область определения. Обозначается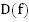 
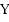– область значений. Обозначается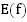 
Теперь напомним определения конкретных функций y = tg t, y = ctg t
Каждому действительному числу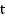 
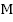на числовой окружности. Эта точка 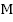будет иметь две координаты. То есть, 
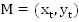. Назовем 
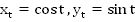(Рис.1).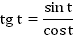
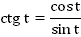
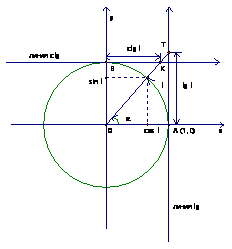
Рис. 1.
Из рассмотрения подобных треугольников, мы говорили, что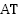 
– линия тангенсов, а 
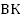– линия котангенсов (Рис. 1). Таким образом, мы определили функции 
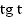и 
.
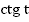Функции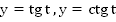 
периодические. Наименьшим положительным периодом для данных функций является число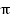 
Продлив прямую 
, получим вторую точку 
а также угол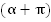 
, точк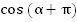и 
и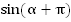 
(Рис. 2).
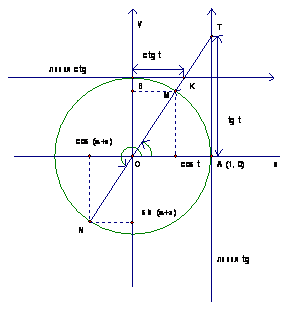
Рис. 2.
Отсюда:
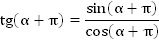
По формулам приведения, получим:
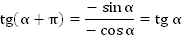
Аналогично, для котангенса:
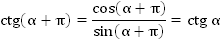
Сделаем выводы:
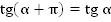
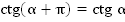
для любого допустимого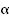 
Мы знаем, как по заданному значению аргумента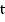 
получить 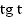. Для этого можно воспользоваться линией тангенсов. Мы знаем также, что наименьший период – .
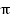Приведем конкретные примеры для тангенса (Рис. 3).
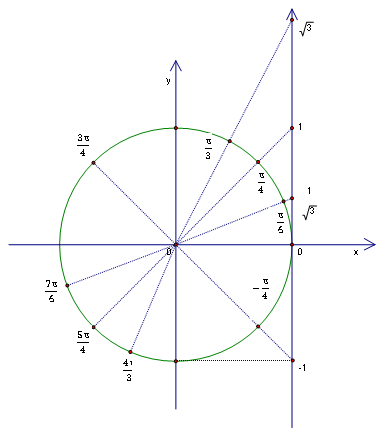
Рис. 3.
Из рисунка видно, что:
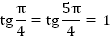
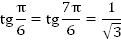
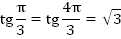
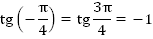
Примеры можно продолжать.
Приведем аналогичные примеры для котангенса (Рис. 4).
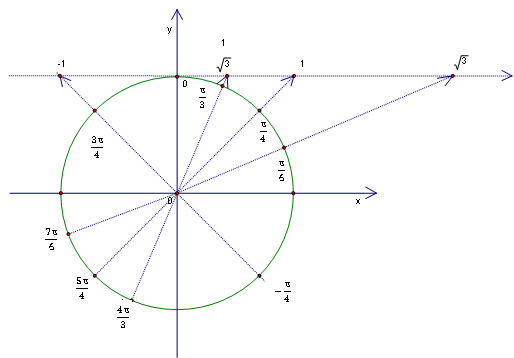
Рис. 4.
Из рисунка видно, что:
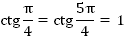
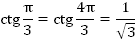
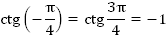
Построим график функции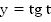 
. Он частично отображен на Рис. 5:
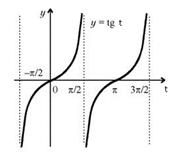
Рис. 5.
Охарактеризуем основные свойства функции:
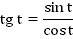
1. Область определения: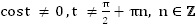 
2. Область значения: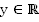 
3. Функция нечетная, то есть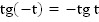 
, график функции симметричен относительно начала координат
4. Наименьшим периодом является число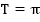 
5. На промежутке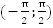
функция монотонно возрастает. Значит, любому значению 
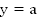соответствует единственное значение аргумента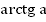 
Таковы основные свойства функции .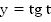
Аналогично рассмотрим функцию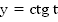 
.
Построим график функции 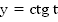. Он частично отображен на Рис. 6:
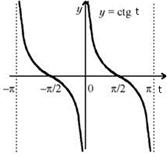
Рис. 6.
Охарактеризуем основные свойства функции:
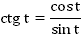
1. Область определения: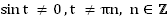 
2. Область значения: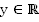
3. Функция нечетная, то есть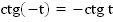 
, график функции симметричен относительно начала координат
4. Наименьшим периодом является число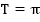
5. На промежутке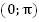
функция монотонно убывает. Значит, каждое значение 
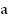она принимает только при одном значении аргумента, которое называется 
.
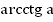Таковы основные свойства функции .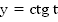
Спецификой тригонометрических функций является наличие у них периода. Рассмотрим и обсудим одну из задач, связанную с периодом.
Для начала напомним, что:
1. 
2. 
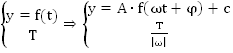
Приведем пару примеров:
3. 
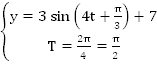
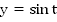– функция периодическая, наименьший период которой равен 
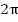. Данная функция тоже периодическая, наименьший период 
.
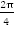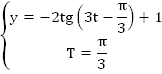
Важно, что коэффициент, стоящий перед параметром 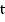, равен 3. Поэтому данная функция имеет наименьший положительный период, равный 
.
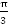Рассмотрим формулы, связывающие между собой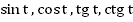 
. Эти формулы являются следствием определений этих функций.
Имеем единичную числовую окружность, заданное число 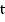, точка на окружности 
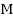имеет две координаты: 
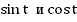. Получаем 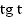на линии тангенсов и
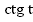на линии котангенсов (Рис. 1).
Вспомним уравнение окружности:
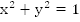
Сразу же получаем основное тригонометрическое тождество, которое справедливо для любого числа :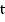
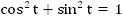
Преобразуем это тождество, поделив его части на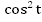
:
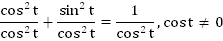
Получаем следующую формулу:
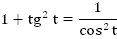
Аналогично, поделив исходное тождество на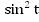 
, получим:
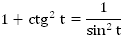
И наконец:
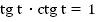
Таковы основные формулы, связывающие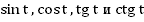
.
Теперь рассмотрим конкретную вычислительную задачу.
Дано:
.
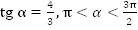Найти:
.
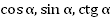Прокомментируем условие задачи. Известен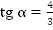 
, который не задает однозначно угол, но данный угол лежит в 3 четверти, а такой угол только один (Рис. 7).
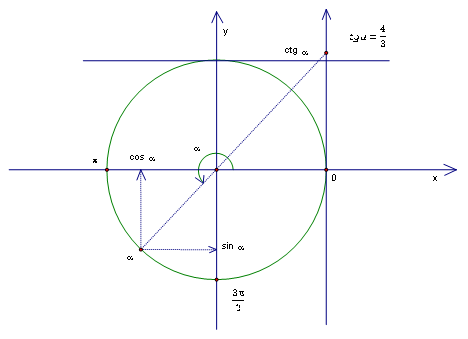
Рис. 7.
Решение:
1. Найдем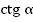 
.
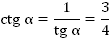
2. Так как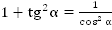 
, то:
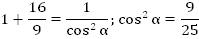
Отсюда:
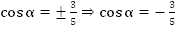, так как угол находится в 3 четверти.
3. Найдем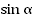 
.
Так как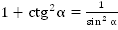 
, то:
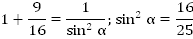
Отсюда:
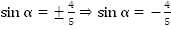, так как угол находится в 3 четверти.
Ответ: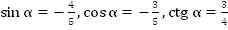 
.
Список литературы
1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Подготовка к ЕГЭ по математике (Источник).
2. Математика.ру (Источник).
3. Википедия (Источник).
4. Школьный сайт «Школьная жизнь» (Источник).
Домашнее задание
1. Определите наименьший положительный период функций: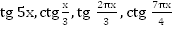 
.
2. Найдите значения всех тригонометрических функций, если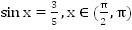 
.
3. Постройте график функции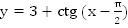 
.
4. Алгебра и начала анализа, Мордоквич А.Г.: № 93-97
interneturok.ru
| 1. | Определение значения функции y = tgx и y = ctgx | 1 вид — рецептивный | лёгкое | 1 Б. | Определение значения функции y = tgx и y = ctgx при заданном значении аргумента. |
| 2. | Определение значения тригонометрической функции | 1 вид — рецептивный | лёгкое | 1 Б. | Находится значение тригонометрической функции y = tgx при применении свойства периодичности и чётности функции. |
| 3. | Определение знака выражения | 2 вид — интерпретация | лёгкое | 1 Б. | Определяется знак разности (tgx — tgy) с применением свойств функции y = tgx на заданном промежутке. |
| 4. | Свойства функции y = tgx | 1 вид — рецептивный | среднее | 1 Б. | Сравниваются числа с использованием свойства возрастания функции. |
| 5. | Область определения и множество значений тригонометрических функций | 1 вид — рецептивный | среднее | 2 Б. | Находится область определения и множество значений функции y = tg ax, идёт сравнение с областью определения и множеством значений функции y = cos ax. |
| 6. | Сравнение свойств тригонометрических функций | 1 вид — рецептивный | среднее | 1 Б. | Задание для домашней работы; сравниваются свойства функций y = sinx; y = cosx; y = tgx. |
| 7. | Работа с графиком функции y = tgx | 2 вид — интерпретация | сложное | 6 Б. | Используя график функции y = tgx, находим корни уравнения tgx = a, принадлежащие определённому промежутку. |
| 8. | Нахождение корней уравнения tgx = а с использованием графика | 3 вид — анализ | сложное | 10 Б. | Для нахождения числа корней и самих корней уравнения сначала надо преобразовать левую часть уравнения, решить его, проанализировать график функции y = tgx. Можно предложить для домашнего задания. |
| 9. | Доказать равенство с применением свойств функции y = tgx | 3 вид — анализ | сложное | 1 Б. | Предлагается доказать равенство с применением свойств периодичности и чётности функции y = tgx. |
www.yaklass.ru
y = ctgx
Рассмотрим функцию y = ctg x.
Функция называется котангенс и она является обратной к тангенсу, то есть:
и наоборот.
Функция котангенс определена (область определения) на всей числовой прямой, кроме точек , .
Котангенс может принимать значения всей числовой прямой, поэтому говорят, что множество значений функции — все действительные числа.
Котангенс — функция периодическая с периодом, равным Пи.
График котангенса называется тангенсоидой, и он симметричен относительно начала координат, вследствие чего функция является нечетной.
График котангенса строится аналогично графику тангенса, только котангенс является зеркальным отображение тангенса относительно оси ординат.
Ветвь котангенса, которая находится в промежутке между прямой и , называется главной ветвью графика функции котангенс.
Котангенс является убывающей функцией на всех промежутках , .
Функция не имеет экстремумов, то есть нет наибольшего и наименьшего значения на всем множестве ее значений.
Нулями функции котангенс (то есть когда ctg x = 0) являются точки , .
Котангенс принимает положительные значения на промежутках от до , а отрицательны — на промежутках от до , .
ru.solverbook.com
Свойства и графики тригонометрических функций
Тригонометрические функции и их графики
ГБПОУ ИО «ИРКПО»
Тема: «Свойства и графики тригонометрических функций»
Иркутск
2016
Тема: Свойства и графики тригонометрических функций.
Тип урока: Изучение нового материала.
Цели:
Учебные:
Обеспечить усвоение свойств и графиков тригонометрических функций y=sinx, y=cosx, y=tgx, y=ctgx;
Формирование умения учащихся исследовать тригонометрические функции;
Формирование умения учащихся строить графики тригонометрических функций.
Развивающие:
Развитие логического мышления;
Развитие познавательных процессов: умения наблюдать и обобщать, формулировать свойства, правила;
Воспитательные:
Воспитание аккуратности при построении графиков;
Воспитание отдельные качества личности: настойчивость, трудолюбие.
Оборудование: демонстрационный проектор, мультимедийная презентация, раздаточный материал.
Структура урока
Организационный момент (5 мин)
Изучение нового материала (50 мин)
Первичное закрепление изученного материала (25 мин)
Постановка домашнего задания (5 мин)
Подведение итогов урока (5 мин)
Ход урока
Учитель
Ученик
Организационный момент
Здравствуйте, садитесь.
Сегодня на занятии мы начинаем изучение новой темы: «Свойства и графики тригонометрических функций». Целью нашего занятия будет: изучить, какие функции называются тригонометрическими и какими свойствами и графиками они обладают.
Здороваются, садятся.
Слушают учителя.
Актуализация опорных знаний
Формирование новых знаний и умений
(Рассказывая теорию, показываю соответствующие слайды из презентации).
Откройте свои тетради, запишите число, сегодня 21.03.16, и тему занятия: «Свойства и графики тригонометрических функций».
Как вы думаете, какие функции называются тригонометрическими?
Не совсем верно. Правильнее будет сказать: тригонометрическими функциями называются функции вида: y=sinx, y=cosx, y=tgx, y=ctgx. Запишите это определение.
Рассмотрим основополагающую тригонометрическую функцию y=sinx. Запишите подзаголовок: Свойства функции y=sinx и ее график.
Для построения графика функции y=sinx, составим ее таблицу значений. Для каких углов синус легко определяется?
Составьте таблицу значений и напишите ее у себя в тетрадях.
У каждого из вас лежат на столах листы, на которых начерчены системы координат (Приложение 1), отметим на первой системе координат полученные точки. Для удобства, возьмем за 
3 ед. Соедините их, и получим график функции y=sinx, так называемую синусоиду. С чем у вас ассоциируется график функции y=sinx?
Исследуем данный график. Посмотрите внимательно на график и скажите:
Какова область определения данной функции?
А область значения…?
На каком промежутке функция y=sinx возрастает, а на каком убывает?
Вы заметили, что функция снова возрастает и убывает через определенный промежуток?
Значит, она обладает чем…? И каков же ее период?
При каком значении х, у=0?
Также эту функцию можно определить на четность или нечетность. Как вы думаете, какой функцией, четной или нечетной, она является и почему?
Правильно, молодцы!
Вот мы с вами и сформулировали основные свойства функции y=sinx. Запишите их в тетрадь.
Запишите следующий подзаголовок: «Свойства функции у=cosx и ее график».
Для построения графика функции у=cosx, воспользуемся формулой приведения cosx=sin(
+ x). Т. е. строим синусоиду, сдвинутую по оси Ох влево на…?
Получим график функции у=cosx. Начертите эту функцию.
Т. к. график функции у=cosx, есть преобразованная синусоида, то и свойства функции у=cosx будут схожи со свойствами функции y=sinx. Запишите их, а затем найдите и назовите отличия.
Молодцы!
Аналогично рассматривают пункты:
(см. Слайды презентации)
Записывают число и тему
Отвечают: sinx, cosx, tgx, ctgx
Записывают определение под диктовку учителя.
Записывают в тетради подзаголовок.
Отвечают: Для 0,
, ,
Составляют таблицу значений и пишут ее в тетрадях.
Отмечают на системе координат полученные точки, соединяют их и получают график функции y=sinx.
Отвечают: с волной на реке.
Отвечают: она бесконечна, т. е. х любое действительное число.
А область значения от -1 до 1, т.к. у принадлежит от -1 до 1.
Убывает на промежутке от до 
, а возрастает от — до .
Да.
Периодом, он равен 2.
При х=.
Она является нечетной функцией, т. к. sin(-x)=-sinx.
Записывают свойства функции в тетрадь.
Записывают новый подзаголовок.
Отвечают: на .
Чертят на листах полученную функцию.
Записывают свойства.
Называют различия:
1. убывает при х
;
2. возрастает при х
;
3. четная, т.к. cos(-x)=cosx;
4. у=0, при х=+n.
Применение знаний, формирование умений и навыков
Решим несколько примеров для усвоения и закрепления полученных знаний.
(Первый пример решаю у доски, объясняю)
Пример 1.
Найдите область определения и область значений функции 
.
Решение:
а) Найдем область определения функции 
: 
имеет смысл при любом значении 
, следовательно, областью определения данной функции является множество действительных чисел, т.е. 
.
б) Найдем область значений функции : 
До множим все части неравенства на 3, получим 
.
Прибавим ко всем частям неравенства число -1: 
, получим 
.
Значит 
.
Ответ: ,
На доске записаны задания:
Задание 1. Найти множество значений функции:
а) y=2cosx
Ответ: Е(у): 
б) у=2-3sinx
Ответ: Е(у): 
Второе задание направлено на определение четности и нечетности функции. Вспомним правило: Если y(-x) = y (x), то функция четная, а если y(-x) = —y (x), то функция нечетная.
Задание 2. Определите, является ли функция четной или нечетной?
а) y=x2 + cosx
y(-x)=(-x)2 + cos(-x) = x2 + cosx = = y(x) – четная
б) y = x3 – sinx
y(-x) = (-x)3 – sin(-x) = -x3 + sin x = = -(x3 — sinx) = -y(x) — нечетная
Задание 3. Найти наименьшее и наибольшее значения функции 
на отрезке 
.
Решение:
По графику функции определяем, что на отрезке 
— наименьшее значение функции; 
— наибольшее значение функции.
Задание 4. Решить задания маршрутный лист №1
Упр.11.1 (а,б), упр.11.2 (а,в), 11.3 (а,б), 11.4 (а,б)
Слушают учителя.
Записывают. Отвечают на вопросы учителя в процессе решения.
Студенты решают в тетрадях, один студент у доски.
Постановка домашнего задания
Запишите домашнее задание. Они аналогичны тем, что мы делали в классе.
Практикум. Тумина Т.К. стр.15, упр11.1 (в,г,ж,з), упр.11.2 (б,г), упр.11.3 (в,г), упр.11.4 (в,г)
Записывают домашнее задание.
Итог занятия
Сегодня на занятии вы узнали, какие функции называются тригонометрическими, научились строить их график, и по графику определять свойства данных функций.
Отмечает присутствующих, ставит оценки ребятам, кто активно работал у доски и с места.
Всем спасибо, все свободны!
Слушают учителя
И напоследок притча:
«Однажды царь решил выбрать из своих придворных первого помощника. Он подвёл всех к огромному дверному замку. Кто откроет тот и будет первым помощником. Никто не притронулся даже к замку. Лишь один визирь подошёл и толкнул замок, который открылся. Он не был закрыт на ключ.
Ты получишь эту должность, потому что полагаешься не только на то, что видишь и слышишь, но надеешься на собственные силы и не боишься сделать попытку»
Пример 11
1) Не выполняя построения, ответьте на вопрос, принадлежит ли графику функции
точка с координатами 
?Решение:
Данная точка принадлежит графику функции , так как 
.
2) Найти наименьшее и наибольшее значения функции на отрезке .
Решение:
По графику функции определяем, что на отрезке — наименьшее значение функции; — наибольшее значение функции.
3) Найти область определения функции 
.
Решение:
Областью определения функции является множество 
всех действительных чисел, кроме 
. То есть 
.
4) Найдите множество значений функции 
.
Решение:
Домножим на 3 все части неравенства:
Прибавим -1 ко всем частям неравенства:
Значит 
Упражнение 11 (Упр.11.1 (а,б), упр.11.2 (а,в), 11.3 (а,б), 11.4 (а,б))
1. Не выполняя построения, ответьте на вопрос, принадлежит ли графику функции точка с координатами:
точка с координатами: 2. Найдите наименьшее и наибольшее значения функций и : 3. Найдите область определения функции: 4. Найдите множество значений функции: Пример 11 1) Не выполняя построения, ответьте на вопрос, принадлежит ли графику функции точка с координатами ?Решение:
Данная точка принадлежит графику функции , так как .
2) Найти наименьшее и наибольшее значения функции на отрезке .
Решение:
По графику функции определяем, что на отрезке — наименьшее значение функции; — наибольшее значение функции.
3) Найти область определения функции .
Решение:
Областью определения функции является множество всех действительных чисел, кроме . То есть .
4) Найдите множество значений функции .
Решение:
Домножим на 3 все части неравенства:
Прибавим -1 ко всем частям неравенства:
Значит
Упражнение 11 (Упр.11.1 (а,б), упр.11.2 (а,в), 11.3 (а,б), 11.4 (а,б))
1. Не выполняя построения, ответьте на вопрос, принадлежит ли графику функции точка с координатами:
точка с координатами: 2. Найдите наименьшее и наибольшее значения функций и : 3. Найдите область определения функции: 4. Найдите множество значений функции:infourok.ru
«Функции y = tgx, y = ctgx, их свойства и графики”(10 класс)
Тема: «Функции y = tgx, y = ctgx, их свойства и графики”
Цели: 1. Изучит свойства функций y = tgx, y = ctgx; выработать у учащихся умения изображать схематически и читать графики этих функций. Сформировать прочные навыки в умении решать графически уравнения, выполнять преобразования графиков.
Оргмомент. Сообщение темы, целей и задач урока. Приглашение к сотрудничеству.
Актулизация знаний. Устная работа.
1.Вычислите: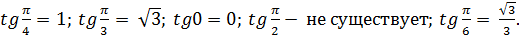 
2.Докажите, что число является периодом для функции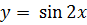 
.
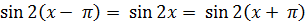
3.Докажите, что функция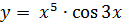 
нечётная. Доказательство: 
.
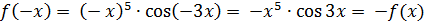4.Прочитайте по графику функцию.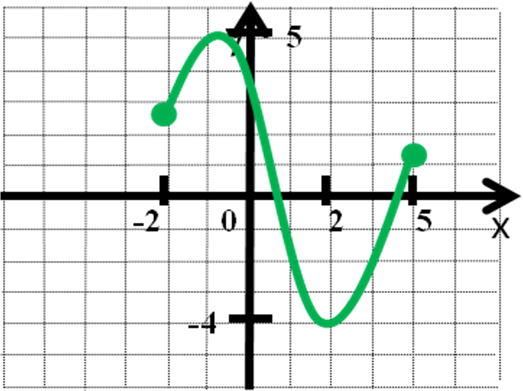 
D(f) = [ -2; 5]. Функция не является ни чётной, ни нечётной. Функция возрастает на промежутках [ -2; -1], [2; 5], убывает на промежутке [ -1; 2]. Функция ограничена снизу и сверху.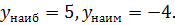 
Функция непрерывна на всей области определения. E(f) = [ -4; 5].
Изучение нового материала. Начинаем со свойств функции y = tgx. Свойство 1. Какова область определения функции y = tgx? (Все действительные числа, кроме чисел вида
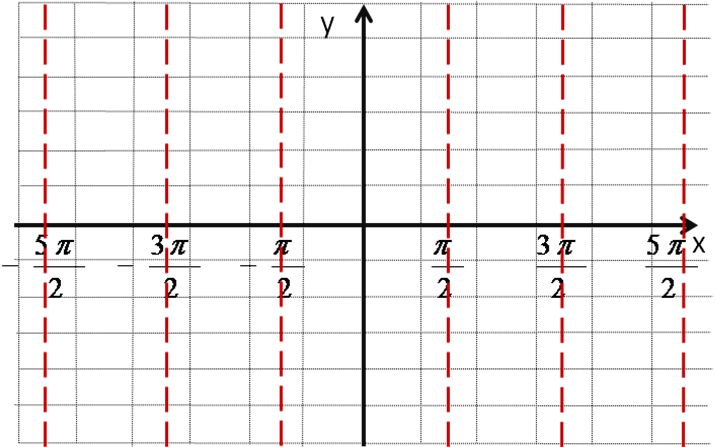
Свойство 2. Функция периодическая с периодом , т.к.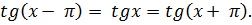 
Свойство 3. Функция нечётная, т.к.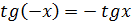 
. График нечётной функции симметричен относительно начала координат.
Составим таблицу основных значений:
x
0
/6
/4
/3
tgx
0
1
Построим график функции в первой четверти:
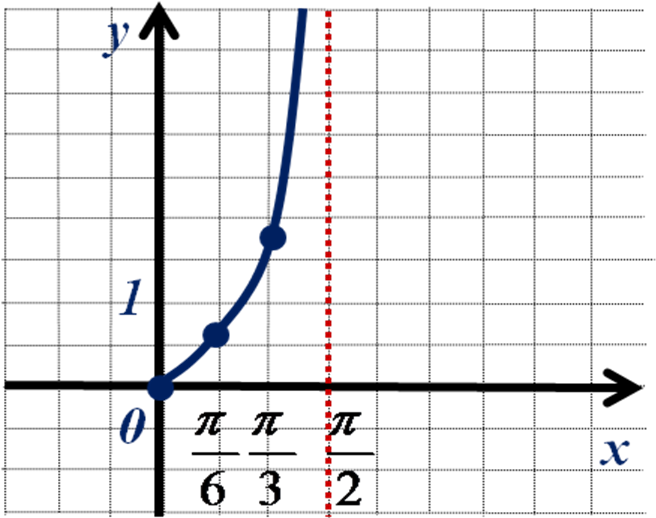
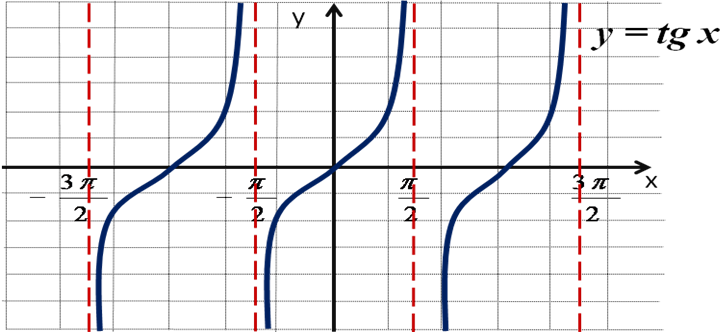
Используя свойства функции, строим полностью график функции y = tgx.
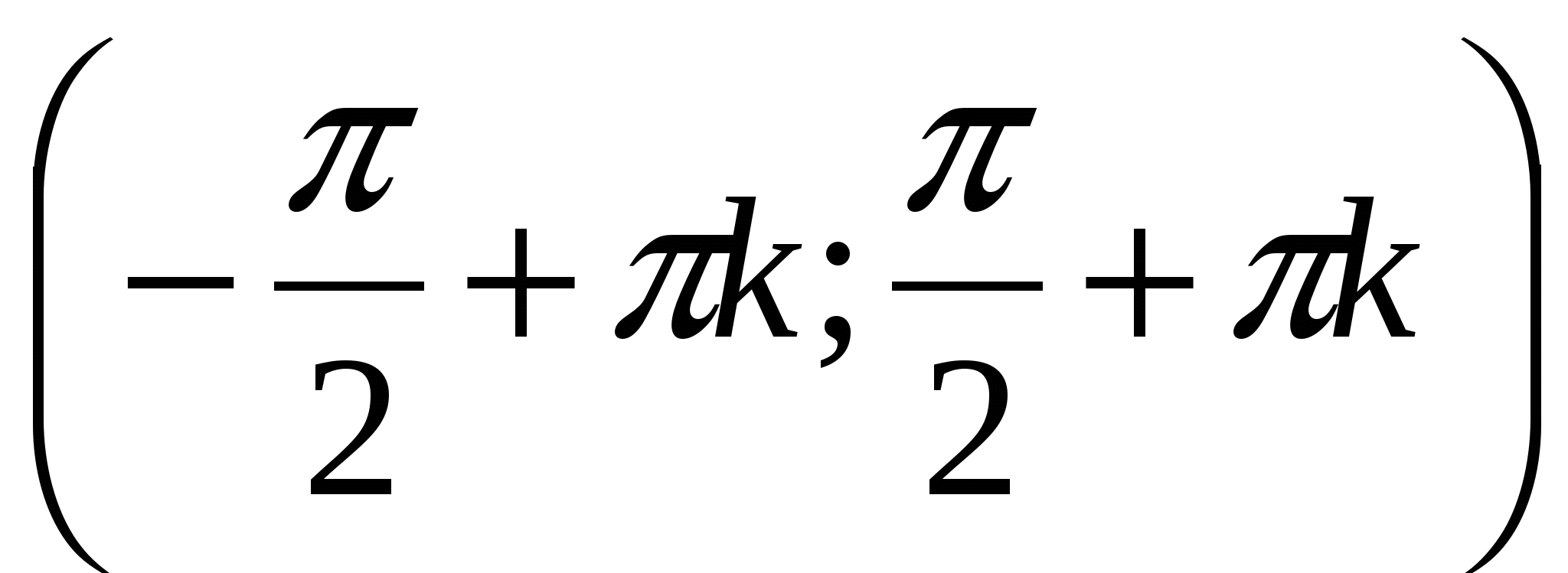
Свойство 4. Функция возрастает на всём интервале вида:
Г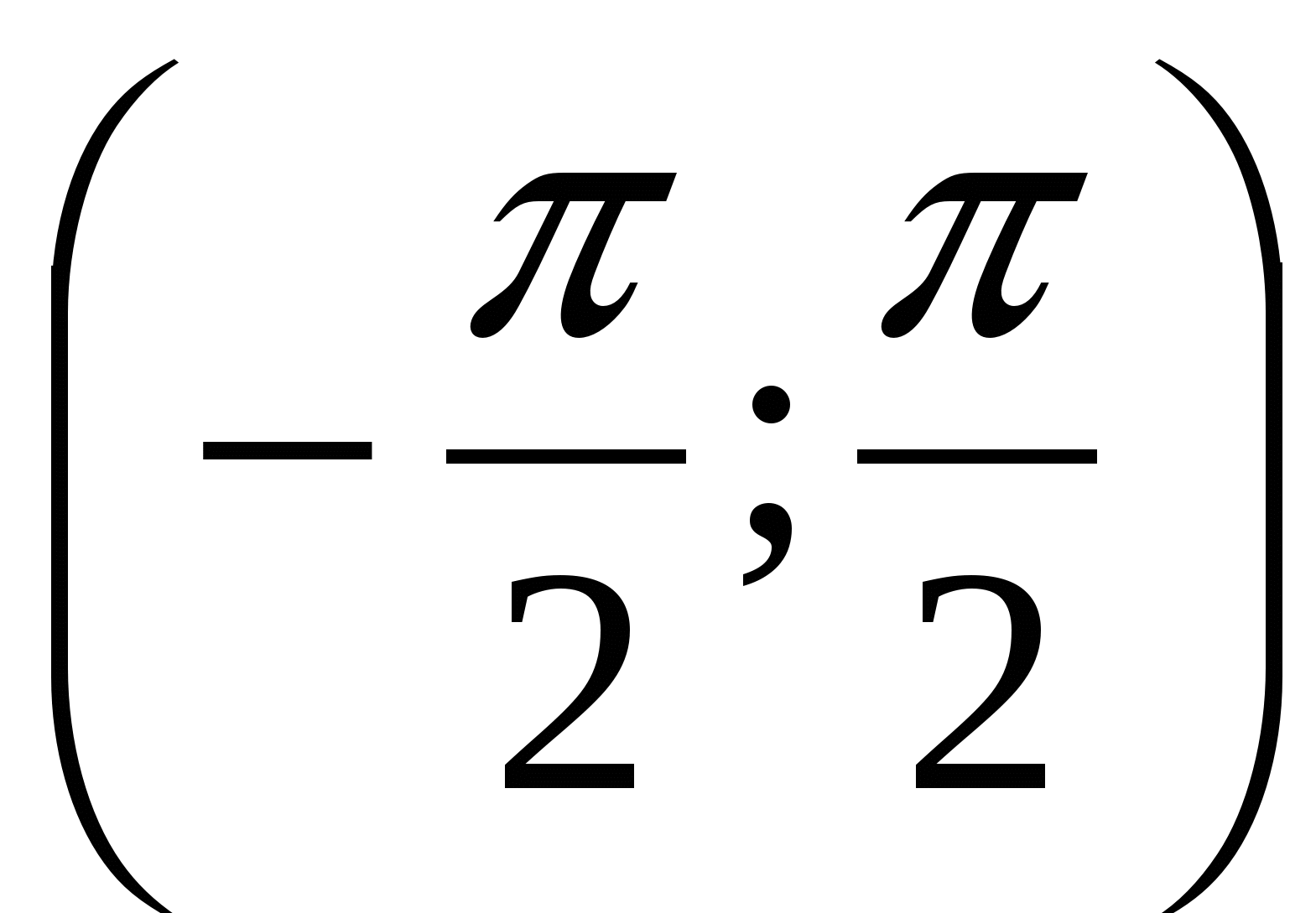
рафик функции y = tgx называют тангенсоидой, а ветвь на промежутке называют главной ветвью.
Свойство 5. Функция не ограничена ни снизу, ни сверху.
Свойство 6. Функция не имеет ни наибольшего, ни наименьшего значений.
С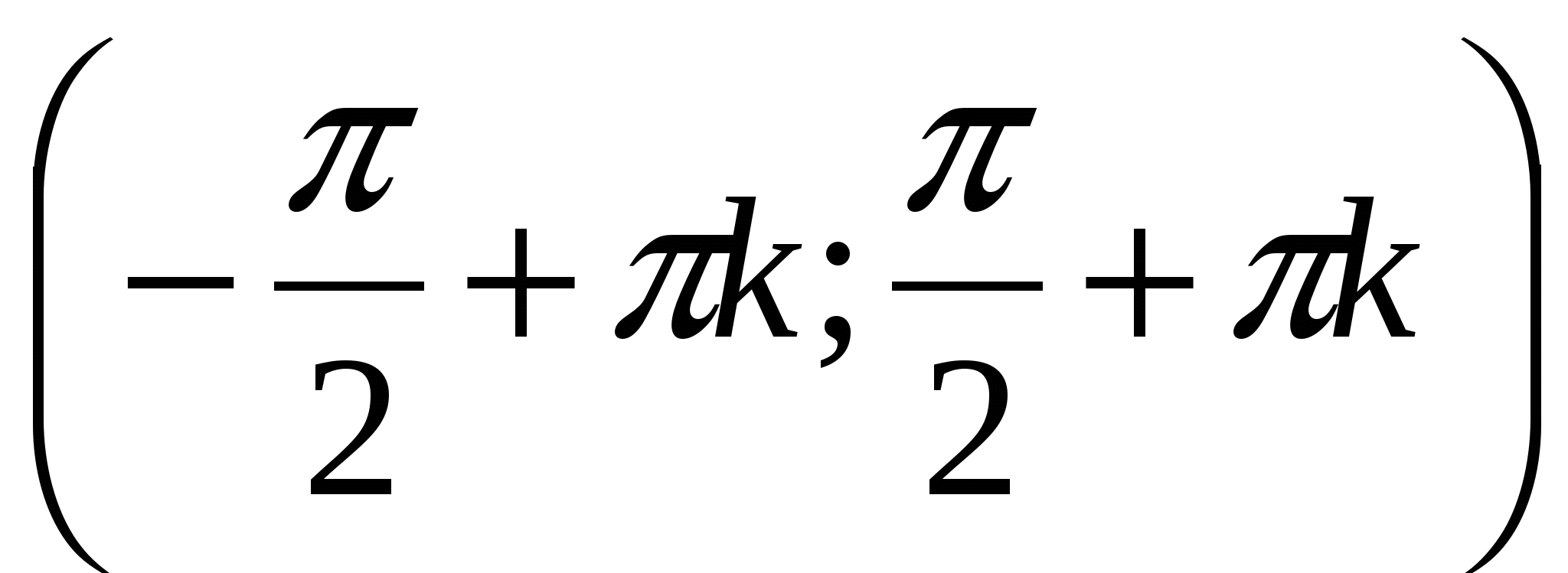войство 7.Функция y = tgx непрерывна на любом промежутке вида
Свойство 8. E(f) = ( — ; + ).
Рассмотрим пример: решите уравнение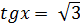 
. Решим это уравнение графически. Построим в одной системе координат графики функци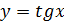й 
и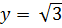 
.
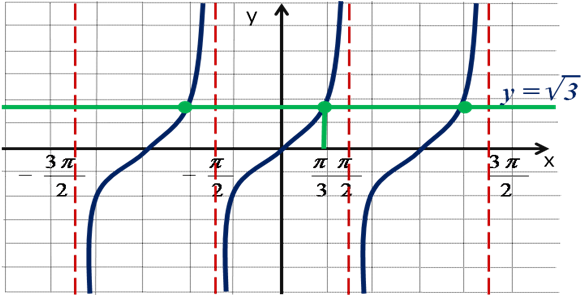
Пример 2. Построить график функции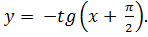 
Составим план построения: 1) Построим главную тангенсоиду.
2) Отобразим эту ветвь симметрично относительно оси х. 3) Сдвинем полученную ветвь на /2 влево. 4) зная одну ветвь, построим весь график.
Т.к.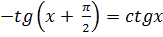 
, то построен график функции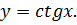 
По графику полученной функции описать её свойства. Как быстро это сделать? (Большинство свойств у функций y = tgx и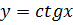 
совпадают).
Свойство 1. D(f) – все действительные числа, кроме чисел вида x = k.
Свойство 2. Функция периодическая с периодом .
Свойство 3. Функция нечётная.
Свойство 4. Функция убывает на всём интервале вида: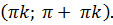 
Свойство 5. Функция не ограничена ни снизу, ни сверху.
Свойство 6. Функция не имеет ни наибольшего, ни наименьшего значений.
Свойство 7.Функция y = tgx непрерывна на любом промежутке вида: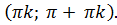
Свойство 8. E(f) = ( — ; + ).
График функции 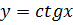так же называется тангенсоидой.
Закрепление изученного материала. № 254,255,257,258 – устно. № 261в, 262в – письменно.
Итог урока.
— С какими функциями мы сегодня с вами познакомились?
— Что можно сказать о них?
— Какими похожими свойствами они обладают? В чём различие?
— Как называются графики этих функций?
Домашнее задание.
infourok.ru
График тригонометрических функций. Тангенс. Котангенс
График функции y=tgx
Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции 
.
Надеюсь, вы помните, где располагается ось тангенсов…
Глядя на картинку, хорошо видно, что значения тангенса в I и III четвертях совпадают с соответствующими значениями тангенса II и IV четвертей. (Например, 
и т.д.)
Переносим основные значения углов, представленные на круге, например, из I и IV четвертей и соответствующие им значения тангенса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения тангенса угла.
Нанесенные на координатную плоскость точки подсказывают нам плавную кривую. Это и есть график функции на 
.
Обратите внимание! Тангенс в точках 
не существует. Мы лишь можем сколь угодно близко «подбираться» к этим значениям.
Указанный выше фрагмент графика тангенса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :
График функции является симметричным относительно начала координат.
График функции y=ctgx
Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и 
.
Поступим несколько иначе.
Согласно формулам приведения 
или, что тоже самое, что 
.
Из чего мы делаем вывод, что график функции будет получен смещением графика функции на 
единиц влево и при этом график 
«опрокидывается» относительно оси (ox) за счет коэффициента -1.
График функции является симметричным относительно начала координат.
egemaximum.ru
Тригонометрические функции: свойства и их графики
Основными тригонометрическими функциями являются функции y=sin(x), y=cos(x), y=tg(x), y=ctg(x). Рассмотрим каждую из них в отдельности.
Y = sin(x)
График функции y=sin(x).
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = cos(x)
График функции y=cos(x).
Основные свойства:
1. Область определения вся числовая ось.
2. Функция ограниченная. Множество значений – отрезок [-1;1].
3. Функция четная.
4.Функция периодическая с наименьшим положительным периодом равным 2*π.
Y = tg(x)
График функции y=tg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π/2 +π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Y = ctg(x)
График функции y=ctg(x).
Основные свойства:
1. Область определения вся числовая ось, за исключением точек вида x=π*k, где k – целое.
2. Функция неограниченная. Множество значение вся числовая прямая.
3. Функция нечетная.
4.Функция периодическая с наименьшим положительным периодом равным π.
Нужна помощь в учебе?
Предыдущая тема: Электронный учебник по физике: все темы школьной программы
Следующая тема:   Периодичность тригонометрических функций: четные и нечетные
Все неприличные комментарии будут удаляться.
www.nado5.ru