Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения, в которых выражение, зависящее от y, входит только в левую часть, а выражение, зависящее от x — только в правую часть, это дифференциальные уравнения с разделяющимися переменными, в которых переменные уже разделены.
В левой части уравнения может находиться производная от игрека и в этом случае решением дифференциального
уравнения будет функция игрек, выраженная через значение интеграла от правой части уравнения. Пример такого уравнения —
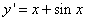 .
.
В левой части уравнения может быть и дифференциал функции от игрека и тогда для получения решения уравнения
следует проинтегрировать обе части уравнения. Пример такого уравнения —
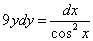 .
.
Пример 1.
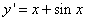
Решение. Пример очень простой. Непосредственно находим функцию по её производной, интегрируя:
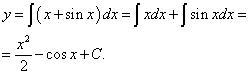
Таким образом, получили функцию — решение данного уравнения.
Пример 2. Найти общее решение дифференциального уравнения
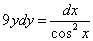
Решение. Интегрируем обе части уравнения:
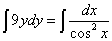 .
.
Оба интеграла — табличные. Идём к решению:
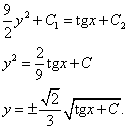
Функция — решение уравнения — получена. Как видим, нужно только уверенно знать табличные интегралы и неплохо расправляться с дробями и корнями.
Дифференциальные уравнения с разделяющимися переменными, в которых требуется разделить переменные, имеют вид
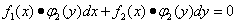 .
.
В таком уравнении 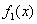 и
и
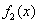 — функции только переменной x,
а
— функции только переменной x,
а 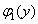 и
и 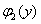 —
функции только переменной y.
—
функции только переменной y.
Поделив члены уравнения на произведение 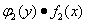 ,
после сокращения получим
,
после сокращения получим
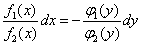
Как видим, левая часть уравнения зависит только от x, а правая только от y, то есть переменные разделены.
Левая часть полученного уравнения — дифференциал некоторой функции переменной x, а правая часть — дифференциал некоторой функции переменной y. Для получения решения исходного дифференциального уравнения следует интегрировать обе части уравнения. При этом при разделении переменных не обязательно переносить один его член в правую часть, можно почленно интегрировать без такого переноса.
Пример 3. Найти общее решение дифференциального уравнения
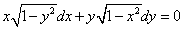 .
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим уравнение
почленно на произведение 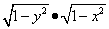
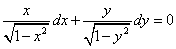 .
.
Почленно интегрируем:
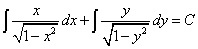 ,
,
откуда, используя метод замены переменной (подстановки), получаем
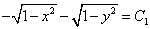 или
или 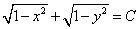 ,
,
поскольку левая часть равенства есть сумма арифметических значений корней. Таким образом, получили общий интеграл данного уравнения. Выразим из него y и найдём общее решение уравнения:
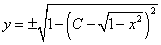 .
.
Есть задачи, в которых для разделения переменных уравнение нужно не делить почленно на произведение некоторых функций, а почленно умножать. Таков следующий пример.
Пример 4. Найти общее решение дифференциального уравнения
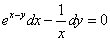 .
.
Решение. Бывает, что забвение элементарной (школьной) математики мешает даже близко подойти к началу решения, задача выглядит абсолютно тупиковой. В нашем примере для начала всего-то нужно вспомнить свойства степеней.
Так как 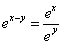 , то
перепишем данное уравнение в виде
, то
перепишем данное уравнение в виде
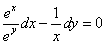 .
.
Это уже уравнение с разделяющимися переменными. Умножив его почленно на произведение 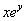 , получаем
, получаем
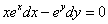
Почленно интегрируем:
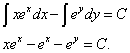
Первый интеграл находим интегрированием по частям, а второй — табличный. Следовательно,
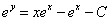 .
.
Логарифимруя обе части равенства, получаем общее решение уравнения:
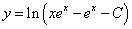 .
.
Решить примеры самостоятельно, а затем посмотреть правильные решения
Продолжаем решать примеры вместе
Пример 7. Найти общее решение дифференциального уравнения
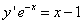 .
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим уравнение
почленно на 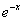
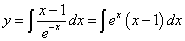 .
.
Чтобы найти y, требуется найти интеграл. Интегрируем по частям.
Пусть 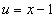 ,
, 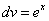 .
.
Тогда 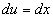 ,
, 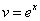 .
.
Находим общее решение уравнения:
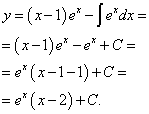
Пример 8. Найти частное решение дифференциального уравнения
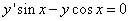 ,
,
удовлетворяющее условию 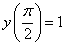 .
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим уравнение
почленно на 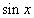 и получим
и получим
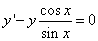
или
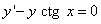 .
.
Записываем производную y в виде 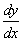 и получаем
и получаем
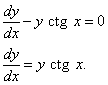
Разделяем dy и dx и получаем уравнение:
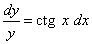 , которое почленно интегрируя:
, которое почленно интегрируя:
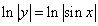 ,
,
находим общее решение уравнения:
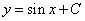 .
.Чтобы найти частное решение уравнения, подставляем в общее решение значения y и x из начального условия:
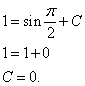 .
.
Таким образом частное решение данного дифференциального уравнения:
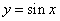 .
.
В некоторых случаях ответ (функцию) можно выразить явно. Для этого следует воспользоваться тем свойством логарифма, что сумма логарифмов равна логарифму произведения логарифмируемых выражений. Обычно это следует делать в тех случаях, когда слева искомая функция под логарифмом находится вместе с каким-нибудь слагаемым. Рассмотрим два таких примера.
Пример 9. Найти общее решение дифференциального уравнения
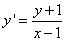 .
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных запишем производную
«игрека» в виде 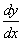 и получим
и получим
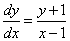 .
.
Разделяем «игреки» и «иксы»:
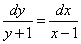 .
.
Почленно интегрируем и, так как в левой части «игрек» присутствует со слагаемым, в правой части константу интегрирования записываем также под знаком логарифма:
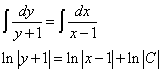 .
.
Теперь по свойству логарифма 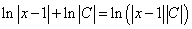 имеем
имеем
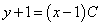 .
.Находим общее решение уравнения:
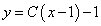
Пример 10. Найти частное решение дифференциального уравнения
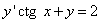 ,
,
удовлетворяющее условию 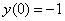 .
.
Это уравнение с разделяющимися переменными. Решение. Для разделения переменных поделим уравнение
почленно на 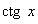 и получим
и получим
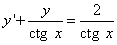
или
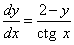 .
.
Разделяем dy и dx и получаем уравнение:
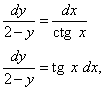
которое почленно интегрируя:
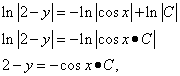
находим общее решение уравнения:
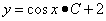 .
.
Чтобы найти частное решение уравнения, подставляем в общее решение значения y и x из начального условия:
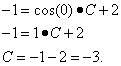 .
.
Таким образом частное решение данного дифференциального уравнения:
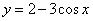 .
.
Выводы. В дифференциальных уравнениях с разделяющимися переменными, как в тех, в которых переменные уже разделены, так и в тех, где переменные требуется разделить, существуют однозначные способы решения, на основе которых может быть построен простой алгоритм. Если недостаточно уверенно освоен материал по нахождению производной и решению интегралов, то требуется его повторить. Во многих задачах на путь к решению уравнения наводят знания и приёмы из элементарной (школьной) математики.

Всё по теме «Дифференциальные уравнения»
Поделиться с друзьями
Дифференциальные уравнения первого порядка с разделяющимися переменными
Дифференциальное уравнение 1-го порядка с неизвестной функцией , разрешенное относительно производной имеет вид:
где – данная функция. В некоторых случаях выгодно за искомую функцию считать переменную и записывать уравнение в виде:
где
Учитывая, что и , то дифференциальные уравнения можно записать в симметрической форме:
где и – известные функции
Под решениями дифференциального уравнения понимаются функция вида или , удовлетворяющие этому уравнению.
Общий интеграл уравнений имеет вид , где – произвольная постоянная.
Уравнением с разделяющимися переменными называется уравнение 1-го порядка вида
или
Разделив обе части уравнения (*) на и умножив на , будем иметь
Отсюда, интегрируя, получим общий интеграл уравнения (*) в виде:
Аналогично, разделив обе части уравнения (**) на и проинтегрировав, получим общий интеграл уравнения (**) в виде
Если для некоторого значения мы имеем , то функция является также, как непосредственно легко убедиться, решением уравнения (*). Аналогично прямые и будут интегральными кривыми уравнения (**), если и являются соответственно корнями уравнения и , на левые части которых приходилось делить исходное уравнение.
Методы решения других видов дифференциальных уравнений:
Дифференциальные уравнения с разделенными и разделяющимися переменными | Математика
ОПРЕДЕЛЕНИЕ 11.2.7 Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его правая часть есть произведение двух функций, одна из которых зависит от , а другая от . .
Предположим, что функции и непрерывны на интервале и что .
Умножая обе части уравнения на и деля на , запишем его в виде: .
Почленное интегрирование последнего уравнения приводит к соотношению , которое представляет собой общий интеграл данного уравнения в указанной области.
ОПРЕДЕЛЕНИЕ 11.2.8 Дифференциальное уравнение
называется дифференциальным уравнением с разделяющимися переменными в симметричной относительно и дифференциальной форме.
Функции непрерывны соответственно в интервалах и не равны тождественно нулю.
Для нахождения всех решений такого уравнения достаточно разделить обе части уравнения на произведение и проинтегрировать полученное соотношение: . Полученное соотношение является общим интегралом данного уравнения, где произвольная постоянная.
ОПРЕДЕЛЕНИЕ 11.2.9 Уравнение вида называется дифференциальным уравнением с разделенными переменными.
Почленное интегрирование данного уравнения приводит к соотношению , которое определяет (в неявной форме) решение исходного уравнения.
ПРИМЕР 11.2.1. Найти общее решение уравнения .
Решение.
Данное уравнение есть уравнение с разделяющимися переменными функции и непрерывна всюду и .
Разделяя переменными и интегрируя , получим
общий интеграл данного уравнения во всей плоскости .
Разрешая относительно , находим общее решение , .
ПРИМЕР 11.2.2. Найти общий интеграл уравнения
.
Решение.
Преобразуем данное уравнение
. Данное уравнение есть уравнение с разделяющимися переменными в дифференциальной форме симметричное относительно и .
Функции и не равны нулю в рассматриваемой области. Разделим обе части уравнения на , получим
.
, где . Получили общий интеграл.
ПРИМЕР 11.2.3. Проинтегрировать уравнение .
Решение.
Данное уравнение — есть уравнение с разделенными переменными. Проинтегрируем данное уравнение
(так как левая часть выражается через натуральный логарифм, то постоянную удобнее в данном случае записать как ).
общее решение, с геометрической точки зрения определяет семейство гипербол.
ПРИМЕР 11.2.4. Найти кривую, обладающую тем свойством, что отрезок любой ее касательной, заключенный между осями координат, делится пополам в точке касания.
Решение.
Пусть уравнение искомой кривой, произвольная точка кривой.
рис 11.2.1
, т.е.
. Из
, так как , то , тогда . Получили дифференциальное уравнение с разделяющими переменными, интегрируя его, получим
семейство интегральных кривых, удовлетворяющих условию задачи.
ПРИМЕР 11.2.5. Материальная точка с массой г погружается в жидкость без начальной скорости. Сила сопротивления жидкости пропорциональна скорости погружения . Коэффициент пропорциональности . Найти зависимость погружения от времени.
Решение.
В момент времени точка находится под действием силы тяжести и силы сопротивления жидкости . Сила P направлена в сторону движения, а в сторону противоположную движению, поэтому их равнодействующая .
Так как материальная точка погружается в жидкость под действием силы , то по второму закону Ньютона эта же сила равна . Приравнивая оба выражения для , получим , но по условию г, а . сократим на , .
Получили уравнение с разделяющими переменными. Разделив переменные и проинтегрировав, получим
. .
; ; ;
или , где .
Для нахождения воспользуемся начальным условием .
.Тогда частное решение будет иметь вид
.
Задачи и примеры для самостоятельного решения
Решите уравнения:
11.2.14 Кривая проходит через точку . В произвольной точке этой кривой проведена касательная. Точка пересечения касательной с осью имеет абсциссу вдвое большую, чем абсцисса точки касания. Найти кривую.
Ответ:
11.2.15 Составить уравнение кривой, проходящей через точку , если угловой коэффициент касательной в любой точке кривой равен произведению координат точки касания.
Ответ: .
11.2.16 Найти время, в течение которого вся вода вытекает из конической воронки, если известно, что половина воды вытекает в мин.
Ответ: мин.
11.2.17 В комнате, где температура , некоторое тело остыло за мин от до . Найти закон охлаждения тела; через сколько минут оно остынет до ? Повышением температуры в комнате пренебречь.
Ответ: мин.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Задача 1. \(\sqrt{y^2+1}dx=xydy.\)
Решение. Это уравнение с разделяющимися переменными. Деля обе его части на произведение \(\sqrt{y^2+1}\cdot x\), получаем
$$\frac{dx}{x}=\frac{ydy}{\sqrt{y^2+1}},\; x\neq 0,$$
откуда
$$\int {\frac{dx}{x}}=\int {\frac{ydy}{\sqrt{y^2+1}}}+C,$$
или
$$\ln\left|x \right|-\sqrt{y^2+1}=C.$$
Таким образом, все решения данного уравнения имеют вид
$$\ln\left|x \right|-\sqrt{y^2+1}=C,\; x=0.$$
Задача 2. \((x^2-1)y’+2xy^2=0,\; y(0)=1.\)
Решение. Сначала находим все решения этого уравнения. Имеем
$$(x^2-1)dy+2xy^2dx=0,$$
откуда, разделив переменные \(x\) и \(y\), получаем
$$\frac{dy}{y^2}+\frac{2xdx}{x^2-1}=0.$$
Интегрируя обе части полученного уравнения, находим
$$-\frac{1}{y}+ \ln \left|x^2-1 \right|=C.$$
Для получения всех решений исходного уравнения к последнему семейству интегральных кривых присоединим еше решение \(y=0.\)
Далее, из совокупности всех интегральных кривых выделим ту кривую, которая проходит через точку \((0,1)\). Полагая \(x=0\) и \(y=1\), находим \(C=-1.\) Таким образом, функция
$$y=\frac{1}{1+ \ln \left|x^2-1 \right|}$$
является решением поставленной задачи.
Задача 3. \(xy’+y=y^2,\; y(1)=0,5.\)
Решение. Записывая уравнение в виде
$$xdy+(y-y^2)dx=0$$
и разделяя переменные, имеем
$$\frac{dy}{y-y^2}+\frac{dx}{x}=0.$$
Интегрируя, получаем
$$xy(1-y)=C.$$
Заметим, что несмотря на деление обеих частей уравнения на \(x(y-y^2)\), его решения \(x=0,\: y=0\) и \(y=1\) не были потеряны. Наконец, подставив \(x=1,\: y=0,5\), находим \(C=\frac{1}{4}\). Следовательно, дифференцируемая кривая
$$4xy(1-y)-1=0$$
— решение поставленной задачи.
Задача 4. \(e^{-s}\left(1+\frac{ds}{dt} \right)=1.\)
Решение. Переписав уравнение в виде
$$\frac{ds}{dt}=e^s-1,$$
разделяем переменные \(s\) и \(t\):
$$\frac{ds}{e^s-1}=dt.$$
Проинтегрировав полученное уравнение, находим \(\ln \left|\frac{e^s-1}{e^s} \right|=t+ \ln C,\) или \(s=-\ln (1+Ce^t).\)
2012-01-17 • Просмотров [ 10575 ]
Уравнения с разделяющимися переменными
Обыкновенные дифференциальные уравнения.
Решение различных геометрических, физических и инженерных задач часто приводят к уравнениям, которые связывают независимые переменные, характеризующие ту ил иную задачу, с какой – либо функцией этих переменных и производными этой функции различных порядков.
В качестве примера можно рассмотреть простейший случай равноускоренного движения материальной точки.
Известно, что перемещение материальной точки при равноускоренном движении является функцией времени и выражается по формуле:
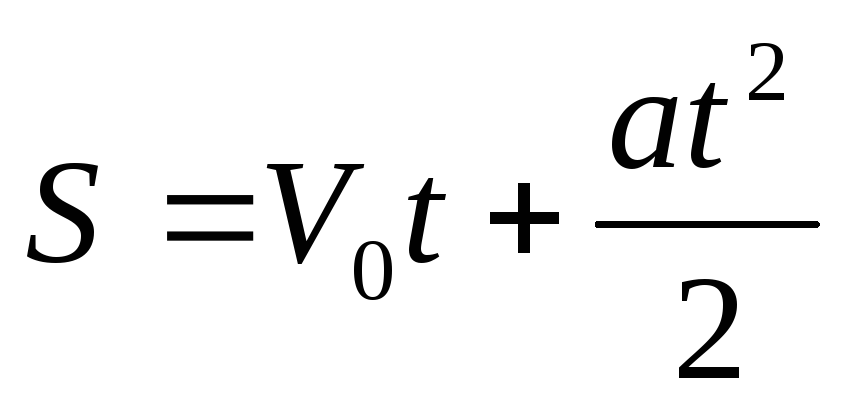
В свою очередь ускорение a является производной по времени t от скорости V, которая также является производной по времени t от перемещения S. Т.е.
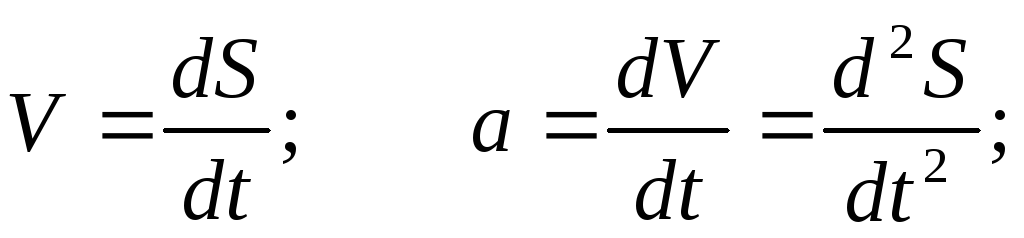
Тогда
получаем: 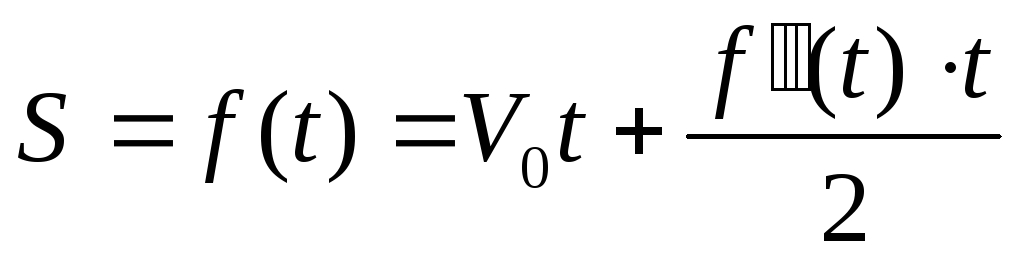 — уравнение связывает функцию f(t)
с независимой переменной t
и производной второго порядка функции
f(t).
— уравнение связывает функцию f(t)
с независимой переменной t
и производной второго порядка функции
f(t).
Определение. Дифференциальным уравнением называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции.
Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Определение. Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения.
Пример.
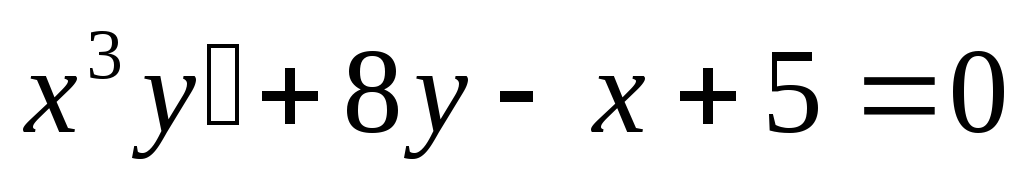 —
обыкновенное дифференциальное уравнение
1 – го порядка. В общем виде записывается
—
обыкновенное дифференциальное уравнение
1 – го порядка. В общем виде записывается 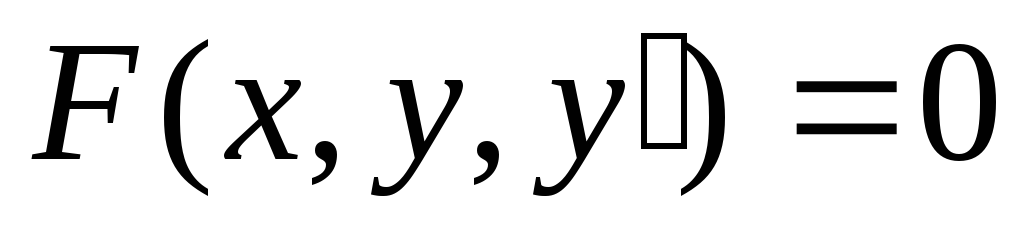 .
.
—
обыкновенное дифференциальное уравнение
2 – го порядка. В общем виде записывается 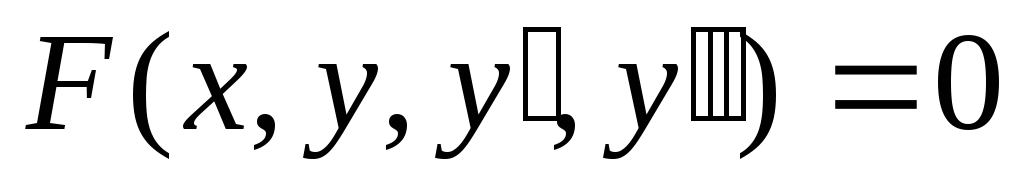
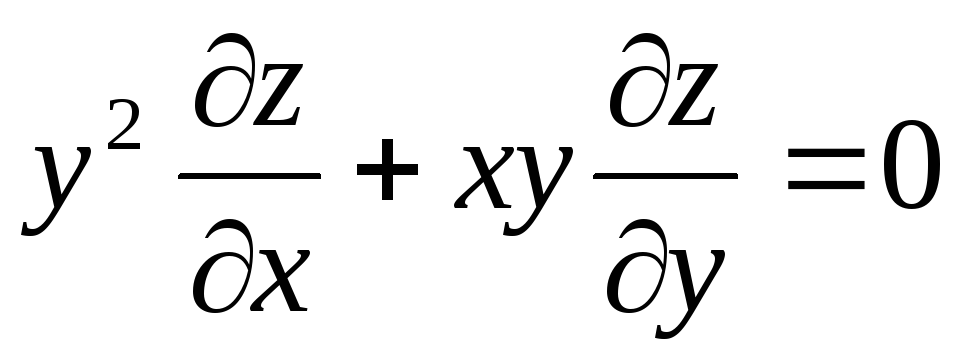 —
дифференциальное уравнение в частных
производных первого порядка.
—
дифференциальное уравнение в частных
производных первого порядка.
Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.
Свойства общего решения.
1) Т.к. постоянная С – произвольная величина, то вообще говоря дифференциальное уравнение имеет бесконечное множество решений.
2) При каких- либо начальных условиях х = х0, у(х0) = у0 существует такое значение С = С0, при котором решением дифференциального уравнения является функция у = (х, С0).
Определение. Решение вида у = (х, С0) называется частным решением дифференциального уравнения.
Определение. Задачей Коши (Огюстен Луи Коши (1789-1857)- французский математик) называется нахождение любого частного решения дифференциального уравнения вида у = (х, С0), удовлетворяющего начальным условиям у(х0) = у0.
Теорема Коши. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка)
Если
функция f(x, y)
непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную
частную производную 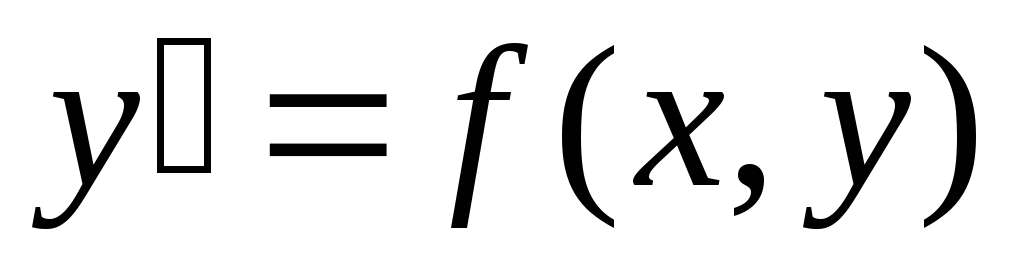 ,
то какова бы не была точка (х0,
у0)
в области D,
существует единственное решение
,
то какова бы не была точка (х0,
у0)
в области D,
существует единственное решение 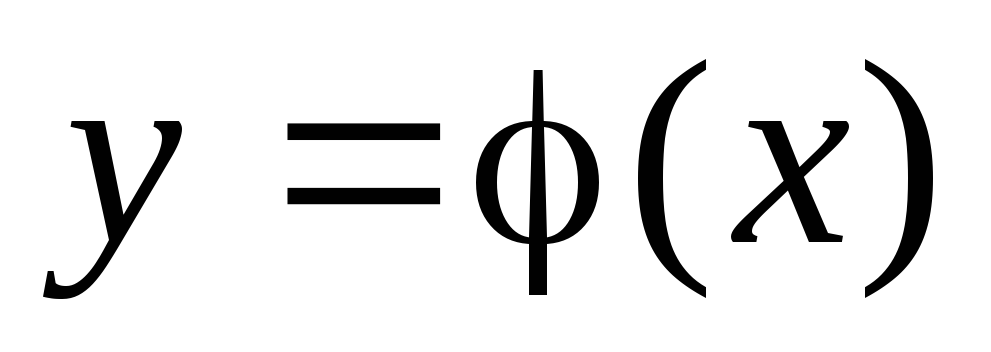 уравнения
уравнения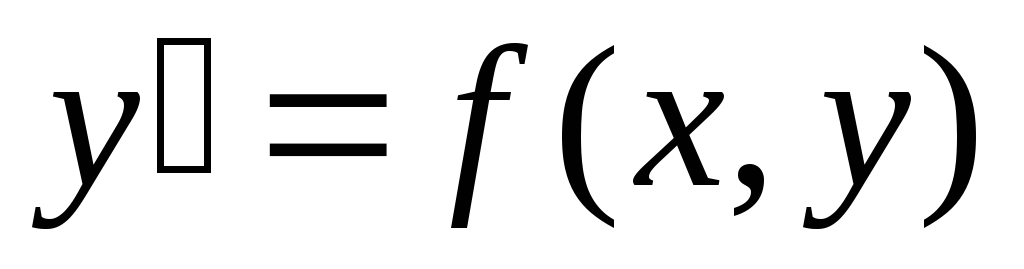 ,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
,
определенное в некотором интервале,
содержащем точку х0,
принимающее при х = х0 значение (х0)
= у0,
т.е. существует единственное решение
дифференциального уравнения.
Определение. Интегралом дифференциального
уравнения называется любое уравнение,
не содержащее производных, для которого
данное дифференциальное уравнение
является следствием.
Пример. Найти общее решение дифференциального
уравнения 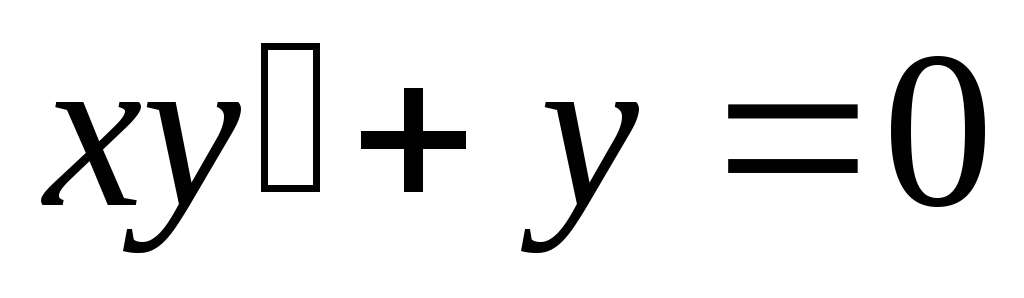 .
.
Общее решение дифференциального уравнения ищется с помощью интегрирования левой и правой частей уравнения, которое предварительно преобразовано следующим образом:
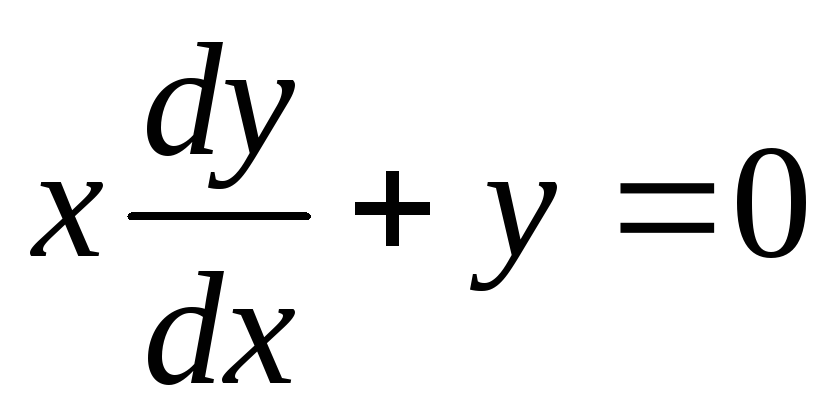
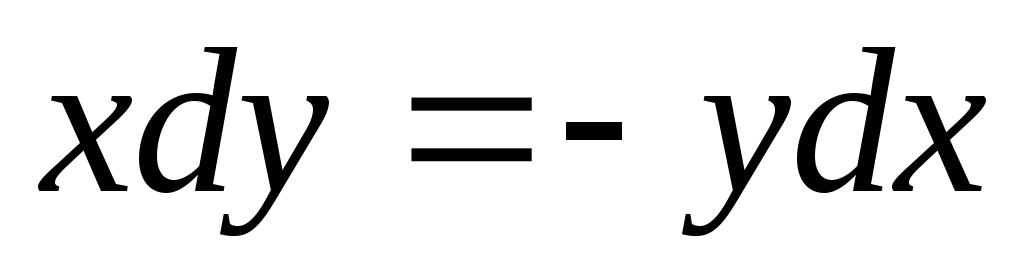
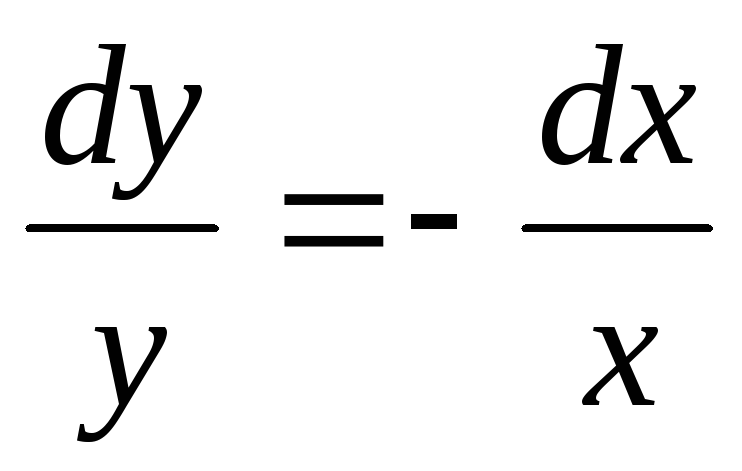
Теперь
интегрируем: 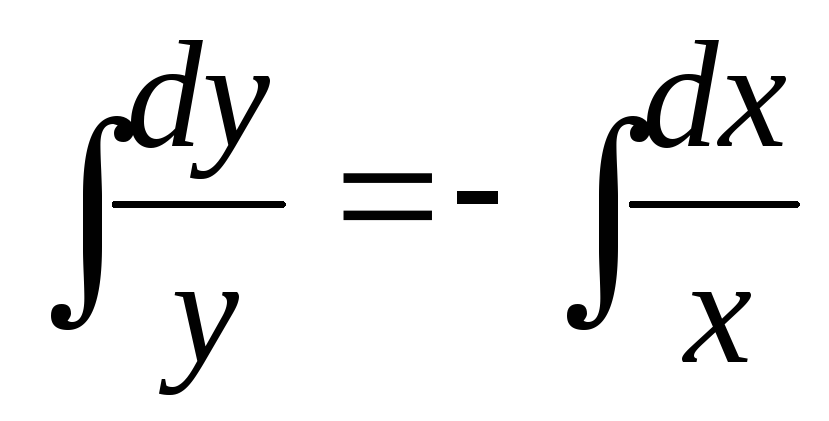
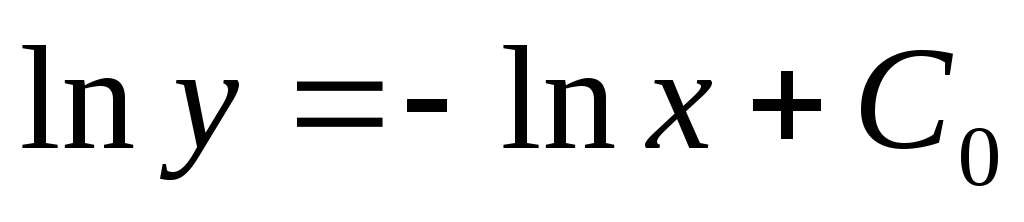
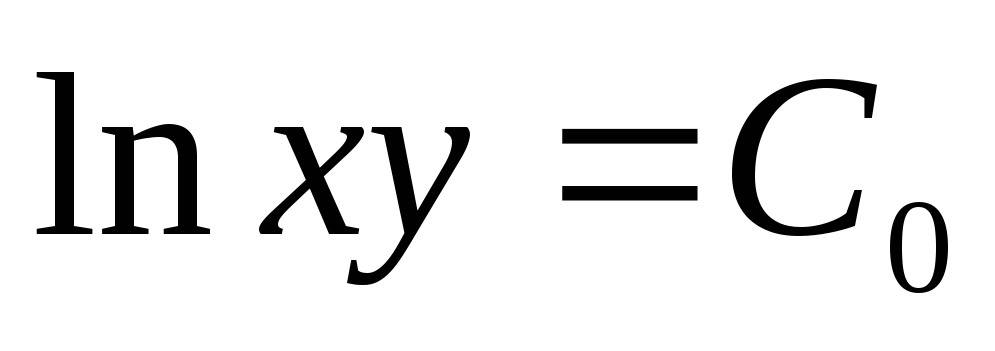
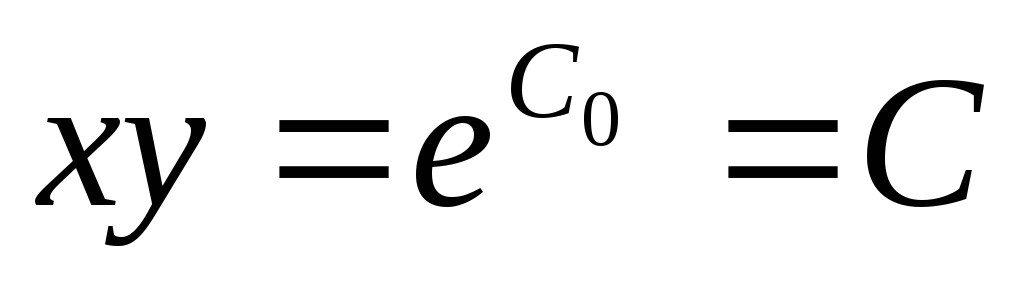
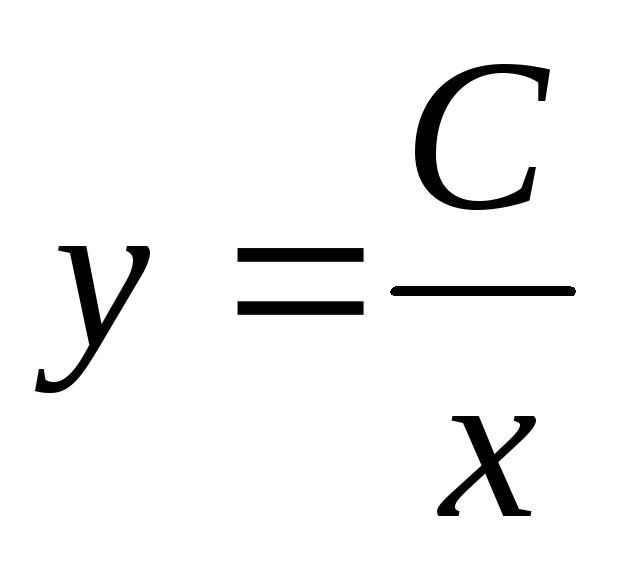 —
это общее решение исходного дифференциального
уравнения.
—
это общее решение исходного дифференциального
уравнения.
Допустим, заданы некоторые начальные условия: x0 = 1; y0 = 2, тогда имеем
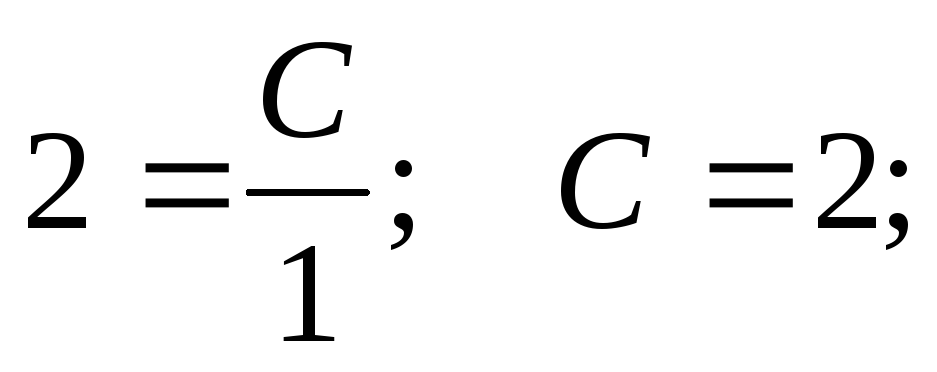
При подстановке полученного значения постоянной в общее решение получаем частное решение при заданных начальных условиях (решение задачи Коши).
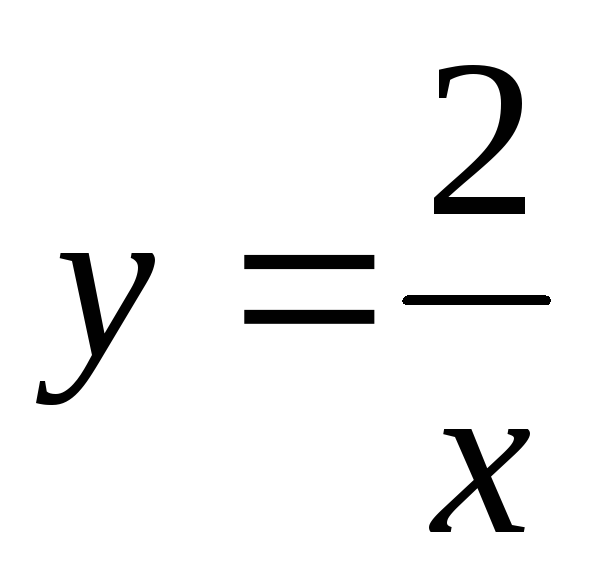
Определение. Интегральной кривой называется график y = (x) решения дифференциального уравнения на плоскости ХОY.
Определение. Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши (см. Теорема Коши. ) не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых.
Особые решения не зависят от постоянной С.
Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.
Отметим, что не каждое дифференциальное уравнение имеет особые решения.
Пример. Найти общее решение дифференциального
уравнения: 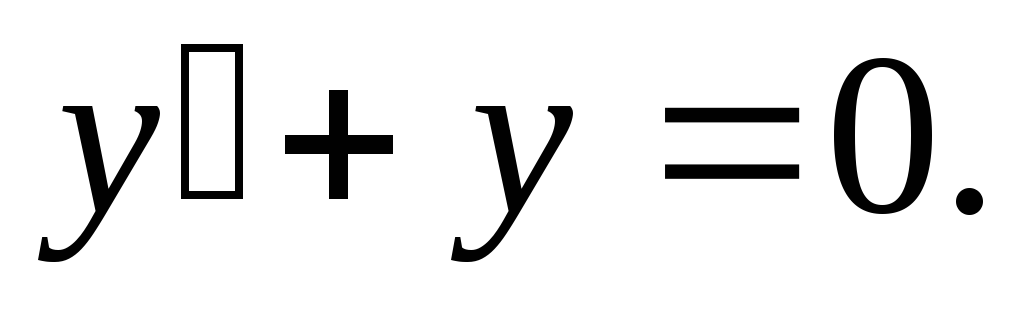 Найти особое решение, если оно существует.
Найти особое решение, если оно существует.
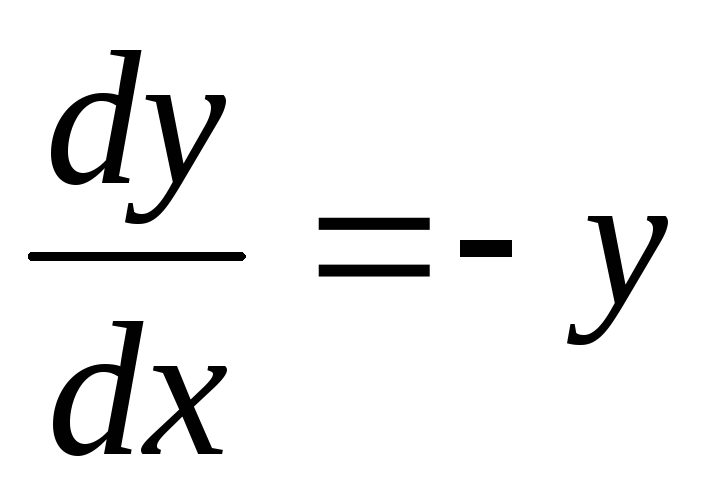
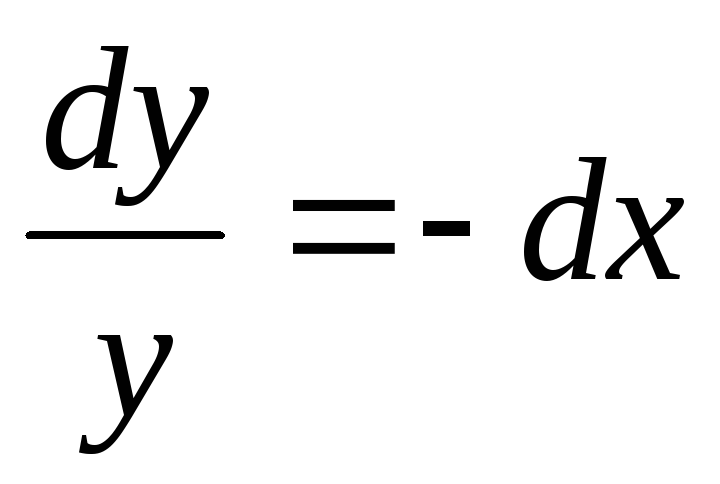
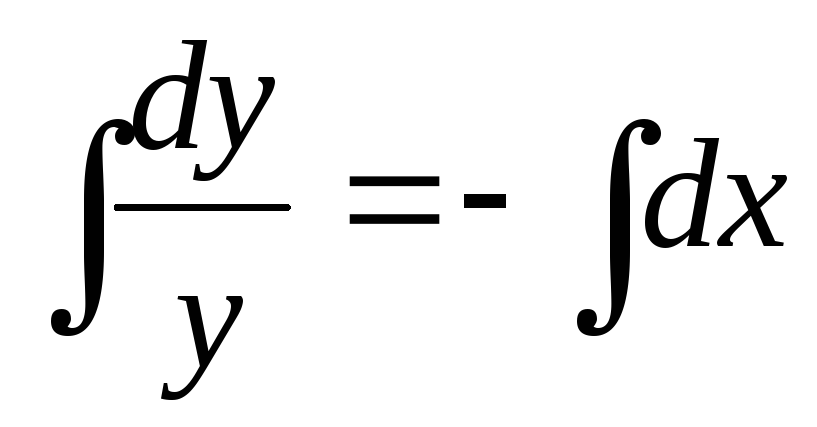
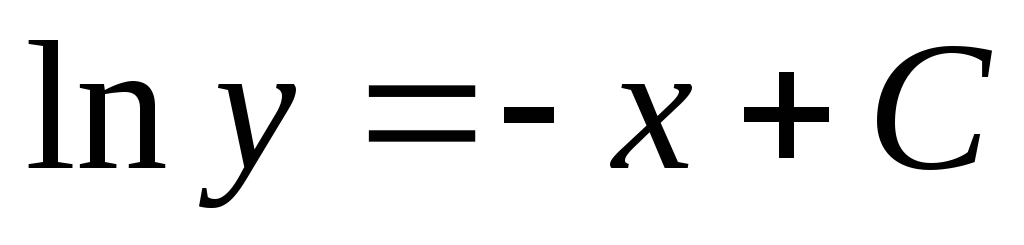
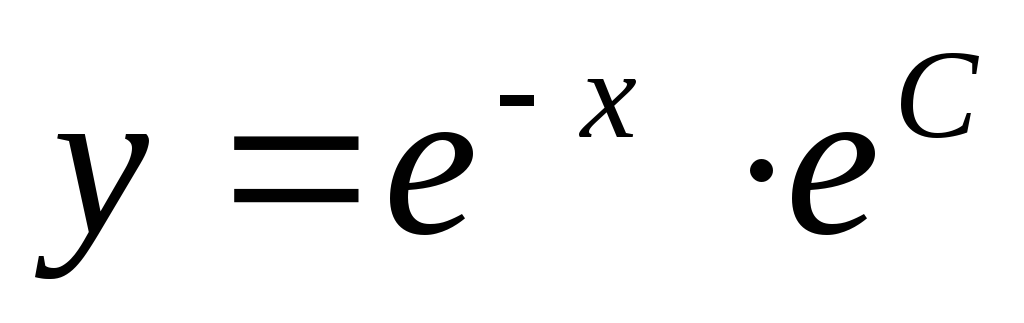
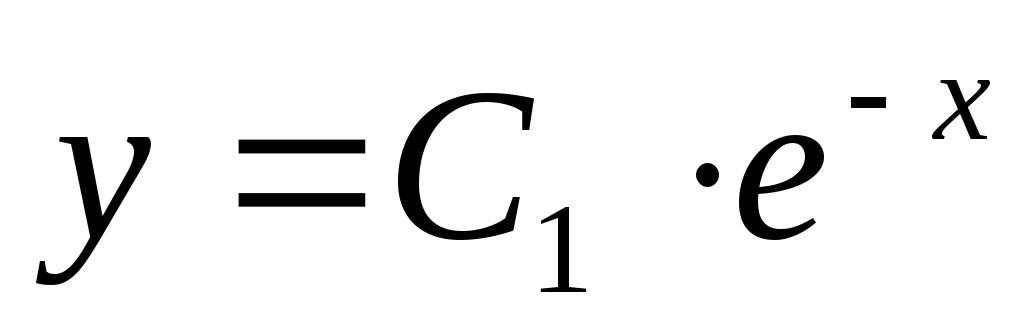
Данное дифференциальное уравнение имеет также особое решение у = 0. Это решение невозможно получить из общего, однако при подстановке в исходное уравнение получаем тождество. Мнение, что решение y = 0 можно получить из общего решения при С1 = 0 ошибочно, ведь C1 = eC 0.
Далее рассмотрим подробнее приемы и методы, которые используются при решении дифференциальных уравнений различных типов.
Дифференциальные уравнения первого порядка.
Определение. Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида:
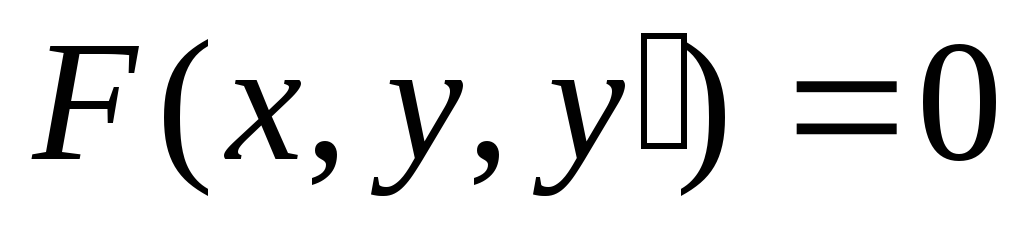
Если
такое соотношение преобразовать к виду 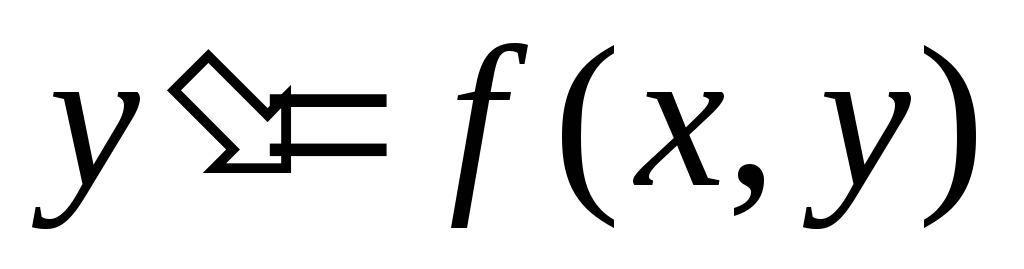 то это дифференциальное уравнение
первого порядка будет называться
уравнением,разрешенным
относительно производной.
то это дифференциальное уравнение
первого порядка будет называться
уравнением,разрешенным
относительно производной.
Преобразуем такое выражение далее:
Функцию
f(x,y)
представим в виде: 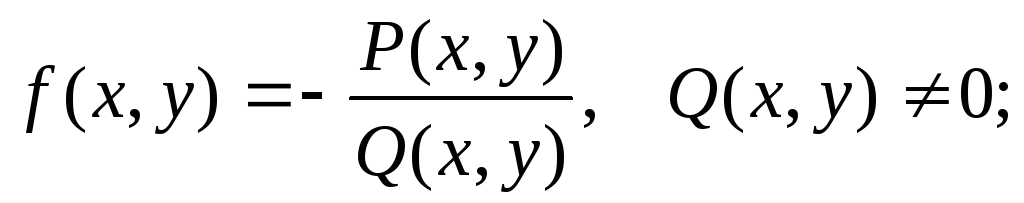 тогда при подстановке в полученное выше
уравнение имеем:
тогда при подстановке в полученное выше
уравнение имеем:
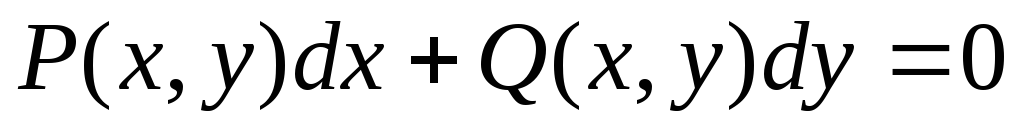
Далее рассмотрим подробнее типы уравнений первого порядка и методы их решения.
Уравнения вида y’ = f(x).
Пусть функция f(x) – определена и непрерывна на некотором интервале
a
< x
< b.
В таком случае все решения данного
дифференциального уравнения находятся
как 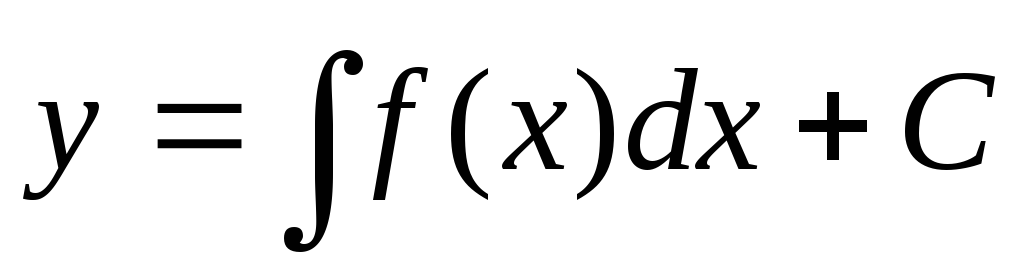 .
Если заданы начальные условия х0 и у0,
то можно определить постоянную С.
.
Если заданы начальные условия х0 и у0,
то можно определить постоянную С.
Определение. Дифференциальное уравнение 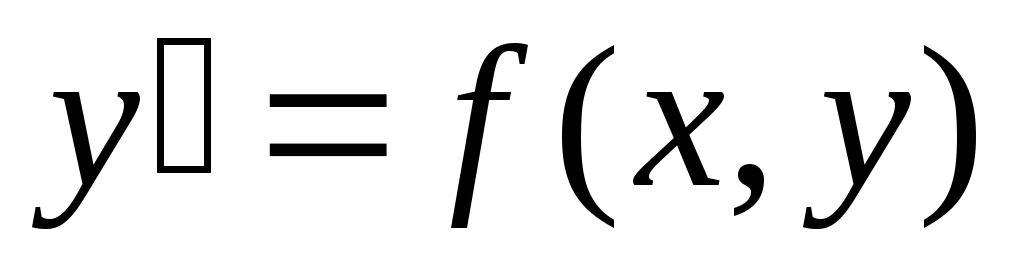 называетсяуравнением
с разделяющимися переменными,
если его можно записать в виде
называетсяуравнением
с разделяющимися переменными,
если его можно записать в виде
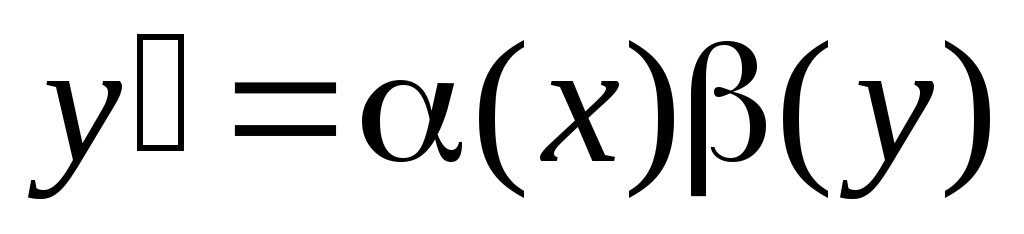 .
.
Такое уравнение можно представить также в виде:
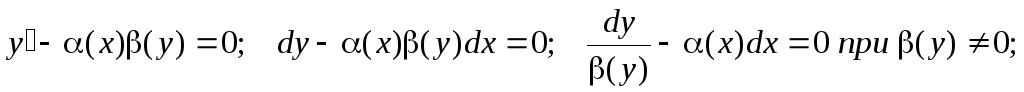
Перейдем
к новым обозначениям 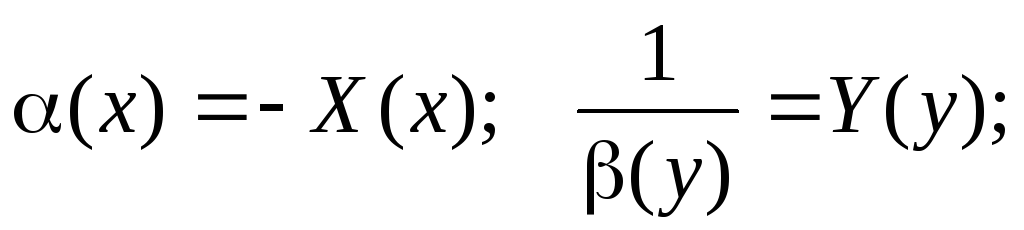
Получаем: 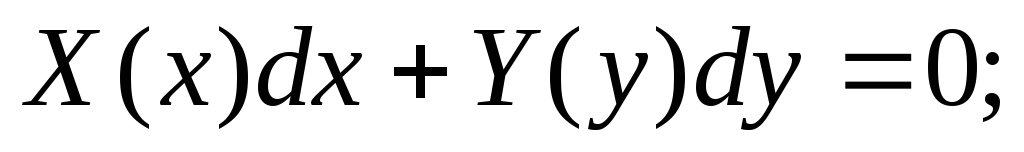
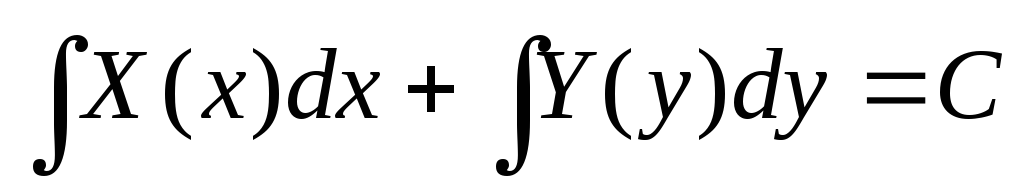
После нахождения соответствующих интегралов получается общее решение дифференциального уравнения с разделяющимися переменными.
Если заданы начальные условия, то при их подстановке в общее решение находится постоянная величина С, а, соответственно, и частное решение.
Пример. Найти общее решение дифференциального
уравнения: 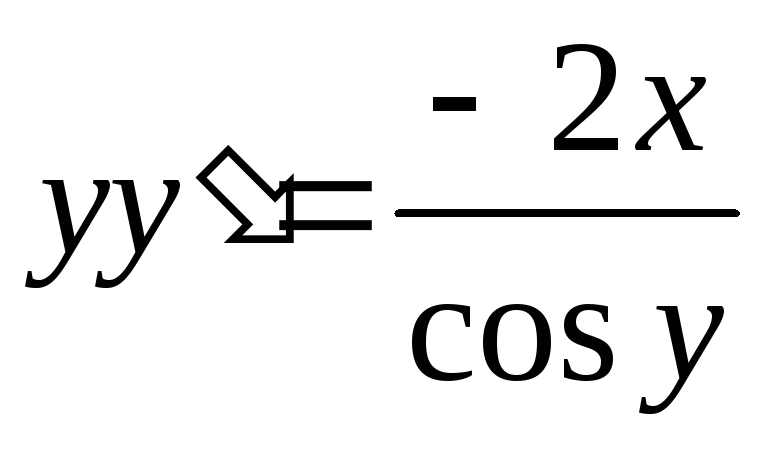
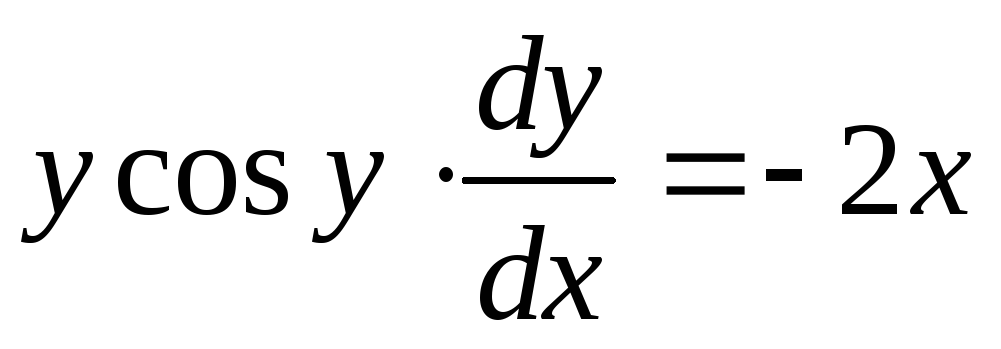
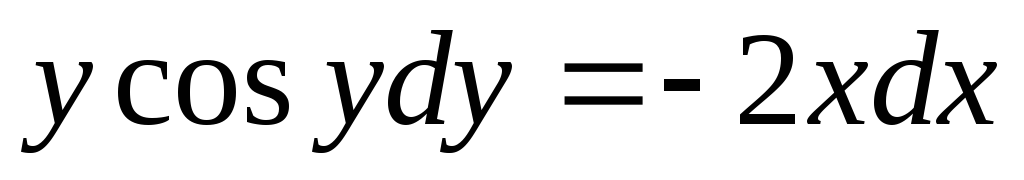
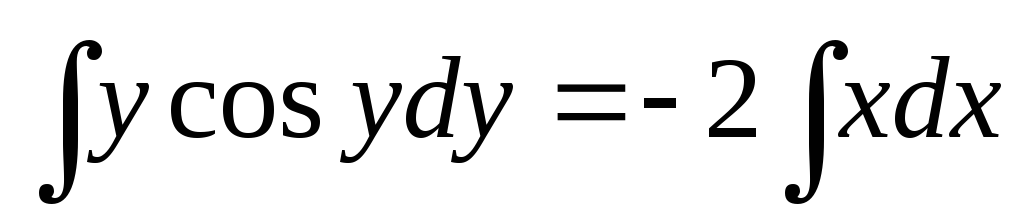
Интеграл, стоящий в левой части, берется по частям (см. Интегрирование по частям.):
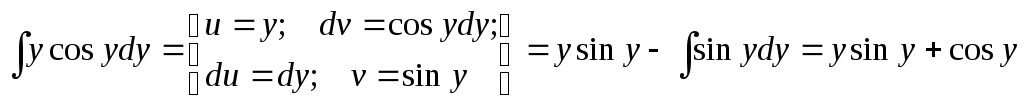

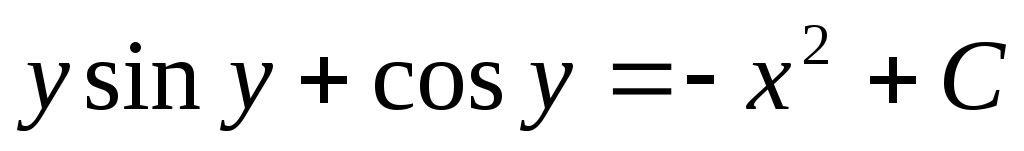
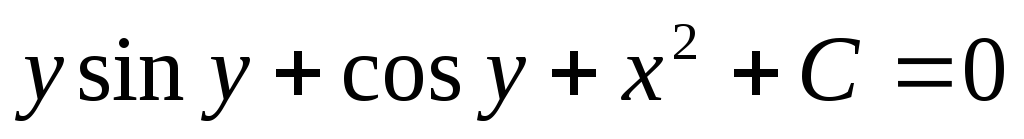
это есть общий интеграл исходного дифференциального уравнения, т.к. искомая функция и не выражена через независимую переменную. В этом и заключается отличие общего (частного) интеграла от общего (частного) решения.
Чтобы проверить правильность полученного ответа продифференцируем его по переменной х.
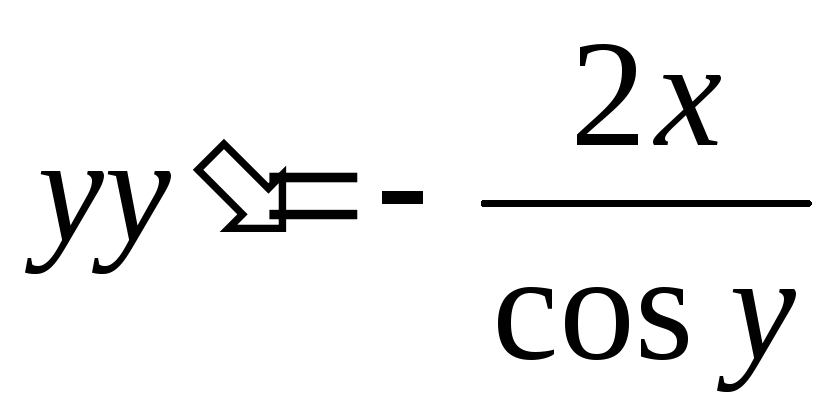 —
верно
—
верно
Пример. Найти решение дифференциального
уравнения 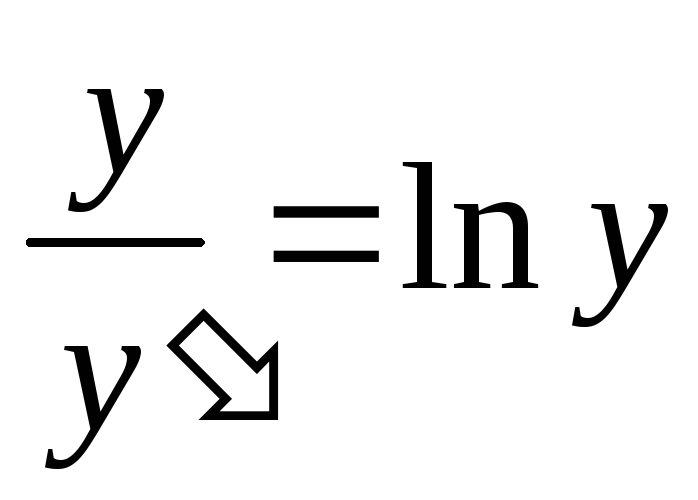 при условии у(2) = 1.
при условии у(2) = 1.
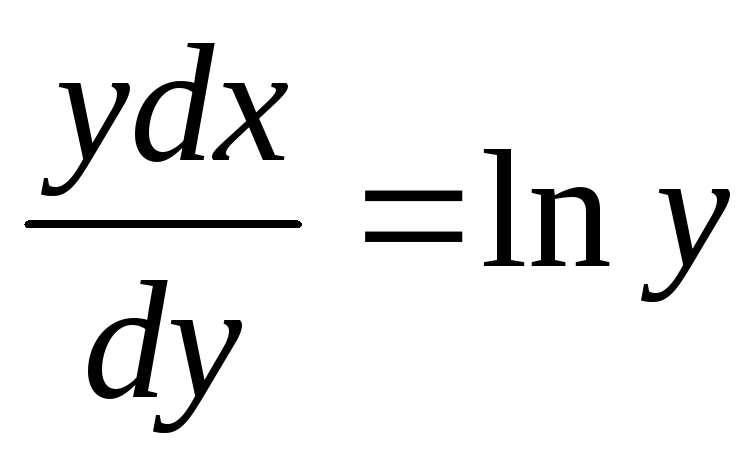

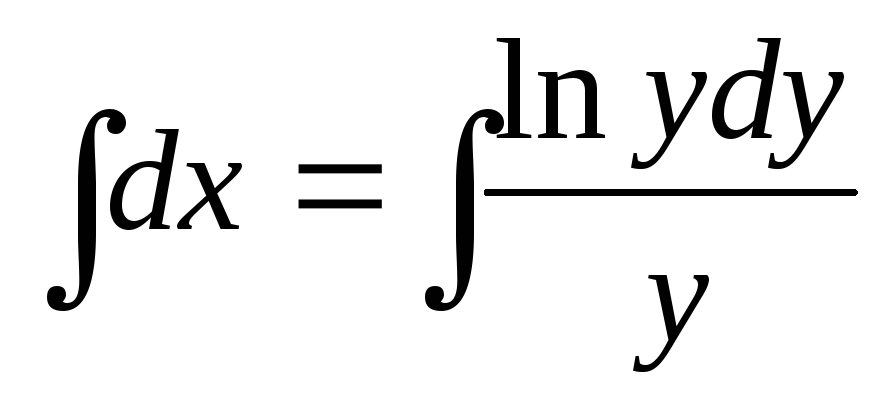
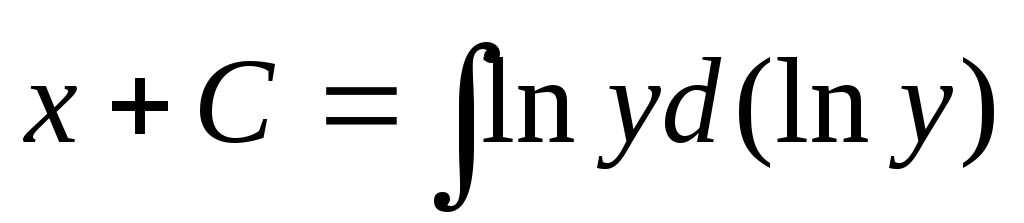
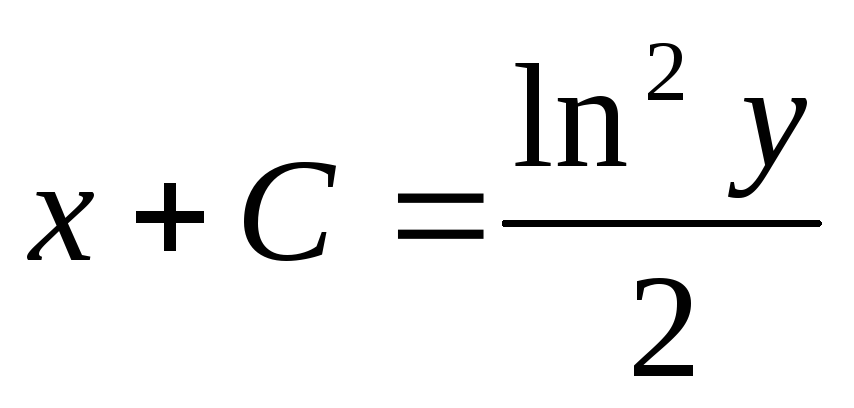
при
у(2) = 1 получаем 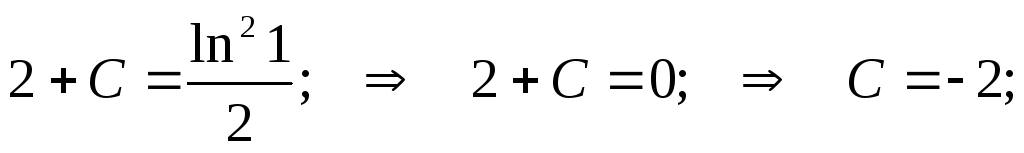
Итого: 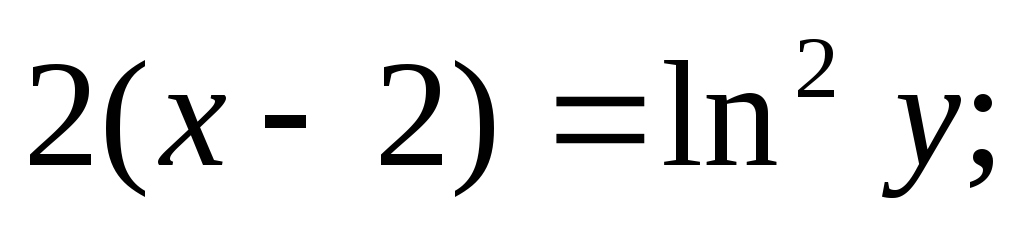 или
или 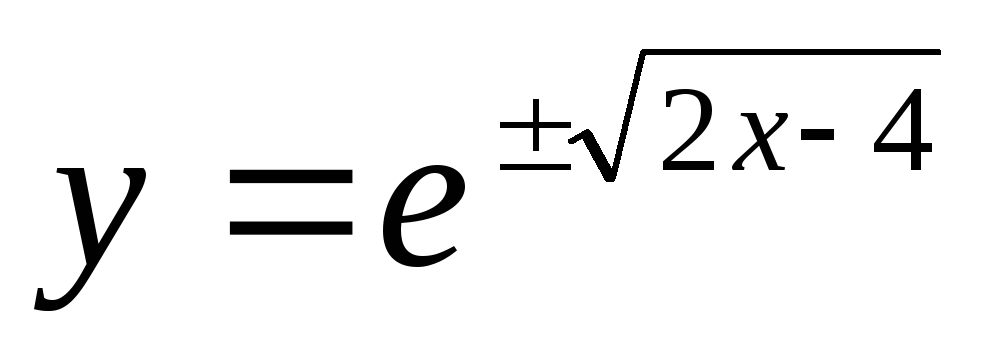 — частное решение;
— частное решение;
Проверка: 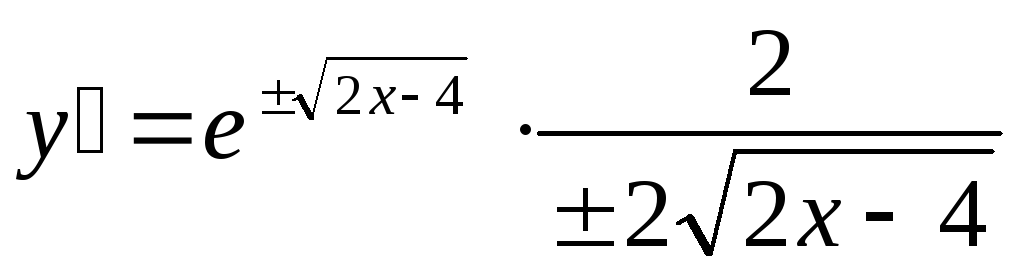 , итого
, итого
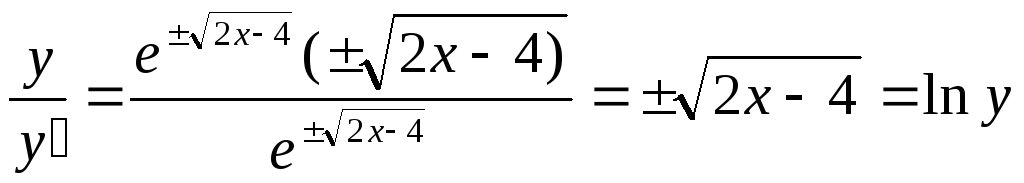 —
верно.
—
верно.
Пример. Решить уравнение 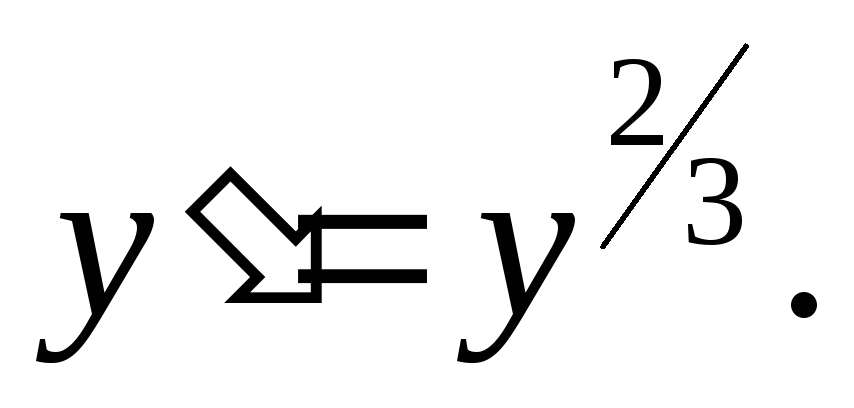
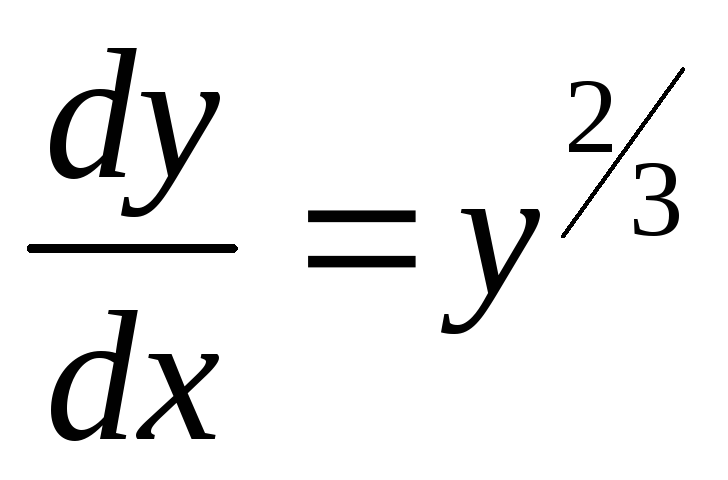
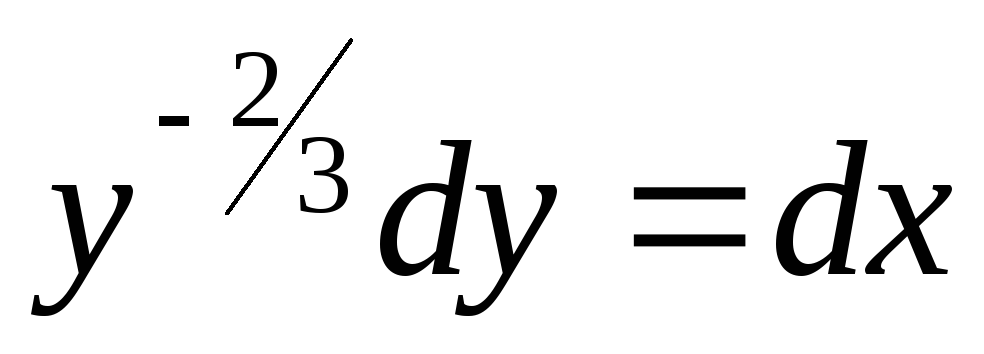

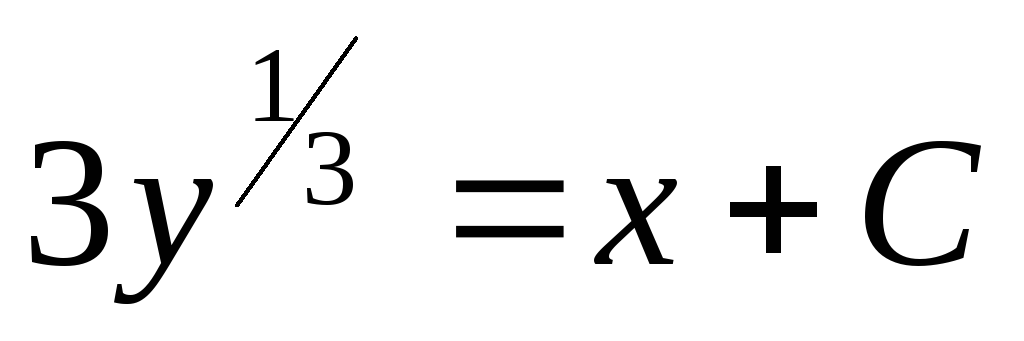
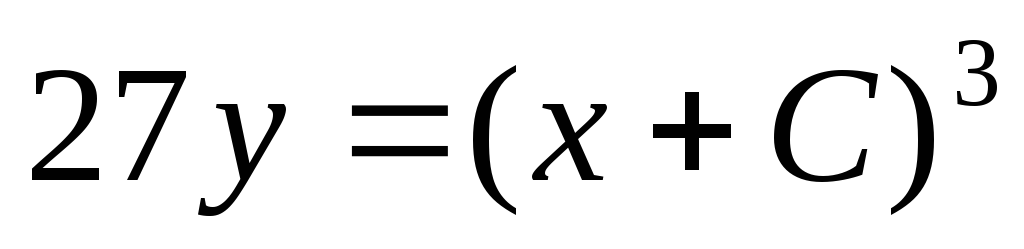 —
общий интеграл
—
общий интеграл
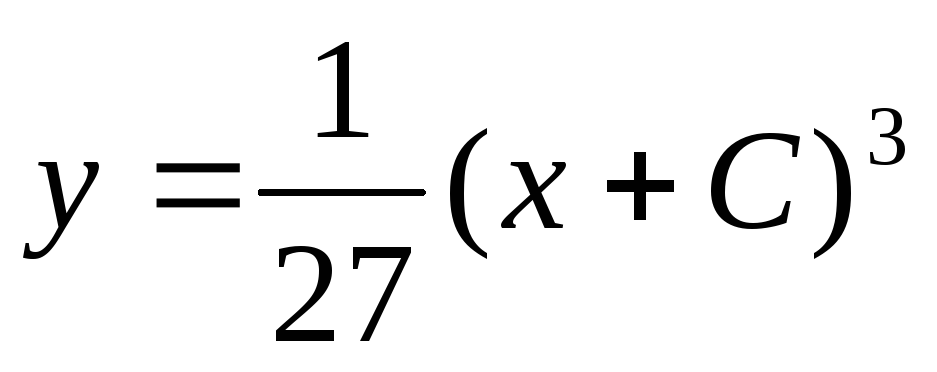 —
общее решение
—
общее решение
Пример. Решить уравнение 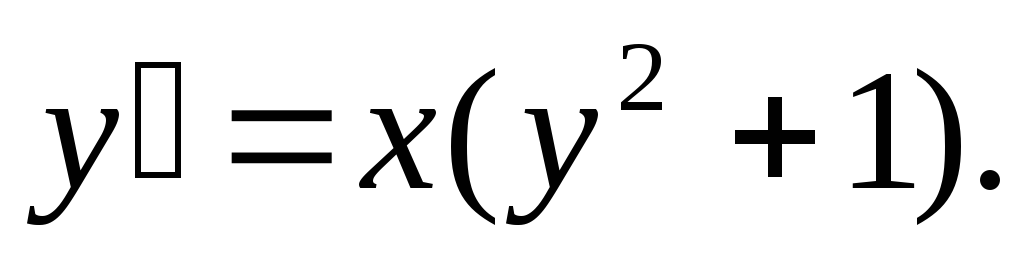
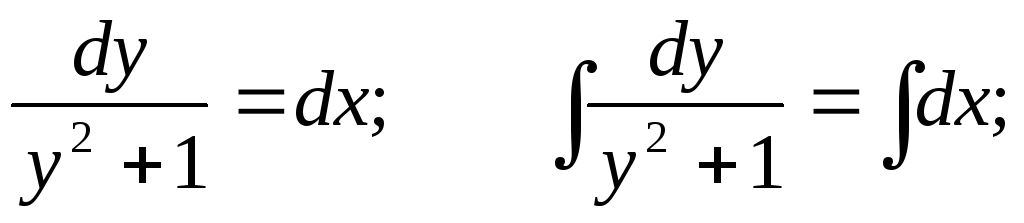
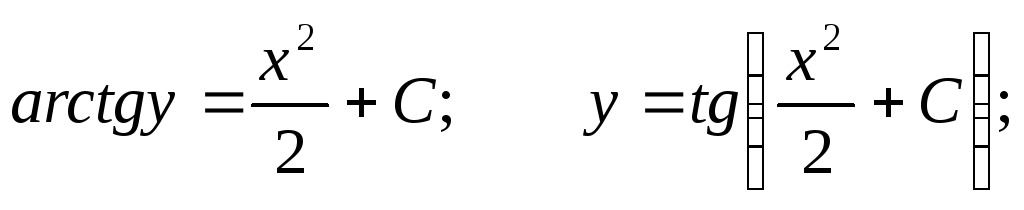
Пример. Решить уравнение 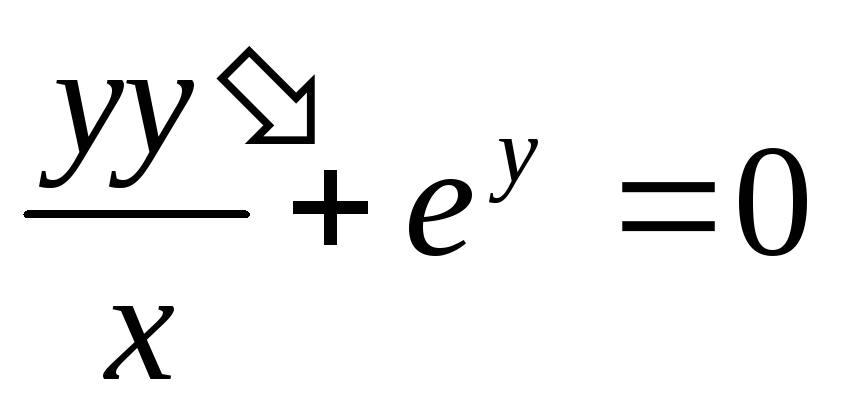 при
условии у(1) = 0.
при
условии у(1) = 0.
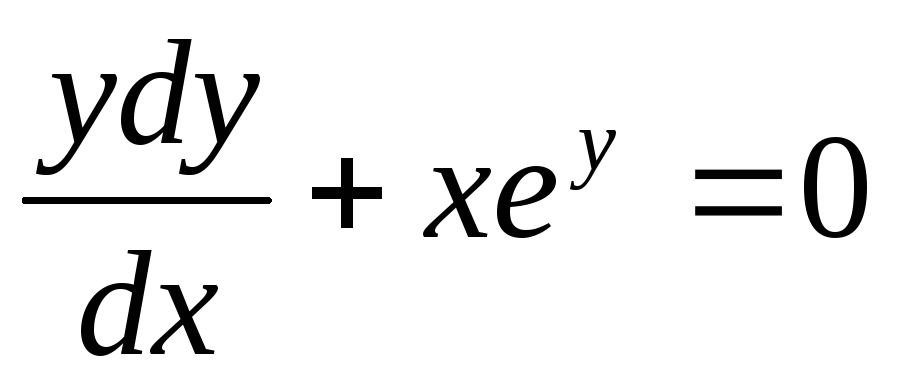

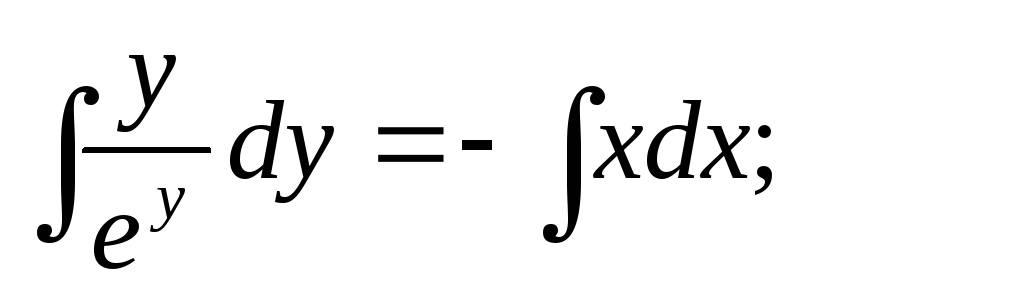
Интеграл, стоящий в левой части будем брать по частям (см. Интегрирование по частям. ).
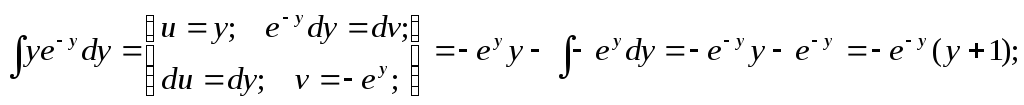
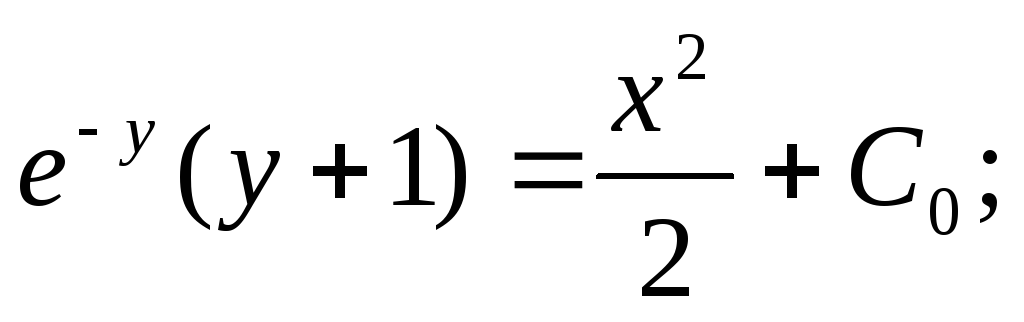
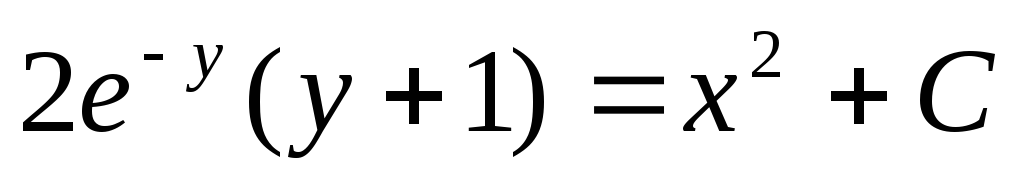
Если
у(1) = 0, то 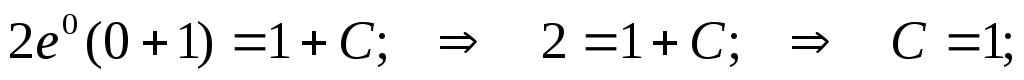
Итого,
частный интеграл: 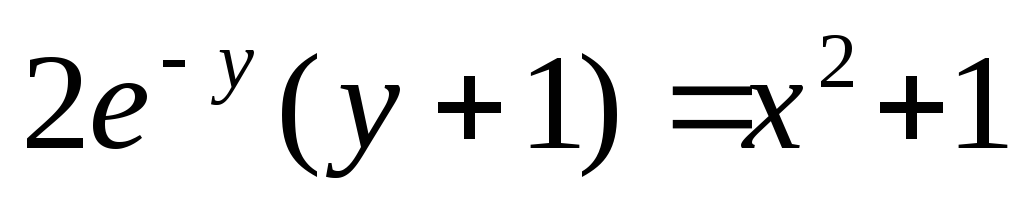 .
.
Пример. Решить уравнение 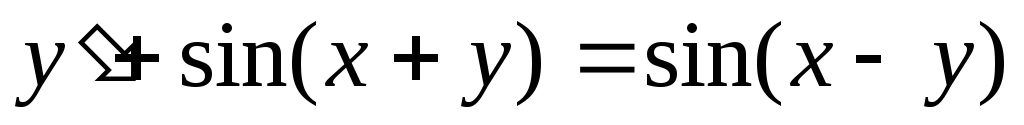 .
.
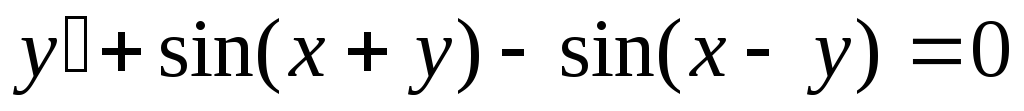
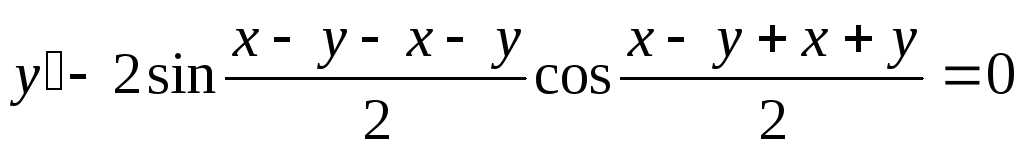

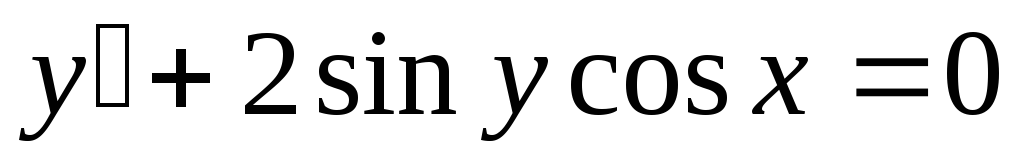
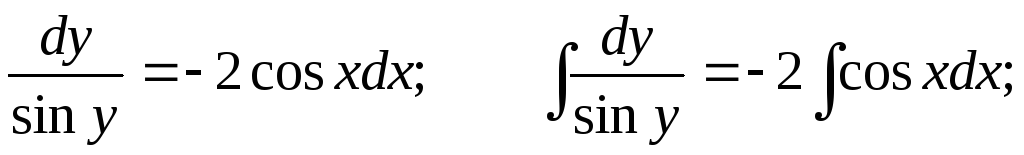
Для нахождения интеграла, стоящего в левой части уравнения см. Таблица основных интегралов. п.16. Получаем общий интеграл:
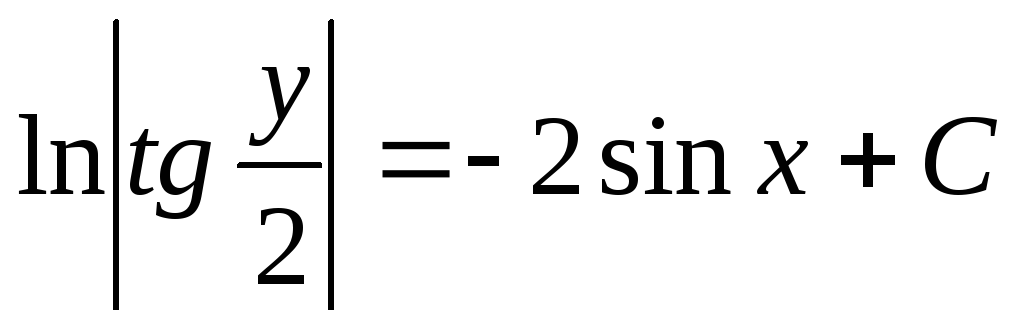
Пример. Решить уравнение 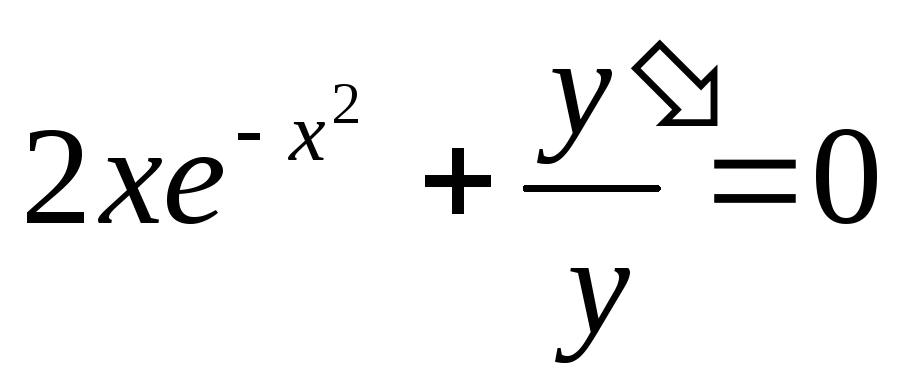
Преобразуем заданное уравнение:
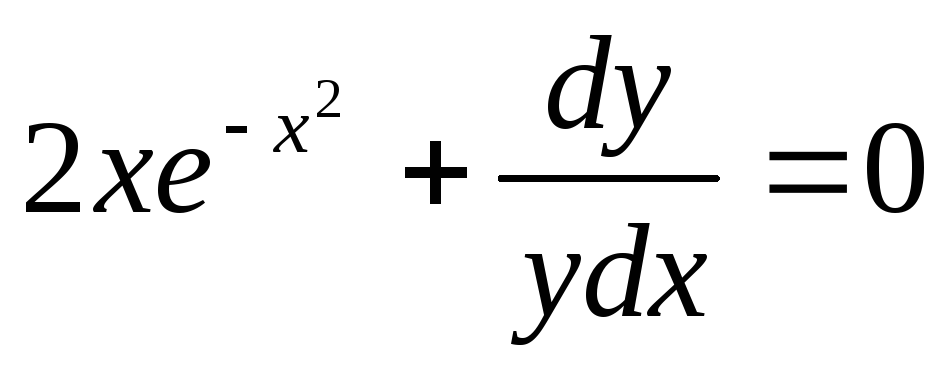
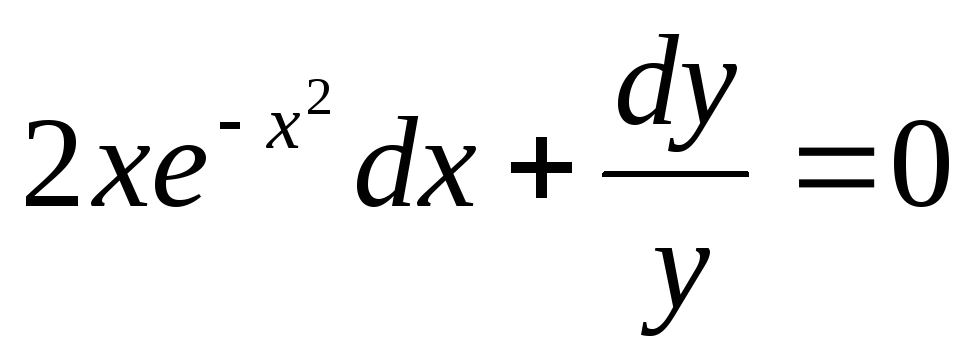
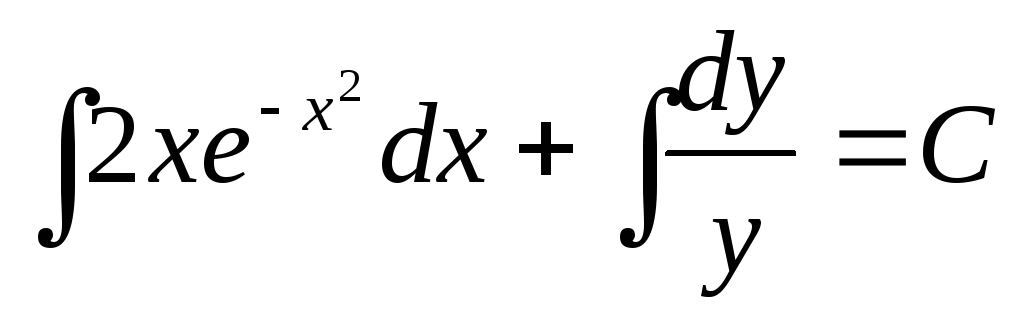
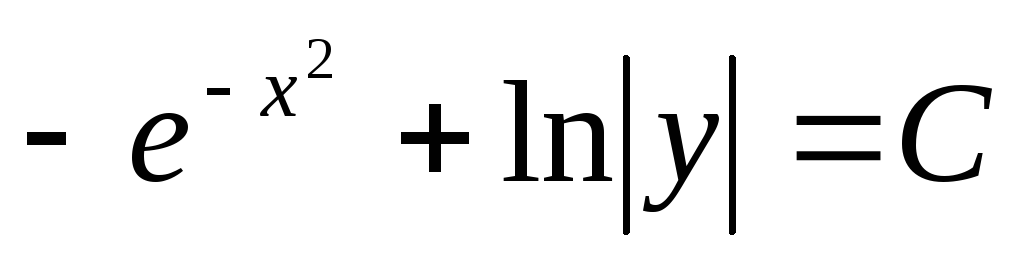
 Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.
Получили
общий интеграл данного дифференциального
уравнения. Если из этого соотношения
выразить искомую функцию у, то получим
общее решение.
Пример. Решить уравнение  .
.
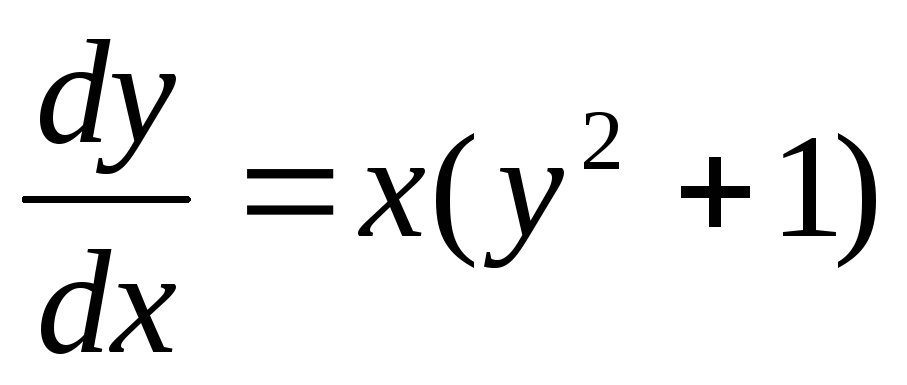
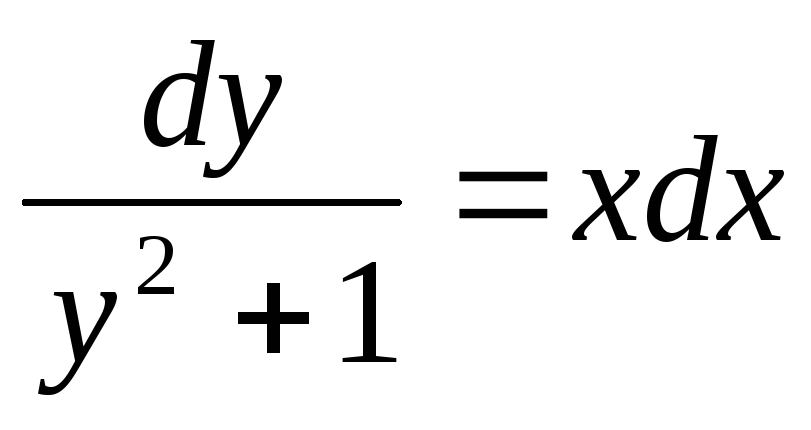
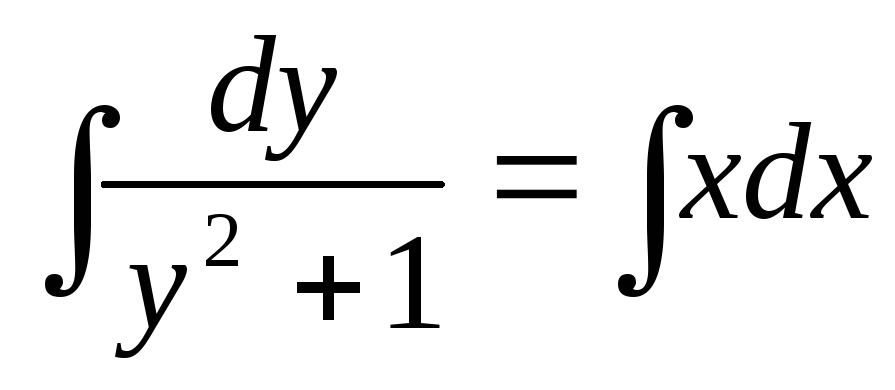 ;
; 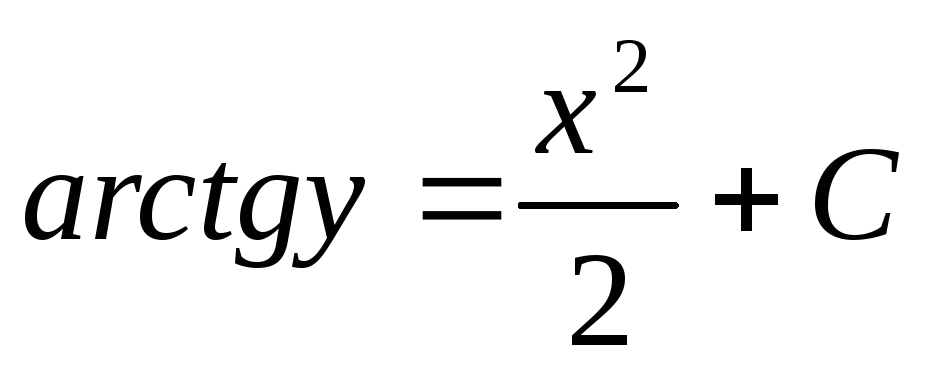 ;
;
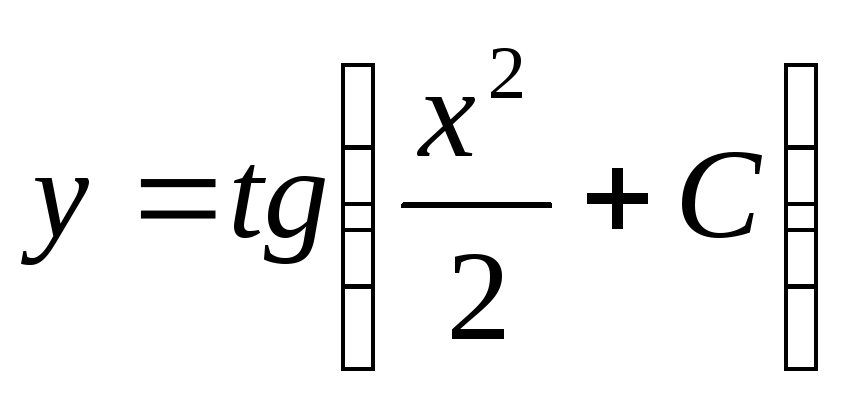
Допустим, заданы некоторые начальные условия х0 и у0. Тогда:

Получаем
частное решение 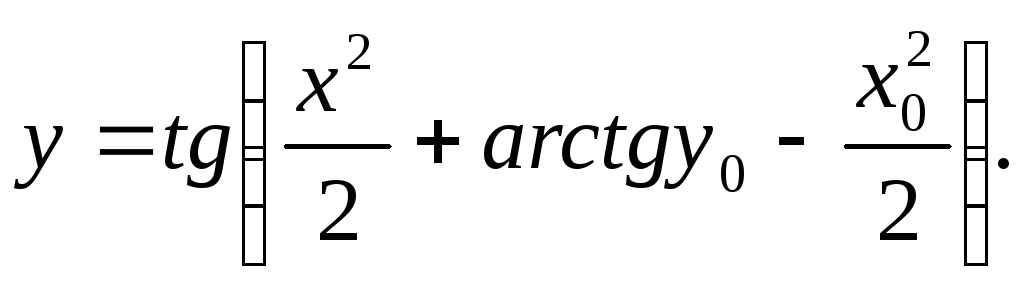
Однородные уравнения.
Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:
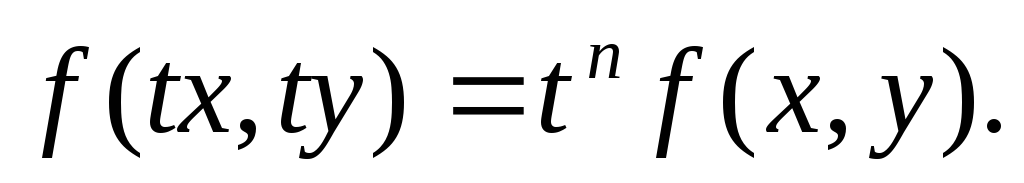
Пример. Является ли однородной функция 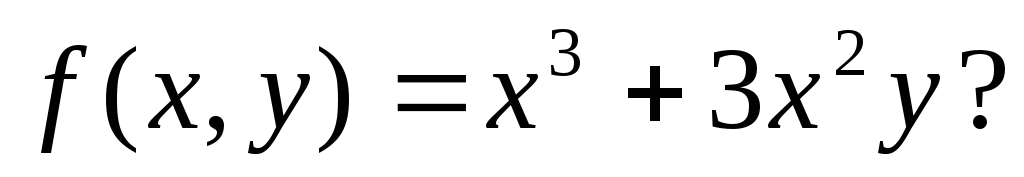
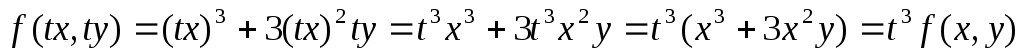
Таким образом, функция f(x, y) является однородной 3- го порядка.
Определение. Дифференциальное уравнение вида 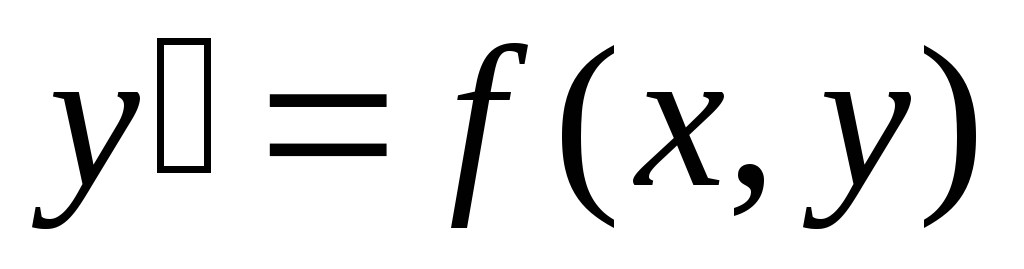 называетсяоднородным,
если его правая часть f(x,
y)
есть однородная функция нулевого
измерения относительно своих аргументов.
называетсяоднородным,
если его правая часть f(x,
y)
есть однородная функция нулевого
измерения относительно своих аргументов.
Любое
уравнение вида  является однородным, если функцииP(x, y) и Q(x, y) – однородные функции одинакового
измерения.
является однородным, если функцииP(x, y) и Q(x, y) – однородные функции одинакового
измерения.
Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.
Рассмотрим
однородное уравнение 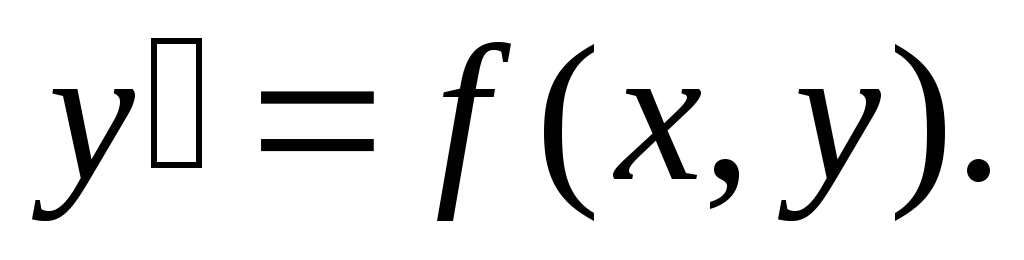
Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:
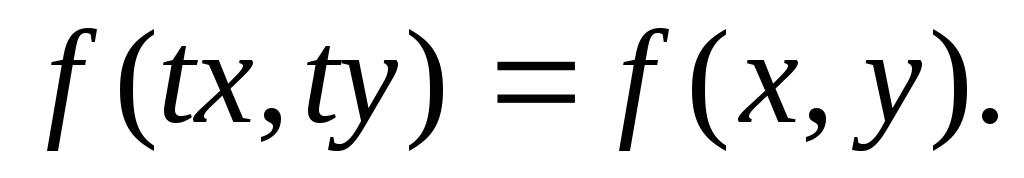
Т.к.
параметр t
вообще говоря произвольный, предположим,
что 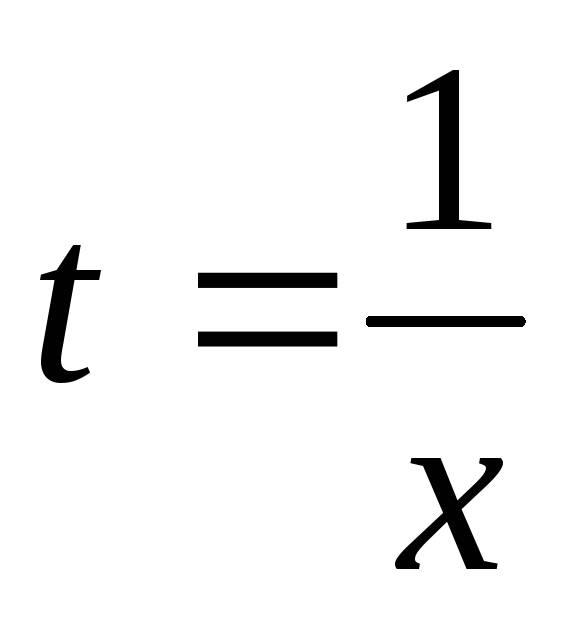 .
Получаем:
.
Получаем:
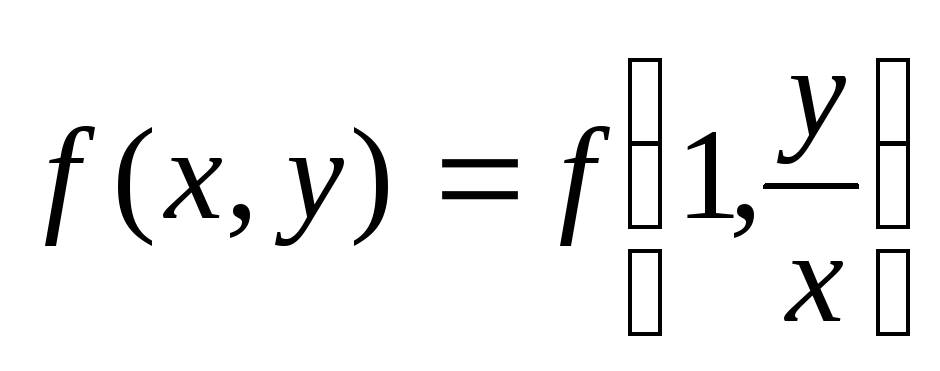
Правая
часть полученного равенства зависит
фактически только от одного аргумента 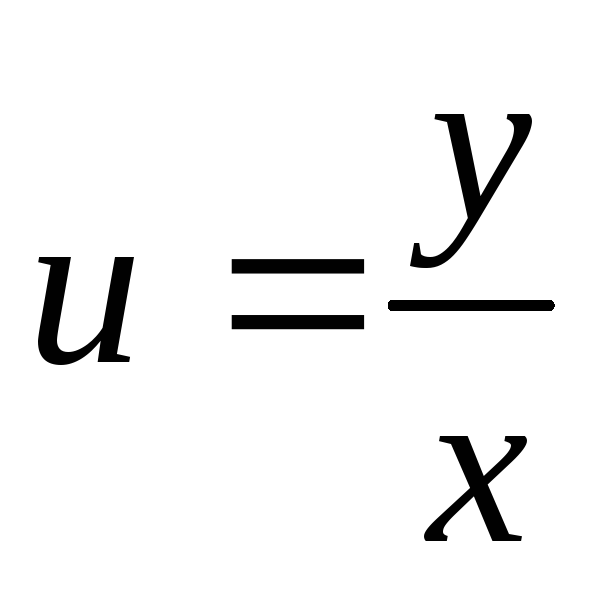 ,
т.е.
,
т.е.
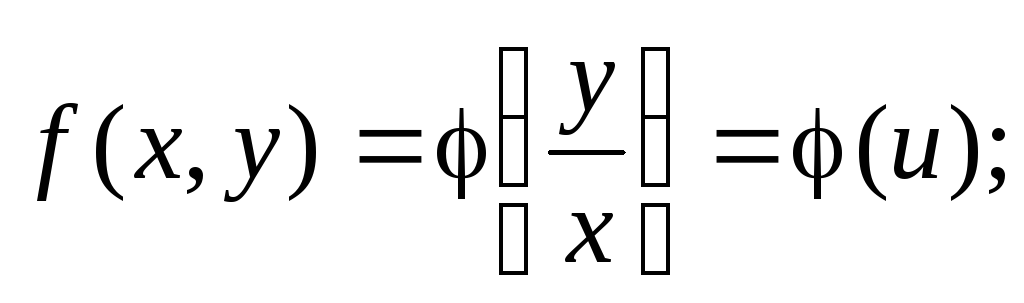
Исходное дифференциальное уравнение таким образом можно записать в виде:
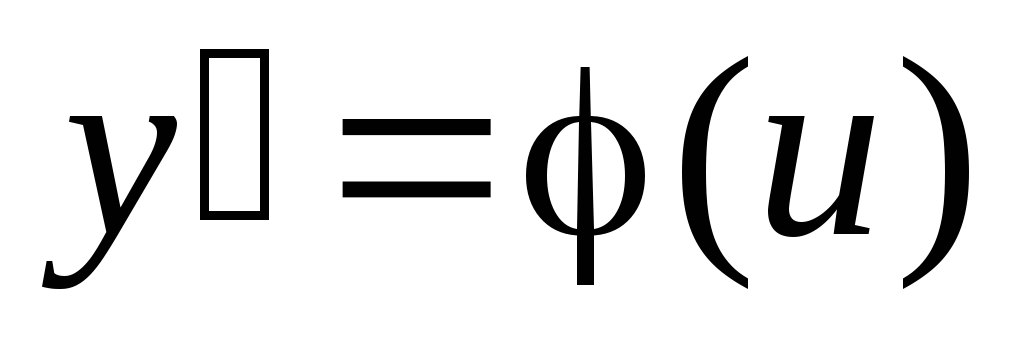
Далее
заменяем y
= ux, 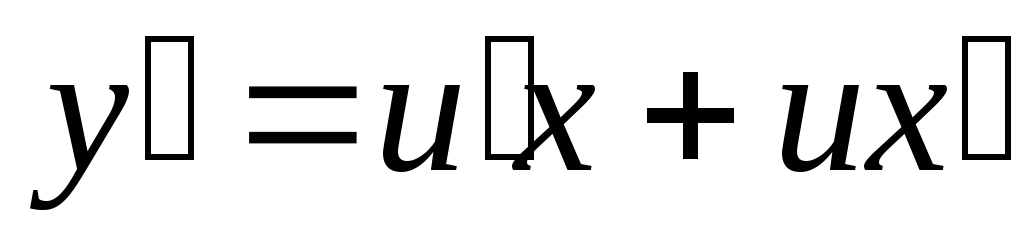 .
.

таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.
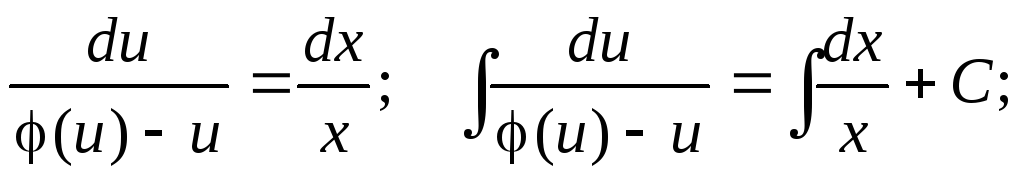
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.
Пример. Решить уравнение 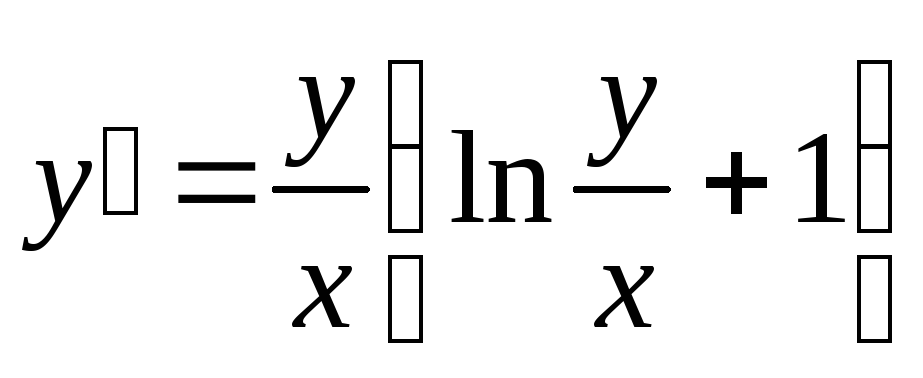 .
.
Введем вспомогательную функцию u.
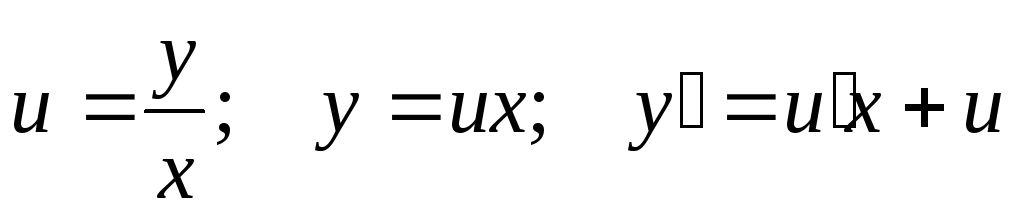 .
.
Отметим,
что введенная нами функция u всегда положительна, т.к. в противном
случае теряет смысл исходное
дифференциальное уравнение, содержащее 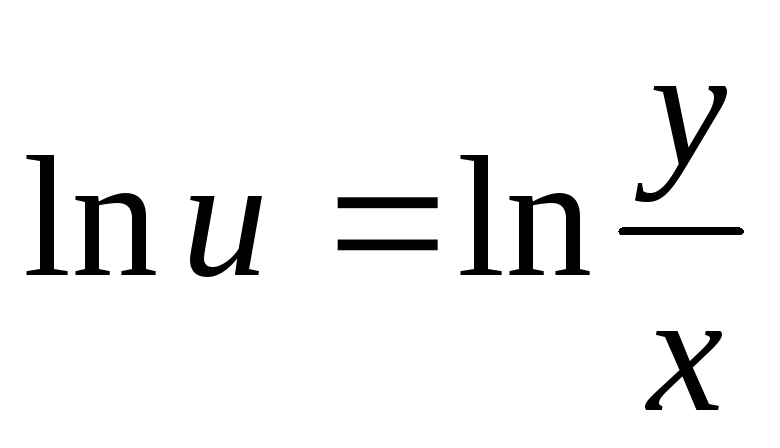 .
.
Подставляем в исходное уравнение:
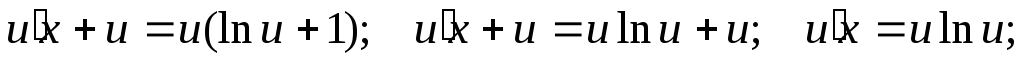
Разделяем
переменные: 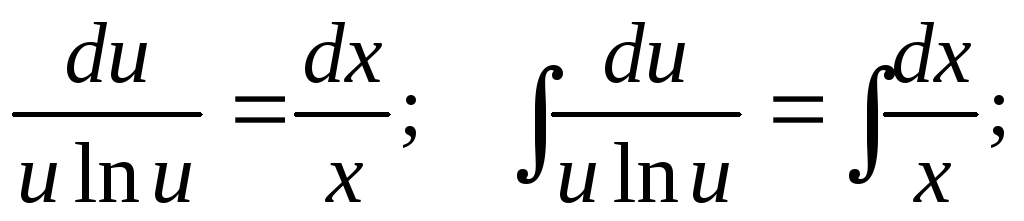
Интегрируя,
получаем: 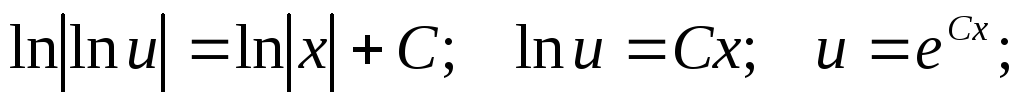
Переходя от вспомогательной функции обратно к функции у, получаем общее решение:
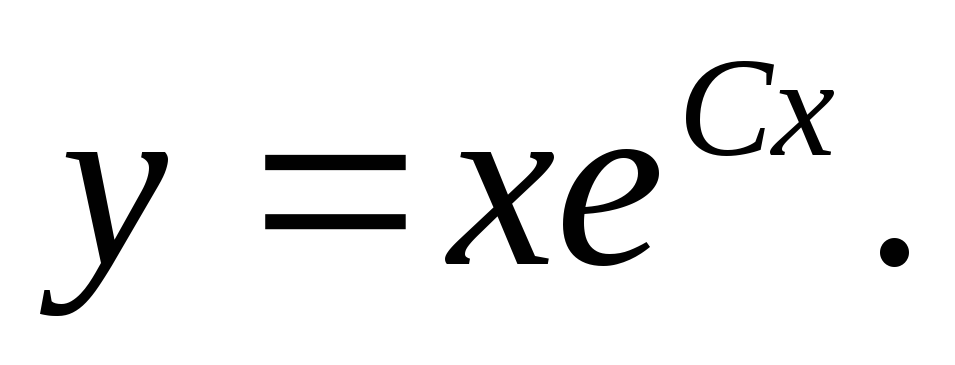
Уравнения, приводящиеся к однородным.
Кроме уравнений, описанных выше, существует класс уравнений, которые с помощью определенных подстановок могут приведены к однородным.
Это
уравнения вида 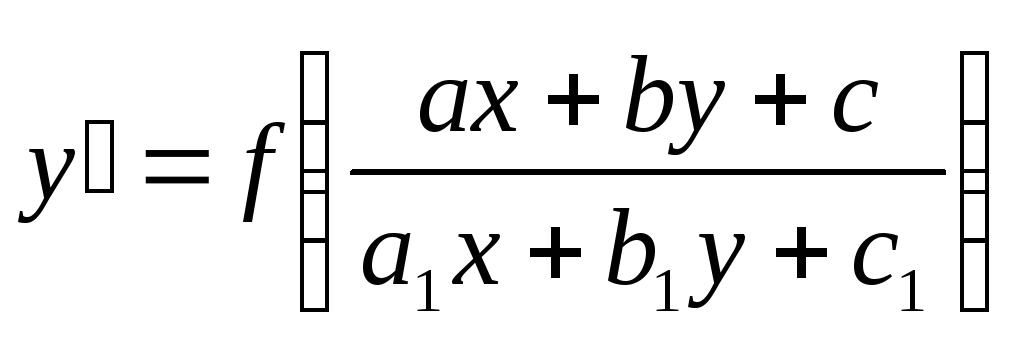 .
.
Если
определитель  то переменные могут быть разделены
подстановкой
то переменные могут быть разделены
подстановкой

где
и
— решения системы уравнений 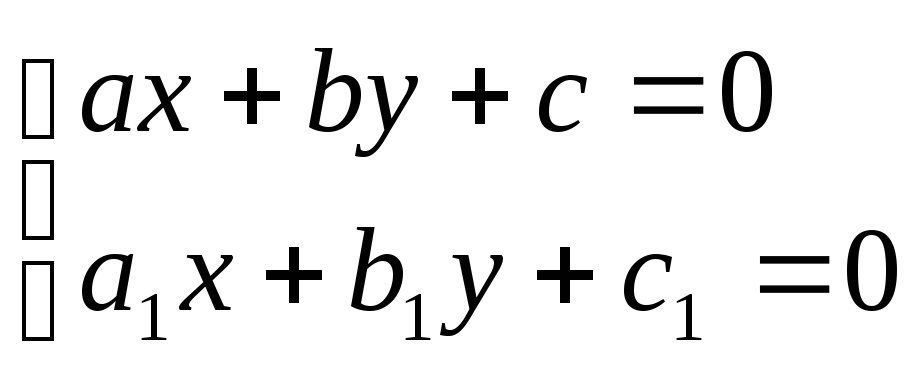
Пример. Решить уравнение 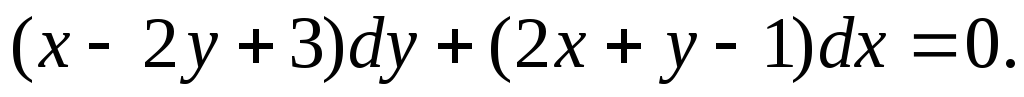
Получаем 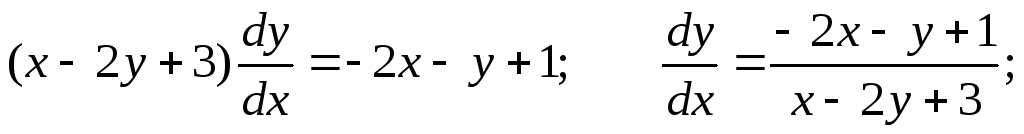
Находим
значение определителя 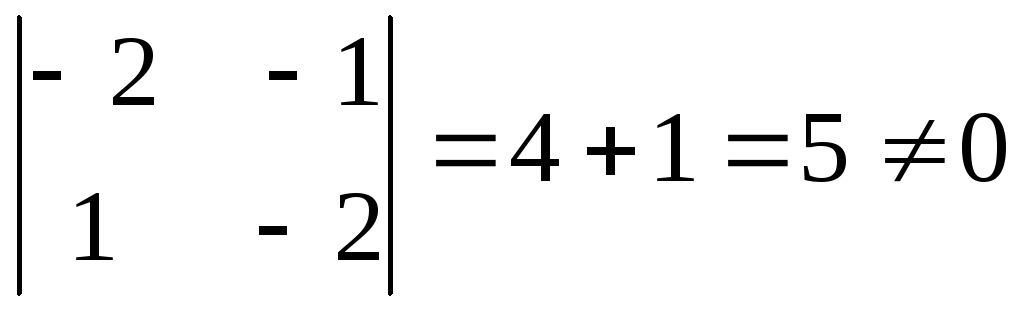 .
.
Решаем
систему уравнений 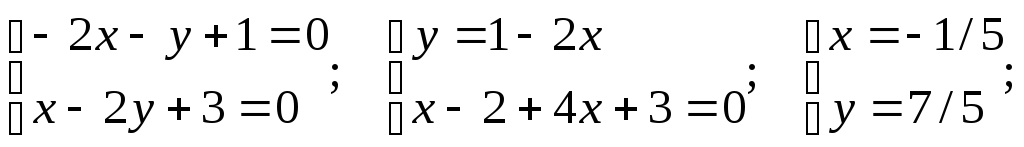
Применяем
подстановку 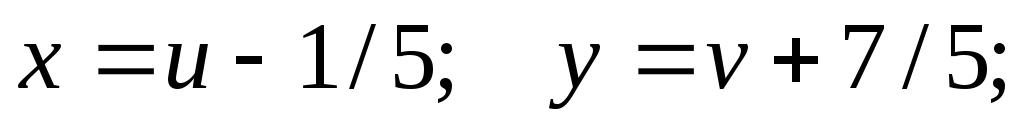 в исходное уравнение:
в исходное уравнение:
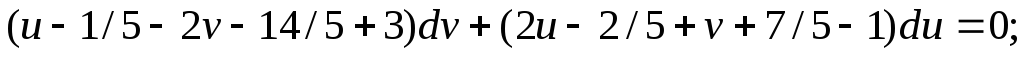
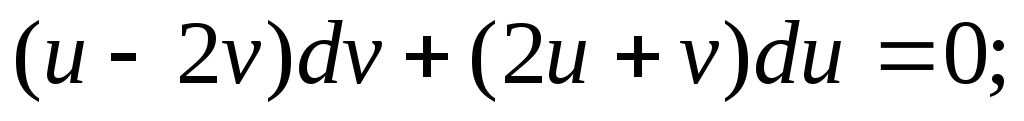
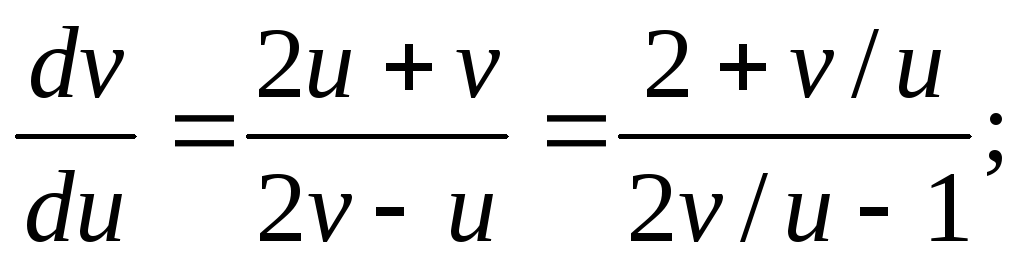
Заменяем
переменную 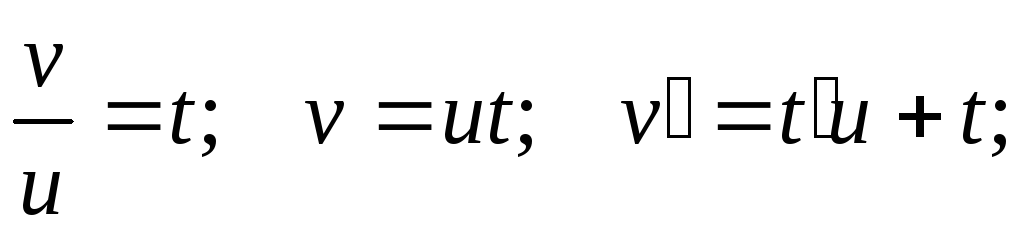 при подстановке в выражение, записанное
выше, имеем:
при подстановке в выражение, записанное
выше, имеем:
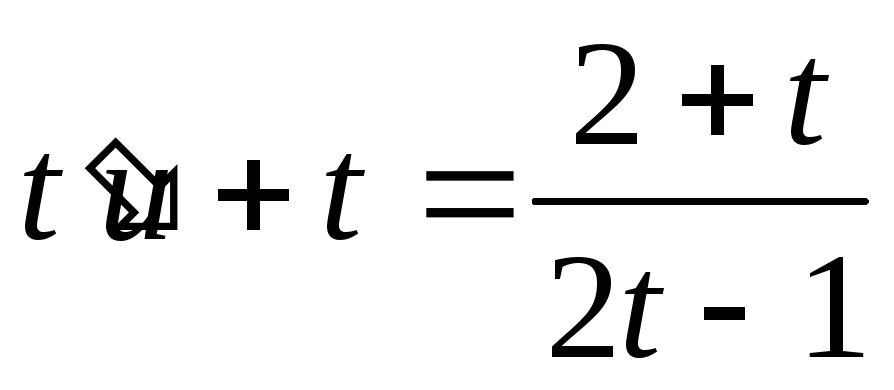
Решение дифференциальных уравнений
Математические модели происходящих процессов чаще всего описываются дифференциальными уравнениями. Поэтому остро стоит проблема нахождения их решения. Будем считать, что искомые функции рассматриваемых дифференциальных уравнений зависят от одной переменной.
Методы решения дифференциальных уравнений
1. К простейшим дифференциальным уравнениям первого порядка относятся уравнения вида
Решение таких уравнений находится с помощью операции интегрирования:
2. Дифференциальные уравнения вида
сводятся к дифференциальным уравнениям делением обеих частей равенства на . В результате получаем дифференциальное уравнение
Тогда, согласно выше написанному, его решение
3. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида или .
Например.
Дифференциальное уравнение или называется дифференциальным уравнением с разделенными переменными.
Например.
Общее решение такого уравнения ищется с помощью интегрирования обеих частей равенства :
Дифференциальные уравнения с разделяющимися переменными сводятся к дифференциальным уравнениям с разделенными переменными делением на произведение :
Подробнее о дифференциальных уравнениях с разделяющимися переменными читайте в отдельной статье.
4. Дифференциальные уравнения вида
сводятся к дифференциальным уравнениям с разделяющимися переменными с помощью замены
5. Однородным дифференциальным уравнением n-го порядка называется уравнение , удовлетворяющее условию
Однородные дифференциальные уравнения можно свисти к уравнению вида или , которое с помощью замены
(или ) сводится к дифференциальному уравнению с разделяющимися переменными.
Подробнее об однородных дифференциальных уравнениях читайте в отдельной статье.
6. Дифференциальные уравнения , где коэффициенты – некоторые действительные числа.
Если , то данное уравнение является однородным и методика получения его решения описана выше.
Рассмотрим случай, когда хотя бы одно из чисел или отлично от нуля. Выполним заменой (введем новые переменные)
Здесь – некоторые числа. При этом
Подставляя эти выражения в исходное дифференциальное уравнение, будем иметь:
или
Величины будем выбирать так, чтобы свободные коэффициенты в числителе и знаменателе последнего дифференциального уравнения равнялись нулю. То есть h и k найдем из системы
С учетом этого уравнение сводится к дифференциальному уравнению
которое является однородным.