Дискриминант. Решение, примеры

Важно! В корнях четной кратности функция знак не меняет.

Обратите внимание! Любое нелинейное неравенство школьного курса алгебры нужно решать с помощью метода интервалов.

Предлагаю вам подробный алгоритм решения неравенств методом интервалов , следуя которому вы сможете избежать ошибок прирешении нелинейных неравенств .

Решение квадратных уравнений с отрицательными дискриминантами

Как мы знаем,

i 2 = — 1.

Вместе с тем

(- i ) 2 = (- 1 i ) 2 = (- 1) 2 i 2 = -1.

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда

(а + bi

) 2 = — 1,

а 2 + 2аbi — b 2 = — 1

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

{	а 2 — b 2 = — 1 ab = 0 (1)

Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = — 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: —b 2 = — 1,

b = ± 1.

Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i и —i , Условно это записывается в виде:

√-1 = ± i .

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а . Такими числами являются √ai и -√ai . Условно это записывается так:

√— а = ± √ai .

Под √a здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому

√-4 = + 2i , √-9= ± 3i

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение

x 2 + 2х + 5 = 0; тогда

х 1,2 = — 1 ± √1 -5 = — 1 ± √-4 = — 1 ± 2i .

Итак, данное уравнение имеет два корня: х 1 = — 1 +2i , х 2 = — 1 — 2i . Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

Понятие комплексного числа

Комплексным числом называется выражение вида a + ib , где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:

1. Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда
   
   a = b и c = d .
2. Суммой двух комплексных чисел a + ib и c + id называется комплексное число
   a + c + i (b + d).
3. Произведением двух комплексных чисел a + ib и c + id называется комплексное число
   ac – bd + i (ad + bc).

Комплексные числа часто обозначают одной буквой, например, z = a + ib . Действительное число a называется действительной частью комплексного числа z , действительная часть обозначается a = Re z . Действительное число b называется мнимой частью комплексного числа z , мнимая часть обозначается b = Im z . Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.

Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,

Следовательно, комплексные числа вида a + i · 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что , а именно

В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi , например, 0 + i 3 = 3 i . Чисто мнимое число i1 = 1 i = i обладает удивительным свойством:
Таким образом,

№ 4 .1. В математике числовая функция — это функция, области определения и значений которой являются подмножествами числовых множеств — как правило, множествавещественных чисел или множества комплексных чисел .

График функции

Фрагмент графика функции

Способы задания функции

[править]Аналитический способ

Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента.

[править]Табличный способ

Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:

[править]Графический способ

Осциллограмма задаёт значение некоторой функции графически.

Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.

[править]Рекурсивный способ

Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.

• факториал;
• числа Фибоначчи;
• функция Аккермана.

[править]Словесный способ

Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.

• функция, возвращающая цифру в записи числа пи по её номеру;
• функция, возвращающая число атомов во вселенной в определённый момент времени;
• функция, принимающая в качестве аргумента человека, и возвращающая число людей, которое родится на свет после его рождени

Среди всего курса школьной программы алгебры одной из самых объемных тем является тема о квадратных уравнениях. При этом под квадратным уравнением понимается уравнение вида ax 2 + bx + c = 0, где a ≠ 0 (читается: а умножить на икс в квадрате плюс бэ икс плюс цэ равно нулю, где а неравно нулю). При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).

Формула (уравнение) дискриминанта квадратного уравнения

Общепринятая формула дискриминанта квадратного уравнения выглядит следующим образом: D = b 2 – 4ac. Вычисляя дискриминант по указанной формуле, можно не только определить наличие и количество корней у квадратного уравнения, но и выбрать способ нахождения этих корней, которых существует несколько в зависимости от типа квадратного уравнения.

Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю

Дискриминант, как следует из формулы, обозначается латинской буквой D. В случае, когда дискриминант равен нулю, следует сделать вывод, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, имеет только один корень, который вычисляется по упрощенной формуле. Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.

Решение квадратного уравнения через дискриминант

Если при вычислении дискриминанта по вышеприведенной формуле получается положительное значение (D больше нуля), то квадратное уравнение имеет два корня, которые вычисляются по следующим формулам: x 1 = (–b + vD)/2a, x 2 = (–b – vD)/2a. Чаще всего, дискриминант отдельно не высчитывается, а в значение D, из которого извлекается корень, просто подставляется подкоренное выражение в виде формулы дискриминанта. Если переменная b имеет четное значение, то для вычисления корней квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно также использовать следующие формулы: x 1 = (–k + v(k2 – ac))/a, x 2 = (–k + v(k2 – ac))/a, где k = b/2.

В некоторых случаях для практического решения квадратных уравнений можно использовать Теорему Виета, которая гласит, что для суммы корней квадратного уравнения вида x 2 + px + q = 0 будет справедливо значение x 1 + x 2 = –p, а для произведения корней указанного уравнения – выражение x 1 x x 2 = q.

Может ли дискриминант быть меньше нуля

При вычислении значения дискриминанта можно столкнуться с ситуацией, которая не попадает ни под один из описанных случаев – когда дискриминант имеет отрицательное значение (то есть меньше нуля). В этом случае принято считать, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, действительных корней не имеет, следовательно, его решение будет ограничиваться вычислением дискриминанта, а приводимые выше формулы корней квадратного уравнения в данном случае применяться не будут.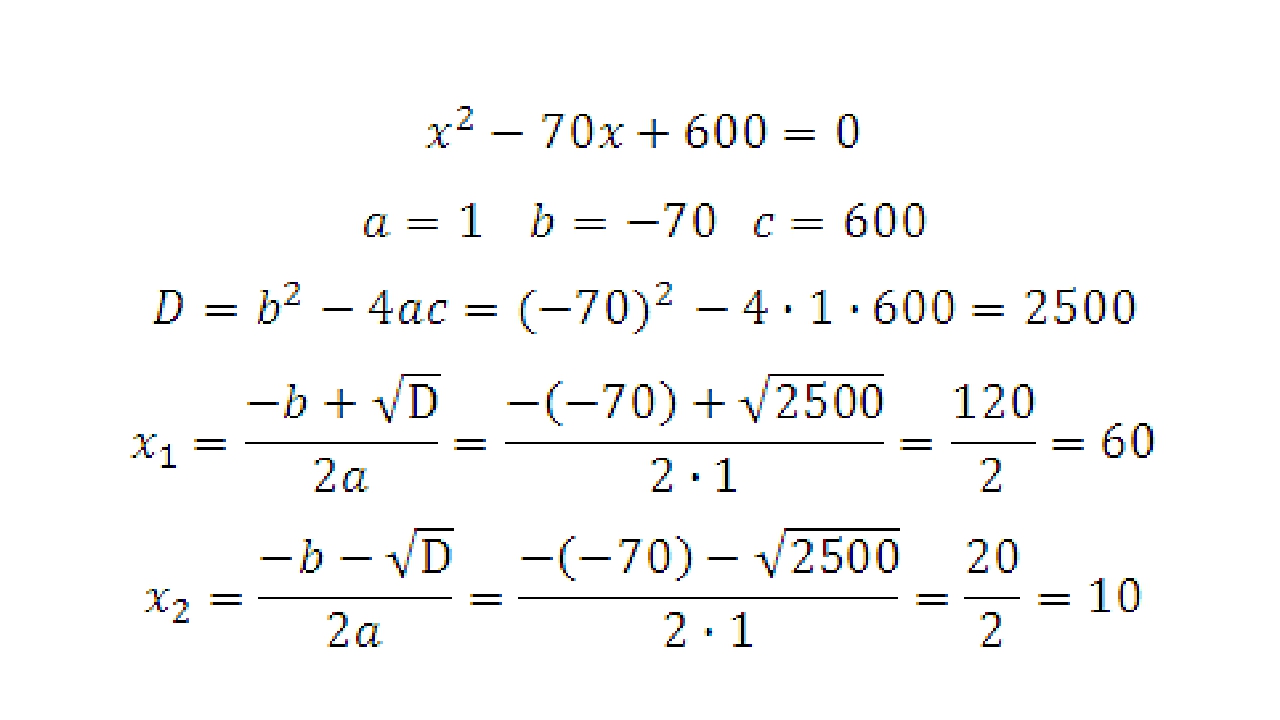 При этом в ответе к квадратному уравнению записывается, что «уравнение действительных корней не имеет».

Поясняющее видео:

КОМПЛЕКСНЫЕ ЧИСЛА XI

§ 253. Извлечение корней квадратных из отрицательных чисел.
Решение квадратных уравнений с отрицательными дискриминантами

Как мы знаем,

i 2 = — 1.

Вместе с тем

(- i ) 2 = (- 1 i ) 2 = (- 1) 2 i 2 = -1.

Таким образом, существуют по крайней мере два значения корня квадратного из — 1, а именно i и — i . Но, может быть, есть еще какие-нибудь комплексные числа, квадраты которых равны — 1?

Чтобы выяснить этот вопрос, предположим, что квадрат комплексного числа а + bi равен — 1. Тогда

(а + bi ) 2 = — 1,

а 2 + 2аbi — b 2 = — 1

Два комплексных числа равны тогда и только тогда, когда равны их действительные части и коэффициенты при мнимых частях. Поэтому

{	а 2 — b 2 = — 1 ab = 0 (1)

Согласно второму уравнению системы (1) хотя бы одно из чисел а и b должно равняться нулю. Если b = 0, то из первого уравнения получается а 2 = — 1. Число а действительное, и поэтому а 2 > 0. Неотрицательное число а 2 не может равняться отрицательному числу — 1. Поэтому равенство b = 0 в данном случае невозможно. Остается признать, что а = 0, но тогда из первого уравнения системы получаем: — b 2 = — 1, b = ± 1.

Следовательно, комплексными числами, квадраты которых равны -1, являются только числа i и —i , Условно это записывается в виде:

√-1 = ± i .

Аналогичными рассуждениями учащиеся могут убедиться в том, что существует ровно два числа, квадраты которых равны отрицательному числу —а . Такими числами являются √a i и -√a i . Условно это записывается так:

√— а = ± √a i .

Под √a здесь подразумевается арифметический, то есть положительный, корень. Например, √4 = 2, √9 =.3; поэтому

√-4 = + 2i , √-9 = ± 3i

Если раньше при рассмотрении квадратных уравнений с отрицательными дискриминантами мы говорили, что такие уравнения не имеют корней, то теперь так говорить уже нельзя. Квадратные уравнения с отрицательными дискриминантами имеют комплексные корни. Эти корни получаются по известным нам формулам. Пусть, например, дано уравнение x 2 + 2х + 5 = 0; тогда

х 1,2 = — 1 ± √1 -5 = — 1 ± √-4 = — 1 ± 2i .

Итак, данное уравнение имеет два корня: х 1 = — 1 +2i , х 2 = — 1 — 2i . Эти корни являются взаимно сопряженными. Интересно отметить, что сумма их равна — 2, а произведение 5, так что выполняется теорема Виета.

Упражнения

2022. (У с т н о.) Решить уравнения:

а) x 2 = — 16; б) x 2 = — 2; в) 3x 2 = — 5.

2023. Найти все комплексные числа, квадраты которых равны:

а) i ; б) 1 / 2 — √ 3 / 2 i ;

2024. Решить квадратные уравнения:

а) x 2 — 2x + 2 = 0; б) 4x 2 + 4x + 5 = 0; в) x 2 — 14x + 74 = 0.

Решить системы уравнений (№ 2025, 2026):

2027. Доказать, что корни квадратного уравнения с действительными коэффициентами и отрицательным дискриминантом являются взаимно сопряженными.

2028. Доказать, что теорема Виета верна для любых квадратных уравнений, а не только для уравнений с неотрицательным дискриминантом.

2029. Составить квадратное уравнение с действительными коэффициентами, корнями которого являются:

a) х 1 = 5 — i , х 2 = 5 + i ; б) х 1 = 3i , х 2 = — 3i .

2030. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен (3 — i ) (2i — 4).

2031. Составить квадратное уравнение с действительными коэффициентами, один из корней которого равен 32 — i
1- 3i .

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2 – 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2 + х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет .

Решить уравнение 2х 2 + 5х – 7 = 0 .

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1 .

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2 + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение. 2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
D Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра. .

Общая формула для нахождения корней квадратного уравнения :

Корни уравнения находим по формуле
Если коэффициент при переменной в квадрате парный то целесообразно исчислять не дискриминант, а четвертую его часть
В таких случаях корни уравнения находят по формуле

Вторая способ нахождения корней — это Теорема Виета.

Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
Суть формул Виета заключается в том, что сумма корней уравнения равна коэффициенту при переменной, взятому с противоположным знаком. Произведение корней уравнения равно свободном члену. Формулами теорема Виета имеет запись.
Вывод формулы Виета достаточно прост. Распишем квадратное уравнение через простые множители
Как видите все гениальное одновременно является простым. Эффективно использовать формулу Виета когда разница корней по модулю или разница модулей корней равна 1, 2. Например, следующие уравнения по теореме Виета имеют корни

До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».

Давайте попробуем разобраться,

что описывает дискриминант?

В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
Так вот физический смысл квадратного уравнения — это нули параболы, то есть точки пересечения графика функции с осью абсцисс Ox
Свойства парабол которые описаны ниже попрошу Вас запомнить. Придет время сдавать экзамены, тесты, или вступительные экзамены и Вы будете благодарны за справочный материал. Знак при переменной в квадрате соответствует тому, будут ли ветки параболы на графике идти вверх (a>0) ,

или парабола ветвями вниз (a

Вершина параболы лежит посередине между корнями

Физический смысл дискриминанта:

Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox .
Если дискриминант равен нулю (D=0) то парабола в вершине касается оси абсцисс.
И последний случай, когда дискриминант меньше нуля (D

Неполные квадратные уравнения

Что значит если дискриминант отрицательный. Решение квадратных уравнений, формула корней, примеры

В современном обществе умение производить действия с уравнениями, содержащими переменную, возведённую в квадрат, может пригодиться во многих областях деятельности и широко применяется на практике в научных и технических разработках. Свидетельством тому может служить конструирование морских и речных судов, самолётов и ракет. При помощи подобных расчётов определяют траектории перемещения самых разных тел, в том числе и космических объектов. Примеры с решением квадратных уравнений находят применение не только в экономическом прогнозировании, при проектировании и строительстве зданий, но и в самых обычных житейских обстоятельствах. Они могут понадобиться в туристических походах, на спортивных состязаниях, в магазинах при совершении покупок и в других весьма распространённых ситуациях.

Разобьём выражение на составляющие множители

Степень уравнения определяется максимальным значением степени у переменной, которую содержит данное выражение. В случае, если она равна 2, то подобное уравнение как раз и называется квадратным.

Если изъясняться языком формул, то указанные выражения, как бы они ни выглядели, всегда можно привести к виду, когда левая часть выражения состоит из трёх слагаемых. Среди них: ax 2 (то есть переменная, возведённая в квадрат со своим коэффициентом), bx (неизвестное без квадрата со своим коэффициентом) и c (свободная составляющая, то есть обычное число). Всё это в правой части приравнивается 0. В случае, когда у подобного многочлена отсутствует одно из его составляющих слагаемых, за исключением ax 2 , оно называется неполным квадратным уравнением. Примеры с решением таких задач, значение переменных в которых найти несложно, следует рассмотреть в первую очередь.

Если выражение на вид выглядит таким образом, что слагаемых у выражения в правой части два, точнее ax 2 и bx, легче всего отыскать х вынесением переменной за скобки. Теперь наше уравнение будет выглядеть так: x(ax+b). Далее становится очевидно, что или х=0, или задача сводится к нахождению переменной из следующего выражения: ax+b=0. Указанное продиктовано одним из свойств умножения. Правило гласит, что произведение двух множителей даёт в результате 0, только если один из них равен нулю.

Пример

x=0 или 8х — 3 = 0

В результате получаем два корня уравнения: 0 и 0,375.

Уравнения такого рода могут описывать перемещение тел под действием силы тяжести, начавших движение из определённой точки, принятой за начало координат. Здесь математическая запись принимает следующую форму: y = v 0 t + gt 2 /2. Подставив необходимые значения, приравняв правую часть 0 и найдя возможные неизвестные, можно узнать время, проходящее с момента подъёма тела до момента его падения, а также многие другие величины. Но об этом мы поговорим позднее.

Разложение выражения на множители

Описанное выше правило даёт возможность решать указанные задачи и в более сложных случаях. Рассмотрим примеры с решением квадратных уравнений такого типа.

X 2 — 33x + 200 = 0

Этот квадратный трёхчлен является полным. Для начала преобразуем выражение и разложим его на множители. Их получается два: (x-8) и (x-25) = 0. В результате имеем два корня 8 и 25.

Примеры с решением квадратных уравнений в 9 классе позволяют данным методом находить переменную в выражениях не только второго, но даже третьего и четвёртого порядков.

Например: 2x 3 + 2x 2 — 18x — 18 = 0. При разложении правой части на множители с переменной, их получается три, то есть (x+1),(x-3) и (x+3).

В результате становится очевидно, что данное уравнение имеет три корня: -3; -1; 3.

Извлечение квадратного корня

Другим случаем неполного уравнения второго порядка является выражение, на языке букв представленное таким образом, что правая часть строится из составляющих ax 2 и c. Здесь для получения значения переменной свободный член переносится в правую сторону, а после этого из обеих частей равенства извлекается квадратный корень. Следует обратить внимание, что и в данном случае корней уравнения обычно бывает два. Исключением могут служить лишь только равенства, вообще не содержащие слагаемое с, где переменная равна нулю, а также варианты выражений, когда правая часть оказывается отрицательной. В последнем случае решений вообще не существует, так как указанные выше действия невозможно производить с корнями. Примеры решений квадратных уравнений такого типа необходимо рассмотреть.

В данном случае корнями уравнения окажутся числа -4 и 4.

Вычисление пощади земельного участка

Потребность в подобного рода вычислениях появилась в глубокой древности, ведь развитие математики во многом в те далёкие времена было обусловлено необходимостью определять с наибольшей точностью площади и периметры земельных участков.

Примеры с решением квадратных уравнений, составленных на основе задач такого рода, следует рассмотреть и нам.

Итак, допустим имеется прямоугольный участок земли, длина которого на 16 метров больше, чем ширина. Следует найти длину, ширину и периметр участка, если известно, что его площадь равна 612 м 2 .

Приступая к делу, сначала составим необходимое уравнение. Обозначим за х ширину участка, тогда его длина окажется (х+16). Из написанного следует, что площадь определяется выражением х(х+16), что, согласно условию нашей задачи, составляет 612. Это значит, что х(х+16) = 612.

Решение полных квадратных уравнений, а данное выражение является именно таковым, не может производиться прежним способом. Почему? Хотя левая часть его по-прежнему содержит два множителя, произведение их совсем не равно 0, поэтому здесь применяются другие методы.

Дискриминант

Прежде всего произведём необходимые преобразования, тогда внешний вид данного выражения будет выглядеть таким образом: x 2 + 16x — 612 = 0.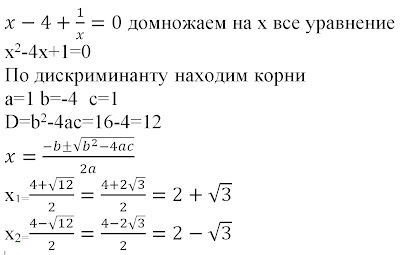 Это значит, мы получили выражение в форме, соответствующей указанному ранее стандарту, где a=1, b=16, c=-612.

Это может стать примером решения квадратных уравнений через дискриминант. Здесь необходимые расчёты производятся по схеме: D = b 2 — 4ac. Данная вспомогательная величина не просто даёт возможность найти искомые величины в уравнении второго порядка, она определяет количество возможных вариантов. В случае, если D>0, их два; при D=0 существует один корень. В случае, если D

О корнях и их формуле

В нашем случае дискриминант равен: 256 — 4(-612) = 2704. Это говорит о том, что ответ у нашей задачи существует. Если знать, к , решение квадратных уравнений нужно продолжать с применением ниже приведённой формулы. Она позволяет вычислить корни.

Это значит, что в представленном случае: x 1 =18, x 2 =-34. Второй вариант в данной дилемме не может являться решением, потому что размеры земельного участка не могут измеряться в отрицательных величинах, значит х (то есть ширина участка) равна 18 м. Отсюда вычисляем длину: 18+16=34, и периметр 2(34+18)=104(м 2).

Примеры и задачи

Продолжаем изучение квадратных уравнений. Примеры и подробное решение нескольких из них будут приведены далее.

1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1

Перенесём всё в левую часть равенства, сделаем преобразование, то есть получим вид уравнения, который принято именовать стандартным, и приравняем его нулю.

15x 2 + 20x + 5 — 12x 2 — 27x — 1 = 0

Сложив подобные, определим дискриминант: D = 49 — 48 = 1. Значит у нашего уравнения будет два корня. Вычислим их согласно приведённой выше формуле, а это значит, что первый из них буде равен 4/3, а второй 1.

2) Теперь раскроем загадки другого рода.

Выясним, есть ли вообще здесь корни x 2 — 4x + 5 = 1? Для получения исчерпывающего ответа приведём многочлен к соответствующему привычному виду и вычислим дискриминант. В указанном примере решение квадратного уравнения производить не обязательно, ведь суть задачи заключается совсем не в этом. В данном случае D = 16 — 20 = -4, а значит, корней действительно нет.

Теорема Виета

Квадратные уравнения удобно решать через указанные выше формулы и дискриминант, когда из значения последнего извлекается квадратный корень. Но это бывает не всегда. Однако способов для получения значений переменных в данном случае существует множество. Пример: решения квадратных уравнений по теореме Виета. Она названа в честь который жил в XVI веке во Франции и сделал блестящую карьеру благодаря своему математическому таланту и связям при дворе. Портрет его можно увидеть в статье.

Закономерность, которую заметил прославленный француз, заключалась в следующем. Он доказал, что корни уравнения в сумме численно равны -p=b/a, а их произведение соответствует q=c/a.

Теперь рассмотрим конкретные задачи.

3x 2 + 21x — 54 = 0

Для простоты преобразуем выражение:

x 2 + 7x — 18 = 0

Воспользуемся теоремой Виета, это даст нам следующее: сумма корней равна -7, а их произведение -18. Отсюда получим, что корнями уравнения являются числа -9 и 2. Сделав проверку, убедимся, что эти значения переменных действительно подходят в выражение.

График и уравнение параболы

Понятия квадратичная функция и квадратные уравнения тесно связаны. Примеры подобного уже были приведены ранее. Теперь рассмотрим некоторые математические загадки немного подробнее. Любое уравнение описываемого типа можно представить наглядно. Подобная зависимость, нарисованная в виде графика, называется параболой. Различные её виды представлены на рисунке ниже.

Любая парабола имеет вершину, то есть точку, из которой выходят её ветви. В случае если a>0, они уходят высоко в бесконечность, а когда a

Наглядные изображения функций помогают решать любые уравнения, в том числе и квадратные. Этот метод называется графическим. А значением переменной х является координата абсцисс в точках, где происходит пересечение линии графика с 0x. Координаты вершины можно узнать по только что приведённой формуле x 0 = -b/2a. И, подставив полученное значение в изначальное уравнение функции, можно узнать y 0 , то есть вторую координату вершины параболы, принадлежащую оси ординат.

Пересечение ветвей параболы с осью абсцисс

Примеров с решением квадратных уравнений очень много, но существуют и общие закономерности. Рассмотрим их. Понятно, что пересечение графика с осью 0x при a>0 возможно только если у 0 принимает отрицательные значения. А для a0. В противном случае D

По графику параболы можно определить и корни. Верно также обратное. То есть если получить наглядное изображение квадратичной функции нелегко, можно приравнять правую часть выражения к 0 и решить полученное уравнение. А зная точки пересечения с осью 0x, легче построить график.

Из истории

С помощью уравнений, содержащих переменную, возведённую в квадрат, в старину не только делали математические расчёты и определяли площади геометрических фигур. Подобные вычисления древним были нужны для грандиозных открытий в области физики и астрономии, а также для составления астрологических прогнозов.

Как предполагают современные деятели науки, одними из первых решением квадратных уравнений занялись жители Вавилона. Произошло это за четыре столетия до наступления нашей эры. Разумеется, их вычисления в корне отличались от ныне принятых и оказывались гораздо примитивней. К примеру, месопотамские математики понятия не имели о существовании отрицательных чисел. Незнакомы им были также другие тонкости из тех, которые знает любой школьник современности.

Возможно, ещё раньше учёных Вавилона решением квадратных уравнений занялся мудрец из Индии Баудхаяма. Произошло это примерно за восемь столетий до наступления эры Христа. Правда, уравнения второго порядка, способы решения которых он привёл, были самыми наипростейшими. Кроме него, подобными вопросами интересовались в старину и китайские математики. В Европе квадратные уравнения начали решать лишь в начале XIII столетия, но зато позднее их использовали в своих работах такие великие учёные, как Ньютон, Декарт и многие другие.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий . Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Квадратное уравнение это уравнение которое выглядит как ax 2 + dx + c = 0 . В нем значение а,в и с любые числа, при этом а не равно нулю.

Все квадратные уравнения разделяются на несколько видов, а именно:

Уравнения в которых только один корень.
-Уравнения с двумя разными корнями.
-Уравнения в которых корней нет совсем.

Это и различает линейные уравнения в которых корень всегда единый, от квадратных. Для того что бы понять какое количество корней в выражении и нужен Дискриминант квадратного уравнения .

Допустим наше уравнение ax 2 + dx + c =0. Значит дискриминант квадратного уравнения —

D = b 2 — 4 ac

И это нужно запомнить навсегда. С помощью этого уравнения мы и определяем количество корней в квадратном уравнении. И делаем мы это следующим образом:

Когда D меньше нуля, в уравнении нет корней.
— Когда D равно нулю, имеется только один корень.
— Когда D больше нуля, соответственно, в уравнении два корня.
Запомните что дискриминант показывает сколько корней в уравнении, не меняя знаков.

Рассмотрим для наглядности:

Нужно выяснить какое количество корней в данном квадратном уравнении.

1) х 2 — 8х + 12 = 0
2)5х 2 + 3х + 7 = 0
3) х 2 -6х + 9 = 0

Вписываем значения в первое уравнение, находим дискриминант.
а = 1, b = -8, c = 12
D = (-8) 2 — 4 * 1 * 12 = 64 — 48 = 16
Дискриминант со знаком плюс, значит в данном равенстве два корня.

Делаем тоже самое со вторым уравнением
a = 1, b = 3, c = 7
D = 3 2 — 4 * 5 * 7 = 9 — 140 = — 131
Значение минусовое, значит корней в данном равенстве нет.

Следующее уравнение разложим по аналогии.
а = 1, b = -6, с = 9
D = (-6) 2 — 4 * 1 * 9 = 36 — 36 = 0
как следствие имеем один корень в уравнении.

Важно что в каждом уравнении мы выписывали коэффициенты. Конечно это не много длительный процесс, но это помогло нам не запутаться и предотвратило появление ошибок. Если очень часто решать подобные уравнения, то вычисления сможете производить мысленно и заранее знать сколько у уравнения корней.

Рассмотрим еще один пример:

1) х 2 — 2х — 3 = 0
2) 15 — 2х — х 2 = 0
3) х 2 + 12х + 36 = 0

Раскладываем первое
а = 1, b = -2, с = -3
D =(-2) 2 — 4 * 1 * (-3) = 16, что больше нуля, значит два корня, выведем их
х 1 = 2+?16/2 * 1 = 3, х 2 = 2-?16/2 * 1 = -1.

Раскладываем второе
а = -1, b = -2, с = 15
D = (-2) 2 — 4 * 4 * (-1) * 15 = 64, что больше нуля и так же имеет два корня. Выведем их:
х 1 = 2+?64/2 * (-1) = -5, х 2 = 2-?64/2 *(-1) = 3.

Раскладываем третье
а = 1, b = 12, с = 36
D = 12 2 — 4 * 1 * 36 =0, что равно нулю и имеет один корень
х = -12 + ?0/2 * 1 = -6.
Решать данные уравнения не сложно.

Если нам дано неполное квадратное уравнение. Такое как

1х 2 + 9х = 0
2х 2 — 16 = 0

Данные уравнения отличаются от тех что были выше, так как оно не полное, в нем нет третьего значения. Но не смотря на это оно проще чем полное квадратное уравнение и в нем дискриминант искать не нужно.

Что делать когда срочно нужна дипломная работа или реферат, а времени на его написание нет? Всё это и многое другое можно заказать на сайте Deeplom.by (http://deeplom.by/) и получить высший балл.

Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:

Квадратное уравнение – это уравнение вида:

где коэффициенты a, b и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х 1 = 3 х 2 = 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1: Решить 2x 2 +8 x –192=0

а=2 b=8 c= –192

D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2: Решить x 2 –22 x+121 = 0

а=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3: Решить x 2 –8x+72 = 0

а=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

а x 2 + bx + c =0 выполняется равенство

a + b + с = 0, то

— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство

a + с = b , то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001 x 2 –4995 x – 6=0

Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит

Пример 2: 2501 x 2 +2507 x +6=0

Выполняется равенство a + с = b , значит

Закономерности коэффициентов.

1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = –6 х 2 = –1/6.

2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

х 1 = 15 х 2 = 1/15.

3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны

аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

х 1 = – 17 х 2 = 1/17.

4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.

Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.

х 1 = 10 х 2 = – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а ± b+c ≠ 0, то используется прием переброски, например:

2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим

х 1 = 5 х 2 = 0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:

У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х 1 = 5 х 2 = 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

примеры решения уравнений. Решение квадратных уравнений

Квадратные уравнения часто появляются во время решения различных задач физики и математики. В данной статье мы рассмотрим, как решать эти равенства универсальным способом «через дискриминант». Примеры использования полученных знаний также даются в статье.

О каких уравнениях пойдет речь?

На рисунке ниже изображена формула, в которой x — неизвестная переменная, а латинские символы a, b, c представляют собой некоторые известные числа.

Каждый из этих символов называется коэффициентом. Как можно заметить, число «a» стоит перед переменной x, возведенной в квадрат. Это максимальная степень представленного выражения, поэтому оно называется квадратным уравнением. Часто используют другое его название: уравнение второго порядка. Само значение a — это квадратный коэффициент (стоящий при переменной в квадрате), b — это линейный коэффициент (он находится рядом с переменной, возведенной в первую степень), наконец, число c — свободный член.

Отметим, что вид уравнения, который изображен на рисунке выше, является общим классическим квадратным выражением. Помимо него существуют другие уравнения второго порядка, в которых коэффициенты b, c могут быть нулевыми.

Когда ставят задачу решить рассматриваемое равенство, то это означает, что такие значения переменной x нужно найти, которые бы ему удовлетворяли. Здесь первым делом нужно запомнить следующую вещь: поскольку максимальная степень икса — это 2, то данный тип выражений не может иметь больше, чем 2 решения. Это означает, что если при решении уравнения были найдены 2 значения x, которые ему удовлетворяют, то можно быть уверенным, что не существует никакого 3-го числа, подставляя которое вместо x, равенство также бы являлось истиной. Решения уравнения в математике называют его корнями.

Способы решения уравнений второго порядка

Решения уравнений этого типа требует знания некоторой теории о них. В школьном курсе алгебры рассматривают 4 различных метода решения. Перечислим их:

• с помощью факторизации;
• используя формулу для полного квадрата;
• применяя график соответствующей квадратичной функции;
• используя уравнение дискриминанта.

Плюс первого метода заключается в его простоте, однако, он не для всех уравнений может применяться. Второй способ является универсальным, однако несколько громоздким. Третий метод отличается своей наглядностью, но он не всегда удобен и применим. И, наконец, использование уравнения дискриминанта — это универсальный и достаточно простой способ нахождения корней абсолютно любого уравнения второго порядка. Поэтому в статье рассмотрим только его.

Формула для получения корней уравнения

Обратимся к общему виду квадратного уравнения. Запишем его: a*x²+ b*x + c =0. Перед тем как пользоваться способом его решения «через дискриминант», следует приводить равенство всегда к записанному виду. То есть оно должно состоять из трех слагаемых (или меньше, если b или c равен 0).

Например, если имеется выражение: x²-9*x+8 = -5*x+7*x², то сначала следует перенести все его члены в одну сторону равенства и сложить слагаемые, содержащие переменную x в одинаковых степенях.

В данном случае эта операция приведет к следующему выражению: -6*x²-4*x+8=0, которое эквивалентно уравнению 6*x²+4*x-8=0 (здесь левую и правую части равенства мы умножили на -1).

В примере выше a = 6, b=4, c=-8. Заметим, что все члены рассматриваемого равенства всегда суммируются между собой, поэтому если появляется знак «-«, то это означает, что отрицательным является соответствующий коэффициент, как число c в данном случае.

Разобрав этот момент, перейдем теперь к самой формуле, которая дает возможность получения корней квадратного уравнения. Она имеет вид, который представлен на фото ниже.

Как видно из этого выражения, оно позволяет получать два корня (следует обратить внимание на знак «±»). Для этого в него достаточно подставить коэффициенты b, c, и a.

Понятие о дискриминанте

В предыдущем пункте была приведена формула, которая позволяет быстро решить любое уравнение второго порядка. В ней подкоренное выражение называют дискриминантом, то есть D = b²-4*a*c.

Почему эту часть формулы выделяют, и она даже имеет собственное название? Дело в том, что дискриминант связывает в единое выражение все три коэффициента уравнения. Последний факт означает, что он полностью несет информацию о корнях, которую можно выразить следующим списком:

1. D>0: равенство имеет 2 различных решения, причем оба они представляют собой действительные числа.
2. D=0: у уравнения всего один корень, и он является действительным числом.

Задача на определение дискриминанта

Приведем простой пример, как найти дискриминант. Пусть дано такое равенство: 2*x² — 4+5*x-9*x² = 3*x-5*x²+7.

Приведем его к стандартному виду, получаем: (2*x²-9*x²+5*x²) + (5*x-3*x) + (- 4-7) = 0, откуда приходим к равенству: -2*x²+2*x-11 = 0. Здесь a=-2, b=2, c=-11.

Теперь можно воспользоваться названной формулой для дискриминанта: D = 2² — 4*(-2)*(-11) = -84. Полученное число является ответом на поставленную задачу. Поскольку в примере дискриминант меньше нуля, то можно сказать, что данное квадратное уравнение не имеет действительных корней. Его решением будут только числа комплексного типа.

Пример неравенства через дискриминант

Решим задачи несколько иного типа: дано равенство -3*x²-6*x+c = 0. Необходимо найти такие значения c, для которых D>0.

В данном случае известно лишь 2 из 3 коэффициентов, поэтому рассчитать точное значение дискриминанта не получится, однако известно, что он является положительным. Последний факт используем при составлении неравенства: D= (-6)²-4*(-3)*c>0 => 36+12*c>0. Решение полученного неравенства приводит к результату: c>-3.

Проверим полученное число. Для этого вычислим D для 2 случаев: c=-2 и c=-4. Число -2 удовлетворяет полученному результату (-2>-3), соответствующий дискриминант будет иметь значение: D = 12>0. В свою очередь, число -4 не удовлетворяет неравенству (-4Таким образом, любые числа c, которые больше -3, будут удовлетворять условию.

Пример решения уравнения

Приведем задачу, которая заключается не только в нахождении дискриминанта, но и в решении уравнения. Необходимо найти корни для равенства -2*x²+7-9*x = 0.

В этом примере дискриминант равен следующему значению: D = 81-4*(-2)*7= 137. Тогда корни уравнения определятся так: x = (9±√137)/(-4). Это точные значения корней, если вычислить приближенно корень, тогда получатся числа: x = -5,176 и x = 0,676.

Геометрическая задача

Решим задачу, которая потребует не только умения вычислять дискриминант, но и применения навыков абстрактного мышления и знания, как составлять квадратные уравнения.

У Боба было пуховое одеяло размером 5 x 4 метра. Мальчик захотел пришить к нему по всему периметру сплошную полосу из красивой ткани. Какой толщины будет эта полоса, если известно, что у Боба имеется 10 м² ткани.

Пусть полоса будет иметь толщину x м, тогда площадь ткани по длинной стороне одеяла составит (5+2*x)*x, а поскольку длинных сторон 2, то имеем: 2*x*(5+2*x). По короткой стороне площадь пришитой ткани составит 4*x, так как этих сторон 2, то получаем значение 8*x. Отметим, что к длинной стороне было добавлено значение 2*x, поскольку длина одеяла увеличилась на это число. Общая пришитая к одеялу площадь ткани равна 10 м². Поэтому получаем равенство: 2*x*(5+2*x) + 8*x = 10 => 4*x²+18*x-10 = 0.

Для этого примера дискриминант равен: D = 18²-4*4*(-10) = 484. Его корень равен 22. Воспользовавшись формулой, находим искомые корни: x = (-18±22)/(2*4) = (-5; 0,5). Очевидно, что из двух корней подходит по условию задачи только число 0,5.

Таким образом, полоса из ткани, которую пришьет Боб к своему одеялу, будет иметь ширину 50 см.

Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.

С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье «Решение неполных квадратных уравнений».

Какие же квадратные уравнения называются полными? Это уравнения вида ах 2 + b x + c = 0 , где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.

D = b 2 – 4ас.

В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.

Если дискриминант отрицательное число (D

Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),

тогда х 1 = (-b — √D)/2a , и х 2 = (-b + √D)/2a .

Например. Решить уравнение х 2 – 4х + 4= 0.

D = 4 2 – 4 · 4 = 0

x = (- (-4))/2 = 2

Ответ: 2.

Решить уравнение 2х 2 + х + 3 = 0.

D = 1 2 – 4 · 2 · 3 = – 23

Ответ: корней нет .

Решить уравнение 2х 2 + 5х – 7 = 0 .

D = 5 2 – 4 · 2 · (–7) = 81

х 1 = (-5 — √81)/(2·2)= (-5 — 9)/4= – 3,5

х 2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1

Ответ: – 3,5 ; 1 .

Итак представим решение полных квадратных уравнений схемой на рисунке1.

По этим формулам можно решать любое полное квадратное уравнение. Нужно только внимательно следить за тем, чтобы уравнение было записано многочленом стандартного вида

ах 2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х 2 = 0, ошибочно можно решить, что

а = 1, b = 3 и с = 2. Тогда

D = 3 2 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).

Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах 2 , затем с меньшим – bx , а затем свободный член с.

При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.

Полное квадратное уравнение называется приведенным, если коэффициент при х 2 равен единице и уравнение примет вид х 2 + px + q = 0 . Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а , стоящий при х 2 .

На рисунке 3 приведена схема решения приведенных квадратных
уравнений. Рассмотрим на примере применение рассмотренных в данной статье формул.

Пример. Решить уравнение

3х 2 + 6х – 6 = 0.

Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.

D = 6 2 – 4 · 3 · (– 6) = 36 + 72 = 108

√D = √108 = √(36 · 3) = 6√3

х 1 = (-6 — 6√3)/(2 · 3) = (6 (-1- √(3)))/6 = –1 – √3

х 2 = (-6 + 6√3)/(2 · 3) = (6 (-1+ √(3)))/6 = –1 + √3

Ответ: –1 – √3; –1 + √3

Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам, приведенным на схеме рисунка D 1 = 3 2 – 3 · (– 6) = 9 + 18 = 27

√(D 1) = √27 = √(9 · 3) = 3√3

х 1 = (-3 — 3√3)/3 = (3 (-1 — √(3)))/3 = – 1 – √3

х 2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3

Ответ: –1 – √3; –1 + √3 . Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x 2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного
уравнения рисунок 3.

D 2 = 2 2 – 4 · (– 2) = 4 + 8 = 12

√(D 2) = √12 = √(4 · 3) = 2√3

х 1 = (-2 — 2√3)/2 = (2 (-1 — √(3)))/2 = – 1 – √3

х 2 = (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3

Ответ: –1 – √3; –1 + √3.

Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Среди всего курса школьной программы алгебры одной из самых объемных тем является тема о квадратных уравнениях. При этом под квадратным уравнением понимается уравнение вида ax 2 + bx + c = 0, где a ≠ 0 (читается: а умножить на икс в квадрате плюс бэ икс плюс цэ равно нулю, где а неравно нулю). При этом основное место занимают формулы нахождения дискриминанта квадратного уравнения указанного вида, под которым понимается выражение, позволяющее определить наличие или отсутствие корней у квадратного уравнения, а также их количество (при наличии).

Формула (уравнение) дискриминанта квадратного уравнения

Общепринятая формула дискриминанта квадратного уравнения выглядит следующим образом: D = b 2 – 4ac. Вычисляя дискриминант по указанной формуле, можно не только определить наличие и количество корней у квадратного уравнения, но и выбрать способ нахождения этих корней, которых существует несколько в зависимости от типа квадратного уравнения.

Что значит если дискриминант равен нулю \ Формула корней квадратного уравнения если дискриминант равен нулю

Дискриминант, как следует из формулы, обозначается латинской буквой D. В случае, когда дискриминант равен нулю, следует сделать вывод, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, имеет только один корень, который вычисляется по упрощенной формуле. Данная формула применяется только при нулевом дискриминанте и выглядит следующим образом: x = –b/2a, где х – корень квадратного уравнения, b и а – соответствующие переменные квадратного уравнения. Для нахождения корня квадратного уравнения необходимо отрицательное значение переменной b разделить на удвоенное значение переменной а. Полученной выражение будет решением квадратного уравнения.

Решение квадратного уравнения через дискриминант

Если при вычислении дискриминанта по вышеприведенной формуле получается положительное значение (D больше нуля), то квадратное уравнение имеет два корня, которые вычисляются по следующим формулам: x 1 = (–b + vD)/2a, x 2 = (–b – vD)/2a. Чаще всего, дискриминант отдельно не высчитывается, а в значение D, из которого извлекается корень, просто подставляется подкоренное выражение в виде формулы дискриминанта. Если переменная b имеет четное значение, то для вычисления корней квадратного уравнения вида ax 2 + bx + c = 0, где a ≠ 0, можно также использовать следующие формулы: x 1 = (–k + v(k2 – ac))/a, x 2 = (–k + v(k2 – ac))/a, где k = b/2.

В некоторых случаях для практического решения квадратных уравнений можно использовать Теорему Виета, которая гласит, что для суммы корней квадратного уравнения вида x 2 + px + q = 0 будет справедливо значение x 1 + x 2 = –p, а для произведения корней указанного уравнения – выражение x 1 x x 2 = q.

Может ли дискриминант быть меньше нуля

При вычислении значения дискриминанта можно столкнуться с ситуацией, которая не попадает ни под один из описанных случаев – когда дискриминант имеет отрицательное значение (то есть меньше нуля). В этом случае принято считать, что квадратное уравнение вида ax 2 + bx + c = 0, где a ≠ 0, действительных корней не имеет, следовательно, его решение будет ограничиваться вычислением дискриминанта, а приводимые выше формулы корней квадратного уравнения в данном случае применяться не будут. При этом в ответе к квадратному уравнению записывается, что «уравнение действительных корней не имеет».

Поясняющее видео:

Дискриминант — многозначный термин. В данной статье речь пойдёт о дискриминанте многочлена, который позволяет определить, есть ли у данного многочлена действительные решения. Формула для квадратного многочлена встречается в школьном курсе алгебры и анализа. Как найти дискриминант? Что нужно для решения уравнения?

Квадратным многочленом или уравнением второй степени называется i * w ^ 2 + j * w + k равный 0, где «i» и «j» — первый и второй коэффициент соответственно, «k» — константа, которую иногда именуют «свободным членом», а «w» — переменная. Его корнями окажутся все значения переменной, при которых оно превращается в тождество. Такое равенство допустимо переписать, как произведение i, (w — w1) и (w — w2) равное 0. В этом случае очевидно, что если коэффициент «i» не обращается в ноль, то функция в левой части станет нулевой только в случае, если x принимает значение w1 или w2. Эти значения являются результатом приравнивания многочлена к нулю.

Для нахождения значения переменной, при котором квадратный многочлен обращается в ноль, используется вспомогательная конструкция, построенная на его коэффициентах и названная дискриминантом. Эта конструкция рассчитывается согласно формуле D равняется j * j — 4 * i * k. Зачем она используется?

1. Она говорит, имеются ли действительные результаты.
2. Она помогает их высчитать.

Как это значение показывает наличие вещественных корней:

• Если оно положительное, то можно найти два корня в области действительных чисел.
• Если дискриминант равен нулю, то оба решения совпадают. (1/2).
• Нахождение результата в соответствии с формулой (-j +/- d) / (2 * i).
• Подстановка полученного результата в исходное равенство для проверки.

Некоторые частные случаи

В зависимости от коэффициентов решение может несколько упрощаться. Очевидно, что если коэффициент перед переменной во второй степени равен нулю, то получается линейное равенство. Когда коэффициент перед переменной в первой степени нулевой, то возможны два варианта:

1. многочлен раскладывается в разность квадратов при отрицательном свободном члене;
2. при положительной константе действительных решений найти нельзя.

Если свободный член нулевой, то корни будут {0; -j}

Но есть и другие частные случаи, упрощающие нахождение решения.

Приведенное уравнение второй степени

Приведенным именуют такой квадратный трёхчлен, где коэффициент перед старшим членом — единица. Для данной ситуации применима теорема Виета, гласящая, что сумма корней равняется коэффициенту при переменной в первой степени, помноженному на -1, а произведение соответствует константе «k». 2 + 18 * i * j * k * m.

Допустим, дискриминант превосходит ноль . Это значит, что имеется три корня в области действительных чисел. При нулевом есть кратные решения. Если D

Видео

Наше видео подробно расскажет о вычислении дискриминанта.

Не получили ответ на свой вопрос? Предложите авторам тему.

Использование дискриминанта видео | Shmoop

Дискриминант является частью квадратичной формулы, но это не значит, что он не важен сам по себе; на самом деле, однажды он даже принимал гостей The Tonight Show . Дискриминант определяет количество решений в квадратной формуле. Если дискриминант положительный, есть два решения. Если дискриминант равен нулю, действительное решение будет одно. Если оно отрицательное, реальных решений не будет.

Русский язык2 Язык квадратичных уравнений квадратичных уравнений квадратичных уравнений транскрипта 00:28 Если B2 — 4ac положительный и больше нуля, будет два разных, реальных решения. 00:38 Если b2 – 4ac равно нулю, будет одно отличное реальное решение. 00:45 Но если b2 – 4ac отрицательно и меньше нуля, реальных решений нет. 00:56 Нет. Даже не пытайся придумать. Этого не произойдет. 01:00 Давайте возьмем квадратное число для пары примеров. 01:08 Наш первый пример: х в квадрате плюс три-х плюс пять равно нулю. 01:14 Подставив этих плохих парней в дискриминант, b в квадрате минус 4ac, мы получим три в квадрате 01:20 минус четыре раза один раз пять. 01:23 Это упрощается до девяти минус двадцать, что составляет минус одиннадцать. 01:28 Это меньше нуля… реальных решений нет. 01:33 Что означает «нет реальных решений»? Если мы посмотрим на график, то увидим, что парабола 01:37 не касается оси x ни при каких значениях x. 01:50 Для нашего второго примера у нас есть уравнение… 01:53 x-квадрат минус шесть-x минус десять равно нулю. 01:57 Если подставить это в дискриминант, получится… 02:00 шесть в квадрате минус четыре раза минус десять раз один. 02:05 Это тридцать шесть плюс сорок, то есть семьдесят шесть. 02:09 Семьдесят шесть больше нуля.Таким образом, есть два различных, реальных решения этой проблемы. 02:16 Глядя на график, мы видим, что есть два действительных решения, потому что парабола 02:21 касается оси x в двух различных значениях x. Итак, 02:28 Magic Discriminant Ball может не помочь вам с некоторыми из самых важных вопросов в жизни… 02:32 … тест по математике. Нахождение дискриминанта квадратного уравнения с использованием семейства TI-84 Plus или TI-Nspire в портативных устройствах с режимом TI-84 Plus. Управление настройками файлов cookie Вы можете контролировать свои предпочтения относительно того, как мы используем файлы cookie для сбора и использования информации, когда вы находитесь на веб-сайтах TI, настраивая статус этих категорий. Категория Описание Разрешить Аналитические и эксплуатационные файлы cookie Эти файлы cookie, в том числе файлы cookie из Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI, а также отслеживать, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, упрощая поиск информации на сайте). Рекламные и маркетинговые файлы cookie Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами. Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах.Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламу, чтобы она лучше соответствовала вашим интересам, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. Функциональные файлы cookie Эти файлы cookie помогают определить, кто вы, и сохраняют информацию о вашей деятельности и учетной записи, чтобы обеспечить расширенные функциональные возможности, включая более персонализированный и актуальный опыт на наших сайтах.Если вы не разрешите использование этих файлов cookie, некоторые или все функции и службы сайта могут работать неправильно. Если вы не разрешите эти файлы cookie, некоторые или все функции и службы сайта могут работать неправильно. Файлы cookie социальных сетей Эти файлы cookie позволяют идентифицировать пользователей и контент, связанный с онлайн-социальными сетями, такими как Facebook, Twitter и другие платформы социальных сетей, и помогают TI улучшить охват социальных сетей. Строго необходимо Эти файлы cookie необходимы для работы сайтов TI или для выполнения ваших запросов (например, для отслеживания того, какие товары вы положили в свою корзину на TI.com, для доступа к защищенным областям сайта TI или для управления настроенными настройки файлов cookie). Всегда включен Дискриминантный анализ — Статистические решения Количественные результаты Статистический анализ Во время исследования у исследователя часто возникают вопросы, на которые необходимо ответить.Эти вопросы включают в себя такие вопросы, как «отличаются ли группы?», «по каким переменным группы наиболее различаются?», «можно ли предсказать, к какой группе принадлежит человек, используя такие переменные?» и т. д. При ответе на такие вопросы дискриминантный анализ весьма полезно. Statistics Solutions — лидер в стране в области дискриминантного анализа и статистики диссертаций. Используйте календарь ниже, чтобы запланировать бесплатную 30-минутную консультацию. Узнайте, как мы помогаем редактировать главы вашей диссертации Согласование теоретической основы, сбор статей, обобщение пробелов, формулирование четкой методологии и плана данных, а также описание теоретических и практических последствий вашего исследования являются частью наших комплексных услуг по редактированию диссертации. Своевременно привнесите опыт редактирования диссертации в главы 1–5. Отслеживайте все изменения, а затем работайте с вами над научными работами. Постоянная поддержка для рассмотрения отзывов комитетов, сокращение количества исправлений. Дискриминантный анализ — это метод, который используется исследователем для анализа данных исследования, когда критерий или зависимая переменная являются категориальными, а предиктор или независимая переменная носит интервальный характер.Термин категориальная переменная означает, что зависимая переменная делится на ряд категорий. Например, три марки компьютеров: Компьютер A, Компьютер B и Компьютер C могут быть категориальной зависимой переменной. Целью дискриминантного анализа является разработка дискриминантных функций, которые представляют собой не что иное, как линейную комбинацию независимых переменных, которая будет идеально различать категории зависимой переменной. Это позволяет исследователю изучить, существуют ли значительные различия между группами с точки зрения переменных-предикторов.Он также оценивает точность классификации. Дискриминантный анализ описывается количеством категорий, которыми обладает зависимая переменная. Как и в статистике, предполагается все до бесконечности, поэтому в этом случае, когда зависимая переменная имеет две категории, используется двухгрупповой дискриминантный анализ. Если зависимая переменная имеет три или более трех категорий, то используется тип множественного дискриминантного анализа. Основное различие между типами дискриминантного анализа заключается в том, что для двух групп можно вывести только одну дискриминантную функцию. С другой стороны, в случае множественного дискриминантного анализа можно вычислить более одной дискриминантной функции. Есть много примеров, которые могут объяснить, когда дискриминантный анализ подходит. Его можно использовать, чтобы узнать, различаются ли интенсивные, средние и легкие потребители безалкогольных напитков с точки зрения потребления замороженных продуктов. В области психологии его можно использовать для различения чувствительных к цене и нечувствительных к цене покупателей продуктов питания с точки зрения их психологических атрибутов или характеристик.В сфере бизнеса его можно использовать для понимания характеристик или атрибутов покупателя, обладающего лояльностью к магазину, и покупателя, у которого нет лояльности к магазину. Intellectus позволяет проводить и интерпретировать анализ за считанные минуты. Нажмите на ссылку ниже, чтобы создать бесплатную учетную запись, и начните анализировать свои данные прямо сейчас! Для исследователя важно понимать взаимосвязь дискриминантного анализа с регрессионным и дисперсионным анализом (ANOVA), который имеет много сходств и различий.Часто мы можем найти сходства и различия с людьми, с которыми мы сталкиваемся. Точно так же есть некоторые сходства и различия в дискриминантном анализе и двух других процедурах. Сходство состоит в том, что число зависимых переменных в дискриминантном анализе равно единице, а в двух других процедурах число независимых переменных в дискриминантном анализе кратно. Разница является категориальной или бинарной в дискриминантном анализе, но метрической в ​​двух других процедурах. Природа независимых переменных является категориальной в дисперсионном анализе (ANOVA), но метрической в ​​регрессионном и дискриминантном анализе. При проведении дискриминантного анализа выполняются следующие шаги: • Перед проведением формулируется задача. • Оцениваются коэффициенты дискриминантной функции. • Следующим шагом является определение значимости этих дискриминантных функций. • Необходимо интерпретировать полученные результаты. • Последним и самым важным шагом является оценка достоверности. Statistics Solutions может помочь вам с количественным анализом, помогая вам разработать методологию и разделы результатов. Услуги, которые мы предлагаем, включают: План анализа данных Отредактируйте свои исследовательские вопросы и нулевые/альтернативные гипотезы Напишите свой план анализа данных; указать конкретные статистические данные для решения вопросов исследования, допущения статистических данных и обосновать, почему они являются надлежащими статистическими данными; предоставить ссылки Обоснуйте объем выборки/анализ мощности, предоставьте ссылки Объясните вам свой план анализа данных, чтобы вы чувствовали себя комфортно и уверенно Два часа дополнительной поддержки со статистиком Секция количественных результатов (Описательная статистика, двумерный и многомерный анализ, моделирование структурными уравнениями, анализ путей, HLM, кластерный анализ) Очистить и закодировать набор данных Провести описательную статистику (т. д., среднее значение, стандартное отклонение, частота и процент, в зависимости от обстоятельств) Проведите анализ, чтобы изучить каждый из ваших вопросов исследования Результаты записи Обеспечьте APA 6 th издание таблиц и рисунков Объясните выводы главы 4 Текущая поддержка всей статистики главы результатов Пожалуйста, позвоните по номеру 727-442-4290, чтобы запросить расценки с учетом специфики вашего исследования, запланируйте с помощью календаря на этой странице или напишите по электронной почте [email protected] Алгоритм и блок-схема для нахождения всех корней квадратного уравнения Что такое квадратные уравнения? Квадратные уравнения — это полиномиальные уравнения 2-й степени от одной переменной типа: f(x) = ax 2 + bx + c, где a, b, c, ∈ R и a ≠ 0.Это общая форма квадратного уравнения, где «а» называется старшим коэффициентом, а «с» называется абсолютным членом f (x). Квадратное уравнение всегда будет иметь два корня. Природа корней может быть как реальной, так и мнимой. Общая форма квадратного уравнения: ax 2 + bx + c Пример: 4x 2 + 6x + 12 Корни квадратного уравнения находятся по квадратной формуле: Член b 2 — 4ac известен как дискриминант квадратного уравнения.Это говорит о природе корней. Если дискриминант > 0 Если дискриминант = 0 Если дискриминант Мы собираемся использовать описанную выше логику для решения этой проблемы. Давайте взглянем на алгоритм и блок-схему, чтобы лучше понять. Алгоритм поиска всех корней квадратного уравнения: Шаг 1. Начните Шаг 2. Считайте коэффициенты уравнения, a, b и c от пользователя. Шаг 3. Вычислить дискриминант = (b * b) – (4 * a * c) Шаг 4. Если дискриминант > 0: 4.1: Вычислить root1 = (-b + sqrt(дискриминант)) / (2 * a) 4.2: Вычислить root2 = (-b — sqrt(дискриминант)) / (2 * a) 4.3: Показать «Корни настоящие и разные» 4.4: Показать root1 и root2 Шаг 5: В противном случае, если дискриминант = 0: 5.1: Вычислить root1 = -b / (2 *a) 5.2: корень2 = корень1 5.3: Отображение «Корни действительны и равны» 5.4: Показать root1 и root2 Шаг 6. Еще: 6.1: Вычисление реального = -b / (2 * a) 6.2: Вычислить мнимую = sqrt (-дискриминант) / (2 * a) 6.3: Дисплей «Корни мнимые» 6.4: Отображение реального, «±», мнимого, «i» Шаг 7. Стоп Объяснение: Алгоритм начинается с получения коэффициентов уравнения a, b и c от пользователя. После этого по заданной формуле вычисляется дискриминант. Теперь проверим, больше ли дискриминант 0. Если да, то корни уравнения действительны и различны. Если дискриминант равен 0, то корни вещественные и равные. Если дискриминант меньше 0, то корни мнимые и разные. Мы сравним вычисленный дискриминант с каждым из условий и в зависимости от того, какое из них выполнено, мы вычислим два корня по соответствующей формуле, а затем отобразим это. Примечание. Пожалуйста, обратитесь к таблице в начале, чтобы увидеть соответствующую формулу. Например: Давайте рассмотрим уравнение: 6x² + 11x — 35 = 0, . Здесь дискриминант = 961 Следовательно, дискриминант > 0; корни настоящие и разные. Итак, root1 = 938, root2 = -81? Блок-схема для нахождения всех корней квадратного уравнения: Блок-схема удаления водяных знаков сверху . Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт