| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) ) |
|
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) ) |
|
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень 3) | |
| 24 | Найти точное значение | csc(60 град. ) ) |
|
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) |
|
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) |
|
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) |
|
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) ) |
|
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) ) |
|
| 77 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) |
|
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) |
|
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
7) Производные функции sin x, cos x, tg x, ctg x, ax, logax, xa, arcsin x, arctg x, arcos(x) arcctg(x), sh x, ch x, th x, cth x (вывод формул).
Теорема 6. (производная логарифмической функции)Доказательство
Вначале докажем теорему для функции y = ln x. Если аргумент x получит приращение Δx, то функция y = ln x получит приращение
Если аргумент x получит приращение Δx, то функция y = ln x получит приращение Воспользовавшись вторым замечательным пределом, свойствами предела функции и свойствами логарифмической функции, получаем
Теперь, так как то, вынося постоянную за знак производной, получаемТеорема доказана.
Теорема 7. (производная степенной функции)Теорема доказана.
Теорема 8. (производная показательной функции)Доказательство
Так как , то, дифференцируя это равенство, получаемТеорема доказана.
Теорема 9. (производные тригонометрических функций)Доказательство
Если аргумент x получит приращение Δx, то функция y = sin x получит приращение
Воспользовавшись первым замечательным пределом и свойствами предела функции, получаем
Утверждение 1) доказано. Утверждение 2) доказывается аналогично, заметим только, что приращение функции y = cos x можно записать так:
Утверждение 2) доказывается аналогично, заметим только, что приращение функции y = cos x можно записать так:
Для доказательства утверждения 3) используем утверждения 1), 2) данной теоремы и теорему 3. Имеемs
Утверждение 3) доказано. Утверждение 4) доказывается аналогично.
Теорема доказана.
Теорема 10. (производные обратных тригонометрических функций)Доказательство
Если y = arcsin x, то x = sin y. Получаем . Тогда и утверждение 1) доказано. Остальные утверждения теоремы доказываются аналогично.Теорема доказана.
Властивості sin(x), cos(x),tg(x), ctg(x)
Наведені та структуровані основні характеристики тригонометричних функцій sin(x), cos(x), tg(x), ctg(x), які є вкрай необхідними при дослідженні графіків та поведінки цих функцій, спрощенні тригонометричних виразів, обчисленні рівнянь та нерівностей.
Основну частину присутніх тут формул Ви повинні вміти легко застосовувати на практичних, а для цього частину матеріалу потрібно завчити та знати.
Це не стосується всіх формул, але частину основних тригонометричних тотожностей, а також формули синуса чи косинуса подвійного кута слід запам’ятати.
Cинус y=sin(x)
Область визначення: D(y): x∈R
Область допустимих значень: E(y):y∈[-1;1], тобто -1≤sin(x)≤1.
Функція непарна: sin(-a)=sin(a).
Функція періодична з найменшим додатним періодом 2Pi: sin(a+2Pi)=sin(a).
Точки перетину з осями координат: (0,0) на осі Oy; (Pi·k;0), k∈Z на осі Ox.
Проміжки знакопостійності:
y>0, якщо x∈(2Pi·k;Pi+2Pi·k), k∈Z;
y<0, якщо x∈(Pi+2Pi·k;2Pi+2Pi·k), k∈Z.
Проміжки зростання: [-Pi/2+2Pi·k; Pi/2+2Pi·k], k∈Z, звідси ymax=1 у точках xmax=Pi/2+2Pi·k.
Проміжки спадання: [Pi/2+2Pi·k; 3Pi/2+2Pi·k], k∈Z, звідси ymin=-1 у точках xmin=-Pi/2+2Pi·k.
Косинус y=cos(x)
Область визначення: D(y): x∈R
Область значень: E(y):y∈[-1;1], тобто -1≤cos(x)≤1.
Функція парна: cos(-a)=cos(a).
Функція періодична з найменшим додатним періодом 2Pi: cos(a+2Pi)=cos(a).
Точки перетину з осями координат: (0;1) на осі Oy, (Pi/2+Pi·k;0), k∈Z на осі Ox;
Проміжки знакопостійності:
y>0, якщо x∈(-Pi/2+2Pi·k;Pi/2+2Pi·k), k∈Z;
y<0, якщо x∈(Pi/2+2Pi·k;3Pi/2+2Pi·k), k∈Z.
Проміжки зростання: [Pi+2Pi·k; 2Pi·k], k∈Z, звідси ymax=1 у точках xmax= 2Pi·k.
Проміжки спадання: [2Pi·k; Pi+2Pi·k], k∈Z, звідси ymin=-1 у точках xmin= Pi+2Pi·k.
Тангенс y=tg(x)
Область визначення: D(y):x≠Pi/2+Pi·k, k∈Z;
Область значень: E(y): y∈R, тобто -∞≤tg(x)≤+∞.
Функція непарна tg(-a)=-tg(a).
Функція періодична з найменшим додатним періодом Pi: tg(a+Pi)=tg(a).
Точки перетину з осями координат: (0;0) на осі Oy; (Pi·k;0), k∈Z на осі Ox.
Проміжки знакопостійності:
y>0, якщо x∈(Pi·k;Pi/2+Pi·k), k∈Z;
y<0, якщо x∈(-Pi/2+Pi·k; Pi·k), k∈Z .
Проміжки зростання: (-Pi/2+Pi·k; Pi/2+Pi·k), k∈Z.
Найменших і найбільших значень функція не має .
Котангенс y=ctg(x)
Область визначення: D(y):x≠ Pi·k, k∈Z;
Область значень: E(y): y∈R, тобто -∞≤ctg(x)≤+∞.
Функція непарна ctg(-a)=-ctg(a).
Функція періодична з найменшим додатним періодом Pi: ctg(a+Pi)=ctg(a).
Точки перетину з осями координат:
не перетинає вісь Oy;
(Pi/2+Pi·k;0), k∈Z на осі Ox
Проміжки знакопостійності:
y>0, якщо x∈(Pi·k;Pi/2+Pi·k), k∈Z;
y<0, якщо x∈(Pi/2+Pi·k;Pi+Pi·k), k∈Z.
Проміжки спадання: (Pi·k;Pi+Pi·k), k∈Z.
Найменших і найбільших значень функція не має.
Значення тригонометричних функцій для деяких кутів:
α | 0 | π/6 | π/4 | π/3 | π/2 | π | 3π/2 |
sinα | 0 | 1/2 | √2/2 | √3/2 | 1 | 0 | -1 |
cosα | 1 | √3/2 | √2/2 | 1/2 | 0 | -1 | 0 |
tgα | 0 | √3/3 | 1 | √3 | — | 0 | — |
ctgα | — | √3 | 1 | √3/3 | 0 | — | 0 |
Формули зведення:
Функція | 900+α | 1800+α | 2700+α | -α | 900-α | 1800-α | 2700-α |
sinα | cosα | -sinα | -cosα | -sinα | cosα | sinα | -cosα |
cosα | -sinα | -cosα | sinα | cosα | sinα | -cosα | -sinα |
tgα | -ctgα | tgα | -ctgα | -tgα | ctgα | -tgα | ctgα |
ctgα | -tgα | ctgα | -tgα | -ctgα | tgα | -ctgα | tgα |
Знаки тригонометричних функцій:
Зв’язок між тригонометричними функціями одного аргументу:
У наведених формулах перед знаком радикала слід взяти знак «плюс» або «мінус»
залежно від того, в якій чверті лежить кут α саме так, щоб знак тригонометричної
функції, який стоїть у лівій частині збігався зі знаком величини, що стоїть у правій
частині рівності.
Основні тригонометричні тотожності
Універсальна тригонометрична підстановка
Тригонометричні функції суми і різниці аргументів
Тригонометричні функції подвійного, потрійного і половинного
аргументів
Перетворення суми тригонометричних функцій у добуток
Перетворення добутку тригонометричних функцій у суму
Далі будуть наведені відповіді до поширених на практиці прикладів з тригонометрії на знаходження значень тригонометричних виразів, розв’язування рівнянь та нерівностей на яких буде показано всю силу наведених вище формул.
Самостійна робота «Тригонометричні функції» | Тест з алгебри – «На Урок»
Запитання 1
Найменший додатний період для функції y=sin x дорівнює
варіанти відповідей
Запитання 2
Найменший додатний період для функції y=cos x дорівнює
варіанти відповідей
Запитання 3
Найменший додатний період для функції y=tg x дорівнює
варіанти відповідей
Запитання 4
Оберіть графік функції y=sin x
варіанти відповідей
Запитання 5
Оберіть графік функції y=cos x
варіанти відповідей
Запитання 6
Оберіть графік функції y=tg x
варіанти відповідей
Запитання 7
Оберіть непарні функції
варіанти відповідей
синус, косинус, тангенс, котангенс.
синус, косинус, котангенс.
синус, косинус, тангенс.
синус, тангенс, котангенс.
Запитання 8
Перетворіть у радіани 1800
варіанти відповідей
Запитання 9
Обчисліть sin π+cos π/3+tg π/4
варіанти відповідей
Запитання 10
Обчислити sin(-405⁰)
варіанти відповідей
Запитання 11
Перетворіть у градусну міру кут π/10
варіанти відповідей
Запитання 12
Яка градусна міра кута 2π/3?
варіанти відповідей
Запитання 13
На одиничному колі синус — це …
варіанти відповідей
абсциса точки
частка абсциси і ординати
ордината точки
частка ординати і абсциси
Запитання 14
На одиничному колі зображено точку Р(-0,8; 0,6) і кут α
Визначте cosα.
варіанти відповідей
Запитання 15
Встановіть знак виразу sin2100
варіанти відповідей
Запитання 16
У якій чверті знаходиться кут 393°?
варіанти відповідей
Запитання 17
Спростіть вираз sinα⋅ctgα
варіанти відповідей
Запитання 18
Спростити вираз
(1 — sin2β) : (1 — cos2β)
варіанти відповідей
Запитання 19
варіанти відповідей
Запитання 20
Спростити вираз і вказати правильну відповідь
6 — 6sin2α =
варіанти відповідей
Запитання 21
варіанти відповідей
Запитання 22
варіанти відповідей
Запитання 23
Знайдіть значення виразу 3·cos90º – 3·sin90º
варіанти відповідей
Запитання 24
tg (3π/2 − α) = …
варіанти відповідей
Запитання 25
Обчисліть cos2α, якщо sin α = 5/13
варіанти відповідей
Запитання 26
Знайдіть значення виразу: cos45⁰sin45⁰-sin90⁰cos120⁰
варіанти відповідей
Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома
Натисніть «Подобається», щоб слідкувати за оновленнями на Facebook
Следующие инструкции
работать с углами и тригонометрическими функциями. Существует шесть основных
тригонометрические функции, которые проще всего вводятся
рассматривая прямоугольный треугольник, один из других углов которого
равно x, как показано на рисунке ниже: Существует шесть основных
тригонометрические функции, которые проще всего вводятся
рассматривая прямоугольный треугольник, один из других углов которого
равно x, как показано на рисунке ниже:Основные функции определяются с точки зрения длины гипотенузы (самая длинная сторона), сторона, лежащая против угла x, и сторона, примыкающая к углу x. под углом х. Синус x, записанный как sin(x) , определяется как:
Косинус x, записанный как cos(x) , определяется как:
Тангенс x, записанный как tan(x) , определяется как:
Обратите внимание, что tan(x) не определено, где x = 0. Используя эти функции, если угол и длина одной стороны прямоугольного треугольника известны, длину двух других сторон легко вычислить.
Остальные три функции — это секанс, косеканс и котангенс.
обратны синусу, косинусу и тангенсу соответственно. Примечания:Тригонометрические функции поддерживаются C-Script для переменных var , и lite-C для var (в чистом режиме) и для double . Функции var использовать углы в градусов (0…360) для совместимости с Gamestudio; их двойные аналоги однако используйте углы в радиан (0…2 pi) для совместимости с C. Всегда будьте уверены, какое представление угла
вы хотите использовать! Всегда будьте уверены, какое представление угла
вы хотите использовать!Некоторые полезные функции:
Подставляя x = y в приведенные выше формулы, мы получаем:
|
Как решить Sin X = Tan X?
Как построить график Y = Sin X + Cos X?
Математика
График y = sin x +, потому что x находится на сайте www. ies.co.jp. Этот сайт разделен…
ies.co.jp. Этот сайт разделен…
Как решить: (tan X + Cot X)/сек в квадрате X?
Математика
(tan x+cotx)/сек sqd x = (tanx+(1/tanx))/(1+tan sqdx) …
Как решить: Cos(2x)/(1+sin(2x)) = (cot(x)-1) / (cot(x)+1)?
Математика
R=((cosx/sinx)-1) / ((cosx/sinx)+1) =((cosx-sinx)/sinx) / ((cosx+sinx)/sinx) =((cosx-sinx)/sinx) *…
Как решить: (csc X + Sec X)/(sin X+ Cos X)= (cot X+ Tan X)?
Математика
Это личность. Это верно для всех значений X. Возможно, вы хотите продемонстрировать, что это правда. Мы используем…
Решите для X, Tan X + Tan 2x + Tan 3x = Tan X Tan 2x Tan 3x?
Математика
Tan x + tan 2x+ tan3x=tanx.tan 2x.tan 3x tanx+ tan 2x= -tan 3x +tan x.загар2x.загар 3x tanx+tan2x= -tan…
Решить, тангенс x + тангенс 2x + тангенс 3x = тангенс x тангенс 2x тангенс 3x?
Математика
График левой и правой частей уравнения быстро показывает решения, которые
х = {0,. ..
..
Как решить Sec(-x)cot X?
Математика
Речь идет о тригонометрических функциях…
Если tan x = 0,76 и cos x = 0,22, чему равно sin x?
Геометрия
Используя фундаментальное тождество…,tan(x) = sin(x)/cos(x)cos(x) * tan(x) = sin(x)0,22 * 0,76= 0,1672======[. ..
sin(15 градусов+x)+sin(45 градусов-x)=1 Чему равно x при решении?
Математика
Х = 42…
Как найти производную от y = sin(tan x²)?
Математика
Используйте цепное правило, т.е.e.,d/dx f(g(x))=f′(g(x))×g′(x)= cos(tanx²) d/dx (tanx²)= cos(tanx²) •…
Производные триггерные функции
| Доказательства: Производная Триггерные функции |
| (Математика | Исчисление | производные | Таблица Из | Триггерные функции) |
| sin(x) = cos(x) cos(x) = -sin(x) tan(x) = sec ^2 (x) csc(x) = -csc(x) детская кроватка(х) сек(х) = сек(х) tan(x) кроватка(x) = -csc ^2 (x) |
Доказательства производных триггерных функций
Доказательство sin(x) : алгебраический метод Дано : lim(d->0) sin(d)/d = 1. 2 (d) / ( d(cos(d) + 1) + cos(x) lim sin(d)/d
2 (d) / ( d(cos(d) + 1) + cos(x) lim sin(d)/d = sin(x) lim (-sin(d)) * lim sin(d)/d * lim 1/(cos(d)+1) + cos(x) lim sin(d)/d
= sin(x) * 0 * 1 * 1/2 + cos(x) * 1 = cos(x) В.Э.Д.
Доказательство cos(x) : из производной синуса
Это может быть получено точно так же, как sin(x) или проще из результата sin(x)
Учитывая : грех (х) = потому что (х); Правило цепи.
Решить :
cos(x) = sin(x + PI/2)
кос(х) = грех (х + PI / 2)
= грех(и) * (x + PI/2) (Установить и = х + PI/2)
= cos(u) * 1 = cos(x + PI/2) = -sin(x) В.2 (x) В.Э.Д.
A) tanx cosx + cotxsinxsinxcosxb) C04 corx4 =sinx Janr…
Хорошо. При проверке этого тождества совершенно ясно, что левая сторона сложнее. Итак, я собираюсь умножить левый член на ко-секвенцию над самим собой. Потому что вот эта штука в синем — одна из них. И затем в правом члене я собираюсь умножить это на ко-знак X над СО-знаком X, потому что синим тоже один правильный, и я умножаю его здесь. Хорошо, если умножить это здесь, это не изменит термин.Просто меняется внешний вид. И я собираюсь получить хуй в квадрате от Х над со поиском Х умножить на знак Х минус поиск и на Х умножить на знак Х на одно и то же. Итак, я описываю для вас больше шагов, потому что я хочу, чтобы вы увидели, что это действительно дает мне одинаковый знаменатель или один и тот же знаменатель в обоих терминах, поэтому я могу объединить это в одну дробь. Итак, давайте сделаем это. Так что некоторые из вас могут просто пропустить этот шаг, и это совершенно нормально. Хорошо, но у нас Cosi соединяет Times со знаком X.Все это должно быть равносильно совместному изменению Innovex. Итак, я вижу, что поиск X и второй знак X являются взаимными, поэтому я могу написать пару способов, которыми я могу написать поиск X больше, чем его взаимный, гм, второй знак, который на единицу превышает поиск X. другой способ написать знак со, правильно, Это должно быть равно единице. Поэтому, когда я умножаю что-то на обратное, оно всегда будет единицей. Так что это просто будет единицей, а затем останется петух в квадрате X минус один над Cosi Connects Times Co знаком X.Ну, хм, я мог бы сделать что-то в знаменателе здесь, потому что это можно переписать как один над знаком X Times Co знак X над единицей. И когда я умножаю прямо, как вы делаете с умножением дробей, я записываю числитель назад. Я получаю кознак X над знаком X, и я знаю, что это кокасание. Она должна быть кокасательной. Это еще одно соотношение тождества. Co Seacon в квадрате X минус один относительно котангенса действий должен быть равен котангенсу x, не пишущего каждый раз, но я просто привожу его справа.
Хорошо, но у нас Cosi соединяет Times со знаком X.Все это должно быть равносильно совместному изменению Innovex. Итак, я вижу, что поиск X и второй знак X являются взаимными, поэтому я могу написать пару способов, которыми я могу написать поиск X больше, чем его взаимный, гм, второй знак, который на единицу превышает поиск X. другой способ написать знак со, правильно, Это должно быть равно единице. Поэтому, когда я умножаю что-то на обратное, оно всегда будет единицей. Так что это просто будет единицей, а затем останется петух в квадрате X минус один над Cosi Connects Times Co знаком X.Ну, хм, я мог бы сделать что-то в знаменателе здесь, потому что это можно переписать как один над знаком X Times Co знак X над единицей. И когда я умножаю прямо, как вы делаете с умножением дробей, я записываю числитель назад. Я получаю кознак X над знаком X, и я знаю, что это кокасание. Она должна быть кокасательной. Это еще одно соотношение тождества. Co Seacon в квадрате X минус один относительно котангенса действий должен быть равен котангенсу x, не пишущего каждый раз, но я просто привожу его справа. Я ничего не делаю для этого. Эм, и мы очень близки. У нас есть петух в квадрате X минус один. Это почти пифагорейское тождество, которое мы знаем о том, что один плюс котангенс в квадрате X равен ко-квадрату Seacon к досаде. Я не хочу это писать. Cosi получено в квадрате X. Хорошо, мы знаем, что это правда, потому что это тождество трубочного Агрона. Итак, я возьму этот берег Дикона в квадрате X и подставлю сюда это выражение. Когда я это делаю, я получаю один плюс котангенс в квадрате от скорости X. Это выражение, которое я подставил, а затем вычел один.Так что это просто сходит на нет. Я ничего не делал с этим плюсом. Крутая вещь здесь в том, что у меня есть положительный, а отрицательный отменяет, у меня остается котангенс, возведенный в квадрат X, над котангенсом X должен быть равен котангенсу X, и действительно, это потому, что котангенс, возведенный в квадрат над котангенсом , отменяет квадрат, и я остаюсь с котангенсом X над тем, который равен котангенсу X. И у меня также есть проверка этого тождества
Я ничего не делаю для этого. Эм, и мы очень близки. У нас есть петух в квадрате X минус один. Это почти пифагорейское тождество, которое мы знаем о том, что один плюс котангенс в квадрате X равен ко-квадрату Seacon к досаде. Я не хочу это писать. Cosi получено в квадрате X. Хорошо, мы знаем, что это правда, потому что это тождество трубочного Агрона. Итак, я возьму этот берег Дикона в квадрате X и подставлю сюда это выражение. Когда я это делаю, я получаю один плюс котангенс в квадрате от скорости X. Это выражение, которое я подставил, а затем вычел один.Так что это просто сходит на нет. Я ничего не делал с этим плюсом. Крутая вещь здесь в том, что у меня есть положительный, а отрицательный отменяет, у меня остается котангенс, возведенный в квадрат X, над котангенсом X должен быть равен котангенсу X, и действительно, это потому, что котангенс, возведенный в квадрат над котангенсом , отменяет квадрат, и я остаюсь с котангенсом X над тем, который равен котангенсу X. И у меня также есть проверка этого тождества
Единица обратного синуса. Этот результат достаточно важен, чтобы его можно было выделить в виде теоремы, которую мы сформулируем далее.2π может встречаться в нескольких местах, но в целом идея одна и та же. у, грех(т)*н. ¯. Этот вопрос не показывает каких-либо исследовательских усилий; непонятно или бесполезно. 13, часть (б) Предположим, что R — кольцо с единицей и a2R — единица кольца R. Если sin(θ) = cos(θ), то sin2(θ) = cos2(θ). Вы, наверное, уже это знаете, но тригонометрические функции, такие как Sin(), Cos() и ATan2(), очень медленные. е я Икс знак равно потому что Икс + я грех Икс. Но это показывает, что если x является корнем уравнения, то и 1/x является корнем, поскольку обратным cis (2πn/7) является cis ((2π(7−n)/7).Для комплексного числа z = a + bi z = a + b i комплексно-сопряженное число обозначается ¯. 25 s я п — 1 . обучение обратному рендерингу. В математике, в области теории чисел, гауссовский период — это своего рода сумма корней из единицы. РЕШЕНИЕ: Предположим, что b; c2R и что ab= ba= 1 и что ac= ca= 1.
Этот результат достаточно важен, чтобы его можно было выделить в виде теоремы, которую мы сформулируем далее.2π может встречаться в нескольких местах, но в целом идея одна и та же. у, грех(т)*н. ¯. Этот вопрос не показывает каких-либо исследовательских усилий; непонятно или бесполезно. 13, часть (б) Предположим, что R — кольцо с единицей и a2R — единица кольца R. Если sin(θ) = cos(θ), то sin2(θ) = cos2(θ). Вы, наверное, уже это знаете, но тригонометрические функции, такие как Sin(), Cos() и ATan2(), очень медленные. е я Икс знак равно потому что Икс + я грех Икс. Но это показывает, что если x является корнем уравнения, то и 1/x является корнем, поскольку обратным cis (2πn/7) является cis ((2π(7−n)/7).Для комплексного числа z = a + bi z = a + b i комплексно-сопряженное число обозначается ¯. 25 s я п — 1 . обучение обратному рендерингу. В математике, в области теории чисел, гауссовский период — это своего рода сумма корней из единицы. РЕШЕНИЕ: Предположим, что b; c2R и что ab= ba= 1 и что ac= ca= 1. Тщательная проверка вычисления интеграла, выполненного выше: обнаруживает проблему. Посмотрите на (основную камеру). Можем ли мы показать, что сумма значений симметричного косинуса равна нулю, используя корни из единицы? 3.Лучшее решение этой проблемы (помимо Transform. Next). В этой программе компилятор C# неявно преобразует. Очень часто в Unity вам может понадобиться анимировать кнопку, переместить объект в новое положение, плавно затухать звук или графика или, возможно, , постепенно меняйте цвет чего-либо с течением времени. Но я здесь потерялся. Когда оно подпрыгивает вверх и вниз, его движение, если его изобразить во времени, представляет собой синусоидальную волну. Такие функции … sin 2 kx/L sin 2 jx/L Конечное преобразование Фурье можно определить как действие вычисления многочлена степени n-1 в n корнях из единицы, то есть в n решениях уравнения xn =1.Вы услышите чистую синусоидальную волну, дискретизированную с частотой 44. (Точнее говоря, они представляют собой один из возможных наборов трех углов Тейта-Брайана, или морских углов, или углов Кардана, поскольку они описывают повороты вокруг трех разных… Алгоритм определяется следующим образом: —— sx = sin(A) // Настройка — выполняется только один раз cx = cos(A) sy = sin(B) cy = cos(B) sz = sin(C) cz = cos (C) x1 = x * cz + y * sz // Вращение каждой вершины y1 = y * cz — x * sz z1 = z x2 = x1 * cy + z1 * sy y2 = z1 z2 = z1 * cy — x1 * sy x3 = x2 y3 = y2 * cx + z1 * sx z3 = z2 * cx — x1 * sx xr = x3 + D Тригонометрическая функция.
Тщательная проверка вычисления интеграла, выполненного выше: обнаруживает проблему. Посмотрите на (основную камеру). Можем ли мы показать, что сумма значений симметричного косинуса равна нулю, используя корни из единицы? 3.Лучшее решение этой проблемы (помимо Transform. Next). В этой программе компилятор C# неявно преобразует. Очень часто в Unity вам может понадобиться анимировать кнопку, переместить объект в новое положение, плавно затухать звук или графика или, возможно, , постепенно меняйте цвет чего-либо с течением времени. Но я здесь потерялся. Когда оно подпрыгивает вверх и вниз, его движение, если его изобразить во времени, представляет собой синусоидальную волну. Такие функции … sin 2 kx/L sin 2 jx/L Конечное преобразование Фурье можно определить как действие вычисления многочлена степени n-1 в n корнях из единицы, то есть в n решениях уравнения xn =1.Вы услышите чистую синусоидальную волну, дискретизированную с частотой 44. (Точнее говоря, они представляют собой один из возможных наборов трех углов Тейта-Брайана, или морских углов, или углов Кардана, поскольку они описывают повороты вокруг трех разных… Алгоритм определяется следующим образом: —— sx = sin(A) // Настройка — выполняется только один раз cx = cos(A) sy = sin(B) cy = cos(B) sz = sin(C) cz = cos (C) x1 = x * cz + y * sz // Вращение каждой вершины y1 = y * cz — x * sz z1 = z x2 = x1 * cy + z1 * sy y2 = z1 z2 = z1 * cy — x1 * sy x3 = x2 y3 = y2 * cx + z1 * sx z3 = z2 * cx — x1 * sx xr = x3 + D Тригонометрическая функция.

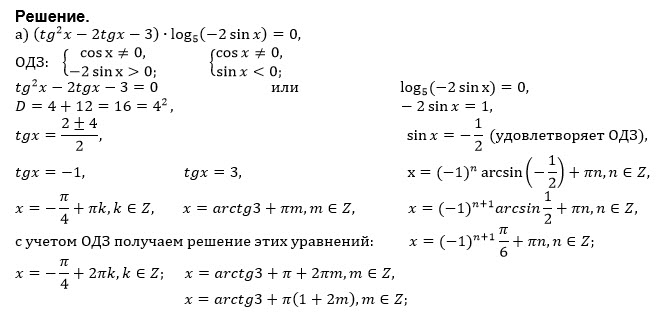 Это важно, поскольку используется обозначение sin -1 (x).
чтобы указать функцию обратного синуса, или арксинус — то есть,
угол, синус которого равен х. Аналогичные обозначения применяются к арккосинусу .
и арктангенс . Беглый просмотр приведенной выше таблицы показывает
что дуговые функции могут давать несколько ответов для любого заданного значения
— обычно требуется физическое обследование проблемы, чтобы
определить, в какой диапазон попадает угол.
Это важно, поскольку используется обозначение sin -1 (x).
чтобы указать функцию обратного синуса, или арксинус — то есть,
угол, синус которого равен х. Аналогичные обозначения применяются к арккосинусу .
и арктангенс . Беглый просмотр приведенной выше таблицы показывает
что дуговые функции могут давать несколько ответов для любого заданного значения
— обычно требуется физическое обследование проблемы, чтобы
определить, в какой диапазон попадает угол. 2 (x) В.Э.Д.
2 (x) В.Э.Д.