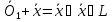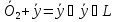Доказательство от противного — Википедия

Материал из Википедии — свободной энциклопедии

Доказательство «от противного» (лат. contradictio in contrarium) в математике — вид доказательства, при котором «доказывание» некоторого суждения (тезиса доказательства) осуществляется через опровержение отрицания этого суждения — антитезиса. Этот способ доказательства основывается на истинности закона двойного отрицания в классической логике.

Доказательство утверждения A{\displaystyle A} проводится следующим образом. Сначала принимают предположение, что утверждение A{\displaystyle A} неверно, а затем доказывают, что при таком предположении было бы верно некоторое утверждение B{\displaystyle B}, которое заведомо неверно.

Из определения импликации следует, что, если B{\displaystyle B} ложно, то формула ¬A⇒B{\displaystyle \neg A\Rightarrow B} истинна тогда и только тогда, когда ¬A{\displaystyle \neg A} ложно, следовательно утверждение A{\displaystyle A} истинно.

Полученное противоречие показывает, что исходное предположение было неверным, и поэтому верно утверждение ¬¬A{\displaystyle \neg \neg A}, которое по закону двойного отрицания равносильно утверждению A{\displaystyle A}.

В интуиционистской логике доказательство от противного не принимается, также как не действует закон исключённого третьего.

Доказательство иррациональности числа 2{\displaystyle {\sqrt {2}}}.

Допустим противное: число 2{\displaystyle {\sqrt {2}}} рационально, то есть представляется в виде несократимой дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} — целое число, а n{\displaystyle n} — натуральное. Возведём предполагаемое равенство в квадрат:

2=mn{\displaystyle {\sqrt {2}}={\frac {m}{n}}} ⇒{\displaystyle \Rightarrow } 2=m2n2{\displaystyle 2={\frac {m^{2}}{n^{2}}}}, откуда m2=2n2{\displaystyle m^{2}=2n^{2}}.

Отсюда следует, что m2{\displaystyle m^{2}} чётно, значит, чётно и m{\displaystyle m}; следовательно, m2{\displaystyle m^{2}} делится на 4, а значит, n2{\displaystyle n^{2}} и n{\displaystyle n} тоже чётны. Полученное утверждение противоречит несократимости дроби mn{\displaystyle {\frac {m}{n}}}. Значит, исходное предположение было неверным, и 2{\displaystyle {\sqrt {2}}} — иррациональное число.

Другие примеры

Врач, убеждая пациента в том, что тот не болен гриппом, может рассуждать следующим образом: «Если бы вы действительно были больны гриппом, то у вас была бы повышена температура, был заложен нос и т. д. Но ничего этого нет. Следовательно, нет и гриппа».

Вопрос 1. Методы математических доказательств (метод непосредственной проверки, метод доказательства от противного, метод математической индукции).

1) Метод непосредственной проверки:

Этим методом обычно доказывают равенства или некоторые другие соотношения, а само доказательство заключается в осуществлении последовательности действий, существо и порядок которых определяются

самой формулировкой доказываемого утверждения.

2) Метод доказательства от противного:

Для доказательства этим методом некоторого утверждения А допускают, что утверждение А ложно, то есть истинно его отрицание A*. Далее, с использованием утверждения А* доказывают некоторое заведомо ложное утверждение F и из этого делают вывод о том, что сделанное предположение о ложности А неверно, и поэтому А — истинно. В основе этого метода лежит логическое правило (А* => F, F == л) => А.

3) Метод полной математической индукции:

Этот метод применяют для доказательства таких утверждений, в формулировке которых участвует числовой параметр n, принимающий все значения из множества N натуральных чисел. Процесс доказательства методом полной математической индукции состоит из двух этапов.

А) Доказывают, что утверждение A(t) истинно при t = 1 (это чаще всего удается сделать непосредственной проверкой).

Б) Исходя из допущения, что утверждение A(t) верно для произвольного фиксированного значения t = n доказывают его истинность при t = n + 1.

1 МЕТОД.

Теорема:

Модуль смешанного произведения численно равен объёму параллелепипеда, построенного на векторах ,,.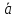

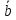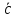Доказательство:

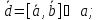
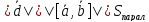
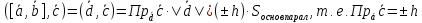
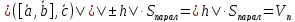
Доказано.

2 Метод.

Докажем одно из следствий аксиом линейного пространства.

Например: Единственность ноль вектора.

Допустим, что есть 2 ноль вектора .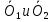

По определению:

1. 

2. 

Положим:

=>

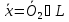
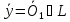
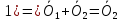
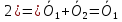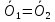
Предположение оказалось неверным => ноль вектор единственен

Доказано.

3 Метод.

Доказать методом математической индукции, что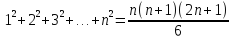

Доказательство:

1) Проверяем верность данной формулы при n=1. Левая часть = 1. Правая часть 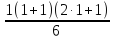=1. Значит формула верна для n=1.

2) Предполагая, что данная ф-ия верна для некоторого n>1, докажем что при n+1 имеет место такая же формула: .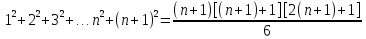

Действительно:

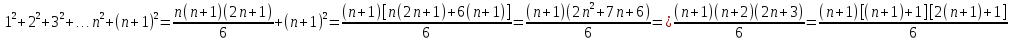
ч.т.д.

Делаем вывод на основании математической индукции, что формула верна для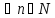

.

Вопрос 2. Формула Бинома Ньютона.

Для любого натурального числа n справедлива формула:

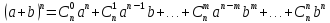– формула Бинома Ньютона.

Доказательство:

Метод математической индукции.

1) Проверяем верность формулы при n=1:

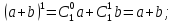
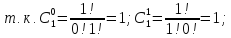
2) Предполагая, что формула верна для некоторого n, покажем, что она верна для n+1 т.е. докажем справедливость формулы:

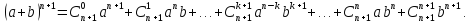
Действительно, используя сначала свойства степени с натуральным показателем, далее исходную формулу Бинома Ньютона и правило перемножения многочленов получим:

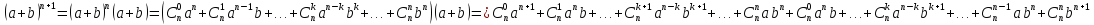
Приводя подобные члены имеем:

,

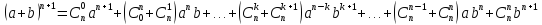откуда в силу того, что

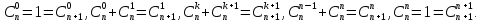
Из 1) и 2) на основании метода математической индукции заключаем, что формула верна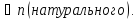

Теорема Доказана.

Следствия:

1)Число всех членов разложения на единицу больше показателя Бинома. Это видно из самой формулы.

2)Сумма показателей степени при a и b в любом слагаемом разложения равна n – показателю степени Бинома.

3)Биномиальные коэффициенты, равноудалённые от концов разложения равны между собой, т.к.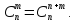

4) Общий член разложения имеет вид:

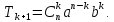
Положив k=0,1,2…n получаем первый, второй и другие члены разложения.

Например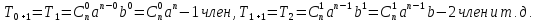

5)Сумма всех биномиальных коэффициентов равна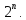

Действительно, полагая a=b=1 получим:

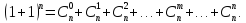
6)Число всех подмножеств n-элементного множества равно .

Также формула имеет вид

Доведение до абсурда — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 ноября 2018; проверки требуют 3 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 ноября 2018; проверки требуют 3 правки.

Доведение до абсурда (лат. reductio ad absurdum), или апагогия («сведе́ние», др.-греч. Εις άτοπον απαγωγή), — логический приём, которым доказывается несостоятельность какого-нибудь мнения таким образом, что или в нём самом, или же в вытекающих из него следствиях обнаруживается противоречие.

Частным случаем доведения до абсурда является доказательство от противного.

Метод приведения к абсурду используется в математической логике в виде умозаключения^[1]. Если требуется доказать истинность некоторого утверждения A{\displaystyle {\mathfrak {A}}}, то образуют отрицание этого утверждения A¯{\displaystyle {\overline {\mathfrak {A}}}} и находят такое утверждение B{\displaystyle {\mathfrak {B}}}, что оказывается возможным одновременно доказать выводимости A¯⊢B{\displaystyle {\overline {\mathfrak {A}}}\vdash {\mathfrak {B}}} и A¯⊢B¯{\displaystyle {\overline {\mathfrak {A}}}\vdash {\overline {\mathfrak {B}}}}, то есть прийти к абсурду. На основании этого делают логическое заключение, что утверждение A{\displaystyle {\mathfrak {A}}} истинно.

Метод приведения к абсурду основан на тождественно истинном высказывании: ((A¯⇒B)∧(A¯⇒B¯))⇒A{\displaystyle (({\overline {\mathfrak {A}}}\Rightarrow {\mathfrak {B}})\land ({\overline {\mathfrak {A}}}\Rightarrow {\overline {\mathfrak {B}}}))\Rightarrow {\mathfrak {A}}}. Следовательно, формула A{\displaystyle {\mathfrak {A}}} выводима из формул A¯⇒B{\displaystyle {\overline {\mathfrak {A}}}\Rightarrow {\mathfrak {B}}} и A¯⇒B¯{\displaystyle {\overline {\mathfrak {A}}}\Rightarrow {\overline {\mathfrak {B}}}}.

Необходимо различать логическое безэмоциональное упрощение высказывания и приём пропаганды, когда софист опровергает мнение, искусственно усиленное до абсурда. Также абсурдность обсуждаемого высказывания должна оцениваться в контексте цели беседы (решаемой проблемы).

Примеры[править | править код]

• Земля не может быть плоской; в противном случае мы бы обнаружили, что люди падают с края. Пример утверждает, что отрицание предпосылки привело бы к нелепому выводу вопреки свидетельству наших чувств.
• Нет наименьшего положительного рационального числа, потому что, если бы оно было, то его можно было бы разделить на два, чтобы получить меньшее. Это математическое доказательство от противоречия, в котором утверждается, что отрицание предпосылки приведет к логическому противоречию (существует «наименьшее» число, и все же число меньше его).

• В 2011 году власти Австрии разрешили пастафарианину Нико Альму сфотографироваться на водительское удостоверение с дуршлагом на голове как религиозным головным убором. Нико Альм подал соответствующее заявление три года назад, тем самым используя аргумент reductio ad absurdum (сведение к абсурду) против разрешения мусульманам фотографироваться на документы в хиджабах. Так как фотографии с головными уборами разрешены в Австрии только из религиозных побуждений, он обосновал свой поступок принадлежностью к пастафарианству ^[2]. «Моя главная цель — заставить людей задуматься над адекватностью системы», — заявил он^[3].

• Эдельман С.Л. Математическая логика. — М.: Высшая школа, 1975. — 176 с.

Доказательство от противного Википедия

Доказательство «от противного» (лат. contradictio in contrarium) в математике — вид доказательства, при котором «доказывание» некоторого суждения (тезиса доказательства) осуществляется через опровержение отрицания этого суждения — антитезиса. Этот способ доказательства основывается на истинности закона двойного отрицания в классической логике.

Схема доказательства

Доказательство утверждения A{\displaystyle A} проводится следующим образом. Сначала принимают предположение, что утверждение A{\displaystyle A} неверно, а затем доказывают, что при таком предположении было бы верно некоторое утверждение B{\displaystyle B}, которое заведомо неверно.

Из определения импликации следует, что, если B{\displaystyle B} ложно, то формула ¬A⇒B{\displaystyle \neg A\Rightarrow B} истинна тогда и только тогда, когда ¬A{\displaystyle \neg A} ложно, следовательно утверждение A{\displaystyle A} истинно.

Полученное противоречие показывает, что исходное предположение было неверным, и поэтому верно утверждение ¬¬A{\displaystyle \neg \neg A}, которое по закону двойного отрицания равносильно утверждению A{\displaystyle A}.

В интуиционистской логике доказательство от противного не принимается, также как не действует закон исключённого третьего.

Пример

Доказательство иррациональности числа 2{\displaystyle {\sqrt {2}}}.

Допустим противное: число 2{\displaystyle {\sqrt {2}}} рационально, то есть представляется в виде несократимой дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} — целое число, а n{\displaystyle n} — натуральное. Возведём предполагаемое равенство в квадрат:

2=mn{\displaystyle {\sqrt {2}}={\frac {m}{n}}} ⇒{\displaystyle \Rightarrow } 2=m2n2{\displaystyle 2={\frac {m^{2}}{n^{2}}}}, откуда m2=2n2{\displaystyle m^{2}=2n^{2}}.

Отсюда следует, что m2{\displaystyle m^{2}} чётно, значит, чётно и m{\displaystyle m}; следовательно, m2{\displaystyle m^{2}} делится на 4, а значит, n2{\displaystyle n^{2}} и n{\displaystyle n} тоже чётны. Полученное утверждение противоречит несократимости дроби mn{\displaystyle {\frac {m}{n}}}. Значит, исходное предположение было неверным, и 2{\displaystyle {\sqrt {2}}} — иррациональное число.

Другие примеры

Врач, убеждая пациента в том, что тот не болен гриппом, может рассуждать следующим образом: «Если бы вы действительно были больны гриппом, то у вас была бы повышена температура, был заложен нос и т. д. Но ничего этого нет. Следовательно, нет и гриппа».

См. также

Доказательство от противного Википедия

Доказательство «от противного» (лат. contradictio in contrarium) в математике — вид доказательства, при котором «доказывание» некоторого суждения (тезиса доказательства) осуществляется через опровержение отрицания этого суждения — антитезиса. Этот способ доказательства основывается на истинности закона двойного отрицания в классической логике.

Схема доказательства[ | ]

Доказательство утверждения A{\displaystyle A} проводится следующим образом. Сначала принимают предположение, что утверждение A{\displaystyle A} неверно, а затем доказывают, что при таком предположении было бы верно некоторое утверждение B{\displaystyle B}, которое заведомо неверно.

Из определения импликации следует, что, если B{\displaystyle B} ложно, то формула ¬A⇒B{\displaystyle \neg A\Rightarrow B} истинна тогда и только тогда, когда ¬A{\displaystyle \neg A} ложно, следовательно утверждение A{\displaystyle A} истинно.

Полученное противоречие показывает, что исходное предположение было неверным, и поэтому верно утверждение ¬¬A{\displaystyle \neg \neg A}, которое по закону двойного отрицания равносильно утверждению A{\displaystyle A}.

В интуиционистской логике доказательство от противного не принимается, также как не действует закон исключённого третьего.

Пример[ |

Доказательство от противного — Карта знаний

• Доказательство «от противного» (лат. contradictio in contrarium) в математике — вид доказательства, при котором «доказывание» некоторого суждения (тезиса доказательства) осуществляется через опровержение отрицания этого суждения — антитезиса. Этот способ доказательства основывается на истинности закона двойного отрицания в классической логике.

Источник: Википедия

Связанные понятия

Парадоксы импликации — это парадоксы, возникающие в связи с содержанием условных утверждений классической логики. Главная функция этих утверждений — обоснование одних утверждений ссылкой на другие. Логическая ошибка — в логике, философии и прочих науках, изучающих познание, ошибка, связанная с нарушением логической правильности умозаключений. Ошибочность обусловлена каким-либо логическим недочётом в доказательстве, что делает доказательство в целом неверным. Парадокс лжеца — семейство логических парадоксов, классический вариант которого гласит… Зако́н доста́точного основа́ния — принцип, согласно которому каждое осмысленное выражение (понятие, суждение) может считаться достоверным только в том случае, если оно было доказано, то есть были приведены достаточные основания, в силу которых его можно считать истинным. Парадокс Ябло (англ. Yablo’s paradox) — это логический парадокс, похожий на парадокс лжеца. Был опубликован Стефаном Ябло в 1993 году. Важность этого парадокса в том, что, хотя он похож на парадокс лжеца и разные его варианты, этот парадокс, по крайней мере на первый взгляд, избегает самореференции. Правда, многие считают, что это только на первый взгляд, и самореференция «спрятана» внутри парадокса.

Упоминания в литературе

Это необходимо в точных науках, юридической практике. Большое применение находит закон исключенного третьего в процессе доказательства, например доказательства от противного. Кому не нужна социология? (доказательство от противного.) Доказательство от противного представляет собой некоторый мысленный эксперимент, при котором в исследуемую модель искусственно вводится параметр виртуальной абберации. Например, утверждается, что параллельные прямые пересекутся, или скорость звука будет меньше/больше 1/3 км/с[21], и анализируются последствия с выводом о том, что подобное невозможно. Они могут сопровождаться прямыми доказательствами или доводами, которые обосновывают справедливость выдвинутого тезиса, а также доводами или доказательствами от противного, когда истинность выдвигаемого тезиса доказывается методом опровержения различных предположений, противоположных доказываемому.

Связанные понятия (продолжение)

Доказательство — это процесс (метод) установления истины, логическая операция обоснования истинности утверждения с помощью фактов и связанных с ними суждений. С помощью совокупности логических приёмов истинность какого-либо суждения обосновывается исходя из других истинных суждений. Логический квадрат — это схематичный способ классификации суждений. Он имеет форму геометрического квадрата, чья система классификации включает все атрибутивные (единичные, общие и частные) суждения. Причем общие и единичные суждения рассматриваются как тождественные объему субъекта. Аксио́ма (др.-греч. ἀξίωμα «утверждение, положение») или постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами. Мнимый парадокс — ложный парадокс, возникающий из-за неверного хода рассуждений. Математическое доказательство — рассуждение с целью обоснования истинности какого-либо утверждения (теоремы), цепочка логических умозаключений, показывающая, что при условии истинности некоторого набора аксиом и правил вывода утверждение верно. В зависимости от контекста, может иметься в виду доказательство в рамках некоторой формальной системы (построенная по специальным правилам последовательность утверждений, записанная на формальном языке) или текст на естественном языке, по которому при необходимости… Опровержение — рассуждение, направленное против тезиса с целью установления факта его ложности (иногда недоказанности). Недоказу́емые утвержде́ния в какой-либо теории — утверждения, которые нельзя ни доказать, ни опровергнуть в рамках этой теории. Теорема Гёделя о неполноте говорит, что в каждой достаточно сложной непротиворечивой теории, включающей в себя формальную арифметику, имеется недоказуемое утверждение. Однако нахождение достаточно простых утверждений такого рода и доказательство их недоказуемости — сложная задача. Гипотеза в математике — утверждение, которое на основе доступной информации представляется с высокой вероятностью верным, но для которого не удаётся получить математическое доказательство. Математическая гипотеза является открытой математической проблемой, и каждую нерешённую математическую проблему, которая является проблемой разрешимости, можно сформулировать в форме гипотезы. Однако в виде гипотезы может быть сформулирована не всякая математическая проблема. Например, конкретное решение некоторой… Тезис Дюэма — Куайна — утверждение о невозможности окончательного определения истинности научной теории. Инду́кция (лат. inductio — наведение, от лат. inducere — влечь за собой, установить) — процесс логического вывода на основе перехода от частного положения к общему. Индуктивное умозаключение связывает частные предпосылки с заключением не строго через законы логики, а скорее через некоторые фактические, психологические или математические представления.Объективным основанием индуктивного умозаключения является всеобщая связь явлений в природе.

Подробнее: Индуктивное умозаключение

Онтологи́ческий аргуме́нт, или Онтологическое доказательство бытия Бога, — одна из категорий аргументов, относящихся к вопросу существования Бога, появившаяся в христианской теологии. Не существует точных критериев для классификации онтологических аргументов, но аргументы типично начинаются с определения Бога, а заканчиваются подведением итогов о необходимости его существования, используя главным образом причины априори и эмпирические наблюдения. Парадо́кс во́ронов (англ. Raven paradox), известный также как парадокс Гемпеля (нем. Hempels paradox) или во́роны Гемпеля — парадокс подтверждения, сформулированный немецким математиком Карлом Густавом Гемпелем в 1940-х годах, для иллюстрации того, что индуктивная логика иногда входит в противоречие с интуицией. Наиболее распространённый метод разрешения этого парадокса состоит в применении теоремы Байеса, которая соотносит условную и предельную вероятность стохастических событий. Доказа́тельство — рассуждение по определенным правилам, обосновывающее какое-либо утверждение. В разных областях науки и человеческой деятельности этот термин имеет разные значения. Саморефере́нция (самоотносимость) — явление, которое возникает в системах высказываний в тех случаях, когда некое понятие ссылается само на себя. Иначе говоря, если какое-либо выражение является одновременно самой функцией и аргументом этой функции. Конти́нуум-гипо́теза (проблема континуума, первая проблема Гильберта) — выдвинутое в 1877 году Георгом Кантором предположение о том, что любое бесконечное подмножество континуума является либо счётным, либо континуальным. Другими словами, гипотеза предполагает, что мощность континуума — наименьшая, превосходящая мощность счётного множества, и «промежуточных» мощностей между счетным множеством и континуумом нет, в частности, это предположение означает, что для любого бесконечного множества действительных… Не следует путать с фальсификацией.Фальсифици́руемость (принципиальная опровержимость утверждения, опроверга́емость, крите́рий По́ппера) — критерий научности эмпирической или иной теории, претендующей на научность. Сформулирован К. Р. Поппером в 1935 году. Теория удовлетворяет критерию Поппера (является фальсифицируемой и, соответственно, научной) в том случае, если существует возможность её экспериментального или иного опровержения. Согласно этому критерию, высказывания или системы высказываний…

Подробнее: Фальсифицируемость

Противоположные суждения — так называются два суждения, имеющие одно и то же подлежащее и сказуемое, но различающиеся между собой по количеству или качеству. Если назвать A — общеутвердительные суждения; E — общеотрицательные; I — частноутвердительные; O — частноотрицательные, то можно составить квадрат, на котором все отношения противоположности будут выяснены графически. Основания математики — математическая система, разработанная с целью обеспечить вывод математического знания из небольшого числа чётко сформулированных аксиом с помощью логических правил вывода, тем самым гарантируя надёжность математических истин. Основания математики включают в себя три компонента. Доведение до абсурда (лат. reductio ad absurdum), или апагогия («сведе́ние», др.-греч. Εις άτοπον απαγωγή), — логический приём, которым доказывается несостоятельность какого-нибудь мнения таким образом, что или в нём самом, или же в вытекающих из него следствиях обнаруживается противоречие. Неконструктивное доказательство (неэффективное доказательство) — класс математических доказательств, доказывающих лишь существование в заданном (как правило, бесконечном) множестве элемента, удовлетворяющего заданным свойствам, но не дающее никакой информации о других свойствах элемента, то есть не позволяющие ни предъявить его, ни приблизительно описать. Доказательства, которые доказывают существование элемента, предъявляя способ получения этого элемента, называются конструктивными. Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел. Для этого сначала проверяется истинность утверждения с номером 1 — база (базис) индукции, а затем доказывается, что если верно утверждение с номером n, то верно и следующее утверждение с номером n + 1 — шаг индукции, или индукционный переход. Презу́мпция (от лат. praesumptio — предположение, ожидание, надежда) — предположение, которое считается истинным до тех пор, пока ложность такого предположения не будет бесспорно доказана. Презумпции широко используются в юриспруденции и в естественных науках, во втором случае — зачастую неявно. Алгоритмическая разрешимость — свойство формальной теории обладать алгоритмом, определяющим по данной формуле, выводима она из множества аксиом данной теории или нет. Теория называется разрешимой, если такой алгоритм существует, и неразрешимой, в противном случае. Вопрос о выводимости в формальной теории является частным, но вместе с тем важнейшим случаем более общей проблемы разрешимости. «Философский зомби» (англ. philosophical zombie, также употребляются англ. p-zombie, англ. p-zed) — гипотетическое существо, которое неотличимо от нормального человека за исключением того, что у него отсутствует сознательный опыт, квалиа (лат. qualia), или способность ощущать (англ. sentience). Когда зомби, например, колет себя острым предметом, то он не чувствует боли. В то же время он ведёт себя так, как будто действительно её чувствует (он может сказать «ай» и отскочить от раздражителя, или сказать… Те́зис Чёрча — Тью́ринга — это гипотеза, постулирующая эквивалентность между интуитивным понятием алгоритмической вычислимости и строго формализованными понятиями частично рекурсивной функции и функции, вычислимой на машине Тьюринга. В связи с интуитивностью исходного понятия алгоритмической вычислимости, данный тезис носит характер суждения об этом понятии и его невозможно строго доказать или опровергнуть. Перед точным определением вычислимой функции математики часто использовали неофициальный термин… Программа Гильберта в математике была сформулирована немецким математиком Давидом Гильбертом в начале 20-го века. Гильберт предположил, что согласованность более сложных систем, таких как реальный анализ, может быть доказана в терминах более простых систем. В конечном счете, непротиворечивость всей математики может быть сведена к простой арифметике. Достове́рность — термин, имеющий различные значения и применяемый в философии, теории судебных доказательств, гносеологии, логике, теории вероятностей, психологии, естествознании и других областях. Единого определения термина не существует, хотя собственное его определение пытались давать многие известные философы (Локк, Лейбниц, Фихте, Кант, Гегель и другие). Дефляционная теория истины или дефляционизм (от лат. deflatio — «сдувание») — семейство теорий, объединяемых заявлениями о том, что утверждения, объявляющие истинность некоего высказывания, не придают свойство истинности такому высказыванию. Логическая вероятность — логическое отношение между двумя предложениями, степень подтверждения гипотезы H свидетельством E. «Тогда́ и то́лько тогда́» — логическая связка эквиваленции между утверждениями, применяемая в логике, математике, философии. Чтобы быть эквиваленцией, связка должна быть идентична стандартному материальному условному высказыванию («только тогда» эквивалентно «если … то»), соединённому со своей противоположностью, откуда и название связки. В результате истинность одного утверждения требует такой же истинности другого, то есть либо оба они истинны, либо оба ложны. Можно спорить о том, передаёт ли выражение… Индуктивное логическое программирование (Inductive Logic Programming, ILP) — раздел машинного обучения, который использует логическое программирование как форму представления примеров, фоновых знаний и гипотез. Получив описания уже известных фоновых знаний и набор примеров, представленных как логическая база фактов, система ILP может породить логическую программу в форме гипотез, объясняющую все положительные примеры и ни одного отрицательного. Сомнение — психическое состояние или состояние ума, в котором возникает воздержание от окончательно определённого суждения, или/и раздвоения (троения и т. п.) его становления, из-за неспособности сознания сделать дискретный однозначный вывод. Если ум не может обнаружить причин, аргументов, которые бы позволили ему прийти к однозначному решению относительно правильности или ошибочности своего мнения, тогда сомнение является отрицательным (то есть фактически блокирование дальнейшего анализа и выводов… Аргументы за и против существования богов, и в частности, Бога авраамических религий предлагались философами, теологами и учёными на протяжении нескольких тысячелетий. В настоящее время в философской терминологии эти вопросы рассматриваются в рамках гносеологии и онтологии.

Подробнее: Вопрос существования Бога

Двухчастная инвенция (лат. inventio — изобретение, выдумка) Льюиса Кэрролла (другое название — «Что черепаха сказала Ахиллесу», англ. What the Tortoise Said to Achilles) — логический парадокс в форме диалога, описанный Кэрроллом в 1895 году.

Подробнее: Парадокс Кэрролла

Силлогистика (др.-греч. συλλογιστικός умозаключающий) — теория логического вывода, исследующая умозаключения, состоящие из т. н. категорических высказываний (суждений). В силлогистике рассматриваются, например, выводы заключения из одной посылки (т. н. непосредственные умозаключения), «сложные силлогизмы», или полисиллогизмы, имеющие не менее трёх посылок. Однако основное внимание силлогистика уделяет теории категорического силлогизма, имеющего ровно две посылки и одно заключение указанного вида…

Подробнее: Силлогистические теории

Заключе́ние — логическая противоположность основанию в логическом выводе. Суждение, считающееся истинным в том случае, когда истинными признаются его предпосылки.В быту понятие используется примерно с тем же значением, обозначая, в широком смысле, любой предположительно правильный вывод или следствие из чего-нибудь, как, например, во фразе «Я пришел к заключению, что вы были правы» или в выражении «заключение экспертов». Верифика́ция (от лат. verum «истинный» + facere «делать») в различных сферах деятельности человека может подразумевать… Теорема Цермело — теорема теории множеств, утверждающая, что на всяком множестве можно ввести такое отношение порядка, что множество будет вполне упорядоченным. Парадокс Скулема — противоречивое рассуждение, описанное впервые норвежским математиком Туральфом Скулемом, связанное с использованием теоремы Лёвенгейма — Скулема для аксиоматической теории множеств. Гипо́теза (др.-греч. ὑπόθεσις «предположение» от ὑπό «снизу, под» + θέσις «тезис») — предположение или догадка; утверждение, предполагающее доказательство, в отличие от аксиом, постулатов, не требующих доказательств. Гипотеза считается научной, если она удовлетворяет научному методу, то есть объясняет все факты, которые гипотеза призвана объяснить; не является логически противоречивой; принципиально проверяема, то есть потенциально может быть проверена критическим экспериментом; не противоречит ранее… Логика первого порядка, называемая иногда логикой или исчислением предикатов — формальное исчисление, допускающее высказывания относительно переменных, фиксированных функций и предикатов. Расширяет логику высказываний. В свою очередь является частным случаем логики высших порядков. Нулевая гипотеза — принимаемое по умолчанию предположение о том, что не существует связи между двумя наблюдаемыми событиями, феноменами. Так, нулевая гипотеза считается верной до того момента, пока нельзя доказать обратное. Опровержение нулевой гипотезы, то есть приход к заключению о том, что связь между двумя событиями, феноменами существует, — главная задача современной науки. Статистика как наука даёт чёткие условия, при наступлении которых нулевая гипотеза может быть отвергнута.

ДОКАЗАТЕЛЬСТВО ОТ ПРОТИВНОГО

ДОКАЗАТЕЛЬСТВО ОТ ПРОТИВНОГО

— косвенное доказательство, при котором истинность тезиса обосновывается не прямо — с помощью аргументов, а посредством антитезиса — положения, противоречащего тезису. Показывая, что антитезис ложен, мы тем самым обосновываем истинность противоположного ему положения — тезиса. Напр., врач, убеждая пациента в том, что тот не болен гриппом, может рассуждать следующим образом: «Если бы вы действительно были больны гриппом, то у вас была бы повышена температура, был заложен нос и т.д. Но ничего этого нет. Следовательно, нет и гриппа». Доказательство некоторого положения от противного — это обоснование истинности данного положения, опирающееся на демонстрацию ложности «противного» (противоречащего) положения и закон исключенного третьего.
Общая структура Д. от п. описывается следующим образом. Нужно доказать некоторое высказывание А. В процессе доказательства сначала формулируется противоположное ему высказывание не-А и предполагается, что оно истинно: допустим, что А ложно, тогда должно быть истинно не-А. Затем из этого якобы истинного антитезиса выводятся следствия — до тех пор, пока либо не получится противоречие, либо такое следствие, которое явным образом противоречит известному истинному высказыванию. Если показано, что не-А ложно, то тем самым обоснована истинность тезиса А (см. ДОКАЗАТЕЛЬСТВО ).

Поделитесь на страничке