Эдс самоиндукции
Изменение тока в катушке вызывает изменение потока сцепления самоиндукции, а следовательно возникает ЭДС.
Явление, при котором ЭДС возникает в контуре или в катушке в результате изменения тока в этом контуре или катушке, называется самоиндукцией.
ЭДС самоиндукции
обозначается 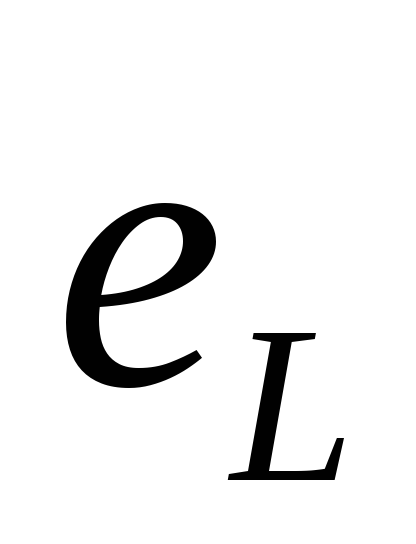 .
.
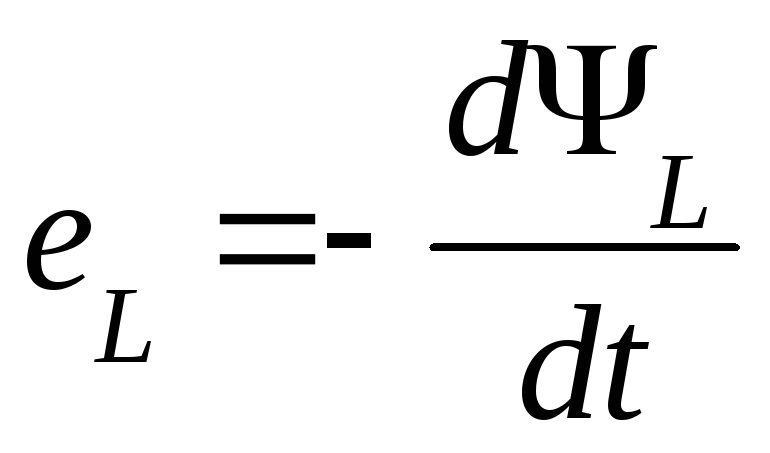
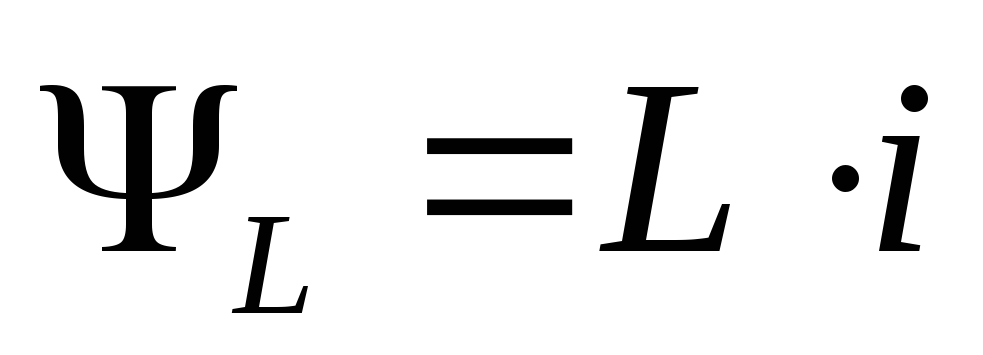
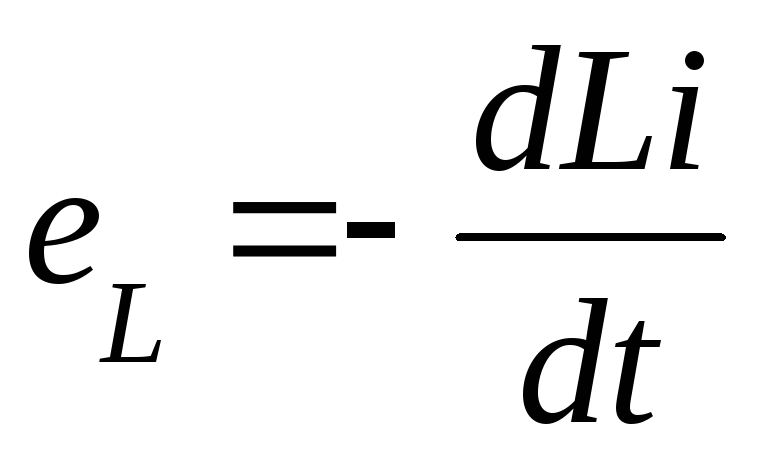
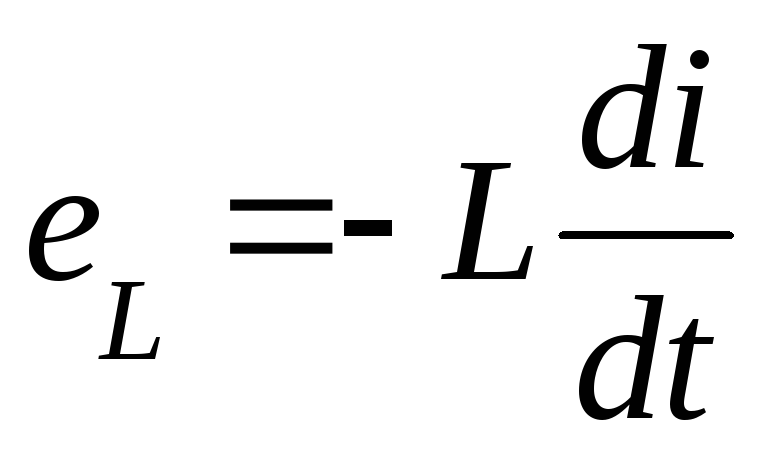
Т.о. ЭДС самоиндукции пропорциональна индуктивности катушки и скорости изменения тока в ней.
Если 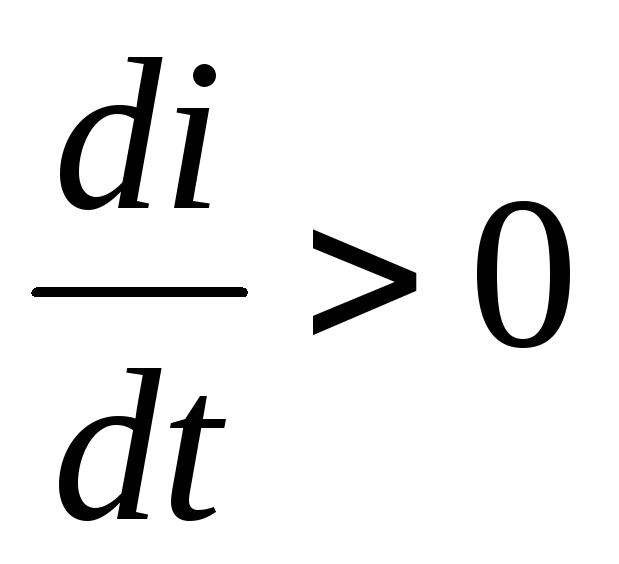 (ток нарастает), то
(ток нарастает), то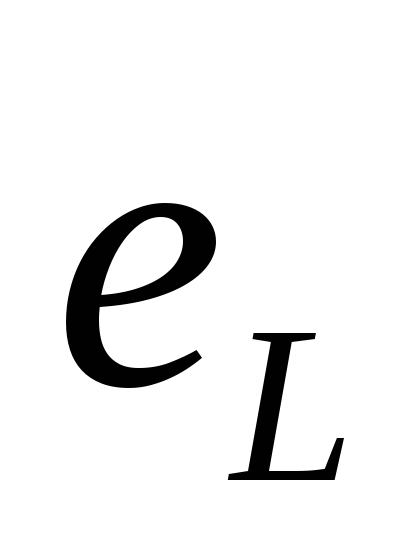 — отрицательна, т.е. направлена навстречу
току (противо ЭДС), если же
— отрицательна, т.е. направлена навстречу
току (противо ЭДС), если же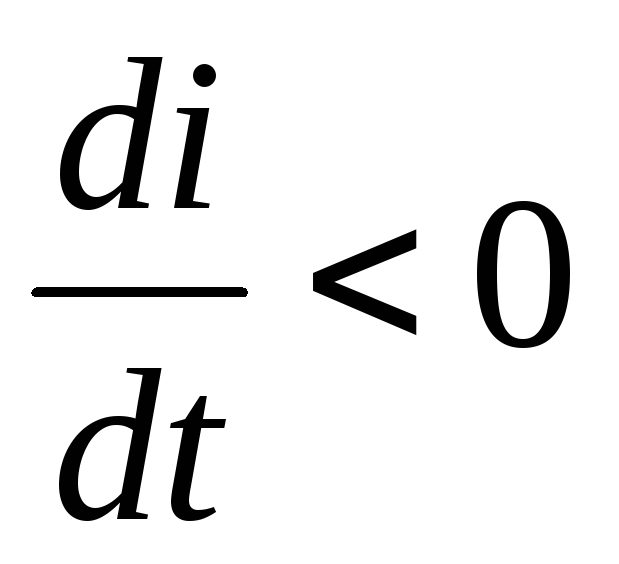 (ток убывает), то
(ток убывает), то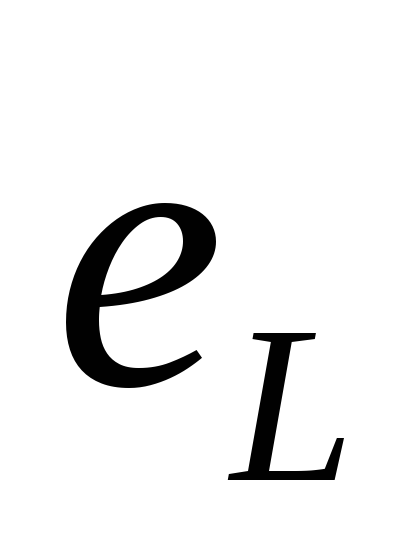 — положительна, т.е. направлена согласно
с током.
— положительна, т.е. направлена согласно
с током.
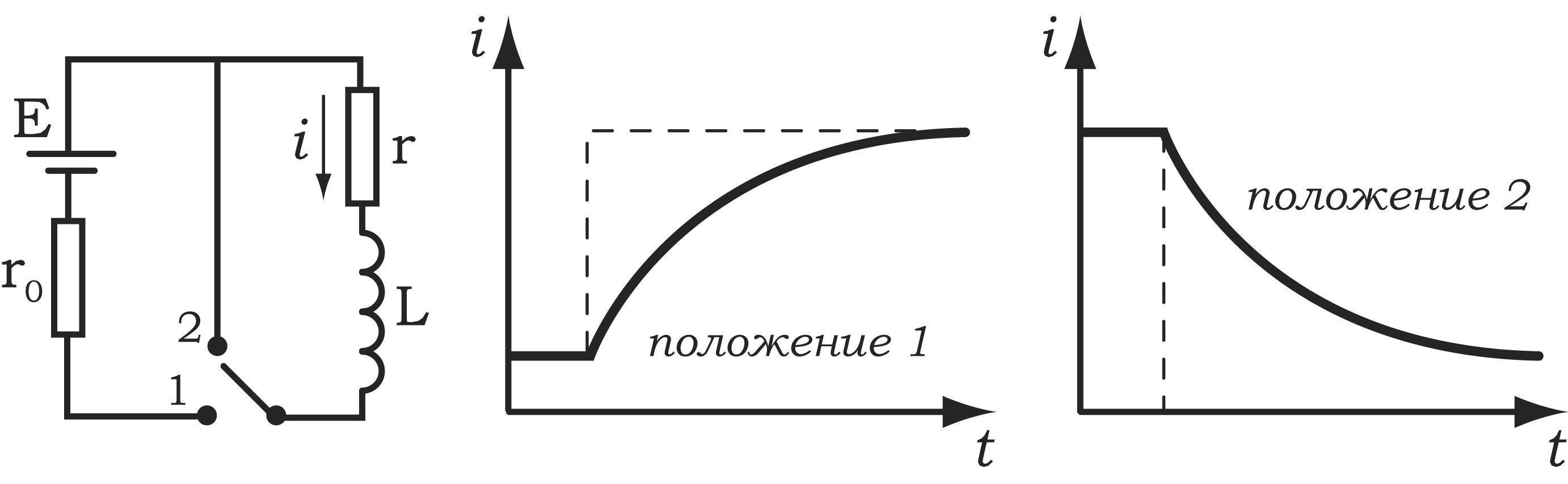
Время нарастания и уменьшения тока характеризуется постоянным временем.
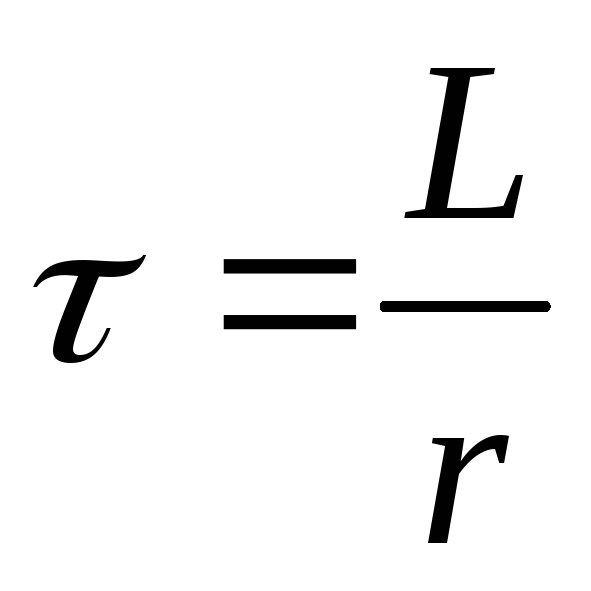

При включении катушки в электрическую цепь вокруг катушки создается магнитное поле, в котором запасается часть энергии, израсходованной источниками.
Величина этой
энергии определяется как: 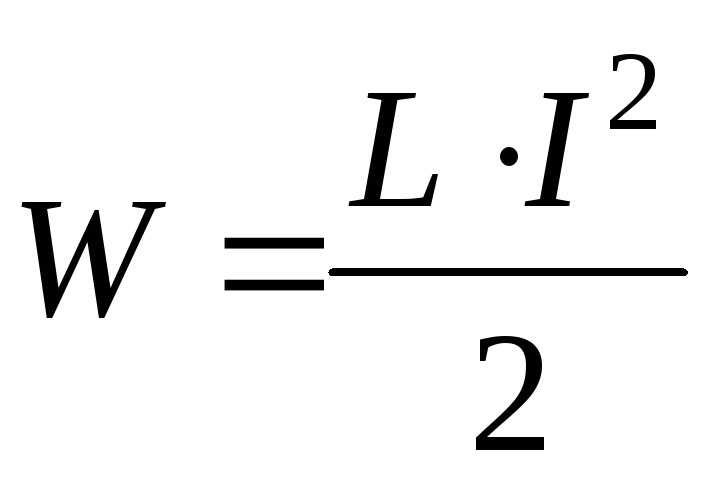
Явление взаимоиндукции
| Если две катушки с током расположены близко друг от друга, то часть магнитного потока первой катушки пронизывает витки второй и наоборот. Такие контуры и катушки называют индуктивно- или магнитосвязанными. |
Магнитный поток 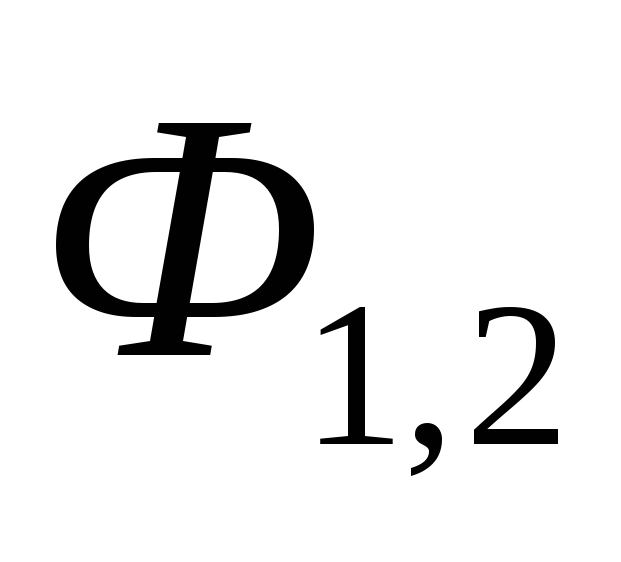
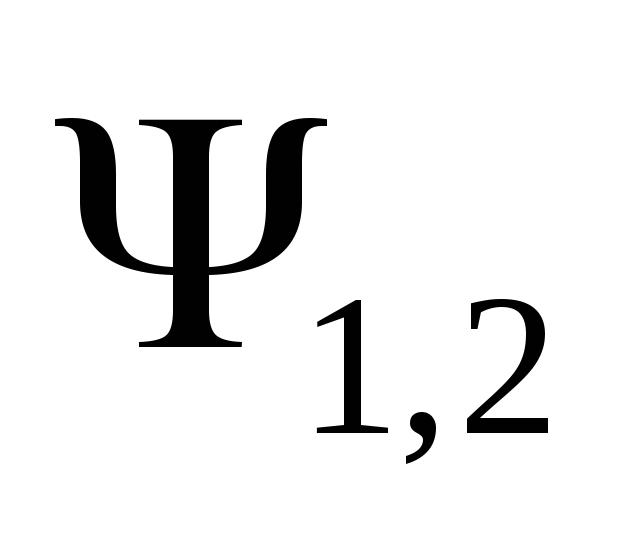 пропорциональны току в катушкеI1,
т. е.
пропорциональны току в катушкеI1,
т. е. 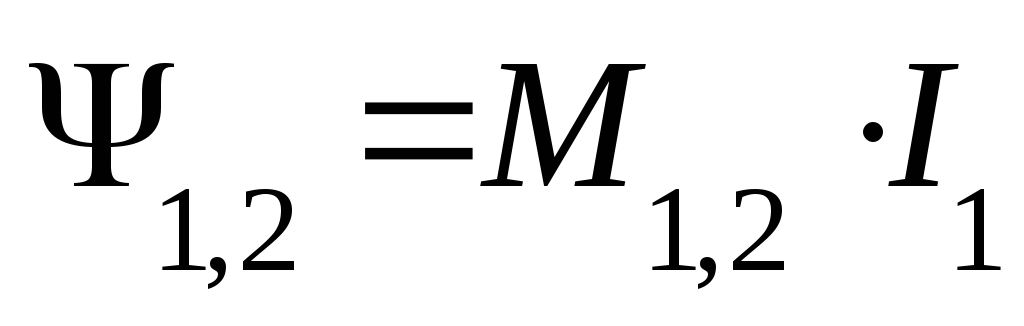
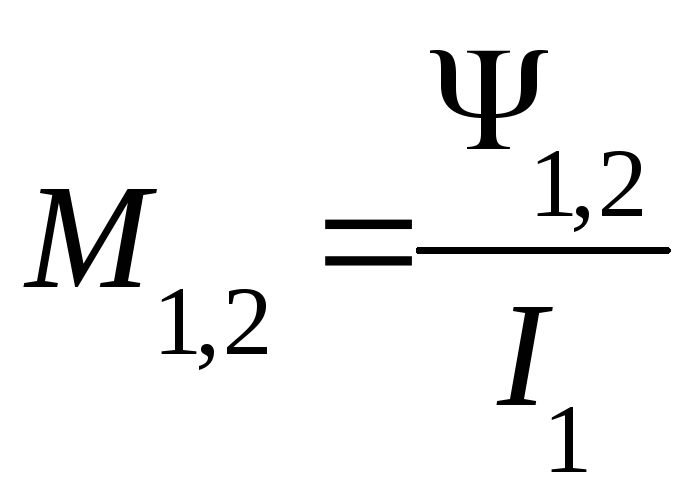
М– взаимная индуктивность двух катушек, равная отношению потокосцепления одной катушки к току другой.
ЭДС, возникающая
при этом в другой катушке будет равна: 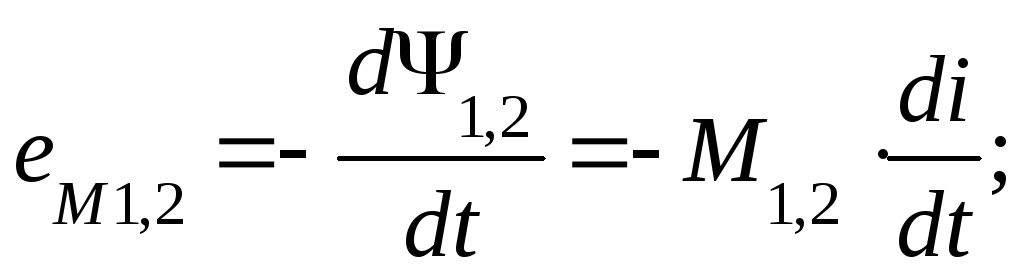
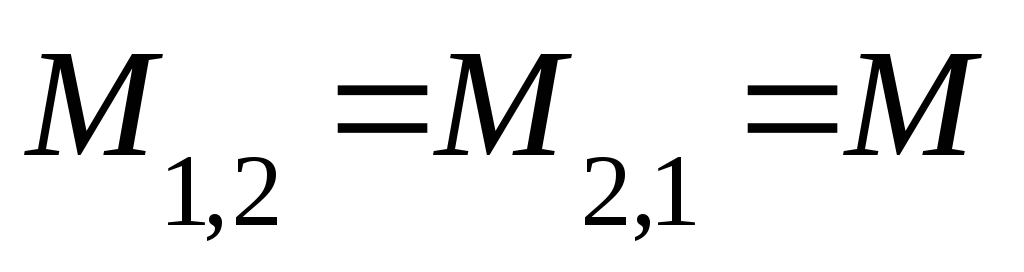
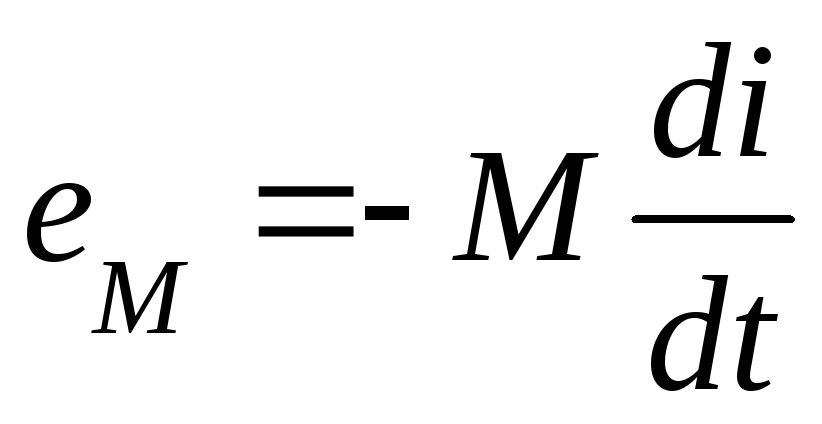
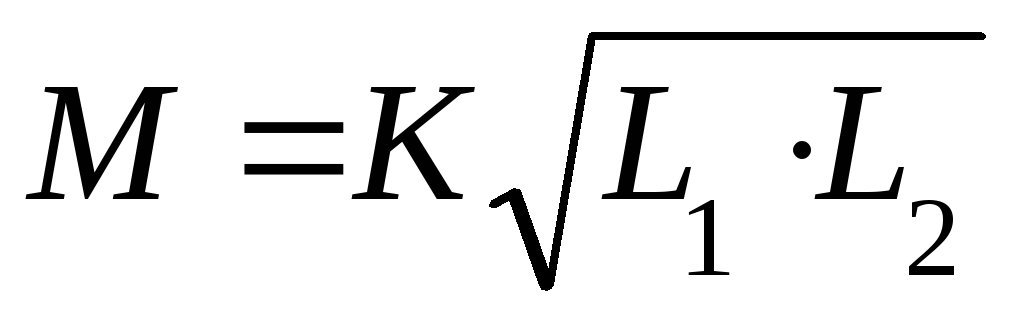 ,
,где K– коэффициент связи двух катушек, зависящий от взаимного их расположения (чем ближе катушка, тем большеKи наоборот).
Однофазный переменный ток
Переменнымназывают такой электрический ток, который с течением времени изменяется по величине и по направлению.
Основным достоинством переменного тока является возможность его трансформации, а также то, то электрические машины и аппараты переменного тока значительно проще и дешевле, чем постоянного тока.
Время, в течении которого ток делает полный цикл своих изменений называется периодом.
Величина, обратная
периоду и численно равная числу периодов
за секунду, называется частотой  .
.
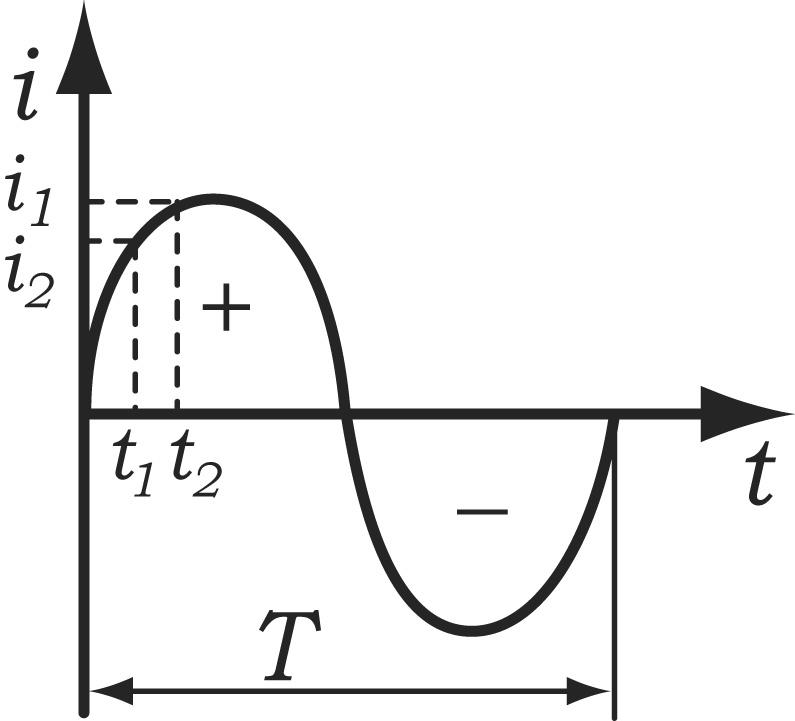
Значение переменного тока в любой момент времени называется мгновенным значением.
Наибольшее из
мгновенных значений называется максимальным, илиамплитудным 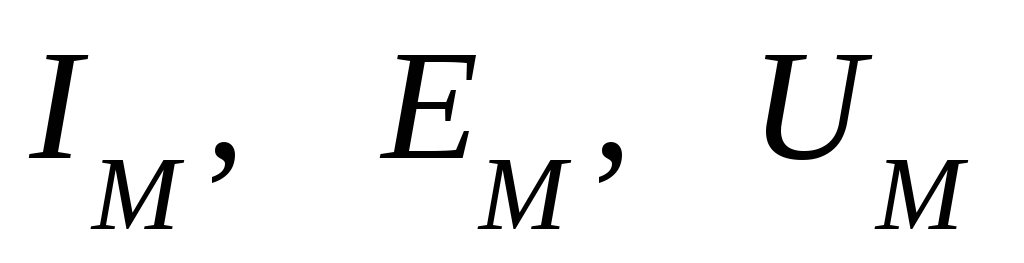 .
.
Получение синусоидальной ЭДС
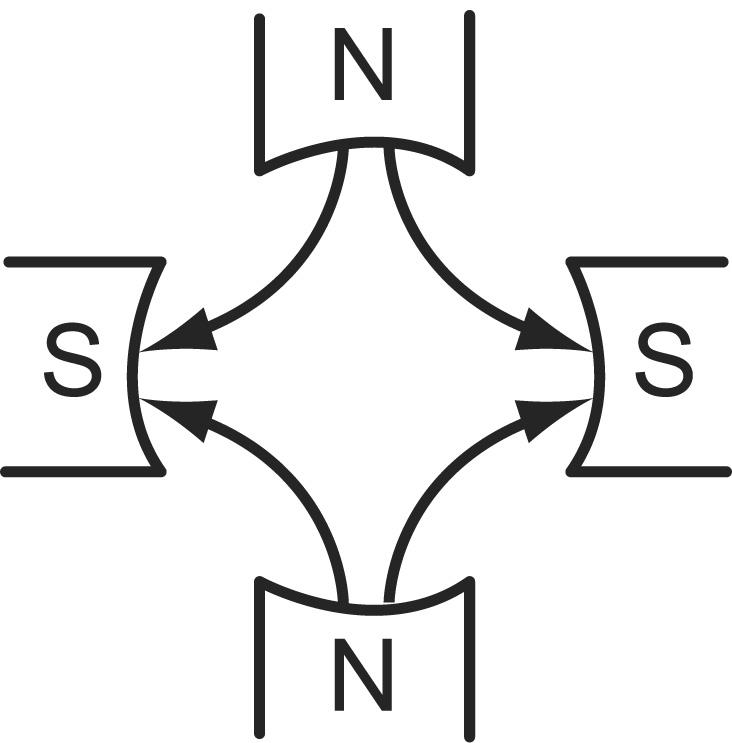
Простейший генератор
переменного тока представляет собой
магнитную систему, состоящую из двух
полюсов, причем, форма полюсов такова,
что магнитная индукция в воздушном
зазоре распределяется по синусоидальному
закону, т.е. значение магнитной индукции
в любой точке 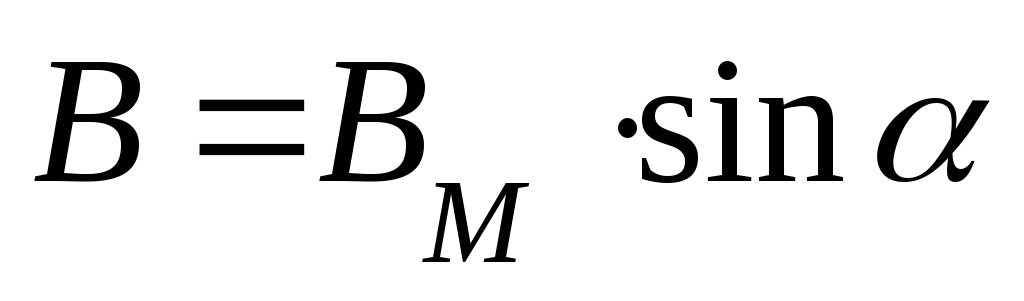 .
.
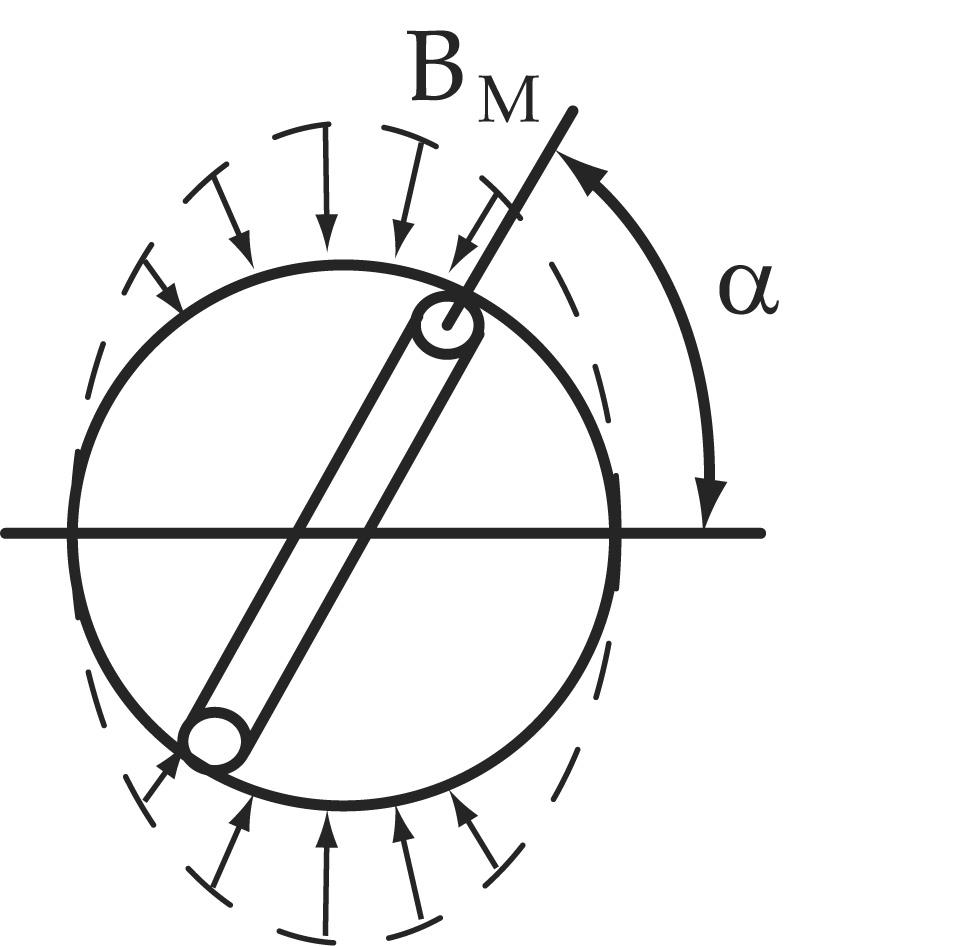
Допустим, за время tрамка развернулась
на угол, тогда
угловая скорость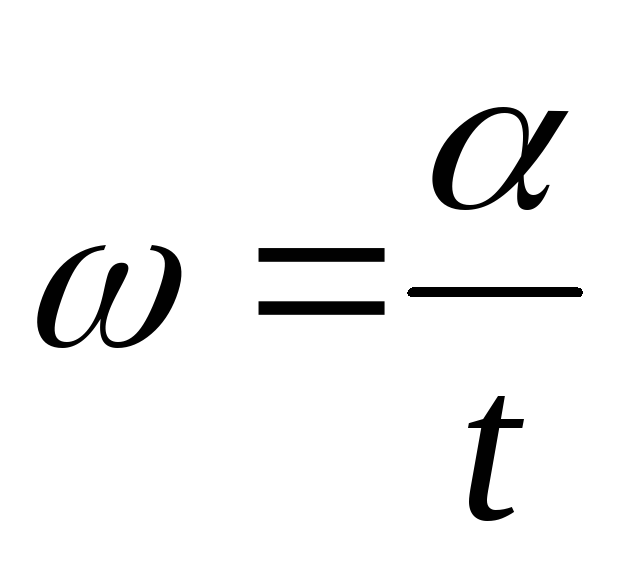 .
.
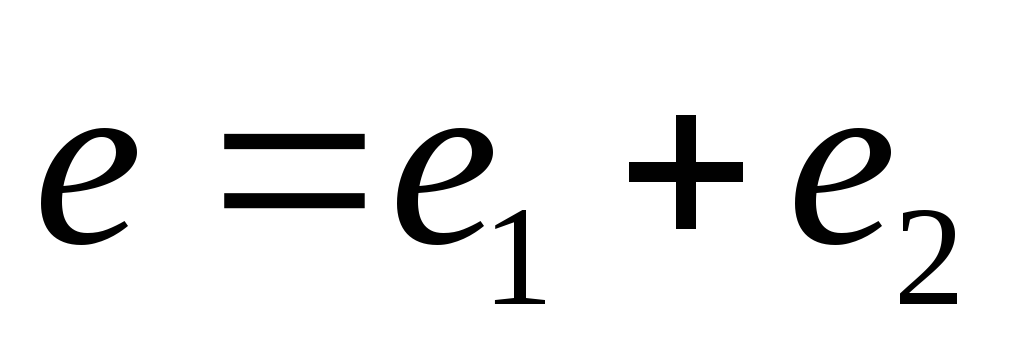
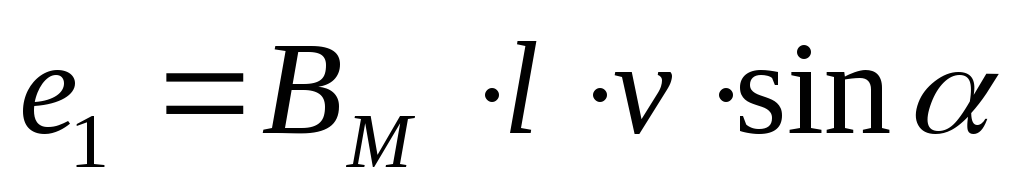
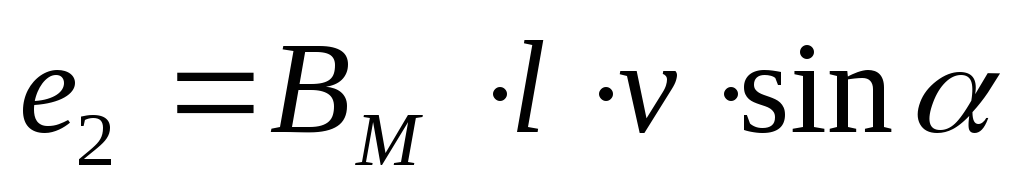
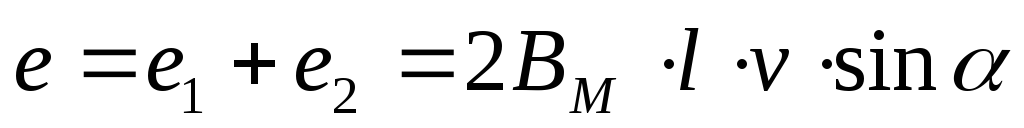
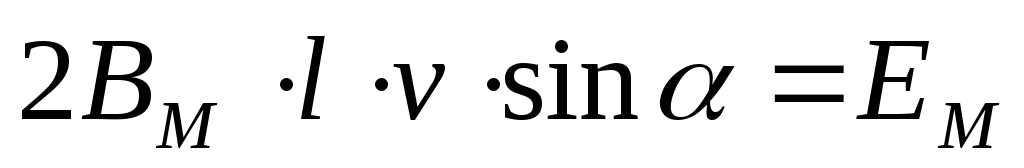
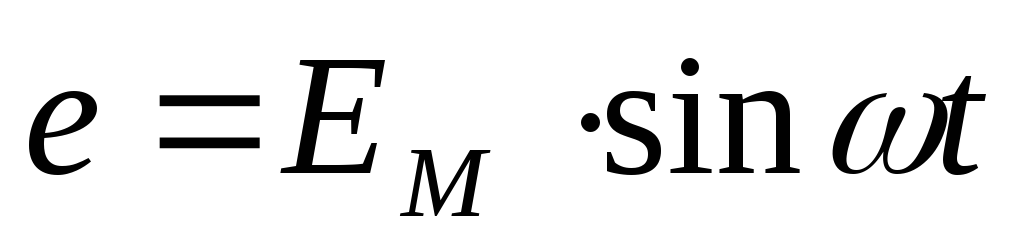
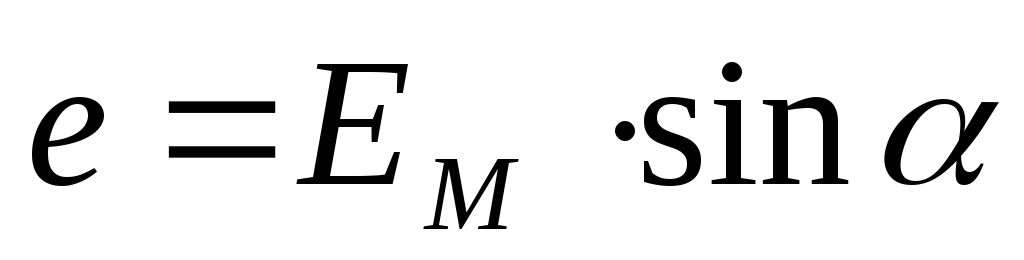

За один оборот
рамка развернется на угол  ,
а время оборота – период (Т), тогда
угловая частота
,
а время оборота – период (Т), тогда
угловая частота определяется:
определяется:
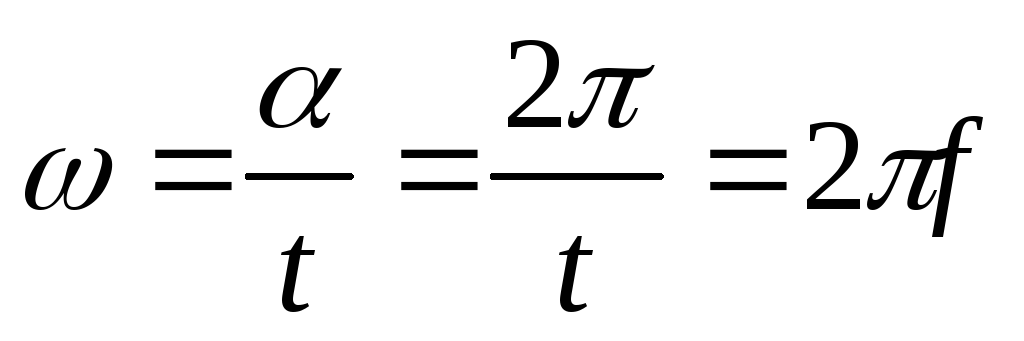
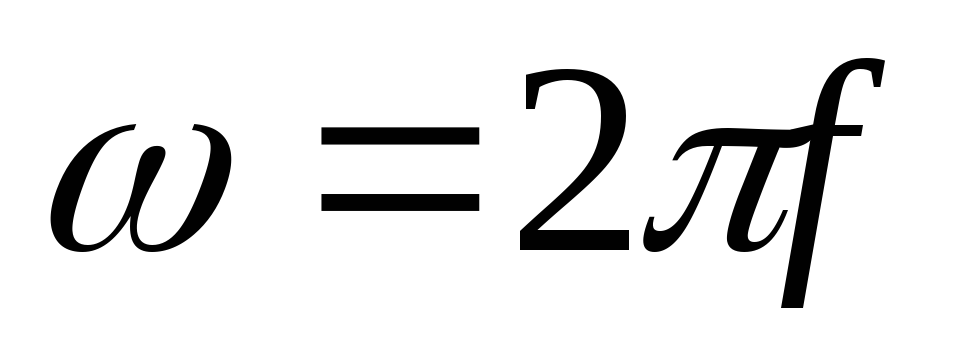
Многополюсные генераторы
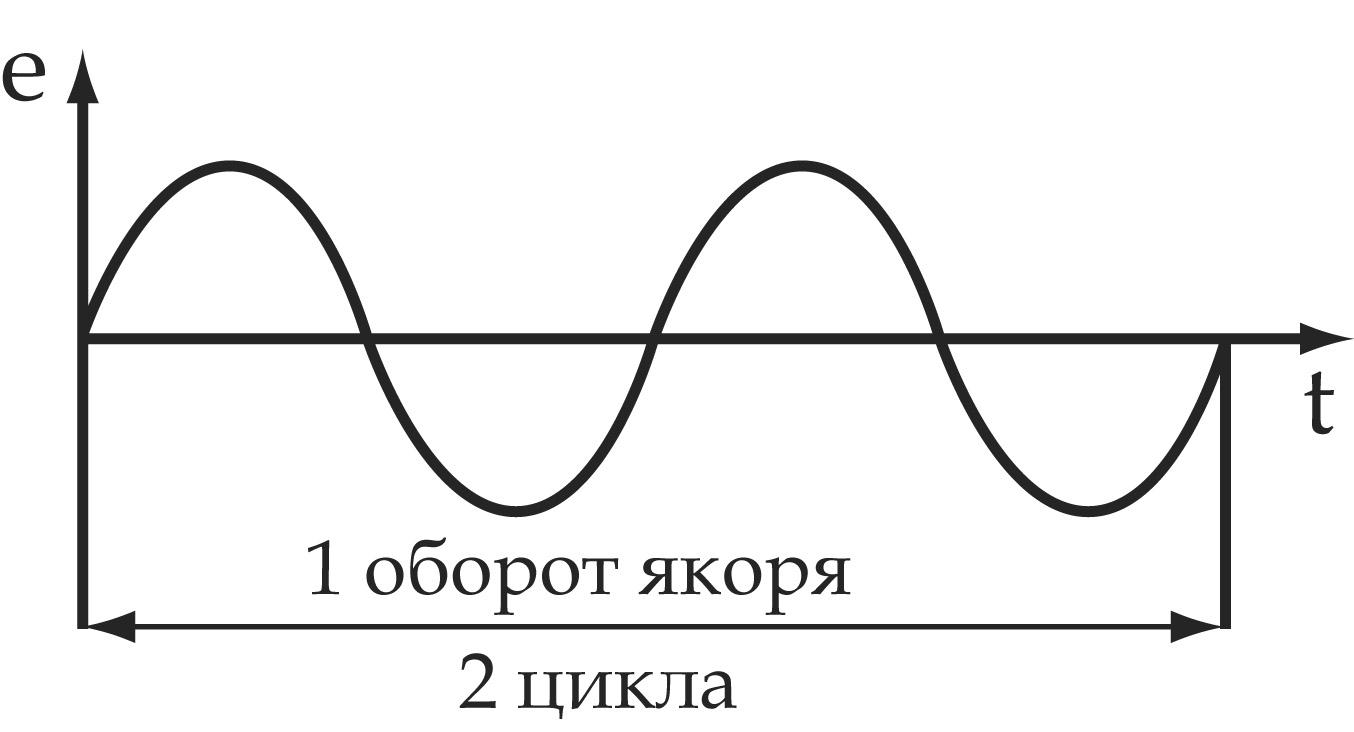
| Для получения промышленной частоты 50Гц якорь двухполюсного генератора должен вращаться со скоростью 50 об/с или 3000 об/мин. Если скорость вращения меньше, то необходимо увеличить число пар полюсов. У многополюсных генераторов за 1 оборот якоря ЭДС совершает Р циклов своих |
изменений,
где Р – число пар полюсов. Если число
оборотов в минуту n,
то число циклов в минуту будет 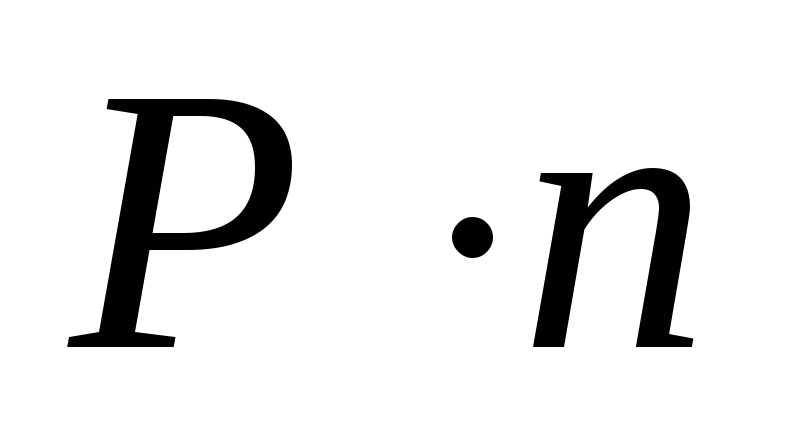 ,
а в секунду
,
а в секунду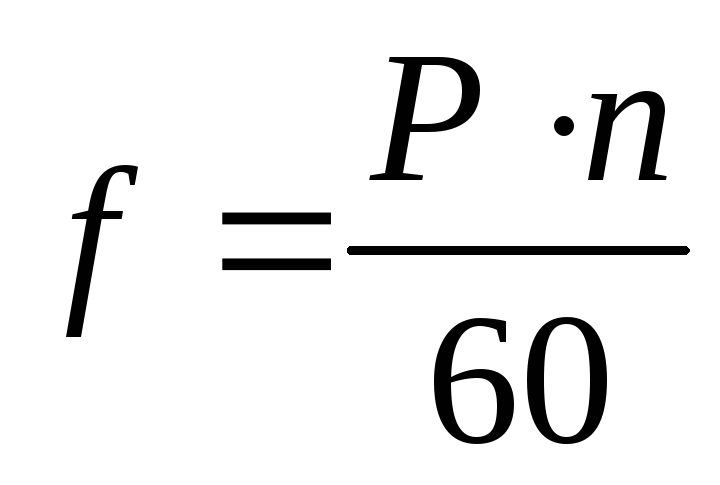
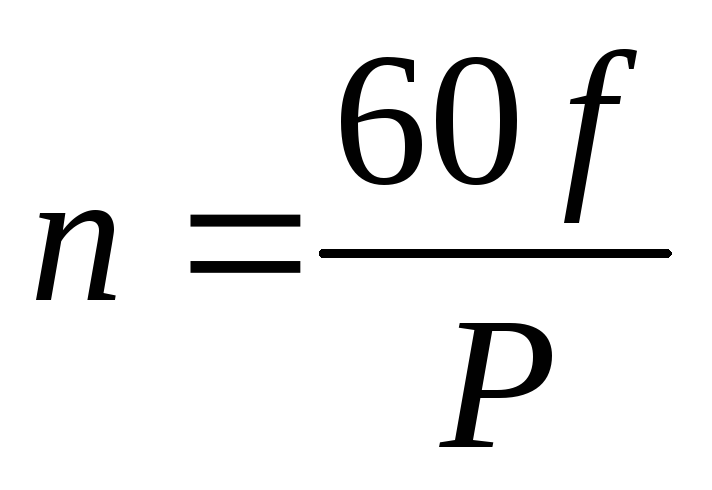
studfile.net
Эдс индукции
Причиной электродвижущей силы может стать изменение магнитного поля в окружающем пространстве. Это явление называетсяэлектромагнитной индукцией. Величина ЭДС индукции в контуре определяется выражением
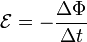
где 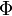 — поток
магнитного поля через
замкнутую поверхность
— поток
магнитного поля через
замкнутую поверхность 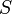 ,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).
,
ограниченную контуром. Знак «−» перед
выражением показывает, что индукционный
ток, созданный ЭДС индукции, препятствует
изменению магнитного потока в контуре
(см. правило
Ленца).
41. Индуктивность, ее единица СИ. Индуктивность длинного соленоида.
Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность [1], краем которой является этот контур.[2][3][4].
В формуле
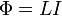
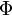 —
магнитный
поток,
—
магнитный
поток,  —
ток в контуре,
—
ток в контуре, 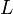 —
индуктивность.
—
индуктивность.
Нередко говорят об индуктивности прямого длинного провода(см.). В этом случае и других (особенно — в не отвечающих квазистационарному приближению) случаях, когда замкнутый контур непросто адекватно и однозначно указать, приведенное выше определение требует особых уточнений; отчасти полезным для этого оказывается подход (упоминаемый ниже), связывающий индуктивность с энергией магнитного поля.
Через индуктивность выражается ЭДС самоиндукции в контуре, возникающая при изменении в нём тока[4]:
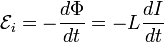 .
.
Из этой формулы следует, что индуктивность численно равна ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
При заданной силе тока индуктивность определяет энергию магнитного поля, создаваемого этим током[4]:
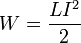 .
.
Обозначение и единицы измерения
В системе единиц СИ индуктивность измеряется в генри[7], сокращенно Гн, в системе СГС — в сантиметрах (1 Гн = 109см)[4]. Контур обладает индуктивностью в один генри, если при изменении тока на один ампер в секунду на выводах контура будет возникать напряжение в один вольт. Реальный, не сверхпроводящий, контур обладает омическим сопротивлением R, поэтому на нём будет дополнительно возникать напряжение U=I*R, где I — сила тока, протекающего по контуру в данное мгновение времени.
Символ  ,
используемый для обозначения индуктивности,
был взят в честь Ленца
Эмилия Христиановича (Heinrich
Friedrich Emil Lenz)[источник не указан 1017 дней].
Единица измерения индуктивности названа
в честь Джозефа
Генри (Joseph
Henry)[8].
Сам термин индуктивность был
предложен Оливером
Хевисайдом (Oliver
Heaviside) в феврале 1886
года[источник не указан 1017 дней].
,
используемый для обозначения индуктивности,
был взят в честь Ленца
Эмилия Христиановича (Heinrich
Friedrich Emil Lenz)[источник не указан 1017 дней].
Единица измерения индуктивности названа
в честь Джозефа
Генри (Joseph
Henry)[8].
Сам термин индуктивность был
предложен Оливером
Хевисайдом (Oliver
Heaviside) в феврале 1886
года[источник не указан 1017 дней].
Электрический
ток, который течет в замкнутом контуре,
создает вокруг себя магнитное поле,
индукция которого, согласно закону
Био-Савара-Лапласа, пропорциональна
току. Сцепленный с контуром магнитный
поток Ф поэтому прямо пропорционален
току I в контуре: 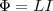 (1) где
коэффициент пропорциональности L
называетсяиндуктивностью
контура. При
изменении в контуре силы тока будет
также изменяться и сцепленный с ним
магнитный поток; значит, в контуре будет
индуцироваться э.д.с. Возникновение
э.д.с. индукции в проводящем контуре при
изменении в нем силы тока
называетсясамоиндукцией. Из
выражения (1) задается единица
индуктивности генри (Гн):
1 Гн — индуктивность контура, магнитный
поток самоиндукции которого при токе
в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В
(1) где
коэффициент пропорциональности L
называетсяиндуктивностью
контура. При
изменении в контуре силы тока будет
также изменяться и сцепленный с ним
магнитный поток; значит, в контуре будет
индуцироваться э.д.с. Возникновение
э.д.с. индукции в проводящем контуре при
изменении в нем силы тока
называетсясамоиндукцией. Из
выражения (1) задается единица
индуктивности генри (Гн):
1 Гн — индуктивность контура, магнитный
поток самоиндукции которого при токе
в 1 А равен 1 Вб: 1 Гн = 1 Вб/с = 1 В
·c/А .
Вычислим
индуктивность бесконечно длинного
соленоида. Полный магнитный поток сквозь
соленоид (потокосцепление) равен
μ0μ(N2I/l)S
. Подставив в (1), найдем 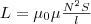 (2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна
(2) т.
е. индуктивность соленоида зависит от
длиныl солениода,
числа его витков N, его , площади S и
магнитной проницаемости μ вещества, из
которого изготовлен сердечник
соленоида. Доказано, что
индуктивность контура зависит в общем
случае только от геометрической формы
контура, его размеров и магнитной
проницаемости среды, в которой он
расположен, и можно провести аналог
индуктивности контура с электрической
емкостью уединенного проводника, которая
также зависит только от формы проводника,
его размеров и диэлектрической
проницаемости среды. Найдем,
применяя к явлению самоиндукции закон
Фарадея, что э.д.с. самоиндукции
равна 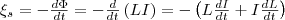 Если
контур не претерпевает деформаций и
магнитная проницаемость среды остается
неизменной (в дальнейшем будет показано,
что последнее условие выполняется не
всегда), то L = const и
Если
контур не претерпевает деформаций и
магнитная проницаемость среды остается
неизменной (в дальнейшем будет показано,
что последнее условие выполняется не
всегда), то L = const и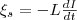 (3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем. Если
ток со временем увеличивается, то
(dI/dt<0) и ξs>0
т. е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его увеличение. Если ток со
временем уменьшается, то (dI/dt>0) и ξs<0
т. е. индукционный ток имеет такое же
направление, как и уменьшающийся ток в
контуре, и замедляет его уменьшение.
Значит, контур, обладая определенной
индуктивностью, имеет электрическую
инертность, заключающуюся в том, что
любое изменение тока уменьшается тем
сильнее, чем больше индуктивность
контура.
(3) где
знак минус, определяемый правилом Ленца,
говорит о том, чтоналичие
индуктивности в контуре приводит к
замедлению изменения тока в нем. Если
ток со временем увеличивается, то
(dI/dt<0) и ξs>0
т. е. ток самоиндукции направлен навстречу
току, обусловленному внешним источником,
и замедляет его увеличение. Если ток со
временем уменьшается, то (dI/dt>0) и ξs<0
т. е. индукционный ток имеет такое же
направление, как и уменьшающийся ток в
контуре, и замедляет его уменьшение.
Значит, контур, обладая определенной
индуктивностью, имеет электрическую
инертность, заключающуюся в том, что
любое изменение тока уменьшается тем
сильнее, чем больше индуктивность
контура.
42. Ток при размыкании и замыкании цепи.
При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Рассмотрим
процесс выключения тока в цепи, содержащей
источник тока с э.д.с. 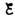 ,
резистор сопротивлением R и
катушку индуктивностью L. Под
действием внешней э. д. с. в цепи течет
постоянный ток
,
резистор сопротивлением R и
катушку индуктивностью L. Под
действием внешней э. д. с. в цепи течет
постоянный ток
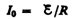
(внутренним сопротивлением источника тока пренебрегаем).
В
момент времени t=0
отключим источник тока. Ток в катушке
индуктивностью L начнет
уменьшаться, что приведет к возникновению
э.д.с. самоиндукции 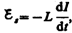 препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=
препятствующей,
согласно правилу Ленца, уменьшению
тока. В каждый момент времени ток в
цепи определяется законом Ома I=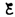 s/R, или
s/R, или
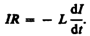 (127.1)
(127.1)
Разделив
в выражении (127.1) переменные,
получим 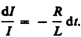 Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
Интегрируя
это уравнение по I (от I0 до I)
и t (от
0 до t),
находим ln (I /I0)
= –Rt/L, или
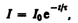 (127.2)
(127.2)
где =L/R — постоянная, называемая временем релаксации. Из (127.2) следует, что есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника тока сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1 на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При
замыкании цепи помимо внешней э. д.
с.  возникает
э. д. с. самоиндукции
возникает
э. д. с. самоиндукции 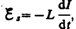 препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома,
препятствующая,
согласно правилу Ленца, возрастанию
тока. По закону Ома, 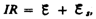 или
или
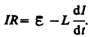
Введя
новую переменную 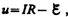 преобразуем
это уравнение к виду
преобразуем
это уравнение к виду
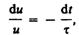
где — время релаксации.

В
момент замыкания (t=0)
сила тока I =
0 и u =
–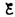 .
Следовательно, интегрируя по и (от
–
.
Следовательно, интегрируя по и (от
–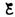 до IR–
до IR–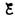 )
и t (от
0 до t),
находим ln[(IR–
)
и t (от
0 до t),
находим ln[(IR–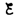 )]/–
)]/–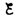 = —t/, или
= —t/, или
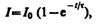 (127.3)
(127.3)
где 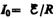 —
установившийся ток (при t).
—
установившийся ток (при t).
Таким
образом, в процессе включения источника
тока нарастание силы тока в цепи задается
функцией (127.3) и определяется кривой 2
на рис. 183. Сила тока возрастает от
начального значения I=0
и асимптотически стремится к установившемуся
значению 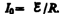 . Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
. Скорость
нарастания тока определяется тем же
временем релаксации =L/R, что
и убывание тока. Установление тока
происходит тем быстрее, чем меньше
индуктивность цепи и больше ее
сопротивление.
Оценим
значение э.д.с. самоиндукции 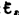 , возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток
, возникающей
при мгновенном увеличении сопротивления
цепи постоянного тока от R0 до R.
Предположим, что мы размыкаем контур,
когда в нем течет установившийся ток 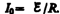 .
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
.
При размыкании цепи ток изменяется по
формуле (127.2). Подставив в нее выражение
дляI0 и ,
получим
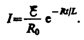
Э.д.с. самоиндукции
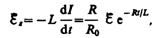
т. е. при значительном увеличении сопротивления цепи (R/R0>>1), обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
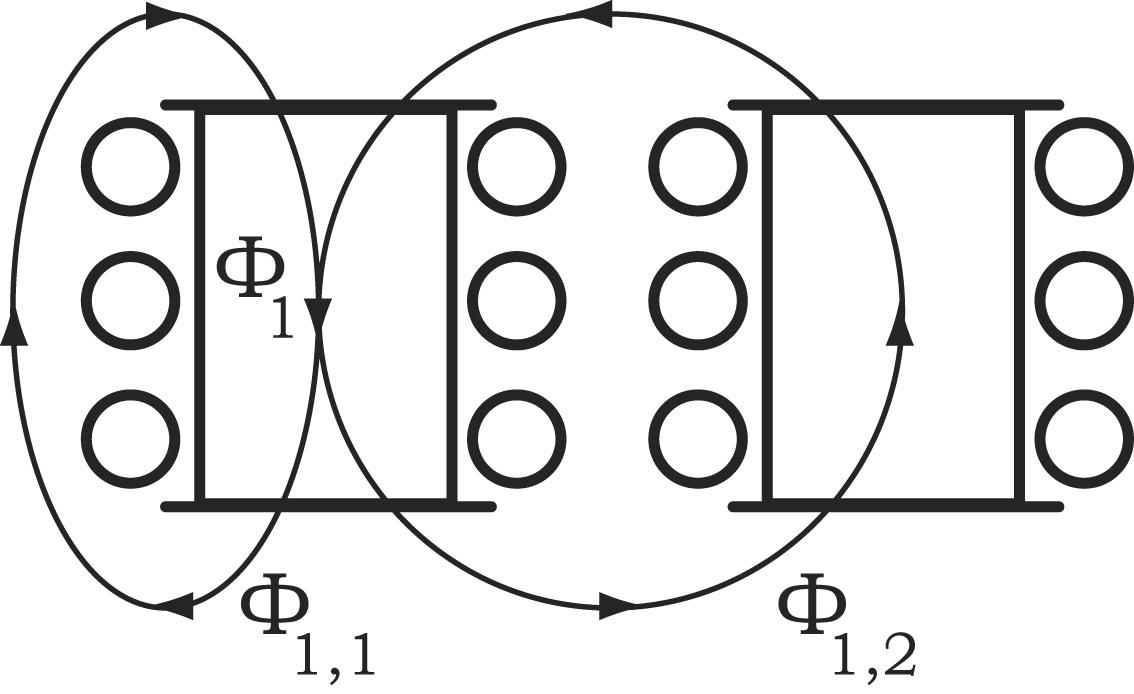
43. Явление взаимной индукции. Трансформатор.
Рассмотрим
два неподвижных контура (1 и 2), которые
расположены достаточно близко друг от
друга (рис. 1). Если в контуре 1 протекает
ток I1,
то магнитный поток, который создавается
этим током (поле, создающее этот поток,
на рисунке изображено сплошными линиями),
прямо пропорционален I1.
Обозначим через Ф21 часть
потока,пронизывающая контур 2.
Тогда  (1) где
L21 —
коэффициент пропорциональности.
(1) где
L21 —
коэффициент пропорциональности.
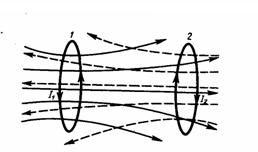
Рис.1
Если
ток I1 меняет
свое значение, то в контуре 2 индуцируется
э.д.с. ξi2 ,
которая по закону Фарадея будет равна
и противоположна по знаку скорости
изменения магнитного потока Ф21,
который создается током в первом контуре
и пронизыващет второй: 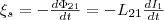 Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то
Аналогичным
образом, при протекании в контуре 2 тока
I2 магнитный
поток (его поле изображено на рис. 1
штрихами) пронизывает первый контур.
Если Ф12 —
часть этого потока, который пронизывает
контур 1, то 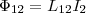 Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый:
Если
ток I2 меняет
свое значение, то в контуре 1 индуцируется
э.д.с. ξi1 ,
которая равна и противоположна по знаку
скорости изменения магнитного потока
Ф12,
который создается током во втором
контуре и пронизывает первый: 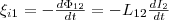 Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е.
Явление
возникновения э.д.с. в одном из контуров
при изменении силы тока в другом
называется взаимной
индукцией.
Коэффициенты пропорциональности L21 и
L12 называются взаимной
индуктивностью контуров.
Расчеты, которые подтверждены опытом,
показывают, что L21 и
L12 равны
друг другу, т. е. 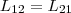 (2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
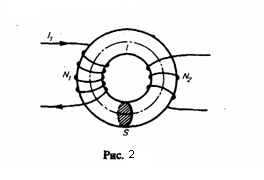
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S
(2) Коэффициенты
пропорциональности L12 и
L21 зависят
от размеров, геометрической формы,
взаимного расположения контуров и от
магнитной проницаемости среды, окружающей
контуры. Единица взаимной индуктивности
та же, что и для индуктивности, — генри
(Гн). Найдем
взаимную индуктивность двух катушек,
которые намотаны на общий тороидальный
сердечник. Этот случай имеет большое
практическое значение (рис. 2). Магнитная
индукция поля, которое создавается
первой катушкой с числом витков N1,
током I1 и
магнитной проницаемостью μ сердечника,
B = μμ0(N1I1/l)
где l —
длина сердечника по средней линии.
Магнитный поток сквозь один виток второй
катушки Ф2 =
BS = μμ0(N1I1/l)S
Значит,
полный магнитный поток (потокосцепление)
сквозь вторичную обмотку, которая
содержит N2 витков, 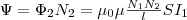 Поток
Ψ создается током I1,
поэтому, используя (1), найдем
Поток
Ψ создается током I1,
поэтому, используя (1), найдем 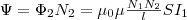 (3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник,
(3) Если
рассчитать магнитный поток, который
создавается катушкой 2 сквозь катушку
1, то для L12 получим
выражение в соответствии с формулой
(3). Значит, взаимная индуктивность двух
катушек, которые намотаны на общий
тороидальный сердечник, 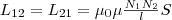
Трансформа́тор (от лат. transformo — преобразовывать) — это статическое электромагнитное устройство, имеющее две или более индуктивно связанных обмоток на каком-либо магнитопроводе и предназначенное для преобразования посредствомэлектромагнитной индукции одной или нескольких систем (напряжений) переменного тока в одну или несколько других систем (напряжений) переменного тока без изменения частоты системы (напряжения) переменного тока
studfile.net
ЭДС самоиндукции и индуктивность цепи
Дата публикации: .
Категория: Электротехника.
При замыкании выключателя в цепи, представленной на рисунке 1, возникнет электрический ток, направление которого показано одинарными стрелками. С появлением тока возникает магнитное поле, индукционные линии которого пересекают проводник и индуктируют в нем электродвижущую силу (ЭДС). Как было указано в статье «Явление электромагнитной индукции», эта ЭДС называется ЭДС самоиндукции. Так как всякая индуктированная ЭДС по правилу Ленца направлена против причины, ее вызвавшей, а этой причиной будет ЭДС батареи элементов, то ЭДС самоиндукции катушки будет направлена против ЭДС батареи. Направление ЭДС самоиндукции на рисунке 1 показано двойными стрелками.
Таким образом, ток устанавливается в цепи не сразу. Только когда магнитный поток установится, пересечение проводника магнитными линиями прекратится и ЭДС самоиндукции исчезнет. Тогда в цепи будет протекать постоянный ток.
 |  |
| Рисунок 1. Электродвижущая сила самоиндукции в момент замыкания цепи направлена против ЭДС источника напряжения | Рисунок 2. График постоянного тока |
На рисунке 2 дано графическое изображение постоянного тока. По горизонтальной оси отложено время, по вертикальной оси – ток. Из рисунка видно, что если в первый момент времени ток равен 6 А, то в третий, седьмой и так далее моменты времени он также и будет равен 6 А.
На рисунке 3 показано, как устанавливается ток в цепи после включения. ЭДС самоиндукции, направленная в момент включения против ЭДС батареи элементов, ослабляет ток в цепи, и поэтому в момент включения ток равен нулю. Далее в первый момент времени ток равен 2 А, во второй момент времени – 4 А, в третий – 5 А, и только спустя некоторое время в цепи устанавливается ток 6 А.
 |  |
| Рисунок 3. График нарастания тока в цепи с учетом ЭДС самоиндукции | Рисунок 4. ЭДС самоиндукции в момент размыкания цепи направлена одинаково с ЭДС источника напряжения |
При размыкании цепи (рисунок 4) исчезающий ток, направление которого показано одинарной стрелкой, будет уменьшать свое магнитное поле. Это поле, уменьшаясь от некоторой величины до нуля, будет вновь пересекать проводник и индуктировать в нем ЭДС самоиндукции.
При выключении электрической цепи с индуктивностью ЭДС самоиндукции будет направлена в ту же сторону, что и ЭДС источника напряжения. Направление ЭДС самоиндукции показано на рисунке 4 двойной стрелкой. В результате действия ЭДС самоиндукции ток в цепи исчезает не сразу.
Таким образом, ЭДС самоиндукции всегда направлена против причины, ее вызвавшей. Отмечая это ее свойство, говорят что ЭДС самоиндукции имеет реактивный характер.
Графически изменение тока в нашей цепи с учетом ЭДС самоиндукции при замыкании ее и при последующем размыкании в восьмой момент времени показано на рисунке 5.
 |  |
| Рисунок 5. График нарастания и исчезновения тока в цепи с учетом ЭДС самоиндукции | Рисунок 6. Индукционные токи при размыкании цепи |
При размыкании цепей, содержащих большое количество витков и массивные стальные сердечники или, как говорят, обладающих большой индуктивностью, ЭДС самоиндукции может быть во много раз больше ЭДС источника напряжения. Тогда в момент размыкания воздушный промежуток между ножом и неподвижным зажимом рубильника будет пробит и появившаяся электрическая дуга будет плавить медные части рубильника, а при отсутствии кожуха на рубильнике может ожечь руки человека (рисунок 6).
В самой цепи ЭДС самоиндукции может пробить изоляцию витков катушек, электромагнитов и так далее. Во избежание этого в некоторых выключающих приспособлениях устраивают защиту от ЭДС самоиндукции в виде специального контакта, который замыкает накоротко обмотку электромагнита при выключении.
Следует учитывать, что ЭДС самоиндукции проявляет себя не только в моменты включения и выключения цепи, но также и при всяких изменениях тока.
Величина ЭДС самоиндукции зависит от скорости изменения тока в цепи. Так, например, если для одной и той же цепи в одном случае в течение 1 секунды ток в цепи изменился с 50 до 40 А (то есть на 10 А), а в другом случае с 50 до 20 А (то есть на 30 А), то во втором случае в цепи будет индуктироваться втрое большая ЭДС самоиндукции.
Величина ЭДС самоиндукции зависит от индуктивности самой цепи. Цепями с большой индуктивностью являются обмотки генераторов, электродвигателей, трансформаторов и индукционных катушек, обладающих стальными сердечниками. Меньшей индуктивностью обладают прямолинейные проводники. Короткие прямолинейные проводники, лампы накаливания и электронагревательные приборы (печи, плитки) индуктивностью практически не обладают и появления ЭДС самоиндукции в них почти не наблюдается.
Магнитный поток, пронизывающий контур и индуктирующий в нем ЭДС самоиндукции, пропорционален току, протекающему по контуру:
Ф = L × I ,
где L – коэффициент пропорциональности. Он называется индуктивностью. Определим размерность индуктивности:

Ом × сек иначе называется генри (Гн).
1 генри = 103; миллигенри (мГн) = 106 микрогенри (мкГн).
Индуктивность, кроме генри, измеряют в сантиметрах:
1 генри = 109 см.
Так, например, 1 км линии телеграфа обладает индуктивностью 0,002 Гн. Индуктивность обмоток больших электромагнитов достигает нескольких сотен генри.
Если ток в контуре изменился на Δi, то магнитный поток изменится на величину Δ Ф:
Δ Ф = L × Δ i .
Величина ЭДС самоиндукции, которая появится в контуре, будет равна (формула ЭДС самоиндукции):

При равномерном изменении тока по времени выражение  будет постоянным и его можно заменить выражением
будет постоянным и его можно заменить выражением  . Тогда абсолютная величина ЭДС самоиндукции, возникающая в контуре, может быть найдена так:
. Тогда абсолютная величина ЭДС самоиндукции, возникающая в контуре, может быть найдена так:

На основании последней формулы можно дать определение единицы индуктивности – генри:

Проводник обладает индуктивностью 1 Гн, если при равномерном изменении тока на 1 А в 1 секунду в нем индуктируется ЭДС самоиндукции 1 В.
Как мы убедились выше, ЭДС самоиндукции возникает в цепи постоянного тока только в моменты его включения, выключения и при всяком его изменении. Если же величина тока в цепи неизменна, то магнитный поток проводника постоянен и ЭДС самоиндукции возникнуть не может (так как  . В моменты изменения тока в цепи ЭДС самоиндукции мешает изменениям тока, то есть оказывает ему своеобразное сопротивление.
. В моменты изменения тока в цепи ЭДС самоиндукции мешает изменениям тока, то есть оказывает ему своеобразное сопротивление.
 |
| Рисунок 7. Бифилярная обмотка катушки |
Часто на практике встречаются случаи, когда нужно изготовить катушку, не обладающую индуктивностью (добавочные сопротивления к электроизмерительным приборам, сопротивления штепсельных реостатов и тому подобные). В этом случае применяют бифилярную обмотку катушки (рисунок 7)
Как нетрудно видеть из чертежа, в соседних проводниках токи проходят в противоположных направлениях. Следовательно, магнитные поля соседних проводников взаимно уничтожаются. Общий магнитный поток и индуктивность катушки будут равны нулю. Для еще более полного уяснения понятия индуктивности приведем пример из области механики.
Как известно из физики, по второму закону Ньютона ускорение, полученное телом под действием силы, пропорционально самой силе и обратно пропорционально массе тела:

или

Сравним последнюю формулу с формулой ЭДС самоиндукции, взяв абсолютное значение ЭДС:

Если в этих формулах изменения скорости во времени  уподобить изменению тока во времени
уподобить изменению тока во времени  , механическую силу – электродвижущей силе самоиндукции, то масса тела будет соответствовать индуктивности цепи.
, механическую силу – электродвижущей силе самоиндукции, то масса тела будет соответствовать индуктивности цепи.
При равномерном прямолинейном движении a = 0, поэтому F = 0, то есть если на тело не действуют силы, его движение будет прямолинейным и равномерным (первый закон Ньютона).
В цепях постоянного тока величина тока не меняется  и поэтому eL = 0.
и поэтому eL = 0.
Источник: Кузнецов М.И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560с.
www.electromechanics.ru
Электромагнитная индукция – FIZI4KA

Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.


Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь \( S \) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции \( B \), площади поверхности \( S \), пронизываемой данным потоком, и косинуса угла \( \alpha \) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
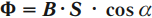
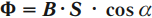


Обозначение – \( \Phi \), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:


Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла \( \alpha \) магнитный поток может быть положительным (\( \alpha \) < 90°) или отрицательным (\( \alpha \) > 90°). Если \( \alpha \) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
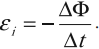
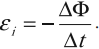
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из \( N \) витков, то ЭДС индукции:
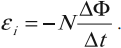
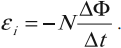
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением \( R \):
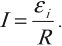
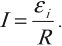
При движении проводника длиной \( l \) со скоростью \( v \) в постоянном однородном магнитном поле с индукцией \( \vec{B} \) ЭДС электромагнитной индукции равна:


где \( \alpha \) – угол между векторами \( \vec{B} \) и \( \vec{v} \).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
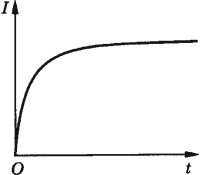

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции \( \varepsilon_{is} \), возникающая в катушке с индуктивностью \( L \), по закону электромагнитной индукции равна:


ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
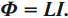
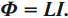
Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током:
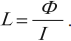
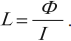
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
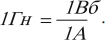
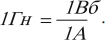
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
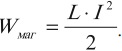
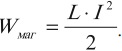
Основные формулы раздела «Электромагнитная индукция»


Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3 (60%) 2 votesfizi4ka.ru
ЭДС самоиндукции — это… Что такое ЭДС самоиндукции?
- ЭДС самоиндукции
Самоиндукция — явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.
При изменении тока в контуре меняется поток магнитной индукции через поверхность, ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.
Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L:
 .
.
За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи, при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.
Wikimedia Foundation. 2010.
Смотреть что такое «ЭДС самоиндукции» в других словарях:
эдс самоиндукции — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN self induced emfFaraday voltageinductance voltageself induction… … Справочник технического переводчика
Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре [1]при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется[2] и магнитный поток через поверхность, ограниченную этим контуром[3]. Изменение… … Википедия
ИНДУКТИВНОСТЬ — (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… … Физическая энциклопедия
реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ — раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… … Энциклопедия Кольера
электрический трансформатор — электрический машина, не имеющая подвижных частей и преобразующая переменный ток одного напряжения в переменный ток другого напряжения. В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь
Импульсный стабилизатор напряжения — Импульсный стабилизатор напряжения это стабилизатор напряжения, в котором регулирующий элемент работает в ключевом режиме[1], то есть большую часть времени он находится либо в режиме отсечки, когда его сопротивление максимально, либо в… … Википедия
Катушка индуктивности — У этого термина существуют и другие значения, см. Катушка (значения). Катушка индуктивности (дроссель) на материнской плате компьютера … Википедия
Индуктивность — Размерность L2MT−2I−2 Единицы измерения СИ Гн СГС … Википедия
Диод — У этого термина существуют и другие значения, см. Диод (значения). Четыре диода и диодный мост. Диод (от др. греч … Википедия
biograf.academic.ru
Самоиндукция — Основы электроники
Общеизвестно, что поезд, отходящий от станции, не может сразу развить нужную скорость.
Требуемая скорость достигается лишь по истечении некоторого промежутка времени. За этот промежуток значительная часть энергии локомотива затрачивается на преодоление инерции поезда т. е. на образование запаса кинетической энергии, и очень незначительная часть — на преодоление трения.
В силу того что движущийся поезд обладает запасом кинетической энергии, он не может остановиться мгновенно и будет по инерции двигаться еще некоторое время, т. е. до тех пор, пока не израсходуется на трение весь запас кинетической энергии, сообщенной ему локомотивом в начале движения.
Аналогичные явления имеют место и в замкнутой электрической цепи при включении и выключении тока.
В момент включения постоянного тока (рисунок 1) вокруг проводника образуется магнитное силовое поле.
Рисунок 1. Инерция электрического тока. При включении тока вокруг проводника появляется магнитное поле.
В первые мгновения после включения тока значительная часть энергии источника тока затрачивается на создание этого магнитного поля и лишь незначительная часть — на преодоление сопротивления проводника, вернее на нагревание током проводника. Поэтому в момент замыкания цепи ток не сразу достигает предельной своей величины. Предельная сила тока устанавливается в цепи лишь после окончания процесса образования вокруг проводника магнитного поля (рисунок 2).
Рисунок 2. Влияние ЭДС самоиндукции на ток в цепи. При включении источника тока, ток в цепи устанавливается не сразу.
Если, не разрывая замкнутой цепи, выключить из нее источник тока, то ток в цепи прекратится не сразу, а будет протекать в ней, еще некоторое время уменьшаясь постепенно (рисунок 3) до тех пор, пока не исчезнет магнитное поле вокруг проводника, т. е. пока не израсходуется весь запас энергии, заключенной в магнитном поле.
Рисунок 2. Влияние ЭДС самоиндукции на ток в цепи. При выключении источника тока, ток в цепи прекращается не сразу.
Итак, магнитное поле является носителем энергии. Оно накопляет в себе энергию при включении источника постоянного тока и отдает ее обратно в цепь после выключения источника тока. Энергия магнитного поля, таким образом, имеет много общего с кинетической энергией движущегося предмета. Магнитное поле служит причиной «инерции» электрического тока.
Мы знаем, что всякий раз, когда изменяется магнитный поток, пронизывающий площадь, ограниченную замкнутой электрической цепью, в этой цепи появляется ЭДС индукции.
Кроме того, нам известно, что всякое изменение силы тока в цепи влечет за собой изменение числа магнитных силовых линий, охватываемых этой цепью. Если замкнутая цепь неподвижна, то число магнитных силовых линий, пронизывающих данную площадь, может измениться только тогда, когда новые линии войдут снаружи в пределы этой площади или когда существующие уже линии выйдут за пределы этой площади. И в том и в другом случае магнитные силовые линии при своем движении должны пересечь проводник. Пересекая проводник, магнитные силовые линии наводят в нем ЭДС индукции. Но так как в этом случае проводник индуктирует ЭДС в самом себе, то эта ЭДС называется ЭДС самоиндукции.
При включении источника постоянного тока в какую-либо замкнутую цепь площадь, ограниченную этой цепью, начинают пронизывать извне магнитные силовые линии. Каждая магнитная силовая линия, приходящая извне, пересекая проводник, наводит в нем ЭДС самоиндукции.
Электродвижущая сила самоиндукции, действуя против ЭДС источника тока, задерживает нарастание тока в цепи. Через несколько мгновений, когда возрастание магнитного потока вокруг цепи прекратится, ЭДС самоиндукции исчезнет и в цепи устанавливается сила тока, определяемая по закону Ома:
I=U/R
При выключении источника тока из замкнутой цепи магнитные силовые линии должны исчезнуть из пространства, ограниченного проводником. Каждая уходящая магнитная силовая линия при пересечении проводника наводит в нем ЭДС самоиндукции, имеющую одинаковое направление с ЭДС источника тока; поэтому ток в цепи прекратится не сразу, а будет протекать в том же направлении, постепенно уменьшаясь до того момента, пока полностью не исчезнет магнитный поток внутри цепи. Ток, протекающий по цепи после выключения из нее источника тока, называется током самоиндукции.
Если при выключении источника цепь разрывается, то ток самоиндукции проявляется в виде искры в месте размыкания цепи.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
www.sxemotehnika.ru
1.2. Явление электромагнитной индукции и самоиндукции
(основные величины и закономерности)
Индукция
магнитного поля  – силовая характеристика магнитного
поля. Характеризует влияние магнитного
поля на движущиеся заряды и токи. Единица
измерения – тесла,
– силовая характеристика магнитного
поля. Характеризует влияние магнитного
поля на движущиеся заряды и токи. Единица
измерения – тесла,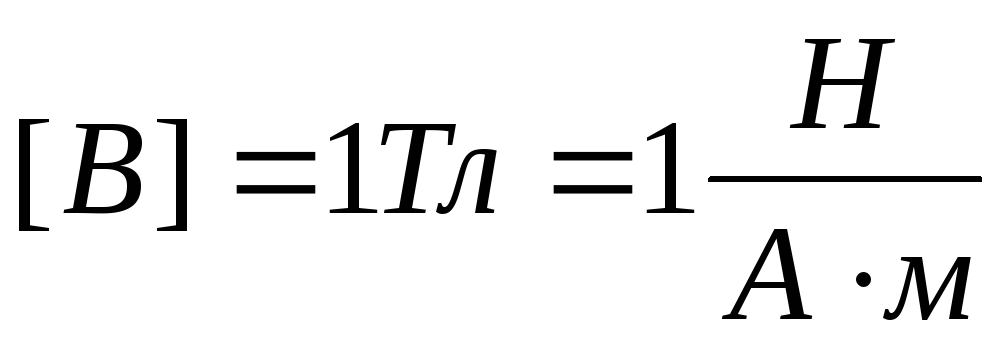 .
.
П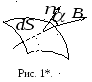 отоком вектора магнитной индукции (магнитным потоком) через площадку
отоком вектора магнитной индукции (магнитным потоком) через площадку 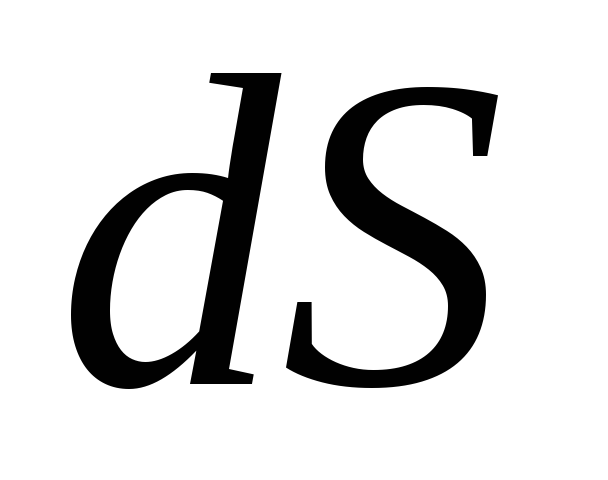 (или магнитным потоком) называется
произведение
(или магнитным потоком) называется
произведение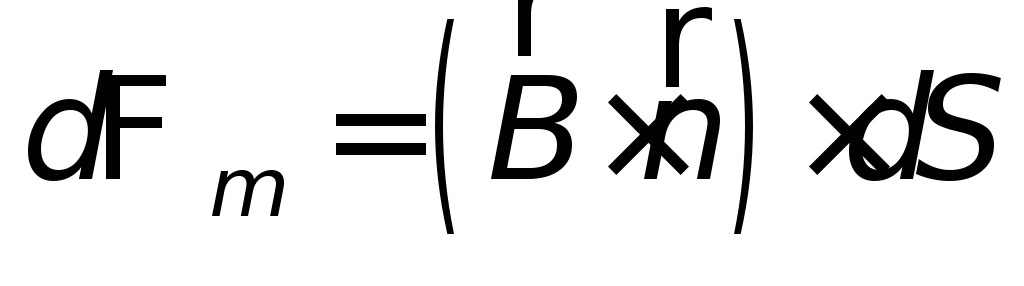 ,
или
,
или
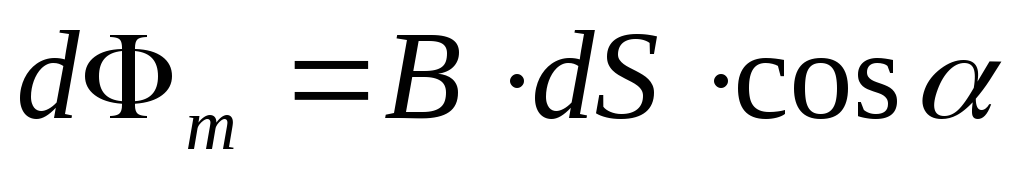 ,
(8*)
,
(8*)
где 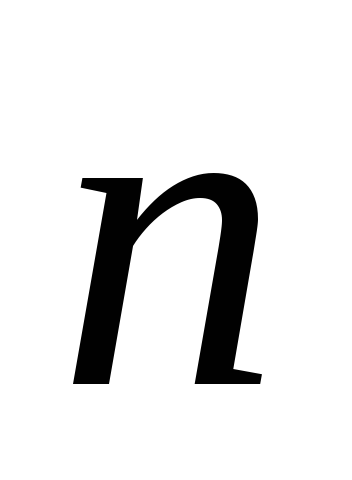 – единичный вектор – нормаль к этой
площадке,
– единичный вектор – нормаль к этой
площадке, – вектор магнитной индукции,
– вектор магнитной индукции, – угол между векторами
– угол между векторами и
и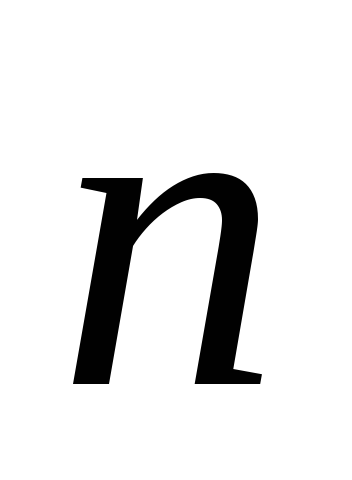 (рис. 1). (Магнитный поток можно трактовать,
как количество линий магнитной индукции,
которые пересекают поверхность
(рис. 1). (Магнитный поток можно трактовать,
как количество линий магнитной индукции,
которые пересекают поверхность ).
Единица измерения магнитного потока –
вебер:
).
Единица измерения магнитного потока –
вебер: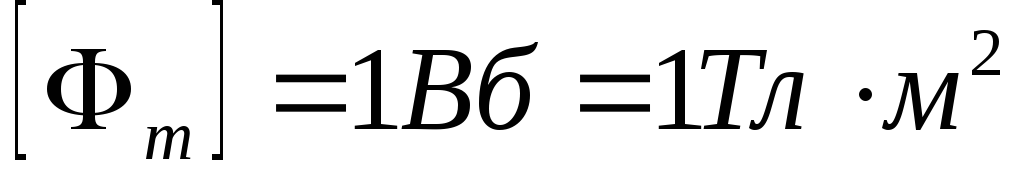 .
.
Явление электромагнитной индукции состоит в возникновении ЭДС в замкнутом проводящем контуре при изменении магнитного потока, который пронизывает этот контур. (Например, когда в замкнутый контур (без батарейки) вносят магнит, в контуре возникает ЭДС и ток, который называют индукционным).
Закон Фарадея: ЭДС индукции, которая возникает в замкнутом проводящем контуре, равняется скорости изменения магнитного потока:
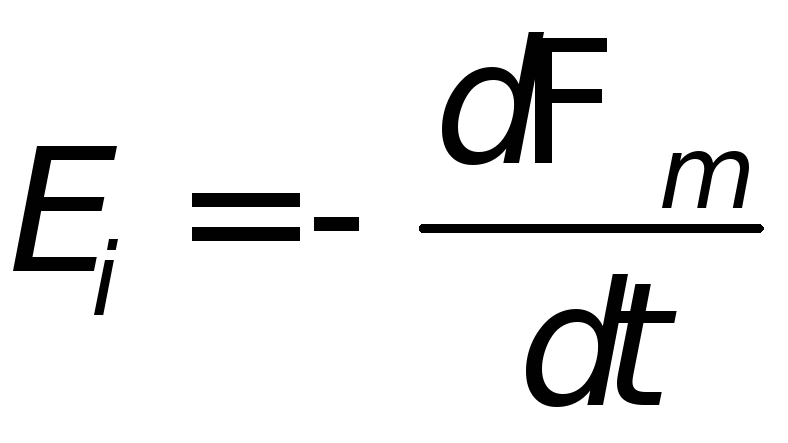
 .
(9*)
.
(9*)
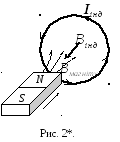
Эта ЭДС порождает индукционный ток. Знак „–” указывает на направление индукционного тока согласно правилу Ленца: при изменении магнитного потока, который пронизывает контур, в нём возникает индукционный ток такого направления, который своим магнитным полем противодействует первичному изменению магнитного потока. На рис. 2* магнитный поток, который пронизывает контур, благодаря внесению магнита, увеличивается. Поэтому индукционный ток должен иметь такое направление, чтобы его магнитное поле было противоположным полю магнита. Направление этого тока можно определить по правилу буравчика.
Если
ток проходит по замкнутому контуру, он
создает магнитное поле (и, следовательно,
магнитный поток) через этот же контур.
Когда ток в контуре меняется – меняется
и магнитный поток через этот контур,
поэтому должна возникать ЭДС индукции
(самоиндукции). То есть явление
самоиндукции состоит в возникновении ЭДС самоиндукции
в замкнутом контуре при изменении тока
в этом контуре.
Когда по контуру течет ток 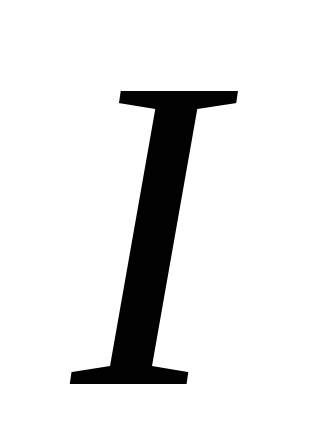 ,
то созданный им магнитный поток будет
пропорциональным силе тока:
,
то созданный им магнитный поток будет
пропорциональным силе тока: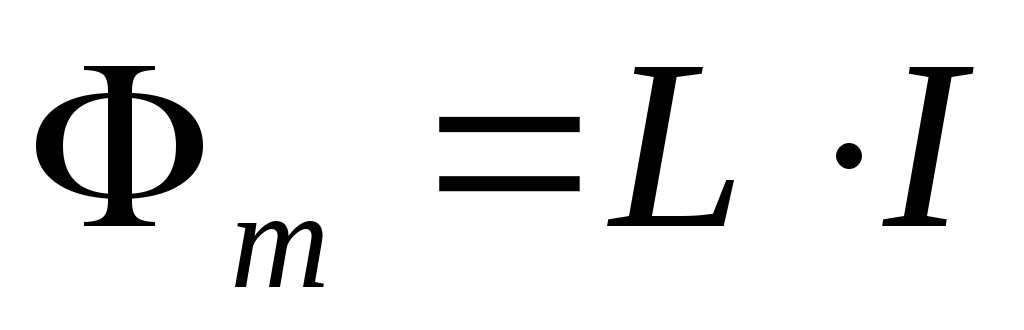 ,
где коэффициент пропорциональности
,
где коэффициент пропорциональности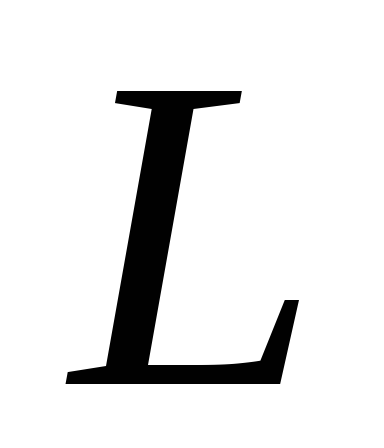 называютиндуктивностью контура. То есть индуктивность
контура численно равняется магнитному потоку,
который пронизывает контур при силе
тока
называютиндуктивностью контура. То есть индуктивность
контура численно равняется магнитному потоку,
который пронизывает контур при силе
тока 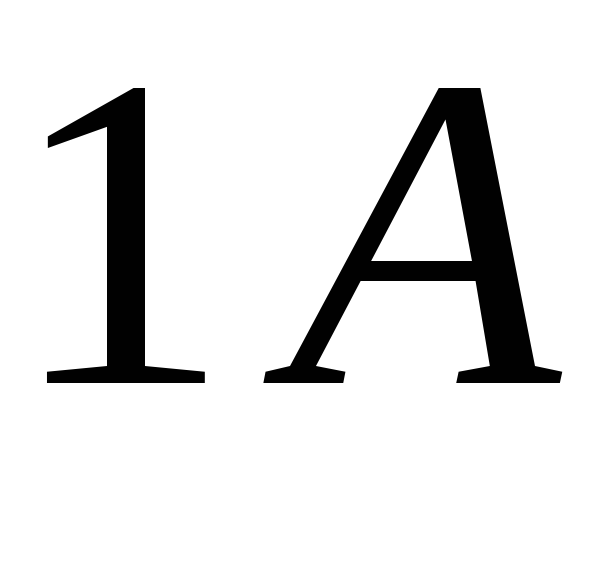
| (10*) |
(Индуктивность
зависит от формы, размеров контура и
среды, но не зависит от силы тока). Единица
измерения индуктивности – генри: 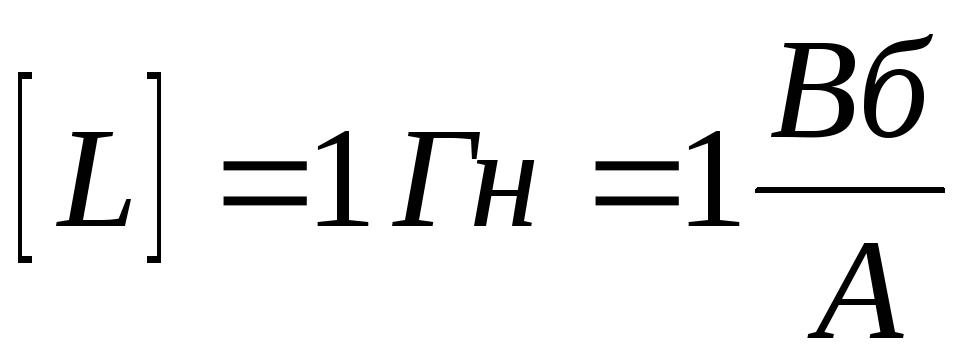 .
.
Поскольку
магнитный поток равняется 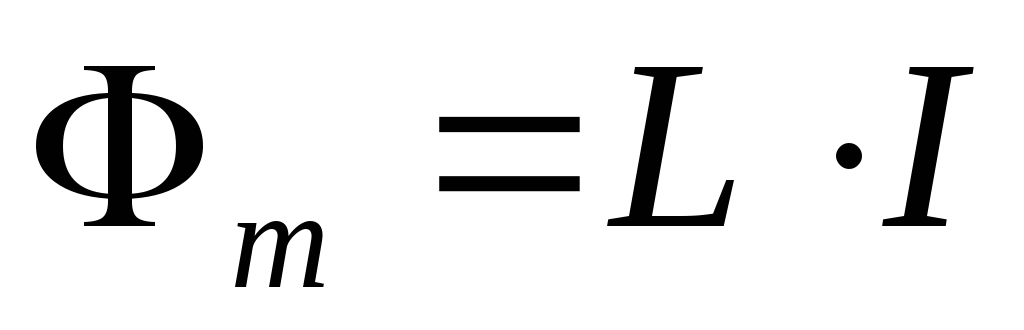 ,
то по закону Фарадея (9*) ЭДС самоиндукции
,
то по закону Фарадея (9*) ЭДС самоиндукции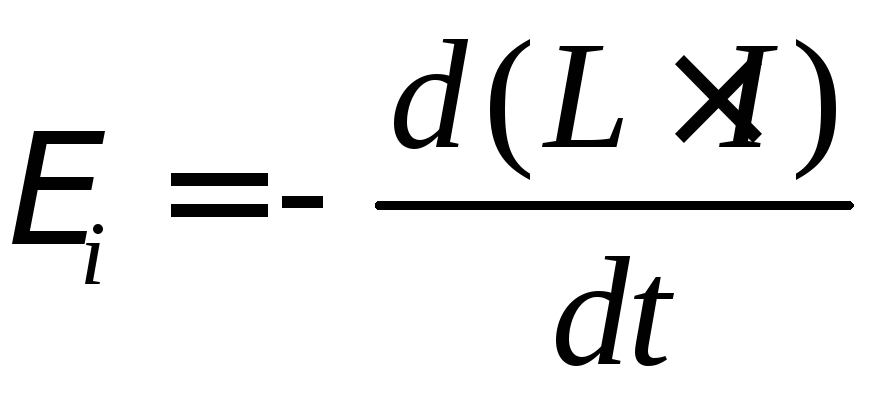 .
Если индуктивность
.
Если индуктивность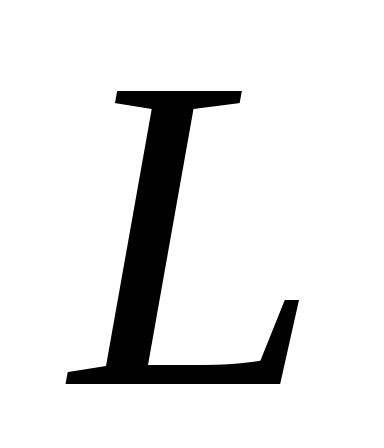 постоянная, то ее можно вынести за знак
производной. Тогда ЭДС самоиндукции
равняется
постоянная, то ее можно вынести за знак
производной. Тогда ЭДС самоиндукции
равняется
| (11*) |
Знак
„–” в этом выражении означает, что ток
самоиндукции противодействует начальному
изменению тока. (Например, когда ток 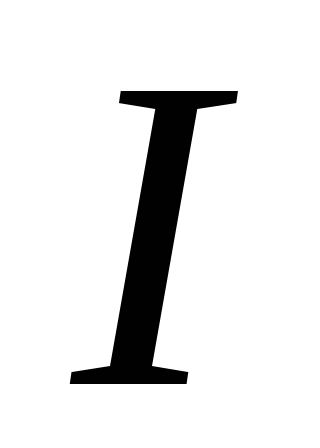 в контуре увеличивается, ток самоиндукции
в контуре увеличивается, ток самоиндукции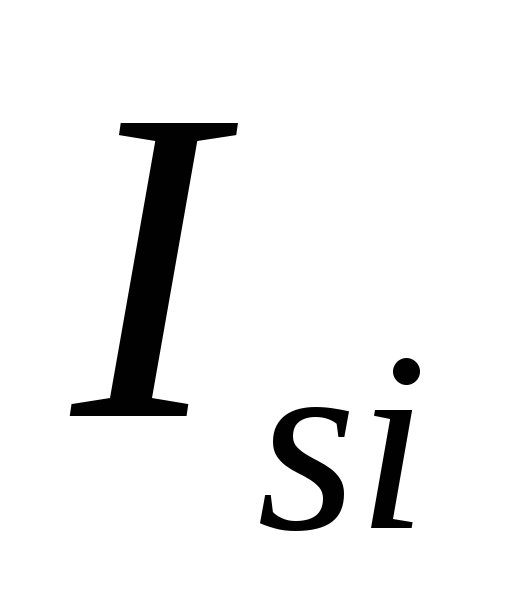 противоположен начальному току
противоположен начальному току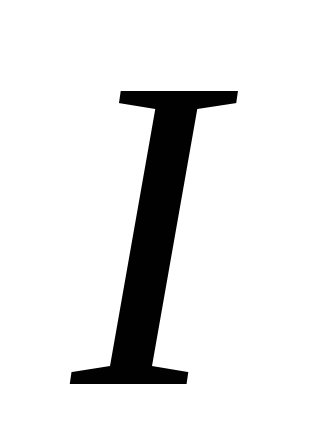 .
Когда ток
.
Когда ток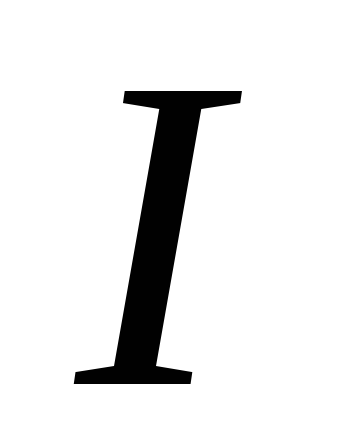 в
контуре уменьшается, то
в
контуре уменьшается, то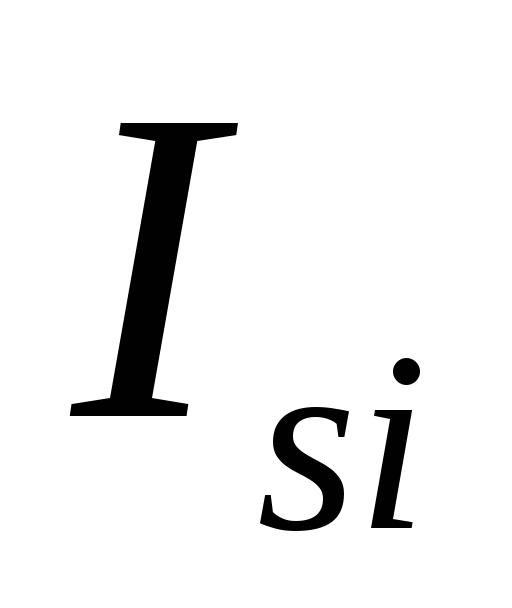 направлен в ту же сторону, что и
направлен в ту же сторону, что и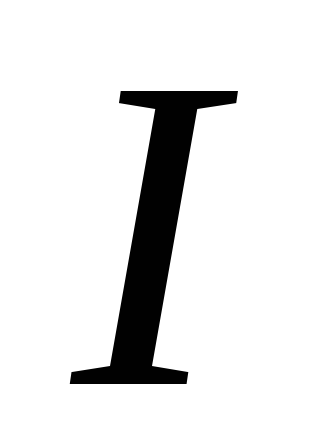 ).
).
2. Индуктивность, емкость и активное сопротивление в цепи переменного тока
Р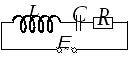 ассмотрим
контур, который включает в себя
индуктивность
ассмотрим
контур, который включает в себя
индуктивность 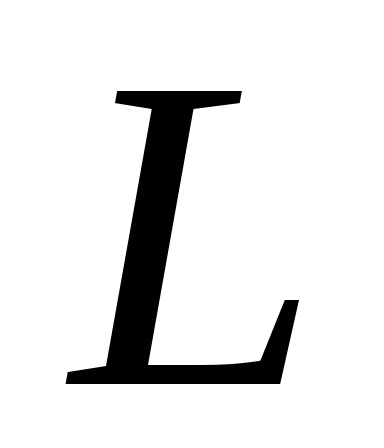 ,
емкость
,
емкость и активное сопротивление
и активное сопротивление .
Пусть в этот контур включен источник
ЭДС, которая изменяется по гармоничному
закону (синуса или косинуса) с амплитудой
.
Пусть в этот контур включен источник
ЭДС, которая изменяется по гармоничному
закону (синуса или косинуса) с амплитудой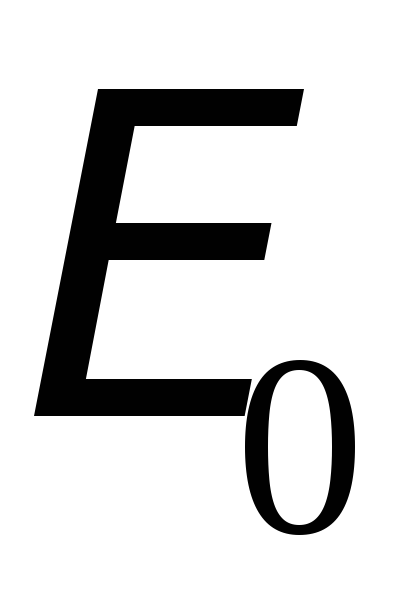 и циклической частотой
и циклической частотой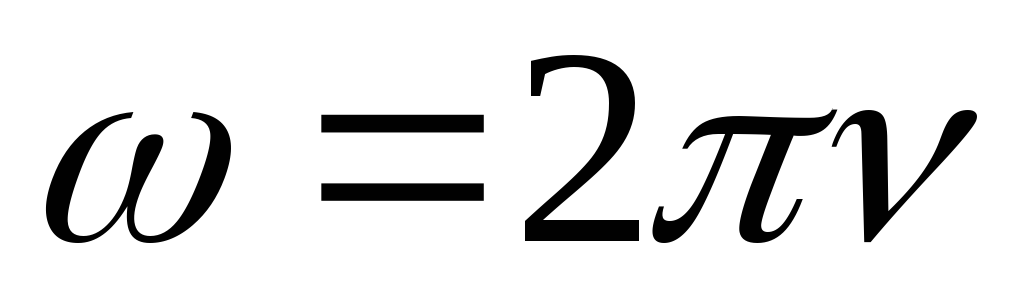 ,
где
,
где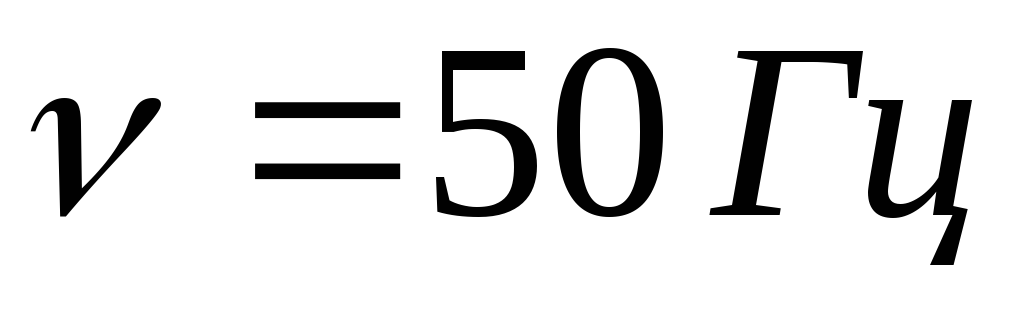 – линейная частота. Выясним, как влияют
– линейная частота. Выясним, как влияют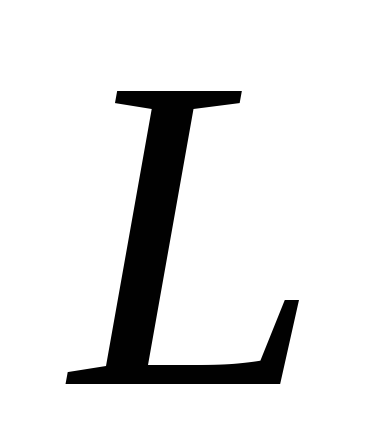 ,
, и
и отдельно и вместе на ток в этом цепи и
какие падениянапряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
отдельно и вместе на ток в этом цепи и
какие падениянапряжения будут на этих элементах. Ток на всех
элементах цепи будет одинаковым (ток
неразрывный). Пусть он меняется по закону
синуса
| (1) |
где  – амплитудное значение силы тока (пока
еще неизвестное).
– амплитудное значение силы тока (пока
еще неизвестное).
2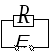 .1.Активное
сопротивление в цепи переменного тока
.1.Активное
сопротивление в цепи переменного тока
Рассмотрим электрическую цепь, которая состоит только из источника переменного тока и активного сопротивления R. Падение напряжения на активном сопротивлении определяется из закона Ома и выражения (1)
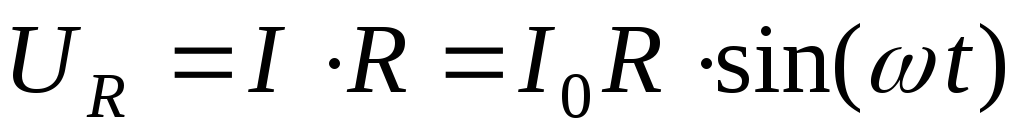
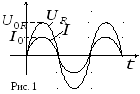 .
(2)
.
(2)
Величина 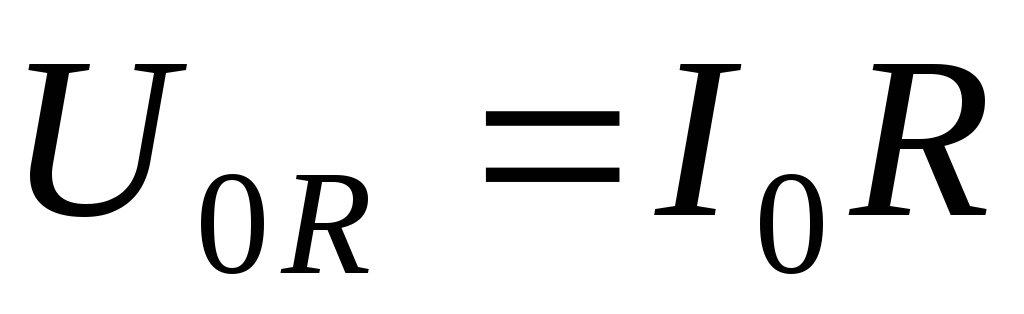 будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
будет представлять собой амплитудное
значение напряжения на активном
сопротивлении. Сравнивая выражения (1)
и (2) видим, что колебания напряжения и
тока на активном сопротивлении происходит
с одинаковой фазой (по закону синуса,
рис.1). Заметим, что в цепи с активным
сопротивлением происходит необратимый
процесс преобразования электрической
энергии в тепловую.
studfile.net
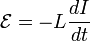 .
.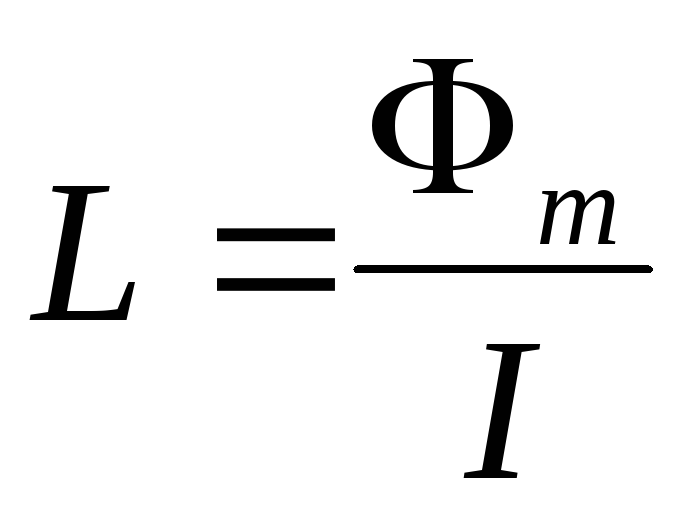 .
.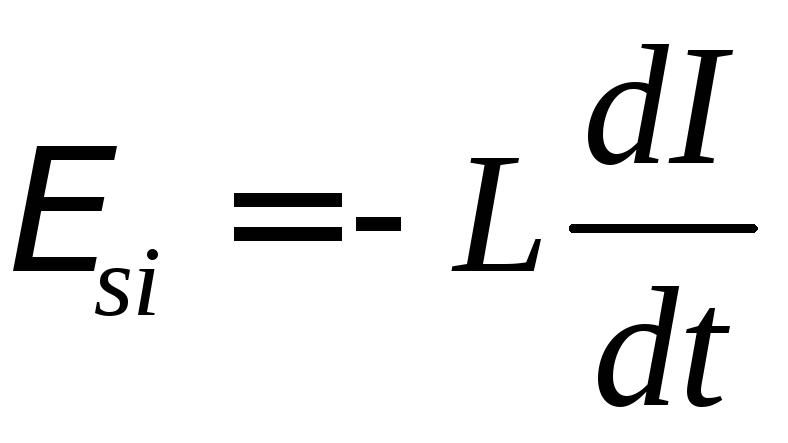 .
.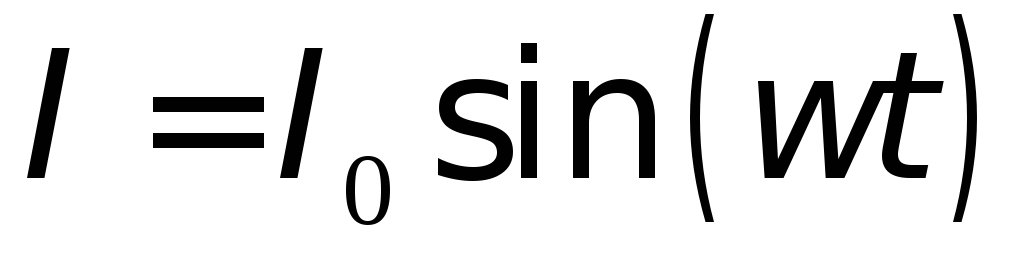 ,.
,.