определение, формула, применение на практике
«Самоиндукция останавливает рост напряжения в индуктивных цепях». Если ваша работа или увлечение связаны с электричеством вы наверняка слышали подобные высказывания. На самом деле это явление присуще индуктивным цепям, как в явном виде, например, катушек, так и в неявном, такие как паразитные параметры кабеля. В этой статье мы простыми словами расскажем о том, что такое самоиндукция и где она применяется.
Определение
Самоиндукцией называется появление в проводнике электродвижущей силы (ЭДС), направленной в противоположную сторону относительно напряжения источника питания при протекании тока. При этом оно возникает в момент, когда сила тока в цепи изменяется. Изменяющийся электрической ток порождает изменяющееся магнитное поле, оно в свою очередь наводит ЭДС в проводнике.
Это похоже на формулировку закона электромагнитной индукции Фарадея, где сказано:
При прохождении магнитного потока через проводник, в последнем возникает ЭДС.
То есть:
E=dФ/dt,
Где E – ЭДС самоиндукции, измеряется в вольтах, Ф – магнитный поток, единица измерения – Вб (вебер, он же равен В/с)
Индуктивность
Мы уже сказали о том, что самоиндукция присуща индуктивным цепям, поэтому рассмотрим явление самоиндукции на примере катушки индуктивности.
Катушка индуктивности – это элемент, который представляет собой катушку из изолированного проводника. Для увеличения индуктивности увеличивают число витков или внутрь катушки помещают сердечник из магнитомягкого или другого материала.
Единица измерения индуктивности – Генри (Гн). Индуктивность характеризует то, насколько сильно проводник противодействует электрическому току. Так как вокруг каждого проводника, по которому протекает ток, образуется магнитное поле, и, если поместить проводник в переменное поле – в нем возникнет ток. В свою очередь магнитные поля каждого витка катушки складываются.
Согласно закону электромагнитной индукции Фарадея, если катушку будет пронизывать переменный магнитный поток, то в ней возникнет ток и ЭДС самоиндукции. Они будут препятствовать току, который протекал в индуктивности от источника питания к нагрузке. Их еще называют экстратоки ЭДС самоиндукции.
Формула ЭДС самоиндукции на индуктивности имеет вид:
То есть чем больше индуктивность, и чем больше и быстрее изменился ток – тем сильнее будет всплеск ЭДС.
При возрастании тока в катушке возникает ЭДС самоиндукции, которая направлена против напряжения источника питания, соответственно возрастание тока замедлится. То же самое происходит при убывании – самоиндукция приведет к появлению ЭДС, которое будет поддерживать ток в катушке в том же направлении, что и до этого. Отсюда следует, что напряжение на выводах катушки будет противоположным полярности источника питания.
На рисунке ниже вы видите, что при включении/отключении индуктивной цепи ток не резко возникает, а изменяется постепенно. Об этом говорят и законы коммутации.
Другое определение индуктивности звучит так: магнитный поток пропорционален току, но в его формуле индуктивность выступает в качестве коэффициента пропорциональности.
Ф=L*I
Трансформатор и взаимоиндукция
Если расположить две катушки в непосредственной близости, например, на одном сердечнике, то будет наблюдаться явление взаимоиндукции. Пропустим переменный ток по первой, тогда её переменный поток будет пронизывать витки второй и на её выводах появится ЭДС.
Это ЭДС будет зависеть от длины провода, соответственно количества витков, а также от величины магнитной проницаемости среды. Если их расположить просто около друг друга — ЭДС будет низким, а если взять сердечник из магнитомягкой стали – ЭДС будет значительно больше. Собственно, так и устроен трансформатор.
Интересно: такое взаимное влияние катушек друг на друга называют индуктивной связью.
Польза и вред
Если вам понятна теоретическая часть, стоит рассмотреть где применяется явление самоиндукции на практике. Рассмотрим на примерах того, что мы видим в быту и технике. Одно из полезнейших применений – это трансформатор, принцип его работы мы уже рассмотрели. Сейчас встречаются все реже, но ранее ежедневно использовались люминесцентные трубчатые лампы в светильниках. Принцип их работы основан на явлении самоиндукции. Её схемы вы можете увидеть ниже.
После подачи напряжения ток протекает по цепи: фаза — дроссель — спираль — стартер — спираль — ноль.
Или наоборот (фаза и ноль). После срабатывания стартера, его контакты размыкаются, тогда дроссель (катушка с большой индуктивностью) стремится поддержать ток в том же направлении, наводит ЭДС самоиндукции большой величины и происходит розжиг ламп.
Аналогично это явление применяется в цепи зажигания автомобиля или мотоцикла, которые работают на бензине. В них в разрыв между катушкой индуктивности и минусом (массой) устанавливают механический (прерыватель) или полупроводниковый ключ (транзистор в ЭБУ). Этот ключ в момент, когда в цилиндре должна образоваться искра для зажигания топлива, разрывает цепь питания катушки. Тогда энергия, запасенная в сердечнике катушки, вызывает рост ЭДС самоиндукции и напряжение на электроде свечи возрастает до тех пор, пока не наступит пробой искрового промежутка, или пока не сгорит катушка.
В них в разрыв между катушкой индуктивности и минусом (массой) устанавливают механический (прерыватель) или полупроводниковый ключ (транзистор в ЭБУ). Этот ключ в момент, когда в цилиндре должна образоваться искра для зажигания топлива, разрывает цепь питания катушки. Тогда энергия, запасенная в сердечнике катушки, вызывает рост ЭДС самоиндукции и напряжение на электроде свечи возрастает до тех пор, пока не наступит пробой искрового промежутка, или пока не сгорит катушка.
В блоках питания и аудиотехнике часто возникает необходимость убрать из сигнала лишние пульсации, шумы или частоты. Для этого используются фильтры разных конфигурации. Один из вариантов это LC, LR-фильтры. Благодаря препятствию роста тока и сопротивлению переменного тока, соответственно, возможно добиться поставленных целей.
Вред ЭДС самоиндукции приносит контактам выключателей, рубильников, розеток, автоматов и прочего. Вы могли заметить что, когда вытаскиваете вилку работающего пылесоса из розетки, очень часто заметна вспышка внутри неё. Это и есть сопротивление изменению тока в катушке (обмотке двигателя в данном случае).
Это и есть сопротивление изменению тока в катушке (обмотке двигателя в данном случае).
В полупроводниковых ключах дело обстоит более критично – даже небольшая индуктивность в цепи может привести к их пробою, при достижении пиковых значений Uкэ или Uси. Для их защиты устанавливают снабберные цепи, на которых и рассеивается энергия индуктивных всплесков.
Заключение
Подведем итоги. Условиями возникновения ЭДС самоиндукции является: наличие индуктивности в цепи и изменение тока в нагрузке. Это может происходить как в работе, при смене режимов или возмущающих воздействиях, так и при коммутации приборов. Это явление может нанести вред контактам реле и пускателей, так как приводит к образованию дуги при размыкании индуктивных цепей, например, электродвигателей. Чтобы снизить негативное влияние большая часть коммутационной аппаратуры оснащается дугогасительными камерами.
В полезных целях явление ЭДС используется довольно часто, от фильтра для сглаживания пульсаций тока и фильтра частот в аудиоаппаратуре, до трансформаторов и высоковольтных катушек зажигания в автомобилях.
Напоследок рекомендуем просмотреть полезное видео по теме, на которых кратко и подробно рассматривается явление самоиндукции:
Надеемся, теперь вам стало понятно, что такое самоиндукция, как она проявляется и где ее можно использовать. Если возникли вопросы, задавайте их в комментариях под статьей!
Материалы по теме:
Формула ЭДС индукции, E
Закон Фарадея – Максвелла для электромагнитной индукции
Основной формулой, которая определяет ЭДС индукции, является закон Фарадея – Максвелла, больше известный как основной закон электромагнитной индукции (или закон Фарадея). Этот закон утверждает, что ЭДС индукции в контуре, находящемся в переменном магнитном поле, равна по величине и противоположна по знаку скорости изменения магнитного потока () через поверхность, которую ограничивает данный контур:
где – скорость изменения магнитного потока. Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.
Полная производная в законе (1) охватывает весь спектр причин изменения магнитного потока через поверхность контура. Знак минус в формуле (1) соответствует правилу Ленца. Формула (1) для ЭДС индукции записана для системы СИ.
В случае равномерного изменения магнитного потока формулу ЭДС индукции можно записать как:
Частные случаи формул ЭДС индукции
Если контур содержит N витков, которые соединяются последовательно, то ЭДС индукции вычисляют как:
где – потокосцепление.
При движении прямолинейного проводника в однородном магнитном поле в нем возникает ЭДС индукции, которая равна:
где v – скорость движения проводника; l – длина проводника; B – модуль вектора магнитной индукции поля; .
При вращении с постоянной скоростью в однородном магнитном поле плоского контура вокруг оси, которая лежит в плоскости контура в нем возникает ЭДС индукции, равная:
где S – площадь, которую ограничивает виток; – поток самоиндукции витка; — угловая скорость; () – угол поворота контура. Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .
Следует учесть, что формула (5) справедлива, если ось вращения составляет прямой угол с направлением вектора внешнего поля .
Если во вращающейся рамке имеется N витков и самоиндукцией рассматриваемой системы можно пренебречь, то:
В стационарном проводнике, который находится в переменном магнитном поле, ЭДС индукции находят по формуле:
Примеры решения задач по теме «ЭДС индукции»
Методы защиты устройств (датчиков, приборов, контроллеров) с транзисторными выходами от токов самоиндукции
Введение
В данной статье будет рассмотрено явление самоиндукции, проявляющееся зачастую при коммутации индуктивных нагрузок. Также будут рассмотрены способы защиты и используемое для этого оборудование.
Техника безопасности
ВНИМАНИЕ! К работам по монтажу, наладке, ремонту и обслуживанию технологического оборудования допускаются лица, имеющие техническое образование и специальную подготовку (обучение и проверку знаний) по безопасному производству работ в электроустановках с группой не ниже 2 для ремонтного персонала, а также имеющие опыт работ по обслуживанию оборудования, в конструкцию которого вносятся изменения и дополнения, либо производится модернизация.
1. Электромагнитная индукция. Определение. Физический смысл
Электромагнитная индукция — явление возникновения электрического тока, при изменении во времени магнитного поля. Изменение магнитного поля, в силу закона электромагнитной индукции, приводит к возбуждению в контуре индуктивной электродвижущей силы (ЭДС). Процесс возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию, а при убывании тока — препятствует убыванию. Величина ЭДС самоиндукции определяется уравнением:
E=−L×dI/dtE= -L times dI / dtгде:
E — ЭДС самоиндукции
L — индуктивность катушки
dI/dt — изменение тока во времени.
Знак «минус» означает, что ЭДС самоиндукции действует так, что индукционный ток препятствует изменению магнитного потока. Этот факт отражён в правиле Ленца:
Индукционный ток всегда имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Явление самоиндукции можно наблюдать при включении и последующем выключении катушек соленоидов, промежуточных реле, электромагнитных пускателей. При подаче напряжения на катушку создается электромагнитное
поле, в следствии чего образуется электродвижущая сила, которая препятствует мгновенному росту тока в катушке. Согласно принципу суперпозиции, основной ток в катушке можно представить в виде суммы токов, один из
которых вызван внешним напряжением и сонаправлен с основным током, а второй вызван ЭДС самоиндукции и имеет противоположное направление основному току. Скорость изменения тока через катушку ограничена и
определяется индуктивностью катушки. При протекании тока катушка «запасает» энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдает запасенную энергию, стремясь поддержать
величину тока в цепи. Это, в свою очередь, вызывает всплеск напряжения обратной полярности на катушке. Данный всплеск может достигать значений во много раз превышающих номинальное напряжение источника питания, что
может помешать нормальной работе электронных устройств, вплоть до их разрушения.
При протекании тока катушка «запасает» энергию в своём магнитном поле. При отключении внешнего источника тока катушка отдает запасенную энергию, стремясь поддержать
величину тока в цепи. Это, в свою очередь, вызывает всплеск напряжения обратной полярности на катушке. Данный всплеск может достигать значений во много раз превышающих номинальное напряжение источника питания, что
может помешать нормальной работе электронных устройств, вплоть до их разрушения.
Разберем более подробно, почему скачок ЭДС самоиндукции будет иметь обратную полярность. На рисунке 1 изображены две схемы, на которых стрелками обозначено направление движения тока, а так же потенциалы на всех элементах схемы при закрытом и открытом ключе.
а — закрытый ключб — открытый ключРисунок 1 — Направление тока при закрытом и открытом ключе
При закрытом ключе потенциалы на всех элементах совпадают с потенциалом источника питания (рисунок 1, а). Во время размыкания ключа, из схемы исключается источник питания, и ЭДС самоиндукции стремится поддержать ток в катушке. Для того, что бы сохранить направление тока в катушке, ЭДС меняет свой потенциал на противоположный по знаку источнику питания (рисунок 1, б). Именно поэтому всплеск ЭДС самоиндукции будет иметь обратную полярность.
Для того, что бы сохранить направление тока в катушке, ЭДС меняет свой потенциал на противоположный по знаку источнику питания (рисунок 1, б). Именно поэтому всплеск ЭДС самоиндукции будет иметь обратную полярность.
Более наглядно этот всплеск показан на рисунке 2. На графике изображено напряжение источника питания Uпит, ток возникающий в катушке I, ЭДС самоиндукции.
Рисунок 2 — График изменения тока и напряжения при коммутации2. Теоретический расчет ЭДС самоиндукции
Рассмотрим явление самоиндукции на примере работы электромагнитной катушки при пропускании через нее постоянного тока. Включение катушки происходит при помощи бесконтактного датчика. Катушку можно заменить на последовательно соединенные активное Rk и индуктивное Lk сопротивления (рисунок 3).
Рисунок 3 — Эквивалентная схема электромагнитной катушкиТогда электрическая схема будет иметь вид, представленный на рисунке 4.
Рисунок 4 — Схема включения электромагнитной катушкиПри сработавшем датчики падение напряжения U на катушке составляет 24 В. При коммутации индуктивной нагрузки в первый момент времени ток остается равным току до коммутации, а после изменяется по экспоненциальному закону. Таким образом, при переходе управляющего транзистора в закрытое состояние катушка начинает генерировать ЭДС самоиндукции, предотвращающую падение тока. Попробуем рассчитать величину генерируемого катушкой напряжения.
При коммутации индуктивной нагрузки в первый момент времени ток остается равным току до коммутации, а после изменяется по экспоненциальному закону. Таким образом, при переходе управляющего транзистора в закрытое состояние катушка начинает генерировать ЭДС самоиндукции, предотвращающую падение тока. Попробуем рассчитать величину генерируемого катушкой напряжения.
На рисунке 5 показано направление тока при открытом транзисторе. Переход транзистора в закрытое состояние фактически означает что цепь катушки с генерируемым ЭДС самоиндукции замыкается через подтягивающий резистор. Обозначим его Ro. По документации датчика это сопротивление составляет 5,1 кОм.
Рисунок 5 — Направление тока при открытом транзистореРисунок 6 — Направление тока после перехода транзистора в закрытое состояниеНа рисунке 6 видно что ток на резисторе Ro поменял направление — это обусловлено возникновением ЭДС самоиндукции в катушке. Для полученного замкнутого контура выполняется следующее уравнение:
UR0+URk+ULk=0U_R0+U_Rk+U_Lk=0Выражая напряжение через ток и сопротивление, получим:
I×R0+I×Rk+ULk=0I times R_0 + I times R_k +U_Lk=0 ULk=−I×(Rk+R0)U_Lk= -I times ( R_k + R_0 )При этом ток в цепи стремится к значению тока при открытом транзисторе:
Подставим данное выражение в предыдущую формулу, получим величину генерируемого напряжения самоиндукции:
ULk=−U×(Rk+R0)/Rk=−U×(1+R0/Rk)U_Lk= -U times ( R_k + R_0 ) / R_k = -U times ( 1 + R_0 / R_k )Все переменные из этой формулы известны:
U = 24В — напряжение питания
Ro = 5,1кОм — сопротивление подтягивающего резистора датчика
Rk = 900 Ом — активное сопротивление катушки (данные из документации).
Подставив значения в формулу, рассчитаем примерное значение напряжения самоиндукции:
ULk=−U×(1+R0/Rk)=−24×(1+5100/900)=−160ВU_Lk= -U times ( 1 + R_0/R_k ) = -24 times ( 1 + 5100 / 900 )=-160 ВДанный расчет упрощен и не учитывает индуктивность катушки, от которой так же зависит ЭДС самоиндукции. Но даже из упрощенного расчета видно, что величина генерируемого напряжения оказывается во много раз больше номинального напряжения 24В.
Воздействие ЭДС самоиндукции может повредить устройства, имеющие общие с индуктивной нагрузкой цепи питания. На рисунке 7 приведена некорректная схема, на которой от одного источника питания подключен бесконтактный датчик и катушка соленоидного клапана.
Рисунок 7 — Некорректная схема подключенияНа первый взгляд, данная схема может работать без каких-либо сбоев. Однако, при выключении катушки клапана возникает всплеск напряжения в результате самоиндукции. Всплеск распространяется по цепи питания на клемму «минус» датчика. В результате, разница потенциалов между коллектором и эмиттером закрытого транзистора превышает максимальное значение, что приводит к его пробою.
В результате, разница потенциалов между коллектором и эмиттером закрытого транзистора превышает максимальное значение, что приводит к его пробою.
3. Практическое измерение ЭДС самоиндукции
Чтобы проверить правдивость приведенных выше теоретических расчетов, проведем измерение ЭДС самоиндукции. Для проведения измерений необходимо собрать схему, для которой мы проводили расчеты. При помощи осциллографа на клеммах катушки произведем измерение напряжения (рисунок 8).
Рисунок 8 — Измерение ЭДС самоиндукцииНа рисунке 9 изображена осциллограмма значений напряжения самоиндукции катушки с питанием 24 В. На графике видно, что реальный всплеск напряжения при отключении катушки в несколько раз больше напряжения питания и составляет 128 В. Как следствие, транзисторный ключ выйдет из строя. Возникающий скачок ЭДС приводит к пробою транзисторных ключей, бесконтактных датчиков, слаботочных коммутирующих элементов и другим нежелательным эффектам в схемах управления.
Рисунок 9 — ЭДС самоиндукции при выключении катушки с питанием 24 В4.
 Методы и средства защиты от ЭДС самоиндукции
Методы и средства защиты от ЭДС самоиндукцииДля подавления ЭДС самоиндукции и предотвращения выхода из строя оборудования необходимо принимать специальные меры. Для подавления пиков напряжения на катушке во время выключения, необходимо параллельно катушке включить в схему диод (для постоянного напряжения) или варистор (для переменного напряжения). ЭДС самоиндукции будет ограничиваться этими элементами, тем самым они будут обеспечивать защиту схемы.
Диод включается параллельно катушке против напряжения питания (рисунок 10). Таким образом, в установившемся режиме он не оказывает никакого воздействия на работу схемы. Однако при отключении питания на катушке возникает ЭДС самоиндукции, имеющая полярность, противоположную рабочему напряжению. Диод открывается и шунтирует катушку индуктивности.
а — включение диода в схему PNPб — включение диода в схему NPNРисунок 10 — Схема включения диода для защиты от самоиндукции
Варистор также включается параллельно катушке (рисунок 11).
При увеличении напряжения выше пороговой величины, сопротивление варистора резко уменьшается, шунтируя индуктивную нагрузку. Соответственно, при броске тока варистор быстро срабатывает и обеспечивает надежную защиту схемы.
На рисунке 12 изображен график напряжения во время включения и выключения индуктивной катушки с использованием защитного диода для напряжения 24 В.
Рисунок 12 — ЭДС самоиндукции с использованием диодаНа графике видно, что использование защитных диодов сглаживает переходную характеристику напряжения.
Для защиты от ЭДС самоиндукции существует целый ряд готовых устройств. Их выбор зависит от применяемой катушки и типа напряжения питания. Для гашения ЭДС самоиндукции на катушках промежуточных реле используют модули FINDER серии 99 (рисунок 13):
Рисунок 13 — Защитный модуль Finder/99.02.9.024.9999.02.0.230.98 Finder/ Модуль защитный(светодиод+варистор)~/=110…240
99. 02.9.024.99 Finder/ Модуль защитный(светодиод+диод), =6…24В
02.9.024.99 Finder/ Модуль защитный(светодиод+диод), =6…24В
Модули устанавливаются непосредственно на колодку реле, не требуют дополнительного изменения схемы управления.
В случае подключения катушек пускателей, либо катушек соленоидных клапанов, необходимо использовать защитные клеммники Klemsan серии WG-EKI (рисунок 14):
Рисунок 14 – Защитный клеммник WG-EKI110 220 Клеммник WG-EKI с варистором (0,5…2,5 мм2, рабочее напряжение до 30В, рабочий ток до 10А)
110 040 Клеммник WG-EKI с защитным диодом (0,5…2,5 мм2, рабочее напряжение до 1000В, рабочий ток до 10А, ток диода 1А)
Клеммники позволяют осуществить подключение индуктивной катушки без дополнительного изменения схемы. Клеммник имеет два яруса, соединенных между собой защитным диодом либо варистором. Для осуществления защиты необходимо провести провода питания катушки через этот клеммник. При использовании клеммника с защитным диодом необходимо соблюдать полярность при подключении (рисунок 15).
Заключение
В рамках данной статьи было рассмотрено явление самоиндукции, приведен теоретический расчет ЭДС и практическое подтверждение этого расчета. Применяя модули Finder серии 99 и клеммники Klemsan серии WG-EKI, можно избавиться от пагубного воздействия самоиндукции и сохранить целостность коммутирующих элементов цепей управления.
Инженер ООО «КИП-Сервис»
Хоровец Г.Н.
Список использованной литературы:
- Сивухин, Д.В. Общий курс физики. Электричество. Том III / Сивухин Д.В — М.: Наука, 1977. — 724.с.
- Калашников, С.Г. Электричество / Калашников С.Г. — 6-е изд., стереот. — М.: Физматлит, 2003.-624.с.
- Алексеев Н.И., Кравцов А.В. Лабораторный практикум по общей физике (электричество и магнетизм). Самоиндукция / Лицей No1580 при МГТУ им. Н.Э. Баумана, 2012. — 16 с.
Читайте также:
Электричество и магнетизм
Рассмотрим снова контур с током, но не станем его помещать на этот раз во внешнее магнитное поле. Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока
Ток сам создает свое собственное поле В, которое пронизывает контур. Это поле, как следует из закона Био — Савара — Лапласа, пропорционально силе тока
Собственное магнитное поле контура с током обуславливает наличие магнитного потока Y через поверхность, опирающуюся на этот контур, который также будет пропорционален силе тока в контуре
Введем коэффициент пропорциональности L
|
|
(8.16) |
Коэффициент пропорциональности L называется индуктивностью контура.
|
Индуктивность контурачисленно равна магнитному потоку, собственного магнитного поля через поверхность, опирающуюся на контур, при условии протекания в контуре единичного тока. |
Индуктивность контура определяется формой и размерами контура, а также свойствами окружающей среды.
|
В системе СИ единицей измерения индуктивности является генри (Гн)
|
Если в проводящем контуре протекает переменный электрический ток, то магнитное поле этого тока также меняется с течением времени. Собственный магнитный поток, создаваемый этим полем, также является переменным. Изменение магнитного потока влечет за собой возникновение ЭДС электромагнитной индукции.
|
Явление возникновения ЭДС индукции в замкнутом проводящем контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции. |
Видео 8. 13. Закон Фарадея. Явление самоиндукции.
13. Закон Фарадея. Явление самоиндукции.
Возникающая при этом ЭДС называется ЭДС самоиндукции. Явление самоиндукции является частным случаем электромагнитной индукции.
Явление самоиндукции является, в частности, причиной явления, которое называют «экстра токи замыкания и размыкания». Оно состоит в следующем. Собственное магнитное поле в цепи постоянного тока изменяется в моменты замыкания или размыкания цепи. Это означает, что в такие моменты в цепи должна возникать ЭДС самоиндукции. Направление токов самоиндукции следует из правила Ленца. При замыкании цепи ЭДС самоиндукции вызывает ток, препятствующий увеличению основного тока в цепи, что делает конечной скорость роста силы тока, а при размыкании ток самоиндукции, препятствуя его уменьшению, делает конечной скорость убывания тока. Если бы не ЭДС самоиндукции, то при замыкании цепи ток мгновенно нарастал бы до своего стационарного значения, а при размыкании цепи, мгновенно убывал бы до нуля.
Выведем формулу для ЭДС самоиндукции . Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
Для этого надо продифференцировать полный магнитный поток, охватываемый проводящим контуром, по времени
|
|
(8.17) |
Если контур не меняет свою форму, и рядом с контуром нет ферромагнетиков, то его индуктивность от времени не зависит. Однако, даже при неизменной форме контура, при наличии ферромагнетиков, например, ферромагнитного сердечника, индуктивность контура зависит от силы тока в нём и, тем самым, от времени, если ток переменный. Таким образом, в присутствии ферромагнетиков
,
что необходимо учитывать при дифференцировании
Подставляя это выражение в (8.17), получаем для неподвижного контура всреде
|
|
(8. |
Если же индуктивность контура не зависит от силы тока в нём, то имеем
|
|
(8.19) |
Мы приходим к закону самоиндукции. В этом простейшем случае:
|
В отсутствие ферромагнетиков ЭДС самоиндукции в цепи прямопропорциональна скорости изменения силы тока в этой цепи. |
Будем считать катушку длинной, а магнитное поле внутри нее — однородным. Пропустим через соленоид ток I. Тогда магнитная индукциявнутри соленоида равна, как мы знаем (см. (6.20)), равна
где — магнитная проницаемость сердечника, a n — число витков на единицу длины.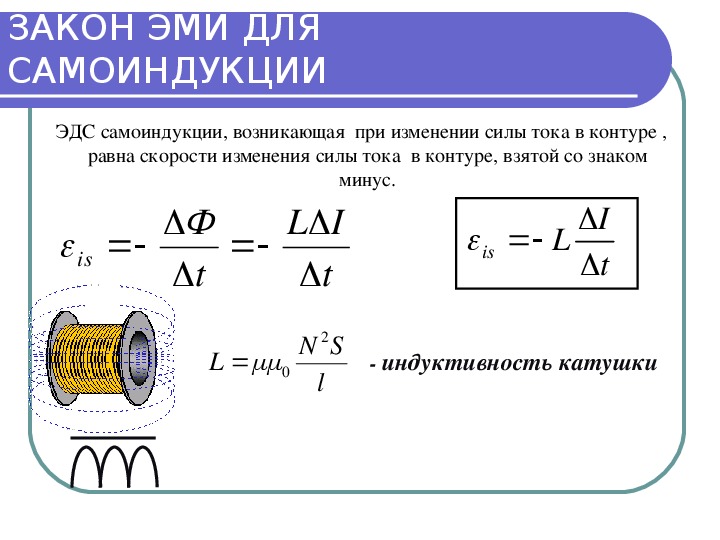 Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
Полное число витков в катушке равно , где l — ее длина. Пусть S — площадь поперечного сечения соленоида. Полный магнитный поток (потокосцепление) определяется как
|
|
(8.20) |
где V — объем соленоида: V = Sl. Согласно определению индуктивности как коэффициента пропорциональности между и I, получаем величину индуктивности длинного соленоида (рис. 8.31)
|
|
(8.21) |
Рис. 8.31. Индуктивность соленоида
При замыкании или размыкании цепи (то есть в случаях, когда ток в цепи меняется по величине) в ней вследствие явления самоиндукции возникают дополнительные токи, которые по правилу Ленца всегда направлены так, чтобы воспрепятствовать причине их вызывающей, то есть чтобы воспрепятствовать нарастанию или убыванию тока в цепи. Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Следовательно, как уже было сказано,при замыкании цепи ЭДС самоиндукции будет замедлять скорость нарастания тока, а при размыкании, напротив, замедлять скорость уменьшения тока в ней.
Самоиндукция. Индуктивность. Энергия магнитного поля тока
Самоиндукция. Индуктивность. Энергия магнитного поля тока
- Подробности
- Просмотров: 640
Самоиндукция
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.
Это явление называется самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции
Проявление явления самоиндукции
Замыкание цепи
При замыкании в эл. цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.
Размыкание цепи
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.
Вывод:
в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От чего зависит ЭДС самоиндукции?
Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность — физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
ЭДС САМОИНДУКЦИИ
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.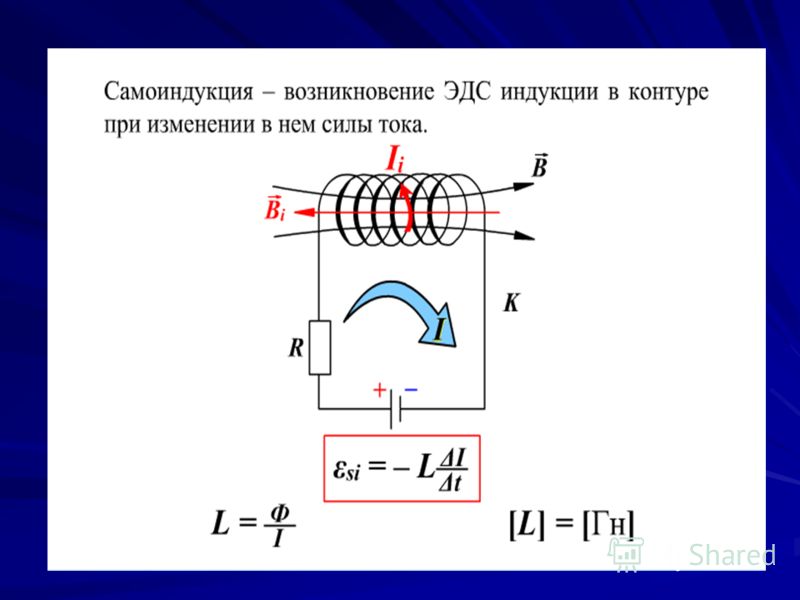
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? — выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
по теме «Электромагнитная индукция»
1. Перечислить 6 способов получения индукционного тока.
Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток ( определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле ( причина появления, чертеж, формула, входящие величины, их ед. измерения).
8. Самоиндукция (кратко проявление в электротехнике, определение).
9. ЭДС самоиндукции (ее действие и формула).
10. Индуктивность (определение, формулы, ед. измерения).
11. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).
Электромагнитное поле — Класс!ная физика
Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера —
Действие магнитного поля на движущийся заряд. Магнитные свойства вещества —
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца —
ЭДС электромагнитной индукции. Вихревое электрическое поле —
ЭДС индукции в движущихся проводниках
Магнитные свойства вещества —
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца —
ЭДС электромагнитной индукции. Вихревое электрическое поле —
ЭДС индукции в движущихся проводниках
—
Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе
Электродвижущая сила индукции. Закон Фарадея-Ленца
1. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
По определению Фарадея общим для этих
опытов является то, что: если поток вектора
индукции, пронизывающий замкнутый,
проводящий контур меняется, то в контуре
возникает электрический ток.
Это явление называют явлением
электромагнитной индукции, а ток –
индукционным.
При этом, явление совершенно не зависит
от способа изменения потока вектора
магнитной индукции.
2. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
 1. Электродвижущая сила индукции. Закон
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
Итак, движущиеся заряды (ток) создают магнитное
поле, а движущееся магнитное поле создает
(вихревое) электрическое поле и, собственно
индукционный ток.
Ленц установил общее правило нахождения
направления тока: индукционный ток всегда
направлен так, что магнитное поле этого тока
препятствует изменению магнитного потока,
вызывающего индукционный ток — правило Ленца.
3. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
Заполнение всего пространства
однородным магнетиком приводит при
прочих равных условиях к увеличению
индукции в µ раз.
Индукционный ток
обусловлен изменением
потока вектора B , а не потока вектора E .
4. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
Для создания тока в цепи необходимо
наличие ЭДС.

Поэтому явление электромагнитной
индукции свидетельствует о том, что при
изменении магнитного потока в контуре
возникает ЭДС индукции .
5. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
Для определения величины и природы ЭДС
индукции рассмотрим перемещение
подвижного участка 1 – 2 контура с током в
магнитном поле
6. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
Пусть сначала магнитное поле
отсутствует.
Батарея с ЭДС равной ε0 создает ток
I0 .
За время dt батарея совершает
работу
dA ε 0 I 0 dt
– эта работа будет переходить в тепло,
которое можно найти по закону
Джоуля-Ленца.
7. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
Поместим контур в однородное
магнитное поле с индукцией B .

Линии B параллельны n и связаны с
направлением тока «правилом
буравчика».
Поток Ф, сцепленный с контуром, ˃0 .
8. 1. Электродвижущая сила индукции. Закон Фарадея – Ленца.
1. Электродвижущая сила индукции. ЗаконФарадея – Ленца.
Каждый элемент контура
испытывает
механическую силу dF .
Подвижная сторона
рамки будет
испытывать силу F0 .
Под действием этой силы участок 1 – 2
будет перемещаться со скоростью dx/dt .
При этом изменится и поток магнитной
индукции.
Тогда в результате электромагнитной
индукции, ток в контуре изменится и станет
равным I I 0 I i .
9. Величина ЭДС индукции
F0Изменится и сила
,
которая
теперь
станет равна F – результирующая
сила. Эта сила за время dt произведет
работу dA: dA Fdx IdФ.
Как и в случае, когда все элементы
рамки неподвижны, источником
работы является ε0.
10. Величина ЭДС индукции
При неподвижном контуре эта работасводилась только лишь к выделению тепла.

В нашем случае тепло тоже будет
выделяться, но уже в другом количестве,
так как ток изменился.
Кроме того, совершается механическая
работа.
Общая работа за время dt, равна:
0 Idt I 2 Rdt IdФ .
11. Величина ЭДС индукции
Отсюда:I
dФ
dt .
R
0
Полученное выражение мы вправе
рассматривать как закон Ома для контура, в
котором кроме источника действует эдс
индукции , которая равна:
dФ
i
dt
ЭДС индукции контура равна скорости
изменения потока магнитной индукции,
пронизывающей этот контур.
.
12. Величина ЭДС индукции
Это выражение для ЭДС индукции контураявляется совершенно универсальным, не
зависящим от способа изменения потока
магнитной индукции и носит название закон
Фарадея.
Знак минус – математическое выражение
правила Ленца о направлении
индукционного тока: индукционный ток
всегда направлен так, чтобы своим полем
противодействовать изменению начального
магнитного поля.

13. Природа ЭДС индукции
Ответим на вопрос, что являетсяпричиной движения зарядов,
причиной возникновения
индукционного тока. Рассмотрим
рисунок
14. Природа ЭДС индукции
1) Если перемещать проводник воднородном магнитном поле , то под
действием силы Лоренца, электроны
будут отклоняться вниз, а
положительные заряды вверх –
возникает разность потенциалов, под
действием которой течет ток.
Как мы знаем, для положительных
зарядов F q [B, ], для электронов F e[B, ].
л
л
15. Природа ЭДС индукции
2) Если проводник неподвижен, аизменяется магнитное поле, какая сила
возбуждает индукционный ток в этом
случае?
Возьмем обыкновенный трансформатор.
Как только мы замкнули цепь первичной
обмотки, во вторичной обмотке сразу
возникает ток.
Но ведь сила Лоренца здесь ни причем, т.к.
она действует на движущиеся заряды, а они
в начале покоились (находились в тепловом,
хаотическом движении).

16. Природа ЭДС индукции
Ответ был дан Дж. Максвеллом в1860 г.: всякое переменное магнитное
поле возбуждает в окружающем
пространстве электрическое поле.
Оно и является причиной
возникновения индукционного тока в
проводнике.
То есть, возникает только при
наличии переменного магнитного
поля (на постоянном токе
трансформатор не работает).
17. Природа ЭДС индукции
Сущность явления электромагнитнойиндукции совсем не в появлении
индукционного тока (ток появляется
тогда, когда есть заряды и замкнута
цепь), а в возникновении вихревого
электрического поля (не только в
проводнике, но и в окружающем
пространстве, в вакууме).
18. Природа ЭДС индукции
Это поле имеет совершенно инуюструктуру, нежели поле, создаваемое
зарядами.
Так как оно не создается зарядами,
то силовые линии не могут
начинаться и заканчиваться на
зарядах, как это было у нас в
электростатике.

Это поле вихревое, силовые линии
его замкнуты.
19. Циркуляция вектора напряженности вихревого электрического поля
Чему равнациркуляция
вектора
вихревого
электрического
поля в случае
изображенном
на рисунке?
20. Циркуляция вектора напряженности вихревого электрического поля
Работу вихревого электрического поля поперемещению заряда вдоль замкнутого
контура L можно подсчитать по формуле
dA q E’ d l .
С другой стороны, работа по перемещению
L
единичного заряда вдоль замкнутой цепи
равна ЭДС, действующей в этой цепи:
dA i
Следовательно:
dФ
E
‘
d
l
.
d
t
L
21. Циркуляция вектора напряженности вихревого электрического поля
Эти выражения для циркуляциисправедливы всегда, независимо от
того, выполнен контур в виде
линейного проводника, диэлектрика
или речь идет о контуре (мысленном)
в вакууме.
Если контур выполнен из диэлектрика,
то каждый элемент его поляризуется
в соответствии с действующим
электрическим полем .

22. Циркуляция вектора напряженности вихревого электрического поля
Если заряд q движется в вакууме по контуру,то при каждом обходе контура
механическая энергия его возрастает на
величину
m 2
qE ‘ d l q i ;
2 L
(при движении заряда в проводнике из-за
сопротивления устанавливается
динамическое равновесие).
На использовании этого факта основан
оригинальный ускоритель электронов –
бетатрон.
23. Токи Фуко (вихревые токи)
До сих пор мы рассматривалииндукционные токи в линейных
проводниках.
Но индукционные токи будут возникать и в
толще сплошных проводников при
изменении в них потока вектора магнитной
индукции .
Они будут циркулировать в веществе
проводника (напомним, что линии –
замкнуты).
Так как электрическое поле вихревое и токи
называются вихревыми – токи Фуко.
24. Токи Фуко (вихревые токи)
Если медную пластину отклонить от положенияравновесия и отпустить так, чтобы она вошла со
скоростью υ в пространство между полосами
магнита, то пластина практически остановится в
момент ее вхождения в магнитное поле.

Замедление движения связано с возбуждением в
пластине
вихревых
токов,
препятствующих
изменению потока вектора магнитной индукции.
Поскольку
пластина
обладает
конечным
сопротивлением,
токи
индукции
постепенно
затухают и пластина медленно двигается в
магнитном поле.
Если электромагнит отключить, то медная пластина
будет совершать обычные колебания, характерные
для маятника.
25. Токи Фуко (вихревые токи)
Тормозящее действие тока Фуко используется длясоздания магнитных успокоителей – демпферов.
Если под качающейся в горизонтальной плоскости
магнитной стрелкой расположить массивную медную
пластину, то возбуждаемые в медной пластине токи Фуко
будут тормозить колебание стрелки.
Магнитные успокоители такого рода используются в
сейсмографах, гальванометрах и других приборах.
Токи Фуко применяются в электрометаллургии для плавки
металлов.
Металл помещают в переменное магнитное поле,
создаваемое током частотой 500 2000 Гц.

В результате индуктивного разогрева металл плавится, а
тигль в котором он находится при этом остается холодным.
Например, при подведенной мощности 600 кВт тонна
металла плавится за 40 – 50 минут.
26. Скин-эффект
Если быстропеременный высокочастотный токпротекает по проводнику, то вихревые токи,
индуцируемые в проводнике, препятствуют
равномерному распределению плотности тока по
поперечному сечению проводника – плотность тока
на оси провода оказывается меньше, чем у его
поверхности.
Ток как бы вытесняется на поверхность провода, при
этом вихревые токи по оси проводника текут против
направления основного тока, а на поверхности – в
том же направлении.
Это явление называется скин-эффектом (от англ.
skin – кожа, оболочка).
27. Скин-эффект
При нарастании тока в проводе ЭДСиндукции направлена против тока.
Электрическое поле самоиндукции
максимально на оси провода, что
приводит к неравномерному
распределению плотности тока.

Плотность тока убывает от
поверхности к оси провода примерно
по экспоненциальному закону.
28. Скин-эффект
29. Скин-эффект
При частоте ν 50 Гц,r0 10 мм – токпрактически равномерно распределен
по объему проводов, исключая очень
толстые кабели.
Но при высокочастотных колебаниях
ν 100 МГц 108 Гц
глубина проникновения равна
– ток почти целиком течет по
поверхности провода.
r0 7 10 3 мм
30. Скин-эффект
По этой причине с целью уменьшения потерьповерхность высокочастотных контуров серебрят.
Провода для переменных токов высокой частоты,
учитывая скин-эффект, сплетают из большого числа
тонких проводящих нитей, изолированных друг от
друга эмалевым покрытием – литцендратом.
ВЧ-токи используются для закалки поверхностей
деталей: поверхностный слой разогревается быстро
в ВЧ поле, закаливается и становится прочным, но не
хрупким, так как внутренняя часть детали – не
разогревалась и не закаливалась.

31. САМОИНДУКЦИЯ И ВЗАИМНАЯ ИНДУКЦИЯ
1. Явление самоиндукции2. Влияние самоиндукции на ток при
замыкании и размыкании цепи,
содержащей индуктивность
3. Взаимная индукция
4. Индуктивность трансформатора
5. Энергия магнитного поля
32. Явление самоиндукции
До сих пор мы рассматривали изменяющиесямагнитные поля не обращая внимание на то, что
является их источником.
На практике, чаще всего магнитные поля создаются с
помощью различного рода соленоидов, т.е.
многовитковых контуров с током.
Здесь возможны два случая: при изменении тока в
контуре изменяется магнитный поток,
пронизывающий: а) этот же контур; б) соседний
контур.
ЭДС индукции, возникающая в самом же контуре
называется ЭДС самоиндукции, а само явление –
самоиндукция.
33. Явление самоиндукции
Если же ЭДС индукции возникаетв соседнем контуре, то говорят о
явлении взаимной индукции.
Ясно, что природа явления одна
и та же, а разные названия
использованы для того, чтобы
подчеркнуть место
возникновения ЭДС индукции.

34. Явление самоиндукции
Явление самоиндукции открыламериканский ученый Дж. Генри в
1831 г.
Явление самоиндукции можно
определить следующим образом.
Ток I, текущий в любом контуре
создает магнитный поток Ψ,
пронизывающий этот же контур. При
изменении I, будет изменяться Ψ,
следовательно в контуре будет
наводится ЭДС индукции.
35. Явление самоиндукции
Т.к. магнитная индукция Впропорциональна току I ( B μμ 0 nI ),
следовательно Ψ LI ,
где L – коэффициент
пропорциональности, названный
индуктивностью контура.
36. Явление самоиндукции
За единицу индуктивности в СИпринимается индуктивность
такого контура, у которого при
токе I 1 A возникает полный поток
Ψ 1 Вб
Эта единица называется Генри
(Гн).
37. Явление самоиндукции
Вычислим индуктивность соленоида L.Если длина соленоида l гораздо больше его
диаметра d (), то к нему можно применить
формулы для бесконечно длинного
соленоида.

N
B
μμ
I
,
0
Тогда
l
здесь N – число витков.
Поток через каждый из витков Ф BS.
Потокосцепление
N
N 2S
Ψ NBS μμ 0 I
l
NS μμ 0
l
I.
38. Явление самоиндукции
Так какLI
Lсол
N 2S
0
0 n 2 lS ,
l
n N / l, l S V
Lсол 0 n 2V .
При изменении тока в контуре в нем
возникает ЭДС самоиндукции, равная
dΨ
d
dI
IL L ,
i
dt
dt
dt
39. Явление самоиндукции
Явление самоиндукции играетважную роль в электротехнике и
радиотехнике.
Как мы увидим дальше, благодаря
самоиндукции происходит
перезарядка конденсатора,
соединенного последовательно с
катушкой индуктивности, в
результате в такой LC-цепочке
(колебательном контуре) возникают
электромагнитные колебания.
40. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
Рассмотрим несколько случаев влияния ЭДСсамоиндукции на ток в цепи.

Случай 1.
По правилу Ленца, токи возникающие в цепях
вследствие самоиндукции всегда направлены так,
чтобы препятствовать изменению тока, текущего в
цепи.
Это приводит к тому, что при замыкании ключа К
установление тока I2 в цепи содержащей
индуктивность L, будет происходить не мгновенно, а
постепенно.
41. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
Сила тока в этой цепи будет удовлетворятьуравнению
R
t
I 2 I 0 1 e L
.
42. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
Скорость возрастания тока будетхарактеризоваться постоянной времени
L
цепи
τ
.
R
В цепи, содержащей только активное
сопротивление R ток установится
практически мгновенно
(пунктирная кривая ).
43. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
Случай 2.
При переводе ключа из положения 1 в 2 в
момент времени t0 , ток начнет уменьшаться
но ЭДС самоиндукции будет поддерживать
ток в цепи, т.е. препятствовать резкому
уменьшению тока.
В этом случае убывание тока в цепи можно
описать уравнением
I I 0e
R
t
L
I 0e
t
.
44. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
45. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
Оба эти случая говорят, что чем большеиндуктивность цепи L и чем меньше сопротивление
R, тем больше постоянная времени и тем медленнее
изменяется ток в цепи.
Случай 3.
Размыкание цепи содержащей индуктивность L.
Сначала цепь замкнута. В цепи течет
установившийся ток. Поэтому рисуем зависимость
i (t ) . При размыкании цепи в момент времени t0 , R .
Это приводит к резкому возрастанию ЭДС индукции,
определяемой по формуле:
i L
dI
.

dt
46. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
47. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
Происходит этот скачек вследствие большойвеличины скорости изменения тока
dI
dt
i резко возрастает по сравнению с 0 и даже может
быть в несколько раз больше . (Нельзя резко
размыкать цепь, состоящую из трансформатора и
других индуктивностей).
48. Взаимная индукция
Возьмем два контура, расположенныенедалеко друг от друга
В первом контуре течет ток I1 . Он создает
магнитный поток, который пронизывает и
витки второго контура.
Ψ2 L21I1.
49. Взаимная индукция
При изменении тока I1 во втором контуренаводится ЭДС индукции
i 2 L21
Аналогично, ток I 2 второго контура создает
магнитный поток пронизывающий первый
контур
Ψ1 L12 I 2 .
И при изменении тока I 2 наводится ЭДС
i 1 L12
dI1
.

dt
dI 2
.
dt
Контуры называются связанными, а
явление – взаимной индукцией.
50. Индуктивность трансформатора
Трансформатор является типичнымпримером двух связанных контуров.
Рассмотрим индуктивность трансформатора
и найдем коэффициент трансформации.
Рассчитаем взаимную индуктивность двух
катушек и , намотанных на общий
сердечник
51. Индуктивность трансформатора
Когда в первой катушке идет ток , всердечнике возникает магнитная индукция
и магнитный поток Ф через поперечное
сечение S.
Магнитное поле тороида можно рассчитать
по формуле
N1
Β μμ 0 I1
l
.
Через вторую обмотку проходит полный
магнитный поток Ψ2 сцепленный со второй
NN
обмоткой
Ψ N BS μμ 1 2 SI ,
2
2
0
l
1
52. Индуктивность трансформатора
здесь Ψ2 N 2Ф – потокосцепление котороеможно найти по формуле:
Ψ 2 L21I1.
По определению взаимная индуктивность
двух катушек равна:
Ψ2
N1N 2
L12 L21
μμ 0
S.

I1
l
К первичной обмотке подключена
переменная ЭДС E1 . По закону Ома ток в этой
цепи будет определятся алгебраической
суммой внешней ЭДС и ЭДС индукции.
53. Индуктивность трансформатора
К первичной обмотке подключенапеременная ЭДС 1.
По закону Ома ток в этой цепи будет
определяться алгебраической суммой
внешней ЭДС и ЭДС индукции.
d( N 1Ф)
1
I1 R1 ,
dt
где R1 – сопротивление обмотки, которое
делают малым, так что
I1R1 0
54. Индуктивность трансформатора
Тогда1
d( N 1Ф)
dФ
N1
.
dt
dt
Во второй обмотке, по аналогии
1 N1
Отсюда
.
2
N2
Если пренебречь потерями, т.е.
предположить, что R 0 , то
1 I1 2 I 2 .
dФ
2 N2
dt
Коэффициент трансформации
1 N2
.
2 N1
55. Энергия магнитного поля
Сначала замкнем соленоид L на источникЭДС , в нем будет протекать ток .

Затем переключим ключ в положение 2 –
замкнем соленоид на сопротивление R.
В цепи будет течь убывающий ток I.
При этом будет совершена работа:
56. Энергия магнитного поля
Определим ееdA i Idt ;
dA L
dI
Idt LIdI ;
dt
LI 2
A L IdI
;
2
I
0
LI 2
A
.
2
57. Энергия магнитного поля
Эта работа пойдет на нагреваниепроводников.
Но откуда взялась эта энергия?
Поскольку других изменений кроме
исчезновения магнитного поля в окружном
пространстве не произошло, остается
заключить, что энергия была локализована
в магнитном поле.
Значит, проводник, с индуктивностью L, по
которой течет ток I, обладает энергией
LI 2
W
.
2
58. Энергия магнитного поля
Обозначим w – плотность энергии,или энергия в объеме V, тогда
W 0 H
w
,
V
2
2
B2
w
.
2 0
BH
w
2
Энергия однородного магнитного
поля в длинном соленоиде может
быть рассчитана по формуле:
W
1
0 n2 I 2V
2
w
1
0 n 2 I 2
2
59.
 Контрольные вопросы 1.
Контрольные вопросы 1.2.
3.
4.
5.
6.
Дайте определение явления
электромагнитной индукции.
Сформулируйте правило Ленца.
Циркуляция вектора напряженности
вихревого электрического поля.
Определение: токи Фуко, скин – эффект.
Явление самоиндукции.
Взаимная индукция
60. Контрольные вопросы
1. Взаимная индуктивность двух катушек –трансформатора.
2. Энергия магнитного поля, объемная плотность
энергии магнитного поля, объемная плотность
энергии магнитного поля соленоида.
3. Диамагнетики, парамагнетики, ферромагнетики.
4. Орбитальный магнитный момент электрона,
орбитальный момент импульса электрона.
5. Гиромагнитное отношение орбитальных моментов,
гиромагнитное отношение спиновых моментов.
Чему равно эдс самоиндукции. Что такое самоиндукция — объяснение простыми словами
Магнитное поле
контура, в котором сила тока изменяется,
индуцирует ток не только в других
контурах, но и в себе самом. Это
явление получило название самоиндукции.
Это
явление получило название самоиндукции.
Опытным путём установлено, что магнитный поток вектора магнитной индукции поля, создаваемого текущим в контуре током, пропорционален силе этого тока:
где L– индуктивность контура. Постоянная характеристика контура, которая зависит от его формы и размеров, а так же от магнитной проницаемости среды, в которой находится контур. [L] = Гн (Генри,
1Гн = Вб/А).
Если за время dtток в контуре изменится наdI, то магнитный поток, связанный с этим током, изменится наdФ =LdIв результате чего в этом контуре появится ЭДС самоиндукции:
Знак минус показывает, что ЭДС самоиндукции (а, следовательно, и ток самоиндукции) всегда препятствует изменению силы тока, который вызвал самоиндукцию.
Наглядным примером явления самоиндукции служат экстратоки замыкания и размыкания, возникающие при включении и выключении электрических цепей, обладающей значительной индуктивностью.
Энергия магнитного поля
Магнитное поле
обладает потенциальной энергией, которая
в момент его образования (или изменения)
пополняется за счёт энергии тока в цепи,
совершающего при этом работу против
ЭДС самоиндукции, возникающей вследствие
изменения поля.
Работа dAза бесконечно малый промежуток времениdt, в течении которого ЭДС самоиндукциии токIможно считать постоянными, равняется:
. (5)
Знак минус указывает, что элементарная работа совершается током против ЭДС самоиндукции. Чтобы определить работу при изменении тока от 0 до I, проинтегрируем правую часть, получим:
. (6)
Эта работа численно равна приросту потенциальной энергии ΔW п магнитного поля, связанного с этой цепью, т.е.A= -ΔW п.
Выразим энергию магнитного поля через его характеристики на примере соленоида. Будем считать, что магнитное поле соленоида однородно и в основном расположено внутри его. Подставим в (5) значение индуктивности соленоида, выраженное через его параметры и значение силы тока I, выраженное из формулы индукции магнитного поля соленоида:
, (7)
где N – общее число витков соленоида; ℓ – его длина; S – площадь сечения внутреннего канала соленоида.
, (8)
После подстановки имеем:
Разделив обе части на V, получим объёмную плотность энергии поля:
(10)
или, с учётом, что
получим,
. (11)
(11)
Переменный ток
2.1 Переменный ток и его основные характеристики
Переменным называется ток, изменяющийся с течением времени и по величине и по направлению. Примером переменного тока может служить потребляемый промышленный ток. Этот ток является синусоидальным, т.е. мгновенное значение его параметров меняются со временем по закону синуса (или косинуса):
i = I 0 sinωt, u = U 0 sin(ωt + φ 0). (12)
Переменный синусоидальный ток можно получить, если вращать рамку (контур) с постоянной скоростью
в однородном магнитном поле с индукцией B (рис.5). При этом магнитный поток, пронизывающий контур, изменяется по закону
где S– площадь контура, α = ωt– угол поворота рамки за время t. Изменение потока приводит к возникновению ЭДС индукции
, (17)
направление которой определяется по правилу Ленца.
Если контур замкнут (рис.5), то по нему идёт ток:
. (18)
График изменения электродвижущей
силыи индукционного токаi представлен на рис. 6.
6.
Переменный
ток характеризуется периодом Т, частотой
ν = 1/Т, циклической частотой
и фазой φ = (ωt
+ φ 0)
Графически значения напряжения и силы
переменного тока на участке цепи будут
представляться двумя синусоидами, в
общем случае сдвинутыми по фазе на φ.
Для характеристики переменного тока вводятся понятия действующего (эффективного) значения тока и напряжения. Эффективным значением силы переменного тока называется сила такого постоянного тока, который выделяет в данном проводнике столько же тепла за время одного периода, сколько выделяет тепла и данный переменный ток.
,
. (13)
Приборы, включенные в цепь переменного тока (амперметр, вольтметр), показывают эффективные значения тока и напряжения.
Согласно закону Фарадея ℰ is = – . Если Ф = LI , то ℰ is = = – . При условии, что индуктивность контура в процессе изменения тока не меняется (т.е. не меняются геометрические размеры контура и магнитные свойства среды), то
ℰ is = – . (13.2)
(13.2)
Из этой формулы видно, что если индуктивность катушки L достаточно велика, а время изменения тока мало, то величина ℰ is может достигнуть большой величины и превысить ЭДС источника тока при размыкании цепи. Именно этот эффект мы наблюдали в опыте 1.
Из формулы (13.2) можно выразить L :
L = – ℰ is /(DI /Dt ),
т.е. индуктивность имеет еще один физический смысл: она численно равна ЭДС самоиндукции при скорости изменения тока через контур 1 А в 1 с.
Читатель : Но тогда получится, что размерность индуктивности
[L ] = Гн = .
СТОП! Решите самостоятельно: А3, А4, В3–В5, С1, С2.
Задача 13.2. Какова индуктивность катушки с железным сердечником, если за время Dt = 0,50 с ток в цепи изменился от I 1 = = 10,0 А до I 2 = 5,0 А, а возникшая при этом ЭДС самоиндукции по модулю равна |ℰ is | = 25 В?
Ответ : L = ℰ is » 2,5 Гн.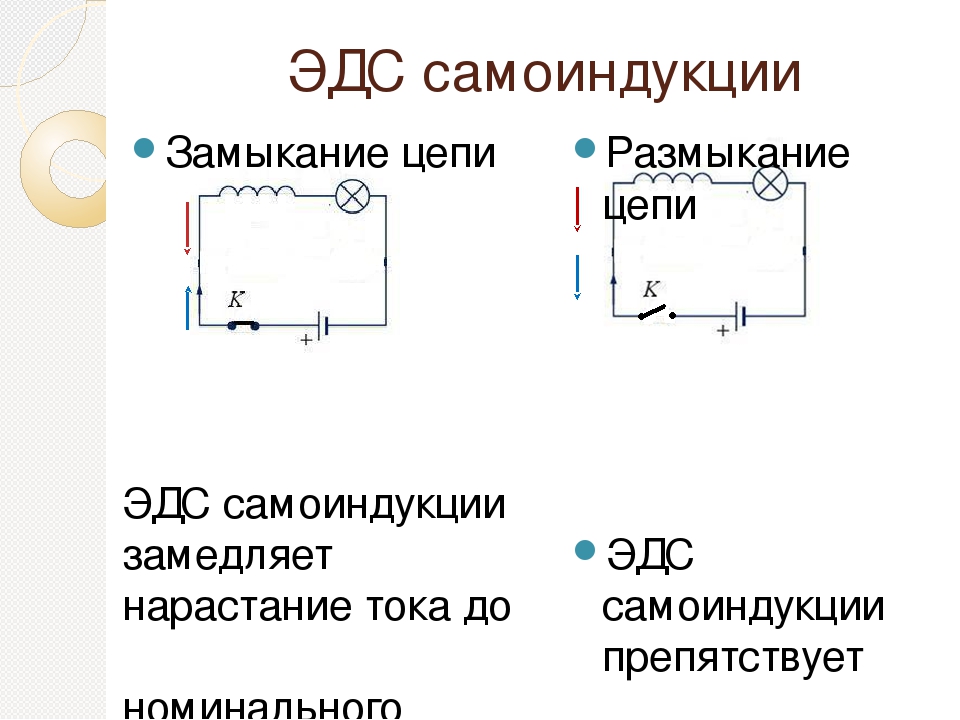
СТОП! Решите самостоятельно: А5, А6, В6.
Читатель : А какой смысл имеет знак минус в формуле (13.2)?
| Рис. 13.6 |
Автор : Рассмотрим какой-либо проводящий контур, по которому течет ток. Выберем направление обхода контура – по или против часовой стрелки (рис. 13.6). Вспомним: если направление тока совпадает с выбранным направлением обхода, то сила тока считается положительной, а если нет – отрицательной.
Изменение тока DI = I кон – I нач – также величина алгебраическая (отрицательная или положительная). ЭДС самоиндукции – это работа, совершаемая вихревым полем при перемещении единичного положительного заряда по контуру вдоль направления обхода контура . Если напряженность вихревого поля направлена вдоль направления обхода контура, то эта работа положительна, а если против – отрицательна. Таким образом, знак минус в формуле (13.2) показывает, что величины DI и ℰ is всегда имеют разные знаки.
Покажем это на примерах (рис. 13.7):
а) I > 0 и DI > 0, значит, ℰ is
б) I > 0 и DI is >
в) I I| > 0, т.е. модуль тока возрастает, а сам ток становится все «более отрицательным». Значит, DI is > 0, т.е. ЭДС самоиндукции «включена» вдоль направления обхода;
г) I I| I > 0, тогда ℰ is
В задачах, по возможности, следует выбирать такое направление обхода, чтобы ток был положительным.
Задача 13.3. В цепи на рис. 13.8, а L 1 = 0,02 Гн и L 2 = 0,005 Гн. В некоторый момент ток I 1 = 0,1 А и возрастает со скоростью 10 А/с, а ток I 2 = 0,2 А и возрастает со скоростью 20 А/с. Найти сопротивление R .
| а б Рис. 13.8 Решение. Так как оба тока возрастают, то в обеих катушках возникают ЭДС самоиндукции ℰ is 1 | |
| L 1 = 0,02 Гн L 2 = 0,005 Гн I 1 = 0,1 А I 2 = 0,2 А DI 1 /Dt = 10 А/с DI 2 /Dt = 20 А/с | |
| R = ? | |
и ℰ is 2 , включенные навстречу токам I 1 и I 2 (рис. 13.8, б ), где
13.8, б ), где
|ℰ is 1 | = ; |ℰ is 2 | = .
Выберем направление обхода по часовой стрелке (см. рис. 13.8,б ) и применим второе правило Кирхгофа
–|ℰ is 1 | + |ℰ is 2 | = I 1 R – I 2 R ,
R = |ℰ is 2 | – |ℰ is 1 | / (I 1 – I 2) = =
1 Ом.
Ответ : R = » 1 Ом.
СТОП! Решите самостоятельно: В7, В8, С3.
Задача 13.4. Катушка сопротивлением R = 20 Ом и индуктивностью L = 0,010 Гн находится в переменном магнитном поле. Когда создаваемый этим полем магнитный поток увеличился на DФ = = 0,001 Вб, ток в катушке возрос на DI = 0,050 А. Какой заряд прошел за это время по катушке?
дукции |ℰ is | = . Причем ℰ is «включилась» навстречу ℰ i , так как ток в цепи возрастал (рис. 13.9).
Возьмем направление обхода контура по часовой стрелке. Тогда согласно второму правилу Кирхгофа получим:
|ℰ i | – |ℰ is | = IR ,
I = (|ℰ i | – |ℰ is |)/R = .
Заряд q , прошедший по катушке за время Dt , равна
q = I Dt =
Ответ : 25 мкКл.
СТОП! Решите самостоятельно: В9, В10, С4.
Задача 13.5. Катушка с индуктивностью L и электрическим сопротивлением R подключена через ключ к источнику тока с ЭДС ℰ. В момент t = 0 ключ замыкают. Как изменяется со временем сила тока I в цепи сразу же после замыкания ключа? Через длительное время после замыкания? Оцените характерное время t возрастания тока в такой цепи. Внутренним сопротивлением источника тока можно пренебречь.
Рис. 13.10
| Рис. 13.11 |
Сразу же после замыкания ключа I = 0, поэтому можно считать » ℰ/L , т.е. ток возрастает с постоянной скоростью (I = (ℰ/L )t ;рис. 13.11).
9.4. Явление электромагнитной индукции
9.4.3. Среднее значение электродвижущей силы самоиндукции
При изменении потока, сцепленного с замкнутым проводящим контуром, через площадь, ограниченную данным контуром, в нем появляется вихревое электрическое поле и течет индукционный ток — явление электромагнитной самоиндукции.
Модуль средней ЭДС самоиндукции за определенный промежуток времени рассчитывают по формуле
〈 | ℰ i s | 〉 = | Δ Ф s | Δ t ,
где ΔФ s — изменение магнитного потока, сцепленного с контуром, за время Δt .
Если сила тока в контуре изменяется с течением времени I = I (t ), то
∆Ф s = L ∆I ,
где L — индуктивность контура; ΔI — изменение силы тока в контуре за время Δt ;
〈 | ℰ i s | 〉 = L | Δ I | Δ t ,
где ΔI /Δt — скорость изменения силы тока в контуре.
Если индуктивность контура изменяется с течением времени L = L (t ), то
- изменение потока, сцепленного с контуром, определяется формулой
∆Ф s = ∆LI ,
где ΔL — изменение индуктивности контура за время Δt ; I — сила тока в контуре;
- модуль средней ЭДС самоиндукции за определенный промежуток времени рассчитывается по формуле
〈 | ℰ i s | 〉 = I | Δ L | Δ t .
Пример 16. В замкнутом проводящем контуре с индуктивностью 20 мГн течет ток силой 1,4 А. Найти среднее значение ЭДС самоиндукции, возникающей в контуре, при равномерном уменьшении в нем силы тока на 20 % за 80 мс.
В замкнутом проводящем контуре с индуктивностью 20 мГн течет ток силой 1,4 А. Найти среднее значение ЭДС самоиндукции, возникающей в контуре, при равномерном уменьшении в нем силы тока на 20 % за 80 мс.
Решение . Появление ЭДС самоиндукции в контуре вызвано изменением потока, сцепленного с контуром, при изменении в нем силы тока.
Поток, сцепленный с контуром, определяется формулами:
- при силе тока I 1
Ф s 1 = LI 1 ,
где L — индуктивность контура, L = 20 мГн; I 1 — первоначальная сила тока в контуре, I 1 = 1,4 А;
- при силе тока I 2
Ф s 2 = LI 2 ,
где I 2 — конечная сила тока в контуре.
Изменение потока, сцепленного с контуром, определяется разностью:
Δ Ф s = Ф s 2 − Ф s 1 = L I 2 − L I 1 = L (I 2 − I 1) ,
где I 2 = 0,8I 1 .
Среднее значение ЭДС самоиндукции, возникающей в контуре, при изменении в нем силы тока:
〈 ℰ s i 〉 = | Δ Ф s Δ t | = | L (I 2 − I 1) Δ t | = | − 0,2 L I 1 Δ t | = 0,2 L I 1 Δ t ,
где ∆t
— интервал времени, за который происходит уменьшение силы тока, ∆t
= 80 мс.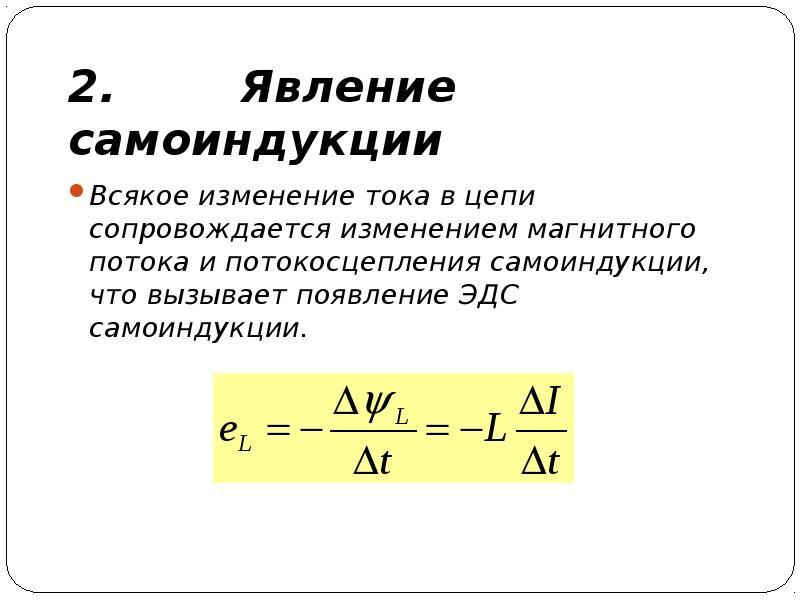
Расчет дает значение:
〈 ℰ s i 〉 = 0,2 ⋅ 20 ⋅ 10 − 3 ⋅ 1,4 80 ⋅ 10 − 3 = 70 ⋅ 10 − 3 с = 70 мВ.
При изменении силы тока в контуре в нем возникает ЭДС самоиндукции, среднее значение которой равно 70 мВ.
На данном уроке мы узнаем, как и кем было открыто явление самоиндукции, рассмотрим опыт, с помощью которого продемонстрируем это явление, определим, что самоиндукция — это частный случай электромагнитной индукции. В конце урока введем физическую величину, показывающую зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, т. е. индуктивность.
Генри изобретал плоские катушки из полосовой меди, с помощью которых добивался силовых эффектов, выраженных более ярко, чем при использовании проволочных соленоидов. Ученый заметил, что при нахождении в цепи мощной катушки ток в этой цепи достигает своего максимального значения гораздо медленнее, чем без катушки.
Рис. 2. Схема экспериментальной установки Д. Генри
Генри
На рис. 2 изображена электрическая схема экспериментальной установки, на основе которой можно продемонстрировать явление самоиндукции. Электрическая цепь состоит из двух параллельно соединенных лампочек, подключенных через ключ к источнику постоянного тока. Последовательно с одной из лампочек подключена катушка. После замыкания цепи видно, что лампочка, которая соединена последовательно с катушкой, загорается медленнее, чем вторая лампочка (рис. 3).
Рис. 3. Различный накал лампочек в момент включения цепи
При отключении источника лампочка, подключенная последовательно с катушкой, гаснет медленнее, чем вторая лампочка.
Почему лампочки гаснут не одновременно
При замыкании ключа (рис. 4) из-за возникновения ЭДС самоиндукции ток в лампочке с катушкой нарастает медленнее, поэтому эта лампочка загорается медленнее.
Рис. 4. Замыкание ключа
При размыкании ключа (рис. 5) возникающая ЭДС самоиндукции мешает убыванию тока. Поэтому ток еще некоторое время продолжает течь. Для существования тока нужен замкнутый контур. Такой контур в цепи есть, он содержит обе лампочки. Поэтому при размыкании цепи лампочки должны некоторое время светиться одинаково, и наблюдаемое запаздывание может быть вызвано другими причинами.
Поэтому ток еще некоторое время продолжает течь. Для существования тока нужен замкнутый контур. Такой контур в цепи есть, он содержит обе лампочки. Поэтому при размыкании цепи лампочки должны некоторое время светиться одинаково, и наблюдаемое запаздывание может быть вызвано другими причинами.
Рис. 5. Размыкание ключа
Рассмотрим процессы, происходящие в данной цепи при замыкании и размыкании ключа.
1. Замыкание ключа.
В цепи находится токопроводящий виток. Пусть ток в этом витке течет против часовой стрелки. Тогда магнитное поле будет направлено вверх (рис. 6).
Таким образом, виток оказывается в пространстве собственного магнитного поля. При возрастании тока виток окажется в пространстве изменяющегося магнитного поля собственного тока. Если ток возрастает, то созданный этим током магнитный поток также возрастает. Как известно, при возрастании магнитного потока, пронизывающего плоскость контура, в этом контуре возникает электродвижущая сила индукции и, как следствие, индукционный ток. По правилу Ленца, этот ток будет направлен таким образом, чтобы своим магнитным полем препятствовать изменению магнитного потока, пронизывающего плоскость контура.
По правилу Ленца, этот ток будет направлен таким образом, чтобы своим магнитным полем препятствовать изменению магнитного потока, пронизывающего плоскость контура.
То есть для рассматриваемого на рис. 6 витка индукционный ток должен быть направлен по часовой стрелке (рис. 7), тем самым препятствуя нарастанию собственного тока витка. Следовательно, при замыкании ключа ток в цепи возрастает не мгновенно благодаря тому, что в этой цепи возникает тормозящий индукционный ток, направленный в противоположную сторону.
2. Размыкание ключа
При размыкании ключа ток в цепи уменьшается, что приводит к уменьшению магнитного потока сквозь плоскость витка. Уменьшение магнитного потока приводит к появлению ЭДС индукции и индукционного тока. В этом случае индукционный ток направлен в ту же сторону, что и собственный ток витка. Это приводит к замедлению убывания собственного тока.
Вывод: при изменении тока в проводнике возникает электромагнитная индукция в этом же проводнике, что порождает индукционный ток, направленный таким образом, чтобы препятствовать любому изменению собственного тока в проводнике (рис. 8). В этом заключается суть явления самоиндукции. Самоиндукция — это частный случай электромагнитной индукции.
8). В этом заключается суть явления самоиндукции. Самоиндукция — это частный случай электромагнитной индукции.
Рис. 8. Момент включения и выключения цепи
Формула для нахождения магнитной индукции прямого проводника с током:
где — магнитная индукция; — магнитная постоянная; — сила тока; — расстояние от проводника до точки.
Поток магнитной индукции через площадку равен:
где — площадь поверхности, которая пронизывается магнитным потоком.
Таким образом, поток магнитной индукции пропорционален величине тока в проводнике.
Для катушки, в которой — число витков, а — длина, индукция магнитного поля определяется следующим соотношением:
Магнитный поток, созданный катушкой с числом витков N , равен:
Подставив в данное выражение формулу индукции магнитного поля, получаем:
Отношение числа витков к длине катушки обозначим числом :
Получаем окончательное выражение для магнитного потока:
Из полученного соотношения видно, что значение потока зависит от величины тока и от геометрии катушки (радиус, длина, число витков). Величина, равная , называется индуктивностью:
Величина, равная , называется индуктивностью:
Единицей измерения индуктивности является генри:
Следовательно, поток магнитной индукции, вызванный током в катушке, равен:
С учетом формулы для ЭДС индукции , получаем, что ЭДС самоиндукции равна произведению скорости изменения тока на индуктивность, взятому со знаком «-»:
Самоиндукция — это явление возникновения электромагнитной индукции в проводнике при изменении силы тока, протекающего сквозь этот проводник.
Электродвижущая сила самоиндукции прямо пропорциональна скорости изменения тока, протекающего сквозь проводник, взятой со знаком минус. Коэффициент пропорциональности называется индуктивностью , которая зависит от геометрических параметров проводника.
Проводник имеет индуктивность, равную 1 Гн, если при скорости изменения тока в проводнике, равной 1 А в секунду, в этом проводнике возникает электродвижущая сила самоиндукции, равная 1 В.
С явлением самоиндукции человек сталкивается ежедневно. Каждый раз, включая или выключая свет, мы тем самым замыкаем или размыкаем цепь, при этом возбуждая индукционные токи. Иногда эти токи могут достигать таких больших величин, что внутри выключателя проскакивает искра, которую мы можем увидеть.
Каждый раз, включая или выключая свет, мы тем самым замыкаем или размыкаем цепь, при этом возбуждая индукционные токи. Иногда эти токи могут достигать таких больших величин, что внутри выключателя проскакивает искра, которую мы можем увидеть.
Список литературы
- Мякишев Г.Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. — М.: Просвещение, 2010.
- Касьянов В.А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. — М.: Дрофа, 2005.
- Генденштейн Л.Э., Дик Ю.И., Физика 11. — М.: Мнемозина.
- Интернет-портал Myshared.ru ().
- Интернет-портал Physics.ru ().
- Интернет-портал Festival.1september.ru ().
Домашнее задание
- Вопросы в конце параграфа 15 (стр. 45) — Мякишев Г.Я. Физика 11 (см. список рекомендованной литературы)
- Индуктивность какого проводника равна 1 Генри?
Физика для науки и техники II
com/video/738» frameborder=»0″ title=»9.7 Self Induction» webkitallowfullscreen=»» mozallowfullscreen=»» allowfullscreen=»»/>
от Office of Academic Technologies на Vimeo.
9.7 Самоиндукция
Рассмотрим две простые схемы. Катушка, которая подключена к клеммам блока питания, аккумулятор, выключатель, и, допустим, это наша схема номер один. Аналогичную катушку размещаем напротив этой, и в этой схеме у нас нет источника питания. Мы можем разместить здесь гальванометр для определения тока, и давайте назовем его второй схемой.
Допустим, источник питания, батарея, генерирует ε вольт электродвижущей силы. Конечно, когда переключатель выключен, по этой цепи не будет протекать ток. Когда мы включаем переключатель во включенное положение, то через эту цепь будет течь определенный ток от положительного конца к отрицательному концу, поэтому, как только переключатель замкнут.
Что ж, во время этого процесса, как только мы включим этот переключатель, ток начнется с 0 и начнет нарастать до своего максимального значения.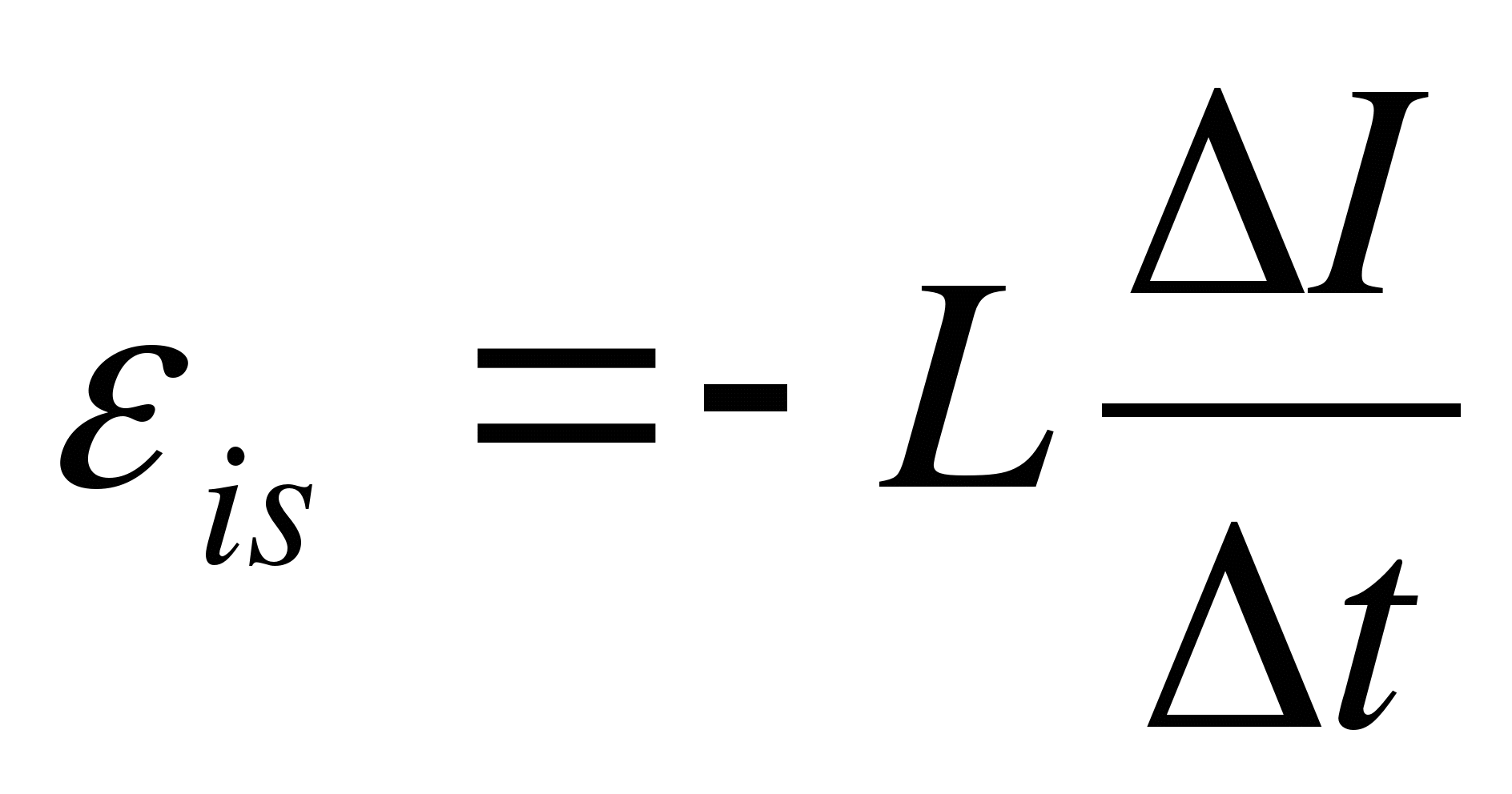 Тогда он достигнет своего максимального значения и, следовательно, будет течь по этому контуру при этом постоянном значении. Но во время нарастания тока, другими словами, когда он идет от 0 до своего максимального значения, тогда соответствующее магнитное поле, которое он генерирует, также будет начинаться с 0 и увеличиваться до своего максимального значения, потому что, как вы помните, величина тока прямо пропорциональна силе создаваемого им магнитного поля.
Тогда он достигнет своего максимального значения и, следовательно, будет течь по этому контуру при этом постоянном значении. Но во время нарастания тока, другими словами, когда он идет от 0 до своего максимального значения, тогда соответствующее магнитное поле, которое он генерирует, также будет начинаться с 0 и увеличиваться до своего максимального значения, потому что, как вы помните, величина тока прямо пропорциональна силе создаваемого им магнитного поля.
Ну, поэтому во время этого процесса, когда магнитное поле поднимается с увеличением тока, оно будет генерировать линии магнитного поля через этот первый контур, скажем, первую катушку, и эти линии будут проходить через область, окруженную второй катушкой.По мере увеличения тока это магнитное поле будет увеличиваться. Следовательно, поток через область, окруженную второй катушкой, будет увеличиваться, и в результате этого увеличения потока, согласно закону Фарадея, мы получим индуцированную ЭДС и, следовательно, индуцированный ток.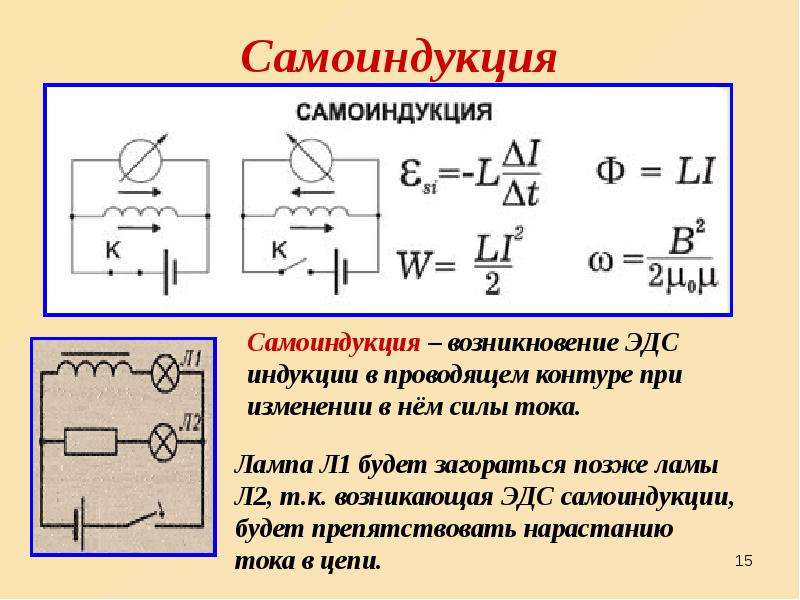 Этот ток появится из закона Ленца, так что он будет противодействовать своей причине, поэтому он будет генерировать магнитное поле в направлении, противоположном этому. Это магнитное поле индуцированного тока. Чтобы иметь возможность генерировать магнитное поле в этом направлении, используя правило правой руки, индуцированный ток должен течь в направлении против часовой стрелки по всей этой цепи.
Этот ток появится из закона Ленца, так что он будет противодействовать своей причине, поэтому он будет генерировать магнитное поле в направлении, противоположном этому. Это магнитное поле индуцированного тока. Чтобы иметь возможность генерировать магнитное поле в этом направлении, используя правило правой руки, индуцированный ток должен течь в направлении против часовой стрелки по всей этой цепи.
Конечно, этот ток будет обнаружен гальванометром вот здесь, и стрелка гальванометра будет двигаться в одном направлении. Он отклонится от своего исходного 0, в какой бы точке или месте он ни находился. Ну, если мы будем следовать этому случаю, то магнитное поле этого индуцированного тока вдоль этого второго контура будет проходить через область, окруженную первым контуром, вот так. Поскольку ток накапливается в первом, поэтому индуцированное i будет генерировать второй.Магнитное поле этого второго будет проходить через область, окруженную первой катушкой. Следовательно, это вызовет изменение потока через первую катушку, и этот поток будет индуцировать электродвижущую силу вдоль первой катушки и, следовательно, также ток, и этот ток будет проявляться так, что будет противодействовать своей причине.
Если мы проследим катушки, исходные катушки, и это вернется к тому факту, что i индуцируется во второй катушке, и что происходит, что исходный ток i проявляется как увеличение от его максимума ценность.Следовательно, ток, возникающий в первой катушке, будет противодействовать этой причине. Другими словами, он попытается противостоять увеличению этого исходного тока. Для этого он должен генерировать магнитное поле, противоположное направлению исходного тока. Поэтому он должен работать в направлении, противоположном первоначальному току. И по этой причине мы не сможем в конечном итоге получить случай, когда ток сразу пойдет от 0 до своего максимального значения.Для достижения этого значения потребуется некоторое время.
Ну, здесь мы можем констатировать, что индуцированная электродвижущая сила возникает и в катушке, если мы изменим ток в той же самой катушке. Это называется самоиндукцией, а создаваемая ЭДС, электродвижущая сила, называется «ЭДС самоиндукции». Поэтому теперь, как только мы изменим ток в первой катушке, мы индуцируем ток через вторую катушку, и магнитное поле этого тока вызовет изменение потока через первую катушку.Таким образом, мы получим i , индуцированных вдоль первой катушки. И если ток увеличивается в первой катушке, этот индуцированный ток будет течь в направлении, противоположном направлению исходного тока.
Поэтому теперь, как только мы изменим ток в первой катушке, мы индуцируем ток через вторую катушку, и магнитное поле этого тока вызовет изменение потока через первую катушку.Таким образом, мы получим i , индуцированных вдоль первой катушки. И если ток увеличивается в первой катушке, этот индуцированный ток будет течь в направлении, противоположном направлению исходного тока.
Таким образом, первоначальный ток сразу достигает своего максимального значения. Или, если i уменьшается, если первоначальный ток уменьшается от своего максимального значения до 0, то уменьшение магнитного поля будет генерировать или индуцировать электрический ток вдоль второй катушки.Этот ток будет течь в таком направлении, что он будет противодействовать своей причине, и, следовательно, он будет течь в таком направлении, что создаваемое им магнитное поле будет в том же направлении, что и первоначальное магнитное поле. Это магнитное поле, опять же, будет генерировать изменение магнитного потока через область, окруженную первой катушкой. Это вызовет индуцированный ток вдоль первого, и в этом случае, опять же, он проявится против своей первоначальной причины, а именно уменьшения первоначального тока.
Это вызовет индуцированный ток вдоль первого, и в этом случае, опять же, он проявится против своей первоначальной причины, а именно уменьшения первоначального тока.
Следовательно, в этом случае этот ток будет отображаться в том же направлении, что и исходный ток. Поэтому позвольте мне выключить выключатель, ток не сразу упадет до 0 и пройдет некоторое время, и мы называем это электродвижущей силой, которая появляется в результате изменения тока в том же состоянии, что и сила самоиндукции. электродвижущая сила и связанный с ней ток как ток самоиндукции.
Хорошо. Если вспомнить определение индуктивности, то для любой катушки индуктивности имеем L равно количеству потокосцеплений, деленному на ток.Отсюда, если мы сделаем перекрестное умножение, Li будет равно N умножить на Φ B . Итак, по закону Фарадея индуцированная электродвижущая сила равна – Н , умноженное на число витков, умноженное на изменение магнитного потока. Мы можем поместить это N в оператор производной, так как это константа, и записать эту связь d of NΦ B на dt . Но NΦ B по определению индуктивности равно L время i .Поэтому ε становится равным – d из Li на dt .
Мы можем поместить это N в оператор производной, так как это константа, и записать эту связь d of NΦ B на dt . Но NΦ B по определению индуктивности равно L время i .Поэтому ε становится равным – d из Li на dt .
Поскольку индуктивность постоянна, мы можем взять ее за пределы оператора производной. Тогда ЭДС индукции становится равной – L di на dt , и это выражение для электродвижущей силы самоиндукции. Это просто говорит нам, что если ток меняется, то мы получим ЭДС самоиндукции через ту же катушку. Если через любой индуктор протекает постоянный ток, то ЭДС самоиндукции будет равна 0.
Таким образом, мы можем резюмировать, сказав, что, таким образом, в любом индукторе — это может быть простой соленоид катушки или тороид — ЭДС самоиндукции возникает всякий раз, когда ток изменяется во времени. Величина электродвижущей силы не влияет на индуцированную электродвижущую силу. Имеет значение только скорость изменения тока. Другими словами, поскольку мы генерируем электродвижущую силу самоиндукции в самой первой катушке, ЭДС самоиндукции, а также связанный с ней индуцированный ток не имеют ничего общего с величиной исходного тока.Это напрямую зависит от того, насколько быстро или медленно изменяется этот первоначальный ток.
Имеет значение только скорость изменения тока. Другими словами, поскольку мы генерируем электродвижущую силу самоиндукции в самой первой катушке, ЭДС самоиндукции, а также связанный с ней индуцированный ток не имеют ничего общего с величиной исходного тока.Это напрямую зависит от того, насколько быстро или медленно изменяется этот первоначальный ток.
Что ж, направление самоиндуцированной электродвижущей силы опять-таки определяется законом Ленца, другими словами, самоиндуцированные действия противодействуют вызывающему ее изменению. Таким образом, если мы добавим, мы можем сказать, что направление самоиндуцируемой электродвижущей силы определяется законом Ленца. То есть противостоит своему делу.
В этом смысле, если вы посмотрите на пару интересных случаев, предполагая, что у нас есть индуктор, может быть соленоид, тороид или простая катушка, и давайте предположим, что ток течет слева направо, и предположим, что i повышается.Следовательно, мы придем к самоиндуцированной электродвижущей силе, и она проявится так, что будет противодействовать своей причине. Очевидно, чтобы иметь возможность протекать ток в этом направлении, мы должны иметь нашу исходную стрелку ЭДС. Он указывает вправо, чтобы ток протекал слева направо. Таким образом, если i увеличивается, мы получим ЭДС самоиндукции вдоль этой катушки индуктивности, которая будет противодействовать своей причине. Другими словами, он будет вести себя так, как будто у нас есть другой источник питания, противодействующий этому току.Другими словами, генерация индуцированного тока в направлении, противоположном первоначальному току.
Очевидно, чтобы иметь возможность протекать ток в этом направлении, мы должны иметь нашу исходную стрелку ЭДС. Он указывает вправо, чтобы ток протекал слева направо. Таким образом, если i увеличивается, мы получим ЭДС самоиндукции вдоль этой катушки индуктивности, которая будет противодействовать своей причине. Другими словами, он будет вести себя так, как будто у нас есть другой источник питания, противодействующий этому току.Другими словами, генерация индуцированного тока в направлении, противоположном первоначальному току.
С другой стороны, если мы рассмотрим тот же индуктор, в этом случае ток убывает, опять же, в том же направлении. Итак, еще раз, стрелка ЭДС указывает в направлении протекания тока, но теперь ток становится все меньше и меньше, поэтому мы получим ЭДС самоиндукции через эту катушку индуктивности, но эта ЭДС проявится каким-то образом. что он попытается противостоять своему делу. Для этого он будет генерировать индуцированный ток, который будет течь в том же направлении, что и первоначальный ток. Следовательно, он будет вести себя так, как если бы у нас была индуцированная электродвижущая сила ε′ , и он генерирует ток в том же направлении, что и этот первоначальный. Принимая во внимание, что в предыдущем случае этот индуцированный ток будет иметь направление, противоположное направлению исходного тока.
Следовательно, он будет вести себя так, как если бы у нас была индуцированная электродвижущая сила ε′ , и он генерирует ток в том же направлении, что и этот первоначальный. Принимая во внимание, что в предыдущем случае этот индуцированный ток будет иметь направление, противоположное направлению исходного тока.
Хотя это не очень хорошее представление, но оно поможет вам понять, потому что, помните, мы не можем реально использовать стрелки ЭДС из-за электродвижущей силы, генерируемой в результате индукции.Что ж, именно из-за этих причин для первого случая мы можем рассматривать этот случай как момент, когда мы включаем переключатель, так что ток увеличивается от его, от 0 до его максимального значения. В то время как во втором случае мы можем визуализировать это как момент, когда мы выключаем переключатель, чтобы ток уменьшался от своего максимального значения до 0. В обоих случаях ни максимальное значение, ни 0 значение тока не будут достигнуты немедленно. Это займет некоторое время из-за самоиндуцированной электродвижущей силы.
Индуктивность – Гиперучебник по физике
Обсуждение
введение
Готов? Вот так.
Пуск с соленоидом. Пропустите через него ток, и вы получите электромагнит. Поле внутри задается формулой…
| B = μ 0 nI = μ 0 | Н | я |
| ℓ |
Соленоид одновременно является и устройством для улавливания флюса.
Φ B = НБА
Статическая ситуация, безусловно, достаточно интересна, но когда дело доходит до потока, нас действительно волнует скорость изменения во времени. Это то, что дает нам электромагнитную индукцию, или индуцированную электродвижущую силу, или называйте это как хотите. Эта ситуация описывается законом Фарадея.
Давайте еще раз пройдемся по этим уравнениям, но с изменением во времени. Соленоид с переменным током, протекающим через него, будет генерировать изменяющееся магнитное поле.
| дБ | = мк 0 | Н | ДИ | |
| дт | ℓ | дт |
Это изменяющееся магнитное поле захватывается тем самым соленоидом, который его создал. Захваченное поле называется потоком, а изменяющийся поток создает ЭДС — в данном случае ЭДС самоиндукции или противоЭДС.
| ℰ = — | г Φ В | = − N | ⎛ ⎜ ⎝ | мк 0 | Н | ДИ | ⎞ ⎟ ⎠ | А | |
| дт | ℓ | дт |
Немного переставив вещи, мы получим это уравнение…
| ℰ = — | мк 0 АН 2 | ДИ | |
| ℓ | дт |
, что может показаться не таким уж большим, пока вы не поймете, что члены в первой дроби во многом определяются геометрией соленоида. Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.
Если бы мы выбрали другую конфигурацию проводов, произошло бы то же самое.
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения тока во времени ( dI / dt ), умноженной на константу ( L ). Эта константа называется индуктивностью (или, точнее, собственной индуктивностью ) и определяется геометрией схемы (или, чаще, геометрией отдельных элементов схемы).Например, индуктивность соленоида (определенная выше) находится по формуле…
Обозначение L для индуктивности было выбрано в честь Генриха Ленца (1804–1865), чья новаторская работа в области электромагнитной индукции сыграла важную роль в разработке окончательной теории. Если вы помните, закон Ленца гласит, что индуцированный ток в цепи всегда действует таким образом, что противостоит изменению, которое изначально его создало. Это наблюдение объясняет, почему во всех версиях закона Фарадея стоит знак минус.Ленц поставил нам знак минус, и мы чтим его символом L .
Индуктивность лучше всего определяется ее ролью в уравнении, полученном из закона индукции Фарадея. Некоторым это не нравится, и они предпочитают определения, написанные в форме подлежащее-глагол-дополнение простого предложения.
По-английски мы бы прочитали это как «собственная индуктивность ( L ) — это отношение противо-ЭДС (ℰ) к скорости изменения тока, производящего ее ( dI / dt ).Как я уже сказал, мне не особенно нравятся такого рода определения, но они помогают нам определить соответствующие единицы.
| ⎡ ⎢ ⎣ | Н = | В | = | Дж/К | = | (кг·м 2 /с 2 )/(А с) | = | кг м 2 | ⎤ ⎥ ⎦ |
| А/с | А/с | А/с | А 2 с 2 |
Единицей индуктивности является генри , названный в честь Джозефа Генри (1797–1878), американского ученого, открывшего электромагнитную индукцию независимо и примерно в то же время, что и Майкл Фарадей (1791–1867) в Англии. Фарадей опубликовал свои открытия первым, и поэтому ему приписывают большую часть заслуг. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое послужило основой для телеграфа). Цепь с собственной индуктивностью в один генри будет испытывать противо-ЭДС в один вольт при изменении тока со скоростью один ампер в секунду.
Фарадей опубликовал свои открытия первым, и поэтому ему приписывают большую часть заслуг. Генри также открыл самоиндукцию и взаимную индуктивность (которые будут описаны позже в этом разделе) и изобрел электромеханическое реле (которое послужило основой для телеграфа). Цепь с собственной индуктивностью в один генри будет испытывать противо-ЭДС в один вольт при изменении тока со скоростью один ампер в секунду.
Индуктивность это нечто. Индуктивность — это сопротивление элемента цепи изменению тока.Индуктивность в цепи является аналогом массы в механической системе.
| ⇕ | |||||
| |||||
| ⇕ | |||||
индуктивный петлевой детектор
Движение на некоторых перекрестках контролируется с помощью индуктивных петлевых извещателей (ИЛД).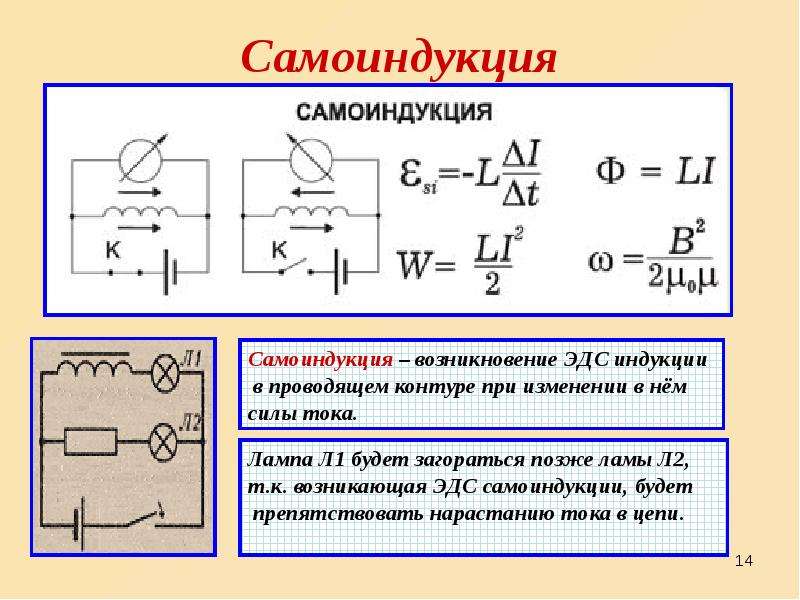 ILD представляет собой петлю проводящего провода, встроенную всего в несколько сантиметров под тротуар. Когда транспортное средство проходит через поле, оно действует как проводник, изменяя индуктивность контура. Изменение индуктивности петли указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, мониторинга транспортного потока или автоматического цитирования.
ILD представляет собой петлю проводящего провода, встроенную всего в несколько сантиметров под тротуар. Когда транспортное средство проходит через поле, оно действует как проводник, изменяя индуктивность контура. Изменение индуктивности петли указывает на наличие автомобиля наверху. Затем эту информацию можно использовать для активации сигналов светофора, мониторинга транспортного потока или автоматического цитирования.
примеры
индуктивность зависит от геометрии
соленоид ( A площадь поперечного сечения, N количество витков, ℓ длины, n количество витков на длину)
| Φ В | = N | Б | А | ||
| Φ В | = N | мк 0 NI | А | ||
| ℓ | |||||
| Φ В | = | мк 0 АН 2 | я | ||
| ℓ | |||||
| г Φ В | = | мк 0 АН 2 | ДИ | ||
| дт | ℓ | дт | |||
| Л | = | мк 0 АН 2 | = | мк 0 Ан 2 | |
| ℓ |
коаксиальные проводники ( a внутренний радиус, b внешний радиус, ℓ длины)
| Φ В | = | ⌠ ⌡ | Б | · | д А | ||||
| б | б | ||||||||
| Φ В | = | ⌠ ⌡ | мк 0 I | л др | = | мк 0 л | ⌠ ⌡ | др | |
| 2π р | 2π | р | |||||||
| и | и | ||||||||
| Φ В | = | мк 0 ℓ | по | ⎛ ⎜ ⎝ | и | ⎞ ⎟ ⎠ | я | ||
| 2π | б | ||||||||
| г Φ В | = | мк 0 ℓ | по | ⎛ ⎜ ⎝ | и | ⎞ ⎟ ⎠ | ДИ | ||
| дт | 2π | б | дт | ||||||
| Л | = | мк 0 ℓ | по | ⎛ ⎜ ⎝ | и | ⎞ ⎟ ⎠ | |||
| 2π | б | ||||||||
тор ( A площадь поперечного сечения, R радиус вращения, N количество витков)
| Φ В | = | Н | Б | А | |
| Φ В | ≈ | Н | мк 0 NI | А | |
| 2π R | |||||
| Φ В | ≈ | Н | мк 0 нет данных | я | |
| 2π R | |||||
| г Φ В | ≈ | мк 0 АН 2 | ДИ | ||
| дт | 2π Р | дт | |||
| Л | ≈ | мк 0 АН 2 | |||
| 2π R | |||||
прямоугольная петля ( ширина , высота , радиус проволоки a )
| Φ В | = | Н | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ В | = | Н |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Φ В | = | 2 | мк 0 С 2 | ⎡ ⎢ ⎣ | у лн | ⎛ ⎜ ⎝ | х | ⎞ ⎟ ⎠ | + | x ln | ⎛ ⎜ ⎝ | г | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | я | |||||||||||||||||||||||||||||||||||||||||||||||||
| 2π | и | и | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| г Φ В | = | мк 0 С 2 | ⎡ ⎢ ⎣ | у лн | ⎛ ⎜ ⎝ | х | ⎞ ⎟ ⎠ | + | x ln | ⎛ ⎜ ⎝ | г | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | ДИ | ||||||||||||||||||||||||||||||||||||||||||||||||||
| дт | № | и | и | дт | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Л | = | мк 0 С 2 | ⎡ ⎢ ⎣ | у лн | ⎛ ⎜ ⎝ | х | ⎞ ⎟ ⎠ | + | x ln | ⎛ ⎜ ⎝ | г | ⎞ ⎟ ⎠ | ⎤ ⎥ ⎦ | |||||||||||||||||||||||||||||||||||||||||||||||||||
| № | и | и | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Эта формула не работает, так как игнорирует краевые эффекты. Вы можете найти точную формулу (а также сценарии, которые рассчитают индуктивность для вас) в Интернете на нескольких сайтах по электротехнике.
Вы можете найти точную формулу (а также сценарии, которые рассчитают индуктивность для вас) в Интернете на нескольких сайтах по электротехнике.
Молекулярные выражения: электричество и магнетизм
Индуктивность
Индуктивность — это свойство электрической цепи, при котором изменяющееся магнитное поле создает электродвижущую силу или напряжение в этой цепи или в соседней цепи. Индуктивность также определяется как свойство электрической цепи, противодействующее любому изменению тока.В 1831 году английский ученый Майкл Фарадей обнаружил, что изменение магнитного поля в цепи индуцирует ток в соседней цепи. Джозеф Генри, американский ученый, независимо сделал это открытие примерно в то же время. Генерация электродвижущей силы и тока изменяющимся магнитным полем называется электромагнитной индукцией. Работа электрических генераторов основана на принципе индуктивности.
Линии магнитного поля Чтобы лучше понять индуктивность, полезно иметь представление о силовых линиях магнитного поля. Все магниты окружены магнитным полем, также называемым магнитным потоком. Магнитное поле можно представить состоящим из силовых линий или линий потока. Силы магнитного притяжения и отталкивания движутся по силовым линиям. Образец линий магнитного поля можно наблюдать в нашем интерактивном учебном пособии по Java «Линии магнитного поля».
Все магниты окружены магнитным полем, также называемым магнитным потоком. Магнитное поле можно представить состоящим из силовых линий или линий потока. Силы магнитного притяжения и отталкивания движутся по силовым линиям. Образец линий магнитного поля можно наблюдать в нашем интерактивном учебном пособии по Java «Линии магнитного поля».
| Интерактивное руководство по Java | ||
Фарадей открыл электромагнитную индукцию в ходе эксперимента с использованием двух катушек проволоки, намотанных на противоположные стороны кольца из мягкого железа, подобно установке для эксперимента, показанной на рис. 1 ниже.
Первая катушка справа подключена к батарее. Вторая катушка содержит компас, который действует как гальванометр для определения протекания тока. Когда переключатель замкнут, ток проходит через первую катушку, и железное кольцо намагничивается. Когда переключатель замыкается в первый раз, компас во второй катушке на мгновение отклоняется и сразу же возвращается в исходное положение. Отклонение компаса является признаком того, что была индуцирована электродвижущая сила, вызывающая мгновенное протекание тока во второй катушке.Фарадей также заметил, что при размыкании переключателя компас снова на мгновение отклоняется, но в противоположном направлении.
Вторая катушка содержит компас, который действует как гальванометр для определения протекания тока. Когда переключатель замкнут, ток проходит через первую катушку, и железное кольцо намагничивается. Когда переключатель замыкается в первый раз, компас во второй катушке на мгновение отклоняется и сразу же возвращается в исходное положение. Отклонение компаса является признаком того, что была индуцирована электродвижущая сила, вызывающая мгновенное протекание тока во второй катушке.Фарадей также заметил, что при размыкании переключателя компас снова на мгновение отклоняется, но в противоположном направлении.
Фарадей знал, что катушка проволоки с текущим по ней электрическим током создает магнитное поле. Поэтому он предположил, что изменяющееся магнитное поле индуцирует ток во второй катушке. Замыкание и размыкание переключателя вызывают изменение магнитного поля: расширение и сжатие соответственно. Вы можете провести эксперимент Фарадея в нашем интерактивном учебном пособии по Java Faraday’s Experiment.
| Интерактивное руководство по Java | ||
Фарадей продемонстрировал, что его гипотеза верна, перемещая простой стержневой магнит вперед и назад внутри катушки. Он заметил, что ток в катушке индуцируется только во время движения магнита. Он также заметил, что в катушке индуцируется ток, когда сама катушка перемещается рядом с неподвижным постоянным магнитом.Он обнаружил, что это относительное движение между проводником и магнитным полем, которое производит ток. Для генерации тока либо проводник может двигаться через поле, либо поле может проходить мимо проводника. Для возникновения электромагнитной индукции необходимо изменение магнитного потока. Проведите этот эксперимент в нашем Faraday’s 2nd Experiment Interactive Java Tutorial.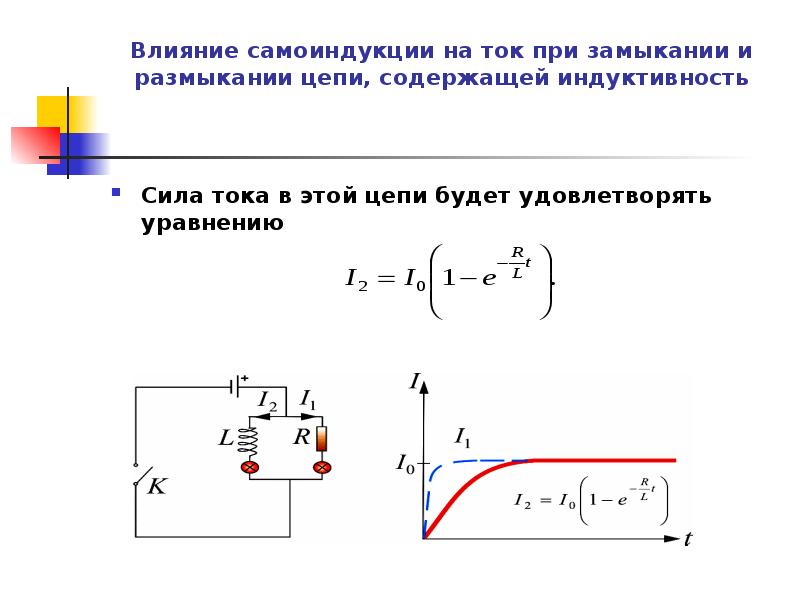
| Интерактивное руководство по Java | ||
Связь между изменением магнитного потока и индуцированной электродвижущей силой известна как закон электромагнитной индукции Фарадея:
Величина электромагнитной силы, индуцированной в цепи, пропорциональна скорости изменения магнитного потока, пересекающего цепь.
Математически закон Фарадея записывается так:
E = — (DF/Dt)
, где E — индуцированная электродвижущая сила в вольтах, DF — изменение магнитной силы в веберах, а Dt — количество времени в секундах, в течение которого происходит изменение магнитной силы.
Из приведенной выше формулы видно, что величина индуцированного напряжения определяется двумя факторами:
- Величина магнитного потока
Чем больше число силовых линий магнитного поля, пересекающих проводник, тем больше индуцированное напряжение. - Скорость, с которой силовые линии магнитного поля пересекают проводник
Чем быстрее линии поля пересекают проводник или проводник пересекает линии поля, тем больше индуцированное напряжение. Вы можете наблюдать это, изменяя скорость, с которой вы перемещаете магнит, в нашем Фарадеевском 2-м интерактивном учебном пособии по Java.
Знак минус в законе Фарадея относится к направлению или полярности индуцированного напряжения.В 1833 году русский физик Генрих Ленц открыл направленные отношения между силами, напряжениями и токами электромагнитной индукции. Закон Ленца гласит:
Индуцированная электродвижущая сила генерирует ток, который индуцирует встречное магнитное поле, противодействующее магнитному полю, генерирующему ток.
Например, когда внешнее магнитное поле приближается к кольцеобразному проводнику, ток, возникающий в кольце, индуцирует свое собственное магнитное поле в противовес приближающемуся внешнему магнитному полю.С другой стороны, когда внешнее магнитное поле удаляется от кольца, индуцированное магнитное поле в кольце меняет направление и препятствует изменению направления внешнего магнитного поля. Вы можете увидеть закон Ленца в действии в нашем интерактивном учебном пособии по Java Lenz’s Law.
| Интерактивное руководство по Java | ||
Мы знаем, что ток, протекающий по проводнику, создает магнитное поле вокруг проводника.Когда ток увеличивается, уменьшается или меняет направление, магнитное поле изменяется. Магнитное поле расширяется, сжимается или меняет направление в ответ на изменения протекающего тока. Изменяющееся магнитное поле индуцирует дополнительную электродвижущую силу или напряжение в проводнике. Индукция этого дополнительного напряжения называется самоиндукцией, потому что она индуцируется внутри самого проводника. Направление самоиндуцируемой электродвижущей силы, или напряжения, противоположно направлению тока, вызвавшего ее.Это согласуется с законом Ленца, который можно выразить следующим образом:
Магнитное поле расширяется, сжимается или меняет направление в ответ на изменения протекающего тока. Изменяющееся магнитное поле индуцирует дополнительную электродвижущую силу или напряжение в проводнике. Индукция этого дополнительного напряжения называется самоиндукцией, потому что она индуцируется внутри самого проводника. Направление самоиндуцируемой электродвижущей силы, или напряжения, противоположно направлению тока, вызвавшего ее.Это согласуется с законом Ленца, который можно выразить следующим образом:
Наведенная электродвижущая сила (напряжение) в любой цепи всегда имеет направление, противоположное вызвавшему ее току.
Эффект самоиндукции в цепи заключается в противодействии любому изменению тока, протекающего в цепи. Например, когда на цепь подается напряжение, ток начинает течь во всех частях цепи. Этот ток создает вокруг себя магнитное поле.По мере расширения поля в цепи создается встречное напряжение, иногда называемое обратным напряжением. Это обратное напряжение вызывает протекание тока в направлении, противоположном основному протеканию тока. Индуктивность на этом этапе препятствует накоплению тока. Когда индуцированное магнитное поле становится устойчивым, оно перестает индуцировать обратное напряжение.
Это обратное напряжение вызывает протекание тока в направлении, противоположном основному протеканию тока. Индуктивность на этом этапе препятствует накоплению тока. Когда индуцированное магнитное поле становится устойчивым, оно перестает индуцировать обратное напряжение.
Когда ток в цепи отключается, индуцированное магнитное поле начинает разрушаться. Когда поле разрушается, оно генерирует напряжение в направлении, которое на мгновение продлевает течение основного тока.Когда индуцированное магнитное поле полностью разрушается, индуцированное напряжение и ток прекращаются. Опять же, самоиндукция противостоит изменениям в протекании тока. Он противостоит нарастанию и задерживает прорыв тока. Вы можете увидеть влияние самоиндукции на ток в нашем интерактивном учебном пособии по Java Self-Inductance.
| Интерактивное руководство по Java | ||
| gif»/> | ||
В эксперименте Фарадея с двумя катушками на проводящем железном кольце он обнаружил, что изменяющееся магнитное поле в одной катушке индуцирует электродвижущую силу или напряжение во второй катушке.Это явление называется взаимной индуктивностью. Взаимная индуктивность возникает, когда изменяющееся магнитное поле в одной цепи индуцирует напряжение в соседней цепи.
В соответствии с законом Ленца направление индуцированной электродвижущей силы, или напряжения, противоположно направлению тока, вызвавшего ее. Снова взглянув на эксперимент Фарадея ниже, мы обнаружим, что когда напряжение подается на катушку справа, в железном кольце индуцируется магнитное поле. По мере расширения поля во второй катушке слева генерируется напряжение.Это вторичное напряжение вызывает протекание тока во второй катушке. Этот вторичный ток течет в направлении, противоположном току первой катушки. Когда индуцированное магнитное поле в кольце становится устойчивым, ток во второй катушке перестает течь.
Когда ток в первой катушке отключается, индуцированное магнитное поле в кольце начинает разрушаться. Когда поле спадает, оно снова генерирует напряжение во второй катушке.Результирующий ток во второй катушке течет в направлении, противоположном ранее индуцированному току. Когда магнитное поле в кольце полностью схлопывается, наведенное напряжение и ток во вторичной обмотке прекращаются. Вы можете провести этот эксперимент в нашем Faraday’s Experiment Interactive Java Tutorial.
| Интерактивное руководство по Java | ||
Катушки индуктивности — это электрические устройства, предназначенные для обеспечения индуктивности в цепи. Катушка индуктивности — это просто катушка провода. Самоиндукция возникает в цепи, даже если проводники идеально прямые. Однако собственная индуктивность в прямом проводнике очень мала. Индуктивность гораздо более значительна, когда проводники скручены, потому что магнитное поле каждого витка катушки пересекает соседние витки катушки. Для увеличения индуктивности индуктор может иметь железный сердечник. Помещение железа внутрь катушки значительно увеличивает силу ее магнитных полей.
Катушка индуктивности — это просто катушка провода. Самоиндукция возникает в цепи, даже если проводники идеально прямые. Однако собственная индуктивность в прямом проводнике очень мала. Индуктивность гораздо более значительна, когда проводники скручены, потому что магнитное поле каждого витка катушки пересекает соседние витки катушки. Для увеличения индуктивности индуктор может иметь железный сердечник. Помещение железа внутрь катушки значительно увеличивает силу ее магнитных полей.
На индуктивность катушки влияют три фактора:
- Количество витков в катушке
Чем больше витков в катушке, тем больше индуктивность.Это верно, потому что чем больше витков в катушке, тем больше число взаимодействий магнитного поля. - Площадь поперечного сечения катушки
Чем больше площадь поперечного сечения катушки, тем больше индуктивность. Этот фактор тесно связан с количеством витков в катушке. Он включает в себя рассмотрение расстояния между витками. Поскольку магнитное поле становится слабее по мере его удаления, близко расположенные витки обеспечивают взаимодействие там, где поля наиболее сильны.
Он включает в себя рассмотрение расстояния между витками. Поскольку магнитное поле становится слабее по мере его удаления, близко расположенные витки обеспечивают взаимодействие там, где поля наиболее сильны. - Проницаемость сердечника
Проницаемость относится к способности материала проводить магнитные силовые линии. Железо обладает гораздо большей проницаемостью, чем воздух. Следовательно, катушка с железным сердечником имеет большую индуктивность, чем катушка с сердечником, содержащим только воздух.
Закон Фарадея можно использовать для определения полной индуцированной электродвижущей силы или напряжения в катушке.Предполагая, что витки катушки намотаны близко друг к другу, общее индуктивное напряжение катушки можно рассчитать по следующей формуле:
E = — N (DF/Dt)
, где E — индуцированная электродвижущая сила в вольтах, N — число витков в катушке, DF — изменение магнитной силы в веберах, а Dt — количество времени в секундах, в течение которого происходит изменение магнитной силы.
Символом индуктивности является заглавная буква L в честь Генриха Ленца. Единицей измерения индуктивности является генри, названный в честь Джозефа Генри и сокращенно обозначаемый как ч . Один генри индуктивности существует, когда один вольт электродвижущей силы индуцируется, когда ток изменяется со скоростью один ампер в секунду. Математически это записывается как:
L = E/(DI/Dt)
, где L — индуктивность в генри, E — индуцированная электродвижущая сила в вольтах, DI — изменение тока в амперах, а Dt — время в секундах, в течение которого происходит изменение тока. .
Катушки индуктивности в последовательных цепях Последовательная цепь — это цепь, в которой ток имеет только один путь. В последовательной цепи весь ток проходит через каждый из компонентов цепи. В схеме на рис. 2 последовательно соединены три катушки индуктивности.
Если катушки индуктивности экранированы или расположены достаточно далеко друг от друга, чтобы предотвратить взаимную индуктивность, общая индуктивность цепи суммируется. Общая индуктивность такой цепи равна сумме всех катушек индуктивности в цепи.Поэтому используйте следующую формулу для расчета общей индуктивности последовательной цепи:
Л Т = Л 1 + Л 2 + Л 3 . . .
, где L T — общая индуктивность в цепи, а от L 1 до L 3 . . . — номинальная индуктивность отдельных катушек индуктивности в цепи.
Используя эту формулу, общую индуктивность последовательной цепи на рис. 2 можно рассчитать следующим образом:
L T = 50 + 40 + 20
Д Т = 110 м ч
Катушки индуктивности в параллельных цепях Параллельная цепь — это цепь, компоненты которой расположены таким образом, что путь прохождения тока разделен. Схема на рисунке 3 имеет три катушки индуктивности, соединенные параллельно.
Схема на рисунке 3 имеет три катушки индуктивности, соединенные параллельно.
Параллельное размещение индукторов всегда уменьшает общую индуктивность цепи. Если катушки индуктивности экранированы или расположены достаточно далеко друг от друга, чтобы предотвратить взаимную индуктивность, общую индуктивность цепи можно рассчитать по следующей формуле:
L T = 1 ÷ (1/л 1 + 1/л 2 + 1/л 3 . . .)
, где L T — это общая индуктивность в цепи, а от L 1 до L 3 .. . — номинальная индуктивность отдельных катушек индуктивности в цепи.
Используя эту формулу, общую или индуктивность указанной выше параллельной цепи можно рассчитать следующим образом:
L T = 1 ÷ (1/5 + 1/15 + 1/30)
L T = 1 ÷ (0,2 + 0,066 + 0,033)
L T = 1 ÷ 0,299
Л Т = 3. 344 мч
344 мч
Эффект самоиндукции в катушке заключается в противодействии любому изменению тока в катушке. Например, когда на катушку подается напряжение, в катушке начинает течь ток. Этот ток создает вокруг себя магнитное поле. По мере расширения поля в катушке создается встречное напряжение, иногда называемое обратным напряжением. Это обратное напряжение противодействует протеканию основного тока. Это сопротивление протеканию тока называется индуктивным сопротивлением и измеряется в омах.
Величина индуктивного сопротивления в цепи зависит от частоты и величины переменного тока, а также величины индуктивности. Индуктивное сопротивление цепи можно рассчитать по следующей формуле:
Х Д = 2 пфл
, где X L — индуктивное реактивное сопротивление в омах, 2p — константа, полученная расчетным путем, которая обычно округляется до 6,28, f — частота подаваемого переменного тока в герцах, а L — индуктивность цепи в генри.
Работа трансформаторов основана на принципе взаимной индуктивности. Трансформаторы используются для увеличения или уменьшения напряжения и тока переменного тока (AC) в цепях. Трансформатор обычно состоит из двух катушек провода, электрически изолированных друг от друга, намотанных на один и тот же сердечник. Одна катушка называется первичной катушкой; другая называется вторичной катушкой. Первичная катушка является входной катушкой трансформатора, а вторичная катушка является выходной катушкой.Когда переменное напряжение подается на первичную катушку, оно индуцирует изменяющееся магнитное поле в сердечнике. Взаимная индукция вызывает наведение напряжения во вторичной обмотке.
Количество витков первичной и вторичной обмотки трансформатора определяет, как влияет напряжение в цепи. Когда количество витков первичной катушки больше, чем количество витков вторичной катушки, индуцированное напряжение во вторичной катушке меньше, чем приложенное напряжение первичной катушки. Когда количество витков первичной катушки меньше, чем количество витков вторичной катушки, индуцированное напряжение во вторичной катушке больше, чем приложенное напряжение первой катушки. Если выходное напряжение трансформатора больше, чем входное напряжение, он называется повышающим трансформатором. Если выходное напряжение трансформатора меньше входного, он называется понижающим трансформатором. Узнайте о влиянии различных входных напряжений и количества обмоток трансформатора в нашем интерактивном учебном пособии по Java Transformer.
Когда количество витков первичной катушки меньше, чем количество витков вторичной катушки, индуцированное напряжение во вторичной катушке больше, чем приложенное напряжение первой катушки. Если выходное напряжение трансформатора больше, чем входное напряжение, он называется повышающим трансформатором. Если выходное напряжение трансформатора меньше входного, он называется понижающим трансформатором. Узнайте о влиянии различных входных напряжений и количества обмоток трансформатора в нашем интерактивном учебном пособии по Java Transformer.
| Интерактивное руководство по Java | ||
Повышающий трансформатор повышает напряжение. Однако увеличение напряжения сопровождается уменьшением тока. Противоположное верно для понижающего трансформатора. Понижающий трансформатор снижает напряжение, но увеличивает ток. Это свойство трансформаторов делает их очень полезными и выгодными для передачи электроэнергии на большие расстояния.Повышающие трансформаторы используются на электростанциях для выработки очень высоких напряжений. Выходной ток уменьшается, что значительно снижает потери мощности из-за сопротивления в линиях передачи. Когда мощность достигает потребителей, понижающие трансформаторы используются для снижения напряжения и увеличения тока до соответствующих уровней для потребительских приложений.
Противоположное верно для понижающего трансформатора. Понижающий трансформатор снижает напряжение, но увеличивает ток. Это свойство трансформаторов делает их очень полезными и выгодными для передачи электроэнергии на большие расстояния.Повышающие трансформаторы используются на электростанциях для выработки очень высоких напряжений. Выходной ток уменьшается, что значительно снижает потери мощности из-за сопротивления в линиях передачи. Когда мощность достигает потребителей, понижающие трансформаторы используются для снижения напряжения и увеличения тока до соответствующих уровней для потребительских приложений.
Свойства катушек индуктивности делают их очень полезными в различных приложениях.Например, катушки индуктивности сопротивляются любым изменениям тока. Поэтому катушки индуктивности можно использовать для защиты цепей от скачков тока. Катушки индуктивности также используются для стабилизации постоянного тока и для контроля или устранения переменного тока. Катушки индуктивности, используемые для устранения переменного тока выше определенной частоты, называются дросселями.
Катушки индуктивности, используемые для устранения переменного тока выше определенной частоты, называются дросселями.
Одним из наиболее распространенных применений электромагнитной индуктивности является генерация электрического тока. Чтобы узнать, как работает генератор, посетите нашу брошюру «Генераторы и двигатели».
Радиоприемники Катушки индуктивностимогут использоваться в цепях с конденсаторами для генерирования и изоляции высокочастотных токов. Например, катушки индуктивности используются с конденсаторами в схемах настройки радиоприемников. На рисунке 4 переменный конденсатор подключен к схеме антенна-трансформатор. Передаваемые радиоволны вызывают протекание индуцированного тока в антенне через первичную катушку индуктивности на землю.
Во вторичной катушке индуктивности индуцируется вторичный ток в противоположном направлении.Этот ток течет к конденсатору. Всплеск тока на конденсаторе индуцирует противодействующую электродвижущую силу. Эта противодействующая электродвижущая сила называется емкостным сопротивлением. Индуцированный ток через катушку также индуцирует противодействующую электродвижущую силу. Это называется индуктивным реактивным сопротивлением. Таким образом, в цепи есть как емкостные, так и индуктивные реактивные сопротивления.
Эта противодействующая электродвижущая сила называется емкостным сопротивлением. Индуцированный ток через катушку также индуцирует противодействующую электродвижущую силу. Это называется индуктивным реактивным сопротивлением. Таким образом, в цепи есть как емкостные, так и индуктивные реактивные сопротивления.
На более высоких частотах индуктивное сопротивление больше, а емкостное сопротивление меньше. На более низких частотах все наоборот.Переменный конденсатор используется для выравнивания индуктивного и емкостного сопротивлений. Состояние, при котором реактивные сопротивления уравниваются, называется резонансом. Конкретная частота, которая выделяется уравновешенными реактивными сопротивлениями, называется резонансной частотой.
Радиоконтур настраивают регулировкой емкости переменного конденсатора для уравнивания индуктивного и емкостного сопротивлений контура на нужную резонансную частоту, или, другими словами, для настройки на нужную радиостанцию.Наш Radio Receiver Interactive Java Tutorial демонстрирует, как катушки индуктивности и переменный конденсатор используются для настройки на радиочастоты.
| Интерактивное руководство по Java | ||
Работа металлоискателя основана на принципе электромагнитной индукции. Металлодетекторы содержат одну или несколько катушек индуктивности.Когда металл проходит через магнитное поле, создаваемое катушкой или катушками, поле индуцирует электрические токи в металле. Эти токи называются вихревыми токами. Эти вихревые токи, в свою очередь, индуцируют собственное магнитное поле, которое генерирует ток в детекторе, питающий сигнал, указывающий на присутствие металла. Наблюдайте за магнитными полями и вихревыми токами, генерируемыми металлоискателем, в нашем учебном пособии по Java для металлодетектора .
| Интерактивное руководство по Java | ||
| gif»/> | ||
НАЗАД В ЭЛЕКТРИЧЕСТВО И МАГНИТИЗМ
Вопросы или комментарии? Отправить нам письмо.
© 1995-2021 автор Майкл В. Дэвидсон и Университет штата Флорида. Все права защищены. Никакие изображения, графика, программное обеспечение, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения владельцев авторских прав. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами.
Этот веб-сайт поддерживается нашим
Группа графического и веб-программирования
в сотрудничестве с Optical Microscopy в
Национальной лаборатории сильного магнитного поля.
Последнее изменение: пятница, 13 ноября 2015 г., 13:18
Количество обращений с 29 марта 1999 г.: 265584
индуктивность| электроника | Британика
индуктивность , свойство проводника (часто в форме катушки), измеряемое величиной индуцированной в нем электродвижущей силы или напряжения по сравнению со скоростью изменения электрического тока, создающего напряжение . Постоянный ток создает стационарное магнитное поле; постоянно меняющийся ток, переменный ток или флуктуирующий постоянный ток создают переменное магнитное поле, которое, в свою очередь, индуцирует электродвижущую силу в проводнике, находящемся в поле.Величина индуцированной электродвижущей силы пропорциональна скорости изменения электрического тока. Коэффициент пропорциональности называется индуктивностью и определяется как значение электродвижущей силы, индуцируемой в проводнике, деленное на величину скорости изменения тока, вызывающего индукцию.
Постоянный ток создает стационарное магнитное поле; постоянно меняющийся ток, переменный ток или флуктуирующий постоянный ток создают переменное магнитное поле, которое, в свою очередь, индуцирует электродвижущую силу в проводнике, находящемся в поле.Величина индуцированной электродвижущей силы пропорциональна скорости изменения электрического тока. Коэффициент пропорциональности называется индуктивностью и определяется как значение электродвижущей силы, индуцируемой в проводнике, деленное на величину скорости изменения тока, вызывающего индукцию.
Если электродвижущая сила индуцируется в проводнике, отличном от того, в котором изменяется ток, явление называется взаимной индукцией, примером которого является трансформатор.Однако изменяющееся магнитное поле, вызванное переменным током в проводнике, также индуцирует электродвижущую силу в самом проводнике, по которому течет изменяющийся ток. Такое явление называется самоиндукцией, а отношение индуцированной электродвижущей силы и скорости изменения тока определяется как самоиндукция.
Британская викторина
Электричество: короткие замыкания и постоянные токи
В чем разница между электрическим проводником и изолятором? Кто изобрел аккумулятор? Почувствуйте, как ваши клетки горят, пока вы перезаряжаете свою умственную батарею, отвечая на вопросы этой викторины.
Самоиндуцируемая электродвижущая сила противодействует вызывающему ее изменению. Следовательно, когда ток начинает течь через катушку с проводом, он испытывает сопротивление своему течению в дополнение к сопротивлению металлического провода. С другой стороны, когда электрическая цепь с постоянным током и катушкой внезапно размыкается, разрушающееся и, следовательно, уменьшающееся магнитное поле вызывает индуцированную электродвижущую силу, которая стремится поддерживать ток и магнитное поле и может вызвать искру. между контактами выключателя.Таким образом, самоиндукцию катушки или просто ее индуктивность можно рассматривать как электромагнитную инерцию, свойство, которое противодействует изменениям как токов, так и магнитных полей.
между контактами выключателя.Таким образом, самоиндукцию катушки или просто ее индуктивность можно рассматривать как электромагнитную инерцию, свойство, которое противодействует изменениям как токов, так и магнитных полей.
Индуктивность зависит от размера и формы данного проводника, количества витков, если это катушка, и типа материала вблизи проводника. Катушка, намотанная на сердечник из мягкого железа, гораздо эффективнее подавляет возрастание тока, чем такая же катушка с воздушным сердечником. Железный сердечник увеличивает индуктивность; при той же скорости изменения тока в катушке присутствует большая противодействующая электродвижущая сила (противоэдс), которая подавляет ток.
Единицей магнитной индуктивности является генри, названный в честь американского физика 19 века Джозефа Генри, впервые обнаружившего явление самоиндукции. Один генри равен одному вольту, деленному на один ампер в секунду. Если ток, изменяющийся со скоростью один ампер в секунду, индуцирует электродвижущую силу в один вольт, цепь имеет индуктивность в один генри, что является относительно большой индуктивностью.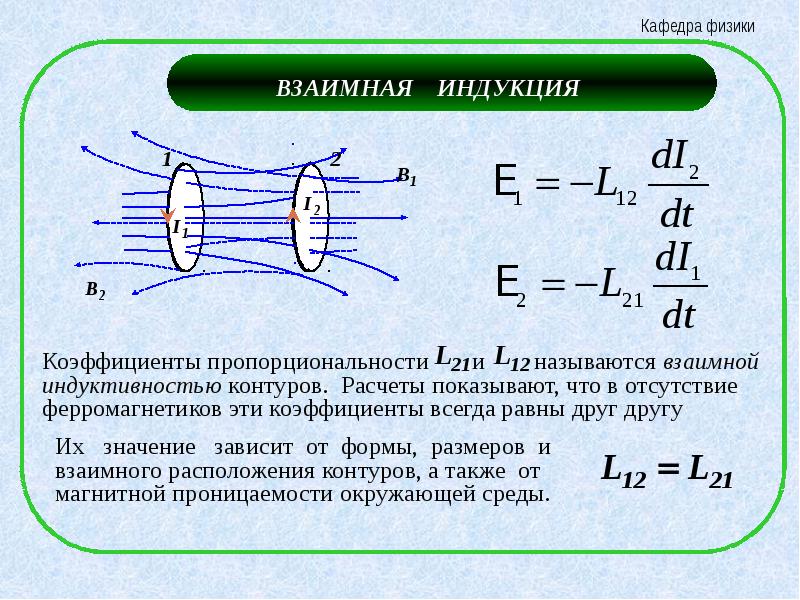
14.2 Самоиндукция и катушки индуктивности — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Соотнести скорость изменения тока с ЭДС индукции, создаваемой этим током в той же цепи
- Расчет собственной индуктивности цилиндрического соленоида
- Расчет собственной индуктивности прямоугольного тороида
Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи.Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ положительный, и это явление называется самоиндукцией .
Катушки индуктивности
На рис. 14.5 показаны некоторые силовые линии магнитного поля, вызванные током в круглой проволочной петле. Если ток постоянен, магнитный поток через контур также постоянен.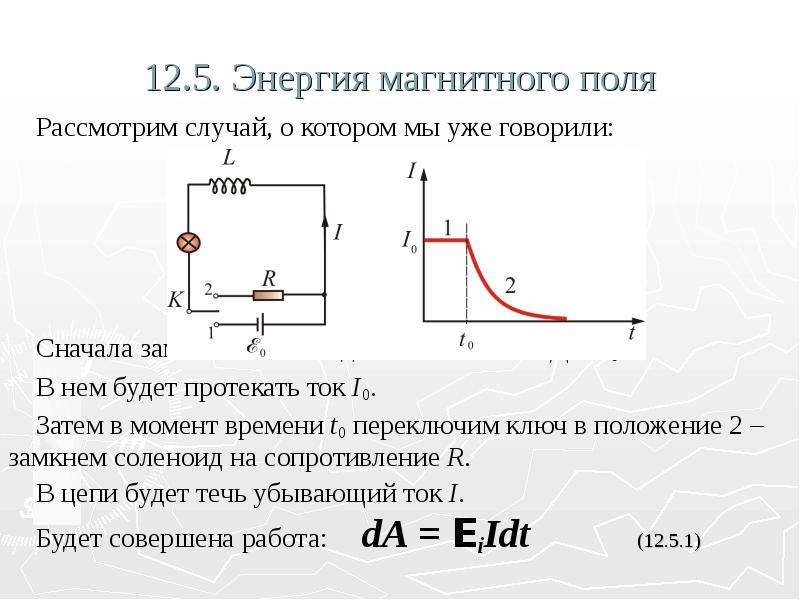 Однако если бы ток I менялся во времени, скажем, сразу после замыкания ключа S, то соответственно изменялся бы и магнитный поток ΦmΦm.Тогда закон Фарадея говорит нам, что в цепи будет индуцироваться ЭДС εε, где
Однако если бы ток I менялся во времени, скажем, сразу после замыкания ключа S, то соответственно изменялся бы и магнитный поток ΦmΦm.Тогда закон Фарадея говорит нам, что в цепи будет индуцироваться ЭДС εε, где
14,6
Поскольку магнитное поле, создаваемое проводом с током, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть
Фигура 14,5 Магнитное поле создается током I в контуре. Если бы I изменялись со временем, магнитный поток через контур также менялся бы и в контуре индуцировалась бы ЭДС.
Это также может быть записано как
., где константа пропорциональности L известна как самоиндукция проволочной петли. Если в петле N витков, это уравнение принимает вид
. По соглашению положительное направление нормали к контуру связано с током по правилу правой руки, поэтому на рис.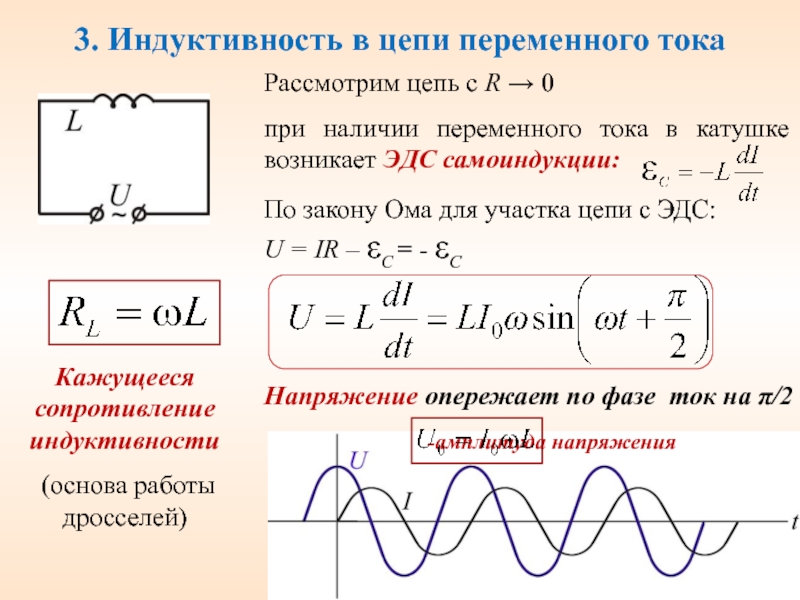 14.5 нормаль направлена вниз. При таком соглашении ΦmΦm является положительным в уравнении 14.9, поэтому L всегда имеет положительное значение .
14.5 нормаль направлена вниз. При таком соглашении ΦmΦm является положительным в уравнении 14.9, поэтому L всегда имеет положительное значение .
Для контура с Н витками ε=-NdΦm/dt,ε=-NdΦm/dt, поэтому ЭДС индукции может быть записана через самоиндукцию как
ε=-LdIdt.ε=-LdIdt.14.10
При использовании этого уравнения для определения L проще всего игнорировать знаки εanddI/dt, εanddI/dt и вычислить L как
L=|ε||dI/dt|.L=|ε||dI/dt|. Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией.Например, помимо проволочной петли длинный прямой провод обладает собственной индуктивностью, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно обнаружить при подключении к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и собственной индуктивностью, что может иметь нежелательные последствия.
Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и собственной индуктивностью, что может иметь нежелательные последствия.
Элемент цепи, используемый для обеспечения собственной индуктивности, известен как индуктор.Он представлен символом, показанным на рис. 14.6, который напоминает катушку проволоки, основную форму катушки индуктивности. На рис. 14.7 показаны несколько типов катушек индуктивности, обычно используемых в цепях.
Фигура 14,6 Символ, используемый для обозначения катушки индуктивности в цепи.
Фигура 14,7 Различные индукторы. Независимо от того, заключены ли они в капсулу, как показаны три верхние, или намотаны на катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку провода.(кредит: Уинделл Оскей)
В соответствии с законом Ленца отрицательный знак в уравнении 14.10 указывает на то, что ЭДС индукции на катушке индуктивности всегда имеет полярность, которая противодействует изменению тока. Например, если бы ток, протекающий от А к В на рис. 14.8(а), увеличивался, ЭДС индукции (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от А до В уменьшался, то ЭДС индукции имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (рис. 14.8(б)). Наконец, если бы ток через индуктор был постоянным, в катушке не индуцировалась бы ЭДС.
Например, если бы ток, протекающий от А к В на рис. 14.8(а), увеличивался, ЭДС индукции (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от А до В уменьшался, то ЭДС индукции имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (рис. 14.8(б)). Наконец, если бы ток через индуктор был постоянным, в катушке не индуцировалась бы ЭДС.
Фигура 14,8 Индуцированная ЭДС на катушке индуктивности всегда противодействует изменению тока. Это можно представить как воображаемую батарею, заставляющую течь ток, противодействующий изменению в (а) и усиливающий изменение в (б).
Одним из распространенных применений индуктивности является определение сигналов светофора, когда транспортные средства ожидают на перекрестке.Электрическая цепь с индуктором размещается на дороге под местом, где остановится ожидающий автомобиль. Кузов автомобиля увеличивает индуктивность, и цепь меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал от катушки передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути (рисунок 14.9). Металлодетекторы можно настроить на чувствительность, а также они могут обнаруживать наличие металла на человеке.
Кузов автомобиля увеличивает индуктивность, и цепь меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал от катушки передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути (рисунок 14.9). Металлодетекторы можно настроить на чувствительность, а также они могут обнаруживать наличие металла на человеке.
Фигура 14,9 Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но и могут указать их приблизительную высоту над полом. (кредит: Alexbuirds/Wikimedia Commons)
Во вспышках фотокамер обнаружены большие наведенные напряжения. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор , чтобы индуцировать большие напряжения. Напомним из книги «Колебания об колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения. Также вспомните (из электромагнитной индукции об электромагнитной индукции), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки.
Напомним из книги «Колебания об колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения. Также вспомните (из электромагнитной индукции об электромагнитной индукции), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки.
Пример 14.2
Самоиндукция катушки
ЭДС индукции 20 мВ измеряется на катушке из 50 тесно намотанных витков, при этом ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Чему равна собственная индуктивность катушки? б) Чему равен поток через каждый виток катушки при силе тока 5,0 А?Стратегия
Обе части этой задачи дают всю информацию, необходимую для определения собственной индуктивности в части (а) или потока через каждый виток катушки в части (б).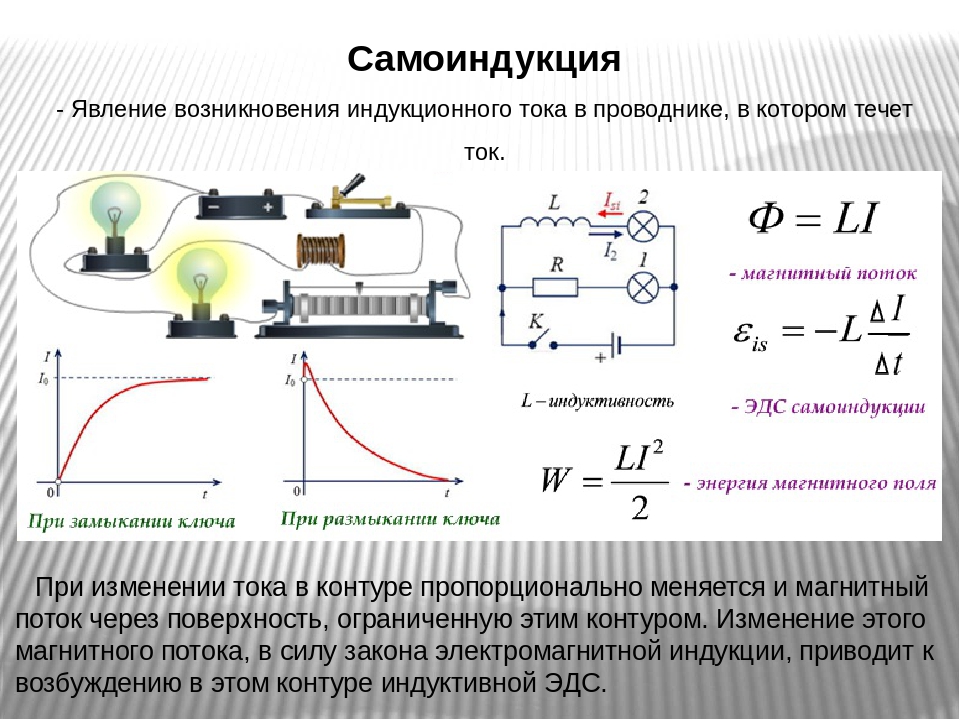 Необходимые уравнения: Уравнение 14.10 для части (а) и Уравнение 14.9 для части (б).
Необходимые уравнения: Уравнение 14.10 для части (а) и Уравнение 14.9 для части (б).Решение
- Игнорируя отрицательный знак и используя величины, мы имеем из уравнения 14.10, L=εdI/dt=20 мВ 5,0 А/0,10 с=4,0×10-2H.L=εdI/dt=20 мВ 5,0 А/0,10 с=4,0×10-2H.
- Из уравнения 14.9 поток выражается через ток как Φm=LI/N, Φm=LI/N, поэтому Φm=(4,0×10-2H)(5,0A)50 витков=4,0×10-3Wb. Φm=(4,0×10-2H)(5,0A)50витков=4,0×10-3Wb.
Значение
Собственная индуктивность и поток, рассчитанные в частях (а) и (б), являются типичными значениями для катушек, используемых в современных устройствах.Если ток не меняется во времени, поток не меняется во времени, поэтому ЭДС не индуцируется.Проверьте свое понимание 14.2
Проверьте свое понимание Ток течет через катушку индуктивности на рис. 14.8 от B к A вместо от A к B , как показано.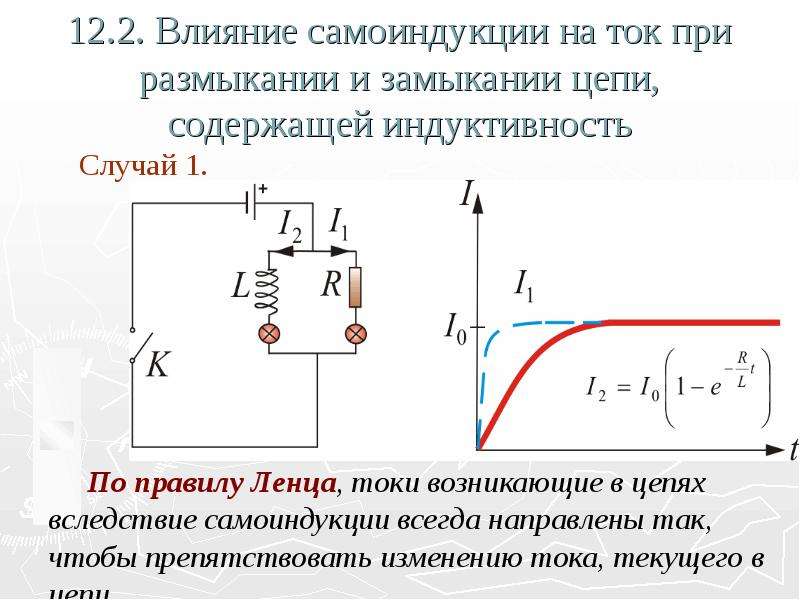 Ток увеличивается или уменьшается, чтобы создать ЭДС, указанную на диаграмме (а)? На схеме (б)?
Ток увеличивается или уменьшается, чтобы создать ЭДС, указанную на диаграмме (а)? На схеме (б)?
Проверьте свое понимание 14.3
Проверьте свои знания Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?
Хороший подход к расчету собственной индуктивности катушки индуктивности состоит из следующих шагов:
Стратегия решения проблем
Самоиндукция
- Предположим, что ток I протекает через индуктор.
- Определите магнитное поле B→B→, создаваемое током.Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
- Получите магнитный поток, Φm.Φm.
- При известном потоке собственная индуктивность может быть найдена из уравнения 14.9, L=NΦm/IL=NΦm/I.
Чтобы продемонстрировать эту процедуру, мы теперь рассчитаем собственные индуктивности двух катушек индуктивности.
Цилиндрический соленоид
Рассмотрим длинный цилиндрический соленоид с длиной l , площадью поперечного сечения A и N витков провода.Мы предполагаем, что длина соленоида настолько больше его диаметра, что мы можем принять магнитное поле равным B=µ0nIB=µ0nI во всей внутренней части соленоида, т. е. пренебрегаем концевыми эффектами в соленоиде. При токе I , протекающем через катушки, магнитное поле, создаваемое внутри соленоида, равно
B=μ0(Nl)I, B=μ0(Nl)I,14.11
, поэтому магнитный поток через один виток равен
. Φm=BA=μ0NAlI.Φm=BA=μ0NAlI.14.12
Используя уравнение 14.9, находим для собственной индуктивности соленоида
Lсоленоид=NΦmI=μ0N2Al.Lсоленоид=NΦmI=μ0N2Al.14.13
Если n=N/ln=N/l — число витков на единицу длины соленоида, мы можем записать уравнение 14. 13 как
13 как
14.14
, где V=AlV=Al — объем соленоида. Обратите внимание, что собственная индуктивность длинного соленоида зависит только от его физических свойств (таких как число витков провода на единицу длины и объем), а не от магнитного поля или тока.Это справедливо для катушек индуктивности в целом.
Прямоугольный тороид
Тороид с прямоугольным поперечным сечением показан на рис. 14.10. Внутренний и внешний радиусы тороида равны R1 и R2, hR1 и R2, а h — высота тороида. Применяя закон Ампера так же, как в примере 13.8, для тороида с круглым поперечным сечением, мы находим, что магнитное поле внутри прямоугольного тороида также равно
B=μ0NI2πr, B=μ0NI2πr,14.15
, где r — расстояние от центральной оси тороида.Поскольку поле изменяется внутри тороида, мы должны вычислить поток путем интегрирования по поперечному сечению тороида. Используя бесконечно малый элемент площади поперечного сечения da=hdrda=hdr, показанный на рис. 14.10, мы получаем
Используя бесконечно малый элемент площади поперечного сечения da=hdrda=hdr, показанный на рис. 14.10, мы получаем
14.16
Фигура 14.10 Расчет самоиндукции прямоугольного тороида.
Теперь из уравнения 14.16 получаем для собственной индуктивности прямоугольного тороида
L=NΦmI=μ0N2h3πlnR2R1.L=NΦmI=μ0N2h3πlnR2R1.14.17
Как и ожидалось, собственная индуктивность является константой, определяемой только физическими свойствами тороида.
Проверьте свое понимание 14,4
Проверьте свои знания (a) Рассчитайте собственную индуктивность соленоида, который туго намотан проволокой диаметром 0,10 см, имеет площадь поперечного сечения 0,90 см20,90 см2 и длину 40 см. (b) Если ток через соленоид равномерно уменьшается от 10 до 0 А в 0.10 с, чему равна ЭДС между концами соленоида?
Проверьте свое понимание 14,5
Проверьте свои знания (a) Каков магнитный поток через один виток соленоида с собственной индуктивностью 8,0×10−5H8,0×10−5H, когда через него протекает ток силой 3,0 А? Предположим, что соленоид имеет 1000 витков и намотан из проволоки диаметром 1,0 мм. б) Чему равна площадь поперечного сечения соленоида?
б) Чему равна площадь поперечного сечения соленоида?
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ
ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯРисунок 32.1 показан стержень из проводящего материала, перемещаемый с скорость v в однородном магнитном поле B. Магнитная сила, действующая на свободный электрон в стержне будет направлен вверх и имеет величину, равную
(32.1)
Рисунок 32.1. Движущийся проводник в магнитном поле. В результате действия магнитной силы электроны начнут накапливаются в верхней части стержня. Распределение заряда стержня будет поэтому измениться, и вершина стержня будет иметь избыток электронов (отрицательный заряд), а в нижней части стержня будет дефицит электронов (положительный заряд).Это распределение заряда создаст электрическое поле в стержень. Сила этого электрического поля будет увеличиваться до тех пор, пока Электростатическая сила, создаваемая этим полем, по величине равна магнитная сила. В этот момент восходящий поток электронов остановится и (32. 2)
2)
или
(32.3)
Наведенное электрическое поле создаст разность потенциалов [Delta]V между концами стержня, равно
(32.4)
где L — длина стержня. Если концы стержня соединить цепи, обеспечивающей обратный путь для накопленного заряда, стержень будет источник ЭДС. Поскольку ЭДС связана с движением стержня через магнитное поле называется ЭДС движения . Уравнение (32.4) показывает, что величина ЭДС пропорциональна скорости v. Глядя на рис. 32.1 мы видим, что vL — это площадь, охватываемая стержнем за второй.Величина BvL представляет собой магнитный поток, охватываемый стержнем за второй. Таким образом,
(32.5)
Хотя эта формула была выведена для частного случая, показанного на рис. 32.1, она действует в целом. Оно справедливо для стержней и проволоки произвольной формы, движущихся через произвольные магнитные поля.
Уравнение (32.5) связывает ЭДС индукции со скоростью, с которой
меняется магнитный поток. В системе, показанной на рисунке 32.1 приложенный флюс
изменяется при движении стержня. Вложенный магнитный поток также может быть
изменяется, если изменяется сила окружающего магнитного поля. В обоих случаях
результатом будет ЭДС индукции. Связь между ЭДС индукции и
изменение магнитного потока известно как закон индукции Фарадея:
В системе, показанной на рисунке 32.1 приложенный флюс
изменяется при движении стержня. Вложенный магнитный поток также может быть
изменяется, если изменяется сила окружающего магнитного поля. В обоих случаях
результатом будет ЭДС индукции. Связь между ЭДС индукции и
изменение магнитного потока известно как закон индукции Фарадея:
ЭДС индукции вдоль движущейся или изменяющейся математической траектории в постоянном или изменение магнитного поля равно скорости, с которой магнитный поток проходит через путь.»
Если рассматривать замкнутый путь, то закон Фарадея можно сформулировать так:
ЭДС индукции вокруг замкнутого математического пути в магнитном поле равна к скорости изменения магнитного потока, пересекаемого областью внутри путь »
или
(32.6)
Знак минус в уравнении (32.6) показывает, как полярность ЭДС индукции связаны со знаком потока и со скоростью изменения потока.Знак поток фиксируется по правилу правой руки:
«Согните пальцы правой руки в том направлении, в котором мы
расчет ЭДС по пути; магнитный поток положителен, если
линии магнитного поля указывают в направлении большого пальца, а отрицательные
в противном случае. »
»
Пример: Задача 32.13
Металлический стержень длины L и массы m свободно скользит без трения. на двух параллельных металлических дорожках.Дорожки соединены одним концом так, что они и стержень образуют замкнутый контур (см. рис. 32.2). Стержень имеет сопротивление R, а дорожки имеют незначительное сопротивление. Однородное магнитное поле есть перпендикулярно плоскости этого контура. Магнитное поле увеличивается с постоянной скоростью дБ/dt. Первоначально магнитное поле имеет напряженность B 0 и стержень покоится на расстоянии x 0 от соединенные концы рельсов. Выразите ускорение стержня при этом мгновенный в терминах заданных величин.
Рисунок 32.2. Задача 32.13.Магнитный поток [Phi], окруженный стержнем и дорожками в момент времени t = 0 с, равен предоставлено
(32.7)
Магнитное поле увеличивается с постоянной скоростью, и, следовательно, приложенный магнитный поток также увеличивается:
(32. 8)
8)
Закон индукции Фарадея теперь можно использовать для определения ЭДС индукции:
(32.9)
Под действием ЭДС индукции по стержню потечет ток с величина равна
(32.10)
Направление тока вдоль провода, а значит, перпендикулярно магнитное поле. Сила, с которой магнитное поле действует на стержень, равна предоставлено
(32.11)
(см. главу 31). Комбинируя уравнения (32.10) и (32.11), получаем для силы на провод
(32.12)
Таким образом, ускорение стержня в момент времени t = 0 с равно
(32.13)
Пример: Задача 32.12
а) Длинный соленоид имеет 300 витков провода на метр и имеет радиус 3,0 см. Если сила тока в проводе увеличивается со скоростью 50 А/с, то при какой С какой скоростью увеличивается напряженность магнитного поля в соленоиде?
б) Соленоид окружен катушкой со 120 витками.Радиус этого катушка 6,0 см. Какая ЭДС индукции будет создаваться в этой катушке, пока ток в соленоиде увеличивается?
а) Магнитное поле в соленоиде обсуждалось в главе 31. Если
соленоид имеет n витков на метр, и если I — ток через каждую катушку, чем
поле внутри соленоида равно
Если
соленоид имеет n витков на метр, и если I — ток через каждую катушку, чем
поле внутри соленоида равно
(32.14)
Следовательно,
(32.15)
В этой задаче n = 300 витков/метр и dI/dt = 50 А/с.Изменение в Таким образом, магнитное поле равно
(32.16)
Это уравнение показывает, что магнитное поле увеличивается со скоростью 0,019 т/с.
б) Поскольку магнитное поле в соленоиде меняется, магнитный поток окруженный окружающей катушкой, также изменится. Поток, заключенный в одна обмотка этой катушки
(32.17)
где г в = 3.0 см — радиус соленоида. Здесь у нас есть считалось, что напряженность магнитного поля вне соленоида равна нулю. Общий поток, создаваемый внешними катушками, равен
. (32.18)
Скорость изменения магнитного потока из-за этого изменения магнитного поля равна предоставлено
(32.19)
В результате изменения тока в соленоиде будет индуцироваться ЭДС во внешней катушке со значением, равным
(32. 20)
20)
Если концы катушки соединить, то через нее потечет ток. проводник. Направление тока в катушке можно определить с помощью Закон Ленца , который гласит, что
«ЭДС индуцирования всегда имеют такую полярность, чтобы противодействовать изменение, которое их порождает»Применим закон Ленца к задаче 32.12. Направление магнитного поля может быть определена по правилу правой руки и направлена вправо.Если ток в соленоиде увеличивается, поток также будет увеличиваться. Электрический ток во внешней катушке будет течь в таком направлении, чтобы противодействовать этому изменению. Это означает, что ток в этой катушке будет течь против часовой стрелки (т. поле, создаваемое индуцированным током, направлено противоположно полю генерируется большим соленоидом).
Стержень, движущийся в магнитном поле, будет испытывать ЭДС индукции.
магнитная сила, действующая на свободные электроны.ЭДС индукции будет
пропорциональна линейной скорости v стержня.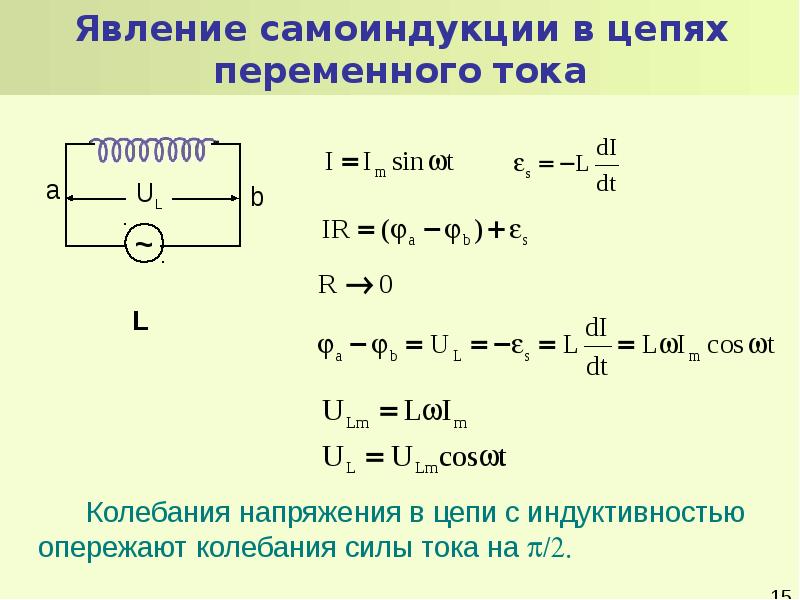 Если мы посмотрим на стержень из
системе отсчета, в которой стержень покоится, магнитная сила будет равна нулю.
Однако должна существовать ЭДС индукции. Так как эта ЭДС не может быть
создаваемое магнитным полем, оно должно быть связано с электрическим полем, которое
существует в подвижной системе отсчета. Величина этого электрического поля
должна быть такой, чтобы создавалась та же ЭДС индукции, что и в
система отсчета, в которой движется стержень.Для этого необходимо, чтобы
Если мы посмотрим на стержень из
системе отсчета, в которой стержень покоится, магнитная сила будет равна нулю.
Однако должна существовать ЭДС индукции. Так как эта ЭДС не может быть
создаваемое магнитным полем, оно должно быть связано с электрическим полем, которое
существует в подвижной системе отсчета. Величина этого электрического поля
должна быть такой, чтобы создавалась та же ЭДС индукции, что и в
система отсчета, в которой движется стержень.Для этого необходимо, чтобы
(32.21)
Электрическое поле E’, существующее в системе отсчета движущегося стержня, равно называется индуцированным электрическим полем . ЭДС, возникающая между концы стержня равны
(32.22)
что эквивалентно уравнению (32.4). Если индуцированное электрическое поле является позиционным зависимы, то уравнение (32.22) нужно заменить интегральным выражением
(32.23)
где интеграл простирается от одного конца стержня до другого конца
стержень.
Разница между индуцированным электрическим полем и электрическим полем генерируемое распределением статического заряда, заключается в том, что в первом случае поле не является консервативным и интеграл по замкнутому пути равен
(32.24)
который отличен от нуля, если магнитный поток зависит от времени.
Изменение тока в проводнике (например, в катушке) вызывает изменение магнитного поля. поле.Это зависящее от времени магнитное поле может индуцировать ток за секунду. проводник, если он находится в этом поле. ЭДС, индуцируемая в эту секунду проводник, [эпсилон] 2 , будет зависеть от магнитного потока через этот кондуктор:
(32.25)
Поток [Phi] B1 зависит от силы магнитного поля генерируется проводником 1 и, следовательно, пропорциональна току I 1 через этот провод:
(32.26)
Здесь константа L 21 зависит от размера двух катушек, от
расстояние между ними и количество витков в каждой катушке.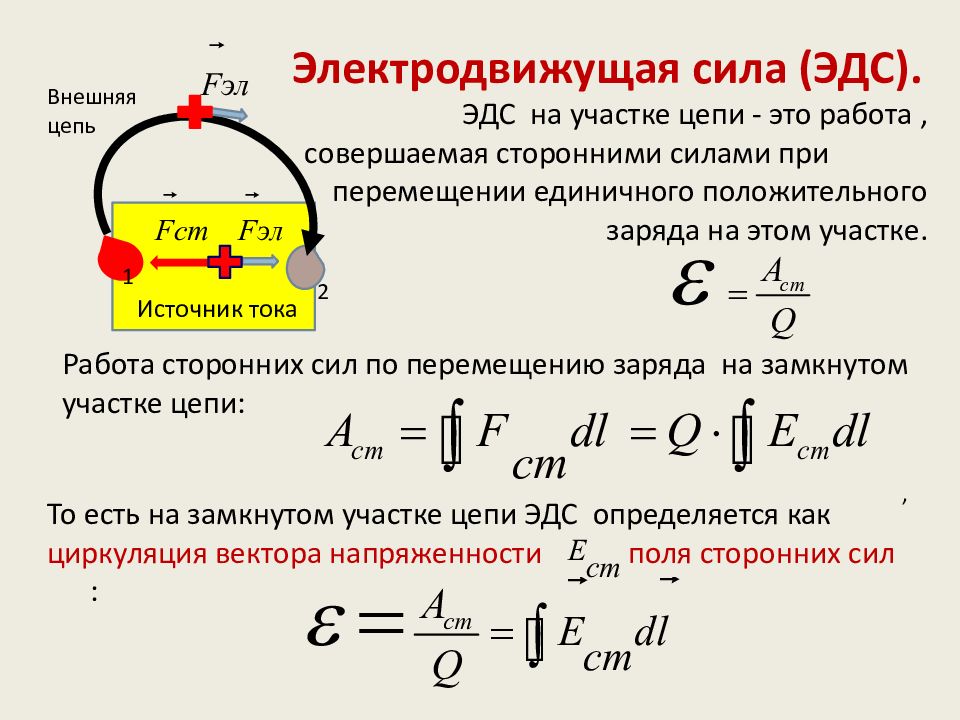 То
константа L 21 называется взаимной индуктивностью двух катушек.
Используя эту константу, уравнение (32.25) можно переписать как
То
константа L 21 называется взаимной индуктивностью двух катушек.
Используя эту константу, уравнение (32.25) можно переписать как
(32.27)
Единицей индуктивности является Генри (Гн), и из уравнения (32.27) мы заключаем, что
(32.28)
При изменении магнитного поля, создаваемого катушкой (из-за изменения тока) магнитный поток, охватываемый катушкой, также изменится.Это изменение в потоке будет индуцировать ЭДС в катушке, а поскольку ЭДС возникает из-за изменения ток через катушку называется ЭДС самоиндукции. То ЭДС самоиндукции равна
(32.29)
В уравнении (32.29) L называется собственной индуктивностью катушки. ЭДС самоиндукции будет действовать в таком направлении, чтобы противодействовать изменению Текущий.
Пример: Задача 32.32
Длинный соленоид радиуса R имеет n витков на единицу длины.циркуляр
катушка провода радиуса R’ с n’ витками окружает соленоид. Что
взаимная индукция? Имеет ли значение форма витка проволоки?
Что
взаимная индукция? Имеет ли значение форма витка проволоки?
Поле внутри соленоида предполагается бесконечно длинным. соленоид и имеет силу, равную
(32.30)
Поток, заключенный во внешней катушке, равен
(32.31)
ЭДС индукции во внешней катушке равна
(32.32)
Таким образом, взаимная индуктивность L 12 равна
(32.33)
Если через катушку индуктивности протекает постоянный ток, то магнитное поле, не зависящее от времени,
поле создано. Если вдруг источник тока отключится, изменение
в замкнутом магнитном потоке создаст ЭДС самоиндукции, которая попытается
чтобы ток протекал в исходном направлении. Электрическая энергия
создаваемая ЭДС самоиндукции первоначально сохранялась в катушке индуктивности в
форма магнитной энергии.Количество магнитной энергии, запасенной в магнитном
поле можно определить, рассчитав общую мощность, отдаваемую мощностью
источник для создания магнитного поля. Предположим, что после того, как батарея
подключенный к индуктору, ток увеличивается со скоростью dI/dt. То
ЭДС самоиндукции, создаваемая этим зависящим от времени током, равна
Предположим, что после того, как батарея
подключенный к индуктору, ток увеличивается со скоростью dI/dt. То
ЭДС самоиндукции, создаваемая этим зависящим от времени током, равна
(32.34)
Ток должен доставлять дополнительную мощность, чтобы преодолеть эту ЭДС самоиндукции. То требуемая мощность будет зависеть от времени и равна
(32.35)
Работа, совершаемая током, накапливается в катушке индуктивности в виде магнитной энергии. То Таким образом, изменение dU магнитной энергии индуктора равно
(32.36)
Полная энергия, запасенная в магнитном поле индуктора, когда ток достигает своего конечного значения, можно получить, интегрируя уравнение (32.36) между I = 0 и I = I f .
(32.37)
Для соленоида длины l собственная индуктивность равна
(32.38)
Таким образом, запасенная в соленоиде магнитная энергия равна
(32.39)
где V — объем соленоида. Магнитная энергия может быть выражена в
условия B и V:
Магнитная энергия может быть выражена в
условия B и V:
(32.40)
где B = u 0 n I — магнитное поле в соленоиде. Общая магнитная энергия индуктора теперь может быть выражена через плотность магнитной энергии u, которая определяется как
(32.41)
Магнитная энергия, запасенная в магнитном поле, равна плотности энергии время громкости. Хотя мы вывели формулу для магнитной энергии плотность для частного случая очень длинного соленоида, его вывод верен для любого произвольного магнитного поля.
Пример: Задача 32.46
Тороид квадратного сечения имеет внутренний радиус R 1 и внешний радиус R 2 .Тороид имеет N витков провода, по которому ток I ; Предположим, что N очень велико.
а) Найдите плотность магнитной энергии как функцию радиуса.
б) Интегрируя плотность энергии, найти полную магнитную энергию, запасенную в соленоид.
в) Определите самоиндукцию по формуле U = L . я 2 /2.
я 2 /2.
а) Примените закон Ампера, используя сферическую петлю Ампера с радиусом r
(32.42)
Ток, заключенный в петле Ампера, равен
(32.43)
Используя закон Ампера, мы можем определить магнитное поле B:
(32.44)
Таким образом, плотность магнитной энергии равна
(32.45)
б) Предположим, что высота тороида равна h. Рассмотрим кусочек тор, показанный на рис. 32.3.
Рисунок 32.3. Сечение тороида задачи 32.46. Объем dV этого среза равен(32.46)
Магнитная энергия, запасенная в этом сегменте, равна
(32.47)
Полная магнитная энергия, запасенная в тороиде, может быть получена путем интегрирования уравнение (32.47) относительно r между r = R 1 и r = R 2 :
(32.48)
в) Магнитная энергия, запасенная в катушке индуктивности L, равна 0. 5 л
я 2 . Сравнивая это с уравнением (32.48), мы заключаем, что
индуктивность L тороида равна
5 л
я 2 . Сравнивая это с уравнением (32.48), мы заключаем, что
индуктивность L тороида равна
(32.49)
Цепь RL состоит из резистора и катушки индуктивности, соединенных последовательно с аккумулятор (см. рис. 32.4). Применяя к этому второе правило Крихгофа одноконтурной схемы получаем следующее дифференциальное уравнение
(32.50)
Рисунок 32.4. Цепь RL. Это дифференциальное уравнение имеет решение(32.51)
Это решение справедливо, если батарея подключена в момент времени t = 0. Уравнение (32.51) показывает, что ток при t = 0 с равен 0 и неуклонно растет, достигая конечное значение e /R при t = [бесконечность]. Постоянная времени цепи RL Л/П. Если ток достиг устойчивого значения и батарея внезапно отключен, проводник может генерировать ток через резистор, который будет постепенно затухать в зависимости от времени.Если начальный ток равен [эпсилон]/R, ток в момент времени t будет равен
(32.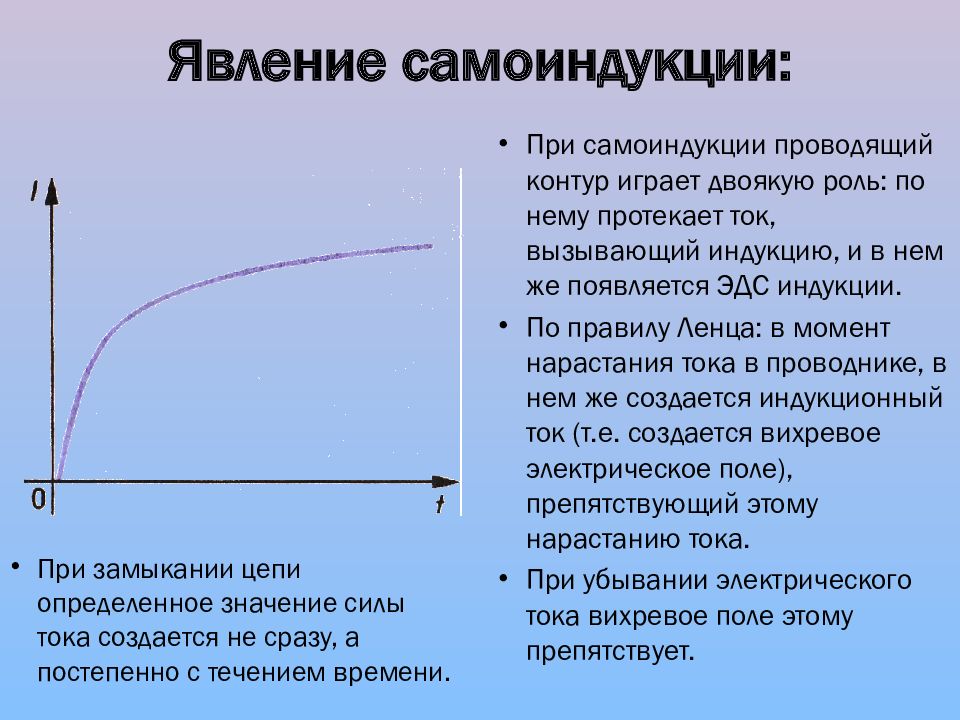 52)
52)
Пример: Задача 32.54
Какое тепло Джоуля рассеивается током в уравнении (32.52) в резистор в интервале времени между t = 0 и t = [бесконечность] ? Сравнить с начальная магнитная энергия в индукторе.
Ток через резистор задается уравнением (32.51). Мощность рассеивается при этом ток в резисторе равен
(32.53)
Полная энергия, рассеиваемая этим током в резисторе между t = 0 и t = [бесконечность] равно
(32.54)
Магнитная энергия, запасенная в индукторе, равна
(32.55)
и мы заключаем, что вся магнитная энергия, запасенная в индукторе, рассеивается как джоулево тепло в резисторе.
Присылайте комментарии, вопросы и/или предложения по электронной почте по адресу [email protected] и/или посетите домашнюю страницу Фрэнка Вольфса.
индуктивность
индуктивностьВзаимная и собственная индуктивность
Проблема:
Для запуска электропоезда нужно 12 В, а напряжение на выходе 120 В. Каково отношение числа витков первичной обмотки к числу
включает вторичную обмотку трансформатора, который вы используете?
Каково отношение числа витков первичной обмотки к числу
включает вторичную обмотку трансформатора, который вы используете?
Решение:
- Концепты:
Взаимная индуктивность, собственная индуктивность, трансформатор - Рассуждение:
Прототип трансформатора имеет первичную и вторичную обмотки. намотаны по обе стороны железного кольца.Если ток в первичной меняется катушка, меняется поток через вторичную катушку и ЭДС наводится во вторичной обмотке. ЭДС, индуцируемая во вторичной обмотке, равна пропорциональна числу витков N 2 вторичной обмотки, так как количество витков определяет общий магнитный поток, проходящий через эта катушка. ЭДС индукции также пропорциональна напряжению В 1 через первичную катушку, так как это определяет величину первичной тока и связанного с ним магнитного поля.Индуцированное напряжение равно обратно пропорциональна, однако, количеству витков N 1 первичная катушка. Отношения принимают форму
Отношения принимают формуВ 2 /Н 2 = В 1 /Н 1 .
Отношение количества витков на двух катушках определяет отношение напряжения. Самоиндукция является причиной того, что ЭДС, индуцируемая в вторичная обмотка обратно пропорциональна числу витков первичная катушка.Если первичная обмотка имеет больше витков, ее труднее производить быстрое изменение тока, протекающего через него, из-за обратного ЭДС, создаваемая самоиндукцией. Этот эффект ограничивает ток и поэтому величина магнитного поля, создаваемого первичной катушкой, что, в свою очередь, ограничивает магнитный поток, проходящий через вторичную катушку.
Предположим, что одно и то же поле B пронизывает обе катушки и поток на виток Φ B одинаково для обеих катушек.Общий поток за виток обусловлен токи в обеих катушках. В хорошо спроектированном трансформаторе сопротивление катушек мало, и мы пренебрегаем здесь. Тогда ЭДС индукции в первичная обмотка должна точно уравновешивать приложенное напряжение V p .
V p = N 1 dΦ B /dt.
Поскольку Φ B одинакова для вторичной обмотки, ЭДС индукции в вторичная обмотка ε с = N 2 dΦ B /dt.Пока нет нагрузки подключены, измеряем выходное напряжение V s = N 2 dΦ B /dt.
V p /N p = V s /N s . - Детали расчета:
N 1 /N 2 = V 1 /V 2 . Ты нуждаешься в трансформатор с в десять раз большим числом витков на первичной обмотке, чем на вторичная катушка.
Проблема:
Большая катушка радиуса а лежит в плоскости х-у с центром в точке
Происхождение.Коаксиальная малая катушка радиуса b << a с
ось, параллельная оси z, лежит на расстоянии z выше большой
катушка. По маленькой катушке течет постоянный ток I.
а) Найдите магнитный поток, связанный с большой катушкой.
(b) Если маленькая катушка движется вдоль оси z с постоянной скоростью против = v 0 k , что
это ЭДС ε
индуцируется в большой катушке как
функция времени? Пусть z = 0 при t = 0,
Решение:
- Концепты:
Флюс F = ∫ A B ∙ n дА, F = MI, M = взаимная индуктивность, ε = -∂F/∂t = ЭДС индукции - Рассуждение:
Найдя взаимную индуктивность катушек как функцию катушки разделения, можно найти поток через большую катушку и ЭДС индукции. - Детали расчета:
(а) Поток через большую катушку из-за тока I в малой катушка F = MI. Чтобы найти M, мы вычисляем поток через маленькую катушку за счет тока I в большой катушке.
[При расчете взаимной индуктивности можно рассчитать поток через цепи 1 из-за тока в цепи 2 или потока через цепь 2 из-за ток в цепи 1. В данной задаче одним из этих расчетов является часто намного проще, чем другие. ]
]
То поле на оси токовой петли радиуса a равно B = к мк 0 Ia 2 /[2(а 2 + z 2 ) 3/2 ] (единицы СИ), если ток течет в ф направление.
Поток через петлю радиуса b равен F = ∫ А В ∙ н дА.
Ф = πb 2 μ 0 Ia 2 /[2(a 2 + z 2 ) 3/2 ]. (Поскольку b << a, B почти постоянно по площади, если малый петля.)
F = МИ, М = πb 2 a 2 μ 0 /[2(a 2 + z 2 ) 3/2 ].
(б) ε = -∂F/∂t = -(πb 2 a 2 μ 0 I/2)(∂/∂t)(1/(a 2 + z 2 ) 3/2 )
= (3πb 2 a 2 μ 0 I/4)(1/(a 2 + з 2 ) 5/2 )2зв 0 .
ε = (3πb 2 а 2 μ 0 I/2)(zv 0 /(а 2 + z 2 ) 5/2 ).
Проблема:
Тороидальная катушка из N витков имеет квадратное поперечное сечение, каждая сторона
квадрат имеет длину a и внутренний радиус b.
а) Найдите индуктивность катушки.
б) Найти взаимную индуктивность системы, состоящей из катушки и
длинный прямой провод вдоль оси симметрии катушки.(Предположить, что
проводники, замыкающие цепь, частью которой является длинный прямой провод
расположены далеко от катушки, так что их влиянием можно пренебречь.)
в) Найти отношение собственной индуктивности катушки к взаимной
индуктивность системы.
Решение:
- Концепты:
Закон Ампера, магнитный поток, взаимная индуктивность, собственная индуктивность - Рассуждение
Закон Ампера можно использовать для нахождения магнитных полей, создаваемых катушкой и к проводу.Найдя поток этих полей через катушку, мы можем найти самоиндукцию и взаимную индуктивность. - Детали расчета:
(а) Закон Ампера дает магнитное поле внутри тора из-за тока Я в обмотках. Симметрия диктует, что магнитное поле направлено в
в
( φ /φ)-направление.
Симметрия диктует, что магнитное поле направлено в
в
( φ /φ)-направление.
Б = ( φ /φ) μ 0 NI/(2πr). Здесь N — число витков обмоток.
Поток этого поля через обмотки равен
F = ∫ В ∙d А = [μ 0 N 2 I/(2π)]a∫ b b+a (1/r)dr = [μ 0 N 2 I/(2π)]a пер((б+а)/б).
F = LI, L = [μ 0 N 2 a/(2π)] пер((б+а)/б).
(b) Закон Ампера дает магнитное поле внутри тора из-за ток I в проводе.
Б = ( φ /φ)μ 0 I/(2πr).
Поток этого поля через обмотки равен
F = ∫ В ∙d А = [μ 0 NI/(2π)]a∫ b b+a (1/r)dr = [μ 0 NI/(2π)]a пер((б+а)/б).
F = MI, M = [μ 0 Na/(2π)] пер((б+а)/б).
(в) L/M = N.
Проблема:
По длинному кабелю течет ток в одном направлении, равномерно распределенный по всей его длине. круглое сечение.Ток возвращается по поверхности (есть
очень тонкая изолирующая оболочка, разделяющая токи). Найдите себя
индуктивность на единицу длины.
круглое сечение.Ток возвращается по поверхности (есть
очень тонкая изолирующая оболочка, разделяющая токи). Найдите себя
индуктивность на единицу длины.
Решение:
- Концепты:
Собственная индуктивность, Ампер U = ½LI 2 = (1/(2µ 0 ))∫ B 2 dV. - Рассуждение:
Находим магнитное поле произвести по току из закона Ампера и решить
½LI 2 = (1/(2μ 0 ))∫ B 2 дВ для собственной индуктивности L. - Детали расчета:
Предположим, что провод имеет радиус a и концентричен с осью z. Предположим, что по ней течет ток I.
Для круговой петли Γ радиуса r, концентрично оси z и лежащей в плоскости xy, мы имеем
2πrB = μ 0 I через Г .
В = В ( φ / φ).
я через Γ = Ir 2 /a 2 .
r < a: B = μ 0 Ir/(2πa 2 )
r > a: B = 0.

 18)
18) Он включает в себя рассмотрение расстояния между витками. Поскольку магнитное поле становится слабее по мере его удаления, близко расположенные витки обеспечивают взаимодействие там, где поля наиболее сильны.
Он включает в себя рассмотрение расстояния между витками. Поскольку магнитное поле становится слабее по мере его удаления, близко расположенные витки обеспечивают взаимодействие там, где поля наиболее сильны. Отношения принимают форму
Отношения принимают форму
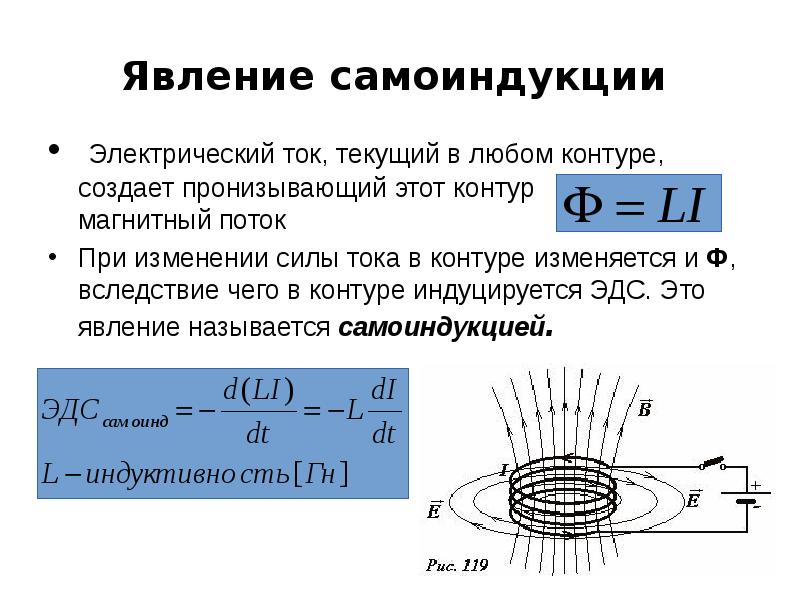 ]
] 
 Симметрия диктует, что магнитное поле направлено в
в
( φ /φ)-направление.
Симметрия диктует, что магнитное поле направлено в
в
( φ /φ)-направление. 