Трапеция. Свойства — презентация онлайн
Найдите все неизвестные углы параллелограмма.СК – биссектриса угла ВСD.
1800 – (200+200)
В
200
К
А
400
1400
D
С
1. Определение: Трапецией называется
четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
В
A
основание
основание
С
D
№ 387.
Найдите углы трапеции.
боковой стороне.
В
основание
С
1170
360
A
основание
D
3. Свойство углов трапеции:
Сумма углов прилежащих к боковой стороне равна 1800
2. Виды трапеций:
1) Произвольная. Боковые стороны не равны. Углы
при основаниях не равны.
2) Трапеция, один из углов которой прямой,
называется прямоугольной.
3) Трапеция называется равнобедренной, если ее
боковые стороны равны.
С
В
В
С
D
A
A
D
4. Высота трапеции- перпендикуляр,опущенный
из вершины на противоположную сторону.

В
С
С
В
A
М
D
A
Н
N
D
№ 392 (а)
В
4
С
300
?6
A
М
7
600
3
D
Найти ВС.
В
?
С
450
A
45
30
М
15 15
15
0
D
5. Свойство биссектрис трапеции.
Биссектрисы углов при боковых сторонах трапеции
перпендикулярны.
10. 6.Определение средней линии трапеции
Средней линией трапеции называетсяотрезок, соединяющий середины её
боковых сторон.
B
M
A
C
MN – средняя линия
трапеции ABCD
N
D
11. Свойство средней линии трапеции
BM
A
Средняя линия трапеции
параллельна основаниям и
равна их полусумме.
C
N
D
1)MN || BC, MN || AD
2) MN = ½ (BC + AD)
B
M
A
4,3 см
?
7,7 см
C
N
D
B
M
C
15 см
AB = 16 см
CD = 18 см
N
P ABCD = ?
A
D
7.
 Равнобедренная трапеция. Трапеция называется
Равнобедренная трапеция. Трапеция называетсяравнобедренной, если ее боковые стороны равны.
В
A
С
D
Из равнобедренной трапеции можно построить красивый
паркет.
Из равнобедренной трапеции можно построить красивый
паркет.
8. Свойства равнобедренной трапеции.
8.1. Свойство углов. В равнобедренной трапеции
углы при каждом основании равны.
Дано:
С =1800- 1
В =1800- 3
АВСD – р/б трапеция
Доказать:
А = D
B = C
2
3
A
Е
1
D
8.2. Свойство высот равнобокой трапеции.
Высоты равнобедренной трапеции отсекают
равные прямоугольные треугольники.
В
A
Н
С
N
D
8. Свойства равнобедренной трапеции.
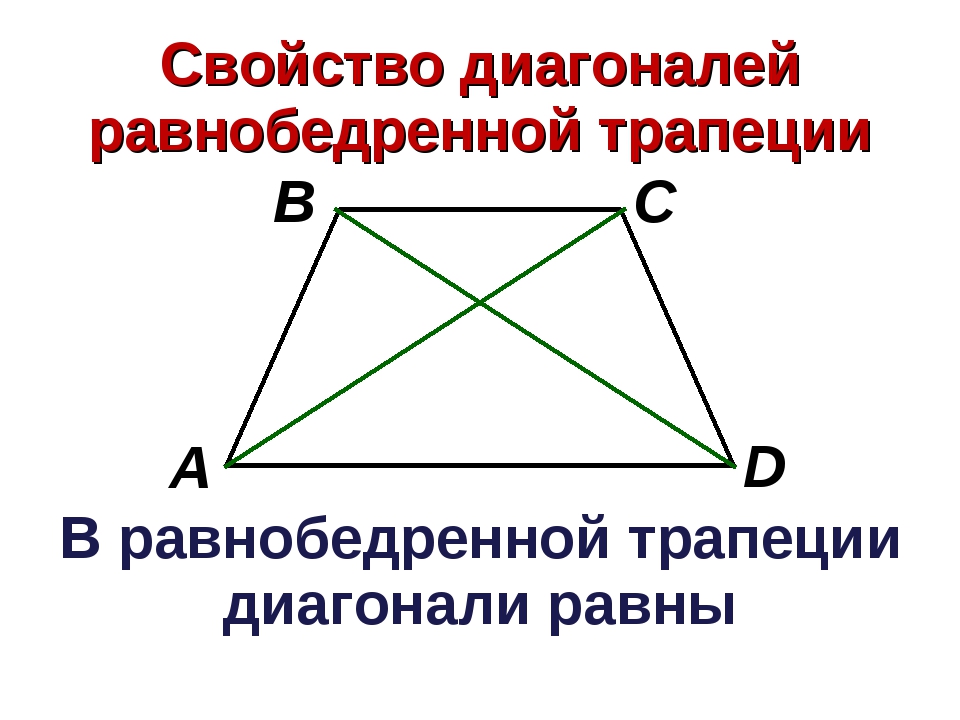
8.3. Свойство диагоналей. В равнобедренной
трапеции диагонали раны.
В
A
Дано:
АВСD – р/б трапеция
АC = BD
С
D
8. Свойства равнобедренной трапеции.
8.4. Свойство диагоналей. Если в равнобедренной
трапеции диагонали перпендикулярны, то высота,
проведенная через точку пересечения диагоналей
равна средней линии.

№ 390.
Найдите углы трапеции
В
1120
680
A
С
D
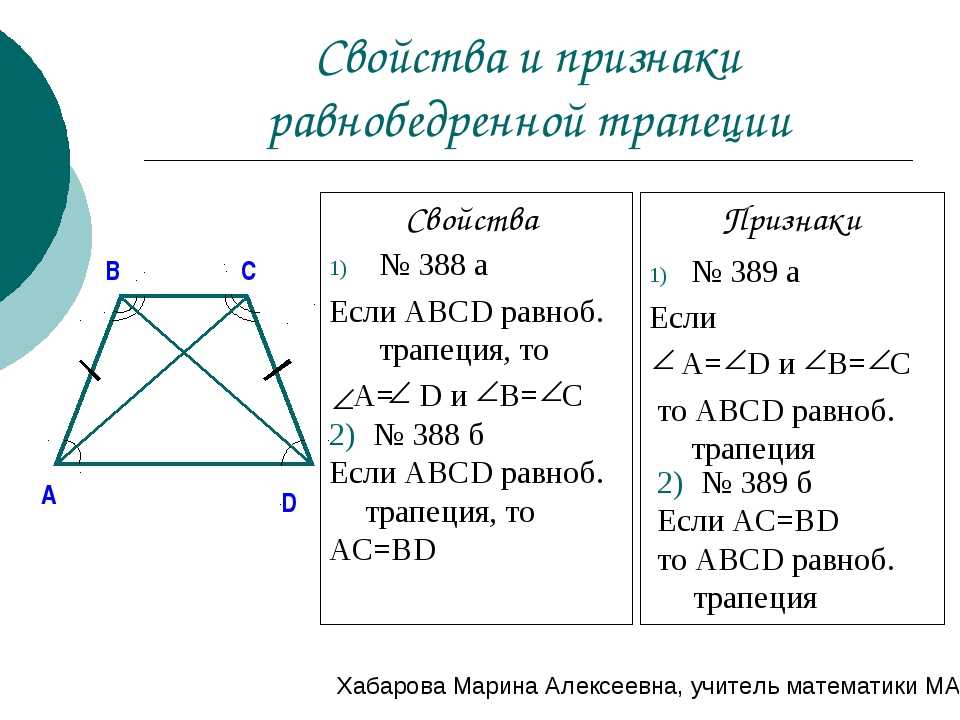
Свойства равнобедренной трапеции.
В равнобедренной трапеции углы при каждом основании
равны.
В равнобедренной трапеции диагонали равны.
Признаки равнобедренной трапеции.
Если углы при основании трапеции равны, то она
равнобедренная.
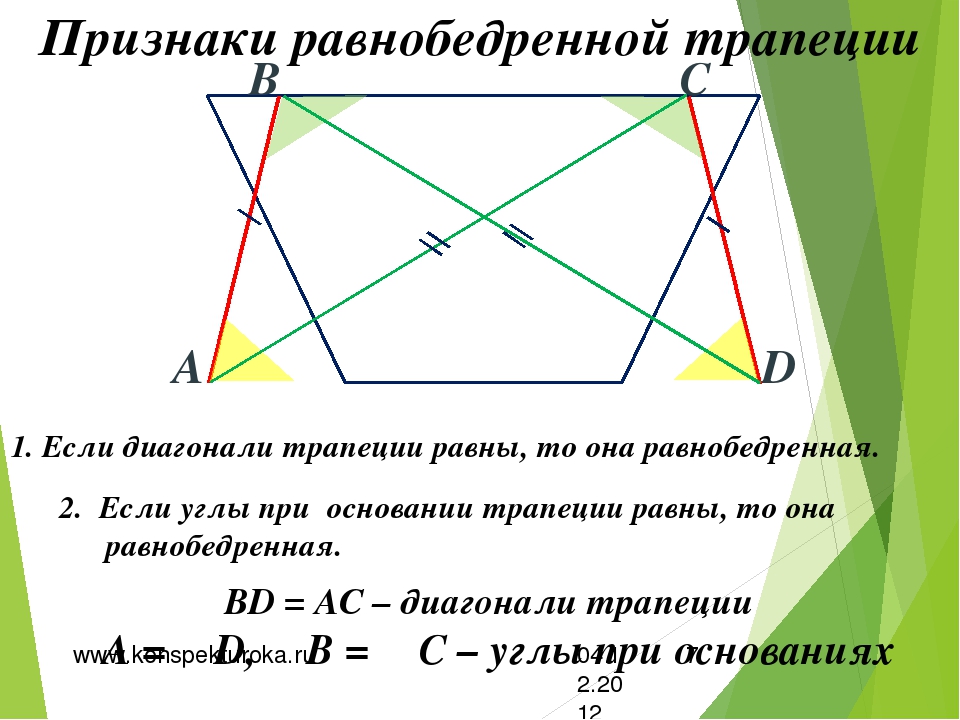
Если диагонали трапеции равны, то она равнобедренная.
9. Признаки равнобедренной трапеции.
9.1 Если углы при основании трапеции равны, то она
равнобедренная.
Дано:
С
В
АВСD – р/б трапеция
Доказать:
3
2
A
1
Е
D
А = D
B = C
Признаки равнобедренной трапеции.
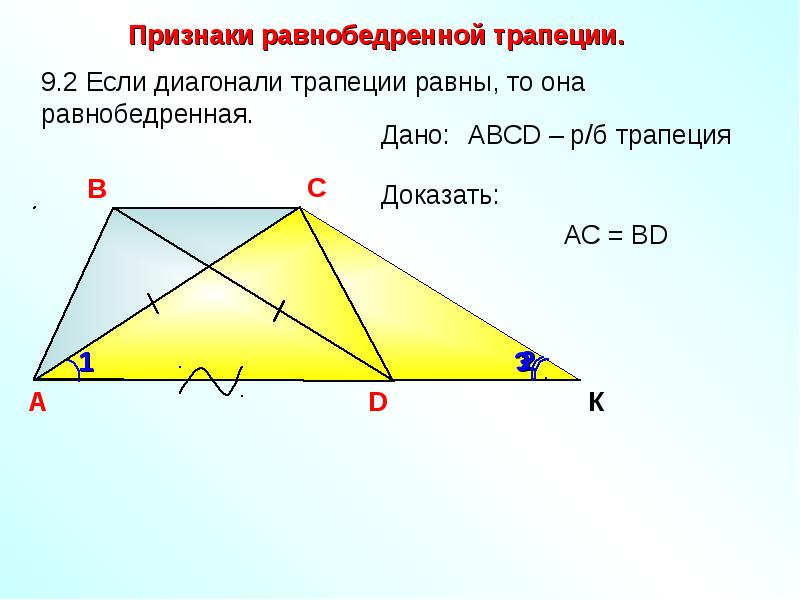
9.2 Если диагонали трапеции равны, то она
равнобедренная.
Дано: АВСD – р/б трапеция
В
С
Доказать:
АC = BD
2
1
A
D
К
Решение задач на готовых чартежах
АВСD – трапеция. Найти АОВ.
1800
В
С
О
A
D
Решение задач на готовых чартежах
АВСD – трапеция.
 Найти углы трапеции.
Найти углы трапеции.В
х
С
2х
D
A
Из АСD: х+2х=90
Решение задач на готовых чартежах
АВСD – трапеция. ВЕ II СD
Найти углы трапеции.
В
С
0
750 65
400
A
1150
650
Е
D
№ 384
Через середину М стороны АВ треугольника АВС
проведена прямая, параллельная стороне ВС.
Эта прямая пересекает сторону АС в точке N.
Докажите, что AN = NC.
В
М
3
А
1
2
N
D
С
Эта задача поможет нам
доказать теорему Фалеса
Фалес Милетский
Древнегреческий ученый
(ок. 625 – 547 гг. до н. э.)
Если на одной из двух прямых отложить последовательно
несколько равных отрезков и через их концы провести
параллельные прямые, пересекающие вторую прямую, то
они отсекут на второй прямой равные между собой отрезки.
А1
В1
А2
В2
А3
В3
А4
В4
А5
l1
В5
l2
1 случай
l1 II l2
2 случай
А1
В1
А2
С
А3
D
А4
В2
В3
В4
А5
l1
В5
l
l2
Е
М
М1
М3
М2
М4
К
К1
К2
К3
МК II М1К1 II М2К2 II М3К3 II М4К4
ЕМ = ММ1 = М1М2 = М2М3 = М3М4
КК4 – К1К2 = 14 см
Найти: ЕК4
К4
Дано: АС II EF
Найти: PАВС
B
F
E
5
4
A
12
C
Дано: АВСD – трапеция, МК II ВE II СD, АD = 16 cм
Найти: АК
B
10
C
M
A
K
E
16
D
Если трапеция равнобедренная то диагонали.
 Полезные свойства трапеции
Полезные свойства трапецииСоблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.

Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
 К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже .
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
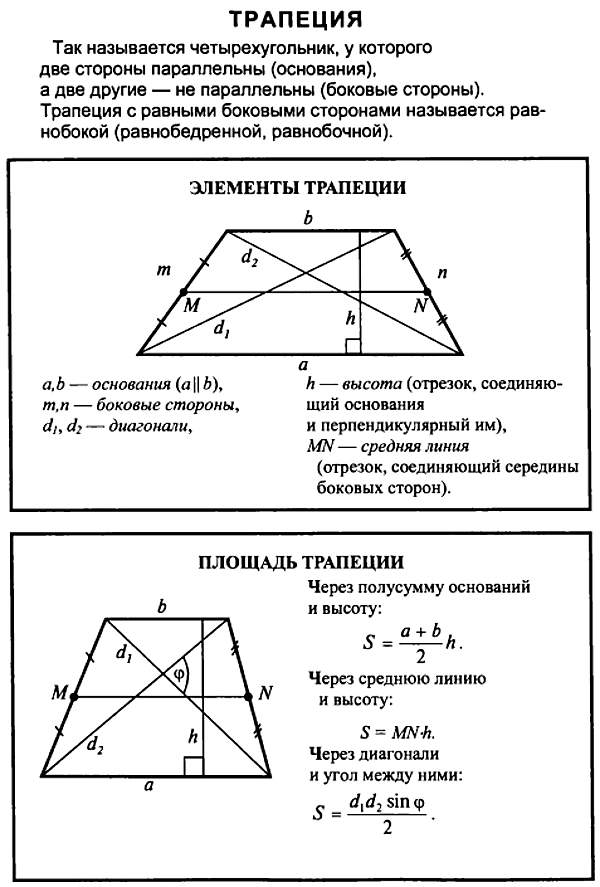
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу;
- боковые стороны AB и CD — два непараллельных элемента;
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
- высота трапеции CH — перпендикулярный основаниям отрезок;
- средняя линия EF — линия, соединяющая середины боковых сторон.
Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника.
Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.

- При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2 .
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры.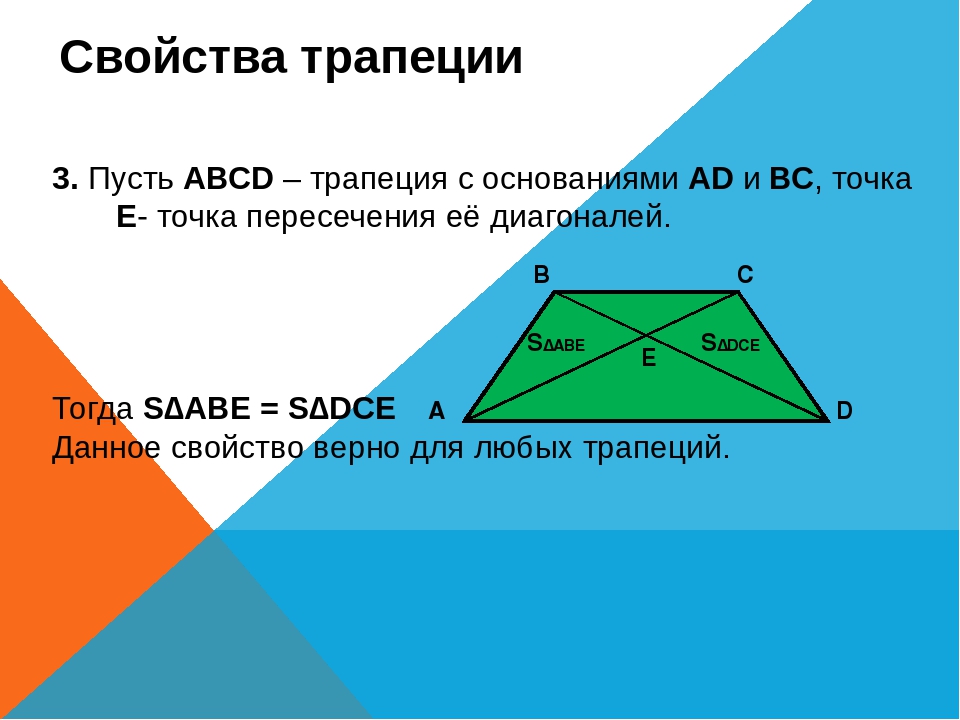 Радиус её можно найти через высоту, и он будет равен r = h/2.
Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения , которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.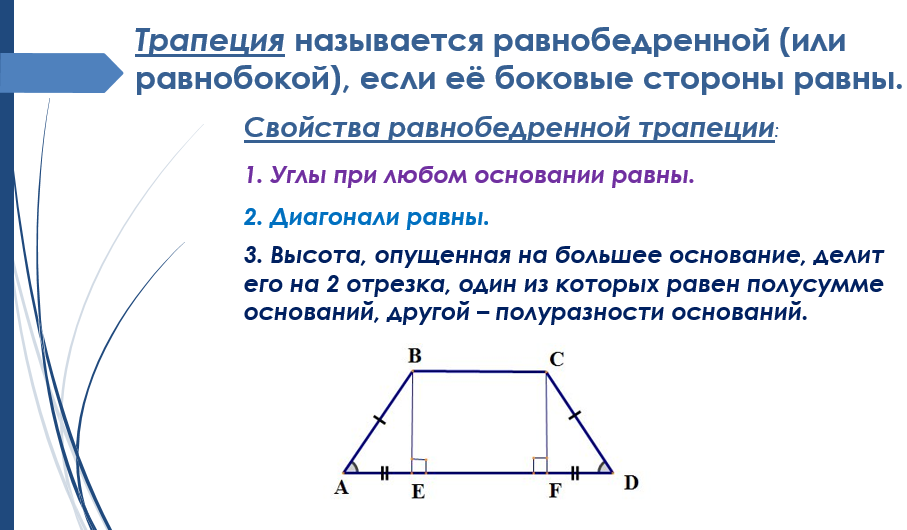 \circ\)
.
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN»\parallel AD\) (\(N»\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\) ) точка \(N»\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\) и \(N»\) — середины отрезков \(BB»\) и \(CC»\) соответственно. Значит, \(MM»\) – средняя линия \(\triangle ABB»\) , \(NN»\) — средняя линия \(\triangle DCC»\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Значит, \(B»M»N»C»\) и \(BM»N»C\) – равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.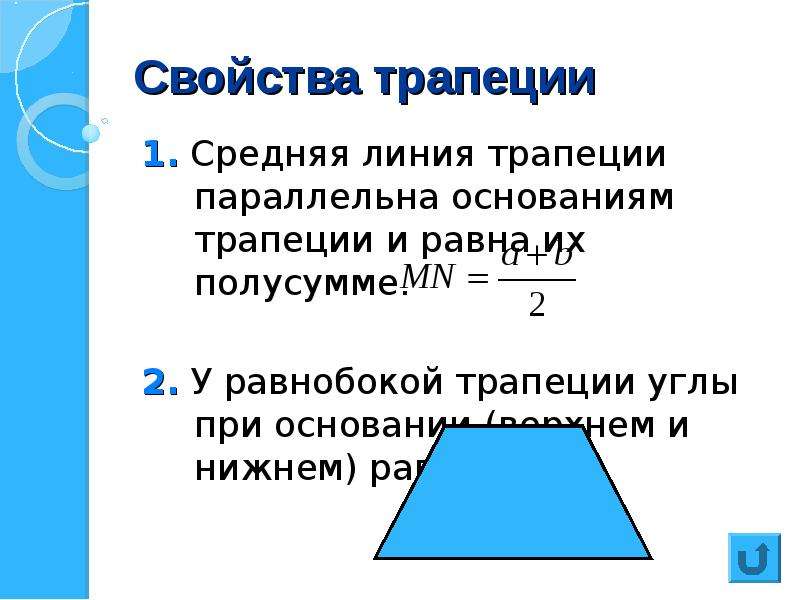
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
.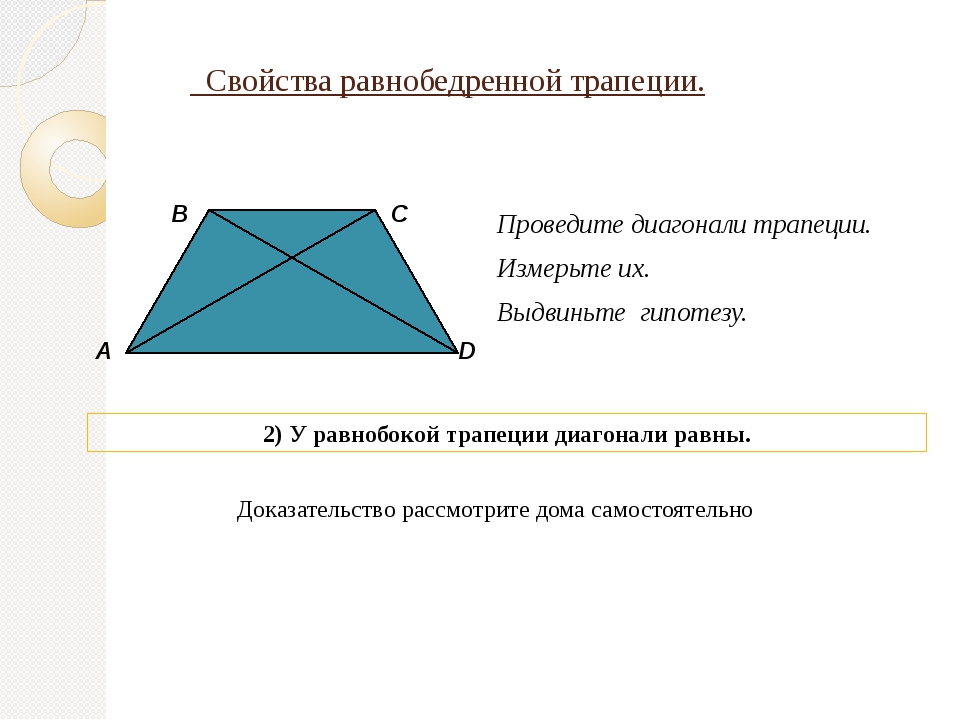 Докажем, что \(M\)
– середина \(AD\)
.
Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.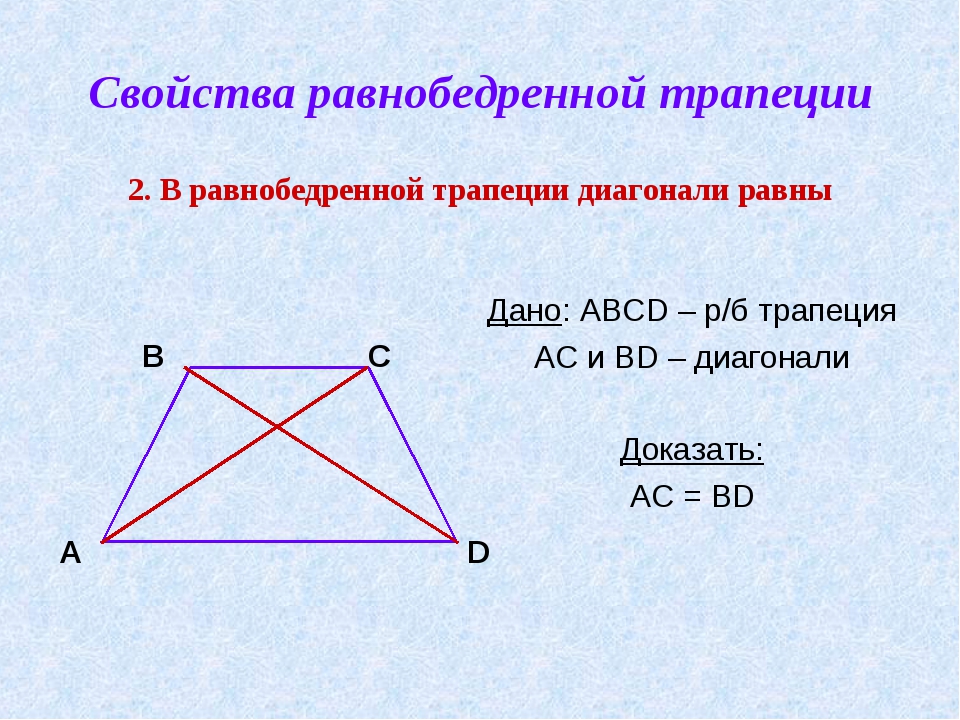
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.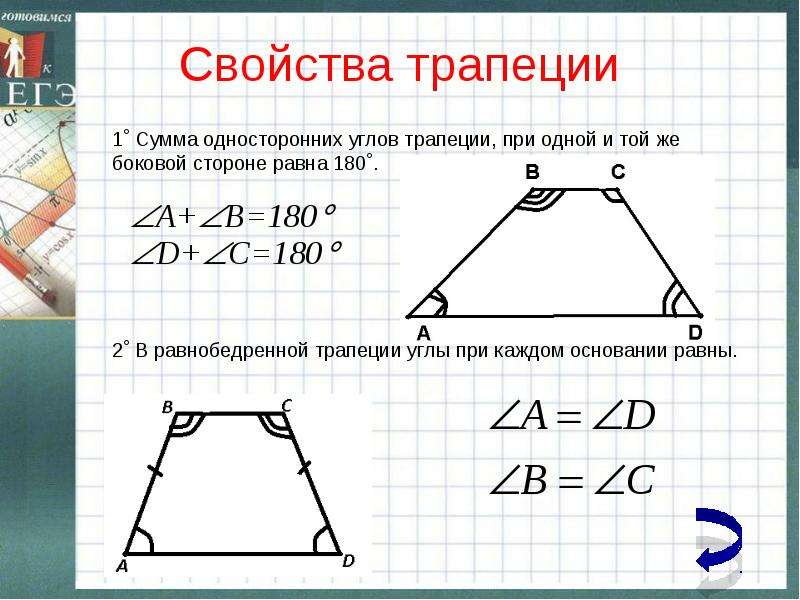
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE — BE = DE — CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Рассмотрим несколько направлений решения задач, в которых трапеция вписана в окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию .
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции лежит внутри трапеции.
Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Кстати, использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
Средняя линия прямоугольной трапеции. Запоминаем и применяем свойства трапеции
В курсе геометрии за 8-й класс подразумевается изучение свойств и признаков выпуклых четырёхугольников. К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
К ним относятся параллелограммы, частными случаями которых являются квадраты, прямоугольники и ромбы, и трапеции. И если решение задач на различные вариации параллелограмма чаще всего не вызывает сильных затруднений, то разобраться, какой четырёхугольник называется трапецией, несколько сложнее.
Определение и виды
В отличие от других четырёхугольников, изучаемых в школьной программе, трапецией принято называть такую фигуру, две противоположные стороны которой параллельны друг другу, а две другие — нет. Существует и другое определение: это четырёхугольник с парой сторон, которые не равны между собой и параллельны.
Различные виды указаны на рисунке ниже .
На изображении под номером 1 изображена произвольная трапеция. Номером 2 обозначен частный случай — прямоугольная трапеция, одна из сторон которой перпендикулярна её основаниям. Последняя фигура — тоже особый случай: это равнобедренная (равнобокая) трапеция, т. е. четырёхугольник с равными боковыми сторонами.
Важнейшие свойства и формулы
Для описания свойств четырёхугольника принято выделять определённые элементы. В качестве примера можно рассмотреть произвольную трапецию ABCD.
В её состав входят:
- основания BC и AD — две стороны, параллельные по отношению друг к другу;
- боковые стороны AB и CD — два непараллельных элемента;
- диагонали AC и BD — отрезки, соединяющие противоположные вершины фигуры;
- высота трапеции CH — перпендикулярный основаниям отрезок;
- средняя линия EF — линия, соединяющая середины боковых сторон.
Основные свойства элементов
Чтобы решить задачи по геометрии или доказать какие-либо утверждения, наиболее часто используют свойства, которые связывают различные элементы четырёхугольника. Они формулируются следующим образом:
Кроме того, часто полезно знать и применять следующие утверждения:
- Биссектриса, проведённая из произвольного угла, отделяет на основании отрезок, длина которого равна боковой стороне фигуры.

- При проведении диагоналей образуются 4 треугольника; из них 2 треугольника, образованных основаниями и отрезками диагоналей, обладают подобием, а оставшаяся пара имеет одинаковую площадь.
- Через точку пересечения диагоналей O, середины оснований, а также точку, в которой пересекаются продолжения боковых сторон, можно провести прямую.
Вычисление периметра и площади
Периметр рассчитывается как сумма длин всех четырёх сторон (аналогично любой другой геометрической фигуре):
P = AD + BC + AB + CD.
Вписанная и описанная окружность
Окружность возможно описать около трапеции только в том случае, когда боковые стороны четырёхугольника равны.
Чтобы вычислить радиус описанной окружности, необходимо знать длины диагонали, боковой стороны и большего основания. Величина p, используемая в формуле, рассчитывается как полусумма всех вышеперечисленных элементов: p = (a + c + d)/2 .
Для вписанной окружности условие будет следующим: сумма оснований должна совпадать с суммой боковых сторон фигуры. Радиус её можно найти через высоту, и он будет равен r = h/2.
Радиус её можно найти через высоту, и он будет равен r = h/2.
Частные случаи
Рассмотрим часто встречаемый случай — равнобокую (равностороннюю) трапецию. Её признаки — равенство боковых сторон или равенство противолежащих углов. К ней применимы все утверждения , которые характерны для произвольной трапеции. Другие свойства равнобедренной трапеции:
Прямоугольная трапеция встречается в задачах не так часто. Её признаки — наличие двух смежных углов, равных 90 градусов, и наличие боковой стороны, перпендикулярной основаниям. Высота в таком четырёхугольнике одновременно является одной из его сторон.
Все рассмотренные свойства и формулы обычно используются для решения планиметрических задач. Однако также их приходится применять в некоторых задачах из курса стереометрии, например, при определении площади поверхности усечённой пирамиды, внешне напоминающей объёмную трапецию.
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a — b) * tg α;
c = √ (d 2 — (a — b) 2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a — b) /cosα;
d = c / sin α;
d = √ (c 2 + (а — b) 2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно. Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с 2 + b 2)
или по-другому, заменив «с» на «h»:
d1 = √ (h 2 + b 2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с 2 + b 2) или d 2 = √ (h 2 + а 2).
Задача №1
Условие . Площадь прямоугольной трапеции известна и равна 120 дм 2 . Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с 2 + (а — b) 2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а — b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d 2 = с 2 + (a — b) 2 или (a + b) 2 = с 2 + (a — b) 2 .
Необходимо сделать преобразования, подставив вместо с его значение из условия — 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см 2 .
Ответ. Искомая площадь 36 см 2 .
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции , которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Поэтому ознакомимся с ними более детально.
Вконтакте
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т.е. пересекаются под углом 90° (как это показано на рис.1).
Если сложить все градусные меры внутренних , то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей. Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией.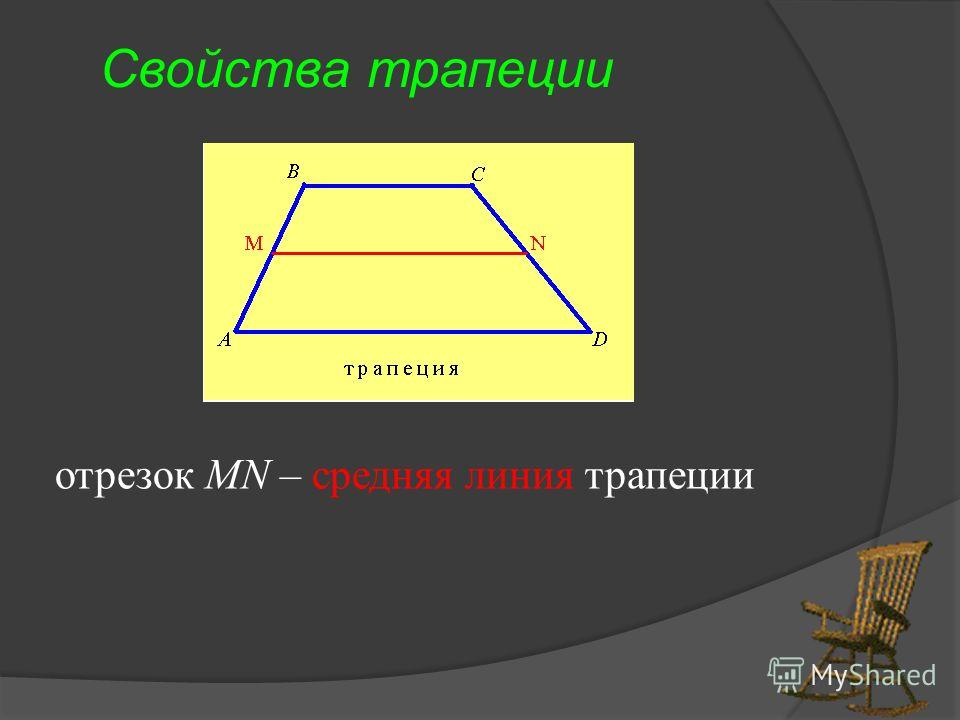 Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см. Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет . Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.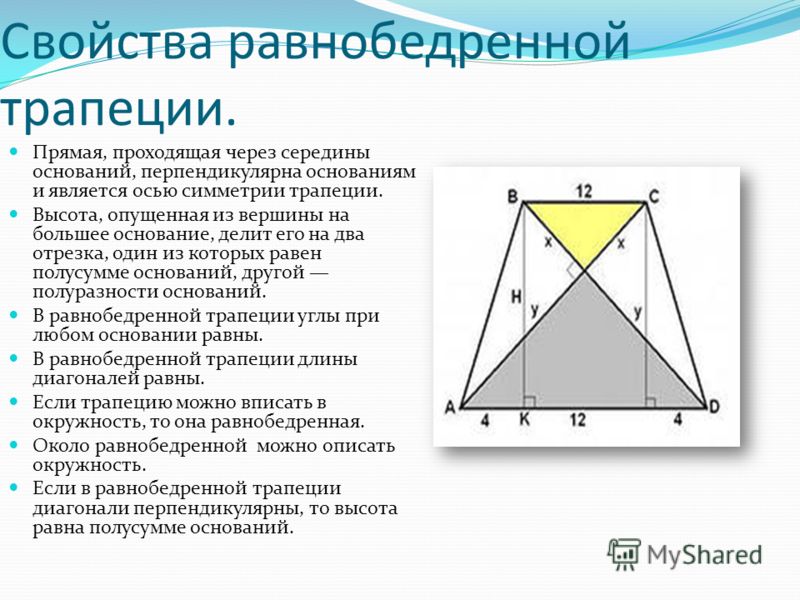
Важно! При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная . ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого.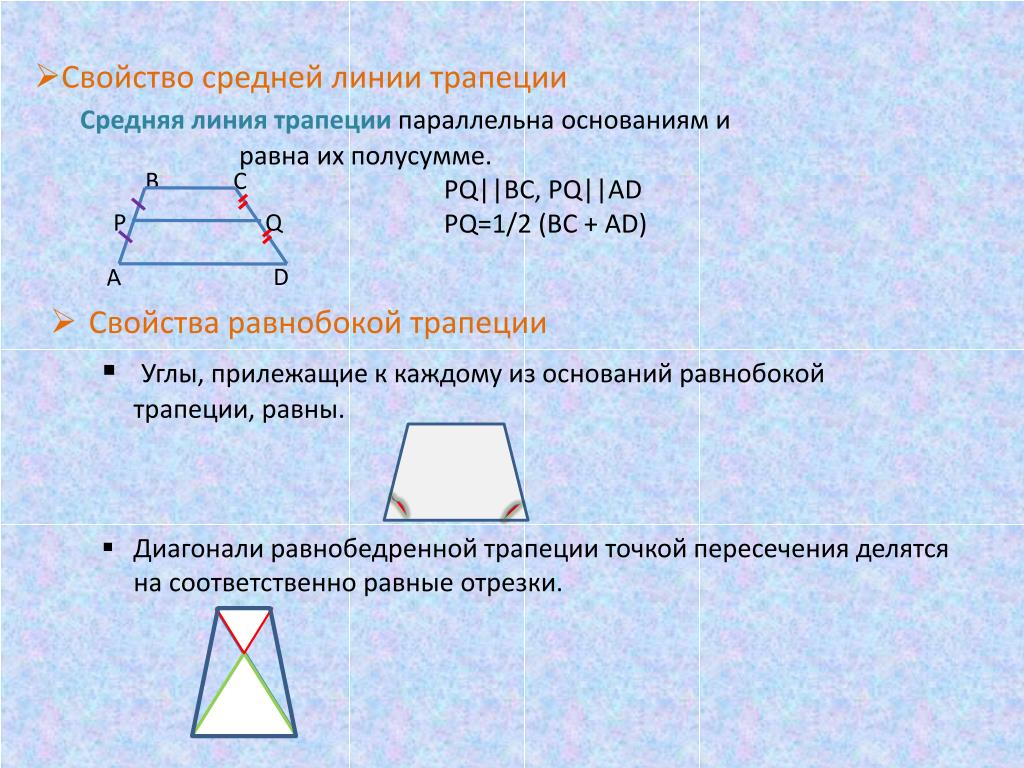 Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.
- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.
- Вокруг любой правильной трапеции можно построить .
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции :
Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может, потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой.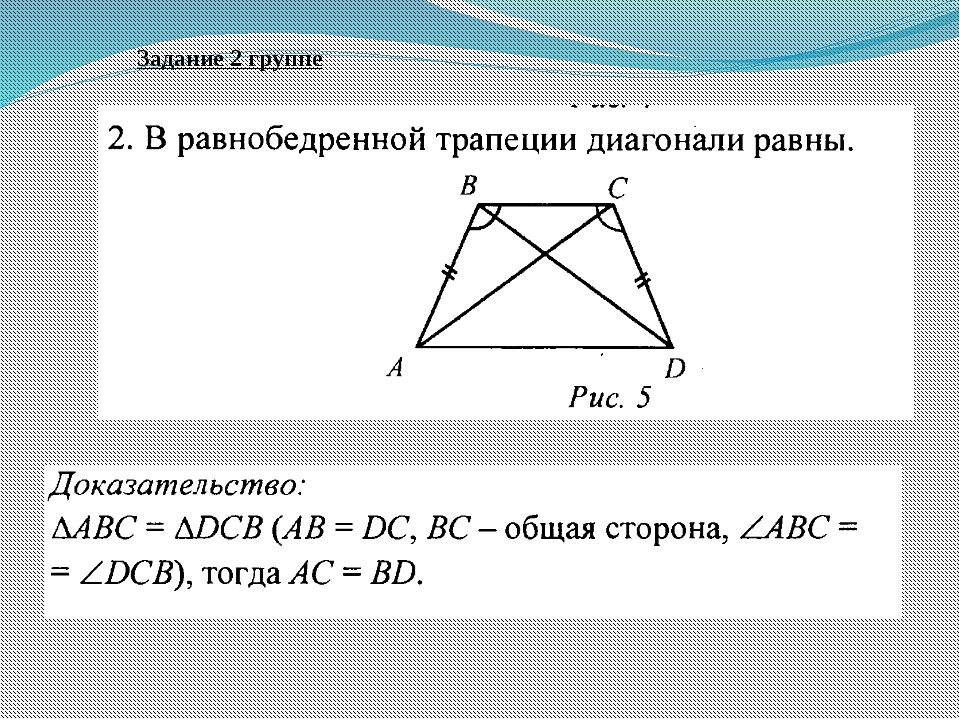 При этом, перпендикулярная сторона также будет являться и высотой.
При этом, перпендикулярная сторона также будет являться и высотой.
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией. Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
Важно! Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур.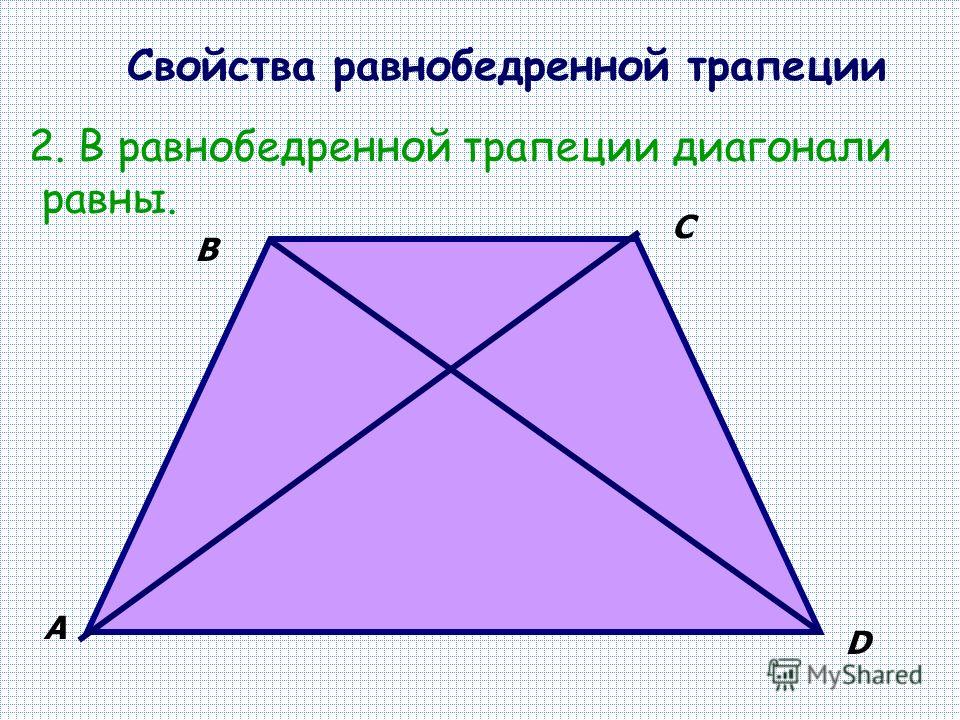 Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции, следует определиться какие даны входные значения. Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .
Как было установлено, DF=CH , отсюда .
Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников. Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Важно! В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как :
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии.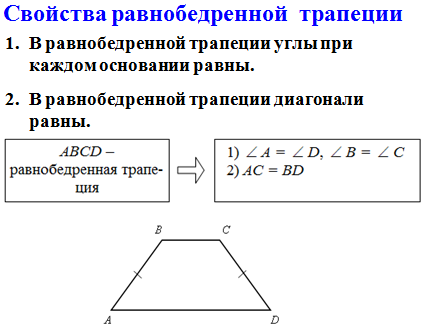 Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.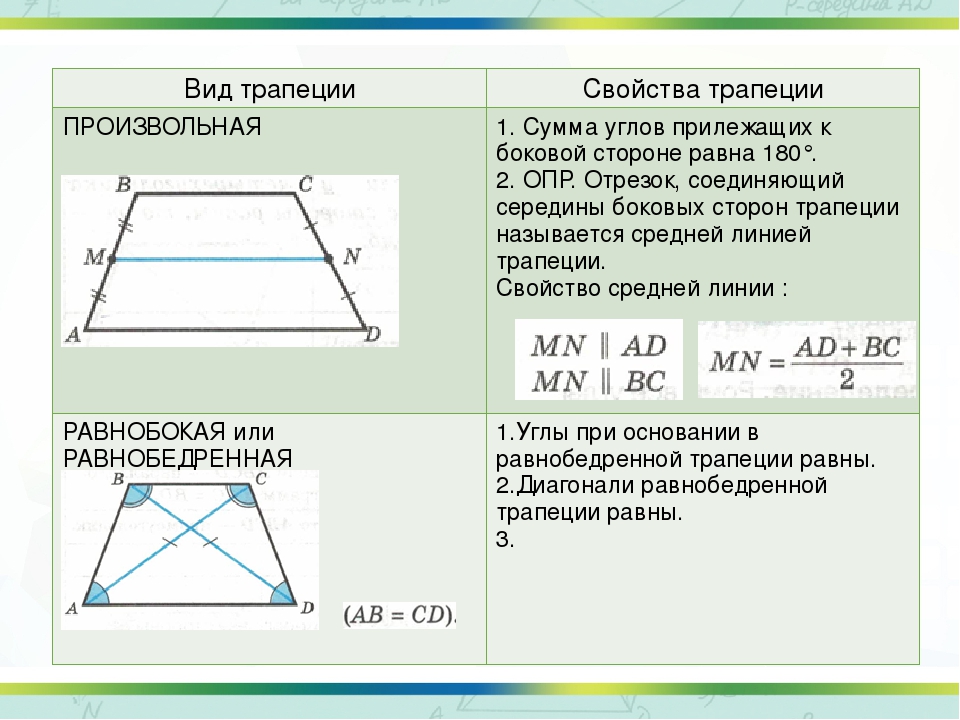
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ).
 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ . - А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.

- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка.
 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.

- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.

Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию.
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной.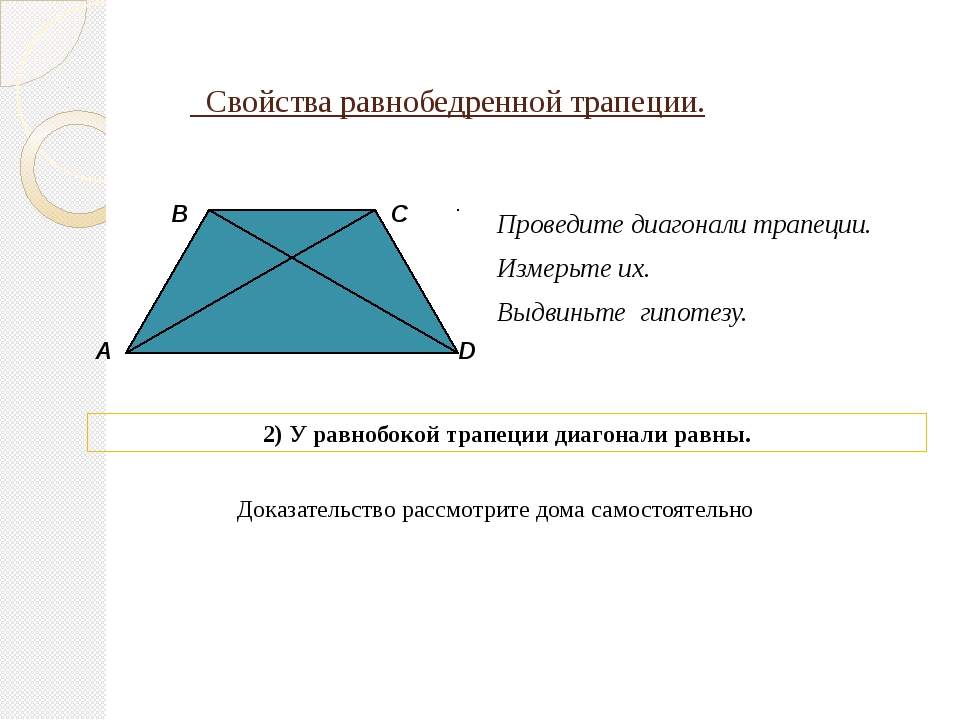 Но вы сами убедились, что разница огромна.
Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Тест по геометрии «Трапеция и её свойства. Площадь трапеции» — 4ЕГЭ
Задания рассматривают весь базовый материал темы.Всего 14 заданий. Ответы прилагаются.
trapeciya-t.pdf
Вопрос №1
В равнобедренной трапеции синус острого угла при основании равен 0,6. Найдите периметр трапеции, если длины оснований соответственно равны 14 см и 30 см.
Вопрос №2
Основания равнобедренной трапеции равны 3 м и 8 м, угол при основании 60°. Найдите диагональ.
Вопрос №3
Меньшее основание равнобедренной трапеции равно 6 м, а большее 12 м, угол при основании 60°. Найдите радиус окружности, описанной около трапеции.
Найдите радиус окружности, описанной около трапеции.
Вопрос №4
Основания трапеции равны 10 м и 31 м, а боковые стороны 20 м и 13 м. Найдите высоту трапеции.
Вопрос №5
Найдите радиус окружности, вписанной в равнобедренную трапецию, у которой сумма оснований равна 20, а разность оснований равна 12.
Вопрос №6
Диагонали трапеции АВКН пересекаются в точке О, основания ВК и АН равны соответственно 5 и 15. Площадь треугольника КОВ равна 4. Найдите площадь трапеции.
Вопрос №7
В трапеции АВМТ с основаниями АВ и МТ диагонали пересекаются в точке С, причем СМ = 2∙ АС. Площадь треугольника СМТ равна 24. Найдите площадь трапеции.
Вопрос №8
Найдите площадь равнобедренной трапеции, если ее основания равны 7 и 25, а диагональ перпендикулярна боковой стороне.
Вопрос №9
Прямоугольная трапеция с острым углом 30° описана около окружности. Площадь трапеции равна 96. Найдите большую боковую сторону трапеции.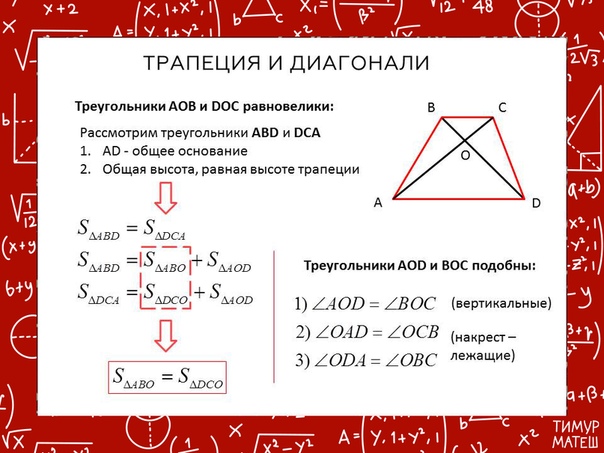
Вопрос №10
В трапеции разность параллельных сторон равна 12, а высота равна 6. Найдите длину большего основания, если площадь трапеции равна 132.
Вопрос №11
В трапеции АВСD с основаниями АD = 2 см и ВС = 1 см, боковые стороны АВ и СD равны 1 см. Найдите квадрат диагонали трапеции.
Вопрос №12
Основания равнобокой трапеции равны 3 и 5. Найдите площадь трапеции, если ее диагонали взаимно перпендикулярны.
Вопрос №13
В прямоугольную трапецию вписана окружность радиуса 3. Найдите площадь трапеции, если ее меньшее основание равно 4.
Вопрос №14
Боковые стороны трапеции равны 9 и 12, а основания трапеции равны 30 и 15. Найдите угол, образованный продолжением боковых сторон трапеции.
Ответы
Вопрос №1 — 64 см
Вопрос №2 — 7 м
Вопрос №3 — 6 м
Вопрос №4 — 12 м
Вопрос №5 — 4
Вопрос №6 — 64
Вопрос №7 — 54
Вопрос №8 — 192
Вопрос №9 — 16
Вопрос №10 — 28
Вопрос №11 — 3
Вопрос №12 — 16
Вопрос №13 — 24
Вопрос №14 — 90
Автор: Воробьева Елена Александровна.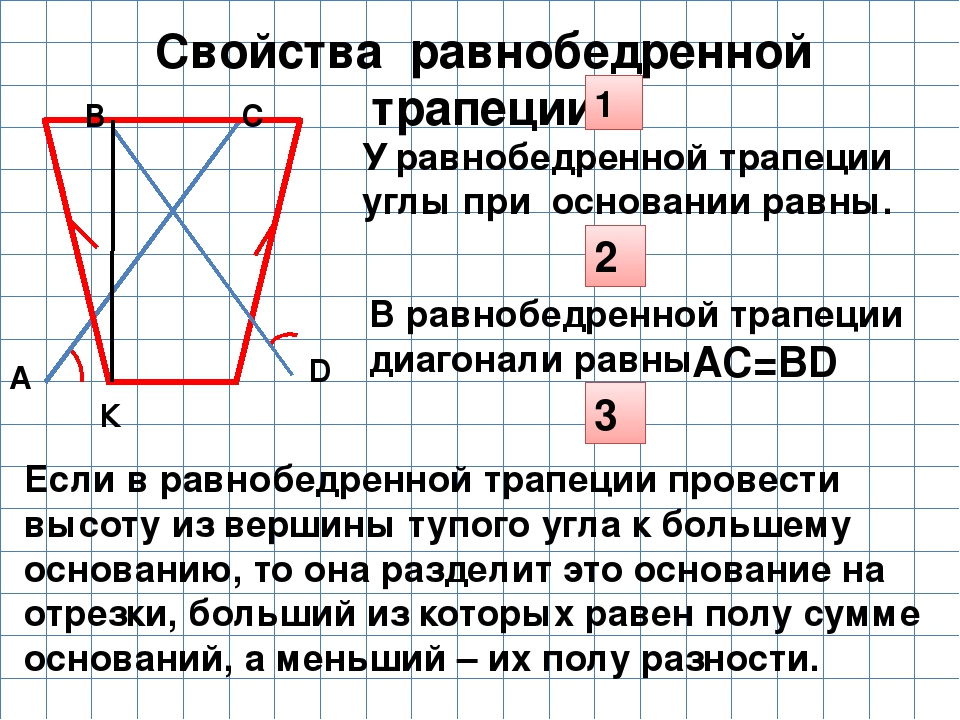
Разработка урока геометрии по теме «Трапеция» в 8 классе — К уроку — Математика, алгебра, геометрия
Учитель: Юртина Ирина Вячеславовна.
Город: Сургут, ХМАО – Югра
Предмет: геометрия
Класс: 8
Тема урока: Трапеция.
Место урока в теме: изучение нового материала.
Цели урока:
Обучающие: формирование понятия о трапеции, её видах, свойствах и признаках.
Развивающие: формирование у обучающихся ключевых компетентностей: информационной, коммуникативной, интеллектуальной, социальной, учебно-познавательной.
Воспитательные: формировать ответственное и осознанное отношение к своей деятельности.
Приемы: «Корзина понятий», «Кластер», «Зигзаг», «Шесть шляп мышления».
Ход урока:
Вызов.
— Какую важную тему из курса 8 класса мы с вами начали изучать? (Ответ: четырехугольники).
Прием: «Корзина понятий» (4 минуты):
— Запишите на листах бумаги все что мы изучили о четырехугольниках. (3 мин)
-Обсудите с соседом по парте свою информацию. (1 мин).
Затем происходит зачитывание работы пар.
-Попробуем систематизировать данную информацию.
Прием: «Кластер»
На большом листе ватмана заранее изображена структура кластера, который необходимо заполнить (данная схема будет продолжать заполняться на протяжении нескольких уроков при изучении тем о прямоугольнике, ромбе и квадрате) . В процессе зачитывания работ пар, кластер заполняется учителем следующим образом:
Кроме того, ребята проговаривают определение параллелограмма, его элементов, свойства и признаки. Отвечают на вопрос: для чего необходимо использовать признаки, а для чего применять свойства?
— Как вы думаете, у всех ли четырехугольников
противоположные стороны параллельны?
(Выслушиваются ответы учеников).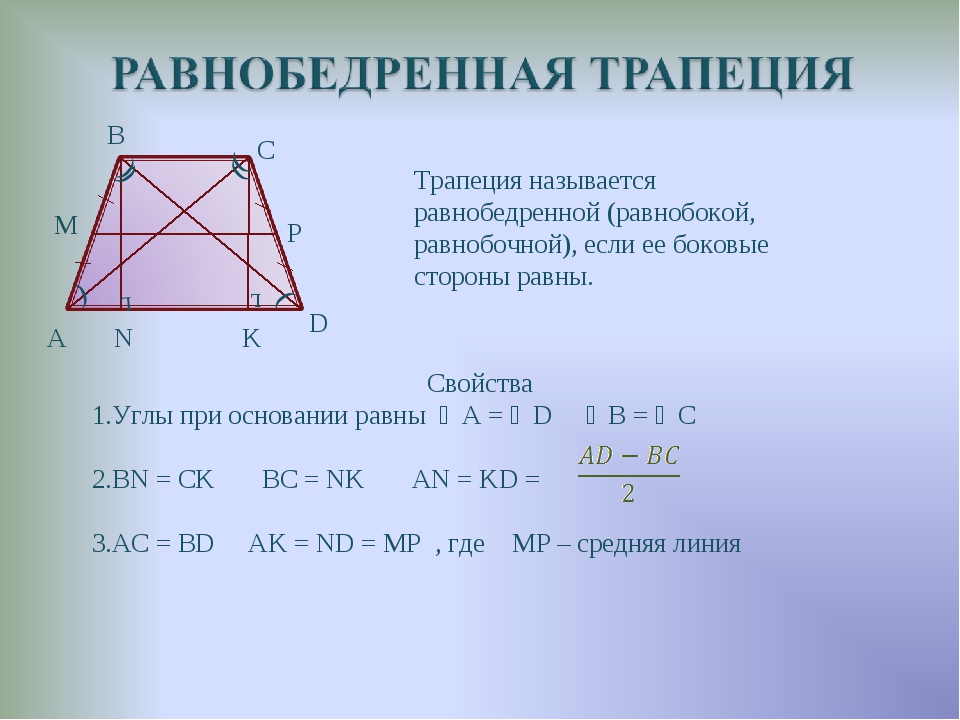
-А может ли существовать четырехугольник, у которого только одна пара сторон параллельна?
— А как такие четырехугольники называются? (Ученики могут ответить, а могут и не ответить)
— Запишем тему урока: Трапеция.
Осмысление.
А) Прием «Зигзаг».
Смысловая стадия: (5 мин)
Для этого приема класс заранее разделен на 6 групп по 4 человека в каждой группе (соеденены по две парты каждого ряда). Каждый ученик имеет свой порядковый номер в группе. Каждой группе выдаются 4 текста разного содержания. Каждый учащийся работает со своим текстом, записывая в тетрадь опорный конспект или план своего рассказа.
Текст №1
Трапецией называется четырехугольник, у которого одна пара параллельных сторон.
Основаниями трапеции называют её
параллельные стороны.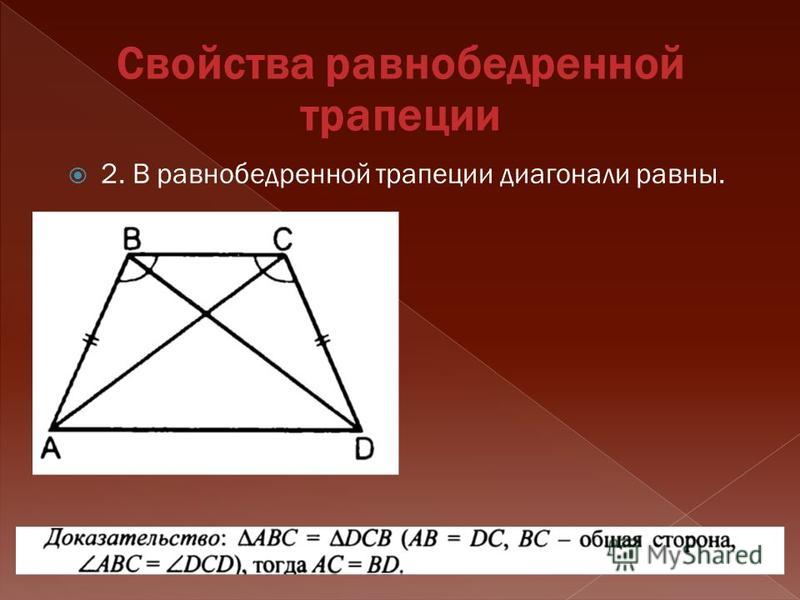 Параллельные
стороны не могут быть равными, так как
в противном случае мы имели бы
параллелограмм.(почему?). Поэтому одну
из них мы назовем большим, вторую –
малым основаниями трапеции.
Параллельные
стороны не могут быть равными, так как
в противном случае мы имели бы
параллелограмм.(почему?). Поэтому одну
из них мы назовем большим, вторую –
малым основаниями трапеции.
Боковыми сторонами трапеции называют непараллельные стороны.
Высотой трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон.
Задание: Обозначьте трапецию, укажите все её элементы.
Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Текст №2
Трапецией называется четырехугольник,
у которого одна пара параллельных
сторон.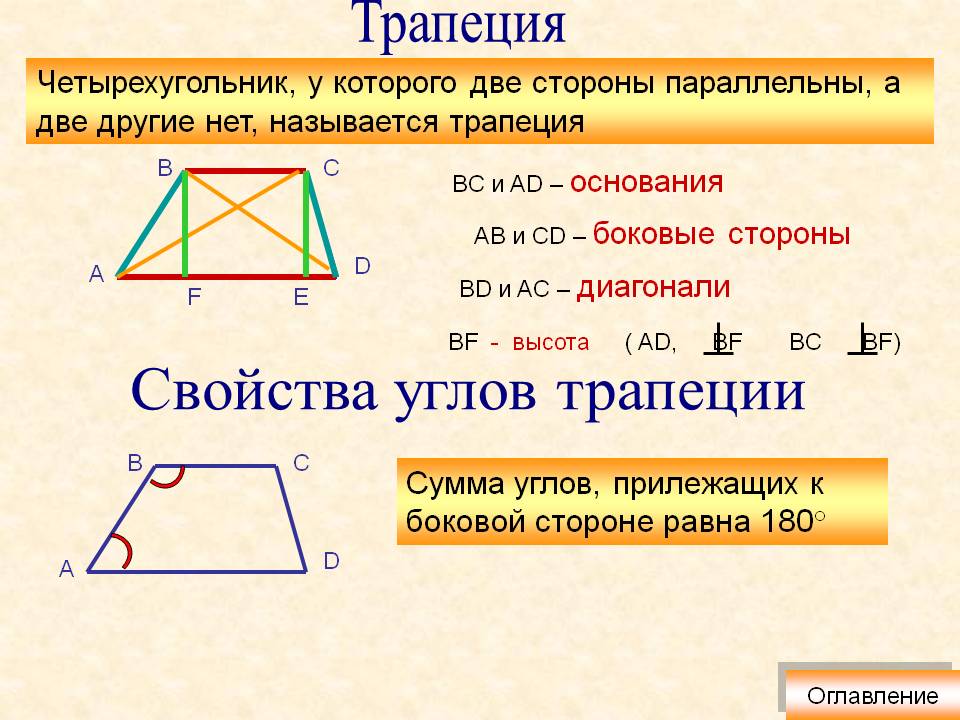
Диагоналями трапеции называются отрезки, соединяющие противоположные вершины.
Фигуры называются равновеликими, если у них одинаковая площадь.
Теорема (свойство трапеции):
Диагонали делят трапецию на 4 части, две из которых, прилежащие к боковым сторонам, равновелики.
А В Дано: АВДС – трапеция, АД и СВ – диагонали.
Доказать: SАОС = SВОД
С К Р Д
Доказательство: 1) SСАД = SСВД, так как у них равные высоты АК и ВР и общее основание СД.
2) SСАО +SСОД =SВОД +SСОД
3) SСАО = SВОД
Текст №3
Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Теорема (свойства равнобокой трапеции):
У равнобедренной трапеции: а) углы при
основании равны; б) сумма противолежащих
углов равна 180°; в) диагонали равны.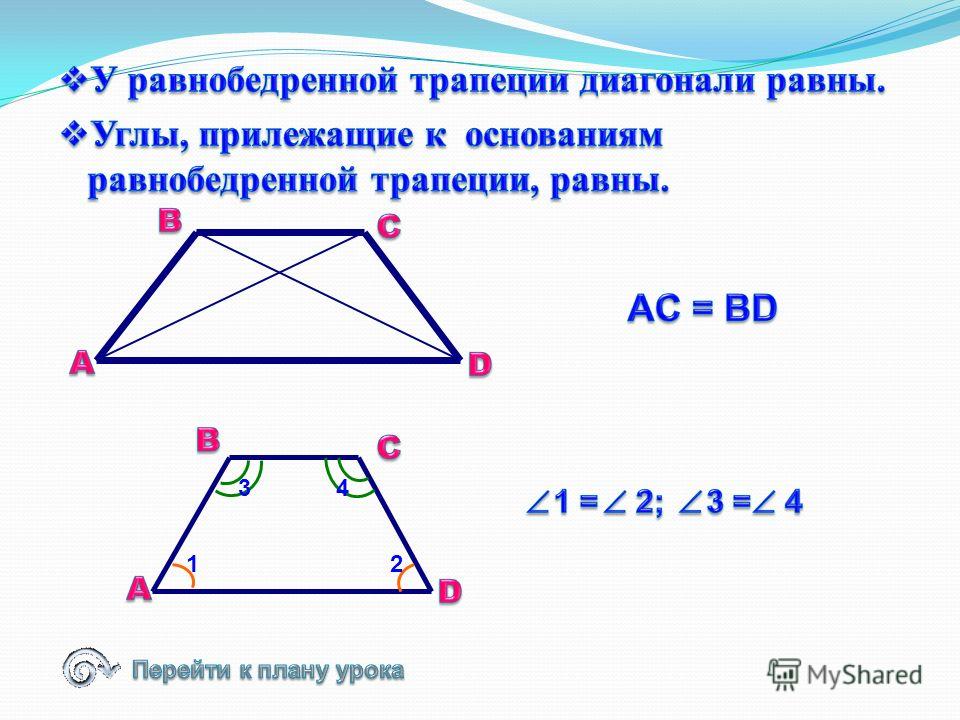
В С
А К М Д
Дано: АВСД – трапеция. АВ = СД.
Доказать: а)
б)
в) АС = ВД.
Доказательство: а) Проведем ВК ┴ АД, СМ ┴ АД. ВК = СМ (по определению). ∆АВК = ∆ДСМ (по катету и гипотенузе)(каким?). Значит,
б) так как то
в) ∆АВД = ∆ДСА (1 признак) (почему?), значит АС = ВД.
Текст №4
Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Теорема (признаки равнобедренной трапеции):
Трапеция является равнобедренной тогда и только тогда, когда: а) углы при основании равны;
б) сумма противолежащих углов равна 180°; в) диагонали равны.
В С
А К М Д
Дано: АВСД – трапеция.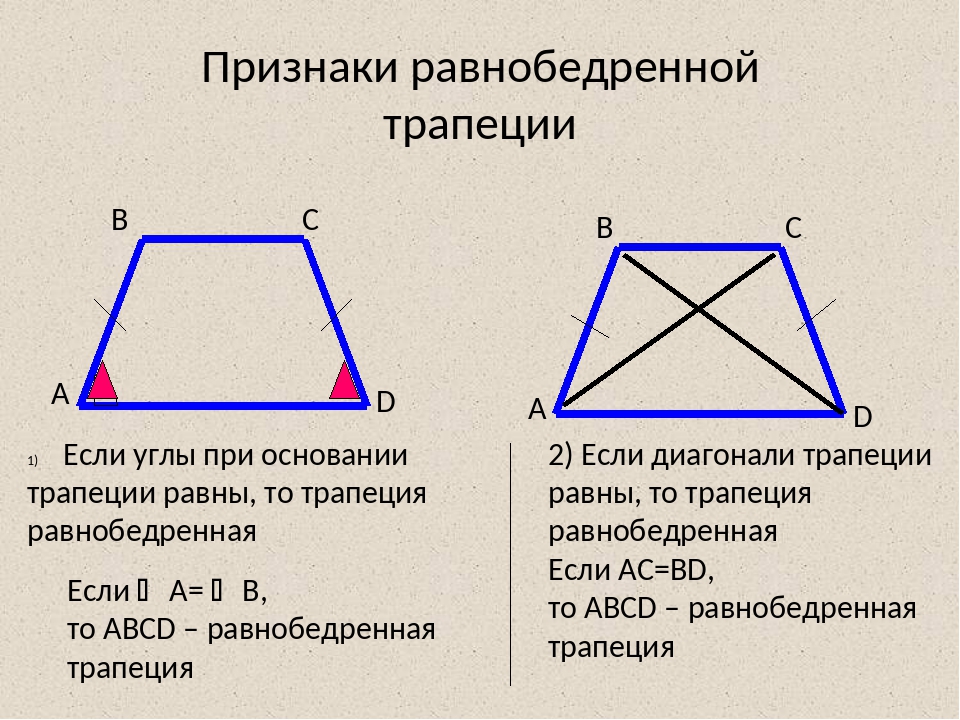 АД || ВС. а)
АД || ВС. а)
б)
в) АС = ВД.
Доказать: АВ = СД.
Доказательство: Проведем ВК ┴ АД, СМ ┴ АД. ВК = СМ (по определению).
А) ∆АВК = ∆ДСМ (по катету и острому углу) (каким?).
Значит, АВ = СД.
Б) (почему?), то .
∆АВК = ∆ДСМ (по катету и острому углу) (каким?).
Значит, АВ = СД.
В) ∆ДВК = ∆АСМ (по катету и гипотенузе) (каким?).
Значит, АВ = СД.
По окончании работы учащиеся переходят в группы экспертов, таких групп 4 – по количеству учеников первоначальных групп. (в 1ю группу садятся 1е номера, во 2ю – 2е номера, в 3ю – 3и номера и в 4ю группу – 4е номера.)
Стадия размышления: (5 мин)
В новых группах ребята обсуждают общий
для них текст, делают замечания, дописывают
опорный конспект и т. д. ( то есть
дорабатывают свою индивидуальную
работу) и готовятся к выступлению
(решают, кто будет отвечать у доски).
д. ( то есть
дорабатывают свою индивидуальную
работу) и готовятся к выступлению
(решают, кто будет отвечать у доски).
Затем учащиеся возвращаются в прежние группы и по очереди рассказывают свой текст, используя опорный конспект.(3 мин).
Стадия усвоения: (10 мин)
Возвращаемся к заполнению кластера, причем заканчивают его заполнять сами ученики, которые выходят выступать к доске по изученному тексту.
Б) Закрепление темы в ходе решения задач.
Учебник «Геометрия 7-9», Атанасян Л.С. и др., глава 5, пункт 44, №387, № 390. К доске выходят учащиеся по желанию. (5 – 7 минут).
Домашнее задание: составить и решить две задачи на использование свойств или признаков трапеции.
3. Рефлексия:
Прием «Шесть шляп мышления»:
Так как класс разбит на 6 групп, то считаю
уместным закончить урок данным приемом. (3 — 5 мин).
(3 — 5 мин).
Логично предположить, что 3 группа (черная шляпа) выскажет предположение о том, что решили мало задач, а 6 группа (синяя шляпа) эту идею поддержит. Таким образом, будет логичный переход к теме следующего урока: «Решение задач по теме «Трапеция».
Какими свойствами обладает трапеция? – Кухня
Свойства трапеции
- Это 2D-форма.
- Основания трапеции параллельны друг другу.
- Длина обеих диагоналей одинакова.
- Диагонали трапеции всегда пересекаются.
- Сумма смежных внутренних углов составляет 180°.
- Сумма всех внутренних углов трапеции всегда равна 360°.
Какое свойство трапеции?
Трапеция обладает следующими свойствами: Как и у других четырехугольников, сумма всех четырех углов трапеции равна 360° Трапеция имеет две параллельные стороны и две непараллельные стороны.Диагонали правильной трапеции пересекаются пополам.
Какие свойства трапеции для 8 класса?
Свойства трапеции
- Четырехсторонняя замкнутая фигура с суммой внутренних углов 360°.

- Одна пара параллельных сторон, которые должны быть противоположны друг другу.
- Одна пара непараллельных сторон.
- Сумма углов смежных сторон равна 180°.
- Диагонали трапеции пересекаются пополам.
Какими свойствами обладают углы трапеции?
Трапеция и ее свойства
- Угол: Сумма углов другого четырехугольника, подобного трапеции, равна 360°.
- Два угла по одну сторону смежные, то есть сумма углов двух смежных сторон равна 180°.
- Его диагонали делятся пополам.
Сколько сторон у трапеции равны?
Трапеция разделится на две неравные части, если разрезать ее на две стороны из середины непараллельных сторон.В равнобедренной трапеции две непараллельные стороны равны и образуют равные углы при основаниях.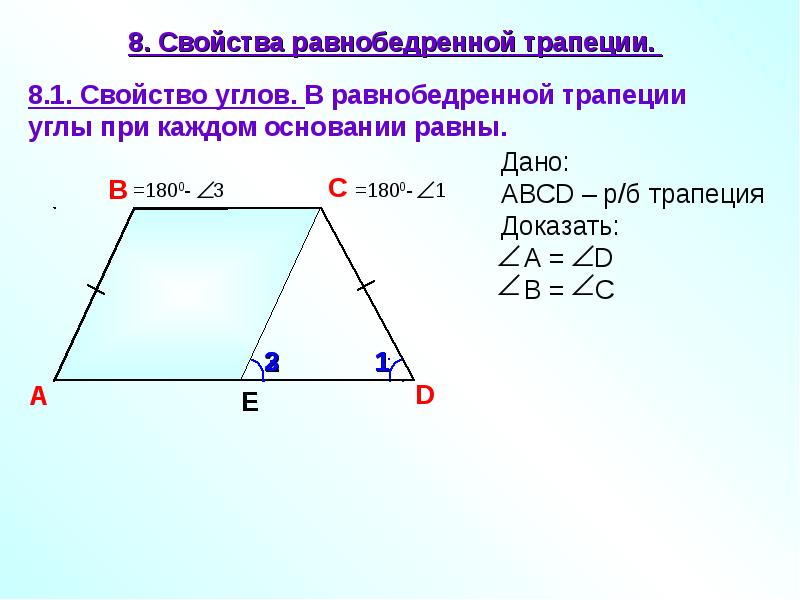
Какие 3 свойства трапеции?
Каковы три атрибута трапеции?
- Углы при основании и диагонали равны, если трапеция равнобедренная.
- Точка пересечения диагоналей лежит на одной прямой с серединами двух противоположных сторон.
- Противоположные стороны равнобедренной трапеции равны.
Что такое равнобедренная трапеция и ее свойства?
: Что такое равнобедренная трапеция и ее свойства?
Квадрат, Прямоугольник, Ромб, Трапеция, Параллелограмм
Четырехугольник просто означает «четыре стороны»
( четырехугольник означает четыре, боковой означает сторону).
Четырехугольник имеет четыре стороны , он двумерный (плоская форма), замкнутый (линии соединяются), и имеет прямых сторон.
Попробуйте сами
геометрия/изображения/geom-quad.js?mode=выбрать
(Также см. это в интерактивном четырехугольнике)
Свойства
Четырехугольник имеет:
- четыре стороны (кромки)
- четыре вершины (углы)
- внутренних углов, которые в сумме составляют 360 градусов :
Попробуйте нарисовать четырехугольник и измерьте углы. Они должны добавить к 360°
Они должны добавить к 360°
Типы четырехугольников
Существуют особые типы четырехугольников:
Некоторые типы также включены в определение других типов! Например, квадрат , ромб и прямоугольник также являются параллелограммами . Подробности смотрите ниже.
Рассмотрим каждый тип по очереди:
Прямоугольник
квадратики в каждом углу означают «прямой угол»
Прямоугольник — это четырехсторонняя фигура, в которой каждый угол прямой (90°).
Также противоположные стороны параллельны и имеют одинаковую длину.
Площадь
квадратики в каждом углу означают «прямой угол»
Квадрат имеет равные стороны (обозначены буквой «s») и каждый угол прямой (90°)
Также параллельны противоположные стороны.
Квадрат также соответствует определению прямоугольника (все углы равны 90°) и ромба (все стороны имеют одинаковую длину).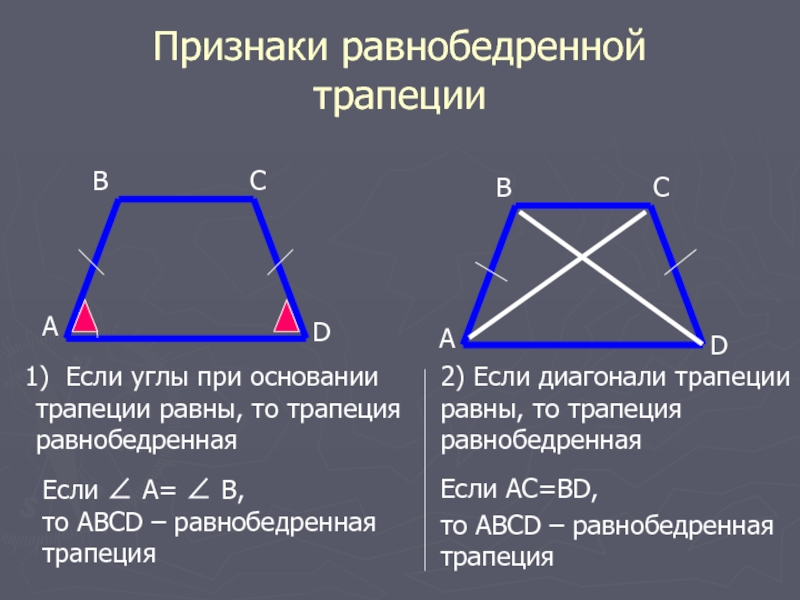
Ромб
Ромб — это четырехгранная фигура, все стороны которой имеют одинаковую длину (обозначены буквой «s»).
Также противоположные стороны параллельны и противоположные углы равны.
Еще одна интересная вещь: диагонали (штриховые линии) сходятся посередине под прямым углом. Другими словами, они «делят пополам» друг друга под прямым углом.
Ромб иногда называют ромбом или ромбом .
Параллелограмм
У параллелограмма противоположные стороны параллельны и равны по длине. Также противоположные углы равны (углы «А» равны, а углы «В» такие же).
ПРИМЕЧАНИЕ. Квадраты, прямоугольники и ромбы Параллелограммы!
Пример:
A параллелограмм с:
- все стороны равны и
- углов «А» и «В» как прямые углы
— это квадрат !
Трапеция (Великобритания: Трапеция)
Трапеция | Равнобедренная трапеция |
У трапеции (называемой в Великобритании трапецией) пара противоположных сторон параллельна.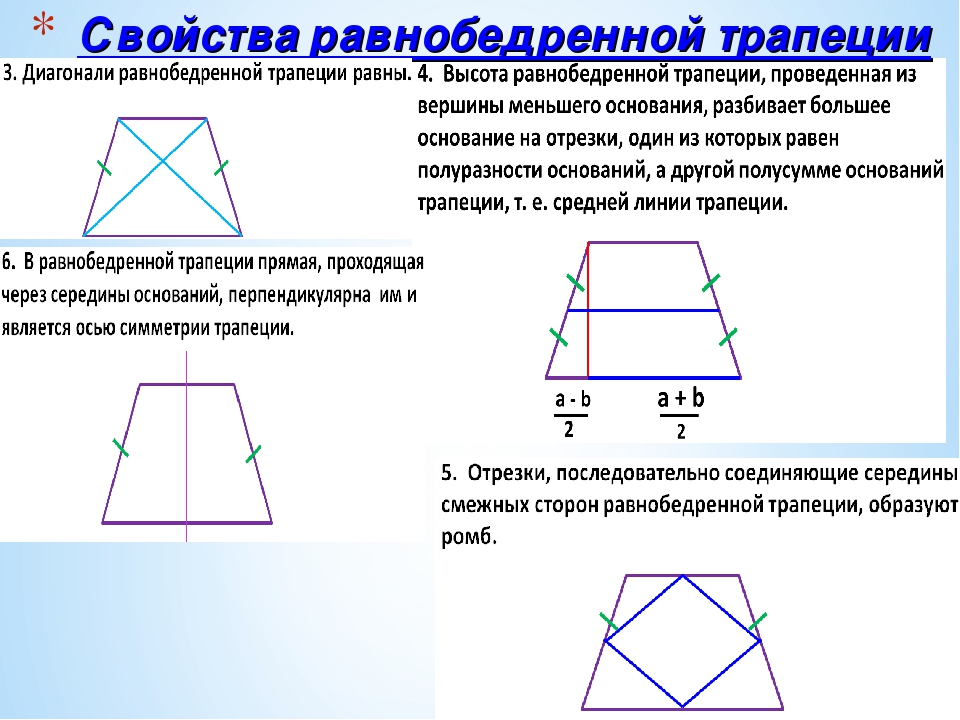
И трапеция (называемая трапецией в Великобритании) является четырехугольником без параллельных сторон:
| Трапеция | Трапеция | |
| В США: | пара параллельных сторон | НЕТ параллельных сторон |
| В Великобритании: | НЕТ параллельных сторон | пара параллельных сторон |
| (определения для США и Великобритании поменяны местами!) | ||
Равнобедренная трапеция , как показано выше, имеет левую и правую стороны одинаковой длины, которые соединяются с основанием под одинаковыми углами.
Воздушный змей
Эй, это похоже на воздушного змея (обычно).
Он имеет две пары сторон:
Каждая пара состоит из двух соединенных сторон одинаковой длины.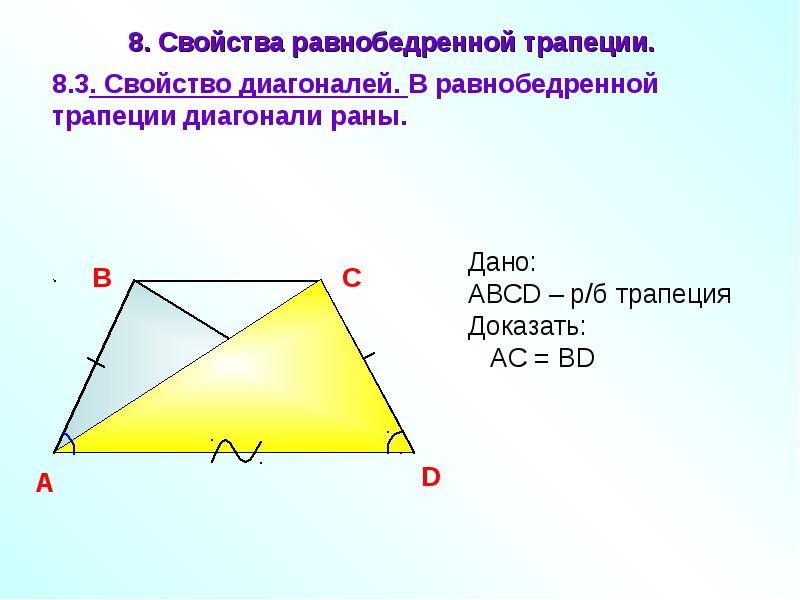
Также:
- углы, где встречаются две пары равны.
- диагонали, показанные выше пунктирными линиями, пересекаются в прямой угол.
- одна из диагоналей делит пополам (равнополовину) другую.
… и это все для специальных четырехугольников.
Неправильные четырехугольники
Единственный правильный (все стороны равны и все углы равны) четырехугольник является квадратом. Итак, все остальные четырехугольники неправильные .
Карта «Семейное древо»
Определения четырехугольника: включительно .
Пример: квадрат также является прямоугольником.
Итак, мы включаем квадрат в определение прямоугольника.
(Мы, , не говорим : «Если все углы равны 90°, это прямоугольник, за исключением случаев, когда все стороны равны, тогда это квадрат».)
Это может показаться странным, поскольку в повседневной жизни мы думаем о квадрате как о , а не о как о прямоугольнике.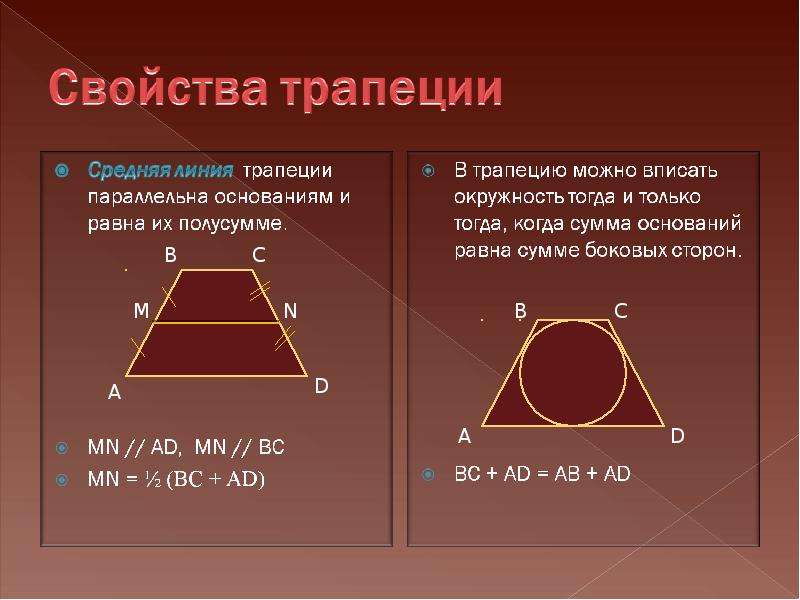 .. но в математике равно .
.. но в математике равно .
Используя приведенную ниже таблицу, мы можем ответить на такие вопросы, как:
- Является ли квадрат разновидностью прямоугольника? (Да)
- Является ли прямоугольник разновидностью воздушного змея? (№)
Сложные четырехугольники
О да! когда две стороны пересекаются, мы называем это «сложным» или «самопересекающимся» четырехугольником, например:
У них по-прежнему 4 стороны, но две стороны пересекаются.
Полигон
Четырехугольник — это многоугольник. На самом деле это 4-сторонний многоугольник, точно так же, как треугольник — 3-сторонний многоугольник, пятиугольник — 5-сторонний многоугольник и так далее.
Играй с ними
Теперь, когда вы знаете различные типы, вы можете поиграть с интерактивными четырехугольниками.
Другие названия
Четырехугольник иногда можно назвать:
- a Четырехугольник (« четыре угла «), так что это звучит как «треугольник»
- a Tetragon (« четыре многоугольника «), так что это звучит как «пятиугольник», «шестиугольник» и т.
 д.
д.
621 622 623 624 763 764, 2128, 2129, 3230, 3231
Площадь трапеции – определение, формулы, свойства и примеры решения
Четырехугольник – это двумерная замкнутая фигура, имеющая четыре стороны, четыре угла и четыре вершины. Согласно евклидовой геометрии, четырехугольник — это многоугольник, имеющий 4 стороны и 4 вершины. Четырехугольников семь, а именно:
Квадрат: все стороны равны, а углы составляют 90°.Диагонали пересекаются друг с другом. Сумма всех внутренних углов равна ∠A + ∠B + ∠C + ∠D = 360°.
Прямоугольник: пары сторон равны, и все ребра находятся под углом 90°. Диагонали пересекаются. Сумма внутренних углов равна ∠A + ∠B + ∠C + ∠D = 360°.
Ромб: Похож на квадрат. Все стороны равны. Он имеет форму алмаза. Противоположные углы равны. Сумма внутренних углов равна ∠A + ∠B + ∠C + ∠D = 360°.

Трапеция: имеет пару параллельных сторон.Сумма внутренних углов равна ∠A + ∠B + ∠C + ∠D = 360°.
Воздушный змей: Две пары сторон одинаковой длины, примыкающих друг к другу. Сумма внутренних углов равна ∠A + ∠B + ∠C + ∠D = 360°.
Параллелограмм: Противоположные стороны параллельны и равны по длине. Сумма внутренних углов равна ∠A + ∠B + ∠C + ∠D = 360°.
Равнобедренная трапеция: тоже самое, что и трапеция. Разница лишь в том, что непараллельные стороны имеют одинаковую длину. Сумма внутренних углов равна ∠A + ∠B + ∠C + ∠D = 360°.
Эта статья посвящена трапеции, ее основной концепции, свойствам, площади, применению, формулам и выводу площади трапеции.
Трапеция Определение:
Трапеция представляет собой двумерную замкнутую фигуру, имеющую пару параллельных сторон.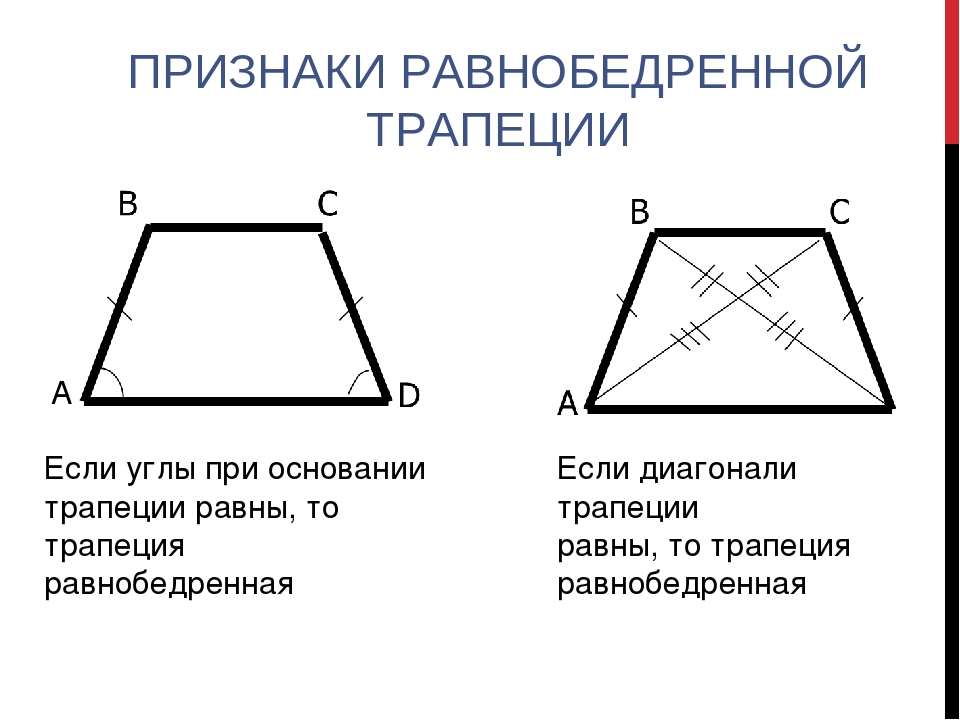 У него 4 стороны и 4 вершины. Параллельные стороны трапеции являются основаниями, а непараллельные стороны называются катетами.
У него 4 стороны и 4 вершины. Параллельные стороны трапеции являются основаниями, а непараллельные стороны называются катетами.
Различные типы трапеций:
Разносторонняя трапеция: Все стороны и углы имеют разную величину.Просто трапеция является разносторонней трапецией, как показано на рисунке ниже.
Равнобедренная трапеция: Если в трапеции любые две пары сторон равны, то есть основания или катеты, то трапеция равнобедренная.
Прямая трапеция: по крайней мере два угла прямые, т. е. 90°.
Основное различие между трапецией и трапецией показано ниже. Это различие связано только с британской и американской версиями.
Разница между трапецией и трапецией
| | | | | | USA | |
Trapezoid | Четырехугольник с одной парой параллельных сторон. | |||||
Трапеция | Четырехугольник с одной парой параллельных сторон. | Четырехугольник без параллельных сторон. |
Основные понятия трапеции:
Основания — параллельные стороны трапеции, а непараллельные стороны — стороны.
Линия, проведенная из середины непараллельных сторон, является средней точкой.
Стрелки и знаки равенства, показанные на рисунке, означают, что линии параллельны, а длины сторон равны соответственно.
Трапеция разделится на две неравные части, если разрезать ее на две стороны из середины непараллельных сторон.
В равнобедренной трапеции две непараллельные стороны равны и образуют равные углы при основаниях.

Свойства трапеции:
Вот некоторые из свойств трапеции:
Ровно одна пара противоположных сторон параллельна.
Диагонали пересекаются.
Сумма внутренних углов трапеции равна 360°, т. е. ∠A + ∠B + ∠C + ∠D = 360°.
За исключением равнобедренной трапеции, у трапеции непараллельные стороны неравны.
Линия, соединяющая середины непараллельных сторон, всегда параллельна основаниям трапеции.
Середина сегмента = (AB + CD)/2
Площадь трапеции:
Площадь трапеции рассчитывается как половина суммы параллельных сторон и высоты.Формула площади трапеции записывается так:
\[\frac{1}{2}\] \[\times\] сумма параллельных сторон \[\times\] умноженная на расстояние между ними
\[= \ frac{1}{2} \times (b_{1} \times b_{2}) \times h\]
Периметр трапеции:
Периметр трапеции равен сумме всех четырех сторон . Математически это дается как
Математически это дается как
Периметр = AB + BC + CD + DA.
Вычисление площади трапеции:
Вывод площади трапеции приведен ниже.
Получение: площадь трапеции
Получение:
Здесь пусть одна сторона будет «b1», а другая сторона будет «b2»
Расстояние между параллельными сторонами равно «h»
Из рисунка можно видно, что есть два треугольника и один прямоугольник.
Следовательно, площадь трапеции равна
Площадь = площадь треугольника 1 + площадь прямоугольника + площадь треугольника 2
\[Площадь = \frac{1}{2} \times AE \times DE + DE \times EF + \frac{1}{2} \times FB \times CF\]
\[= \frac{ah}{2} + b_{1} h \frac{bh}{2}\]
\ [= \frac{ah + 2b_{1}h + bh}{2}\]
Упрощая приведенное выше уравнение, мы получаем,
\[= \frac{h}{2} (a + 2 b_{ 1} + b)\]
Из рисунка мы знаем
\[= b_{2} = a + b_{1} + b\]
Следовательно,
\[Площадь = \frac{h} {2} [b_{1} + (a + b_{1} + b)]\]
Подставляя значение из приведенного выше уравнения, мы получаем
\[= \frac{h}{2} [b_{ 1} + b_{2}]\]
\[= \frac{1}{2} [b_{1} + b_{2}] \times h\]
— требуемое уравнение. Следовательно, площадь трапеции была получена, где b1 и b2 — основания, а h — высота.
Следовательно, площадь трапеции была получена, где b1 и b2 — основания, а h — высота.
Применение трапеции:
Концепция трапеции имеет широкий спектр применений. Он используется в физике для решения различных вопросов, основанных на трапеции, тогда как в математике он используется в различных приложениях, например, для решения различных вопросов, основанных на площади поверхности или для нахождения площади или периметра сложной фигуры. Формулу трапеции можно использовать в строительстве так же, как форма крыши трапециевидная.Он имеет множество применений в повседневной жизни.
Пример:
Длины параллельных сторон трапеции относятся как 5:2, а расстояние между ними равно 20 см. Найдите длину параллельных сторон, если площадь трапеции 325 см².
Раствор:
Пусть X = Общее соотношение
Параллельные стороны = 5x и 2x
Высота = 20 см
площадь трапеции = 325 см2
Тогда из формулы площади трапеции
\ [область = \frac{1}{2} [b_{1} + b_{2}] \times h\]
\[325 = \frac{1}{2} \times (5x + 2x) \times 20\ ]
= х = 4.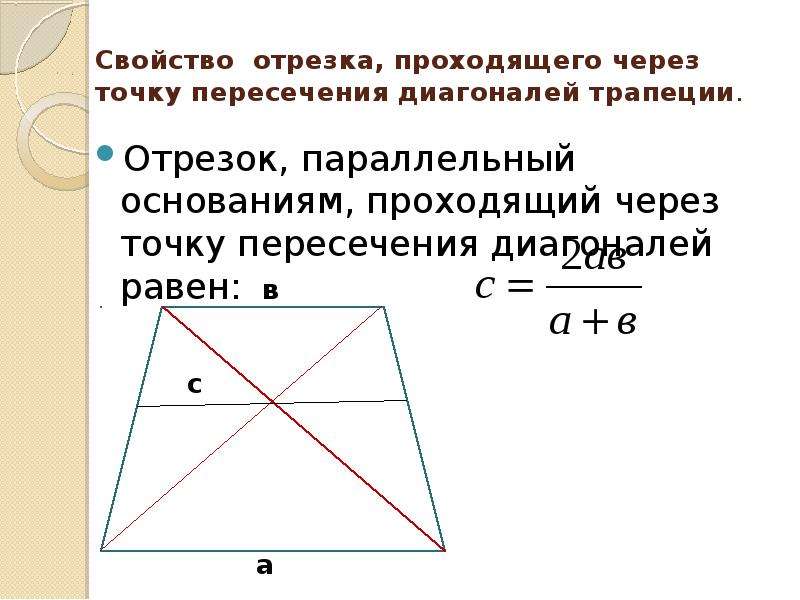 {2}\]
{2}\]
Следовательно, площадь трапеции равна 275 см2.
Пример:
Найдите периметр и площадь трапеции, параллельные стороны которой равны 10 см и 25 см. Расстояние между основаниями равно 30 см, а длина непараллельной стороны по 20 см каждая.
Решение:
Дано:
Длина параллельных сторон = 10 см и 25 см
Высота = 30 см
\[Площадь = \frac{1}{2} [b_{1} + b_{2 }] \times h\]
\[= \frac{1}{2} (10 + 25) \times 30\]
= 1050 см2
Периметр = сумма всех сторон
= 10 + 25 + 20 + 20
= 75 см
Следовательно, площадь и периметр равны 1050 см2 и 75 см соответственно.
Что такое Трапеция? Определение и свойства — WTSkills
Трапеция (геометрия) Трапеция – это четырехугольник, у которого две стороны параллельны , а две другие стороны не параллельны .
Это один из неправильных четырехугольников с параллельными противоположными сторонами.
На самом деле слово «Трапеция» означает «Столик» по-гречески.
Ключевое слово для трапеции
(a) одна пара параллельных сторон
(b) одна пара непараллельных сторон
Трапеция состоит из следующих компонентов
(a) Основание
Параллельные стороны называются основанием.
(b) Нога
Стороны, которые не параллельны, называются Ногами
(c) Высота
Перпендикулярное расстояние между параллельными линиями называется высотой
(d) Четыре угла трапеции
Примеры трапеции Типы трапецийТрапеции классифицируются по сторонам и углам.
(01) Разнонаправленная трапеция
Это трапеция, у которой все углы и стороны разной величины
(02) Равнобедренная трапеция
Это трапеция, у которой непараллельные стороны равны
Дана трапеция ABCD, у которой стороны AB и CD параллельны, а стороны AD и BC непараллельны.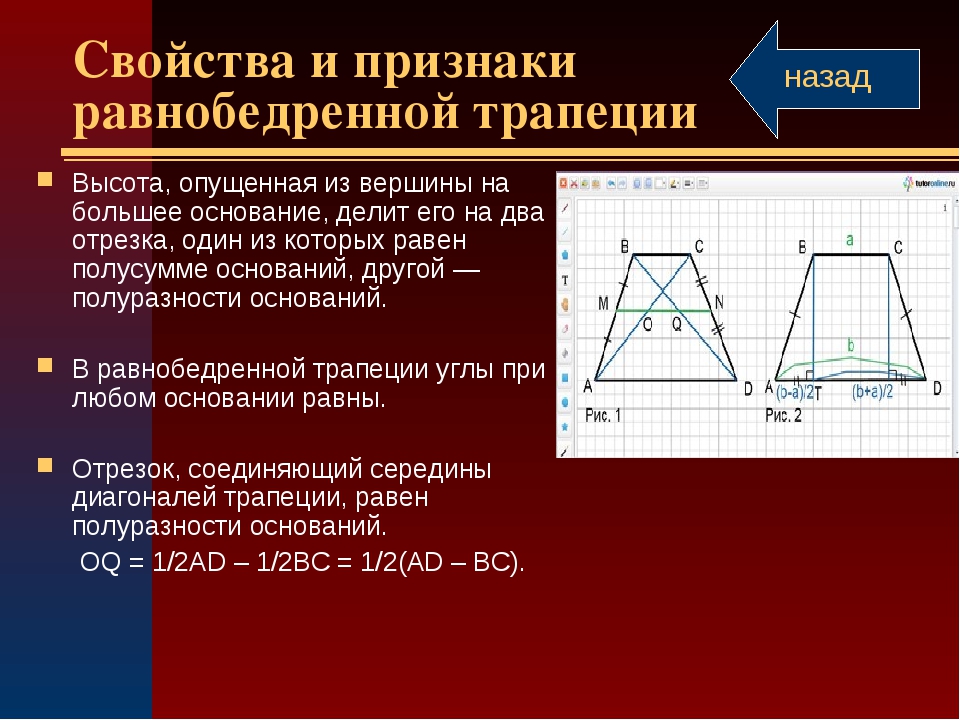
В равнобедренной трапеции непараллельные стороны равны
, т.е. AD = BC
(03) Правая трапеция
Трапеция, имеющая не менее двух прямых углов, называется прямой трапецией
Выше приведена правильная трапеция ABCD, в которой ∠A = ∠D = 90 градусов
Свойства трапеции(01) Одна пара сторон параллельна друг другу
В приведенной выше трапеции ABCD стороны AB и CD параллельны
i.е. АВ II CD
(02) Смежные углы между параллельными линиями дополнительные
Выше приведена трапеция ABCD с линией AB II CD
В соответствии со свойством угла трапеции
∠1 + ∠ 2 = 180 и ∠3 + ∠ 4 = 180
Доказательство
Прямые AB и CD — параллельные прямые, а AD — поперечная
Итак,
∠1 + ∠ 2 = 180 { Свойство внутреннего угла одной стороны }
Точно так же считайте AB и CD параллельными прямыми, а BC поперечными
∠3 + ∠ 4 = 180 {Свойство внутреннего угла той же стороны}
(03) Диагонали трапеции
За исключением равнобедренной трапеции, диагонали не делят друг друга пополам
(04) В трапеции диагонали делят друг друга пропорционально
ABCD — трапеция, в которой прямая AB параллельна CD (AB II CD)
AC и BD — две диагонали, пересекающиеся в точке O
Согласно свойству трапеций диагонали делят друг друга пропорционально.
\mathsf{\frac{DO}{OB} \ =\ \frac{CO}{OA}}
Доказательство
Берем треугольники AOB и DOC
Рассматриваем AB и CD как параллельные прямые, а BD как трансверсальные
∠ 1 = ∠ 3 {Альтернативные внутренние углы} }
∠ 5 = ∠ 6 { Вертикально противоположные углы}
Следовательно, по подобию AAA, ▵AOB и ▵DOC подобны.
В подобных треугольниках отношения соответствующих сторон одинаковы
\mathsf{\frac{DO}{OC} \ =\ \frac{OB}{OA}}
При переходе на другую сторону получаем:
\mathsf{\frac{DO}{OB} \ =\ \frac{CO}{OA}}
Отсюда доказано
(05) Трапециевидная диагональ Свойство
Сумма квадратов диагоналей = сумма квадратов непараллельных сторон + удвоенное произведение параллельных сторон
Дана трапеция ABCD с параллельными сторонами AB и CD.{2} \ +\ 2\ АВ\ .\ CD}
(06) Теорема о средней линии трапеции
Длина линии, соединяющей середину непараллельной стороны, равна половине суммы параллельных сторон
ABCD — трапеция с параллельными сторонами AB и CD
E и F — середины непараллельных сторон AD и BC соответственно
Согласно теореме о срединном отрезке
EF = 1/2 (AB + CD)
(07) Формула площади трапеции
Площадь трапеции находится по формуле:
\mathsf{Площадь\ =\ \frac{1}{2} \ ( сумма\ параллелей\ сторон) \ \times \ height}\\\ \\ \mathsf {Площадь\ =\ \frac{1}{2} \ ( AB+CD) \ \times \ h}
(08) Периметр трапеции
Периметр любой фигуры равен общей длине границы.
В случае трапеции периметр равен сумме всех сторон
Периметр = (a + b + c + d) см
(01) ABCD — трапеция, в которой AB || CD, AB = 16 см и CD = 12 см, а расстояние между параллельными сторонами 10 см. Найдите площадь трапеции
Дано
AB = 16 см
CD = 12 см
Высота (h) = 10 см
Мы это знаем;
Площадь трапеции = (1/2) x (сумма параллельных сторон) x высота
Площадь = (1/2) (AB + CD) x h
Площадь = (1/2) (16 + 12) x 10 = 140 кв.см
Отсюда 140 кв.см — площадь трапеции
(02) ABCD — трапеция, в которой AB II CD. Диагонали пересекаются в точке O.
При условии, что AO = 3, OC = x – 3, OD = 3x – 19, OB = x – 5
Найдите значения x
Использование диагонального свойства трапеции
\mathsf{\frac{DO}{OB} \ =\ \frac{CO}{OA}}
\mathsf{\frac{3x-19}{x-5} \ =\ \frac{x-3}{3}}\\\ \\ \mathsf{3( 3x-19) \ =( x- 5) \ ( x-3)}\\\ \\ \mathsf{9x\ -57\ =\ x^{2} -8x+15}\\\ \\ \mathsf{x^{2} -17x+ 72\ =\ 0}\
При решении квадратного уравнения получаем;
х = 9 и х = 8
Следовательно, и 8, и 9 являются решением для x
. Часто задаваемые вопросы – Трапеция
Часто задаваемые вопросы – Трапеция (01) Чем трапеция отличается от параллелограмма
В параллелограмме противоположные стороны равны и параллельны, а в трапеции параллельна только одна пара сторон.
(02) Равны ли диагонали в трапеции?
НЕТ!!
Они не равны и не делят друг друга пополам
(03) В Трапеции равны ли противоположные пары углов?
У трапеции такого свойства нет.
Свойство трапеции, связанное с углом:
(a) Альтернативные углы являются дополнительными
(b) Сумма всех углов составляет 360 градусов
(04) Любое другое название Трапеции?
В некоторых странах их еще называют трапециевидными.
Краткое описание трапецииСвойства четырехугольников: определение, формулы, свойства
Свойства четырехугольников: Четырехугольник — это четырехугольник, ограниченный четырьмя конечными отрезками.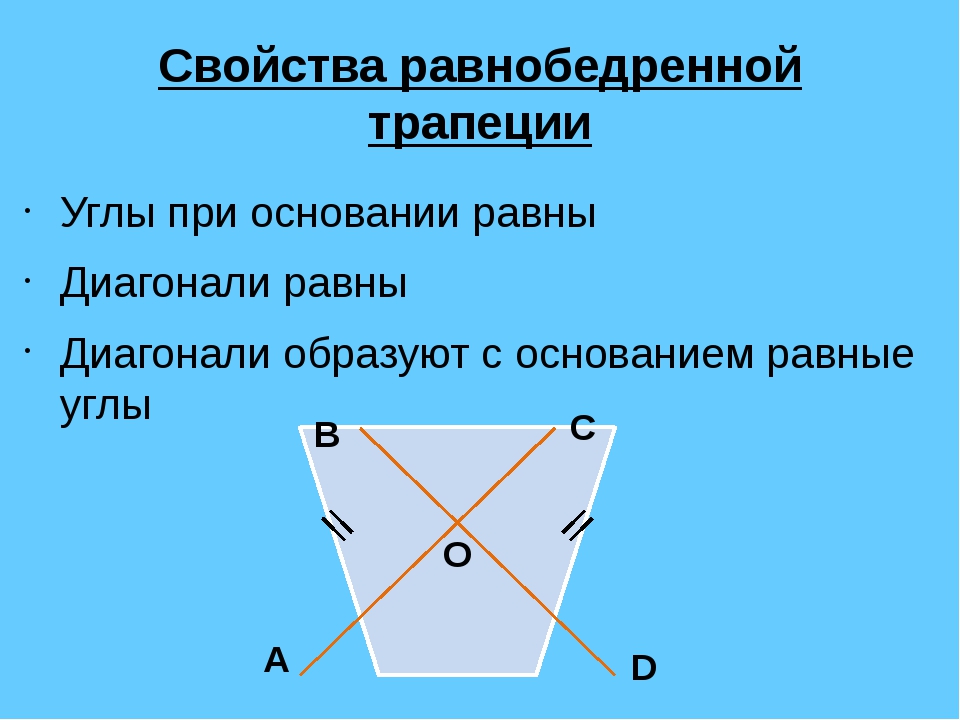 Термин «четырехугольник» происходит от латинских слов «quadra» (четыре) и «Latus» (стороны). Четыре стороны четырехугольника могут быть, а могут и не быть равными. Четырехугольник содержит две диагонали, которые позволяют классифицировать его как вогнутый или выпуклый.Диагонали в выпуклых четырехугольниках всегда лежат внутри границы многоугольника. Это означает, что если размеры находятся внутри границ многоугольника, он называется выпуклым четырехугольником. Выпуклые четырехугольники делятся на шесть категорий в зависимости от их сторон и углов, а именно: трапеция, параллелограмм, квадрат, прямоугольник, ромб, воздушный змей.
Термин «четырехугольник» происходит от латинских слов «quadra» (четыре) и «Latus» (стороны). Четыре стороны четырехугольника могут быть, а могут и не быть равными. Четырехугольник содержит две диагонали, которые позволяют классифицировать его как вогнутый или выпуклый.Диагонали в выпуклых четырехугольниках всегда лежат внутри границы многоугольника. Это означает, что если размеры находятся внутри границ многоугольника, он называется выпуклым четырехугольником. Выпуклые четырехугольники делятся на шесть категорий в зависимости от их сторон и углов, а именно: трапеция, параллелограмм, квадрат, прямоугольник, ромб, воздушный змей.
Хотя четырехугольник имеет четыре стороны, четыре угла и четыре вершины, длины сторон и углов различаются. Следует отметить, что сумма внутренних углов четырехугольника всегда равна 360°.На этой странице давайте подробно обсудим все о свойствах четырехугольника, его определении, решенных задачах. Читайте дальше, чтобы узнать больше.
Свойства четырехугольников
Четырехугольник – это замкнутая двумерная фигура, образованная соединением четырех точек, среди которых три точки не лежат на одной прямой.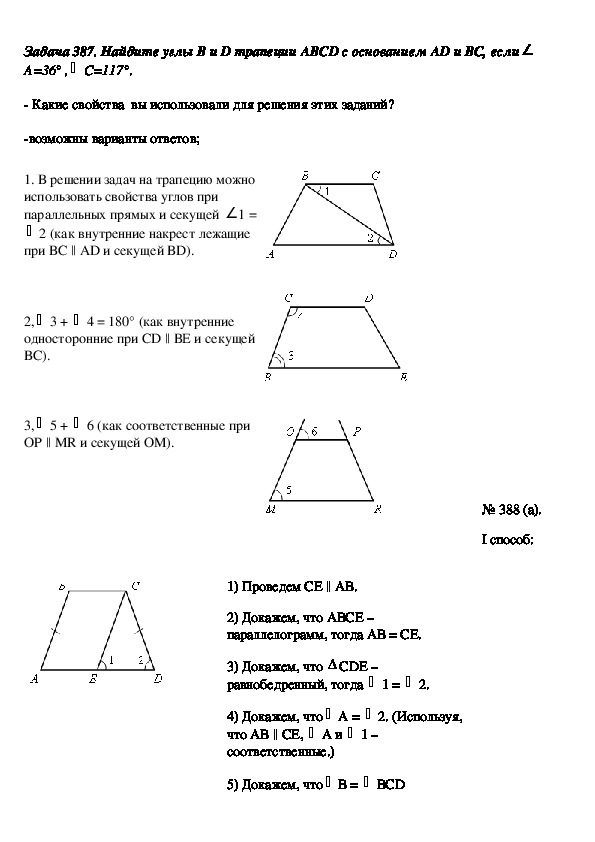 Четырехугольник имеет четыре стороны, четыре угла и четыре вершины или угла. Разберем свойства любого четырехугольника на примере:
Четырехугольник имеет четыре стороны, четыре угла и четыре вершины или угла. Разберем свойства любого четырехугольника на примере:
Изучите концепции 10-го экзамена CBSE
Пусть \(PQRS\) – четырехугольник.Мы должны назвать четырехугольник по порядку
\(PQRS,\,QRSP,\,RSPQ,\,SPQR\), а не \(PSQR,\,SRPQ,\,RSQP,\,SPRQ\).
- \(PQ,\,QR,\,RS\) и \(SP\) — \(4\) стороны.
- Точки \(P,\,Q,\,R\) и \(S\) являются \(4\) вершинами или углами.
- \(∠PQR,\,∠QRS,\,∠RSP\) и \(∠SPQ\) — это \(4\) углы.
- \(PS\) и \(QR\) — противоположные стороны.
- \(PQ\) и \(QR\) — смежные стороны.
- \(∠Q\) и \(∠S\) — противоположные углы.
- \(∠Q\) и \(∠R\) смежные углы.\круг\).
Специальные четырехугольники состоят из четырехсторонних фигур квадрата, прямоугольника, параллелограмма, ромба, трапеции и воздушного змея. Итак, свойства четырехугольника будут совокупностью свойств всех этих фигур.
Свойства параллелограмма Четырехугольник называется параллелограммом, если обе пары его противоположных сторон параллельны.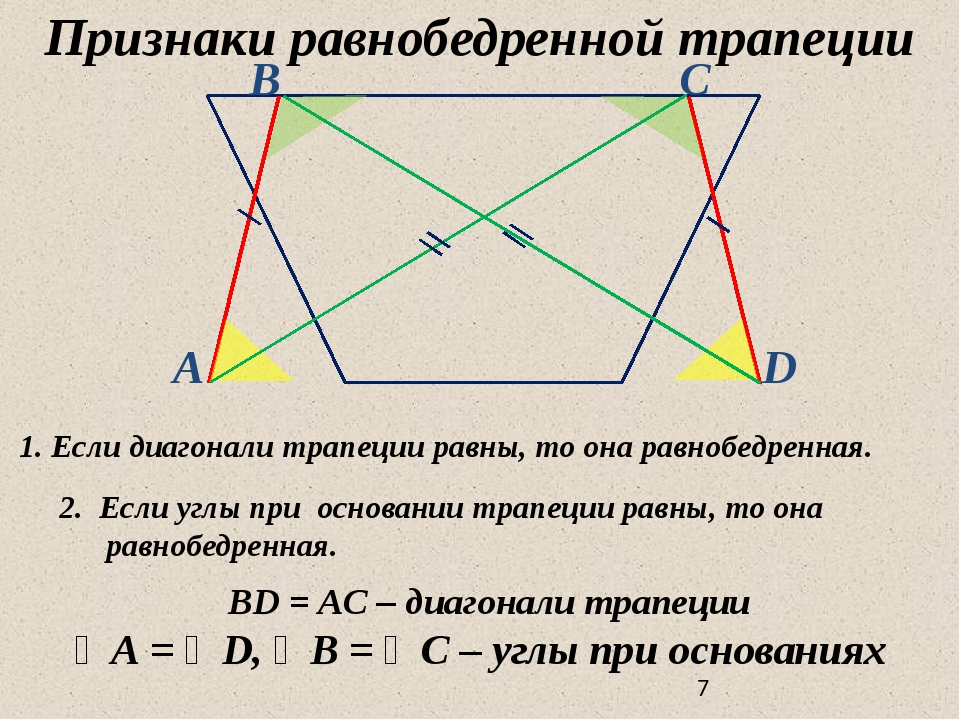
Свойства параллелограмма следующие:
- Четырехугольник называется параллелограммом, если обе пары его противоположных сторон параллельны и равны.
- Диагонали параллелограмма делят друг друга пополам.
- Противоположные углы равны.
- Пара смежных углов дополнительные.
Четырехугольник называется воздушным змеем, если у него есть две пары равных смежных сторон, но неравные противоположные стороны.
Свойства воздушного змея указаны ниже:
- Четырехугольник называется воздушным змеем, если он имеет \(2\) пар равных смежных сторон, но неравные противоположные стороны.
- Большая диагональ воздушного змея делит меньшую диагональ пополам.
- Только одна пара противоположных углов имеет одинаковую меру.
Практические вопросы 10-го экзамена CBSE
Получить формулы алгебры снизу:
Свойства ромба Тип четырехугольника, у которого все стороны равны, называется ромбом. \circ\).\circ\) т. е. под прямым углом.
\circ\).\circ\) т. е. под прямым углом.
Тип четырехугольника, имеющего ровно одну пару параллельных сторон, называется трапецией.
Свойства трапеции указаны ниже:
- Тип четырехугольника, имеющего ровно одну пару параллельных сторон, называется трапецией.
- Он имеет две параллельные стороны и две непараллельные стороны
- Два угла, образованные парой параллельных сторон и любыми непараллельными сторонами, являются дополнительными.
- Трапеции бывают двух типов: разносторонняя трапеция и равнобедренная трапеция
- У разносторонней трапеции непараллельные стороны разной длины
- У равнобедренной трапеции непараллельные стороны одинаковы по длине
- У равнобедренной трапеции диагонали делят друг друга пополам.
Формулы периметра четырехугольников:
| Название четырехстороннего | Perimeter Formula |
| ROMBUS | \ (4 \ Times \ RM {сторона} \) |
| квадратный | \ (4 \ times \ RM {сторона }\) |
| Прямоугольник | \(2 \times \left( {{\rm{Длина}} + {\rm{Ширина}}} \right)\) |
| Параллелограмм | \(2 \times \left( {\rm{Sum}}\,{\rm{of}}\,{\rm{the}}\,{\rm{смежные}}\,{\rm{стороны}}} \right)\) |
| Воздушный змей | \(2 \times (a + b) \) где \(a\) и \(b\) — длины неравных сторон |
Площадь любой формы — это пространство, которое она занимает. Формулы площади некоторых четырехугольников приведены ниже:
Формулы площади некоторых четырехугольников приведены ниже:
| Имя четырехстороннего | площадь Формулы |
| площадь | \ RM {сторона} \) |
| Прямоугольник | \ (\ Rm { Длина} \times \rm{Ширина}\) |
| Параллелограмм | \(\rm{Основание} \times \rm{Высота}\) |
| Ромб | \(\frac{1}{2 } \times {\text{Продукт}}\,{\text{из}}\,{\text{}}\,{\text{диагонали}}\) |
| Воздушный змей | \(\ frac {1}{2} \times {\text{Продукт}}\,{\text{из}}\,{\text{диагонали}}\,{\text{диагонали}}\) |
Другие важные статьи по математике:
Решенные примеры – свойства четырехугольников В.1. Сколько сторон и вершин у четырехугольника?
Ответ: Четырехугольник имеет \(4\) сторон и \(4\) вершин.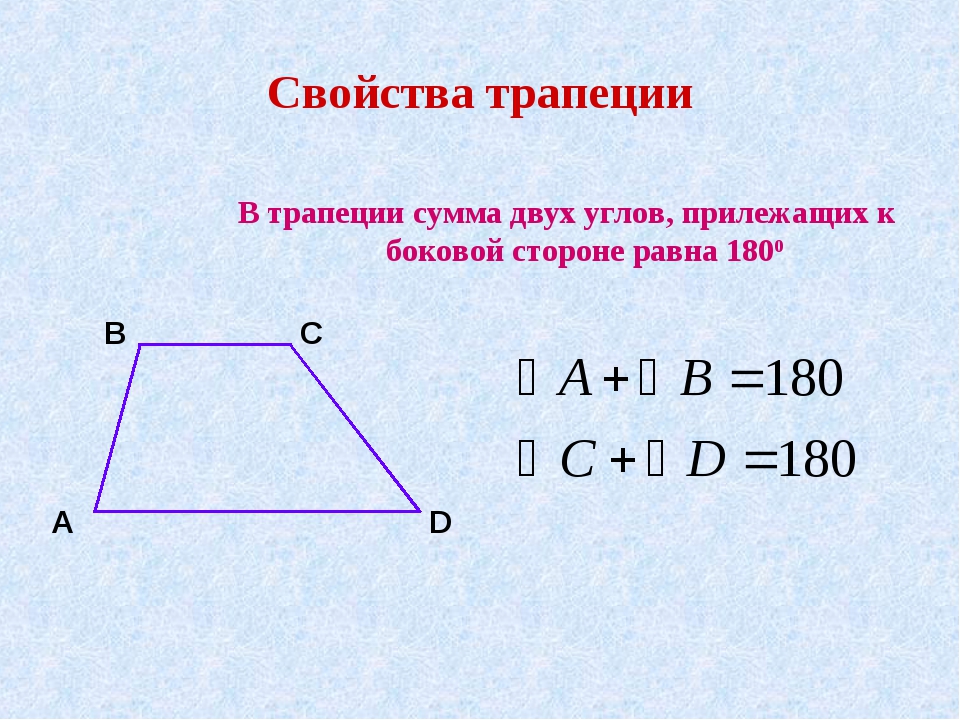 2\).
2\).
Q.4. Найдите периметр приведенной ниже фигуры.
Ответ: Даны длины сторон фигуры \(3\;\rm{см},\,3\;\rm{см},\,5\;\rm{см} \) и \(4\;\rm{см}\).
Мы знаем, что периметр фигуры \(=\) сумма длин всех сторон
Теперь периметр фигуры \(ABCD = 3\;\rm{см} + 3\;\rm{см} + 5\ ;\rm{см} + 4\;\rm{см} = 15\;\rm{см}\)
Следовательно, периметр данной фигуры равен \(15\;\rm{см}\).2\).
Получите математические формулы для классов с 6 по 12 ниже:
Сводка В этой статье мы рассмотрели термин четырехугольник. Мы говорили о свойствах четырехугольника, которые включали свойства квадрата, свойства ромба, свойства прямоугольника, свойства параллелограмма, свойства воздушного змея, свойства трапеции. Затем мы взглянули на формулы периметра и площади четырехугольников.Затем мы обсудили решенные примеры вместе с несколькими часто задаваемыми вопросами.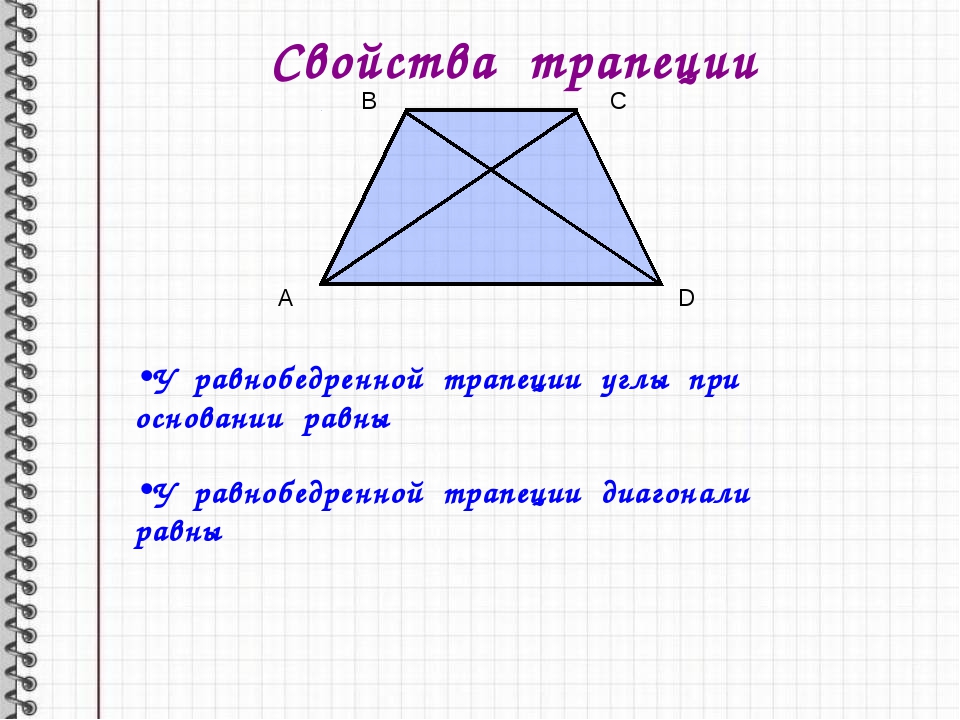
Часто задаваемые вопросы
Q.1. Какие бывают четырехугольники и их свойства?
Ответ: Типы четырехугольников и их свойства приведены ниже:
| Название четырехугольников | Свойства четырехугольников |
| Параллелограмм | Противоположные стороны параллельны и равны.\круг\). |
| Ромб | Все стороны равны, и противоположные углы тоже равны. |
| Трапеция | Имеет одну пару параллельных сторон и одну пару непараллельных сторон. Непараллельные стороны могут быть или не быть равными по длине. |
В 2. Какие семь четырехугольников?
Ответ: Ниже приведены семь четырехугольников:
1. Воздушный змей
2.Параллелограмм
3. Трапеция (США) и Трапеция (Великобритания)
4.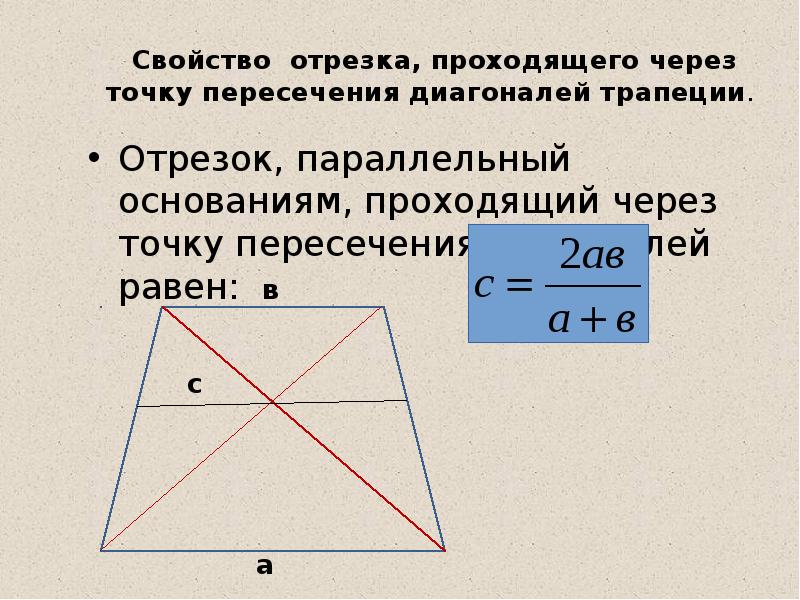 Равнобедренная трапеция
Равнобедренная трапеция
5. Прямоугольник
6. Квадрат и
7. Ромб
Q.3. Каковы свойства четырехугольного воздушного змея?
Ответ: Четырехугольником называется воздушный змей с двумя парами равных смежных сторон, но неравными противоположными сторонами.
1. Четырехугольником называется воздушный змей с двумя парами равных смежных сторон, но неравными противоположными сторонами.
2. Большая диагональ воздушного змея делит меньшую диагональ пополам под прямым углом.\круг\).
3. Противоположные стороны параллельны друг другу.
4. Диагонали прямоугольника делят друг друга пополам, но не перпендикулярно.
Q.5. Какие шесть специальных четырехугольников?
Ответ: Четырехугольники делятся на следующие шесть (\(6\)) типов:
1. Квадрат
2. Прямоугольник
3. Ромб
4. Трапеция
5. Параллелограмм 9081
Q.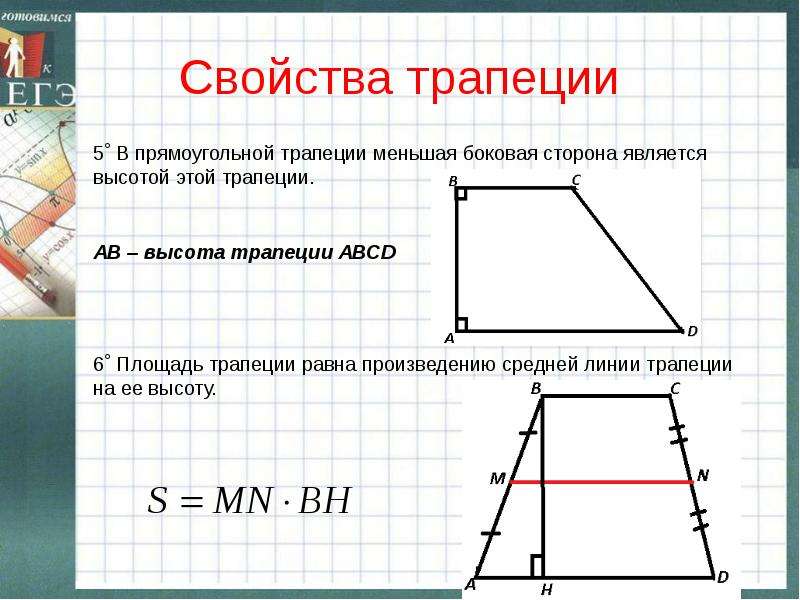 6. Как классифицировать четырехугольники?
6. Как классифицировать четырехугольники?
Ответ: Четырехугольники классифицируются и идентифицируются на основе длин и углов сторон.\круг\).
Q.8. Что означает четырехугольник?
Ответ: Слово «четырехугольник» происходит от двух латинских слов «quadri» означает «четыре» и «latus» означает стороны. Итак, четырехугольник – это плоская замкнутая фигура, имеющая четыре стороны.
Q.9. Каковы \(4\) свойства четырехугольника?
Ответ: Четырехугольник — это двумерная замкнутая фигура, имеющая четыре стороны, ребра или стороны.\круг\).
Теперь у вас есть вся необходимая информация о свойствах четырехугольников. Практикуйте больше вопросов и осваивайте эту концепцию. Вы можете использовать NCERT Solutions для математики, предоставленные Embibe, для подготовки к экзамену.
Мы надеемся, что эта подробная статья о свойствах четырехугольников поможет вам. Если у вас есть какие-либо вопросы относительно этой статьи, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее.
617 Просмотров
Иллюстративная математика
Задача
Ниже приведены изображения четырех четырехугольников: квадрата, прямоугольника, трапеции и параллелограмма.
Для каждого четырехугольника найдите и проведите все оси симметрии.
Комментарий к IM
Это задание дает учащимся возможность поэкспериментировать с отражениями плоскости и их влиянием на определенные типы четырехугольников. Это и то, и другое
интересно и важно, что эти типы четырехугольников можно отличить по их линиям симметрии.С этой точки зрения здесь отсутствуют только изображения ромба и общего четырехугольника, которые не вписываются ни в одну из рассматриваемых здесь специальных категорий.
Это задание лучше всего подходит для обучения, хотя его можно адаптировать и для оценивания. Если учащиеся еще не усвоили терминологию трапеций и параллелограммов, учитель может начать с объяснения значения этих терминов. В 4.G.2 говорится, что учащиеся должны классифицировать фигуры на основе наличия или отсутствия параллельных и перпендикулярных линий, поэтому это задание будет хорошо работать в модуле, который касается всех стандартов кластера 4.Г.А.
Учащиеся должны сначала попытаться визуализировать линии симметрии, а затем они могут сделать или получить вырезки четырех четырехугольников или обвести их на кальке. Студентам полезно поэкспериментировать и посмотреть, что пойдет не так, например, при отражении прямоугольника (который не является квадратом) относительно диагонали. Это упражнение помогает развить навыки визуализации, а также получить опыт работы с различными формами и их поведением при отражении.
Ученики должны вернуться к этой задаче как в средней, так и в старшей школе, чтобы проанализировать ее с более сложной точки зрения, поскольку они разрабатывают инструменты для этого. В восьмом классе четырехугольникам можно присвоить координаты, и учащиеся могут исследовать свойства отражений в системе координат. В старших классах учащиеся могут использовать абстрактные определения отражений и различных четырехугольников, чтобы доказать, что эти четырехугольники на самом деле характеризуются количеством линий симметрии, которые они имеют.
В восьмом классе четырехугольникам можно присвоить координаты, и учащиеся могут исследовать свойства отражений в системе координат. В старших классах учащиеся могут использовать абстрактные определения отражений и различных четырехугольников, чтобы доказать, что эти четырехугольники на самом деле характеризуются количеством линий симметрии, которые они имеют.
Решение
Линии симметрии для каждого из четырех четырехугольников показаны ниже:
Когда геометрическая фигура складывается вокруг линии симметрии, две половины совпадают, поэтому, если у учащихся есть копии четырехугольников, они могут проверить линии симметрии путем складывания.Квадрат можно сложить пополам либо по диагонали, либо по горизонтальному сегменту, который делит квадрат пополам, либо по вертикальному сегменту, который делит квадрат пополам. Значит, у квадрата четыре оси симметрии. В прямоугольнике их всего две, так как его можно сложить пополам по горизонтали или вертикали: учащимся следует предложить попробовать сложить прямоугольник пополам по диагонали, чтобы понять, почему это не работает. Трапеция имеет только вертикальную линию симметрии. У параллелограмма нет линий симметрии, и, как и в случае с прямоугольником, учащиеся должны поэкспериментировать, сложив копию, чтобы увидеть, что происходит с линиями, проходящими через диагонали, а также с горизонтальными и вертикальными линиями.
Трапеция имеет только вертикальную линию симметрии. У параллелограмма нет линий симметрии, и, как и в случае с прямоугольником, учащиеся должны поэкспериментировать, сложив копию, чтобы увидеть, что происходит с линиями, проходящими через диагонали, а также с горизонтальными и вертикальными линиями.
Указанные линии симметрии являются единственными для фигур. Один из способов показать это — отметить, что для четырехугольника линия симметрии должна либо совпадать с двумя вершинами на одной стороне линии с двумя вершинами на другой, либо должна проходить через две вершины, а затем две другие вершины соединяются. вверх при сгибании по линии. Это ограничивает число возможных линий симметрии, и тогда эксперименты покажут, что возможны только те, что показаны на картинках.
Разница между параллелограммом и прямоугольником
Геометрия относится к классификации форм и фигур, что также может быть описано как пространственная ориентация объекта. Существует широкий спектр различных геометрических фигур, включая двумерные четырехугольники. Это относится ко всем четырехсторонним геометрическим фигурам, которые далее делятся на четыре категории, а именно трапеции, равнобедренные трапеции, воздушные змеи и параллелограммы. Это все простые фигуры, которые не пересекаются сами с собой и состоят из области, ограниченной четырьмя сторонами.
Это относится ко всем четырехсторонним геометрическим фигурам, которые далее делятся на четыре категории, а именно трапеции, равнобедренные трапеции, воздушные змеи и параллелограммы. Это все простые фигуры, которые не пересекаются сами с собой и состоят из области, ограниченной четырьмя сторонами.
Что такое параллелограмм?
Параллелограмм классифицируется как замкнутый четырехугольник с конгруэнтными или подобными противоположными сторонами, которые параллельны, также известный как четырехугольник. Две параллельные стороны известны как основания параллелограмма, а расстояние между парой называется высотой. Площадь параллелограмма можно описать как (1/2) h (2 b ), а точнее bh , где h — высота, а b — основание.Еще одна особенность, отличающая параллелограммы, — две пары параллельных прямых. Диагонали — еще одна особенность, которую следует учитывать; при проведении между противоположными углами линии точно делят друг друга пополам. Каждая из этих диагоналей стремится разделить параллелограмм на два равных треугольника, а пересечение обеих диагоналей делит его на четыре треугольника, причем противоположные треугольники равны. Если сложить квадраты сторон, получится сумма диагоналей. Параллелограмм также имеет дополнительные смежные углы.
Каждая из этих диагоналей стремится разделить параллелограмм на два равных треугольника, а пересечение обеих диагоналей делит его на четыре треугольника, причем противоположные треугольники равны. Если сложить квадраты сторон, получится сумма диагоналей. Параллелограмм также имеет дополнительные смежные углы.
Что такое прямоугольник?
Прямоугольник часто называют частным случаем параллелограмма, так как он имеет аналогичные свойства, но с высотой, такой же, как одна из параллельных сторон. Это означает, что формула для прямоугольника lw ( длина x ширина) вместо bh. Прямоугольники также имеют две противоположные параллельные стороны, хотя у него также есть перпендикулярные последовательные стороны, что означает, что противоположные углы всегда равны 90°.Диагонали всегда делят друг друга пополам и дают отрезки прямой равной длины. Другими словами, параллелограмм, у которого противоположные стороны равны и углы равны 90°, называется прямоугольником.
Параллелограмм Против. Прямоугольник
1. Классификация
Это оба четырехугольника, причем прямоугольник классифицируется как разновидность параллелограмма. Параллелограммы и прямоугольники имеют два набора параллельных сторон, хотя у прямоугольника есть последовательные стороны, которые перпендикулярны.
2. Уголки
Противоположные внутренние углы параллелограмма и прямоугольника равны. Основное отличие состоит в том, что у прямоугольника углы всегда равны 90°, а у параллелограмма могут быть разными. Другими словами, углы прямоугольника всегда равны или равноугольны.
3. Диагонали
В случае параллелограмма диагонали не равны, и он делит фигуру пополам на два конгруэнтных треугольника. Прямоугольник имеет равные диагонали, что делит прямоугольник пополам на два равных прямоугольных треугольника.
4 . Формулы Формула для вычисления площади параллелограмма: bh ( ширина x высота ), а площадь прямоугольника вычисляется как lw ( длина x ширина ).
Существует «закон параллелограмма», который применяется к параллелограммам, где сумма квадратов всех сторон эквивалентна сумме квадратов диагоналей. Прямоугольники, с другой стороны, подчиняются «закону Пифагора», согласно которому квадраты двух смежных сторон, сложенные вместе, равны квадрату диагонали.
Параллелограмм против прямоугольника: сравнительная таблица
Резюме параллелограмма против. Прямоугольник
Есть определенные критерии, которые идентифицируют четырехугольник как параллелограмм. Наиболее очевидным является наличие двух пар параллельных сторон. Прямоугольник известен как частный случай параллелограмма, поскольку он соответствует основной классификации параллелограмма, но имеет особенности, которые выделяют его. Сюда входят противоположные стороны равной длины, пересекающиеся под углом 90° во всех случаях.Таким образом, диагонали равны и делят прямоугольник на прямоугольные треугольники, тогда как диагонали параллелограмма не равны и делят его пополам на два конгруэнтных треугольника с углами, зависящими от угла параллелограмма.

 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.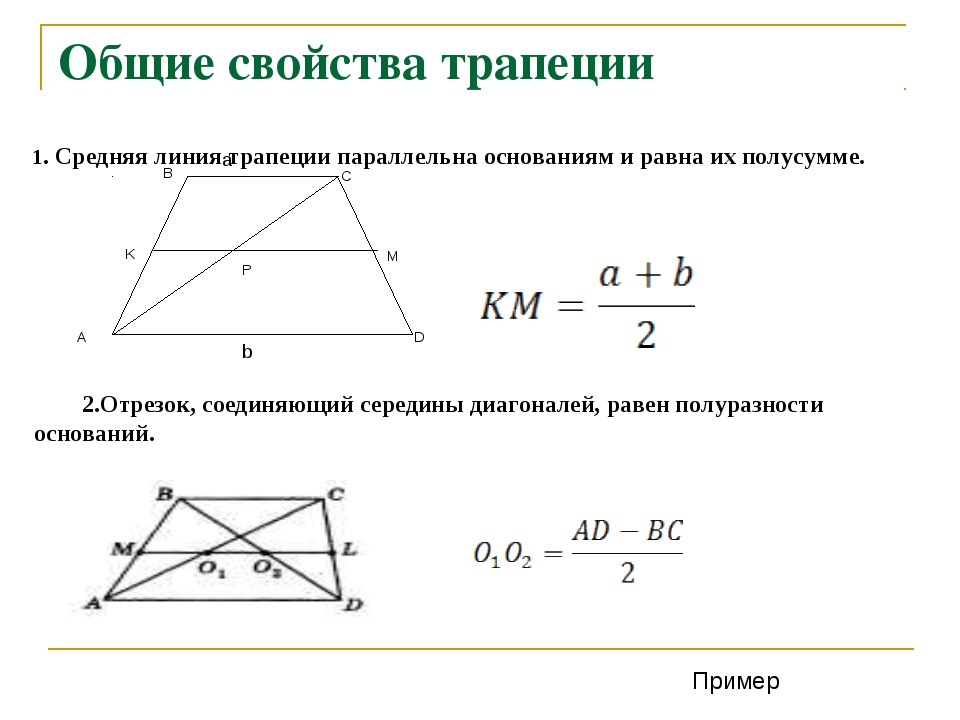
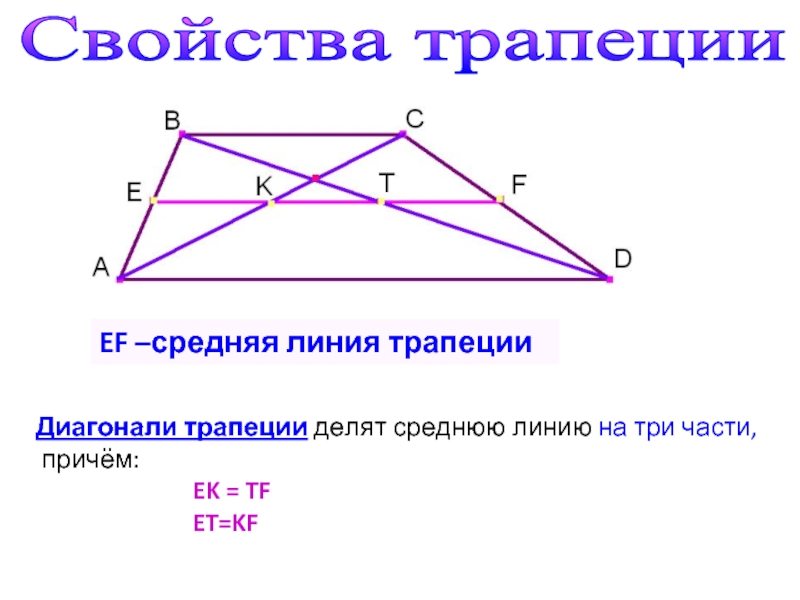
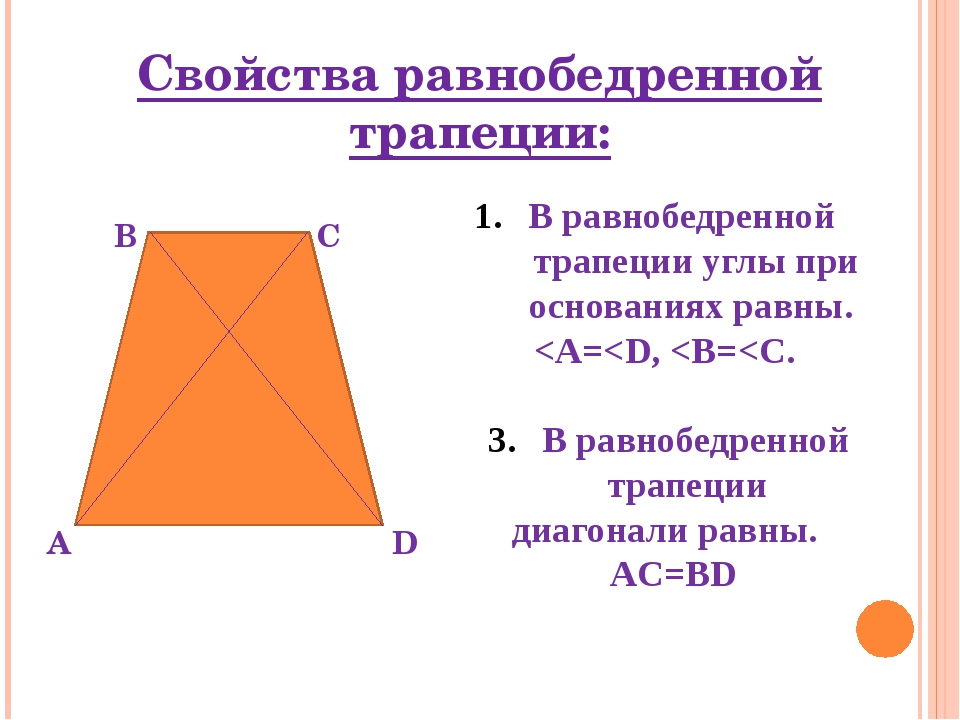
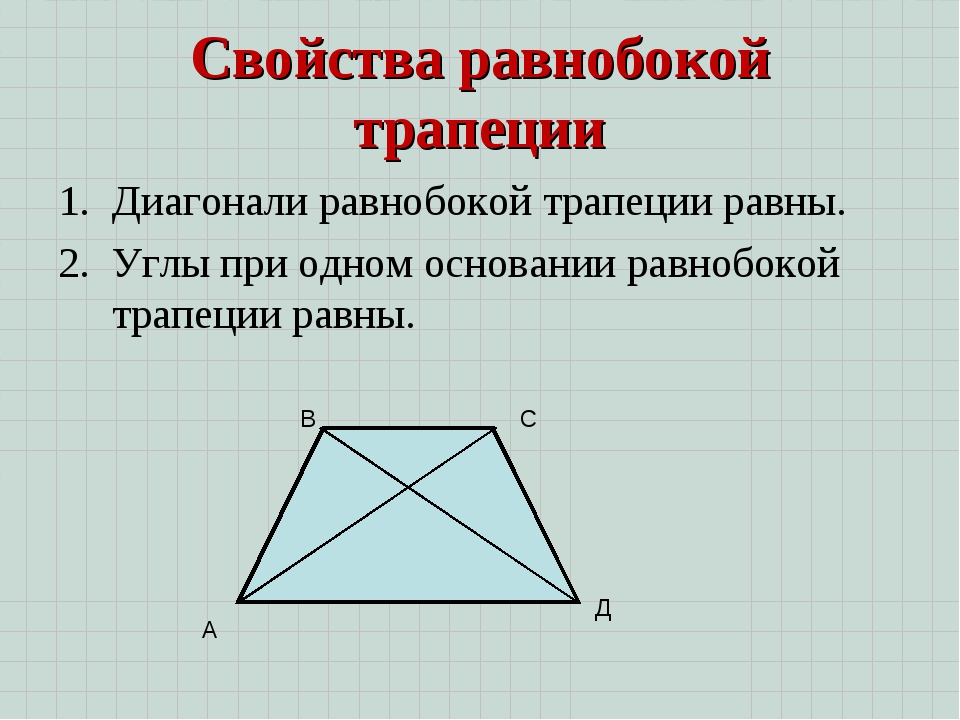 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .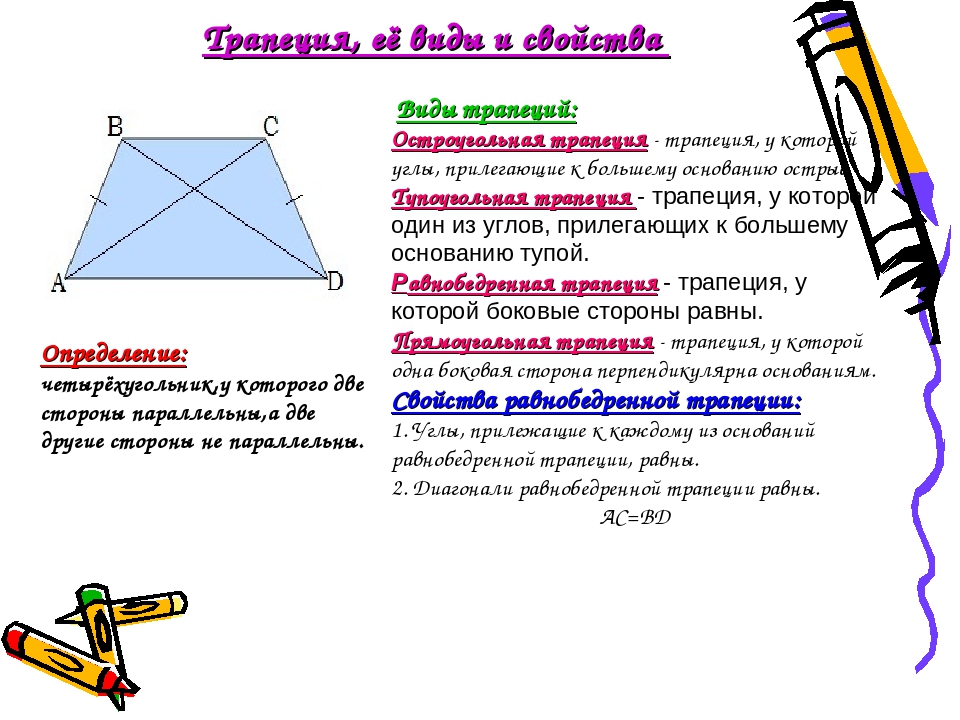

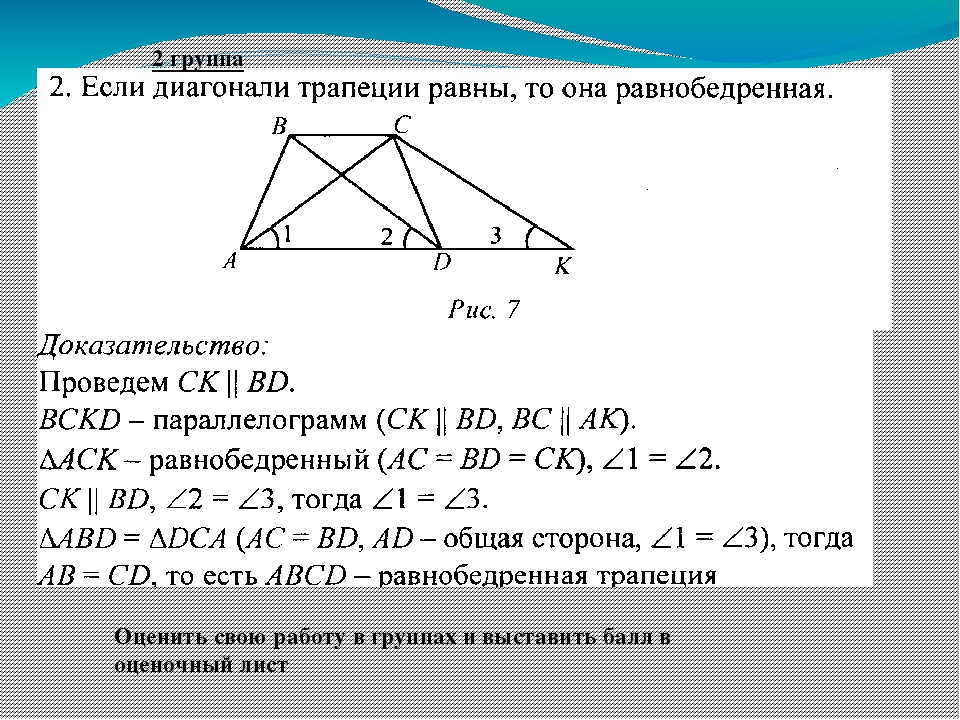 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
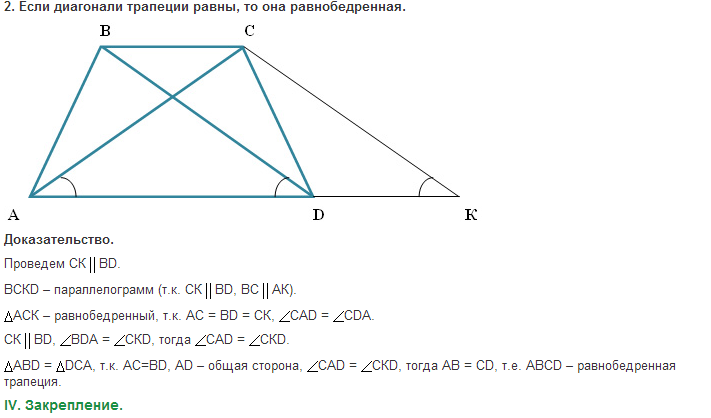 д.
д.