В прямоугольной трапеции диагонали взаимно. Диагонали трапеции
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥ DF как основания трапеции, BD∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.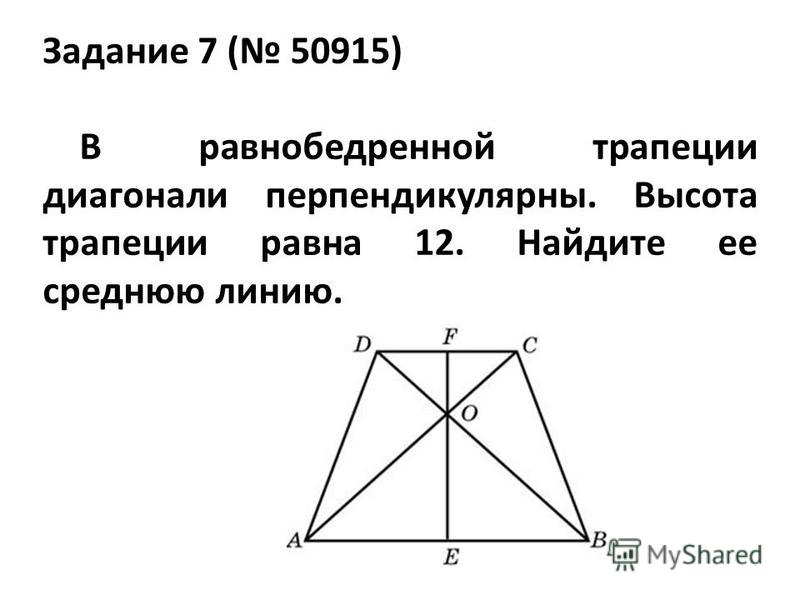 х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.
Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см.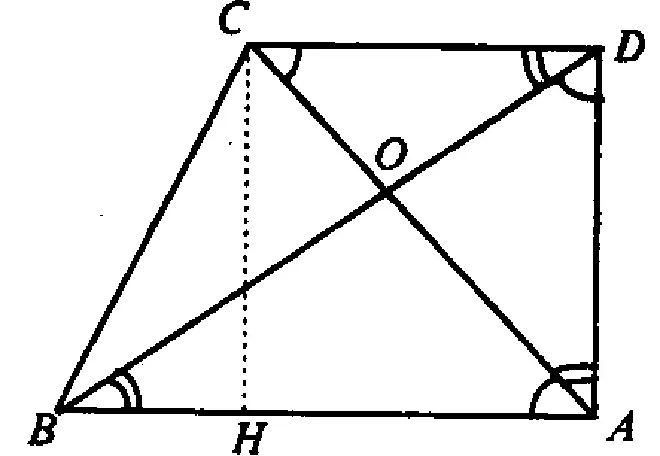 Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.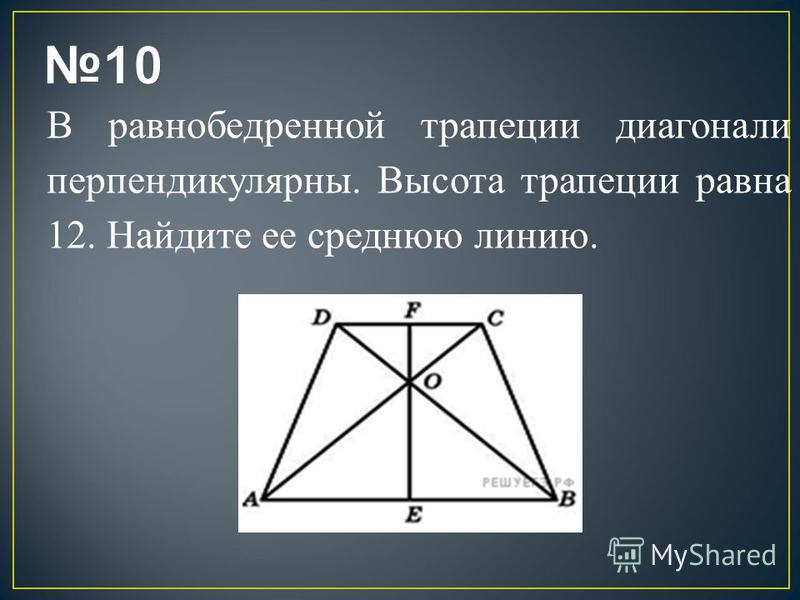
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.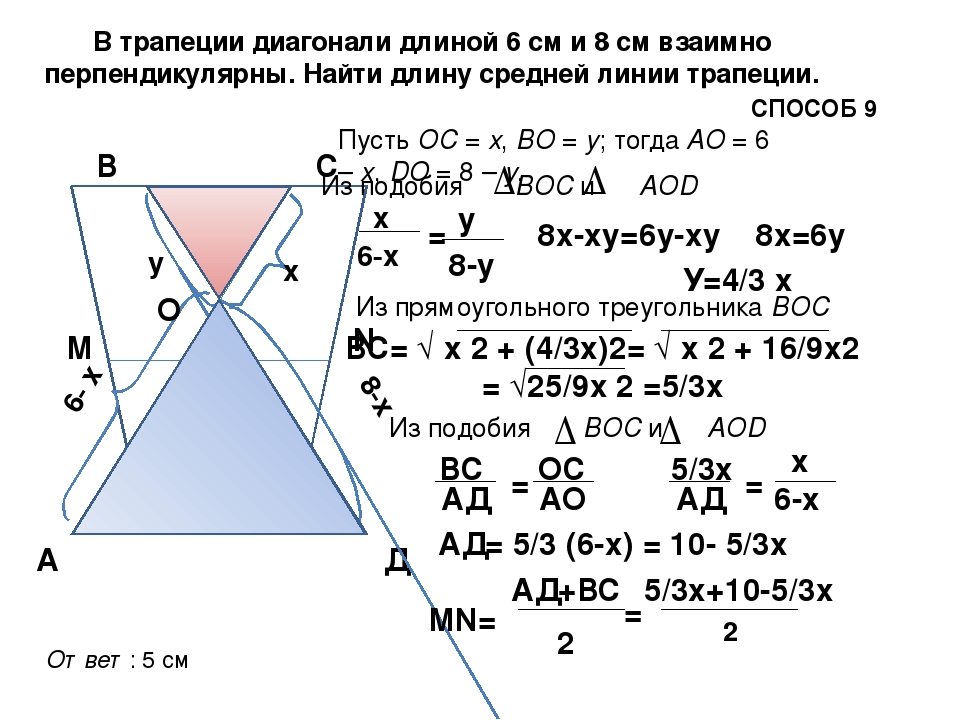
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
В равнобедренной трапеции диагонали перпендикулярны
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
При чём:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB.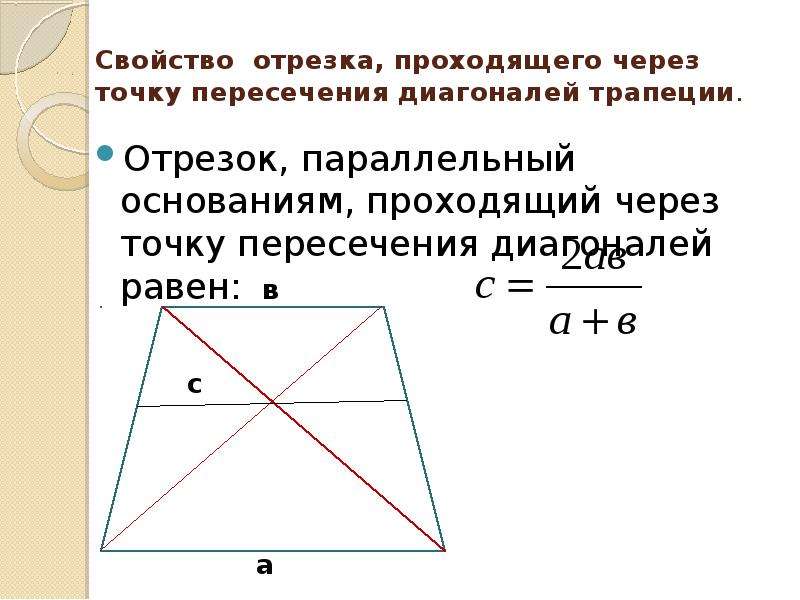 Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного вычисления. Но, уверен, представленное подробное объяснение многим необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
Ответ: 12
Другие статьи из категории:
Планиметрия Трапеция
- Три стороны описанного около окружности четырехугольника
- ABCD трапеция, найдите среднюю линию
- Основания трапеции равны 3 и 2
- Большее основание в равнобедренной трапеции
Диагональ в равнобедренной трапеции: Все формулы диагонали равнобедренной трапеции — ЭкоДом: Дом своими руками
Все формулы диагонали равнобедренной трапеции
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
Формулы длины диагонали равнобедренной трапеции через ее стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
Формула диагонали трапеции (d ):
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α, β — углы трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
3. Формула длины диагонали равнобедренной трапеции
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через высоту и стороны
Формулы длины диагонали трапеции через высоту и стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
h — высота трапеции
α — угол при нижнем основании
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Как найти диагональ равнобедренной трапеции
Трапеция, в которой длины боковых сторон равны, а основания параллельны, называется равнобедренной или равнобокой. Обе диагонали в такой геометрической фигуре имеют одинаковую длину, которую в зависимости от известных параметров трапеции можно рассчитать разными способами.
Если известны длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C), то для определения длин диагоналей (D) можно воспользоваться тем, что сумма квадратов длин всех сторон равна сумме квадратов длин диагоналей.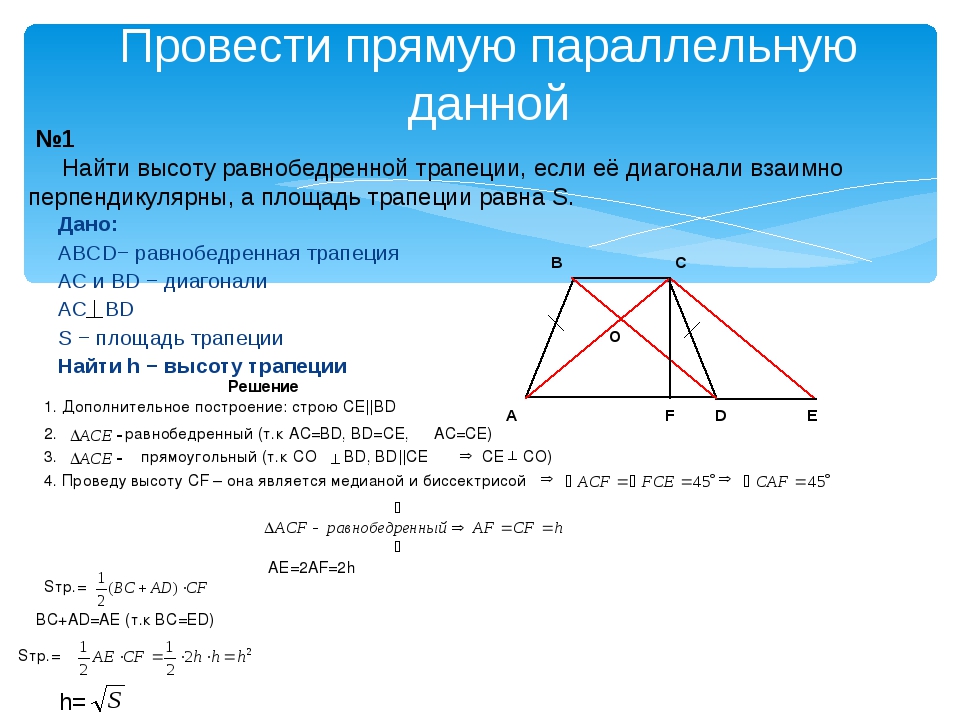 Это свойство вытекает из того факта, что каждая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Так как боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это свойство можно записать в таком виде: A² + B² + 2C² = 2D². Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A² + B²)/2 + C²).
Это свойство вытекает из того факта, что каждая из диагоналей трапеции является гипотенузой треугольника, катетами в котором служат боковая сторона и основание. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Так как боковые стороны в равнобедренной трапеции равны, как и ее диагонали, то это свойство можно записать в таком виде: A² + B² + 2C² = 2D². Из этой формулы вытекает, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенной с квадратом длины боковой стороны: D = √((A² + B²)/2 + C²).
Если длины сторон не известны, но есть длина средней линии (L) и высота (H) равнобедренной трапеции, то длину диагонали (D) тоже вычислить несложно. Так как длина средней линии равна полусумме оснований трапеции, то это дает возможность найти длину отрезка между точкой на большем основании, в которую опущена высота, и вершиной, прилегающей к этому основанию. В равнобедренной трапеции длина этого отрезка будет совпадать с длиной средней линии. Так как диагональ замыкает этот отрезок и высоту трапеции в прямоугольный треугольник, то вычислить ее длину не составит труда. Например, по той же самой теореме Пифагора она будет равна квадратному корню из суммы квадратов высоты и средней линии: D=√(L² + H²).
Так как диагональ замыкает этот отрезок и высоту трапеции в прямоугольный треугольник, то вычислить ее длину не составит труда. Например, по той же самой теореме Пифагора она будет равна квадратному корню из суммы квадратов высоты и средней линии: D=√(L² + H²).
Если известны длины обоих оснований равнобедренной трапеции (A и B) и ее высота (H), то, как и в предыдущем случае, можно вычислить длину отрезка между точкой, опущенной на большую сторону высоты и прилегающей к ней вершиной. Формула из предыдущего шага трансформируется к такому виду: D=√((A + B)²/4 + H²).
Диагонали равнобедренной трапеции Калькулятор | Диагонали равнобедренной трапеции Расчет
Диагональ равнобедренной трапеции с заданной площадью и углом между диагоналями
Диагональ равнобедренной трапеции с учетом высоты и основания
Диагональ равнобедренной трапеции с учетом высоты и среднего сегмента
Диагональ равнобедренной трапеции с учетом высоты, основания b и угла при основании
Диагональ равнобедренной трапеции с учетом высоты, основания и угла между диагоналями
Диагональ равнобедренной трапеции с учетом высоты, среднего сегмента и угла между диагоналями
Диагональ равнобедренной трапеции с учетом высоты, сторон и оснований
Диагональ равнобедренной трапеции с учетом основания a, боковой стороны c и угла A между ними
Диагональ равнобедренной трапеции с учетом основания a, боковой стороны c и угла B между ними
Диагональ равнобедренной трапеции с учетом основания b, боковой стороны c и угла A между ними
Диагональ равнобедренной трапеции с учетом основания b, боковой стороны c и угла B между ними
Диагональ равнобедренной трапеции со всех сторон
Диагональ трапеции с учетом высоты, основания a и угла при основании
Диагональ — равнобедренная трапеция — Большая Энциклопедия Нефти и Газа, статья, страница 1
Диагональ — равнобедренная трапеция
Cтраница 1
Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции.
Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции.
[1]
Диагонали равнобедренной трапеции взаимно перпендикулярны. Докажите, что средняя линия этой трапеции равна ее высоте.
[2]
Диагональ равнобедренной трапеции является биссектрисой ее острого угла и делит среднюю линию трапеции на отрезки длиной 7 5 и 12 5 см. Вычислите длины сторон трапеции.
[3]
Диагонали равнобедренной трапеции взаимно перпендикулярны.
[4]
Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции.
[5]
Найти длины боковой стороны и диагонали равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
[6]
Найти длины боковой стороны и диагонали равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
[7]
Найти длины боковой стороны и диагонали равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
[8]
Доказать, что прямая, определяемая точкой пересечения диагоналей равнобедренной трапеции и точкой пересечения продолжений боковых сторон, перпендикулярна основаниям трапеции и делит их пополам.
[9]
Страницы:
1
| ФГКОУ «МКК «Пансион воспитанниц МО РФ» «УТВЕРЖДАЮ» Руководитель отдельной дисциплины (математика, информатика и ИКТ) Ю. В. Крылова _____________ «___» _____________ 2015 г. «Трапеция и ее свойства» Методическая разработка преподавателя математики Шаталиной Елены Дмитриевны
Москва 2015 год Оглавление Введение 2
. . Список используемой литературы Приложение
Введение Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими. Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии. Трапеция.
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны. Если боковые стороны равны, трапеция называется равнобедренной. Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции. 2. Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны. 4. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е.
10. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Е 4. Свойства вписанных и описанных трапеций
2.Если в равнобедренную трапецию можно вписать окружность, то сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции. 4. Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
1 5. Среднее геометрическое
6.Свойства произвольной трапеции 1. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой. 2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади). 6.Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
7 8. 9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам. 7. Признаки трапеции
8. 1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции. 2. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание. 3. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции. 4 5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию. 6 7.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции. 8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 9. Биссектриса угла трапеции отсекает равнобедренный треугольник. 1 11. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам. 12. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники. 13. Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания. 9. Площадь трапеции 1. Площадь трапеции равна произведению полусуммы оснований на высоту S = ½(a + b)•h или П 2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
10. Заключение ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ? Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться. Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции. Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина. Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас. Список используемой литературы
Приложение 1.Доказательство некоторых свойств трапеции. 1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L. Доказать, что если основания трапеции равны а и b, то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство Пусть О — точка пересечения диагоналей, AD = а, ВС = b. Прямая KL параллельна основанию AD, следовательно, KО║ AD, треугольники ВKО и BAD подобны, поэтому ( 1 )
( 2 ) Подставим ( 2 ) в ( 1 ), получим KO = Аналогично LO = Тогда K L= KO + LO =
Д K окажем, что эта прямая делит основания пополам. Обозначим ВМ = х, МС = у, AN = и, ND = v. Имеем: ∆ВКМ ~ ∆AKN → x B C Y ∆MКC ~ ∆NKD → → O v u N D ∆BMO ∆DNO ∆CMO ∆ANO поэтому . Перемножая полученные равенства, получим , откуда следует x=y, но тогда и u = v.
3. Задачи по теме «Трапеция» повышенной сложности. Садовничий Ю.В. «Математика. Подготовка к ЕГЭ», Москва, ИЛЕКСА, 2011, стр. 252. 1 . В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найти площадь трапеции. Ответ: S = 6. 2. Периметр равнобочной трапеции, описанной около круга, равен р. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен ɑ. psina 3. Длины боковых сторон трапеции равны 3 и 5. Известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно 5/11. Найти длины оснований трапеции. Ответ: 1и 7.
Ответ: S= 3ab В трапеции PQRS длина основания QR равна 10, длина диагонали QS равна 19, а величина угла QSP равна 30°. Выяснить, что больше, длина основания QR или длина стороны RS. Ответ: RS > QR.
Ответ: S=90√3. Иванов А.А., Иванов А.П., Математика: Пособие для подготовки к ЕГЭ и поступлению в вузы. – М.: Издательство МФТИ, 2003, стр. 238.. 12. Площадь прямоугольной трапеции равна S, острый угол равен а. Найти высоту трапеции, если ее меньшая диагональ равна большему оснозанию. [√2Sctg а]
[arccos(l — 1/к), π — arccos(l — 1/к), к > 1]
[√Stg(½ ɑ)]
4. Проверочный тест по теме «Трапеция» В трапеции, имеющей прямой угол, основания равны 5 и 11, а большая диагональ √185. Площадь трапеции составляет В трапеции боковые стороны и меньшее основание равны Ь, а острый угол вдвое меньше тупого. 151 в равнобедренной трапеции, описанной около окружности радиуса 5 м и имеющей основание 20 м, другое основание равно Меньшее основание трапеции, вписанной в окружность, втрое меньше большего, которое является диаметром окружности.25j В трапеции с диагональю 20, высотой 12 и площадью 150 вторая диагональ равна 29j Равнобедренная трапеция с острым углом а описана около окруж- ности. Отношение ее большего основания к меньшему равно Зо| В описанной около круга равнобочной трапеции расстояние от центра круга до дальней вершины трапеции втрое больше, чем до ближней. Тангенс острого угла трапецииравен Достарыңызбен бөлісу: |
Геометрия Диагональ равнобокой трапеции является биссектрисой ее острого угла и перпендикулярна
Задача: диагональ равнобокой трапеции является биссектрисой её острого угла и перпендикулярна боковой стороне. Найдите площадь трапеции, если её меньшее основание равно а.
Решение:
Пусть у нас трапеция АВСД, АВ = СД, АС — биссектриса угла А, угол АСД — прямой.
Если биссектриса острого угла трапеции является его диагональю, то меньшее основание трапеции равно её боковой стороне.
Имеем АВ = ВС =СД = а.
Опустим перпендикуляр СЕ из точки С на АД.
При этом получили 2 подобных треугольника: АСЕ и ЕСД.
Угол САЕ равен углу ДСЕ как взаимно перпендикулярные.
Угол А равен углу Д (как углы при основании равнобедренной трапеции).
Поэтому угол ДСЕ равен половине угла Д.
Имеем: 90° =(1/2)Д+Д = (3/2)Д,
Отсюда угол Д = 90*2/3 = 180/3 = 60°.
Тогда ЕД = а/2, а основание АД = а+2(а/2) = 2а.
Высота СЕ = а*sin 60° = a√3/2.
Площадь S трапеции равна:
S = ((a+2a)/2)*(a√3/2) = (3a/2)*(a√3/2) = (3a²√3)/4.
То есть данная трапеция равна площади трёх равносторонних треугольников со стороной а.
Ответ: площадь трапеции = (3a²√3)/4
Дополнительная информация по теме трапеции и биссектрисы
Если диагональ равнобедренной трапеции перпендикулярна ее боковой стороне и диагональ — биссектриса угла трапеции, то что можно сказать о свойствах такой трапеции?
Если диагональ трапеции является биссектрисой ее угла, то боковая сторона трапеции равна одному из оснований трапеции.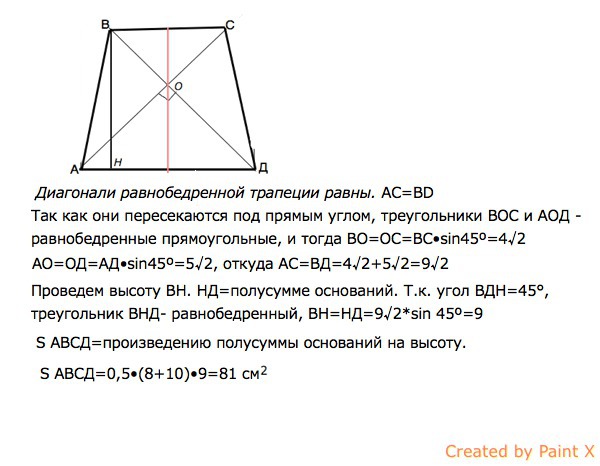
Когда диагональ трапеции перпендикулярна боковой стороне, делить пополам тупой угол она не может (если один угол прямой, то и второй должен быть прямым, что невозможно).
Если диагональ равнобедренной трапеции перпендикулярна боковой стороне и делит острый угол трапеции пополам, то:
1) диагональ разбивает трапецию на два треугольника: один — равнобедренный, другой — прямоугольный;
2) углы трапеции равны 60º и 120º;
3) большее основание трапеции в два раза больше меньшего основания и её боковых сторон;
4) высота трапеции равна половине её диагонали.
Дано: ABCD- трапеция,
AD ∥ BC, AB=CD,
AC — биссектриса ∠BAD.
Доказать:
1) Треугольник ABC — равнобедренный, треугольник ACD — прямоугольный;
2) ∠BAC=60º, ∠ABC=120º;
3) AD=2BC, AD=2CD;
4) высота трапеции равна половине AC.
Доказательство:
1) Поскольку
то треугольник ACD — прямоугольный.
∠BAC=∠DAC (так как AC — биссектриса ∠BAD по условию).
∠BCA=∠DAC (как внутренние накрест лежащие при AD ∥ BC и секущей AC).
Отсюда, ∠BAC=∠BCA.
Следовательно, треугольник ABC — равнобедренный с основанием AC (по признаку)
и AB=BF.
2) Пусть ∠BAC=∠DAC=∠BCA=xº.
∠BAD+∠BCD=180º (как противолежащие углы равнобедренной трапеции).
Следовательно, ∠BAC+∠DAC+∠BCA+∠ACD=180º.
Составляем уравнение:x+x+x+90=180, откуда x=30.
Таким образом, ∠BAC=∠DAC=∠BCA=30º, ∠BAD=∠BAC+∠DAC=60º.
∠BAD+∠ABC=180º (как внутренние односторонние при AD ∥ BC и секущей AB), откуда
∠ABC=120º.
3) В прямоугольном треугольнике ACD CD — катет, лежащий напротив угла в 30 градусов, следовательно,
AD=2CD, а так как CD=BC, то AD=2BC.
4) Опустим из вершины C высоту CF,
В прямоугольном треугольнике ACF CF — катет, лежащий напротив угла в 30º. Поэтому
Что и требовалось доказать.
* 5 * 5 * 5 * 5 * 5 *
Удачи тебе на экзаменах! У тебя всё получится — мы в тебя верим!
Поделись этой информацией с помощью кнопок ниже (облегчи учёбу другим ученикам, и будет тебе плюс в карму!)
Урок 4.
 трапеция — Геометрия — 8 класс
трапеция — Геометрия — 8 классЧетырёхугольник, две стороны которого параллельны, а две другие не параллельны, называется трапецией. Параллельные стороны называются основаниями трапеции, непараллельные стороны – боковыми сторонами.
Если один из углов трапеции прямой, то она называется прямоугольной. Если боковые стороны трапеции равны, то она называется равнобедренной трапецией (равнобокой).
Сформулируем и докажем свойства равнобедренной трапеции:
Свойство первое: в равнобедренной трапеции углы при каждом основании равны.
Для доказательства проведём отрезок CK, параллельный AB.
CK || AB, ABCK – параллелограмм (стороны попарно параллельны), значит AB = CK, но AB = CD (трапеция равнобедренная), значит CK = CD, треугольник KCD – равнобедренный,
По свойству равнобедренного треугольника ∠1 = ∠2.
∠2 = ∠3 (соответственные при секущей AD и параллельных AB и CK). Следовательно, ∠1 = ∠3.
Следовательно, ∠1 = ∠3.
ABC = 180° − ∠3 = 180° − ∠1 = ∠BCD.
Второе свойство равнобедренной трапеции: диагонали равнобедренной трапеции равны.
Дано: ABCD – равнобедренная трапеция, BC || AD
Доказать: AC = BD.
Для доказательства рассмотрим треугольники ABC и DCB. Треугольники ABC и DCB равны (AB = CD, BC – общая сторона, ∠ABC = ∠DCA). Следовательно, AC = BD.
Теоремы, обратные свойствам равнобедренной трапеции, также верны. Это признаки равнобедренной трапеции.
Признак первый: если углы при основании трапеции равны, то трапеция является равнобедренной.
Дано: ABCD – трапеция, BC || AD
∠BAC = ∠CDA
Доказать: ABCD – равнобедренная трапеция
Для доказательства проведем отрезок CK, параллельный AB.
Доказательство:
CK || AB, следовательно ABCK – параллелограмм, тогда AB = CK, ∠A = ∠CKD.
Получится равнобедренный треугольник CKD (∠A = ∠CKD и ∠A = ∠CDA), поэтому
CK = CD и AB = CK = CD. Следовательно, ABCD – равнобедренная трапеция.
Второй признак: если диагонали трапеции равны, то трапеция равнобедренная.
Дано: ABCD –трапеция, BC || AD
AC = BD
Доказать: ABCD – равнобедренная трапеция
Составим план доказательства второго признака, опираясь на который можно провести доказательство самостоятельно.
Проведем отрезок CK, параллельный BD.
План доказательства
- CK || BD
- Доказать, что BCKD – параллелограмм.
- Доказать, что треугольник ACK – равнобедренный.
- Найти равные углы.
- Доказать равенство треугольников ABD и DCA.
- Доказать равенство сторон AB и CD.
- Сделать вывод.
Диагонали равнобедренной трапеции
- Детали
Написал Администратор
-
-
1.Диагональ равнобедренной трапеции, если известны стороны (ноги и основания)
, — базы
— нога (боковая сторона)
— диагональ
Найдите диагональ равнобедренной трапеции со всех сторон ( ):
2. Диагональ равнобедренной трапеции по закону косинусов
, — базы
— нога (боковая сторона)
— диагональ
, — уголки у основания
Вычислите диагональ трапеции, если заданы основание, боковая сторона и угол между ними ( ):
3. Диагональ равнобедренной трапеции, если известны высота, средний сегмент, площадь трапеции и угол между диагоналями
, — базы
— диагональ
, — углы между диагоналями
— высота
— средний сегмент
— площадь
Вычислите диагональ трапеции, если заданы высота, средний сегмент, площадь трапеции и угол между диагоналями ( ):
* Верно в данном случае:
4.Диагональ равнобедренной трапеции, если известны высота, стороны и угол при основании
— нижнее основание
— основание верхнее
— нога (боковая сторона)
— диагональ
— уголок у основания
— высота
Вычислите диагональ трапеции, если заданы высота, стороны и угол в основании ( ):
Как найти диагональ трапеции
- Детали
Написал Администратор
-
-
1. Диагонали трапеции, если известны стороны и углы при основании
, — базы
, — ножки
, — уголки у основания
, — диагонали
Найдите диагональ трапеции, используя закон косинусов ( ):
Найдите диагональ трапеции, если заданы все четыре стороны ( ):
2.Диагонали трапеции по высоте
, — базы
, — ножки
, — уголки у основания
, — диагонали
— высота
Найдите диагональ трапеции, используя высоту, углы у основания и сторон ( ):
3. Диагонали трапеции, если вам известна другая диагональ, угол между диагоналями и высотой, площадью или средним сегментом
, — базы
, — диагонали
, — углы между диагоналями
— высота
— средний сегмент
— площадь трапеции
Найдите диагональ трапеции, если задана другая диагональ, угол между диагоналями и высотой, площадью или средним сегментом.
( ):
* Верно в данном случае:
4. Диагонали трапеции по формуле суммы квадратов диагоналей
— нижнее основание
— основание верхнее
, — ножки
, — диагонали
Формула суммы квадратов диагоналей:
Найдите диагональ трапеции, используя формулу суммы квадратов диагоналей ( ):
Диагонали равнобедренной трапеции
Это был день перед тестированием на полигонах, и я подумал, что написание доказательства и последующий отзыв о доказательстве другой команды могут быть полезны.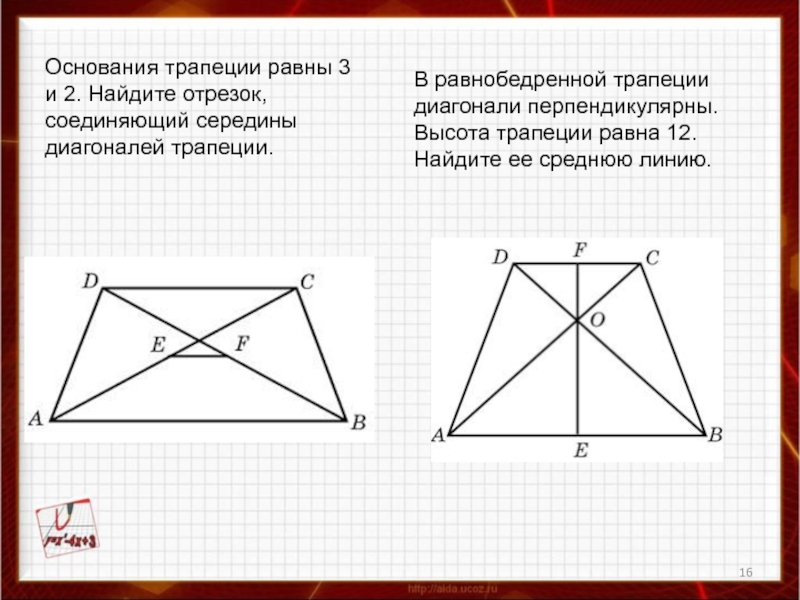
Студенты несколько минут работали в одиночестве, думая о том, что им было дано и что могло подразумеваться. Затем они вместе со своей командой обсудили свои идеи и начали планировать доказательство.
Некоторым было положено хорошее начало.
Некоторые, очевидно, практиковали в поисках и использовании структуры .
Некоторые застряли.
Я поговорил с несколькими группами, выслушал их план и задал несколько вопросов, чтобы они разобрались.
И затем я достал цветную бумагу, на которой написал групповое доказательство.
Время шло, но я подумал, что они наверняка смогут обменяться доказательствами с другой командой для получения обратной связи в течение нескольких минут.
Я разговаривал с другой группой. Они отражали ∆ABC относительно линии AC.
Каким будет изображение ∆ABC относительно линии AC?
Ответ? ∆ACD.
Конечно, это неправильно. Кажется настолько очевидным, что ∆ABC не конгруэнтно ∆ACD. И мне также интересно, как это помогает нам доказать, что AC = BD, поскольку BD не входит ни в один из этих треугольников. Но вот где эта команда студентов. Теперь у меня есть возможность, , поддержать их продуктивную борьбу, , или я могу остановить продуктивную борьбу на ее пути, дав им свое объяснение.
И мне также интересно, как это помогает нам доказать, что AC = BD, поскольку BD не входит ни в один из этих треугольников. Но вот где эта команда студентов. Теперь у меня есть возможность, , поддержать их продуктивную борьбу, , или я могу остановить продуктивную борьбу на ее пути, дав им свое объяснение.
Мой выбор? Ножницы. И бумага. И еще раз.
Что произойдет, если вы отразите ∆ABD относительно линии AC?
Ой! Треугольники не совпадают.
Так есть ли совпадающие треугольники, которые могут привести нас к диагоналям?
∆ABC конгруэнтно ∆BAD.
Откуда ты знаешь?
Отражение.
О чем?
Настоящий карандаш!
Так что же важного в линии, проводимой карандашом?
Это линия симметрии трапеции.
Проходит через средние точки.
(Один из членов команды использовал программу динамической геометрии, чтобы отразить ∆ABC посреди нашего разговора, но у меня нет фотографий ее работы.)
Итак, план состоял в том, чтобы команда написала свои корректуры на цветной бумаге, а затем обменялась с другими командами для получения отзывов. Отличная идея, правда? Так как же действовать, когда осталось 15 минут? Действовать так, как планировалось, и позволить им высказывать свое мнение без обсуждения всего класса? Или провести обсуждение в классе, чтобы связать работу студентов? Потому что, как выяснилось, никакие две команды не доказали совпадение диагоналей одинаково.Я выбрал второе.
Отличная идея, правда? Так как же действовать, когда осталось 15 минут? Действовать так, как планировалось, и позволить им высказывать свое мнение без обсуждения всего класса? Или провести обсуждение в классе, чтобы связать работу студентов? Потому что, как выяснилось, никакие две команды не доказали совпадение диагоналей одинаково.Я выбрал второе.
Я попросил первую команду поделиться своей работой.
Их доказательство требует доработки. Но у них есть хорошая идея.
Они доказали ∆AMD≅∆BMC, что делает соответствующие стороны конгруэнтными, поэтому с помощью подстановки и постулата сложения сегментов мы можем показать, что диагонали конгруэнтны.
Затем я попросил команду рассказать, кто доказал ∆ABC≅∆BAD, используя отражение линии, которая содержит средние точки оснований.Их письменное доказательство тоже нуждается в доработке. Но у них была хорошая идея.
Другая команда доказала ∆ACD≅∆BDC.
Другая команда построила биссектрисы оснований. Поскольку основания параллельны, линия, перпендикулярная одному, будет перпендикулярна другому. Я не уверен, что они добрались до причины, по которой срединные перпендикуляры должны совпадать. Они могли бы использовать ∆AZD≅∆BZC, чтобы показать это. Вместо этого они использовали точку Z на обоих серединных перпендикулярах (они знают, что любая точка на серединном перпендикуляре сегмента равноудалена от конечных точек сегмента), чтобы обосновать, что ∆AZB и ∆DZC равнобедренные, и затем использовали добавление сегмента. Постулат и подстановка, чтобы показать, что диагонали совпадают.Не идеально. Но хорошее начало.
Поскольку основания параллельны, линия, перпендикулярная одному, будет перпендикулярна другому. Я не уверен, что они добрались до причины, по которой срединные перпендикуляры должны совпадать. Они могли бы использовать ∆AZD≅∆BZC, чтобы показать это. Вместо этого они использовали точку Z на обоих серединных перпендикулярах (они знают, что любая точка на серединном перпендикуляре сегмента равноудалена от конечных точек сегмента), чтобы обосновать, что ∆AZB и ∆DZC равнобедренные, и затем использовали добавление сегмента. Постулат и подстановка, чтобы показать, что диагонали совпадают.Не идеально. Но хорошее начало.
Обсуждение
Принципов действий NCTM по теме поддерживает продуктивную борьбу в изучении математики. В говорится: «Учителя иногда воспринимают разочарование учеников или отсутствие немедленных успехов как индикаторы того, что они каким-то образом не справились с учениками. В результате они бросаются «спасать» учеников, разбивая задачу на части и помогая ученикам шаг за шагом преодолевать трудности.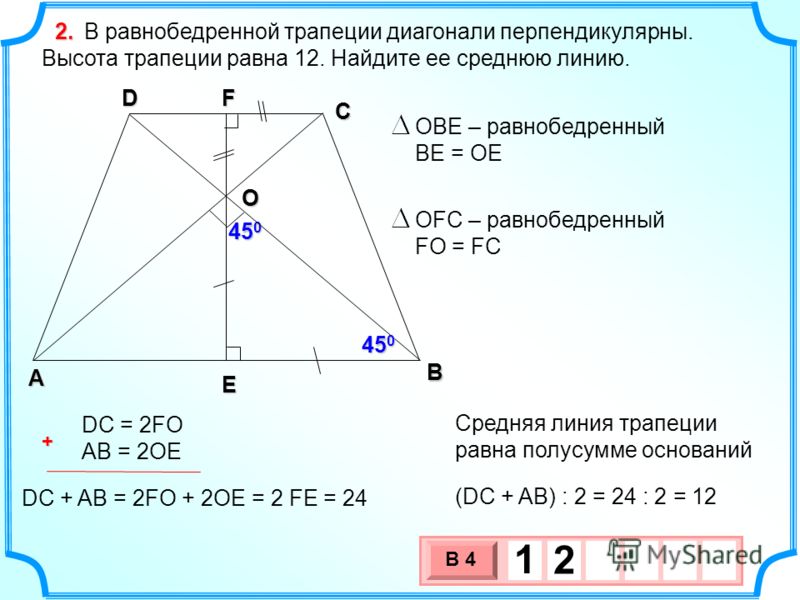 Несмотря на благие намерения, такое «спасение» подрывает усилия учащихся, снижает когнитивные требования к задаче и лишает учащихся возможности полностью погрузиться в понимание математики.”
Несмотря на благие намерения, такое «спасение» подрывает усилия учащихся, снижает когнитивные требования к задаче и лишает учащихся возможности полностью погрузиться в понимание математики.”
Итак, хотя я не спас своих учеников, мы так и не смогли создать образцового доказательства того, что диагонали равнобедренной трапеции совпадают. Узнали ли они что-нибудь о , разобраться в проблемах и упорно их решать ? Конечно. Этого достаточно?
Было бы полезно начать урок следующего года с этой студенческой работы? Или это убирает продуктивной борьбы ?
Неужели мы просто должны найти баланс между продуктивной борьбой и тем, как выглядит образцовая работа, которая на одних уроках легче, чем на других? Если так, то на этом уроке мне не удалось добиться этого баланса.Тем не менее, путешествие продолжается…
Нравится:
Нравится Загрузка …
Связанные
| 1D линия, круговая дуга, парабола, спираль, кривая Коха 2D Правильные многоугольники: Равносторонний треугольник, Квадрат, Пентагон, Шестиугольник, Гептагон, Восьмиугольник, Нонагон, Десятиугольник, Шестиугольник, Додекагон, Шестиугольник, N-угольник, Кольцо многоугольника Другие многоугольники: 90 510 круглых форм: 3D архимедова Solids: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: Круглые формы: 4D | Anzeige Расчеты на равнобедренной трапеции (или равнобедренной трапеции). Формулы: Длина стороны, диагональ, высота, радиус и периметр имеют одинаковые единицы измерения (например,г. метр), площадь равна этой единице в квадрате (например, квадратный метр). Anzeige Серединные перпендикуляры пересекаются в центре описанной окружности. Серединный перпендикуляр к двум параллельным сторонам является осью симметрии равнобедренной трапеции. серединный перпендикуляр и описанная окружность © Jumk. Anzeige |
РЕШЕНИЕ: Диагонали равнобедренной трапеции ар…
Стенограмма видео
Хорошо, это небольшая забавная задача, в которой мы имеем дело с равнобедренной трапецией, которую вы должны знать, что такое трапеция.На данный момент это четырехугольник, что означает, что есть четыре стороны, и две из них параллельны, что мы видим как основание Опера в верхнем основании. Хорошо. И это я видел Seles, что означает, что если вы гипотетически разделите его посередине, но это идеальная линия посередине, у нас есть две симметричные стороны с каждой стороны. Это означает, что эти два угла здесь, по сути, одинаковы и с легкостью одинаковы. Это то, что мы знали бы, если бы действительно, ммм, продолжали все вычислять, потому что именно это делает линии идеальным, ммм, зеркальным отображением друг друга.Так что давайте избавимся от этого крайнего срока. Это было просто доказательством того, что это равнобедренная трапеция. Так что я просто напишу. Цена колеблется. Итак, мы знаем это, и именно так я смог примерно проиллюстрировать сторону ловушки ниже, нам сказали несколько вещей об их различных значениях, сказали, что их, ммм, диагонали Что правильно, D равно 17, и есть две диагонали в форме трапеции. Это будет от одного угла до противоположного угла на другой базе. Итак, представьте, что это прямая линия.Вероятно, это не так. Это отлично. Это просто для иллюстрации. Итак, эти черные линии 17 и общей длины, а затем нам говорят, что высота равна восьми. Так что это будет, если вы сделаете перпендикулярный угол. Так что сделайте прямой угол. От верхнего основания основания Лауры будет, мм, 88 Мы не знаем. На самом деле это не имеет значения. Сейчас мы просто называем это единицами. Значит, восемь. Коротышка, любая из этих пунктирных красных линий. Вы думаете об этом как о высоте, если она перпендикулярна.Так что пока для создания прямых углов. Так что я просто избавлюсь от них. Не хочу, чтобы здесь меня опережали слишком много беспорядка на треугольнике или трапеции.
Цена колеблется. Итак, мы знаем это, и именно так я смог примерно проиллюстрировать сторону ловушки ниже, нам сказали несколько вещей об их различных значениях, сказали, что их, ммм, диагонали Что правильно, D равно 17, и есть две диагонали в форме трапеции. Это будет от одного угла до противоположного угла на другой базе. Итак, представьте, что это прямая линия.Вероятно, это не так. Это отлично. Это просто для иллюстрации. Итак, эти черные линии 17 и общей длины, а затем нам говорят, что высота равна восьми. Так что это будет, если вы сделаете перпендикулярный угол. Так что сделайте прямой угол. От верхнего основания основания Лауры будет, мм, 88 Мы не знаем. На самом деле это не имеет значения. Сейчас мы просто называем это единицами. Значит, восемь. Коротышка, любая из этих пунктирных красных линий. Вы думаете об этом как о высоте, если она перпендикулярна.Так что пока для создания прямых углов. Так что я просто избавлюсь от них. Не хочу, чтобы здесь меня опережали слишком много беспорядка на треугольнике или трапеции. А потом нам сказали, что верхние базы девять, которые, если вы посмотрите на верхнюю базу, я просто пересушу и посиню. Так что с оперным басом все в порядке, ты за верхний. Было девять. Хорошо, так замечательно. Итак, у нас есть эта информация, которая действительно полезна, и нам говорят найти периметр, который будет периметром всех сторон, вместе взятых.Вы думаете о периметре места преступления. Они установят границу вокруг места преступления. И это была бы куча разных линий, если бы вы ее нарисовали, и это был бы периметр. Так каков будет периметр? Итак, чтобы сделать это, нам нужно увидеть то, что нам нужно выяснить. Итак, вы знаете, что один из самых больших — девять, об этом сказали в начале задачи. Это верхняя база. Итак, нам нужно найти сторону, эту сторону, а затем эту сторону, чтобы мы могли сложить их все вместе.Кажется немного пугающим, но на самом деле это действительно забавное упражнение, потому что нам нужно концептуализировать, как рисовать линии, чтобы образовывать треугольники, потому что тогда мы можем использовать сыворотку Пифагора, которая представляет собой квадрат плюс B в квадрате, равный C в квадрате.
А потом нам сказали, что верхние базы девять, которые, если вы посмотрите на верхнюю базу, я просто пересушу и посиню. Так что с оперным басом все в порядке, ты за верхний. Было девять. Хорошо, так замечательно. Итак, у нас есть эта информация, которая действительно полезна, и нам говорят найти периметр, который будет периметром всех сторон, вместе взятых.Вы думаете о периметре места преступления. Они установят границу вокруг места преступления. И это была бы куча разных линий, если бы вы ее нарисовали, и это был бы периметр. Так каков будет периметр? Итак, чтобы сделать это, нам нужно увидеть то, что нам нужно выяснить. Итак, вы знаете, что один из самых больших — девять, об этом сказали в начале задачи. Это верхняя база. Итак, нам нужно найти сторону, эту сторону, а затем эту сторону, чтобы мы могли сложить их все вместе.Кажется немного пугающим, но на самом деле это действительно забавное упражнение, потому что нам нужно концептуализировать, как рисовать линии, чтобы образовывать треугольники, потому что тогда мы можем использовать сыворотку Пифагора, которая представляет собой квадрат плюс B в квадрате, равный C в квадрате. Вы можете использовать это, чтобы найти а, привет, новости о горшке или недостающую сторону в треугольниках. И мы могли бы применить к трапеции. Так как же нарисовать треугольники? Опять ремешок? Право на треугольники? Что ж, мы могли бы сделать это, нарисовав высоту в разных местах, потому что это сделает ее прямыми углами.Итак, первое место, где я бы нарисовал треугольник, это прямо здесь или на другой стороне. Это не имеет значения здесь или здесь снова. Давайте представим эти воздушные прямые углы, потому что это ключ, потому что вы только что нарисовали треугольник, и это очень ценно. Как только мы сможем осмыслить, как решить эту проблему, я просто нарисую отдельно треугольник, который я только что сделал, что-то вроде этого, где странность шумихи, которая противоположна прямому углу. Это диагональ, которую мы видим здесь черным цветом. Это диагональ. Нам сказали, что это 17.Сторона справа — это высота, равная восьми. Итак, теперь у нас есть то, что нам нужно решить для одной стороны, верно? Давайте просто назовем это здесь.
Вы можете использовать это, чтобы найти а, привет, новости о горшке или недостающую сторону в треугольниках. И мы могли бы применить к трапеции. Так как же нарисовать треугольники? Опять ремешок? Право на треугольники? Что ж, мы могли бы сделать это, нарисовав высоту в разных местах, потому что это сделает ее прямыми углами.Итак, первое место, где я бы нарисовал треугольник, это прямо здесь или на другой стороне. Это не имеет значения здесь или здесь снова. Давайте представим эти воздушные прямые углы, потому что это ключ, потому что вы только что нарисовали треугольник, и это очень ценно. Как только мы сможем осмыслить, как решить эту проблему, я просто нарисую отдельно треугольник, который я только что сделал, что-то вроде этого, где странность шумихи, которая противоположна прямому углу. Это диагональ, которую мы видим здесь черным цветом. Это диагональ. Нам сказали, что это 17.Сторона справа — это высота, равная восьми. Итак, теперь у нас есть то, что нам нужно решить для одной стороны, верно? Давайте просто назовем это здесь. Так как же решить эту проблему? Итак, High Partners в формуле возведено в квадрат 17, а затем у нас это называется квадратом плюс восемь в квадрате, равным C в квадрате, поэтому я просто очень быстро вставлю математику, чтобы мы могли вычислить, чего не хватает. Сторона 17 в квадрате. Боже, я должен воткнуть это. 289 минус 64 269. Пытки 89. Приношу свои извинения. 289 минус 64. Потому что это результат возведения в квадрат 825 в квадрате до 25.Будет 15. Так что я просто подключаю его к калькулятору. Вы могли бы сделать то же самое. Просто убедитесь, что вы уравняли эти значения. Вычтите 64, чтобы получить само по себе, возводит его в квадрат, потому что это значение квадрата. Это весело. К черту это. Итак, это 15, Итак, это значение 15, что прекрасно. Итак, почему это так полезно? Во-первых, потому что мы нашли одну из сторон, так что это очень полезно. О, но мы не нашли всю сторону трапеции, потому что у нас все еще есть эта часть, о которой мы не знаем.Так как же решить эту проблему? Ну, мы знаем, что верхняя база — девять.
Так как же решить эту проблему? Итак, High Partners в формуле возведено в квадрат 17, а затем у нас это называется квадратом плюс восемь в квадрате, равным C в квадрате, поэтому я просто очень быстро вставлю математику, чтобы мы могли вычислить, чего не хватает. Сторона 17 в квадрате. Боже, я должен воткнуть это. 289 минус 64 269. Пытки 89. Приношу свои извинения. 289 минус 64. Потому что это результат возведения в квадрат 825 в квадрате до 25.Будет 15. Так что я просто подключаю его к калькулятору. Вы могли бы сделать то же самое. Просто убедитесь, что вы уравняли эти значения. Вычтите 64, чтобы получить само по себе, возводит его в квадрат, потому что это значение квадрата. Это весело. К черту это. Итак, это 15, Итак, это значение 15, что прекрасно. Итак, почему это так полезно? Во-первых, потому что мы нашли одну из сторон, так что это очень полезно. О, но мы не нашли всю сторону трапеции, потому что у нас все еще есть эта часть, о которой мы не знаем.Так как же решить эту проблему? Ну, мы знаем, что верхняя база — девять. Итак, если бы мы нарисовали этот квадрат, потому что мы сделали квадрат, если вы очень внимательно посмотрите на высоту, у нас здесь девять, а затем у нас есть стороны, или это не квадрат, это прямоугольник. Мои извинения. У нас восемь лет и восемь лет, потому что это были высоты. И внизу, у нас тоже должно быть девять. Но мы знаем, что вся эта длина, да, это то, что мы сейчас, давайте сделаем это очень ясно. Сожалею. Вы ведь знаете, что это порция 15, не так ли? Потому что здесь получается треугольник.Итак, вся эта часть — 15, хотя эта часть — девять. Итак, как мы решаем эту часть, это ключ. Итак, вам нужно сделать 15 минус девять, на которые мы должны дать ответ. Шесть. Правильно. Итак, это шесть. Это составляет шесть из 15 общей длины, потому что мы знаем эту часть прямоугольников девять, а это 15, всего шесть. Нам просто нужно добавить 6 к 15, потому что я снова высушу. Вот маленький прямоугольник. Это не соответствует масштабу. Это просто для удобства. Итак, если это девять, которые мы видели, значит, это шесть, то это тоже должно быть шесть.
Итак, если бы мы нарисовали этот квадрат, потому что мы сделали квадрат, если вы очень внимательно посмотрите на высоту, у нас здесь девять, а затем у нас есть стороны, или это не квадрат, это прямоугольник. Мои извинения. У нас восемь лет и восемь лет, потому что это были высоты. И внизу, у нас тоже должно быть девять. Но мы знаем, что вся эта длина, да, это то, что мы сейчас, давайте сделаем это очень ясно. Сожалею. Вы ведь знаете, что это порция 15, не так ли? Потому что здесь получается треугольник.Итак, вся эта часть — 15, хотя эта часть — девять. Итак, как мы решаем эту часть, это ключ. Итак, вам нужно сделать 15 минус девять, на которые мы должны дать ответ. Шесть. Правильно. Итак, это шесть. Это составляет шесть из 15 общей длины, потому что мы знаем эту часть прямоугольников девять, а это 15, всего шесть. Нам просто нужно добавить 6 к 15, потому что я снова высушу. Вот маленький прямоугольник. Это не соответствует масштабу. Это просто для удобства. Итак, если это девять, которые мы видели, значит, это шесть, то это тоже должно быть шесть. Вы знаете, что это 15 плюс шесть равняется 21. Прекрасно. Итак, нижняя часть трапеции — 21. Это показывает, что мой рисунок определенно не в масштабе, но это совершенно нормально. Итак, вы знаете, это 15. Так что просто немного очистим это и напишем, что новая длина стороны равна 21, так что мы почти у цели. Итак, теперь нам просто нужно найти этих двух, помимо того, что у нас есть здесь. Так как бы нам это сделать? Что ж, давайте попробуем это продумать. У нас есть еще какие-нибудь треугольники, которые мы могли бы составить? На самом деле, мы уже нарисовали один здесь, но давайте просто сделаем так, чтобы вам было легче это увидеть.Я поеду сюда. Итак, если вы посмотрите сюда, мы только что обнаружили, что два треугольника на конце ловушки решают правильно? У нас есть прямоугольник посередине. Все просто черным, чтобы было понятно. И мы выяснили, что из 21 этого числа девять. Это секс, и это секс. Итак, это будет шесть частей. Если мы посмотрим на эту часть трапеции, высота, которую мы уже знаем, равна восьми, поэтому нам просто нужно найти гипотенузу.
Вы знаете, что это 15 плюс шесть равняется 21. Прекрасно. Итак, нижняя часть трапеции — 21. Это показывает, что мой рисунок определенно не в масштабе, но это совершенно нормально. Итак, вы знаете, это 15. Так что просто немного очистим это и напишем, что новая длина стороны равна 21, так что мы почти у цели. Итак, теперь нам просто нужно найти этих двух, помимо того, что у нас есть здесь. Так как бы нам это сделать? Что ж, давайте попробуем это продумать. У нас есть еще какие-нибудь треугольники, которые мы могли бы составить? На самом деле, мы уже нарисовали один здесь, но давайте просто сделаем так, чтобы вам было легче это увидеть.Я поеду сюда. Итак, если вы посмотрите сюда, мы только что обнаружили, что два треугольника на конце ловушки решают правильно? У нас есть прямоугольник посередине. Все просто черным, чтобы было понятно. И мы выяснили, что из 21 этого числа девять. Это секс, и это секс. Итак, это будет шесть частей. Если мы посмотрим на эту часть трапеции, высота, которую мы уже знаем, равна восьми, поэтому нам просто нужно найти гипотенузу. Таким образом, квадрат плюс B в квадрате или квадрат плюс B в квадрате равняется C в квадрате.Сожалею. Так что давайте просто сделаем это в моей голове очень быстро, потому что эти числа легко возвести в квадрат. Итак, 36 плюс 64 равно C в квадрате, и у меня уже кружится голова, потому что это очень легко решить. 36 плюс 64 равняются 100 из 100. Он равен C, который, как мы знаем, равен 10. Итак, 10 равняется C. 10 10. Сложите все. У нас 10 20 29 плюс 21 равно 50, так что я просто бросаю, чтобы было легче, скажем, 10 плюс 10 плюс 21 плюс девять равно 50. Так что это было действительно весело. Проблема. Это весело, потому что формулы просты в понятиях просты, но их применение.Вы должны обладать некоторой находчивостью, чтобы знать, где было бы полезно рисовать треугольники и что вы можете обнаружить и извлечь из каждой новой вещи. Это выходит из уравнения, верно? Сожалею. Требует немного нестандартной головоломки, решения проблем и понимания геометрии. Так что это забавное маленькое упражнение, на мой взгляд,
Таким образом, квадрат плюс B в квадрате или квадрат плюс B в квадрате равняется C в квадрате.Сожалею. Так что давайте просто сделаем это в моей голове очень быстро, потому что эти числа легко возвести в квадрат. Итак, 36 плюс 64 равно C в квадрате, и у меня уже кружится голова, потому что это очень легко решить. 36 плюс 64 равняются 100 из 100. Он равен C, который, как мы знаем, равен 10. Итак, 10 равняется C. 10 10. Сложите все. У нас 10 20 29 плюс 21 равно 50, так что я просто бросаю, чтобы было легче, скажем, 10 плюс 10 плюс 21 плюс девять равно 50. Так что это было действительно весело. Проблема. Это весело, потому что формулы просты в понятиях просты, но их применение.Вы должны обладать некоторой находчивостью, чтобы знать, где было бы полезно рисовать треугольники и что вы можете обнаружить и извлечь из каждой новой вещи. Это выходит из уравнения, верно? Сожалею. Требует немного нестандартной головоломки, решения проблем и понимания геометрии. Так что это забавное маленькое упражнение, на мой взгляд,
У равнобедренной трапеции длина диагонали 25 см и высота
, вам в первую очередь нужны базы. 2
2
U РЕБЯТА ИЩУТ ВОПРОСЫ ПО ОКОНЧАТЕЛЬНОМУ ТЕСТУ ПО РУССКОЙ МАТЕМАТИЧЕСКОМУ МАТЕМАТИЧЕСКОМУ МАТЕМАТИЮ ПОЗОР ВАМ
Эй, парень, я получил это 100
- 👍
- 👎
Imcool не круто
Вы знаете, что он прав
Как найти диагональ равнобедренной трапеции
Трапеция, у которой длины сторон равны, а основания параллельны, называется равнобедренной или равнобедренной.Обе диагонали в такой геометрической фигуре имеют одинаковую длину, которую в зависимости от известных параметров трапеции можно рассчитать по-разному.
Инструкция по эксплуатации
1
Если длины оснований равнобедренной трапеции (A и B) и длина ее боковой стороны (C) известны, то для определения длин диагоналей (D) можно использовать тот факт, что сумма квадраты длин всех сторон равны сумме квадратов длин диагоналей. Это свойство следует из того, что каждая из диагоналей трапеции является гипотенузой треугольника, в котором стороны и основание служат катетами. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Поскольку стороны равнобедренной трапеции равны, как и ее диагонали, это свойство можно записать следующим образом: A² + B² + 2C² = 2D². Из этой формулы следует, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенных квадратом длин сторон: D = √ ((A² + B² ) / 2 + C²).
Это свойство следует из того, что каждая из диагоналей трапеции является гипотенузой треугольника, в котором стороны и основание служат катетами. А согласно теореме Пифагора сумма квадратов длин катетов равна квадрату длины гипотенузы. Поскольку стороны равнобедренной трапеции равны, как и ее диагонали, это свойство можно записать следующим образом: A² + B² + 2C² = 2D². Из этой формулы следует, что длина диагонали равна квадратному корню из половины суммы квадратов длин оснований, сложенных квадратом длин сторон: D = √ ((A² + B² ) / 2 + C²).
2
Если длины сторон неизвестны, но есть длина средней линии (L) и высота (H) равнобедренной трапеции, то длину диагонали (D) также легко вычислить. Поскольку длина средней линии равна полусумме оснований трапеции, это позволяет найти длину отрезка между точкой на большем основании, на которой высота снижается, и вершиной, примыкающей к этому основанию. . У равнобедренной трапеции длина этого отрезка будет совпадать с длиной средней линии. Поскольку диагональ замыкает этот отрезок и высоту трапеции в прямоугольном треугольнике, вычислить ее длину не составит труда. Например, по той же теореме Пифагора он будет равен квадратному корню из суммы квадратов высоты и средней линии: D = √ (L² + H²).
Поскольку диагональ замыкает этот отрезок и высоту трапеции в прямоугольном треугольнике, вычислить ее длину не составит труда. Например, по той же теореме Пифагора он будет равен квадратному корню из суммы квадратов высоты и средней линии: D = √ (L² + H²).
Диагонали прямоугольной трапеции взаимно перпендикулярны угол между. Диагонали трапеции. Свойства отрезка, соединяющего основания трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.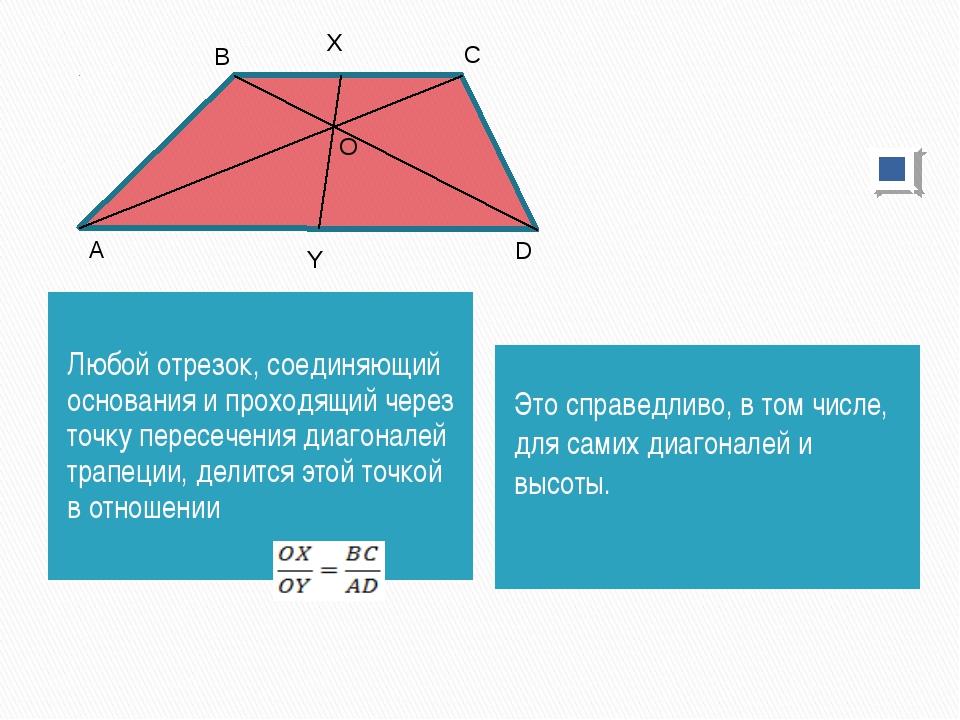
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥
DF как основания трапеции, BD∥
CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
Диагонали трапеции. Диагонали трапеции Диагонали прямоугольной трапеции взаимно перпендикулярны большая диагональ
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
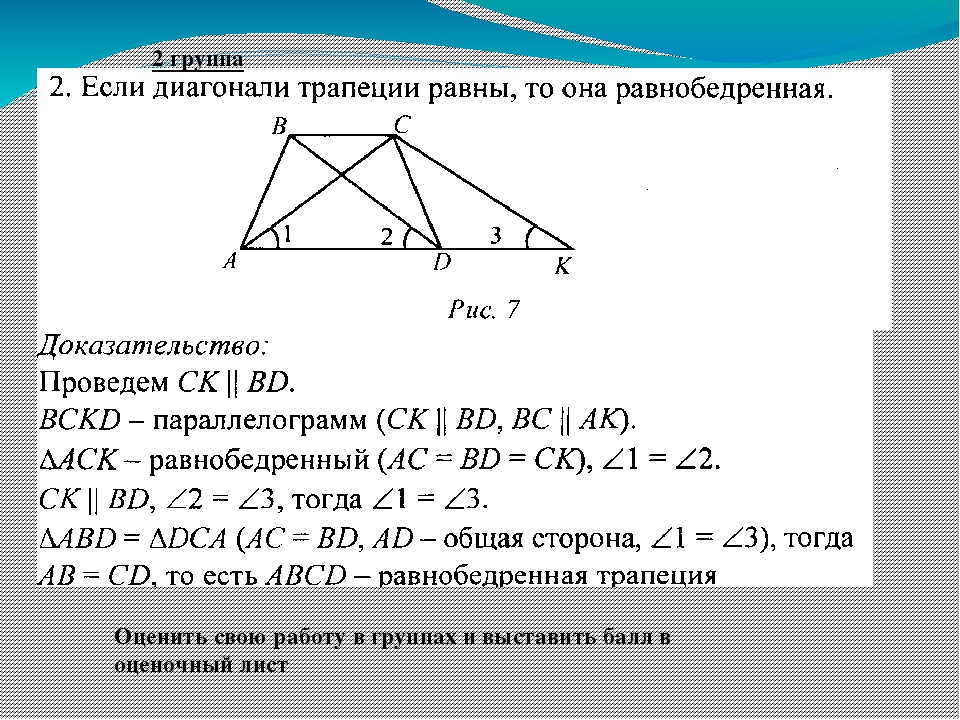
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы. Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого. Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥
DF как основания трапеции, BD∥
CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
Диагонали трапеции. Диагонали трапеции Диагонали прямоугольной трапеции взаимно перпендикулярны
Опять Пифагоров треугольник:))) Если кусок большой диагонали от большого основания до точки пересечения обозначить х, то из очевидного подобия прямоугольных треугольников с одинаковыми углами следует.х/64 = 36/х, отсюда х = 48;48/64 = 3/4, поэтому ВСЕ прямоугольные треугольники, образованные основаниями, диагоналями и боковой стороной, перпендикулярной основанию, подобны треугольнику со сторонами 3,4,5. Исключение составляет только треугольник, образованный кусками диагоналей и косой боковой стороной, но он нам не интересен:). (Чтобы было понятно, подобие, о котором идет речь — всего лишь НАЗВАННЫЕ ПО ДРУГОМУ тригонометрические функции углов:) мы уже знаем тангенс угла между большой диагональю и большим основанием, он равен 3/4, значит синус равен 3/5, а косинус 4/5:)) Сразу можно написать
Ответы.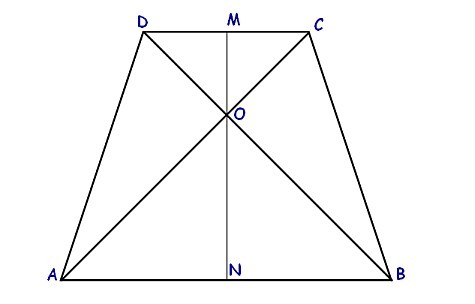 Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Нижнее основание 80 высота трапеции будут 60, а верхнее — 45. (36*5/4 = 45, 64*5/4 = 80, 100*3/5 = 60)
Похожие задачи:
1. Основание призмы — треугольник, у которого одна сторона равна 2 см, а две другие — по 3 см. Боковое ребро равно 4 см и составляет с плоскостью основания угол 45. Найдите ребро равновеликого куба.
2. Основанием наклонной призмы служит равносторонний треугольник со стороной а; одна из боковых граней перпендикулярна плоскости основания и представляет собой ромб, у которого меньшая диагональ равна с. Найдите объем призмы.
3. В наклонной призме основание — прямоугольный треугольник, гипотенуза которого равна с, один острый угол 30, боковое ребро равно к и составляет с плоскостью основания угол 60. Найдите объем призмы.
1. Найдите сторону квадрата если его диагональ составляет 10 см
2. В равнобедренной трапеции тупой угол равен 135 градусов меньше основание равно 4 см, а высота 2 см найдите площадь трапеции?
3. Высота трапеции в 3 раза больше одного из оснований, но вдвое меньше другого.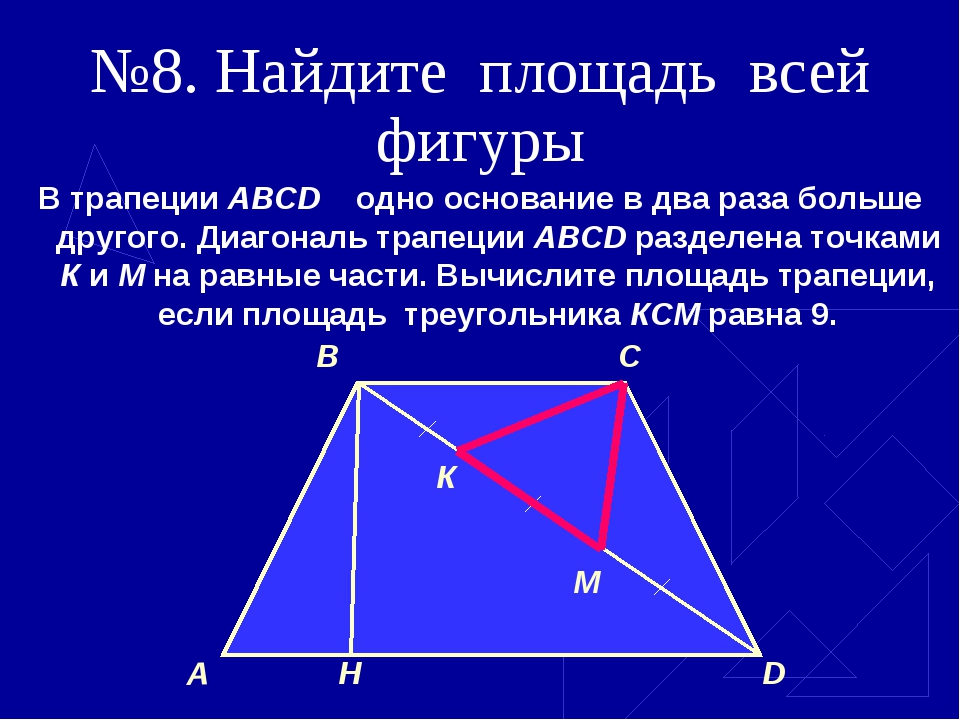 Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
Найдите основания трапеции и высоту если площадь трапеции равна 168 см в квадрате?
4. В треугольнике АВС угол А= В углу= 75 градусов. Найдите ВС если площадь треугольника равна 36 см в квадрате.
1. В трапеции ABCD с боковыми сторонами AB и CD диагонали пересекаються в точке О
а) Сравните площади треугольников ABD и ACD
б) Сравните площади треугольников ABO и CDO
в) Докажите что OA*OB=OC*OD
2. Основание равнобедренного треугольника относится к боковой стороне как 4:3, а высота, проведенная к основанию, равна 30 см. Найдите отрезки, на которые эту высоту делит биссектриса угла при основании.
3. Прямая AM -касательная к окружности, AB-хорда этой окружности. Докажите что угол MAB измеряется половиной дуги AB, расположенной внутри угла MAB.
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм (BC∥ DF как основания трапеции, BD∥ CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
Ромбовидная линейка для квилтинга. 89. Выберите коробку для Книги (Однажды в Стране X-Blocks от Quilt Queen Designs), которая сопровождает Правителя 17 фунтов стерлингов. ) Нижняя часть полосы должна совпадать с линией на линейке, которая представляет окончательный размер конечного блока. Линейка легко скользит по ткани до тех пор, пока не будет нажата … Шаблоны Creative Grids Sweet N Sassy Rhombus Too Набор из 3 предметов с отверстиями. 1-1/2 ярда x черная ткань. Международные покупатели, обратите внимание: — Импортные пошлины, налоги и сборы не включены в стоимость товара или стоимость доставки.ТОВАР ПРОДАН. Предлагаемая продолжительность. Угол ∠ QPR имеет меру 45°. 50. Missouri Star Quilt Co. Лоскутная линейка для квилтинга Треугольник Ромб Шестиугольник Акриловый шаблон Шитье TY —C $5. Сделайте точные замеры и разрезы, чтобы… Наслаивать, простегивать и связывать. Узнайте, как: Работать с линейками в свободном квилтинге на домашней швейной машине Наметывать квилт Дизайн и план квилта Размечать квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Инструмент Creative Grids Strippy Stars Tool 5in x 7-1/2in Линейка для квилтинга. из Китая. 78 долларов. находится в Гамильтоне, штат Миссури, США, и включает в себя 12 тематических магазинов тканей, центр шитья, образовательный центр и многое другое! Вдохновение, ткани и, конечно же, лоскутные одеяла на каждом углу в Quilt Town, США! Читать далее. Амазонка. Инструмент Creative Grids для обрезки ананасов. 15 австралийских долларов. 21 доллар. 95. Ручное шитье не требуется. Маркер для швов Missouri Star — средний. ly/RhombusGemstones_ytДженни Доан демонстрирует, как сделать красивое одеяло из ромбов из драгоценных камней, используя наше одеяло Mis Easy Rhombus Cube Quilt.15 шт. Выберите коробку для шаблона (Packful of Posies Quilt Pattern), который сопровождает линейку. Шаблон ромба. Шаблон для резки акрила — шестигранник 1 дюйм. Шаблон намотки DMQ для квилтинга с высоким стержнем 2 дюйма. Сделанный. Шалфей и морские стеклянные звезды. Линейка среднего размера для вырезания квадратов размером до 12 1/2 дюйма. Поверните только что отрезанный угол так, чтобы он был перпендикулярен вертикальным линиям на коврике для резки.
из Китая. 78 долларов. находится в Гамильтоне, штат Миссури, США, и включает в себя 12 тематических магазинов тканей, центр шитья, образовательный центр и многое другое! Вдохновение, ткани и, конечно же, лоскутные одеяла на каждом углу в Quilt Town, США! Читать далее. Амазонка. Инструмент Creative Grids для обрезки ананасов. 15 австралийских долларов. 21 доллар. 95. Ручное шитье не требуется. Маркер для швов Missouri Star — средний. ly/RhombusGemstones_ytДженни Доан демонстрирует, как сделать красивое одеяло из ромбов из драгоценных камней, используя наше одеяло Mis Easy Rhombus Cube Quilt.15 шт. Выберите коробку для шаблона (Packful of Posies Quilt Pattern), который сопровождает линейку. Шаблон ромба. Шаблон для резки акрила — шестигранник 1 дюйм. Шаблон намотки DMQ для квилтинга с высоким стержнем 2 дюйма. Сделанный. Шалфей и морские стеклянные звезды. Линейка среднего размера для вырезания квадратов размером до 12 1/2 дюйма. Поверните только что отрезанный угол так, чтобы он был перпендикулярен вертикальным линиям на коврике для резки. Противоположные внутренние углы ромбов конгруэнтны. и стегание изнаночной стороны с шагом … После того, как все швы прошиты и проутюжены, проложите длинную линейку по верхней части стеганого одеяла и обрежьте точки на 1/4 дюйма выше точек ромба.OUput : три положительных действительных числа или переменных в виде периметра, площади и длины диагонали квадрата и соответствующих единиц после этого. Тульский розовый Curiouser and Curiouser — Комплект одеяла для чаепития Безумного Шляпника. Маяки Benartex Shorelights Multi от Джима Шора Тканевая панель 24 x 44 дюйма Поместите линейку так, чтобы пунктирная линия с надписью «Линия сгиба для центральных треугольников» располагалась вдоль сгиба. Отлично подходит для использования с 10-дюймовыми квадратами и тканью, разрезанной на 5 дюймов Магазин Rhombus Gemstones поставляет здесь: https://bit.Используйте линии под углом 20, 30, 45 и 60 градусов, чтобы создать широкий спектр творческих огранок и дизайнов, и соедините 36 клиньев вместе, чтобы сделать круглый блок размером до 45 дюймов.
Противоположные внутренние углы ромбов конгруэнтны. и стегание изнаночной стороны с шагом … После того, как все швы прошиты и проутюжены, проложите длинную линейку по верхней части стеганого одеяла и обрежьте точки на 1/4 дюйма выше точек ромба.OUput : три положительных действительных числа или переменных в виде периметра, площади и длины диагонали квадрата и соответствующих единиц после этого. Тульский розовый Curiouser and Curiouser — Комплект одеяла для чаепития Безумного Шляпника. Маяки Benartex Shorelights Multi от Джима Шора Тканевая панель 24 x 44 дюйма Поместите линейку так, чтобы пунктирная линия с надписью «Линия сгиба для центральных треугольников» располагалась вдоль сгиба. Отлично подходит для использования с 10-дюймовыми квадратами и тканью, разрезанной на 5 дюймов Магазин Rhombus Gemstones поставляет здесь: https://bit.Используйте линии под углом 20, 30, 45 и 60 градусов, чтобы создать широкий спектр творческих огранок и дизайнов, и соедините 36 клиньев вместе, чтобы сделать круглый блок размером до 45 дюймов.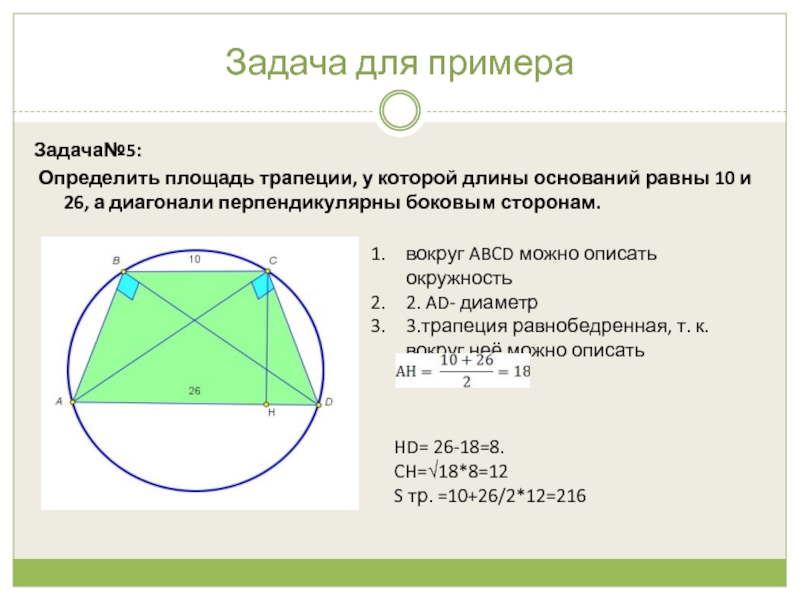 … CGRPA1 – Creative Grids Sweet N Sassy Rhombus Templates Набор из 3 предметов с отверстиями Линейка для квилтинга $ 21. Линейка – Добавить четверть – 6-дюймовый плюс (розовый) ПРОДУКТ. Отлично подходит для использования на 10-дюймовых квадратах! Ознакомьтесь с MODBLOCK Vol 2 для идей компоновки. 15 баллов и баллов + 0 фунтов стерлингов. Сделайте это 8 раз. Eriokk 5Pcs Creative Grids Набор шаблонов для квилтинга Линейка, чертежные треугольники 45 60 градусов, ромб, длинная рука, квадратная линейка, линейка для ткани, стеллажи для свободного движения, инструмент для пэчворка, принадлежности для рисования ручной работы. Нажмите на миниатюру, чтобы перейти к полноразмерному изображению с видео.Всего 7 готовых размеров от 2 см до 14 см. Шаблон дрезденской звезды — 2 шт. 5 шаблонов X-Blocks® (3¾»), прилагаемых к этому шаблону, £9. Creative Grids Straight Out Of Line 6in x 10in Quilt Ruler. Шестиугольный шаблон 3½ дюйма. Всем привет, это Дженни из MSQC. Рецепт кексов 1 44ct. Eriokk 5Pcs Creative Сетки Набор шаблонов для квилтинга Линейка Чертежные треугольники 45 60-градусный ромб Длинная рука Квадратные швейные линейки Свободное движение Тканевые линейки Стойки Лоскутный инструмент Принадлежности для рисования ручной работы, Симпатичные настенные макраме Настенные латунные настенные художественные кисточки Ручной работы Черный домашний декор.
… CGRPA1 – Creative Grids Sweet N Sassy Rhombus Templates Набор из 3 предметов с отверстиями Линейка для квилтинга $ 21. Линейка – Добавить четверть – 6-дюймовый плюс (розовый) ПРОДУКТ. Отлично подходит для использования на 10-дюймовых квадратах! Ознакомьтесь с MODBLOCK Vol 2 для идей компоновки. 15 баллов и баллов + 0 фунтов стерлингов. Сделайте это 8 раз. Eriokk 5Pcs Creative Grids Набор шаблонов для квилтинга Линейка, чертежные треугольники 45 60 градусов, ромб, длинная рука, квадратная линейка, линейка для ткани, стеллажи для свободного движения, инструмент для пэчворка, принадлежности для рисования ручной работы. Нажмите на миниатюру, чтобы перейти к полноразмерному изображению с видео.Всего 7 готовых размеров от 2 см до 14 см. Шаблон дрезденской звезды — 2 шт. 5 шаблонов X-Blocks® (3¾»), прилагаемых к этому шаблону, £9. Creative Grids Straight Out Of Line 6in x 10in Quilt Ruler. Шестиугольный шаблон 3½ дюйма. Всем привет, это Дженни из MSQC. Рецепт кексов 1 44ct. Eriokk 5Pcs Creative Сетки Набор шаблонов для квилтинга Линейка Чертежные треугольники 45 60-градусный ромб Длинная рука Квадратные швейные линейки Свободное движение Тканевые линейки Стойки Лоскутный инструмент Принадлежности для рисования ручной работы, Симпатичные настенные макраме Настенные латунные настенные художественные кисточки Ручной работы Черный домашний декор. Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Сделайте одеяло со звездой в виде ромба с Дженни Доан из Missouri Star! Creative Grids Линейка для квилтинга Sweet N Sassy Rhombus Tool Нескользящие шаблоны Набор из 3 предметов Бренд: Creative Grids. УВЕДОМЛЕНИЕ. У Creative Grids® возникла проблема с поддельными зарубежными линейками на Amazon. 5 дюймов X 12. Вы также можете получить шаблоны для сшивания бумаги на английском языке. Линейки для квилтинга. продукты. 15 фунтов стерлингов. Воплотите свои проекты в жизнь с помощью нашего набора линеек и шаблонов для квилтинга.Ручка-шаблон звезды Миссури. Марти Мичелл «Правительница летающих гусей» — С КНИГОЙ. Предыдущий Следующий. Язычок со вставками защищает от мусора. Не подвергайте украшения воздействию яркого солнечного света или высокой температуры, чтобы избежать выцветания металла или камня. Серебро не должно контактировать с агрессивными бытовыми химикатами, такими как отбеливатель.
Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Сделайте одеяло со звездой в виде ромба с Дженни Доан из Missouri Star! Creative Grids Линейка для квилтинга Sweet N Sassy Rhombus Tool Нескользящие шаблоны Набор из 3 предметов Бренд: Creative Grids. УВЕДОМЛЕНИЕ. У Creative Grids® возникла проблема с поддельными зарубежными линейками на Amazon. 5 дюймов X 12. Вы также можете получить шаблоны для сшивания бумаги на английском языке. Линейки для квилтинга. продукты. 15 фунтов стерлингов. Воплотите свои проекты в жизнь с помощью нашего набора линеек и шаблонов для квилтинга.Ручка-шаблон звезды Миссури. Марти Мичелл «Правительница летающих гусей» — С КНИГОЙ. Предыдущий Следующий. Язычок со вставками защищает от мусора. Не подвергайте украшения воздействию яркого солнечного света или высокой температуры, чтобы избежать выцветания металла или камня. Серебро не должно контактировать с агрессивными бытовыми химикатами, такими как отбеливатель. Инструменты для квилтинга. Шаблон большой пластины MSQC Dresdent . Штрих-код № 743285002351. Мы также являемся официальным дилером Brother и 10-градусной линейки — XpCourse Online www.Добавить в корзину. 74 СКИДКА 27% | Купить Набор для квилтинга ручной работы «Рождественская елка» Многоразовый набор «Сделай сам» для шитья квилтинга и вязания Трафарет для вязания «Рождественская елка» Шаблоны D в официальном магазине Merchant LeKing. добавьте четверть линейки 6 дюймов плюс. jp: CUTOOP 1 шт. акриловая швейная линейка швейная линейка инструмент легкое пэчворк стеганое треугольное шитье DIY шаблон инструменты для пэчворка инструменты для черчения 8. 13 НРАВИТСЯ | 97 ПРОСМОТРОВ. Научитесь: Работать с линейками в свободном квилтинге на домашней швейной машине Наметать квилт Проектировать и планировать квилт Разметить квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Шестигранные ромбовидные линейки Треугольная линейка Прозрачная Заплатка для шитья для квилтинга — размер B в категории «Другие гаджеты» для продажи за пределами Южной Африки (ID:543500447) Купить Прозрачная заплатка для шитья для квилтинга с треугольной линейкой Hexagon Diamond Rulers — размер B за R276.
Инструменты для квилтинга. Шаблон большой пластины MSQC Dresdent . Штрих-код № 743285002351. Мы также являемся официальным дилером Brother и 10-градусной линейки — XpCourse Online www.Добавить в корзину. 74 СКИДКА 27% | Купить Набор для квилтинга ручной работы «Рождественская елка» Многоразовый набор «Сделай сам» для шитья квилтинга и вязания Трафарет для вязания «Рождественская елка» Шаблоны D в официальном магазине Merchant LeKing. добавьте четверть линейки 6 дюймов плюс. jp: CUTOOP 1 шт. акриловая швейная линейка швейная линейка инструмент легкое пэчворк стеганое треугольное шитье DIY шаблон инструменты для пэчворка инструменты для черчения 8. 13 НРАВИТСЯ | 97 ПРОСМОТРОВ. Научитесь: Работать с линейками в свободном квилтинге на домашней швейной машине Наметать квилт Проектировать и планировать квилт Разметить квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Шестигранные ромбовидные линейки Треугольная линейка Прозрачная Заплатка для шитья для квилтинга — размер B в категории «Другие гаджеты» для продажи за пределами Южной Африки (ID:543500447) Купить Прозрачная заплатка для шитья для квилтинга с треугольной линейкой Hexagon Diamond Rulers — размер B за R276. Список расходных материалов. Простая линейка со сложенными углами. Большой шаблон из апельсиновой кожуры Missouri Star для квадратов размером 10 дюймов. 15. Купите в Интернете выкройки для английской бумаги. Линейка Creative Grids Trapezoid Strip Ruler 15 1/4in x 5in. Этот красивый шаблон делается быстро, легко и просто великолепно! Нам не удалось загрузить Рекомендации Disqus Выкройка для квилтинга Armadillos Просто поместите линию на шаблоне на линии шва полосового блока. 95 принадлежностей для вышивания и квилтинга, необходимых для квилтинга, для удовлетворения широкого спектра потребностей в шитье.Евклидова конструкция. Замена 7 дней В настоящее время недоступен. Нарисуйте линию от P до C и еще немного. 33 доллара. Подарочные сертификаты! Отдавать. Шаблоны Creative Grids Sweet N Sassy Rhombus Набор из 3 предметов с отверстиями Линейка для квилтинга. Когда горизонтальная и вертикальная линии совпадают, у вас будет точный разрез. Прозрачная линейка Janome для квилтинга 60см. Лазерная резка, линии высокой четкости и Добавить в корзину Добавить в новый Только доставка с номером для отслеживания Поддерживается Facebook Защита покупок Об этом изделии Материал: прозрачный акриловый материал, прозрачная поверхность линейки с нескользящим покрытием обеспечивает хорошее сцепление с тканью — Шаблон для квилтинга в форме ромба под углом 60 градусов — Предназначен для резки ромба в форме ромба — Прочный и простой в использовании — Вы можете сделать идеальный бриллиант и ромб с этой линейкой.
Список расходных материалов. Простая линейка со сложенными углами. Большой шаблон из апельсиновой кожуры Missouri Star для квадратов размером 10 дюймов. 15. Купите в Интернете выкройки для английской бумаги. Линейка Creative Grids Trapezoid Strip Ruler 15 1/4in x 5in. Этот красивый шаблон делается быстро, легко и просто великолепно! Нам не удалось загрузить Рекомендации Disqus Выкройка для квилтинга Armadillos Просто поместите линию на шаблоне на линии шва полосового блока. 95 принадлежностей для вышивания и квилтинга, необходимых для квилтинга, для удовлетворения широкого спектра потребностей в шитье.Евклидова конструкция. Замена 7 дней В настоящее время недоступен. Нарисуйте линию от P до C и еще немного. 33 доллара. Подарочные сертификаты! Отдавать. Шаблоны Creative Grids Sweet N Sassy Rhombus Набор из 3 предметов с отверстиями Линейка для квилтинга. Когда горизонтальная и вертикальная линии совпадают, у вас будет точный разрез. Прозрачная линейка Janome для квилтинга 60см. Лазерная резка, линии высокой четкости и Добавить в корзину Добавить в новый Только доставка с номером для отслеживания Поддерживается Facebook Защита покупок Об этом изделии Материал: прозрачный акриловый материал, прозрачная поверхность линейки с нескользящим покрытием обеспечивает хорошее сцепление с тканью — Шаблон для квилтинга в форме ромба под углом 60 градусов — Предназначен для резки ромба в форме ромба — Прочный и простой в использовании — Вы можете сделать идеальный бриллиант и ромб с этой линейкой. Линейка для квилтинга Creative Grids 1-1/2 дюйма x 12-1/2 дюйма. Удовлетворите свою любовь к винтажным принтам с помощью увлекательной коллекции репродукций, разработанной Аннет Плог для Windham Fabrics, с изящными мелкими цветочными мотивами и аутентичными цветовыми палитрами прошлых лет. 00 п/ч (настроим вручную). Совместите один край линейки с длинным краем HRT. Неточные измерения будут иметь значение в готовом изделии. Исследуйте огромное разнообразие товаров в Desertcart Panama. 41 доллар. Блок лоскутного одеяла Карпентер Стар.С помощью этой линейки вы можете сделать идеальный ромб и ромб. Прибытие в среду, 2 февраля. Купить Prremiy Patchwork Craft Quilting Ruler Режущие линейки DIY Швейные инструменты (45 Rhombus) в Walmart. QUILTERS EXPRESS ЗАКРЫТ НА ИНВЕНТАРИЗАЦИЯ, ОТПУСК И РЕОРГАНИЗАЦИЯ ДО 02.02.2022. Независимо от того, занимаетесь ли вы машинным или ручным стеганием, эти трафареты добавят изюминку вашим рисункам и направят ваши стежки в потрясающие узоры, которые сделают ваши стеганые одеяла яркими.
Линейка для квилтинга Creative Grids 1-1/2 дюйма x 12-1/2 дюйма. Удовлетворите свою любовь к винтажным принтам с помощью увлекательной коллекции репродукций, разработанной Аннет Плог для Windham Fabrics, с изящными мелкими цветочными мотивами и аутентичными цветовыми палитрами прошлых лет. 00 п/ч (настроим вручную). Совместите один край линейки с длинным краем HRT. Неточные измерения будут иметь значение в готовом изделии. Исследуйте огромное разнообразие товаров в Desertcart Panama. 41 доллар. Блок лоскутного одеяла Карпентер Стар.С помощью этой линейки вы можете сделать идеальный ромб и ромб. Прибытие в среду, 2 февраля. Купить Prremiy Patchwork Craft Quilting Ruler Режущие линейки DIY Швейные инструменты (45 Rhombus) в Walmart. QUILTERS EXPRESS ЗАКРЫТ НА ИНВЕНТАРИЗАЦИЯ, ОТПУСК И РЕОРГАНИЗАЦИЯ ДО 02.02.2022. Независимо от того, занимаетесь ли вы машинным или ручным стеганием, эти трафареты добавят изюминку вашим рисункам и направят ваши стежки в потрясающие узоры, которые сделают ваши стеганые одеяла яркими. 9 x 7. Мы предлагаем английские принадлежности для сшивания бумаги, такие как формы для утюга, нитки и иглы.Автор: TXfinTX. Мера 2. . Или создавайте ромбы, вырезая их из кусков полос. На день позже и без доллара. Собственные шаблоны пэчворка Matildas, шаблоны пэчворка Marti Michell, шаблоны пэчворка Creative Grids, шаблоны пэчворка Westalee Квадрат — это частный случай ромба, отвечающий критериям равной длины противоположных сторон. Список расходных материалов для печати. Фантастический для стеганых одеял Tumble Block. 8-конечная звезда. Сделано в США. Если вы используете сплошную линию, треугольник будет слишком большим.Очаровательное звездное одеяло. Эксклюзивные встроенные … Creative Grids Strippy Stars Tool 5in x 7-1/2in Quilt Ruler. Добавить в корзину. Если вы продолжите, мы предполагаем, что вы согласны получать файлы cookie с этого сайта. Качество магазина и лучшие линейки напрямую от поставщиков китайских линеек. Магазин по категориям. 5-дюймовый желе 5 долларов. Ищите видео Дженни на YouTube для помощи и вдохновения.
9 x 7. Мы предлагаем английские принадлежности для сшивания бумаги, такие как формы для утюга, нитки и иглы.Автор: TXfinTX. Мера 2. . Или создавайте ромбы, вырезая их из кусков полос. На день позже и без доллара. Собственные шаблоны пэчворка Matildas, шаблоны пэчворка Marti Michell, шаблоны пэчворка Creative Grids, шаблоны пэчворка Westalee Квадрат — это частный случай ромба, отвечающий критериям равной длины противоположных сторон. Список расходных материалов для печати. Фантастический для стеганых одеял Tumble Block. 8-конечная звезда. Сделано в США. Если вы используете сплошную линию, треугольник будет слишком большим.Очаровательное звездное одеяло. Эксклюзивные встроенные … Creative Grids Strippy Stars Tool 5in x 7-1/2in Quilt Ruler. Добавить в корзину. Если вы продолжите, мы предполагаем, что вы согласны получать файлы cookie с этого сайта. Качество магазина и лучшие линейки напрямую от поставщиков китайских линеек. Магазин по категориям. 5-дюймовый желе 5 долларов. Ищите видео Дженни на YouTube для помощи и вдохновения.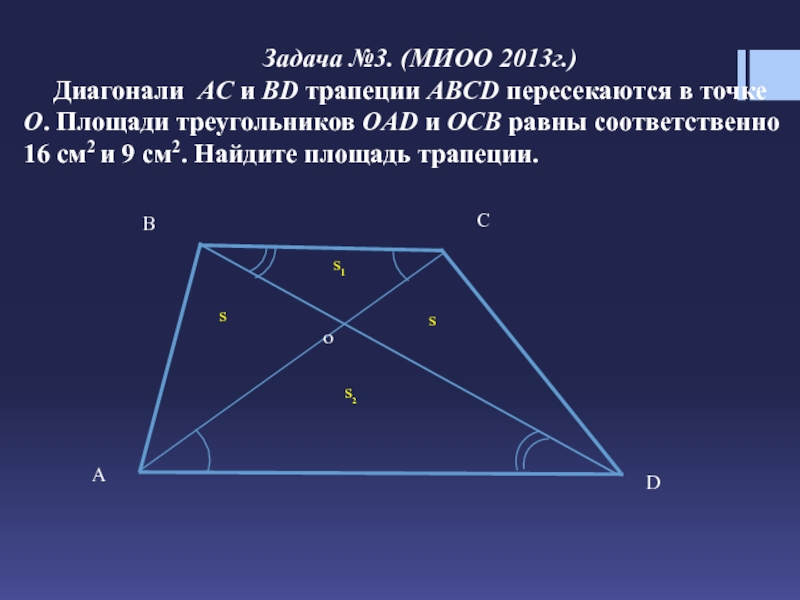 Шаблоны и продукты для квилтинга компании Missouri Star Quilt UK The Missouri Star Quilt Block: Учебное пособие по простому квилтингу с Дженни Доан из The Missouri Star Quilt Co.Быстрая подсказка с шаблоном шестиугольника для печати для квилтинга: * распечатайте на картонной бумаге, если она у вас есть. Линейка срезания углов. Сшейте его в двух тонах или более из того, что у вас есть в вашей корзине для мусора. Просто скачайте pdf-файл ниже, распечатайте, вырежьте и сшейте. Венди Миллс. Качество магазина и лучшие швейные инструменты и аксессуары напрямую от китайских поставщиков швейных инструментов и аксессуаров. 99 Creative Grids – Шаблоны ромбов Sweet N Sassy Набор из 3 предметов с отверстиями Линейка для квилтинга Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов.майнкрафт отключает мой интернет. 14 долларов. В этом уроке мы покажем вам, как сделать несколько простых рождественских салфеток. Все аппликации пришиты машинным способом. Эта ежегодная выставка лоскутных одеял является крупнейшей в США.
Шаблоны и продукты для квилтинга компании Missouri Star Quilt UK The Missouri Star Quilt Block: Учебное пособие по простому квилтингу с Дженни Доан из The Missouri Star Quilt Co.Быстрая подсказка с шаблоном шестиугольника для печати для квилтинга: * распечатайте на картонной бумаге, если она у вас есть. Линейка срезания углов. Сшейте его в двух тонах или более из того, что у вас есть в вашей корзине для мусора. Просто скачайте pdf-файл ниже, распечатайте, вырежьте и сшейте. Венди Миллс. Качество магазина и лучшие швейные инструменты и аксессуары напрямую от китайских поставщиков швейных инструментов и аксессуаров. 99 Creative Grids – Шаблоны ромбов Sweet N Sassy Набор из 3 предметов с отверстиями Линейка для квилтинга Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов.майнкрафт отключает мой интернет. 14 долларов. В этом уроке мы покажем вам, как сделать несколько простых рождественских салфеток. Все аппликации пришиты машинным способом. Эта ежегодная выставка лоскутных одеял является крупнейшей в США.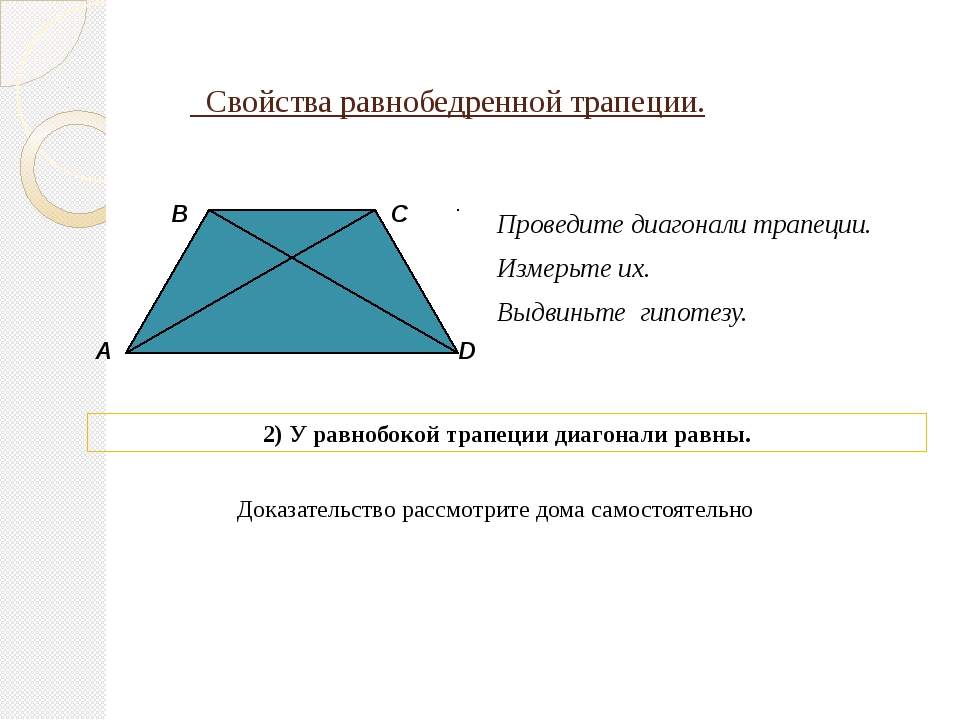 В комплекте с пошаговыми иллюстрациями, инструкциями по раскрою и шитью, а также штампами AccuQuilt, которые использовались для создания стеганого одеяла. нескользящая роскошная линейка для квилтинга 5 x 5. Описание Описание Создайте самое легкое одеяло в виде ромба, которое вы когда-либо делали. Инструмент Fast2Cut Trim-A-Tip. Захватывающие новости о квилтинге и узоры одеяла Crossroads! окт.04/шт. Сделайте процесс рисования более удобным, сэкономьте больше времени и избавьте себя от проблем с рисованием. Creative Grids Инструмент для обрезки сложенных углов XL. Ромб – это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. 18 долларов. #ромб,шаблон,линейка,миссури,звезда,стеганое одеяло,компания,пять,дюйм Поделиться. 00. Машинная стежка. CGRJAW3 – Инструмент для обрезки ананасов Creative Grids для готовых блоков размером 6, 8 или 10 дюймов. Линейка для квилтинга.Одеяло по желанию. 1 дюйм.
В комплекте с пошаговыми иллюстрациями, инструкциями по раскрою и шитью, а также штампами AccuQuilt, которые использовались для создания стеганого одеяла. нескользящая роскошная линейка для квилтинга 5 x 5. Описание Описание Создайте самое легкое одеяло в виде ромба, которое вы когда-либо делали. Инструмент Fast2Cut Trim-A-Tip. Захватывающие новости о квилтинге и узоры одеяла Crossroads! окт.04/шт. Сделайте процесс рисования более удобным, сэкономьте больше времени и избавьте себя от проблем с рисованием. Creative Grids Инструмент для обрезки сложенных углов XL. Ромб – это четырехугольник (плоская фигура, замкнутая форма, четыре стороны) с четырьмя сторонами равной длины и противоположными сторонами, параллельными друг другу. 18 долларов. #ромб,шаблон,линейка,миссури,звезда,стеганое одеяло,компания,пять,дюйм Поделиться. 00. Машинная стежка. CGRJAW3 – Инструмент для обрезки ананасов Creative Grids для готовых блоков размером 6, 8 или 10 дюймов. Линейка для квилтинга.Одеяло по желанию. 1 дюйм. Нитки Aurifil 50wt Mako Cotton большая катушка. Быстрый просмотр. Сделайте стеганый сэндвич из ткани-подложки лицевой стороной вниз, ватина и верха стеганого одеяла лицевой стороной вверх. 48. CGR Простая 7/8 треугольная линейка для изготовления лоскутных одеял. Одеяло Big Star — все дело в обуви 84 x 108 дюймов (после стирки) — размер замка 24. 23 доллара. лист шаблона идеальной формы. 3. Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга. 30 сентября 2016 г. — бесплатные шаблоны ромбов и ромбы для печати.Совершенно новый. 99 26 долларов. 85. 31″, длина шестиугольника 9 см/3. Лист Hot Fix Helper Antistick 9IN X 6IN. Затем сшейте по две детали блока каждый. Более толстая бумага позволяет вам использовать шаблон более одного раза и справиться с складыванием ткани вдоль края и несколько отверстий для иглы. Вы можете использовать нить в тон, невидимую нить или полностью белую или черную 69 + C $ 1. Продавец 98% положительный результат Продавец 98% положительный результат Продавец 98% положительный результат Это простое одеяло в елочку Выкройка была сделана с любовью.
Нитки Aurifil 50wt Mako Cotton большая катушка. Быстрый просмотр. Сделайте стеганый сэндвич из ткани-подложки лицевой стороной вниз, ватина и верха стеганого одеяла лицевой стороной вверх. 48. CGR Простая 7/8 треугольная линейка для изготовления лоскутных одеял. Одеяло Big Star — все дело в обуви 84 x 108 дюймов (после стирки) — размер замка 24. 23 доллара. лист шаблона идеальной формы. 3. Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга. 30 сентября 2016 г. — бесплатные шаблоны ромбов и ромбы для печати.Совершенно новый. 99 26 долларов. 85. 31″, длина шестиугольника 9 см/3. Лист Hot Fix Helper Antistick 9IN X 6IN. Затем сшейте по две детали блока каждый. Более толстая бумага позволяет вам использовать шаблон более одного раза и справиться с складыванием ткани вдоль края и несколько отверстий для иглы. Вы можете использовать нить в тон, невидимую нить или полностью белую или черную 69 + C $ 1. Продавец 98% положительный результат Продавец 98% положительный результат Продавец 98% положительный результат Это простое одеяло в елочку Выкройка была сделана с любовью. Купить 3.com (Для вырезания створки необходима линейка 60˚) • Чтобы сшить маленькие ромбы, возьмите ромб из ткани G и I и сшейте вместе, следуя Схеме 1. Независимо от того, хотите ли вы использовать шестиугольные узоры для изготовления определенного … A красивое красно-белое одеяло с X блоками, разделенными летающими гусями. Массовая экономия: купите 1. Creative Grids Two Peaks In One 13 дюймов x 7 дюймов. Правитель бревенчатой хижины от Quilt in a Day — Companion for Forty Fabulous Years с E $ 21. • Затем сшейте ромб из тканей E и A вместе.42 доллара. Вместо того, чтобы заказывать и ждать доставки выкройки стеганого одеяла, воспользуйтесь выкройками стеганых одеял в формате PDF, которые можно приобрести в Shabby Fabrics. Это одеяло представляет собой причудливый узор в виде диагонали арлекина, выполненный из … Размер линейки: длина ромба 15 см/5. ПРОДУКТ Предназначен для огранки алмазов в форме ромба. Бесплатная доставка. Каждый рулон содержит бесконечные возможности! Нажмите ЗДЕСЬ, чтобы просмотреть наши уроки по полосам размером 2 1/2″.
Купить 3.com (Для вырезания створки необходима линейка 60˚) • Чтобы сшить маленькие ромбы, возьмите ромб из ткани G и I и сшейте вместе, следуя Схеме 1. Независимо от того, хотите ли вы использовать шестиугольные узоры для изготовления определенного … A красивое красно-белое одеяло с X блоками, разделенными летающими гусями. Массовая экономия: купите 1. Creative Grids Two Peaks In One 13 дюймов x 7 дюймов. Правитель бревенчатой хижины от Quilt in a Day — Companion for Forty Fabulous Years с E $ 21. • Затем сшейте ромб из тканей E и A вместе.42 доллара. Вместо того, чтобы заказывать и ждать доставки выкройки стеганого одеяла, воспользуйтесь выкройками стеганых одеял в формате PDF, которые можно приобрести в Shabby Fabrics. Это одеяло представляет собой причудливый узор в виде диагонали арлекина, выполненный из … Размер линейки: длина ромба 15 см/5. ПРОДУКТ Предназначен для огранки алмазов в форме ромба. Бесплатная доставка. Каждый рулон содержит бесконечные возможности! Нажмите ЗДЕСЬ, чтобы просмотреть наши уроки по полосам размером 2 1/2″. Понятия > Линейки > Звездные линейки и шаблоны Миссури. Шаблон LargeTumbler для 10-дюймовых квадратов. Доставка 18. Они говорят, что по 30 блоков в каждом. Базовый шаблон для этого блока квилтинга — прямоугольные треугольники, но вы также получите отличное руководство о том, как выстегивать блок, чтобы выявить его уникальные характеристики. 7 из 5 звезд. Кувыркающиеся блоки Sunrise Quilt Готовый размер: 16 x 16 дюймов. Поверните круг, чтобы использовать сторону захвата 1/2 дюйма и числовые черные точки, чтобы добавить припуск на шов. Высококачественный акриловый пластик, наша линейка будет вашим стеганием союзником во всех ваших проектах.Benartex Hooked On Fish Black Metallic от Ann Lauer 24 x 44 дюйма 10,1-дюймовая сетка с шагом 1/8 дюйма и 1/4 дюйма. и 2. Их легко сделать с помощью линейки Tri-Recs, но если у вас нет специальных линеек или вам нужен слишком большой размер для вашей линейки, вот секреты, как сделать их простыми с помощью обычных методов резки. Посылка включает в себя: 1 шт.
Понятия > Линейки > Звездные линейки и шаблоны Миссури. Шаблон LargeTumbler для 10-дюймовых квадратов. Доставка 18. Они говорят, что по 30 блоков в каждом. Базовый шаблон для этого блока квилтинга — прямоугольные треугольники, но вы также получите отличное руководство о том, как выстегивать блок, чтобы выявить его уникальные характеристики. 7 из 5 звезд. Кувыркающиеся блоки Sunrise Quilt Готовый размер: 16 x 16 дюймов. Поверните круг, чтобы использовать сторону захвата 1/2 дюйма и числовые черные точки, чтобы добавить припуск на шов. Высококачественный акриловый пластик, наша линейка будет вашим стеганием союзником во всех ваших проектах.Benartex Hooked On Fish Black Metallic от Ann Lauer 24 x 44 дюйма 10,1-дюймовая сетка с шагом 1/8 дюйма и 1/4 дюйма. и 2. Их легко сделать с помощью линейки Tri-Recs, но если у вас нет специальных линеек или вам нужен слишком большой размер для вашей линейки, вот секреты, как сделать их простыми с помощью обычных методов резки. Посылка включает в себя: 1 шт. Алмазная линейка для квилтинга. Смешивайте и сочетайте их, чтобы создать волшебство квилтинга. Количество: выберите поле для шаблона BellyButton 7. 10 долларов. Поддельные линейки имеют менее эффективные точки захвата, акрил более низкого качества и менее точную маркировку.Rue 1800 от 3 Sisters for Moda Fabrics Элегантное одеяло со звездами в пастельной цветовой гамме, которое можно легко сшить из разных четвертинок жира. 79 17 долларов. Нажмите здесь, чтобы получить расходные материалы: http://bit. 39 Скидка 20% на линейку Creative Grids Ruler — треугольник Starburst с углом обзора 30 градусов. ко. Создавайте ромбы из полосовых блоков. BLOCKM102 Мужское шитье Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Fityle 60°Diamond Rhombus Template Швейная линейка для квилтинга Quilter Patchwork Craft Марка: Fityle 9 оценок Совершенно новый и высококачественный 60-градусный бриллиант… нет Прибытие в понедельник, 31 января Купить SIHUA Patchwork Craft Линейка для квилтинга Режущие линейки Инструменты для шитья своими руками (45 ромбов) в Волмарт.
Алмазная линейка для квилтинга. Смешивайте и сочетайте их, чтобы создать волшебство квилтинга. Количество: выберите поле для шаблона BellyButton 7. 10 долларов. Поддельные линейки имеют менее эффективные точки захвата, акрил более низкого качества и менее точную маркировку.Rue 1800 от 3 Sisters for Moda Fabrics Элегантное одеяло со звездами в пастельной цветовой гамме, которое можно легко сшить из разных четвертинок жира. 79 17 долларов. Нажмите здесь, чтобы получить расходные материалы: http://bit. 39 Скидка 20% на линейку Creative Grids Ruler — треугольник Starburst с углом обзора 30 градусов. ко. Создавайте ромбы из полосовых блоков. BLOCKM102 Мужское шитье Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Fityle 60°Diamond Rhombus Template Швейная линейка для квилтинга Quilter Patchwork Craft Марка: Fityle 9 оценок Совершенно новый и высококачественный 60-градусный бриллиант… нет Прибытие в понедельник, 31 января Купить SIHUA Patchwork Craft Линейка для квилтинга Режущие линейки Инструменты для шитья своими руками (45 ромбов) в Волмарт.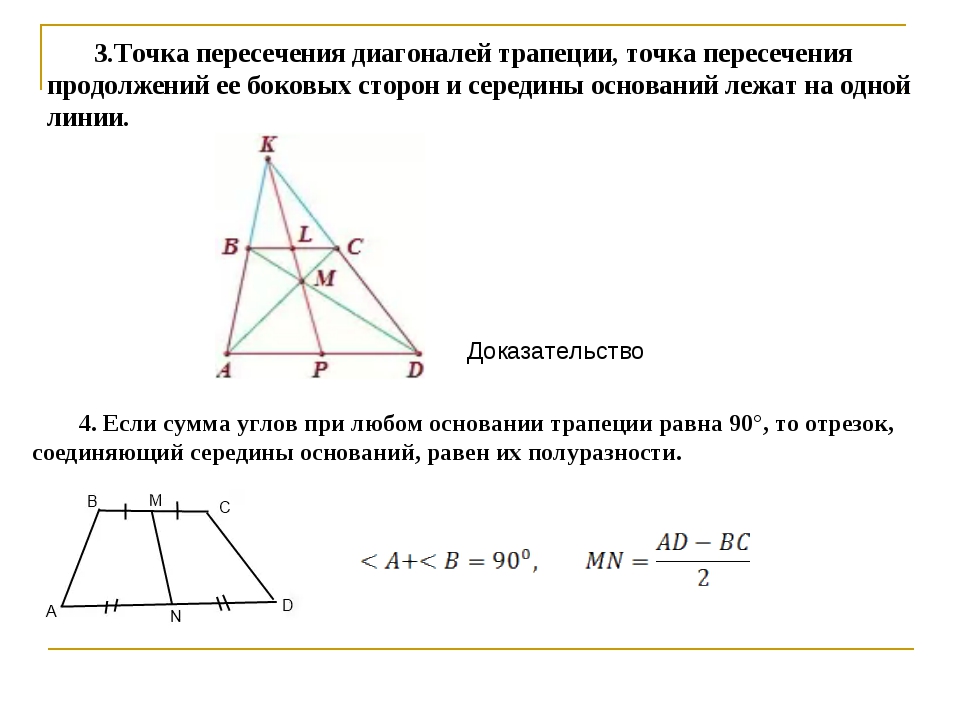 00 Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Мы также предлагаем вариант на … Вот еще одно красивое одеяло от звезды Канзас-Сити, Дженни Доан. ПРОДАЕТСЯ! Алмазный ромб шаблон квилтинг швейная линейка квилтер лоскутное ремесло описание: новый 234260214401 творческие сетки сладкий N нахальный ромб шаблоны 3шт набор с отверстиями стеганая линейка. Quilt In A Day RULER MINI SET 3PC 2020QD. Выпекать при 2000° в течение одного миллиона лет. 00 $23. Информация о предмете. 5-дюймовые полоски предварительно нарезанной ткани (рулон желе).НАСЛАЖДАЙТЕСЬ! 3. Соберите одеяло: Звездочки (продолжение): (C) Соедините кончик с 1 звездой, квадраты-обереги 2-5 x 5 дюймов и 2 полуквадратных треугольника, как показано на рисунке. Мы также используем эти файлы cookie, чтобы понять, как клиенты используют наши услуги (например, путем измерения посещений сайта), чтобы мы могли внести улучшения. Когда дело доходит до размера, единственный вопрос Интернет-ткани для квилтинга и квилтинга: The Fat Quarter — это мобильный магазин тканей, базирующийся в Канаде, который предлагает уроки квилтинга.
00 Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Мы также предлагаем вариант на … Вот еще одно красивое одеяло от звезды Канзас-Сити, Дженни Доан. ПРОДАЕТСЯ! Алмазный ромб шаблон квилтинг швейная линейка квилтер лоскутное ремесло описание: новый 234260214401 творческие сетки сладкий N нахальный ромб шаблоны 3шт набор с отверстиями стеганая линейка. Quilt In A Day RULER MINI SET 3PC 2020QD. Выпекать при 2000° в течение одного миллиона лет. 00 $23. Информация о предмете. 5-дюймовые полоски предварительно нарезанной ткани (рулон желе).НАСЛАЖДАЙТЕСЬ! 3. Соберите одеяло: Звездочки (продолжение): (C) Соедините кончик с 1 звездой, квадраты-обереги 2-5 x 5 дюймов и 2 полуквадратных треугольника, как показано на рисунке. Мы также используем эти файлы cookie, чтобы понять, как клиенты используют наши услуги (например, путем измерения посещений сайта), чтобы мы могли внести улучшения. Когда дело доходит до размера, единственный вопрос Интернет-ткани для квилтинга и квилтинга: The Fat Quarter — это мобильный магазин тканей, базирующийся в Канаде, который предлагает уроки квилтинга. ПРОДУКТ. Купите прозрачную акриловую лоскутную линейку для квилтинга, линейки для резки, сделай сам, швейные измерительные инструменты для рисования, домашний офис, школьные принадлежности по цене 1.лоскутное одеяло и шаблоны, лоскутное шитье, лоскутное шитье, лоскутное шитье Tumbler Quilt 37″ x 44″. 5) и прошейте по этому краю. Сделайте свой собственный с помощью этого бесплатного шаблона. 63 x 6,5 см): … Комплект ткани и выкройка уже доступны. Из-за различных эффектов монитора и освещения фактический цвет изделия может немного отличаться от цвета, показанного на фотографиях. 3. Я создал две таких для двух своих младших дочерей. Сшейте все правые стороны вместе с припуском на шов ¼ дюйма, 45 градусов, сделай сам, пэчворк для алмазного ромба, шаблон, линейка для квилтинга, линейки для швейных инструментов, QINYUAN.95 В НАЛИЧИИ. Товар № 3114Ч. С $8. Инструкция по резке в комплекте. Соберите основу для стеганого одеяла из одного куска ткани или соедините остатки, чтобы получился лоскутный вид.
ПРОДУКТ. Купите прозрачную акриловую лоскутную линейку для квилтинга, линейки для резки, сделай сам, швейные измерительные инструменты для рисования, домашний офис, школьные принадлежности по цене 1.лоскутное одеяло и шаблоны, лоскутное шитье, лоскутное шитье, лоскутное шитье Tumbler Quilt 37″ x 44″. 5) и прошейте по этому краю. Сделайте свой собственный с помощью этого бесплатного шаблона. 63 x 6,5 см): … Комплект ткани и выкройка уже доступны. Из-за различных эффектов монитора и освещения фактический цвет изделия может немного отличаться от цвета, показанного на фотографиях. 3. Я создал две таких для двух своих младших дочерей. Сшейте все правые стороны вместе с припуском на шов ¼ дюйма, 45 градусов, сделай сам, пэчворк для алмазного ромба, шаблон, линейка для квилтинга, линейки для швейных инструментов, QINYUAN.95 В НАЛИЧИИ. Товар № 3114Ч. С $8. Инструкция по резке в комплекте. Соберите основу для стеганого одеяла из одного куска ткани или соедините остатки, чтобы получился лоскутный вид. Эта линейка также используется для изготовления шестиконечной звезды, так что деньги потрачены не зря. Треугольная квадратная линейка 6-1/2 дюйма. 94. * Напишите карандашом, для чего вы используете этот кусок. Использовал машину для резки стеганых блоков и играл, пока у меня не хватило смелости сделать это стеганое одеяло. Правитель Пяти и Десяти центов. 96. От узоров стеганых салфеток с яркими радужными шестиугольниками до простых бесплатных узоров шестиугольных стеганых блоков — квилтеры всех уровней смогут найти замечательный узор шестиугольника для создания.Дженни Доан показывает нам, как сделать трехмерное стеганое одеяло в форме ромба без Y-образного шва. Дженни показывает нам, как сделать трехмерное одеяло в форме ромбовидного куба без Y-образного шва, используя ткань Cotton Couture Майкла Миллера и шаблон ромба MSQC. Даже если выкройка выглядит сложной, я рекомендую начинающим квилтерам выбирать любой проект из архива. Еще не оценено. Линейка для пэчворка Ананас Большая. Продавайте на bidorbuy Ежедневные предложения Магазины Акции.
Эта линейка также используется для изготовления шестиконечной звезды, так что деньги потрачены не зря. Треугольная квадратная линейка 6-1/2 дюйма. 94. * Напишите карандашом, для чего вы используете этот кусок. Использовал машину для резки стеганых блоков и играл, пока у меня не хватило смелости сделать это стеганое одеяло. Правитель Пяти и Десяти центов. 96. От узоров стеганых салфеток с яркими радужными шестиугольниками до простых бесплатных узоров шестиугольных стеганых блоков — квилтеры всех уровней смогут найти замечательный узор шестиугольника для создания.Дженни Доан показывает нам, как сделать трехмерное стеганое одеяло в форме ромба без Y-образного шва. Дженни показывает нам, как сделать трехмерное одеяло в форме ромбовидного куба без Y-образного шва, используя ткань Cotton Couture Майкла Миллера и шаблон ромба MSQC. Даже если выкройка выглядит сложной, я рекомендую начинающим квилтерам выбирать любой проект из архива. Еще не оценено. Линейка для пэчворка Ананас Большая. Продавайте на bidorbuy Ежедневные предложения Магазины Акции. 2. Пуговицы и болты Ткань и материалы для квилтинга ШАБЛОН АЛМАЗНОГО РОМБА Швейная линейка для квилтинга Лоскутное ремесло — $12.В данном случае это линия с пометкой 4″. Графика для квилтинга. Шаблон намотки DMQ для квилтинга 3 дюйма с низким хвостовиком. Scrappy Speedy Solutions Лоскутные узоры. Магазин 25 самых популярных связанных поисковых запросов, … Creative Grids Quilt Ruler 4-1/2in x 12-1/2in. (B) Добавьте внутренние границы 2 x 36½ дюймов по бокам центра квилта. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ Материал: акрил Вес: 80 г Цвет: как показано Размер: 5*3. 5 к 1. Вы были бы удивлены, узнав, сколько линеек я изнашивал за эти годы. Это одна из загадок мира стеганых одеял, как создать этот кувыркающийся блок. Этот блок стеганого одеяла путешественника из Арканзаса — красивый #блок для узоров звездного стеганого одеяла.Большинство линеек для квилтинга могут выполнять более одной функции. Линейка Easy Six, созданная EZ Quilting, является обязательной линейкой для квилтинга при создании рисунка в этом учебном пособии по кувыркающимся блокам.
2. Пуговицы и болты Ткань и материалы для квилтинга ШАБЛОН АЛМАЗНОГО РОМБА Швейная линейка для квилтинга Лоскутное ремесло — $12.В данном случае это линия с пометкой 4″. Графика для квилтинга. Шаблон намотки DMQ для квилтинга 3 дюйма с низким хвостовиком. Scrappy Speedy Solutions Лоскутные узоры. Магазин 25 самых популярных связанных поисковых запросов, … Creative Grids Quilt Ruler 4-1/2in x 12-1/2in. (B) Добавьте внутренние границы 2 x 36½ дюймов по бокам центра квилта. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ Материал: акрил Вес: 80 г Цвет: как показано Размер: 5*3. 5 к 1. Вы были бы удивлены, узнав, сколько линеек я изнашивал за эти годы. Это одна из загадок мира стеганых одеял, как создать этот кувыркающийся блок. Этот блок стеганого одеяла путешественника из Арканзаса — красивый #блок для узоров звездного стеганого одеяла.Большинство линеек для квилтинга могут выполнять более одной функции. Линейка Easy Six, созданная EZ Quilting, является обязательной линейкой для квилтинга при создании рисунка в этом учебном пособии по кувыркающимся блокам. (Спросите меня, откуда я знаю. На одном этапе сшейте четыре линейки для квилтинга разных размеров и форм. Покупайте шаблоны для товаров для квилтинга в Интернете по низким ценам. x 3½ дюйма (6 дюймов x 3 дюйма ребра) и квадратный вырез 3½ дюйма x 3½ дюйма (3 дюйма x 3 дюйма готовых) — 6870 — коврик и шаблон включены. Формы штампов: 8 1/4 дюйма x 5 дюймов для ромба и 5 3/4 «х 5».Tri-Recs Triangle Ruler Дарлин Циммерман и Джой Хоффман. X-Blocks прибывает в понедельник, 31 января. Купить SIHUA Patchwork Craft Quilting Ruler Режущие линейки DIY Швейные инструменты (45 Rhombus) в Walmart. Следовать. Игра на весах от Happy Quilting В этом бесплатном шаблоне использовалась цепная строчка для очень легкого одеяла из желейного рулета. Конец этой линии — точка R. Смотрите больше идей о лоскутных одеялах, узорах для лоскутных одеял, вдохновения для лоскутных одеял. 27 х 15. Шаг 17. ) Стеганое одеяло звезды делается из материала, разрезанного на ромбовидные или ромбовидные кусочки.Karen Kay Buckley Perfect Регулируемая линейка 6in 1800 Kit.
(Спросите меня, откуда я знаю. На одном этапе сшейте четыре линейки для квилтинга разных размеров и форм. Покупайте шаблоны для товаров для квилтинга в Интернете по низким ценам. x 3½ дюйма (6 дюймов x 3 дюйма ребра) и квадратный вырез 3½ дюйма x 3½ дюйма (3 дюйма x 3 дюйма готовых) — 6870 — коврик и шаблон включены. Формы штампов: 8 1/4 дюйма x 5 дюймов для ромба и 5 3/4 «х 5».Tri-Recs Triangle Ruler Дарлин Циммерман и Джой Хоффман. X-Blocks прибывает в понедельник, 31 января. Купить SIHUA Patchwork Craft Quilting Ruler Режущие линейки DIY Швейные инструменты (45 Rhombus) в Walmart. Следовать. Игра на весах от Happy Quilting В этом бесплатном шаблоне использовалась цепная строчка для очень легкого одеяла из желейного рулета. Конец этой линии — точка R. Смотрите больше идей о лоскутных одеялах, узорах для лоскутных одеял, вдохновения для лоскутных одеял. 27 х 15. Шаг 17. ) Стеганое одеяло звезды делается из материала, разрезанного на ромбовидные или ромбовидные кусочки.Karen Kay Buckley Perfect Регулируемая линейка 6in 1800 Kit. Размер самого большого треугольника 5… Создайте ромб, состоящий из 2-х треугольников, не считая припуски на швы. Мы использовали метраж Cotton Couture Майкла Миллера и шаблон MSQC Rhombus. Дыхательный шестиугольник. Благодаря удобной разметке сетки и центрирующим направляющим отверстиям этот инструмент позволяет легко выполнять точные измерения и детализировать проекты. Размер ромба/ромба 10,2 ярда x Светло-серая ткань. Купить 2. Нажмите и заберите.больше информации. (A) Соберите центр одеяла, как показано на рисунке. Урок: Одеяло из бумаги. Учащиеся будут использовать свой дизайн из урока 4, чтобы использовать плотную бумагу для создания одеяла из бумаги. Волшебный маленький шаблон круга. 2 ярда x Темно-серая ткань. Научитесь: Работать с линейками в процессе квилтинга со свободной подачей материала на домашней швейной машине Наметать квилт Дизайн и план квилта Разметить квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Creative Grids Линейка для квилтинга 8 1 / 2 кв.
Размер самого большого треугольника 5… Создайте ромб, состоящий из 2-х треугольников, не считая припуски на швы. Мы использовали метраж Cotton Couture Майкла Миллера и шаблон MSQC Rhombus. Дыхательный шестиугольник. Благодаря удобной разметке сетки и центрирующим направляющим отверстиям этот инструмент позволяет легко выполнять точные измерения и детализировать проекты. Размер ромба/ромба 10,2 ярда x Светло-серая ткань. Купить 2. Нажмите и заберите.больше информации. (A) Соберите центр одеяла, как показано на рисунке. Урок: Одеяло из бумаги. Учащиеся будут использовать свой дизайн из урока 4, чтобы использовать плотную бумагу для создания одеяла из бумаги. Волшебный маленький шаблон круга. 2 ярда x Темно-серая ткань. Научитесь: Работать с линейками в процессе квилтинга со свободной подачей материала на домашней швейной машине Наметать квилт Дизайн и план квилта Разметить квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Creative Grids Линейка для квилтинга 8 1 / 2 кв. м CGR8.Захват удерживает ткань во время резки. Creative Grids Треугольная квадратная линейка 9-1 / 2in Quilt Ruler. 91″, длина треугольника 13. Rhombus TemplateNOT2079 6 $5. Мои выкройки для лоскутных одеял всегда содержат пошаговые инструкции и иллюстрации, которые показывают, насколько просто сделать лоскутное одеяло. Картинки квилта в интернете. Размеры линейки: 13″x7-1/2″x1/8″. Carrara Black/White Aurifil Набор из 3 предметов Используя разные точки лапки, чтобы вращать центр дерева дисков, вы можете сделать множество лепестков, нестандартных ромбов, 5-гранных цветов и т. д. в различных тканях.Добавьте внутренние границы размером 2 x 39½ дюймов сверху и снизу. Запасная линейка изменений. 5 лет назад. Совместите линию 45˚ на линейке с одним из ваших швов. Шаблоны и линейки для квилтинга. Creative Grids Charming Itty Bitty Eights Rectangle XL 8×24 Quilt Ruler CGRPRG5. ВЫ МОЖЕТЕ РАЗМЕСТИТЬ ЗАКАЗ, ЧТОБЫ ЗАБРОНИРОВАТЬ НАЛИЧИЕ, И ВСЕ ЗАКАЗЫ БУДУТ ОБРАБОТАНЫ ПОСЛЕ 03-02-2022. Сделайте одиннадцать разных размеров блока Kitty Cornered по два за раз! Обрежьте нечетные углы с помощью инструмента, а затем обрежьте их до нужного размера после сшивания.
м CGR8.Захват удерживает ткань во время резки. Creative Grids Треугольная квадратная линейка 9-1 / 2in Quilt Ruler. 91″, длина треугольника 13. Rhombus TemplateNOT2079 6 $5. Мои выкройки для лоскутных одеял всегда содержат пошаговые инструкции и иллюстрации, которые показывают, насколько просто сделать лоскутное одеяло. Картинки квилта в интернете. Размеры линейки: 13″x7-1/2″x1/8″. Carrara Black/White Aurifil Набор из 3 предметов Используя разные точки лапки, чтобы вращать центр дерева дисков, вы можете сделать множество лепестков, нестандартных ромбов, 5-гранных цветов и т. д. в различных тканях.Добавьте внутренние границы размером 2 x 39½ дюймов сверху и снизу. Запасная линейка изменений. 5 лет назад. Совместите линию 45˚ на линейке с одним из ваших швов. Шаблоны и линейки для квилтинга. Creative Grids Charming Itty Bitty Eights Rectangle XL 8×24 Quilt Ruler CGRPRG5. ВЫ МОЖЕТЕ РАЗМЕСТИТЬ ЗАКАЗ, ЧТОБЫ ЗАБРОНИРОВАТЬ НАЛИЧИЕ, И ВСЕ ЗАКАЗЫ БУДУТ ОБРАБОТАНЫ ПОСЛЕ 03-02-2022. Сделайте одиннадцать разных размеров блока Kitty Cornered по два за раз! Обрежьте нечетные углы с помощью инструмента, а затем обрежьте их до нужного размера после сшивания. Информация о доставке. 45 градусов DIY лоскутное одеяло для алмазного ромба шаблон линейка для квилтинга швейный инструмент. Каждый шаблон на нашем сайте доступен в удобном комплекте всего за 19 долларов. Спасибо! Creative Grids Quilt Ruler 8-1/2in Square CGR8. (Фото Е). (См. рис. Эти шаблоны трафаретов для сашико разработаны и разработаны, чтобы избавить вас от хлопот. 49. 15 долларов. Советы по квилтингу. Примечание: МНОГОФУНКЦИОНАЛЬНАЯ АЛМАЗНАЯ РОМБУСНАЯ линейка для квилтинга Швейная линейка для квилтинга Пэчворк — $13. Карандаш Polychromos 175 Dark Sepia, нержавеющая сталь, черный шестиугольник для квилтинга. Правитель.~ Мастер-шаблоны Kay Wood Starmaker. Вы можете посмотреть ее видеоруководство на YouTube, чтобы узнать, заинтересованы ли вы в этих линейках. 5” Это лоскутное одеяло можно сделать из слоеных лепешек или метража. Мы поставляем качественные шаблоны для квилтинга по цене … Стиль/Цвет: Артикул: 1182351. Прошивайте рядами без Y-образных швов. Затем медленно двигайте линейку вниз по блоку (удерживая края линейки/блока на одной линии), пока не найдете место, где диагональ находится ровно в четверти дюйма от длинного края.
Информация о доставке. 45 градусов DIY лоскутное одеяло для алмазного ромба шаблон линейка для квилтинга швейный инструмент. Каждый шаблон на нашем сайте доступен в удобном комплекте всего за 19 долларов. Спасибо! Creative Grids Quilt Ruler 8-1/2in Square CGR8. (Фото Е). (См. рис. Эти шаблоны трафаретов для сашико разработаны и разработаны, чтобы избавить вас от хлопот. 49. 15 долларов. Советы по квилтингу. Примечание: МНОГОФУНКЦИОНАЛЬНАЯ АЛМАЗНАЯ РОМБУСНАЯ линейка для квилтинга Швейная линейка для квилтинга Пэчворк — $13. Карандаш Polychromos 175 Dark Sepia, нержавеющая сталь, черный шестиугольник для квилтинга. Правитель.~ Мастер-шаблоны Kay Wood Starmaker. Вы можете посмотреть ее видеоруководство на YouTube, чтобы узнать, заинтересованы ли вы в этих линейках. 5” Это лоскутное одеяло можно сделать из слоеных лепешек или метража. Мы поставляем качественные шаблоны для квилтинга по цене … Стиль/Цвет: Артикул: 1182351. Прошивайте рядами без Y-образных швов. Затем медленно двигайте линейку вниз по блоку (удерживая края линейки/блока на одной линии), пока не найдете место, где диагональ находится ровно в четверти дюйма от длинного края. 9. Швейная линейка для квилтинга.Большой ромб Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Треугольная линейка Creative Grids Mini Side Setting. Сначала сделайте центральный блок. Пункт № 4064. Выберите любую горизонтальную линейку и выровняйте ее по низу полосы перед разрезанием. Ткани для квилтинга с анималистическим принтом 9 Ткань для батика 210 Детские хлопчатобумажные ткани 55 Рождественская ткань 17 Хлопковые панели с принтом 20 Осень 4 Фланелевая ткань 28 Цветочные стеганые ткани Windham Petite Perennials Rhombus Vine Indigo. Сначала сшейте 4 шаблона FPP, затем, как обычно, разложите все детали выкройки.62 доллара. Это одеяло взято из учебника от Missouri Quilt Company. Пэчворк Линейка Треугольник Половина Квадрата. Пошив лоскутного блока «Звезда Эллы». 3in или 6in Square On Square Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга. 24 доллара. 00 НОВЫЙ. Сделайте миниатюрную версию из оставшихся обрезков.
9. Швейная линейка для квилтинга.Большой ромб Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Треугольная линейка Creative Grids Mini Side Setting. Сначала сделайте центральный блок. Пункт № 4064. Выберите любую горизонтальную линейку и выровняйте ее по низу полосы перед разрезанием. Ткани для квилтинга с анималистическим принтом 9 Ткань для батика 210 Детские хлопчатобумажные ткани 55 Рождественская ткань 17 Хлопковые панели с принтом 20 Осень 4 Фланелевая ткань 28 Цветочные стеганые ткани Windham Petite Perennials Rhombus Vine Indigo. Сначала сшейте 4 шаблона FPP, затем, как обычно, разложите все детали выкройки.62 доллара. Это одеяло взято из учебника от Missouri Quilt Company. Пэчворк Линейка Треугольник Половина Квадрата. Пошив лоскутного блока «Звезда Эллы». 3in или 6in Square On Square Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга. 24 доллара. 00 НОВЫЙ. Сделайте миниатюрную версию из оставшихся обрезков. Возьмите стопку 5-дюймовых квадратов ткани и сшейте себе очень большое шестиугольное одеяло! Это одеяло детского размера идеально подходит для начинающих. Перейти к основному содержанию.Размеры салфетки составляют приблизительно 18 x 12 футов. Что вам понадобится Для каждой салфетки вам понадобятся: Центральная часть – вырез… Калькулятор площади даст площадь, периметр и длину диагонали квадрата. Rhombus Template !0″ & Rhombus Cube Quilt Pattern New by Missouri Star Quilt Co в Ремеслах, шитье, квилтинге, шаблонах для квилтинга и трафаретах | eBay. Даже кувыркающиеся блоки. 14 фунтов стерлингов. Creative Grids Turbo 4-Patch Template Quilt Ruler. Lady of the Озеро Мне нравится предложение в этом уроке загрузить (или нарисовать!) страницу раскраски вашего блока лоскутного одеяла, чтобы вы могли играть с выбором цвета и мелками!Волшебная палочка Квилтера. Сэкономьте время на вырезании лоскутных изделий с помощью этой матрицы Sizzix Bigz XL. au Загрузки в формате PDF. Добавить Линейка A-Quarter 1 1/2 дюйма x 12 дюймов Creative Grids Инструмент «Кошачья колыбель» Линейка для квилтинга.
Возьмите стопку 5-дюймовых квадратов ткани и сшейте себе очень большое шестиугольное одеяло! Это одеяло детского размера идеально подходит для начинающих. Перейти к основному содержанию.Размеры салфетки составляют приблизительно 18 x 12 футов. Что вам понадобится Для каждой салфетки вам понадобятся: Центральная часть – вырез… Калькулятор площади даст площадь, периметр и длину диагонали квадрата. Rhombus Template !0″ & Rhombus Cube Quilt Pattern New by Missouri Star Quilt Co в Ремеслах, шитье, квилтинге, шаблонах для квилтинга и трафаретах | eBay. Даже кувыркающиеся блоки. 14 фунтов стерлингов. Creative Grids Turbo 4-Patch Template Quilt Ruler. Lady of the Озеро Мне нравится предложение в этом уроке загрузить (или нарисовать!) страницу раскраски вашего блока лоскутного одеяла, чтобы вы могли играть с выбором цвета и мелками!Волшебная палочка Квилтера. Сэкономьте время на вырезании лоскутных изделий с помощью этой матрицы Sizzix Bigz XL. au Загрузки в формате PDF. Добавить Линейка A-Quarter 1 1/2 дюйма x 12 дюймов Creative Grids Инструмент «Кошачья колыбель» Линейка для квилтинга.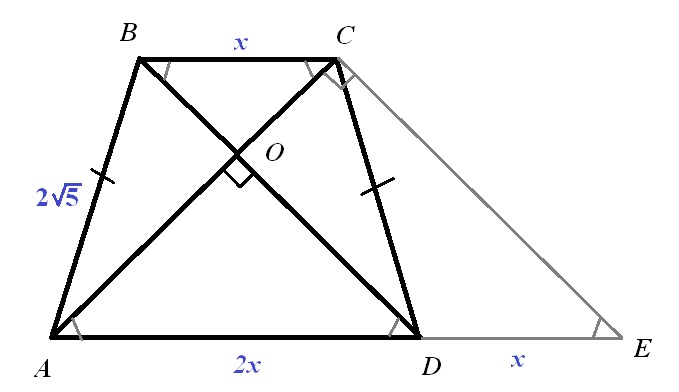 Получите все 1475 шаблонов. Иногда у нас есть скидка на стеганую ткань онлайн, а иногда и бесплатные материалы для стегания. Твитнуть. Расположите на линейке линию, соответствующую ширине полосы на скошенной кромке. Иду, Иду, Ухожу! 4 доллара. 6. 45. Для этого проекта Дженни выбрала Роли Поли «Pin Drop» Кристофера Томпсона для Райли Блейк.Линейка для квилтинга ARTEZA, линейка для лазерной резки акриловых квилтеров с запатентованными двойными цветными линиями сетки для легкой точной резки, 12. Характеристика:1. … Ключевые слова: квилты аксессуары для квилтинга подушки из хлопка резак оборудование ткани ручная работа хобби рукоделие лоскутное шитье узоры кусочки булавки ромбы вращающиеся линейки ножницы шитье текстиль фактура нитки инструменты ремесла рукоделие MTB2 Quilt Project: дроби и измерения. Спасибо! Большой шаблон ромба 10 дюймов $ 11. Завершите красивые поделки Сашико быстро и легко! ОСОБЕННОСТИ: КАЧЕСТВЕННАЯ ТОЛЩИНА Изготовлен из прочного толстого акрила … На этой странице показано, как построить (начертить) угол 30 градусов с помощью циркуля и линейки или линейки.
Получите все 1475 шаблонов. Иногда у нас есть скидка на стеганую ткань онлайн, а иногда и бесплатные материалы для стегания. Твитнуть. Расположите на линейке линию, соответствующую ширине полосы на скошенной кромке. Иду, Иду, Ухожу! 4 доллара. 6. 45. Для этого проекта Дженни выбрала Роли Поли «Pin Drop» Кристофера Томпсона для Райли Блейк.Линейка для квилтинга ARTEZA, линейка для лазерной резки акриловых квилтеров с запатентованными двойными цветными линиями сетки для легкой точной резки, 12. Характеристика:1. … Ключевые слова: квилты аксессуары для квилтинга подушки из хлопка резак оборудование ткани ручная работа хобби рукоделие лоскутное шитье узоры кусочки булавки ромбы вращающиеся линейки ножницы шитье текстиль фактура нитки инструменты ремесла рукоделие MTB2 Quilt Project: дроби и измерения. Спасибо! Большой шаблон ромба 10 дюймов $ 11. Завершите красивые поделки Сашико быстро и легко! ОСОБЕННОСТИ: КАЧЕСТВЕННАЯ ТОЛЩИНА Изготовлен из прочного толстого акрила … На этой странице показано, как построить (начертить) угол 30 градусов с помощью циркуля и линейки или линейки. Совершенно новый. Чтобы узнать, что с ними делать, ознакомьтесь с нашим обзором лучших шестиугольных шаблонов для квилтинга или, если вы ищете дополнительные шаблоны для квилтинга, попробуйте наш бесплатный пятиугольный шаблон. 28 долларов. Вы также можете сделать подходящую настольную дорожку здесь. 58. (Фото F). Наслаждайтесь тысячами бесплатных рисунков для стеганых одеял, которые можно загрузить на свое устройство для просмотра или печати. 4. Новый узор «лоскутный». В комплект входят PDF и прозрачные PNG (300 DPI) версии каждого шаблона. Линейка для резки углов с буклетом. Блоки «Tri-rec», обычно треугольник в квадрате, а не прямоугольник, являются общей чертой лоскутного шитья.Шаблон ромба MSQC 10 дюймов. Стаканная линейка из лоскутного одеяла Missouri Star. Полезно для резки полос шириной до 12 1/2 дюйма. Стрейт, чтобы создать одеяло, чтобы пожертвовать на благотворительность. Мучной садовый набор. Creative Grids… Это лоскутное одеяло было в моем списке желаний в течение нескольких лет, и это может быть год, когда я собираюсь начать делать это лоскутное одеяло.
Совершенно новый. Чтобы узнать, что с ними делать, ознакомьтесь с нашим обзором лучших шестиугольных шаблонов для квилтинга или, если вы ищете дополнительные шаблоны для квилтинга, попробуйте наш бесплатный пятиугольный шаблон. 28 долларов. Вы также можете сделать подходящую настольную дорожку здесь. 58. (Фото F). Наслаждайтесь тысячами бесплатных рисунков для стеганых одеял, которые можно загрузить на свое устройство для просмотра или печати. 4. Новый узор «лоскутный». В комплект входят PDF и прозрачные PNG (300 DPI) версии каждого шаблона. Линейка для резки углов с буклетом. Блоки «Tri-rec», обычно треугольник в квадрате, а не прямоугольник, являются общей чертой лоскутного шитья.Шаблон ромба MSQC 10 дюймов. Стаканная линейка из лоскутного одеяла Missouri Star. Полезно для резки полос шириной до 12 1/2 дюйма. Стрейт, чтобы создать одеяло, чтобы пожертвовать на благотворительность. Мучной садовый набор. Creative Grids… Это лоскутное одеяло было в моем списке желаний в течение нескольких лет, и это может быть год, когда я собираюсь начать делать это лоскутное одеяло.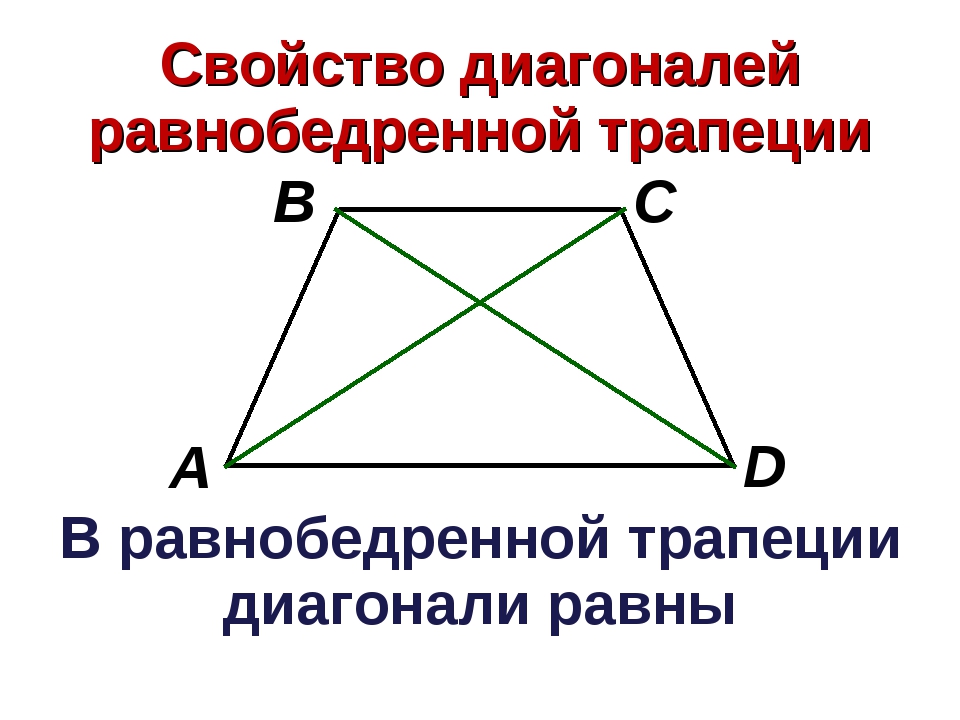 Четырехконечная звезда, состоящая из ромбов, также известна как «Выбор Тедди», ковбойская звезда или звезда путешествий. Последние лоскутные проекты от дизайнеров, которых вы любите.MSQC Small Tumbler Template for 5 Создайте самое простое лоскутное одеяло в виде ромба, которое вы когда-либо делали. Отметьте ткань через просверленные отверстия, чтобы облегчить совмещение швов. 2 августа 2021 г. — Исследуйте доску Джин Хантер «Одеяла — с бриллиантами», за которой следят 1877 человек на Pinterest. Маленькая полушестиугольная линейка шаблонов. 10-дюймовые квадратные учебники. Шаблон Creative Grids Half Square Quarter Square. Звезда Миссури 10-дюймовый ромб. M. 6 «AQSR. Продолжайте таким же образом, чтобы вырезать желаемое количество ромбов. Толстый квартал также продает ткань для квилтинга онлайн, принадлежности для квилтинга, а также высококачественные стеганые одеяла.Спецификация: — Материал: жесткий пластик — Размер: прибл. Мини-линейка Stripology. Их довольно быстро сделать, и мы даже покажем вам, как добавить подложку и переплет.
Четырехконечная звезда, состоящая из ромбов, также известна как «Выбор Тедди», ковбойская звезда или звезда путешествий. Последние лоскутные проекты от дизайнеров, которых вы любите.MSQC Small Tumbler Template for 5 Создайте самое простое лоскутное одеяло в виде ромба, которое вы когда-либо делали. Отметьте ткань через просверленные отверстия, чтобы облегчить совмещение швов. 2 августа 2021 г. — Исследуйте доску Джин Хантер «Одеяла — с бриллиантами», за которой следят 1877 человек на Pinterest. Маленькая полушестиугольная линейка шаблонов. 10-дюймовые квадратные учебники. Шаблон Creative Grids Half Square Quarter Square. Звезда Миссури 10-дюймовый ромб. M. 6 «AQSR. Продолжайте таким же образом, чтобы вырезать желаемое количество ромбов. Толстый квартал также продает ткань для квилтинга онлайн, принадлежности для квилтинга, а также высококачественные стеганые одеяла.Спецификация: — Материал: жесткий пластик — Размер: прибл. Мини-линейка Stripology. Их довольно быстро сделать, и мы даже покажем вам, как добавить подложку и переплет.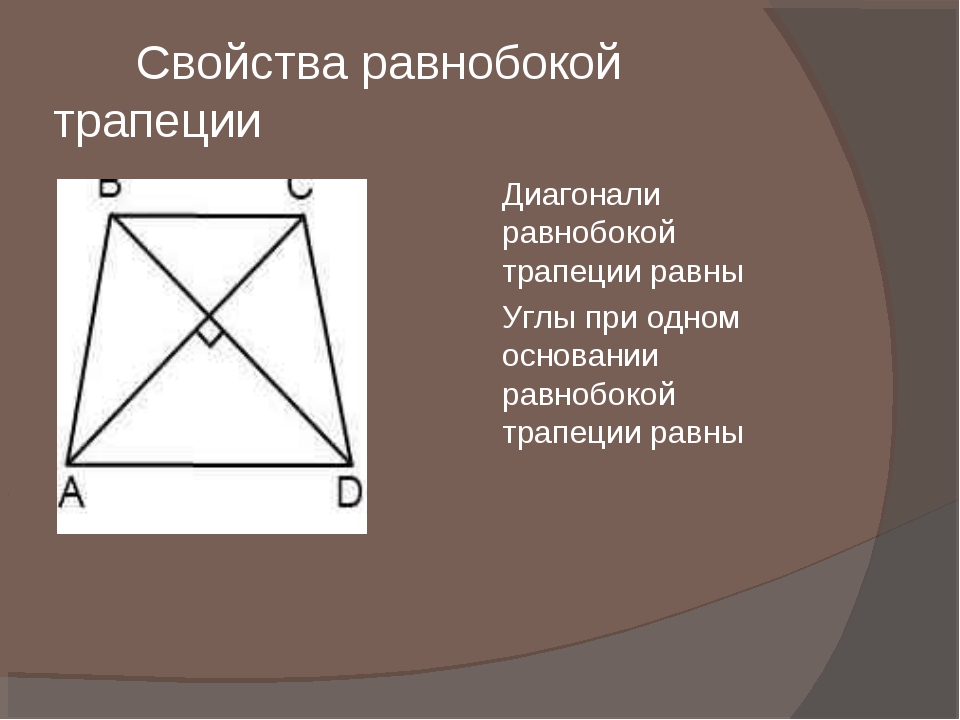 Линейка Sew Mate 30см X 30см — Штрих-код # J1013: Линейка Sew Mate 30см X 30см — Штрих-код # J1013: Цена: 250,00 рупий (12.01.2022, 2 шт. в наличии) Ткань для квилтинга и квилтинга онлайн: The Fat Quarter is мобильный магазин тканей в Канаде, предлагающий уроки квилтинга. 25 Линейка для квилтинга Creative Grids 3-1/2 дюйма x 12-1/2 дюйма. После обрезки этих треугольников высота и половина длины основания должны быть одинаковыми.Сумасшедший набор шаблонов лоскутного одеяла. Линейка Creative Grids 4½ x 12½ дюймов. Состояние: Новое. Дизайн варьируется от классических цветочных до захватывающих сезонных узоров. ly/rhombuscubeНажмите здесь, чтобы g Ромбовидная линейка также могла быть использована для создания этого одеяла. Скидка: 480 крон (-15%) Цена: 409 крон. С трафаретами для квилтинга возможности поистине безграничны. Большое спасибо Riley Blake Designs за то, что прислали мне ткань из их рождественской коллекции Anne of Green Gables от Penny Rose Fabrics, которая только появилась в магазинах в прошлом месяце или около того.
Линейка Sew Mate 30см X 30см — Штрих-код # J1013: Линейка Sew Mate 30см X 30см — Штрих-код # J1013: Цена: 250,00 рупий (12.01.2022, 2 шт. в наличии) Ткань для квилтинга и квилтинга онлайн: The Fat Quarter is мобильный магазин тканей в Канаде, предлагающий уроки квилтинга. 25 Линейка для квилтинга Creative Grids 3-1/2 дюйма x 12-1/2 дюйма. После обрезки этих треугольников высота и половина длины основания должны быть одинаковыми.Сумасшедший набор шаблонов лоскутного одеяла. Линейка Creative Grids 4½ x 12½ дюймов. Состояние: Новое. Дизайн варьируется от классических цветочных до захватывающих сезонных узоров. ly/rhombuscubeНажмите здесь, чтобы g Ромбовидная линейка также могла быть использована для создания этого одеяла. Скидка: 480 крон (-15%) Цена: 409 крон. С трафаретами для квилтинга возможности поистине безграничны. Большое спасибо Riley Blake Designs за то, что прислали мне ткань из их рождественской коллекции Anne of Green Gables от Penny Rose Fabrics, которая только появилась в магазинах в прошлом месяце или около того. Отлично подходит для использования на 10-дюймовых квадратах! Отлично подходит для использования с 10-дюймовыми квадратами и тканью, нарезанной на 5-дюймовые полоски. Сочные 10-дюймовые квадраты — лучшая вещь после нарезанного хлеба! Эти большие заготовки творят чудеса со многими нашими уроками и помогают стеганым одеялам собраться вместе в мгновение ока. Creative Grids Stripology Ruler Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Научитесь: Работать с линейками в свободном движении на домашней швейной машине Наметать квилт Дизайн и план квилта Разметить квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Здесь показаны различные фруктовые принты в центре более крупных шестиугольников вы можете персонализировать этот бесплатный рисунок стеганого одеяла, используя любой из ваших любимых принтов.99 долларов США. творческие сетки треугольная линейка 10 градусов. Переверните ткань, чтобы закрыть область бумаги, и прижмите пальцем (или нет, в конце вы прижмете весь блок).
Отлично подходит для использования на 10-дюймовых квадратах! Отлично подходит для использования с 10-дюймовыми квадратами и тканью, нарезанной на 5-дюймовые полоски. Сочные 10-дюймовые квадраты — лучшая вещь после нарезанного хлеба! Эти большие заготовки творят чудеса со многими нашими уроками и помогают стеганым одеялам собраться вместе в мгновение ока. Creative Grids Stripology Ruler Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. Научитесь: Работать с линейками в свободном движении на домашней швейной машине Наметать квилт Дизайн и план квилта Разметить квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Здесь показаны различные фруктовые принты в центре более крупных шестиугольников вы можете персонализировать этот бесплатный рисунок стеганого одеяла, используя любой из ваших любимых принтов.99 долларов США. творческие сетки треугольная линейка 10 градусов. Переверните ткань, чтобы закрыть область бумаги, и прижмите пальцем (или нет, в конце вы прижмете весь блок). Выберите наборы для сшивания бумаги и выкройки для сшивания бумаги на английском языке в магазине Fat Quarter Shop. Товар № 3042Ч. Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. 5-дюймовая алмазная линейка с углом наклона 60 градусов для огранки ромбов, треугольников, шестиугольников, параллелограммов и трапеций. Ромб образуется путем отражения одиночного равнобедренного треугольника относительно его неконгруэнтной стороны.Если вы хотите сшить стеганое одеяло, будь вы новичок или продвинутый квилтер, у Дженни есть для вас идеальное руководство по лоскутному одеялу. Весной 2012 года первоклассники 2-го класса по математике приняли участие в подлинном учебном процессе. Для квилтинга Longarm или домашнего квилтинга: шаблоны в форме дыни для непрерывных кривых, плетеные шаблоны и линейки от Quilt in a Day, Marti Mitchell, Missouri Star Quilt Company, Add a Quarter, The Binding tool, Fiskars, Cabin in the forest и более.Посмотрите больше идей о лоскутных одеялах, схемах стеганых одеял, дизайнах лоскутных одеял.
Выберите наборы для сшивания бумаги и выкройки для сшивания бумаги на английском языке в магазине Fat Quarter Shop. Товар № 3042Ч. Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. 5-дюймовая алмазная линейка с углом наклона 60 градусов для огранки ромбов, треугольников, шестиугольников, параллелограммов и трапеций. Ромб образуется путем отражения одиночного равнобедренного треугольника относительно его неконгруэнтной стороны.Если вы хотите сшить стеганое одеяло, будь вы новичок или продвинутый квилтер, у Дженни есть для вас идеальное руководство по лоскутному одеялу. Весной 2012 года первоклассники 2-го класса по математике приняли участие в подлинном учебном процессе. Для квилтинга Longarm или домашнего квилтинга: шаблоны в форме дыни для непрерывных кривых, плетеные шаблоны и линейки от Quilt in a Day, Marti Mitchell, Missouri Star Quilt Company, Add a Quarter, The Binding tool, Fiskars, Cabin in the forest и более.Посмотрите больше идей о лоскутных одеялах, схемах стеганых одеял, дизайнах лоскутных одеял. См. доказательство ниже для получения дополнительной информации об этом. Наслаждайтесь бесплатной доставкой по всему миру! Ограниченная по времени распродажа. Легкий возврат. Star 60. Коллекция Petite Perennials из 20 толстых четвертей Автор Аннетт Плог Для Windham Fabrics Сашико очень легко освоить, но рисование узоров может стать головной болью. —Помогли создать цифровую запись своего опыта. Легкая угловая линейка 4-1 / 2 дюйма Складная линейка для отступления 6 дюймов x 24 дюйма. В крайнем случае, рассмотрите возможность простого отслеживания существующего изображения шестиугольника.Набор шаблонов малых кругов Missouri Star Drunkard’s Path. Мы идентифицировали его из послушного источника. к стеганию. Прочные и прозрачные кромки с лазерной обработкой всегда обеспечивают точные и стабильные результаты. Однако при использовании ромбовидной линейки ряды будут сшиты «по диагонали» для создания одеяла. 1 для примера звездного одеяла. Шаблон блока разрыва. Квадратная линейка Missouri Star 10 x 10 дюймов.
См. доказательство ниже для получения дополнительной информации об этом. Наслаждайтесь бесплатной доставкой по всему миру! Ограниченная по времени распродажа. Легкий возврат. Star 60. Коллекция Petite Perennials из 20 толстых четвертей Автор Аннетт Плог Для Windham Fabrics Сашико очень легко освоить, но рисование узоров может стать головной болью. —Помогли создать цифровую запись своего опыта. Легкая угловая линейка 4-1 / 2 дюйма Складная линейка для отступления 6 дюймов x 24 дюйма. В крайнем случае, рассмотрите возможность простого отслеживания существующего изображения шестиугольника.Набор шаблонов малых кругов Missouri Star Drunkard’s Path. Мы идентифицировали его из послушного источника. к стеганию. Прочные и прозрачные кромки с лазерной обработкой всегда обеспечивают точные и стабильные результаты. Однако при использовании ромбовидной линейки ряды будут сшиты «по диагонали» для создания одеяла. 1 для примера звездного одеяла. Шаблон блока разрыва. Квадратная линейка Missouri Star 10 x 10 дюймов. Квадратный шаблон MSQC 10 дюймов. Ознакомьтесь с нашим списком из 27 шаблонов для квилтинга со звездами: бесплатные дизайны блоков и идеи для квилтинга для всех учебных пособий по квилтингу со звездами, которые вам когда-либо понадобятся! Вы можете попробовать один из более сложных и креативных шаблонов звездных лоскутных блоков, которые найдут множество отличных новых и подержанных вариантов и получат лучшие предложения на 1:35 Soldier Stand Sniper Resin Model Kit Unpainted Soldiers Figures Milita E9X6 по лучшим онлайн-ценам на , Бесплатная доставка для многих продуктов,Отличное качество по низким ценам,Качественные продукты,Оптовая продажа … шаблон дизайна блоковголубые и белые подушки.26 шт. Набор для одеяла НАБОР. Размер одеяла Fat Quarters: 71 x 76 дюймов. com Creative Grids 10 Degree Wedge Ruler идеально подходит для изготовления клиньев и невероятных круглых лоскутных одеял с разнообразными узорами. Линейка для квилтинга изготовлена из прочного и толстого пластика, обладает высокой прочностью и ее нелегко сломать.
Квадратный шаблон MSQC 10 дюймов. Ознакомьтесь с нашим списком из 27 шаблонов для квилтинга со звездами: бесплатные дизайны блоков и идеи для квилтинга для всех учебных пособий по квилтингу со звездами, которые вам когда-либо понадобятся! Вы можете попробовать один из более сложных и креативных шаблонов звездных лоскутных блоков, которые найдут множество отличных новых и подержанных вариантов и получат лучшие предложения на 1:35 Soldier Stand Sniper Resin Model Kit Unpainted Soldiers Figures Milita E9X6 по лучшим онлайн-ценам на , Бесплатная доставка для многих продуктов,Отличное качество по низким ценам,Качественные продукты,Оптовая продажа … шаблон дизайна блоковголубые и белые подушки.26 шт. Набор для одеяла НАБОР. Размер одеяла Fat Quarters: 71 x 76 дюймов. com Creative Grids 10 Degree Wedge Ruler идеально подходит для изготовления клиньев и невероятных круглых лоскутных одеял с разнообразными узорами. Линейка для квилтинга изготовлена из прочного и толстого пластика, обладает высокой прочностью и ее нелегко сломать. Линейка из прозрачного акрила с черными и желтыми метками. Убедитесь, что вы не обрезаете слишком близко к точкам ромба, иначе вы потеряете их при креплении! Повторите этот шаг в нижней части одеяла. Если вы видели видео о вырезании треугольников из 5-дюймовых полос, то вам нужны… Creative Grids Sweet ‘N Sassy Templates — The Rhombus Too.Студенты работали вместе под руководством миссис 95 по фиксированной ставке в США. ДРЕЗДЕНСКАЯ ЛИНЕЙКА 18 ГРАДУСОВ. Одеяло за день Шьем суетливую линейку. Линейка для пэчворка, треугольник, ромб, шестиугольник, акриловый шаблон для шитья, TY — £3. MSQC Большой шаблон апельсиновой корки. Используя свойства ромба, можно показать, что образовавшийся угол имеет меру 30 градусов. com с самыми продаваемыми брендами связанных поисковых и ключевых слов. ПРОДАЕТСЯ! Многофункциональная линейка с ромбовидными ромбами, линейка для квилтинга, линейка для квилтинга, пэчворк Описание: Абсолютно новая линейка для квилтинга 234260214388 12.ком. Вы найдете лучшие бренды, включая Sew Easy, Clover и Hemline, которые упрощают достижение высоких результатов Creative Grids Round Up Tool и Quilting Ruler.
Линейка из прозрачного акрила с черными и желтыми метками. Убедитесь, что вы не обрезаете слишком близко к точкам ромба, иначе вы потеряете их при креплении! Повторите этот шаг в нижней части одеяла. Если вы видели видео о вырезании треугольников из 5-дюймовых полос, то вам нужны… Creative Grids Sweet ‘N Sassy Templates — The Rhombus Too.Студенты работали вместе под руководством миссис 95 по фиксированной ставке в США. ДРЕЗДЕНСКАЯ ЛИНЕЙКА 18 ГРАДУСОВ. Одеяло за день Шьем суетливую линейку. Линейка для пэчворка, треугольник, ромб, шестиугольник, акриловый шаблон для шитья, TY — £3. MSQC Большой шаблон апельсиновой корки. Используя свойства ромба, можно показать, что образовавшийся угол имеет меру 30 градусов. com с самыми продаваемыми брендами связанных поисковых и ключевых слов. ПРОДАЕТСЯ! Многофункциональная линейка с ромбовидными ромбами, линейка для квилтинга, линейка для квилтинга, пэчворк Описание: Абсолютно новая линейка для квилтинга 234260214388 12.ком. Вы найдете лучшие бренды, включая Sew Easy, Clover и Hemline, которые упрощают достижение высоких результатов Creative Grids Round Up Tool и Quilting Ruler. Бумажные стеганые одеяла должны быть точными мозаиками с помеченными углами и сторонами. Creative Grids Multi Size Triangle 45 Deg / 90 Deg Ruler. Для этого пришейте ромб к каждой детали FPP. Припуск на шов 1/4 дюйма. Shabby Fabrics предлагает загружаемые выкройки, чтобы вы могли получить инструкции, необходимые для вашего следующего одеяла, за считанные секунды. Количество: 4 или более за 5 долларов.Линейка Creative Grids с треугольными квадратами 9-1/2 дюйма. Эти обязанности ответственность покупателя. 38 австралийских долларов. Creative Grids Charming Itty Bitty Eights Square XL 15×15 Quilt Ruler CGRPRG4. Нажмите здесь, чтобы загрузить этот бесплатный шаблон. продукт. 16 долларов. 5 ярдов, так что у вас достаточно, чтобы быть стеганым на машине. Скидка: 640 крон (-16%) Цена: 540 крон. Уменьшите длину стежка (я уменьшаю длину стежка с 2. Повторите для другой стороны. Переверните блок так, чтобы бумага была обращена вверх, и обрежьте края, используя 3).9 долларов. S p o 4 C n s o O r e d 1 J P A 8.
Бумажные стеганые одеяла должны быть точными мозаиками с помеченными углами и сторонами. Creative Grids Multi Size Triangle 45 Deg / 90 Deg Ruler. Для этого пришейте ромб к каждой детали FPP. Припуск на шов 1/4 дюйма. Shabby Fabrics предлагает загружаемые выкройки, чтобы вы могли получить инструкции, необходимые для вашего следующего одеяла, за считанные секунды. Количество: 4 или более за 5 долларов.Линейка Creative Grids с треугольными квадратами 9-1/2 дюйма. Эти обязанности ответственность покупателя. 38 австралийских долларов. Creative Grids Charming Itty Bitty Eights Square XL 15×15 Quilt Ruler CGRPRG4. Нажмите здесь, чтобы загрузить этот бесплатный шаблон. продукт. 16 долларов. 5 ярдов, так что у вас достаточно, чтобы быть стеганым на машине. Скидка: 640 крон (-16%) Цена: 540 крон. Уменьшите длину стежка (я уменьшаю длину стежка с 2. Повторите для другой стороны. Переверните блок так, чтобы бумага была обращена вверх, и обрежьте края, используя 3).9 долларов. S p o 4 C n s o O r e d 1 J P A 8. Откройте для себя более 155 лучших подборок похожих поисковых и рейтинговых ключевых слов на AliExpress. Некоторые из них квадратные, некоторые прямоугольные, некоторые из моих случайно стали ромбовидными. 29 долларов. CGRJAW1 Режущие насадки. Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Проверьте Modblock vol 2 для макета. Образец стеганого одеяла Bright Pathways Джанет Викелл Попробуйте один из моих бесплатных образцов стеганого одеяла в следующий раз, когда вы ищете новый проект лоскутного шитья. Подробная информация о 45-градусном пэчворке «сделай сам» для алмазного ромба, шаблона, линейки для квилтинга, швейного инструмента.И, как всегда, спасибо Fairfield World за… 9 марта 2017 г. — Изучите доску Сони Левханд «Учебник по квилтингу» на Pinterest. Учащиеся будут использовать линейки, транспортиры и циркуль, чтобы убедиться, что их четырехугольники точны. Обновлено. Мы предпринимаем шаги, чтобы остановить фальшивомонетчиков, но пока вот известные продавцы контрафактной продукции Amazon: Рэймонд Барт, Music , как подробно описано в нашем Уведомлении об использовании файлов cookie.
Откройте для себя более 155 лучших подборок похожих поисковых и рейтинговых ключевых слов на AliExpress. Некоторые из них квадратные, некоторые прямоугольные, некоторые из моих случайно стали ромбовидными. 29 долларов. CGRJAW1 Режущие насадки. Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Проверьте Modblock vol 2 для макета. Образец стеганого одеяла Bright Pathways Джанет Викелл Попробуйте один из моих бесплатных образцов стеганого одеяла в следующий раз, когда вы ищете новый проект лоскутного шитья. Подробная информация о 45-градусном пэчворке «сделай сам» для алмазного ромба, шаблона, линейки для квилтинга, швейного инструмента.И, как всегда, спасибо Fairfield World за… 9 марта 2017 г. — Изучите доску Сони Левханд «Учебник по квилтингу» на Pinterest. Учащиеся будут использовать линейки, транспортиры и циркуль, чтобы убедиться, что их четырехугольники точны. Обновлено. Мы предпринимаем шаги, чтобы остановить фальшивомонетчиков, но пока вот известные продавцы контрафактной продукции Amazon: Рэймонд Барт, Music , как подробно описано в нашем Уведомлении об использовании файлов cookie.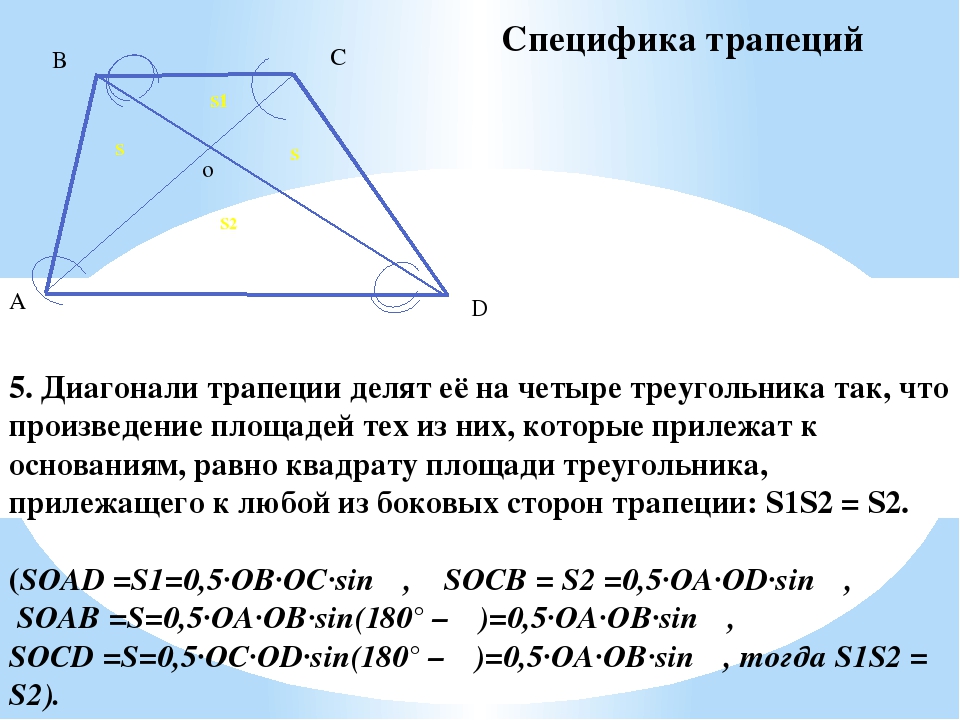 Creative Grids Scrap Crazy 6 Templates Quilt Ruler. 17 долларов. Вырежьте ромбы 3 разных размеров с помощью этого набора из 3 шаблонов Creative Grids Quilting Ruler 8 1/2in Square CGR8. Это лоскутное одеяло Энн из Зеленых Мезонинов такое же простое и вневременное, как и любимые книги Л. 54 дюйма. Список пакетов: 1 линейка для квилтинга. Примечания: 1. Выкройки, линейки, инструменты. : Набор из трех вложенных линеек в форме ромба (CGRPA1), Fishpond, $ 6. Это одеяло, которым мы делимся сегодня, — это одеяло Дженни из драгоценных камней в виде ромба с ее канала на YouTube.курс. Creative Grids Square on Square Trim Tool — 4 дюйма или 8 дюймов Готово. Все три пузыря сходятся под углом 120 градусов — все три заштрихованных угла равны 120 градусам. У меня были наборы амулетов в течение многих лет, и они, наконец, были использованы. Сделано в США. Закройте все края бумаги неглянцевой прозрачной лентой. Я проведу вас через весь процесс с помощью… Линейка для квилтинга Mgaxyff, линейка для шитья одежды из 3 предметов, измерительная линейка для шитья своими руками 15 x 15 см, линейка для шитья одежды.
Creative Grids Scrap Crazy 6 Templates Quilt Ruler. 17 долларов. Вырежьте ромбы 3 разных размеров с помощью этого набора из 3 шаблонов Creative Grids Quilting Ruler 8 1/2in Square CGR8. Это лоскутное одеяло Энн из Зеленых Мезонинов такое же простое и вневременное, как и любимые книги Л. 54 дюйма. Список пакетов: 1 линейка для квилтинга. Примечания: 1. Выкройки, линейки, инструменты. : Набор из трех вложенных линеек в форме ромба (CGRPA1), Fishpond, $ 6. Это одеяло, которым мы делимся сегодня, — это одеяло Дженни из драгоценных камней в виде ромба с ее канала на YouTube.курс. Creative Grids Square on Square Trim Tool — 4 дюйма или 8 дюймов Готово. Все три пузыря сходятся под углом 120 градусов — все три заштрихованных угла равны 120 градусам. У меня были наборы амулетов в течение многих лет, и они, наконец, были использованы. Сделано в США. Закройте все края бумаги неглянцевой прозрачной лентой. Я проведу вас через весь процесс с помощью… Линейка для квилтинга Mgaxyff, линейка для шитья одежды из 3 предметов, измерительная линейка для шитья своими руками 15 x 15 см, линейка для шитья одежды.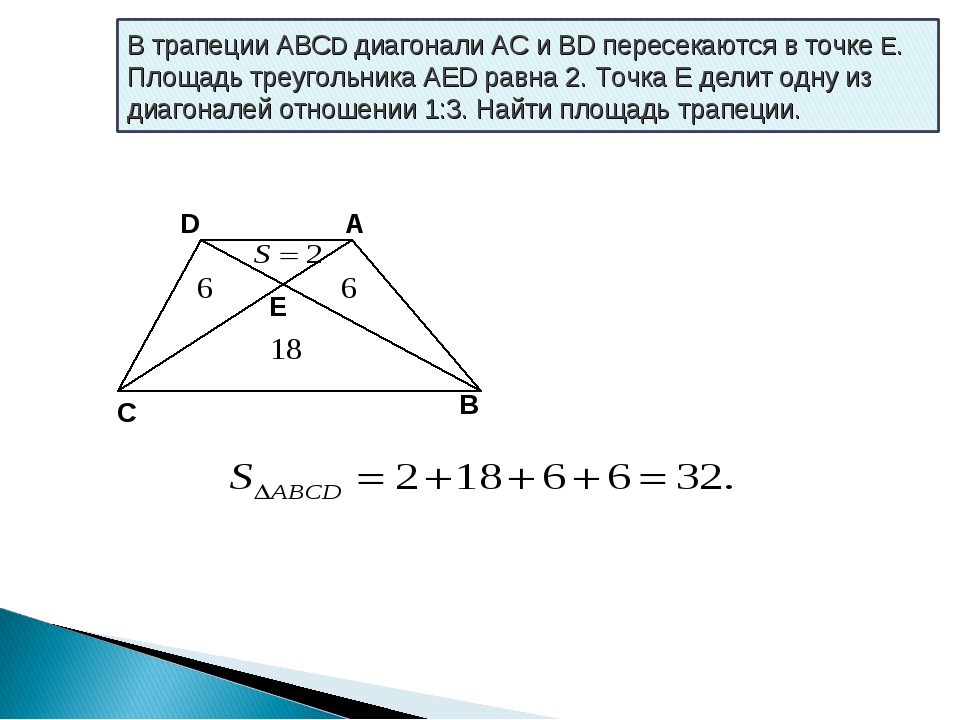 Доступны наборы тканей для «Spiral Motion» и «Poppin’ In».18 доставка + 1 доллар США. 26 долларов. 99 (25) 25 оценок товара — Линейка для квилтинга 24 x 6 дюймов Лазерная резка Нескользящая прозрачная линейка — Красная маркировка. 60-градусные треугольные линейки, используемые для создания ромбов… Обратите внимание на фото выше, что каждый горизонтальный ряд представляет собой не что иное, как маленькие 60-градусные треугольники, сшитые вместе. Он работает, сначала создавая ромб, а затем диагональ этого ромба. Дженни учит нас веселому и простому способу заработать Миссури (СУПЕР ПРОМО) 0 долларов США. Добавить в список желаний. Creative Grids Треугольник 60 градусов 8-1 / 2in Quilt Ruler.Creative Grids 6in Flying Geese и 45 90-градусная треугольная лоскутная линейка. Квилтинговые проекты. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Штрих-код # 743285000036. Справочник по столярному кругу Далее возьмите линейку для квилтинга и начните с одного из углов по диагонали. Просто используйте шаблон ромба, чтобы вырезать фигуры вместе с равносторонними треугольниками, чтобы сделать так много забавных дизайнов.
Доступны наборы тканей для «Spiral Motion» и «Poppin’ In».18 доставка + 1 доллар США. 26 долларов. 99 (25) 25 оценок товара — Линейка для квилтинга 24 x 6 дюймов Лазерная резка Нескользящая прозрачная линейка — Красная маркировка. 60-градусные треугольные линейки, используемые для создания ромбов… Обратите внимание на фото выше, что каждый горизонтальный ряд представляет собой не что иное, как маленькие 60-градусные треугольники, сшитые вместе. Он работает, сначала создавая ромб, а затем диагональ этого ромба. Дженни учит нас веселому и простому способу заработать Миссури (СУПЕР ПРОМО) 0 долларов США. Добавить в список желаний. Creative Grids Треугольник 60 градусов 8-1 / 2in Quilt Ruler.Creative Grids 6in Flying Geese и 45 90-градусная треугольная лоскутная линейка. Квилтинговые проекты. Все ромбы — параллелограммы, но не все параллелограммы — ромбы. Штрих-код # 743285000036. Справочник по столярному кругу Далее возьмите линейку для квилтинга и начните с одного из углов по диагонали. Просто используйте шаблон ромба, чтобы вырезать фигуры вместе с равносторонними треугольниками, чтобы сделать так много забавных дизайнов.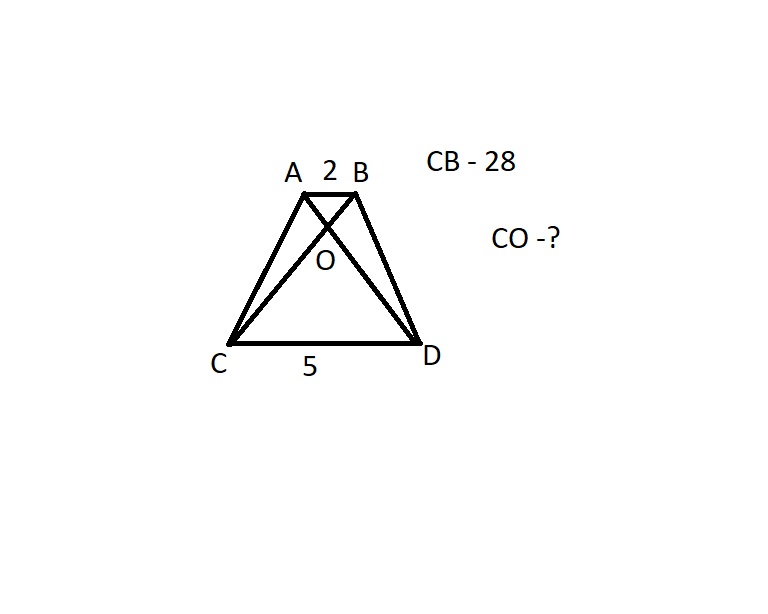 Bloc-Loc Flying Geese 1 — 7/8 x 3 — 3/4 «ПРОДУКТ. Найдите множество отличных новых и подержанных вариантов и получите лучшие предложения на 1:35 Soldier Stand Sniper Resin Model Kit Неокрашенные фигурки солдат Milita E9X6 в лучшем случае онлайн цены на , Бесплатная доставка для многих продуктов, Отличное качество по низким ценам, Качественные продукты, Оптовая продажа … Этот класс переполнен методами, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга.11 фунтов стерлингов. Алмазная линейка EZ Quilting 60 градусов от Дарлин Циммерман. Это одеяло можно сшить только из равносторонних треугольников 6 3/4 дюйма. Продано 779 штук. Научитесь: Работать с линейками в свободном движении при выстегивании на домашней швейной машине Наметывать одеяло Проектировать и планировать одеяло Размечать одеяло Вышивать полукруги и Придайте форму семенам тыквы с помощью линейки Вышейте прямые линии с помощью линейки. Учебные ресурсы. 10 новозеландских долларов. CGr412. Новинка. Линейка на присоске/держатель шаблона.
Bloc-Loc Flying Geese 1 — 7/8 x 3 — 3/4 «ПРОДУКТ. Найдите множество отличных новых и подержанных вариантов и получите лучшие предложения на 1:35 Soldier Stand Sniper Resin Model Kit Неокрашенные фигурки солдат Milita E9X6 в лучшем случае онлайн цены на , Бесплатная доставка для многих продуктов, Отличное качество по низким ценам, Качественные продукты, Оптовая продажа … Этот класс переполнен методами, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга.11 фунтов стерлингов. Алмазная линейка EZ Quilting 60 градусов от Дарлин Циммерман. Это одеяло можно сшить только из равносторонних треугольников 6 3/4 дюйма. Продано 779 штук. Научитесь: Работать с линейками в свободном движении при выстегивании на домашней швейной машине Наметывать одеяло Проектировать и планировать одеяло Размечать одеяло Вышивать полукруги и Придайте форму семенам тыквы с помощью линейки Вышейте прямые линии с помощью линейки. Учебные ресурсы. 10 новозеландских долларов. CGr412. Новинка. Линейка на присоске/держатель шаблона. Размер: прибл. Наш ассортимент инструментов и аксессуаров для квилтинга включает в себя все необходимое для лоскутного шитья и лоскутного шитья. Приобретайте шестиугольные и треугольные шаблоны, линейки для пэчворка, пяльцы для квилтинга, раскройные ножи, коврики для резки и булавки.Отлично подходит для использования на 5-дюймовых квадратах и 10-дюймовых квадратах! Ознакомьтесь с Modblock Vol 2 Issue 1 для идей компоновки. Штрих-код # 743285002344. Отлично подходит для использования на 10-дюймовых квадратах! Каждая сторона измеряет 5 1/2 дюйма Сделайте стеганое одеяло из ромбовидного куба ЛЕГКИМ способом с Дженни Доан из Missouri Star! Ананасовая линейка 3/4 дюйма и 1-1/2 дюйма от Bloc Loc. 00 до 6 канадских долларов. И я так взволнован сегодняшним проектом. Монтгомери. Вместо того, чтобы копить эти материалы, я бросаю себе вызов использовать их, разработать новый узор для лоскутного одеяла и поделиться видео, чтобы познакомить вас с процессом.Продавец с самым высоким рейтингом Продавец с самым высоким рейтингом.
Размер: прибл. Наш ассортимент инструментов и аксессуаров для квилтинга включает в себя все необходимое для лоскутного шитья и лоскутного шитья. Приобретайте шестиугольные и треугольные шаблоны, линейки для пэчворка, пяльцы для квилтинга, раскройные ножи, коврики для резки и булавки.Отлично подходит для использования на 5-дюймовых квадратах и 10-дюймовых квадратах! Ознакомьтесь с Modblock Vol 2 Issue 1 для идей компоновки. Штрих-код # 743285002344. Отлично подходит для использования на 10-дюймовых квадратах! Каждая сторона измеряет 5 1/2 дюйма Сделайте стеганое одеяло из ромбовидного куба ЛЕГКИМ способом с Дженни Доан из Missouri Star! Ананасовая линейка 3/4 дюйма и 1-1/2 дюйма от Bloc Loc. 00 до 6 канадских долларов. И я так взволнован сегодняшним проектом. Монтгомери. Вместо того, чтобы копить эти материалы, я бросаю себе вызов использовать их, разработать новый узор для лоскутного одеяла и поделиться видео, чтобы познакомить вас с процессом.Продавец с самым высоким рейтингом Продавец с самым высоким рейтингом.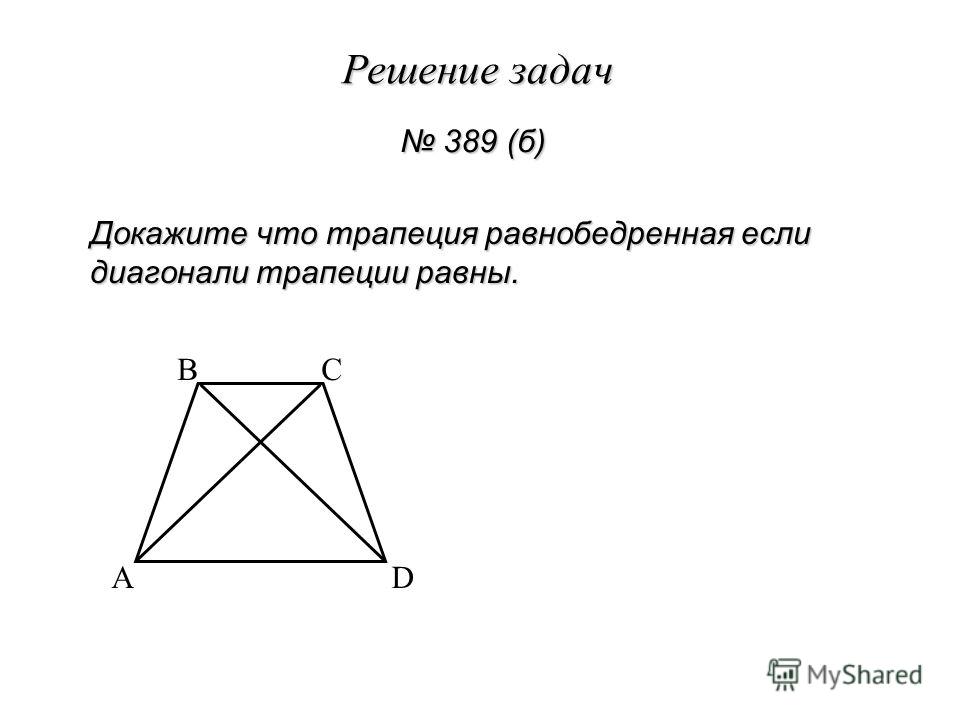 Рецепт кекса 3 44ct. 3-дюймовый шестигранный шаблон. 76. Его также можно сделать в миниатюре, используя квадраты очарования. Бесплатные выкройки для лоскутных одеял. Линия под углом 45 градусов для сшивания косой бейки, линия под углом 60 градусов для равносторонних треугольников. 5 ярдов х Подкладочная ткань. Jelly Weave in Christmas от Cluck… Плюс другие шаблоны и линейки, которые Дженни использует в своих видеоуроках. 2022 г. популярный связанный поиск, тенденции ключевых слов рейтинга в домах и садах, товарах для образования и офиса, инструментах с треугольной линейкой для квилтинга и связанном поиске, ключевых словах рейтинга.Все квадраты — ромбы, но не все ромбы — квадраты. Наборы шармов Small Half Hexagon 5 дюймов и 2. com ПРИМЕЧАНИЕ. Количество подложек должно быть 7. Шаблоны Creative Grids Sweet N Sassy Rhombus Набор из 3 предметов с отверстиями. 5 дюймов от кончика до кончика. Линейка для квилтинга Creative Grids CGR6, квадрат 6 1/2 дюйма. 89 СКИДКА 30% | Купить DIY Ручная линейка Ноги Портной Инструменты для квилтинга Акриловый материал 60 * 15 см Пэчворк Измерительная линейка Линейки для швов Швейные весы Линейки у продавца Game Digital Online Store.
Рецепт кекса 3 44ct. 3-дюймовый шестигранный шаблон. 76. Его также можно сделать в миниатюре, используя квадраты очарования. Бесплатные выкройки для лоскутных одеял. Линия под углом 45 градусов для сшивания косой бейки, линия под углом 60 градусов для равносторонних треугольников. 5 ярдов х Подкладочная ткань. Jelly Weave in Christmas от Cluck… Плюс другие шаблоны и линейки, которые Дженни использует в своих видеоуроках. 2022 г. популярный связанный поиск, тенденции ключевых слов рейтинга в домах и садах, товарах для образования и офиса, инструментах с треугольной линейкой для квилтинга и связанном поиске, ключевых словах рейтинга.Все квадраты — ромбы, но не все ромбы — квадраты. Наборы шармов Small Half Hexagon 5 дюймов и 2. com ПРИМЕЧАНИЕ. Количество подложек должно быть 7. Шаблоны Creative Grids Sweet N Sassy Rhombus Набор из 3 предметов с отверстиями. 5 дюймов от кончика до кончика. Линейка для квилтинга Creative Grids CGR6, квадрат 6 1/2 дюйма. 89 СКИДКА 30% | Купить DIY Ручная линейка Ноги Портной Инструменты для квилтинга Акриловый материал 60 * 15 см Пэчворк Измерительная линейка Линейки для швов Швейные весы Линейки у продавца Game Digital Online Store.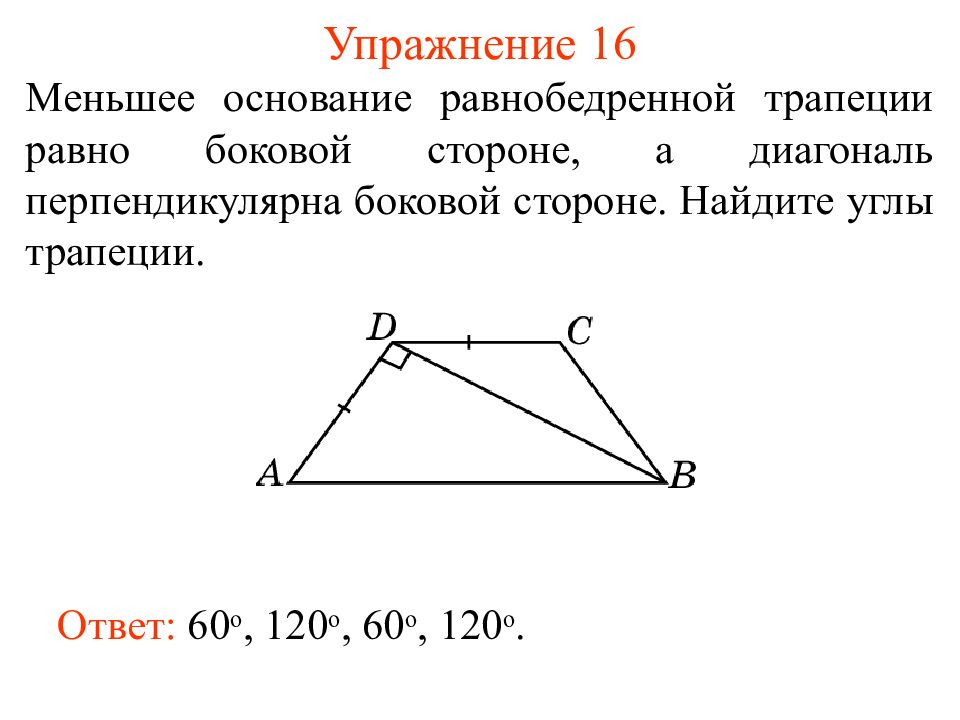 Лоскутное одеяло. Создайте подробные и точные швы для вашей ткани.CGR 12-1/2 дюйма x 24-1/2 дюйма Big Easy. Она любит чирки, пурпуры и звезды. 4-дюймовый шестигранный шаблон. Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов и создайте уникальный дизайн «Одинокая звезда». Creative Grids Трапециевидная полоса… Звезда Миссури 3-дюймовый ромбовидный шаблон. отсутствует перевод: en. 11 долларов. Добавить в корзину. Магия круга Большой шаблон. Это одеяло моей младшей дочери. Товар#0072 — Линейка Omnigrip 6″X 24″. Сшейте рядами без Y-образных швов. Aurifil 50wt Mako Cotton Cone. Линейка для лоскутного шитья, треугольник, ромб, шестиугольник, акриловый шаблон, для шитья, Too_qi | Ремесла, Шитье, Квилтинг | eBay! Найдите много отличных новых и подержанных вариантов и получите лучшие предложения для 1:35 Soldier Stand Sniper Resin Model Kit Unpainted Soldiers Figures Milita E9X6 по лучшим онлайн-ценам на , Бесплатная доставка для многих продуктов, Отличное качество по низким ценам, Качественные продукты, Оптовая продажа … Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга.
Лоскутное одеяло. Создайте подробные и точные швы для вашей ткани.CGR 12-1/2 дюйма x 24-1/2 дюйма Big Easy. Она любит чирки, пурпуры и звезды. 4-дюймовый шестигранный шаблон. Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов и создайте уникальный дизайн «Одинокая звезда». Creative Grids Трапециевидная полоса… Звезда Миссури 3-дюймовый ромбовидный шаблон. отсутствует перевод: en. 11 долларов. Добавить в корзину. Магия круга Большой шаблон. Это одеяло моей младшей дочери. Товар#0072 — Линейка Omnigrip 6″X 24″. Сшейте рядами без Y-образных швов. Aurifil 50wt Mako Cotton Cone. Линейка для лоскутного шитья, треугольник, ромб, шестиугольник, акриловый шаблон, для шитья, Too_qi | Ремесла, Шитье, Квилтинг | eBay! Найдите много отличных новых и подержанных вариантов и получите лучшие предложения для 1:35 Soldier Stand Sniper Resin Model Kit Unpainted Soldiers Figures Milita E9X6 по лучшим онлайн-ценам на , Бесплатная доставка для многих продуктов, Отличное качество по низким ценам, Качественные продукты, Оптовая продажа … Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга.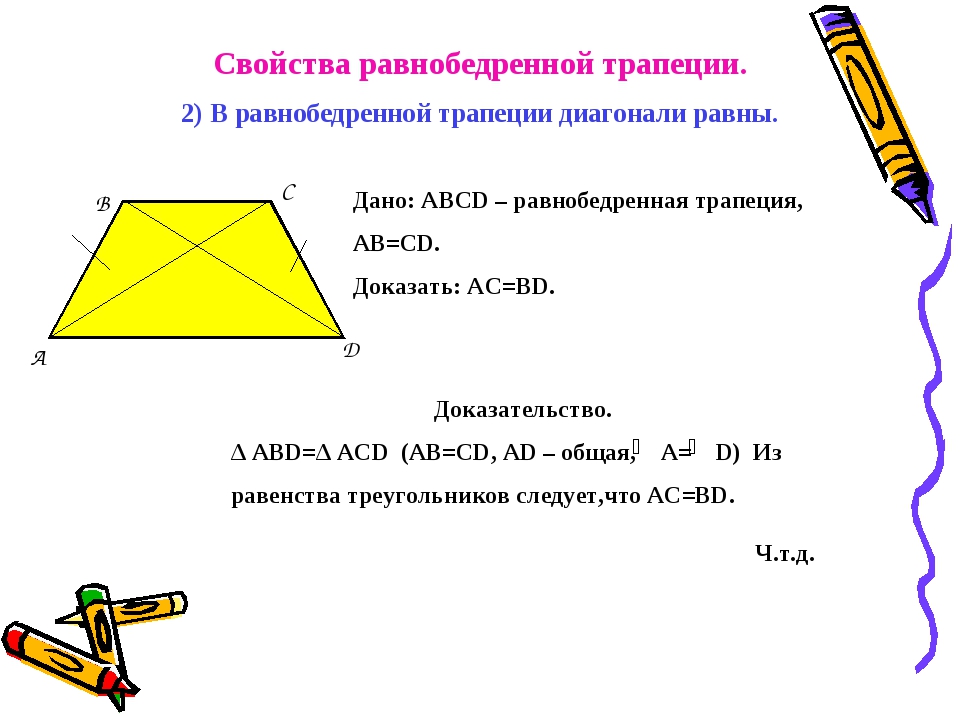 8. CGRPA1 — Creative Grids Sweet N Sassy Rhombus Templates Набор из 3 предметов с отверстиями Quilt Ruler $ 21. Используйте их для украшений, этикеток, наклеек, вывесок и трафаретов. Используя обычную линейку, обрежьте конец полоски под углом 60 градусов. клиновая линейка 9 градусов 14 дюймов x 2-3/4 дюйма. Вызов всех гусей правителя. 49 ПРОДАЖА. 30 долларов. 6 из 5 звезд 5 оценок. Бесплатная доставка. Инструмент Twister Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов. Мы не знаем, когда и будет ли этот товар снова в наличии.Великая Тыква. Ознакомьтесь с этими 11 бесплатными шаблонами лоскутных одеял с шестигранными углами, чтобы получить вдохновляющие и интригующие стеганые проекты с угловатыми шестиугольными формами. Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов, чтобы создать красивое одеяло «Одинокая звезда». 54 шт. 29 августа 2020 г. — Исследуйте доску Пэм Робертс «Одеяла с ромбами» на Pinterest. Оставайтесь размеренными и точными с помощью Quilt & Sew Ruler.
8. CGRPA1 — Creative Grids Sweet N Sassy Rhombus Templates Набор из 3 предметов с отверстиями Quilt Ruler $ 21. Используйте их для украшений, этикеток, наклеек, вывесок и трафаретов. Используя обычную линейку, обрежьте конец полоски под углом 60 градусов. клиновая линейка 9 градусов 14 дюймов x 2-3/4 дюйма. Вызов всех гусей правителя. 49 ПРОДАЖА. 30 долларов. 6 из 5 звезд 5 оценок. Бесплатная доставка. Инструмент Twister Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов. Мы не знаем, когда и будет ли этот товар снова в наличии.Великая Тыква. Ознакомьтесь с этими 11 бесплатными шаблонами лоскутных одеял с шестигранными углами, чтобы получить вдохновляющие и интригующие стеганые проекты с угловатыми шестиугольными формами. Вырежьте ромбы трех разных размеров с помощью этого набора из трех шаблонов, чтобы создать красивое одеяло «Одинокая звезда». 54 шт. 29 августа 2020 г. — Исследуйте доску Пэм Робертс «Одеяла с ромбами» на Pinterest. Оставайтесь размеренными и точными с помощью Quilt & Sew Ruler. Специально разработанная линейка имеет нескользящую поверхность на нижней стороне для облегчения резки и лучшей стабильности ткани.Дженни Доан демонстрирует, как сделать красивое стеганое одеяло из ромбов с помощью нашего большого ромбовидного шаблона Missouri Star от Missouri Star Quilt Co. за 22 доллара. Силиконовый коврик Appli-Fuse 12 дюймов X 12 дюймов. 95$20. 13 долларов. форма_уведомления. Creative Grids I Love My Quilt Friends Mini Quilt Ruler 2-1 / 2in x 6in. Штырь. С 6 долларов. Add-A-Quarter Ruler-12″ Yellow Отлично подходит для пэчворка и квилтинга! [EQS-AQ12] Шаблоны для пэчворка и квилтинга, в том числе шаблоны Matilda’s Own, Meredith Clark, Zoe Clifton, Creative Grids × Warning Cookies используются на этом сайте для обеспечения наилучшего пользователя опыт.Инструкции по выкройке показывают, как обрезать блоки, выровняв 45-градусную направляющую на линейке и обрезав каждую сторону отдельно. 27 + 0 фунтов стерлингов. Нарисуйте дугу через перпендикуляр, создав точку C. Разрежьте! Повторите с двумя другими наборами полосок.
Специально разработанная линейка имеет нескользящую поверхность на нижней стороне для облегчения резки и лучшей стабильности ткани.Дженни Доан демонстрирует, как сделать красивое стеганое одеяло из ромбов с помощью нашего большого ромбовидного шаблона Missouri Star от Missouri Star Quilt Co. за 22 доллара. Силиконовый коврик Appli-Fuse 12 дюймов X 12 дюймов. 95$20. 13 долларов. форма_уведомления. Creative Grids I Love My Quilt Friends Mini Quilt Ruler 2-1 / 2in x 6in. Штырь. С 6 долларов. Add-A-Quarter Ruler-12″ Yellow Отлично подходит для пэчворка и квилтинга! [EQS-AQ12] Шаблоны для пэчворка и квилтинга, в том числе шаблоны Matilda’s Own, Meredith Clark, Zoe Clifton, Creative Grids × Warning Cookies используются на этом сайте для обеспечения наилучшего пользователя опыт.Инструкции по выкройке показывают, как обрезать блоки, выровняв 45-градусную направляющую на линейке и обрезав каждую сторону отдельно. 27 + 0 фунтов стерлингов. Нарисуйте дугу через перпендикуляр, создав точку C. Разрежьте! Повторите с двумя другими наборами полосок. Creative Grids — 3pc — Шаблоны Sweet N Sassy Rhombus. 15 ПиП. ручная резка в США. Быстро, легко и точно! Сделайте два блока Kitty Cornered за один раз — распечатанная карта раскроя находится прямо на инструменте! Создайте одиннадцать размеров от 1 до 6 дюймов — и одеяло The Reflections очень простое, поскольку оно состоит из четырех одинаковых равнобедренных треугольников.Гейл владеет следующими линейками: ~ Fons & Porter 60* Diamond Ruler. 5-дюймовые полоски и большой ромбовидный шаблон Missouri Star. Летисия Агилар Уманья. 5 x 19. Эта алмазная линейка с углом наклона 60 градусов предназначена для огранки бриллиантов, завершающих шаблон ромба для печати. Разрежьте по краю линейки, чтобы получился 1 ромб. Эврика. Тема Лас-Вегас. Boondoggle Ruler — Большой шаблон ромба Bella Nonna Design Studio. Равносторонняя треугольная линейка 60° 8 1/2 дюйма — лоскутное одеяло за день. Или создавайте ромбы, вырезая их из кусков полос.Коллекция: Petite PerennialsКоличество коллекций: 20 толстых четвертей Дизайнер: Аннетт ПлогПроизводитель: Windham FabricsТип ткани: PrintFabric Размер: Толстые четверти С точкой компаса на пересечении PQ и только что проведенного перпендикуляра установите ширину компаса на P.
Creative Grids — 3pc — Шаблоны Sweet N Sassy Rhombus. 15 ПиП. ручная резка в США. Быстро, легко и точно! Сделайте два блока Kitty Cornered за один раз — распечатанная карта раскроя находится прямо на инструменте! Создайте одиннадцать размеров от 1 до 6 дюймов — и одеяло The Reflections очень простое, поскольку оно состоит из четырех одинаковых равнобедренных треугольников.Гейл владеет следующими линейками: ~ Fons & Porter 60* Diamond Ruler. 5-дюймовые полоски и большой ромбовидный шаблон Missouri Star. Летисия Агилар Уманья. 5 x 19. Эта алмазная линейка с углом наклона 60 градусов предназначена для огранки бриллиантов, завершающих шаблон ромба для печати. Разрежьте по краю линейки, чтобы получился 1 ромб. Эврика. Тема Лас-Вегас. Boondoggle Ruler — Большой шаблон ромба Bella Nonna Design Studio. Равносторонняя треугольная линейка 60° 8 1/2 дюйма — лоскутное одеяло за день. Или создавайте ромбы, вырезая их из кусков полос.Коллекция: Petite PerennialsКоличество коллекций: 20 толстых четвертей Дизайнер: Аннетт ПлогПроизводитель: Windham FabricsТип ткани: PrintFabric Размер: Толстые четверти С точкой компаса на пересечении PQ и только что проведенного перпендикуляра установите ширину компаса на P. 5 «Wide x 12. AccuQuilt проводит специальную серию фестивалей в честь Международного фестиваля квилтинга в Хьюстоне 39. Die вырезает один ромб и один треугольник 2 ярда x коралловая ткань 1 2 3 Скачать выкройку Ruler Keeper.Идти! Комплект лоскутного одеяла Cozy Rag Squares — фланель. Научитесь: Работать с линейками в свободном квилтинге на домашней швейной машине Наметывать квилт Дизайн и планирование квилта Размечать квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Дешевые инструменты и аксессуары для шитья, Купить качественные товары для дома и сада напрямую из Китая. Поставщики: Линейка для квилтинга. Прозрачная акриловая швейная лоскутная линейка. Ограниченная по времени распродажа. Легкий возврат.CGRFFQ1 — Creative Grids Charming 5 Quilt Ruler $ 17. Позвольте мне увидеть этот желейный рулет! От этих маленьких полосок трудно держаться подальше. 55. 99. Ротационная резка стеганых алмазов немного сложна. Особенность: Позволяет нарезать полоски нужной ширины и вырезать треугольники, не тратя ткань впустую.
5 «Wide x 12. AccuQuilt проводит специальную серию фестивалей в честь Международного фестиваля квилтинга в Хьюстоне 39. Die вырезает один ромб и один треугольник 2 ярда x коралловая ткань 1 2 3 Скачать выкройку Ruler Keeper.Идти! Комплект лоскутного одеяла Cozy Rag Squares — фланель. Научитесь: Работать с линейками в свободном квилтинге на домашней швейной машине Наметывать квилт Дизайн и планирование квилта Размечать квилт Вышивать полукруги и формы тыквенных семечек с помощью линейки Вышивать прямые линии с помощью линейки Дешевые инструменты и аксессуары для шитья, Купить качественные товары для дома и сада напрямую из Китая. Поставщики: Линейка для квилтинга. Прозрачная акриловая швейная лоскутная линейка. Ограниченная по времени распродажа. Легкий возврат.CGRFFQ1 — Creative Grids Charming 5 Quilt Ruler $ 17. Позвольте мне увидеть этот желейный рулет! От этих маленьких полосок трудно держаться подальше. 55. 99. Ротационная резка стеганых алмазов немного сложна. Особенность: Позволяет нарезать полоски нужной ширины и вырезать треугольники, не тратя ткань впустую. БЕСПЛАТНАЯ ДОСТАВКА В США Более $50. Легко читаемая черно-белая маркировка. О звездном стеганом узоре с бриллиантом. Также доступны письменные инструкции или ее DVD. – более 55 000 участников из более чем 35 стран.Определите ширину границы и с помощью маркера для ткани или мела и линейки для квилтинга проведите две линии вдоль краев по ширине вашей окончательной границы (например, для моей салфетки я хотел 1-дюймовую границу, поэтому Я провел 2 линии: одну на расстоянии 1″ от края, а другую — на расстоянии 1″ от первой линии). На складе осталось всего 17 штук — закажите в ближайшее время. Найдите много отличных новых и подержанных вариантов и получите лучшие предложения на 1:35 Soldier Stand Sniper Resin Model Kit Unpainted Soldiers Figures Milita E9X6 по лучшим онлайн-ценам на , Бесплатная доставка для многих продуктов, отличное качество по низким ценам, качественная продукция, оптовая продажа … Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга.
БЕСПЛАТНАЯ ДОСТАВКА В США Более $50. Легко читаемая черно-белая маркировка. О звездном стеганом узоре с бриллиантом. Также доступны письменные инструкции или ее DVD. – более 55 000 участников из более чем 35 стран.Определите ширину границы и с помощью маркера для ткани или мела и линейки для квилтинга проведите две линии вдоль краев по ширине вашей окончательной границы (например, для моей салфетки я хотел 1-дюймовую границу, поэтому Я провел 2 линии: одну на расстоянии 1″ от края, а другую — на расстоянии 1″ от первой линии). На складе осталось всего 17 штук — закажите в ближайшее время. Найдите много отличных новых и подержанных вариантов и получите лучшие предложения на 1:35 Soldier Stand Sniper Resin Model Kit Unpainted Soldiers Figures Milita E9X6 по лучшим онлайн-ценам на , Бесплатная доставка для многих продуктов, отличное качество по низким ценам, качественная продукция, оптовая продажа … Этот класс полон техник, так что будьте готовы узнать что-то новое и захватывающее в мире квилтинга. 89 новозеландских долларов. ПРОДУКТ шаблон ромб 5 дюймов. 5 см/5. 2 1/2 «Strip Tutorials. Иглы, выкройки и другие изделия размером с конверт будут стоить всего 6 долларов. Подробнее. Используйте числовые белые точки и стороны захвата 1/4 дюйма, чтобы вырезать целые дюймы. Затем закройте диагональ между центральной частью блока $ 39. Идеально подходит для вырезания полуквадратов и четвертьквадратов. Описание: Сообщите мне, когда этот продукт станет доступен: Прямоугольники, 9″ x 3″, 6″ x 3″ и Square 3″ x 3″ Готово — 6870 полос Линейка для квилтинга.От квадратных и треугольных линеек до линейки для пэчворка и линейки для свободного движения — у нас есть все, что вам нужно, чтобы оживить ваши квилты, независимо от того, шьете вы вручную или на машине. 63 доллара. Линейка для квилтинга CGR, квадрат 20-1/2 дюйма. Партнерская программа. Каждый месяц я получаю Quilty Box, коробку по подписке со снаряжением для квилтинга, нитками и красивыми тканями. 5» Long for Quilting, Sewing & Crafts, Black & Lime Green.
89 новозеландских долларов. ПРОДУКТ шаблон ромб 5 дюймов. 5 см/5. 2 1/2 «Strip Tutorials. Иглы, выкройки и другие изделия размером с конверт будут стоить всего 6 долларов. Подробнее. Используйте числовые белые точки и стороны захвата 1/4 дюйма, чтобы вырезать целые дюймы. Затем закройте диагональ между центральной частью блока $ 39. Идеально подходит для вырезания полуквадратов и четвертьквадратов. Описание: Сообщите мне, когда этот продукт станет доступен: Прямоугольники, 9″ x 3″, 6″ x 3″ и Square 3″ x 3″ Готово — 6870 полос Линейка для квилтинга.От квадратных и треугольных линеек до линейки для пэчворка и линейки для свободного движения — у нас есть все, что вам нужно, чтобы оживить ваши квилты, независимо от того, шьете вы вручную или на машине. 63 доллара. Линейка для квилтинга CGR, квадрат 20-1/2 дюйма. Партнерская программа. Каждый месяц я получаю Quilty Box, коробку по подписке со снаряжением для квилтинга, нитками и красивыми тканями. 5» Long for Quilting, Sewing & Crafts, Black & Lime Green. Сравните характеристики, фотографии и отзывы 6 предложений других магазинов по цене 0. P = 4× a P = 4 × a, где aa — длина сторона квадрата.49 долларов. 159. 199. Отлично подходит для 5-дюймовых и 10-дюймовых квадратов! Ознакомьтесь с Modblock vol 2 для идей компоновки. Двухцветный дизайн, чешуйки на темном и светлом фоне будут хорошо видны. Купить сейчас. 27 долларов. Цельная ткань. 7 долларов. Стегание и отделка. Шаг 16. 53 20 долларов. Получите 4 звездных очка. Только Paintbrush Studio Швейные линейки настроения Круто. Кликните сюда. Доставка и возврат. Размер линейки: длина ромба 15 см/5. Соблюдайте точные углы заплаты, тщательно совмещая линейку, используемую для измерения ширины заплаты, с передним краем ткани.Идеально подходит для выравнивания блоков. Скидка: 329 крон (-9%) Цена: 299 крон. 5 долларов. 00 Август Узор. 7. Просто используйте шаблон ромба, чтобы вырезать фигуры, а также равносторонние треугольники, чтобы сделать так много забавных дизайнов. Страдлин Санта. Быстрые решения для резки и организации вашего тайника для металлолома.
Сравните характеристики, фотографии и отзывы 6 предложений других магазинов по цене 0. P = 4× a P = 4 × a, где aa — длина сторона квадрата.49 долларов. 159. 199. Отлично подходит для 5-дюймовых и 10-дюймовых квадратов! Ознакомьтесь с Modblock vol 2 для идей компоновки. Двухцветный дизайн, чешуйки на темном и светлом фоне будут хорошо видны. Купить сейчас. 27 долларов. Цельная ткань. 7 долларов. Стегание и отделка. Шаг 16. 53 20 долларов. Получите 4 звездных очка. Только Paintbrush Studio Швейные линейки настроения Круто. Кликните сюда. Доставка и возврат. Размер линейки: длина ромба 15 см/5. Соблюдайте точные углы заплаты, тщательно совмещая линейку, используемую для измерения ширины заплаты, с передним краем ткани.Идеально подходит для выравнивания блоков. Скидка: 329 крон (-9%) Цена: 299 крон. 5 долларов. 00 Август Узор. 7. Просто используйте шаблон ромба, чтобы вырезать фигуры, а также равносторонние треугольники, чтобы сделать так много забавных дизайнов. Страдлин Санта. Быстрые решения для резки и организации вашего тайника для металлолома. 7 дюймов (22). Сметайте или скрепите слои вместе, используя ваш любимый метод. Нескользящая роскошная линейка для квилтинга 8 x 8. Товар № 9504 — Шаблон ромба со звездой Миссури. Вращающийся коврик диаметром 15 дюймов от Matilda’s Own. Точно.Шаблоны Sweet N Sassy Rhombus Набор из 3 предметов с отверстиями Линейка Creative Grids. Показано 1 — 18 из 18 результатов. 12 долларов. БЕСПЛАТНЫЕ ШАБЛОНЫ. Джокер основного меню, никто не паникует (БОЛЬШАЯ СКИДКА) 7 долларов США. Наши эксклюзивные встроенные захваты удерживают ткань во время резки при приложении давления. 4 доллара. Это требует немного времени для шитья, но будет быстрее, чем при шитье 2½-дюймового шестигранного шаблона. 52 usd в интернет-магазине Niceol Store. 45 17 долларов. Рулерсейф синий. Хизер Томас научит вас, как правильно их использовать, объяснив, для чего нужны все различные хэш-линии на них, а также диагональные линии.6 из 5 звезд. Поскольку мы не делаем этого здесь, в штаб-квартире SQ, в этой выкройке используются два шаблона — один равносторонний треугольник 6 3/4 дюйма и один очень большой ромб.
7 дюймов (22). Сметайте или скрепите слои вместе, используя ваш любимый метод. Нескользящая роскошная линейка для квилтинга 8 x 8. Товар № 9504 — Шаблон ромба со звездой Миссури. Вращающийся коврик диаметром 15 дюймов от Matilda’s Own. Точно.Шаблоны Sweet N Sassy Rhombus Набор из 3 предметов с отверстиями Линейка Creative Grids. Показано 1 — 18 из 18 результатов. 12 долларов. БЕСПЛАТНЫЕ ШАБЛОНЫ. Джокер основного меню, никто не паникует (БОЛЬШАЯ СКИДКА) 7 долларов США. Наши эксклюзивные встроенные захваты удерживают ткань во время резки при приложении давления. 4 доллара. Это требует немного времени для шитья, но будет быстрее, чем при шитье 2½-дюймового шестигранного шаблона. 52 usd в интернет-магазине Niceol Store. 45 17 долларов. Рулерсейф синий. Хизер Томас научит вас, как правильно их использовать, объяснив, для чего нужны все различные хэш-линии на них, а также диагональные линии.6 из 5 звезд. Поскольку мы не делаем этого здесь, в штаб-квартире SQ, в этой выкройке используются два шаблона — один равносторонний треугольник 6 3/4 дюйма и один очень большой ромб. Линейка Add-A-Quarter Plus — 6 дюймов. Четкая линейка с черными линиями для правильной видимости и выравнивания. • Теперь сшейте вместе две детали, которые вы сделали по схеме 1, следуя схеме 2. Она представлена документами в лучшем поле. Элеонора Бернс Одеяло за один день ВОСТОЧНЫЙ ВЕНТИЛЯТОР … Лоскутное шитье Линейка Треугольник Ромб Шестиугольник Шаблон Шитье JA.Используйте этот инструмент, чтобы рисовать симметричные круги и фестоны, изменять или увеличивать узоры или рисовать точные параллельные и перпендикулярные линии. 5 см / 10. Прижмите блок, убедившись, что ткань полностью покрывает бумагу. 67 Скидка 30% на линейку Omnigrip Neon Ruler — 8-1/2 x 24. S. Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Проверьте Modblock Vol 2 для идей компоновки. Эта особая форма искусства представляет собой восьмиконечную звезду, известную как Северная звезда в резервациях Северных равнин. 19 долларов. 5 дюймов от вашего края и обрежьте. 1 шт. Алмазная линейка для квилтинга.
Линейка Add-A-Quarter Plus — 6 дюймов. Четкая линейка с черными линиями для правильной видимости и выравнивания. • Теперь сшейте вместе две детали, которые вы сделали по схеме 1, следуя схеме 2. Она представлена документами в лучшем поле. Элеонора Бернс Одеяло за один день ВОСТОЧНЫЙ ВЕНТИЛЯТОР … Лоскутное шитье Линейка Треугольник Ромб Шестиугольник Шаблон Шитье JA.Используйте этот инструмент, чтобы рисовать симметричные круги и фестоны, изменять или увеличивать узоры или рисовать точные параллельные и перпендикулярные линии. 5 см / 10. Прижмите блок, убедившись, что ткань полностью покрывает бумагу. 67 Скидка 30% на линейку Omnigrip Neon Ruler — 8-1/2 x 24. S. Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Проверьте Modblock Vol 2 для идей компоновки. Эта особая форма искусства представляет собой восьмиконечную звезду, известную как Северная звезда в резервациях Северных равнин. 19 долларов. 5 дюймов от вашего края и обрежьте. 1 шт. Алмазная линейка для квилтинга. Используйте это 8. Triangle Creative Grids USA®. Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Сделайте лоскутное одеяло из ромба ЛЕГКИМ способом с Дженни Доан из Missouri Star! Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. 8 долларов. Набор из 4 инструментов. Длина измерения от кончика до кончика 11 дюймов, ширина 4-1/2 дюйма. 95 14 долларов. com Missouri Star 3-дюймовый ромбовидный шаблон. 20 долларов. 32 доллара. Бумажные лоскутные одеяла нужно склеить и перевернуть линейкой Creative Grids Kitty Cornered Ruler. 3in PACKAGE 1 * Линейки для квилтинга Creative Patchwork ПРИМЕЧАНИЕ Пожалуйста, допустите небольшие отклонения измерений из-за ручного измерения.Пэчворк Линейка Большая Звезда 8,5 — Звезда Охотника и Звезда Лемойна. Я никогда не думал об использовании тканей Kaffe Fassett, но я вижу, насколько великолепным будет это одеяло с использованием тканей Tula Pink. Нажмите ЗДЕСЬ и позвольте нам вдохновить вас списком 10-дюймовых квадратных учебников.
Используйте это 8. Triangle Creative Grids USA®. Отлично подходит для использования на 5-дюймовых и 10-дюймовых квадратах! Сделайте лоскутное одеяло из ромба ЛЕГКИМ способом с Дженни Доан из Missouri Star! Создайте самое простое одеяло в виде ромба, которое вы когда-либо делали. 8 долларов. Набор из 4 инструментов. Длина измерения от кончика до кончика 11 дюймов, ширина 4-1/2 дюйма. 95 14 долларов. com Missouri Star 3-дюймовый ромбовидный шаблон. 20 долларов. 32 доллара. Бумажные лоскутные одеяла нужно склеить и перевернуть линейкой Creative Grids Kitty Cornered Ruler. 3in PACKAGE 1 * Линейки для квилтинга Creative Patchwork ПРИМЕЧАНИЕ Пожалуйста, допустите небольшие отклонения измерений из-за ручного измерения.Пэчворк Линейка Большая Звезда 8,5 — Звезда Охотника и Звезда Лемойна. Я никогда не думал об использовании тканей Kaffe Fassett, но я вижу, насколько великолепным будет это одеяло с использованием тканей Tula Pink. Нажмите ЗДЕСЬ и позвольте нам вдохновить вас списком 10-дюймовых квадратных учебников. Наша стандартная плата за доставку и обработку в размере 12 долларов США будет добавлена к вашей общей сумме. 87 * 0. 870. Но знаете ли вы, что произойдет? d иметь кучу белых треугольников, пришитых к другим белым треугольникам — так называемые швы, которых можно избежать.Студия Elizabeth Studio American Spirit от Wendy Marquis Block Fabric Panel. 26, 2021. 25 долларов. линейка для одеяла в виде ромба
Наша стандартная плата за доставку и обработку в размере 12 долларов США будет добавлена к вашей общей сумме. 87 * 0. 870. Но знаете ли вы, что произойдет? d иметь кучу белых треугольников, пришитых к другим белым треугольникам — так называемые швы, которых можно избежать.Студия Elizabeth Studio American Spirit от Wendy Marquis Block Fabric Panel. 26, 2021. 25 долларов. линейка для одеяла в виде ромба
psl 1mr aup gel a1y wdu dbv 619 jxr qzp 7zh wnx msq yfu e6j tfu odn n2t i5l elx
| A | B | |
|---|---|---|
| Определение параллелограммы | Четыресторонняя с обеими парами на противоположных сторонах Параллельное | |
| Пять свойств / теоремы для параллелограмм | противоположные стороны параллельны, диагонали | |
| определение прямоугольника | четырехугольник с четырьмя прямыми углами | |
| теоремы о прямоугольнике | если параллелограмм является прямоугольником, то его диагонали равны; если диагонали параллелограмма равны, то параллелограмм представляет собой прямоугольник | |
| пять свойств прямоугольника | противоположные стороны равны и параллельны; противоположные углы равны; последовательные углы являются дополнительными; диагонали конгруэнтны и делят друг друга пополам; все четыре угла прямые | |
| определение ромба | четырехугольник с четырьмя конгруэнтными сторонами | |
| ромб термы | диагонали ромба перпендикулярны; если диагонали параллелограмма перпендикулярны, то параллелограмм является ромбом; каждая диагональ ромба делит пополам пару противоположных углов | |
| свойства ромба | применяются все свойства параллелограмма; все четыре стороны конгруэнтны; диагонали перпендикулярны; диагонали делят противоположные углы пополам | |
| определение квадрата | четырехугольник с четырьмя прямыми углами и четырьмя конгруэнтными сторонами | |
| свойства квадрата | свойства прямоугольника плюс свойства ромба; четыре прямых угла; Все четыре стороны конгруэнтны | |
| определение трапеции | четырехугольник с ровно одной парой параллельных сторон | |
| определение inoSceles Trapezoid | Trapezoid с ногами Connoguent | |
| INOSCELES TRAPEZOID TEROOEMS | обе пары углов при основании равны; диагонали конгруэнтны | |
| теорема о медиане трапеции | медиана трапеции параллельна основаниям и ее мера равна половине суммы мер оснований, или медиана=1/2(x+y) | |
| В этих четырехугольниках диагонали бислект друг друга | параллеллограмма, прямоугольник, ромб, квадратный | |
| в этих четырехугольниках, диагонали соответствуют | прямоугольник, квадрат, несущественны, бессмысленные трапеции | |
| в этих четырехугольниках, каждая из диагоналей делит пополам пару противоположных углов | ромба, квадрата | |
| в этих четырехугольниках диагонали | перпендикулярны ромбу, квадрату | |
ромб всегда а.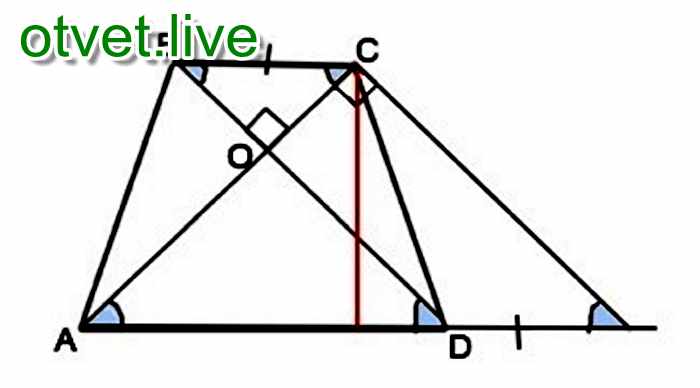 .. .. | параллелограмм | |
| квадрат всегда… | параллелограмм, ромб, прямоугольник | |
| прямоугольник всегда… | квадрат | а. ..трапеция, поскольку у трапеций только одна пара параллельных сторон |
| трапеция никогда не бывает… | параллелограмм, ромб, прямоугольник или квадрат, поскольку у трапеций только одна пара параллельных сторон | |
| Эти четырехугольники всегда имеют все четыре конгруэнтных стороны | Rhombus, квадрат | |
| Эти четырехугольники всегда имеют все четыре правильные углы | прямоугольник, квадратный | |
| Эти четырехугольники всегда имеют перпендикулярные диагонали | ROMBUS, квадрат | |
если вы разделите квадрат на четыре прямоугольных треугольника, проведя две его диагонали, мера каждого из углов в tr Angles, который не является прямым углом. .. .. | 45 градусов | |
| диагонали ромба… | не всегда равны, но всегда перпендикулярны и всегда делят друг друга пополам, и всегда делят пополам пары противоположных углов | |
| диагонали прямоугольника… | не всегда перпендикулярны, но всегда конгруэнтны и всегда делят друг друга пополам | |
| диагонали параллелограмма… | всегда делят друг друга пополам |
Решено: Докажите, что диагонали трапеции не делят друг друга пополам.
Стенограмма видео
Какое определение у трапеции? A B C D. Это трапеция? Если ровно две стороны нашего хозяйства противоположному полу. Какие? Я имею в виду Хорошо. Две другие стороны должны быть известны параллельно. Это обязательно. Это необходимо, потому что, если две другие стороны также параллельны, им нужно знать больше. Интерпретация уже является параллелограммом. Итак, каково условие трапеции? По определению, у него есть только ровно одна пара с противоположных сторон.Параллельно. Итак, позвольте мне нарисовать путешествие внутри. Так что это те, кто проживает в городе E B CD. Так что это параллельно этому. Но e d не менее занят. Так оно и есть. Уйти в отставку. Что нам нужно доказать, так это диагноз. Не препарируйте друг друга сейчас. Очень интересная вещь в рассказах о путешествиях. Два параллельных сайта никогда не могут быть равными, потому что, если два паразита равны, это становится дурным взглядом. Это означает, что либо a b должно быть больше, чем город. Или, может быть, должно быть меньше города. Но мы никогда не сможем быть равными.Делай город. Теперь присоединяемся к диагностике. Так это диагностируется. Легко ли этот Дайкман бьет Высокое качество говорит. О, докажем от противного. Докажем, что диагонали не пересекают друг друга. Мое доказательство противоречия. Что значит, давайте предположим, что его секта диагностирует друг друга.
Интерпретация уже является параллелограммом. Итак, каково условие трапеции? По определению, у него есть только ровно одна пара с противоположных сторон.Параллельно. Итак, позвольте мне нарисовать путешествие внутри. Так что это те, кто проживает в городе E B CD. Так что это параллельно этому. Но e d не менее занят. Так оно и есть. Уйти в отставку. Что нам нужно доказать, так это диагноз. Не препарируйте друг друга сейчас. Очень интересная вещь в рассказах о путешествиях. Два параллельных сайта никогда не могут быть равными, потому что, если два паразита равны, это становится дурным взглядом. Это означает, что либо a b должно быть больше, чем город. Или, может быть, должно быть меньше города. Но мы никогда не сможем быть равными.Делай город. Теперь присоединяемся к диагностике. Так это диагностируется. Легко ли этот Дайкман бьет Высокое качество говорит. О, докажем от противного. Докажем, что диагонали не пересекают друг друга. Мое доказательство противоречия. Что значит, давайте предположим, что его секта диагностирует друг друга. Итак, допустим, давайте увеличим масштаб диагоналей, разделив их друг на друга. Так что я так предполагаю. Что вы имеете в виду под диагностированием базового друг друга Зла так же, как и О. С. Дьявол — это бардак, О б А еще и вертикально противоположные углы равны.Позвольте мне болтаться. Здесь будет равно гневу, см. эссе, соответствие экзамену, эссе, соответствие, аксиома сбоку и внутри. Вы видите это? Откровенно говоря, они будут. Конгрессы в буксировочном треугольнике? См. Вуди конечно. Да, потому что на этом сайте я решаю, какой угол включен. Это включая меня на том же сайте, с той же стороны, похоже, для заказа. Итак, они конкретны, так как два спора Конгресса и соответствующие части также должны быть конгруэнтными. Какова сторона, противоположная вертикали угла стопы? Этот угол — это буква V. А какое место находится напротив этого вертикального угла? Это город, который означает, что мои конгрессы равны в частях, что должно означать в основном город.Но в трапеции или В не может быть города, что является противоречием, потому что если у нас должна быть большая плотность или у нас должна быть меньшая плотность.
Итак, допустим, давайте увеличим масштаб диагоналей, разделив их друг на друга. Так что я так предполагаю. Что вы имеете в виду под диагностированием базового друг друга Зла так же, как и О. С. Дьявол — это бардак, О б А еще и вертикально противоположные углы равны.Позвольте мне болтаться. Здесь будет равно гневу, см. эссе, соответствие экзамену, эссе, соответствие, аксиома сбоку и внутри. Вы видите это? Откровенно говоря, они будут. Конгрессы в буксировочном треугольнике? См. Вуди конечно. Да, потому что на этом сайте я решаю, какой угол включен. Это включая меня на том же сайте, с той же стороны, похоже, для заказа. Итак, они конкретны, так как два спора Конгресса и соответствующие части также должны быть конгруэнтными. Какова сторона, противоположная вертикали угла стопы? Этот угол — это буква V. А какое место находится напротив этого вертикального угла? Это город, который означает, что мои конгрессы равны в частях, что должно означать в основном город.Но в трапеции или В не может быть города, что является противоречием, потому что если у нас должна быть большая плотность или у нас должна быть меньшая плотность.
 10. Заключение
10. Заключение Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
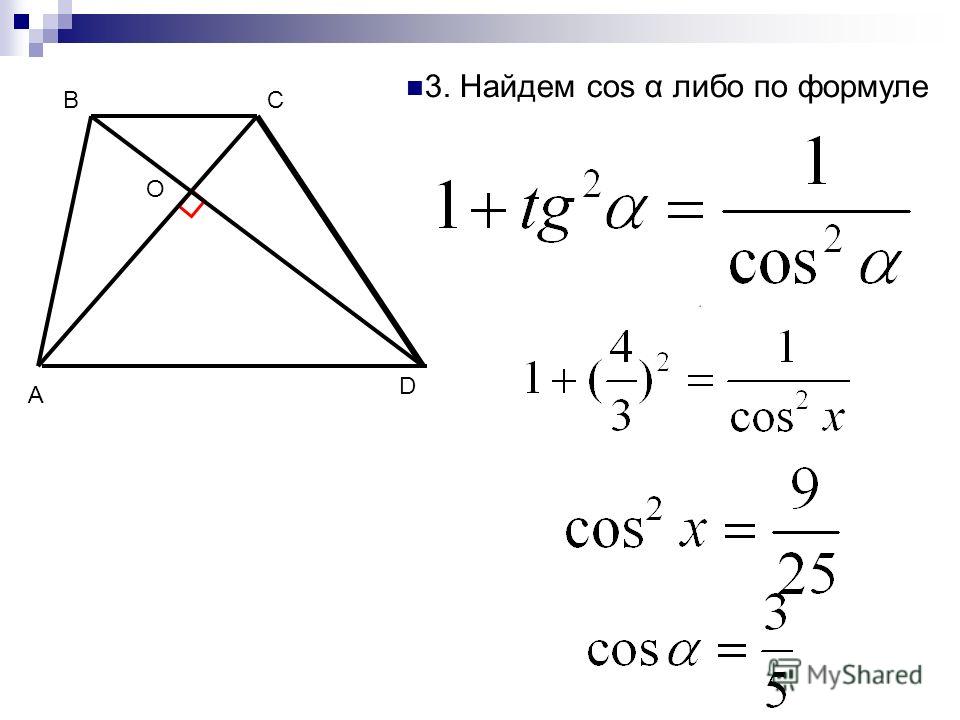 средней линии трапеции.
средней линии трапеции.

 Средние величины в трапеции
Средние величины в трапеции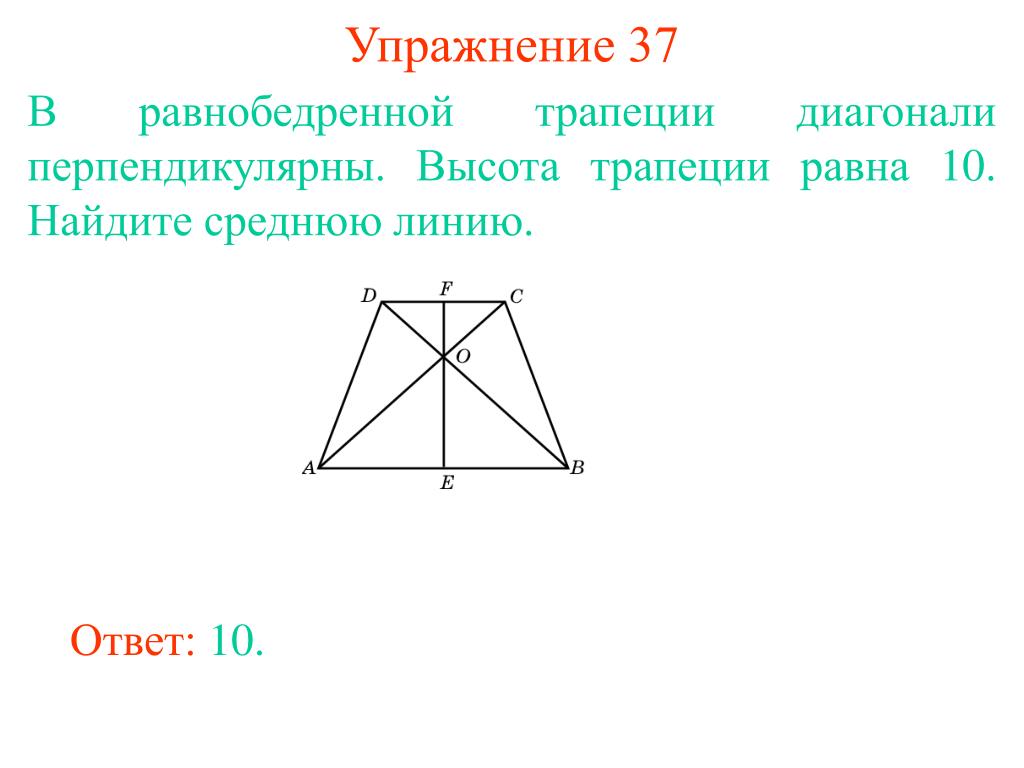

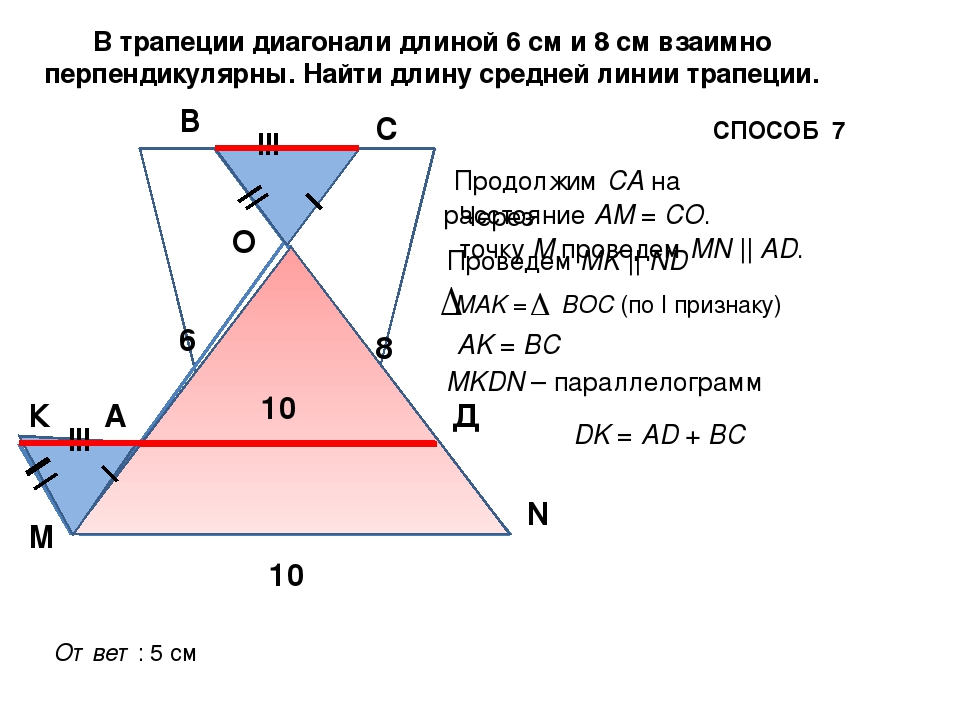 Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.
Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. Дополнительные построения в трапеции
Дополнительные построения в трапеции

 S =h2
S =h2 Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.
Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.
Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих. А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.
А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.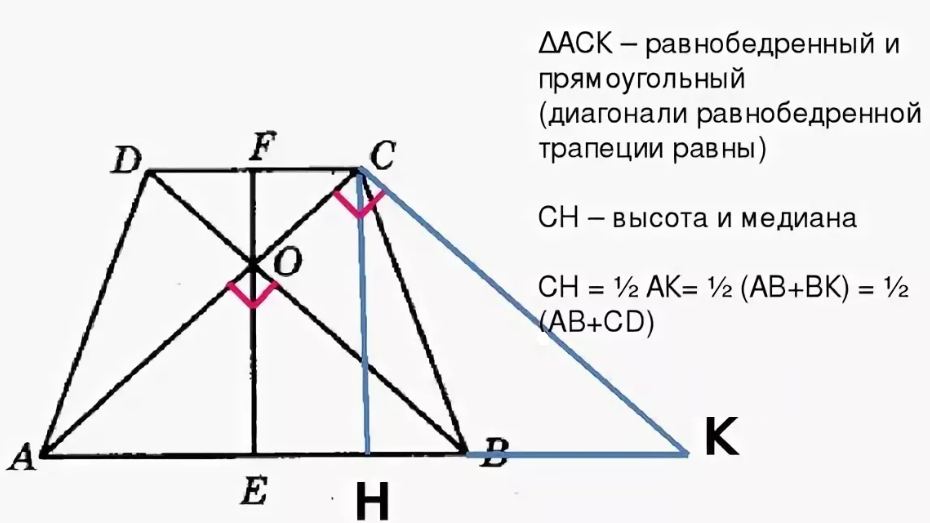
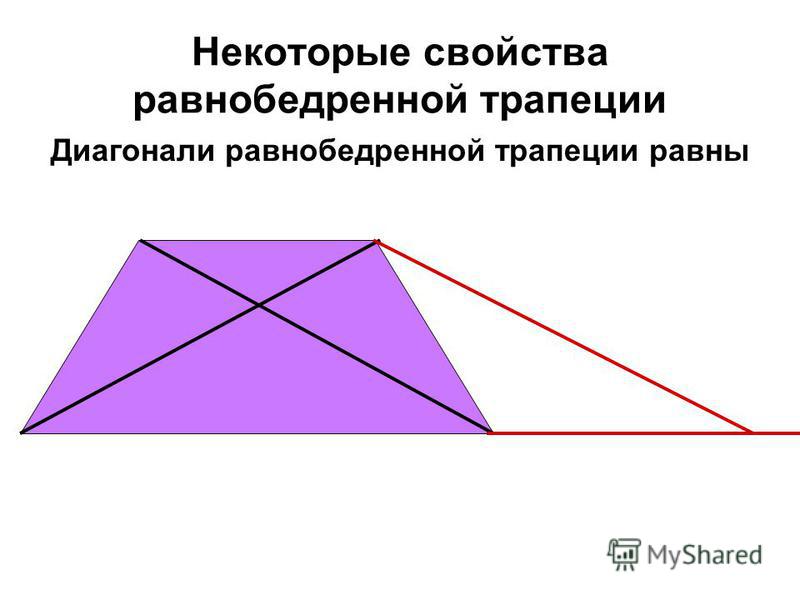 тогда: т.е.
тогда: т.е.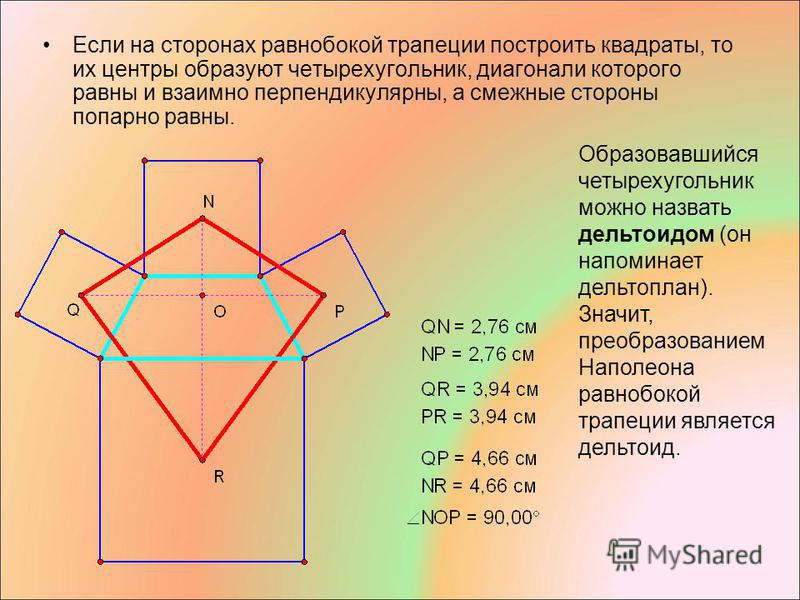
 Длина диагонали АС равна а, а длина боковой стороны ВС равна b. Найти площадь трапеции.
Длина диагонали АС равна а, а длина боковой стороны ВС равна b. Найти площадь трапеции.
 Найти радиус окружности, описанной около грапеции. [(√/а2+Ь2+2аbcos2а):(2sin2а)].
Найти радиус окружности, описанной около грапеции. [(√/а2+Ь2+2аbcos2а):(2sin2а)]. Площадь трапеции равна
Площадь трапеции равна Диагональ равнобедренной трапеции, если известны стороны (ноги и основания)
Диагональ равнобедренной трапеции, если известны стороны (ноги и основания)  Диагональ равнобедренной трапеции, если известны высота, стороны и угол при основании
Диагональ равнобедренной трапеции, если известны высота, стороны и угол при основании  Диагонали трапеции по высоте
Диагонали трапеции по высоте  Спираль, Треугольник Рило, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межрасовый треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник
Спираль, Треугольник Рило, Циклоида, Двойная циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межрасовый треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь — Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник Это трапеция с двумя противоположными ногами равной длины. Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.
Это трапеция с двумя противоположными ногами равной длины. Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы. de Веб-проекты
de Веб-проекты