Презентация «Интересные свойства трапеции»
Слайды и текст этой презентации
Слайд 1

Проектная работа « Интересные свойства трапеции » конкурс проектных работ среди обучающихся школ Правобережного района
Выполнила :
Тараева Залина
ученица 8 класса
МКОУ СОШ с. Н.Батако
Руководитель: Гагиева А.О.
20.11.2012 года
г.Беслан
2012
Слайд 2

Цель работы:
Рассмотреть свойства трапеции, которые в школьном курсе геометрии не изучаются, но при решении геометрических задач ЕГЭ из развернутой части С 4 бывает необходимо знать и уметь применять именно эти свойства .
Слайд 3
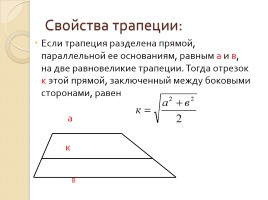
Свойства трапеции:
Если трапеция разделена прямой, параллельной ее основаниям, равным a и в, на две равновеликие трапеции. Тогда отрезок к этой прямой, заключенный между боковыми сторонами, равен
a
В
к
Слайд 4
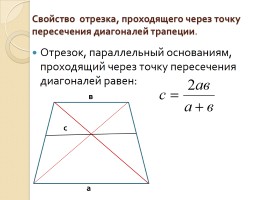
Свойство отрезка, проходящего через точку пересечения диагоналей трапеции.
Отрезок, параллельный основаниям, проходящий через точку пересечения диагоналей равен:
а
в
с
Слайд 5

Свойства трапеции:
Отрезок прямой, параллельной основаниям трапеции, заключенный внутри трапеции, разбивается ее диагоналями на три части. Тогда отрезки, прилегающие к боковым сторонам, равны между собой.
МР=ОК
Р
М
О
К
Слайд 6

Свойства равнобедренной трапеции:
Если в трапецию можно вписать окружность, то радиус окружности есть среднее пропорциональное отрезков, на которые точка касания делит боковую сторону.
О
О
Слайд 7

Свойства равнобедренной трапеции:
Если центр описанной окружности лежит на основании трапеции, то её диагональ перпендикулярна боковой стороне
О
А
В
С
Д
Слайд 8

Свойства равнобедренной трапеции:
В равнобедренную трапецию можно вписать окружность, если боковая сторона равна её средней линии.
С
В
А
Д
h
Слайд 9

1)Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства:
1. Сумма оснований трапеции равна сумме боковых сторон.
2. Расстояния от вершины трапеции до точек касания вписанной окружности равны.
3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен
Слайд 10

Свойства прямоугольной трапеции, в которую вписана окружность:
1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r).
2) Если в прямоугольную трапецию вписана окружность, то площадь трапеции равна произведению ее оснований: S=AD*BC
Слайд 11

Доказательство :
Площадь трапеции равна произведению полусуммы ее оснований на высоту:
Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а
Слайд 12

I. Биссектрисы углов при боковой стороне трапеции пересекаются под углом 90º .
1)∠ABC+∠BAD=180º(как внутренние односторонние при AD∥BC и секущей AB).
2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам).
3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º.
Вывод: Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Это утверждение применяется при решении задач на трапецию, в которую вписана окружность.
Слайд 13

I I .Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS
Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.
Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD.
Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS.
Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Слайд 14
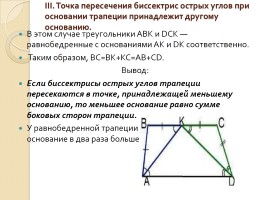
III. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.
Таким образом, BC=BK+KC=AB+CD.
Вывод:
Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.
У равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
Слайд 15

IV.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.
Отсюда AD=AF+FD=AB+CD.
Вывод:
Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.
У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Слайд 16

Если равнобедеренную трапецию со сторонами а,в,с,d можно вписать и около неё можно описать окружности, то площадь трапеции равна
Площадь трапеции
Тип урока: совершенствование знаний, умений и навыков.
Цель обучающая:
доказать теорему о площади трапеции разными способами, отрабатывать применение данной формулы при решении задач различного уровня сложности.
Цель воспитательная:
воспитывать трудолюбие, уважение друг к другу, активность на уроке.
Цель развивающая:
развивать логическое мышление, интерес к предмету, умение работать в группах.
Цель методическая:
Показать применение методов дифференцированной работы при проверке домашнего задания.
Оборудование: интерактивная доска, раздаточный материал, учебники, чертежные принадлежности.
Ход урока
Актуализация знаний учащихся.
- Дать определение трапеции.
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. - Виды трапеций: прямоугольная(Рисунок1), равнобедренная (Рисунок2).
Свойства площадей.
- Равные многоугольники имеют равные площади.
- Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Формулы площади прямоугольника, квадрата, прямоугольного треугольника, треугольника, параллелограмма.
S=ab (Рисунок3),
S=a2(Рисунок4),
S=1/2 ab (Рисунок5),
S=1/2 ah (Рисунок6),
S=ah (Рисунок7).
Проверка домашнего задания:
| Уровень А | Уровень Б | Уровень В | |
|---|---|---|---|
| 1. | 4 см и 10 см | h=5 см, а=15 см, b=25 см | 22 см2 |
| 2. | 24 см2 | 32 см2 | 81 см2 |
Уровень А1
- Дано:
АВСD-трапеция (Рисунок8)
AD-ВС=6 см
h=8 см; Sтрап.=56 см2
Найти: ВС и АD
Решение:
Пусть ВС=х, тогда АD=6+х
Sтрап.=((х+6+х):2)*8
(х+3)*8=56
x=4
ВС=4см; АD=10 см
Ответ: 4 см; 10 см. - Дано:
АВСD — прямоугольная трапеция (Рисунок9)
ABCH — квадрат
Sкв=16 см2
<BCD=135°
Sтрапеции-?
Решение:
ВС=4 (по усл.Sкв=16)
CHD — прямоугольный треугольник
Значит h=4; AD=8
Sтрап=4*((4+8):2)
Sтрап=24 см2
Ответ: 24.
Уровень Б1.
- Дано:
Sтрап=100 см2(Рисунок10)
Высота в 3 раза меньше одного из оснований и в 5 раз меньше другого
Найти: BH, BC, AD
Решение:
Пусть BH=х см, ВС=3х см, AD=5х см
((3х+5х):2)*x=100
х2=25
х=5
х=-5
x>0, значит BH=5 cм; AD=25 см, BC=15 см
Ответ: 5 см, 25 см, 15 см. - Дано:
ABCD — равнобедренная трапеция (Рисунок11)
<A=45°, ВС=BH
AD=12 см
Найти: Sтрап
Решение:
Д.п. BH перпендикулярно AD, CK перпендикулярно AD.
Пусть ВС=BH=х, тогда HK=AH=KD=х, т.к.треугольник ABH-прямоугольный,
значит 3х=12
х=4
Sтрап=(4+12):2*4
Sтрап=32см2
Ответ: 32 см2.
Уровень В1.
- Дано: ABCD — равнобед. nрапеция (Рисунок13)
<A=30°
BC+AD=22 cм
Р=30 см
Найти:Sтрап
Решение:
AB+CD=30-22=8 см
AB=CD=4 см
Д.п. BH перпендикулярно AD, CK перпендикулярно AD
Треугольник ABH — прямоугольный
BH=АВ:2=2 см(по св-ву прямоугольного треугольника)
Sтрап=22*2:2=22 см2
Ответ: 22см2 - Дано:
ABCD — равнобедр. трапеция (Рисунок12)
АС перпендикулярно BD
BC+AD=18 cм
Найти:Sтрап
Решение:
Пусть BC=х, тогда AD=18-х
Треугольник BOC-прямоугольный, равнобедренный
Значит <4=<2=<1=<3=45°
Треугольник BOH-прямоугольный, р/б
Значит BH=HO=х:2
Треугольник AOK-прямоугольный, р/б, значит AH=KO=(18-х):2
Sтрап=9*9; Sтрап=81 см2
Ответ: 81 см2.
Различные способы доказательства теоремы о площади трапеции:
Sтрап=
I способ.(Рисунок16)
Док-во:
S=S1+S2+S3 (по 2-у свойству площадей)
S1=ah
S2=1/2ch; S3=1/2h*(b-c-a)
S3=1/2hb-1/2hc-1/2ah
S1+S2+S3=ah+1/2ch+1/2hb-1/2ch-1/2ah=1/2ah+1/2bh=1/2h(a+b), ч.т.д.
II способ.(Рисунок14)
Док – во:
- Достроим трапецию до параллелограмма.
- Sтрап=Sпар–Sтр
Sпаp=bh
Sтр=1/2h*(b–a)=1/2bh-1/2ah
Sпар–Sтр=bh-1/2bh+1/2ah=1/2bh+1/2ah=1/2h(a+b), ч.т.д.
Решение задач.
- В трапеции ABCD (Рисунок15) BC и AD – основания. BC:AD=3:4. Площадь трапеции 70 см2. Найдите площадь треугольника ABC.
Решение:- Sтрап=7xh/2=70
xh=20 - SACD=4xh/2
2xh=2*20
SACD=40 - SABC=70–40
SABC=30 (см2)
- Sтрап=7xh/2=70
- Высота больше меньшего основания на 6 см, разность оснований 12 см. Найти основания трапеции, если ее площадь 64 см2(Рисунок17).
Решение:
Пусть BC=x; тогда BH=(6+x) см
AD=(12+x) см
Sтрап=
(x+6)2=64
x+6=8 или x+6=-8
x=2 или x=-14, x>0
BC=2 см
AD=14 см
Ответ: 2 см, 14 см.
Рефлексия деятельности на уроке.
Что нового узнали, самооценка учениками собственной деятельности.
Интересные факты:история трапеции.
«Трапеция» — слово греческое, означавшее в древности «столик» (по-гречески, «трапедзион» — столик, обеденный стол). В начале термин «трапеция» применяется не в современном, в другом смысле — любой четырехугольник. Трапеция в нашем смысле слова встречается впервые у древнегреческого математика Пасидона. В средние века трапецией называли, по Евклиду, любой четырехугольник (кроме трапеции), лишь в XVIII веке слово приобретает современный смысл.
Созвездие-трапеция.
Четыре яркие звезды созвездия α, β, γ и δ располагаются в вершинах трапеции – туловища льва. А голову льва образуют звезды, располагающиеся в виде серпа. Поэтому этот астеризм и называется «серп».
Итог урока: подведение итогов, выставление оценок.
Литература:
- Учеб. для 7-9 кл. общеобразоват. учреждений./ Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадюмцев и др.- 5-е изд. — М.: Просвешение, 1995.- 335 с.
- Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. — 7-е изд., испр. и доп. — М.: Илекса, — 2007,- 208 с.
- Задачи по геометрии: Пособие для учащихся 7-11 кл. общеобразоват. учреждений/ Б.Г.Зив, В.М.Мейлер, А.Г.Баханский. — 4-е изд. — М.: Просвещение, 2001.- 271 с.
- Шарыгин И.Ф. 2200 задач по геометрии. – М. Дрофа, 1999г.
- Атанасян Л.С. Изучение геометрии в 7-9 кл.: Просвещение, 2005.- 384 с.
Новый факт геометрии трапеции!!! | Беляев-сан
На Московской математической олимпиаде 2011 года для 8 класса
появилась задача, претендующая на звание нового замечательного
факта геометрии трапеции. Задача такая:
Из концов средней линии трапеции опущены перпендикуляры на её
диагонали. Доказать, что точка пересечения этих перпендикуляров
равноудалена от вершин одного из оснований.
Доказательство.
Выберем обозначения (и проведём перпендикуляры) как на рисунке.
Пусть — середина основания (для основания
рассуждения аналогичны), тогда прямые и параллельны
диагоналям и соответственно. Ясно, что прямые и
содержат высоты треугольника , следовательно, —
его ортоцентр. Значит, перпендикулярен , а значит и ,
то есть медиана треугольника является его высотой, то
есть он равнобедренный: , что и требовалось доказать.
Понравилось это:
Нравится Загрузка…
Похожее
Четырехугольники. Основные теоремы, формулы и свойства. Виртуальный справочник репетитра по математике
Здесь ученики и репетиторы по математике и могут найти основные свойства и формулы площадей четырехугольников, изучаемых в школе по основной программе. Регулярно пользуюсь этими теоретическими сведениями на тематических и обзорных занятиях по геометрии (планиметрии), а также при подготовке к ЕГЭ по математкие. Все математические понятия и факты иллюстрированы с цветовыми выделениями главных особенностей изучаемого.
1) Площади четырехугольников
Площадь параллелограмма

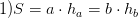
произведение основания на высоту
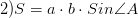
пороизведение сторон на синус угла между ними
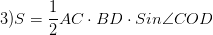
полупроизведение диагоналей на синус угла между ними
Площадь трапеции


произведение полусуммы оснований на высоту
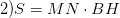
произведение средней линии на высоту

полупроизведение диагоналей на синус угла между ними
Площадь произвольного четырехугольника
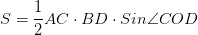
Площадь произвольного четырехугольника равна полупроизведению его диагоналей на синус угла между ними
2) Свойства параллелограмма
 В параллелограмме:
В параллелограмме: противолежащие стороны и углы равны
противолежащие стороны и углы равны
 диагонали пересекаются и в точке пересечения делятся пополам
диагонали пересекаются и в точке пересечения делятся пополам
3) сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон, то есть

3) Cредняя линия в трапеции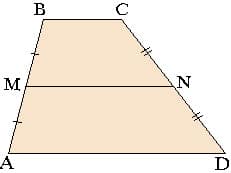
Теорема о средней линии: Средняя линия трапеции параллельна основаниям и равна их полусумме.
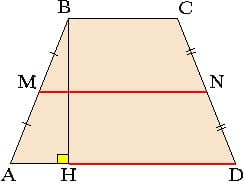
То есть 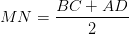 и
и

4) Средняя линия в равнобедренной трапеции
Средняя линия в равнобедренной трапеции равна отрезку нижнего основания, соединяющему вершину основания с снованием проведенной к ней высоты.
То есть 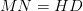
5) Теорема с сдвиге диагонали в трапеции
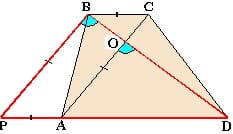
Теорема: Если в трапеции через вершину В, как показано на рисунке слева , провести отрезок параллельный одной из диагоналей, то окажутся верными следующие факты:
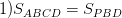
 трапеция
трапеция  — равнобедренная
— равнобедренная 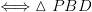 равнобедренный
равнобедренный
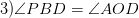
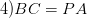
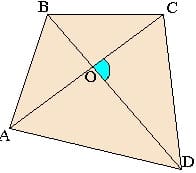
6) Четыре замечательные точки в трапеции

Теорема: В любой трапеции точка пересечения диагоналей, точка пеерсечения продолжений боковых сторон и середины оснований лежат на одной прямой.
То есть точки M, N, K и P лежат на одной прямой
Комментарий репетитора по математкие: Знаний этих свойств по четырехугольникам вполне достаточно для решения задачи С4 на ЕГЭ, то есть ничего сверх этих фактов по четырехугольникам абитуриент знать не обязан. Однако сильным ученикам для решения сложных задач части С или олимпиадных геометрических задач, а также для качественной подготовки к экзамену по математике в МГУ необходимо расширить список. Я бы не советовал репетиторам ограничиваться только задачами на применение этих свойств, так как составителями ЕГЭ по математике закладывается проверка сразу нескольких навыков работы с теорией. В течении всего времени подготовки к ЕГЭ репетитору по математкие необходимо отбирать тренировочные задачи на одновременное использование этих свойств с другими планиметрическими фактами внутри одной задачи, ибо на экзамене может встретиться многоходовая комбинация.
Колпаков Александр Николаевич. Репетитор по математике.
Метки: Геометрия, Справочник репетитора
Трапеция — Циклопедия
Трапеция Трапеция. Определения // Артем МатЛектор [2:24] Трапеция // Мрия Урок [14:07] Трапеция. Решение задач // Доступная математика [21:22]Трапеция (от греческого слова trapezion — «столик») — четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Четырехугольник является трапецией, если его параллельные стороны не равны.[1]
Равнобедренная трапеция
Прямоугольная трапеция
Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной[1].
Свойства трапеции[1]:
- ее средняя линия параллельна основаниям и равна их полусумме;
- если трапеция равнобокая, то ее диагонали равны и углы при основании равны;
- если трапеция равнобокая, то около нее можно описать окружность;
- если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
Площадь трапеции равна произведению длины ее высоты на полусумму длин оснований.
Геометрия факты интересные. Интересные факты о геометрии
Геометрия факты интересные. Интересные факты о геометрии
- Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
- Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
- С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
- Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
- Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
- Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
- В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
- Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
- Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).
- Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
- Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
- Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
- Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
- При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
- Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.
Интересные факты о стереометрии. Стереометрия
Стереоме́трия (от др.-греч. «твёрдый; объёмный, пространственный» + «измеряю») — раздел евклидовой геометрии , в котором изучаются свойства фигур в пространстве. Основными (простейшими) фигурами в пространстве являются точки , прямые и плоскости . В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые . Это одно из немногих существенных отличий стереометрии от планиметрии , так как во многих случаях задачи по стереометрии решаются путём рассмотрения различных плоскостей, в которых выполняются планиметрические законы.
Не стоит путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), а в стереометрии — свойства фигур в пространстве (свойства пространственных фигур).
Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников . Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми и невыпуклыми . Выпуклый многогранник расположен по одну сторону относительно плоскости, проходящей через любую его грань .
Источник: https://interesnyefakty.com/novosti/interesnye-fakty-geometriya-interesnye-fakty-o-geometrii
Интересные факты о углах. 10 интересных фактов о математике, которые удивляют
Человек может и не быть математиком.
Более того, он может даже не знать эту науку на минимальном уровне, но тяжело отрицать – математику человек видит практически везде.
Цифры, фигуры и математические законы преследуют человека повсюду, поэтому нелишним будет узнать кое-что об этой науке.
1. Абрахам де Муавр (математик из Англии) в своей глубокой старости вдруг понял, что его сон увеличивается на 15 минут в каждый последующий день. После этого он составил прогрессию и определил тот день, когда сон займет весь день. Случилось это 27 ноября в 1754 году, и это был день его смерти.
2. Религиозные и верующие евреи стараются всеми силами избегать любых знаков, которые связаны с крестом или символику Христа. К примеру, вместо плюса в школах используют перевернутую «Т».
3. Подлинность денежной купюры евро всегда можно узнать по ее серийному номеру – это буква и 11 цифр. Необходимо поменять букву на то число, которое является порядковым номером этой буквы в алфавите. После этого необходимо сложить все числа и складывать результаты до тех пор, пока не будет одна цифра. И если в итоге получится 8, это говорит о подлинности купюры. Другой способ – сложение всех цифр, без буквы. Итоговый результат, состоящий их буквы и цифры, должен подходить под ту страну, на территории которой появилась купюра. К примеру, Германия – это Х2.
4. Есть версия, что Альфред Нобель отказался включать математику в длинный список наук для своей премии по личным причинам – жена Альфреда спала с математиком. Но в действительности Нобель был холостым. Нет достоверных доказательств того, почему математику не включили, однако есть предположения. К примеру, уже тогда существовала своя премия, но созданная шведским королем. Другая версия – математика является чисто теоретическим предметом, поэтому математики не способны сделать ничего действительно важного для людей и человечества в целом.
5. Есть такая фигура, как треугольник Рело. Она образовывается через пересечение трех идентичных по радиусу кругов, причем центры этих кругов расположены в вершинах треугольника с равными сторонами. Сверло, созданное на основе этого треугольника, дает возможность сверлить только квадратные отверстия. При этом стоит помнить, что сверление таких отверстий с использованием треугольника Рело может иметь погрешность в 2 процента.
6. В русской литература и математике 0 не относится к спискам натуральных чисел, однако на западе 0 является одним из представителей множества таких чисел.
7. Джордж Данциг, математик из Америки, будучи всего лишь университетским аспирантом, один раз опоздал на занятие и, увидев несколько уравнений и подумал о том, что эти уравнения являются общими домашними задачами, которые необходимо выполнить. Это задание показалось ему намного сложнее того, что давали обычно, но он их выполнил и принес результаты преподавателю. И только после этого он узнал, что смог решить 2 нерешаемых уравнения статистики. Причем это были те задачи, которые не могли решить ученые в течение нескольких лет.
8. Если сложить все числа в рулетке, получится 666.
9. Небезызвестная Софья Ковалевская познакомилась с этой наукой о числах в далеком детстве – в ее комнате не было обоев, были лишь лекции ученого Остроградского об исчислениях.
10. В Индиане (штат США) в 1897-ом году выпустили билль, согласно которому число Пи будет равно 3,2. Однако билль не превратился в закон благодаря тому, что в этот процесс вовремя вмешался университетский профессор.
Интересные факты о трапеции. Презентация 8 класса на тему: «Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина.». Скачать бесплатно и без регистрации. — Транскрипт:
1 Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина
2 Цели: 1.Узнать интересную информацию о геометрической фигуре «трапеция»; 2.Показать, что она встречается в нашей жизни чаще, чем нам кажется.
3 То, что мы знаем о трапеции: Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции ее средняя линия параллельна основаниям и равна их полусумме; если трапеция равнобедренная, то ее диагонали равны и углы при основании равны; / 5
4 А вот то, что мы еще не знаем: ее средняя линия равна полусумме оснований; если трапеция равнобедренная, то около нее можно описать окружность; если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
9 Задача 1. Треугольник из трапеций! Сложите из трех одинаковых трапеций равносторонний треугольник. Трапеции нельзя накладывать друг на друга, разрезать. Треугольник должен получиться целый (без отверстий внутри) и без лишних частей снаружи фигуры.
11 Задача 2. Четыре из одной! Разрежьте данную фигуру на четыре равные и одинаковые по форме части, не повторяющие, однако, исходную форму.
13 Итак: С помощью этой презентации вы узнали, как часто встречается трапеция в нашей жизни! Вы решили несколько интересных задач, связанных с трапецией. Мы надеемся, что вам было интересно!
Интересные факты о конусе. Конусы
Брюхоногие моллюски рода конус обладают раковиной, длина которой 15 20 см, а форма напоминает коническую. Раковины этих животных окрашены в красивые тона и имеют на поверхности изысканный узор, чем и привлекают коллекционеров, стремящихся заполучить такую раковину. Эти раковины привлекают внимание и охотников за моллюсками, так как на рынках они высоко ценятся туристами.

K наиболее распространенным и брюхоногих моллюсков рода конус относятся:
- , живущие в зоне от Полинезии до Индийского океана;
- , обитающий в зоне Полинезии, и вплоть, до восточного побережья Африки;
- обитающие в регионе от Красного моря до Полинезии;
- — житель берегов Австралии и восточного побережья Африки.
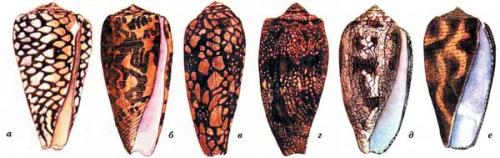
Ловцы конусов могут получить уколы от этих животных, когда они складывают моллюсков в сетчатые мешки, а также могут пострадать и при неосторожной транспортировке мешка, который они, как правило, привязывают к поясу. Сказанное относится к ловцам-профессионалам. Что же касается неопытных коллекционеров, то они получают уколы во время очистки раковины от сидящего там моллюска. Конусы обладают хорошо выраженным и сформированным ядовитым аппаратом, оснащенным шипом, достаточно острым, чтобы проколоть кожу или одежду. Шип выступает из края раковины и расположен около головной части моллюска. Заканчивается такой шип зубцом, к которому проходит проток, соединенный с ядовитой железой животного. При уколе в ранку поступает очень сильный по действию на организм яд.

Готовясь напасть , моллюск выдвигает зубы в переднюю часть головы, чтобы вонзить их в тело жертвы. К зубам подходит яд из канала радулы и глотки. В хоботке расположен один из зубов радулы. При уколе пузырек сжимается и яд под давлением вгоняется в свернутые, похожие на острый полый гарпун — зубы радулы.
Конусы обычно предпочитают держаться или свободно . Тропические виды этих моллюсков представляют реальную угрозу для человека, так как их яд, попавший в организм, часто вызывает гибель пострадавших. Самым отравления при уколе конуса считается побледнение кожных покровов, а затем кожа становится синюшной и немеет. Вокруг ранки появляется зуд, но чаще возникают острая боль или жжение, которые из местных очагов довольно быстро распространяются по всему телу, особенно резко это выражается вокруг рта. При тяжелых поражениях случается паралич. Пострадавший может потерять сознание и погибнуть в результате остановки сердца.
Б. Холстед считает, что при развивающихся симптомах отравления ядом расстройства дыхания обычно не бывает, а В. Н. Орлова и Д. Б. Гелашвили указывают, что в тяжелых случаях человек погибает не от остановки сердца, а от паралича дыхательной мускулатуры.
Для предупреждения поражений этими моллюсками можно порекомендовать единственный способ, а именно, быть крайне аккуратным при прикосновении к раковинам неизвестных моллюсков. Брать их необходимо очень осторожно, избегая мягких тканей животного.
Интересное в геометрии. Интересные факты о геометрии
Интересное в геометрии. Интересные факты о геометрии
- Неоценимый вклад в развитие этой науки сделали древнегреческие учёные Евклид и Пифагор. Открытые ими принципы и сейчас являются базой для неё. Поэтому, собственно, классическая геометрия и называется евклидовой.
- Вышеупомянутый Евклид сам доказал 465 геометрических теорем.
- С помощью геометрических формул можно легко вычислить объём пирамиды. Что интересно, формула для вычисления объёма полной пирамиды появилась позже, чем формула для усечённой.
- Одна из известных геометрических задач называется «задача Наполеона». Её назвали в честь французского императора, который был очень сведущ в этой науке, и который является автором ряда научных трудов (см. 11 интересных фактов о Наполеоне ).
- Если сделать на любой верёвке двенадцать узлов, отделённых друг от друга одинаковым расстоянием, и растянуть эту верёвку в форме треугольника, в итоге мы получим прямой угол. Эту простейшую формулу знали ещё тысячи лет назад в Древнем Египте, и пользовались ей при строительных работах.
- Помимо евклидовой геометрии, ещё существуют геометрии Римана и Лобачевского.
- В геометрии Лобачевского сумма всех углов треугольника всегда меньше 180 градусов, а в геометрии Римана — больше.
- Древнегреческий учёный Архимед первым создал формулы для вычисления объёма вписанных в цилиндр шара и конуса.
- Одна из теорем Пифагору называлась «ослиный мост». Её легко запомнить, но не так-то просто понять, и тех учеников, которые её просто зубрили на память, Пифагор называл ослами ( 25 интересных фактов о Пифагоре ).
- Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса «А» с центрами в вершинах равностороннего треугольника со стороной «А». Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия, правда, с 2% погрешностью.
- Евклидова геометрия отличается от геометрии Лобачевского в том числе и тем, что в последней можно провести не менее двух не пересекающихся прямых, лежащих в той же плоскости, через любую точку, не лежащую на этой прямой.
- Основы фрактальной геометрии заложил ещё Леонардо да Винчи, известный учёный и деятель искусства Эпохи Возрождения.
- Различные виды неевклидовых геометрий применяются в основном в астрономии, астрофизике и других науках, имеющих весьма опосредованное отношение к повседневной жизни.
- При помощи геометрии Эратосфен, древнегреческий учёный, рассчитал окружность Земли и, как показали более поздние исследования, практически не ошибся.
- Круг имеет наибольшую площадь среди всех геометрических фигур с одинаковой длиной периметра.
Интересные факты о углах. Интересные факты об угле
Человек применяет уголь в качестве горючего с старейших времен. С момента изобретения его применяли для самых различных целей. Это было и приготовление еды, и производство.
Благодаря углю стало вероятно изготавливать сталь. С углем связано множество любопытных фактов, а его роль в нашей жизни велика.

Образование угля в недрах почвы – весьма продолжительный процесс. Тут большое количество неспециализированного с нефтью. Уголь образуется из погибших растений, каковые по тем либо иным обстоятельствам выяснялись под почвой. Тут без кислорода они не гнили, и их остатки не теряли находившийся в них углерод – базу угля. Потом в течение миллионов лет под действием самых различных факторов эти остатки преобразовывались в торф, а из него в уголь.
А предстоящий процесс ведет к образованию графита.
Прежде, чем углубляться в интересные факты о разработка интересных ситуаций и добычи, которые связаны с углем, поболтаем об углях, нужных для того чтобы:
По большому счету главное отличие японской кухни от европейской – доминирование морепродуктов. Их применяют везде. А также для шашлыков, каковые японцы именуют «тэмпора». Действительно, наряду с этим они не частенько применяют уголь для их изготовление. Считается, что он способен впитывать запахи и после этого отдавать их подготавливающемуся блюду.
Углю по большей части предпочитают открытый пламя. А в дополнение довольно часто применяют имбирь, что кроме этого ликвидирует запахи.
В Северной Африке во франкоговорящих государствах обожают применять сухой кустарники и другие небольшие растения. Тут пустыня, и больших деревьев нет. Угли делают, к примеру, из саксаула.
Они получаются тёплыми и владеющими своеобразным запахом.
У нас же в Российской Федерации привычнее применять уголь для шашлыка в брикетах. Лично от себя могу дать совет компанию Хороший уголь, которая специализирутеся на производстве угля для кальяна и барбекю наивысшего качества.
Шахты, в которых добывают уголь, являются достаточно страшным местом. В них выделяются разные газы. Очень страшен метан. Он вытесняет часть кислорода совершает воздушное пространство взрывоопасным. Раньше, в то время, когда индикаторов метана не существовало, применяли канареек.
Их забирали в шахту, и в случае если птицам становилось не хорошо, это означало, что в шахте скопился метан.
Среди вторых опасностей выделяются пожары в шахтах. Как в случаях с горящим торфом, они смогут длить достаточно продолжительно. Рекордным оказался пожар на месторождении Люхуангоу в Китае.
На его устранение ушло целых 130 лет, и совсем его потушили лишь в 2004 году. Было стёрто с лица земли около 260 млн. тысячь киллограм угля.
С его месторождениями и углём связано множество забавных обстановок. В нем довольно часто обнаружили сокровища. Так в первой половине 90-ых годов XIX века повезло некой госпоже Калп, отыскавшей в громадном куске угля древнюю золотую цепочку.
Уголь хранит множество древних артефактов. Шахтеры неоднократно обнаружили останки древних сооружений. Как, к примеру, в американском городе Хаммондвилле, где во второй половине 60-ых годов XIX века нашли останки стенки с иероглифами.
Уголь играет громадную роль в жизни людей а также целых городов. Весьма интересно проследить судьбу японского города Хасима, находящегося на одноименном острове, что был некогда богат углем. Начиная с 30-х годов века прошлого, данный город продолжительное время считался самым многолюдным в мире. Остров владел береговой линией всего в 1 км, но его население составляло более 5 тыс. человек.
Но к середине 70-х уголь тут закончился. Люди начали покидать это место. Город стал полностью закинутым.
на данный момент в том месте кроме того выполняют экстремальные экскурсии.
В Российской Федерации находятся огромные запасы угля. Ученые заявляют о 4 триллионах тысячь киллограм запасов. Это чуть менее трети от общемировых.
Уголь может иметь не только привычную жёсткую форму. Сейчас имеются разработке, превращающие его в жидкое горючее, весьма похожее на нефть.
В индустрии уголь применяют не только в качестве горючего. Он есть сырьем для производства разных материалов. К примеру, из каменного угля делают неестественный графит.
И вдобавок из угля добывают содержащиеся в нем нужные материалы: свинец, серу, галлий, цинк и другие.
Интересные факты о трапеции. Презентация 8 класса на тему: «Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина.». Скачать бесплатно и без регистрации. — Транскрипт:
1 Замечательная трапеция!!! Работу выполнили ученицы 8б класса ГОУ СОШ 223 Кузуб Ольга, Харитонова Полина
2 Цели: 1.Узнать интересную информацию о геометрической фигуре «трапеция»; 2.Показать, что она встречается в нашей жизни чаще, чем нам кажется.
3 То, что мы знаем о трапеции: Трапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной, если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной. Свойства трапеции ее средняя линия параллельна основаниям и равна их полусумме; если трапеция равнобедренная, то ее диагонали равны и углы при основании равны; / 5
4 А вот то, что мы еще не знаем: ее средняя линия равна полусумме оснований; если трапеция равнобедренная, то около нее можно описать окружность; если сумма оснований равна сумме боковых сторон, то в нее можно вписать окружность.
9 Задача 1. Треугольник из трапеций! Сложите из трех одинаковых трапеций равносторонний треугольник. Трапеции нельзя накладывать друг на друга, разрезать. Треугольник должен получиться целый (без отверстий внутри) и без лишних частей снаружи фигуры.
11 Задача 2. Четыре из одной! Разрежьте данную фигуру на четыре равные и одинаковые по форме части, не повторяющие, однако, исходную форму.
13 Итак: С помощью этой презентации вы узнали, как часто встречается трапеция в нашей жизни! Вы решили несколько интересных задач, связанных с трапецией. Мы надеемся, что вам было интересно!
Интересные факты о конусе. Есть много интересных фактов о конусе

Есть много интересных фактов о конусе. Во многих религиях и учениях , конус имеет культовое значение. Имеется множество обрядов ,в которых затрагивается магические свойства конуса , например, у ведьм и колдуний имеется ритуал — «конус силы».
Слайд 22 из презентации «Конус»Размеры: 720 х 540 пикселей, формат: .jpg. Чтобы бесплатно скачать слайд для использования на уроке, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как…». Скачать всю презентацию «Конус.ppt» можно в zip-архиве размером 786 КБ.
Похожие презентации
краткое содержание других презентаций на тему слайда
«Конус и усечённый конус» — Одна из частей представляет собой конус, а другая называется усеченным конусом. Осевое сечение. Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Используя формулу (2), получаем. Усеченный конус. Боковая поверхность. В. Для вычисления площади SКОН полной поверхности конуса получается формула.
«Цилиндр конус шар» — Объём шара радиуса R равен . Определение цилиндра. Объём шара Теорема. Найти объём и площадь поверхности шара. Виды тел вращения. Объём шарового сегмента. Шаровой сегмент. Сечения шара. Сечения цилиндра. — Шаровые сегменты. Объём шарового сектора. Задача № 3. Сечение конуса. Тела вращения. Завершить работу.
«Конус» — Конус, усеченный конус. Усеченный конус – геометрическое тело, отсеченное от конуса плоскостью, параллельной основанию. Доказательство Пусть b – плоскость перпендикулярная оси конуса и пересекающая конус. Формулы. Теорема. Геометрия. Усеченный конус.
«Урок конус» — Кусты в королевском саду. Объем конуса. Проблемно-поисковый семинар работа в группах. Тема урока: «Конус. Карликовое дерево. Работа в группах 6) 5 мин: Коррекция. Задача №2: Стог сена имеет форму цилиндра с коническим верхом. Вопрос №8: По какой формуле можно вычислить объем цилиндра? Развивающие задачи урока.
«Объём конуса» — 1. Высота конуса равна 8 см. 2. В правильную треугольную пирамиду вписан конус. Объем конуса равен V. Найдите объем пирамиды. Решение задач. 3. В конус вписана правильная треугольная пирамида. Объем конуса.
«Конус геометрия» — Основание. R-радиус основания. Образующие. H-высота. Вершина. Конус. L-образующая. Применение конуса и усеченного конуса в повседневной жизни. Центр основания. С конусом люди знакомы с глубокой древности. Конус в переводе с греческого «konos» означает «сосновая шишка».