Сборник задач по геометрии 10 класс

Календарно – тематическое планирование

№

Тема урока

Кол-во часов

Хар-ка деят-ти уч-ся или виды учебной деят-ти

Виды контроля ,измерители

Планируемые результаты освоения материала

Дата проведения

план

факт

1 четверть

Повторение (4 часа)

1

Повторение

4

Объяснительно-иллюстративный репродуктивный

ФО

Знать наиболее важные темы курса геометрии 7-9 классов;

совершенствовать навыки решения задач.

02.09

2

Повторение

Репродуктивный

ИО

03.09

3

Повторение

Репродуктивный

ФО

09.09

4

Повторение

Эвристический

МД

10.09

Введение (аксиомы стереометрии и их следствия) 3 часа

5

Предмет стереометрии. Аксиомы стереометрии.

1

Эвристический

ФО

Знать : основные понятия стереометрии, аксиомы стереометрии и их следствия

Уметь : решать задачи на применение аксиом стереометрии и их следствий

16.09

6

Некоторые следствия из аксиом

1

Эвристический

УО

17.09

7

Решение задач на применение аксиом стереометрии и их следствий

1

Проблемное изложение

ИО

23.09

Параллельность прямых и плоскостей(18 час)

8

Параллельные прямые в пространстве. Параллельность трех прямых.

1

Объяснительно-иллюстративный репродуктивный

ФО

Знать : определение параллельных прямых , прямой и плоскости. Взаимное расположение прямых в пространстве

24.09

9

Параллельность прямой и плоскости.

1

Объяснительно-иллюстративный репродуктивный

УО

Знать : признак параллельности прямой и плоскости

Уметь описывать взаимное расположение прямой и плоскости.

30.09

10

Решение задач на параллельность прямой и плоскости

1

Эвристический

ИО

Знать : признак параллельности прямой и плоскости,

Уметь применять признак параллельности прямой и плоскости

при решение задач

1.10

11

Скрещивающиеся прямые.

1

Объяснительно-иллюстративный репродуктивный

Знать : определение и признак скрещивающихся прямых, как определяется угол между прямыми

Уметь находить на моделях параллелепипеда параллельные , скрещивающиеся и пересекающиеся прямые, определять взаимное расположение прямой и плоскости, решать простейшие стереометрические задачи

7.10

12

Скрещивающиеся прямые.

1

Объяснительно-иллюстративный репродуктивный

ФО

8.10

13

Углы с сонаправленными сторонами. Угол между прямыми

1

Проблемное изложение

ФО

14.10

14

Решение задач по теме «Параллельность прямой и плоскости»

1

Исследовательский

МД

15.10

15

Параллельные плоскости. Признак параллельности двух плоскостей

1

Объяснительно-иллюстративный репродуктивный

ФО

Знать : определение и признак, свойства параллельности двух плоскостей

Уметь применять признак ,свойства параллельности двух плоскостей при решение задач

21.10

16

Параллельные плоскости. Признак параллельности двух плоскостей

1

Репродуктивный

СР

22.10

17

Резерв

1

28.10

18

Контрольная работа №1по теме «Параллельность прямой и плоскости»

1

Контролирующий

КР

29.10

По плану 18 ч.; фактически _____

2 четверть

19

Свойства параллельных плоскостей.

2

Репродуктивный

ФО

Знать : определение и признак, свойства параллельности двух плоскостей

Уметь применять признак ,свойства параллельности двух плоскостей при решение задач

11.11

20

Свойства параллельных плоскостей.

Репродуктивный

СР

12.11

21

Параллельность плоскостей

2

Репродуктивный

ФО

18.11

22

Параллельность плоскостей

Репродуктивный

СР

19.11

23

Тетраэдр. Параллелепипед. Свойства граней и диагоналей параллелепипеда.

1

Объяснительно-иллюстративный репродуктивный

ФО

Знать : элементы тетраэдра и параллелепипеда, свойства противоположных граней и его диагоналей.

Уметь распознавать на чертежах и моделях тетраэдр, параллелепипед и изображать на плоскости , строить сечения тетраэдра и параллелепипеда плоскостью, параллельной грани, строить диагональные сечения, применять свойства параллельности прямой и плоскости, параллельности двух плоскостей при док-ве подобия треугольников в прост-ве

25.11

24

Решение задач по теме «Параллельность плоскостей, тетраэдр, параллелепипед»

1

познавательный

ФО

26.11

25

Контрольная работа №2 по теме «Параллельность плоскостей»

1

Контролирующий

КР

2.12

Перпендикулярность прямых и плоскостей (17 часов)

26

Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости.

1

Объяснительно-иллюстративный репродуктивный

ФО

Знать : определение и признак перпендикулярности прямой и плоскости, Т о параллельных прямых перпендикулярных к 3 прямой

Уметь распознавать на чертежах и моделях перпендикулярные прямые в пространстве, использовать при решении стереометрических задач Т. Пифагора

3.12

27

Признак перпендикулярности прямой и плоскости

2

Объяснительно-иллюстративный репродуктивный

ФО

Знать признак перпендикулярности прямой и плоскости,

Уметь применять признак при решении стереометрических задач

9.12

28

Признак перпендикулярности прямой и плоскости

Репродуктивный

СР

10.12

29

Теорема о прямой, перпендикулярной к плоскости

1

Репродуктивный

ФО

Знать теорему о прямой, перпендикулярной к плоскости

Уметь применять теорему при решении стереометрических задач

16.12

30

Решение задач на перпендикулярность прямой и плоскости

2

Познавательный

ФО

Уметь решать стереометрические задачи

17.12

31

Решение задач на перпендикулярность прямой и плоскости

Репродуктивный

СР

23.12

32

Контрольная работа №3 по теме :«Перпендикулярность прямых и плоскостей»

1

контролирующий

КР

Знать : определение прямоугольного параллелепипеда

Уметь находить измерения прямоугольного параллелепипеда, находить угол между гранью и диагональным сечением прямоугольного параллелепипеда,

24.12

По плану 14 ч.; фактически _____

3 четверть

33

Расстояние от точки до плоскости. Теорема о трех перпендикулярах

2

Эвристический

ФО

Знать : определение расстояний от точки до плоскости, от прямой до плоскости, Т .о трех перпендикулярах, определение угла между прямой и плоскостью.

Уметь находить наклонную или её проекцию, применяя Т. Пифагора, применять Т .о трех перпендикулярах при решении стереометрических задач

13.01

34

Расстояние от точки до плоскости. Теорема о трех перпендикулярах

Репродуктивный

СР

14.01

35

Угол между прямой и плоскостью.

1

Проблемное изложение

ФО

20.01

36

Решение задач на применение теоремы о трех перпендикулярах, на угол между прямой и плоскостью

1

исследовательский

ИО

21.01

37

Двугранный угол. Признак перпендикулярности двух плоскостей.

2

Объяснительно-иллюстративный репродуктивный

ФО

Знать : определение двугранного угла, перпендикулярности 2 –х плоскостей, признак перпендикулярности 2 –х плоскостей

Уметь строить линейный угол двугранного угла , распознавать на чертежах и моделях взаимное расположение плоскостей в пространстве, выполнять чертеж по условию задачи

27.01

38

Двугранный угол. Признак перпендикулярности двух плоскостей.

Эвристический

ДМ

28.01

39

Прямоугольный параллелепипед

2

Репродуктивный

ФО

Знать : определение прямоугольного параллелепипеда, куба, свойства прямоугольного параллелепипеда, куба

Уметь применять свойства прямоугольного параллелепипеда при нахождении его диагонали

3.02

40

Прямоугольный параллелепипед

Эвристический

Тест

4.02

41

Решение задач по теме «Двугранный угол. Перпендикулярность плоскостей»

1

Познавательный

ФО

Знать : определение прямоугольного параллелепипеда, куба, свойства прямоугольного параллелепипеда, куба

Уметь находить диагональ куба, находить угол между диагональю куба и плоскостью одной из его граней, находить измерения прямоугольного параллелепипеда, находить угол между гранью и диагональным сечением прямоугольного параллелепипеда, куба

10.02

42

Контрольная работа №3 по теме :«Перпендикулярность прямых и плоскостей»

1

контролирующий

КР

Знать : определение прямоугольного параллелепипеда, куба, свойства прямоугольного параллелепипеда, куба

Уметь находить

диагональ куба, находить угол между диагональю куба и плоскостью одной из его граней, находить измерения прямоугольного параллелепипеда, находить угол между гранью и диагональным сечением прямоугольного параллелепипеда, куба

11.02

Многогранники (10 часов)

43

Понятие многогранника

1

Репродуктивный

ФО

Знать элементы многогранника

17.02

44

Геометрическое тело. Теорема Эйлера

3

Объяснительно-иллюстративный репродуктивный

ФО

Знать : определение призмы, формулу площади поверхности призмы

Уметь : изображать призму, выполнять чертеж по условию задачи ,находить площадь поверхности призмы, строить сечение, находить площадь поверхности правильной п- угольгой призмы , при п= 3, 4, 6

18.02

45

Призма. Пространственная теорема Пифагора

Исследовательский

тест

24.02

46

Пирамида.

1

Объяснительно-иллюстративный репродуктивный

ФО

Знать : определение пирамиды, её элементов, определение правильной пирамиды, определение усеченной пирамиды,

Уметь : изображать пирамиду выполнять чертеж по условию задачи ,находить площадь поверхности пирамиды, строить сечение пирамиды плоскостью, решать задачи на нахождение апофемы, бокового ребра, площади основания правильной пирамиды

25.02

47

Правильная пирамида.

1

Репродуктивный

ДМ

03.03

48

Усеченная пирамида.

1

Репродуктивный

ФО

04.03

49

Симметрия в пространстве

1

Репродуктивный

Тест

10.03

50

Понятие правильного многогранника Элементы симметрии правильных многогранников.

1

Репродуктивный

ИО

Иметь представление о правильных многогранниках

Уметь распознавать на чертежах и моделях правильные многогранники

11.03

51

Урок обобщения ,систематизации коррекции

знаний

1

Познавательный

ФО

Знать основные многогранники

Уметь распознавать на чертежах и моделях правильные многогранники, строить сечение призмы ,пирамиды плоскостью, находить площадь поверхности пирамиды , призмы

17.03

52

Контрольная работа №4 по теме «Многогранники»

1

контролирующий

КР

18.03

По плану 20 ч.; фактически _____

3 четверть

Векторы в пространстве (10часов)

53

Понятие вектора в пространстве

2

Объяснительно-иллюстративный репродуктивный

ФО

Знать : определение вектора в пространстве

Уметь распознавать на чертежах и моделях сонаправленные, противоположно направленные, равные вектора

31.03

54

Понятие вектора в пространстве

Репродуктивный

ФО

1.04

55

Сложение и вычитание векторов. Умножение вектора на число

3

Объяснительно-иллюстративный репродуктивный

ФО

Знать : правило сложения и вычитания векторов, умножение вектора на число

Уметь находить сумму и разность векторов с помощью правила треугольника и многоугольника

7.04

56

Сложение и вычитание векторов. Умножение вектора на число

8.04

57

Сложение и вычитание векторов. Умножение вектора на число

эвристический

ПР

14.04

58

Компланарные вектора

2

Репродуктивный

ФО

Знать : определение компланарных векторов

Уметь распознавать на моделях находить компланарные вектора

15.04

59

Компланарные вектора

эвристический

ПР

21.04

60

Решение задач по теме «Векторы в пространстве»

2

Познавательный

ФО

Знать : определение компланарных векторов, Т. Разложении любого вектора по 3-м некомпланарным векторам,

Уметь распознавать на моделях находить компланарные вектора,

22.04

61

Решение задач по теме «Векторы в пространстве»

Познавательный

СР

28.04

62

Контрольная работа №5 по теме:«Векторы в пространстве»

1

Контролирующий

КР

29.04

Итоговое повторение ( 5 часов)

63

Повторение

5

Познавательный

ФО

ЗНАТЬ :основополагающие аксиомы стереометрии, признаки взаимного расположения прямых и плоскостей в 1прост-ве, основные пространственные формы

Уметь решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин и проводить доказательные рассуждения в ходе решения задач;

систематизировать, анализировать и классифицировать информацию, использовать разнообразные информационные источники, включая учебную и справочную литературу, иметь навыки поиска необходимой

информации

5.05

64

Повторение

Исследовательский

ПР

06.05

65

Повторение

Репродуктивный

СР

12.05

66

Повторение

Познавательный

ФО

13.05

67

Итоговая административная контрольная работа № 6

1

контролирующий

КР

Проверить умение обобщения и систематизации знаний по основным темам

курса геометрии

10 класса.

Уметь проводить самооценку собственных действий

19.05

68-70

Резерв

3

20.05

26.05

27.05

По плану 18 ч.; фактически _____

ГДЗ по геометрии за 10 класс, решебник и ответы онлайн

Решение есть!

• 1 класс
  • Математика
  • Английский язык
  • Русский язык
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир

• 2 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир
  • Человек и мир

• 3 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир

• 4 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Информатика
  • Музыка
  • Литература
  • Окружающий мир

• 5 класс
  • Математика
  • Английский язык
  • Русский язык
  • Немецкий язык
  • Украинский язык
  • Биология
  • История
  • Информатика
  • ОБЖ
  • География
  • Музыка
  • Литература
  • Обществознание
  • Технология
  • Естествознание

Дидактический материал по Геометрии 10 класс.

Математические диктанты по геометрии

10 класс

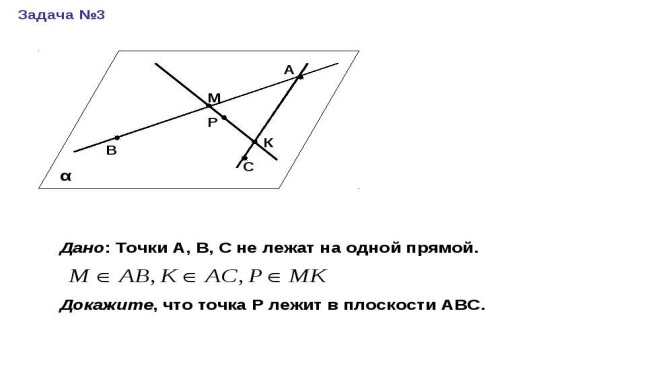
Аксиомы стереометрии

1. Запишите основные фигуры стереометрии.

2. Постройте плоскость α, прямую СД, лежащую в данной плоскости и точку А, не лежащую в плоскости. Сделайте соответствующие записи.

3. Верно ли, что: а) любые три точки лежат в одной плоскости; б) через любые три точки проходит плоскость и притом только одна.

4. Верно ли, что прямая лежит в плоскости треугольника, если она пересекает две стороны треугольника?

5. Закончите предложение: Если две плоскости имеют общую точку, то они…

6. Можно ли через точку пересечения двух прямых провести третью прямую, не лежащую с ними в одной плоскости?

7. Верно ли, что если две точки окружности лежат в одной плоскости, то и вся окружность лежит в этой плоскости?

8. Два диаметра окружности принадлежат одной плоскости. Принадлежит ли вся окружность этой плоскости?

9. Могут ли прямая и плоскость иметь только одну общую точку? Только две общие точки?

Диктант «Аксиомы стереометрии»

1. Сформулируйте аксиому стереометрии С₁.

2. Заполните пропуски, чтобы получилось верное утверждение:

а) Через прямую и не лежащую на ней точку можно провести ________________________ и притом только одну;

б) Если А  а, а  α, то А … α.

3. «Да» и «нет» не говорите, лучше сразу напишите

а) Могут ли прямая и плоскость иметь только одну общую точку?

б) Могут ли прямая и плоскость иметь только две общие точки?

в) Можно ли через любые три точки провести единственную плоскость?

4. Верны ли следующие утверждения:

а) Если прямая пересекает две смежные стороны квадрата, то она лежит в плоскости этого квадрата.

б) Если две точки окружности лежат в одной плоскости, то и вся окружность лежит в этой плоскости.

в) Если две противоположные вершины параллелограмма лежат в одной плоскости, то и весь параллелограмм лежит в этой плоскости.

г) Если две прямые пересекаются в точке А, то все прямые, не проходящие через точку А и пересекающие данные прямые, лежат в одной плоскости

Диктант «Взаимное расположение прямых»

1. Закончите предложения:

а) Две прямые в пространстве называются параллельными, если ________________________________________________________ .

б) Две прямые называются скрещивающимися, если ________________________________________________________ .

2. Заполните пропуски, чтобы получилось верное утверждение:

а) Две пересекающиеся прямые лежат в _______________ плоскости;

б) Если прямые а и в имеют две общую точку, то они ___________________ .

в) Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то данные прямые _______________________________ .

г) Через точку пересечения двух данных прямых можно провести третью ______________________ , не лежащую с ними в одной плоскости.

д) Если прямая пересекает две пересекающиеся прямые и не проходит через точку их пересечения, то она лежит в ________________________ этих прямых.

3. Прямые а и b параллельны. Прямая с пересекает прямую а, но не пересекает b. Как расположены прямые с и b?

4. «Да» и «нет» не говорите, лучше сразу напишите

а) Прямые c и d принадлежат плоскости β. Могут ли прямые c и d быть параллельными?

б) Прямые а и b принадлежат одной плоскости. Могут ли эти прямые пересекаться?

Диктант «Параллельные прямые в пространстве. Параллельность прямой и плоскости»

1. Закончите предложения:

а) Признак параллельности прямых в пространстве _________________________________________________ .

б) Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом __________________________ .

в) Прямая и плоскость называются параллельными, если ___________________________________________________________ .

2. Известно, что две прямые с и d параллельны прямой к. Как взаимно расположены прямые с и d?

3. Через концы отрезка МN и его середину К проведены параллельные прямые, пересекающие плоскость α в точках М_1, N₁ и К₁. Найдите длину отрезка КК₁, если отрезок МN не пересекает α и ММ₁ = 6 см, NN₁=2 см.

4. Прямые а и b не лежат в одной плоскости. Можно ли провести прямую с, параллельную прямым а и b?

5. Сколько можно провести через данную точку прямых, параллельных данной плоскости?

6. Две прямые параллельны некоторой плоскости. Могут ли эти прямые быть скрещивающимися?

7. Сторона АВ параллелограмма АВСD принадлежит плоскости α. Как расположены по отношению к плоскости α остальные стороны?

8. Прямые а и b – параллельны. Прямая а не лежит в плоскости α, прямая b принадлежит α. Какое взаимное расположение прямой а и плоскости α?

Параллельные прямые в пространстве.

Параллельность прямой и плоскости

1. Всегда ли две непересекающиеся прямые в пространстве параллельны?

2. Всегда ли через две параллельные прямые можно провести плоскость?

3. Каким может быть взаимное расположение прямой и плоскости?

4. Верно ли, что если прямая, не лежащая в плоскости, параллельна ей, то она параллельная любой прямой, лежащей в этой плоскости?

5. Сколько можно провести через данную точку прямых, параллельных данной плоскости?

6. Две прямые параллельны некоторой плоскости. Могут ли эти прямые а) пересекаться? б) быть скрещивающимися?

7. Три вершины ромба лежат в плоскости. Принадлежит ли этой плоскости четвертая вершина ромба?

8. Средняя линия трапеции лежит в некоторой плоскости. Пересекают ли основания трапеции эту плоскость?

9. Сколько можно провести через данную точку прямых, параллельных данной плоскости?

10. Две смежные стороны параллелограмма пересекают плоскость. Пересекают ли эту плоскость две другие стороны параллелограмма?

Диктант 4 «Параллельность плоскостей»

1. Закончите предложения:

а) Две плоскости называются параллельными, если _________________.

б) Признак параллельности плоскостей:__________________________ .

2. Сколько случаев взаимного расположения плоскостей в пространстве и какие?

3. Будут ли параллельны плоскости, если прямая, лежащая в одной плоскости, параллельна другой плоскости?

4. Будут ли параллельны плоскости, если две прямые, лежащие в одной плоскости, соответственно параллельны двум прямым другой плоскости?

5. Каким может быть взаимное расположение прямых а и b, каждая из которых лежит в одной из параллельных плоскостей?

6. Заполните пропуски, чтобы получилось верное утверждение:

а) Если одна из противоположных сторон параллелограмма пересекает плоскость α, то и другая сторона ________________________ эту плоскость.

б) Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом ___________________________ .

в) Противоположные грани куба лежат в _________________ плоскостях.

г) Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями ____________________________ .

Параллельные плоскости

1. Закончите предложение: Две плоскости называются параллельными, если…

2. Верно ли, что две плоскости параллельны, если две прямые, лежащие в одной плоскости, параллельные двум прямым, лежащим в другой плоскости?

3. Сформулируйте Аксиому 3.

4. Верно ли, что если две стороны треугольника параллельны плоскости, то и третья сторона параллельна этой плоскости?

5. Две стороны трапеции лежат в параллельных плоскостях. Могут ли эти стороны быть боковыми сторонами трапеции?

6. Как называются вершины параллелепипеда, не принадлежащие одной грани?

7. Какие фигуры являются гранями параллелепипеда?

8. Постройте сечение тетраэдра плоскостью, проходящей черед данные точки.

Диктант «Перпендикулярность прямых и плоскостей»

1. Заполните пропуски, чтобы получилось верное утверждение:

а) Две прямые называются перпендикулярными, если ________________ .

б) Прямая и плоскость называются перпендикулярными, если __________ .

в) Две прямые, перпендикулярные одной и той же плоскости __________________________________________ .

г) Если две плоскости перпендикуляры прямой, то они ________________ .

2. Сколько перпендикуляров можно провести через данную точку к данной прямой на плоскости?

3. Сколько перпендикуляров можно провести через данную точку к данной прямой в пространстве?

4. Прямые а и b – пересекаются. При каком условии можно провести через а плоскость, перпендикулярную b?

5.Прямая проходит через вершину А треугольника АВС перпендикулярно сторонам АВ и АС. Как она расположена относительно стороны ВС?

2. Вставьте пропущенное слово

а) Если плоскость перпендикулярна одной из двух параллельных прямых, то она _________________________________________ и другой.

б) Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая ________________________ этой плоскости.

Диктант «Перпендикулярность и наклонная.

Теорема о 3 перпендикулярах»

1. Закончите предложения:

а) Перпендикуляром, опущенным из данной точки на данную плоскость, называется__________________________________________________ .

б) Основанием перпендикуляра называется _________________________ .

в) Расстоянием между прямой и плоскостью называется ____________________ .

г) Наклонной, проведенной из данной точки к данной плоскости, называется ____________________________________________________ .

д) Основанием наклонной называется ______________________________ .

е) Проекцией наклонной на плоскость называется _____________________ .

ж) Теорема о трех перпендикулярах: ________________________________ .

2. Может ли наклонная быть короче перпендикуляра, проведенного из той же точки и к той же плоскости?

3. Если наклонные, проведенные из одной точки к плоскости равны, то что можно сказать об их проекциях?

4. Точка А не лежит в плоскости α. Сколько наклонных заданной длины можно провести из этой точки к данной плоскости?

Диктант 7 «Перпендикулярность плоскостей»

1. Закончите предложения:

а) Две пересекающиеся плоскости называются перпендикулярными, если ________________________________ .

б) Признак перпендикулярности двух плоскостей: _____________________ .

в) Две смежные грани прямоугольного параллелепипеда лежат в _______________________________ плоскостях.

г) Если прямая, лежащая в одной из двух перпендикулярных плоскостей, перпендикулярна их линии пересечения, то она перпендикулярна и другой__________________________________________ .

д) Плоскость, перпендикулярная прямой, по которой пересекаются две данные плоскости, перпендикулярна каждой из этих ________________ .

е) В прямоугольном параллелепипеде все шесть граней ________________ .

ж) Длины ребер прямоугольного параллелепипеда, имеющие общую вершину, называются ___________________________________ .

2. Сколько можно провести плоскостей через данную точку, перпендикулярных данной плоскости?

3. Сколько существует плоскостей, проходящих через данную прямую (не перпендикулярную плоскости) и перпендикулярных данной плоскости?

4. Прямые а и b – параллельные и лежат в плоскости α. Через каждую из этих прямых проведена плоскость, перпендикулярная α. Каково взаимное расположение полученных плоскостей?

Перпендикулярность прямой и плоскости

1. Закончите предложение: а)Прямая называется перпендикулярной к плоскости, если … б) Если плоскость перпендикулярна к одной из двух параллельных прямых, то она…

2. Закончите предложение: Две прямые, перпендикулярные одной и той же плоскости …

3. Можно ли утверждать, что прямая, проходящая через центр круга перпендикулярно диаметру, перпендикулярна плоскости круга?

4. Можно ли утверждать, что прямая перпендикулярна плоскости, если она перпендикулярна лежащим в этой плоскости двум сторонам квадрата; двум сторонам треугольника?

5. Закончите предложение: если одна из двух параллельных прямых перпендикулярна плоскости, то …

6. Установите взаимное положение прямых а и b

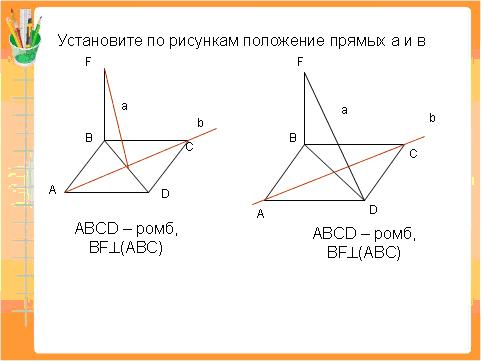
7. Запишите теорему, обратную теореме о трёх перпендикулярах.

Многогранники

1. Запишите известные вам многогранники.

2. Равны ли многоугольники, лежащие в основаниях призмы?

3. Какими фигурами являются боковые грани призмы?

4. Что называется кубом?

5. Призма имеет 30 граней. Какой многоугольник лежит в её основании?

6. Закончите предложение: Призма называется прямой, если…

7. Может ли быть наклонной призма, основанием которой является прямоугольник?

8. Что называется апофемой пирамиды?

9. Чему равна площадь боковой поверхности правильной пирамиды?

10. Боковые рёбра пирамиды равны между собой. Может ли основанием пирамиды быть ромб? Прямоугольник?

11. Боковые рёбра пирамиды равны между собой. Как расположена проекция вершины пирамиды на основание, если основание прямоугольник? Прямоугольный треугольник?

Параллельность прямой и плоскости».

1. Могут ли две различные прямые в пространстве иметь более одной общей точки? (Пояснить)

2. Могут ли вершины замкнутой ломаной линии, состоящей из 4 звеньев, не принадлежать одной плоскости? (Пояснить)

3. Прямые a и b параллельны плоскости α. Укажите взаимное положение этих прямых.

4. Плоскости α и β пересекаются по прямой m. Прямая a параллельна плоскости α и плоскости β. Каково взаимное положение прямых a и m?

5. Верно ли утверждение: если прямая параллельна плоскости, то она параллельна любой прямой, лежащей в этой плоскости.

Математический диктант. (Геом.10кл.урок 13-14)

1. Верно ли утверждение , что если прямая , не лежащая в плоскости , параллельна ей , то она параллельна любой прямой , лежащей в этой плоскости .

2. Верно ли утверждение , что если две прямые параллельны одной и той же плоскости , то они параллельны между собой .

3. Каким может быть взаимное расположение двух прямых , из которых одна параллеьна некоторой плоскости , а другая пересекает эту плоскость.

4. Верно ли утверждение параллельности прямой и плоскости “Прямая , параллельная какой либо прямой на плоскости , параллельна и самой плоскости “.

5. Прямые а и в параллельны . Какой положение может занимать прямая а относительно плоскости , проходящей через прямую в .

6. Одна из двух параллельных прямых параллельна некоторой плоскости . Можно ли утверждать , что и вторая прямая параллельна этой плоскости .

7. Даны две пересекающие плоскости . Существует ли плоскость , пересекающая две данные плоскости по параллельным прямым.

8. Верно ли утверждение : если две прямые не имеют общих точек , то они параллельны .

9. Две прямые параллельны некоторой плоскости . Могут ли эти прямые

а) пересекаться б) быть скрещивающимися

10. Могут ли скрещивающиеся прямые а и в быть параллельными прямой с .

11. Даны две скрещивающиеся прямые а и в . Точки А и А₁ лежат на прямой а , точки В и В₁ лежат на прямой в . Как будут расположены прямые АВ и А₁В_{1 .}

12. Прямая а скрещивается с прямой в , а прямая в скрещивается с прямой с . Следует ли из этого , что прямые а и с скрещиваются .

13. Каково должны быть взаимное расположение трех прямых , чтобы можно провести плоскость , содержащую все прямые .

Математический диктант

1. Какие две прямые в пространстве называются параллельными

2. Сформулируйте признак параллельности прямой и плоскости

3. Дан куб АВСДА₁В₁С₁Д₁. назовите четыре пары параллельных прямых , четыре пары пересекающих прямых.

4. Какие возможны случаи взаимного расположения прямой и плоскости.

5. Верно ли утверждение :если одна из двух параллельных прямых параллельна плоскости, то вторая прямая не пересекает эту плоскость .

Математический диктант

1. Могут ли прямая и плоскость не иметь общих точек?

2. Верно ли, что если две прямые не пересекаются, то они параллельны?

3. Плоскости α и β параллельны , прямая m лежит в плоскости α. Верно ли , что прямая m параллельна плоскости β?

4. Верно ли , что если прямая m параллельна одной из двух параллельных плоскостей, с другой плоскостью прямая mимеет только одну общую точку?

5. Верно ли, что боковые стороны трапеции параллельны плоскости α и плоскости трапеции?

6. Верно ли, что плоскости параллельны , если прямая лежащая в одной плоскости , параллельна другой плоскости?

7. Верно ли, что линия пересечения двух плоскостей параллельна одной из этих плоскостей?

8. Верно ли, что любые четыре точки лежат в одной плоскости?

9. Верно ли , что если две стороны треугольника параллельны плоскости α, то и третья сторона параллельны плоскости α?

Диктант Векторы в пространстве

1. Что называется вектором в пространстве? (Что такое модуль вектора?)

2. Какие векторы называются противоположно направленными (коллинеарными)?

3. Что называется суммой векторов х и у ? (Что называется скалярным произведением вектора х и вектора у?)

4. Как записать в координатах условие равенства вектора а и b? (Как определяется произведение вектора а на число ?)

5. Какие векторы называются равными? (Запишите условие перпендикулярности векторов.)

6. Что такое абсолютная величина вектора? (Каково направление нулевого вектора?)

7. Найдите сумму вектора х (1; -4; -5) и вектора у (3; 4; -5). (Найдите произведение числа – 3 на вектор b (4; 3; 10).)

8. Каковы координаты вектора с началом в точке (3; 2; -5) и концом в точке (-5; 2; 3;)? (Найдите координаты вектора, противоположного вектору b (7; 8; 9).)

9. Найдите скалярное произведение вектора а (1; 31; 2) и вектора b (-1; 0; 3)).

Векторы в пространстве

Вариант 1

1. Вектором в пространстве называется …

2. Вектор обозначается …

3. Длиной вектора называется …

4. Два вектора в пространстве называются одинаково направленными, если …

5. Для того, чтобы сложить два вектора, нужно

Вариант 2

1. Вектором на плоскости называется …

2. Вектор изображается …

3. Модулем вектора называется …

4. Два вектора в пространстве называются противоположно направленными, если …

5. При умножении вектора на число …

Диктант Углы между прямыми и плоскостями

1. Чему равен угол между прямой и параллельной ей плоскостью? (Чему равен угол прямой и пересекающей ее плоскостью?)

2. Чему равен угол между пересекающими плоскостями? (Чему равен угол между скрещивающимися прямыми?)

3. Что называется углом между скрещивающимися прямыми? (Что называется углом между двумя прямыми?)

4. Чему равен угол между параллельными плоскостями? (Чему равен угол между параллельными прямыми?)

5. Что называется углом между прямой и плоскостью? (Чему равен угол между двумя пересекающимися прямыми?)

6. Что называется углом между плоскостями? (Чему равен угол между перпендикулярными прямыми?)

7. В кубе А…D покажите угол между гранью ВВ С и диагональю АС (между плоскостью АВС и прямой ВD).

8. В кубе А…D покажите угол между пересекающимися плоскостями (между скрещивающимися прямыми).

Диктант Перпендикуляр и наклонная.

1. Сформулируйте условие теоремы о трех перпендикулярах (заключение теоремы о трех перпендикулярах).

2. Дайте определение перпендикуляра к плоскости (определение наклонной к плоскости).

3. Дайте определение проекции наклонной (перпендикулярной плоскостей).

4. Сформулируйте признак перпендикулярности плоскости. (Что называется основанием наклонной?)

5. Что называется расстоянием от прямой до параллельной ей плоскости? (Что называется основанием перпендикуляра?)

6. Что называется расстоянием между параллельными плоскостями? (Сформулируйте признак перпендикулярности плоскостей.)

7. Покажите на рисунке угол между проекцией наклонной и прямой, проведенной через основание наклонной (угол между наклонной и прямой, проведенной через основание наклонной).

8. Сделайте рисунок к теореме о трех перпендикулярах (к обратной теореме о трех перпендикулярах).

Диктант Свойства перпендикулярных прямой и плоскости.

1. Дайте определение прямой, перпендикулярной плоскости. (Какие прямые в пространстве называются перпендикулярными?)

2. Сколько прямых, перпендикулярных плоскости, можно провести через любую точку плоскости? (Что можно сказать о нескольких перпендикулярах к одной плоскости?)

3. Сколько плоскостей, перпендикулярных данной прямой, можно провести через точку вне данной прямой? (Сколько прямых, перпендикулярных плоскости, можно провести через точку, не лежащую в данной плоскости?)

4. Что можно сказать о прямой, параллельной перпендикуляру к плоскости? (Сколько плоскостей, перпендикулярных данной прямой, можно провести через точку вне данной прямой?)

5. Постройте прямую, перпендикулярную плоскости. (Постройте через данной прямой перпендикулярную ей плоскость.)

6. Постройте в пространстве три проходящие через одну точку взаимно перпендикулярные прямые. (Постройте через точку плоскости прямую, перпендикулярную плоскости.)

Диктант «Углы в пространстве»

1. Закончите предложения:

а) Углом между скрещивающимися прямыми называется угол между __________________________________________ .

б) Углом между прямой и плоскостью называется угол между этой прямой и ____________________________________________________ .

2. Ответьте на вопросы

а) Чему равен угол между параллельными прямыми?

б) В каком случае скрещивающиеся прямые перпендикулярны?

в) Что называется проекцией наклонной на плоскость?

г) Чему равен угол между параллельными плоскостями?

3. Справедливо ли утверждение?

а) Любая прямая на плоскости, перпендикулярная проекции наклонной, перпендикулярна и наклонной.

б) Плоскость, пересекающая параллельные плоскости, пересекает их под равными углами.

в) Прямая, проходящая через центр круга, перпендикулярна диаметру.

4. Точка А отстоит от плоскости на расстоянии 12см. Найдите длины наклонных, проведенных из этой точки, если они образуют с плоскостью углы 30⁰.

Диктант Пространственные фигуры

Вариант 1

1. Гранями многогранника называются …

2. Вершинами многогранника называются …

3. Куб – многогранник, у которого …

4. Прямая призма – призма, у которой …

5. Правильная пирамида – пирамида, у которой …

Вариант 2

1. Ребрами многогранника называются …

2. Диагоналями многогранника называются …

3. Параллелепипед – многогранник, у которого …

4. Пирамида – многогранник, у которого …

5. Правильная призма – призма, у которой …

Диктант Моделирование многогранников

Вариант 1

1. Развертка многогранника – это …

2. Для удобства склейки развертку многогранника нужно …

3. Развертка прямого параллелепипеда состоит из …

4. Развертка треугольной призмы состоит из …

5. Развертка правильной шестиугольной пирамиды состоит из …

Вариант 2

1. Чтобы получить развертку многогранника нужно …

2. Геометрический конструктор состоит из …

3. Развертка прямого параллелепипеда состоит из …

4. Развертка прямой пятиугольной призмы состоит из …

5. Развертка правильной четырехугольной пирамиды состоит из …

Диктант Скрещивающиеся прямые

Вариант 1

1. Две прямые в пространстве называются скрещивающимися, если …

2. Два отрезка называются скрещивающимися, если …

3. В тетраэдре имеется … пар скрещивающихся ребер.

4. Через точку, принадлежащую прямой, можно провести … прямых, скрещивающихся с этой прямой.

5. Даны две скрещивающиеся прямые и третья прямая, их пересекающая. Плоскости, проходящие через первую и третью прямые и через вторую и третью прямые …

Вариант 2

1. Две прямые в пространстве называются параллельными, если …

2. Две прямые в пространстве скрещиваются, если они не пересекаются и …

3. Две прямые скрещиваются, если одна из них лежит в плоскости, а другая …

4. Через точку, не принадлежащую прямой, можно провести … прямых, скрещивающихся с этой прямой.

5. В четырехугольной пирамиде имеется … пар скрещивающихся ребер.

«Решение задач по геометрии». 10-й класс

Пояснительная записка

 Курс разработан в рамках Концепции профильного обучения на старшей ступени общего образования и соответствует федеральному компоненту государственного среднего (полного) общего образования по математике. При разработке данного курса учитывалось, что курс должен быть направлен на удовлетворение  интересов и потребностей обучающихся, на формирование у них новых видов познавательной деятельности. Математические  знания, представление о роли математики в современном мире стали необходимыми компонентами общей культуры. Кроме того, математика является профилирующим предметом на вступительных экзаменах в ВУЗы по многим специальностям.
Научиться решать задачи по геометрии гораздо сложнее, чем по алгебре. Это связано с тем, что для успешного решения пространственных задач требуется не только знание основных теорем, определений, свойств и признаков, но и развитое пространственное воображение, умение выполнять необходимые построения, эффективно использовать алгебру и тригонометрию. При выполнении экзаменационных заданий наибольшие затруднения вызывают задания по стереометрии (С2) и планиметрии (С4).
Умение решать задачи – один из основных показателей математического развития учащихся, глубины усвоения ими учебного материала. При изучении стереометрии в старших классах необходима систематизация полученных учащимися знаний в основной школе. Дополнительные знания углубляют знания учащихся по основному курсу, предоставляют возможность удовлетворить свои познавательные интересы, дают возможность научиться решать более трудные задачи. В старших классах углубление основного курса выполняет функцию подготовки к продолжению образования и к сдаче экзамена по математике в форме ЕГЭ. Поэтому данный курс является дополнением и углублением базового курса геометрии.
Данный курс предназначен для учащихся 10-11 классов и рассчитан  на помощь в создании системы ранее приобретенных знаний, на приобретение опыта решения стереометрических задач, на подготовку к сдаче ЕГЭ.
Данный курс построен таким образом, что изучение нового материала опирается на материал пройденный. Первостепенная роль отводится рисунку, помогающему сделать задачу более зримой и понятной. Пространственные способности учащихся развиваются в процессе решения задач группы С  вариантов ЕГЭ.
В программу курса входят некоторые теоремы, которые не входят в программу общеобразовательного курса. Они помогают решить разнообразные нестандартные геометрические задачи.

Цель: эффективная подготовка выпускников к сдаче ЕГЭ по математике и повышение уровня математической культуры.

Задачи курса:

• Развивать пространственное воображение, математические  способности
• Обобщить, углубить, расширить знания учащихся
• Познакомить с разнообразными приемами и методами решения задач
• Развивать умение правильно строить чертеж и использовать его для решения задач
• Формировать навыки исследовательской деятельности
• Приобщать учащихся к работе с различными источниками информации, развивать умение анализировать полученную информацию

Данный курс рассчитан на 68 часов (34 в 10 классе и 34 в 11 классе) и предполагает компактное изложение теории, решение задач и самостоятельную работу.

Содержание курса

1. Треугольники (10 часов)
Метрические соотношения в прямоугольном треугольнике. Свойства проекций катетов. Метрические соотношения в произвольном треугольнике. Свойства медиан, биссектрис высот. Теоремы о площадях треугольника.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений
Формы контроля: самостоятельная работа
2.Четырехугольники (10 часов)
Метрические соотношения в четырехугольнике. Свойства произвольного четырехугольника. Свойства параллелограмма. Теоремы о площадях четырехугольников. Свойства биссектрисы параллелограмма, трапеции.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений
Формы контроля: самостоятельная работа
3.Окружность (5 часов)
Метрические соотношения между длинами хорд. Свойства вписанных углов. Углы между хордами, касательными и секущими.
Окружности и треугольники (2 ч.). Окружности, вписанные и описанные около треугольников. Окружности, описанные и вписанные в прямоугольные треугольники.
Окружности и четырехугольники (3 ч.) Четырехугольники , вписанные и описанные около окружности. Площади четырехугольников описанных  и вписанных в окружность.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений
Формы контроля: самостоятельная работа
4. Расстояние в пространстве (9 часов).
Тема 4.1 (3 часа) Расстояние между точками, расстояние от точки до  прямой в пространстве. Пропедевтический  материал (теорема Пифагора, свойства равнобедренного треугольника, подобие треугольников, тригонометрические функции углов треугольника).
Введение в тему. Определение расстояния между точками, расстояние от  точки до прямой.
Тема 4.2 Расстояние между прямыми в пространстве (общий перпендикуляр, расстояние между параллельными плоскостями, скрещивающиеся прямые) (3 ч.) Определение расстояния между непересекающимися прямыми в пространстве как длины общего перпендикуляра. Решение задач на нахождение расстояния между параллельными и скрещивающимися прямыми.
Тема 4.3 Расстояние от точки до плоскости в пространстве (длина перпендикуляра, длина  высоты пирамиды) (3 часа)
Определение расстояния от точки до плоскости как длина перпендикуляра. Решение задач на нахождение расстояния от точки до плоскости
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений
Формы контроля: опрос, самостоятельная работа
5. Углы в пространстве (16 часов)
Тема 5.1 Угол между  прямыми  в пространстве (5 часа)
Пропедевтический материал (теорема о трех перпендикулярах, признак перпендикулярности прямой и плоскости, тригонометрические функции углов треугольника, теорема косинусов)
Определение угла между пересекающимися  прямыми, угла между скрещивающимися прямыми. Теоремы об углах между прямой и плоскостью
Тема 5.2 Угол между прямой и плоскостью (5 часа)
Пропедевтический материал (методы нахождения углов между пересекающимися прямыми.
Пропедевтический материал (методы нахождения углов между пересекающимися прямыми, тригонометрические функции углов, теорема косинусов). Определение угла между наклонной и плоскостью. Теорема о трех перпендикулярах.
Тема 5.3 Угол между плоскостями. (6 часа)
Пропедевтический материал (методы нахождения углов между пересекающимися прямыми, тригонометрические функции углов). Определение двугранного угла, линейного угла двугранного угла, угла между пересекающимися плоскостями
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений
Формы контроля: опрос, самостоятельная работа
6. Координатный метод (16 часов)
Прямоугольная система координат в пространстве. Применение метода координат к решению задач на вычисление расстояния от точки до плоскости, угла между плоскостями. Периметр и площадь сечения. Объем пирамиды.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений
Формы контроля: самостоятельная работа
7. Защита проектов. Подведение итогов.(2 часа)
Примерные темы проектов:
«Различные способы нахождения расстояния  между скрещивающимися прямыми», «Различные способы нахождения расстояния от точки до плоскости», «Применение векторного и координатного методов при нахождении расстояний в пространстве», «Решение задач повышенной сложности».

Требования к уровню подготовки учащихся

– овладение математическими знаниями и умениями, необходимыми для успешного освоения программы по геометрии
– развитие логического мышления, пространственного воображения, интуиции, творческой активности
– умение правильно выполнять чертежи, развитие «геометрического видения»
– сформированные навыки исследовательской деятельности
– умение работать с различными источниками информации, анализировать полученную информацию
– умение работать в группе

Освоение учащимися программы курса проверяется в ходе выполнения самостоятельных работ по каждой теме. Также в ходе изучения курса предполагается подготовить групповой проект по данной теме и защитить его.

Календарно-тематическое  планирование

№	Наименование тем курса	Всего часов	лекция	практика	Форма контроля	Дата
1	Треугольники	10
1.1	Решение задач на свойства биссектрисы углов треугольника	2	0,5	1,5
1.2	Решение задач на свойства медиан треугольника	2	0,5	1,5
1.3	Решение задач на свойства высот треугольника	2	0,5	1,5
1.4	Решение задач на свойства описанной около треугольника окружности	1	–	1
1.5	Решение задач на свойства вписанной в треугольник окружности	1	–	1
1.6	Решение задач на площадь треугольника	2	0,5	1,5	С.р
2	Четырехугольники	10
2.1	Решение задач на свойства параллелограмма	2	0,5	1,5
2.2	Решение задач на вычисление площади параллелограмма	2	0,5	1,5
2.3	Решение задач на свойства ромба	2	0,5	1,5
2.4	Решение задач на свойства трапеции	2	0,5	1,5
2.5	Решение задач на вычисление площади ромба и трапеции	2	0,5	1,5	С.р
3	Окружности	5
3.1	Окружности	2	0,5	1,5
3.2	Окружности и четырехугольники	3	1	2	С.р
4	Расстояние в пространстве	9
4.1	Расстояние между двумя точками. Расстояние от точки до прямой.	3
4.2	Расстояние между  прямыми.  Общий перпендикуляр. Расстояние между параллельными плоскостями и скрещивающимися прямыми.	3
4.3	Расстояние от точки до плоскости. Длина перпендикуляра.	3			С.р
5	Углы в пространстве	16
5.1	Угол между  прямыми	5	1	4
5.2	Угол между прямой и плоскостью	5	1	4
5.3	Угол между плоскостями	6	1	5	С.р
6	Координатный метод	16
6.1	Прямоугольная система координат в пространстве	2
6.2	Расстояние между двумя точками.	2	0,5	1,5
6.3	Расстояние между  прямыми.	2	0,5	1,5
6.4	Расстояние от точки до плоскости	2	0,5	1,5
6.5	Угол между прямыми.	2	0,5	1,5
6.6	Угол между прямой и плоскостью.	2	0,5	1,5

Методическая разработка (геометрия, 10 класс) по теме: Решение задач по теме «Многогранники», геометрия, 10 класс

МБОУ «Западнодвинская СОШ №1»

Урок по геометрии в 10 классе

Решение задач по теме «Многогранники».

Разработала и провела учитель высшей категории Макарова Р. Б.

«Вдохновение нужно в геометрии не меньше, чем в поэзии» .А.С. Пушкин

Тип урока: комплексное применение знаний

Дидактическая цель урока: проверить уровень теоретических знаний по теме «Многогранники», умение применить полученные знания на практике.

Задачи урока:

образовательные:

— организовать работу обучающихся на уроке по проверке качества усвоения теоретического материала и умение применить его на практике; 

развивающие:

— развивать у ребят активность, умение работать с литературой, компьютером, ЦОРами, умение рассуждать, объяснять, делать выводы, творчески мыслить и действовать,  работать самостоятельно и в группах;

воспитательные:

— воспитывать чувство ответственности и коллективизма, а также интерес к предмету через современные технологии преподавания. 

Формы организации познавательной деятельности: индивидуальная, групповая, работа в парах.

Методы и приемы обучения:  исследовательский, словесный, наглядный (демонстрация компьютерных презентаций и моделей многогранников), инновационный, практический.

Оборудование: компьютер, мультимедийный проектор, презентация  по теме урока, ноутбуки с выходом в Интернет, интерактивная доска, листы контроля, карточки для проверки формул площадей, карточки с разноуровневыми заданиями, модели многогранников, презентация (приложение 6).

ХОД УРОКА.

    Учащиеся  распределены на 3 группы, в каждой определен лидер. Группе выданы:  лист контроля (приложение 4), тест, индивидуальные рабочие листы, карточки с домашним заданием, модели многогранников, карточки для проверки формул площадей.

ДЕЯТЕЛЬНОСТЬ УЧИТЕЛЯ	ДЕЯТЕЛЬНОСТЬ ОБУЧАЮЩИХСЯ	КОММЕНТАРИИ
Постановка целей урока (3 минуты)
— Добрый день, ребята! Тема сегодняшнего урока «Решение задач по теме «Многогранники»».     Увлекательный раздел геометрии – теория многогранников. Многогранники выделяются необычными свойствами, красивыми формами, которые находят широкое применение в конструировании сложных и красивых многогранных поверхностей для реальных архитектурных сооружений.    Исходя из темы урока, поставьте перед собой цели. Учитель обобщает сказанное. Повторить теоретический материал по теме «Многогранники». Применять знания при решении задач. Вы распределены на 3 группы и в каждой группе определен лидер, который будет помогать организовывать работу в группе и делать соответствующие пометки в листе контроля для самооценки и взаимооценке по итогам урока.     Эпиграфом к нашему уроку я взяла слова А. С. Пушкина «Вдохновение нужно в геометрии не меньше, чем в поэзии». Желаю и вам вдохновиться на предстоящую работу и получить удовольствие от работы на уроке.	Учащиеся предлагают цели урока Рассматривают листы контроля.	Слайд 1 Слайд 2 Слайд 3
Актуализация знаний (12 мин)
Прошу лидеров выбрать по одному ученику – знатоку формул площадей многоугольников. Вам предлагается карточка, на которой необходимо записать формулы площадей предложенных вам фигур.                                                                              приложение 1	Лидер выбирает одного представителя, который выполняет задание на карточке отдельно от своей группы.	Слайд 4 Слайды 5-12 Слайд 13
Пока ребята работают, остальным предлагаю ответить на вопросы по теме «Многогранники». Лидеров групп прошу фиксировать правильные ответы в листе контроля. (фронтальный опрос)                                                                              приложение 2	Дают ответы на поставленные вопросы. Лидер контролирует работу.
Молодцы! Вы показали хорошие знания теоретического материала.    Предлагаю учащимся, работавшим самостоятельно, вернуться в свою группу и обратиться за помощью, если она вам необходима. Проверьте свои записи с помощью слайда.    Сколько ошибок вами допущено? Какие формулы вызвали затруднения?	Участники группы проверяют формулы на карточке, при необходимости дополняют, исправляют.  Количество правильных формул фиксируют в листе контроля.
Решение задач (25 мин)
Теоретический материал мы будем применять при отработке навыков по решению задач различного уровня сложности. В том числе и задач демоверсии ЕГЭ по математике 2013.     При решении геометрических задач необходимо хорошо уметь определять на чертеже взаимное расположение прямых, плоскостей, уметь определять линейный угол двугранного угла. Эти навыки я предлагаю закрепить при выполнении первых четырех заданий теста (вариант 1)  на сайте:  «WEB-сайт «Геометрия». Решение геометрических заданий частей А, В, С ЕГЭ» http://geometry.far.ru/var1.php    Для удобства работы группы данные задания вынесены на отдельные листы на ваших столах (тест) (приложение 3).  На работу отводится 5 минут.                                                                  Учитель контролирует работу групп, оказывает помощь при необходимости.	Учащиеся выходят в Интернет и группой выполняют четыре задания теста с онлайн проверкой. Лидеры отмечают результаты теста в листе контроля.	Слайд 14 (пустой) Слайд 15 (проверка теста) Слайд 16 (пустой) Слайды 17-21
Молодцы! Вы показали хорошие навыки определения взаимного расположения прямых и плоскостей по заданному чертежу.    Продолжаем решать задачи. На ваших столах лежат рабочие листы (приложение 5) с задачами двух уровней. Прочитайте задачи и выберите для себя соответствующий уровень. Предлагаю лидерам разделить свою команду на микро группы (по 2-3 человека) в соответствии с выбранным уровнем задач. Цель группы – решить как можно больше задач различных уровней и обсудить их решение в группе с последующей защитой у доски. На работу отводится 12 минут.   При затруднении учитель помогает разделится на микро группы и оказывает консультации по решению задач.        Предлагаю закончить решение задач. Приступаем к проверке решения задач.	Лидер группы помогает определится с уровнем задач и делит учащихся на микро группы.     По мере решения задач учащиеся из различных групп приглашаются к интерактивной доске и к обычной доске, где коротко записывают решение задач. Каждая группа защищает свое решение. Другие группы слушают, задают вопросы, предлагают свое решение.
Подведение итогов, домашнее задание (5мин)
Наш урок подходит к концу. Прошу обсудить работу своей группы и ее членов (что получилось, какие были затруднения, достигли ли вы поставленных целей)    Заслушать лидеров с анализом работы группы. Оценить самых активных учащихся. Остальные получат оценки после просмотра учителем рабочих листов, листов контроля, выполненной домашней работы.    Домашнее задание на рабочих листах (задачи разных уровней)   Прошу в листах контроля в виде смайликов выразить свое настроение по итогам урока.    Спасибо за урок.	Обсуждают, в листы контроля ставят самооценки, взаимооценки. Просматривают домашнее задание. Ставят смайлики.	Слайд 22 (пустой) Слайд 23   Слайд 24

Тест по геометрии (10 класс) на тему: Геометрия 10 класс. Тематические тесты

1	Точки М, Р, К – середины ребер DA, DB, DC тетраэдра DABC. Назовите прямую, параллельную плоскости FАB. 1) МР             2) РК             3) МК              4)  МК и РК
2	АВСDA1B1C1D1 – прямоугольный параллелепипед. Какая из прямых параллельна плоскости  A1AD? 1) а                   2) b                 3) p                 4)  m
3	В тетраэдре DАВС AM = MD, AN = NB. Плоскости какой грани параллельна прямая MN? 1) DAB             2) DBC            3) DAC            4)  ABC
4	Выберите верные высказывания: 1) Параллельные прямые не имеют общих точек. 2) Если прямая параллельна данной плоскости, то она параллельна любой прямой, лежащей в этой плоскости. 3) Если прямая параллельна линии пересечения двух плоскостей и не принадлежит ни одной из них, то она параллельна каждой из этих плоскостей. 4)  Существует параллелепипед, у которого все углы граней острые. Ответ: ______
5	Точки А, В, С и D – середины ребер прямоугольного параллелепипеда. Назовите параллельные прямые. 1) a || n                           2) a || b                3) b || c                           4)  a || c
6	Точки А и D – середины ребер параллелепипеда. Выберите верные высказывания: 1) Прямые СD и MN пересекаются. 2) Прямые АВ и MN скрещивающиеся 3) Прямые АВ и СD параллельные. 4) Прямые АВ и MN пересекаются Ответ: ______
7	Определите взаимное расположение прямых.                 1) a и b – пересекающиеся прямые 2) a и b – параллельные прямые 3) a и b – скрещивающиеся прямые
8	Точки А и В – середины ребер параллелепипеда. Определите взаимное расположение прямых.                 1) a и b – пересекающиеся прямые 2) a и b – параллельные прямые 3) a и b – скрещивающиеся прямые
9	Два равнобедренных треугольника АВС и АВD с общим основанием АВ расположены так, что точка С не лежит в плоскости АВD. Определите взаимное расположение прямых, содержащих медианы треугольников, проведенных к сторонам ВС и ВD. 1) они параллельны                  2) скрещиваются                   3) пересекаются
10	В тетраэдре DАВС АВ = ВС = АС = 10; DA = DB = DC = 20. Через середину ребра ВС плоскость, параллельная АС и ВD. Найдите периметр сечения. Ответ: ____

Поурочные разработки по геометрии 10 класс

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА

Введение. АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ

Урок 1. Предмет стереометрии. Аксиомы стереометрии

Урок 2. Некоторые следствия из аксиом

Урок 3. Решение задач на применение аксиом стереометрии и их следствий

Урок 4. Решение задач на применение аксиом стереометрии и их следствий

Урок 5. Решение задач на применение аксиом стереометрии и их следствий. Самостоятельная работа

Глава I. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

§ 1. ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ, ПРЯМОЙ И ПЛОСКОСТИ

Урок 6. Параллельные прямые в пространстве

Урок 7. Параллельность прямой и плоскости

Урок 8. Решение задач по теме «Параллельность прямой и плоскости»

Урок 9. Решение задач по теме «Параллельность прямой и плоскости»

Урок 10. Решение задач по теме «Параллельность прямой и плоскости»

§ 2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ

Урок 11. Скрещивающиеся прямые

Урок 12. Углы с сонаправленными сторонами. Угол между прямыми

Урок 13. Решение задач по теме «Взаимное расположение прямых в пространстве. Угол между двумя прямыми»

Урок 14. Решение задач по теме «Параллельность прямых и плоскостей»

Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»

§ 3. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ

Урок 16. Параллельные плоскости

Урок 17. Свойства параллельных плоскостей

§ 4. ТЕТРАЭДР. ПАРАЛЛЕЛЕПИПЕД

Урок 18. Тетраэдр

Урок 19. Параллелепипед

Урок 20. Задачи на построение сечений

Урок 21. Задачи на построение сечений

Урок 22. Закрепление свойств параллелепипеда

Урок 23. Контрольная работа № 1

Урок 24. Зачет № 1

Глава II. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

§ 1. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Урок 25. Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости

Урок 26. Признак перпендикулярности прямой и плоскости

Урок 27. Теорема о прямой, перпендикулярной к плоскости

Урок 28. Решение задач на перпендикулярность прямой и плоскости

Урок 29. Решение задач на перпендикулярность прямой и плоскости

Урок 30. Решение задач на перпендикулярность прямой и плоскости

§ 2. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Урок 31. Расстояние от точки до плоскости. Теорема о трех перпендикулярах

Урок 32. Угол между прямой и плоскостью

Урок 33. Повторение теории. Решение задач на применение теоремы о трех перпендикулярах (ТПП), на угол между прямой и плоскостью

Урок 34. Решение задач на применение ТТП, на угол между прямой и плоскостью

Урок 35. Повторение (решение задач на теорему о 3-х перпендикулярах)

Урок 36. Угол между прямой и плоскостью (повторение)

§ 3. ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ

Урок 37. Двугранный угол

Урок 38. Признак перпендикулярности двух плоскостей

Урок 39. Прямоугольный параллелепипед

Урок 40. Решение задач на свойства прямоугольного параллелепипеда

Урок 41. Перпендикулярность прямых и плоскостей (повторение)

Урок 42. Решение задач

Урок 43. Контрольная работа по теме «Перпендикулярность прямых и плоскости»

Урок 44. Зачет № 2

Глава III. МНОГОГРАННИКИ

§ 1. ПОНЯТИЕ МНОГОГРАННИКА. ПРИЗМА

Урок 45. Понятие многогранника

Урок 46. Призма. Площадь поверхности призмы

Урок 47. Повторение теории, решение задач на вычисление площади поверхности призмы

Урок 48. Решение задач на вычисление площади поверхности призмы

§ 2. ПИРАМИДА

Урок 49. Пирамида

Урок 50. Правильная пирамида

Урок 51. Решение задач по теме «Пирамида»

Урок 52. Решение задач по теме «Пирамида». Самостоятельная работа

Урок 53. Усеченная пирамида. Площади поверхности усеченной пирамиды

§ 3. ПРАВИЛЬНЫЕ МНОГОГРАННИКИ

Урок 54. Симметрия в пространстве. Понятие правильного многогранника. Элементы симметрии правильных многогранников

Урок 55. Контрольная работе № 3.1 по теме «Многогранники»

Урок 56. Зачет № 3 по теме «Многогранники. Площадь поверхности призмы, пирамиды»

Глава IV. ВЕКТОРЫ В ПРОСТРАНСТВЕ

§ 1. ПОНЯТИЕ ВЕКТОРА В ПРОСТРАНСТВЕ

Урок 57. Понятие векторов. Равенство векторов

§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО

Урок 58. Сложение и вычитание векторов. Сумма нескольких векторов

Урок 59. Умножение вектора на число

§ 3. КОМПЛАНАРНЫЕ ВЕКТОРЫ

Урок 60. Компланарные векторы. Правило параллелепипеда

Урок 61. Разложение вектора по трем некомпланарным векторам

Урок 62. Зачет по теме «Векторы в пространстве»

ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ

Урок 63. Итоговое повторение. Аксиомы стереометрии и их следствия

Урок 64. Параллельность прямых и плоскостей

Урок 65. Повторение (теорема о трех перпендикулярах, угол между прямой и плоскостью)

Урок 66. Контрольная работа № 5

Урок 67. Повторение. Векторы в пространстве, их применение к решению задач

Урок 68. Заключительный урок-беседа по курсу геометрии

ПРИЛОЖЕНИЯ

Приложение 1. Контрольные и самостоятельные работы

Урок 5. Самостоятельная работа

Урок 9. Самостоятельная работа обучающего характера

Урок 10. Проверочная самостоятельная работа

Урок 14. Работа по карточкам

Урок 15. Контрольная работа по теме «Аксиомы стереометрии. Взаимное расположение прямых, прямой и плоскости»

Урок 17. Самостоятельная работа

Урок 23. Контрольная работа № 1

Урок 30. Самостоятельная работа

Урок 53. Тест

Урок 55. Контрольная работа № 3.1 по теме «Многогранники»

Урок 63. Теоретический тест с последующей самопроверкой

Урок 66. Контрольная работа № 5

Урок 67. Мини-тест по теории

Приложение 2. Плакаты № 1, 2, 3, 4, рекомендуемые к урокам № 51, 52, 53