Теорема Фалеса — Википедия
Материал из Википедии — свободной энциклопедии
- Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.
Теорема Фалеса — теорема планиметрии о параллельных и секущих.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Формулировки
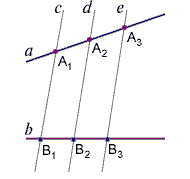
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
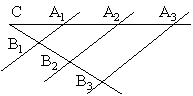В обратной теореме Фалеса важно, что равные отрезки начинаются от вершиныТаким образом (см. рис.) из того, что CB1CA1=B1B2A1A2=…{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots }, следует, что A1B1||A2B2||…{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots }.
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.
Лемма Соллертинского
Следующее утверждение, двойственно к лемме Соллертинского:
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть f{\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых Xf(X){\displaystyle Xf(X)} будет коника (возможно, вырожденная). |
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers[es] представила песню, посвящённую теореме[1].
Литература
- Атанасян Л. C. и др. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.
Примечания
См. также
Теорема Фалеса — Википедия. Что такое Теорема Фалеса
- Эта теорема о параллельных прямых. Смотри также Теорема Фалеса об угле, опирающемся на диаметр окружности.
Теорема Фалеса — теорема планиметрии о параллельных и секущих.
Вне русскоязычной литературы теоремой Фалеса иногда называют другую теорему планиметрии, а именно, утверждение о том, что вписанный угол, опирающийся на диаметр окружности, является прямым. Открытие этой теоремы действительно приписывается Фалесу, о чём есть свидетельство Прокла.
Формулировки
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
- Более общая формулировка, также называемая теорема о пропорциональных отрезках
Параллельные прямые отсекают на секущих пропорциональные отрезки:
- A1A2B1B2=A2A3B2B3=A1A3B1B3.{\displaystyle {\frac {A_{1}A_{2}}{B_{1}B_{2}}}={\frac {A_{2}A_{3}}{B_{2}B_{3}}}={\frac {A_{1}A_{3}}{B_{1}B_{3}}}.}
Замечания
- В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также не важно, где находятся отрезки на секущих.
- Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках, поскольку равные отрезки можно считать пропорциональными отрезками с коэффициентом пропорциональности, равным 1.
Доказательство в случае секущих
Доказательство в случае параллельных прямых
Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по второму признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD. ■
Вариации и обобщения
Обратная теорема
Если в теореме Фалеса равные отрезки начинаются от вершины (часто в школьной литературе используется такая формулировка), то обратная теорема также окажется верной. Для пересекающихся секущих она формулируется так:
Если прямые, пересекающие две другие прямые(параллельные или нет), отсекают на обеих из них равные (или пропорциональные) между собой отрезки, начиная от вершины, то такие прямые параллельны. |
В обратной теореме Фалеса важно, что равные отрезки начинаются от вершиныТаким образом (см. рис.) из того, что CB1CA1=B1B2A1A2=…{\displaystyle {\frac {CB_{1}}{CA_{1}}}={\frac {B_{1}B_{2}}{A_{1}A_{2}}}=\ldots }, следует, что A1B1||A2B2||…{\displaystyle A_{1}B_{1}||A_{2}B_{2}||\ldots }.
Если секущие параллельны, то необходимо требовать равенство отрезков на обеих секущих между собой, иначе данное утверждение становится неверным (контрпример — трапеция, пересекаемая линией, проходящей через середины оснований).
Этой теоремой пользуются в навигации: столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется направление с одного судна на другое.
Лемма Соллертинского
Следующее утверждение, двойственно к лемме Соллертинского:
В случае теоремы Фалеса коникой будет бесконечно удалённая точка, соответствующая направлению параллельных прямых.
Это утверждение, в свою очередь, является предельным случаем следующего утверждения:
Пусть f{\displaystyle f} — проективное преобразование коники. Тогда огибающей множества прямых Xf(X){\displaystyle Xf(X)} будет коника (возможно, вырожденная). |
Теорема Фалеса в культуре
Аргентинская музыкальная группа Les Luthiers[es] представила песню, посвящённую теореме[1].
Литература
- Атанасян Л. C. и др. Геометрия 7-9. — Изд. 3-е. — М.: Просвещение, 1992.
Примечания
См. также
Обсуждение:Теорема Фалеса — Википедия
Материал из Википедии — свободной энциклопедии
Про столкновение судов[править код]
«Столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохраняется курс судов друг на друга» — поясните, пожалуйста. Я не понимаю этой формулировки, или же при чём тут теорема Фалеса. —gul 09:02, 8 февраля 2010 (UTC)
- Имеется в виду одинаковое влияние ветра. Т.е. они едут друг на друга, но ветер их сносит. А т.к. сносит всегда на одну и ту же величину (угол?), то вместо отрезка получается треугольник. infovarius 21:29, 8 февраля 2010 (UTC)
- Спасибо. Возможно, стоит это пояснить в статье? А то вряд ли так, как оно сформулировано, только мне непонятно, а остальные читатели сразу понимают, что речь идёт о влиянии ветра.
- И есть ли этому утверждению пруфлинк? Одинаковое влияние ветра на разные суда мне представляется допустимым для абстрактной математической задачи, но слишком далёким от реальности для того, чтобы применяться в современной морской навигации. Кроме того, насколько я понимаю, при условии сохранения курса судов друг на друга они столкнутся даже при разном влиянии ветра, но их пути не будут прямыми, а теорема Фалеса — применимой. Может, речь о влиянии не ветра, а течения? Но тогда для обоснования столкновения проще перейти в систему отсчёта, связанную с водой, без всякой теоремы Фалеса. И непонятно, откуда в реальной навигации может взяться и второе столь странное условие — сохранение курса судов друг на друга. — gul 14:17, 14 февраля 2010 (UTC)
А разве курс на что-то — это не полярный угол вектора, соединяющего точку наблюдения с этим чем-то? Тогда утверждение о постоянстве курса означает параллельность линии, соединяющей суда, в зависимости от времени? deevrod (обс) 06:13, 14 ноября 2011 (UTC)
Неверное использование термина «Секущая»[править код]
Согласно тексту «секущие» имеются в виду прямые, которые делятся на отрезки, иными словами — прямые, на которых отсекаются отрезки. Это — неправильное применение термина «секушая». Кроме того, не совсем верно применение названия «пересекающиеся прямые» к не параллельным прямым, пересечение несомненно есть, но в контексте данной задачи оно может быть сколь угодно «далеко» от места построения. Обычно говорят «пересекающиеся» прямые, если точка пересечения находится в области видимости/области построения задачи, иначе просто говорят «не параллельные прямые».
теорема фалеса — с русского на все языки
См. также в других словарях:
Теорема Фалеса — Эта теорема о параллельных прямых. Об угле, опирающемся на диаметр, см. другую теорему. Теорема Фалеса одна из теорем планиметрии. Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести… … Википедия
Теорема Фалеса (значения) — Фалесу Милетскому приписывается несколько теорем: Теорема Фалеса о пропорциональных (равных) отрезках и параллельных прямых. Утверждение о вписанном угле, опирающемся на диаметр окружности. В англоязычной литературе именуется теоремой Фалеса … Википедия
ТЕОРЕМА — Пифагора. Жарг. шк. Шутл. Учительница математики. ВМН 2003, 131. Теорема Пофигатора. Жарг. шк. Шутл. Теорема Пифагора. ВМН 2003, 108. Теорема Фаллоса. Жарг. студ. (матем.). Шутл. Теорема Фалеса. (Запись 2003 г.). Теорема хана банаха. Жарг. студ.… … Большой словарь русских поговорок
Теорема Фаллоса — Жарг. студ. (матем.). Шутл. Теорема Фалеса. (Запись 2003 г.) … Большой словарь русских поговорок
Теорема о биссектрисе — одна из теорем геометрии … Википедия
Фалес Милетский — Θαλῆς ὁ Μιλήσιος Θαλῆς ὁ Μιλήσιος … Википедия
Фалес — Θαλῆς ὁ Μιλήσιος Фалес Милетский Дата и место рождения: 640/624 до н. э. Да … Википедия
Прямоугольный треугольник — Прямоугольный треугольник это треугольник, в котором один угол прямой (то есть составляет 90 градусов). Соотношения между сторонами и … Википедия
Трапеция — У этого термина существуют и другие значения, см. Трапеция (значения). Трапеция (от др. греч. τραπέζιον «столик»; … Википедия
ЕВКЛИД — [греч. Εὐκλείδες] (кон. IV нач. III в. до Р. Х.), древнегреч. математик и педагог, представитель александрийской математической школы, широкую известность приобрел благодаря сочинению по основам математики, озаглавленному «Начала» (Στοιχεῖα, букв … Православная энциклопедия
Угол, опирающийся на диаметр окружности — У этого термина существуют и другие значения, см. Теорема Фалеса. прямой Теоремой Фалеса в западной литературе называют следующее утверждение планиметрии … Википедия