Ампер, Андре-Мари — Википедия

В Википедии есть статьи о других людях с фамилией Ампер.

Андре-Мари́ Ампе́р (фр. André-Marie Ampère; 20 января^[7][8]1775 — 10 июня 1836) — французский физик, математик и естествоиспытатель.

Джеймс Максвелл назвал Ампера «Ньютоном электричества». Ампер создал первую теорию, которая выражала связь электрических и магнитных явлений, ввёл в физику понятие электрического тока и проницательно предположил, что магнетизм вызван электрическими токами «на молекулярном уровне». Внёс значительный вклад в механику, теорию вероятностей, математический анализ.

Член Парижской академии наук (1814). Член многих других научных обществ, в частности — иностранный член Лондонского королевского общества (1827)^[9], иностранный^[10][11] почётный^[11] член Петербургской академии наук (1830).

Детство[править | править код]

Андре-Мари Ампер родился в Лионе, в приходе Сент-Низье в семье крупного коммерсанта и уважаемого гражданина Жан-Жака Ампера и Жанны-Антуанетты Сарсей-де-Сатьер. Вскоре после рождения сына семья Амперов прекратила заниматься торговлей и перебралась в своё имение в Полоймье-де-Мондоре в окрестностях Лиона

[12].

Способность считать появилась у будущего великого физика с самых первых лет, для чего он, не зная цифр, использовал турецкие бобы и кремни. В раннем детстве юный Ампер быстро освоил чтение и начал буквально «глотать» все книги вокруг без разбора: стихи, романы, философские сочинения, исторические труды и т. п. Из всех писателей он предпочитал Вольтера, Гомера, Лукана, Тассо, Фенелона, Томаса и Корнеля^[12]. Одной из главных книг его детства была французская энциклопедия Дидро и д’Аламбера, которую он полностью прочел и после цитировал её уже в зрелом возрасте. Андре получил домашнее образование, читал на латинском Эйлера и Бернулли.

Когда Амперу было 18 лет, в 1793 году, его отца гильотинировали по приговору комиссаров Конвента^[13]

[14]. Это событие глубоко потрясло юношу, и он находился в состоянии близком к безрассудному почти год^[15][13][16].

Зрелые годы[править | править код]

В 1799 году Ампер женится и становится репетитором в Политехнической школе в Париже, затем, с 1801 года, занимает кафедру физики в Бурке, где он проявил себя и на литературном поприще, впервые выступив с сочинением: «Considerations sur la thèorie mathematique du jeu» («Рассуждения о математической теории игр», Лион, 1802), благодаря этому сочинению, Ампер, в 1805 году, получает предложение занять место на кафедре математики в парижской Политехнической школе. В этот период Ампер публикует ряд математических исследований, посвященных математическому анализу и теоретической физике, что принесло ему авторитет в научном мире^[15].

В 1814 он был избран членом Академии наук, а с 1824 занимал должность профессора экспериментальной физики в Коллеж де Франс. Ампер умер от пневмонии 10 июня 1836 в Марселе.

Его имя внесено в список величайших учёных Франции, помещённый на первом этаже Эйфелевой башни.

Могила Ампера (дата рождения указана ошибочно 21 вместо 20) и его сына

Сын Андре Мари, Жан-Жак Ампер (1800—1864), был известным филологом.

Математика, механика и физика обязаны Амперу важными исследованиями. Его основные физические работы выполнены в области электродинамики. В 1820 он установил правило для определения направления действия магнитного поля на магнитную стрелку, известное ныне как правило Ампера; провёл множество опытов по исследованию взаимодействия между магнитом и электрическим током; для этих целей создал ряд приборов; обнаружил, что магнитное поле Земли влияет на движущиеся проводники с током. В том же году открыл взаимодействие между электрическими токами, сформулировал закон этого явления (закон Ампера), развил теорию магнетизма, предложил использовать электромагнитные процессы для передачи сигналов.

Согласно теории Ампера, магнитные взаимодействия являются результатом происходящих в телах взаимодействий так называемых круговых молекулярных токов, эквивалентных маленьким плоским магнитам, или магнитным листкам. Это утверждение носит название теоремы Ампера. Таким образом, большой магнит, по представлениям Ампера, состоит из множества таких элементарных магнитиков. В этом заключается суть глубокого убеждения учёного в чисто токовом происхождении магнетизма и тесной связи его с электрическими процессами.

В 1822 Ампером был открыт магнитный эффект соленоида (катушки с током), откуда следовала идея эквивалентности соленоида постоянному магниту. Также им было предложено усиливать магнитное поле с помощью железного сердечника, помещаемого внутрь соленоида. Идеи Ампера были изложены им в работах «Свод электродинамических наблюдений» (фр. «Récueil d’observations électrodynamiques», Париж, 1822),

«Краткий курс теории электродинамических явлений» (фр. «Precis de la thèorie des phenômenes électrodynamiques», Париж, 1824), «Теория электродинамических явлений» (фр. «Thèorie des phenômenes électrodynamiques»). В 1826 году им была доказана теорема о циркуляции магнитного поля. В 1829 Ампер изобрёл такие устройства как коммутатор и электромагнитный телеграф.

В механике ему принадлежит формулировка термина «кинематика».

В 1830 году ввёл в научный оборот термин «кибернетика».

Разносторонний талант Ампера оставил след и в истории развития химии, которая отводит ему одну из почетных страниц и считает его, совместно с Авогадро, автором важнейшего закона современной химии.

В честь учёного единица силы электрического тока названа «ампером», а соответствующие измерительные приборы — «амперметрами».

Некоторые исследования Ампера относятся к ботанике, а также к философии, в частности «Наброски по философии науки» (фр.

«Essais sur la philosophie des Sciences», 2 т., 1834—43; 2-е издание, 1857).

1. ↑ http://www.ampere.cnrs.fr/unevieenimages/index.php?limite=0
2. ↑ http://books.google.de/books?id=rwEoAAAAYAAJ&pg=PA389&hl=de#v=snippet&q=1775&f=false
3. ↑ http://amperemusee.fr
4. ↑ Немецкая национальная библиотека, Берлинская государственная библиотека, Баварская государственная библиотека и др. Record #118645048 // Общий нормативный контроль (GND) — 2012—2016.
5. ↑ идентификатор BNF: платформа открытых данных — 2011.
6. ↑ Roux P. d. Nouveau Dictionnaire des œuvres de tous les temps et tous les pays — 2 — Éditions Robert Laffont, 1994. — Vol. 1. — P. 82. — ISBN 978-2-221-06888-5
7. ↑ Акт крещения (фр.)
8. ↑ в некоторых источниках ошибочно 21 или 22 января, в том числе на могиле 21 Ампер Андре Мари // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
9. ↑ Ampere; Andre-Marie (1775—1836) (англ.)
10. ↑ Советский энциклопедический словарь / Гл. ред. А. М. Прохоров. — М.: Сов. энциклопедия, 1986. — С. 51. — 1600 с. — 2 500 000 экз. — ISBN ИБ№115.
11. ↑ ^{1 2} Профиль Андре-Мари Ампера на сайте РАН
12. ↑ ^{1 2} Ф. Араго. Детство Ампера. Его необыкновенная память и преждевременно раскрывшиеся дарования. Его любимые чтения и сочинение о первоначальном языке // Биографии знаменитых астрономов, физиков и геометров. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2000. — Т. 2. — С. 192. — 464 с. — ISBN 5-93972-018-8.
13. ↑ ^{1 2} Amelia Fedo. 1793: Jean-Jacques Ampère, father of a savant, for Joseph Chalier (англ.), ExecutedToday.com (22 ноября 2013). Дата обращения 8 февраля 2018.
14. ↑ Ennemond Fayard. Histoire des tribunaux révolutionnaires de Lyon et de Feurs. — H. Georg, 1888. — 390 с.
15. ↑ ^{1 2} Забаринский П. П., Полак Л. С. Андре Мари Ампер // Наука и Жизнь : журнал. — 1936. — Июнь (№ 6). — С. 49—52.
16. ↑ François Arago, Pierre Flourens. Œuvres complètes de François Arago. — Gide et J. Baudry, 1854. — С. 11. — 720 с.

Сочинения

• Ампер А. М. Электродинамика. М.: Изд-во АН СССР, 1954.

О нём

• Белькинд Л. Д. Андре-Мари Ампер. М.: Наука, 1968.
• Храмов Ю. А. Ампер Андре Мари // Физики: Биографический справочник / Под ред. А. И. Ахиезера. — Изд. 2-е, испр. и дополн. — М.: Наука, 1983. — С. 14—15. — 400 с. — 200 000 экз. (в пер.)

Закон электромагнитной индукции Фарадея — Википедия

Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.

[1] Закон гласит:

или другими словами:

Генерируемая ЭДС пропорциональна скорости изменения магнитного потока.

При этом индукционный ток направлен таким образом, что его действие противоположно действию причины, вызвавшей этот ток (правило Ленца).^[2]

Электромагнитная индукция была обнаружена независимо друг от друга Майклом Фарадеем и Джозефом Генри в 1831 году, однако Фарадей первым опубликовал результаты своих экспериментов^[3][4].

В первой экспериментальной демонстрации электромагнитной индукции (август 1831) Фарадей обмотал двумя проводами противоположные стороны железного тора (конструкция похожа на современный трансформатор). Основываясь на своей оценке недавно обнаруженного свойства электромагнита, он ожидал, что при включении тока в одном проводе особого рода волна пройдёт сквозь тор и вызовет некоторое электрическое влияние на его противоположной стороне. Он подключил один провод к гальванометру и смотрел на него, когда другой провод подключал к батарее. В самом деле, он увидел кратковременный всплеск тока (который он назвал «волной электричества»), когда подключал провод к батарее, и другой такой же всплеск, когда отключал его.

[5] В течение двух месяцев Фарадей нашёл несколько других проявлений электромагнитной индукции. Например, он увидел всплески тока, когда быстро вставлял магнит в катушку и вытаскивал его обратно, он генерировал постоянный ток во вращающемся вблизи магнита медном диске со скользящим электрическим проводом («диск Фарадея»)^[6].

Фарадей объяснил электромагнитную индукцию с использованием концепции так называемых силовых линий. Однако, большинство учёных того времени отклонили его теоретические идеи, в основном потому, что они не были сформулированы математически.

[7] Исключение составил Максвелл, который использовал идеи Фарадея в качестве основы для своей количественной электромагнитной теории.^[7][8][9] В работах Максвелла аспект изменения во времени электромагнитной индукции выражен в виде дифференциальных уравнений. Оливер Хевисайд назвал это законом Фарадея, хотя он несколько отличается по форме от первоначального варианта закона Фарадея и не учитывает индуцирование ЭДС при движении. Версия Хевисайда является формой признанной сегодня группы уравнений, известных как уравнения Максвелла.

Эмилий Христианович Ленц сформулировал в 1834 году закон (правило Ленца), который описывает «поток через цепь» и даёт направление индуцированной ЭДС и тока в результате электромагнитной индукции.

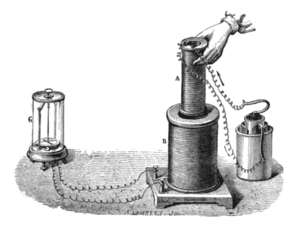Эксперимент Фарадея, показывающий индукцию между витками провода: жидкостная батарея (справа) даёт ток, который протекает через небольшую катушку (A), создавая магнитное поле. Когда катушки неподвижны, ток не индуцируется. Но когда маленькая катушка вставляется или извлекается из большой катушки (B), магнитный поток через катушку изменяется, вызывая ток, который регистрируется гальванометром (G).^[10]

Закон Фарадея как два различных явления[править | править код]

Некоторые физики отмечают, что закон Фарадея в одном уравнении описывает два разных явления: двигательную ЭДС, генерируемую действием магнитной силы на движущийся провод, и трансформаторную ЭДС, генерируемую действием электрической силы вследствие изменения магнитного поля. Джеймс Клерк Максвелл обратил внимание на этот факт в своей работе О физических силовых линиях в 1861 году. Во второй половине части II этого труда Максвелл даёт отдельное физическое объяснение для каждого из этих двух явлений. Ссылка на эти два аспекта электромагнитной индукции имеется в некоторых современных учебниках.^[11] Как пишет Ричард Фейнман:^[12]

Таким образом, «правило потока» о том, что ЭДС в цепи равна скорости изменения магнитного потока через контур, применяется независимо от причины изменения потока: то ли потому что поле изменяется, то ли потому что цепь движется (или и то, и другое)…. В нашем объяснении правила мы использовали два совершенно различных закона для двух случаев  –    v×B{\displaystyle {\stackrel {\mathbf {v\times B} }{}}}   для «движущейся цепи» и   ∇ x E = −∂ tB{\displaystyle {\stackrel {\mathbf {\nabla \ x\ E\ =\ -\partial _{\ t}B} }{}}}   для «меняющегося поля».

Мы не знаем никакого аналогичного положения в физике, когда такие простые и точные общие принципы требовали бы для своего реального понимания анализа с точки зрения двух различных явлений.

— Ричард Фейнман,   Фейнмановские лекции по физике

Отражение этой очевидной дихотомии было одним из основных путей, которые привели Эйнштейна к разработке специальной теории относительности:

Известно, что электродинамика Максвелла — как её обычно понимают в настоящее время — при применении к движущимся телам приводит к асимметрии, которая, как кажется, не присуща этому явлению. Возьмем, к примеру, электродинамическое взаимодействие магнита и проводника. Наблюдаемое явление зависит только от относительного движения проводника и магнита, тогда как обычное мнение рисует резкое различие между этими двумя случаями, в которых либо одно, либо другое тело находится в движении. Ибо, если магнит находится в движении, а проводник покоится, в окрестности магнита возникает электрическое поле с определенной плотностью энергии, создавая ток там, где расположен проводник. Но если магнит покоится, а проводник движется, то в окрестности магнита никакое электрическое поле не возникает. В проводнике, однако, мы находим электродвижущую силу, для которой не существует соответствующей энергии самой по себе, но которая вызывает — предполагая равенство относительного движения в двух обсуждаемых случаях — электрические токи по тому же направлению и той же интенсивности, как в первом случае.

Примеры подобного рода вместе с неудачной попыткой обнаружить какое-либо движение Земли относительно «светоносной среды» предполагают, что явления электродинамики, а также механики не обладают свойствами, соответствующими идее абсолютного покоя.

— Альберт Эйнштейн, К электродинамике движущихся тел^[13]

Поток через поверхность и ЭДС в контуре[править | править код]

Определение поверхностного интеграла предполагает, что поверхность Σ поделена на мелкие элементы. Каждый элемент связан с вектором dA, величина которого равна площади элемента, а направление — по нормали к элементу во внешнюю сторону. Векторное поле F(r, t) определено во всём пространстве, а поверхность Σ ограничена кривой ∂Σ, движущейся со скоростью v. По этой поверхности производится интегрирование поля.

Закон электромагнитной индукции Фарадея использует понятие магнитного потока Φ_B через замкнутую поверхность Σ, который определён через поверхностный интеграл:

 :Φ=∬SBn⋅dS,{\displaystyle \Phi =\iint \limits _{S}\mathbf {B_{n}} \cdot d\mathbf {S} ,}

где dS — площадь элемента поверхности Σ(t), B — магнитное поле, а B·dS — скалярное произведение B и dS. Предполагается, что поверхность имеет «устье», очерченное замкнутой кривой, обозначенной ∂Σ(t). Закон индукции Фарадея утверждает, что когда поток изменяется, то при перемещении единичного положительного пробного заряда по замкнутой кривой ∂Σ возникает ЭДС E{\displaystyle {\mathcal {E}}}, величина которой определяется по формуле:

|E|=|dΦdt| ,{\displaystyle |{\mathcal {E}}|=\left|{{d\Phi } \over dt}\right|\ ,}

где |E|{\displaystyle |{\mathcal {E}}|} — величина электродвижущей силы (ЭДС) в вольтах, а Φ_B — магнитный поток в веберах. Направление электродвижущей силы определяется законом Ленца.

Для плотно намотанной катушки индуктивности, содержащей N витков, каждый с одинаковым магнитным потоком Φ_B, закон индукции Фарадея утверждает, что:

|E|=N|dΦBdt|,{\displaystyle |{\mathcal {E}}|=N\left|{{d\Phi _{B}} \over dt}\right|,}

где N — число витков провода, Φ_B — магнитный поток в веберах на один виток.

При выборе пути ∂Σ(t) для нахождения ЭДС заметим, что путь должен удовлетворять двум основным требованиям: (i) путь должен быть замкнутым, и (ii) путь должен охватывать относительное движение частей контура (источник происхождения t-зависимости в ∂Σ(t)). К требованиям не относится то, что путь должен совпадать с линией тока, но, конечно, ЭДС, которая находится по закону потока, будет считаться по выбранному пути. Если путь не совпадает с линией тока, то подсчитанная ЭДС, возможно, будет не та ЭДС, которая вызывает ток.

Пример 1: пространственно меняющееся магнитное поле[править | править код]

Рис. 3. Замкнутый прямоугольный провод движется вдоль оси x со скоростью v в магнитном поле, которое изменяется вдоль x.

Рассмотрим случай на рисунке 3, на котором прямоугольная замкнутая проволочная петля, расположенная в плоскости xy, перемещается в направлении оси x со скоростью v. Центр петли x_C удовлетворяет условию v = dx_C / dt. Петля имеет длину ℓ в направлении оси y и ширину w в направлении оси x. Зависящее от времени пространственно меняющееся магнитное поле B(x) показано в направлении z. Магнитное поле на левой стороне равно B(x_C − w / 2), а на правой стороне B(x_C + w / 2). Электродвижущую силу можно найти либо с помощью закона Лоренца, либо, что эквивалентно, используя вышеизложенный закон индукции Фарадея.

Закон Лоренца[править | править код]

Заряд q в проводнике на левой стороне петли испытывает силу Лоренца q v × B k = −q v B(x_C − w / 2) j   (j, k — единичные векторы в направлениях y и z; см. векторное произведение векторов), что вызывает ЭДС (работу на единицу заряда) v ℓ B(x_C − w / 2) по всей длине левой стороны петли. На правой стороне петля аналогичное рассуждение показывает, что ЭДС равна v ℓ B(x_C + w / 2). Две противоположные друг другу ЭДС толкают положительный заряд по направлению к нижней части петли. В случае, когда поле B возрастает вдоль х, сила на правой стороне будет больше, а ток будет течь по часовой стрелке. Используя правило правой руки, мы получаем, что поле B, создаваемое током, противоположно приложенному полю.^[14] ЭДС, вызывающая ток, должна увеличиваться по направлению против часовой стрелки (в отличие от тока). Складывая ЭДС в направлении против часовой стрелки вдоль петли мы находим:

E=vℓ[B(xC+w/2)−B(xC−w/2)] .{\displaystyle {\mathcal {E}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ .}

Закон Фарадея[править | править код]

В любой точке петли магнитный поток через неё равен:

ΦB=±∫0ℓdy∫xC−w/2xC+w/2B(x)dx{\displaystyle \Phi _{B}=\pm \int _{0}^{\ell }dy\int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx}

=±ℓ∫xC−w/2xC+w/2B(x)dx .{\displaystyle \qquad =\pm \ell \int _{x_{C}-w/2}^{x_{C}+w/2}B(x)dx\ .}

Выбор знака определяется по принципу, имеет ли нормаль к поверхности в данной точке то же направление, что и B, или противоположное. Если нормаль к поверхности имеет то же направление, что и поле B наведённого тока, этот знак отрицательный. Производная по времени от потока (найденная с помощью методов дифференцирования сложной функции или по правилу Лейбница дифференцирования интеграла) равна:

dΦBdt=(−)ddxC[∫0ℓdy ∫xC−w/2xC+w/2dxB(x)]dxCdt {\displaystyle {\frac {d\Phi _{B}}{dt}}=(-){\frac {d}{dx_{C}}}\left[\int _{0}^{\ell }dy\ \int _{x_{C}-w/2}^{x_{C}+w/2}dxB(x)\right]{\frac {dx_{C}}{dt}}\ }

=(−)vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle \qquad =(-)v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

(где v = dx_C / dt является скоростью движения петли в направлении оси х), что приводит к:

E=−dΦBdt=vℓ[B(xC+w/2)−B(xC−w/2)] ,{\displaystyle {\mathcal {E}}=-{\frac {d\Phi _{B}}{dt}}=v\ell [B(x_{C}+w/2)-B(x_{C}-w/2)]\ ,}

как и в предыдущем случае.

Эквивалентность этих двух подходов является общеизвестной, и в зависимости от решаемой задачи более практичным может оказаться либо тот, либо другой метод.

Пример 2: проводник, движущийся в постоянном магнитном поле[править | править код]

Рис. 4. Два проводника замкнутые на проводящие обода образуют «рамку» вращающуюся с угловой скоростью ω в радиальном, направленном наружу магнитном поле B фиксированной величины. Ток подается щётками, касающимися верхнего и нижнего дисков с проводящими ободами.

На рис. 4 показан шпиндель, образованный двумя дисками с проводящими ободами, и проводники, расположенные вертикально между этими ободами. ток скользящими контактами подается на проводящие обода. Эта конструкция вращается в магнитном поле, которое направлено радиально наружу и имеет одно и то же значение в любом направлении. то есть мгновенная скорость проводников, ток в них и магнитная индукция, образуют правую тройку, что заставляет проводники вращаться.

Сила Лоренца[править | править код]

В этом случае на проводники действует Сила Ампера, а на единичный заряд в проводнике Сила Лоренца — поток вектора магнитной индукции B , ток в проводниках, соединяющих проводящие обода, направлен нормально к вектору магнитной индукции, тогда сила, действующая на заряд в проводнике, будет равна

F=qBv,{\displaystyle F=qBv\,,}

где v = скорости движущегося заряда^[15]

Следовательно, сила действующая на проводники

F=IBℓ,{\displaystyle {\mathcal {F}}=IB\ell ,}

где l — длина проводников

Здесь мы использовали B как некую данность, на самом деле она зависит от геометрических размеров ободов конструкции, и это значение можно вычислить, используя Закон Био — Савара — Лапласа . Данный эффект используется и в другом устройстве, называемом Рельсотрон

Закон Фарадея[править | править код]

Интуитивно привлекательный, но ошибочный подход к использованию правила потока выражает поток через цепь по формуле Φ_B = B w ℓ, где w — ширина движущейся петли.

Ошибочность такого подхода в том, что это не рамка в обычном понимании этого слова. Прямоугольник на рисунке образован отдельными проводниками, замкнутыми на обод. Как видно на рисунке, ток по обоим проводникам течет в одном направлении, то есть здесь отсутствует понятие «замкнутый контур»

Наиболее простое и понятное объяснение этому эффекту дает понятие сила Ампера. То есть вертикальный проводник может быть вообще один, чтобы не вводить в заблуждение. Или же проводник конечной толщины может быть расположен на оси, соединяющей обода. Диаметр проводника должен быть конечным и отличаться от нуля, чтобы момент силы Ампера был ненулевой.

Рис. 6. Иллюстрация теоремы Кельвина-Стокса с помощью поверхности Σ, её границы ∂Σ и ориентации n , установленной правилом правой руки.

Переменное магнитное поле создаёт электрическое поле, описываемое уравнением Фарадея — Максвелла:

∇×E=−∂B∂t,{\displaystyle \nabla \times \mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}},}

где:

∇×{\displaystyle \nabla \times } обозначает ротор

E — электрическое поле

B — плотность магнитного потока.

Это уравнение присутствует в современной системе уравнений Максвелла, часто его называют законом Фарадея. Однако, поскольку оно содержит только частные производные по времени, его применение ограничено ситуациями, когда заряд покоится в переменном по времени магнитном поле. Оно не учитывает^{[уточнить]} электромагнитную индукцию в случаях, когда заряженная частица движется в магнитном поле.

В другом виде закон Фарадея может быть записан через интегральную форму теоремы Кельвина-Стокса:^[16]

∮∂Σ⁡E⋅dℓ=−∫Σ∂∂tB⋅dA.{\displaystyle \oint _{\partial \Sigma }\mathbf {E} \cdot d{\boldsymbol {\ell }}=-\int _{\Sigma }{\partial \over {\partial t}}\mathbf {B} \cdot d\mathbf {A} .}

Для выполнения интегрирования требуется независимая от времени поверхность Σ (рассматриваемая в данном контексте как часть интерпретации частных производных). Как показано на рис. 6:

Σ — поверхность, ограниченная замкнутым контуром ∂Σ, причём, как Σ, так и ∂Σ являются фиксированными, не зависящими от времени,

E — электрическое поле,

dℓ — бесконечно малый элемент контура ∂Σ,

B — магнитное поле,

dA — бесконечно малый элемент вектора поверхности Σ.

Элементы dℓ и dA имеют неопределённые знаки. Чтобы установить правильные знаки, используется правило правой руки, как описано в статье о теореме Кельвина-Стокса. Для плоской поверхности Σ положительное направление элемента пути dℓ кривой ∂Σ определяется правилом правой руки, по которому на это направление указывают четыре пальца правой руки, когда большой палец указывает в направлении нормали n к поверхности Σ.

Интеграл по ∂Σ называется интеграл по пути или криволинейным интегралом. Поверхностный интеграл в правой части уравнения Фарадея-Максвелла является явным выражением для магнитного потока Φ_B через Σ. Обратите внимание, что ненулевой интеграл по пути для E отличается от поведения электрического поля, создаваемого зарядами. Генерируемое зарядом E-поле может быть выражено как градиент скалярного поля, которое является решением уравнения Пуассона и имеет нулевой интеграл по пути.

Интегральное уравнение справедливо для любого пути ∂Σ в пространстве и любой поверхности Σ, для которой этот путь является границей.

Рис. 7. Площадь заметания элемента вектора dℓ кривой ∂Σ за время dt при движении со скоростью v.

Используя^[17]

ddt∫AB dA=∫A(∂B∂t+v div B+rot(B×v))dA{\displaystyle {\frac {\text{d}}{{\text{d}}t}}\int \limits _{A}{\mathbf {B} }{\text{ d}}\mathbf {A} =\int \limits _{A}{\left({\frac {\partial \mathbf {B} }{\partial t}}+\mathbf {v} \ {\text{div}}\ \mathbf {B} +{\text{rot}}\;(\mathbf {B} \times \mathbf {v} )\right)\;{\text{d}}}\mathbf {A} }

и принимая во внимание divB=0{\displaystyle {\text{div}}\mathbf {B} =0} (Ряд Гаусса), B×v=−v×B{\displaystyle \mathbf {B} \times \mathbf {v} =-\mathbf {v} \times \mathbf {B} } (Векторное произведение) и ∫ArotXdA=∮∂A⁡Xdℓ{\displaystyle \int _{A}{\text{rot}}\;\mathbf {X} \;\mathrm {d} \mathbf {A} =\oint _{\partial A}\mathbf {X} \;{\text{d}}{\boldsymbol {\ell }}} (теорема Кельвина — Стокса), мы находим, что полная производная магнитного потока может быть выражена

∫Σ∂B∂tdA=ddt∫ΣB dA+∮∂Σ⁡v×Bdℓ.{\displaystyle \int \limits _{\Sigma }{\frac {\partial \mathbf {B} }{\partial t}}{\textrm {d}}\mathbf {A} ={\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{ d}}\mathbf {A} +\oint _{\partial \Sigma }\mathbf {v} \times \mathbf {B} \,{\text{d}}{\boldsymbol {\ell }}.}

Добавляя член ∮⁡v×Bdℓ{\displaystyle \oint \mathbf {v} \times \mathbf {B} \mathrm {d} \mathbf {\ell } } к обеим частям уравнения Фарадея-Максвелла и вводя вышеприведённое уравнение, мы получаем:

∮∂Σ⁡(E+v×B)dℓ=−∫Σ∂∂tBdA⏟induced emf+∮∂Σ⁡v×Bdℓ⏟motional emf=−ddt∫ΣB dA,{\displaystyle \oint \limits _{\partial \Sigma }{(\mathbf {E} +\mathbf {v} \times \mathbf {B} )}{\text{d}}\ell =\underbrace {-\int \limits _{\Sigma }{\frac {\partial }{\partial t}}\mathbf {B} {\text{d}}\mathbf {A} } _{{\text{induced}}\ {\text{emf}}}+\underbrace {\oint \limits _{\partial \Sigma }{\mathbf {v} }\times \mathbf {B} {\text{d}}\ell } _{{\text{motional}}\ {\text{emf}}}=-{\frac {\text{d}}{{\text{d}}t}}\int \limits _{\Sigma }{\mathbf {B} }{\text{ d}}\mathbf {A} ,}

что и является законом Фарадея. Таким образом, закон Фарадея и уравнения Фарадея-Максвелла физически эквивалентны.

Рис. 7 показывает интерпретацию вклада магнитной силы в ЭДС в левой части уравнения. Площадь, заметаемая сегментом dℓ кривой ∂Σ за время dt при движении со скоростью v, равна:

dA=−dℓ×vdt ,{\displaystyle d\mathbf {A} =-d{\boldsymbol {\ell \times v}}dt\ ,}

так что изменение магнитного потока ΔΦ_B через часть поверхности, ограниченной ∂Σ за время dt, равно:

dΔΦBdt

Андре-Мари Ампер: биография, вклад в науку

Многие наверняка часто слышали слово «ампер», моментально относя это понятие к физике. Ампер является единицей измерения силы электрического тока. Но задумывались ли вы, почему и в чью честь была названа единица силы тока? Сегодня мы изложим информацию о биографии Андре Мари Ампера, выдающегося физика и гениального ученого, а также о его вкладе в науку, личной жизни, семье и карьере.

Основные сведения из жизни ученого

В краткой биографии Андре Мари Ампера сказано, что он был французским физиком и одним из основателей электродинамики. Он также был признанным математиком, интересующимся и другими областями науки, такими как история, философия и естественные науки. Рожденный в разгар французской эпохи Просвещения, он вырос в интеллектуально стимулирующей атмосфере. Франция его молодости была отмечена широко распространенными событиями в области науки и искусства, и Французская революция, начавшаяся тогда, когда он был юношей, также оказала значительное влияние в формировании его будущей жизни.

Сын процветающего предпринимателя, он был воодушевлен для образования, поиска себя и получения знаний с ранней юности, увлекался математикой и пограничными с ней науками. Будучи гениальным ученым, обладающим обширными и ценными знаниями в различных областях, также преподавал философию и астрономию в Парижском университете.

Интересы

Наряду с академической карьерой, Ампер также занимался научными экспериментами в различных областях и был особенно заинтригован работами Ханса Христиана Эрстеда, который обнаружил связь между электричеством и магнетизмом. Биография Ампера отражает то, как сильно он повлиял на науку. Став последователем Эрстеда, посредством усердной лабораторной деятельности, Ампер сделал еще несколько открытий в этой области, которые внесли огромный вклад в становление электромагнетизма и электродинамики как наук. Ампер считается одним из основателей этой отрасли теоретической физики. Биография Ампера кратко будет изложена в этой статье.

Семья Андре Мари

Ампер родился 20 января 1775 года в семье Жан-Жака Ампера и Жанны Антуанетты Десутье-Сарси Ампер. Жан-Жак был успешным предпринимателем. У Андре Ампера было две сестры.

Отец ученого был ценителем философии Жана-Жака Руссо, который считал, что молодые мальчики должны избегать формального обучения и вместо этого им следует «обучаться у окружающей среды». Таким образом, он не стал отправлять своего сына в школу и вместо этого позволил ему просвещать себя с помощью книг в своей неплохо укомплектованной библиотеке.

В детстве Ампер был очень любознателен, что явилось хорошей почвой для развития его дальнейшей ненасытной жажды знаний. Под руководством своего отца он читал книги по математике, истории, философии и естественным наукам, а также поэзию. Наряду с его интересом к наукам он также был заинтересован католической верой, поскольку его мать была очень набожной женщиной.

Он был особенно увлечен математикой и начал серьезно изучать этот предмет, когда ему было 13 лет. Его отец всячески поощрял его интеллектуальные занятия, находил специализированные книги по этому предмету для сына и организовал для него возможность получать уроки математики от аббата Дабурона. В это время Андре начал изучать физику.

Французская революция началась в 1789 году, когда Андре было 14. Его отец был призван на государственную службу недавно пришедшим к власти правительством и был отправлен в маленький городок недалеко от Лиона.

Семья Ампера потерпела трагедию, когда одна из его сестер умерла в 1792 году. Еще одно несчастье, касающееся его семьи, произошло, когда фракция якобинцев захватила контроль над революционным правительством в 1792 году и гильотинировала отца Андре в ноябре 1793 года. Переживая эти ужасные потери, он оставил учебу на год. Карьера Ампер начал работать частным преподавателем математики в Лионе в 1797 году. Он оказался отличным учителем, и ученики начали быстро стекаться к нему, с целью перенять знания и стать последователем талантливого преподавателя. Его успех в качестве учителя привлек к Амперу внимание интеллектуалов Лионы — они были поражены багажом знаний молодого человека.

Карьера

В 1799 году он нашел постоянную работу в качестве учителя математики. В течение нескольких лет был назначен профессором физики и химии в Школе Сентрале в Бург-ан-Брессе в 1802 году. За это время Андре также исследовал математику и подготовил к публикации труд под названием «Исследования математической теории игр», 1802.

Ампер стал преподавателем в новой, недавно учрежденной Политехнической школе в 1804 году. Помимо многочисленных талантов в разных сферах, у него был еще и преподавательский дар. В связи с этим Андре стал профессором математики в школе в 1809 году, несмотря на отсутствие базового образования в широком смысле этого понятия (ведь он обучался индивидуально). Ампер был избран во Французскую академию наук в 1814 году. Биография Ампера демонстрирует нам, что упорный труд всегда вознаграждается.

Он также занимался научными исследованиями наряду с его академической карьерой и преподавал такие дисциплины, как философия и астрономия, в Парижском университете в 1819-20 годах.

Ампер был сильно впечатлен открытиями Эрстеда касательно электромагнитизма, поэтому перенял исследовательскую инициативу и стал работать над дальнейшими открытиями. После тщательных экспериментов Ампер показал, что два параллельные провода, несущие электрические токи, притягивают или отталкивают друг друга, в зависимости от того, протекают ли токи в одном и том же или противоположном направлении.

Одаренный от природы, имеющий массу знаний и навыков в области точных наук, Ампер применял математику в обобщении физических законов из экспериментальных результатов. После долгих лет интенсивных исследований и экспериментов Ампер опубликовал «Размышление о математической теории электродинамических явлений, уникально выведенных из опыта в 1827 году. Новая наука, «электродинамика» была названа таковой и обобщена в этой работе, которая стала известной как ее основополагающий трактат.

Это краткая биография Андре Ампера.

Основные работы

Ученый вывел закон (названный в его честь), который гласит, что взаимное действие двух длин токопроводящей проволоки пропорционально их длинам и интенсивности их токов.

Ампер изобрел астатическую иглу — почти первостепенную по важности составляющую современного астатического гальванометра.

Награды и достижения

В 1827 году Ампер стал членом Королевского общества и членом Королевской Академии наук в Швеции в 1828 году. Но это лишь капля в море. Великий ученый внес неоценимый вклад в развитие науки.

Личная жизнь и наследие

Андре Мари Ампер женился на Кэтрин-Антуанетт Каррон в 1799 году. Сын родился у них год спустя, назвали его в честь деда ─ Жан-Жаком.

Однако в молодой семье случилась трагедия — жена ученого заболела раком и умерла в 1803 году.

Андре сочетался браком с Жанне-Франсуазой Пото в 1806 году. Этот союз казался многим неудачным с самого начала. И действительно, пара рассталась вскоре после рождения дочери.

Ампер умер в городе Марселе 10 июня 1836 года от пневмонии. Биография Ампера довольно трагична, если рассматривать сферы жизни, не связанные с его профессиональной деятельностью.

В краткой биографии Андре Ампера сказано, что его имя одно из 72 имен, записанных на Эйфелевой башне.

Великие достижения

Жизнь величайшего ученого тесным образом связана с научной деятельностью. Экспромтом рассмотрим 5 важнейших событий в биографии Андре Мари Ампера, касающиеся его научной деятельности.

1. Открытие, касающееся фтора. В 1810 году Андре-Мари Ампер предположил, что фтористоводородная кислота представляет собой соединение водорода и неизвестного элемента, свойства которого, по его словам, были похожи на хлор. Он придумал термин «фтор» для этого элемента, предположив, что F может быть изолирован электролизом. Спустя 76 лет французский химик Анри Моисан окончательно изолировал фтор (сделал это путем электролиза по предложению Ампера.
2. Предложил свою версию идентификации элементов. В 1816 году Ампер предложил указать химические элементы в соответствии с их свойствами. В то время было известно только 48 элементов, и Андре попытался поместить их в 15 групп. Он успешно группировал щелочные металлы, щелочноземельные металлы и галогены. Спустя 53 года после попытки ученого организовать элементы, российский химик Дмитрий Менделеев опубликовал свою знаменитую периодическую таблицу.
3. Придумал «правило правой руки». Андре-Мари Ампер разработал правило, известное как правило правой руки, чтобы определить направление отклонения стрелки компаса относительно направления, в котором электрический ток протекал вдоль провода. В этом правиле, если предполагается, что правая рука наблюдателя захватывает провод, через который протекает ток, большим пальцем, направленным вдоль провода в направлении тока. Затем пальцы, скручивающиеся вокруг провода, указывают направление, в котором стрелка компаса будет отклоняться. Правило Ампера все еще используется учениками для расчета направления магнитных силовых линий.
4. Эрстед экспериментальным путем указал на связь между электричеством и магнетизмом в 1820 году. Спустя незначительное время Андре-Мари Ампер обнаружил, что два параллельных провода с электрическим током отталкивают или притягивают друг друга. Это зависит от того, совпадает или разнится ли их направление, соответственно. Таким образом, Ампер впервые показал, что магнитное притяжение и отталкивание могут быть получены без использования магнитов.
5. Андре-Мари Ампер применил математику к своим экспериментам с электромагнетизмом, чтобы сформулировать физические законы. Наиболее важный из них — это силовой закон Ампера (сформулирован в 1823 году) — показывает, что возникновение притяжения или отталкивания между двумя проводами, несущими токи, напрямую зависит от длин и интенсивности проходящего через них тока. Физическое происхождение этой силы состоит в том, что каждый провод генерирует магнитное поле.

Кибернетика

Существует множество определений кибернетики. Норберт Винер, математик, инженер и социальный философ, придумал слово «кибернетика» происходящее из греческого языка, означает «рулевой». Он определил его как науку о связи и управлении живыми организмами и машинами. Ампер же, еще до Винера, нарек кибернетику наукой правительства. Важным элементом этой науки Андре назвал отрасль, которая должна изучать законы, их происхождение и воздействие на социум.

Мы рассмотрели биографию Мари Ампера.

Ампер — Википедия

Ампе́р (русское обозначение: А; международное: A) — единица измерения силы электрического тока в Международной системе единиц (СИ), одна из семи основных единиц СИ. В амперах измеряется также магнитодвижущая сила и разность магнитных потенциалов (устаревшее наименование — ампер-виток)^[1]. Кроме того, ампер является единицей силы тока и относится к числу основных единиц в системе единиц МКСА.

16 ноября 2018 года на XXVI Генеральной конференции мер и весов было принято новое определение ампера, основанное на использовании численного значения элементарного электрического заряда. Формулировка, вступившая в силу 20 мая 2019 года, гласит^[2]:

Ампер, символ А, есть единица электрического тока в СИ. Она определена путём фиксации численного значения элементарного заряда равным 1,602 176 634⋅10⁻¹⁹, когда он выражен единицей Кл, которая равна А·с, где секунда определена через ΔνCs{\displaystyle \Delta \nu _{\mathrm {Cs} }}^[3].

Происхождение[править | править код]

Единица измерения, принятая на 1-м Международном конгрессе электриков^[4] (1881 г., Париж), названа в честь французского физика Андре Ампера. Она была первоначально определена как одна десятая единицы тока системы СГСМ (эта единица, известная в настоящее время как абампер или био, определяла ток, создающий силу в 2 дины на сантиметр длины между двумя тонкими проводниками на расстоянии в 1 см).

Международный ампер[править | править код]

В 1893 году было принято определение единицы измерения силы тока как тока, необходимого для электрохимического осаждения 1,118 миллиграммов серебра в секунду из раствора нитрата серебра. Предполагалось, что величина единицы при этом не изменится, однако оказалось, что она изменилась на 0,015%. Эта единица стала известна как международный ампер.

Определение 1948 года[править | править код]

Определение ампера, предложенное Международным комитетом мер и весов в 1946 году и принятое IX Генеральной конференцией по мерам и весам (ГКМВ) в 1948 году, гласит^[5][6]:

Ампер — сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2⋅10⁻⁷ньютона.

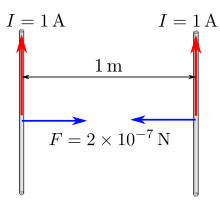Иллюстрация к определению ампера 1948 года.

Таким образом, фактически было возвращено изначальное определение.

Из определения ампера следует, что магнитная постоянная μ0{\displaystyle \mu _{0}} равна 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Гн/ м или, что то же самое, 4π×10−7{\displaystyle 4\pi \times 10^{-7}} Н/А² точно. Это утверждение становится понятным, если учесть, что сила взаимодействия двух расположенных на расстоянии d{\displaystyle d} друг от друга бесконечных параллельных проводников, по которым текут токи I1{\displaystyle I_{1}} и I2{\displaystyle I_{2}}, приходящаяся на единицу длины, выражается соотношением:

F=μ04π2I1I2d.{\displaystyle F={\frac {\mu _{0}}{4\pi }}{\frac {2I_{1}I_{2}}{d}}.}

Магнитодвижущая сила 1 ампер (ампер-виток) — это такая магнитодвижущая сила, которую создаёт замкнутый контур, по которому протекает ток, равный 1 амперу.

Определение 2018 года[править | править код]

В 2018 году было принято и на следующий год вступило в силу нынешнее определение ампера. Величина ампера не изменилась при смене определения. Однако изменения определения привело к тому, что указанное выше выражение для магнитной постоянной перестало быть точным, а стало выполняться лишь численно (но с огромной точностью).

В соответствии с полным официальным описанием СИ, содержащемся в действующей редакции Брошюры СИ (фр. Brochure SI, англ. The SI Brochure), опубликованной Международным бюро мер и весов (МБМВ), десятичные кратные и дольные единицы ампера образуются с помощью стандартных приставок СИ^[5]. «Положение о единицах величин, допускаемых к применению в Российской Федерации», принятое Правительством Российской Федерации, предусматривает использование в России тех же приставок^[7].

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 А	декаампер	даА	daA	10−1 А	дециампер	дА	dA
102 А	гектоампер	гА	hA	10−2 А	сантиампер	сА	cA
103 А	килоампер	кА	kA	10−3 А	миллиампер	мА	mA
106 А	мегаампер	МА	MA	10−6 А	микроампер	мкА	µA
109 А	гигаампер	ГА	GA	10−9 А	наноампер	нА	nA
1012 А	тераампер	ТА	TA	10−12 А	пикоампер	пА	pA
1015 А	петаампер	ПА	PA	10−15 А	фемтоампер	фА	fA
1018 А	эксаампер	ЭА	EA	10−18 А	аттоампер	аА	aA
1021 А	зеттаампер	ЗА	ZA	10−21 А	зептоампер	зА	zA
1024 А	иоттаампер	ИА	YA	10−24 А	иоктоампер	иА	yA
применять не рекомендуется

Если сила тока в проводнике равна 1 амперу, то за одну секунду через поперечное сечение проходит заряд, равный 1 кулону^[8].

Если конденсатор ёмкостью в 1 фарад заряжать током 1 ампер, то напряжение на обкладках будет возрастать на 1 вольт каждую секунду.

1. ↑ Магнитодвижущая сила (неопр.). Большая советская энциклопедия. Архивировано 21 августа 2011 года.
2. ↑ Le Système international d’unités (SI) / The International System of Units (SI). — BIPM, 2019. — P. 20, 132. — ISBN 978-92-822-2272-0.
3. ↑ ΔνCs{\displaystyle \Delta \nu _{\mathrm {Cs} }} — частота излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.
4. ↑ History of the ampere, Sizes, <http://www.sizes.com/units/ampHist.htm> 
5. ↑ ^{1 2} The SI brochure Описание СИ на сайте Международного бюро мер и весов.
6. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации. Основные единицы Международной системы единиц (СИ) (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018. Архивировано 18 сентября 2017 года.
7. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации (неопр.) (недоступная ссылка). Дата обращения 28 декабря 2014. Архивировано 5 марта 2016 года.
8. ↑ Bodanis, David (2005), Electric Universe, New York: Three Rivers Press, ISBN 978-0-307-33598-2 

• Краткий словарь физических терминов / Сост. А. И. Болсун, рец. М. А. Ельяшевич. — Мн.: Вышэйшая школа, 1979. — С. 23—24. — 416 с. — 30 000 экз.

Закон Ампера и его применение

Урок 3. Закон Ампера и его применение

Цель: сформулировать закон Ампера и показать его практическую применимость.

Ход урока

I. Организационный момент

II. Актуализация знаний

— Опишите опыт Эрстеда.

— Каким является магнитное поле?

— Что можно сказать об основных линиях магнитного поля?

— Что такое соленоид?

— Сформулируйте правила для определения направлений силовых линий магнитного поля?

— Что можно сказать о магнитных монополях?

III. Выполнение лабораторной работы

Лабораторная работа по теме «Изучение свойств постоянных магнитов»

Цели: получить картины силовых линий магнитного поля вокруг постоянных магнитов.

Оборудование: магнит полюсовой (2 шт.), магнит подковообразный, магнитная стрелка, скрепки, медный провод, ластик, железные опилки.

Ход работы

1. Найдите северный полюс стрелки, установите полюса полюсового магнита и подковообразного. Обозначьте северный и южный полюса магнитов.

2. Положите лист картона на полюсовой магнит и равномерно посыпьте его железными опилками. Не двигая магнит и картонку, осторожно постучите по картонке, чтобы опилки могли перемещаться. Обратите внимание, как выстроились опилки на листе. Сделайте рисунок в тетради.

3. Получите картину магнитного поля двух полюсовых магнитов, расположенных параллельно друг другу, и подковообразного магнита.

4. Что можно сказать о линиях магнитной индукции?

IV. Изучение нового материала

1. Проведение эксперимента.

По двум параллельным проводникам пропускаем электрический ток. В том случае, если ток направлен в одну сторону, наблюдается притяжение проводников, если в разные стороны, то отталкивание.

Притяжение или отталкивание электрически нейтральных проводников при пропускании через них электрического тока называют магнитным взаимодействием токов.

На проводник с током в магнитном поле действует сила, которая получила название силы Ампера. Направление этой силы можно найти при помощи правила левой руки. Математическая запись имеет следующий вид:

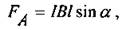
где I — сила тока в проводнике; В — магнитная индукция; l — длина проводника; α — угол между направлением проводника и направлением вектора магнитной индукции.

2. Работа с учебником.

Учащиеся открывают с. 900 учебника, читают § 64 и отвечают на следующие вопросы:

— Как устроен измерительный прибор магнитоэлектрической системы?

— Каково устройство электродвигателя постоянного тока?

— От чего зависит вращающийся магнит электродвигателя постоянного тока?

— Как можно изменить направление вращения якоря электродвигателя?

— Как можно изменить скорость вращения якоря электродвигателя?

V. Решение задач

1. Какая сила действует на каждый метр длины воздушных проводов троллейбусной линии, расположенных на расстоянии 52 м друг от друга, если сила тока в проводах — 2000 А? (Ответ: 1,5 Н.)

2. Вычислите индукцию магнитного поля на расстоянии 10 м от длинного прямого проводника при силе тока в проводнике 20 А. (Ответ: 4 · 10^-5 Тл.)

3. Вычислите индукцию магнитного поля внутри цилиндрической катушки длиной 10 м, содержащей 200 витков провода, при силе тока в катушке 5 А. (Ответ: 1,3 · 10^-2 Тл.)

Задачи повышенной сложности:

1. В вертикально однородном магнитном поле на двух тонких лентах горизонтально подвешен проводник длиной 20 см и массой 20,4 г. Индукция магнитного поля равна 0,5 Тл. На какой угол от вертикали отклонятся ленты, если сила тока в проводнике равна 2 А. (Ответ: 45°.)

2. Прямолинейный проводник массой 2 кг и длиной 50 см помещен в однородное магнитное поле перпендикулярно линиям индукции. Индукция поля равна 15 Тл. Какой силы ток должен проходить по нему, чтобы он висел не падая? (Ответ: 2,7 Тл.)

3. Проводящий стержень лежит на горизонтальной поверхности перпендикулярно однородному горизонтальному магнитному полю с индукцией 0,2 Тл. Какую силу в горизонтальном направлении нужно приложить перпендикулярному проводнику для его равномерного поступательного движения? Сила тока в проводнике — 10 А, масса — 100 г, длина — 25 см, коэффициент трения — 0,1. (Ответ: 0,548 Н или 0,402 Н.)

VI. Подведение итогов урока

Дополнительный материал Андре-Мари Ампер

Андре-Мари Ампер родился 20 января 1775 г. в Лионе в семье образованного коммерсанта. Отец его вскоре переселился с семьей в имение Полемье, расположенное в окрестностях Лиона, и лично руководил воспитанием сына. Уже к 14 годам Ампер прочитал все 20 томов знаменитой «Энциклопедии» Дидро и д’Аламбера. Проявляя с детства большую склонность к

математическим наукам, Ампер к 18 годам в совершенстве изучил основные труды Эйлера, Бернулли и Лагранжа. К тому времени он хорошо владел латынью, греческим и итальянским языками. Иными словами, Ампер получил глубокое и энциклопедическое образование.

В 1793 г. в Лионе вспыхнул контрреволюционный мятеж. Отец Ампера — жирондист, исполнявший обязанности судьи при мятежниках, после подавления мятежа был казнён как сообщник аристократов. Имущество его было конфисковано. Юный Ампер начал свою трудовую деятельность с частных уроков. В 1801 г. он занял должность преподавателя физики и химии центральной школы в городе Бурге. Здесь он написал первый научный труд, посвященный теории вероятности «Опыт математической теории игры». Эта работа привлекла внимание д’Аламбера и Лапласа. И Ампер стал преподавать математику и астрономию в Лионском лицее. В 1805 г. Ампер был назначен репетитором по математике в знаменитой Политехнической школе в Париже и с 1809 г. заведовал кафедрой высшей математики и механики. В этот период Ампер публикует ряд математических трудов по теории рядов. В 1813 г. его избирают членом Института (т. е. Парижской Академии наук) на место скончавшегося Лагранжа. Вскоре после избрания Ампер представил в Академию свое исследование о преломлении света. К этому же времени относится его знаменитое «Письмо к г. Бертолле», в котором Ампер сформулировал открытый им независимо от Авогадро химический закон, именуемый ныне законом Авогадро-Ампера.

В 1816 г. Ампер опубликовал свою классификацию химических элементов, первую в истории химии серьезную попытку расположить химические элементы по их сходству между собой.

Открытие Эрстедом в 1820 г. действия электрического тока на магнитную стрелку привлекает внимание Ампера к явлениям электромагнетизма. Ампер ставит многочисленные опыты, изобретает для этой цели сложные приборы, которые изготавливает за свой счет, что сильно подрывает его материальное положение.

С 1820 по 1826 г. Ампер опубликовал ряд теоретических и экспериментальных трудов по электродинамике и почти еженедельно выступал с докладами к Академии наук.

В 1822 г. он выпустил «Сборник наблюдений по электромагнетизму», в 1823 г. — «Конспект теории электродинамических явлений» и, наконец, в 1826 г. — знаменитую «Теорию электродинамических явлений, выведенных исключительно из опыта». Ампер получает всемирную известность как выдающийся физик.

Андре-Мари Ампер (краткая биография)

Содержание статьи:
1. Семья Андре Ампера и юные годы
2. Первые самостоятельные шаги
3. Закон Ампера
4. Телеграфный прибор Ампера
5. Закон о циркуляции, наука кибернетика и другие открытия
6. Смерть и почитание великого ученого

В конце XVIII столетии во Франции родился мальчик, которому суждено было войти в историю всемирной науки в области физики, математики, химии и тем самым пополнить список великих людей Франции.

Семья Андре Ампера и юные годы

Андре Мари Ампер родился в Лионе (административный центр современного региона Овернь – Рона – Альпы) в 1775 году в семье ремесленников.

Жанна Антуанетта Десютье-Сарсе Ампер, дочь шелкового предпринимателя, была его матерью.

Отец, Жан Жак Ампер, для того времени считался образованным человеком, имел богатую библиотеку, владел несколькими языками и увлекался изучением трудов популярных философов Древней Греции.

В 1789 году произошла Французская революция, и Жан Жак был назначен в Лионе на должность королевского прокурора. Через несколько лет к власти пришли якобинцы (ультрарадикальная партия) и началось преследование, а затем и аресты убежденных сторонников революции.

Среди них был и отец будущего ученого. В конце 1793 года Жан Жак Ампер был арестован, и по приговору суда казнен.
Андре Ампер с детства стремился к знаниям и, привитая отцом любовь к книгам, помогла в 12 лет самостоятельно освоить математику и чтение, учитывая, что из-за материальных трудностей он не учился в школе.

В четырнадцатилетнем возрасте Андре полностью изучил французское справочное пособие (энциклопедия в 28 томах) по физике.
Особенно он уделял внимание изучению различных физических явлений. Библиографы Ампера отмечают, что талант Андре Мари удивлял современников: чтобы прочитать в подледнике книги швейцарских математика Леонарда Эйлера и физика Даниила Бернулли, юноша выучил латынь.

Первые самостоятельные шаги

После исполнения смертельного приговора убежденному стороннику французской революции Жан Жаку Амперу, якобинское правосудие конфисковало все семейное имущество, и Андре вынужден был в 1802 году устроиться преподавателем математики в частный пансионат. Мизерная зарплата учителя вынудила его параллельно преподавать в школе в городке Бурга (предместье Лиона).

Примерно в это время, на заседании Лионской академии, в присутствии изобретателя первого источника постоянного тока итальянского физика Алессандро Вольта, Ампер высказывает предположение, где научно объясняет связь магнитных и электрических явлений.
Благодаря этой гипотезе молодой учитель привлекает внимание ученый совет Академии наук и его приглашают преподавателем в престижный Лионский лицей.

После смерти жены Катрин Каррон, в 1804 году Андре Мари вместе с сыном, названным в честь деда Жан Жаком, будущего историка французской литературы, переезжает в Париж и начинает работать преподавателем физики и математики в Политехнической школе.
В течение трех лет Ампер становится одним из лучших репетиторов Парижского колледжа и в 1807 году 32-летний Андре Мари получает должность профессора математического анализа.

Кроме этого он являлся экзаменатором по механике, а через год его назначают главным инспектором высших учебных заведений Парижа.

Закон Ампера

В 1814 году при единогласном голосовании он становится членом Французской академии наук.

В 1820 году на одном из заседаний датский физик Ханс Христиан Эрстед сообщил членам совета академии об открытии, в котором говорилось о влиянии электричества на магнитную стрелку.

Раньше считалось, что в природе электрические и магнитные явления существуют параллельно и независимы между собой. Датчанином было доказано обратное: эти явления связаны между собой — электричество, пропущенное через проводник, создает магнитный заряд, который приводит в движение тело, обладающее собственным магнитным полем.

Молодой ученый не согласился с выводами Ханса Христиана и начал разрабатывать свою теорию на основе многочисленных экспериментов, на основании которых им была выдвинута теория, что магнитных зарядов вообще не существует в природе. Они появляются благодаря перемещению в одну сторону электрических зарядов.

Затем после двухнедельных опытов, ученым было определено «правило Ампера», впоследствии названное в физике «законом Ампера».
Суть закона заключался в том, что расположенные параллельно проводники, при условии протекания тока в одном направлении – притягиваются, благодаря созданному магнитному полю, и отталкиваются, если пропустить ток в одном из проводников в противоположное направление.

Эта природная закономерность считается одной из важных явлений в современной электротехнике, без которой невозможен научно-технический прогресс.

Телеграфный прибор Ампера

Развитие технического прогресса в XVIII столетии подтолкнуло ученых создать устройство, способное передавать сигналы на определенные расстояния.

Идея первой системы приспособления для передачи сообщений по проводам принадлежит шотландскому физику Чарльзу Морису, который в 1753 году рекомендовал, основываясь на ряде опытов, провести изолированные между собой провода. Каждый проводник должен был соответствовать определенной букве алфавита или знака.

По этим проводам должен передаваться электрический заряд на металлические шарики, расположенные на приемной точке. Принимающий сигналы оператор, по шарикам, которые притягиваются к металлическому предмету, должен был расшифровать посланное сообщение.
В 1829 году Ампер предложил более упрощенный телеграф, на основе воздействия электрического тока на магнит (опыт Эрстеда).
Но по ряду технических причин того времени идея ученого (как и Чарльза Мориса) не была осуществлена.

Современные физики считают, что польза от идеи Андре Мари имеет большое значение – по этому принципу сейчас работают современные электромагнитные станции (коммутаторы).

Закон о циркуляции, наука кибернетика и другие открытия

Магнитный эффект катушки с током был сформулирован ученым в 1822 году, а через четыре года Андре Мари озвучил и доказал теорему о циркуляции магнитного поля, впоследствии названной законом Ампера о циркуляции и сейчас считается основным в науке о свойствах и закономерностях электромагнитного поля (электродинамика).

В 1830 году Ампер становится почетным членом Петербургской Академии наук.

В этом же году ученый закончил научный трактат «Опыт о философии наук», где впервые дал понятие о новой науке, основанной на общих законах управления в биологической, технической и социальной природе, названной им «кибернетика».

Первая часть этого труда вышла из печати в 1834 году. Вторая часть рукописи, была издана через семь лет после его смерти.

Благодаря разностороннему таланту Андре Мари Ампера были в свое время сделаны открытия в области математики и химии.

Работа над дифференциальными уравнениями с частными производными получили в математике имя Монжа-Ампера. В области химии им был сформулирован закон молярных объемов газа.

Смерть и почитание великого ученого

После одной из инспекторских командировок заболел пневмонией, давшая осложнения, в результате которой французский ученый Андре Мари Ампер в 1836 году 10 июня скончался и похоронен в Париже на кладбище Монмартр.

Современников поражает факт, что Андре Мари Ампер никогда не учился в школе, но благодаря стремлению к знаниям стал одним из образованных людей своей эпохи и вошел в список великих ученых Франции.

В 1881 году в Париже проходил первый Международный конгресс физиков, где в память о великом ученом, было решено единицу силы тока назвать ампером.

Взаимодействие параллельных токов. Закон Ампера.

Взаимодействие параллельных токов. Закон Ампера.

Закон Ампера — закон взаимодействия постоянных токов. Установлен Андре Мари Ампером в 1820. 

Из закона Ампера следует, что параллельные проводники с постоянными токами, текущими в одном направлении, притягиваются, а в противоположном — отталкиваются. 

Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. 

Сила , с которой магнитное поле действует на элемент проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длины проводника на магнитную индукцию : . Направление силы определяется по правилу вычисления векторного произведения, которое удобно запомнить при помощи правила левой руки:

     

— руку вдоль тока

— разворачиваем ладонь навстречу магнитным линям (перпендикулярно) (рука по-прежнему вытянута вдоль тока)

— отогнутый на 90 градусов большой палец покажет направление силы Ампера

(Направление магнитного поля провода с током по правилу буравчика или правой руки:

Модуль силы Ампера можно найти по формуле: ,

где α — угол между векторами магнитной индукции и тока.

Сила dF максимальна когда элемент проводника с током расположен перпендикулярно линиям магнитной индукции (): .

Наиболее известным примером, иллюстрирующим силу Ампера, является следующая задача. В вакууме на расстоянии r друг от друга расположены два бесконечных параллельных проводника, в которых в одном направлении текут токи I1 и I2. Требуется найти силу, действующую на единицу длины проводника.

Бесконечный проводник с током I1 в точке на расстоянии r создаёт магнитное поле с индукцией:

Теперь по закону Ампера найдём силу, с которой первый проводник действует на второй:

По правилу буравчика поле тока I1 в месте нахождения второго проводника

По правилу буравчика, направлена в сторону первого проводника (аналогично и для , а значит, проводники притягиваются).

Модуль данной силы (r — расстояние между проводниками):

Интегрируя, получаем для проводника единичной длины (пределы l от 0 до 1):