Метод трапеций — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 мая 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 мая 2019; проверки требует 1 правка. Аппроксимация функции линейной зависимостью при интегрировании методом трапеций
Аппроксимация функции линейной зависимостью при интегрировании методом трапецийМетод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.
Если отрезок [a,b]{\displaystyle \left[a,b\right]} является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле
- ∫abf(x)dx=f(a)+f(b)2(b−a)+E(f),E(f)=−f″(ξ)12(b−a)3.{\displaystyle \int _{a}^{b}f(x)\,dx={\frac {f(a)+f(b)}{2}}(b-a)+E(f),\qquad E(f)=-{\frac {f»(\xi )}{12}}\left(b-a\right)^{3}.}
Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной
- |E(f)|⩽(b−a)312n2maxx∈[a,b]|f″(x)|,(b−a)312n2=nh412.{\displaystyle \left|E(f)\right|\leqslant {\frac {\left(b-a\right)^{3}}{12n^{2}}}\max _{x\in [a,b]}\left|f»(x)\right|,{\frac {(b-a)^{3}}{12n^{2}}}={\frac {nh^{3}}{12}}.}
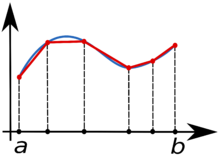 Применение составной формулы трапеций
Применение составной формулы трапецийЕсли отрезок [a,b]{\displaystyle \left[a,b\right]} разбивается узлами интегрирования и на каждом из элементарных отрезков применяется формула трапеций, то суммирование даст составную формулу трапеций
- ∫abf(x)dx≈∑i=0n−1f(xi)+f(xi+1)2(xi+1−xi)={\displaystyle \int _{a}^{b}f(x)\,dx\approx \sum _{i=0}^{n-1}{\frac {f(x_{i})+f(x_{i+1})}{2}}(x_{i+1}-x_{i})=}
- =f(a)2(x1−a)+∑i=1n−2f(xi)2(xi+1−xi−1)+f(b)2(b−xn−1).{\displaystyle ={\frac {f(a)}{2}}(x_{1}-a)+\sum _{i=1}^{n-2}{\frac {f(x_{i})}{2}}(x_{i+1}-x_{i-1})+{\frac {f(b)}{2}}(b-x_{n-1}).}
- xj=a+jh,h=(b−a)/N,N−{\displaystyle x_{j}=a+jh,h=(b-a)/N,N-}четное
 Применение формулы трапеций для равномерной сетки
Применение формулы трапеций для равномерной сеткиВ случае равномерной сетки
- ∫abf(x)dx=h(f0+fn2+∑i=1n−1fi)+En(f),{\displaystyle \int _{a}^{b}f(x)\,dx=h\left({\frac {f_{0}+f_{n}}{2}}+\sum _{i=1}^{n-1}f_{i}\right)+E_{n}(f),}
- En(f)=−f″(ξ)12(b−a)h3.{\displaystyle E_{n}(f)=-{\frac {f»(\xi )}{12}}(b-a)h^{2}.}
где h{\displaystyle h} — шаг сетки.
- Метод трапеций быстро сходится для осциллирующих функций, поскольку погрешность за период аннулируется.
- Метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников.
- Демидович Б.П., Марон И.А. Основы вычислительной математики. — 2. — Физ-Мат. Лит., 1963. — С. 659.
Формула трапеций
Точность
расчетов с помощью теоремы о среднем
существенно зависит, как было показано,
от визуального
назначения по графику точки 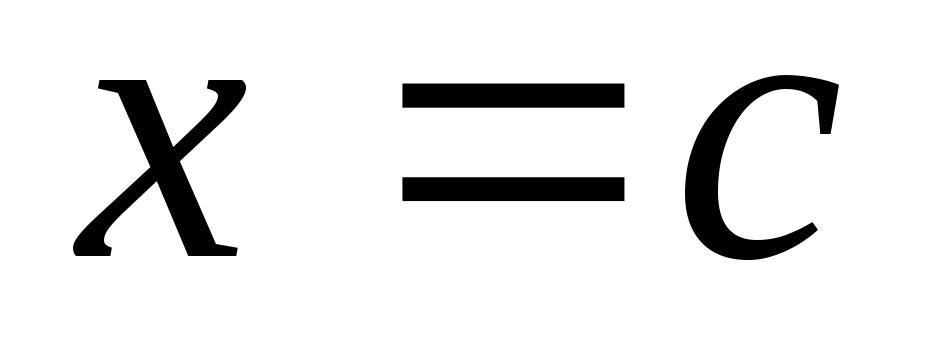 .
Действительно, выбрав, в том же примере,
точки
.
Действительно, выбрав, в том же примере,
точки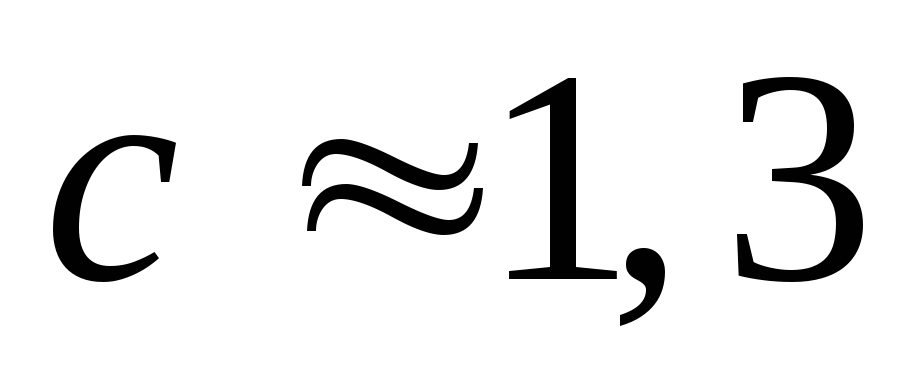 или
или ,
можно получить другие значения интеграла,
причем погрешность может и увеличиться.
Субъективные факторы, масштаб графика
и качество рисования сильно влияют на
результат. Этонеприемлемо в ответственных расчетах, поэтому
теорема о среднем применяется только
для быстрой качественной оценки интеграла.
,
можно получить другие значения интеграла,
причем погрешность может и увеличиться.
Субъективные факторы, масштаб графика
и качество рисования сильно влияют на
результат. Этонеприемлемо в ответственных расчетах, поэтому
теорема о среднем применяется только
для быстрой качественной оценки интеграла.
В
этом разделе рассмотрим один из самых
популярных способов приближенного
интегрирования – формулу
трапеций.
Основная идея построения этой формулы
исходит из того, что кривую 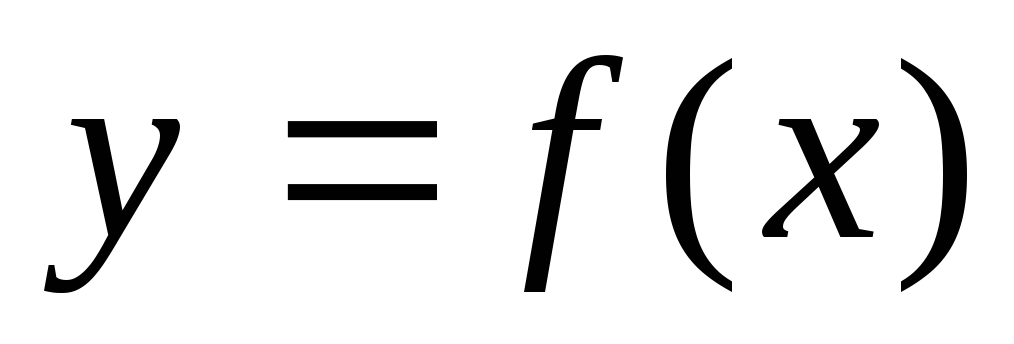 можно приближенно заменить ломаной
линией, как показано на рисунке.
можно приближенно заменить ломаной
линией, как показано на рисунке.
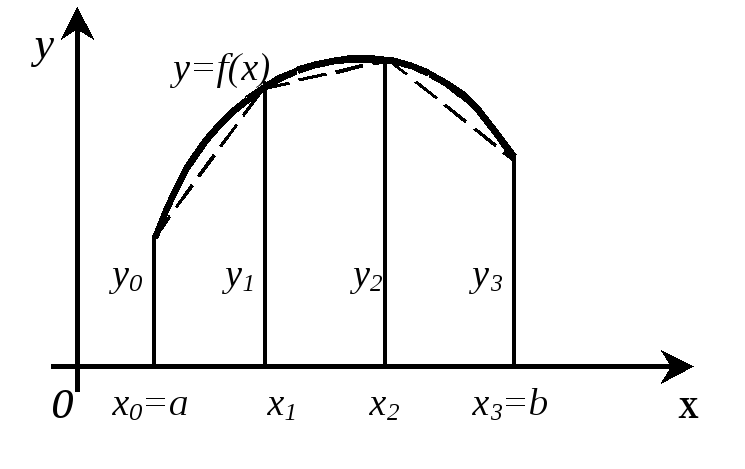
Тогда из геометрического смысла определенного интеграла следует, что площадь криволинейной трапеции заменяется суммой площадей нескольких прямоугольных трапеций. Ясно, что чем точнее проводится ломаная (т.е., чем больше прямолинейных отрезков в ее составе), тем ближе она к реальной кривой и сумма площадей элементарных трапеций сходится к точному значению площади криволинейной трапеции и, следовательно, к значению данного интеграла.
Примем,
для определенности (и в соответствии с
рисунком), что интервал интегрирования
разбит на 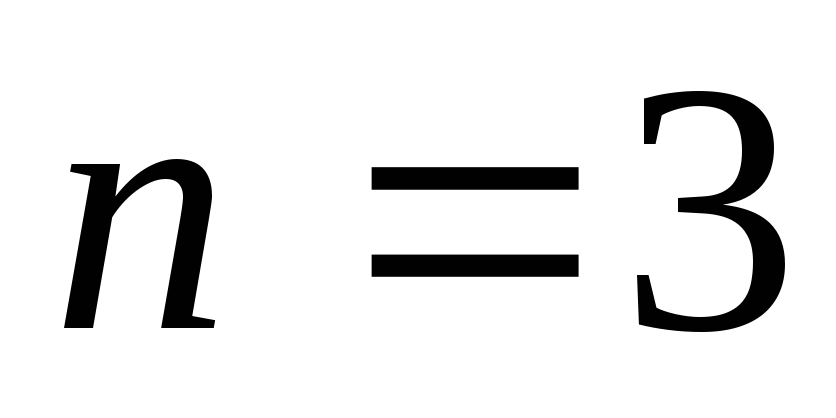 равные (это необязательно, но очень удобно)
части. Длина каждой из этих частей
вычисляется по формуле
равные (это необязательно, но очень удобно)
части. Длина каждой из этих частей
вычисляется по формуле 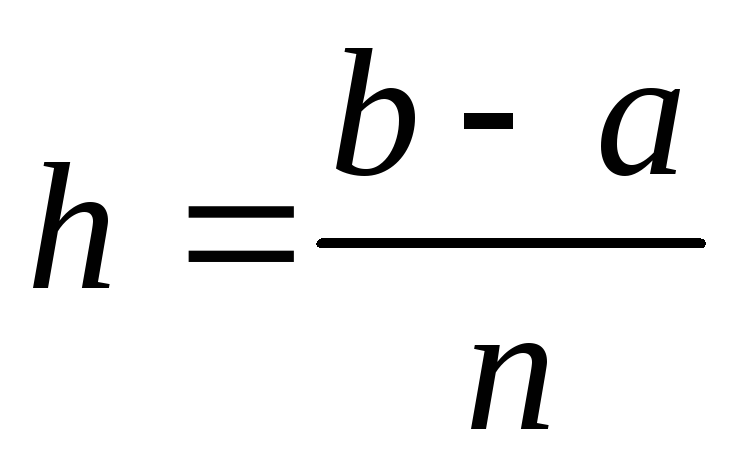 и называетсяшагом.
Абсциссы точек разбиения, если задано
и называетсяшагом.
Абсциссы точек разбиения, если задано 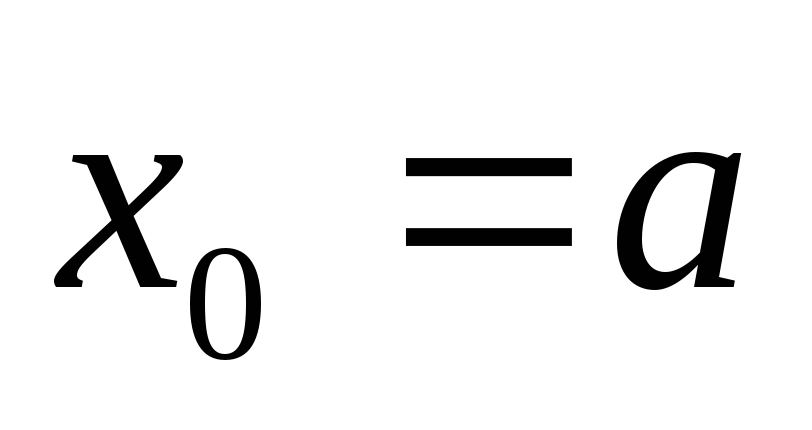 ,
определятся по формуле
,
определятся по формуле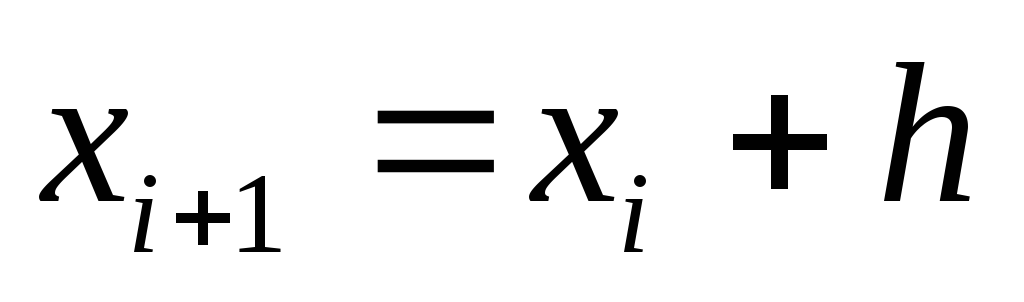
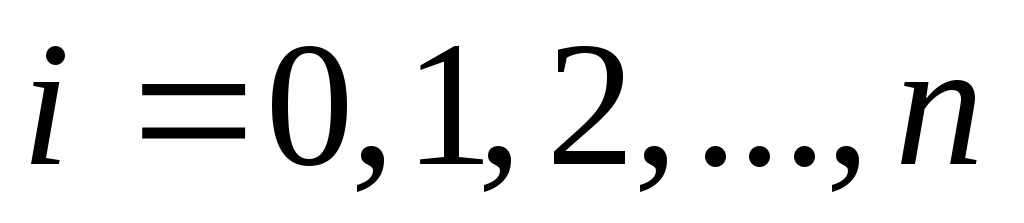 .
По известным абсциссам легко вычислить
ординаты
.
По известным абсциссам легко вычислить
ординаты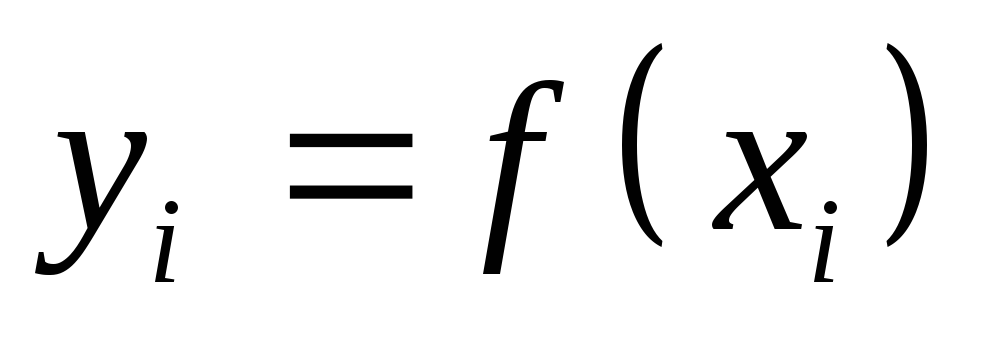 .
Таким образом,
.
Таким образом, 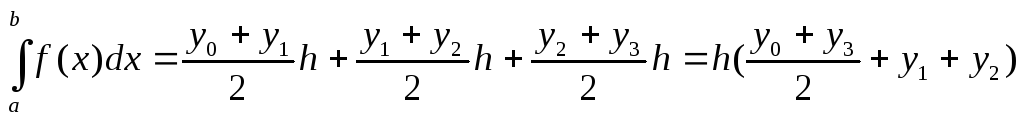 .
.
Это
и есть формула трапеций для случая  .
Отметим, что первое слагаемое в скобках
является полусуммой начальной и конечной
ординат, к которой прибавляются все
промежуточные ординаты. Для произвольного
числа
.
Отметим, что первое слагаемое в скобках
является полусуммой начальной и конечной
ординат, к которой прибавляются все
промежуточные ординаты. Для произвольного
числа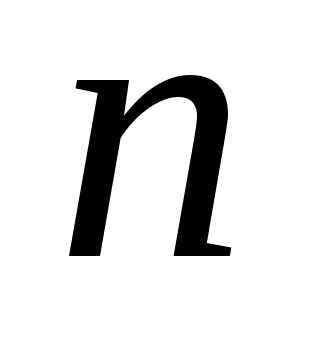 разбиений
интервала интегрированияобщая
формула трапеций имеет вид
разбиений
интервала интегрированияобщая
формула трапеций имеет вид
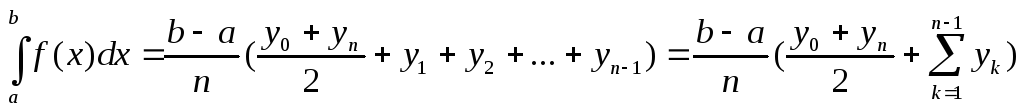 .
.
Точность формулы трапеций зависит от принимаемого
(самостоятельно)
числа разбиений 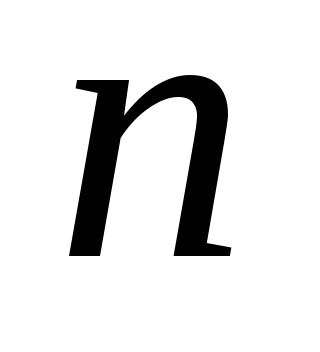 .
Хотя в учебной литературе приводятся
способы оценки погрешности этой формулы,
на практике удобно произвести два
расчета (в ответственных задачах) при
разных значениях
.
Хотя в учебной литературе приводятся
способы оценки погрешности этой формулы,
на практике удобно произвести два
расчета (в ответственных задачах) при
разных значениях .
На пример, при
.
На пример, при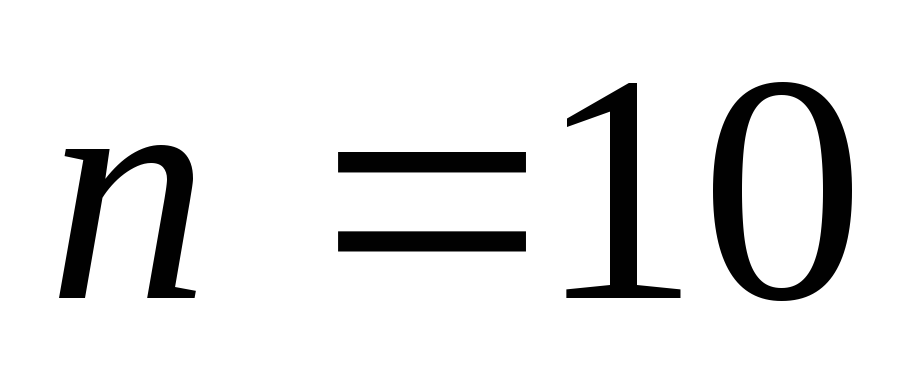 и
и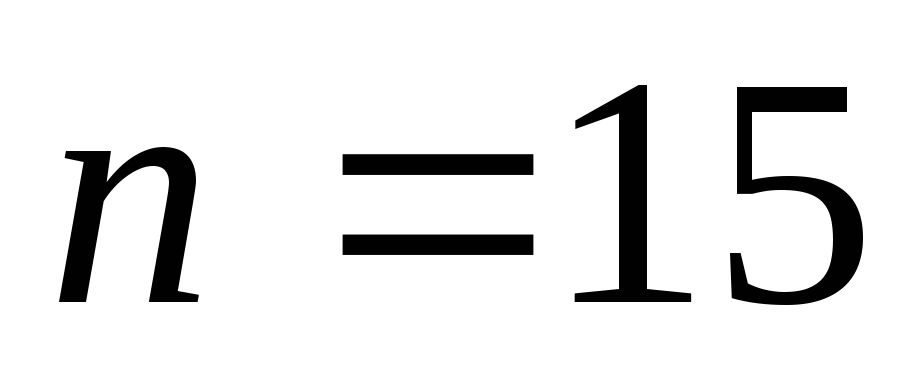 .
Если результаты близки, то расчет
заканчивается, иначе рекомендуется
повторить вычисления при
.
Если результаты близки, то расчет
заканчивается, иначе рекомендуется
повторить вычисления при или
или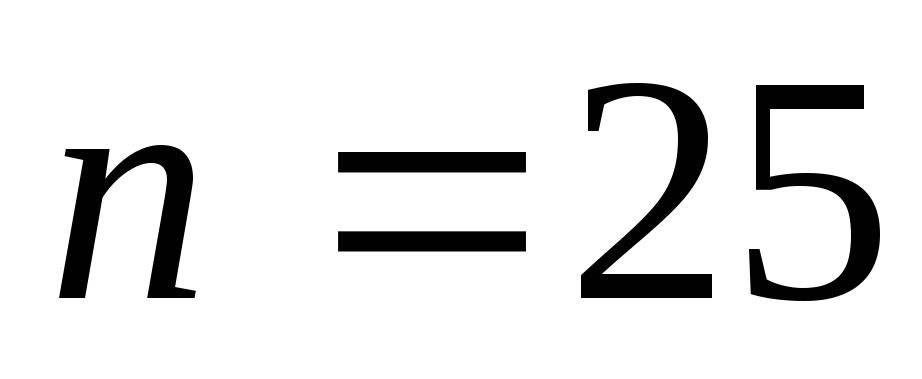
Отметим,
что имеется большой ряд и других способов
численного интегрирования или, иначе, квадратурных
формул:
прямоугольников, Симпсона, Гаусса и
т.д. Они строятся на той же идее
представления криволинейной трапеции
элементарными площадями различной
формы, поэтому, после освоения формулы
трапеций, разобраться в аналогичных
формулах не составит особого труда.
Многие формулы не так просты, как формула
трапеций, но позволяют получить результат
высокой точности при малом числе
разбиений  .
.
С помощью формулы трапеций (или аналогичных) можно вычислять, с нужной на практике точностью, как «неберущиеся» интегралы, так и интегралы от сложных или громоздких функций.
Функции нескольких переменных Основные понятия
В предыдущих разделах изучались функции одной переменной. Однако многим явлениям присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности, введения понятия функции нескольких переменных.
Определение.
Пусть имеется n переменных величин, и каждому набору
их значений (х1,
х2, …, хn) из некоторого множества Х соответствует
одно вполне определенное значение
переменной величины z.
Тогда говорят, что задана функция
нескольких переменных z=f(х1,х2,…,хn). Например,
формула 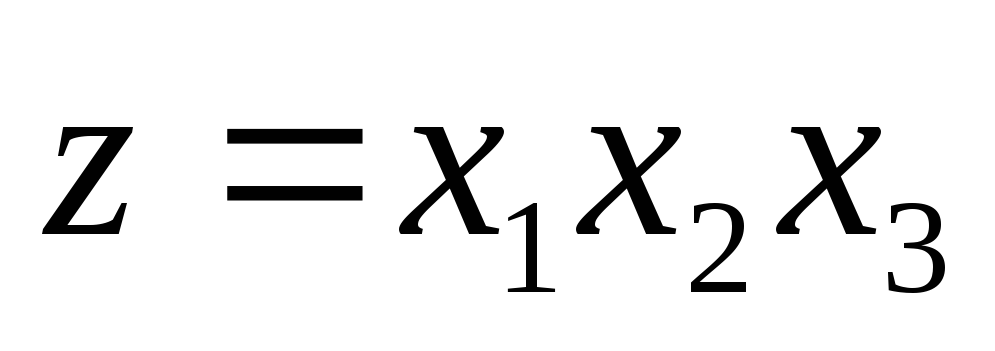
Переменные х1, х2, …, хn называются независимыми переменными (или аргументами), z — зависимой переменной, а символ f означает закон соответствия. Множество X называется областью определения функции.
Частный случай
функции двух аргументов определяется соотношением z=f(x, у). Основное внимание мы уделим именно этому случаю, т.к. функции трех и более переменных легко вводятся по аналогии. 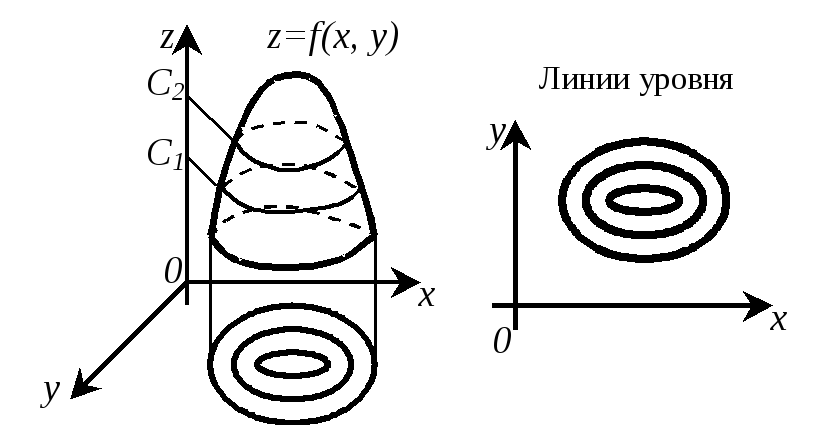
График функции двух переменных z=f(x, у) представляет собой некоторую поверхность в трехмерном пространстве. Как видно из рисунка, график функции двух переменных — значительно более сложный объект, чем график функции одной переменной. Как правило, построение поверхности оказывается непростой задачей. В то же время поверхность в пространстве обладает гораздо меньшей наглядностью, чем линия на плоскости. Поэтому в случае двух переменных для изучения поведения функции желательно использовать другие, более наглядные инструменты. Важнейшим из них являются линии уровня.
Линией уровня функции двух переменных z=f(x, у) называется множество точек на плоскости, в которых функция принимает одно и то же значение f(x, y)=С. Число С в этом случае называется уровнем. На рисунке показаны сечения функции двумя плоскостями С1 и С2, а также проекции этих сечений на плоскость XoY. Эти проекции изображаются на отдельном чертеже и являются линиями уровня.
Многие примеры линий уровня хорошо известны и привычны. Например, параллели и меридианы на глобусе — это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм
— линий уровня температуры. Построение линий уровня оказывается существенно более легкой задачей, чем построение графиков самих функций.Все определения и большая часть понятий анализа, определенных ранее для функций одной переменной, может быть перенесена на случай многих переменных без существенных изменений. Несколько увеличивается объем формул, т.к. надо учитывать несколько аргументов. Проиллюстрируем сказанное на примере классического определения предела функции.
Число А называется пределом функции z=f(x,
у) при 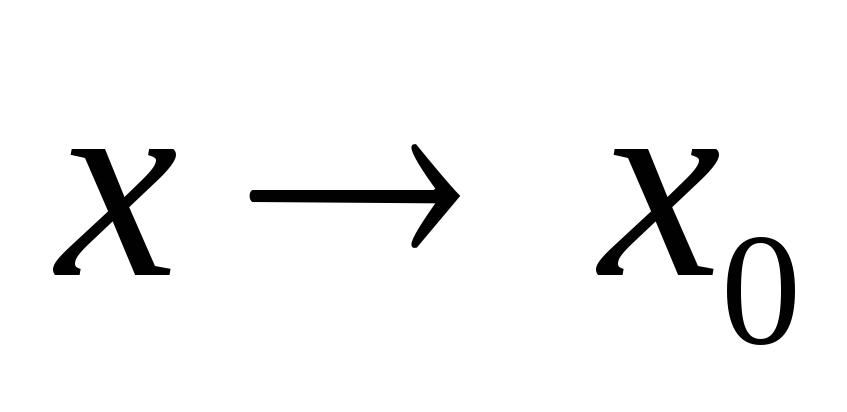 и
и 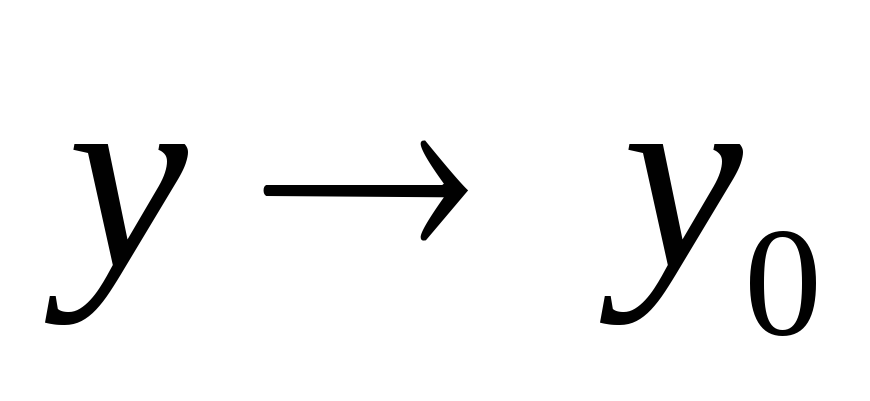
 ,
найдется положительное число
,
найдется положительное число ,
такое, что для всех точекM(х,
у),
отстоящих от точки M0(х0,
у0) на расстояние меньшее, чем
,
такое, что для всех точекM(х,
у),
отстоящих от точки M0(х0,
у0) на расстояние меньшее, чем  ,
выполняется неравенство
,
выполняется неравенство 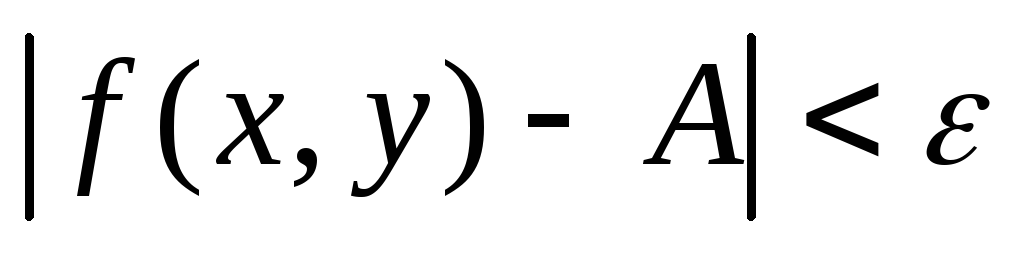 .
. Обозначается
предел так: 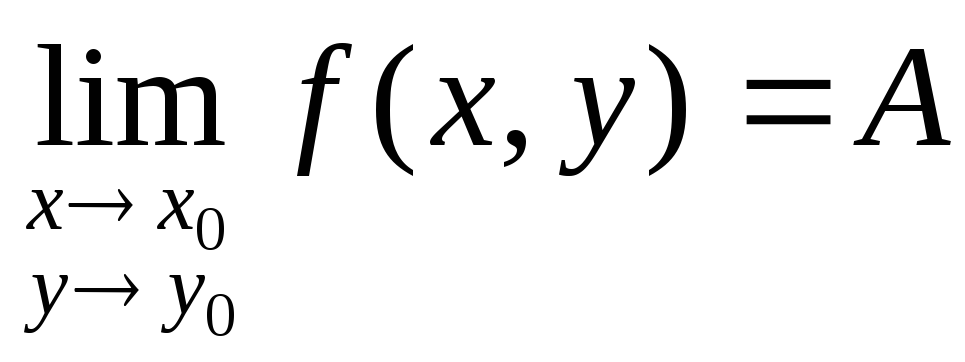 .
.
Вычисление пределов функций двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной. Причина заключается в том, что на линии существуют всего два направления, по которым аргумент может стремиться к предельной точке, а именно — справа и слева. На плоскости же таких направлений — бесконечное множество, и пределы функции по разным направлениям могут не совпадать.
формула трапеций — с английского на русский
См. также в других словарях:
Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
ТРАПЕЦИЙ ФОРМУЛА — формула для приближенного вычисления определенных интегралов (квадратурная формула), имеющая вид:где h = (b a) /n, fk = f (a + kh), k=1,…, n 1 … Большой Энциклопедический словарь
Трапеций формула — формула для приближённого вычисления определённых интегралов, имеющая вид где fm=f (a+mh), m = 0, 1,…, n. Геометрически применение Т. ф. означает замену площади криволинейной трапеции, ограниченной осью Ox, графиком… … Большая советская энциклопедия
трапеций формула — формула для приближённого вычисления определённых интегралов (квадратурная формула), имеющая вид: , где h = (b a)/n, fk = f(a + kh), k = 1, …, п 1. * * * ТРАПЕЦИЙ ФОРМУЛА ТРАПЕЦИЙ ФОРМУЛА, формула для приближенного вычисления определенных… … Энциклопедический словарь
ТРАПЕЦИЙ ФОРМУЛА — частный случай Ньютона Котеса квадратурной формулы, в к рой берется два узла: Если подинтегральная функция f(х)сильно отличается от линейной, то формула (1) дает малую точность. Промежуток [ а, b]разбивается на пчастичных промежутков [ х i, xi+1] … Математическая энциклопедия
ТРАПЕЦИЙ ФОРМУЛА — ф ла для приближённого вычисления определ. интегралов (квадратурная ф ла), имеющая вид: h = (b a)/n, fk = f(a + kh), k=1,…,n 1. > где h = (b a)/n, fk = f(a + kh), k=1,…,n 1 … Естествознание. Энциклопедический словарь
Трапеций формула — … Википедия
КВАДРАТУРНАЯ ФОРМУЛА — формула, служа щая для приближённого вычисления определ. интегралов по значениям подынтегральной функции в конечном числе точек. Примеры К. ф. прямоугольников формула, трапеций формула, Симпсона формула … Естествознание. Энциклопедический словарь
Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Формула трапеций — с русского на все языки
Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
ТРАПЕЦИЙ ФОРМУЛА — формула для приближенного вычисления определенных интегралов (квадратурная формула), имеющая вид:где h = (b a) /n, fk = f (a + kh), k=1,…, n 1 … Большой Энциклопедический словарь
Трапеций формула — формула для приближённого вычисления определённых интегралов, имеющая вид где fm=f (a+mh), m = 0, 1,…, n. Геометрически применение Т. ф. означает замену площади криволинейной трапеции, ограниченной осью Ox, графиком… … Большая советская энциклопедия
трапеций формула — формула для приближённого вычисления определённых интегралов (квадратурная формула), имеющая вид: , где h = (b a)/n, fk = f(a + kh), k = 1, …, п 1. * * * ТРАПЕЦИЙ ФОРМУЛА ТРАПЕЦИЙ ФОРМУЛА, формула для приближенного вычисления определенных… … Энциклопедический словарь
ТРАПЕЦИЙ ФОРМУЛА — частный случай Ньютона Котеса квадратурной формулы, в к рой берется два узла: Если подинтегральная функция f(х)сильно отличается от линейной, то формула (1) дает малую точность. Промежуток [ а, b]разбивается на пчастичных промежутков [ х i, xi+1] … Математическая энциклопедия
ТРАПЕЦИЙ ФОРМУЛА — ф ла для приближённого вычисления определ. интегралов (квадратурная ф ла), имеющая вид: h = (b a)/n, fk = f(a + kh), k=1,…,n 1. > где h = (b a)/n, fk = f(a + kh), k=1,…,n 1 … Естествознание. Энциклопедический словарь
Трапеций формула — … Википедия
КВАДРАТУРНАЯ ФОРМУЛА — формула, служа щая для приближённого вычисления определ. интегралов по значениям подынтегральной функции в конечном числе точек. Примеры К. ф. прямоугольников формула, трапеций формула, Симпсона формула … Естествознание. Энциклопедический словарь
Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
формула трапеций — со всех языков на украинский
См. также в других словарях:
Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
ТРАПЕЦИЙ ФОРМУЛА — формула для приближенного вычисления определенных интегралов (квадратурная формула), имеющая вид:где h = (b a) /n, fk = f (a + kh), k=1,…, n 1 … Большой Энциклопедический словарь
Трапеций формула — формула для приближённого вычисления определённых интегралов, имеющая вид где fm=f (a+mh), m = 0, 1,…, n. Геометрически применение Т. ф. означает замену площади криволинейной трапеции, ограниченной осью Ox, графиком… … Большая советская энциклопедия
трапеций формула — формула для приближённого вычисления определённых интегралов (квадратурная формула), имеющая вид: , где h = (b a)/n, fk = f(a + kh), k = 1, …, п 1. * * * ТРАПЕЦИЙ ФОРМУЛА ТРАПЕЦИЙ ФОРМУЛА, формула для приближенного вычисления определенных… … Энциклопедический словарь
ТРАПЕЦИЙ ФОРМУЛА — частный случай Ньютона Котеса квадратурной формулы, в к рой берется два узла: Если подинтегральная функция f(х)сильно отличается от линейной, то формула (1) дает малую точность. Промежуток [ а, b]разбивается на пчастичных промежутков [ х i, xi+1] … Математическая энциклопедия
ТРАПЕЦИЙ ФОРМУЛА — ф ла для приближённого вычисления определ. интегралов (квадратурная ф ла), имеющая вид: h = (b a)/n, fk = f(a + kh), k=1,…,n 1. > где h = (b a)/n, fk = f(a + kh), k=1,…,n 1 … Естествознание. Энциклопедический словарь
Трапеций формула — … Википедия
КВАДРАТУРНАЯ ФОРМУЛА — формула, служа щая для приближённого вычисления определ. интегралов по значениям подынтегральной функции в конечном числе точек. Примеры К. ф. прямоугольников формула, трапеций формула, Симпсона формула … Естествознание. Энциклопедический словарь
Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
формула+трапеций — с русского на все языки
Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
ТРАПЕЦИЙ ФОРМУЛА — формула для приближенного вычисления определенных интегралов (квадратурная формула), имеющая вид:где h = (b a) /n, fk = f (a + kh), k=1,…, n 1 … Большой Энциклопедический словарь
Трапеций формула — формула для приближённого вычисления определённых интегралов, имеющая вид где fm=f (a+mh), m = 0, 1,…, n. Геометрически применение Т. ф. означает замену площади криволинейной трапеции, ограниченной осью Ox, графиком… … Большая советская энциклопедия
трапеций формула — формула для приближённого вычисления определённых интегралов (квадратурная формула), имеющая вид: , где h = (b a)/n, fk = f(a + kh), k = 1, …, п 1. * * * ТРАПЕЦИЙ ФОРМУЛА ТРАПЕЦИЙ ФОРМУЛА, формула для приближенного вычисления определенных… … Энциклопедический словарь
ТРАПЕЦИЙ ФОРМУЛА — частный случай Ньютона Котеса квадратурной формулы, в к рой берется два узла: Если подинтегральная функция f(х)сильно отличается от линейной, то формула (1) дает малую точность. Промежуток [ а, b]разбивается на пчастичных промежутков [ х i, xi+1] … Математическая энциклопедия
ТРАПЕЦИЙ ФОРМУЛА — ф ла для приближённого вычисления определ. интегралов (квадратурная ф ла), имеющая вид: h = (b a)/n, fk = f(a + kh), k=1,…,n 1. > где h = (b a)/n, fk = f(a + kh), k=1,…,n 1 … Естествознание. Энциклопедический словарь
Трапеций формула — … Википедия
КВАДРАТУРНАЯ ФОРМУЛА — формула, служа щая для приближённого вычисления определ. интегралов по значениям подынтегральной функции в конечном числе точек. Примеры К. ф. прямоугольников формула, трапеций формула, Симпсона формула … Естествознание. Энциклопедический словарь
Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
формула трапеций — с русского на английский
Формула трапеций — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Формула прямоугольников — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
ТРАПЕЦИЙ ФОРМУЛА — формула для приближенного вычисления определенных интегралов (квадратурная формула), имеющая вид:где h = (b a) /n, fk = f (a + kh), k=1,…, n 1 … Большой Энциклопедический словарь
Трапеций формула — формула для приближённого вычисления определённых интегралов, имеющая вид где fm=f (a+mh), m = 0, 1,…, n. Геометрически применение Т. ф. означает замену площади криволинейной трапеции, ограниченной осью Ox, графиком… … Большая советская энциклопедия
трапеций формула — формула для приближённого вычисления определённых интегралов (квадратурная формула), имеющая вид: , где h = (b a)/n, fk = f(a + kh), k = 1, …, п 1. * * * ТРАПЕЦИЙ ФОРМУЛА ТРАПЕЦИЙ ФОРМУЛА, формула для приближенного вычисления определенных… … Энциклопедический словарь
ТРАПЕЦИЙ ФОРМУЛА — частный случай Ньютона Котеса квадратурной формулы, в к рой берется два узла: Если подинтегральная функция f(х)сильно отличается от линейной, то формула (1) дает малую точность. Промежуток [ а, b]разбивается на пчастичных промежутков [ х i, xi+1] … Математическая энциклопедия
ТРАПЕЦИЙ ФОРМУЛА — ф ла для приближённого вычисления определ. интегралов (квадратурная ф ла), имеющая вид: h = (b a)/n, fk = f(a + kh), k=1,…,n 1. > где h = (b a)/n, fk = f(a + kh), k=1,…,n 1 … Естествознание. Энциклопедический словарь
Трапеций формула — … Википедия
КВАДРАТУРНАЯ ФОРМУЛА — формула, служа щая для приближённого вычисления определ. интегралов по значениям подынтегральной функции в конечном числе точек. Примеры К. ф. прямоугольников формула, трапеций формула, Симпсона формула … Естествознание. Энциклопедический словарь
Квадратурная формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Прямоугольников формула — Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия