У р о к 4 (49) Решение квадратных уравнений с четным вторым коэффициентом
Цели: вывести формулу (II) нахождения корней квадратного уравнения с четным вторым коэффициентом; формировать умения применять формулы I и II для решения квадратных уравнений.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Назовите коэффициенты a, b, c уравнений:
а) 4х2 – 5х – 7 = 0; г) 8 – 9х2 = 0;
б) х2 + 2 – 3х = 0; д) 11х2 = 0;
в) 3х2 + 2х = 0; е) 17 – х2 – х = 0.
2. Решите уравнение:
а) 2х2 – 18 = 0; в)
б) 3х2 – 12х = 0; г) 3,6х2 = 0.
3. Сколько корней имеет уравнение:
а) 6х2 – 5х = 0; в) 3х2 – 4 = 0;
б) х2 – 4х + 4 = 0; г) 2х2 + 7 = 0?
III. Объяснение нового материала.
С о з д а н и е п р о б л е м н о й с и т у а ц и и.
Предложить учащимся для решения квадратное уравнение 15х2 – 34х + + 15 = 0. Используя формулу нахождения корней квадратного уравнения, получаем:
D = (–34)2 – 4 · 15 · 15 = 1156 – 900 = 256.
;
Решая это уравнение, учащиеся вынуждены проводить вычисления достаточно громоздкие, в отличие от ранее решаемых уравнений.
Можно теперь сообщить учащимся, что для решения квадратных уравнений, у которых второй коэффициент четный, существует другая формула корней, позволяющая упростить вычисления.
Вывод этой формулы проводится согласно пункту учебника. Причём в сильном классе можно предложить учащимся проделать это самостоятельно, записав только общий вид такого уравнения:
ax2 + 2 ∙ k ∙ x + c = 0 (b = 2k).
После вывода формулы возвращаемся к решенному уравнению и применяем новую формулу:
D = (–17)2 – 15 · 15 = 289 – 225 = 64;
.
Как видим, вычисления можно произвести «в уме», так как все значения квадратов чисел – табличные.
На доску можно вынести п л а к а т:
(обращаем внимание учащихся, что D1 в четыре раза меньше, чем D)
Р е ш е н и е к в а д р а т н о г о у р а в н е н и я a2 + 2kx + c = 0, a ≠ 0; D1 = k2 – ac. Если D1 < 0, то уравнение не имеет корней. Если D1 = 0, то x = Если D1 > 0, то x = |
.
.IV. Формирование умений и навыков.
Все у п р а ж н е н и я, решаемые на этом уроке, можно разбить на три группы:
1-я г р у п п а. Упражнения на непосредственное применение формулы (II) корней квадратного уравнения.
2-я г р у п п а. Упражнения с выбором формулы (I или II) корней квадратного уравнения в зависимости от второго коэффициента.
3-я г р у п п а. Упражнения повышенной трудности.
1. № 539 (б, г, ж), № 540 (в, з).
При решении этих упражнений демонстрируем учащимся применение новой формулы для случая, когда корни уравнения являются иррациональными. Для этого вызываем двух учеников к доске и параллельно проводим решение по разным формулам.
№ 539 (ж).
7z2 – 20z + 14 = 0.
Ф о р м у л а I | Ф о р м у л а II |
D = (–20)2 – 4 · 7 · 14 = = 400 – 392 = 8. | D1 = (–10)2 – 7 · 14 = = 100 – 98 = 2. |
(Ещё
раз замечаем, что D1 = | |
x = Вынесем множитель из-под знака корня: x = ,
то естьx = | x = |
.)
.
.
.Таким образом, получаем такие же корни.
2. № 541 (б, в, ж), № 546 (а, г), № 550 (б), № 552 (а, в), № 553 (а).
3. № 554, № 555.
Эти упражнения можно предложить сильным в учебе учащимся, сократив для них количество заданий из 1-й и 2-й группы.
№ 554.
Р е ш е н и е
а) х2 – 5х + 6 = 0;
D = (–5)2 – 4 · 1 · 6 = 25 – 24 = 1, D > 0.
= 3.6х2 – 5х + 1 = 0;
D = (–5)2 – 4 · 6 · 1 = 25 – 24 = 1, D > 0.
x1 =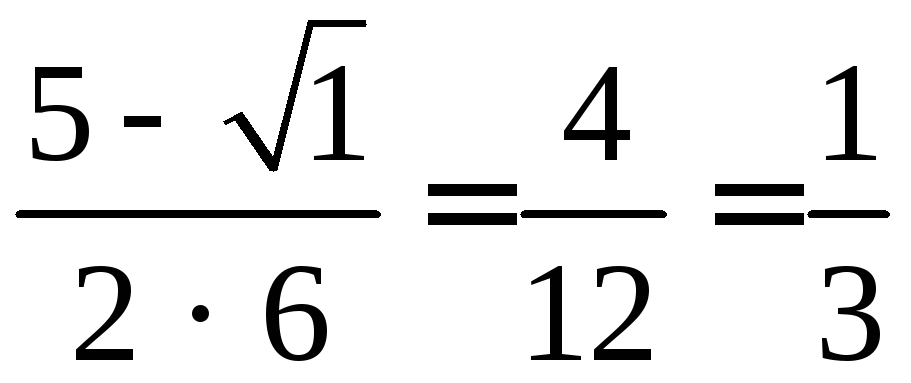 
;x2 =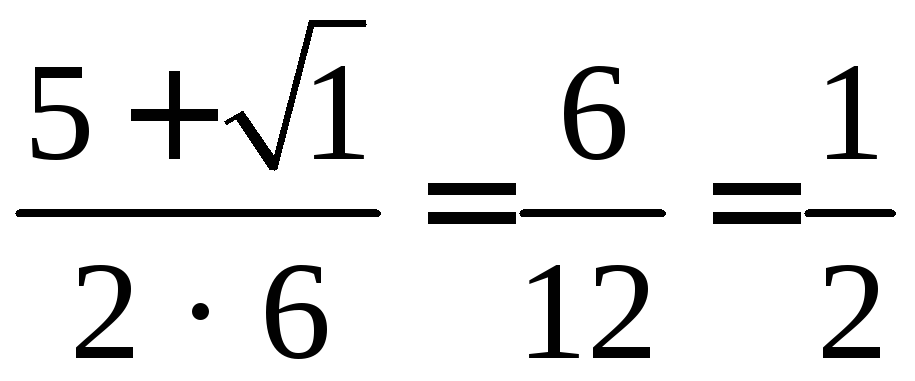 
.
б) 2х2 – 13х + 6 = 0;
D = (–13)2 – 4 · 2 · 6 = 169 – 48 = 121, D > 0.
x1 =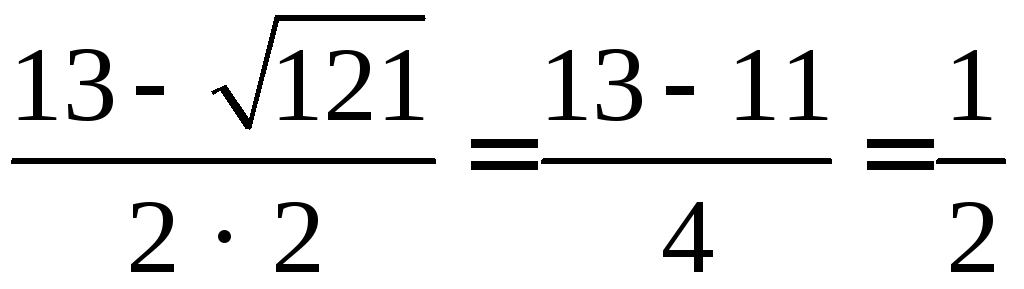 
;x2 = 
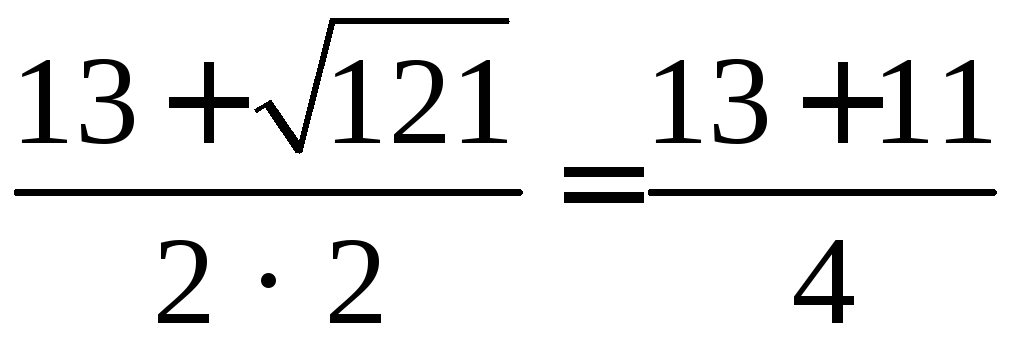= 6.
D = (–13)2 – 4 · 6 · 2 = 169 – 48 = 121, D > 0.
x1 = 
;x2 = 
= 2.
Можно предположить, что корни уравнений ax2 + bx + c = 0 и cx2 + + bx + a = 0 являются взаимно-обратными числами. Докажем это.
ax2 + bx + c = 0. | cx2 + bx + a = 0. |
x1 = x2 = | x3 = x4 = |
.
;
.(Мы предполагаем, что b2 – 4ac ≥ 0, то есть корни существуют.)
Вычислим x1 ∙ x4 = 
=
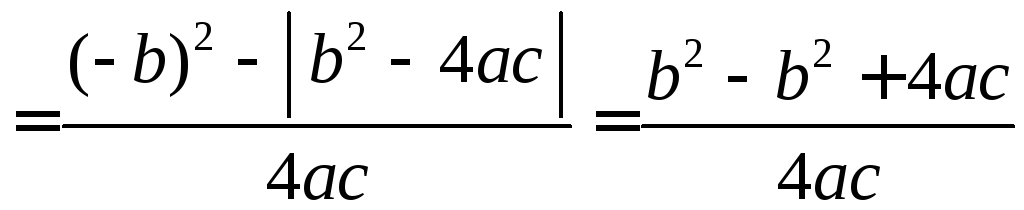= 1. Значит, х1
Аналогично доказывается, что x2 и x3 – взаимно-обратные числа.
№ 555.
Р е ш е н и е
х2 – ах + (а – 4) = 0.
D = (–а)2 – 4 · 1 · (а – 4) = а2 – 4а + 16.
Чтобы определить количество корней, необходимо оценить дискриминант. Выделим в выражении квадрат двучлена:
D = (а2 – 2 · 2 · а + 4) + 12 = (а – 2)2 + 12.
Дискриминант принимает положительные значения при любом а (точнее D ≥ 12), значит, при любом а уравнение имеет два корня.
О т в е т: а) нет; б) нет; в) при любом а.
8.8-3. Квадратные уравнения с чётным вторым коэффициентом — математика в тестах
Алгебра. 8 класс. Параграф 8. Тест 3.
Вариант 1.
Решить уравнения.
1. 3x2-10x+3=0.
3. 5x2+14x-3=0.
A) -3; -0,2; B) 0,2; 3; C) -3; 0,2; D) -3; 0,5.
4. 5x2-18x+9=0.
A) -3; -0,6; B) -0,6; 3; C) 3; D) 0,6; 3.
5. 5x2-18x-8=0.
A) 0,4; 4; B) -4; -0,4; C) -0,4; 4; D) -4; 0,2.
6. 7x2+82x+55=0.
7. 9x2+12x-5=0.
9. 7(x2+2x-2)=(1-x)(1+x).
A) -2,5; -0,75; B) -0,75; 2,5; C) 0,75; 2,5; D) -2,5; 0,75.
10. 6x(x+4)+2x(x-1)= -15.
A) -1,5; 1,25; B) -1,5; -1,25; C) 1,25; 1,5; D) -2,5; 1,25.
Вариант 2.
Решить уравнения.
1. 3x2+14x-5=0.
3. 5x2-36x+7=0.
A) -7; 0,2; B) -0,2; 7; C) -7; 0,2; D) 0,2; 7.
4. 5x2-22x+8=0.
A) -4; -0,4; B) -0,4; 4; C) 0,4; 4; D) -4; 0,4.
5. 5x2+12x-9=0.
A) -3; 0,6; B) -3; -0,6; C) -0,6; 3; D) 0,6; 3.
6. 7x2+62x+48=0.
7. 9x2-6x-8=0.
9. 5(x2+x+3)=3х(9-x).
A) -1,5; -1,25; B) -1,25; 1,5; C) -1,5; 1,25; D) 1,25; 1,5.
10. 2x(x+5)+2(x2-18)= 6х-1.
A) -3,5; -2,5; B) 2,5; 3,5; C) -3,5; 2,5; D) -2,5; 3,5.
Поделиться новостью в соцсетях « Предыдущая запись Следующая запись »
mathem-test.ru
Что это за формула для нахождения дискреминанта?
Называется формула для нахождения корней квадратного уравнения с чётным коэффициентом при х. Если коэффициент при х есть чётное число, то вместо дискриминанта удобнее вычислить его четверть. В данном случае через D1 обозначили D/4. Иногда это обозначают через d, но чаще оставляют просто D/4, чтобы меньше было путаницы и вопросов. Иногда обозначают половину чётного коэффициента при х буквой k: k = b/2 В этом случае формула для корней квадратного уравнения принимает простой вид: x1,2 = (-k +- sqrt(D1) / a, где D1 = D/4 = k^2 — ac. Эта формула проще тем, что: 1. В квадрат возводится не сам коэффициент b, а его половина. 2. Из этого квадрата вычитается не 4aс, а просто ac 3. В знаменателе содержится не 2а, а просто а. Если а = 1, т. е. уравнение приведённое, как в данном случае, то формула ещё упрощается: x1,2 = -k +- sqrt(D1), где D1 = k^2 — c Эту формулу и применили. Она легко выводится из общей формулы путём соответствующих подстановок и упрощений и применима для уравнений такого вида: x^2 + 2kx + c = 0 В данном случае k = 1, c = -120.
Я формулу дискриминанта и нахождения корней по нему помню до сих пор, а вам должно быть стыдно 🙂 <img src=»//otvet.imgsmail.ru/download/u_85a85f637e0814757e86b06ef89f3558_800.jpg» alt=»» data-lsrc=»//otvet.imgsmail.ru/download/u_85a85f637e0814757e86b06ef89f3558_120x120.jpg» data-big=»1″>
стандартная формула 4+480-сократи на 4 и всё,чем меньше число, тем легче считать
touch.otvet.mail.ru
напишите формулу квадратного уровнение где второе число чётное
..ну формула квадратного уравнения ах2+bx+c=0..не поняла что тебе нужно..
если число четное, то через коэффициент, К= -в / 2а…. потом х1= -K +,-корень из D/a
по такиому условию могу предложить только ax^2 +2bx + с =0
х2+2х-3=0 ну вот только так… . Задание какое-то странное…
формулу для квадратного уравнения с четным вторым коэффициентом
touch.otvet.mail.ru
План-конспект урока по алгебре (8 класс) по теме: Решение квадратных уравнений
Конспект урока по алгебре в 8 классе
на тему «Решение квадратных уравнений по формуле №2
с чётным вторым коэффициентом»
Цели урока:
1. Вывести формулу корней квадратного уравнения с четным вторым
коэффициентом.
2. Продолжить формирование навыка решений квадратных уравнений .
3.Расширение знаний и навыков решения квадратных уравнений.
4.Развитие интеллекта , сознательного отношения к учебе.
СОДЕРЖАНИЕ УРОКА:
I .ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ
1.В парах по заранее приготовленным заданиям на доске проверяют правильность выполненных уравнений.
№542 а)5х2= 9х+2
5х2 — 9х-2 =0
Д=b2 – 4ac=81+40=121,Д >0 ,2 корня :
х1,2 =
Х1,2 = ; х1=2; х2=-0,2
б)-х2 =5х -14
-х2 —5х +14 =0
х2 +5х — 14=0,
Д=b2 – 4ac=25+56= 81; Д >0 ,2 корня : х1,2 === — 7; 2
в) 6х+9 =х2
х2 – 6х – 9=0
Д=b2 – 4ac=35+36=72; Д >0 ,2 корня : х1,2 === 3 +3;3 — 3;
г ) z -5 = z2 -25
z2 –z -20 =0
Д=b2 – 4ac=1+80=81; Д >0 ,2 корня : х1,2 === 5 ; — 4
д ) у2 =52у -576
у2 -52у +76 =0
Д=b2 – 4ac=2704 -2304=400; Д >0 ,2 корня : х1,2 === 36 ; -16
е ) 15 у2 -30 =22у +7
15 у2 -22у -37 =0
Д=b2 – 4ac=484 +2220=2704; Д >0 ,2 корня : х1,2 === -1; 2
ж ) 25p2 -10p +1=0
Д=b2 – 4ac=100-100=0; Д =0 ,1 корень : х= = 0,2
з ) 299х2 +100х =500- 101х2
400х2 +100х-500 =0| : 100
4х2 + х -5 =0
Д=b2 – 4ac=1+80 =81; Д >0 ,2 корня : х1,2 === 1; -1
№543
а) 25=26х-х2
х2 -26х +25 =0
Д=b2 – 4ac=676-100 =576; Д >0 ,2 корня : х1,2 === 25 ;1
б)3х2 =10 -29х
3х2 +29х -10 =0
Д=b2 – 4ac=841+120= 961; Д >0 ,2 корня : х1,2 === -10 ;
в )у2 = 4у +96
у2 — 4у -96 =0
Д=b2 – 4ac=16+384= 400; Д >0 ,2 корня : х1,2 === -8 ;12
г ) 3p2 +3=10р
3p2 — 10р +3 =0
Д=b2 – 4ac=100-36= 64; Д >0 ,2 корня : х1,2 === 3 ;
д ) х2 -20х=20х+100
х2 -40х -100 =0
Д=b2 – 4ac=1600+400= 2000; Д >0 ,2 корня :
х1,2 ===20+10; 20 -10;
е ) 25х2 -13 х =10х2 -7
15х2 -13х +7 =0
Д=b2 – 4ac=169 -420= -259; Дкорней нет
II. УСТНЫЕ УПРАЖНЕНИЯ
1.Докажите ,что -1 является корнем уравнения : х3 +1=0, х2 -1=0,х2+х =0,х2+3х+2=0.
2.Укажите коэффициенты квадратного уравнения:
2х2 -5х+10 = 0 , 2+х+х2=0 , х2 +3х -0,5 =0 , 5х2 -4х =3 , 0,5х2 –х -3 =0 , 8х -7 =х2
1-3х-2х2 =0 , 11-2х2 =4х.
3.Замените уравнение равносильным ему приведённым квадратным уравнением:
3х2-6х -12 =0; х2 -3х +6=0; -х2+2х -2 =0; 10х2 -20х +30 =0.
4.Имеет ли квадратное уравнение корни ; если имеет, то сколько; рациональными или иррациональными числами являются корни: 4х2-12х +9 =0 , 2х2+3х -9 =0;
5х2-х+2=0 ; 4х2+7х -1 =0; х2-3х +5 =0; 3х2+2х -2 =0; 3х2-11х +10=0; 25х2+10х+1=0
5.Подберите какие-нибудь значения с , при которых уравнение имеет корни:
х2-3х +с =0; 5х2- 2х +с =0.
III.АКТУАЛИЗАЦИЯ ОПОРНЫХ ЗНАНИЙ :
(проводится в виде диктанта с взаимопроверкой в парах, двое учащихся выполняют задания на отворотах доски)
1.Запишите общий вид квадратного уравнения и формулу дискриминанта:
2.При каком условии полное квадратное уравнение :
Имеет единственный корень | не имеет корней
3.Вычислите дискриминант квадратного уравнения :
3х2 -8х — 3=0 | 2х2 -3х -2=0
4.Решите квадратное уравнение :
х2-4х+9=0 | х2-6х+5=0
5. Подберите какое-нибудь значение с , при котором уравнение имеет корни:
х2 -3х +с=0; | х2-2х+с=0.
IV. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА:
Поручить уч-ся самостоятельно изучить в течение 5 минут вывод формулы из п.21(стр.115).Затем сильный ученик выполняет вывод на доске , дети записывают в тетради. Для квадратных уравнений, у которых второй коэффициент является четным числом , формулу корней удобно записывать в другом виде:
ах2 +2kх +с =0
D=b2 – 4ac=4k2-4ас =4(k2 –ас),D1 = k2 –ас; если D1>0, то
х1,2 ===, где D1 = k2 –ас ,
если D1
Привести вторую запись данной формулы при условии , если в приведенном квадратном уравнении второй коэффициент чётный :
х2 +2kх +с =0; , где b =2k , то есть : х1,2 = (формулаII)
Для быстрого запоминания формулы привожу стихотворные строки:
« …б со знаком взяв обратным , мы на два его поделим ,
И от корня аккуратно знаком „минус-плюс” отделим ,
а под корнем очень кстати – половина б в квадрате, минус це (с) и вот решенье небольшого уравненья»
V. ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО:
Решить на доске : №539 (а,б,в,ж)
а )3х2 -14х+16=0 б) 5х2 -16х+3=0
Д1=72-3·16=1, х1,2 == 2 ;2 Д1=82-15=49, х1,2 == ;3
в ) х2 +2х-80=0 ж)7z2 -20z+14=0
х1,2 = -1=-19 =8; -10 Д1=102-7∙14=2, х1,2 =.
Обучающая самостоятельная работа :№539 (г, д , е, з) с последующей проверкой. Ответы :
г | 23; -1 |
д | 5,5; 3,5 |
е | -1; 2 |
з | 5+ 5 ; 5 — 5 |
VI. ИТОГ УРОКА:
1.воспроизвести буквенную запись формулы на доске.
2.Словесная формулировка нового правила :
А ) Что означаетД1 ?
Б)Как быстро запомнить формулу корней?
VII . Приёмы устного решения некоторых квадратных уравнений
Сообщение о случаях устного решения отдельных видов квадратных уравнений готовится с помощью учителя заранее сильным учеником.
В сообщении ученика приводятся приёмы для квадратных уравнений ах2+bх+с =0:
1.Если а+b+с=0 , то х1 =1 , х2 =;
2.Если а+ с =b , то х1 = -1; х2 =.
Решаем устно :
1) х2 +17х-18=0, 2) х2 -19х+18=0; 3)13х2 -29х+16=0 ; 4) х2 +2009х-2010=0;
5) х2 -5х-6=0 ; 6)17 х2 -19х-36=0; 7) х2 +17х+16=0
1 | 2 | 3 | 4 | 5 | 6 | 7 |
1; -18 | 1;18 | 1; | 1,-2010 | -1;6 | -1; | -1;-16 |
VII .ДОМАШНЕЕ ЗАДАНИЕ :
запомнить выведенные формулы п21учебника,№540,№543.
nsportal.ru