Первообразная и интеграл | Формулы с примерами
ФормулаПервообразная формула

Основное свойство первообразной

Неопределенный интеграл, формула

Простейшие правила интегрирования, формулы

Таблица интегралов, формулы

Определенный интеграл функции, формула

Формула Ньютона Лейбница

Свойства определенного интеграла, формулы

Площадь фигуры, ограниченной линиями, формула

Объем тела, площадь поперечного сечения которого задается функцией S (x), формула

Объем тела, образованного вращением вокруг оси OX криволинейной трапеции, ограниченной линиями

Работа переменной силы F (x) при прямолинейном перемещении материальной точки вдоль оси OX из точки a в точку b, формула

formula-xyz.ru
Первообразная функции ℹ️ понятие, правила нахождения, формулы, основные свойства, виды, геометрический и физический смысл, таблица интегралов, примеры решений

Основная информация

Первообразная некоторой функции находится при помощи операции интегрирования. Последняя является обратной для вычисления производной. Например, существует какое-то выражение Z(p). Его производной является некоторая функция z(р), то есть [Z(p)]’ = z(p). Нахождение Z(p) осуществляется по таблице первообразных или интегралов. Когда такой нет под рукой, то можно применить и таблицу производных. При этом следует учитывать константу.
Табличные значения специалисты не рекомендуют заучивать, поскольку такие действия приводят к потере драгоценного времени. Они считают, что в процессе нахождения интегралов информация отложится в голове. Для начала рекомендуется рассмотреть неопределенный интеграл, а затем переходить к другим его видам.
Применение интеграла

Интеграл — один из основных элементов высшей математики. Его обозначают «∫». После этого символа следует подынтегральное выражение, которое записывается в следующем виде: (функция)d(переменная). Следует отметить, что совокупность символов «d(переменная)» обозначает, по какой переменной следует осуществлять операцию интегрирования.
При помощи операции поиска первообразной можно находить площади некоторых фигур, величину пути при неравномерном движении и множество других параметров, для которых невозможно применить общие формулы и соотношения.
Алгебраический смысл интеграла заключается в представлении некоторой суммы в виде маленьких слагаемых. Их бывает много видов: неопределенный, определенный, двойной и так далее. Однако конечным результатом является некоторая производная. Следует отметить, что идет строгое разделение по переменным, по которым выполняется интегрирование. В этом случае их нужно классифицировать на два вида: определенный и неопределенный.
Неопределенным интегралом произвольной функции z(p) называется выражение, представленное в виде ее первообразной с учтенной константой Z(p) + C, то есть ∫(z(p)) dp = Z(p) + С. У него отсутствуют ограничения в виде некоторых числовых значений границ. Первообразная находится в общем виде. Во втором случае также следует найти исходную функцию, но по формуле Ньютона-Лейбница подставляются числовые значения. Далее находится конкретная числовая величина.
Чтобы найти первообразную, необходимо руководствоваться некоторыми правилами. Математики рекомендуют их знать, поскольку это поможет в дальнейшем обучении.
Методика нахождения
Существуют определенные правила нахождения первообразных. Для нахождения интеграла простейшей функции необходимо воспользоваться таблицей первообразных (рис. 1). Далее нужно найти соответствующее выражение и записать результат. Однако задания не всегда могут быть простыми, поскольку некоторые выражения следует упростить, а другие — решаются только при помощи формул интегрирования по частям.
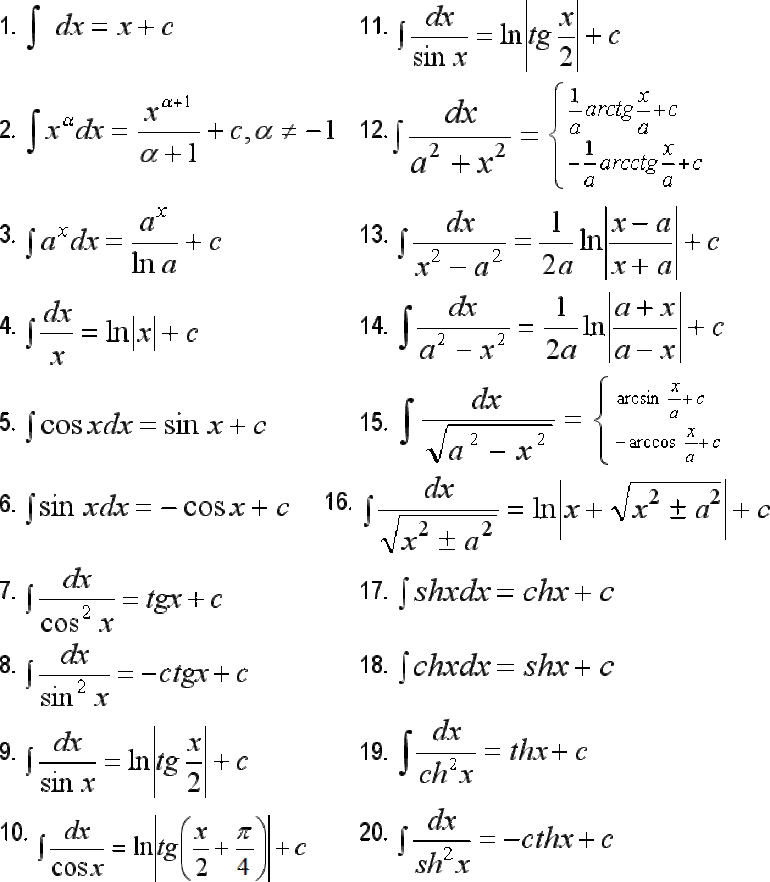
Рисунок 1. Таблица первообразных.
Методика нахождения первообразной для простой табличной функции состоит из двух этапов. Для этой цели следует воспользоваться обыкновенным алгоритмом, который рекомендуют математики всего мира:
- Упростить выражение под знаком интеграла. Операция подразумевает такие элементы (следует применять по необходимости): приведение подобных слагаемых, вынесение общего множителя за скобки, использование формул сокращенного умножения, раскрытие скобок и так далее.
- Определение первообразной по таблице (рис. 1).

Если первый метод не подходит, то следует воспользоваться формулой первообразной, которая позволяет выполнять операцию интегрирования по частям. Прибегать к такому варианту следует в том случае, когда функция является сложной и ее нет в таблицах производных и интегралов.
Однако для начала следует рассмотреть теорию. Необходимо предположить, что существуют две функции: m = m(y) и n = n(y). У них есть некоторые производные, которые являются непрерывными. Чтобы вывести формулу, нужно рассмотреть свойство дифференциалов: d(mn) = mdn + ndm. Далее необходимо взять неопределенный интеграл от правой и левой частей: ∫d(mn) = ∫(mdn + ndm). После этого получится такое тождество: ps = ∫pds + ∫sdp. Из соотношения можно вывести формулу нахождения первообразной при помощи методики интегрирования по частям: ∫mdn = mn — ∫ndm.
Суть соотношения заключается в упрощении сложного выражения и сведении его к табличному значению. Следует отметить, что методика может применяться много раз и без каких-либо ограничений. Специалисты выделили отдельные подынтегральные функции, к которым нужно применять эту методику:
- Произведение натурального логарифма на многочлен.
- Многочлен, умноженный на показательную или степенную функции (экспонента также входит в эту группу).
- Выражение, умноженное на любые из тригонометрических прямых и обратных функций. Первое должно быть представлено в виде многочлена. К прямым относятся синус, косинус, тангенс и котангенс, а к обратным — арксинус, арктангенс, арккосинус и арккотангенс.
- Дробь с неизвестными: только числитель и знаменатель.
Если по какой-то причине интеграл невозможно взять, то это объясняется только наличием ошибок при интегрировании. Специалисты рекомендуют пересмотреть ход решения или начать его заново. Иногда необходимо осуществить замену подынтегрального выражения, но этот способ не будет рассматриваться, поскольку он является очень сложным.
Геометрический смысл
У интеграла есть определенный геометрический смысл, который заключается в нахождении площади криволинейной трапеции. К последним принадлежат плоские фигуры, ограниченные некоторым заданным графиком, а также прямыми или другими графиками. Основные требования — непрерывность и конечное значение S (площади) должно быть больше нуля. Как правило, в подынтегральную часть идет сама функция, а границами являются значения переменных.
В качестве ограничителей могут выступать также и оси декартовой системы координат. Чтобы вычислить площадь этой фигуры, необходимо выполнить такие операции:

- Найти первообразную в общем виде.
- Подставить значения ограничителей в формулу Ньютона-Лейбница (p1 = a и p2 = b).
- Произвести необходимые вычисления.
Во втором пункте соотношение имеет такой вид: S = Z(а) — Z(b). Необходимо отметить, что величина «а» является верхней границей, а «b» — нижней. Площадь S не может быть отрицательной величиной. Если по каким-то причинам S < 0, тогда следует проверить саму функцию на непрерывность и поменять границы местами.
Во время процесса интегрирования вся фигура разбивается на множество мелких элементов прямоугольной формы. Далее высчитывается площадь каждого элемента, а затем выполняется операция сложения. В результате получается искомое значение площади криволинейной трапеции.
У интеграла есть также и физический смысл. В этом случае необходимо связать понятие материальной точки (тела) со скоростью ее движения V(t) за время t из точки а в точку b. Интеграл (определенный) в этом случае эквивалентен пути: ∫[V(t)] dt |(a;b).
Следует также сформулировать основное свойство первообразной: произвольная первообразная непрерывной и дифференцируемой функции z(p) на некотором промежутке записывается в виде выражения Z(p) + C, где С — произвольная постоянная величина. На основании этого утверждения математики сформулировали два вспомогательных свойства:
- С — любое число, поскольку производная константы равна 0.
- Для любой подынтегральной функции z(p) существует некоторая первообразная Z(p) + C, которая также является дифференцируемой и непрерывной на заданном промежутке.
Свойства и определения необходимы для доказательства тождеств и теорем. Несмотря на то что при дифференцировании константа обращается в нулевое значение, следует всегда ее учитывать. В задачах некоторого вида нужно найти постоянную величину. Примером таких упражнений является решение дифференциальных уравнений.
Важные рекомендации

Для нахождения первообразной существует несколько методов. Они делятся на следующие группы: автоматизированные и ручные. Первый тип применяется для быстрого нахождения исходной функции, а также вычисления площади криволинейной трапеции. Это можно решать при помощи специальных программ или интернет-сервисов. Примером последних является калькулятор интегралов (Integral Calculator). Приложение поддерживает все современные операционные системы и платформы: Windows, Linux, Android и Mac.
Приложение считается одним из лучших, поскольку его функциональные возможности не ограничиваются только нахождением производных. Оно обладает такими дополнительными возможностями: нахождение производных, построение графиков, решение дифференциальных уравнений, вычисление значений тригонометрических функций и так далее.
Математики все же не рекомендуют использовать различные сервисы для решения задач, поскольку следует научиться выполнять такие операции в ручном режиме. Это объясняется тем, что не всегда под рукой будет соответствующее программное обеспечение. Кроме того, на экзаменах, зачетах и контрольных запрещается их использовать. Специалисты считают, что их применение целесообразно, когда нужно проверить результат решения.
Основные алгоритмы
Алгоритмизация решения задач применяется во всех областях науки, поскольку позволяет не только избежать ошибок, но и написать отдельные веб-приложения для решения задач определенного вида. Этот подход также необходим при написании курсовых и дипломных работ, в которых нужно разрабатывать схемы в виде программных продуктов. Реализуются они на различных языках программирования. Полный алгоритм или инструкция нахождения первообразной для неопределенного интеграла имеет такой вид:

- Подынтегральное выражение нужно упростить. Вынесение константы за знак интеграла также входит в этот пункт.
- Найти первообразную по таблице, изображенной на рисунке 1.
- Записать ответ.
- Осуществить проверку при помощи Integral Calculator или другого сервиса. Если решения совпадают, то задача решена верно. В противном случае следует перейти в первый пункт, поскольку от правильности выполнения операции упрощения тождества зависит конечный результат.
Когда следует найти первообразную с учетом значений границ, то следует воспользоваться алгоритмом:

- Выполнить первый и второй пункты алгоритма нахождения первообразной для неопределенного интеграла.
- Вычислить значение при помощи формулы Ньютона-Лейбница, внимательно проверив соответствующие границы.
- Осуществить подстановку значений.
- Произвести необходимые вычисления.
- Если получено отрицательное значение при нахождении площади, то следует пересмотреть график функции и ограничивающие прямые или другие графики-ограничители. Далее следует выполнить повторное нахождение решения, то есть вернуться к первому пункту.
- Результат — положительное число. Необходимо перейти к 7 пункту.
- Проверка при помощи онлайн-сервиса.
- Ответ не совпадает: осуществить поиск ошибки, переходя в предыдущий пункт.
- Результаты совпадают: записать ответ.
Когда представлена сложная функция (не является табличной), тогда можно также применять любой из алгоритмов. Однако следует свести ее к табличной, применив формулу интегрирования по частям.
Примеры решения
Для практического применения следует разобрать такое выражение: (p — 1)(p+1) — (p+2)^2 + p^3. Необходимо найти его первообразную. Выполнять это задание необходимо по первому алгоритму:
- Раскрытие скобок и приведение подобных слагаемых: (p — 1)(p+1) — (p+2)^2 + p^3 = р^2 — 1 — p^2 — 4p — 4 + p^3 = p^3 — 4p — 1.
- Результат состоит из суммы разности элементарных первообразных: ∫(p^3 — 4p — 1) dx = (p^4) / 4 — (4 * p^2) / 2 — p + C (степенные функции).
- Проверка: результаты совпадают.
Далее нужно решить пример с использованием интегрирования по частям. Например, дана некоторая подынтегральная функция p * ln(p). Она является сложной, поскольку ее нет в таблице. Следует также отметить, что нужно учитывать характер ln(p). Неизвестная величина р должна быть под знаком модуля, то есть p = |p|. Если р < 0, то функция является неопределенностью. Алгоритм интегрирования имеет такой вид:
- Обозначения: m = ln(p), dm = 1 / dp, dn = dp и n = p.
- Результат операции интегрирования: ∫p * ln(p) dp = p * ln(p) — ∫dp = p * ln(p) — p + C, где p >= 0.
Проверив результат при расчетах и на калькуляторе интегралов, можно сделать вывод, что задача решена правильно. Кроме того, следует проверять подынтегральное выражение. Например, если дана функция с корнем четной степени (квадрат, четвертая и так далее), то необходимо указывать, что функция должна быть больше или равна 0.
nauka.club
Таблица первообразных и правила их нахождения
На этой странице вы найдёте:
1. Собственно, таблицу первообразных — её можно скачать в формате PDF и распечатать;
2. Видео, посвящённое тому, как этой таблицей пользоваться;
3. Кучу примеров вычисления первообразной из различных учебников и контрольных работ.
В самом видео мы разберём множество задач, где требуется посчитать первообразные функций, зачастую довольно сложных, но главное — не являющихся степенными. Все функции, сведённые в таблицу, предложенную выше, необходимо знать наизусть, подобно производным. Без них невозможно дальнейшее изучение интегралов и их применение для решения практических задач.
Сегодня мы продолжаем заниматься первообразными и переходим у чуть более сложной теме. Если в прошлый раз мы рассматривали первообразные только от степенных функций и чуть более сложных конструкций, то сегодня мы разберем тригонометрию и многое другое.
Как я говорил на прошлом занятии, первообразные в отличие от производных, никогда не решаются «напролом» с помощью каких-либо стандартных правил. Более того, плохая новость состоит в том, что в отличие от производной, первообразная вообще может не считаться. Если мы напишем совершенно случайную функцию и попытаемся найти ее производную, то это с очень большой вероятностью у нас получится, а вот первообразная практически никогда в этом случае не посчитается. Но есть и хорошая новость: существует довольно обширный класс функций, называемых элементарными, первообразные от которых очень легко считаются. А все прочие более сложные конструкции, которые дают на всевозможных контрольных, самостоятельных и экзаменах, на самом деле, составляются из этих элементарных функций путем сложения, вычитания и других несложных действий. Первообразные таких функций давно посчитаны и сведены в специальные таблицы. Именно с такими функциями и таблицами мы будем сегодня работать.
Но начнем мы, как всегда, с повторения: вспомним, что такое первообразная, почему их бесконечно много и как определить их общий вид. Для этого я подобрал две простенькие задачки.
Решение легких примеров
Пример № 1
\[f\left( x \right)=\frac{1}{1+{{x}^{2}}}\]
\[M=\left( \sqrt{3};\frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)\]
Сразу заметим, что $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$ и вообще наличие $\text{ }\!\!\pi\!\!\text{ }$ сразу намекает нам, что искомая первообразная функции связана с тригонометрией. И, действительно, если мы посмотрим в таблицу, то обнаружим, что $\frac{1}{1+{{x}^{2}}}$ — не что иное как $\text{arctg}x$. Так и запишем:
\[F\left( x \right)=\text{arctg}x+C\]
Для того чтобы найти, необходимо записать следующее:
\[\frac{\pi }{6}=\text{arctg}\sqrt{3}+C\]
\[\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}+C\]
\[C=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}-\frac{\text{ }\!\!\pi\!\!\text{ }}{3}=-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}\]
Теперь мы окончательно можем посчитать именно ту первообразную, которая нас и интересует:
\[F\left( x \right)=\text{arctg}x-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}\]
Пример № 2
\[f\left( x \right)=\frac{1}{\sqrt{1-{{x}^{2}}}}\]
\[M=\left( \frac{1}{2};\text{ }\!\!\pi\!\!\text{ } \right)\]
Здесь также речь идет о тригонометрических функциях. Если мы посмотрим в таблицу, то, действительно, так и получится:
\[F\left( x \right)=\arcsin x+C\]
Нам нужно среди всего множества первообразных найти ту, которая проходит через указанную точку:
\[\text{ }\!\!\pi\!\!\text{ }=\arcsin \frac{1}{2}+C\]
\[\text{ }\!\!\pi\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}+C\]
\[C=\text{ }\!\!\pi\!\!\text{ }-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{6\text{ }\!\!\pi\!\!\text{ }-\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}\]
Давайте окончательно запишем:
\[F\left( x \right)=\arcsin x+\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}\]
Вот так все просто. Единственная проблема состоит в том, для того чтобы считать первообразные простых функций, нужно выучить таблицу первообразных. Однако после изучения таблицы производных для вас, я думаю, это не будет проблемой.
Поэтому идем далее и переходим к более сложным конструкциям — первообразным показательных функций.
Решение задач, содержащих показательную функцию
Для начала запишем такие формулы:
\[{{e}^{x}}\to {{e}^{x}}\]
\[{{a}^{x}}\to \frac{{{a}^{x}}}{\ln a}\]
Давайте посмотрим, как это все работает на практике.
Пример № 1
\[f\left( x \right)={{\left( {{e}^{x}}+{{e}^{-x}} \right)}^{2}}\]
Если мы посмотрим на содержимое скобок, то заметим, что в таблице первообразных нет такого выражения, чтобы ${{e}^{x}}$ стояло в квадрате, поэтому этот квадрат необходимо раскрыть. Для этого воспользуемся формулами сокращенного умножения:
\[f\left( x \right)={{\left( {{e}^{x}} \right)}^{2}}+2\cdot {{e}^{x}}\cdot {{e}^{-x}}+{{\left( {{e}^{-x}} \right)}^{2}}\]
\[f\left( x \right)={{e}^{2x}}+2+{{e}^{-2x}}\]
Давайте найдем первообразную для каждого из слагаемых:
\[{{e}^{2x}}={{\left( {{e}^{2}} \right)}^{x}}\to \frac{{{\left( {{e}^{2}} \right)}^{x}}}{\ln {{e}^{2}}}=\frac{{{e}^{2x}}}{2}\]
\[2\to 2x\]
\[{{e}^{-2x}}={{\left( {{e}^{-2}} \right)}^{x}}\to \frac{{{\left( {{e}^{-2}} \right)}^{x}}}{\ln {{e}^{-2}}}=\frac{1}{-2{{e}^{2x}}}\]
А теперь соберем все слагаемые в единое выражение и получим общую первообразную:
\[F\left( x \right)=\frac{{{e}^{2x}}}{2}+2x-\frac{1}{2{{e}^{2x}}}+C\]
Пример № 2
\[f\left( x \right)={{\left( {{2}^{x}}-{{2}^{-x}} \right)}^{3}}\]
На этот раз степень уже побольше, поэтому формула сокращенного умножения будет довольно сложной. Итак раскроем скобки:
\[f\left( x \right)={{\left( {{2}^{x}} \right)}^{3}}-3\cdot {{\left( {{2}^{x}} \right)}^{2}}\cdot {{2}^{-x}}+3\cdot {{2}^{x}}\cdot {{\left( {{2}^{-x}} \right)}^{2}}-{{\left( {{2}^{-x}} \right)}^{3}}\]
\[f\left( x \right)={{2}^{3x}}-3\cdot {{2}^{x}}+3\cdot {{2}^{-x}}-{{2}^{-3x}}\]
\[f\left( x \right)={{8}^{x}}-3\cdot {{2}^{x}}+3\cdot {{\left( \frac{1}{2} \right)}^{x}}-{{\left( \frac{1}{8} \right)}^{x}}\]
Теперь от этой конструкции попробуем взять первообразную от нашей формулы:
\[F\left( x \right)=\frac{{{8}^{x}}}{\ln 8}-3\cdot \frac{{{2}^{x}}}{\ln 2}+3\cdot \frac{{{\left( \frac{1}{2} \right)}^{x}}}{\ln \frac{1}{2}}-\frac{{{\left( \frac{1}{8} \right)}^{x}}}{\ln \frac{1}{8}}+C\]
\[F\left( x \right)=\frac{{{8}^{x}}}{\ln 8}-\frac{3\cdot {{2}^{x}}}{\ln 2}-\frac{3\cdot {{\left( \frac{1}{2} \right)}^{x}}}{2}+\frac{{{\left( \frac{1}{8} \right)}^{x}}}{3\ln 2}+C\]
Как видите, в первообразных показательной функции нет ничего сложного и сверхъестественного. Все один считаются через таблицы, однако внимательные ученики наверняка заметят, что первообразная ${{e}^{2x}}$ намного ближе просто к ${{e}^{x}}$ нежели к ${{a}^{x}}$. Так, может быть, существует какой-то более специальное правило, позволяющее, зная первообразную ${{e}^{x}}$, найти ${{e}^{2x}}$? Да, такое правило существует. И, более того, оно является неотъемлемой частью работы с таблицей первообразных. Его мы сейчас разберем на примере тех же самых выражений, с которыми мы только что работали.
Правила работы с таблицей первообразных
Еще раз выпишем нашу функцию:
\[f\left( x \right)={{\left( {{e}^{x}}+{{e}^{-x}} \right)}^{2}}={{e}^{2x}}+2+{{e}^{-2x}}\]
В предыдущем случае мы использовали для решения следующую формулу:
\[{{a}^{x}}\to \frac{{{a}^{x}}}{\operatorname{lna}}\]
Но сейчас поступим несколько иначе: вспомним, на каком сновании ${{e}^{x}}\to {{e}^{x}}$. Как уже и говорил, потому что производная ${{e}^{x}}$ — это не что иное как ${{e}^{x}}$, поэтому ее первообразная будет равна тому же самому ${{e}^{x}}$. Но проблема в том, что у нас ${{e}^{2x}}$ и ${{e}^{-2x}}$. Сейчас попытаемся найти производную ${{e}^{2x}}$:
\[{{\left( {{e}^{2x}} \right)}^{\prime }}={{e}^{2x}}\cdot {{\left( 2x \right)}^{\prime }}=2\cdot {{e}^{2x}}\]
Давайте еще раз перепишем нашу конструкцию:
\[{{\left( {{e}^{2x}} \right)}^{\prime }}=2\cdot {{e}^{2x}}\]
\[{{e}^{2x}}={{\left( \frac{{{e}^{2x}}}{2} \right)}^{\prime }}\]
А это значит, что при нахождении первообразной ${{e}^{2x}}$ мы получим следующее:
\[{{e}^{2x}}\to \frac{{{e}^{2x}}}{2}\]
Как видите, мы получили тот же результат, что и ранее, однако не воспользовались формулой для нахождения ${{a}^{x}}$. Сейчас это может показаться глупостью: зачем усложнять вычисления, когда есть стандартная формула? Однако в чуть более сложных выражениях вы убедитесь, что этот прием очень эффективен, т.е. использование производных для нахождения первообразных.
Давайте в качестве разминки аналогичным способом найдем первообразную от ${{e}^{2x}}$:
\[{{\left( {{e}^{-2x}} \right)}^{\prime }}={{e}^{-2x}}\cdot \left( -2 \right)\]
\[{{e}^{-2x}}={{\left( \frac{{{e}^{-2x}}}{-2} \right)}^{\prime }}\]
При вычислении наша конструкция запишется следующим образом:
\[{{e}^{-2x}}\to -\frac{{{e}^{-2x}}}{2}\]
\[{{e}^{-2x}}\to -\frac{1}{2\cdot {{e}^{2x}}}\]
Мы получили точно тот же результат, но пошли при этом по другому пути. Именно этот путь, который сейчас кажется нам чуть более сложным, в дальнейшем окажется более эффективным для вычисления более сложных первообразных и использование таблиц.
Обратите внимание! Это очень важный момент: первообразные как и производные можно посчитать множеством различных способов. Однако если все вычисления и выкладки будут равны, то ответ получится одним и тем же. Мы убедились в этом только что на примере ${{e}^{-2x}}$ — с одной стороны мы посчитали эту первообразную «напролом», воспользовавшись определением и посчитав ее с помощью преобразований, с другой стороны, мы вспомнили, что ${{e}^{-2x}}$ может быть представлено как ${{\left( {{e}^{-2}} \right)}^{x}}$ и уже потом воспользовались первообразной для функции ${{a}^{x}}$. Тем не менее, после всех преобразований результат получился одним и тем же, как и предполагалось.
А теперь, когда мы все это поняли, пора перейти к чему-то более существенному. Сейчас мы разберем две простенькие конструкций, однако прием, который будет заложен при их решении, является более мощным и полезным инструментом, нежели простое «беганье» между соседними первообразными из таблицы.
Решение задач: находим первообразную функции
Пример № 1
\[f\left( x \right)=\frac{1=x+{{x}^{2}}}{x\sqrt{x}}\]
Давайте сумму, которая стоит в числители, разложи на три отдельных дроби:
\[f\left( x \right)=\frac{1}{x\sqrt{x}}+\frac{x}{x\sqrt{x}}+\frac{{{x}^{2}}}{x\sqrt{x}}\]
Это довольно естественный и понятный переход — у большинства учеников проблем с ним не возникает. Перепишем наше выражение следующим образом:
\[f\left( x \right)=\frac{1}{{{x}^{1}}\cdot {{x}^{\frac{1}{2}}}}+\frac{1}{{{x}^{\frac{1}{2}}}}+{{x}^{\frac{1}{2}}}\]
\[f\left( x \right)={{x}^{-\frac{3}{2}}}+{{x}^{-\frac{1}{2}}}+{{x}^{\frac{1}{2}}}\]
А теперь вспомним такую формулу:
\[{{x}^{n}}\to \frac{{{x}^{n+1}}}{n+1}\]
В нашем случае мы получим следующее:
\[F\left( x \right)=\frac{{{x}^{-\frac{3}{2}+1}}}{-\frac{3}{2}+1}+\frac{{{x}^{-\frac{1}{2}+1}}}{-\frac{1}{2}+1}+\frac{{{x}^{\frac{1}{2}+1}}}{\frac{1}{2}+1}+C\]
\[F\left( x \right)=\frac{{{x}^{-\frac{1}{2}}}}{-\frac{1}{2}}+\frac{{{x}^{\frac{1}{2}}}}{\frac{1}{2}}+\frac{{{x}^{\frac{3}{2}}}}{\frac{3}{2}}+C\]
Чтобы избавиться от всех этих трехэтажных дробей, предлагаю поступить следующим образом:
\[F\left( x \right)=\frac{-2}{{{x}^{\frac{1}{2}}}}+2\cdot {{x}^{\frac{1}{2}}}+\frac{2{{x}^{\frac{3}{2}}}}{3}+C\]
\[F\left( x \right)=-\frac{2}{\sqrt{x}}+2\cdot \sqrt{x}+\frac{2x\sqrt{x}}{3}+C\]
Пример № 2
\[f\left( x \right)=\frac{{{x}^{2}}}{{{x}^{2}}+1}\]
В отличие от предыдущей дроби в знаменателе стоит не произведение, а сумма. В этом случае мы уже не можем разделить нашу дробь на сумму нескольких простых дробей, а нужно каким-то образом постараться сделать так, чтобы в числителе стояло примерно такое же выражение как в знаменателе. В данном случае сделать это довольно просто:
\[f\left( x \right)=\frac{{{x}^{2}}+1-1}{{{x}^{2}}+1}\]
Такая запись, которая на языке математики называется «добавление нуля», позволит нам вновь разделить дробь на два кусочка:
\[f\left( x \right)=\frac{{{x}^{2}}+1}{{{x}^{2}}+1}-\frac{1}{{{x}^{2}}+1}\]
Теперь найдем то, что искали:
\[F\left( x \right)=x-\text{arctg}x+C\]
Вот и все вычисления. Несмотря на кажущуюся большую сложность, чем в предыдущей задаче, объем вычислений получился даже меньшим.
Нюансы решения
И вот в этом кроется основная сложность работы с табличными первообразными, особенно это заметно на второй задаче. Дело в том, что для того чтобы выделить какие-то элементы, которые легко считаются через таблицу, нам нужно знать, что конкретно мы ищем, и именно в поиске этих элементов и состоит все вычисление первообразных.
Другими словами, недостаточно просто зазубрить таблицу первообразных — нужно уметь видеть что-то, чего пока еще нет, но что подразумевал автор и составитель этой задачи. Именно поэтому многие математики, учителя и профессора постоянно спорят: «А что такое взятие первообразных или интегрирование — это просто инструмент либо это настоящее искусство?» На самом деле, лично на мой взгляд, интегрирование — это никакое не искусство — в нем нет ничего возвышенного, это просто практика и еще раз практика. И чтобы попрактиковаться, давайте решим еще три более серьезных примера.
Тренируемся в интегрировании на практике
Задача № 1
\[f\left( x \right)=\frac{{{x}^{4}}}{{{x}^{2}}+1}\]
Запишем такие формулы:
\[{{x}^{n}}\to \frac{{{x}^{n+1}}}{n+1}\]
\[\frac{1}{x}\to \ln x\]
\[\frac{1}{1+{{x}^{2}}}\to \text{arctg}x\]
Давайте запишем следующее:
\[f\left( x \right)=\frac{{{x}^{4}}+{{x}^{2}}}{{{x}^{2}}+1}-\frac{{{x}^{2}}}{{{x}^{2}}+1}\]
\[f\left( x \right)=\frac{{{x}^{2}}\left( {{x}^{2}}+1 \right)}{{{x}^{2}}+1}-\frac{{{x}^{2}}+1-1}{{{x}^{2}}+1}\]
\[f\left( x \right)={{x}^{2}}-1+\frac{1}{{{x}^{2}}+1}\]
\[F\left( x \right)=\frac{{{x}^{3}}}{3}-x+3+\text{arctg}x+C\]
Задача № 2
\[f\left( x \right)=\frac{2{{x}^{2}}-3}{{{x}^{2}}+1}\]
Перепишем следующим образом:
\[f\left( x \right)=\frac{2{{x}^{2}}+2-2-3}{{{x}^{2}}+1}\]
\[f\left( x \right)=\frac{2{{x}^{2}}+2}{{{x}^{2}}+1}-\frac{5}{{{x}^{2}}+1}\]
\[f\left( x \right)=\frac{2\left( {{x}^{2}}+1 \right)}{{{x}^{2}}+1}-\frac{5}{{{x}^{2}}+1}\]
Итого первообразная будет равна:
\[F\left( x \right)=2x-5\text{arctg}x+C\]
Задача № 3
\[f\left( x \right)=\frac{1}{{{x}^{2}}\left( 1+{{x}^{2}} \right)}\]
Сложность этой задачи состоит в том, что в отличие от предыдущих функций сверху вообще отсутствует какая-либо переменная $x$, т.е. нам непонятно, что добавлять, вычитать, чтобы получить хоть что-то похожее на то, что стоит снизу. Однако, на самом деле, это выражение считается даже проще, чем любое выражение из предыдущих конструкций, потому что данную функцию можно переписать следующим образом:
\[f\left( x \right)=\frac{1}{{{x}^{2}}}-\frac{1}{{{x}^{2}}+1}\]
Возможно, вы сейчас спросите: а почему эти функции равны? Давайте проверим:
\[f\left( x \right)=\frac{1}{{{x}^{2}}}-\frac{1}{{{x}^{2}}+1}=\frac{{{x}^{2}}+1-{{x}^{2}}}{{{x}^{2}}\left( {{x}^{2}}+1 \right)}=\frac{1}{{{x}^{2}}\left( {{x}^{2}}+1 \right)}\]
Еще перепишем:
\[f\left( x \right)={{x}^{-2}}-\frac{1}{{{x}^{2}}+1}\]
Найдем:
\[F\left( x \right)=\frac{{{x}^{-1}}}{-1}-\text{arctg}x+C\]
Немного преобразуем наше выражение:
\[F\left( x \right)=-\frac{1}{x}-\text{arctg}x+C\]
И когда я все это объясняю своим ученикам, практически всегда возникает одна и та же проблема: с первой функцией все более-менее понятно, со второй тоже при везении или практике можно разобраться, но каким альтернативным сознанием нужно обладать, чтобы решить третий пример? На самом деле, не пугайтесь. Тот прием, который мы использовали при вычислении последней первообразной, называется «разложение функции на простейшие», и это очень серьезный прием, и ему будет посвящен отдельный видеоурок.
А пока предлагаю вернуться к тому, что мы только что изучили, а именно, к показательным функциям и несколько усложнить задачи с их содержанием.
Более сложные задачи на решение первообразных показательных функций
Задача № 1
\[f\left( x \right)={{2}^{x}}\cdot {{5}^{x}}\]
Заметим следующее:
\[{{2}^{x}}\cdot {{5}^{x}}={{\left( 2\cdot 5 \right)}^{x}}={{10}^{x}}\]
\[f\left( x \right)={{10}^{x}}\]
Чтобы найти первообразной этого выражения, достаточно просто воспользоваться стандартной формулой — ${{a}^{x}}\to \frac{{{a}^{x}}}{\ln a}$.
В нашем случае первообразная будет такая:
\[F\left( x \right)=\frac{{{10}^{x}}}{\ln 10}+C\]
Разумеется, на фоне той конструкции, которую мы решали только что, эта выглядит более простой.
Задача № 2
\[f\left( x \right)=\frac{{{8}^{x}}-{{9}^{x}}}{{{6}^{x}}}\]
Опять же, несложно заметить, что эту функцию несложно разделить на два отдельных слагаемых — две отдельных дроби. Перепишем:
\[f\left( x \right)=\frac{{{8}^{x}}}{{{6}^{x}}}-\frac{{{9}^{x}}}{{{6}^{x}}}={{\left( \frac{8}{6} \right)}^{x}}-{{\left( \frac{9}{6} \right)}^{x}}={{\left( \frac{4}{3} \right)}^{x}}-{{\left( \frac{3}{2} \right)}^{x}}\]
Осталось найти первообразную от каждого от этих слагаемых по вышеописанной формуле:
\[F\left( x \right)\frac{{{\left( \frac{4}{3} \right)}^{x}}}{\ln \frac{4}{3}}-\frac{{{\left( \frac{3}{2} \right)}^{x}}}{\ln \frac{3}{2}}+C\]
Несмотря на кажущуюся большую сложность показательных функций по сравнению со степенными, общий объем вычислений и выкладок получился гораздо проще.
Конечно, для знающих учеников то, что мы только что разобрали (особенно на фоне того, что мы разобрали до этого), может показаться элементарными выражениями. Однако выбирая именно две эти задачи для сегодняшнего видеоурока, я не ставил себе цель рассказать вам еще один сложный и навороченный прием — все, что я хотел вам показать, так это то, что не стоит бояться использовать стандартные приемы алгебры для преобразования исходных функций.
Использование «секретного» приема
В заключение хотелось бы разобрать еще один интересный прием, который, с одной стороны выходит за рамки того, что мы сегодня в основном разбирали, но, с другой стороны, он, во-первых, отнюдь не сложный, т.е. его могут освоить даже начинающие ученики, а, во-вторых, он довольно часто встречается на всевозможных контрольных и самостоятельных работах, т.е. знание его будет очень полезно в дополнение к знанию таблицы первообразных.
Задача № 1
\[f\left( x \right)={{\left( x-5 \right)}^{4}}\]
Очевидно, что перед нами что-то очень похожее на степенную функцию. Как нам поступить в этом случае? Давайте задумаемся: $x-5$ отличается от $x$ не так уж и сильно — просто добавили $-5$. Запишем так:
\[{{x}^{4}}\to \frac{{{x}^{5}}}{5}\]
\[{{\left( \frac{{{x}^{5}}}{5} \right)}^{\prime }}=\frac{5\cdot {{x}^{4}}}{5}={{x}^{4}}\]
Давайте попробуем найти производную от ${{\left( x-5 \right)}^{5}}$:
\[{{\left( {{\left( x-5 \right)}^{5}} \right)}^{\prime }}=5\cdot {{\left( x-5 \right)}^{4}}\cdot {{\left( x-5 \right)}^{\prime }}=5\cdot {{\left( x-5 \right)}^{4}}\]
Отсюда следует:
\[{{\left( x-5 \right)}^{4}}={{\left( \frac{{{\left( x-5 \right)}^{5}}}{5} \right)}^{\prime }}\]
В таблице нет такого значения, поэтому мы сейчас сами вывели эту формулу, используя стандартную формулу первообразной для степенной функции. Давайте так и запишем ответ:
\[F\left( x \right)=\frac{{{\left( x-5 \right)}^{5}}}{5}+C\]
Задача № 2
\[f\left( x \right)={{\left( 4-3x \right)}^{9}}\]
Многим ученикам, которые посмотрят на первое решение, может показаться, что все очень просто: достаточно заменить в степенной функции $x$ на линейное выражение, и все станет на свои места. К сожалению, все не так просто, и сейчас мы в этом убедимся.
По аналогии с первым выражением запишем следующее:
\[{{x}^{9}}\to \frac{{{x}^{10}}}{10}\]
\[{{\left( {{\left( 4-3x \right)}^{10}} \right)}^{\prime }}=10\cdot {{\left( 4-3x \right)}^{9}}\cdot {{\left( 4-3x \right)}^{\prime }}=\]
\[=10\cdot {{\left( 4-3x \right)}^{9}}\cdot \left( -3 \right)=-30\cdot {{\left( 4-3x \right)}^{9}}\]
Возвращаясь к нашей производной, мы можем записать:
\[{{\left( {{\left( 4-3x \right)}^{10}} \right)}^{\prime }}=-30\cdot {{\left( 4-3x \right)}^{9}}\]
\[{{\left( 4-3x \right)}^{9}}={{\left( \frac{{{\left( 4-3x \right)}^{10}}}{-30} \right)}^{\prime }}\]
Отсюда сразу следует:
\[F\left( x \right)=\frac{{{\left( 4-3x \right)}^{10}}}{-30}+C\]
Нюансы решения
Обратите внимание: если в прошлый раз по сути ничего не поменялось, то во втором случае вместо $-10$ появилось $-30$. На что отличается $-10$ и $-30$? Очевидно, что на множитель $-3$. Вопрос: откуда он взялся? Присмотревшись можно увидеть, что она взялась в результате вычислений производной сложной функции — тот коэффициент, который стоял при $x$, появляется в первообразной внизу. Это очень важное правило, которое я изначально вообще не планировал разбирать в сегодняшнем видеоуроке, но без него изложение табличных первообразных было бы неполным.
Итак, давайте еще раз. Пусть есть наша основная степенная функция:
\[{{x}^{n}}\to \frac{{{x}^{n+1}}}{n+1}\]
А теперь вместо $x$ давайте подставим выражение $kx+b$. Что тогда произойдет? Нам нужно найти следующее:
\[{{\left( kx+b \right)}^{n}}\to \frac{{{\left( kx+b \right)}^{n+1}}}{\left( n+1 \right)\cdot k}\]
На каком основании мы это утверждаем? Очень просто. Давайте найдем производную написанной выше конструкции:
\[{{\left( \frac{{{\left( kx+b \right)}^{n+1}}}{\left( n+1 \right)\cdot k} \right)}^{\prime }}=\frac{1}{\left( n+1 \right)\cdot k}\cdot \left( n+1 \right)\cdot {{\left( kx+b \right)}^{n}}\cdot k={{\left( kx+b \right)}^{n}}\]
Это то самое выражение, которое изначально и было. Таким образом, эта формула тоже верна, и ею можно дополнить таблицу первообразных, а лучше просто запомнить всю таблицу.
Выводы из «секретного: приема:
- Обе функции, которые мы только что рассмотрели, на самом деле, могут быть сведены к первообразным, указанным в таблице, путем раскрытия степеней, но если с четвертой степенью мы еще более-менее как-то справимся, то вот девятую степень я бы вообще не рискнул раскрывать.
- Если бы мы раскрыли степени, то мы бы получили такой объем вычислений, что простая задача заняла бы у нас неадекватно большое количество времени.
- Именно поэтому такие задачи, внутри которых стоят линейные выражения, не нужно решать «напролом». Как только вы встречаете первообразную, которая отличается от той, что в таблице, лишь наличием выражения $kx+b$ внутри, сразу вспоминайте написанную выше формулу, подставляйте ее в вашу табличную первообразную, и все у вас получится намного быстрее и проще.
Естественно, в силу сложности и серьезности этого приема мы еще неоднократно вернемся к его рассмотрению в будущих видеоуроках, но на сегодня у меня все. Надеюсь, этот урок действительно поможет тем ученикам, которые хотят разобраться в первообразных и в интегрировании.
До новых встреч!
Смотрите также:
- Первообразная функции

- Интегрирование по частям

- Пробный ЕГЭ 2012. Вариант 3 (без логарифмов)

- Что такое ЕГЭ по математике 2011 и как его сдавать

- Что такое ЕГЭ по математике 2012

- Быстрое возведение чисел в квадрат без калькулятора

www.berdov.com
Первообразная функции. Формула Ньютона-Лейбница — подготовка к ЕГЭ по Математике
Функция F(x), для которой f(x) является производной, называется первообразной функции y = f(x). Функции вида у = F(x) + C образуют множество первообразных функции у = f(x).
Сейчас объясним, что это значит.
Вспомним таблицу производных. В левой колонке — функции, в правой — их производные. Например, — производная от функции , — производная функции . А чем будет являться для функции ? Или — для функции ? Вы уже догадались. Первообразной.
Заметим, кстати, что — производная не только функции , но и функций , — в общем, всех функций вида Здесь C — константа, то есть постоянная величина, и ее производная равна нулю.
Аналогично, функция — производная для всех функций вида , где — константа.
Посмотрим на таблицу первообразных. Каждая функция в левом столбце таблицы является производной для функции в правом столбце.
Таблица первообразных

Первообразная суммы функций равна сумме их первообразных.
Первообразная разности функций — разности первообразных.
Первообразная от функции , где — постоянный множитель, равна произведению на первообразную функции , то есть .
Множество всех первообразных функции называется неопределенным интегралом данной функции. Записывается это так:
Нахождение первообразной называется также интегрированием функции. А нахождение производной — дифференцированием функции. Интегрирование (то есть нахождение первообразной) и дифференцирование (взятие производной) — взаимно-обратные действия.
Но интегралы — отдельная тема. В задачах ЕГЭ по математике неопределенные интегралы не встречаются, а теме «Первообразная» посвящено всего несколько задач в первой части ЕГЭ. Для их решения надо знать только таблицу первообразных и еще одну важную формулу.
Формула для вычисления площади под графиком функции (Формула Ньютона-Лейбница)
Пусть в прямоугольной системе координат задана фигура, ограниченная графиком непрерывной функции , осью и прямыми и . Пусть функция неотрицательна на отрезке [a; b].

Тогда площадь этой фигуры вычисляется по формуле:
Такую фигуру называют еще криволинейной трапецией. А сама формула носит название «Формула Ньютона-Лейбница».
1. Значение первообразной функции в точке 0 равно 6. Найдите .
Найдем первообразную функции с помощью таблицы первообразных. Получим:
При получим:
Значит, и
Ответ: 40,5
2. Значение первообразной функции в точке 0 равно -13. Найдите
Найдем первообразную функции с помощью таблицы первообразных. Получим:
При x = 0 получим: Значит, и
Ответ: -14
3. На рисунке изображен график функции . Найдите значение выражения , где — одна из первообразных функции .

По формуле Ньютона-Лейбница, разность первообразных — это площадь, ограниченная графиком функции, осью X и прямыми y=a и y=b.
В этой задаче нужная фигура ограничена графиком функции, осью и прямыми и . Это квадратик, и площадь его равна 4.
Ответ: 4.
4. На рисунке изображён график некоторой функции . Функция — одна из первообразных функции . Найдите площадь закрашенной фигуры.

Решение. По формуле Ньютона-Лейбница, площадь под графиком функции на отрезке [a,b] равна разности значений первообразной в концах отрезка, то есть
В нашей задаче имеем:
Дальше — просто арифметика.
Ответ: 13,5.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Таблица первообразных
Таблица первообразных («интегралов»). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.
Таблица первообразных («интегралов»). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). | |
Интеграл степенной функции. |
Интеграл степенной функции. |
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
|
|
Интеграл экспоненциальной функции. |
Интеграл экспоненты, где a-постоянное число. |
Интеграл сложной экспоненциальной функции. |
Интеграл экспоненциальной функции. |
|
|
Интеграл, равняющийся натуральному логорифму. | Интеграл : «Длинный логарифм». |
| Интеграл : «Длинный логарифм». |
Интеграл : «Высокий логарифм». |
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму. |
Интеграл : «Высокий логарифм». |
|
|
|
Интеграл косинуса. |
Интеграл синуса. |
Интеграл, равный тангенсу. |
Интеграл, равный котангенсу. |
|
|
Интеграл, равный как арксинусу, так и арккосинусу |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
Интеграл, равный как арксинусу, так и арккосинусу. |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
|
Интеграл равный косекансу. | Интеграл, равный секансу. |
Интеграл, равный арксекансу. |
Интеграл, равный арккосекансу. |
Интеграл, равный арксекансу. |
Интеграл, равный арксекансу. |
|
|
Интеграл, равный гиперболическому синусу. |
Интеграл, равный гиперболическому косинусу. |
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
Интеграл, равный гиперболическому синусу, где sinhx — гиперболический синус в ангийской версии. |
Интеграл, равный гиперболическому косинусу, где sinhx — гиперболический синус в ангийской версии. |
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
Интеграл, равный гиперболическому секансу. |
Интеграл, равный гиперболическому косекансу. |
Формулы интегрирования по частям. Правила интегрирования.
Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования. | |
Интегрирование произведения (функции) на постоянную: |
|
Интегрирование суммы функций: |
|
Формула интегрирования по частям неопределенные интегралы: |
|
Формула интегрирования по частям определенные интегралы: |
|
Формула Ньютона-Лейбница определенные интегралы: | Где F(a),F(b)-значения первообразных в точках b и a соответственно. |
Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.
Если x — независимая переменная, то:
Таблица производных. Табличные производные.»таблица производный»-да, к сожалению, именно так их и ищут в интернете | |
|
|
| |
|
|
|
|
| |
|
|
|
Производная натурального логарифма функции |
| |
|
|
|
|
| |
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|
|
Правила дифференцирования. Производная произведения. Производная частного. Производная сложной функции. | |
Производная произведения (функции) на постоянную: |
|
Производная суммы (функций): |
|
Производная произведения (функций): |
|
Производная частного (функций): |
|
Производная сложной функции: |
|
Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
Основное логарифмическое тождество |
|
Покажем как можно любую функцию вида ab сделать экспоненциальной. Поскольку функция вида ех называется экспоненциальной, то |
|
Любая функция вида a b может быть представлена в виде степени десяти |
|
Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045… ) ln(e)=1; ln(1)=0
При |
| логарифм числа (1+х) разлагается в ряд: |
| ||
Например, | ||
| ||
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:


При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1) ,
где f(x) — функция, имеющая при х=а производные
всех порядков. Rn — остаточный член в ряде Тейлора
определяется выражением
,
где f(x) — функция, имеющая при х=а производные
всех порядков. Rn — остаточный член в ряде Тейлора
определяется выражением 
2)
k-тый коэффициент (при хk) ряда определяется формулой

3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при
a=0 
члены ряда определяются по формуле

Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:

Ряды Тейлора применяются при аппроксимации ( приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Первые члены разложений основных функций в ряды Тейлора и Макларена.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена( =Макларена, Тейлора в окрестностях точки 0)
Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1
studfile.net
Интегрирование по частям ℹ️ правило вычисления для сложных функций, формула, методы и способы нахождения первообразной, примеры решений

Общая информация

В математике существуют функции, которые не поддаются интегрированию простыми методами. Некоторые алгоритмы также неприменимы в этом случае. Специалисты рекомендуют освоить нахождение первообразной на простых примерах. Этот принцип называется переходом от простого к сложному. Невозможно, не зная основ, переходить к решению сложных задач.
На начальных этапах обучения следует руководствоваться некоторыми правилами и алгоритмами. Их нужно освоить, и безошибочно решать простые задачи. Кроме того, следует разобраться в основном предназначении интеграла, и понять его геометрический смысл. Очень часто новички пытаются найти первообразную сложной функции. Некоторые пользуются информацией из интернета, которая бывает недостоверной. Но у них ничего не получается. Объяснение такому поражению — неверное обучение и отсутствие опыта.
Использование интеграла
Во многих дисциплинах применяется интеграл. Он обозначается литерой или символом «∫», и считается единицей дифференциального исчисления. Выражение (функция), которое идет после этого знака, называется подынтегральным. Его ограничением является знак дифференциала, т. е. «dx» или «dy». Под дифференциалом стоит переменная, по которой происходит поиск первообразной. Интегралом функции вида z = y (x) называется функция вида Y (x) с учетом константы «С» (Y (x) + C). Необходимо отметить, что Y (x) + C является первообразной функции y (x), которая была получена при дифференцировании.

Интегрирование очень часто применяется для нахождения площадей разнообразных фигур, когда невозможно воспользоваться какой-либо формулой. Например, площадь криволинейной трапеции следует искать толь при помощи операции интегрирования. Кроме того, при помощи данного метода выполняется нахождение объемов тел, пройденного пути при равноускоренном движении и т. д.
Следует отметить, что интегралы бывают двух типов: неопределенные и определенные. Вторые отличаются от первых конечным результатом, который является не первообразной, а некоторым численным значением. Если интеграл определенный, то необходимо воспользоваться формулой Ньютона — Лейбница, подставив в нее некоторые значения или границы. Она имеет такой вид с ограничениями a и b: F (y) = F (b) — F (a). Значение определенного интеграла соответствует разности первообразных, в которые подставляются верхняя и нижняя границы.
Интегралы бывают также собственными и несобственными. К первому типу относятся определенные интегралы, ограничениями которого являются область интегрирования и его подынтегральное выражение. Несобственный — интеграл определенного типа, который ограничен подынтегральным выражением или областью его интегрирования.
Геометрический смысл интеграла — площадь трапеции криволинейного типа. Стороной или сторонами фигуры являются кривые прямые. В этом случае найти площадь не удастся, поскольку формулы для этого не предусмотрены. Криволинейной называется плоская фигура, которая ограничена системой координат, неотрицательной функцией, а также прямыми. Значения ограничений нужно подставлять в формулу Ньютона — Лейбница. Фигура состоит из множества частей прямоугольной формы. При интегрировании их площади складываются, образуя общую площадь S.
Методика нахождения первообразной
Определение первообразной зависит от самой функции. Если она является элементарной, то для этого используется только простейший алгоритм, состоящий из двух шагов. Первым этапом является упрощение выражения, а вторым — определение исходной функции по таблице интегралов.

Некоторые выражения имеют свойство инвариантности, т. е. остаются неизменными при дифференцировании и интегрировании (экспонента в степени, которой является аргумент — e^x). В случае, когда подынтегральное выражение является сложным, то нужно применять специальный метод интегрирования по частям. Методика позволяет находить решения с высокой долей вероятности. Однако бывают функции очень сложные. При этом нужно применять метод замены, а затем правило интегрирования по частям.
Теорема имеет такую формулировку: первообразная сложной функции F (z, y) соответствует произведению ее составных элементов без интеграла, последнего элемента по первому. Следствие из нее — формула, позволяющая искать производную сложной функции. Пусть даны две непрерывные функции z = z (x) и y = y (x), имеющие производные. Соотношение необходимо рассматривать следующим образом: d (zy) = zdy + ydz. Нужно найти первообразные двух частей: ∫d (zy) = ∫(zdy + ydz). Произведение двух функций равно zy = ∫zdy + ∫ydz. Окончательная формула интегрирования по частям имеет такой вид: ∫zdy = zy — ∫ydz.
Формула применяется, когда невозможно найти первообразную какой-либо функции. Примером для интегрирования по частям является y = x * e^(2x). Однако не во всех случаях можно разобраться, когда стоит применять формулу. Ведь при неверном пути решения задания можно потерять много времени. Специалисты классифицировали функции, которые необходимо интегрировать по частям:

- Любой логарифм, умноженный на переменную или многочлен с неизвестным [z = (x 2 — 2x) * ln (x — 2)].
- Произведение переменной (многочлена с неизвестным) на функцию, имеющую экспоненциальный или показательный вид [f = (y — 2)^(3) — e^y].
- Частное (деление) или произведение аргумента на тригонометрическое выражение [y = x * cos (2x 2 )].
- Дробь, в которой числитель и знаменатель состоит из переменных [v = (x 2 — 3x + 7) / x 4 — 5x 3 + 12x + 7)].
Необходимо также отметить, что в первом и во втором видах сложных функций, необязательно должно быть произведение. Оно может рассматриваться в виде дроби, умноженной на выражение.
Например, уравнение с натуральным логарифмом y = ln (x) / (x 2 — 4) можно записать в виде произведения (1 / (x 2 — 4)) * ln (x). Для нахождения первообразной умножения длинного натурального логарифма на переменную также нужно применять этот метод.
В некоторых случаях необходимо осуществлять замену выражения, которое находится под знаком интеграла, а затем, в зависимости от самой замены, находить значение по таблице первообразных или использоваться способ интегрирования по частям. Очень важно правильно определить алгоритм решения, поскольку он избавит от циклического разложения на множители и прочих операций.
Рекомендации специалистов
Для оптимизации нахождения первообразной или ее вычисления необходимо воспользоваться некоторыми советами математиков. Только правильное решение поможет успешно перейти от простых задач к сложным. К ним можно отнести следующие:

- Нет необходимости заучивать таблицу интегралов.
- Разобраться в основных правилах интегрирования на примере элементарных функций.
- Использовать специализированное программное обеспечение только при проверке решения.
- Действовать по алгоритму, который предназначен для решения конкретного типа задач.
- Больше практики.
Следует отметить, что для нахождения первообразной применяется ручной и автоматизированный способы. Первый из них — решение задач самостоятельно, а второй — использование программного обеспечения. Специалисты рекомендуют универсальное онлайн web-приложение. Оно называется INTEGRAL CALCULATOR. Существует и офлайн-версия, которую поддерживают операционные системы Android, Windows, Mac и Linux. Кроме того, есть обыкновенный онлайн-калькулятор интегралов. Его следует использовать, когда нужно вычислять или находить первообразные.
Основное отличие онлайн от офлайн заключается в том, что в первом случае должно быть соединение с интернетом, а во втором — приложение устанавливается на жесткий диск. Оно позволяет находить первообразные, производные и т. д. При ручном методе решения следует руководствоваться подробным универсальным алгоритмом нахождения первообразной сложной функции по частям для неопределенного интеграла:
- Вынести константу за пределы интеграла.
- Выполнить математические преобразования, которые позволяют упростить подынтегральное выражение.
- Обозначить функции для подготовки к применению формулы интегрирования по частям.
- Выполнить интегрирование по формуле.
- Записать результат.
- Проверить с помощью приложения.
- При неверном решении проверить работоспособность программы, используя табличные значения.
- Найти ошибку, и вернуться в тот пункт алгоритма, в котором она допущена. Иногда требуется выполнить решение с самого начала.
На третьем шаге алгоритма необходимо правильно определить параметры, поскольку это может существенно замедлить решение. Следует выбрать выражение, которое будет легко дифференцироваться и интегрироваться по частям. Например, в функции v = (x 2 ) * sin (2x) части следует выбирать таким образом: z = x 2 и y = sin (2x).

К разбиению на части следует подходить с логической стороны. Нужно выписать формулу ∫zdy = zy — ∫ydz. В ней проще всего найти производную функции x 2, а не sin (2x). Для определенного интеграла алгоритм похож на предыдущий, но имеет некоторые отличия:
- Выполнить первые четыре пункта.
- Вычислить значения по формуле Ньютона — Лейбница.
- Осуществить шаги с 5 по 8-й пункт предыдущего алгоритма.
Специалисты рекомендуют выписать эти алгоритмы на отдельный лист, который должен быть постоянно в поле зрения. При регулярных тренировках надобность в «шпаргалке» отпадает. Если интеграл является собственным, то необходимо внимательно следить за решением, поскольку ограничением является также его подынтегральное выражение.
Примером является определенный интеграл с границами от -1 до 5 вида ∫(1/x)dy. В этом случае переменная не должна быть равна 0, поскольку превращает подынтегральную функцию в пустое множество. Для этого следует рассматривать сумму двух интегралов, а x = 0 следует исключить, взяв предел. Первый интеграл имеет такие границы: нижняя — (-1), а верхняя — x стремится к 0 (х->0). Для второго выражения нижней границей является x->0, а верхней — 5.
Примеры решения
Необходимо вычислить интеграл функции v = x * ln (x). Если границы не обозначены, то интеграл является неопределенным. Для этого следует воспользоваться универсальным алгоритмом нахождения первообразной по частям:

- Преобразования не нужно выполнять. Подынтегральное выражение состоит из произведения функций, которые являются табличными.
- Обозначения: z = ln (x), y = x, dz = [ln (x)]’ = (1/x)dx, dy = [x]’ = dx.
- Подставить в формулу: ∫zdy = zy — ∫ydz = ln (x) * x — ∫(x * (1/x))dx = ln (x) * x — ∫dx = ln (x) * x — x + С= x (ln (x) — 1) + С.
- Если воспользоваться онлайн-калькулятором интегралов, то видно, что решения совпадают. Следовательно, задача решена правильно.
Нужно проинтегрировать функцию u = (x — 9) * e^(3x). Следует обратить внимание на выражение e^(3x), поскольку оно является сложным. Для решения рекомендуется применить также универсальный алгоритм:
- Необходимость в упрощении выражения отсутствует.
- Ввести обозначения: z = x — 9, dy = e^(3x), dz = dx и y = ∫(e^(3x))dx = (1/3) * e^(3x).
- Интегрирование: ∫zdy = zy — ∫ydz = (1/3) * (x — 9) * e^(3x) — (1/3) * ∫(e^(3x))dx =(1/3) * (x — 9) * e^(3x) — (1/3) * (1/3) * e^(3x) + С = [(e^(3x) * (3x — 28)) / 9] + С.
Если проверить результат с помощью INTEGRAL CALCULATOR, то решения совпадут. Очень важно анализировать функции, и следить за знаками. Например, необходимо также учитывать, что e^(-x) является также сложной. Ее первообразная соответствует -e^(-x).
Таким образом, интегрирование по частям следует применять в том случае, когда обыкновенные методы поиска первообразной не дают результата. Метод используется для понижения сложности подынтегрального выражения. Его можно применять неограниченное количество раз для одной функции.
nauka.club
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Интегральное и дифференциальное исчисление. Табличные производные и интегралы. Таблица производных. Таблица интегралов. Таблица первообразных. Найти производную. Найти интеграл. Диффуры. / / Таблица первообразных. Таблица интегралов. Таблица неопределенных интегралов. Формулы интегралов. Формулы первообразных. Поделиться:
| ||||||||
dpva.ru













































 Производная
степенной функции
Производная
степенной функции Производная
степенной функции
Производная
степенной функции Производная
экспоненциальной функции
Производная
экспоненциальной функции Производная
экспоненты
Производная
экспоненты Производная
сложной экспоненциальной функции
Производная
сложной экспоненциальной функции Производная
экспоненциальной функции
Производная
экспоненциальной функции Производная
логарифмической функции
Производная
логарифмической функции Производная
натурального логарифма
Производная
натурального логарифма
 Производная
синуса
Производная
синуса Производная
косинуса
Производная
косинуса Производная
косеканса
Производная
косеканса Производная
секанса
Производная
секанса Производная
арксинуса
Производная
арксинуса Производная
арккосинуса
Производная
арккосинуса Производная
арксинуса
Производная
арксинуса Производная
арккосинуса
Производная
арккосинуса Производная
тангенса
Производная
тангенса Производная
котангенса
Производная
котангенса Производная
арктангенса
Производная
арктангенса Производная
арккотангенса
Производная
арккотангенса Производная
арктангенса
Производная
арктангенса Производная
арккотангенса
Производная
арккотангенса Производная
арксеканса
Производная
арксеканса Производная
арккосеканса
Производная
арккосеканса Производная
арксеканса
Производная
арксеканса Производная
арккосеканса
Производная
арккосеканса Производная
гиперболического синуса
Производная
гиперболического синуса Производная
гиперболического синуса в английской
версии
Производная
гиперболического синуса в английской
версии Производная
гиперболического косинуса
Производная
гиперболического косинуса Производная
гиперболического косинуса в английской
версии
Производная
гиперболического косинуса в английской
версии Производная
гиперболического тангенса
Производная
гиперболического тангенса Производная
гиперболического котангенса
Производная
гиперболического котангенса Производная
гиперболического секанса
Производная
гиперболического секанса Производная
гиперболического косеканса
Производная
гиперболического косеканса











