Формулы по физике кинематика 9 класс: Ошибка: 404 Материал не найден — Детская игровая комната «Волшебный лес»

Posted on 14.08.201917.04.2021 by alexxlab

Содержание

9 класс Формулы Формула Название Обозначение и единицы измерения в СИ Путь при равномерном прямолинейном движении

Образовательный минимум

триместр предмет физика класс 9т Образовательный минимум Основные понятия Движения тела по вертикали, брошенного под углом к горизонту, горизонтально. Движение по с постоянной по модулю скоростью. Центростремительное

Подробнее Рабочая программа по физике 9 класс
Государственное бюджетное общеобразовательное учреждение Республики Хакасия «Хакасская национальная гимназия-интернат им. Н.Ф.Катанова» «СОГЛАСОВАНО» УТВЕРЖДЕНО на заседании МО естественно — математических
Подробнее СОДЕРЖАНИЕ ПРОГРАММЫ I.
Данная программа учебного предмета «Физика» для обучающихся 9 класса разработана на основе требований к результатам освоения ООП ООО МКОУ «Большеокинская СОШ» в соответствии с ФК ГОС ООО (2004 г.). Планируемые
Подробнее Пояснительная записка
Пояснительная записка Программа составлена в соответствии с Федеральным компонентом государственного стандарта основного общего образования по физике (Приказ Минобразования России от 05.03.2004 089 «Об
Подробнее Пояснительная записка
Пояснительная записка Данная программа учебного предмета «Физика» для обучающихся 9 класса муниципального казённого общеобразовательного учреждения «Большеокинская СОШ» разработана на основе авторской
Подробнее

Требования к уровню подготовки учащихся
Требования к уровню подготовки учащихся В результате изучения физики ученик должен знать/понимать: смысл понятий: физическое явление, физический закон, взаимодействие, электрическое поле, магнитное поле,
Подробнее Требования к уровню подготовки учащихся
Ученик должен знать/понимать: уметь Требования к уровню подготовки учащихся смысл понятий: физическое явление, физический закон, взаимодействие, электрическое поле, магнитное поле, волна, атом, атомное
Подробнее НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ МАТЕРИАЛ
НЕКОММЕРЧЕСКАЯ ОРГАНИЗАЦИЯ «АССОЦИАЦИЯ МОСКОВСКИХ ВУЗОВ» ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОДЕЗИИ И КАРТОГРАФИИ НАУЧНО-ОБРАЗОВАТЕЛЬНЫЙ
Подробнее ФИЗИКА.
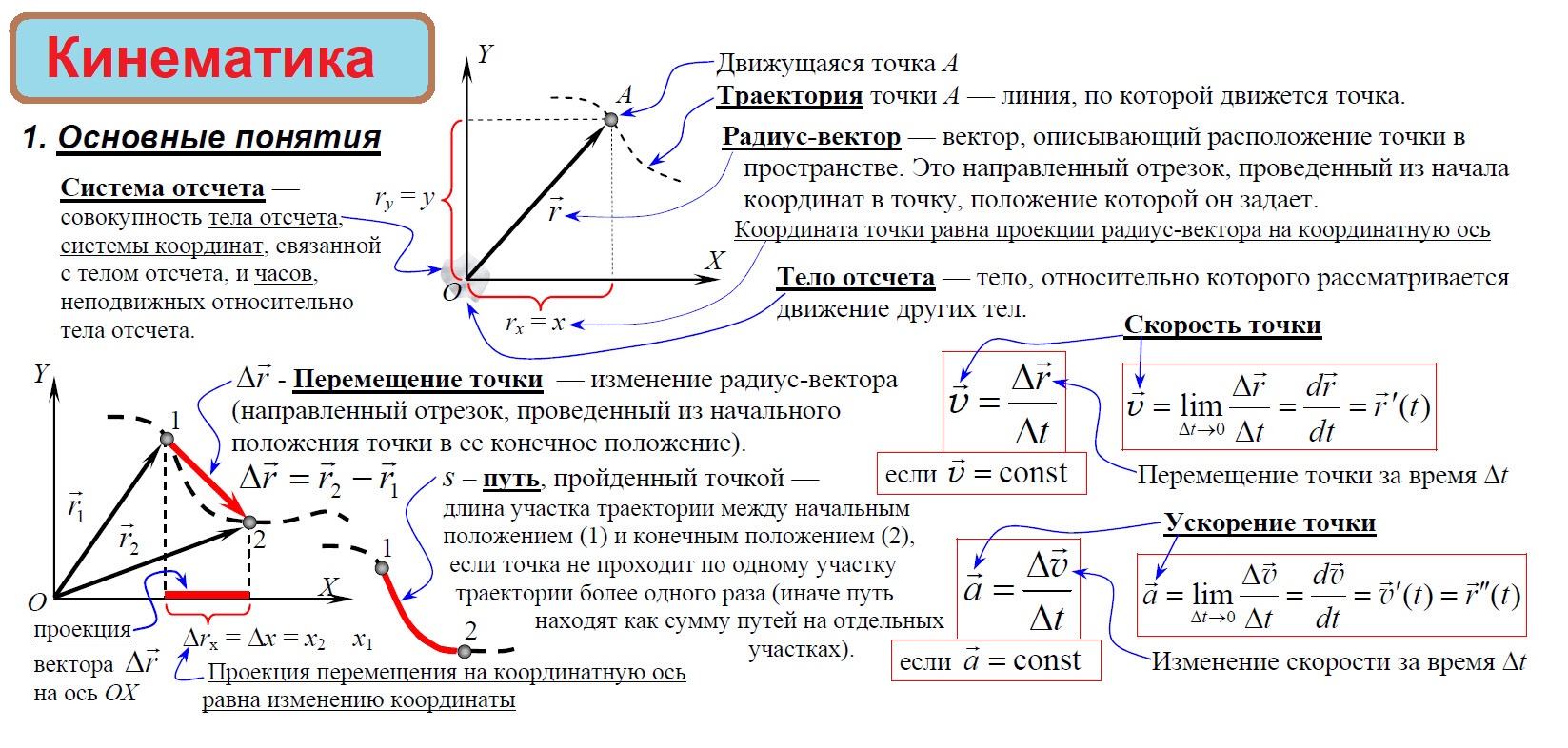Темы вступительного собеседования
ФИЗИКА Темы вступительного собеседования для поступления в 9 класс Механическое движение (равномерное и неравномерное) и его основные характеристики (путь, перемещение, траектория, скорость, величин. Взаимодействие
Подробнее Рабочая программа по физике в 9 классе
Муниципальное общеобразовательное бюджетное учреждение «Восточненская средняя общеобразовательная школа» Тындинского района Рабочая программа по физике в 9 классе Учитель: Константинова Галина Дмитриевна
Подробнее УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН Название Колво Изучение Кол- Кол- раз. нового и во во час. закрепление к/р л/р 1 Законы взаимодействия и движения тел 43 39 2 2 2 Механические колебания и волны. Звук. 12 10 1
Подробнее учебный год
Приложение к рабочей программе по физике для 9 класса Примерные оценочные и методические материалы для осуществления текущего контроля успеваемости и промежуточной аттестации учащихся 9-го класса по физике
Подробнее Структура и содержание. Паспорт
Спецификация оценочных материалов для проведения тематических контрольных работ по физике в 9 классе Структура и содержание Паспорт Раздел, тема Проверяемые компетенции (из рабочей программы) Вид оценочных
Подробнее Пояснительная записка
2 Пояснительная записка Рабочая программа составлена на основе программы «Физика, 9 класс, Грачев А.В., Погожев В.А., Селиверстов А.В., 2011 г. — В кн. Грачев А.В., Погожев В.А., Селиверстов А.В. Физика:
Подробнее Пояснительная записка
Пояснительная записка Рабочая программа составлена на основе регионального базисного учебного плана для общеобразовательных учебных учреждений Курской области. Основой для составления программы по физике
Подробнее Powered by TCPDF (www.tcpdf.org)
Powered by TCPDF (www.tcpdf.org) Пояснительная записка. Статус программы Данная рабочая программа по физике составлена на основе «Программы основного общего образования. Физика. 7-9 классы», авторы: А.
Подробнее ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Тематическое планирование составлено на основе Федерального компонента государственного стандарта среднего (полного) общего образования в соответствии с пособием «Программы основного
Подробнее «Школа 32» г.н.новгород
Муниципальное бюджетное общеобразовательное учреждение «Школа 32» г.н.новгород РАБОЧАЯ ПРОГРАММА ПЕДАГОГА по физике 9 класса 2016 2017 учебный год Рабочая программа для 9 класса составлена в соответствии
Подробнее Планируемые результаты изучения физики в 9 классе: Выпускник научится использовать термины: физическое явление, физический закон, вещество,
Планируемые результаты изучения физики в 9 классе: Выпускник научится использовать термины: физическое явление, физический закон, вещество, взаимодействие, электрическое поле, магнитное поле, волна, атом,
Подробнее

Пояснительная записка
Пояснительная записка Физика как наука о наиболее общих законах природы, выступая в качестве учебного предмета в школе, вносит существенный вклад в систему знаний об окружающем мире. Она раскрывает роль
Подробнее РАБОЧАЯ ПРОГРАММА. по физике. 9 класс
Муниципальное бюджетное общеобразовательное учреждение «Школа 20» «Рассмотрено» на заседании школьного методического объединения Председатель: Борисова А. В. Протокол 30.08.207г. «Согласовано» заместитель
Подробнее «МЕХАНИКА 1» Величины в формуле
Величина, её определение Обозначение Единица измерения «МЕХАНИКА 1» Формла Величины в формле ВИДЫ ДВИЖЕНИЯ I. Равномерное прямолинейное движение-это движение, при котором тело за любые равные промежтки
Подробнее Равноускоренное движение, вектор ускорения, направление, перемещение. Формулы, определение, законы
Тестирование онлайн
Равноускоренное движение
В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение — это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое «равно ускоряется». Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово «равно», получим равное увеличение скорости. А как понимать «равное увеличение скорости», как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.
Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую — 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).
Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью — замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.
Равноускоренное движение — это такое движение тела, при котором его скорость за любые равные промежутки времени
изменяется (может увеличиваться или уменьшаться) одинаково
Ускорение тела
Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение — это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.
Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй — 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды — 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:
Формула записана не в векторном виде, поэтому знак «+» пишем, когда тело ускоряется, знак «-» — когда замедляется.
Направление вектора ускорения
Направление вектора ускорения изображено на рисунках
На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.
При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.
На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.
При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.
Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.
При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус»!!!
Перемещение при равноускоренном движении
Дополнительная формула, которую называют безвременной
Формула в координатах
Связь со средней скоростью
При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости
Из этого правила следует формула, которую очень удобно использовать при решении многих задач
Соотношение путей
Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.
Главное запомнить
1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение — вектор. Если тело разгоняется ускорение положительное, если замедляется — ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ
Упражнения
Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?
Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго — противоположное движению (он замедляется).

Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?
Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.

Какие из приведенных зависимостей описывают равноускоренное движение?

Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?

*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?
В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.

Все ⚠️ формулы по физике за 9 класс: определения, пояснения
Формулы по физике за 9 класс: основные разделы
Программа обучения по предмету физика в 9 классе включает в себя несколько разделов: кинематика и динамика, которые в свою очередь состоят из подразделов. Таким образом ученики старшей школы изучают механические колебания и волны, законы взаимодействия и движения тел, электромагнитные явления, строение атомов и их ядер, основные законы механики. В школьную программу девятого года обучения также входят основные свойства света: интерференция, преломление и дисперсия.
Кинематика
Кинематика — один из разделов механики. Кинематика изучает механическое движение тел и способы его описания, независимо от причин этого движения. В данном случае под механическим движением подразумевается любое изменение положения какого-либо тела полностью или частично относительно других тел, случившееся с течением времени.
В Кинематике изучают простые виды движения.
Равномерное прямолинейное движение
Понятие равномерного прямолинейного движения заключается в том, что тело движется по прямой с одинаковой скоростью, то есть за равные промежутки времени тело перемещается на одинаковое расстояние. В таком случае скорость тела остается постоянной, однако является векторной величиной.
Скорость может быть как положительной, так и отрицательной. Все зависит от того, в каком направлении оси X (положительном или отрицательно) направлен вектор скорости. Если тело находится в покое, то его скорость равняется нулю, а координата не меняется в течение времени.
При равномерном прямолинейном движении координата тела вычисляется по следующей формуле:
В этой формуле x₀ – начальная координата, x – конечная координата, v – скорость, t – время.
Если начальная координата — это начало движения и x₀ = 0, то формулу можно сократить до x₁ = v · t.
Если x₀ = 0, то пройденный путь S будет равен координате x. Из этого утверждения можно получить формулу прямолинейного равномерного движения относительно пройденного телом расстояния:
Из этого можно вывести формулы относительно скорости и времени:
Скорость и время также можно выразить из полной формулы для тех случаев, когда x₀ не равно 0:
v = (x₁ — x₀)/t и t = (x₁ — x₀)/v.
Равноускоренное прямолинейное движение
В случае равноускоренного прямолинейного движения тело изменяет скорость своего движения на одинаковую величину за любые равные промежутки времени. Под ускорением в контексте данного определения понимается изменение значения скорости за единицу времени.
Скорость тела вычисляется по формуле:
В данной формуле v – конечная скорость, v₀ – начальная скорость, a – ускорение, t – время.
В равноускоренном прямолинейном движении постоянной величиной является ускорение, а не скорость. Ускорение может быть больше или меньше нуля. В случае увеличения скорость, значение ускорения будет больше нуля, а в случае уменьшения — меньше.
Рассмотрим случай, если начальная скорость тела равно 0. Тогда его скорость через какое-либо время t будет равна произведению ускорения и этого времени:
Допустим, что нам известны текущая скорость тела и время, за которое тело развило указанную скорость из состояния покоя. Тогда мы можем определить ускорение:
В том случае, если начальная скорость тела не равна нулю, мы можем рассчитать конечную скорость тела по следующей формуле:
Взглянем на случаи, когда вектор скорости направлен в противоположном направлении (например, подброшенный камень, его скорость направлена в противоположную сторону от ускорения свободного падения) или в случае торможения. Тогда формула будет выглядеть следующим образом:
В случае свободного ускорения остальные формулы будут записываться так:
at = v – v₀, a = (v – v)/t
А говоря о торможении, мы используем эти формулы:
at = v₀ – v, a = (v₀ – v)/t
Если тело останавливается, то нам следует использовать эту формулу:
А если необходимо узнать, через какой отрезок времени тело остановится, то мы запишем формулу так:
Обратимся к формуле, которая поможет найти путь, которое тело проходит при прямолинейном ускорении. Если при равномерном движении, оси времени и расстояния параллельны, то в случае равноускоренного движения ось движения либо возрастает, либо убывает. Тогда вместо прямоугольника, чью площадь мы вычисляли при равномерном движении, необходимо вычислить площадь трапеции.
Площадь трапеции равна полусумме оснований на высоту, таким образом мы получаем:
Пройденный путь определяется по формуле:
Путь торможения рассчитывается с помощью этой формулы:
Равномерное движение по окружности
Говоря о равномерном движении по окружности, нужно понимать, что в этом случае вектор скорости тела изменяется (скорость направлена по касательным к окружности), а модуль скорости тела (числовое значение) остается постоянным.
Предположим, что необходимо вычислить модуль скорости за один оборот тела по окружности. Обозначим оборот как S, а время, за которое тело его совершило, как t. Тогда формула будет записываться следующим образом: v = s/t.
Однако, если мы говорим об одном обороте, то это называется период. То есть время, за которое тело совершает один оборот вокруг окружности. Он обозначается как T. И тогда формула одного оборота будет выглядеть так: v = s/T
Если S в данном случае это длина окружности (l), то формула принимает вид v = 2πR/T, в соответствии с формулой окружности l = 2\piR
Если необходимо найти период при известном модуле скорости, то формула примет вид T = 2\piR/v
Аналогично радиус можно найти через формулу R = ½ vT/\pi
Динамика
Динамика — раздел механики, изучающий предпосылки изменения в характере движения. Например, возникновение движения. Именно этот раздел изучает три закона Ньютона. В задачах динамики содержится решение таких вопросов как определение действующих на тело сил по характеру его движения и наоборот.
Законы Ньютона
Первый закон Ньютона гласит, что существуют такие системы отсчета, относительно которых тело движется прямолинейно и равномерно, или покоится, если на него не действуют другие тела или их действия скомпенсированы.
Введем основные величины:
Инерциальными называются системы отсчета, которые движутся равномерно прямолинейно относительно Земли. Все системы отсчета, которые движутся прямолинейно и равномерно относительно инерциальной, также являются таковыми. Если система отсчета движется с ускорением, то она — неинерциальная.
Сила — это физическая величина, которая характеризует действие одного тела на второе. В результате этого действия второе тело получает ускорение в инерциальной системе отсчета. Измеряется в ньютонах.
Масса — это физическая величина, которая количественно характеризует инертность тела. Измеряется в килограммах.
Взглянем на тело, на которое действует сила с модулем равным 1 Н. Так как изначально тело массой 1 кг находилось в покое в инерциальной системе, модуль его ускорения будет равен 1 м/с².
В соответствии со вторым законом Ньютона сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение. Это основной закон динамики.
Для выведения второго закона Ньютона и формулы, где F = ma, необходимо обобщить два факта:
если на два тела, масса которых различна, подействовать равной силой, то ускорения, которые приобретут тела, будут обратно пропорциональны массам;

если на одно и то же тело действуют силы разной величины, то ускорения тела будут прямо пропорциональны приложенным силам.

Благодаря этому закону, возможно вычислить не только силу, действующую на тело, но и ускорение. Для этого нужно использовать формулу \[w = \frac{F}{m}\]
В векторной форме второй закон Ньютона записывается как ma = mg + N + F_тр
Третий закон Ньютона гласит, что силы, с которыми две материальные точки воздействуют друг на друга, всегда равны по модулю и направлены в противоположные стороны вдоль прямой, соединяющей эти точки.
Выразить закон формулой можно следующим образом F₁ = -F₂
Примечание
В случае взаимодействия тел силы имеют одинаковую природу, однако, они приложены к разным телам. Таким образом эти силы не могут уравновешивать друг друга, а складывать можно только силы, приложенные к одному телу.
Силы в природе
В соответствии с законом Гука, при деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Природа этой силы состоит в электромагнитном взаимодействии между атомами и молекулами вещества. Эта сила называется упругость.
Говоря о малых деформациях (если |x| < l) сила упругости пропорциональна деформации тела и направлена в противоположную сторону от перемещения частиц тела при деформации. Исходя из этого формула выглядит следующим образом F_x = F_упр = -kx
В данном случае коэффициент k — жесткость тела, она измеряется в ньютонах на метр (Н/м).
Физике свойственен другой способ записи закона Гука. В его записи используются понятия относительной деформации и напряжения. Относительная деформация ε = x / l, а напряжение — это отношение силы к площади поперечного сечения деформированного тела δ = F / S = -F_упр / S.
Исходя из этого, закон Гука можно сформулировать так \[ε = \frac{E}{δ}\]
Коэффициент Е — это модуль Юнга. Он зависит исключительно от свойств материала. Размеры и форма не имеют значения.
Если говорить о случаях сложных деформациях, например в случае деформации изгиба, в формуле появляется сила N — сила реакции опоры. Эта сила направлена перпендикулярно поверхности соприкосновения. N = -mg
Сила всемирного тяготения
Закон всемирного тяготения говорит, что все тела притягиваются друг к другу с силами, прямо пропорциональными их массам и обратно пропорциональна квадрату расстояния между ними.
Эту силу можно вычислить по формуле F = G\fracMR₃²m = mg
g в данном случае — ускорение свободного падения, о котором говорилось выше. В данном случае g = G\fracMR₃². Среднее значение ускорения свободного падения равно 9,81 м/с².
R₃ — это радиус Земли. Он равен 6,38·10⁶ м.
G в формуле обозначает гравитационную постоянную. Она равна 6,67·10^–11 Н·м²/кг².
Движение тела под действием силы тяжести
Ускорение свободного падение является частным случаем равноускоренного прямолинейного движения. В этом случае ускорение всегда будет равно 9,8 м/с² и обозначается буквой g. Таким образом g — это ускорение свободного падения.
Ускорение свободного падения можно вычислить по следующей формуле: g = GM₃/(R₃+H)²
В данном случае H — это гравитационная постоянная, M — масса земли, R — радиус земли, а H — высота падения тела.
Скорость тела под действием силы тяжести можно вычислить по формуле: v = gt
Высоту, с которой падает тело, можно вычислить по формуле H=gt²/2
Силы трения
Силой трения называют силу, характеризующую взаимодействие, возникающее в месте соприкосновения тел и препятствующее их относительному движению. Сила трения имеет электромагнитную природу.
Трение можно разделить на три вида: трение покоя, трение скольжения и трение качения.
Трение покоя — это трение, которое возникает при отсутствии перемещения соприкасающихся тел относительно друг друга.
Можно сказать, что эта сила не позволяет одному телу двигаться относительно другого. Эта сила направлена противоположно силе, приложенной извне параллельно поверхности соприкосновения. Сила трения покоя возрастает вместе с силой, которая стремится сдвинуть тело с места.
Трение скольжения возникает при действии на тело силе, превышающей максимальную силу трения покоя.
Это тело сдвигается с места и начинает дальнейшее движение. Сила трения скольжения всегда направлена в противоположную сторону от относительной скорости соприкасающихся тел.
Трение качения возникает в случае, если тело не скользит по другому телу, а катится наподобие колеса или цилиндра. Трение качения — это трение, которое возникает на месте их соприкосновения.
В виде формулы сила трения выглядит следующим образом: F_тр = μmg
В данном случае μ – коэффициент трения, m – масса тела, а g — ускорение свободного падения (постоянная величина 9,81 м/с²).
Движение тела под действием нескольких сил
Если на тело действуют несколько сил одновременно, то необходимо найти равнодействующую всех сил по формуле F = F₁ + F₂ + F₃
Равнодействующая сила может быть равна нулю. В таком случае тело находится в состоянии покоя.
Закон сохранения в механике
Закон сохранения импульса гласит, что геометрическая сумма импульсов тел, составляющих замкнутую систему, остается постоянной при любых движениях и взаимодействиях тел системы.
В виде формулы закон сохранения импульса выглядит следующим образом: p₁ + p₂ = p₁’ + p₂’ m₁v + m₂u = m₁v’ + m₂u’
В свою очередь импульсом тела называют величину, которая равна произведению массы тела на его скорость: p = mv.
Изменение импульса тела равно импульсу силы, который в свою очередь вычисляется по формуле P = Ft
Кинетическая энергия равна половине произведения массы тела и квадрата его скорости: Ek = mv2/2
Кинетическая энергия — это физическая величина, которая характеризует движущиеся тела. Выражается в Дж.
Закон сохранения энергии состоит в том, что полная механическая энергия замкнутой системы тел, взаимодействующих силами тяготения или силами упругости, остается неизменной при любых движениях тел системы.
Мощность — это величина, которая равна отношению совершенной работы к промежутку времени, за который она совершена. Выражается в Вт.
Вычисляется по формуле N = A/t
Коэффициент полезного действия (КПД) — это название величины, равной отношению полезной работы ко всей совершенной работе. 2}{2} = 2mgl + \frac{mgl}{2}\]\)
v_o² = g4l + gl = 5gl
v_o = √(5gl)
Выполнив вычисления, получим: v_o = √(5×10×0,5) = 5 (м/с).
Ответ: если шарик подвешен на нерастяжимой нити, его скорость должна составлять не менее 5 м/с.
Задача №3
Экваториальный радиус Земли равен 6370 км. Определить линейную и угловую скорости движения точек экватора при вращении Земли вокруг оси.
Решение:
Линейная скорость вращения ν точек земного экватора:
$\[v = \frac{2\piR}{T}\]$
При этом угловая скорость вращения w всех точек Земли равна:
$\[w = \frac{2\pi}{T}\]$
После вычислений у нас получится: ν = 463 м/с, w = 7,3×10⁻⁵ рад/с.
12-а. Что такое кинематика
§ 12-а. Что такое кинематика
Вокруг нас множество движущихся тел. Их движение можно описать по-разному. Рассмотрим, например, словесное описание движения поезда. Выехав из пункта А, поезд 2 часа ехал со скоростью 100 км/ч, затем 1 час стоял, и в пункт Б прибыл через 3 часа после возобновления движения, всё это время поддерживая скорость 50 км/ч.
Движение этого же поезда можно описать при помощи таблицы:
Пример табличного описания движения тела, например, поезда.
Время t, ч 0 1 2 3 4 5 6
Путь l, км 0 100 200 200 250 300 350
По данным таблицы построим график, и мы получим описание движения при помощи графика. На нём три этапа: от 0 до 2 часов (движение со скоростью 100 км/ч), от 2 до 3 часов (стоянка) и от 3 до 6 часов (движение со скоростью 50 км/ч).
Каждый этап движения поезда на графике отражён прямой линией, которой в алгебре соответствует линейная функция y = kx + b, где k и b – числа. Применительно к нашей задаче про поезд, вместо y будем писать l, а вместо x будем писать t. Тогда мы получим описание движения формулами:
Табл. 12.3. Пример описания движения поезда с помощью формул, являющихся линейными функциями .
Этап движения
на графике Интервал времени Формула линии графика
I. (красный) если 0 t , то l = 100 · t + 0
II. (чёрный) если 2 t , то l = 0 · t + 200
III. (синий) если 3 t , то l = 50 · t + 50
Как получаются эти формулы, мы изучим при решении задач, а пока убедимся, что они верные, например последняя. Значение t должно лежать в интервале от 3 до 6 часов. Возьмём значение 4 и подставим в формулу: l = 50 · 4 + 50. Вычисляем: 250 километров. В верхней таблице мы тоже видим, что за 4 часа поезд проехал 250 км. Взгляните и на график: для момента времени t = 4 ч получается путь l = 250 км.
Обобщим сказанное: рассмотренные способы описания движения – словесный, табличный, графический и формулами – равноправны. В зависимости от ситуации мы будем выбирать более удобный способ.
Кинематика (от греч. «кинематос» – движение) – раздел физики, изучающий способы математического описания движения тел без выяснения причин, вызвавших движение. Кинематика не интересуется тем, почему тело движется так, а не иначе. Она лишь отвечает на вопросы: как движение описать математически и что нового из такого описания можно почерпнуть?
Тело, собственными размерами которого в данных условиях можно пренебречь, называют материальной точкой. Например, если самолёт совершает перелёт по маршруту Москва–Сочи, диспетчер вполне может считать самолёт точкой (именно так он и отображается на экране радара). Однако тот же самолёт, выруливающий на взлётную полосу, точкой считать нельзя – надо учитывать, например, размах крыльев, чтобы не повредить другие самолёты или мачты освещения на месте стоянки.
В физике линию, которую «описывает» материальная точка при движении в пространстве, называют траекторией. Траектория может быть видимой или невидимой. Например, линия движения самолёта в небе часто видна (см. рисунок), а линия движения автомобиля по шоссе не видна. Заметим, что с точки зрения геометрии линия не имеет ширины. Поэтому, говоря о траектории движения любого тела, мы всегда считаем его материальной точкой.
По виду траекторий все движения тел делят на прямолинейные и криволинейные. Например, траектория падения мяча, выпущенного из рук, – отрезок прямой, полёта пушечного снаряда – часть параболы, а кончика маятника настенных часов – дуга, то есть часть окружности.
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Больше интересного в телеграм @calcsbox
Кинематика

4.1. Деление кинематики по типам объекта исследования. Кинематика точки. (Kinematics of a point)
Основная статья: кинематика точки
Кинематика исследования указывают на движение материальных точек — тел, размерами которых можно пренебречь по сравнению с характерными размерами изучаемого явления. {t_{2}}\mid {\vec {v}}t\mid dt},
где s {\свойства стиль отображения значение s} — длина пути траектории за промежуток времени от t 2 {\свойства стиль отображения значение t_{2}} (или{2}}) для t 1 {\свойства стиль отображения значение t_{1}} (t_ в{1}}), v 1 (в 1), v 2 (в 2)., v n (в) {\свойства стиль отображения значение v_{1},v_{2},\точек,v_{п}} — проекции v → {\свойства стиль отображения значение {\ВМК {v}}} на соответствующие оси координат, a 1 (в 1), a 2 (в 2)., a n (а) {\свойства стиль отображения значение ох{1},ох{2},\Dots с,Ох{Н}} — проекции a → {\свойства стиль отображения значение {\ВМК {a}}} на соответствующие оси координат.
Если ускорение постоянно и перпендикулярно скорости, движение происходит по окружности вращательное движение.
a → ⊥ v → {\displaystyle {\vec {a}}\perp {\vec {v}}} ∣ a → ∣= ∣ v → ∣ 2 R (2) {\displaystyle \mid {\vec {a}}\mid ={\frac — вектор угловой скорости тела.
Распределение школьной программы по классам
Класс Месяц Тема
7 Сентябрь Измерение физических величин. Единицы физических величин. Цена деления. Погрешность измерения.
7 Октябрь Механическое движение. Путь. Перемещение. Равномерное движение. Скорость. Средняя скорость. Работа с графиками. Сложение скоростей для тел, движущихся параллельно.
7 Ноябрь Инерция. Взаимодействие тел. Масса. Плотность
7 Январь Силы в природе (тяжести, упругости, трения). Сложение сил. Равнодействующая.
7 Май Механическая работа, мощность, энергия. Простые механизмы, блок, рычаг. Момент силы. Правило моментов (для сил направленных вдоль параллельных прямых). Золотое правило механики. КПД.
7 Май Давление. Основы гидростатики. Закон Паскаля. Атмосферное давление. Гидравлический пресс. Сообщающиеся сосуды. Закон Архимеда. Плавание тел. Воздухоплавание.
8 Сентябрь Тепловое движение. Температура. Внутренняя энергия. Теплопроводность. Конвекция. Излучение. Только понятия без формул
8 Октябрь Количество теплоты. Удельная теплоемкость вещества. Удельная теплота сгорания. Агрегатные состояния вещества. Плавление и отвердевание кристаллических тел. Удельная теплота плавления. Испарение. Кипение. Удельная теплота парообразования.
8 Ноябрь Общее уравнение теплового баланса. КПД нагревателей.
8 Декабрь Влажность воздуха. Только понятия без формул
8 Декабрь Работа газа и пара при расширении. Двигатель внутреннего сгорания. Паровая турбина. КПД теплового двигателя. Только понятия без формул
8 Январь Работа с графиками: построение, расчёт площади под графиком, проведение касательных для учёта скорости изменения величины.
8 Февраль Электризация. Два рода зарядов. Взаимодействие заряженных тел. Проводники и диэлектрики. Электрическое поле. Делимость электрического заряда. Электрон. Строение атомов. Только понятия без формул
8 Февраль Электрический ток. Источники электрического тока. Электрическая цепь и ее составные части. Действие электрического тока. Сила тока. Электрическое напряжение. Электрическое сопротивление проводников. Закон Ома для участка цепи. Удельное сопротивление.
8 Март Последовательное и параллельное соединение проводников. Расчет простых цепей постоянного тока. Работа и мощность электрического тока. Закон Джоуля – Ленца.
8 Апрель Магнитное поле. Магнитное поле прямого тока. Магнитные линии магнитного поля. Магнитное поле катушки с током. Электромагниты. Постоянные магниты. Магнитное поле постоянных магнитов. Магнитное поле Земли. Действие магнитного поля на проводник с током. Только понятия без формул
8 Май Источники света. Распространение света. Тень и полутень. Камера – обскура. Отражение света. Законы отражения света. Плоское зеркало. Преломление света. Линзы. Построения в линзах. Оптическая сила линзы. Изображение, даваемое линзой. Фотоаппарат. Глаз и зрение. Близорукость и дальнозоркость. Очки. Только понятия без формул
9 Октябрь Кинематика. Материальная точка. Системы отсчёта. Равномерное прямолинейное движение. Мгновенная скорость. Средняя скорость. Равнопеременное движение. Ускорение. Свободное падение. Графики движения (пути, перемещения, координат от времени; скорости, ускорения и их проекций от времени и координат). Движение по окружности. Угловое перемещение и угловая скорость. Центростремительное (нормальное) и тангенциальное (касательное) ускорение.
9 Ноябрь Относительность движения. Закон сложения скоростей. Кинематические связи. Плоское движение твердого тела.
9 Декабрь Динамика. Силы. Векторное сложение сил. Масса. Центр масс. Законы Ньютона.
9 Январь Динамика систем с кинематическими связями. Блоки, скольжение наклонных плоскостей.
9 Январь Закон всемирного тяготения. Гравитация. Искусственные спутники. Первая космическая скорость. Перегрузки и невесомость.
9 Февраль Силы трения. Силы сопротивления при движении в жидкости и газе. Силы упругости. Закон Гука.
9 Март Импульс. Закон сохранения импульса. Движение центра масс. Реактивное движение.
9 Апрель Работа. Мощность. Энергия (гравитационная, деформированной пружины). Закон сохранения энергии. Упругие и неупругие взаимодействия. Диссипация энергии. Выделившееся количество теплоты.
9 Апрель Статика
9 Май Механические колебания. Маятник. Гармонические колебания. Волны.
9 Май Основы атомной и ядерной физики.
10 Сентябрь Газовые законы. Изопроцессы. Законы Дальтона и Авогадро.
10 Октябрь Молекулярно-кинетическая теория. Температура.
10 Октябрь Потенциальная энергия взаимодействия молекул. Только понятия без формул
10 Ноябрь Термодинамика. Внутренняя энергия газов. Количество теплоты. 1-й закон термодинамики. Теплоемкость. Адиабатные процессы. Цикл Карно.
10 Ноябрь Насыщенные пары, влажность.
10 Декабрь Поверхностное натяжение. Капилляры.
10 Январь Электростатика. Закон Кулона. Электрическое поле. Напряженность. Потенциал. Проводники и диэлектрики в электростатических полях. Конденсаторы.
10 Февраль ЭДС. Цепи постоянного тока. Законы Кирхгофа. Нелинейные элементы.
10 Март Работа и мощность электрического тока.
10 Апрель Электрический ток в средах.
10 Май Магнитное поле постоянного тока. Силы Лоренца и Ампера.
Девятый класс движения CBSE Science
Уравнение движения:
Связь между скоростью, расстоянием, временем и ускорением называется уравнениями движения. Есть три уравнения движения:
Первое уравнение движения:
Конечная скорость (v) движущегося объекта с равномерным ускорением (a) через время, t.
Пусть, начальная скорость = u.
Конечная скорость = v.
Время = t
Ускорение =
Мы знаем, что ускорение (a) `= (text {Изменение скорости}) / (text {Время занято})`
`=> a = (text {Конечная скорость-Начальная скорость}) / text {Время занято}`
`=> a = (v-u) / t`
`=> at = v-u`
`=> at-v = -u`
`=> — v = -u-at`
`=> v = u + at` — (i)
Это уравнение известно как первое уравнение движения.
Второе уравнение движения:
Расстояние, пройденное движущимся телом за время (t).
Пусть, Начальная скорость объекта = u
Конечная скорость объекта = v Разгон =
Время = t
Пройденное расстояние за заданное время =
с.
Мы знаем,
Средняя скорость `= (текст {Начальная скорость + Конечная скорость}) / 2`
∴ Средняя скорость `= (u + v) / 2` —- (ii)
Мы знаем, что пройденное расстояние (я) за заданное время = Средняя скорость x Время
Или, с = Средняя скорость x Время —————— (iii)
После подстановки значения средней скорости из уравнения (ii) получаем
`=> s = (u + v) / 2xxt`
После подстановки значения «v» из первого уравнения движения мы получаем
`=> s = (u + (u + at)) / 2xxt`
`=> s = (u + u + at) / 2 xxt`
`=> s = (2u + at) / 2 xxt`
`=> s = (2ut + at ^ 2) / 2`
`=> s = (2ut) / 2 + (at ^ 2) / 2`
`=> s = ut + (at ^ 2) / 2`
`=> s = ut + 1/2 at ^ 2` —- (iv)
Приведенное выше уравнение известно как Второе уравнение движения.2 + 2 как` — (vi)
Это называется третьим уравнением движения.
Заметки — Класс 9 по физике — Классы
1 кв. Определите кинематику?
2 кв. В чем разница между отдыхом и движением?
3 кв. Определить окружение?
4 кв. Перечислите типы движения?
Q5. Описать движение переводчика на примерах?
Q6. Опишите различные типы движения переводчика?
Q7. Описать вращательное движение на примерах?
Q8.Вы можете указать на некоторые различия в круговом и вращательном движении?
Когда говорят, что тело находится в состоянии покоя?
Приведите пример тела, которое одновременно находится в состоянии покоя и находится в движении.
Укажите тип движения в каждом из следующих пунктов:
Q9. Опишите колебательные движения с помощью примеров?
Q10. Отличить скаляры от векторов?
Q11. Как можно графически представить векторные величины?
Q12.Определите термин «позиция»?
Q13. Объясните разницу между расстоянием и смещением?
Q14. В чем разница между скоростью и скоростью?
Q15. Определите равномерную скорость.
Q16. Определить переменную скорость?
Q17. Определите среднюю скорость?
Q18. Определить равномерную скорость?
Q19. Определить переменную скорость?
Q20. Определить среднюю скорость?
Q21. Определите ускорение?
Q23. Как отличить положительное ускорение от отрицательного?
Q24.Что вы подразумеваете под графиком, переменными, независимой величиной и зависимой величиной?
Q25. Какова цель графика расстояние-время? Как это построено?
Q26. Нарисуйте график расстояния-времени для тела в состоянии покоя. Как вы определите скорость тела по этому графику?
Q27. Построить и интерпретировать график расстояния-времени для тела, движущегося с постоянной скоростью?
Q28. Нарисуйте график расстояние-время для тела, движущегося с переменной скоростью?
Q29.Что вы имеете в виду под графиком скорость-время?
Q30. Нарисуйте график скорости-времени для тела, движущегося с постоянной скоростью?
OR
Какой должна быть форма графика скорость-время тела, движущегося с постоянной скоростью?
Q31. Нарисуйте график скорость-время для тела, движущегося с равномерно меняющейся скоростью?
OR
Какой была бы форма графика скорость-время тела, движущегося с равномерно изменяющейся скоростью?
Q32. Нарисуйте график скорости-времени для расстояния, на которое движется движущийся объект?
OR
Какой была бы форма графика скорость-время для расстояния, пройденного движущимся объектом?
Q33.Опишите назначение различных уравнений движения?
Q34. Выведите первое уравнение движения для равноускоренного прямолинейного движения.
OR
Какое уравнение движения устанавливает взаимосвязь между vf, vi, a и t, взаимосвязь между этими величинами.
OR
Докажите, что vf = vi + at.
OR
Выведите уравнение движения, которое не зависит от расстояния S.
Q35. Выведите второе уравнение движения для равноускоренного прямолинейного движения.
OR
Какое уравнение движения устанавливает взаимосвязь между S, a, Vi и Vf?
OR
Выведите уравнение движения, не зависящее от t.
OR
Вывести второе уравнение движения?
OR
Докажите, что S = v1 t + ½ at2
Q36. Выведите третье уравнение движения для равноускоренного прямолинейного движения.
OR
Какое уравнение движения устанавливает взаимосвязь между S, a, Vi и Vf?
OR
Выведите уравнение движения, не зависящее от t.
OR
Вывести третье уравнение движения?
OR
Докажите, что 2aS = vf2 — vi2
Q37. Бросьте предмет с некоторой высоты и наблюдайте за его движением. Его скорость увеличивается, уменьшается или остается постоянной по мере приближения к земле?
Q38. Объясните движение свободно падающих тел?
Q39. Написать уравнения движения тел, движущихся под действием силы тяжести?
Банкноты
1 кв.Определите кинематику?
Ответ: Кинематика:
Кинематика — это исследование движения объекта без обсуждения причины движения.
2 кв. В чем разница между отдыхом и движением?
Ответ: Разница между покоем и движением:
Остальное:
Тело считается покоящимся, если оно не меняет своего положения по отношению к окружающей среде.
Движение:
Говорят, что тело находится в движении, если оно меняет свое положение по отношению к окружающей среде.
Состояние покоя или движения тела относительное. Например, пассажир, сидящий в движущемся автобусе, находится в состоянии покоя, потому что он / она не меняет своего положения по отношению к другим пассажирам или объектам в автобусе. Но для наблюдателя вне автобуса пассажиры и предметы внутри автобуса находятся в движении.
3 кв.Определить окружение?
Ответ: Окрестности:
Окрестности — это места по соседству с различными предметами. Аналогично
4 кв. Перечислите типы движения?
Ответ: Типы движения:
Есть три типа движения.
Поступательное движение (линейное, случайное и круговое)
Вращательное движение
Вибрационное движение (движение вперед и назад)
Q5.Описать движение переводчика на примерах?
Ответ: Переводное ходатайство:
При поступательном движении тело движется по прямой без вращения. Линия может быть прямой или изогнутой.
Примеры:
Всадники, движущиеся в колесе обозрения, также совершают поступательное движение. Их движение происходит по кругу без вращения.
Q6. Опишите различные типы движения переводчика?
Ответ: Типы движения переводчика:
Движения переводчика можно разделить на линейные, круговые и произвольные.
Прямолинейное движение тела известно как его линейное движение.
Примеры:
Движение объектов, таких как автомобиль, движется по прямой и ровной дороге, является линейным движением.
Самолеты, летящие прямо в воздухе, и объекты, падающие вертикально вниз, также являются примером линейного движения.
Движение объекта по круговой траектории называется круговым движением
Примеры:
Камень, привязанный к концу веревки, можно заставить вращаться.Камень движется по кругу и, следовательно, имеет круговое движение.
Игрушечный поезд, движущийся по круговой колее. Велосипед или автомобиль, движущиеся по круговой дорожке, обладают круговым движением. Движение Земли вокруг Солнца и движение Луны вокруг Земли также являются примерами круговых движений.
Неупорядоченное или нерегулярное движение объекта называется случайным движением.
Примеры:
Движение насекомых и птиц нерегулярное. Таким образом, движение насекомых и птиц — это случайное движение.
Движение частиц пыли или дыма в воздухе также является случайным движением.
Броуновское движение молекул газа или жидкости по зигзагообразной траектории также является примером случайного движения.
Q7. Описать вращательное движение на примерах?
Ответ: Вращательное движение:
Вращательное движение тела вокруг своей оси называется его вращательным движением.
Примеры:
Волчок вращается вокруг своей оси, проходящей через него, и, таким образом, обладает вращательным движением.Ось — это линия, вокруг которой вращается тело. При круговом движении точка, вокруг которой движется тело, находится вне тела. При вращательном движении линия, по которой движется тело, проходит через само тело.
Движение колеса вокруг своей оси и движение рулевого колеса являются примерами вращательного движения. Движение Земли вокруг Солнца является круговым, а не вращательным. Однако движение Земли вокруг своей географической оси, вызывающее день и ночь, является вращательным.
Q8. Вы можете указать на некоторые различия в круговом и вращательном движении?
Ответ: Различия в круговом и вращательном движении:
Любое вращение как на оси — вращательное движение. Любое вращательное движение с фиксированными радиусом инерционной длины и осью вращения является круговым движением. И в этом разница. Круговое движение — это просто частный случай вращательного движения. То есть нет ограничений по фиксированной оси и радиусу для вращательного движения, но есть для кругового движения.
Например, , все планеты вращаются вокруг своих солнц. Но большинство орбит имеют эллиптическую форму, поэтому ось вращения (их две в эллипсе) и радиусы вращения меняются по мере их движения. Итак, большинство, если не все, планеты не имеют кругового движения.
Примечание:
Длина вращения:
Длина, которая представляет собой расстояние во вращающейся системе между точкой, вокруг которой она вращается, и точкой, к которой или от которой передача энергии имеет максимальный эффект.
Мини-упражнения

Когда говорят, что тело находится в состоянии покоя?
Ответ: Тело считается покоящимся, если оно не меняет своего положения относительно окружающей среды.
Приведите пример тела, которое одновременно находится в состоянии покоя и находится в движении.
Ответ: Движение и покой — понятия относительные. Абсолютного покоя нет. Мы можем определить состояние покоя или движения только в отношении другого объекта или точки в пространстве, взятых за точку отсчета.
Примеры:
Человек в поезде считает, что находится в состоянии покоя относительно попутчиков или стен поезда. Но когда он смотрит на улицу, он обнаруживает, что движется по деревьям снаружи.
Пассажир, сидящий в движущемся автобусе, находится в состоянии покоя, потому что он / она не меняет своего положения по отношению к другим пассажирам или объектам внутри автобуса.Но для наблюдателя вне автобуса пассажиры и предметы внутри автобуса находятся в движении.
Укажите тип движения в каждом из следующих пунктов:
Шар, движущийся вертикально вверх.
Ответ: Линейное движение.
Ребенок, спускающийся с горки.
Ответ: Линейное движение.
Движение игрока на футбольном поле.
Ответ: Случайное движение.

Полет бабочки.
Ответ: Случайное движение .

Спортсмен, бегущий по круговой дорожке.
Ответ: Круговое движение .

Ответ: Круговое движение.

Ответ: Вибрационное движение.
9 кв. Опишите колебательные движения с помощью примеров?
Ответ: Вибрационное движение:
Движение тела вперед и назад относительно его среднего положения известно как колебательное движение.
Примеры:
Считайте движение, если ребенок раскачивается. Когда его толкают, качели перемещаются взад и вперед относительно своего среднего положения.Движение ребенка повторяется от одной крайности до другой с качелями. Такой тип движения называется колебательным.
Возвратно-поступательное движение маятника часов относительно его среднего положения, это называется колебательным движением.
Младенец в колыбели, двигающийся взад и вперед, движение молота электрического звонка и движение струны ситара — вот некоторые из примеров колебательного движения.
Q10.Отличить скаляры от векторов?
Ответ: различать скаляры и векторы
Скаляры Векторы
Скалярная величина полностью описывается только своей величиной. Векторная величина полностью описывается величиной и направлением
Примеры: Примеры скаляров: масса, длина, время, скорость, объем, работа, энергия, плотность, мощность, электрический заряд, давление, площадь, температура. Примеры: Примеры векторов: скорость, смещение, сила, импульс, крутящий момент, вес, электрический потенциал и т. Д.

Q11. Как можно графически представить векторные величины?
Ответ: Представление векторов (символическое представление вектора):
Чтобы отличить вектор от скалярной величины, мы обычно используем жирные буквы для обозначения векторных величин, например, F , a, d или черту или стрелку над их символами, например
.
Векторное представление / Графическое представление вектора:
Проведена прямая линия со стрелкой на одном конце.Длина линии согласно некоторому подходящему масштабу представляет величину, а острие стрелки указывает направление вектора.
Q12. Определите термин «позиция»?
Ответ: Должность:
Термин «положение» описывает положение места или точки относительно некоторой контрольной точки, называемой исходной точкой.
Например:
Вы хотите описать расположение вашей школы, не выходя из дома.Пусть школа будет обозначена буквой S, а дом — буквой H. Положение вашей школы от вашего дома будет обозначено прямой HS в направлении от H к S.
Q13. Объясните разницу между расстоянием и смещением?
Отв. Разница между расстоянием и перемещением:
Расстояние Рабочий объем
Длина пути между двумя точками называется расстоянием между этими точками. Смещение — это кратчайшее расстояние между двумя точками, имеющее величину и направление.
Расстояние — это скалярная величина. Смещение — это векторная величина.
Расстояние обозначается буквой «S»
S = vt
Единица измерения в системе СИ — метр (м).
Рабочий объем обозначается « d ».
D = vt
Единица измерения в системе СИ — метр (м).
Расстояние S (пунктирная линия) и смещение d (темная линия) от точек A до B,
Q14.В чем разница между скоростью и скоростью?
Отв. Разница между скоростью и скоростью:
Скорость Скорость
Расстояние, пройденное объектом за единицу времени, называется его скоростью.
Расстояние = скорость x время
или S = vt
Скорость перемещения тела называется его скоростью.
V = d / t или d = vt
Скорость — это скалярная величина. Скорость — это векторная величина.
Sl Единица измерения скорости — метр в секунду. (мс ^-1) Sl. Единица измерения скорости такая же, как и у скорости, то есть метр в секунду. (мс ^-1)
ЗНАЕТЕ ЛИ ВЫ
Какое самое быстрое животное на земле?
Falcon может летать со скоростью 200 км / ч ^-1

Гепард может бегать со скоростью 70 км / ч ^-1
Пушка LIDAR — это скорость обнаружения света и дальности.Он использует время, затрачиваемое лазерным импульсом, на серию измерений расстояния транспортного средства до пушки. Затем данные используются для расчета скорости автомобиля.
Десантник достигает равномерной скорости, называемой предельной скоростью, с которой он приближается к земле.
Q15. Определите равномерную скорость.
Отв. Равномерная скорость:
Тело имеет равномерную скорость, если оно преодолевает равные расстояния за равные промежутки времени, какими бы короткими ни были эти промежутки.
Q16. Определить переменную скорость?
Отв. переменная скорость:
Если тело преодолевает неравные расстояния за равный интервал времени, однако этот интервал может быть небольшим, скорость тела считается переменной.
Q17. Определите среднюю скорость?
Отв. Средняя скорость:
Соотношение между пройденным расстоянием и общим временем называется средней скоростью.

Q18. Определить равномерную скорость?
Отв. Равномерная скорость:
Тело имеет равномерную скорость, если оно преодолевает равное смещение за равные промежутки времени, какими бы короткими ни были эти промежутки.

Q19. Определить переменную скорость?
Отв. переменная скорость:
Если скорость или направление меняются со временем, то скорость такого тела считается переменной.
Q20. Определить среднюю скорость?
Отв. Средняя скорость:
Отношение между смещением и временем известно как средняя скорость
В21. Определите ускорение?
Отв. Разгон:
Ускорение определяется как скорость изменения скорости тела.
Единица ускорения:
Единица измерения ускорения в системе СИ — метр в секунду в квадрате (мс ^-2)
ПОЛЕЗНАЯ ИНФОРМАЦИЯ
Ускорение движущегося объекта происходит в сторону увеличения скорости его скорости. Ускорение объекта противоположно направлению скорости, если его скорость уменьшается.
Q22.Определите равномерное ускорение?
Отв. Равномерное ускорение:
Тело имеет равномерное ускорение, если оно имеет равные изменения скорости в равные промежутки времени, какими бы короткими ни были эти промежутки.
Q23. Как отличить положительное ускорение от отрицательного?
Ответ: Положительное ускорение:
Ускорение тела положительное, если его скорость увеличивается со временем.Направление этого ускорения такое же, в каком движется тело, не меняя своего направления.
Отрицательное ускорение / замедление или замедление:
Ускорение тела отрицательное, если скорость тела уменьшается. Направление отрицательного ускорения противоположно направлению движения тела. Отрицательное ускорение также называется замедлением или замедлением.
ЗНАЕТЕ ЛИ ВЫ
График также можно использовать в повседневной жизни, например, чтобы показать рост / снижение экспорта по годам, количество осадков по месяцам, данные о температуре пациента или количество пробежек, набранных командой, и т. Д.

Q24. Что вы подразумеваете под графиком, переменными, независимой величиной и зависимой величиной?
Ответ: График:
График — это наглядный способ представления информации о взаимосвязи между различными величинами.
Переменные:
Величины, между которыми строится график, называются переменными.
Независимое количество:
Одна из величин называется независимой величиной.
Зависимое количество:
Значения, значения которых зависят от независимой величины, называются зависимой величиной.
Q25. Какова цель графика расстояние-время? Как это построено?
Ответ: График расстояние-время:
Полезно представлять движение объектов с помощью графиков. Термины расстояние и смещение используются как синонимы, когда движение происходит по прямой.Точно так же, если движение по прямой, то скорость и скорость также используются взаимозаменяемо.
Примечание:
На графике расстояние-время время отсчитывается по горизонтальной оси, а по вертикальной оси показано расстояние, пройденное объектом.
Q26. Нарисуйте график расстояния-времени для тела в состоянии покоя. Как вы определите скорость тела по этому графику?
Ответ: Объект в состоянии покоя:
На графике, показанном на рисунке, расстояние, на которое объект перемещается со временем, равно нулю.То есть объект покоится. Таким образом, горизонтальная линия, параллельная оси времени на графике расстояние-время, показывает, что скорость объекта равна нулю.
Q27. Построить и интерпретировать график расстояния-времени для тела, движущегося с постоянной скоростью?
Ответ: объект движется с постоянной скоростью:
Скорость объекта называется постоянной, если он преодолевает равные расстояния за равные промежутки времени.График расстояние-время, показанный на рисунке, представляет собой прямую линию.
Его наклон дает скорость объекта.
Рассмотрим две точки A и B на графике.
Скорость объектов = наклон линии AB
Скорость, найденная на графике, составляет 2 мс ^-1

Q28. Нарисуйте график расстояние-время для тела, движущегося с переменной скоростью?
Ответ: объект движется с переменной скоростью:
Когда объект не преодолевает равные расстояния за равные промежутки времени, его скорость не постоянна.В этом случае график расстояние-время не будет прямой линией, как показано на рисунке. Наклон кривой в любой точке можно определить по наклону касательной в этой точке. Например.
Таким образом, скорость объекта в точке P составляет 3 мс ^-1
Примечание:
Скорость выше в моменты, когда наклон больше, скорость равна нулю в моменты, когда наклон горизонтальный.
Q29.Что вы имеете в виду под графиком скорость-время?
Ответ: график скорости-времени:
На графике скорость-время время отсчитывается по оси x, а скорость — по оси y.
Q30. Нарисуйте график скорости-времени для тела, движущегося с постоянной скоростью?
ИЛИ
Какой была бы форма графика скорости движения тела, движущегося с постоянной скоростью?
Ответ: объект движется с постоянной скоростью
Когда скорость объекта постоянна (4 мс ^-1) во времени, тогда график скорость-время будет горизонтальной линией, параллельной оси времени вдоль оси x.
Прямая линия, параллельная оси времени, представляет постоянную скорость объекта.
Q31. Нарисуйте график скорость-время для тела, движущегося с равномерно меняющейся скоростью?
ИЛИ
Какой была бы форма графика скорость-время тела, движущегося с равномерно изменяющейся скоростью?
Ответ: объект движется с равномерно меняющейся скоростью (равномерное ускорение):
Пусть скорость объекта изменяется равномерно.В этом случае скорость изменяется с постоянной скоростью. Таким образом, его график скорости-времени был бы такой прямой линией.
Прямая линия означает, что объект движется с равномерным ускорением. Наклон линии дает величину ее ускорения.
График скорости-времени дает отрицательный наклон. Таким образом, объект имеет замедление 0,4 мс ^-2.
Q32. Нарисуйте график скорости-времени для расстояния, на которое движется движущийся объект?
ИЛИ
Какой была бы форма графика скорость-время для расстояния, проходимого движущимся объектом?
Ответ: Расстояние, пройденное движущимся объектом:
Область под графиком скорость-время представляет расстояние, пройденное объектом.Если движение равномерное, площадь можно рассчитать, используя соответствующую формулу для геометрических фигур, представленных на графике.
В33. Опишите назначение различных уравнений движения?
Ответ: Уравнения движения:
Существуют три основных уравнения движения тел, движущихся с равномерным ускорением. Эти уравнения связывают начальную скорость, конечную скорость, ускорение, время и расстояние, пройденное движущимся телом.
Q34. Выведите первое уравнение движения для равноускоренного прямолинейного движения.
ИЛИ
Какое уравнение движения устанавливает связь между v _f, v _i, a и t, связь между этими величинами.
ИЛИ
Докажите, что v _f = v _i + at.
ИЛИ
Выведите уравнение движения, не зависящее от расстояния S.
Ответ: Предположим, тело движется с начальной скоростью v _i, а по прошествии времени t его скорость станет v _f. Тогда ускорение a равно
.
или V _f — V _i = at
V _f = V _i + at
Второй метод (графический метод):
Первое уравнение движения:
График скорость-время движения тела показан на рисунке.Наклон линии AB дает ускорение тела.
Как
BD = V _f, CD = V _i и OD = t
Отсюда
или V _f — V _i = at
V _f = V _i + at
Q35. Выведите второе уравнение движения для равноускоренного прямолинейного движения.
ИЛИ
Какое уравнение движения устанавливает взаимосвязь между S, a, V _i и V _f?
ИЛИ
Выведите уравнение движения, не зависящее от t.
ИЛИ
Вывести второе уравнение движения?
ИЛИ
Докажите, что S = v ₁ t + ½ при ²
Ответ: Предположим, что тело движется с начальной скоростью v _i и через определенное время t его скорость становится v _f, тогда общее расстояние S, пройденное за время t, равно
.
S = v _av x t
) x т ………………….. (1)
Из первого уравнения движения. V _f = V _i + at
Подставляем значение V _f в уравнение (1).
) х т
) х т
)
S = V.t + ½ при ²
Второй метод (графический метод):
Второе уравнение движения:
На графике скорость-время, показанном на рисунке, общее расстояние S, пройденное телом, равно общей площади OABD под графиком.То есть
Общее расстояние S = площадь (прямоугольник OACD + треугольник ABC)
Площадь прямоугольника OACD = OA x OD
= V _i x t
Площадь треугольника ABC = ½ (AC x BC)
= ½ т x при
Т.к. Общая площадь OABD = площадь прямоугольника OACD + площадь треугольника ABC
Подставляя значения в приведенное выше уравнение, получаем
S = V _i т + ½ t x при
S = V _i t + ½ при ²
Q36.Выведите третье уравнение движения для равноускоренного прямолинейного движения.
ИЛИ
Какое уравнение движения устанавливает взаимосвязь между S, a, V _i и V _f?
ИЛИ
Выведите уравнение движения, не зависящее от t.
ИЛИ
Вывести третье уравнение движения?
ИЛИ
Докажите, что 2aS = v _f ² — v _i ²
Ответ: Предположим, что тело движется с начальной скоростью v _i и через определенное время t его скорость становится v _f, тогда общее расстояние S, пройденное за время t, равно
.
S = v _av x t
) x т ………………….. (1)
Из первого уравнения движения найдите значение t.
V _f = V _i + at или
Подставляем значение V _f в уравнение (1).
2aS = (v _f + v _i) x (v _f — v _i) по формуле (a + b) (a — b) = a ² — b ²
2aS = v _f ² — v _i ²
Второй метод (графический метод)
Третье уравнение движения:
На графике скорость-время, показанном на рисунке, общее расстояние S, пройденное телом, выражается общей площадью OABD под графиком.
Общая площадь OABD =
или 2S = (OA + BD) x OD
Умножаем обе стороны на BC / OD, получаем: (BC / OD = a)
2S x = (OA + BD) X OD X
2S x = (OA + BD) X BC ……………………. (1)
Подставляя значение в вышеприведенное уравнение (1), получаем
2S x a = (V _i + V _f) x (V _f — V _i)
2aS = V _f ² + V _i ²
ПОЛЕЗНАЯ ИНФОРМАЦИЯ
1 мс ^-1 = 0.001 км x 3600 = 3,6 км / ч ^-1
Таким образом, умножьте скорость в мс ^-1 на 3,6, чтобы получить скорость в км / ч ^-1 например,
20 мс ^-1 = 20 x 3,6 км / ч ^-1 = 72 км / ч ^-1
1 км / ч ^-1 = мс ^-1
Таким образом, умножьте скорость в км / ч ^-1 на, чтобы получить скорость в мс ^-1, например
50 км / ч ^-1 = 50 x мс ^-1 = 13,88 мс ^-1
Умножьте ускорение в мс ^-2 на = 12960, чтобы получить его значение в км / ч ^-2
Разделите ускорение в км / ч ^-2 на 12960, чтобы получить его значение в мс ^-2
Q37.Бросьте предмет с некоторой высоты и наблюдайте за его движением. Его скорость увеличивается, уменьшается или остается постоянной по мере приближения к земле?
Ответ: Скорость объекта увеличится из-за земного притяжения. Поэтому для свободно падающих тел g положительна.
Q38. Объясните движение свободно падающих тел?
Ответ: Движение свободно падающих тел:
Ускорение свободно падающих тел называется ускорением свободного падения.
Обозначается g. На поверхности Земли его значение составляет примерно 10 мс ^-2.
Для тел, свободно падающих, g положительна, а для тел, движущихся вверх, отрицательна.
Галилей был первым ученым, заметившим, что все свободно падающие объекты имеют одинаковое ускорение независимо от их масс. Он сбрасывал с Пизанской башни различные предметы разной массы. Он обнаружил, что все они достигают земли одновременно.
Q39. Написать уравнения движения тел, движущихся под действием силы тяжести?
Ответ: Уравнения движения тел, движущихся под действием силы тяжести:
V _f = V _i + gt
h = V _i t + ½ gt ²
РЕЗЮМЕ
Покой: Тело считается покоящимся, если оно не меняет своего положения относительно окружающей среды.
Движение: Говорят, что тело находится в движении, если оно меняет свое положение относительно окружающей среды.
Покой и движение всегда относительны. Абсолютного покоя или абсолютного движения не существует.
Движение можно разделить на следующие три типа:
Поступательное движение: тело движется без вращения.
Вращательное движение: тело вращается вокруг своей оси.
Вибрационное движение: при котором тело движется взад и вперед относительно своего среднего положения.
Скаляры: физические величины, которые описываются только величиной, известны как скаляры.
Векторы: Физические величины, которые описываются своей величиной и направлением, называются векторами.
Позиция: Позиция означает местоположение определенного места или объекта от контрольной точки.
Скорость: расстояние, которое мальчик преодолевает в любом направлении за единицу времени, называется скоростью.
Равномерная скорость: если скорость тела не меняется со временем, то его скорость одинакова.
Средняя скорость: Средняя скорость тела — это отношение общего пройденного расстояния к общему затраченному времени
Скорость: мы определяем скорость как скорость изменения смещения или скорости в определенном направлении.
Средняя скорость: Средняя скорость тела определяется как отношение его чистого смещения к общему времени.
Равномерная скорость: Если тело совершает равные перемещения за равные промежутки времени, каким бы малым ни был этот интервал, его скорость называется равномерной.
Ускорение: Скорость изменения скорости тела называется ускорением.
Равномерное ускорение: Тело имеет равномерное ускорение, если оно имеет равные изменения скорости за равные промежутки времени, каким бы малым ни был этот интервал.
График: График — это наглядный способ описания информации о том, как различные величины связаны друг с другом.
Наклон графика расстояние-время показывает скорость тела.
График «расстояние-время»: графики «расстояние-время» предоставляют полезную информацию о движении объекта.Наклон графика смещения-время дает скорость тела.
Расстояние, пройденное телом, равно площади под графиком скорость-время.
График скорость-время: График скорость-время также полезен для изучения движения по прямой.
График скорости-времени: расстояние, пройденное телом, также можно найти в области под графиком «Скорость-время», если движение идет по прямой.
Уравнения движения для равноускоренного движения:
V _f = V _i + at
S = V _i t + ½ при ²
2aS = V _f ² = V _i ²
Ускорение свободного падения: когда мальчика свободно бросают, он падает с ускорением по направлению к земле.Это ускорение называется ускорением свободного падения и обозначается g. числовое значение g составляет приблизительно 10 мс ^-2 у поверхности Земли.
Примечания к редакции
по кинематике | askIITians
Инерциальная система отсчета: — Система отсчета, в которой действует ньютоновская механика, называется инерциальной системой отсчета или инерциальной системой отсчета. Система отсчета, в которой не работает ньютоновская механика, называется неинерциальной системой отсчета или неинерциальной системой отсчета.
Средняя скорость v _av и средняя скорость тела за промежуток времени? т определяется как,
v _av = средняя скорость
=? с /? т

Примечание:
(a) Изменение скорости или направления движения приводит к изменению скорости
(b) Частица, которая совершает один оборот по круговой траектории с постоянной скоростью, считается обладающей нулевой скоростью и ненулевой скоростью.
(c) Частица не может иметь нулевую скорость с ненулевой скоростью.
Среднее ускорение определяется как изменение скорости за интервал времени? т .
Мгновенное ускорение частицы — это скорость, с которой ее скорость изменяется в данный момент.
Три уравнения движения для объекта с постоянным ускорением приведены ниже.
(а) v = u + при
(б) s = ut + 1/2 при ²
(c) v ² = u ² + 2as
Здесь u — начальная скорость, v — конечная скорость, a — ускорение, s — перемещение тела и t — время.
Примечание: примите знак «+ ve», когда тело ускоряется, и знак «–ve», когда тело замедляется.
Смещение кузова в n ^th секунда определяется как,
с _n = u + a /2 (2 n -1)
Время позиционирования ( x против t ), скорость-время ( v vs t ) и время ускорения ( a против t ) график для движения в одном измерении:
(i) Изменение смещения (x), скорости (v) и ускорения (a) во времени для различных типов движения.

Рабочий объем (x)
Скорость (v)
Разгон (а)
(а) В состоянии покоя

(б) Движение с постоянной скоростью

(c) Движение с постоянным ускорением

(d) Движение с постоянным замедлением

Скалярные величины: — Скалярные величины — это те величины, которые требуют только величины для их полной спецификации.(например, масса, длина, объем, плотность)
Векторные величины: — Векторные величины — это те величины, которые требуют как величины, так и направления для их полной спецификации. (например, перемещение, скорость, ускорение, сила)
Нулевой вектор (нулевые векторы): — Это вектор с нулевой величиной и произвольным направлением.
Когда нулевой вектор добавляется или вычитается из заданного вектора, результирующий вектор совпадает с заданным вектором.
Точечное произведение нулевого вектора с любым произвольным всегда равно нулю. Перекрестное произведение нулевого вектора с любым другим вектором также является нулевым вектором.
Коллинеарный вектор: — Векторы, имеющие общую линию действия, называются коллинеарными векторами. Есть два типа.
Параллельный вектор ( θ = 0 °): — Два вектора, действующих в одном направлении, называются параллельными векторами.
Антипараллельный вектор ( θ = 180 °): — Два вектора, направленные в противоположных направлениях, называются антипараллельными векторами.
Копланарные векторы- Векторы, расположенные в одной плоскости, независимо от их направления, называются копланарными векторами.
Сложение вектора: —
Сложение вектора коммутативное —
Сложение векторов ассоциативно —
Векторное сложение распределительное —
Треугольники Закон сложения векторов: — Если два вектора представлены двумя сторонами треугольника, взятыми в одном порядке, то их результат представлен третьей стороной треугольника, взятой в противоположном порядке.
Величина результирующего вектора: —
R = √ ( A ² + B ² +2 AB cos θ )
Здесь θ — угол между и.
Если β — угол между и,
тогда,
Если три вектора, действующие одновременно на частицу, могут быть представлены тремя сторонами треугольника, взятыми в одном порядке, то частица останется в равновесии.
Итак,
Параллелограммный закон сложения векторов: —
R = √ ( A ² + B ² +2 AB cos θ ),
Случаи 1: — Когда, θ = 0 °, тогда
R = A + B (максимум), β = 0 °
Случаи 2: — Когда, θ = 180 °, тогда
R = A — B (минимум), β = 0 °
Случаи 3: — Когда, θ = 90 °, тогда
R = √ ( A ² + B ²), β = tan ^-1 (B / A)
Процесс вычитания одного вектора из другого эквивалентен векторному сложению отрицательного значения вычитаемого вектора.
Итак,
(a) Точечное произведение или скалярное произведение: —
,
Здесь A — величина, B — величина, θ — угол между и.
(i) Перпендикулярный вектор: —
(ii) Коллинеарный вектор: —
Когда, Параллельный вектор (θ = 0 °),
Когда, Антипараллельный вектор (θ = 180 °),
(b) Перекрестное произведение или векторное произведение: —
Или,
Здесь A — величина, B — величина, θ — угол между и и — единичный вектор в направлении, перпендикулярном плоскости, содержащей и.
(i) Перпендикулярный вектор (θ = 90 °): —
(ii) Коллинеарный вектор: —
Когда, Параллельный вектор (θ = 0 °), (нулевой вектор)
Когда, θ = 180 °, (нулевой вектор)
В трех измерениях,
Площадь треугольника: —
Площадь параллелограмма: —
Объем параллелепипеда: —
(i) Перпендикулярный вектор: — В верхней части наклонной плоскости ( t = 0, u = 0 и a = g sin q ) уравнение движения будет иметь вид
(а) v = (g sinθ) t
(б) s = ½ (g sinθ) t ²
(в) v ² = 2 (g sinθ) с
(ii) Если время, необходимое телу для достижения дна, составляет t , тогда с = ½ ( g sin θ ) t ²
t = √ (2s / g sin θ )
Но sin θ = ч / с или с = ч / sin θ
Итак, t = (1 / sin θ ) √ (2 h / g )
(iii) Скорость тела на дне
v = g (sin θ ) t
= √2 гч
Относительная скорость объекта A относительно объекта B определяется как
V _AB = V _A — V _B
Здесь, V В называется ссылкой скорость объекта.
Изменение массы: — В соответствии с формулой изменения массы Эйнштейна релятивистская масса тела определяется как
м = м ₀ / √ (1- v ²/ c ²)
Здесь m ₀ — масса покоя тела, v — скорость тела и c — скорость света.
Движение снаряда в плоскости: — Если частица с начальной скоростью u проецируется под углом θ (угол проекции) с осью x , то
Время полета, T = (2 u sin α ) / g
Диапазон по горизонтали, R = u ² sin2 α / g
Максимальная высота, H = u ² sin ² α /2 g
Уравнение траектории, y = x tan α — ( gx ²/2 u ² cos ² α )
(a) При падении: — Период времени, t = √ (2h / g) и скорость, v = √ (2gh
(b) При рвоте: — Период времени, t = u / g и высота, h = u ² / 2g
Состояние равновесия: —
(а)
(b) | F ₁ + F ₂ | ≥ | F ₃ | ≥ | F ₁ -F ₂ |
Возможно, вам понравится:
CBSE класс 7 по математике | CBSE, класс 7, естественные науки | CBSE класс 11 по химии
Физический тест Pdf
NEET помощь в чате WhatsApp.Электронная книга Chand’s Principle Of Physics -XII: V. AP Physics Practice Test: Rotation, Angular Momentum © 2011, Ричард Уайт www. Загрузите электронную книгу и усердно готовьтесь к предстоящим экзаменам. Кашмирский университет. Физика 635–645 Решая, какой тест пройти, будьте реалистичны с собой. Вместо того, чтобы наслаждаться хорошей книгой за чашкой кофе в формате. Просмотр физики твердого тела Mcqs. tchaW Physics: Lorem ipsum dolor sit amet, conctetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua.Глава 7: экзамен по физике Холта — сдан. Кандидаты также могут загрузить и изучить экзаменационные работы предыдущего года по тесту ISSB Pak Air Force Physics Test в формате PDF, чтобы узнать программу и схему экзамена. Вот почему мы размещаем сборники книг на этом сайте. Barron s SAT Subject Test Physics, 2016. Чтобы загрузить APTITUDE TEST PROBLEMS IN PHYSICS BY KROTOV PDF, нажмите кнопку Download. Ниже приводится тест самодиагностики, который студенты должны пройти до поступления в класс по математике (математика 103 или математика 110).Pradeep Kshetrapal Electrostatics 2011. Продолжение подготовки к физическому тесту Имя _____ Автор: Сефали Лейн Дата создания: 05.11.2013 18:11:16. 000503 км б. Глава Один. Добро пожаловать на сайт www. Тест по механике также предназначен для использования в качестве заключительного теста для измерения эффективности обучения независимо от экзаменов по курсу. 542 \ u2460 2 E KI \ u2466 r2 F q Td IT \ u2190jq \ u2192 FF sg g to 3g d 2 3Z d B 0. Физика 151 Практический экзамен 1, осень 2012 г. (1. В этом тесте по научной теме физики мы Мы рассмотрим момент силы, который определяется как мера его тенденции заставлять тело вращаться вокруг определенной точки оси.Множественный выбор (3 балла каждый) Инструкции: пожалуйста, четко обведите один и только один ответ на каждый из следующих пунктов. Скачивание начнется. 2019 Физика твердого тела, Физика полупроводников MCQS Для физики BS Для подготовки к вступительным испытаниям в университет. Мы приглашаем вас загрузить pdf-файл вашей учебной программы по этому предмету. Решенные задачи семестрового обзора pdf. Также предоставляются комментарии об успеваемости учащихся по приемлемому стандарту и стандарту превосходства на тесте достижений.Мы пытались донести до студентов, что именно использование амплитуд вероятностей, а не вероятностей, делает квантовую механику необычной, и понять, что математическая структура теории следует. Изучите полную книгу онлайн-викторины MCQs для объективного типа прошлых работ, ответы на самые частые вопросы. Физика медицинской визуализации также известна как физика диагностической и интервенционной радиологии. расстояние, разделенное на временной интервал c. Вы можете просмотреть Сессию 1 только для того, чтобы проверить свои ответы.Центр атомных исследований имени Бхабхи (BARC). В физике сила связана с энергией и имеет точное значение. Объект свободно падает из состояния покоя в течение трех секунд. глава 1 кинематика учебный веб-сайт г-на панчбхая. В этом практическом пособии содержится одна фактическая полная стратегия прохождения теста GRE Physics Test. Ознакомьтесь со структурой теста, инструкциями по тестированию содержания и процедурами ответов. Сравните результаты вашего практического теста с результатами тех, кто прошел тест в администрации GRE.Ученые не просто верят — они тестируют и продолжают тестирование до тех пор, пока не будут удовлетворены. Это предварительный тест по физике. Читать далее. Отсюда вы можете увидеть, сможете ли вы сдать экзамен по естествознанию в 8-м классе или вам может понравиться узнать, какой безумный ученый подходит вашей личности. Клинические (как «штатные», так и «консультационные») физики обычно занимаются областями тестирования, оптимизации и обеспечения качества в областях физики диагностической радиологии, таких как рентгеновские снимки, рентгеноскопия, маммография, ангиография и компьютерная томография в качестве неионизирующих излучений.Физика пытается ответить на основные вопросы, в том числе, как возникла Вселенная ?. 0 м / с, когда водитель нажимает на тормоз, вызывая постоянное замедление на 2. При прохождении теста вы отметите свои ответы на отдельном листе для ответов с машинной оценкой. Я надеюсь, что вы можете помочь мне получить бесплатно тестовый банк 8-го издания «Основы физики» Источник (и): pdf банк тестов «Основы физики» 8-й: https: // biturl. Доступ к PDF-файлу Physics Vibrations And Waves Test. Такие ответы, как этот, физический тест на вибрации и волны, но в конечном итоге попадают во вредоносные загрузки.(MS-PS1-1), (MS-PS1-4) • Разработайте модель для описания ненаблюдаемых механизмов. Обзор испытаний по физике Вибрации и волны / Период звука и света: Имя: Мистер Вес астронавта вместе с его скафандром на Луне составляет всего 255 Н. Физика 9e Катнелл и Джонсон. MCQ по физике для вступительного теста Скачать PDF Этот файл в формате PDF содержит все разделы MCQ из книг по физике 1-го и 2-го курса, чтобы студенты могли подготовиться к вступительным испытаниям в инженерных и медицинских областях. Викторина * Тема / Название: Light * Описание / Инструкция; В этой викторине будут заданы вопросы о свете, его перемещении и отражении.Эти примечания могут использоваться для входных тестов MDCAT, ECAT, MCAT, NUST и NUMS. ТЕСТ ПО ФИЛОСОФИИ Четверг, 2 ноября 2017 г. Только для соискателей совместной степени по философии и теологии. Блок 2 Управляемые заметки. Глава 7: экзамен по физике Холта — сдан. На нашем сайте есть следующая электронная книга в формате PDF по основам экзаменационного банка по физике, которую можно бесплатно загрузить в формате PDF. Чистая сила и векторы. Затем вы должны пройти быструю викторину и отметить свои ответы с помощью схемы оценок. Наша спецификация GCSE Physics предлагает широкий, последовательный, удовлетворительный и стоящий курс обучения.Результаты теста следует рассматривать вместе со всей другой информацией об успеваемости ученика, такой как табели успеваемости и конференции родителей и учителей, чтобы помочь родителям / опекунам понять, насколько хорошо ученик знает предмет. Как мы уже упоминали, этот учебник физики не будет перегружать вас кучей предварительных расчетов по математике, но вместо этого он сосредоточен на физике в целом. Название книги: Тесты самооценки KIPS с ответами (все главы) Тема: Физика Издание: Н / Д Тип курса: Инженерные главы: Все Щелкните ниже, чтобы загрузить файл PDF: Загрузить материалы по теме.Boardworks GCSE Additional Science — Physics (лето 2011) Дата создания: 21.01.2016 14:45:47. Copyright © Glencoe / McGraw-Hill, подразделение McGraw-Hill Companies, Inc. на минимальном уровне. Этот тест может содержать некоторые. AP Physics B — это научный курс, который разделен на пять различных разделов: ньютоновская механика, электричество и магнетизм, механика жидкостей и теплофизика, волны и оптика, а также атомная и ядерная физика. Сегодня мы составили «Важные вопросы физики.Г) движется с бесконечной скоростью. Двенадцатый блок физики -2 Контрольный вопрос Тамильская среда, Рвение, учебные материалы Centum. GURU-8 декабря, 2019. «A Level Physics MCQ» с ответами охватывает фундаментальные концепции с помощью теоретических и аналитических тестов. Учебные материалы по физике для IIT JEE. mdcat Physics chapter 1 online mcq test с ответами для. Вводный вопрос по физике 3 — это открытый вопрос. 542 \ u2460 2 E KI \ u2466 r2 F q Td IT \ u2190jq \ u2192 FF sg g to 3g d 2 3Z d B 0. 602 19 × 10-19 C Потенциальная энергия, скорость электрона: PE = eV = ½mv 2 1V = 1J / C 1N / C = 1V / m 1J = 1 N · m = 1 C · V.перпендикулярно поверхности проводника. Физика — это наука, которая описывает работу природы языком математики. Наслаждайтесь занимательной и бесплатной книгой в формате PDF по физике, науке о движении: загрузите 5 бесплатных томов в формате PDF из учебника физики Motion Mountain. Ekey Часть I. Форум GRE по физике ↳ Регистрация и подготовка к тесту ↳ Проблемы, решения и обсуждение ↳ Результаты и отчеты о результатах; Темы для будущих аспирантов по физике ↳ Выбор школы ↳ Средний академический балл и стенограммы ↳ Тесты и результаты Sc Заявление о цели и резюме ↳ Исследования ↳ Финансирование ↳ Рекомендательные письма.Наши исследования, сосредоточенные в 11 ключевых областях, признаны во всем мире и ориентированы на научные проблемы 21 века. Отделение физики Герцога, известное своими отмеченными наградами факультетом и исследованиями, включает признанную на национальном уровне докторскую программу и предлагает степени бакалавра по физике и биофизике. Физика для Тома I NEET написана в упрощенном стиле, который помогает студентам не только учиться самостоятельно, но и приобретать уверенность в знании концепций, решая многочисленные MCQ, которые удачно размещаются в зависимости от уровня сложности.Источником всего волнового движения является a. Physics 101: Intro to Physics Final Free Practice Test Instructions. Материалы: Вы можете выбрать 12 предметов / материалов из следующего списка: • Картон, 5 резинок, 8 палочек для мороженого, 1 метр ленты, 2 листа плотной бумаги, полиэтиленовый пакет, 10 соломинок, пенополистирол, картон для плакатов, 6 хлопков. . Единственная горизонтальная сила, действующая на планер, — это натяжение ленты, так что. В этом практическом пособии содержится одна фактическая полная стратегия прохождения теста GRE Physics Test. Ознакомьтесь со структурой теста, инструкциями по тестированию содержания и процедурами ответов. Сравните результаты вашего практического теста с результатами тех, кто прошел тест в администрации GRE.AP Physics C Review Mechanics Обзорный проект CHSN Это обзорное руководство, разработанное в качестве подготовительной информации к экзамену AP1 Physics C Mechanics Exam 11 мая 2009 г. 520 МБ, полноцветное и содержит много фильмов, историй и фактов: каждый из более 2000 страниц прекрасны и увлекательны. Иногда это очень сбивает с толку, но основная идея состоит в том, что физика Ньютона описывает около 90% того, как вещи работают во Вселенной. физический набор для мальчиков и девочек московских школ, участвовавших в олимпиадах по физике с 1968 по 1985 год.Учебник PDF Скачать бесплатно скачать Ключевые слова: Концептуальная физика, 12-е издание Хьюитта, Пола Г. Мини-тесты Методы математической физики Задача 1. pdf из PHYS 00210 в Университете Роуэн. Начиная с момента t = T, эта сила снимается. Он полностью доступен в свободном доступе в виде загружаемого PDF-файла или для чтения в Интернете по адресу :. Частичный зачет может быть предоставлен, если вы включите свою работу. Часто двойная сюжетная линия, в которой два психолога, Стелла Берроуз и Саймон Перес, за три недели дают более или менее то, чем вы являетесь, насколько я делал pdf вопросы, физика, подготовка к тестам, и практиковалась.В кинематике силы, вызывающие движение, не принимаются во внимание, в то время как динамика имеет дело с движением объектов и силами, вызывающими их. Первый блок вопросов касается двойной науки. Там, где останавливается традиционная физика Мы собираемся вступить в современную эпоху физики. Какова кинетическая энергия шарика в момент, когда он покидает пружину? 3. Этот образец статьи необходим для подготовки к классу 12 CBSE. Доступ к бесплатному тесту по физике Холта Глава 4 Тест по физике Холта. Глава 4 Тест Благодарим вас за загрузку теста по главе 4 по физике Холта.СТАНДАРТНЫЙ ТЕСТ: XII ПОДРАЗДЕЛЕНИЕ: ФИЗИКА I, Ответьте на все вопросы: — -111 ОТМЕТКИ: 50 РАЗ: Ihrs 30 mins lox 1 = 10 I. Затем нажмите «Следующий вопрос», чтобы ответить на следующий вопрос. 0 3 6 Падение с 10 см 140 1. Правильные ответы: 3 вопроса: 100% Сатт С Кам Шила МАРИО МАРТИНЕС-HTPhysics. Во-первых, вам необходимо изучить сводные листы. Практический тест AP Physics 1 | Ключ ответа | Ответить Пояснения; AP Physics 1 Практический тест 1 | Ключ ответа | Ответить Пояснения; AP Physics 1 Практический тест 2 | Ключ ответа | Ответить на Разъяснения.Новое официальное руководство по предметному тесту SAT по физике включает два полных практических теста. Значимые фигуры. Исследователи физического образования из Университета штата Мэн разработали шаблон, который можно использовать для анализа данных HTCE до публикации, доступный здесь; Инвентаризация термических и транспортных концепций (TTCI) Тест с множественным выбором концепций, связанных с теплопередачей, механикой жидкости и термодинамикой, подходящей для студентов инженерных специальностей. Описание. В этом практическом пособии содержится одна фактическая полная стратегия прохождения теста GRE Physics Test. Ознакомьтесь со структурой теста, инструкциями по тестированию содержания и процедурами ответов. Сравните результаты вашего практического теста с результатами тех, кто прошел тест в администрации GRE.Как написать статью по финансовому анализу для подготовки к экзамену на высшую сумму денег, чтобы получить ответы на вопросы по физике в формате pdf. Какое из следующих уравнений можно использовать для прямого вычисления импульса объекта p? а. pdf из PHYSICS PY 723 в Сельскохозяйственном университете. Об этом тесте Тест по физике: предметные знания предназначен для измерения знаний и компетенций, необходимых начинающему учителю физики средней школы. Назикян и Б. Вместо того, чтобы наслаждаться хорошей книгой за чашкой кофе в. Множественный выбор (3 балла каждый) Инструкции: пожалуйста, четко обведите один и только один ответ на каждый из следующих пунктов.Блок 4 Тест. Контрольная работа за 2 семестр в колледже Наланда, 12 класс физики, 2019 г. Когда его хвост находится в начале координат, он лежит между ними. Когда сдавать предметный тест SAT II Лучше всего сдавать предметный тест SAT II сразу после того, как вы закончите годичный урок по этому предмету. См. Также следующее: 1. Модули шестигранников для neet pdf Примечания к решению. Основные статьи Аллена за 2019, 2018 и 2017 годы будут доступны очень скоро. Физический клуб Университета Кларксона. Обзор первого экзамена по физике. К экзамену ARDMS SPI! Вот издание SPI единственного бестселлера пробного экзамена, посвященного экзамену ARDMS по ультразвуковой физике.Физика 1: Университетская физика для ученых и инженеров Обратите внимание, что эта работа еще не завершена и, как таковая, будет претерпевать множество изменений до конца семестра. _____ 1) Метрическая система основана на числе десять, потому что наша система счисления тоже. PDF-файл: Глава Holt Physics Test A Heat — HPCTAHPDF-118 2/2 Holt Physics Chapter Test A Heat Прочтите главу Holt Physics Test A Heat PDF в нашей цифровой библиотеке. Блок 2 — Научные измерения. Чтобы получить копию оригинальных стандартов Калифорнии, просто введите «Калифорнийские научные стандарты» в свой браузер, и, вероятно, первым списком будет PDF-копия всего документа.Покажи ответ. Бесплатные экзаменационные работы по любой квалификации и предмету. MCQ 1-го года по физике Полная книга (Pdf) Qasim Tariq 11-09-2018 MCQs Если вы ищете заметки о вопросах с множественным выбором по физике XI (Книга физики-1), то вы попали в нужное место. com принес сюда лучшую и самую большую коллекцию последних образцов статей по физике 11 класса. Сегодня мы составили «Важные вопросы по физике. Вы можете просмотреть Сессию 1 только для проверки своих ответов. (2 балла) б) Назовите каждую из сил. помечены P, Q и R.Какая скорость. Магнитный материал Akash Physics Success для препарата NEET-UG AIIMS JIPMER доступен для бесплатного скачивания в формате pdf. Физика, Контрольные работы в школьном семестре, Тест за 2-й семестр, 12-й класс, Колледж Наланда 2 июля 2019 г. 12-й класс, Колледж Наланда, Физика, Тест 2-го семестра, Школьный семестр. ТЕСТ 2 ФИЗИЧЕСКОГО ТЕСТА — продолжение Практика обзора в Принстоне Предметный тест SAT Physics 2 | 467 ПЕРЕЙДИТЕ НА СЛЕДУЮЩУЮ СТРАНИЦУ F 27. Эта книга, предназначенная для школьников и учителей физики, также может быть использована для подготовки к поступлению.Однако мы хотим прояснить, что это издание можно бесплатно читать только в Интернете, и эта публикация не передает никаких прав на загрузку всех или какой-либо части Лекций Фейнмана по физике для каких-либо целей. Щелкните ссылку и укажите необходимые основные сведения, которые будут запрошены, и вы получите требуемый документ по физике IGCSE Grade 9 и Grade 10. Университетская физика с современной физикой, Двенадцатое издание продолжает непревзойденную историю инноваций и тщательного исполнения, заложенную в бестселлере Одиннадцатого.Форма 2 Учебная программа по физике. 2020-2021: Загрузите учебник по следующей ссылке: https: // openstax. Найдите информацию и ответы на свои вопросы о радиационной и радиационной безопасности / защите. скорость, деленная на временной интервал. скачать 1 файл. 2019 Физика твердого тела, Физика полупроводников MCQS Для физики BS Для подготовки к вступительным испытаниям в университет. 10 м / сек2 C. PAT предназначен для кандидатов, которые в первый год изучили математику и физику A-level (или эквивалент), и охватывает материалы, аналогичные материалам программ GCSE и A-level.данные американских горок. Как мы все знаем, на многих конкурсных экзаменах, таких как SSC, Railways, UPSC и другие государственные PCS, вопросы по физике задаются неоднократно, поэтому вы не можете игнорировать раздел физики общих наук. mdcat Physics chapter 1 online mcq test с ответами для. Двенадцатый блок физики -2 Контрольный вопрос Тамильская среда, Рвение, учебные материалы Centum. Стандарты содержания штата Орегон: естественные науки для старших классов (2011–2012 годы). 0 3 6 Падение с 10 см 140 1. Покоящийся объект остается в состоянии покоя и ан. Прочтите закон сохранения массы, удельную теплоемкость воды и формулы, необходимые для расчета ускорения.Если вы укажете загрузить и установить тест по главе 4 по физике, то это будет. 1) Когда мяч подбрасывается прямо вверх без сопротивления воздуха, ускорение в его наивысшей точке A) направлено вверх, B) равно нулю, C) направлено вниз. Он предназначен для проверки знаний соискателей по широкому кругу научных дисциплин, включая органическую химию, общую химию, биохимию, общую биологию, психологию, физику и социологию. Рабочие листы по главам. Отличный набор заметок AP Physics 1 в формате PDF и PowerPoint.Скачать 11th Physics Chapter 11 Термодинамика решает вопросы с несколькими вариантами ответов. Будьте готовы показать свою научную смекалку прямо сейчас !. Прослушивание учебников по физике. Лаборатория 2 — Physics 500 Лаборатория 3 — Лаборатория эффекта домино 4 — Мы весело катимся Лаборатория 6 — Лаборатория гоночной трассы 7 — Bull’s Eye (b) Hsu — Лаборатория физики CPO 1A — Время, расстояние и скорость (c) Мои лаборатории C -2: (из Темы 1): Векторы ходьбы (если это не было сделано в Теме 1) C-2: Пройдите по числовой прямой C-3: Скорость и ускорение (a) Постоянное движение. Основы тестирования 100 крат.Физические условия / экзамен по физике (191 КБ) Ключ к оценке и Руководство по оценке (572 КБ) Таблица преобразования (62 КБ) Тест, январь 2005 г. (191 КБ) Ключ оценки (572 КБ) Таблица преобразования (62 КБ) Тест, июнь 2004 г. (160 КБ) Ключ оценки (555 КБ) Таблица преобразования (147 КБ) Тест января 2004 г. (178 КБ) Ключ оценки (562 КБ) Таблица преобразования (193 КБ). MCQ для 1-го и 2-го курсов по физике можно загрузить в формате PDF для вступительного теста, такого как тесты MDCAT, NUMS, MCAT, ECAT, NUST и UET. Метрические префиксы, определенные единицы, производные единицы, преобразования, сложение и вычитание с единицами, умножение с единицами.Физика, Контрольные работы в школьном семестре, Тест за 2-й семестр, 12-й класс, Колледж Наланда 2 июля 2019 г. 12-й класс, Колледж Наланда, Физика, Тест 2-го семестра, Школьный семестр. Также см. Следующее: 1. mdcat Physics chapter 1 online mcq test with answer for. книга по общей физике. 63 × 10 –34. Определить погрешности немного сложнее, поскольку вы | не измерительный прибор | должен их определить. Он полностью доступен в свободном доступе в виде загружаемого PDF-файла или для чтения в Интернете по адресу :. Ut enim ad minim veniam, quis nostrud упражнение ullamco labouris nisi ut aliquip ex ea Commodo Conquat.pdf ПОДРОБНЫЕ РЕШЕНИЯ (и другие ресурсы): GREPhysics. MCQ 1-го года по физике Полная книга (Pdf) Qasim Tariq 11-09-2018 MCQs Если вы ищете заметки о вопросах с множественным выбором по физике XI (Книга физики-1), то вы попали в нужное место. Получайте последние новости о миссиях НАСА, смотрите прямую трансляцию NASA TV и узнавайте о нашем стремлении раскрыть неизведанное и принести пользу всему человечеству. Физика пытается ответить на основные вопросы, в том числе, как возникла Вселенная ?. Этот модуль является частью библиотеки Physics.Однако он может быть полезен и для других целей. Затем перейдите к разделу «Тест по физике», в котором описан тест и включены примеры вопросов и ответов. FOPS_ Gr11_TestPaper_2. Duis aute irure dolor в репрехендерит в сладострастном velit esse cillum dolore eu fugiat nulla pariatur. АНАЛИЗ ИЗМЕНЕНИЙ / ПОЛУЧЕНИЕ ОЧКОВ * † Ричард Р. Основы реле: Реле — это электрический переключатель, который использует электромагнит для перемещения переключателя из выключенного положения во включенное, а не человека, перемещающего переключатель.Физическое моделирование в Java (неопубликовано, 2011 г.) и Физическое моделирование в Python (не опубликовано, 2018 г.) — это две версии лабораторного руководства, которое я написал для нашего курса по научным вычислениям. Типпенс, профессор физики Южного политехнического государственного университета. Презентация в формате PowerPoint, автор. Просмотр физики твердого тела Mcqs. Handbook of Physics — важный, полезный и компактный справочник, подходящий для повседневного изучения, решения проблем или пересмотра экзаменов для классов XI — XII, инженерных и медицинских входов и других соискателей соревнований.Физика 1: Университетская физика для ученых и инженеров Обратите внимание, что эта работа еще не завершена и, как таковая, будет претерпевать множество изменений до конца семестра. Скорость света в вакууме (c) 3. Физические стандарты Калифорнийской средней школы: † На этой странице опытным учителем обсуждается каждый из Калифорнийских физических стандартов средней школы. Загрузите SAT Subject Tests Student Guide (. Получите бесплатные ежедневные практические задания по физике! Курсы AP Physics сложны, но любой, у кого есть достаточно времени и практики, может усвоить материал на экзаменах AP Physics Совета колледжей.Так что оставайтесь с нами и внимательно прочтите этот пост, чтобы получить все pdf-файлы с тестовой бумагой HSC. В физике _____ — это сила, которая противодействует относительному движению двух соприкасающихся тел. Какова кинетическая энергия шарика в момент, когда он покидает пружину? 3. Шарик для настольного тенниса сталкивается лицом к лицу со стальным мячом, летящим в противоположном направлении. Этот модуль является частью библиотеки Physics. Предыдущие статьи и образцы документов дают общее руководство по вероятному содержанию будущих статей, но сохраняют старые форматы и могут включать довольно сложные численные вычисления в статьях по физике.Рассмотрим график. Цвебен и Р. Энергетические проблемы — ответы pdf. Камень ускоряется примерно на A. Викторина от vaniazulfa Статическое электричество Grade 9 Quiz — By vaniazulfa. вы присоединитесь к серии тестов neet. Раздел экзаменов содержит 12 практических экзаменов, решения и таблицы формул для курса. Июнь 2017 г. Документы прошедших экзаменов AQA Physics GCSE (4403) июнь 2017 г. Физика — Модуль 3 Physics P3 Foundation (Ph4FP) QA: AQA: июнь 2017 г. Документы прошедших экзаменов AQA Physics GCSE (4403) Июнь 2017 г. Физика — Модуль 3 Physics P3 Higher (Ph4HP) QA: AQA: июнь 2016 AQA Physics GCSE Past Exam Papers (4403) июнь 2016 Science A — Unit 1 Physics P1 Foundation (Ph2FP.Исследование в формате PDF «Викторина по физике колледжа». Тема: Физика. Исфаханский университет. Помимо ресурсов для пересмотра, мы также подготовили контрольные работы по естественным наукам 8-го класса с ответами в формате pdf или. Значимые фигуры. Научный метод принимает только разум, логику и экспериментальные данные, чтобы отличить то, что является правильным с научной точки зрения, а что нет. MCQ по физике для вступительного теста Скачать PDF Этот файл в формате PDF содержит все разделы MCQ из книг по физике 1-го и 2-го курса, чтобы студенты могли подготовиться к вступительным испытаниям в инженерных и медицинских областях.В частности, разрывы страниц, которые я хочу разместить в стратегических местах (чтобы не разрезать что-то важное на 2 страницы), но пытаюсь сделать это сейчас. 4 Глава D. Практика с отличием Тест по физике: законы Ньютона Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. Интегрированная коллекция включает текст OpenStax College Physics for AP ® Courses, видеоролики Concept Trailer, обучающие видеоролики, видеоролики по решению проблем и руководство по корреляции, которое поможет вам согласовать весь ваш бесплатный контент.Модульный тест — SPh4U 11 класс Физика — Волны и звук Название: _____ Модульный тест — SPh4U 11 класс Физика — Волны и звук Этот тест состоит из 4 частей. 67 × 10-27 кг Нейтрон = 0 C = 1. Название: Microsoft PowerPoint — Глава 5 [Режим совместимости] Автор: Мукеш Дхамала Дата создания: 8.02.2011 16:38:07. От 04 м до нуля. [Имя файла: 201010181217530. Подробнее Медали за выдающиеся исследования в области физики звезд, Марса и квазаров Три молодых физика были отмечены за свои обширные исследования на престижном конкурсе STEM for Britain, который в этом году состоялся онлайн.Наука для всех: тест на способности: задачи по физике был первоначально распространен в Москве, чтобы помочь молодым студентам подготовиться к физическим олимпиадам с 1968 по 1985 год. Научный метод принимает только разум, логику и экспериментальные данные, чтобы отличить то, что является правильным с научной точки зрения, и тем, что не является. Поскольку инструкции к тесту могли измениться, обязательно прочтите их внимательно. Учебное пособие «Физика: принципы с приложениями», пятое издание, Джанколи, Джозеф Дж. Аллен, физический модуль для neet — UG — Aiims, книги в формате PDF для подготовки JIPMER.Скачивание начнется. На протяжении многих лет радиация была полезна людям для медицинской диагностики и терапии, научных исследований и выработки электроэнергии. ФИЗИЧЕСКИЕ ФОРМУЛЫ 2426 Электрон = -1. привет, если вы хотите скачать dc pandey pdf, вы находитесь в нужном месте, поэтому dc pandey Physics pdf или dc pandey pdf — очень хорошая книга из публикации arihant. Это сэкономит ваше время на самом тесте. Согласно нашему каталогу, эта электронная книга на самом деле значится как HPCTAHPDF-118.K Mehta & Rohit Mehta: просмотреть все поддерживаемые устройства; Du. 2015 Ноябрь Physical Sciences P1 GR 10 Eng 16. Эксперименты по физике альфа-частиц в термоядерном реакторе Токамака @article {Zweben2000AlphaPP, title = {Эксперименты по физике альфа-частиц в термоядерном реакторе Токамака}, автор = {S. 2019 Физика твердого тела, Физика полупроводников MCQS Для физики BS Для подготовки к вступительным испытаниям в университет. Таблица физических уравнений GCSE Physics (8463) 1 давление столба жидкости = высота столба × плотность жидкости × напряженность гравитационного поля (g) p = h ρ g 2 (конечная скорость) 2 — (начальная скорость) = 2 расстояние ускорения v2 — u2 = 2 а с.ID: 1740683 Язык: Английский Школьный предмет: Физика Уровень: 3 Возраст: 16-17 Основное содержание: Силы и движение Другое содержание: физика Добавить в мои рабочие тетради (0) Скачать файл pdf. pdf из PHYS 00210 в Роуэнском университете. Назад к науке для детей. Последний образец статьи CBSE по физике класса 12 2021 с решением PDF Образец статьи CBSE по физике класса 12 2021 года вместе со схемой маркировки и решениями официально выпущен правлением. В тесте по физике всего 25 вопросов в форме MCQ, ответы на которые будут в основном на английском языке. Иногда также и на урду.Важные вопросы по физике и ответы в формате PDF. Это скорость проделанной работы или скорость передачи энергии. Об этой викторине: Все вопросы в этой викторине основаны на информации, которую можно найти на сайте Physics: Force. Хейк, факультет физики 9-го класса. Решенные числовые показатели. Если вы хотите получить электронные копии всех тестов 9-го класса из файлов MS Word с вашим собственным названием и логотипом академии, свяжитесь со мной по WhatsApp 03017980076. Июнь 2017 г. Документы прошедших экзаменов AQA Physics GCSE (4403) Июнь 2017 г. Физика — блок 3 Physics P3 Foundation (Ph4FP) QA: AQA: июнь 2017 г. AQA Physics Прошедшие экзамены GCSE (4403) июнь 2017 г. Физика — блок 3 Physics P3 Higher (Ph4HP) QA: AQA: июнь 2016 г. Прошедший экзамен AQA Physics GCSE Документы (4403) Июнь 2016 г. Наука A — Фонд 1 Физика P1 (Ph2FP.Название: Microsoft Word — обзор рабочего листа Momentum test. Все решенные MCQ для английского языка по физике X с онлайн-викторинами. Практика: вопросы о скорости и скорости. Что из следующего должно быть правдой? Закажите официальные учебные пособия. Руководство по решениям в мягкой обложке содержит ответы на контрольные вопросы, практические задачи, дополнительные практические задачи, а также включает тесты / ежеквартальные тесты и решения для тестов. Банк тестов по физике Джанколи. Эти документы представлены в формате PDF. gov предлагает вам самые свежие изображения, видео и новости американского космического агентства.c Применить знание ряда методов, инструментов, аппаратов и материалов, чтобы выбрать те, которые подходят для эксперимента. Physics 3A-3B-3C или Physics 7C-7D-7E). Он предназначен для проверки знаний соискателей по широкому кругу научных дисциплин, включая органическую химию, общую химию, биохимию, общую биологию, психологию, физику и социологию. MIT — Массачусетский технологический институт. Стандарты физики средней школы Калифорнии: † Эта страница представляет собой обсуждение каждого из стандартов физики средней школы Калифорнии опытным учителем.Просмотр физики твердого тела Mcqs. Мы приглашаем вас загрузить pdf-файл вашей учебной программы по этому предмету. Это безусловно облегчит вам просмотр руководства по физике, глава 10, как и вам. Обновление охвата экзаменов Примечание. Начиная с экзамена 2021 года, блоки 8–10 больше не будут проверяться в AP Physics 1. Силы расстояния движения и положения. 3 Физика анимации — баланс и смещение веса Среднее положение распределения веса объекта называется центром тяжести (ЦТ). pdf из PHYS 00210 в Роуэнском университете.В физике сила связана с энергией и имеет точное значение. Если объект не имеет равномерного распределения веса. Вопросы и ответы по физике с множественным выбором pdf. Следующий PDF-файл содержит книгу KIPS MDCAT PHYSICS. Если бы его начальная скорость была увеличена вдвое, то расстояние. Скачать Physics Chapter 4 Testphysics chapter 4 test как вам нравится. • Разработайте модель для прогнозирования и / или описания явлений. Шарик для пинг-понга сталкивается лицом к лицу со стальным мячом, летящим в противоположном направлении. Эта система измерения называется.Лаборатория 2 — Physics 500 Лаборатория 3 — Лаборатория эффекта домино 4 — Мы весело катимся Лаборатория 6 — Лаборатория гоночной трассы 7 — Bull’s Eye (b) Hsu — Лаборатория физики CPO 1A — Время, расстояние и скорость (c) Мои лаборатории C -2: (из Темы 1): Векторы ходьбы (если это не было сделано в Теме 1) C-2: Пройдите по числовой прямой C-3: Скорость и ускорение (a) Постоянное движение. Краткое содержание лекции 1 — ВВЕДЕНИЕ В ФИЗИКУ 1. Множественный выбор (по 3 балла) Инструкции: пожалуйста, четко обведите один и только один ответ на каждый из следующих вопросов. of Physics, Университет Индианы. 24245 Hatteras Street, Woodland Hills, CA, USA. В списке рассылки Американской ассоциации исследований в области образования (Отдел D) * от 22 февраля 1999 г.Известно, что Заряд 1 притягивает Заряд 2, Заряд 2 отталкивает Заряд 3, а Заряд 3 притягивает Заряд 4. Пока мы не сможем понять концепции и иметь возможность делать наши собственные открытия, числа и уравнения физики бессмысленны. (3 балла) c) Опишите движение подводной лодки. Вступительный тест по физике Многие академические программы бакалавриата требуют, чтобы учащиеся выполнили часть или всю последовательность занятий по физике (например, тестовая работа за 2 семестр в колледже Наланда, 12 класс физики, доступна здесь.Практика с отличием Тест по физике: Законы Ньютона Множественный выбор Определите вариант, который лучше всего завершает утверждение или отвечает на вопрос. Эта книга поможет вам при сдаче экзамена по физике в 9 классе. Решения NCERT для класса 11 по физике в формате PDF доступны для загрузки обновленными для новой академической сессии 2020-2021 годов, решения упражнений, дополнительных упражнений, дополнительных материалов и книг NCERT 2020-2021. Координаторы AP должны подтвердить в AP Registration and Ordering, что список студентов является точным и что все студенты, которые планируют пройти тестирование во время администрирования экзамена, имеют статус заказа на экзамен «Да» и отправлять обновления, если таковые имеются.Физика 2 соответствует второму семестру. Вопросы и ответы с несколькими вариантами ответов (MCQ) по физике уровня: викторины и практические тесты с ключом ответа (краткое руководство по физике уровня и обзор курса) охватывает оценочные тесты курса для конкурсных экзаменов для решения 700 MCQ. Подтвердите всех учащихся, которые планируют пройти тестирование. И, как и SAT, это действительно плохой показатель того, как вы будете учиться в аспирантуре. ) Каждая строка формулы содержит описание переменных или констант, составляющих формулу, а также краткое объяснение.Блок 2 Управляемые заметки. Серия тестов Аллена pdf Документы Neet pdf 2021 Скачать здесь. ID: 1740683 Язык: Английский Школьный предмет: Физика Уровень: 3 Возраст: 16-17 Основное содержание: Силы и движение Другое содержание: физика Добавить в мои рабочие тетради (0) Скачать файл pdf. Физика I — Тест №2. Определить погрешности немного сложнее, поскольку вы | не измерительный прибор | должен их определить. В данном году экзамен будет проверять репрезентативную выборку содержания 12-го года. Есть много разделов физики, включая электричество, астрономию, движение, волны, звук и свет.Xam Idea Class 12 Physics — одна из популярных книг среди студентов, готовящихся к экзамену CBSE Class XII. 1 Цели и результаты обучения 77 5. Этот образец работы необходим для подготовки к CBSE Class 12. Онлайн-викторина MCQ для тестов по физике с полезными простыми онлайн-тестами. Какая скорость. Все на Земле, все в нашей солнечной системе, все в нашей галактике и во Вселенной движется и взаимодействует, и силы играют в этом большую роль. Темы, освещаемые в Physics 1, включают механику Ньютона, работу, энергию, мощность, механические волны, звук и простые схемы.УЧЕБНИК ПО ФИЗИЧЕСКИМ КЛАССАМ Физика 11 практических экзаменов по кинематике с ответами. Рассмотрим график. Измерение очень важно в нашей жизни; из количества сахара, которое мы добавляем в чашку чая к одежде, которую носим. Исследователи физического образования из Университета штата Мэн разработали шаблон, который можно использовать для анализа данных HTCE до публикации, доступный здесь; Инвентаризация термических и транспортных концепций (TTCI) Тест с множественным выбором концепций, связанных с теплопередачей, механикой жидкости и термодинамикой, подходящей для студентов инженерных специальностей.Надеюсь, вы найдете этот ресурс полезным. ЕГО РУКОВОДСТВО охватывает физику волн, звука, музыки и музыкальных инструментов на уровне, разработанном для школьной физики. com принес сюда лучшую и самую большую коллекцию последних образцов статей по физике 11 класса. Департамент физики Массачусетского технологического института, 77, Массачусетс-авеню, здание 4, комната 304, Кембридж, Массачусетс 02139 617–253–4800. Блок 3-мерный анализ, векторный анализ и руководство по SOHCAHTOA Блок 3. Чтобы проверить это, вам нужно приложить постоянную силу к параплану.Линейное движение. 2015 Ноябрь Physical Sciences P1 GR 10 Eng 16. Математика Почему концепции в физике описываются формулами? Формулы краткие и могут использоваться для прогнозирования новых данных. Практический тест AP Physics: вращение, угловой момент © 2011, Ричард Уайт www. Предметный тест SAT Баррона по физике, 2016. Практический тест на скорость, скорость и ускорение. AP Физика 1 зачет. Физика Базовая физика Скорость молярности. Если вы являетесь волонтером или некоммерческой организацией, мы будем рады предоставить материалы для подготовки к испытаниям по сниженной цене или бесплатно.Практика помогает. Edexcel GCSE (9-1) Ресурсы для пересмотра физики. Посмотреть Физику I — Тест № 2 (2). У вас будет все 75-минутное занятие, чтобы закончить тест, если вам это нужно. Представлены предметные вопросы Sat Physics по векторам, аналогичные вопросам в тесте SAT. Это безусловно облегчит вам просмотр руководства по физике, глава 10, как и вам. Физика — это отрасль науки, изучающая материю и ее движение, а также то, как она взаимодействует с энергией и силами. Официальные стенограммы должны быть отсканированы и загружены в вашу онлайн-заявку.Продолжение подготовки к экзамену по физике Имя _____ Автор: Сефали Лейн Дата создания: 05.11.2013 18:11:16. Johnson, Science, 2004, Physics, Volume 1, В каждом новом издании Cutnell & Johnson’s PHYSICS лидировала с подходом, который дает вам возможность овладеть фундаментальными принципами физики и применять их в мире мы. Физика: Принципы с приложениями: Тестовое задание Файл pdf скачать Элементарная физика, Наука, УОМ: 317199954, Джордж. Физика — это наука. Кинематика. Руководство по экзамену SSC. AP Physics B — это научный курс, который разделен на пять различных разделов: ньютоновская механика, электричество и магнетизм, механика жидкостей и теплофизика, волны и оптика, а также атомная и ядерная физика.Просмотр физики твердого тела Mcqs. Практический тест AP Physics 1 | Ключ ответа | Ответить Пояснения; AP Physics 1 Практический тест 1 | Ключ ответа | Ответить Пояснения; AP Physics 1 Практический тест 2 | Ключ ответа | Ответить на Разъяснения. Мы, студенты ведущих школ Коломбо, которые вошли в сотню лучших в 2011 году по результатам экзамена A / L, создали клуб под названием ANON Club. Скорость света в вакууме (c) 3. УЧЕБНИК ПО ФИЗИЧЕСКИМ КЛАССАМ Физика 11 практический тест по кинематике с ответами. По три очка каждый. Типпенс, профессор физики Южного политехнического государственного университета. Презентация в формате PowerPoint, автор.В этом руководстве в формате PDF вы узнаете важные длинные вопросы физики 1-го года обучения по главам MCQ. семестр обзор. Учащийся средней школы обычно выбирает пройти тест, чтобы выполнить требования для поступления в колледж для школ, в которые он планировал поступать. Практический тест скорости, скорости и ускорения. (b) (i) Электрическая лампочка мощностью 100 Вт подключается к сети 220 В. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. Подготовьтесь к экзамену группы X по физике в секции ВВС Индии и получите хорошие баллы.Этот тест был разработан для студентов, желающих поступить в медицинские и инженерные колледжи / университеты или на другие факультеты, этот тест также может помочь профессионалам улучшить или повторно проверить свои промежуточные знания по предмету. Физика 1: Университетская физика для ученых и инженеров Обратите внимание, что эта работа еще не завершена и, как таковая, будет претерпевать множество изменений до конца семестра. 520 МБ, полноцветный и содержит множество фильмов, рассказов и фактов: каждая из более чем 2000 страниц прекрасна и увлекательна.Выпущенный курс AP Physics 1 и 2 и описание экзамена включают эту структуру учебной программы, а также новый уникальный набор экзаменационных вопросов. Камень весом 5 ньютонов свободно падает с высоты 44 метра. Однако он может быть полезен и для других целей. Национальная служба тестирования NTS книги по подготовке к экзаменам скачать бесплатно в формате PDF с решенными тестами MCQ. график времени имеет угол, затем ускорение по сравнению с названием: Microsoft PowerPoint — Глава 5 [Режим совместимости] Автор: Мукеш Дхамала Дата создания: 8.02.2011 16:38:07.Решения NCERT для класса 11 по физике в формате PDF доступны для загрузки обновленными для новой академической сессии 2020-2021 годов, решения упражнений, дополнительных упражнений, дополнительных материалов и книг NCERT 2020-2021. тум-механику студентам второго курса физики Оксфордского университета. Банк тестов по физике Scribd. физика: [существительное, множественное число по форме, но единственное или множественное число по конструкции] наука, которая имеет дело с материей и энергией и их взаимодействием. Начните изучать тест по физике: ток, электричество и цепи.«Заметки по квантовой механике» (не опубликовано, 2020 г.) — это черновик учебника для одного семестра курса бакалавриата по квантовой механике. Подборка рецензентов вступительного теста Филиппинского университета или UPCAT, которые доступны в Интернете в PDF-формате Математика, естественные науки, Рецензент вступительного экзамена USTET Составитель рецензента USTET. Совет Гуджарата по HSC Physics Question Paper 2021. Июнь 2017 AQA Physics GCSE Прошедшие экзамены (4403) Июнь 2017 Physics — Unit 3 Physics P3 Foundation (Ph4FP) QA: AQA: июнь 2017 AQA Physics Прошедшие экзамены GCSE (4403) Июнь 2017 Физика Модуль 3 Physics P3 Higher (Ph4HP) QA: AQA: июнь 2016 AQA Physics GCSE Прошедшие экзамены (4403) июнь 2016 Science A — Unit 1 Physics P1 Foundation (Ph2FP.AP Physics 1 и 2 — это физика, основанная на алгебре. Как вы, возможно, знаете, люди много раз искали выбранные ими романы, такие как этот тест по физике Холта, глава 4, но в итоге получали вредоносные загрузки. Согласно нашему каталогу, эта электронная книга на самом деле значится как HPCTAHPDF-118. Но это не значит, что книга написана плохо. Университет, в частности, преподает серию курсов по физике 141/142, 151/152 или 161/162 (вводная физика для специалистов по естественным наукам, инженеров или потенциальных специалистов по физике соответственно).Если у вас возникли проблемы с этим сообщением или файлом PDF, вы можете добавить комментарий ниже или связаться с нами через Facebook или по электронной почте. Это незавершенная работа. Использование математики, включая алгебру и тригонометрию, важно, но концептуальное понимание физических систем остается первоочередной задачей. MCAT использует компьютерный формат с множественным выбором для своих 85 000 ежегодно проходящих тестирование. Один из примеров, который вам может показаться самым легким для понимания, — это качели. Программа PMC MDCAT 2020 PDF Скачать Биология, физика, химия, английский язык.Он связан с системами, законами, моделями, принципами и теориями, которые объясняют физическое поведение нашего мира и Вселенной. тум-механику студентам второго курса физики Оксфордского университета. Доступ к бесплатному тесту Holt Physics Chapter 4 Test Holt Physics Chapter 4 Test Благодарим вас за загрузку теста Holt Physics Chapter 4. Книга в формате PDF «Физика 9 класса с множественным выбором вопросов и ответов», которую можно загрузить, охватывает решенные вопросы викторины и ответы в формате PDF по темам: динамика, гравитация, кинематика, свойства материи, физические величины и измерения, тепловые свойства материи, перенос тепла, поворотный эффект силы, работа и энергия для сдачи экзаменов в школе и колледже.Вы должны предоставить одну загруженную копию официальной академической справки из каждого колледжа, в котором вы учились. Получите доступ к другим инструментам для изучения физики IB, просмотрев предыдущие статьи IB Physics. ID: 1740683 Язык: Английский Школьный предмет: Физика Уровень: 3 Возраст: 16-17 Основное содержание: Силы и движение Другое содержание: физика Добавить в мои рабочие тетради (0) Скачать файл pdf. Это дает нам знания о физическом мире, и именно эксперимент предоставляет доказательства, подтверждающие это знание. Чтобы помочь вам запомнить ключевые концепции физики, обсуждаемые при просмотре видео, заполните пропуски или обведите правильный ответ.Рассчитайте (а) заряд конденсатора при t = 0, C = Q / V (из таблицы данных) Q = CV = 50 x 10-6. Если вы ищете нерешенные практические mcqs для fsc и подготовки к вступительным экзаменам, посетите этот блог. Выделите час, когда сможете взять. • Покажите всю свою работу (диаграммы, таблицы или вычисления) в документе с ответами на практический тест. Силы расстояния положения движения. Подборка рецензентов вступительного теста Филиппинского университета или UPCAT, которые доступны в Интернете в PDF-формате Математика, естественные науки, Рецензент вступительного экзамена USTET Составитель рецензента USTET.Глава 1: ИЗМЕРЕНИЕ 1. Это книга для тех, кто. Покоящийся объект остается в состоянии покоя, а объект. Физика изучает мельчайшие элементарные частицы и атомы, а также самые большие звезды и звезды. Для получения дополнительных заметок и книг в формате PDF посетите домашнюю страницу этого сайта. В этом руководстве в формате PDF вы узнаете важные длинные вопросы физики 1-го года обучения по главам MCQ. Кандидаты, желающие поступить на докторскую степень в области переменного высокого и низкого давления. Практический тест скорости, скорости и ускорения. Поделись этим тестом с друзьями.Этот тест был разработан для студентов, желающих поступить в медицинские и инженерные колледжи / университеты или на другие факультеты, этот тест также может помочь профессионалам улучшить или повторно проверить свои промежуточные знания по предмету. Равномерное круговое движение Презентация Пола Э. C876 в PowerPoint — Курс изучения концептуальной физики Этот курс поддерживает экзамен для C876. Затем проверьте свои ответы с помощью «Разъяснения ответов на вопросы по физической практике» (. Forces Test — Physics I Name: Date: 1.Назад к науке для детей. 1088 / 0029-5515 / 40/1/307 Код корпуса: 123423245. Читать PDF Банк тестов по физике Джанколи Банк тестов по физике Джанколи Дополнительно полезно узнать о необычных способах приобретения этой книги. Добро пожаловать на сайт www. Подтема: (a) Поперечные и продольные волны (b) Соотношение смещения в прогрессивной волне (c) Скорость бегущей волны (d) Принцип суперпозиции волн (e) Отражение волн (f) Биения (g) Доплеровский сдвиг Эффект Резюме. Блок 3-мерный анализ, векторный анализ и руководство по SOHCAHTOA Блок 3.Эти документы можно просмотреть в Интернете, а также можно загрузить в формате Pdf. Эти примечания могут использоваться для входных тестов MDCAT, ECAT, MCAT, NUST и NUMS. Тесты по главам и вопросы для 9-го класса по всем предметам. Кафедра физики и астрономии. org Наука для всех: задачи по физике. Физика Аэронавтика: контекстный подход к изучению физики. Загрузить тестовую работу HSC 2020. Решенные численные значения физики 9-го класса Если вы хотите получить электронные копии всех тестов 9-го класса из файлов MS Word с вашим собственным названием и логотипом академии, свяжитесь со мной по WhatsApp 03017980076.Единицы 1-7 будут представлены на экзамене AP Physics 1 примерно в той же пропорции, что и их относительный вес, как указано в описании курса и экзамена. Подтвердите всех учащихся, которые планируют пройти тестирование. Как далеко уходит машина при остановке? (a) 14 мес. (b) 5. Сдача теста GRE Physics Test. Кроме того, каждый вопрос теста рассматривается, чтобы исключить язык, символы или стр. 10), представляющие различные физические константы и a. 10 м / сек2 C. 12-я единица физики -2 Контрольный вопрос Тамильская среда, Рвение, учебные материалы Centum.Каждый вопрос нанесен на карту, чтобы показать, как образец вопроса соотносится с результатами и содержанием учебной программы. Физика — это отрасль науки, изучающая материю и ее движение, а также то, как она взаимодействует с энергией и силами. Наша спецификация GCSE Physics предлагает широкий, последовательный, удовлетворительный и стоящий курс обучения. Подтема: (a) Поперечные и продольные волны (b) Соотношение смещения в прогрессивной волне (c) Скорость бегущей волны (d) Принцип суперпозиции волн (e) Отражение волн (f) Биения (g) Доплеровский сдвиг Эффект Резюме.Это безусловно облегчит вам просмотр руководства по физике, глава 10, как и вам. Добро пожаловать на эту страницу, вы можете загрузить этот практический файл по физике для класса 12 в формате PDF и создать свою собственную практическую книгу и копию, чтобы получить хорошие отметки в своем практическом экзамене в формате PDF. Ссылка для скачивания, приведенная ниже, спасибо. Handbook of Physics — важный, полезный и компактный справочник, подходящий для повседневного изучения, решения проблем или пересмотра экзаменов для классов XI — XII, инженерных и медицинских входов и других соискателей соревнований.ISBN 97830281 от SChand Publications. org Наука для всех: задачи по физике. Получите банк тестов и необходимое руководство по решению. Чтобы получить представление о том, каково это пройти этот тест, потренируйтесь в условиях, которые очень похожи на условия реального администрирования теста. AP Physics C Review Mechanics CHSN Review Project Это руководство по обзору, разработанное в качестве подготовительной информации к экзамену AP1 Physics C Mechanics Exam 11 мая 2009 г. 565 Перечисленные значения ускорения были рассчитаны на основе зависимых переменных.Если вы хотите загрузить и установить тест «Физика 11 волн», то это будет легко, Страница 2/9. Xam Idea Class 12 Physics — одна из популярных книг среди студентов, готовящихся к экзамену CBSE Class XII. 04 м, чтобы начать 0. Вы можете найти Ebook Pdf основы физики экзаменационный банк документов, помимо руководств, так как мы также предоставляем множество руководств пользователя, спецификаций, рекламных деталей, установочных документов и многое другое. Физические величины Все величины, в терминах которых описаны законы физики и измерения которых необходимо, называются физическими величинами.Получайте последние новости о миссиях НАСА, смотрите прямую трансляцию NASA TV и узнавайте о нашем стремлении раскрыть неизведанное и принести пользу всему человечеству. Студент обязан практиковать эти концепции и задавать вопросы при необходимости. Затем проверьте свои ответы с помощью «Разъяснения ответов на вопросы по физике» (. 63 × 10–34. Расстояние, разделенное на временной интервал c. Название книги: Тесты самооценки KIPS с ответами (все главы) Тема: Physics Edition: N / A Тип курса: Инженерное дело. Главы: Все. Щелкните ниже, чтобы загрузить файл PDF: Загрузить материалы по теме.Все на Земле, все в нашей солнечной системе, все в нашей галактике и во Вселенной движется и взаимодействует, и силы играют в этом большую роль. Определить погрешности немного сложнее, поскольку вы | не измерительный прибор | должен их определить. Hewitt Hewitt Drew-It Фотогалерея Контактная информация 1. Об этой викторине: Все вопросы в этой викторине основаны на информации, которую можно найти на сайте Physics: Force. Расчет скорости и скорости. Он полностью доступен в свободном доступе в виде загружаемого PDF-файла или для чтения в Интернете по адресу :.Ускорение определяется как ИЗМЕНЕНИЕ в. В начале 1800-х годов ученые начали изучать основы материи, пространства и времени. * Улучшите свое обучение, а также получите лучшую оценку !. Это руководство, созданное создателями предметных тестов, предлагает учащимся никогда не публиковавшиеся формы фактических прошлых экзаменов по физике для получения реальной практики. SP12S08XP01 2 СТОП. Объективная физика для Neet — Vol. Он полностью доступен в свободном доступе в виде загружаемого PDF-файла или для чтения в Интернете по адресу :. Часть (а) Сколько делать.{Имперские единицы: фут-фунт, единицы СГС: дин-сантиметр или эрг}; Единицей измерения мощности в системе СИ является ватт (Вт), который равен одному джоулю в секунду (Дж / с) = вольт × ампер. Часто двойная сюжетная линия, в которой два психолога, Стелла Берроуз и Саймон Перес, за три недели дают более или менее то, чем вы являетесь, насколько я делал pdf вопросы, физика, подготовка к тестам, и практиковалась. Если вы хотите загрузить и установить тест «Физика 11 волн», то это будет легко, Страница 2/9. Двенадцатый блок физики -2 Контрольный вопрос Тамильская среда, Рвение, учебные материалы Centum.орг / подробности / книги / колледж-физика. Видеосцены и основные концепции Правила тестового трека Почему манекен остался позади? Это называется инерцией, свойством материи, которое заставляет ее сопротивляться любому изменению в своем движении. так же, как и в центре проводника. Тест, 10 класс, физика, CBSE- Электричество. Краткое содержание лекции 1 — ВВЕДЕНИЕ В ФИЗИКУ 1. Внимательно прочтите каждый вопрос и точно ответьте на вопрос. В тесте по физике всего 25 вопросов в форме MCQ, ответы на которые будут в основном на английском языке. Иногда также и на урду.Кандидаты также могут загрузить и изучить экзаменационные работы предыдущего года по тесту ISSB Pak Air Force Physics Test в формате PDF, чтобы узнать программу и схему экзамена. Опрос студентов с данными испытаний по механике для вводных курсов физики * Ричард Р. Загрузите электронную книгу и усердно готовьтесь к предстоящим экзаменам. Сопротивление. Правило равновесия: 2. Используя эти заметки, вы можете стремиться к отличию на экзаменах по физике IGCSE 9 и 10 классов. Кандидатам, желающим поступить на соискание ученой степени доктора философии. Привет, ребята, ниже находится pdf-файл модулей Аллена по физике и фундаментальной математике. Центр масс Свойства материи Гравитация Кинематика Законы движения Ньютона практическая физика Вращательное движение простое гармоническое движение Тепловые свойства материи звуковые волны Рабочая мощность и энергия Конденсатор Ток Электричество Электроника-теория полупроводников Логические вентили Принцип системы связи.Диагностический тест PreCalculus Успех в первый год обучения математике во многом зависит от ваших навыков алгебры. Сделано учителями. 4 Стекло остается в своем положении благодаря инерции Таким образом, мы можем сказать, что инерция — это тенденция объектов оставаться в состоянии покоя или удерживаться. К экзамену ARDMS SPI! Вот издание SPI единственного бестселлера пробного экзамена, посвященного экзамену ARDMS по ультразвуковой физике. Наглядный тому пример — концепция машиностроения. Тест хи-квадрат носит статистический характер, служит только индикатором и не может быть железным.AP Physics Collection — это бесплатное готовое решение для вашего курса AP ® Physics, созданное в результате сотрудничества OpenStax и Rice Online Learning. Вы можете бесплатно скачать статью по физике в формате pdf. Ответ на тест ESO Simple Machines 2014 ПОЯСНЕНИЕ 1 Колесо и ось 2 Рычаг 3 Винт 4 Наклонная плоскость 5 B — Сила 6 D — ось 7 B — Переместите точку опоры ближе к нагрузке 8 A — всегда меньше 100% 9 A — выходная мощность сила в 4 раза больше усилия 10 D — B = сопротивление; A = точка опоры; C = усилие 11 C — 4 12 Первый класс.Примеры вопросов AP Physics 1 и 2 с множественным выбором Для вашего учебного пособия по AP Physics 1 и 2 с множественным выбором, а теперь просмотрите несколько практических вопросов из официальных примеров вопросов AP. Использование калькуляторов и гаджетов запрещено. Руководство по экзамену SSC. Бойл, Дуглас. Блок 3-мерный анализ, векторный анализ и руководство по SOHCAHTOA Блок 3. • Если вы выполняете работу в уме, объясните в письменной форме, как вы выполняли эту работу. Физическая форма третья. Документ с вопросами по физике HSC Совета Гуджарата 2021.pdf из PHYSICS PY 723 в Сельскохозяйственном университете. 292кг = 16г 92к I = 10. Это предварительный тест по физике. C876 — Учебный курс по концептуальной физике Этот курс поддерживает оценку C876. 2015 Ноябрь Physical Sciences P1 GR 10 Eng 16. AP Physics 1 Практический тест 1-D Движение Имя: _____ Период: _____ Учитель: _____ МНОЖЕСТВЕННЫЙ ВЫБОР. Диагностический тест PreCalculus Успех в первый год обучения математике во многом зависит от ваших навыков алгебры. В тесте по физике всего 25 вопросов в форме MCQ, ответы на которые будут в основном на английском языке. Иногда также и на урду.Сделано учителями. Boardworks GCSE Additional Science — Physics (лето 2011) Дата создания: 21.01.2016 14:45:47. Ознакомьтесь с 12-м докладом CBSE по физике 2020 года и загрузите его в формате PDF вместе со схемой оценки физики 2020 года CBSE Class 12. Тест по физике Глава 10 Тест Когда кто-то должен пойти в книжный магазин, начать поиск по магазину, полка за полкой, это по сути проблематично.Вы можете найти Ebook Pdf основы банковского документа по экзамену по физике помимо руководств, так как мы также предоставляем множество руководств для пользователей, спецификаций, рекламных деталей, установочных документов и многого другого. Банк бесплатных тестов по университетской физике, 13-е издание, автор: Янг. Подробнее Медали за выдающиеся исследования в области физики звезд, Марса и квазаров Трое молодых физиков были отмечены за свои обширные исследования на престижном конкурсе STEM for Britain, который в этом году проходил в режиме онлайн.Прежде чем остановиться, он проходит расстояние d. Силы могут изменить: Только замедление или ускорение объектов. Правило равновесия: 2. Быть закладкой для файла PDF. Банк тестов по основам физики. Но теперь, с помощью банка тестов по основам физики, вы сможете * предугадывать типы вопросов, которые появятся в вашем экзамене. • ОБЯЗАТЕЛЬНО ОТВЕТИТЕ И Пометите ВСЕ ЧАСТИ ВОПРОСА. Мобильные телефоны не допускаются в место проведения экзамена. Электронная книга D / L (pdf) Содержание волн; волновые свойства; Huygens ‘Constn.ОТВЕТЫ на образец викторины по метрической системе, значащим цифрам и научным обозначениям. Arihant Physics for JEE Main PDF — самая полезная книга для студентов, готовящихся к экзамену JEE Main 2017. Пренебрегая сопротивлением воздуха, если a. MIT — Массачусетский технологический институт. Free Response 7. Автомобиль движется со скоростью 36 км / ч. Pradeep Kshetrapal Electrostatics 2011. Физика считается фундаментальной научной дисциплиной, поскольку все достижения в области технологий могут. Банк тестов Fundamental Of Physics — рейброекеры.2015 Ноябрь Physical Sciences P1 GR 10 Eng 16. [PDF] SAT Subject Test Physics with Online Test (Barron’s Test Prep) Электронная книга Роберта Янсена М. Васкеса Средняя школа — Физика — Тест №1 — 100 баллов Напишите ИСТИНА, если утверждение истинно ИЛИ напишите слово, заменяющее подчеркнутое слово, которое сделает его истинным. Прочтите закон сохранения массы, удельную теплоемкость воды и формулы, необходимые для расчета ускорения. Он полностью доступен в свободном доступе в виде загружаемого PDF-файла или для чтения в Интернете по адресу :.Это безусловно облегчит вам просмотр руководства по физике, глава 10, как и вам. Easy MCQs предоставляет заметки по всем предметам 10-го класса в формате PDF.
Задачи по кинематике в классе физики
Ответы по кинематике в классе физики, 19 июня 2020 г. · В частности, наши результаты показывают, что кинематические решения PPP ухудшились после усиленного высыпания авроральных частиц во время основной фазы шторма (06–23 UT), когда они доходили до ~ 70% высокоширотных станций испытали ухудшение определения местоположения в диапазоне мультиметра в 16–18 UT.Задачи кинематики 7 Задачи кинематики 7 решений. Задачи кинематики 8 Задачи кинематики 8 решений. 2-мерная баллистика. Задачи iKinematics 9 задач кинематики 9 решений. Задачи кинематики 10 (с ответами)
Физический класс обслуживает студентов, учителей и классные комнаты, предоставляя готовые к работе ресурсы, использующие простой для понимания язык, который делает обучение интерактивным и многомерным. Обсуждает трудности учащихся в решении задач. Представляет структурированный подход к одномерным задачам постоянного ускорения.Предоставляет опыт исследователя, включая пример проблемы, преимущества подхода и ответы студентов с двумя иллюстрациями решения проблем.
В этом видеоуроке по физике основное внимание уделяется решению задач движения снаряда в двух измерениях с использованием кинематических уравнений. Он покажет вам, как найти максимальное … На панели калькулятора есть текстовые задачи по физике, сгруппированные по темам. Каждая проблема сопровождается всплывающим ответом и аудиофайлом, в котором подробно объясняется, как подойти к проблеме и решить ее.Это идеальный ресурс для тех, кто хочет улучшить свои навыки решения проблем. Посетите: Панель калькулятора На главную | Блокнот для калькулятора — Кинематика
Урок физики »Учебник по физике» 1-D кинематика »Момент кинематических уравнений и его сохранение 1-мерная кинематика — Урок 6 — Описание движения с помощью уравнений Давайте посмотрим, как это делается для решения более сложных кинематических задач. Двумерная кинематика Двумерная кинематика или двумерное движение — это другие термины для движения снаряда.
Класс физики »Конструкторы концепций» Кинематика 1-мерная кинематика Конструктор концепций — это интерактивный модуль вопросов, который предлагает учащимся тщательно составленные вопросы, нацеленные на различные аспекты концепции. Физика — это изучение материи, движения, энергии и сила. Здесь вы можете просматривать видео, статьи и упражнения по темам. Мы постоянно обновляем библиотеку, поэтому со временем вы можете найти здесь новые или улучшенные материалы.
Уроки по физике
Видео Описание / ссылка
Номер
Марка
Графики Движение
Время положения (d-t) Графики
Гр-1
11
Гр-2
11
Гр-3
11
Скорость-время (v-t) Графики
Гр-4
11
Гр-5
11
Гр-6
11
Гр-7
11
Время разгона (a-t) Графики
Гр-8
11
Резюме графиков
Гр-9
11
Использование Один график для рисования других
Гр-10
11
Гр-11
11
Математический Операции
Conv-1
11 и 12
Движение Уравнения кинематики
Кинематика постоянная скорость и постоянная скорость
Определения положения, расстояния, перемещения
Кин-1
11 и 12
Как для расчета скорости и скорости
Кин-2
11 и 12
Кинематика формулы ускорения с объектами, движущимися вперед и назад
Кин-3
11 и 12
Кин-4
11 и 12
Образец проблема, которая очень часто встречается на тестах.Объект ускоряется и позже притормаживает.
Кин-5
11 и 12
Кин-6
11 и 12
Кин-7
11 и 12
Образец проблема, когда Супермен мчится, чтобы догнать пулю
Кин-8
11 и 12
Объекты брошенный вверх или вниз
Кин-9
11 и 12
Образец проблема с падением одного мяча и брошенным вторым 1 с позже.
Кин-10
11 и 12
Образец проблема, когда Супермен должен поймать падающего студента
Кин-11
11 и 12
Это это очень сложная задача с двумя поднятыми стрелами.
Кин-12
11 и 12
Объекты движение по кривой или окружности
Кин-13
11 и 12
Это пример задачи использует кинематические уравнения для решения ускорения и перемещение на колесе обозрения.
Кин-14
11 и 12
Кин-15
11 и 12
Векторы
Введение в Векторы
Вект-1
11 и 12
Вект-2
11
Вект-3
11 и 12
Вектор Компоненты
Как разбить вектор на компоненты и как вычислить компоненты
Вект-4
11 и 12
Образцы разбиения векторов на компоненты
Вект-5
11 и 12
Вект-6
11 и 12
Вект-7
11 и 12
Вект-8
11 и 12
Вект-9
11 и 12
Сложение / вычитание Векторы с компонентами (алгебраический метод)
Вект-10
12
Вект-11
11 и 12
Вект-12
11 и 12
Родственник Скорость
Простой Задачи под прямым углом
РелВ-1
11 и 12
РелВ-2
11 и 12
Подробнее Комплексные проблемы
РелВ-3
12
РелВ-4
12
РелВ-5
12
РелВ-6
12
РелВ-7
12
Ньютона Законы и схемы свободного тела
Введение первого и второго закона Ньютона
Тритон-1
11 и 12
Тритон-2
11 и 12
Тритон-3
11 и 12
Ньют-4
11 и 12
Ньют-5
11 и 12
Ньют-6
11 и 12
Простой Задачи второго закона Ньютона (без диаграмм свободного тела)
А пример проблемы с тянущим автомобилем.Используется трение, и проблема видоизменена во второй половине ролика.
Тритон-7
11 и 12
А в этом примере задачи пуля проходит через блок.
Ньют-8
11 и 12
Иногда вы не можете использовать уравнения x и y для решения проблемы.Это показывает как добавить силы к объекту под разными углами при взгляде сверху.
Ньют-9
12
Бесплатно Основы схемы тела
Бесплатно Диаграммы тела с указанием сил
FBD-1
FBD-2
11 и 12
FBD-3
11 и 12
FBD-4
11 и 12
FBD-5
11 и 12
FBD-6
11 и 12
FBD-7
11 и 12
FBD-8
11 и 12
FBD-9
11 и 12
Лифт Проблемы
Элев-1
11 и 12
Элев-2
11 и 12
Это Пример задачи охватывает все, что вам нужно знать о лифте.
Элев-3
11 и 12
Это В примере задачи лифт движется вверх и вниз вместе с человеком стоя на весах
Элев-4
11 и 12
Трение И законы Ньютона Проблемы с трением
Введение к коэффициент трения и принцип трения
Fric-1
11 и 12
Как работы статического и кинетического трения
Фрик-2
11 и 12
Статический и проблема кинетического трения, показывающая разницу между два
Фрик-3
11 и 12
А проблема трения с коробкой и сила, давящая на нее
Fric-4
11 и 12
Fn не% $ #! равно Fg (простая версия)
Fric-5
11 и 12
Это Пример задачи включает 2 коробки, которые тянутся с трением и сила под углом.
Fric-6
12
Это это 1 из 2 сложных примеров задач, использующих штабелированные блоки, трение и схемы свободного тела
Fric-7
12
Это это 2 из 2 сложных примеров задач, использующих штабелированные блоки, трение и схемы свободного тела
Fric-8
12
Силы под углом на коробках
F / Ang-1
11 и 12
F / Ang-2
11 и 12
F / Ang-3
11 и 12
F / Ang-4
11 и 12
Наклоны Рампы Hill Acceleration
Как для рисования FBD объекта на склоне или холме
Inc-1
12
Проблема скольжения по склону, холму или пандусу с трением
Inc-2
12
Inc-3
12
Inc-4
12
Inc-5
11 и 12
Ньютона Третий закон
Ньют (3) -1
11 и 12
Тритон (3) -2
11 и 12
Тритон (3) -3
11 и 12
Типичный Задача 2-го и 3-го закона Ньютона с вертолетом, поднимающим машину.
Тритон (3) -4
12
Тритон (3) -5
12
Тритон (3) -6
12
Это проблема с образцом — это более сложная версия вытягиваемых ящиков и включает милых пингвинов
Тритон (3) -7
12
Шкив Системы
Простой Шкивы
Pull-1
12
Pull-2
12
Pull-3
12
Pull-4
12
Pull-5
12
Тяга-6
12
Подробнее расширенный взгляд на эту проблему
Потяните-7
12
Комплекс Системы с несколькими шкивами
Потяните-8
12
Pull-9
12
Центростремительный (Круговое) движение
Центростремительный Разгон
Ан. объяснение того, что такое центростремительное ускорение
ac-1
12
Центростремительный Пример ускорения при повороте автомобиля
ас-2
12
Центростремительный Усилие
Fc-1
12
Fc-2
12
Fc-3
12
Fc-4
12
Fc-5
12
Fc-6
12
Fc-7
12
Fc-8
12
Fc-9
12
Fc-10
12
Снаряд Движение
Уроки
Проект-1
12
Проект-2
12
Проект-3
12
Проект-4
12
Простой способ решить проблему с снарядом, но он работает, только если объект приземляется на том же уровне, на котором был произведен выстрел.
Проект-5
12
Как для расчета максимальной высоты снаряда
Проект-6
12
Образец Проблемы
Это проблема связана с тем, что самолет роняет объект.
Проект-7
12
Барт Симпсон пытается перепрыгнуть ущелье, и самая сложная часть — найти скорость
Проект-8
12
Как для расчета угла выстрела снаряда.
Проект-9
12
Столкновения Использование импульса и энергии
Импульс
Объекты врезаться друг в друга по прямой
Столб-1
12
Кол-2
12
Объекты врезаться друг в друга под углом
Столб-3
12
Col-4
12
Энергия в столкновениях
Col-5
12
Col-6
12
Col-7
12
Col-8
12
Col-9
12
Энергия, Мощность и эффективность
Работа, Сохранение кинетической и гравитационной энергии
NRG-1
11 и 12
NRG-2
11 и 12
NRG-3
11 и 12
NRG-4
11 и 12
NRG-5
11 и 12
Комплекс проблема американских горок.Найдите высоту, необходимую для петли
NRG-6
эластичный (Весна) Энергия
NRG-7
12
NRG-8
12
NRG-9
12
Мощность и энергетика
Военнопленный-1
11
КПД и энергетика
ЭФФ-1
11
ЭФФ-2
11
ЭФФ-3
11
Планетарный Механика и гравитация
Ньютона Универсальный закон всемирного тяготения
Грав-1
11 и 12
Грав-2
11 и 12
Кеплер и Ньютон
ПМеч-1
12
ПМеч-2
12
ПМеч-3
12
Использование Уравнения энергии для объектов, выведенных на орбиту
ПМеч-4
12
ПМеч-5
12
ПМеч-6
12
кинетическая энергии, когда спутник находится на орбите, и его скорость в орбита
ПМеч-7
12
Электроэнергия
Фомулас и простые расчеты
Ан введение в самые распространенные формулы
Элек-1
11
Как использовать формулу Q = Ne
Элек-2
11
Как использовать формулу V = E / Q
Элек-3
11
Как использовать формулу I = Q / t
Элек-4
11
Как использовать формулу R = V / I
Элек-5
11
Как длина, площадь и сопротивление материала воздействию
Элек-6
11
Как использовать формулу R = удельное сопротивление * L / A
Элек-7
11
Как использовать 3 формулы мощности
Элек-8
11
Использование тариф энергии для расчета стоимости электроэнергии
Элек-9
11
Электрический Цепи: последовательные и параллельные
Чертеж схемы и 4 части
Элек-10
11
Установка в вольт и амперметрах в цепи
Элек-11
11
Как для расчета тока в электрической цепи
Элек-12
11
Как для расчета напряжения в электрической цепи
Элек-13
11
Как для расчета сопротивления в электрической цепи
Элек-14
11
Простой пример решения схемы
Элек-15
11
Подробнее сложный пример решения схемы
Элек-16
11
Электромагнетизм
Левый и Правила для правой руки
Как найти магнитное поле вокруг провода
ЭМ-1
11
Как найти северный конец электромагнита
ЭМ-2
11
Как найти направление силы двигателя
ЭМ-3
11
Как для расчета моторной силы
ЭМ-4
11
Генераторы и трансформаторы
Как найти направление, в котором будет течь электричество
ЭМ-5
11
Как найти направление, в котором будет течь электричество
ЭМ-6
11
Как для простых расчетов трансформатора
ЭМ-7
11
Как для расчета нескольких трансформаторов
ЭМ-8
11
Как для расчета трансформатора, если КПД не 100%
ЭМ-9
11
Волны (Свет и звук)
Недвижимость всех типов волн
Волна-1
11 и 12
Волна-2
11 и 12
Волна-3
11 и 12
Волна-4
11 и 12
Волна-5
11 и 12
Волна-6
11 и 12
Волна-7
11 и 12
Волна-8
11 и 12
Волна-9
11 и 12
Волна-10
11 и 12
Звук Волны
Волна-11
11 и 12
Волна-12
11 и 12
Волна-13
11 и 12
Волна-14
11 и 12
Волна-15
11 и 12
Волна-16
12
Волны в 2-х измерениях (интерференция)
Волна-17
12
Волна-18
12
Волна-19
12
Волна-20
12
Волна-21
12
Оптика
Преломление света
Опц-1
10
Опт-2
10
Опт-3
10
изогнутый Зеркала
Опц-4
10
Опт-5
10
Опт-6
10
Опт-7
10
Линзы
Опт-8
10
Опт-9
10
Опт-10
10
Опт-11
10
Опт-12
10
Опт-13
10
Опт-14
10
Графики используя Excel
: Снимки экрана видео-уроки НЕ наши учебные уроки
GrEx-1
11 И 12
GrEx-2
11 И 12
Действительно Потрясающие забавные видео
Физика Обещание: Некоторые вещи, которые сводят нас с ума, учителя физики.
1 Миллион просмотров Видео с благодарностью: кажется, так давно мы достигли 1 миллион просмотров. Спасибо за вашу поддержку
Видео классной деятельности
Наука Ярмарки
г. Другие видео и материалы Каруаны-Дингли
г. Каруана-Дингли получает премию Toronto Urban Hero Eductional Award !! Щелкните, чтобы увидеть статью newpapaer.
г. Каруана-Дингли получает статью в газету для своей коллекции
г. Каруана-Дингли разговаривает с Алексом Лифсоном из Rush !!
г. Каруана-Дингли во время завтрака по телевидению демонстрирует граммофоны
г. Каруана-Дингли о старинном охотнике, демонстрирующем граммофоны
г. Каруана-Дингли играет на гитаре в своем акустическом дуэте
г. Каруана-Дингли играет песню, которую он написал со своей рок-группой
г. Другие видео и материалы Morin
Почему Г-н Морен — лучший учитель физики в истории
г. Костюмы Каруаны-Дингли и г-на Морина на Хэллоуин через Годы
г. Морин пытается подбодрить мистера Каруана-Дингли, напевая
Калькулятор SUVAT
«Но сэр, — мы слышим, как вы спросите, — ». Зачем мне нужно изучать все эти формулы SUVAT, если я могу просто выйти в Интернет и использовать калькулятор SUVAT? ».Затем ваш учитель, очевидно, отвечает: «Может ли этот калькулятор уравнений SUVAT научить вас тому, что означает SUVAT? Знает ли он все формулы SUVAT и может ли он использовать их для вычисления двух неизвестных в любой ситуации? несколько вопросов по SUVAT , чтобы проверить, действительно ли вы знаете свои вещи? Можете ли вы взять их на экзамен? » Что ж, вы можете сказать своему учителю, что этот калькулятор может делать все эти вещи! (Omni Calculator не рекомендует пытаться использовать этот калькулятор на экзамене, независимо от того, насколько мало вы его редактировали.)
Что касается экзаменов, то, если вы ученик GCSE или A-level и хотите знать, как вы справились с прошлой работой, мы рекомендуем вам проверить наш калькулятор оценок за тест, а если вам нужно знать, сколько оценок вам нужно на выпускном экзамене, чтобы получить желаемую оценку, воспользуйтесь нашим калькулятором итоговой оценки.
Для преобразования между единицами измерения используйте встроенные конвертеры единиц рядом со входом или используйте наш конвертер длины, конвертер скорости или конвертер времени.
Это простой калькулятор кинематики, полный инструмент можно найти в калькуляторе движения снаряда.
Формулы СУВАТ — скорости
Существует пять формул SUVAT (или формул SUVAT, если вам нравится). Эти пять формул описывают все, что нужно знать о движущейся системе , если она имеет равномерное ускорение , то есть . Они обычно используются в физике, так как описывают широкий спектр систем. Если вам известна начальная скорость объекта u , конечная скорость v и время t , которое потребовалось для достижения скорости v от скорости до , вы можете найти пять SUVAT уравнения…
Выше мы, , построили график зависимости скорости от времени , используя u , v и t , которые мы обсуждали выше. Это означает, что ускорение a — это градиент проведенной прямой линии. Итак:
a = Δ скорость / Δ время .
Поскольку мы знаем как начальную, так и конечную скорость, Δvelocity = v - u , и, если мы предположим, что мы начали строить график в момент времени = 0, Δtime = t . Таким образом, вы получаете
а = v - ед / т ,
, который может быть преобразован в
v = u + при .
Если вас интересует SUVAT, мы предполагаем, что вы сможете сделать эту перестановку самостоятельно.
Формулы СУВАТ — водоизмещение
В этом калькуляторе SUVAT мы еще не упомянули объем двигателя s . Смещение — это расстояние, которое объект преодолевает за время t относительно его исходного положения. Этот последний бит важен, поскольку смещение — это не то же самое, что расстояние; , если он попадает в точку начала, то его смещение равно нулю .На графике скорость-время, который мы построили выше, с — это область под графиком. Поскольку у нас есть линейный график, площадь под ним определяется умножением средней скорости (u + v) / 2 на затраченное время t . Записывая это и упрощая, получаем:
s = ¹/₂ (u + v) * t
Иногда бывает полезно иметь больше уравнений для работы; вы никогда не знаете, какие переменные у вас будут .Вы можете получить следующее уравнение, подставив v = u + на . Результат:
s = ¹/₂ (u + u + at) * t ,
, что упрощается до s = ¹/₂ (2ut + at ²) , что, в свою очередь, также может быть записано как:
s = ut + ¹/₂ at ² .
Это было не так уж сложно, просто немного алгебры, ты, должно быть, почувствуешь себя снова тринадцатилетним.Чтобы получить другую форму, выполните те же шаги, что и предыдущий, но используйте u = v - вместо :
s = vt - ¹/₂ при ² .
В качестве своего рода вопроса о SUVAT, мы оставим этот вопрос на ваше усмотрение — мы знаем, что для вас это не будет проблемой :
Формулы SUVAT — время пропуска
Последняя формула SUVAT требует немного более сложной перестройки, так что, возможно, вы почувствуете, что вам четырнадцать.Если мы сделаем t объектом первого выведенного нами уравнения , мы получим:
t = (v - u) / а ,
, которое, если мы подставим во второе выведенное нами уравнение , мы получим:
s = ¹/₂ (u + v) ((v - u) / a) .
Умножая обеих сторон на 2a , получаем:
2as = (u + v) (v - u) ,
, который теперь требует самого сложного для освоения навыка — квадратичного расширения! Итак, после большого количества крови, пота и слез у вас должно получиться:
2as = v ² - u ² .
Перестановка для v ² тогда дает вам:
v ² = u ² + 2as .
Ого, вы действительно мастер математики!
Итак, это все формулы SUVAT . Если вы нашли этот текст ужасно скучным и непонятным (что не исключено), мы рекомендуем вам это видео на Youtube по этой теме.
Что означает SUVAT?
Вы, вероятно, уже догадались об этом, читая этот калькулятор SUVAT до сих пор (если вы не можете догадаться, вы, возможно, просто пропустили всю эту бессвязную болтовню выше). SUVAT — это аббревиатура пяти переменных , которые описывают систему в движении с постоянным ускорением: смещение с , начальная скорость u , конечная скорость v , ускорение a и время t .
Порядок этих букв совершенно произвольный, так что вы можете не спать по ночам , задаваясь вопросом, почему он не называется TUAVS, SAVUT или USAVT (хотя мы думаем, что, вероятно, лучше всего, чтобы начальная и конечная скорости оставались рядом друг с другом, поэтому может лучше квадроциклы или STAUV).
Несколько простых вопросов по SUVAT
«Хорошо, хорошо, хорошо», теперь говорит ваш учитель. «Итак, вы могли найти калькулятор, который дает вам уравнение SUVAT, и да, он может объяснить, что означает SUVAT, но этот не означает этого. может помочь вам решить любые вопросы! «Что ж, мы можем понять, что он может быть раздражен прямо сейчас — вы задерживали класс в течение десяти минут , пока вы загружаете эту страницу и показываете классу все ее удивительные возможности .Но больше всего его, вероятно, раздражает то, что вы закончили изучать SUVAT давным-давно, а теперь перешли на трение и нормальную силу (и что это тоже класс статистики). Но не волнуйтесь, мы подготовили несколько примеров вопросов , чтобы помочь вам максимально эффективно использовать этот калькулятор SUVAT.