Урок 48. функции. свойства функций и их графики. исследование функций — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №48. Функции. Свойства функций и их графики. Исследование функций.
Перечень вопросов, рассматриваемых в теме:
- функция, аргумент функции, значение функции
- график функции, преобразование графика функции
- свойства функции, исследование свойств функции
Глоссарий по теме урока
Определение
Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент,
у — зависимая переменная, значение функции
Определение
Множество значений аргумента функции называется областью определения функции и обозначается D(y).
Определение
Множество значений, которые принимает сама функция, называется множеством значений функции и обозначается Е(у).
Определение
Функция у = f(х) называется четной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
- для любого х из области определения выполняется равенство f(-х)=f(х).
Функция у = f(х) называется нечетной, если она обладает двумя свойствами:
- область определения этой функции симметрична относительно 0;
для любого х из области определения выполняется равенство f(-х)=-f(х).
Определение
Значения аргумента, при которых значение функции равно 0, называются корнями (нулями) функции.
Определение
Функция у=f(x) возрастает на промежутке (а; в), если для любых х1, х2 из этого промежутка, таких, что х1<х2, выполняется неравенство у1<у2.
Функция у=f(x) убывает на промежутке (а; в), если для любых х1, х 2 из этого промежутка, таких что, х1<х2, выполняется неравенство у1>у2.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл.– М.: Просвещение, 2015. С. 98-118, 271-307.
Дополнительная литература:
Шахмейстер А.Х. Построение и преобразование графиков. Параметры. Ч.2-3. СПб.: Петроглиф; М.: МЦНМО, 2016. 392 с. С.73-307.
Открытые электронные ресурсы:
Образовательный портал “Решу ЕГЭ”.
https://mathb-ege.sdamgia.ru/test?theme=177
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Теоретический материал для самостоятельного изучения
1. Исследование функции и построение графика
Схема исследования функции на примере функции
1) Область определения функции
Знаменатель дроби не равен нулю:
Получили область определения
D(y)=
- Множество значений функции
Отыскание Е(у) можно свести к решению уравнения с параметром у. Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Все значения параметра у, при которых уравнение имеет хотя бы одно решение, и составят Е (у).
Получили
- Четность / нечетность функции
D(y)= — симметрична относительно нуля
,
следовательно, функция четная и ее график симметричен относительно оси ОУ
- Нули функции
Для нахождения нулей функции необходимо решить уравнение
Уравнение не имеет действительных корней, значит, нулей у данной функции нет, ее график не пересекает ось ОХ
- Промежутки знакопостоянства
у>0 при
у<0 при
- Монотонность
Найдем производную
Найдем точки, в которых производная равна нулю или не существует: х=0, х=-1, х=1.
Определим знаки производной в полученных промежутках.
точки -1, 1 – выколоты, 0 — закрашена
Производная положительна, а значит, функция возрастает при .
Производная отрицательна, а значит, функция убывает при
- Экстремум
х=0 – стационарная точка.
В ней производная меняет знак с плюса на минус, следовательно, х=0 – точка максимума.
Значение функции в точке максимума
- Дополнительные точки
у(0,5)= у(-0,5)=-5/3; у(2)=у(-2)=5/3; у(3)= у(-3)=5/4
- Отразим найденные свойства графически, построим график функции
2. Решение задачи на оптимизацию
Задачи на отыскание наибольших или наименьших значений величин решаются по определенному плану.
В решении таких задач выделяют 3 основных этапа:
1 этап. «Перевод» задачи на язык функций:
- вводят независимую переменную х
- выявляют оптимизируемую величину у, для которой надо найти наибольшее или наименьшее значение
- выражают у через х и другие известные величины
- устанавливают по условию задачи границы изменения переменной х
2 этап. Исследуют составленную функцию на наибольшее или наименьшее значение (в зависимости от условия задачи) с помощью производной или элементарными средствами.
3 этап. Интерпретация найденного решения для поставленной задачи – «перевод» полученного математического результата на язык задачи.
Рассмотрим план решения на примере задачи.
Задача. В распоряжении начальника имеется бригада рабочих в составе 24 человек. Их нужно распределить на день на два объекта. Если на первом объекте работает t человек, то их суточная зарплата составляет 4t2 у.е. Если на втором объекте работает t человек, то их суточная зарплата составляет t2 у.е. Как нужно распределить на эти объекты бригаду рабочих, чтобы выплаты на их суточную зарплату оказались наименьшими? Сколько у.е. в этом случае придется заплатить рабочим?
Решение:
1 этап. Ведем переменную, выразим нужные компоненты, составим искомую функцию.
Пусть на 1 объект направлено х рабочих, суточная зарплата которых составит 4x2 у.е.
Тогда на 2 объект направлено (24 — x) рабочих – суточная заработная плата (24 — x)2 (у. е.)
е.)
Всем рабочим нужно заплатить 4x
Причем 0≤ x ≤ 24, x ϵ N.
2 этап.
Рассмотрим функцию f(x)=5x2-48x+576.
Функция квадратичная, старший коэффициент положителен, следовательно, наименьшее значение в вершине при x0 = 4,8 .
3 этап. Перевод на язык задачи
Поскольку x ϵ N, подходящим будет ближайшее к вершине натуральное значение, x=5 (рабочих) – на 1 объекте.
24-5=19 (рабочих) – на 2 объекте.
Наименьшее значение f(5)=125+240-576=461 (у.е.) – наименьшая суточная выплата.
Примечание: исследовать функцию также можно было с помощью производной.
Ответ: 5 рабочих на 1 объекте, 19 – на втором, 461 у.е. – наименьшая суточная выплата.
Примеры и разбор решения заданий тренировочного модуля
1. Исследуйте функции на четность.
Функции |
у=0 |
у=sin(x+5π/2) |
у=lg(x+10) |
Решение:
- у=0
область определения – множество действительных чисел – симметрична относительно нуля
у(-х)=0, что можно интерпретировать и как у(х), и как –у(х). К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.
К тому же график этой функции – прямая, совпадающая с осью ОХ, — симметричен относительно оси ОУ и относительно начала координат.
Данная функция одновременно четна и нечетна.
- у=sin(x+5π/2)
область определения – множество действительных чисел – симметрична относительно нуля
преобразуем функцию, применив формулы приведения: sin(x+5π/2)=cos x
у= cos x – четная функция, значит, исходная функция также четная
- у=lg(x+10)
логарифмируемое выражение должно быть положительным
x+10>0; x>-10
D(y): x>-10
Область определения несимметрична относительно 0, значит, в проверке второго условия нет необходимости, — функция общего вида.
Найдем область определения D(f)
Проверим второе условие
Полученное в результате подстановки –х в функцию выражение, очевидно, не равно f(x), не дает пока понимания о выполнении условия нечетности.
Зайдем с другого конца, выразим -f(x):
домножим на сопряженное
Теперь можем сделать вывод: f(-x)=-f(x), функция нечётная.
Ответ:
Функции | Четность / нечетность |
у=0 | и четная, и нечетная |
у=sin(x+5π/2) | четная |
у=lg(x+10) | общего вида |
нечетная |
2.
Решение:
Используем функциональный подход при решении данной задачи. Представим каждое из уравнений как функции. Построим их графики. Единственное решение системы будем интерпретировать как единственную точку пересечения графиков функций первого и второго уравнений.
Второе уравнение проще, но содержит параметр. Перепишем его в явном виде для функции, выразив у: у=-х+а.
В таком виде понятно, что данное уравнение задает множество прямых, параллельных у=-х.
Первое уравнение содержит квадратные корни, что накладывает ограничения: х≥-4, у<7
Сгруппируем в скобках первое, третье и пятое слагаемые, второе и четвертое, получим:
Приравнивая каждый из множителей числителя к нулю, получаем прямые: у=4, у=х+3, х=-4, точнее, с учетом ограничений, части прямых.
Выполним построения выделенных функций.
Условию задачи удовлетворяют только такие прямые второго уравнения у=-х+а, которые пересекают графики первого уравнения только в одной точке.
Анализируя рисунок, получаем: а ≤ -5, а ≥11, а=5.
Ответ:
Сложная функция
Сложная функцияПример 1. Дана функция f(x) = 3x2 – 4. Найти:
Решение: f(4) = 3•42 – 4 = 48 – 4 = 44;
f(a3 + 1) = 3(a3 + 1)2 – 4 = 3(a6 + 2a3 + 1) – 4 =
= 3a6 + 6a3 – 1;
f(t) = 3t2 – 4;
Пример 2. Найти функцию f(x),
если f(x + 1) = x2 + 2x + 2.
Найти функцию f(x),
если f(x + 1) = x2 + 2x + 2.
Решение. Пусть x + 1 = a, тогда x = a – 1; f(a) = (a – 1)2 + 2(a – 1) + 2 = a2 – 2a + 1 + 2a – 2 + 2 = a2 + 1.
Ответ: f(x) = x2 + 1.
Пример 3. F(2x – 1) = 4x – 7; F(g(x)) = x3. Найти g(x).
Решение. Пусть 2x – 1 = a, тогда
т. е. F(x) = 2x – 5. Значит,
F(g(x)) = 2g(x) – 5. 2g(x) – 5 = x3.
Ответ:
Пример № 229г (из учебника
«алгебра, 10–11» А.Н. Колмогорова). Найти такую
функцию f, что
Найти такую
функцию f, что
f(g(x)) = x, g(x) = x2 + 1, x Ј 0.
Решение. По условию f(x2 + 1) = x, x Ј 0.
Пусть x2 + 1 = t, тогда
Ответ:
Пример 4. Найти F(x), если F(sin x) + F(cos x) = 3.
Решение. Перепишем данное уравнение в виде
F(sin x) + F(cos x) = 3(sin2 x + cos2 x).
В выражении sin x заменим букву x на m, получим sin m. Допустим, что cos x = sin m, выразим x через m:
x = arccos (sin m).
Уравнение примет вид
F(sin m) + F(cos (arccos (sin m))) = 3(sin2 m + sin2 m),
2F(sin m) = 3•2sin2 m,
т. е. F(sin m) = 3sin2 m; F(x) = 3x2.
е. F(sin m) = 3sin2 m; F(x) = 3x2.
Ответ: F(x) = 3x2.
Пример 5. Найти функцию f(x), если
Решение. В дроби
заменив x на m, получим
Пусть
Выразим x через m, получим
Найдем значение дроби через m:
и значение дроби в правой части данного уравнения тоже при
Получим новое уравнение (при аргументе m)
или, заменив букву m на x,
Вместе с данным уравнением составим систему
Эта система, линейная относительно неизвестных
и
решается любым из возможных
способов. Ее решение (после упрощения):
Ее решение (после упрощения):
или
Найдем f(t), если допустим, что
Выразим x через t:
Тогда
Аналогичный результат получим из первого уравнения последней системы.
Ответ:
Пример 6. Найти функцию f(x), если
Решение. Пусть
тогда
Получим новое уравнение с переменной t
Заменив t на x, запишем
Составим систему с данным уравнением, переставив слагаемые
Исключим из системы неизвестное
Ответ:
Пример 7. Найти функции F(x) и g(x) из системы уравнений
Решение. Пусть
Пусть
Тогда
и первое уравнение примет вид
Заменим t на x. Получим систему
Вычитая уравнения почленно, находим
а затем и
Пусть 2x + 1 = a, тогда
Следовательно,
Ответ:
Пример 8. Найти функции F(x) и g(x) из системы уравнений
Решение. Пусть
откуда
и второе уравнение перепишется в виде
Система примет вид
Исключим функцию F(•):
Значит,
Пусть
тогда
F(a) = 2a + 3.
Ответ: F(x) = 2x + 3, g(x) = 0.
Упражнения для самостоятельной работы
1. Найдите функцию F(x) из уравнений:
2. Найдите g(x), если
1) F(x – 1) = 2x – 3, F(g(x)) = 3x – 4.
2) F(x) = x3, F(g(x)) = 2x + 1.
3. Найдите F(x) и g(x) из систем уравнений:
Ответы
М Селиванова,
г. Реутов
Новые функции департамента развития территории помогут решать проблемы округов комплексно и более оперативно
Как известно, в администрации города начал работу департамент развития территорий, который объединил деятельность управлений округами и забрал ряд функций некоторых структурных подразделений и подведомственных учреждений мэрии. Как отмечают специалисты, модернизация позволит решать проблемы комплексно и в более сжатые сроки.
Как отмечают специалисты, модернизация позволит решать проблемы комплексно и в более сжатые сроки.
— Если раньше, проблемами территорий занимались одновременно несколько департаментов и управлений, и чтобы решить ту или иную задачу сотрудникам округов приходилось связываться с коллегами, синхронизировать работу, то теперь основные полномочия сконцентрированы в рамках одного департамента, — отметил председатель нового ведомства Антон Затонских.
Одна из функций, которой не было у управлений округами, – контроль за земляными работами. Раньше при обнаружении раскопки специалистам было необходимо запрашивать информацию у коллег из управления главного смотрителя. Теперь следить за проведением ремонтов на сетях, соблюдением требований по ограждению производственных участков и сроками выполнения работ они будут самостоятельно. А в случае выявления нарушений, смогут выдавать предписания и протоколы на штрафы.
В числе новых полномочий содержание мест накопления твердых коммунальных отходов, если это не включено в обязанности других лиц, а также организация вывоза и утилизации временных сооружений и разукомплектованных транспортных средств. До этого сотрудники территориальных управлений могли вести работу по поиску собственника объекта. Если же хозяин не появлялся в течение 30 дней, то машина или гараж признавались бесхозными. Их вывозом занимался департамент дорожного хозяйства и благоустройства по заявке сотрудников округов. Сейчас весь цикл от выявления конструкций и до утилизации будет курировать департамент развития территории.
До этого сотрудники территориальных управлений могли вести работу по поиску собственника объекта. Если же хозяин не появлялся в течение 30 дней, то машина или гараж признавались бесхозными. Их вывозом занимался департамент дорожного хозяйства и благоустройства по заявке сотрудников округов. Сейчас весь цикл от выявления конструкций и до утилизации будет курировать департамент развития территории.
Кроме того, консолидированы возможности специалистов управлений округами по работе с рекламными конструкциями на территории Липецка. В рамках предшествующих полномочий они могли только выдать предписание о демонтаже самовольно установленных элементов или составить протокол за неисполнение требований. Новые функции позволяют выдавать разрешения на установку рекламных конструкций или аннулировать их, вносить изменения в Схему размещения рекламы.
Кто придумал линейную функцию. Как решать линейные функции
1)
Область определения функции и область
значений функции .
Область определения функции — это множество всех допустимых действительных значений аргумента x (переменной x ), при которых функция y = f(x) определена. Область значений функции — это множество всех действительных значений y , которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции .
Нуль функции – такое значение аргумента, при котором значение функции равно нулю.
3) Промежутки знакопостоянства функции .
Промежутки знакопостоянства функции – такие множества значений аргумента, на которых значения функции только положительны или только отрицательны.
4) Монотонность функции .
Возрастающая функция (в некотором промежутке) — функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая
функция (в некотором промежутке) —
функция, у которой большему значению
аргумента из этого промежутка
соответствует меньшее значение функции.
5) Четность (нечетность) функции .
Четная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения выполняется равенство f(-x) = f(x) . График четной функции симметричен относительно оси ординат.
Нечетная функция — функция, у которой область определения симметрична относительно начала координат и для любого х из области определения справедливо равенство f(-x) = — f(x ). График нечетной функции симметричен относительно начала координат.
6) Ограниченная и неограниченная функции .
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция — неограниченная.
7) Периодическость функции .
Функция
f(x) — периодическая, если существует
такое отличное от нуля число T, что для
любого x из области определения функции
имеет место: f(x+T) = f(x). Такое наименьшее
число называется периодом функции. Все
тригонометрические функции являются
периодическими. (Тригонометрические
формулы).
Такое наименьшее
число называется периодом функции. Все
тригонометрические функции являются
периодическими. (Тригонометрические
формулы).
19. Основные элементарные функции, их свойства и графики. Применение функ-ций в экономике.
Основные элементарные функции. Их свойства и графики
1. Линейная функция.
Линейной функцией называется функция вида , где х — переменная, а и b — действительные числа.
Число а называют угловым коэффициентом прямой, он равен тангенсу угла наклона этой прямой к положительному направлению оси абсцисс. Графиком линейной функции является прямая линия. Она определяется двумя точками.
Свойства линейной функции
1. Область определения — множество всех действительных чисел: Д(y)=R
2. Множество значений — множество всех действительных чисел: Е(у)=R
3. Функция принимает нулевое значение при или.
4. Функция возрастает (убывает) на всей области определения.
5. Линейная функция
непрерывная на всей области определения,
дифференцируемая и
.
2. Квадратичная функция.
Функция вида , где х — переменная, коэффициенты а, b, с — действительные числа, называетсяквадратичной.
Научитесь брать производные от функций. Производная характеризует скорость изменения функции в определенной точке, лежащей на графике этой функции. В данном случае графиком может быть как прямая, так и кривая линия. То есть производная характеризует скорость изменения функции в конкретный момент времени. Вспомните общие правила, по которым берутся производные, и только потом переходите к следующему шагу.
- Прочитайте статью .
- Как брать простейшие производные, например, производную показательного уравнения, описано . Вычисления, представленные в следующих шагах, будут основаны на описанных в ней методах.
Научитесь различать задачи, в которых угловой коэффициент требуется вычислить через производную функции. В задачах не всегда предлагается найти угловой коэффициент или производную функции. {2}+6x}
в точке А(4,2) равен 22.
{2}+6x}
в точке А(4,2) равен 22.
Если возможно, проверьте полученный ответ на графике. Помните, что угловой коэффициент можно вычислить не в каждой точке. Дифференциальное исчисление рассматривает сложные функции и сложные графики, где угловой коэффициент можно вычислить не в каждой точке, а в некоторых случаях точки вообще не лежат на графиках. Если возможно, используйте графический калькулятор, чтобы проверить правильность вычисления углового коэффициента данной вам функции. В противном случае проведите касательную к графику в данной вам точке и подумайте, соответствует ли найденное вами значение углового коэффициента тому, что вы видите на графике.
- Касательная будет иметь тот же угловой коэффициент, что и график функции в определенной точке. Для того, чтобы провести касательную в данной точке, двигайтесь вправо/влево по оси Х (в нашем примере на 22 значения вправо), а затем вверх на единицу по оси Y. Отметьте точку, а затем соедините ее с данной вам точкой.
 В нашем примере соедините точки с координатами (4,2) и (26,3).
В нашем примере соедините точки с координатами (4,2) и (26,3).
Рассмотрим функцию y=k/y. Графиком этой функции является линия, называемая в математике гиперболой. Общий вид гиперболы, представлен на рисунке ниже. (На графике представлена функция y равно k разделить на x, у которой k равно единице.)
Видно, что график состоит из двух частей. Эти части называют ветвями гиперболы. Стоит отметить также, что каждая ветвь гиперболы подходит в одном из направлений все ближе и ближе к осям координат. Оси координат в таком случае называют асимптотами.
Вообще любые прямые линии, к которым бесконечно приближается график функции, но не достигает их, называются асимптотами. У гиперболы, как и у параболы, есть оси симметрии. Для гиперболы, представленной на рисунке выше, это прямая y=x.
Теперь разберемся с двумя общими случаями гипербол. Графиком функции y = k/x, при k ≠0, будет являться гипербола, ветви которой расположены либо в первом и третьем координатных углах, при k>0, либо во втором и четвертом координатных углах, при k
Основные свойства функции y = k/x, при k>0
График функции y = k/x, при k>0
5. y>0 при x>0; y6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).
y>0 при x>0; y6. Функция убывает как на промежутке (-∞;0), так и на промежутке (0;+∞).
10. Область значений функции два открытых промежутка (-∞;0) и (0;+∞).
Основные свойства функции y = k/x, при k
График функции y = k/x, при k
1. Точка (0;0) центр симметрии гиперболы.
2. Оси координат — асимптоты гиперболы.
4. Область определения функции все х, кроме х=0.
5. y>0 при x0.
6. Функция возрастает как на промежутке (-∞;0), так и на промежутке (0;+∞).
7. Функция не ограничена ни снизу, ни сверху.
8. У функции нет ни наибольшего, ни наименьшего значений.
9. Функция непрерывна на промежутке (-∞;0) и на промежутке (0;+∞). Имеет разрыв в точке х=0.
Линейная функция – это функция вида
x-аргумент (независимая переменная),
y- функция (зависимая переменная),
k и b- некоторые постоянные числа
Графиком линейной функции является прямая .
Для построения графика достаточно двух точек, т. к. через две точки можно провести прямую и притом только одну.
к. через две точки можно провести прямую и притом только одну.
Если k˃0, то график расположен в 1-й и 3-й координатных четвертях. Если k˂0, то график расположен в 2-й и 4-й координатных четвертях.
Число k называют угловым коэффициентом прямой графика функции y(x)=kx+b. Если k˃0, то угол наклона прямой y(x)= kx+b к положительному направлению Ох — острый; если k˂0, то этот угол- тупой.
Коэффициент b показывает точку пересечения графика с осью ОУ (0; b).
y(x)=k∙x— частный случай типичной функции носит название прямая пропорциональность. Графиком является прямая, проходящая через начало координат, поэтому для построения этого графика достаточно одной точки.
График линейной функции
Где коэффициент k = 3, следовательно
График функции будет возрастать и иметь острый угол с осью Ох т.к. коэффициент k имеет знак плюс.
ООФ линейной функции
ОЗФ линейной функции
Кроме случая, где
Так же линейная функция вида
Является функцией общего вида.
Б) Если k=0; b≠0,
В этом случае графиком является прямая параллельная оси Ох и проходящая через точку (0;b).
В) Если k≠0; b≠0, то линейная функция имеет вид y(x)=k∙x+b.
Пример 1 . Построить график функции y(x)= -2x+5
Пример 2 . Найдём нули функции у=3х+1, у=0;
– нули функции.
Ответ: или (;0)
Пример 3 . Определить значение функции y=-x+3 для x=1 и x=-1
y(-1)=-(-1)+3=1+3=4
Ответ: y_1=2; y_2=4.
Пример 4 . Определить координаты их точки пересечения или доказать, что графики не пересекаются. Пусть даны функции y 1 =10∙x-8 и y 2 =-3∙x+5.
Если графики функций пересекаются, то значение функций в этой точке равны
Подставим х=1, то y 1 (1)=10∙1-8=2.
Замечание. Подставить полученное значение аргумента можно и в функцию y 2 =-3∙x+5, тогда получим тот же самый ответ y 2 (1)=-3∙1+5=2.
y=2- ордината точки пересечения.
(1;2)- точка пересечения графиков функций у=10х-8 и у=-3х+5.
Ответ: (1;2)
Пример 5 .
Построить графики функций y 1 (x)= x+3 и y 2 (x)= x-1.
Можно заметить, что коэффициент k=1 для обеих функций.
Из выше сказанного следует, что если коэффициенты линейной функции равны, то их графики в системе координат расположены параллельно.
Пример 6 .
Построим два графика функции.
Первый график имеет формулу
Второй график имеет формулу
В данном случае перед нами график двух прямых, пересекающихся в точке (0;4). Это значит, что коэффициент b, отвечающий за высоту подъёма графика над осью Ох, если х=0. Значит мы может полагать, что коэффициент bу обоих графиков равен 4.
Редакторы: Агеева Любовь Александровна, Гаврилина Анна Викторовна
Инструкция
Если графиком является прямая линия, проходящая через начало координат и образующая с осью ОX угол α (угол наклона прямой к положительной полуоси ОХ). Функция, описывающая эту прямую, будет иметь вид y = kx. Коэффициент пропорциональности k равен tg α. Если прямая проходит через 2-ю и 4-ю координатные четверти, то k 0 и функция возрастает.Пусть представляет собой прямую линию, располагающуюся различным образом относительно осей координат. Это линейная функция, и она имеет вид y = kx + b, где переменные x и y стоят в первой степени, а k и b могут принимать как положительные, так и отрицательные значения или равны нулю. Прямая параллельна прямой y = kx и отсекает на оси |b| единиц. Если прямая параллельна оси абсцисс, то k = 0, если оси ординат, то уравнение имеет вид x = const.
Коэффициент пропорциональности k равен tg α. Если прямая проходит через 2-ю и 4-ю координатные четверти, то k 0 и функция возрастает.Пусть представляет собой прямую линию, располагающуюся различным образом относительно осей координат. Это линейная функция, и она имеет вид y = kx + b, где переменные x и y стоят в первой степени, а k и b могут принимать как положительные, так и отрицательные значения или равны нулю. Прямая параллельна прямой y = kx и отсекает на оси |b| единиц. Если прямая параллельна оси абсцисс, то k = 0, если оси ординат, то уравнение имеет вид x = const.
Кривая, состоящая из двух ветвей, располагающихся в разных четвертях и симметричных относительно начала координат, гиперболой. Этот график обратную зависимость переменной y от x и описывается уравнением y = k/x. Здесь k ≠ 0 — коэффициент пропорциональности. При этом если k > 0, функция убывает; если же k координатные углы.
Квадратичная функция имеет вид y = ax2 + bx + с, где a, b и c – величины постоянные и a 0. При выполнении условия b = с = 0, уравнение функции выглядит, как y = ax2 (простейший случай ), а ее график является параболой, проходящей через начало координат. График функции y = ax2 + bx + с имеет ту же форму, что и простейший случай функции, однако ее вершина (точка пересечения с осью OY) лежит не в начале координат.
При выполнении условия b = с = 0, уравнение функции выглядит, как y = ax2 (простейший случай ), а ее график является параболой, проходящей через начало координат. График функции y = ax2 + bx + с имеет ту же форму, что и простейший случай функции, однако ее вершина (точка пересечения с осью OY) лежит не в начале координат.
Параболой является также график степенной функции, выраженной уравнением y = xⁿ, если n – любое четное число. Если n — любое нечетное число, график такой степенной функции будет иметь вид кубической параболы.
В случае, если n – любое , уравнение функции приобретает вид. Графиком функции при нечетном n будет гипербола, а при четном n их ветви будут симметричны относительно оси ОУ.
Еще в школьные годы подробно изучаются функции и строятся их графики. Но, к сожалению, читать график функции и находить ее тип по представленному чертежу практически не учат. В действительности это довольно просто, если помнить основные виды функций.
Инструкция
Если представленным графиком является , которая через начало координат и с осью ОX угол α (который является углом наклона прямой к положительной полуоси), то функция, описывающая такую прямую, будет представлена как y = kx. При этом коэффициент пропорциональности k равен тангенсу угла α.
При этом коэффициент пропорциональности k равен тангенсу угла α.
Если заданная прямая проходит через вторую и четвертую координатные четверти, то k равен 0, и функция возрастает. Пусть представленный график является прямой линией, располагающейся любым образом относительно осей координат. Тогда функцией такого графика будет линейная, которая представлена видом y = kx + b, где переменные y и х стоят в первой , а b и k могут принимать как отрицательные, так и положительные значения или .
Если прямая параллельна прямой с графиком y = kx и отсекает на оси ординат b единиц, тогда уравнение имеет вид x = const, если график параллелен оси абсцисс, то k = 0.
Кривая линия, которая состоит из двух ветвей, симметричных относительно начала координат и располагающихся в разных четвертях, гиперболой. Такой график показывает обратную зависимость переменной y от переменной x и описывается уравнением вида y = k/x, где k не должен быть равен нулю, так как является коэффициентом обратной пропорциональности. При этом, если значение k больше нуля, функция убывает; если же k меньше нуля – возрастает.
При этом, если значение k больше нуля, функция убывает; если же k меньше нуля – возрастает.
Если предложенным графиком является парабола, проходящая через начало координат, ее функция при выполнении условия, что b = с = 0, будет иметь вид y = ax2. Это самый простой случай квадратичной функции. График функции вида y = ax2 + bx + с будет иметь такой же вид, что и простейший случай, однако вершина (точка, где график пересекается с осью ординат) будет находиться не в начале координат. В квадратичной функции, представленной видом y = ax2 + bx + с, значения величин a, b и c – постоянные, при этом a не равно нулю.
Параболой также может являться график степенной функции, выраженной уравнением вида y = xⁿ, только если n является любым четным числом. Если же значение n — нечетное число, такой график степенной функции будет представлен кубической параболой. В случае, если переменная n является любым отрицательным числом, уравнение функции приобретает вид .
Видео по теме
Координата абсолютно любой точки на плоскости определяется двумя ее величинами: по оси абсцисс и оси ординат. Совокупность множества таких точек и представляет собой график функции. По нему вы видите, как меняется значение Y в зависимости от изменения значения Х. Также вы можете определить, на каком участке (промежутке) функция возрастает, а на каком убывает.
Совокупность множества таких точек и представляет собой график функции. По нему вы видите, как меняется значение Y в зависимости от изменения значения Х. Также вы можете определить, на каком участке (промежутке) функция возрастает, а на каком убывает.
Инструкция
Что можно сказать о функции, если ее график представляет собой прямую линию? Посмотрите, проходит ли эта прямая через точку начала отсчета координат (то есть, ту, где величины Х и Y равны 0). Если проходит, то такая функция описывается уравнением y = kx. Легко понять, что чем больше будет значение k, тем ближе к оси ординат будет располагаться эта прямая. А сама ось Y фактически соответствует бесконечно большому значению k.
примеры решения производных
Производная функции является основным понятием дифференциального исчисления.
Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого
ряда задач по математике, физике и другим наукам, в особенности при изучении скорости различного рода процессов. Именно поэтому мы собрали на сайте более 200 примеров решения производных и постоянно добавляем новые! Список тем находится в правом меню.
Именно поэтому мы собрали на сайте более 200 примеров решения производных и постоянно добавляем новые! Список тем находится в правом меню.
Перед изучением примеров вычисления производных советуем изучить теоретический материал по теме: прочитать определения, правила дифференцирования, таблицу производных и другой материал по производным.
Таблица производных и правила дифференцирования
Основные ссылки — таблица производных, правила дифференцирования и примеры решений (10 шт).
ПримерЗадание. Найти производную функции
Решение. Так как производная суммы равна сумме производных, то
Воспользуемся формулами для производных показательной и обратной тригонометрической функций:
Ответ.
Больше примеров решений →
Производные сложных функций
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Найти производную функции
Найти производную функции
Решение. По правилу дифференцирования сложной функции:
В свою очередь производная также берется по правилу дифференцирования сложной функции:
Ответ.
Больше примеров решений →
Применение дифференциала в приближенных вычислениях
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Геометрический смысл производной
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Механический смысл производной
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Точка движется по закону . Чему равна скорость в момент времени ?
Решение. Найдем скорость точки как первую производную от перемещения:
В момент времени скорость равна
Ответ.
Больше примеров решений →
Уравнение касательной, нормали и угол между прямыми
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Записать уравнение касательной к графику функции в точке
Решение. Найдем значение функции в заданной точке:
Найдем производную заданной функции по правилу дифференцирования произведения:
Вычислим её значение в заданной точке
Используя формулу
запишем уравнение касательной:
Ответ. Уравнение касательной:
Больше примеров решений →
Производные высших порядков
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Найти производную второго порядка от функции
Решение. Находим первую производную как производную сложной функции:
Находим первую производную как производную сложной функции:
Вторую производную находим как от произведения, предварительно вынеся по правилам дифференцирования коэффициент 3 за знак производной. Также будем учитывать, что первый множитель — — есть сложной функцией:
Ответ.
Больше примеров решений →
Механическое смысл второй производной
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Уравнение движения материальной точки вдоль оси имеет вид (м). Найти ускорение точки в момент времени c.
Решение. Ускорение заданной точки найдем, взяв вторую производную от перемещения по времени:
Первая производная
(м/с)
вторая производная
(м/с2)
В момент времени c
(м/с2)
Ответ. (м/с2)
(м/с2)
Больше примеров решений →
Дифференциалы высших порядков
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Найти дифференциал третьего порядка функции
Решение. По формуле
Найдем третью производную заданной функции:
Тогда
Ответ.
Больше примеров решений →
Производная функции, заданной неявно
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Производная функции, заданной параметрически
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Логарифмическое дифференцирование
Основные ссылки — теоретический материал и примеры решений (10 шт).
ПримерЗадание. Найти производную функции
Найти производную функции
Решение. Применим логарифмическое дифференцирование:
Тогда, продифференцировав левую и правую часть, будем иметь:
Отсюда получаем, что
Ответ.
Больше примеров решений →
Формулы Маклорена и Тейлора
Основные ссылки — теоретический материал и примеры решений (10 шт).
Больше примеров решений →
Вы поняли, как решать? Нет?
Помощь с решением
График линейной функции в 7 классе, определения, понятия, урок по алгебре
Дата публикации: .
График линейной функции
График функции – это такое понятие в математике, которое дает наглядное геометрическое представление о функции.

Графиком линейной функции всегда является прямая. Как проще всего её построить?
Возьмем линейную функцию с двумя переменными, например, ax + by + с =0, где b ≠ 0.
Определим, чему равен y?
by = -ax — c
y = -$\frac{a}{b}x — \frac{c}{b}$.
Введём обозначения: k = -$\frac{a}{b}$ и m = — $\frac{c}{b}$.
Получаем запись нашего уравнения y = kx + m. Это уравнение называется линейным уравнением c двумя переменными, о таких уравнениях мы уже рассказывали.
Здесь х – независимая переменная; у – зависимая переменная.
Как мы уже говорили, графиком линейной функции y = kx + m является прямая.
Построим график этой функции. Для примера, возьмём уравнение y = x + 2.
Составим небольшую таблицу.
Х 0 2
У 2 4
Отметим эти точки на координатной плоскости и получим вот такой график.
Давайте посмотрим, как на практике можно использовать график функции? Рассчитаем, на сколько дней хватит запаса яблок, если известно первоначальное количество яблок и количество яблок, которое магазин продает каждый день?
Задача.
На складе магазина находится 60 кг яблок. Каждый день магазин продает 12 кг этих фруктов. Сколько кг яблок останется на складе магазина через 2 дня, через 3 дня, через 5 дней?
Решение.
Построим математическую модель задачи: y= 60 — 12x.
Составим таблицу.
Х 2 3
У 36 24
По этим точкам построим график.
По графику можно предположить, какое количество яблок будет находится на складе магазина в любой день (от 1 до 5). Нужно помнить, что количество фруктов не может быть отрицательным.
Как решать линейные функции — видео и расшифровка урока
Проверка вашего ответа и примеров
Чтобы проверить свой ответ, просто подставьте значения f( x ) и x в исходную функцию. В упрощенном виде обе стороны знака равенства должны совпадать.
- f( х ) = 3 х — 1; f(3) = 8
- 8 = 3(3) — 1
- 8 = 9 — 1
- 8 = 8
Отлично!
Вот еще несколько примеров.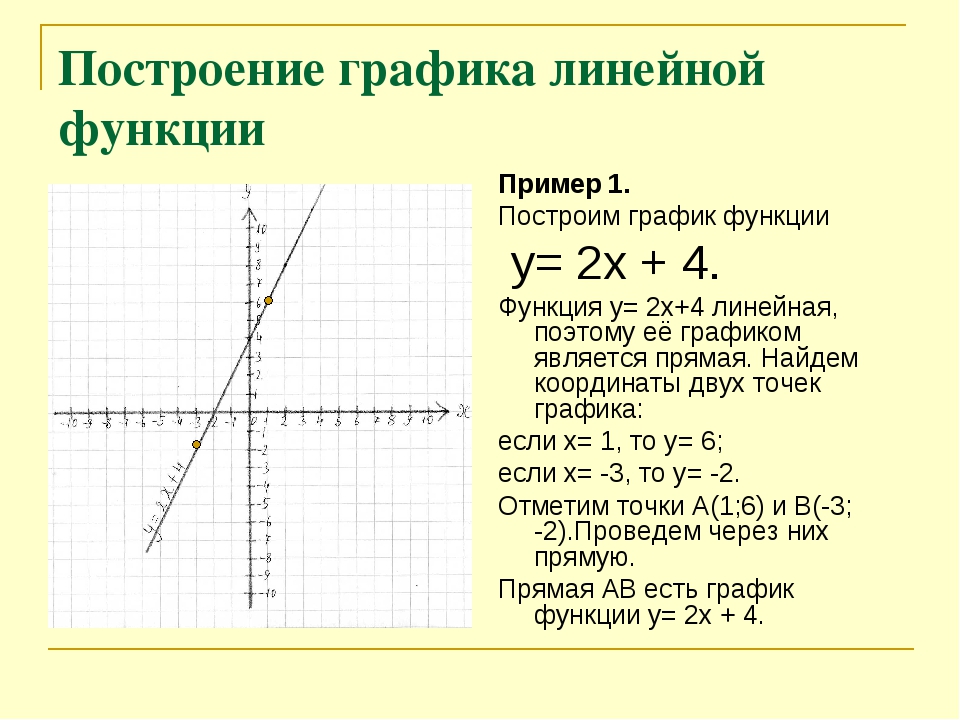 Допустим, вам дано значение x . Таким же образом можно найти f( x ). Просто следуйте инструкциям, чтобы выделить неизвестное f( x ).
Допустим, вам дано значение x . Таким же образом можно найти f( x ). Просто следуйте инструкциям, чтобы выделить неизвестное f( x ).
Если f( x ) = 5 x — 1, чему равно f(2)? Здесь нам сообщают, что x = 2 заменой 2 в формате функции f( x ).
Шаг 1
Замена. Итак:
Шаг 2
Изолируйте переменную. Здесь переменная f( x ) уже была выделена, поэтому мы можем перейти к упрощению.Итак:
Шаг 3
Упрощение. Итак:
Шаг 4
У нас есть ответ! Например, для f( x ) = 5 x — 1, f(2) = 9,
Теперь давайте рассмотрим более сложный пример: решим f( x ) = 4( x + 2) когда f( x ) = 24.
Шаг 1
Замена. Или:
Шаг 2
Упрощение. Здесь нам нужно сначала упростить, чтобы изолировать переменную. Или:
Не забудьте распределить 4 между обоими терминами в скобках.
Шаг 3
Изолируйте переменный член. Или:
Или:
- 24 — 8 = 4 x + 8 — 8
- 16 = 4 х
Шаг 4
Продолжайте изолировать.
Итак, наш окончательный ответ для функции f( x ) = 4( x +2), f(4) = 24. мы узнали на этом уроке. В этом уроке мы узнали, что линейная функция — это функция вида f( x ) = x + b .Это похоже на обычное линейное уравнение, но вместо использования y линейная функция обозначается как f( x ). Чтобы решить линейную функцию, вам дадут значение f( x ) и попросят найти x . Мы также изучили шаги для решения этой проблемы, а именно:
- Шаг 1: Подставьте значение f( x ) в задачу.
- Шаг 2: Изолируйте переменную.
- Шаг 3: Продолжайте изолировать переменную.
- Шаг 4: Подтверждение ответа.
Все просто!
Алгебра — Обратные функции
Показать мобильное уведомление Показать все примечания Скрыть все примечания Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-7: Обратные функции
В последнем примере из предыдущего раздела мы рассмотрели две функции \(f\left( x \right) = 3x — 2\) и \(g\left( x \right) = \frac{x}{3 } + \frac{2}{3}\) и увидел, что
\[\left( {f \circ g} \right)\left( x \right) = \left( {g \circ f} \right)\left( x \right) = x\], и, как отмечалось в этом разделе, это означает, что это очень специальные функции.Давайте посмотрим, что делает их такими особенными. Рассмотрим следующие оценки.
\[\require{color} \begin{align*}f\left( {\color{ProcessBlue} — 1} \right) & = 3\left({- 1} \right) — 2 = {\color{Red } — 5} & \hspace{0. 25in} \Rightarrow \hspace{0.25in}g\left( {\color{Red} — 5} \right) & = \frac{{ — 5}}{3} + \ frac{2}{3} = \ frac{{ — 3}}{3} = {\color{ProcessBlue} — 1}\\ & & \\ g\left ({\color{ProcessBlue} 2} \right) & = \frac{2}{3} + \frac{2}{3} = { \color{Red}\frac{4}{3}} & \hspace{0.25in} \Rightarrow \hspace{0.25in}f\left( {\color{Red} \frac{4}{3}} \right) & = 3\left({\frac{4}{3}} \right ) — 2 знак равно 4 — 2 знак равно {\ цвет {ProcessBlue} 2} \ конец {выравнивание *} \]
25in} \Rightarrow \hspace{0.25in}g\left( {\color{Red} — 5} \right) & = \frac{{ — 5}}{3} + \ frac{2}{3} = \ frac{{ — 3}}{3} = {\color{ProcessBlue} — 1}\\ & & \\ g\left ({\color{ProcessBlue} 2} \right) & = \frac{2}{3} + \frac{2}{3} = { \color{Red}\frac{4}{3}} & \hspace{0.25in} \Rightarrow \hspace{0.25in}f\left( {\color{Red} \frac{4}{3}} \right) & = 3\left({\frac{4}{3}} \right ) — 2 знак равно 4 — 2 знак равно {\ цвет {ProcessBlue} 2} \ конец {выравнивание *} \]В первом случае мы подставили \(x = — 1\) в \(f\left( x \right)\) и получили значение -5. Затем мы развернулись и подставили \(x = — 5\) к \(g\left( x \right)\) и получили значение -1, число, с которого мы начали.
Во втором случае мы сделали нечто подобное. Здесь мы подставили \(x = 2\) к \(g\left( x \right)\) и получили значение \(\frac{4}{3}\), мы развернулись и подставили это к \( f\left( x \right)\) и получил значение 2, которое снова является числом, с которого мы начали.
Обратите внимание, что здесь мы действительно выполняем композицию функций. Первый случай действительно
Первый случай действительно
, а второй случай действительно
\[\ влево ( {е \ circ g} \ вправо) \ влево ( 2 \ вправо) = е \ влево [ {г \ влево ( 2 \ вправо)} \ вправо] = е \ влево [ {\ гидроразрыва {4} {3}} \справа] = 2\]Обратите также внимание, что они оба согласуются с формулой для композиций, которую мы нашли в предыдущем разделе.Мы получаем обратно из вычисления функции число, которое мы изначально вставили в композицию.
Итак, что же здесь происходит? В некотором смысле мы можем думать об этих двух функциях как об отмене того, что другая сделала с числом. В первом случае мы подставили \(x = — 1\) в \(f\left( x \right)\), а затем подставили результат этой функции обратно в \(g\left( x \right)\) и каким-то образом \(g\left( x \right)\) отменил то, что \(f\left( x \right)\) сделал с \(x = — 1\), и вернул нам исходный \(x \), с которого мы начали.
Пары функций, демонстрирующие такое поведение, называются обратными функциями . Прежде чем формально определить обратные функции и обозначения, которые мы собираемся использовать для них, нам нужно получить определение.
Функция называется однозначной , если никакие два значения \(x\) не дают одинаковых \(y\). Это довольно простое определение однозначности, но для демонстрации того, что это означает, нужен пример функции, которая не является взаимно однозначной.2}\) во взаимно однозначную функцию, если мы ограничимся \(0 \le x < \infty \). Иногда это можно сделать с помощью функций.
Демонстрация однозначности функции часто является утомительным и трудным процессом. По большей части мы будем предполагать, что функции, с которыми мы будем иметь дело в этом разделе, являются взаимно однозначными. Однако нам нужно было поговорить о функциях «один к одному», поскольку только функции «один к одному» могут быть обратными функциями. { — 1}}\left( x \right)\).{ — 1}} \circ f} \right)\left( x \right) = x\) верны. Для всех функций, которые мы будем рассматривать в этом разделе, если одна из них истинна, то и другая тоже будет истинна. Однако существуют функции (однако они выходят далеко за рамки этого курса), для которых возможно, что только одно из них будет истинным. Это связано с тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять оба.
{ — 1}}\left( x \right)\).{ — 1}} \circ f} \right)\left( x \right) = x\) верны. Для всех функций, которые мы будем рассматривать в этом разделе, если одна из них истинна, то и другая тоже будет истинна. Однако существуют функции (однако они выходят далеко за рамки этого курса), для которых возможно, что только одно из них будет истинным. Это связано с тем, что во всех задачах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять оба.
Давайте поработаем над некоторыми примерами.{ — 1}}\влево( х \вправо)\). Показать решение
Теперь мы уже знаем, что является обратной для этой функции, так как мы уже поработали с ней. Тем не менее, было бы неплохо начать с этого, поскольку мы знаем, что мы должны получить. Это будет хорошей проверкой процесса.
Итак, приступим. Сначала мы заменим \(f\left( x \right)\) на \(y\).
\[у = 3x — 2\] Затем замените все \(x\) на \(y\) и все y на на \(x\). { — 1}}\left( x \right) = \frac{{4 + 5x}}{{2x — 1}}\]
{ — 1}}\left( x \right) = \frac{{4 + 5x}}{{2x — 1}}\]
Наконец, нам нужно выполнить проверку.{ — 1}}} \right)\left( x \right) & = \frac{{2x — 1}}{{2x — 1}}\,\,\frac{{\frac{{4 + 5x} }{{2x — 1}} + 4}}{{2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5}}\\ & = \frac{ {\ влево ( {2x — 1} \ вправо) \ влево ( {\ гидроразрыва {{4 + 5x}} {{2x — 1}} + 4} \ вправо)}} {{\ влево ( {2x — 1} \right)\left( {2\left( {\frac{{4 + 5x}}{{2x — 1}}} \right) — 5} \right)}}\\ & = \frac{{4 + 5x + 4\влево( {2x — 1} \вправо)}}{{2\влево( {4 + 5x} \вправо) — 5\влево( {2x — 1} \вправо)}}\\ & = \ frac{{4 + 5x + 8x — 4}}{{8 + 10x — 10x + 5}}\\ & = \frac{{13x}}{{13}}\\ & = x\end{align*} \]
Вау.Было много работы, но в итоге все получилось. Мы сделали всю нашу работу правильно, и на самом деле мы имеем обратное.
Есть еще одна последняя тема, которую нам нужно быстро обсудить, прежде чем мы покинем этот раздел. Существует интересная связь между графиком функции и ее обратной.
Вот график функции и обратной из первых двух примеров. Мы не будем рассматривать последний пример, так как это функция, график которой мы еще не обсуждали.
В обоих случаях мы видим, что график обратной функции является отражением фактической функции относительно линии \(y = x\). Это всегда будет иметь место с графиками функции и ее обратной.
Функции Как решить математическую задачу
Решение математической задачи состоит из трех шагов.
- Выясните, в чем проблема.
- Решите проблему.
- Проверьте ответ.
Эти шаги позволяют нам решать проблемы, с которыми мы раньше не сталкивались, и это хорошо, иначе у нас будут проблемы на экзаменах.
Пример задачи
Нарисуйте зависимость, описываемую неравенством y ≤ 4 – 2 — x .
Это похоже на построение графика линейного неравенства, за исключением того, что неравенство не является линейным. Здесь нам нужно спросить: «Чье это нелинейное неравенство?»
Здесь нам нужно спросить: «Чье это нелинейное неравенство?»
Так что же нам делать? Давайте пройдемся по нашим шагам решения проблемы.
1. Выясните, в чем проблема.
Ну, задача говорит что-нибудь нарисовать. Вероятно, нам понадобится построить график
y = 4 – 2 – x
, поэтому сначала нам нужно выяснить, как это выглядит. Затем, поскольку нас просят построить график неравенства, нам нужно выяснить, какую часть графика закрасить. Мы можем использовать для этого древесный уголь, просто чтобы быть более художественным.
2.Решать проблему.
Сначала построим график y = 4 – 2 — x .
Это экспоненциальная функция. Мы могли бы переписать уравнение как
y = (-1)2 — x + 4
, что немного больше похоже на экспоненциальные функции, с которыми мы работали ранее. Близость иногда порождает презрение, но в данном случае порождает радость, так как это облегчит решение.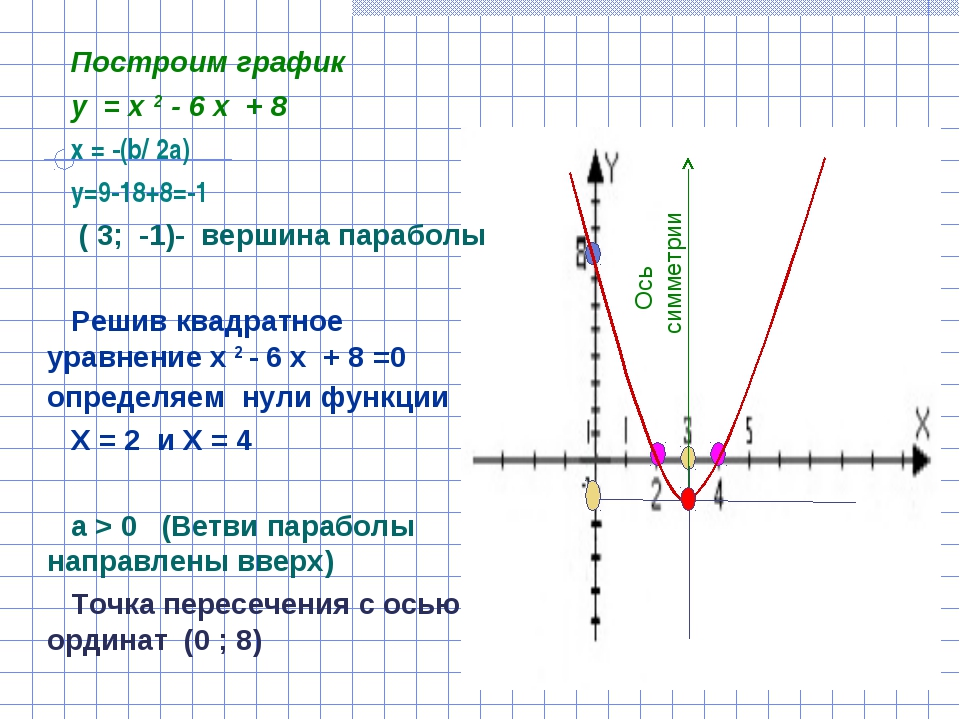 Давайте сначала сделаем легкий бит. y -перехват:
Давайте сначала сделаем легкий бит. y -перехват:
y = (-1)2 0 + 4 = 3
Поскольку постоянный член равен 4, асимптота равна y = 4. Теперь самое интересное часть, как будто уже не катаешься по полу с неудержимым животным смехом уже. Поскольку показатель степени равен — x вместо x , экспоненциальная кривая будет перевернута. Поскольку экспоненциальный член умножается на отрицательное число, кривая также будет повернута слева направо.Собрав все вместе, график выглядит так:
Теперь у нас есть график y = 4 – 2 — x , что очень хорошо, но не то, о чем просила задача. Мы должны изобразить неравенство, а это значит, что нам нужно немного заштриховать. Мы знаем, что в глубине души вы бунтарь, но в этом нет ничего лишнего. Чтобы определить, где нам нужно заштриховать, давайте представим это как линейное неравенство. Нам нужны точки на этой кривой или те точки, где y на меньше , чем они были бы на кривой. Это означает, что мы хотим заштриховать нижнюю часть графика:
Это означает, что мы хотим заштриховать нижнюю часть графика:
3. Проверьте ответ.
Чтобы проверить наш ответ, давайте возьмем одну точку в заштрихованной области и убедимся, что она должна быть включена в отношение, затем возьмем одну точку вместо в заштрихованной области и убедимся, что она не должна быть включена в отношение . Тогда давайте удостоверимся, что они разделены, так как они неизменно начнут драться каждый раз, когда окажутся на расстоянии пяти футов друг от друга.
Во-первых, точка (3, 0) в настоящее время находится в заштрихованной части графика. Должна ли эта точка действительно быть в отношении? Когда x = 3, правая часть неравенства равна
.
Значение y = 0, безусловно, меньше или равно , так что да, этот пункт действительно должен быть включен.
Точка (-4, 0) не находится в заштрихованной части графика. Когда x = -4, правая часть неравенства равна
4 – 2 {-(-4)} = 4 – 16 = -12.
Значение y = 0 заведомо не меньше -12, поэтому точка (-4, 0) не в соотношении. Хотя мы не можем проверить бесконечное количество точек, проверка того, что эти две оказались на правильных сторонах неравенства, обнадеживает. Однако, если вы перфекционист и решительно настроены проверять бесконечное количество точек, удачи. Осенью проверим, как у вас дела.
Нули функции – объяснение и примеры
Одна из самых распространенных проблем, с которыми мы сталкиваемся на наших базовых и продвинутых занятиях по алгебре, — это нахождение нулей определенных функций. Сложность будет меняться по мере того, как мы продвигаемся и овладеваем искусством нахождения нулей функций.
Судя по названию, нули функции — это значения x, где f(x) равно нулю.
Мы встречаем нули на уроках математики и в повседневной жизни. Например, если мы хотим узнать сумму, которую нам нужно продать, чтобы выйти в ноль, мы в конечном итоге найдем нули в уравнении, которое мы составили. Это всего лишь один из многих примеров задач и моделей, где нам нужно найти нули f(x).
Это всего лишь один из многих примеров задач и моделей, где нам нужно найти нули f(x).
Широко применяя функции и их нули, мы должны научиться манипулировать различными выражениями и уравнениями, чтобы находить их нули.В этой статье мы научимся:
- Знать, что представляет ноль функции.
- Научитесь находить нули общих функций.
- Определение нулей функции по ее графику.
Давайте продолжим и начнем с понимания основного определения нуля.
Что такое ноль функции?
Понимание того, что обозначают нули, может помочь нам узнать, когда находить нули функций по их выражениям, и научиться находить их по графику функции.В общем, нули функции — это значение x, когда сама функция становится нулевой .
Нули функции могут принимать разные формы — если они возвращают значение y, равное 0, мы будем считать это нулем функции.
Нули определения функции
Нули функции — это значения x, когда f(x) равно 0 . Отсюда и его название. Это означает, что когда f(x) = 0, x является нулем функции. Когда график проходит через x = a, говорят, что a является нулем функции.Следовательно, (a, 0) является нулем функции .
Отсюда и его название. Это означает, что когда f(x) = 0, x является нулем функции. Когда график проходит через x = a, говорят, что a является нулем функции.Следовательно, (a, 0) является нулем функции .
- Функция f(x) = x + 3 имеет нуль при x = -3, поскольку f(-3) = 0.
- Функция g(x) = x 2 – 4 имеет два нуля: x = -4 и x = 4. Это означает, что f(-4) = 0 и f(4) = 0.
- График h(x) проходит через (-5, 0), поэтому x = -5 равно ноль h(x) и h(-5) = 0.
Когда задан график функции, ее реальные нули будут представлены точками пересечения x. Это имеет смысл, поскольку нули — это значения x, когда y или f(x) равны 0.
Х-пересечения функции: (x 1 , 0), (x 2 , 0), (x 3 , 0) и (x 4 , 0). Это означает, что для графа, показанного выше, его действительные нули равны {x 1 , x 2 , x 3 , x 4 } .
Однако бывают случаи, когда график не проходит через точку пересечения x. Это не означает, что у функции нет нулей, но вместо этого нули функций могут иметь сложную форму.
Это не означает, что у функции нет нулей, но вместо этого нули функций могут иметь сложную форму.
Как найти нули функции
?Поиск нулей функции может быть таким же простым, как изолировать x в одной части уравнения, чтобы многократно манипулировать выражением, чтобы найти все нули уравнения.
В общем случае, если задана функция f(x), ее нули можно найти, установив функцию в ноль . Значения x, которые представляют заданное уравнение, являются нулями функции. Чтобы найти нули функции, найдите значения x, при которых f(x) = 0.
Как найти нули квадратичной функции?
Существует множество сложных уравнений, которые в конечном итоге можно свести к квадратным уравнениям. Вот почему на наших промежуточных занятиях по алгебре мы потратим много времени на изучение нулей квадратичных функций.
Чтобы найти нули квадратичной функции, мы приравниваем данную функцию к 0 и находим значения x, которые удовлетворяют уравнению. Вот несколько важных напоминаний при нахождении нулей квадратной функции:
Вот несколько важных напоминаний при нахождении нулей квадратной функции:
- Убедитесь, что квадратное уравнение имеет стандартную форму (ax 2 + bx + c = 0).
- По возможности множьте, но не стесняйтесь использовать квадратную формулу.
- Квадратичная функция может иметь не более двух нулей.
В прошлом мы узнали о различных стратегиях поиска нулей квадратичных функций, поэтому вот руководство о том, как выбрать лучшую стратегию:
Как найти нули полиномиальной функции?
Тот же процесс применяется для полиномиальных функций – приравнять полиномиальную функцию к 0 и найти значения x, которые удовлетворяют уравнению .Это руководство может помочь вам найти наилучшую стратегию при поиске нулей полиномиальных функций.
Нужен дополнительный обзор по решению полиномиальных уравнений? Не беспокойтесь, перейдите по этой ссылке здесь и освежите свои знания о решении полиномиальных уравнений.
Как найти нули рациональной функции?
Рациональные функции — это функции, которые имеют полиномиальное выражение как в числителе, так и в знаменателе. Применяя тот же принцип при нахождении нулей других функций, мы приравниваем рациональную функцию к 0.
Допустим, у нас есть рациональная функция f(x) с числителем p(x) и знаменателем q(x).
f(x) = p(x)/q(x)
Чтобы найти его ноль, приравняем рациональное выражение к нулю.
p(x)/q(x) = 0
Поскольку q(x) никогда не может быть равно нулю, мы упрощаем уравнение до p(x) = 0. Что это означает для всех рациональных функций?
При нахождении нуля рациональных функций мы приравниваем числитель к 0 и находим х .
Как найти нули других функций?
Как вы уже догадались, правило остается тем же для всех видов функций .Получив уникальную функцию, не забудьте приравнять ее выражение к 0, чтобы найти ее нули.
Вот еще несколько функций, которые вы уже можете столкнуться в прошлом:
| тип функции | Пример | |
F (x) = log 2 2x Узнайте, как решать логарифмические уравнения здесь. | ||
| Степенная функция | f(x) = 3x 1/3 Здесь потренируйтесь решать уравнения, включающие степенные функции. | |
| Экспоненциальная функция | F (x) = 2 x + 1 | |
| Тригонометрическая функция | F (x) = -3 sin x |
zeros из любых из этих функций вернуть значения x, где функция равна нулю. Имея график этих функций, мы можем найти их действительные нули, проверив x-пересечения графика.
На приведенном выше графике показана зависимость f(x) = -3 sin x от -3π до 3π. Все точки пересечения x на графике являются нулями функции между интервалами.Следовательно, нули между данными интервалами равны: {- 3 π, -2 π , – π, 0, π, 2}.
Готовы применить то, что мы только что узнали? Давайте продолжим и попробуем решить некоторые из этих задач.
Пример 1
Функция f(x) имеет следующую таблицу значений, показанную ниже.
Основываясь на таблице, каковы нули f(x)?
Решение
Всегда возвращайтесь к тому факту, что нули функций — это значения x, когда значение функции равно нулю.
Мы видим, что когда x = -1, y = 0, а когда x = 1, y = 0. Следовательно, нули f(x) равны -1 и 1.
Пример 2
График f(x) показан ниже. Используя этот график, каковы нули f(x)?
Решение
График f(x) проходит через ось x в точках (-4, 0), (-1, 0), (1, 0) и (3, 0). Это x-перехваты и, следовательно, это действительные нули f (x).
Следовательно, нулей f(x) равны {-4, -1, 1, 3} .
Пример 3
Чему равны нули g(x) = –x 3 – 3x 2 + x + 3?
Решение
Найдите ноль g(x), приравняв кубическое выражение к 0. и факторизовать выражение.
и факторизовать выражение.
–x 3 + x – 3x 2 + 3 = 0
-x(x 2 – 1) – 3(x 2 – 1) = 0
(-
) (x 2 – 1) = 0Применить свойство разности двух квадратов, a 2 – b 2 = (a – b),(a + b) ко второму фактору.
(-x-3)(x – 1)(x + 1) = 0
Приравняйте каждый множитель к 0, чтобы найти x.
-x- 3 = 0 -x = 3 x = 3 x — 1 = 0 x — 1 = 0 x = 1 | x + 1 = 0 x = -1 |
Следовательно, нулей g(x) равны {-1, 1, 3}.
пример 4
Решение
Приравняйте выражение h(x) к 0, чтобы найти его нули.Это приведет к полиномиальному уравнению.
–2x 4 – 2x 3 + 14x 2 + 2x – 12 = 0
Разделите обе части уравнения на -2, чтобы упростить уравнение.
x 4 + x 3 – 7x 2 – x + 6 = 0
Перечислите возможные рациональные множители выражения, используя теорему о рациональных нулях. Для нашего случая имеем p = 1 и q = 6.
| Факторы p | ±1 |
| Коэффициенты q ±167 ± 9,560 9,560 | |
| Возможные нули (p/q) | ±1/6, ±1/3, ±1/2, ±1 |
Давайте продолжим и воспользуемся синтетическим делением, чтобы убедиться, что x = 1 и x = -1 может удовлетворять уравнению.
Это означает, что x = 1 является решением и h(x) можно переписать как -2(x – 1)(x 3 + 2x 2 -5x – 6). Используйте кубическое выражение в следующем синтетическом делении и посмотрите, является ли x = -1 также решением.
Следовательно, x = -1 является решением и (x + 1) является множителем h(x). Отсюда имеем h(x) = -2(x – 1)(x + 1)(x 2 + x – 6).
Чтобы найти два оставшихся нуля h(x), приравняем квадратное выражение к 0.
х + 2 = 0
х = -2
х – 3 = 0
х = 3
7 Отсюда 1, 1, 3}.Пример 5
Решение
Функция g(x) является рациональной функцией, поэтому, чтобы найти ее нуль, приравняйте числитель к 0. который удовлетворяет уравнению для нахождения нулей g(x).
Пусть a = x 2 и сведем уравнение к квадратному уравнению.
(x 2 ) 2 — 10x 2 + 9 = 0
A 2 — 10A + 9 = 0
(A — 1) (A — 9) = 0
Приравнете каждый умножьте на 0, чтобы найти a, затем подставьте x 2 обратно, чтобы найти возможные значения нулей g(x).
A — 1 = 0 x 2 — 1 = 0 x 2 = 1 x = ± 1 0 | A — 9 = 0 x 2 – 9 = 0 x 2 = 9 x = ± 3 |
Следовательно, нули g(x) равны {-3, -1, 1, 3}.
Композиция функций — определение, домен, составная функция
Композиция функций — это процесс объединения двух или более функций в одну функцию. Функция представляет некоторую работу. Возьмем приготовление хлеба. Пусть x — мука, кухонный комбайн выполняет функцию приготовления теста с использованием муки (и пусть эта функция равна g(x)) и пусть печь выполняет функцию приготовления хлеба (и пусть эта функция равна f (Икс)).Для приготовления хлеба выход g(x) нужно поместить в функцию f(x) (т. е. приготовленное тесто нужно поставить в печь). Результат обозначается f(g(x)) и представляет собой композицию функций f(x) и g(x).
Давайте посмотрим, что такое композиция функций в математике вместе с ее вычислением. Давайте также посмотрим, как найти его домен и диапазон.
Что такое композиция функций?
Композиция функций f(x) и g(x), где g(x) действует первой, представляется как f(g(x)) или (f ∘ g)(x).Он объединяет две или более функций, чтобы получить другую функцию. В составе функций выход одной функции, находящейся внутри скобок, становится входом внешней функции. то есть
- В f(g(x)), g(x) является входом f(x).
- В g(f(x)), f(x) является входом g(x).
Мы можем понять это, используя следующую цифру:
, т. е. чтобы найти f(g(x)) (которое читается как «f от g от x»), мы должны сначала найти g(x), а затем подставить результат в f(x).
Символ композиции функций
Символ композиции функций ∘. Его также можно показать без использования этого символа, но с помощью скобок. то есть
- (f ∘ g)(x) = f(g(x)) и читается как «f of g of x». Здесь g — внутренняя функция, а f — внешняя функция.
- (g ∘ f)(x) = g(f(x)) и читается как «g of f of x».
 Здесь f — внутренняя функция, а g — внешняя функция.
Здесь f — внутренняя функция, а g — внешняя функция.
Как решать составные функции?
Используя BODMAS, мы всегда сначала упрощаем то, что находится в скобках.Таким образом, чтобы найти f (g (x)), сначала необходимо вычислить g (x) и подставить его в f (x). Точно так же, чтобы найти g (f (x)), сначала нужно вычислить f (x) и подставить его в g (x). т. е. при нахождении составных функций порядок имеет значение. Это означает, что f(g(x)) НЕ может быть равно g(f(x)). Для любых двух функций f(x) и g(x) мы находим составную функцию f(g(a)) с помощью следующих шагов:
- Найдите g(a), подставив x = a в g(x).
- Найдите f(g(a)) подстановкой x = g(a) в f(x).
Мы можем понять эти шаги, используя приведенный ниже пример. Здесь мы находим f(g(-1)) при f(x) = x 2 — 2x и g(x) = x — 5.
Мы можем обобщить этот процесс с помощью простых математических вычислений, как показано ниже:
ф(г(-1)) = ф(-1-5)
= f(-6)
= (-6) 2 — 2 (-6)
= 36 + 12
= 48
Нахождение составной функции по графику
Чтобы найти составную функцию двух функций (которые не определены алгебраически), показанную графически, мы должны вспомнить, что если (x, y) — точка на функции f(x), то f(x) = y. Используя это, чтобы найти f (g (a)) (т. Е. f (g (x)) при x = a):
Используя это, чтобы найти f (g (a)) (т. Е. f (g (x)) при x = a):
- Сначала найдите g(a) (т. е. координату y на графике g(x), соответствующую x = a)
- Найти f(g(a)) (т.е. координату y на графике f(x), соответствующую g(a))
Пример: Найдите f(g(5)) на следующем графике.
Решение:
f(g(5)) = f(3) (Поскольку g(5) = 3, так как (5, 3) принадлежит g(x))
= 2 (Поскольку f(3) = 2, так как (3, 2) принадлежит f(x))
Следовательно, f(g(5)) = 2.
Поиск составной функции из таблицы
Мы уже видели, как найти составную функцию, если задан график функций. Иногда точки на графике функций изображают таблицами. Таким образом, мы применяем ту же процедуру, что описана в предыдущем разделе.
Пример: Найдите g(f(-3)) с помощью следующих таблиц.
| х | ф(х) |
|---|---|
| -1 | -4 |
| -2 | -3 |
| -3 | -2 |
| -4 | -1 |
| х | г(х) |
|---|---|
| -4 | 1 |
| -3 | 0 |
| -2 | -1 |
| -1 | -2 |
Решение:
Из таблицы f(x), f(-3) = -2.
Таким образом, g(f(-3))=g(-2).
Из таблицы g(x), g(-2) = -1.
Таким образом, g(f(-3)) = -1.
Домен составных функций
В общем случае, если g : X → Y и f : Y → Z, то f ∘ g : X → Z. т. е. областью определения f ∘ g является X, а область значений — Z. Но когда функции определены алгебраически, здесь — шаги по нахождению области определения составной функции f(g(x)).
- Найти область определения внутренней функции g(x) (пусть это будет A)
- Найдите область определения функции, полученной путем нахождения f(g(x)) (пусть это будет B)
- Найдите пересечение A и B и A ∩ B дает область определения f(g(x))
Пример: Найдите область определения f(g(x)) при f(x) = 1/(x+2) и g(x) = 1/(x+3).
Решение:
В f(g(x)) внутренней функцией является g(x), а ее областью определения является A = {x | х ≠ -3}.
Теперь вычислим f(g(x)).
\(\ начало {выровнено}
f(g(x)) &=f\left(\frac{1}{x+3}\right) \\
&=\frac{1}{\frac{1}{x+3}+2} \\
&=\frac{1}{\frac{1+2 x+6}{x+3}} \\
&=\фракция{х+3}{2х+7}
\конец{выровнено}\)
Его домен B = {x : x ≠ -7/2}
Таким образом, область определения f(g(x)) равна A ∩ B = {x : x ≠ -3 и x ≠ -7/2}.
В интервальной записи это (-∞, -7/2) U (-7/2, -3) U (-3, ∞).
Набор составных функций
Диапазон составной функции вычисляется так же, как диапазон любой другой функции. Это не зависит от внутренних или внешних функций. Вычислим диапазон f(g(x)), показанный в последнем примере. Мы получили f(g(x)) = \(\frac{x+3}{2 x+7}\). Предположим, что y = \(\frac{x+3}{2 x+7}\). Это рациональная функция. Следовательно, мы решаем это для x и устанавливаем знаменатель не равным нулю, чтобы найти диапазон.
(2х + 7) у = х + 3
2ху + 7у = х + 3
2xy — x = 3 — 7y
х (2г — 1) = 3 — 7г
х = (3 — 7 лет) / (2 года — 1)
Для диапазона 2y — 1 ≠ 0, что дает y ≠ 1/2.
Следовательно, диапазон = {y : y ≠ 1/2}.
☛ Похожие темы:
Часто задаваемые вопросы о составе функций
Что такое определение составной функции?
Составная функция из двух функций объединяет данные две функции в заданном порядке.т. е. для любых заданных двух функций f(x) и g(x) может быть 4 составные функции:
- f(g(x)), который заменяет g(x) на f(x)
- g(f(x)) который заменяет f(x) на g(x)
- f(f(x)), которая заменяет f(x) на себя
- g(g(x)), который заменяет g(x) на себя
Как найти состав функций?
Чтобы вычислить составную функцию f(g(x)) при некотором x = a, сначала вычислите g(a), подставив x = a в функцию g(x).Затем подставьте g(a) в функцию f(x), подставив x = g(a). Точно так же мы можем вычислить и g(f(a)).
Важен ли порядок в составных функциях?
Да, в составных функциях порядок действительно важен. т. е. f (g (x)) ≠ g (f (x)) (т. е. они могут не быть равными все время). Но иногда они могут быть равны.
т. е. f (g (x)) ≠ g (f (x)) (т. е. они могут не быть равными все время). Но иногда они могут быть равны.
Как найти область определения составной функции?
Чтобы найти область определения составной функции, найдите область определения внутренней функции и область определения результирующей функции.Возьмите пересечение обоих доменов.
Как найти диапазон составной функции?
Диапазон составной функции не зависит от внутренних или внешних функций. Его диапазон вычисляется так же, как мы вычисляем диапазон любой другой функции.
Как найти состав функций из графиков?
Если даны графики двух функций f(x) и g(x), то найти g(f(a)):
- Найти f(a) (используя точку (a, f(a)) на f(x))
- Найти g(f(a)) (используя точку (f(a), g(f(a)) ) на графике g(x))
Как разбить состав функций?
Мы можем разбить составную функцию на две функции с помощью некоторого наблюдения.Не забудьте перепроверить свой ответ после взлома. Если f(g(x)) = sin(x + 1), то можно сказать, что g(x) = x + 1 и f(x) = sin x. Давайте перепроверим ответ.
Если f(g(x)) = sin(x + 1), то можно сказать, что g(x) = x + 1 и f(x) = sin x. Давайте перепроверим ответ.
f(g(x)) = f (x + 1) = sin (x + 1) и, следовательно, наш ответ правильный.
Кусочные функции
Функция может быть разделена на части
Мы можем создавать функции, которые ведут себя по-разному в зависимости от входного значения (x).
Функция, состоящая из 3 частей
Пример:
- , когда x меньше 2, это дает x 2 ,
- , когда x ровно 2, это дает 6
- , когда x больше 2 и меньше или равно 6, это дает строку 10-x
Выглядит так:
(сплошная точка означает «включая»,
открытая точка означает «не включая»)
И вот как мы это пишем:
Домен (все значения, которые могут быть переданы в функцию) — это все действительные числа до 6 включительно, что можно записать так:
Dom(f) = (-∞, 6] (с использованием интервальной нотации)
Дом(f) = {х | x ≤ 6} (с использованием нотации Set Builder)
Вот несколько значений для примера:
| Х | Д |
|---|---|
| −4 | 16 |
| −2 | 4 |
| 0 | 0 |
| 1 | 1 |
| 2 | 6 |
| 3 | 7 |
Пример: Вот еще одна кусочная функция:
| который выглядит так: |
Что такое h(−1)?
x ≤ 1, поэтому мы используем h(x) = 2, поэтому h(−1) = 2
Что такое h(1)?
x ≤ 1, поэтому мы используем h(x) = 2, поэтому h(1) = 2
Что такое h(4)?
x > 1, поэтому мы используем h(x) = x, поэтому h(4) = 4
Кусочные функции позволяют нам создавать функции, которые делают все, что мы хотим!
Пример: Плата за услуги врача зависит от продолжительности лечения.

- До 6 минут стоит 50 долларов США
- Более 6 и до 15 минут стоит 80 долларов США
- Более 15 минут стоит 80 долларов плюс 5 долларов за минуту сверх 15 минут
Что мы можем написать так:
Вы заходите на 12 минут, какая плата? $80
Вы заходите на 20 минут, какая плата? 80 долларов + 5 долларов (20-15) = 105 долларов
Функция абсолютного значения
Функция абсолютного значения — известная кусочная функция.
Состоит из двух частей:
- ниже нуля: -x
- от 0 и далее: x
f(x) = |x|
Функция этажа
Функция Floor — это особая кусочная функция. Он имеет бесконечное количество частей:
Функция этажа
Операции над функциями
Функции
с перекрытием
домены
можно складывать, вычитать, умножать и делить. Если
ф
(
Икс
)
и
г
(
Икс
)
две функции, то для всех
Икс
в области определения обеих функций сумма, разность, произведение и частное определяются следующим образом.
Если
ф
(
Икс
)
и
г
(
Икс
)
две функции, то для всех
Икс
в области определения обеих функций сумма, разность, произведение и частное определяются следующим образом.
( ф + г ) ( Икс ) знак равно ф ( Икс ) + г ( Икс ) ( ф − г ) ( Икс ) знак равно ф ( Икс ) − г ( Икс ) ( ф г ) ( Икс ) знак равно ф ( Икс ) × г ( Икс ) ( ф г ) ( Икс ) знак равно ф ( Икс ) г ( Икс ) , г ( Икс ) ≠ 0
Пример :
Позволять ф ( Икс ) знак равно 2 Икс + 1 и г ( Икс ) знак равно Икс 2 − 4
Находить
(
ф
+
г
)
(
Икс
)
,
(
ф
−
г
)
(
Икс
)
,
(
ф
г
)
(
Икс
)
и
(
ф
г
)
(
Икс
)
.
( ф + г ) ( Икс ) знак равно ф ( Икс ) + г ( Икс ) знак равно ( 2 Икс + 1 ) + ( Икс 2 − 4 ) знак равно Икс 2 + 2 Икс − 3
( ф − г ) ( Икс ) знак равно ф ( Икс ) − г ( Икс ) знак равно ( 2 Икс + 1 ) − ( Икс 2 − 4 ) знак равно − Икс 2 + 2 Икс + 5
( ф г ) ( Икс ) знак равно ф ( Икс ) × г ( Икс ) знак равно ( 2 Икс + 1 ) ( Икс 2 − 4 ) знак равно 2 Икс 3 + Икс 2 − 8 Икс − 4
( ф г ) ( Икс ) знак равно ф ( Икс ) г ( Икс ) знак равно 2 Икс + 1 Икс 2 − 4 , Икс ≠ ± 2
Другой способ объединения двух функций для создания новой функции называется
состав функций
. В композиции функций мы заменяем целую функцию на другую функцию.
В композиции функций мы заменяем целую функцию на другую функцию.
Обозначение функции ф с участием г является ( ф ∘ г ) ( Икс ) знак равно ф ( г ( Икс ) ) и читается ф из г из Икс .Это означает, что везде, где есть Икс в функции ф , она заменяется функцией г ( Икс ) . Домен ф ∘ г это совокупность всех Икс в области г такой, что г ( Икс ) находится в сфере ф .
Пример 1:
Позволять
ф
(
Икс
)
знак равно
Икс
2
и
г
(
Икс
)
знак равно
Икс
−
3
. Находить
ф
(
г
(
Икс
)
)
.
Находить
ф
(
г
(
Икс
)
)
.
ф ( г ( Икс ) ) знак равно ф ( Икс − 3 ) знак равно ( Икс − 3 ) 2 знак равно Икс 2 − 6 Икс + 9
Пример 2:
Позволять
ф
(
Икс
)
знак равно
2
Икс
−
1
и
г
(
Икс
)
знак равно
Икс
+
2
. Находить
ф
(
г
(
Икс
)
)
.
Находить
ф
(
г
(
Икс
)
)
.
ф ( г ( Икс ) ) знак равно ф ( Икс + 2 ) знак равно 2 ( Икс + 2 ) − 1 знак равно 2 Икс + 3
Порядок имеет значение при поиске композиции функций.
Пример 3:
Позволять ф ( Икс ) знак равно 3 Икс + 1 и г ( Икс ) знак равно 2 Икс − 3 .
Находить ф ( г ( Икс ) ) и г ( ф ( Икс ) ) .
ф ( г ( Икс ) ) знак равно ф ( 2 Икс − 3 ) знак равно 3 ( 2 Икс − 3 ) + 1 знак равно 6 Икс − 8 г ( ф ( Икс ) ) знак равно ф ( 3 Икс + 1 ) знак равно 2 ( 3 Икс + 1 ) − 3 знак равно 6 Икс − 1
С
6
Икс
−
8
≠
2
Икс
−
1
,
ф
(
г
(
Икс
)
)
≠
г
(
ф
(
Икс
)
)
.

 В нашем примере соедините точки с координатами (4,2) и (26,3).
В нашем примере соедините точки с координатами (4,2) и (26,3).
 Здесь f — внутренняя функция, а g — внешняя функция.
Здесь f — внутренняя функция, а g — внешняя функция.