Графики функций с модулями. 10 класс
1. Графики функций с модулями.
Проект:Угарина Сергея, ученика
10п класса.
2. Цель работы:
Научитсястроить графики функций
с модулями.
Хорошая подготовка к ЕГЭ.
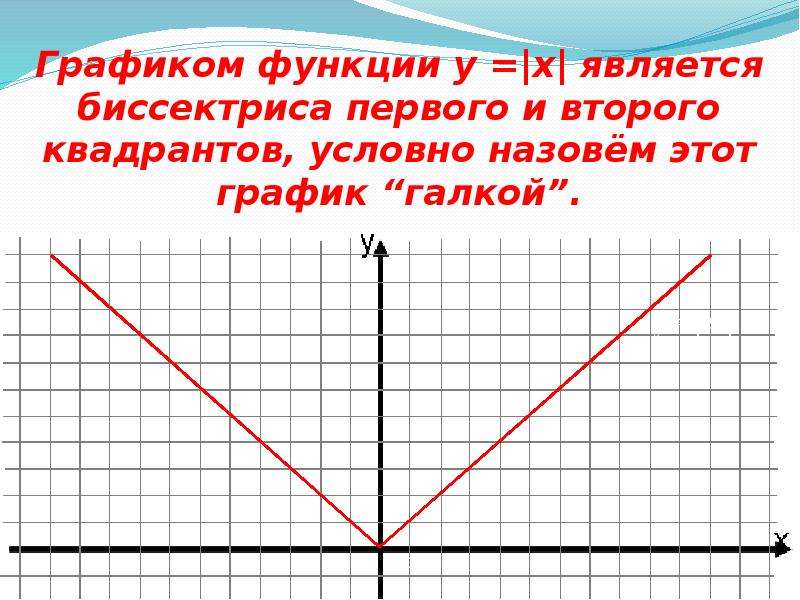
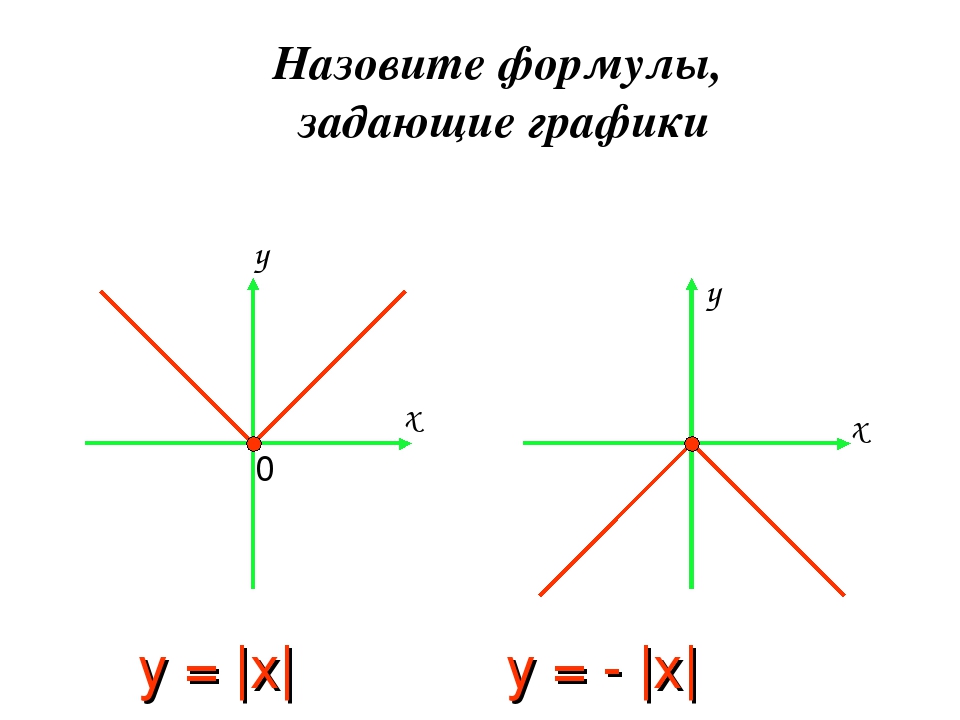
3. 1 ФУНКЦИЯ С МОДУЛЕМ
Y=lXlСтроим график функции у = x
Из-за модуля положительная
часть графика отразится
вдоль оси У.
x 1 2
y 1 2
4. 2 функция с модулем.
У=l10х+4lСтроим график функции
у=10х+4
Подставляем модуль и
функция станет
положительной во всей
области определения.
Положительная часть
первой функции
отразится от х=-0,4
х
у
0
4
-1
-6
5. 3 функция с модулем
У=lx²-4lСтроим график функции у= х²-4
Это квадратичная функция,
графиком является парабола.
Чтобы построить параболу надо
найти как можно больше точек.
Сейчас строим график функции
у=lх²-4l, тогда отрицательная
сторона графика функции
у=х²-4 отразится по оси Х.

Областью определения будут все
числа, функция будет равняться
нулю в точках х = ±2.
х 1 2 -1 -2
у -4 0 -3 0
6. 4 функция с модулем
У=2х²-5lхl-7Строим гр.функции
у=2х²-5х-7, приравняем
нулю и получим два
корня х=3,5 и х’=-1
Найдём вершину
функции. В точке х=1,5
у=-10
Строим график функции
у=2х²-5lхl-7.
7. 5 функция с модулем
У=l2х²-5х-7lСтроим график функции
у=2х²-5х-7
Всё также ,как и в
предыдущем слайде.
Потом строим график
функции у=l2х²-5х-7l
Функция станет только
положительным.
Отрицательная сторона
первой функции
отразится по оси Х
8. 6 функция с модулем
У=l2х²-5lхl-7l – сложнаяфункция. Строим сперва
график функции у=2х²5lхl-7 как в 4-ом слайде.
Потом всю эту функцию
берём под модуль.
Функция у=l2х²-5lхl-7l
будет положительным на
всей области
определения. Функция
будет равняться нулю в
точках х=±3,5
9.
 7 функция с модулем У=lх²+хl
7 функция с модулем У=lх²+хlСтроим гр.ф у=х²+х
Эта квадратичная функция,
графиком является
парабола. Чтобы построить
параболу надо как можно
больше точек.
Строим гр.ф у=lх²+хl
Отрицательная сторона
отразится в положительную
сторону по оси Х.
х 1 -1 0 -2
у 2 0 0 2
10. 8 функция с модулем
У=lх³+х²-lхl+1l – сложнаяфункция.
Строи график функции
у=х³+х²-х+1. Это кубическая
функция, графиком является
гипербола. Чтобы построить
гиперболу надо найти как
можно больше точек. Потом
строим гр.ф. у=х³+х²-lхl+1 Изза модуль х, первая функция от
х=0 понижется резко. Потом
строим гр.ф. у=lх³+х²-lхl+1l
х
у
0
1
1
2
-1 2 -2
2 11 -1
Графики
функций с модулями
очень много встречаются на Е.Г.Э.
В средней школе графики функций
с модулями обучают в 10, 11
классах.
Вывод:Графики
функций надо
обязательно уметь строить, чтобы
функциями на экзамене.

Открытый урок в 8 классе «Построение графиков функций, содержащих модули»
Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику в 19 веке английским учёным Р. Котесом учеником Ньютона. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля — символ, которым это понятие обозначается при написании.
Геометрический смысл модуля заключается в том, что это расстояние от нуля до данного числа.
Необходимо указать номера примеров, где есть ошибка.
Постройте схематично график функцииРазработка проекта, плана выхода из создавшегося затруднения, поиск оптимального решения
Основные виды:
y = x2 – 8|x| + 12.
y = |x2 – 8x + 12|.
y = |x2 – 8|x| + 12|.
Изучение новой темы по плану:
1) Построение графика функции
2) Построение графика функции
3) Построение графика функции
Реализация выбранного плана.
 «Открытие новых знаний»
«Открытие новых знаний»
Целесообразно рассматривать построение графиков в следующей последовательности:
Построение графиков следует осуществлять двумя способами:
на основании определения модуля;
на основании правил (алгоритмов) геометрического преобразования графиков функций.
Построение графика функции
Следовательно, график функции состоит из двух графиков: — в правой полуплоскости, — в левой полуплоскости.
Исходя из этого, можно сформулировать правило (алгоритм).
График функции получается из графика функции следующим образом: при x0 график сохраняется, а при x<0 часть графика в правой полуплоскости отображается симметрично относительно оси Oy.
Построение графика функции
Отсюда вытекает алгоритм построения графиков функции .
а) Строим график функции f(x).
б) Часть графика, лежащая над осью Ox, сохраняется, часть его, лежащая под осью Ox, отображается симметрично относительно оси Ox.
Построение графика функции
Правило (алгоритм) построения.
Чтобы построить график функции , надо сначала построить график функции y=f(x) при x>0, затем при x<0 построить изображение, симметричное ему относительно оси Oy, а затем на интервалах, где , построить изображение, симметричное графику относительно оси Ox.
Первичное закрепление новых знаний
(построение графиков функций на примерах)
Пример 1.
Построить график функции
Построение.
1-й способ.
Построим, опираясь на определение модуля действительного числа.
2-й способ.
Построим, используя способы преобразования графика функции.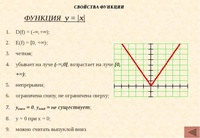
а) Строим график функции для x>0.
б) Достраиваем его левую часть для x<0, симметрично построенной относительно оси Oy.
Пример 2.
Построить график функции
Построение.
1-й способ.
Строим график кусочной функции по определению модуля.
2-й способ.
Строим на основе преобразования графика уже известной нам функции.
а) Строим график функции y=x-2.
б) График нижней полуплоскости отображаем вверх симметрично относительно оси Ox.
Пример 3.
Построить график функции .
Построение.
1-й способ.
Построим на основе определения модуля действительного числа.
2-й способ.
Построим на основе простейших способов преобразования графика функции.
1) Строим график функции .
2) График функции , получаем из графика функции отражением симметрично (при ) относительно оси Oy.
3) График функции , получаем из графика функции отображением симметрично оси Ox нижней части графика.
Включение в систему знаний и умений
(построение графиков, задание – установи соответствие)
1. Начнем с построения графика
В “основе” его лежит график функции
и все мы знаем, как он выглядит:
Теперь построим график
Чтобы получить этот график, достаточно всего лишь сдвинуть полученный ранее график на три единицы вправо. Заметим, что, если бы в знаменателе дроби стояло бы выражение х+3, то мы сдвинули бы график влево:
Теперь необходимо умножить на два все ординаты, чтобы получить график функции
Наконец, сдвигаем график вверх на две единицы:
Последнее, что нам осталось сделать, это построить график данной функции, если она заключена под знак модуля. Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):
Для этого отражаем симметрично вверх всю часть графика, ординаты которой отрицательны (ту часть, что лежит ниже оси х):
2. Теперь построим график функции
Выражение, стоящее под знаком модуля, меняет знак в точке х=2/3.
При х<2/3 функция запишется так:
При х>2/3 функция запишется так:
То есть точка х=2/3 делит нашу координатную плоскость на две области, в одной из которых (правее) мы строим функцию
а в другой (левее) – график функции
Строим:
3. Теперь можем построить график, похожий на один из предыдущих, и все же отличающийся:
В основе опять знакомый нам график функции
но, если в знаменателе x стоит под знаком модуля,
то график имеет вид:
Теперь произведем сдвиг на три единицы,
при этом сдвинутся обе части: правая – вправо, левая – влево (своеобразное зеркало : отходишь дальше – видно больше)
График этой функции, умноженной на два,
выглядит так:
Теперь можно поднять график по оси у:
и тогда он будет таким:
Наконец, строим окончательный вид графика, отражая все, что ниже оси абсцисс, вверх:
Очень интересно выглядит график функции
В точках 2 и (-2) знак подмодульного выражения меняет знак, поэтому функция состоит из трех кусков (точки 2 и (-2) выколоты).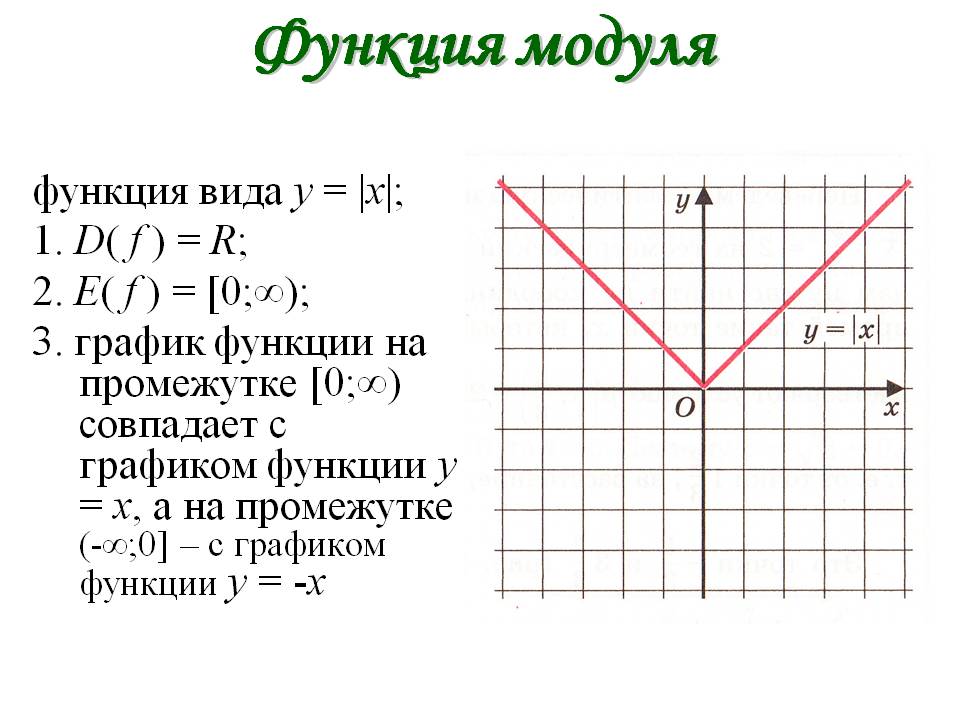 На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:
На участках (-∞; -2) и (2; ∞) справедливо первое уравнение, а на участке (-2;2) – второе:
Установите соответствие между функцией и графиком функций, содержащих модуль.
y = |x2 – 8|x| + 12|
y = x2 – 8|x| + 12.
y = |x2 – 8x + 12|.
Ответы:
Пример 1.
y = x2 – 8|x| + 12.
Решение.
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
1).
Пример 2.
y = |x2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
y = |x2 – 8|x| + 12|
Для построения графика функции y = |x2 – 8|x| + 12| проводят комбинацию преобразований:
y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|.
Ответ: рисунок 3.
Рефлексия, самоанализ, выставление оценок, домашнее задание, рефлексия чувств и эмоций.

Выводы:
Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.

Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Ответы:
Математический диктант
Устная работа с таблицейНеобходимо указать номера примеров, где есть ошибка (истинно/ложно)
Установите соответствие между функцией и графиком функций, содержащих модуль.
12-13правильных ответов – 5
10-11 правильных ответов -4
7-9 правильных ответов – 3
Меньше 7 ответов – очень плохо! Учи!!!
Оценка _________
Индивидуальная карточка учащегося _____ класса дата ________
Фамилия, имя ___________________________________
Математический диктант
Ответы:
Устная работа с таблицей
Необходимо указать номера примеров, где есть ошибка (истинно/ложно)
Ответы:
Установите соответствие между функцией и графиком функций, содержащих модуль.
y = |x2 – 8|x| + 12|
y = x2 – 8|x| + 12.
y = |x2 – 8x + 12|.
12-13правильных ответов – 5
10-11 правильных ответов -4
7-9 правильных ответов – 3
Меньше 7 ответов – очень плохо! Учи!!!
Оценка _________
как построить – сложное простыми словами — ЕГЭ/ОГЭ
График модуля, как построить – очень просто. Особенно, если знать несколько закономерностей. О них расскажу в статье. С помощью них вы поймете как построить график модуля легко и играючи. Без поиска пробных точек.
На самом деле построение графиков функций с модулями – это удовольствие. Раньше они вызывали у вас в лучшем случае пренебрежение? Забудьте – после прочтения статьи вы будете первым по скорости построения графика.
Построение различных видов графиков, содержащих модуль:
- Воландеморт среди модулей
- Как калькулятор может помочь при построении графика?
- Как построить график модуля и одновременно решить уравнение
- Война среди модулей
Господа, перед тем, как мы приступим к светской беседе с модулем.
Подмечайте фишки каждой функции, но главное – держите в голове его «неотрицательность».
Главный миф о сложности графиков модуля – полный модуль по правой частиЗабудьте сказки про сложность модуля – ведь теперь вы скоро узнаете о методе «Зеркало».
Модуль всей правой части y = |f(x)| отражает график относительно оси X. Все, что было под осью Ox зеркально отражается наверх.
Почему так? Обратите внимание, что значение функции (то есть y) является результатом вычисления модуля. Оно не может быть отрицательным. Согласны? Значит, его заменяют на противоположное ему по знаку. А в построении функций эти зеркальные превращения и есть смена знака у функции.
Уже чувствуете себя как Алиса в Зазеркалье? Ничего страшного – объясню на примере:
Пример: y = |X – 3|
Видите, график функции y = |X – 3| состоит из двух ветвей. Первая y = X – 3, а вторая y = – (X – 3) = 3 – X. Все по определению модуля – не придраться. Зеркально отраженная функция и есть противоположная по знаку той, которую отражали.
Первая y = X – 3, а вторая y = – (X – 3) = 3 – X. Все по определению модуля – не придраться. Зеркально отраженная функция и есть противоположная по знаку той, которую отражали.
Можете так себя проверять – сначала просто отзеркальте конец, который улетает в отрицательную бесконечность (под ось Ох). А потом посмотрите, действительно ли он совпадает с минусовой версией подмодульного выражения. Уверяю, если вы были аккуратны – совпадет.
*Читайте понятное определение модуля в статье «Простая инструкция: как решать любые уравнения с модулем». После ее прочтения вы научитесь расправляться со всеми видами уравнений с модулем с помощью всего 1 инструкции!
А теперь перейдем к функции, которая заставляет поежиться от недовольства слишком многих. Если б они знали, что ее настолько просто начертитить…то стали бы решать уравнения с ней только графически.
Воландеморт среди модульных функций — Полный модуль по правой частиМодуль всей левой части |y| = f(x) отражает график относительно оси X.
Все, что было над осью Oх зеркально отражается вниз.
Смотрим, что является результатом вычисления подмодульного выражения? Ага, все, что стоит справа. Значит, в данном случае Рубиконом является ось Oy – отзеркаливаем относительно нее.
Пример: |y| = X – 3
Мы разобрали две базы графиков с модулями. Дальше уже идут вариации с дополнительными математическими па: поднимите график, опустите, сузьте – расширьте. Давайте и их разберем!
Как калькулятор может помочь при построении графика? — График содержащий модуль
Это пример сложной функции, такие функции строятся по этапам. Сложной – не потому что она поддается только сильнейшим умам. Просто
С такими функциями работает способ «калькулятор».
Представьте, что вам нужно вычислить выражение: (217 – 327)/72. С чего вы начнете? Вероятно, с возведения в степень, продолжите подсчетом числителя и только потом перейдете к делению. Будете идти от малого к большому.
Тот же метод работает и со сложной функцией. Начните с ядра и продолжайте справляться со всеми остальными прибамбасами вокруг него.
Пример: y = |x–3| + 5 ( ядром является график прямой y=x-3)
1. Y = X – 3 {строим график прямой}
2. Y = |X –3| {отражаем график относительно оси X}
3. Y = |X – 3| + 5 {поднимаем график 2. на +5}.
Вспомните суперспособности графиков – положительное число поднимает график, а отрицательное опускает (вверх/вниз относительно оси Ox). Причем, нет ничего страшного в том, что модульная галка окажется под прямой Ox (в отрицательной области) – это необходимые последующие действия с графиком.
Иногда в качестве «потустороннего члена» выступает переменная. Тут уж хитрить с отражениями и подниманиями – не получится. Придется раскрывать алгебраически модуль для каждого интервала – и уже по вычисленному выражению чертить ветви графика.
О том, как легко раскрыть модуль – написано в статье – Решение уравнений с модулем.
А мы двигаемся навстречу забора из модуля. По правде, такой вид функций очень полезно уметь чертить. Этот скилл способен сэкономить вам время. Ведь частенько по графику намного точнее и проще найти корни уравнения такого вида.
Пример: y = ||X–2|–3|
{Порядок действий как при работе со сложной функцией – пользуемся методом «Калькулятор»}
1. Y = X – 2
2. Y = |X – 2|
3. Y = |X – 2|–3
4. Y = ||X – 2|–3|
Согласитесь, что раскрывать уравнения такого типа довольно муторно. Да и велик риск просчитаться. Начертить график и по нему оценить корни (иногда точно их посчитать) супер просто.
Да и велик риск просчитаться. Начертить график и по нему оценить корни (иногда точно их посчитать) супер просто.
Поэтому графический метод решения уравнений нужно эксплуатировать на все 100% именно в этом случае.
Теперь нас ждет один из самых непредсказуемых графиков из всего рода модулей. Никогда не знаешь, что именно он приподнесет. Но и с этой неприятной неожиданностью научимся работать)
Война среди модулей — Несколько модулей
Что делать если в бой вступает сразу несколько модулей? – К сожалению, бороться с ними приходится с помощью арифметики и алгебры. Приходится аккуратно раскрывать на разных областях. Так же, как при решении модульных уравнений – алгебраически.
*Подробнее о том, как раскрывать модуль читайте в статье «Простая инструкция: как решать любые уравнения с модулем». В ней на пальцах объяснено, как раскрыть забор из модулей и НЕ запутаться.
Y = |X–2|+|X+2|
I ) X ∈ (–∞;–2] {1 модуль с «–» , 2 модуль с «–»}
Y1 = – (X – 2) – (X + 2)
Y1 = – X + 2 – X – 2
Y1 = –2X
II ) X ∈ (–2;2] {1 модуль с «–» , 2 модуль с «+»}
Y2 = – (X – 2) + (X + 2)
Y2 = – X + 2 + X + 2
Y2 = 4
III) X ∈ (2; +∞) {1 модуль с «+» , 2 модуль с «+»}
Y
Y3 = 2X
Вот такая галочка получилась из трех кусочков различных функций.
Вы уже заметили, что все модульные функции являются кусочно заданными? Их особенностью является то, что они существуют только на определенных интервалах.
Главное в модулях – понять закономерности. Дальше все пойдет как по маслу. Надеюсь, мне удалось хоть немного прояснить график модуля, как его построить и не надорваться в счете.
Остались вопросы? – обращайтесь! Я с удовольствием проведу первую консультацию бесплатно. Запишитесь на первое бесплатное занятие: напишите мне на почту или в сообщениях ВКонтакте)
Запишитесь на первое бесплатное занятие: напишите мне на почту или в сообщениях ВКонтакте)
До встречи, Ваш Михаил
График функции 2 в степени модуль х. График функции
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Урок на тему: «График и свойства функции $y=x^3$.
 3$.
3$.2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Построение графиков содержащих знак модуля построение графика функции содержащей переменную или функцию под знаком модуля согласно определению модуля
Построение графиков, содержащих знак модуля
Построение графика функции, содержащей переменную
или функцию под знаком модуля согласно определению модуля:
x, если х>=0 f(x), если f(x)>=0
|x| = ; |f(x) | =
-x, если x<0 -f(x), если f(x)<0
Пример:
Построить
график функции у=|2x-3|-х.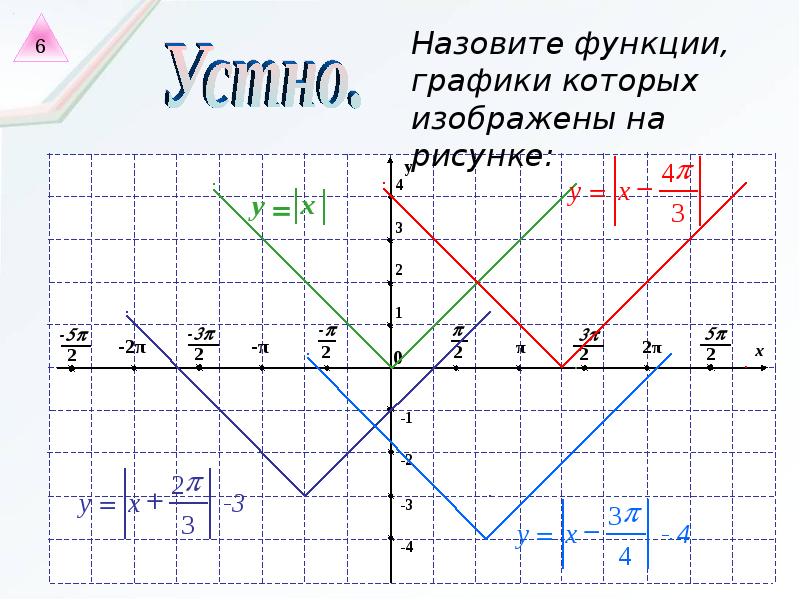
Рассмотрим два случая.
2х-3>=0 2х-3<0
y=2x-3-x или y=-2x+3-x
x>= x<
y=x-3 y= -3x+3
Таким образом, чтобы построить график функции у=|2x-3|-x, надо построить графики функций, заданными различными выражениями на различных промежутках.
х-3, х>=
у=
— 3х+3, х<
График изображен ниже:
y=|2x-3|-x
Построить график:
Y=|X|+X
Y=|X| · (X-2)
Y=|X+4| · X
Y=
Y=
Y=2–1)
Y=2+4X+3)
Y=
Y=
Y=X — 1 — |X-1|
Y=|3X-4|-X
Y=
13. Y=
Y=
Y=
Y=
Y=X2 — 2|X+1|-1
Y=X+
Y=|X2-4X+3|+2X
Y=
Y=|X2-4|+4X
Y=
Элементарные преобразования графика функции у=f(x)
Если формула зависимости имеют вид |y| = f(x):
Надо построить график у = f(x)
Часть графика, расположенную выше оси Ох (и на самой оси) оставить без изменения
Часть графика расположенную ниже оси Ох стереть
Для оставленной части построить симметричную относительно оси Ох
Пример:
Построить график |y| = 2х-1
Построить график:
Y|=5X-4
|Y|=9-X2
|Y|=
|Y|=(X+4)2-5
|Y|=
|Y|=X+2
|Y|=X2-6X+8
|Y|=X2-4X
X|Y|=2
|Y|=
|Y| · (X+1)=1
|Y|=1-
|Y|=|2X-X2|
Y2=-2X
|Y|=8+2X-X2
Y2=0,5X
Элементарные преобразования графика функции у=f(x)
Если формула зависимости у = f(|x|):
Надо построить график функции у = f(x), часть графика расположенную правее оси Оу(и на самой оси) оставить без изменения
Часть графика расположенную левее оси Оу стереть
Построить для оставленной части симметричную относительно оси Оу
Пример:
Построить график у=2|x|-1
Построить график:
Y=5|X|-5
Y=9-|X|2
Y=
Y=
Y=
Y=(|X|+4)2-5
Y=
Y=
Y=|X|-1
Y=
Y=X2-|X|-6
Y=-X2+6|X|-8
Постройте график.
 С его помощью укажите пути функции,
интервалы знакопостоянства, промежутки
монотонности, наибольшее и наименьшее
значения функции, область значений
функции:
С его помощью укажите пути функции,
интервалы знакопостоянства, промежутки
монотонности, наибольшее и наименьшее
значения функции, область значений
функции:
2-, если |X|<=4
у= , если |X|>4
Y=X2-|X|-2
Решите уравнение X2+3|X|-18=0 графически.
Y=|X|-X2
Y=
Элементарные преобразования графика функции у=f(x)
Если формула зависимости имеет вид у = |f(x)|,
График функции у = f(x) выше оси Ох (и на самой оси Ох) оставить без изменения
Для части графика расположенной ниже оси Ох строят симметричную относительно
оси Ох
Часть графика расположенная ниже оси Ох стирается.
Пример:
Построить график функции у=|2x-1|
Построить график:
Y=|5X-4|
Y=|9 -X2|
Y=
Y=|(X-4)2-5)|
Y=|X+2|
Y=|X-1|
Y=|X2+2X|
Y=
Y=||
Y=||X2-3|-1|
Y=|X2-1|
Y=|X+1|-2
Y=4+|X-3|
Y=3 ∙ |X-2|
Найдите наибольшее и наименьшее значение функции Y=:
а)на отрезке [-2;2]
б)на луче [0;+ )
в)на луче (- ;3]
г)на отрезке [-5;0]
16. Найдите
наименьшее и наибольшее значение функции
Y=:
Найдите
наименьшее и наибольшее значение функции
Y=:
а)на луче (- ;5]
б)на отрезке [4;7]
в)на луче [2;+ )
г)на полуинтервале [-1;6]
17.Решите уравнение графически:
а)|X2-9|=5 б)|X-2|=X2 в)|X+1|= -2X2
г)|X2-1|=|X2-X+1| д)|X-3|=X2+1 е)|X+5|=-X-1
ё) -2(X+2)2 ж) з)(X+3)2
и)-X
Построение графиков уравнений, содержащих несколько модулей
Пример: построить график функции
1). Найти те значения переменной, при которых выражение, стоящее под знаком модуля, равно нулю. ; ; .
2). Числовую прямую разбивают на промежутки точками, соответствующими найденным значениям переменной
0 1
3). На каждом
промежутке определяют знак выражения,
стоящего под знаком модуля (берут числа
из промежутка и ставят в под модульное
выражение). Определяют знак выражения
стоящего под знаком модуля
Определяют знак выражения
стоящего под знаком модуля
− 0 − 1 +
− + +
4). Берут промежуток, раскрывают модуль (пользуясь определением модуля) на данном промежутке и упрощают
Составляют формулу кусочной функции
y
Строят график кусочной функции
1
x
0 1
1). Найдите промежутки убывания функции и ее наибольшее значение на отрезке . Ответ: , .
2). Найдите множество значений функции и ее наименьшее значение на отрезке . Ответ: , .
3). Найдите
множество значений функции и значения, которые функция принимает
ровно три раза.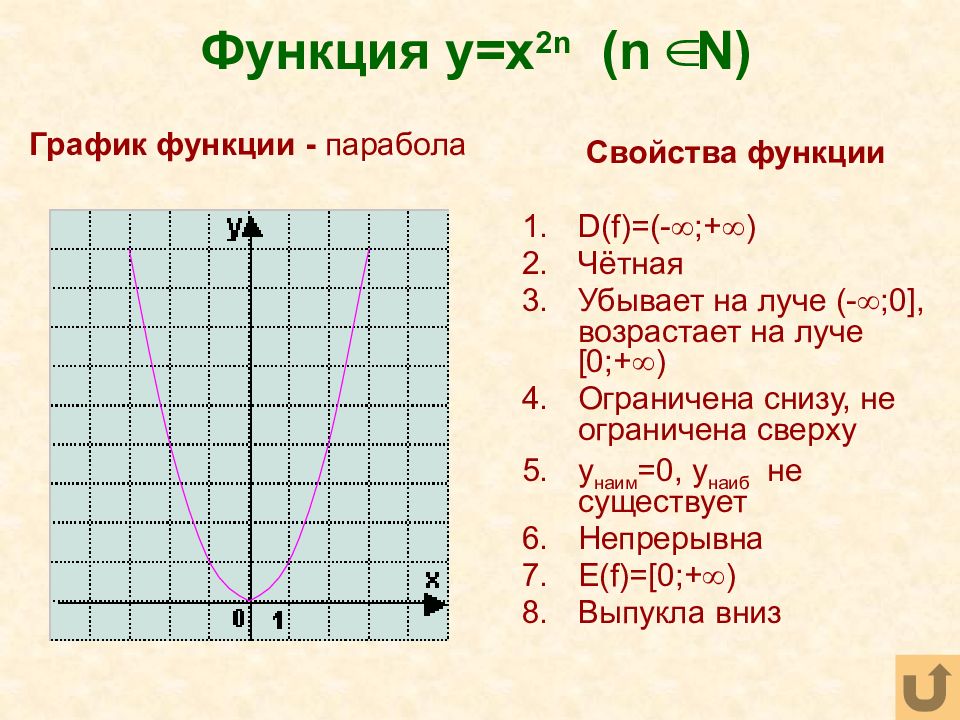 Ответ: ; ; .
Ответ: ; ; .
4). Найдите все значения , при которых значения функции положительны и значения, принимаемые функцией ровно 2 раза. Ответ: ; , .
5). Постройте график функции и для каждого укажите количество общих точек этого графика и прямой .
а). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При , бесконечное множество точек.
б). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При ,, три точки;
При , четыре точки.
6). Найдите
наибольшее и наименьшее значения функции на отрезке . Ответ: ; .
7). Найдите наименьшее значение функции
а). .Ответ: при .
б). .Ответ: при .
9). Докажите, что если , то наименьшее значение функции равно .
10). Исследуйте функцию на промежутки монотонности
а). . Ответ: На промежутках ; функция убывает. На промежутках возрастает.
б). . Ответ: На промежутках ; функция убывает. На промежутках и возрастает. На промежутках и функция постоянна.
11). Постройте графики функций
1). 2).
3). 4).
Решение неравенств, содержащих знак модуля
Неравенства вида
> , где > 0
Если выражение,
стоящее под знаком модуля , обозначить
через t (f(x)
= t), то данное неравенство
примет вид > . Используя геометрический смысл
модуля (модуль на числовой прямой
представляет собой расстояние от точки,
которая изображает данное число, до
точки ноль). Изображаем на числовой
прямой все точки, расстояние от которых
до ноля больше .
Используя геометрический смысл
модуля (модуль на числовой прямой
представляет собой расстояние от точки,
которая изображает данное число, до
точки ноль). Изображаем на числовой
прямой все точки, расстояние от которых
до ноля больше .
———∙——————∙—————∙————►t
— 0
t < — или t >
Решаем совокупность неравенств
Пример:
Решите неравенство > 11
Решение: > 11
Пусть , >11
———∙——————∙—————∙————►t
-11 0 11
; ;
Ответ: ; ;
Неравенство
вида > ,
где < 0 верно при всех из области допустимых значений
неравенства.
Решите неравенства
1). > 11. Ответ:
2). . Ответ:
3). . Ответ: : .
4). . Ответ: . .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). >2. Ответ: .
Неравенства вида
>
Учитывая свойство модуля =
и свойство
неравенства: если обе части неравенства
неотрицательны, то при возведении в
квадрат получаем неравенство равносильное
данному .
Неравенство > можно заменить равносильным неравенством > это — >0 (—) ∙ (+) >0
Далее решать методом интервалов или заменить совокупностью систем
Аналогично решаются неравенства вида < .
Решите неравенства
1). . Ответ: .
2). Найти целочисленные решения неравенства .
Ответ: -8; -7; -6; … -1;0.
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
12). . Ответ: .
13). . Ответ: .
14). . Ответ: .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
20). . Ответ: .
21). . Ответ: .
22). . Ответ: .
23). . Ответ: .
Решение неравенств вида
;
Неравенство
Доказательство:
.
Неравенство
Доказательство:
.
.
Решите неравенства
1). . Ответ: .
2). . Ответ: .
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). . Ответ: или .
7). . Ответ: .
8). . Ответ: ; .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
12). . Ответ: или .
13). . Ответ: ; .
14). . Ответ: или .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
20). . Ответ: ; .
Решение неравенств, содержащих несколько модулей методом интервалов
Суть метода состоит в следующем:
Пример:
1). Находят те
значения переменной при которых
выражения, стоящие под знаком модуля
равно нулю.
Находят те
значения переменной при которых
выражения, стоящие под знаком модуля
равно нулю.
2). Числовую ось разбивают на промежутки точками, соответствующими значениям переменной
1
3). На каждом промежутке, определяют знак выражения, стоящего под знаком модуля (берут число из промежутка, ставят в подмодульное выражение, определяют знак выражения, стоящего под знаком модуля)
— 0 + 1 +
-1 — — +
4). Берут промежуток, раскрывают каждый модуль, пользуясь определением модуля на данном промежутке, и решают неравенство
5). Проверяют,
принадлежат ли найденные решения
неравенства рассматриваемому промежутку;
если принадлежат, то их включают в ответ
Проверяют,
принадлежат ли найденные решения
неравенства рассматриваемому промежутку;
если принадлежат, то их включают в ответ
0
2
Если нет – отбрасывают. Так поступают с каждым промежутком.
6). Объединяют все решения исходного неравенства, найденные на всех промежутках, и учитывая область допустимых значений первоначального неравенства, выписывают ответ.
Ответ: -2<<3
Решите неравенство
1). Ответ:
2). Ответ:
3). Ответ:
4). Ответ:
5).Укажите целочисленные решения неравенства Ответ: 3;4
6). Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
Ответ:
10). Ответ:
11). Ответ:
12). Ответ:
13). Ответ:
14). Ответ:
15). Ответ:
16). Ответ:
Решение неравенств, содержащих знак модуля, методом введения новой переменной.
1). Найти область значений переменной, входящей в неравенство.
2). Если в уравнении неоднократно встречается фиксированное выражение, зависящее от неизвестной величины, то имеет смысл обозначить это выражение, какой либо буквой. Когда вводится обозначение желательно сразу отбросить все или некоторые значения при которых уравнение = не имеет решений , т.е. полезно сразу указать область значений функции = .
3). Решить
неравенство относительно введенной
неизвестной.
4). Решить неравенство относительно исходной переменной.
5). Учитывая область допустимых значений исходного неравенства записать ответ.
Пример:
Учитывая свойство модулей имеем Пусть = , , тогда неравенство примет вид =1; =-3. f
Учитывая, что имеем
Учитывая область допустимых значений исходного неравенства Ответ:
Решите неравенства
1). Ответ:
2). Ответ:
3). Ответ:
4). Ответ:
5). Ответ:
6). Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
Ответ:
Изображение на координатной плоскости множества точек, координаты которых удовлетворяют данному неравенству
Чтобы на координатной плоскости изобразить множество точек, координаты которых удовлетворяют неравенству надо:
1). Построить множество точек, координаты которых удовлетворяют уравнению (если неравенство строгое, то линия изображается пунктирной, если не строгое, то сплошной).
2). График или графики уравнений разбивают координатную плоскость на части.
3). Взять координаты точки, принадлежащей каждой части по очереди и поставить в неравенство. Если координаты точки удовлетворяют неравенству, то эту часть координатной плоскости заштриховать.
Пример: Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству .
1). Построим график уравнения .
или
III II I
-1 0 1
Прямые и изображаем сплошными линиями, так как неравенство не строгое. Прямые разбивают координатную плоскость на три области. Неравенству удовлетворяют координаты точек, принадлежащих II части, поэтому заштриховываем II часть.
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству.
1). .
2). .
3). .
4). .
5). .
6). .
7). .
8). .
9). .
10). .
11). .
12). .
13). .
.
14). .
15). .
16). .
17). .
18). .
19).
20). .
21). .
22). .
23. .
24). .
Изобразите на координатной плоскости множество точек, удовлетворяющих условию
а) . б).
в) г)
д) е) .
Системы неравенств с параметрами, содержащие знак модуля
1). Найдите все значения параметра , при которых система неравенств имеет единственное решение.
а). Ответ: При .
б). Ответ: При .
2). При каких значениях параметра система неравенств имеет ровно одно решение?. Для всех таких найдите это решение.
а). Ответ: При , ;
При , .
б). Ответ: При , ;
При , .
3). При каких значениях параметра система не имеет решения.
а). Ответ: При .
б). Ответ: При .
4). Для каждого значения параметра решите систему неравенств.
а). Ответ: При , ;
При , ;
При , ;
При , .
б). Ответ: При и , ;
При , ;
При , ;
При , ;
При , .
Нестандартные уравнения и неравенства, содержащие знак модуля
К
нестандартным ,обычно относятся такие
уравнения и неравенства, где традиционные
алгоритмы решения не проходят.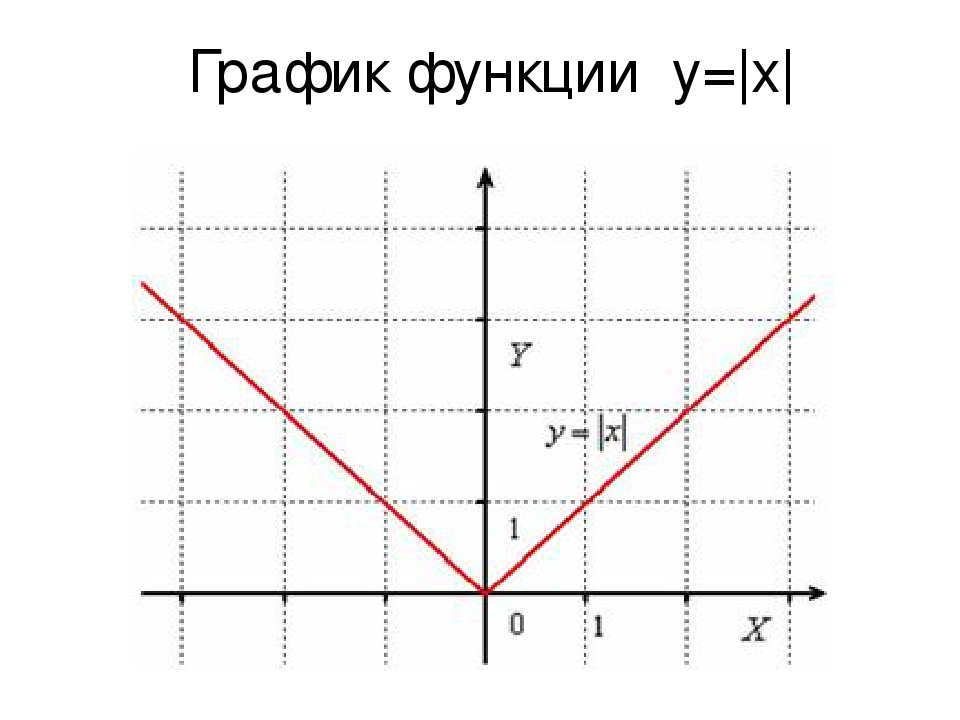 Во многих
случаях, решение таких уравнений и
неравенств осуществляется на функциональном
уровне, т.е с помощью графиков, или за
счет сопоставления некоторых свойств
функций, содержащихся в левой и правой
частях уравнения или неравенства.
Во многих
случаях, решение таких уравнений и
неравенств осуществляется на функциональном
уровне, т.е с помощью графиков, или за
счет сопоставления некоторых свойств
функций, содержащихся в левой и правой
частях уравнения или неравенства.
Если, например, наименьшее значение одной из функций совпадает с наибольшим значением функции , то уравнение = заменяют равносильной системой , где — наименьшее значение или наибольшее значение .
Решение системы является решением уравнения = .
1). Решите уравнение
Уравнение необходимо решить графически. Ответ:
2). Решите неравенство
. Применить метод оценки. Ответ:
3). Решите уравнение
. Решить уравнение графически. Ответ:
4). Решите уравнение
.
Применить свойство: сумма неотрицательных
функций равна нулю тогда и только тогда,
когда все функции одновременно равны
нулю.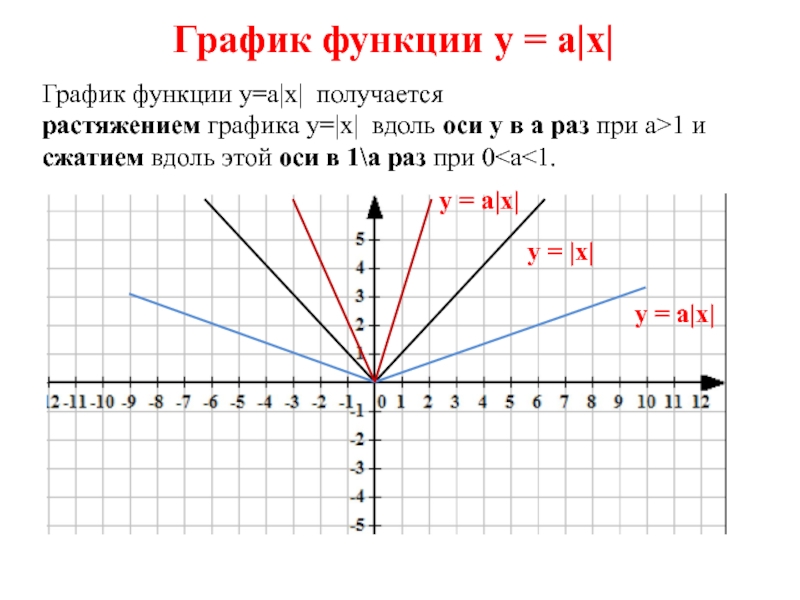 Ответ:
Ответ:
5). Решите уравнение
.Область допустимых значений (ОДЗ) уравнения состоит из конечного числа значений. Для решения достаточно проверить все эти значения. Ответ:
Применение свойства = для любого
при нахождении значения выражения
Вычислите:
1). Ответ: -6
2). , если t = -10; t = 127. Ответ: -8; 127
3). ∙ . Ответ: 0,125
4). −. Ответ: -6
5). − . Ответ: 2
6). − . Ответ: 8
7). + . Ответ: 2
8). + . Ответ: 6
9). + . Ответ: 2
10). + . Ответ: 10
11). − . Ответ: -3
Ответ: -3
12). − . Ответ: -6
13). − − 0,5. Ответ: 0
14). + . Ответ:1
15). + Ответ: 1
16). . Ответ: 8
17). Найти и , если = — . Ответ: 28; -2
18). Найти и , если = — . Ответ: 40; -2
19). Сравните значение выражения
с числом . Ответ:
20). Сравните значение выражения
с числом . Ответ:
21).
Докажите, что выражение ∙ является корнем уравнения =
1.
22). Докажите, что выражение является корнем уравнения = 1.
23). Удовлетворяет ли число − неравенству 7+58+13>0 .
Ответ: нет
24). Удовлетворяет ли число − неравенству 11+26-730 .
Ответ: да
Л и т е р а т у р а
1). Алгебра: 8; 9; 10 – 11 класс.
Авторы: А.Г.Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.
2). Задания по математике для подготовки к письменному экзамену в 9 классе.
Авторы: Л.И. Звавич, Д.И.Аверьянов, Б.П. Пигарёв, Т.Н. Грушанина.
3). Сборник
задач по алгебре 8 – 9 класс.
Сборник
задач по алгебре 8 – 9 класс.
Авторы: М.Л. Галицкий,А.М. Гольдман, Л.И. Звавич.
4). Сборник для проведения письменного экзамена за курс средней школы 11 класс.
Авторы: Г.В. Дорофеев, Г.К.Муравин, Е.А.Седова.
5). Алгебраический тренажер.
Авторы: А.Г. Мерзляк,В.Б.Полонский, М.С.Якир
6). Материалы ЦТ и ЭГЭ за 2002 – 2005 годы.
7). Математика. Самостоятельные и контрольные работы 8; 9; 10 – 11 классы.
Авторы: А.П. Ершова, В.В. Голобородько.
8). Различные сборники для поступающих в В У З Ы.
Урок алгебры в 8-м классе по теме: «Модуль и квадратичная функция»
“Великое множество функций
Любой может школьник назвать.
Но лишь о немногих сегодня
Решили мы вам рассказать”
Изучение квадратичной функции с модулем
позволяет углубить знания учащихся в
преобразовании графиков квадратичной функции.
Учащиеся с большим интересом выполняют любые
задания с модулем.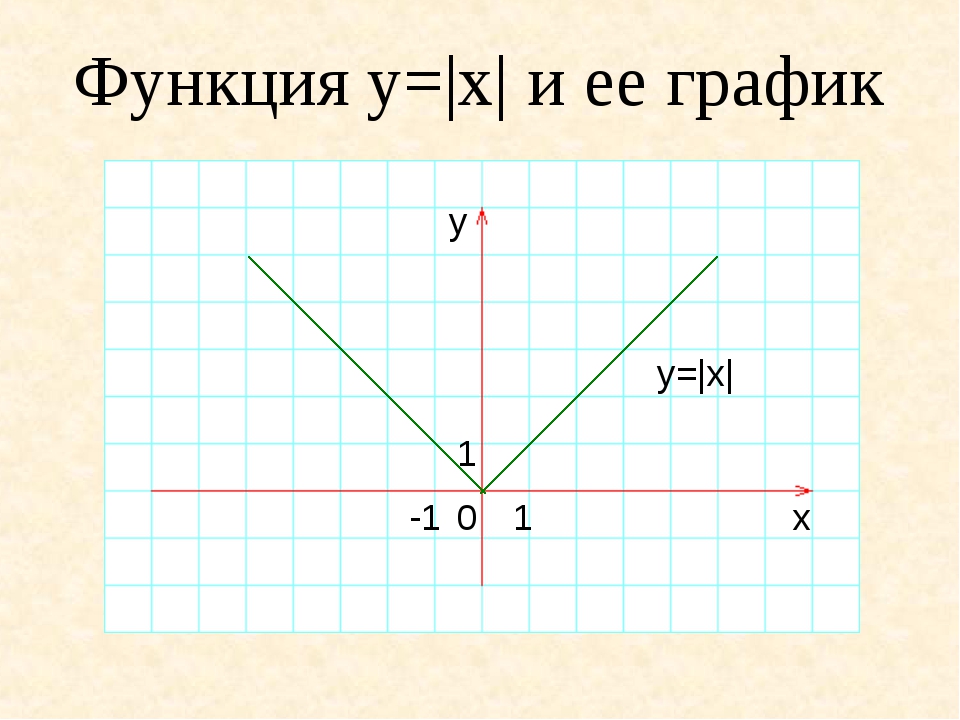 Рассмотренные приемы
построения графиков функции являются общими и
применяются не только к квадратичной, но и к
другим функциям.
Рассмотренные приемы
построения графиков функции являются общими и
применяются не только к квадратичной, но и к
другим функциям.
Ход урока
I. Вводное слово учителя
Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. Математика рассматривает абстрактные переменные величины, изучает законы их взаимосвязи, не углубляясь в природу задачи. Например, в соотношении Y = Х2 математик или геодезист увидит зависимость площади квадрата от его стороны, а физик, авиаконструктор или кораблестроитель может увидеть зависимость силы Y сопротивления воздуха или воды от скорости Х движения.
Математика же изучает эту зависимость в
отвлеченном виде, и она устанавливает, например,
что увеличение Х в 2 раза приведет к увеличению Y в
4 раза, и это заключение может применяться в любой
конкретной ситуации.
Модуль и квадратичная функция
Построение графиков функций:
- Y = АХ2 + ВX + C,
- Y = АХ2 + ВX + C ,
- Y = АХ2 + ВХ + С
II. Устная работа
1) Дать определение модуля числа Х
2) Дать определение квадратичной функции, рассказать все, что известно об этой функции (график, свойства).
3) Найти на рисунке график функции Y = –Х2 + 4Х – 3.
4) На каком рисунке изображен график функции Y = –(Х + 1)(2 – Х)?
5) Вспомнить, как построить график функции Y = Х
По определению модуля
График функции Y = Х симметричен относительно оси У.
III. Построение графиков функций:
Y = АХ2 + ВX + C,
Y = АХ2 + ВX + C,
Y = АХ2 + ВХ + С
Работа проводится в группах, т. к. графики в К–1
в) и К–3 в) одинаковы, их необходимо сравнить и
сделать вывод (всего 3 группы). Каждой группе
выдается карточка, в ней 3 задания. Учащиеся
должны построить графики квадратичной функции,
содержащей модуль, используя определение модуля
и сделать вывод: как построить график данной
функции, используя график квадратичной функции и
симметрию относительно осей координат.
к. графики в К–1
в) и К–3 в) одинаковы, их необходимо сравнить и
сделать вывод (всего 3 группы). Каждой группе
выдается карточка, в ней 3 задания. Учащиеся
должны построить графики квадратичной функции,
содержащей модуль, используя определение модуля
и сделать вывод: как построить график данной
функции, используя график квадратичной функции и
симметрию относительно осей координат.
Работа в группах.
Задание: построить график функции, используя:
а) определение модуля;
б) график функции Y = АХ2 + ВХ + С;
в) симметрию относительно осей координат.
а) Y = Х2 – 4 Х + 3
б) Y = Х2 – 4 Х + 3
в) Y = Х2 – 4 Х + 3
а) Y = Х2 + 2 Х – 3
б) Y = Х2 + 2 Х – 3
в) Y = Х2 + 2 Х – 3
а) Y = –Х2 + 4 Х – 3
б) Y = –Х2 + 4 Х – 3
в) Y = –Х2 + 4 Х – 3
IV.
 Учащиеся делают вывод о расположении
графиков указанных функций
Учащиеся делают вывод о расположении
графиков указанных функцийВопрос: а) Как построить график функции Y = f (X)?
(1 способ. Построить график функции Y = f (X), если Х 0 и Y = f (–Х), если Х<
0.
2 способ. Построить график функции Y = f (X) и
отобразить правую часть графика симметрично
относительно оси Y).
б) Как построить график функции Y = f (X) ?
(Построить график функции Y = f (X) и точки с отрицательными ординатами симметрично отобразить относительно оси Х).
в) Как построить график функции Y = f (X) ?
(Построить график функции Y = f (X), если Х 0 и эту часть графика симметрично отобразить относительно оси Y, а потом точки с отрицательными ординатами отобразить симметрично относительно оси Х.)
г) Почему графики функций Y = –Х2 + 4X – 3 и Y = Х2 – 4X + 3 одинаковы?
(Так как А = А , –А = А)
V.
У рассмотренных функций под знаком модуля была
независимая переменная. Теперь рассмотрим
функции, где под знаком модуля стоит либо сама
функция, либо и функция, и независимая переменная
одновременно, т.е. зависимости вида
Теперь рассмотрим
функции, где под знаком модуля стоит либо сама
функция, либо и функция, и независимая переменная
одновременно, т.е. зависимости вида
Y = АХ2 + ВX+ C и Y = АХ2 + ВX + C
Приведем конкретные примеры.
а) Y = Х2 – 4X+ 3
По определению
Построим график функции Y = f (X) и берем ту его часть, которая расположена выше оси Х, т.к. Х2 – 4X+ 3 0 и добавим к ней ее симметричное отображение относительно оси Х.
б) Y = Х2 – 4X+ 3
Сначала строим график функции Y = Х2 – 4X+ 3 , а затем множество точек, координаты которых удовлетворяют условию Y = Х2 – 4X+ 3 , т.е. график функции Y = Х2 – 4X+ 3 отображаем относительно оси Х.
VI.
 Творческое задание
Творческое заданиеДана функция Y = Х2 + 2X– 3
Выполнить всевозможные преобразования данной квадратичной функции с модулем.
1 Модуль действительного числа Функция
” 1 ”
Модуль действительного числа Функция y= lхl Алгебра, 8 класс 2
Модуль действительного числа ЧИСЛА положительные неположительные отрицательные неотрицательные 2 -7 3
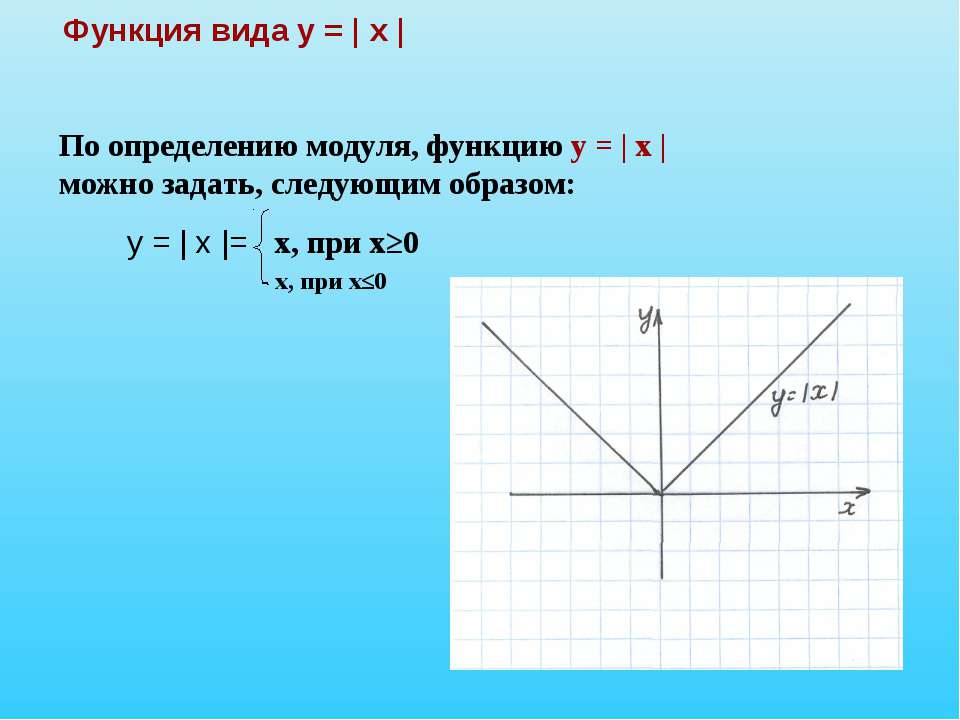
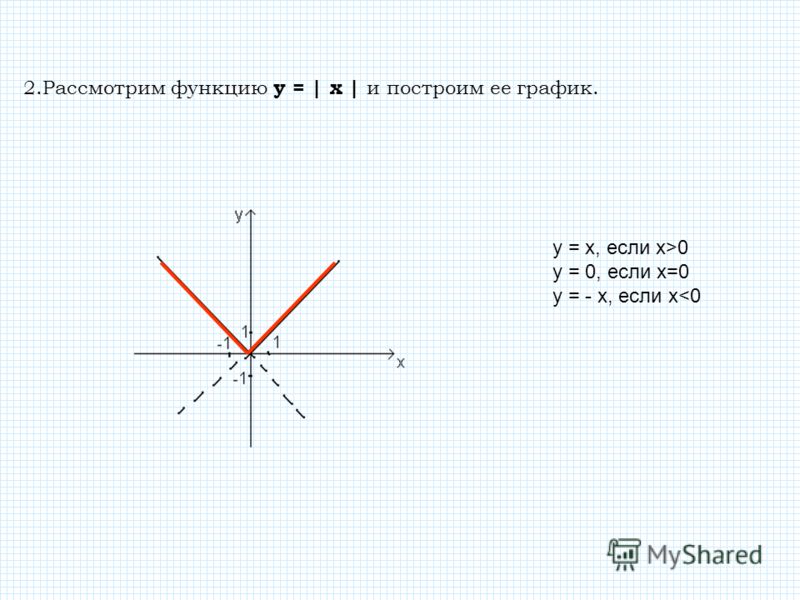
Модуль действительного числа |x|= Х, если Х 0, -Х, если Х
Модуль действительного числа 1) |а|=5 а = 5 или а = — 5 2) |х — 2|=5 х – 2 = 5 или х – 2 = — 5 х=-3 х=7 3) |2 х+3|=4 2 х+3= 4 или 2 х+3= — 4 2 х= 1 2 х= — 7 х= 0, 5 х= — 3, 5 |х — 4|= — 2 5 4)
Функция y= lхl y = |x| y= Х, если Х 0, -Х, если Х
Работа с учебником по стр. 177 -181 1. Сформулировать свойства модуля 2. В чем состоит геометрический смысл модуля? 3. Описать свойства функции y = |x| по плану 1) D (y) 2) Нули функции 3) Ограниченность 4) yн/б, yн/м 5) Монотонность 6) E (y) 4. Как получить из графика функции y = |x| график функции y = |x+2| y = |x-3| ? 7
Описать свойства функции y = |x| по плану 1) D (y) 2) Нули функции 3) Ограниченность 4) yн/б, yн/м 5) Монотонность 6) E (y) 4. Как получить из графика функции y = |x| график функции y = |x+2| y = |x-3| ? 7
Модуль действительного числа |x|= Х, если Х 0, -Х, если Х
Свойства функции y = |x| 1) D (y): (- ∞; + ∞) 2) Нули функции: х=0 3) Ограничена снизу (y=0) Не ограничена сверху 4) yн/б – нет, yн/м = 0 5) Монотонность: убыв. на (- ∞; 0 ] возр. на [ 0; + ∞) 9 6) E (y): [ 0; + ∞)
Алгоритм построения графика функции y = lkх+bl 1. Построить график функции y =kx+b. 2. Отобразить часть графика, лежащую в нижней полуплоскости, симметрично относительно оси Ox (в верхнюю полуплоскость). 10
Алгоритм построения графика функции y = lkх+bl ПРИМЕР № 1 y = lх — 2 l Ø y=х– 2 x y 0 -2 2 0 Ø отобрази «нижнюю» часть в верхнюю полуплоскость 11
Алгоритм построения графика функции y = lkх+bl ПРИМЕР № 2 y = l- 2 х – 3 l Ø y=-2 х– 3 x y 0 -3 -2 1 Ø отобрази «нижнюю» часть в верхнюю полуплоскость 12
Самостоятельная работа 1. Построить график функции y = |x+1| « 2 — 3» 2. Решить уравнение: а) |x|=2 б) |x|=0 1 вариант « 4 — 5» 13 1. Построить график функции: y = |x-2| y = |x+3| 2. Решить уравнение: « 3 — 4» 2 вариант |x-2|=3 |x+3|=2 1. Построить график функции: y = |2 x+1| y = |4 x+1| 2. Решить уравнение: |2 x+1|=5 |4 x+1|=3
Построить график функции y = |x+1| « 2 — 3» 2. Решить уравнение: а) |x|=2 б) |x|=0 1 вариант « 4 — 5» 13 1. Построить график функции: y = |x-2| y = |x+3| 2. Решить уравнение: « 3 — 4» 2 вариант |x-2|=3 |x+3|=2 1. Построить график функции: y = |2 x+1| y = |4 x+1| 2. Решить уравнение: |2 x+1|=5 |4 x+1|=3
Решение самостоятельной работы « 2 — 3» « 3 — 4» 14 « 4 — 5»
Советы великих 1) |-3| 2)Число, противоположное числу (-6) 3) Выражение, противоположное выражению 5 — 7 4) |- 4 : 2| 5) Выражение, противоположное выражению — 2+3 6) |3 — 2| 7) |- 3 2| 8) | 7 — 5| Варианты ответов: -3 15 3 — 2 1___ 3 — 2 1 -6 6 2 — 3 7 — 5 2 -3 2 3 5 — 7 А Е Г Ж И К Н Т Ш Э Я
Советы великих «Очень просто. Все знают, что сделать это невозможно. Случайно находится один невежда, который этого не знает. Он-то и делает ИЗОБРЕТЕНИЯ» 16
Функция модуля— График, свойства и решенные примеры
Функция модуля обычно относится к функции, которая дает положительное значение любой переменной или числа. Также известная как функция абсолютного значения, она может генерировать неотрицательное значение для любой независимой переменной, независимо от того, положительное оно или отрицательное. Обычно представляет собой: y = | x |, где x представляет действительное число, а y = f (x), представляя все положительные действительные числа, включая 0, и f: R → R и x ∈ R
Также известная как функция абсолютного значения, она может генерировать неотрицательное значение для любой независимой переменной, независимо от того, положительное оно или отрицательное. Обычно представляет собой: y = | x |, где x представляет действительное число, а y = f (x), представляя все положительные действительные числа, включая 0, и f: R → R и x ∈ R
Выражение, в котором модуль может быть определен следующим образом:
f (x) = \ [\ left \ {\ begin {matrix} x & if x \ geq 0 \\ -x & if x <0 \ end {matrix} \ right.\]
Здесь x представляет любое неотрицательное число, а функция генерирует положительный эквивалент x. Для отрицательного числа, x <0, функция генерирует (-x), где
— (- x) = положительное значение x.
Однако для модульной функции существуют разные случаи, и они могут означать по-разному для разных контекстов.
Случай 1:
Для y = | x |, где x — действительное число, т. е. x> 0, поскольку переменные могут иметь только действительные значения. Здесь функция модуля действительной переменной остается положительным значением действительного числа.
е. x> 0, поскольку переменные могут иметь только действительные значения. Здесь функция модуля действительной переменной остается положительным значением действительного числа.
Для x = 2,
y = | 2 | т.е. = 2.
Случай 2:
Для y = | f (x) | здесь мы используем f (x) вместо | x |, и поэтому модуль изменяет значение и свойства функции, изменяя общую функцию. Вот несколько примеров:
| f (x) | = а; a> 0 => f (x) = \ [\ pm \] a
| f (x) | = а; а = 0 => е (х) = 0
| е (х) | = а; a <0 => Нет решения этого уравнения
График функции модуля
В функции модуля, каждый раз | x | = 4, значение x = ± 4
Для построения графика нам нужно сначала взять определенные значения,
Когда x = -5, затем y = | -5 | = 5
Аналогично, для x = -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 соответствующие значения y будут = -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
(Изображение будет добавлено в ближайшее время)
Здесь для x> 0 график представляет собой линию, где y = x.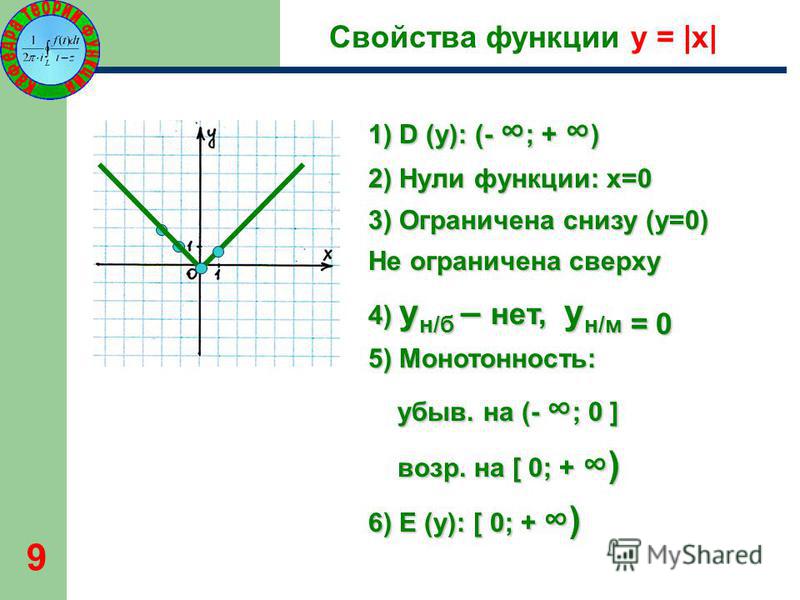 Аналогично для x <0 график представляет собой линию, где y = -x.
Аналогично для x <0 график представляет собой линию, где y = -x.
Здесь обе линии графика соответствуют определению функций модуля. График определяет область и диапазон функции модуля, т.е.
область = R (или действительные числа)
Диапазон = [0, ∞]; где диапазон функции модуля — это верхняя половина вещественных чисел (R +), включая 0.
Поскольку функция модуля понимается как неотрицательное значение, можно сказать, что модуль переменной аналогичен корня квадратного из квадрата переменной.{2}} \]
Вот некоторые другие неотрицательные выражения, которые могут объяснить неотрицательное значение функции модуля:
Четный показатель степени выражения или переменной может быть определен как: x2n, где n ∈ Z
Четный корень переменной может быть определен как: x1 / 2n, где n ∈ Z
Значение y может быть определено как: y = 1-sinx, или, y = 1- cosx, (поскольку sinx ≤ 1 и cosx ≤1)
Свойства функции модуля
Поскольку функция модуля может быть эффективной для поиска неравенства между числами, вот следующие свойства функции модуля:
Здесь x лежит между -a и a, не считая конечных точек интервала, i. е.
е.
| x | <а; a> 0 ⇒ -a | x | > а; a> 0 x <- a или x> a ⇒ x ∈ (- ∞, a) ∪ (a, ∞) Поскольку неравенства могут быть полезны для выражения интервалов в компактной форме, вот пример тригонометрической функции cosec диапазон, который определяется как x ∈ (−∞, -1] ∪ [1, ∞}, представленный как: | x | ≥ 1 | f (x) | | xy | = 0, ⇔ x = y. | x + y | ≤ | x | + | y | | xy | ≥ || x | — | y || | xy | = | x | * | y | | x / y | = | x | / | y |, где | y | ≠ 0. x2 ≤ p2 ⇔ | x | ≤ p ⇔ -p ≤ x ≤ p x2 ≥ p2 ⇔ | x | ≥ p ⇔ x ≤ -p, x ≥ p x2 x2> p2 ⇔ | x | > p ⇔ x <-p, x> p p2 ≤ x2 ≤ q2 ⇔ p ≤ | x | ≤ q ⇔ x ∈ [-q, -p] ∪ [p, q] p2 Пример 1: функция f определена на R как: f (x) = \ [\ left \ {\ begin {matrix} \ frac {| x |} {x}, & x \ neq 0 \\ 0, & x = 0 \ end {matrix} \ right. Постройте график Решение: Когда x является положительным целым числом, функция может быть определена как: f (x) = \ [\ frac {| x |} {x} \] = \ [\ frac {x} {x} \] = 1 Когда x является отрицательным целым числом, функция может быть определена как: f (x) = \ [\ frac {| x |} {x} \] = \ [\ frac {-x} {x} \] = -1 Следовательно, f можно переопределить как: f (x) = \ [\ left \ {\ begin {matrix} 1, & & x > 0 \\ 0 & & x = 0 \\ -1 & & x <0 \ end {matrix} \ right.\] (Изображение будет добавлено в ближайшее время) Закрашенная точка в точке (0,0) и полые точки в точке (0,1), (0, -1) обозначают, что f (0) имеет значение 0 вместо 1 или -1. Такая функция также известна как функция Signum. Цели обучения Авиалайнер меняет высоту по мере увеличения расстояния от точки старта полета. Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования. В этом разделе мы разберем такие отношения. Отношение — это набор упорядоченных пар.Набор первых компонентов каждой упорядоченной пары называется областью, а набор вторых компонентов каждой упорядоченной пары называется диапазоном. Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. \ [\ {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10) \} \ tag {1.1.1} \] Домен \ (\ {1, 2, 3, 4, 5 \} \). Диапазон равен \ (\ {2, 4, 6, 8, 10 \} \). Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой \ (x \).Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой \ (y \). Функция \ (f \) — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене. Другими словами, никакие \ (x \) — значения не повторяются. Для нашего примера, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене, {1, 2, 3, 4, 5}, связан ровно с одним элементом в диапазон, \ (\ {2, 4, 6, 8, 10 \} \). Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами. Это будет выглядеть как \ [\ mathrm {\ {(нечетное, 1), (четное, 2), (нечетное, 3), (четное, 4), (нечетное, 5) \}} \ tag {1.1.2} \] Обратите внимание, что каждый элемент в домене {четный, нечетный} не связан ровно с одним элементом в диапазоне \ (\ {1, 2, 3, 4, 5 \} \). Например, термин «нечетный» соответствует трем значениям из области \ (\ {1, 3, 5 \} \), а термин «четный» соответствует двум значениям из диапазона \ (\ {2, 4 \} \).Это нарушает определение функции, поэтому это отношение не является функцией. На рисунке \ (\ PageIndex {1} \) сравниваются отношения, которые являются функциями, а не функциями. Функция Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа». Входные значения составляют область , а выходные значения составляют диапазон . Практическое руководство. Учитывая взаимосвязь между двумя величинами, определите, является ли взаимосвязь функцией Пример \ (\ PageIndex {1} \): определение того, являются ли прайс-листы меню функциями Меню кофейни, показанное на рисунке \ (\ PageIndex {2} \), состоит из предметов и их цен. Раствор Каждый элемент в меню имеет только одну цену, поэтому цена зависит от элемента. Следовательно, товар не зависит от цены. Пример \ (\ PageIndex {2} \): определение того, являются ли правила оценки класса функциями В конкретном классе математики общая процентная оценка соответствует среднему баллу.Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице \ (\ PageIndex {1} \) показано возможное правило назначения оценок. Решение Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл. В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла. Упражнение \ (\ PageIndex {2} \) Таблица \ (\ PageIndex {2} \) перечисляет пять величайших бейсболистов всех времен в порядке рангов. Есть да.(Примечание: если бы два игрока были разделены, скажем, на 4-м месте, то имя не зависело бы от ранга. Как только мы определим, что отношение является функцией, нам необходимо отобразить и определить функциональные отношения, чтобы мы могли понимать и использовать их, а иногда также, чтобы мы могли программировать их в компьютерах. Есть разные способы представления функций. Стандартные обозначения функций — это одно из представлений, облегчающих работу с функциями. Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных \ (h \) для роста и \ (a \) для возраста. Буквы \ (f \), \ (g \) и \ (h \) часто используются для обозначения функций точно так же, как мы используем \ (x \), \ (y \) и \ (z \) для обозначения числа и \ (A \), \ (B \) и \ (C \) для представления множеств. \ [\ begin {array} {ll} h \ text {is} f \ text {of} a \; \; \; \; \; \; & \ text {Назовем функцию} f \ text {; высота является функцией возраста.} \\ h = f (a) & \ text {Мы используем круглые скобки для обозначения ввода функции. Помните, мы можем использовать любую букву для названия функции; запись \ (h (a) \) показывает нам, что \ (h \) зависит от \ (a \). Значение \ (a \) необходимо поместить в функцию \ (h \), чтобы получить результат. Скобки указывают, что возраст вводится в функцию; они не указывают на умножение. Мы также можем дать алгебраическое выражение в качестве входных данных для функции.Например, \ (f (a + b) \) означает «сначала сложите \ (a \) и \ (b \), и результат будет входом для функции \ (f \)». Для получения правильного результата операции необходимо выполнять именно в таком порядке. Обозначение функции Обозначение \ (y = f (x) \) определяет функцию с именем \ (f \). Это читается как «\ (y \) является функцией \ (x \)». Буква \ (x \) представляет входное значение или независимую переменную. Буква \ (y \) или \ (f (x) \) представляет выходное значение или зависимую переменную. Пример \ (\ PageIndex {3} \): Использование обозначения функций для дней в месяце Используйте обозначение функции для представления функции, входом которой является название месяца, а выходом — количество дней в этом месяце. Раствор Использование обозначения функций для дней в месяце Используйте обозначение функции для представления функции, входом которой является название месяца, а выходом — количество дней в этом месяце. Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию \ (f \), мы напишем \ (\ text {days} = f (\ text {month}) \) или \ (d = f (m) \). Название месяца — это вход для «правила», которое связывает определенное число (выход) с каждым входом. Например, \ (f (\ text {March}) = 31 \), потому что в марте 31 день. Обозначение \ (d = f (m) \) напоминает нам, что количество дней, \ (d \) (выход), зависит от названия месяца \ (m \) (вход). Анализ Обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа в качестве входов и выходов. Пример \ (\ PageIndex {3B} \): интерпретация обозначения функции Функция \ (N = f (y) \) дает количество полицейских \ (N \) в городе в году \ (y \). Что означает \ (f (2005) = 300 \)? Раствор Когда мы читаем \ (f (2005) = 300 \), мы видим, что входной год — 2005. Выходное значение, количество полицейских \ ((N) \), равно 300.Помните, \ (N = f (y) \). Утверждение \ (f (2005) = 300 \) говорит нам, что в 2005 году в городе было 300 полицейских. Упражнение \ (\ PageIndex {3} \) Используйте обозначение функций, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях \ (d \). \ (ш = е (г) \) Вопросы и ответы Вместо обозначения, такого как \ (y = f (x) \), можем ли мы использовать тот же символ для вывода, что и для функции, например, \ (y = y (x) \), что означает «\ (y \) является функцией \ (x \)? » Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, например физике и инженерии.Однако, исследуя математику, нам нравится проводить различие между такой функцией, как \ (f \) , которая является правилом или процедурой, и выходом y, который мы получаем, применяя \ (f \) к конкретному ввод \ (x \) . Вот почему мы обычно используем такие обозначения, как \ (y = f (x), P = W (d) \) и т. Д. Общий метод представления функций — в виде таблицы. В строках или столбцах таблицы отображаются соответствующие входные и выходные значения. Таблица \ (\ PageIndex {3} \) перечисляет входное число каждого месяца (\ (\ text {Январь} = 1 \), \ (\ text {Февраль} = 2 \) и т. Д.) И вывод значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце \ (f \), где \ (D = f (m) \) идентифицирует месяцы целым числом, а не именем. Номер месяца, \ (м \) (ввод) Таблица \ (\ PageIndex {4} \) определяет функцию \ (Q = g (n) \). \ (п \) Таблица \ (\ PageIndex {5} \) отображает возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Сразу видно, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма. Возраст в годах, \ (a \) (ввод) Как: по таблице входных и выходных значений определить, представляет ли таблица функцию Пример \ (\ PageIndex {5} \): определение таблиц, представляющих функции Какая таблица, Таблица \ (\ PageIndex {6} \), Таблица \ (\ PageIndex {7} \) или Таблица \ (\ PageIndex {8} \), представляет функцию (если есть)? Выход Выход Выход Решение Таблица \ (\ PageIndex {6} \) и Таблица \ (\ PageIndex {7} \) определяют функции. Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции. Функция, представленная таблицей \ (\ PageIndex {6} \), может быть представлена записью \ [f (2) = 1 \ text {,} f (5) = 3 \ text {и} f (8) = 6 \ nonumber \] Аналогично выписки \ [g (−3) = 5 \ text {,} g (0) = 1 \ text {и} g (4) = 5 \ nonumber \] представляют функцию в таблице \ (\ PageIndex {7} \). Таблица \ (\ PageIndex {8} \) не может быть выражена подобным образом, потому что она не представляет функцию. Упражнение \ (\ PageIndex {5} \) Представляет ли Таблица \ (\ PageIndex {9} \) функцию? Выход да Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию. Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем вход. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение. Когда у нас есть функция в форме формулы, вычислить ее обычно несложно.2 + 2p − 3 = 0 & \ text {Вычтите по 3 с каждой стороны.} \\ (p + 3) (p − 1) = 0 & \ text {Factor.} \ End {array} \ nonumber \] Если \ ((p + 3) (p − 1) = 0 \), либо \ ((p + 3) = 0 \), либо \ ((p − 1) = 0 \) (или оба они равны \ (0 \)). Мы установим каждый множитель равным \ (0 \) и решим относительно \ (p \) в каждом случае. \ [(p + 3) = 0, \; p = −3 \ nonumber \] \ [(p − 1) = 0, \, p = 1 \ nonumber \] Это дает нам два решения. Упражнение \ (\ PageIndex {7} \) Дана функция \ (g (m) = \ sqrt {m − 4} \), решить \ (g (m) = 2 \). \ (м = 8 \) Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения . Если можно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме.Например, уравнение \ (2n + 6p = 12 \) выражает функциональную связь между \ (n \) и \ (p \). Мы можем переписать его, чтобы решить, является ли \ (p \) функцией \ (n \). Как: Для данной функции в форме уравнения напишите ее алгебраическую формулу. Пример \ (\ PageIndex {8A} \): поиск уравнения функции Выразите отношение \ (2n + 6p = 12 \) как функцию \ (p = f (n) \), если это возможно. Раствор Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где \ (p \) является функцией \ (n \), что означает запись его как \ (p = [\ text {выражение с участием} п] \). \ [\ begin {align *} 2n + 6p & = 12 \\ 6p & = 12−2n && \ text {Вычтите 2n с обеих сторон.} \\ p & = \ dfrac {12−2n} {6} & & \ text {Разделите обе стороны на 6 и упростите.} \\ p & = \ frac {12} {6} — \ frac {2n} {6} \\ p & = 2− \ frac {1} {3} n \ end {align *} \] Следовательно, \ (p \) как функция от \ (n \) записывается как \ [p = f (n) = 2− \ frac {1} {3} n \ nonumber \] Анализ Важно отметить, что не все отношения, выраженные уравнением, также можно выразить как функцию с формулой. Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Функция, которая связывает тип питомца с продолжительностью его памяти, легче визуализировать с помощью таблицы (Table \ (\ PageIndex {10} \)). Память для домашних животных интервал в часах Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию \ (P \). Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца.Мы можем оценить функцию \ (P \) при входном значении «золотая рыбка». Мы бы написали \ (P (золотая рыбка) = 2160 \). Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции P кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции. Как сделать: для данной функции, представленной в виде таблицы, определить конкретные выходные и входные значения 1.Найдите данный вход в строке (или столбце) входных значений. Пример \ (\ PageIndex {9} \): Вычисление и решение табличной функции Использование таблицы \ (\ PageIndex {11} \), а. Оцените \ (g (3) \). \ (п \) Решение а. \ (п \) Когда мы вводим 2 в функцию \ (g \), на выходе получаем 6.Когда мы вводим 4 в функцию \ (g \), наш результат также равен 6. Упражнение \ (\ PageIndex {1} \) Используя Table \ (\ PageIndex {12} \), вычислите \ (g (1) \). \ (г (1) = 8 \) Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров заданного выходного значения на графике и наблюдения за соответствующими входными значениями. Пример \ (\ PageIndex {10} \): чтение значений функций из графика Учитывая график на рисунке \ (\ PageIndex {7} \), Раствор Чтобы оценить \ (f (2) \), найдите точку на кривой, где \ (x = 2 \), затем прочтите координату y этой точки.Точка имеет координаты \ ((2,1) \), поэтому \ (f (2) = 1 \). См. Рисунок \ (\ PageIndex {8} \). Чтобы решить \ (f (x) = 4 \), мы находим выходное значение 4 на вертикальной оси. Двигаясь горизонтально по прямой \ (y = 4 \), мы обнаруживаем две точки кривой с выходным значением 4: \ ((- 1,4) \) и \ ((3,4) \). Эти точки представляют два решения \ (f (x) = 4 \): −1 или 3. Это означает \ (f (−1) = 4 \) и \ (f (3) = 4 \), или когда вход — -1 или 3, выход — 4.См. Рисунок \ (\ PageIndex {9} \). Упражнение \ (\ PageIndex {10} \) Учитывая график на рисунке \ (\ PageIndex {7} \), решите \ (f (x) = 1 \). \ (x = 0 \) или \ (x = 2 \) Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям.Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов. Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в Таблице \ (\ PageIndex {13} \). Эта система оценок представляет собой функцию «один-к-одному», потому что каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве. Чтобы визуализировать эту концепцию, давайте еще раз посмотрим на две простые функции, изображенные на рисунках \ (\ PageIndex {1a} \) и \ (\ PageIndex {1b} \). Индивидуальные функции Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.2 \). Поскольку площади и радиусы являются положительными числами, существует ровно одно решение: \ (\ sqrt {\ frac {A} {\ pi}} \). Таким образом, площадь круга однозначно зависит от радиуса круга. Упражнение \ (\ PageIndex {11A} \) а. г. нет, потому что несколько номеров банковских счетов могут иметь одинаковый баланс; г. нет, потому что один и тот же выход может соответствовать более чем одному входу. Упражнение \ (\ PageIndex {11B} \) Оцените следующее: а.Да, буквенная оценка является функцией процентной оценки; Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Наиболее распространенные графики называют входное значение \ (x \) и выходное значение \ (y \), и мы говорим, что \ (y \) является функцией \ (x \), или \ (y = f (x) \), когда функция названа \ (f \). График функции — это совокупность всех точек \ ((x, y) \) на плоскости, которая удовлетворяет уравнению \ (y = f (x) \). Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующим выходным значением.Например, черные точки на графике на рисунке \ (\ PageIndex {10} \) говорят нам, что \ (f (0) = 2 \) и \ (f (6) = 1 \). Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, тогда график не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения.См. Рисунок \ (\ PageIndex {11} \) . Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию Пример \ (\ PageIndex {12} \): Применение теста вертикальной линии Какой из графиков на рисунке \ (\ PageIndex {12} \) представляет (ы) функцию \ (y = f (x) \)? Раствор Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) рисунка \ (\ PageIndex {12} \). Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что не более чем значений x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке \ (\ PageIndex {13} \). Упражнение \ (\ PageIndex {12} \) Представляет ли график на рисунке \ (\ PageIndex {14} \) функцию? да После того, как мы определили, что график определяет функцию, простой способ определить, является ли функция взаимно однозначной, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию. Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию Пример \ (\ PageIndex {13} \): Применение теста горизонтальной линии Рассмотрим функции, показанные на рисунке \ (\ PageIndex {12a} \) и рисунке \ (\ PageIndex {12b} \). Раствор Функция на рисунке \ (\ PageIndex {12a} \) не является взаимно однозначной. Горизонтальная линия, показанная на рисунке \ (\ PageIndex {15} \), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках.) Функция на рисунке \ (\ PageIndex {12b} \) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза. Упражнение \ (\ PageIndex {13} \) Является ли график, показанный на рисунке \ (\ PageIndex {13} \), взаимно однозначным? Нет, потому что он не проходит тест горизонтальной линии. В этом тексте мы будем исследовать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем. В этой книге мы будем часто видеть эти функции набора инструментов, комбинации функций набора инструментов, их графики и их преобразования. Будет очень полезно, если мы сможем быстро распознать эти функции набора инструментов и их возможности по имени, формуле, графику и основным свойствам таблицы. Графики и примерные значения таблицы включены в каждую функцию, показанную в Таблице \ (\ PageIndex {14} \). зависимая переменная домен функция проверка горизонтальной линии независимая переменная ввод взаимно однозначная функция вывод диапазон отношение проверка вертикальной линии Фигуры, созданные, обработанные и визуализированные библиотекой Python plotly, представлены древовидными структурами данных, которые автоматически сериализуются в JSON для визуализации с помощью Plotly. Основные классы, определенные в Примечание: все функции в Plotly Express, который является рекомендуемой точкой входа в библиотеку Каждый атрибут фигуры, не являющийся листом, представлен экземпляром класса в иерархии Объекты, содержащиеся в списке, который является значением атрибута Объекты графиков имеют несколько преимуществ по сравнению с простыми словарями Python: Рекомендуемый способ создания фигур — использование функций в модуле plotly.express, вместе известных как Plotly Express, которые все возвращают экземпляры Тем не менее, некоторые виды фигур еще невозможно создать с помощью Plotly Express, например фигуры, использующие определенные типы трехмерных трасс, такие как сетка Обратите внимание, что фигуры, созданные Plotly Express в одном вызове функции , легко настроить во время создания и манипулировать после создания с помощью методов Фигуры, полученные с помощью Plotly Express, всегда можно построить с нуля, используя графические объекты, но этот подход обычно требует 5–100 строк кода, а не 1 . Вот простой пример того, как создать один и тот же объект-фигуру из одних и тех же данных, один раз с помощью Plotly Express, а другой — без него. Данные в этом примере представлены в «длинной форме», но Plotly Express также принимает данные в «широкой форме», и экономия количества строк от Plotly Express по объектам графа сопоставима.Для более сложных фигур, таких как солнечные лучи, параллельные координаты, фасеточные графики или анимация, требуется гораздо больше строк кода графических объектов для конкретных фигур, тогда как переключение с одного представления на другое с помощью Plotly Express обычно включает изменение всего нескольких символов. Обратный
Функции: Определение «инверсии» / Разделы: Определение
/ Инвертирование графика, обратная функция — это функция ?,
Нахождение обратного, Доказательство
обратное Охват вашего учебника
Обратные функции, вероятно, состояли из двух частей.В первой части было много
фигурных скобок и списков точек; во второй части есть лоты « y =»
или « f ( x ) =»
функции, для которых вам нужно найти обратные, если это возможно. Первое
часть будет отображаться в вашем домашнем задании и, возможно, на тесте; Вторая часть
обязательно появится на вашем тесте, и вы даже можете использовать его позже
классы. Обратная функция
имеет все те же характеристики, что и исходная функция, за исключением того, что x и y ‘s
были отменены.Это то, что они пытались объяснить своим
наборы точек. Например, предположим, что ваша функция состоит из этих
точки: {
(1, 0), (3, 5), (0, 4)}.
Тогда обратное дается этим набором точек: {
(0, 1), (5, 3), (4, 0)}.
(Обратите внимание, что порядок точек не имеет значения; вы можете переставить
указывает, поэтому x находятся «в порядке» или нет. Выбор за вами.) Как только вы нашли обратное
функции, тогда возникает вопрос: «Является ли эта обратная
функция? «Используя набор точек сверху, функция выше
графики вроде этого: Вы знаете, что это
функция (и вы можете быстро проверить, используя Вертикальный
Line Test): вы
не иметь двух разных точек с одинаковым значением x . Поскольку синие точки (
точки обратного) не имеют двух точек с общим значением x ,
эта инверсия также является функцией. Находка
обратная к графику Наверное, ваш учебник
подробно рассказывал о том, что обратное — это «отражение в линии. y = x «.Он пытался сказать, что вы можете взять на себя свою функцию, нарисовать
линия г
= x (что является
от нижнего левого угла к верхнему правому диагонали) положите на эту линию двустороннее зеркало,
и вы могли «видеть» обратное отражение в зеркале. Практически
говоря, это свойство «отражения» может помочь вам нарисовать обратное: Нарисуйте точки и
линия отражения: Отражение точек
по линии: Вы можете увидеть на последней
изображение, что существует определенная графическая взаимосвязь между точками
функции и точки обратного. Предположим, вам дано
этот график: Обратите внимание, что у меня
НЕ сказал вам, что это за функция! Теперь нарисуйте отражение.
линия: (Было бы хорошо
идея использовать для этого линейку; вы захотите быть аккуратным!). Теперь взгляните на график,
и проведем диагонали от известных точек на графике до их «отражений»
на другой стороне линии: Обратите внимание, что точки
собственно по линии г
= x нет
переехать; то есть там, где функция пересекает диагональ, обратная
тоже пересечется. А теперь нарисуйте немного
сюжетные точки: . Даже не зная, что
функция была, вы можете нарисовать обратное (фиолетовая линия). Верх
| 1 | 2 | 3
| 4 | 5 | 6
| 7 | Возвращение
к указателю Вперед >> Цитируйте эту статью
как: Стапель, Элизабет.
«Обратные функции: определение« обратного »/ Построение обратного
Из графика ». Используется инструкция Экспортируемые модули находятся в строгом режиме, независимо от того,
объявлять их таковыми или нет. Оператор экспорта не может использоваться во встроенных скриптах. Есть два типа экспорта: Идентификатор для экспорта (чтобы его можно было импортировать через Существует два разных типа экспорта: с именем и по умолчанию . У вас может быть несколько именованных экспортов для каждого модуля, но только один
экспорт по умолчанию. Каждый тип соответствует одному из приведенных выше синтаксисов: Именованный экспорт: Экспорт по умолчанию: Именованный экспорт полезен для экспорта нескольких значений. При импорте обязательно
использовать то же имя соответствующего объекта. Но экспорт по умолчанию можно импортировать с любым именем, например: Вы также можете переименовать именованный экспорт, чтобы избежать конфликтов имен: Также можно «импортировать / экспортировать» из разных модулей в родительском модуле, поэтому
что они доступны для импорта из этого модуля.Другими словами, можно создать
единый модуль, концентрирующий различные экспортные данные из разных модулей. Этого можно добиться с помощью синтаксиса «экспорт из»: Что сравнимо с комбинацией импорта и экспорта: Но где Примечание: Следующее синтаксически недопустимо, несмотря на его импорт
эквивалент: Правильный способ сделать это — переименовать экспорт: Синтаксис «экспорт из» позволяет опустить В модуль Тогда в модуле верхнего уровня, включенном в вашу HTML-страницу, мы могли бы иметь: Важно отметить следующее: Вопросы о функции модуля (решено)
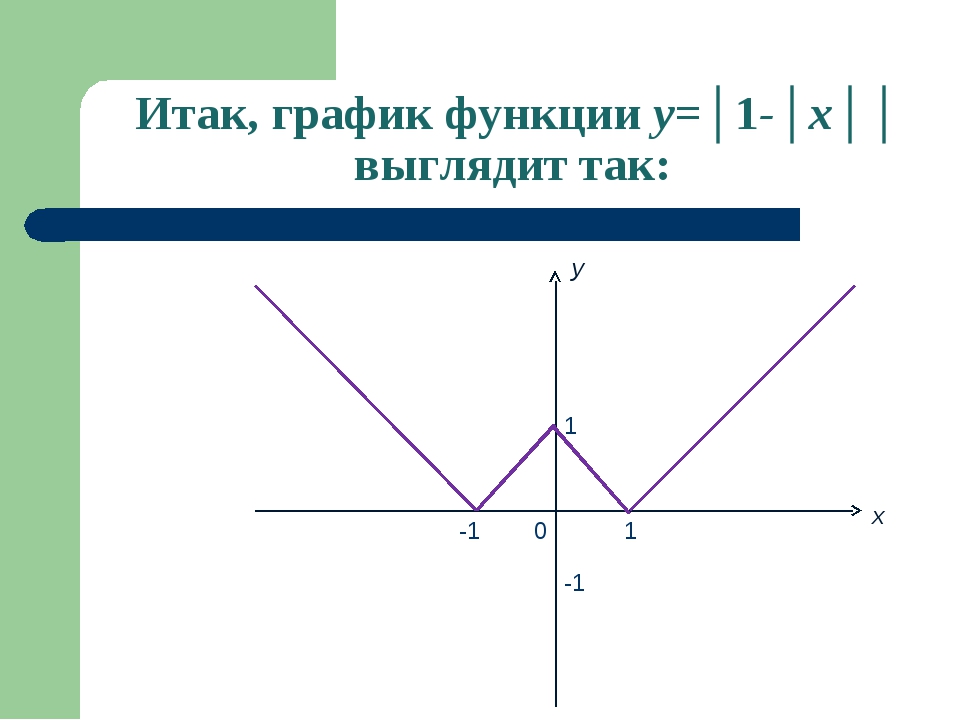 \]
\] 1.1: Четыре способа представления функции

Определение того, представляет ли отношение функцию
 Второе число в каждой паре вдвое больше первого.
Второе число в каждой паре вдвое больше первого.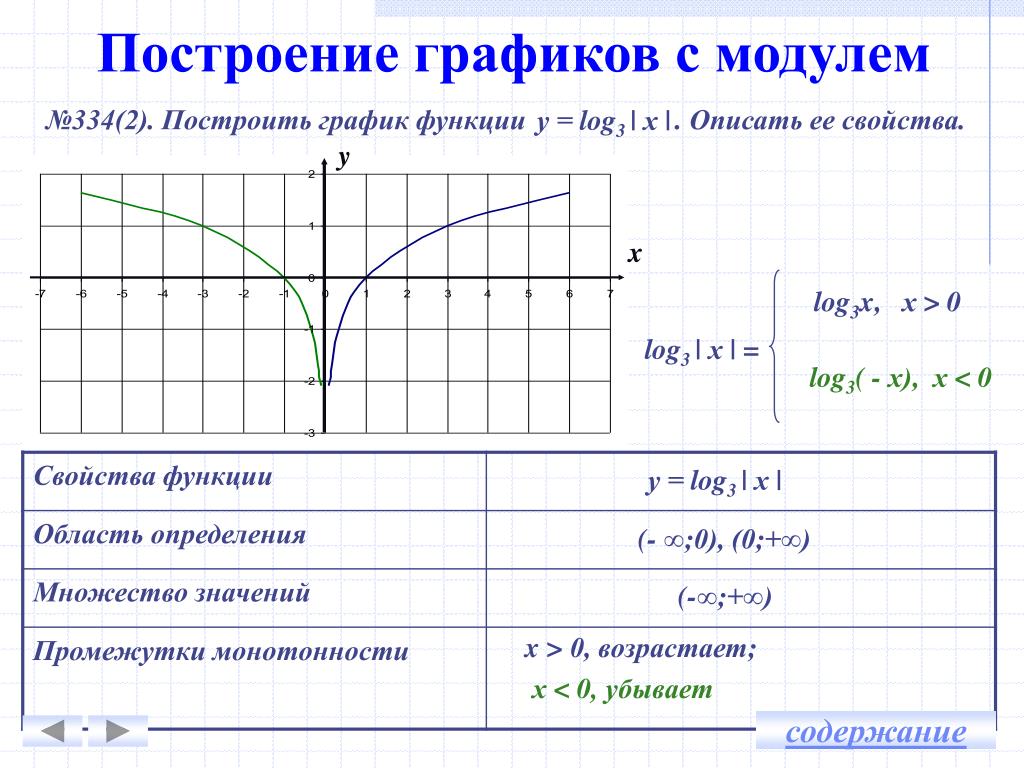
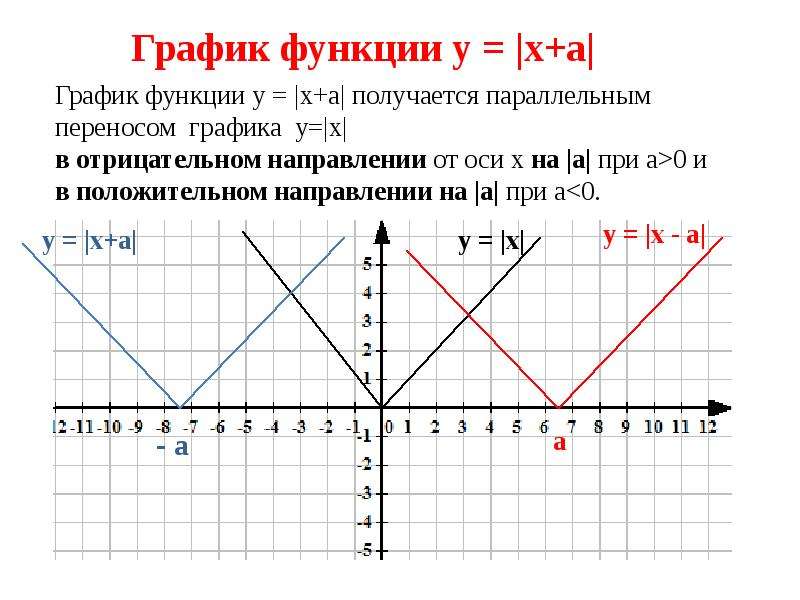 В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход \ (q \) связан с двумя разными выходами.
В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход \ (q \) связан с двумя разными выходами.
Рисунок \ (\ PageIndex {2} \): меню с ценами на пончики из кафе, где простой пончик стоит 1 доллар.49, пончик с желе и шоколадный пончик — 1,99 доллара.
Рисунок \ (\ PageIndex {3} \): меню с ценами на пончики из кафе, где простой пончик стоит 1,49 доллара, а пончик с желе и шоколадный пончик — 1,99 доллара.
Рисунок \ (\ PageIndex {4} \): Связь цен с пончиками.
Процентное содержание 0–56 57–61 62–66 67–71 72–77 78–86 87–91 92–100 Средний балл 0.  0
0 1,0 1,5 2,0 2,5 3,0 3,5 4,0 
Игрок Рейтинг Бэйб Рут 1 Уилли Мейс 2 Тай Кобб 3 Уолтер Джонсон 4 Хэнк Аарон 5  )
) Использование обозначения функций
 } \\ f (a) & \ text {Мы называем функцию} f \ text {; выражение читается как «} f \ text {of} a \ text {.»} \ end {array} \]
} \\ f (a) & \ text {Мы называем функцию} f \ text {; выражение читается как «} f \ text {of} a \ text {.»} \ end {array} \]

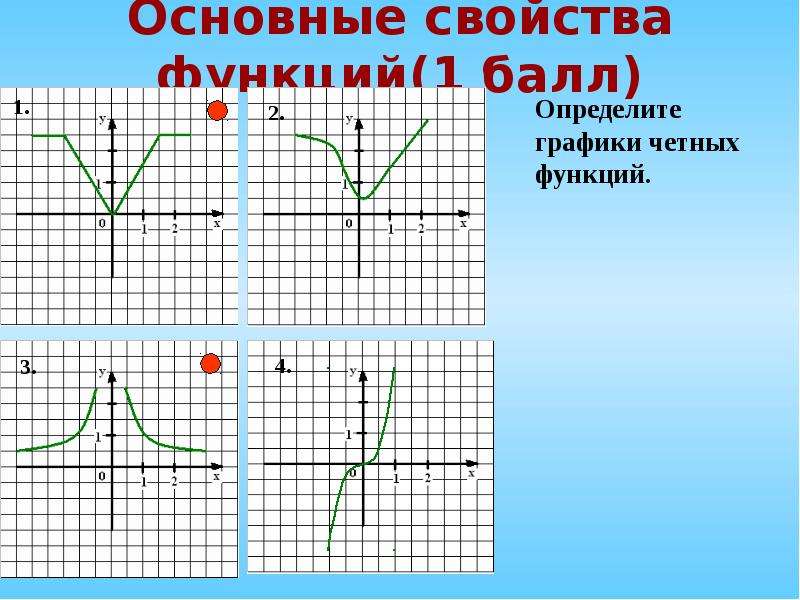
Представление функций с помощью таблиц
 В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.
В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений. 1 2 3 4 5 6 7 8 9 10 11 12 Количество дней в месяце, \ (D \) (вывод) 31 28 31 30 31 30 31 31 30 31 30 31 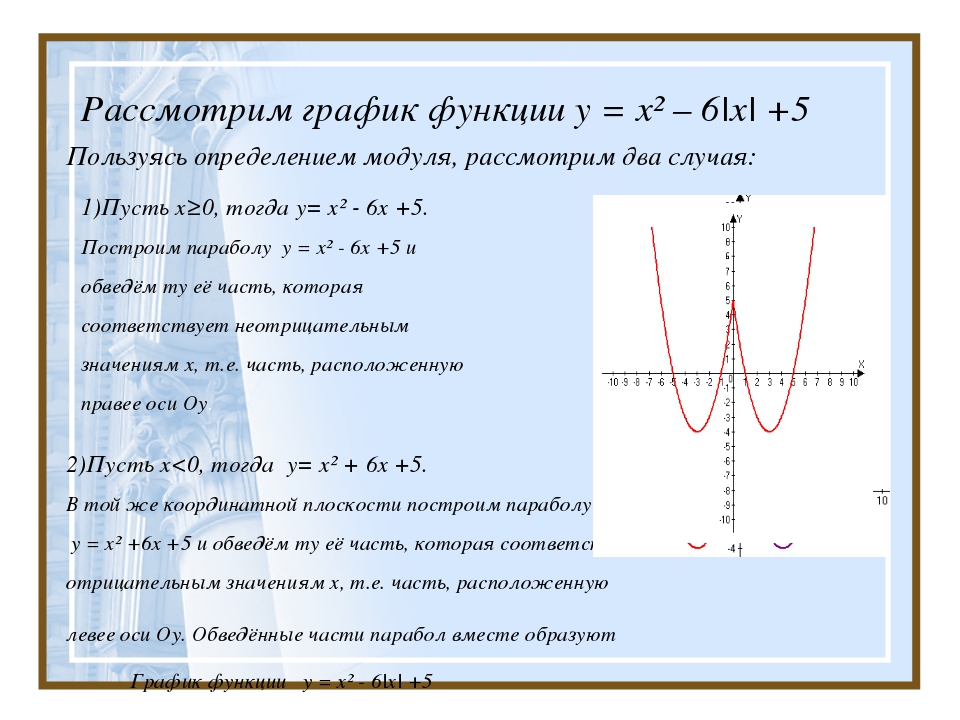 Помните, это обозначение говорит нам, что \ (g \) — это имя функции, которая принимает входные данные \ (n \) и дает результат \ (Q \).
Помните, это обозначение говорит нам, что \ (g \) — это имя функции, которая принимает входные данные \ (n \) и дает результат \ (Q \). 1 2 3 4 5 \ (Q \) 8 6 7 6 8 
5 5 6 7 8 9 10 Высота в дюймах, \ (h \) (выход) 40 42 44 47 50 52 54 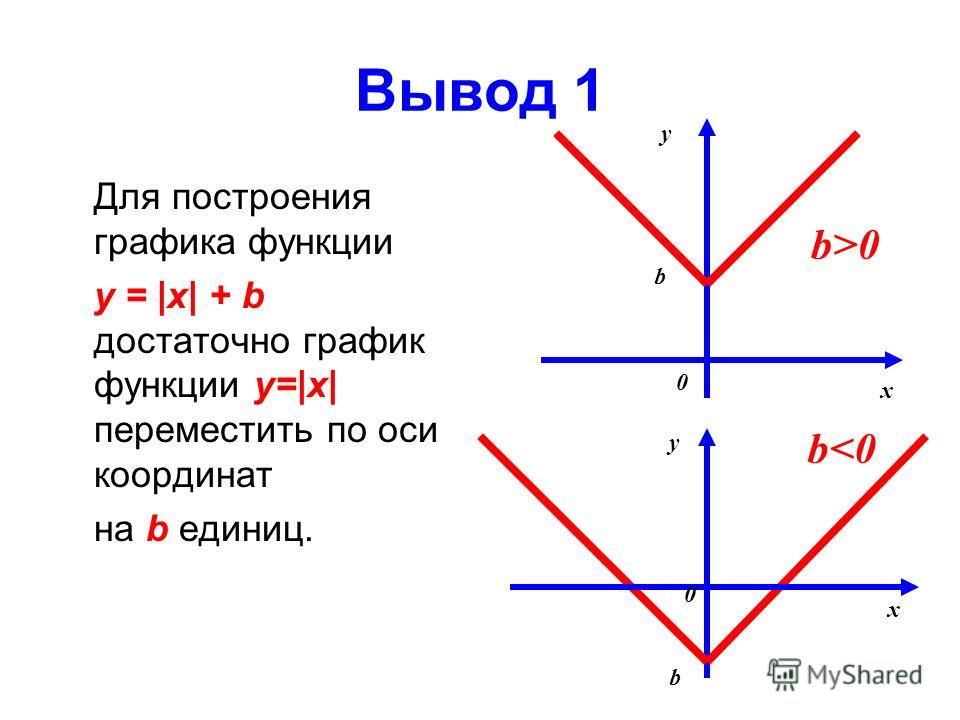
Ввод 2 1 5 3 8 6 Ввод -3 5 0 1 4 5 Ввод 1 0 5 2 5 4 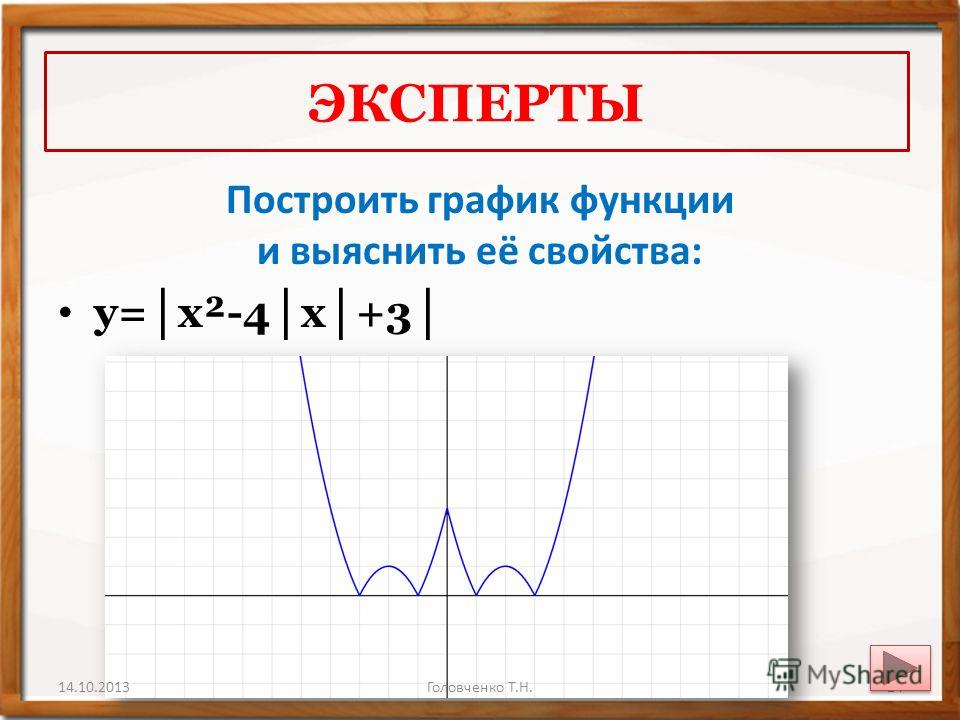 В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица \ (\ PageIndex {8} \) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.
В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица \ (\ PageIndex {8} \) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям. Ввод 1 10 2 100 3 1000 Поиск входных и выходных значений функции
 Вычисление всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Вычисление всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению. Вычисление функций в алгебраических формах
 Выход \ (h (p) = 3 \), когда вход либо \ (p = 1 \), либо \ (p = −3 \). Мы также можем проверить, построив график, как на рисунке \ (\ PageIndex {6} \).2 + 2п \)
Выход \ (h (p) = 3 \), когда вход либо \ (p = 1 \), либо \ (p = −3 \). Мы также можем проверить, построив график, как на рисунке \ (\ PageIndex {6} \).2 + 2п \) Вычисление функций, выраженных в формулах

 2 = 1 \) функцию с \ (x \) на входе и \ (y \) на выходе? Если это так, представьте отношение как функцию \ (y = f (x) \).y \), если мы хотим выразить y как функцию от x, не существует простой алгебраической формулы, включающей только \ (x \), которая равна \ (y \). Однако каждый \ (x \) определяет уникальное значение для \ (y \), и существуют математические процедуры, с помощью которых \ (y \) может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для \ (y \) как функции от \ (x \), даже если формулу нельзя записать явно.
2 = 1 \) функцию с \ (x \) на входе и \ (y \) на выходе? Если это так, представьте отношение как функцию \ (y = f (x) \).y \), если мы хотим выразить y как функцию от x, не существует простой алгебраической формулы, включающей только \ (x \), которая равна \ (y \). Однако каждый \ (x \) определяет уникальное значение для \ (y \), и существуют математические процедуры, с помощью которых \ (y \) может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для \ (y \) как функции от \ (x \), даже если формулу нельзя записать явно. Оценка функции, заданной в табличной форме
 Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.
Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов. Щенок 0,008 Взрослая собака 0. 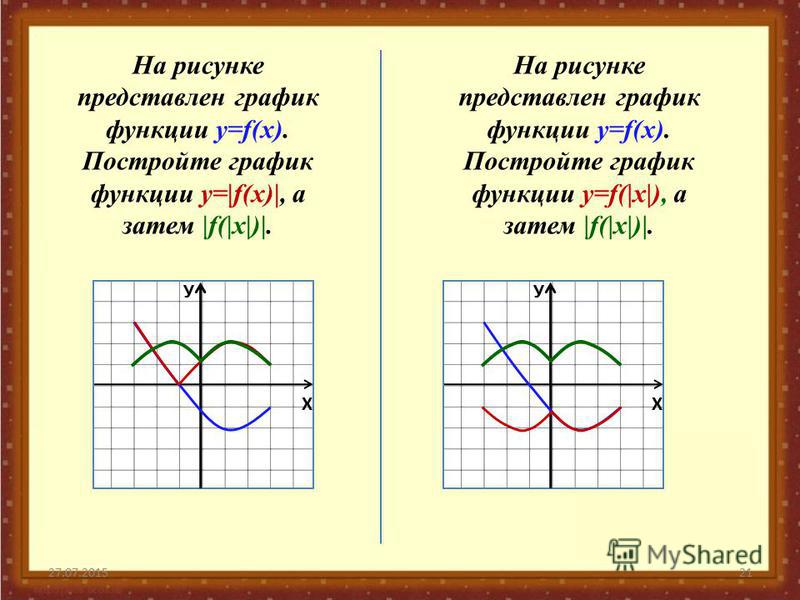 083
083 Кот 3 Золотая рыбка 2160 Бета-рыба 3600 
2. Определите соответствующее выходное значение в паре с этим входным значением.
3. Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
4. Определите входные значения, соответствующие заданному выходному значению.
г. Решите \ (g (n) = 6 \). 1 2 3 4 5 \ (г (п) \) 8 6 7 6 8  Вычисление \ (g (3) \) означает определение выходного значения функции \ (g \) для входного значения \ (n = 3 \). Выходное значение таблицы, соответствующее \ (n = 3 \), равно 7, поэтому \ (g (3) = 7 \).
Вычисление \ (g (3) \) означает определение выходного значения функции \ (g \) для входного значения \ (n = 3 \). Выходное значение таблицы, соответствующее \ (n = 3 \), равно 7, поэтому \ (g (3) = 7 \).
г. Решение \ (g (n) = 6 \) означает определение входных значений n, которые производят выходное значение 6. Таблица \ (\ PageIndex {12} \) показывает два решения: 2 и 4. 1 2 3 4 5 \ (г (п) \) 8 6 7 6 8 
Поиск значений функций из графика
Рисунок \ (\ PageIndex {7} \): График положительной параболы с центром в \ ((1, 0) \).

Определение того, является ли функция взаимно однозначной
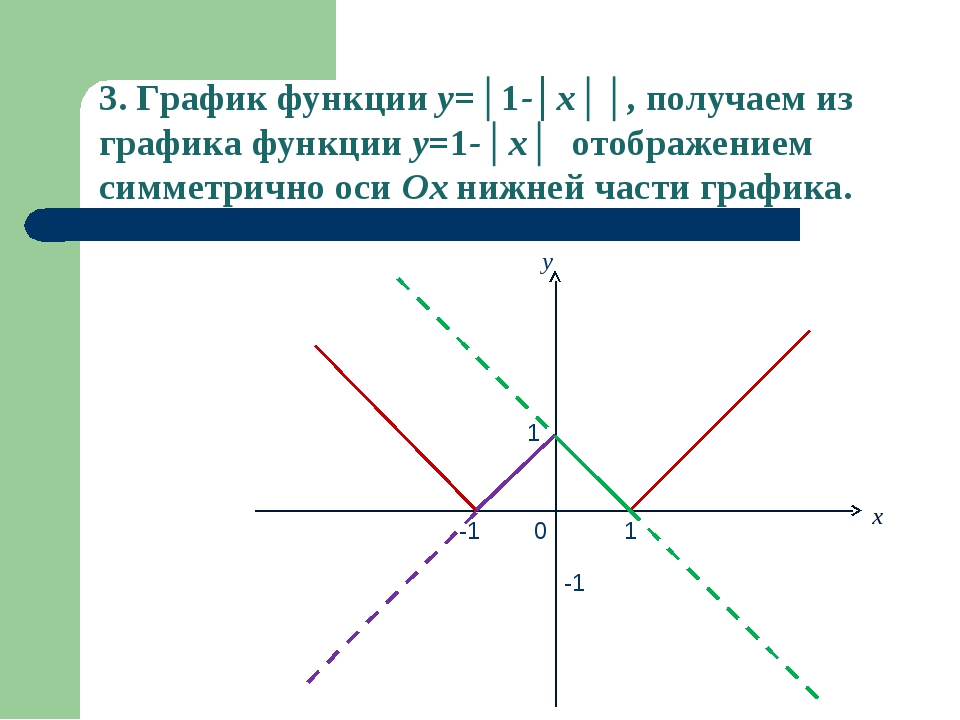
Letter Grade Средний балл A 4,0 B 3,0 С 2,0 D 1,0  Функция в части (a) показывает взаимосвязь, которая не является взаимно-однозначной, потому что входы \ (q \) и \ (r \) оба дают выход \ (n \). Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом.
Функция в части (a) показывает взаимосвязь, которая не является взаимно-однозначной, потому что входы \ (q \) и \ (r \) оба дают выход \ (n \). Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом. да, потому что на каждом банковском счете в любой момент времени имеется единый баланс;
да, потому что на каждом банковском счете в любой момент времени имеется единый баланс;
г. Нет, не один на один. Мы могли бы получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке. Использование теста вертикальной линии
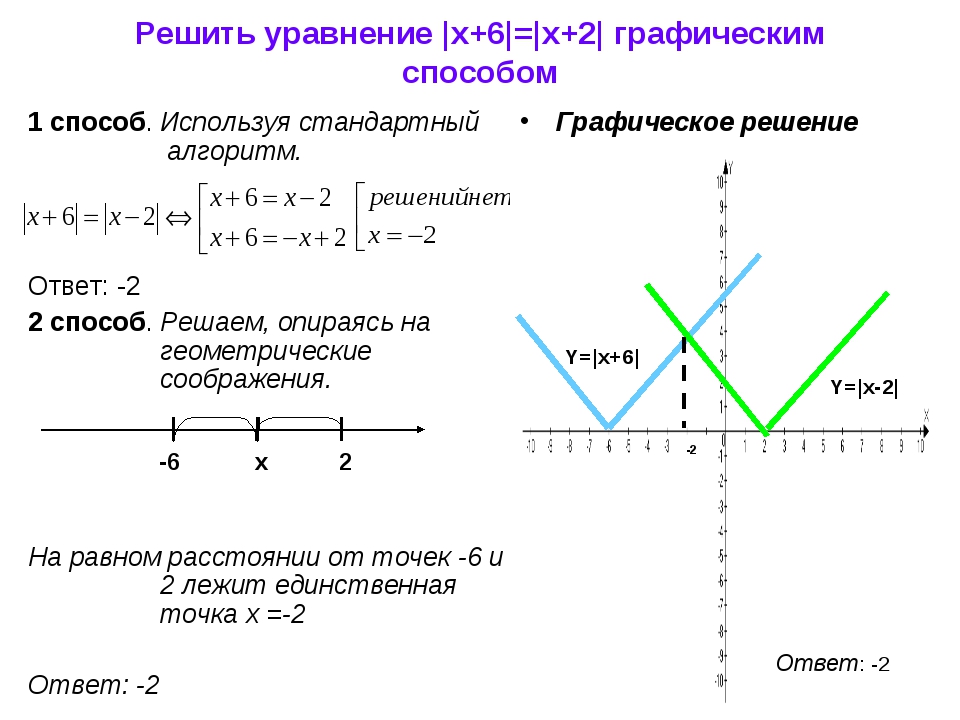 Графики отображают огромное количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений.По соглашению, графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Графики отображают огромное количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений.По соглашению, графики обычно строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси. Однако множество всех точек \ ((x, y) \), удовлетворяющих \ (y = f (x) \), является кривой. Показанная кривая включает \ ((0,2) \) и \ ((6,1) \), потому что кривая проходит через эти точки
Однако множество всех точек \ ((x, y) \), удовлетворяющих \ (y = f (x) \), является кривой. Показанная кривая включает \ ((0,2) \) и \ ((6,1) \), потому что кривая проходит через эти точки

Использование теста горизонтальной линии
 Являются ли какие-либо функции взаимно однозначными?
Являются ли какие-либо функции взаимно однозначными? Учимся читать, начинаем с алфавита. Изучая арифметику, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать x в качестве входной переменной и \ (y = f (x) \) в качестве выходной переменной.
Учимся читать, начинаем с алфавита. Изучая арифметику, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. Некоторые из этих функций запрограммированы на отдельные кнопки на многих калькуляторах. Для этих определений мы будем использовать x в качестве входной переменной и \ (y = f (x) \) в качестве выходной переменной. Ключевые уравнения
Ключевые понятия
 Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу.
Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу.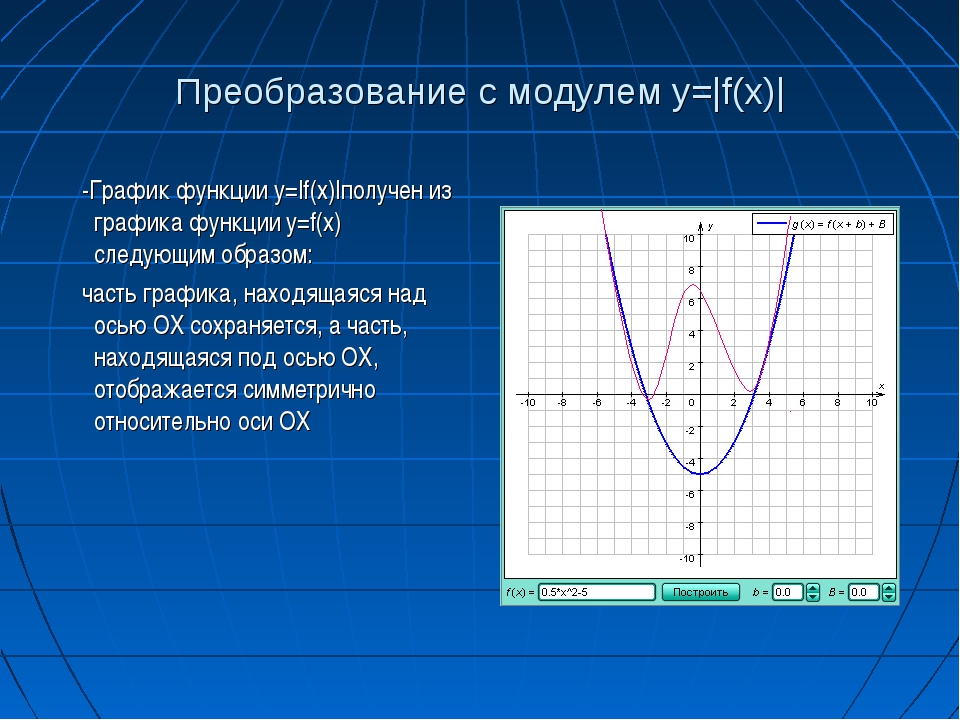
Глоссарий
выходная переменная
набор всех возможных входных значений для отношения
отношение, в котором каждое входное значение дает уникальное выходное значение
метод проверки взаимно однозначности функции путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза
входная переменная
каждый объект или значение в домене, который относится к другому объекту или значению посредством отношения, известного как функция
функция, для которой каждое значение вывода связано с уникальным значением ввода
каждый объект или значение в диапазоне, который создается, когда входное значение вводится в функцию
набор выходных значений, которые являются результатом входных значений в отношении
набор упорядоченных пар
метод проверки того, представляет ли график функцию, путем определения того, пересекает ли вертикальная линия график не более одного раза Авторы и авторство
Графических объектов
Что такое объекты графика? ¶
 js библиотека JavaScript. Эти деревья состоят из именованных узлов, называемых «атрибутами», а их структура определяется схемой рисунка Plotly.js, которая доступна в машиночитаемой форме. Модуль
js библиотека JavaScript. Эти деревья состоят из именованных узлов, называемых «атрибутами», а их структура определяется схемой рисунка Plotly.js, которая доступна в машиночитаемой форме. Модуль plotly.graph_objects (обычно импортируемый как go ) содержит автоматически сгенерированную иерархию классов Python, которые представляют нелистовые узлы в этой схеме рисунка. Термин «объекты графа» относится к экземплярам этих классов. графически.Модуль graph_objects — это Figure и ipywidgets -совместимый вариант, называемый FigureWidget , которые оба представляют собой целые фигуры. Экземпляры этих классов имеют множество удобных методов для Python-манипулирования их атрибутами (например, .update_layout () или .add_trace () , которые все принимают нотацию «магического подчеркивания»), а также их рендеринга (например, .) и экспорт их в различные форматы (например,  show ()
show () .to_json () или .write_image () или .write_html () ). plotly , построены поверх графических объектов и все возвращают экземпляры plotly.graph_objects.Figure . plotly.graph_objects . Например, фигура и фиг. может иметь атрибут макета.поле , которое содержит атрибуты t , l , b и r , которые являются листьями дерева: у них нет дочерних элементов. Поле в fig.layout является объектом класса plotly.graph_objects.Layout , а fig.layout.margin является объектом класса plotly.graph_objects., который представляет узел  layout.Margin
layout.Margin margin , и он имеет поля t , l , b и r , содержащие значения соответствующих конечных узлов.Обратите внимание, что указание всех этих значений может быть выполнено без создания промежуточных объектов с использованием нотации «магического подчеркивания»: go.Figure (layout_margin = dict (t = 10, b = 10, r = 10, l = 10)) . data , называются «трассировками» и могут относиться к одному из более чем 40 возможных типов, каждый из которых имеет соответствующий класс в plotly.graph_objects . Например, трассировки типа , разброс представлены экземплярами класса графически.Граф_объекты.Разброс . Это означает, что фигура, построенная как go.Figure (data = [go.Scatter (x = [1,2], y = [3,4)]) , будет иметь представление JSON {"data": [{ «тип»: «разброс», «х»: [1,2], «у»: [3,4]}]} .
Объекты графиков по сравнению со словарями¶
fig ["layout"] ), так и с помощью доступа к свойствам в стиле класса (например, fig ["layout"] ). г.
г. рис. Макет ). .update_layout () , .add_trace () и т. Д.). go.Figure (layout_title_text = «The Title») , а не dict (layout = dict (title = dict (text = «The Title»))) ) для более компактного кода..show () ) и функции экспорта ( .write_image () ), которые автоматически вызывают соответствующие функции из модуля plotly.io . Когда использовать объекты графика или Plotly Express¶
plotly., поэтому каждая фигура, созданная с помощью библиотеки  graph_objects.Figure
graph_objects.Figure plotly , фактически использует графические объекты под капотом, если только не создается вручную из словарей. или изоповерхность . Кроме того, некоторые фигуры сложно создавать, начиная с фигуры, созданной с помощью Plotly Express, например фигуры с частями разных типов, двухосные графики или фасеточные графики с несколькими различными типами трасс. Чтобы построить такие фигуры, может быть проще начать с пустого графически.graph_objects. Изобразите объект (или объект, сконфигурированный с подзаголовками с помощью функции make_subplots ()) и постепенно добавляйте трассировки и обновляйте атрибуты, как указано выше. На каждой странице документации plotly вверху отображается опция Plotly Express, если существует функция Plotly Express для создания рассматриваемого типа диаграммы, а затем — версия графических объектов ниже.
update_ * и add_ * . Сравнение графических объектов и графического выражения¶
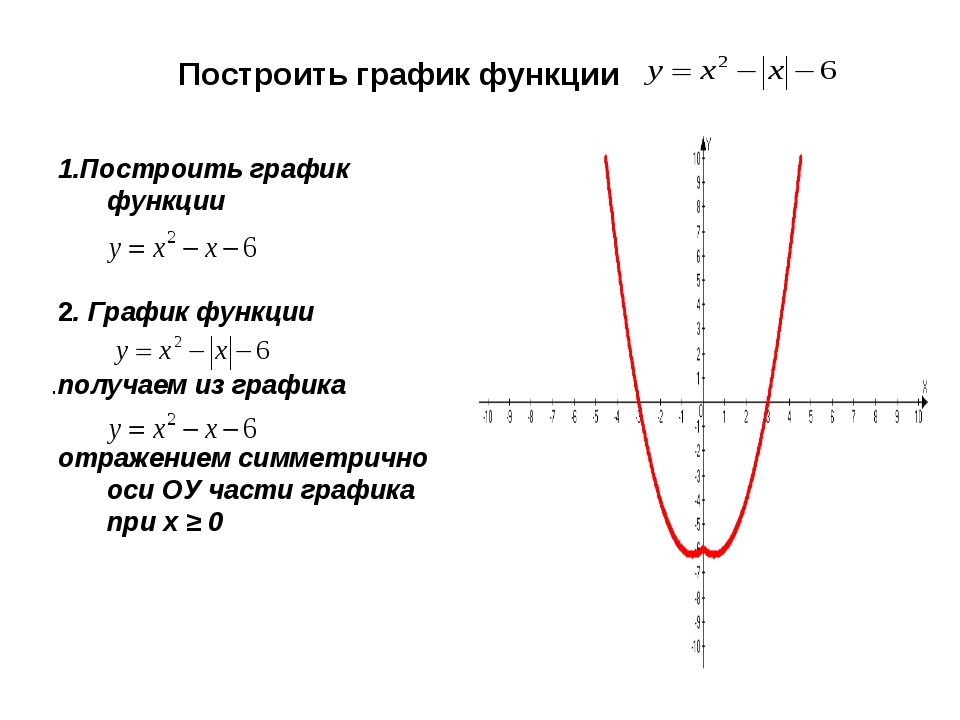
Обратные функции: Определение / Чертеж Обратные
Чертеж
Обратное из графика (стр.
1 из 7) 
 Обратный график — синие точки ниже:
Обратный график — синие точки ниже: Вы можете использовать это отношение
если вам дается случайный график и просят построить обратный график. авторское право
Элизабет Стапель 2000-2011 Все права защищены
Вы можете использовать это отношение
если вам дается случайный график и просят построить обратный график. авторское право
Элизабет Стапель 2000-2011 Все права защищены
 .. и подключите
точек:
.. и подключите
точек:
Purplemath .Доступно с https://www.purplemath.com/modules/invrsfcn.htm .
Дата обращения [Дата] [Месяц] 2016 г. экспорт — JavaScript | MDN
экспорт при создании модулей JavaScript для экспорта живых привязок к функциям, объектам или
примитивные значения из модуля, чтобы они могли использоваться другими программами с импорт выписка. Значение импортированной привязки
может быть изменен в модуле, который его экспортирует. Когда модуль обновляет значение
привязка, которую он экспортирует, обновление будет отображаться в импортированном значении.
Значение импортированной привязки
может быть изменен в модуле, который его экспортирует. Когда модуль обновляет значение
привязка, которую он экспортирует, обновление будет отображаться в импортированном значении.
экспорт let name1, name2,…, nameN;
экспорт let name1 =…, name2 =…,…, nameN;
функция экспорта functionName () {...}
экспорт класса ClassName {...}
экспорт {имя1, имя2,…, имяN};
экспорт {переменная1 как имя1, переменная2 как имя2,…, имяN};
экспорт const {имя1, имя2: бар} = o;
экспортировать выражение по умолчанию;
функция экспорта по умолчанию (…) {…}
экспортировать функцию по умолчанию name1 (…) {…}
экспорт {имя1 по умолчанию,…};
экспорт * из…;
экспорт * как name1 из…;
экспорт {имя1, имя2,…, имяN} из…;
экспорт {импорт1 как имя1, импорт2 как имя2,…, имяN} из…;
экспорт {по умолчанию,…} из…;
наименование N импортировать в другом скрипте).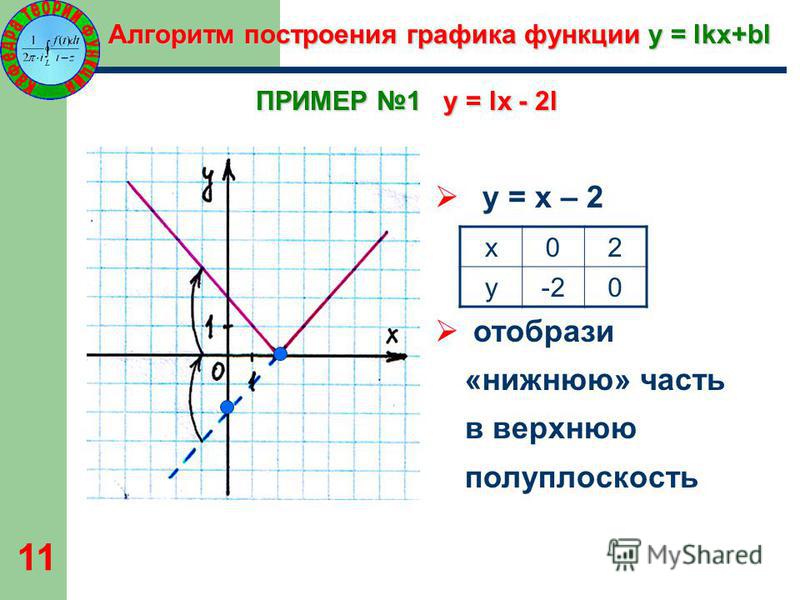
экспорт {myFunction, myVariable};
экспорт let myVariable = Math.sqrt (2);
функция экспорта myFunction () {};
экспорт {myFunction по умолчанию};
функция экспорта по умолчанию () {}
экспорт класса по умолчанию {.. }
пусть k; экспорт по умолчанию k = 12;
импортировать m из './test';
console.  log (м);
log (м);
экспорт {myFunction as function1,
myVariable как переменная};
Реэкспорт / агрегирование
экспорт {по умолчанию как функция1,
function2} из bar.js;
import {по умолчанию как function1,
function2} из bar.js;
экспорт {функция1, функция2};
function1 и function2 недоступны
внутри текущего модуля.
импортировать DefaultExport из bar.  js;
js;
экспорт DefaultExport из bar.js;
экспорт {по умолчанию как DefaultExport} из bar.js;
как маркер ; тем не мение
это будет означать, что элемент по умолчанию не может быть импортирован как именованный импорт:
экспорт {по умолчанию, функция2} из панели.js ';
Использование именованного экспорта
my-module.js мы могли бы включить следующий код:
function cube (x) {
вернуть х * х * х;
}
const foo = Math.PI + Math.SQRT2;
var graph = {
опции: {
белый цвет',
толщина: '2px'
},
draw: function () {
console.log ('Из функции рисования графика');
}
}
экспорт {cube, foo, graph};
импортировать {cube, foo, graph} из '.  /my-module.js ';
graph.options = {
цвет синий',
толщина: '3px'
};
graph.draw ();
console.log (куб (3));
console.log (foo);
/my-module.js ';
graph.options = {
цвет синий',
толщина: '3px'
};
graph.draw ();
console.log (куб (3));
console.log (foo);
 «Открытие новых знаний»
«Открытие новых знаний»
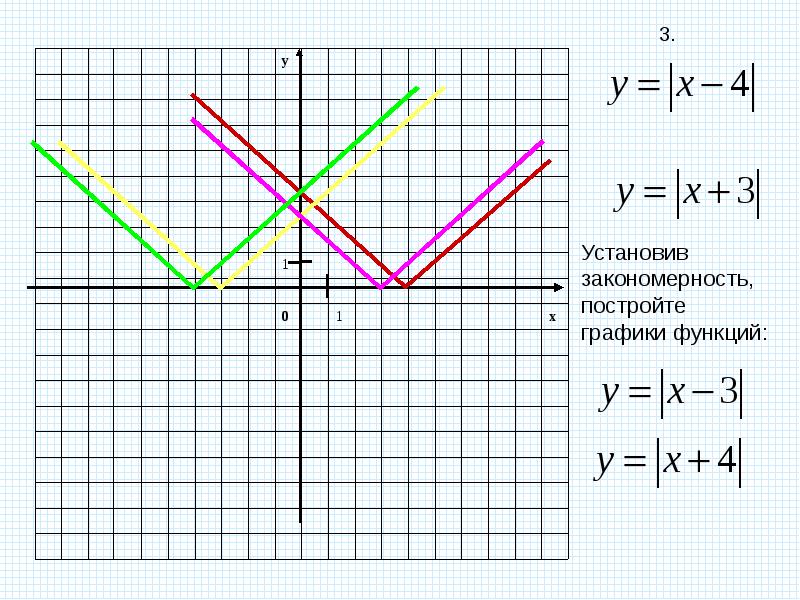
 Все, что было над осью Oх зеркально отражается вниз.
Все, что было над осью Oх зеркально отражается вниз. д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. С его помощью укажите пути функции,
интервалы знакопостоянства, промежутки
монотонности, наибольшее и наименьшее
значения функции, область значений
функции:
С его помощью укажите пути функции,
интервалы знакопостоянства, промежутки
монотонности, наибольшее и наименьшее
значения функции, область значений
функции: