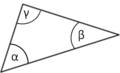Історія геометрії — Вікіпедія

Геометрія — (від дав.-гр. γεωμετρία; гео- «земля», -метрон «вимірювання» або одним словом означає землемірство) виникла як область знань пов’язана із вивченням просторових вимірювань.

Першими «землемірами» були стародавні єгиптяни. Сільське господарство могло розвиватись лише біля річки Ніл. Щороку Ніл розливався, приносячи на землі, які були залиті водою, плодючий мул. Кожен селянин мав наділ землі певної площі, однак розливи ріки не дозволяли раз і назавжди визначити межі кожного наділу, тому після чергового розливу доводилось визначати земельну ділянку заново. Це виконували землеміри — люди, що за допомогою шнура відміряли кожному селянину ділянку з площею, яка була йому приписана. Стародавні єгиптяни не знали циркуля, його винайшли греки. Однак це їм особливо не перешкоджало. Так, прямий кут вони будували мотузкою, що має довжину 12 мір. За допомогою цієї мотузки можна побудувати трикутник зі сторонами 3, 4 і 5 мір. Такий трикутник за теоремою Піфагора є прямокутним. Тому прямокутний трикутник також називають єгипетським.

У Стародавній Греції, починаючи з 7 століття до н. е., з часів Фалеса Мілетського, починається новий етап розвитку геометрії. Вона набуває характерного для неї абстрактного напряму, у ній виникає доведення. Грецький мислитель мілетської школи Анаксимандр здійснив першу спробу створення систематичного курсу для викладання геометрії. Перетворення це відбулося шляхом абстрагування від будь-яких властивостей тіл, крім взаємного положення і величини. Наукою геометрія стала, коли від набору рецептів перейшли до встановлення загальних закономірностей. Подальші спроби побудови систематичних курсів математики належать Гіппократу Хіоському, Феодору Кіренському, Архіту Тарентському, Евдоксу Кнідському та багатьом іншим вченим. Вони створили математичну основу для подальшого розвитку науки, теоретичного природознавства і філософії Давньої Греції. Греки склали перші систематичні і доказові праці з геометрії, великий внесок зробили Евклід, Архімед, Аполлоній Перзький.

Центральне місце серед них займають складені близько 300 до н. е. «Начала» Евкліда. Ця праця і понині залишається зразковим викладенням у дусі аксіоматичного методу: всі положення виводяться логічним шляхом з невеликого числа явно зазначених і не доводимих припущень — аксіом. Геометрія греків, звана сьогодні евклідовою, або елементарною, займалася вивченням простих форм: прямих, площин, відрізків, правильних багатокутників і багатогранників, конічних перерізів, а також куль, циліндрів, призм, пірамід і конусів. Обчислюються їхні площі і об’єми. Перетворення в основному обмежувалися геометричною подібністю.

Середні віки небагато дали геометрії, і наступною великою подією в її історії стало відкриття Рене Декартом (1596—1650) і П’єром Ферма (1601—1665) в XVII столітті координатного методу («Міркування про метод», 1637). Точкам зіставляються набори чисел, це дозволяє вивчати відносини між формами методами алгебри. Так з’явилася аналітична геометрія, що вивчає фігури і перетворення, які в координатах задаються алгебраїчними рівняннями. Приблизно одночасно з цим Блезом Паскалем і Жераром Дезаргом (1591—1661) почато дослідження властивостей плоских фігур, що не міняються при проектуванні з однієї площини на іншу. Цей розділ отримав назву проективної геометрії. Метод координат лежить з розвитком математичного аналізу ліг в основу нового підходу, що з’явився трохи пізніше, — диференціальної геометрії, де фігури і перетворення все ще задаються в координатах, але вже довільними досить гладкими функціями. Властивості цих фігур вивчаються за допомогою моці й гнучкості апарату аналізу.

Остаточне оформлення і систематичний виклад цих нових напрямів геометрії дані в XVIII — на початку XIX століття Леонардом Ейлером (1707—1783) для аналітичної геометрії (1748), Гаспаром Монжем для диференціальної геометрії (1795), Жан-Віктором Понселе для проективної геометрії (1822), причому саме вчення про геометричне зображення (у прямому зв’язку із завданнями креслення) було ще раніше (1799) розвинене і приведене в систему Монжем у вигляді нарисної геометрії. У всіх цих нових дисциплінах основи (аксіоми, початкові поняття) геометрії залишалися незмінними, коло ж фігур, що вивчаються, і їхніх властивостей, а також використаних методів розширювався.

XIX сторіччя дало два значних прориви у розвитку науки. Дослідження Миколи Лобачевського, Яноша Больяї і Карла Гауса відкрили несуперечність неевклідової геометрії, в якій знаменитий п’ятий постулат Евкліда замінений на зворотне твердження. Фелікс Клейн зв’язав всі види геометрій, згідно з ним геометрія вивчає всі ті властивості фігур, які інваріантні щодо перетворень з певної групи. При цьому кожна група задає свою геометрію. Так, ізометрії (руху) задає евклідову геометрію, група афінних перетворень — афінну геометрію, група проективних перетворень — проективну геометрію, група конформних перетворень — конформну геометрію тощо.

Двома визначними майстрами досліджень в геометрії цього часу були Бернгард Андре де Ріман, який працював переважно з інструментами математичного аналізу і ввів Ріманові поверхні, та Анрієс Пунаанкарде, засновник алгебраїчної топології і геометричної теорії динамічних систем.

Наслідком цих великих змін в геометричних поглядах концепція «простору» стала значно багатша і різноманітніша, і перетворилася на природну основу таких різних теорій, як комплексний аналіз чи класична механіка. Традиційні види геометрій були визнані як загальний однорідний простір, такий простір, який має достатню кількість симетрій, так щоб погляд з одної чи іншої точки давав той самий вид.

Афінна геометрія — Вікіпедія

Афі́нна геоме́трія (лат. affinis — споріднений) — розділ геометрії, що вивчає властивості геометричних фігур, інваріантні (незмінні) відносно афінних перетворень, тобто таких взаємно однозначних точкових відображень евклідової площини на евклідову площину або евклідового простору на самого себе, при яких прямі переходять у прямі. Афінне перетворення зберігає величину відношення двох відрізків прямої, паралельність прямих і площин.

У декартових координатах афінне перетворення площини в себе виражається формулами:

• х’ = а₁х + b₁y + с₁
• у’ = а₂х + b₂у + с₂

причому a₁b₂ — a₂b₁ ≠ 0.

Тут х, у — координати довільної точки М; х’, у’ — координати її образу.

Афінні перетворення, а значить і афінна геометрія, широко застосовуються в геометрії і прикладних науках (теорія пружності та ін.).

У 1748 році Ейлер ввів термін «афінний»(лат. affinis ‘зв’язний’).Властивості геометричних фігур, які переходять одна в одну при афінних перетвореннях, вивчалися А. Ф. Мебіусом в першій половині XIX століття: у 1827 році вийшла його книга «Барицентричне обчислення».

Після Ерлангенської програми Фелікса Кляйна, афінна геометрія була визнана як узагальнення Евклідової геометрії.

У 1912 році Б. Е. Вільсон і Гілберт Ньютон Льюїс розробили афінну геометрію для вираження спеціальної теорії відносності.

У 1984 році «афінні площини, пов’язані з Лоренцевим векторним простором L2» були описані Г. Бірманом і Кацумі Номідзу у статті під назвою «Тригонометрія в геометрії Лоренца».

Були висунуті кілька аксіоматичних підходів до афінної геометрії:

Закон Паппа[ред. | ред. код]

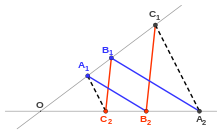Закон Паппа: якщо червоні прямі паралельні і сині прямі паралельні, то пунктирні чорні прямі повинні бути паралельні.

Оскільки афінна геометрія має справу з паралельними прямими, одна з властивостей паралельних прямих, зазначених Паппа Олександрівським, була прийнята як передумова:

• Якщо A,B,C{\displaystyle A,B,C} знаходяться на одній прямій, а A′,B′,C′{\displaystyle A’,B’,C’} на інший, то

(AB′∥A′B ∧ BC′∥B′C)⇒CA′∥C′A.{\displaystyle (AB’\parallel A’B\ \land \ BC’\parallel B’C)\Rightarrow CA’\parallel C’A.}

Повна система аксіом передбачає точку, пряму і пряму, що містить точку; примітивні поняття:

• Дві точки лежать на одній прямій.

• Для будь-якої прямої L і будь-якої точки p, яка не належить L, є тільки одна пряма, що містить p і не містить жодної точки прямої L. Ця пряма називається паралельною до прямої L.

• Кожна пряма містить принаймні дві точки.

• Існують принаймні три точки, які не належать одній прямій.

Згідно Г. С. М. Коксетера: Цікавість цих п’яти аксіом посилюється тим, що вони можуть бути поширені на величезну кількість тверджень, проведених не тільки в Евклідовій геометрії, але і в геометрії Мінковського простору і часу (у простому випадку 1 + 1 вимірах, в той час як спеціальна теорія відносності вимагає 1 + 3)Розширення геометрії Евкліда або Мінковського досягається шляхом додавання різних додаткових аксіом ортогональності тощо.

Різні типи афінної геометрії відповідають тому, що інтерпретація береться для обертання. Геометрія Евкліда відповідає звичайній ідеї обертання, в той час як геометрія Мінковського відповідає гіперболічному оберту. Що стосується перпендикулярних ліній, вони залишаються перпендикулярними, якщо площина піддається звичайному обертанню. У геометрії Мінковського, лінії, які є гіперболічно-ортогональними залишаться в цьому відношенні, якщо площина піддається гіперболічному обертанню.

Впорядкована структура[ред. | ред. код]

Аксіоматика афінної геометрії може бути побудована з аксіом впорядкованої геометрії шляхом додавання двох додаткових аксіом:

1. (Афінна аксіома паралельності) дана точка A і пряма r, яка не проходить через точку А, існує не більше однієї прямої, яка проходить через точку А, що не задовольняє прямій r.
2. (Теорема Дезарга) дано сім різних точок A, A’, B, B’, C, C’, O, таких що AA’, BB’, та CC’ відмінні прямі, які проходять через точку O та AB паралельна A’B’ та BC паралельна B’C’, тоді AC паралельна A’C’.

Афінне поняття паралельності утворює відношення еквівалентності для прямих. Так як аксіоми впорядкованої геометрії, представленої тут, включають в себе властивості, які передбачають структуру дійсних чисел, ці властивості переносяться, так що це аксіоматизація афінної геометрії над полем дійсних чисел.

Геометрично, афінне перетворення (спорідненості) зберігає колінеарність: так воно перетворить паралельні прямі в паралельні прямі і збереже відношення відстаней уздовж паралельних прямих.

Ми визначаємо, як афінну теорему будь-який геометричний результат, який інваріантний щодо афінної групи (в Ерлангенській програмі Фелікса Кляйна, це його основна група перетворень симетрії для афінної геометрії). Розглянемо в лінійному просторі V, загальну лінійну групу GL(V).Це не вся афінна група, тому що ми повинні дозволити також перетворення вектора v із V. (Подібне перетворення карти будь-якого w із V в w + v.) Афінна група породжена загальною лінійною групою, а перетворення і справді їх напівпрямий добуток V⋊GL(V){\displaystyle V\rtimes \mathrm {GL} (V)}.

Наприклад, теореми з планіметрії про збіг прямих в трикутнику, що з’єднують кожну вершину з серединою протилежної сторони (у центр ваги або барицентр) залежать від поняття медіани і центра ваги як афінних інваріантів. Інші приклади теорем Чеви і Менелая.

Афінні інваріанти також можуть допомогти в обчисленні. Наприклад, прямі, які ділять площину трикутника на дві рівні частини, утворюють обгортку всередині трикутника. Відношення площі обгортки до площі трикутника є афінним інваріантом, і тому необхідно обчислювати простий випадок, такий як, одиничний рівнобедрений прямокутний трикутник дає 34loge⁡(2)−12,{\displaystyle {\tfrac {3}{4}}\log _{e}(2)-{\tfrac {1}{2}},} тобто 0.019860… або менше, ніж 2 %, для всіх трикутників. Знайомі формули, такі як: половина добутку основи на висоту — площа трикутника, або одна третя частина основи на висоту — об’єм піраміди, також афінні інваріанти. Остання є менш очевидною, ніж перша, в загальному випадку легко бачити, для однієї шостої частини одиничного куба, утвореного гранню (площа 1) і середньою точкою куба (висота 1/2). Отже, вона вірна для всіх пірамід, навіть для косих, вершина яких знаходиться не прямо над центром основи, і з основою паралелограм замість квадрата. Формула надалі узагальнюється на піраміди, основа яких може бути поділена на паралелограми, дозволяючи нескінченно багато паралелограмів (з урахуванням конвергенції). Такий же підхід показує, що чотиривимірна піраміда має об’єм 4D — одна чверть добутку 3D-об’єму основи її паралелепіпеда на висоту, і так далі для більш високих розмірностей.

Евклідова геометрія — Вікіпедія

Евклі́дова геоме́трія — геометрична теорія, заснована на системі аксіом, вперше викладеній у підручнику «Начала» Евкліда (давньогрецькою: Στοιχεῖα Stoicheia, III століття до н. е.). Метод Евкліда полягає в прийнятті невеликого набору інтуїтивно зрозумілих аксіом і виведення з них багатьох інших теорем. Хоча багато визначень Евкліда були висловлені іншими математиками, Евклід був першим, хто показав, як ці пропозиції могли б використовуватися у всеосяжну дедуктивну та логічну систему. «Начала» починаються з планіметрії, яка і до сьогодні вивчається у середній школі як аксіоматика і базується на доведеннях. Більша частина «Начал» вказує на доведення того, що зараз називають алгеброю та теорією чисел.

Більше двох тисяч років прикметник «евклідова» був непотрібним, оскільки жодна інша форма геометрії ще не існувала. Аксіоми Евкліда здавались настільки очевидними (за винятком аксіоми паралельності), що будь-яка теорема, що випливала з них, вважалася вірною в абсолютному, часто метафізичному сенсі. Сьогодні відомо багато інших несуперечливих неевклідових геометрій, перші з яких з’явилися на початку 19 ст. Зокрема, із загальної теорії відносності Альберта Ейнштейна слідує що фізичний простір неевклідовий, а евклідовий простір для нього існує лише там, де слабке гравітаційне поле.

Евклідова геометрія є прикладом аналітичної геометрії, оскільки вона логічно йде від аксіом до тверджень без використання координат(на відміну від аналітичної геометрії, яка їх використовує).

«Начала» вважаються систематизацією попередніх знань з геометрії. Оскільки його новіші видання були одразу загальновизнаними, і не було попиту у минулих версіях, на сьогодні майже всі вони втрачені. «Начала» складаються з 13 книг: У I-IV та VI книгах йдеться про планіметрію. Доведено багато результатів щодо плоских фігур, наприклад: теорема Піфагора «У прямокутному трикутнику сума квадратів катетів дорівнює квадрату гітотенузи». (Книга I, постулат 47). V і VII-X книги стосуються теорії чисел, причому числа геометрично обробляються через їхні подання у вигляді ліній різної довжини. У них вводяться такі поняття, як прості, раціональні та ірраціональні числа. Також доводиться нескінченність простих чисел. XI-XIII книги стосуються cтереометрії. Типовим прикладом є співвідношення 1/3 між об’ємом конуса та циліндра з однаковою висотою та основою.

Аксіоматика[ред. | ред. код]

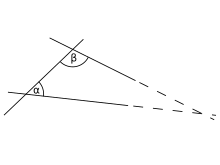Про паралельні прямі (Постулат 5): Якщо пряма, що перетинає дві інші прямі, утворює внутрішні односторонні кути, які менші, ніж два прямі кути, то ці дві прямі перетнуться як завгодно далеко з тієї сторони, де кути (давньогрецькою:Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ’ ἄπειρον συμπίπτειν, ἐφ’ ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες).

Проблема повної аксіоматизації елементарної геометрії — одна з проблем геометрії, що виникла у Стародавній Греції у зв’язку з критикою цієї першої спроби побудувати повну систему аксіом так, щоб всі твердження евклідової геометрії з цих аксіом були чисто логічним висновком без додаткових пояснень.

У «Началах» Евкліда, була дана наступна аксіоматика:

1. Від усякої точки до всякої точки можна провести пряму лінію.
2. Обмежену лінію можна безперервно продовжувати до прямої.
3. З усякого центра довільним розхилом циркуля може бути описане коло.
4. Усі прямі кути рівні між собою.
5. Якщо пряма, що перетинає дві прямі, утворює внутрішні односторонні кути, які менші ніж два прямі кути, то ці дві прямі, продовжені необмежено, зустрінуться з тієї сторони, де кути менші за два прямі (див. Аксіома паралельності Евкліда).

Дослідження системи аксіом Евкліда в другій половині XIX століття показало її неповноту. У 1899 році Давид Гільберт запропонував першу достатньо строгу аксіоматику евклідової геометрії. Спроби поліпшення евклідової аксіоматики робилися і до Гільберта, проте підхід Гільберта, при всій його консервативності у виборі понять, виявився найуспішнішим.

Евклідова геометрія базується на конструктивному доведенні. Аксіоми 1, 2, 3 та 5 стверджують про існування та унікальність певних геометричних фігур, і ці твердження носять конструктивний характер: тобто ми не лише сказали про існування певних речей, але й довели це. У цьому сенсі Евклі́дова геометрія більш конкретна, ніж багато сучасних аксіоматичних систем, таких як теорія множин, які часто стверджують про існування об’єктів, не кажучи, як їх побудувати, або навіть стверджують про існування об’єктів, які не можуть бути побудовані в рамках теорії. Іншими словами, лінії на папері є моделями об’єктів, визначених у формальній системі, а не прикладами цих об’єктів. Наприклад, Евклі́дова пряма не має ширини, але будь-яка реальна намальована лінія матиме. Хоча майже всі сучасні математики вважають неконструктивні методи настільки ж конструктивними, конструктивні докази Евкліда часто витісняють помилкові неконструктивні.

Евклід часто використовував у своїй праці доведення від супротивного. Евклідова геометрія використовує також метод суперпозицій, в якому фігура переміщується на іншу точку простору. Наприклад, пропозиція I.4, конгруенція трикутників бічним кутом, доведена шляхом переміщення одного з двох трикутників так, що одна з його сторін збігається з такою ж за розміром стороною іншого трикутнику, доводить, що інші сторони також збігаються. Деякі сучасні методи додають шостий постулат — жорсткість трикутника, яку можна використовувати як альтернативу суперпозиції.

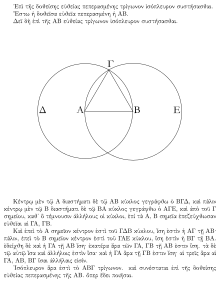Одне з доведень із «Елементів» Евкліда: враховуючи лінійний сегмент, існує рівносторонній трикутник, який включає сегмент як одну з його сторін. Конструктивне доведення: рівносторонній трикутник ΑΒΓ зроблений шляхом нанесення кругів Δ і Ε, центрованих по точкам А і В, і взяття одного перетину кругів як третьої вершини трикутника.

Система вимірювання та арифметика[ред. | ред. код]

Евклідова геометрія має два основних типи вимірювань: кут і відстань. Кутова шкала абсолютна, і Евклід використовує прямий кут як його базову одиницю так, що, наприклад, кут у 45° градусів називають половиною прямого кута. Шкала відстані відносна: один довільно вибраний сегмент лінії з певною ненульовою довжиною береться за одиницю, а інші відстані виражаються відносно нього. Додавання відстаней представлено конструкцією, в якій один рядок сегмента копіюється на кінці іншого сегмента лінії, щоб збільшити його довжину, і аналогічно для віднімання.

Вимірювання площі та об’єму визначаються за допомогою поняття відстані. Наприклад, прямокутник з шириною 3 і довжиною 4 має ділянку, яка дорівнює 12. Через те, що ця геометрична інтерпретація множення була обмежена трьома вимірами, не було прямого способу інтерпретації добутку з чотирьох або більше значень, і Евклід уникав таких добутків, хоча саме вони вказані у доведенні книги IX, пропозиції 20.

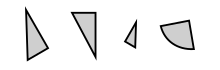Приклад конгруентності: дві фігури ліворуч є конгруентними, а третя — подібною до них. Остання фігура не конгруентна з ними. Конгруентність змінює деякі властивості, такі як місце розташування та орієнтація, але залишають інші незмінними, наприклад, відстані та кути. Останні властивості називаються інваріантами, і їх вивчення є сутністю геометрії.

Евклід трактує пари ліній або пари фігур на площині як «рівні» (ἴσος), якщо їх довжини, площі або об’єми рівні, аналогічно для кутів. Більш сильний термін «конгруентний» означає, що фігура буде однакова за розміром і формою щодо іншої фігури. Інше визначення конгруентності двох фігур полягає в тому, що їх можна сумістити одну з іншою за допомогою руху (допускається віддзеркалення фігури). Наприклад, прямокутник 2×6 і прямокутник 3×4 рівні, але не конгруентні, а буква R конгруентна зі своїм дзеркальним відображенням. Фігури, які будуть конгруентними, за винятком їх різного розміру, називаються подібними. Відповідні кути в парі подібних фігур є конгруентними, а відповідні сторони пропорційні одна одній.

Позначення та термінологія[ред. | ред. код]

Означення точок та фігур[ред. | ред. код]

Точки зазвичай називають «великими літерами алфавіту». Інші фігури, такі як лінії, трикутники або кола, називаються переліком достатньої кількості точок, щоб однозначно їх вибирати з відповідного значення, наприклад, трикутник ABC, як правило, буде трикутником з вершинами в точках A, B і C .

Комплементарні та суміжні кути[ред. | ред. код]

Кути, сума яких є прямим кутом, називаються комплементарними. Комплементарні кути утворюються, коли промінь ділиться однією вершиною і орієнтований у напрямку, що знаходиться між двома вихідними променями, які утворюють правий кут. Кількість променів між двома променями є нескінченною.

Кути, сума яких дорівнює 180 градусів, називають суміжними. Суміжні кути утворюються, коли промінь ділиться однією вершиною і орієнтований у напрямку між двома вихідними променями, які утворюють прямий кут (кут 180 градусів). Кількість променів між двома оригінальними променями є нескінченною.

Сучасні версії фігур Евкліда[ред. | ред. код]

У сучасній термінології кути, як правило, вимірюються в градусах чи в радіанах.

Сучасні шкільні підручники часто визначають окремі фігури: лінії (нескінченні), промені (напівнескінченні) та лінійні сегменти (кінцевої довжини). Евклід, замість того, щоб говорити про промінь як про об’єкт, що поширюється до нескінченності в одному напрямку, зазвичай використовує такі означення, як «лінія, проведена до достатньої довжини», хоча іноді вона називається «нескінченною». «Лінія» в «Началах» може бути як прямою, так і криволінійною, і при необхідності він використовував більш конкретний термін «пряма лінія».

Деякі важливі або відомі результати[ред. | ред. код]

• 

  Tеорема про суму кутів у трикутнику доводить, що сума трьох кутів будь-якого трикутника (у цьому випадку кутів α, β і γ) завжди дорівнює 180 градусів.

• 

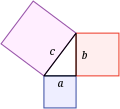
  Теорема Піфагора вказує на те, що сума квадратів катетів (a і b) дорівнює квадрату гіпотенузи(c).

Теорема про рівнобедренний трикутник[ред. | ред. код]

Теорема про міст віслюків стверджує, що трикутник, в якому дві сторони (бічні) рівні між собою, а також кути при основі рівні між собою, називають рівнобедренним. За означенням, правильний трикутник також є рівнобедреним, але обернене твердження не є правильним. Одне з походжень назви цієї теореми: геометрична фігура схожа на крутий міст, водночас схожу лише на віслюка.

Конгруентність трикутників[ред. | ред. код]

Конгруентність трикутників визначається шляхом визначення двох сторін і кута між ними (SAS), двома кутами та сторони між ними (ASA) або двома кутами та відповідною суміжною стороною ( AAS). Проте, якщо вказати дві сторони та сусідній кут (SSA), можна отримати два різні можливі трикутники, якщо вказаний кут не є прямим.

Tеорема про суму кутів у трикутнику[ред. | ред. код]

Сума кутів трикутника дорівнює куту 180 градусів. Наслідком з цього є те, що рівносторонній трикутник має три внутрішні кути по 60 градусів. Крім того, кожен трикутник має принаймні 2 гострі кути.

Теорема Піфагора[ред. | ред. код]

У знаменитій теоремі Піфагора (книга I, постулат 47) сказано, що в будь-якому прямокутному трикутнику квадрат гіпотенузи (сторони, протилежної прямокутному куту), дорівнює сумі квадратів катетів (сторін, які перетинаються під прямим кутом).

Теорема Фалеса[ред. | ред. код]

Теорема Фалеса, названа на честь Фалеса з Мілета, говорить, що якщо А, В та С є точками в колі, де лінія АС є діаметром кола, то кут АВС — прямий кут. Кантор вважав, що Фалес довів свою теорему за допомогою книги Евкліда I, Постулату 32.

Через фундаментальний статус евклідової геометрії в математиці, було б неможливо не дати більш репрезентативну вибірку застосувань його «Начал» у цьому розділі.

Застосування евклідової стереометрії полягає у визначенні механізмів пакування, таких як проблема пошуку найефективнішого пакування куль n розмірностей.

Геометрична оптика використовує евклідову геометрію для аналізу фокусування світла об’єктивами та дзеркалами.

Застосування в описі структури простору[ред. | ред. код]

Евклід вважав, що його аксіоми були очевидними твердженнями про фізичну реальність. Евклідові доведення залежали від припущень, які, можливо, не були очевидними в його основних аксіомах. Враховуючи фізичний опис простору, постулат 2 стверджує, що простір однорідний і необмежений; постулат 4 (про рівність прямокутників) говорить про те, що простір є ізотропним, а фігури можуть бути перенесені в будь-яке місце, зберігаючи конгруентність, і постулат 5 (Аксіома паралельності Евкліда), вказує на те, що простір не має власної кривизни. Але теорія відносності Ейнштейна суттєво змінює цю точку зору.

Неоднозначний характер аксіом, сформульований Евклідом, дає змогу різним аналітикам не погодитися з деякими їхніми наслідками для структури простору, наприклад, чи є вона нескінченною і яка її топологія. Сучасні, переформулювання системи, як правило, спрямовані на відокремлення цих питань. Інтерпретуючи аксіоми Евкліда у стилі більш сучасного підходу, аксіоми 1-4 узгоджуються або з нескінченним, або зі скінченними просторами (як в геометрії Рімана), і всі п’ять аксіом збігаються з різними топологіями (наприклад, площиною, циліндром , чи тором для двовимірної евклідової геометрії).

Класичні теореми[ред. | ред. код]

Аналітична геометрія — Вікіпедія

Аналіти́чна геоме́трія — розділ геометрії, в якому властивості геометричних об’єктів (точок, ліній, поверхонь) установлюють засобами алгебри за допомогою методу координат, тобто шляхом дослідження властивостей рівнянь, які і визначають ці об’єкти. Основні положення аналітичної геометрії вперше сформулював філософ і математик Рене Декарт 1637 року. Лейбніц, Ісаак Ньютон і Леонард Ейлер надали аналітичній геометрії сучасної структури.

Стародавня Греція[ред. | ред. код]

Грецький математик Менехм розв’язував задачі і доводив теореми використовуючи методи, які дуже подібні до використання координат, і іноді висловлювалася думка, що саме він започаткував аналітичну геометрію.^[1]

Аполлоній Перзький, в книзі On Determinate Section, розв’язує задачі у спосіб, який би можна було назвати аналітичною геометрією для одного виміру; де він знаходить точки на прямій, які співвідносяться із іншими.^[2] У роботі Conics Аполлоній далі розвинув метод, так що він ще більше нагадує аналітичну геометрію. Так що іноді вважають, що його робота попередила роботи Декарта приблизно на 1800 років. Його застосування прямих відліку, діаметра і дотичної істотно не відрізняється від сучасного використання координатної системи відліку, де відстані виміряні здовж діаметру від точки дотику є абсцисами, а відрізки паралельні дотичній і поділені між віссю і кривою є ординатами. Далі він побудував відношення між абсцисами і відповідними ординатами, які є еквівалентними теоретичним рівнянням кривих. Однак, хоча Аполлоній впритул наблизився до понять аналітичної геометрії, він не зміг це довести до логічного завершення, оскільки він не брав до уваги від’ємні величини і кожного разу його система координат була прив’язана до даної кривої. Таким чином, рівняння визначалися кривими, а не криві — рівняннями. Координати, змінні і рівняння були допоміжними поняттями, які застосовувалися до певної окремої геометричної ситуації.^[3]

Західна Європа[ред. | ред. код]

Створення аналітичної геометрії зазвичай приписують Рене Декарту, який виклав її основи в La Geometrie (Геометрія) , одного з трьох додатків, опублікованих в 1637 році разом зі своїм трактатом Міркування про метод. Спочатку робота не була добре прийнята, але після переведення латинською та додавання коментарів ван Схотена в 1649, трактат Декарта отримав належне визнання.

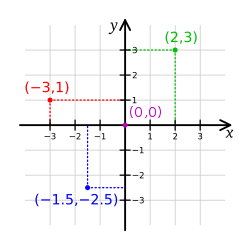Ілюстрація декартової системи координат. Чотири відмічені точки позначені їх координатами: (2,3) зеленим, (−3,1) червоним, (−1.5,−2.5) синім, і початок координат (0,0) пурпуровим.

В аналітичній геометрії, двовимірний простір задається системою координат, в якій кожна точка маж пару координат у формі дійсних чисел. Аналогічним чином, Евклідів простір представлено координатами, де кожна точка має три координати. Значення координат залежить від вибору точки початкового відліку. Існує велика кількість різних систем координат, але найбільш загальними є наступні:^[4]

Декартові координати (на площині або в просторі)[ред. | ред. код]

Найбільш поширеною системою координат, яку використовують є Декартова система координат, в якій кожна точка має x-координату, яка задає її горизонтальну позиції та y-координату, яка задає її вертикальну позицію. Вони як правило записуються як впорядкована пара (x, y). Цю систему можна використовувати і для тривимірної геометрії, де кожна точка в Евклідовому просторі представляється впорядкованою трійкою координат (x, y, z).

Полярні координати (на площині)[ред. | ред. код]

У полярній системі координат, кожна точка на площині представлена її відстанню r від початку координат і її кутом θ від полярної осі.

Циліндричні координати (у просторі)[ред. | ред. код]

У циліндричних координатах, кожна точка простору задається її висотою z, радіусом r від осі z та кутом θ відносно її проекції на площину xy по відношенню до горизонтальної осі.

Сферичні координати (у просторі)[ред. | ред. код]

У сферичних координатах, кожна точка в просторі представлена її відстанню ρ від початку відліку, кутом θ її проекції на xy-площину по відношенню до горизонтальної осі, і кутом φ яку вона утворює із віссю z. Назви кутів у фізиці як правило можуть бути обернені навпаки.^[4]

Характерною особливістю аналітичної геометрії є визначення геометричних фігур рівняннями. Нехай на площині з осями координат OX і OY (прямокутна декартова система координат) маємо лінію l. Якщо вздовж l пересувати точку M, то координати x, y цієї точки будуть змінюватись, але між ними існуватиме певна залежність, яку можна записати у вигляді рівняння:

f(x,y)=0{\displaystyle f(x,y)=0\,},

де f(x,y){\displaystyle f(x,y)} є математичний вираз, що містить змінні x і y або одну з них.

Наприклад, з прямокутного трикутника OMP виводимо, що рівняння кола K радіуса г з центром в початку координат 0 є

x2+y2−r2=0{\displaystyle x^{2}+y^{2}-r^{2}=0}.

Розглянемо ще пряму АВ. Якщо М є довільна її точка і OA = a, OB = b, то PA = a — x. З подібності прямокутних трикутників MPA і BOA маємо:

ya−x=ba{\displaystyle {\frac {y}{a-x}}={\frac {b}{a}}}.

Звідси дістаємо рівняння прямої АВ:

bx+ay−ab=0{\displaystyle bx+ay-ab=0\,}.

В аналітичній геометрії приймають, що рівняння визначає геометричну фігуру як множину точок, координати х та у яких справджують це рівняння. Інакше кажучи, рівняння розглядають як засіб для поділу точок площини на 2 класи: до 1-го належать точки, координати яких справджують дане рівняння (ці точки утворюють визначену рівнянням фігуру), до 2-го — всі інші точки площини. Якщо рівняння алгебраїчне, то воно визначає лінію — дійсну чи уявну (див. нижче), яку називають алгебраїчною, а степінь рівняння — порядком цієї лінії. Порядок алгебраїчної лінії не залежить від того, як розміщені відносно неї осі координат. Прямі і тільки прямі є лініями 1-го порядку; конічні перерізи (тобто лінії, що утворюються при перетині конуса площиною) і тільки вони є лініями 2-го порядку. Аналогічно рівняння f(x,y,z)=0{\displaystyle f(x,y,z)=0}, де x,y,z{\displaystyle x,y,z} — декартові координати точки у просторі, визначає просторову фігуру, зокрема алгебраїчну поверхню n-го порядку, якщо воно є алгебраїчним рівнянням n-го степеня. В сучасних курсах аналітичної геометрії вивчаються тільки лінії і поверхні 1-го та 2-го порядків.

Застосування в аналітичній геометрії алгебраїчних методів привело до поняття уявної фігури. Сукупність двох чисел x,y,{\displaystyle x,y,} з яких принаймні одне уявне, можна розглядати як уявну точку. Якщо рівняння (наприклад , x2+y2+1=0{\displaystyle x^{2}+y^{2}+1=0}) справджують лише координати уявних точок, то вважають, що воно визначає уявну фігуру. Хоч поняттям нескінченно віддалених і уявних точок не відповідають жодні реальні образи, проте запровадження їх дозволило глибше досліджувати властивості фігур.

В сучасних курсах аналітичної геометрії широко використовується апарат векторного числення.

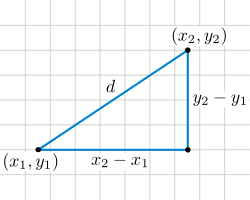Формула відстані на площині слідує із теореми Піфагора.

В аналітичній геометрії, геометричні поняття такі як міри відстані і кута визначають за допомогою формул. Ці визначення узгоджені із Евклідовою геометрією, яка є в основі них. Наприклад, при використанні Декартових координат на площині, відстань між двома точками (x₁, y₁) і (x₂, y₂) визначається формулою

d=(x2−x1)2+(y2−y1)2,{\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}},}

яку можна розглядати як ще одну версію теореми Піфагора. Аналогічно, кут, який пряма утворює із горизонталлю можна визначити за допомогою формули

θ=arctg(m),{\displaystyle \theta =\mathrm {arctg} (m),}

де m це нахил (кутовий коефіцієнт) прямої.

В трьох вимірах, відстань визначається за допомогою узагальненої теореми Піфагора:

d=(x2−x1)2+(y2−y1)2+(z2−z1)2,{\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}},}

а кут між двома векторами задається скалярним добутком. Скалярний добуток двох Евклідових векторів A і B визначається як^[5]

A⋅B=def‖A‖‖B‖cos⁡θ,{\displaystyle \mathbf {A} \cdot \mathbf {B} {\stackrel {\mathrm {def} }{=}}\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,}

де θ це кут між A і B.

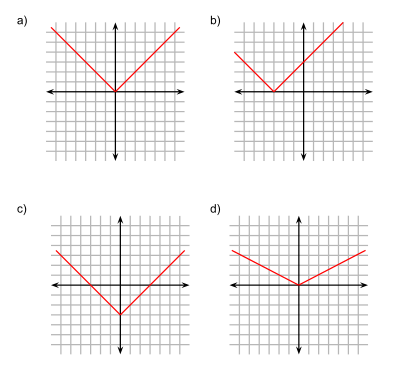a) y = f(x) = |x|       b) y = f(x+3)       c) y = f(x)-3       d) y = 1/2 f(x)

Перетворення застосовуються до початкової функції з метою перетворити її на нову функцію із подібними характеристиками.

Графік функції R(x,y){\displaystyle R(x,y)} змінюється за допомогою стандартних перетворень наступним чином:

Існують і інші стандартні перетворення, які як правило не вивчаються в рамках елементарної аналітичної геометрії, оскільки перетворення змінюють форму об’єктів у такий спосіб, який не розглядається часто. Наприклад, таким перетворенням є перетворення скосу.

Наприклад, початкова функція y=1/x{\displaystyle y=1/x} має горизонтальну і вертикальну асимптоту, і займає перший і другий квадрант, і всі форми її перетворення мають горизонтальну і вертикальну асимптоту, і займають або 1-й і 3-й або 2-й і 4-й квадрант. В загальному випадку, якщо дана функція y=f(x){\displaystyle y=f(x)}, то її можна трансформувати у вигляд y=af(b(x−k))+h{\displaystyle y=af(b(x-k))+h}. В новій перетвореній функції, a{\displaystyle a} це коефіцієнт вертикального розтягування функції, якщо він більший за 1, або вертикального стискання, якщо він менший за 1, а для від’ємних значень a{\displaystyle a}, функція буде відображена по осі x{\displaystyle x}. Коефіцієнт b{\displaystyle b} стискає графік функції по горизонталі, якщо він більший за 1 і розтягує функцію горизонтально, якщо він менший за 1, і так само як a{\displaystyle a}, відображає функцію по осі y{\displaystyle y}, коли він від’ємний. Значення k{\displaystyle k} і h{\displaystyle h} задають переміщення, h{\displaystyle h} — вертикальне, і k{\displaystyle k} — горизонтальне. Додатні значення h{\displaystyle h} і k{\displaystyle k} означають, що функція переміщується в додатному напрямку відповідної осі, а від’ємне значення, що вона переміщується в сторону від’ємного напрямку.

Перетворення можна застосувати до будь-якого геометричного рівняння, не залежно від того чи задає це рівняння функцію, чи ні.

Знаходження перетинів геометричних об’єктів[ред. | ред. код]

Для двох геометричних об’єкта P і Q, які представлені рівняннями P(x,y){\displaystyle P(x,y)} і Q(x,y){\displaystyle Q(x,y)} перетином є набір всіх таких точок (x,y){\displaystyle (x,y)}, які відповідають двом рівнянням одночасно.

Наприклад, P{\displaystyle P} може бути колом із радіусом 1 і з центром в координатах (0,0){\displaystyle (0,0)}: P={(x,y)|x2+y2=1}{\displaystyle P=\{(x,y)|x^{2}+y^{2}=1\}}, а Q{\displaystyle Q} може бути колом із радіусом 1 і центром в (1,0):Q={(x,y)|(x−1)2+y2=1}{\displaystyle (1,0):Q=\{(x,y)|(x-1)^{2}+y^{2}=1\}}. Перетином цих кіл є множина точок, при якій обидва рівняння виконуються. Чи точка з координатами (0,0){\displaystyle (0,0)} робить обидва ці рівняння вірними? Підставивши (0,0){\displaystyle (0,0)} для (x,y){\displaystyle (x,y)}, рівняння для Q{\displaystyle Q} буде наступним (0−1)2+02=1{\displaystyle (0-1)^{2}+0^{2}=1} або (−1)2=1{\displaystyle (-1)^{2}=1}, що є вірним, тож (0,0){\displaystyle (0,0)} відповідає рівнянню Q{\displaystyle Q}. З іншого боку, використавши (0,0){\displaystyle (0,0)} для (x,y){\displaystyle (x,y)} в рівнянні P{\displaystyle P} отримаємо 02+02=1{\displaystyle 0^{2}+0^{2}=1} або 0=1{\displaystyle 0=1}, що є хибним. (0,0){\displaystyle (0,0)} не належить P{\displaystyle P}, то ж ця точка не є перетином.

Перетин фігур P{\displaystyle P} і Q{\displaystyle Q} можна знайти розв’язавши одночасні рівняння:

x2+y2=1{\displaystyle x^{2}+y^{2}=1}

(x−1)2+y2=1.{\displaystyle (x-1)^{2}+y^{2}=1.}

Традиційними методами пошуку перетинів за допомогою таких рівнянь є заміна і скорочення.

Метод заміни: (метод підстановки) Необхідно розв’язати рівняння відносно y{\displaystyle y}, спочатку виразимо його через x{\displaystyle x}, а потім підставляємо отриманий вираз для y{\displaystyle y} в друге рівняння:

x2+y2=1{\displaystyle x^{2}+y^{2}=1}

y2=1−x2{\displaystyle y^{2}=1-x^{2}}.

Потім, після підстановки отриманого значення для y2{\displaystyle y^{2}} в інше рівняння, маємо розв’язок для x{\displaystyle x}:

(x−1)2+(1−x2)=1{\displaystyle (x-1)^{2}+(1-x^{2})=1}

Що таке геометрія? Наука геометрія

Геометрія є важливою частиною математики, яку починають вивчати в школах з 7 класу в якості окремого предмета. Що таке геометрія? Що вона вивчає? Які корисні висновки можна з неї витягти? Всі ці питання докладно розглядаються в статті.

Поняття про геометрію

Під цією наукою розуміють гілка математики, що займається вивченням властивостей різних фігур на площині і в просторі. Саме слово «геометрія» з давньогрецької мови означає «вимірювання землі», тобто будь-які реальні або уявлювані об’єкти, які мають кінцеву довжину вздовж хоча б однієї з трьох осей координат (наш простір є тривимірним), піддаються вивченню даної наукою. Можна сказати, що геометрія — математика простору і площини.

В ході свого розвитку геометрія обзавелася набором понять, якими вона оперує з метою вирішення різних завдань. До таких понять належать точка, пряма, площина, поверхня, відрізок, коло, крива, кут та інші. Основою цієї науки є аксіоми, тобто концепції, що зв’язують геометричні поняття в рамках тверджень, які приймаються в якості істинних. На підставі аксіом будуються і доводяться теореми.

Коли з’явилася ця наука

Що таке геометрія з точки зору історії? Тут слід сказати, що вона є дуже давнім вченням. Так, її використовували стародавні вавілоняни при визначенні периметрів та площ простіших фігур (прямокутників, трапецій та ін). Розвинена вона була і в Стародавньому Єгипті. Досить згадати знамениті піраміди, будівництво яких було б неможливо без знання властивостей об’ємних фігур, а також без уміння орієнтуватися на місцевості. Зазначимо, що знамените число «пі» (його приблизне значення), без якого неможливо визначити параметри кола, було відомо єгипетським жерцям.

Розрізнені знання про властивості плоских і об’ємних тіл були зібрані в єдину науку тільки за часів Античної Греції завдяки діяльності її філософів. Найважливішим працею, на якому ґрунтуються сучасні геометричні навчання, є «Елементи» Евкліда, які були їм складені приблизно в 300 році до нашої ери. Близько 2000 років цей трактат був основою для кожного вченого, який займався дослідженням просторових властивостей тел.

У XVIII столітті французький математик і філософ Рене Декарт заклав основи так званої аналітичної науки геометрії, яка описувала за допомогою чисельних функцій будь-просторовий елемент (пряму, площину і так далі). З цього часу починають з’являтися багато гілки в геометрії, причиною існування яких є п’ятий постулат в «Елементах» Евкліда.

Евклідова геометрія

Що таке геометрія Евкліда? Це досить струнке вчення про просторові властивості ідеальних об’єктів (точок, прямих, площин і т. д.), яке грунтується на 5 постулатах або аксіомах, викладених у праці під назвою «Елементи». Аксіоми наведено нижче:

1. Якщо дано дві точки, то можна провести лише одну пряму, яка їх з’єднає.
2. Кожен відрізок можна продовжити нескінченно з будь-якого його кінця.
3. Будь-яка точка простору дозволяє накреслити коло довільного радіуса так, щоб сама точка знаходилася в центрі.
4. Усі прямі кути є подібними або конгруэнтными.
5. Через кожну точку, яка не належить даній прямій, можна провести лише одну лінію, паралельну їй.

Евклідова геометрія становить основу будь-якого сучасного шкільного курсу по цій науці. Більше того, саме нею людство користується в процесі своєї життєдіяльності при конструюванні будівель і споруд та при складанні топографічних карт. Тут важливо зазначити, що набір постулатів в «Елементах» не є повним. Він був розширений німецьким математиком Давидом Гильбертом на початку XX століття.

Види евклідової геометрії

Ми розібралися, що таке геометрія. Розглянемо, які бувають види. В рамках класичного вчення прийнято виділяти два види цієї математичної науки:

• Планіметрія. Вона вивчає властивість плоских об’єктів. Наприклад, розрахунок площі трикутника або знаходження його невідомих кутів, визначення периметра трапеції або довжини кола — це завдання планіметрії.
• Стереометрія. Об’єктами вивчення цієї гілки геометрії є просторові фігури (всі точки, які їх утворюють, лежать у різних площинах, а не в одній). Так, визначення об’єму піраміди або циліндра, вивчення властивостей симетрії куба і конуса — це приклади задач стереометрії.

Неевклидовы геометрії

Що таке геометрія в її широкому розумінні? Крім звичної нам науки про просторові властивості тіл, існують також неевклидовы геометрії, у яких п’ятий постулат в «Елементах» порушується. До них відносяться еліптична і гіперболічна геометрія, які були створені в XIX столітті німецьким математиком Георгом Риманом і російським ученим Миколою Лобачевским.

Спочатку вважали, що неевклидовы геометрії мають вузьку сферу застосування (наприклад, в астрономії при вивченні небесної сфери), а саме фізичне простір являється евклідовим. Помилковість останнього твердження показав Альберт Ейнштейн на початку XX століття, розробивши свою теорію відносності, в якій він узагальнив поняття простору і часу.

Геометрія в школі

Як було сказано вище, вивчення геометрії в школі починається з 7 класу. При цьому школярам демонструють основи планіметрії. Геометрія 9 класу вже включає вивчення тривимірних тіл, тобто стереометрії.

Головне завдання шкільного курсу полягає в тому, щоб розвинути у школярів абстрактне мислення і уяву, а також навчити їх мислити логічно.

Багато досліджень показали, що при вивченні цієї науки у школярів спостерігаються проблеми з абстрактним мисленням. Коли формулюється для них геометрична задача, вони часто не розуміють її суть. У старшокласників до проблеми з уявою додаються труднощі розуміння математичних формул для визначення об’єму та площі поверхні розверстки просторових фігур. Часто старшокласники при вивченні геометрії 9 класу не знають, якою формулою слід скористатися в конкретному випадку.

Шкільні підручники

Існує велика кількість навчальних посібників для навчання школярів цій науці. Одні з них дають тільки базові знання, наприклад, підручники Л. С. Атанасяна або А. В. Погорєлова. Інші переслідують мета поглибленого вивчення науки. Тут можна виділити підручник А. Д. Александрова або повний курс геометрії Бевза Р. П.

Оскільки в останні роки для здачі всіх екзаменів у школі запроваджено єдиний стандарт ЄДІ, стали необхідні підручники і решебники, які дозволяють учневі швидко самостійно розібратися з необхідною темою. Гарним прикладом таких посібників можна назвати геометрію Єршової А. П., Голобородько Ст. Ст.

Будь-який з названих вище підручників має як позитивні, так і негативні відгуки з боку вчителів, тому викладання геометрії в школі часто здійснюється з використанням кількох підручників.

Загрузка…

Дивіться також:

Проєктивна геометрія — Вікіпедія

Проєкти́вна геоме́трія — розділ геометрії, який вивчає проєктивні площини та проєктивний простір.

При аксіоматичній побудові проєктивної площини постулюється обов’язковий перетин двох різних прямих, замість аксіоми існування єдиної паралельної у геометрії Евкліда. Таким чином на проєктивній площині дві різні точки визначають пряму, дві різні прямі визначають точку. Це породжує головну особливість проєктивної геометрії — принцип дуальності, який додає витончену симетрію для багатьох конструкцій. Проєктивна геометрія може вивчатися як з чисто геометричної точки зору, так з аналітичної (за допомогою однорідних координат) і з алгебраїчної, розглядаючи проєктивну площину як структуру над полем. Часто, і історично, дійсна проєктивна площина розглядається як Евклідова площина з додаванням «прямої у нескінченності».

Проєктивна геометрія доповнює Евклідову, надаючи красиві і прості рішення для багатьох завдань, ускладнених присутністю паралельних прямих. Особливо проста й витончена проєктивна теорія конічних перетинів.

Хоча деякі результати, які тепер зараховані до проєктивної геометрії, виходять з робіт таких давньогрецьких геометрів, як Папп Александрійський, проєктивної геометрії як така народилася в XVII століття з прямої перспективи в живописі і архітектурному кресленні. Ідея безмежно далеких точок, в яких перетинаються паралельні прямі, з’явилася незалежно у французького архітектора Жерара Дезарга і у німецького астронома Йоганна Кеплера. Дезарга навіть запропонував, що може існувати пряма, що складається виключно з нескінченно віддалених точок.

В XIX столітті інтерес до цієї області відродився завдяки працям Жана-Віктора Понселе та Мішеля Шаля. Понселе вивів проєктивний простір з Евклідового, додавши пряму в нескінченності, на якій перетинаються всі площини, паралельні даній, і довів принцип дуальності. Шаль продовжив і значно поглибив праці Понселе. Пізніше Карл фон Штаудта створив чисто синтетичну аксіоматизацію, об’єднуючи ці прямі з рештою.

У кінці XIX століття Фелікс Клейн запропонував використовувати для проєктивної геометрії однорідні координати, які раніше запровадили Мебіус, Плюккер, і Фейєрбах.

Основні, залишені без визначення в стандартній аксіоматизації, поняття проєктивної геометрії — це точка та пряма. Сукупність точок на прямій називається рядом, а сукупність прямих, що проходять крізь точку — пучком. Сукупність точок на прямих у пучку A, що перетинаються з прямою BC, визначає площину ABC. Принцип дуальності свідчить, що будь-яка конструкція проєктивної геометрії в n-вимірному просторі залишається вірною, якщо в усіх випадках замінити (k)-вимірні конструкції на (n— k-1)-вимірні. Так, будь-яка конструкція в проєктивній площині залишається вірною, якщо замінити точки на прямі і прямі на точки.

Перетворення ряду прямих X в пучок точки x, що не знаходиться в цьому ряду, або навпаки, ідентифікує кожну точку в ряді з прямою з пучка, що її перетинає, і позначається X⌅x . Послідовність з декількох таких перетворень (з ряду в пучок, потім назад в ряд, і так далі) називається проєктивністю’. Перспективність — це послідовність з двох проєктивностей (пишетьсяX⌆X). Перспективність двох прямих проходить крізь центр O, а перспективність двох точок — крізь вісь o. Точка інваріантна по відношенню до проєктивності, якщо проєктивність перетворює її в ту ж точку.

Трикутник  — це частина площини, обмежена трьома точками, з’єднаними попарно прямими. Повний чотирикутник  — це частина площини, обмежена чотирма точками (вершини), що знаходяться в цій площині, з яких жодні три не колінеарними, з’єднаними попарно прямими. Перетин двох із цих прямих, які не є вершинами, називається діагональною точкою. Повний чотиригранник визначається аналогічно, але з точками замість прямих і прямими замість точок. Аналогічно можна визначити повний n-кутник і повний n-гранник.

Два трикутники перспективні якщо вони можуть бути з’єднані за допомогою перспективності, тобто їхні грані перетинаються на колінеарними точках (перспективність крізь пряму) або їхні вершини з’єднані конкурентними прямими (перспективність крізь точку).

Є три головних підходи до проєктивної геометрії: незалежна аксіоматизація, доповнення Евклідової геометрії, і структура над полем.

Аксіоматизація[ред. | ред. код]

Проєктивний простір можна визначити за допомогою різного набору аксіом. Коксетер надає такі:

1. Існує пряма і точка не на ній.
2. На кожній прямий є принаймні три точки.
3. Через дві точки можна провести рівно одну пряму.
4. Якщо A, B, C, і D — різні точки і AB і CD перетинаються, то AC і BD перетинаються.
5. Якщо ABC — площина, то існує принаймні одна точка не в площині ABC.
6. Дві різні площини перетинаються принаймні в двох точках.
7. Три діагональні точки повного чотирикутника не є колінеарними.
8. Якщо три точки на прямій X інваріантні по відношенню до проєктивної φ, то всі точки на X інваріантні по відношенню до φ.

Проєктивна площина (без третього виміру) визначається дещо іншими аксіомами:

1. Через дві точки можна провести рівно одну пряму.
2. Будь-які дві прямі перетинаються.
3. Існує чотири точки, з яких немає трьох колінеарних.
4. Три діагональні точки повних чотирикутників не є колінеарними.
5. Якщо три точки на прямій X інваріантні по відношенню до проєктивної φ, то всі точки на X інваріантні по відношенню до φ.
6. Теорема Дезарга: Якщо два трикутника перспективні крізь точку, то вони перспективні крізь пряму.

При наявності третього виміру, теорема Дезарга може бути доведена.

Доповнення Евклідової геометрії[ред. | ред. код]

Історично, проєктивний простір був вперше визначено, як доповнення евклідового простору ідеальним елементом — нескінченно віддаленої площини. Кожна точка на цій площині відповідає напрямку в просторі і є місцем перетину всіх прямих цього напрямку.

Проєктивна геометрія починається тоді, коли ми забуваємо про нескінченну віддаленість «ідеальних» точок, прямих і площини, і починаємо розглядати їх абсолютно на рівних умовах зі «звичайними» евклідовими точками, прямими і площинами.

Структура над полем[ред. | ред. код]

N-вимірний проєктивний простір над полем F визначається за допомогою системи однорідних координат над F, тобто множини ненульових (n+1) — векторів з елементів F. Точка і пряма визначаються як множина векторів, що відрізняються множенням на константу. Точка x знаходиться на прямій X якщо скалярний добуток X ⋅ x = 0. Таким чином, маючи пряму X, ми можемо визначити лінійне рівняння X ⋅ x = 0, що визначає ряд точок на X . З цього випливає, що точки x, y, і z є колінеарними, якщо X ⋅ x = X ⋅ y = X ⋅ z = 0 для будь-якої прямої X.

Однорідні координати дають можливість наглядно представити модель проєктивного простору. Оскільки однорідний вектор визначає (і тотожний) прямій, що проходить через початок координат, то точками n-вимірного проєктивного простору є прямі, що проходять через початок координат n+1-мірного евклідового простору. У найпростішому випадку,

• точки 2-мірної проєктивної площини — прямі, що проходять через початок координат 3-мірного евклідового простору
• прямі цієї 2-мірної проєктивної площини — це площини 3-мірного евклідового простору, що проходять через початок координат.

Кожні дві проєктивні точки (тобто дві різні евклідові прямі) визначають проєктивну пряму (тобто евклідову площину, що проходять через початок координат). Кожні дві проєктивні прямі (тобто дві евклідові площини, що проходять через початок координат) перетинаються у проєктивній точці (іншими словами, перетином двох евклідових площин, що проходять через початок координат, є евклідова пряма, що проходять через початок координат).

• Буземан Г., Келли П. Проективная геометрия и проективные метрики. M., 1957.
• Бэр Р. Линейная алгебра и проективная геометрия. М., 1955.
• Вольберг А. О. Основные идеи проективной геометрии. М.-Л.: Учпедгиз, 1949.
• Глаголев Н. А. Проективная геометрия. М.-Л., 1936.
• Хартсхорн Р. Основы проективной геометрии. М., 1970.
• Юнг Дж. В. Проективная геометрия. М.: ИЛ, 1949.

Ріманова геометрія — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Ріманова геометрія є розділом диференціальної геометрії, який вивчає ріманові многовиди, гладкі многовиди з рімановою метрикою, тобто зі скалярним добутком на дотичному просторі в кожній точці, яка змінюється плавно від точки до точки. Це зокрема, дозволяє ввести локальні поняття кута, довжини кривої, площі поверхні та об’єму. З цих локальних глобальні величини можуть бути отримані шляхом інтегрування локальних складових.

Ріманова геометрія виникла з бачення Бернгарда Рімана, викладеного в його інавгураційній лекції Ueber die Hypothesen, welche der Geometrie zu Grunde liegen (Про гіпотези, що лежать в основі геометрії). Це дуже широке і абстрактне узагальнення диференціальної геометрії поверхонь в R³. Розвиток ріманової геометрії є результатом синтезу різних результатів, що стосуються геометрії поверхонь і поведінки геодезичних ліній на них, з методами, які можуть бути застосовані для вивчення диференційовних многовидів вищих розмірностей. Це уможливило загальну теорію відносності Ейнштейна, яка глибоко вплинула на теорію груп і теорію представлень, так само як і на аналіз^[en], і стимулювала розвиток алгебричної і диференціальної топології.

Ріманова геометрія була вперше винесена на загал Бернгардом Ріманом у дев’ятнадцятому столітті. Вона має справу з широким спектром геометрій, метричні властивості яких змінюються від точки до точки, в тому числі стандартних типів неевклідової геометрії.

На будь-якому гладкому многовиді можна ввести ріманову метрику, яка часто допомагає вирішити проблеми диференціальної топології. Вона також слугує початковим рівнем для більш складної структури — псевдоріманових многовидів, які (в чотирьох вимірах) є основними об’єктами загальної теорії відносності. Інші узагальнення ріманової геометрії включають фінслерову геометрію.

Існує близька аналогія диференціальної геометрії з математичними структурами дефектів у звичайних кристалах. Дислокації та дисклінації породжують кривину і скрут.^[1][2]

Наступні статті містять корисний вступний матеріал до ріманової геометрії:

Класичні теореми в рімановій геометрії[ред. | ред. код]

Далі наведено неповний список найбільш класичних теорем в рімановій геометрії. Вибір зроблений залежно від її важливості, краси і простоти формулювання. Більшість результатів можна знайти в класичній монографії Джеффа Чігера^[en] і Д. Ебіна (див. нижче).

Наведені формулювання далеко не самі точні або більш загальні. Цей список орієнтований на тих, кому відомі основні визначення і хоче знати, про що ці визначення.

Загальні теореми[ред. | ред. код]

1. Теорема Гауса — Бонне — інтеграл від Гаусової кривини на компактному 2-вимірному рімановому многовиді M дорівнює 2πχ(M) де χ(M) позначає Ейлерову характеристику M. Ця теорема має узагальнення на будь-якому компактному парномірному рімановому мновиді, див. узагальнену теорему Гауса-Бонне^[en].
2. Теорема Неша про регулярні вкладення^[en], також її називають фундаментальною теоремою геометрії Рімана^[en]. Вона стверджує, що кожен Ріманів многовид можна ізометрично вкласти в Евклідів простір Rⁿ.

Геометрія в цілому[ред. | ред. код]

У всіх наступних теоремах ми припускаємо деяку локальну поведінку простору (зазвичай сформульовані припущенням про кривину), щоб отримати деяку інформацію про глобальну структуру простору, в тому числі будь-яку інформацію про топологічний тип многовиду або про поведінку точок на «достатньо великих» відстанях.

Затиснена секційна кривина[ред. | ред. код]

1. Теорема про сферу^[en]. Якщо M є компактний однозв’язний n-вимірний ріманів многовид з секційною кривиною затиснутою між 1/4 і 1, то M дифеоморфний сфері.
2. Теорема скінченності Чігера. Для заданих констант C, D і V, існує скінченне число (з точністю до дифеоморфізмів) — компактних n-мірних ріманових многовидів з секційною кривиною |K| ≤ C, діаметром ≤ D та об’ємом ≥ V.
3. Майже плоскі многовиди Громова^[en]. Існує ε_n >0 таке, що якщо n-мірний рімановий многовид має метрику з секційною кривиною |K| ≤ ε_n та діаметр ≤ 1, то його скінченне покриття дифеоморфне нільмноговиду.

Секційні кривини обмежені знизу[ред. | ред. код]

1. Теорема душі^[en] Чігера-Громолла. Якщо M є некомпактний повний n-мірний ріманів многовид невід’ємної кривини, то M містить компактний, цілком геодезичний підмноговид S такий, що M дифеоморфне нормальному шаруванню S (S називається душею M.) Зокрема, якщо M має строго додатну кривину всюди, то воно дифеоморфно Rⁿ. Г. Перельман в 1994 році дав дивно елегантний/короткий доказ гіпотези: M дифеоморфно Rⁿ якщо воно має додатну кривину хоча б в одній точці.
2. Теорема Громова про число Бетті. Існує константа C = C(n) така, що якщо M є компактним зв’язним n-мірним рімановим многовидом з додатною секційною кривиною, то сума його чисел Бетті максимально C.
3. Теорема обмеженості Грува-Петерсена. Для заданих констант C, D і V, існує скінченне число гомотопних типів компактних n-мірних Ріманових многовидів з секційною кривиною K ≥ C, діаметром ≤ D та об’ємом ≥ V.

Секційні кривини обмежені зверху[ред. | ред. код]

1. Теорема Адамара — Картана стверджує, що повний однозв’язний Ріманів многовид M з від’ємною секційною кривиною дифеоморфний Евклідовому простору Rⁿ з n = dim M за допомогою експоненціального відображення^[en] в будь-якій точці. Це означає, що будь-які дві точки однозв’язних повних ріманових многовидів з від’ємною секційною кривиною з’єднані єдиною геодезичною кривою.
2. Геодезичний потік будь-якого компактного ріманового многовиду з від’ємною секційною кривиною ергодичний.
3. Якщо M є повним рімановим многовидом з секційною кривиною, обмеженою зверху строго від’ємною константою k то це CAT(k) простір^[en]. Тому, його фундаментальна група Γ = π₁(M) є гіперболічною групою Громова^[en]. Це має багато наслідків для структури фундаментальної групи:

Кривина Річчі обмежена знизу[ред. | ред. код]

1. Теорема Майерса. Якщо компактний ріманів многовид має додатну кривину Річчі, то його фундаментальна група скінченна.
2. Теорема розщеплення^[en]. Якщо повний n-мірний Ріманів многовид має невід’ємну кривину Річчі і пряму лінію (тобто геодезичну, яка мінімізує відстань на кожному відрізку), то він ізометрічний прямому добутку числової прямої R{\displaystyle \mathbb {R} } та повного (n-1)-мірного ріманового многовиду, з невід’ємною кривиною Річчі.
3. Нерівність Бішопа-Громова^[en]. Об’єм метричної кулі з радіусом r в повному n-вимірному рімановому многовиді з додатною кривиною Річчі не перевищує об’єм кулі того ж радіуса r в Евклідовому просторі.
4. Теорема Громова про компактність^[en]. Множина ріманових многовидів з додатними кривинами Річчі, діаметром не більше D є пред-компактом в метриці Громова-Хаусдорфа^[en].

Від’ємна кривина Річчі[ред. | ред. код]

1. Ізометрична група компактного ріманового многовиду з від’ємною кривиною Річчі є дискретною.
2. На будь-якому гладкому многовиду вимірності n≥3 можна ввести ріманову метрику з від’ємною кривиною Річчі^[3] (Це невірно для поверхонь.)

Додатна скалярна кривина[ред. | ред. код]

1. n-мірний тор не допускає метрику з додатною скалярною кривиною.
2. Якщо радіус ін’єктивності компактного n-мірного ріманового многовиду ≥ π тоді середня скалярна кривина не перевищує n(n-1).

Книги

• Берже, Марсель (2000). Ріманова геометрія протягом другої половини ХХ століття. Цикл університетських лекцій 17. Род-Айленд: Американське математичне товариство. ISBN 0-8218-2052-4. . (Наводиться історичний огляд, в тому числі сотні посилань.)
• Чігер, Джефф (2008). Теореми порівняння в Рімановій геометрії. Провіденс: AMS Chelsea Publishing. ; Переглянутий передрук оригіналу 1975 року.
• Галлот, Сильвестр; Халін, Домінік; Лафонтен, Жак (2004). Ріманова геометрія. Університетський текст (вид. третє). Берлін: Спрінгер-Верлаг. .
• Йост, Юрген (2002). Ріманова геометрія і геометричний аналіз. Берлін: Спрінгер-Верлаг. ISBN 3-540-42627-2. .
• Петерсен, Пітер (2006). Ріманова геометрія. Берлін: Спрінгер-Верлаг. ISBN 0-387-98212-4. 

Документи

• Брендл, Саймон; Шоен, Річард М. (2007). Класифікація многовидів із слабкими 1/4-затисненими кривинами. arXiv:0705.3963.