Отрезок — Википедия

Материал из Википедии — свободной энциклопедии

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A{\displaystyle \;A} и B{\displaystyle \;B}, обозначается символом AB{\displaystyle AB}. Расстояние между концами отрезка называют его длиной и обозначают AB{\displaystyle AB} или |AB|{\displaystyle |AB|}.

Направленный отрезок[править | править код]

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB{\displaystyle AB} и BA{\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки AB{\displaystyle AB} и BA{\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел {x}{\displaystyle \{x\}}, удовлетворяющих неравенству a≤x≤b{\displaystyle a\leq x\leq b}, где заранее заданные вещественные числа a{\displaystyle a} и b{\displaystyle b} (a<b){\displaystyle (a<b)} называются

концами (граничными точками) отрезка. В противоположность им, остальные числа x{\displaystyle x}, удовлетворяющие неравенству a<x<b{\displaystyle a<x<b}, называются внутренними точками отрезка^[1].

Отрезок обычно обозначается [a,b]{\displaystyle [a,b]}:

[a,b]={x∈R∣a≤x≤b}{\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}.

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число b−a{\displaystyle b-a} называется длиной числового отрезка [a,b]{\displaystyle [a,b]}.

Стягивающаяся система сегментов[править | править код]

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой {[a,b]|a,b∈R∧a<b}{\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}}.

Система сегментов обозначается {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }}. Подразумевается, что каждому натуральному числу n{\displaystyle n} поставлен в соответствие отрезок [an,bn]{\displaystyle [a_{n},b_{n}]}.

Система сегментов {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  ∀n∈N:[an+1,bn+1]⊆[an,bn]{\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}

• соответствующая последовательность длин отрезков бесконечно мала.

  limn→∞(bn−an)=0{\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

∀{[an,bn]}n=1∞ ∃!c∈R ∀n∈N:c∈[an,bn]{\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}

Этот факт следует из свойств монотонной последовательности.

ru.wikipedia.org

Отрезок — Википедия. Что такое Отрезок

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок в геометрии

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A{\displaystyle \;A} и B{\displaystyle \;B}, обозначается символом AB{\displaystyle AB}. Расстояние между концами отрезка называют его длиной и обозначают AB{\displaystyle AB} или |AB|{\displaystyle |AB|}.

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB{\displaystyle AB} и BA{\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки AB{\displaystyle AB} и BA{\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел {x}{\displaystyle \{x\}}, удовлетворяющих неравенству a≤x≤b{\displaystyle a\leq x\leq b}, где заранее заданные вещественные числа a{\displaystyle a} и b{\displaystyle b} (a<b){\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x{\displaystyle x}, удовлетворяющие неравенству a<x<b{\displaystyle a<x<b}, называются внутренними точками отрезка^[1].

Отрезок обычно обозначается [a,b]{\displaystyle [a,b]}:

[a,b]={x∈R∣a≤x≤b}{\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}.

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число b−a{\displaystyle b-a} называется длиной числового отрезка [a,b]{\displaystyle [a,b]}.

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой {[a,b]|a,b∈R∧a<b}{\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}}.

Система сегментов обозначается {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }}. Подразумевается, что каждому натуральному числу n{\displaystyle n} поставлен в соответствие отрезок [an,bn]{\displaystyle [a_{n},b_{n}]}.

Система сегментов {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  ∀n∈N:[an+1,bn+1]⊆[an,bn]{\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}

• соответствующая последовательность длин отрезков бесконечно мала.

  limn→∞(bn−an)=0{\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

∀{[an,bn]}n=1∞ ∃!c∈R ∀n∈N:c∈[an,bn]{\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}

Этот факт следует из свойств монотонной последовательности.

См. также

Примечания

wiki.sc

Отрезок — Википедия

Материал из Википедии — свободной энциклопедии

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок в геометрии

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A{\displaystyle \;A} и B{\displaystyle \;B}, обозначается символом AB{\displaystyle AB}. Расстояние между концами отрезка называют его длиной и обозначают AB{\displaystyle AB} или |AB|{\displaystyle |AB|}.

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB{\displaystyle AB} и BA{\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки AB{\displaystyle AB} и BA{\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел {x}{\displaystyle \{x\}}, удовлетворяющих неравенству a≤x≤b{\displaystyle a\leq x\leq b}, где заранее заданные вещественные числа a{\displaystyle a} и b{\displaystyle b} (a<b){\displaystyle (a<b)} называются концами (граничными точками) отрезка. В противоположность им, остальные числа x{\displaystyle x}, удовлетворяющие неравенству a<x<b{\displaystyle a<x<b}, называются внутренними точками отрезка^[1].

Отрезок обычно обозначается [a,b]{\displaystyle [a,b]}:

[a,b]={x∈R∣a≤x≤b}{\displaystyle [a,b]=\{x\in \mathbb {R} \mid a\leq x\leq b\}}.

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число b−a{\displaystyle b-a} называется длиной числового отрезка [a,b]{\displaystyle [a,b]}.

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой {[a,b]|a,b∈R∧a<b}{\displaystyle \{[a,b]|a,b\in \mathbb {R} \land a<b\}}.

Система сегментов обозначается {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }}. Подразумевается, что каждому натуральному числу n{\displaystyle n} поставлен в соответствие отрезок [an,bn]{\displaystyle [a_{n},b_{n}]}.

Система сегментов {[an,bn]}n=1∞{\displaystyle \{[a_{n},b_{n}]\}_{n=1}^{\infty }} называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  ∀n∈N:[an+1,bn+1]⊆[an,bn]{\displaystyle \forall n\in \mathbb {N} \colon [a_{n+1},b_{n+1}]\subseteq [a_{n},b_{n}]}

• соответствующая последовательность длин отрезков бесконечно мала.

  limn→∞(bn−an)=0{\displaystyle \lim _{n\to \infty }(b_{n}-a_{n})=0}

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

∀{[an,bn]}n=1∞ ∃!c∈R ∀n∈N:c∈[an,bn]{\displaystyle \forall \{[a_{n},b_{n}]\}_{n=1}^{\infty }~\exists !c\in \mathbb {R} ~\forall n\in N\colon c\in [a_{n},b_{n}]}

Этот факт следует из свойств монотонной последовательности.

См. также

Примечания

wikipedia.green

Середина отрезка — Википедия

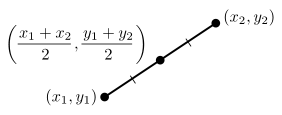Средняя точка отрезка с вершинами (x₁, y₁) и (x₂, y₂)

Середина отрезка — точка на заданном отрезке, находящаяся на равном расстоянии от обоих концов данного отрезка. Является центром масс как всего отрезка, так и его конечных точек.

Средняя точка отрезка в n{\displaystyle n}-мерном пространстве, концами которого являются точки A=(a1,a2,…,an){\displaystyle A=(a_{1},a_{2},\dots ,a_{n})} и B=(b1,b2,…,bn){\displaystyle B=(b_{1},b_{2},\dots ,b_{n})}, задаётся формулой:

A+B2{\displaystyle {\frac {A+B}{2}}}.

Таким образом, i{\displaystyle i}-я координата средней точки (i=1,2,…,n{\displaystyle i=1,2,\dots ,n}) равна:

ai+bi2{\displaystyle {\frac {a_{i}+b_{i}}{2}}}.

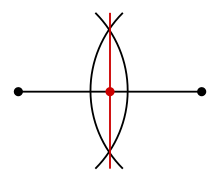Построение с помощью циркуля и линейки

Если заданы две точки, нахождение середины образованного ими отрезка может быть осуществлено с помощью циркуля и линейки. Для нахождения середины отрезка на плоскости можно сначала построить две дуги равного (и достаточно большого) радиуса с центрами в концах отрезка, а затем через точки пересечения этих дуг провести прямую. Точка, где полученная прямая пересекает отрезок, является его серединой.

Построение с помощью одного циркуля

С использованием теоремы Мора — Маскерони возможно также нахождение середины отрезка с помощью одного только циркуля: на первом шаге для отрезка (AB){\displaystyle (AB)} строится точка C{\displaystyle C}, симметричная точке A{\displaystyle A} относительно точки B{\displaystyle B}; на втором шаге строится инверсия точки C{\displaystyle C} относительно окружности радиуса |AB|{\displaystyle |AB|} с центром в точке A{\displaystyle A}; полученная точка является серединой отрезка (AB){\displaystyle (AB)}^[1][2][3].

Можно также построить середину отрезка с помощью только линейки при условии, что на плоскости имеется окружность с отмеченным центром^[4].

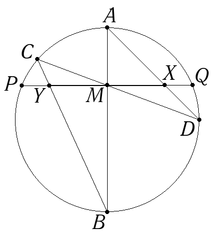
Середина любого диаметра окружности является центром окружности. Перпендикуляр к любой хорде, проходящий через её середину, проходит через центр окружности. Теорема о бабочке утверждает, что если M{\displaystyle M} является серединой хорды PQ{\displaystyle PQ} и через середину проходят две другие хорды AB{\displaystyle AB} и CD{\displaystyle CD}, то AD{\displaystyle AD} и BC{\displaystyle BC} пересекают хорду PQ{\displaystyle PQ} в точках X{\displaystyle X} и Y{\displaystyle Y} соответственно таким образом, что M{\displaystyle M} является серединой отрезка XY{\displaystyle XY}.

Центр эллипса является серединой отрезка, соединяющего два фокуса эллипса.

Середина отрезка, соединяющего вершины гиперболы, является центром гиперболы.

Перпендикуляры к серединам сторон треугольника пересекаются в одной точке, и эта точка является центром описанной окружности. Центр девяти точек треугольника — середина отрезка, соединяющего центра описанной окружности с ортоцентром данного треугольника. Вершины серединного треугольника данного треугольника лежат в серединах сторон треугольника.

В прямоугольном треугольнике центр описанной окружности является серединой гипотенузы. В равнобедренном треугольнике медиана, высота и биссектриса угла при вершине совпадают с прямой Эйлера и осью симметрии, и эта прямая проходит через середину основания.

Две бимедианы выпуклого четырёхугольника — это отрезки, соединяющие середины противоположных сторон. Две бимедианы и отрезок, соединяющий середины диагоналей, пересекаются в одной точке, которая является серединой этих трёх отрезков^[5]. Теорема Брахмагупты утверждает, что если вписанный в окружность четырёхугольник является ортодиагональным (то есть, имеющий перпендикулярные диагонали), то перпендикуляры к сторонам из точки пересечения диагоналей всегда проходят через середину противоположной стороны. Теорема Вариньона утверждает, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма, а если четырёхугольник к тому же является самонепересекающимся, то площадь параллелограмма равна половине площади четырёхугольника. Прямая Ньютона — линия, соединяющая середины двух диагоналей выпуклого четырёхугольника, не являющегося параллелограммом. Отрезки, соединяющие середины противоположных сторон выпуклого четырёхугольника, пересекаются в точке, лежащей на прямой Ньютона.

Правильный многоугольник имеет вписанную окружность, которая касается всех сторон многоугольника в серединах его сторон. В правильном многоугольнике с чётным числом сторон середины диагоналей, соединяющих противоположные центры, являются центром многоугольника. Серединный многоугольник — многоугольник, вершины которого — середины рёбер исходного многоугольника. Растянутый многоугольник серединных точек вписанного многоугольника P является другим вписанным многоугольником, вписанным в ту же окружность, и его вершины являются серединами дуг между вершинами P^[6]. Повторение операции создания многоугольника растянутых средних точек приводит к последовательности многоугольников, форма которых сходится к правильному многоугольнику

[6]^[7].

Середина отрезка является аффинным инвариантом, поэтому координатные формулы^[⇨] применимы к любой аффинной системе координат.

Середину отрезка невозможно определить в проективной геометрии: любая внутренняя точка отрезка может быть проективно отображена в любую другую точку внутри (того же или любого другого) проективного отрезка. Закрепление одной такой точки в качестве середины определяет аффинную структуру на проективной прямой, содержащей этот отрезок. Четвёртая точка гармонической четвёрки для такой «средней точки» и двух конечных точек является бесконечно удалённой точкой^[8].

Понятие середины отрезка можно ввести на геодезических в римановом многообразии, но в отличие от аффинного случая, середина отрезка может быть не единственной.

1. ↑ Костовский, 1984, с. 20.
2. ↑ Курант, Роббинс, 2001, с. 172—179.
3. ↑ Wolfram mathworld (неопр.) (недоступная ссылка) (29 September 2010).
   Дата обращения 20 июля 2015. Архивировано 25 ноября 2016 года.
4. ↑ Адлер, 1940, с. 67—72.
5. ↑ Altshiller-Court, 2007.
6. ↑ ^{1 2} Ding, Jiu, Zhang, 2003, с. 255—270.
7. ↑ Gomez-Martin, Taslakian, Toussaint, 2008.
8. ↑ Coxeter, 1949, с. 119.

• А. Н. Костовский. Геометрические построения одним циркулем. — М.: «Наука» Главная редакция физико-математической литературы, 1984. — (Популярные лекции по математике).
• Август Адлер. Теория геометрических построений. — Ленинград: Государственное учебно-педагогическое издательство Наркомпроса РСФСР, Ленинградское отделение, 1940.
• Р. Курант, Г. Роббинс. Что такое математика?. — 3-е. — МЦНМО, 2001. — ISBN 5–900916–45–6.
• Jiu Ding, L. Richard Hitt, Xin-Min Zhang. Markov chains and dynamic geometry of polygons // Linear Algebra and its Applications. — 2003. — Т. 367. — DOI:10.1016/S0024-3795(02)00634-1.
• Francisco Gomez-Martin, Perouz Taslakian, Godfried T. Toussaint. 18th Fall Workshop on Computational Geometry. — 2008.
• H. S. M. Coxeter. The Real Projective Plane. — New York, Toronto, London: McGraw-Hill, 1949.
• Х. С. М. Коксетер. Действительная проективная плоскость. — М.: Физматлит, 1959.
• Nathan Altshiller-Court. College Geometry. — Mineola, New York: Dover Publ., 2007. — ISBN 0-486-45805-9.

ru.wikipedia.org

Отрезок Википедия

Эта статья — о понятии в геометрии и математическом анализе. О насильно отрезанных от крестьянских наделов землях см. Отрезки (земля). Отрезок AB (выделен красным)

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок в геометрии[ | ]

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки A{\displaystyle \;A} и B{\displaystyle \;B}, обозначается символом AB{\displaystyle AB}. Расстояние между концами отрезка называют его длиной и обозначают AB{\displaystyle AB} или |AB|{\displaystyle |AB|}.

Направленный отрезок[ | ]

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки AB{\displaystyle AB} и BA{\displaystyle BA} представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется

направленным. Например, направленные отрезки AB{\displaystyle AB} и BA{\displaystyle BA} не совпадают. Отдельного обозначения для направленных отрезков нет — то, что у отрезка важно его направление, обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

ru-wiki.ru

Отрезок — Традиция

Материал из свободной русской энциклопедии «Традиция»

Отрезок — множество точек на прямой, расположенных между двумя точками А и В, включая сами точки А и В. Иначе говоря, отрезок есть множество точек на прямой, координаты которых удовлетворяют условиям а≤х≤b (где а и b — координаты концов)^[1]

Отрезок в геометрии[править]

В геометрии отрезок прямой — это часть прямой, состоящее из двух различных точек и всех точек, лежащих между ними. Отрезок прямой, соединяющий две точки \(\;A\) и \(\;B\) (которые называются

концами отрезка), обозначается следующим образом — \([A;\;B]\). Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок \(\;AB\)». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. При аксиоматическом обосновании элементарной геометрии отрезок прямой определяется как система двух точек A и B и доказывается, что между ними существует бесконечное число точек.

Расстояние между концами отрезка называют его длиной и обозначают как \(\;|AB|\).

На вопрос о разрешимости построения отрезка с помощью циркуля и линейка отвечает следующая теорема:

Для того чтобы циркулем и линейкой можно было построить отрезок, длина которого является заданной положительной функцией длин данных отрезков, необходимо и достаточно, чтобы длину искомого отрезка можно было выразить через длины данных отрезков при помощи конечного числа действий сложения, вычитания, умножения, деления и извлечения арифметического квадратного корня.

Отрезок числовой прямой[править]

Отрезок числовой (координатной) прямой или числовой отрезок — множество вещественных чисел, удовлетворяющих неравенству \(a\le x\le b\), где числа \(a\,\) и \(b\,\) \((a\) называются концами отрезка. Обычно обозначается \([a,b]=\{x\in\mathbb R|a\le x\le b\}\). Число \(b-a\,\) называется длиной числового отрезка.

Отрезок является замкнутым промежутком.

Направленный отрезок[править]

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки \(AB\) и \(BA\) представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, выше указанные направленные отрезки не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

При написании этой статьи использовались материалы страницы «Отрезок» Русской Википедии.

traditio.wiki

Отрезок — Википедия (с комментариями)

Материал из Википедии — свободной энциклопедии

Отре́зком называются два близких понятия: в геометрии и математическом анализе.

Отрезок в геометрии

Отрезок прямой — часть прямой, ограниченная двумя точками. Точнее: это множество, состоящее из двух различных точек данной прямой (которые называются концами отрезка) и всех точек, лежащих между ними (которые называются его внутренними точками). Отрезок, концами которого являются точки <math>\;A</math> и <math>\;B</math>, обозначается символом <math>AB</math>. Расстояние между концами отрезка называют его длиной и обозначают <math>|AB|</math>.

Направленный отрезок

Обычно у отрезка прямой неважно, в каком порядке рассматриваются его концы: то есть отрезки <math>AB</math> и <math>BA</math> представляют собой один и тот же отрезок. Если у отрезка определить направление, то есть порядок перечисления его концов, то такой отрезок называется направленным. Например, направленные отрезки <math>AB</math> и <math>BA</math> не совпадают. Особого обозначения у направленных отрезков нет — то, что у отрезка важно его направление обычно указывается особо.

Дальнейшее обобщение приводит к понятию вектора — класса всех равных по длине и сонаправленных направленных отрезков.

Отрезок числовой прямой

Отрезок числовой (координатной) прямой (иначе числовой отрезок, сегмент) — множество вещественных чисел <math>\{x\}</math>, удовлетворяющих неравенству <math>a \le x \le b</math>, где заранее заданные вещественные числа <math>a</math> и <math>b</math> <math>(a<b)</math> называются концами (граничными точками) отрезка. В противоположность им, остальные числа <math>x</math>, удовлетворяющие неравенству <math>a<x<b</math>, называются внутренними точками отрезка^[1].

Отрезок обычно обозначается <math>[a, b]</math>:

<math>[a,b] = \{ x \in \mathbb{R} \mid a \le x \le b \}</math>.

Любой отрезок, по определению, заведомо включён в множество вещественных чисел. Отрезок является замкнутым промежутком.

Число <math>b-a</math> называется длиной числового отрезка <math>[a, b]</math>.

Стягивающаяся система сегментов

Система сегментов — это бесконечная последовательность элементов множества отрезков на числовой прямой <math>\{[a, b] | a, b \in \R \land a < b\}</math>.

Система сегментов обозначается <math>\{[a_n, b_n]\}_{n = 1}^{\infty}</math>. Подразумевается, что каждому натуральному числу <math>n</math> поставлен в соответствие отрезок <math>[a_n, b_n]</math>.

Система сегментов <math>\{[a_n, b_n]\}_{n = 1}^{\infty}</math> называется стягивающейся, если^[2]

• каждый следующий отрезок содержится в предыдущем;

  <math>\forall n \in \N \colon [a_{n+1}, b_{n+1}] \subseteq [a_n, b_n]</math>

• соответствующая последовательность длин отрезков бесконечно мала.

  <math>\lim_{n \to \infty} (b_n — a_n) = 0</math>

У любой стягивающейся системы сегментов существует единственная точка, принадлежащая всем сегментам этой системы.

<math>\forall \{[a_n, b_n]\}_{n = 1}^{\infty} ~ \exists ! c \in \R ~ \forall n \in N \colon c \in [a_n, b_n]</math>

Этот факт следует из свойств монотонной последовательности.

См. также

Напишите отзыв о статье «Отрезок»

Примечания

Отрывок, характеризующий Отрезок

Когда всё было готово, сабли воткнуты в снег, означая барьер, до которого следовало сходиться, и пистолеты заряжены, Несвицкий подошел к Пьеру.
– Я бы не исполнил своей обязанности, граф, – сказал он робким голосом, – и не оправдал бы того доверия и чести, которые вы мне сделали, выбрав меня своим секундантом, ежели бы я в эту важную минуту, очень важную минуту, не сказал вам всю правду. Я полагаю, что дело это не имеет достаточно причин, и что не стоит того, чтобы за него проливать кровь… Вы были неправы, не совсем правы, вы погорячились…
– Ах да, ужасно глупо… – сказал Пьер.
– Так позвольте мне передать ваше сожаление, и я уверен, что наши противники согласятся принять ваше извинение, – сказал Несвицкий (так же как и другие участники дела и как и все в подобных делах, не веря еще, чтобы дело дошло до действительной дуэли). – Вы знаете, граф, гораздо благороднее сознать свою ошибку, чем довести дело до непоправимого. Обиды ни с одной стороны не было. Позвольте мне переговорить…
– Нет, об чем же говорить! – сказал Пьер, – всё равно… Так готово? – прибавил он. – Вы мне скажите только, как куда ходить, и стрелять куда? – сказал он, неестественно кротко улыбаясь. – Он взял в руки пистолет, стал расспрашивать о способе спуска, так как он до сих пор не держал в руках пистолета, в чем он не хотел сознаваться. – Ах да, вот так, я знаю, я забыл только, – говорил он.
– Никаких извинений, ничего решительно, – говорил Долохов Денисову, который с своей стороны тоже сделал попытку примирения, и тоже подошел к назначенному месту.
Место для поединка было выбрано шагах в 80 ти от дороги, на которой остались сани, на небольшой полянке соснового леса, покрытой истаявшим от стоявших последние дни оттепелей снегом. Противники стояли шагах в 40 ка друг от друга, у краев поляны. Секунданты, размеряя шаги, проложили, отпечатавшиеся по мокрому, глубокому снегу, следы от того места, где они стояли, до сабель Несвицкого и Денисова, означавших барьер и воткнутых в 10 ти шагах друг от друга. Оттепель и туман продолжались; за 40 шагов ничего не было видно. Минуты три всё было уже готово, и всё таки медлили начинать, все молчали.

– Ну, начинать! – сказал Долохов.
– Что же, – сказал Пьер, всё так же улыбаясь. – Становилось страшно. Очевидно было, что дело, начавшееся так легко, уже ничем не могло быть предотвращено, что оно шло само собою, уже независимо от воли людей, и должно было совершиться. Денисов первый вышел вперед до барьера и провозгласил:
– Так как п’отивники отказались от п’ими’ения, то не угодно ли начинать: взять пистолеты и по слову т’и начинать сходиться.
– Г…’аз! Два! Т’и!… – сердито прокричал Денисов и отошел в сторону. Оба пошли по протоптанным дорожкам всё ближе и ближе, в тумане узнавая друг друга. Противники имели право, сходясь до барьера, стрелять, когда кто захочет. Долохов шел медленно, не поднимая пистолета, вглядываясь своими светлыми, блестящими, голубыми глазами в лицо своего противника. Рот его, как и всегда, имел на себе подобие улыбки.
– Так когда хочу – могу стрелять! – сказал Пьер, при слове три быстрыми шагами пошел вперед, сбиваясь с протоптанной дорожки и шагая по цельному снегу. Пьер держал пистолет, вытянув вперед правую руку, видимо боясь как бы из этого пистолета не убить самого себя. Левую руку он старательно отставлял назад, потому что ему хотелось поддержать ею правую руку, а он знал, что этого нельзя было. Пройдя шагов шесть и сбившись с дорожки в снег, Пьер оглянулся под ноги, опять быстро взглянул на Долохова, и потянув пальцем, как его учили, выстрелил. Никак не ожидая такого сильного звука, Пьер вздрогнул от своего выстрела, потом улыбнулся сам своему впечатлению и остановился. Дым, особенно густой от тумана, помешал ему видеть в первое мгновение; но другого выстрела, которого он ждал, не последовало. Только слышны были торопливые шаги Долохова, и из за дыма показалась его фигура. Одной рукой он держался за левый бок, другой сжимал опущенный пистолет. Лицо его было бледно. Ростов подбежал и что то сказал ему.

wiki-org.ru