Урок 27. неравенства с двумя переменными — Алгебра — 9 класс

Рассмотрим неравенство.
3x² – y<0
При значениях переменной икс равен 1, а игрик равен пяти, оно обращается в верное исловое неравенство.
Говорят, что пара чисел 1 и 5 являются решением этого неравенства
Рассмотрим еще одно неравенство с двумя переменными
6x + 2y>8,
Заменим его на равносильное неравенство
3x + y>4,
Перенесем слагаемое три икс в правую часть неравенства
Рассмотрим функцию игрик равен 4 минус три икс
y>4 – 3x,
Это линейная функция, графиком которой является прямая. Изобразим ее на координатной плоскости
Решением данного неравенства будет являться множество точек координатной плоскости, расположенных строго выше прямой игрик равен 4 минус 3 икс.
А чтобы показать, что самая прямая не принадлежит полуплоскости, изображаем ее штриховой линией.

Можно сделать вывод, что прямая разбивает плоскость на две полуплоскости: ту, которая расположена выше прямой и на ту, которая расположена ниже. Первая удовлетворяет данному нам неравенству, а вторая неравенству игрик меньше четыре икс минус три икс.
Изобразим на координатной плоскости множество решений еще одного неравенства.
y ≥ (x – 3)²
Для этого изобразим график функции игрик равно икс минус три во второй степени. Графиком данной функции является парабола.
Чтобы точно определить, какая именно часть плоскости будет содержать в себе множество решений неравенства, выберем произвольную точку в любой части плоскости и подставим в неравенство. Например, точку с координатами 3 и 2
Подставим координаты этой точки в изначальное неравенство и получим верное числовое неравенство, а значит все точки этой части плоскости являются множеством решения неравенства.
Точки, принадлежащие параболе, также являются решением неравенства, так как знак неравенства нестрогий.

Технологическая карта урока алгебры в 9 классе «Неравенства с двумя переменными»

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СРЕДНЯЯ ШКОЛА №23 г. ЙОШКАР-ОЛЫ»

РАЗРАБОТКА УРОКА

ПО АЛГЕБРЕ

В 9 КЛАССЕ ПО ТЕМЕ

«Неравенства с двумя переменными»

УЧИТЕЛЬ МАТЕМАТИКИ

Луценко Ольга Александровна

ЯНВАРЬ 2016

ФИО учителя Луценко Ольга Александровна

Класс_9 Предмет «Алгебра»

Тема урока : Неравенства с двумя переменными

Место и роль урока в изучаемой теме_ Закрепление пройденного материала

Цели урока

образовательные: сформулировать определение неравенства, применять свойства неравенства. Изображать графики функций: квадратичной, линейной, обратной пропорциональности, изображать окружность в системе координат по её уравнению. Находить решение неравенства с двумя переменными графически, определяя его как часть множества точек координатной плоскости. Выполнять задания по повторению пройденного материала для подготовки к государственному обязательному экзамену по математике.

развивающие: применять полученные знания при решении неравенства графически (простейшие случаи). Правильно использовать термины: левая часть неравенства, правая часть неравенства, график функции, парабола, гипербола, прямая линия, окружность, круг, координатная плоскость, прямоугольная система координат ХОУ

воспитательные: вести эстетически и математически корректные чертежи в координатной плоскости , оформлять грамотно записи при выполнении заданий, работать самостоятельно в группа и парах, сопереживать, помогать друг другу, вести диалог.

Учебник Алгебра 9, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В. Суворова, Москва «Просвещение» 2013

Технологическая карта урока

1.Организация начала урока

(1 мин)

Подготовка учащихся к работе на уроке. Готовность класса и оборудования, быстрое включение учащихся в режим работы.

Приветствует обучающихся, проверяет их готовность к уроку

Приветствуют учителя, проверяют свою готовность к уроку

Приветствуя друг друга, настраиваются на совместное сотрудничество.

Настраиваются на работу на уроке, готовятся к получению новых знаний.

2.Проверка выполнения домашнего задания

(9 мин)

Проверка правильности и осознанности выполнения домашнего задания обучающимися, выявление пробелов и их коррекция. Сочетание контроля, самоконтроля и взаимоконтроля для установления правильности выполнения задания и коррекции пробелов.

Контрольные вопросы: -Что такое функция? -На предложенных вам карточках примеры нескольких зависимостей между переменными, укажите, какие из них не являются функциями. (Приложение1) -Дать устно краткую характеристику расположения графиков предложенных зависимостей в системе координат.

Проверка решения домашнего задания № 486 Ответы: а) прямая х = 3 и часть координатной плоскости, расположенная справа от этой прямой, б) часть координатной плоскости, расположенная ниже прямой у = — 1 в) часть координатной плоскости, расположенная между прямыми х = 1 и х = 4, г) прямые у = -3, у = 3 и часть координатной плоскости, расположенная между ними.

Проводит фронтальный опрос, отвечает на вопросы учащихся

Предлагает сверить результаты выполнения домашнего задания.

( Решение на слайде)

Работают в парах. Выполняют задания, готовят ответы на вопросы.

Задают вопросы, сравнивают результаты, полученные при выполнении домашнего задания.

Общаются, находят ошибки и устраняют их с помощью диалогового общения.

Проверяют эстетичность и корректность выполнения записей в тетрадях

Взаимоценка выполнения Д/з

3.Подготовка к основному этапу урока

(9 мин)

(1 мин)

Мотивация , актуализация опорных знаний и умений.

Создание проблемной ситуации. Фиксация новой учебной задачи

Подведение детей к формулированию темы и постановке цели урока.

Индивидуальные задания каждому (на карточках) Задания на два варианта.

(Приложение 2)

Ответы( на слайде) :

1 вариант.

1) график-парабола, вершина которой находится в т.(0;4) и ветви направлены вниз; 2) А(1;3)принадлежит графику данной функции, В(0; 5) не принадлежит графику данной функции; 3)неравенство верно, т.к. прямая у = 5 не пересекает параболу и расположена выше вершины параболы. 4) а) окружность с радиусом 3; б)круг с радиусом 3 без границы; 5) вторая и четвертая четверти координатной плоскости, включая оси ОХ и ОУ.

2 вариант

1) график-парабола, вершина которой находится в т.(0;- 4) и ветви направлены вверх; 2) А(1;- 3) принадлежит графику данной функции, В(0;- 5) не принадлежит графику данной функции; 3)неравенство верно, т.к. прямая у = — 5 не пересекает параболу и расположена ниже вершины параболы. 4) а) окружность с радиусом 2; б)круг с радиусом 2 без границы 5) первая и третья четверти координатной плоскости, включая оси ОХ и ОУ

Физминутка В положении сидя носочки ног потянуть вперед, откинувшись на спинку стула и отведя руки за спинку стула, голову наклонить назад (повторить трижды)

Организация погружения в проблему

Проводит фронтальный опрос. Предлагает учащимся назвать тему урока и цели

Готовность учащихся к активной учебно-познавательной деятельности на основе опорных знаний. Пытаются решить задания известным способом. Задания выполняют самостоятельно. Сверяют ответы

Фиксируют проблему.

Слушают учителя. Строят понятные для собеседника высказывания

Принимают и сохраняют учебную цель .

4Усвоение новых знаний и способов действий

(8 мин)

.

Организация работы в группах

Самостоятельная работа в группах-парах

Задание № 487(а. в ) Изобразить на координатной плоскости множество решений неравенства, дать устное обоснование. Работу выполняем в рабочих тетрадях. Ответы: а) у ≤ х² – 4. Решением неравенства является множество точек параболы, ветви которой направлены вверх, и точки координатной плоскости, расположенные во внешней области параболы; в) х

² + у²≤ 25 Решением является множество точек круга с радиусом 5 и центром (0;0)

Организует работу учащихся в группах. Организует диалог с обучающимися.

Записывают в тетрадях неравенства, выполняют построения кривых в координатной плоскости. Объясняют результаты сравнений.

Формулируют тему и цель урока

Строят понятные для собеседника высказывания

Обосновывают решения, приводят примеры, учатся анализировать

5.Первичная проверка понимания

(3 мин)

Установление правильности и осознанности усвоения учебного материала учащимися

Повторение: — Какое выражение называется неравенством?

— Сколько решений имеет неравенство? – Что собою представляет решение неравенства с одной переменной на числовой оси? – Что собою представляет решение неравенства с двумя переменными на координатной плоскости?

Выявляет пробелы и неверные решения, проводит коррекцию.

Усваивают сущность новых знаний и способов действий на репродуктивном уровне

Учатся коллективному усвоению знаний методом проб и ошибок.

Ликвидируют типичные ошибки и неверные представления о неравенствах и их решениях.

6.Закрепление знаний и способов действий

(5 мин)

Обеспечение усвоения новых знаний и способов действий на уровне применения в измененной ситуации..

Выполнение задания № 487 (б,г). Работают в тетрадях и два ученика выполняют работу на обратной стороне классной доски.

Ответы: б) у ≥ (х – 2)² – 1 Решением является множество точек параболы, ветви которой направлены вверх, а вершина в точке (2; — 1), и точки координатной плоскости, находящиеся во внутренней области параболы.

г) (х – 1)² + (у – 2)² ≤ 4 Решением является множество точек круга с радиусом 2 и центром (1;2)

Проводит коррекционную работу, дает консультацию по просьбе учащихся

Прослушивание информации одноклассников, выполнение заданий, требующих применения знаний в знакомой и измененной ситуациях

Учатся слушать, проверять, исправлять ошибки и анализировать работу одноклассников

Проверяют правильность выполнения своих заданий, корректируют записи и рисунки, следят за эстетикой письма в тетрадях

7.Обобщение и систематизация знаний

(2 мин)

Формирование целостной системы ведущих знаний по теме, курсу.

Обобщение рассматриваемого теоретического и практического материала на уроке по теме «Неравенства с двумя переменными»

Контролирует правильность произношения терминов и их применение в построении определений

Активная и продуктивная деятельности учащихся по классификации и систематизации, выявлению внутрипредметных связей

Взаимопроверка правильности высказываний одноклассников

Постановка задач для себя по усвоению материала

8.Информация о домашнем задании

(1 мин)

Обеспечение понимания цели, содержания и способов выполнения домашнего задания.

Задание на дом: № 490,491

Ответы к № 490 : а) (х – 2)²+ у²≤ 9 б) х² + (у – 4)² ≥ 4; к № 491 а) у > х² – 9; б) у< (х + 2)²

Реализует необходимые и достаточные условия для успешного выполнения домашнего задания всеми учащимися в соответствии с уровнем их развития

Проводят сверку соответствующих записей в тетрадях и дневниках.

Настраиваются на верное выполнение домашнего задания

Оценивают свои возможности для выполнения домашнего задания

9. Контроль и самопроверка знаний (4 мин)

Получение достоверной информации о достижении всеми учащимися планируемых результатов обучения, об уровне подготовки к государственному обязательному экзамену по математике

Тест (самостоятельная работа) по повторению (Приложение 3)

Ответы во всех заданиях под № 1

Наблюдает за самостоятельным выполнением заданий учащимися

Выявляют качество и уровень овладения знаниями и способами действий по решению неравенств и уравнений.

Обеспечивают коррекцию записей и верных ответов.

Выполняют работу индивидуально

10.Подведение итогов знаний (1 мин)

Подведение итогов усвоения знаний. Выставление оценок.

(Приложение 4 – маршрутный лист урока)

Комментирует и выставляет оценки за урок

Сдают учителю маршрутные листы на выставление оценок

Проводят оценку своих возможностей на успешное усвоение материала урока

Анализируют и сравнивают результаты своей деятельности за урок с другими учащимися

11.Рефлексия (1 мин)

Мобилизация учащихся на рефлексию своего поведения (мотивации, способов деятельности, общения).

— Я узнал на уроке….

-Мне было трудно …

— Мне было понятно ….

— На уроке мне понравилось…

Предлагает учащимся проанализировать их деятельность на уроке. А также оценить усвоение материала за урок.

Мотивируют свои успехи и учебную деятельность

Усваивают принципы саморегуля

ции и сотрудничества. Прогнозируют способы саморегуляции и сотрудничества.

Осмысливают свои действия и дают самооценку.

ПРИЛОЖЕНИЕ 1

1. y = 2x — 3

2. y = 2x² – 8x + 3

3. 3x + 2y = 5

4. x² + y² = 9

5. y = (x – 2)² – 3

6. y = 2/x

7. (x – 3)² + (y – 1)² = 9

ПРИЛОЖЕНИЕ 2

I вариант

1.Изобразите график функции y = — x² + 4

2.Принадлежат ли графику функции точки: A (1; 3), B (0;5)

3.Верно ли неравенство: — х² + 4 < 5

Пользуясь графиком, докажите истинность неравенства. Как интерпретировать это геометрически?

4.Изобразите решение уравнения и неравенства на координатной плоскости: а) х² + у² = 9; б) х² + у² < 9

5.Изобразите на координатной плоскости множество решений неравенства ху ≤ 0

II вариант

1.Изобразите график функции y = x² — 4

2.Принадлежат ли графику функции точки: A (1;- 3), B (0;- 5)

3.Верно ли неравенство: х² – 4 > — 5

Пользуясь графиком, докажите истинность неравенства. Как интерпретировать это геометрически?

4.Изобразите решение уравнения и неравенства на координатной плоскости: а) х² + у² = 4; б) х² + у² < 4

5.Изобразите на координатной плоскости множество решений неравенства ху ≥ 0

ПРИЛОЖЕНИЕ 3

(пример одного варианта)

1.Решите неравенство х² – х — 12≤ 0 Выбрать вариант ответа 1) [- 3;4] 2) [3; — 4] 3) [3;4] 4) [ -∞;-3]U [4;+ ∞ ]

2.Какое из приведенных ниже неравенств является верным при любых a и b, удовлетворяющих условиям a>0, b <0? 1) (a – b)/a> 1 2) 2a + b > 0; 3) a + b < 0; 4) (b²/a) > 1

3.Решите уравнение (5х – 3)² = (5х + 6)²

Выбрать вариант ответа: 1) – 0,3 2) 0,3 3) 3 4) – 3

Фамилия, имя уч –ся:

ПРИЛОЖЕНИЕ 4

МАРШРУТНЫЙ ЛИСТ УРОКА

Класс

Число

Тема урока:

№ п/п

Оценка

Самооценка

1

Проверка домашней работы

2

Работа по карточкам

3

Самостоятельная работа в парах, выполнение № 487 (а,в)

4

Повторение (ответы на вопросы)

5

Работа в тетрадях, № 487 (б.г)

6

Участие в обобщении знаний

7

Получение домашнего задания, корректировка

8

Тест (самостоятельная работа)

9

Отметка итоговая

10

Рефлексия (анализ собственной деятельности на уроке, мотивация успехов)

Урок по теме «Неравенства с двумя переменными», 9 класс

Технологическая урока по алгебре в 9 классе по теме:

«Неравенства с двумя переменными ».

Учитель: Ускова Вера Владимировна, МКОУ Семилукская СОШ №1 с УИОП

Цели урока:

образовательные: давать определение неравенства, знать его части, применять свойства неравенства при переносе слагаемых из одной части неравенства в другую и деления обеих частей неравенства на отрицательное число. Изображать графики функций: квадратичной, линейной, обратной пропорциональности, изображать окружность в системе координат по её уравнению. Находить решение неравенства с двумя переменными графически, определяя его как часть множества точек координатной плоскости.

развивающие: применять полученные знания при решении неравенства графически (простейшие случаи). Правильно использовать в речи термины: левая часть неравенства, правая часть неравенства, график функции, парабола, гипербола, прямая линия, окружность, круг, координатная плоскость, прямоугольная система координат ХОУ

воспитательные: вести эстетические и математически корректные чертежи в координатной плоскости и записи при выполнении заданий, работать самостоятельно и парах, сопереживать, помогать друг другу, вести диалог.

Оборудование: мультимедийный проектор, интерактивная доска, презентация к уроку, раздаточный материал.

1.Организация начала урока

Приветствует обучающихся, проверяет их готовность к уроку

Приветствуют учителя, проверяют свою готовность к уроку

Приветствуя друг друга, настраиваются на совместное сотрудничество.

Настраиваются на работу на уроке, готовятся к получению новых знаний.

2.Проверка выполнения домашнего задания

№477,№479.

Предлагает сверить результаты выполнения домашнего задания

Задают вопросы, сравнивают результаты, полученные при выполнении домашнего задания.

Общаются, находят ошибки и устраняют их с помощью диалогового общения.

Проверяют эстетичность и корректность выполнения записей в тетрадях

3.Подготовка к основному этапу урока .

Работа по карточкам – трое учеников у доски :

Карточка 1. Построить график функции:

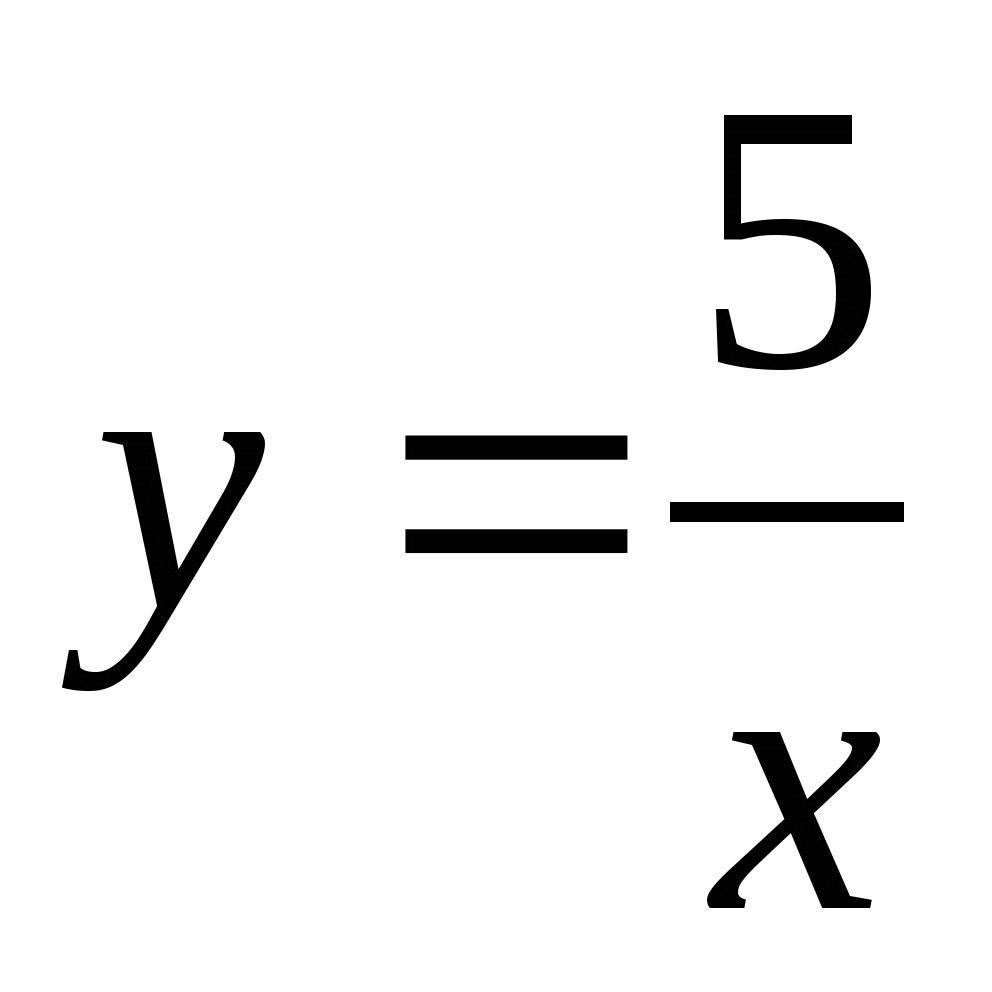
Карточка 2. Построить график функции:

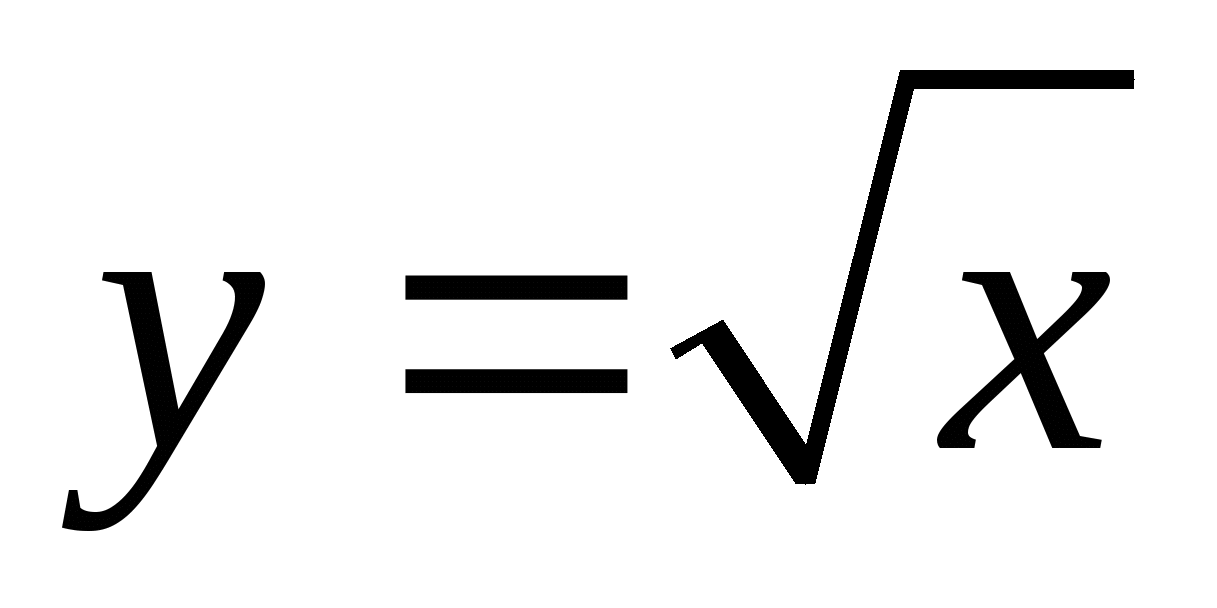
Карточка 3. Построить график функции:

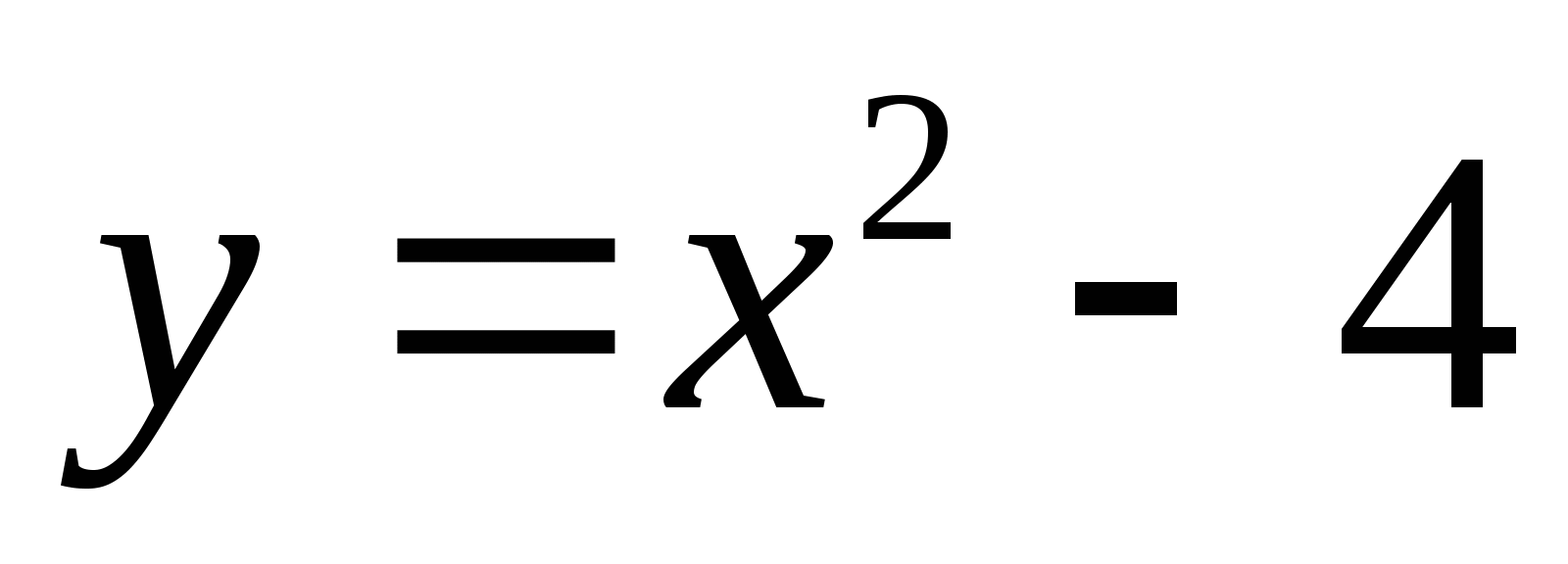
(Приложение 2) Работу выполнить в парах на листах.

Ответы: 1вариант 1) график-парабола, вершина которой находится в т.(0;- 4) и ветви направлены вверх; 2) А(1;- 3) принадлежит графику данной функции, В(0;- 5) не принадлежит графику данной функции; 3)неравенство верно, т.к. прямая у = — 5 не пересекает параболу и расположена ниже вершины параболы. 4) а) окружность с радиусом 2; б)круг с радиусом 2 без границы 5) первая и третья четверти координатной плоскости, включая оси ОХ и ОУ 2 вариант. 1) график-парабола, вершина которой находится в т.(0;4) и ветви направлены вниз; 2) А(1;3)принадлежит графику данной функции, В(0; 5) не принадлежит графику данной функции; 3)неравенство верно, т.к. прямая у = 5 не пересекает параболу и расположена выше вершины параболы. 4) а) окружность с радиусом 3; б)круг с радиусом 3 без границы; 5) вторая и четвертая четверти координатной плоскости, включая оси ОХ и ОУ.

Организация погружения в проблему

Проводит фронтальный опрос. Предлагает учащимся назвать тему урока и цели

Готовность учащихся к активной учебно-познавательной деятельности на основе опорных знаний. Пытаются решить задания известным способом. Задания выполняют самостоятельно. Сверяют ответы

Фиксируют проблему.

Слушают учителя. Строят понятные для собеседника высказывания

Принимают и сохраняют учебную цель .

4Усвоение новых знаний и способов действий

1) Слайд 1.Выполните устно следующее упражнение:

Учащиеся находят отличия в записанных неравенствах (в 2-х неравенствах- по 1 переменной, в остальных – по две)

2) Слайд 2.Определение неравенства с двумя переменными (заучивание определения и тут же опрос по цепочке).

3) Рассмотрим неравенство

2х² – у < 6.

При х = 2, у = 5 это неравенство обращается в верное числовое неравенство

2 • 2² — 5 < 6.

Говорят, что пара (2; 5) является решением этого неравенства.

Слайд 3.Определение решения неравенства с двумя переменными (заучивание определения и тут же опрос по цепочке).

4) Рассмотрим на примерах, как изображается на координатной плоскости мно­жество решений неравенства с двумя переменными.

Слайды 4 — 7. Задание 1. Изучить алгоритм нахождения множества решений неравенства

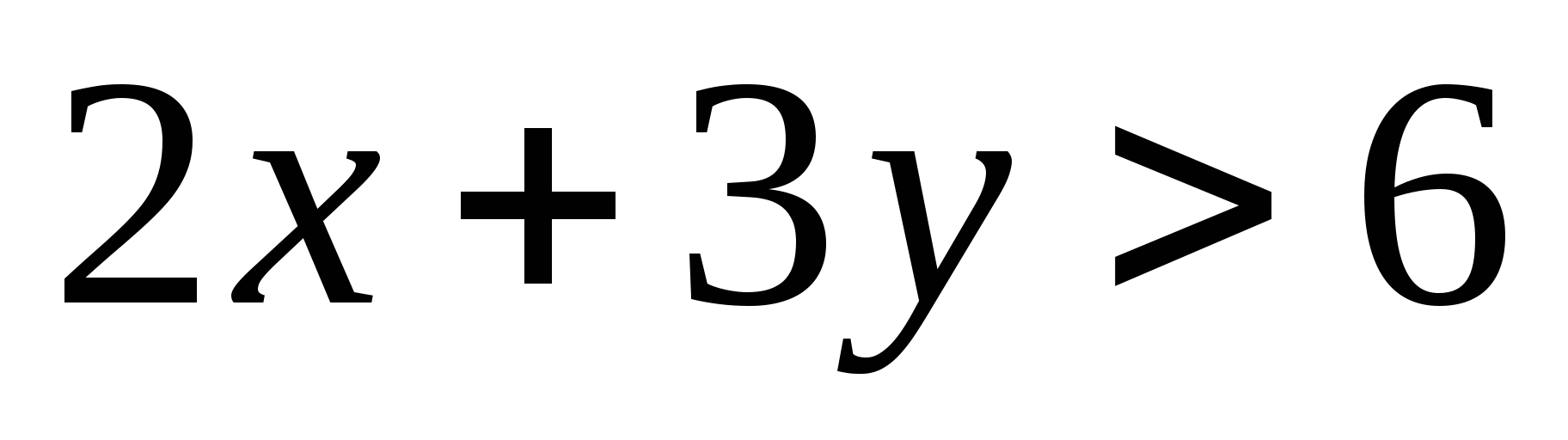(объяснение учителем по слайдам)

(Алгоритм (есть запись на слайде 9)

5) Повторение алгоритма учащимися.

Самостоятельная работа в группах-парах

Задание № 487(а. в ) Изобразить на координатной плоскости множество решений неравенства, дать устное обоснование Работу выполняем в рабочих тетрадях.

Ответы: а) у ≤ х² – 4. Решением неравенства является множество точек параболы, ветви которой направлены вверх, и точки координатной плоскости, расположенные во внешней области параболы;

в) х² + у²≤ 25 Решением является множество точек круга с радиусом 5 и центром (0;0)

Организует работу учащихся в группах. Организует диалог с обучающимися.

Записывают в тетрадях неравенства, выполняют построения кривых в координатной плоскости. Объясняют результаты сравнений.

Формулируют тему и цель урока

Строят понятные для собеседника высказывания

Обосновывают решения, приводят примеры, учатся анализировать

5.Физминутка

В положении сидя носочки ног потянуть вперед, откинувшись на спинку стула и отведя руки за спинку стула, голову наклонить назад (повторить трижды)

6.Закрепление знаний и способов действий

Слайды 8 – 11. (Открыть только 8 слайд, когда учащиеся перепишут задание, открыть алгоритм выполнения задания на 9 слайде)

Задание 2. Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству

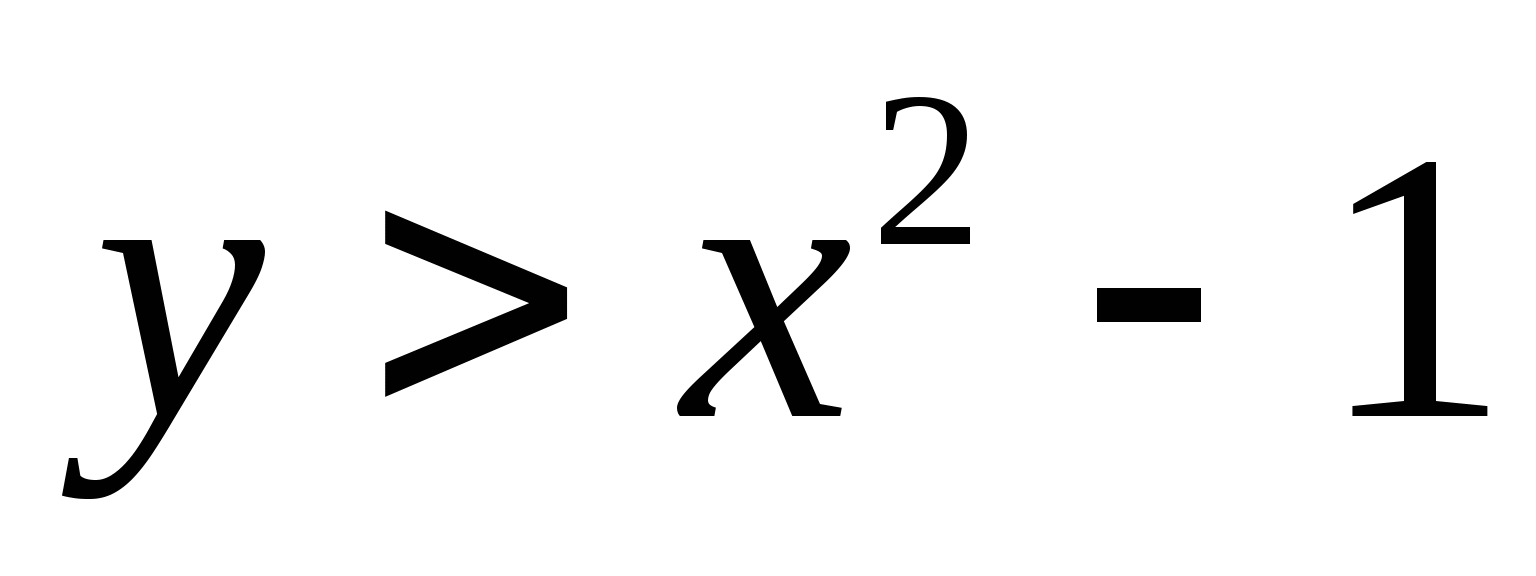(К доске вызывается 1 ученик)

Проверка – на 10,11 слайдах.

Проводит коррекционную работу, дает консультацию по просьбе учащихся

Прослушивание информации одноклассников, выполнение заданий, требующих применения знаний в знакомой и измененной ситуациях

Учатся слушать, проверять, исправлять ошибки и анализировать работу одноклассников

Проверяют правильность выполнения своих заданий, корректируют записи и рисунки, следят за эстетикой письма в тетрадях

7.Информация о домашнем задании

п.21, выучить правила, №482, №484

Реализует необходимые и достаточные условия для успешного выполнения домашнего задания всеми учащимися в соответствии с уровнем их развития

Проводят сверку соответствующих записей в тетрадях и дневниках.

Настраиваются на верное выполнение домашнего задания

Оценивают свои возможности для выполнения домашнего задания

8. Контроль и самопроверка знаний

Тест (самостоятельная работа) по повторению (Приложение 3)

Ответы во всех заданиях под № 1

Наблюдает за самостоятельным выполнением заданий учащимися

Выявляют качество и уровень овладения знаниями и способами действий по решению неравенств и уравнений.

Обеспечивают коррекцию записей и верных ответов.

Выполняют работу индивидуально

10.Подведение итогов знаний

Комментирует и выставляет оценки за урок

Слушают учителя

Проводят оценку своих возможностей на успешное усвоение материала урока

Анализируют и сравнивают результаты своей деятельности за урок с другими учащимися

11.Рефлексия

Предлагает учащимся проанализировать их деятельность на уроке. А также оценить усвоение материала за урок.

Мотивируют свои успехи и учебную деятельность

Усваивают принципы саморегуляции и сотрудничества. Прогнозируют способы саморегуляции и сотрудничества.

Осмысливают свои действия и дают самооценку.

ПРИЛОЖЕНИЕ 1

1. y = 5x + 3

2. y = 2x² – 8x + 3

3. 2x + 3y = 7

4. x² + y² = 16

5. y = (x – 2)² – 1

6. y = 5/x

7. (x – 1)² + (y – 2)² = 4

ПРИЛОЖЕНИЕ 2

I вариант

1.Изобразите график функции y = x² — 4

2.Принадлежат ли графику функции точки: A (1;- 3), B (0;- 5)

3.Верно ли неравенство: х² – 4 > — 5

Пользуясь графиком, докажите истинность неравенства. Как интерпретировать это геометрически?

4.Изобразите решение уравнения и неравенства на координатной плоскости: а) х² + у² = 4; б) х² + у² < 4

5.Изобразите на координатной плоскости множество решений неравенства ху ≥ 0

II вариант

1.Изобразите график функции y = — x² + 4

2.Принадлежат ли графику функции точки: A (1; 3), B (0;5)

3.Верно ли неравенство: — х² + 4 < 5

Пользуясь графиком, докажите истинность неравенства. Как интерпретировать это геометрически?

4.Изобразите решение уравнения и неравенства на координатной плоскости: а) х² + у² = 9; б) х² + у² < 9

5.Изобразите на координатной плоскости множество решений неравенства ху ≤ 0

ПРИЛОЖЕНИЕ 3

1.Решите неравенство х² – х — 12≤ 0 Выбрать вариант ответа 1) [- 3;4] 2) [3; — 4] 3) [3;4] 4) [ -∞;-3]U [4;+ ∞ ]

2.Какое из приведенных ниже неравенств является верным при любых a и b, удовлетворяющих условиям a>0, b <0? 1) (a – b)/a> 1 2) 2a + b > 0; 3) a + b < 0; 4) (b²/a) > 1

3.Решите уравнение (5х – 3)² = (5х + 6)²

Выбрать вариант ответа: 1) – 0,3 2) 0,3 3) 3 4) – 3

Фамилия, имя уч –ся:

«Решение неравенств и систем неравенств с двумя переменными»

Методическая разработка урока

по математике

«Решение неравенств и систем неравенств

с двумя переменными»

(9 класс)

Учитель: Супрун А.В.

г. Донецк

2017 г.

Тема: «Решение неравенств и систем неравенств с двумя переменными»

Цели урока:

1. образовательные: систематизация знаний и умений по теме «Решение неравенств с двумя переменными», применение полученных знаний на практике;

2. развивающие: развитие мышления, памяти, самостоятельной творческой деятельности учащихся, графической грамотности;

3. воспитательные: воспитание ответственности за свою учёбу и интереса к изучаемому предмету.

Тип урока: обобщение и систематизация знаний.

Формы, методы, приёмы работы: фронтальная беседа, работа учащихся в парах, индивидуальная работа.

Ресурсы: раздаточный материал.

План урока

I – Организационный момент.

Приветствие учащихся, проверка готовности к уроку. Сообщение темы и цели урока.

II – Проверка домашнего задания.

Работа в парах, взаимопроверка. Проверка по образцу решения домашнего задания. Учитель предлагает проверить и оценить выполнение домашнего задания. Выяснить ошибки, исправить их, используя метод «Пресс». Оценить работу (2 балла).

1. x²+y²>4

3)

III – Актуализация знаний учащихся.

Фронтальная беседа с классом, отработка теории по теме «Неравенства с двумя переменными, уравнения с двумя переменными и их графики».

1.

1. Что называется графиком уравнения с двумя переменными?

2. Что называется решением неравенства с двумя переменными?

3. Что называется графиком неравенства с двумя переменными?

4. Что является графиком неравенства x≥2, y≤-3, y>x², x²+y²≤4, y≥|x|, |x|+|y|≤2

2.Практическая работа «Задание на двоих» (работа в парах).

Установить соответствие между графиком неравенства и формулой. Оценить работу (1 задание – 1 балл).

a)

б)

в)

IV – Практическое применение полученных знаний, усовершенство- вание умений и навыков.

Знакомство с заданиями. Установить шаги решения.

Изобразить на координатной плоскости XY множество решений неравенства или системы неравенств:

1. y≤x²-2|x|–3

2. |y-3x|≤4

Индивидуальное задание (повышенной трудности)

|x+1|-|y-1|≤2

V –Рефлексия. Итог урока.

Мы повторили построение и преобразование графиков уравнений с двумя переменными, рассмотрели примеры графического решения неравенств и систем неравенств с двумя переменными.

VI –Домашнее задание:

П. 20, № 20.11 (1), № 20.9 (4)

Дополнительное задание: решить систему уравнений с двумя переменными.

x²+y²=17

x+xy+y=9

VII –Закрепление.

Самостоятельная работа по вариантам

Изобразите на координатной плоскости XY множество решений системы неравенств:

I вариант

1)

3б

2)

4б

II вариант

1)

2)

Конспект урока алгебры в 9 классе «Системы неравенств с двумя переменными»

Урок алгебры по теме «Системы неравенств с двумя переменными». 9-й класс

Цели:

• Образовательные – ввести понятие решения системы неравенств с двумя переменными; формировать умение решать системы неравенств с двумя переменными, отработать навыки построения множества решений систем неравенств на координатной плоскости;

• Развивающие – формирование графической и функциональной культуры учащихся;

• Воспитательные – воспитание интереса к математике и повышение мотивации учебной деятельности через внедрение компьютерных технологий в процесс обучения, побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей учебной деятельности.

Ход урока

ОГЭ-34в

Актуализация знаний.

Учитель. На доске вы видите два неравенства

х²+3ху –у²<20 и (х-3)²+(у-4)²<2

• Как они называются? [Неравенства с двумя переменными]

• Что является решением такого неравенства? [Пара чисел, которые удовлетворяют неравенству]

• Определите, является ли пара чисел (-2;3) решением какого либо из этих неравенств? [Являются решением только первого неравенства]

• Найдите свою пару чисел которая являлась бы решением второго неравенства [Например 3 и 4, 4 и 4, 3 и 5 и т.д.]

Проверка домашнего задания.

Учитель Давайте вспомним , как решаются такие неравенства.

На примере неравенств х²+2 > у  рассказать о решении неравенств с двумя переменными.

Двое учащихся рассказывают и показывают решение неравенств на доске.

• Чем отличается решение строгого неравенства от нестрогого? [линия функии штриховая]

• Как можно проверить правильно ли вы выбрали множество? [Правило пробной точки]

Новая тема.

Учитель. Тема сегодняшнего урока «Системы неравенств с двумя переменными»

• Как вы думаете, каковы цели сегодняшнего урока?

• Чему вы должны научиться к концу сегодняшнего урока?

Рассмотрим систему неравенств с двумя переменными.

№496

• Как вы думаете, что же может, является решением такой системы? [Пара чисел]

• Какие из пар (4;2), (-5;1), (-2;-1) являются решением этой системы? [Первая]

• Как по-вашему, сколько решений может иметь такая система? [Множество]

• Что значит решить систему?c[Найти все решения, или доказать, что таких решений нет]

Учитель. Давайте выясним, какое множество точек задает на координатной плоскости система. Как это сделать? [Решить по отдельности каждое неравенство и найти их пересечение решений.]

Пример 1

Ребята в тетрадях рисуют графики функций, а учитель поэтапно показывает графики на доске

Закрепление.

№497 а, в на обычной доске [Одновременное решение на доске и в тетрадях]

Итоги урока.

– Что называется решением системы неравенств с двумя переменными?

– Как решаются системы линейных неравенств с двумя переменными?

– Как проверить верно ли выбрано решение?

Домашнее задание.

№ 497 (б, г),

Огэ35в

План-конспект урока по алгебре (9 класс) по теме: Решение неравенств и систем неравенств с двумя переменными

Решение неравенств и систем неравенств с двумя переменными

Повторение. Подготовка к ГИА. 9  класс.

Цели урока:

— Повторение понятия решения неравенства  и системы неравенств с двумя переменными.

— Повторение алгоритма решения неравенства с двумя переменными.

— Повторение алгоритма решения системы неравенства с двумя переменными.

— Использование технологии уровневой дифференциации.

Приборы и материалы: распечатанные по вариантам разноуровневые самостоятельные и домашние задания.

План урока:

1. Организационный момент.
2. Повторение понятия решения неравенства  и алгоритма решения неравенства с двумя переменными и закреплениеэтой темы.
3. Физкультминутка.
4. Повторение понятия решения системы неравенств и  алгоритма решения системы неравенства с двумя переменными.
5. Самостоятельная работа.
6. Домашняя работа.

Ход урока:

1. Организационный момент.

2. Повторение понятия решения неравенства  и алгоритма решения неравенства с двумя переменными.

Решением неравенств с двумя переменными называется пара значений переменных, обращающая данное неравенство в верное числовое неравенство.

Выполняя упражнение № 554 из учебника «Алгебра» 9 класса,

рассмотрим, как изображается на координатной плоскости множество решений неравенства с двумя переменными.

Изобразите на координатной плоскости множество решений неравенства:

а) у ≥ |х|;                                                              б) у ≤ |х — 2|.

Решение:

а) Построим график функции , причем он будет изображаться в виде сплошной линии, так как неравенство было нестрогое. В случае строгого неравенства график рисуют штриховой линией. График разбил координатную плоскость на две части: верхнюю и нижнюю. Выберем любую точку на плоскости. Например А(1; 3) из верхней полуплоскости. Подставим значения х и у  в неравенство у ≥ |х|. 3 ≥ |1| — верно. Значит координаты точек верхней области удовлетворяют данному неравенству, поэтому выделим эту часть плоскости штриховкой. Решением неравенства являются координаты точек, принадлежащих графику функции  и координаты точек, расположенных выше него.

Задание б) все учащиеся выполняют самостоятельно с последующей самопроверкой. Для этого два ученика одновременно выполняют решение на внутренних частях доски. Затем открывают своё решение и все учащиеся проверяют верность выполненного задания.

3. Физкультминутка.

4. Повторение понятия решения системы неравенств и  алгоритма решения системы неравенства с двумя переменными и закреплениеэтой темы.

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений входящих в неё неравенств. На координатной плоскости множество решений системы неравенств изображается множеством точек, представляющих собой общую часть множеств, задаваемых неравенствами, входящими в систему.

Пример. Изобразите на координатной плоскости множество решений системы      Решение.

. 

Решением системы является часть плоскости с двойной штриховкой.

5. Самостоятельная работа (разноуровневая).

Вариант А 1.

№1. Изобразите на координатной плоскости множество решений неравенства у ≥  |х — 3|.      

 №2. Изобразите на координатной плоскости множество решений системы  

Вариант А 2.

№1. Изобразите на координатной плоскости множество решений неравенства у ≤ |х — 4|. №2.  Изобразите на координатной плоскости множество решений системы  

                                                   

Вариант Б 1.

№1. Изобразите на координатной плоскости множество решений неравенства у ≥  |х + 3|.      

 №2. Изобразите на координатной плоскости множество решений системы  

Вариант Б 2.

№1. Изобразите на координатной плоскости множество решений неравенства у ≤ |х + 4|. №2.  Изобразите на координатной плоскости множество решений системы

 

6. Домашнее задание:

№1 Решите неравенства:  а) ,            б) .

№2 Изобразите на координатной плоскости множество решений системы

а)                          б)  

Презентация к уроку по алгебре (9 класс) по теме: Презентация по теме «Решение неравенств с двумя переменными»

По теме: методические разработки, презентации и конспекты

Методическая разработка урока алгебры для 9 класса по теме «Системы неравенств с двумя переменными в задачах линейного программирования»

Данная разработка может применяться как обобщающий урок по теме «Системы неравенств с двумя переменными» в 9 классе (алгебра 9 под ред. Теляковского) и как урок повторения по данной теме в 10 классе. …

Урок.»Неравенства с двумя переменными.»

9 класс. Тема урока:»Неравенства с двумя переменными.» Объяснение нового материала….

Открытый урок по теме «Неравенства с двумя переменными»

Данный урок проводился в рамках месячника открытых уроков. Рассчитан на среднего уровня класс, разработан по учебнику Макарычева Ю.Н. и др. — М. : Просвещение, 2010, пункт 21, относится к уроку изучен…

Решение неравенств и систем неравенств с двумя переменными

Алгебра.Повторение. Подготовка к ГИА. 9  класс….

Презентация к уроку «Неравенства с двумя переменными».

Предлагаемая вашему вниманию презентация содержит иллюстрации к решению некоторых заданий из параграфа «Неравенства с двумя переменными»  учебника алгебры для 9 класса Ю.Н.Макарычева и др. Сами р…

Разработка урока по алгебре в 9 классе по теме: «Неравенства с двумя переменными»

Урок закрепления пройденного материала по теме :»Неравенства с двумя переменными» в 9 классе, учебник Алгебра 9, Ю.Н.Макарычев, Н.Г.Миндюк и др. Разработка урока в форме технологической…

Презентации к урокам по теме «Системы неравенств с двумя переменными» в 9 классе

Разработка трёх уроков по теме «Системы неравенств с двумя переменными» 9 класс….