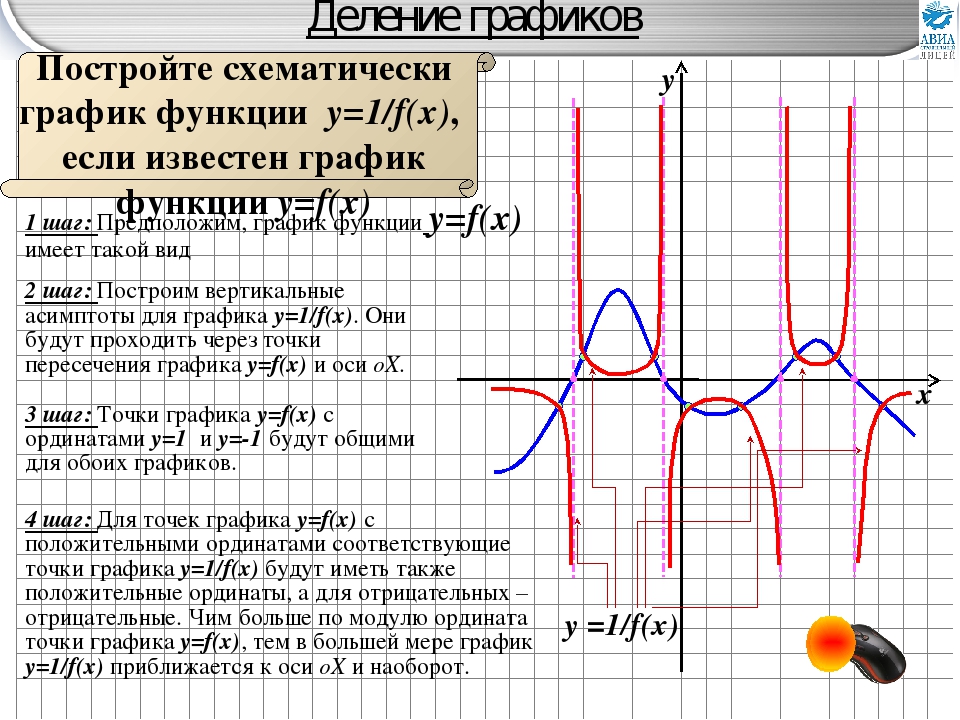
3 6 Risolvere per ? cos(x)=1/2 7 Risolvere per x sin(x)=-1/2 8 Преобразовать из градусов в радианы 225 9 Risolvere per ? cos(x)=( квадратный корень 2)/2 10 Risolvere per x cos(x)=( квадратный корень 3)/2 11 Risolvere per x sin(x)=( квадратный корень 3)/2 12 График g(x)=3/4* корень пятой степени x 13 Найти центр и радиус x^2+y^2=9 14 Преобразовать из градусов в радианы 120 град. {3}}\right)\right) = \infty$$
— пределы не равны, зн.
$$x_{3} = 0$$
— является точкой перегиба

Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках

(-oo, -(sqrt(3)*sqrt(-(4 + 3*sqrt(2))**(1/3) - 2**(2/3) + 2**(1/3)*(4 + 3*sqrt(2))**(2/3)) + 3*(4 + 3*sqrt(2))**(1/6))/(3*(4 + 3*sqrt(2))**(1/6))]

Выпуклая на промежутках

[-(-sqrt(3)*sqrt(-(4 + 3*sqrt(2))**(1/3) - 2**(2/3) + 2**(1/3)*(4 + 3*sqrt(2))**(2/3)) + 3*(4 + 3*sqrt(2))**(1/6))/(3*(4 + 3*sqrt(2))**(1/6)), oo)

Задание №7. Производная. Поведение функции. Первообразная

Необходимая теория:

Производная функции

Таблица производных

Первообразная функции

Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих встречаются вопросы о первообразной.

Геометрический смысл производной 

Вспомним, что производная — это скорость изменения функции.

Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.

1. На рисунке изображён график функции и касательная к нему в точке с абсциссой Найдите значение производной функции в точке

Производная функции в точке равна тангенсу угла наклона касательной, проведенной в точке .

Достроив до прямоугольного треугольника АВС, получим:

Ответ: 0,25.

2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке

Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке образует тупой угол с положительным направлением оси . Поэтому из прямоугольного треугольника мы найдём тангенс угла , смежного с углом .

Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку , имеем:

Ответ: −0, 25.

Касательная к графику функции

3. Прямая является касательной к графику функции

Найдите абсциссу точки касания.

Запишем условие касания функции и прямой в точке

При значения выражений и равны.

При этом производная функции равна угловому коэффициенту касательной, то есть .

Из второго уравнения находим или Первому уравнению удовлетворяет только .

Физический смысл производной

Мы помним, что производная — это скорость изменения функции.

Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.

Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.

4. Материальная точка движется прямолинейно по закону , где — расстояние от точки отсчета в метрах, — время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени

с.

Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:

Найдем скорость материальной точки как производную от координаты по времени:

В момент времени получим:

.

Ответ: 3

Применение производной к исследованию функций

Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.

Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.

Или наоборот. Нарисован график производной — а спрашивают о поведении функции.

И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.

Если , то функция возрастает.

Если , то функция убывает.

В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».

В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».

 

5. На рисунке изображен график функции , определенной на интервале Найдите количество точек, в которых производная функции равна 0.

Производная функции в точках максимума и минимума функции Таких точек на графике 5.

Ответ: 5.

6. На рисунке изображён график — производной функции , определённой на интервале .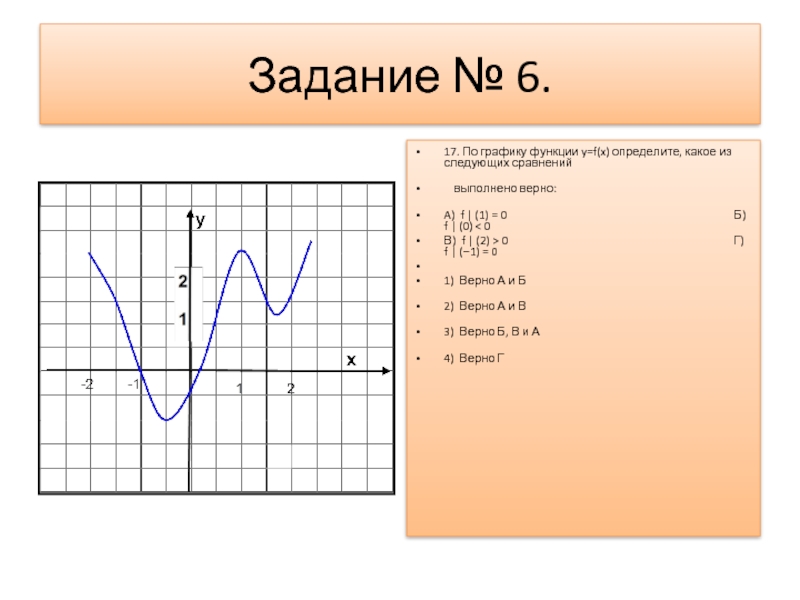 В какой точке отрезка функция принимает наибольшее значение?

Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?

Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.

На отрезке производная функции положительна.

Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.

Ответ: 3.

7. На рисунке изображён график функции , определённой на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой

Прямая параллельна оси абсцисс. Найдем на графике функции точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.

Ответ: 7.

8. На рисунке изображен график производной функции

, определенной на интервале Найдите количество точек максимума функции на отрезке

Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это

Ответ: 1.

9. На рисунке изображен график производной функции , определенной на интервале Найдите точку экстремума функции на отрезке

Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке В этой точке производная меняет знак с минуса на плюс.

Значит, является точкой экстремума.

Первообразная и формула Ньютона-Лейбница

Функция , для которой является производной, называется первообразной функции Функции вида образуют множество первообразных функции

10. На рисунке изображён график — одной из первообразных некоторой функции , определённой на интервале Пользуясь рисунком, определите количество решений уравнения на отрезке

Функция для которой является производной, называется первообразной функции

Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции равна нулю. Это точки максимума и минимума функции На отрезке таких точек 4.

Ответ: 4.

Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье

Первообразная функции. Формула Ньютона-Лейбница.

 

Параграф 2.1. Понятие числовой функции. Простейшие свойства числовых функций.

 

---

Работу выполнил: Косярский А.А. студент группы 45.2

Пункт 2.1. Понятие числовой функции. Простейшие свойства числовых функций.

 

1. Понятие числовой функции

Числовой функцией с областью определения D называется зависимость, при которой каждому числу x
из множества D (области определения) ставится в соответствие единственное число y.
Записывается это соотвествие так: y=f(x)
Обозначения и термины
D(f) — область определения
E(f) — область значений
x — аргумент (независимая переменная)
y — функция (зависимая переменная)
f — функция
f(x0) — значение функции f в точке x0

2. График функции

 

Графиком функции f называется множество всех точек координатной плоскости
с координатами (x; f (x)), где первая координата x

«пробегает» всю область определения функции, а вторая координата
равна соответствующему значению функции f в точке x

 

3. Возрастающие и убывающие функции

 

Функция f(x) возрастающая на множестве P:
если x2 > x1, то f(x2) > f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)

 

 

 

 

 

Функция f(x) убывающая на множестве P:
если x2 > x1, то f(x2) < f(x1)
для любых x1 и x2, лежащих во множестве P
(при увеличении аргумента соотвествующие точки графика поднимаются)

 

 

 

4. Чётные и нечётные функции

 

Функция f(x) чётная:
если f(-x) = f(x)
для любых x из области определения.
График чётной функции симметричен относительно Oy

 

 

Функция f(x) нечётная:
если f(-x) = -f(x)
для любых x из области определения.
График нечётной функции симметричен относительно начала координат

 

 

Объяснение и обоснование

1. Понятие функции. С понятием функции вы ознакомились в курсе алгебры.
Напомним, что зависимость переменной y от переменной x называется функцией, если
каждому значению x соответствуе единственное значение y.
В курсе алгебры и начал математического анализа мы будем пользоваться
следующим определением числовой функции.

 

Числовой функцией с областью определения D называется зависимость,
при которой каждому числу x из множества D ставится в соответствие
единственное число y.

 

Функции обозначают латинскими (иногда греческими) буквами. Рассмотрим
произвольную функцию f. Число y, соответствующее числу x (на рисунке 9 это
показано стрелкой), называют значением функции f в точке x и обозначают f (x).

Область определения функции f — это множество тех значений, которые
может принимать аргумент x. Она обозначается D(f).

Область значений функции f — это множество, состоящее из всех чисел
f(x), где x принадлежит области определения. её обозначают E(f).

Чаще всего функцию задают с помощью какой-либо формулы. Если нет
дополнительных ограничений, то областью определения функции, заданной
формулой, считается множество всех значений переменной, при которых эта
формула имеет смысл.

Например, если функция задана формулой y = √x + 1, то её область
определения: x ≥ 0, то есть D(y) = [0;+∞), а область значений:
y ≥ 1, то есть E(y) = [1;+∞).

Функция может задаваться не только при помощи формул, но и сс помощью
таблицы, графика или словесного описания. Например, на рисунке 10
графически задана функция y = f(x) с областью определения
D(f) = [-1;3] и множеством значений E(f) = [1;4]

2. График функции. Напомним, что
графиком функции y = f(x) называется множество точек
координатной плоскости с координатами (x;f(x)), где первая координата
x «пробегает» всю область определения функции, а вторая координата —
это соответствующее значение функции f точке x.

 

 

На рисунках к пункту 4 табицы 2 приведены графики функций y = x²
и y = 1/x, а на рисунке 11 — график функции y = |x|.

 

Приведём также график функции y = [x], где [x] — обозначение
целой части числа x, то есть наибольшего целого числа,
не превосходящего x (рис. 12). Область определения этой функции
D(y) = R — множество всех действительных чисел, а область
значений E(y) = Z — множество всех целых чисел.

На рисунке 13 приведён график ещё одной числовой функции y = {x},
где {x} — обозначение дробной части числа x ( по определению
{x} = x — [x]).

 

 

 

3. Возрастающие и убывающие функции. Важными характеристиками
функций являются их возрастание и убывание.

Функция f(x) называется возрастающей на множестве P, если
большему значению аргумента из этого множества соответствует
большее значение функции.

То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) > f(x1).
Например, функция f(x) = 2x возрастающая ( на всей области
определения — на множестве R), поскольку при x2 > x1 имеем
2⋅ > 2⋅, то есть f(x2) > f(x1). У возрастающей
функции при увеличении аргумента соотвествующие точки графика
поднимаются (рисунок 14).

На рисунке 15 приведён график ещё одной возрастающей функции
y = x³. Действительно, при x2 > x1 имеем x2³ > x1³,
то есть f(x2) > f(x1).

Функция f(x) называется убывающей на множестве P, если
большему значению аргумента из этого множества соответствует
меньшее значение функции.

То есть для любых двух значений x1 и x2 из множества P, если
x2 > x1, то f(x2) < f(x1).

Например, функция f(x) = -2x убывающая ( на всей области
определения — на множестве R), поскольку при x2 > x1 имеем
-2⋅ < -2⋅, то есть f(x2) < f(x1). У убывающей
функции при увеличении аргумента соотвествующие точки графика
опускаются (рисунок 16).

 

Рассматривая график функции y = x² (рис. 17), видим, что
на всей области определения эта функция не является ни возрастающей,
ни убывающей. Однако можно выделить промежутки области определения,
где эта функция возрастает и где убывает. Так как на промежутке
(-∞;0] — убывает, а на промежутке [0;+∞) функция
y = x² возрастает.(Докажите самостоятельно).

отметим, что для возрастающих и убывающих функций выполняются
свойства, обратные утверждениям, содержащимся в определении.

Если функция возрастает, то большему значению функции
соответствует большее значение аргумента.
Если функция убывает, то большему значению функции
соответствует меньшее значение аргумента.

 

Обоснуем первое из этих свойств методом от противного. Пусть
функция f(x)возрастает и f(x2) > f(x1). Допустим, что
аргумент x2 не больше аргумента x1, то есть x2≤x1.
Из этого предположения получаем: если x2≤x1 и f(x)
возрастает, то f(x2)≤f(x1), что противоречит
условию f(x2) > f(x1). Таким образом, наше предположение
неверно, и если f(x2) > f(x1), то x2 > x1, ч.т.д.
Аналогично обосновывается и второе свойство.

Например, если x² > 8, то есть x² > 2², то,
учитывая возрастание функции f(x) = x², получаем x > 2.

4. Чётные и нечётные функции. Рассмотрим функции, области
определения которых симметричны относительно начала координат, то
есть содержат вместе с каждым числом x и число (-x). Для таких
функций вводятся понятия чётности и нечётности.
Функция f называется чётной, если для любого x из её области определения
f(-x) = f(x).

Например, функция y = x² (то есть функция f(x) = x²) —
чётная, поскольку f(-x) = (-x)² = x² = f(x).

Если функция f(x) чётная, то ее графику вместе с каждой точкой
M с координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;f(x)). Точки M и M1
расположены симметрично относительно оси Oy (рис. 18), поэтому
и весь график чётной функции расположен симметрично относительно оси OY.

Например, график четной функции y = x² (рис. 17)
симметричен относительно Oy.
Функция f называется нечётной, если для любого x из её области определения
f(-x) = -f(x).
Например, функция y = 1/x ( то есть функция f(x) = 1/x) — нечётная,
поскольку f(-x) = 1/(-x) = -1/x = -f(x).

 

 

Если функци f(x) нечётная, то её графику вместе с каждой точкой M с
координатами (x;y) = (x;f(x)) принадлежит также точка M1 с
координатами (-x;y) = (-x;f(-x))=(-x;-f(x)). Точки M и M1
расположены симметрично относительно начала координат (рис. 19), поэтому
и весь график нечётной функции расположен симметрично относительно начала координат.

Например, график нечётной функции y = 1/x (см. пункт 4 табл. 2) симметричен относительно
начала координат, то есть точки O.

 

 

 

ВОПРОСЫ ДЛЯ КОНТРОЛЯ:

1. Что называется числовой функцией? Приведите примеры таких функций.
2. На примерах объясните, что такое область определния функции и область
значений функции. Какие ограничения необходимо учесть при нахождении
области определения функции y = √x/x ? Найдите её область определения.
3. Что называется графиком функции y = f(x)? Приведите примеры.
4. Какая функция называется возрастающей? Приведите примеры.
5. Какая функция называется убывающей? Приведите примеры.
6. Какая функция называется чётной? Приведите примеры. Как расположен
график чётной функции на координатной плоскости? Приведите примеры.
7. Какая функция называется нечётной? Как расположен график нечётной
функции на координатной плоскости? Приведите примеры.

---

УПРАЖНЕНИЕ 1. Найдите область определения функции: 1.y = x² + x         2.y = x/(x² + x)          3. y= √(x+5)
РЕШЕНИЕ 1) Ограничений для нахождения значений выражения x² + x нет, таким образом D(y) = R. 2) Область определения функции y = x/(x² + x) задаётся ограничением x² + x ≠ 0, поскольку знаменатель не может быть равным нулю. Выясним, когда x² + x = 0. Имеем x(x + 1) = 0, x = 0 или x = -1. Тогда область определения можно задать ограничениями x ≠ 0, x ≠ -1 или записать так: D(y) = (-∞;-1) ∪ (-1;0) ∪ (0;+∞) 3) Область определения функции y= √(x+5) задаётся ограничением x + 5 ≥ 0, то есть x ≥ -5, поскольку под знаком квадратного корня должно стоять неотрицательное выражение. Таким образом, D(y) = [-5;+∞)	КОММЕНТАРИЙ Поскольку все функции заданы формулами, то их области определения — это множество всех значений переменной x, при которых формула имеет смысл, то есть имеет смысл выражение, которое стоит в правой части формулы y = f(x). В курсе алгебры встречались только два ограничения, которые необходимо учитывать при нахождении области определения: 1)если выражение записано в виде дроби A/B, то знаменатель B ≠ 0 2)если запись выражения содержит квадратный корень √ A, то подкоренное выражение A ≥ 0. В других случаях, которые вам приходилось рассматривать, областью определения выражения были все действительные числа.
УПРАЖНЕНИЕ 2. Найдите область определения функции: y = x² — 3
РЕШЕНИЕ Составим уравнение x² — 3 = a. Оно равносильно уравнению x² = a +3, которое имеет решения, если a + 3 ≥ 0, то есть при a ≥-3. Все эти числа и составят область значений функции. Таким образом, область значений заданной функции E(f) = [-3;+∞), то есть y ≥ -3.	КОММЕНТАРИЙ Обозначим значение заданной функции f(x) ( то есть x² — 3) через a и выясним, для каких a можно найти соответствующее значение x ( при этом значении x значение f(x) = a). Тогда все числа a, для которых существует хотя бы один корень уравнения f(x) = a, войдут в область значений функции f(x). Множество всех таких a и составит область значений функции.
УПРАЖНЕНИЕ 3. Докажите, что при k ≠ 0 областью значений линейной функции y = kx + b является множество всех действительных чисел.
ДОКАЗАТЕЛЬСТВО Если kx + b = a (где k ≠ 0), то решение этого уравнения x = (a — b)/k существует для любого a ∈ R (k ≠ 0 по условию). Таким образом, значением заданной функции может быть любое действительное число. Итак, ее область значений E(f) = R.	КОММЕНТАРИЙ Обозначим значение заданной функции f(x), то есть kx + b, через a и выясним, для каких a можно найти соответствующее значение x, такое, что f(x) = a. Множество всех таких значений a и будет составлять область значений функции f(x).
УПРАЖНЕНИЕ 4. Докажите, что линейная функция y = kx + b при k > 0 является возрастающей, а при k < 0 — убывающей.
ДОКАЗАТЕЛЬСТВО Пусть x2 > x1 (тогда x2 — x1 >0). Рассмотрим разность f(x2) — f(x1) = kx2 + b — (kx1 + b) = k(x2 — x1). Поскольку x2 — x1 > 0, то при k > 0 имеем f(x2) — f(x1) > 0, таким образом, f(x2) > f(x1) и, значит, функция возрастает. При k < 0 имеем f(x2) — f(x1) < 0, таким образом, f(x2) < f(x1), значит, функция убывает.	КОММЕНТАРИЙ Для обснования возрастания или убывания функцииполезно помнить, что для доказательства неравенсства f(x2) > f(x1) или f(x2) < f(x1) достаточно найти знак разноссти f(x2) — f(x1). Функция f(x) = kx + b будет возрастающей, если из неравенства x2 > x1 будет следовать неравенство f(x2) > f(x1), а для доказательства последнего неравенства достаточно найти знак разности f(x2) — f(x1) (аналогичные рассуждения применимы и для убывания функции)
УПРАЖНЕНИЕ 5. Докажите, что: 1.Сумма двух возрастающих на множестве P функций всегда является возрастающей функцией на этом множестве. 2.Сумма двух убывающих на множестве P функций всегда является убывающей функцией на этом множестве.
ДОКАЗАТЕЛЬСТВО 1) Пусть функции f(x) и g(x) являются возрастающими на одном и том же множестве P. Если x2 > x1, то f(x2) > f(x1) и g(x2) > g(x1). Складывая почленно эти нервенства, получаем: f(x2) + g(x2) > f(x1) + g(x1) Это и означает, что сумма двух возрастающих функций есть функция возрастающая. 2) Пусть функции f(x) и g(x) являются убывающими на одном и том же множестве P. Если x2 > x1, то f(x2) < f(x1) и g(x2) < g(x1). Складывая почленно эти нервенства, получаем: f(x2) + g(x2) < f(x1) + g(x1) Это и означает, что сумма двух убывающих функций есть функция убывающая.	КОММЕНТАРИЙ Для доказательства того, что сумма двух возрастающих функций f(x) и g(x) является возрастающей функцией, достаточно доказать, что на множестве P из неравенства x2 >x1 следует неравенство: f(x2) + g(x2) > f(x1) + g(x1) Аналогино, для доказательства того, что сумма двух убывающих функций f(x) и g(x) является убывающей функцией, достаточно доказать, что на множестве P из неравенства x2 > x1 следует неравенство: f(x2) + g(x2) < f(x1) + g(x1)
УПРАЖНЕНИЕ 6. Докажите, что возрастающая или убывающая функция принимает каждое свое значение только в одной точке её области определения.
ДОКАЗАТЕЛЬСТВО Пусть функция f(x) является возрастающей и f(x1) = f(x2) (1) Допустим x1 ≠ x2. Если x1 ≠ x2, то x1 > x2 или x1 x2 имеем f(x1) > f(x2), что противоречит равенству (1). Таким образом, наше предположение неверно, и равенство f(x1) = f(x2) возможно только при x1 = x2. То есть возрастающая функция принимает каждое свое значение только в одной точке её области определения. Аналогично доказывается утверждение и для убывающей функции.	КОММЕНТАРИЙ Докажем это утверждение методом от противного. Для этого достаточно допустить, что выполняется противоположное утверждение (функция может принимать одно и то же значение хотя бы в двух точках), и получить противоречие. Это будет означать, что наше предположение неверно, а верно данное утверждение.
УПРАЖНЕНИЕ 7. Исследуйте, какие из данных функций являются четными, какие нечётными, а какие ни чётными, ни нечётными. 1. y = 1/(x + 1)      2. y = x²      3. y = x³ + x
РЕШЕНИЕ 1) Область определения функции y = 1/(x+1): x ≠ -1, то есть она не симметрична относительно точки O (точка x = 1 принадлежит области определения, а точка x = -1 — нет). Таким образом, заданная функция не является ни чётной, ни нечётной. 2) Область определения функции y = x²: D(y) = R, то есть она симметрична относительно точки O. f(-x)=(-x) ² = x ²$; = f(x), следовательно, функция чётная. 3) Область определения функции y = x³ + x: D(y) = R, то есть она симметричная относительно точки . f(-x)=(-x)² + (-x) = — (x³ + x) = -f(x), значит функция нечётная.	КОММЕНТАРИЙ Для исследования функции y = f(x) на чётность или нечётность достаточно, во-первых, убедиться, что область опредления этой функции симметричная относительно точки O ( вместе с каждой точкой x содержит и точку -x), и, во-вторых, сравнить значения f(-x) и f(x).

 

5. Обоснуйте, что заданная функция является возрастающей (на её области определения):
1) y = 3x 2) y = x + 5 3) y = x³ 4) y = x⁵ 5) y = √(x)

6. Докажите, что на заданном промежутке функция возрастает:
1) y = -2/x, где x > 0 2) y = 1/x, где x < 0

7. Обоснуйте, что заданная функция является убывающей (на её области определения):
1) y = -3x 2) y = -x -1 3) y = -x³ 4) y = -x⁵

8. Докажите, что на заданном промежутке функция убывает:
1) y = 3/x, где x < 0 2) y = 5/x, где x > 0

9. Докажите, что функция y = x² на промежутке [0; + ∞) возрастает, а на промежутке (- ∞;0] убывает.

10. Используя утверждения, приведённые в примере 5, укажите какие из данных функций являются возрастающими, а какие — убывающими.
1) y = x³ + x 2) y = -x -x⁵ 3) y = x + √ (x) 4) y = -x³-x⁵

11. Используя утверждения, приведённые в примере 6:
1) Обоснуйте, что уравнение x³ + x = 10 имеет единственный корень x = 2;
2) Подберите корень уравнения √(x) + x = 6 и докажите, что других корней это уравнение не имеет.

12. Обоснуйте, что заданная функция является чётной:
1) y = x⁶ 2) y = 1/x² + 1 3) y = √ (x² + 1) 4) y = √ (|x| + x⁴)

13. Обоснуйте, что заданная функция является нечётной:
1) y = x⁵ 2) y = -1/x³ 3) y = x |x| 4) y = x³ — x

Возрастание и убывание функций | Алгебра

Определения

1) Функция y=f(x) называется возрастающей на некотором промежутке, если  бо́льшему значению аргумента из этого промежутка соответствует бо́льшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

   

2) Функция y=f(x) называется убывающей на некотором промежутке, если бо́льшему значению аргумента из этого промежутка соответствует меньшее значение функции.

То есть для любых двух значений x₁,x₂ из этого промежутка выполняется условие

   

Предполагается, что промежуток принадлежит области определения функции y=f(x). Обычно промежуток — это отрезок, интервал или полуинтервал.

График функции на промежутках возрастания «идёт вверх» (чем правее x, тем выше y).

На промежутках убывания график «идёт вниз» (чем правее x, тем ниже y).

Пример 1.

Пользуясь графиком, найти промежутки возрастания и убывания функции y=f(x), определённой на отрезке [x₁;x₅]:

Функция y=f(x) возрастает на промежутках [x₂;x₃] и [x₄;x₅]

Функция y=f(x) убывает на промежутках [x₁;x₂] и [x₃;x₄].

Кратко это записывают так:

   

   

3) Функцию, возрастающую на промежутке либо убывающую на промежутке, называют монотонной функцией на этом промежутке (или строго монотонной).

4) Если функция возрастает на всей своей области определения, то её называют возрастающей.

Если функция убывает на всей своей области определения, то её называют убывающей.

Например, y=√x, y=x³ — возрастающие функции.

Линейная функция y=kx+b возрастающая при k>0 и убывающая при k<0.

 

5) Если для любых двух значений x₁,x₂ из некоторого промежутка выполняется условие

   

то функция y=f(x) называется неубывающей на этом промежутке.

6) Если для любых двух значений x₁,x₂ из некоторого промежутка выполняется условие

   

то функция y=f(x) называется невозрастающей на этом промежутке.

7) Функцию, невозрастающую на промежутке либо неубывающую на промежутке, называют не строго монотонной функцией на этом промежутке.

Пример 2.

Пользуясь графиком, найти промежутки, на которых  функции y=g(x), определённая на отрезке [x₁;x₃], является невозрастающей и неубывающей:

Функция y=g(x) является неубывающей на промежутке [x₁;x₂].

Функция y=g(x) является невозрастающей на промежутке [x₂;x₃].

 

Возрастание и убывание функции можно определять как с помощью графика, так и аналитически.

Как доказать, что функция возрастает или убывает, с помощью задающей эту функцию формулы?

Для этого при условии x₂>x₁ на промежутке надо доказать выполнение одного из неравенств: f(x₂)>f(x₁) либо f(x₂)>f(x₁), то есть определить f(x₂)-f(x₁)>0 или f(x₂)-f(x₁)<0.

Примеры.

1) Доказать, что функция f(x)=x²+4x убывает на промежутке (-∞;-2).

Доказательство:

Функция определена на всей числовой прямой.

Пусть x₂>x₁.

f(x₁)=x₁²+4x₁, f(x₂)=x₂²+4x₂,

f(x₂)-f(x₁)=(x₂²+4x₂)-(x₁²+4x₁)=x₂²+4x₂-x₁²-4x₁=

группирует первое слагаемое с третьим, второе — с четвертым. В первых скобках — разность квадратов, из вторых выносим общий множитель 4 за скобки:

=(x₂²-x₁²)+(4x₂-4x₁)=(x₂-x₁)(x₂+x₁)+4(x₂-x₁)=

Теперь выносим общий множитель (x₂-x₁) за скобки:

=(x₂-x₁)(x₂+x₁+4).

Так как x₂>x₁, то x₂-x₁>0. Следовательно, знак произведения зависит от знака второго множителя.

Для x₁, x₂ ∈(-∞;-2) x₂+x₁+4<0. Значит, (x₂-x₁)(x₂+x₁+4)<0 и f(x₂)<f(x₁). Отсюда следует, что функция функция f(x)=x²+4x убывает на промежутке (-∞;-2).

Что и требовалось доказать.

2) Доказать, что функция

   

возрастает на промежутке (2;+∞).

Доказательство:

Функция определена при x∈(-∞;2) и (2;+∞).

Пусть x₂>x₁.

   

   

Так как x₂>x₁, то x₂-x₁>0.

Для x₁, x₂ ∈ (2;+∞) (2-x₁)(2-x₂)>0. Значит,

   

Отсюда y(x₂)-y(x₁)>0. Поэтому данная функция возрастает на промежутке (2;+∞).

Что и требовалось доказать.

 

Исследование функции на монотонность гораздо удобнее проводить с помощью производной  (начала математического анализа — производную и её применение —  проходят в школьном курсе алгебры в 10-11 классах).

Построение графиков в MathCad | Cl-Box

При решении задач в MathCad часто возникает необходимость построить график, будь то график функции или график по каким либо расчетным данным. В этой статье мы разберем как строятся графики в MathCad. В этой статье мы не будем рассматривать само решение задач, его Вы можете найти в других статьях, ссылка в конце статьи.

1. Построение графика функции в MathCad

1.1. Рассмотрим построение на примере функции sin, для этого введем в Маткад следующее (думаю как пользоваться инструментами ввода информации подробно рассматривать не надо, а если вдруг возникнут какие-либо трудности с вводом советую почитать статью Расчаты в  MathCad ):

Не забываем что необходимо ставить не знак «равно» а именно знак «определения».

1.2. Теперь нам нужно создать сам график, для этого нажимаем на пункт меню Добавить, выбираем строку Графики, и в появившемся списке выбираем X—Y график

1.3. Теперь, в появившемся поле графика заполняем наименование осей (в нашем варианте названиями будут f(x) и х)

После ввоза названий полей кликаем в любой области вне поля графика

В итоге мы получаем готовый график функции синуса:

2. Построение графика в MathCad по данным

2.1. Для начала введем данные графика, для этого вводим определитель (у меня это w и r) и добавляем матрицу нужным размером (в моем случае 6х1, это 6 строк, 1 столбик) и вводим в нее свои данные для графика. Вот что получилось у меня:

2.2. Теперь повторяем действия указанные в пункте 1.2. этой статьи (т.е. добавляем график)

2.3. Как и в пункте 1.3. этой статьи заполняем название осей, только на этот раз у нас будут определители наших данных

2.4. При необходимости совместить два графика на одном делаем следующее: добавляем еще один блок данных, ставим курсор после определителя w в графике и нажимаем поставить запятую (напоминаю, что запятая на русской раскладке и на английской раскладке это разные клавиши, и так как мы работаем в Маткаде используя английскую раскладку нам нужна запятая именно английской раскладки), после этого вводим определитель во вторую (появившеюся) строку на нашем графике.

Теперь у нас получилось два пересекающихся графика (конечно же то как он будет выглядеть зависит от данных)

3. Форматирование графика в MathCad

Созданный график по умолчанию очень бледный и Вам наверное захочется сделать его немого поярче.

3.1. На графике нажимаем ПКМ (правой клавишей мыши) и в контекстном меню выбираем пункт Формат…

В открывшемся диалоговом окне переходим на вкладку Графики

Тут мы видим табличку строка трассировка 1 соответствует первой кривой нашего графика, трассировка 2 соответственно второй. Столбик Линия соответствует типу линии на нашем графике (сплошная, прерывистая, точка-тире и т.п.). Столбик Линия Вес соответствует толщине нашей линии. И Цвет соответственно цвету. Я в своем примере изменю только толщину линии, и по второму графику тип линии с точек на пунктир для этого в двух верхних строках столбика Линия Вес поставлю цифру 2 и в столбике Линия поменяю тип линии, после чего нажму Применить

Вот что получилось:

Я думаю не надо объяснять как изменять размер графика, если это необходимо.

 

автор: Admin

Mathscene — Функции 1 — Урок 3

Mathscene — Функции 1 — Урок 3

2007 Rasmus ehf и Jhann sak

Функции Я

Печать

Урок 3

.

Функции второй степени

---

Давайте снова посмотрим на многочлены второй степени.Самая простая форма функции — f (x) = х ² . График представляет собой параболу часто называют основной параболой.

Обратите внимание, что график симметричен относительно оси y- ось. Ось ординат называется осью симметрии этой функции.

Теперь посмотрим, как коэффициенты влияют на внешний вид графика.

Коэффициент x ² равен обычно называется a. Если мы посмотрим на параболы с разными значениями a мы видим, что некоторые шире, а некоторые уже основной параболы, где a = 1.

Вот графики парабол, где a = 4, 2, ог.

а = 4 а = 2 а = а =

Вот параболы с отрицательные значения

а = −4 а = −2 а = — а = —

Если значение a равно положительный график изгибается вверх (как улыбка!) Чем больше значение уже график.

Как становится мало график становится более плоским и плоским до тех пор, пока, когда a не станет отрицательным, он не станет меньше ( как хмурый взгляд! ).

---

Пример 1

Теперь нарисуем график из f (x) = x ² + 1 и сравните его с g (x) = x ² .

x	f (х) = х 2 + 1
-2	(-2) 2 + 1 = 5
-1	(-1) 2 + 1 = 2
0	0 + 1 = 1
1	1 2 + 1 = 2
2	2 2 + 1 = 5

Значения функции ( y) в таблице значений для f (x) = x ² +1 все на единицу выше соответствующих значений в таблице значений для g (x) = x ² , а график переведен по вертикали на 1 единицу.

Обратите внимание, что график f (x) = x ² + 1 не пересекает ось абсцисс. Это говорит нам о том, что уравнение x ² + 1 = 0 не имеет решения. Мы уже знаем это, поскольку число в квадрате никогда не бывает отрицательный, поэтому x ² никогда не может быть равно -1.

---

Пример 2

Нарисуйте график f (x) = x ² — 1 и сравните с g (x) = х ² .

x	f (х) = х 2 — 1
-2	(-2) 2 — 1 = 3
-1	(-1) 2 — 1 = 0
0	0 — 1 = -1
1	1 2 — 1 = 0
2	2 2 — 1 = 3

Теперь значения функции в все таблицы f (x) на единицу ниже соответствующих значений в таблице для g (x) = x ² и график сдвинулась на одну единицу.

Обратите внимание, что в этом примере график f (x) = x ² — 1 пересекает ось x в двух местах.

Это означает, что уравнение x ² — 1 = 0 имеет два решения,

x ² — 1 = 0

х ² = 1

х = 1

, которые равны x = −1 и x = 1.

---

Пример 3

Нарисуйте график f (x) = (x + 1) ² (или f (x) = x ² + 2x + 1) и сравните это к основной параболе g (x) = x ² .

x	f (х) = (х + 1) 2
-3	(-3 + 1) 2 = 4
-2	(-2 + 1) 2 = 1
-1	(-1 + 1) 2 = 0
0	(0 + 1) 2 = 1
1	(1 + 1) 2 = 4

Здесь мы прибавили 1 к x и мы видим, что функция значения в таблице значений сдвинуты на одну строку вверх по сравнению с базовыми функция.

График f (x) — это так же, как если бы мы переместили график g (x) = x ² на одну единицу Слева.

Мы говорим, что основной граф переведено на -1 единиц по горизонтали. Ось симметрии теперь x = -1.

---

Пример 4

Нарисуйте график f (x) = (x — 2) ² — 1 (или f (x) = x ² — 4x + 3) и сравните его с базовым графиком g (x) = x ² .

Если использовать тот же метод, что и в предыдущем Например, мы можем предположить, что график переместился на две единицы вправо и одну блок вниз. Теперь проверим это, составив таблицу значения, начиная с x = 0 и рисование графика.

x	f (х) = (х — 2) 2 — 1
0	(0–2) 2 — 1 = 3
1	(1-2) 2 — 1 = 0
2	(2–2) 2 — 1 = -1
3	(3–2) 2 — 1 = 0
4	(4–2) 2 — 1 = 3

Обратите внимание, что ось симметрии теперь x = 2.

Мы можем найти, где график пересекает ось Y без рисования графика. Мы делаем это, вычисляя f (0) = 3 или путем умножения скобок и видя, что постоянный член (член без x) равен 3.

f (x) = (x — 2) ² — 1 = x ² — 4x + 4 — 1 = x ² — 4x + 3 или

f (0) = (x — 2) ² — 1 = 4 — 1 = 3

---

Пример 5

Найдите график зависимости f (x) = (x — 2) ² — 1 пересекает ось абсцисс.Положим y = f (x) = 0, а затем решим уравнение для x.

(x — 2) 2 — 1 = 0	Первый переместите -1 над знаком равенства.
(x — 2) 2 = 1	Далее, извлеките квадратный корень из обеих частей уравнения. Помните + и -.
x — 2 = 1 = 1	Наконец переместите 2 на другую сторону и упростите результат.
х = 2 1

Точки пересечения х = 2 -1 = 1 и x = 2 + 1 = 3.

Легко видеть, что запись функции как f (x) = (x — 2) ² — 1 дает нам много информации.

Он сообщает нам, как переводится основной график вертикально и горизонтально.

Он также сообщает нам, где находится ось симметрии.

Наконец, мы можем легко найти точки пересечение с осями x и y.

Общий вид уравнения, записанного в этом путь:

f (x) = a (x + r) ² + s

a — коэффициент x ² как мы уже видели.

г. ось симметрии имеет уравнение x = −r (или, можно сказать, то же значение как r, но с обратным знаком).

Поэтому важно знать, как перепишите функцию

f (x) = ax ² + bx + c в виде f (x) = a (x + r) ² + s

---

Пример 6

Теперь давайте посмотрим, как мы можем изменить секунду функция степени от одной формы к другой.

Записываем f (x) = x ² — 4x + 3 в виде f (x) = (x — 2) ² — 1.

По сравнению с общей формой:

f (x) = ах ² + bx + c

f (х) = х ² — 4x + 3

Здесь a = 1

og b = −4

и c = 3 (поэтому график пересекает ось y в 3).

Посмотрите на правило для квадрата скобки:

(x q) ² = p ² 2xq + q ² .

Мы видим, что коэффициент при x составляет 2кв.

В нашем примере коэффициент при x равен −4, что означает 2q = — 4 и, следовательно, q = −2.

Если посчитать (х — 2) ² получаем x ² — 4x + 4.

(х — 2) ² = x ² — 4x + 4.

Если мы вычтем 1 с обеих сторон мы получили :

(х — 2) ² −1 = x ² — 4x + 4−1 = x ² — 4x + 3

Обобщая метод:

f (x) = x 2 — 4x + 3	Половина коэффициент при x равен −4 / 2 = −2, который мы возводим в квадрат (4) и добавить к уравнению.
= (x 2 — 4x + 2 2 ) — 2 2 + 3
= (x — 2) 2 — 4 + 3	Если мы прибавив 4 к уравнению, мы также должны вычесть 4, чтобы уравнение без изменений Теперь упростим −4 + ​​3 = −1
= (x — 2) 2 — 1

Из приведенного выше примера можно сделать вывод, что график полинома второй степени, где a = 1 (f (x) = x ² + bx + c) имеет ось симметрии в:

x = ^−b / ₂ и обрезает y ось, где y = c.

---

Пример 7

Найдите ось симметрии графика f (x) = 2x ² — 12x + 10.

В этом случае a = 2, поэтому правило из предыдущего примера не применяется. Ни один так же легко переписать функцию, как раньше.

Вместо этого мы переводим функцию вниз на 10 единиц путем вычитания 10 из уравнения. Перемещение графика по вертикали не изменить положение оси симметрии.

Назовем эту новую функцию g (x) и найдем, где g (x) отсекает ось x.

2x ² — 12x = 0

2х (х — 6) = 0

Это уравнение имеет решения x = 0 и 6, поэтому график g (x) пересекает ось x в 0 и 6. Ось симметрии должна быть посередине этих двух точек, что находится в x = 3 .

---

Пример 8

Перепишем функцию f (x) = 2x ² — 12x + 10 в виде
f (x) = a (x + r) ² + s.

f (x) = 2x 2 — 12x + 10	Дубль 2 вне скобки. Половина коэффициента при x равно −6 / 2 = −3, поэтому добавьте 3 2 внутри скобок. Мы действительно добавили 18, поэтому теперь нам нужно вычесть 23 2 = 18 за пределами скобки.
= 2 (x 2 — 6x + 3 2 ) — 2 3 2 + 10
= 2 (x 2 — 6x + 9) — 18 + 10
= 2 (х — 3) 2 — 8

Теперь мы, как и раньше, видим, что ось симметрии находится в x = 3.

Коэффициенты x В приведенном выше примере (f (x) = 2x ² — 12x + 10) равны a = 2, b = −12 и c = 10. Чтобы найти ось симметрии, мы множитель 2 вынес за скобки. Это соответствует делению на 2. Тогда мы завершил квадрат делением коэффициента при x (−6) на 2.

Общая формула оси симметрии функция
f (x) = ax ² + bx + c — это следовательно:

---

Пример 9

Найдите вершину параболы f (x) = 2x ² — 12x + 10.

Вершина (в которой вращается парабола) лежит на оси симметрии, поэтому мы знаем значение x вершины (3).

Мы нашли значение y путем вычисления f (3).

f (3) = 23 ² — 123 + 10 = 18 — 36 + 10 = −8.

Вершина параболы равна (3, −8).

Примечание: Если a> 0, вершина является точкой минимума. Если a <0 вершина является точкой максимума.

---

Попробуйте выполнить тест 3 по функциям I.
Не забудьте использовать контрольный список, чтобы отслеживать свою работу.

1,7 — Обратные функции

1,7 — Обратные функции

Обозначение

Функция, обратная f, обозначается f ^-1 (если ваш браузер не поддерживает надстрочные индексы, это выглядит как f с показателем -1) и произносится как «f инверсия».Хотя обратная функция выглядит как вы возводите функцию в степень -1, это не так. Обратная функция не означает обратная функция.

Обратные

Функция обычно сообщает вам, что такое y, если вы знаете, что такое x. Обратная функция скажет вы, каким должен быть x, чтобы получить это значение y.

Функция f ^-1 является обратной функцией f, если

• для каждого x в области f, f ^-1 [f (x)] = x и
• для каждого x в области f ^-1 , f [f ^-1 (x)] = x

Область f — это диапазон f ^-1 , а диапазон f — это область f ^-1 .

График обратной функции

Обратная функция функции отличается от функции тем, что все координаты x и y были переключены. То есть, если (4,6) — точка на графике функции, то (6,4) — точка на графике обратной функции.

Точки на функции идентичности (y = x) останутся в функции идентичности при переключении. Все координаты других точек будут изменены, и их местоположение будет перемещено.

График функции и обратная ей функция являются зеркальным отображением друг друга.Они размышляют о функция тождества y = x.

Существование обратной функции

Функция говорит, что для каждого x существует ровно один y. То есть значения y могут дублироваться, но x значения не могут быть повторены.

Если функция имеет инверсию, которая также является функцией, тогда может быть только один y для каждого x.

Однозначная функция — это функция, в которой для каждого x есть ровно один y, а для каждого y, есть ровно один x.У однозначной функции есть обратная функция, которая также является функцией.

Есть функции, у которых есть инверсии, которые не являются функциями. Есть и обратные для связи. По большей части мы не обращаем на них внимания и имеем дело только с функциями, обратными к которым являются также функции.

Если обратная функция также является функцией, то обратная зависимость должна проходить вертикальную линию. контрольная работа. Поскольку все координаты x и y переключаются при нахождении обратного, говоря что обратная функция должна пройти проверку вертикальной линии — это то же самое, что сказать, что исходная функция должна пройти тест горизонтальной линии.

Если функция проходит как тест вертикальной линии (так что это в первую очередь функция), так и проверка горизонтальной линии (так что его обратная функция является функцией), тогда функция взаимно однозначна и имеет обратная функция.

Неформальный поиск инверсий

Инверсия некоторых функций, особенно тех, где есть только одно вхождение независимая переменная, может быть решена путем отмены операций. Чтобы отменить операции, вы должен не только изменить порядок, но и использовать обратную операцию.

Пример 1

Функция f (x) = 5x-2

1. Начать с x: x
2. Умножить на 5: 5x
3. Вычесть 2: 5x-2

Обратное f

^-1 (x) = (x + 2) / 5

1. Начать с x: x
2. Добавить 2: x + 2
3. Разделить на 5: (x + 2) / 5

Пример 2

Функция f (x) = 2 (x-3)

² -5, x≥3

Обратите внимание, что на x есть ограничение.

1. Начать с x: x
2. Вычесть 3: x-3
3. Квадрат: (x-3) ²
4. Умножить на 2: 2 (x-3) ²
5. Вычесть 5: 2 (x-3) ² -5

Обратное f

^-1 (x) = 3 + sqrt [(x + 5) / 2]

1. Начать с x: x
2. Добавить 5: x + 5
3. Разделить на 2: (x + 5) / 2
4. Извлеките квадратный корень: ± sqrt [(x + 5) / 2]
5. Добавить 3: 3 ± sqrt [(x + 5) / 2]
6. Подождите! Эта инверсия не является функцией, потому что для каждого x есть два значения y.Это из-за ±, которое появилось, когда мы извлекли квадратный корень из обеих частей. Теперь вернемся к исходной области x≥3. Это означает, что для обратного диапазон y≥3. Поскольку y должно быть не меньше 3, нам нужен положительный квадратный корень, а не отрицательный. Без ограничения на x в исходная функция, у нее не было бы обратная функция: 3 + sqrt [(x + 5) / 2]

Пример 3

Функция f (x) = x

² — 4x + 6, x≤2

Уххх ????

Что происходит, когда встречается более одного раза независимая переменная в функции? Ты не знаю, что вы сделали с x, потому что вы сделали это с двумя разных x, и вы не сделали одно и то же с обоими их.

Формальный поиск инверсий

Нельзя сказать, что последний пример не может быть выполнен, но он включает в себя завершение квадрата до получить f (x) = (x-2) ² +2, а затем инвертировать его, чтобы получить f ^-1 (x) = 2-sqrt (x-2).

Однако есть другой способ, который не слишком полагается на неформальность и будет работать независимо от того, Вы не можете точно определить, что вы сделали с одним x.

1. Начать с функции
2. Заменить f (x) на y, если необходимо
3. Поменяйте местами x и y.На данный момент вы имеете дело с инверсией
4. Решить для y
5. Замените y на f ^-1 (x), если обратная функция также является функцией, в противном случае оставьте ее как y

Пример 4

Функция f (x) = x

² / (x ² +1), x≥0

Ограничение важно сделать 1-1.

1. Начните с функции: f (x) = x ² / (x ² +1), x≥0
2. Заменить f (x) на y: y = x ² / (x ² +1), x≥0
3. Поменяйте местами x и y: x = y ² / (y ² +1), y ≥0
4. Решите для y:
   1. Умножаем на знаменатель: x (y ² +1) = y ²
   2. Распределить: xy ² + x = y ²
   3. Переместите y в одну сторону, а все остальное в другую: xy ² -y ² = -x
   4. Фактор: y ² (x-1) = — x
   5. Разделить на коэффициент при y ² : y ² = -x / (x-1)
   6. Упростите правую часть: y ² = x / (1-x)
   7. Извлеките квадратный корень: y = ± sqrt [x / (1-x)]
   8. Поскольку y≥0, нам нужен положительный квадратный корень: y = sqrt [x / (1-x)]
5. Назовите это f ^-1 (x): f ^-1 (x) = sqrt [x / (1-x)]
   

Для этой последней функции подразумеваемая область обратного преобразования — [0,1).Это означает, что диапазон исходная функция также должна быть [0,1). Проверьте это на своем калькуляторе, и вы увидите, что это так.

Иногда в инструкциях говорится, что если функция не является взаимно однозначной, то не находите обратную функция (потому что ее нет). Поэтому всегда проверяйте, прежде чем тратить время на поиск обратная функция. Теперь, если вы должны найти обратное, независимо от того, функция или нет, тогда вперед.

Хороший материал!

Индивидуальные функции — замечательные вещи.

При решении уравнений вы можете прибавить одно и то же к обеим сторонам, вычесть одно и то же из обе стороны, умножьте обе стороны на одно и то же ненулевое значение и разделите обе стороны на одно и то же отличная от нуля вещь, и вы все равно получите то же самое решение, не беспокоясь о необходимости проверять свой ответ.

Вы также можете применить взаимно однозначную функцию к обеим сторонам уравнения, не беспокоясь о введении посторонних решений (решений, которые работают после выполнения чего-то, что не работало раньше).Это не обязательно верно для функций, которые не являются взаимно однозначными, как функция возведения в квадрат, где вы всегда должны проверять ответы после возведения в квадрат обеих сторон уравнения. Например, уравнение sqrt (x) = -2 не имеет решения, но если вы возведете в квадрат обе стороны, вы получите x = 4, но оно не проверяется в исходной задаче. Благодаря индивидуальным функциям вы не будете предлагать никаких посторонних решений.

Вау! Говорить о мощный. Вы не цените этого сейчас, и книга не справится с этим должным образом, пока вы не получите к главе 4 и имеют дело с логарифмическими и экспоненциальными функциями, и даже тогда они не делают как бы то ни было.

Ладно, попробуем сейчас. Поверьте мне на слово, что exp (x) является взаимно однозначной функцией и является инверсия ln (x).

ln (x) = 3

Найдите x.

ехр [ln (x)] = ехр [3]

«Погодите, мистер Джонс» — вот ваш ответ. Вы никогда не видели такого зверя. Это хорошо. Возьмите обратную функцию и примените ее к обеим сторонам.

х = ехр (3)

Вернитесь к определению инверсии в верхней части этого документа.x и находится на клавише [2 ^nd ] [ln].

Вау — больше сплоченности. Обратную функцию можно найти, взяв функцию [2 ^nd ]. Посмотрите у него для прочего на калькуляторе.

Квадратный корень — это величина, обратная квадрату. Если вы посмотрите на три тригонометрических ключа [sin], [cos] и [tan], их инверсии находятся с помощью клавиши [2 ^nd ].

Режим мыльницы включен.

Я вам говорю — все сходится.Для тех, кто помнит строчку, которую Ганнибал Смит использовал в A-Team: «Мне нравится, когда план слагается».

Математика — один из самых совместных предметов. Все дополняет еще. Я надеюсь, что вы получите от этого курса гораздо больше, чем просто механику математика, но понимание, понимание и оценка того, как работает система. Имея такой прочный фундамент, математика может быть менее напряженной и даже приятной. У тебя есть перестать иметь дело с концепциями как с отдельными вещами, не связанными друг с другом и стоящими отдельно.Все они связаны друг с другом и переплетены. Вы не можете их разделить и понять.

Режим мыльницы выключен.

Использование преобразований в графические функции

Вертикальный и горизонтальный перевод

Когда график функции изменяется по внешнему виду и / или местоположению, мы называем это преобразованием. Есть два типа преобразований. Жесткое преобразование — набор операций, которые изменяют положение графика в координатной плоскости, но оставляют неизменными размер и форму.изменяет положение функции в координатной плоскости, но оставляет размер и форму графика неизменными. Нежесткое преобразование — набор операций, которые изменяют размер и / или форму графа в координатной плоскости. изменяет размер и / или форму графика.

Вертикальный сдвиг — жесткое преобразование, которое сдвигает график вверх или вниз. — жесткое преобразование, которое сдвигает граф вверх или вниз относительно исходного графа. Это происходит, когда к какой-либо функции добавляется константа.Если мы добавим положительную константу к каждой координате y , график сдвинется вверх. Если мы добавим отрицательную константу, график сместится вниз. Например, рассмотрим функции g (x) = x2−3 и h (x) = x2 + 3. Начните с вычисления некоторых значений независимой переменной x .

Теперь постройте точки и сравните графики функций g и h с основным графиком f (x) = x2, который показан ниже с помощью пунктирной серой кривой.

Функция g сдвигает основной график на 3 единицы вниз, а функция h сдвигает основной график на 3 единицы вверх. В общем, это описывает вертикальные переводы; если k — любое положительное действительное число:

Вертикальный сдвиг вверх k единиц:	F (x) = f (x) + k
Вертикальное смещение вниз k единиц:	F (x) = f (x) −k

Пример 1

Нарисуйте график функции g (x) = x + 4.

Решение:

Начните с базовой функции, определенной как f (x) = x, и сдвиньте график на 4 единицы вверх.

Ответ:

Горизонтальный сдвиг — жесткое преобразование, которое сдвигает график влево или вправо. — жесткое преобразование, которое сдвигает граф влево или вправо относительно исходного графа. Это происходит, когда мы добавляем или вычитаем константы из координаты x перед применением функции.Например, рассмотрим функции, определенные как g (x) = (x + 3) 2 и h (x) = (x − 3) 2, и создадим следующие таблицы:

Здесь мы складываем и вычитаем координаты x , а затем возводим результат в квадрат. Это дает горизонтальный перевод.

Обратите внимание, что это противоположное тому, что вы могли ожидать. В общем, это описывает горизонтальные переводы; если h — любое положительное действительное число:

Горизонтальный сдвиг влево ч единиц:	F (x) = f (x + h)
Горизонтальный сдвиг вправо ч единиц:	F (x) = f (x − h)

Пример 2

Нарисуйте график функции g (x) = (x − 4) 3.

Решение:

Начните с базовой функции кубирования, определяемой как f (x) = x3, и сдвиньте график на 4 единицы вправо.

Ответ:

Часто встречаются комбинации переводов.

Пример 3

Нарисуйте график функции g (x) = | x + 3 | −5.

Решение:

Начните с функции абсолютного значения и примените следующие преобразования.

y = | x | Базовая функция y = | x + 3 | Горизонтальный сдвиг влево на 3 единицы y = | x + 3 | −5 Вертикальный сдвиг вниз на 5 единиц

Ответ:

Порядок, в котором мы применяем горизонтальный и вертикальный переводы, не влияет на окончательный график.

Пример 4

Нарисуйте график функции g (x) = 1x − 5 + 3.

Решение:

Начните с обратной функции и определите переводы.

y = 1x Основная функция y = 1x − 5 Горизонтальный сдвиг вправо 5 единиц y = 1x − 5 + 3 Вертикальный сдвиг вверх на 3 единицы

Позаботьтесь о том, чтобы сместить вертикальную асимптоту от оси y на 5 единиц вправо и сместить горизонтальную асимптоту от оси x вверх на 3 единицы.

Ответ:

Попробуй! Нарисуйте график функции g (x) = (x − 2) 2 + 1.

Ответ:

Отражения

Отражение Преобразование, которое создает зеркальное отображение графика вокруг оси. представляет собой преобразование, при котором зеркальное отображение графика создается вокруг оси. В этом разделе мы рассмотрим отражения относительно осей x и y . График функции отражается относительно оси x- , если каждая координата y умножается на -1.График функции отражается относительно оси y , если каждая координата x умножается на -1 перед применением функции. Например, рассмотрим g (x) = — x и h (x) = — x.

Сравните график g и h с базовой функцией квадратного корня, определяемой f (x) = x, показанной ниже серым пунктиром:

Первая функция g имеет отрицательный фактор, который появляется «внутри» функции; это дает отражение относительно оси y .Вторая функция h имеет отрицательный фактор, который появляется «вне» функции; это дает отражение относительно оси x . В общем, правда, что:

Отражение относительно оси y :	F (x) = f (−x)
Отражение относительно оси x :	F (x) = — f (x)

При рисовании графиков с отражением сначала рассмотрите отражение, а затем примените вертикальный и / или горизонтальный перенос.

Пример 5

Нарисуйте график функции g (x) = — (x + 5) 2 + 3.

Решение:

Начните с функции возведения в квадрат, а затем определите преобразования, начиная с любых отражений.

y = x2 Основная функция. Y = −x2 Отражение относительно оси x. Y = — (x + 5) 2 Сдвиг по горизонтали влево на 5 единиц. Y = — (x + 5) 2 + 3 Сдвиг по вертикали на 3 единицы.

Используйте эти переводы, чтобы нарисовать график.

Ответ:

Попробуй! Нарисуйте график функции g (x) = — | x | +3.

Ответ:

Расширения

Горизонтальные и вертикальные переводы, а также отражения называются жесткими преобразованиями, потому что форма основного графа остается неизменной или жесткой. Функции, умноженные на действительное число, отличное от 1, в зависимости от действительного числа, кажутся растянутыми по вертикали или по горизонтали. Этот тип нежесткого преобразования называется расширением. Нежесткое преобразование, производимое умножением функций на ненулевое действительное число, которое, по-видимому, растягивает график либо по вертикали, либо по горизонтали.. Например, мы можем умножить функцию возведения в квадрат f (x) = x2 на 4 и 14, чтобы увидеть, что происходит с графиком.

Сравните график для g и h с базовой функцией возведения в квадрат, определяемой f (x) = x2, показанной ниже серым пунктиром:

Функция g круче, чем базовая функция возведения в квадрат, и ее график выглядит растянутым по вертикали. Функция h не такая крутая, как базовая функция возведения в квадрат, и кажется, что она растянута по горизонтали.

В общем имеем:

Если множитель a представляет собой ненулевую дробь между -1 и 1, он растянет график по горизонтали. В противном случае график будет растянут по вертикали. Если коэффициент a отрицательный, то он также будет производить отражение.

Пример 6

Нарисуйте график функции g (x) = — 2 | x − 5 | −3.

Решение:

Здесь мы начинаем с произведения −2 и основной функции абсолютного значения: y = −2 | x |.Это приводит к отражению и расширению.

xyy = −2 | x | ← Расширение и отражение − 1−2y = −2 | −1 | = −2⋅1 = −200y = −2 | 0 | = −2⋅0 = 01−2y = −2 | 1 | = −2⋅1 = −2

Используйте точки {(−1, −2), (0, 0), (1, −2)}, чтобы построить график функции отражения и расширения y = −2 | x |. Затем переместите этот график на 5 единиц вправо и на 3 единицы вниз.

y = −2 | x | Базовый график с растяжением и отражением относительно оси x. Y = −2 | x − 5 | Сдвиг вправо на 5 единиц. Y = −2 | x − 5 | −3 Сдвиг на 3 единицы вниз.

Ответ:

Таким образом, с учетом положительных вещественных чисел h и k :

Вертикальный сдвиг вверх k единиц:	F (x) = f (x) + к
Вертикальное смещение вниз k единиц:	F (x) = f (x) −k

Горизонтальный сдвиг влево ч единиц:	F (x) = f (x + h)
Горизонтальный сдвиг вправо ч единиц:	F (x) = f (x − h)

Отражение относительно оси y :	F (x) = f (−x)
Отражение относительно оси x :	F (x) = — f (x)

Основные выводы

• Идентификация преобразований позволяет быстро набросать график функций.Этот навык будет полезен по мере нашего прогресса в изучении математики. Часто геометрическое понимание проблемы приводит к более элегантному решению.
• Если к функции добавить положительную константу, f (x) + k, график сдвинется вверх. Если из функции f (x) −k вычесть положительную константу, график сдвинется вниз. Основная форма графика останется прежней.
• Если положительная константа добавляется к значению в области до применения функции, f (x + h), график сдвинется влево.Если положительная константа вычтена из значения в области до применения функции, f (x − h), график сдвинется вправо. Основная форма останется прежней.
• Умножение функции на отрицательную константу -f (x) отражает ее график на оси x . Умножение значений в области на -1 перед применением функции f (-x) отражает график относительно оси y .
• При применении нескольких преобразований сначала примените отражения.
• Умножение функции на константу, отличную от 1, a⋅f (x), дает расширение. Если положительное число константы больше 1, график будет казаться растянутым по вертикали. Если положительная константа представляет собой дробную часть меньше 1, график будет казаться растянутым по горизонтали.

Ответы

7. у = х; Сдвинуть вверх на 3 единицы; домен: ℝ; диапазон: ℝ

9. у = х2; Сдвинуть вверх на 1 единицу; домен: ℝ; диапазон: [1, ∞)

11. у = х2; Сдвиг вправо на 5 единиц; домен: ℝ; диапазон: [0, ∞)

13. у = х2; Сдвиг вправо на 5 единиц и на 2 единицы вверх; домен: ℝ; диапазон: [2, ∞)

15. у = | х |; Сдвиг влево на 4 единицы; домен: ℝ; диапазон: [0, ∞)

17. у = | х |; Сдвинуть вправо на 1 единицу и вниз на 3 единицы; домен: ℝ; диапазон: [−3, ∞)

19. у = х; Сдвинуть вниз на 5 единиц; домен: [0, ∞); диапазон: [−5, ∞)

21. у = х; Сдвиг вправо на 2 единицы и на 1 единицу вверх; домен: [2, ∞); диапазон: [1, ∞)

23. у = х3; Сдвиг вправо на 2 единицы; домен: ℝ; диапазон: ℝ

25. у = х3; Сдвиг вправо на 1 единицу и вниз на 4 единицы; домен: ℝ; диапазон: ℝ

27. y = 1x; Сдвиг вправо на 2 единицы; область: (−∞, 2) ∪ (2, ∞); диапазон: (−∞, 0) ∪ (0, ∞)

29. y = 1x; Сдвинуть вверх на 5 единиц; область: (−∞, 0) ∪ (0, ∞); диапазон: (−∞, 1) ∪ (1, ∞)

31. y = 1x; Сдвинуть влево на 1 единицу и вниз на 2 единицы; область: (−∞, −1) ∪ (−1, ∞); диапазон: (−∞, −2) ∪ (−2, ∞)

33. Базовый график y = −4; домен: ℝ; диапазон: {−4}

35. у = х3; Сдвинуть вверх на 6 единиц и вправо на 2 единицы; домен: ℝ; диапазон: ℝ

обратных функций

обратных функций

---

Содержание: Эта страница соответствует § 1.7 (стр.150) текста.

Предлагаемые задачи из текста

с.158 # 1-4, 5, 8, 9, 12, 13, 15, 18, 21, 22, 27, 31, 34, 37, 46, 48, 51, 71, 74, 83

Определение обратной функции

Графики обратных функций

Существование инверсии

Поиск инверсий

---

Определение обратной функции

Прежде чем определять инверсию функции, нам нужно иметь правильный мысленный образ функции.

Рассмотрим функцию f (x) = 2x + 1. Мы знаем, как вычислить f при 3, f (3) = 2 * 3 + 1 = 7. В этом разделе это помогает думать о f как о преобразовании 3 в 7, а f превращает 5 в 11 и т. д.

Теперь, когда мы думаем о f как о «действующем» на числа и преобразующем их, мы можем определить обратное к f как функция, которая «отменяет» то, что сделала f. Другими словами, функция, обратная f, должна вернуть 7 к 3, и вернем -3 к -2 и т. Д.

Пусть g (x) = (x — 1) / 2.Тогда g (7) = 3, g (-3) = -2 и g (11) = 5, поэтому кажется, что g отменяет то, что сделал f, по крайней мере для этих трех значений. Чтобы доказать, что g является обратным к f, мы должны показать, что это верно для любого значения x в область f. Другими словами, g должен вернуть f (x) к x для всех значений x в области определения f. Итак, g (f (x)) = x должно выполняться для всех x в области определения f. Чтобы проверить это условие, убедитесь, что формула для g (f (x)) упрощается до x.

г (f (x)) = g (2x + 1) = (2x + 1 -1) / 2 = 2x / 2 = x.

Это упрощение показывает, что если мы выберем любое число и позволим f действовать им, то применение g к результату восстанавливает наш оригинальный номер. Нам также нужно увидеть, что этот процесс работает в обратном порядке, или что f также отменяет то, что делает g.

f (g (x)) = f ((x — 1) / 2) = 2 (x — 1) / 2 + 1 = x — 1 + 1 = x.

Обозначив f ^-1 , обратное f, мы только что показали, что g = f ^-1 . (1/3)

Используйте калькулятор для вычисления значений f (g (4)) и g (f (-3)). g — величина, обратная f, но из-за округления ошибка, калькулятор может не вернуть точное значение, с которого вы начали. Попробуйте f (g (-2)). Ответы будут отличаться для разные компьютеры. Однако на нашей тестовой машине f (g (4)) вернул 4; g (f (-3)) вернул 3; но, f (g (-2)) вернул -1.9999999999999991, что довольно близко к -2.

Калькулятор может дать нам хорошее представление о том, что g является обратной величиной f, но мы не можем проверить все возможные значения. из х.

(b) Докажите, что g является обратным к f, упростив формулы для f (g (x) и g (f (x)).

Вернуться к содержанию

Графики обратных функций

Мы видели примеры отражений в плоскости. Отражение точки (a, b) относительно оси x равно (a, -b), а отражение (a, b) вокруг оси y равно (-a, b). Теперь мы хотим поразмышлять о прямой y = x.

Отражением точки (a, b) относительно прямой y = x является точка (b, a) .

Пусть f (x) = x ³ + 2. Тогда f (2) = 10 и точка (2,10) находится на графике f. Обратное к f должно возьмите 10 обратно к 2, то есть f ^-1 (10) = 2, поэтому точка (10,2) находится на графике f ^-1 . Точка (10,2) — отражение на прямой y = x точки (2,10). Тот же аргумент можно сделать для всех пунктов графики f и f ^-1 .

График f ^-1 является отражением относительно линии y = x графика f.

Вернуться к содержанию

Существование инверсии

Некоторые функции не имеют обратных функций. Например, рассмотрим f (x) = x ² . Есть два числа что f принимает значение 4, f (2) = 4 и f (-2) = 4. Если бы f имел обратный, то тот факт, что f (2) = 4, означал бы, что Функция, обратная f, возвращает 4 к 2. С другой стороны, поскольку f (-2) = 4, функция, обратная f, должна привести 4 к -2.Следовательно, не существует функции, обратной f.

Посмотрите на ту же проблему с точки зрения графиков. Если бы у f был обратный, то его график был бы отражением график функции f относительно прямой y = x. График f и его отражение относительно y = x показаны ниже.

Обратите внимание, что отраженный график не проходит тест вертикальной линии, так что это не график функции.

Это обобщает следующим образом: функция f имеет обратную тогда и только тогда, когда ее график отражается относительно line y = x, результат — график функции (проходит тест вертикальной линии).Но это можно упростить. Прежде чем отображать график, мы можем сказать, пересечется ли какая-либо вертикальная линия более одного раза, посмотрев как горизонтальные линии пересекают исходный график!

Тест горизонтальной линии

Пусть f — функция.

Если какая-либо горизонтальная линия пересекает график f более одного раза, то f не имеет обратной.

Если ни одна горизонтальная линия не пересекает график f более одного раза, тогда f действительно имеет обратный.

Свойство иметь обратное очень важно в математике, и у него есть название.

Определение : Функция f равна взаимно однозначно тогда и только тогда, когда f имеет обратный.

Следующее определение эквивалентно, и оно чаще всего дается для однозначного определения.

Альтернативное определение : Функция f равна однозначно , если для каждого a и b в своем домене f (a) = f (b) влечет a = b.(1/3) (кубический корень из x). Ответ

Вернуться к содержанию

Поиск инверсий

Пример 1. Сначала рассмотрим простой пример f (x) = 3x + 2 .

График f представляет собой линию с наклоном 3, поэтому он проходит тест горизонтальной линии и имеет инверсию.

Есть два шага, необходимые для вычисления f для числа x. Сначала мы умножаем x на 3, затем прибавляем 2.

Думая об обратной функции как об отмене того, что сделала f, мы должны отменить эти шаги в обратном порядке.

Шаги, необходимые для вычисления f ^-1 , состоят в том, чтобы сначала отменить прибавление 2 путем вычитания 2. Затем мы отменим умножение на 3 путем деления на 3.

Следовательно, f ^-1 (x) = (x — 2) / 3.

Шаги по поиску обратной функции f.

1. Замените f (x) на y в уравнении, описывающем функцию.
2. Поменять местами x и y. Другими словами, замените каждый x на y и наоборот.
3. Решить относительно y.
4. Заменить y на f ^-1 (x).

Пример 2. f (x) = 6 — x / 2

Шаг 1	у = 6 — х / 2.
Шаг 2	х = 6 — у / 2.
Шаг 3	х = 6 — у / 2. у / 2 = 6 — х. y = 12 — 2x.
Шаг 4	f -1 (x) = 12 — 2x.

Шаг 2 часто сбивает студентов с толку. Мы могли бы пропустить шаг 2 и найти x вместо y, но тогда мы бы получили с формулой в y вместо x. Формула будет такой же, но переменная будет другой. Избежать это мы просто меняем местами x и y перед тем, как решить.

Пример 3. f (x) = x ³ + 2

Это функция, с которой мы работали в упражнении 1. Из ее графика (показанного выше) мы видим, что у нее есть обратный. (Фактически, обратное ему было дано в упражнении 1.)

Шаг 1	y = x 3 + 2.
Шаг 2	х = у 3 + 2.
Шаг 3	х — 2 = у 3 .(1/3).

Упражнение 3:

График f (x) = 1 — 2x ³ , чтобы увидеть, что у него есть обратное. Найдите f ^-1 (x). Ответ

Вернуться к содержанию

---

Область и диапазон рациональных функций

В домен из функция ж Икс — это набор всех значений, для которых определена функция, а диапазон функции — это набор всех значений, которые ж берет.

Рациональная функция — это функция вида ж Икс знак равно п Икс q Икс , где п Икс а также q Икс являются многочленами и q Икс ≠ 0 .

Область определения рациональной функции состоит из всех действительных чисел Икс кроме тех, для которых знаменатель 0 . Чтобы найти эти Икс значения, которые нужно исключить из области определения рациональной функции, приравнять знаменатель к нулю и решить для Икс .

Например, домен родительская функция ж Икс знак равно 1 Икс это набор всех действительных чисел, кроме Икс знак равно 0 . Или область определения функции ж Икс знак равно 1 Икс — 4 это набор всех действительных чисел, кроме Икс знак равно 4 .

Теперь рассмотрим функцию ж Икс знак равно Икс + 1 Икс — 2 Икс — 2 .По упрощению, когда Икс ≠ 2 он становится линейной функцией ж Икс знак равно Икс + 1 . Но исходная функция не определена в Икс знак равно 2 . Это оставляет график с дырой, когда Икс знак равно 2 .

Один из способов найти диапазон рациональной функции — найти область определения обратной функции.

Другой способ — нарисовать график и определить диапазон.

Снова рассмотрим родительскую функцию ж Икс знак равно 1 Икс . Мы знаем, что функция не определена, когда Икс знак равно 0 .

В виде Икс → 0 по обе стороны от нуля, ж Икс → ∞ . Аналогично, как Икс → ± ∞ , ж Икс → 0 .

График приближается Икс -ось как Икс стремится к положительной или отрицательной бесконечности, но никогда не касается Икс -ось.То есть функция может принимать все реальные значения, кроме 0 .

Итак, диапазон функции — это набор действительных чисел, кроме 0 .

Пример 1:

Найдите домен и диапазон функции y знак равно 1 Икс + 3 — 5 .

Чтобы найти исключенное значение в области определения функции, приравняйте знаменатель к нулю и решите для Икс .

Икс + 3 знак равно 0 ⇒ Икс знак равно — 3

Итак, область определения функции — это действительные числа, кроме — 3 .

Диапазон функции такой же, как и область определения обратной функции. Итак, чтобы найти диапазон, определите обратную функцию.

Поменять местами Икс а также y .

Икс знак равно 1 y + 3 — 5

Решение для y ты получаешь,

Икс + 5 знак равно 1 y + 3 ⇒ y + 3 знак равно 1 Икс + 5 ⇒ y знак равно 1 Икс + 5 — 3

Итак, обратная функция ж — 1 Икс знак равно 1 Икс + 5 — 3 .

Исключенное значение в области определения обратной функции можно определить, приравняв знаменатель к нулю и решив для Икс .

Икс + 5 знак равно 0 ⇒ Икс знак равно — 5

Итак, область определения обратной функции — это набор действительных чисел, кроме — 5 . То есть диапазон данной функции — это набор действительных чисел, кроме — 5 .

Следовательно, область определения данной функции равна { Икс ∈ ℝ | Икс ≠ — 3 } и диапазон { y ∈ ℝ | y ≠ — 5 } .

Пример 2:

Найдите домен и диапазон функции y знак равно Икс 2 — 3 Икс — 4 Икс + 1 .

Используйте графический калькулятор, чтобы построить график функции.

Когда вы множите числитель и отменяете ненулевые общие множители, функция сводится к линейной функции, как показано.

y знак равно Икс + 1 Икс — 4 Икс + 1 знак равно Икс + 1 Икс — 4 Икс + 1 знак равно Икс — 4

Итак, график линейный с дырой в Икс знак равно — 1 .

Используйте график, чтобы определить домен и диапазон.

Функция не определена для Икс знак равно — 1 . Итак, домен { Икс ∈ ℝ | Икс ≠ — 1 } или же — ∞ , — 1 ∪ — 1 , ∞ .

Диапазон функции: { y ∈ ℝ | y ≠ k где y — 1 знак равно k } .

Для Икс ≠ — 1 , функция упрощается до y знак равно Икс — 4 .Функция не определена в Икс знак равно — 1 или функция не принимает значение — 1 — 4 знак равно — 5 . Это, k знак равно — 5 .

Следовательно, диапазон функции равен { y ∈ ℝ | y ≠ — 5 } или же — ∞ , — 5 ∪ — 5 , ∞ .

Асимптоты рациональной функции:

An асимптота это линия, к которой график функции приближается, но никогда не касается. В родительской функции ж Икс знак равно 1 Икс , как Икс — а также y -оси — это асимптоты. График родительской функции будет приближаться к асимптотам, но никогда не касается их.

Чтобы найти вертикальную асимптоту рациональной функции, приравняйте знаменатель к нулю и решите относительно Икс .

Если степень многочлена в числителе меньше степени знаменателя, то горизонтальная асимптота — это Икс -ось или y знак равно 0 .

Функция ж Икс знак равно а Икс , а ≠ 0 имеет тот же домен, диапазон и асимптоты, что и ж Икс знак равно 1 Икс .

Теперь график функции ж Икс знак равно а Икс — б + c , а ≠ 0 гипербола, симметричная относительно точки б , c .Вертикальная асимптота функции равна Икс знак равно б а горизонтальная асимптота равна y знак равно c .

В более общем виде функция ж Икс знак равно а Икс + б c Икс + d имеет вертикальную асимптоту при Икс знак равно — d c и горизонтальная асимптота при y знак равно а c .В более общем смысле, если и числитель, и знаменатель имеют одинаковую степень, то горизонтальная асимптота будет иметь вид y знак равно k где k — отношение старшего коэффициента числителя к знаменателю.

Если степень знаменателя на единицу меньше степени числителя, то функция имеет наклонную асимптоту.

Пример 3:

Найдите вертикальную и горизонтальную асимптоты функции ж Икс знак равно 5 Икс — 1 .

Чтобы найти вертикальную асимптоту, приравняйте знаменатель к нулю и решите относительно Икс .

Икс — 1 знак равно 0 ⇒ Икс знак равно 1

Итак, вертикальная асимптота равна Икс знак равно 1

Поскольку степень многочлена в числителе меньше степени знаменателя, горизонтальная асимптота имеет вид y знак равно 0 .2 (1-х)?

Ответ:

График функции f — это совокупность всех точек на плоскости вида (x, f (x)). Мы также могли бы определить график f как график уравнения y = f (x). Итак, график функции — это частный случай графика уравнения.

Пример 1.

Пусть f (x) = x2 — 3.

Напомним, когда мы вводили графики уравнений, мы отметили, что если мы можем решить уравнение относительно y, то легко найти точки, которые находятся на график.Мы просто выбираем число для x, а затем вычисляем соответствующее значение y. Графики функций — это графики уравнений, которые были решены относительно y!

График f (x) в этом примере — график y = x2 — 3. На графике легко создавать точки. Выберите значение для первой координаты, затем оцените f для этого числа, чтобы найти вторую координату. В следующей таблице показаны несколько значений x и функции f, вычисленных с этими числами.

x

-2

-1

0

1

2

f (x)

1

-2

-3

-2

1

Каждый столбец чисел в таблице хранятся координаты точки на графике f.2, что мы и хотим!

График f показан ниже.

Упражнение 2:

Постройте график кусочно-определенной функции

Ответ

Мы видели, что некоторые уравнения для x и y не описывают y как функцию от x. Алгебраический способ узнать, определяет ли уравнение y как функцию от x, состоит в решении относительно y. Если нет единственного решения, тогда y не является функцией x.

Предположим, что нам дан график уравнения. Есть простой способ узнать, описывает ли это уравнение y как функцию от x.

Вернуться к содержанию

Тест вертикальной линии

Набор точек на плоскости является графиком функции тогда и только тогда, когда ни одна вертикальная линия не пересекает график более чем в одной точке.

Пример 3.

График уравнения y2 = x + 5 показан ниже.

Согласно тесту вертикальной линии, этот график не является графиком функции, потому что есть много вертикальных линий, которые встречаются с ним более одного раза.

Подумайте о тесте вертикальной линии таким образом.Точки на графике функции f имеют вид (x, f (x)), поэтому, когда вы знаете первую координату, определяется вторая. Следовательно, на графике функции не может быть двух точек с одинаковой первой координатой.

Все точки на вертикальной линии имеют одинаковую первую координату, поэтому, если вертикальная линия дважды попадает в график, то на графике есть две точки с одинаковой первой координатой. В таком случае график не является графиком функции.

Алгебра — обратные функции

Показать мобильное уведомление Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана ( i.е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 3-7: Обратные функции

В последнем примере из предыдущего раздела мы рассмотрели две функции \ (f \ left (x \ right) = 3x — 2 \) и \ (g \ left (x \ right) = \ frac {x} {3 } + \ frac {2} {3} \) и увидел, что

\ [\ left ({f \ circ g} \ right) \ left (x \ right) = \ left ({g \ circ f} \ right) \ left (x \ right) = x \]

, и, как указано в этом разделе, это означает, что это особые функции.Посмотрим, что делает их такими особенными. Рассмотрим следующие оценки.

\ [\ require {color} \ begin {align *} f \ left ({\ color {ProcessBlue} — 1} \ right) & = 3 \ left ({- 1} \ right) — 2 = {\ color {Красный } — 5} & \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} g \ left ({\ color {Red} — 5} \ right) & = \ frac {{- 5}} {3} + \ frac {2} {3} = \ frac {{- 3}} {3} = {\ color {ProcessBlue} — 1} \\ & & \\ g \ left ({\ color {ProcessBlue} 2} \ right) & = \ frac {2} {3} + \ frac {2} {3} = {\ color {Red} \ frac {4} {3}} & \ hspace {0.25 дюймов} \ Rightarrow \ hspace {0,25 дюйма} f \ left ({\ color {Red} \ frac {4} {3}} \ right) & = 3 \ left ({\ frac {4} {3}} \ right ) — 2 = 4 — 2 = {\ color {ProcessBlue} 2} \ end {align *} \]

В первом случае мы подключили \ (x = — 1 \) к \ (f \ left (x \ right) \) и получили значение -5. Затем мы развернулись и подключили \ (x = — 5 \) к \ (g \ left (x \ right) \) и получили значение -1, число, с которого мы начали.

Во втором случае мы сделали нечто подобное. Здесь мы подключили \ (x = 2 \) к \ (g \ left (x \ right) \) и получили значение \ (\ frac {4} {3} \), мы развернулись и вставили это в \ ( f \ left (x \ right) \) и получил значение 2, которое снова является числом, с которого мы начали.

Обратите внимание, что здесь мы действительно выполняем некоторую композицию функций. Первый корпус действительно,

\ [\ left ({g \ circ f} \ right) \ left ({- 1} \ right) = g \ left [{f \ left ({- 1} \ right)} \ right] = g \ left [ {- 5} \ right] = — 1 \]

а второй корпус действительно

\ [\ left ({f \ circ g} \ right) \ left (2 \ right) = f \ left [{g \ left (2 \ right)} \ right] = f \ left [{\ frac {4} {3}} \ right] = 2 \]

Также обратите внимание, что оба они согласуются с формулой композиций, которые мы нашли в предыдущем разделе.Мы возвращаем из оценки функции число, которое мы изначально вставили в композицию.

Итак, что здесь происходит? В некотором смысле мы можем думать об этих двух функциях как об отмене того, что другой сделал с числом. В первом случае мы вставили \ (x = — 1 \) в \ (f \ left (x \ right) \), а затем вставили результат этой оценки функции обратно в \ (g \ left (x \ right) \) и каким-то образом \ (g \ left (x \ right) \) отменил то, что \ (f \ left (x \ right) \) сделал с \ (x = — 1 \), и вернул нам оригинал \ (x \), с которой мы начали.

Пары функций

, которые демонстрируют такое поведение, называются обратными функциями . Прежде чем формально определять обратные функции и обозначения, которые мы собираемся использовать для них, нам нужно получить определение.

Функция называется однозначно , если никакие два значения \ (x \) не дают одинаковых \ (y \). Это довольно простое определение «один-к-одному», но для того, чтобы показать, что это означает, используется пример функции, которая не является взаимно-однозначной.2} \) во взаимно однозначную функцию, если мы ограничимся \ (0 \ le x <\ infty \). Иногда это можно сделать с помощью функций.

Демонстрация того, что функция является индивидуальной, часто бывает утомительным и трудным процессом. По большей части мы будем предполагать, что функции, с которыми мы будем иметь дело в этом разделе, взаимно однозначны. Однако нам нужно было поговорить о взаимно-однозначных функциях, поскольку только однозначные функции могут быть обратными.

Теперь давайте формально определим, что такое обратные функции.

Обратные функции

Даны две взаимно однозначные функции \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \), если

\ [\ left ({f \ circ g} \ right) \ left (x \ right) = x \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} {\ mbox {AND}} \ hspace {0,25 дюйма} \ hspace {0,25 дюйма} \ left ({g \ circ f} \ right) \ left (x \ right) = x \]

, то мы говорим, что \ (f \ left (x \ right) \) и \ (g \ left (x \ right) \) являются обратными друг другу. Более конкретно, мы скажем, что \ (g \ left (x \ right) \) — это , обратный к \ (f \ left (x \ right) \), и обозначим его как

. {- 1}} \ left (x \ right) \).{- 1}} \ circ f} \ right) \ left (x \ right) = x \) верны. Для всех функций, которые мы собираемся рассмотреть в этом разделе, если одна из них истинна, то другая также будет истинной. Однако есть функции (однако они выходят далеко за рамки этого курса), для которых возможно только одно из них. Это вызвано тем, что во всех проблемах здесь мы будем проверять только одну из них. Нам просто нужно всегда помнить, что технически мы должны проверять и то, и другое.

Давайте поработаем несколько примеров.{- 1}} \ left (x \ right) \). Показать решение

Теперь мы уже знаем, что является обратным к этой функции, поскольку мы уже поработали с ней. Однако было бы неплохо начать именно с этого, поскольку мы знаем, что должны получить. Это будет хорошей проверкой процесса.

Итак, приступим. Сначала заменим \ (f \ left (x \ right) \) на \ (y \).

\ [y = 3x — 2 \]

Затем замените все \ (x \) на \ (y \), а все y на на \ (x \). {- 1}} \ left (x \ right) = \ frac {{4 + 5x}} {{2x — 1}} \]

Наконец, нам нужно провести проверку.{- 1}}} \ right) \ left (x \ right) & = \ frac {{2x — 1}} {{2x — 1}} \, \, \ frac {{\ frac {{4 + 5x} } {{2x — 1}} + 4}} {{2 \ left ({\ frac {{4 + 5x}} {{2x — 1}}} \ right) — 5}} \\ & = \ frac { {\ left ({2x — 1} \ right) \ left ({\ frac {{4 + 5x}} {{2x — 1}} + 4} \ right)}} {{\ left ({2x — 1}) \ right) \ left ({2 \ left ({\ frac {{4 + 5x}} {{2x — 1}}} \ right) — 5} \ right)}} \\ & = \ frac {{4 + 5x + 4 \ left ({2x — 1} \ right)}} {{2 \ left ({4 + 5x} \ right) — 5 \ left ({2x — 1} \ right)}} \\ & = \ frac {{4 + 5x + 8x — 4}} {{8 + 10x — 10x + 5}} \\ & = \ frac {{13x}} {{13}} \\ & = x \ end {align *} \]

Вау.Это было много работы, но в конце концов все получилось. Мы сделали всю нашу работу правильно, и у нас действительно есть обратное.

Есть еще одна последняя тема, которую нам нужно быстро обсудить, прежде чем мы покинем этот раздел.