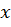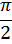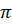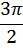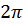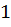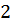Преобразование графиков функций у= f(x) в y=-f(x); y=f(-x); y=-f(-x); y=f(x-a); y=f(x)+b; y=f(ax); y=kf(x); y=|f(x)|; y=f(|x|). Построение графика обратной функции. Примерно 7-9 класс (13-15 лет)

Преобразование графиков функций у= f(x) в y=-f(x):
График функции y=-f(x) получается преобразованием симметрии графика функции у= f(x) относительно оси x Точки пересечения графика с осью x остаются неизменными
Преобразование графиков функций у= f(x) в  y=f(-x):
График функции y=f(-x) получается преобразованием симметрии графика функции у= f(x) относительно оси y Точки пересечения графика с осью y остаются неизменными
Преобразование графиков функций у= f(x) в y=-f(-x):
График функции y=-f(-x) получается преобразованием симметрии графика функции у= f(x) относительно начала координат
Преобразование графиков функций у= f(x) в y=f(x-a):
График функции y=f(x-a)

dpva.ru

Как построить график функции у = f(x + t), если известен график функции у = f(x)

В этом уроке вы узнаете, как построить график функции y = f (x + t), если известен график функции y = f(x)

Конкретизируем задачу.

Дано:

Кривая 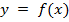; график этой функции нам известен

 (действительное число)

Построить:

Это и есть задача нашего урока. Рассмотрение этой задачи начнем с простейших примеров.

Пример 1. Построить а) у = (х – 1)²; б)

у = (х + 1)²

Дано:

у = х²(графиком данной функции является парабола (рис. 1).

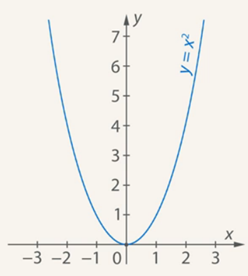
Рис. 1. Парабола

Решение:

Поясним характер кривых, их взаимное расположение поясним с помощью таблицы.

х	-2	-1	0	1	2
у = х2	4	1	0	1	4
у = (х – 1)2	9	4	1	0	1
у = (х + 1)2	1	0	1	4	9

Строим график функции у = (х – 1)² (рис. 2):

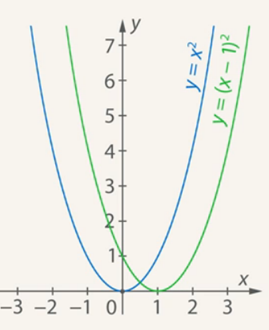
Рис. 2. График функции

у = (х – 1)²

Следует заметить, что кривая а) была получена сдвигом на 1 единицу вправо. Кривая же б) будет получена сдвигом на 1 единицу влево (что можно проверить, поставив полученные в таблице точки на координатную прямую) (рис. 3):

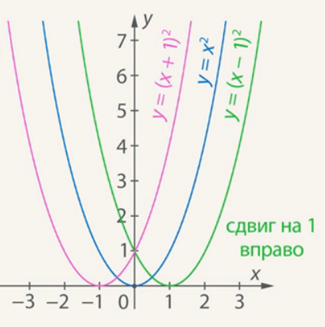
Рис. 3. Сдвиг графика

Заметим еще раз, что если к х прибавляется 1 единица, то сдвиг исходной прямой идет влево вдоль оси Ох, а если отнимается – то сдвиг графика идет вправо.

Вспомнить, когда сдвиг идет направо, а когда – налево, нам помогает самая характерная точка параболы – вершина параболы.

Значение у = 0 достигается этими функциями (рис. 4):

при х = 0, если у = х²

при х = 1, если у = (х – 1)²

при х = -1, если у = (х + 1)

2

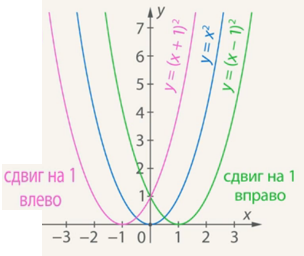
Рис. 4. Случаи, когда у = 0

Если у нас у = (х – 1)², то кривая сдвигается на 1 единицу вправо.

Если у нас у = (х + 1)², то кривая сдвигается на 1 единицу влево.

Мы рассмотрели конкретный случай с конкретными числами. Но вместо чисел, можно взять любое действительное число; вместо функции у = х²можно взять любую функцию. Получим важное правило.

Чтобы получить у = f(x + t), надо кривую у = f(x):

— сдвинуть на 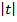 единиц вправо, если t

< 0,

— сдвинуть на 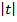 единиц влево, если t > 0

 Это правило является центральным, и нам необходимо закрепить его на примерах.

Дано:

 

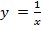
Построить:

а)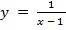

б)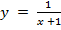

Решение:

а) Строим график функции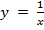

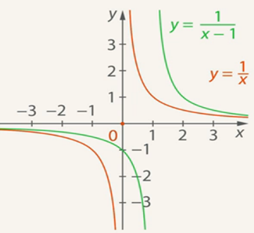
 и сдвигаем его на 1 единицу вправо (согласно правилу) (рис. 5):

Рис. 5. Иллюстрация к примеру а)

Эта гипербола не существует в точке 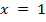 (вертикальная асимптота проходит в точке ).

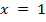Точка пересечения с осью Оу – -1, потому что у(0) = -1.

Задача а) решена.

б) Строим график функции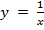

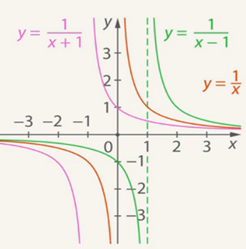
 и сдвигаем его на 1 единицу влево (согласно правилу) (рис. 6):

Рис. 6. Иллюстрация к примеру б)

Эта гипербола не существует в точке .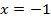

Точка пересечения с осью Оу – 1, потому что у(0) = 1.

В построении графика 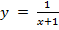 помогла точка разрыва графика (то есть точка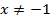

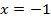; вертикальная асимптота проходит в точке , что означает невозможность существования функции в данной точке.).

Обе задачи решены.

Из этой задачи мы можем сделать вывод, что, если правило забыто, то нам может помочь характерная особенность (например, точка разрыва в примере 1). Но иногда сдвигать график утомительно, тогда мы поступаем следующим образом:

Дано:

 

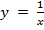
Построить:

а)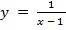

Решение:

Можно сдвинуть ось Оу. Кривая тогда останется на месте, однако масштаб по оси

Ох придется изменить. Если сдвигать всю кривую для построения графика функции, то кривую надо сдвинуть на 1 единицу вправо. Но если мы сдвигаем ось Оу, то ее надо сдвинуть на 1 единицу влево.

Получим новую ось Oу(рис. 7):

      

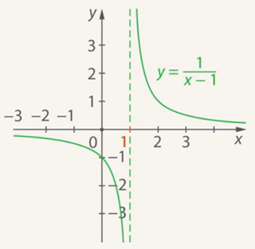
Рис. 7. Иллюстрация к примеру 2

Асимптота проходит в точке 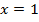, потому что в точке  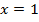функции не существует.

Задача решена сдвигом оси Оу. Итак, если затруднительно сдвигать кривую, то можно сдвинуть ось в ту или иную сторону.

         

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5 издание. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Домашнее задание

1. № 19.11, 19.18, 19.24 стр. 116–120. Мордкович А.Г. Алгебра 8 класс. Задачник для учащихся общеобразовательных школ.– 12-е изд. – М.: Мнемозина, 2010. – 273 стр.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Urokimatematiki.ru (Источник).
2. Интернет-портал Festival.1september.ru (Источник).
3. Интернет-портал Yaklass.ru (Источник).

interneturok.ru

Как построить график функции y=f(kx), если известен график функции y=f(x)

На этом уроке мы рассмотрим построение модификаций графика вида у = f(k∙x). Вначале мы вспомним, как строится график вида у = m*f(x) и общее правило построения таких графиков. Далее мы рассмотрим построение модификаций графиков вида у = f(k∙x) при k>1 на примере функции синуса и сформулируем правило построения. И рассмотрим построение графиков при 0<k<1. В конце урока мы сформулируем общее правило для построения графиков данной модификации при k>0.

Тема: Тригонометрические функции

Урок: Как построить график функции y=f(kx), если известен график функции y=f(x)

Ранее мы рассматривали, как построить график функции 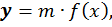 когда на число m умножалась вся функция, при этом необходимо было сжать или растянуть исходную кривую в m раз вдоль оси y.

Теперь вместо аргумента x в функцию подставим аргумент 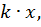 и исходную кривую необходимо будет в  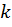раз сжать или растянуть вдоль оси x.

Вспомним правило построения графика функции  

Дан график 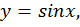 необходимо получить график функции

	0		0		0
	0		0		0

Рассмотрим функцию

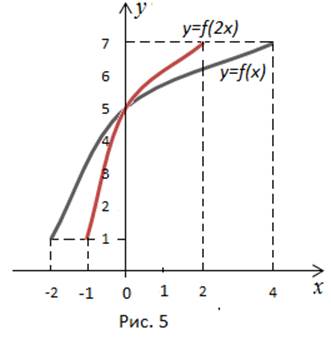
Дан график функции 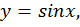 необходимо построить график функции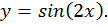

           

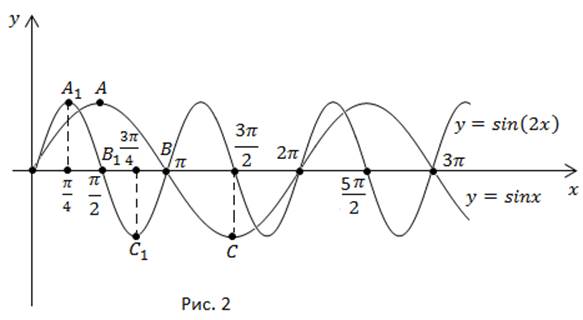
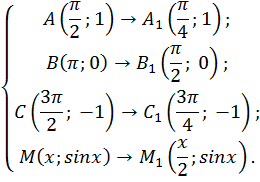
На рисунке видно, что кривая сжимается к оси y  в 2 раза. Если исходная функция имела период 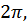 то период функции равен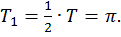

Чтобы сохранить фиксированное значение функции, аргумент следует уменьшить в два раза. Происходит сжатие в 2 раза вдоль оси x (или к оси y).

Рассмотрим функцию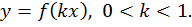

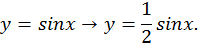
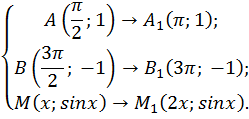
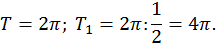
Кривая  получена растяжением кривой 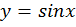 в 2 раза вдоль оси x (или от оси y).

Мы рассмотрели построение графика функции 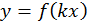 по известному графику  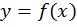при 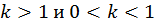 (рис. 4).

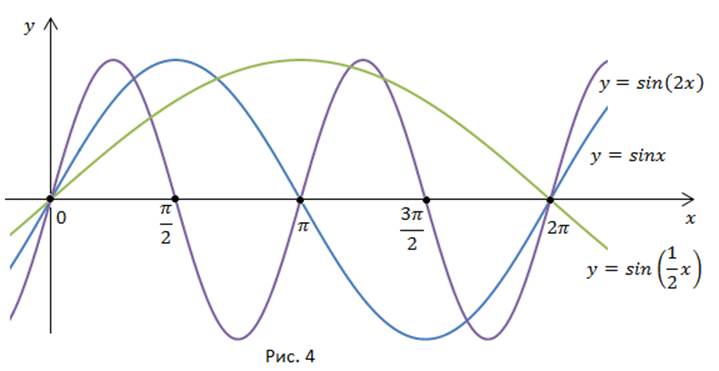
Сформулируем правило для

Чтобы получить кривую 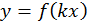 необходимо:

1. Оставить на месте точку 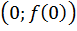 пересечения с осью y, если такая точка существует.

2. Остальные точки исходной кривой сжать или растянуть в 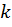 раз вдоль оси x (или к оси y) .

Мы повторили правило преобразования графика функции, когда число m  умножается на саму функцию и вывели правило получения графика функции 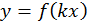 для

На следующем уроке мы продолжим рассмотрение этого правила, в частности, для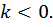

Список литературы

1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2009.

2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.

4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.

5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.

6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.

7. Саакян С.М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.

8. Карп А.П. Сборник задач по алгебре и началам анализа : учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.

 

Домашнее задание

Алгебра и начала анализа, 10 класс (в двух частях). Задачник  для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. –М.: Мнемозина, 2007.

№№ 18.1 – 18.6.

 

Дополнительные веб-ресурсы

1. Математика (Источник).

2. Интернет-портал Problems.ru (Источник).

3. Образовательный портал для подготовки к экзаменам (Источник).

interneturok.ru

Графики функций и их модификация

Графиком функции у=f(х), где , называется множество всех точек координатной плоскости хОу вида (х;f(х)) или графиком функции называется множество всех точек, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции.

Параллельный перенос (сдвиг) вдоль оси абсцисс

График функции у=f(х+а) получаем с помощью параллельного переноса (сдвига) последнего вдоль оси Ох на |а| единиц масштаба в направлении, имеющем знак, противоположный знаку числа а.

Например, для построения графика функции у=f(х+2) вспомогательную ось ординат графика функции у=f(х) переносим параллельно вдоль оси абсцисс на две единицы масштаба вправо или сам график переносим на две единицы влево.

Параллельный перенос (сдвиг) вдоль оси ординат

График функции у=f(х+b) получаем из графика функции у=f(х) с помощью параллельного переноса (сдвига) последнего вдоль оси Оу на |b| единиц масштаба в направлении, имеющем знак числа b.

Например, для построения графика функции у=f(х)-4 вспомогательную ось абсцисс графика функции у=f(х) поднимаем вдоль оси ординат на четыре единицы или сам график переносим на 4 единицы вниз.

Растяжение или сжатие по оси абсцисс

График функции у=f(kх) получаем из графика функции у=f(х ) с помощью сжатия по оси абсцисс исходного графика пропорционально коэффициенту k при аргументе: если k>1, то график сжимается в k раз, а если 0<k<1, то график растягивается в раз.

Построим графики функций у=f(2х) и

Растяжение или сжатие по оси ординат

График функции у=mf(х) получаем из графика функции у=f(х) с помощью растяжения этого графика по оси ординат пропорционально m при функции (если m>1, то график растягивается в m раз, если 0<m<1, то график сжимается в раз).

Построим графики функций у=3f(х) и у=f(х).

Построение графика функции у=-f(х)

График функции у=-f(х) получаем из графика функции у=f(х) с помощью симметрии относительно оси абсцисс.

Построим график этой функции.

Построение графика функции у=f(-х)

График функции у=f(-х) получаем из графика функции у=f(х) с помощью симметрии относительно оси ординат.

Построим график этой функции.

Построение графика функции у=|f(х)|

Для построения графика функции у=|f(х)|, надо построить график функции у=f(х), далее оставить без изменения все части построенного графика, которые лежат выше оси абсцисс или на оси, а части, расположенные ниже её, отобразить симметрично относительно этой оси.

Строим график этой функции:

Построение графика функции у= f(|х|)

Для построения графика функции у=f(|х|), надо построить график функции у=f(х) для х?0, а затем отобразить построенную часть симметрично относительно оси ординат. Обе части в совокупности дадут график функции у=f(|х|).

Построение графика функции y=-f(-х)

Для построения графика функции y=-f(-х), надо построить график функции у = f(х), затем выполнить симметрию относительно начала координат. В результате получим график заданной функции.

urok.1sept.ru