График функции — Википедия. Что такое График функции

Материал из Википедии — свободной энциклопедии

График функции — понятие в математике, которое даёт представление о геометрическом образе функции.

Наиболее наглядны графики вещественнозначных функций вещественного переменного.

В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:

точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.

Таким образом, функция может быть адекватно описана своим графиком.

Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и тоже подмножество плоскости).

График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:

Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}

В частности, при рассмотрении динамических систем, изображающая точка

(t,f(t)){\displaystyle (t,f(t))},

представляет собою график решения соответствующего дифференциального уравнения.

Примеры

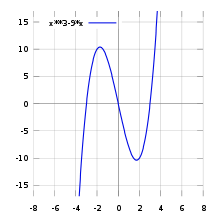График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}

• График кубического многочлена вещественной переменной

  f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}

это множество

{(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.

• График функции

  f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}

это множество из трёх точек {(1,a), (2,d), (3,c)}.

См. также

Литература

Ссылки

график функции — это… Что такое график функции?



график функции

1) Computers: diagram of function, diagram of the function, plot of the function

2) Engineering: function chart, function curve, graph of a function, graph of function

3) Mathematics: function graph

4) Economy: plot of function, plotted function

5) Geophysics: crossplot

Универсальный русско-английский словарь. Академик.ру. 2011.

• график финансирования
• график функции взаимной корреляции

Смотреть что такое «график функции» в других словарях:

• график функции — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] график функции 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами, где x… …   Справочник технического переводчика

• График функции — [ graph of a function ] — 1. Один из основных (наряду с таблицей,  формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости  с прямоугольными координатами., где x — любая точка области определения этой функции,… …   Экономико-математический словарь

• График функции — Для термина «График» см. другие значения. График функции  множество точек, у которых абсциссы являются допустимыми значениями аргумента , а ординаты  соответствующими значениями функции . Обычно рассматриваются графики вещественных… …   Википедия

• график функции — ▲ изображение ↑ графический, функция (математическая) график изображение функции при помощи линии на плоскости. … грамма. номограмма. кардиограмма. эхограмма. диаграмма наглядное графическое изображение соотношения каких л. величин. круговая… …   Идеографический словарь русского языка

• график — 1. ГРАФИК, а; м. [от греч. graphikos начерченный] 1. Чертёж, диаграмма и т.п., изображающие с помощью линий количественные показатели развития, состояния и т.п. чего л. Г. изменения атмосферного давления. Г. заболеваемости гриппом. Г. проведённых …   Энциклопедический словарь

• Функции Бесселя — в математике  семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где   произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя  функции целых… …   Википедия

• ГРАФИК

  — (от греч. graphikos начертанный) 1) чертеж, применяемый для наглядного изображения зависимости какой либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции. График функции …   Большой Энциклопедический словарь

• График —         геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г. изменения атмосферного давления со временем. Г. применяют как для наглядного изображения функциональных зависимостей и… …   Большая советская энциклопедия

• График — График: График функции  множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты соответствующими значениями функции . График  деятель искусств, занимающийся графикой. График базальной… …   Википедия

• График (значения) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов …   Википедия

• График (знач.) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов …   Википедия

График функции — Википедия

Материал из Википедии — свободной энциклопедии

График функции — понятие в математике, которое даёт представление о геометрическом образе функции.

Наиболее наглядны графики вещественнозначных функций вещественного переменного.

В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:

точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.

Таким образом, функция может быть адекватно описана своим графиком.

Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и то же подмножество плоскости).

График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:

Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}

В частности, при рассмотрении динамических систем, изображающая точка

(t,f(t)){\displaystyle (t,f(t))},

представляет собою график решения соответствующего дифференциального уравнения.

Примеры

График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}

• График кубического многочлена вещественной переменной

  f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}

это множество

{(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.

• График функции

  f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}

это множество из трёх точек {(1,a), (2,d), (3,c)}.

См. также

Литература

Ссылки

График функции — Википедия

Материал из Википедии — свободной энциклопедии

График функции — понятие в математике, которое даёт представление о геометрическом образе функции.

Наиболее наглядны графики вещественнозначных функций вещественного переменного.

В этом случае, график функции — это геометрическое место точек плоскости, абсциссы (x) и ординаты (y) которых связаны указанной функцией:

точка (x,y){\displaystyle (x,y)} располагается (или находится) на графике функции f{\displaystyle f} тогда и только тогда, когда y=f(x){\displaystyle y=f(x)}.

Таким образом, функция может быть адекватно описана своим графиком.

Из определения графика функции следует, что далеко не всякое множество точек плоскости может быть графиком некоторой функции: никакая прямая, параллельная оси ординат, не может пересекать график функции более чем в одной точке. Если функция обратима, то график обратной функции (как подмножество плоскости) будет совпадать с графиком самой функции (это, попросту, одно и тоже подмножество плоскости).

График гладкой (требуемое количество раз дифференцируемой функции) является плоской кривой той же степени гладкости.

При рассмотрении отображения произвольного вида f:X→Y{\displaystyle f:X\to Y}, действующего из множества X{\displaystyle X} в множество Y{\displaystyle Y}, графиком функции называется следующее множество упорядоченных пар:

Γf={(x,f(x))∈X×Y∣x∈X}.{\displaystyle \Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}.}

В частности, при рассмотрении динамических систем, изображающая точка

(t,f(t)){\displaystyle (t,f(t))},

представляет собою график решения соответствующего дифференциального уравнения.

Примеры

График f(x)=x3−9x{\displaystyle f(x)=x^{3}-9x}

• График кубического многочлена вещественной переменной

  f(x)=x3−9x{\displaystyle f(x)={{x^{3}}-9x}}

это множество

{(x,x3−9x)∈R2 |x∈R}{\displaystyle \{(x,x^{3}-9x)\in \mathbb {R} ^{2}\ |x\in \mathbb {R} \}}.

• График функции

  f(x)={a,x=1d,x=2c,x=3.{\displaystyle f(x)=\left\{{\begin{matrix}a,&x=1\\d,&x=2\\c,&x=3.\end{matrix}}\right.}

это множество из трёх точек {(1,a), (2,d), (3,c)}.

См. также

Литература

Ссылки