Равновесие фаз — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 декабря 2016; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 декабря 2016; проверки требуют 2 правки.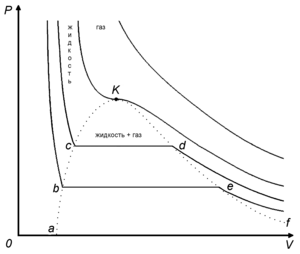

Равнове́сие фаз в термодинамике — состояние, при котором фазы в термодинамической системе находятся в состоянии теплового, механического и химического равновесия.

Типы фазовых равновесий:

Тепловое равновесие означает, что все фазы вещества в системе имеют одинаковую температуру.

Механическое равновесие означает равенство давлений по разные стороны границы раздела соприкасающихся фаз. Строго говоря, в реальных системах эти давления равны лишь приближенно, разность давлений создается поверхностным натяжением.

Химическое равновесие выражается в равенстве химических потенциалов всех фаз вещества.

Рассмотрим химически однородную систему (состоящую из частиц одного типа). Пусть в этой системе имеется граница раздела между фазами 1 и 2. Как было указано выше, для равновесия фаз требуется равенство температур и давлений на границе раздела фаз. Известно (см. статью Термодинамические потенциалы), что состояние термодинамического равновесия в системе с постоянными температурой и давлением соответствует точке минимума потенциала Гиббса.

Потенциал Гиббса такой системы будет равен

• G=μ1N1+μ2N2{\displaystyle G=\mu _{1}N_{1}+\mu _{2}N_{2}},

где μ1{\displaystyle \mu _{1}} и μ2{\displaystyle \mu _{2}} — химические потенциалы, а N1{\displaystyle N_{1}} и N2{\displaystyle N_{2}} — числа частиц в первой и второй фазах соответственно.

При этом сумма N=N1+N2{\displaystyle N=N_{1}+N_{2}} (полное число частиц в системе) меняться не может, поэтому можно записать

• G=μ1N1+μ2(N−N1)=μ2N+(μ1−μ2)N1{\displaystyle G=\mu _{1}N_{1}+\mu _{2}(N-N_{1})=\mu _{2}N+(\mu _{1}-\mu _{2})N_{1}}.

Предположим, что μ1≠μ2{\displaystyle \mu _{1}\neq \mu _{2}}, для определенности, μ1<μ2{\displaystyle \mu _{1}<\mu _{2}}. Тогда, очевидно, минимум потенциала Гиббса достигается при N1=N{\displaystyle N_{1}=N} (все вещество перешло в первую фазу).

Таким образом, равновесие фаз возможно только в том случае, когда химические потенциалы этих фаз по разные стороны границы раздела равны:

• μ1=μ2{\displaystyle \mu _{1}=\mu _{2}}.

Из условия равновесия фаз можно получить зависимость давления в равновесной системе от температуры. Если говорить о равновесии жидкость — пар, то под давлением понимают давление насыщенных паров, а зависимость P=P(T){\displaystyle P=P(T)} называется кривой испарения

.

Из условия равенства химических потенциалов следует условие равенства удельных термодинамических потенциалов:

• g1=g2{\displaystyle g_{1}=g_{2}},

где gi=Gimi{\displaystyle g_{i}={\frac {G_{i}}{m_{i}}}}, Gi{\displaystyle G_{i}} — потенциал Гиббса i-й фазы, mi{\displaystyle m_{i}} — её масса.

Отсюда:

• dg1=dg2{\displaystyle dg_{1}=dg_{2}},

а значит,

• v1dP−s1dT=v2dP−s2dT{\displaystyle v_{1}dP-s_{1}dT=v_{2}dP-s_{2}dT},

где v1{\displaystyle v_{1}} и s1{\displaystyle s_{1}} — удельные объем и энтропия фаз. Отсюда следует, что

• dPdT=s2−s1v2−v1{\displaystyle {\frac {dP}{dT}}={\frac {s_{2}-s_{1}}{v_{2}-v_{1}}}},

и окончательно

• dPdT=qT(v2−v1){\displaystyle {\frac {dP}{dT}}={\frac {q}{T(v_{2}-v_{1})}}},

где q{\displaystyle q} — удельная теплота фазового перехода (например, удельная теплота плавления или удельная теплота испарения).

Последнее уравнение называется

уравнением Клапейрона — Клаузиуса.

Основной закон гетерогенных равновесий, согласно которому в гетерогенной (макроскопически неоднородной) физико-химической системе, находящейся в устойчивом термодинамическом равновесии, число фаз не может превышать числа компонентов, увеличенного на 2. Установлено Дж. У. Гиббсом в 1873—76^[1].

• Базаров И. П. Термодинамика. (недоступная ссылка) М.: Высшая школа, 1991. 376 с.
• Сивухин Д. В. Общий курс физики. — М.: Наука, 1975. — Т. II. Термодинамика и молекулярная физика. — 519 с.

равновесие — это… Что такое равновесие?

равновесие — равновесие …   Орфографический словарь-справочник

РАВНОВЕСИЕ — (equilibrium) Ситуация, в которой ни у кого нет непосредственной причины к внесению изменений в свои действия, в результате чего может сохраняться, по крайней мере временно, статус кво. Данная концепция нашла широкое применение в экономической… …   Экономический словарь

РАВНОВЕСИЕ — РАВНОВЕСИЕ, равновесия, мн. нет, ср. (книжн.). 1. Состояние неподвижности, покоя, в котором находится какое нибудь тело под воздействием равных, противоположно направленных и потому взаимно уничтожающихся сил (мех.). Равновесие сил. Устойчивое… …   Толковый словарь Ушакова

равновесие — Динамические условия физического, химического, механического или атомного баланса. [http://www.manual steel.ru/eng a.html] равновесие Общее понятие, относимое к различным ситуациям, характеризующимся взаимодействием разнонаправленных сил,… …   Справочник технического переводчика

Равновесие — [equilibrium] общее понятие, относимое к различным ситуациям, характеризующимся взаимодействием разнонаправленных сил, воздействие которых взаимно погашается таким образом, что наблюдаемые свойства системы остаются неизменными. Среди… …   Экономико-математический словарь

РАВНОВЕСИЕ — механической системы, состояние механической системы, находящейся под действием сил, при котором все ее точки покоятся по отношению к рассматриваемой системе отсчета. Равновесие имеет место, когда все действующие на тело силы взаимно уравновешены …   Современная энциклопедия

РАВНОВЕСИЕ — механической системы состояние механической системы, находящейся под действием сил, при котором все ее точки покоятся по отношению к рассматриваемой системе отсчета. Равновесие имеет место, когда все действующие на тело силы взаимно уравновешены …   Большой Энциклопедический словарь

РАВНОВЕСИЕ — (equilibrium) Ситуация, в которой все факторы, оказывающие влияние на экономическую переменную, полностью уравновешивают друг друга таким образом, что переменная величина в результате не изменяется. Равновесие является фундаментальным… …   Словарь бизнес-терминов

равновесие — баланс, устойчивость; пондерация, экилибр, изостазия Словарь русских синонимов. равновесие экилибр (устар.) Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова. 2011 …   Словарь синонимов

равновесие — механической системы; равновесие Состояние механической системы, при котором все её точки под действием приложенных сил остаются в покое по отношению к рассматриваемой системе отсчёта равновесное состояние; равновесие Состояние термодинамической… …   Политехнический терминологический толковый словарь

равновесие — – состояние системы, при котором ее параметры не зависят от времени. Словарь по аналитической химии [3] • фазовое равновесие химическое равновесие …   Химические термины

Экономическое равновесие — Википедия

Материал из Википедии — свободной энциклопедии

Цена при рыночном равновесии:

P — цена

Q — количество товара

S — предложение

D — спрос

P₀ — цена при рыночном равновесии

A — нехватка при P<P₀

B — избыток при P>P₀

Экономическое равновесие (англ. economic equilibrium) — состояние экономики, при котором произведенная продукция реализована, а спрос удовлетворен в условиях, когда имеющиеся трудовые ресурсы и производственные мощности используются в полном объёме, а нарушаемые пропорции быстро восстанавливаются^[1]. В экономике, экономическое равновесие характеризует состояние, в котором экономические силы сбалансированы и, в отсутствие внешних воздействий, (сбалансированные) величины экономических переменных не будут изменяться.

Согласно К. Р. Макконнеллу и С. Л. Брю, равновесная цена (англ. equilibrium price) — цена на конкурентном рынке, при которой величина спроса и величина предложения равны, то есть цена, при которой нет дефицита или избытка товаров и услуг, а значит на рынке нет тенденций роста или снижения

[2].

Рыночное равновесие (англ. market equilibrium) — ситуация на рынке, когда спрос на товар равен его предложению. Объём продукта и его цену в такой ситуации называют равновесными или соответствующими состоянию расчистки рынков^ru_en. Такая цена имеет тенденцию в отсутствие изменений спроса и предложения оставаться неизменной. Рыночное равновесие характеризуется равновесной ценой и равновесным объёмом.

Механизм достижения рыночного равновесия[править | править код]

На конкурентном рынке, на котором имеется большое количество покупателей и продавцов, с помощью метода перебора определяем равновесную цену, исключая цены, при которых формируется излишек или нехватка продукта. Так при высокой цене производители желают производить большое количество продукта, но покупатели готовы приобрести только малое количество продукта, возникает перепроизводство. При малой цене покупатели готовы приобрести большое количество продукта, но производители готовы производить малое количество товара, возникает дефицит товара и услуги. При некой средней цене, равновесной цене производители готовы производить ровно столько сколько потребители желают и в состоянии приобрести. На рынке не возникает избыток, при котором рынок толкал бы цену на продукт вниз, не возникает и нехватка продукта, при котором рынок не вызывает повышение цены на продукт. При такой равновесной цене (или цене рыночного клиринга) величина спроса и предложения уравновешиваются. Графически это показано на рисунке

Цена при рыночном равновесии, где на горизонтальной оси указаны величины спроса и предложения. Равновесная цена возникает на пересечение кривых спроса и предложения. При любой цене, превышающей равновесную цену, величина предложения окажется больше величины спроса, а возникший избыток вызовет конкурентное сбивание цены продавцами. Снижение цены позволит сократить предложение и одновременно побудит покупателей покупать её в большем количестве. При любой цене, которая ниже равновесной, приводит к нехватке продукта, когда величина спроса превысит величину предложения. Повышение цены позволит производителей увеличить предложение, а потребителей покупать продукт, в результате излишек исчезает ^[3].

Согласно К. Р. Макконнеллу и С. Л. Брю, уравновешивающая функция цен — способность конкурентных сил предложения и спроса устанавливать цену на уровне, на котором решение о продаже и решение о покупке синхронизируются. Если конкурентные силы автоматически не могут согласовать решение о предложении и спроса, то в таком случае требуется административное регулирование со стороны государства для устранения нехватки или избытка^[3].

Равновесие бывает устойчивым и неустойчивым. Если после нарушения равновесия рынок приходит в состояние равновесия и устанавливаются прежние равновесные цена и объём, то равновесие называют устойчивым. Если после нарушения равновесия устанавливается новое равновесие и изменяется уровень цен и объём спроса и предложения, то равновесие называют неустойчивым.

Устойчивость равновесия. Виды устойчивости[править | править код]

Устойчивость равновесия — способность рынка приходить в состояние равновесия путём установления прежней равновесной цены и равновесного объёма.

Виды устойчивости

• Абсолютная
• Относительная
• Локальная (колебания цен происходят, но в определённых пределах)
• Глобальная (Устанавливается при любых колебаниях)

• Распределительная
• Информационная
• Стимулирующая
• Балансирующая
• Нормирующая. Она нормирует распределение товаров, давая сигнал потребителю о том, доступен ли ему данный товар и на какой объём потребления он может рассчитывать при данном уровне дохода. Одновременно она воздействует на производителя, показывая, сможет ли он окупить затраты или ему следует воздержаться от производства товара.

Статика — Википедия

Ста́тика (от греч. στατός, «неподвижный») — раздел механики, в котором изучаются условия равновесия механических систем под действием приложенных к ним сил и моментов.

Система сил, приложенная к телу или материальной точке, называется уравновешенной или эквивалентной нулю, если тело под действием этой системы находится в состоянии покоя или движется по инерции.^[1]

1. Аксиома о добавлении (отбрасывании) системы двух сил, эквивалентной нулю. Не нарушая механического состояния тела, к нему можно приложить или отбросить уравновешенную систему сил.
2. Аксиома о равенстве сил действия и противодействия. (Закон классической механики о действии и противодействии). При всяком действии одного тела на другое со стороны другого тела имеется равное противодействие, такое же по величине, но противоположное по направлению.
3. Аксиома о равновесии системы двух сил. Две силы, приложенные к одному и тому же телу, взаимно уравновешены (их действие эквивалентно нулю) тогда и только тогда, когда они равны по величине и действуют по одной прямой в противоположные стороны.
4. Аксиома параллелограмма двух сил. Равнодействующая двух сил, приложенных к одной точке, приложена к той же точке и равна диагонали параллелограмма, построенного на этих силах как сторонах.
5. Аксиома затвердевания. Если деформируемое тело находилось в равновесии, то оно будет находиться в равновесии и после его превращения в абсолютно твёрдое тело (затвердевания).
6. Аксиома освобождаемости от связей. Механическое состояние системы не изменится, если освободить её от связей и приложить к точкам системы силы, равные действовавшим на них силам реакций связей.
7. Аксиома параллелепипеда трёх сил. Три силы, действующие в одной точке тела или на материальную точку, можно заменить одной равнодействующей силой, равной по модулю и направлению диагонали параллелепипеда, построенного на заданных силах^[2].

Следствия[править | править код]

1. При переносе силы вдоль её линии действия, действие этой силы на тело не меняется.
2. Сумма всех внутренних сил равна нулю.

Про тело говорят, что оно находится в равновесии, если оно покоится или движется равномерно и прямолинейно относительно выбранной инерциальной системы отсчёта^[3].

В статике материальные тела считают абсолютно твёрдыми, т.к. изменение размеров тел обычно мало по сравнению с начальными размерами.

Связи[править | править код]

На тело влияют внешние силы, а также другие материальные тела, ограничивающие перемещение данного тела в пространстве. Такие тела называют связями. Сила, с которой связь действует на тело, ограничивая его перемещение, называется реакцией связи. Для записи условия равновесия системы связи убирают, а реакции связей заменяют на равные им силы^[1].

Например, если тело закреплено на шарнире, то шарнир является связью. Реакцией связи при этом будет сила, проходящая через ось шарнира.

Системы сил[править | править код]

Если систему сил, действующих на твёрдое тело, можно заменить на другую систему сил, не изменяя механического состояния тела, то такие системы сил называются эквивалентными.

Для любой системы сил, приложенных к твёрдому телу, можно найти эквивалентную систему сил, состоящую из силы, приложенной в заданной точке (центре приведения), и пары сил (теорема Пуансо). Эта сила называется главным вектором системы сил, а момент, создаваемый парой сил — главным моментом относительно выбранного центра приведения. Главный вектор равен векторной сумме всех сил системы и не зависит от выбранного центра приведения. Главный момент равен сумме моментов всех сил системы относительно центра приведения.

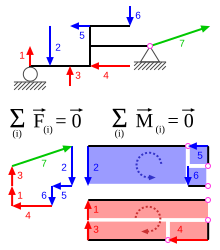Пример статического равновесия при равенстве нулю суммы всех сил. 1 — сила реакции нормального давления, 7 — сила реакции в шарнире.

Твёрдое тело находится в равновесии, если сумма всех сил, приложенных к данному телу, и их моментов равны нулю или главный вектор и главный момент системы сил, приложенных к телу, равны нулю.^[1]

Для записи условия равновесия системы, состоящей из твёрдых тел, систему разделяют на отдельные части, и записывают уравнения равновесия как для всей системы, так и для её частей^[1]. При этом возможны несколько эквивалентных вариантов записи условий равновесия в зависимости от выбора частей системы, для которых записываются уравнения.

Из второго закона Ньютона следует, что если геометрическая сумма всех внешних сил, приложенных к телу, равна нулю, то тело находится в состоянии покоя или совершает равномерное прямолинейное движение. В этом случае принято говорить, что силы, приложенные к телу, уравновешивают друг друга. При вычислении равнодействующей все силы, действующие на тело, можно прикладывать к центру масс.

Чтобы невращающееся тело находилось в равновесии, необходимо, чтобы равнодействующая всех сил, приложенных к телу, была равна нулю.

Рисунок 1.14.1. Равновесие твердого тела под действием трех сил. При вычислении равнодействующей все силы приводятся к одной точке C На рис. 1.14.1 дан пример равновесия твердого тела под действием трех сил. Точка пересечения O линий действия сил и не совпадает с точкой приложения силы тяжести (центр масс C), но при равновесии эти точки обязательно находятся на одной вертикали. При вычислении равнодействующей все силы приводятся к одной точке.

Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил.

Вращающее действие силы зависит не только от её величины, но и от расстояния между линией действия силы и осью вращения.

Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы.

Произведение модуля силы на плечо d называется моментом силы M. Положительными считаются моменты тех сил, которые стремятся повернуть тело против часовой стрелки (рис. 1.14.2).

Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

Статика является разделом теоретической механики.

Статика является базой для науки о сопротивлении материалов.

1. ↑ ^{1 2 3 4} Под редакцией Колесникова К. С. Курс теоретической механики. — Москва: Издательство МГТУ им. Н.Э. Баумана, 2005. — С. 173-176. ISBN 5-7038-1371-9
2. ↑ Тарасов, 2012, с. 27.
3. ↑ Под редакцией Колесникова К. С. Курс теоретической механики. — Москва: Издательство МГТУ им. Н.Э. Баумана, 2005. — С. 173-224. ISBN 5-7038-1371-9

• Д. Сивухин, Курс общей физики. Механика.

• Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М.: ТрансЛит, 2012. — ISBN 978-5-94976-455-8 страниц = 560.

Химическое равновесие — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 мая 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 2 мая 2019; проверки требует 1 правка.

Химическое равновесие — состояние химической системы, в которой протекает одна или несколько химических реакций, причём скорости в каждой паре прямой-обратной реакции равны между собой. Для системы, находящейся в химическом равновесии, концентрации реагентов, температура и другие параметры системы не изменяются со временем^[1].

А₂ + В₂ ⇄ 2AB

Принцип работы: если на систему воздействовать, то она противодействует.

Положение химического равновесия зависит от следующих параметров реакции: температуры, давления и концентрации. Влияние, которое оказывают эти факторы на химическую реакцию, подчиняется закономерности, которая была высказана в общем виде в 1884 году французским учёным Ле Шателье.

Влияние температуры[править | править код]

При увеличении температуры химическое равновесие смещается в сторону эндотермической (поглощение) реакции, а при понижении — в сторону экзотермической (выделение) реакции.

• CaCO3↽−−⇀CaO+CO2−Q{\displaystyle {\ce {CaCO3 <=> CaO + CO2 — Q}}}

При повышении температуры, равновесие смещается в сторону оксида кальция, при понижении — в сторону карбоната.

• N2+3h3↽−−⇀2Nh4+Q{\displaystyle {\ce {N2 + 3 h3 <=> 2 Nh4 + Q}}}

При повышении температуры, равновесие смещается в сторону простых веществ, при понижении — в сторону аммиака.

Влияние давления[править | править код]

При повышении давления химическое равновесие смещается в сторону меньшего объёма веществ, а при понижении — в сторону большего объёма. Этот принцип действует только на газы, то есть если в реакции участвуют твёрдые вещества, то они в расчёт не берутся.

CaCO3↽−−⇀CaO+CO2↑{\displaystyle {\ce {CaCO3 <=> CaO + CO2 ^}}}

При повышении давления, равновесие смещается в сторону карбоната кальция, а при понижении — в сторону оксидов.

Влияние концентраций реагентов и продуктов[править | править код]

При увеличении концентрации одного из исходных веществ или удаления из реакционной смеси продуктов, химическое равновесие смещается в сторону продуктов реакции, и наоборот.

HF↽−−⇀H++F−{\displaystyle {\ce {HF <=> H+ + F-}}}

При подкислении раствора (увеличении концентрации H⁺) или введении соли, содержащей одноименный ион, будет увеличиваться концентрация недиссоциированной кислоты, а добавление щёлочи свяжет H⁺ в молекулы воды и увеличит концентрацию фторид-ионов.

Катализаторы не влияют на смещение химического равновесия

Сильное равновесие — Википедия

Материал из Википедии — свободной энциклопедии

Сильное равновесие — принцип оптимальности в теории игр, очищение равновесия Нэша. Кроме устойчивости ситуации в игре к индивидуальным отклонениям участников, требует также устойчивости к групповым отклонениям.

Пусть задана игра в нормальной форме Γ=⟨I,{Xi}i∈I,{Hi}i∈I⟩{\displaystyle \Gamma =\langle I,\{X_{i}\}_{i\in I},\{H_{i}\}_{i\in I}\rangle }. Ситуация x=(x1,x2,…,xn){\displaystyle x=(x_{1},x_{2},\dots ,x_{n})} называется сильным равновесием в игре Γ, если для любой коалиции игроков S⊆I{\displaystyle S\subseteq I} и любого набора стратегий {ys;s∈S}{\displaystyle \{y_{s};s\in S\}} найдётся участник коалиции S такой, что

Hi(x)>Hi(x−S,yS).{\displaystyle H_{i}(x)>H_{i}(x_{-S},y_{S}).}

Сильное равновесие всегда Парето-эффективно, но существует намного реже, нежели равновесие Нэша, в связи с чем не получило широкого распространения.

• Губко М. В., Новиков Д. А. Теория игр в управлении организационными системами. — М., 2005.
• Петросян Л. А., Зенкевич Н. А., Семина Е. А. Теория игр: Учеб. пособие для ун-тов. — М.: Высш. шк., Книжный дом «Университет», 1998. — С. 304. — ISBN 5-06-001005-8, 5-8013-0007-4.

Принцип детального равновесия — Википедия

Материал из Википедии — свободной энциклопедии

Принцип детального равновесия — общее положение статистики, справедливое для многих случайных (марковских) процессов и физических систем, находящихся в состоянии термодинамического равновесия. Его суть заключается в равенстве вероятностей прямого (n→m){\displaystyle (n\rightarrow m)} и обратного (m→n){\displaystyle (m\rightarrow n)} переходов между дискретными состояниями системы m{\displaystyle m} и n{\displaystyle n}.

Марковская цепь, для которой выполняется принцип детального равновесия, называется обратимой.

Принцип детального равновесия, в частности, справедлив в приложении к статистической физике и квантовой механике, поскольку он является следствием основных принципов квантовой механики, например, симметрии квантовых уравнений движения относительно обращения времени.

В квантовой механике математическим выражением принципа детального равновесия является равенство матричных элементов перехода для прямого и обратного процессов |Tab|2=|Tba|2{\displaystyle |T_{ab}|^{2}=|T_{ba}|^{2}}^[1]

В общем случае, принцип детального равновесия можно сформулировать как равенство вероятностей перехода, отнесённых к конечному состоянию:

wmnPm=wnmPn{\displaystyle {\frac {w_{mn}}{P_{m}}}={\frac {w_{nm}}{P_{n}}}},

где

В отличие от обычного стационарного состояния, для которого достаточно выполнения условия:

dPndt=∑m≠n(wnm⋅Pm−wmn⋅Pn)=0{\displaystyle {\frac {dP_{n}}{dt}}=\sum _{m\neq n}\left(w_{nm}\cdot P_{m}-w_{mn}\cdot P_{n}\right)=0},

детальное равновесие требует равенства нулю каждого из членов суммы, то есть:

wnm⋅Pm=wmn⋅Pn{\displaystyle w_{nm}\cdot P_{m}=w_{mn}\cdot P_{n}},

Для замкнутых изолированных систем принцип детального равновесия сводится к равенству:

wmn=wnm.{\displaystyle w_{mn}=w_{nm}.}

Если же система не изолирована и взаимодействует с другой большой системой (термостатом), то согласно принципу детального равновесия:

wmnwnm=exp⁡En−EmkT.{\displaystyle {\frac {w_{mn}}{w_{nm}}}=\exp {\frac {E_{n}-E_{m}}{kT}}.}

Для газа, подчиняющегося статистике Больцмана, принцип детального равновесия принимает вид:

ff1=f′f1′.{\displaystyle ff_{1}=f^{\prime }f_{1}^{\prime }.}

Для квантовых газов:

ff1(1±f′)(1±f1′)=f′f1′(1±f)(1±f1),{\displaystyle ff_{1}(1\pm f^{\prime })(1\pm f_{1}^{\prime })=f^{\prime }f_{1}^{\prime }(1\pm f)(1\pm f_{1}),}

где знак «+» соответствует бозонам, а знак «−» — фермионам.