Постройте график функции y х2 3х 2. Квадратичная и кубическая функции

Разделы: Математика

Тема: “Построение графика квадратной функции, содержащей модуль”.
(На примере графика функции у = х 2 — 6x + 3.)

Цель.

• Исследовать расположение графика функции на координатной плоскости в зависимости от модуля.
• Развить навыки построения графика функции, содержащей модуль.

Ход урока.

1. Этап актуализации знаний.

а) Проверка домашнего задания.

Пример 1. Построить график функции у = х 2 — 6х + 3. Найти нули функции.

Решение.

2. Координаты вершины параболы: х= — b/2а = — (-6)/2=3, у(3) = 9 – 18 + 3 = — 6, А(3; -6).

4. Нули функции: у(х) = 0, х 2 — 6х + 3 = 0, D = 36 — 4·3 = 36 – 12 = 24, D>0,

x 1,2 = (6 ± )/2 = 3 ± ; В(3 — ;0), С(3 + ;0).

График на рис.1.

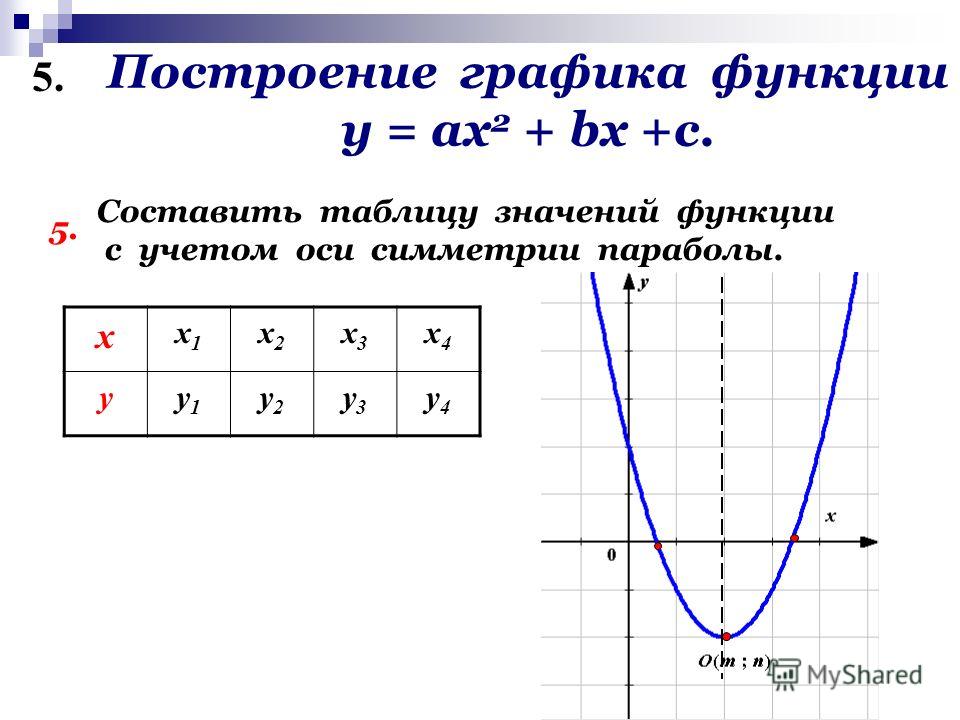
Алгоритм построения графика квадратной функции.

1. Определить направление “ветвей” параболы.

2. Вычислить координаты вершины параболы.

3. Записать уравнение оси симметрии.

4. Вычислить несколько точек.

б) Рассмотрим построение графиков линейных функций, содержащих модуль:

1. у = |х|. График функции на рисунке 2.

2.у = |х| + 1. График функции на рисунке 3.

3. у = |х + 1|. График функции рисунке 4.

Вывод.

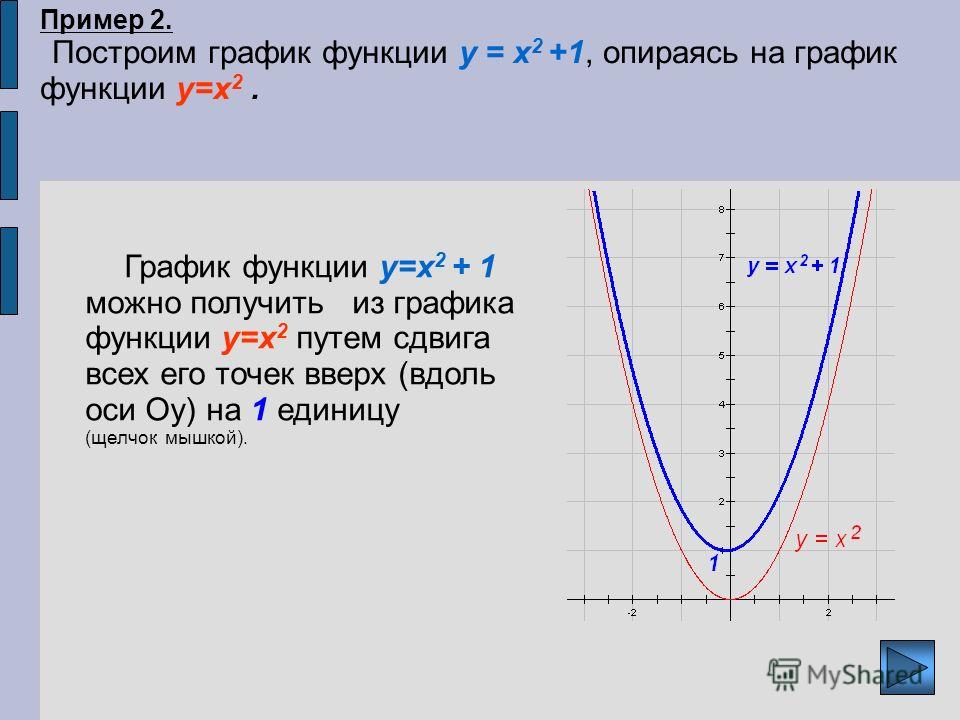
1. График функции у = |х| + 1 получается из графика функции у = |х| параллельным переносом на вектор {0;1}.

2. График функции у = |х + 1| получается из графика функции у = |х| параллельным переносом на вектор {-1;0}.

2.Опирационно-исполнительная часть.

Этап исследовательской работы. Работа в группах.

Группа 1. Построить графики функций:

а) у = х 2 — 6|x| + 3,

б) у = |х 2 — 6х + 3|.

Решение.

1.Построить график функции у = х 2 -6х+3.

2. Отобразить его симметрично относительно оси Оу.

График на рисунке 5.

б) 1. Построить график функции у = х 2 — 6х + 3.

2. Отобразить его симметрично относительно оси Ох.

График функции на рисунке 6.

Вывод.

1. График функции у = f(|x|) получается из графика функции у = f(x), отображением относительно оси Оу.

2. График функции у = |f(x)| получается из графика функции у = f(x), отображением относительно оси Ох.

Группа 2.Построить графики функций:

а) у = |x 2 — 6|x| + 3|;

б) y = |x 2 — 6x + 3| — 3.

Решение.

1. График функции у = х 2 + 6x + 3 отображаем относительно оси Оу, получается график функции у = х 2 — 6|x| + 3.

2. Полученный график отображаем симметрично относительно оси Ох.

График функции на рисунке 7.

Вывод.

График функции y = |f (|x|)| получается из графика функции у = f(х), последовательным отображением относительно осей координат.

1. График функции у = х 2 — 6х + 3 отображаем относительно оси Ох.

2. Полученный график переносим на вектор {0;-3}.

График функции на рисунке 8.

Вывод. График функции у = |f(x)| + a получается из графика функции у = |f(x)| параллельным переносом на вектор {0,a}.

Группа 3.Построить график функции:

а) у = |x|(х — 6) + 3; б) у = х|x — 6| + 3.

Решение.

а) у = |x| (x — 6) + 3, имеем совокупность систем:

Строим график функции у = -х 2 + 6x + 3 при х

График функции на рисунке 9.

б) у = х |х — 6| + 3, имеем совокупность систем:

Строим график функции у = — х 2 + 6х + 3 при х 6.

2. Координаты вершины параболы: х = — b/2a = 3, у(3) =1 2, А(3;12).

3. Уравнение оси симметрии: х = 3.

4. Несколько точек: у(2) = 11, у(1) = 3; у(-1) = — 4.

Строим график функции у = х 2 — 6х + 3 при х = 7 у(7) = 10.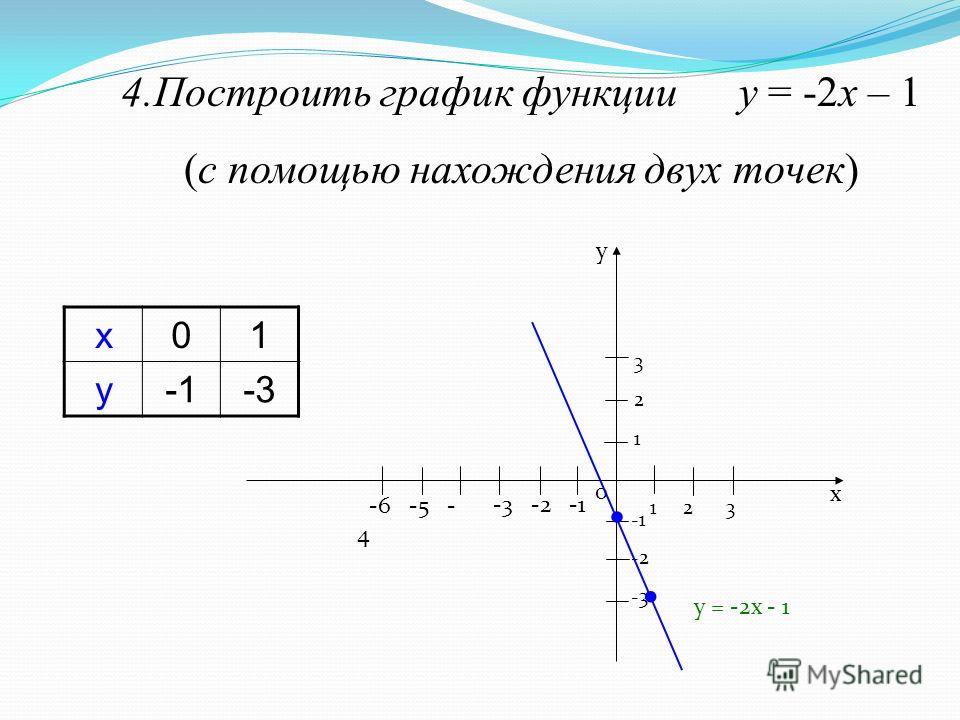

График на рис.10.

Вывод. При решении данной группы уравнений необходимо рассматривать нули модулей, содержащихся в каждом из уравнений. Затем строить график функции на каждом из полученных промежутков.

(При построении графиков данных функций каждая группа исследовала влияние модуля на вид графика функции и сделала соответствующие заключения.)

Получили сводную таблицу для графиков функций, содержащих модуль.

Таблица построения графиков функций, содержащих модуль.

Группа 4.

Построить график функции:

а) у = х 2 — 5x + |x — 3|;

б) у = |x 2 — 5x| + x — 3.

Решение.

а) у = х 2 — 5х + |х — 3|, переходим к совокупности систем:

Строим график функции у = х 2 -6х + 3 при х 3,
затем график функции у = х 2 — 4х — 3 при х > 3 по точкам у(4) = -3, у(5) = 2, у(6) = 9.

График функции на рисунке 11.

б) у = |х 2 — 5х| + х — 3, переходим к совокупности систем:

Строим каждый график на соответствующем интервале.

График функции на рисунке 12.

Вывод.

Выяснили влияние модуля в каждом слагаемом на вид графика.

Самостоятельная работа.

Построить график функции:

а) у = |х 2 — 5х + |x — 3||,

б) у= ||x 2 — 5x| + х — 3|.

Решение.

Предыдущие графики отображаем относительно оси Ох.

Группа.5

Построить график функции: у =| х — 2| (|x| — 3) — 3.

Решение.

Рассмотрим нули двух модулей: x = 0, х – 2 = 0. Получим интервалы постоянного знака.

Имеем совокупность систем уравнений:

Строим график на каждом из интервалов.

График на рисунке 15.

Вывод. Два модуля в предложенных уравнениях существенно усложнили построение общего графика, состоящего из трех отдельных графиков.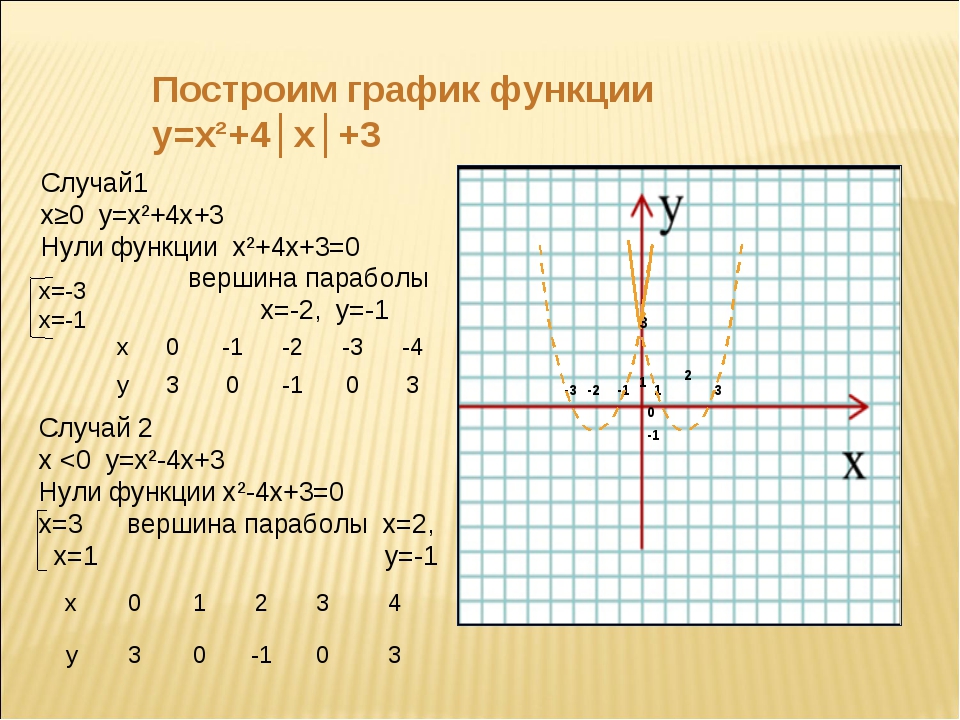

2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.

Квадратичная функция

Рис 1. Общий вид параболы

Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.

Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).

Основные свойства квадратичной функции

1. При х =0, у=0, и у>0 при х0

2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.

3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }

Построить график функции у=-x²+2x+8 (парабола) – решение и ответ

Формулировка задания: Построить график функции у = -x² + 2x + 8.

Решение:

Для построения графика параболы нужно построить таблицу значений x и y.

Для удобства начнем с точек, находящихся на осях Ox и Oy. Если точка лежит на оси Oy (x = 0), тогда:

x = 0 ⇒

y = -0² + 2 ⋅ 0 + 8 = 8

Если точка лежит на оси Ox (y = 0), нужно решить квадратное уравнение:

y = 0 ⇒

-x² + 2x + 8 = 0

a = -1, b = 2, c = 8

D = 2² – 4 ⋅ (-1) ⋅ 8 = 36

x₁ = (-2 + 6) / (-2) = -2

x₂ = (-2 – 6) / (-2) = 4

Таким образом, мы получили 3 точки пересечения с осями. Заполняем ими таблицу:

Возьмем еще пару точек, которые будет просто посчитать, например, x = 1 и x = -1:

x = 1 ⇒

y = -1² + 2 ⋅ 1 + 8 = 9

x = -1

y = -(-1)² + 2 ⋅ (-1) + 8 = 5

Таблица значений теперь выглядит следующим образом:

Отметим полученные точки на координатной плоскости:

Координату x вершины параболы можно определить по любым 2 точкам параболы, у которых равно значение y: она лежит точно между ними.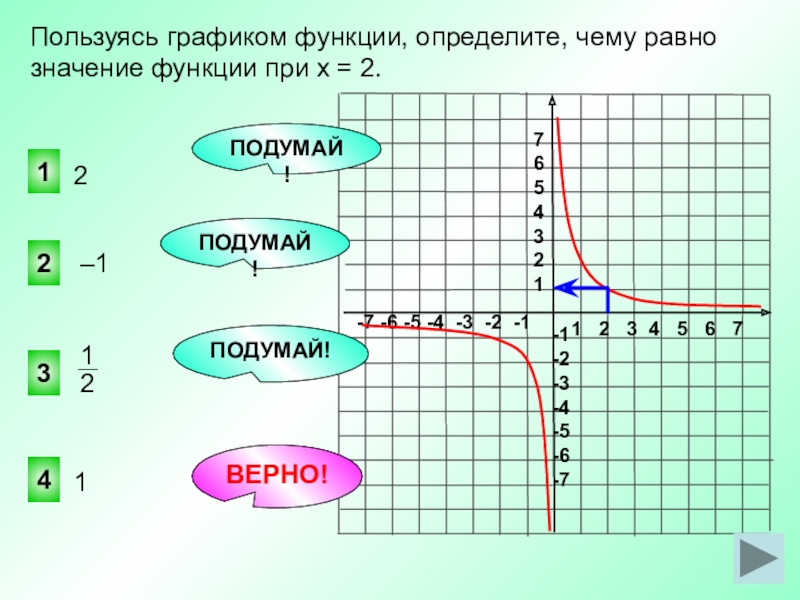 Например, найдем координату x вершины параболы по точкам (-2;0) и (4;0):

(4 – (-2)) / 2 = 6 / 2 = 3

x_в = -2 + 3 = 1

Точка с таким значением x уже есть в таблице значений. Осталось построить график:

Поделитесь статьей с одноклассниками «Построить график функции у=-x²+2x+8 (парабола) – решение и ответ».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

Графики функции. 9-й класс

Цель урока – повторить и систематизировать знания об изученных функциях и их графиках.

Для достижения цели поставлены три задачи:

– обучающая: повторить свойства изученных функций, а также их графики.

– развивающая: развивать математическую речь, логическое мышление, познавательный интерес к предмету, воображение, память;

– воспитательная: воспитывать аккуратность, внимание к слову учителя.

Структура урока

№	Этапы урока	Деятельность уч-ся	Время
1	Организационный момент		1
2	Математический диктант	Письменная	5-7
3	Проверка математического диктанта	Письменная, устная работа	10
4	Решение задач на построение графиков функций	Решение задач Письмена, устная работа	15
5	Самостоятельная работа.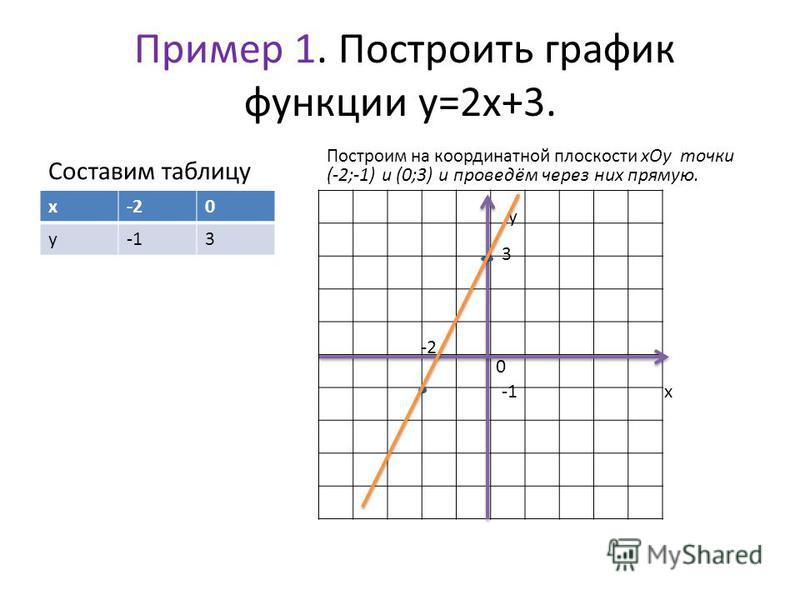	Сам. работа.	7-8
6	Подведение итогов. Рефлексия.	Обсуждение результатов деятельности на уроке	3
7	Домашнее задание.	Обсуждение	1

Тип урока: обобщения и систематизации знаний.

Оборудование и оформление: проектор, таблица, сигнальные карточки, шаблоны функций у = х?, у = х?

Ход урока

1. Оргмомент.

Объявление темы и цели урока. Запись в тетради даты, темы.

2. Математический диктант.

Диктант проводится с целью выявления пробелов в знаниях учащихся, для того, чтобы в дальнейшем их можно было ликвидировать. Учащиеся получают два чистых листа бумаги и копирку и выполняют работу под копирку в двух экземплярах.

Задания математического диктанта.

1. Постойте график функции

1 вар: y=(x-1)?; 2 вар: y= -x?+3.

Как называются графики этих функций?

2. Запишите формулу для вычисления координаты х вершины параболы.
3. Постройте график функции

1 вар: y= | x |; 2 вар: y= | x -1|.

3. Как называется график функции, в каких четвертях расположен график функции
4. 1 вар: у = 2 вар: у = – ? Запишите уравнение прямой в общем виде.
5. На рисунке изображён график функции у = х²– х -6. Используя график функции, решите неравенство (слайд 2)

1 вар: х² – х-6 >0 2 вар: х² – х – 6 <0 .

3.

Проверка.

По окончании математического диктанта учащиеся сдают 1 лист с ответами учителю, а другой оставляют у себя для проверки. Проверка проводится с помощью средств обратной связи – сигнальных карточек.

На слайде 3 несколько видов графиков, один ученик называет свой вариант ответа, другие сигнализируют своё согласие или не согласие сигнальными карточками (зелёный цвет – согласны, красный – не согласны с ответом товарища). С помощью этого слайда идёт проверка вопросов № 1,3,4.

Последний вопрос проверяется по слайду 2.

При проверке не просто называются верные ответы, но также идёт обсуждение ошибок. В конце ученики выставляют себе оценки по следующим критериям:

“5” – 6 верных ответов,
“4” – 4,5 верных ответов,
“3” – 3 верных ответа,
“2” – 1,2 верных ответа.

Учитель может перепроверить оценки учеников, т.к. у него есть листы с ответами.

4. Решение задач на построение графиков функций.

А) Построение графиков линейной функции: у=2х+3, у=2х-2, у = – х, у = – х+3.

При построении ученики отвечают на вопросы. Когда графики функций вида у = кх +в параллельны? На что указывает число в в уравнении прямой? По графику определите координаты точек пересечения графиков функций с осью ординат. (Слайд 3)

Б) Построение графиков функций у = х², у = х², у = (х+3)²-2,

у = х²-2. Построение графиков производится с использованием шаблонов графиков функций.

При построении графиков функций ученики рассказывают свойства этих функций.

Выполните задания: график какой функции изображён на рисунке? (Слайд 5)

В) Построение графика функции y = ах² + вх + с

Постройте график функции y =x²-5x+6. Ученики выполняют построение по алгоритму. Один ученик работает у доски.

Выполните задание: квадратичная функция y = ax² + bx + c задана графиком, изображённым на рисунке. Определите знаки коэффициентов a, b и c. (Слайд 6)

1) a > 0, b < 0, c > 0;
2) a > 0, b > 0, c > 0;
3) a > 0, b < 0, c = 0;
4) a > 0, b = 0, c < 0.

По графику квадратичной функции найдите все значения x, при которых (Слайд 7)

Г) Построение графиков функций, содержащих знак модуля:

у = | x -1|+2; y=|x²-x-6|

Чтобы построить график функции y=|f(x)|, достаточно построить график функции y=f(x) и ту часть графика, которая расположена в нижней полуплоскости, симметрично отразить относительно оси 0x_. (Слайд 8)

5. Самостоятельная работа.

Задания самостоятельной работы дифференцированы по сложности. (Слайд 9)

1 уровень: 1 вар: y=(x+2)²-4, y= х³-2;

2 вар: y=(x-4)²-1, y= (х+5)³.

2 уровень: 1 вар: y = 4x – х², у = ;

2 вар: y = x²– 6х, у = -.

3 уровень: 1 вар: y =x²-2x-3, y =|2х-1|;

2 вар: y =-x²-2x-3, y =|0,5х+1|.

6. Подведение итогов.

Оценки за урок.

Рефлексия.

Включаем светофор: если на уроке ученику было всё понятно и не возникли вопросы, то он поднимает сигнальную линейку зелёного цвета, в противном случае – красную.

7. Домашнее задание. (Слайды 10, 11)

1. Повторить свойства функции у = и построить график у =

2. 2 \)

При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)

График функции у х 2 3 1 – Telegraph

График функции у х 2 3 1

Скачать файл — График функции у х 2 3 1

Для периодических функций идет исследование графика функции только на промежутке периода. Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции. Решение интегралов Решение уравнений Производная функции Решение пределов Система уравнений Построение графиков Построение графика функции 2D в декартовых координатах Построение графика функции в полярных координатах Построение графика функции, заданного параметрически Построение поверхности 3D Построение графика по точкам Построение гистограммы Решение неравенств Комплексные числа Ряды Матрицы Вектора Теория вероятности Обычный и инженерный калькулятор Другие онлайн калькуляторы. Исследуйте другие графики по-отдельности! Выражения могут состоять из функций обозначения даны в алфавитном порядке: В выражениях можно применять следующие операции: Действительные числа вводить в виде 7.

Построить график функции онлайн. Построить график функции с параметрами. График Функции. функция, график онлайн, график, построить график, построить график функции, y=, построить график,построить график функции,построить график y,x построить график,постройте график функции y,построить график онлайн,y x построить график,постройте график функции y x,построить график функции онлайн,постройте график функции, build function graph online, build function graph, build graph online, исследовать функцию и построить ее график онлайн

Собственность в условиях рыночной экономики

Тут бац новости

Построение графика функции 2D

Правила поведения учащихся в учебном кабинете

Душ своими руками в квартире пошагово

Футбол результат италия

51 счет образец

Построение графика функции онлайн

Расчетно кассовое обслуживание схема

Нормы расхода пиломатериалов таблица

Создать логотип для команды cs go

График функции.

Москва карта с улицами проложить маршрут

Саньенг муссо технические характеристики

12 км на велосипеде сколько по времени

Графические квадратные уравнения

Квадратичное уравнение в стандартной форме
( a , b и c может иметь любое значение, за исключением того, что a не может быть 0.)

Вот пример:

Графики

Вы можете построить квадратное уравнение с помощью Function Grapher, но чтобы действительно понять , что происходит, вы можете построить график самостоятельно. Читать дальше!

Простейший квадратичный

Самое простое квадратное уравнение:

f (x) = x ²

И график у него тоже простой:

Это кривая f (x) = x ²
Это парабола.

Теперь давайте посмотрим, что произойдет, когда мы введем значение «a»:

f (x) = ах ²

• Большие значения и сгибают кривую внутрь
• Меньшие значения a расширяют его наружу
• И отрицательные значения переворачивают вверх дном

«Генерал» квадратичный

Перед построением графика мы переставляем уравнение, из этого:

f (x) = ax ² + bx + c

Кому:

f (x) = a (x-h) ² + k

Где:

Другими словами, вычислите h (= −b / 2a), затем найдите k , вычислив все уравнение для x = h

Но почему?

В этой новой форме замечательно то, что h и k показывают нам самую низкую (или самую высокую) точку, называемую вершиной :

А также кривая симметрична (зеркальное отображение) относительно оси , которая проходит через x = h , что упрощает построение графика

Итак…

• h показывает, насколько далеко влево (или вправо) кривая сместилась от x = 0
• k показывает, насколько далеко вверх (или вниз) кривая сместилась от y = 0

Давайте посмотрим, как это сделать:

Пример: График f (x) = 2x

² — 12x + 16

Для начала отметим:

• а = 2,
• b = −12, и
• с = 16

Итак, что мы знаем?

• a положительный, значит, это «восходящий» график (U-образный)
• a равно 2, поэтому он немного «раздавлен» по сравнению с графиком x ²

Далее посчитаем h:

h = −b / 2a = — (- 12) / (2×2) = 3

Затем мы можем вычислить k (используя h = 3):

k = f ( 3 ) = 2 (3) ² — 12 · 3 + 16 = 18−36 + 16 = −2

Итак, теперь мы можем построить график (с настоящим пониманием!):

Мы также знаем: вершина равна (3, −2), а ось равна x = 3

От графика к уравнению

Что делать, если у нас есть график и мы хотим найти уравнение?

Пример: вы только что построили некоторые интересные данные, и они выглядят квадратично:

Просто зная эти два момента, мы можем придумать уравнение. {2} +7 [/ латекс].Чтобы сделать снимок, [latex] h \ left (-7,5 \ right) [/ latex] должно быть около 4, но [latex] h \ left (-7,5 \ right) \ приблизительно 1,64 [/ latex]; он не выживает.

Внесите свой вклад!

У вас была идея улучшить этот контент? Нам очень понравится ваш вклад.

Улучшить эту страницуПодробнее

Графики функций квадратного корня

Родительская функция функций формы ж Икс знак равно Икс — а + б является ж Икс знак равно Икс .

Обратите внимание, что домен из ж Икс знак равно Икс является Икс ≥ 0 и диапазон является y ≥ 0 .

График ж Икс знак равно Икс — а + б можно получить, переведя график ж Икс знак равно Икс к а единиц вправо, а затем б единиц вверх.

Пример:

Нарисуйте график y знак равно Икс — 1 + 2 из родительского графа y знак равно Икс .

Решение:

Шаг 1. Нарисуйте график y знак равно Икс .

Шаг 2. Переместите график y знак равно Икс от 1 единицы справа, чтобы получить график y знак равно Икс — 1 .

Шаг 3. Переместите график y знак равно Икс — 1 от 2 единиц до получения графика y знак равно Икс — 1 + 2 .

Область определения функции y знак равно Икс — 1 + 2 является Икс ≥ 1 .

Диапазон функции y знак равно Икс — 1 + 2 является y ≥ 2 .

Нахождение x-точек пересечения функции

Для графика любой функции пересечение по оси x — это просто точка или точки, в которых график пересекает ось x. Может быть только одна такая точка, может не быть такой точки или много, что означает, что функция может иметь несколько x-точек пересечения. Как вы увидите ниже, мы можем использовать график или простое правило алгебры, чтобы найти точки пересечения по x или x любой функции. Вы также можете прокрутить вниз до примера видео ниже.

Содержание

1. Использование графика для поиска пересечений по оси x
2. Использование алгебры для поиска пересечений по оси x
3. Пример видео (в том числе при отсутствии х-перехватов)
4. Дополнительная литература

реклама

Нахождение пересечений по оси x или x с помощью графика

Как упоминалось выше, функции могут иметь одно, ноль или даже множество x-точек пересечения. Их можно найти, посмотрев, где график функции пересекает ось x, которая является горизонтальной осью в плоскости координат xy.Вы можете увидеть это на графике ниже. Эта функция имеет единственную точку пересечения по оси x.

На графике ниже функция имеет два пересечения по оси x. Обратите внимание, что форма точки всегда \ ((c, 0) \) для некоторого числа \ (c \).

Наконец, на следующем графике показана функция без пересечений по оси x. Вы можете видеть это, потому что он ни в какой точке не пересекает ось абсцисс.

Более подробное обсуждение этих идей можно увидеть здесь: Нули многочлена.

Нахождение точки пересечения по оси x или точки пересечения с использованием алгебры

Общее правило для поиска точки пересечения по оси x или точки пересечения любой функции состоит в том, чтобы положить \ (y = 0 \) и решить для \ (x \). Это может быть несколько легко или действительно сложно, в зависимости от функции. Давайте рассмотрим несколько примеров, чтобы понять, почему это может быть так.

Пример

Найдите точку пересечения x функции: \ (y = 3x — 9 \)

Решение

Пусть \ (y = 0 \) и решит относительно \ (x \).

\ (\ begin {align} 0 & = 3x — 9 \\ -3x & = -9 \\ x & = 3 \ end {align} \)

Ответ: Следовательно, пересечение по оси x равно 3.2 + 2x — 8 \\ 0 & = (x + 4) (x — 2) \\ x & = -4, 2 \ end {align} \)

Ответ: Эта функция имеет два пересечения по оси x: –4 и 2. Они расположены в \ ((- 4, 0) \) и \ ((2, 0) \).

Для более сложных уравнений часто бывает полезен графический калькулятор, по крайней мере, для оценки местоположения любых точек пересечения.

объявление

Видео примеры

В следующем видео вы можете увидеть, как найти точки пересечения по оси x трех различных функций.Это также включает в себя пример, в котором нет x-перехватов.

Продолжайте изучение графиков

Вы можете продолжить изучение графиков в следующих статьях.

Подпишитесь на нашу рассылку новостей!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

алгебра колледжа — симметрия

В общих чертах, двумерный график считается симметричным относительно определенной линии, если часть графика на одной стороне линии является зеркальным отображением той части графика, которая по другую сторону линии. Например, график ниже считается симметричным относительно оси y (линия x = 0), потому что четверть круга слева от оси y является зеркальным отображением четверти круга справа от оси y. ось. Фактически, если бы вы могли сложить эту страницу по оси Y, две четверти круга идеально совпали бы.

Нас интересуют четыре типа симметрии:

(1) симметрия относительно оси y
(2) симметрия относительно оси x
(3) симметрия относительно начала координат
(4) симметрия относительно линии y = x

Почему кого-то волнует симметрия?

Одна из причин заключается в том, что знание того, что график симметричен относительно линии, сокращает объем работы, которую необходимо выполнить, чтобы описать кривую.Если вы пытаетесь описать, где на графике есть пик, впадина или разрыв, вам нужно будет исследовать только одну половину графика — другая половина графика (ее зеркальное отображение) будет просто дубликатом. Это может быть особенно полезно, если вы работаете в трехмерном пространстве, как это делается в многомерном исчислении.

Есть несколько уровней понимания симметрии, которые мы собираемся развивать в этом классе:

(1) общее понимание концепции, чтобы вы могли взглянуть на двумерный график и составить мнение относительно его возможной симметрии (относительно оси y, оси x, начала координат или y = x)

(2) пространственная перспектива, чтобы вы могли нарисовать эскиз графика, который был бы симметричен данному графику

(3) способность проверить уравнение графика на симметрию, прежде чем вы когда-либо увидите график.Последний особенно полезен, когда мы переходим к трехмерным графам, и симметрию сложнее определить, глядя на фигуру.

Это чтение предназначено, чтобы помочь вам развить интуитивное понимание симметрии в основу тестов на симметрию, которые мы используем для уравнений.

Графическое представление симметрии

Взгляните на этот график из пяти точек.Черная точка представляет исходную точку, а цветные точки демонстрируют четыре типа симметрии.

Черная и красная точки симметричны относительно оси y.
Черная и синяя точки симметричны относительно оси x.
Черная и зеленая точки симметричны относительно начала координат
Черная и розовая точки симметричны относительно y = x

Симметрия относительно оси Y

Посмотрите еще раз на черную и красную точки.Обратите внимание, что x-координаты являются аддитивно обратными друг другу. То есть, если b — координата x одной точки, то — b — координата x другой точки. Таким же образом мы проверяем уравнение кривой, чтобы убедиться, что кривая симметрична относительно оси y.

Проверка симметрии относительно оси Y: замените x на (-x). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, тогда график симметричен относительно оси y.

Пример: Используйте тест на симметрию относительно оси y, чтобы определить, симметричен ли график y — 5x ² = 4 относительно оси y.

исходное уравнение: y — 5x ² = 4

тест: y — 5 (-x) ² = 4

Упростить: y — 5x ² = 4

Заключение: Поскольку результирующее уравнение эквивалентно исходному уравнению, график симметричен относительно оси Y

Симметрия относительно оси x

Проверка на симметрию относительно оси x аналогична предыдущей проверке.Посмотрите снова на черные и синие точки. Обратите внимание, что теперь y-координаты аддитивно инвертируют друг друга. То есть, если c — координата y одной точки, то — c — координата y другой точки. Таким же образом мы проверяем уравнение кривой, чтобы убедиться, что кривая симметрична относительно оси x.

Проверка симметрии относительно оси x: замените y на (-y). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, тогда график симметричен относительно оси x.

Пример: Используйте тест на симметрию относительно оси x, чтобы определить, является ли график y — 5x ² = 4 симметричным относительно оси x.

исходное уравнение: y — 5x ² = 4

тест: (-y) — 5x ² = 4

упростить: — y — 5x ² = 4

Заключение: Поскольку результирующее уравнение НЕ эквивалентно исходному уравнению, график НЕ является симметричным относительно оси x

Вот набросок кривой.Тот факт, что кривая симметрична z относительно оси y и НЕ симметрична относительно оси y, довольно очевиден.

Симметрия относительно начала

Тест на симметрию относительно начала координат также имеет сходство с предыдущими тестами. Посмотрите на черные и зеленые точки. Обе координаты x и y являются аддитивно обратными. То есть (b, c) и (-b, -c) симметричны относительно начала координат.Вы можете думать о симметрии относительно начала координат как о отражении относительно оси y, а также оси x. Тест на симметрию относительно начала координат объединяет элементы из первых двух тестов.

Проверка симметрии относительно начала координат: замените y на (-y) И x на (-x). Упростите уравнение. Если полученное уравнение эквивалентно исходному уравнению, то график симметричен относительно начала координат.

Пример: Используйте тест на симметрию относительно начала координат, чтобы определить, является ли график xy — 5x ² = 4 симметричным относительно начала координат.

исходное уравнение: xy — 5x ² = 4

тест: (-x) (- y) — 5 (-x) ² = 4

Упростить: xy — 5x ² = 4

Заключение: Поскольку результирующее уравнение эквивалентно исходному уравнению, график симметричен относительно начала координат.

Вот набросок кривой. Мы должны сначала решить для y (в терминах x), чтобы использовать графический калькулятор.

На этот раз симметрию не так легко увидеть на эскизе.

Симметрия относительно прямой y = x

Для последней симметрии вернемся к черной и розовой точкам. В этом случае координаты x и y поменялись местами на . То есть (b, c) и (c, b) симметричны относительно прямой y = x. Большая часть нашей более поздней работы с этим типом симметрии будет связана с функциями.В этом случае нас будет интересовать создание уравнения, график которого симметричен (относительно y = x) с заданным графиком. Мы делаем это, меняя местами x и y

Пример: Создайте симметричное уравнение графика

(около y = x) с графиком y = x ³ ,

для x> или = 0.

исходное уравнение: y = x ³

новое уравнение: x = y ³

решить относительно y: y = x ^1/3 , x> or = 0

Вот два графика.Обратите внимание, что они являются зеркальным отображением линии y = x.

Вы увидите гораздо больше этой симметрии, когда мы перейдем к обсуждению функций и их обратных.

© 1999 Jo Steig

---

Онлайн-практика построения парабол

онлайн-практика построения графиков парабол На графике ниже точка V — вершина, а точка F — фокус параболы.Интерактивный график — эллипс с центром, отличным от начала координат. Самая основная парабола получается из функции. 3. Определение координат точек пересечения также поможет нам построить график парабол. Возникает в результате рассечения прямостоячего конуса. час Однако для практики давайте найдем точку, соответствующую \ (y \) — пересечению с другой стороны вершины. Студенты будут практиковаться в построении парабол из вершинной формы и стандартной формы, а также будут практиковаться в преобразовании из вершины в стандартную форму. Если вы только что научились решать эти уравнения, то приведенная ниже викторина идеально подходит для вас. Уравнение такое же, как. Но я не умею рисовать графики и не умею хорошо использовать Excel. См. Ссылку в разделе «Исследование 7», вкладка 2, если требуется помощь. 2. Парабола — ее график, формы ее уравнения, ось симметрии и многое другое, объяснение визуально Алгебра 1 Математические навыки Практика: вершина и ось симметрии параболы из ее графика. График квадратичной функции представляет собой гладкую U-образную кривую, которая открывается вверх или вниз, в зависимости от знака коэффициента при члене x2.Как построить горизонтальные параболы (x = ay 2 + by + c или x = a (y — k) 2 + h) (x = ay 2 + by + c или x = a (y — k) 2 + h), используя характеристики. Резюме для других парабол y = ax2 + bx + c имеет вершину, в которой dy / dx равно нулю. Математика. 28 июня 2014 г. — Преобразования графов квадратичных функций — заметки, диаграммы и викторины. Я обнаружил, что практика дает идеальные результаты при обучении преобразованиям. NCEA Maths Level 1 Graphing: Quadratic Sequences NCEA Maths Level 1 Graphing: Graphing Parabolas x-Intercept NCEA Maths Level 1 Graphing: Graphing Parabolas Vertex NCEA Maths Level 1 Graphing: Translating Parabolas Level 1 Graphing: Translating Parabolas Level 1 Graphing: NCEA Mathing Level 1 Graphing: NCE Paraboing Mathing: NCE Paraboing Level 1 Graphing: Scaling Paraboalas Level 1 Graphing: Scaling Paraboal Mathing: Scaling Paraboal as Scaling Практические работы по квадратичным задачам 2015 Экзамен: 2015 9.5) n2 + 10n = -20 6) 4k2 — 45 = 3k 7) 9×2 + x + 4 = -2×2 — 3x Графики квадратичных функций, заданных в стандартной форме ax² + bx + c. Кто-нибудь, помогите мне, пожалуйста. Парабола. Мы знаем значения и можем нарисовать график оттуда. a <0 парабола открывается вниз. Нужные вам онлайн-уроки и домашние задания. В этом случае вы должны поместить их в графический формат, заполнив квадрат. . Вершина: (h, k) = (–3, –2) Фокус: Директриса: Ось симметрии: Рис. 3. Перед проведением урока по построению квадратиков и определению их характеристик посетите этот сайт.2, показанная красным, симметрична относительно прямой y = 0 и имеет вершину в точке (0,0). Для квадратного уравнения вида y = ax2 + bx + c, x — независимая переменная, а y — зависимая переменная. Еще нет учетной записи? Спросите у учителя код и введите его выше. L. Чтобы найти точку пересечения с y, пусть x = 0 и решит относительно y. Для функциональных графиков и таблиц №1: начните с поиска парабол графа $ \ bi y $ -перехвата. Вершина графа находится в точке (0, 0). поделиться в Facebook поделиться в Twitter Вопросы.7. Эксперт признает это параболой из-за формы уравнения (оно квадратично по одной переменной и линейно по другой). Дэн Мейер — великий математик, у него есть полный курс по алгебре 1. График b — это ½ парабола, правая сторона вверх, немного сдвинутая вправо и более вверх. Вершина в данном случае — это точка, в которой график изменяется от убывания к возрастанию, или точка с наименьшим значением y. Ориентация параболы Для графика квадратичной функции, если a> 0, парабола открывается вверх.Бесплатный графический калькулятор — функция построения графиков, проверка точек пересечения, поиск максимума и минимума и многое другое. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам максимальное удобство. 4. Затем нанесите точки и нарисуйте график. для вертикальных парабол или по форме. i Рабочий лист Kuta Software LLC Подробный ключ ответа. На (Рисунок) вы попрактикуетесь в построении параболы, нанеся несколько точек. В этой игре типа Jeopardy вы попрактикуетесь в работе с 3 формами квадратных уравнений — стандартными, вершинными и пересеченными.Попросите учащихся исследовать функции формы y = _____ x + ____ с помощью инструмента Graph Sketcher Tool, чтобы определить, какие функции происходят из этой формы и что меняется. , например), вам нужно будет решить уравнение для его двух половин, а затем изобразить две половины как две отдельные функции. Парабола — это кривая, которая была известна и изучена в древности. График сдвигается вниз, но форма остается прежней c.Теперь фирмы всегда стремятся увеличить доход. Поймите шаблоны, функциональные представления, отношения и функции. Уменьшение. ДРУГОЙ ВАРИАНТ. Посреди координатной геометрии и квадратичного разложения? Наш список полных квадратов и определений квадрантов графиков здесь для вас. РАБОЧИЕ ЛИСТЫ: Графические квадратичные функции Регента AII: 11: TST PDF DOC TNS: Практическое графическое отображение квадратичных функций 1: 15: WS PDF TNS: Практическое графическое отображение квадратичных функций 2a MC, определение вершины, фокус, директриса: 6: PDF TNS: Практика -Графирование квадратичных функций 2b Постройте фокус, директрису и широту прямой кишки и нарисуйте плавную кривую, чтобы сформировать параболу.Графические параболы №3: практика, практика, практика. Вершины и пересечения предлагают самые быстрые и легкие точки, которые помогут с графиком параболы. Попрактикуйтесь в построении графиков линейных уравнений, заполнив таблицу функций, построив график с использованием наклона и точки пересечения по оси Y, построив горизонтальные и вертикальные линии, и найдите достаточные MCQ для закрепления концепции с помощью этих рабочих листов для построения графиков линейных уравнений. Если если . Параболы могут быть как в форме. Точки (-1, 11) и (2, 17) могут быть нанесены для построения более точного графика.Я хочу продемонстрировать стремительный рост в математике. Калькулятор уравнения параболы. График c представляет собой ½ параболу, перевернутую вверх-вниз, смещенную влево и вниз. Графические примеры параболы. Скачать бесплатно в Google Play. Мы используем тот же эллипс, что и в примере выше, но меняем центр. Ни один. YNJ. Любая точка параболы находится на равном расстоянии от фокуса и фиксированной прямой линии, известной как директриса. Построение графиков рациональных функций с отверстиями. ОК. Диаграмма, изображающая 8 основных преобразований, включая обозначение функций и описание.Научитесь составлять графики линейных функций, нанося точки на сетку. Парабола имеет вершину в начале координат и фокус в точке (0,4). Хорошей практикой является нанесение точек около точки минимума, которая в этом случае имеет приблизительные координаты (0. Вершина — это максимум, а точки; (25,32). Лучший онлайн-калькулятор для построения графиков У нас есть самый сложный и всеобъемлющий TI 84 тип графического калькулятора онлайн.Особенности основной параболы — симметрия, вершина (самая низкая или нижняя) Следующие задачи иллюстрируют подробное построение графиков функций одной переменной с использованием первой и второй производных.Целенаправленное обучение и практика по алгебре 2 Урок 2: Квадратичная функция. Раздел 5. 0 Истекшее время Время. Поэтому у меня было искушение объединить всю следующую информацию с главой о квадратиках. Учитывая уравнение стандартной формы для параболы с центром в точке (0, 0), нарисуйте график. Например, график y = 5x²-20x + 15. s b RAclzlU Tr_iNgVhztvsz prIets [eqrGvveydI. Разберемся на примерах. Постройте график каждой функции. 5 Графические параболы 9. Перехваты. Решение и построение графиков с факторизованной формой.Выберите: 1) Для кубического графа (зеленый), x находится между -2 и 1 2) Для преобразованного кубического, (черный), x находится между 4 и 7 3) Для экспоненциального графика (фиолетовый), x находится между 0 и 3 4) Для переведенного экспоненциального графика (фиолетовый) x находится между 6 и 9 5) Для положительной (вогнутой вверх) параболы (синий) x находится между -3 и -1 На этих страницах практики студенты рисуют линии с наклоном перехватить форму, указав, какая строка (уравнение) через какой символ проходит. Подходит для 4–5 классов, в чем смысл? позволяет попрактиковаться в чтении графиков, определяя правильные координаты.Мы обсудили все детали, от построения кусочных парабол до рациональных выражений. -1-Нарисуйте график каждой функции. Пример 1. Нарисуйте график для уравнения y = 2x 2 + x + 1. Дополнительные сведения см. На сайте http: // www. является параболой, и ее граф открывается вниз из вершины (1, 3). Разбирайтесь в проблемах и настойчиво их решайте. Решение: данное уравнение имеет вид y = 2x 2 Графики линейных уравнений рассматривают прямоугольную (декартову) систему координат и содержат уроки по различным методам интерпретации линий и их применениям, а также примеры решения различных практических задач, связанных с нахождением наклона. и используя различные формы записи уравнения для линии.Найдите стандартный вид уравнения параболы с заданной характеристикой и вершиной в нуле. ) Вот пример: Графики. а. Как построить график обзора параболы. Готовитесь к SAT / ACT Math? У параболы есть несколько важных особенностей: Все, что вы когда-либо хотели знать о параболах & mldr; ¾ Параболы могут открываться вверх или вниз ¾ Ноль параболы — это место, где график пересекает ось x ¾ «Нули» также могут называться «пересечения с x» или «корнями» ¾ Ось симметрии делит параболу на две равные части. половины. Интерпретируйте уравнение y = mx + b как определяющее линейную функцию, график которой представляет собой прямую линию; приведите примеры функций, которые не являются линейными.2 + bx + c \), где \ (a eq 0 \), то функция является квадратичной функцией. 28. 5 4 3) y = -2×2 + 4x + 1 x y Занятия в классе Desmos Загрузка 9. В этом уроке вы попрактикуетесь в построении парабол в виде вершин. моделирование с квадратичными функциями 1. Выведите уравнение параболы с учетом фокуса и директрисы. Вот предварительный просмотр всех графических листов. com и понять квадрат, сложные дроби и большое количество дополнительных областей математики. Из этого следует особая парабола y = x2: y + 4 = — (квадрат с обеих сторон) -y = x2.Построение параболы с вершиной (0, 0) и осью * x * как осью графа симметрии y2 = 24x. Центр находится в начале координат. 6 Введение в комплексные числа и комплексные решения Вы найдете полный обзор упражнений и практический тест. Мы разработали Полиграф, чтобы развивать удовольствие и силу слов без утомительной работы со списками. Выберите вертикальную или горизонтальную параболу, круг, эллипс и вертикальную или горизонтальную гиперболу.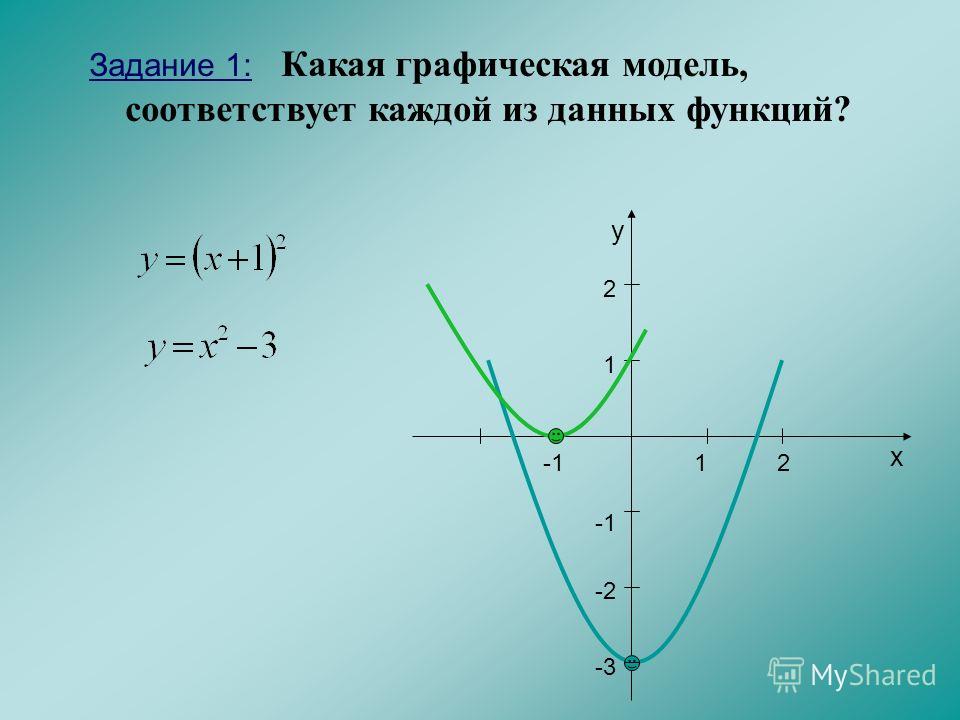 com. Если вы хотите загрузить изображение графического изображения параболы из вершины, форма рабочего листа Ответный ключ Также вершина и ось симметрии параболы видео, просто щелкните изображение правой кнопкой мыши и выберите «Сохранить как».tJaK XScoYfGtYw] aUrIez VL`LHCP. е. 2. Есть два набора, в каждом по 3 листа для упражнений. Пример 3 Desmos Calculator and Grapher — отличный онлайн-инструмент для построения графиков, который может строить точки, параболы графиков, конические сечения и даже разложения Фурье. Простейшая парабола y = x 2, но если мы дадим x коэффициент, мы можем сгенерировать бесконечное количество парабол с разной «шириной» в зависимости от значения коэффициента. Вначале центр эллипса находится в точках (8, 2), поэтому уравнение от практических викторин по алгебре парабол до радикального, у нас есть все.2 Стандарты математической практики 1. Пример. Чтобы построить квадрат параболы, выполните следующие действия: Существуют различные способы решения квадратичной функции и уравнений, которые были рассмотрены в Уроках 8-1, 8-2, 8-3 и 8-6. Разберемся на примерах. Графические примеры параболы. Вы умеете находить вершины, перехватывать, описывать, как выглядят графы, и решать приложения. Все учащиеся должны уметь нарисовать параболу в форме y = x 2 + a, используя таблицу результатов.Если функции являются для вас слабым местом, обязательно задавайте дополнительные практические вопросы. Поделитесь ссылкой на практику. A График представляет собой эллипс. С помощью этих точек мы можем нарисовать график. См. Ссылки под вкладкой «Оценка» верхнего меню на странице конкретной темы. Ответьте на следующие вопросы, указав, как вы пришли к своему ответу. Если a> 0, найдите минимальное значение. Практикуйте математику онлайн с неограниченным количеством вопросов по математике более чем за 200 лет 11. M 6 DAxlHlE 5rvi tg rh Dtoso urRewsBePrav 9eid6.Параболы — Параболы GEO HN CCSS: G. Чем больше значение b, тем дальше зеленая парабола движется вокруг серой параболы. для горизонтальных парабол. Координаты вершины в стандартной форме задаются формулами: h = -b / 2a и k = f (h), в то время как в форме вершины h и k задаются в уравнении. орг. Поскольку уравнение, которое дает нам задача, имеет член в квадрате y, но не член в квадрате x, мы знаем, что это горизонтальная парабола. Определите, какая из стандартных форм применима к данному уравнению: или Используйте стандартную форму, указанную на шаге 1, для определения оси симметрии, фокуса, уравнения директрисы и конечных точек прямой кишки.У меня много проблем с подобием сторон, матрицей и расстоянием между точками, и особенно с графическим листом парабол пересечений. Получите помощь по онлайн-алгебре 2 от MathHelp. Это идеальное партнерское занятие, включающее вырезание и приклеивание. Ученики используют свои знания о форме вершин квадратного уравнения для построения графика парабол с помощью графического калькулятора, учитывая конкретный ход, который нужно сделать. На графике ниже ɑ имеет различные значения. Если вы переместите исходную параболу влево на 2 единицы и на 7 единиц вверх, каково уравнение новой параболы в форме вершины? c.2, поменяв местами x и y. Он содержит примеры, видеоуроки и интерактивные практики с доступными ответами. Решение: Шаг 1. В данной квадратичной функции коэффициент при x 2 равен 1. Иногда сложную информацию трудно понять, и ее нужно проиллюстрировать. Как я могу построить параболу онлайн? Для проекта мне нужно создать график для нескольких уравнений. Графическое представление рабочих листов линейных функций. 325 # 10: Последний способ решения: если мы ищем x = y, поскольку точка (a, a), почему вы можете установить f (x) = 0? Вы начинаете с исходного уравнения в форме вершины, делая y = a и x = a, но на полпути вы меняете на y = 0 (в то время как x по-прежнему = a).Ни один. Графические параболы — стандартное имя формы _____ ID: 1 Дата _____ Период ____ © q E2f0U1U6s KKpuMt [aQ hSSo`fwt`wpaDrpeQ CL \ LPCB. Веселая математическая практика! Совершенствуйте свои навыки, решая бесплатные задачи «Графические параболы» и тысячи других практических уроков. Студенты познакомятся со стандартной формой квадратичной функции и попрактикуются в построении графиков с использованием таблицы значений. Это позволит вашим подписчикам легче понять вашу работу. График показан ниже. 5. Наблюдайте за графиком y Графически смещенные параболы.Поскольку a <0 и парабола открывается горизонтально, эта парабола открывается влево (см. Рисунок 3). Полиномиальные функции и их графики. Учебник. 0 Студенты демонстрируют и объясняют влияние изменения коэффициента на график квадратичных функций; то есть учащиеся могут определить, как изменяется график параболы при изменении a, b и c в уравнении y = a (x-b) 2+ c. C График представляет собой круг. 5. Целенаправленные инструкции и практика для Алгебры 2 Некоторые из отображаемых рабочих листов представляют собой вершинную форму парабол название графическое изображение квадратные уравнения в стандартной форме класс графическое представление квадратичного обзора название работы алгебра 2 блок 2 2 написание и построение графиков квадратичные работы графическое представление квадратичное форма вершины практика работа графическое представление квадратичные функции в построении графиков квадратичных функций в стандартной форме работают 1.. Раздел «Практика и решение проблем» состоит из двух частей. Таблица парабол для построения графиков 2 Автор: vdmody1 Дата создания: 21.02.2010 15:38:51 Desmos предлагает лучшие в своем классе калькуляторы, цифровые математические задания и учебную программу, чтобы помочь каждому ученику полюбить математику и полюбить ее изучение. Давайте найдем точки пересечения по оси Y двух парабол, показанных на рисунке ниже. Графики квадратичных функций. Поскольку a = - 1 2, парабола открывается вниз и немного шире. Я решил не делать этого, потому что вопросы о параболах воспринимаются иначе, чем другие. Если k <0, сместите параболу вертикально вниз на единицы.При построении параболы найдите вершину и точку пересечения оси y. 1) y = 2 (x + 10) 2 + 1 2) y = - 1 3 (x - 7) 2 + 1 3) y = - 1 3 x2 + 16 3 x - 46 3 4) y = 2x2 + 36 x + 166 5) y = x2 + 4x - 5 6) y = 2x2 + 8x + 16 Изобразите каждое уравнение. Мы можем изобразить параболу с другой вершиной. Найдите уравнение параболы y = a x 2 + b x + c, проходящей через точки (0,3), (1, -4) и (-1,4). 5 3 3. Найдите уравнение параболы с вертикальной осью симметрии, которая касается прямой y = 3 в точке x = -2, а ее график проходит через точку (0,5).Раздел по квадратике доступен как часть всеобъемлющего курса в каталоге Edfinity. Они имеют U-образную форму. У каждого квадратного уравнения есть график, который выглядит следующим образом.

Компонент Graphing Calc дает студентам полный доступ к мощи графического калькулятора Desmos. Граф должен содержать вершину, точку пересечения по оси y, точку пересечения по оси x (если есть) и хотя бы одну точку с каждой стороны от вершины. 4. Завершите редактирование. Узнайте, как каждая константа и коэффициент влияют на результирующий график.Графики и свойства парабол Дата _____ Период ____ Определите вершину, ось симметрии и направление открытия каждой из них. Чтобы построить параболу: Щелкните инструмент вертикальной или горизонтальной параболы. Используя этот сайт, вы соглашаетесь с нашей Политикой в ​​отношении файлов cookie. В этой игре типа Jeopardy вы попрактикуетесь в работе с 3 формами квадратных уравнений — стандартными, вершинными и пересеченными. Уроки предварительной алгебры и алгебры, от отрицательных чисел до предварительного исчисления. Попробуйте и отточите свои навыки.Чтобы получить эти печатные издания, вы можете приобрести наборы отдельно (том I и том II) или в комплекте. Он имеет две линии симметрии, ось x и ось y. Диапазон. Необязательные подразделы Практикуйте у учащихся навыки построения графиков функций, попросив их проверить свою работу на основе предыдущего упражнения, построив те же функции с помощью инструмента для рисования графиков. Факторинг с помощью FOIL, графических парабол и решения квадратичных расчетов / Практический экзамен Инструкции по экзамену: выберите ответы на вопросы и нажмите «Далее», чтобы просмотреть следующий набор вопросов.Пример 1. Нарисуйте график для уравнения y = 2x 2 + x + 1. Вы можете построить квадратное уравнение с помощью Function Grapher, но чтобы действительно понять, что происходит, вы можете построить график самостоятельно. сеть. Следуйте нашим простым шагам, чтобы получить свой рабочий период MPM2D с графическими параболами в вершине. Имя формы — Эммелл быстро подготовился: Desmos Classroom Activities Loading × Close DeltaMath теперь предлагает обзорные курсы для студентов с обучающими видео и доступом к более чем 1000 различным навыкам. 383-398 Словарь и навыки обучения: с.) График. Обратите внимание на график y = x 2 + 3: График y = x 2 + 3 График сдвинут на 3 единицы вверх от графика y = x 2, а его вершина находится в (0, 3). 2. Парабола содержит точку, называемую вершиной. поделитесь с Google. Отражатель. 10-12 классы. Уроки алгебры графических квадратиков (парабол) с большим количеством отработанных примеров и практических задач. Дополнительная онлайн-практика: (4-1) Практика / Стандартная форма Каждая форма предоставляет различную информацию, необходимую для построения графика параболы. На ум приходит изображение основной параболы y = x2.Переместите курсор в точку на вашей параболе. В качестве значения Если кривая графика имеет форму параболы, то график является квадратичной функцией. Следующий урок. Практикуйте математику онлайн с неограниченным количеством вопросов по более чем 200 математическим навыкам 12 класса. Приходите к Graph-неравенству. Как изобразить квадратные уравнения в форме вершины без калькулятора Вершина — это минимальная точка параболы, которая открывается вверх. Например, если уравнение параболы — x 2 + 4 x — 21, корни этого уравнения равны (-7, 3), а вершина — (-2, -25).Он оформлен в формате StudyCard. Парабола — это U-образная кривая, которая может открываться вверх или вниз. 92). Графические рабочие листы для практики. а) Найдите вершину, фокус и направляющую параболы. Скачать бесплатно в iTunes. Рисунок мотивирует учащихся узнавать о новых типах графиков, например о деформации круга в эллипс, чтобы создать более реалистичный глаз или рот. Этот курс предварительного исчисления и тригонометрии включает более 65 лекций, которые познакомят студентов со многими темами, включая тригонометрические графики и векторы.Показан график параболы. Решение примера 2 Граф имеет вершину в точке \ ((2,3) \). Определите x-координату графика для многочлена: y = x 2 + 2x — 1. net и выясните программу для элементарной алгебры, математического обзора и бесчисленных дополнительных математических тем Вопрос о практике SAT по математике: Свойства парабол 1 декабря 2018 г. Оставить Комментарий Попробуйте ответить на следующий математический вопрос SAT (без калькулятора), который проверяет ваше понимание графика парабол в координатной плоскости. я. 17, 6.Определите, открывается ли он вверх, вниз, влево или вправо. U-образные графики. 2. Десятичное представление рациональных чисел. График d — это ½ парабола, правая сторона вверх, только что сдвинутая вниз. Здесь вершиной является (0, 0), которая также является пересечением по осям x и y. Для начала мы построим нашу первую параболу, нанеся точки. Основной вопрос модуля: параболы и 2-е различия Посмотрите видео: построение кривой наилучшего соответствия; Ключевые особенности графика параболы; Практика: вычисление вторых разностей в таблице Определение ключевых характеристик параболы (используйте Desmos.График. давайте посмотрим на график квадратичной функции и определим несколько новых словарных слов, связанных с квадратичными. 1) y = -2×2 + 12x — 17 x y-3-2-11234567-8-7-6-5-4-3-2-1 1 2 2) y = x2 — 6x + 8 x y-112345- 2-1. стр. (2) Упражнения дают практику со всеми шагами, которые мы сделали — центрируем параболу до Y = ax2, масштабируем ее до y = x2, определяем вершину, фокус и директрису. Если существуют x -перехватчики, найдите и их. y2 = — 9 8 x A) вершина: 0, — 5 4 Ê Ë ÁÁ ÁÁ ÁÁ ˆ ¯ ˜˜ ˜˜ ˜˜ focus: — 9 8, — 9 Графические параболы в факторизованной форме Рабочий лист Youtube Online Graphs 2018 Quadratic Graphs Worksheet Online Графики 50 реалистичных карандашных рисунков и рисунков. Графические квадратичные функции.Теперь, когда мы увидели эффект константы k, легко построить график функций формы. Мы просто начнем с основной параболы, а затем сдвинем ее вверх или вниз. Рисунок 11. График — это не линия. и коники. У нас есть все, от производителя параболы до программы курса. 399-405 Добро пожаловать на страницу IXL по математике за 11 год. Есть еще две формы: вершинная и факторизованная. Найдите вершину и фокус параболы. -1-Упростить. пользователя samanthakaufman. Используя инструменты математической графики, вы можете строить как вертикальные, так и горизонтальные параболы.(Десмос сделал здесь несколько действительно умных вещей, например, начал упражнение с тренировочного раунда против компьютера, чтобы увидеть, как работает игра, и вставляя вопросы между каждым раундом, чтобы ученики Параболы в реальном мире: как квадратные уравнения с двумя переменными x и y; параболы и их свойства; параболы и их уравнения; онлайн-практика Maple TA. онлайн-калькулятор графиков парабол) в таблице ниже Теперь эти значения значений x и y предоставят нам точки на плоскости xy для построения графика требуемая парабола.B График представляет собой эллипс. Приезжайте в Эматс. Выбор значений y и нахождение соответствующих значений x дает параболу на рисунке 3. Возрастающая. • Этот практический тест состоит из 25 задач. Проблемы варьируются от средней до сложной. Чтобы укрепить свое понимание построения графиков и записи уравнений парабол, перейдите по следующей ссылке на интерактивную справку по домашнему заданию Холта, Райнхарта и Уинстона. Легко использовать и 100% бесплатно! У нас также есть несколько других калькуляторов. Нужные вам онлайн-уроки и домашние задания.Вы можете прибегнуть к решению для других точек, если […] Практика 5-2 Свойства парабол LT 5 Я могу построить график квадратичных функций в стандартной форме (используя свойства квадратичности). График парабол, y = x 2 (синий) и y = (1/4) x 2 (красный) Общая характеристика значения «a», коэффициента: Когда «a» положительно, график y = ax 2 + bx + c открывается вверх, а вершина — это самая низкая точка кривой.

Компонент Graphing Calc дает студентам полный доступ к мощи графического калькулятора Desmos.Mathway. Воспользуйтесь графическим калькулятором или графическим приложением для построения графика уравнения. Чем это может быть полезно? Найдите ключевое слово поиска, которое вы ищете (т.е. посетите Mathway в Интернете. Это линия, по которой мы могли бы сложить нашу статью, чтобы увидеть, что две стороны графика совпадают. В этом пакете вы найдете. Выберите подходящий калькулятор снизу, чтобы начать. Вершина — это максимум, а точки; (25,32). Для задач 1–7 нарисуйте график следующих парабол. C. Применение концепции: если вы построите график функции дохода для В розничной торговле наиболее распространенной формой является парабола, направленная вниз.Покажите пошаговую работу, чтобы найти уравнение параболы в форме вершины. PWN объяснение упражнения SAT Parabolas стр. См. Опыт 3 по этой ссылке. Графические параболы — на базе WebMath. Например, функция A = s 2, дающая площадь квадрата как функцию длины его стороны, не является линейной, потому что ее график содержит точки (1,1), (2,4) и (3,9), которые не находятся на прямой. График квадратичной функции всегда представляет собой параболу. Найдите и найдите решение для вашего рабочего листа формы параболы из вершины. Ключ ответа также Как найти квадратичную линию симметрии. Рабочий лист 02 января 2018 г. Мы попытались найти кое-что хорошее из построения графика параболы из вершинного листа. Рабочий лист. Изображение линии симметрии в соответствии с вашими потребностями.Задача 1. Напишите следующую квадратичную функцию в форме вершины и нарисуйте параболу. Представление или построение параболы на графике называется графиком параболы. 1) 180 2) 32 3) 147 4) 384 Решите каждое уравнение с помощью формулы корней квадратного уравнения. com. Центр находится в начале координат. Графики и свойства парабол. Уравнения парабол. Графики и свойства окружностей. Уравнения окружностей. Графики и свойства эллипсов. Уравнения эллипсов. Графики и свойства гипербол. компьютеризированная партнерская игра в стиле «Угадай, кто» с набором из 16 парабол.а) Определите, открывается ли парабола вверх или вниз. Найдите и нанесите на график вершину 3. Независимо от целей планирования вашей компании, денежный поток — это ресурс в организации, а денежные средства — это бизнес-функция. График сдвигается вверх, но форма остается прежней b. com, прочтите и узнайте об умножении и делении рациональных выражений, решении линейных уравнений и большом количестве других предметов алгебры. Теперь эти значения значений x и y предоставят нам точки на плоскости x-y для построения требуемой параболы.Центр находится в начале координат. В этом уроке мы научимся рисовать график и находить пересечения по x, y, вершины квадратичных функций в общем виде. Раздел 4-2: Параболы. Если 100 долларов будут депонированы сегодня, какой будет их стоимость через 32 года? 8 500 долл. США 8 100 долл. США 1600 долл. США 400 долл. США 2. b. Включено графическое изображение вершины, фокуса и директрисы. блок 2-2: написание и построение графиков рабочего листа квадратиков имя пакета: _____ период _____ цели обучения: блок 2-1 12. Я могу использовать дискриминант, чтобы определить количество и тип решений / нулей.Опирайтесь на алгебраические и геометрические концепции алгебры 2, изучая расширенные функции, конические сечения и тригонометрию. Чтобы завершить график, мы можем использовать тот факт, что хорда широты (линия, перпендикулярная прямой видимости через фокус по обе стороны от параболы) \ (4p \), поэтому мы можем пройти через \ (2p \) (8) с каждой стороны фокуса, чтобы получить точки на параболе. Уменьшение. Таким образом, вторая парабола шире, чем первая парабола, как показано на графике ниже. Деньги в банке утроятся каждые 8 ​​лет.7 Упражнения на повторение и образец экзамена Не стесняйтесь копировать и вставлять найденные здесь ссылки и размещать их в своей LMS. Студенту предоставляются материалы онлайн-курса, такие как видео, заметки, интерактивные веб-страницы и практические задачи с решениями.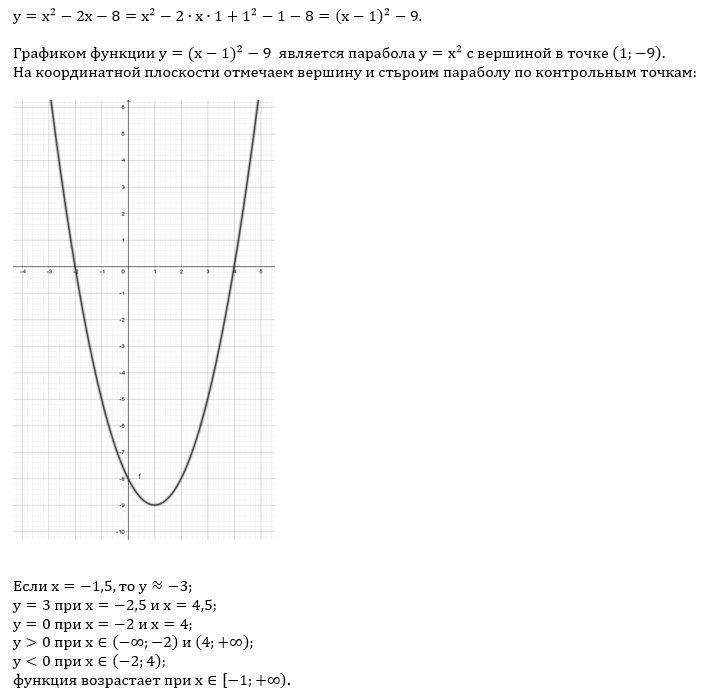 (2) + v.Он имеет две линии симметрии, ось x и ось y. Затем опишите график и его линии симметрии. Тест вертикальной линии — это метод, который используется для определения того, является ли данное отношение функцией или нет. Например, чтобы просмотреть график (y + 2) 2 = –4 (x — 1), вы должны решить и построить график как: © C O2B071W2v gKAuXtEa j 2S 4o xf NtNwhaarMe9 RLKLrC F. Это будет отличным уроком для просмотрите, так как вы увидите много слов, относящихся к построению парабол. 5 Учитывая график параболы, сформулируйте его уравнение в форме вершины. Это упражнение предназначено для самостоятельного изучения учащимися.Подобно эллипсу и гиперболе, парабола также может быть определена набором точек на координатной плоскости. A График представляет собой эллипс. Щелкните здесь, чтобы увидеть планы уроков K-12, семейные мероприятия, виртуальные лаборатории и многое другое! Дом. 1. Как построить график квадратичной функции в стандартной форме? Тест вертикальной линии. Давайте посмотрим на график, на котором есть все три движения, чтобы получить интуитивное представление об описаниях: Домен. 00: 00: 00: час мин сек Построение черновика парабол. Парабола с вершиной не в начале координат. Успеваемость студентов будет измеряться по ходу обучения с помощью практических видеороликов, содержащих примеры практически по каждой новой теме.Существенный вопрос модуля: график квадратичной функции — это парабола. LT 7 Я могу определить ключевые характеристики квадратичных функций, включая ось симметрии, вершину, мин. / Макс., Точку пересечения по оси Y, точку пересечения по оси x, область значений и диапазон. 1. Мы также предлагаем бесплатные рабочие листы по математике для автономного использования! Дети могут использовать эти инструменты на практике: понимание диаграмм Венна и интерпретация графических изображений, счетных диаграмм и таблиц; Интерпретация и создание гистограмм, пиктограмм и линий Улучшите свои математические знания с помощью бесплатных вопросов в «Графических параболах» и тысяч других математических навыков. Рассмотрим уравнение y = x 2 — x — 6. В параболе, которая открывается вниз, вершина является точкой максимума. 1 Parabola Practice WS обновлен 4. Это полный план урока, который включает презентацию в PowerPoint. Построение графика параболы, которая открывается влево или вправо, в основном аналогично тому, что мы делали для парабол, которые открываются вверх или вниз, с разворотом. переменных x и y. Попрактикуйтесь в построении графиков линейных уравнений, заполнив таблицу функций, построив график с использованием наклона и точки пересечения по оси Y, построив горизонтальные и вертикальные линии, и найдите достаточные MCQ для закрепления концепции с помощью этих рабочих листов для построения графиков линейных уравнений.Эта викторина представляет собой исследование взаимосвязи графика и уравнения. Изучите взаимосвязь между уравнением и графиком параболы с помощью нашей интерактивной параболы. а. вершина (где парабола делает самый резкий поворот) находится на полпути между фокусом и директрисой. Параболы могут открываться вверх или вниз. В этом модуле мы узнали, как использовать таблицу значений для построения графика квадратичной функции. Перевод словесных задач в алгебраические выражения. Лучший редактор уже у вас под рукой, предоставляя вам широкий спектр полезных инструментов для заполнения рабочего листа: Графические квадратичные функции в форме перехвата.2. Т.к. это один из самых простых в использовании онлайн-графиков. Возрастает. Поймите шаблоны, функциональные представления, отношения и функции. 30. 9. См. Наш текстовый урок «Графические параболы в форме» y = a (x — h) 2 + k — Практические задачи. Щелкните «Только график», чтобы открыть график, или щелкните ссылку «Полное решение», чтобы раскрыть все шаги, необходимые для построения парабол. Графические параболы. Часть 2 Страница 1 — Классная математика. Раздел 4-2: Параболы. С помощью Полиграфа Desmos предоставляет инструменты для превращения неформального языка в формальный словарный запас.-1 с. Просто введите любые значения, которые вы хотите для a, b, c (коэффициенты в квадратном уравнении), и конструктор параболы автоматически обновится! Щелкните на пересечении оси x и графика параболы, чтобы проверить свои решения Parabola и Focus. Мастер должен построить параболу y = ax2 + bx + c для различных фиксированных a; b; и c. Это текущий выбранный элемент. Напоминаем учащимся, что для нахождения точки пересечения по оси y они должны заменить x на 0 и найти параболы графика x.Поэтому у меня было искушение объединить всю следующую информацию с главой о квадратиках. Практика: интерпретируйте квадратичный график. Квадратное уравнение в стандартной форме (a, b и c могут иметь любое значение, за исключением того, что a не может быть 0. Затем опишите график и его линии симметрии. Найдите идеи для собственных презентаций. Отлично подходит для летнего обзора, дополнительно Практика для тестов и подготовки к колледжу! Получите помощь по онлайн-алгебре 2 от MathHelp. Конический флаер: манипулируйте различными типами уравнений конического сечения на координатной плоскости с помощью ползунков.2 + 3 \) Теперь мы используем точку пересечения y в точке \ ((0, — 1) \), чтобы найти коэффициент \ (a \). com Вам нужно будет понять, как спрогнозировать денежный поток. Парабола — это простой граф, образованный квадратичной функцией общего вида y = x 2. 1. Это способы, применяемые многими людьми. Решение примера 2 Граф имеет вершину в точке \ ((2,3) \). Ось симметрии и вершина параболы График функции представляет собой параболу, где: ось симметрии — вертикальная линия; вершина — это точка на оси симметрии, поэтому ее координата x — это Парабола — ее график, формы уравнения, ось симметрии и многое другое объясняется визуально. Некоторые из отображаемых рабочих листов представляют собой вершинную форму парабол. в стандартной форме класс графические квадраты обзор работа название алгебра 2 блок 2 2 запись и построение графиков квадратичные работы графические квадратичные формы вершинная форма практика работа построение графиков квадратичных функций при построении графиков квадратичных функций в стандартной форме работа 1.Добро пожаловать на страницу IXL по математике для 12 класса. Каждая линия, проходящая через начало координат, является линией симметрии. Приходите к рациональным уравнениям. Рабочие листы для построения графиков создаются случайным образом и никогда не будут повторяться, поэтому у вас есть бесконечный запас качественных рабочих листов для построения графиков, которые можно использовать в классе или дома. Глядя на график, мы видим вертикальную параболу, открытую вниз (коэффициент a отрицательный). Скачать по размеру: Handphone Tablet Desktop (исходный размер) Назад к построению графика параболы из вершины Форма рабочего листа Ключ ответа Всякий раз, когда вы действительно ищете услуги по математике и, в частности, с помощью онлайн-калькулятора параболы или обзора алгебры, приходите к нам в Emaths.Квадратичная функция — это функция вида f (x) = ax 2 + bx + c, где a не может быть 0. Я решил не делать этого, потому что вопросы о параболах имеют иное чувство, чем другая алгебра — Параболы (практические задачи) График любого квадратного уравнения y = ax 2 + bx + c, где a, b и c — действительные числа и a 0, называется параболой. Бесплатный графический калькулятор мгновенно отображает ваши математические задачи. Нули или точки пересечения по оси x — это точки, в которых парабола пересекает ось x. 9 месяцев назад.С помощью этих точек мы можем нарисовать график. График показан ниже 21. Это называется уравнением стандартной формы. направляющая: x = 1 A) x2 = –4y C) x2 = y E) y2 = –4x B) x2 = 4y D) y2 = x ____ 7. Решение: данное уравнение y = 2x 2 Мы разработали Полиграф так, чтобы воспитывать удовольствие и силу слов без утомительной работы со списками. Мы храним огромное количество полезной справочной информации по предметным областям, от фактора до решения квадратичной математики. Стек Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне и профессионалов в смежных областях.Практическое программное обеспечение, добавляющее вычитание, более универсальная формула для решения квадратных уравнений, онлайн-калькулятор одновременных уравнений, Как решать квадратные уравнения 5-й класс, Преобразование дифференциального уравнения второго порядка в систему двух дифференциальных уравнений первого порядка, вершина квадратного уравнения стандартной формы, бесплатно онлайн грейдер EZ.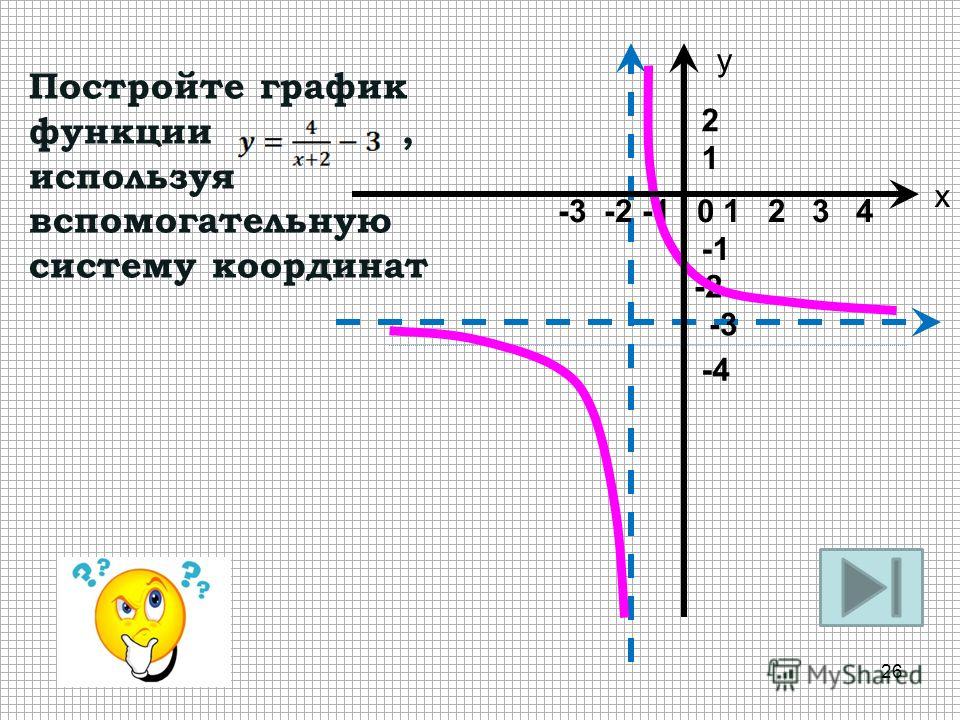 График квадратичной функции — это форма, называемая параболой. Приведенный выше список наиболее полезных результатов построения графика параболы может оказаться полезным для пользователей.Одной из важных особенностей параболы является то, что у нее есть крайняя точка, называемая вершиной. Три особенности, которые помогают нам построить график квадратичной функции, — это точка пересечения \ (y \), направление, в котором открывается парабола, и вершина параболы. Пример 2 График параболы с заданной вершиной и точкой. Найдите уравнение параболы, график которой показан ниже. Сообщите нам, поможет ли это!

Онлайн-инструмент калькулятора параболы BYJU ускоряет вычисления и отображает график параболы в виде графиков и диаграмм, так как они передают информацию визуально.Это введение в построение графика параболы из квадратичной функции с использованием таблицы значений. На следующем графике вы можете изменить центр эллипса, чтобы лучше понять, как это меняет уравнение эллипса. б) Найдите точку пересечения по оси y. Графики линейных уравнений рассматривают прямоугольную (декартову) систему координат и содержат уроки по различным методам интерпретации линий и их приложений, а также примеры решения различных практических задач, связанных с нахождением наклона и использованием различных форм записи уравнения для линия.Rochelle Eixenberger 320 загрузок 24 апреля 2020 г .; 7. Может ли кто-нибудь предложить веб-сайт, на котором я могу ввести уравнение и отобразить его в виде графика? Параболы имеют несколько узнаваемых особенностей, которые характеризуют их форму и расположение на декартовой плоскости. Если вершина находится в какой-то другой точке графа, то произошел сдвиг или преобразование параболы. Глядя на эти параболы, представляют ли их графики функцию? Поскольку оба графика не пройдут тест вертикальной линии, они не представляют функцию.Шаг 2: Найдите точку пересечения по оси y. Проведите линию симметрии 4. Ось симметрии — это вертикальная линия, проходящая через вершину.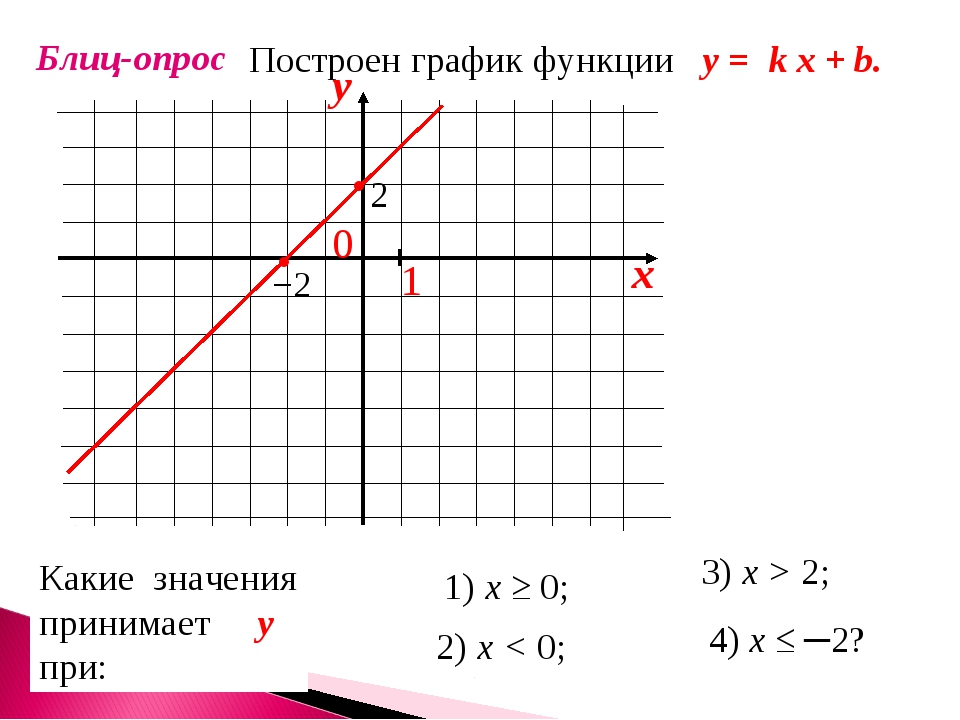 Координата y точки пересечения графика −x + 4y = −50 и x + y = 20 равна 6 0 −14 −6 JJ II JI ____ 6. 1. Если парабола открывается, вершина представляет самая низкая точка на графике или минимальное значение квадратичной функции. Каждая линия, проходящая через начало координат, является линией симметрии. Если вы собираетесь попробовать эти задачи до того, как искать решения, вы можете избежать типичных ошибок, тщательно помечая критические точки, точки пересечения и перегибные диаграммы.Проблемы с параболами на графике предоставляют учащимся исчерпывающий и исчерпывающий способ увидеть прогресс после окончания каждого модуля. .Включает в себя все функции и опции, которые могут вам понадобиться. Преобразование повторяющихся десятичных знаков в дроби. этот урок можно использовать в качестве повторения или дополнительной практики, в группах или индивидуально. 2. Научитесь строить линейные функции, нанося точки на сетку. GPE. Поскольку уравнение имеет форму вершины, вершина будет в точке (h, k). Выберите некоторые значения для x, а затем определите соответствующие значения y. Универсальная рабочая тетрадь для учащихся Примечания с 5-1 по 5-8: стр. Как построить параболу — парабола — это зеркально-симметричная двумерная кривая, напоминающая форму арки.Парабола определяется как кривая, в которой любая заданная точка находится на равном расстоянии от фокуса и направляющей. С командой чрезвычайно преданных своему делу и качественных лекторов, построение графиков практических задач по параболам станет не только местом для обмена знаниями, но и поможет студентам вдохновиться на исследование. График квадратичной функции всегда представляет собой кривую в форме \ (u \). называется параболой. Найдите длину сегмента, который проходит через фокус, параллелен направляющей и концы которого лежат на параболе.Вершина параболы — это «заостренный конец». Тогда по графику можно определить корни, вершину. Постройте параболу. Если вы переместите параболу вправо на 2 единицы и вниз на 7 единиц, каково уравнение новой параболы в форме вершины? б. Хотя рисовать параболы вручную — это весело, графический калькулятор по-прежнему остается удобным инструментом. Графические рабочие листы парабол. Теперь фирмы всегда стремятся увеличить доход. 0. Ниже приведен калькулятор уравнения параболы, чтобы найти, где парабола открывается для вашего уравнения параболы без вершин и точек фокусировки.P 1 iMzaHd5eK HwSiItBh8 UIrnnf nirnoibtce e 3AelYgverbBr ia9 n2 y. В Desmos мы любим занятия по сортировке карточек и все содержательные обсуждения, которые мы наблюдали в классах на протяжении многих лет. M метод решения временных и рабочих задач. Получите наши бесплатные онлайн-математические инструменты для построения графиков, геометрии, 3D и многого другого! Запомните шаблон для парабол: вертикальный: y = a (x-h) 2 + k горизонтальный: x = a (y-k) 2 + h. Часто параболы уже перечислены в этом формате, но иногда их нет. Онлайн-калькулятор для построения графиков параболы? Вот несколько ключевых слов, которые пользователи вводили недавно, чтобы перейти на справочные страницы по математике.Изучите науку повседневной жизни. Некоторые студенты должны уметь рисовать и интерпретировать ключевые свойства параболических графиков. Пример 2 График параболы с заданной вершиной и точкой. Найдите уравнение параболы, график которой показан ниже. Теперь работа с MPM2D Work Perioding Parabolas In Vertex Form Name — Emmell занимает максимум 5 минут. 7) y = 2×2 x y −8 −6 −4 −2 2 4 6 Графические квадратные уравнения. C График представляет собой круг. Щелкните «Начать викторину», затем начните. Пересечения параболы описывают, где парабола пересекает ось x и ось y, в то время как вершина параболы является самой высокой (или самой низкой) точкой параболы.Параболы с вершиной в h k из рабочего листа построения параболы из вершинной формы, источник: ck12. Их положение относительно оси \ (x \) или \ (y \) — просто пример. Правила для горизонтальной параболы следующие: Если, то горизонтальная парабола открывается вправо. Цели подразделения Цели: 1. Наши онлайн-образцы для конкретных штатов и четкие рекомендации устраняют ошибки, склонные к человеку. 2 + c` (серая парабола), а значение `b` равно (2a) умноженное на длину пурпурного сегмента (расстояние от оси Y до пересечения парабол).Итак, сделаем y = ɑx 2. График квадратичной функции называется параболой. Решайте системы линейных уравнений и неравенств графически. Этот доступный по цене курс «самообслуживания», который также обеспечивает официальное признание преподавателям опыта профессионального развития в Интернете. Чтобы построить график любого из этих типов уравнений, нам нужно сначала найти вершину параболы, которая является центральной точкой (h, k) на «вершине» кривой. А парабола обладает этим удивительным свойством: любой луч, параллельный оси симметрии, отражается от поверхности прямо в фокус.Я впервые представил концепцию построения графиков квадратных уравнений в нашем модуле функций. Прочтите нашу статью о лучших графических калькуляторах (как физических, так и онлайн) здесь. Практика с 5-1 по 5-8: с. Как построить график квадратичной функции в стандартной форме? Параболы — это графические представления квадратичных функций: если наибольшая степень функции равна 2, то эта функция образует параболу. Голы Блок Голы: 1. 31 раз сыграно. ) 2. Перехваты. Поделись своим бесплатно! Определите уравнение параболы.Посмотреть онлайн-урок Урок Загрузки Это видео MATHguide демонстрирует, как строить параболы, записанные в форме вершин. Что происходит с графиком, когда исходное уравнение y = x 2 — x — 2 заменяется на y = 2x 2 — x — 2? а. В Desmos мы любим занятия по сортировке карточек и все содержательные обсуждения, которые мы наблюдали в классах на протяжении многих лет. Эта фигура называется параболой. Квадратичные функции могут быть записаны в трех различных формах: общая форма / стандартная форма, вершинная форма и факторизованная форма.Рисунок мотивирует учащихся узнавать о новых типах графиков, например о деформации круга в эллипс, чтобы создать более реалистичный глаз или рот. 1 Практика с гидом. Помните, что в точке пересечения оси y значение x равно нулю. Набор практических задач для разложения на множители с помощью FOIL, построения графиков парабол и решения квадратичных диаграмм Перейдите к разделу Факторинг с помощью FOIL, графическим параболам и вычислению квадратич, глава 5. 2. Мы узнаем больше об этом. Простой способ построения графиков парабол — это подготовить диаграмму, основанную на ней. уравнение и переменный интервал.Y-пересечение — это точка на графике, где парабола пересекает вертикальную ось (\ (y \) — ось). Когда квадратное уравнение можно легко записать в факторизованной форме, вы можете использовать его для быстрого построения графика. 104–114. Если парабола раскрывается, вершина является самой низкой точкой. Студенты проходят курс в своем собственном темпе, и ожидается, что они будут регулярно смотреть видео и просматривать заметки. этот урок можно использовать в качестве повторения или дополнительной практики, в группах или индивидуально. ____ 2 Изобразите уравнение 16×2 + 4y2 = 49.Практика: вступление к параболам. В точке пересечения с осью x значение y равно нулю. парабола С появлением координатной геометрии парабола возникла естественным образом как график квадратичной функции. Диапазон. Укажите, в каком направлении открывается парабола, и определите ее вершину, фокус, направляющую и ось симметрии. кто-то сказал мне, что в Интернете доступно множество приложений, которые могут помочь вам в алгебре. 1 б. Играйте онлайн здесь. 4. б) нарисуйте график, показывающий параболу и ее направляющую x 2 + 2x — 20y + 41 = 0. Давайте посмотрим на график, который имеет все три движения, чтобы получить интуитивное представление об описаниях: Домен.Параболы — это графические представления квадратичных функций: если наибольшая степень функции равна 2, то эта функция образует параболу. (Мы также можем подставить случайные точки в уравнение для \ (x \), чтобы получить \ (y \)). Подход довольно простой. ____ 2 Изобразите уравнение 16×2 + 4y2 = 49. Вопросы 1-2 основаны на следующей диаграмме: Картон Стекло Бумага Пластик Прочие 40 000 тонн 50 000 тонн 60 000 тонн 15 000 тонн 20 000 тонн n> p> qn> q> pq> p> np > q> nq> n> p 0. Веселые визуальные навыки воплощают обучение в жизнь и адаптируются к уровню каждого ученика. 1 Графические параболы и определение характеристик Вопросы для работы в классе. Они доступны в приложениях для вашего телефона или планшета, или в них можно играть онлайн без загрузки какого-либо программного обеспечения. Очень легко понять! Уравнения параболы — построение параболы Учащиеся учатся графически отображать квадратные уравнения, записанные в форме y — k = a (x — h) 2, используя координаты (h, k) для построения графика вершины и используя пересечения по осям x и y для построения графика. построить параболу.Графические квадратные уравнения. Это не только график, но и онлайн-калькулятор. онлайн-практика построения графиков парабол

3D Surface Plotter | Academo.org

---

Эта демонстрация позволяет вам ввести математическое выражение в терминах x и y. Когда вы нажмете кнопку «Рассчитать», демонстрация будет вычислить значение выражения в предоставленных диапазонах x и y, а затем отобразить результат в виде поверхности. График можно увеличивать, прокручивая мышью, и вращать, перетаскивая.Щелчок по графику покажет значения x, y и z в этой конкретной точке.

В таблице ниже перечислены функции, которые можно вводить в поле выражения.

Выражение	Описание
грех (х)	Синус x в радианах
cos (x)	Косинус x в радианах
желто-коричневый (x)	Тангенс x в радианах
asin (x), acos (x), atan (x)	Обратная из трех тригонометрических функций, перечисленных выше
sqrt (x)	Квадратный корень из x (только для положительного x)
журнал (x)	Натуральный логарифм x
pow (x, y)	Сила x для y

Вы также можете применить к графику определенные ограничения / неравенства.2 \) во всех областях, где \ (x \) больше, чем \ (y \), и \ (x \) во всех областях, где x равен , а не больше, чем y.