Урок по алгебре и началам анализа на тему «Сложная функция»







Департамент внутренней и кадровой политики Белгородской области
среднего профессионального образования
«Белгородский политехнический колледж»
Методическая разработка
открытого урока
по дисциплине ОДп.10 «Математика»
Тема: «Сложная функция»
Подготовила
преподаватель математики
Съедина В.В.
Белгород — 2014
Пояснительная записка
Урок разработан для обучающихся 1 курса специальностей среднего профессионального образования, реализующих образовательные программы среднего (полного) общего образования.
Разработка может быть использована в рамках изучения раздела «Функции, их свойства и графики», а также отдельные элементы урока могут быть использованы при изучении темы «Производная сложной функции»
Разработка урока снабжена авторской презентацией, которая на всех этапах урока помогает визуализировать учебный материал, а также осуществить первичное закрепление и контроль усвоения во время объяснения нового материала, во время первичного закрепления и отработки навыков при решении задач путем «дозированной» информации, выводящейся на слайдах поэтапно.
Урок рассчитан на 1 академический час (45 минут).
Приложения к конспекту урока;
— презентация «Сложная функция»;
— индивидуальные карты-модули для учащихся.
Конспект открытого урока по математике
на тему: «Сложная функция»
Тип урока – изучение нового материала
Цели урока:
создать условия для формирования нового понятия «сложная функция», обеспечить развитие умения по распознаванию сложных функций, создать условия для освоения навыков построения графика сложной функции.
создать условия для развития познавательного интереса учащихся, развития аналитического мышления, расширения кругозора учащихся.
создать условия для развития математической культуры, культуры речи, создать условия для воспитания целеустремленности, аккуратности
Целью изучения данной темы является формирование общих и профессиональных компетенций обучающихся:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 8 Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ПК 6.4 Контролировать ход и оценивать результаты выполнения работ
ПК 6.5 Вести утвержденную учетно – отчетную документацию
Оборудование:
Презентация «Сложная функция»;
Экран, проектор, доска;
Индивидуальные карты-модули;
Учебники:
Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2010, Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2009.
Структура урока:
I. Организационный момент — 0,5 мин.
II. Этап подготовки учащихся к активному сознательному усвоению знаний – 4,5 мин.
III. Этап усвоения новых знаний – 30 мин.
IV. Этап закрепления новых знаний – 8 мин.
V. Этап информирования учащихся о домашнем задании и инструктажа по его выполнению — 2 мин.
Ход занятия
I. Организационный момент
II. Этап подготовки учащихся к активному сознательному усвоению знаний
Слайд 1.
Тема нашего занятия «Сложная функция». С понятием «функция» вы уже знакомы, да и понятие «сложный» так же известен вам. Однако часто в повседневной речи мы часто считаем слова «сложный» и «трудный» синонимами. Но на самом деле «сложный» и «Трудный» далеко не всегда означают одно и то же.
В толковом словаре В.И. Даля можно найти такое определение «Сложный, составной, сложенный или составленный из разных частей…».
Наша с вами задача убедиться, что сложная функция – это не значит трудная!
Слайд 2.
Итак, цель нашего сегодняшнего занятия разобраться, что же такое «Сложная функция», как распознать сложную функцию и научиться строить график сложной функции.Прежде чем рассматривать сложную функцию, давайте вспомним основные понятия, которые нам сегодня потребуются при изучении нового материала. Перед каждым из вас лежат индивидуальные карты, прочтите 5 вопросов, которые там приведены, подумайте и ответьте на них. У вас в распоряжении 1,5 мин.
Вводная беседа по ранее изученному материалу:
1. Что значит задать функцию?
2. Что такое аргумент функции?
3. Что такое значение функции?
4. Что называют областью определения функции?
5. Что называют областью значений функции?
Слайд 3.
Итак, еще раз обращаю ваше внимание, что функция, это прежде всего некоторое соответствие между множеством Х (независимых переменных) и множеством У (значений функции), при этом обязательно нужно помнить что каждому значению х соответствует
III. Этап усвоения новых знаний
Достаточно часто мы сталкиваемся с задачами, где значение функции зависит не непосредственно от аргумента, через «промежуточную» функцию. Такие функции называют сложными
Слайд 4.
Или говорят, что «сложная функция – это композиция двух и более функций». Термин «сложная» функция не является понятием сложности начертания или исследования, а указывает на вид или «конструкцию» функциональной зависимости.
Рассмотреть слайд, обратить внимание на промежуточный шаг x0→ t0 →y0.
Слайд 5.
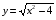 Сложную функцию можно задать формулой y=f(g(x)), где g(x) – внутренняя функция, f(t) – внешняя функция. Обратите внимание, эта формула есть в ваших индивидуальных картах .
Сложную функцию можно задать формулой y=f(g(x)), где g(x) – внутренняя функция, f(t) – внешняя функция. Обратите внимание, эта формула есть в ваших индивидуальных картах .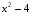
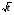 Рассмотрим пример сложной функции
Рассмотрим пример сложной функции
g(x) = – внутренняя функция, f(t) = – внешняя функция.
Для определения какая функция является внутренней, а какая внешней нужно задать вопрос: «в каком порядке будут выполнены действия при необходимости вычисления значения функции по заданному аргументу?»
Найдите y(2)-?
1) Сначала нужно найти значение подкоренного выражения 22-4=0, то есть g(x) = x2-4 – будет внутренней функцией;
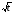 2) затем уже находим значение корня
2) затем уже находим значение корня 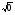 =0, то есть f(t) = будет внешней функцией.
=0, то есть f(t) = будет внешней функцией.
Слайд 6.
Перед вами на экране и в индивидуальных картах приведены примеры сложных функций: y = sin2x, y = (x3 – 1 )5 , y = cos(7x + 2), 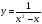 ,
,
y = sin2x + sin x .
Вам необходимо определить какая функция является внутренней, а какая внешней, и заполнить таблицу. На выполнение задания вам дается 3 минуты.
Слайд 7.
Самопроверка (2 мин.). Проверьте правильность выполненного задания (около каждой функции проставьте «+» или « — » и подсчитайте количество правильных ответов).
Слайд 8.
Помимо умения различать в заданных функциях внутреннюю и внешнюю функции необходимо уметь составлять композицию функций.
На экране приведены три элементарных функции. Вам необходимо составить композицию этих функций по заданным формулам.
Например y=h(f(x))=[ f(x)=t=x2 , h(t)=sin t ] =sin x2
Рассуждая аналогично, составьте, пожалуйста, композицию из функций в соответствии с заданием, на выполнение этого задания вам дается 3 минуты.
Проверка (1 мин.) – опрос по цепочке, сверка с доской (около каждой функции проставьте «+» или « — » и подсчитайте количество правильных ответов).
Слайд 9.
Итак, мы с вами рассмотрели, как в аналитически заданной функции определить внутреннюю и внешнюю функции.
Что бы еще раз убедиться, что сложная функция является композицией двух функций, построим график функции  .
.
Фронтальная беседа (2 мин):
1. Определите внутреннюю и внешнюю функции.
2. Укажите область определения каждой функции
3. Что можно сказать о четности этой функции.
Подведение итога опроса слайд 10 .
Слайд 11.
Как мы уже говорили, сложная функция – это композиция функций. Построим графики внутренней и внешней функции в координатных осях XOG и GOУ. Для этого составим таблицы значений каждой функции. Заполните таблицы в индивидуальных картах (2 минуты).
Слайд 12.
Проверьте правильность своих вычислений, и как показано на экране, постройте графики двух функций в разных системах координат (на построение у вас — 3 минуты).
Посмотрите на экран, вот что у вас должно было получиться.
Слайд 13.
А теперь рассмотрим как, используя полученные графики, построить график сложной функции.
Возьмем некоторое х0=0 и по первому графику найдем соответствующее ему значение g0=-1, затем по второму графику для g0=-1, найдем у0=1/2 и построим в новой системе координат точку с координатами (0:1/2). Аналогично, можно построить и другие точки x1=1 →g1=0 →y1=1→(1;1), учитывая четность функции, получаем точку (-1;1). И строим эскиз графика сложной функции.
Проделайте эту операцию самостоятельно в своих индивидуальных картах, для удобства можете использовать вспомогательную таблицу. На выполнение работы 5 мин. (пройти для проверки и корректировки выполнения задания, проверить выполнение заданий по определению внутренней и внешней функции, составлению сложных функций).
IV. Этап закрепления новых знаний
Используя имеющиеся графики, постройте график функции y=(2x)2-1
(на выполнение 4 минуты) – первый справившийся учащийся на доске выполняет чертеж графика
Итак, мы рассмотрели понятие сложной функции как композицию двух функций, внешней и внутренней. Научились распознавать эти функции в конкретно заданной функции, а также составлять композицию двух функций. А также посмотрели, как с помощью графиков элементарных функций можно построить график сложной функции.
Фронтальный опрос:
1. Объясните понятие «сложная функция»
2. Как распознать внешнюю и внутреннюю функции?
3. Можно ли утверждать, что график сложной функции — это обязательно сложная кривая, для построения которой необходимы сложные вычисления и преобразования?
Хочется отметить, что слова «сложный», «сложенный» связаны с глаголом «сложить», «складывать». В словаре В.И. Даля читаем, что «СКЛАД» — это стройность, красота, порядок, устройство, а «складный ум – логичный, ясный и верный». Мне хотелось, что бы сложная функция оказалась для вас в первую очередь не трудной, а интересно устроенной.
По итогам работы на уроке выставляются отметки активным учащимся.
V. Этап информирования учащихся о домашнем задании и инструктажа по его выполнению
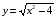 В ваших индивидуальных картах записано домашнее задание: построить график функции
В ваших индивидуальных картах записано домашнее задание: построить график функции
Построение выполнить в рабочих тетрадях.
Индивидуальные карты сдать для проверки на следующем уроке.
Спасибо за урок.
Заключение
Данная разработка была опробована на группе 1 курса с достаточно высоким уровнем подготовки, цели и задачи урока были достигнуты в полном объеме.
Использование индивидуальных карт-модулей позволило сократить время, как при объяснении нового материала, так и при закреплении, что позволило рассмотреть на уроке достаточно большой объем материала.
При изучении материала была использована презентация, в которой пошагово рассмотрены все этапы урока, что позволило увеличить плотность урока и оптимально увеличить его темп. Чередование проверки и самопроверки в ходе объяснения нового материала, позволило в ходе урока проводить коррекцию усвоения и реализовать индивидуальный подход к каждому учащемуся.
Литература
1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2010.
2. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2007.
3. Башмаков М.И. Математика: учебник для 10 кл. – М., 2007.
4. Колмогоров А.Н. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2009.
Приложение 1.
Фамилия, имя учащегося______________________________________
Тема занятия: «Сложная функция»
Цель:
Познакомить с понятием «сложная функция»;
Научить распознавать сложные функции;
Научить строить график сложной функции;
Ход занятия:
1. Ответьте на вопросы:
1. Что значит задать функцию?
2. Что такое аргумент функции?
3. Что такое значение функции?
4. Что называют областью определения функции?
5. Что называют областью значений функции?
2. Сложная функция – это композиция двух и более функций.
Формула для задания сложной функции
y=f(g(x)) – сложная функция
g(x) – внутренняя функция
f(t) – внешняя функция
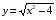
Пример.
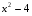
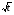 g(x) = – внутренняя функция, f(t) = – внешняя функция
g(x) = – внутренняя функция, f(t) = – внешняя функция
3. Заполните таблицу
Сложная функция
y=f(g(x))
Внешняя функция
f(t)
Внутренняя функция
g(x)
1. y = sin2x
2. y = (x3 – 1 )5
3. y = cos(7x + 2)
4. 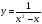
5. y = sin2x + sin x
4. Составьте сложную функцию, если f(x)=x2, g(x)=2x-4, h(x)=sin x
пример: y=h(f(x))=sin x2
y2=g(f(x)) ____________________________________
y3= f(h(x)) ____________________________________
y4=h(g(x)) _____________________________________
5. Пример. Построить график функции 
Решение
— Определим внутреннюю и внешнюю функции y=f(g(x)): g(x)=x2-1, f(g)=2g.
— Построим на разных координатных плоскостях графики функций g(x)=x2-1и f(g)=2g, для этого составим таблицы значений каждой функции
g(x)=x2-1 f(g)=2g
х
-2
-1
0
1
2
g
-2
-1
0
1
2
3
g
y
Примечание 1 клетка=1 Примечание 1 клетка=0,5
Учитывая, что сложная функция есть композиция двух функций, т.е. составим вспомогательную таблицу
x
-2
-1
0
1
2
g
f
Построим график сложной функции: 1 клетка = 0,5
Задания для самостоятельной работы:
В рабочих тетрадях постройте график функции y=(2x)2-1
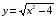 Домашнее задание:
Домашнее задание:
Построить график функции
Проект на тему «Преобразование графиков функции»
ДАГЕСТАНСКИЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ
ПЕДАГОГИЧЕСКИХ КАДРОВ
КАФЕДРА ФИЗИКО- МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ И ИКТ
Проект
на тему:
« Построение и преобразования
графиков функций
в школьном курсе математики»
Автор проекта:
Рабаданова П.А.
учитель математики
МБОУ « Кочубейская СОШ»
Тарумовский район
2015 г.
СОДЕРЖАНИЕ
1. Введение……………………………………………………………….….3
2. Глава I. Обзор литературы по теме проекта………………………….….5
3. Глава II. Эмпирическая часть:
3.1. Основные методы преобразования графиков функции……….….7
3.2. Построение графиков четной и нечетной функций……………..10
3.3. Построение графика обратной функции…………………………11
3.4. Деформация (сжатие и растяжение) графиков………………….12
3.5.Комбинация переноса, отражения и деформации……………………13
4.Задания для самостоятельного решения………………………..……14
5.Заключение………………………………………………………………15
6. Выводы…………………………………………………………..………17
ВВЕДЕНИЕ
Преобразование графиков функции является одним из фундаментальных математических понятий, непосредственно связанные с практической деятельностью. В графиках отражены изменчивость и динамичность реального мира, взаимные отношения реальных объектов и явлений.
Функциональная линия является базовой тематикой, рассматриваемая в Основном и Едином государственных экзаменах. Так же многие математические понятия рассматриваются графическими методами. Например, квадратичная функция вводится и изучается в тесной связи с квадратными уравнениями и неравенствами. Отсюда следует, что обучение учащихся построению и преобразованию графиков функции является одной из главных задач обучению математике в школе.
Исследование функции дает возможность найти область определения и область значения функции, области убывания или возрастания, асимптоты, интервалы знакопостоянства и др. Однако для построения графиков многих функций можно использовать ряд методов, облегчающие построение. Поэтому учащиеся должны иметь компетенции построения графиков по методическим схемам.
Выше сказанное определяет актуальность темы исследования.
Объектом исследования является изучение преобразование графиков функциональной линии в школьной математике.
Предмет исследования – процесс построение и преобразование графиков функции в общеобразовательной школе.
Цель исследования: образовательная — заключается в выявлении методической схемы построения и преобразования графиков функции; развивающая — развитие абстрактного, алгоритмического, логического мышления, пространственного воображения; воспитательная – воспитание графической культуры школьников, формирование навыков умственного труда.
Цели обусловили решение следующих задач:
1. Проанализировать учебно-методическую по исследуемой проблеме.
2. Выявить методические схемы преобразования графиков функции в школьном курсе математики.
3. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в общеобразовательной школе, способствующие: осмысленному усвоению учебного материала; повышению познавательной активности учащихся; развитию их творческих способностей.
ГИПОТЕЗА исследования: формирование графических навыков в процессе изучения функций и воспитание графической культуры учащихся будет эффективным, если учащиеся владеют методической схемой построения и преобразования графиков функции в школьном курсе математики.
ГЛАВА I. ОБЗОР ЛИТЕРАТУРЫ ПО ТЕМЕ ПРОЕКТА.
При подготовке к проекту мы изучили следующую литературу:
Сивашинский, И. Х. Теоремы и задачи по алгебре, элементарным функциям — М., 2002. — 115 с.
Гельфанд, И. М., Глаголева, Е. Г., Шноль, Э. Э. Функции и графики (основные приемы) — М., 1985. — 120 с
В.З.Зайцев, В.В. Рыжков, М.И. Сканави. Элементарная математика- М., 2010(переиздание). — 590 с.
Кузьмин, М. К. Построение графика функции — Ж. Математика в школе. — 2003. — №5. — С. 61-62.
Шилов Г.Е. Как строить графики? — М., 1982.
Исаак Танатар . Геометрические преобразования графиков функций — МЦНМО, 2012
В [2] отмечено, что умение с помощью графика «прочитать» поведение функции на некотором множестве находит применение не только в курсе математики, но и в любой практической деятельности человека, в которой ему приходится иметь дело с теми или иными графическими изображениями зависимостей. Поэтому учащиеся должны уметь по графику функции определить некоторые ее свойства.
В [3] строго изложен теоретический материал преобразования графиков. Сопровождается методика иллюстрацией рисунками, различной сложности примерами и их решениями, что дает возможность углублено расширить знания и построении графиков сложных функций.
[6] представляет электронный учебный курс, объем и содержание которого соответствуют требованиям к курсу математики старших классов средней школы. Теоретический материал подкреплен графическими анимационными иллюстрациями, которые дают наглядные представления об изучаемой теме. Курс включает три модуля: модуль изучения теоретического материала, модуль самопроверки и модуль контроля знаний.
Из [1] , [5] , [7] использованы для эмпирической части проекта методические схемы построения графиков, примеры для самостоятельной работы.
Выводы к 1 главе
Изучение учебно-методической литературы позволило:
1. Выявить методическую схему изучения, построения и преобразования графиков функции в школьном курсе математики.
2. Отобрать наиболее эффективные методы и средства построение и преобразование графиков функции в школьной математике, способствующие:
осмысленному усвоению учебного материала;
повышению познавательной активности учащихся;
развитию их творческих способностей.
3. показать, что функциональная линия оказывает существенное влияние при изучении различных понятий в математике.
Глава 2. ЭМПИРИЧЕСКАЯ ЧАСТЬ
В этой главе мы рассмотрим основные методы преобразования графиков функций, дадим методические схемы построения различных комбинаций графиков для различных функций.
2.1. ОСНОВНЫЕ МЕТОДЫ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ
Перенос вдоль оси ординат
f(x) 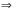 f(x)+b.
f(x)+b.
Для построения графика функции y = f(x) + b следует:
1. построить график функции y=f(x)
2. перенести ось абсцисс на |b| единиц вверх при b>0 или на |b| единиц вниз при b < 0. Полученный в новой системе координат график является графиком функции y = f(x) + b.

2. Перенос вдоль оси абсцисс
f(x) 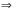 f(x+a).
f(x+a).
Для построения графика функции y = f(x+a) следует:
построить график функции y=f(x)
перенести ось ординат на |а| единиц вправо при а>0 или на |а| единиц влево при а<0.
Полученный в новой системе координат график является графиком функции y=f(x+a).



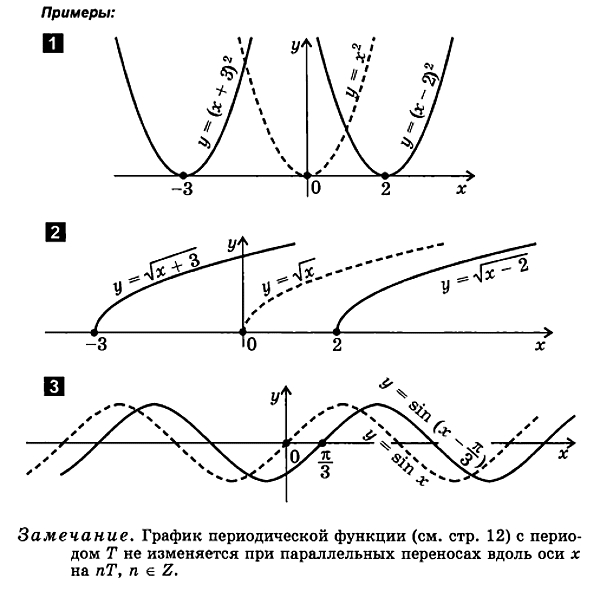
3. Построение графика функции вида y=f(-x)
f(x) 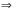 f(-x).
f(-x).
Для построения графика функции y = f(-х) следует:
построить график функции y = f(x)
отразить его относительно оси ординат
полученный график является графиком функции y = f(-х).
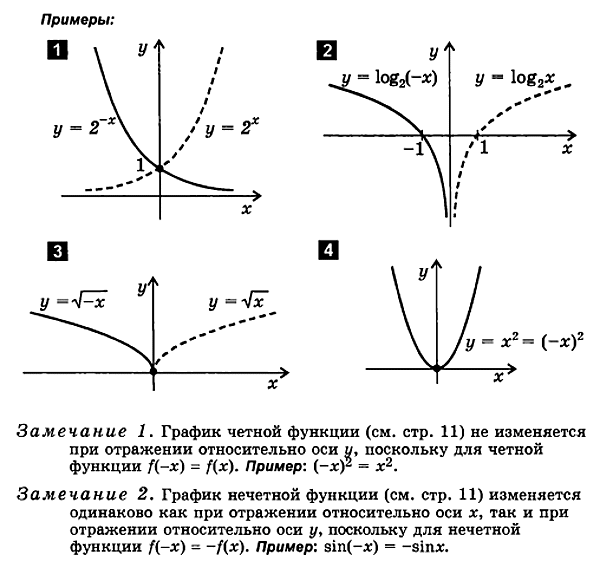
4. Построение графика функции вида у = —f(x)
f(x) 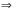 — f(x)
— f(x)
Для построения графика функции у = -f(x) следует:
построить график функции y=f(x)
отразить его относительно оси абсцисс
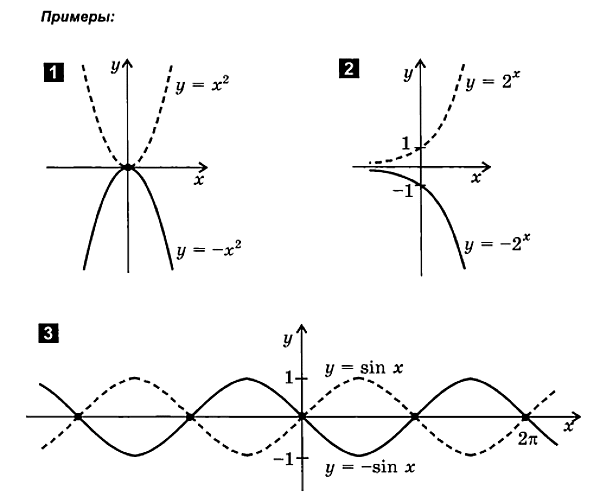
2.2. Построение графиков четной и нечетной функций
При построении графиков четной и нечетной функции удобно пользоваться следующими свойствами:
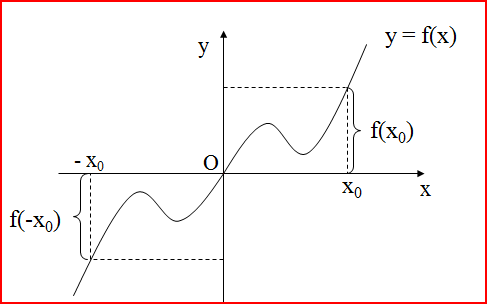
1.График четной функции симметричен относительно оси ординат.
2. График нечетной функции симметричен относительно начала координат.
Для построения графиков четной и нечетной функции достаточно построить только правую ветвь графика для положительных значений аргумента. Левая ветвь достраивается симметрично относительно начала координат для нечетной функции и относительно оси ординат для четной функции.
Для построения графика четной функции y = f(x) следует:
построить ветвь графика этой функции только в области положительных значений аргумента х≥О.
Отразить этот ветвь относительно оси ординат в область отрицательных значений х .
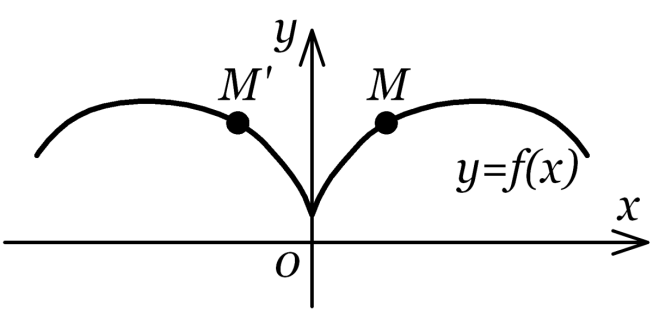
Для построения графика нечетной функции y=f(x) следует:
строить ветвь графика этой функции только в области положительных значений аргумента (х≥0).
Отразить этот ветвь относительно начало координат в область отрицательных значений х .
2.3. Построение графика обратной функции
Как уже отмечалось, прямая и обратная функции выражают одну и ту же зависимость между переменными х и у, с тем только отличием, что в обратной функции эти переменные поменялись ролями, что равносильно изменению обозначений осей координат. Поэтому график обратной функции симметричен графику прямой функции относительно биссектрисы I и III координатных углов, т. е. относительно прямой у = х. Таким образом, получаем следующее правило.
Для построения графика функции у = 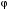 (х), обратной по отношению к функции y = f(x), следует построить график y = f(x) и отразить его относительно прямой у = х.
(х), обратной по отношению к функции y = f(x), следует построить график y = f(x) и отразить его относительно прямой у = х.

2.4. Деформация (сжатие и растяжение) графиков
1. Сжатие (растяжение) графика вдоль оси ординат
f(x) 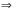 A∙f(x).
A∙f(x).
Для построения графика функции y=A∙f(x) следует:
построить график функции y=f(x)
увеличить его ординаты в А раз при А>1 (произвести растяжение графика вдоль оси ординат) или уменьшить его ординаты в
 раз при А < 1 (произвести сжатие графика вдоль оси ординат)
раз при А < 1 (произвести сжатие графика вдоль оси ординат)полученный график является графиком функции y = A∙f(x).
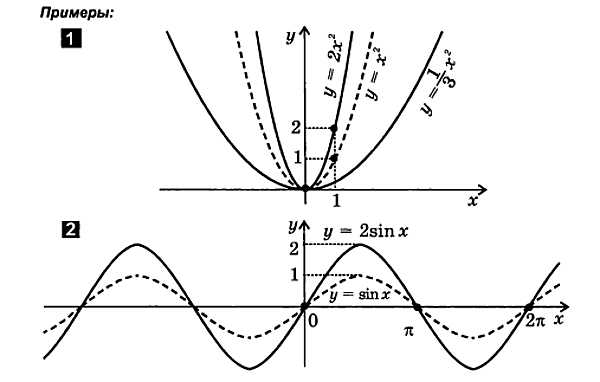
8. Сжатие (растяжение) графика вдоль оси абсцисс
f(x)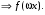
Для построения графика функции у = f(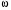 x) следует:
x) следует:
построить график функции y=f(x)
уменьшить его абсциссы в
 раз при
раз при  >1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в
>1 (произвести сжатие графика вдоль оси абсцисс) или увеличить его абсциссы в  раз при
раз при  < 1 (произвести растяжение графика вдоль оси абсцисс).
< 1 (произвести растяжение графика вдоль оси абсцисс).полученный график является графиком функции y=f(
 x).
x).
2.5. Комбинация переноса, отражения и деформации
Очень часто при построении графиков функций применяют комбинацию приемов.
Последовательное применение ряда таких приемов позволяет существенно упростить построение графика исходной функции и нередко свести его в конце концов к построению одной из простейших элементарных функций. Рассмотрим, как с учетом изложенного следует строить графики функций.
Отметим, что порядок упрощения целесообразно проводить в следующей последовательности.
Использование четности или нечетности функции.
Перенос осей.
Отражение и деформация.
Построение же графика выполняется в обратной последовательности.
Пример. Построить график функции 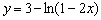
Построение проведем по следующим шагам:
1. построим график натурального логарифма 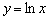 :
:
2. сожмём к оси OY в 2 раза: 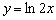 ;
;
3. отобразим симметрично относительно оси OY: 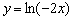 ;
;
4. сдвинем вдоль оси OX на 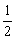 (!!!) вправо:
(!!!) вправо: 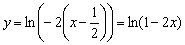 :
:
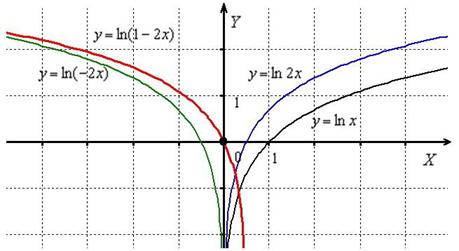
5. отобразим симметрично относительно оси OX: 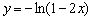 ;
;
6. сдвинем вдоль оси OY на 3 единицы вверх: 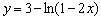 :
:
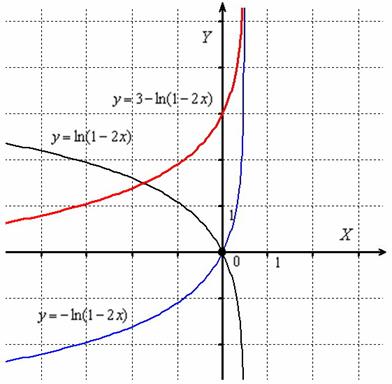
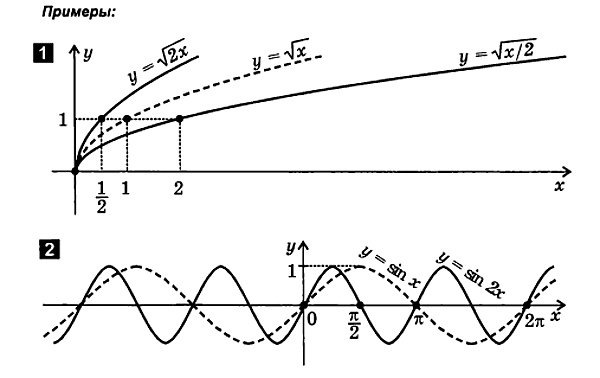
ПРИМЕРЫ ПОСТРОЕНИЯ и ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИИ
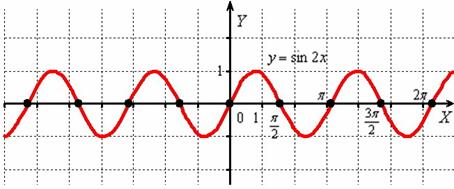
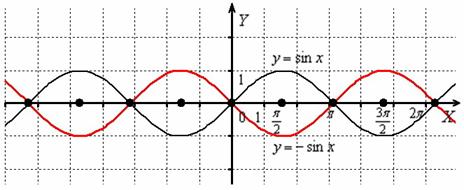
Пример 1. Построить график функции 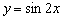 .
.
Сначала изобразим график синуса, его период равен 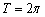 :
:
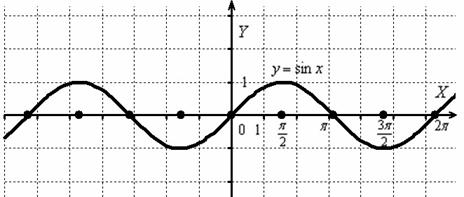
график функции 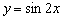 получается путём сжатия графика
получается путём сжатия графика 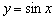 к оси ординат в два раза.
к оси ординат в два раза.
Пример 2. Построить график функции 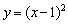
Построим параболу 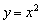 и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
и сдвигаем её вдоль оси абсцисс на 1 единицу вправо:
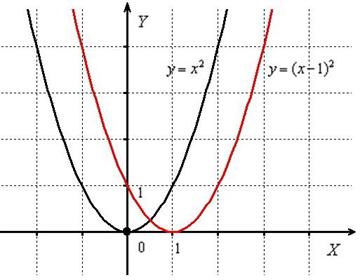
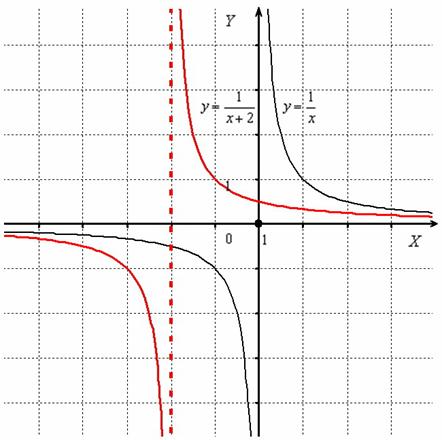
Пример 3.Построить график функции 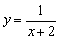
Гиперболу 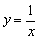 (чёрный цвет) сдвинем вдоль оси
(чёрный цвет) сдвинем вдоль оси  на 2 единицы влево:
на 2 единицы влево:
Пример 4.Построить график функции 
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Построить график функции у = 2х + 3.
Построить график функции у =
 .
.Построить график функции y = log2(x+2).
Построить график функции у = sin (x —
 ).
).Построить график функции y = log
 (-х).
(-х).Построить график функции y= arccos(-х).
Построить график функции у = -cos x.
Построить график функции у = —
 .
.Построить график функции y =
 .
.Построить график функции y = x|x|.
Построить график функции
 .
.Построить график функции у=
 .
.Построить график функции у = 2cosх.
Построить график функции y = sin
 x.
x.
ЗАКЛЮЧЕНИЕ
Во время работы над проектной работой были проанализирована различная учебно-методическая литература по данной проблеме. Результаты исследования позволили выявить наиболее характерные положительные стороны изучения, построения и преобразования графиков функции в школьном курсе математики
Основной целью проекта является формирование у учащихся умений и навыков в чтении и выполнении чертежей, в формировании у них рациональных приемов самостоятельной деятельности.
Необходимость усовершенствования графического образования в целом диктуется не только современными требованиями производства, но и ролью графики в развитии технического мышления и познавательных способностей учащихся. Способность человека к переработке графической информации является одним из показателей его умственного развития. Поэтому графическая подготовка должна стать неотъемлемым элементом общеобразовательной подготовки.
Выводы
Таким образом, разработанный проект « Построение и преобразование графиков функции», посвященный одному из центральных понятий математики — функциональной зависимости, ориентирован на систематизацию и расширение знаний учащихся. Изучение конкретных способов преобразования графиков функций проводится аналитико-графическим путем по строгим методическим схемам. Собранный материал можно использовать на уроках и для самоподготовки учащихся. Для проведения занятий могут использоваться разнообразные формы и методы организации и обучения.
Презентация к уроку по алгебре (11 класс) по теме: Построение графиков сложных функций без применения производной
Пояснительная записка к работе
«Построение графиков сложных функций»
Выполнил: Черемисин Дмитрий ученик 11Б класса
Преподаватель: Черемисина Галина Артуровна
Образовательное учреждение: МОУ-гимназия №13 п. Краснообска Новосибирского района Новосибирской области
Предмет: алгебра, алгебра и начала анализа
Тема: график сложной функции
Класс: 9 — 10 — 11 классы
Цель руководителя:
- привить навыки эффективного использования ИКТ в школе и в жизни;
- продолжать формировать интерес к математике посредством рассмотрения внепрограммного материала;
- воспитывать осознанное отношение к процессу работы, прививать чувство ответственности за качество выполняемого проекта;
- содействовать развитию у учащихся умения систематизировать материал;
- осуществлять самоконтроль за процессом выполнения и оформления работы
Самостоятельная работа старшеклассника-гимназиста – это особым образом организованная деятельность, включающая в свою структуру такие компоненты, как:
- уяснение цели поставленной учебной задачи;
- четкое и системное планирование самостоятельной работы;
- поиск необходимой учебной и научной информации;
- освоение информации и её логическая переработка;
- выработка собственной позиции;
- представление, обоснование и защита полученного результата;
- проведение самоанализа и самоконтроля.
Этот проект позволит учителю эффективно использовать ИТ в процессе преподавания, делая с их помощью уроки более увлекательными и насыщенными.
Цель работы:
- Овладеть умением представлять сложную функцию в виде композиции двух функций
- Освоить приём построения эскиза графика функции без применения производной
- Показать возможность использования схемы построения графиков сложных функций вида y = f(φ(x))
В работе рассматриваются функции вида y = f(φ(x)), где φ(x) – любая из основных элементарных функций, а f – любая из следующих операций над ними: прибавление к функции какого-либо числа, умножение функции на число, деление единицы на функцию, возведение функции в положительную степень, извлечение корня из функции, нахождение показательной функции от функции, логарифмирование функции, нахождение модуля функции, нахождение тригонометрических функций от функции.
Эта работа может быть предложена в качестве развивающего компонента на уроках алгебры (демонстрация презентации при изучении темы «Исследование функции» и в рамках предметной недели).
Разрешение на публикацию работы моего сына есть!
Сложная функция
Ключевые слова: сложная функция , композиция функций , внешняя и внутренняя функция , график сложной функции , свойства функций
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
“Сложный,
составной, сложенный или
составленный из разных
частей…”.
Толковый словарь
В.И. Даля.
Мы часто в повседневной речи считаем слова “сложный” и “трудный” синонимами. Иногда можно услышать от тех учеников, которым нелегко дается математика, что сложная функция потому так называется, что она “трудная”. Но на самом деле “сложный” и “трудный” далеко не всегда означают одно и то же.
Понятие сложной функции встречается в курсе алгебры и начал математического анализа в 10 классе [3]. Для сложной функции выводится формула дифференцирования. Ученики без предварительной подготовки этот материал воспринимают с большим трудом. На чисто формальном уровне можно дать много примеров на нахождение внутренней и внешней функции для данных сложных функций. При определенной практике они начинают хорошо различаться и производную можно вычислять. Беда в том, что при этом учащиеся погружаются в технику дифференцирования, а само понятие сложной функции как композиции нескольких функций отходит на задний план.
Чтобы сложная функция предстала в более наглядном виде, и сделана данная презентация.
В зависимости от подготовленности класса этот материал может быть предложен и на факультативных занятиях, и на уроках, причем в некоторых случаях непосредственно в теме “Производная”, а в некоторых и раньше. Самое главное, чтобы основные свойства функций (в первую очередь – монотонность) к этому времени учащимися были хорошо усвоены и чтобы графики элементарных функций стали легко узнаваемы.
К этому времени учащимся будет и легче воспринимать само понятие функции как соответствие между множествами.
Несмотря на весь абстрактный характер понятия “функция” с ним нужно разобраться, постепенно вводя логические уточнения и учитывая возможности класса. А сложную функцию нужно изучать как композицию двух функций. Это понятие важно для определения взаимно обратных функций. В связи с этим в сильных классах данный материал целесообразно вводить до того, как изучаются обратные функции — например, обратные тригонометрические функции. Для классов со слабой подготовкой, где обратные тригонометрические функции вводятся на более простом уровне, разговор о сложной функции пойдет в теме “Производная”. Но и в этом случае должно быть подробное рассмотрение определения этой функции.
Поведение элементарных функций лучше всего иллюстрируется с помощью графика, поэтому и для исследования сложной функции наилучший, как мне кажется, подход — это дать представление о ее графике, построенном с использованием графиков внутренней и внешней функций.
При построении графиков сложных функций в презентации для большей наглядности используются анимационные эффекты, дающие представление о последовательных шагах, которыми характеризуется композиция нескольких соответствий.
Важно подчеркнуть, что при исследовании функций с помощью производной ученики получают более совершенный аппарат для построения графика, но и элементарные методы имеют свои преимущества: они позволяют учащимся на более простом материале воспринимать основные функциональные изменения и дают возможность “прочувствовать” поведение сложной функции. Построение графиков без производной может осуществляться с разных точек зрения. Примеры получения достаточно трудных графиков описаны, например, в [1]. Те приемы, которые предложены в данной презентации, с одной стороны, касаются именно сложных функций, но с другой демонстрируют достаточно наглядные рассуждения, которые могут помочь в исследовании функций при решении различных задач. Например, изученные приемы могут пригодиться в тех случаях, когда требуется узнать промежутки монотонности сложной функции, множество ее значений. Причем предложенный метод достаточно нагляден и не использует громоздких преобразований с формулами.
В предлагаемой презентации можно выделить три части:
- Введение понятия сложной функции.
- Построение графиков сложных функций.
- Нахождение множества значений сложной функции.
1. Для того чтобы подробно описать, как “действует” сложная функция, сначала нужно повторить определение функции как соответствия между множествами, при котором каждому элементу первого множества соответствует не более одного элемента второго множества. То, что на слайде изображены круги Эйлера, не случайно: на них более ярко можно показать соответствие между элементами множеств.
Понятие функции к 10 классу должно быть сформировано, но ученикам с низкой мотивацией иногда трудно его запоминать, и в данном случае можно подробнее остановиться на контрольных вопросах, например, почему окружность или вертикальная прямая в системе координат не могут быть графиками функций (хотя их и можно задать уравнениями).
Сложную функцию рассматриваем как композицию двух функций, то есть как последовательное выполнение двух соответствий. По рисунку можно проследить, как некоторому элементу множества Х соответствует элемент множества Т, этот закон устанавливается внутренней функцией. А затем для элемента множества Т внешняя функция указывает соответствующее значение элемента из множества У. Таким образом, для первоначального х0 мы находим t0, а затем у0. Устанавливается зависимость: x0t0у0.
После того, как чертеж с тремя множествами и соответствиями подробно разобран, переходим к рассмотрению конкретных сложных функций. Рассматриваем примеры, где сложная функция задается формулой. Ученикам предлагается назвать внутреннюю и внешнюю функцию.
Аналогичные задания приводятся и в учебнике [3], но практика показывает, что если ограничиваться только рассмотрением формул, то от восприятия учеников ускользает структура самой композиции функций, последовательность в переходе от одного шага к другому, в итоге исчезает математическая суть сложной функции.
Восполнить этот пробел помогают графики.
2. Построим график функции (пример 1).
Укажем область определения: D(y) = (-∞; -2] U (2; +∞). Заметим, что это четная функция.
Внутренняя функция: g(x) = x2 – 4, построим график в системе координат (х,t). Для простоты изложения мы строим всю параболу, но в дальнейшем рассматриваем только те х, которые входят в множество D(y).
Внешняя функция: f(t) =, построим график в системе координат (t,y).
График исходной сложной функции будем строить в системе координат (х,у).
Для наглядности на рисунке отмечено некоторое произвольное значение х0, для него с помощью графика g(x) можно указать t0=g(x0), а для t0 по графику внешней функции находим значение у0=f(t0), таким образом получаем цепочку соответствий: x0t0у0, аналогичную той, которая была изображена на рисунке с кругами Эйлера.
После того, как два вспомогательных графика построены, переходим к главной задаче – построению графика сложной функции.
Пусть переменная х изменяется от 2 до бесконечности. По графику g(x) хорошо видно, что при этом переменная t изменяется от 0 до бесконечности. В силу возрастания квадратичной функции на данном участке об этом можно было догадаться и без графика, но график помогает в дальнейших рассуждениях.
Итак, переменная t изменяется от 0 до бесконечности. Переходим в систему координат с графиком внешней функции f(t). Значения функции, то есть у, меняются от 0 до бесконечности.
Все эти изменения приводятся в таблице на слайде.
Значит, для функции при увеличении аргумента от 2 до бесконечности получаем возрастание функции от 0 до бесконечности. И то, что мы выделили этот участок монотонности, уже очень важно! Можно хотя бы схематично изобразить график при х≥2.
Чтобы детям лучше был понятен этот переход, соответствующие участки на чертежах подчинены анимационным эффектам (слайд 10). Участки появляются по щелчку мыши последовательно, друг за другом, в определенном цвете. В результате в системе координат (х,у) выделяется промежуток [2; +∞) на оси абсцисс, а по оси ординат ему соответствует промежуток [0; +∞), функция возрастает. И появляется первый участок искомого графика.
В силу четности исходной функции получаем и второй участок графика, при х≤-2, отражая первый участок относительно оси ординат.
Но можно и другим способом получить ту же линию при х≤-2: рассмотреть изменение х от минус бесконечности до -2, тогда переменная t изменяется от +∞ до 0, а переменная у при этом изменяется от +∞ до 0. Значит, при изменении аргумента от -∞ до -2 значения сложной функции убывают – это мы и видим на графике. Данные рассуждения можно провести устно, но они хорошо иллюстрируются изображениями на слайдах.
Заметим, что в этих рассуждениях приходится намеренно отказываться от термина “промежутки” и от соответствующих скобок для их указания, потому что мы говорим именно об изменении величины, а не просто о множестве, на котором ее рассматриваем, то есть если переменная уменьшается, она изменяется, начиная с большего значения (а в промежутках на первом месте указывается меньшее значение).
Еще один вариант применения указанного способа построения графика – это подготовительный этап в изучении свойств растяжения и сжатия графиков. Например, чтобы ученик осмысленно и “своими руками” получил график у=sin2x, можно рассматривать данную функцию как сложную. Это построение разобрано в презентации (пример 2).
Не исключено, что гармонические колебания будут уже известны ученикам к моменту изучения сложной функции и, в частности, поведение графика у=sin2x. В этом случае можно предложить ученикам самостоятельно найти ответ на вопрос, как пользуясь свойствами внутренней и внешней функции, прийти к итоговому графику. Второй способ решения уже известной задачи ничуть не умаляет первый, а только лучше закрепляет полученную информацию.
В классах, где тригонометрические сведения усвоены не достаточно хорошо, весьма полезной будет повторение значений синуса для определенных углов и заполнение предложенной таблицы. В классах с высокой мотивацией в обучении эта работа достаточно легкая, таблицу можно заполнять устно, а в тетрадях только построить сам график, но действовать поэтапно.
Итак, рассматриваем функцию у=sin2x.
Замечаем, что она всюду определена, нечетная, периодична с наименьшим положительным периодом π.
Изображаем графики внутренней и внешней функции.
Начинаем с анализа изменения переменной х. Для каждого участка изменения указываем, как изменяется переменная t, а затем переменная у.
Рассматриваем участки изменения для переменной х: от 0 до π/4; от π/4 до π/2; от π/2 до 3π/4; от 3π/4 до π.
То, что нужны именно эти участки, можно объяснить поведением рассматриваемых функций. Мы должны указать такой участок для x, на котором характер изменения t не меняется – либо только увеличивается, либо только уменьшается, то есть важна монотонность внутренней функции, а при соответствующих t монотонность внешней функции тоже дает однозначный ответ, то есть можно определенно указать, что значения у либо увеличиваются, либо уменьшаются. Для простоты расчетов участки монотонности иногда дробятся на два — в данном случае учитываются нули — пересечение графика с осью абсцисс. Но характер монотонности на каждом отдельном участке постоянен.
Если у учеников появляются вопросы, то графические иллюстрации позволяют быстрее их разрешить, поэ
Урок в 10 классе по алгебре на тему «Построение графика сложной функции»
ОТКРЫТЫЙ УРОК
Построение графика сложной функции
Алгебра 10 класс
Подготовила:
Учитель математики: Ваганова И.Г
2016-2017 уч
«…не давать образцов, ставить ребенка в ситуацию, где его привычные способы действия с очевидностью непригодны и мотивировать поиск существенных особенностей новой ситуации , в которой надо действовать – вот основания нетрадиционной педагогики, основанной на психологической теории учебной деятельности…»
Г.А.Цукерман , доктор психологических наук
Проблемно-деятельностный метод обучения – это организация учебного процесса, в котором главное место отводится активной , разносторонней, самостоятельной ,познавательной деятельности школьника . Преподаватель не сообщает готовых знаний ,а организует учеников на их поиск .
Тип урока : открытие нового знания
Цели урока:
Образовательная: активизация знаний о свойствах функции на примерах элементарных и квадратичной функций, о пределах;
Учебная задача: построить график сложной функции на основе имеющихся знаний и указать способы его построения.
Форма работы: фронтальная, групповая
Оборудование: мультимедиа-проектор, интерактивная доска.
Урок построен на основе технологии проблемно-деятельностного подхода. Работа на уроке сопровождается мультимедийной презентацией
Ход урока
I этап. Мотивационно-ориентировочная часть.
Организационный момент. Мы сегодня с вами будем работать в группах , каждая группа за выполнение задания получит определенное количество баллов. Но у каждого есть возможность заработать свои дополнительные баллы в ходе фронтальной работы. Поэтому каждый получает листок критериев, по которому будет выставляться оценка за работу на уроке.
Листок критериев Ф.И.____________________________
БаллМаксимальное количество баллов
1. Построение графика квадратичной функции
5 баллов
2.Свойства функций
10 баллов
3. Нахождение свойств для предложенной функции
7 баллов
4. Построение графика данной функции
5 баллов
5. Построение графика функции( сам работа)
10 баллов
итого
37 баллов
Дополнительные баллы
Оценка
37 и больше -5
36-30 баллов — 4
29- 20 баллов — 3
Меньше 19 -2
Актуализация.
У: Мы с вами давно занимаемся построением графиков функций. И вы знаете , что при решении многих сложных задач — это необходимо знать и уметь применять.
У:И так как называется эта группа функций.(слайд 1)
У: Правильно. Элементарные функции. Можем мы построить их графики сразу, не делая дополнительных вычислений , рассуждений?
УЧ: Да. ( Называют функцию , график )
У: А как построить график этой функции и какая это функция ? (слайд 2)
У = х2 +4х + 3
УЧ: Квадратичная функция , графиком является парабола
У: Можем мы построить эту функцию?
УЧ: Да.
У: Можем сразу построить ?
УЧ: Нет
У: Что для этого нужно знать?
УЧ: Схему построения графика квадратичной функции (координаты вершины параболы , точки пересечения графика с осями координат )
У: Я вам предлагаю выполнить
1 задание : Построить график квадратичной функции
У: Обменяйтесь тетрадями и оцените работу другой группы .Полученные баллы занесите каждый в свой лист критерия.
У: Следующее задание : построить график функции у=
У: Какая это функция?
УЧ: Сложная
У: Можете построить график этой функции ?
Уч: Нет.
Проблема : Как построить график сложной функции?
Цель урока : Разработать схему построения графика сложной функции.
Чтобы ответить на этот вопрос , нужно разработать план нашего урока.
План :
1. Обобщить свойства сложных функций
2.Применить эти знания для определения свойств искомой функции
3.Попытаться построить график искомой функции и выяснить ,что еще не хватает для его построения
4.Вывести способ построения графика сложной функции
Итак, идем по плану.1 Этап.
2 задание .Давайте вспомним свойства функций. Для этого работая в группах на отдельных листах перечислите свойства, и подчеркните те , которые по вашему мнению могут помочь при построении сложной функции и которые можно найти для любой функции.
Сверим правильные ответы. Слайд 3.
1. Область определения (выявить точки разрыва )
2. Область значений
3. Четность
4. Периодичность
5. Знакопостоянство
6. Нули функции
7. Выпуклость ( вогнутость )
8. Ограниченность
9. Монотонность
10. Наибольшее и наименьшее значение
11 Точки экстремума
Обменяйтесь тетрадями и занесите в листок баллы за это задание.
Дайте определения свойств и укажите приемы их нахождения. Учащиеся дают определения и рассказывают , как можно их найти (устно отвечают , получают дополнительные баллы).
Переходим к 2 этапу нашего плана.
3 задание : Вам предстоит для нашей функции найти перечисленные свойства ( работают в тетрадях в группах ).
Обменяйтесь своими работами и оцените работу группы ( слайд 4 )
1. Область определения – вся числовая
2. Функция общего вида
3. Непериодическая
4. нули функции х=2 (2;0)
5. промежутки возрастания ( -1; 5) промежутки убывания ( ∞ ;-1) и ( 5; ∞ )
6. точки экстремума х=-1 ( минимум ) и х=5 ( максимум)
7. промежутки знакопостоянства у>0 при х (2;∞ ) и у<0 при ( ∞ ;2)
Занесите баллы в листок критериев.
И с этим этапом мы с вами справились и переходим к другому шагу нашего урока.
У; Отметьте найденные точки на координатной плоскости.
У: Можно построить график ?
УЧ: Нет.
У: Почему ?
УЧ: Мало данных.
У: Что можно и хочется еще найти , глядя на координатную плоскость ?
УЧ: Значение функции в точках экстремума ?
У: Находим и отмечаем точки на плоскости.
У: А сейчас можно построить однозначно график ?
УЧ: Нет ?
У: Почему ?
УЧ: Не знаем точки пересечения графика с осью ординат и как ведет себя функция в близи оси абсцисс .
У: Как найти точки пересечения графика с осью ординат ?
УЧ: Подставить в уравнение функции х=0 и решить его.
У: А как исследовать поведение функции в окрестности оси абсцисс? И кто нам в этом может помочь?
УЧ: Предел. Нужно найти предел функции при х→+∞ и при х→-∞ (горизонтальные асимтоты)
У: Какие прямые называются асимтотами?
Какие еще асимтоты мы знаем и как их найти?
УЧ: Вертикальные. Точки разрыва.
Учащиеся находят предел, называют уравнения асимтот и получают дополнительные баллы .
У:4 задание. А теперь по найденным вычислениям постройте график функции.
Обменяйтесь тетрадями и сравните свои графики .
Полученные баллы занесите в листок.
Перейдем к следующему этапу нашего урока .
И следующее для вас задание : составьте, на основе всех рассуждений , схему построения графика сложной функции.
Проверим свои результаты с предложенной схемой . Слайд 5.
Схема построения графика сложной функции.
1.Определить четность функции. 2.Найти область определения.
3. Определить период (если это возможно)
4. Найти нули функции
5. Координаты точек пересечения графика с осью ординат
6.Найти промежутки знакопостоянства ( если это возможно )
7. Найти промежутки монотонности
8. Найти координаты точек экстремума
9. Найти горизонтальные и вертикальные асимтоты.
У: Я думаю ,что мы с вами успешно справились с такой сложной задачей. Ответили на все вопросы нашего урока и прошли все его этапы..
И для закрепления , я вам предлагаю самостоятельно выполнить построение графика функции
5 задание : У=
Сравним график . Заносим результаты в листок и подводим итог .Выставляем оценку за урок по предложенному критерию.
Рефлексия: Вспомните, какую задачу мы поставили перед собой сегодня на уроке?
Построить график сложной функции.
Достигли мы этой цели?
Каким способом мы это сделали, с помощью каких знаний?
Использовали свойства функций и объединили их в схему для построения графика сложной функции..
4. Задание на дом.
Построить график функций: 1) У= 2) У = х3 +6х2 — 3
Листок критериев Ф.И.____________________________
БаллМаксимальное количество баллов
1. Построение графика квадратичной функции
5 баллов
2.Свойства функций
10 баллов
3. Нахождение свойств для предложенной функции
7 баллов
4. Построение графика данной функции
5 баллов
5. Построение графика функции( сам работа)
10 баллов
итого
37 баллов
Дополнительные баллы
Оценка
37 и больше -5
36-30 баллов — 4
29- 20 баллов — 3
Меньше 19 -2
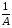 раз при А < 1 (произвести сжатие графика вдоль оси ординат)
раз при А < 1 (произвести сжатие графика вдоль оси ординат)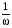 раз при
раз при 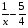 .
.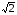 ).
).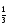 (-х).
(-х).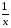 .
.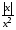 .
.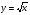 .
. .
.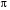 x.
x.