3. Основные понятия аксиоматической теории. Аксиомы, пастулаты, теоремы.
Аксиоматическая теория — результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка, причем все условия, регулирующие употребление этих слов в теории, явно высказаны посредством аксиом и правил, позволяющих вывести одну фразу из других.
В множестве формул выделяется подмножество аксиом, и задается конечное число правил вывода — таких правил, с помощью которых (и только с помощью их) из аксиом и ранее выведенных теорем можно образовать новые теоремы. Все аксиомы также входят в число теорем. Таким способом задается формальная теория (формальная аксиоматическая теория, формальное (логическое) исчисление).
Формальная теория считается определенной, если:
Задано конечное или счётное множество произвольных символов.
Имеется подмножество выражений, называемых формулами.
Выделено подмножество формул, называемых аксиомами.
Имеется конечное множество отношений между формулами, называемых правилами вывода.
Чаще всего имеется возможность эффективно выяснять, является ли данная формула аксиомой; в таком случае теория называется эффективно аксиоматизированной или аксиоматической.
Множество аксиом может быть конечным или бесконечным. Если число аксиом конечно, то теория называется конечно аксиоматизируемой. Если множество аксиом бесконечно, то, как правило, оно задаётся с помощью конечного числа схем аксиом и правил порождения конкретных аксиом из схемы аксиом.
Обычно аксиомы делятся на два вида: логические аксиомы (общие для целого класса формальных теорий) и нелогические
или собственные аксиомы (определяющие специфику и содержание конкретной теории).Для каждого правила вывода R и для каждой формулы A эффективно решается вопрос о том, находится ли выбранный набор формул в отношении R с формулой A, и если да, то A называется непосредственным следствием данных формул по правилу R.
Вывод — всякая последовательность формул такая, что всякая формула последовательности есть либо аксиома, либо непосредственное следствие каких-либо предыдущих формул по одному из правил вывода.
Формула называется теоремой, если существует вывод, в котором эта формула является последней.
Теория, для которой существует эффективный алгоритм, позволяющий узнавать по данной формуле, существует ли её вывод, называется разрешимой; в противном случае теория называется неразрешимой.
Теория, в которой не все формулы являются теоремами, называется абсолютно
Аксио́ма или постула́т — исходное положение какой-либо теории, принимаемое в рамках данной теории истинным без требования доказательства и используемое при доказательстве других её положений, которые, в свою очередь, называются теоремами
Теоре́ма — утверждение, выводимое в рамках рассматриваемой теории из множества аксиом посредством использования конечного множества правил вывода.
4. Аксиоматический метод, его сущность. Примеры применения аксиоматического метода в языкознании.
Аксиоматический метод — это такой способ построения математической теории, при котором в основу кладутся некоторые положения, принимаемые без доказательства (аксиомы), а все остальные выводятся из них чисто логическим путем.
Основные понятия делятся на два вида: одни обозначают объекты, которыми занимается теория, другие обозначают отношения между ними.
В этом случае аксиомы представляют собой формулы этого языка (последовательности символов), а теоремы получаются как преобразования исходных последовательностей символов в новые последовательности по строго определённым логическим правилам исходных последовательностей символов в новые последовательности. Такую теорию называют исчислением, или формальной аксиоматической теорией.
Например, аксиома может иметь статус утверждения, или статус предположения, или статус лингвистического соглашения о желаемом употреблении терминов.
studfile.net
аксиомы-определения-теоремы-1 четверть 7кл
1 четверть геометрия 7 класс
ПРЯМЫЕ И ОТРЕЗКИ
Основные геометрические фигуры: точка, прямая, плоскость, пространство.
Аксиома 1. Через любые две точки можно провести прямую, и только одну.
Аксиома 3. Прямая, проходящая через две точки плоскости, лежит в этой плоскости.
Определение 1. Любое множество точек называется геометрической фигурой. Часть любой геометрической фигуры также является геометрической фигурой.
Аксиома 4. Для любых двух точек А и В пространства однозначно определено некоторое неотрицательное число АВ, называемое расстоянием между ними и обладающее следующими свойствами:
1) АВ = ВА;
2) АВ = 0 тогда и только тогда, когда точки А и В совпадают;
3) АС = АВ + ВС, причём равенство достигается в том и только в том случае, когда точка В лежит на отрезке АС.
Определение 2. Точка X лежит между точками А и В, если эти точки различны и АХ + ХВ = АВ.
Для любых трёх точек, не лежащих на одной прямой, расстояние АС меньше суммы расстояний АВ и ВС.
Определение 3.
Отрезки равны, если равны их длины.УГЛЫ
Определение 4. Углом называется фигура, состоящая из двух различных лучей с общим началом и ограниченной ими части плоскости.
Определение 5. Развёрнутым углом называется угол, сторонами которого являются дополнительные лучи одной прямой. Два луча с общим началом, дополняющие друг друга до прямой, называются дополнительными.
Определение 6. Фигура называется выпуклой, если любые две её точки можно соединить отрезком, принадлежащим этой фигуре.
Определение 7. Угол, равный 90°, называется прямым углом. Угол, меньший 90°, называется острым углом. Угол, больший 90°, называется тупым углом.
Определение 8. Углы равны, если равны их величины.
Определение 9. Углы называются равными, если их можно совместить наложением друг на друга.
Определение 10. Биссектрисой угла называется луч, который исходит из вершины угла и делит угол пополам.
Определение 11. Два угла называются смежными, если у них одна сторона общая, а другие стороны этих углов являются дополнительными лучами.
Теорема 1. Сумма смежных углов равна 180°.
Следствие 1. Если два угла равны, то смежные с ними углы тоже равны.
Следствие 2. Угол, смежный с прямым углом, есть прямой угол.
Следствие 3. Угол, смежный с острым углом, — тупой; угол, смежный с тупым углом, — острый.
Трёхгранный угол — фигура, состоящая из трёх углов и части пространства, ограниченной этими плоскими углами. Лучи называются рёбрами трёхгранного угла, а углы, ограничивающие трёхгранный угол, — его гранями. Эти углы-грани образуют поверхность трёхгранного угла.
В трёхгранном угле каждый плоский угол меньше суммы двух других плоских углов.
Многогранные углы бывают выпуклыми и невыпуклыми.
Определение 12. Многогранный угол называется выпуклым, если он лежит по одну сторону от каждой плоскости, содержащей его грань.
studfile.net
Раздел 3. Логическое следование. Применение алгебры высказываний к логико-математической практике
3.1 Логическое следование
Определение 1. Формула B называется логическим следствием формул A1, A2, …, An, если при любых значениях входящих в них элементарных высказываний формула B принимает значение «истинно» всякий раз, когда формулы A1, A2, …, Anпринимают значение «истинно». Обозначается A1, A2, …, An╞ B
Из определения логического следования вытекает, что:
Тавтология логически следует из любой формулы.
Из противоречия логически следует любая формула.
Теорема
1. Из A логически следует B тогда и только тогда, когда тавтологией
является 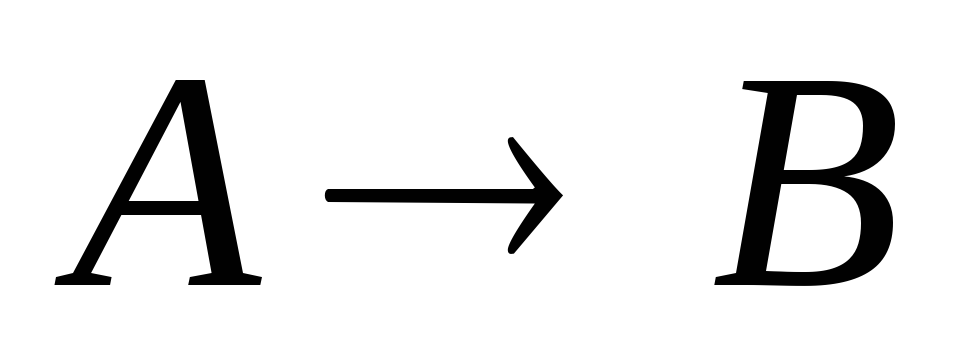 .
.
Теорема
2. A1,
A2,…,
An╞
Bтогда
и только тогда, когда является тавтологией
A1&A2&
…& An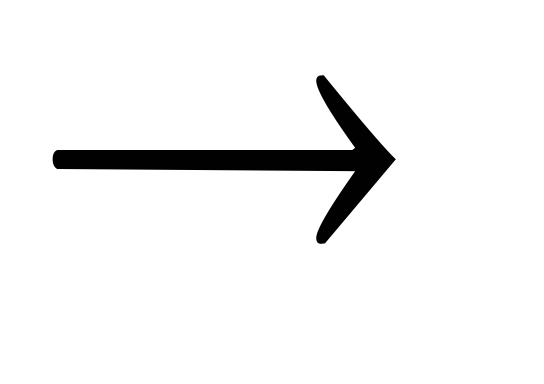 B.
B.
Теорема
3. Из формул A1,
A2,…,
An , B логически следует C тогда и только
тогда, когда из формул A1,
A2,
…, An логически
следует B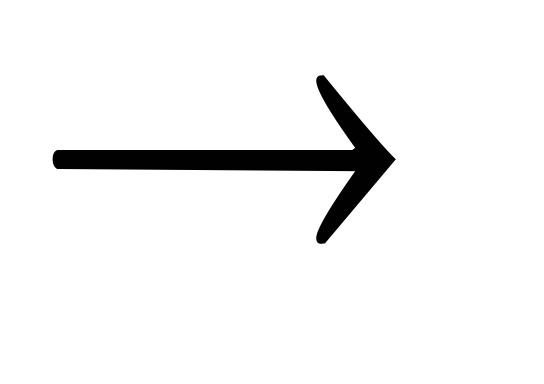
Следствие
1.
Из A и B логически следует C тогда и только
тогда, когда тавтологией является A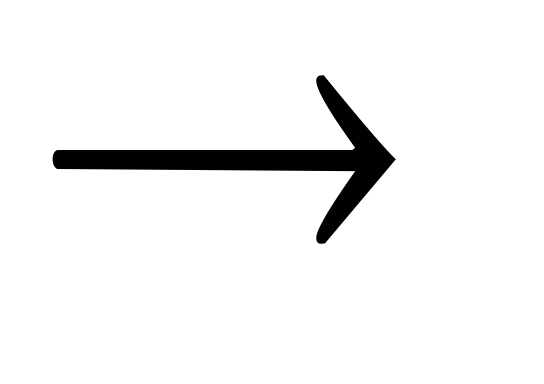 (B
(B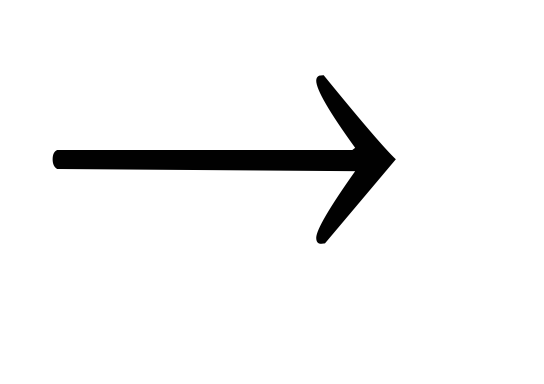 C).
C).
Следствие
2. Из формул A1,
A2,
…, An логически следует B тогда и только тогда,
когда тавтологией является A1 (A2
(A2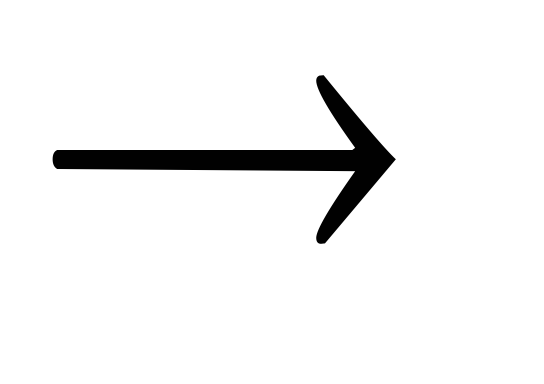 …
(An
…
(An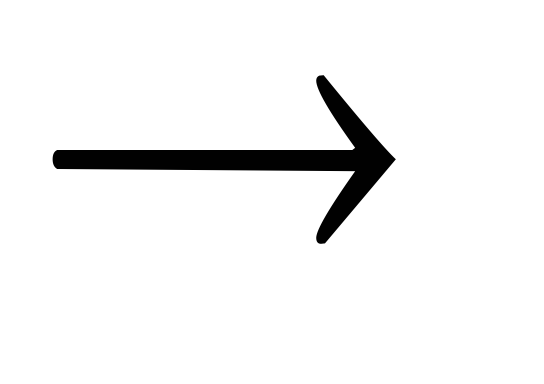 B)…).
B)…).
Отношение логического следования играет в математике большую роль.
Теоремы. Необходимые и достаточные условия
Теорема –
это предложение, истинность которого
доказывается на основе аксиом или ранее
доказанных теорем. Теоремы часто
формулируются в виде импликаций
(следования). Импликативная структура
наиболее удобна для выделения условия
и заключения теоремы (того, что дано, и
того, что необходимо доказать). Если
импликация  выражает некоторую теорему, то основание
импликацииА выражает условие,
а следствие В – заключение теоремы. Условие или заключение в свою
очередь может не быть элементарным
высказыванием, а иметь определенную
логическую структуру, чаще всего
конъюнктивную или дизъюнктивную.
Рассмотрим примеры:
выражает некоторую теорему, то основание
импликацииА выражает условие,
а следствие В – заключение теоремы. Условие или заключение в свою
очередь может не быть элементарным
высказыванием, а иметь определенную
логическую структуру, чаще всего
конъюнктивную или дизъюнктивную.
Рассмотрим примеры:
1.
Теорема «Если диагонали параллелограмма взаимно
перпендикулярны или делят его углы пополам, то этот параллелограмм – ромб» имеет
структуру 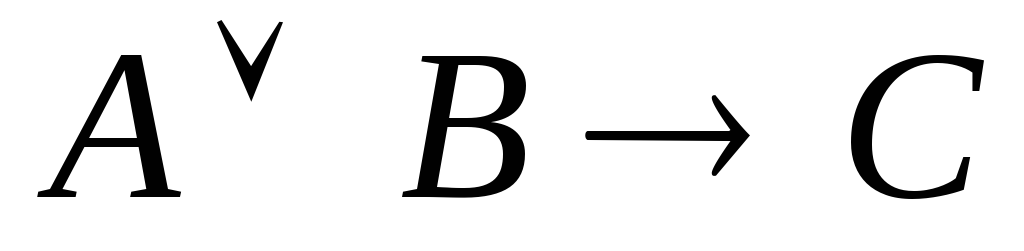 ,
гдеА = «диагонали параллелограмма взаимно
перпендикулярны»; В = «(диагонали параллелограмма) делят его
углы пополам»; С = «этот параллелограмм – ромб».
,
гдеА = «диагонали параллелограмма взаимно
перпендикулярны»; В = «(диагонали параллелограмма) делят его
углы пополам»; С = «этот параллелограмм – ромб».
2.
Теорема о средней линии трапеции
(«средняя линия трапеции параллельна
основаниям и равна их полусумме») после
соответствующей переформулировки
(«если четырехугольник – трапеция, то его средняя линия параллельна основаниям и равна их полусумме») имеет структуру: 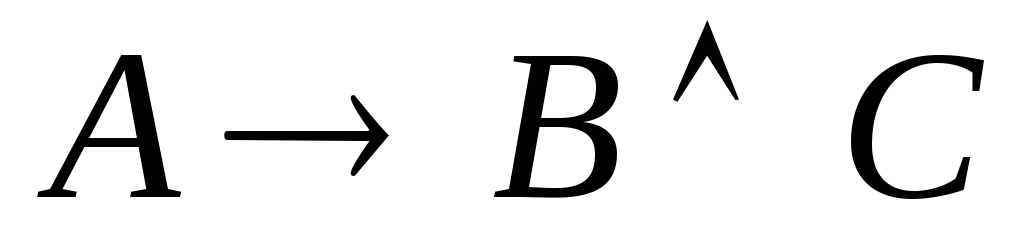 ,
гдеА = «четырехугольник – трапеция»; В = «его средняя линия параллельна
основаниям»; С = «(его средняя линия) равна полусумме
оснований».
,
гдеА = «четырехугольник – трапеция»; В = «его средняя линия параллельна
основаниям»; С = «(его средняя линия) равна полусумме
оснований».
Для
каждого предложения, сформулированного
в виде импликации 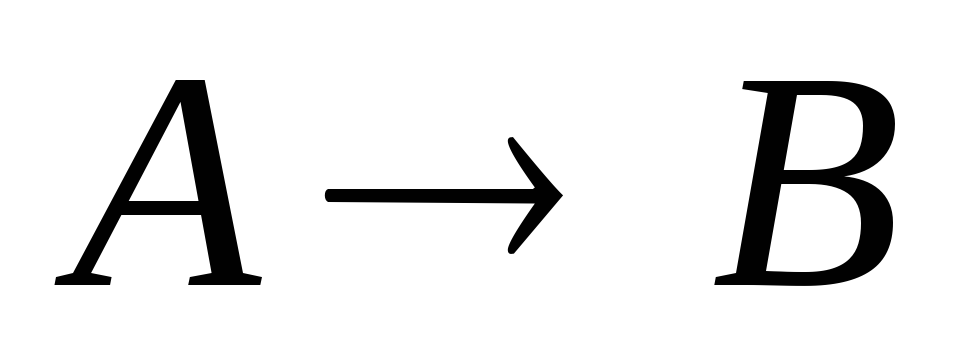 можно составить обратное ему предложение,
противоположное и обратно-противоположное
предложение. Рассмотрим их более
подробно.
можно составить обратное ему предложение,
противоположное и обратно-противоположное
предложение. Рассмотрим их более
подробно.
1.
Обратное предложение 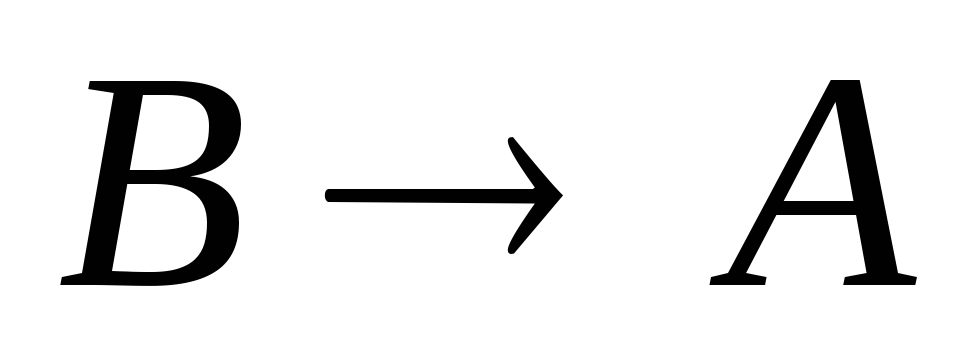 .
Для всякой теоремы «еслиА,
то В»
можно сформулировать обратное ей
предложение «если В,
то А».
При этом не для всякой теоремы, обратное
ей предложение также является теоремой.
Пусть, например, даны две теоремы: «Если
два квадрата равны, то их площади равны»;
«Если два прямоугольника равны, то их
площади равны». Предложение «Если
площади двух квадратов равны, то эти
квадраты равны», обратное первой из
этих теорем, также является теоремой.
Предложение «Если площади двух
прямоугольников равны, то эти прямоугольники
равны», обратное второй теореме, теоремой
не является, её легко опровергнуть.
.
Для всякой теоремы «еслиА,
то В»
можно сформулировать обратное ей
предложение «если В,
то А».
При этом не для всякой теоремы, обратное
ей предложение также является теоремой.
Пусть, например, даны две теоремы: «Если
два квадрата равны, то их площади равны»;
«Если два прямоугольника равны, то их
площади равны». Предложение «Если
площади двух квадратов равны, то эти
квадраты равны», обратное первой из
этих теорем, также является теоремой.
Предложение «Если площади двух
прямоугольников равны, то эти прямоугольники
равны», обратное второй теореме, теоремой
не является, её легко опровергнуть.
Эти
примеры свидетельствуют о неравносильности
предложений вида 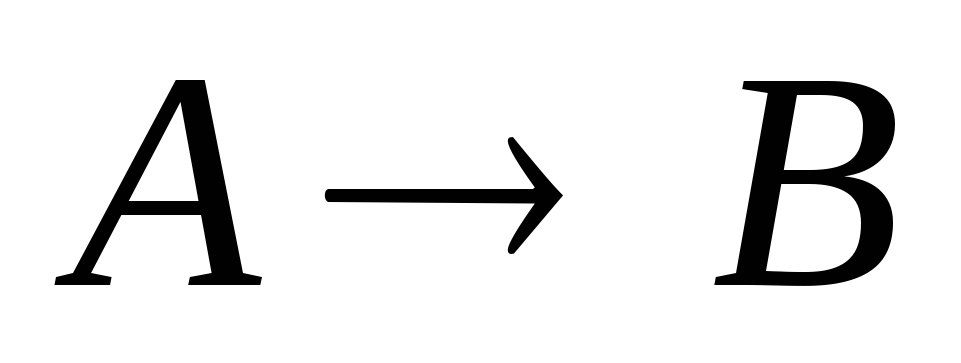 и
и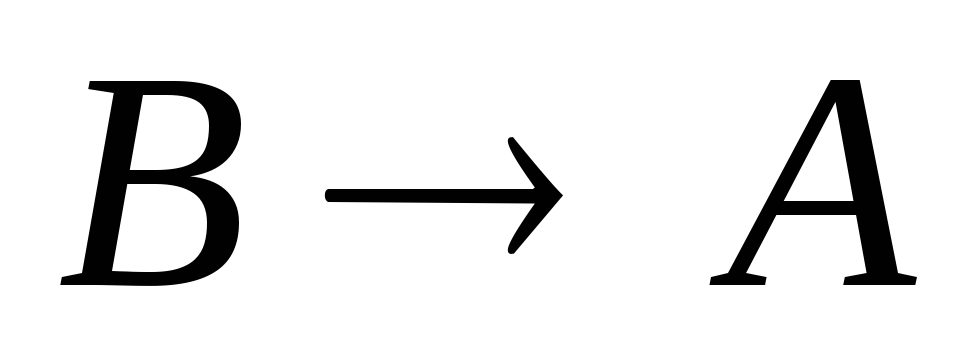 .
В неравносильности предложений такого
вида можно также убедиться, сравнив
таблицы истинности формул
.
В неравносильности предложений такого
вида можно также убедиться, сравнив
таблицы истинности формул и
и :
:
X | Y |
|
|
1 | 1 | 1 | 1 |
1 | 0 | 0 | 1 |
0 | 1 | 1 | 0 |
0 | 0 | 1 | 1 |
Поскольку два последних столбца в таблице не одинаковы, эквиваленция этих формул не является тавтологией, то есть они не равносильны. Более того, из таблицы видно, что одновременно с истинностью предложения вида «если А, то В», предложение вида «если В, то А» может быть как истинным, так и ложным.
Таким образом, если доказана истинность какого-либо предложения, то независимо от этого обратное ему предложение требует доказательства или опровержения.
2.
Противоположные предложения 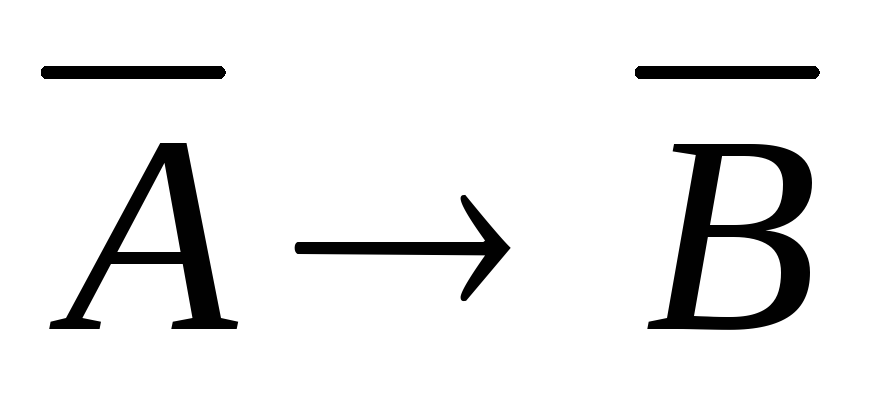 .
Для всякой теоремы, сформулированной
в виде импликации
.
Для всякой теоремы, сформулированной
в виде импликации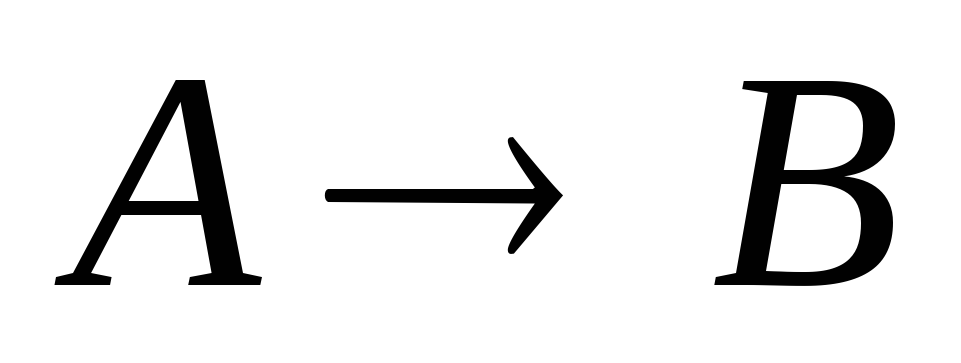 ,
можно составить противоположное
предложение
,
можно составить противоположное
предложение .
Предложение, противоположное данной
теореме, может быть также теоремой, но
может ею и не быть. В этом легко убедиться,
сравнив таблицы истинности формул
.
Предложение, противоположное данной
теореме, может быть также теоремой, но
может ею и не быть. В этом легко убедиться,
сравнив таблицы истинности формул и
и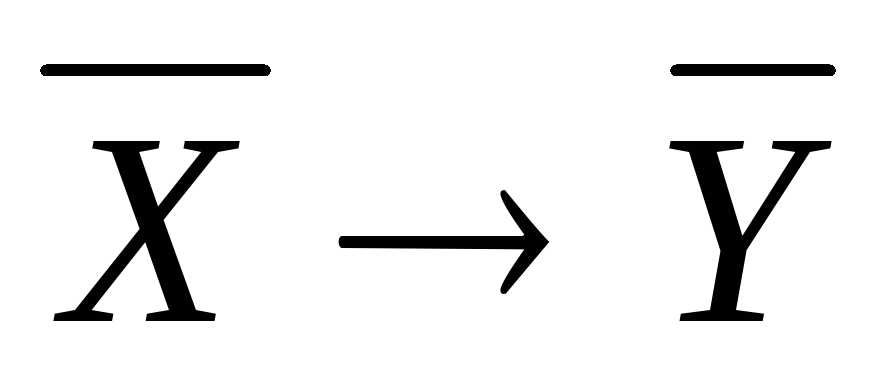 :
:
X | Y |
|
|
|
|
1 | 1 | 1 | 0 | 0 | 1 |
1 | 0 | 0 | 0 | 1 | 1 |
0 | 1 | 1 | 1 | 0 | 0 |
0 | 0 | 1 | 1 | 1 | 1 |
В
том случае, когда предложение 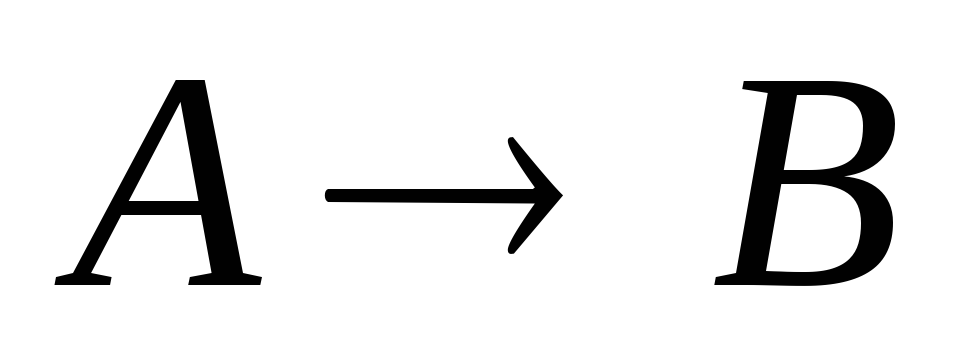 истинно, предложение
истинно, предложение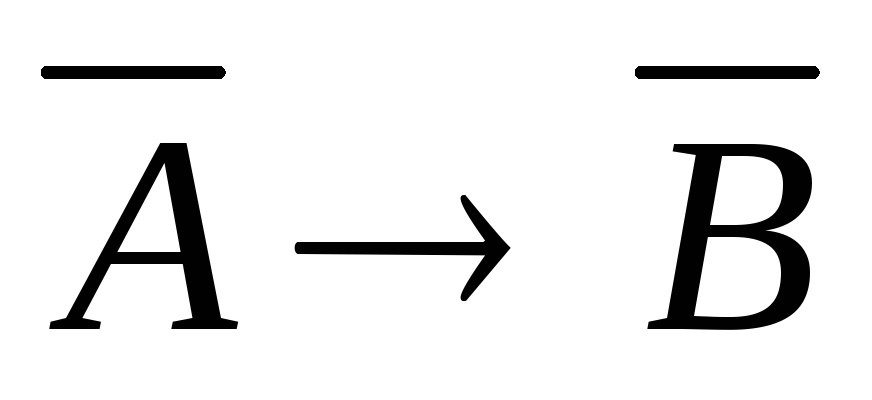 может быть как истинным, так и ложным.
Следовательно, предложение, противоположное
доказанной теореме, в свою очередь
требует доказательства или опровержения.
Для наглядности рассмотрим теоремы,
приведенные выше, и составим для каждой
противоположное предложение. Предложение,
противоположное первой теореме «Если
квадраты не равны, то их площади не
равны», очевидно, является теоремой.
Предложение «Если прямоугольники не
равны, то их площади не равны» легко
опровергается примером (Прямоугольники
со сторонами 3х4 и 2х6 не равны, но площадь
каждого из них равна 12).
может быть как истинным, так и ложным.
Следовательно, предложение, противоположное
доказанной теореме, в свою очередь
требует доказательства или опровержения.
Для наглядности рассмотрим теоремы,
приведенные выше, и составим для каждой
противоположное предложение. Предложение,
противоположное первой теореме «Если
квадраты не равны, то их площади не
равны», очевидно, является теоремой.
Предложение «Если прямоугольники не
равны, то их площади не равны» легко
опровергается примером (Прямоугольники
со сторонами 3х4 и 2х6 не равны, но площадь
каждого из них равна 12).
Если
условие или заключение данной теоремы
представляет собой конъюнкцию или
дизъюнкцию, то при составлении предложения,
противоположного данной теореме, нужно
учитывать соответствующий закон де
Моргана. Иногда конъюнкция или дизъюнкция
в формулировке теоремы присутствует
неявно, «замаскированно». Поэтому, чтобы
правильно сформулировать предложение,
противоположное данной теореме, нужно
сначала тщательно проанализировать её
формулировку и выявить подразумеваемые
конъюнкции или дизъюнкции (если таковые
имеются). Например, в заключении теоремы
«Если треугольник АВС равнобедренный, то два его угла равны»
скрыта дизъюнкция: «Если в треугольнике АВС  или
или ,
или
,
или ,
то
,
то или
или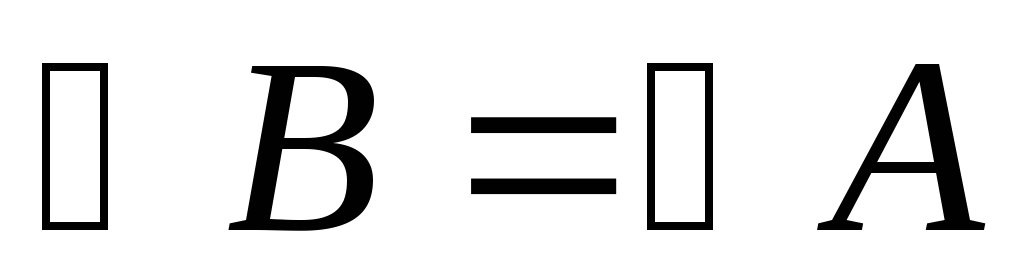 ,
или
,
или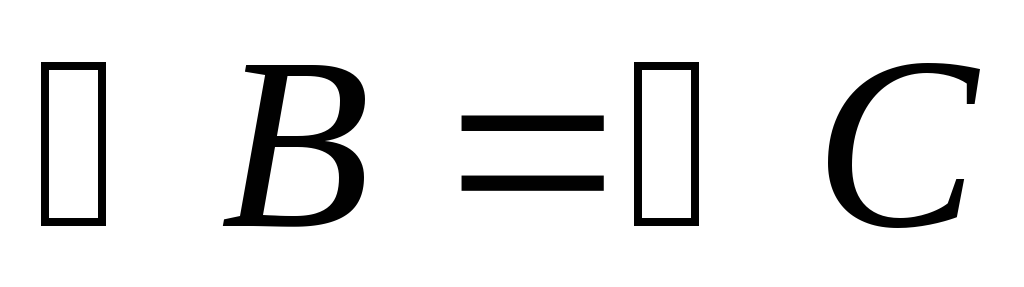 ».
Отрицание этой дизъюнкции дает конъюнкцию:
«Если в треугольникеАВС
».
Отрицание этой дизъюнкции дает конъюнкцию:
«Если в треугольникеАВС 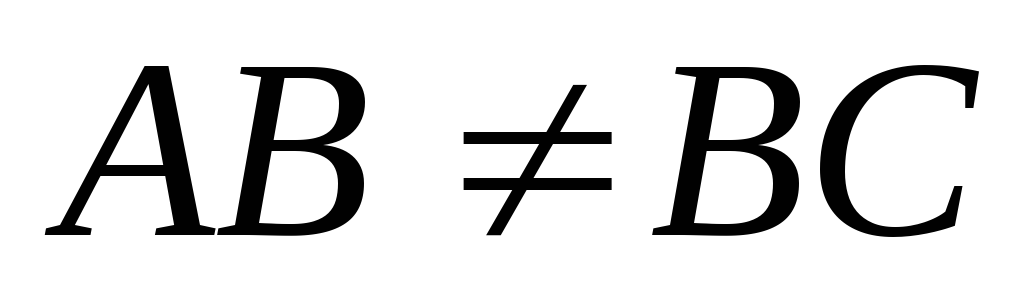 и
и ,
и
,
и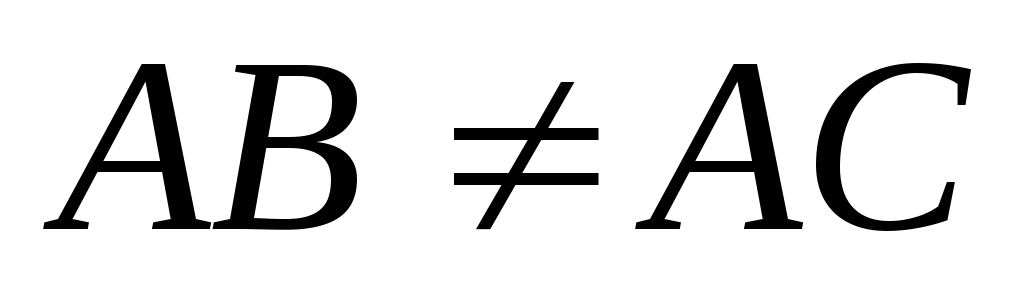 ,
то
,
то и
и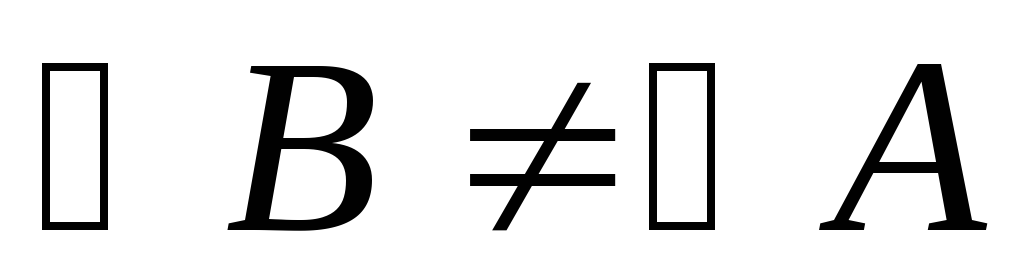 ,
и
,
и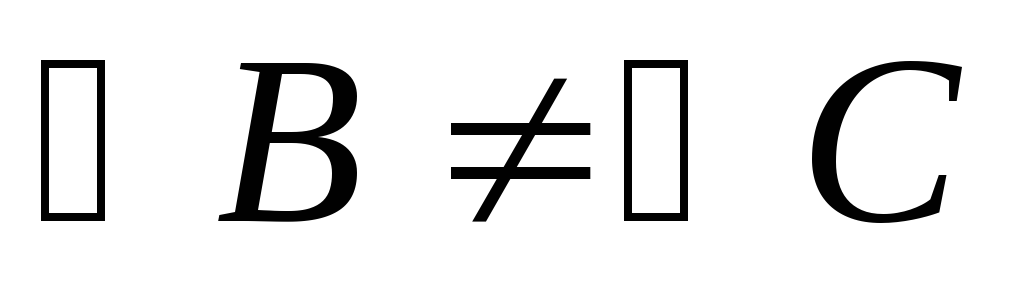 »,
что короче можно выразить так: «Если
треугольник не равнобедренный, то
никакие два его угла не равны».
»,
что короче можно выразить так: «Если
треугольник не равнобедренный, то
никакие два его угла не равны».
3.
Обратно-противоположные предложения.
Закон контрапозиции. Для каждой теоремы вида 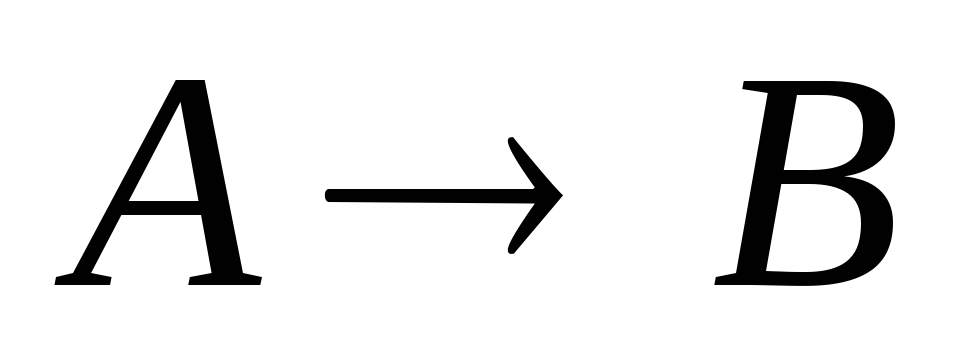 можно сформулировать обратно-противоположное
предложение вида
можно сформулировать обратно-противоположное
предложение вида ,
при этом имеет место следующая
равносильность:
,
при этом имеет место следующая
равносильность: ,
которая носит название закона
контрапозиции. Согласно ему: 1)два
предложения вида
,
которая носит название закона
контрапозиции. Согласно ему: 1)два
предложения вида  и
и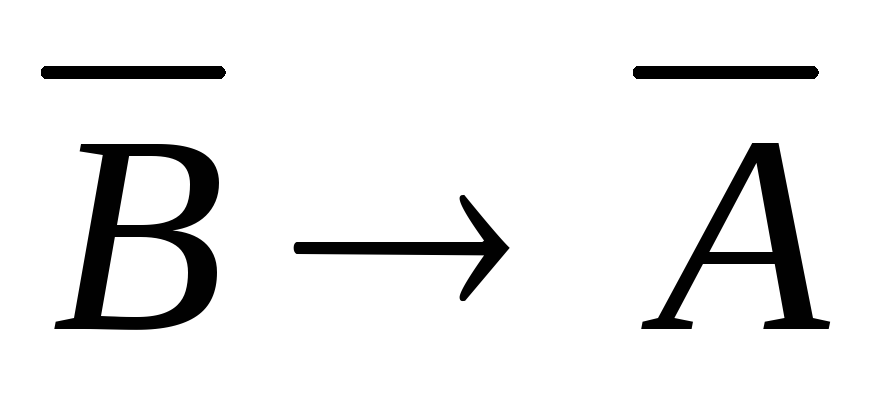 одновременно истинны или одновременно
ложны;
2) предложение,
обратно-противоположное данной теореме,
также является теоремой;
3) вместо
данной теоремы можно доказывать
обратно-противоположную ей теорему.
одновременно истинны или одновременно
ложны;
2) предложение,
обратно-противоположное данной теореме,
также является теоремой;
3) вместо
данной теоремы можно доказывать
обратно-противоположную ей теорему.
Пусть,
например, требуется доказать утверждение
«Если  нечетно, тот нечетно». Сформулируем и докажем
обратно-противоположную теорему: «Если т четно, то
нечетно, тот нечетно». Сформулируем и докажем
обратно-противоположную теорему: «Если т четно, то 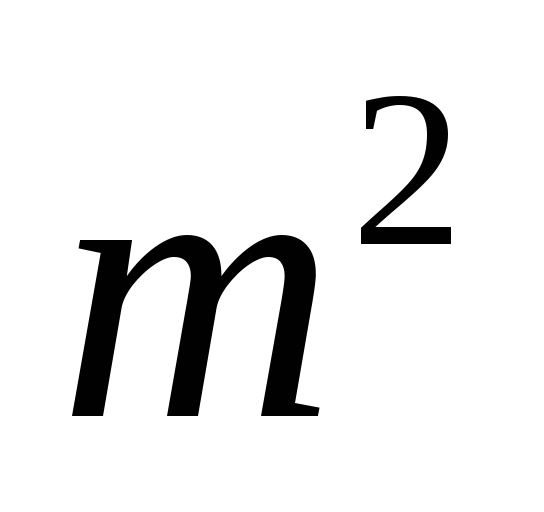 четно»; действительно, еслит четно, то
четно»; действительно, еслит четно, то 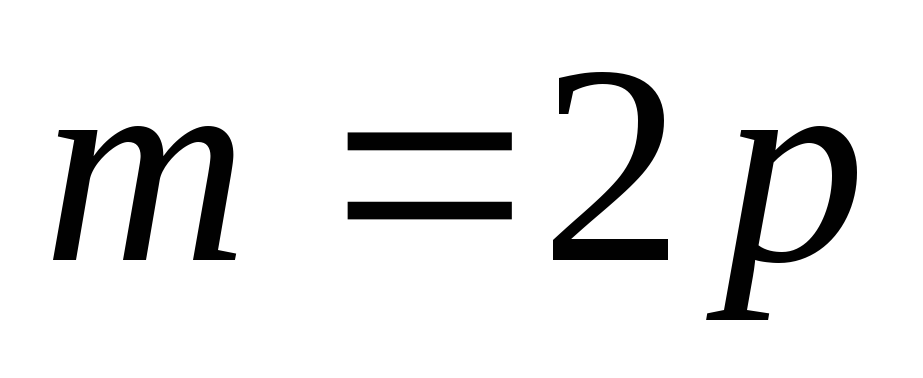 (р – натуральное число), откуда
(р – натуральное число), откуда 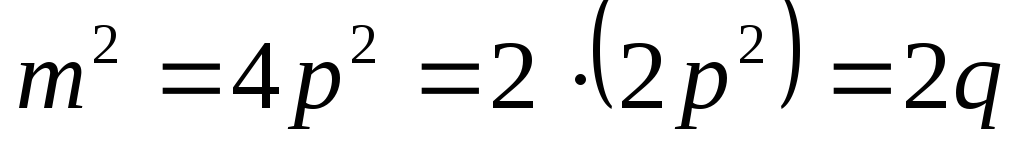 ,
то есть
,
то есть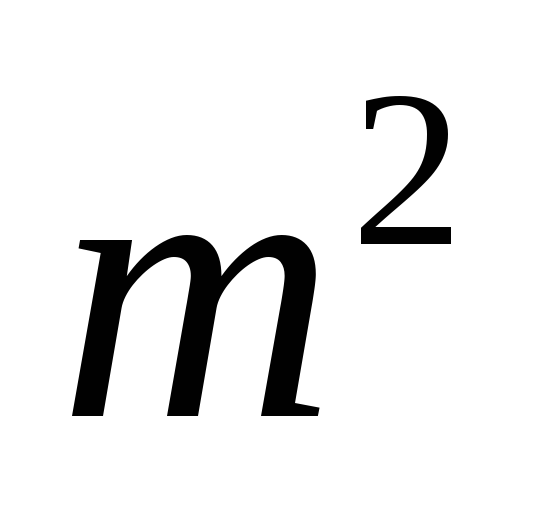 четно.
четно.
Если
в равносильность  подставитьY вместо Х и Х вместо Y,
то получим
подставитьY вместо Х и Х вместо Y,
то получим 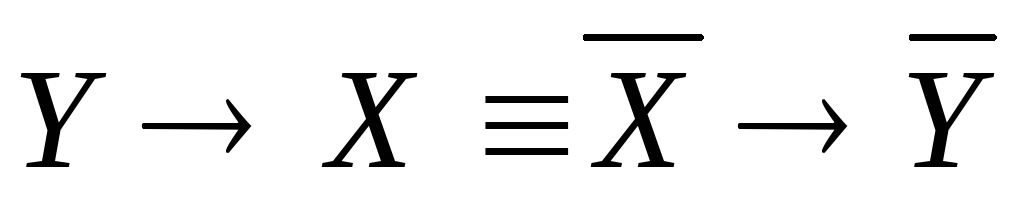 .
Из этой равносильности следует: 1)предложение,
обратное данному и противоположное
данному одновременно истинны или
одновременно ложны;
2) из
двух предложений – обратного данной
теореме и противоположного ей –
достаточно доказать или опровергнуть
только одно из них; тем самым будет
доказано или опровергнуто и второе.
.
Из этой равносильности следует: 1)предложение,
обратное данному и противоположное
данному одновременно истинны или
одновременно ложны;
2) из
двух предложений – обратного данной
теореме и противоположного ей –
достаточно доказать или опровергнуть
только одно из них; тем самым будет
доказано или опровергнуто и второе.
Часто
в формулировках теорем используются
выражения «необходимо», «достаточно»
«необходимо и достаточно» (признак).
Если
предложение 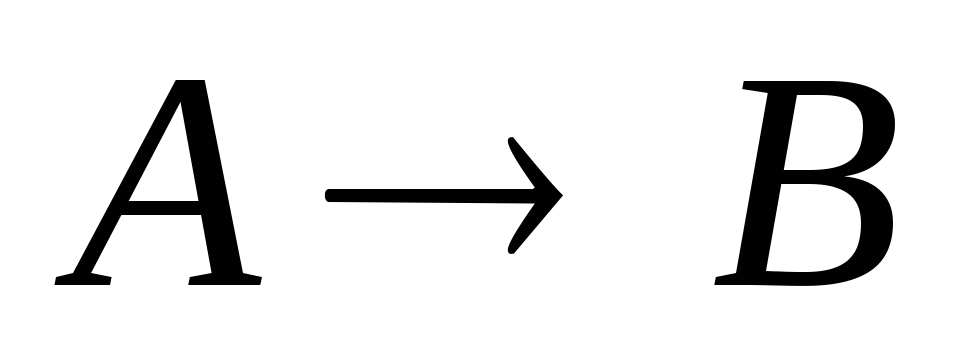 – теорема,
то A называется достаточным условием для B,
а B – необходимым условием для A.
Например, теорему «Если квадраты равны,
то их площади равны» можно сформулировать
в виде необходимого условия: «Для того
чтобы квадраты были равны, необходимо,
чтобы их площади были равны»; или
достаточного условия: «Для того чтобы
площади двух квадратов были равны, достаточно,
чтобы они были равны».
– теорема,
то A называется достаточным условием для B,
а B – необходимым условием для A.
Например, теорему «Если квадраты равны,
то их площади равны» можно сформулировать
в виде необходимого условия: «Для того
чтобы квадраты были равны, необходимо,
чтобы их площади были равны»; или
достаточного условия: «Для того чтобы
площади двух квадратов были равны, достаточно,
чтобы они были равны».
Если
вместе с 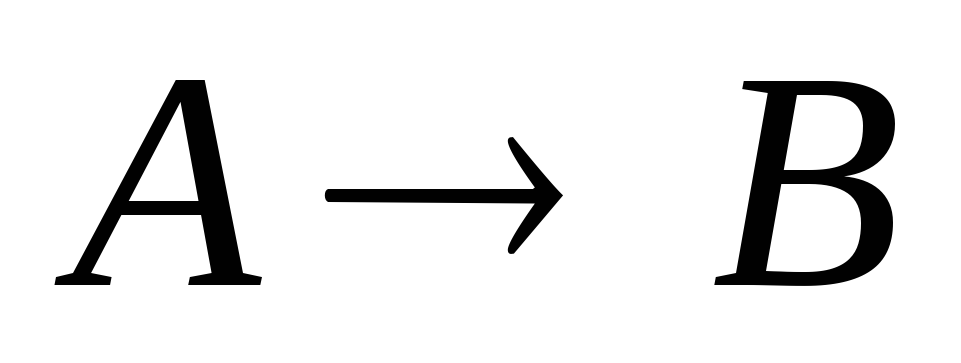 предложение
предложение  также является теоремой,
то A называется необходимым
и достаточным условием для B,
а B – необходимым
и достаточным условием для A.
В
логике это выражение соответствует
эквиваленции, которая, как известно,
представима в виде конъюнкции двух
импликаций. Одна из этих импликаций
выражает теорему, доказывающую необходимость признака,
другая выражает теорему, доказывающую достаточность признака.
Например, признак перпендикулярности
двух плоскостей:
также является теоремой,
то A называется необходимым
и достаточным условием для B,
а B – необходимым
и достаточным условием для A.
В
логике это выражение соответствует
эквиваленции, которая, как известно,
представима в виде конъюнкции двух
импликаций. Одна из этих импликаций
выражает теорему, доказывающую необходимость признака,
другая выражает теорему, доказывающую достаточность признака.
Например, признак перпендикулярности
двух плоскостей:
«Для
того чтобы две плоскости были
перпендикулярны, необходимо
и достаточно,
чтобы одна из них проходила через прямую,
перпендикулярную к другой», может быть
сформулирован и так: «Две плоскости
перпендикулярны, ЕСЛИ И ТОЛЬКО ЕСЛИ
одна из них проходит через прямую,
перпендикулярную к другой»:  или
или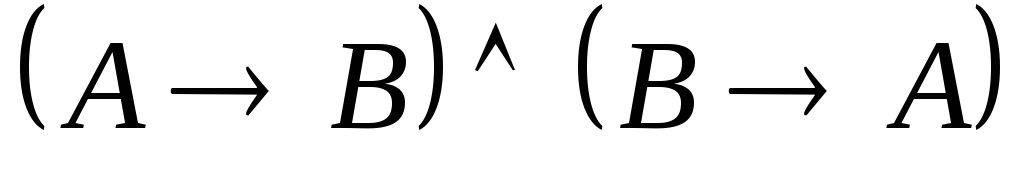 .
.
Если
же 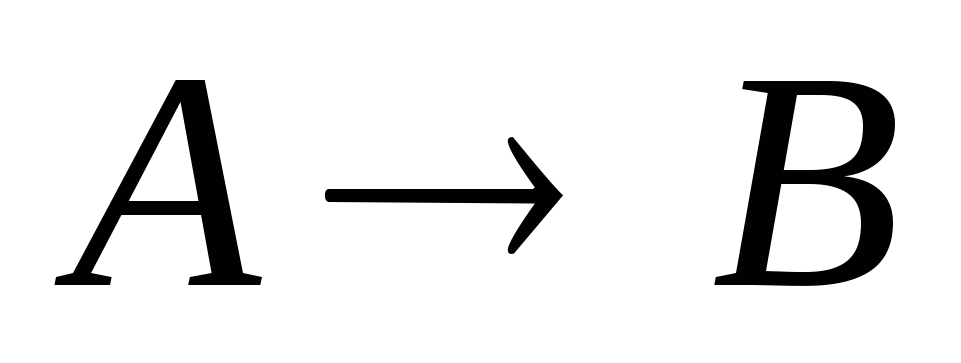 – теорема, а предложение
– теорема, а предложение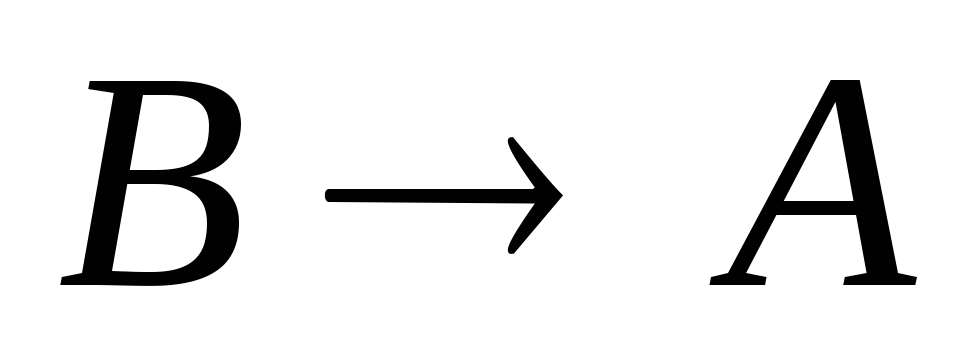 теоремой не является, тоА называется достаточным,
но не необходимым условием для В,
а В – необходимым,
но не достаточным условием для А.
теоремой не является, тоА называется достаточным,
но не необходимым условием для В,
а В – необходимым,
но не достаточным условием для А.
Умозаключение – это мысль, в ходе которой из одного или нескольких суждений выводится новое суждение.
При этом исходные суждения называются посылками, а полученное суждение – заключением или следствием. Аристотель приводил такой пример умозаключения: “Все люди смертны.” и “Сократ – человек.” — посылки. “Сократ смертен” – заключение. Переход от посылок к заключению происходит по правилом вывода и законам логики.
ПРАВИЛО 1: Если посылки умозаключения истинны, то истинно и заключение.
ПРАВИЛО 2: Если умозаключение справедливо во всех случаях, то оно справедливо и в каждом частном случае. (Это правило ДЕДУКЦИИ – переход от общего к частному)
Приведите пример дедуктивного вывода. С именем какого литературного героя связано понятие дедукции?
ПРАВИЛО 3: Если умозаключение справедливо в некоторых частных случаях, то оно справедливо во всех случаях. (Это правило ИНДУКЦИИ – переход от частного к общему.)
studfile.net
Основные аксиомы стереометрии и следствия из них
Раздел геометрии, в котором изучаются фигуры, расположенные в пространстве, называется стереометрией.
Основными понятиями стереометрии являются точка, прямая и плоскость. Пространство состоит из бесконечного множества точек. Прямые и плоскости состоят из бесконечного множества точек пространства и не совпадают со всем пространством.
Сформулируем основные аксиомы стереометрии. Напомним, аксиомы — это предложения, принимаемые без доказательства. Аксиомы геометрии являются абстракцией соответствующих свойств окружающего нас реального мира.
Будем предполагать, что для любой плоскости пространства выполняются все аксиомы, определения и теоремы планиметрии. Кроме того, будем предполагать справедливыми следующие аксиомы стереометрии:
1. Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.2. Если две различные точки прямой принадлежат плоскости, то все точки прямой принадлежат этой плоскости.
3. Если две различные плоскости пересекаются, то они пересекаются по прямой.
Используя эти аксиомы, докажем следующие утверждения:
Следствие 1. Через прямую и не принадлежащую ей точку проходит единственная плоскость.
Доказательство. На данной прямой l возьмем какие-нибудь две точки А и В (рис.).
Тогда по аксиоме 1 через данную точку М и точки А и В проходит единственная плоскость р и все точки прямой l принадлежат плоскости р.
Следовательно, плоскость р проходит через прямую l и не принадлежащую ей точку М. Другой такой плоскости нет, так как она должна проходить через три точки А, В, М, не лежащие на одной прямой, и, следовательно, должна совпасть с плоскостью р.
Следствие 2. Через две пересекающиеся прямые проходит единственная плоскость.
Доказательство. Действительно, пусть прямые 11 и 12 пересекаются в точке М (рис.).
razdupli.ru
2.2. Аксиома выбора, лемма Цорна, теорема Цермело
Одной из аксиом аксиоматической системы Цермело – Френкеля является аксиома выбора. Фактически мы ею уже пользовались: например, когда доказывали, что всякое бесконечное множество имеет счётное подмножество. Дадим точную формулировку этой аксиомы.
Аксиома
выбора. Если  – непустое множество, то в каждом его
непустом подмножестве можно выбрать
по одному элементу. Иными словами,
существуетфункция
выбора
– непустое множество, то в каждом его
непустом подмножестве можно выбрать
по одному элементу. Иными словами,
существуетфункция
выбора 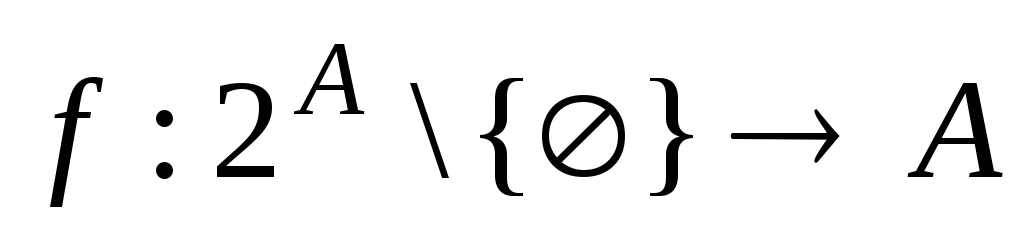 такая, что
такая, что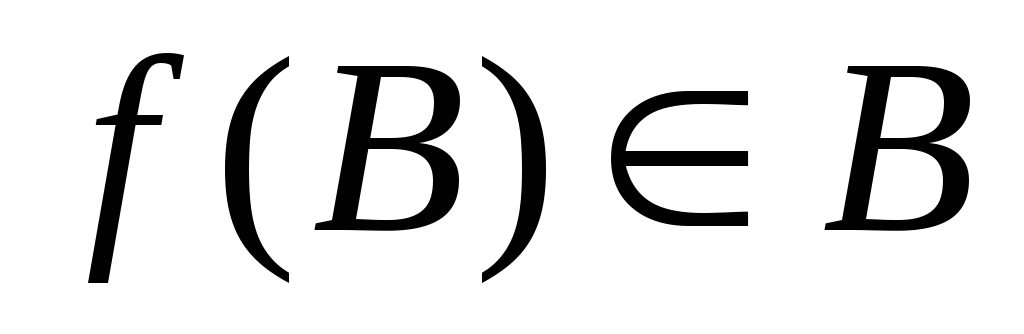 при любом непустом
при любом непустом
Замечание. Хотя аксиома выбора кажется интуитивно очевидной, не все математики её принимают. В частности, интуиционисты и конструктивисты её отвергают за её неконструктивный характер (в самом деле, аксиома утверждает, что можно выбрать по одному элементу, но как это сделать, она не говорит).
Вполне упорядоченные множества
Определение.
Множество  называетсявполне
упорядоченным,
если оно линейно упорядочено и любое
непустое его подмножество имеет
наименьший элемент.
называетсявполне
упорядоченным,
если оно линейно упорядочено и любое
непустое его подмножество имеет
наименьший элемент.
Утверждение.
Линейно упорядоченное множество является
вполне упорядоченным, если и только
если оно не содержит бесконечных
убывающих последовательностей элементов 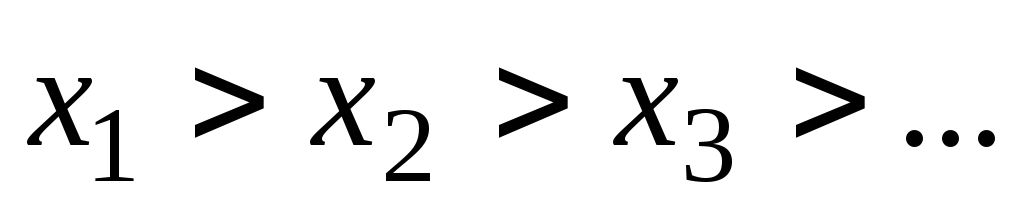
Доказательство.
Необходимость. Пусть  вполне упорядочено и в нём есть убывающая
цепь
вполне упорядочено и в нём есть убывающая
цепь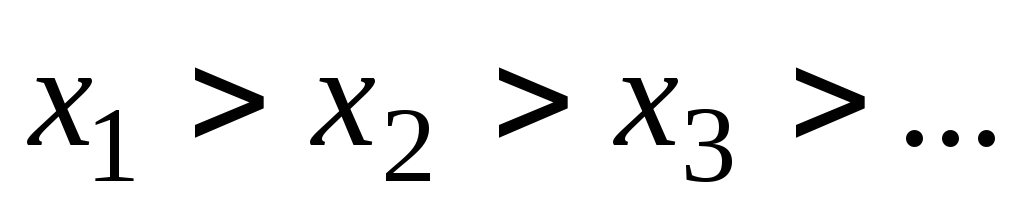 Тогда множество
Тогда множество
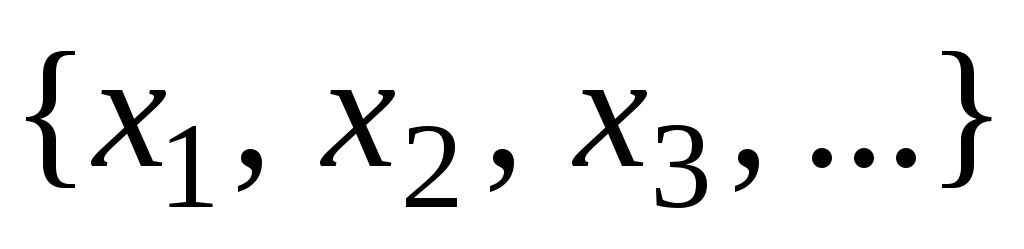 не имеет наименьшего элемента –
противоречие.
не имеет наименьшего элемента –
противоречие.
Достаточность.
Пусть  – линейно упорядоченное множество без
бесконечных убывающих цепей элементов.
Рассмотрим какое-нибудь непустое
подмножество
– линейно упорядоченное множество без
бесконечных убывающих цепей элементов.
Рассмотрим какое-нибудь непустое
подмножество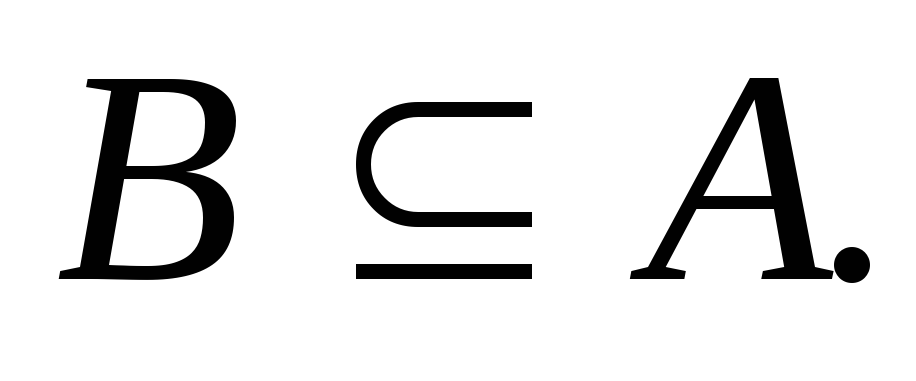 Пусть
Пусть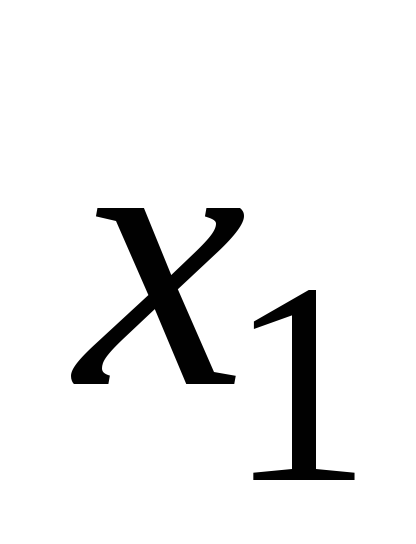 – какой-нибудь элемент из
– какой-нибудь элемент из Если он не наименьший, то существует
Если он не наименьший, то существует такое, что
такое, что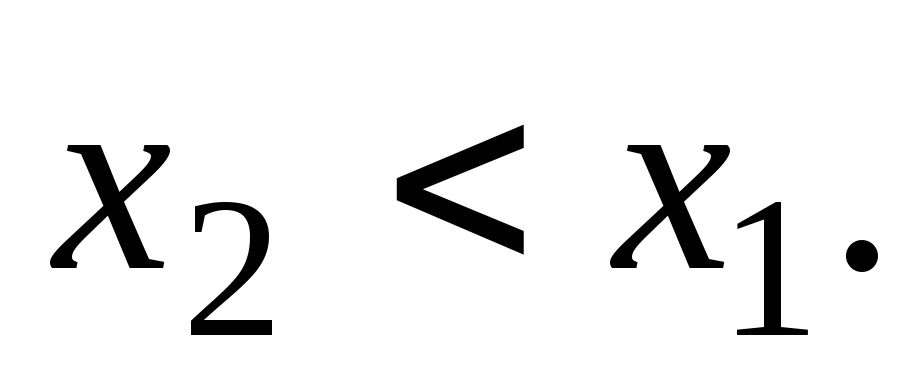 Если
Если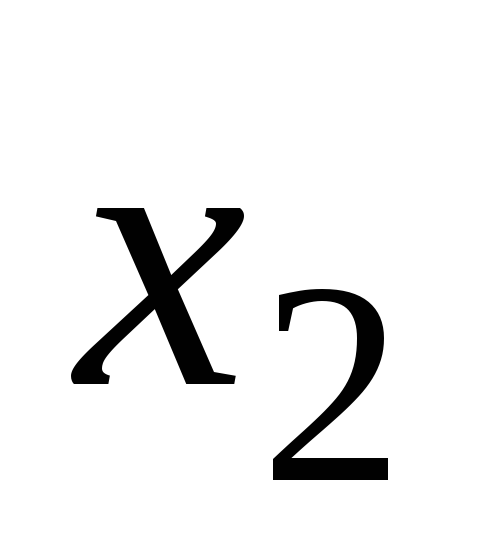 не наименьший, то существует
не наименьший, то существует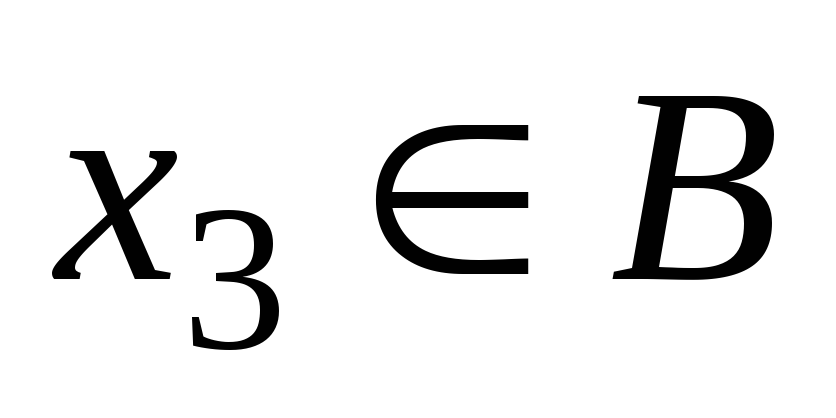 такое, что
такое, что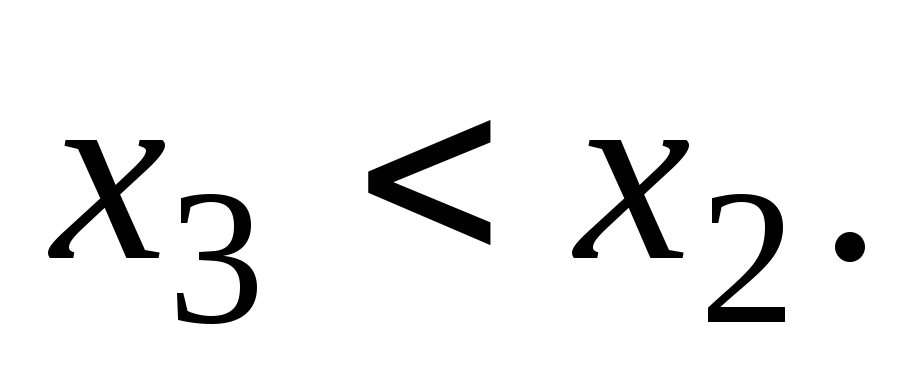 И т.д. Если
И т.д. Если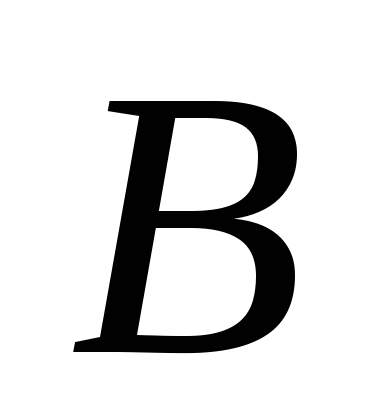 не имеет наименьшего элемента, то
существует бесконечная убывающая цепь
не имеет наименьшего элемента, то
существует бесконечная убывающая цепь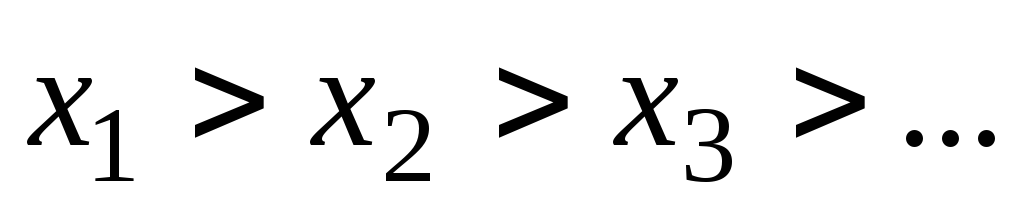 ,
что противоречит условию.
,
что противоречит условию.
Пример 1. Множество N натуральных чисел с обычным отношением порядка является вполне упорядоченным.
Пример
2. Множество N N с отношением
лексикографического порядка
N с отношением
лексикографического порядка 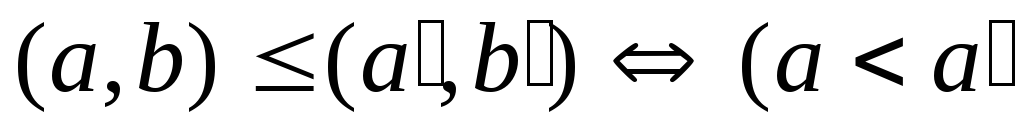 или
или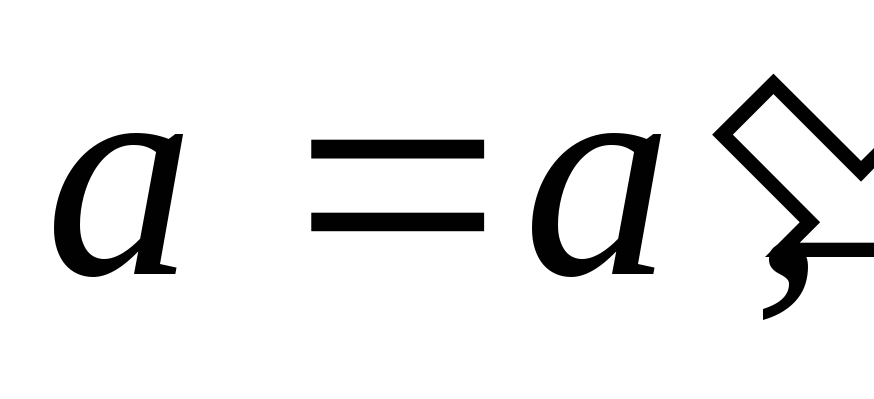
 является вполне упорядоченным.
является вполне упорядоченным.
Докажем
это. То, что это множество линейно
упорядочено, очевидно. Осталось доказать,
что любое непустое подмножество имеет
наименьший элемент. Пусть 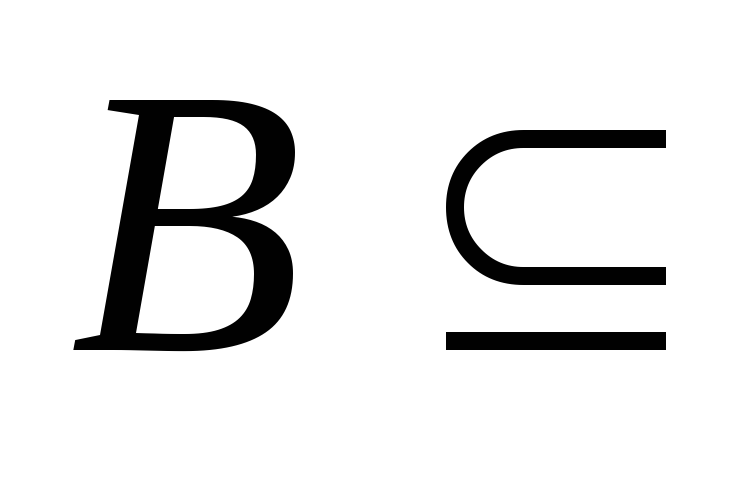 N
N N – непустое
подмножество. Выберем элемент
N – непустое
подмножество. Выберем элемент  у которого
у которого – наименьшее среди
– наименьшее среди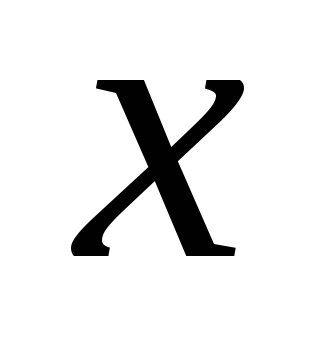 таких, что
таких, что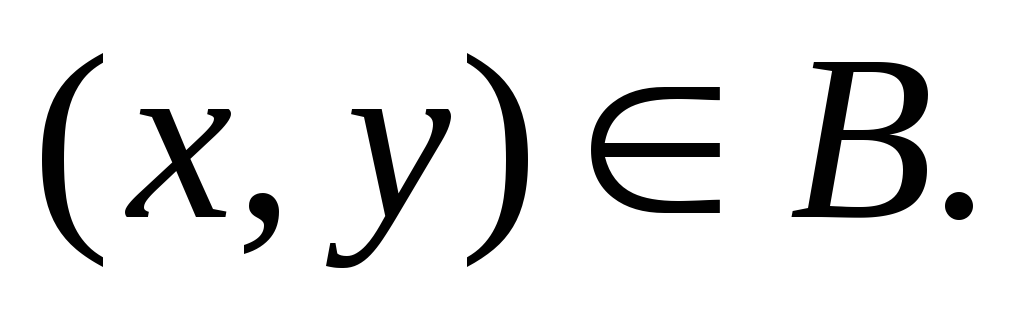 Рассмотрим теперь лишь те элементы из
Рассмотрим теперь лишь те элементы из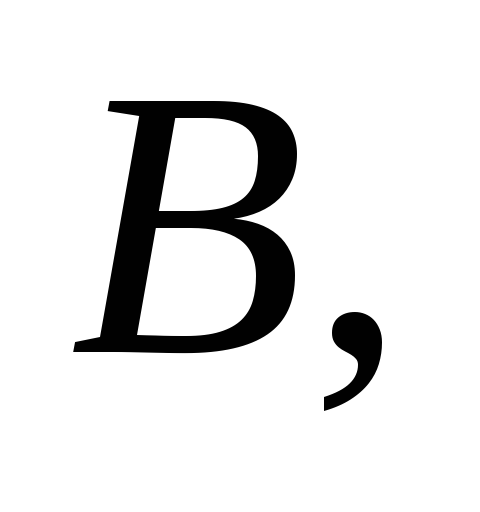 которые имеют вид
которые имеют вид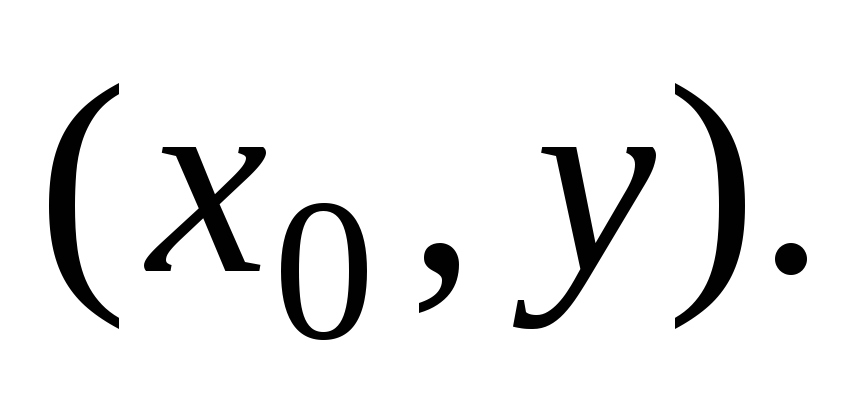 Среди всех таких
Среди всех таких выберем наименьшее
выберем наименьшее Нетрудно проверить, что
Нетрудно проверить, что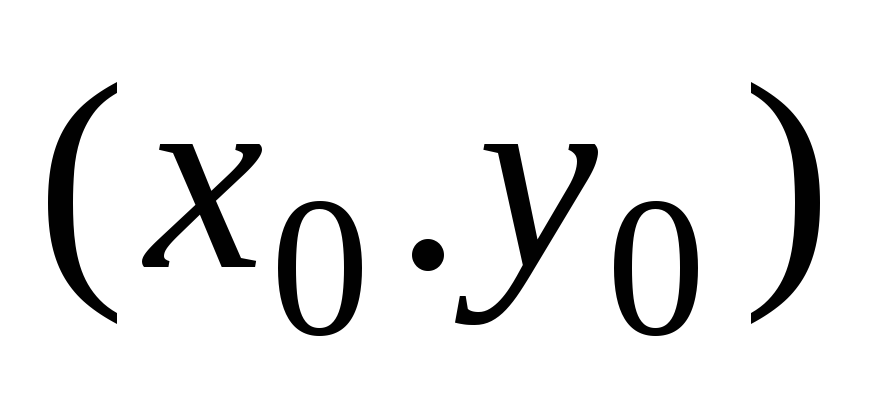 – наименьший элемент в
– наименьший элемент в
Пример
3. Множество 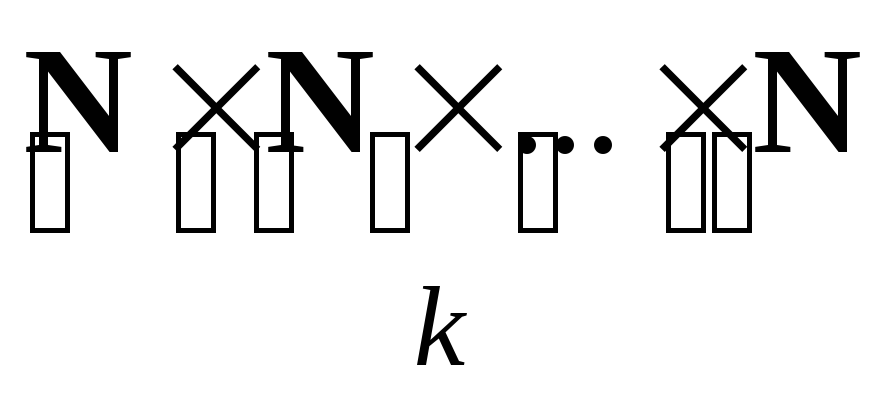 с лексикографическим порядком
с лексикографическим порядком
Доказательство проводится аналогично примеру 2.
Свойства вполне упорядоченных множеств
любое подмножество вполне упорядоченного множества вполне упорядочено;
если
 и
и – два непересекающихся вполне
упорядоченных множества, то порядок
на множестве
– два непересекающихся вполне
упорядоченных множества, то порядок
на множестве определённый следующим образом:
определённый следующим образом:
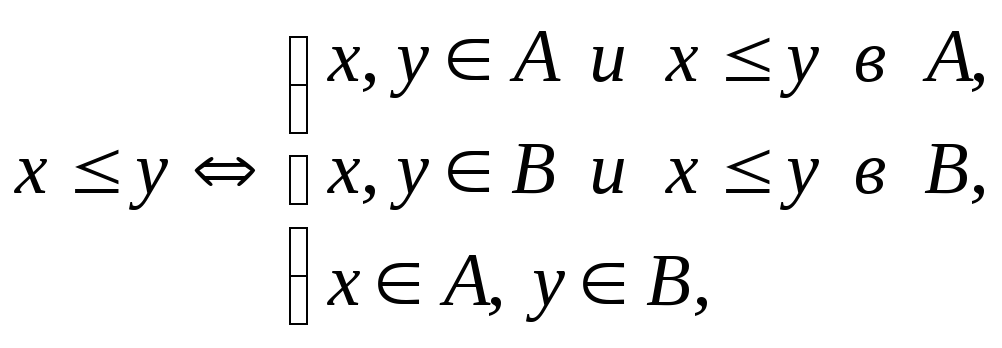
превращает 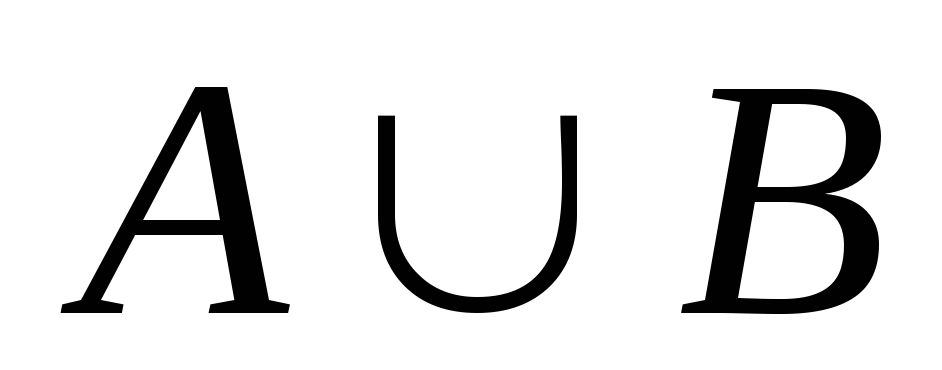 во вполне упорядоченное множество.
во вполне упорядоченное множество.
Доказательство очевидно.
Определение.
Пусть  – линейно упорядоченное множество.Начальным
отрезком множества
– линейно упорядоченное множество.Начальным
отрезком множества  назовём такое подмножество
назовём такое подмножество что
что
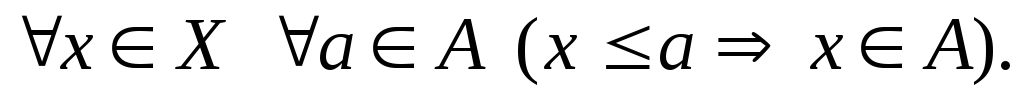
Лемма
1. Для любых
двух начальных отрезков  линейно упорядоченного множества
линейно упорядоченного множества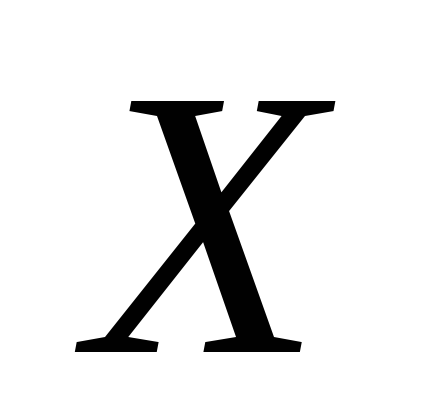 либо
либо либо
либо
Доказательство.
Пусть 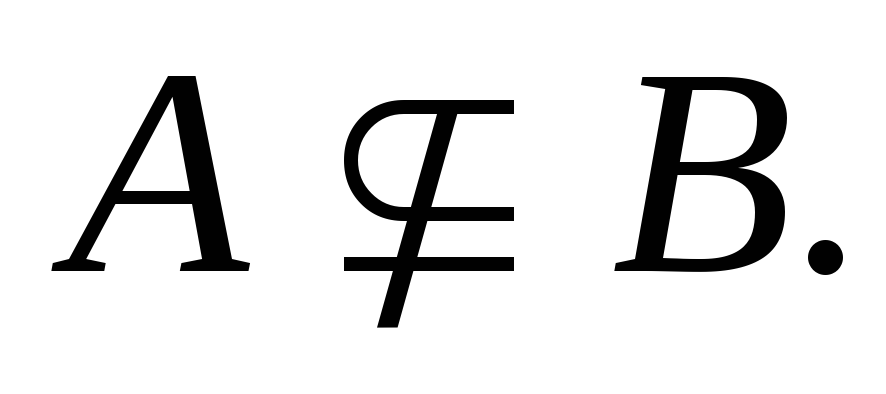 Тогда существует
Тогда существует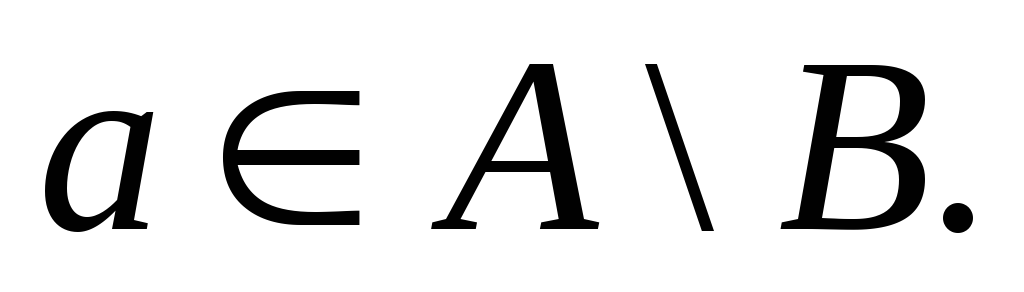 Возьмём любой элемент
Возьмём любой элемент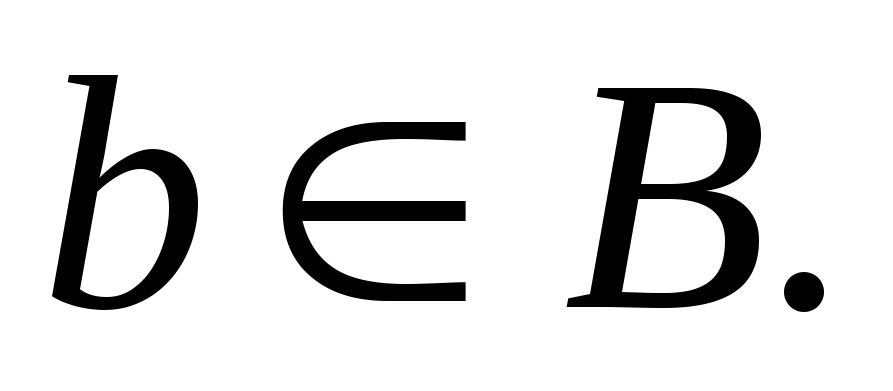 Если бы
Если бы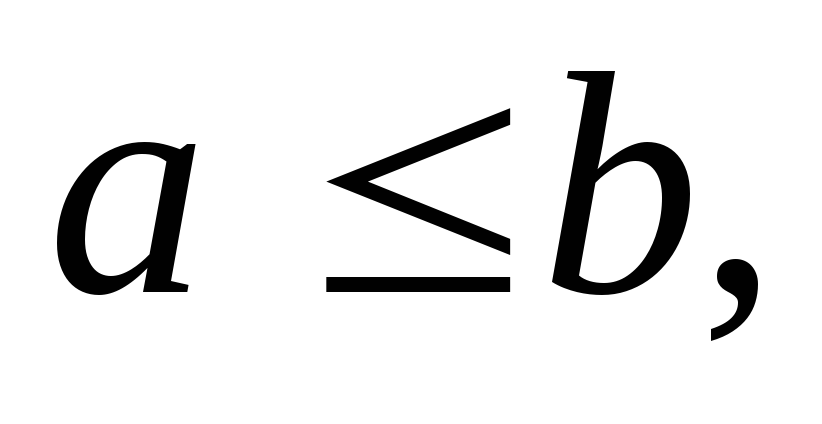 то
то что невозможно. Значит,
что невозможно. Значит,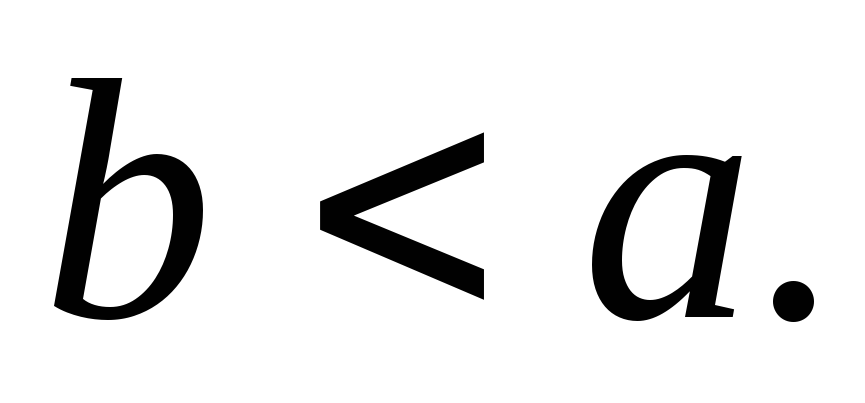 Отсюда следует, что
Отсюда следует, что Итак, любой элемент
Итак, любой элемент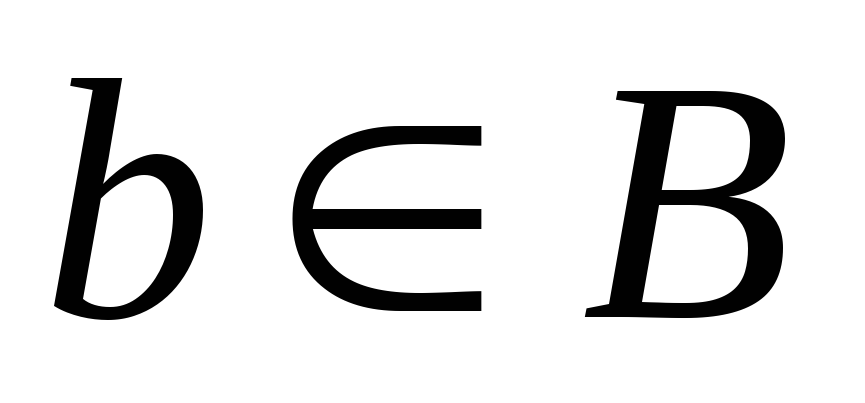 лежит в
лежит в Следовательно,
Следовательно,
Определение. Два линейно упорядоченных множества называются изоморфными, если между ними существует взаимно однозначное соответствие, сохраняющее порядок.
Теорема 1. Для любых двух вполне упорядоченных множеств одно из них изоморфно начальному отрезку другого.
Доказательство.
Пусть 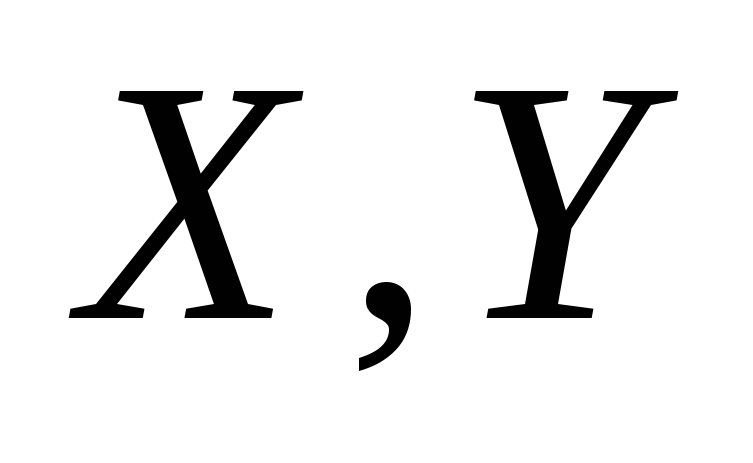 – вполне упорядоченные множества.
Рассмотрим изоморфизмы
– вполне упорядоченные множества.
Рассмотрим изоморфизмы где
где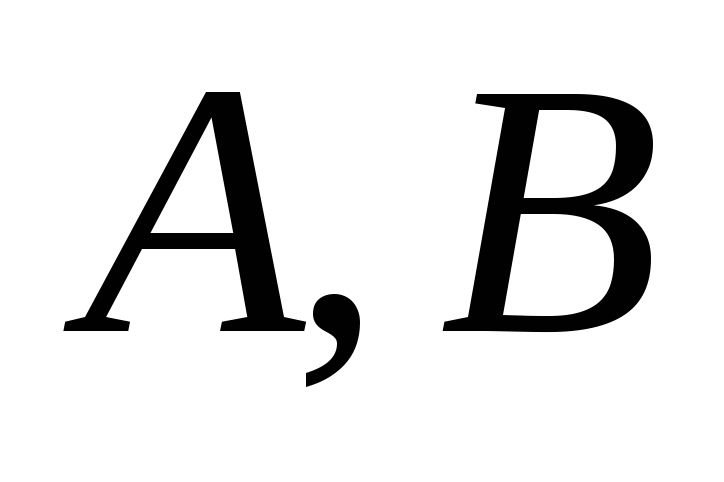 – начальные отрезки множеств
– начальные отрезки множеств Такие изоморфизмы есть. Например, если
Такие изоморфизмы есть. Например, если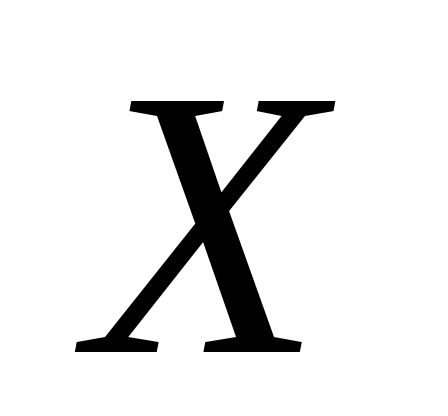 и
и непусты, а
непусты, а и
и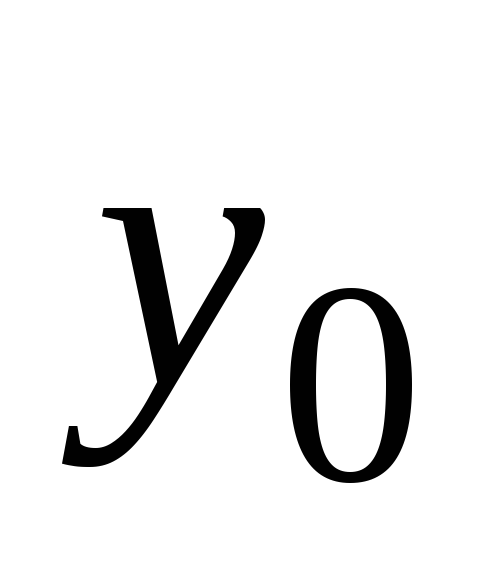 – наименьшие элементы множеств
– наименьшие элементы множеств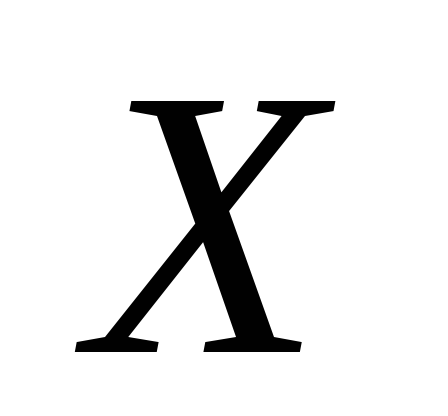 и
и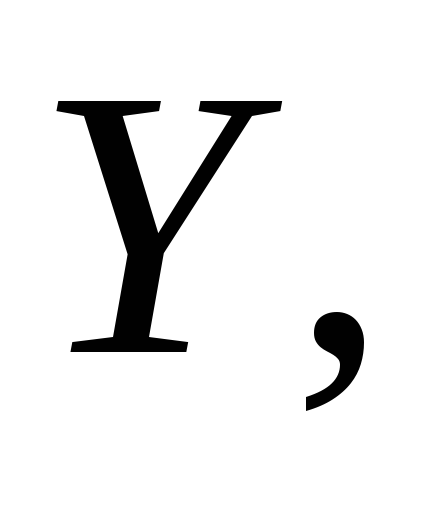 то
то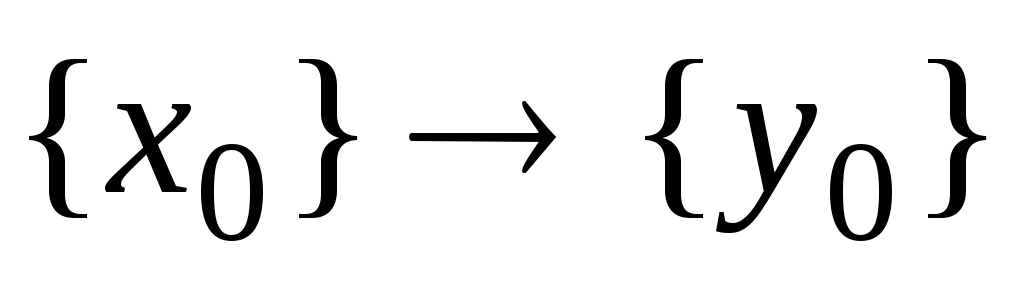 – изоморфизм начальных отрезков. Докажем
теперь, что для каждого начального
отрезка
– изоморфизм начальных отрезков. Докажем
теперь, что для каждого начального
отрезка множества
множества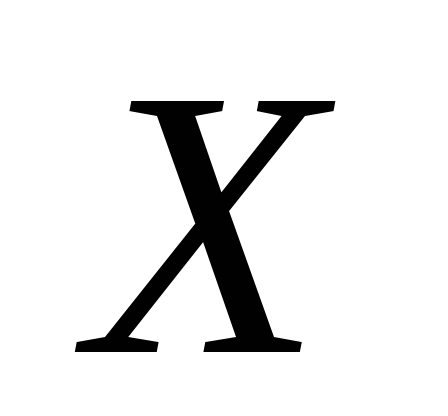 изоморфизм
изоморфизм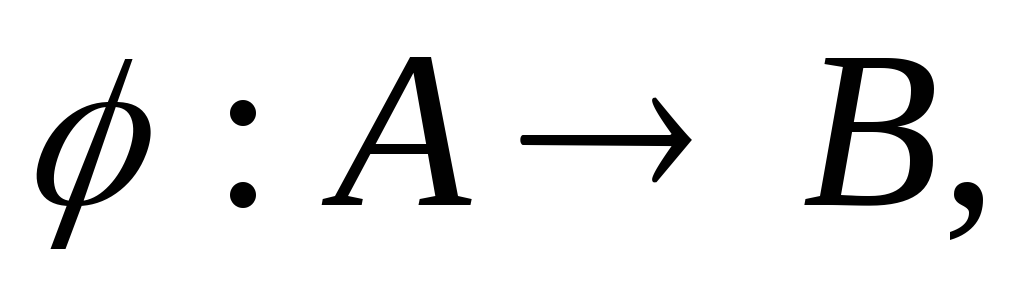 где
где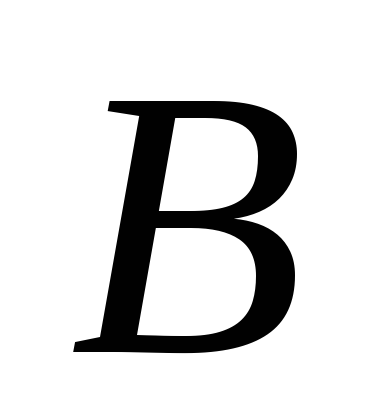 – начальный отрезок множества
– начальный отрезок множества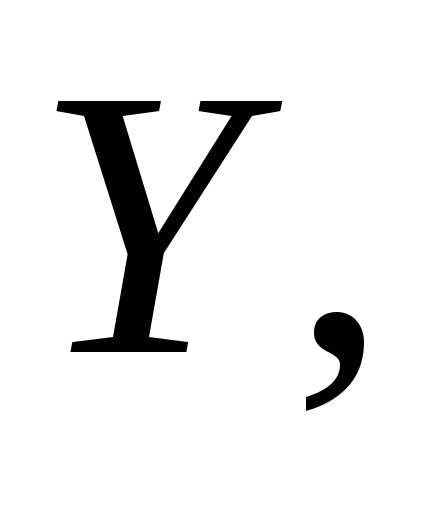 если существует, то однозначен.
Действительно, пусть
если существует, то однозначен.
Действительно, пусть
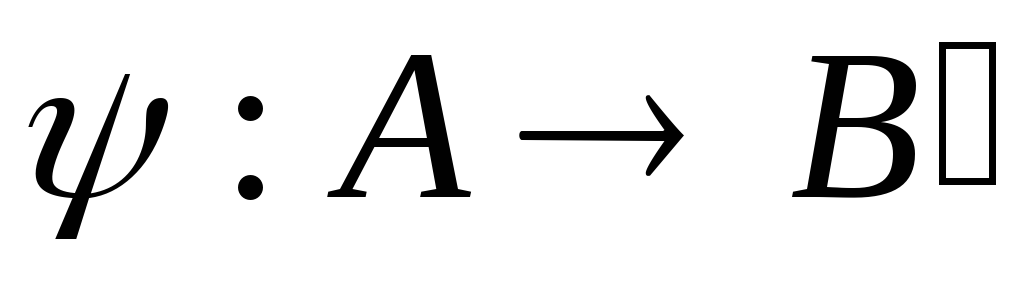 – изоморфизмы, где
– изоморфизмы, где – начальный отрезок множества
– начальный отрезок множества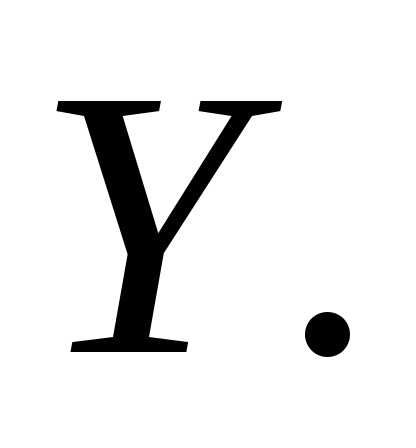 Пусть
Пусть – наименьший элемент из
– наименьший элемент из такой, что
такой, что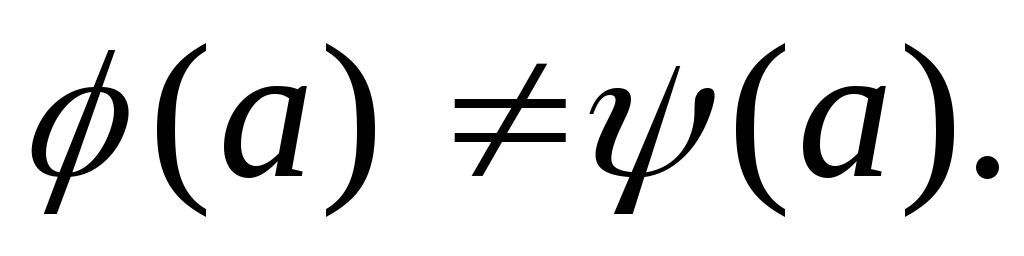 Мы можем считать, что
Мы можем считать, что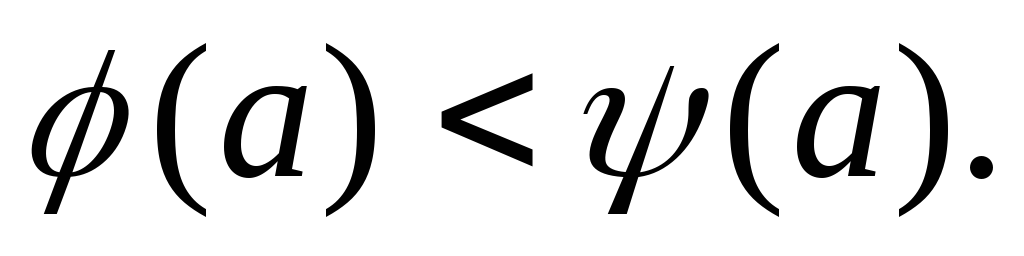 Положим
Положим
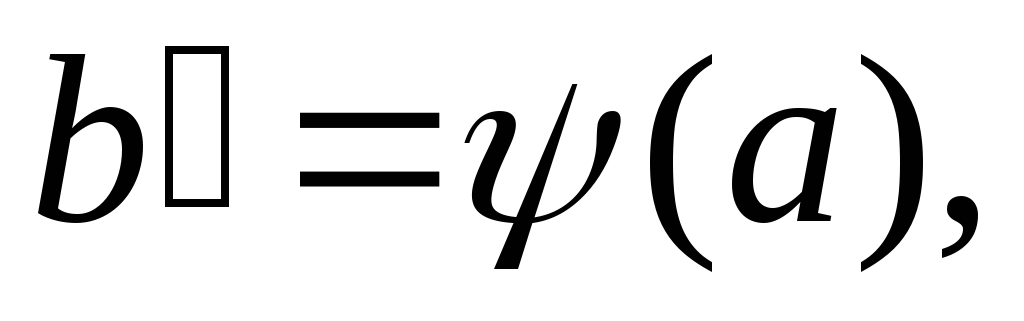
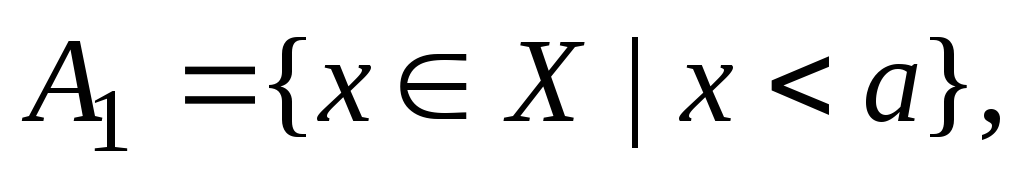
 Очевидно,
Очевидно, отображает взаимно однозначно
отображает взаимно однозначно на
на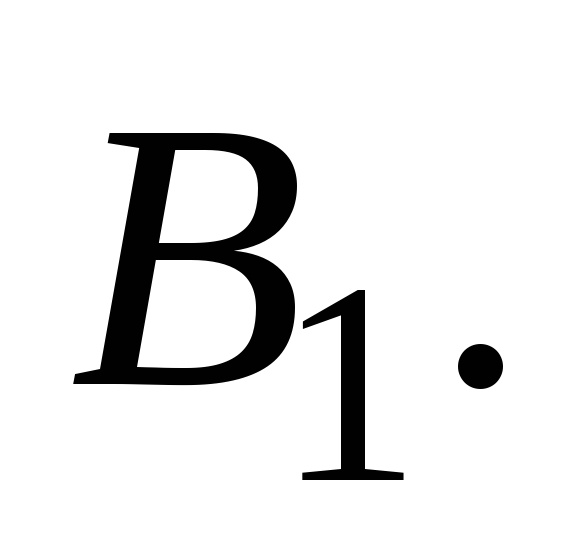 Для
Для
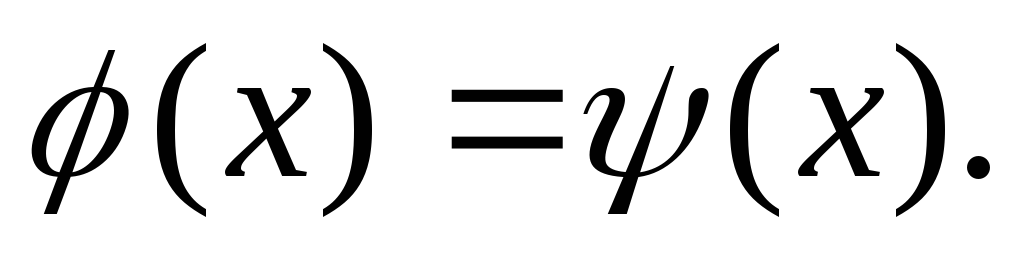 По условию
По условию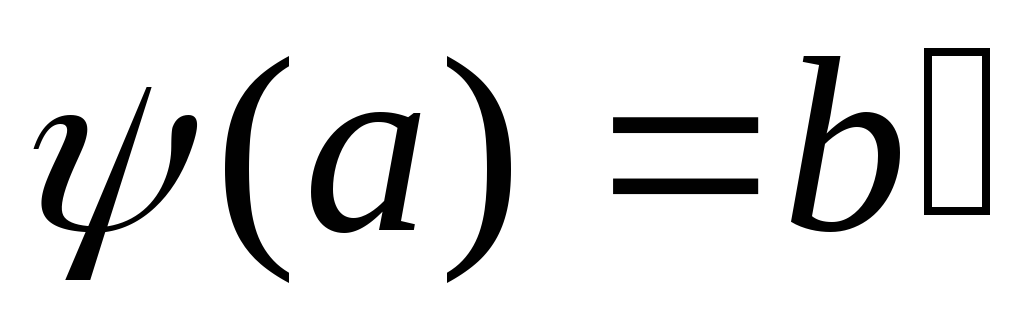 и
и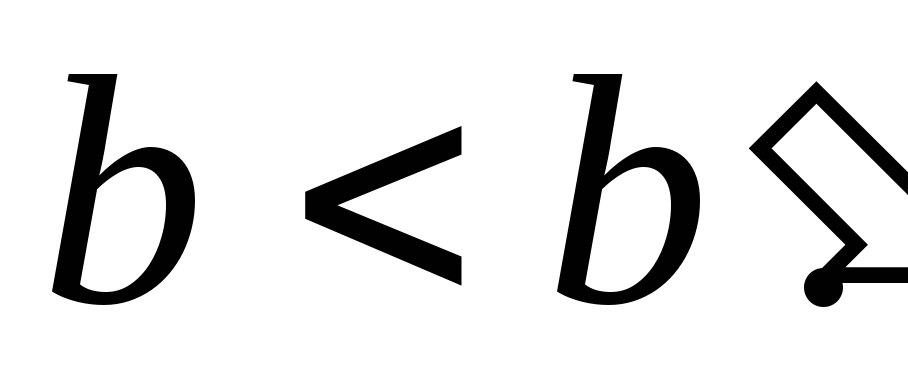 Поэтому
Поэтому при некотором
при некотором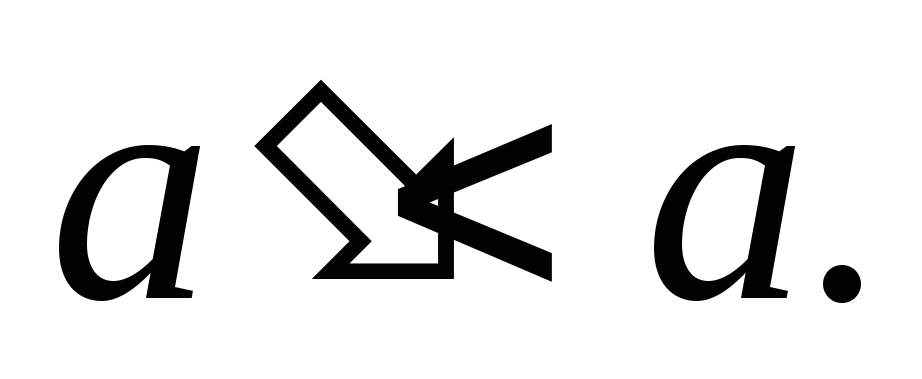 Имеем:что противоречит равенству
Имеем:что противоречит равенству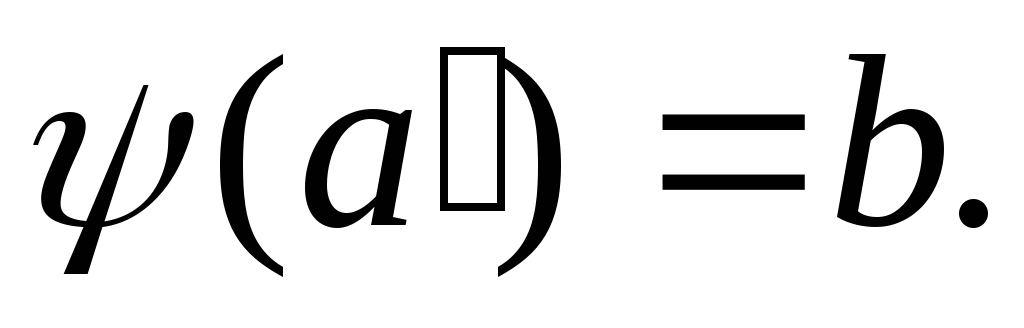
Пусть  – объединение всех начальных отрезков
– объединение всех начальных отрезков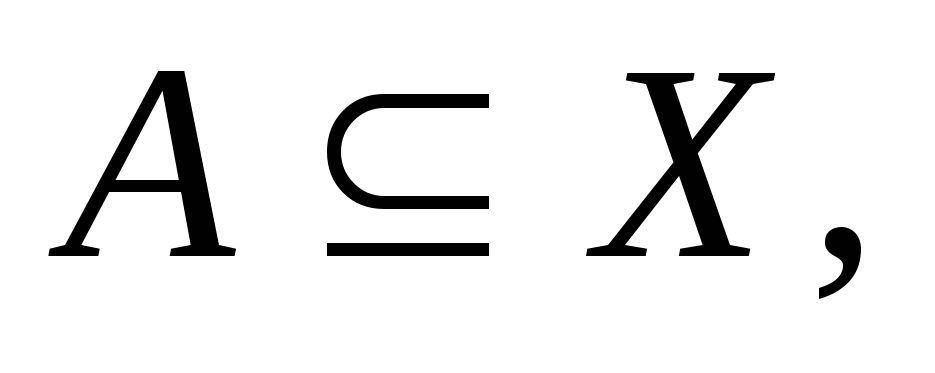 для которых существует изоморфизм
для которых существует изоморфизм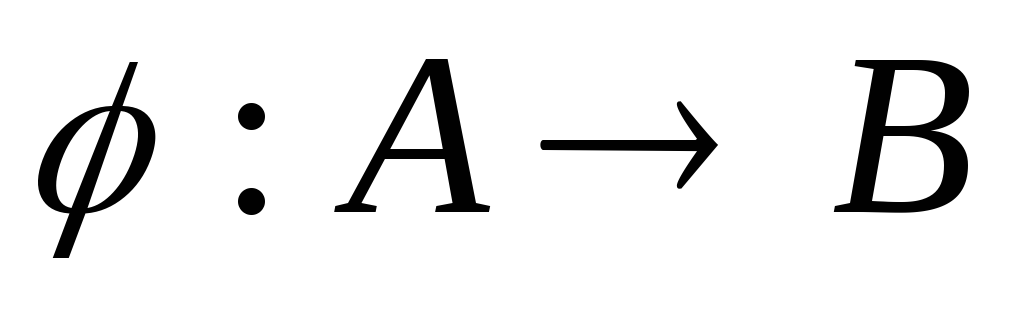 на начальный отрезок
на начальный отрезок множества
множества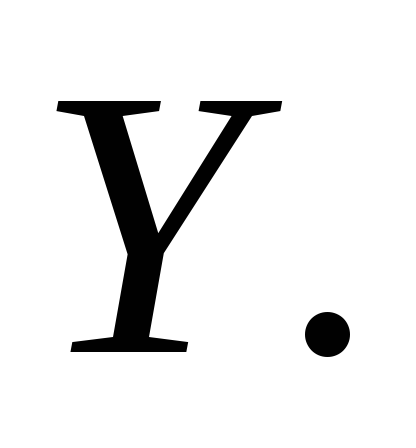 Рассмотрим отображение
Рассмотрим отображение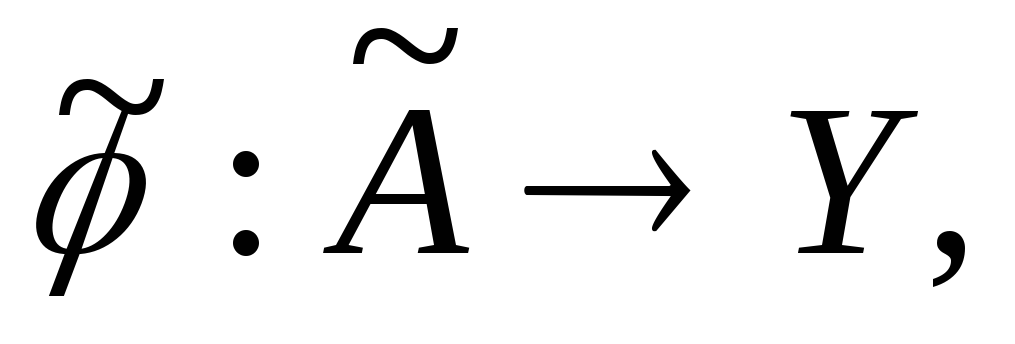 определённое следующим образом: если
определённое следующим образом: если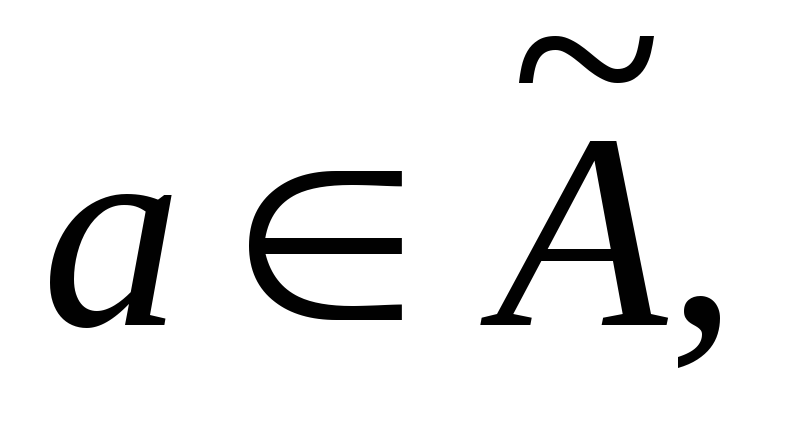 то
то для некоторого
для некоторого для которого есть изоморфизм
для которого есть изоморфизм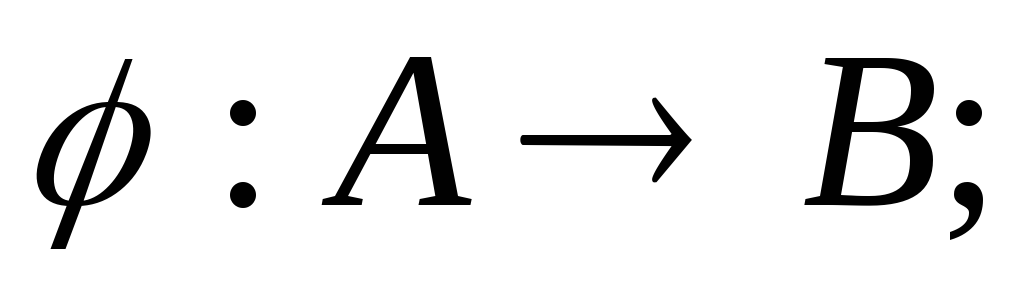 положим
положим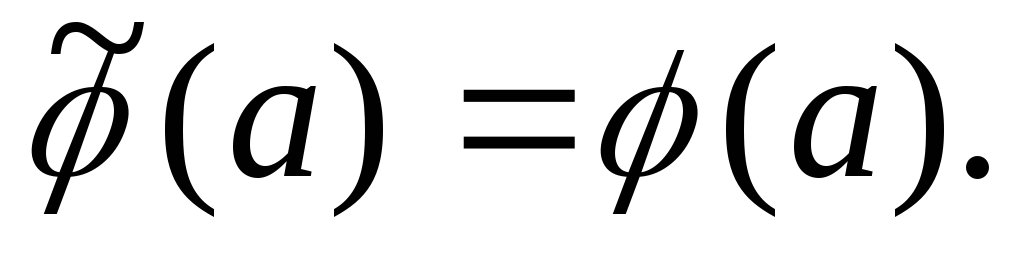 Это определение является корректным,
так как если
Это определение является корректным,
так как если и
и – изоморфизм, то либо
– изоморфизм, то либо либо
либо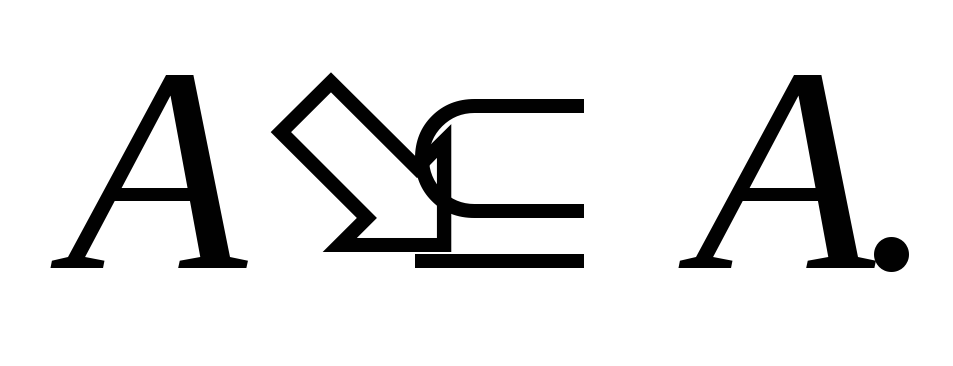 Если
Если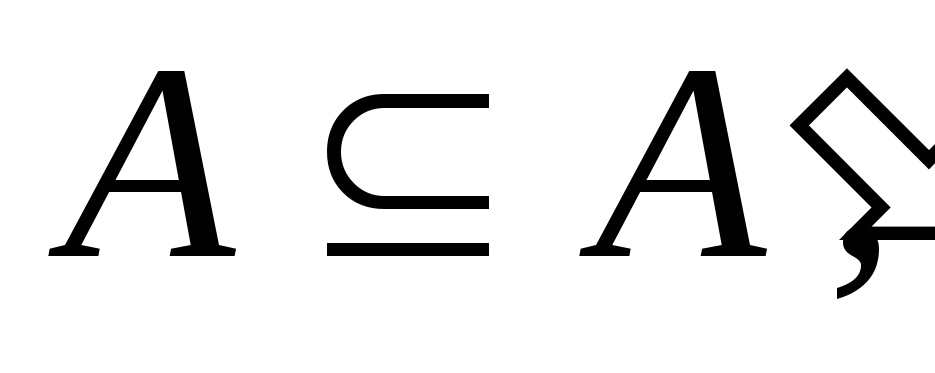 то
то и
и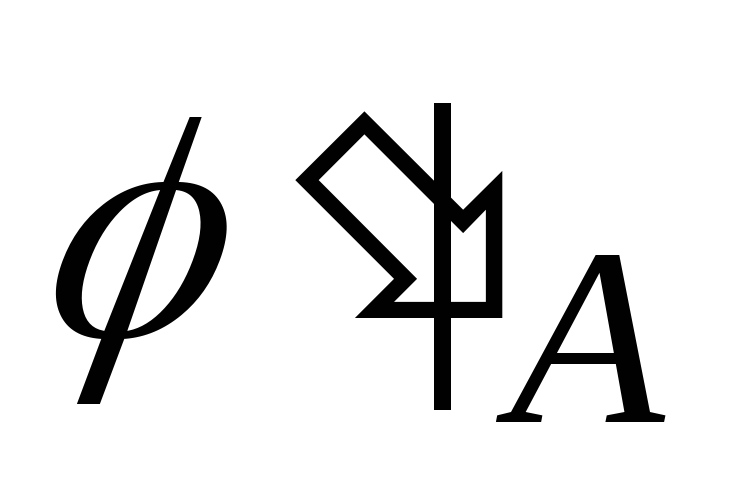 – изоморфизмы начального отрезка
– изоморфизмы начального отрезка на начальный отрезок
на начальный отрезок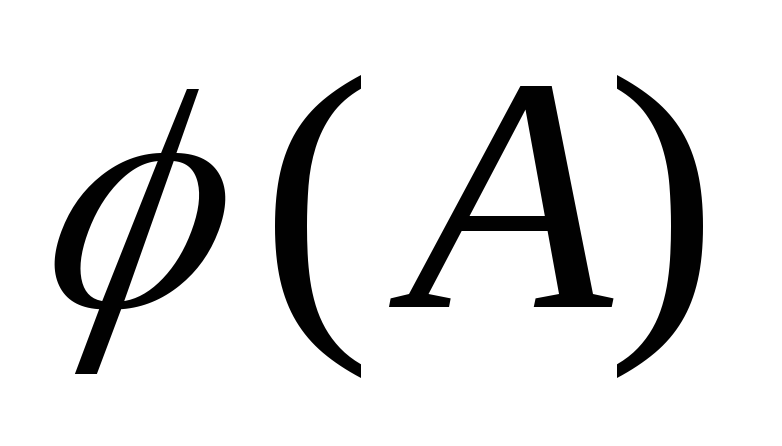 или
или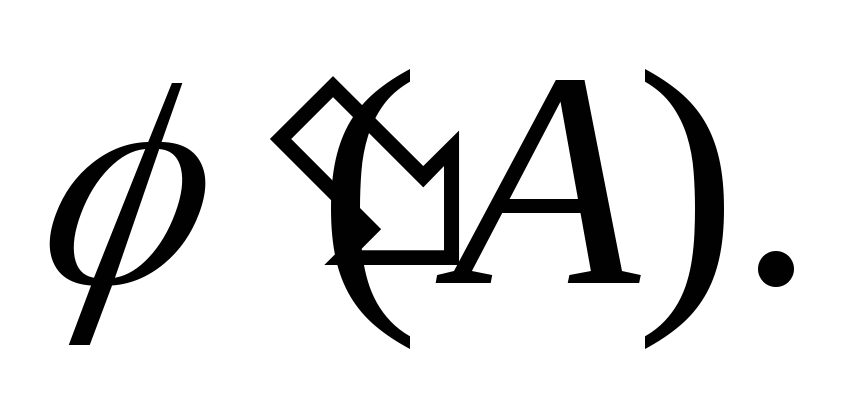 Поэтому
Поэтому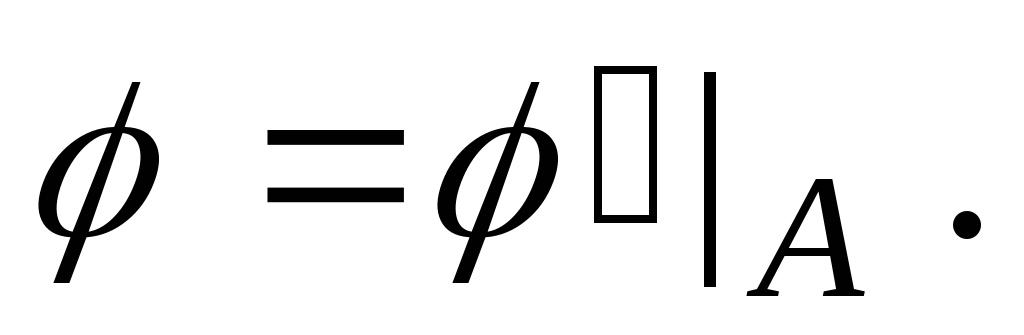 Значит,
Значит,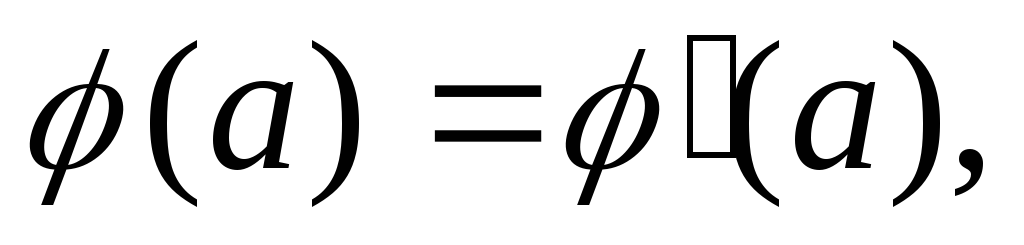 что доказывает корректность определения
отображения
что доказывает корректность определения
отображения
Очевидно,  – наибольший начальный отрезок в
– наибольший начальный отрезок в отображающийся на начальный отрезок в
отображающийся на начальный отрезок в Пусть
Пусть Докажем, что либо
Докажем, что либо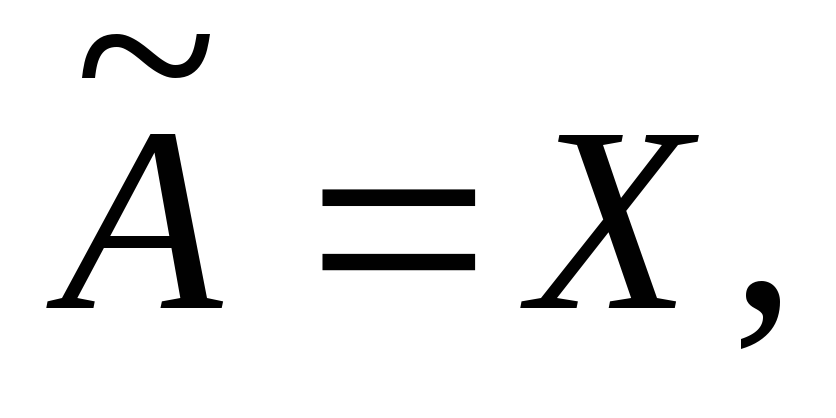 либо
либо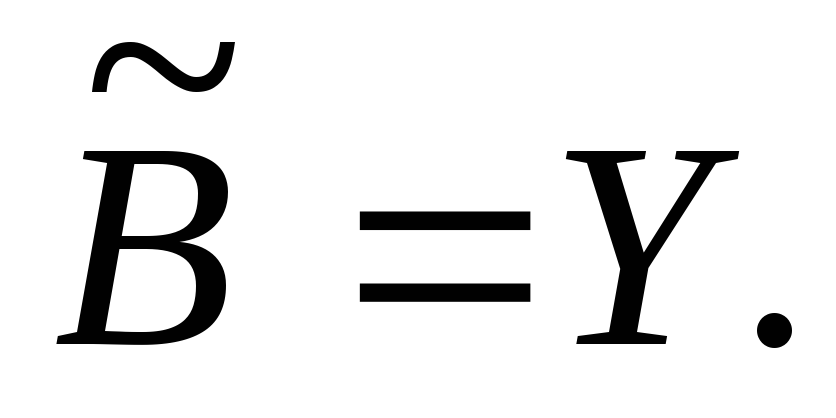 Предположим, что
Предположим, что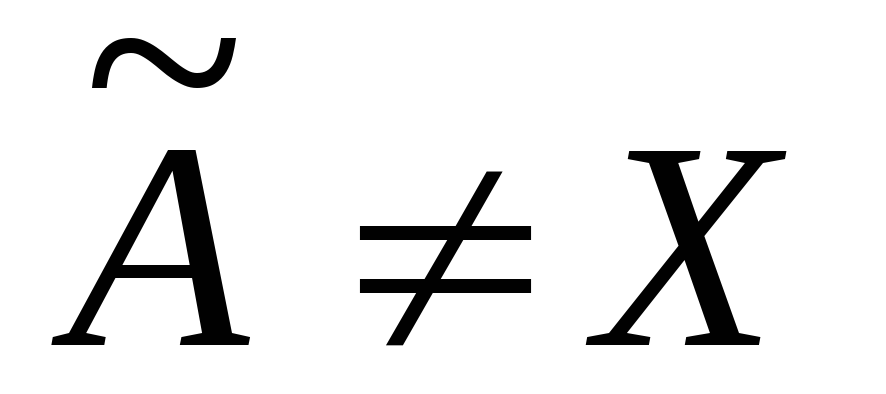 и
и Пусть
Пусть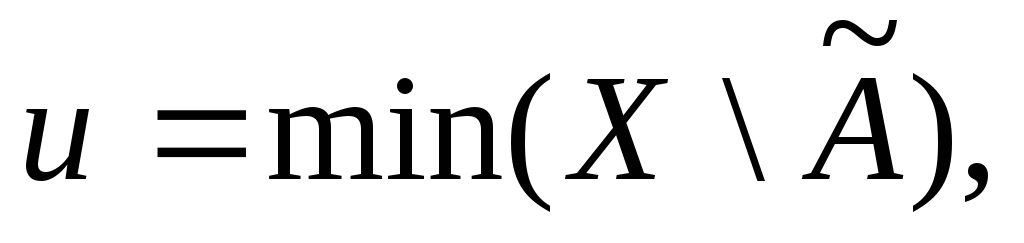
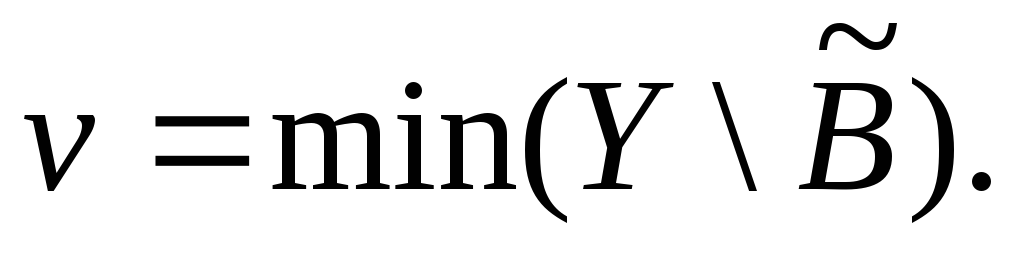 Положим
Положим
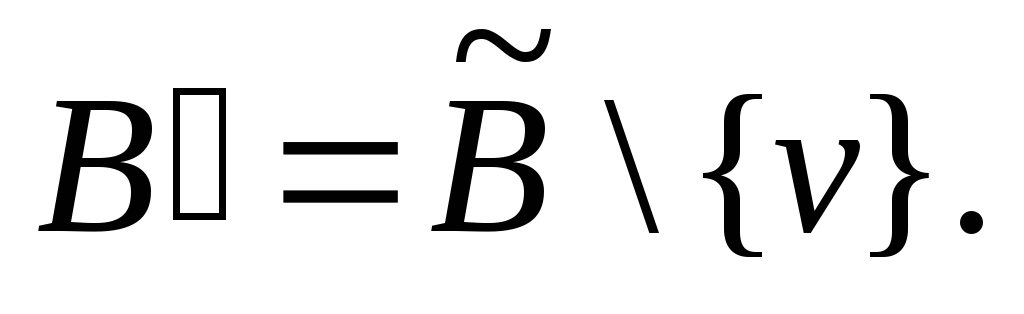 Очевидно,
Очевидно, и
и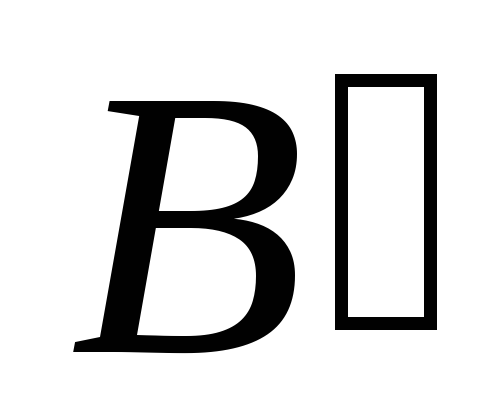 – начальные отрезки множеств
– начальные отрезки множеств и
и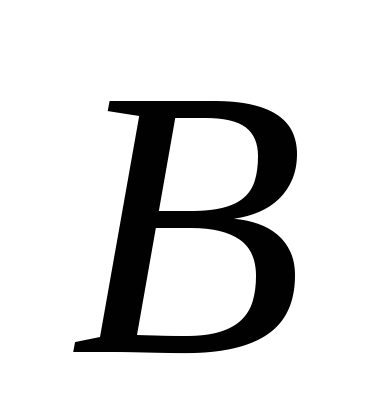 соответственно. Определим отображение
соответственно. Определим отображение полагая
полагая для
для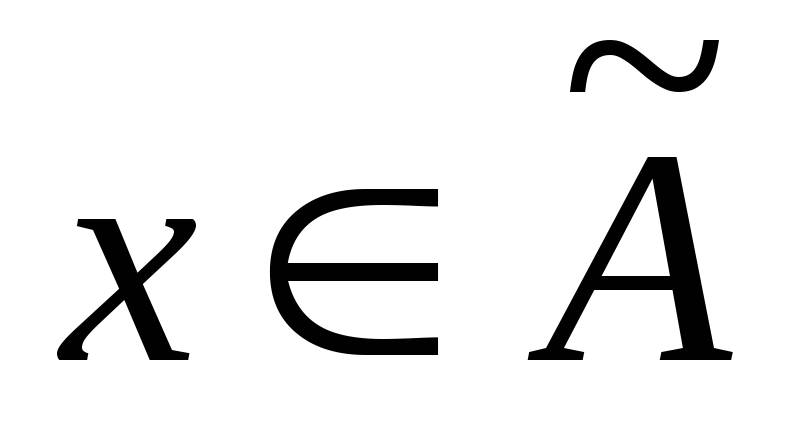 и
и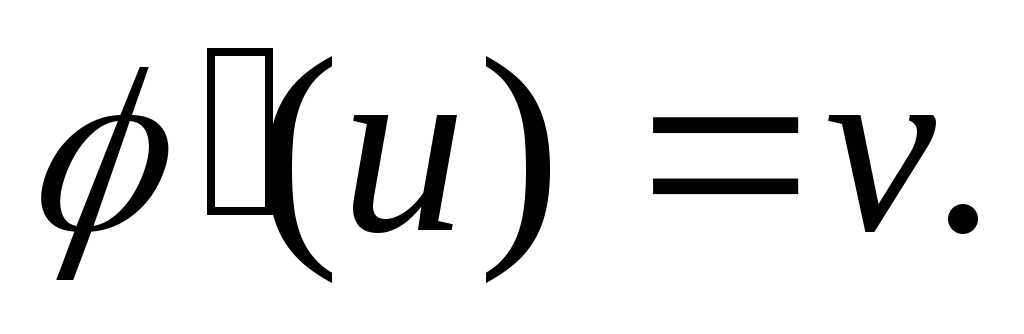 Очевидно,
Очевидно,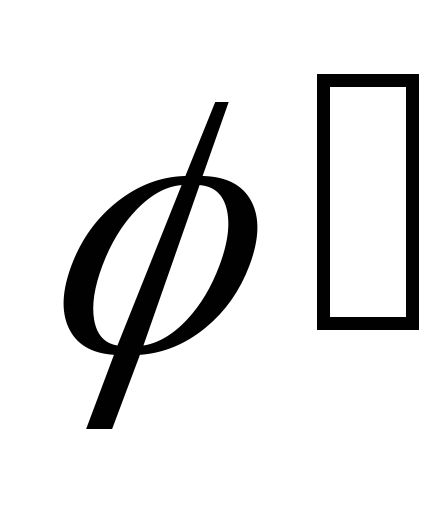 – изоморфизм начальных отрезков
– изоморфизм начальных отрезков и
и Так как
Так как – наибольший начальный отрезок,
изоморфный начальному отрезку в
– наибольший начальный отрезок,
изоморфный начальному отрезку в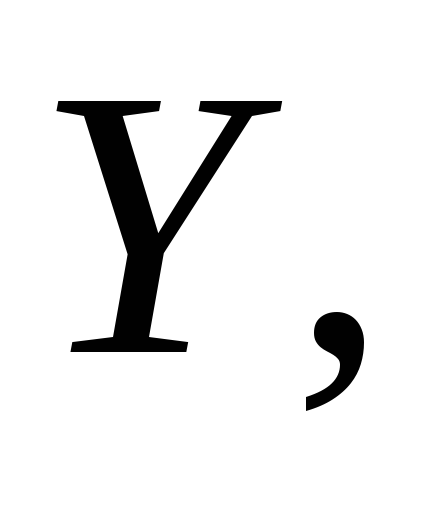 то
то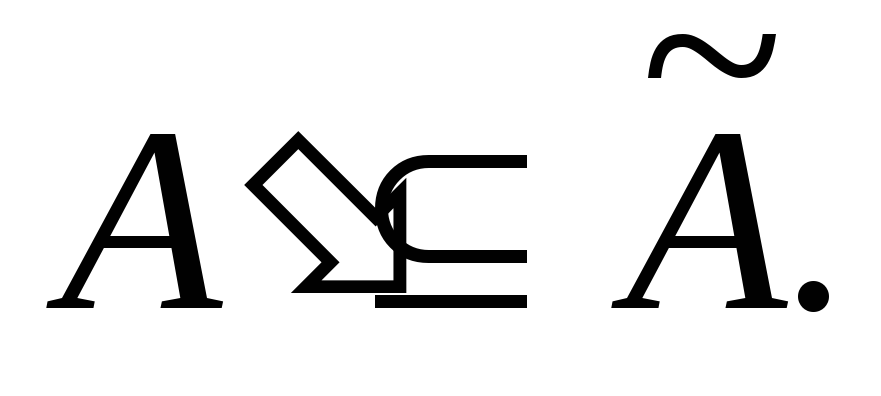 Однако,
Однако, Мы получили противоречие. Следовательно,
Мы получили противоречие. Следовательно,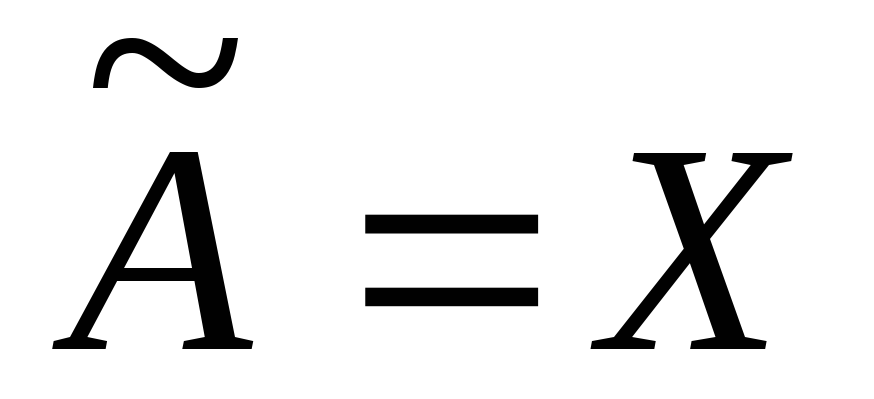 или
или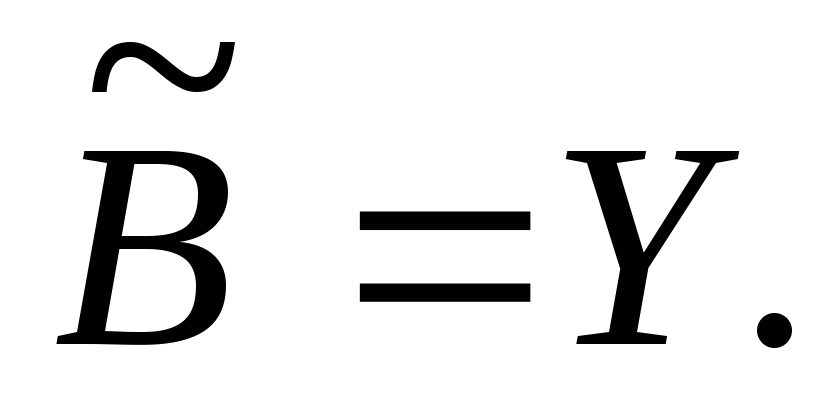 В первом случае множество
В первом случае множество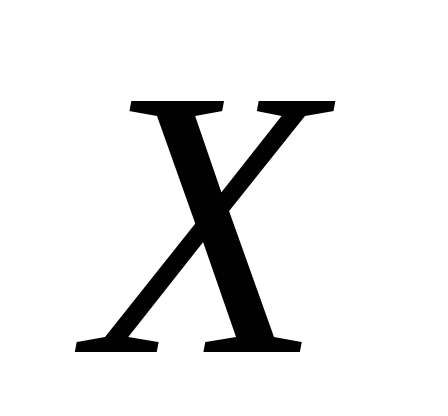 изоморфно начальному отрезку множестваво втором случае наоборот. Теорема
доказана.
изоморфно начальному отрезку множестваво втором случае наоборот. Теорема
доказана.
Лемма
2. Пусть  – вполне упорядоченные множества и
множество
– вполне упорядоченные множества и
множество изоморфно начальному отрезку множества
изоморфно начальному отрезку множества Тогда этот изоморфизм
Тогда этот изоморфизм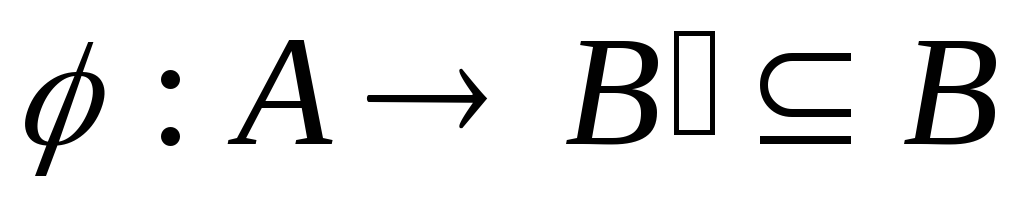 определяется единственным образом.
определяется единственным образом.
Доказательство.
Пусть 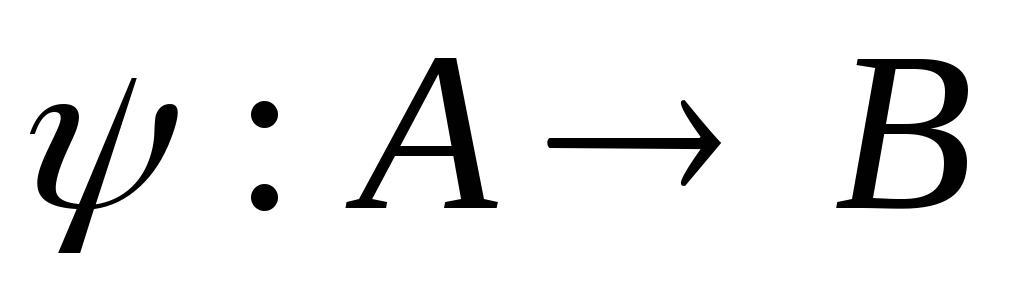 – вложение, сохраняющее порядок, и
– вложение, сохраняющее порядок, и – начальный отрезок множества
– начальный отрезок множества Надо доказать, что
Надо доказать, что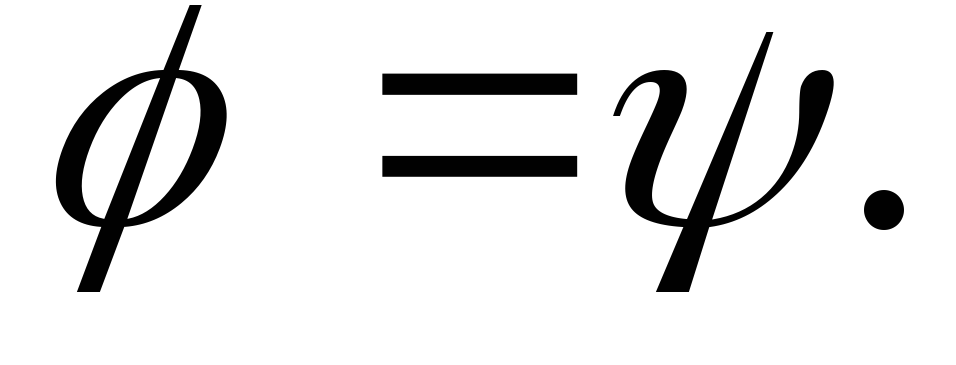 Пусть
Пусть и
и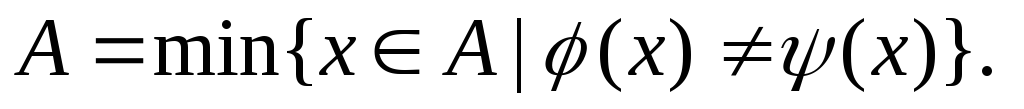 Можно считать, что
Можно считать, что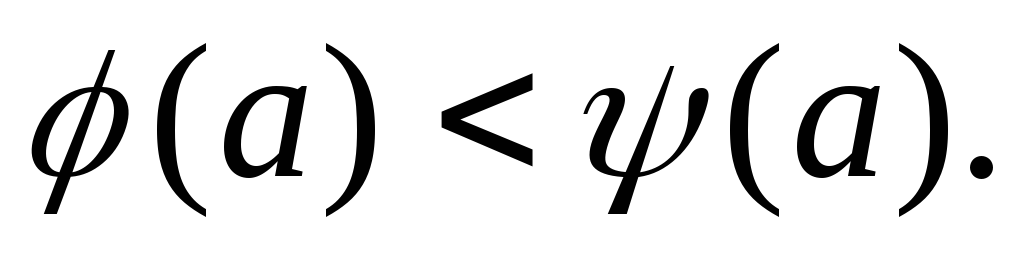 Так как
Так как – начальный отрезок,
– начальный отрезок,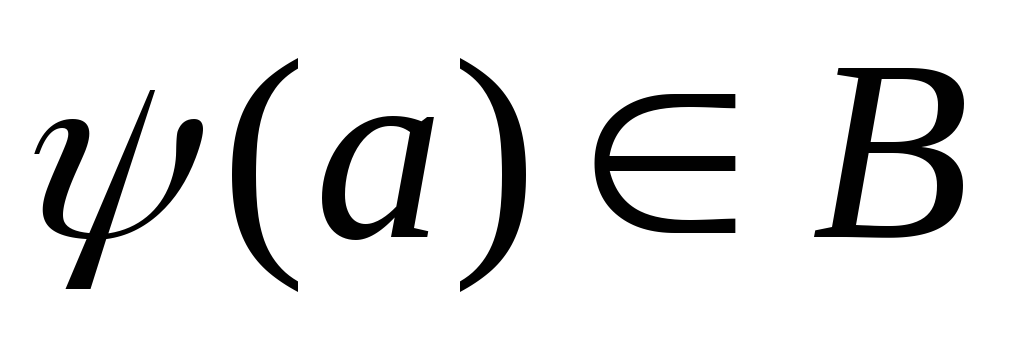 и
и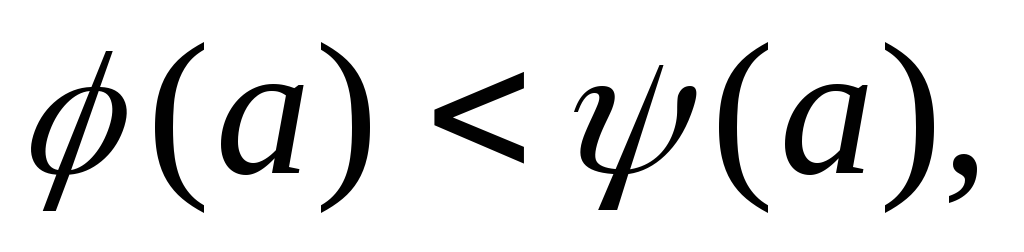 то
то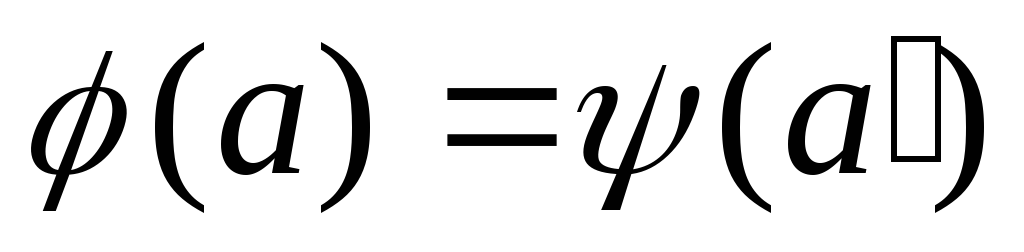 для некоторого
для некоторого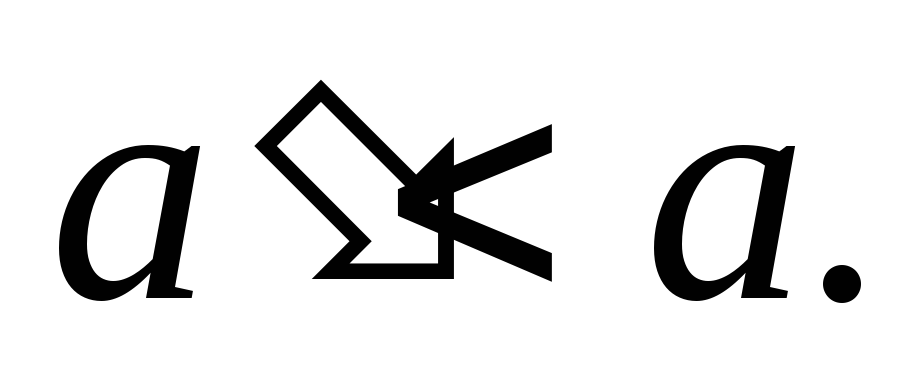 Так как
Так как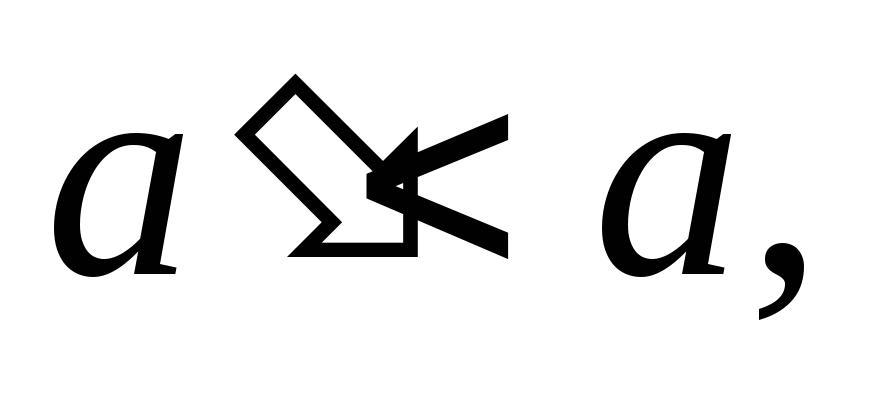 то
то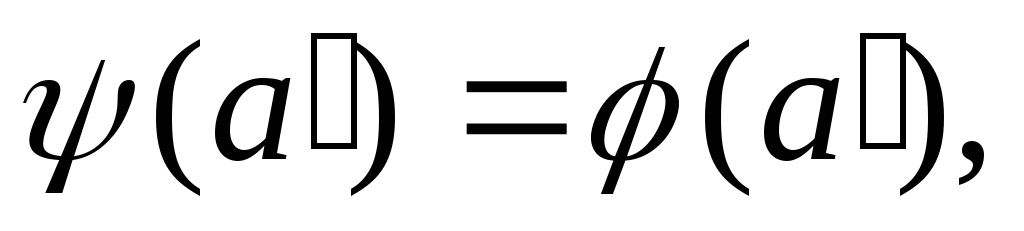 значит,
значит,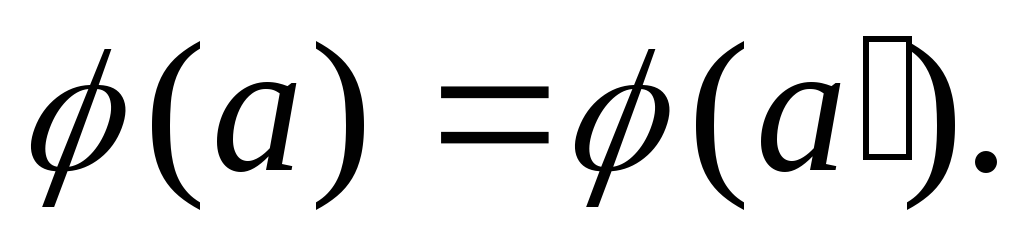 Так как
Так как – вложение, то
– вложение, то но это невозможно. Таким образом,
но это невозможно. Таким образом,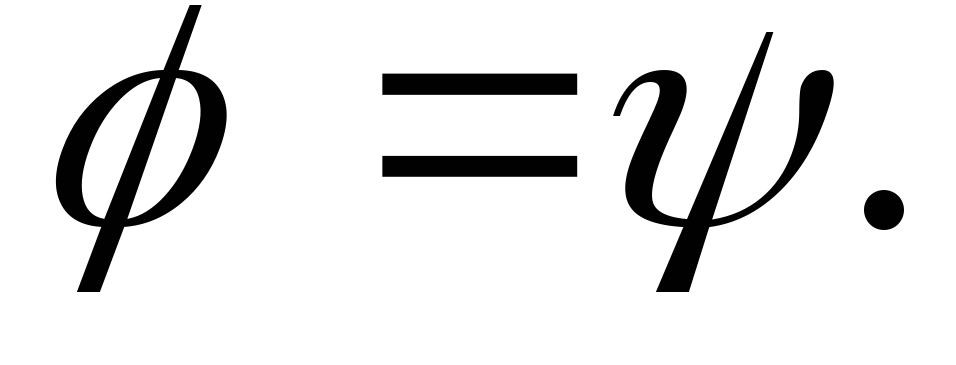
Следствие.
Вполне упорядоченное множество  не может быть изоморфно своему начальному
отрезку, отличному от
не может быть изоморфно своему начальному
отрезку, отличному от
Доказательство.
Пусть  – вполне упорядоченное множество и
– вполне упорядоченное множество и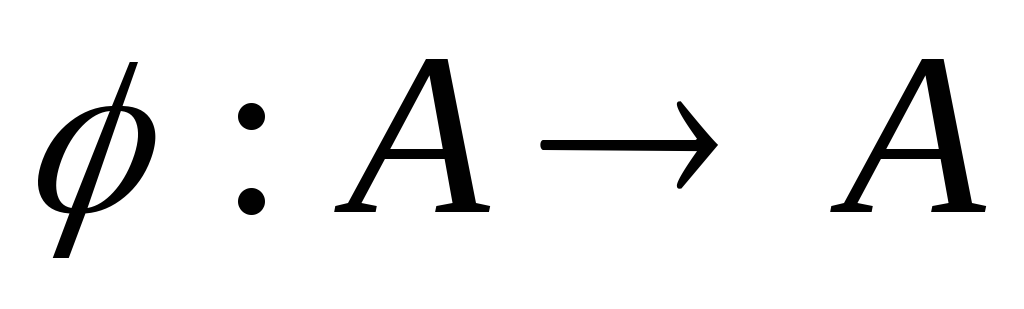 – вложение, сохраняющее порядок, причём
– вложение, сохраняющее порядок, причём – начальный отрезок множества
– начальный отрезок множества Тождественное отображение
Тождественное отображение
 тоже является изоморфизмом
тоже является изоморфизмом на начальный отрезок
на начальный отрезок откуда по лемме получаем:
откуда по лемме получаем: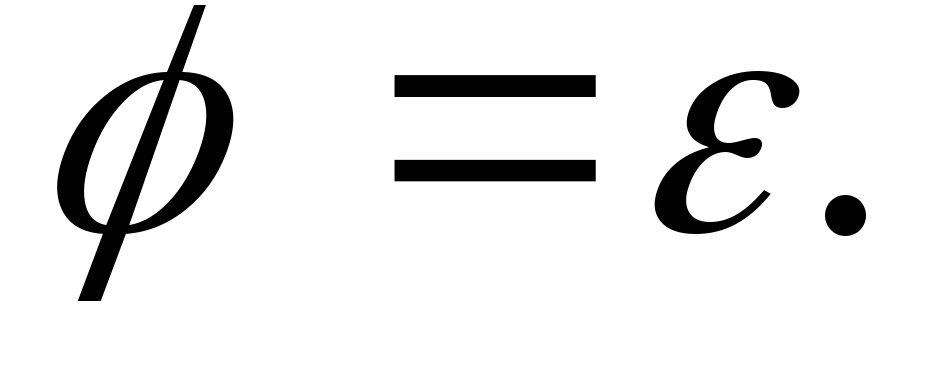 Следовательно,
Следовательно,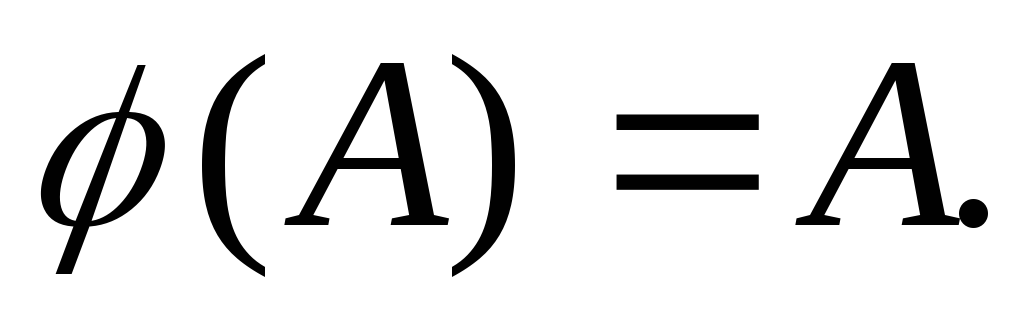
studfile.net




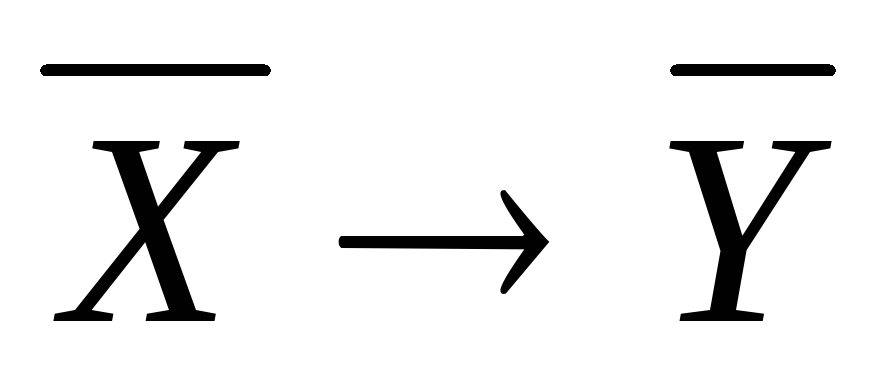
 и
и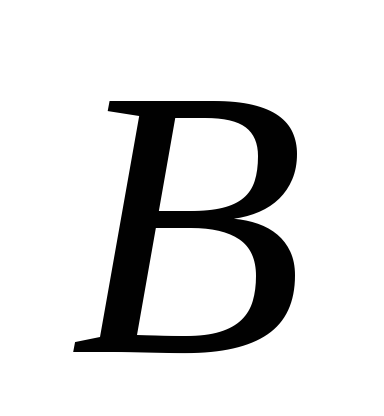 – два непересекающихся вполне
упорядоченных множества, то порядок
на множестве
– два непересекающихся вполне
упорядоченных множества, то порядок
на множестве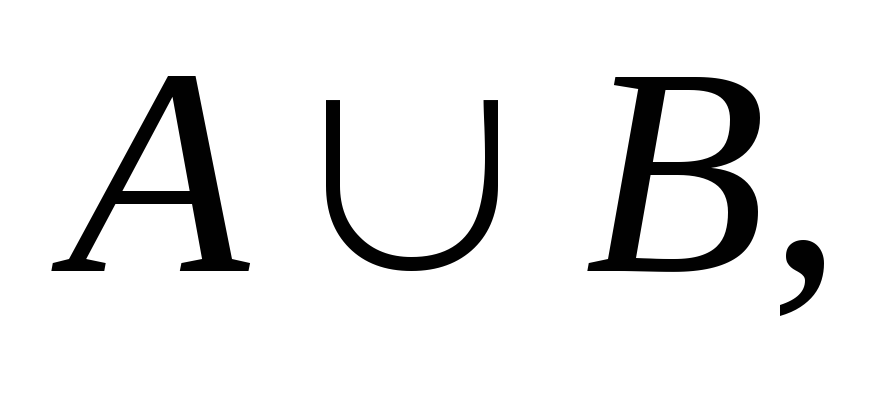 определённый следующим образом:
определённый следующим образом: