Геометрия — Википедия

Геоме́трия (от др.-греч. γεωμετρία, от γῆ — земля и μετρέω — измеряю) — раздел математики, изучающий пространственные структуры и отношения, а также их обобщения^[1].

Геометрия как систематическая наука появилась в Древней Греции, её аксиоматические построения описаны в «Началах» Евклида. Евклидова геометрия занималась изучением простейших фигур на плоскости и в пространстве, вычислением их площади и объёма. Предложенный Декартом в 1637 году координатный метод лёг в основу аналитической и дифференциальной геометрии, а задачи, связанные с черчением, привели к созданию начертательной и проективной геометрии. При этом все построения оставались в рамках аксиоматического подхода Евклида. Коренные изменения связаны с работами Лобачевского в 1829 году, который отказался от аксиомы параллельности и создал новую неевклидову геометрию, определив таким образом путь дальнейшего развития науки и создания новых теорий.

Классификация геометрии, предложенная Клейном в «Эрлангенской программе» в 1872 году и содержащая в своей основе инвариантность геометрических объектов относительно различных групп преобразований, сохраняется до сих пор.

Геометрия занимается взаимным расположением тел, которое выражается в прикосновении или прилегании друг к другу, расположением «между», «внутри» и так далее; величиной тел, то есть понятиями о равенстве тел, «больше» или «меньше»; а также преобразованиями тел. Геометрическое тело представляет собой абстракцию ещё со времён Евклида, который полагал, что «линия есть длина без ширины», «поверхность есть то, что имеет длину и ширину». Точка представляет собой абстракцию, связанную с неограниченным уменьшением всех размеров тела, или пределом бесконечного деления. Расположение, размеры и преобразования геометрических фигур определяются пространственными отношениями

[2].

Исследуя реальные предметы, геометрия рассматривает только их форму и взаимное расположение, отвлекаясь от других свойств предметов, таких как плотность, вес, цвет. Это позволяет перейти от пространственных отношений между реальными объектами к любым отношениям и формам, возникающим при рассмотрении однородных объектов, и сходным с пространственными. В частности, геометрия позволяет рассматривать расстояния между функциями^[1].

Классификацию различных разделов геометрии предложил Феликс Клейн в своей «Эрлангенской программе» (1872). Согласно Клейну, каждый раздел изучает те свойства геометрических объектов, которые сохраняются (инвариантны) при действии некоторой группы преобразований, специфичной для каждого раздела. В соответствии с этой классификацией, в классической геометрии можно выделить следующие основные разделы.

• Евклидова геометрия, в которой предполагается, что размеры отрезков и углов при перемещении фигур на плоскости не меняются. Другими словами, это теория тех свойств фигур, которые сохраняются при их переносе, вращении и отражении.
  • Планиметрия — раздел евклидовой геометрии, исследующий фигуры на плоскости.
  • Стереометрия — раздел евклидовой геометрии, в котором изучаются фигуры в пространстве.
• Проективная геометрия, изучающая проективные свойства фигур, то есть свойства, сохраняющиеся при их проективных преобразованиях.
• Аффинная геометрия, изучающая свойства фигур, сохраняющиеся при аффинных преобразованиях.
• Начертательная геометрия — инженерная дисциплина, в основе которой лежит метод проекций. Этот метод использует две и более проекций (ортогональных или косоугольных), что позволяет представить трехмерный объект на плоскости.

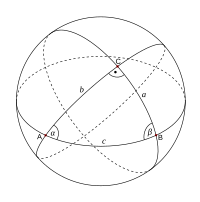Сферический треугольник

Современная геометрия включает в себя следующие дополнительные разделы.

По используемым методам выделяют также такие инструментальные подразделы.

Аксиомы евклидовой геометрии, сформулированные в III—IV веке до н. э., составляли основу геометрии до второй половины XIX века, так как хорошо описывали физическое пространство и отождествлялись с ним^[1]. Пяти постулатов Евклида было недостаточно для полного описания геометрии и в 1899 году Гильберт предложил свою систему аксиом. Гильберт разделил аксиомы на несколько групп: аксиомы принадлежности, конгруэнтности, непрерывности (в том числе аксиома Архимеда), полноты и параллельности. Позднее Шур заменил аксиомы конгруэнтности аксиомами движения, а вместо аксиомы полноты стали использовать аксиому Кантора. Система аксиом евклидовой геометрии позволяет доказать все известные школьные теоремы^[3].

Существуют и другие системы аксиом, в основе которых, помимо точки, прямой и плоскости, лежит не движение, а конгруэнтность, как у Гильберта, или расстояние, как у Кагана. Другая система аксиом связана с понятием вектора. Все они выводятся одна из другой, то есть аксиомы в одной системе можно доказать как теоремы в другой

[3].

Для доказательства непротиворечивости и полноты аксиом евклидовой геометрии строят её арифметическую модель и показывают, что любая модель изоморфна арифметической, а значит они изоморфны между собой^[4]. Независимость аксиом евклидовой геометрии показать сложнее из-за большого количества аксиом. Аксиома параллельности не зависит от других, так как на противоположном утверждении строится геометрия Лобачевского. Аналогично была показана независимость аксиомы Архимеда (в качестве координат вместо тройки вещественных чисел используется тройка комплексных чисел), аксиомы Кантора (в качестве координат вместо тройки любых вещественных чисел используются вещественные числа, построенные определённым образом), а также одной из аксиом принадлежности, которая фактически определяет размерность пространства (вместо трёхмерного пространства можно построить четырёхмерное, и любое многомерное пространство с конечным числом измерений)

[5].

Постулаты Евклида[править | править код]

Постулаты Евклида

Постулаты Евклида представляют собой правила построения с помощью идеального циркуля и идеальной линейки^[6]:

1. Всякие две точки можно соединить прямой линией;
2. Ограниченную прямую линию можно неограниченно продолжить;
3. Из всякого центра всяким радиусом можно описать окружность;
4. Все прямые углы равны между собой;
5. Если прямая падает на две прямые и образует внутренние односторонние углы в сумме меньше двух прямых, то при неограниченном продолжении этих двух прямых они пересекутся с той стороны, где углы меньше двух прямых.

Другая формулировка пятого постулата (аксиомы параллельности), гласит

[7]: Через точку вне прямой в их плоскости можно провести не более одной прямой, не пересекающей данную прямую.

Аксиомы евклидовой геометрии[править | править код]

В «Энциклопедии элементарной математики» предлагается следующая система аксиом^[3]:

• Аксиомы принадлежности:

1. Через каждые две различные точки проходит прямая и притом одна;
2. На каждой прямой имеется по крайней мере две точки;
3. Существуют три точки, не лежащие на одной прямой;
4. Через каждые три точки не лежащие на одной прямой проходит плоскость и притом только одна;
5. На каждой плоскости имеется по крайней мере одна точка;
6. Если две точки лежат на плоскости, то и проходящая через них прямая лежит на этой плоскости;
7. Если две плоскости имеют общую точку, они имеют по крайней мере ещё одну общую точку;
8. Существуют четыре точки, не лежащие на одной плоскости.
   • Аксиомы порядка:
9. Из любых трёх различных точек прямой одна и только одна лежит между двумя другими;
10. Для всяких двух точек прямой существует на этой прямой такая третья точка, что вторая точка лежит между первой и третьей;
11. Если прямая l, лежащая в плоскости ABC, не проходит ни через одну из точек A, B, C и содержит одну точку отрезка AB, то она имеет общую точку с хотя бы одним из отрезков AC, BC;
    • Аксиомы движения:
12. Всякое движение является взаимно однозначным отображением пространства на себя;
13. Пусть f — произвольное движение. Тогда, если точки A, B, C расположены на одной прямой, причём C лежит между A и B, то точки f(A), f(B), f(C) также расположены на одной прямой, причём f(C) лежит между f(A) и f(B);
14. Два движения, произведённые один за другим, равносильны некоторому одному движению;
15. Для всяких двух реперов, взятых в определённом порядке, существует одно и только одно движение, переводящее первый репер во второй;
    • Аксиомы непрерывности:
16. Аксиома Архимеда. Пусть A₀, A₁, B — три точки, лежащие на одной прямой, причём точка A₁ находится между A₀ и B. Пусть далее f — движение, переводящее точку A₀ в A₁ и луч A₀B в A₁B. Положим f(A₁)=A₂, f(A₂)=A₃, …. Тогда существует такое натуральное число n, что точка B находится на отрезке A_n-1A_n.
17. Аксиома Кантора. Пусть A₁, A₂, … и B₁, B₂, … — такие две последовательности точек, расположенных на одной прямой l, что для любого n точки A_n и B_n различны между собой и лежат на отрезке A_n-1B_n-1
    . Тогда на прямой l существует такая точка C, которая находится на отрезке A_nB_n при всех значениях n.
    • Аксиома параллельности:
18. Через точку A, не лежащую на прямой l, можно провести в их плоскости не более одной прямой, не пересекающей прямую l.

Если убрать из системы аксиомы 4-8, относящиеся к пространственной геометрии, то получится система аксиом евклидовой плоскости^[3].

Преобразованием множества называют его взаимно-однозначное отображение на себя. В таком смысле этот термин используется в геометрии, хотя иногда его используют и как синоним отображения или отображения множества в себя.

Говоря о «геометрических преобразованиях», обычно имеют в виду некоторые конкретные типы преобразований, играющие фундаментальную роль в геометрии — движения, преобразования подобия, аффинные, проективные, круговые преобразования (в последних двух случаях плоскость или пространство дополняют бесконечно удаленными точками). Эту фундаментальную роль выявил немецкий математик Феликс Клейн в своей лекции в университете г. Эрланген в 1872 г., известной как Эрлангенская программа. Согласно концепции Клейна, геометрия изучает свойства фигур, сохраняющиеся при всех преобразованиях некоторой группы преобразований. Рассматривая группы преобразований указанных выше видов, получают разные геометрии — евклидову (для преобразований подобия), аффинную и т. д.

Муза геометрии, Лувр

Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтян ремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину^[2]. При этом античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии. Центральное место среди них занимают написанные в III веке до н. э. «Начала» Евклида. Этот труд более двух тысячелетий считался образцовым изложением в духе аксиоматического метода: все положения выводятся логическим путём из небольшого числа явно указанных и не доказываемых предположений — аксиом^[2]. Первые же доказательства геометрических утверждений появились в работах Фалеса и использовали, по всей видимости, принцип наложения, когда фигуры, равенство которых необходимо доказать, накладывались друг на друга^[8].

Геометрия греков, называемая сегодня евклидовой или элементарной, занималась изучением простейших форм: прямых, плоскостей, отрезков, правильных многоугольников и многогранников, конических сечений, а также шаров, цилиндров, призм, пирамид и конусов. Вычислялись их площади и объёмы. Преобразования в основном ограничивались подобием. В Греции в работах Гиппарха и Менелая также появились тригонометрия и геометрия на сфере^[2].

Средние века немного дали геометрии^[1], и следующим великим событием в её истории стало открытие Декартом в XVII веке координатного метода (трактат «Геометрия», 1637). Точкам пространства сопоставляются наборы чисел, это позволяет изучать отношения между геометрическими формами методами алгебры. Так появилась аналитическая геометрия, изучающая фигуры и преобразования, которые в координатах задаются алгебраическими уравнениями. Систематическое изложение аналитической геометрии было предложено Эйлером в 1748 году. В начале XVII века Паскалем и Дезаргом начато исследование свойств плоских фигур, не меняющихся при проектировании с одной плоскости на другую. Этот раздел получил название проективной геометрии и был впервые обобщён Понселе в 1822 году. Ещё раньше, в 1799 году Монж развил начертательную геометрию, связанную напрямую с задачами черчения. Метод координат лежит в основе появившейся несколько позже дифференциальной геометрии, где фигуры и преобразования все ещё задаются в координатах, но уже произвольными достаточно гладкими функциями. Дифференциальная геометрия была систематизирована Монжем в 1795 году^[2], её развитием, в частности теорией кривых и теорией поверхностей, занимался Гаусс. На стыке геометрии, алгебры и анализа возникли векторное исчисление, тензорное исчисление, метод дифференциальных форм^[1].

В 1826 году Лобачевский, отказавшись от аксиомы параллельности Евклида построил неевклидову геометрию, названную его именем. Аксиома Лобачевского гласит, что через точку, не лежащую на прямой можно провести более одной прямой, параллельной данной. Лобачевский, используя эту аксиому вместе с другими положениями, построил новую геометрию, которая в силу отсутствия наглядности, оставалась гипотетической до 1868 года, когда было дано её полное обоснование. Лобачевский, таким образом, открыл принципы построения новых геометрических теорий и способствовал развитию аксиоматического метода^[2].

Следующим шагом явилось определение абстрактного математического пространства. Проективные, аффинные и конформные преобразования, сохраняющиеся при этом свойства фигур, привели к созданию проективной, аффинной и конформной геометрий. Переход от трёхмерного пространства к n-мерному впервые был осуществлён в работах Грассмана и Кэли в 1844 году и привёл к созданию многомерной геометрии. Другим обобщением пространства стала риманова геометрия, предложенная Риманом в 1854 году^[2]. Ф. Клейн в «Эрлангенской программе» систематизировал все виды однородных геометрий; согласно ему, геометрия изучает все те свойства фигур, которые инвариантны относительно преобразований из некоторой группы. При этом каждая группа задаёт свою геометрию. Так, изометрии (движения) задаёт евклидову геометрию, группа аффинных преобразований — аффинную геометрию.

В 70-х годах XIX века возникла теория множеств, с точки зрения которой фигура определяется как множество точек. Данный подход позволил по новому взглянуть на евклидову геометрию и проанализировать её основы, которые подверглись некоторым уточнениям в работах Гильберта^[2].

Со времён Древней Греции в основе геометрии лежат философские понятия. Определяя точку как «то, что не имеет частей», подход к ней отличается у Пифагора, который отождествляет точку с числовой единицей и у которого точка имеет только положение в пространстве и не имеет размера, и у Демокрита, который строя атомистическую теорию, даёт точке «сверхчувственно малый» размер. К атомистическим представлениям восходят также определения линии и поверхности, где неделимыми являются «ширина» и «глубина», соответственно^[6].

Геометрия является пятым из семи свободных искусств по уровню обучения. Ей предшествует тривиум, состоящий из Грамматики, Риторики и Диалектики, а также Арифметика — старшая наука в квадривиуме, к которому также относятся Музыка и Астрономия^[9]. Марциан Капелла в своём трактате «Свадьба Философии и Меркурия» создал визуальные образы всех семи искусств и в том числе Геометрии. Искусства олицетворяли женщины с соответствующими атрибутами, которые сопровождались известными представителями сферы. Геометрия держит в своих руках глобус и циркуль, которым она может мерить, реже угольник, линейку или компасы. Её сопровождает Евклид^[10][11].

В честь геометрии назван астероид (376) Геометрия, открытый в 1893 году.

1. ↑ ^{1 2 3 4 5} Геометрия // Математическая энциклопедия : в 5 т.. — М. : Советская Энциклопедия, 1982. — Т. 1.
2. ↑ ^{1 2 3 4 5 6 7 8} БСЭ, 1971.
3. ↑ ^{1 2 3 4} Геометрия, 1963, с. 32—41.
4. ↑ Геометрия, 1963, с. 41—44.
5. ↑ Геометрия, 1963, с. 44—48.
6. ↑ ^{1 2} Геометрия, 1963, с. 12—17.
7. ↑ Геометрия, 1963, с. 18—21.
8. ↑ Геометрия, 1963, с. 12.
9. ↑ Liberal Arts (англ.). Encyclopædia Britannica. Дата обращения 20 марта 2012. Архивировано 27 мая 2012 года.
10. ↑ Семь свободных искусств (неопр.). Simbolarium. Дата обращения 20 марта 2012. Архивировано 27 мая 2012 года.
11. ↑ The Seven Liberal Arts (неопр.). Catholic Encyclopedia. Дата обращения 20 марта 2013. Архивировано 3 апреля 2013 года.

• Комацу, Мацуо. Многообразие геометрии. — М. : Знание, 1981.
• Левитин, К. Е. Геометрическая рапсодия. — 3-е изд., перераб. и доп. — М. : ИД «Камерон», 2004. — 216 с. — ISBN 5-9594-0023-5.
• Шаль, Мишель. Исторический обзор происхождения и развития геометрических методов : в 2 т.. — М. : М. Катков, 1883.
• Граве Д. А. Геометрия // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
• Геометрия // Газлифт — Гоголево. — М. : Советская энциклопедия, 1971. — (Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров ; 1969—1978, т. 6).
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. I : С древнейших времён до начала Нового времени.
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1970. — Т. II : Математика XVII столетия.
• История математики : в 3 т. / под ред. А. П. Юшкевича. — М. : Наука, 1972. — Т. III : Математика XVIII столетия.
• Математика XIX века / ред. А. Н. Колмогоров, А. П. Юшкевич. — М. : Наука, 1981. — Т. 2 : Геометрия. Теория аналитических функций.
• Энциклопедия элементарной математики / под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М. : Физматгиз, 1963. — Кн. 4 : Геометрия. — 568 с.
• Энциклопедия элементарной математики / под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М. : Наука, 1966. — Кн. 5 : Геометрия. — 624 с.

Предмет стереометрии

Материал урока.

В курсе геометрии базовой школы, мы с вами в основном знакомились с плоскими фигурами, напомню, что раздел геометрии, который занимается изучением свойств плоских фигур называется планиметрия. Основными фигурами планиметрии являются точка и прямая. У плоских фигур есть только два измерения: длина и ширина, эти измерения используются для нахождения площади фигур.

Но мы уже знаем, что есть такой раздел геометрии, который занимается изучением объемных фигур, он называется стереометрия.

Напомним, что если в планиметрии мы говорили о квадрате, то в стереометрии мы будем говорить о кубе, который состоит из квадратов.

Если в планиметрии мы говорили о прямоугольном треугольнике, то в стереометрии из треугольника, вращая его вокруг одного из катетов, мы получим конус.

С некоторыми фигурами стереометрии мы уже знакомы: это призма, пирамида, цилиндр, конус, шар.

В курсе геометрии десятого и одиннадцатого классов, мы будем работать именно со стереометрией, то есть изучать свойства фигур в пространстве.

На прежде чем приступить к изучению стереометрии, давайте, еще раз вспомним как все начиналось.

Слово стереометрия происходит от двух древнегреческих слов «стереос» – «твердый, пространственный» и слово «метрио» – измеряю. В отличии от планиметрии основными фигурами стереометрии являются точка, прямая и плоскость.

Точки, как и в планиметрии обозначаются заглавными буквами латинского алфавита. Прямые обозначаются строчными буквами латинского алфавита.

Плоскость может изображаться разными способами, но чаще всего она изображается параллелограммом. Для обозначения плоскости используются строчные буквы греческого алфавита.

Наряду с этими понятиями в стереометрии рассматриваются геометрические тела и их поверхности. У геометрических тел три измерения: длина, ширина и высота. Эти измерения позволяют вычислить объем фигуры, то есть геометрические тело обладают вместимостью. Практически каждый окружающий нас предмет можно представить в виде геометрических тел.

Стереометрия, как и планиметрия, возникла и развивалась вместе с человеком. Геометрия была очень нужна строителям, которые возводили на реках дамбы, перекидывали с одного берега на другой мосты, виадуки, создавали многоэтажные здания и величественные храмы.

Ярким примером этого являются египетские пирамиды, сооруженные за два четыре тысячелетия до нашей эры. До сих пор эти пирамиды поражают точностью своих метрических соотношений.

Считается, что геометрия появилась в древнем Египте около 2000 лет до нашей эры.

Сначала геометрия была интуитивной. То есть факты признавались существующими и никак не доказывались. Но в 600 году до нашей эры греческий ученый Фалес выдвинул и развил идею о том, что должны быть пути, доказывающие справедливость тех или иных фактов. В геометрии факты называются теоремами. Фалес открыл доказательства теорем, которые люди принимали на веру до этого.

Начиная с VIIвека до нашей эры в Древней Греции создаются философские школы, в которых происходит постепенный переход от практической к теоретической геометрии.

Одной из самых первых и самых известных геометрических школ была пифагорейская, она существовала в VI-V веках до нашей эры. Названа она была в честь своего основателя древнегреческого ученого Пифагора.

Пифагорейцы использовали правильные многогранники для философских теорий. Так огню они придавали форму тетраэдра (пирамиды), земле – форму гексаэдра (куба), воздуху – форму октаэдра (фигуры, которая образована восьмью равносторонними треугольниками), воде – форму икосаэдра (фигуры, которая образована двадцатью равносторонними треугольниками).

По их мнению, вся вселенная имеет форму додекаэдра (фигуры, которая состоит из двенадцати правильных пятиугольников).

Нетрудно заметить, что названия многогранников тоже имеют древнегреческое происхождение. Первая часть названия показывает количество граней из которых состоит фигура, а слово «эдр» произошло от древнегреческого слова «эдра» – грань.

Еще одной известной школой, которая занималась вопросами геометрии, является Александрийская философская школа. Выходцем этой школы был знаменитый ученый Евклид, который жил около 300 года до нашей эры.

Евклид является автором «Начала», работы, которая состоит из тринадцати книг и содержит изложение планиметрии, стереометрии, ряда вопросов теории чисел. Этой работой Евклид создал фундамент дальнейшего развития математики. До сих пор этот труд считается основой изучения курса геометрии.

Он сформулировал пять постулатов:

1.  Через две точки можно провести прямую.

2.  Отрезок прямой можно продолжить неограниченно.

3.  Из всякого центра любым расстоянием можно описать окружность.

4.  Все прямые углы равны между собой.

5.  Всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними внутренние односторонние углы, сумма которых меньше 2-х прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше 2-х прямых.

В девятнадцатом веке в геометрии появились новые методы, которые позволили переводить геометрические задачи на язык алгебры и наоборот. Возникли и развиваются новые направления геометрических исследований: геометрия Лобачевского, проективная геометрия, топология, компьютерная геометрия и так далее.

В 1829 году русский математик Николай Лобачевский написал работу «О началах геометрии», в которой заявил, что можно построить геометрию такую же содержательную и свободную от противоречий, как и евклидова.

Если геометрию Евклида можно назвать геометрией земных пространств и расстояний, то геометрия Лобачевского – геометрия гигантских межпланетных и исчезающих малых атомных пространств, она включает геометрию Евклида как составную часть, как частный случай. Основное отличие геометрии Лобачевского от геометрии Евклида заключается в так называемом «пятом постулате». Евклид утверждал, что «Через точку, не лежащую на данной прямой, проходит не более одной прямой, лежащей с данной прямой в одной плоскости и не пересекающей её». В геометрии Лобачевского вместо этой аксиомы принимается другая аксиома: «Через точку, не лежащую на данной прямой, проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости и не пересекающие её».

В 1899 году немецкий математик Давид Гильберт написал труд «Основания геометрии». Эта работа стала образцом для дальнейших работ по аксиоматическому построению геометрии.

Но математикой в целом и геометрией в частности интересовались не только ученые. Существует так называемое математическое искусство Эшера.

Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.

Правильные геометрические тела — многогранники — имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.

 Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из одинаковых правильных многоугольников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями.

На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

Вернемся к геометрическим телам. Геометрические тела, как и все геометрические фигуры являются воображаемыми объектами.

Геометрическое тело – часть пространства, отделенное от остальной части пространства границей этого тела.

Все геометрические тела делятся на два больших класса: тела вращения (из названия понятно, что к ним относятся тела, которые получаются вращением плоских фигур вокруг одного из своего элемента) к ним относятся шар (получается вращением полукруга вокруг диаметра), цилиндр (получается вращением прямоугольника вокруг одной из своих сторон), конус (получается вращением прямоугольного треугольника вокруг одного из своих катетов).

Ко второй группе геометрических тел, относятся многогранники – тела, ограниченные конечным числом плоских многоугольников, любые два смежные из которых не лежат в одной плоскости.

Многогранники в свою очередь делятся на призмы (это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы), пирамиды (многогранник, составленный из n угольника А₁А₂ и так далее А_n и n треугольников). С некоторыми видами многогранниками, мы с вами уже встречались, с остальными познакомимся в этом году.

Напомним, что многогранники бывают выпуклыми (то есть многогранник расположен по одну сторону от плоскости каждой его грани). Мы помним, что все грани выпуклого многогранника являются выпуклыми многоугольниками.

И невыпуклыми, когда многогранник лежит по разные стороны хотя бы от одной плоскости, проходящей через грань.

Давайте повторим основные элементы фигур, с которыми мы уже знакомы.

Начнем с тел вращения. У цилиндра есть ось, высота, основания цилиндра, радиус цилиндра, боковая или цилиндрическая поверхность, образующая.

У конуса также есть ось, высота, основание, радиус, коническая или боковая поверхность, образующая.

У шара или сферы (напомним, что сфера – оболочка шара, по аналогии с окружностью и кругом в планиметрии) есть центр, радиус, хорда, диаметр.

Теперь рассмотрим многогранники.

Призма имеет два основания, боковые грани, боковые ребра, у призмы есть диагональ – отрезок соединяющий две вершины призмы, не принадлежащие одной грани.

У пирамиды, в отличии от призмы – одно основание, есть боковые грани, вершина, боковые ребра, высота.

Закончить наш сегодняшний урок хочется цитатой Галилео Галилея «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

Стереометрия. Страница 1

Главная > Учебные материалы > Математика:  Стереометрия. Страница 1             1.Основные фигуры стереометрии. 2.Группа дополнительных аксиом стереометрии. 3.Плоскость, проходящая через данную прямую и точку. 4.Пересечение прямой с плоскостью. 5.Существование плоскости, проходящей через три данные точки. 6.Примеры.       1 2 3 4 5 6 7 8           1. Основные фигуры стереометрии    Стереометрия — это раздел геометрии, изучающий геометрические фигуры и их свойства в пространстве. Основные фигуры в пространстве — это точка, прямая, плоскость. Плоскости обозначаются греческими буквами α, β, γ.    Аксиомы планиметрии описывают свойства простейших геометрических фигур на плоскости. Так как стереометрия изучает фигуры в пространстве и в пространстве может быть великое множество плоскостей, то аксиомы стереометрии состоят из аксиом планиметрии с уточнением «на» или «в заданной плоскости» и 3-х дополнительных аксиом.       2. Группа дополнительных аксиом стереометрии        1. Для любой плоскости в пространстве, существуют точки принадлежащие данной плоскости и точки не принадлежащие ей.          2. Две различные плоскости, имеющие одну общую точку, пересекаются по прямой, проходящей через эту точку.          3. Через две различные прямые, имеющие общую точку, можно провести только одну плоскость.   (Рис.1)   Рис. 1. Аксиомы стереометрии.               Пример    Даны три попарно пересекающиеся плоскости. Две прямые пересечения из них пересекаются. Доказать, что три прямые пересечения этих плоскостей пересекаются в одной точке.               Доказательство.    Пусть даны три попарно пересекающиеся плоскости α, β и γ. Плоскость α пересекает плоскость β по прямой а. А плоскость β пересекает плоскость γ по прямой с (Рис. 2 а).    а ∈ α,β    c ∈ β,γ     точка Е ∈ а,с (прямые пересекаются в точке Е по условию задачи)     Тогда плоскости α и γ пересекаются по прямой b.     b ∈ α,γ     Отсюда следует, что, т.к. прямые b,с ∈ γ, то они либо параллельны, либо пересекаются в какой-то точке Е1.    Если они параллельны, то у них нет общих точек, а следовательно, плоскости α и β пересекаются по прямой а, параллельной b и с (Рис. 2 б). А это противоречит условию задачи. Следовательно, прямые b и с пересекаются в какой-то точке Е1. т.Е1 ∈ b,с Следовательно, т.Е1 ∈ α,β,γ.    Отсюда можно сделать вывод, что точка Е1 принадлежит трем плоскостям α,β,γ и, следовательно, она лежит одновременно на трех прямых а, b и с. А это возможно только, если три прямые пересекаются в одной точке. И, следовательно, прямая b пересекает прямую с в точке Е1, которая является точкой пересечения прямых а и с. Таким образом, точки Е и Е1 совпадают.     Рис.2. Даны три попарно пересекающиеся плоскости…                     3. Плоскость, проходящая через данную прямую и точку    Теорема: Через прямую и не лежащую на ней точку можно провести только одну плоскость. Доказательство.        Пусть АВ данная прямая и Е не принадлежащая ей точка. (Рис.3) Проведем через точки А и Е прямую. Тогда прямые АВ и АЕ пересекаются в точке А. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость α, проведенная через эти прямые, единственная. Т.к. точка Е принадлежит прямой АЕ, то она принадлежит плоскости α.    Если допустить, что существует еще одна плоскость α’, проходящая через прямую АВ и точку Е, то эта плоскость пересекает плоскость α по прямой, на которой лежат точки А, В, и Е согласно аксиоме 2. А это противоречит условию, т.к. точки А, В, и Е не лежат на одной прямой. Следовательно, плоскость α единственная.   Рис. 3 Плоскость, проходящая через данную прямую и точку.             4. Пересечение прямой с плоскостью    Теорема: Если две точки прямой принадлежат плоскости, то и вся прямая принадлежит данной плоскости. Доказательство.        Пусть а — данная прямая, А и В принадлежащие этой прямой точки, α — данная плоскость. Точки А и В принадлежат плоскости α. Согласно аксиоме 1, существует точка С, не лежащая на прямой а. (Рис.4)    Проведем через прямую а и точку С плоскость β. Тогда, если плоскости α и β совпадают, то прямая а принадлежит плоскости α, что и утверждает данная теорема. Если плоскости α и β не совпадают, то они пересекаются по прямой а’. Таким образом, имеем: точки А и В ∈ а, α прямая а ∈ β следовательно, точки А и В ∈β    Отсюда следует, что две точки А и В принадлежат двум плоскостям: α и β. И, согласно аксиоме, они могут лежать только на прямой а’, которая является прямой пересечения этих плоскостей. Т.к. через две точки можно провести только одну прямую, и по условию теоремы эта прямая есть а, то следовательно, она и является прямой пересечения двух плоскостей. Т.е. прямые а и а’ совпадают. А следовательно, прямая а принадлежит плоскости α.    Из данной теоремы следует, что плоскость и не принадлежащая ей прямая, либо не пересекаются, либо пересекаются в одной точке.     Рис. 4 Пересечение прямой с плоскостью.             5. Существование плоскости, проходящей через три данные точки    Теорема. Через три точки, не лежащие на данной прямой, можно провести только одну плоскость. Рис.5        Доказательство. Пусть А, В, С три точки, не лежащие на одной прямой. Проведем через точки А,С и В,С прямые. Тогда они пересекаются в точке С. Согласно аксиоме: через две пересекающиеся прямые можно провести только одну плоскость, плоскость, проведенная через эти прямые, единственная. По теореме о пересечении прямой с плоскостью, обе прямые целиком принадлежат данной плоскости.   Рис. 5 Существование плоскости, проходящей через три данные точки.                       6.Пример 1      Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.                  Доказательство:    Пусть дана данная прямая а и точка О, не принадлежащая прямой а. И даны пересекающие ее прямые b, c, d в точках B, C, D, которые пересекаются в точке О. Проведем через прямую а и точку О плоскость α (Рис.6).     По теореме о пересечении прямой и плоскости, если провести прямую b, проходящую через точку О и точку В прямой а, то она целиком будет принадлежать плоскости α, так как две точки прямой b принадлежат плоскости α.     Если допустить, что прямая b не принадлежит плоскости α, то в этом случае мы можем провести плоскость α’, проходящую через точки В и О. Тогда плоскости α и α’ пересекаются по прямой b’, проходящей через точки В и О. А так как через две точки можно провести только одну прямую, то прямые b и b’ совпадают. Следовательно, прямая b целиком принадлежит плоскости α.    Точно так же доказывается, что прямые с и d принадлежат плоскости α. Отсюда можно сделать вывод, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.   Рис.6 Задача. Докажите, что все прямые, пересекающие данную прямую…                         Пример 2      Даны две непересекающиеся плоскости. Докажите, что прямая, пересекающая одну из этих плоскостей, пересекает и другую.                  Доказательство:    Пусть даны две непересекающиеся плоскости α и α’. И прямая а, которая пересекает плоскость α в точке В (Рис.7). Необходимо доказать, что прямая а пересекает плоскость α’ в точке В’.    Возьмем на плоскости α’ точку А и проведем через нее и прямую а плоскость β. Тогда плоскость β будет пересекать плоскости α и α’ по параллельным прямым b и b’. Точка В принадлежит прямой b, так как она принадлежит плоскости α и лежит на прямой а. И следовательно, она принадлежит двум плоскостям α и β.    Таким образом получается, что на плоскости β лежат две параллельные прямые b и b’. Одну из них пересекает прямая а в точке В. Следовательно, прямая а пересекает и вторую прямую b’. Так как согласно аксеоме, через точку В, не лежащей на данной прямой b’, можно провести только одну, параллельную прямой b’, прямую b. Отсюда следует, что прямая а не параллельна прямой b’, она ее пересекает в точке B’.   Рис.7 Задача. Даны две непересекающиеся плоскости…                         Пример 3      Даны две плоскости, пересекающиеся по прямой а. И прямая b, которая лежит в одной из этих плоскостей и пересекает другую. Докажите, что прямые а и b пересекаются.                  Доказательство:    Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Прямая b лежит в плоскости β и пересекает плоскость α в точке А (Рис.8). Необходимо доказать, что прямая b пересекает прямую а.    По условию задачи, прямая b лежит в плоскости β и пересекает плоскость α в точке А. Следовательно, точка А принадлежит двум плоскостям α и β.    Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что, так как точка А принадлежит двум плоскостям, то она лежит на прямой а, потому что прямая а является прямой пересечения двух плоскостей α и β.    Таким образом, точка А принадлежит двум прямым а и b. А следовательно, эти прямые пересекаются.   Рис.8 Задача. Даны две плоскости, пересекающиеся по прямой а…                         Пример 4      Точки А, В, С лежат в каждой из двух различных плоскостей. Докажите, что эти точки лежат на одной прямой.                  Доказательство:    Пусть даны две пересекающиеся плоскости α и β. Прямая а, является их прямой пересечения. Точки А, В, С одновременно принадлежат двум плоскостям α и β (Рис.9). Необходимо доказать, что все три точки принадлежат прямой а.    Согласно аксиоме стереометрии, если две плоскости имеют одну общую точку, то они пересекаются по прямой, проходящей через эту точку. Отсюда следует, что все три точки А, В и С лежат на прямой пересечения двух плоскостей, т.е. прямой а, так как они принадлежат обоим плоскостям α и β.    Пусть дана точка D, принадлежащая только плоскости β. Тогда она не может лежать на прямой а, так как она не принадлежит плоскости α. Точно так же точка Е не может принадлежать прямой а, так как она принадлежит только плоскости α. Точка F не принадлежит плоскостям α и β, а следовательно, и прямой а.    Отсюда можно сделать вывод, что, если точка принадлежит обоим плоскостям α и β, то она обязательно лежит на прямой а. Так как прямая а — это множество точек, принадлежащих двум пересекающимся плоскостям α и β.   Рис.9 Задача. Точки А, В, С лежат в каждой из двух различных плоскостей…                         Пример 5      Даны четыре точки. Известно, что прямая, проходящая через любые две из этих точек, не пересекается с прямой, проходящей через другие две точки. Докажите, что данные четыре точки не лежат в одной плоскости.                  Доказательство:     Пусть даны четыре точки А, В, С, D. Допустим, что все четыре точки лежат в одной плоскости α.     Прямая АВ не пересекается с прямой CD. Прямая АС также не пересекается с прямой BD. Если провести прямую AD, то точки В и С окажутся в разных полуплоскостях. Следовательно, прямая AD пересекается с прямой ВС в точке О (Рис.10 а).     Допустим, что прямая AB не пересекает прямую DС (Рис.10 б). АD не пересекает прямую BC. Тогда, если провести прямую АС, то точки B и D окажутся в разных полуплоскостях. И прямая АС будет пересекать прямую BD в точке О.     Теперь допустим, что прямая AC не пересекает прямую ВD (Рис.10 в). АD не пересекает прямую ВC. Тогда, если провести прямую АВ, то точки D и C окажутся в разны полуплоскостях. А следовательно, прямая АВ будет пересекать прямую СD в точке О.     Отсюда можно сделать вывод, для того, чтобы выполнялось условие, при котором прямые АВ, АС, АD, одновременно не пересекали бы прямые CD, BD, BC, необходимо чтобы четыре точки А, В, С и D лежали в разных плоскостях.   Рис.10 Задача. Даны четыре точки. Известно, что прямая…                                         1 2 3 4 5 6 7 8                       Содержание                   Страница 1   Страница 5     1.Основные фигуры стереометрии. 2.Группа дополнительных аксиом стереометрии. 3.Плоскость, проходящая через данную прямую и точку. 4.Пересечение прямой с плоскостью. 5.Существование плоскости, проходящей через три данные точки.   1.Двухгранный, трехгранный углы. 2.Призма и построение ее сечений. 3.Параллелепипед. 4.Прямоугольный параллелепипед. 5.Пирамида. 6.Усеченная пирамида. 7.Правильные многогранники.               Страница 2   Страница 6     1.Параллельность прямых в пространстве. 2.Признак параллельности прямых. 3.Признак параллельности плоскостей. 4.Свойства параллельных плоскостей.   1.Цилиндр. 2.Конус. 3.Вписанная и описанная призма. 4.Вписанная и описанная пирамида. 5.Шар. 6.Симметрия шара.               Страница 3   Страница 7     1.Перпендикулярность прямых в пространстве. 2.Признак перпендикулярности прямой и плоскости. 3.Теорема о трех перпендикулярах. 4.Признак перпендикулярности плоскостей. 5.Расстояние между скрещивающимися прямыми.   1.Объем. Объем прямоугольного параллелепипеда. 2.Наклонный параллелепипед. 3.Объем пирамиды. 4.Объем призмы. 5.Равновеликие тела. 6.Объемы подобных тел.               Страница 4   Страница 8     1.Декартовы координаты в пространстве. 2.Расстояние между двумя точками. 3.Преобразование симметрии в пространстве. 4.Движение в пространстве. 5.Угол между прямой и плоскостью. 6.Угол между плоскостями. 7.Векторы в пространстве. 8.Площадь ортогональной проекции многоугольника.   1.Площадь боковой поверхности цилиндра. 2.Объем цилиндра. 3.Площадь боковой поверхности конуса. 4.Объем конуса. 5.Объем тел вращения. 6.Объем шара. 7.Объем шарового сегмента и сектора. 8.Площадь сферы.                 Комментарий:

Стереометрия | Наука | Fandom

Стереометрия (от др.-греч. στερεός, «стереос» — «твёрдый, пространственный» и μετρέω — «измеряю») — это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путем рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Не стоит путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), а в стереометрии — свойства фигур в пространстве (свойства пространственных фигур).

Аксиомы стереометрии Править

• В каждой прямой и в каждой плоскости имеются по крайней мере две точки.
• В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
• Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
• Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
• Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
• Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
• Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
  1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;
  2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
• Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников. Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми и невыпуклыми . Выпуклый многогранник расположен по одну сторону относительно плоскости, проходящей через любую его грань .

• В. В. Прасолов, И.Ф. Шарыгин. Задачи по стереометрии. — М.: Наука, 1989.
• И.Ф. Шарыгин. Задачи по геометрии (стереометрия). М.: Наука, 1984. — 160 с. (Библиотечка «Квант», Вып.31).

СТЕРЕОМЕТРИЯ — это… Что такое СТЕРЕОМЕТРИЯ?

1. стереометрия — стереометрия …   Орфографический словарь-справочник

2. СТЕРЕОМЕТРИЯ — (греч., от stereos плотный, и metreo меряю). Часть геометрии, трактующая о свойстве твердых тел, находящихся не на плоскостях, противоположная планиметрии. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910.… …   Словарь иностранных слов русского языка

3. Стереометрия — (от др. греч. στερεός, «стереос»  «твёрдый, пространственный» и μετρέω  «измеряю»)  это раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве являются точка, прямая и плоскость. В… …   Википедия

4. СТЕРЕОМЕТРИЯ — СТЕРЕОМЕТРИЯ, часть ГЕОМЕТРИИ, в которой изучаются фигуры в трехмерном пространстве. Стереометрия включает изучение плоскостей, объемных геометрических тел, их всевозможных сечений и пересечений, а также измерение объемов и площадей тел …   Научно-технический энциклопедический словарь

5. стереометрия — и, ж. stéréometrie, нем. Stereometrie <гр. stereos телесный + metreo измеряю. Раздел геометрии, изучающий объемные фигуры. Крысин 1998. || Название игрушки по Фребелю. Возьмем хотя стереометрию. Игрушка эта стоит 2 р. 50 к., что очень дорого.… …   Исторический словарь галлицизмов русского языка

6. стереометрия — (неправильно стереометрия) …   Словарь трудностей произношения и ударения в современном русском языке

7. СТЕРЕОМЕТРИЯ — (от стерео… и …метрия) часть элементарной геометрии, в которой изучаются фигуры в пространстве …   Большой Энциклопедический словарь

8. СТЕРЕОМЕТРИЯ — СТЕРЕОМЕТРИЯ, и, жен. Раздел геометрии, изучающий фигуры, лежащие в пространстве. | прил. стереометрический, ая, ое. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 …   Толковый словарь Ожегова

9. СТЕРЕОМЕТРИЯ — жен., греч. часть геометрии, измеренье тел, толщ. метрический чертеж. графия, черченье тел, толщ. Стереографическая проекция земного шара, перспективный чертеж, как бы пришлось смотреть на прозрачное тело. Стереотип, неразборная форма для печати… …   Толковый словарь Даля

10. стереометрия — сущ., кол во синонимов: 2 • геометрия (9) • математика (29) Словарь синонимов ASIS. В.Н. Тришин. 2013 …   Словарь синонимов

Стереометрия — Википедия. Что такое Стереометрия

Материал из Википедии — свободной энциклопедии

Стереометрия (от др.-греч. στερεός, «стереос» — «твёрдый, объёмный, пространственный» и μετρέω, «метрео» — «измеряю») — раздел геометрии, в котором изучаются свойства фигур в пространстве. Основными (простейшими) фигурами в пространстве являются точки, прямые и плоскости. В стереометрии появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это одно из немногих существенных отличий стереометрии от планиметрии, так как во многих случаях задачи по стереометрии решаются путём рассмотрения различных плоскостей, в которых выполняются планиметрические законы.

Не стоит путать этот раздел с планиметрией, поскольку в планиметрии изучаются свойства фигур на плоскости (свойства плоских фигур), а в стереометрии — свойства фигур в пространстве (свойства пространственных фигур).

Аксиомы стереометрии

• На каждой прямой и в каждой плоскости имеются по крайней мере две точки.
• В пространстве существуют плоскости. В каждой плоскости пространства выполняются все аксиомы планиметрии.
• Через любые три точки, не принадлежащие одной прямой, можно провести плоскость, и притом только одну.
• Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
• Если две точки прямой лежат на одной плоскости, то все точки данной прямой лежат в этой плоскости.
• Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
• Любая плоскость α разбивает множество не принадлежащих ей точек пространства на два непустых множества так, что:
  1. любые две точки, принадлежащие разным множествам, разделены плоскостью α;
  2. любые две точки, принадлежащие одному и тому же множеству, не разделены плоскостью α.
• Расстояние между любыми двумя точками пространства одно и то же на любой плоскости, содержащей эти точки.

Многогранник

Многогранник представляет собой тело, поверхность которого состоит из конечного числа плоских многоугольников. Эти многоугольники называются гранями многогранника, а стороны и вершины многоугольников называются соответственно ребрами и вершинами многогранника. Многогранники могут быть выпуклыми и невыпуклыми . Выпуклый многогранник расположен по одну сторону относительно плоскости, проходящей через любую его грань .

Литература

• В. В. Прасолов, И. Ф. Шарыгин. Задачи по стереометрии. — М.: Наука, 1989.
• И. Ф. Шарыгин. Задачи по геометрии (стереометрия). М.: Наука, 1984. — 160 с. (Библиотечка «Квант», Выпуск 31).

Стереометрия

К основным из них относятся — точка, прямая и плоскость. Точка и прямая известны из планиметрии.

Например, поверхность стола дает представление о части плоскости.

В геометрии считают, что плоскость ровная и неограниченная, не имеет краев и толщины.

На рисунках часть плоскости чаще всего изображают в виде произвольной замкнутой фигуры и обозначают буквами греческого алфавита $\alpha ,\; \beta ,\; \gamma ,\; \ldots $ и т.д.



Примеры других популярных фигур стереометрии:



Аксиомы стереометрии

В стереометрии справедливы все аксиомы планиметрии, а именно:

1. все точки или принадлежат данной прямой, или не принадлежат ей;
2. через любые $2$-е точки можно провести $1$-ну прямую;
3. только одна из $3$-х точек на прямой может лежать между $2$-мя другими;
4. длина любого отрезка прямой отлична от нуля;
5. длина отрезка складывается из длин частей, на которые он делится любой его точкой;
6. любой угол имеет определенную меру, отличную от нуля;
7. мера угла складывается из мер углов, на которые он делится любым лучем, проходящим между его сторонами;
8. аксиома Эвклида — через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Дополнительные аксиомы стереометрии



На рисунках ниже представлены два случая, когда прямая $s$ не принадлежит плоскости.

На рисунке плоскости $\alpha $ и $\beta $ имеют общую точку R, то есть точка R принадлежит как плоскости $\alpha $, так и плоскости $\beta $. Точка R принадлежит также прямой $s$. Значит, плоскости $\alpha $ и $\beta $ пересекаются по прямой $s$.

На рисунке точки M, N и K не лежат на $1$-ной прямой. Поэтому существует единственная плоскость $\alpha $, которой принадлежат все эти точки.

Следствия из аксиом стереометрии.