Правила из курса математики 5 класса — Сайт учителя математики Косыхиной Н.В.
1
Натуральные числа
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 и т. д., которые используют при счете предметов, называют натуральными.
Сравнение натуральных чисел
- Число 0 меньше любого натурального числа.
- Из двух натуральных чисел, которые имеют разное количество цифр большим является то, у которого количество цифр больше.
- Из двух натуральных чисел с одинаковым количеством цифр большим является то, у которого больше первая (при чтении слева направо) из неодинаковых цифр.
Свойства сложения
Переместительный закон: а + b = b + а. Сочетательный закон: (а + b) + с = а + (b + с)
Формула пути
S = ⱱt, где s — пройденный путь, ⱱ — скорость движения, t — время, за которое пройден путь s.
Корень уравнения
Корнем (решением) уравнения называют число, которое при подстановке его вместо буквы превращает уравнение в верное числовое равенство.
Решение уравнений
Решить уравнение — это значит найти все его корни или убедиться, что их вообще нет.
2
Отрезок
Отрезок — часть прямой, ограниченная двумя точками(концами) и все точки между этими концами(внутренние точки отрезка)
Свойство длины отрезка
Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ.
Равные отрезки
Два отрезка называют равными, если они совмещаются при наложении.
Свойство прямой
Через две точки проходит только одна прямая.
Измерить отрезок
Измерить отрезок означает подсчитать, сколько единичных отрезков в нем помещается
Ломаная
Ломаная — геометрическая фигура, состоящая из отрезков, последовательно соединенных друг с другом
Луч
Луч (полупрямая) — это геометрическая фигура, часть прямой, состоящая из точки(начала луча) и всех точек прямой, лежащих по одну сторону от начала луча.В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
Угол
Фигуру, образованную двумя лучами, имеющими общее начало, называют углом.Равные углы
Два угла называют равными, если они совмещаются при наложении.
Биссектриса угла
Луч, который делит угол на два равных угла, называется биссектрисой угла.
Свойство величины угла
Если между сторонами угла ABC провести луч BD, то градусная мера угла ABC равна сумме градусных мер углов ABD и DBC, то есть ∠ABC = ∠ABD+ ∠DBC.
Развернутый угол
Угол, стороны которого образуют прямую, называют развернутым. Градусная мера развернутого угла равна 180°.
Прямой угол
Угол, градусная мера которого равна 90°, называют прямым.
Острый угол
Угол, градусная мера которого меньше 90°, называют острым.
Тупой угол
Угол, градусная мера которого больше 90°, но меньше 180°, называют тупым.
Равные многоугольники
Два многоугольники называют равными, если они совмещаются при наложении.
Равные фигуры
Две фигуры называют равными, если они совмещаются при наложении.
Остроугольный треугольник
Если все углы треугольника острые, то его называют остроугольным треугольником.
Прямоугольный треугольник
Если один из углов треугольника прямой, то его называют прямоугольным треугольником.
Тупоугольный треугольник
Если один из углов треугольника тупой, то его называют тупоугольным треугольником.
Равнобедренный треугольник
Если две стороны треугольника равны, то его называют равнобедренным треугольником.
Равносторонний треугольник
Если три стороны треугольника равны, то его называют равносторонним треугольником.
Разносторонний треугольник
Если три стороны треугольника имеют разную длину, то его называют разносторонним треугольником.
Периметр равностороннего треугольника
Если сторона равностороннего треугольника равна а, то его периметр Р вычисляют по формуле Р = 3а.
Прямоугольник
Если в четырехугольнике все углы прямые, то его называют прямоугольником.
Свойство прямоугольника
Противоположные стороны прямоугольника равны.
Периметр прямоугольника
Если соседние стороны прямоугольника равны а и b, то его периметр Р вычисляют по формуле Р = 2а + 2 b.
Квадрат
Прямоугольник, у которого все стороны равны, называют квадратом.
Периметр квадрата
Если сторона квадрата равна а, то его периметр Р вычисляют по формуле Р = 4а.
3
Умножение
• Произведением числа а на натуральное число b, которое не равно 1, называют сумму, состоящую из b слагаемых, каждый из которых равен а.
• В равенства а ∙ b = с числа а и b называют множителями, а число с и запись а ∙ b — произведением.
• Если один из двух множителей равен 1, то произведение равно второму множителю.
• Если один из множителей равен нулю, то произведение равно нулю.
• Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Свойства умножения
• Переместительный закон умножения: ab = bа.
• Сочетательный закон умножения: (ab) с = а (bс).
• Распределительное свойство умножения относительно сложения:
a (b + с) = ab + ас.
• Распределительное свойство умножения относительно вычитания:
а (b — с) = аb — ас.
Деление
• Для натуральных чисел а, b и с равенство а : b = с является правильным, если является правильным равенство b ∙ с = а.
• В равенстве а : b = с число а называют делимым, число b — делителем, число с и запись a : b — частным от деления, отношением, долей.
• На ноль делить нельзя.
• Для любого натурального числа а правильными являются равенства: 0:а = 0; а:а=1; а:1 = а.
Деление с остатком
• а = bq + г, где а — делимое, b — делитель, q — неполное частное, r — остаток, r < b.
• Если остаток равен нулю, то говорят, что число а делится нацело на число b.
Свойства площади фигуры
1) Равные фигуры имеют равные площади;
2) площадь фигуры равна сумме площадей фигур, из которых она состоит.
Площадь прямоугольника
Площадь прямоугольника равна произведению длин его соседних сторон, выраженных в одних и тех же единицах.
Площадь квадрата
S = а*a( a в квадрате), где S — площадь квадрата, а — длина его стороны.
Свойства объема фигуры
1) Равные фигуры имеют равные объемы;
2) объем фигуры равен сумме объемов фигур, из которых она состоит.
Объем прямоугольного параллелепипеда
V = abc, где V — объем параллелепипеда, а, b и с — его измерения, выраженные в одних и тех же единицах;
V = Sh, где S — площадь основания параллелепипеда, h — его высота.
Объем куба
, где V — объем куба, а — длина его ребра.
4
Правильный дробь
Дробь, числитель которой меньше знаменателя, называют правильной
Неправильная дробь
Дробь, числитель которой больше знаменателя или равен ему, называют неправильной.
Сравнение дробей
• Из двух дробей с одинаковыми знаменателями больше та, числитель которой больше, и меньше та, числитель которой меньше.
• Из двух дробей с одинаковыми числительнями больше та, знаменатель которого меньше, и меньшая та, знаменатель которой больше.
• Все правильные дроби меньше единицы, а неправильные — больше или равны единице.
• Любая неправильная дробь больше любой правильной дроби.
Сложение и вычитание дробей с одинаковыми знаменателями
• Чтобы найти разницу двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Сложение и вычитание смешанных чисел
• Чтобы найти сумму двух смешанных чисел, надо отдельно сложить их целые и дробные части.
• Чтобы найти разность двух смешанных чисел, надо от целой и дробной части уменьшаемого вычесть соответственно целую и дробную части вычитаемого.
Преобразование неправильной дроби в смешанное число
Чтобы неправильную дробь, числитель которой не делится нацело на знаменатель, преобразовать в смешанное число, нужно числитель разделить на знаменатель; полученный неполное частное записать как целую часть смешанного числа, а остаток — как числитель его дробной части.
Преобразование смешанного числа в неправильную дробь
Преобразование смешанного числа в неправильную дробь — нужно целую часть числа умножить на знаменатель дробной части и к полученному произведению прибавить числитель дробной части; эту сумму записать как числитель неправильной дроби, а в его знаменателе записать знаменатель дробной части смешанного числа.
5
Свойства десятичной дроби
• Если к десятичной дроби справа приписать любое количество нулей, то получим дробь, равную данной.
• Значение дроби, которая заканчивается нулями, не изменится, если последние нули в его записи отбросить.
Сравнение десятичных дробей
• Из двух десятичных дробей больше та, у которой целая часть больше.
• Чтобы сравнить две десятичные дроби с равными целыми частями и разным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно.
Округление десятичных дробей
Для того чтобы десятичную дробь округлить до единиц, десятых, сотых и т. д., надо все следующие за этим разрядом цифры отбросить. Если при этом первая из цифр, которые отвергают равна 0, 1, 2, или 4, то последнюю из цифр, которые оставляют, не меняют; если же первая из цифр, которые отвергают, равна 5, 6, 7, 8 или 9, то последнюю из цифр, которые оставляют, увеличивают на единицу.
Сложение десятичных дробей
Чтобы найти сумму двух десятичных дробей, нужно:
1) уравнять количество цифр после запятых;
2) записать слагаемые друг под другом так, чтобы каждый разряд второго слагаемого оказался под соответствующим разрядом первого слагаемого;
3) сложить полученные числа так, как складывают натуральные числа;
4) поставить в полученной сумме запятую под запятыми.
Вычитание десятичных дробей
Чтобы найти разность двух десятичных дробей, нужно:
1) уравнять количество цифр после запятых;
2) записать вычитаемое под уменьшаемым так, чтобы каждый разряд вычитаемого оказался под соответствующим разрядом уменьшаемого;
3) выполнить вычитание так, как вычитают натуральные числа;
4) поставить в полученной разности запятую под запятыми
Умножение десятичных дробей
Чтобы перемножить две десятичные дроби, надо:
1) перемножить их как натуральные числа, не обращая внимания на запятые;
2) в полученном произведении отделить запятой справа столько цифр, сколько их стоит после запятых в обоих множителях вместе.
Чтобы умножить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую вправо на 1, 2, 3 и т. д. цифры.<.span>
Чтобы умножить десятичную дробь на 0,1; 0,01; 0,001 и т. д., надо в этой дроби перенести запятую влево соответственно на 1, 2, 3 и т. д. цифры.<.span>
Деление десятичных дробей
• Чтобы разделить десятичную дробь на десятичную, надо:
1) перенести в делимом и в делителе запятую вправо на столько цифр, сколько их содержится после запятой в делителе;
2) выполнить деление на натуральное число.
Чтобы разделить десятичную дробь на 10, 100, 1000 и т. д., надо в этой дроби перенести запятую влево на 1, 2, 3 и т. д. цифры.
Среднее арифметическое
Средним арифметическим нескольких чисел называют результат деления сумму этих чисел на количество слагаемых.
Процент
Процентом называют сотую часть величины или числа.
blackseaweb.ru
Правила по математике
ЧИСЛА И ЦИФРЫ.
Числа – это единицы счёта. С помощью чисел можно сосчитать количество предметов и определить различные величины (длину, ширину, высоту и т.д.).
Для записи чисел используются специальные знаки – цифры.
Цифр – десять:
1 2 3 4 5 6 7 8 9 0
НАТУРАЛЬНЫЕ ЧИСЛА.
Числа, которые используются при счёте, называются натуральными.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …, □
1 – самое маленькое число.
□ – самого большого числа не существует.
Число 0 (нуль) обозначает отсутствие предмета. Нуль не является натуральным число.
СРАВНЕНИЕ ЧИСЕЛ.
Правило 1.
Из двух натуральных чисел больше то, которое в натуральном ряду расположено правее, а меньше то, которое расположено левее:
…, 10, 11, 12, 13, 14, 15,
14 > 11
Правило 2.
Из двух натуральных чисел с разным количеством разрядов больше то число, в котором разрядов больше.
28 < 145 782 < 1263
Правило 3.
Из двух натуральных чисел с одинаковым количеством разрядов больше то, у которого больше цифра старшего разряда.
4 5 861 и 4 7 361
45 861 < 47 361 47361 > 45 681
СЛОЖЕНИЕ.
Сложение – это математическое действие.
Числа, которые складываются, называются слагаемыми.
Результат сложение называется суммой.
|
|
|
2 + 3 = 5 |
сумма |
Правило 1.
Если одно из слагаемых равно 0, сумма равна второму слагаемому:
a + 0 = a 0 + a = a
5 + 0 = 5 0 + 5 = 5
Правило 2.
Если оба слагаемых равны 0, то и сумма равна 0: 0 + 0 = 0
ВЫЧИТАНИЕ.
Вычитание – действие, обратное сложению.
Правило 1.
Если к разности прибавить вычитаемое, то получится уменьшаемое.
Правило 2.
Если из уменьшаемого вычесть разность, то получится вычитаемое.
ЗАКОНЫ СЛОЖЕНИЯ.
Закон 1.
Переместительный закон сложения.
От перемены мест слагаемых значение суммы не меняется:
a + b = b + a
4 + 2 = 2 + 4
Закон 2.
Сочетательный закон сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел или ко второму числу прибавить сумму первого и третьего чисел:
(a + b) + c = a + (b + c) = (a + c) + b
(2 + 4) + 8 = 2 + (4 + 8) = (2 + 8) + 4
УМНОЖЕНИЕ.
Умножение – это сложение одинаковых слагаемых.
2 + 2 + 2 = 2 · 3 = 6
2 – слагаемое
3 – число, которое показывает, сколько раз повторяется слагаемое 2 (по два три раза)
· , × — знаки умножения.
a · b = a + a + a + … + a
b раз
ДЕЛЕНИЕ.
Деление – это действие, обратное умножению.
6 : 2 = 3 6 : 3 = 2
ЗАКОНЫ УМНОЖЕНИЯ.
Закон 1.
Переместительный закон умножения.
От перестановки множителей произведение не меняется:
a · b = b · a
4 · 2 = 2 · 4
8 = 8
Закон 2.
Сочетательный закон умножения.
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел или второе число умножить на произведении первого и третьего чисел:
(a · b) · c = a · (b · c) = (a · c) · b
(2 · 4) · 8 = 2 · (4 · 8) = (2 · 8) · 4
Закон 3.
Распределительный закон умножения.
Относительно сложения
Произведение суммы на число равно сумме произведений каждого слагаемого на это число.
(a + b + c) · d = a · d + b · d + c · d
(2 + 5 + 3) · 2 = 2 · 2 + 5 · 2 + 3 · 2 = 20
Относительно вычитания
Чтобы умножить разность на число, достаточно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе произведение.
(a — b) · d = a · d — b · d
(15 — 5) · 4 = 15 · 4 — 5 · 4 = 60 -+ 20 = 40
СВОЙСТВА ДЕЛЕНИЯ.
Правило 1.
Чтобы разделить сумму на число, достаточно разделить каждое слагаемое на это число, а полученные результаты сложить.
(a + b) : c = a : c + b : c
Правило 2.
Чтобы разделить разность на число, достаточно разделить на это число уменьшаемое и вычитаемое, а затем из первого частного вычесть второе частное.
(a — b) : c = a : c — b : c
Правило 3.
Частное от деления произведений двух множителей на число равно произведению одного из множителей на частное от деления второго множителя на это число.
(a · b) : c = (a : c) · b = a · (b : c)
Правило 4.
Чтобы разделить число на частное, достаточно разделить это число на делимое и полученный результат умножить на делитель.
a · (b : c) = (a : b) · c
Правило 5.
Чтобы разделить частное на число, достаточно умножить делитель на это число и разделить делимое на полученный результат
Можно так же разделить делимое на это число, а полученный результат разделить на делитель.
(a : b) : c = a : (b · c)
или
(a : b) : c = (a : c) : b
НАХОЖДЕНИЕ КОМПОНЕНТОВ ДЕЛЕНИЯ.
Правило.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
a : ? = c ? = a : c
Чтобы найти неизвестное делимое, нужно частное умножить на делитель.
? : b = c ? = c · b
ОСОБЫЕ СЛУЧАИ УМНОЖЕНИЯ.
a · 1 = a 4 · 1 = 4 | 1 · a = a 1 · 4 = 4 |
0 · a = 0 0 · 6 = 0 | a · 0 = 0 6 · 0 = 0 |
ОСОБЫЕ СЛУЧАИ ДЕЛЕНИЯ.
a : 1 = a 8 : 1 = 8 | 0 : a = 0 0 : 6 = 0 | a : a = 1 8 : 8 = 1 |
На нуль делить НЕЛЬЗЯ!
| ||
Нуль можно делить на любое число, получится 0.
ПРИЗНАКИ ДЕЛИМОСТИ.
На 2 делятся все чётные числа, то есть числа, которые оканчиваются цифрами 0, 2, 4, 6, 8.
На 3 делятся все числа, сумма цифр которых делится на 3.
На 5 делятся все числа, которые оканчиваются на 0 или 5.
На 6 делятся числа, которые делятся одновременно и на 2, и на 3.
На 9 делятся числа, сумма цифр которых делится на 9.
ИМЕНОВАННЫЕ ЧИСЛА.
Именованные числа – это числа, полученные при измерении величин и сопровождающиеся названием единиц измерения.
Например: 2 кг, 4 см, 8 л
Именованные числа бывают простые и составные.
Простые именованные числа: 7 м, 18 т, 21 кг – в них входит только одн единица измерения.
Составные именованные числа: 2 м 4 см, 24 кг 45 г, 8 км 520 м – в них входят несколько единиц измерения.
ПРЕОБРАЗОВАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Чтобы перейти от одних единиц измерения к другим, пользуйся таблицей величин.
Таблица величин.
Единицы измерения длины 1 см = 10 мм 1 дм = 10 см 1 м = 10 дм = 100 см = 1000 мм 1 км = 1000 м = 10000 дм = 100000 см |
Единицы измерения массы 1 кг = 1000 г 1 ц = 100 кг 1 т = 10 ц = 1000 кг |
Единицы измерения времени 1 мин = 60 с 1 ч = 60 мин = 3600 с 1 сутки = 24 часа 1 неделя = 7 дней 1 месяц = 30 или 31 день (в феврале 28 или 29 дней) 1 год = 12 месяцев = 52 недели = 365 или 366 дней 1 век (столетие) = 100 лет |
Единицы измерения площади 1 мм2 1 см2 = 100 мм2 1 дм2 = 100 см2 1 м2 = 100 дм2 = 10000 см2 1 км2 = 1000000 м2 1 ар (1 а) = 1 сотка = 100 м2 1 гектар (1 га) = 10000 м2 |
СЛОЖЕНИЕ И ВЫЧИТАНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Правило.
Складывать и вычитать можно именованные числа, выраженные в одинаковых единицах измерения.
УМНОЖЕНИЕ И ДЕЛЕНИЕ ИМЕНОВАННЫХ ЧИСЕЛ.
Запомни!
При умножении и делении составные именованные числа сначала заменяют простыми, а затем выполняют вычисления. В ответе простое именованное число заменяют составным.
ВЫРАЖЕНИЯ.
Математическое выражение – это фраза, записанная с помощью чисел, знаков и букв.
Выражение, записанное только с помощью чисел и знаков, называется числовым.
Выражение, в котором кроме чисел и знаков есть буквы, называется буквенным.
Любое числовое выражение имеет значение. Найти значение числового выражения – значит найти его ответ.
ПОРЯДОК ДЕЙСТВИЙ В ВЫРАЖЕНИЯХ.
Правило 1.
В выражениях без скобок, где выполняются только сложение и вычитание, действия выполняются в том порядке, в котором они записаны (то есть слева направо).
1 2
70 — 26 + 10 = 54
1 2
90 — 20 — 15 = 55
1 2
42 + 18 — 19 = 41
Правило 2.
В выражениях без скобок, где выполняются только умножение и деление, действия выполняются в том порядке, в котором они записаны.
1 2
4 · 10 : 5 = 8
1 2
60 : 10 · 3 = 18
1 2
36 : 9 · 3 = 12
Правило 3.
В выражениях со скобками первым выполняется действие в скобках, затем умножение или деление и только потом сложение или вычитание.
1 2
80 — (46 — 14) = 48
1 2
6 · (30 — 20) = 60
1 2
90 : (2 · 5) = 9
Правило 4.
В выражениях, где есть действия первой и второй ступеней (то есть +, -, ·, :), сначала выполняются умножение и деление, а затем по порядку сложение и вычитание.
1 3 2
6 · 5 + 40 : 2 = 20
2 1 3
72 – 24 : 6 + 2 = 70
УРАВНЕНИЯ.
Уравнение – это равенство, которое содержит в себе неизвестное (переменную), значение которого нужно найти, чтобы равенство было верным.
x + 3 = 5 5 · x = 20 | y — 2 = 7 8 : a = 2 |
Решить уравнение – значит найти все значения переменной, при которых уравнение превращается в верное равенство.
x + 3 = 5
x = 5 — 3
x = 2
2 + 3 = 5
5 = 5
Значение переменной, при котором уравнение превращается в верное равенство, называется корнем уравнения: y — 2 = 7
y = 9 — корень уравнения, так как 9 — 2 = 7
РЕШЕНИЕ ПРОСТЕЙШИХ УРАВНЕНИЙ.
Правило 1.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
x + 3 = 5
x = 5 — 3
Правило 2.
Чтобы найти неизвестное уменьшаемое, нужно к вычитаемому прибавить разность.
x — 3 = 5
x = 5 + 3
Правило 3.
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
8 — x = 5
x = 8 — 5
Правило 4.
Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель.
x · 3 = 15
x = 15 : 3
Правило 5.
Чтобы найти неизвестное делимое, нужно к вычитаемому прибавить разность.
x : 3 = 5
x = 5 · 3
Правило 6.
Чтобы найти неизвестный делитель, нужно делимое разделить на частное.
8 : x = 2
x = 8 : 2
УЧИМСЯ РЕШАТЬ ЗАДАЧИ.
Как работать над задачей.
1. Прочитай внимательно условие задачи и представь то, о чём идёт речь.
2. Запиши кратко задачу или сделай к ней рисунок, схему, чертёж.
3. Объясни, что означает каждое число.
4. Устно составь план решения задачи.
5. Реши задачу и найди ответ.
6. Проверь решение, составив обратную задачу.
7. Запиши ответ.
Знак | Действие | Знак | Действие |
+ | Увеличить на … | — | Найти разность |
— | Уменьшить на … | · (х) | Увеличить в несколько раз |
— | На сколько больше? | : | Уменьшить в несколько раз |
— | На сколько меньше? | : | Во сколько раз больше? |
+ | Найти сумму | : | Во сколько раз меньше? |
ЗАДАЧИ НА НАХОЖДЕНИЕ СУММЫ ДВУХ ЧИСЕЛ.
Запомни!
Задачи этого вида решаются сложением, потому что находим сумму.
Задача.
Белочка припасла для маленьких друзей 4 гриба и 5 орехов. Сколько всего гостинцев приготовила белочка?
Краткое условие:
Грибов — □
Орехов — □
Решение:
4 + 5 = 9 (гост.)
Ответ: 9 гостинцев.

ЗАДАЧИ НА НАХОЖДЕНИЕ ОСТАТКА.
Запомни!
Задачи этого вида решаются вычитанием, потому что находим остаток.
Задача.
На ветке было 7 ягод рябины. Снегирь склевал 3 ягоды. Сколько ягод осталось?
Краткое условие:
Было – 7 яг.
Склевал – 3 яг.
Осталось — ? яг.
Решение:
7 — 3 = 4 (яг.)
Ответ: 4 ягоды.

ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА
НА НЕСКОЛЬКО ЕДИНИЦ.
Задача.
Во дворе гуляло 6 утят, а гусят на 2 больше. Сколько гуляло гусят?
Краткое условие:
Утят – 6 пт.
Гусят – ? пт., на 2 больше (>)
Решение:
6 + 2 = 8 (гус.)
Ответ: 8 гусят.
ЗАДАЧИ НА УМЕНЬШЕНИЕ ЧИСЛА
НА НЕСКОЛЬКО ЕДИНИЦ.
Задача.
На столе лежало 9 столовых ложек, а чайных на 3 меньше. Сколько чайных ложек лежало на столе?
Краткое условие:
Стол. – 9 лож.
Чайн. – ? лож., на 3 меньше (<)
Решение:
9 — 3 = 6 (лож.)
Ответ: 6 чайных ложек.
ЗАДАЧИ НА РАЗНОСТНОЕ СРАВНЕНИЕ ДВУХ ЧИСЕЛ.
Правило.
Чтобы узнать, на сколько одно число больше (меньше) другого, нужно из большего числа вычесть меньшее.
Задача.
В одной корзине 7 яблок, а в другой – 10 груш. На сколько груш больше, чем яблок?
Краткое условие:
Яб. – 7 шт.
Гр. – 10 шт., на ? шт. больше (>)
Решение:
10 — 7 = 3 (гр.)
Ответ: на 3 груши.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО СЛАГАЕМОГО.
Задача.
Два петушка нашли 8 червячков. Первый нашёл 5. Сколько червячков нашёл второй петушок?
Краткое условие:
1 пет. – 5 чер. 8 чер.
2 пет. — ? чер.
Решение:
8 — 5 = 3 (чер.)
Ответ: 3 червячка.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО УМЕНЬШАЕМОГО.
Задача.
На тарелке лежали пряники. Когда дети взяли 4 пряника, на тарелке осталось 8. Сколько пряников было на тарелке?
Краткое условие:
Было – ? пр.
Взяли – 4 пр.
Осталось – 8 пр.
Решение:
8 + 4 = 12 (пр.)
Ответ: 12 пряников.
ЗАДАЧИ НА НАХОЖДЕНИЕ
НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО.
Задача.
В вазе стояло 7 гвоздик. Когда несколько гвоздик отдали, в вазе осталось 5 гвоздик. Сколько гвоздик отдали?
Краткое условие:
Было – 7 гв.
Отдали – ? гв.
Осталось – 5 гв.
Решение:
7 — 5 = 2 (гв.)
Ответ: 2 гвоздики.
ЗАДАЧИ НА НАХОЖДЕНИЕ
ПРОИЗВЕДЕНИЯ ДВУХ ЧИСЕЛ.
Задача.
В одной коробке 6 карандашей. Сколько карандашей в 4 коробках?
Краткое условие:
1 кор. – 6 кар.
4 кор. — ? кар.
Решение:
6 · 4 = 24 (кар.)
Ответ: 24 карандаша.
ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТНОГО ДВУХ ЧИСЕЛ.
Задача 1.
ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ.
15 шариков раздали 5 ученикам поровну. Сколько шариков получил каждый ученик?
Краткое условие:
15 шар. – 5 уч.
Поровну шар. – 1 уч.
Решение:
15 : 5 = 3 (шар.)
Ответ: 3 шарика.
Задача 2.
ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ.
12 лимонов разложили в пакеты по 4 лимона в каждый. Сколько получилось пакетов с лимонами?
Краткое условие:
12 лим. – ? пак.
4 лим. – 1 пак.
Решение
12 : 4 = 3 (пак.)
Ответ: 3 пакета.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ.
Задача.
У Тани было 4 ириски, а карамелек в 2 раза больше. Сколько карамелек было у Тани?
Краткое условие:
Ириски – 4 шт.
Карамельки – ? шт., в 2 раза больше (>)
Решение:
4 · 2 = 8 (кар.)
Ответ: 8 карамелек.
ЗАДАЧИ НА УМЕНЬШЕНИЕ ЧИСЛА
В НЕСКОЛЬКО РАЗ.
Задача.
На одной полке стоит 12 книг, а на второй – в 3 раза меньше. Сколько книг на второй полке?
Краткое условие:
I – 12 кн.
II – ? кн., в 3 раза меньше (<)
Решение:
12 : 3 = 4 (кн.)
Ответ: 4 книг.
ЗАДАЧИ НА КРАТНОЕ СРАВНЕНИЕ ДВУХ ЧИСЕЛ.
Правило.
Чтобы узнать, во сколько раз одно число больше (меньше) другого, нужно большее число разделить на меньшее.
Задача.
Петя почистил 27 картофелин, а Коля – 9. Во сколько раз больше картофелин почистил Петя, чем Коля?
Краткое условие:
Петя – 27 кар. во ? раз больше (>)
Коля – 9 кар.,
Решение:
27 : 9 = 3 (гр.)
Ответ: в 3 раза больше.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО МНОЖИТЕЛЯ.
Задача.
20 яблок разложили в сетки по 5 яблок в каждую. Сколько потребовалось сеток?
Краткое условие:
1 сет. – 5 яб.
? сет. – 20 яб.
Решение:
1-ый способ: 20 : 5 = 4 (сет.)
2-ой способ: запишем решение задачи, составив уравнение.
х · 5 = 20
х = 20 : 5
х = 4 (сет.)
Ответ: 4 сетки.
ЗАДАЧИ В КОСВЕННОЙ ФОРМЕ.
Правило.
При решении задач в косвенной форме помни: если одна величина на несколько единиц (в несколько раз) больше, то другая на столько же единиц (во столько же раз) меньше.
Задача.
Брату 5 лет, он на 2 года старше сестры. Сколько лет сестре?
Краткое условие:
Брат – 5 лет, на 2 года больше (>)
Сестра – ? лет
Если брат старше на 2 года, значит, сестра на 2 года младше. Чтобы стало меньше, нужно вычитать.
Решение:
5 — 2 = 3 (г.)
Ответ: 3 года.
Задача.
У Нины 7 марок. Это на 4 марки меньше, чес у Тани. Сколько марок у Тани?
Краткое условие:
Нина – 7 мар., на 4 мар. меньше (<)
Таня – ? мар.
Если у Нины на 4 марки меньше, значит, у Тани на 4 марки больше. Чтобы стало больше, нужно прибавлять.
Решение:
7 + 4 = 11 (мар.)
Ответ: 11 марок.
loseva-nn-shat-schtugoles.edumsko.ru
Математика 6 класс: все темы, правила и формулы
Математика 6 класс: все темы, правила и формулы.
Краткий курс математики за 6 класс.
«Математика 6 класс: все темы, правила и формулы» — это краткое повторение математики за 6 класс (основные понятия, формулы и определения). Вся информация, самое главное и всё, что нужно знать вкратце. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского) — М.: Просвещение, 2014.
Делимость чисел
- Пусть а и b — натуральные числа и при делении а на b в частном получается q и в остатке r. Тогда а = bq + r, где q и r — натуральные числа или нули, причём r < b. Например:

- Если натуральное число а делится на натуральное число b, то а называют кратным b, а b — делителем а. Это означает, что а = bq, где q — натуральное число. Например, 62 кратно 31, 31 — делитель 62, так как 62 = 31 • 2.
- Простым числом называется такое натуральное число, которое имеет только два делителя — единицу и само это число. Составным числом называется такое натуральное число, которое имеет более двух делителей.
Например, числа 2, 7, 43, 109 — простые, а числа 4, 12, 35 — составные. Число 1 не является ни простым, ни составным. Всякое составное число можно разложить на простые множители, и притом единственным способом. Например, 630 = 2 • 32 • 5 • 7.
- Чтобы найти наименьшее общее кратное (НОК) нескольких чисел, надо разложить эти числа на простые множители и найти произведение всех получившихся простых множителей, взяв каждый из них с наибольшим показателем. Например, 72 = 23 • 32; 180 = 22 • 32 • 5 и 600 = 23 • 3 • 52. Наименьшее общее кратное чисел 72, 180 и 600 равно 23 • 32 • 52 = 1800.
Чтобы найти наибольший общий делитель (НОД) нескольких чисел, надо разложить эти числа на простые множители и найти произведение общих простых множителей, взяв каждый из них с наименьшим показателем. Например, наибольший общий делитель чисел 72, 180 и 600 равен 22 • 3, т. е. числу 12.
- Если число оканчивается цифрой 0 или цифрой 5, то оно делится на 5. Если число оканчивается любой другой цифрой, то оно не делится на 5.
- Если число оканчивается чётной цифрой, то оно делится на 2. Если число оканчивается нечётной цифрой, то оно но делится на 2.
- Если сумма цифр числа делится на 3, то и число делится на 3. Если сумма цифр числа не делится на 3, то число не делится на 3.
- Если сумма цифр числа делится на 9, то и число делится на 9. Если сумма цифр числа не делится на 9, то и число не делится на 9.
Обыкновенные дроби
- Правильной дробью называется дробь, у которой числитель меньше знаменателя. Неправильной дробью называется дробь, у которой числитель больше знаменателя или равен ему.
- Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
- Чтобы привести дроби к наименьшему общему знаменателю, надо найти наименьшее общее кратное знаменателей дробей; вычислить дополнительные множители, разделив наименьшее общее кратное на каждый знаменатель; умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множитель. Например, приведём к наименьшему общему знаменателю дроби 1/6, 7/12, 5/18. Наименьший общий знаменатель равен 36:

- При сложении дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби и оставляют тот же знаменатель. При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитают числитель второй дроби и оставляют тот же знаменатель. Например,
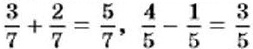
При сложении и вычитании дробей с разными знаменателями сначала их приводят к общему знаменателю.
- Чтобы перемножить две дроби, надо перемножить отдельно их числители и знаменатели; первое произведение сделать числителем, а второе — знаменателем. Чтобы разделить одну дробь на другую, надо делимое умножить на дробь, обратную делителю.
Например, 
Десятичные дроби
- При округлении десятичной дроби до какого-нибудь разряда все следующие за этим разрядом цифры заменяют нулями, а если они стоят после запятой, то их отбрасывают. Если первая следующая за этим разрядом цифра 5, б, 7, 8 или 9, то к последней оставшейся цифре прибавляют 1. Если первая следующая за этим разрядом цифра 0, 1, 2, 3 или 4, то последнюю оставшуюся цифру не изменяют.
Например, 4,376 ≈ 4,4; 2,8195 ≈ 2,820; 10,1425 ≈ 10,14.
- Сложение и вычитание десятичных дробей выполняют поразрядно. При этом дроби записывают одну под другой так, чтобы запятая оказалась под запятой.
Например: 
- Чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимания на запятые, а затем в полученном произведении отделить занятой справа столько цифр, сколько их стоит после занятой в обоих множителях вместе.
- Чтобы разделить десятичную дробь на десятичную, надо в делимом и делителе перенести запятые вправо на столько цифр, сколько их после запятой в делителе, а затем выполнить деление на натуральное число.
Например: 
- Чтобы умножить десятичную дробь на 10n, надо в этой дроби перенести запятую на n цифр вправо. Чтобы разделить десятичную дробь на 10n, надо в этой дроби перенести запятую на n цифр влево.
Например, 8,373 • 100 = 837,3; 3,4 : 1000 = 0,0034.
Положительные и отрицательные числа
- Модулем положительного числа и нуля называется само это число. Модулем отрицательного числа называется противоположное ему положительное число. Модуль числа а обозначают |а|. Например, |3,6| = 3,6; |0| = 0; |–2,8| = 2,8.
- Чтобы сложить два отрицательных числа, надо сложить их модули и перед полученным результатом поставить знак «минус».
- Чтобы сложить два числа с разными знаками, надо из большего модуля вычесть меньший и перед полученным результатом поставить знак того слагаемого, модуль которого больше.
- Сумма двух противоположных чисел равна нулю.
Например, –3,4+ (–1,8) = –5,2; 2,5 + (–4,1) = –1,6; –3,6 + 3,6 = 0.
- Чтобы из одного числа вычесть другое, достаточно к уменьшаемому прибавить число, противоположное вычитаемому.
Например, –5 – 1,9 = –5 + (–1,9) = –6,9.
- Чтобы перемножить два отрицательных числа, надо перемножить их модули. Чтобы перемножить два числа с разными знаками, надо перемножить их модули и перед полученным результатом поставить знак «минус».
Например, –1,2 • (–8) = 9,6, –3 • 1,2 = –3,6.
- Чтобы разделить отрицательное число на отрицательное, надо модуль делимого разделить на модуль делителя. Чтобы разделить два числа с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным результатом поставить знак «минус».
Например, –4,8 : (–2,4) = 2, 5,5 : (–5) = –1,1.
- Средним арифметическим нескольких чисел называется частное от деления суммы этих чисел на число слагаемых.
Пропорции
- Равенство двух отношений называют пропорцией. Например, равенство 2,5 : 5 = 3,5 : 7 — пропорция. Числа 2,5 и 7 — крайние члены пропорции. Числа 5 и 3,5 — средние члены пропорции. Если пропорция верна, то произведение её крайних членов равно произведению средних членов. В пропорции можно менять местами крайние члены или средние члены.
- Две величины называются прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
- Если величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
- Две величины называются обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.
- Если величины обратно пропорциональны, то отношение значений одной из величин равно обратному отношению соответствующих значений другой величины.
Свойства действий над числами
- Переместительное свойство сложения. От перестановки слагаемых значение суммы не изменяется.
Сочетательное свойство сложения. Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего.
Переместительное свойство умножения. От перестановки множителей значение произведения не изменяется.
Сочетательное свойство умножения. Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
Распределительное свойство умножения. Чтобы умножить число на сумму, можно умножить ото число на каждое слагаемое и сложить полученные результаты.
Преобразование выражений
- Слагаемые, которые имеют одинаковую буквенную часть, называются подобными слагаемыми.
- Для того чтобы привести подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Например, 5а – 7а + 4а = 2а.
- Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки.
Например, 3х + (2а – у) = 3х + 2а – у.
- Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки.
Например, 5а – (2х – 3у) = 5а – 2х + 3у.
«Математика 6 класс: все темы, правила и формулы» — это краткое повторение алгебры за 6 класс (основные понятия, формулы и определения). Краткий курс: вся информация, самое главное и всё, что нужно знать вкратце.
uchitel.pro
Правила математики из курса 5-6 классов — Сайт учителя математики Косыхиной Н.В.
1.Основное свойство дроби
Если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получим дробь, равную данной:
Если числитель и знаменатель данной дроби разделить на их общий делитель (или на одно и то же натуральное число), то получим дробь, равную данной:
2.Сокращение дробей
- Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют сокращением дроби.
- Дробь, числитель и знаменатель которой — взаимно простые числа, называют несократимой.
- Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получим несократимую дробь.
3.Приведение дробей к наименьшему общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю, надо:
- найти наименьший общий знаменатель данных дробей;
- найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
4. Целые числа. Рациональные числа
- Все натуральные числа, противоположные им числа и число 0 называют целыми числами.
- Натуральные числа называют целыми положительными числами. Числа -1, -2, -3, … называют целыми отрицательными числами.
- Объединив натуральные числа с целыми отрицательными и нулем, получим целые числа.
- Объединив целые числа с дробными, получим рациональные числа:
5. Модуль числа
- Модулем числа a называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.
- Модуль числа а обозначают так: | а | (читают: «модуль а»).
- Модуль положительного числа равен этому числу; модуль отрицательного числа равен числу, противоположному данному;
| 0 | = 0.
- Модуль числа принимает только неотрицательные значения.
- Модули противоположных чисел равны: | а | = | -а |.
6. Сложение. Свойства сложения
- Числа, которые складывают, называют слагаемыми, а результат сложения — суммой.
- От перестановки слагаемых сумма не изменяется:
а + b = b + а — переместительное свойство сложения.
- Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел:
(a+ b) + с = а + (b + с) — сочетательное свойство сложения.
7. Вычитание. Свойства вычитания
- Из числа а число b — значит найти такое число, которое в сумме с числом b дает число а.
- Равенство а-b = с верно, если верно равенство b + с = а.
- В равенстве а-b = с число а называют уменьшаемым, b — вычитаемым, с — разностью.
- Разность а-b показывает, на сколько число а больше числа b или на сколько число b меньше числа а.
- Для любого числа а верны равенства:
а-0= а, а-а = 0
8. Сложение и вычитание дробей
- Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
- Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
- Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а потом применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
9. Сложение рациональных чисел
- Чтобы сложить два числа с разными знаками, надо:
-
найти модули слагаемых;
-
из большего модуля вычесть меньший модуль;
-
перед полученным числом поставить знак слагаемого с большим модулем.
- Чтобы сложить два отрицательных числа, надо:
- найти модули слагаемых;
- сложить модули слагаемых;
- перед полученным числом поставить знак «-».
- Сумма двух противоположных чисел равна нулю. Для любого рационального числа а:
а + 0 = 0 + а = а.
10. Вычитание рациональных чисел
- Чтобы найти разность двух чисел, можно к уменьшаемому прибавить число, противоположное вычитаемому.
11. Умножение. Свойства умножения
- Произведением числа а на натуральное число b не равное 1, называют сумму, состоящую из b слагаемых, каждое из которых равно а:
- Если один из двух множителей равен 1, то произведение равно второму множителю:
- Если один из множителей равен нулю, то произведение равно нулю:
- Если произведение равно нулю, то хотя бы один из множителей равен нулю.
- От перестановки множителей произведение не изменяется:
аb = bа — переместительное свойство умножения.
- Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел:
(аb)с = а(bс) — сочетательное свойство умножения.
- Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить: а (b + с) = аb + ас — распределительное свойство умножения относительно сложения.
- Чтобы число умножить на разность двух чисел, можно это число умножить на уменьшаемое, отдельно на вычитаемое и полученные произведения вычесть: а (b — с) = аb — ас — распределительное свойство умножения относительно вычитания.
12. Умножение обыкновенных дробей
- Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:
Считают, что .
- Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
- Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
13. Умножение рациональных чисел
- Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».
- Чтобы умножить два отрицательных числа, надо умножить их модули.
- Для любого рационального числа а:
- Если произведение аb — положительное, то числа а и b имеют одинаковые знаки;
если произведение аb — отрицательное, то числа а и b имеют разные знаки.
14. Деление. Свойства деления
- Разделить число а на число b — значит найти такое число, произведение которого с числом b равно а.
- Равенство а:b=с верно, если верно равенство bс = а.
- В равенстве а:b = с число а называют делимым, число b — делителем, число с — частным.
- При любых значениях а верно равенство
a : 1 = а.
- Если а не равно 0, то справедливы такие равенства:
На нуль делить нельзя!
15. Делимость натуральных чисел
- Если натуральное число а делится нацело на натуральное число b, то число а называют кратным числа b, число b — делителем числа а.
- Для любого натурального числа а каждое из чисел а • 1, а • 2, а • 3, а • 4, … является кратным числа а.
- Наименьшим делителем любого натурального числа а является число 1, а наибольшим — само число а.
- Среди чисел, кратных а, наибольшего нет, а наименьшее есть — это само число а.
- Если каждое из чисел а и b делится нацело на число k, то и сумма а + k также делится нацело на число k.
- Если число а делится нацело на число к, а число b не делится нацело на число к, то сумма а + b также не делится нацело на число к.
- Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число.
- Натуральное число, имеющее более двух делителей, называют составным.
- Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.
- Если наибольший общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми.
16. Признаки делимости натуральных чисел
- Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.
- Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.
- Если натуральное число разделить на 10, то остаток равен числу, записанному последней цифрой этого числа.
- Если запись натурального числа оканчивается четной цифрой, то это число делится нацело на 2.
- Если запись натурального числа оканчивается нечетной цифрой, то это число не делится нацело на 2.
- Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.
- Если запись натурального числа оканчивается любой цифрой, отличной от цифр 0 и 5, то это число не делится нацело на 5.
- Если сумма цифр натурального числа делится нацело на 9, то и само число делится нацело на 9.
- Если сумма цифр натурального числа не делится нацело на 9, то и само число не делится нацело на 9.
- Если сумма цифр натурального числа делится нацело на 3, то и само число делится нацело на 3.
- Если сумма цифр натурального числа не делится нацело на 3, то и само число не делится нацело на 3.
17. Деление с остатком
- Остаток всегда меньше делителя.
- Чтобы найти делимое, надо делитель умножить на неполное частное и прибавить остаток.
а=bq +r, где а — делимое, b — делитель, q — неполное частное, r — остаток, r < b.
18. Деление обыкновенных дробей
- Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
19. Деление рациональных чисел
- Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
- Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.
20. Нахождение дроби от числа
- Чтобы найти дробь от числа, можно число умножить на эту дробь.
- Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.
21. Нахождение числа по его дроби
- Чтобы найти число по значению его дроби, можно это значение разделить на эту дробь.
- Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
22. Степень числа
- Степенью числа а с натуральным показателем п, большим 1, называют произведение п множителей, каждый из которых равен а:
Число а при этом называют основанием степени.
- Степенью числа а с показателем 1 называют само число a
- Вторую степень числа называют также квадратом числа. Например, запись читают: «а в квадрате». Третью степень называют кубом числа, а запись читают: «а в кубе».
- Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем другие действия.
23. Числовые и буквенные выражения
- Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением.
- Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.
24. Раскрытие скобок
- Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
- Если перед скобками стоит знак « + », тотпри раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.
25. Приведение подобных слагаемых
- Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
26. Формулы
- Равенства вида у = 3x, Р=2(а + b) называют формулами.
- Равенство , где S — пройденный путь, V — скорость движения,t — время, за которое пройден путь S, называют формулой пути.
27. Уравнения
- Корнем уравнения называют значение переменной, при котором уравнение обращается в верное числовое равенство.
- Решить уравнение — значит найти все его корни или убедиться, что их вообще нет. Поэтому корень часто называют решением уравнения.
- Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
- Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
- Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
- Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
- Чтобы найти неизвестное делимое, надо делитель умножить на частное.
- Чтобы найти неизвестный делитель, надо делимое разделить на частное.
28. Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
- Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.
- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
29. Отношения
- Частное двух чисел а и b, не равных нулю, еще называют отношением чисел а и b, или отношением числа а к числу b.
- Числа а и b называют членами отношения, число а — предыдущим членом отношения, а число b — последующим.
- Отношение положительных чисел а и b показывает, во сколько раз число а больше числа b, или какую часть число а составляет от числа b.
- Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
30. Пропорции
- Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:
или
Числа а и d называют крайними членами пропорции, а числа b и с — средними членами пропорции.
31. Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов:
Если a, b, c и d числа, не равные нулю, и ab = cd, то отношение и и могут образовывать пропорцию
32. Процентное отношение двух чисел
- Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
- Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
33. Прямая пропорциональная зависимость
- Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
- Если величины у и х прямо пропорциональны, то их соответствующие значения удовлетворяют равенству , где k -число, постоянное для данных величин.
Данная информация взята из Учебника «Алгебра 7 класс» А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
blackseaweb.ru
Порядок выполнения действий в выражениях без скобок и со скобками
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Давайте проверим
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Запишем.
8-3+4=5+4=9
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
8-3+4=8-7=1
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
Потренируемся.
Рассмотрим выражение
38-10+6
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий
Рассмотрим второе выражение
24:3*2
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассмотрим выражение.
18:2-2*3+12:3
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
1 4 2 5 3
18:2-2*3+12:3
Вычислим значение выражения.
1 4 2 5 3
18:2-2*3+12:3=9-6+4=3+4=7
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Рассмотрим выражение.
30 + 6 * (13 — 9)
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
3 2 1
30 + 6 * (13 — 9)
Вычислим значение выражения.
3 2 1
30+6*(13-9)=30+6*4=30+24=54
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).
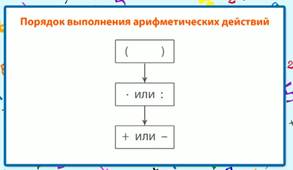
Рис. 4. Порядок действий
Потренируемся.
Рассмотрим выражения, установим порядок действий и выполним вычисления.
43 — (20 — 7) +15
32 + 9 * (19 — 16)
2 * 9 — 18:3
Будем действовать по правилу. В выражении 43 — (20 — 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 — (20 — 7) +15 =43 — 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 — 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 — 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
2*9-18:3=18-6=12
Узнаем, правильно ли определен порядок действий в следующих выражениях.
4 3 1 2
37 + 9 — 6 : 2 * 3 =
3 1 2
18 : (11 — 5) + 47=
1 3 2
7 * 3 — (16 + 4)=
Рассуждаем так.
3 4 1 2
37 + 9 — 6 : 2 * 3 =
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
3 4 1 2
37+9-6:2*3 =37+9-3*3=37+9-9=46-9=37
Продолжаем рассуждать.
3 1 2
18:(11-5)+47=
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
2 1 3
18:(11-5)+47=18:6+47=3+47=50
Рассуждаем далее.
1 3 2
7*3-(16+4)=
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
2 3 1
7*3-(16+4)=7*3-20=21-20=1
Выполним задание.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).
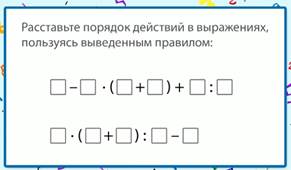
Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).
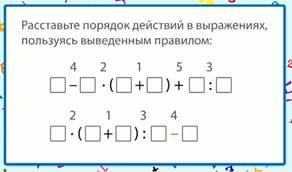
Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник).
- Sosnovoborsk-soobchestva.ru (Источник).
- Openclass.ru (Источник).
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
68+2-50+43
(36-18):(72:8)
35:5+6*2
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
25+30:6-3*5+45
15+6*5-48:6-10
20+8*5-45:9+12
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
interneturok.ru
Основные правила по математике во 2 классе
ПРАВИЛА ПО МАТЕМАТИКЕ 2 класс
ВопросПравило
Пример
Компоненты сложения:
Слагаемое + слагаемое = сумма
2 + 3 = 5
Как найти неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, надо
из суммы вычесть известное слагаемое
? + 3 = 5
5 — 3 = 2
Переместительное свойство сложения
От перестановки слагаемых сумма не меняется.
a + b= b + a
Сочетательное свойство сложение
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.
(a + b) + c = a + (b + c)
Вычитание суммы из числа
Чтобы вычесть суммы из числа, можно сначала вычесть одно слагаемое, а потом другое.
а – (b + c) = (a – c) — b
Вычитание числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого и прибавить второе слагаемое.
(a + b) – c = f + (b – c)
Компоненты
вычитания
Уменьшаемое – вычитаемое = разность
7 – 4 = 3
Как найти уменьшаемое?
Чтобы найти уменьшаемое, надо
к разности прибавить вычитаемое.
? – 4 = 3
4 + 3 = 7
Как найти неизвестное вычитаемое?
Чтобы найти вычитаемое, надо
из уменьшаемого вычесть разность.
7 — ? = 3
7 – 3 = 4
Как узнать, на сколько одно число больше или меньше другого?
Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего вычесть меньшее.
На сколько 8 больше 5?
8 – 5 = 3
Однозначные числа
Числа, которые записывают одной цифрой называют однозначными (содержат только разряд единиц)
2, 3, 6. 8
Двузначные числа
Числа, которые записывают двумя цифрами
называют двузначными.
(содержат разряд десятков и разряд единиц)
24 = 2 десятка 4 единицы
38 = 3 десятка 8 единиц
50 = 5 десятков 0 единиц
Трёхзначные числа
Числа, которые записывают тремя цифрами
называют трехзначными.
(содержат разряд сотен, разряд десятков и разряд единиц)
723 = 7 сотен 2 десятка 3 единицы
100 = 1 сотня о десятков о единиц
Какие числа называют круглыми?
У круглых двузначных и трехзначных чисел в разряде единиц записывают 0
10, 20, 30, 40, 50, 600
Как к двузначному числу прибавить двузначное число?
Чтобы сложить двузначные числа надо
к десяткам прибавить десятки, к единицам — единицы
23 + 35 = 58
2 дес + 3 дес = 5 дес
3 ед + 5 ед = 8 ед
5 дес 8 ед = 58
Как из двузначного числа вычесть двузначное число?
Чтобы вычесть из двузначного числа двузначное число надо
из десятков вычесть десятки, из единиц — единицы
32 — 21 = 11
3 дес — 2 дес = 1 дес
2 ед — 1 ед = 1 ед
1 дес 1 ед = 11
Как к трехзначному числу прибавить трехзначное число?
Чтобы сложить трехзначные числа надо
к сотням прибавить сотни, к десяткам прибавить десятки, к единицам — единицы
123 + 135 = 258
1 сот + 1 сот = 2 сот
2 дес + 3 дес = 5 дес
3 ед + 5 ед = 8 ед
2 сот 5 дес 8 ед = 158
Как из трехзначного числа вычесть трехзначное число?
Чтобы вычесть из трехзначного числа трехзначное число, надо
из сотен вычесть сотни, из десятков вычесть десятки, из единиц — единицы
132 — 121 = 11
1 сот- 1 сот = 0 сот
3 дес — 2 дес = 1 дес
2 ед — 1 ед = 1 ед
1 дес 1 ед = 11
Как найти часть?
Чтобы найти часть, надо из целого вычесть известную часть.
76 – 12 = 64
Как найти целое?
Чтобы найти целое, надо части сложить.
12 + 64 = 76
Что называют разностью?
Разностью называют то, на сколько одно число больше или меньше другого.
12 < 23
Как найти разность?
Чтобы найти разность, надо из большего числа вычесть меньшее.
12 < 23
23 – 12 = 11
Что называют умножением?
Умножение – это сложение одинаковых слагаемых.
5 + 5 + 5 + 5…
Как называются компоненты умножения?
Множитель множитель = произведение
а b = с
Переместительное свойство умножения
От перестановки множителей произведение не изменяется.
а b = b а
Взаимосвязь компонентов умножения
При увеличении множителей произведение увеличивается.
При уменьшении множителей произведение уменьшается.
2 3 = 6
3 4 = 12
1 2 = 2
Что называют делением?
Деление – это действие, обратное умножению.
а b = с
с : а = б
с : б = а
Название компонентов деления
Делимое : делитель = частное
с : а = б
Особые случаи умножения
При умножении любого числа на 0 получится 0.
При умножении любого числа на 1 получится то же самое число.
2 0 = 0
2 1 = 2
Особые случаи деления
При делении числа на себя получается 1.
При делении числа на 1 получается то же самое число.
При делении нуля на любое число, получится 0.
Делить на 0 нельзя!
2 : 2 = 1
2 : 1 = 2
0 : а = 0
Четные числа
Числа, которые делятся на 2, называют четными.
2, 4, 6, 8, 10…
Нечетные числа
Числа, которые не делятся на 2, называют нечетными.
1, 3, 5, 7, 9, 11…
Как найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
а ? = с
с : а = б
? b = с
с : б = а
Увеличение и уменьшение на несколько единиц
Увеличить число на а единиц значит прибавить а единиц.
Уменьшить число на а единиц – вычесть а единиц.
с + а
с — а
Увеличение и уменьшение в несколько раз
Увеличить число в а раз значит умножить его на а.
Уменьшить число в а раз – разделить его на а.
с а
с : а
Порядок действий
1. В выражении со скобками первым выполняется действие в скобках.
2. В выражении со скобками вторым выполняется деление или умножение.
3. Последним выполняется действие сложение или вычитание.
Все действия выполняются слева направо!
4 2 1 5 3
с – d · (b – а) + m : n
Кратное
Кратное чисел а и б– это число с, которое делится на а и б.
12 : 2
12 : 6
12 – кратное чисел 2 и 6.
Делитель
Делитель – это число (а или б), на которое делится с.
12 : 2
12 : 6
2 и 6 делители числа 12.
Уравнение
Уравнение – это равенство с неизвестным компонентом.
23 + х = 41
Что значит решить уравнение?
Решить уравнение – значит найти значение неизвестного компонента (корня).
х = ?
Прямоугольник
Четырехугольник, у которого все углы прямые, называют прямоугольником.

Квадрат
Квадрат – это прямоугольник, у которого все стороны равны.

Длина прямоугольника
Противоположные стороны у прямоугольника равны. Большая сторона называется длиной.

Ширина прямоугольника
Меньшая сторона прямоугольника называется шириной.
Мерка
Мерка – это единица измерения величин.
м, см, кг, г, л, ч….
Величина
Величина – это такое свойство предметов, которое можно измерить и результаты измерений выразить числом.
длина, масса, ёмкость, время, площадь
Периметр
Периметр прямоугольника – это сумма длин всех его сторон.
P = a + a + b + b
Площадь
Площадь – это часть плоскости, которую занимает геометрическая фигура.

Площадь прямоугольника
Площадь прямоугольника равняется произведению его длины и ширины.
S = a b
Как найти сторону прямоугольника?
Чтобы найти длину одной стороны прямоугольника, надо площадь разделить на длину известной стороны.
а = S : b
b = S : а
Виды углов
Острый (меньше прямого угла), прямой, тупой(больше прямого угла).






infourok.ru
Порядок действий в математике, последовательность выполнения умножения, сложения, деления, вычитания, правила очередности арифметических действий
Основные операции в математике
Базовыми формами вычисления являются:- Сложение +
- Умножение х или ∗
- Вычитание —
- Деление ÷ или /
15 — 3 + 7 = 19
При наличии скобок сначала выполняется действие, в них заключенное.15 — (3 + 7) = 5
При появлении знаков или первыми выполняются они, лишь затем сложение или вычитание.2 + 2 х 2 = 2 + 4 = 6
2 + 2 ÷ 2 = 2 + 1 = 3
Скобки могут частично ослабить эти правила, так как действие в них заключенное всегда выполняется в первую очередь.(2 + 2) х 2 = 4 х 2 = 8
(2 + 2) ÷ 2 = 4 ÷ 2 = 2
Если в скобки заключено сложное выражение, внутри них работают стандартные правила.(4 + 7 — 1) + 5 = (11 — 1) + 5 = 15
(5 + 3 х 2) — 4 = (5 + 6) — 4 = 11 — 4 = 7
При появлении двух и более знаков или нужно учитывать их очередность.5 х 2 — 8 ÷ 4 = 10 — 2 = 8
Решение примеров с множественными скобками
Вариант 1:5 + 8 ÷ 2 + 3 х (15 — 6 х 2 + 1) + 3 х (6 — 4) = ?
Распишем все расчеты поэтапно:- 6 х 2 = 12
- 15 — 12 + 1 = 4
- 6 — 4 = 2
- 8 ÷ 2=4
5 + 4 + 3 х 4 + 3 х 2 = ?
Снова расписываем:- 3 х 4 = 12
- 3 х 2 = 6
- 6 ÷ 2 = 3
- 10 — 3 х 3 = 10 — 9 = 1
- 5 + 2 = 7
- 11 — 7 = 4
- 50 — 4 = 46
- 46 х 4 = 184
Законы сложения и умножения Также описывают общие принципы проведения вычислений.
Переместительный:a + b = a + b
Сочетательный:(a + b) + c = a + (b + c)
a х (b х c) = (a х b) х c
Распределительный:
a х (b + c)=a х b + a х c
(a + b) х c= a х c + b х c
Законы нуля:a + 0 = a
a х 0=0
Правило единицы:a х 1 = a
Знание этих законов поможет проводить необходимые вычисления быстрее.Важно! В случае замены + и х на — и ÷ соответственно эти правила перестают действовать.Несмотря на легкость понимания, очередность выполнения операций жизненно важна, так как все сложные формулы (логарифмы, интегралы и так далее) по сути представляют собой сокращенную форму написания длинной цепи простых вычислений. Чтобы закрепить материал статьи, рекомендуем посмотреть видео ниже. Рекомендуем посмотреть видео о порядке дейсивий в математике
nauka.club