1- 5_Дискретная математика_2
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Заочный факультет (дистанционная форма обучения)
Кафедра автоматизированных систем управления (АСУ)
Контрольная работа № 1
Дата выполнения работы _ _
Дата проверки _ _
Оценка _ _
И. О. Фамилия преподавателя _ _
Подпись преподавателя _ _
2003 г.
На множестве Х ={х/х € N, х < 12} задано отношение R: х и y имеют один и тот же остаток путем деления на 5 (х € Х, у € Х).
Покажите, что R – отношение эквивалентности.
Запишите все классы эквивалентности, на которые разбивается множество данным отношением.
Решение.
Заданное отношение R обладает свойствами рефлекторности, симметричности и перанзитивности, следовательно, R- отношение эквивалентности.
Классы эквивалентности, на которые разбивается данное множество отношением R:
{1, 6, 11}, {2, 7}, {3, 8}, {4,9}, {5,10}.
№ 15
Рассмотрите на множестве людей следующие отношения, укажите среди них отношения эквивалентности:
а) ״ х похож на у″;
б) ″х и у живут в одном доме″;
в) ″х и у — друзья″;
г) ″х живет этажом выше, чем х″.
Решение.
а) отношение не обладает свойством рефлекторности, следовательно, отношение не является эквивалентным.
б) отношение эквивалентное.
в) отношение не обладает свойством пуанзиативности, следовательно, не эквивалентное.
г) отношение не является эквивалентным, так как не выполняется свойство симмепуаничности для данного отношения.
№ 24
Известно, что из 100 студентов живописью увлекается 28,
Спортом – 42, музыкой – 30, живописью и музыкой – 8, спортом и музыкой – 3.
Определите количество студентов:
а) увлекающихся только спортом;
б) ничем не увлекающихся.
Решение.





живопись 7 спорт


 28
42
28
42
5 3 2

музыка
30

а) Количество студентов увлекающихся только спортом: 42-10-2=30 (человек).
б) Для определения количества студентов ничем не увлекающихся используем формулу включений и исключений:
100-28-42-30+10+8+5-3=20 (человек).
2. Составьте список элементов множества А, заданного относительным способом:
А={х/х2-8х+15=0}.
Решение.
х2-8х+15=0;
Д/4=16-15=1;
х= 4+1; х1 = 5; х2 = 3.
Итак, А = {5, 3}.
3. Докажите, что {{1, 2}, {2, 3}} ≠ {1, 2, 3}
Доказательство.
Два множества равны в том и только в том случае, когда они состоят из одних и тех же элементов.
Множества {{1, 2}, {2, 3}} и {1, 2, 3} не равны, так как элементами первого множества являются {1, 2}и {2, 3}, а элементами второго – 1, 2, 3.
4. Докажите тождество:
А ∩ (В/ С) = (А ∩ В) /(А ∩ С)
Доказательство.
Преобразуем правую часть равенства.
Представим разность множеств с помощью операции дополнения.
( А∩В)
/(А ∩ С)=(А∩В) А∩С.
А∩В)
/(А ∩ С)=(А∩В) А∩С.




(А ∩В) ∩ (А∩С)= (А∩В) ∩ (АU
С) = (по свойству димумбутивности) = (А ∩
В) ∩ АU(А∩В)  ∩
С.
∩
С.




Так как (А ∩ В) ∩ А= (А ∩ А) ∩ В= Ø, то (А ∩ В) ∩ (АU С)= (А ∩В) ∩ С (по свойству ассоциативности)= А ∩ (В ∩С)= А ∩ (В/С).
Итак, (А ∩ В)/ (А ∩ С)= А ∩ (В/С), что и требовалось доказать.
Литература
Сафьянова Е. Н.
Дискретная математика часть 1: Учебное пособие. Томск, 2000 г.
2. Роберт Р. Столл Множества. Логика. Москва. Изд. «Просвещение». 1968 г.
studfile.net
III. Интегральное исчисление
1) Найти интегралы:
a)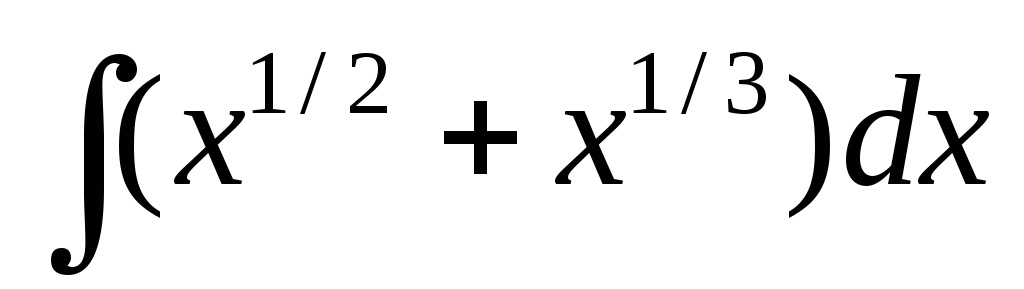 ;
б)
;
б)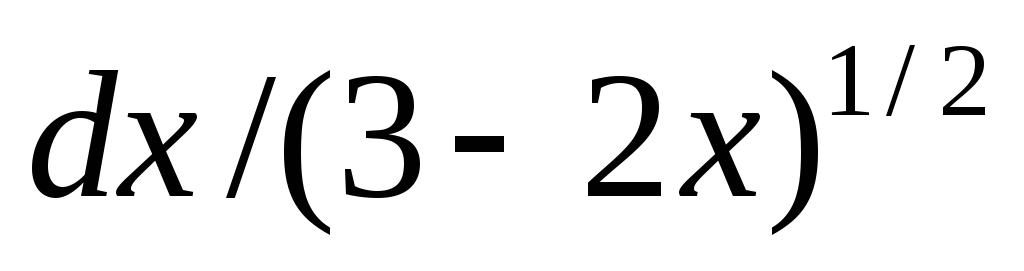
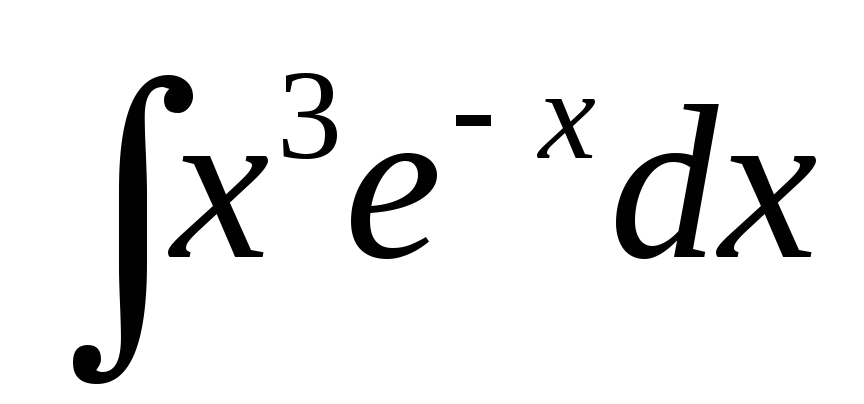 .
.2) Вычислить в интегралы:
a)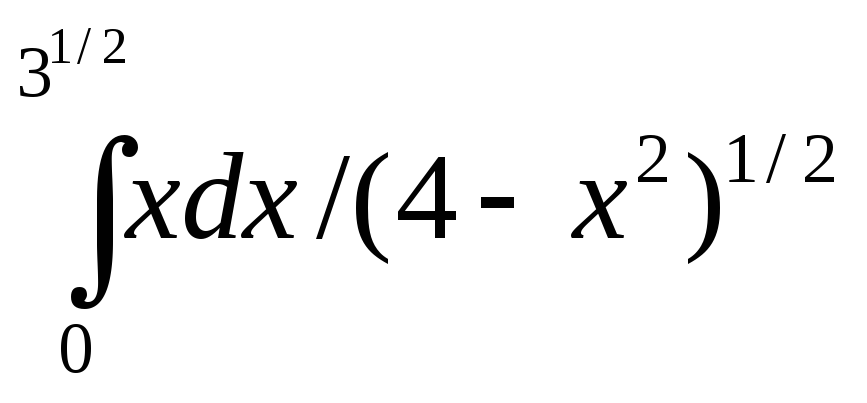 ;
б)
;
б) 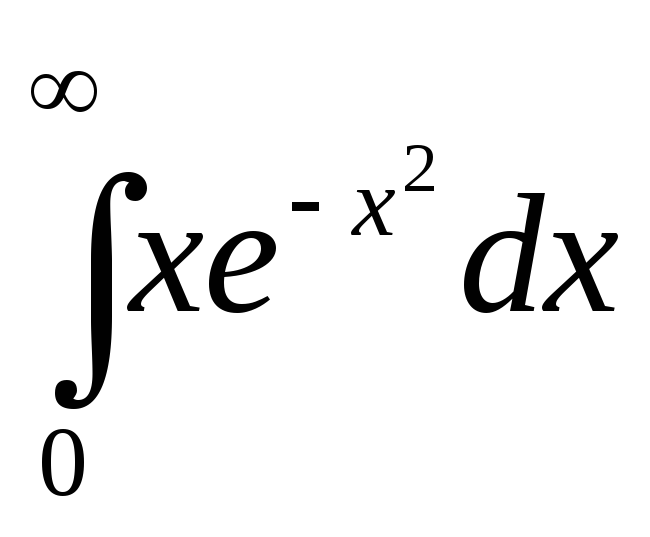
3) Найти общий интеграл: х + ху + у'{у + ух) = 0
4) Исследовать сходимость числовых рядов:
a)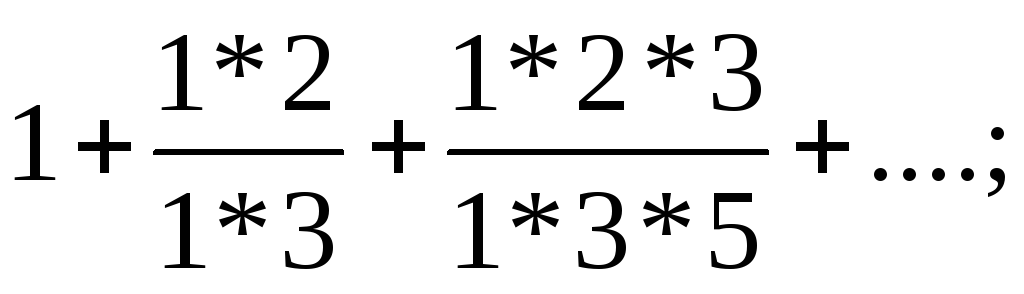 б)
б)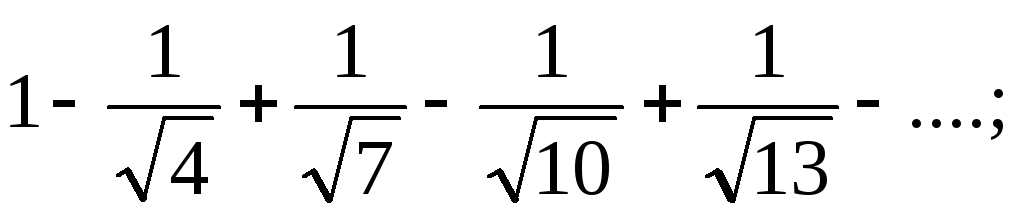
Вариант 22
Контрольная работа по курсу «Математический анализ»
I. Множества
1) Каждый из учеников класса в зимние каникулы ровно 2 раза был в театре. При этом спектакли А,В и С видели соответственно 25,12 и 23 ученика.
Сколько учеников в классе?
Сколько из них видели спектакли А и В, А и С, С и В?
Сколько человек не видели спектакль А?
2) Множества А, В и С являются подмножествами U. Указать штриховкой множества:
а)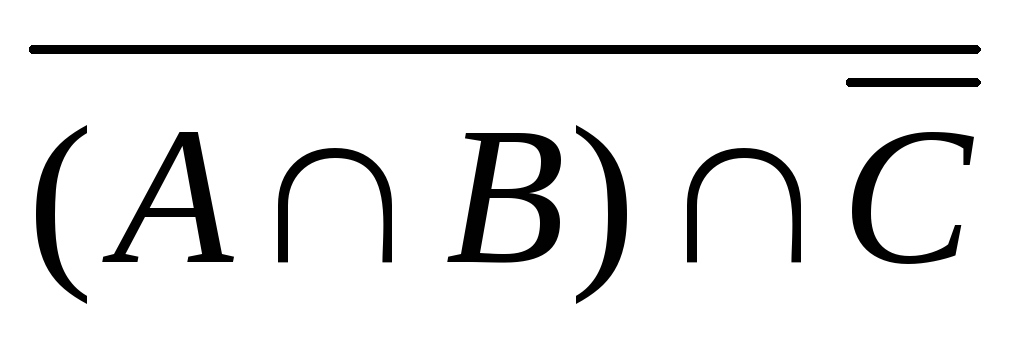 ; б)
; б)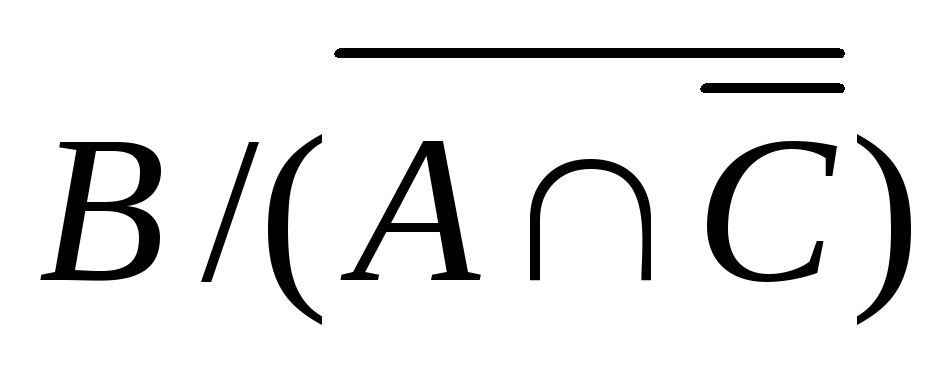
II. Дифференциальное исчисление
1) Найти область определения действительных значений функций:
а) y = |x|-у; б) у = (х + 2)1/2; в) у = 6/х
2) Найти пределы:
a)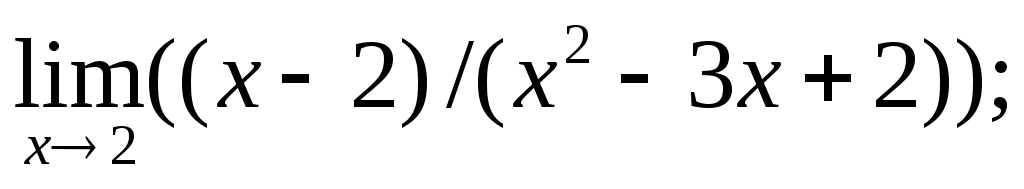 б)
б) 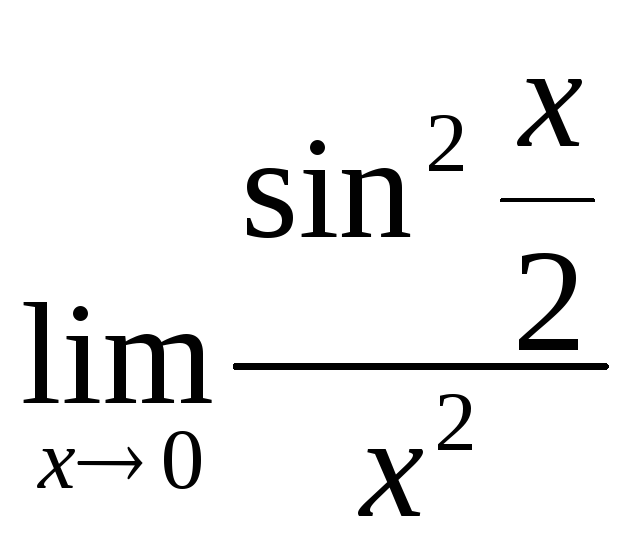
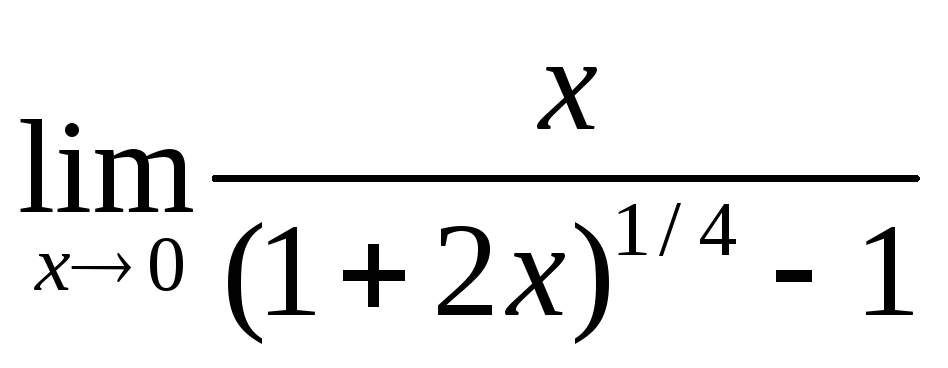
3) Найти производные функций:
а) у = (а1/2 –х1/2)2; 6)y = sin4x; в) у = х + ctgx; г) у = cos2 х
4) Найти пределы, используя правило Лопиталя:
а) 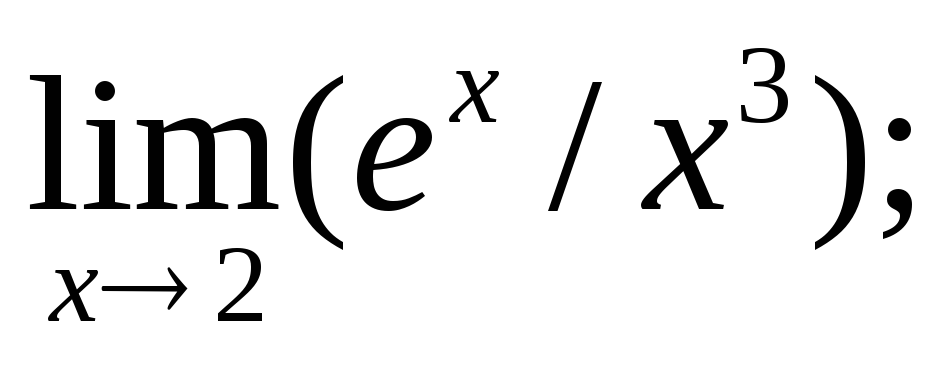 б)
б) 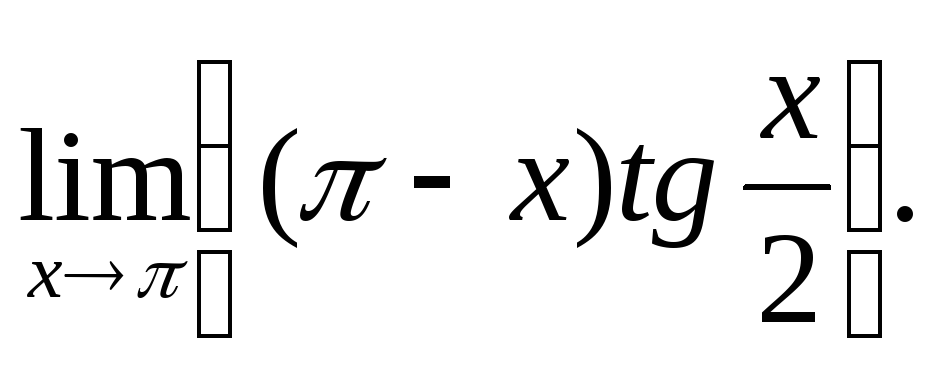
5) Выполнить полное исследование функции и построить ее график:
а) у = 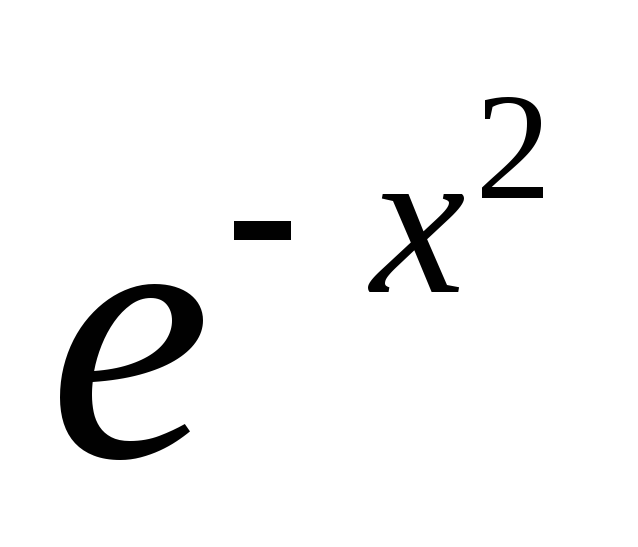 ; б) e
=
; б) e
= 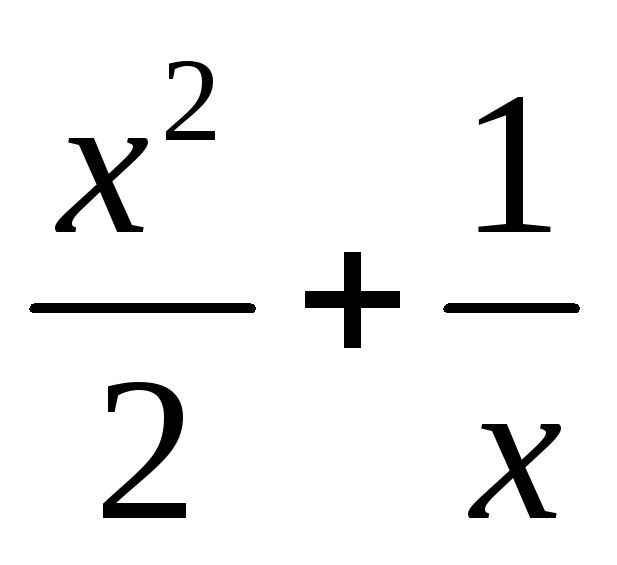
6) Для функций многих переменных:
а) Указать область
определения функции: z
= 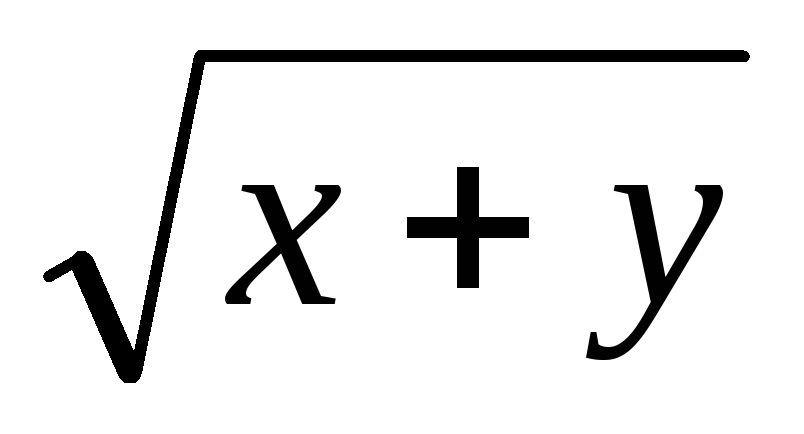 ;
;
б) Найти частные производные функции: z = у2 /х;
в) Исследовать на экстремум функцию: z = х2 + (у — l)2
III. Интегральное исчисление
1) Найти интегралы:
a) 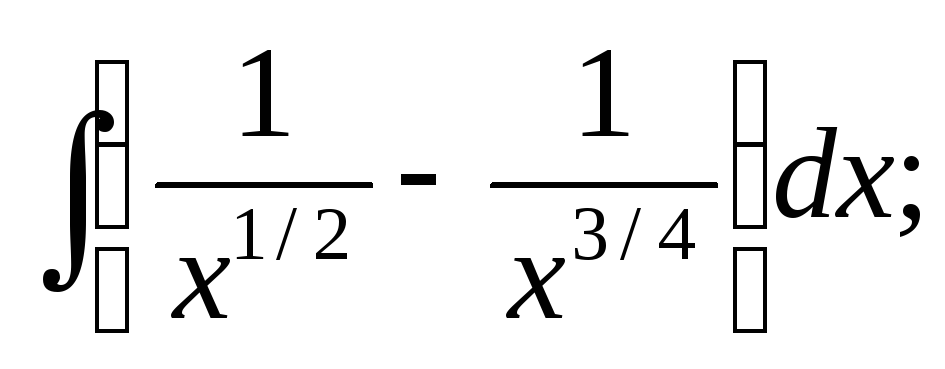 б)
б) 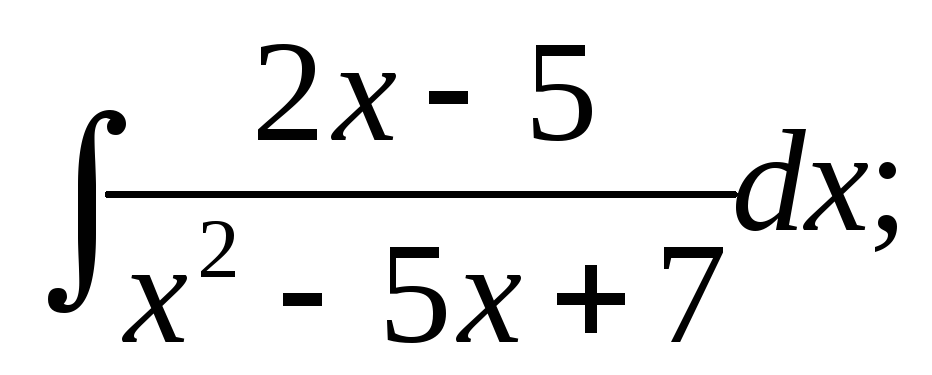 в)
в) 
2) Вычислить интегралы:
а)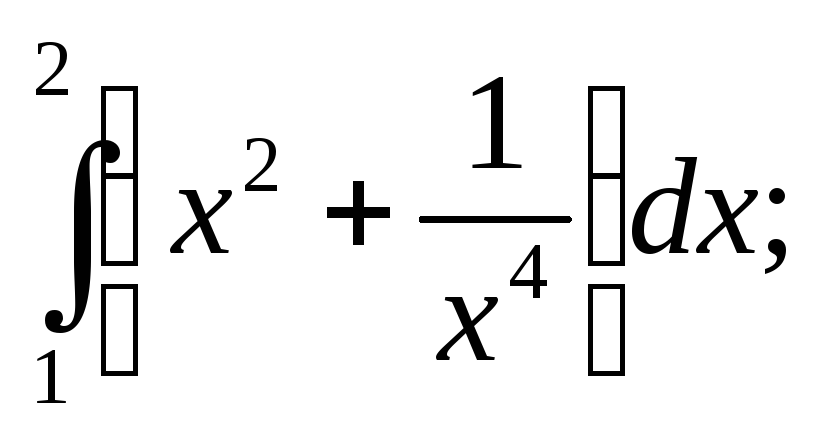 б)
б)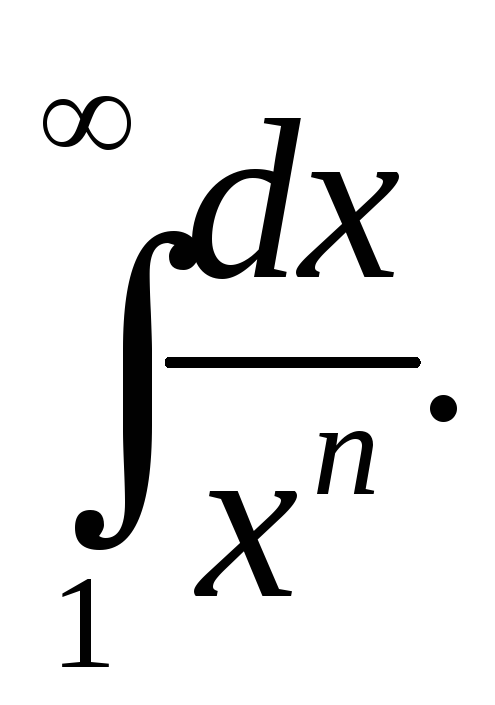
3) Найти общий интеграл: х + ху + у'(у + ух) = о
4) Исследовать сходимость числовых рядов:
а) 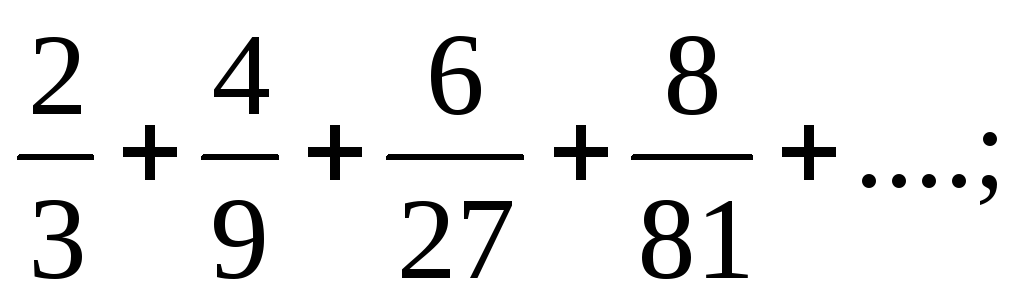 б)
б) 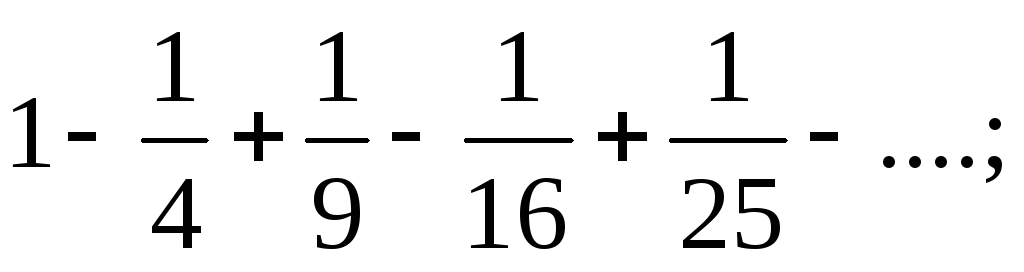
Вариант 23
Контрольная работа по курсу «Математический анализ»
I. Множества
Известно, что из 100 студентов увлекаются живописью 28 человек;
Спортом 42;музыкой 30; живописью и спортом 10; живописью и музыкой 5; Сколько студентов увлекаются только живописью?
Сколько студентов ничем не увлекаются?
Сколько человек имеют ровно 2 увлечения?
2)Множества А,В и С являются подмножествами U. Указать штриховкой множества:
а) 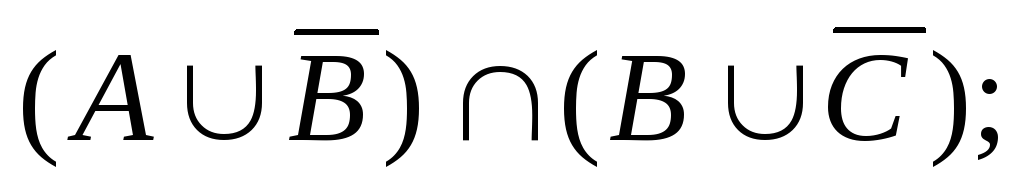 б)
б) 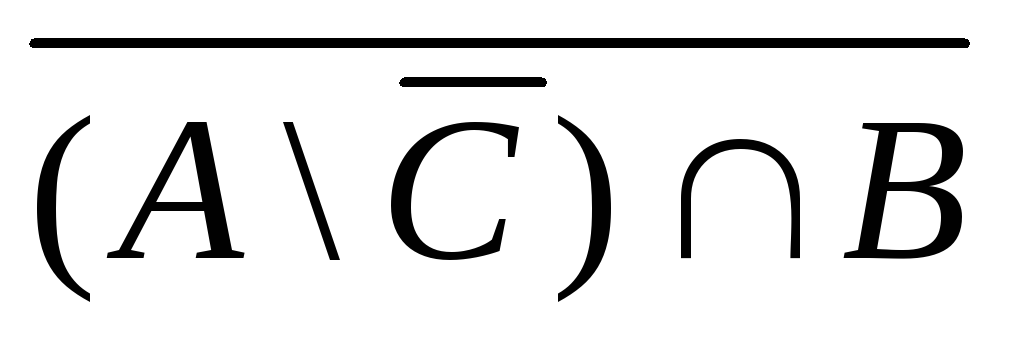
Дифференциальное исчисление
Найти область определения действительных значений функций:
а) y = 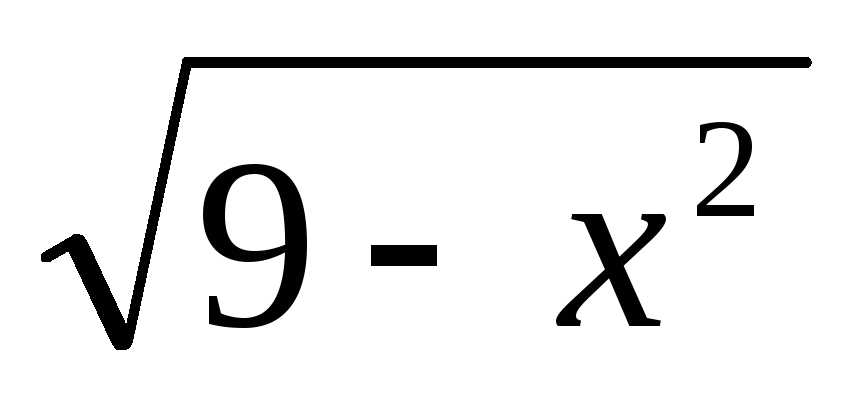 ;
б) y =
;
б) y =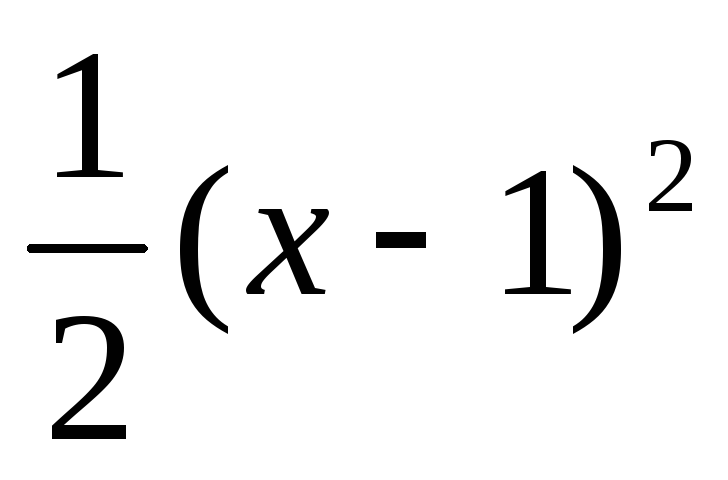 ;
в) y =
;
в) y =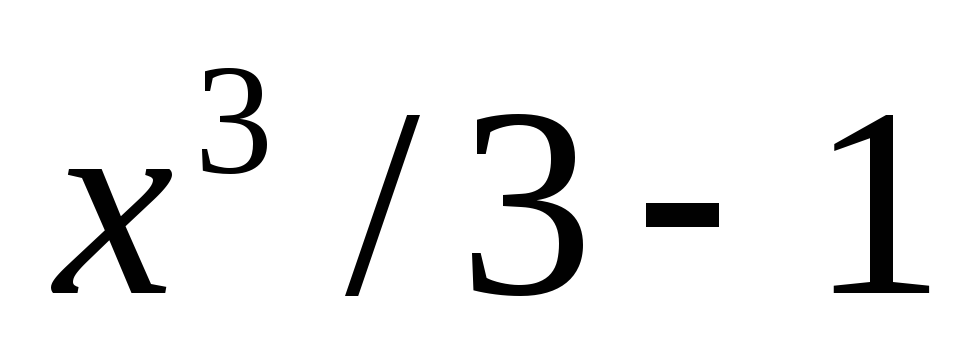
2) Найти пределы:
а) 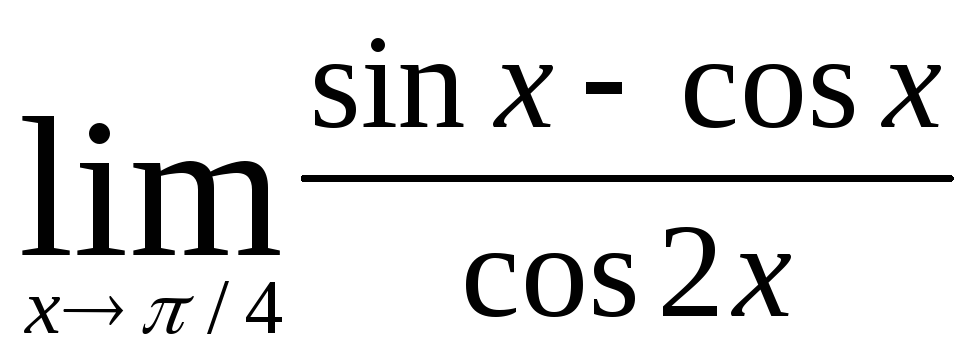 ; б)
; б) 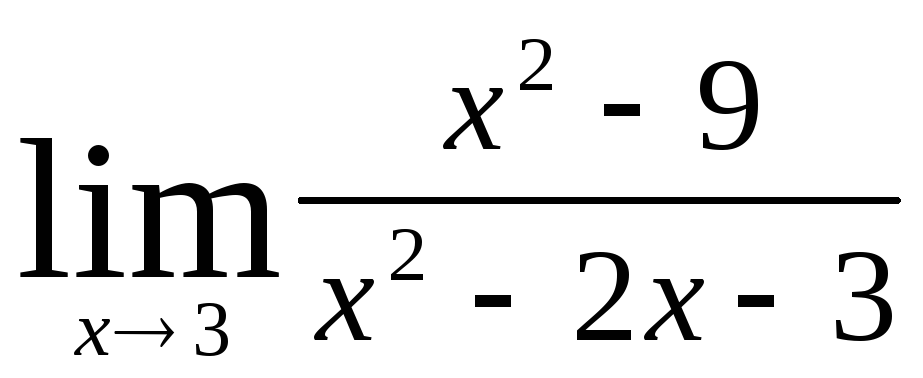 ;
в)
;
в)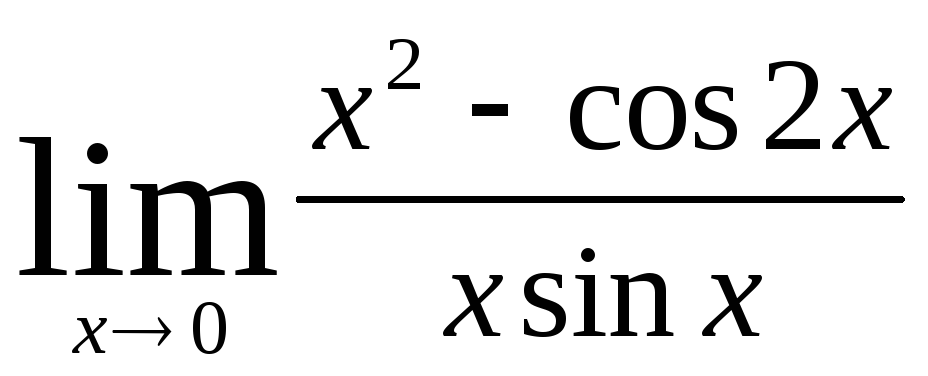



3)Найти производные функций:
а) у =10/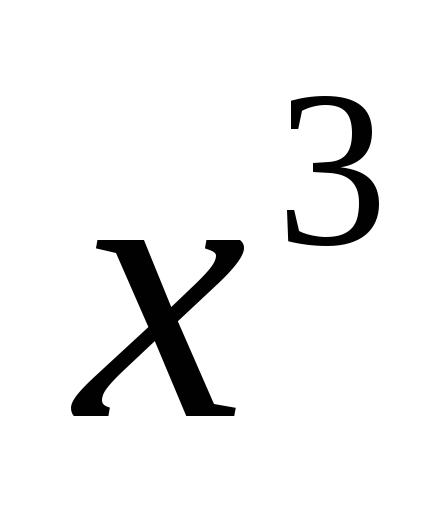 ;
б) у =
;
б) у =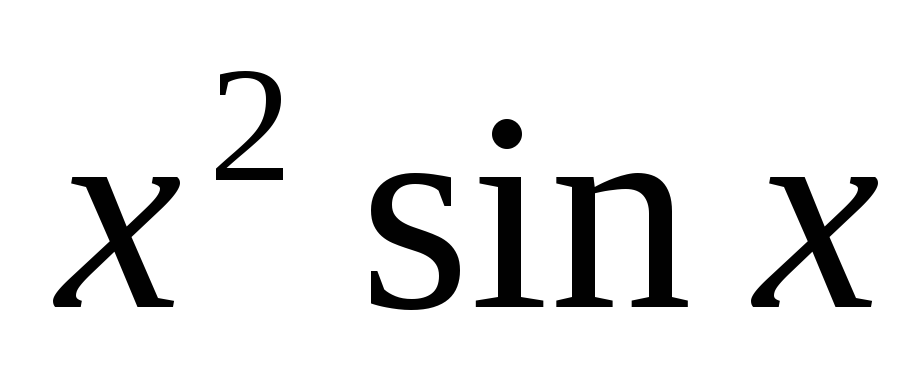 ;
в) у =sin
;
в) у =sin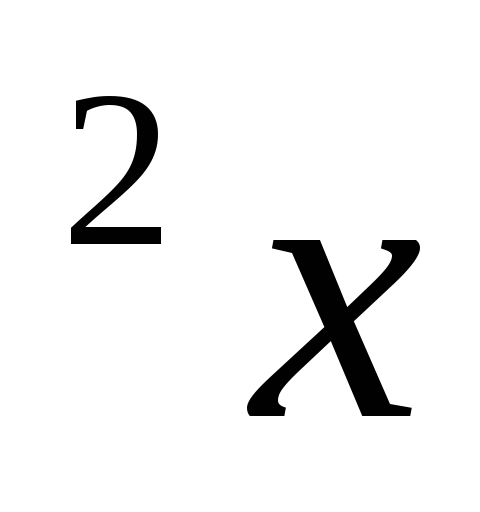 ;
;
г) у = 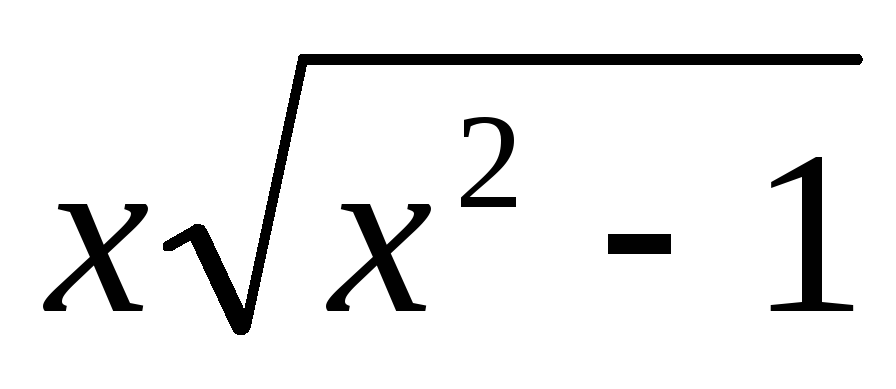 ;
;
4) Найти пределы, используя правило Лопиталя:
а) 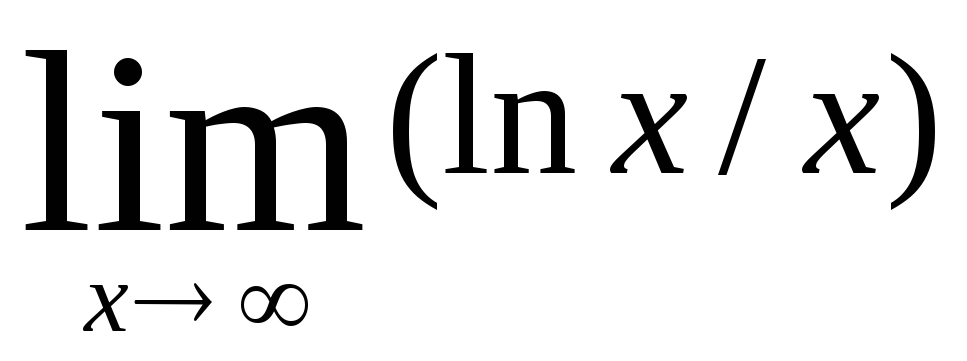 ;
б)
;
б) 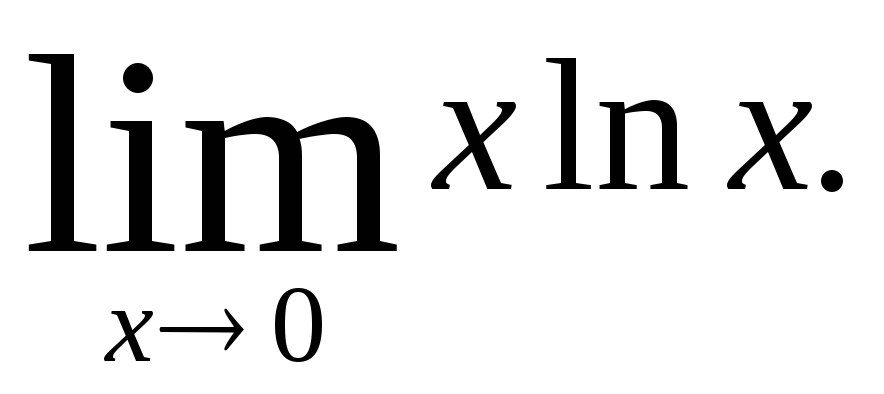
5) Выполнить полное исследование функции и построить её график:
а) у =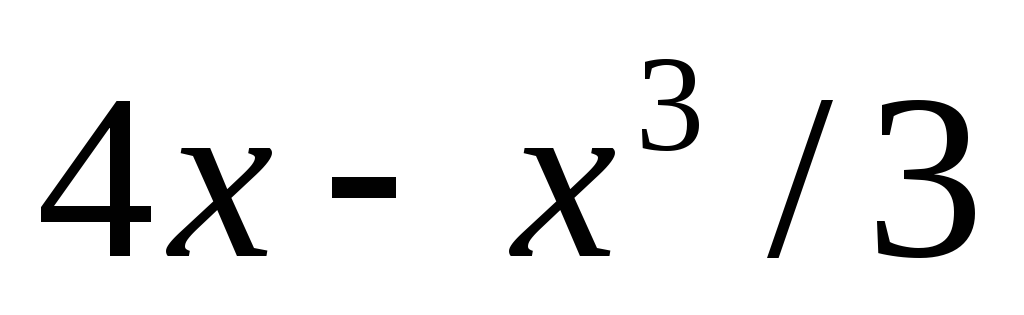 ;
б) у =
;
б) у =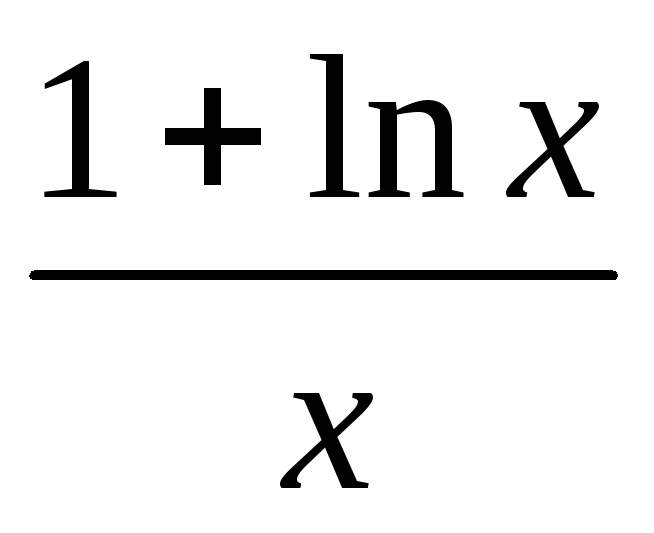 .
.
6) Для функций многих переменных:
а) Указать область
определения функции: 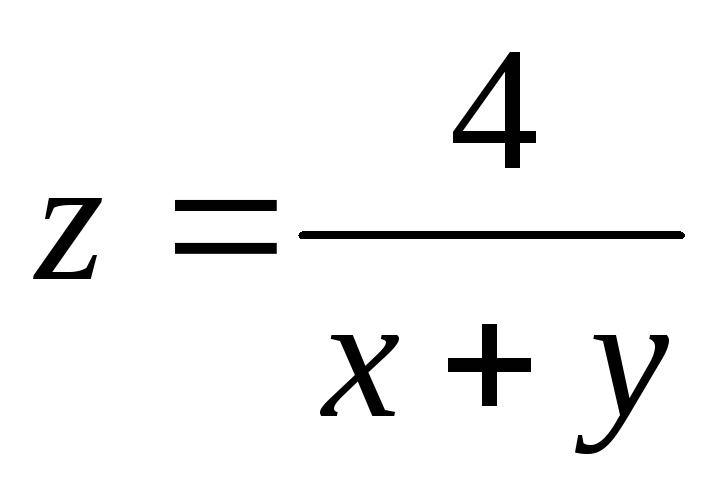 ;
;
б) Найти частные
производные функции: 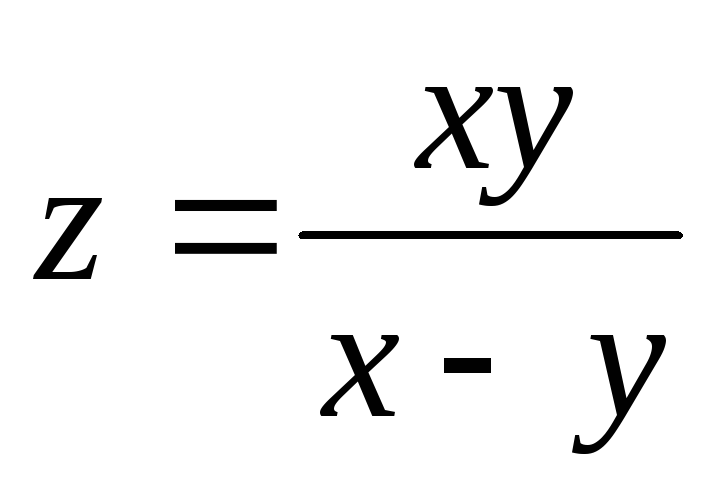 ;
;
в) Исследовать на
экстремум функцию: 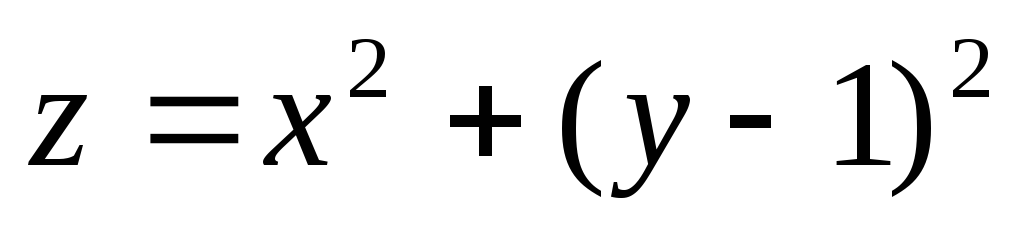
Интегральное исчисление и ряды
Найти интегралы:
а) 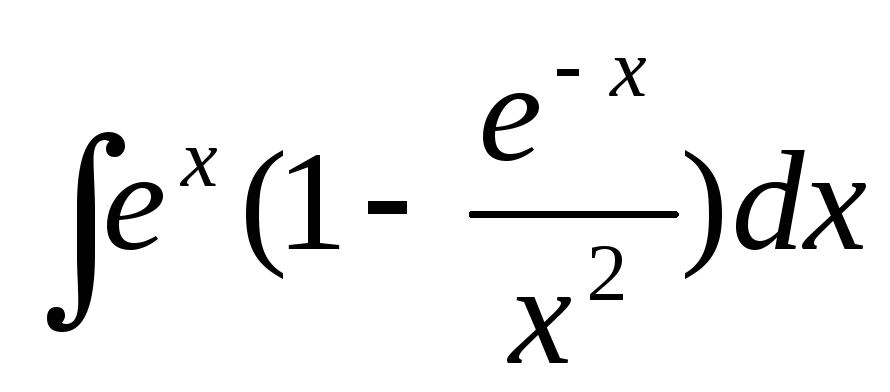 ;
б)
;
б) 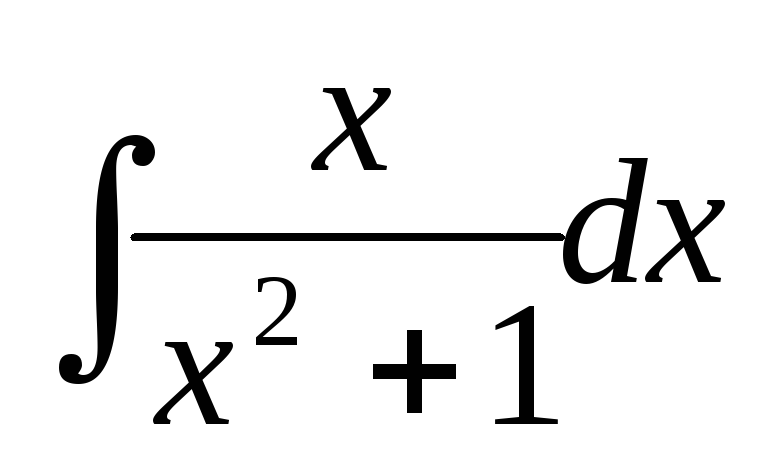 ;
в)
;
в)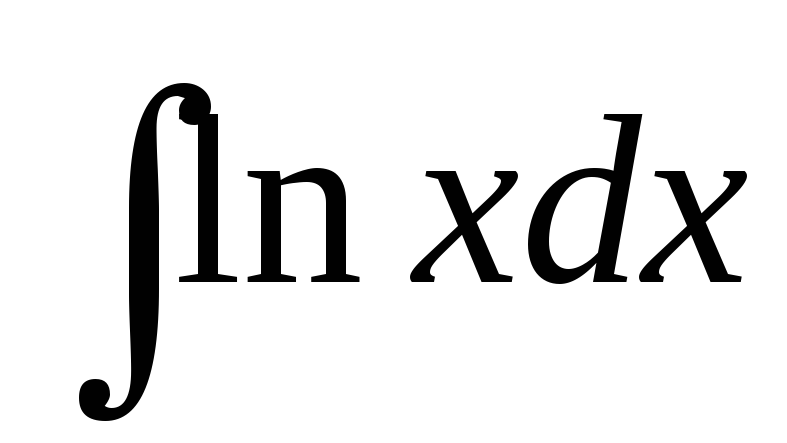
2) Вычислить интегралы:
а) 
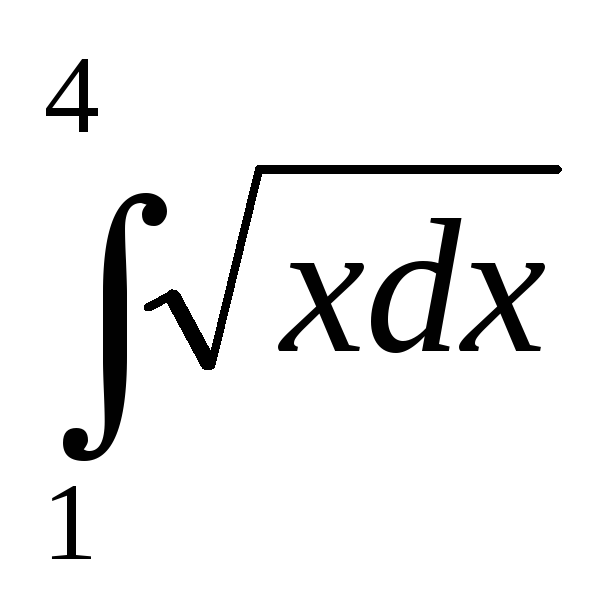 ;
б)
;
б)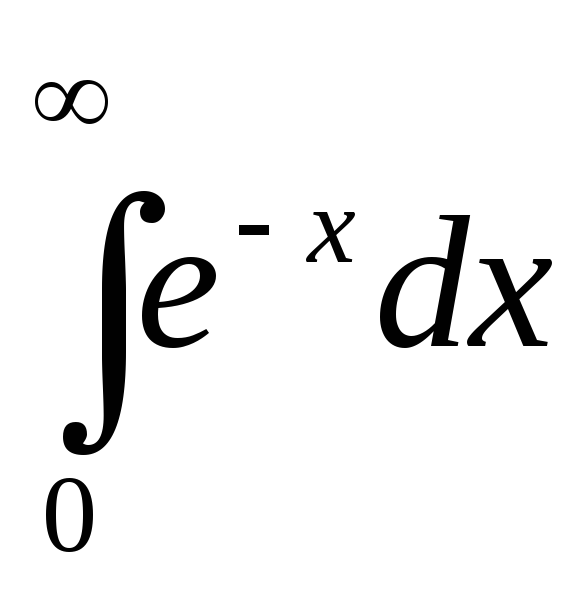 ;
;
3) Найти общий интеграл: 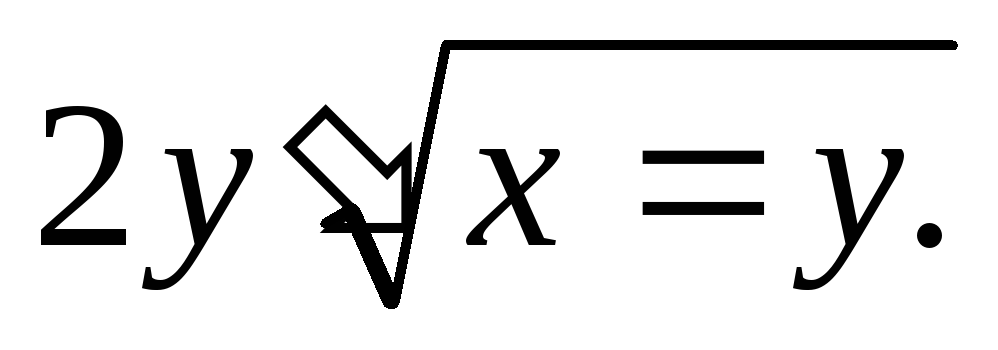
4) Исследовать сходимость числовых рядов
а) 1+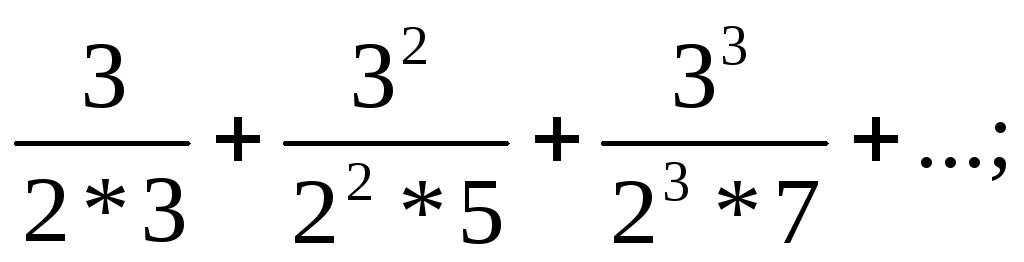 б) 1-
б) 1-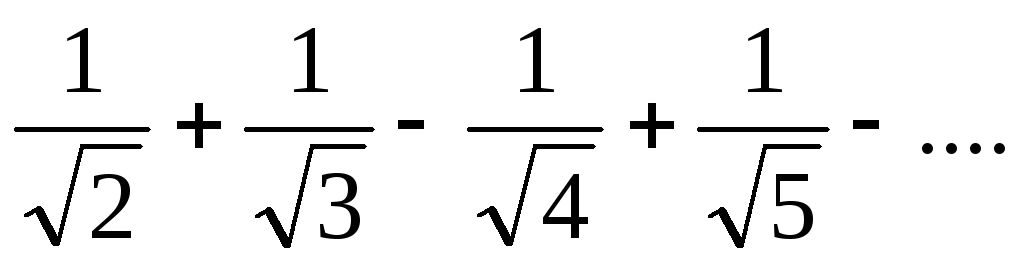
Вариант 24
Контрольная работа по курсу «Математический анализ»
Множества
В группе студентов 40 человек каждый просмотрел либо все три фильма, либо один из трёх. В итоге фильм А увидели 13 человек, фильм В-16, фильм С- 19 человек.
Сколько студентов осмотрели только фильм В?
Сколько студентов посмотрели все три фильма?
Задать множество перечислением его элементов:
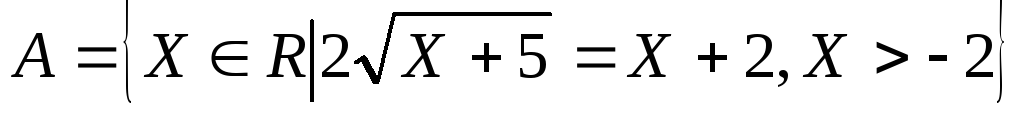
Дифференциальное исчисление
1)Найти область определения действительных значений функций:
а) 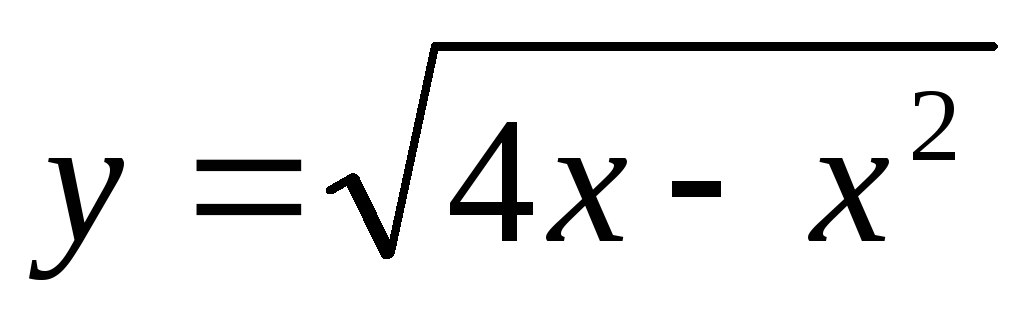 ;
б)
;
б) 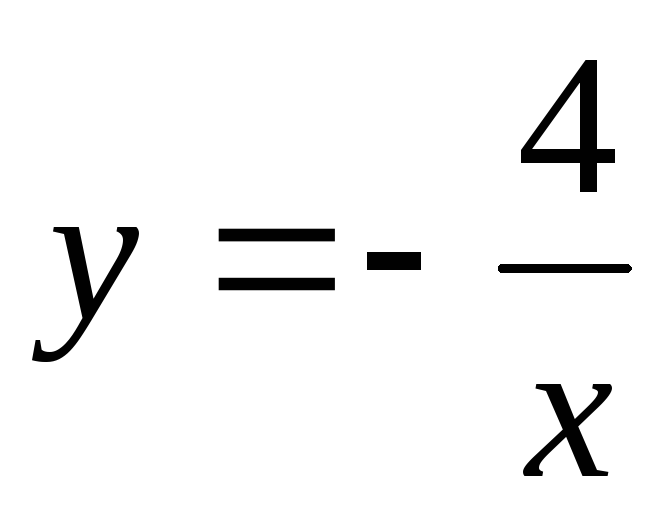 ;
в)
;
в) 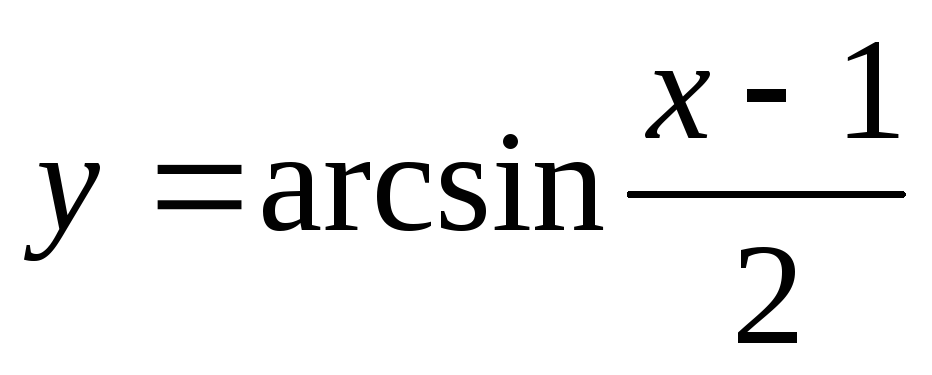 .
.
2) Найти пределы:
а) 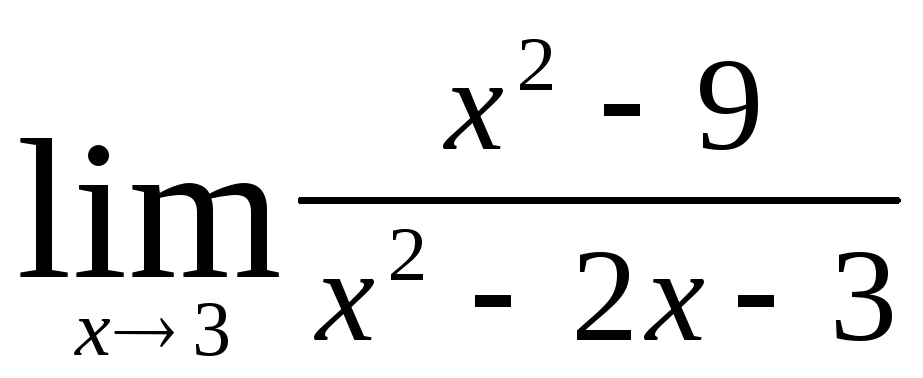 ;
б)
;
б) 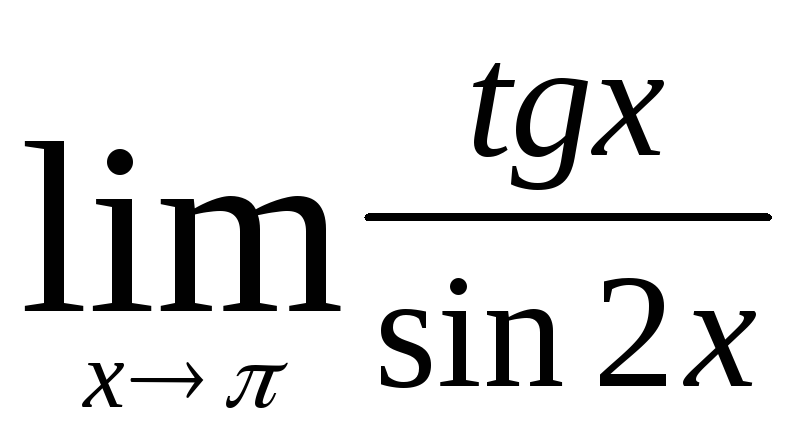 ;
в)
;
в) 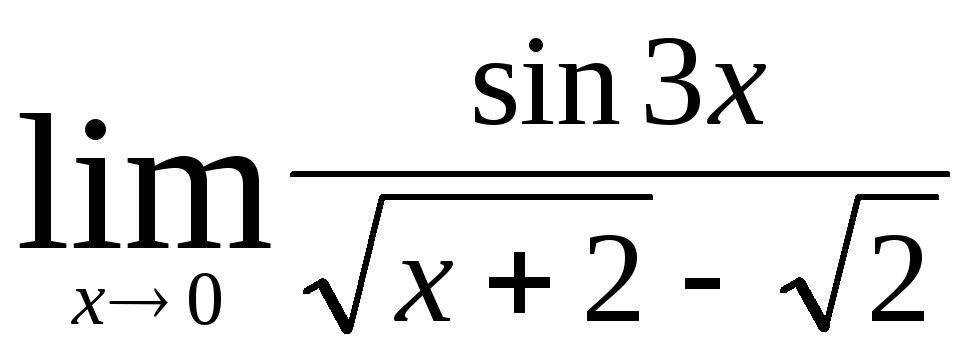 ;
г)
;
г)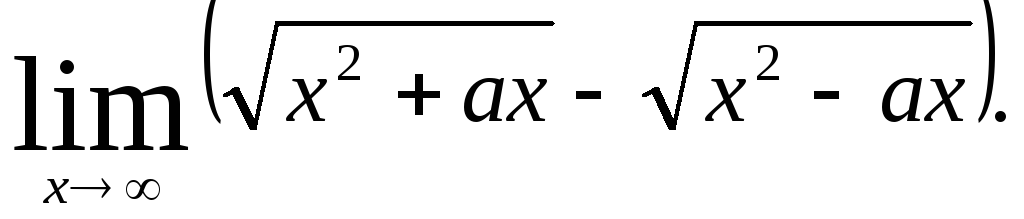
3) Найти производные функций:
а)  ;
б)
;
б) 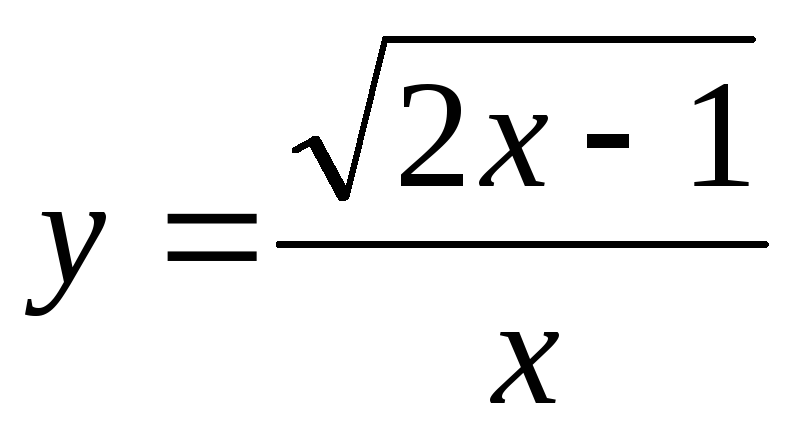 ;
в)
;
в) 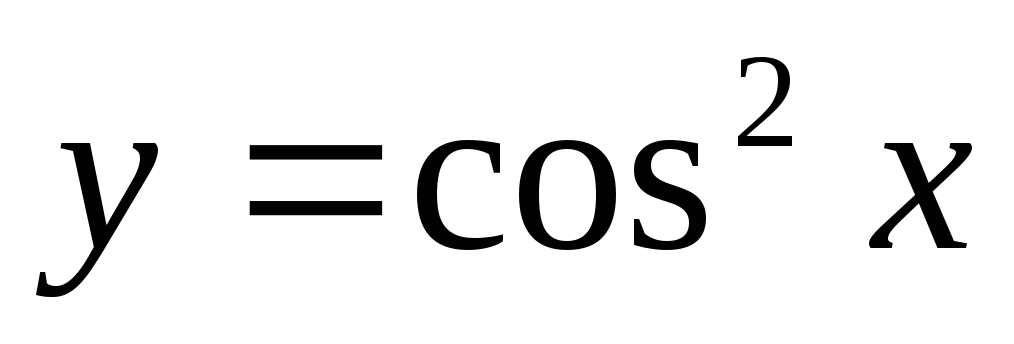 ;
;
г) 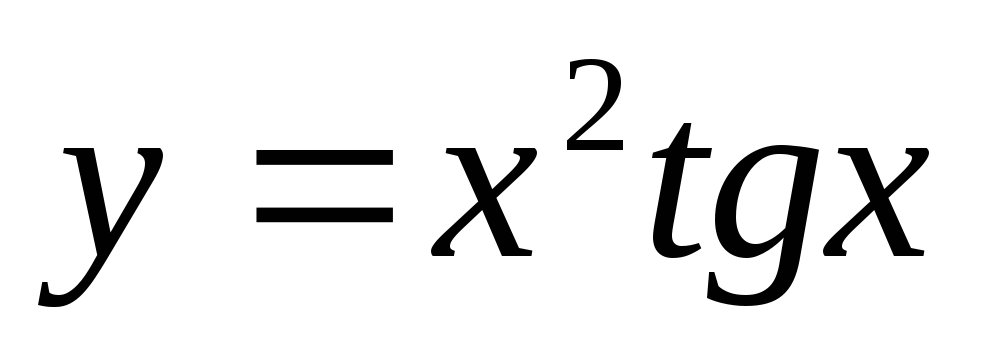 .
.
4) Найти пределы, используя правило Лопиталя:
а) 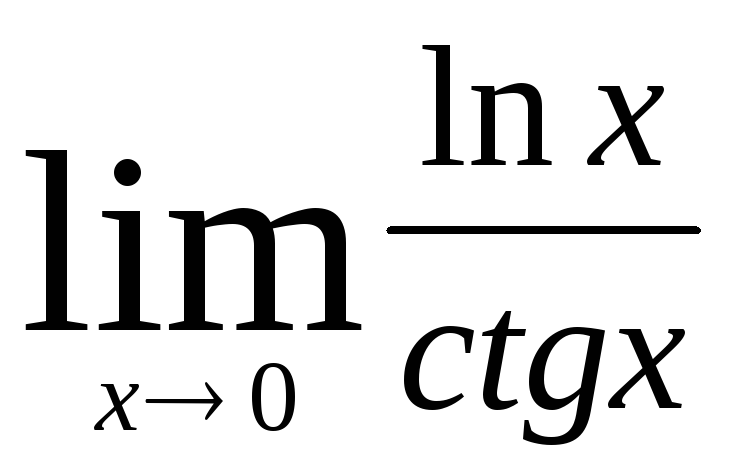 ;
б)
;
б) 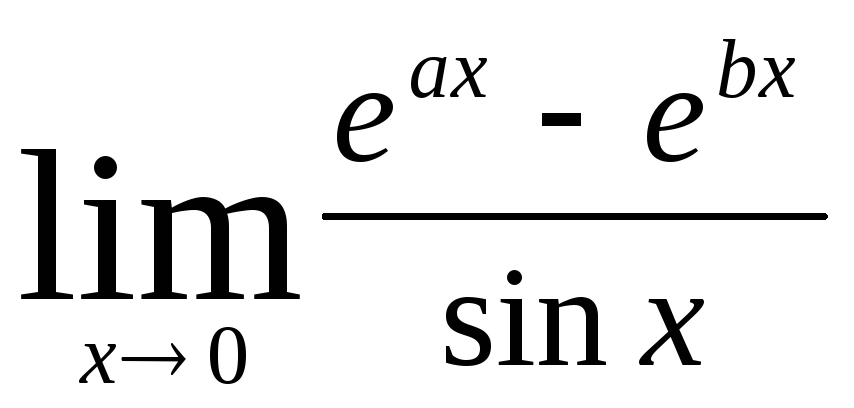 .
.
5) Выполнить полное исследовании функции и построить её график:
а) 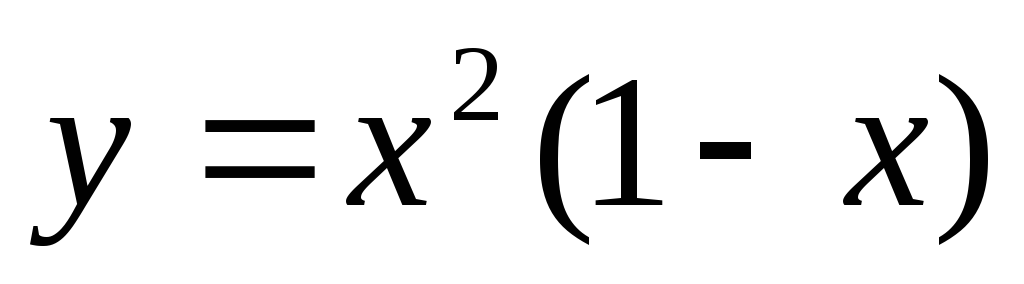 ;
б)
;
б) 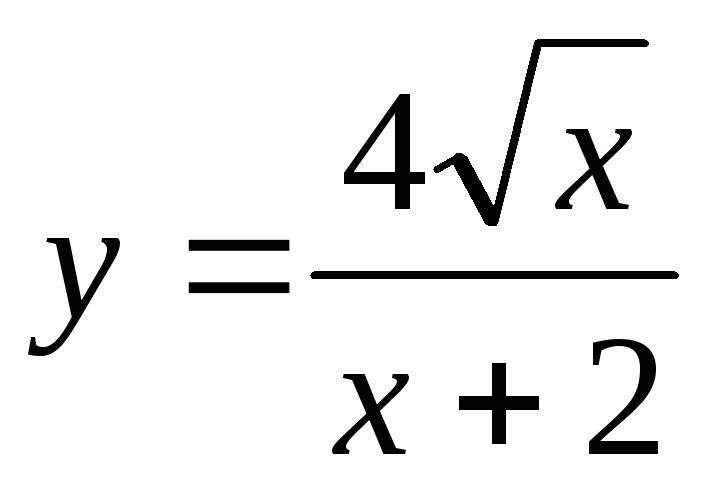 .
.
6) Для функций многих переменных:
а) Указать область определения
функции: 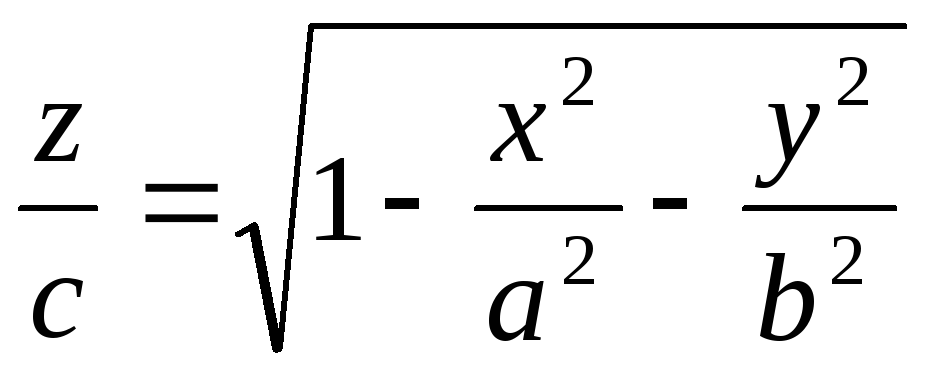 ;
;
б) Найти частные производные
функции: 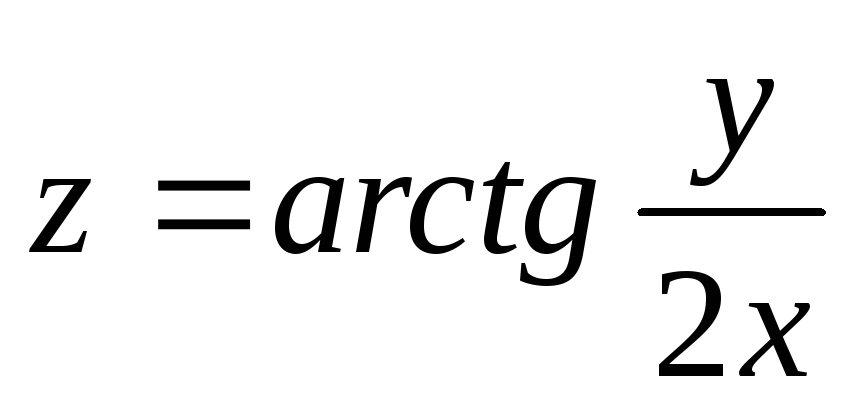 ;
;
в) Исследовать на экстремум
функцию: 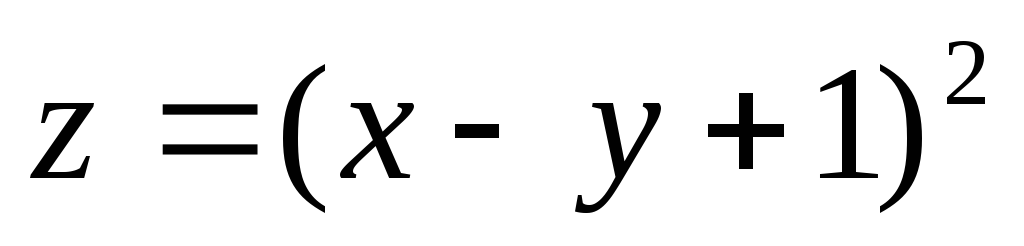 .
.
III. Интегральное исчисление
1) Найти интегралы:
а) 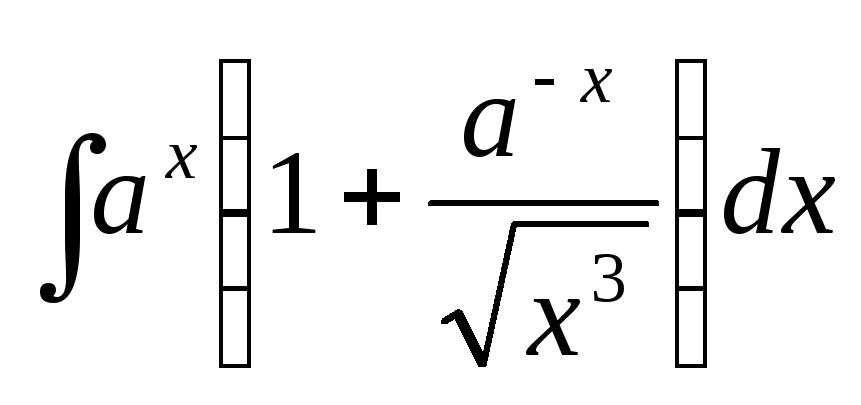 ;
б)
;
б) 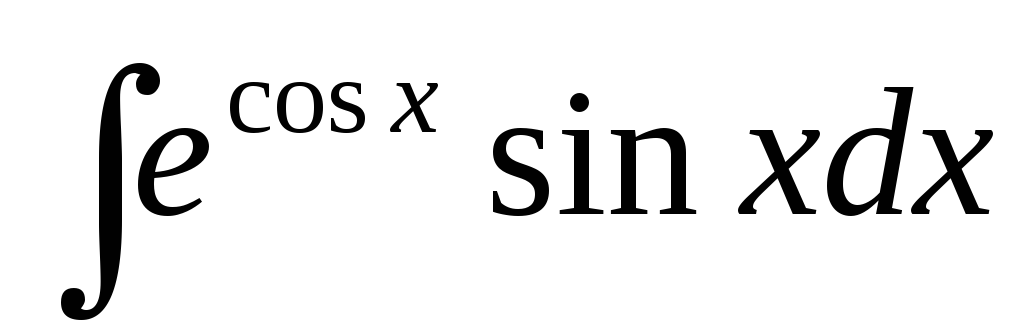 ;
в)
;
в) 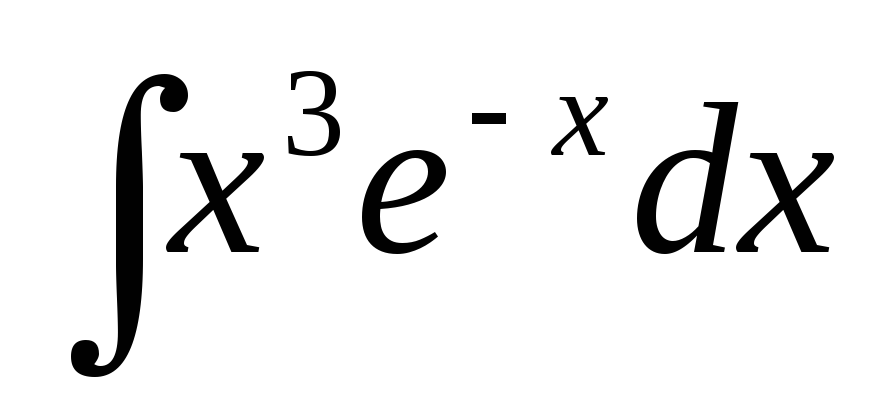 .
.
2) Вычислить интегралы:
а) 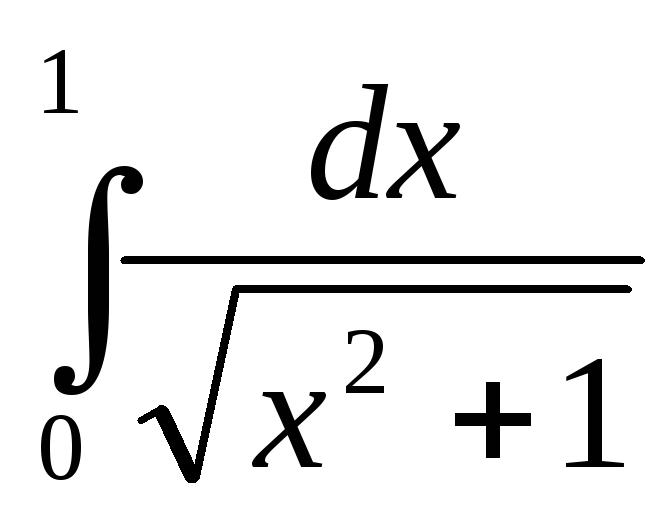 ;
б)
;
б) 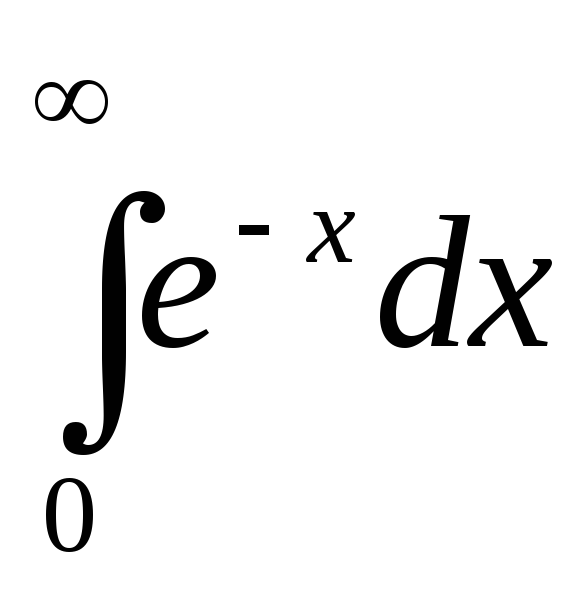 .
.
3) Найти общий интеграл: 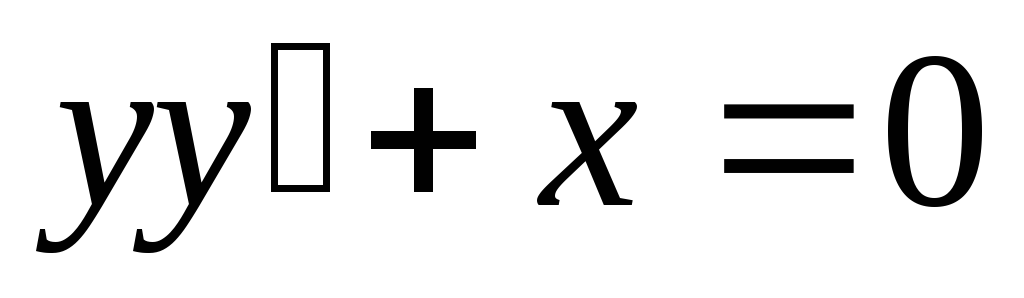 .
.
4) Исследовать сходимость числовых рядов:
а) 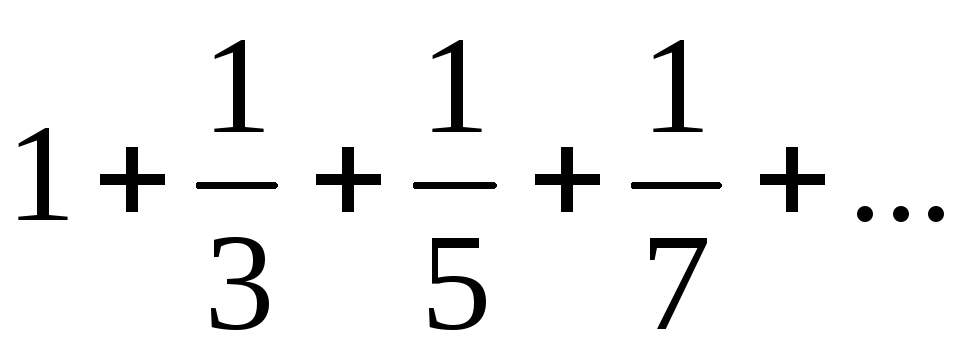 ;
б)
;
б) 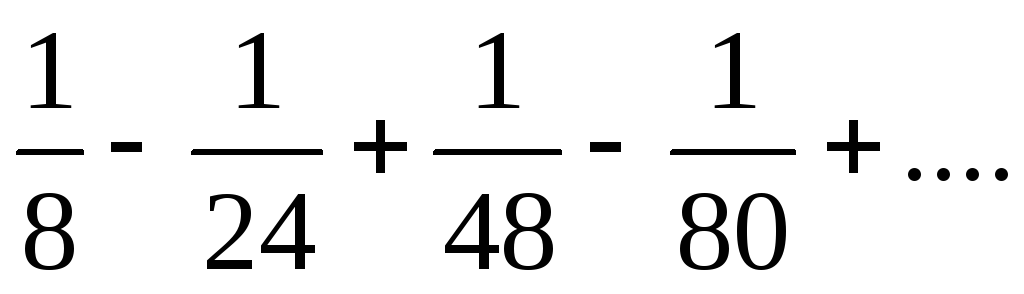
studfile.net
Вариант № 2
Даны три варианта множеств:
a). A ={2, 4, 5, 6}, B={ 1, 5, 6 }, C={ 4, 6}. E={1, 2, … , 9},
b). A = { a : a [2, 4] }, B={b: b (4, 7],}, C = { c: c [ 3, 9) }, E – вся числовая ось.
c). A ={(i, p), (j, j)}, B={(i, p), (5, 6 )}, C={(-4, 6), (5, 6 )}. E ={(i, p), (j, j), (i, i), (-4, 6), (5, 6)}
1. Выполнить над множествами следующие операции и дать графическую интерпретацию.
A C B для варианта множеств а).
B A C для варианта множеств b).
C \ B A для варианта множеств c).
2. Выяснить выполняется ли соотношение (графически):
A\(CB)=(A\B)\C.
3. Найдите произведение множеств AC,BAиC2 и их мощности для варианта множествc).
Найдите проекцию множеств ACBна 2, 3 составляющие, то есть Пр2,3ACBдля варианта множествa).
Дано множество M={m:m=x+y,xA,yB} для варианта множеств а). и отношениеR={(a,b):a,bM,a+b- нечетное}
Записать отношение в явном виде и найти обратное отношение R-1,
представить Rлинейным способом,
выяснить какими свойствами обладает данное отношение,
6. Известно, что из 100 студентов живописью увлекаются 28 чел., спортом – 42 чел., музыкой – 30 чел., живописью и спортом – 10 чел., живописью и музыкой — 8 чел., спортом и музыкой – 5. живописью, спортом и музыкой – 3 чел. Определить a). сколько человек увлекается только спортом, b). сколько человек ничем не увлекается, c). сколько человек увлекается хотя бы живописью и музыкой ?
7. Сколькими способами можно выбрать из полной колоды карт (содержащей 52 карты) по одной карте каждой масти так, чтобы карты красных мастей и карты чёрных мастей образовывали пары( например, девятки пик и треф и валеты бубен и червей)?
Вариант № 3
Даны три варианта множеств:
a). A ={2, 4, 5, 6}, B={ 1, 5, 6 }, C={ 4, 6}. E={1, 2, … , 9},
b). A = { a : a [2, 4] }, B={b: b (4, 7],}, C = { c: c [ 3, 9) }, E – вся числовая ось.
c). A ={(i, p), (j, j)}, B={(i, p), (5, 6 )}, C={(-4, 6), (5, 6 )}. E ={(i, p), (j, j), (i, i), (-4, 6), (5, 6)}
1. Выполнить над множествами следующие операции и дать графическую интерпретацию.
B(CA) для варианта множеств а).
B (A \ C) для варианта множеств b).
C B A для варианта множеств c).
2. Выяснить выполняется ли соотношение (графически):
A\BC=AB\CB
3. Найдите произведение множеств CB,ACиB2 и их мощности для варианта множествc).
Найдите проекцию множеств CABна 2, 3 составляющие, то есть Пр2,3CABдля варианта множествa).
Дано множество M={m:m=x+y,xB,yC} для варианта множеств а). и отношение R={(a, b): a, b M, I a-b I < 9}
Записать отношение в явном виде, найти обратное отношение R-1 ,
представить Rкоординатным способом,
выяснить какими свойствами обладает данное отношение,
6. В отделе НИИ работает несколько человек, причем каждый из них знает хотя бы один иностранный язык. 10 чел. знают английский, 9 чел. – немецкий, 7 чел. – французский, 4 чел. знают и английский, и немецкий, 2 – английский и французский, 2 — немецкий и французский, а один человек знает все три языка. Определить a). сколько человек работает в отделе?b). сколько человек знают ровно два языка?c). сколько человек знают только английский?
7. Рота состоит из 3 офицеров, 6 сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, 2 сержантов и 20 рядовых? Та же задача, если в отряд должен войти командир роты и старший из сержантов.
studfile.net
Вариант № 6
Даны три варианта множеств:
a). A ={2, 4, 5, 6}, B={ 1, 5, 6 }, C={ 4, 6}. E={1, 2, … , 9},
b). A = { a : a [1, 5] }, B={b: b (4, 6],}, C = { c: c [ 3, 9) }, E – вся числовая ось.
c). A ={(a, p), (c, c)}, B={(a, p), (1, 6 )}, C={(-4, 6), (1, 6 )}. E ={(a, p), (c, c), (a, a), (-4, 6), (1, 6)}
1. Выполнить над множествами следующие операции и дать графическую интерпретацию.
A C B для варианта множеств а).
B A C для варианта множеств b).
C \ B A для варианта множеств c).
2. Выяснить выполняется ли соотношение (графически):
A\(CB)=(A\B)\C.
3. Найдите произведение множеств AC,BAиC2 и их мощности для варианта множествc).
4. Найдите проекцию множеств ACBна 2, 3 составляющие, то есть Пр2,3ACBдля варианта множествa).
5. Дано множество M={m:m=x+y,xA,yB} для варианта множеств а). и отношениеR={(a,b):a,bM,a+b- нечетное}
Записать отношение в явном виде, найти обратное отношение R-1 .
представить Rлинейным способом,
выяснить какими свойствами обладает данное отношение,
Известно, что из 100 студентов живописью увлекаются 28 чел., спортом –42 чел., музыкой – 30 чел., живописью и спортом – 10 чел., живописью и музыкой — 8 чел., спортом и музыкой – 5. живописью, спортом и музыкой –3 чел. Определить a). сколько человек увлекается только музыкой, b). сколько человек ничем не увлекается, c). сколько человек увлекается хотя бы живописью и музыкой ?
Надо послать 7 срочных писем. Сколькими способами это можно сделать, если для передачи писем можно послать 3 курьеров и каждое письмо можно дать любому из 3 курьеров?
Вариант № 7
Даны три варианта множеств:
a). A ={2, 4, 5, 6}, B={ 1, 5, 6 }, C={ 4, 6}. E={1, 2, … , 9},
b). A = { a : a [1, 5] }, B={b: b (4, 6],}, C = { c: c [ 3, 9) }, E – вся числовая ось.
c). A ={(a, p), (c, c)}, B={(a, p), (1, 6 )}, C={(-4, 6), (1, 6 )}. E ={(a, p), (c, c), (a, a), (-4, 6), (1, 6)}
1. Выполнить над множествами следующие операции и дать графическую интерпретацию.
B(CA) для варианта множеств а).
B (A \ C) для варианта множеств b).
C B A для варианта множеств c).
2. Выяснить выполняется ли соотношение (графически):
A\BC=AB\CB
3. Найдите произведение множеств CB,ACиB2 и их мощности для варианта множествc).
4. Найдите проекцию множеств CABна 2, 3 составляющие, то есть Пр2,3CABдля варианта множествa).
5. Дано множество M={m:m=x+y,xB,yC} для варианта множеств а). и отношение R={(a, b): a, b M, I a-b I < 9}
Записать отношение в явном виде, найти обратное отношение R-1
представить Rкоординатным способом,
выяснить какими свойствами обладает данное отношение,
В отделе НИИ работает несколько человек, причем каждый из них знает хотя бы один иностранный язык. 10 чел. знают английский, 9 чел. – немецкий, 7 чел. – французский, 4 чел. знают и английский, и немецкий, 2 – английский и французский, 2 — немецкий и французский, а один человек знает все три языка. Сколько человек работает в отделе? Сколько человек знают ровно два языка? Сколько человек знают только немецкий?
Рота состоит из 5 офицеров, 8 сержантов и 80 рядовых. Сколькими способами можно выделить из них отряд, состоящий из одного офицера, 2 сержантов и 20 рядовых? Та же задача, если в отряд должен войти командир роты и старший из сержантов.
studfile.net
Вариант № 10
Даны три варианта множеств:
a). A ={2, 4, 5, 6}, B={ 1, 5, 6 }, C={ 4, 6}. E={0,1, 2, … , 9},
b). A = { a : a [2, 4] }, B={b: b (4, 7],}, C = { c: c [ 3, 9) }, E – вся числовая ось.
c). A ={(i, p), (j, j)}, B={(i, p), (5, 6 )}, C={(-4, 6), (5, 6 )}. E ={(i, p), (j, j), (i, i), (-4, 6), (5, 6)}
1. Выполнить над множествами следующие операции и дать графическую интерпретацию.
A C B для варианта множеств а).
B A C для варианта множеств b).
C \ B A для варианта множеств c).
2. Выяснить выполняется ли соотношение (графически):
A\(CB)=(A\B) C.
3. Найдите произведение множеств AC,BAиC2 и их мощности для варианта множествc).
Найдите проекцию множеств ACBна 2, 3 составляющие, то есть Пр2,3ACBдля варианта множествa).
Дано множество M={m:m=x+y,xA,yB} для варианта множеств а). и отношениеR={(a,b):a,bM,a+b- нечетное}
Записать отношение в явном виде и найти обратное отношение R-1,
представить Rлинейным способом,
выяснить какими свойствами обладает данное отношение,
6. Известно, что из 100 студентов живописью увлекаются 28 чел., спортом –42 чел., музыкой – 30 чел., живописью и спортом – 10 чел., живописью и музыкой — 8 чел., спортом и музыкой – 5. живописью, спортом и музыкой –3 чел. Определить a). сколько человек увлекается только спортом, b). сколько человек ничем не увлекается, c). сколько человек увлекается хотя бы спортом или музыкой ?
7. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков: русского, английского, французского, немецкого, итальянского, на любой другой из этих 5 языков?
Тема 2 «Математическая логика и схемы» Вариант № 1
1. Упростить выражение
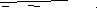
y(a,b,c)= (a bc)ac bc
2. Построить алгебраическими преобразованиями СДНФ

 f(x1,x2,x3,)=x1x2 (x1x2)x3 x2x3
f(x1,x2,x3,)=x1x2 (x1x2)x3 x2x3
3. Построить алгебраическими преобразованиями СКНФ


 f(x,y,z)=x(yz xz) xyz.
f(x,y,z)=x(yz xz) xyz.
4. Минимизировать функции по картам Карно и найти сложность по Квайну:
а) Найти мин. сумму б). Найти мин произведение
0
0
0
1
0
1
0
—
0
1
1
0
0
—
0
0
1
0
0
1
1
—
0
1
1
0
1
0
1
1
0
—
5. Для данного выражения выполнить преобразование в базис операции штрих Шеффера. Дать схемную реализацию в базисе (И-НЕ).

y(a,b,c) = (ab c)(ab abc) (a bc)
Вариант № 2
1. Упростить выражение


 y(a,b,c
) = (a bc)ac bc
y(a,b,c
) = (a bc)ac bc
2. Построить алгебраическими преобразованиями СДНФ

f(x,y,z) = (xy xyz)xy
3. Построить алгебраическими преобразованиями СКНФ
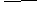
в) f(x,y,z)=x(yz xz) xyz.
4. Минимизировать функции по картам Карно и найти сложность по Квайну:
а) Найти мин. сумму б). Найти мин произведение
1
1
0
0
0
1
1
—
1
0
0
1
—
0
1
0
0
1
0
0
1
1
—
1
1
0
0
1
1
0
1
—
5. Для данного выражения выполнить преобразование в базис операции стрелка Пирса. Дать схемную реализацию в базисе (ИЛИ-НЕ).
f(a,b,c,d)= ab bc cd
studfile.net
2 5-30(1курс
Вариант 25
Контрольная работа по курсу « Математический анализ»
I. Множества
Среди абитуриентов, выдержавших экзамены в ВУЗ, оценку «отлично» получили: по математике – 48 человек, по физике – 37,по языку – 42, по математике или физике – 75, математике или языку – 76, по физике или языку – 66 человек. По трём предметам получили отличную оценку 4 человека.
Сколько абитуриентов получили хотя бы одну пятёрку?
Сколько среди них получивших только одну пятёрку?
Сколько человек не получили пятёрку по языку?
Задать множество перечислением его элементов:
исчисле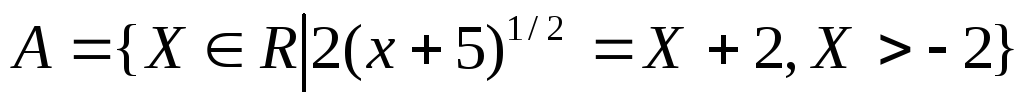
Дифференциальное исчисление
Найти область определения действительных значений функций:
а) 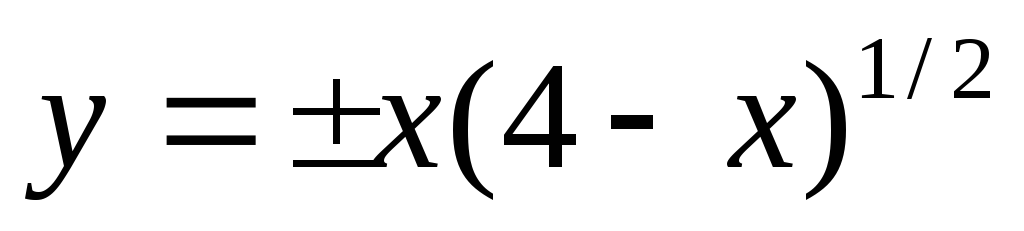 ;
б)
;
б) 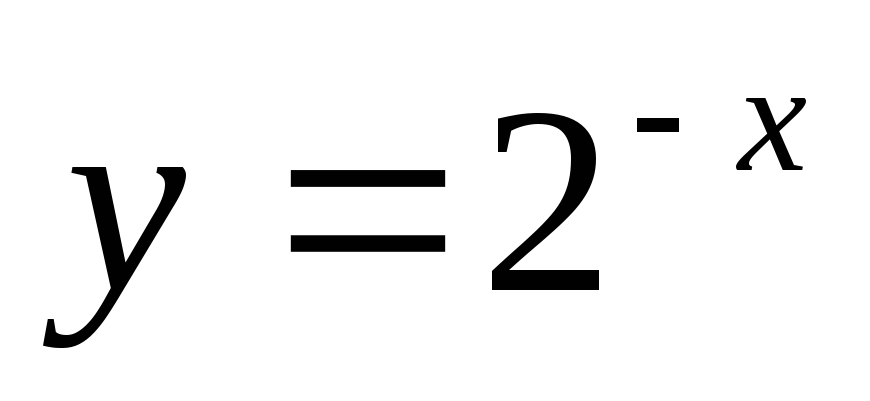 ;
в)
;
в) 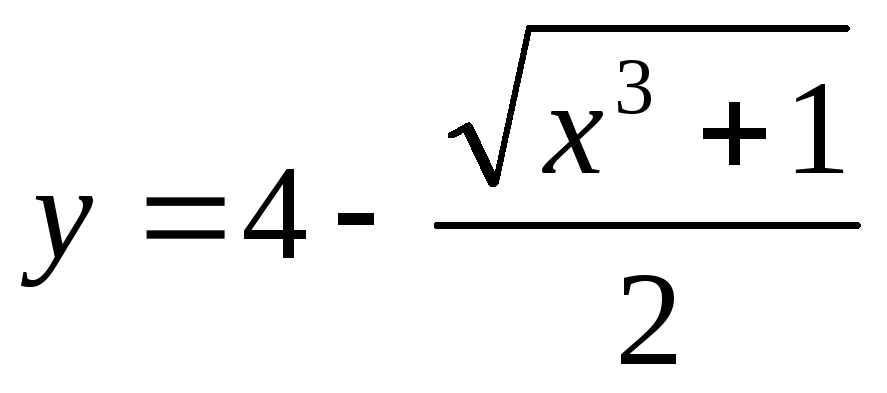 .
.
2) Найти пределы:
а) 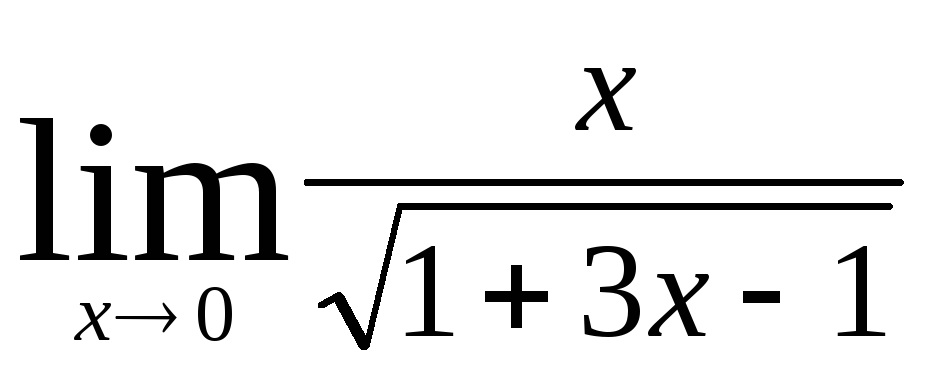 ;
б)
;
б) 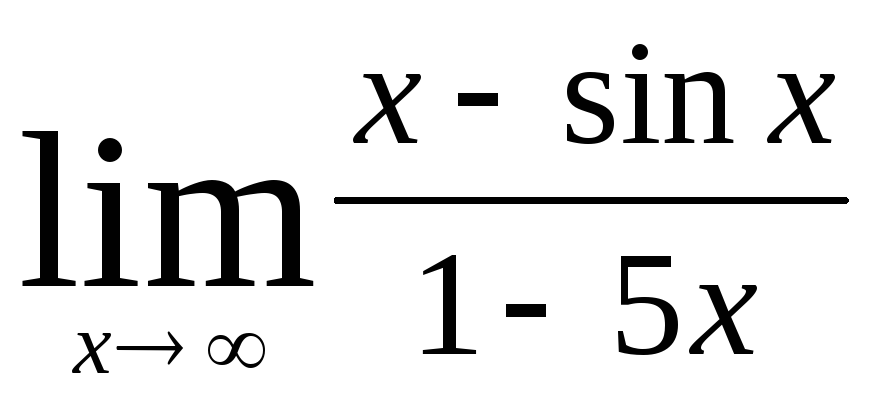 ;
в)
;
в) 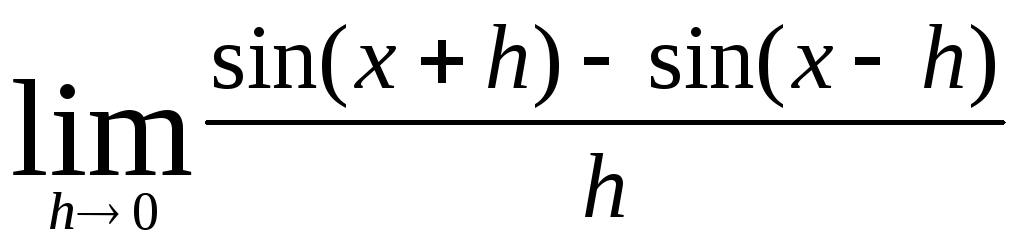 ;
;
г) 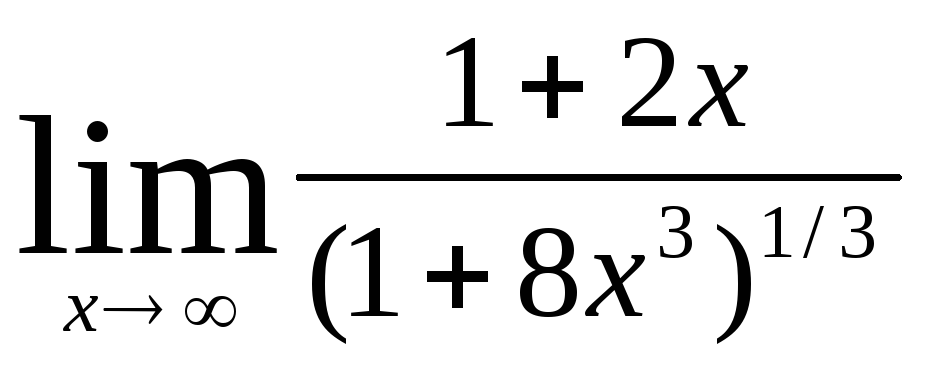 .
.
3) Найти производные функций:
а) 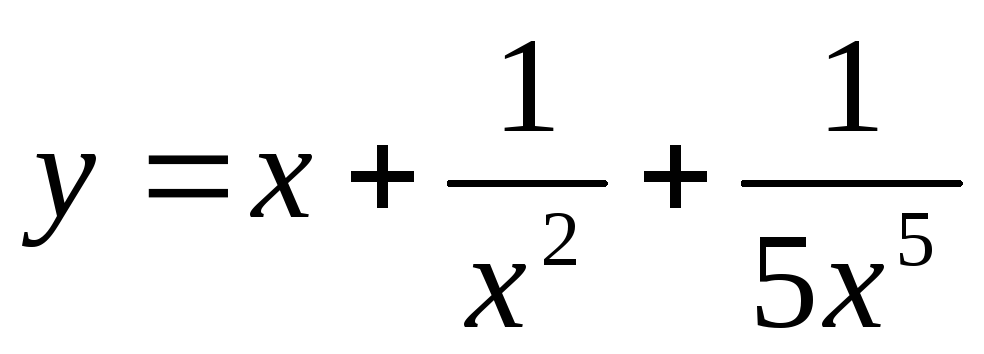 ;
б)
;
б) 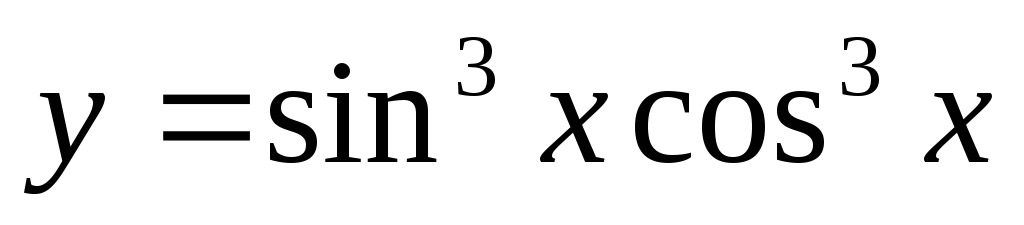 ;
в)
;
в) 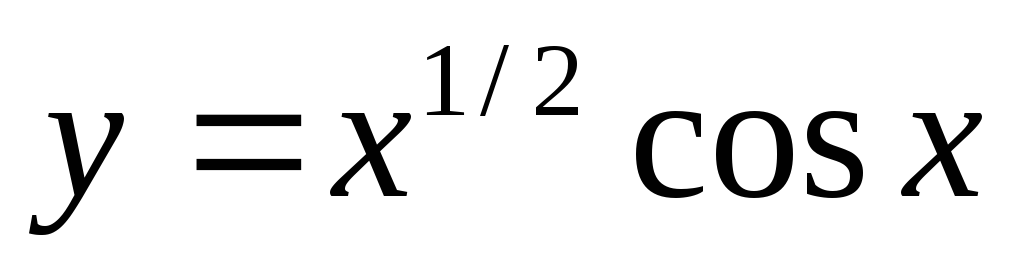 ;
;
г) 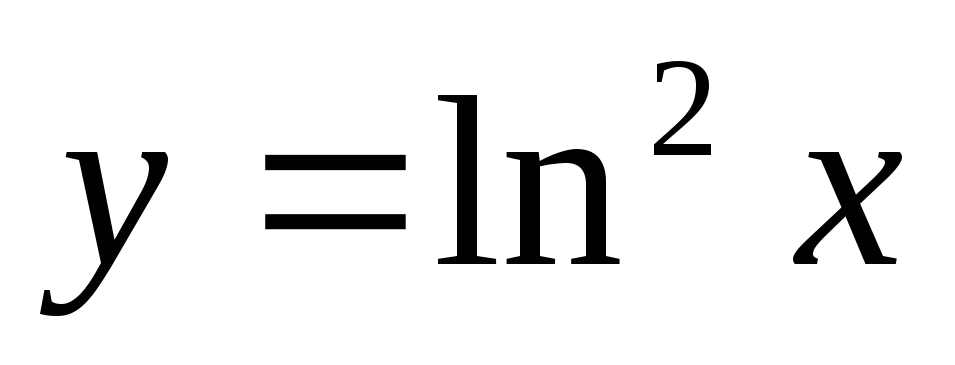 .
.
4) Найти пределы, используя правило Лопиталя:
а) 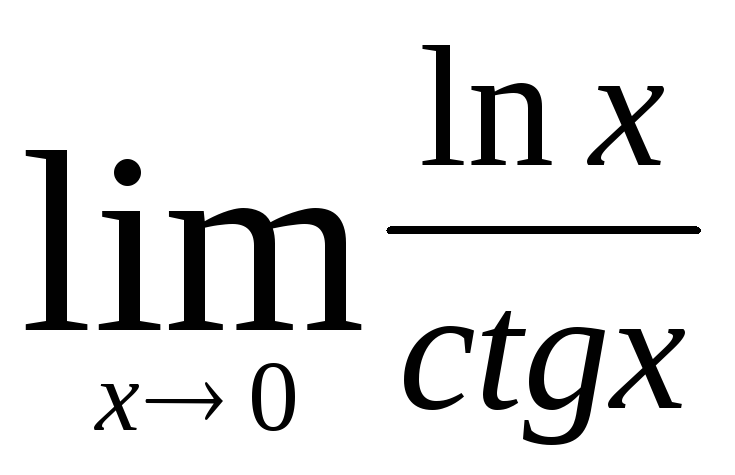 ;
б)
;
б) 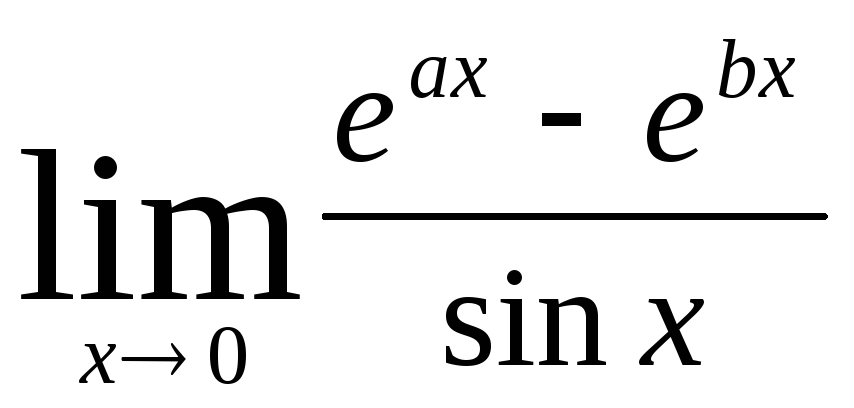 .
.
5) Выполнить полное исследование функции о построить её график:
а) 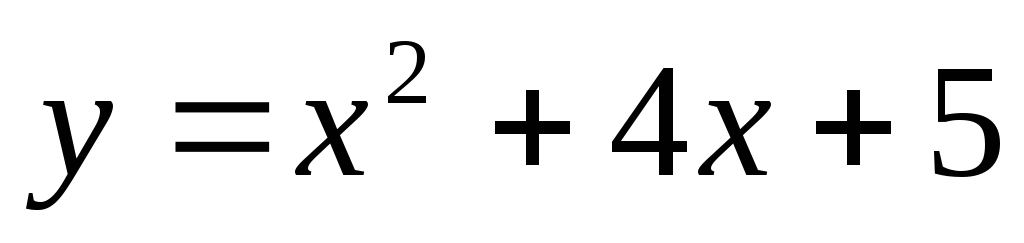 ;
б)
;
б) 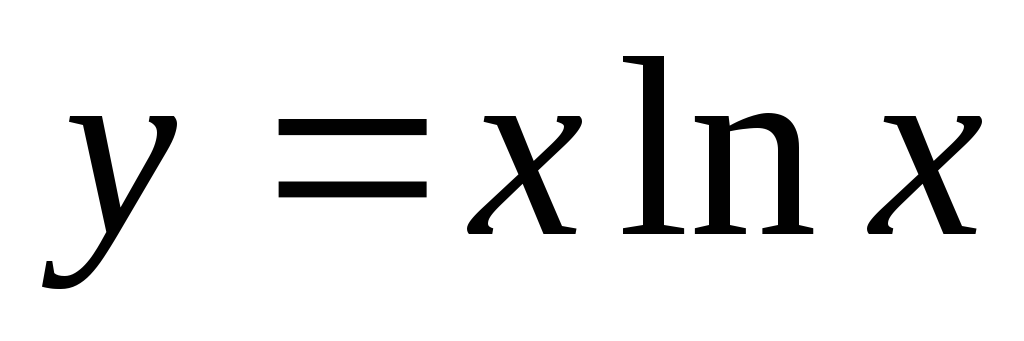 .
.
6) Для функций многих переменных:
а) Указать область определения
функции: 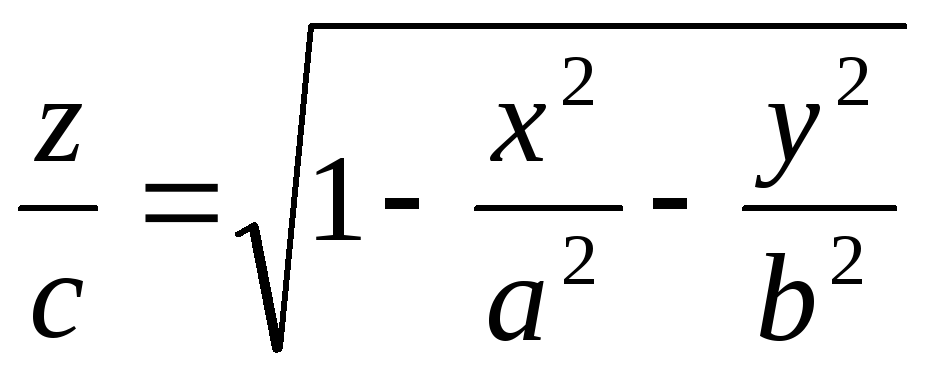 ;
;
б) Найти частные производные
функции: 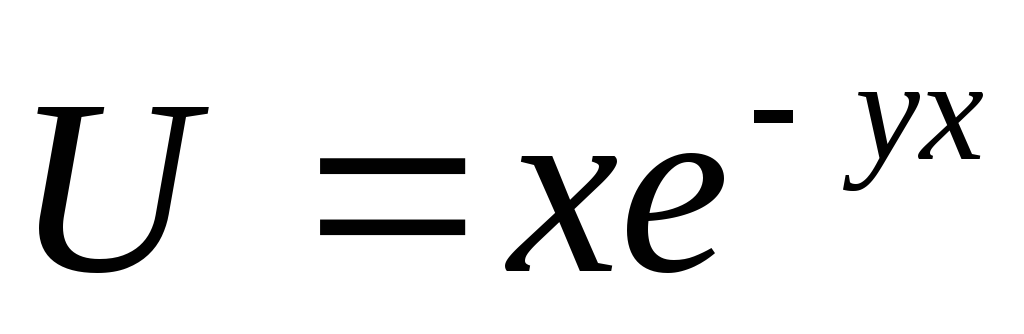 ;
;
в) Исследовать на экстремум функцию: 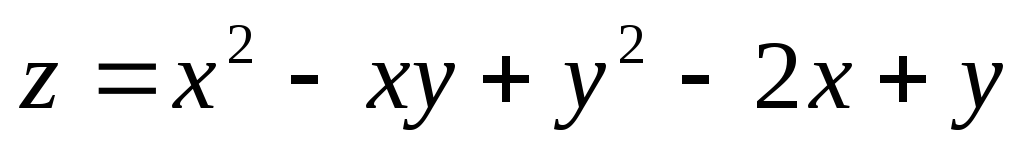 .
.
III. Интегральное исчисление и ряды
Найти интегралы:
а) 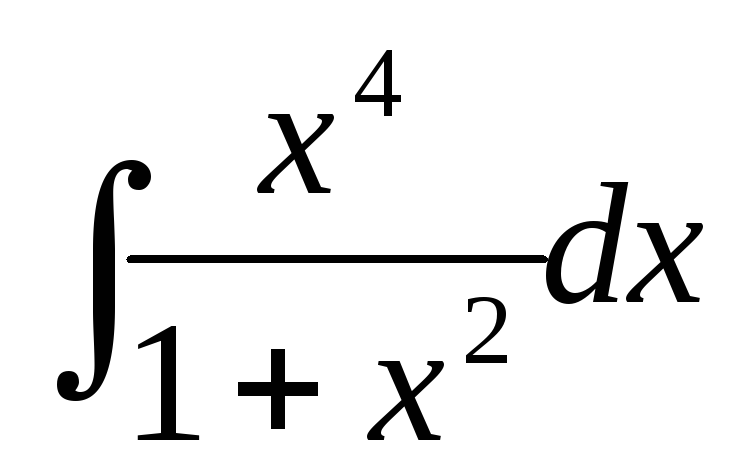 ;
б)
;
б) 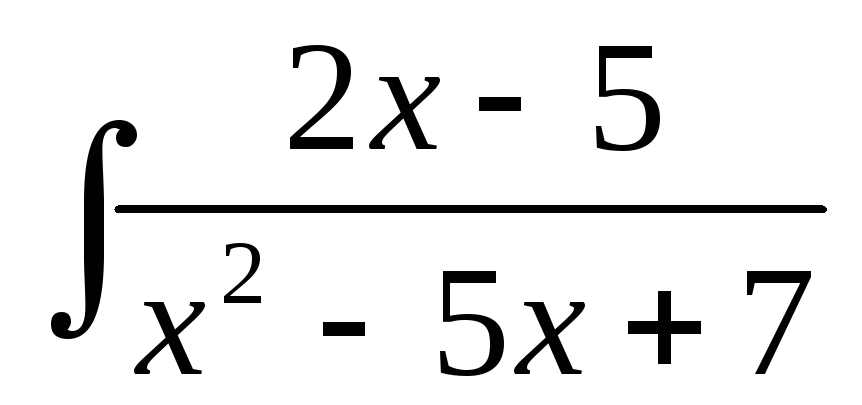 ;
в)
;
в) 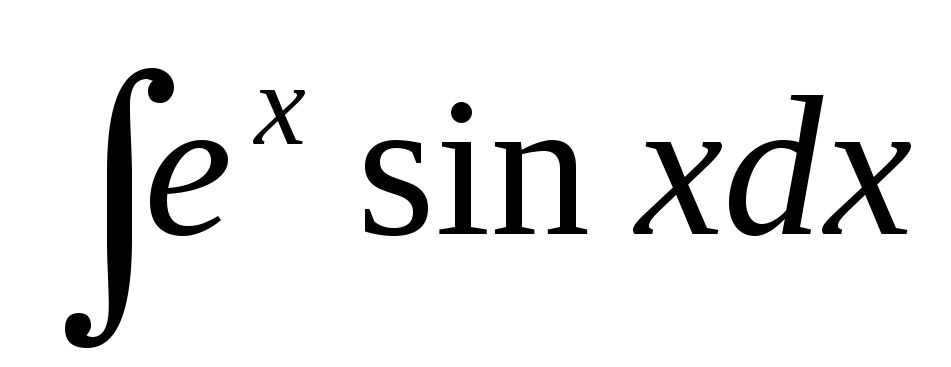 .
.
2) Вычислить интегралы:
а) 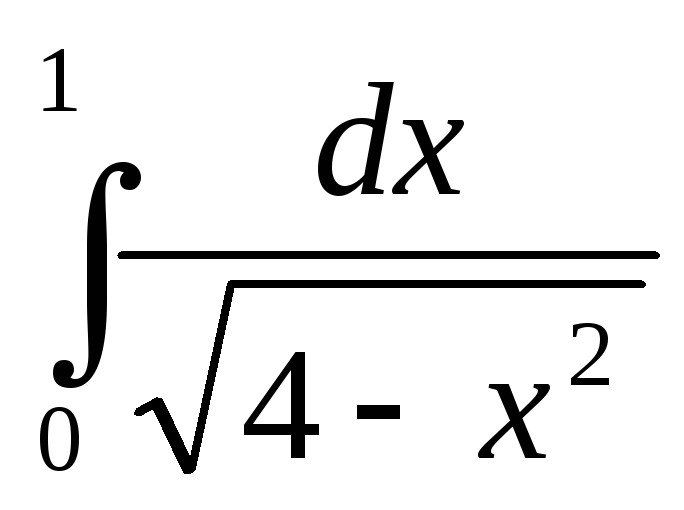 ;
б)
;
б) 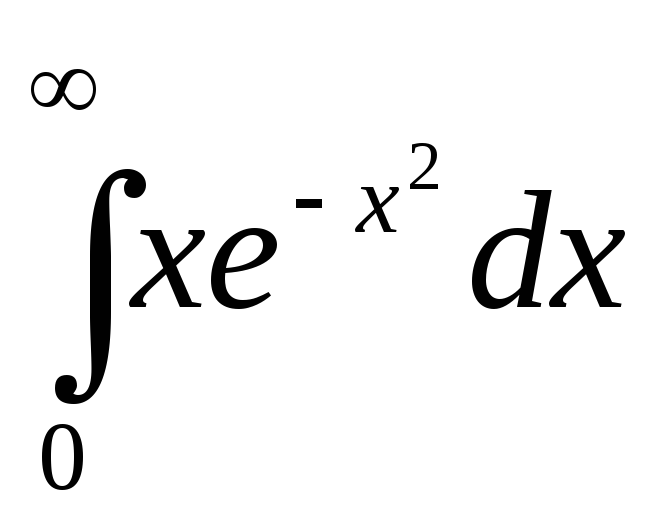 .
.
3) Найти общий интеграл: 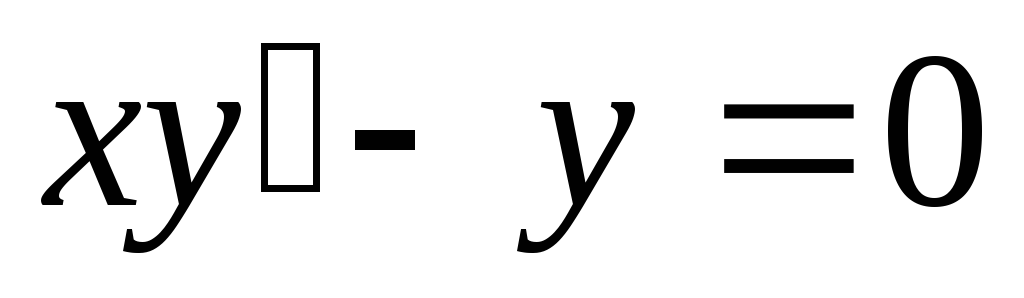 .
.
4) Исследовать сходимость числовых рядов:
а) 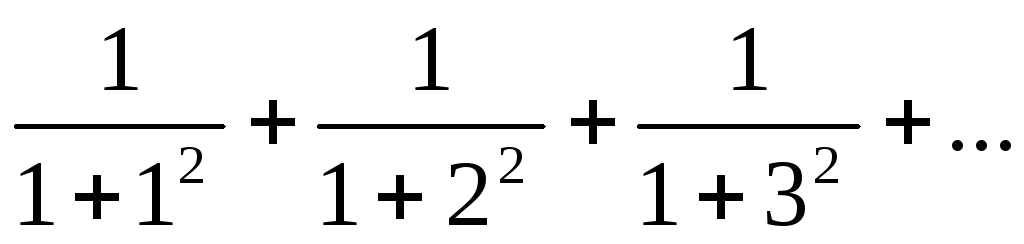 ;
б)
;
б) 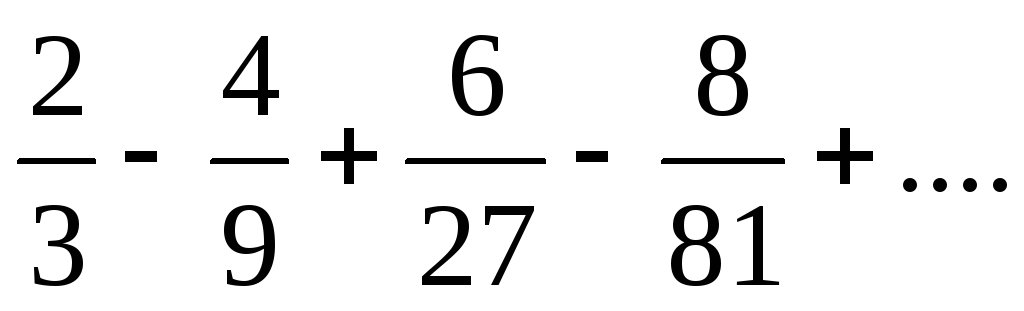
Вариант 26
Контрольная работа по курсу «Математический анализ»
I. Множества.
М – подмножество множества натуральных чисел N. Каждый элемент множества М есть число кратное или 2 или 3. Найти число элементов во множестве М, если среди них имеются: 70 чисел, кратных 2; 60 чисел, кратных 3; 32 числа, кратных 6. Сколько элементов множества М кратны только 2?
Задать множество перечислением его элементов:
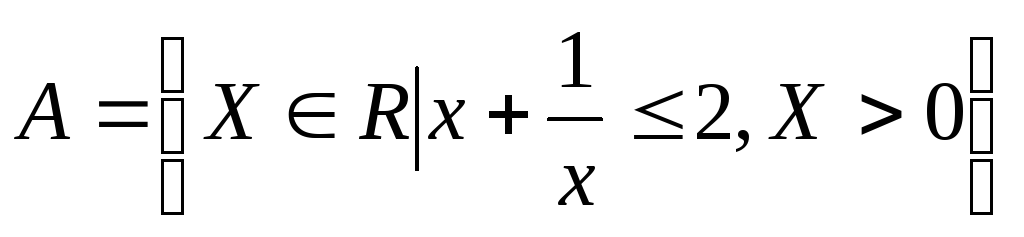
Дифференциальное исчисление
Найти область определения действительных значений функций:
а) 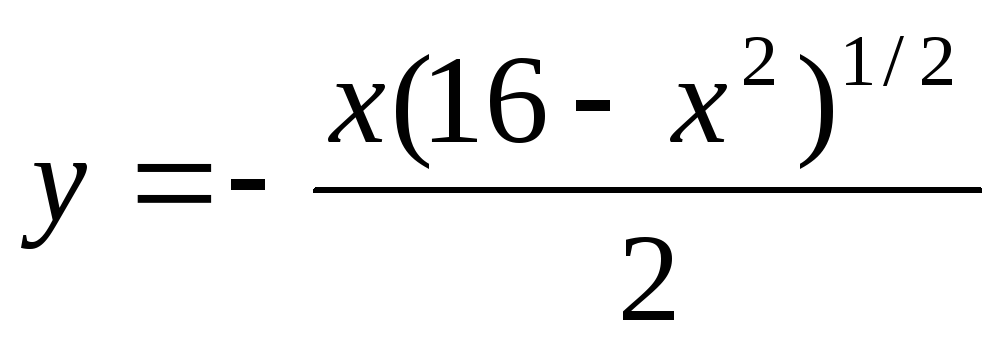 ;
б)
;
б) 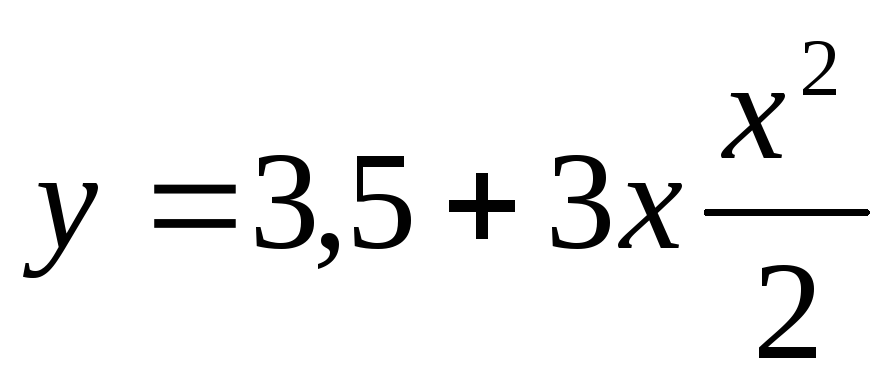 ;
в)
;
в) 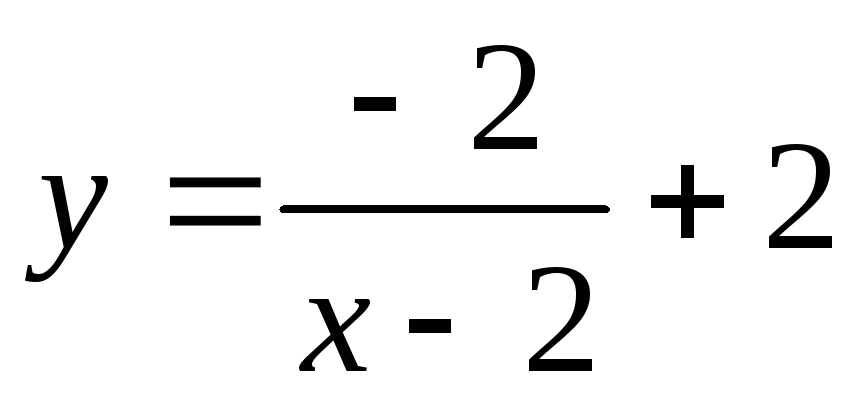
Найти пределы:
а) 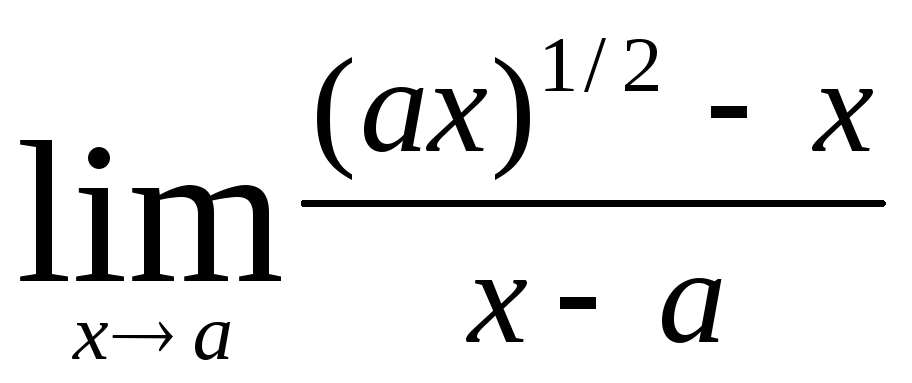 ;
б)
;
б) 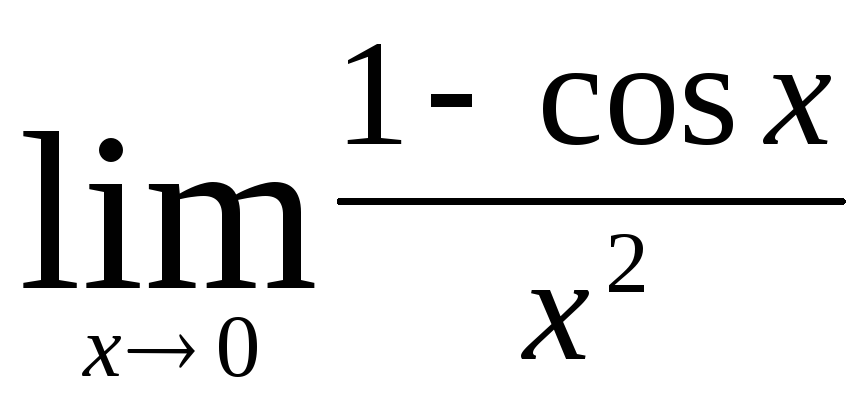 ; в)
; в) 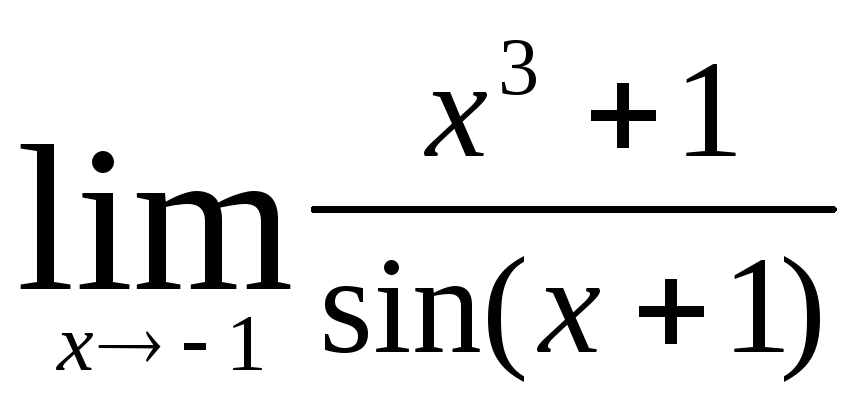 ;
г)
;
г) 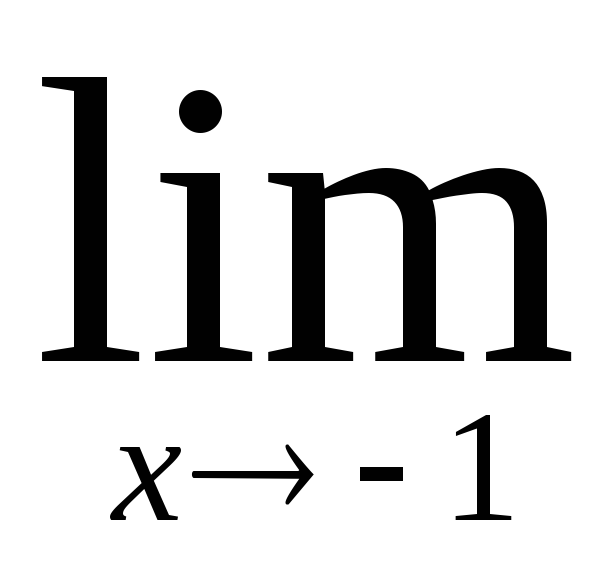
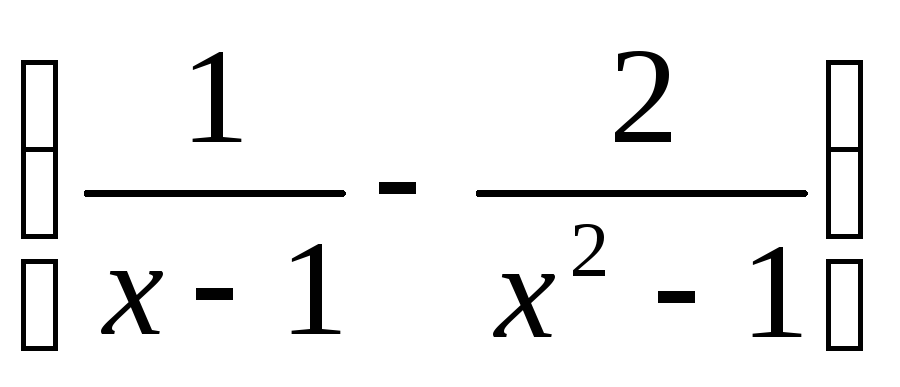 .
.
3) Найти производные функций:
а) 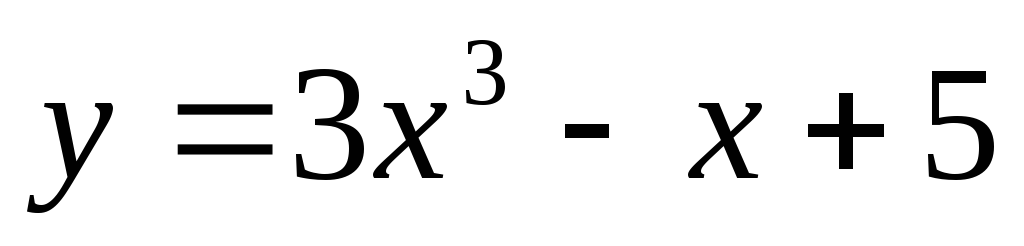 ;
б)
;
б) 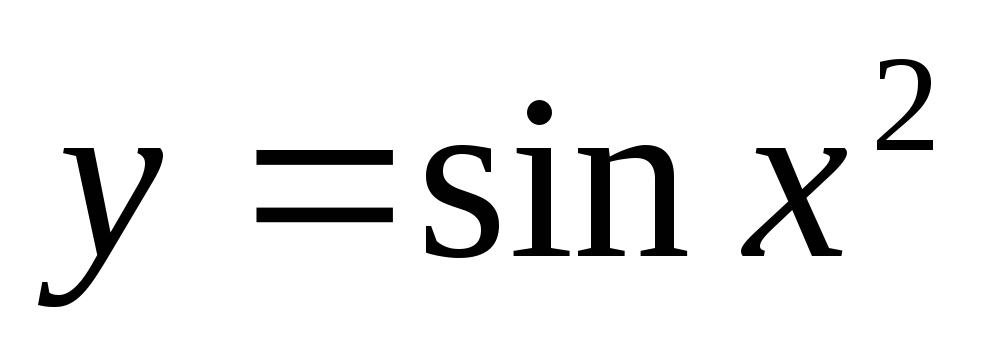 ;
в)
;
в) 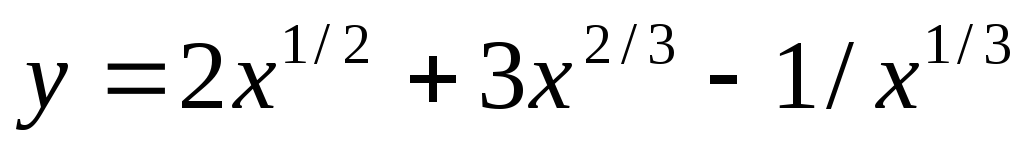 ;
г)
;
г) 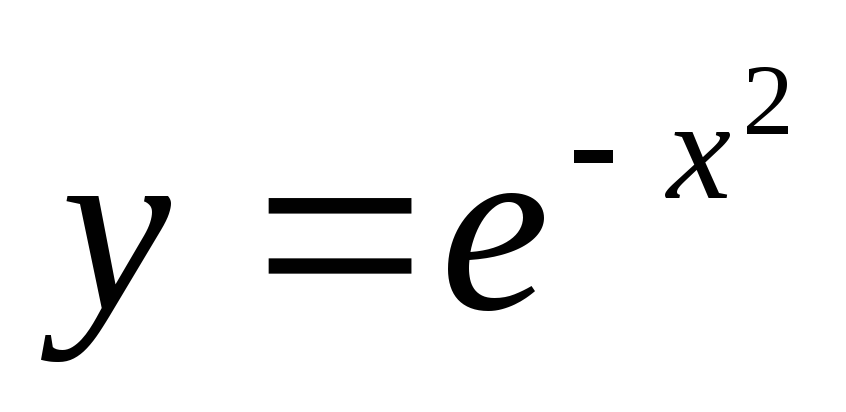
4) Найти пределы, используя правило Лопиталя:
а) 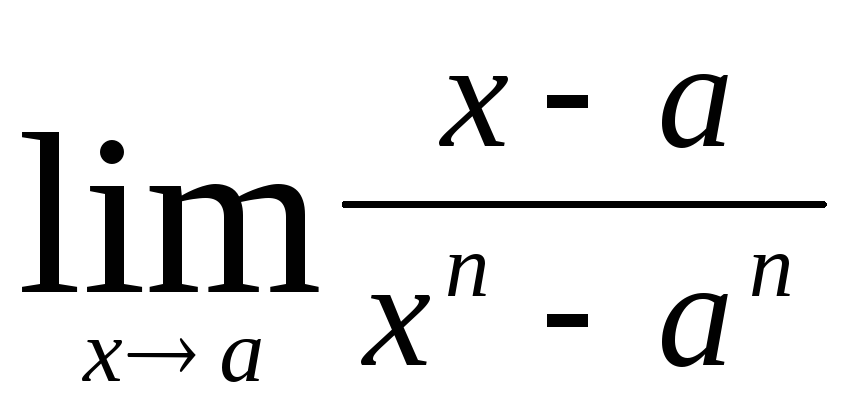 ;
б)
;
б) 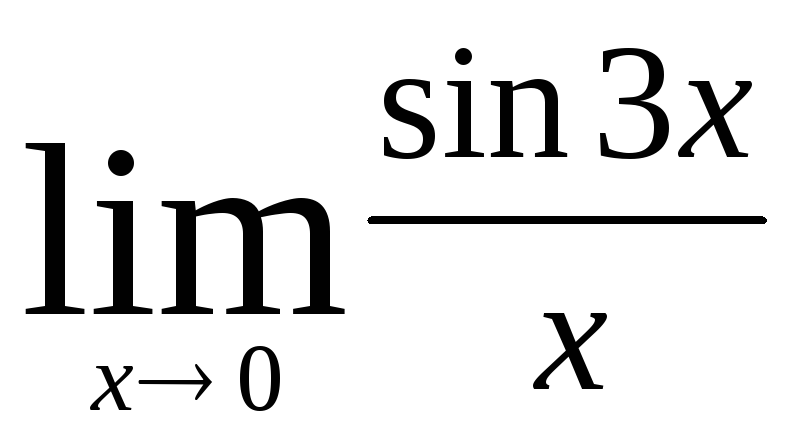 .
.
5) Выполнить полное исследование функции и построить график:
а) 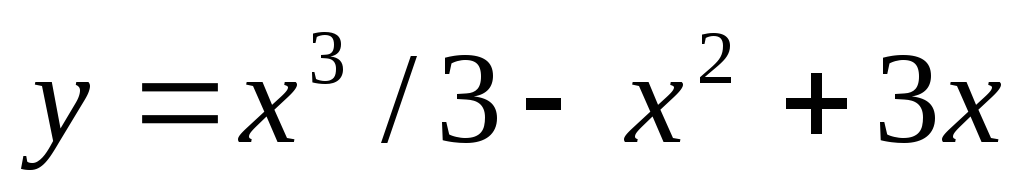 ;
б)
;
б) 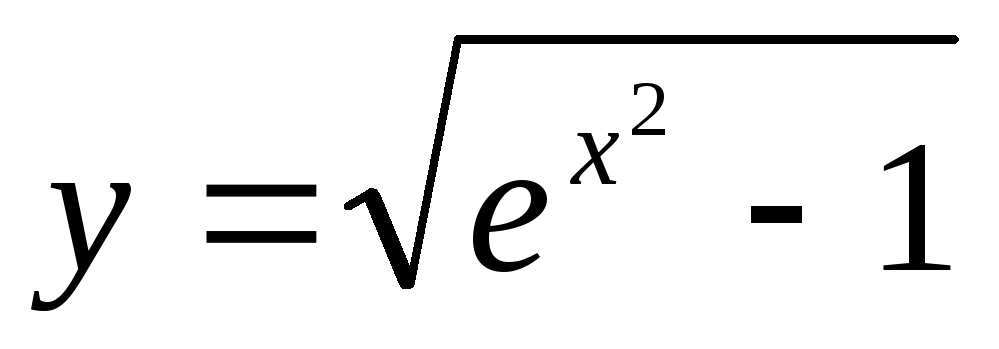 .
.
6) Для функций многих переменных:
а) Указать область
определения функции: 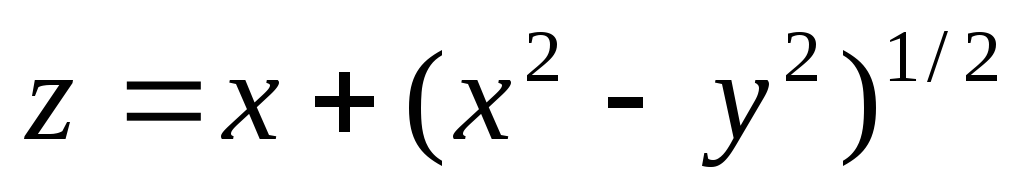 ;
;
б) Найти частные производные
функции: 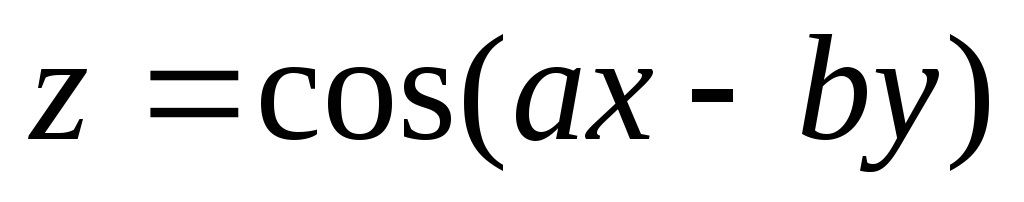 ;
;
в) Исследовать на экстремум
функцию: 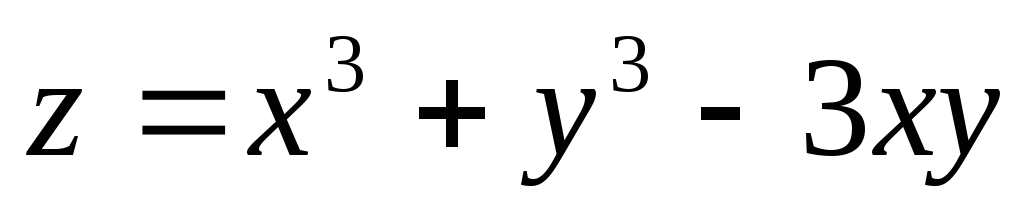 .
.
III. Интегральное исчисление и ряды
Найти интегралы:
а) 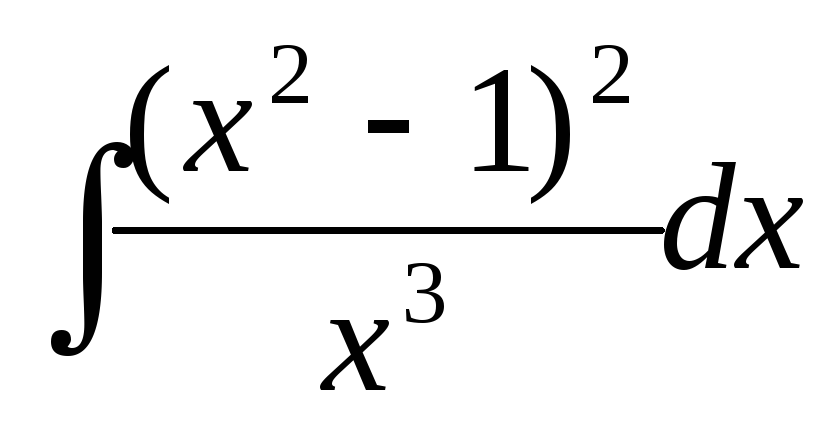 ;
б)
;
б) 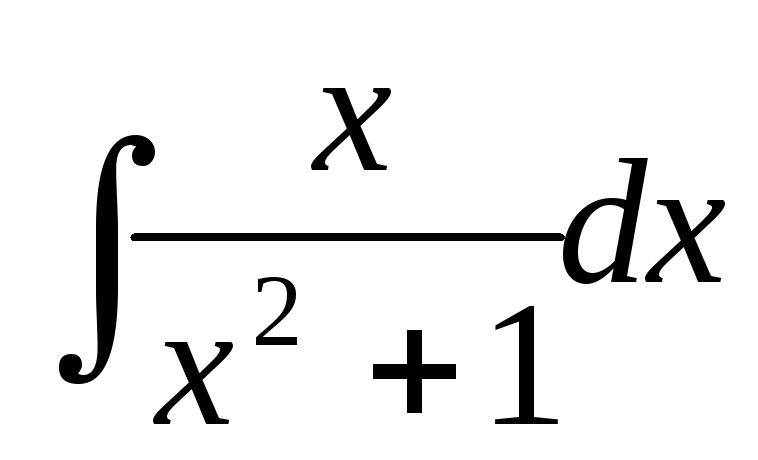 ;
в)
;
в)  .
.
2) Вычислить интегралы:
а) 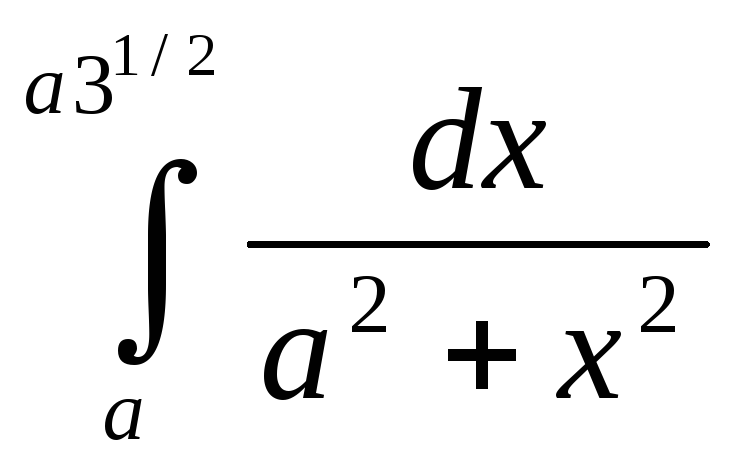 ;
б)
;
б) 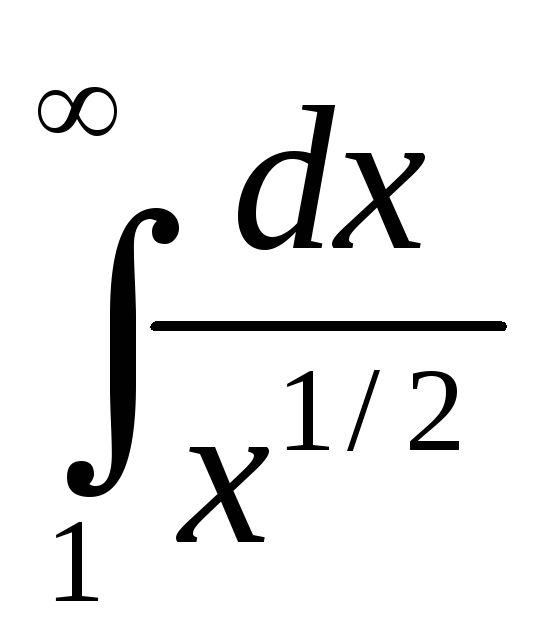 .
.
3) Найти общий интеграл: 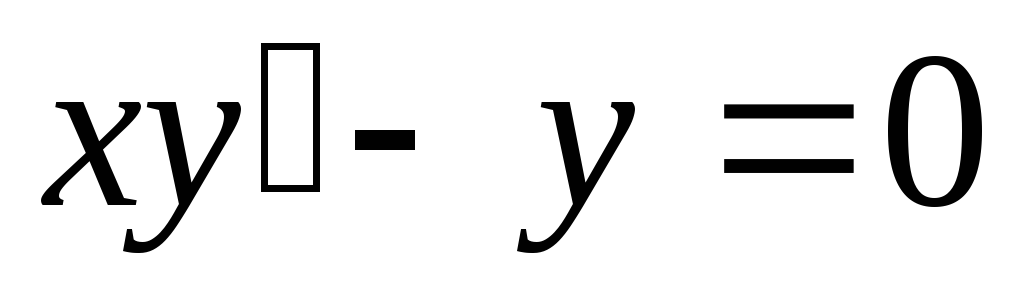 .
.
4) Исследовать сходимость числовых рядов:
а) 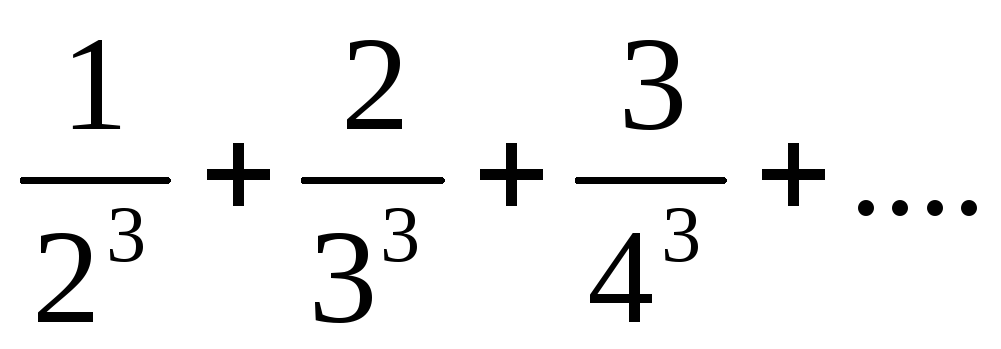 ;
б)
;
б) 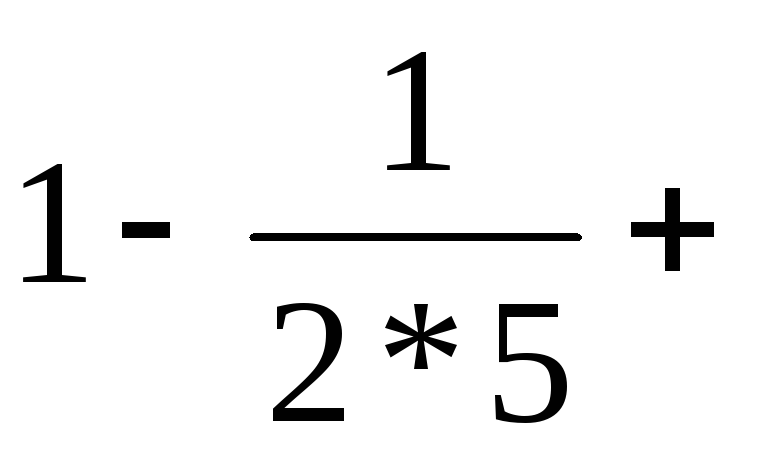
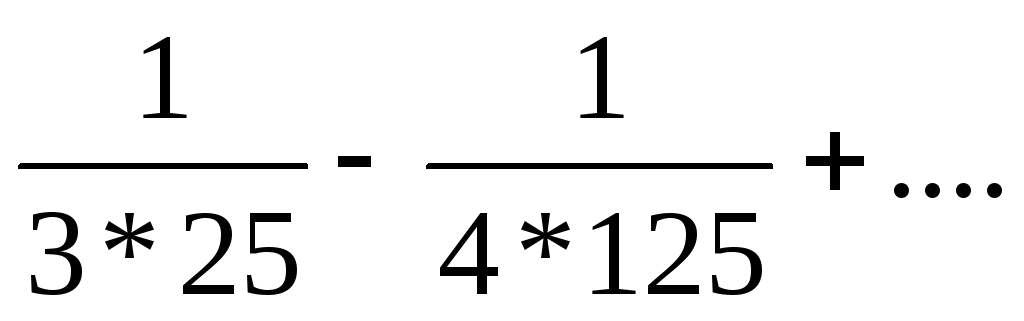
Вариант 27
Контрольная работа по курсу «Математический анализ»
I . Множества
1) В группе из 50 студентов 40 человек сдали экзамен по математике, 27 студентов сдали экзамен по экономике, 5 человек не сдали ни того, ни другого экзамена.
Сколько студентов сдали оба экзамена?
Сколько студентов сдали только экономику?
2) Задать множество перечислением его элементов:
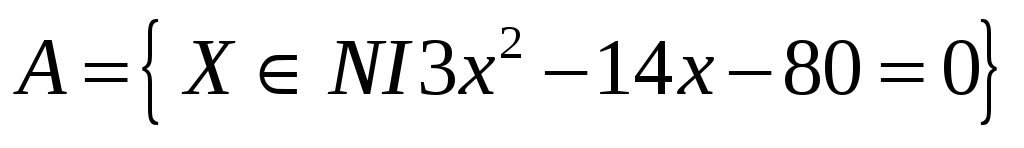
Дифференциальное исчисление
Найти область определения действительных значений функций:
а) y= 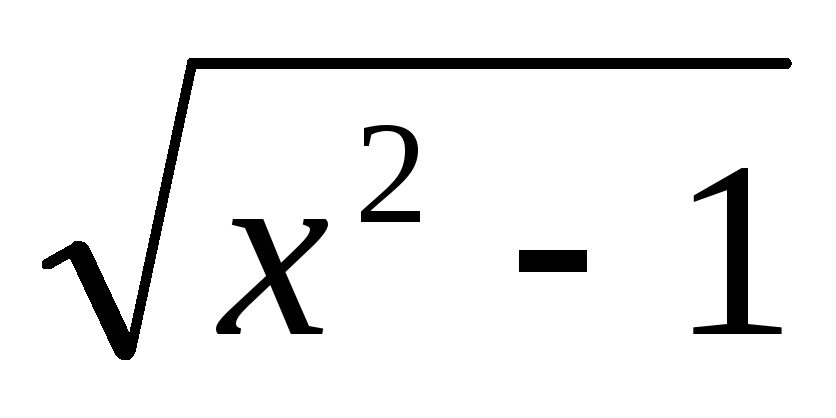 б)
б)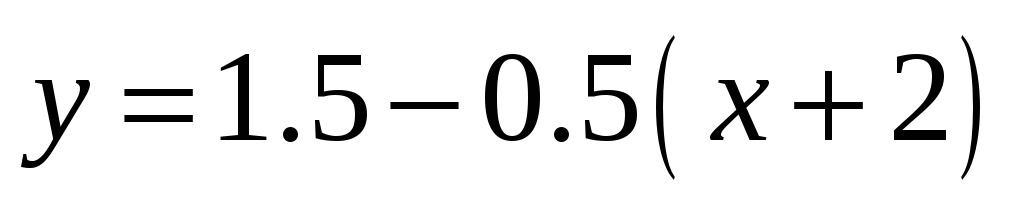 2;в)y = lg
(10x-1).
2;в)y = lg
(10x-1).
2) Найти пределы:
а)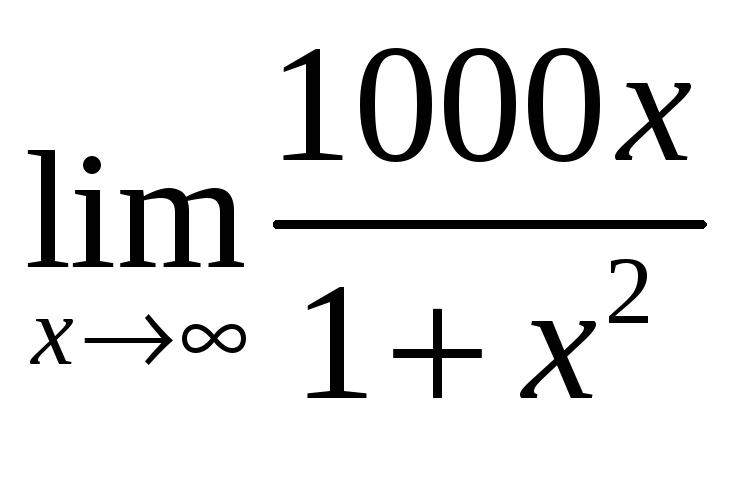 ;
б)
;
б)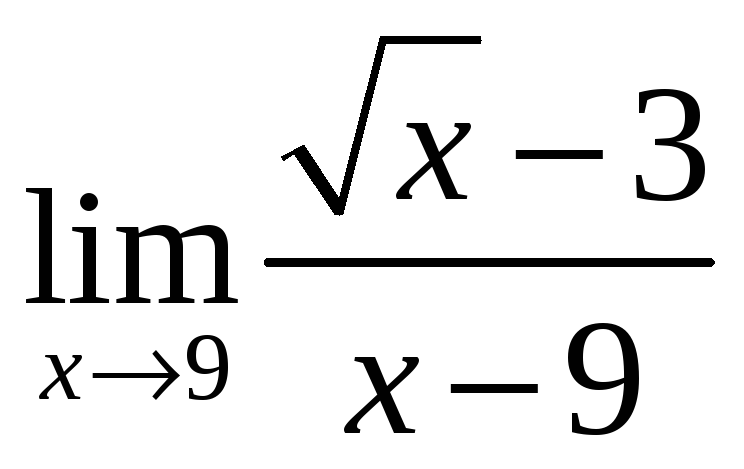 ;
в)
;
в) 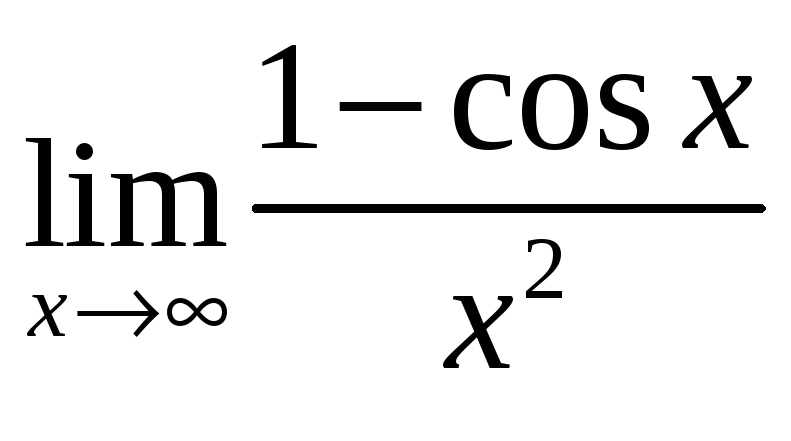 ;
г)
;
г) 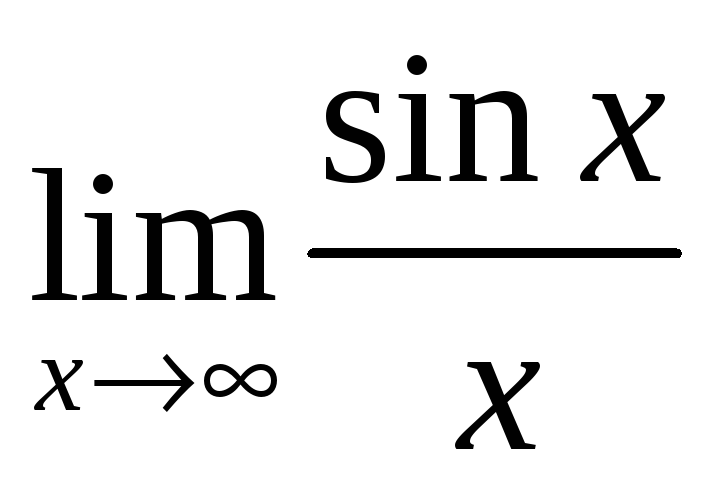
3) Найти производные функций:
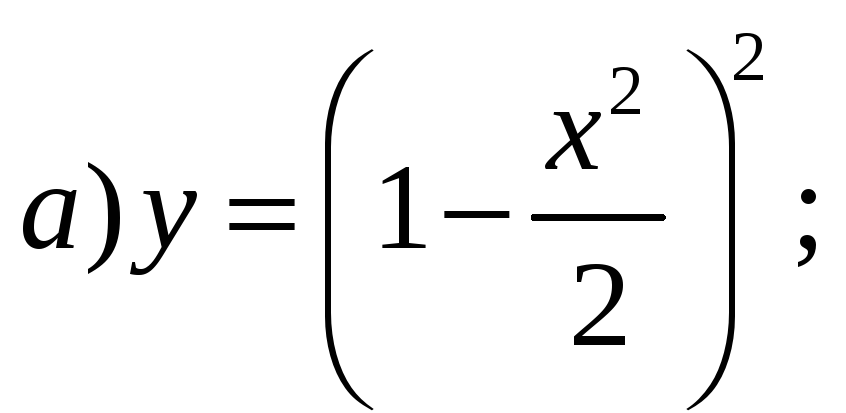
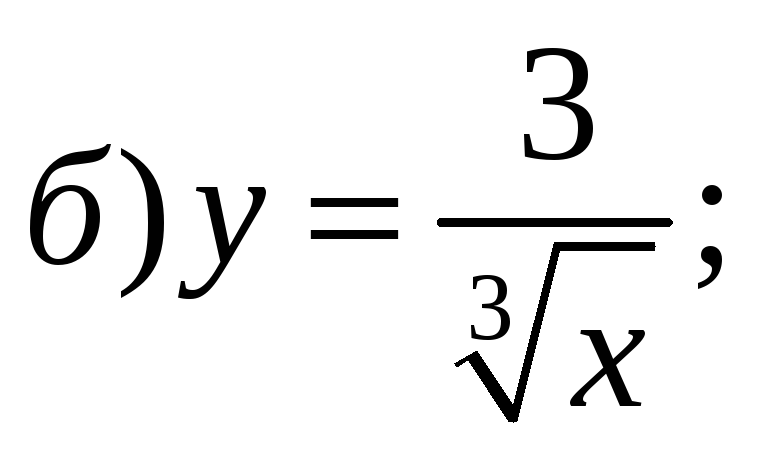
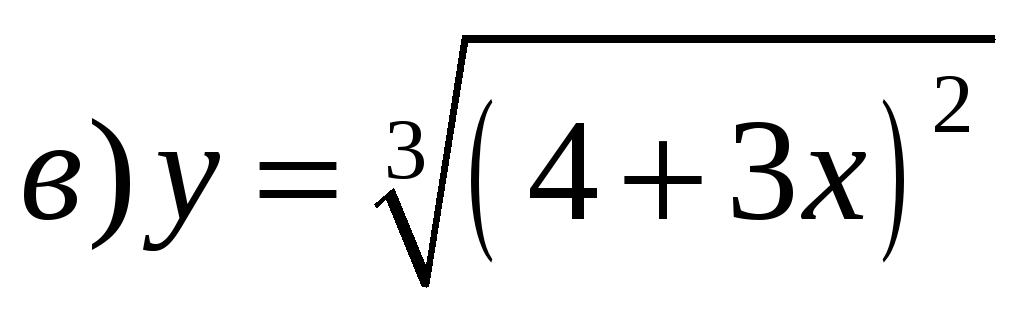 ;
г)
;
г) 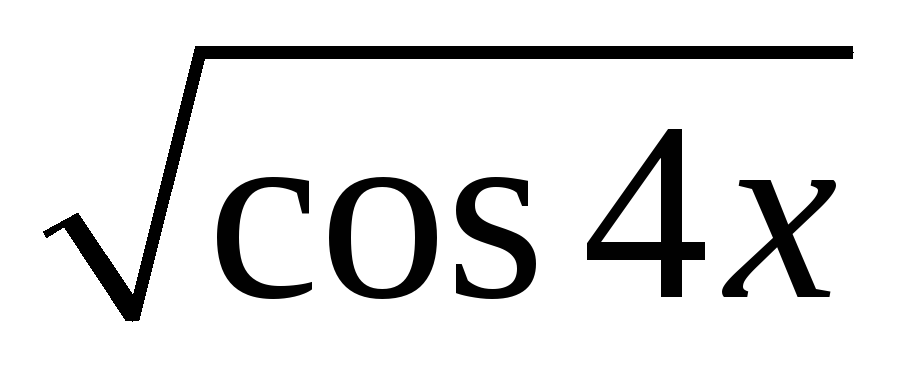
Найти пределы, используя правило Лопиталя:
а) 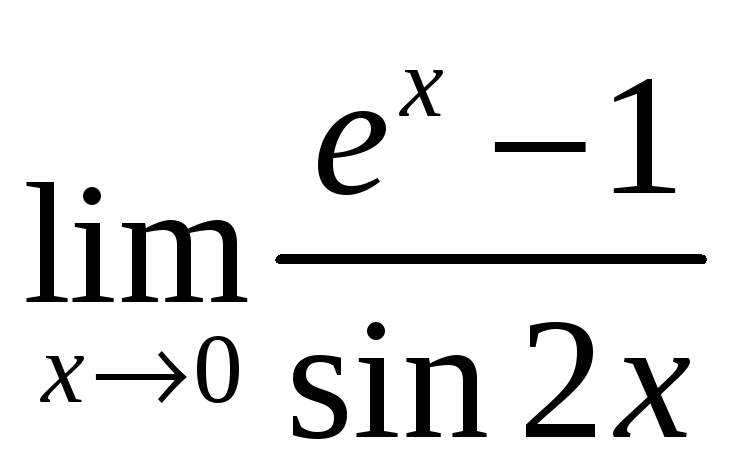 ;
б)
;
б) 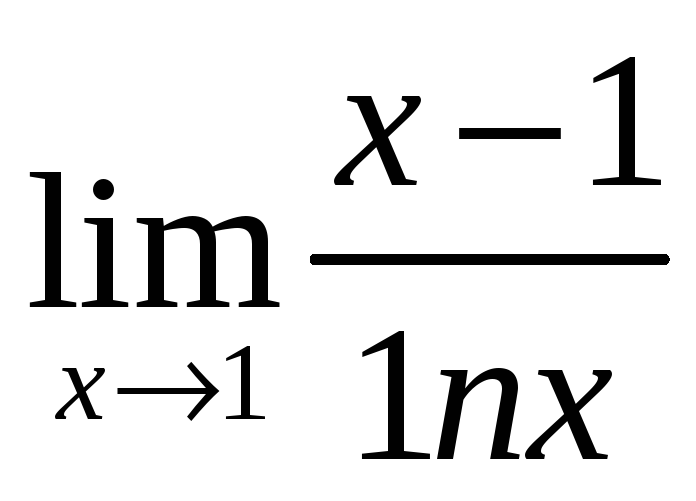
Выполнить полное исследование функции и построить ее график:
а)y=x/2+2/x; б)y=1+2x2-x4/4
Для функций многих переменных:
а) Указать область определения
функции: 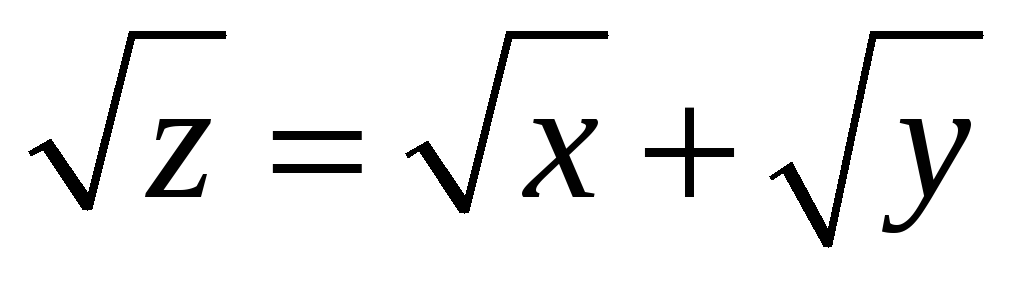 ;
;
б) Найти частные производные функции: z = x2 y-3;
в) Исследовать на экстремум функцию : z = x4 + y4 — x2 — 2xy -y2
Интегральное исчисление и ряды
Найти интегралы:
а)  (x2+2x+1/
x)dx; б)
(x2+2x+1/
x)dx; б) 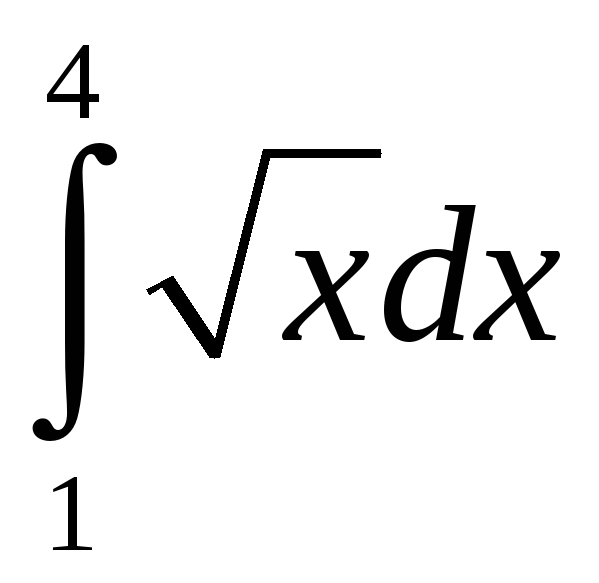 ;
в)
;
в) x2 cos xdx.
x2 cos xdx.
Вычислить интегралы:

Найти общий интеграл:
(x2+x)y/= 2y+1
Исследовать сходимость числовых рядов:
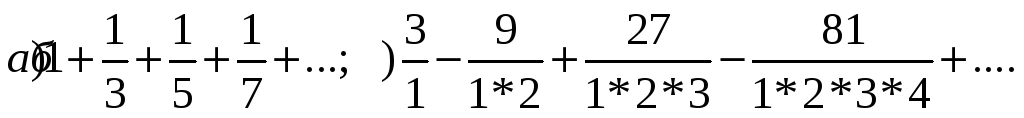
Контрольная работа по курсу «Математический анализ» Вариант 28
I. Множества
1) Известно, что из 100 студентов увлекаются живописью 28 человек, спортом 42, музыкой30; живописью и спортом 10; живописью и музыкой 5; спортом и музыкой 8; и живописью и спортом и музыкой 3 человека.
Сколько студентов увлекаются только живописью?
Сколько студентов ничем не увлекаются?
Сколько человек не увлекаются музыкой?
2) Указать штриховкой множества:
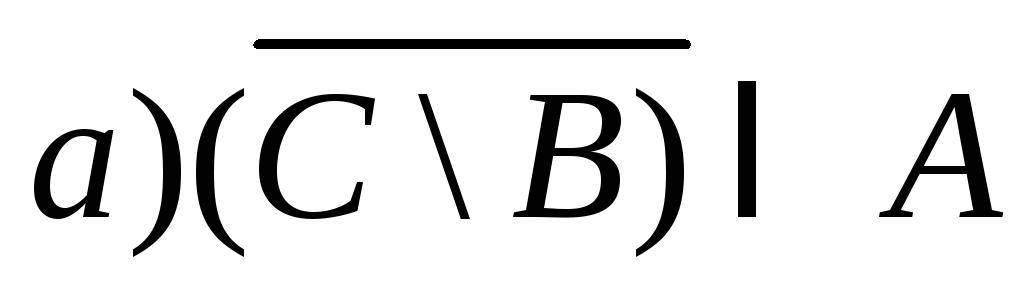 ;
; 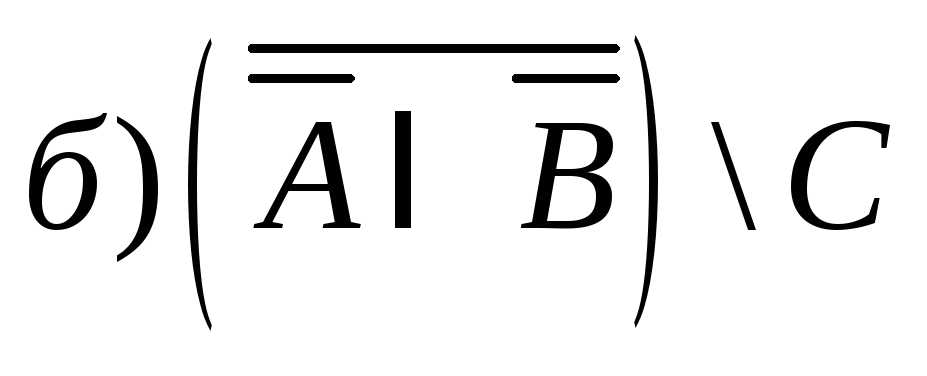
II. Дифференциальное исчисление
Найти область определения действительных значений функций:
а) y=x-4+Ix-2I;
б) y=1-cosx;
в) 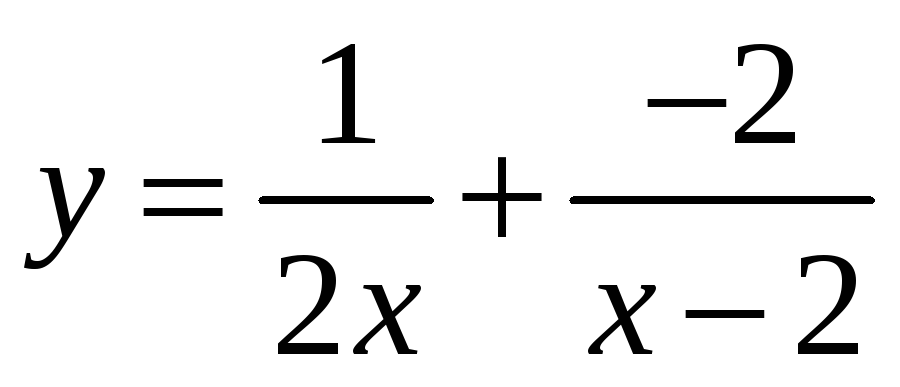 ;
;
2) Найти пределы:
а) 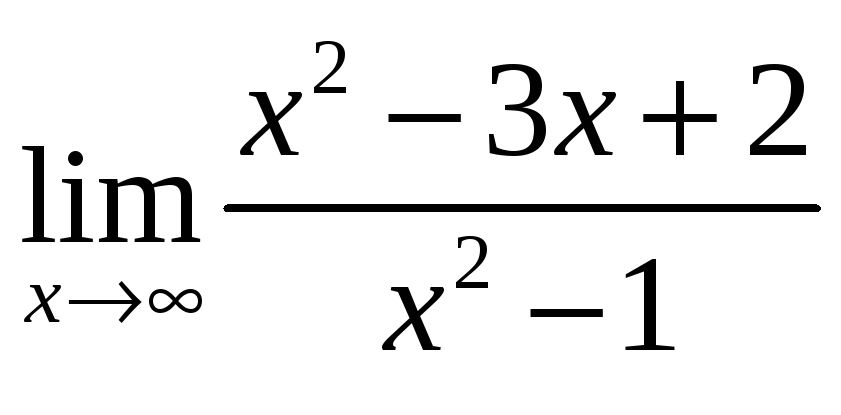 ;
б)
;
б) 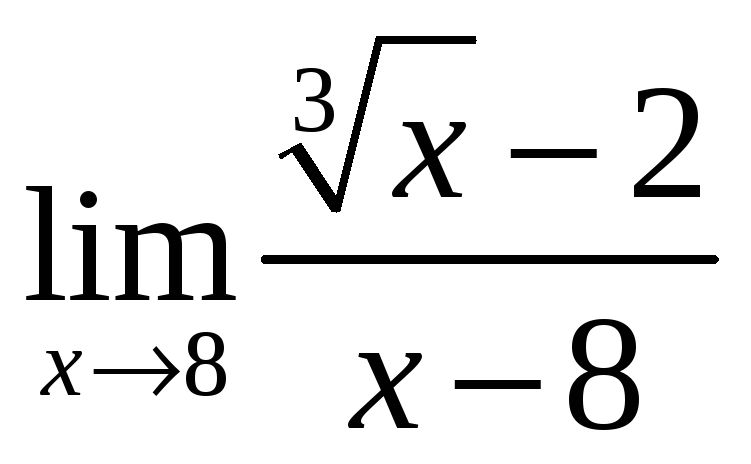 ;
в)
;
в) 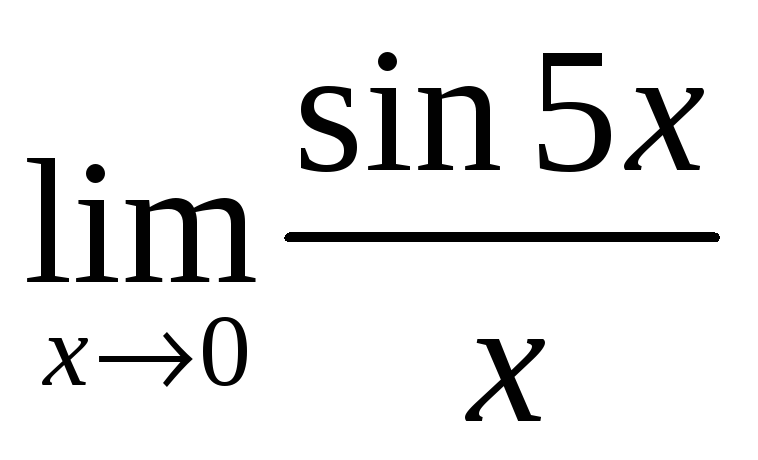 ;
г)
;
г) 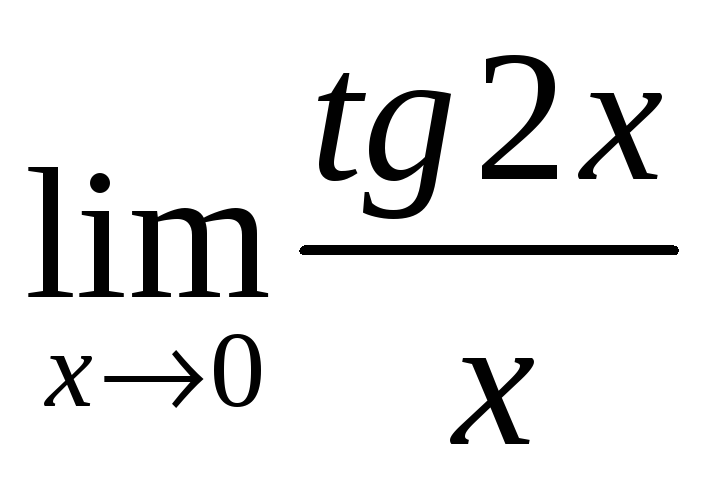 ;
;
3) Найти производные функций:
а)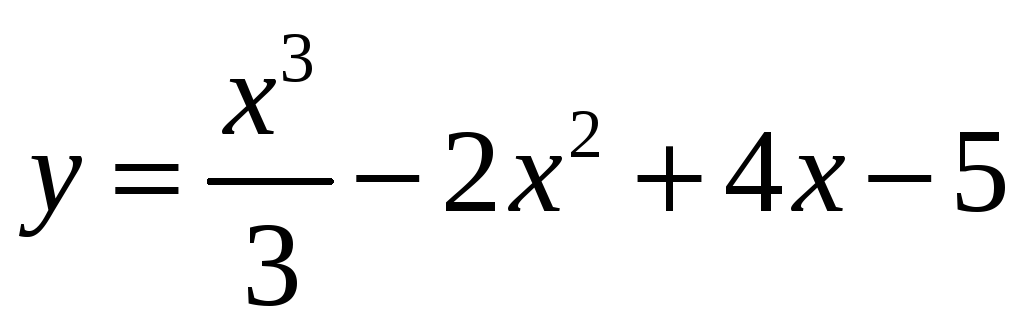 ;
б) y=sin 6x;
в)
;
б) y=sin 6x;
в) 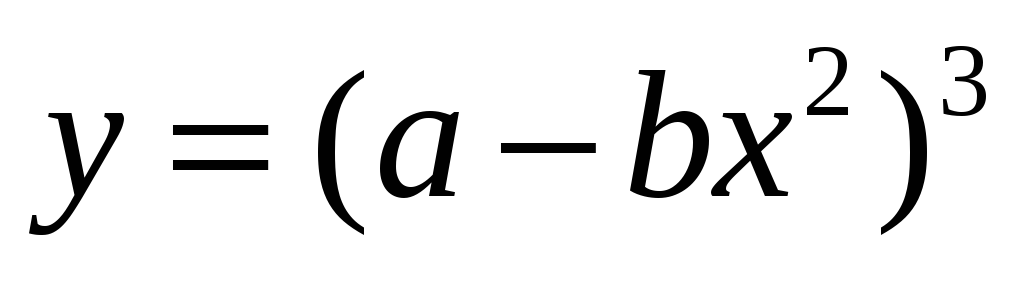 ;
г)
;
г) 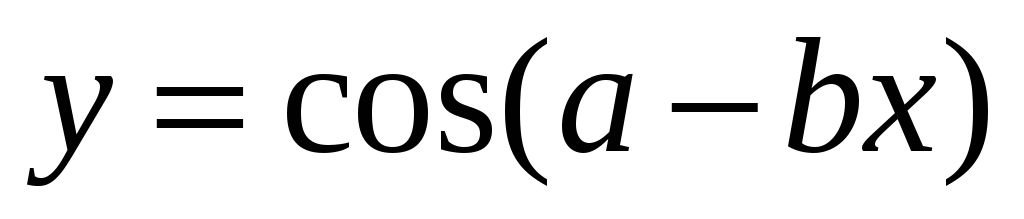 ;
;
4) Найти пределы, используя правило Лопиталя:
а) 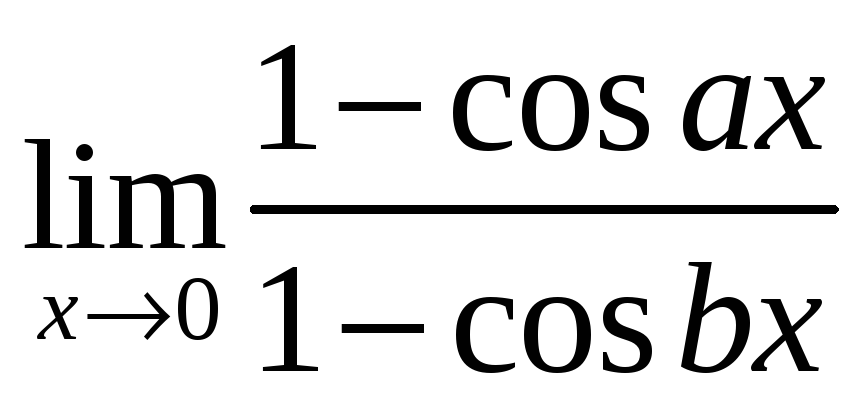 ;
б)
;
б) 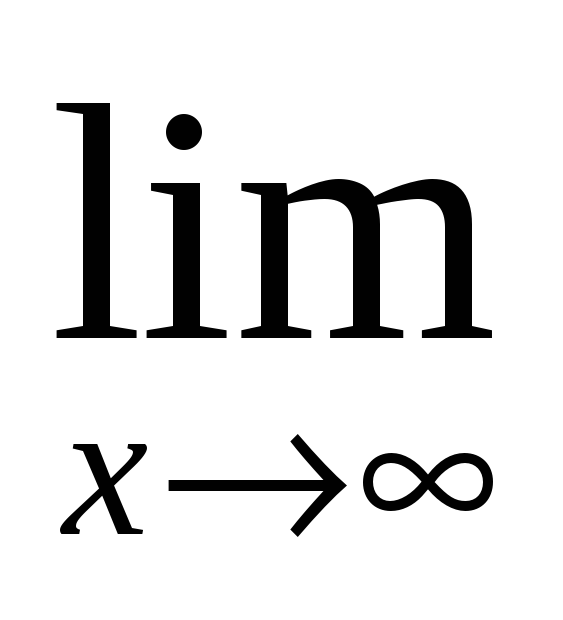 xne—x
xne—x
5) Выполнить полное исследование функции и построить ее график:
а) y=x 4 /4-x3; б) 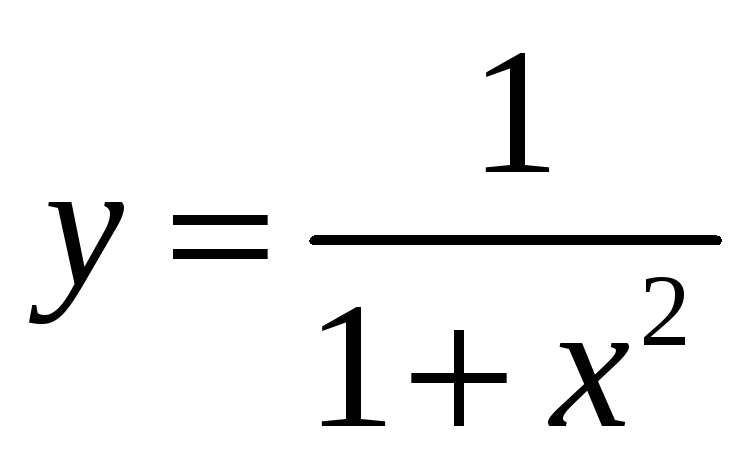 ;
;
6) Для функций многих переменных:
а) Указать область
определения функции: 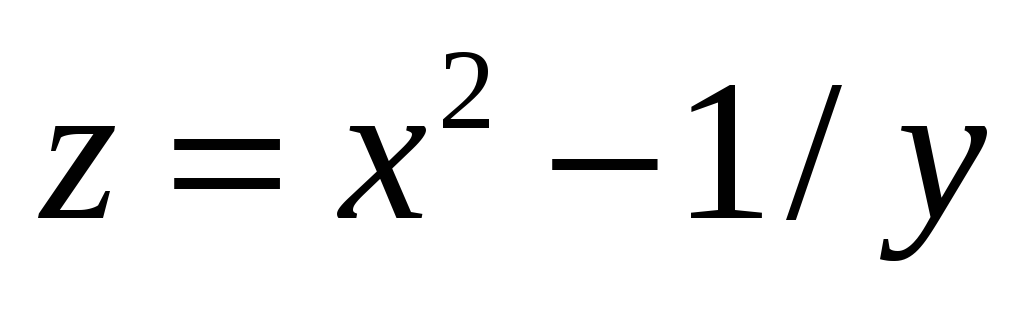 ;
;
б) Найти частные производные
функции: 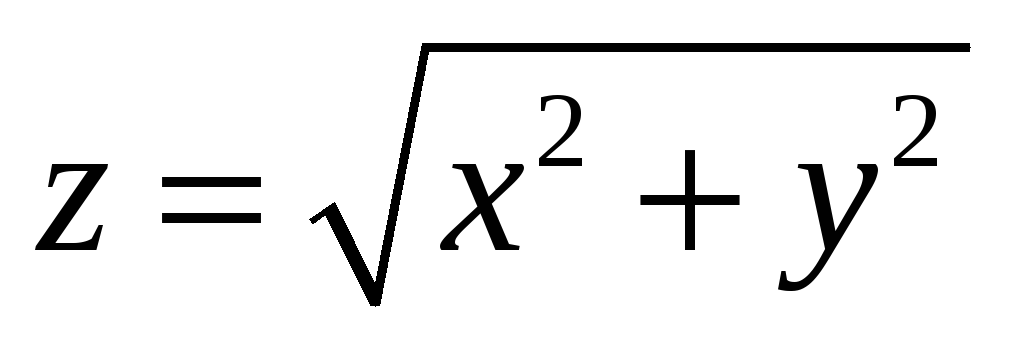 ;
;
в) Исследовать на экстремум
функцию: 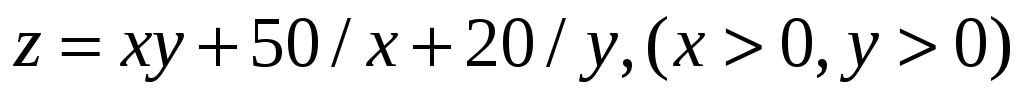
III. Интегральное исчисление и ряды
1) Найти интегралы:
а) 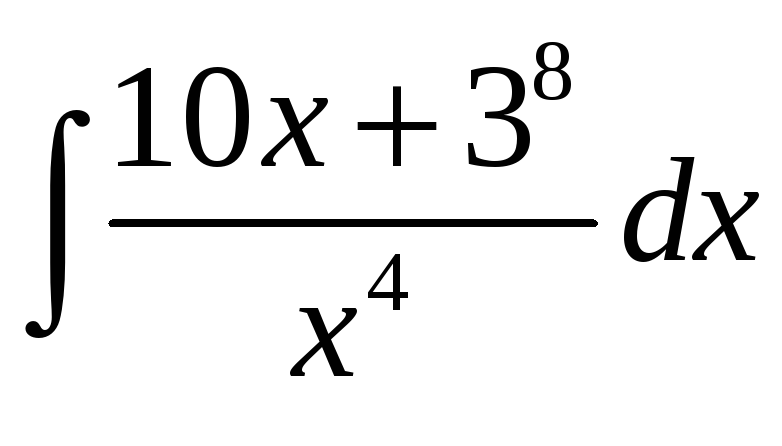 ;
б)
;
б) 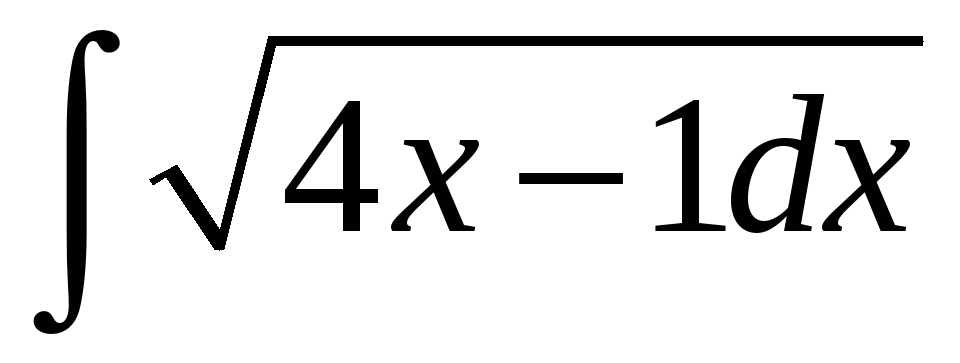 ;
в)
;
в) 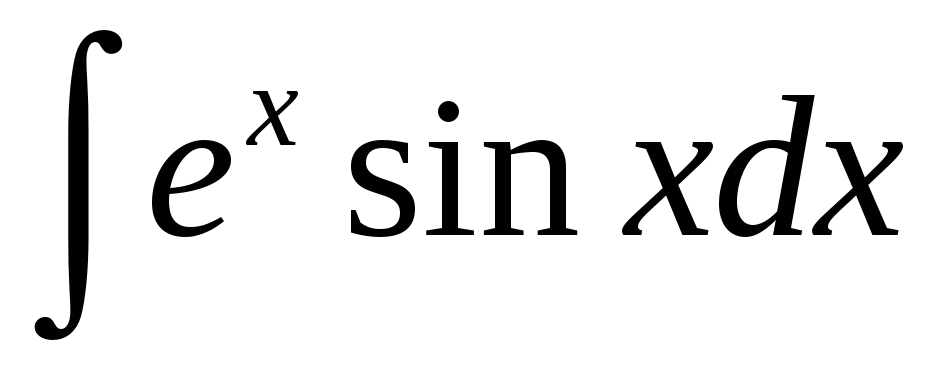 ;
;
Вычислить интегралы:
а) 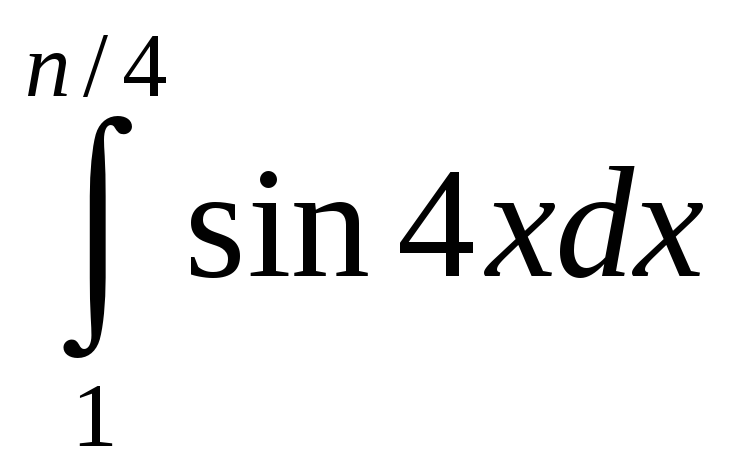 ;
б)
;
б) 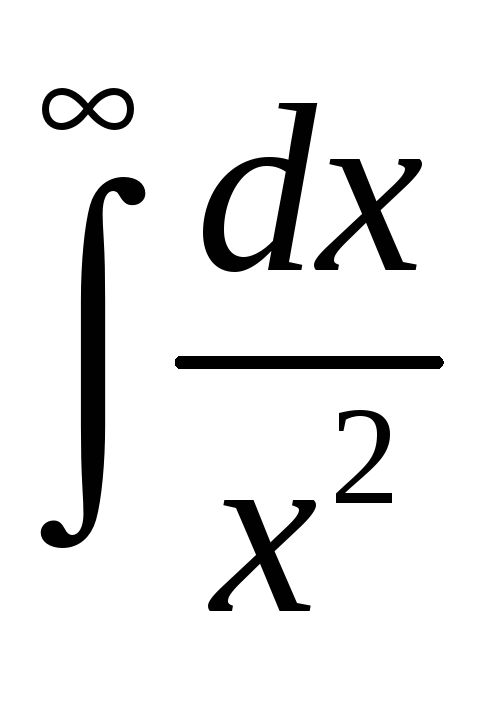
Найти общий интеграл:
yy/+x=0
Исследовать сходимость числовых рядов:
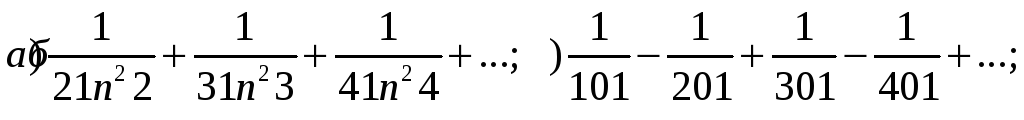
Вариант29
Контрольная работа по курсу «Математический анализ»
I. Множества
1) В коллоквиуме по математике приняло участие 40 студентов. Им были предложены задачи из 3-х разделов: по множествам, по алгебре, по анализу. По множествам решили задачу 20 человек, по алгебре-18, По матем. анализу-18. Не решили ни одной задачи 3 человека. По анализу и по алгебре справились с заданием 7 человек, по множествам и анализу- 8 , по алгебре и анализу – 9 чел..
Сколько студентов решили все задачи?
Сколько студентов решили ровно 2 задачи?
Сколько человек решили задачу только по множествам?
2) Задать множество перечислением его элементов.
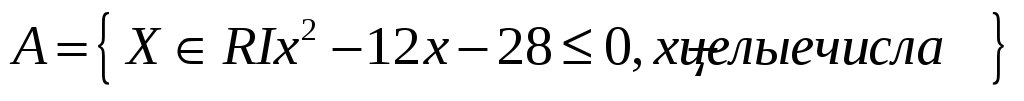
II. Дифференциальное исчисление
1) Найти область определения действительных значений функций:
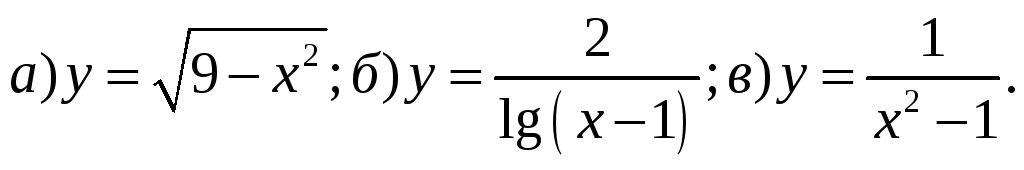
2) Найти пределы:
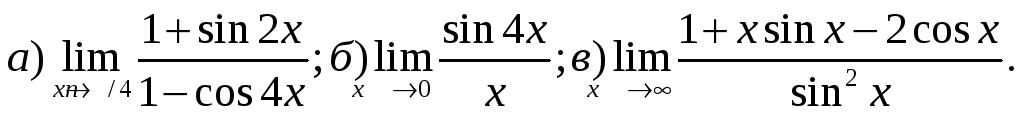
3) Найти производные функций:
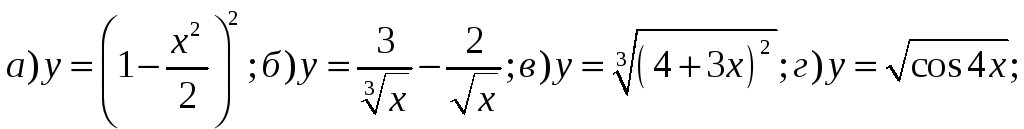
4) Найти пределы, используя правило Лопиталя:
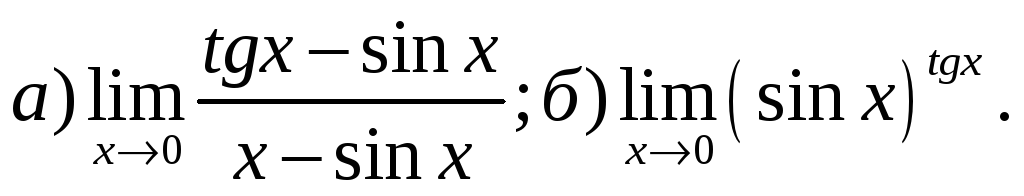
5) Выполнить полное исследование функции и построить ее график:
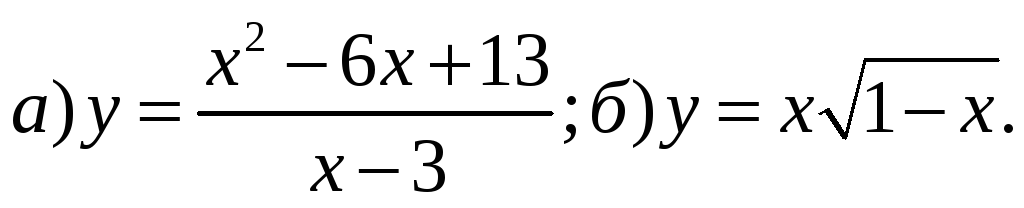
6) Для функций многих переменных:
а) Указать область
определения функции: 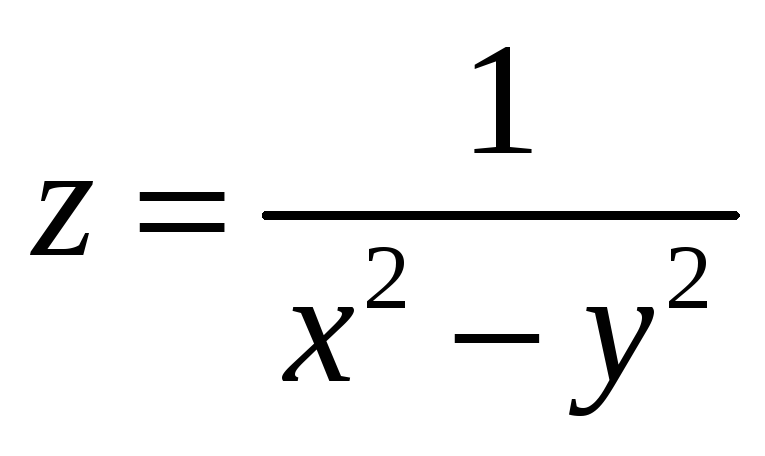 ;
;
б) Найти частные производные
функции: 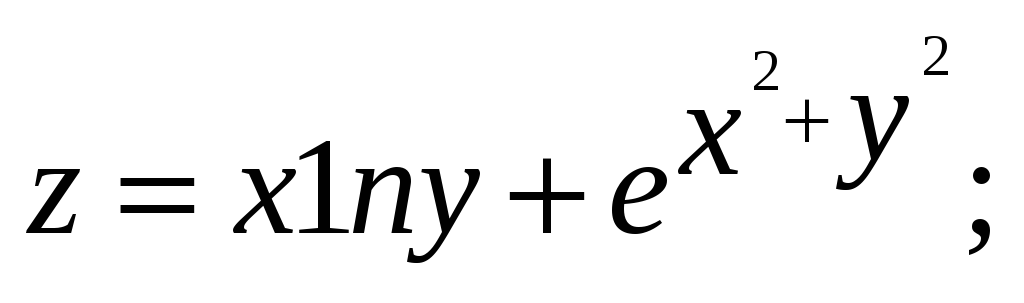
в) Исследовать на экстремум
функцию: 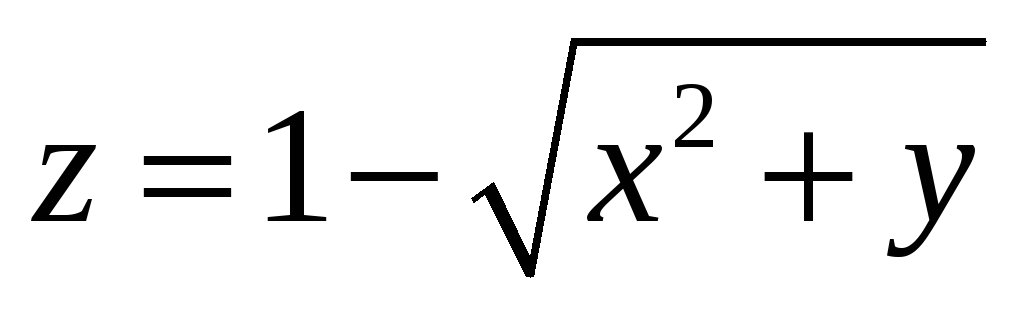 ;
;
III. Интегральное исчисление и ряды
1) Найти интегралы:
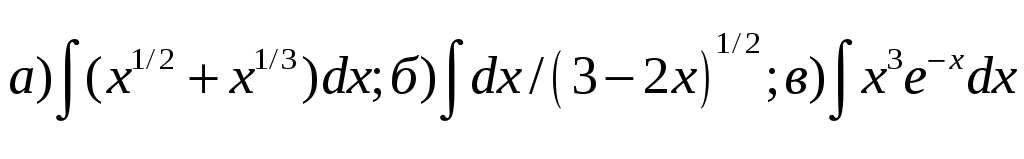
2) Вычислить интегралы:
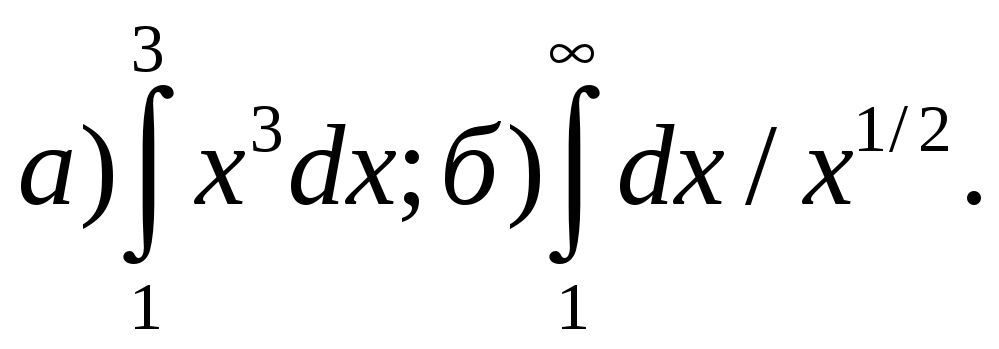
Найти общий интеграл:

Исследовать сходимость числовых рядов:
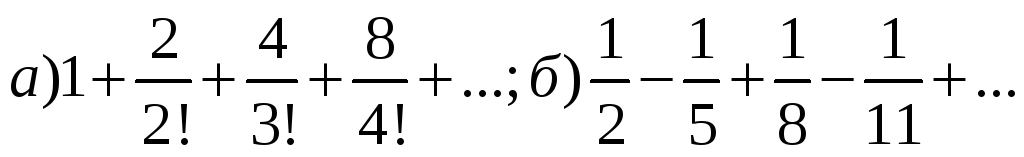
Вариант 30
Контрольная работа по курсу «Математический анализ»
Множества
1) Среди абитуриентов, выдержавших экзамены в ВУЗ, оценку «отлично» получили: по матеметике-48 человек, по физике-37, по языку-42. по математике или физике-75, математике или языку-76, по физике или языку-66 человек. По всем трем предметам получили отличную оценку 4 человека.
Сколько абитуриентов получили хотя бы одну пятерку?
Сколько среди них получивших только одну пятерку?
Сколько человек не получили пятерку по языку?
2) Задать множество перечислением его элементов:
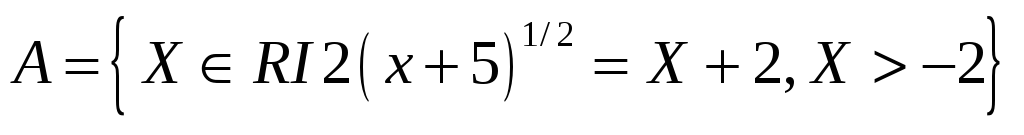
II. Дифференциальное исчисление
1) Найти область определения действительных значений функций:

2) Найти пределы:
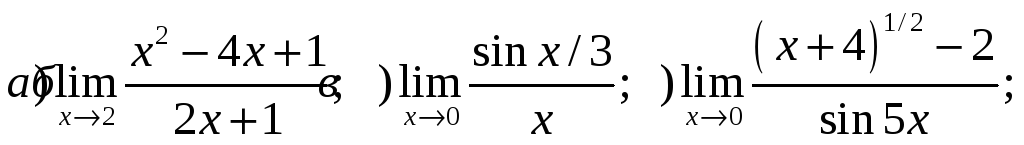
3) Найти производные функций:
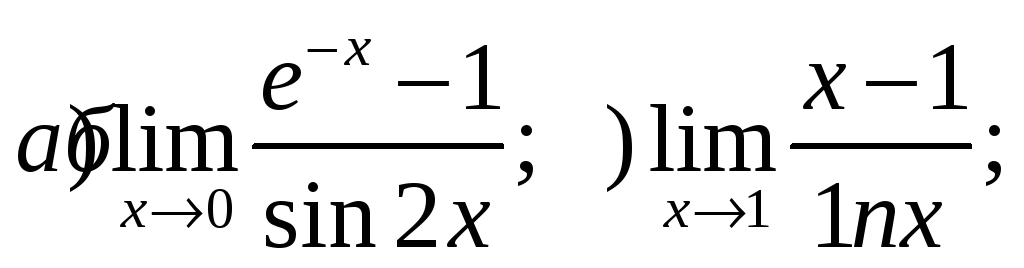
4) Найти пределы, используя правило Лопиталя:
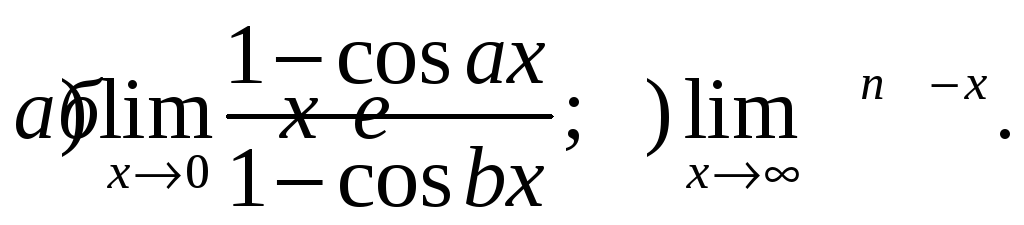
Выполнить полное исследование функции и построить ее график:
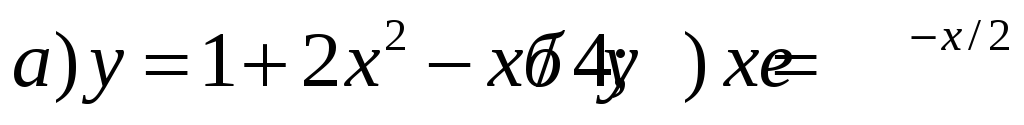
Для функций многих переменных:
а) Указать область
определения функции: 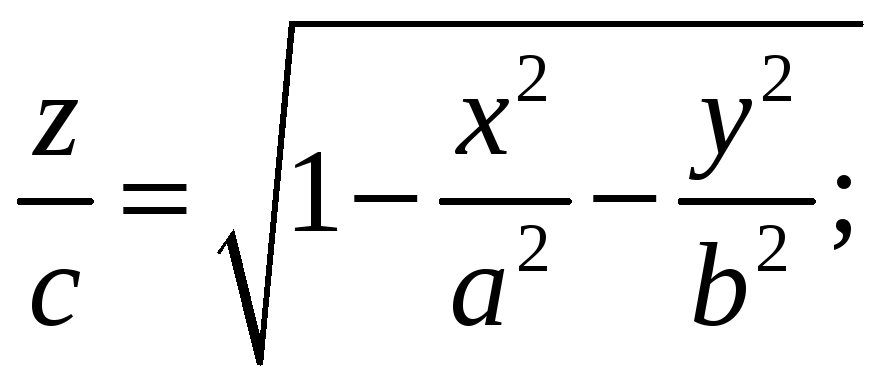
б) Найти частные производные
функции: 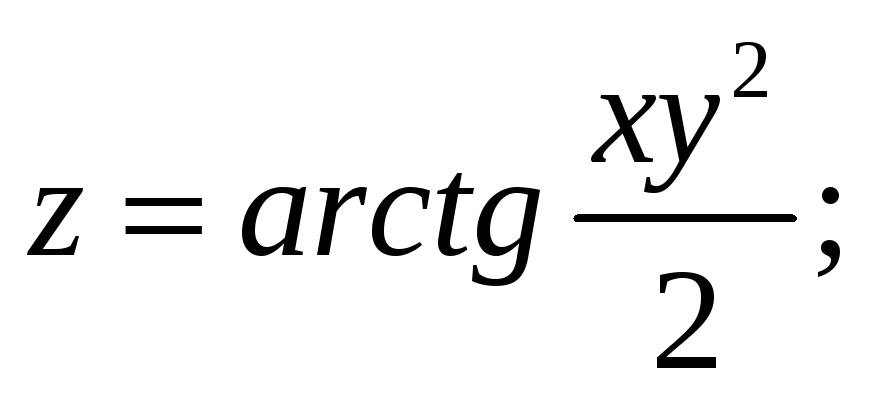
в) Исследовать на экстремум
функцию: 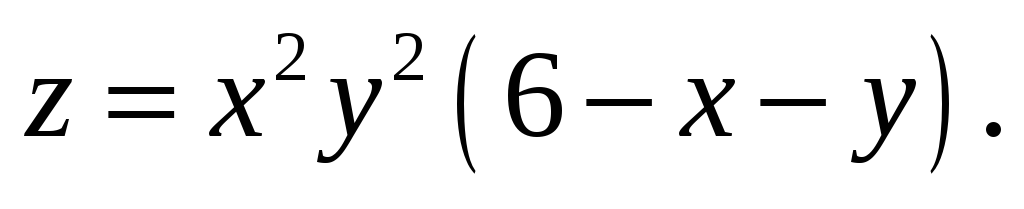
III. Интегральное исчисление и ряды
Найти интегралы:
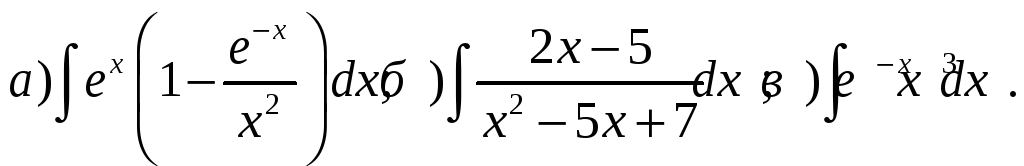
Вычислить интегралы:
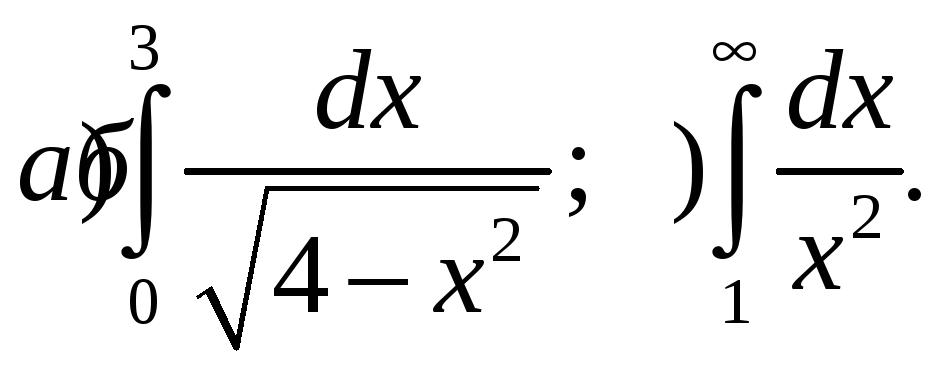
Найти общий интеграл:
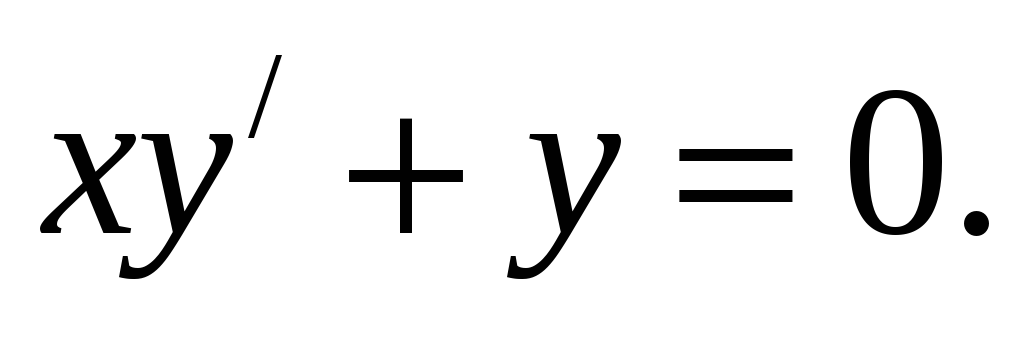
Исследовать сходимость числовых рядов:
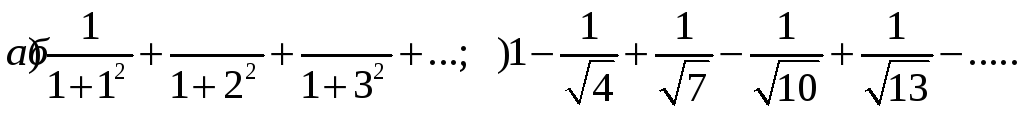
studfile.net
2. Какие из нижеперечисленных отношений являются отношениями порядка, строгого порядка, полного порядка, эквивалентности? Обоснуйте Ваши выводы.
Контрольная работа № 1
1. На множестве X = {x | xN, x < 10}, где N – множество натуральных чисел, задано отношение R: «x и y имеют один и тот же остаток при делении на 2» (xX, yX). Докажите, что R – отношение эквивалентности. Определите, на какие классы эквивалентности разбивается множество данным отношением.
Решение:
Отношение
рефлексивно, если 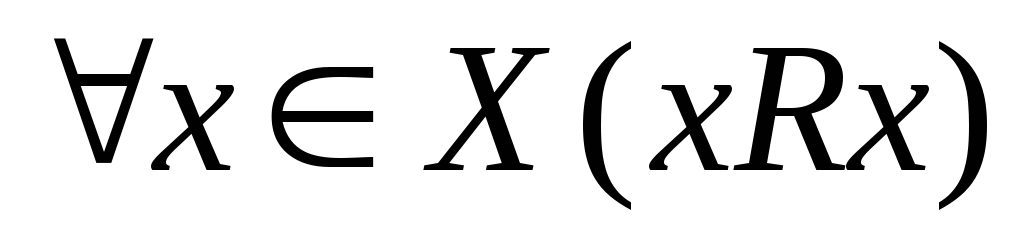 .
.
Отношение
симметрично, если 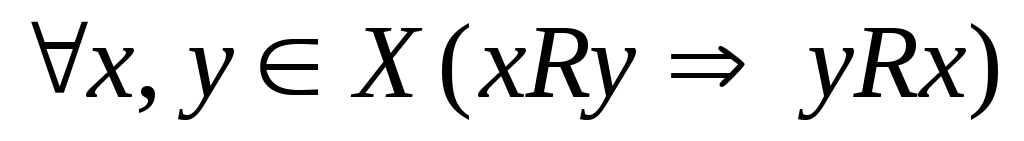 .
.
Отношение
транзитивно, если 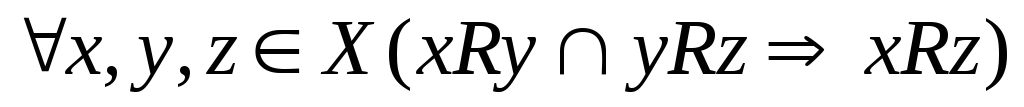 .
.
Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Проверим эти свойства для заданного отношения:
Рефлексивность: выполнена – два одинаковых числа дают одинаковый остаток при делении на 2.
Симметричность: выполнена – если х дает такой же остаток при делении на 2, что и у, то и у дает такой же остаток при делении на 2, что и х.
Транзитивность: выполнена — если х дает такой же остаток при делении на 2, что и у, а у — такой же остаток, что и z, то остатки эти одинаковы у всех трех чисел.
Следовательно, заданное отношение является отношением эквивалентности. Очевидно, что множество X = {x | x N, x < 10} разбивается заданным отношением на два класса (по количеству различных остатков при делении на 2 – 0 и 1: четных и нечетных чисел. К первому классу относятся элементы множества Х: 2, 4, 6 и 8, к второму — элементы множества Х: 1, 3, 5, 7 и 9.
а) «число x больше или равно у» — на множестве R (вещественных чисел).
б) «число х меньше числа у в 2 раза» — на множестве R.
в) «число х делится на число у без остатка» — на множестве R.
г) «х и y — оба учатся в ТУСУРе» — на множестве людей.
д) «х является братом y» — на множестве людей.
е) «окружность х имеет больший радиус, чем окружность у» — на множестве окружностей.
Решение:
Отношение
рефлексивно, если 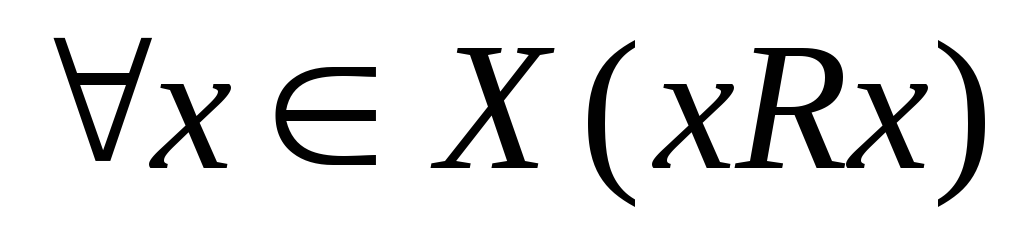 .
.
Отношение
антирефлексивно, если 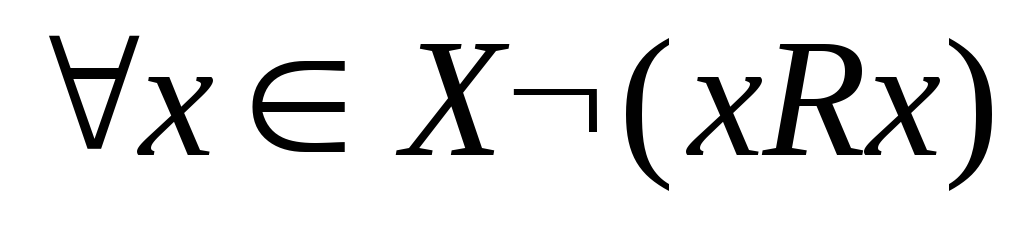 .
.
Отношение
симметрично, если 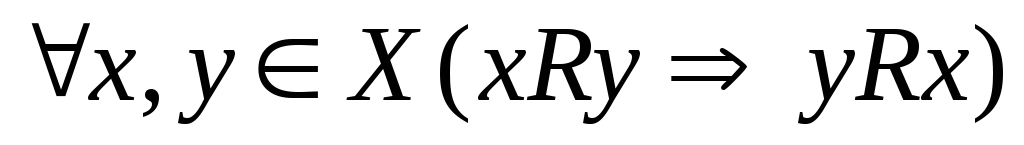 .
.
Отношение
антисимметрично, если 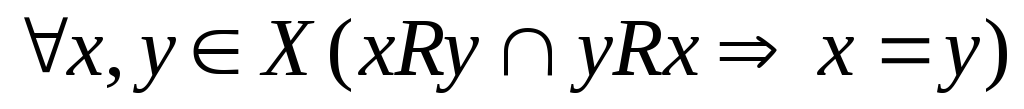 .
.
Отношение
транзитивно, если 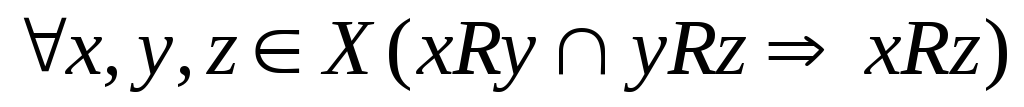 .
.
Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Отношения порядка – отношения, отношения, обладающие только некоторыми из трёх свойств отношения эквивалентности: отношение рефлексивное и транзитивное, но антисимметричное (≤) образует порядок (нестрогий), отношение транзитивное, но антирефлексивное и антисимметричное (<) — строгий порядок.
Рассмотрим свойства заданных отношений:
а) «число x больше или равно у» — на множестве R (вещественных чисел):
—
рефлексивно: 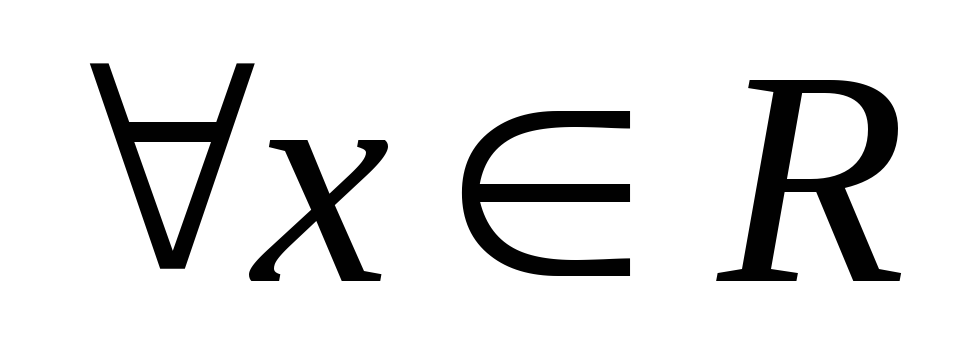 x≥x,
x≥x,
—
антисимметрично: 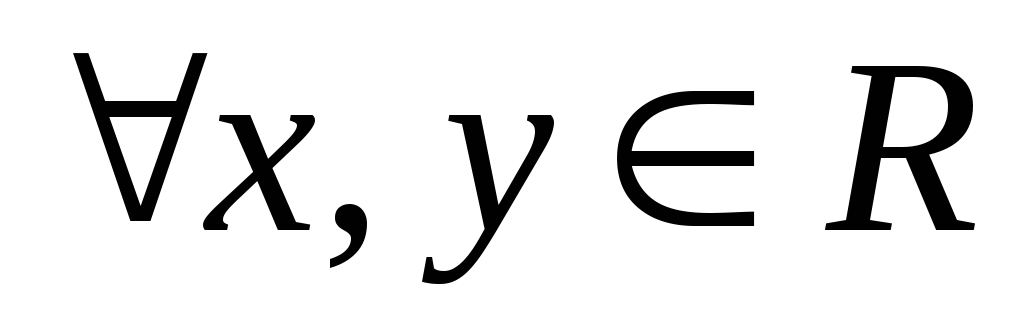 если x≥у и у≥x,
то x=у,
если x≥у и у≥x,
то x=у,
—
транзитивно: 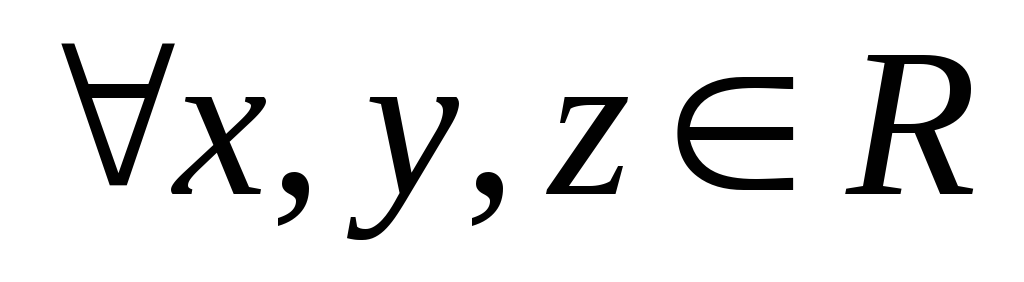 если x≥у и у≥z,
то x≥z,
если x≥у и у≥z,
то x≥z,
Поскольку любые два элемента R сравнимы, то отношение а) является отношением полного порядка.
б) «число х меньше числа у в 2 раза» — на множестве R.
— антирефлексивно: x=x/2,выполнено только для х=0,
— не является симметричным и не является антисимметричным: если x=у/2, то y≠x/2,
— не является транзитивным: если если x=у/2 и у=z/2, то x≠z/2,
следовательно, отношение б) не является отношением порядка или эквивалентности.
в) «число х делится на число у без остатка» — на множестве R:
Поскольку любое вещественное число х можно разделить на другое отличное от нуля вещественное число и получить вещественное число, то будем считать, что вещественное число х делится на другое вещественное число у без остатка, если частное от их деления является целым числом. Тогда отношение в)
— рефлексивно: любое отличное от нуля вещественное число делится на самого себя без остатка,
— антисимметрично: если x делится нацело на у и у делится нацело на x, то x=у,
— транзитивно: если если x делится нацело на у и у делится нацело на z, то x делится нацело на z,
Поскольку вещественное число можно разделить нацело не на все вещественные числа, то отношение в) является отношением порядка.
г) «х и y — оба учатся в ТУСУРе» — на множестве людей:
— рефлексивно: для любого студента:x и x — оба учатся в ТУСУРе
— симметрично: для любых двух студентов:если x и у — оба учатся в ТУСУРе, то это верно и в другом порядке перечисления студентов,
— транзитивно: для любых трех студентов:если x и у — оба учатся в ТУСУРе, если у и z — оба учатся в ТУСУРе, то и х и z — оба учатся в ТУСУРе.
Следовательно, отношение г) – отношение эквивалентности, разбивающее множество людей на два класса – студентов ТУСУРа и не-студентов ТУСУРа.
д) «х является братом y» — на множестве людей.
— антирефлексивно: никакой человек не является своим братом,
— не является симметричным (достаточно рассмотреть брата и сестру) и не является антисимметричным (достаточно рассмотреть двух братьев),
— транзитивно: если x — брат у и у – брат z, то x – брат z,
следовательно, отношение д) не является отношением порядка или эквивалентности.
е) «окружность х имеет больший радиус, чем окружность у» — на множестве окружностей.
— антирефлексивно: утверждение «окружность х имеет больший радиус, чем ее собственный» абсурдно,
— не является симметричным (если радиус окружности х строго больше радиуса окружности у, то радиус окружности у не может быть строго больше радиуса окружности х) и не является антисимметричным (из-за строгости неравенства),
— транзитивно: если радиус окружности х строго больше радиуса окружности у, а радиус окружности у строго больше радиуса окружности z, т то радиус окружности х строго больше радиуса окружности z, следовательно, отношение е) является отношением полного порядка.
3. На множестве М = {1, 2, 3, 4, 5, 6, 7, 8} задано отношение x – y 3. Выпишите пары, принадлежащие этому отношению. Определите его свойства.
Решение:
Для перечисления пар, принадлежащих этому отношению, составим таблицу, в которой знаком «+» отметим эти пары:
х | у | |||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
1 | + | + | + | + | ||||
2 | + | + | + | + | + | |||
3 | + | + | + | + | + | + | ||
4 | + | + | + | + | + | + | + | |
5 | + | + | + | + | + | + | + | + |
6 | + | + | + | + | + | + | + | + |
7 | + | + | + | + | + | + | + | + |
8 | + | + | + | + | + | + | + | |
Отсюда получаем пары, принадлежащие отношению:
(1,1) (1,2) (1,3) (1,4)
(2,1) (2,2) (2,3) (2,4) (2,5)
(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)
(4,1) (4,2) (4,3) (4,4) (4,5) (4,6) (4,7)
(5,1) (5,2) (5,3) (5,4) (5,5) (5,6) (5,7) (5,8)
(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) (6,7) (6,8)
(7,1) (7,2) (7,3) (7,4) (7,5) (7,6) (7,7) (7,8)
(8,1) (8,2) (8,3) (8,4) (8,5) (8,6) (8,7) (8,8)
Определим свойства отношения:
—
на диагонали матрицы стоят знаки «+» — 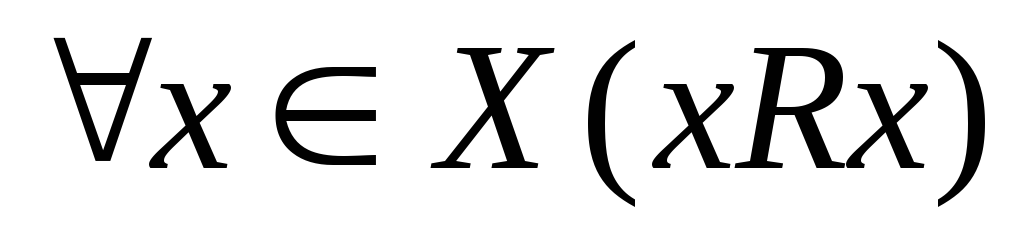 — отношение рефлексивно;
— отношение рефлексивно;
—
матрица не симметрична относительно
главной диагонали – свойство 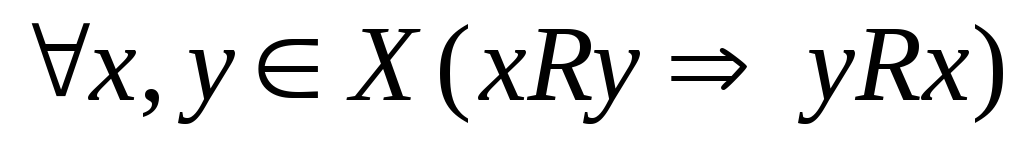 не выполнено — отношение несимметрично;
не выполнено — отношение несимметрично;
—
матрица имеет знаки «+», симметричные
относительно главной диагонали –
свойство 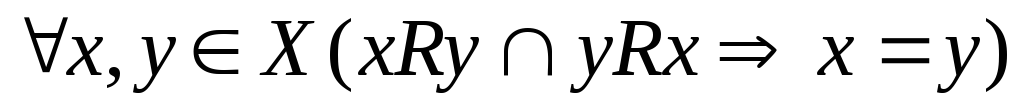 не выполнено — отношение неантисимметрично;
не выполнено — отношение неантисимметрично;
— пары (1,4) и (4,7) показывают, что отношение нетранзитивно – пара (1,7) не принадлежит этому отношению.
Ответ: отношение – рефлексивное, несимметричное, нетранзитивное.
4. Известно, что из 100 студентов живописью увлекается 16, спортом 59, музыкой 43, живописью и спортом 11, живописью и музыкой 10, спортом и музыкой 31, живописью, спортом и музыкой 5. Определите количество студентов:
а) увлекающихся только живописью;
б) ничем не увлекающихся.
Решение:
Обозначим через U, P, S и М множество всех студентов и студентов, увлекающихся живописью, спортом и музыкой, соответственно. Будем также обозначать через [X] мощность множества Х, т.е. число студентов в нем.
Тогда, по условию, [U] = 100, [P] = 16, [S] = 59, [M] = 43, [P∩S]=11, [P∩M]=10, [S∩M]=31, [P∩S∩M]=5.
Заметим, что если какое-либо множество представлено как объединение взаимно не пересекающихся множеств:
X = X1 X2
X2 …
…  Xn
Xn
ио верно равенство
[X] = [X1] + [X2] + … + [Xn]
a)
множество
студентов, увлекающихся только живописью
– это множество 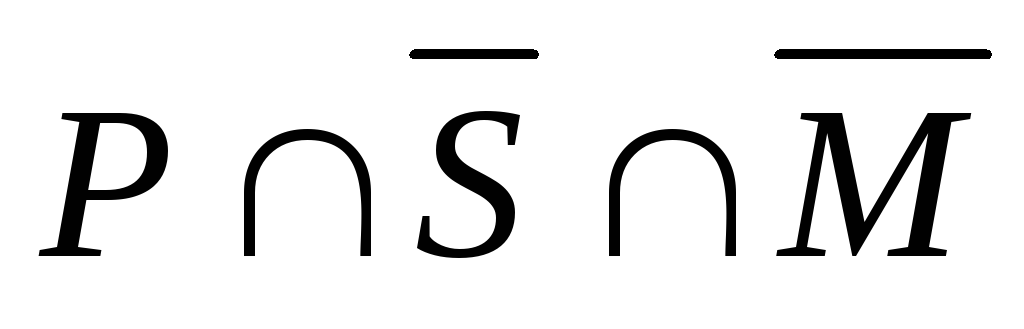 .
Найдем его мощность. Для этого запишем:
.
Найдем его мощность. Для этого запишем:
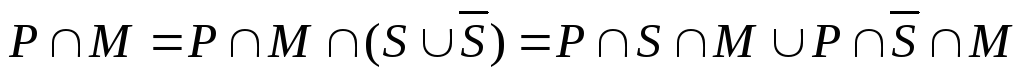
В
правой части этого равенства –
непересекающиеся множества. Следовательно, 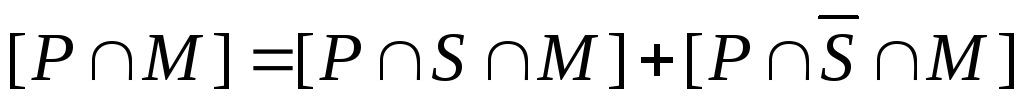 .
Поскольку, по условию,
.
Поскольку, по условию,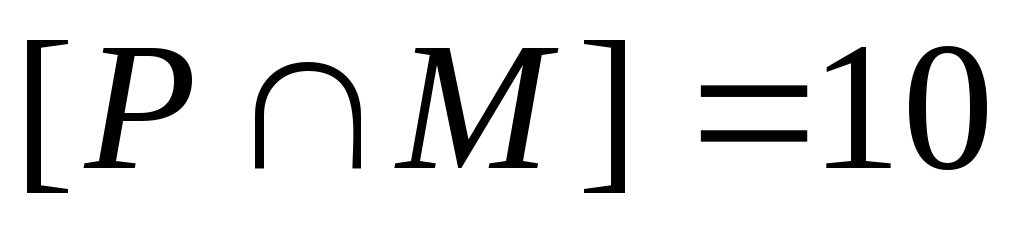 ,
,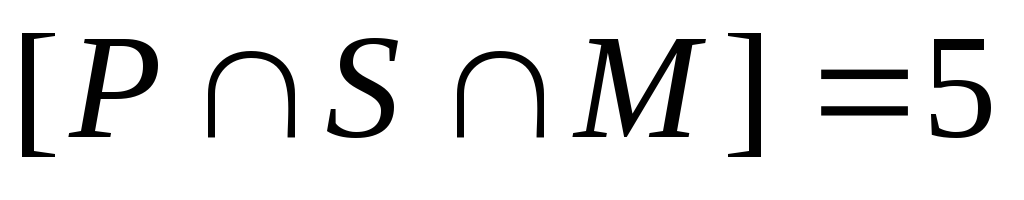 ,
то отсюда получаем:
,
то отсюда получаем: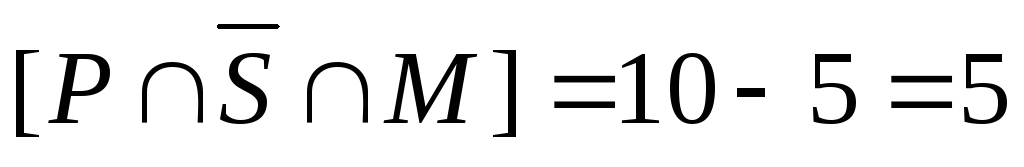 .
.
Аналогично можем написать:
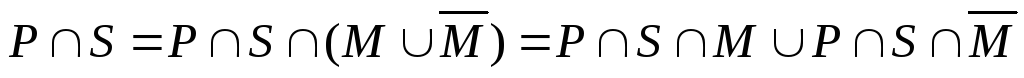 →
→
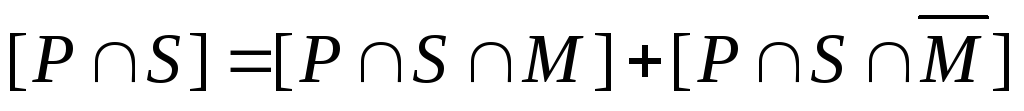 →
→
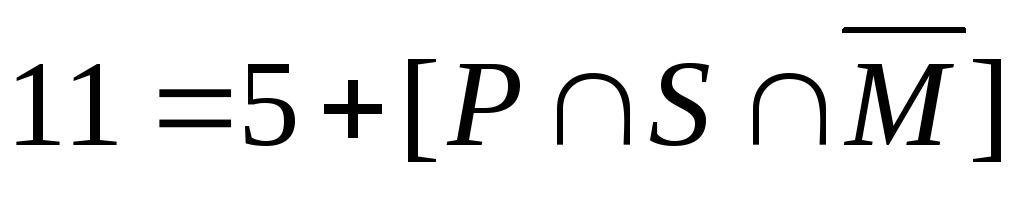 →
→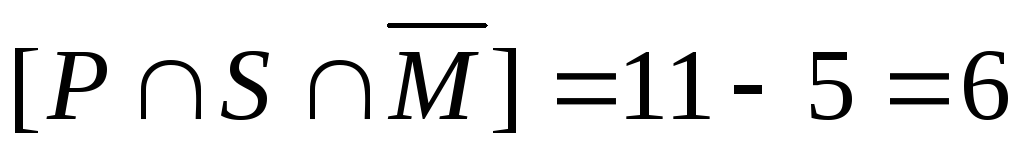
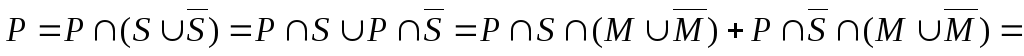
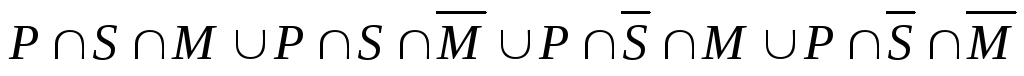 →
→
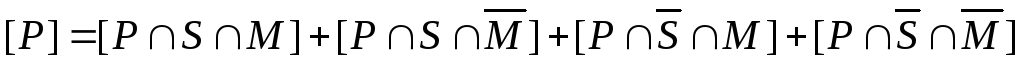 →
→
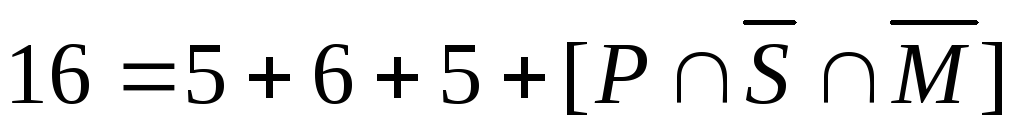 →
→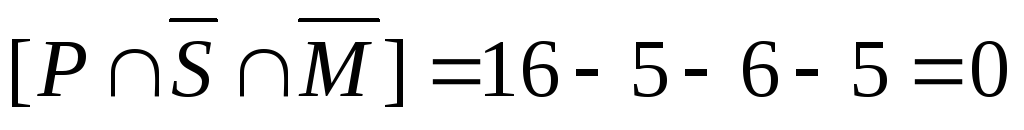
Таким
образом, получили 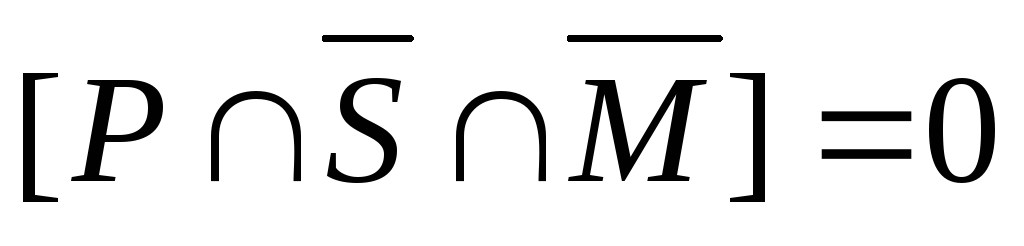 ,
что означает, что число студентов,
которые увлекаются живописью и не
увлекаются спортом и музыкой, т.е.
увлекаются только живописью, равно 0.
,
что означает, что число студентов,
которые увлекаются живописью и не
увлекаются спортом и музыкой, т.е.
увлекаются только живописью, равно 0.
б)
множество
студентов, которые ничем не увлекаются
– это множество 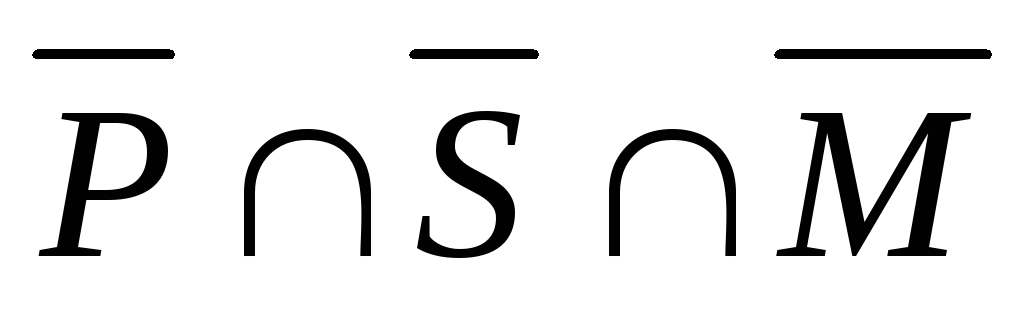 .
Найдем его мощность. Для этого запишем:
.
Найдем его мощность. Для этого запишем:
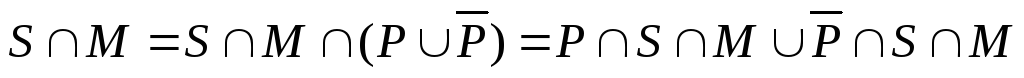 →
→
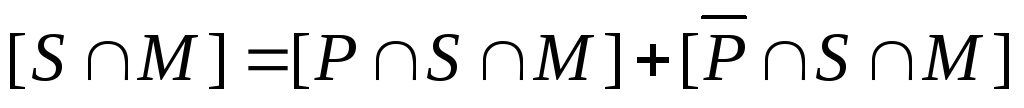 →
→
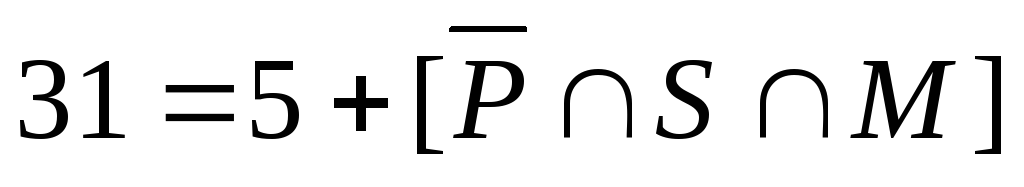 →
→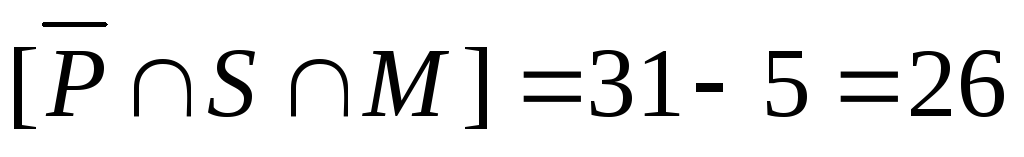
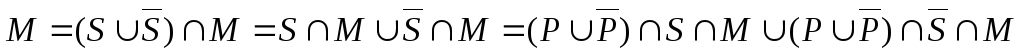 =
=
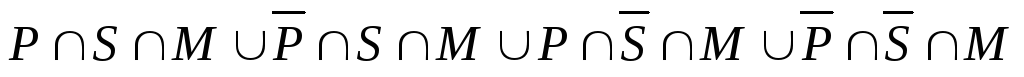 →
→
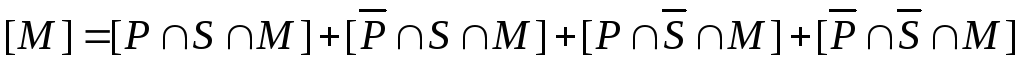 →
→
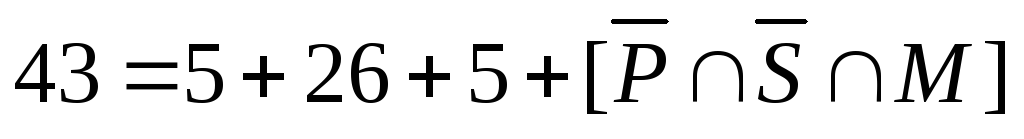 →
→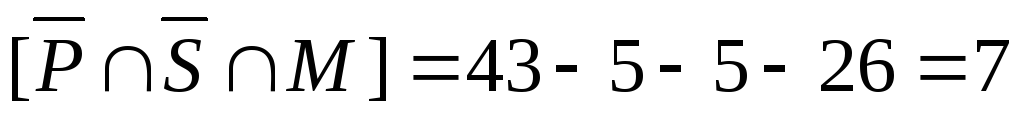
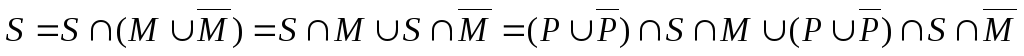 =
=
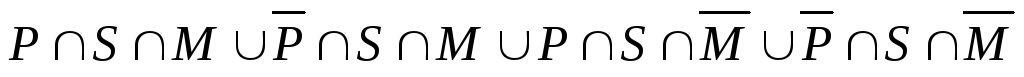 →
→
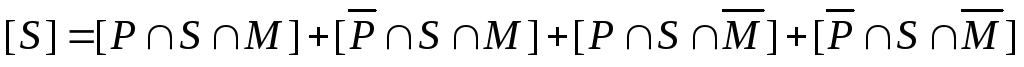 →
→
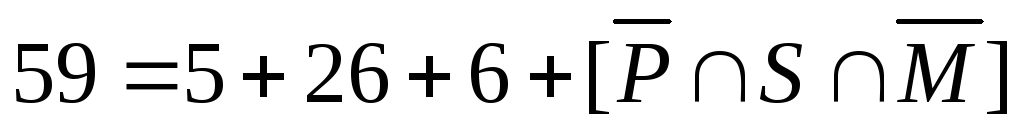 →
→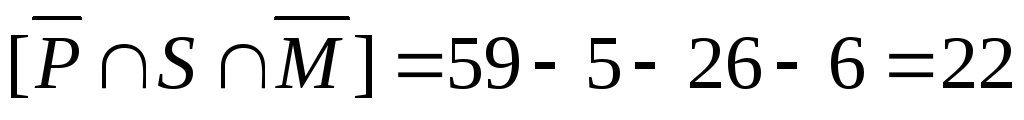
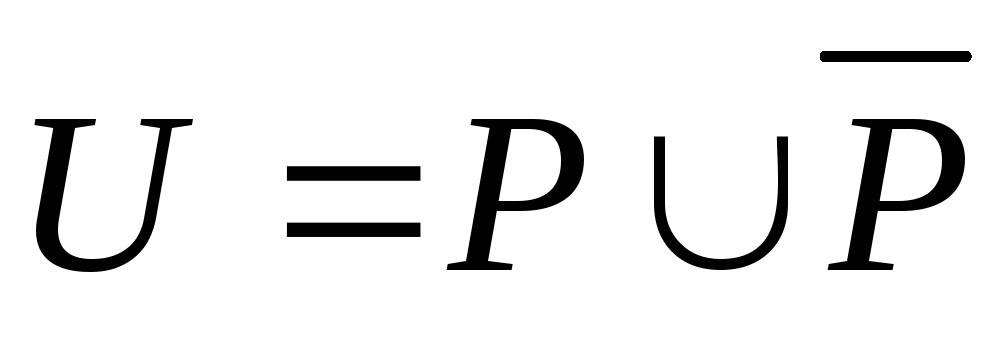 →
→ 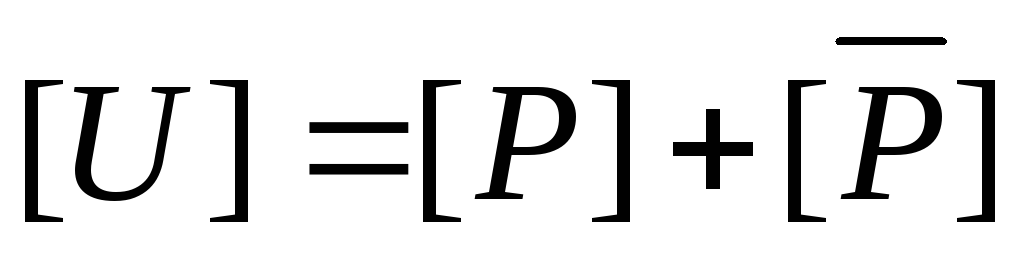 →
→ 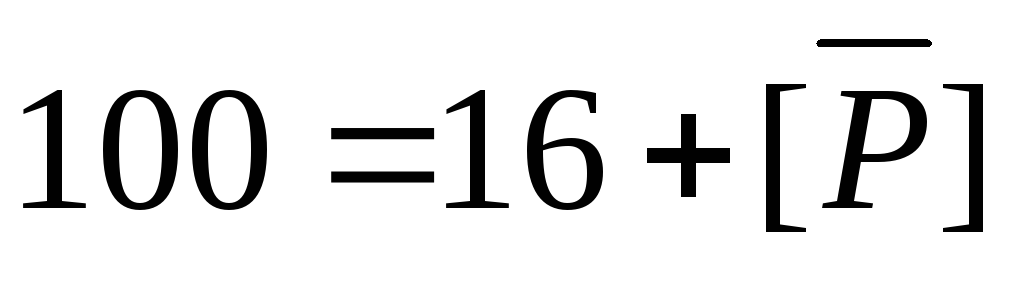 →
→ 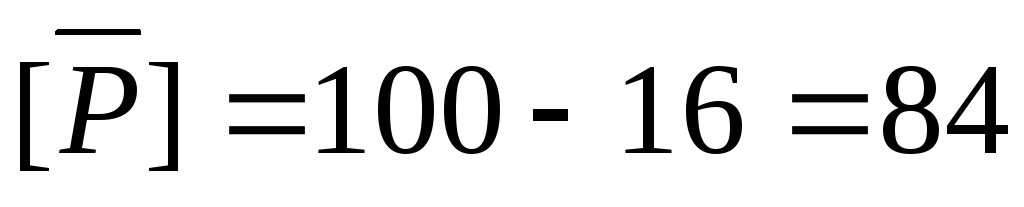
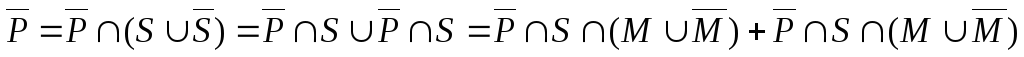 =
=
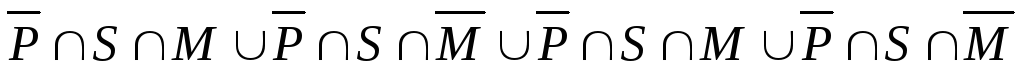 →
→
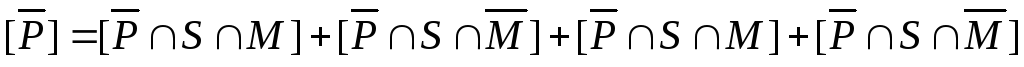 →
→
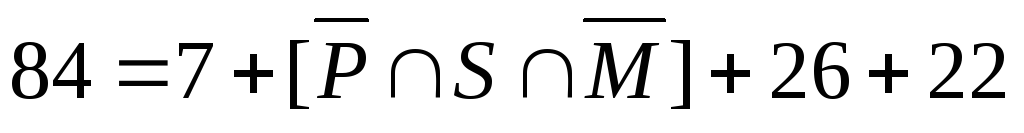 →
→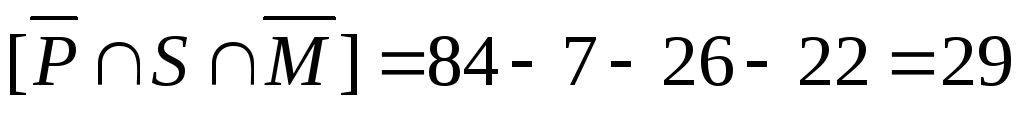
Таким образом, число студентов, которые ничем не увлекаются, равно 29.
Ответ: а) 0; б) 29.
5. Докажите тождество: ( А \ В ) ∩ ( А \ С ) = ( А \ В ) \ С.
Решение:
Тождество следует из следующих равенств:
( А \ В ) ∩ ( А \ С ) =
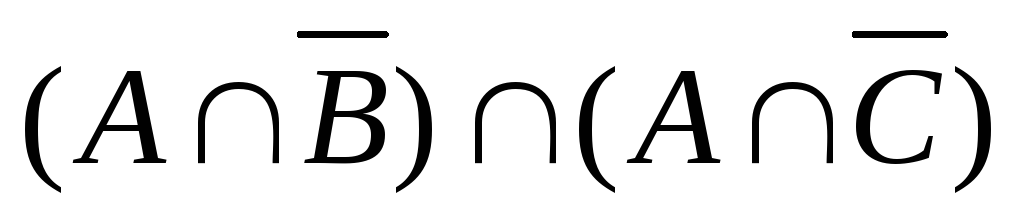 =
=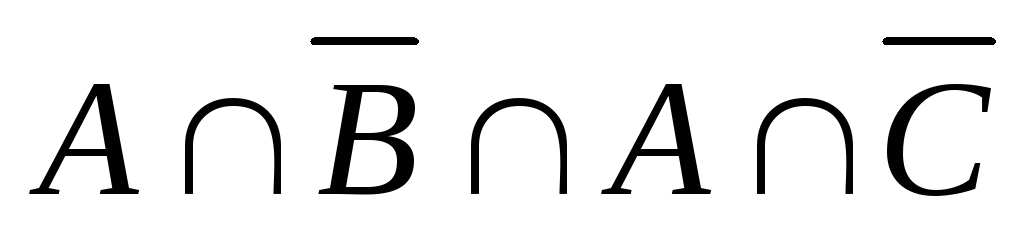 =
=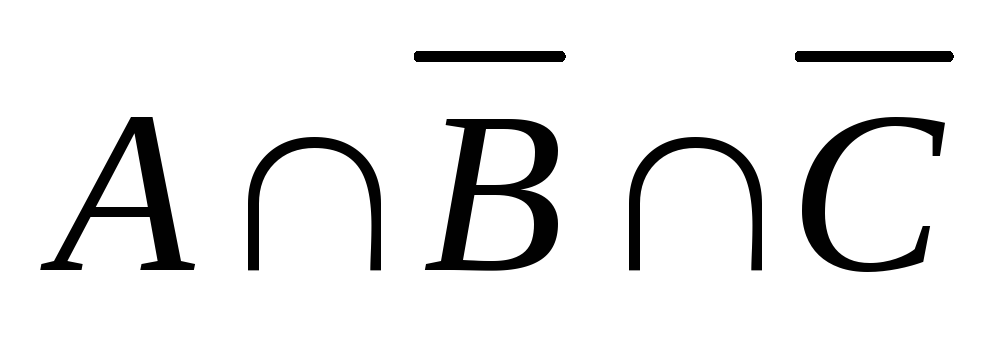
( А \ В ) \ С =
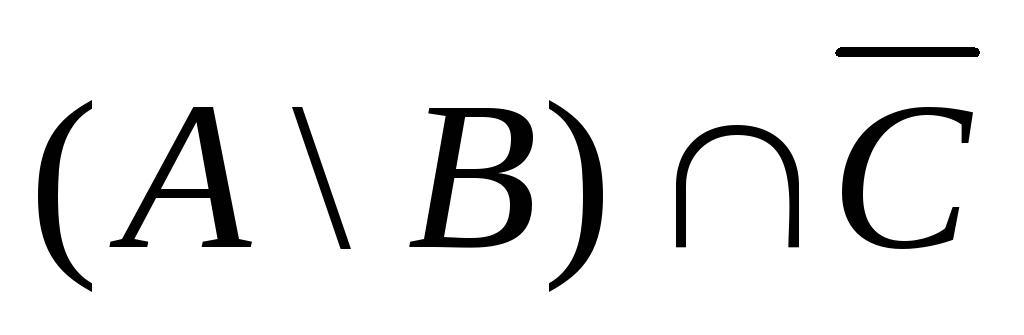 =
= 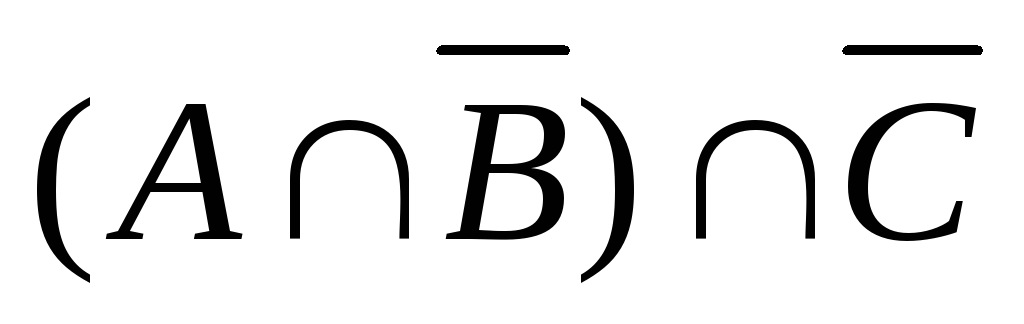 =
=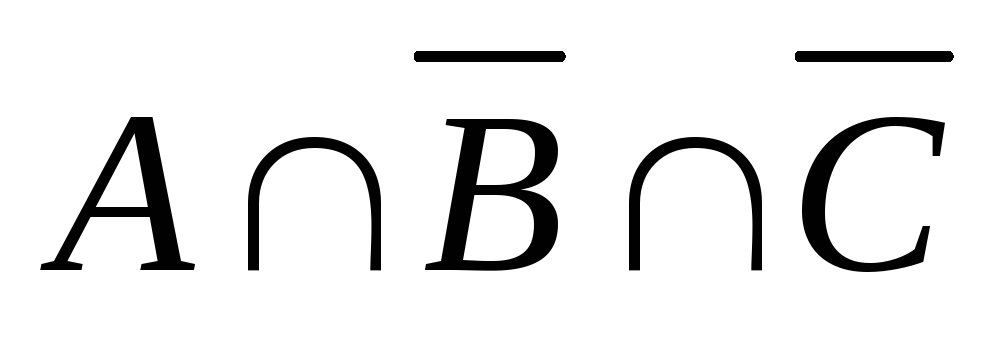
studfile.net