Как из большого числа извлечь корень. Как найти корень из числа
Для вычисления квадратного корня без калькулятора существует несколько методов.
Как найти корень из числа – 1 способ
- Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
- Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.
- Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя.

- Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
- В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
- Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
- Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18.
- Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.
Как найти корень из числа – 2 способ
- Другой способ заключается в делении в столбик. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
- В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
- Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
- При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную.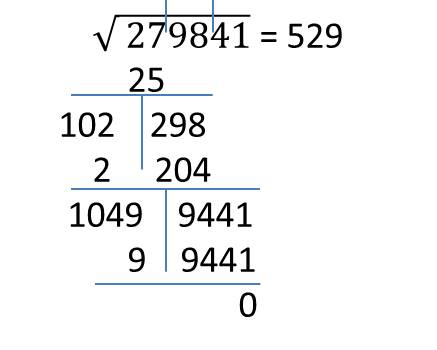 Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число.
 Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400. - Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа.
Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7.
 Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3.
 Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5. - Рассмотрим другой пример: √88.
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
- Для примера вычислим квадратный корень числа 780,14.
 Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
- Для примера вычислим квадратный корень числа 780,14.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.

- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4.
 Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.

- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Понимание процесса
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки.
 Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки.
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Извлечение корня – обратная операция возведению степени. То есть Извлекая корень из числа Х, получим число, которое в квадрате даст то самое число Х.
Извлечение корня довольно-таки несложная операция. Таблица квадратов сможет облегчить работу по извлечению. Потому что, наизусть помнить все квадраты и корни невозможно, а числа могут встретиться большие.
Извлечение корня из числа
Извлечение квадратного корня из числа – просто. Тем более что это можно делать не сразу, а постепенно. Например, возьмем выражение √256. Изначально, незнающему человеку сложно дать ответ сразу. Тогда будем делать по шагам. Сначала разделим на просто число 4, из которого вынесем за корень выделенный квадрат.
Изобразим: √(644), тогда это будет равносильно 2√64. А как известно, по таблице умножения 64=8 8. Ответ будет 2*8=16.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Извлечение комплексного корня
Корень квадратный не может вычисляться из отрицательных чисел, потому что любое число в квадрате – положительное число!
Комплексное число – число i, которое в квадрате равно -1. То есть i2=-1.
В математике существует число, которое получается при извлечении корня из числа -1.
То есть есть возможность вычислить корень из отрицательного числа, но это уже относится к высшей математике, не школьной.
Рассмотрим пример такого извлечения корня: √(-49)=7*√(-1)=7i.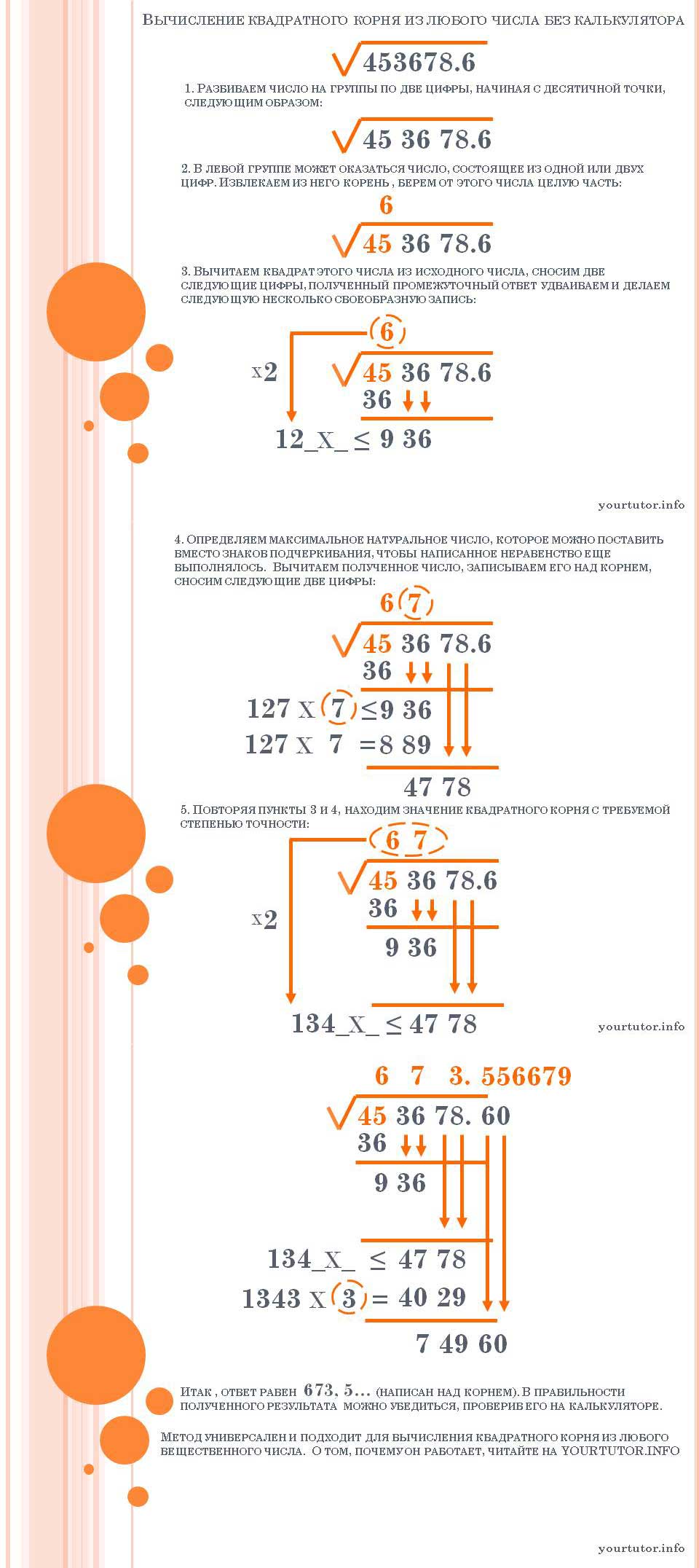
Калькулятор корня онлайн
С помощью нашего калькулятора, Вы сможете посчитать извлечение числа из квадратного корня:
Преобразование выражений, содержащих операцию извлечения корня
Суть преобразования подкоренных выражений в разложении подкоренного числа на более простые, из которых можно извлечь корень. Такие как 4, 9, 25 и так далее.
Приведем пример, √625. Поделим подкоренное выражение на число 5. Получим √(1255), повторим операцию √(25 25), но мы знаем, что 25 это 52. А значит ответом будет 5*5=25.
Но бывают числа, у которых корень таким методом не вычислить и просто нужно знать ответ или иметь таблицу квадратов под рукой.
√289=√(17*17)=17
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Инструкция
Подберите подкоренному числу такой множитель, вынесение которого из под корня действительно выражение — иначе операция потеряет . Например, если под знаком корня с показателем, равным трем (кубический корень), стоит число 128, то из под знака можно вынести, например, число 5. При этом подкоренное число 128 придется разделить на 5 в кубе: ³√128 = 5∗³√(128/5³) = 5∗³√(128/125) = 5∗³√1.024. Если наличие дробного числа под знаком корня не противоречит условиям задачи, то можно в таком виде. Если же нужен более простой вариант, то сначала разбейте подкоренное выражение на такие целочисленные множители, кубический корень одного из которых будет являться целым число м. Например: ³√128 = ³√(64∗2) = ³√(4³∗2) = 4∗³√2.
Используйте для подбора множителей подкоренного числа , если вычислять в уме степени числа не представляется возможным. Особенно это актуально к корня м с показателем степени больше двух. 3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
Источники:
- как вынести из под корня
- Квадратный корень из произведения
Вынести из-под корня один из сомножителей необходимо в ситуациях, когда нужно упростить математическое выражение. Бывают случаи, когда выполнить нужные вычисления с помощью калькулятора невозможно. Например, если вместо чисел используются буквенные обозначения переменных.
Инструкция
Разложите подкоренное выражение на простые сомножители. Посмотрите, какой из сомножителей повторяется столько же раз, указано в показателей корня , или больше. Например, вам нужно извлечь корень из числа а в четвертой степени. В этом случае число можно представить как а*а*а*а = а*(а*а*а)=а*а3. Показателю корня в этом случае будет соответствовать сомножитель а3. Его и нужно вынести за знак .
Извлеките корень получившихся подкоренных в отдельности там, где это возможно. Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Видео по теме
Обратите внимание
Будьте внимательны при записи подкоренного выражения в виде сомножителей – ошибка на этом этапе приведёт к неправильным результатам.
Полезный совет
При извлечении корней удобно пользоваться специальными таблицами или таблицами логарифмических корней – этим вы значительно сократите время на нахождение правильного решения.
Источники:
- знак извлечения корня в 2019
Упрощение алгебраических выражений требуется во многих разделах математики, в том числе при решении уравнений высших степеней, дифференцировании и интегрировании. При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
Инструкция
Вынесение общего множителя за скобки – один из самых распространенных способов разложения . Этот прием применяется для упрощения структуры длинных алгебраических выражений, т.е. многочленов. Общим может быть число, одночлен или двучлен, а для его поиска применяется распределительное свойство умножения.
Число.Посмотрите внимательно на коэффициенты при каждом многочлена, можно ли разделить их на одно и то же число. Например, в выражении 12 z³ + 16 z² – 4 очевидным является множитель 4. После преобразования получится 4 (3 z³ + 4 z² — 1). Иными , это число является наименьшим общим целочисленным делителем всех коэффициентов.
Одночлен.Определите, ли одна и та же переменная в каждый из слагаемых многочлена. Предположим, что это так, теперь посмотрите на коэффициенты, как в предыдущем случае. 4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Как извлечь корень из числа 2. Извлечение корней: способы, примеры, решения
Извлечение корня из большого числа. Дорогие друзья! В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.
Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:
Вычисляем:
Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.
Попробуй-ка сходу найди эти делители.
Суть рассматриваемого нами метода — это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.
Извлечём корень из 190969.
Сначала определим — между какими числами (кратными ста) лежит наш результат.
Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500, так как
400 2 =160000 и 500 2 =250000
Действительно:
посредине, ближе к 160 000 или к 250 000?
Число 190969 находится примерно посредине, но все же ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:
Действительно, он меньше 450, так как 190 969
Теперь проверим число 440:
Значит наш результат меньше 440, так как 190 969
Проверяем число 430:
Мы установили, что результат данного корня лежит в пределах от 430 до 440.
Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце.
Например, 21 на 21 равно 441.
Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.
Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.
Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.
Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.
Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.
*Только они при возведении в квадрат могут дать 9 в конце.
Проверяем:
Значит результат корня будет равен 437.
То есть, мы как бы «нащупали» верный ответ.
Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.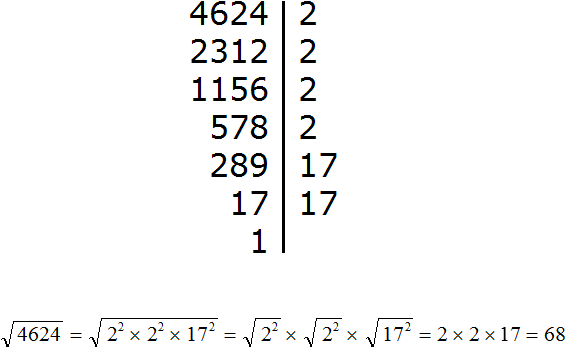
Извлеките самостоятельно корень из 148996
Такой дискриминант получается в задаче:
Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.
Посмотреть решение
Результат корня находится между числами 300 и 400:
300 2 =90000 400 2 =160000
Действительно, 90000
Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.
Вычислим разности 148996 — 90000=58996 и 160000 — 148996=11004.
Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.
Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.
*Только эти числа при возведении в квадрат дают в конце 6.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Библиографическое описание: Прямостанов С. М., Лысогорова Л. В. Методы извлечения квадратного корня // Юный ученый. 2017. №2.2. С. 76-77..02.2019).
Ключевые слова : квадратный корень, извлечение квадратного корня.
На уроках математики я познакомился с понятием квадратного корня, и операцией извлечения квадратного корн. Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Рассмотрим следующие способы:
Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. Таким образом
Таким образом
- Канадский метод. Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность — не более двух — трёх знаков после запятой.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например:
=5,92
- Столбиком. Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком
Алгоритм извлечения квадратного корня
1.От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
2.Извлечение начинается слева направо, и подбираем число, квадрат которого не превосходит числа, стоящего в первой грани. Это число возводим в квадрат и записывает под числом, стоящим в первой грани.
Это число возводим в квадрат и записывает под числом, стоящим в первой грани.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа.
4.К получившейся разности сносим следующую грань, полученное число будет делимым . Образовываем делитель . Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.
5.К получившейся разности сносим следующую грань и выполняем действия по алгоритму. Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Данным способом можно извлекать числа с разной точностью, например с точностью до тысячных. (Рис.2)
Рассматривая различные способы извлечения квадратного корня, можно сделать вывод: в каждом конкретном случае нужно определиться с выбором наиболее эффективного для того, чтобы меньше затратить времени для решения
Литература:
- Киселев А.
 Элементы алгебры и анализа. Часть первая.-М.-1928 г
Элементы алгебры и анализа. Часть первая.-М.-1928 г
Ключевые слова: квадратный корень, извлечение квадратного корня .
Аннотация: В статье описываются способы извлечения квадратного корня, и приведены примеры извлечения корней.
Желательно инженерный – такой, в котором имеется кнопочка со знаком корня: «√». Обычно для извлечения корня достаточно набрать само число, а потом нажать на кнопку: «√».
В большинстве современных мобильных телефонов имеется приложение «калькулятор» с функцией извлечения корня. Порядок нахождения корня числа с помощью телефонного калькулятора аналогичен вышеизложенному.
Пример.
Найти из 2.
Включаем калькулятор (если он выключен) и последовательно нажимаем кнопки с изображением двойки и корня («2» «√»). Нажимать на клавишу «=», как правило, не нужно. В результате получаем число типа 1,4142 (количество знаков и «округленность» зависит от разрядности и настроек калькулятора).
Примечание: при попытке найти корень калькулятор обычно выдает об ошибке.
Если есть доступ к компьютеру, то найти корень числа очень просто.
1. Можно воспользоваться приложением «Калькулятор», имеющемся практически на любом компьютере. Для Windows ХР эту программу можно запустить следующим образом:
«Пуск» — «Все программы» — «Стандартные» — «Калькулятор».
Вид лучше установить «обычный». Кстати, в отличие от реального калькулятора кнопка для извлечения корня помечена как «sqrt», а не «√».
Если добраться до калькулятора указанным способом не , то можно запустить стандартный калькулятор «вручную»:
«Пуск» — «Выполнить» — «calc».
2. Для нахождения корня числа можно также воспользоваться некоторыми программами, установленными на компьютере. Кроме того, программы собственный встроенный калькулятор.
Например, для приложения MS Excel можно проделать следующую последовательность действий:
Запускаем MS Excel.
Записываем в любую клетку число, из которого нужно извлечь корень.
Помещаем указатель клетки на другое место
Нажимаем кнопочку выбора функции (fx)
Выбираем функцию «КОРЕНЬ»
В качестве аргумента функции указываем клетку с числом
Нажимаем «ОК» или «Еnter»
Преимуществом данного способа является то, что теперь достаточно ввести в клетку с числом любое значение, как в с функцией тут же появляется .
Примечание.
Имеется несколько других, более экзотических способа найти корень числа. Например, «уголком», с помощью логарифмической линейки или таблиц Брадиса. Однако, в этой статье эти методы не рассматриваются ввиду их сложности и практической бесполезности.
Видео по теме
Источники:
- как находить корень числа
Иногда возникают ситуации, когда приходится выполнять какие-либо математические вычисления, в том числе извлекать корни квадратные и корни большей степени из числа. Корень степени «n» из числа «a» представляет собой число, n-я степень которого и есть число «a».
Инструкция
Чтобы найти корень «n» из , сделайте следующее.
Нажмите на своем компьютере «Пуск» — «Все программы» — «Стандартные». Затем войдите в подраздел «Служебные» и выберите «Калькулятор». Можете сделать это вручную: нажмите «Пуск», введите «calk» в строку «выполнить» и нажмите «Enter». Откроется . Для извлечения корня квадратного из какого-либо числа, введите это в строку калькулятора и нажмите кнопку с надписью «sqrt». Калькулятор произведет извлечение из введенного числа корня второй степени, называемого квадратным.
Калькулятор произведет извлечение из введенного числа корня второй степени, называемого квадратным.
Для того чтобы извлечь корень, степень которого выше второй, нужно воспользоваться другим видом калькулятора. Для этого в интерфейсе калькулятора нажмите кнопку «Вид» и в меню выберите строку «Инженерный» или «Научный». Этот вид калькулятора имеет необходимую для вычисления корня n-й степени функцию.
Для извлечения корня третьей степени (), на «инженерном» калькуляторе наберите нужное число и нажмите кнопку «3√». Для получения корня, степень которого выше 3-й, наберите нужное число, нажмите кнопку со значком «y√x» и затем введите число – показатель степени. После этого нажмите знак равенства (кнопка «=») и вы получите искомый корень.
Если на вашем калькуляторе отсутствует функция «y√x», следующее.
Для извлечения кубического корня введите подкоренное выражение, потом поставьте в чек боксе, который расположен рядом с надписью «Inv», отметку. Этим действием вы переведете функции кнопок калькулятора на обратные, т. е., щелкнув по кнопке для возведения в куб, вы произведете извлечение корня кубического. На кнопке, которая вам
е., щелкнув по кнопке для возведения в куб, вы произведете извлечение корня кубического. На кнопке, которая вам
Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т. д. Что же представляют собой эти таблицы?
д. Что же представляют собой эти таблицы?
Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т. д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители. Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169
.
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5 , а квадратный корень из знаменателя равен 13 . Тогда . На этом извлечение корня из обыкновенной дроби 25/169 завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Приведем краткую запись решения: .
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n
-ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
. Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Инструкция
Подберите подкоренному числу такой множитель, вынесение которого из под корня действительно выражение — иначе операция потеряет . Например, если под знаком корня с показателем, равным трем (кубический корень), стоит число 128, то из под знака можно вынести, например, число 5. При этом подкоренное число 128 придется разделить на 5 в кубе: ³√128 = 5∗³√(128/5³) = 5∗³√(128/125) = 5∗³√1.024. Если наличие дробного числа под знаком корня не противоречит условиям задачи, то можно в таком виде. Если же нужен более простой вариант, то сначала разбейте подкоренное выражение на такие целочисленные множители, кубический корень одного из которых будет являться целым число м. Например: ³√128 = ³√(64∗2) = ³√(4³∗2) = 4∗³√2.
Например, если под знаком корня с показателем, равным трем (кубический корень), стоит число 128, то из под знака можно вынести, например, число 5. При этом подкоренное число 128 придется разделить на 5 в кубе: ³√128 = 5∗³√(128/5³) = 5∗³√(128/125) = 5∗³√1.024. Если наличие дробного числа под знаком корня не противоречит условиям задачи, то можно в таком виде. Если же нужен более простой вариант, то сначала разбейте подкоренное выражение на такие целочисленные множители, кубический корень одного из которых будет являться целым число м. Например: ³√128 = ³√(64∗2) = ³√(4³∗2) = 4∗³√2.
Используйте для подбора множителей подкоренного числа , если вычислять в уме степени числа не представляется возможным. Особенно это актуально к корня м с показателем степени больше двух. Если есть доступ в интернет, то можно производить вычисления встроенными в поисковые системы Google и Nigma вычислителями. Например, если надо найти наибольший целочисленный множитель, который можно вынести из под знака кубического корня для числа 250, то перейдя на сайт Google введите запрос «6^3», чтобы проверить, нельзя ли вынести из под знака корня шестерку. 3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
3. Результатом будет 125, а это позволяет разбить 250 на множители 125 и 2, а значит вынести из под знака корня число 5, оставив там число 2.
Источники:
- как вынести из под корня
- Квадратный корень из произведения
Вынести из-под корня один из сомножителей необходимо в ситуациях, когда нужно упростить математическое выражение. Бывают случаи, когда выполнить нужные вычисления с помощью калькулятора невозможно. Например, если вместо чисел используются буквенные обозначения переменных.
Инструкция
Разложите подкоренное выражение на простые сомножители. Посмотрите, какой из сомножителей повторяется столько же раз, указано в показателей корня , или больше. Например, вам нужно извлечь корень из числа а в четвертой степени. В этом случае число можно представить как а*а*а*а = а*(а*а*а)=а*а3. Показателю корня в этом случае будет соответствовать сомножитель а3. Его и нужно вынести за знак .
Извлеките корень получившихся подкоренных в отдельности там, где это возможно. Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Извлечение корня представляет собой алгебраическое действие, обратное возведению в степень. Извлечение корня произвольной степени из числа найти такое число, которое при возведении его в эту произвольную степень даст в результате данное число. Если извлечение корня произвести нельзя, оставьте подкоренное выражение под знаком корня так, как оно есть. В результате проведения перечисленных действий вы произведете вынесение из-под знака корня .
Видео по теме
Обратите внимание
Будьте внимательны при записи подкоренного выражения в виде сомножителей – ошибка на этом этапе приведёт к неправильным результатам.
Полезный совет
При извлечении корней удобно пользоваться специальными таблицами или таблицами логарифмических корней – этим вы значительно сократите время на нахождение правильного решения.
Источники:
- знак извлечения корня в 2019
Упрощение алгебраических выражений требуется во многих разделах математики, в том числе при решении уравнений высших степеней, дифференцировании и интегрировании. При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
При этом используется несколько методов, включая разложение на множители. Чтобы применить этот способ, нужно найти и вынести общий множитель за скобки .
Инструкция
Вынесение общего множителя за скобки – один из самых распространенных способов разложения . Этот прием применяется для упрощения структуры длинных алгебраических выражений, т.е. многочленов. Общим может быть число, одночлен или двучлен, а для его поиска применяется распределительное свойство умножения.
Число.Посмотрите внимательно на коэффициенты при каждом многочлена, можно ли разделить их на одно и то же число. Например, в выражении 12 z³ + 16 z² – 4 очевидным является множитель 4. После преобразования получится 4 (3 z³ + 4 z² — 1). Иными , это число является наименьшим общим целочисленным делителем всех коэффициентов.
Одночлен.Определите, ли одна и та же переменная в каждый из слагаемых многочлена. Предположим, что это так, теперь посмотрите на коэффициенты, как в предыдущем случае. 4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
4 – 2 z³ + z² — 4 z + 4 = 0. Путем простой подстановки найдите z1 = 1 и z2 = 2, значит, за скобки можно вынести двучлены (z — 1) и (z — 2). Для того, чтобы найти оставшееся выражение, воспользуйтесь последовательным делением в столбик.
Исследовательская работа по алгебре на тему «Извлечение квадратных корней из больших чисел без калькулятора».
МБОУ «Гимназия «№ 1»
Наименование предмета: Алгебра
Исследовательская работа
Тема: Извлечение квадратных корней из больших чисел без калькулятора
Автор работы: Боронилов Никита
8 «В» класс
Руководитель:
Яновская Светлана Ивановна,
учитель математики
г. Находка
2019 г.
Оглавление
Введение 3-4 Глава 1. История квадратного корня 4 Глава 2. Способ использования таблицы квадратов двузначных чисел 5
История квадратного корня 4 Глава 2. Способ использования таблицы квадратов двузначных чисел 5
Глава 3. Формула Древнего Вавилона 5 Глава 4. Канадский метод 5 Глава 5. Способ разложения на простые множители 6 Глава 6. Метод вычетов нечётного числа 6 Глава 7. Метод подбора угадыванием (метод оценки) 6-7 Глава 8. Метод отбрасывания полного квадрата 7 Глава 9. Извлечение квадратного корня уголком 7-9 Глава 10. Практическая часть. Диаграммы 8-9
(анкетирования среди учащихся 8-11 класса).
Заключение 10 Список литературы 11
Введение
Актуальность исследования. В этом году я изучал тему квадратные корни. Всё хорошо пока под рукой таблица квадратов, но однажды на уроке геометрии при решении задачи надо было извлечь квадратный корень из большого числа, а таблицы квадратов нет. Пришлось число разложить на простые множители. Корень был извлечён, но вопрос существуют ли другие способы для извлечения квадратного корня, остался. Я решил изучить этот вопрос глубже, чем он изложен в школьной программе.
Я решил изучить этот вопрос глубже, чем он изложен в школьной программе.
Практическая значимость: данный материал можно использовать в 8, 9, 10, 11 классах на уроках, олимпиадах, ОГЭ и ЕГЭ.
Цель работы: найти и показать те способы извлечения квадратных корней, которыми можно будет воспользоваться, не имея под рукой калькулятора.
Задачи:
Изучить литературу по данному вопросу.
Рассмотреть особенности каждого найденного способа и его алгоритм.
Показать практическое применение полученных знаний и оценить
степень сложности в использовании различных способов и алгоритмов.
Объект исследования: математические символы – квадратные корни.
Предмет исследования: особенности способов извлечения квадратных корней без калькулятора.
Методы исследования:
Поиск способов и алгоритмов извлечения квадратных корней из больших чисел без калькулятора.
Сравнение найденных способов.
Анализ полученных способов.
Все знают, что извлечь квадратный корень из большого числа без калькулятора — это сложная задача. Когда нет под рукой калькулятора, то начинаем методом подбора стараться вспомнить данные из таблицы квадратов целых чисел, но это не всегда помогает. Также на экзаменах ОГЭ и ЕГЭ пользование калькулятором запрещено и нет таблицы квадратов целых чисел, а надо извлечь корень из чисел больше 100 или 1000.
Но изучая информацию по данной теме, я узнал, что извлекать корни из таких чисел возможно и без таблицы и калькулятора, люди научились делать это задолго до изобретения микрокалькулятора. Исследуя эту тему, я нашел несколько способов решения данной проблемы.
Глава 1. История квадратного корня
Термин корень имеет долгую и сложную историю. Извлечение квадратного корня древние греки понимали строго геометрически. При переводе греческое слово «сторона» превратилась в «мула» (основание, корень). Поэтому при переводе с индийского на арабский использовался термин «джизр» (корень растения).
Современное обозначение впервые употребил немецкий математик Кристоф Рудольф, из школы алгебраистов в 1525 году. Черта над подкоренным выражением вначале отсутствовала; её позже ввёл Декарт для иной цели (вместо скобок), и эта черта вскоре слилась со знаком корня.
Арифметическим квадратным корнем из числа a называется неотрицательное число, квадрат которого равен данному числу a.
Теорема о последней цифре квадрата числа
Если числа оканчиваются на цифру от 1 до 9 и когда мы возводим их в квадрат, то на конце полученного числа будут стоять цифры:
…12=…1 …62=…6
…22=…4 …72=…9
…32=…9 …82=…4
…42=…6 …92=…1
…52=…5
Если в конце числа стоят цифры 2,3,7,8, то полный квадратный корень извлечь из него нельзя.
Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки умножаем на следующее, т.е. это же число плюс единица и к полученному числу справа приписываем 25. Например,
152 = (1∙(1+1))25 = 225
252 = (2∙(2+1))25 = 625
852 = (8∙(8+1))25 = 7225
Глава 2. Способ использования таблицы квадратов двузначных чисел.
Быстро, просто, доступно на экзамене. Но сразу понятно, что корни, большие 100 уже этим способом извлечь невозможно. Способ удобен для заданий с маленькими корнями и при наличии таблицы.
Глава 3. Формула Древнего Вавилона.
Число x представлено в виде суммы , где ближайший к числу х точный квадрат натурального числа .
Извлечем с помощью этой формулы квадратный корень, например из числа 40:
.
Этот способ удобен для нахождения приближённого значения квадратного корня.
Глава 4. Канадский метод.
Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность – не более двух – трёх знаков после запятой. Вот их формула: , где X — число, из которого необходимо извлечь квадратный корень, а S — число ближайшего точного квадрата.
Давайте попробуем извлечь квадратный корень из 40
.
Глава 5. Способ разложения на простые множители
Для извлечения квадратного корня можно разложить число на простые множители и извлечь квадратный корень из произведения.
Таким способом принято пользоваться при решении заданий с корнями
70563528
1764
882
441
147
49
7
2
2
2
2
3
3
7
7
.
Практика показывает, что очень редко предлагаются задания с полным разложением. Чаще мы видим, что корень до конца не извлечь.
Поэтому, этот способ лишь частично решает проблему извлечения без калькулятора.
Глава 6. Метод вычетов нечётного числа.
Суть метода: из подкоренного выражения нужно последовательно вычитать нечетные числа пока разность не станет равной 0 и посчитать количество вычитаний. Например, посчитаем:
256-1, 255-3, 252-5, 247-7, 240-9, 231-11, 220-13, 207-15, 192-17, 175-19, 156-21, 135-23,
112-25, 87-27, 60-29, 31-31
Общее количество вычитаний равно 16.
Российские ученые называют этот метод извлечения арифметического квадратного корня «методом черепахи» из-за его медлительности.
Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее.
Глава 7. Метод подбора угадыванием (метод оценки).
Данный метод эффективно применяется при вычислении квадратных корней из чисел в диапазоне от 100 до 10 000.
Алгоритм извлечения квадратного корня методом оценки.
Рассмотрим пример извлечения квадратного корня из числа 7056.
Шаг №1 — ограничение корней.
6400 < 7056 < 8100, 802 < 7056 < 902, 80 < < 90.
Шаг №2 – «отсев» лишних чисел. У нас есть 10 чисел — «кандидатов» на корень.
Квадратный корень из 7056 обязательно заканчивается на 4 или на 6, получаем:
80<<90;
=…4 или = …6
Известно, что корень лежит в пределах от 80 до 90, на котором есть только два числа, оканчивающихся на 4 и 6, это числа 84 и 86.
Шаг №3 — финальные вычисления. Итак, у нас осталось 2 числа «кандидата». Чтобы узнать, какое из них является корнем, необходимо взять «золотую середину» — число 85, и возвести его в квадрат 852 = (8∙(8+1))25 = 7225, 7225 > 7056, значит, = 84.
Глава 8. Метод отбрасывания полного квадрата.
Этот способ применим только для извлечения квадратного корня из точного квадрата, а алгоритм нахождения зависит от величины подкоренного числа. Выделяем из числа квадрат, который оканчивается той же цифрой, что и данное число.
Извлечение корней до числа . Число 2209 представим в виде суммы, выделив из этого числа квадрат 9, затем выделенный квадрат отбрасываем, к числу сотен первого слагаемого (22) прибавляем всегда 25. Получим ответ 47.
Так можно извлекать только квадратные корни до числа.
.
Извлечение корней после 75²= 5625, вычисляются следующим образом:
.
Глава 9. Извлечение квадратного корня уголком.
Для извлечения квадратного корня уголком рассмотрим алгоритм:
1-й шаг. Число 7056 разбиваем на грани справа налево, каждая из которых должна содержать две цифры. Получаем две грани: .
2-й шаг. Извлекаем квадратный корень из первой грани 70, получаем ≈ 8 с остатком. Цифра 8 –это первая цифра результата.
3-й шаг. Число 8 возводим в квадрат (82 = 64) и число 64 вычитаем из первой грани, получаем 70 — 64=6. Число 6 – первый остаток.
4-й шаг. К остатку 6 приписываем вторую грань 56, получаем число 656.
5-й шаг. Удваиваем первую цифру результата 8 и, записывая слева, получаем-16
К числу 16 нужно приписать такую наибольшую цифру, чтобы произведение числа, которое мы получим, на эту цифру было бы либо равно числу 656, либо меньше. Это цифра 4. Она находится путем подбора: так как 164 ∙ 4 = 656, то цифра 4 – это вторая цифра результата.
6-й шаг. Находим остаток 656 – 656 = 0. Так как остаток равен нулю, то мы получили точное значение корня – 84.
64
= 8 4
64
16 *
*
6 56
16 4
4
6 56
6 56
0
Глава 10. Практическая часть. Диаграммы (анкетирования среди учащихся 8-11 класса).
Получив результаты анкетирования, учащихся я свел все данные в диаграммы. В опросе участвовало 150 учащихся.
Диаграмма № 1 — сложно ли Вам извлекать квадратный корень из числа меньше 100, если нет таблицы квадратов?
Диаграмма № 2 — сложно ли Вам извлекать квадратный корень из числа больше 100, если нет таблицы квадратов?
Диаграмма № 3 – каким образом Вы извлекаете корень их числа больше 100?
Диаграмма № 4 – интересно Вам было бы знать простые способы извлечение корней?
Заключение
В ходе исследования было выявлено, что современной науке известно много способов извлечения квадратного корня, начиная со способа математиков Древнего Вавилона и заканчивая способом степенных рядов сложных степеней из разделов высшей математики. Были изучены и отработаны на практике все найденные способы. Предположение, что существует не менее двух способов извлечения квадратных корней без калькулятора, подтвердилось.
Были изучены и отработаны на практике все найденные способы. Предположение, что существует не менее двух способов извлечения квадратных корней без калькулятора, подтвердилось.
Описанные в работе методы извлечения корней встречаются во многих источниках. Тем не менее, разобраться в них оказалось для меня непростой задачей, что вызвало немалый интерес. Представленные алгоритмы позволят всем, кто заинтересуется данной темой, быстрее овладеть навыками вычисления квадратного корня, их можно использовать при проверке своего решения и не зависеть от наличия в кармане калькулятора. Тем более на экзамене в 9 и 11 классах применение калькулятора не допускается.
Таким образом, цель работы достигнута, задачи выполнены.
Литература и сайты Интернета:
И.Н. Сергеев, С.Н. Олехник, С.Б.Гашков «Примени математику». – М.: Наука, 1990
Керимов З., «Как найти целый корень?» Научно-популярный физико-математический журнал «Квант» №2, 1980
Петраков И.
 С. «математические кружки в 8-10 классах»; Книга для учителя. – М.: Просвещение,1987
С. «математические кружки в 8-10 классах»; Книга для учителя. – М.: Просвещение,1987Тихонов А.Н., Костомаров Д.П. «Рассказы о прикладной математики». — М.: Наука. Главная редакция физико — математической литературы, 1979
Ткачева М.В. Домашняя математика. Книга для учащихся 8 класса учебных заведений. – Москва, Просвещение, 1994г.
Жохов В.И., Погодин В.Н. Справочные таблицы по математике. — М.: ООО «Издательство «РОСМЭН-ПРЕСС», 2004.-120 с.
http://translate.google.ru/translate
http://www.murderousmaths.co.uk/books/sqroot.htm
http://ru.wikipedia.ord /wiki /teorema/
Секрет Великого Искоренителя / Хабр
В недавнем выпуске ТВ-шоу «Удивительные люди» победа была присуждена человеку, продемонстрировавшему, казалось бы, невозможное – извлечение в уме, за 5 минут, корня 9999-й степени из числа, состоящего (по заявлению ведущего) из 80000 цифр.
Но действительно ли продемонстрированное вычисление является проявлением каких-то сверхчеловеческих способностей, как это утверждают победитель и организаторы шоу, или же оно вполне доступно для простого человека?
Для начала нужно выяснить, какое число было задано. Это число было представлено в виде групп цифр размером 100×10 каждая, итого 80 групп на 3 досках. Разглядеть 80000 цифр на экране телевизора невозможно, да и не нужно — ведь нам известно как оно было вычислено:
Здесь и далее:
N — число, из которого извлекается корень;
n — корень;
p — степень корня.
Искомое число можно вычислить, например в python-е (питон умеет работать с большими числами «из коробки», результат получается точный до последней цифры), введя:
print pow(97865891, 9999)получаем Мега-число
210335540071638032532739663973635434663372108457406858001703392643029151656083742751640376426791077714196778186065289364749034720165933751686797625910631225474106658835747402678181714967525210402729964930655343263625370038127202036866249844305294242775799178796718598140271488101691237901734711171152610089501868734349674332673601523846325339786422267496931214540052423682650897003825602727088350321272684789553784049604844344511310854050324323724591262523177971970050524236938168746375618364673692482371242971048044942709465265649843521663164393435959538027792695306764542409188571585725304834625127648653541193162202479709507736963966074488381352178970445923936865562577475854897818580039537243201170306111308309918486726414302755908440285682235379064882406128975920207920432586531093248310807047636441903019772222932346055626467194352601484259214219342497122037161514727391430820841453590747934224417389419095273664732031953337679197470616556369968678435458495942638360216564942870186895685023592589792115560236327156737137012110149447376262029785185561767691367181883299704843642958949306571215848528182421059693246251361088097645084421719152444391616024607832156199790237661440581682756626823677529020510409099683905497199120466769510719993333643904962825051610038015804758608783016155471376568321958755332624670528927940604335327599382019332597827023323997773199677882914167279319866531787311921635334456473863829255808841099292408346055769570039672620711202074070070673812495566474145641082620359279159338657572425266357505822495336897967693639314900314290249367150262633188420168378955974472423967382343138062080175950158111990114559412153261256052629315142047520112764918902555739837488919799007948006770860765073243640147993596043206352980209238245729853139481037883567345445963509066124887873644335694680513495741010769431941752449255737273632673689819847204282621677468462879043666756667421734851016716393895564861648132039616776148077806532373673853643156270540121136542259989632842175488339713629360341100155172715602252557738055370720880738652338250962797326589218730381769944353313505464826453922964327185869813793659014291967130928237196921187665962071909336283470925644386196569677471161235069509925581114984150188256839091946155205818440718538954551429342289736458633265011321352650498190963717413143011853346331408442678643172598541717891654493407348073727339472332168205651270580746774721160586571551979795780561597901725359187762042374069574192931295149132467832472306578126963158718717127705944514515296411721695459236216488268272167542767726244704048694759005159430962590217235054235678537723331008287246961413647899671290829385774002521045334769160797813230251496231169548527639471905683941861004045260664674884614009377750904441027236041612835720886288486931151635146627309266689158573737127435599754013623937907803063754708798333177583307460688347675740120546087923558906997583583880701604856148665646967573750901124966227920162180218857724266512374037214253667809192329369392269006750604426305295257387287219049772505896632809682706107415141476687664896744234540738194333171919824427926327543317179763685345222608536350826879138422414168716000142265763545078146336941103177829466967498884990032144376815285934041750747449575999585020809251193743929477351361700197308730553842941853710390478341279621007804374143865287619682290365794066460879018360751643834596631633259817326228977075486996921307518075718754766447312331588472106426159132191515467396528886098403786124466783718071289340914571344236861734586396315582367496187077697808293536523369633263923691467197212291629930926083542537740660926060001864782880412791564684091008987662256293465352421269854242125141412433698137623148026943991906301639415744505467387671843129830747671576275340132874798278962734723260202017768436029966492203814154140292836012113077416426414785793120315315709001159413818908581100324941133726826797990824006893008668065373085760109140756068508034305153757600266730238414112116462621008889715400166474873371305149358614828097695679622351600637076799746990700406189402786350554594604176192150216922310784471641453304995836230435755809525343819592640735498880484316560635850075436903028124690377384472376812817940249666758843122788201412472270207826729360243835157188525704332471808163295484616721166864230612880100036208490486485850341517749191466832406723247070967679237973833918402096366590817191994100478468993140561838636978675174426042278070284517382209705626467452462800119874470128128750058530087701794859182977785347871700946719959355896736870995234161333614408021449894027976294775581474690319249850561225727767372581154695835727845884550323160354336152468001652682561979743607205979081718955120759349579581887846226008930622184030825830708403659211576985063148856876943766906009812044838024027146406075047500833405724459904573648031952945463288464632958811165775473158189318607792262862905692841064349528989870171854373327680642570865853973419708321557579158079357587980212229876221894120319376829646408217367062380359819285413622601892002305337568666205150408064060139159141953970480256334892541199432531827639535833540025250538289693547572515178807991976093485278783569410960559679733081272224591203370213515838211941180251996584799846769604719217670645134410180116995607818965862792527418227485213954559313050477950015329956417157304379571113138831946161360814464126104927878225198373053742431945241886627345732562064705859706566012143913927681362690196106238471858603434367898906321680936651927093732984028393764106346211776091778508456932534449188662534946161567362277508060715631565182198667322523675993874168524801809472781617863092897066740336313754659405281997629361546415189015849429322037410725109814880957545392089383429216332419787949516145491413435424276380617419025571568059388603097583419022736128847580299972841131101097670355899988525729091428652522113221808244040319434057267169636165871151507320659446598537342097651380083859201360676070754558221760373543492534761995998463669003169344710492613243551972705431377912126859118081854582102658027319208442132001581824645375668614397351718414142436780741384428033987640555504720720930681030506576898610263903395994570054209988922068135965509336908049110573940506462399575238618529065783043204256977762438852837304034995901391382512252929140004817019448038862933169949590075539495890986562373176934517928393324371963894265315942619961945967758111887853496285363902869208661357785022525823034454868802711616920864963543043615864580131451914803855171989260313182622375144777283657231897379751195860942565287752071227855756837521894628570878373280532911150158082361962557645361887880290289959360982720826230626481836277812178289165737472053819602383307668519750442555488209029756917225295452832349430529285046947222271419454006253846351933503534505186734810131045964814818797696757351871721806517372131246341954983014347968823759896930579917772358682638268897869635553308061139212339537958525936322449411951430515282624122931852973464525162649191386798203189398630376581971102329132340807994161457249227494639644857828494406426112290113881410103022052106225140912071781020444586751509026468932377945882427517511024676429175587556874661944451029469712758616773921687871829527150000216929884040927450645275172445071921084578188159825263374825250823175045545320937075663603639227161786436443233122372856764162357132228396781214372554806029457729871942082370639416751551389232805111326417038702289452877420274686862287227816272534636673560148532830673111990065345366457224381061492747743435415207604829019717685702340822674932573636021167868772610023996312101386145503608072295542307658014736950393622820919540164525303886345869918008239340158152757664320434457191827492293413669868014493712231411051493634795600864869576150269871539515725178553137359842386558216270107217591971853994110755945799608969292039971470494583057308560544297959634254650745186933299435174609702962867406592285454860279379934970608318602333423838174099002624590351538069075780567431057656452107252951880294153465453499127899268361518548216121147483565299268491738529095892982642520679846324842854488572722749699464775458261961695934425159016675652437944676740009213764757967318827919947425730618635352493455341720105021115834786840258649705181130221081554049037343863443010077605040408829280768568870134107746447827176689113422463860271943917886097930231215078254238711356004519581245081975854784250384881999824224374052652182652736601651664698982339107346231968543021939710428376104125091683648482567732777426853148602042599785853298274299087800244351837171374400390824139961093896921917195142989474882650809290264566526191656974983960344226631727828680016892869374576726393025170725586545655610068080764344732052585497638855418440931098463785515530822250788422976260983300304235343835706850922727145753389423473987008668682114074136629928164216150026269218416360508312301718647013679135111358412532057899005692665112032017478904096162118653656166993523082959311729815573009609764637585534100523077050668066331161680158009086610004203209148067799667765132748995186740383771707068039382746814304877584053195600796711439410189634331429139539237807146289468808415971615213815755261553498276659056675528315820989832465685669388061504324331782274529418066472967445071988642738456213381469266888359492299435555262034833514229641376512683723567185282061321879209868594067961743997261850014686512182039841581239650488982405335668298036323320345193313056502006754596754246534116969812181652386096003592647125283038814916827950324630073103574690135957054044916255476063542474319579126628834847756947042072668641889049220257128944386049622338809583554578177608387949951367966924815578504135242368251240172808399970313916583811867158130485226770202975692322842469176109085821369775238035954116099584364252726446555929237020401873254971131133198598729242891173747853557802441553433818997838164861246344540016179039917798126931258157840031327700932992714503590017930446702291501799405625905799150164644171386868610612103109786406104722388544949945417069608602919623163567704516690804637413441005664512407275579985703528647411870808458674030657070424981620870174315412412470674055942061024430136994739515141536174740855793467146605572243009502707291598581301421453456013008152956222572776555302085389846905846199520592061159792431033601651522723813324118314576276324282134663660857447866488359711339723903371895562396470880790061402612527457247788388761274794415586281534323495758546751064509565228542942932729033049153192830668677554932517511598119669040963741756622871319599403099064838823892141315024706884343781920067051669221929139839325030899781689732101461363917778214718847620273351893167987812874955553400051765120713877176227810720395357877253984577686101236355898894128039643020891322224773583609865340889916965212059549287125510569094483704574497859230879879503474120314066194481951186811090060058942430838589586736459881556773229310839958411528847666948822538297666229233794404374210422956150339965289162390797553709032852832364106132223591505027089586796565535642099203598780264153566018932902130722432620298858714262147771680020731827374307520392827424990750303050847224269893492957730118784281782042137074682911827273646253903586599888459013665228407067385227304462643642436987279927113270267586017820530043543829398987477664168778918935081067252781854215789568549567083212211024181623174362787797182535475060382804515948162503791064348629342675144643292850896774459728767601528570711638334968474862613995095816341982078944736450887084876838676063746702936566967118901503880873150052540741523357923447647309630111615120040254368715417474274763876817670651422830686096849606235963795313389165845282807938609304571935306361150065124725981553653532110051758588587874871747099570056475400219424135697033545543868124831695277667302718266962967850401136185535140080592275076975402260748292614606230761897659017076901714703053564557592060469606612899318737907821260330836962755056325912059253676741279025898988584558413598893247293525272193037841707303820773953622098259907103335877691574641017660016127552621778286858108102815166307245946198743788186471821326715463646387400718114187710653092561714922779474146343215813454913444496551862183901618650381246088730004165313828863162718728567401547868909487222065760446155143409190462110951330495796049729930394915890492353498707541221217712216126921944497423481948003802339641861446828401355318810606160374046679613793173856248855837789938508254028919135171428563079965567725780592817268857125298640630910398432961749981720763002952977339847537387581029923508856469541659777866539667625820996332453532289730047719148570304132322374401615735928816295228264504525949836821176698727499026194241429415292317413952354087626934840956690336248001979397322222791391860406641624618999930999159424757210152715125641650593178046712746405766353205239616210168684735978279160085673405282412058186078751967956897950460110664657254029080728862081812732580820250330105526211836904019552701503774917777652206613812091206437655851955278782775695357826986730428837740276561415525919392562250520131897362668531915655757351288352519258333189789195902189608745637951039948192029870079363775659180509149007213921771956987041313755122711403533435036151272787223869999701754712159194391535560759185044300427247847303272721285678655159866294784377583649356037949146754399040432936956104342302170361481234236196841162071143726364143006367776287633963195899354679599352861986748704130251652171173757705010188169070340076996979122376958944464097237403171819515794685829380984271229177158447978773994151215672359360393883346392507501963592163015479457694356445541479601556848981553551434609814460412748915301783700352137967130803300435993033590809573983316986327713983611582325223451878267821591965835228455305332202059490799087992372976839916801235395817656170646496819353948908019035420196479797313595059254958853641124052807035348843991484183070980836356892705616931127777772629655540478972862842607346725626440901180275442235117729794510634296642011106662339051168886913650439659501450705342774512467638709544567249501499502087361671511442286573088318961468359663658403723201681834585941655177691427835167481149188362676849300651985832605926036168038696694638850738284971683302855983833519374488696225101267578853305296945083767184143568286680837938518050917010296256193831319570084411288677354955363841535566148908598866042377410523305796259415224249596807527370694011557233115620196267879414703400068447872378498907998278020385685076806683948030166370965129019936846878809725921780533905442920807261383640547434872982512361327780209597189617413762389425076051408252080121092516089626418558112416006447746481322431110875272805006000350622740077099226280861518511795167856789333811393390797069085568618868114538494025598345959757297337037228158167107283832028844453876923342669736953601121542229026341897956345115400937829389717351574684609988401981101917595415015896396196012795092224621167118704785297203038858752867991946270293433684789925112565742049861999416415244292573400727434668552291043027213055491337869351470664097489324098106809470944579344572378051253385371982734878774250225744426143034756063996959877932154907891706201905239682767350939153744647013138332041010214260443741926317777950093351444690574638969076826094686449373818612823341793805564067578015508377912403745847806524491702584239598485369237916874244288341089635658358446958628117676471391372274647455793250246356769565559606153112581453081389308210268237126361319692925004549293625436362425169184086119207903879462656745835903002656071977397620756981196009576455149070207599863946550054419266864139147575718653474472828328181769304720176560180026092040248893933367521242300023918606436830735263962166233781024571892262112539379762509757268856232576475246452692117620963445376630260052530203728713657765975035527615800169991881224331963933281959012648526614615094497542535141599340926164660691336254230714947454017885625475633024265342883720692583839077214847966889540370715112999858002042180207596873087597808422046355288382698113353320218487064934649064217680923812601914308221647891165267079056584000968016266929721598737021040186025754342967639343996141167682124453307929244823724952187353933245611926494402555506293966202579866477482809680208478572969088316856060852468473736234713753720351881807041542835576368333732447134793166928624780021690999557869939427925240668779722351554676793072223303224640769134106859416169174924003063964323060560121483481964008492854908289494841810664060560799528127685525342385069831286007496675454134796185197552632057132041839682739490460388786867032167545856518903466993252219338076181016343520191536349039997094419947753458035618210455965106504157317116481031290499603936924858800714982612120210933457136692941488604167704584174512191706096340162873593949859046779020484372236734823384994414859304899938920407181178458464629560780036767028002717510845700209416162827745594922803208570174525856950220785607434349553122752936812935885455178585314981142452928456759951260252081451036174806294427356866059230921303677546127671047674122051102094007369329008057045060205742973655752339550400664425472516891468297876418075947498109293647619766109336843615649220467485081693753593654854948952284130056591642325661732361205395508187754082278686102065257798223124048292827602074945402200216801490032727208689040327380981797078499851598741290995178558219313811014114529786860168259452365397758271270744210354303286163741798836889991788524164702293084491724480565423364534899830783834263533969313275214682562307855587165401105915364052240037912868431831185625635564122700295963393855128399306165125122677554987956333314159814495433701804362130328060344810374276199483410482267582719091160821785165846304273653045333425728620179998708504396861646009470511958892680168010351767538380814701014764956641898990849274449710402928054101990275639956001359443544091951147156056559306232716956751644935084993213370415272493000870542802868528185016575955360766746801358946726408676976596310991501636106580105045350084792899638245961930005243154524508892081347697924630488903144222258443990852668973251918307832026544133480125912303265579176276695797441831085482582880054957504446601786629315734302840444669176342269300900177445000820781578533028239404703161546789220569461168071815046918353230790821948509062597070235693914234416122784081055562301511416811235161591895415866170772024556011519541654300645435856227921462505815754965407432491613701820624859847156320655703736727774536588710082248211936378741957137111067345411698716556567810424866534705748661008896062571746641378800289307525363655690384174866609192853361013524590844935487827390726722875218825063536879611873447080888959122226001650491928778914156754605391569391710115758493559317102815040515184136350229619408207944280443276280230910453711192593351882155076715702924555141229409907478569014087406573801680752249187384171323571922574742662479561200133993186152399989673092962177107065731439901527277922809641782608379753639124259997205897244283422179531876853785079420862722545449807987345697986403989848038781297076926729278146835665305676272258408644799450390907431512256540018048156253734817147170415169791647712500397879085472075425383193506715835360795755347877463498722242649786935433484912554935845030115938002821031408769883112047813301131450418473371512721338266926070889121928504048324914704854340510665989291331434029062518573121442606782029361642766408917256709769255418401509220325337790495564825912679292976181903936535932250609356326148480532402786046072355642667392633518661719273832130524352494375139279655450146426070306459827530051578357011741600719549156994799159526515065518036866529392583548806229480826146069475418420540930017615854992639849718511726305196573182053679103825353514947067075086392298592298689851657731066798021504513605482078793080019720183365259275448124433385679914246002208795696674000008569536274851547084070207391236769874944182989538477381439029254509910486412744719676377155941131179584029334833292214570159384027809882658372962400460567493645024905329583775583850418570130815558235950476076982731172883101662006249829171712725785565422771596152231975290203938222826661133616490651636831933504712365797339276975467394484948547984772051280130912030216928551136076145202667205850357033534453918725676166970117770596892106876125515631612551016236559617385207275800911658593082276254129302873163865824152375267274167752886115095987334612940190031568079852912314185926945621498091065972994900079630390466120927812649564761926469376509181928999422273123685138496092109969092120147875920308158340347496238605363630211327998952385094963366561293467932775200079545853828074869260748157952299234659497819546900223128231869321849908537731606395653737957332598065062725375955691314103835517012156166859453183444813646586938967652279238502417502036301298599054863391998803163669313646657900633952622046362305268021685944722209665633359355956384025079353735678774405662707810541353193341861857711729881534308672477524880457993653696838406462826930700484223322824463991129910410844863154277294089064868894922129815751239308963156894062248139349407230947711313751253206948543513764205731546608738752709603045131168636634497566180140339384149619366337201116504207796773475972235230089758263156077324942019580878855517681659957433955922533897652153029192934587084375334095421115184427584192574714799621434884852640023060497401715506147824696227359146234778903191645661821579754805622679987357040045394371461143249416709747783011182548959970861093634209991739960629200700886885521626447445450469889434508175416553673592597213863454569334673572174069379400221117030946424556799478763613218251690443781652809376925661580364981116940492381839301237597751379320103698246531834776532651486409386135897885023248403741543683733815723349646891718359694281304107290563811039605700823138689930275968180666653463011321251577838987455570777998076142912040115238991754940165935860149571288692821897535591705586906696805447545820514292569501829895177041877235312873612369904083564608416423243326896439001139713676935906231789402192872026210332967453772594633044640841278949605816869769016950719249202871793794104152515245608295731767686305253552179855030756687670848738129499157604630925582111852873268731759621343841178112644675593015879366222414020747649707722827650928093505618062419528700535755495822020983488609169214406236106475036689070379888726137033100809197831388416724592321066507759465722219032864337609999807936512347174218808853983730952696781152455212513655967566283616608945098673037553875900783602430572761186494966035447197453392206821666749646267584102239849249813695450530810495419157365019406804545776297607763442642035927736398869679667132249175119810866353765195714857153975893846488005491402091988782979925641279601619604585199390713794577119027540081666823733885798138025326148763731759864440607725076992597991172876000160200947343479144961195927691974493885772128025759517977182219389367426715761770236588706566323710183240946227666301891494947872774704776327137488153615385443261364421144942792128993549380383854509365081625587046911931354004396390273987655892624255452978614028311345842472024864006651221542777171327469990892482323349809786610991443770335540488876269262630811850744630661840490328974948923628419712720337325979195420342304937347672237283687451629003815133468214504962291320365562572289506624184126966699854923035262011210791332782038200450732732754385342078352686291081168563023507026229499384588338772802849751717174859790560355810649336589660262693241678934021481925001090182835010867884262837910178143118913461243339625863740916212378447032677068493944666216461273054875088074041589292506054886955006327659956618160028139683813291222128429895887449901748329606888994683097408444365068313310973849212301612452806443028485680057928595828106068478048548853801131835890396561816314170409601353196165454924128384042312509228816192030442129974710247583151664739009854578256535365783411529640387041367590408027354846712291311868109748165454384587216696620006743422691003584027003563259578841142192410991039301557189293856848073321330966434611317680966572961546847033020711059028340706302467439175488341980858487506946551208295658969764840018593308029216292463051196162385969033014650534158910171779488310797884371046020410152680772550010805414126567732465027378215133302402217411127907606893498096164515717901260864689238370510470830574502318123732683123843518146629428957353054210840724860066170639735749231690139674193315155832184254942853236598727186775483329282914082895245083130163722326035028227722008472677737811931340924222465637794453532355383264651333068787155074116565793263806166573740036615038225690876978110250955657455714736147408387176786615726058500559474673829740995606778612352147365922374258348833647337182696844999459906112526529449431012302516104919699558827880397409082569810254545047998222083738267040774108003669403751069108467981602957449031229782287067735294567318458037254909304229095745003919056416360481392013187670620216980878735608813941941314920823273426638838654988885283053921178369500582018919380854586413078345731151836050697594201994143640053319669173034467665170689866290767129714766072533220745804416165250266856466751494912760614200887641734678101498510054445023312007375881304785435405149542915522356871947329595637383988251612211534860061248799443335324237752117420681517400659848975730007375534644644382529456250172501308167457148889415007023767166290222919852308698425664839378757013205351522465842165242774436948344656087320180314288037868599286665538342435572066786008150624905511004326972082451343506598215779182042333172888657177223890698476961741747320313269618933941898418331173347780814955853452254204544951617798998906513178065388411141289606064502994914310290386635566265478354411369181355905616987501287873286289697403547915746212571324393194766250670527257146582499638916123854179049596488023502496056384640919062380604975889068266759796998562572531428361246171522373603641357953839059422403613525698722678093528327621256285344791547309416172823537084375081801737222618937000097532913469743883649092994196076765952141468033805865055395156906388247966901364673121502799081816638313804656955437723475613509139294906812810443514455400899934766215346599318680147138730590744486569294621783134454261544852606909784826333313679395051631576968958869480549663650176905699400531638132996047595408769113511504986165160567725185777217315708378307883701164057444004136532919304268957366471108723016596800580616386948257097527022760947631181136346145070245160631722608610197595611706688123372455005120850332996763255735762091463643949988706730974991382794055083642537528659671284899692887260742658472488159326576920619531863789597945342212815396283709594347736969010138699199526620452017664543672690809093185561726962064891734714423635965519381939576906699162124684389324122603560745855509239452834671014678333370238372302166702911866717823821187476014577234143055505662379579883085200815895144646022805565123075911364495964345039754002477720055810196290679230576261703868293401116283159959457152327774907265304507891032027843375793130939357244126491497881540556263297428004207758601736775907120467984888958377139579569419820580574336098936586513242510249426650972830487493393205763206045934282049110978259093522774083410053114073746640337839207559113398173285959677285536580863118010486639081158736453987533505977053607928780578051547407388537635701065786984970451876045944187092736995913177724624095258276231195768736772743665904801323574780996481461201982059951461391001806168880314722134277348396274014018292974254163002919993079476292078780025597642358365340619754791447154516037857558181581723591157790720171859150060378347496914186597274665376438712642529454495977901152816028828470415113057736586683513692805723854045510981726157830891011204894834403249420978614752300238574515622453485099976642775262900933106636270974563244580174940476349357727618676586879873422912296716064715576105192146588545087935564273033230296449695345458761143643984131923378439497320487277079117104101925717007950940400266384653967011674110963965071597153712563189550959791165250487266991364814170396758374857881029096565339616399206078036624784930020932882782668016892547046073197930310240840352799135464830523235908137545765313014077162306209156271841350357608830183318305231955072832500242713613463475305413237005286758450962194657163307050838184355270756151161916152745936609433968653307864932451533868466696794678479489584214421495865320685610452919718902109878382211731210471410678475329227886417090209436885086549982569058829559900105258842856471129645336400479386390260523607278448077778787784446206684370674935969358671168408670261394005687835317805218022558078442731315331325602178537992005290465337543468068338729159546489982404421569239802821575269455400676604707790965086388373279056714146235074179056466027777985946386227844513069687148348911289640461652515140957839818519768002490588365815805470261532901163349311507139001710195306025835027467667680367346123150310876820497817173929061619921036266453935497972571049646159536249837506128648152733753883292698469161782225386873723029977325358097456613218639277662555403382368876277446685909382758471680177215635441498992775992765999346198404630734201142633967012498675354748759787199715681774374643477375456512976558813665652004393109927526134291246917799093417419521296672538119930133213412973814056294815542198211635239376947241854349504403125582478319285063791543047303843181129687353893900668067200942391783961625942120092923186487930877330537870345275105735546877201065680656722006444721397274049128933958350012229845077831095767253061281168317204900012775730243652884761785317700982670969200543389203716608231147386781792288090184188807071401624759620275257627469136324871491724416171538012611830979643237275760429865728816779470660063569036544593797126631556470961466528675191375998993866931999268910353872369054505767401020027425066737238115066795546085279998276330030030016188058520320635388052818565148049539233888328216048005056695893046046955019958250465577314876880070774298716410221095727303107173865537775419577165428054389231832230455089833399145284797439970709183087444481882822251459448097090766201235015703249245488676763276126301739643249699496730748100928338033126550502530010690219594202385321410761302948694524335010051592501478277144444224139154896174907408364375876265902075610363707765926020678312593766833594970014524657372488820234174037200138736873157401756870984583750125695827652896110350311307707102865102943540855212239791142504361661062069553565326753298754056290630151390838967299220831495236558538340913057374256597165656256401604973959096902023699457165056790560514395234471568452250120476289708342224717752089675284587024914253082802570901865756408687711559321199308178955148600542729847326642520496693585343238650266491391087144051892312516476298470402900167186906407742541861381949680653274196722960624075745898278631254308025659531416967820418046653152860950033964538136875753014154834271823087072857194144011674513986748751164071519344795627947360211176312868539635004751568889209759141496050489017061074173200213038880413713293336375291347492049878395469425134277627765903143625609081130014458497845871658964385296545221991846594514075623188314813739099584027596985296996702047853767638411351204316744906665586771321445915400009804878506706021818219501029859201463485331321268650790756874515196940824832752870596638319590852566702271865613103214725668910533020300571065037279030270178023167330845100958412888977972736906058305002813958614402957699250545618496237372717871176741102967218493605534595449450986522950087517844836135418355273673389846944804268959611350190692675761462722596713501399672509722434741465478377173180020154598411508316185994998204755654607013376030498679353754316013275757707698583476594035251446465349027364125579431364055646514159504922964385829392962740087951910131388626735671106511807698912159502225342069598966770101100264356143529009560949848327369799704485364673404732111627907438663416371674568685663873940597873230684544386421880708483948881839597965520780328432406991519566491565353770524203740365177387639359276731462110576132098466270676856529297016757313620942574173230959370976957942496524727741170878842034343084661789748078304412789885424193700049782794126235552878808244313355830718092458536091191898399419027819100279025070868535523497331995605009023729462019464883101429312565852706520872876537768247514925002934417523289479760723569204883368481587936631167801894451102834568506433480062298646519452966050564188992748476983570415156430797191924652025338688680906978889819275355285276603344662336751827447170611439253315306199741403398221363593895493373519048870663844030501146050061283683036248844192443948498308566581908481108199827414060875494878544706600069712457462414274964664006478788073350557244191011918802401495254749183613311442267227245493591068987565560825372374916165729768047674488309531306652209984268282412688157258396685006628857171962302574265601562203202907861756649880625333268255182560825444912463219962041809816413369684384125961417500441693621453821423154557806735213318712453832995434020283175747584563419725275053022859838324536038232532626765219389634824871026396405808209667707815298854774781970736173933836407251171268924019744455362284416485105078184365769711752453686038674302839120686258198375053250332438409776876887583164224237182425221914390186834986996815159625241167219583085327362698280128731815915940740209195195077048533314992079794519080463932405512981681014387550012084886383064469014964891364551240282978446812516694613993695883517973111140059570266316855435504905502022872589049822908571256721162410281118642948879935817564853919916715828613028886202785249882142472919215118541899759269064657934873955606788985153135033433197390953094598877355729851722191275191048159744520673649887763836883694644610870140673671712499933428848976431751964756723431322189352090691885128245576638621398906305961311070945553397770509489537412917485125315294470719544627967736882892825444828147368735810256796016138096716150699310609749407502997830127755526579304020946727411705417173190984607772278479734054475262763196997246327003008022827614413847286790323574563293238638554183579831877587341664849728216267677992588455899666405396179421670579077826299278621258198743981515517692296313786035781134660214336778990597320756366127600775994836348667484340932397494471512148124704138142715810608580526073810692905196409004908834541850092266200510856867228168899931071881334424257998762534356062173312830331992457469498323264378079680041085671632477400395447499018931578502470690498394120963063598760963016324460025539329175109621020529865538212232402230735845284480574320302733600273339167787718449153088942777401917545406934748569108967425966778415554712843017215718599621069990207371173560181644328698783235811825989963062281774790812420414565837613101040852019172953435587427913009254178358745449080270074782839353674113392089177878476828637963439505843079630811384527493406173328590073234556888578690082571395497664977116262381926036343096783141927662341563764730054361658451818662467083772462850973369418411469626342409868586617753468273443886934180818622607309154316763689488556888230807065545774079030514262518404163030472675976645340782311267227627941040182221281063107077299792198654093762839399287771864457366752606126202063520431370170892888713616660143572265616325449192549091834381958050360045146258891665741679969395729822093991129782894127792230324556176495448265172760085874676375245241653760213274144070617734525457626628535350932909927363849362904954318933142930113941244537109346351548082079334818343529027405441772030596569826920101099251889475925113556692244138284156641970667897878855435006608086870333752226107055425211629750830047901519802698531443226571726529778060656400009990460346095267591460117439919417517281401498229783246777392318656111038478959059440558973654144934753923976320934661178683841529852320145900583476321761735068468816582836220949996011976517083270949896238393627585348031512555010668989993343551340461778375205129059863523732165376784578969971711244724457177967074053605725705975556318855656928261371469280812758870645562934788132619910400981806956299721723049607435467124112836031620444705007790902286745779805205433886679369792433333371925665431466677297049770128379531367542174200818816078423437436460134838333889086786936956783313142864961271954285256146211645673571172197254289824155385121727296069055767594311294546545021715517729125899372619012058343295466458312050913045026617983682976917634256269058157978046571698204719508541126320271857480831576281404546397214973236103157820262716800589237986741904040707927354142945000361323900978689223835756928681389930976922732204680803245966657134206605147718726509717371692446833075169980538887606340949918756522102691516681572851787992559447419351078956052657994593714338387736940545578271871497485688442319095744166517733823983561813229765729468292443150711460324220291157747980008771639138578080977070128471512856142715021532835865885254848521086938523602297046485464441470012538384954169695034573114826947872952396066353645586238839840073675529936653571974732803533004513822953126932946994401867031279931448320708439097097123329288827984147624992816600808071169729937545049570486475584657847693782176141509280991055376028050914295617096308594476912013198828582959963929299029892064581232944525230322295057520197039376148694675110300737207510360312536642819665868667538650550876050739504029178598609015901074229298589923764571204804434708845756043432339924267896323700888709855776224200404581291916089362704835551155238063127723253781012074310947173747734666171259530700271806965192844036271824859299472464472572041643495007955168975614649627039265345729434404778784603659587135744341244034798072888738560979573273934625142653502940763594224960637614123856526671255095944781896288676184491764391934275899416033783773810406377044375737108941979742675538126540152876136442968158574319317581733803747311294958078635112038610501833671587496901328979569281381228900953186059606221075961472498247004693588452619547184742286164165590427972838463736919462297203617247228170817926730668094450107744748070263431760569242723353426030984777320042122873366332795579825433675596279296456465787763349462170597304675087858542516681531379075664928423148778563348490415112562543241353536913333818080076663404111351699030253669083108191207618945520753069010057601955326942758810515469510664444878865760503531152915430168609122146089175757352311071844255946521029376483685966988188577467790709727422195869451360076756968818269168721257877846565363518319230037294576412384715306495579126496377049797232499911490463894806071579924115395924647675447935758624195397873391774408035900201344209883051073379001800397000401207946867649826731743226293340438466115210216435089263708909432763696717315879357644326960162467379881265871397643148411314566935364892622949937864056715472358966414941399640666197638623941856467060707737122202327100441367422628528776109281206940003353834812593182428900910001483668264925035264332893695987116851240191831774623482957220896446658750327020870395165081937039688925252399891333353560338818000671526999783301227897915316578376365477737709955629189024870364882457895232419951253435504354063915569573833121379682745234883744576427120054036399593229656816621008675209422707344423588618110789698532970673525961052601645792785942131993433943575496871990555683499113923427904972775459755768410729671419907676055861452644737502541409655809405630570996172656903297185179922450372933453270750762051185332036623272321168874039782695508060812591111204482776405233757862586089297014205670705694114574910823182711789445161716884465120814314596055047400863714012958950570058803635324801578753348313002958985749730342671979181308386997698177567866956630028036840091908284835520009070375979502446597831613908488259715759867048758194872894584639436089885660714403314804007233057329012551333162451287498501323086888519970411089987302530986768952942777977809048430969366150271682989057975727634979812287088536711222058670455765718003457327568173422734717671105252099402422167787662642678184742143638334410392446814925440162665664051136828941694811407134612314263909457130434452792652715188630417484814612708761505306178360849176761832381491138318586976692770614151983645849332677607444885623849821431503774733165612634859886945399892067253805733332396838219797870242784775165365863996922867190876948935593491345934412987589414038816033208342928214580400007959237717105435394330179510730254193500652310488006505828056620677955561457346914975564642447117317762659366937559701172751788059507576351219610467981408599720777922619345954100690746990826553275615428458340600114040641697207192199060680244484787710075253493851966631900130532316591856272133389684450576553975439608155181110433444633762478593750376966496187788750547042515233431711196274631659165579260912036079009139330806793563080660315687372555199004770376184075111340920868453125377259580954584218268023350264767318555296323889819380145004422408266215154275388776290613172502223515230590816339614810438119638074540756970021179992122892387720756456231095748342204469896872311392637511802459803216027556623559418217642090544713925207039569111324271420445238170512051677346011931100835972243780545066190794258194849917633136863188058985032116335129419859574200925533654380543783775465945868320688168752798384931443199110128348149859889524805574016795079482352015408433351154682051617839342615443199511981878888677801349206685244792499615677999015956659983979859598615271960815055160426173971095269475758338816349572070385093241677926157603450333524741082844359582762692176704237764548140924151074082107795682325601025479683469557526528251560734816041896772990940742538864072423883604813013751743752395873910706195533877284181149368280613224147734833857352733634683439933405249734962582207332205723589720920121823448165300734573647743416396437081829350717591111135071111111003828938851024210238168839176364873735960522719809686387614219589335950356665790593295380066391634427739525482858247683315457497418084084626827786123827460764533474409461624151550776330895864715796920752539536335060100862418208414763288883277064367275106443063978213520693298737995091154537507085306000832931380856646317678374668587055646653948793515909268830326128995244220608402243906136347051904986082225262660910867159461659268495548830951473331934027493541735772797469626271569855677334030894033670868796138866685174956180440284644415425999389772012201861406185319710728647112923136612732282617982935700237395353615245798760985820281354784396727510311187581347761360360087117641907892643238508098959463491410834295249087864599065260882532468859249090792463720857555624406453851328173667530691044746502507702660759529565276143036492852588051951967457944467003348626455889112169756409450102554942768483358910574318120606359377381641879096645662856973344806721971467855672827498400900952930057711815197141502006177662637398792648287027379819498132129151722533567849183937370958312192150668075651755208985976562737758734831681718399808570580159615700970958163822194228697807503804554165514051162900315583463580816281645401077452800791564893139240319127399218876733413564460081664523054271512479102556948186447540388836396234874289851485248157452253830897621168574187831669609151669758142905509756991075875900488019575148933666300164593534493202806636277449606783743284868751425783143845952316878193122024443947013017190855882483222148559740950389647932329936522005819018527988801771702963522868650591029098923058079127527352176238439412764911420723419391370755498116701745108465999193483960456815464772001514973503798023782699801381634744493674116077893399484891235758228048166400737682179746327541665756624047005400937561556546444254465088968972137807529228581498828688994581492368506828081959528592976918331710523299386809507609632792246480899277539346707579440886468778247366811774120593358316435733162714650474312492418586339485777421453793928550249482289663245945531727274439428458066154679562662635505366160030924931638083028373357707880872068769816715506967216043069591096712730056350429655832466482664937938767198548631541441146863993780154943508270002387095797695039112081508368057789886348443707033118092740541326544839625644004516353009178110977518035004607710458330876045257310895920401524384228166486073354323962659764689993484416447604824304702457334975660327834005157354355312098111293238738186518115137266241737089253591398293018002235744762437142668024096364817617270189951088919979881190119927682647044877502625813807984091268568934052809901518817026441122898354389913428183037570215923063274205800902088348842960965222675351424885269351853862092477309824480015551767526757678445705290935677761629467902053121863258183647610911323877171568235603569757746481953144347578268473729099908173908573153279199273493559038433709832886595333217964187601810671168129720645089122500843572990960782144664673316222252895289476137961197747929356636617630440988397303759514590170559179077083386287850814625149374454065799918163135544489057849050678651897097871400706520437919810568787544916957267144438880617244280565365955472875276864649688136655430140507890922736318347795859391019075892210170383645038651788460461249638760173636693317091332008395168952334740190484849856904380155938288279433249225729311471918320754760130068291850537438568433992608391249888277028996867989749690457125662176829432930937341088382860635919516467048179755047227380769611780249320390978172058659729775680898444014455843025421849759942145444892480721427035159651152650925362002643956900038136548179014034524086238124156007271372408390394377523206419445689414166870300912668306466702968189291548040674156656934074559942878983377097083852851555007829802432412745345168042281891963938479849396924775727389855998677940771560428385628817340464705224705962538820948427198560920841242607661165696666092693350162612793858890631420592448688115563186638512387843342951738419792929781634618168634235047016350498205632926387031807842985533338847396524779746479750704632272523611270521024518400307847350943668447726847557648551098413900810237634511669780084738601116413753366882323454245075587077812541666200127653953319495384502529814812221570750971259512051005333699536777686364301321965711237491383540969304188951002459919519725571862959160886797989179458134870108777705085517894785411035120611562501869366874552206590885537657024489583825418128812987291013218323165465722745480300970960810366583802373433657710929793219803979319423099539997542625598323463744336262405647772202444065574117716553847252602513175795410358155030082884944646452211069113586304907437556075917585326596128350030910335676888414425066982048881860713085779076814002939743852646400879829857018552048656517713085382952174369080164068388184238599179329682036808599687387982907671549731803335223756207887180109156622349710412857950241623547580609011838457552790281038264971157559297850213590564928816637754354851264779229264492156112050716645293483307279086348231854997745189372851874818445301122822703726604610288963536852826959476402548423204044608364112501128431227613897593697496226846745116674999998513269900619913842467425159561867369228700779863651542821973559324151090153403459063213445259670810096109706425706734366940264232081367587986849852488412032499343807619072930690420623505842766882216904088802728590935503196826679300166989186423534191719872806491596375431186902061286726926598611629306262884639274671737155420419456883706610443054944333463073223550250239630068906089737140934394672084119135240455004394511626271241372477943457420405964353552661217589390042471096762182625779718930787689222766893453747585963962033837213012372680071433017783095475545510546020479914287107066791852298011835345763122770317645118960896462309351319393600379603170265814947189392526828914606002552005927914832851830965725821737241557904920030245942986669883482126245110320090546348992569223455492540760266916884230863938005598327203538032526745781429051159364232030577545320594477740643670945440643870858149584140910932752637897815393431388092545839584371120872444902581411485349083895882430861084173305330614144561408227484452901847845550008551035091298347386913888383171324403490561396727074205634649810720706911801477809681670553784467101212509790060322567467468680436732876345288271832008630588355079915039324390282188083019096730641538924415211140654125188971729090879142364048245341546641793361578025124260355145500149247182190764757287258173422004121894977931346157639988144067286659325924089851398344626524654112817954589320179260873494002075613982789208726010954728563036311969208137006360775826953402643911571350316394207870124108994000812421926873996661508026715505945935673256722542122913687099535310895589065852588159689256436896231671710736829052004685897913466701015273517462118060794947757009738685359079791082593050559957068610241130009415222915272633087555549748705810175479115756766001811786439413635687584535945397943084706302115859698355408149636971195548310321727140954277599798022910444539195878638621656005010594951194294740164860692880055734501402257630790362538930301012102712815688382498446060402000320537555181379997906748835899434164049498217895959238960488393691760739237059182992395810122581720155153785597782691388182824751124729854597656207368097227087755181220330442741850659198684395088849986928228581077736229048686703446164139531634556509059641224497132973479797017694300708192092792345480884830373258173161047146121993200364595881911573282778758817807122811057969625216097040942780808399328994297253934426850945160704258021114700263711736619613657773741046748566202334194009115681520352768761278501739980184186958505260216174550985510789845805214037603495972873386961979215094695844570185820572153024450723322017543900732377022490781304459573750292643792245691111991942821702864033476971130572159080788505862563579371544051908872718106151850136731207552821243156985956007492740976329179894016994558158767953061448083650905824974457570403044476544719127185243716272833221165567038003397624881154130580470519245580551839421713825048792818095694112269654025123383651415302514595259998987940956622550305183934397468115355076961261214122643408040817771309494592305757374315436497074792047038636751540352356657132850173831872431001120116605004167473200292879495067852539191741525805761536278689513155056133206199619341894254130520275059536622675198929302574801161881717904156013878796800347617887190682061661844583358541958716761834783287116530635503823803073505398123211955434982328063690530382049766621743292915647802898595953271131672971342003239970295699975920038818591488653617513720229027770643019254815774077380803753535415658627433331162235239393588419432695007577629646120375328570730864351318672803207928411406262558136911206429036626243023448045839978831786363994396652720635058247479154858019182923390533334525146854511616893714428183236833013467864218946626491678545006884126879864725737429595637364033132584990528981835018344571566187720756506551439566974613606139928378145804060856227736087237287895562014580572465195375338505881006520500164990979068988278312530919048895075397170131873116229771678231979009067885846925839076510461501241430432937108188810539700665852373719938737751180525556743553867431104652920992540242317849551834975899641820700192270627326334346010032636159267718560750009493194885236922137106213487816212238205944539213217564490346003409837152277372752851708251906760643318274298196704793089923969196609536804891950787430382474954303743881473511177608074281573764568690347284016128084809575483340657806278183585395633200251786603170902976220218348116665723845519967237718459082813757267478043594739309921574419753500342985804659745504740590018985057191439815651530827574605839912152073122353922333066963593823090502092617018408273361213021480932936981503610449591900238592828150198727207205777976097265467287598939876147424021488558052011052405594134845608023157513573433475667077727075822991712371314624675761699116820346468604529323107554823536805940294460374543741688769823370117066931406606133206458735941868942855926451116563883889827976641407703606288630335636650725811919447686038364910535378911727674200400420035458999351098629759740940102445387852385009316249069889986496982210543527955042271991982632030610113504749213919122027972580012729900920610265300562217603382691106106694668577892122984649667557348373894785664881586548992808368980234740461915987450516939574180690051656736274331779318376183728468565548615363054942254067220819527963083827231271990842960732608195361743981831687571188117537587034264747666026956535871780552814109211888890067271484963677860644110303794630789057003362931627673370262554416492012111261796526604082776444197844221748125325053078584474495118565772701929551571682122677344815606957394933686937266941110471080830401223881543740880988328196432604114158864895895990907302172391970892432180579092532698708888634575950981300701125065082346030027108880107891582213656568326811659097358347808500360229989947933022264233546571090928294511691266672439318976624176593594164999227430851991225657563218069130880433372787952654854870600631892964939434969312387455853950650736377148093818439854894778030295566217674109390342420195332391513837724005246875362615424421938100989775579602176478512116147568355437821252155996606843147642298432856466998029965860505006318455380424962562314372962741746585103820207248613090426111162086088728802011579685948724292775692241684327596329918368856033882971002883071177372061949985195058899264749676406066418173886611004863115834293734114759457761614384150303955065611218424748981740771856475208880122263789415923600975560941402621807364429068537424107218795248676235502464177255746048746058626280497943994661049351402038238436971477657243771422946088746948350584076225170624120170504622060707371955430050113282466869911914832292596612952792148801237957088912369695128105258118981891765594256819170809320446014003922201038965710466799329696484839203262056491975289077421082833925537196974733030094190585034955048018045848881813100224402006073599368559836326342781180547654759565947589503895370817364199075193833475006419248057254630858003775378872667446863270426534431737101053564497230339578717181209914420735625838283261292051836215089773906437314203533924389530232300075998041940225387647025565684135632045790860425551393505876151150235561757098082355658560001583430038585473535753812684413738280069731914885039037119382983736644202663208706697456913995797223375149207147896242117212110477449902298989857121782253264865754084289644364926715180195629509664442716016740263129877997990537783536392210960782520147256937675735485846403021133955064565664239386285695584803656317674737702171745041855840091385015127004056442979936149010212035129569799971652465969549057820040121995412360974727101250095985554359020241242573456744692062570898825327431178043663767412133782068805607203214156402665482585951348011718891616434324845809508013959509680266888309647357569346262486641342870149647250676607290061845377603054848398739390954492663640365761475844752540736854261557584198477665241668320825774051740789956508737307380674743294265106675074958072639110043772832225668635430238685218397071414479521914947074681528775820644927515665948303839654573978028919690457257758101093317478772751047615921311787043338836443997283844904703073827088440082616512091716946051364424615238309436585894539790916438703367648566954282220067015611880420012739317721099976785294344838294076739806439375502099367526105436182259156696992428245230987600044471571940404311937831938945787157960426577649880537850511502313606241927299812576855854430039796299485875575189935460670394949294605842300960454694325808353052350163078132761762219476303674001673426395015856902492984823312832770946543775689613161019597517762474775715171972176628882707750725269469955409478900437381821896063742370425623314959247976637435164495263410415886304151771400601703903883071666714812345830079463640269448626166619297970864635784044928609266550017540295872311638453991194098832022545121012913033572068541348337603160023406908948398917176334094991827278065325238072005314522214353221241750611622535324634495578632321123370123077158272561752943136000048919162284932915254529735374311568948472978273736335115232078747945680851175576588264788680127222187969784819618319387779060873686272347872409763560709642866473651876187445567585320170603433939006048822204641187446551396355519813925701442855337723405824237080097168389632703609605146967859175825276087218207758037439443588719851275642695973070690884075869520012796444992684196983684933798753600182066279006952912505784232128875910832176013485055774175252839133618694587430515574083811804327257610752864301612934174969233612274282292915429959317689277267909682827836409237823220540516869897900414047074134335146120138374899625163724545531703999364700342486395107297724848688987879886554160212331351476592017759228981992229654369762830155776380286156619957393990526149859595851639776966577604669708842146357025493582248234020432665613419737138928161634430471955193194586114959961050094169491839382085507090289866702655686959480166123726973993818785343135775801395396180147043809707130103588738075132270938929073742136552520748403482346363735956700434642677429828164837727971965363988158430048314252913653459374022117890710829071523059917981669612489201786955804649593103233959616978329334176855902040315477528578371988362847732353673279006113576373992420160313099992384892136530909763583260762156814469130530045240248293679622627458837149637101777095867827800778608350555077935444621168548579379657918162949443337573245630956406240024413561660375381595037587487383810742376514394312432682071062982917522063028438917914372959489190885479293627500917679593633062357230625189150508741419986616980367648041892769404605546524302426775866422444706050846902982282698209727777789880393136528312188642964343974534589560263794630786483613602648009845019850236837759176679658639191219864699955774459385101789051929254007678906311204873054971528838295011239428670316001061122815867634457501197301194406362697525520863790003708716001664870569229068586485012222606371882139346939359263666483981307018713597414139017113527097657883193764289267771642611531850647981405017847160480869898344147113173141178520050091336072298753410254901705985974411055139164190663700796552248285036134429347189166801410539623389920357612164705524314763055291001167930871046769424526179926358961663258275058994314063148929027224320405929648289955612122967543639109036633664243571342596876998968050294529443057759483772582729744166158020316771793673196844750283383978789057432541683898514383463080559620807464226920829160017898657336364812663150012086330969018718725994440845542914588949592633905940314740088177374202434849453507783974083610719345984364838506636642723635618376617411852012363396296031834473492692988964693155912991949904337192560408636601667026004048126423460802623921347727351625734140063655339210851197760299605410935248525704459632010521627432393086118902641320459085199921923277363310159558090794864035887204298460604624595694828630430248692715054773644071273325138454320450306535500113346131251969692907295387875058546849380857238191054903866009722244037558538345053636608361957823498827484333308147050455398235053874233866736867780594634678612383223047461255616187032986114197868183847000277755721279502722203861034775757320672916481915830830018450183021031199711542278823138562762220989681640881723185878345260677675896655405553256401261274279470381534696755863601397671801806089077675387603363092702946018956345119973025960091861659954657716589249349620146100146087260593046534238247870179526226748289632825658166323991133686247833439285089230728290375194171495072704976207257636352147821946579811143572655802436304960612002708608879029643944713403195666809117322505434756642544035357709752493902747130747965487015754781960987311075444725492349318136335122817809270988562923975418261494958601052829535828687652669661426902811217969332580248404996576921638415484134147947679086353330685170583970945593660426228061590647440408801410600741955196278477967874673490101380406829785048570276851862758959334807395861148895290557185640562663561065774343463136139167859847426299647538763737790807517232074862024778049652031490628419303328227599603095411454797893232828649788630034503642596335889338370587890236109570412563149788180511357954226080584200607128547377692326470848657199152739786083060798150693844140349997792544876494609860098390627177873295123636022113227939295342210518926787059924925242983619890870036495797761614233721055246784403672938049114384914789372043841829952837500168580583897515690130609522500671172631464869396998752408295224874009428688044937052892390789323414581344885765030459358049993415396799158278994905387289297384388211231048428276105561004344221468782499660534744506425686768964753628149530478236114399662306146029360871327549731234957735697652923438769172663695869398440861378076914583079925641061653832965860045620402655793979525704373922487901060435945116027411989441050228391684055771424450471597086279303547939826323682458803242878976365153761059247107230167487314224279923477593029177491612065429095444112443224418165196349823586753836625393028259404441904417088237205465186661403895280981920618760832585235878683886509389716846938854384354406113260505412481490893072100131060047924138184977197551161255573331439320386807552306892076419285717437156095057081360010584854760407710024671663429353267948144197512602526794361250299377035729893128141589195062975040060600827095784789273398902160247731190522768691943313195520250096932300268669412914610119245705742447885969823030835636916657929879726230869334837687929269793270405140622616369572474670566335961812491267660670725770134237119425789560917044049296350970260172054102111432162382578408300339436901671839203167955623201411765692702803281417817538839801120167068989101816566147316602939016899388137597776968317390088941537571029669290645074640522057073376077224053650590062481245454759247558955702725324614637416373412407726256515722965902073434818441630791558078098924225400367899801390356512542617168536112378179737281917896507425704856583184995671433566154809642726547000304918518149151955526322433108055204534769895863979196889028281938722527983716336758468481525602965708253761064804983606339689455845783745812730327117911665467434204930739329374990448780903529015627237923267755339515368281563210950938632664924017796500742172411998428601752152734107956857972160454135607342073292104755741717309794528983091958064387952768660086462490723237880851265055850836893595203512944920897215870686990980259695120436537978130663736713385819138567036735886483561759116779912894359204702912845342026328952355445854083605179682744691696680050110553981178852515089784546032160993102656730845996920817990848968855742405487007247789802353280881430121637623448998239135663330722178839455449531996265748471310528681726441199451147931004004692051504619857768423797641588997017704802766337686513556656165300619731934857168608112318518577529832886853944202140979887948060083536051628489870541082362222487583414414629020982721515615652000155199323397080199433228940780187242943441638269342833728439074513917309836736337389759976504190713510514596498950980846363863789888484546471995973345961906943234671716669571209696738814805534676355059363546958042175169875272727048316385925626392457499882024862953061167031669201823574595059764052254749015351870802728728166309547194369591303522338142918209689574459742997273381476021313515827757477089485192901819290505354368870543611868864524786713230563216958295361537684321369955475233610101220374365366078599128087778720308461032855761148054701468963799412384740768553670608540804079173881803689655635622779814631914088769405498397966869395515285360604176229501866262827186144709964428786535999110306498592401409559589088915841028411037330356607717965182025097866945964344066223736763187914797524907370784201037142541413422558981791336371414628295157412441606904650796998330968981469505359729803979598701159372191842701540958561496456176380066244424480246809093752330276901273761176902140572637718905902356681904541600860616309123962152557714526625059803663580946422345816150731459088827495257733126445639276087166894420738548175314748293328739428807074150545476286363790155061270311836543077935921061088367354006044274067023879026827122584694961719833490340268006237263089726708935718827088736502377133574550442715408815970461665418239082466837188751773340689978811499669216836108984612325753868933657733475093356973018896875309330894182451414254251089361947223018921925524059288199131580992651181151513563599841896271380932441185358550145244152091725106690798425776611000077944850021211008348302481533903431259423561251435481513521053612315522897912055560479169022417623500879286913339902421182407396768449216708040759363061886729061813415418376246107581158824909104116381833609380434937661765294421614817041394067965745784825004386877685628443312751366072668814683795239961112055822254895620037477754418639727606046107800979155742079016805690838852571483965760136741619387259641339511168726155623949477567307091365336279521383473302712325574992144014852669454502438381380871317766395619256996035365890226202738760338529380138510684377258854105135749010982031880054565760518072266015415861764434799301283444595344651006168565883393675751412267972292389240070816658639407898309022173496806889587582129369266032547207576547805007468782575775935390365062969711643659584146890393044126970755806339136475930438556142818117318384952667791471076565131369606953944479830087623645761660783666115249487563913321598948291378016335099181688432324008505924974069992779627211587669473508057459895980885865616701771741661434287685075308454834828925119969949800983632513163779215987564016989791019688088355310909519900840899952679172232928206206808726936848703472529050446697248321144256488840278993786614074054349228992350594256399644697119895598325058797345612732701680542205960022531491852841070257085176350141718440203470357913260602597575873385586860535684917240664166352964048755846013105513257179485267868184300927136705567479978724837900325269927863112533694322201259653766501581186197421395680918649329078304129957094096198516405062034264855995980786632390949076004293327498012170975914791240995222049912018637458696936331418606443909107023186319387400805832184539212149355552355338840205311807432354569886769222975563919538782307714754729283449140597397587187203519506971183950606236442073088327157211485258843404211773097153667356266349212555079851373264115961841034070831778106435785154288547301637829765634888731758034861599003798273577201244931054647303906360804210599972867941818494047247001956252938910042237768321395111860505304170470872998633108374156296423539485204044647316780966746121991083192914976440546627327045962533666474241025887660346506086987070083811250433575907928144251976513710969414788609891197071018915404503272797532041376434743606049640743147986386122245155776943192938857868669308813960946515938964737156317657297118325555594115812754833157360610575264317844376409667090842711207630650122957567695447996493968007097127030084865824624184974065799363913387519214617632014002286965496199263107216685473959636761030197757795560120279869062386389547954833465714106613675289243976184099374167028381327006792559887385482345448593725746414828598131814535659313061349048987783193209719120372790176071821024227987968521510006134879197895998745473870302808943728759200954014570423636386849814726409568991395155510373385885111673724545252161666594712931368614314445805766848870402001112899557993206155093013118487135763097065721312480590676052667322463373390522043112688061221241705388680405950107581594968033391164145007539449916359923846844465661324065574667398887110292468008820482412768194563041812936826658188107428063134534470180937216982494245527607124886456890072509561384791920900155155021283135467367669329966699140220087440120213400648941136059577539591941735409527306290191061263593282183321617481512837681688689080396640010522927991978306787381192272296268932899648287726815424652032108384592976690075408171203522151264313606822779765808749818873399803336431842355958649163065776630790660216036763606568451780580194030307756360087538576271533951011144355299280082942675072377015533037427200346071848417190587457883290412844696677871427723463586024071755391775024485142647034026758404806315606249558757088578300668001399649234724094463642726196142155106263684268915536377411197555751891497682216508018058914696309443313840252732367998054861321662002841787271590910351360540372967487297952369174556111354866715038758709595604841225118414544369833987400861727145985442826976428142541572134523545352571994988322000172377258229907968494774147167221921406074833910171295350579552780586464322446935029113027891822433518088892025765005077730019294806824731797830046736052772042975614811396637381928349564485313583625799353533130801722802058021331945231616914556055744706960503568895004682246021511458423365256217142524368859878696778436796519980358012734960463668736182318989831462457345578966478245746178259350493818714738780923047662287934278934840330800209390690008353415035492752387787205296841534779941351368348846556881394736880355751685052294737824021767251131235246146106600941181409702152710484154112811742444374435950347480843376490283956645437807987597521624818052232095059768405329019202954061444496544884655390494629652354193625239216276474472531013469363334679874555057791237502523314270465190215836157894269956078174317619341087370108926771947247115221831235214542695055951938626045283555535017194237436284536438435468067985997628275814002553291344770687188616122698570632967363908472016249413104967672352351172951279622872827788086865730279876248066377095893682721926073097068500663138430851140544480883480120865208808766535139661984116887763556724830253293600286279038486473230443080777315504791990550780871471292211621785370695786045842167505636208424268496095536754900359355436696128749845462904444016529978078918184686924955660619369345127433966621276831029250171929925776125391256734357743751000906590758612374485600944762399201901493053884062467227681803834376796182505859105910985248843622192840063806500574193851574015279306358523044455430423244515152948654498955578470111451844335396382918148504489643546768814678862370041222882289678040894201315891282619234680002061549660018936523700234354915350491134974026222366360013453380046541713144371085779035282562116996739656842519449455227031360429012122182480708315121761161913327702522639200945417236969163395662300212274879417770438668082212291805364326620649928966664442130847424129061648980441825768000514757959739795384516860522123348801820809079089264975169103130342953682872787907293447976765401175153037410778655617909902064304424909605489481617273585851372115321099254947557974077525126972355204698146873747997154860722486753641633090758049601346846046272829598358787990268944480083621096209177506325566729169825854512173423994741283922698963076940305613764375530079864403140662352292048032540101185311068465517385885747739092089407386898781665951317895616900776873145663981743612981919459195789831859738500556933758580410355304126542066008456604049726084950949517735240219026984982308103171464053281299990136296549603101103760906078911747690808091025266651091205411315879643384579844121978267705742785602028387503152847141551655026654855860267978807343870169129763558461633133898457680493831820585548676508279698078557418314775204734311165602803540937909937247096105137781471878598477844970558779464967386547823870051236492196499639741513652908485756734584693260019304747981914313140283972307613344295182333256446479979556752874370756817960510912884960936251955467528739410237572647702646422460018887566780558419375384835874315597233764355411076256930270157850952312046323793706772705275418616636973066631955390811550042333165700404963930605095350210378273372182172766708513184926530421825905666623807282817710428699968382018798469944485578289189729264776478094511042502624437420067811486623426212113822209160090521009892013685286410396910965019699138784567685638040293182415249224308835740927203871069747755978987014088565811604554318688914305358932984342208839137343220477720935733276648878604732265974659645161187649625144004992835257258232088257754989208947341191527838618500739386349624894704159327846361032481896848538370256846476815572114919209890356576077230803422889161350827125760728731485376803461819666933004211014761179905704081383944600945001069265713102050196789082617822892039667411364808202079185630528680751188818618425945828505261510777762132027959550523827438851960567258944802641719764679545615304112789526261351772676504976896994849669546690650885628839870134061312531280856495034080025266964977381097821053570357747941707837171004302883574579404177764807003373024978787855334168550040704643560956136428500733506200711317325872261346385512979027133714334507554969489820029716799945587779582892099934281698460151804332944737649623314619968652777201754395036276216646501209022780857984883675955702092963474472523372216596599337363715689337874407744947546443732858677746290419684290644980701987204583619835253721332775533128759287031985770826890062385219457006847233617774205201590302356034926821544153553370414274455936214272915836678577262703420150257229401769905714648538129572691541281600030987899788908826483573441882413508465870353458851019892354415663112224880609285913062250035525892069179543576193015217118171519368522445442234905670936570542792634966370567024114377007666274089023128379423182505178352829828673351932753139325116173849524336831315137414555009275348194640714777720560870020422958169916192363871817823889486963959994286650567739727075511775860452738659410755322914299508408154851600908793896922436338552354337359936838160111671754722984667141570799684908476940435898456729519565377791971727655518238684707757847011850930764722601900473319970706395852537581918056319469805524823179814345683763746803472774351911437333981892946611180294982959045238086862167891514373923531188666958816211740828115880450009703843573652147970539389287084965681201305266584259696558512298427594345667100607648335963246297741630861513801004506365299418640407808092789940224443649834353428635586540302917264150004146649521830253492608075831248736257950589660600917575930359895742756490502525468397216171235748369855326832519457017269157444414960561300074754815348712267195152283877851712283866051225406132888939260895766657746518068813743015434147998462119643126352034221619071896382693767272230309484398700313046208030147671437344071625311987385994723700035009436736919174758128794091251090096789424752721467076906148261735775866869689263571741168335049645633710986016247661832969595919117713533612419310708162316685719169472258657949962628305310633410734906970266095227585348072292491313018312439957314245059552367231711849530400147974007070135014887009308007099336588332059167884493286948248921134083968438339578001495895215176562248218479329486893541273654082132796118864575797857353508761173010712295164822547587690733656768826222641334875883122942027130371710127538529881139529273451655200785127810265731685275306378758728882493391723928422988418620625717330505696991173322459951235429367366858858443931971079851515935832779559792920578209075018154132666323452659409673630198244670047587691841252845665145617062417698691275636081655073531218186131375357916531461864825608440678090302766663711499867911194038164971388225203014699065005836631804959346313789077432695062069266551469012367972609971412920737194960225647840783005193172190465048773087919500282596382154590435347676486466869156909373055892855352783336223004728416662550545274307012632793636172418080292546645601475886421532482801610185985033213743117861807027077898935696639455025119937469204184911957784390871710611343589759837550769009224612253777669224542354513382299185768598274800690681851532760745739936456930283433937072262836706913749197993783820396782571900975819867286191247970871165499081082501869438598534499746318469715649056288929900822465092740321089817033002190693640740792356713855355682472697823178394557429990661910252834449860139010039495211876394367763763428308954238705690645653060072468577184480991210159007760558605186977439857345698847176263593172595302236811402399315028253827621274819599078802925399231100277946211971177053548283574398686252442220081265662755112370663084601055293339904964402367277073847422679184254258546466245536151778789091350777742761263686129809662068092639486202864098751406519760226812776375632483871407957598045812008193125985614284342787853580340320176838715247145448988921424578620433166800292077489745491102694261284632330279504859630051750736557056758770771000944005479061042514200571584680690279200087549044160612507905729017524100425384047975050603777062141769276590066068886367409038119815603376219484867605841098625136046379722958797467654982568914639928213865890677191528673539716999942104861534872093426899344153055706918287512581571714907892794761601892088285048582459163550525933968253401003364299242497957468348734162414518073683167490607953435241985782083852615105018600878936568457835341497121761837277061620135719704632999462472827219713293663470850562406442082018341827010425408998837129733598120514053350026795930238750957350682767084097641144175251745835284666186956108108094720207249667905377020477032545945843803003036902265325324439865005497112135727895191713602849317598130374164614715594589503221160141126918558373911142363679666593312893013997385282408331132106230614796807744290254219848595049167258366711315765362776614559396856230009594245966898015724213719769249223501732030530919737866899146666990373444459734090558814343130951923719485071269251353464692848332697709251504433896961590644012707252241516978239889206065823846279646914750629758216960732216074623519278400817825536720927790663411634673962602141257435164734021797667858304519343418613584552749249261040968944760536002249292230209504521904490342330491114994047233869463394674919379501573821986350849240767158833212346163843574629988534481929695346467367434276187710462393616707693913358160823921974674512028311458789151810935917096864676065395719895431689483247514128108690790756622452387409706564369099472208274326252543435615654637545743633204951708298957232732433424747717978766844019978219036760993456941857303023452519721761021655900845579233650697865367271828315210451317016685952324676358590808283462410484173082348940802462687507861320858539106444238556518433063906190973754616872582998631998024302420188439599632205523928128511975956396515909675272717261757528300738174016877833224843806494079193064126562446900784771619474963434911204529306057908194217263026313737579976422558014332777602432419017438415018399275354820008667960559396712998290134220059721032841634134464867563851603891626562587315202327033691159517875164316342236428767156744748248249598858420132127972849710163356776463582168887589670344866701728836540829587899896040478340040671153952994765538190870090231541164900673913919203365195284291822829182361554798570228806614819970391840628865815903433179569538901729067211
Используя кадры из шоу, где видны читаемые фрагменты заданного числа:
можно убедиться, что было задано именно это число. Ну что же, значит, по крайней мере, тут обмана нет – названный победителем ответ действительно является верным.
Ну что же, значит, по крайней мере, тут обмана нет – названный победителем ответ действительно является верным.
Однако найденное число состоит из 79899 цифр, а не 80000, как это заявлял ведущий, к слову, не использовавший никаких намеков типа «примерно» или «около», которые указали бы на приблизительность заявленного числа цифр. Но математика-то точная наука! Впрочем, на кадре, где хоть как-то можно разглядеть последний блок цифр, видно, что у него отсутствует одна строка и одна цифра на последней строке, так что все сходится.
Теперь разберемся, как же можно выполнить это задание, если очевидно, что даже прочитать все эти цифры невозможно за отведенные на решение 5 минут. Сам победитель, объясняя свой метод вычисления, говорит, что оперирует какими-то зрительными образами, вообще не считает чисел, и т.д. в стиле Рен-ТВ и ТВ-3, но посмотрим, что по поводу извлечения корней говорит простая школьная математика.
Для вычисления произвольных степеней и корней можно использовать свойства логарифмов понижать порядок действия.
Поскольку мы считаем в десятичной системе, удобно использовать десятичные логарифмы. Для получения конечного результата нужно будет возвести 10 в полученную степень. Получается такая формула вычисления корня:
Из той же школьной математики известна
экспоненциальная формапредставления числа. В этой форме заданное число выглядит примерно так:
В принципе этого уже достаточно для вычисления – подставив это число в приведенную выше формулу, получаем ответ с нужной точностью. Однако не любой калькулятор может переварить такую степень. Формулу можно слегка оптимизировать – логарифм и степень сокращаются, умножение становится сложением при выносе за пределы логарифма и формула с подставленными числами будет выглядеть так:
Теперь никаких гигантских степеней, результат – самое большое число, которым приходится оперировать. Видно, что точность результата даже избыточна – 5 девяток в дробной части, значит, точности в 8 первых цифр заданного числа даже много. Получается, что все гигантское число вовсе и не нужно – достаточно знать первые несколько цифр и общее количество цифр в числе. Для 5 первых цифр (2.1034 – округляем по правилам) ответ будет 97865891.2, чего вполне достаточно при знании, что искомый результат является целым числом. После округления до целого получаем верный ответ. На самом деле даже отношения 79898/9999 достаточно чтобы определить порядок результата и даже получить первые 3 цифры.
Получается, что все гигантское число вовсе и не нужно – достаточно знать первые несколько цифр и общее количество цифр в числе. Для 5 первых цифр (2.1034 – округляем по правилам) ответ будет 97865891.2, чего вполне достаточно при знании, что искомый результат является целым числом. После округления до целого получаем верный ответ. На самом деле даже отношения 79898/9999 достаточно чтобы определить порядок результата и даже получить первые 3 цифры.
Теперь очевидно, что ничего сверхчеловеческого в продемонстрированном на шоу вычислении нет, вполне достаточно школьной математики и калькулятора. Да, вычисление в уме дробных логарифмов и степеней – это не то, что умеет делать каждый человек, но ради миллиона вечнодеревянных можно и научиться. К слову, на том же шоу был человек, оперировавший дробными числами сходной разрядности в реалтайме, тогда как у победителя на выполнение 4-х математических операций было отведено 5 минут, и он их полностью использовал.
Как сам Великий Искоренитель объяснял свои вычисления, уже было сказано выше – зрительные образы и т. д. Ну да, видимо воображал логарифмическую линейку. Наверное, не стоит его строго судить за это — это как судить фокусника за использование слова “магия”. Однако на шоу, помимо зрителей и ведущих, были приглашены эксперты, с целью дать научную оценку выступлению. И тут – как в ужастиках – уберите слабонервных, стариков и детей от экрана. Иначе они могут получить инфаркт от приступа смеха или черепно-мозговую травму от фейспалма.
д. Ну да, видимо воображал логарифмическую линейку. Наверное, не стоит его строго судить за это — это как судить фокусника за использование слова “магия”. Однако на шоу, помимо зрителей и ведущих, были приглашены эксперты, с целью дать научную оценку выступлению. И тут – как в ужастиках – уберите слабонервных, стариков и детей от экрана. Иначе они могут получить инфаркт от приступа смеха или черепно-мозговую травму от фейспалма.
Приглашенные эксперты, профессора математики и информатики, руководители ВУЗов, в такт участнику стали пороть отборную ахинею в стиле Рен-ТВ. Один предлагал на основе этого разработать супер алгоритм сжатия данных (видимо, слава архиватора Бабушкина не дает покоя), другой говорил что-то про запредельную вычислительную сложность O(n*log(n)) (и откуда только он это взял?), хотя из приведенного выше очевидно, что сложность этого вычисления – O(1). Интересно, они продемонстрировали свои реальные знания, или им заплатили, чтобы они несли эту чушь и позорились в эфире на всю страну? Судя по интро перед выступлением, этот участник решал схожие примеры с корнями и на предыдущем шоу, так что на подготовку была минимум неделя – могли бы хоть загуглить если в голове ничего не осталось.
Но все же, я надеюсь, от этой клоунады будет и реальная польза. Этот пример можно использовать для преподавания ученикам логарифмов и степеней – ведь опустить всем классом на уроке математики двух профессоров этой самой математики – это же так весело! А знания, полученные таким образом, усваиваются в разы лучше стандартной зубрежки, и прививают ученикам интерес к предмету.
Извлекаем корень из большого числа без калькулятора – Оценок.нет
Если легко определяются делители 2, 3, 4 и так далее, то раскладываем число на множители и легко извлекаем корень.
Вычисляем:
НО! Что делать, если число из которого мы извлекаем корень, является произведением простых чисел?Например, 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.
Рассмотрим пример
Извлечем корень из 190969.
Сначала определим, между какими числами лежит наш результат.
Результат этого корня из данного числа лежит в пределах от 400 до 500,
так как 4002 = 160000 и 5002 = 250000.
Действительно,
Далее смотрим, где стоит это число:
посередине, ближе к 160 000 или к 250 000?
Число 190969 находится примерно посередине, но все, же ближе к 160000. Поэтому результат нашего корня будет меньше 450. Проверим:
Значит наш результат меньше 440, так как 190 969 < 193 600.
Проверяем число 430:
Мы установили, что результат корня лежит в пределах от 430 до 440.
Далее используются свойства произведений чисел.
Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце. Например, 21 на 21 равно 441.
Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.
Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.
Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.
Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.
Так как число 190969 на конце имеет 9, то это произведение либо числа 433, либо 437. Только они при возведении в квадрат могут дать 9 на конце.
Проверяем:
Результат корня равен 437.
То есть, мы как бы «нащупали» ответ.
Как видите, максимум, что потребуется, это произвести 5 действий столбиком.
Извлекать квадратный. Формулы корней. Свойства корней. Как умножать корни? Примеры
Извлечение корня из большого числа. Дорогие друзья!
В этой статье мы с вами разберём как извлекать корень из большого числа без калькулятора. Это необходимо не только для решения некоторых типов задач ЕГЭ (есть такие — на движение), но и для общего математического развития этот аналитический приём знать желательно.
Казалось бы, всё просто: разложи на множители, да извлекай. Проблемы нет. Например число 291600 при разложении даст произведение:
Вычисляем:
Есть одно НО! Способ хорош если легко определяются делители 2, 3, 4 и так далее. А что делать если число, из которого мы извлекаем корень является произведением простых чисел? Например 152881 является произведением чисел 17, 17, 23, 23. Попробуй-ка сходу найди эти делители.
Суть рассматриваемого нами метода — это чистый анализ. Корень при наработанном навыке находится быстро. Если навык не отработан, а просто понят подход, то немного медленнее, но всё же определяется.
Извлечём корень из 190969.
Сначала определим — между какими числами (кратными ста) лежит наш результат.
Очевидно, что результат корня из данного числа лежит в пределах от 400 до 500, так как
400 2 =160000 и 500 2 =250000
Действительно:
посредине, ближе к 160 000 или к 250 000?
Число 190969 находится примерно посредине, но все же ближе к 160000. Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:
Можно сделать вывод, что результат нашего корня будет меньше 450. Проверим:
Действительно, он меньше 450, так как 190 969
Теперь проверим число 440:
Значит наш результат меньше 440, так как 190 969
Проверяем число 430:
Мы установили, что результат данного корня лежит в пределах от 430 до 440.
Произведение чисел имеющих на конце 1 или 9 дают число с 1 в конце. Например, 21 на 21 равно 441.
Произведение чисел имеющих на конце 2 или 8 дают число с 4 в конце. Например, 18 на 18 равно 324.
Произведение чисел имеющих на конце 5 дают число с 5 в конце. Например, 25 на 25 равно 625.
Произведение чисел имеющих на конце 4 или 6 дают число с 6 в конце. Например 26 на 26 равно 676.
Произведение чисел имеющих на конце 3 или 7 дают число с 9 в конце. Например, 17 на 17 равно 289.
Так как число 190969 заканчивается цифрой 9, то это произведение либо числа 433, либо 437.
*Только они при возведении в квадрат могут дать 9 в конце.
Проверяем:
Значит результат корня будет равен 437.
То есть, мы как бы «нащупали» верный ответ.
Как видите, максимум что потребуется это осуществить 5 действий столбиком. Возможно, вы сразу попадёте в точку, или сделаете всего три действия. Всё зависит о того, как точно вы сделаете начальную оценку числа.
Извлеките самостоятельно корень из 148996
Такой дискриминант получается в задаче:
Теплоход проходит по течению реки до пункта назначения 336 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.
Посмотреть решение
Результат корня находится между числами 300 и 400:
300 2 =90000 400 2 =160000
Действительно, 90000
Суть дальнейших рассуждений сводится к тому, чтобы определить, как число 148996 расположено (отстоит) относительно этих чисел.
Вычислим разности 148996 — 90000=58996 и 160000 — 148996=11004.
Получается, что 148996 близко (на много ближе) к 160000. Поэтому, результат корня однозначно будет больше 350 и даже 360.
Можем сделать вывод, что наш результат больше 370. Далее ясно: так как 148996 оканчивается цифрой 6, то это означает, что в квадрат надо возводить число, оканчивающееся либо на 4, либо на 6. *Только эти числа при возведении в квадрат дают в конце 6.
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
В математике вопрос о том, как извлекать корень, считается относительно несложным. Если возвести в квадрат числа из натурального ряда: 1, 2, 3, 4, 5 …n, то у нас получится следующий ряд квадратов: 1, 4, 9, 16 …n 2 . Ряд квадратов является бесконечным, и если внимательно посмотреть на него, то вы увидите, что в нем нет очень многих целых чисел. Почему это так, объясним немного позже.
Корень из числа: правила вычисления и примеры
Итак, мы возвели число 2 в квадрат, то есть умножили его само на себя и получили 4. А как извлечь корень из числа 4? Сразу скажем, что корни могут быть квадратными, кубическими и какой угодно степени до бесконечности.
А как извлечь корень из числа 4? Сразу скажем, что корни могут быть квадратными, кубическими и какой угодно степени до бесконечности.
Степень корня – всегда натуральное число, то есть нельзя решить такое уравнение: корень в степени 3,6 из n.
Квадратный корень
Вернемся к вопросу о том, как извлечь корень квадратный из 4. Так как возводили мы число 2 именно в квадрат, то и корень будем извлекать квадратный. Для того чтобы правильно извлечь корень из 4, нужно просто правильно подобрать число, которое при возведении в квадрат дало бы число 4. И это, конечно же, 2. Посмотрите на пример:
- 2 2 =4
- Корень из 4 = 2
Этот пример довольно простой. Попробуем извлечь корень квадратный из 64. Какое число при умножении самого на себя дает 64? Очевидно, что это 8.
- 8 2 =64
- Корень из 64=8
Кубический корень
Как выше было сказано, корни бывают не только квадратными, на примере попробуем более понятно объяснить, как извлечь кубический корень или корень третьей степени. Принцип извлечения кубического корня тот же самый, что и у квадратного, разница лишь в том, что искомое число изначально было умножено само на себя не единожды, а дважды. То есть, допустим, мы взяли следующий пример:
Принцип извлечения кубического корня тот же самый, что и у квадратного, разница лишь в том, что искомое число изначально было умножено само на себя не единожды, а дважды. То есть, допустим, мы взяли следующий пример:
- 3x3x3=27
- Естественно, кубическим корнем из числа 27 будет тройка:
- Корень 3 из 27 = 3
Допустим, необходимо найти кубический корень из 64. Для решения этого уравнения достаточно найти такое число, которое при возведении в третью степень дало бы 64.
- 4 3 =64
- Корень 3 из 64 = 4
Извлечь корень из числа на калькуляторе
Конечно, лучше всего учиться извлекать квадратные, кубические и корни другой степени на практике, путем решения многих примеров и запоминания таблицы квадратов и кубов небольших чисел. В будущем это очень облегчит и сократит время решения уравнений. Хотя, нужно отметить, что порой требуется извлечь корень из такого большого числа, что подобрать правильное число, возведенное в квадрат, будет стоить очень больших трудов, если вообще это возможно. На помощь в извлечении квадратного корня придет обычный калькулятор. Как на калькуляторе извлечь корень? Очень просто введите число, из которого хотите найти результат. Теперь внимательно посмотрите на кнопки калькулятора. Даже на самом простом из них найдется клавиша со значком корня. Нажав на нее, вы немедленно получите готовый результат.
На помощь в извлечении квадратного корня придет обычный калькулятор. Как на калькуляторе извлечь корень? Очень просто введите число, из которого хотите найти результат. Теперь внимательно посмотрите на кнопки калькулятора. Даже на самом простом из них найдется клавиша со значком корня. Нажав на нее, вы немедленно получите готовый результат.
Не из каждого числа можно извлечь целый корень, рассмотрим следующий пример:
Корень из 1859 = 43,116122…
Вы можете параллельно попробовать решить этот пример на калькуляторе. Как видите, полученное число не является целым, более того, набор цифр после запятой является не конечным. Более точный результат могут дать специальные инженерные калькуляторы, на дисплее же обычных полный результат просто не умещается. А если вы продолжите начатый ранее ряд квадратов, то не найдете в нем числа 1859 именно потому, что число, которое возвели в квадрат для его получения, не является целым.
Если вам необходимо извлечь корень третьей степени на простом калькуляторе, то необходимо нажать дважды на кнопку со знаком корня. Для примера возьмем использованное выше число 1859 и извлечем из него кубический корень:
Для примера возьмем использованное выше число 1859 и извлечем из него кубический корень:
Корень 3 из 1859 = 6,5662867…
То есть, если число 6,5662867… возвести в третью степень, то мы получим приблизительно 1859. Таким образом, извлекать корни из чисел не сложно, достаточно лишь запомнить выше приведенные алгоритмы.
Библиографическое описание: Прямостанов С. М., Лысогорова Л. В. Методы извлечения квадратного корня // Юный ученый. 2017. №2.2. С. 76-77..02.2019).
Ключевые слова : квадратный корень, извлечение квадратного корня.
На уроках математики я познакомился с понятием квадратного корня, и операцией извлечения квадратного корн. Мне стало интересно извлечение квадратного корня возможно только по таблице квадратов, с помощью калькулятора или есть способ извлечения вручную. Я нашел несколько способов: формула Древнего Вавилона, через решение уравнений, способ отбрасывания полного квадрата, метод Ньютона, геометрический метод, графический метод (, ), метод подбора угадыванием, метод вычетов нечётного числа.
Рассмотрим следующие способы:
Разложим на простые множители, используя признаки делимости 27225=5*5*3*3*11*11. Таким образом
- Канадский метод. Этот быстрый метод был открыт молодыми учёными одного из ведущих университетов Канады в 20 веке. Его точность — не более двух — трёх знаков после запятой.
где х-число, из которого надо извлечь корень, с-число ближайшего квадрата), например:
=5,92
- Столбиком. Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр. Для ручного извлечения корня применяется запись, похожая на деление столбиком
Алгоритм извлечения квадратного корня
1.От запятой отдельно дробную и отдельно целую части делим на грани по две цифры в каждой грани (целую часть — справа налево; дробную — слева направо). Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
Возможно, что в целой части может оказаться одна цифра, а в дробной — нули.
2.Извлечение начинается слева направо, и подбираем число, квадрат которого не превосходит числа, стоящего в первой грани. Это число возводим в квадрат и записывает под числом, стоящим в первой грани.
3.Находим разность между числом, стоящим в первой грани, и квадратом подобранного первого числа.
4.К получившейся разности сносим следующую грань, полученное число будет делимым . Образовываем делитель . Первую подобранную цифру ответа удваиваем (умножаем на 2), получаем число десятков делителя, а число единиц должно быть таким, чтобы его произведение на весь делитель не превосходило делимого. Подобранную цифру записываем в ответ.
5.К получившейся разности сносим следующую грань и выполняем действия по алгоритму. Если данная грань окажется гранью дробной части, то в ответе ставим запятую. (Рис. 1.)
Данным способом можно извлекать числа с разной точностью, например с точностью до тысячных. (Рис.2)
(Рис.2)
Рассматривая различные способы извлечения квадратного корня, можно сделать вывод: в каждом конкретном случае нужно определиться с выбором наиболее эффективного для того, чтобы меньше затратить времени для решения
Литература:
- Киселев А. Элементы алгебры и анализа. Часть первая.-М.-1928 г
Ключевые слова: квадратный корень, извлечение квадратного корня .
Аннотация: В статье описываются способы извлечения квадратного корня, и приведены примеры извлечения корней.
Что такое квадратный корень?
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня ) в математике обозначается вот таким значком:
Это действие (извлечение квадратного корня ) в математике обозначается вот таким значком:
Сам значок называется красивым словом «радикал «.
Как извлечь корень? Это лучше рассмотреть на примерах .
Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:
А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:
Уловили, что такое квадратный корень? Тогда считаем примеры :
Ответы (в беспорядке): 6; 1; 4; 9; 5.
Решили? Действительно, уж куда проще-то?!
Но… Что делает человек, когда видит какое-нибудь задание с корнями?
Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень …
Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах. ..
..
Пунктик первый. Корни надо узнавать в лицо!
Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…
В этом и есть сложность извлечения корней . Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.
Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да. ..
..
Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём туда и обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.
И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…
Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.
Пунктик второй. Корень, я тебя не знаю!
Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзя их извлекать.
Попробуем вычислить вот такой корень:
Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.
Что, не подбирается? 2 2 даёт +4. (-2) 2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.
(-2) 2 даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.
Такая же история будет с любым отрицательным числом. Отсюда вывод:
Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла ! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно! Или, другими словами:
Квадратные корни из отрицательных чисел извлечь нельзя!
Зато из всех остальных — можно. Например, вполне можно вычислить
На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!
Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:
Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:
Только число это совсем неровное… Вот оно:
Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называют иррациональными . Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:
Если при решении примера у вас получилось что-то неизвлекаемое, типа:
то так и оставляем. Это и будет ответ.
Нужно чётко понимать, что под значками
Конечно, если корень из числа извлекается ровно , вы обязаны это сделать. Ответ задания в виде, например
вполне себе полноценный ответ.
И, конечно, надо знать на память приблизительные значения:
Это знание здорово помогает оценить ситуацию в сложных заданиях.
Пунктик третий. Самый хитрый.
Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах. .. Разберёмся с этим пунктиком как следует!
.. Разберёмся с этим пунктиком как следует!
Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!
Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…
Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ
правильный, а ответ
грубейшая ошибка. Вот так.
Так в чём же дело?
Действительно, (-2) 2 = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.
Но! В школьном курсе математики принято считать за квадратные корни только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: из числа а — это неотрицательное число, квадрат которого равен а . Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические . Хотя особо об этом не упоминается.
Хотя особо об этом не упоминается.
Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.
Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.
Уравнение простое, пишем ответ (как учили):
Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:
Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный ! Непорядок. Это первая (но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:
Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня . Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения . Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.
Вот так. Если вы просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:
Потому, что это — арифметический квадратный корень .
Но если вы решаете какое-нибудь квадратное уравнение, типа:
то всегда получается два ответа (с плюсом и минусом):
Потому, что это — решение уравнения.
Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)
Всё это — в следующих уроках.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Ученики всегда спрашивают: «Почему нельзя пользоваться калькулятором на экзамене по математике? Как извлечь корень квадратный из числа без калькулятора?» Попробуем ответить на этот вопрос.
Как же извлечь корень квадратный из числа без помощи калькулятора?
Действие извлечения корня квадратного обратно действию возведения в квадрат.
√81= 9 9 2 =81
Если из положительного числа извлечь корень квадратный и результат возвести в квадрат, получим то же число.
Из небольших чисел, являющихся точными квадратами натуральных чисел, например 1, 4, 9, 16, 25, …,100 квадратные корни можно извлечь устно. Обычно в школе учат таблицу квадратов натуральных чисел до двадцати. Зная эту таблицу легко извлечь корни квадратные из чисел 121,144, 169, 196, 225, 256, 289, 324, 361, 400. Из чисел больших 400 можно извлекать методом подбора используя, некоторые подсказки. Давайте попробуем на примере рассмотреть этот метод.
Пример: Извлечь корень из числа 676 .
Замечаем, что 20 2 = 400, а 30 2 = 900, значит 20
Точные квадраты натуральных чисел оканчиваются цифрами 0; 1; 4; 5; 6; 9.
Цифру 6 дают 4 2 и 6 2 .
Значит, если из 676 извлекается корень, то это либо 24, либо 26.
Осталось проверить: 24 2 = 576, 26 2 = 676.
Ответ: √676 = 26 .
Еще пример: √6889 .
Так как 80 2 = 6400, а 90 2 = 8100, то 80 Цифру 9 дают 3 2 и 7 2 , то √6889 равен либо 83, либо 87.
Проверяем: 83 2 = 6889.
Ответ: √6889 = 83 .
Если затрудняетесь решать методом подбора, то можно подкоренное выражение разложить на множители.
Например, найти √893025 .
Разложим число 893025 на множители, вспомните, вы делали это в шестом классе.
Получаем: √893025 = √3 6 ∙5 2 ∙7 2 = 3 3 ∙5 ∙7 = 945.
Еще пример: √20736 . Разложим число 20736 на множители:
Получаем √20736 = √2 8 ∙3 4 = 2 4 ∙3 2 = 144.
Конечно, разложение на множители требует знания признаков делимости и навыков разложения на множители.
И, наконец, есть же правило извлечение корней квадратных . Давайте познакомимся с этим правилом на примерах.
Вычислите √279841 .
Чтобы извлечь корень из многоцифрового целого числа, разбиваем его справа налево на грани, содержащие по 2 цифры (в левой крайней грани может оказаться и одна цифра). Записываем так 27’98’41
Чтобы получить первую цифру корня (5), извлекаем квадратный корень из наибольшего точного квадрата, содержащегося в первой слева грани (27).
Потом вычитают из первой грани квадрат первой цифры корня (25) и к разности приписывают (сносят) следующую грань (98).
Слева от полученного числа 298 пишут удвоенную цифру корня (10), делят на нее число всех десятков раннее полученного числа (29/2 ≈ 2), испытывают частное (102 ∙2 = 204 должно быть не больше 298) и записывают (2) после первой цифры корня.
Потом вычитают от 298 полученное частное 204 и к разности (94) приписывают (сносят) следующую грань (41).
Слева от полученного числа 9441 пишут удвоенное произведение цифр корня (52 ∙2 = 104), делят на это произведение число всех десятков числа 9441 (944/104 ≈ 9), испытывают частное (1049 ∙9 = 9441) должно быть 9441 и записывают его (9) после второй цифры корня.
Получили ответ √279841 = 529.
Аналогично извлекают корни из десятичных дробей . Только подкоренное число надо разбивать на грани так, чтобы запятая была между гранями.
Пример . Найдите значение √0,00956484.
Только надо помнить, что если десятичная дробь имеет нечетное число десятичных знаков, из нее точно квадратный корень не извлекается .
Итак, теперь вы познакомились с тремя способами извлечения корня. Выбирайте тот, который вам больше подходит и практикуйтесь. Чтобы научиться решать задачи, их надо решать. А если у Вас возникнут вопросы, записывайтесь на мои уроки .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Вопрос: Как извлечь квадратный корень без калькулятора? — Образование и коммуникации
Содержание статьи:
Извлечение квадратного корня без калькулятора и таблиц.
Видео взято с канала: Andrei Gradient
ЕГЭ.
 Простое извлечение корня без калькулятора 1 способ.
Простое извлечение корня без калькулятора 1 способ.Видео взято с канала: из МАТЕМАТИКИ в АЛГЕБРУ 6,7,8 КЛАСС
Как извлечь квадратный корень из любого числа без калькулятора
Видео взято с канала: Зульфия Абубакирова
Как вычислять корни без Калькулятора ЕГЭ Математика 2018
Видео взято с канала: eXtraTeam
Извлечение корня в столбик sqrt2
Видео взято с канала: Valery Volkov
Квадратный корень. Как извлекать корень без калькулятора. 2 простых способа
Видео взято с канала: Математик МГУ
#140. КАК ИЗВЛЕКАТЬ КОРНИ В СТОЛБИК? В ШКОЛЕ НЕ ПОКАЖУТ!
Показать описаниеВы знали, что квадратные арифметические корни можно извлекать в столбик? Например, можно найти корень из 2, 3, 5 и т.д. с любой наперед заданной точностью. На самом деле, конечно, в некоторых школах дают эту тему, она есть и в некоторых учебниках. Но для большинства она оказывается в новинку, так что надеюсь видео будет полезным!
ЗАДАЧНИК КО ВСЕМ РОЛИКАМ: https://vk. com/wall-135395111_14984.
com/wall-135395111_14984.
МОИ КУРСЫ: https://vk.com/market-135395111.
УСКОРИТЬ ПРОЦЕСС СОЗДАНИЯ НОВОГО ВИДЕО: http://www.donationalerts.ru/r/wildmathing.
VK: https://vk.com/wildmathing.
В этом видео разбирается алгоритм извлечения квадратных арифметических корней в столбик, который описан в книге «Математика — абитуриенту» (В.В.Ткачука). И если вы не знаете, как быстро вычислить квадратный арифметический корень из больших чисел. Как достаточно точно оценить значение корня из двух, трех, пяти и т.д. — вы попали по адресу! Если вам интересна математика, обязательно подпишитесь на канал: тут есть, что посмотреть!
ПОПУЛЯРНЫЕ ВОПРОСЫ:
— Что делать, если возникают нули? Например, такая проблема при извлечение корня из 254016..
— Все то же самое. Сначала разбиваем цифры числа на пары: 25’40’16, затем извлекаем с недостатком корень из 25 — получаем 5. Вычитаем, сносим две новые цифры — 40. Теперь ищем наибольшую цифру ★, которая удовлетворяет неравенству 10★ × ★ ≤40. e? https://youtu.be/sCvh80kqFZg.
e? https://youtu.be/sCvh80kqFZg.
4. Математические анекдоты: https://youtu.be/ZwSSv3BcVy4.
#Математика #арифметика #школа
Видео взято с канала: Wild Mathing
Как вычислить квадратный корень без калькулятора : Learnmath
Простой и эффективный способ вычисления квадратного корня называется методом Герона.
Интуиция такова: предположим, что у вас есть прямоугольник с площадью А. Если вы возьмете среднее значение длин его сторон и сформируете новый прямоугольник той же площади, используя эту длину в качестве одной из сторон, то новый прямоугольник будет быть «более квадратным», чем тот, с которого вы начали. Вы можете повторять этот процесс столько раз, сколько пожелаете, пока прямоугольник не станет как можно ближе к квадрату.
Записано алгебраически, если вы хотите извлечь квадратный корень из x, это означает, что вы начинаете с предположения g_1. Неважно, какое это предположение, вы всегда можете предположить, что g_1 = 1, если хотите, или вы можете сделать грубую оценку, отбросив половину цифр x.
В любом случае, если у вас есть предположение g_n, вы постоянно создаете новое предположение g_(n+1) = (g_n + (x / g_n)) / 2.
• • •
Например, предположим, что мы хотим найдите √7, что означает x = 7. Начнем с g_1 = 1 (было бы немного лучше начать с 2 или 3, но мы будем использовать 1 для ясности).Тогда получаем:
г_2 = (1 + (7/1))/2 = 4
г_3 = (4 + (7/4))/2 = 23/8
г_4 = (23/8 + ( 7 / (23/8))) / 2
= (23/8 + 56/23) / 2
= (23² + 8·56) / (16·23)
= (529 + 448) / 368
= 977 / 368
g_5 = (977/368 + (7 / (977/368))) / 2
= (977² + 7·368²) / (2·368·977)
= 1
Теперь, если выполняем деление в длину, находим:
g_5 ≈ 2,64576704…
(g_5)² ≈ 7,00008325…
Вероятно, этого достаточно для большинства реальных приложений.Если еще раз улучшить предположение, то получим:
g_6 = (1
7/719072 + (7 / (17/719072))) / 2= (17² + 7·719072²) / (2·719072·17)
= 7238946623297/273606497/2736064645568
G_6 ≈ 2. 6457513111113 …
6457513111113 …
(G_6) ² ≈ 70000000002475 …
Сравнение с истинным значением:
√7 ≈ 2.64575131106459 …
У нас уже есть 10 цифр. Каждая итерация по сути удваивает количество правильных цифр, поэтому, если мы сделаем еще один шаг для вычисления g_7, у него будет около 20 правильных цифр, у g_8 будет около 40 и так далее.
И единственной математикой, которую нам нужно было выполнить, было целочисленное умножение и сложение, а затем одно последнее деление в длинную сторону, если нам нужно десятичное расширение.
Как найти корень четвертой степени из числа — Видео и стенограмма урока
Нахождение корня четвертой степени
Итак, как это связано с нахождением корня четвертой степени из 256? Ну, это та же концепция, но вместо того, чтобы выяснять, какое число можно умножить само на себя дважды, чтобы получить 256, мы хотим выяснить, какое число можно умножить само на себя 4 раза, чтобы получить 256.
Нахождение корня четвертой степени числа противоположно умножению числа само на себя 4 раза. Другими словами, это противоположно использованию показателя степени 4. Давайте посмотрим на это математически.
Другими словами, это противоположно использованию показателя степени 4. Давайте посмотрим на это математически.
х 4 = 256
Чтобы найти корень четвертой степени из 256, нам нужно выяснить, сколько в этом уравнении х . Какое число можно возвести в степень 4, чтобы оно равнялось 256? Давайте подумаем об этом. . . Если я подставлю 2, то получу следующее:
24 = 2 x 2 x 2 x 2 = 16
Таким образом, очевидно, что 2 не является корнем четвертой степени из 256.Давайте перейдем к числу 4.
44 = 4 x 4 x 4 x 4 = 256
4, умноженное само на себя в 4 раза, дает нам искомое число, 256! Таким образом, корень четвертой степени из 256 равен 4! Уууу!! Мы решили это.
Символы
Мы обсуждали идею нахождения корня числа в четвертой степени, но в mathpo/ у нас часто есть изящные символы, которые говорят нам, что делать. Всякий раз, когда вы видите радикальный символ в математике, вы знаете, что имеете дело с корнями. Радикальные символы выглядят как галочки с прикрепленной горизонтальной линией. Небольшое число над флажком (если оно есть), называемое индексом , говорит вам, какой корень нужно найти. Большое число под подкоренным символом называется подкоренным числом и и говорит вам, из чего брать корень.
Небольшое число над флажком (если оно есть), называемое индексом , говорит вам, какой корень нужно найти. Большое число под подкоренным символом называется подкоренным числом и и говорит вам, из чего брать корень.
Примеры
Вам задают вопрос по тесту, в котором предлагается найти корень четвертой степени из числа 1296. Теперь вы знаете, что вам нужно найти число, которое умножится само на себя 4 раза и будет равно 1296.Лучший способ сделать это — просто поиграть с цифрами и проверить. Итак, давайте выберем число для начала. Мы знаем, что 4 умножается само на себя 4 раза равно 256, так что давайте возьмем большее число. Мы можем попробовать 5,5 в четвертой степени равно 625. Хммм. . . становится ближе. Попробуем 6! 6 в четвертой степени равно 1296. Таким образом, корень четвертой степени из 1296 равен 6!
Давайте посмотрим на другой пример:
Теперь вам нужно найти корень четвертой степени из 14 641. Итак, давайте подумаем. . . Мы, очевидно, знаем, что их ответ должен быть больше 6 из нашего последнего примера. Мы можем начать с простого числа, такого как 10. 10 в четвертой степени равно 10 000. Это довольно близко! Почему бы нам не попробовать увеличить число еще на один? 11 в четвертой степени равно 14 641. Это означает, что наш ответ 11! Корень четвертой степени из 14 641 равен 11. Не слишком сложно!
Итак, давайте подумаем. . . Мы, очевидно, знаем, что их ответ должен быть больше 6 из нашего последнего примера. Мы можем начать с простого числа, такого как 10. 10 в четвертой степени равно 10 000. Это довольно близко! Почему бы нам не попробовать увеличить число еще на один? 11 в четвертой степени равно 14 641. Это означает, что наш ответ 11! Корень четвертой степени из 14 641 равен 11. Не слишком сложно!
Краткое содержание урока
Нахождение корня четвертой степени числа аналогично нахождению других корней. Все, что вам нужно сделать, это найти число, которое умножается на себя четыре раза, чтобы получить число, из которого вы извлекаете корень четвертой степени.Вы можете представить это как противоположность возведению числа в степень 4.
В математической записи подкоренных символов выглядят как галочки с прикрепленной горизонтальной чертой. Небольшое число над флажком (если оно есть), называемое индексом , говорит вам, какой корень нужно найти. Большое число под подкоренным символом называется подкоренным числом и и говорит вам, из чего брать корень.
Большое число под подкоренным символом называется подкоренным числом и и говорит вам, из чего брать корень.
Как вычислить квадратный корень в уме
Купить сейчас
Как партнер Amazon и книжный магазин.org, QDT зарабатывает на соответствующих покупках.
Если вы читали статью, опубликованную на прошлой неделе, то вычисление квадратного корня из 16, 81 и любого другого числа, являющегося полным квадратом, должно быть легким, поскольку вы знаете, что вам просто нужно найти число, которое было возведено в квадрат, чтобы получить идеальный квадрат. квадратный. Выяснить, что представляет собой квадратный корень из отрицательного числа, такого как –1 или –42, также должно быть легко, поскольку мы видели, что отрицательные числа на самом деле не имеют квадратных корней (по крайней мере, ни одно из чисел, о которых мы пока знаем).И выяснить, какой квадратный корень из несовершенного квадрата, такого как π или 55, тоже не составит труда, поскольку вы всегда можете воспользоваться калькулятором.
Но что, если у вас нет под рукой калькулятора, когда вам действительно нужно найти этот квадратный корень? Что ты можешь сделать? Продолжайте читать, потому что сегодня мы научимся легко вычислять квадратные корни в уме.
Резюме: что такое квадратные корни?
Прежде чем мы углубимся в детали того, как вычислять квадратные корни в уме и как точно вычислять их значения без калькулятора, давайте быстро вспомним, что такое квадратные корни.Идея на самом деле очень проста: всякий раз, когда вы умножаете число само на себя — и имейте в виду, что это относится к любому числу, будь то целое, рациональное или иррациональное, — это называется возведением числа в квадрат.
В качестве примера с целыми числами 15 x 15 — это квадрат 15, что равно 225. Когда мы находим квадратный корень из числа 225, все, что мы делаем, — это выясняем, на что было то исходное число, на которое мы умножили сам, чтобы получить 225. При работе с числами, которые не являются идеальными квадратами, механика нахождения квадратных корней отличается, но идея остается той же. Например, чему равен квадратный корень из 343? Используя калькулятор, я нахожу, что ответ составляет примерно 18,52. Если мы умножим 18,52 на 18,52, мы получим 342,99, что очень близко к 343. Итак, как видите, независимо от того, с каким типом числа мы имеем дело, значение квадратного корня одинаково.
Например, чему равен квадратный корень из 343? Используя калькулятор, я нахожу, что ответ составляет примерно 18,52. Если мы умножим 18,52 на 18,52, мы получим 342,99, что очень близко к 343. Итак, как видите, независимо от того, с каким типом числа мы имеем дело, значение квадратного корня одинаково.
Страницы
Использование калькулятора количественных показателей GRE (для сдающих тест)
Иногда вычисления, которые вам необходимо выполнить, чтобы ответить на вопрос в разделе «Количественное мышление» общего теста GRE ® , требуют много времени, например деление в длинных числах, или требуют извлечения квадратных корней.Для таких расчетов вы можете использовать калькулятор, прилагаемый к вашему тесту.
Хотя калькулятор может сократить время, необходимое для выполнения вычислений, имейте в виду, что калькулятор дает результаты, которые дополняют, но не заменяют ваши знания математики. Вы должны использовать свои математические знания, чтобы определить, являются ли результаты калькулятора разумными и как их можно использовать для ответа на вопрос.
Вы должны использовать свои математические знания, чтобы определить, являются ли результаты калькулятора разумными и как их можно использовать для ответа на вопрос.
Вот некоторые общие рекомендации по использованию калькулятора в мере количественного рассуждения:
Рекомендации, относящиеся к экранному калькулятору
Ниже приведены некоторые примеры расчетов с помощью калькулятора.
Вычислить
Пояснение
Введите , чтобы получить 7,365. Либо введите , чтобы получить 3,365, а затем введите , чтобы получить 7,365.
Вычислить
Пояснение
Поскольку деление имеет приоритет над сложением в порядке операций, вам необходимо переопределить этот приоритет, чтобы вычислить эту дробь. Вот два способа сделать это. Вы можете использовать круглые скобки для сложения в числителе, введя , чтобы получить Или вы можете использовать знак равенства после 9.3, введя , чтобы получить тот же результат.
. Во втором случае обратите внимание, что нажатие первой кнопки обязательно, потому что без нее вместо нее будет ошибочно вычисляться . Между прочим, точное значение выражения является повторяющимся десятичным числом , где цифры 285714 повторяются без конца, но калькулятор округляет десятичное число до
Во втором случае обратите внимание, что нажатие первой кнопки обязательно, потому что без нее вместо нее будет ошибочно вычисляться . Между прочим, точное значение выражения является повторяющимся десятичным числом , где цифры 285714 повторяются без конца, но калькулятор округляет десятичное число доНайдите с точностью до 0,01 длину гипотенузы прямоугольного треугольника с катетами 21 и 54; то есть воспользуемся теоремой Пифагора и вычислим
Пояснение
Введите , чтобы получить 57.939624. Опять же, нажатие перед важно, потому что это приведет к ошибочному вычислению Это связано с тем, что квадратный корень будет иметь приоритет над умножением в порядке операций. Обратите внимание, что можно использовать круглые скобки, как в , но они не обязательны, поскольку умножение уже имеет приоритет над сложением. Между прочим, точный ответ — это бесконечное, неповторяющееся десятичное число или иррациональное число, но калькулятор округляет десятичное число до 57,939624.
 Наконец, обратите внимание, что задача требует ответа с точностью до 0.01, поэтому правильный ответ 57,94.
Наконец, обратите внимание, что задача требует ответа с точностью до 0.01, поэтому правильный ответ 57,94.Вычислить
Пояснение
Введите , чтобы получить
Перевести 6 миль в час в футы в секунду.
Пояснение
Решение этой задачи использует коэффициенты преобразования и следующим образом:
Введите , чтобы получить 8.8. Или введите , чтобы получить результат 31 680, а затем введите , чтобы получить 8,8 фута в секунду.На мероприятии по сбору средств 43 участника пожертвовали по 60 долларов каждый, 21 участник пожертвовал по 80 долларов каждый и 16 участников пожертвовали по 100 долларов каждый.Каково было среднее (среднее арифметическое) пожертвование на одного участника в долларах?
Пояснение
Решением этой проблемы является вычисление средневзвешенного значения. Вы можете использовать кнопки памяти и скобки для этого вычисления следующим образом:
Введите
, чтобы получить 73,25 или 73,25 доллара США на участника.

При первом нажатии кнопки число на дисплее калькулятора сохраняется в памяти, а слева от дисплея появляется буква M, указывающая на то, что функция памяти используется.Каждое последующее использование кнопки добавляет число на текущем дисплее к числу, хранящемуся в памяти, и заменяет число, хранящееся в памяти, суммой. При нажатии кнопки в приведенном выше расчете отображается текущее значение в памяти, 5 860. Чтобы очистить память, используйте кнопку , и значок M рядом с дисплеем исчезнет.
См. также:
Нахождение квадратных корней из чисел, не являющихся полными квадратами, без калькулятора
Там есть несколько способов вычисления квадратных корней без калькулятора.Вот метод угадать и разделить.
Шаг 1: Оцените/найдите идеальный квадратный корень, максимально близкий к можно на ваш номер.
Шаг 2: Разделите число на квадратный корень.
Шаг 3: вычислить среднее значение результата шага 2. и корень.
Шаг 4: Используйте результат шага 3, чтобы повторить шаги 2 и
3, пока не получите число, достаточно точное для вас.
Вычислите квадратный корень из 10 (√ 10) с точностью до 4 знаков после запятой.
1. Найти идеальное квадратное число ближе к 10.3 2 = 9 и 4 2 = 16, так что возьми 3.
2. Разделить 10 на 3. 10÷3 = 3,33 (ответ можно округлить)
3. Среднее 3,33 и 3. (3,33 + 3)÷2 = 3,1667
Повторите шаг 2: 10÷3,1667 = 3,1579
Повторите шаг 3: в среднем 3,1579 и 3.1667.
(3,1579 + 3,1667)÷2 = 3,1623
Пытаться ответ —> 3,1623 в квадрате равно 10? 3,1623 х 3,1623 = 10,0001
Если это достаточно точно для вас, вы можете остановиться! В противном случае вы можете повторить шаги 2 и 3.
Вот еще пример: √ 695. знак равно- Пусть сначала предположим, что корень равен 25.
- 695 ÷ 25 = 27,8
- (25 + 27,8) ÷ 2 = 26,4
- 695 ÷ 26,4 = 26,3257
- (26,4 + 26,3257) ÷ 2 = 26,36285
- 695 ÷ 26,36285 = 26,3628553
Последние два результата примерно равны, поэтому
теперь у вас есть хорошая оценка корня из 695. Вы можете продолжить
процесс, пока вы не будете удовлетворены точностью.
Вы можете продолжить
процесс, пока вы не будете удовлетворены точностью.
Итак, √24,6=?
- Давайте попробуйте 5, так как 5 2 = 25, что довольно близко к 24,6.
- Разделить 24,6 на 5. 24,6 ÷ 5 = 4,92
- (5 + 4,92) ÷ 2 = 4,96
Вы можете остановиться здесь. 4.96 очень близко 4,9598, что является фактическим квадратным корнем из 24,6. Повторите шаги 2 и 3 для любого желаемый уровень точности. Чем дальше, тем сложнее длинное деление становится. Но первые несколько циклов дают довольно близкий ответ.
- 24,6 / 4,96 = 4,9596
- (4,96 + 4,9596) ÷ 2 = 4,9598
Еще несколько примеров, решенных лаконично,
√ 2613 =?
√2500 = 50
2613 ÷ 50 = 52,26
(52,26 + 50) ÷ 2 = 51,13 (примерный ответ)
√6673 =?
√6400 = 80
6673 ÷ 80 = 83,41
(83,41 + 80) ÷ 2 = 81,70 (примерный ответ)
√89108 =?
√9,00,00 = 300
89108 ÷ 300 = 297. 03
03
(297,03 + 300) ÷ 2 = 298,51 (примерный ответ)
Другой аналогичный и простой способ аппроксимации квадратного корня числа состоит в том, чтобы использовать следующее уравнение:Чем ближе известный квадрат к неизвестному, тем точнее приближение. Например, чтобы вычислить квадратный корень из 15, мы могли бы начать с зная, что ближайший полный квадрат равен 16 (4 2 ).
Так
мы оценили квадратный корень из 15 как 3,875. Фактический квадратный корень из 15
это 3.872983…
Квадратный корень из 90 (√90)
В этой статье мы собираемся вычислить квадратный корень из 90, узнать, что такое квадратный корень, и ответить на некоторые из часто задаваемых вопросов. Мы также рассмотрим различные методы вычисления квадратного корня из 90 (как с компьютером/калькулятором, так и без него).
Квадратный корень из 90 Определение
В математической форме мы можем представить квадратный корень из 90, используя знак радикала, например: √90. Это обычно называют квадратным корнем из 90 в радикальной форме.
Это обычно называют квадратным корнем из 90 в радикальной форме.
Так что же такое квадратный корень? В этом случае квадратный корень из 90 — это количество (которое мы будем называть q), которое при умножении само на себя будет равно 90.
√90 = q × q = q 2
Является ли 90 идеальным квадратом?
В математике мы называем 90 полным квадратом, если квадратный корень из 90 является целым числом.
В этом случае, как мы увидим в приведенных ниже вычислениях, мы видим, что 90 не является идеальным квадратом.
Чтобы узнать больше о идеальных квадратах, вы можете прочитать о них и посмотреть список из 1000 из них в нашем разделе Что такое идеальный квадрат? статья.
Является ли квадратный корень из 90 рациональным или иррациональным?
Обычный вопрос состоит в том, является ли квадратный корень из 90 рациональным или иррациональным. Рациональные числа можно записать в виде дроби, а иррациональные — нет.
Быстрый способ проверить это — посмотреть, является ли число 90 правильным квадратом. Если да, то это рациональное число. Если это не идеальный квадрат, то это иррациональное число.
Если да, то это рациональное число. Если это не идеальный квадрат, то это иррациональное число.
Мы уже знаем, является ли 90 полным квадратом, поэтому мы также можем видеть, что √90 — иррациональное число.
Можно ли упростить квадратный корень из 90?
90 можно упростить, только если вы можете уменьшить 90 внутри радикального символа. Это процесс, который называется упрощением сурда. В этом примере квадратный корень из 90 можно упростить.
√90 = 3√10.
Как вычислить квадратный корень из 90 с помощью калькулятора
Если у вас есть калькулятор, то проще всего вычислить квадратный корень из 90 с помощью этого калькулятора. На большинстве калькуляторов это можно сделать, набрав 90 и нажав клавишу √x.Вы должны получить следующий результат:
√90 ≈ 9,4868
Как вычислить квадратный корень из 90 с помощью компьютера
На компьютере вы также можете вычислить квадратный корень из 90 с помощью Excel, Numbers или Google Sheets и функции SQRT, например:
SQRT(90) ≈ 9,486832980505
Что такое квадратный корень из 90 с округлением?
Иногда вам может понадобиться округлить квадратный корень из 90 до определенного числа знаков после запятой. Вот решения для этого, если это необходимо.
Вот решения для этого, если это необходимо.
10-й: √90 ≈ 9,5
100-й: √90 ≈ 9,49
1000-й: √90 ≈ 9,487
Что такое квадратный корень из 90 в виде дроби?
Ранее в этой статье мы рассмотрели, что только рациональное число может быть представлено в виде дроби, а иррациональное число — нет.
Как мы сказали выше, поскольку квадратный корень из 90 является иррациональным числом, мы не можем превратить его в точную дробь. Однако мы можем превратить его в приблизительную дробь, используя квадратный корень из 90, округленный до сотых.
√90
≈ 9,5/1
≈ 949/100
≈ 9 49/100
Что такое квадратный корень из 90, записанный с показателем степени?
Все вычисления квадратного корня могут быть преобразованы в число (называемое основанием) с дробной степенью. Давайте посмотрим, как это сделать с квадратным корнем из 90:
.√b = b ½
√90 = 90 ½
Как найти квадратный корень из 90 с помощью длинного деления
Наконец, мы можем использовать метод деления в длину для вычисления квадратного корня из 90. Это очень полезно для задач на длинное деление, и именно так математики вычисляли квадратный корень из числа до того, как были изобретены калькуляторы и компьютеры.
Это очень полезно для задач на длинное деление, и именно так математики вычисляли квадратный корень из числа до того, как были изобретены калькуляторы и компьютеры.
Шаг 1
Задайте 90 парами из двух цифр справа налево и присоедините один набор 00, потому что нам нужен один десятичный знак:
Этап 2
Начиная с первого набора: самый большой полный квадрат, меньше или равный 90, равен 81, а квадратный корень из 81 равен 9. Поэтому ставим 9 сверху и 81 снизу вот так:
Этап 3
Рассчитайте 90 минус 81 и поместите разницу ниже.Затем переместитесь вниз к следующему набору чисел.
Этап 4
Удвойте число, выделенное зеленым сверху: 9 × 2 = 18. Затем используйте 18 и нижнее число, чтобы решить эту задачу:
18? × ? ≤ 900
Знаки вопроса «пробел» и такие же «пробел». Путем проб и ошибок мы обнаружили, что наибольшее число, которое может быть пустым, равно 4.
Теперь введите 4 сверху:
Вот и все! Ответ показан вверху зеленым цветом. Квадратный корень из 90 с точностью до одной цифры после запятой равен 9.5.
Обратите внимание, что последние два шага фактически повторяют два предыдущих. Чтобы добавить десятичные знаки к вашему ответу, вы можете просто добавить больше наборов 00 и повторить последние два шага.
Квадратный корень из 90 с точностью до одной цифры после запятой равен 9.5.
Обратите внимание, что последние два шага фактически повторяют два предыдущих. Чтобы добавить десятичные знаки к вашему ответу, вы можете просто добавить больше наборов 00 и повторить последние два шага.
Расчет с большими числами
√Вигинтиллионная, [-63]Новемдециллионная, [-60]Октадециллионная, [-57]Септендециллионная, [-54]Сексдециллионная, [-51]Квиндециллионная, [-48]Кваттуордециллионная, [-45]Тредециллионная, [-42]Двадециллионная , [-39]Ундециллионная, [-36]Дециллионная, [-33]Немиллионная, [-30]Октиллионная, [-27]Септиллионная, [-24]Секстиллионная, [-21]Квинтиллионная, [-18]Квадриллионная, [ -15]Триллионная, [-12]Миллиардная, [-9]Миллионная, [-6]Тысячная, [-3]—, [0]Тысячная, [3]Миллионная, [6]Миллиардная, [9]Триллионная, [ 12]квадриллион, [15]квинтиллион, [18]секстиллион, [21]септиллион, [24]октиллион, [27]нониллион, [30]дециллион, [33]ундециллион, [36]дуодециллион, [39]тредециллион, [ 42]Quattuordecillion, [45]Quindecillion, [48]Sexdecillion, [51]Septendecillion, [54]Octodecillion, [57]Novemdecillion, [60]Vigintillion, [63] 12345678910+, плюс-, минус*, раз /, деленное на
√Вигинтиллионная, [-63]ноябрь-дециллионная, [-60]октадециллионная, [-57]септендециллионная, [-54]секдециллионная, [-51]квиндециллионная, [-48]кваттюор дециллионная, [-45]тредециллионная, [-42]дудециллионная, [-39]ундециллионная, [-36]дециллионная, [-33]немиллионная, [-30]октиллионная, [-27]септиллионная, [-24]сектиллионная, [-21]Квинтиллионная, [-18]Квадриллионная, [-15]Триллионная, [-12]Миллиардная, [-9]Миллионная, [-6]Тысячная, [-3]—, [0]Тысячная, [3] Миллион, [6]миллиард, [9]триллион, [12]квадриллион, [15]квинтиллион, [18]секстиллион, [21]септиллион, [24]октиллион, [27]нониллион, [30]дециллион, [33] Ундециллион, [36]Дуодециллион, [39]Тредециллион, [42]Кваттуордециллион, [45]Квиндециллион, [48]Сексдециллион, [51]Септендециллион, [54]Октодециллион, [57]Новемдециллион, [60]Вигинтиллион, [63] 12345678910
=
= Вигинтиллионный, [-63]Ноябрь-дециллионный, [-60]Октадециллионный, [-57]Септендециллионный, [-54]Сексдециллионный, [-51]Квиндециллионный, [-44]Квадециллионный, [-44]Квадециллионный ]Тредециллионная, [-42]Дудециллионная, [-39]Ундециллионная, [-36]Дециллионная, [-33]Немиллионная, [-30]Октиллионная, [-27]Септиллионная, [-24]Секстиллионная, [ -21]Квинтиллионная, [-18]Квадриллионная, [-15]Триллионная, [-12]Миллиардная, [-9]Миллионная, [-6]Тысячная, [-3]—, [0]Тысячная, [3]Миллионная , [6]миллиард, [9]триллион, [12]квадриллион, [15]квинтиллион, [18]секстиллион, [21]септиллион, [24]октиллион, [27]нониллион, [30]дециллион, [33]ундециллион , [36]Дудециллион, [39]Тредециллион, [42]Кваттуордециллион, [45]Квиндециллион, [48]Сексдециллион, [51]Септендециллион, [54]Октодециллион, [57]Новемдециллион, [60]Вигинтиллион, [63]
.


 Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.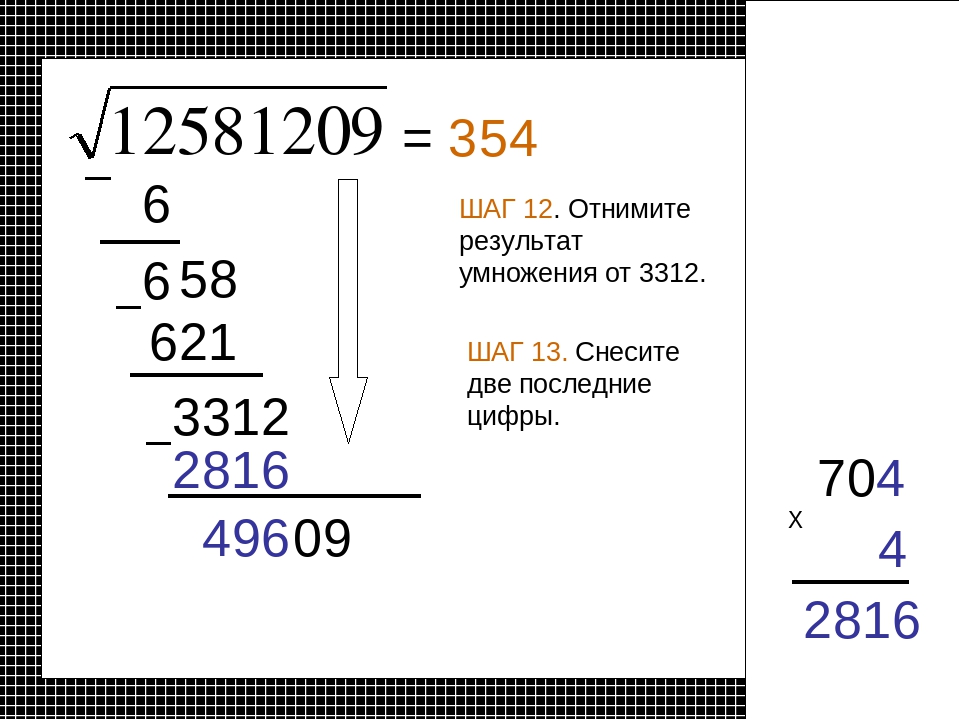 Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
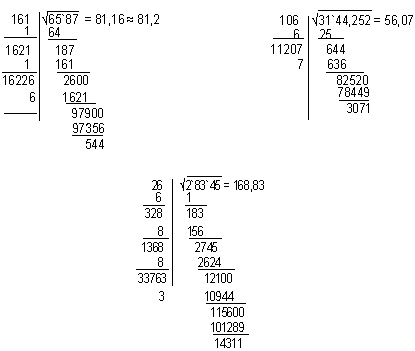 Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
 Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
 Например, 21 на 21 равно 441.
Например, 21 на 21 равно 441.  Элементы алгебры и анализа. Часть первая.-М.-1928 г
Элементы алгебры и анализа. Часть первая.-М.-1928 г С. «математические кружки в 8-10 классах»; Книга для учителя. – М.: Просвещение,1987
С. «математические кружки в 8-10 классах»; Книга для учителя. – М.: Просвещение,1987 Во втором случае обратите внимание, что нажатие первой кнопки обязательно, потому что без нее вместо нее будет ошибочно вычисляться . Между прочим, точное значение выражения является повторяющимся десятичным числом , где цифры 285714 повторяются без конца, но калькулятор округляет десятичное число до
Во втором случае обратите внимание, что нажатие первой кнопки обязательно, потому что без нее вместо нее будет ошибочно вычисляться . Между прочим, точное значение выражения является повторяющимся десятичным числом , где цифры 285714 повторяются без конца, но калькулятор округляет десятичное число до Наконец, обратите внимание, что задача требует ответа с точностью до 0.01, поэтому правильный ответ 57,94.
Наконец, обратите внимание, что задача требует ответа с точностью до 0.01, поэтому правильный ответ 57,94.