Как построить график функции
В этой статье разобран самый простой метод получения графика функции.
Суть метода: найти несколько точек принадлежащих графику, расставить их на координатной плоскости и соединить. Этот способ не лучший (лучший – построение графиков с помощью элементарных преобразований), но если вы все забыли или ничего не учили, то знайте, что у вас всегда есть план Б – возможность построить график по точкам.
Итак, алгоритм по шагам:
1. Представьте, как выглядит ваш график.
Строить гораздо легче, если вы понимаете, что примерно должны получить в итоге. Поэтому сначала посмотрите на функцию и представьте, как примерно должен выглядеть ее график. Все виды графиков элементарных функций вы можете найти здесь. Этот пункт желательный, но не обязательный.
Пример: Построить график функции \(y=-\)\(\frac{2}{x}\)
Данная функция — гипербола с ветвями расположенными во второй и четвертой четверти.
2. Составьте таблицу точек, принадлежащих графику:
Теперь подставим разные значения «иксов» в функцию, и для каждого икса посчитаем значение «игрека».
Пример: \(y=-\)\(\frac{2}{x}\)
|
при \(x=-1\) |
\(y=-\)\(\frac{2}{-1}\)\(=2\) |
|
|
при \(x=0\) |
\(y\) — не существует (делить на ноль нельзя) |
|
|
при \(x=1\) |
\(y=-\)\(\frac{2}{1}\)\(=-2\) |
|
|
при \(x=2\) |
\(y=-\)\(\frac{2}{2}\)\(=-1\) |
|
|
при \(x=3\) |
\(y=-\)\(\frac{2}{3}\) |
|
|
при \(x=4\) |
\(y=-\)\(\frac{2}{4}\)\(=-\)\(\frac{1}{2}\) |
Результат вычислений удобно представлять в виде таблицы, примерно такой:
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
Как вы могли догадаться, полученные пары «икс» и «игрек» — это точки, лежащие на нашем графике.
4. Постройте координатную плоскость и отметьте на ней точки из таблицы.
Пример:
5. Если нужно, найдите еще несколько точек и нанесите их на координатную плоскость.
Пример: Чтобы построить график мне не хватает нескольких точек из отрицательной части, а также рядом с осью игрек, поэтому я добавлю столбцы с \(x=-2\), \(x=-4\), \(x=\)\(\frac{1}{2}\) и \(x=-\)\(\frac{1}{2}\)
|
при \(x=-2\) |
\(y=-\)\(\frac{2}{-2}\)\(=1\) |
|
|
при \(x=-4\) |
\(y=-\)\(\frac{2}{-4}\)\(=\)\(\frac{1}{2}\) |
|
|
при \(x=\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{\frac{1}{2}}\)\(=-2:\)\(\frac{1}{2}\)\(=-2 \cdot 2=-4\) |
|
|
при \(x=-\)\(\frac{1}{2}\) |
\(y=-\)\(\frac{2}{-\frac{1}{2}}\)\(=-2:(-\)\(\frac{1}{2}\)\()\)\(=-2 \cdot (-2)=4\) |
|
\(x\) |
\(-1\) |
\(0\) |
\(1\) |
\(2\) |
\(3\) |
\(4\) |
\(-2\) |
\(-4\) |
\(\frac{1}{2}\) |
\(-\)\(\frac{1}{2}\) |
|
\(y\) |
\(2\) |
\(-\) |
\(-2\) |
\(-1\) |
\(-\)\(\frac{2}{3}\) |
\(-\)\(\frac{1}{2}\) |
\(1\) |
\(\frac{1}{2}\) |
\(-4\) |
\(4\) |
6.
Постройте график
Теперь аккуратно и плавно соединяем точки.
Готово!
Как построить график функции в Excel
Чтобы правильно построить линейный график функций в Excel необходимо выбрать точечную диаграмму с прямыми отрезками и маркерами. Естественно это не единственный, но весьма быстрый и удобный способ.
Для разного рода данных нужно использовать разные типы графиков. Убедимся в этом, разобрав практический пример с построением математического графика функций в Excel.
Построение графиков функций в Excel
Начнем из анализа и создания графика функций в Excel. Мы убедимся в том, что линейный график в Excel существенно отличается от графика линейной функции, который преподают в школе.
Линейная функция x=y имеет следующие значения: x1=0, x2=1, x3=7. Заполните таблицу этими значениями как показано на рисунке:
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«График»-«График с маркерами».
В результате у нас созданы 2 линии на графике, которые наложены одна сверх другой. Так же мы видим, что линии сломаны, а значит, они не соответствуют презентации школьному графику линейной функции. Излом линий, получается, по причине того, что на оси X у нас после значений: 0, 1 сразу идет значение 7 (упущены 2,3,4,5,6).
Вывод один: данный способ графического построения данных нам не подходит. А значит щелкните по нему левой кнопкой мышки (чтобы сделать его активным) и нажмите клавишу DELETE на клавиатуре, чтобы удалить его.
Как построить график линейной функции в Excel
Чтобы создать правильный график функций в Excel выберите подходящий график.
Выделите диапазон A1:B4 и выберите инструмент: «Вставка»-«Диаграммы»-«Точечная»-«Точечная с прямыми отрезками и маркерами».
Как видно на рисунке данный график содержит одинаковое количество значений на осях X и Y. По умолчанию в шаблоне данного графика цена делений оси X равна 2. При необходимости ее можно изменить.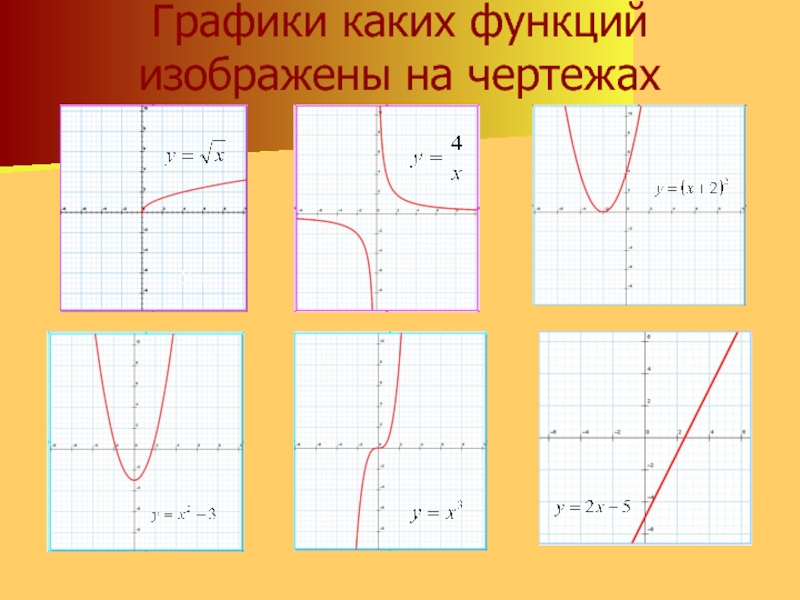
Для этого:
- наведите курсор мышки на любое значение оси X чтобы появилась всплывающая подсказка «Горизонтальная ось (значений)» и сделайте двойной щёлочек левой кнопкой мышки;
- в появившемся окне «Формат оси» выберите пункт опции: «Параметры оси»-«цена основных делений»-«фиксированное» и установите значение 1 вместо 2.
- нажмите на кнопку «Закрыть».
Теперь у нас отображается одинаковое количество значений по всем осям.
Очень важно понимать разницу в предназначениях графиков Excel. В данном примере мы видим, что далеко не все графики подходят для презентации математических функций.
Примечание. В принципе первый способ можно было-бы оптимизировать под отображение линейной функции, если таблицу заполнить всеми значениями 0-7. Но это не всегда работающее решение, особенно в том случае если вместо значений будут формулы изменяющие данные. Одним словом если нужно забить гвоздь лучше взять молоток, чем микроскоп. Несмотря на то, что теоретически гвозди можно забивать и микроскопом.
Не существует универсальных графиков и диаграмм, которыми можно отобразить любой отчет. Для каждого типа отчета наиболее подходящее то или иное графическое представление данных. Выбор зависит от того что и как мы хотим презентовать. На следующих примерах вы убедитесь, что выбор имеет большое значение. Существует даже целая наука «Инфографика», которая учит лаконично презентовать информацию с максимальным использованием графики вместо текста, насколько это только возможно.
Построение графиков функций — урок. Алгебра, 10 класс.
построить график функции y=x2+4×2−4.
Решение 1. Обозначим: f(x)=x2+4×2−4. Область определения этой функции: D(f)=(−∞;−2)∪(−2;2)∪(2;+∞), так как x≠2,x≠−2.
2. Проведём исследование функции на чётность/нечётность:
f(−x)=−x2+4−x2−4=x2+4×2−4=f(x).
Функция чётная. Следовательно, можно построить ветви графика функции для x≥0 и отобразить их симметрично относительно оси ординат.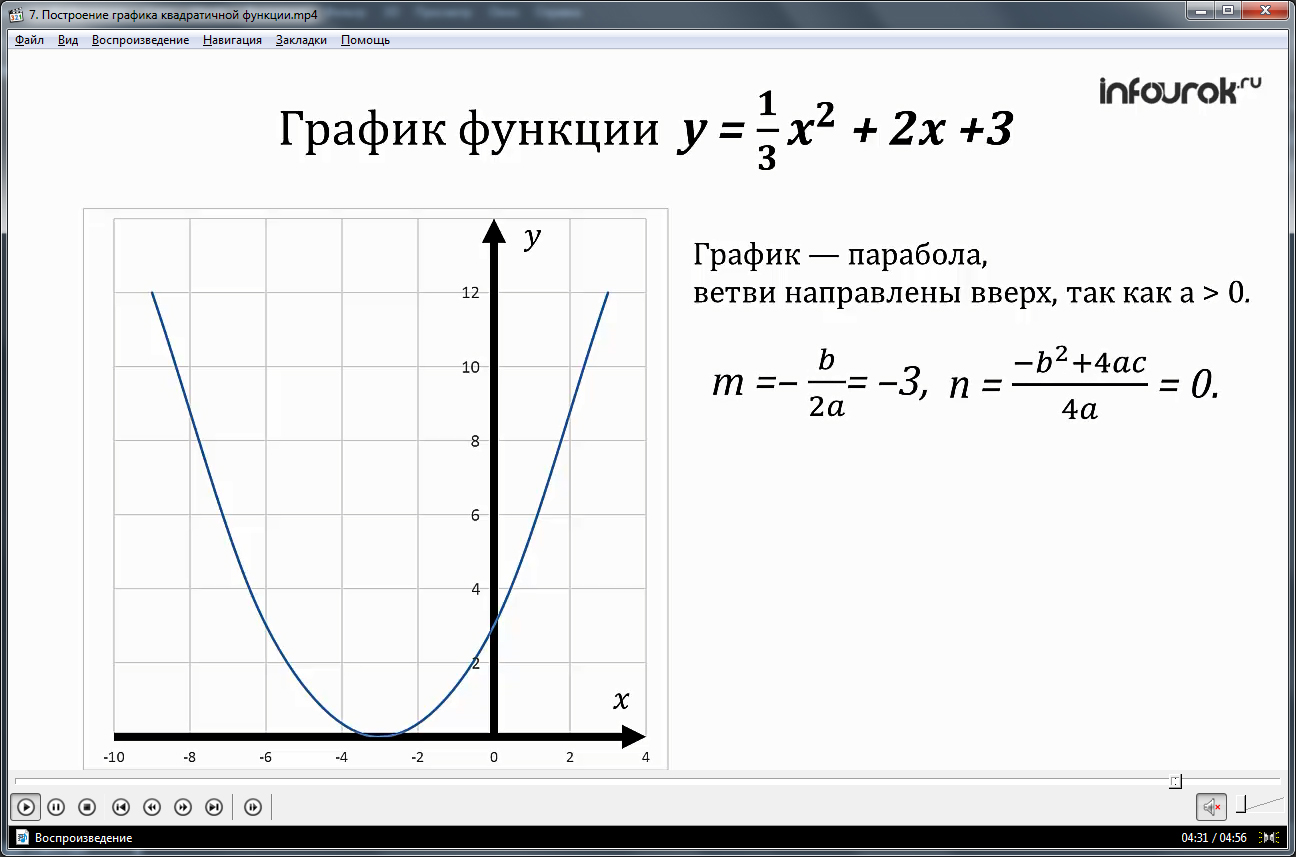
3. Определим асимптоты. Вертикальная асимптота: прямая \(x=1\), т. к. при \(x=1\) знаменатель дроби равен нулю, а числитель при этом не равен нулю. Для определения горизонтальной асимптоты вычисляем limx→∞f(x):
limx→∞x2+4×2−4=limx→∞x2x2+4x2x2x2−4×2=limx→∞1+4×21−4×2=1.
Следовательно, \(y=1\) — горизонтальная асимптота.
4. Определим стационарные и критические точки, точки экстремума и промежутки монотонности функции:
y′=x2+4×2−4′=(x2+4)′⋅(x2−4)−(x2+4)⋅(x2−4)′x2−42=2x⋅(x2−4)−(x2+4)⋅2xx2−42=2×3−8x−2×3−8xx2−42==−16xx2−42.
Производная существует на всей области определения функции, следовательно, критических точек у функции нет.
Стационарные точки определим из уравнения y′=0. Получаем: \(-16x=0\) — откуда получаем, что \(x=0\). При \(x<0\) имеем: y′>0; при \(x>0\) имеем: y′<0. Таким образом, в точке \(x=0\) функция имеет максимум, причём ymax=f(0)=02+402−4=−1.
При \(x>0\) имеем: y′<0. Учитывая точку разрыва \(x=2\), делаем вывод: функция убывает на промежутках 0;2) и (2;+∞).
5. Найдём несколько точек, принадлежащих графику функции f(x)=x2+4×2−4 при x≥0:
\(x\) | \(0\) | \(0.5\) | \(1\) | \(3\) | \(4\) |
\(y\) | \(-1\) | −1715 | −53 | 135 | 53 |
6. Сначала нарисуем часть графика при x≥0, потом — часть, симметричную ей относительно оси \(y\). Полученный график имеет точку максимума \((0;-2)\), горизонтальную асимптоту \(y=1\) и вертикальную асимптоту \(x=2\).
Как построить график функции в Microsoft Excel?
Знаю что в Excel можно построить разные диаграммы, а можно ли в нем строить графики функций?
В Microsoft Excel можно строить даже графики математических функций, конечно это не так просто как построить те же графики в специализированной программе MathCAD.
). То же самое можно реализовать с помощью функции «=B3*B3*B3».
Однако забивать формулу в каждой строке очень неудобно. Создатели Microsoft Excel всё это предусмотрели. Для того, чтобы наша формула появилась в каждой ячейке необходимо «растянуть» её. Растягивание ячеек с формулами и числами — фирменная фишка экзеля (очень полезная).
Щёлкните на ячейке с формулой. В правом нижнем углу ячейки есть маленький квадратик (он отмечен красным цветом на рисунке ниже). Вам нужно навести курсор мышки на него (при этом курсор мышки поменяется), нажать праву кнопку и «растянуть» формулу вниз на столько ячеек, сколько вам нужно.
3. Перейдём непосредственно к построению графика.
Меню «Вставка» → «Диаграмма»:
4. Выбираем любую из точечных диаграмм. Нажимаем «Далее». Следует заметить, что нам необходима именно точечная диаграмма, т.к. другие виды диаграмм не позволяют нам задать и функцию, и аргумент в явном виде (в виде ссылки на группу ячеек).
5.
В появившемся окне нажимаем вкладку «Ряд». Добавляем ряд нажатием кнопки «Добавить».
В появившемся окне надо задать откуда будут взяты числа (а точнее результаты вычислений) для графика. Чтобы выбрать ячейки, нужно щёлкнуть поочередно по кнопкам, обведённым красным овалом на рисунке ниже.
После этого нужно выделить те ячейки, откуда будут взяты значения для x и y.
6. Вот что получилось. Последний шаг — нажимаем «готово» :
Вот таким достаточно простым способом можно строить графики в Microsoft Excel. Стоит заметить, что при любом изменении набора аргументов функции или самой функции график мгновенно перестроится заново
По материалам: how-tos.ru
Как построить график функции в Wolfram|Alpha
Начнем с построения простого 2-мерного графика: plot sin(sqrt(7)x)+19cos(x) для x от -20 до 20Если заменить 7 на (-7), то получим графики действительной и мнимой частей функции: plot sin(sqrt(-7)x)+19cos(x) для x от -5 до 5
В двух предыдущих примерах мы задавали область значений аргумента х.
А что будет, если не задавать область значений х?
Одной из уникальных особенностей Wolfram | Alpha является автоматический выбор подходящего диапазона х для построения графиков функций одной и двух переменных, например, как при построении графика этой функции, содержащей функции Бесселя:
Обращаясь к Wolfram | Alpha, чтобы построить график функции, мы всегда используем префикс plot. Если же мы введем какое-либо одномерное выражение без префикса plot, то получим кроме графика функции в прямоугольных декартовых координатах, еще и много других сведений об этой функции.
Сравните:
Кроме того, изображение построенного графика будет крупнее, если вы используете префикс plot.
Одновременно в Wolfram | Alpha можно строить графики нескольких функций.
Если навести мышь на левый нижний угол изображения, то становятся доступными две ссылки: Save as image и Copyable planetext. Рассмотрим такой график:
Первая ссылка Save as image, которая открывается в левом нижнем углу изображения, позволяет сохранить построенный график, как картинку на компьютере пользователя — при нажатии на Save as image автоматически начнется загрузка изображения:
Вторая ссылка Copyable planetext позволяет увидеть код, аналогичный тому, который используется системой Matematica для построения графиков:
Теперь рассмотрим, как в Wolfram | Alpha построить графики функций двух переменных.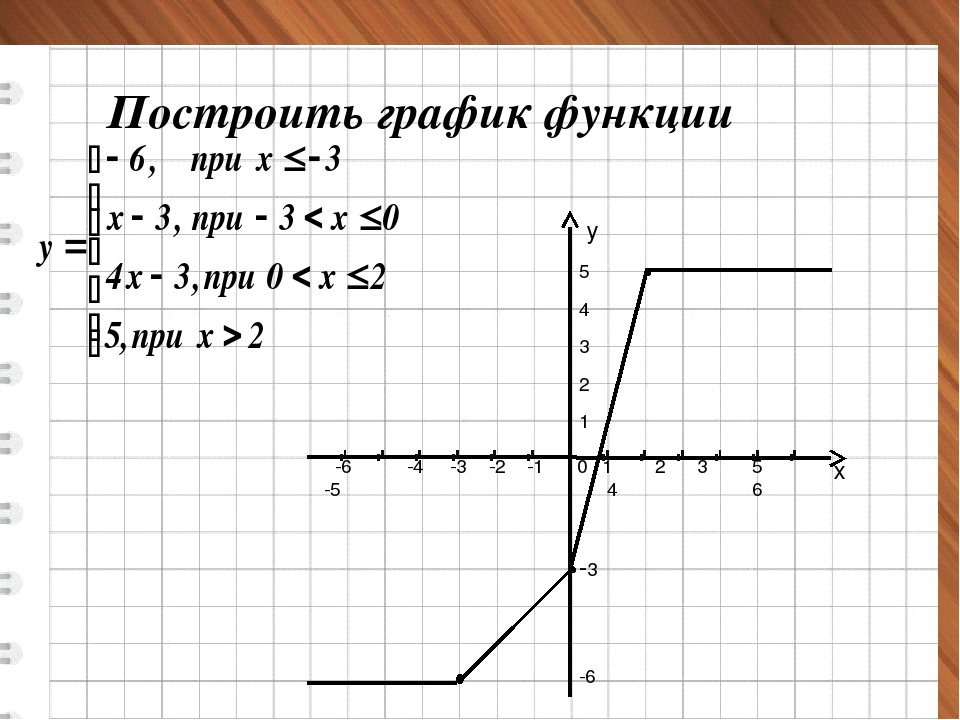
2 cos(x) для x от -6 до 6 и y от -2 до 2
Как и в одномерном случае, Wolfram | Alpha автоматически определяет подходящий диапазон значений аргументов, где функция имеет наиболее характерный вид. В случае, если Wolfram | Alpha не может найти подходящий диапазон, то это скорее всего потому, что система не смогла определить такой диапазон, где функция имеет наиболее интересное поведение. В этом случае, мы можем задать диапазон вручную, как это было сделано выше. Посмотрите следующие примеры:
Wolfram | Alpha строит отдельный график для каждой функции в списке. Вот еще несколько примеров:
Во всех рассмотренных выше примерах Wolfram | Alpha строил также и контурные графики (линии уровня) в дополнение к трехмерным графикам (поверхностям).
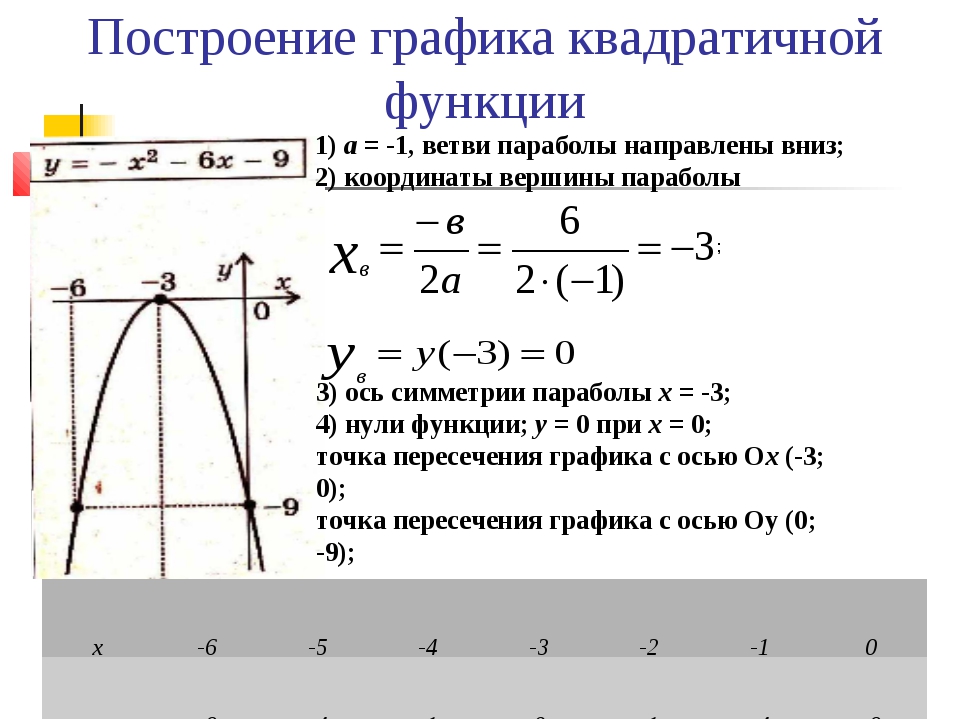Чтобы увидеть связь между трехмерными и контурными графиками, нужно нажать кнопку “Show contour lines”. Отметим, что и трехмерные и контурные графики используют один и тот же диапазон аргументов.Все трехмерные графики строятся с помощью функции plot3d системы Mathematica. Контурные графики были сделаны с помощью ContourPlot. В обоих случаях, чтобы увидеть код системы Mathematica для генерации изображения нужно нажать ссылку Copyable planetext в левом нижнем углу нужного изображения.
Источник by Sam Blake
Опубликовано в блоге Web in Math
График функции у 0 5х 2. Как построить график функций
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Урок алгебры в 9 классе по теме «Построение
графиков функции, аналитическое выражение
которых содержит знак абсолютной величины» был
построен на основе компьютерных технологии,
применяя исследовательскую деятельность
обучения.
Цели урока: Обучающая: Наглядно продемонстрировать учащимся возможности использования компьютера при построении графиков функции с модулями; для самоконтроля, экономии времени при построении графиков функций вида у=f |(х)| , у = | f (х)| , у=|f |(х)| |.
Развивающая: Развитие интеллектуальных умений и мыслительных операций — анализ и синтез сравнение, обобщение. Формирование ИКТ компетентности учащихся.
Воспитывающая: Воспитание познавательного интереса к предмету путем введения новейших технологий обучения. Воспитание самостоятельности при решении учебных задач.
Оборудование: Оборудование: компьютерный класс, интерактивная доска, презентация на тему «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины», раздаточный материал: карточки для работы с графической моделью функций, листы для фиксирования результатов исследования функций, персональные компьютеры. Лист самоконтроля.
Программное обеспечение: презентация Microsoft PowerPoint «Построение графиков функции, аналитическое выражение которых содержит знак абсолютной величины»
Ход урока
1.
Организационный момент
2. Повторение, обобщение и систематизация. Это этап урока сопровождается компьютерной презентацией.
График функции у=f |(х)|
у=f |(х)| — четная функция, т.к. | х | = | -х |, то f |-х| = f | х |
График этой функции симметричен относительно оси координат.
Следовательно, достаточно построить график функции у=f (х) для х>0,а затем достроить его левую часть, симметрично правой относительно оси координат.
Например, пусть графиком функции у=f (х) является кривая, изображенная на рис.1, тогда графиком функции у=f |(х)| будет кривая, изображенная на рис.2.
1. Исследование графика функции у= |х|
Таким образом, искомый график есть ломанная, составленная из двух полупрямых. (Рис.3)
Из сопоставления двух графиков: у=х и у= |х|, учащиеся
сделают вывод, что второй получается из первого
зеркальным отображением относительно ОХ той
части первого графика, которая лежит под осью
абсцисс.
Это положение вытекает из определения
абсолютной величины.
Из сопоставления двух графиков: у = х и у = -х, сделают вывод: функции у = f(|х|) получается из графика у = f (x) при х 0 симметричным отображением относительно оси ОУ.
Можно ли применять этот метод построения графиков для любой функции, содержащей абсолютную величину?
Слайд 3 и 4.
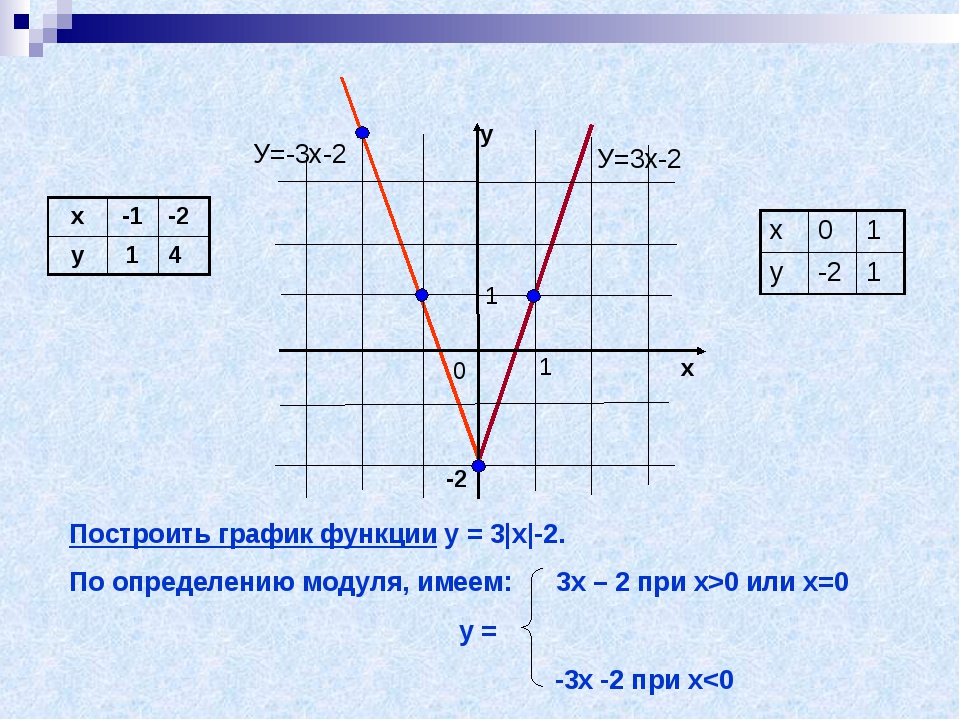
1. Построите график функции у=0,5 х 2 — 2|х| — 2,5
1) Поскольку |х| = х при х 0, у=0,5 х 2 — 2х — 2,5 . Если ху=0,5 х 2 + 2х — 2,5 .
2) Если рассмотрим график у=0,5 х 2 -2х — 2,5 при х
Можно ли применять этот метод построения графиков дл квадратичной функции, для графиков обратной пропорциональности, содержащие абсолютную величину?
1) Поскольку |х| = х при х 0, требуемый график совпадает с параболой у=0,25 х 2 — х — 3. Если ху=0,25 х 2 + х — 3.
2) Если рассмотрим график у=0,25 х 2 — х — 3 при
х 0 и
отобразить его относительно оси ОУ мы получим
тот же самый график.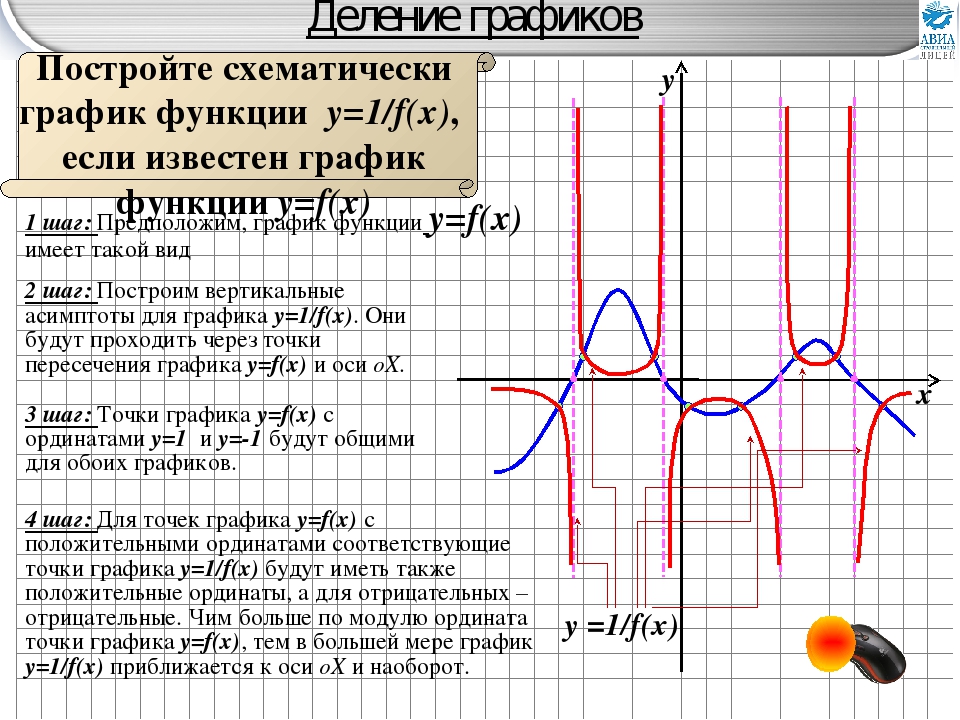
(0; — 3) координаты точки пересечения графика функции с осью ОУ.
у =0, х 2 -х -3 = 0
х 2 -4х -12 = 0
Имеем, х 1 = — 2; х 2 = 6.
(-2; 0) и (6; 0) — координаты точки пересечения графика функции с осью ОХ.
Если х
Значит, часть требуемого графика, соответствующая значениям х0.
б) Поэтому достраиваю для х
На тетрадях ученики доказывают, что график функции у = f |(х)| совпадает с графиком функции у = f (х) на множестве неотрицательных значений аргумента и симметричен ему относительно оси ОУ на множестве отрицательных значений аргумента.
Доказательство: Если х 0, то f |(х)|= f (х), т.е. на множестве неотрицательных значений аргумента графики функции у = f (х) и у = f |(х)| совпадают. Так как у = f |(х)| — чётная функция, то её график симметричен относительно ОУ.
Таким образом, график функции у = f |(х)| можно получить из графика функции у = f (х) следующим образом:
1. построить график функции у = f(х) для х>0;
2.
Для х
Вывод: Для построения графика функции у = f |(х)|
1. построить график функции у = f(х) для х>0;
2. Для х отразить построенную часть
относительно оси ОУ.
Слайд 5
4. Исследовательская работа по построению графика функции у = | f (х)|
Построить график функции у = |х 2 — 2х|
Освободимся от знака модуля по определению
Если х 2 — 2х0,
т.е. если х
0 и х2, то |х 2 —
2х|= х 2 — 2х
Если х 2 — 2х
Видим, что на множестве х
0 и х2 графики функции
у = х 2 — 2х и у = |х 2 — 2х|совпадают, а на множестве (0;2)
графики функции у = -х 2 + 2х и у = |х 2 — 2х| совпадают. Построим их.
График функции у = | f (х)| состоит из части графика функции у = f(х) при у?0 и симметрично отражённой части у = f(х) при у
Построить график функции у = |х 2 — х — 6|
1) Если х 2 — х -6 0, т.е. если х
-2 и х3, то |х 2 — х -6|= х 2 — х -6.
Если х 2 — х -6
Построим их.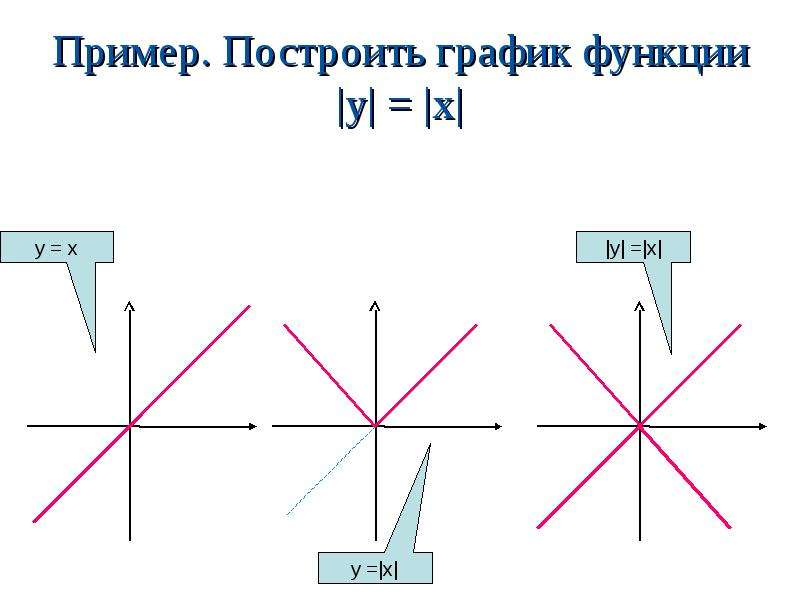
2) Построим у = х 2 — х -6 . Нижнюю часть графика
симметрично отбражаем относительно ОХ.
Сравнивая 1) и 2), видим что графики одинаковые.
Работа на тетрадях.
Докажем, что график функции у = | f (х)| совпадает с графиком функции у = f (х) для f(х) >0 и симметрично отражённой частью у = f(х) при у
Действительно, поопределению абсолютной величины, можно данную функцию рассмотреть как совокупность двух линий:
у = f(х), если f(х) 0; у = — f(х), если f(х)
Для любой функции у = f(х), если f(х) >0, то
| f (х)| = f(х), значит в этой части график функции
у = | f (х)| совпадает с графиком самой функции
Если же f(х) ) симметричнаточке(х; f (х)) относительно оси ОХ. Поэтому для получения требуемого графика отражаем симметрично относительно оси ОХ «отрицательную» часть графика у = f(х).
Вывод: действительно для построения графика функции у = |f(х) | достаточно:
1.Построить график функции у = f(х) ;
F(х)
Вывод: Для построения графика функции у=|f (х) |
1.
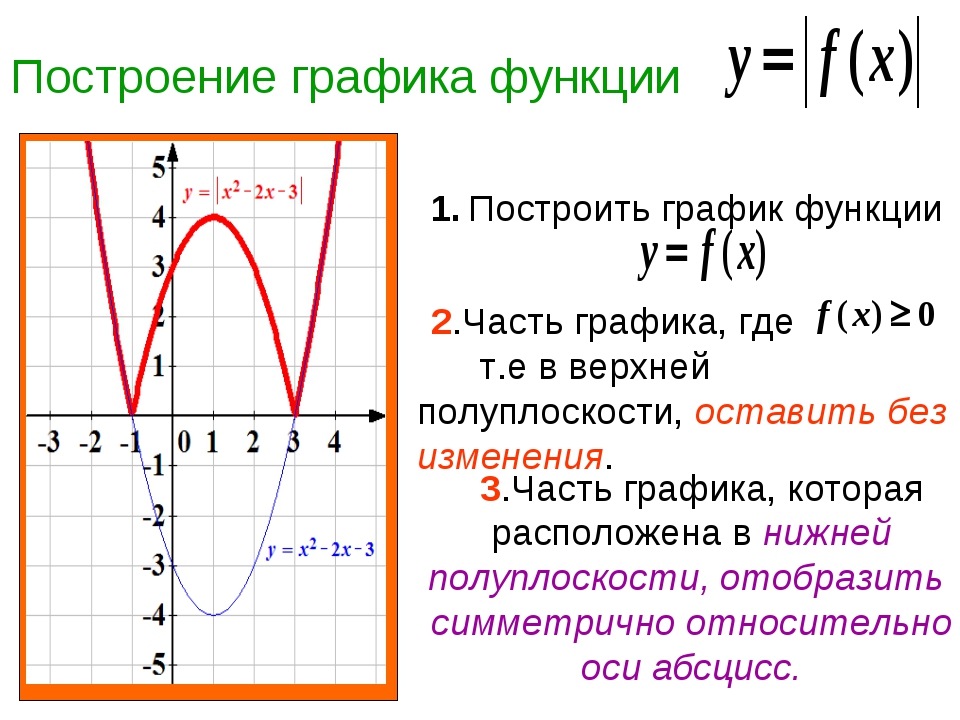Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
Слайды 8-13.
5. Исследовательская работа по построению графиков функции у=|f |(х)| |
Применяя определение абсолютной величины и ранее рассмотренные примеры, построим графиков функции:
у = |2|х| — 3|
у = |х 2 — 5|х||
у = | |х 2 | — 2| и сделал выводы.
Для того чтобы построить график функции у = | f |(х)| надо:
1. Строить график функции у = f(х) для х>0.
2. Строить вторую часть графика, т. е. построенный график симметрично отражать относительно ОУ, т.к. данная функция четная.
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Построить график функции у = | 2|х | — 3| (1-й способ по определению модуля)
1. Строим у = 2|х | — 3 , для 2 |х| — 3 > 0 , | х
|>1,5 т.
е. х1,5
а) у = 2х — 3 , для х>0
б) для х
2. Строим у = —2 |х| + 3 , для 2|х | — 3
а) у = —2х + 3 , для х>0
б) для х
У = | 2|х | — 3|
1) Строим у = 2х-3, для х>0.
2) Строим прямую, симметричную построенной относительно оси ОУ.
3) Участки графика, расположенные в нижней полуплоскости, отображаю симметрично относительно оси ОХ.
Сравнивая оба графика, видим, что они одинаковые.
у = | х 2 — 5|х| |
1. Строим у = х 2 — 5 |х|, для х 2 — 5 |х| > 0 т.е. х >5 и х
а) у = х 2 — 5 х, для х>0
б) для х
2. Строим у = — х 2 + 5 |х| , для х 2 — 5 |х|
а) у = — х 2 + 5 х, для х>0
б) для х
У = | х 2 — 5|х| |
а) Строим график функции у = х 2 — 5 х для х>0.
Б) Строим часть графика, симметричную построенной относительно оси ОУ
в) Часть графика, расположенные в нижней
полуплоскости, преобразовываю на верхнюю
полуплоскость симметрично оси ОХ.
Сравнивая оба графика, видим что они одинаковые. (Рис.10)
3. Подведение итогов урока.
14,15 слайды.
у=f |(х)|
1.Построить график функции у=f (х) для х>0;
2.Построить для х
Алгоритм построения графика функции у=|f (х) |
1.Построить график функции у=f (х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f (х)
Алгоритм построения графика функции у=|f |(х)| |
1. Построить график функции у=f (х) для х>0.
2. Построить кривую графика, симметричную построенной относительно оси ОУ, т.к. данная функция четная.
3. Участки графика, расположенные в нижней полуплоскости, преобразовывать на верхнюю полуплоскость симметрично оси ОХ.
Здравствуйте, Давид.
График функции представляет собой её геометрический образ. Он показывает, где на координатной плоскости находится точка, координаты которой (Х и У) связаны определенным математическим выражением (функцией).
Перед тем, как приступить к построению графика функций, сначала необходимо начертить оси координат ОХ и ОУ. Лучше всего для этого использовать масштабно — координатную бумагу. Далее следует определить тип функции, потому что у различных функций графики очень сильно отличаются. К примеру, линейная функция, о которой пойдет речь ниже, имеет график в виде прямой линии. После этого нужно определить область определения функций, т.е. ограничения для значений Х и У. К примеру, если Х находиться в знаменателе дроби, то его значение не может быть равным 0. Далее надо найти нули функции, то есть места пересечения графика функции с осями координат.
Приступим к построению графика функции, указанной в пункте а) вашего вопроса.
Функция у= — 6х + 4 , график которой требуется построить в первой задаче вашего вопроса, является линейной функцией, т.к. линейные функции представлены выражением y = kx + m. Областью определения линейной функции считается вся прямая ОХ. Параметр m в линейной функции определяет точку, в которой график линейной функции пересекает ось OY.
Для того, чтобы построить график линейной функции достаточно определить хотя бы две её точки, потому что графиком функции является прямая. Если найти больше точек, то можно построить более точный график. Вообще, при построении графика линейной функции необходимо определить точки, в каких график пересечет оси координат Х, У.
Итак, в вашем случае точки пересечения графика функции с осями координат будут такими:
При Х=0, У= -6*0+4=4 Таким образом, мы получили значение параметра m в линейной функции.
У=0, то есть 0= -6*Х+4, то есть 6х=4, следовательно Х=4/6=0,667
При Х= -1, У=-6*-1+4=10
При Х=1, У= -6*1+4=-2
При Х=2, У= -6*2+4=-8
Получив все вышеуказанные точки, вам остается только отметить их на координатной плоскости, соединить прямой линией, как показано в примере на рисунке, который прикреплен к данной статье.
Теперь построим график функции, указанной в пункте б) вашего вопроса.
Сразу видно, что функция у= 0,5х , из второй задачи, также является линейной функцией.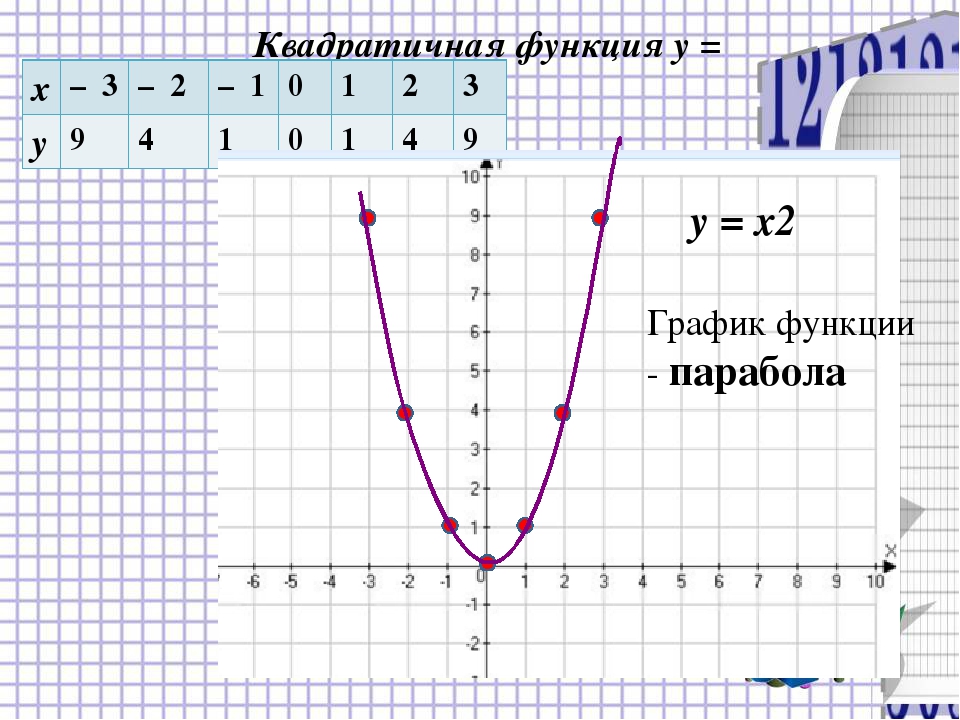
В отличие от первого примера, в данном выражении отсутствует значение m, а это говорит о том, что график функции у= 0,5х проходит через начало осей координат, то есть в их нулевой точке.
При Х=0, У= 0,5*0=0
При Х= 1, У=0,5*1=0,5
При Х=2, У= 0,5*2=1
При Х=3, У=0,5*3=1,5
При Х= -1, У=0,5*-1= -0,5
При Х= -2, У= 0,5*-2= -1
При Х= -3, У=0,5*3= -1,5
Теперь, имея все вышеуказанные значения Х и У вы без труда сможете поставить эти точки на координатной плоскости, соединить их прямой линией при помощи линейки, и у вас получится график линейной функции у=0,5х
Ниже я привела ссылку, перейдя по которой, вы можете найти уроки по математике, алгебре, геометрии и русскому языку. Я бы посоветовала вам прочитать несколько тем, которые касаются построения графиков функций. В данном учебном материале очень наглядно показано, как можно построить графики линейных функций, а в темах, которые расположены далее можно увидеть примеры построения графиков других функций.
Все написано достаточно подробно, поэтому это будет понятно не только тем, кто давно закончил школу и имеет представление о том, как можно построить график функции, но и тем, кто только начинает постигать азы науки. Я считаю, что увидев наглядно на конкретных примерах, как строятся графики функций, вы потом без проблем сможете решить любую задачу по построению графика функций.
Сегодня мы внимательно изучим функции, графиком которых является прямая линия.
Запиши в тетрадь тему урока
«Линейная функция и прямая пропорциональность».
Внимательно выполняй все задания и
старайся запомнить новые для тебя определения.
Запомни определение:
Линейной функцией называется функция, которую можно задать формулой вида
у = kx + b, где х — независимая переменная, k и b — некоторые числа.
Например: если k = 0,5 и b = -2, то у = 0,5х — 2.
Задание:
Построить график линейной функции у = 0,5х — 2.
Составь таблицу значений пар (х, у).
Отметь их на координатной плоскости.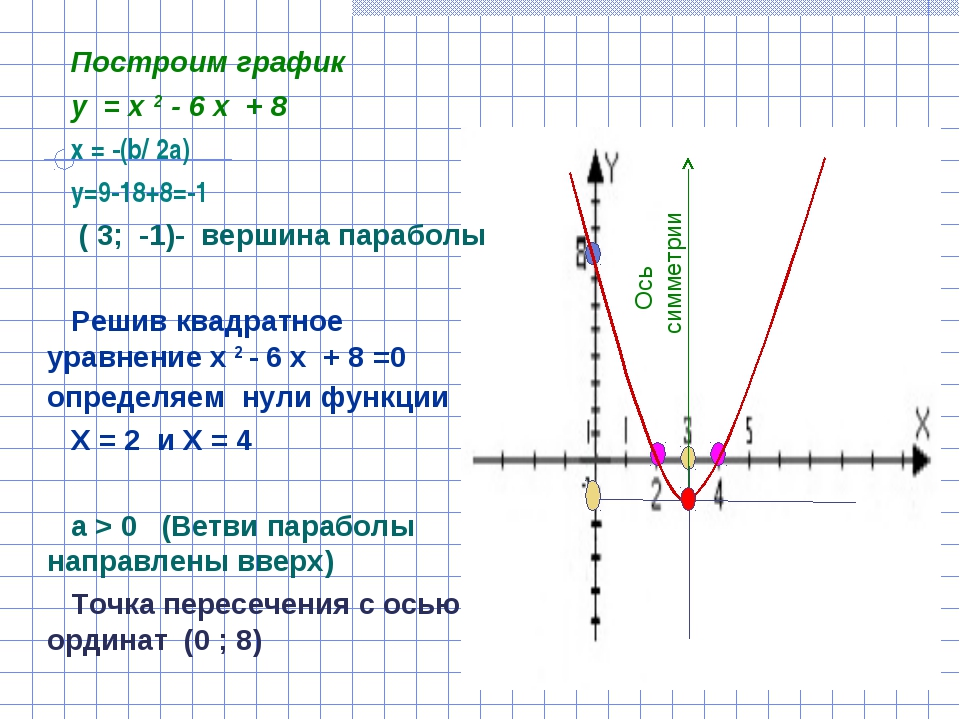
Соедини точки линией.
Проверь решение:
Построим график линейной функции у = 0,5х — 2.
Для построения графика у = -х + 3 вычислим координаты двух точек
Отметим их на координатной плоскости две точки и соединим их прямой.
А сможешь ли ты определить:
принадлежит ли точка А(36; 5) графику линейной функции ?
Да
Нет
А теперь сравни эти два графика и увидим, что у линейной функции у = kx + b,
еще до его построения можно «предугадать» расположение прямой линии на координатной плоскости!
Как?
Просто надо внимательно посмотреть на числа k и b…
И они многое нам расскажут!
Попробуй догадаться…
| Функция у = 0,5х — 2 | Функция у = -х + 3 |
Итак, наблюдаем и делаем выводы:
1) Первый пересекает ось ОУ в точке (0; -2), а второй в (0; 3)
!!! у первого b = -2, а у второго b = 3
Вывод: по числу b в формуле y = kx + b мы определим в какой точке прямая пересечет ось ординат.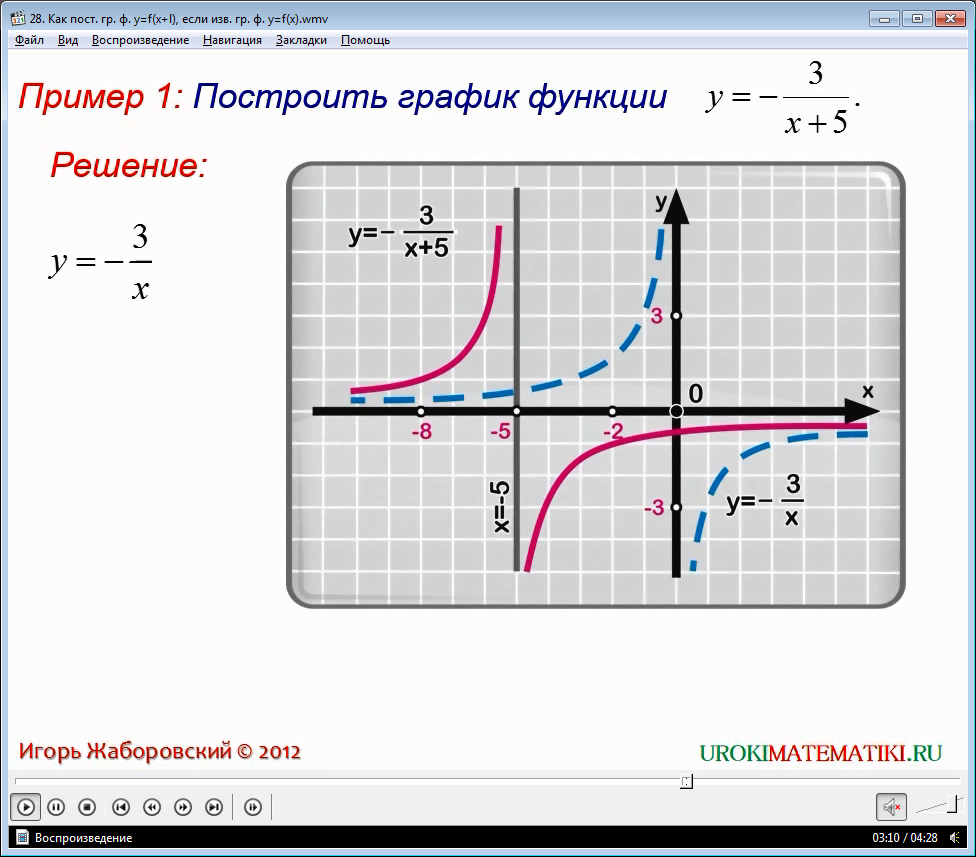
2) Первый наклонен к положительному направлению оси ОХ под острым углом, а второй — под тупым углом.
!!! у первого k > 0, а у второй функции k
Вывод: если в формуле y = kx + b мы видим, что число k > 0 значит график наклонен к положительному направлению оси абсцисс под острым углом;
если же число k Число k (коэффициент при х) называют за это — угловым коэффициентом.
Запомни это все! Нам такие знания еще не раз пригодятся
Если в формуле y = kx + b, мы возьмем b = 0, то получим формулу y = kx.
Запомни определение:
Функция, которую можно задать формулой y = kx, где k — некоторое число не равное 0, х — переменная, называется прямой пропорциональностью.
Выполни в своей тетради задание:
Придумай несколько формул прямой пропорциональности с разными коэффициентами k и построй их графики в одной координатной плоскости.
Поскольку у прямой пропорциональности b = 0, то график пересечет ось ОУ в точке (0; 0).
На одной координатной плоскости мы можем нарисовать и несколько графиков!
У линейной функции график — прямая линия.
А прямые могут быть параллельными или пересекаться в одной точке…
Интересно, а до построения графиков, только посмотрев (внимательно!) на их формулы, мы может сделать вывод:
Графики этих функций — пересекутся,
графики этих функций — расположены параллельно.
Построение графика с помощью элементарных преобразований.
Построение графика функции
y=f(kx) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; b=0)Рассмотрим сначала два частных случая при b=0,т.е. функция имеет вид y=f(kx) .
1. При |k|>1 график функции y=f(x) сжимается в |k| раз вдоль оси OX относительно оси OY.
2. При |k|<1 график функции y=f(x) растягивается в раз вдоль оси OX относительно оси OY . При k<0 полученный график дополнительно отображаем симметрично относительно оси OY.
Рассмотрим примеры:
| Построить график функции | Построить график функции |
Построение графика функции
y=f(x+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0; k=1)При b>0 график функции y=f(x) сдвигается влево вдоль оси OX на b единиц.
При b<0 график функции y=f(x) сдвигается вправо вдоль оси OX на |b| единиц
Рассмотрим примеры:
| Построить график функции ( b>0 ) | Построить график функции ( b<0 ) |
Построение графика функции
y=f(kx+b) с помощью элементарных преобразований графика функции y=f(x) (A=1; B=0)Рассмотрим общий случай : y=f(kx+b) .
Сначала вынесем коэффициент k за скобку: .
Именно число определяет сдвиг вдоль оси OX , а не b ,
как полагают некоторые абитуриенты.
Теперь строим график функции y=f(x) .
Затем строим график функции y=f(kx) , после чего сдвигаем полученный график вдоль оси OX на
единиц влево или вправо в зависимости от знака этого числа.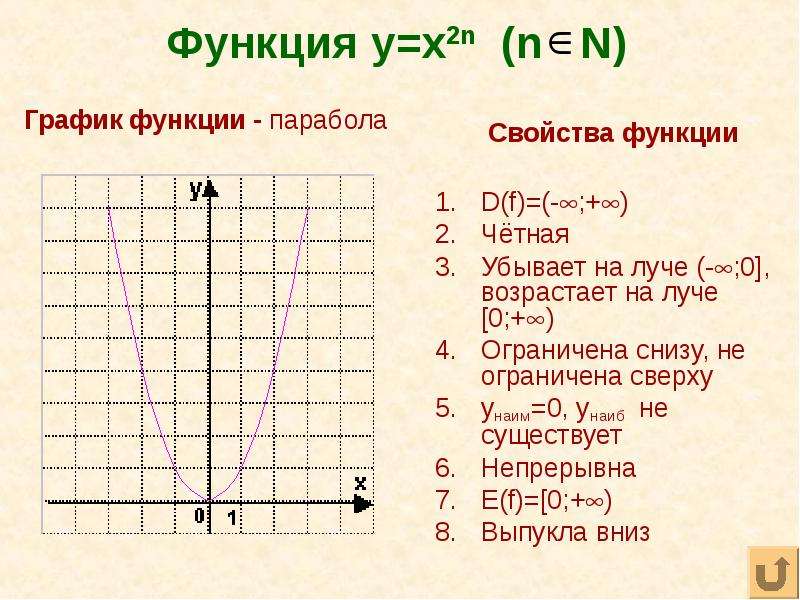
| Рассмотрим пример: построить график функции |
Построение графика функции
y=A·f(kx+b)+B с помощью элементарных преобразоаний графика функции y=f(x)Комбинируя методы построения графиков, рассмотренные в предыдущих случаях, можно по известному графику функции y=f(x) построить график функции y=A·f(kx+b)+B с помощью растяжений, сжатий по горизонтали и вертикали, параллельных переносов вдоль осей координат, а также симметрий относительно координатных осей тех графиков, которые получаются из первоначального графика последовательно применением подходящего преобразования.
Рассмотрим примеры.
| Построить график функции | Построить график функции |
Как нарисовать любой график на глаз
Математические уравнения полезны, но они также неэффективны — для каждого значения x вам нужно выполнить отдельный расчет, чтобы выяснить, что такое y.
Графики берут это уравнение и превращают его в наглядное изображение, во что-то, на что вы можете посмотреть и сразу увидеть, что происходит при разных значениях x, как изменяется функция и многое другое!
Однако, когда вы впервые изучаете графики, все дело в запоминании основных уравнений и того, как будут выглядеть их графики, начиная с формы линейных уравнений с пересечением наклона.Однако по мере того, как вы переходите к более сложным уравнениям, таким как квадратичная и тригонометрия, вас часто просят запоминать формы таких уравнений —
— где вы должны запомнить точную настройку уравнения и то, что означает каждый термин на графике, будь то вершина, наклон, пересечения, масштабирование, горизонтальный или вертикальный сдвиг или многое другое!
Но зачем запоминать все эти a, c, k и h, если это будет полезно только в некоторых конкретных случаях ?!
Вместо этого, в следующий раз, когда вам нужно будет узнать, как должен выглядеть график функции, попробуйте эти шаги, чтобы быстро нарисовать любой график!
Для демонстрации воспользуемся уравнением:
Он похож на полиномиальные уравнения, которые вы, возможно, видели в классе, но он кубический, поэтому у нас нет очевидных форм уравнений, которые можно было бы использовать для построения графика.
Итак, как построить график этой функции?
1. График x = 0
Первое, что мы хотим сделать, это поднять несколько точек на нашем графике, поэтому мы хотим выбрать те, которые будет легко вычислить. Практически для любого уравнения подстановка x = 0 и решение относительно y выполняется быстро и легко на глаз, и почти всегда можно выполнить без калькулятора. Для нашего примера уравнения:
Итак, первая точка, которую мы поставим на нашем графике, — это (0, -4).
а. Если вы легко найдете его, постройте y = 0
Далее, в некоторых случаях y = 0 тоже довольно легко решить.Если вы можете быстро решить для y = 0 , это еще один хороший момент, который нужно решить прямо сейчас. В данном случае:
Итак, теперь у нас есть точка (-2, 0), которую нужно добавить к нашему графику!
г. Бонус: нанесите несколько простых для вычисления точек, например x = 1 & x = -1
В зависимости от графика может быть легко подставить небольшие целые числа, такие как 1 или -1.
Чем больше точек вы можете добавить к своему графику, тем лучше вы сможете увидеть, какую форму он в конечном итоге примет. Однако придерживайтесь тех пунктов, которые легко вычислить.Цель этого метода — быстро найти всего несколько точек — если вы собираетесь вычислять каждую точку на графике, вы не экономите себе время!
Для этого уравнения мы получим:
и
Итак, теперь у нас есть четыре точки: (0, -4), (-2,0), (1, -18) и (-1, -2). Давайте нарисуем эти точки и посмотрим, как они выглядят!
Мы можем увидеть, как график обретает форму, но нам понадобится дополнительная информация, прежде чем мы закончим.
2.Выясните, что происходит, когда x действительно велик (в положительном и отрицательном направлении)
Какая бы линия мы ни рисовали, она должна заканчиваться стрелками на обоих концах, чтобы мы знали, что происходит, когда мы идем дальше по оси x как в положительном, так и в отрицательном направлении.
Это то, что называется «конечным поведением». Чтобы выяснить, что это такое, мы собираемся подставить два числа в наше исходное уравнение — большое положительное число и большое отрицательное число. На самом деле мы не собираемся выбирать число и использовать наш калькулятор, чтобы выяснить, что происходит, мы просто собираемся посмотреть, как части уравнения повлияют на конечный результат.
Например, подставив большое положительное число в нашу кубическую функцию, получим:
Добавление 1 к большому положительному числу почти не изменит его — тогда, когда мы кубим его в куб, оно станет действительно большим положительным числом.
Однако действительно большое положительное число станет отрицательным при умножении на -2, и вычитание 2 не имеет большого значения, поэтому конечным результатом будет действительно большое отрицательное число.
Если мы попробуем то же самое для другой стороны графика, подставив большое отрицательное число для x, мы получим:
Большое отрицательное число в кубе — это действительно большое отрицательное число, но на этот раз, когда оно умножится на -2, оно станет действительно большим положительным числом.
o, для нашего графика мы обнаружили, что при больших положительных значениях x, y является большим и отрицательным значением, а при большом отрицательном значении x, y является большим и положительным. Давайте добавим это к нашему графику со стрелками.
3. Необязательно: найдите любые «важные» значения x
У некоторых уравнений есть необычные особенности или особенности, которые вы можете заметить, взглянув на уравнение — обратите внимание, в частности, на любые точки, где большая часть уравнения может стать нулевой. Это может помочь вам найти корни, асимптоты или другие места, где форма графика изменяется необычным образом.
Например, с уравнением, которое мы рассматривали,
Этот член интересен тем, что если x = -1, вся часть уравнения станет нулевой. Конечно, мы уже нашли эту точку ранее, но это говорит нам, что x = -1 — это «особая» точка в уравнении — возможно, что форма графика здесь каким-то образом изменится.
4.
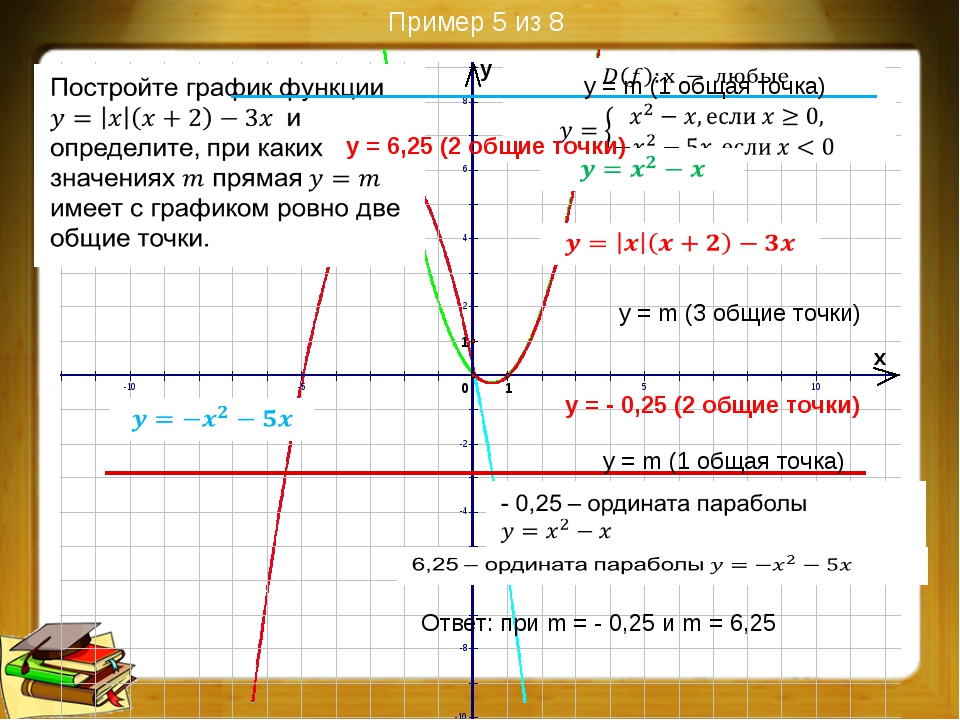Соедините точки и готово!На этом этапе мы сделали все, что могли — у нас есть несколько точек на графике, мы знаем, как он будет выглядеть на концах, и выявили любые необычные точки или особенности.Возможно, мы не знаем, что это такое, но мы готовы что-нибудь нарисовать.
Возможно, мы все еще не знаем точно, как выглядит график, но здесь вы можете использовать основы для каждого основного уравнения. Мы знаем, что наша линия будет гладкой и максимально простой, но при этом будет поражать все наши точки. Если мы в целом знаем, что это за уравнение (полиномиальное, радикальное, экспоненциальное), у нас есть по крайней мере некоторое предположение, какой была бы его общая форма.
В нашем примере у нас достаточно точек, чтобы набросать одну сторону нашего уравнения, но отрицательная сторона немного неясна, поэтому давайте подумаем, что мы можем сказать о другом типе многочлена, квадратном уравнении.
Что касается нашей кубической функции, мы знаем, что квадратичные функции всегда симметричны относительно своей вершины, но это не совсем работает, потому что мы знаем, что в одном направлении мы закончим положительно, а в другом нам нужно пойти отрицательным.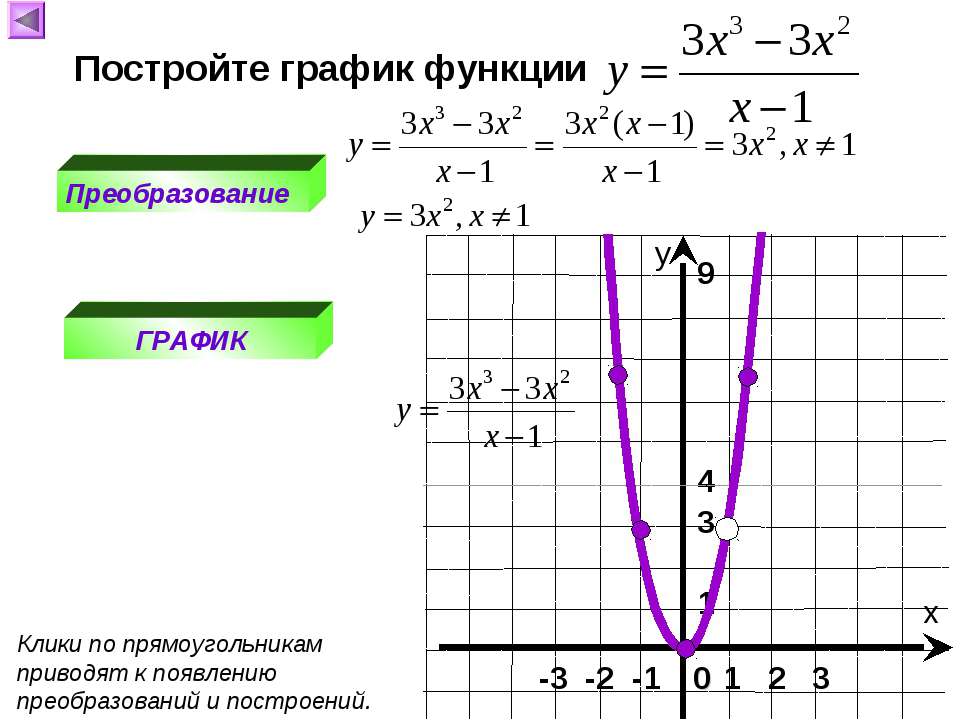
Итак, давайте угадаем что-то подобное — может быть, наша «особая» точка в x = -1 — это , как вершина, но в этой точке форма графика такая же, но движется в противоположном направлении. (Я для справки поставил пунктирную линию в точке x = — 1, но, конечно, это не будет частью настоящего окончательного графика.)
Поехали! Это не идеальный график, но, выполнив несколько быстрых шагов, мы, по крайней мере, в общих чертах узнаем, как этот график будет выглядеть. Если вам интересно, вот как выглядит это уравнение, построенное на компьютере.
Этот метод работает для большого количества функций — многочленов, радикалов, экспонент, логарифмов, триггерных функций и многого другого! Просто будьте осторожны, когда дойдете до функций с несколькими y или членами: в этих случаях графики будут необычными, сложными формами, поэтому нарисуйте много точек (x, y), прежде чем пытаться соединить все точки!
Рисование графиков математических функций с помощью Math Assistant в OneNote
Сначала создайте уравнение, используя рукописный ввод или текст.
На вкладке Draw напишите или введите свое уравнение. Используйте инструмент Lasso Select , чтобы нарисовать круг вокруг уравнения. Затем выберите Math . Это откроет панель Math Assistant.
Из Выберите действие в раскрывающемся меню на панели Math , выберите График в 2D или График с обеих сторон в 2D .
Чтобы настроить график, созданный Math Assistant, выполните одно из следующих действий (если доступно):
Выберите (или нажмите и удерживайте), а затем перетащите график в любом направлении, чтобы переместить его положение.
Щелкайте или касайтесь кнопок лупы + и — столько раз, сколько необходимо, чтобы изменить значения параметров в вашем уравнении, увеличивая или уменьшая масштаб.
Примечание: Если вы используете OneNote на устройстве с сенсорным экраном, вы также можете настроить график пальцами. Используйте один палец, чтобы переместить положение графика, или увеличивайте масштаб двумя пальцами, чтобы изменить уровень увеличения.В OneNote в Интернете вы можете использовать стрелки по бокам графика, чтобы изменить его положение.
Щелкните или коснитесь значка с двойной стрелкой Сбросить , чтобы вернуть график в исходное состояние.
Когда график будет выглядеть так, как вы хотите, щелкните или коснитесь Вставить на странице , чтобы разместить его как снимок экрана на текущей странице.
Примечание: Чтобы изменить способ отображения графика (градусы, радианы, градиенты), щелкните или коснитесь Настройки , когда панель «Математика» открыта.
Расширенные возможности построения графиков
Другие функции могут быть доступны в зависимости от типа вашего графика.
Считывание значений x-y: Наведите указатель мыши на точку на линии графика, чтобы увидеть значения x и y в OneNote для Windows 10. В OneNote в Интернете щелкните строку, чтобы просмотреть значения.
Управление параметрами: Если у вас есть уравнение с параметрами, например ax + b, используйте знаки плюс + и минус — под графиком, чтобы изменить значения a и b.
Ключевые особенности графика: Math Assistant вычисляет интересную информацию о графике, такую как нули, точки пересечения, минимумы, максимумы и многое другое. Используйте флажки, чтобы выбрать, какие функции вы хотите отобразить на графике.
Создавайте математические уравнения с помощью рукописного ввода или текста с помощью Math Assistant в OneNote
Решайте математические уравнения с помощью Math Assistant в OneNote
Типы задач, поддерживаемые Math Assistant
Создайте практическую викторину по математике
Типы задач, которые можно изобразить в 2D
Когда вы используете Math Assistant в OneNote, вы заметите, что раскрывающийся список Выберите действие под уравнением изменяется в зависимости от выбранного вами уравнения.
Следующие типы задач можно изобразить в 2D с помощью Math Assistant.
Выражения (с переменной) | |
Полиномиальные массивы | |
Уравнения | Вы можете График в 2D или Изобразить обе стороны в 2D при работе с уравнениями. Выберите График в 2D , чтобы увидеть решение уравнения. Выберите Обе стороны графика в 2D , чтобы просмотреть график двух функций на противоположных сторонах от знака равенства. |
Системы уравнений | |
Полярные координаты | Чтобы построить график функции в полярных координатах, необходимо выразить r как функцию от тета. |
Неравенства | Вы можете График в 2D или Изобразить обе стороны в 2D при работе с неравенствами. Выберите График в 2D , чтобы увидеть решение неравенства. Выберите Обе стороны графика в 2D , чтобы просмотреть график двух функций на противоположных сторонах знака сравнения. |
Система неравенств |
Узнать больше
Создайте математический тест в Microsoft Forms
Создайте практическую викторину по математике с помощью Math Assistant в OneNote
Решайте математические уравнения с помощью Math Assistant в OneNote
Эскиз кривой
В процессе построения кривой выполняются следующие шаги:
1.
ДоменНайдите область определения функции и определите точки разрыва (если есть).
2. Перехватывает
Определите точки пересечения \ (x- \) и \ (y — \) функции, если это возможно. Чтобы найти точку пересечения \ (x — \), мы устанавливаем \ (y = 0 \) и решаем уравнение для \ (x. \). Точно так же мы устанавливаем \ (x = 0 \), чтобы найти \ (y- \ ) перехват. Найдите интервалы, в которых функция имеет постоянный знак \ (\ left ({f \ left (x \ right) \ gt 0} \ right. \) И \ (\ left. {F \ left (x \ right) \ lt 0} \ вправо).\)
3. Симметрия
Определите, является ли функция четной, нечетной или ни одной, и проверьте периодичность функции. Если \ (f \ left ({- x} \ right) = f \ left (x \ right) \) для всех \ (x \) в области, то \ (f \ left (x \ right) \) является четный и симметричный относительно оси \ (y — \). Если \ (f \ left ({- x} \ right) = -f \ left (x \ right) \) для всех \ (x \) в домене, то \ (f \ left (x \ right) \) нечетное и симметричное относительно начала координат.
4. Асимптоты
Найдите вертикальную, горизонтальную и наклонную (наклонную) асимптоты функции.\ prime \ left (x \ right) \) и найдите критические точки функции. (Помните, что критические точки — это точки, в которых первая производная равна нулю или не существует.) Определите интервалы, в которых функция увеличивается и уменьшается с помощью теста первой производной.
6. Локальный максимум и минимум
Используйте первый или второй производный тест, чтобы классифицировать критические точки как локальный максимум или локальный минимум. Вычислите значения \ (y — \) локальных экстремальных точек.{\ prime \ prime} \ left (x \ right) \ gt 0} \ right). \)
8. График функции
Нарисуйте график \ (f \ left (x \ right) \), используя всю информацию, полученную выше.
Далее мы используем этот алгоритм для исследования функций.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
2}} \ right] + 2 — \ frac {{2 \ sqrt 3}} {3} = \ cancel {1} — \ sqrt 3 + \ cancel {1} - \ frac {{\ sqrt 3}} {9} — \ cancel {3} + 2 \ sqrt 3 — \ cancel {1} + \ cancel {2} — \ frac { {2 \ sqrt 3}} {3} = \ frac {{9 \ sqrt 3 — \ sqrt 3 — 6 \ sqrt 3}} {9} = \ frac {{2 \ sqrt 3}} {9} \ приблизительно 0 , 38; \]
Аналогично находим, что
\ [y \ left ({1 + \ frac {{\ sqrt 3}} {3}} \ right) = — \ frac {{2 \ sqrt 3}} {9} \ приблизительно -0,38.\]
Таким образом, функция имеет локальный максимум в точке
.\ [\ left ({1 — \ frac {{\ sqrt 3}} {3}, \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({0,42; \ ; 0,38} \ вправо). \]
Соответственно, локальный минимум достигается в точке
.\ [\ left ({1 + \ frac {{\ sqrt 3}} {3}, — \ frac {{2 \ sqrt 3}} {9}} \ right) \ приблизительно \ left ({1,58; \; — 0,38} \ вправо) \]
Интервалы увеличения / уменьшения следуют из рисунка \ (1a. \)
Рассмотрим вторую производную:
\ [y ^ {\ prime \ prime} \ left (x \ right) = \ left ({3 {x ^ 2} — 6x + 2} \ right) ^ \ prime = 6x — 6; \]
\ [y ^ {\ prime \ prime} \ left (x \ right) = 0, \; \; \ Rightarrow 6x — 6 = 0, \; \; \ Стрелка вправо x = 1.
2} = \ left ({x + 2} \ right) \ left ({2x — \ cancel {2} + x + \ cancel {2}} \ right) = 3x \ left ({x + 2} \ right) . \]
Стационарных точек
\ [у ‘\ влево (х \ вправо) = 0, \; \; \ Rightarrow 3x \ left ({x + 2} \ right) = 0, \; \; \ Rightarrow {x_1} = 0, \; {x_2} = — 2. \]
Производная меняет знак, как показано на рисунке \ (3a. \). Следовательно, \ (x = -2 \) — точка максимума, а \ (x = 0 \) — точка минимума. В этих экстремальных точках функция имеет следующие значения:
\ [y \ left ({- 2} \ right) = — 4, \; \; y \ left (0 \ right) = 0.3}}} = 0, \; \; \ Rightarrow {x_1} = — \ sqrt 3, \; {x_2} = \ sqrt 3. \]
При прохождении через эти точки вторая производная меняет знак. Следовательно, обе точки являются точками перегиба. Функция строго выпуклая вниз в интервалах \ (\ left ({- \ infty, — \ sqrt 3} \ right) \) и \ (\ left ({\ sqrt 3, + \ infty} \ right) \) и соответственно, строго выпукло вверх на отрезке \ (\ left ({- \ sqrt 3, \ sqrt 3} \ right).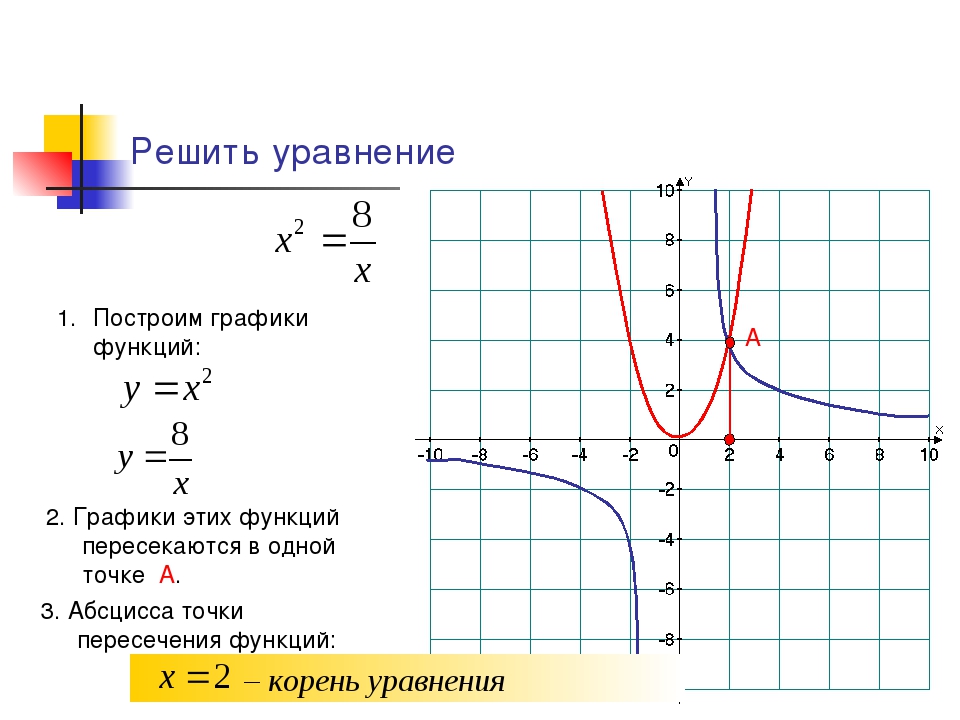
2}}} = \ frac {1} {{1 + 3}} = \ frac {1} {4}.\]
На рисунке \ (4b \) представлен схематический график функции.
Рисунок 4а. Рисунок 4б.См. Другие проблемы на страницах 2, 3.
4. График функции
График функции — это набор всех точек, координаты которых ( x , y ) удовлетворяют функции `y = f (x) `. Это означает, что для каждого значения x существует соответствующее значение y , которое получается, когда мы подставляем в выражение для `f (x)`.
Поскольку количество точек на графике функции не ограничено, сначала мы будем следовать этой процедуре:
- Выберите несколько значений x (минимум 5)
- Получить соответствующие значения функции и занести их в таблицу
- Постройте эти точки, соединив их плавной кривой
Однако вам предлагается изучить общие формы некоторых общих кривых (например, прямую линию,
парабола, тригонометрические и экспоненциальные кривые, с которыми вы встретитесь в следующих главах).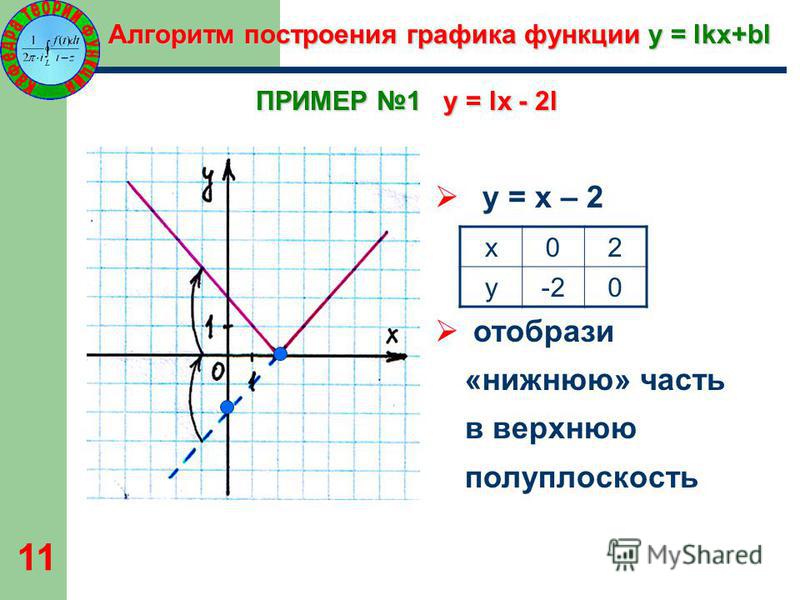
Это намного проще, чем рисовать точки, и это пригодится нам позже!
Пример 1
Мужчина ростом «2 м» бросает мяч прямо вверх, и его высота в момент времени t (в s ) определяется выражением ч = 2 + 9 т — 4,9 т 2 м.
Постройте график функции.
Ответ
Начнем с t = 0, поскольку отрицательные значения времени имеют практического смысла здесь нет.
Выбираем значения `0.С интервалом 5` (если бы мы использовали интервалы `t = 1 \» s «`, мы не увидели бы достаточно деталей на графике).
| т | 0 | 0,5 | 1 | 1,5 | 2 |
| h | 2 | 5,3 | 6,1 | 4,5 | 0,4 |
График снаряда (парабола).
Эта форма называется параболой и является общепринятой.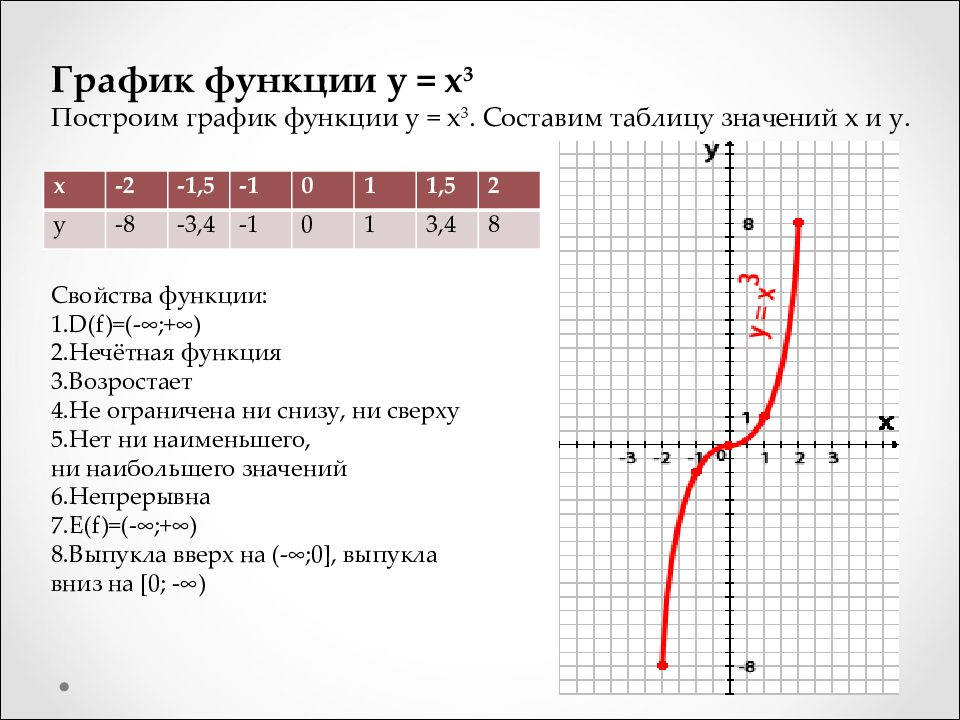
в приложениях математики.
ПРИМЕЧАНИЕ:
(1) На этом графике высота против времени. Мяч пошел прямо вверх, а не вперед. (На нашем графике может создаться впечатление, что мяч двигался в направлении x , а также вверх, но это было не так.)
(2) Мы могли бы написать функцию в этом примере с h ( t ), а не просто h . Следующие два уравнения означают одно и то же.
ч = 2+ 9 т — 4.9 т 2
ч ( т ) = 2 + 9 т — 4,9 т 2
Пример 2
Скорость (в «м / с») мяча в Примере 1 во время т (в с ) дается по
v = 9 — 9,8 t
Нарисуйте график v — t . Что скорость, когда мяч ударяется о землю?
Ответ
Это прямая линия, так как она имеет вид
y = м x + c
Подробнее на Straight Line.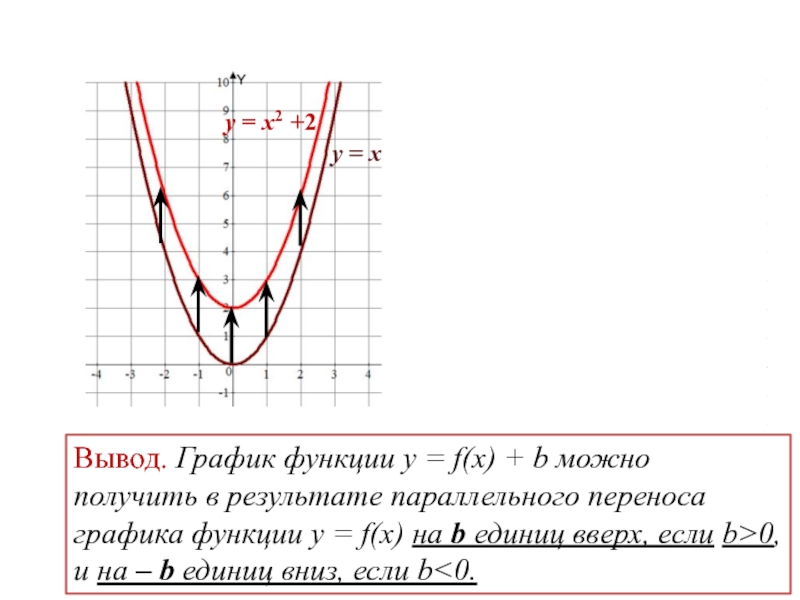
Поскольку мы определили, что это прямая линия, нам нужно только построить 2 очка и присоединяйтесь к ним. Но мы находим 3 точки, просто чтобы убедиться, что у нас правильная линия.
График зависимости `v` от` t` — прямой.
Наш график начинается с `t = 0` (поскольку отрицательные значения времени не имеют значения в этом примере).
В течение первых 0,918 «с» «мяч идет вверх (положительная скорость, то есть синяя линия находится выше оси t ), но замедляется.
После этого мяч приближается к земле и становится быстрее (участок, где синяя линия находится ниже оси t ).
Мяч падает на землю примерно за t = 2,04 с (мы можем см. это из примера 1). Скорость , когда мяч падает на землю с графика, который мы только что нарисовали, имеет значение `-11 \ «м / с» `. График останавливается на этом месте.
На нашем графике предполагается, что мяч приземляется в песок и не отскакивает.
Обычно, как мы сделали здесь, мы берем скорость в до направление быть положительным.
Пример 3
Постройте график функции y = x — x 2 .
Ответ
(a) Определите значения y- для типичного набора значений x и запишите их в таблицу.
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | −6 | -2 | 0 | 0 | -2 | −6 |
(b) Так как y = 0 как для x = 0, так и для x = 1`, проверьте, что происходит между ними.2`, парабола.
Обратите внимание, что кривая продолжается за пределы того, что показано на графике. Это просто общий вопрос, и практических ограничений для значений x или y нет.
Пример 4
Построить график функции `y = 1 + 1 / x`
Ответ
(a) Примечание: y не определен для x = 0 из-за деление на `0`
Следовательно, `x = 0` не находится в области
(б) Составьте таблицу значений:
| x | `-4` | `-3` | `-2` | `-1` | `1` | `2` | `3` | `4` |
| y | `3/4` | `2/3` | `1/2` | `0` | `2` | `3/2` | `4/3` | `5/4` |
(c) Мы знаем, что что-то странное произойдет рядом с x = 0 (поскольку граф там не определен).Итак, мы проверяем, что происходит в некоторых типичных точках между `x = -1` и` x = 1`:
, когда `x = −0,5,` y = 1 + 1 / (- 0,5) = 1-2 = −1`
, когда `x = 0,5, \ y = 1 + 1 / (0,5) = 1 + 2 = 3`
(d) По мере того, как значение x приближается к `0`, точки становятся ближе к y — ось, правда ее не трогают.
Ось y называется асимптотой кривой .
(Чтобы убедиться в этом, нанесите на график точки, где `x = 0.4, x = 0,3, x = 0,2, x = 0,1 и даже x = 0,01.)
График `y = 1 + 1 / x`, гипербола. Это прерывистая функция.
На этой кривой есть еще одна асимптота: y = 1, отмеченная пунктирной линией. Обратите внимание, что кривая не проходит через это значение.
Пример 5
Построить график функции `y = sqrt (x + 1)`
Ответ
(a) Примечание: y не определено для значений x минус чем `-1`. (Попробуйте что-нибудь в своем калькуляторе, например, `x = −4`.)
(b) Мы определяем некоторые значения x и соответствующие значения y и записываем их в таблицу:
| x | –1 | 0 | 1 | 2 | 3 | 4 | 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y | 0 | 1 | 1,4 | 1,7 | 2 | 2. 2`Постройте зависимость мощности от сопротивления. Ответ (a) Отрицательные значения для R не имеют физического значимость, поэтому P не отображается для отрицательных значений из р. (б) Составьте таблицу значений:
Функции
Константы
Вот набросок графика и обратите внимание, как мы обозначили точки в \ (x = 1 \). |
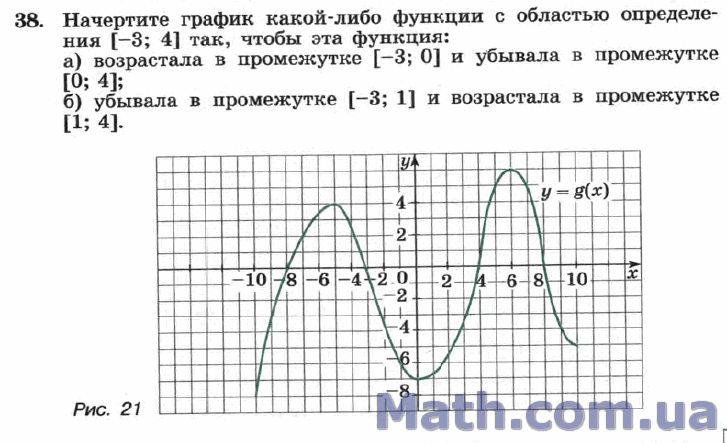(приложение ) Вода вытекает из резервуара в форме перевернутого конуса (т. Е. Вода течет
через заостренный конец конуса и самую широкую часть
конус находится наверху). Объем воды уменьшается с
постоянная скорость.
Эти две числовые линии определяют плоскую поверхность, называемую плоскостью. -axes., и каждая точка на этой плоскости связана с упорядоченной парой пар ( x , y ), которые определяют положение относительно начала координат на прямоугольной координатной плоскости. действительных чисел ( x , y ).Первое число называется координатой x , а второе число называется координатой y . Пересечение двух осей известно как начало координат Точка пересечения осей x и y , обозначенная (0, 0)., Что соответствует точке (0, 0).
Например, упорядоченная пара (-4, 3) представляет позицию на 4 единицы слева от начала координат и на 3 единицы выше во втором квадранте.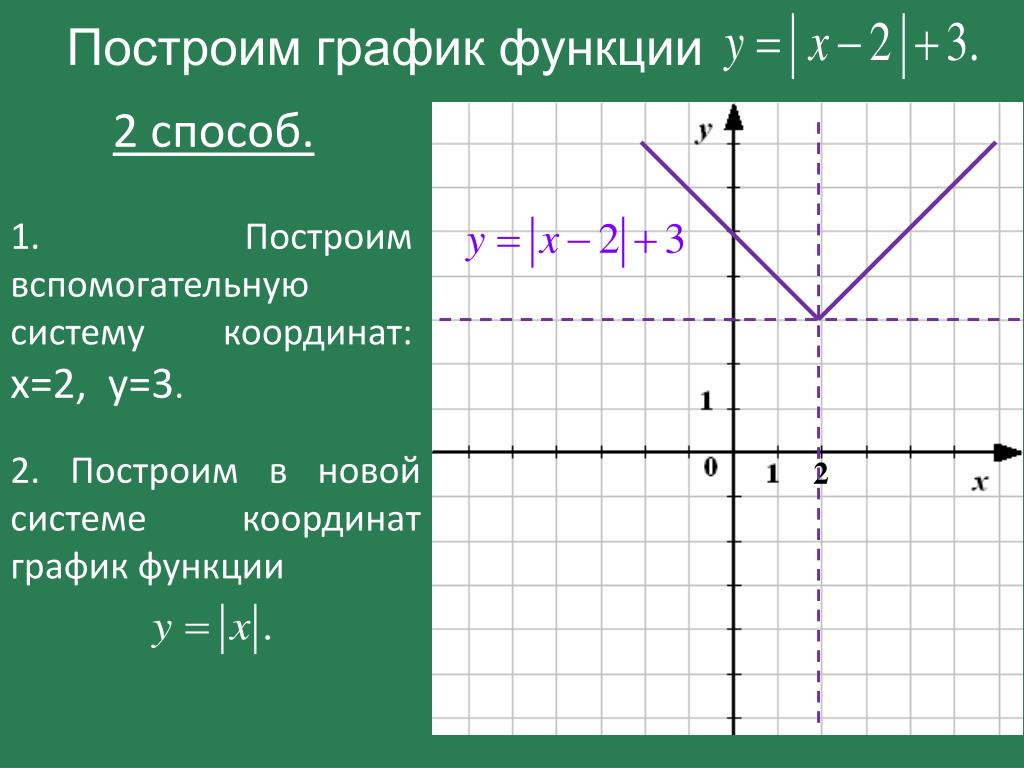
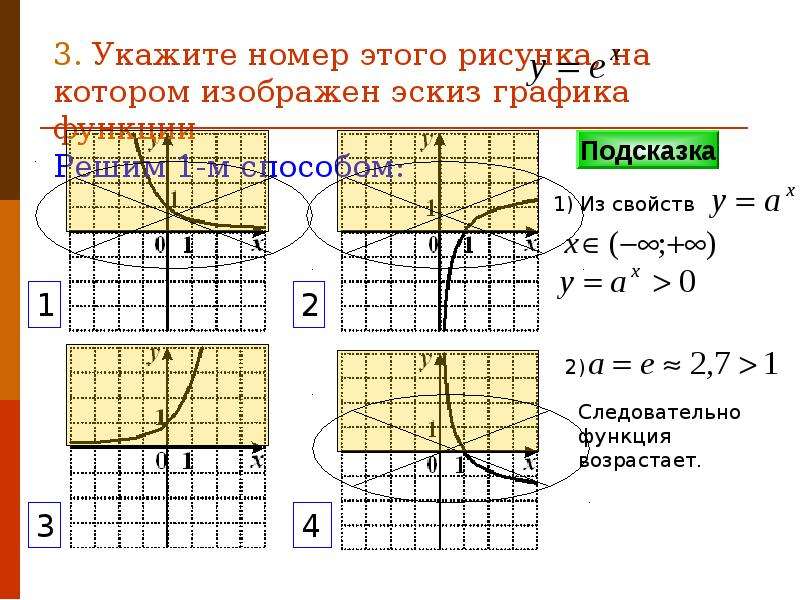. А набор, состоящий из всех вторых компонентов отношения, в данном случае значений y , называется диапазоном. состоящий из всех вторых компонентов отношения.Для отношений, состоящих из точек на плоскости, диапазон представляет собой набор всех значений y . (или codomain Используется при ссылке на диапазон.). Часто мы можем определить область и диапазон отношения, если нам дан его график.
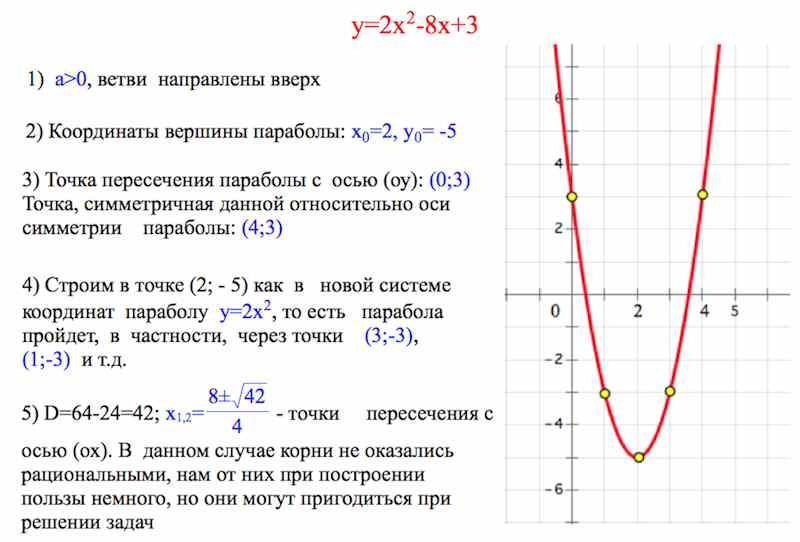Следовательно, область состоит из всех значений x в интервале [−8, ∞). Минимальное значение y , представленное на графике, равно 0; таким образом, диапазон равен [0, ∞).
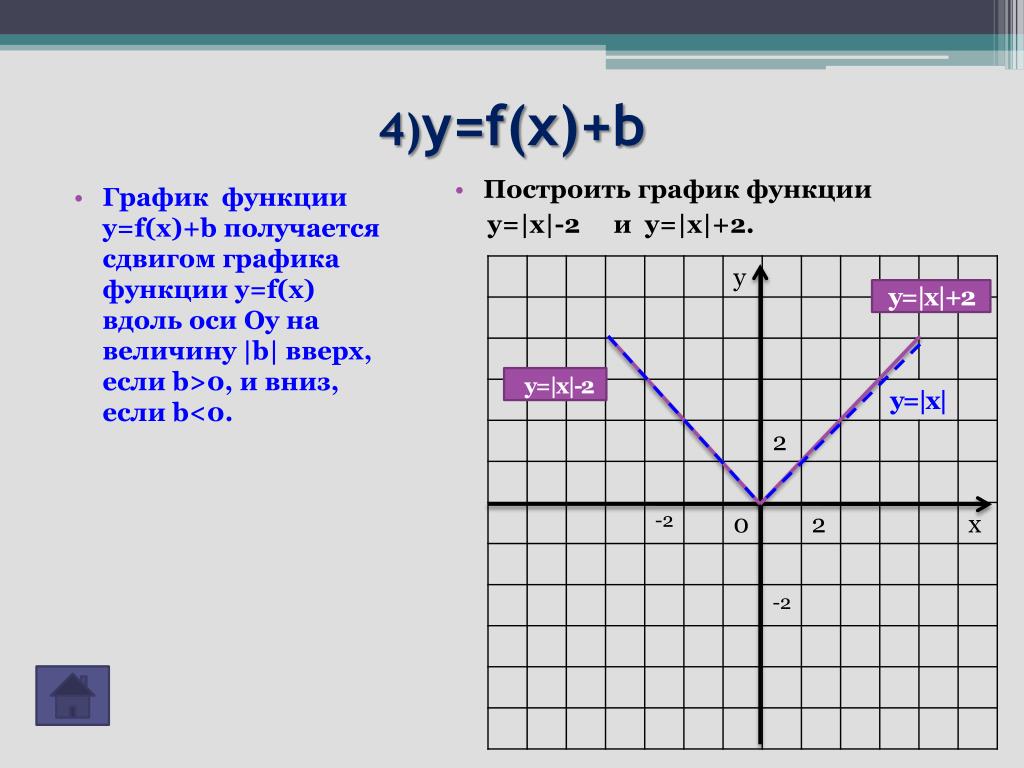
Соответствие между доменом и диапазоном каждого из них можно изобразить следующим образом:
Как мы видим, любая вертикальная линия пересечет график y = | x | −2 только один раз; следовательно, это функция. Вертикальная линия может пересекать график x = | y | +1 более одного раза; следовательно, это не функция. Как показано на рисунке, значение 3 x соответствует более чем одному значению y .
В домене много значений x , которые соответствуют двум значениям y .
Алгебра часто включает функции, поэтому обозначения становятся полезными при выполнении общих задач.Здесь f — это имя функции, а f (x) обозначает значение в диапазоне, связанном со значением x в домене. Функции часто называют разными буквами; некоторые общие названия функций: f , g , h , C и R . Мы определили, что множество решений y = | x | −2 является функцией; следовательно, используя обозначение функций, мы можем написать:
Учитывая значения x в домене, мы можем быстро вычислить соответствующие значения в диапазоне.Как мы видели, функции также выражаются с помощью графиков. В этом случае мы интерпретируем f (−5) = 3 следующим образом:
Мы начинаем с 2 на оси y и затем считываем соответствующее значение x .
Используйте функцию, чтобы определить доход продавца, если он продаст 3 машины в этом месяце. Каков его доход, если он не продаст машины в течение одного месяца?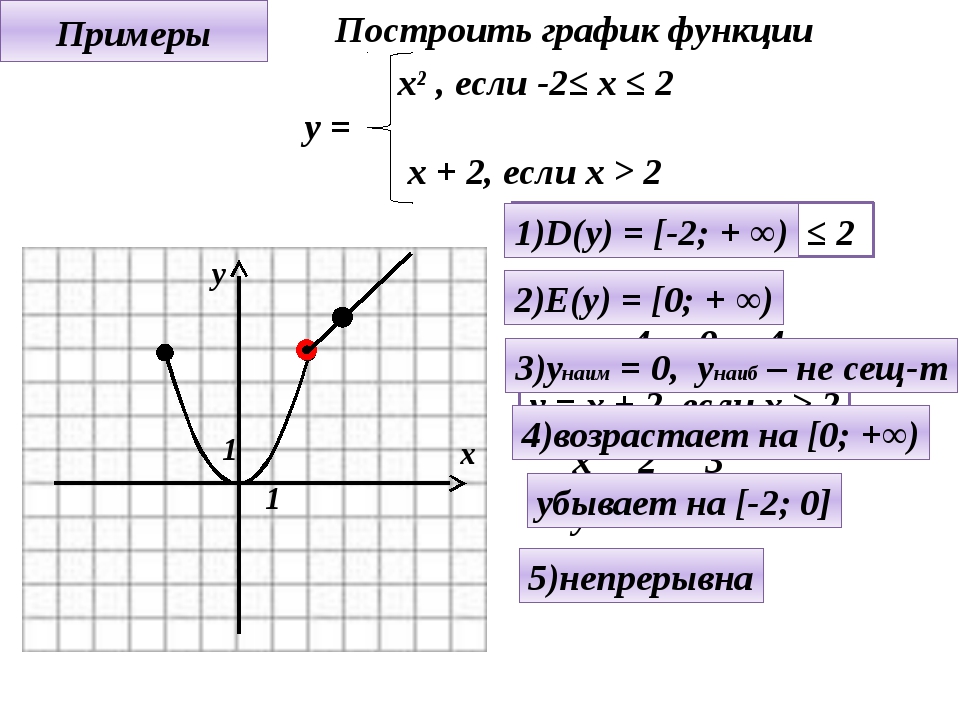
Поделитесь ссылкой на страницу, которая, по вашему мнению, может оказаться полезной для других.
2 
2} + 4 \ hspace {0.25 дюймов} & {\ mbox {on}} \ hspace {0,25 дюйма} x