Сложение дробей — как складывать дроби 🤔
Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Существует два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 − 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x − y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной называют такую дробь, у которой числитель больше знаменателя или равен ему.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
- От перестановки мест слагаемых сумма не меняется: a + b = b + a.
- Чтобы к сумме двух чисел прибавить третье нужно к первому числу прибавить сумму второго и третьего числа: (a + b) + c = a + (b + c).

- Если к числу прибавить ноль, получится само число: a + 0 = 0 + a = a
- При сложении числа можно переставлять и объединять в группы, результат от этого не изменится.
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить сумму двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное знаменателей (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в произведении дают значения знаменателей складываемых дробей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 × 2 × 3 × 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
- 90 : 15 = 6,
- 90 : 18 = 5.
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
- если делимое больше делителя, нужно преобразовать в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, тренируйтесь решать примеры на сложение дробей как можно чаще.
Действия с дробями
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к пиццы прибавить пиццы, то получится пиццы:
Пример 2. Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:
Пример 3. Сложить дроби и .
Сложить дроби и .
Опять же складываем числители, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:
Пример 4. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.
Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Таким образом, пример завершается. К прибавить получается .
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и .
Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения .
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
Осталось сложить эти дроби. Складываем:
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
Получили ответ
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 2. Найти значение выражения .
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от пиццы отрезать пиццы, то получится пиццы:
Пример 3. Найти значение выражения
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выделим в ней целую часть:
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения:
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям и
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Получили ответ
Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.
Пример 2. Найти значение выражения
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке:
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на найденный НОД, то есть на 10
Получили ответ
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь на число 1.
Умножим числитель дроби на число 1
Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:
Пример 2. Найти значение выражения
Умножим числитель дроби на 4
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы
А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
А вот к примеру выражение можно вычислить только первым способом — умножить число 7 на числитель дроби , а знаменатель оставить без изменений:
Связано это с тем, что число 7 и знаменатель дроби не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением деление выполнено только в числителе, поскольку записать это всё равно, что записать . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения .
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:
Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:
Допустим, у нас есть половина пиццы:
Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:
И взять от этих трех кусочков два:
У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:
Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно
Пример 2. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась неправильная дробь. Выделим в ней целую часть:
Пример 3. Найти значение выражения
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь на саму себя, только перевёрнутую:
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь
- обратным числа 3 является дробь
- обратным числа 4 является дробь
Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
Деление дроби на число
Допустим, у нас имеется половина пиццы:
Разделим её поровну на двоих. Сколько пиццы достанется каждому?
Сколько пиццы достанется каждому?
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет пиццы. Значит каждому достанется по пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь на число 2. Здесь делимым является дробь , а делителем число 2.
Чтобы разделить дробь на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь . Значит нужно умножить на
Получили ответ . Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
Пример 2. Найти значение выражения
Умножим первую дробь на число, обратное делителю:
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
Допустим, имелось пиццы:
Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет . Поэтому при делении на 6 получается
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на .
Чтобы разделить число 1 на , нужно это число 1 умножить на дробь, обратную дроби . А обратная дроби это дробь
Выражение можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражения
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь
Допустим, у нас имеются две целые пиццы:
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим на
Чтобы разделить на , нужно умножить на дробь, обратную дроби . А обратная дроби это дробь
Допустим, имеется половина пиццы:
Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
Пример 2. Найти значение выражения
Умножаем первую дробь на дробь обратную второй:
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
Найдите значение выражения:
Решение:
Задание 2. Найдите значение выражения:
Решение:
Задание 3. Найдите значение выражения:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение выражения:
Решение:
Задание 6. Найдите значение выражения:
Решение:
Задание 7. Найдите значение выражения:
Решение:
Задание 8. Найдите значение выражения:
Решение:
Задание 9. Найдите значение выражения:
Решение:
Задание 10. Найдите значение выражения:
Решение:
Задание 11. Найдите значение выражения:
Решение:
Задание 12. Найдите значение выражения:
Решение:
Задание 13. Найдите значение выражения:
Решение:
Задание 14. Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Сложение и вычитание дробей с разными знаменателями
Складывать и вычитать дроби с разными знаменателями можно только тогда, когда в процессе вычисления дроби приведены к одному общему знаменателю.
Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, являющихся знаменателями заданных дробей.
К числителям заданных дробей нужно поставить дополнительные множители, равные отношению НОК и соответствующего знаменателя.
Числители заданных дробей умножаются на свои дополнительные множители, получаются числители дробей с единым общим знаменателем. Знаки действий («+» или «-») в записи дробей, приводимых к общему знаменателю, сохраняются перед каждой дробью. У дробей с общим знаменателем знаки действий сохраняются перед каждым приведенным числителем.
Только теперь можно сложить или вычесть числители и подписать под результатом общий знаменатель.
Внимание! Если в результирующей дроби у числителя и знаменателя есть общие множители, то дробь надо сократить. Неправильную дробь желательно перевести в смешанную дробь. Оставить результат сложения или вычитания, не сократив дробь, где это возможно, — это неоконченное решение примера!
Сложение и вычитание дробей с разными знаменателями. Правило. Чтобы сложить или вычесть дроби с разными знаменателями, нужно их сначала привести к наименьшему общему знаменателю, а потом производить действия сложения или вычитания как с дробями с одинаковыми знаменателями.
Правило. Чтобы сложить или вычесть дроби с разными знаменателями, нужно их сначала привести к наименьшему общему знаменателю, а потом производить действия сложения или вычитания как с дробями с одинаковыми знаменателями.
Порядок действий при сложении и вычитании дробей с разными знаменателями
- найти НОК всех знаменателей;
- проставить к каждой дроби дополнительные множители;
- умножить каждый числитель на дополнительный множитель;
- полученные произведения взять числителями, подписав под каждой дробью общий знаменатель;
- произвести сложение или вычитание числителей дробей, подписав под суммой или разностью общий знаменатель.
Так же производится сложение и вычитание дробей при наличии в числителе букв.
Например:
Запись опубликована в рубрике Математика с метками вычитание, дробь, знаменатель, сложение. Добавьте в закладки постоянную ссылку.
Урок 40. сложение и вычитание дробей — Математика — 6 класс
Математика
6 класс
Урок № 40
Сложение и вычитание дробей
Перечень рассматриваемых вопросов:
- обобщение и систематизация знаний по теме «Сложение и вычитание дробей».

Тезаурус
Сумма дробей с одинаковыми положительными знаменателями есть дробь с тем же знаменателем и числителем, равным сумме числителей.
Разностью двух дробей называют такую дробь, которая в сумме с вычитаемым даёт уменьшаемое.
Наименьший общий положительный знаменатель – это наименьшее положительное число, кратное знаменателям данных дробей.
Наименьшее общее кратное двух чисел – наименьшее натуральное число, которое делится на заданные числа без остатка.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.
 : Просвещение, 2014, стр. 95.
: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
На прошлых уроках мы с вами рассматривали, как выполняют сложение и вычитание дробей любого знака. Сегодня вспомним и закрепим эти правила.
Вспомним основные правила сложения и вычитания дробей любого знака.
Правило сложения дробей с одинаковыми знаменателями
Чтобы сложить две дроби с одинаковыми положительными знаменателями, надо сложить их числители, а знаменатель оставить прежним.
Правило сложения дробей с разными знаменателями
Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби.
Правило вычитания дробей с одинаковыми знаменателями
Чтобы вычесть две дроби с одинаковым положительными знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.
Правило вычитания дробей с разными знаменателями
Чтобы найти разность двух дробей с разными знаменателями, надо привести их к общему положительному знаменателю и выполнить вычитание дробей с одинаковыми знаменателями.
Разность дробей a и b равна сумме уменьшаемого и числа, противоположного вычитаемому.
Дроби можно складывать и вычитать по тем же правилам, что и целые числа, то есть сначала определять знак результата, потом выполнять действия с модулями.
Иногда сложение и вычитание дробей выполняется проще, если привести их к наименьшему общему положительному знаменателю.
Дополнительный материал
Решим задачу.
Какую часть пути прошли туристы за три дня?
Решение.
Найдём, какую часть пути туристы прошли в третий день.
Найдём, какую часть пути туристы прошли за три дня.
Для этого сложим все части.
Разбор заданий тренировочного модуля
№ 1. Разместите нужные подписи под изображениями.
Варианты ответов:
Сложение дробей с разными знаками и разными знаменателями.
Сложение отрицательных дробей с разными знаменателями
Вычитание дробей с одинаковыми знаменателями
Для ответа на вопрос задания вспомним действия с рациональными числами и внимательно посмотрим на знаки между предложенными дробями.
Правильный ответ:
- Вычитание дробей с одинаковыми знаменателями.
- Сложение дробей с разными знаками и разными знаменателями.
- Сложение отрицательных дробей с разными знаменателями
№ 2. Вставьте в текст нужные слова.
Чтобы сложить две дроби с разными …, надо привести их к общему положительному … и … полученные дроби.
Варианты слов для вставки:
знаменателями
числителями
знаменателю
числителю
сложить
вычесть
Для ответа на вопрос задания обратимся к теоретическому материалу урока.
Правильный ответ:
Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби.
Дроби — как объяснить ребенку действия с дробями
Тема дробей — одна из самых непростых для школьников. Понять их неподготовленному ребенку, а тем более выполнять с ними операции, может быть достаточно сложно. Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Но даже самая трудная задача может стать простой и понятной, если правильно к ней подойти. Для детей нужно использовать фантазию, наглядность и элементы игры. А также – сохранять спокойствие и терпеливо объяснять, даже если это потребуется сделать много раз.
Как объяснить суть дробей ребенку?
Слово «дробь» будто говорит само за себя — оно означает дробление, деление. В школьной программе к изучению дробей приступают только в 5 классе, освоив все действия с целыми числами. Но знакомство с ними целесообразно начинать заранее, еще в старшем дошкольном возрасте. Это формирует пространственные представления у детей и тренирует логическое мышление.
Для начала нужно объяснить ребенку понятие долей. Это очень легко сделать на наглядных повседневных примерах. Самый простой и доступный — еда. Например, пирог — целый. Разделить его можно на несколько одинаковых частей. Один кусочек такого пирога и будет называться одной долей из всех возможных. Поделив пирог на четыре части, один кусочек называют одной четвертой частью.
Таким образом делить можно все, что угодно: яблоки, апельсины, плитки шоколада, конфеты в коробке и т. д. Еще один прекрасный наглядный материал для изучения дробей — кубики конструктора Lego. С их помощью можно поделить целое на равные части очень легко. Дети быстро запоминают форму кубиков, и им не требуется постоянно пересчитывать количество выступающих элементов на них.
Если ребенок увидит практическое применение дробей и востребованность их в реальной жизни, ему будет проще понять их и осознать важность получения математических знаний и навыков.
Что нужно знать о дробях?
1. Дробь — число нецелое, оно обозначает количество долей целого.
2. Дробь меньше целого.
3. Чем на большее число долей поделено целое, тем эти доли меньше и наоборот — чем долей меньше, тем они, соответственно, больше.
Для обозначения долей в математике используют понятие обыкновенная дробь. С ее помощью можно записать абсолютно любое необходимое количество долей.
Обыкновенная дробь представляет собой две части, именуемые числителем и знаменателем. Записываются они разделенными горизонтальной чертой либо наклонной вправо линией. Знаменатель пишется внизу либо справа от дробной черты, он показывает общее количество частей от целого, на которое оно было поделено. А числитель пишется вверху или слева от дробной черты и показывает, сколько долей целого сейчас взяли.
Вернемся к нашему пирогу. Очевидно, что разделить его реально на сколько угодно равных частей. В зависимости от того, на сколько частей его разделили, меняется и знаменатель дроби. У пирога, разделенного одной прямой линией на две части, знаменатель будет равен 2, у разделенного на три части — 3 и т. д. Числитель же, в свою очередь, показывает, сколько частей сейчас взято. Если взяли только одну часть из двух, то получится дробь 1/2, только две из трех — 2/3 и т. д.
Что такое смешанные дроби?
В математике выделяют дроби правильные и неправильные. Правильные — те, у которых числитель меньше знаменателя. Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
Например: 1/3, 2/5, 4/12. Но бывает и так, что числитель становится больше знаменателя. Если объяснять предметно, то взято больше частей пирога, чем было тех, на которые он поделен. Такое вполне возможно и в жизни, и в математике.
У таких дробей можно отделить целую часть и оставшуюся после этого дробную. То есть будет видно, сколько взято целых пирогов и плюс определенное количество его частей. Нужно хорошо представить себе описанное, или даже проверить на практике, а не просто заучивать формулы. Тогда сокращение дробей будет выполняться ребенком осмысленно и безошибочно.
Для того чтобы трансформировать неправильную дробь в смешанное число, следует сперва числитель поделить на знаменатель. В результате почти всегда получим целое число и какой-то остаток. Целое число и нужно записать, как целую часть. А остаток — отправить в числитель дробной части. Неизменным остается только знаменатель.
Неправильными называют и дроби с одинаковым числом над и под дробной чертой: 6/6, 12/12 и т. д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
д. Очевидно, что превратить их можно в 1. Наглядно это взято столько кусочков пирога, на сколько он и был поделен, т. е. целый пирог.
Примеры:
- 14/5 = (5*2+4) / 5 = 2 4/5
- 21/6 = (6*3+ 3) / 6 = 3 3/6
Задание:
Выделите целую часть из неправильных дробей:
Можно провести противоположную процедуру — превратить смешанное число в неправильную дробь. Эта операция часто применяется в математических вычислениях, поэтому будет полезным узнать о ней. Для этого нужно сперва умножить целую часть и знаменатель. Затем получившееся число прибавить к числителю, а знаменатель оставить прежним.
Примеры:
- 3 1/8 = (3*8+1) / 8 = 25/8
- 7 4/9 = (7*9+4) / 9 = 67/9
Задание:
1. Преобразовать в смешанное число неправильную дробь:
2. Выполнить обратную первой задачу — смешанное число превратить в неправильную дробь:
Десятичные дроби
Дроби, в знаменателях которых есть числа, кратные десяти — 10, 100, 1000 и т. д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
д. — в математике можно обозначать следующим образом. Сначала пишется целая часть, а потом числитель из дробной части, отделенный запятой.
Например, 5 4/10 попробуем записать в виде десятичной дроби. Пишем целую часть (5), ставим запятую и далее пишем числитель дробной части (4). Получаем: 5,4. Читается эта дробь так: «пять целых и четыре десятых». Число, представленное в таком виде, именуется десятичной дробью.
Существуют также десятичные дроби без целой части. Например: 7/100. Как быть в таком случае? Чтобы записать подобную дробь, пишут ноль, ставят запятую и далее записывают числитель дроби — 0,07. Такая дробь читается как «ноль целых, семь сотых».
Десятичные дроби очень удобны, они используются в точных вычислениях. Десятичная система исчисления применяется человечеством с самых древних времен. Она интуитивна понятна и проста.
Задание:
Преобразовать следующие дроби в десятичные:
Сокращение дробей
Сокращение дробей выполняют для того, чтобы их упростить. Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Если числитель и знаменатель дроби таковы, что делятся на одно и то же число (имеют общий делитель), то можно просто разделить их на это число, упростив тем самым дробь. Эта математическая операция называется сокращением дробей. Чтобы разобраться с этим, рассмотрим пару таких примеров.
Пример 1. Сократить дробь 8/12
Решение будет следующим. Наибольшее число, на которое делятся и 8, и 12, — это 4. Поэтому, чтобы сократить дробь, просто поделим ее числитель и знаменатель на 4:
8/12 = 8:4 / 12:4 = 2/3
Пример 2. Сократить дробь 10/25
Решение. Наибольшее число, на которое делятся и 10, и 25, — это 5. Потому, чтобы сократить дробь, поделим ее числитель и знаменатель на 5:
10/25 = 10:5 / 25:5 = 2/5
Несократимой называется дробь, у которой числитель и знаменатель имеют только один общий делитель — единицу.
Задание:
Сократите следующие дроби:
Сложение дробей
Сначала разберем сложение дробей с одинаковыми знаменателями. В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
В этом случае операция предельно простая. Складываются числители дробей, а знаменатель остается прежним.
Примеры:
- 1/7 + 2/7 = 3/7
- 3/8 + 5/8 = 8/8 = 1
Задание:
Выполни сложение дробей с одинаковыми знаменателями:
Но все усложняется, если нужно сложить дроби с разными знаменателями. В этом случае необходимо привести дроби к наименьшему общему знаменателю. Чтобы это сделать, необходимо найти наименьшее общее кратное. Это такое число, которое делится на оба эти числа без остатка. Например: 3/7 + 2/6. Наименьшее общее кратное для чисел 7 и 6 будет 42.
Далее ищем дополнительные множители для каждой из дробей. Для этого найденное на предыдущем этапе наименьшее общее кратное делим по очереди на знаменатель каждой из дробей:
- 42 / 7 = 6 — это будет дополнительный множитель для 3/7;
- 42 / 6 = 7 — это, соответственно, дополнительный множитель для 2/6.
Обе части каждой из наших дробей, и числитель и знаменатель, умножаем на свой, определенный выше, множитель:
- 3*6 / 7*6 = 18/42;
- 2*7 / 6*7 = 14/42.

Складываем полученные дроби аналогичным образом, как уже разобранные выше дроби с одинаковыми знаменателями:
Если это возможно, то дробь сокращают. Если дробь получилась неправильная, то следует целую часть из нее выделить.
Задание:
Выполни сложение дробей с разными знаменателями:
Вычитание дробей
Эта операция проводится аналогично сложению. Чтобы вычесть две дроби с одинаковыми знаменателями, нужно найти разность их числителей, а знаменатель оставить тем же.
Пример:
7/9 — 2/9 = (7-2) / 9 = 5/9
Задание:
Выполни вычитание дробей с одинаковыми знаменателями:
Для дробей с разными знаменателями также придется найти наименьшее общее кратное и дополнительные множители. Затем, по аналогии со сложением, произвести вычитание.
Пример:
6/7 — 8/10 = (6*10-8*7) / 70 = (60-56) / 70 = 4/70
Задание:
Выполни вычитание дробей с разными знаменателями:
Умножение дробей
Существует два варианта умножения дробей. Рассмотрим каждый из них в деталях.
Рассмотрим каждый из них в деталях.
Умножение обыкновенных дробей
В этом случае числители обеих дробей перемножаются — это будет новый числитель. Знаменатели обеих дробей также перемножаются — это будет новый знаменатель.
Пример:
2/5 * 3/4 = (2*3) / (5*4) = 6/20 = 3/10
Если это возможно, то следует сократить дроби перед перемножением. Это облегчит дальнейшие действия.
Пример:
24/35 * 25/36 = (24*25) / (35*36) = (2*5) / (7*3) = 10/21
Умножение смешанных дробей
Чтобы это сделать, необходимо превратить дроби в неправильные и далее действовать по алгоритму, приведенному в первом пункте.
Пример:
4 2/7 * 5 3/5 = 30/7 * 28/5 = (30*28) / (7*5) = (6*4) / (1*1) = 24/1 = 24
Задание:
Выполните умножение дробей:
- 5/7 * 6/8;
- 6/11 * 2/3;
- 2 3/7 * 4 5/9;
- 4 6/7 * 7 9/10.
Деление дробей
Освоив умножение, с делением также можно справиться легко. Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Правило деления дробей заключается в следующем: при делении одной дроби на другую нужно первую перемножить на обратную (перевернутую) вторую дробь. Или, иными словами, числитель первой умножить на знаменатель второй (это будет новый числитель), а знаменатель первой умножить на числитель второй (это будет новый знаменатель).
Пример:
4/7 : 2/5 = 4/7 * 5/2 = 20/14 = 10/7 = 1 3/7
Бывают ситуации, когда дробь нужно разделить на целое число. В этом случае следует представить дробь как неправильную. Числителем у нее будет это целое число, а знаменателем просто единица. Далее действовать нужно по уже знакомому правилу деления дробей из предыдущего случая.
Пример:
5/9 : 2 = 5/9 : 2/1 = (5*1) / (9*2) = 5/18
Задание:
Выполните деление дробей:
- 6/11 : 3;
- 7/15 : 2;
- 9/12 : 4.
Сравнение дробей
Если сравниваются дроби с одинаковыми знаменателями, то очевидно, что большей будет та, числитель у которой больше.
Пример:
1/5 < 4/5, так как знаменатели одинаковы, а в числителе 1 меньше 5.
Если сравниваются дроби с одинаковыми числителями, то большей будет та, знаменатель у которой меньше.
Пример:
1/2 > 1/8, так как числители одинаковы, а в знаменателе 8 больше 2.
Дроби же с разными знаменателями так просто не сравнишь. Нужно сперва определить их общий знаменатель и привести к нему обе дроби. Правила этой операции были приведены выше. Получим дроби, сравнить которые можно очень легко.
Пример:
Сравниваем дроби 2/5 и 1/10. Для этого приводим их к общему знаменателю — 10. Получаем 4/10 и 1/10. Теперь сравниваем дроби, уже имеющие одинаковые знаменатели: 4/10 > 1/10.
Есть один секрет, который нужно запомнить. Если одна из сравниваемых дробей неправильная, то она всегда больше правильной. Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Если подумать и вспомнить свойства дробей, то все становится понятно. Ведь неправильная дробь всегда будет больше единицы, тогда как правильная, наоборот, всегда будет меньше.
Задание:
Определите, какие дроби изображены на рисунке, и сравните их:
Итак, мы рассмотрели дроби, правила всех действий с ними. Надеемся, что наши объяснения и рекомендации будут очень полезны. Начинайте знакомить детей с дробями еще до школы. Хорошо усвоив эти понятия, ребенок без труда справится затем и с записью дробей, и с действиями с ними.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнееЧитайте также:
| Табличка на двери |
Сложение и вычитание отрицательных дробей.
Отрицательные дроби складываются и вычитаются также как и отрицательные числа, только по правилам сложения дробей. Мы можете добавлять только половинки к половинкам, четверти к четвертям или десятые к десятым и так далее. Вычитание отрицательных дробей следует тем же правилам. Для того чтобы сложить или вычесть две дроби нам нужно привести их к общему знаменателю. Если дробь отрицательная мы можем знак минус поставить в числитель и наоборот. Ниже расписано сложение \(-\frac{7}{6}+\frac{5}{7}\):
Вычитание отрицательных дробей следует тем же правилам. Для того чтобы сложить или вычесть две дроби нам нужно привести их к общему знаменателю. Если дробь отрицательная мы можем знак минус поставить в числитель и наоборот. Ниже расписано сложение \(-\frac{7}{6}+\frac{5}{7}\):
При сложении двух отрицательных дробей результат будет отрицательным. Когда мы вычитаем две отрицательные дроби, то мы к первой отрицательной дроби прибавляем положительную вторую, так как минус на минус дает плюс.
Рассмотрим сложение и вычитание следующих отрицательных дробей.
Задача 1. Вычислите \(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2}).\).
Решение. Приводим к наименьшему общему знаменателю:
\(\frac{1}{4}+(-\frac{3}{10})-(-\frac{1}{2})=\frac{5-3*2+10}{20}=\frac{9}{20}\)
Ответ: \(\frac{9}{20}\).
Задача 2. Вычислите \(\frac{1}{7}-(-\frac{5}{6})-(-\frac{1}{3})\).
Решение. Приводим к наименьшему общему знаменателю:
\(\frac{6-35+14}{42}=-\frac{15}{42}=-\frac{5}{14}\)
Ответ: \(-\frac{5}{14}\).
Задача 3. Вычислите \(\frac{1}{4}+\frac{5}{3}-(-\frac{1}{12})\).
Решение. Приводим к наименьшему общему знаменателю:
\(\frac{3+20+1}{12}=\frac{24}{12}=2.\)
Ответ: \(2.\).
Запишись на бесплатный пробный урок тут и разберись с тем, что тебе непонятно.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Удмуртский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку 1-9 классов. Моя основная задача помочь Вам улучшить свои языковые навыки, приобрести уверенность в себе и избавиться от языкового барьера. В своей практике активно использую TPR (Total Physical Response – метод полного физического реагирования нацелен на восприятие языка через органы чувств),Lead-in, Eliciting(требует от учеников самим предоставлять нужные слова, конструкции и информацию, вместо того, чтобы получать ее от преподавателя).
Моя основная задача помочь Вам улучшить свои языковые навыки, приобрести уверенность в себе и избавиться от языкового барьера. В своей практике активно использую TPR (Total Physical Response – метод полного физического реагирования нацелен на восприятие языка через органы чувств),Lead-in, Eliciting(требует от учеников самим предоставлять нужные слова, конструкции и информацию, вместо того, чтобы получать ее от преподавателя).
Репетитор по математике
Донецкий национальный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 классов. Я люблю математику, поскольку математическое мышление помогает вникать в суть вещей и решать повседневные задачи. Математика тренирует память и развивает ум. С радостью помогу ученикам закрепить школьные знания и узнать новое. Научу правильно задавать вопросы, рассуждать и самостоятельно искать решение задач.
Я люблю математику, поскольку математическое мышление помогает вникать в суть вещей и решать повседневные задачи. Математика тренирует память и развивает ум. С радостью помогу ученикам закрепить школьные знания и узнать новое. Научу правильно задавать вопросы, рассуждать и самостоятельно искать решение задач.
Репетитор по математике
Российский университет дружбы народов
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-9 классов. Подбираю метод работы, отталкиваясь от уровня ученика, говорю с ним на «одном» языке, объясняю сложные вещи на простых примерах. Имею опыт работы по учебникам Школа России, Школа 21 век. Готовлю учеников по программе Петерсона, готовлю к олимпиадам.
Самый главный принцип, которого я придерживаюсь — это индивидуальный подход к ребенку. Занятия провожу в легкой и непринужденной обстановке.
Подбираю метод работы, отталкиваясь от уровня ученика, говорю с ним на «одном» языке, объясняю сложные вещи на простых примерах. Имею опыт работы по учебникам Школа России, Школа 21 век. Готовлю учеников по программе Петерсона, готовлю к олимпиадам.
Самый главный принцип, которого я придерживаюсь — это индивидуальный подход к ребенку. Занятия провожу в легкой и непринужденной обстановке.
Похожие статьи
Добавление дробей
PGSG8gJWt1g
Дробь типа 3 4 говорит, что у нас есть 3 из 4 частей, на которые делится целое.
Чтобы сложить дроби, нужно выполнить три простых шага:
- Шаг 1: Убедитесь, что нижние числа ( знаменатели ) совпадают
- Шаг 2: Сложите верхние числа ( числителей ), поместите этот ответ в знаменатель
- Шаг 3: Упростите дробь (если возможно)
Пример:
Шаг 1 . Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Нижние числа (знаменатели) уже одинаковы. Сразу переходите к шагу 2.
Шаг 2 . Сложите верхние числа и поставьте ответ над тем же знаменателем:
.1 4 + 1 4 знак равно 1 + 1 4 знак равно 2 4
Шаг 3 . Упростите дробь:
2 4 знак равно 1 2
На картинке это выглядит так:
| 1 4 | + | 1 4 | = | 2 4 | = | 1 2 |
. .. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
.. и вы видите, как 2 4 проще, как 1 2 ? (см. Эквивалентные дроби.)
Пример:
Шаг 1 : Нижние числа разные. Видите, как кусочки разного размера?
| 1 3 | + | 1 6 | = | ? | ||
Нам нужно сделать их одинаковыми, прежде чем мы сможем продолжить, потому что мы не можем добавить их вот так.
Число «6» вдвое больше числа «3», поэтому, чтобы сделать нижние числа одинаковыми, мы можем умножить верхнюю и нижнюю части первой дроби на 2 , например:
| × 2 |
| × 2 |
Важно: вы умножаете как сверху, так и снизу на одну и ту же сумму,
, чтобы сохранить значение дроби одинаковым
Теперь дроби имеют одинаковое нижнее число («6»), и наш вопрос выглядит так:
| 2 6 | + | 1 6 | ||||
Нижние числа теперь одинаковы, поэтому мы можем перейти к шагу 2.
Шаг 2 : Сложите верхние числа и поместите их над одним и тем же знаменателем:
2 6 + 1 6 знак равно 2 + 1 6 знак равно 3 6
На картинке это выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | ||
Шаг 3 : Упростить дробь:
3 6 знак равно 1 2
В графической форме весь ответ выглядит так:
| 2 6 | + | 1 6 | = | 3 6 | = | 1 2 |
С ручкой и бумагой
А вот как это сделать ручкой и бумагой (нажмите кнопку воспроизведения):
Стихотворение, которое поможет вам вспомнить
♫ «Если вашей целью является сложение или вычитание,
Нижние числа должны быть одинаковыми!
♫ «Измените низ, используя умножение или деление,
Но то же самое нужно применить к верху,
♫ » И не забудьте упростить,
Пока не пришло время прощаться»
Пример:
1 3 + 1 5
Опять же, нижние цифры разные (ломтики разного размера)!
| 1 3 | + | 1 5 | = | ? | ||
Но давайте попробуем разделить их на более мелкие, чтобы были одинаковыми :
| 5 15 | + | 3 15 | ||||
Первая дробь: умножив верх и низ на 5, мы получили 5 15 :
| × 5 |
| × 5 |
Вторая дробь: умножив верх и низ на 3, мы получили 3 15 :
| × 3 |
| × 3 |
Нижние числа теперь одинаковы, поэтому мы можем добавить верхние числа:
| 5 15 | + | 3 15 | = | 8 15 | ||
Результат настолько прост, насколько это возможно, так что ответ:
1 3 + 1 5 знак равно 8 15
Уравнивание знаменателей
Откуда в предыдущем примере мы узнали, что нужно разрезать их на 1 / 15 тысяч, чтобы знаменатели совпадали? Мы просто перемножили два знаменателя (3 × 5 = 15).
Прочтите о двух основных способах приведения знаменателей в соответствие здесь:
Они оба работают, используйте тот, который вам больше нравится!
Пример: кексы
Вы хотите испечь и продать кексы:
- Друг может поставить ингредиенты, если вы дадите им 1 / 3 продаж
- Прилавок на рынке стоит 1 / 4 продаж
Сколько это вообще?
Нам нужно добавить 1 / 3 и 1 / 4
1 3 + 1 4 = ? ?
Сначала сделайте нижние числа (знаменатели) одинаковыми.
Умножить верх и низ 1 / 3 на 4 :
1×4 3×4 + 1 4 = ? ?
И умножить верх и низ 1 / 4 на 3 :
1×4 3×4 + 1×3 4×3 = ? ?
Теперь делаем вычисления:
4 12 + 3 12 = 4+3 12 = 7 12
0
Ответ: 7 12 сбываний идут в ингридиентах и ценах рынка.
Добавление смешанных фракций
У нас есть специальная (более продвинутая) страница по добавлению смешанных фракций.
930 931, 1399 932, 1400 933, 1401, 1402, 3564, 3565
Калькулятор сложения дробей
Использование калькулятора
Сложите и вычтите правильные и неправильные дроби с помощью этого калькулятора и посмотрите, сколько работы потребуется для решения.
Выберите количество дробей в вашем уравнении, а затем введите числители и знаменатели в доступные поля.Нажмите кнопку «Рассчитать», чтобы решить уравнение и показать работу.
Вы можете складывать и вычитать 3 дроби, 4 дроби, 5 дробей и до 9 дробей за раз.
Как складывать и вычитать дроби
Когда знаменатели совпадают
Когда дроби имеют одинаковые знаменатели, мы просто добавляем или вычитаем числители, как указано, и помещаем результат над общим знаменателем. При необходимости мы можем упростить дробь до меньших членов или смешанных чисел.
При необходимости мы можем упростить дробь до меньших членов или смешанных чисел.
Когда знаменатели не совпадают или отличаются
Если дроби имеют разные знаменатели, первый шаг — найти эквивалентные дроби, чтобы все знаменатели были одинаковыми. Мы находим Наименьший общий знаменатель (LCD) затем перепишите все дроби в уравнении как эквивалентные дроби, используя LCD в качестве знаменателя. Когда все знаменатели одинаковы, просто добавьте или вычтите числители и поместите результат над общим знаменателем.Полученную дробь можно упростить до наименьших членов или записать в виде смешанного числа.
Как работать с отрицательными дробями
Когда уравнение требует добавления отрицательной дроби, мы можем переписать уравнение как вычитание положительной дроби. Точно так же, если уравнение требует вычитания отрицательной дроби, это то же самое, что добавление положительной дроби, и его можно переписать таким образом. Этот калькулятор переписывает отрицательные дроби, когда показывает работу, затраченную на поиск ответа.
Этот калькулятор переписывает отрицательные дроби, когда показывает работу, затраченную на поиск ответа.
Упрощение операций с отрицательными числами
Независимо от того, работаете ли вы с дробями, целыми или десятичными числами, используйте эти рекомендации при сложении и вычитании положительных и отрицательных чисел.
Оригинал
Добавление положительного числа
+
+
Добавление отрицательного числа
+
—
Вычитание положительного числа
−
+
Вычитание отрицательного числа
−
—
Изменения в
+
+
Добавление положительного числа
−
+
Вычитание положительного числа
−
+
Вычитание положительного числа
+
+
Добавление положительного числа
Чтобы ознакомиться с аналогичными и более простыми методами работы с дробями, вы также можете посетить
Помогите с дробями.
Как складывать и вычитать дроби: 3 простых шага
Сложение и вычитание дробей на первый взгляд может показаться пугающим. Мало того, что вы работаете с дробями, которые, как известно, сбивают с толку, так еще и внезапно вам приходится бороться с преобразованием числителей и знаменателей.
А вот складывать и вычитать дроби — полезный навык. Как только вы освоите словарный запас и основы, вы сможете с легкостью складывать и вычитать дроби. Это руководство познакомит вас со всем, что вам нужно знать для сложения и вычитания дробей , включая несколько примеров задач для проверки ваших навыков.
Ключевой словарь для сложения и вычитания дробей
Прежде чем мы приступим к математике сложения и вычитания дробей, вам нужно знать терминологию. Мы будем использовать эти термины на протяжении всего , так что освежите их в памяти, чтобы всегда знать, какую часть дроби мы имеем в виду.
Дробь : Число, не являющееся целым числом; часть целого. Для наших целей дробь будет относиться к числу, записанному с числителем и знаменателем , например, $1/5$ или $147/4$.
Числитель : Верхнее число в дроби, отражающее количество частей целого, например 1 в $1/5$.
Знаменатель : нижнее число в дроби, представляющее общее количество частей, например, 5 в $1/5$.
Общий знаменатель : Когда две дроби имеют одинаковый знаменатель, например, $1/3$ и $2/3$.
Наименьший общий знаменатель : Наименьший знаменатель, которым могут делиться две дроби. Например, наименьший общий знаменатель $1/2$ и $1/5$ равен 10, потому что наименьшее число, в которое входят 2 и 5, равно 10.
Из пирогов получаются отличные дроби.
Как складывать и вычитать дроби?
Теперь, когда у вас есть словарный запас, пришло время применить его на практике. Вы не можете просто складывать или вычитать дроби, как, например, целое число $1/4 — 1/2$ не равно $0/2$.
Вы не можете просто складывать или вычитать дроби, как, например, целое число $1/4 — 1/2$ не равно $0/2$.
Вместо вам нужно будет найти общий знаменатель, прежде чем прибавлять или вычитать . Есть много способов найти общий знаменатель, некоторые из которых проще или эффективнее других.
Один из самых простых способов найти общий знаменатель, хотя и не обязательно лучший, — просто перемножить два знаменателя.
Например, возможный наименьший общий знаменатель для $1/2$ и $1/12$ будет равен 24, что вы найдете, умножив знаменатель 2 на знаменатель 12. Вы можете решить задачу, используя общий знаменатель 24, используя шаги, описанные ниже, но если вы это сделаете, вы столкнетесь с проблемой — вашу дробь нужно будет уменьшить.
Чтобы избавиться от необходимости уменьшать после сложения или вычитания, вместо этого попытайтесь найти наименьший общий знаменатель. Иногда это равносильно умножению двух знаменателей, но чаще всего это не так.
Однако найти наименьший общий знаменатель несложно — вам просто нужно знать таблицу умножения .Например, попробуем найти наименьший общий знаменатель, а не просто общий знаменатель, для тех же дробей, которые мы использовали выше:
.$$1/2\: \ и \: 1/12$$.
Для этого перечислите несколько кратных каждому знаменателю
Кратность 2 : 2, 4, 6, 8, 10, 12 , 14, 16, 18, 20, 22, 24
Кратность 12 : 12 , 24, 36, 48, 60
Затем просмотрите оба списка кратных чисел и найдите наименьшее общее число.В этом случае и 2, и 12 делят кратное 12. Если мы продолжим, мы получим другие кратные, которые они делят, например 24, но 12 является наименьшим, то есть это наименьшее общее кратное .
Вы можете сделать это с любой парой чисел, хотя большие числа могут представлять большую проблему. Для сложения или вычитания вы всегда можете вернуться к простому умножению одного знаменателя на другой, если у вас возникли проблемы с поиском наименьшего общего знаменателя , но имейте в виду, что вам, вероятно, придется уменьшать.
Дроби — самая вкусная часть математики.
Как складывать дроби — метод 1
Теперь, когда вы знаете, как найти общий знаменатель, вы готовы приступить к сложению и вычитанию.
Вернемся к примеру с $1/2$ и $1/12$ — в данном случае рассмотрим эту задачу:
1/2$ + 1/12$
$Помните, что вы не можете добавлять поперек; $1/2 + 1/12$ не равняется $2/14$.
№1: Найдите общий знаменатель
Сначала мы найдем наименьший общий знаменатель, так как обычно это лучший способ.
Мы уже проделали вышеописанную работу, но напомню, что вам нужно выписать ряд кратных каждому числу, пока не найдете совпадение . В этом случае и 2, и 12 кратны 12.
#2: Умножьте, чтобы получить каждый числитель с одним и тем же знаменателем
Всегда помните, что все, что вы делаете со знаменателем, должно быть сделано и с числителем. Итак, давайте посмотрим на эти две дроби, которые нам нужны, чтобы получить знаменатель 12.
$1/12$ легко — это уже больше знаменателя 12, поэтому нам не нужно ничего с ним делать.
$1/2$ нужно немного поработать. Какое число, умноженное на 2, будет равно 12?
Перефразируя этот вопрос как проблему, которую мы можем решить, $2*?=12$. Или, еще проще, мы можем инвертировать операцию , чтобы получить $12/2=?$, что мы можем легко решить.
Итак, теперь мы знаем, что чтобы перейти от знаменателя 2 к знаменателю 12, нам нужно умножить на 6. Опять же, помните, что все, что вы делаете со знаменателем, нужно делать и с числителем, поэтому умножьте верхнее число. и снизу на 6, чтобы получить $ 6/12 $.
#3: Добавьте числители, но оставьте знаменатели в покое
Теперь, когда у вас одинаковые знаменатели, вы можете сложить числители.
В данном случае это будет означать, что $6/12 + 1/12 = 7/12$. Спросите себя, сможете ли вы уменьшить дробь, соединив и числитель, и знаменатель на одно и то же число. В этом случае вы не можете, поэтому ваш ответ прост: $7/12$.
Как складывать дроби — метод 2
В качестве альтернативы мы могли бы просто перемножить два знаменателя, чтобы найти другой общий знаменатель. Это другой способ решения проблемы, но в итоге вы получите тот же ответ.
#1: Умножьте знаменатели вместе
Никаких хитростей — просто умножьте 2 на 12, чтобы получить 24. Это и будет вашим общим знаменателем.
#2: Умножьте, чтобы получить каждый числитель с одним и тем же знаменателем
Как и при нахождении наименьшего общего знаменателя, нам нужно умножить как верхнее, так и нижнее число каждой дроби. В этом случае используйте обратные операции, чтобы узнать, какое число нужно умножить.
Если $1/2$ должно быть $?/24$, вы можете сделать $24÷2$, чтобы выяснить, какое число нужно умножить на 12. Умножьте верх и низ на 12, чтобы получить $12/24$.
Повторите процесс с $1/12$. Если $1/12$ должно быть $?/24$, решите $24÷12$, чтобы получить 2. Теперь умножьте числитель и знаменатель $1/12$ на 2, чтобы получить $2/24$.
Теперь умножьте числитель и знаменатель $1/12$ на 2, чтобы получить $2/24$.
#3: Сложите числители вместе
Теперь вы можете просто добавлять поперек.$12/24 + 2/24 = 14/24$$.
№4: уменьшить
Здесь возникает дополнительный шаг. $14/24$ не является дробью в самой низкой форме, поэтому нам нужно ее уменьшить. Чтобы уменьшить, нужно разделить и числитель, и знаменатель на одно и то же число.
Для этого нам нужно найти наибольший общий делитель. Во многом подобно нахождению наименьшего общего кратного, это означает перечисление чисел до тех пор, пока мы не найдем два множителя, которые являются общими для числителя и знаменателя, исключая 1, например:
14 : 2 , 7
24 : 2 , 3, 4, 6, 8, 12
Какое число у них общее? 2.Это означает, что 2 — это наш наибольший общий множитель, и, следовательно, число, на которое мы будем делить числитель и знаменатель.
$14÷2=7$ и $24÷2=12$ дают нам ответ $7/12$.
Ответ такой же, как и при решении с использованием наименьшего общего кратного, и его нельзя уменьшить дальше, так что это наш окончательный ответ!
Если вы когда-нибудь обнаружите, что записываете множество факторов без особой удачи, есть несколько быстрых способов выяснить потенциальные факторы.
- Если число четное, его можно разделить на 2.
- Если вы можете сложить цифры числа, которое делится на 3, число делится на 3, например, 96 ($9+6=15$ и $1+5=6$, которое делится на 3).
- Если число оканчивается на 5 или 0, оно делится на 5.
- Если вы не знаете, когда прекратить поиск факторов, вычтите меньшее число из большего. Это число будет наибольшим возможным общим делителем, но не самим наибольшим общим делителем.
Например, возьмем 50 и 32.Конечно, мы могли бы просто разделить оба на 2 и продолжать уменьшать оттуда, но если вы сделаете $50-32$, вы получите 18, что говорит нам прекратить поиск наибольшего общего делителя, как только мы достигнем 18.

На практике это выглядит так: это:
50 : 2 , 5, 10
32 : 2 , 4, 8, 16
901,8 выше, что мешает нам тратить больше времени на выяснение факторов, которые нам не нужны. Мы гораздо быстрее увидим, что наибольший общий делитель равен 2, и продолжим решать задачу!
$1/1 — 1/? = ням $
Как вычитать дроби
Как только вы научитесь складывать дроби, вычитание дробей станет легкой задачей! Процесс точно такой же, только вы, естественно, будете вычитать, а не складывать.
№1: Найдите общий знаменатель
Давайте посмотрим на следующий пример:
$2/3-3/10$$
Нам нужно найти наименьшее общее кратное для знаменателей, которое будет выглядеть так:
3 : 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
10 : 10, 20, 30
Первое общее число, которое у них есть, — 30, поэтому мы поместим оба числителя над знаменателем 30.
#2: Умножьте, чтобы получить оба числителя над одним и тем же знаменателем
Во-первых, нам нужно вычислить, на сколько нам нужно умножить числитель и знаменатель каждой дроби, чтобы получить знаменатель 30. Для $2/3$, какое число, умноженное на 3, равно 30? В форме уравнения:
$30÷3=?$$
Наш ответ равен 10, поэтому мы умножим и числитель, и знаменатель на 10, чтобы получить 20/30 долларов.
Далее мы повторим процесс для второй фракции.Какое число нужно умножить на 10, чтобы получить 30? Что ж, $30÷10=3$, поэтому мы умножим верх и низ на 3, чтобы получить $9/30$.
Это делает нашу задачу $20/30-9/30$, что означает, что мы готовы продолжить!
#3: Вычесть числители
Как и при сложении, мы вычтем один числитель из другого, но оставим знаменатели в покое.
$20/30-9/30=11/30$$.
Поскольку мы нашли наименьшее общее кратное, мы уже знаем, что задачу уже нельзя уменьшить.
Однако допустим, что мы только что умножили 3 на 10, чтобы получить знаменатель 30, поэтому нам нужно проверить, можем ли мы уменьшить. Давайте воспользуемся этим маленьким трюком, который мы изучили, чтобы найти наибольший из возможных общих делителей. Что бы ни делили множители 11 и 30, они не могут быть больше, чем 30-11$ или 19.
11 : 11
30 : 2, 3, 5, 6, 10, 15
Поскольку у них нет общих множителей, ответ нельзя сократить дальше.
$1/10$ пицца все еще $10/10$ вкусная.
Примеры сложения и вычитания дробей
Давайте рассмотрим еще несколько примеров задач!
$8/15-4/9$$
#1: Найдите общий знаменатель
15 : 15, 30, 45 , 60
9 : 9, 18, 27, 26, 45
#2: Умножьте, чтобы получить оба числителя на один и тот же знаменатель
$45/15=\bo3$$
$$8÷3=24$$
$15*3=45$$
$24/45$$
$$45÷9=\bo5$$
$4*5=20$$
$9*5=45$$
$20/45$$
#3: Вычесть числители
$24/45-20/45=\bo4/\bo45$$
$6/11+3/4$$
#1: Найдите общий знаменатель
11 : 11, 22, 33, 44
4 : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44
#2: Умножьте, чтобы получить оба числителя на один и тот же знаменатель
$44÷11=\bo4$$
$6*4=24$$
$11*4=44$$
$24/44$$
$44÷4=\bo11$$
$3*11=33$$
$4*11=44$$
$33/44$$
#3: Добавьте числители
$$24/44+33/44=\bo57/\bo44$$ или $$\bo1 \bo13/\bo44$$
$4/7-11/21$$
#1: Найдите общий знаменатель
7 : 7, 14, 21
21 : 21 , 42, 63
#2: Умножьте, чтобы получить оба числителя на один и тот же знаменатель
$$21÷7=\bo3$$
$3*4=12$$
$3*7=21$$
$12/21$$
$11/2$ уже больше 21, так что ничего делать не надо.
#3: Вычесть числители
$$12/21-11/21=\bo1/21$$
$8/9+7/13$$
#1: Найдите общий знаменатель
9 : 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117
13 : 13, 26, 39, 52, 65, 78, 91, 104, 117
#2: Умножьте, чтобы получить оба числителя на один и тот же знаменатель
$117÷9=\bo13$$
$8*13=104$$
$9*13=117$$
$104/117$$
$$117÷13=\bo9$$
$7*9=63$$
$13*9=117$$
$63/117$$
#3: Добавьте числители
$104/117+63/117=\bo167/\bo117$$
Что дальше?
Сложение и вычитание дробей может стать еще проще, если вы начнете преобразовывать десятичные дроби в дроби!
Если вы не знаете, какие уроки математики в средней школе вам следует посещать, это руководство поможет вам составить расписание, чтобы быть уверенным, что вы готовы к поступлению в колледж!
Теперь, когда вы стали экспертом в сложении и вычитании дробей, испытайте себя, научившись переводить градусы Цельсия в градусы Фаренгейта!
Сложение и вычитание дробей с помощью пошагового решения математических задач
Вы много раз сталкивались с дробями с самого начала изучения математики. Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.
Они встречаются в формулах и во многих повседневных практических задачах. Однако арифметические дроби состоят строго из чисел. Теперь мы изучим действия над дробями, компоненты которых являются алгебраическими выражениями.
РЕШЕНИЕ УРАВНЕНИЙ, ВКЛЮЧАЮЩИХ ЗНАКОВЫЕ ЧИСЛА
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Разложите числитель и знаменатель дроби на множители.
- Упростите алгебраические дроби.
Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
При изучении арифметики вам сказали, что дробные ответы всегда следует оставлять в сокращенной или упрощенной форме. Для дроби, до которой вы «уменьшили», разделив числитель и знаменатель на 4. Дробь нельзя уменьшить, потому что никакое число (кроме 1) не будет делить и числитель, и знаменатель. Упрощая дроби таким образом, вы использовали следующее определение.
Дробь в представляет собой упрощенную (или сокращенную) форму , если числитель и знаменатель не содержат общего множителя (кроме 1).
| Дробь, представленная в упрощенной форме, поскольку числитель 2 и знаменатель 3 не имеют общего делителя, кроме единицы. |
Для получения упрощенной формы дроби применяется следующее правило.
Чтобы упростить дробь , полностью разложите числитель и знаменатель, а затем разделите числитель и знаменатель на все общие множители.
| Дробь , однако, не в упрощенной форме, так как числитель и знаменатель имеют общий делитель 2. |
Далее делим на общие множители, получаем
| Помните, множитель, разделенный сам на себя, равен 1. |
Теперь разделите на общий множитель (x + 2) как в числителе, так и в знаменателе, чтобы получить
Мы можем разделить только общие факторы, но не общие термины. |
| В таком выражении, как у некоторых студентов возникает соблазн разделить тройки.Обратите внимание, что это неправильное , поскольку они являются терминами , а не факторами. |
Обратите внимание, что даже если мы смогли разложить числитель и знаменатель на множители, мы все равно не можем разделить, поскольку у них нет общих множителей. Данная дробь уже в упрощенном виде.
Тот факт, что для данной дроби может потребоваться любой из изученных вами методов факторинга, еще раз подчеркивает важность владения факторингом.
Решение Здесь вы можете использовать «пробы и ошибки» для числителя и «группировку» для знаменателя.
| Здесь (x + 2) — общий множитель, поэтому можно разделить и числитель, и знаменатель. |
Обратите внимание, что числитель 2x + 5 можно записать как (2x 4- 5) * 1. Таким образом, при делении множителя (2x + 5) остается множитель 1. Таким образом, при делении множителя (2x + 5) остается множитель 1. |
Решение Проблемы этого типа требуют особого внимания, поскольку они являются распространенной причиной ошибок. На первый взгляд множители могут быть ошибочно приняты за общие, или дробь может быть ошибочно принята за уже упрощенную.Обратите внимание, что факторы нельзя разделить, поскольку знаки не позволяют им быть идентичными. Если, однако, минус 1 факторизуется от одного из множителей, то есть подобные множители, и деление может быть выполнено.
| Любые множители в виде a — b и b — a являются отрицательными по отношению друг к другу, таким образом, 2x — 3 и 3 — 2x являются отрицательными по отношению друг к другу. |
Все это эквивалентные формы одного и того же выражения.Предпочтительной формой будет та, в которой используется наименьшее количество письменных знаков. Всегда проверяйте свой ответ, чтобы убедиться, что он эквивалентен форме, указанной в разделе ответов. |
УМНОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Числители и знаменатели всех умножаемых дробей.
- Определить и разделить на все общие множители.
- Запишите произведение в простейшей форме.
Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
— это определение произведения двух дробей. На словах это означает «умножить числитель на числитель и знаменатель на знаменатель». Вы использовали это правило много раз в арифметике, когда умножали дроби.
Однако помните, что все дробные ответы должны быть в упрощенной форме. Мы могли бы следовать приведенному выше определению, а затем упростить ответ, как в предыдущем разделе.Но с алгебраическими дробями это может привести к очень сложным выражениям. Следующее правило позволяет нам упрощать по мере умножения, поэтому ответ будет в упрощенной форме.
При умножении алгебраических дробей полностью разложите все числители и знаменатели, затем перед умножением разделите на все множители, общие для числителя и знаменателя.
Произведение остальных множителей числителя будет числителем ответа, а произведение остальных множителей знаменателя будет знаменателем ответа.
| Опять же, помните, что общие факторы должны быть совершенно одинаковыми. |
| Мы будем использовать точку * для обозначения умножения, поскольку использование X можно спутать с переменной x. |
| Обратите внимание, что (x + 2) и (2 + x) одинаковы, но (x — 4) и (4 — x) являются отрицательными значениями друг друга. Опять же, есть много возможных форм для окончательных ответов.  Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков. Приведенная здесь форма предпочтительнее, поскольку она содержит наименьшее количество знаков. |
| В этой проблеме много факторов. Будь осторожен! |
ДЕЛЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Заменить задачу на деление связанной задачей на умножение.
- Деление алгебраических дробей.
Деление дробей определяется с помощью умножения.
Чтобы разделить, умножить на величину, обратную делителю.
Чтобы разделить одно алгебраическое выражение на другое , инвертируйте делитель и измените операцию на умножение.
| Делитель следует за знаком. Не инвертируйте неправильную дробь. |
Если знаменатель не указан, считается, что он равен 1. |
После того, как задача на деление заменена на задачу на умножение, она завершается так же, как и в предыдущем разделе.
| Опять же, обратите внимание, что инвертируется только дробь, следующая за знаком. |
ПОИСК НАИМЕНЬШЕГО ОБЩЕГО знаменателя
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Полностью разложить знаменатель дроби на множители.
- Найдите наименьший общий знаменатель двух или более дробей.
Правило сложения и вычитания дробей требует, чтобы объединяемые дроби имели одинаковый знаменатель.В качестве подготовки к выполнению этих операций мы теперь исследуем метод нахождения наименьшего общего знаменателя для любой группы дробей.
общий знаменатель лот двух или более дробей представляет собой выражение, содержащее все множители знаменателя каждой дроби. Наименьший общий знаменатель содержит минимальное количество множителей, чтобы быть общим знаменателем.
Наименьший общий знаменатель содержит минимальное количество множителей, чтобы быть общим знаменателем.
| Наименьший общий знаменатель набора дробей иногда называют наименьшим общим кратным знаменателей. |
Ментальная арифметика позволит вам найти наименьший общий знаменатель для небольших чисел. Если попросить прибавить , то легко получить наименьший общий знаменатель 12. Если спросить, как мы получили 12, мы просто знаем, что 12 — это наименьшее число, которое делится и на 4, и на 6. Однако необходим более сложный метод. если числа больше или если дроби являются алгебраическими дробями.
Пример 1 Найдите наименьший общий знаменатель числа
Решение Эта задача потребовала бы значительного количества предположений или возможностей тестирования, если бы у нас не было общего метода.
| Мы могли бы получить общий знаменатель этих дробей, найдя произведение 12 х 14 х 15 х 18 = 45 360.  Хотя это число является общим знаменателем, оно не является наименьшим общим знаменателем. |
Рассмотрим определение. Из него мы знаем, что общий знаменатель этих чисел должен содержать все множители каждого из них. Другими словами, мы ищем наименьшее число, которое делится на 12, 14, 15 и 18.
Сначала полностью разложите каждое число.
Искомое число должно содержать (2)(2)(3), чтобы оно делилось на 12. Оно должно содержать (2)(7), чтобы делиться на 14, и так далее. Действуйте следующим образом:
Запишите множители первого числа, 12.
(2)(2)(3)
Теперь посмотрите на множители следующего числа, 14, и убедитесь, что нам нужно (2)(7). Но так как у нас уже есть 2, нам нужен только множитель (7). Это дает
(2)(2)(3)(7).
Теперь это число делится и на 12, и на 14. Делители следующего числа, 15, равны (3) и (5).Поскольку у нас уже есть 3, нам нужен только коэффициент 5, что дает
(2)(2)(3)(7)(5).
Теперь это число делится на 12, 14 и 15. Делители следующего числа, 18, равны (2)(3)(3). У нас уже есть 2 и одна 3. Следовательно, нам нужно еще 3.
Делители следующего числа, 18, равны (2)(3)(3). У нас уже есть 2 и одна 3. Следовательно, нам нужно еще 3.
(2)(2)(3)(7)(5)(3) = 1,260
Это число, 1,260, является общим знаменателем 12, 14 , 15 и 18, потому что он содержит все множители каждого и, следовательно, делится на каждый. Это наименьший общий знаменатель, потому что он содержит только те множители, которые необходимы для того, чтобы он делился на 12, 14, 15 и 18.
| Обратите внимание, что 1260 значительно меньше, чем число, полученное простым нахождением произведения всех знаменателей. |
Из предыдущего обсуждения вытекает правило получения наименьшего общего знаменателя для любого количества дробей, будь то числа или алгебраические выражения.
Чтобы найти наименьший общий знаменатель двух или более дробей:
1. Полностью разложить каждый знаменатель на множители.
2. Запишите знаменатель первой дроби в разложенном виде как предлагаемый общий знаменатель.
3. Путем проверки определить, какие факторы второго знаменателя еще не входят в предлагаемый общий знаменатель, и включить их.
4. Повторите третий шаг для каждой фракции.
| После освоения эта пошаговая процедура значительно упростит вашу работу. |
| Обратите внимание, что при нахождении наименьшего общего знаменателя мы не обращаем внимания на числитель. Это всего лишь знаменатель первой дроби. |
При проверке второго знаменателя нам нужен дополнительный множитель (x — 2).Наименьший общий знаменатель равен (3x — 4)(2x + l)(x — 2).
| Опять же, числители не влияют на то, каким будет наименьший общий знаменатель. Иногда наименьший общий знаменатель обозначается аббревиатурой LCD. |
Обратите внимание, что x 2 является множителем в знаменателе первой дроби, но не во второй дроби. |
| Здесь у нас есть три знаменателя. |
Решение
Первый знаменатель: 3(x + 2)
Второй знаменатель: 2(2)(3)
Третий знаменатель: 2(x + 3)(x + 2)
Предлагаемый общий знаменатель: 3( x + 2)
Изучив второй знаменатель, мы видим, что нам нужно включить множители (2) и (2). Теперь у нас есть 2(2)(3)(x + 2). Изучив третий знаменатель, мы видим, что нам нужен множитель (x + 3). Наименьший общий знаменатель равен 2(2)(3)(x + 2)(x + 3) или 12(x + 2)(x + 3).
ЭКВИВАЛЕНТНЫЕ ДРОИ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Понять фундаментальный принцип дробей.
- Заменить дробь эквивалентной дробью.
При дальнейшей подготовке к сложению и вычитанию дробей мы должны иметь возможность заменить заданную дробь дробью с новым знаменателем без изменения значения исходной дроби.
называется фундаментальным принципом дробей .
Когда мы анализируем это утверждение, мы видим две эквивалентные дроби и отмечаем, что числитель и знаменатель умножены на одно и то же ненулевое число, a.
Чтобы преобразовать дробь в эквивалентную дробь , умножьте числитель и знаменатель на одно и то же ненулевое выражение.
| Почему выражение должно быть ненулевым? |
| Вы можете думать об этом процессе как об обратном сокращению дробей. |
Решение Поскольку новый знаменатель находится в факторизованной форме, при проверке мы видим, что первоначальный знаменатель (2x + 3) был умножен на множитель (x — 4).Следовательно, исходный числитель (х + 1) также необходимо умножить на множитель (х — 4), что даст
. Обратите внимание, что в окончательной форме дроби мы умножили множители в числителе, но оставили знаменатель в виде множителей. Это предпочтительный способ написания ответа. Это предпочтительный способ написания ответа. |
Решение Поскольку исходный знаменатель (x — 3) был умножен на (2) и (x + 1), исходный числитель (2x + 1) также необходимо умножить на (2) и (x + 1).
| Опять же, обратите внимание на форму ответа. |
СЛОЖЕНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Сложите дроби с одинаковыми знаменателями.
- Найдите наименьший общий знаменатель двух или более дробей.
- Применить правило сложения дробей.
Теперь мы готовы складывать алгебраические дроби, используя методы, описанные в двух предыдущих разделах.Следует вспомнить следующее правило из арифметики.
Сумма двух или более дробей, имеющих одинаковый знаменатель, равна сумме числителей над их общим знаменателем.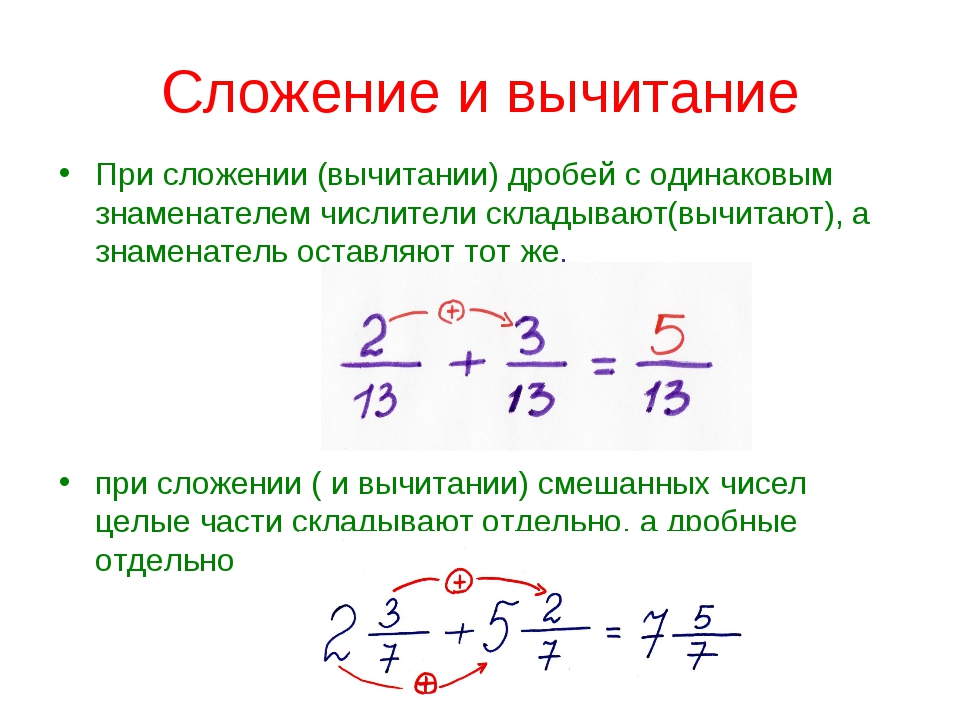
Обратите внимание, что это правило допускает только сумму дробей с одинаковым знаменателем. Другими словами, две или более дроби могут быть сложены только в том случае, если они имеют общий знаменатель. Правило сложения любых двух или более дробей потребует навыков, полученных в последних двух разделах, в дополнение к знанию комбинирования одинаковых терминов.
Чтобы сложить две или более дроби, выполните следующие действия:
Шаг 1 Найдите наименьший общий знаменатель (НОД) для всех дробей, используя метод, описанный в разделе 9-4.
Шаг 2 Замените каждую дробь эквивалентной дробью с наименьшим общим знаменателем (раздел 9-5).
Шаг 3 Найдите сумму числителей и поместите эту сумму на наименьший общий знаменатель.
Шаг 4 Упростите (или уменьшите) дробь, полученную на шаге 3.
Эти четыре шага следует использовать при сложении дробей. |
| Не забудьте умножить числитель и знаменатель на одно и то же выражение. |
Этот ответ в сокращенной форме.
| Опять же, не забудьте умножить числитель на то же выражение, на которое вы умножили знаменатель. |
| Всякий раз, когда знаменатели не имеют общих множителей, LCD является произведением знаменателей. |
| Здесь только первая дробь должна быть изменена по форме. |
Сумма
Обратите внимание, что числитель 3x — 15 можно разложить как 3(x — 5), а множитель (x — 5) соответствует множителю в знаменателе. |
Мы можем использовать меньше письменных шагов, если заметим, что «общий знаменатель» означает, что все дроби имеют один и тот же знаменатель, а если у всех один и тот же знаменатель, то знаменатель необходимо написать только один раз.Чтобы проиллюстрировать это, мы переработаем предыдущий пример.
| Этот ярлык подходит, если вы не забываете умножать числители на необходимые коэффициенты. |
| Опять же, знаменатели не имеют общих множителей, поэтому LCD является произведением всех трех знаменателей. |
ВЫЧИТАНИЕ АЛГЕБРАИЧЕСКИХ ДРОБЕЙ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Вычитание дробей с одинаковыми знаменателями.
- Применить правило вычитания дробей с разными знаменателями.
Вычитание определяется в терминах сложения, поэтому метод вычитания алгебраических дробей будет таким же, как сложение алгебраических дробей, описанный в предыдущем разделе. Вы скоро поймете, почему мы представили их отдельно.
Вы скоро поймете, почему мы представили их отдельно.
Разность любых двух дробей, имеющих один и тот же знаменатель, равна разнице их числителей над их общим знаменателем.
Обратите внимание, что это правило совпадает с правилом сложения двух дробей с одинаковым знаменателем.
Таким образом, шаги для вычитания дробей такие же, как и для сложения дробей.
Чтобы вычесть дроби:
Шаг 1 Найдите наименьший общий знаменатель двух дробей.
Шаг 2 Замените каждую дробь эквивалентной дробью с наименьшим общим знаменателем.
Шаг 3 Найдите разность числителей и поместите этот результат над наименьшим общим знаменателем.
Шаг 4 Упростите (или уменьшите) дробь, полученную на шаге 3.
Очевидный вопрос: «Если эти две операции одинаковы, зачем изучать их по отдельности?» Ответ заключается в том, что вычитание порождает очень распространенную ошибку, которой ученик должен быть готов избежать.
Обратите внимание, что мы вычитаем весь числитель второй дроби. Поэтому будет хорошей практикой заключать весь числитель в круглые скобки со знаком вычитания перед ним. Поэтому будет хорошей практикой заключать весь числитель в круглые скобки со знаком вычитания перед ним. |
Упомянутая ошибка часто возникает из-за того, что знак минус влияет на весь числитель второй дроби, а НЕ только на первый член.
| Это произойдет, если вы не используете круглые скобки. |
Стрелка указывает на ошибку, наиболее часто допускаемую при вычитании дробей. Лучший способ избежать этого — всегда использовать скобки
., и вы, скорее всего, не сможете правильно изменить знак.
| Обратите внимание, мы заключили в скобки числитель второй дроби. Обратите внимание, что сначала мы умножили (x — 4) (2x — 1), а затем умножили (2×2 — 9x + 4) на -l.Умножать и менять знаки одновременно значит вызывать ошибку. |
СЛОЖНЫЕ ДРОИ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Распознавание сложной дроби.

- Упростите сложную дробь.
Дроби определяются как указанное частное двух выражений. В этом разделе мы представим метод упрощения дробей, в которых числитель, знаменатель или оба они сами состоят из дробей.Такие дроби называются сложными фракциями .
Таким образом, если числитель и знаменатель сложной дроби составлены из простых дробей, ее можно упростить, разделив числитель на знаменатель.
Обычно более эффективный метод упрощения сложной дроби включает использование основного принципа дробей. Умножаем и числитель, и знаменатель на общий знаменатель всех отдельных дробей сложной дроби.
| Вспомните, что фундаментальный принцип дробей утверждает |
Мы будем использовать фундаментальный принцип, чтобы снова упростить
ЖК-дисплей 3 и 4 равен 12. Таким образом,
| Отдельные фракции |
| Этот ответ можно записать как смешанное число |
Убедитесь, что каждый член как в числителе, так и в знаменателе умножается на ЖК-дисплей. |
| Нужен ЖКИ отдельных дробей, y не дробь. |
УРАВНЕНИЯ, ИМЕЮЩИЕ АЛГЕБРАИЧЕСКИЕ ДРОИ
ЗАДАЧИ
После завершения этого раздела вы сможете:
- Применить метод решения дробных уравнений.
- Определите, когда дробное уравнение не имеет решения.
В главе 2 мы столкнулись с уравнениями, в которых есть дроби.Однако все эти дроби имели числовые знаменатели. Теперь обсудим уравнения, в знаменателях которых есть дроби с переменными.
Метод решения этих уравнений будет таким же, как и в главе 2, но есть некоторые дополнительные предостережения, к которым вы должны быть готовы.
| Вы можете вернуться к некоторым примерам в главе 3, чтобы освежить свою память. |
Чтобы освежить вашу память, здесь повторяются шаги решения таких уравнений.
Во-первых: Исключите дроби, умножив каждый член уравнения на наименьший общий знаменатель всех дробей в уравнении.
Второй: упростите, объединив одинаковые члены с каждой стороны уравнения.
Третье: Сложите или вычтите необходимые количества, чтобы получить неизвестное количество с одной стороны и числа арифметики с другой.
Четвертое: Разделить на коэффициент неизвестной величины.
Пятое: проверьте свой ответ.
Основное отличие решения уравнений с арифметическими дробями от уравнений с алгебраическими дробями заключается в проверке.Процесс проверки будет заключаться не только в том, чтобы найти возможную ошибку, но и в том, чтобы определить, есть ли у уравнения ответ.
Эта последняя возможность возникает потому, что с алгебраическими дробями мы умножаем на неизвестную величину. Эта неизвестная величина может быть на самом деле равна нулю, что сделает всю работу недействительной.
Помните, мы можем умножать каждую часть уравнения только на ненулевую величину. |
| Это означает, что ни (x — 1), ни (x + 1) не могут быть равны нулю. Если x = 1, то множитель (x — 1) равен нулю и у нас проблемы! |
Поскольку деление на ноль невозможно, мы должны заключить, что x = 1 не является решением. А так как мы не ошиблись в вычислениях, то должны заключить, что это уравнение не имеет решения.
Правильный ответ: «нет решения».
| Проверка необходима в алгебраических уравнениях. В противном случае вы могли бы проделать большую работу — не ошибитесь — и все равно упустить проблемы. Другими словами, x = 1 не является решением, поскольку дает утверждение, не имеющее смысла. |
Помните, что проверка — чрезвычайно важный шаг, так как она определяет, есть решение или нет. |
| Обратите внимание, что в этих примерах, когда у нас есть x 2 членов, они сокращаются, и мы остаемся с линейным уравнением. Если бы они не сокращались, в уравнении было бы член x 2 .Уравнение этого типа (квадратное) будет рассмотрено в главе 11. |
Таким образом, x = -5 является решением.
Таким образом, 11 — это количество, на которое увеличился числитель.
ОБЗОР
Ключевые слова
- Алгебраическая дробь — это указанное отношение двух алгебраических выражений.
- Дробь представляет собой упрощенную форму , если числитель и знаменатель не имеют общего делителя, кроме 1.
- Общий знаменатель для двух или более дробей — это выражение, содержащее все множители знаменателей каждой дроби.
- наименьший общий знаменатель содержит минимальное количество множителей, чтобы быть общим знаменателем.

- Фундаментальный принцип дробей есть
- Сложные дроби — это дроби, в которых числитель или знаменатель (или оба) содержат дробь.
Процедуры
- Чтобы упростить или сократить дроби до наименьших членов, разложите числитель и знаменатель и разделите на все подобные множители.
- Чтобы умножить дроби, умножьте все числители и знаменатели и разделите на все подобные множители перед умножением.
- Чтобы разделить на дробь, переверните делитель, а затем умножьте.
- Чтобы найти наименьший общий знаменатель (НКО), сначала профакторизуйте все знаменатели, а затем найдите знаменатель, который содержит все множители каждого знаменателя, но не содержит ненужных множителей.
- Чтобы преобразовать дробь в эквивалентную дробь, умножьте числитель и знаменатель на одно и то же ненулевое выражение.
- Чтобы сложить дроби, выполните следующие действия:
- Найдите наименьший общий знаменатель.

- Измените каждую дробь на эквивалентную дробь, в знаменателе которой будет ЖК-дисплей.
- Добавьте числители и поместите над ЖК-дисплеем.
- Упростите или сократите ответ.
- Найдите наименьший общий знаменатель.
- Чтобы вычесть дроби, действуйте как сложение, но объединяйте числители путем вычитания.
- Сложные дроби можно упростить, умножив числитель и знаменатель сложной дроби на ЖКД всех дробей в выражении.
- Чтобы решить уравнения, содержащие дроби, сначала удалите все дроби, умножив все уравнение на ЖК-дисплей участвующих дробей. Полученное уравнение затем решается, и решение должно быть проверено в исходном уравнении.
Просмотреть образовательные ресурсы по добавлению дробей
Добавление дробей — еще один математический навык, который ваш ребенок начнет осваивать в четвертом классе вместе с умножением дробей. Изучая, как складывать дроби, ваш ученик также узнает о наименьших общих знаменателях или наименьших общих кратных.Погрузитесь в наши ресурсы, чтобы начать, или прокрутите ниже, чтобы увидеть некоторые основы добавления дробей. Добавление дробей может быть немного сложным, потому что для того, чтобы сложить дроби вместе, их знаменатели должны быть одинаковыми. Сначала найдя общий знаменатель или кратное, дроби можно затем сложить вместе, используя некоторые общие правила.
Добавление дробей может быть немного сложным, потому что для того, чтобы сложить дроби вместе, их знаменатели должны быть одинаковыми. Сначала найдя общий знаменатель или кратное, дроби можно затем сложить вместе, используя некоторые общие правила.Общие правила
- Найдите общий знаменатель, используя метод наименьшего общего знаменателя
- Сложите числители и поднесите сумму к общему знаменателю
- Упростите, если необходимо
Давайте посмотрим на 1 ⁄ 4 + 5 ⁄ 6 :
- Найдите наименьшее общее кратное между 4 и 6.Мы можем найти числа, кратные числу, умножив его на другое число, отличное от 0. Первые три числа, кратные 4, — это 4, 8 и 12, а первые три кратные 6 — это 6, 12 и 18. Наименьшее число, которое является кратным между двумя (наименьшее общее кратное) равно 12.
- Как только вы нашли наименьшее общее кратное для использования в качестве наименьшего общего знаменателя, умножьте знаменатель и числитель каждой дроби на число так, чтобы знаменатель стал Общий знаменатель и числитель изменений для создания эквивалентных фракций: 1 // x = 10 ⁄ 12
- Продолжайте следовать остальным общим правилам: 3 / 12 + 10 / 12 = 13 / 12 = 1 1 / 12
 Однако это не обязательно даст вам наименьший общий знаменатель для работы, а иногда ваши дроби могут выглядеть беспорядочно.
Однако это не обязательно даст вам наименьший общий знаменатель для работы, а иногда ваши дроби могут выглядеть беспорядочно.Теперь, когда у вас есть базовый набор правил, которым нужно следовать при сложении дробей, используйте наши рабочие листы и упражнения для практики!
Добавление дробей: все, что вам нужно знать
Джерри строит небольшой скворечник. Он просматривает планы и определяет длину деревянных блоков, которые ему понадобятся для завершения проекта. К сожалению, не каждое измерение равнялось полному дюйму.Поэтому Джерри нужно использовать дроби для перечисления необходимых ему измерений. Затем ему нужно добавить дроби, чтобы определить, сколько древесины нужно купить.
Дроби используются для обозначения частей целого. Если у вас меньше целого пирога, вы можете использовать дроби, чтобы показать, сколько пирога у вас есть на самом деле. Некоторые дроби включают в себя:
Когда Джерри будет готов сложить дроби вместе, ему нужно знать некоторые вещи, чтобы быть уверенным, что у него будет достаточно дерева.

Как складывать дроби с одинаковыми знаменателями
Складывать дроби довольно просто, если вы начинаете с одинаковыми знаменателями.Знаменатель — это нижнее число, а числитель — это число сверху. Допустим, у вас есть следующая задача:
Поскольку знаменатели одинаковы (6), все, что вам нужно сделать, это сложить числители вместе:
Возможно, вы купили два пирога: вишневый и яблочный. . После того, как несколько ваших гостей угостились десертом, вы обнаружите, что на одном пироге осталось 2 ломтика из 6 ломтиков, которые вы нарезали, а на другом — 3 ломтика из 6. Складывая их вместе, вы знаете, что у вас осталось 5 кусочков, которыми вы можете поделиться с другими.
Упрощение дробей
После сложения дробей важно дать ответ в простейшей форме. Значит, нужно сделать так, чтобы решение сводилось к минимальным условиям. Например,
Прежде чем перейти к следующему уравнению, вам нужно проверить свой ответ и убедиться, что его нельзя упростить дальше.
 Для этого
Для этого- 1. Рассмотрим множители числителя и знаменателя.
- 2. Определите GCF (наибольший общий делитель).Это наибольшее число, которое делится без остатка как на числитель, так и на знаменатель.
- 6 − 1, 2, 3, 6
12 − 1, 2, 3, 4, 6, 12Для приведенного выше примера GCF равен 6.
- 3. Если мы разделим числитель и знаменатель на это число, мы заканчиваем с ½. Это наименьший член, возможный для этого уравнения.
Важно убедиться, что дробь не может быть уменьшена. Это особенно верно, если вы не можете найти GCF, поэтому вы должны продолжать делить верх и низ на одно и то же число, пока не уменьшите дробь настолько, насколько это возможно.
Смешанные числа и неправильные дроби
Смешанное число — это число, которое содержит дробь, а также целое число, например:
Сложение этих чисел может быть затруднено. Чтобы упростить процесс, сначала преобразуйте число в неправильную дробь. У неправильной дроби числитель больше знаменателя.
 Из-за этого важно упростить дробь после нахождения решения, так как вы, вероятно, получите еще одно смешанное число.Посмотрите на это уравнение:
Из-за этого важно упростить дробь после нахождения решения, так как вы, вероятно, получите еще одно смешанное число.Посмотрите на это уравнение:В этом уравнении вы знаете, что 1 = 4/4. Следовательно, 2 = 8/4. Прибавьте дробь к преобразованному целому числу:
После нахождения решения пришло время упростить дробь. В этом случае окончательным решением будет просто целое число 3.
Сложение дробей с разными знаменателями
Важно знать основные принципы сложения дробей, но часто уравнения содержат дроби с разными знаменателями.Что делать, когда это происходит? Прежде чем складывать дроби, нужно иметь одинаковые знаменатели.
Один из самых простых способов найти общие знаменатели — умножить первый знаменатель на второй знаменатель и наоборот. При этом важно умножать числитель и знаменатель на одно и то же число, чтобы значение не изменилось. Если вы не уверены, что это означает, взгляните на этот пример:
Скажем, мы начинаем со следующего уравнения:
Поскольку дроби имеют разные знаменатели, первое, что нам нужно сделать, это преобразовать дроби, чтобы получить общее знаменатели.
 Для этого посмотрите на знаменатели и умножьте каждый на другой знаменатель. И умножьте числитель на то же число, что и его знаменатель, чтобы сохранить то же значение:
Для этого посмотрите на знаменатели и умножьте каждый на другой знаменатель. И умножьте числитель на то же число, что и его знаменатель, чтобы сохранить то же значение: Когда у дробей одинаковый знаменатель, сложите числители вместе:
Окончательное решение представляет собой неправильную дробь, поэтому вам нужно преобразуйте его в смешанное число и упростите решение:
Разделив числитель и знаменатель на 2, вы можете упростить решение до:
Взгляните на следующие 5 практических примеров.Если вам нужно преобразовать знаменатели, обязательно сначала выполните этот шаг. Тогда решайте и упрощайте!
Практические примеры
Практический пример 1 Решение
Поскольку дроби не имеют одинаковых знаменателей, первое, что нужно сделать, это преобразовать дроби. Самый простой способ сделать это — умножить дроби на противоположный знаменатель. Не забудьте умножить числитель и знаменатель на одно и то же число.
 Вы также можете заметить, что оба числа являются множителями 30, поэтому вы можете умножить их на соответствующий множитель, чтобы получить знаменатель 30 (6 х 5 и 10 х 3).
Вы также можете заметить, что оба числа являются множителями 30, поэтому вы можете умножить их на соответствующий множитель, чтобы получить знаменатель 30 (6 х 5 и 10 х 3).После того, как у дробей одинаковые знаменатели, сложите числители. Поскольку сумма является неправильной дробью, замените ее смешанным числом, прежде чем упрощать дробь.
Практический пример 2 Решение
В этой практической задаче вам нужно изменить дроби, чтобы они имели одинаковые знаменатели. Конечно, вы можете умножать знаменатели друг на друга. Однако, поскольку 3 является коэффициентом 12, вы можете умножить только одну из дробей, чтобы получить похожие знаменатели, прежде чем решать уравнение и упрощать.
Так как сумма является неправильной дробью, вам нужно привести уравнение к смешанному числу и упростить конечную дробь.
Практический пример 3 Решение
В практической задаче 3 уравнение имеет смешанное число, поэтому начните с составления неправильной дроби.
 Поскольку 1 = 4/4, мы можем предположить, что 2 = 8/4. Добавьте это число к числителю (3). Затем пришло время убедиться, что у уравнения есть одинаковые знаменатели. Как и в предыдущем примере, 4 является коэффициентом 12.Следовательно, вы можете умножить числитель и знаменатель первой дроби на 3, чтобы преобразовать дробь.
Поскольку 1 = 4/4, мы можем предположить, что 2 = 8/4. Добавьте это число к числителю (3). Затем пришло время убедиться, что у уравнения есть одинаковые знаменатели. Как и в предыдущем примере, 4 является коэффициентом 12.Следовательно, вы можете умножить числитель и знаменатель первой дроби на 3, чтобы преобразовать дробь.Сумма является неправильной дробью. Тридцать восемь можно разделить на 12 три раза (12 × 3 = 36). Это дает вам остаток 2. Затем проверьте, является ли это самой простой формой.
Практический пример 4 Решение
Вы снова можете начать решать уравнение, приведя дроби к одинаковым знаменателям. Умножьте каждую дробь на знаменатель другой дроби, чтобы получить новый знаменатель 56.
После преобразования дроби сложите числители и посмотрите, сможете ли вы упростить дробь.
Решение представляет собой неправильную дробь. Поэтому сначала сделайте из числа смешанное число. Затем упростите решение.
 Делители числа 56 включают 1, 2, 4, 7, 8, 14, 28 и 56. Делители числа 25 включают 1, 5 и 25. Поскольку у них нет общих делителей, окончательное решение будет таким:
Делители числа 56 включают 1, 2, 4, 7, 8, 14, 28 и 56. Делители числа 25 включают 1, 5 и 25. Поскольку у них нет общих делителей, окончательное решение будет таким:Практический пример 5 Решение
Для окончательной практической задачи начните с преобразования смешанного числа в неправильную дробь.Для этого уравнения 1 = 8/8, поэтому 3 = 24/8.
Далее убедитесь, что дроби имеют одинаковые знаменатели. Вы можете умножить каждую дробь на знаменатель другой дроби. Затем сложите продукты вместе.
С решением в виде неправильной дроби упростите его до смешанного числа:
Затем упростите! К делителям числа 51 относятся 1, 3, 17, 51. А к делителям числа 72 относятся 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72. Оба числа можно разделить на 3.Разделите числитель и знаменатель на 3, и вы получите:
Поскольку 17 — простое число, дробь максимально упрощена.
Как вы справились с практическими вопросами? Какие у вас есть вопросы о сложении дробей? Расскажите нам в комментариях ниже.

Джейми окончила Университет имени Бригама Янга в Айдахо по специальности «Английское образование». Она провела несколько лет, обучая и репетиторству студентов в начальной, средней школе и колледже.В настоящее время она работает составителем контрактов и разработчиком учебных программ для курсов онлайн-обучения. В свободное время она любит бегать и проводить время со своими мальчиками!
Посмотреть все сообщения
Сложение дробей с разными знаменателями
Сложение дробей с разными знаменателями- 1 / 2 имеет знаменатель
Число в нижней части дроби, под разделительной чертой.
от «2» и 1 / 4 имеет знаменательЧисло в нижней части дроби, под разделительной чертой.
из «4». - Дроби с разными знаменателями называются в отличие от дробей .
- Мы видим, что 1 / 2 совпадает с 2 / 4 .

- Подобные дроби — это дроби, имеющие одинаковый
знаменательЧисло внизу дроби под разделительной чертой.
. - Мы можем складывать одинаковые дроби, добавляя числители
Число в верхней части дроби над разделительной чертой.
вместе, сохраняя знаменатель прежним. - Считаем количество
четвертиЧетыре равные части. Дроби имеют знаменатель «4».
, что у нас есть всего. - «2» четверти плюс «1» четверть дает «3» четверти.
Этот общий знаменатель остается неизменным в ответе, а затем складываются числители вместе.
- 1 / 2 и 1 / 4 не являются дробями, потому что они имеют разные
знаменателиЧисла внизу дроби, под разделительной чертой.
. - Мы запишем 1 / 2 как
эквивалентную дробьДроби, которые имеют одинаковое значение, но записываются разными числами.
имеет тот же знаменатель, что и 1 / 4 . Здесь 2 из 4 эквивалентны половине.
Здесь 2 из 4 эквивалентны половине. - Чтобы 1 / 2 имели знаменатель «4», мы удваиваем знаменатель.
- Поскольку мы удвоили знаменатель, мы должны удвоить и числитель.
- 1 / 2 совпадает с 2 / 4 .
- Теперь у нас есть , как дроби , мы можем сложить их, сохранив знаменатель и добавив числители.
- Знаменатель ответа останется равным «4».
- 2+1 = 3
- 1 / 12 и 3 / 4 не являются дробями, потому что они имеют разные
знаменателиЧисла внизу дроби, под разделительной чертой.
. - Поскольку «4» — это множитель
, делится точно на. Здесь 4 делится ровно на 12 трижды.
от «12», мы будем писать дроби от «12». - Чтобы число 3 / 4 имело знаменатель «12», мы умножаем знаменатель на 3.

- Поскольку мы умножили знаменатель на 3, мы должны также умножить числитель на 3.
- 3 / 4 совпадает с 9 / 12 .
- Теперь у нас есть , как дроби , мы можем сложить их, сохранив знаменатель и добавив числители.
- Знаменатель ответа останется равным «12».
- 1 + 9 = 10
- Это пример использования «метода бабочки» для сложения дробей.
- Знаменатель находится путем умножения двух знаменателей.
- Умножаем по каждой диагонали, как показано.
- 2 х 7 = 14.
- 3 x 5 = 15.
- Мы добавляем эти результаты, чтобы получить наш числитель 29.
- 2 / 3 + 3 / 29 = 29 / 35
Знаменатель дроби — это число в нижней части дроби, под разделительной чертой.
Подобные дроби — это две или более дроби, имеющие одинаковый знаменатель.

В отличие от дробей — это дроби, у которых разные знаменатели. В знаменателях разные числа.
В этом уроке мы рассмотрим шаги, необходимые для сложения дробей с разными знаменателями путем преобразования дробей в одинаковые дроби.
Шаги для сложения дробей с разными знаменателями:
- Найдите наименьший общий знаменатель, который является первым числом, встречающимся в в обеих таблицах умножения данных знаменателей.
- Перепишите каждую дробь как эквивалентную дробь, содержащую этот общий знаменатель, умножив ее числитель и знаменатель на одно и то же значение.
- Дроби теперь похожи на дроби, и их можно складывать, оставляя прежним знаменатель и добавляя числители.
Чтобы лучше понять эти шаги, мы рассмотрим несколько примеров.
Мы начнем с рассмотрения примеров, в которых изменится только одна дробь.
В следующем примере нас просят сложить дроби
1 ⁄ 2 + 1 ⁄ 4 .

Однако это нелегко рассчитать, потому что дроби делятся на разные размеры. Следовательно, две дроби не похожи друг на друга.
Это потому, что знаменатели разные, а знаменатель говорит нам, на сколько равных частей нужно разделить фигуру.
Формы были разделены на разное количество частей. Чтобы можно было сложить эти две дроби, части должны быть одинакового размера, чтобы мы могли их посчитать.
Знаменатели должны быть одинаковыми.Когда у дробей одинаковые знаменатели, говорят, что они имеют общий знаменатель.
Здесь мы разделили первую фигуру на четыре равные части. Те же пропорции фигуры по-прежнему заштрихованы. Однако общее количество частей изменилось.
Теперь, когда части имеют одинаковый размер, мы можем сложить дроби.
Мы можем видеть, что если мы объединим две четверти с одной четвертью, мы получим три четверти..
Следовательно,
.
Если у двух дробей один и тот же знаменатель , мы можем просто добавить числители и оставить знаменатель одинаковым .
 Чтобы изменить дробь так, чтобы она имела тот же знаменатель, что и другая дробь, нам нужно найти их наименьшее общее кратное .
Чтобы изменить дробь так, чтобы она имела тот же знаменатель, что и другая дробь, нам нужно найти их наименьшее общее кратное .Это означает, что наименьшее число, на которое делятся оба знаменателя.
Мы будем использовать наш предыдущий пример:
Мы ищем наименьшее число , на которое делятся и 2, и 4. Мы можем начать с поиска наибольшего знаменателя и посмотреть, делятся ли на него оба числа. Наибольший знаменатель из двух дробей равен 4.
И 2, и 4 делятся на 4, поскольку 2 x 2 = 4. Итак, наименьшее число, на которое делятся оба знаменателя, равно 4.
Мы изменим одну дробь так, чтобы они были равны обе четверти т.е. обе имеют знаменатель 4 .
Чтобы найти дробь того же размера, но с другими числителем и знаменателем, мы находим эквивалентную дробь .
Мы должны изменить и числитель, и знаменатель на ту же пропорцию . Для этого надо умножить на .
Четверть уже имеет знаменатель 4 , поэтому нам не нужно его менять.
 Мы можем оставить эту дробь прежней.
Мы можем оставить эту дробь прежней.Однако половина имеет другой знаменатель 2 .
Чтобы выяснить, каким будет числитель, мы должны выяснить, на что мы умножаем знаменатель на , чтобы получить 4. Чтобы получить от 2 до 4, мы умножаем на 2 .
Поскольку мы умножили знаменатель на 2, , мы должны также умножить числитель на 2 .
1 х 2 = 2
Таким образом, числитель равен 2 .
Теперь у нас есть
2 ⁄ 4 + 1 ⁄ 4 .
Теперь у нас есть две одинаковые дроби с одинаковыми знаменателями.
Чтобы сложить одинаковые дроби, мы сохраняем знаменатель таким же и добавляем числители .
2 + 1 = 3
Следовательно,
2 ⁄ 4 + 1 ⁄ 4 = 3 ⁄ 4
и так далее,
1 ⁄ 2 + 1 ⁄ 4 = 3 ⁄ 4 .
В приведенном выше примере необходимо было изменить только одну дробь перед их добавлением.
Это произошло потому, что знаменатель одной дроби был множителем другого знаменателя. Это означает, что меньший знаменатель можно умножить на число, чтобы получить больший знаменатель.
Сейчас мы рассмотрим примеры, в которых это не так. Мы будем менять обе дроби, чтобы получить общий знаменатель и сделать их похожими на дроби.
Мы хотим найти наименьший знаменатель, чтобы дроби были как можно более простыми.Это известно как наименьший общий знаменатель .
Чтобы найти наименьший общий знаменатель, выполните следующие действия:
- Перечислите кратные (таблицы умножения) каждого из заданных знаменателей.
- Наименьший общий знаменатель — это первое число, которое появляется в обоих списках.
- Если оба знаменателя нельзя разделить на одно и то же число, то наименьший общий знаменатель равен произведению знаменателей.
Вот пример сложения дробей с разными знаменателями.

1 ⁄ 2 + 1 ⁄ 5 .
Чтобы можно было сложить эти две разные дроби, знаменатели сначала должны быть одинаковыми. Начнем с нахождения наименьшего общего знаменателя.
Это наименьшее число, на которое делятся оба знаменателя: 2 и 5.
Чтобы найти наименьший общий знаменатель, мы перечисляем первые несколько чисел в каждой таблице умножения и продолжаем, пока не найдем число в обоих списках.
Наименьшее число в таблицах умножения на 2 и 5 равно 10. Таким образом, 10 будет нашим наименьшим общим знаменателем.
Обратите внимание, что в этом примере можно было бы перемножить знаменатели 2 и 5, чтобы получить общий знаменатель 10.
Это потому, что не существует целого числа, которое может делиться и на 2, и на 5 точно.
Поскольку мы изменили знаменатели обеих дробей, мы должны изменить и их числители. Мы должны изменить числитель и знаменатель каждой дроби пропорционально, поэтому мы умножаем.

Мы следуем правилу нахождения эквивалентных дробей: на что бы мы ни умножали знаменатель, мы должны умножать и числитель.
Итак, начнем с того, что узнаем, на что мы умножили каждый знаменатель, чтобы получить 10.
Чтобы перейти от 2 к нашему новому знаменателю 10, мы умножили его на 5.
Значит, надо еще и числитель умножить на 5.
1 х 5 = 5
Следовательно, числитель равен 5.
Чтобы получить от 5 до 10, мы умножаем на 2.
Значит, надо еще и числитель умножить на 2.
1 х 2 = 2
Следовательно, числитель равен 2.
Оба знаменателя теперь одинаковы, поэтому у нас есть две одинаковые дроби, и мы можем их сложить.
Чтобы сложить одинаковые дроби, мы складываем числители, но сохраняем знаменатель таким же, как общий знаменатель.
Теперь мы можем сложить числители.
5 + 2 = 7
Следовательно, числитель равен 7.
 И так,
И так,5 ⁄ 10 + 2 ⁄ 10 = 7 ⁄ 10
Следовательно,
1 ⁄ 2 + 1 ⁄ 5 = 7 ⁄ 10
При обучении сложению дробей с разными знаменателями наиболее распространенной ошибкой является сложение вместе числителей и знаменателей без нахождения общего знаменателя.
Чтобы избежать этой очень распространенной ошибки, вернитесь к визуальным моделям, таким как модели столбцов, показанные выше, и постоянно напоминайте им, что мы должны найти общий знаменатель, прежде чем складывать.
Некоторые учащиеся также часто всегда умножают два заданных знаменателя вместе при нахождении наименьшего общего знаменателя.
Хотя это всегда найдет общий знаменатель , оно не даст наименьшего общего знаменателя в некоторых случаях, когда знаменатели имеют общий множитель.
Это может привести к тому, что они получат больший ответ за счет больших умножений, которые необходимо упростить в конце.

Методическая процедура, известная как «метод бабочки» для сложения дробей, показана ниже. Я бы не рекомендовал вводить тему сложения дробей с помощью приведенного ниже метода, но он может упростить структуру для некоторых людей и помочь с мысленным сложением дробей.
В этом примере мы добавляем 2 ⁄ 5 + 3 ⁄ 7 .
Эти дроби имеют разные знаменатели, и у 5 и 7 нет общего множителя.Это означает, что не существует целого числа (кроме 1), которое может делиться точно на 5 и 7.
Знаменатель ответа будет произведением двух знаменателей.
5 х 7 = 35
Мы можем перемножить по диагоналям, а затем сложить эти ответы вместе, чтобы получить числитель.
2 х 7 = 14
и
3 х 5 = 15
14 + 15 = 29
и так, 29 — это числитель нашего ответа.
2 ⁄ 5 + 3 ⁄ 7 = 29 ⁄ 35 .

- 1 / 12 и 3 / 4 не являются дробями, потому что они имеют разные


 : Просвещение, 2014, стр. 95.
: Просвещение, 2014, стр. 95.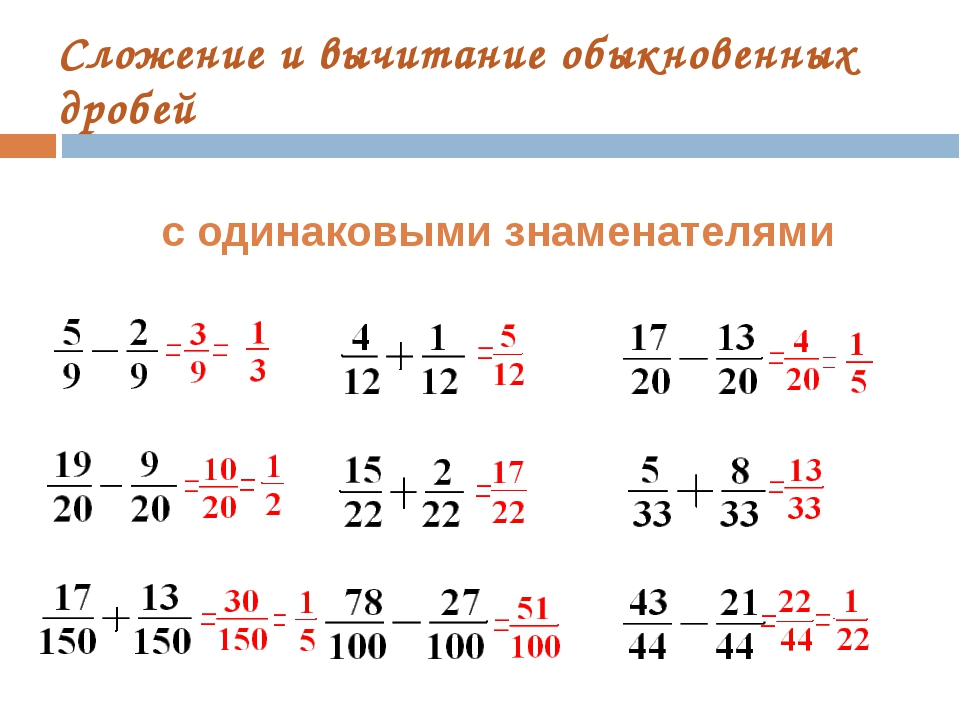





 Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман.
Шок оказался настолько сильным, что «… дискуссии продолжаются и в настоящее время, прийти к общему мнению о сущности парадоксов научному сообществу пока не удалось… к исследованию вопроса привлекались математический анализ, теория множеств, новые физические и философские подходы; ни один из них не стал общепризнанным решением вопроса… » [Википедия, » Апории Зенона «]. Все понимают, что их дурят, но никто не понимает, в чем заключается обман. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Если время останавливается, Ахиллес уже не может перегнать черепаху. Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения.
Но это не полное решение проблемы. На Зеноновскую апорию «Ахиллес и черепаха» очень похоже утверждение Эйнштейна о непреодолимости скорости света. Эту проблему нам ещё предстоит изучить, переосмыслить и решить. И решение нужно искать не в бесконечно больших числах, а в единицах измерения. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
 Вот здесь начнется самое интересное.
Вот здесь начнется самое интересное. Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте.
Как видите, один и тот же набор элементов одновременно является и множеством, и мультимножеством. Как правильно? А вот здесь математик-шаман-шуллер достает из рукава козырный туз и начинает нам рассказывать либо о множестве, либо о мультимножестве. В любом случае он убедит нас в своей правоте. Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
Её не существует. Нет в математике формулы, по которой можно найти сумму цифр любого числа. Ведь цифры — это графические символы, при помощи которых мы записываем числа и на языке математики задача звучит так: «Найти сумму графических символов, изображающих любое число». Математики эту задачу решить не могут, а вот шаманы — элементарно.
 Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел.
Это ещё один аргумент в пользу того, что . Вопрос к математикам: как в математике обозначается то, что не является числом? Что, для математиков ничего, кроме чисел, не существует? Для шаманов я могу такое допустить, но для ученых — нет. Реальность состоит не только из чисел. Какой еще туалет?
Какой еще туалет? Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:
Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения: Если к пиццы прибавить ещё пиццы, то получится пиццы:
Если к пиццы прибавить ещё пиццы, то получится пиццы: В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю. Наименьшее общее кратное этих чисел равно 6
Наименьшее общее кратное этих чисел равно 6 Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца: В результате получили (одну целую пиццу и еще одну шестую пиццы).
В результате получили (одну целую пиццу и еще одну шестую пиццы).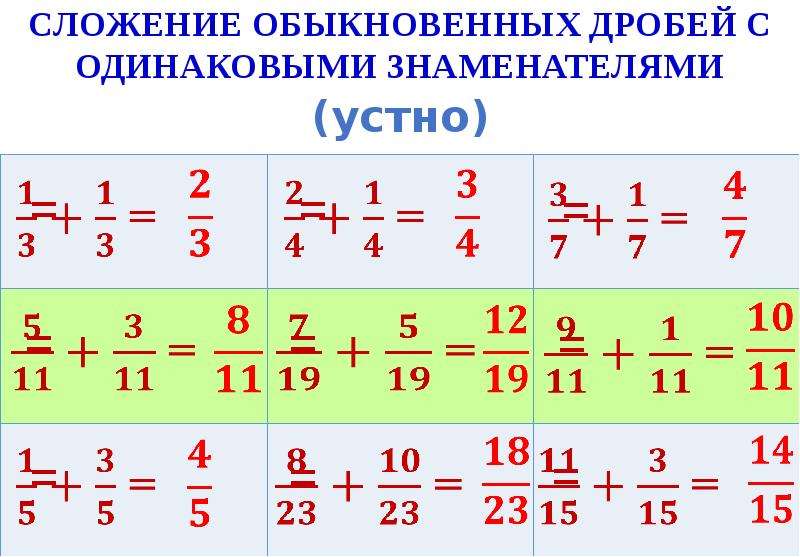 Найти значение выражения .
Найти значение выражения . Умножить числители и знаменатели дробей на свои дополнительные множители
Умножить числители и знаменатели дробей на свои дополнительные множители  Выделяем:
Выделяем: Если от пиццы отрезать пиццы, то получится пиццы:
Если от пиццы отрезать пиццы, то получится пиццы: В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью: Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):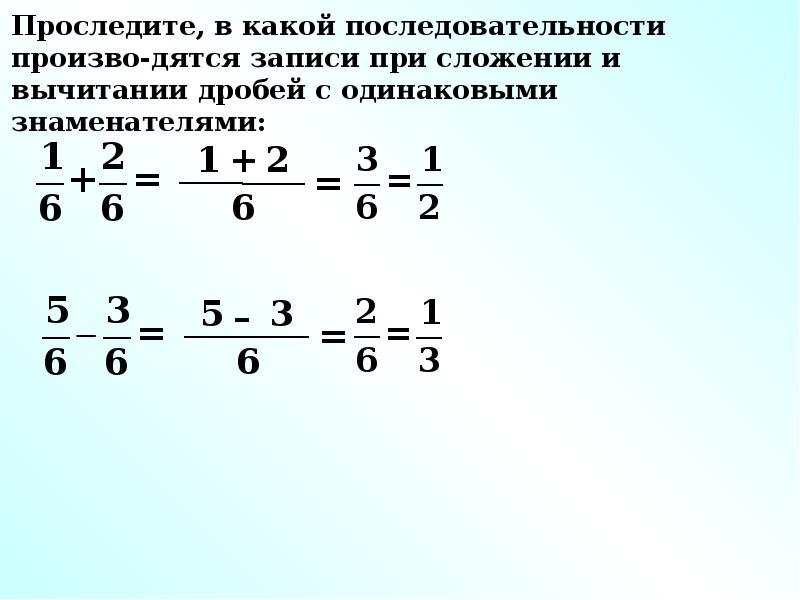 Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью: Не забываем про знак равенства (=) на новой строке:
Не забываем про знак равенства (=) на новой строке: Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:
 Выделим в ней целую часть:
Выделим в ней целую часть:
 Для этого достаточно перевернуть её.
Для этого достаточно перевернуть её. В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.
В каждом виде сложения дробей свои правила и алгоритм действий. Рассмотрим подробно каждый вид сложения.

 В зависимости от типа выражения переходим к алгоритму решения.
В зависимости от типа выражения переходим к алгоритму решения.
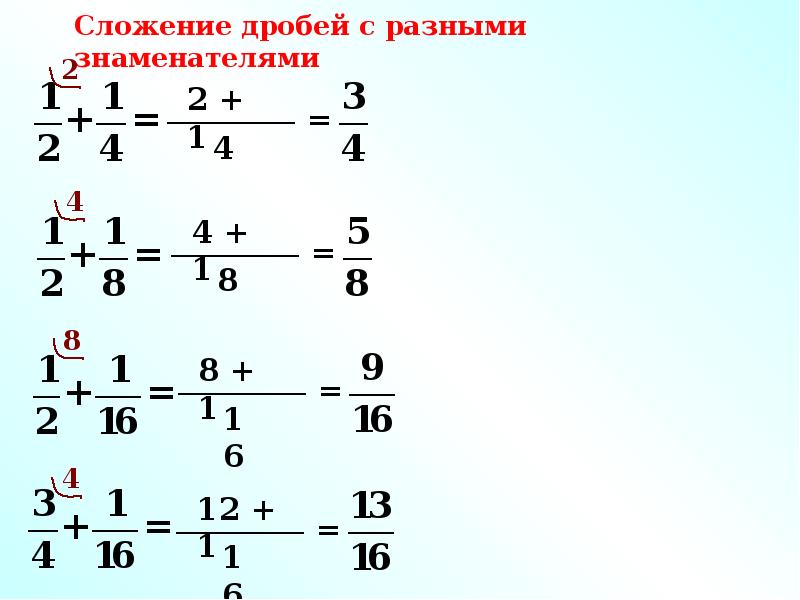 Как вы думаете торт полностью съели или нет?
Как вы думаете торт полностью съели или нет?
 Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.
Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:
Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например: Здесь обнаружатся новые грабли, да…
Здесь обнаружатся новые грабли, да… ..
.. д. А дальше работаем с этим дробями по всем правилам.
д. А дальше работаем с этим дробями по всем правилам.



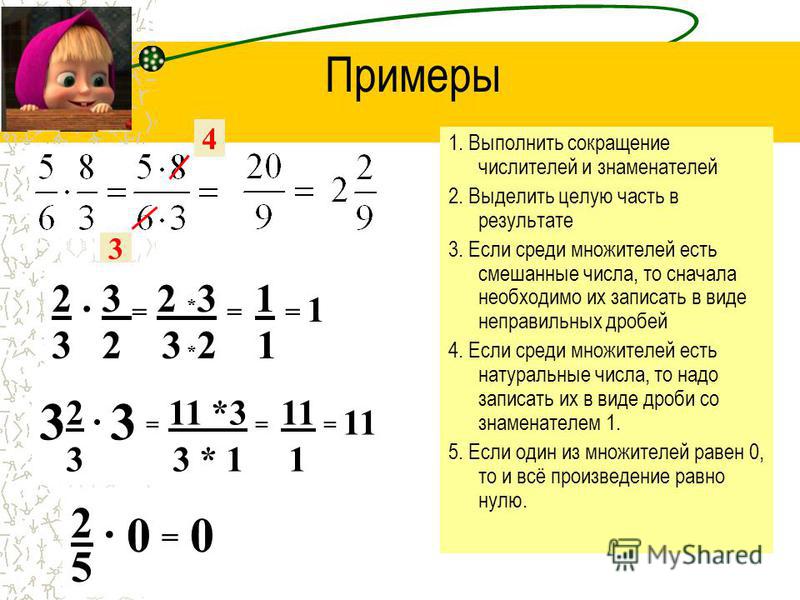 Однако это не обязательно даст вам наименьший общий знаменатель для работы, а иногда ваши дроби могут выглядеть беспорядочно.
Однако это не обязательно даст вам наименьший общий знаменатель для работы, а иногда ваши дроби могут выглядеть беспорядочно.
 Для этого
Для этого Из-за этого важно упростить дробь после нахождения решения, так как вы, вероятно, получите еще одно смешанное число.Посмотрите на это уравнение:
Из-за этого важно упростить дробь после нахождения решения, так как вы, вероятно, получите еще одно смешанное число.Посмотрите на это уравнение: Для этого посмотрите на знаменатели и умножьте каждый на другой знаменатель. И умножьте числитель на то же число, что и его знаменатель, чтобы сохранить то же значение:
Для этого посмотрите на знаменатели и умножьте каждый на другой знаменатель. И умножьте числитель на то же число, что и его знаменатель, чтобы сохранить то же значение:  Вы также можете заметить, что оба числа являются множителями 30, поэтому вы можете умножить их на соответствующий множитель, чтобы получить знаменатель 30 (6 х 5 и 10 х 3).
Вы также можете заметить, что оба числа являются множителями 30, поэтому вы можете умножить их на соответствующий множитель, чтобы получить знаменатель 30 (6 х 5 и 10 х 3). Поскольку 1 = 4/4, мы можем предположить, что 2 = 8/4. Добавьте это число к числителю (3). Затем пришло время убедиться, что у уравнения есть одинаковые знаменатели. Как и в предыдущем примере, 4 является коэффициентом 12.Следовательно, вы можете умножить числитель и знаменатель первой дроби на 3, чтобы преобразовать дробь.
Поскольку 1 = 4/4, мы можем предположить, что 2 = 8/4. Добавьте это число к числителю (3). Затем пришло время убедиться, что у уравнения есть одинаковые знаменатели. Как и в предыдущем примере, 4 является коэффициентом 12.Следовательно, вы можете умножить числитель и знаменатель первой дроби на 3, чтобы преобразовать дробь. Делители числа 56 включают 1, 2, 4, 7, 8, 14, 28 и 56. Делители числа 25 включают 1, 5 и 25. Поскольку у них нет общих делителей, окончательное решение будет таким:
Делители числа 56 включают 1, 2, 4, 7, 8, 14, 28 и 56. Делители числа 25 включают 1, 5 и 25. Поскольку у них нет общих делителей, окончательное решение будет таким:

 Здесь 2 из 4 эквивалентны половине.
Здесь 2 из 4 эквивалентны половине.


 Чтобы изменить дробь так, чтобы она имела тот же знаменатель, что и другая дробь, нам нужно найти их наименьшее общее кратное .
Чтобы изменить дробь так, чтобы она имела тот же знаменатель, что и другая дробь, нам нужно найти их наименьшее общее кратное . Мы можем оставить эту дробь прежней.
Мы можем оставить эту дробь прежней.


 И так,
И так,
