Как разделить одно смешанное число на другое. Деление смешанных дробей
Затем действуем по правилу: первую дробь умножаем на дробь, обратную ко второй (то есть на перевернутую дробь, у которой числитель и знаменатель меняются местами). При умножении дробей числитель умножаем на числитель, знаменатель — на знаменатель.
Рассмотрим примеры на деление смешанных чисел.
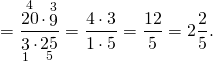
Деление смешанных чисел начинаем с перевода их в неправильные дроби. Затем делим полученные дроби. Для этого первую дробь умножаем на перевернутую вторую. 20 и 25 на 5, 3 и 9 — на 3. Получили неправильную дробь, поэтому необходимо .
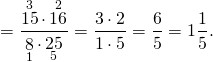
Смешанные числа переводим в неправильные дроби. Далее по правилу деления дробей первое число оставляем и умножаем его на число, обратное ко второму. Сокращаем 15 и 25 на 5, 8 и 16 — на 2. Из полученной неправильной дроби выделяем целую часть.
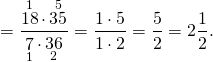
Смешанные числа заменяем неправильными дробями и делим их. Для этого первую дробь переписываем без изменений и умножаем на перевернутую вторую. Сокращаем 18 и 36 на 18, 35 и 7 — на 7. В результате — неправильная дробь. Выделяем из нее целую часть.
На вопрос как разделить между собой два смешанных числа? заданный автором Ѐита Нефедорова лучший ответ это Нужно представить каждое из них в виде неправильной дроби. Это делатеся так. Если число задано в виде a + (b/c), то здесь a — целая часть, b/c — дробная часть, причём b — числитель, с — знаменатель, то тогда a + (b/c) = ac/c + b/c = (ac + b) / c, т. е. целую часть нужно умножить на знаменатель дробной части и прибавить к полученному числу — знаменатель дробной части. Это — числитель полученной неправильной дроби. А её знаменатель — это знаменатель дробной части исходного числа. Результат от деления двух полученных неправильных дробей — это дробь, числитель которой — произведение числителя первой дроби на знаменатель второй, а знаменатель — произведение знаменателя первой дроби на числитель второй. Полученную дробь, если она неправильная, можно при желании перевести в смешанное число, разделив её числитель нацело на знаменатель. Целая часть частного — это целая часть смешанного числа, остаток от деления — это числитель дробной части, знаменатель неправильной дроби — это знаменатель дробной части.
Ответ от Двутавровый [новичек]
Деление смешанных чисел может быть сведено к делению обыкновенных дробей. Для этого достаточно смешанные числа перевести в неправильные дроби.
Запишем правило деления смешанных чисел: чтобы выполнить деление смешанного числа на смешанное число, надо:
перевести смешанные числа в неправильные дроби;
выполнить деление соответствующих обыкновенных дробей.
policom-rt.ru
Деление дробей
Деление обыкновенных дробей
Чтобы разделить две дроби нужно выполнить следующие шаги:
- 1 Перевернуть вторую дробь(поменять числитель и знаменатель местами) и умножить полученные дроби . Следующие шаги, 2—4, в точности повторяют процесс умножения дробей.
- 2 Перемножить числители дробей между собой 5 × 4 = 20.
- 3 Перемножить знаменатели дробей между собой 8 × 3 = 24.
- 4 Сократим полученную дробь , в результате получим .
Деление обыкновенных дробей можно записать в виде:
При деление дробей не имеет значения, имеют ли они одинаковый знаменатель или разный.
Пример Выполните деление дробей
.
Чтобы проверить результат деления дробей, можно воспользоваться калькулятором дробей.
Пример Разделить дроби .
.
Деление дроби на число
Пример Разделим дробь на число
.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
calcs.su
Урок «Деление дробей и смешанных чисел»
План урока
5.2A Действия над обыкновенными дробямиШкола: КГУ «Тимирязевская средняя школа отдела образования акимата Сарыкольского района»
Дата : 19.05.2017
ФИО учителя:Мальгаева А.С.
класс: 5
Участвовали:
Не участвовали:
Тема урока
Деление обыкновенных дробей и смешанных чисел (4 урок)
Цели обучения, достигаемые на этом уроке (Ссылка на учебный план)
5.1.2.23
выполнять деление обыкновенных дробей и смешанных чисел;
Цель урока
делить обыкновенные дроби
делить смешанные числа;
делить натуральные чисела на дробь
делить дроби на натуральное число
Критерии оценивания
делят обыкновенные дроби
делят смешанные числа
делят натуральное число на дробь
делят дробь на натуральное число
делят дробь на смешанное число
Уровень мыслительных навыков
Знание и понимание, применение, анализ, синтез
Языковые задачи
Языковые цели:
Применяют термины :натуральное число, обыкновенная дробь, дробная черта, числитель, знаменатель, правильная и неправильная дробь, смешанное число, множитель, произведение
Сочетания, используемые для диалога и письма:
Чтобы разделить обыкновенные дроби нужно…
Чтобы разделить смешанные числа нужно …
Что бы найти неизвестный множитель нужно…
Воспитание ценностей
Взаимоуважение, взаимопонимание, сотрудничество самостоятельноcть.
Межпредметная связь
биологоия
Предыдущие знания
Основные понятия натуральное число, обыкновенная и неправильная дробь, смешанное число , перевод смешанного числа в неправильную дробь, сложение, вычитание, умножение и деление обыкновенных дробей и смешанных чисел, компоненты умножения
Ход урока
Запланированные этапы урока
Виды упражнений, запланированных на урок:
Ресурсы
Начало урока
1 Организационный момент. (3 мин.) Метод «Дерево дружбы»
Это дерево появилось на свет в тот момент, когда один человек улыбнулся другому. Эта улыбка пустила свои корни глубоко в землю, и на поверхности появились три ростка: доброта, взаимовыручка и искренность. Эти ростки срослись в одно целое, и появилось Дерево Дружбы. Дерево росло и развивалось, на нем набухали новые почки, лопались, превращаясь в изумрудные листья. Некоторые листочки желтели и опадали – это означало, что друзья поссорились. Но если на этом месте появлялась новая почка – друзья мирились!Наше дерево дружбы живет, и будет жить вечно. И каждый раз дерево улыбается, если люди дружат. И сегодняшний наш урок пройдет под девизом о дружбе и взаимовыручке: “Один за всех и все за одного”.
За активную работу на уроке, за хорошие ответы вы будете получать листочки, а в конце урока посмотрим, сможет ли наше дерево улыбнуться нам и порадоваться нашим знаниям.
2. Мотивация и постановка целей
«Дерево познаний».
Каждый учащийся должен отметить на какой веточке он находится на данном этапе урока.

Учитель: Ребята, чем вы с вами занимались на предыдущих уроках?
Дети: Делили обыкновенные дроби и смешанные числа.
Учитель: Сегодня мы продолжим эту работу. Продолжаем совершенствовать вычислительные навыки. Продолжаем учиться делать выбор, оценивать работу свою и работу товарища. Мы будем работать в парах, индивидуально. Из всего услышанного, поставьте перед собой цель на этот урок. (Спросить 2 — 3 детей)
Презентация
Слайд 1
Индивидуальные карточки у каждого учащегося.
Учащийся закрашивает себя зеленым цветом на какой веточке он находится на данном этапе.
Проверка домашнего задания
а) Проверка домашнего задания по готовому решению.
Актуализация знаний
б) Фронтальный опрос— по стратегии «Спроси у товарища» — задают вопрос и кидают мяч, ученик отвечает на вопрос.Если верно мяч кидают следующему учащимуся, в противном случае, если ответ прозвучал неверно, тот ученик который его задает сам на него отвечает. Правильный ответ 1 листочек) — самооценивание.
Предполагаемые вопросы:
Какие обыкновенные дроби можно записать в виде смешанных чисел? (ответ)
Как умножить дробь на натуральное число? (ответ)
Как умножить смешанное число на смешанное число? (ответ)
Как разделить дробь на дробь? (ответ)
Какая дробь называется неправильной дробью? (ответ)
Какие числа называются взаимно обратными? (ответ)
Как умножить дробь на дробь? (ответ)
Как разделить смешанное число на смешанное число? (ответ)
Обратная связь
Учитель корректирует ответы учеников
Слайд 2
Середина урока
Стратегия « Лови ошибку» (устно).
Исправляют ошибки на доске и объясняют почему они были допущены.

Обратная связь:
1. Какие ошибки были допушены.
2. На что нужно обратить внимание.
3. Работа в парах Стратегия: «Думай – объединяйся — делись».
Выполните действия:
 2) 5
2) 5
3)  4)
4) 
Дескриптор: Обучающийся
Правильно делит обыкновенные дроби и смешанные числа
Правильно умножает обыкновенные дроби и смешанные числа
Перевод смешанных чисел в неправильную дробь
Верно прорешивает примеры
Обратная связь:
— В чем испытывали затруднения сложности?
— Какие ошибки были допущены?
— Что нужно знать для того чтобы не допускать таких ошибок?
Восхождение к олимпу (дифференциация по темпу)по вариантам, цепочкой

Обратная связь
Физминутка Игра «Дождь в лесу».
Дети становятся в круг друг за другом – они «превращаются» в деревья в лесу. Учитель читает текст, дети выполняют действия под музыку.
Работа в группах. Учитель делит на дифференцированные группы, раздает карточки учащимся, на которых изображены корень дерева (С), ствол (В) и веточки (А). Затем учащимся предлагается разделиться по виду. Раздаются задания для каждой группы.
Распределяются обязанности внутри групп:
Лидер — отвечает за работу группы в целом
Секретарь – фиксирует результаты
Практик — принимает активное участие в решении,
Эксперт – проверяет, все ли поняли решение задания.
Тайм менеджер – следит за временем
Дизайнер – отвечает за оформление
Обсуждаются правила работы в группе, соблюдение регламента.
Группа №1 – уровень А — базовый – формируются знания в области знание, применение, понимание
Группа №2 – уровень В — продвинутый – понимание, применение, анализ
Группа №3 – уровень В — продвинутый – понимание, применение, анализ, синтез
Стратегия «Снежный ком».
Работа в группе, которая начинается с решения индивидуального задания. Все учащиеся получают аналогичные задания и самостоятельно выполняют их. После этого следует работа в парах. В парах учащиеся предлагают свои способы решения данного задания, из которых выбирается лучшее. Далее две пары объединяются и работа продолжается в группе, где снова происходит обсуждение решений и выбирается лучшее из них. В конце работы все учащиеся попадают в одну группу. На этом последнем этапе уже не происходит обсуждения решений, группы оформляют свое решение на постере и защищают его у доски.
1 группа А: Реши задачу:
Длина одного отрезка равна 6 см. Второй отрезок короче первого в 1
см. Второй отрезок короче первого в 1 раза. Найдите сумму длин этих отрезков.
раза. Найдите сумму длин этих отрезков.
Дескрипторы оценивания решения задачи:
— правильно составляют краткую запись задач;
— верно выполняют вычисления в задаче;
— записывают ответ.
2 группа В. Реши задачу:
За  ч мотоциклист проехал 20
ч мотоциклист проехал 20 км.
км.
«Задача с условием, но без вопроса. Какие вопросы можно поставить?» (Формулируют вопросы и записывают решение с комментированием на постере).
Дескрипторы оценивания решения задачи:
— правильно составляют краткую запись задач;
— правильно формулируют вопросы к задаче;
— верно выполняет вычисления в задаче;
— записывает ответ.
3 группа С.. Реши задачу:
В два вагона погрузили 119 т зерна. В один погрузили зерна в 1 раза больше, чем в другой. Сколько тонн зерна в каждом вагоне?
раза больше, чем в другой. Сколько тонн зерна в каждом вагоне?
Дискрипторы оценивания решения задачи:
— правильно составляют краткую запись задач;
— правильно определяют неизвестное
— верно составляют уравнение
— верно выполняют вычисления в задаче;
— записывают ответ.
Формативное оценивание.
Ученикам выданы листики (зеленые, красные), на которых им необходимо написать свои замечания (на красных) и пожелания (на зеленых) участникам других групп.
Слайд 3
Карточки с заданиями
Карточки с изображениями
Конец урока
Дифференцированное домашнее задание
Уровень А Вычислите: а)  ; б)
; б)  ; в)
; в)  ; г)
; г) 
Уровень В Выполните действия: а)  ; б)
; б) 
Уровень С Решите уравнение: а) ; б) .
Дескриптор: Обучающийся
— правильно делит натуральное число на дробь
— правильно делит смешанные числа
— расставляет порядок действий
— умеет находить неизвестный компонент
Обратная связь: Есть ли у Вас вопросы по выполнению домашнего задания?
Рефлексия. « Дерево познаний»
Каждый учащийся должен отметить на какой веточке он находится на этом этапе урока
 —
—
каждый учащийся закрашивает себя красным цветом на какой веточке он находится в конце урока и прикрепляет все свои заработанные на уроке листики на дерево.
Дифференциация – каким способом вы хотите больше оказывать поддержку? Какие задания вы даете ученикам более способным по сравнению с другими?
Оценивание – как Вы планируете проверять уровень усвоения материала учащимися?
Охрана здоровья и соблюдение техники безопасности
Распределение ролей в групповой работе.
Разноуровневые задания через индивидуальную работу.
Работа групп выполняется через обратную связь, самими учащимися и посредством вопросов от учителя, символические оценки (листики дерева)
Здоровьесберегающие технологии – физ.минутка.
Рефлексия по уроку
Была ли реальной и доступной цель урока или учебные цели?
Все ли учащиесы достигли цели обучения? Если ученики еще не достигли цели, как вы думаете, почему? Правильно проводилась дифференциация на уроке?
Эффективно ли использовали вы время во время этапов урока? Были ли отклонения от плана урока, и почему?
Используйте данный раздел урока для рефлексии. Ответьте на вопросы, которые имеют важное значение в этом столбце.
Итоговая оценка
Какие две вещи прошли действительно хорошо (принимайте в расчет, как преподавание, так и учение)?
1:
2:
Какие две вещи могли бы улучшить Ваш урок (принимайте в расчет, как преподавание, так и учение)?
1:
2:
Что нового я узнал из этого урока о своем классе или об отдельных учениках, что я мог бы использовать при планировании следующего урока?
infourok.ru
 2) 5
2) 5