Доказательство неравенств | Алгебра
Как доказать неравенство? Рассмотрим некоторые способы доказательства неравенств.
Определения
1) Число a больше числа b, если разность a-b — положительное число:
a>b, если a-b>0.
2) Число a меньше числа b, если разность a-b — отрицательное число:
a<b, если a-b<o.
3)a≥b, если a-b>0 или a=b (то есть a-b≥0).
4)a≤b, если a-b<0 или a=b (то есть a-b≤0).
I. Доказательство неравенств с помощью определения.
Сводится к оценке разности левой и правой частей неравенства и сравнение её с нулём.
Примеры.
1) Доказать неравенство: (a+9)(a-2)<a(a+7a).
Доказательство:
Оценим разность левой и правой частей неравенства:
(a+9)(a-2)-a(a+7a)=a²-2a+9a-18-a²-7a=-18<0.
Поскольку разность равна отрицательному числу,
(a+9)(a-2)<a(a+7a).
Что и требовалось доказать.
2) Доказать, что при любом действительном значении переменной x верно неравенство:
9x²+48>30x.
Доказательство:
Оцениваем разность левой и правой частей неравенства:
9x²+48-30x=(3x)²-2·3x·5+5²-5²+48=(3x-5)²+23.
(3x-5)²≥0 при любом значении переменной x.
23>0.
Следовательно, (3x-5)²+23>0 при любом x.
Значит, неравенство 9x²+48>30x выполняется при любом действительном значении x.
Что и требовалось доказать.
3) Доказать неравенство: x²+y²+16x-20y+190>0.
Доказательство:
Выделим полные квадраты в левой части неравенства:
x²+y²+16x-20y=(x²+16x)+(y²-20y)+190=
=(x²+2·x·8+8²)-8²+(y²-2·y·10+10²)-10²+190=(x+8)²+(y-10)²+26.
(x+8)²≥0 при любом значении x,
(y-10)²≥0 при любом значении y,
26>0.
Следовательно, (x+8)²+(y-10)²+26>0 при любых действительных значениях переменных x и y.
А это значит, что x²+y²+16x-20y+190>0.
Что и требовалось доказать.
II. Доказательство неравенств методом «от противного».
Высказываем предположение, что доказываемое неравенство неверно, и приходим к противоречию.
Пример.
Доказать неравенство: (a1b1+a2b2)²≤(a1²+a2²)(b1²+b2²).
Доказательство:
Предположим, что неравенство, которое нам нужно доказать, неверно. Тогда
(a1b1+a2b2)²>(a1²+a2²)(b1²+b2²).
Значит (a1b1+a2b2)²-(a1²+a2²)(b1²+b2²)>0.
Раскрываем скобки и упрощаем:
a1²b1²+2a1
2a1b1a2b2-a1²b2²-a1²b1²>0,
-(a1²b2²-2a1b1a2b2+a1²b1²)>0.
Отсюда
-(a1b2-a1b1)²>0.
Поскольку (a1b2-a1b1)²≥0 при любых действительных значениях переменных, то -(a1b2-a1b1)²≤0. Пришли к противоречию. Значит, наше предположение было неверно. Следовательно,
(a1b1+a2b2)²≤(a1²+a2²)(b1²+b2²).
Что и требовалось доказать.
Замечание.
Неравенство (a1b1+a2b2)²≤(a1²+a2²)(b1²+b2²) является частным случаем неравенства Коши-Буняковского:
(a1b1+a2b2+…+anbn)²≤(a1²+a2²+…+an²)(b1²+b2²+…+bn²).
III. Доказательство неравенств с помощью геометрической интерпретации.
Таким способом, например, можно доказать неравенство о среднем арифметическом и среднем геометрическом (частный случай неравенства Коши).
IV. Доказательство неравенств с использованием очевидных неравенств.
Пример.
Доказать неравенство: a²+b²+c²≥ab+bc+ac.
Доказательство:
Так при любых действительных значениях переменных (a-b)²≥0, (b-c)²≥0 и (a-c)²≥0, то очевидно, что (a-b)²+(b-c)²+(a-c)²≥0.
Раскрываем скобки по формуле квадрата разности и упрощаем:
a²-2ab+b²+b²-2bc+c²+a²-2ac+c²≥0,
2a²+2b²+2c²-2ab-2bc-2ac≥0.
Разделим на 2 обе части неравенства:
a²+b²+c²-ab-bc-ac≥0.
Осталось перенести три слагаемые в правую часть:
a²+b²+c²≥ab+bc+ac.
Что и требовалось доказать.
V. Доказательство неравенств с помощью ранее доказанных неравенств.
Основные неравенства, на которые опираются при доказательстве других неравенств:
- Неравенство Коши:
при a1>0, a2>0, …, an>0 и n>2.
При a1= a2= …= an неравенство превращается в равенство.
В частности, при a1= a, a2=b, n=2:
- Сумма положительных взаимно-обратных чисел не меньше двух:
при x>0
Применяется также аналог неравенства для отрицательных взаимно-обратных чисел:
при x<0
- Неравенство Коши-Буняковского
(a1b1+a2b2+…+anbn)²≤(a1²+a2²+…+an²)(b1²+b2²+…+bn²), где n≥2.
Равенство достигается лишь в случае, когда числа xi и yi пропорциональны, то есть существует число k такое, что для любого i=1,2,…,n выполняется равенство xi=kyi.
- Неравенство Бернулли
где x>-1, n — натуральное число.
Равенство достигается лишь при x=0 и n=1.
- Обобщённое неравенство Бернулли
Если x>-1, n — действительное число:
- При n<0 и n>1
- При 0<n<1
В обоих случаях равенство возможно лишь при x=0.
- Модуль суммы не превосходит суммы модулей
Равенство достигается, если a и b имеют одинаковые знаки (a≥0 и b≤0 либо a≤0, b≤0).
- Модуль разности больше либо равен модуля разности модулей
Примеры.
1) Доказать неравенство при x>0, a>0, b>0, c>0:
Доказательство:
Используем неравенство Коши о среднем арифметическом и среднем геометрическом
для каждого из множителей:
Так как по условию x>0, a>0, b>0, c>0, то x+a>0, x+b>0, x+c>0 и
Значит, полученные неравенства можем почленно перемножить:
Отсюда
Что и требовалось доказать.
2) Доказать неравенство:
Доказательство:
Очевидно, что
то есть
Таким образом, для доказательства нашего неравенства надо показать, что
разделим обе части неравенства на 4 в двадцатой степени (при делении на положительное число знак неравенства не изменяется):
Применим неравенство Бернулли:
Так как в неравенстве
правая часть больше либо равна 6, это равенство верно. Следовательно,
Что и требовалось доказать.
Помимо перечисленных, существуют другие способы доказательства неравенств (метод математической индукции и т.д.).
Умение доказывать неравенства применяется во многих разделах алгебры (например, метод оценки решения уравнений сводится к доказательству неравенств).
Приглашение в мир математики: Как доказывать олимпиадные неравенства
На семинаре координаторов олимпиады «Кенгуру» Вячеслав Андреевич Ясинский прочёл лекцию о том, как можно доказывать олимпиадные симметричные неравенства с помощью собственного метода разностей переменных.Действительно, на математических олимпиадах часто встречаются задания на доказательство неравенств, как, например, такое, с Международной олимпиады по математике 2001 года: $\frac{a}{\sqrt{a^2+8bc}}+\frac{b}{\sqrt{b^2+8ac}}+\frac{c}{\sqrt{c^2+8ab}}\geq 1$ (для положительных a,b,c).
Обычно чтобы доказать олимпиадное неравенство, его нужно привести к одному из базовых: Коши, Коши-Буняковского, Йенсена, неравенству между средними и т.д. Причём часто приходится пробовать различные варианты базового неравенства до достижения успеха.
Однако часто у олимпиадных неравенств (как у приведённого выше) есть одна особенность. При перестановке переменных (например, замене a на b, b на c и c на a) они не изменятся.
Если функция нескольких переменных не меняется при любой их перестановке, то она называется симметрической. Для симметрической функции f от трёх переменных выполняется равенство:
f(x,y,z)= f(x,z,y)= f(y,x,z)= f(y,z,x)= f(z,x,y)= f(z,y,x)
Если же функция не меняется только при циклической перестановке переменных, она называется циклической.
f(x,y,z)= f(y,z,x)= f(z,x,y)
Для неравенств, которые строятся на основе симметрических функций, Вячеслав Андреевич разработал универсальный метод доказательства.
Метод состоит из следующих шагов.
1. Преобразовать неравенство так, чтобы слева оказался симметрический многочлен (обозначим его D), а справа 0.
2. Выразить симметрический многочлен D от переменных a, b, c через базовые симметрические многочлены.
Базовых симметрических многочленов от трёх переменных существует три. Это:
p = a+b+c — сумма;
q = ab+bc+ac — сумма попарных произведений;
r = abc — произведение.
Любой симметрический многочлен можно выразить через базовые.
3. Поскольку многочлен D симметрический, можно, не нарушая общности, считать, что переменные a, b, c упорядочены так: $a\geq b\geq c$
4. Вводим два неотрицательных числа х и у, таки, что x = a-b, y = b-c.
5. Снова преобразовываем многочлен D, выражая p, q и r через c и x, y. Учитываем, что
b = y+c
a = (x+y)+c
Тогда
p = a+b+c = (x+2y)+3c
q = ab+bc+ac = 3c2+2(x+2y)c+(x+y)y
r = abc = (x+y)yc + (x+2y)c2+c3
Обратите внимание, что скобки в выражениях, содержащих x и y, мы не раскрываем.
6. Теперь рассматриваем многочлен D как многочен от с с коэффициентами, выражающимися через х и у. Учитывая неотрицательность коэффициентов оказывается несложно показать, что знак неравенства будет сохраняться для всех допустимых значений с.
Поясним этот метод на примерах.
Пример 1. Доказать неравенство:
$(a+b+c)^2\geq 3(ab+bc+ac)$
Доказательство
Так как неравенство симметрическое (не меняется при любой перестановке переменных a, b, c), то представим его как
$(a+b+c)^2 — 3(ab+bc+ac)\geq 0$
Выразим многочлен в левой части через базовые симметрические:
$p^2 — 3q\geq 0$
Так как многочлен симметрический, можно считать, не ограничивая общности, что $a\geq b\geq c$ и $x = a-b\geq 0$, $y = b-c\geq 0$.
Выразим левую часть через x, y и c, представив её как многочлен относительно с.
p2-3q = ((x+2y)+3c)2-3(3c2+2(x+2y)c+(x+y)y) = (x+2y)2+6(x+2y)c+9c2-9c2-6(x+2y)c-3(x+y)y
После приведения подобных получаем неравенство вообще не содержащее переменную с
$(x+2y)^2-3(x+y)y\geq 0$
Вот теперь можно раскрыть скобки
$x^2+4xy+4y^2-3xy-3y^2\geq 0$
$x^2+xy+y^2\geq 0$ — что является верным как для нотрицательных x, y, так и для любых.
Таким образом, неравенство доказано.
Пример 2 (с Британской математической олимпиады 1999 года)
Доказать, что $7(ab+bc+ac)\leq 2+9abc$ (для положительных чисел, если a+b+c = 1)
Доказательство
Прежде чем начать сводить всё в левую часть, обратим внимание, что степени частей неравенства у нас не сбалансированы. Если в примере 1 обе части неравенства были многосленами второй степени, то тут многочлен второй степени сравнивается с суммой многочленов нулевой и третьей. Использлуем то, что сумма a+b+c по условию равна 1 и домножим левую часть на единицу, а двойку из правой части — на единицу в кубе.
$7(ab+bc+ac)(a+b+c)\leq 2(a+b+c)^3+9abc$
Теперь перенесём всё влево и представим левую часть как симметричный многочkен от a, b, c:
$7(ab+bc+ac)(a+b+c)- 2(a+b+c)^3-9abc\leq 0$
Выразим левую чаcть через базовые симметрические многочлены:
$7qp- 2p^3-9r\leq 0$
Выразим левую часть через x, y и c, представив её как многочлен относительно с.
7qp- 2p3-9r = 7(3c2+2(x+2y)c+(x+y)y)((x+2y)+3c)-2((x+2y)+3c)3-9((x+y)yc + (x+2y)c2+c3) = 7 (3(x+2y)c2+2(x+2y)2c+(x+2y)(x+y)y+9c3+6(x+2y)c2+3(x+y)yс) — 2 ((x+2y)3+9(x+2y)2c+27(x+2y)c2+27c3) — 9((x+y)yc + (x+2y)c2+c3) = 21(x+2y)c2+14(x+2y)2c+7(x+2y)(x+y)y+63c3+42(x+2y)c2+21(x+y)yс-2(x+2y)3-18(x+2y)2c-54(x+2y)c2-54c3-9(x+y)yc -9(x+2y)c2-9c3
Главное — аккуратно и внимательно выполнять преобразования. Как сказал Вячеслав Андреевич, если он выполняет преобразования и его кто-то отвлекает, он выбрасывает листок с формулами и начинает заново.
Для удобства сведения подобных в заключительном многочлене они выделены разными цветами.
Все слагаемые с c3 уничтожатся: 63c3-54c3-9c3 = 0
Это же произойдёт и со второй степенью с: 21(x+2y)c2+42(x+2y)c2-54(x+2y)c2-9(x+2y)c2 = 0
Преобразуем слагаемые с первой степенью с: 14(x+2y)2c+21(x+y)yс-18(x+2y)2c-9(x+y)yc = -4(x+2y)2c+12(x+y)yс = (12(x+y)y — 4(x+2y)2)c = (12xy+12y2 — 4x2-16xy-16y2)c = (- 4x2-4xy-4y2)c = -4 (x2+xy+y2)c — это выражение никогда не будет положительным.
И свободные члены: 7(x+2y)(x+y)y-2(x+2y)3 = 7(x+2y)(xy+y2) — 2(x+2y)(x2+4xy+4y2) = (x+2y) (7xy+7y2-2x2-8xy-8y2) = — (x+2y)(2x2+xy+y2) — и это выражение тоже.
Таким образом, исходное неравенство будет выполняться всегда, а в равенство оно превратится только при условии равенства a=b=c.
На своей лекции Вячеслав Андреевич разобрал ещё много интересных примеров. Попробуйте и вы применить этот метод для доказательства олимпиадных неравенств. Возможно, он поможет добыть несокольо ценных баллов.
А закончим мы эту статью «любимой» фразой из книг по подготовке к олимпиадам. Доказательство первого приведённого в статье неравенства оставляем читателю 🙂
Доказательство неравенств. — Алгебра — 8 класс
Просмотр содержимого документа
«Доказательство неравенств.»
Доказательство неравенств.
Для доказательства неравенств существует несколько способов.
Доказательство неравенств на основе определения.
Метод выделения квадратов.
Метод математической индукции.
Использование специальных и классических неравенств.
Использование элементов математического анализа.
Графический метод.
Идея усиления.
Метод «от противного».
Метод использования тождеств.
Метод введения новых переменных.
Из всех приведённых способов, на данном этапе изучения неравенств нам доступны только два: на основе определения и метод выделения квадратов. Их и рассмотрим.
1. Доказательство неравенств на основе определения.
Число  больше числа
больше числа  , если их разность чисел
, если их разность чисел  и
и  положительна. Исходя из этого определения, можно записать следующие условия:
положительна. Исходя из этого определения, можно записать следующие условия:
 , если разность
, если разность  ;
;
 , если разность
, если разность  ;
;
 , если разность
, если разность  ;
;
 , если разность
, если разность  .
.
Например, доказать неравенство  .
.
Составим разность левой и правой части неравенства:
 .
.
Разность отрицательна, значит, левая часть меньше правой, ч.т.д.
2. Метод выделения квадратов.
Метод заключается в представлении неравенства в виде квадрата суммы (или разности), или в виде суммы (разности) квадратов. Мы ведь знаем, что выражение в квадрате всегда положительно, или, в крайнем случае, равно нулю.
Например, доказать неравенство  .
.
Раскроем скобки в правой части неравенства и перенесём слагаемые в левую часть, и представим число 3 в виде трёх слагаемых, каждое из которых равно1:

 .
.
Значит, неравенство верно.
Доказать неравенство:
Докажите, что для всех действительных значений х и у выполняется неравенство
Докажите, что если , то имеет место неравенство
Докажите, что если , то имеет место неравенство
Докажите неравенства:
Докажите, что если то .
Докажите, что если , то имеет место неравенство
Докажите, что если , то имеет место неравенство
Докажите, что если , то:
Докажите, что если , то .
Докажите, что при любых значениях переменной выполняются неравенства:
2
Доказательство неравенств методом математической индукции.
Доказательство методом математической индукции основано на следующей аксиоме: если предложение, в формулировку которого входит натуральное число п, истинно при п=1 и из его истинности при n=k ( где 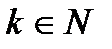 ) следует, что оно истинно и при
) следует, что оно истинно и при 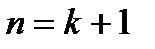 , то оно истинно при всех натуральных значениях п.
, то оно истинно при всех натуральных значениях п.
Таким образом, доказательство по методу математической индукции проводится следующим образом:
1) доказываемое утверждение проверяется при п  =1;
=1;
2) предполагая справедливость утверждения при n=k, доказывается справедливость утверждения для n=k+1.
Некоторые утверждения справедливы не для всех натуральных п, а для п, начиная с некоторого числа р. В таком случае первый шаг доказательства – это проверка справедливости утверждения для п=р  .
.
П р и м е р. Доказать, что если 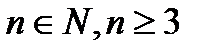 , то
, то
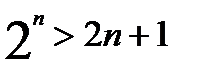
Доказательство. При n=3 неравенство верно: 
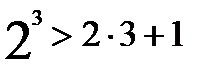 . Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что
. Предположим, что неравенство выполняется при n=k (k>3), т.е. предположим, что 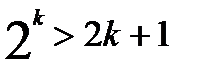 , и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что
, и докажем, что тогда неравенство выполняется и при n=k+1, т. е. докажем, что 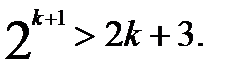
В самом деле, имеем: 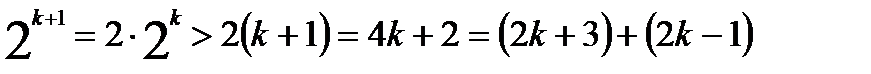 . Итак,
. Итак, 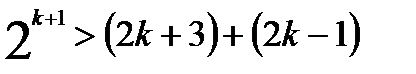 .
.
Но 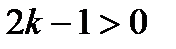
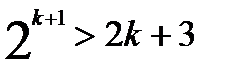 .
.
Согласно методу математической индукции можно сделать вывод о том, что доказываемое неравенство справедливо при всех 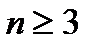 .
.
Доказательство неравенств методом полной индукции.
Полная индукция – это метод рассуждений, при котором вывод делается на основании рассмотрения всех случаев, возможных по условию задачи.
П р и м е р. Доказать, что 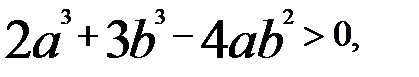 если
если 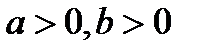 .
.
Доказательство. Рассмотрим случаи:
1) 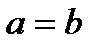
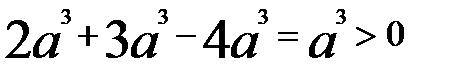 , т.к.
, т.к. 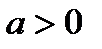
Неравенство верно.
2) 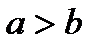 , т.е.
, т.е. 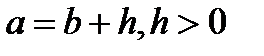 .
.
Тогда 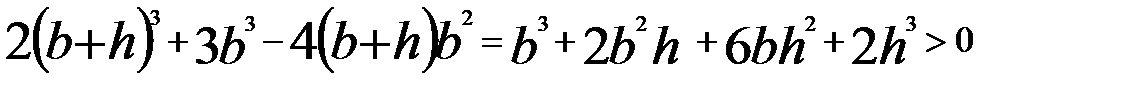 . Неравенство справедливо.
. Неравенство справедливо.
3) 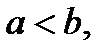 т.е.
т.е. 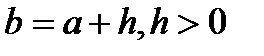 .
.
Тогда 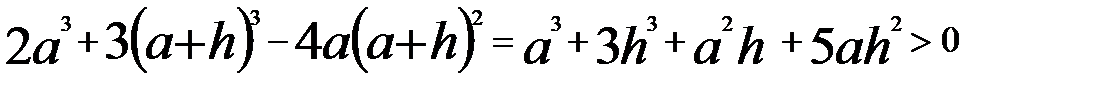 . Неравенство справедливо.
. Неравенство справедливо.
Мы рассмотрели все возможные случаи. Значит неравенство верно для 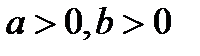 .
.
6. Доказательство неравенств с помощью методов математического анализа.
В этом случае доказательство неравенств сводят к исследованию соответствующих функций с помощью производных.
П р и м е р. Доказать неравенство 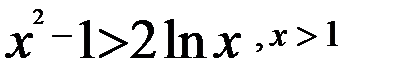
Доказательство. Перепишем неравенство в виде: 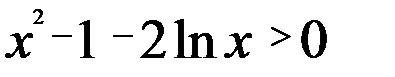 .
.
Рассмотрим функцию 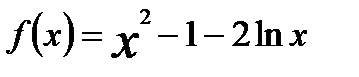 .
.
Найдём производную 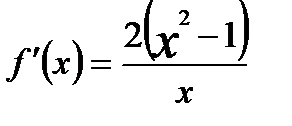 . При
. При 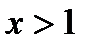 ,
, 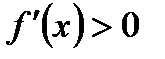 . Это значит, что при
. Это значит, что при 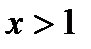
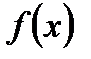 возрастает, причём
возрастает, причём 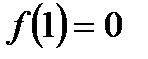 . Поэтому при
. Поэтому при 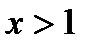
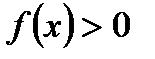 .
.
Литература
1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999
2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Тема: Иррациональные уравнения и неравенства.
План
1. Иррациональные уравнения, основные методы их решения.
2. Иррациональные неравенства.
Иррациональные уравнения.
Иррациональными называются уравнения и неравенства, содержащие переменную под знаком корня или под знаком возведения в дробную степень.
Все корни чётной степени, входящие в уравнение, являются арифметическими, т.е. если подкоренное выражение отрицательно, то корень лишён смысла; если подкоренное выражение равно нулю, то корень также равен нулю; если подкоренное выражение положительно, то значение корня положительно.
Все корни нечётной степени, входящие в уравнение, определены при любом действительном значении подкоренного выражения и в зависимости от знака подкоренного выражения могут принимать как неотрицательные, так и отрицательные значения.
Основные методы решения иррациональных уравнений:
1. возведение обеих частей уравнения в одну и ту же степень;
2. замена переменной;
3. умножение обеих частей уравнения на одну и ту же функцию;
4. применение свойств функций, входящих в уравнение.
Следует помнить, что ряд преобразований, которые применяются при реализации указанных методов, например возведение обеих частей уравнения в чётную степень, приводят к уравнению-следствию. Оно, наряду с корнями исходного уравнения содержит и другие корни, которые называют посторонними. Поэтому после решения уравнения-следствия необходимо найти способ отсеять посторонние корни. Обычно это можно сделать при помощи проверки, которая в данном случае рассматривается как один из этапов решения.
Возможен и другой путь реализации некоторых методов решения иррациональных уравнений – переход к равносильным системам, в которых учитывается область определения уравнения и требование неотрицательности обеих частей уравнения, возводимых в чётную степень.
Рассмотрим несколько примеров.
Пример 1. Решим уравнение 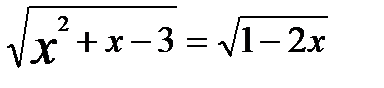 .
.
Решение. Возводим обе части уравнения в квадрат, получаем:
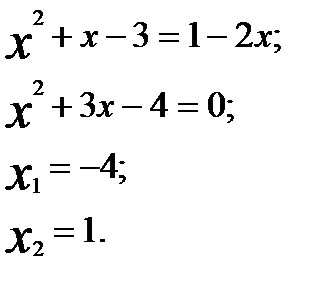
Проверка показывает, что только 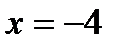 является корнем исходного уравнения.
является корнем исходного уравнения.
Ответ: -4.
Пример 2. Решим уравнение 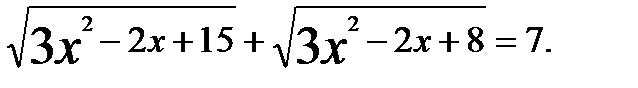
Решение. Выполним замену. Обозначим: 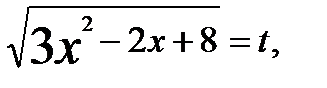 заметим, что
заметим, что 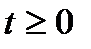 .
.
Тогда 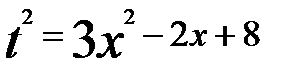 и
и 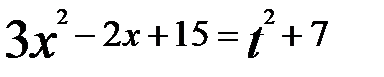 .
.
Исходное уравнение принимает вид:
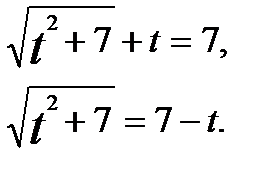
Полученное уравнение равносильно системе:
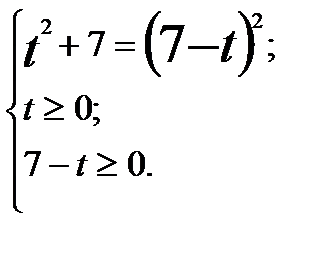
Из получившейся системы, имеем: 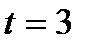 .
.
Возвращаемся к подстановке, получаем:
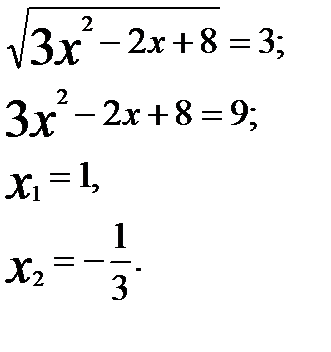
Ответ: 1; 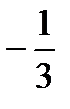 .
.
Пример 3. Решим уравнение 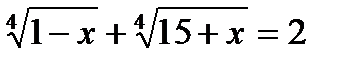 .
.
Решение: Пусть 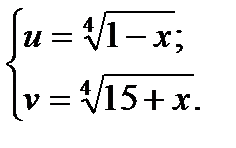
Тогда имеем:
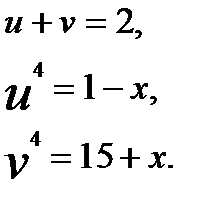
Откуда последовательно получаем:
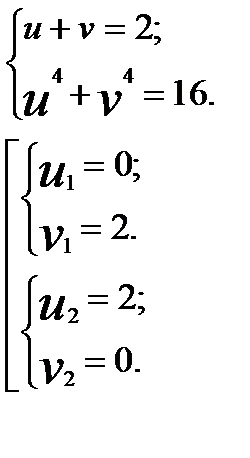
Возвращаясь к первоначальным подстановкам, получим:
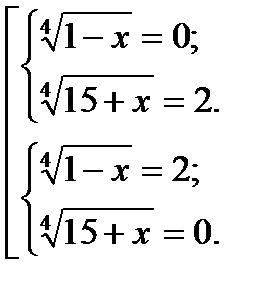
Откуда 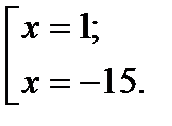
С помощью проверки убеждаемся, что оба корня являются корнями исходного уравнения.
Ответ: 1; -15.
Пример 4. Решим уравнение 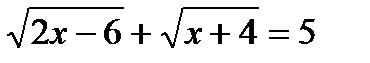 .
.
Решение: Рассмотрим функцию 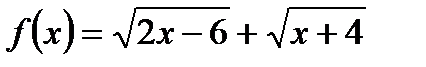 .
.
Исходное уравнение принимает вид: 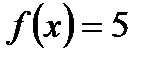 .
.
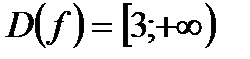 . Функция
. Функция 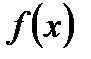 монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что
монотонно возрастает на всей области определения. Поэтому уравнение может иметь не более одного корня. Легко видеть, что 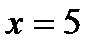 является корнем уравнения.
является корнем уравнения.
Ответ: 5.
Иррациональные неравенства.
Основным методом решения иррациональных неравенств является метод сведения исходного неравенства к равносильной системе рациональных неравенств или совокупности таких систем. При этом используются те же приёмы, что и при решении иррациональных уравнений: возведение обеих частей неравенства в одну и ту же степень, введение новых переменных, использование свойств функций, входящих в обе части неравенства и т.д.
Рассмотрим некоторые виды иррациональных неравенств и подходы к их решению:
1) Неравенство вида 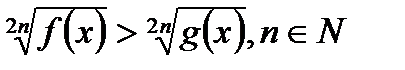 равносильно системе
равносильно системе
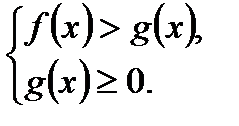
2) Неравенство вида 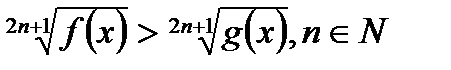 равносильно неравенству
равносильно неравенству 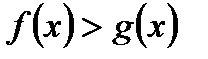 .
.
3) Неравенство вида 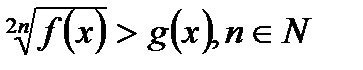 равносильно совокупности систем
равносильно совокупности систем 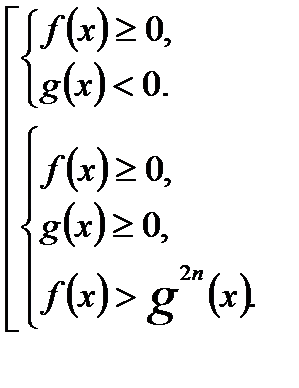
4) Неравенство вида 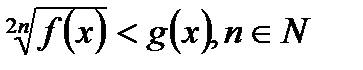 равносильно системе
равносильно системе
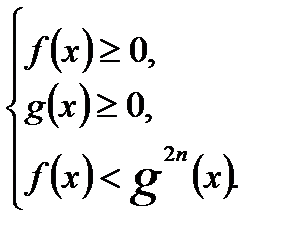
Пример 5. Решим неравенство 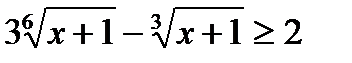 .
.
Решение. Введём новую переменную 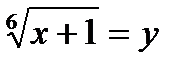 . Тогда исходное неравенство принимает вид:
. Тогда исходное неравенство принимает вид:
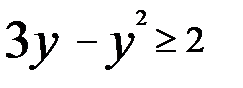 .
.
Решая это неравенство и возвращаясь к исходным переменным, получаем: 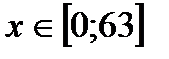 .
.
Ответ: 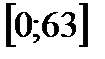 .
.
Пример 6. Решим неравенство 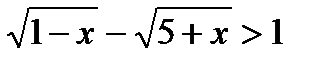 .
.
Решение: Перепишем неравенство в виде: 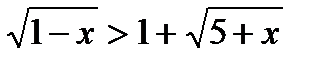 .
.
Это неравенство равносильно системе неравенств:
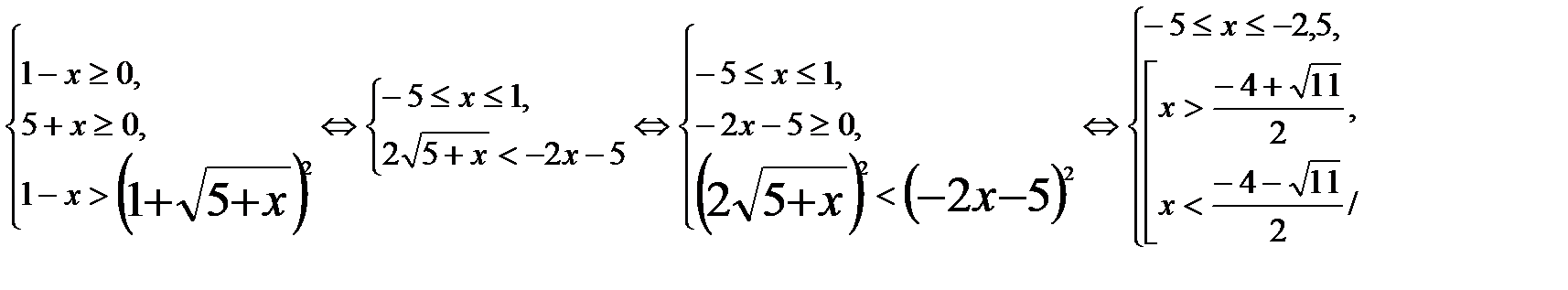 Откуда получаем
Откуда получаем  .
.
Пример 6. Решим неравенство 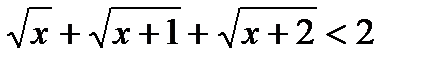 .
.
Решение: Рассмотрим функцию 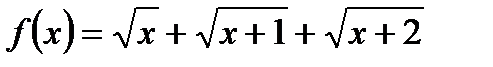 . Область определения этой функции
. Область определения этой функции 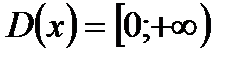 . Функция
. Функция 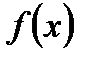 возрастает на всей области определения, причём
возрастает на всей области определения, причём 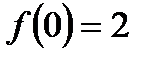 . Значит, неравенство
. Значит, неравенство 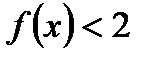 решений не имеет.
решений не имеет.
Ответ: нет решений.
Литература
1. В.Н. Литвиненко, А.Г. Мордкович. Практикум по элементарной математике. Алгебра. Тригонометрия. – М, 1999
2. Рогановский Н.М., Рогановская Е. Н. Элементарная математика- Мн., 2000
Текстовые задачи
План
Материал по математике «Доказательство неравенств»
Доказательство неравенств. Существует несколько методов доказательства неравенств. Мы рассмотрим их на примере неравенства:
 где a – положительное число.
где a – положительное число.
1). Использование известного или ранее доказанного неравенства.
Известно, что ( a – 1 )²  0 .
0 .

2). Оценка знака разности между частями неравенства.
Рассмотрим разность между левой и правой частью:

более того, равенство имеет место только при a = 1 .
3). Доказательство от противного.
Предположим противное:

Умножая обе части неравенства на a , получим: a 2 + 1 a, т.e.
a 2 + 1 – 2a или ( a – 1 ) 2 что неверно. ( Почему ? ) .
Полученное противоречие доказывает справедливость
рассматриваемого неравенства.
4). Метод неопределённого неравенства.
Неравенство называется неопределённым, если у него знак \/ или /\ ,
т.е. когда мы не знаем в какую сторону следует повернуть этот знак,
чтобы получить справедливое неравенство.
Здесь действуют те же правила, что и с обычными неравенствами.
Рассмотрим неопределённое неравенство:

Умножая обе части неравенства на a , получим: a 2+ 1 \/ 2a, т.e.
а 2 + 1 – 2a \/ 0 , или ( a – 1 )2 \/ 0 , но здесь мы уже знаем, как повернуть
знак \/ , чтобы получить верное неравенство ( Как? ). Поворачивая его
в нужном направлении по всей цепочке неравенств снизу вверх, мы
получим требуемое неравенство.
Решение неравенств. Два неравенства, содержащие одни и те же неизвестные, называются равносильными, если они справедливы при одних и тех же значениях этих неизвестных. Такое же определение используется для равносильности двух систем неравенств. Решение неравенств — это процесс перехода от одного неравенства к другому, равносильному неравенству. Для этого используются основные свойства неравенств (см. параграф «Неравенства: общие сведения»). Кроме того, может быть использована замена любого выражения другим, тождественным данному. Неравенства могут быть алгебраические ( содержащие только многочлены ) и трансцендентные ( например, логарифмические или тригонометрические ). Мы рассмотрим здесь один очень важный метод, используемый часто при решении алгебраических неравенств.
Метод интервалов. Решить неравенство: ( x – 3 )( x – 5 ) x – 3 ). Здесь нельзя делить обе части неравенства на ( x – 3 ), так как мы не знаем знака этого двучлена ( он содержит неизвестное x ). Поэтому мы перенесём все члены неравенства в левую часть:
( x – 3 )( x – 5 ) – 2( x – 3 )
разложим её на множители:
( x – 3 )( x – 5 – 2 ) ,
и получим: ( x – 3 )( x – 7 ) x = 3 и x = 7 — корни этого выражения. Поэтому вся числовая ось разделится этими корнями на следующие три интервала:

В интервале I ( x 3 ) оба сомножителя отрицательны, следовательно, их произведение положительно; в интервале II ( 3 x 7 ) первый множитель ( x – 3 ) положителен, а второй ( x – 7 ) отрицателен, поэтому их произведение отрицательно; в интервале III ( x 7 ) оба сомножителя положительны, следовательно, их произведение также положительно. Теперь остаётся выбрать интервал, в котором наше произведение отрицательно. Это интервал II, следовательно, решение неравенства: 3 x 7. Последнее выражение — так называемое двойное неравенство. Оно означает, что x должен быть одновременно больше 3 и меньше 7.
П р и м е р . Решить следующее неравенство методом интервалов:
( x – 1 )( x – 2 )( x – 3 ) … ( x –100 ) 0 .
Р е ш е н и е . Корни левой части неравенства очевидны: 1, 2, 3, …, 100.
Они разбивают числовую ось на 101 интервал:

Так как количество скобок в левой части чётно (равно 100), то
при x
положительно. При переходе через корень происходит смена
знака произведения. Поэтому следующим интервалом, внутри
которого произведение положительно, будет ( 2, 3 ), затем ( 4, 5 ),
затем ( 6, 7 ), … , ( 98, 99 ) и наконец, x 100.
Таким образом, данное неравенство имеет решение:
x x x x 100.
Итак, чтобы решить алгебраическое неравенство, надо перенести все его члены в левую (или правую) часть и решить соответствующее уравнение. После этого найденные корни нанести на числовую ось; в результате она разбивается на некоторое число интервалов. На последнем этапе решения нужно определить, какой знак имеет многочлен внутри каждого из этих интервалов, и выбрать нужные интервалы в соответствии со знаком решаемого неравенства.
Заметим, что большинство трансцендентных неравенств заменой неизвестного приводятся к алгебраическому неравенству. Его надо решить относительно нового неизвестного, а затем путём обратной замены найти решение для исходного неравенства.
Системы неравенств. Чтобы решить систему неравенств, необходимо решить каждое из них, и совместить их решения. Это совмещение приводит к одному из двух возможных случаев: либо система имеет решение, либо нет.
П р и м е р 1. Решить систему неравенств:

Р е ш е н и е. Решение первого неравенства: x x 6.
Таким образом, эта система неравенств не имеет решения.
( Почему ? )
П р и м е р 2. Решить систему неравенств:

Р е ш е н и е. Первое неравенство, как и прежде, даёт: x
второго неравенства в данном примере: x 1.
Таким образом, решение системы неравенств: 1 x
индукция / Как доказывать неравенства? / Математика
Возьмем логарифм с обеих сторон: $${(n!)^2} > {n^n} \Leftrightarrow 2\log n! > n\log n$$
Докажем по индукции $$\log n! \geqslant \frac{1}{2}n\log n,\,\,\,\,\,\forall n \geqslant 2$$
База индукции: $$n = 2 \Leftrightarrow {\log _2}2! = 1 \geqslant \frac{1}{2} \cdot {\text{2}} \cdot {\text{lo}}{{\text{g}}_2}{\text{2 = 1 ВЕРНО}}$$
Индукционная гипотеза: $$\log ((n — 1)!) \geqslant \frac{1}{2}(n — 1)\log (n — 1)$$
Имеем: $$\log n! = \log (n \cdot (n — 1)!) = \log n + \log ((n — 1)!) \geqslant \log n + \frac{1}{2}(n — 1)\log (n — 1)$$
Теперь нам нужно показать, что $%\log (n — 1) \geqslant \log n — \varepsilon $% для очень маленьких значений эпсилона. Для доказательства константы $%\varepsilon $% не достаточно, нужно что-то порядка $%\frac{1}{n}$%. Воспользуемся разложением в ряд Тейлора $%{e^x}$%: $${e^x} = 1 + \frac{x}{{1!}} + \frac{{{x^2}}}{{2!}} + \frac{{{x^3}}}{{3!}} + \ldots $$
Следовательно, для любого $%x > 0$%, получим $%{e^x} > 1 + x$%. Подставив $%\frac{1}{{n — 1}}$% вместо $%x$%, имеем $%{e^{\frac{1}{{n — 1}}}} > 1 + \frac{1}{{n — 1}} = \frac{n}{{n — 1}}$%. Возьмем логарифм с обеих сторон: $$\frac{1}{{n — 1}}\log e > \log \frac{n}{{n — 1}} \Leftrightarrow \log (n — 1) > \log n — \frac{{\log e}}{{n — 1}}$$
Подставим полученное значение в $$\log n! = \log (n \cdot (n — 1)!) = \log n + \log ((n — 1)!) \geqslant \log n + \frac{1}{2}(n — 1)\log (n — 1)$$
$$\eqalign{ & \log n! \geqslant \log n + \frac{1}{2}(n — 1)\log (n — 1) \cr & \,\,\,\,\,\,\,\,\,\,\,\, > \log n + \frac{1}{2}(n — 1)(\log n — \frac{{\log e}}{{n — 1}}) = \log n + \frac{1}{2}(n — 1)\log n — \frac{1}{2}\log e \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}n\log n + \frac{1}{2}\log n — \frac{1}{2}\log e \cr} $$
Теперь достаточно показать, что $$\frac{1}{2}\log n — \frac{1}{2}\log e \geqslant 0 \Leftrightarrow \log n \geqslant \log e \Leftrightarrow n \geqslant e$$
Последнее неравенство выполняется для всех $%n \geqslant 3$%, отсюда следует что, $$\log n! \geqslant \frac{1}{2}n\log n.$$ Это доказывает индукционный шаг.
доказать_неравенство / Неравенство / Математика
Замена: $%x=a-1, y=b-1, z=c-1$%. Ограничение: $%x, y, z \in [-1; \infty)$%. Неравенство: $$(3+x+y)(3+y+z)(3+y+z) \leq 9((1+x)(1+y)+(1+x)(1+z)+(1+y)(1+z))$$
Ясно, что самый простой случай — это неотрицательные $%x, y, z$%. Впрочем, рассмотрим левую часть по порядку. А для начала узнаем, что правая часть нам готовит.
$$R = 9(3+2(x+y+z)+xy+xz+yz)$$ $$L=(3+(x+y))(3+(x+z)(3+(y+z))$$
Левая часть раскладывается на 8 слагаемых.
Первое — это $%27$%. Оно соответствует первому слагаемому в правой части.
Ещё три штуки — это $%9 \cdot 2 \cdot (x+y+z)$%: второе слагаемое в правой части.
Ещё три штуки — позубастее. Это тройка, вынесенная в качестве общего множителя за сумму трёх слагаемых вида $%(w_1+w_2)(w_1+w_3) = w_1^2+w_1 w_2+w_1 w_3+w_2 w_3$%, где $%w_1$% принимает по очереди вид каждой переменной $%x, y, z$%. Стало быть, у нас есть третье слагаемое правой части и ещё вдобавок $%x^2+y^2+z^2$%.
Если считать, что $%x, y, z$% неотрицательны, то неравенство уже выполнено. Если считать, что какие-то (не все) из этих величин лежат в интервале $%[-1; 0)$%, то надо рассмотреть последнее слагаемое левой части $%L_8$%. Заведомо выполняется неравенство, если справедливо: $$|(x+y)(x+z)(y+z)| \leq 3(x^2+y^2+z^2)$$
Можно переписать: $%|L_8|=|x^2(y+z)+y^2(x+z)+z^2(x+y)+2xyz|$%. В самом худшем случае все слагаемые имеют одинаковый знак — этот случай и будем рассматривать. Тогда верно, что $%|L_8|=x^2|y+z|+y^2|x+z|+z^2|x+y|+2|xyz|$%.
Рассмотрим случай, когда ни одна переменная не равна нулю, но все переменные по модулю не больше единицы. Поделим правую часть на $%|xyz|=|x||y||z|$%. Можно утверждать, что: $$\frac{3|x|}{|y||z|}+\frac{3|y|}{|y||z|}+\frac{3|z|}{|x||y|} \geq \frac{(|y+z|+1)|x|}{|y||z|}+\frac{(|x+z|+1)|y|}{|y||z|}+\frac{(|x+y|+1)|z|} {|x||y|}$$
Правая часть означенного неравенства больше левой части предыдущего неравенства, поделёной на $%|x||y||z|$%, если $%\frac{|x|}{|y||z|}+\frac{|y|}{|x||z|}+\frac{|z|}{|x||y|} \geq 2$%, что заведомо верно, так как выражение можно переписать в виде $%\frac{1}{|z|}(\frac{|x|}{|y|}+\frac{|y|}{|x|}+A)$%, где $%A > 0$%. Это значит, что доказано и проверочное неравенство для нашего случая, а с ним и исходное неравенство (то самое, где были заменены переменные).
Если любые две переменные в самом первом неравенстве равны единице, доказательство совершенно очевидно. Если $%|x|=0$%, то надо доказать $%y^2|z|+z^2|y| \leq 3y^2+3z^2$%; здесь тоже всё очевидно.
Добавление:
Рассмотрим теперь неравенство: $$x^2(3+y+z)+y^2(3+x+z)+z^2(3+x+y)+2xyz < 0$$
Надо доказать, что у него нет правильных решений (из ОДЗ: $%x, y, z \in [-1; \infty)$%), и дело в шляпе. Какие у него могли бы быть решения?
Прежде всего: количество отрицательных переменных — нечётное; либо одна, либо три. Если их три, то увеличение модуля любой переменной не нарушает неравенства: первые три слагаемых становятся по модулю меньше, а последнее — больше. Но если $%x=y=z=-1$%, то неравенство не выполняется. Значит, отрицательна всего одна переменная; назовём её $%x$%.
Далее: величина $%(x+y)(x+z)(y+z)$% — тоже отрицательная; следовательно, только одно число может превышать по модулю единицу; пусть это $%z$%. Тот случай, когда ни одно число не превышает по модулю единицу, был уже рассмотрен; осталось рассмотреть случай, когда превышает.
Может ли быть $%z^2(3+x+y) < 2|xyz|$%? Левая часть больше $%2z^2$%. Правая часть меньше $%2z$%. Следовательно, такого быть не может.
Шляпа готова.