Как доказывать теорему?
Если в обычной жизни, для того чтобы на что-то указать, достаточно сказать: «Смотри!» и все сразу становится ясно, то в науке, любой факт, должен подтверждаться для того чтобы его признали. То же самое творится с теоремами в математике, ведь они являются недоказанными утверждениями. Они доказываются путем цепочки логических мышлений и с помощью аксиом, которые не ставятся под сомнение.
Итак, как нужно доказывать теорему? Теорему можно доказать путем логического мышления и выстраивания логической цепочки. Также применяются заранее доказанные теоремы и аксиомы. Все предельно просто, если включить логику и действовать по конкретному алгоритму доказывания теорем.
Каким правилам следовать в доказывание теоремы?
- Нужно найти последовательность аксиом, теорем и т.д., которые могли бы помочь доказывать теорему. Следуя им нужно составить логичную цепочку.
- Нет обязательных правил, которые помогли бы доказать теорему. Правила указывают возможное направление, которое поможет доказать теорему и носят название
- Объекты, о которых речь в теореме нужно заменить другими названиями и определениями, которые могли бы отражать его сущность и указать на конкретные характеристики объекта.
- В случае сложной теоремы допускается разделение теоремы на части и доказательство каждой части по отдельности.
- Доказывать теорему нужно в двух направлениях, от заключения к условиям и от условий к заключению.
- Начиная доказывать теорему нужно идти с отрицанием того что нужно доказать, чтобы в итоге доказать что первоначальное предположение подтвердилось. Итак, начинать нужно со слов «предположим обратное», а в конце дойти до вывода, что «первоначальное подтверждение является верным».
Что касается практической части, с чего и следует начать, это создать графический чертеж теоремы. Для этого нужно создать две графы «Дано» и «Доказано». В первой графе записываете те факты, которые известны, а во второй, то, что следует доказать.
Заметка: если у вашего папы скоро днюха, самое время выбрать подарок отцу на день рождение (http://www.gift-for-man.ru/).
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Как доказывать теоремы?
Как доказывать теоремы?


Процедура доказательства теоремы только кажется сложной. Достаточно уметь логически мыслить, иметь необходимые знания по данной научной дисциплине, и доказать теорему для вас не составит труда. Важно выполнять все действия четко в правильной последовательности.
В некоторых науках, к примеру, в алгебре и геометрии, одним из важнейших умений является умение доказывать теоремы. Это связано с тем, что доказанные теоремы впоследствии пригодятся для того, чтобы решать задачи. Нужно не просто выучить алгоритм доказательства, а суметь понять ее суть. Давайте разберемся, как доказывать теоремы.
Доказательство теорем
Для начала следует сделать чертеж, он должен быть четким и аккуратным. После этого нужно отметить на нем заданные условия. В графе «Дано» нужно записать все величины, которые вам изначально известны, и то, что нужно доказать. После этого можно заняться доказательством. По сути, это цепочка логически выстроенных мыслей, которые позволяют показать то, что какое-либо утверждение является верным. Доказательство теоремы подразумевает использование других теорем, аксиом, применение действия от противного и т.д.Итак, доказательством теоремы является определенная последовательность действий, позволяющих получить утверждение, истинность которого нельзя оспорить. Как правило, наиболее трудным во время доказательства является как раз поиск последовательности логических рассуждений. Если же это удастся, то вы сможете доказать то, что от вас требовалось.
Как доказывать теоремы по геометрии без труда
Чтобы упростить себе задачу, можно разбить теорему на части, и доказывать каждую из них по отдельности, что в итоге приведет вас к результату. В некоторых случаях эффективно использовать метод «доказательства от противного». Тогда нужно начинать со слов «предположим обратное». Следует объяснить, почему в данном случае то или иное заключение невозможно. Заканчивать нужно словами «значит, первоначальное утверждение является верным. Теорема доказана».
Еще больше полезной информации по геометрии можно найти в разделе Геометрия.
/math/ — Как научиться доказывать теоремы?
>>3759Радоваться отсутствию знаний — это так… по-русски, что ли. Я разбираюсь в этом лучше вас, потому что я знаю об этом меньше вас! Невежество — это знание, свобода — это рабство, или как там было?
>>3759
Короткий ответ: да, есть.
Чуть менее короткий ответ: у тебя нет совершенно никакой базы, и поэтому ты задаешь какие-то идиотские вопросы, если уж быть честным, извини. Учитывая, что ты оперируешь понятиями «дерьмо\не дерьмо» и «невозможно слушать впринципе», я сильно сомневаюсь, что я смогу тебе что-то объяснить. Ты какой-то особенный, понятный одному тебе смысл вкладываешь в слово «теория». И мне совершенно непонятно, что ты имел в виду под «музыку идущую в совершенно разных строях».
Давай еще раз. Звуковысотность — только одна из многих составляющих музыки. Ее можно вообще убрать, вообще не использовать, понимаешь? Вообще без нот музыка может быть, окей? И писать такую музыку тоже учатся, никто не умер.
По поводу дерьма\недерьма: я лично видел человека, который утверждал, что Хроматическая фантазия Баха — случайный набор нот. Он вообще не слышал там мелодии, не улавливал совершенно. Для него это было «невозможно слушать впринципе». Улавливаешь? Так и сюда может зайти какой-нибудь анончик и сказать, что дерьмо все эти ваши гомотопии, невозможно понять впринципе их.
Наконец, просить дать какую-то теорию, которая позволит написать заебись)) и недерьмо музыку — это как просить теорию, которая позволит придумать и доказать какую-нибудь заебись и недерьмо теорему. Ну то есть… Ээ… Вот тебе zfc, сиди и придумывай. Осознаешь всю идиотичность такого вопроса? В музыке абсолютно то же самое. Теория — это не алгоритм как сделать «заебись))», это определенная система, в рамках которой можно работать. В любой системе можно доказывать интересные или неинтересные теоремы, в любой системе можно писать интересную или неинтересную музыку. Теория не делает «заебись))», теория дает инструменты.
И все, иди читай Способина-Холопова, слушай Сорабджи и Шенберга, читай Мочидзуку, унижай второкультурщиков и т.п., я съебываю.
Как доказывать теоремы 🚩 доказательство теоремы 🚩 Образование 🚩 Другое
Не только каждый школьник, но и каждый уважающий себя образованный человек должен знать, что такое теорема и доказательство теорем. Может, такие понятия и не встретятся в реальной жизни, но структурировать многие знания, а также делать умозаключения они точно помогут. Именно поэтому мы и рассмотрим в этой статье способы доказательства теорем, а также ознакомимся со столь знаменитой теоремой Пифагора.
Что же такое теорема
Если рассматривать школьный курс математики, то очень часто в нем встречаются такие научные термины, как теорема, аксиома, определение и доказательство. Для того чтобы ориентироваться в программе, нужно ознакомиться с каждым из этих определений. Сейчас же мы рассмотрим, что такое теорема и доказательство теорем.

Итак, теорема – это некое утверждение, которое требует доказательства. Рассматривать данное понятие нужно параллельно с аксиомой, так как последняя доказательства не требует. Ее определение уже является истинным, поэтому воспринимается как должное.
Сфера применения теорем
Ошибочно думать, что теоремы применяются только в математике. На самом деле это далеко не так. Например, существует просто невероятное количество теорем в физике, позволяющих подробно и со всех сторон рассмотреть некоторые явления и понятия. Сюда можно отнести теоремы Ампера, Штейнера и многие другие. Доказательства таких теорем позволяют неплохо разобраться в моментах инерции, статике, динамике, и во многих других понятиях физики.
Использование теорем в математике
Тяжело представить себе такую науку, как математика, без теорем и доказательств. Например, доказательства теорем треугольника позволяют подробно изучить все свойства фигуры. Ведь очень важно разобраться в признаках подобия, свойствах равнобедренного треугольника и во многих других вещах.

Доказательство теоремы площади позволяет понять, как проще всего вычислять площадь фигуры, опираясь на некоторые данные. Ведь, как известно, существует большое количество формул, описывающих, как можно найти площадь треугольника. Но перед тем как их использовать, очень важно доказать, что это возможно и рационально в конкретном случае.
Как доказывать теоремы
Каждый школьник должен знать, что такое теорема, и доказательство теорем. На самом деле доказать какое-либо утверждение не так-то просто. Для этого нужно оперировать многими данными и уметь делать логические выводы. Конечно, если вы неплохо владеете информацией по определенной научной дисциплине, то доказать теорему для вас не составит особого труда. Главное — выполнять процедуру доказательства в определенной логической последовательности.
Для того чтобы научиться доказывать теоремы по таким научным дисциплинам, как геометрия и алгебра, нужно иметь неплохой багаж знаний, а также знать сам алгоритм доказательства. Если вы освоите такую процедуру, то решать математические задачи впоследствии для вас не составит особого труда.
Что нужно знать о доказательстве теорем
Что такое теорема и доказательства теорем? Это вопрос, который волнует многих людей в современном обществе. Очень важно научиться доказывать математические теоремы, это поможет вам в будущем строить логические цепочки и приходить к определенному выводу.

Итак, для того чтобы доказывать теорему правильно, очень важно сделать правильный рисунок. На нем отобразите все данные, которые были указаны в условии. Также очень важно записать всю информацию, которая предоставлялась в задаче. Это поможет вам правильно проанализировать задание и понять, какие именно величины в нем даны. И только после проведения таких процедур можно приступать к самому доказательству. Для этого вам нужно логически выстроить цепочку мыслей, используя другие теоремы, аксиомы или определения. Итогом доказательства должен быть результат, истинность которого не подлежит сомнению.
Основные способы доказательства теорем
В школьном курсе математики существует два способа, как доказать теорему. Чаще всего в задачах используют прямой метод, а также метод доказательства от противного. В первом случае просто анализируют имеющиеся данные и, опираясь на них, делают соответственные выводы. Также очень часто используется и метод от противного. В этом случае мы предполагаем противоположное утверждение и доказываем, что оно неверно. На основе этого мы получаем противоположный результат и говорим о том, что наше суждение было неверным, а значит, указанная в условии информация является правильной.

На самом деле многие математические задачи могут иметь несколько способов решения. Например, теорема Ферма доказательств имеет несколько. Конечно, некоторые рассматриваются только одним способом, но, например, в теореме Пифагора можно рассмотреть сразу несколько из них.
Что представляет собой теорема Пифагора
Конечно, каждый школьник знает о том, что теорема Пифагора касается именно прямоугольного треугольника. И звучит она так: «Квадрат гипотенузы равен сумме квадратов катетов». Несмотря на название данной теоремы, открыта она была не самим Пифагором, а еще задолго до него. Существует несколько способов доказательства данного утверждения, и мы рассмотрим некоторые из них.
Согласно научным данным, в самом начале рассматривался равносторонний прямоугольный треугольник. Затем строились квадраты на всех его сторонах. Квадрат, построенный на гипотенузе, будет состоять из четырех равных между собой треугольников. В то время как фигуры, построенные на катетах, будут состоять только из двух таких же треугольников. Такое доказательство теоремы Пифагора является самым простым.
Рассмотрим еще одно доказательство данной теоремы. В нем нужно использовать знания не только из геометрии, но также и из алгебры. Для того чтобы доказать данную теорему этим способом, нам нужно построить четыре аналогичных прямоугольных треугольника, и подписать их стороны как а, в и с.

Построить эти треугольники нужно таким образом, чтобы в результате у нас получилось два квадрата. Внешний из них будет иметь стороны (а+в), а вот внутренний – с. Для того чтобы найти площадь внутреннего квадрата, нам нужно найти произведение с*с. А вот для того чтобы найти площадь большого квадрата, нужно сложить площади маленьких
Статья «Изучение и доказательство теорем»
Е.В. Петрова,учитель математики СОШ №25 г. Владимира
Доказательство — это рассуждение, которое убеждает. (Ю.А. Шиханович)
Изучение и доказательство теорем.Реализация современной роли математики предполагает улучшение математической подготовки учащихся, важное место в котором отводится умению открывать закономерности, обосновывать их и применять на практике. Формирование алгоритмического, эвристического, абстрактного мышления учащихся осуществляется также главным образом в процессе доказательства. Обучение математике предполагает обучение способам деятельности по приобретению знаний, что требует выявления и освоения в процессе обучения математике различных схем используемых в математике рассуждений. В опытных науках мы постоянно обращаемся к наблюдениям и экспериментам, чтобы проверить те или иные утверждения. Совершенно иначе дело обстоит в математике. Теорема считается доказанной только в том случае, если она логически выведена из других предложений. Поэтому проблема обучения учащихся доказательству всегда являлась одной из центральных в методике преподавания математики.
В настоящее время, идущий процесс гуманизации образования предполагает направленность обучения на развитие личности, на формирование нравственности, чему способствует обучение доказательству, где важная роль отводится обучению поиска способов доказательства, их сравнения, выбора наиболее простого из них.
Что значит доказать теорему, что такое доказательство?
Когда вы убеждаете своего товарища в чем-либо или отстаиваете в споре с ним свое мнение, свою точку зрения, то вы по существу производите доказательство (умело или неумело — это уже другой вопрос).
Математическое доказательство должно представлять собой цепочку логических следствий из исходных аксиом, определений, условий теоремы и ранее доказанных теорем до требуемого заключения. Основную нагрузку по формированию у учащихся умения доказывать несёт курс геометрии. Д. Пойа указывал на важную роль, которую играют доказательства при построении геометрической системы: «Геометрическая система цементирована доказательствами. Каждая теорема связана с предшествующими аксиомами, определениями и теоремами каким-нибудь доказательством. Без понимания таких доказательств нельзя понять самую сущность системы». Исторически сложилось так, что геометрия как учебный предмет имеет большое значение для изучения окружающего мира и создаёт благоприятные условия для приобщения учащихся к творческой исследовательской деятельности. Изучение геометрии способствует развитию умения доказывать, т.е. умения логически мыслить и рассуждать. Развитие логического мышления происходит в ходе изучения приводимых в учебниках и учителем доказательств теорем, при решении задач. Что значит доказать теорему, что такое доказательство? Доказательство в широком смысле — это логическое рассуждение, в процессе которого истинность какой-либо мысли обосновывается с помощью других положений. В математике недопустимо ссылаться, например, на очевидные отношения , иллюстрируемые чертежом. Математическое доказательство должно представлять собой цепочку логических следствий из исходных аксиом, определений, условий теоремы и ранее доказанных теорем до требуемого заключения.
Таким образом, при доказательстве теоремы мы сводим ее к ранее доказанным теоремам, а те в свою очередь еще к другим и т.д. Очевидно, что этот процесс сведения должен быть конечным, и поэтому всякое доказательство в конце концов сводит доказываемою теорему к исходным определениям и принятым без доказательства аксиомам.
Процесс доказательства – сложный процесс мышления, и он формируется лишь постепенно, от простых к более сложным структурам. Следовательно, обучение доказательству представляет собой сложную систему, структура которой обусловлена многочисленными связями между различными ее составляющими.
К 13 – 14 годам мозг школьника становится способным овладеть абстрактным, обоснованным, рассуждающим мышлением. Развитие доказательного мышления, отмечает П. П. Блонский, проходит две стадии. В подростковом возрасте школьник скорее усваивает доказательства, чем самостоятельно пользуется ими, и еще меньше он создает их: в этом возрасте доказывание скорее дело памяти. В юношеском же возрасте уже заметно выступают критическое мышление к даваемым доказательствам и стремление к своим доказательствам. Все вышесказанное приводит к выводу о необходимости исследования индивидуальных познавательных стратегий школьников при изучении и доказательстве теорем.
Над этой проблемой я работаю первый год.Сначала я определила цель, задачи и гипотезу исследования.
Цель: выявить и развить индивидуальные стратегии изучения и доказательства теоремы в 8 классе.
Задачи:
1. Выявить индивидуальные стратегии изучения и доказательства теорем на основе вопросника (с элементами листа анализа).
2. Развить индивидуальные стратегии учащихся через обсуждение полученных результатов, создание банка успешных действий при выполнении изучения и доказательства теорем.
3. Разработать советы по успешному изучению теорем по геометрии.
4. Проанализировать результаты освоения учащимися теорем до и после применения технологии ЦРПС, разработать и апробировать памятку успешной деятельности учеников.
Гипотеза: осмысление учащимися собственных действий при изучении теорем позволит развить навыки доказательстваирешения задач по геометрии, достичь более высоких результатов обучения.
Школьные учебники геометрии показывают готовое доказательство теорем, но не обучают самому процессу доказательства. Учащиеся нередко испытывают трудности в усвоении теорем и воспроизведении их доказательств. Хорошо известен страх многих учащихся перед словом «теорема». Преодолеть его помогает целенаправленная работа в соответствии с теорией поэтапного формирования умственных действий П.Я. Гальперина. Чтобы обеспечить усвоение теорем, их доказательств и научить самостоятельно решать задачи по геометрии, в соответствии с этой теорией необходимо организовать самостоятельную деятельность учащихся. Необходимо научить учащихся доказывать теорему самостоятельно.
Под обучением доказательству надо понимать обучение учащихся анализу готовых доказательств, их воспроизведению, самостоятельному открытию фактов, поиску других путей доказательств, а также опровержению выдвинутых предложений.
Свой эксперимент я начала с вопроса, на который получила неожиданный ответ.
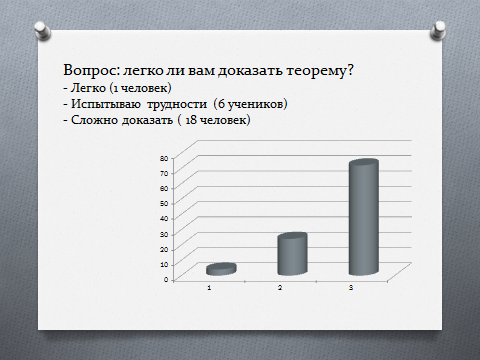
На первом этапе учащимся было предложено описать действия, которые они совершают при знакомстве и доказательстве теоремы. В результате были получены следующие варианты:
***
Читаю по учебнику теорему.
Учу.
В классе доказываю теорему.
***
Учу, как стихотворение. Когда рассказываю, то боюсь сбиться.
. ***
1.Учу по учебнику теорему.
2. Кратко записываю для себя доказательство.
3. Доказываю теорему, используя записи.
4. Рассказываю доказательство маме.
5. В классе доказываю теорему учителю.
После анализа индивидуальных стратегий я поняла, почему ребятам сложно доказать теорему. Это происходит потому, что они в принципе не понимают, что значит « выучить теорему». Далее, я выявила причины затруднений. Это и плохое качество знаний, неумение их применять, неосознанность умственных операций, неумение устанавливать связи между логическими шагами, слабая мотивация и т.д. Реализация требования «доказать теорему» предполагает ряд действий. Без овладения этими действиями в мышлении ученика не возникнет ассоциаций, которые позволили бы ему продвигаться в доказательстве теорем. К числу таких мыслительных операций относятся: выделить условие и заключение теоремы, зафиксировать их словесно и графически, разбить доказательство на части, каждую из которых проанализировать, сделать выводы и двигаться дальше. Следовательно, необходимо сформировать у учащихся в мышлении нужные для осуществления доказательства действия.
При изучении теоремы« Первый признак подобия треугольников», я составила для учащихся вопросник. Эти вопросы заставили задуматься над содержанием теоремы, над этапами доказательства, вызвав при этом в мышлении учащихся нужные ассоциации.
Вопросник.
С какого действия начали знакомство с теоремой?
Как вы понимаете, что это теорема?
Что мотивирует вас на изучение доказательства теоремы?
Сколько раз прочитали теорему?
Что дано?
Что надо доказать?
Поможет ли чертеж при доказательстве теоремы?
С чего вы начали изучать доказательство теоремы?
Можно ли доказательство теоремы разбить на части?
Знание каких фактов ,теорем, определений вам пригодилось?
Что вам мешало при доказательстве теоремы?
А что помогало доказать теорему?
Как вы поняли, что теорема доказана?
Какое открытие вы для себя сделали?
Вы довольны? Что вы при этом испытываете?
Какие советы вы могли бы дать тем ,кому предстоит изучать теорему?
Вот некоторые из ответов на данные вопросы.
Юля:
Открыла учебник, нашла теорему, познакомилась зрительно.
Прочитала.
Стала изучать, т. К. мне интересно.
2 раза прочла теорему.
Дан первый признак подобия треугольников.
Что, если 2 угла одного треугольника равны 2 соответственным углам другого треугольника, то такие треугольники подобны.
Да.
С текста.
Да.
Да.
Несосредоточенность, много новых слов.
Чертеж.
Когда поняла о чем теорема , посмотрела доказательство.
————
Антон:
С открытия учебника.
Там написано, что это теорема.
Знание теоремы и оценка.
2 раза.
Два треугольника.
Подобие треугольников.
Да.
С прочтения.
Да.
Теорема об отношении площадей подобных треугольников.
Незнание некоторых нужных фактов.
Помогла память.
В учебнике написано, что теорема доказана.
Я узнал новую теорему.
Да, я доволен.
Быть внимательным.
Алина:
Я ищу нужную мне теорему в учебнике, читаю ее, пытаюсь вникнуть в текст.
Я понимаю, что это теорема, т. к. к правилу дано доказательство этого факта.
Умение и понимание решения задач.
Я перечитываю теорему, пока не запомню ее, раза 4 -6.
Даны 2 треугольника, обозначены равные углы.
Подобие этих двух треугольников.
Чертеж поможет мне лучше понять, что нужно доказать и разобраться с условием.
Сначала я прочитаю все доказательство, потом сделаю чертеж и , внимательно вчитываясь, начну разбирать доказательство.
Что дано – подход к решению проблемы – доказательство – вывод.
Мне помогла с доказательством теорема о сумме углов треугольника, определение подобных треугольников, теорема об отношении площадей подобных треугольников.
Ничего не мешало.
Знание определения о подобных треугольниках, знание других теорем и фактов.
Дан вывод, и когда мы получили то, что нужно было доказать, заканчиваю словами «теорема доказана».
Я открыла для себя новый признак подобия треугольников и впервые сама смогла разобрать доказательство новой теоремы.
Учите теорему в тишине, вникая в текст. Сначала выучите формулировку теоремы, вспомните материал, который может помочь при доказательстве.
Виктория:
Открыла учебник, нашла нужную мне теорему, прочитала ее, стараясь запомнить ее.
Это предложение, которое надо доказать.
Меня мотивирует: а) получение хорошей оценки, т. к. это очень важно моим родителям и моему будущему; б) Изучение теорем развивает логическое мышление, а логика нужна при решении задач по геометрии. Значит, изучая теоремы, я учусь решать задачи.
Нужно прочитать теорему столько раз, чтобы ее формулировка отложилась в памяти. Я прочитала ее 8 раз.
Дано: 2 треугольника, равные углы в них.
Надо доказать, что два треугольника подобны.
Да. Чертеж мне очень помогает при доказательстве теорем и решении задач . Иногда чертеж подсказывает решение задачи.
Я прочитала несколько раз доказательство теоремы по учебнику, кратко записала его в тетрадь, а затем попыталась устно повторить теорему и доказательство.
Можно, на 2 части.
Мне пригодились знания, которые были получены мною ранее, даже из 7 класса.
Мне ничего не мешало. Главное знать, зачем все это надо.
В доказательстве теоремы мне помог учебник и огромное желание знать то, что еще мне не ведомо.
Логически определила, что доказывать больше нечего.
Сама теорема для меня уже открытие, я же не знала этого свойства раньше.
Довольна, что смогла доказать теорему, чувство удовлетворения, чувство гордости, что я все поняла.
Внимательно прочитай теорему и доказательство, попытайся понять их, прочитай несколько раз, докажи теорему кому-нибудь или зеркалу, я бы посоветовала иметь этот вопросник перед собой – помогает.
Используя этот вопросник ребята сами доказывали теорему. Для учеников данная работа была необычной, интересной и трудной. Мы рассмотрели и обобщили все ответы, отметив их разнообразие, выявили наиболее рациональные действия при выполнении данной работы. На следующий урок все опрошенные учащиеся смогли доказать теорему на положительные отметки.
Далее мы с учениками обсудили стратегии изучения и доказательства теоремы, выявили общие и различные закономерности их действий, создали банк успешных действий, назвав итоговую работу «Мои шаги».
Второй признак подобия треугольников ребята доказали сами, используя перечень «Мои шаги». А вот при изучении третьего признакаподобия (этот урок записан на видео, а конспект урока приведен ниже),мы смогли составить памятку доказательства теоремы, которую успешно применяли при доказательстве других теорем как в этом классе так и в другом классе данной параллели.
Памятка.
При изучении и доказательстве теорем надо:
Внимательно прочитать теорему.
Заменить термины в теореме определениями понятий, которые они обозначают или их признаками.
Развести элементы условия и заключения словами «дано» и «доказать».
Записать все известные величины в графу «Дано».
В графу «Доказательство» записать, что необходимо доказать.
Сделать четкий и аккуратный чертеж. Отметить на нем латинскими буквами то, что изначально известно.
Еще раз прочитать теорему, понимая значение каждого слова в ней, запомнить ее формулировку.
Прочитать полностью текст доказательства, знакомясь с приемами доказательства.
Разбить теорему на части.
Повторно читать доказательство, кратко записывая его шаги.
Доказать каждую часть по отдельности.
Закончить доказательство выводом «следовательно, первоначальное утверждение верно, теорема доказана».
Закрой учебник, докажи кому-нибудь теорему, попробуй.
Положив памятку перед собой, теперь любой ребенок может самостоятельно разобраться с теоремой и доказать ее. Эта памятка помогает извлекать информацию из условия теоремы, вычленять отдельные элементы, комбинировать их, делать самостоятельные выводы, формировать требования каждого этапа доказательства, в процессе работы оценивать свои знания, ликвидировать «пробелы». Не меньший интерес наша работа вызвала у моих коллег – математиков.
Использование технологии ЦРПС позволило добиться положительной динамики в изучении и доказательстве теорем в геометрии. Теперь все ученики 8 класса понимают, что означают слова учителя «выучить теорему». Ребят стала привлекать самостоятельная познавательная деятельность, у них изменилась мотивация, появилась уверенность в себе и собственных силах, возникло ответственное отношение к собственной деятельности. Вот одна из стратегий успешного изучения и доказательства теоремы после знакомства с основными принципами ЦРПС:
Саша:
Внимательно читаю теорему по учебнику.
Вчитываюсь в каждое слово, отмечая новые термины, словосочетания.
Читаю доказательство.
Определяюсь, понятно ли мне все.
Если что-то непонятно, вновь читаю, обращая внимание на каждое слово.
Если все понятно, то выясняю и записываю, что дано и что надо доказать.
Делаю чертеж, соответствующий условию теоремы с указанием всех данных.
Перечитываю вновь внимательно доказательство.
Стараюсь поделить доказательство на логические части.
Доказываю теорему по частям, делая необходимые выводы.
Еще раз читаю теорему.
Закрыв учебник, используя чертеж, доказываю теорему.
Все, теорему выучил и доказал!
Теперь постараюсь применить знания, полученные в ходе изучения теоремы.
Проведенные наблюдения, анализ стратегий, беседы с учащимися позволили определить и перспективы работы – необходимость исследования стратегии эвристического доказательства теорем, доказательства методом «от противного».
Разработка урока
Предмет: геометрия.
Учитель: Петрова Елена Владимировна
Класс: 8 «г»
Тема урока: третий признак подобия треугольников.
Цель урока: составить памятку по изучению и доказательству теорем, апробировать ее при изучении третьего признака подобия треугольников.
Задачи урока, сформулированные на деятельностной основе:
—воспитательная: развитие мотивации для изучения геометрии; формирование уважительного отношения к иному мнению, к иной точке зрения; развитие самостоятельности в решении личностных проблем.
-учебная: Составить памятку, способствующую успешному изучению и доказательству теорем, применить ее для самостоятельного изучения
третьего признака подобия треугольников.
— развивающая: формировать умение анализировать, выделять главное, сравнивать, обобщать, систематизировать, объяснять понятия и доказывать их.
Содержание урока
Этап
Название этапа
Задачи
Деятельность учителя (методы и приёмы обучения)
Деятельность ученика (формы организации УПД)
Ожидаемый результат (знания, умения, способы деятельности)
1.
Мотивирование к учебной деятельности
Создать условия для возникновения внутренней потребности включения в учебную деятельность
У меня есть два треугольника. Стороны одного из них 3 см, 5см и 4 см, а другого 12 см, 20 см и 16 см. Как выяснить, подобны ли эти треугольники?
Проанализировать ситуацию, потытаться решить проблему.
Ученики задумаются над решением этой задачи, но решить не смогут.
2.
Выявление места и причины затруднения.
Выяснить причины: почему мы не можем ответить на поставленный вопрос?
Организовать деятельность учеников так, чтобы подвести их к причине затруднения.
В процессе обсуждения ученики выясняют, что им мешает решить эту задачу, а что могло бы помочь выйти из затруднительного положения.
Ученики осознают, что для решения проблемы, у них недостаточно знаний
3.
Построение проекта выхода из затруднения.
Помочь ученикам найти выход из ситуации
Учитель помогает в постановке цели с помощью подводящего диалога, побуждения к действию.
Учащиеся ставят цели и выбирают способ для достижения цели – изучить еще один признак подобия треугольников.
Проанализировав ситуацию, приходим к выводу о необходимости создания памятки по изучению и доказательству теорем.
4.
Реализация намеченного плана
Создать универсальную памятку.
Учитель руководит процессом
Учащиеся составляют индивидуально свою памятку на основе «мои шаги», выявленных на предыдущих уроках, чтоб успешно изучить теорему; а затем в процессе обсуждения создаем универсальную памятку.
Создание памятки для успешного доказательства лябой теоремы по учебнику.
5.
Реализация построенного проекта.
Разобрать по учебнику третий признак подобия треугольников.
Учитель руководит процессом
Ученики по учебнику разбирают новую для нх теорему и с помощью памятки описывают ее доказательство в тетрадь.
Теорема разобрана и ее доказательство записано в тетрадь.
6.
Первичное закрепление с программированием во внешней речи
Выяснить все непонятные моменты в теореме
Учитель помогает учащимся, фиксируя преодоление возникших затруднений.
Соотносят записи в тетради с планом доказательства, выясняют возникшие вопросы и делают выводы.
.Проанализировать проделанную работу и устно разобрать доказательство
7.
Включение в систему знаний и повторение.
Доказать третий признак подобия треугольников.
Учитель предлагает , используя составленную памятку, доказать теорему у доски.
Ученики по своему желанию доказывают теорему у доски.
Кто-то из ребят сможет ответить у доски.
8.
Рефлексия учебной деятельности на уроке.
Фиксирует степень достижения цели.
Ученики понимают, что теперь и эта задача решаема, т.е. поднимается самооценка ученика.
Ученикам понравится такой вид деятельности и они поймут, что именно такой подход к изучению и доказательству теоремы наиболее эффективен.
Учимся доказывать теорему
Усвоить содержание теорем (правил, формул, тождеств и т. д.), которые изучаются в школе, не так уж трудно. Для этого необходимо систематически пытаться понять смысл теоремы (правил, формул, тождеств и т. д., как можно чаще применять их при решении задач, при доказательстве других теорем. Такая работа, как показывает практика, приводит к непроизвольному усвоению их содержания, запоминанию их формулировок. Значительно труднее научиться доказывать теоремы. При этом речь идет не о запоминании доказательства той или иной теоремы, которая была рассмотрена на уроке. Специально запоминать доказательство не нужно, нужно научиться самому доказывать теоремы. Доказательства теорем в учебнике следует рассматривать как образец (эталон) рассуждений при доказательстве какого-либо утверждения.
Что значит доказать теорему, что такое доказательство?
Доказательство в широком смысле — это логическое рассуждение, в процессе которого истинность какой-либо мысли обосновывается с помощью других положений.
Поэтому, когда вы убеждаете своего товарища в чем-либо или отстаиваете в споре с ним свое мнение, свою точку зрения, то вы по существу производите доказательство (умело или неумело — это уже другой вопрос) . В жизни все время, каждодневно в общении с другими людьми, приходится доказывать те или иные мысли, утверждения, приходится убеждать в чем-то, т. е. доказывать.
Доказательство математических теорем есть частный случай доказательства вообще. Оно отличается от доказательства в житейских условиях или в других науках тем, что оно совершается по возможности чисто дедуктивным способом (от латинского слова дедукция — выведение), т. е. выведением новой доказываемой мысли (утверждения, суждения) из ранее доказанных или принятых без доказательства мыслей (аксиом) по правилам логики без каких-либо ссылок на примеры или опыт. В других науках, в житейских обстоятельствах мы для доказательства часто прибегаем к примерам, к опыту. Мы говорим: «Смотри» — и это может служить доказательством. В математике такой способ доказательства недопустим, ссылаться, например, на очевидные отношения, иллюстрируемые чертежом, не разрешается. Математическое доказательство должно представлять собой цепочку логических следствий из исходных аксиом, определений, условий теоремы и ранее доказанных теорем до требуемого заключения.
Таким образом, при доказательстве теоремы мы сводим ее к ранее доказанным теоремам, а те в свою очередь еще к другим и т. д. Очевидно, что этот процесс сведения должен быть конечным, и поэтому всякое доказательство в конце концов сводит доказываемую теорему к исходным определениям и принятым без доказательства аксиомам.
Следовательно, аксиомы служат не только для косвенного определения первичных понятий, но и в качестве оснований для доказательства всех теорем математики. Вот почему в числе аксиом встречаются и такие, которые указывают особые свойства понятий, имеющих логические определения. Так, например, параллельные прямые в курсе геометрии являются не первичным понятием, а определяемым. Однако одно из свойств параллельных прямых, а именно что ч ерез точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной , мы вынуждены принять за аксиому, ибо, как было установлено великим русским геометром Н. И. Лобачевским (1792—1856), а также немецким математиком К. Ф. Гауссом (1777—1855) и венгерским математиком Я. Больяй (1802—1860), доказать это свойство параллельных прямых на основе лишь остальных аксиом геометрии невозможно.
Всякий шаг доказательства состоит из трех частей:
1) предложение (аксиома, теорема, определение), на основе которого производится этот шаг доказательства; это основание шага доказательства называется посылкой или аргументом;
2) логическое рассуждение, в процессе которого посылка применяется к условиям теоремы или к ранее полученным следствиям;
3) логическое следствие применения посылки к условиям или ранее полученным следствиям.
В последнем шаге доказательства теоремы в качестве следствия получаем утверждение, которое необходимо было доказать. Покажем процесс доказательства на примере такой теоремы: «Диагонали прямоугольника равны».
В этой теореме нам дан произвольный (любой) прямоугольник, Для того чтобы легче было рассуждать в процессе доказательства, поступают следующим образом. Начертим вполне определенный прямоугольник ABCD, но при доказательстве не будем использовать какие-либо частные особенности этого прямоугольника (например, что его сторона АВ примерно в 2 раза больше стороны AD и т. д.). Поэтому наши рассуждения относительно этого определенного прямоугольника будут верны и для любого другого прямоугольника, т. е. они будут иметь общий характер для всех прямоугольников.
Проведем диагонали АС и BD. Рассмотрим полученные треугольники ABC и ABD. У этих треугольников углы ABC и BAD равны как прямые, катет АВ — общий, а катеты ВС и AD равны как противоположные стороны прямоугольника. Следовательно, эти треугольники равны. Отсюда следует, что стороны АС и BD также равны, что и требовалось доказать.
Все доказательство этой теоремы можно изобразить в виде следующей схемы.
Самое трудное в доказательстве — это найти последовательность посылок (аксиом, теорем, определений), применяя которые к условиям теоремы или промежуточным результатам (следствиям) в конечном итоге можно получить нужное следствие — доказываемое положение.
Какими правилами нужно руководствоваться при поиске этой последовательности? Очевидно, что эти правила не могут носить обязательный характер, они лишь указывают возможные пути поиска. Поэтому они называются эвристическими правилами или просто эвристиками (от греческого слова эврика — нахожу, нашел). Многие выдающиеся математики, такие, как Папп (древнегреческий математик, живший в III в.), Блез Паскаль (1623—1662), Рене Декарт (1596—1650), Жак Адамар (1865—1963), Дьердж Пойя (1887) и многие другие, занимались разработкой эвристик для поиска доказательства теорем и решения задач. Вот некоторые эвристические правила, которые полезно помнить:
1. Полезно заменять названия объектов, о которых идет речь в теореме (задаче), их определениями или признаками.
Например, в рассмотренной выше теореме шла речь о прямоугольнике, и мы для доказательства использовали определение прямоугольника.
2. Если можно, то нужно доказываемое положение раздробить на части и доказывать каждую часть в отдельности.
Так, например, доказательство теоремы: «Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм» — можно разделить на две части: сначала доказать, что одна пара противоположных сторон данного четырехугольника параллельна, а затем доказать, что и вторая пара противоположных сторон также параллельна.
Так следует поступать всегда, когда есть возможность доказываемое утверждение разбить на несколько частей более простых утверждений.
3. В поисках доказательства теоремы полезно идти с двух сторон: от условий теоремы к заключению и от заключения к условиям.
Например, нужно доказать такую теорему: «Если некоторая последовательность такова, что любой ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов, то эта последовательность — арифметическая прогрессия».
Пойдем от условия теоремы. Что нам дано? Дано, что каждый член последовательности, начиная со второго (обозначим его a n , где n ³ 2), есть среднее арифметическое предшествующего и последующего членов, т.
a n- 1 и a n+1 . Значит, верно такое равенство:
(1)
Теперь пойдем от заключения. А что нам нужно доказать? Нужно доказать, что эта последовательность — арифметическая прогрессия. А какая последовательность называется арифметической прогрессией? Вспоминаем определение:
a n = a n-1 + d, где n 2, d — постоянное число. (2)
Сопоставляем данное нам условие (1) с заключением (2). Чтобы условие приняло форму заключения, надо преобразовать так:
2a n = a n-1 + a n+1 , (3)
Отсюда a n — a n-1 = a n+1 — a n . (4)
Левая и правая части (4) обозначают одно и то же, а именно разность между двумя последовательными членами заданной последовательности. Если в равенстве (4) п давать последовательно значения 2, 3 и т. д., то получим: а 2 —a 1 = а 3 — a 2 , затем а 3 — a 2 = a 4 — a 3 и т. д. Следовательно, все эти разности равны между собой, а это значит, что разность а п — а п -1 есть постоянное число, которое можно обозначить буквой, например, буквой d:
а п — а п-1 = d.
Отсюда получаем: a n = a n-1 + d, а это значит, что согласно определению (2) данная последовательность есть арифметическая прогрессия, что нам и надо было доказать.
Эту эвристику можно и так сформулировать: надо стараться сблизить условие и заключение теоремы, преобразуя их или заменяя их следствиями.
Известен и ряд более частных эвристических правил, которые применяются при поиске лишь некоторых теорем. Например, такая эвристика: для того чтобы доказать равенство каких-либо отрезков, надо найти или построить фигуры, соответствующими сторонами которых являются эти отрезки; если фигуры окажутся равными, то будут равны и соответствующие отрезки.
Изучая теоремы, нужно не просто запоминать их доказательство, а каждый раз думать и устанавливать, какими методами они доказываются, какими эвристическими правилами руководствовались при нахождении этих доказательств, как догадались (додумались) до этих доказательств.
В ряде случаев для доказательства теорем используется особый прием, называемый «доказательством от противного» или «приведением к нелепости».
Сущность этого приема заключается в том, что предполагают несправедливость (ложность) заключения данной теоремы и доказывают, что такое предположение приводит к противоречию с условием или с ранее доказанными теоремами или аксиомами. А так как любое утверждение может быть либо верным, либо неверным (ничего другого быть не может), то полученное противоречие показывает, что допущение о ложности заключения теоремы неверно и, следовательно, заключение верно, тем самым теорема доказана.
Приведем пример.
Теорема. Две прямые, порознь параллельные третьей, параллельны между собой.
Дано: а||с, b||с.
Доказать: а||b.
Докажем эту теорему методом от противного. Допустим, что заключение теомы неверно, т. е. прямая а непараллельна прямой b. Тогда они пересекаются в некоторой точке М. А так как по условию каждая из этих прямых параллельна прямой с, то получается, что через точку М проведены две прямые а и b, параллельные одной и той же прямой с. А мы знаем по аксиоме параллельности, что через точку вне прямой можно провести не более одной прямой, параллельной данной. Пришли к противоречию с аксиомой. Это показывает, что наше предположение о непараллельности прямых а и b неверно, следовательно, а||b, что и требовалось доказать.
Другой пример.
Теорема. Среднее арифметическое двух положительных чисел не меньше {значит: больше или равно) среднего геометрического этих чисел.
Эту теорему можно так записать:
, где а>0, b>0, (1)
Ее можно доказать как прямым способом, так и способом от противного. Докажем ее способом от противного.
Для этого допустим, что она неверна, т. е. среднее арифметическое меньше среднего геометрического двух положительных чисел: ; (2)
Умножим обе части (2) на 2 и возведем их в квадрат, получим: a 2 + 2ab + b 2 <.4ab или a 2 — 2ab + b 2 < 0. По формуле квадрата разности двух чисел получаем: (а — b) 2 < 0.
В результате получили явную нелепость: квадрат некоторого числа (а — b) отрицателен, чего быть не может. Следовательно, предположение о неверности теоремы привело к противоречию, что доказывает справедливость теоремы.
Таким образом, доказательство от противного некоторой теоремы состоит в том, что мы делаем допущение о неверности заключения теоремы. Затем делаем ряд логических умозаключений на основе этого допущения, в результате которых приходим к явно нелепому положению (к противоречию с условием или ранее доказанными теоремами, аксиомами). Далее рассуждаем так: если бы наше предположение было бы верным, то мы могли бы прийти лишь к верному выводу, а так как мы пришли к неверному выводу, то это означает, что наше предположение было ложным, следовательно, тем самым мы убедились, что заключение теоремы верно.
Заметим, что если в результате рассуждений мы не получили бы нелепости (противоречия), то это еще не означало бы, что предположение верно. Иными словами, если исходить из верности (справедливости) заключения теоремы и из этого предположения получить верное (очевидное) следствие, то это еще не значит, что предположение верно: может случиться, что исходная теорема как раз неверна.
На этом построены многие софизмы (умышленно ложно построенные умозаключения, кажущиеся лишь правильными), этим объясняются многие ошибки, допускаемые, при решении задач.
Рассмотрим, например, такое равенство: а — b = b — a (1), где а и b — произвольные числа. Допустим, что (1) верно, тогда возвысим обе части (1) в квадрат, получим:
a 2 — 2ab + b 2 = b 2 — 2ab + a 2
Перенеся все члены в одну сторону и сделав приведение подобных, придем к совершенно верному равенству: 0 = 0. Но отсюда нельзя делать вывод, что и исходное равенство (1) верно. Если бы мы такой вывод сделали, то пришли бы к такому софизму: 2а = 2b или а = b, т. е. любые произвольные числа равны между собой. Ошибка состоит в том, что из равенства квадратов двух чисел не следует равенство самих этих чисел. Например, (-2) 2 = 2 2 , но -2 2.
Вот пример ошибочного решения задачи.
Задача. Решить уравнение 3 + x + 2 = 0 (1).
Допустим, что уравнение (1) имеет решение и, следовательно, равенство (1) верно. Тогда получим: З = — х — 2. Возведем обе части равенства в квадрат: 9х = х 2 + 4х + 4 или х 2 —5x + 4 = 0, отсюда x 1 =4, х 2 =1. Можно ли найденные значения х считать корнями уравнения (1)? Некоторые ученики отвечают на этот вопрос утвердительно, ибо ведь все преобразования уравнения верные. И все же ни одно из найденных значений х не является корнем (1). Это подтверждает проверка. Подставляя найденные значения х в (1), получаем явно нелепые равенства: 12 = 0 и 6 = 0.
А как все же решить это уравнение. Заметим, что выражение в левой части уравнения имеет смысл, если x 0. Тогда левая часть уравнения при любых допустимых значениях х принимает только положительные значения и ни как не может быть равной 0, следовательно, данное уравнение корней не имеет.
Таким образом вы должны учиться доказывать теоремы (формулы, тождества и т. д.), овладевать общими способами поиска доказательства теорем.
Что такое теорема и доказательство теоремы? Доказательство теоремы Пифагора
Не только каждый школьник, но и каждый уважающий себя образованный человек должен знать, что такое теорема и доказательство теорем. Может, такие понятия и не встретятся в реальной жизни, но структурировать многие знания, а также делать умозаключения они точно помогут. Именно поэтому мы и рассмотрим в этой статье способы доказательства теорем, а также ознакомимся со столь знаменитой теоремой Пифагора.
Что же такое теорема
Если рассматривать школьный курс математики, то очень часто в нем встречаются такие научные термины, как теорема, аксиома, определение и доказательство. Для того чтобы ориентироваться в программе, нужно ознакомиться с каждым из этих определений. Сейчас же мы рассмотрим, что такое теорема и доказательство теорем.

Итак, теорема – это некое утверждение, которое требует доказательства. Рассматривать данное понятие нужно параллельно с аксиомой, так как последняя доказательства не требует. Ее определение уже является истинным, поэтому воспринимается как должное.
Сфера применения теорем
Ошибочно думать, что теоремы применяются только в математике. На самом деле это далеко не так. Например, существует просто невероятное количество теорем в физике, позволяющих подробно и со всех сторон рассмотреть некоторые явления и понятия. Сюда можно отнести теоремы Ампера, Штейнера и многие другие. Доказательства таких теорем позволяют неплохо разобраться в моментах инерции, статике, динамике, и во многих других понятиях физики.
Использование теорем в математике
Тяжело представить себе такую науку, как математика, без теорем и доказательств. Например, доказательства теорем треугольника позволяют подробно изучить все свойства фигуры. Ведь очень важно разобраться в признаках подобия, свойствах равнобедренного треугольника и во многих других вещах.

Доказательство теоремы площади позволяет понять, как проще всего вычислять площадь фигуры, опираясь на некоторые данные. Ведь, как известно, существует большое количество формул, описывающих, как можно найти площадь треугольника. Но перед тем как их использовать, очень важно доказать, что это возможно и рационально в конкретном случае.
Как доказывать теоремы
Каждый школьник должен знать, что такое теорема, и доказательство теорем. На самом деле доказать какое-либо утверждение не так-то просто. Для этого нужно оперировать многими данными и уметь делать логические выводы. Конечно, если вы неплохо владеете информацией по определенной научной дисциплине, то доказать теорему для вас не составит особого труда. Главное — выполнять процедуру доказательства в определенной логической последовательности.
Для того чтобы научиться доказывать теоремы по таким научным дисциплинам, как геометрия и алгебра, нужно иметь неплохой багаж знаний, а также знать сам алгоритм доказательства. Если вы освоите такую процедуру, то решать математические задачи впоследствии для вас не составит особого труда.
Что нужно знать о доказательстве теорем
Что такое теорема и доказательства теорем? Это вопрос, который волнует многих людей в современном обществе. Очень важно научиться доказывать математические теоремы, это поможет вам в будущем строить логические цепочки и приходить к определенному выводу.
Итак, для того чтобы доказывать теорему правильно, очень важно сделать правильный рисунок. На нем отобразите все данные, которые были указаны в условии. Также очень важно записать всю информацию, которая предоставлялась в задаче. Это поможет вам правильно проанализировать задание и понять, какие именно величины в нем даны. И только после проведения таких процедур можно приступать к самому доказательству. Для этого вам нужно логически выстроить цепочку мыслей, используя другие теоремы, аксиомы или определения. Итогом доказательства должен быть результат, истинность которого не подлежит сомнению.
Основные способы доказательства теорем
В школьном курсе математики существует два способа, как доказать теорему. Чаще всего в задачах используют прямой метод, а также метод доказательства от противного. В первом случае просто анализируют имеющиеся данные и, опираясь на них, делают соответственные выводы. Также очень часто используется и метод от противного. В этом случае мы предполагаем противоположное утверждение и доказываем, что оно неверно. На основе этого мы получаем противоположный результат и говорим о том, что наше суждение было неверным, а значит, указанная в условии информация является правильной.
На самом деле многие математические задачи могут иметь несколько способов решения. Например, теорема Ферма доказательств имеет несколько. Конечно, некоторые рассматриваются только одним способом, но, например, в теореме Пифагора можно рассмотреть сразу несколько из них.
Что представляет собой теорема Пифагора
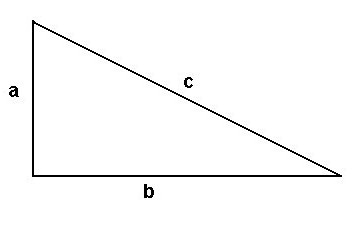
Конечно, каждый школьник знает о том, что теорема Пифагора касается именно прямоугольного треугольника. И звучит она так: «Квадрат гипотенузы равен сумме квадратов катетов». Несмотря на название данной теоремы, открыта она была не самим Пифагором, а еще задолго до него. Существует несколько способов доказательства данного утверждения, и мы рассмотрим некоторые из них.
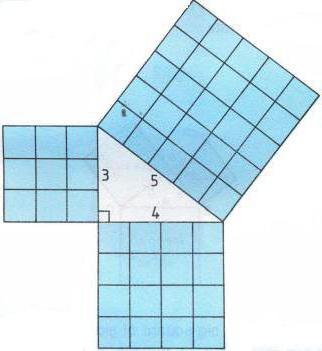
Согласно научным данным, в самом начале рассматривался равносторонний прямоугольный треугольник. Затем строились квадраты на всех его сторонах. Квадрат, построенный на гипотенузе, будет состоять из четырех равных между собой треугольников. В то время как фигуры, построенные на катетах, будут состоять только из двух таких же треугольников. Такое доказательство теоремы Пифагора является самым простым.
Рассмотрим еще одно доказательство данной теоремы. В нем нужно использовать знания не только из геометрии, но также и из алгебры. Для того чтобы доказать данную теорему этим способом, нам нужно построить четыре аналогичных прямоугольных треугольника, и подписать их стороны как а, в и с.

Построить эти треугольники нужно таким образом, чтобы в результате у нас получилось два квадрата. Внешний из них будет иметь стороны (а+в), а вот внутренний – с. Для того чтобы найти площадь внутреннего квадрата, нам нужно найти произведение с*с. А вот для того чтобы найти площадь большого квадрата, нужно сложить площади маленьких квадратов и добавить площади полученных прямоугольных треугольников. Теперь, произведя некоторые алгебраические операции, можно получить такую формулу:
а2+в2=с2
На самом деле существует огромное количество методов доказательства теорем. Перпендикуляр, треугольник, квадрат или любые другие фигуры и их свойства можно рассмотреть с помощью применения различных теорем и доказательств. Теорема Пифагора только является тому подтверждением.
Вместо заключения
Очень важно уметь формулировать теоремы, а также правильно их доказывать. Конечно, такая процедура является достаточно сложной, так как для ее осуществления необходимо не только уметь оперировать большим количеством информации, но также и выстраивать логические цепочки. Математика – это очень интересная наука, которая не имеет ни конца, ни края.
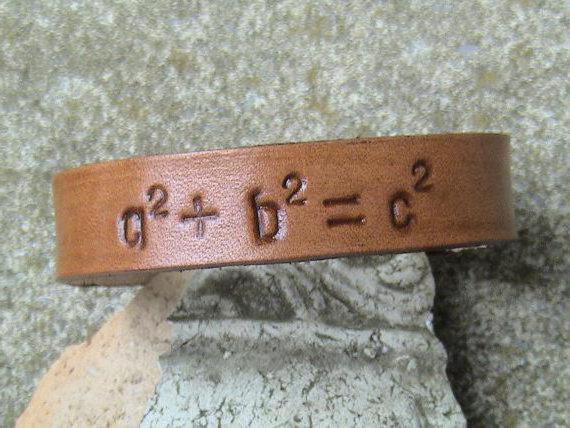
Начните ее изучать, и вы не только повысите уровень своего интеллекта, но и получите огромное количество интересной информации. Займитесь своим образованием уже сегодня. Поняв основные принципы доказательств теорем, вы сможете проводить свое время с большой пользой.