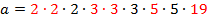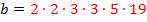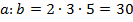Разложение многочленов на множители. Видеоурок. Алгебра 7 Класс
Упрощение выражений чем-то похоже на игру в пятнашки: есть исходные данные (выражение, которое нужно упростить, например 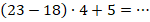 ) и правила игры (набор стандартных действий, которые приведут к необходимому результату, например порядок выполнения действий: 1) действия в скобках; 2) умножение и деление; 3) сложение и вычитание).
) и правила игры (набор стандартных действий, которые приведут к необходимому результату, например порядок выполнения действий: 1) действия в скобках; 2) умножение и деление; 3) сложение и вычитание).
В пятнашках есть начальные положения, при которых можно выиграть, получить нужный результат (см. рис. 1), а есть те, при которых нельзя (см. рис. 2). Для игры обычно предлагаются те варианты, в которых выиграть можно.
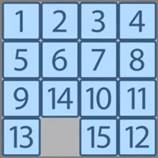
Рис. 1. Положение в пятнашках, при котором можно выиграть
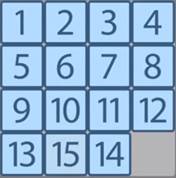
Рис. 2. Положение в пятнашках, при котором нельзя выиграть
Так и с выражениями – есть те, которые упрощаются, есть те, которые нет. Например:
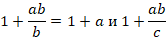
В задачах и примерах вам будут чаще всего встречаться те выражения, которые можно упростить. Нужно только научиться «правилам игры» – методам, которые используются для упрощения выражения, и потренироваться их применять.
Чем больше вы тренируетесь, тем более хорошим «игроком» становитесь (меньше ошибок при упрощении выражений совершаете, быстрее упрощаете, учитесь упрощать более сложные выражения). Все определяет цель – кто-то хочет стать чемпионом, а кому-то достаточно уметь играть в свое удовольствие. Рассмотрим «правила игры» – методы упрощения.
Число 12 можно разложить на множители:
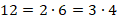
А вот число 17 – нельзя (если не считать  разложением).
разложением).
Разложение чисел на множители мы использовали для сокращения обыкновенных дробей, нахождения общего знаменателя, например:


Действия с алгебраическими дробями не отличаются от действий с обыкновенными. Чтобы сократить дробь или привести дроби к общему знаменателю, нужно научиться раскладывать выражения на множители.
С некоторыми выражениями мы умеем это делать:
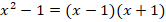
А можно ли разложить на множители 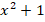 ? Оказывается, нет.
? Оказывается, нет.
Но способов, с помощью которых можно раскладывать на множители, всего два. Рассмотрим их, чтобы научиться раскладывать многочлены на множители и, соответственно, впоследствии упрощать выражения.
Вспомним распределительный закон:
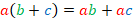
Поскольку это тождество, то по определению равенство выполняется в две стороны: как слева направо, так и наоборот:
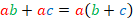
В частности, это означает, что:
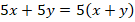
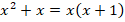
и т. д.
Такая эквивалентная запись получается с помощью вынесения общего множителя за скобки (в первом примере выносится общий множитель 5, во втором – общий множитель 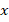 ).
).
Пример 1.
Вычислить значение выражения:
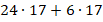
Решение:
Чтобы не выполнять два умножения, вынесем за скобку общий множитель 17.
Вместо трех действий мы сделаем два:

Ответ: 510.
Пример 2.
Упростить выражение:

Решение:
В числителе вынесем за скобки общий множитель 3, в знаменателе – общий множитель 12 и сократим:
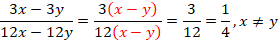
Ответ:  .
.
ОДЗ при преобразованиях выражений
Почему равенство  не является тождеством?
не является тождеством?
Какие бы значения переменных 
 . Кроме одного случая – когда
. Кроме одного случая – когда 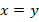 .
.Но тождество – это равенство, которое выполняется на всем множестве значений входящих в него переменных (если это множество отдельно не задано).
Если мы не укажем ограничения на множество значений переменных, то тождественно равными выражения 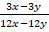 и
и  считать нельзя, ведь, например, при
считать нельзя, ведь, например, при 
 .
.Поэтому данные выражения тождественно равны только при условии, что  .
.
Пример 3.
Вычислить значение выражения 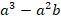 , если
, если 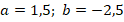 .
.
Решение:
Вспомним распределительный закон:

В примере можно взять 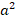 в качестве
в качестве 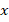 :
:
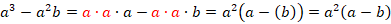
Подставим известные значения 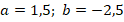 :
:
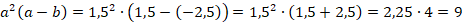
Заметим, что, записав выражение так: 
Ответ: 9.
Пример 4.
Представить в виде произведения многочленов:
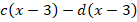
Решение:
Распределительный закон:
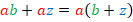
В примере можно взять 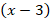 в качестве
в качестве 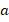 :
:

Ответ: 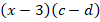 .
.
Пример 5.
Представить в виде произведения многочленов:
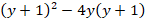
Решение:
Распределительный закон:
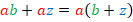
В примере можно взять  в качестве
в качестве 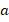 :
:
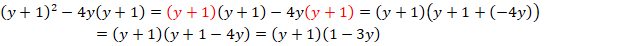
Ответ: 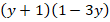 .
.
Операция, которую мы проделали в рассмотренных примерах, называется разложением на множители. В наших примерах слагаемые имели общий множитель, который мы выносили за скобки, но есть выражения, где не все слагаемые имеют общий множитель, например:
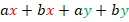
У первых двух слагаемых есть общий множитель 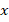 , у вторых двух – общий множитель
, у вторых двух – общий множитель  . Вынесем их за скобки:
. Вынесем их за скобки:
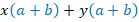
Мы получили выражение, где у слагаемых есть общий множитель, снова вынесем его:

Мы разложили на множители многочлен, выбрав группы слагаемых, у которых был общий множитель, такой метод разложения на множители называют методом группировки.
Всего есть два основных метода разложения на множители:
- Метод группировки.
- Использование формул сокращенного умножения (ФСУ).
Пример 6.
Разложить на множители:
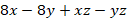

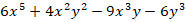
Решение:
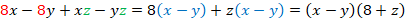
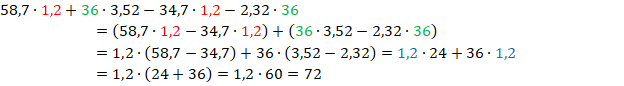
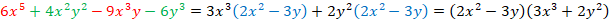
Ответ: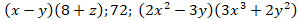 .
.
Кроме метода группировки, в разложении на множители выражений нам помогут ФСУ,
вспомним их:
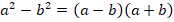
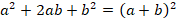
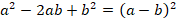
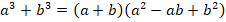
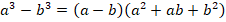
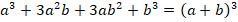

Пример 7.
Разложить на множители:
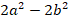
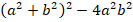

Решение:

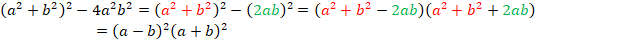
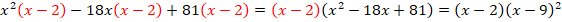
Ответ:  .
.
Использование ФСУ и группировка слагаемых
Мы выделили использование ФСУ в отдельный метод разложения на множители. Однако сами ФСУ получаются методом группировки. Рассмотрим это на примере:
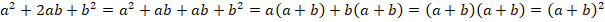
Т. е., обобщив все сказанное, можно сказать, что существует единственный способ разложения многочленов на множители – метод группировки. А вынесение общего множителя и ФСУ можно считать частным случаем этого способа.
Не всегда для разложения выражения на множители можно сразу применить метод группировки. Иногда предварительно одно из слагаемых необходимо эквивалентно представить в виде суммы двух других.
Пример 1.
Разложить многочлен на множители:

Решение:

Ответ: 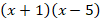 .
.
Пример 2.
Разложить многочлен на множители:

Решение:

Ответ:  .
.
Разложение на множители с помощью выделения полного квадрата
При изучении ФСУ мы рассматривали метод выделения полного квадрата. Напомним его суть.
Пример 1.
Выделить полный квадрат:
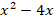
Решение:
Для выделения полного квадрата мы используем ФСУ:

Будем выделять полный квадрат на основе слагаемых, содержащих переменную:

Определим 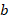 , добавим и вычтем его квадрат (вычитать необходимо для того, чтобы выражение не изменилось):
, добавим и вычтем его квадрат (вычитать необходимо для того, чтобы выражение не изменилось):
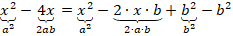
Чтобы получилось  :
:
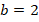
Получим:
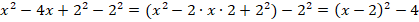
Ответ: 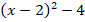 .
.
С помощью этого метода некоторые квадратные трехчлены можно разложить на множители.
Пример 2.
Разложить на множители:

Решение:
Например, выделим полный квадрат в следующем выражении:
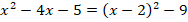
Обратим внимание, что теперь мы можем воспользоваться формулой разности квадратов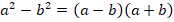 :
:
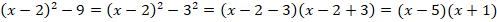
Ответ:  .
.
Пример 3.
Разложить на множители:

Решение:
Выделим полный квадрат:
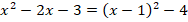
Воспользуемся формулой разности квадратов 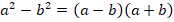 :
:

Ответ:  .
.
Заключение
На этом уроке мы познакомились с двумя основными методами, которые используются для упрощения выражений: группировка слагаемых и применение ФСУ.
Оба этих метода используются для вынесения за скобки общих множителей. Сама операция вынесения общего множителя является применением распределительного закона слева направо:
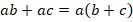
Зачем нужно выносить общий множитель за скобки? Как мы увидели на примерах, это позволяет сократить количество операций, которые нужно сделать для вычисления значения различных выражений или, говоря простым языком, упростить выражения.
Список литературы
- Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. – ФГОС, издательство «Просвещение», 2017.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник. – М.: «Просвещение», 2014.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник. – М.: «Просвещение», 2013.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал mathematics.ru (Источник)
- Интернет-портал youclever.org (Источник)
Домашнее задание
1. Разложить выражение на множители и вычислить:
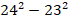
2. Вынести общий множитель за скобки:
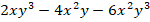
3. Разложить многочлен на множители, используя ФСУ:
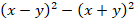
interneturok.ru
Разложение числа на множители. Видеоурок. Математика 6 Класс
Определения:
Простым называют число, которое имеет ровно два различных делителя.
Составным называют число, которое имеет более двух делителей.
Разложить натуральное число на множители – значит представить его в виде произведения натуральных чисел.
Разложить натуральное число на простые множители – значит представить его в виде произведения простых чисел.
Замечания:
- В разложении простого числа один из множителей равен единице, а другой – самому этому числу.
- Говорить о разложении единицы на множители не имеет смысла.
- Составное число можно разложить на множители, каждый из которых отличен от 1.
|
|
Разложим число 150 на множители. Например, 150 – это 15 умножить на 10. 15 – это составное число. Его можно разложить на простые множители 5 и 3. 10 – это составное число. Его можно разложить на простые множители 5 и 2. Записав вместо 15 и 10 их разложения на простые множители, мы получили разложение числа 150. |
|
|
Число 150 можно по-другому разложить на множители. Например, 150 – это произведение чисел 5 и 30. 5 – число простое. 30 – это число составное. Его можно представить как произведение 10 и 3. 10 – число составное. Его можно разложить на простые множители 5 и 2. Мы получили разложение числа 150 на простые множители другим способом. |
|
|
Заметим, что первое и второе разложение одинаковы. Они отличаются только порядком следования множителей. Принято записывать множители в порядке возрастания.
|
|
Всякое составное число можно разложить на простые множители единственным образом с точностью до порядка множителей. |
|
При разложении больших чисел на простые множители используют запись в столбик:
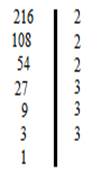 |
Разделим 216 на 2. Получим 108. |
|
Выполним деление. Получим в результате 54. |
|
|
Выполнив деление, получим 27. |
|
|
Не делится на 2. Следующее простое число – это 3. Разделим 27 на 3. Получим 9. Наименьшее простое Число, на которое делится 9, – это 3. Три – само является простым числом, оно делится на себя и на единицу. Разделим 3 на себя. В итоге мы получили 1. |
|
 |
|
- Число делится лишь на те простые числа, которые входят в состав его разложения.
- Число делится лишь на те составные числа, разложение которых на простые множители полностью в нем содержится.
Рассмотрим примеры:
|
|
4900 делится на простые числа 2, 5 и 7. (они входят в разложение числа 4900), но не делится, например, на 13. |
|
1.
2.
|
11 550 В результате деления будет произведение множителей 2, 7 и 11.
11550 не делится на 4 потому, что в разложении четырех есть лишняя двойка. |
Найти частное от деления числа a на число b, если эти числа раскладываются на простые множители следующим образом a=2∙2∙2∙3∙3∙3∙5∙5∙19; b=2∙2∙3∙3∙5∙19
|
|
Разложение числа b полностью содержится в разложении числа a. |
|
|
Результат деления a на b – это произведение оставшихся в разложении числа a трех чисел. Итак, ответ: 30. |
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Matematika-na.ru (Источник).
- Интернет-портал Math-portal.ru (Источник).
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012. № 127, № 129, № 141.
- Другие задания: № 133, № 144.
interneturok.ru
Разложение на множители ℹ️ что значит и как раскладывать на простые множители число, корни, трехчлен, квадратное уравнение, примеры и решения, правило и алгоритм

Термины и понятия
Под разложением в математике понимается операция, которую выполняют для превращения сложного неудобного для вычисления примера в простой. В учебниках и литературе такое преобразование выражений называется тождественным, то есть без изменения сути задания.
Из слова «множители» можно понять, что в превращении используется умножение. Зная, как разложить полином на простые числа, можно быстро решать задачи на действия с корнями и сложными дробями. Например, выражение (3*h*y + 9*y — 8*h — 24) * (3*h — 8) после упрощения примет вид: h + 3 — и быстро решается в уме.
В математике все алгебраические выражения могут быть:

- Одночленными. Это уравнения, состоящие из чисел, натуральных степеней и не содержащие никаких других арифметических действий, кроме умножения. Числовой множитель выражения называют коэффициентом.
- Многочленными. Включающими в себя сумму нескольких одночленов. Если выражение, кроме произведения, не содержит другие арифметические операции, такие как деление, возведение в степень, его называют целым.
Числа часто записывают в так называемом стандартном виде. Например, 296,8 = 2,968 * 102. То есть используется формула приведения: a * 10r, где 1≤а<10, а r — целое число, обозначающее порядок.
Каноническим правилом является следующее: любое простое число можно представить как произведение его составляющих. Так, 12 можно представить как 6 х 2, в свою очередь, 6 — как 3 х 2. Таким образом, будет верной запись: 12 = 3 х 2 х 2. На этом принципе построено упрощение любого выражения. Простые цифры 3, 2, 2 и являются множителями, на которые раскладывают пример.
Существуют пять способов преобразования многочленов (полиномов):
- вынесение общего коэффициента для каждого члена за скобку;
- трансформация по формулам сокращённого умножения;
- способ группирования;
- нахождение и выделения полного квадрата;
- разложение на простые множители.
Какой способ использовать, зависит от вида многочлена. Универсального метода, подходящего к любому решению, не существует. Поэтому для решения задачи нужно правильно определить, какой метод применять лучше всего, особенно это важно для чайников.
Простое разложение
На уроках математики ученикам предлагают разложить на простые множители числа с помощью столбика (двух колонок). Делается это по следующему алгоритму. Исходное число проверяют на возможность деления без остатка на два. Если делится, то рисуют две колонки, в правую вписывают двойку, а в левую число, получившееся после деления на него исходного. В обратном случае вместо двойки используют цифру три. Далее действия повторяют для числа, находящегося уже в правой колонке. Выполняют деление до тех пор, пока в левой колонке не останется единица. Например, число 1176 можно разложить следующим образом:
1176 | 2 (1176 / 2 = 588).

588 | 2 (588 / 2 = 294).
294 | 2 (294 / 2 = 147).
147 | 2 (147 / 3 = 49).
49 | 2 (49 / 7 = 7).
7 | 2 (7 / 7 = 1).
1176 = 2 * 2 * 2 * 3 * 7 * 7 = 23 * 3 * 72.
Для того чтобы понять алгоритм, лучше рассмотреть ещё несколько интересных примеров:
- 7140 = 2 • 2 • 3 • 5 • 7 • 17 = 2 2 • 3 • 5 • 7 • 17;
- 5544 = 2 • 2 • 2 • 3 • 3 • 7 • 11 = 2 3 • 32 • 7 • 11;
- 4104 = 2 • 2 • 2 • 3 • 3 • 3 • 19 = 2 3 • 33 • 19;
- 546 = 2 • 3 • 7 • 13;
- 510 = 2 • 3 • 5 • 17;
- 495 = 3 • 3 • 5 • 11 = 3 2 • 5 • 11;
- 224 = 2 • 2 • 2 • 2 • 2 • 7 = 2 5 • 7;
- 208 = 2 • 2 • 2 • 2 • 13 = 2 4 • 13;
- 156 = 2 • 2 • 3 • 13 = 2 2 • 3 • 13;
- 126 = 2 • 3 • 3 • 7 = 2 • 3 2 • 7;
- 118 = 2 • 59.
Используя метод, можно представить любое число как произведение простых множителей, но с условием, что изначально оно будет кратным двум или трём. В ином же случае простые множители подобрать не получится, как, например, для числа 247, которое можно заменить произведением чисел 13 и 19.
Вынесение коэффициента
Это довольно простой способ разложения многочлена. Выполняют его с помощью перестановки общего множителя за скобку, в которой остаётся сумма выражения. То есть для этого метода необходимо представить искомое в виде произведения нескольких полиномов.
Чтобы выделить общий множитель, следует выполнить:
- для численного выражения — найти число, на которое можно будет разделить без остатка любой коэффициент одночлена;
- для выражения с неизвестным — определить неопределённое число, повторяющееся в каждом одночлене, и вынести его за скобку в наименьшей степени;
- рассчитать многочлен, стоящий в скобках.
Например, пусть дано выражение: 3у2 — 3y + 6 r*y. Согласно правилу, необходимо найти число, на которое без остатка можно разделить каждый из трёх коэффициентов многочлена. Для рассматриваемого примера это будет цифра 3.
Затем определить буквенный множитель, имеющийся в каждом члене выражения. Найденную цифру и повторяющееся неизвестное с наименьшей степенью записать за скобкой. Теперь нужно каждый одночлен разделить на вынесенное значение, а полученный результат записать в скобках: 3y * (y — 1 + 2r). Для проверки правильности действий нужно просто раскрыть скобки путём умножения каждого члена на вынесенный множитель.
Формулы умножения
Довольно часто для упрощения расчётов используют формулы сокращённого умножения. Всего существует семь выражений, которые необходимо выучить. Найти их можно в таблицах любого учебника по алгебре за седьмой класс. Смысл этих теорем в следующем:

- Разность двух членов, стоящих во второй степени, прямо пропорциональна произведению разности этих членов на их сумму. Например, 16 2 — 3 2 = (16 — 3) * (16 + 3) = 247 или 9 * h 2 — 4 * e 2 * h 2 = (3 * h — 2 * e * h) * (3 * h — 2 * e * h).
- Квадрат суммы двух членов можно разложить на квадрат первого элемента и удвоенное произведение его на второй элемент, прибавив квадрат второго члена. Используя это правило, можно быстро находить квадрат числа без использования калькулятора. Например, 114 2 = (100 +14) = 100 2 + 2 * 100 * 14 + 14 2 = 10000 + 2800 + 196 = 12966.
- Квадрат разности двух членов равняется квадрату первого члена с вычетом из него двойного произведения первого на второй с добавлением квадрата второго члена. В этом правиле используют обыкновенное раскрытие скобок. Например, (6 — 3) 2 = 6 2 — 2 * 6 * 3 + 3 2 = (3 — 6) 2 = 9 .
- Кубическая сумма двух выражений определяется кубом первого члена с прибавлением к нему утроенного произведения исходного числа в степени два на второй член, плюс увеличенное в три раза произведение исходного числа на квадрат второго с прибавлением этого элемента в третьей степени. Например, (2h+7e) 3 = (2 * h) 3 + 3 * 2 * h 2 * 7* e + 3 * 2h * (7 * e) 2 + (7 * e) 3.
- Куб разности находится вычитанием из исходного числа утроенного произведения первого члена, возведённого во вторую степень, с прибавлением утроенного произведения исходного члена на второй в степени два минус его куб. Например, (4 * h − 2 * e) 3 = (4 * h) 3 − 3 * (4 * h) 2 * 2 * e + 3 * 4 * h * (2 * e) 2 − (2 * e) 3 .
- Сумма кубов находится как произведение суммы членов на неполный квадрат разности: (5 * h) 3 + 8 3 = (5 * h + 8) * ((5 * h) 2 − 5 * h * 8 + 8 2). Неполным квадратом называют выражение: (h 2 — h * e + e 2).
- Разность кубов равна выражению, полученному перемножением разности двух чисел на неполный квадрат суммы: h4− e3 = (h − e) * ((h 2 +h) * (e + e 2)).
Все эти формулы умножения можно использовать также в обратную сторону, то есть собирать многочлен. Например, для решения примеров типа: «квадратный трёхчлен разложен на множители, найдите а». Если понять смысл этих формул, то запомнить их наизусть будет довольно легко.
Метод группировки
Пожалуй, самый распространённый способ разложения на множители. Его удобно применять для упрощения квадратных уравнений без поиска корней. Разложение этим методом выполняют в следующей последовательности действий:

- выбирают повторяющиеся неизвестные и записывают друг за другом одночлены с одинаковыми множителями;
- в каждой группе находят одинаковый множитель и переносят его за скобку;
- находят общий полином и отделяют его скобками.
Выполнять группировку можно по-разному, но в итоге обязательно должен остаться общий многочлен. Например, выражение 48 * h * e 2 + 32 * h * q — 15 * e 2 — 10 * q2 возможно решить двумя способами.
- Изучив выражение, можно заметить, что во всех членах уравнения повторяются две неизвестные. Выписав их друг за другом, а затем вынеся общий множитель за скобку, можно будет записать: 48 * h * e2 + 15 * e2 + 32 * h * q2 − 1 0 * q2 − 10 * q2 = 3 * e2 (16 * h − 5) + 2 q2 (16 * h — 5) = (16 * h − 5) * (3 * e2 + 2 * q2).
- Во втором способе можно использовать то, что в первых одночленах повторяется неизвестная h. Вынеся её за скобку, получают следующее упрощение: 48 * r * z2 + 32 * r * y2 − 15 * z2 − 10 * y2 = 16 * h * (3 * e2 + 2 q2) − 5 (3 * e2 + 2 q2) = (3 * e2 + 2 * q2) * (16 * h − 5).
Для того чтобы вынести многочлен за скобку, может понадобиться инвертировать все знаки. Следует помнить, что при выносе минуса у всех одночленов, оставшихся под скобкой, знак изменится на противоположный.
Выделение квадрата
По сути, выделение общего квадрата соответствует преобразованию, при котором трёхчлен представляют в виде (k + e)2 или (k — e)2. Метод используется для решения биквадратных уравнений. Для выделения полного квадрата при разложении многочлена на множители применяют две формулы:
- k2 + 2 * k * e + e2 = (k + e)2.
- k2 — 2 * k * e + e2 = (k — e)2.
Например, нужно упростить дробь: (k4 + 4 * e4) / (k4 + 2 * e2 + 2 * k * e). Необходимо разложить числитель, используя формулы для полного квадрата: (k4 + 4 * e4) = (k4 + 4 * e2 * k2 + 4 * e 4). Значит, если отнять от многочлена 4 * k2 * e2, то получится уравнение: (k2 + 2 * e2) * 2 − 4 * k2 * e2. Используя формулу умножения квадратов, верно будет записать: (k2 + 2 e 2 − 2 * k * e) * (k2 + 2 e 2 + 2 * k * e).

Заменив полученным выражением числитель, можно будет его часть взаимно сократить со знаменателем. В итоге получится простое выражение: h3 + 2 * e2 − 2 * h * e.
Неприводимые множители
Решая различные задачи, можно столкнуться со сложными выражениями, которые, как кажется, разложить нельзя. Например, (2 * p2 — 5 * p — 3)/(3 * p — 9). В числителе дроби находится квадратный трёхчлен, который на самом деле можно разложить. Для того чтобы его можно было упростить, используется формула: ar2 + br + p = a (r — r1) * (r — r2), где r1 и r2 корни выражения.
Чтобы найти решения для линейного уравнения, необходимо определить дискриминант. То есть нужно из задачи отделить числитель, найти его решения и подставить найденные значения в формулу разложения.
Для рассматриваемого примера дискриминант квадратного уравнения будет равняться: Д = 25 — 4*2 (-3) = 49. Отсюда p1 = (5 + 7)/4 = 3, p2 = (5 — 7)/4 = -½. Подставив полученные корни в формулу, можно запись: 2 * (p — 3) * (p + ½).
Теперь вместо числителя нужно подставить полученное разложение: (2*p2 — 5*p — 3)/(3*p — 9) = 2*(p — 3) * (p + ½)/3 * (p — 3) = (2 *p + 1)/3.
Использование онлайн-калькуляторов

Порой, для решения сложных заданий нужно затратить много времени. При этом всегда существует риск допустить ошибку при расчётах. Чтобы этого избежать или проверить свой ответ, можно воспользоваться сайтами, предлагающие онлайн-калькуляторы. Использовать их сможет даже пользователь, совершенно не понимающий методов, используемых для упрощения выражений.
Расчёт обычно занимает менее 30 секунд. Приложений для упрощений уравнений достаточно много. Написаны они на Паскале или javascript. Появление ошибки при вычислении невозможно. Нередко на этих сайтах ещё и содержится информация о способах упрощения полиномов.
Для того чтобы получить ответ, необходимо будет с помощью браузера зайти на сайт онлайн-калькулятора и заполнить предлагаемые им поля. После того как упрощаемое выражение будет вписано, следует нажать кнопку «Рассчитать» или «Упростить выражение» и получить ответ с пошаговым решением.
nauka.club


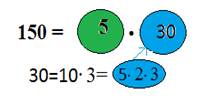
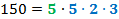
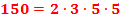
 Наименьшее простое число, на которое делится 216 – это 2.
Наименьшее простое число, на которое делится 216 – это 2. Полученное число 108 делится на 2.
Полученное число 108 делится на 2.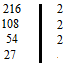 Согласно признаку делимости на 2 число 54 делится на 2.
Согласно признаку делимости на 2 число 54 делится на 2. Число 27 заканчивается на нечетную цифру 7 . Оно
Число 27 заканчивается на нечетную цифру 7 . Оно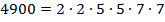
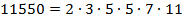
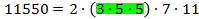
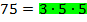


 .
. 75. Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550.
75. Это так, потому что разложение числа 75 полностью содержится в разложении числа 11550.