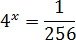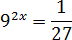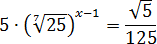Уравнение экспоненты онлайн калькулятор

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Экспонента представляет собой показательную функцию \[y(x) =e^x,\] производная которой равна самой функции. Экспоненту обозначают: \[e^x, exp(x), Exp(x) \]

\[e^x=exp(x)=Exp(x) \]

Экспонента обладает свойствами показательной функции с основанием степени е > 1. Основанием степени экспоненты является число «е». Это иррациональное число. Оно примерно равно:

\[e\approx 2,718281828459045\cdots \]

Выражение числа «е» через предел последовательности. Число «е» можно выразить через предел последовательности. Это, так называемый, второй замечательный предел:

\[e=\lim_{n\to\infty} \left(1+\frac~xn\right)^n\]

Выражение числа е в виде ряда

\[e = 2+1/2!+1/3!+1/3!+ \cdots +1/n!+ \cdots \]

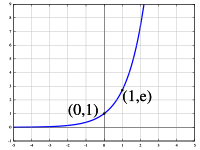
График экспоненты

На графике представлена экспонента, \[e\] в степени \[x:\]

\[y(x) = e^x\]

На графике видно, что экспонента монотонно возрастает.

Так же читайте нашу статью «Решить уравнения с факториалом онлайн решателем»

Что касается основных формул, то они такие же, как и для показательной функции с основанием степени \[е.\]

\[e^p \cdot e^q=e^{p+q}\]

\[ (e^p)^p=e{pq}=(e^p)^p\]

\[e^p=e^{pq}=1/e^p\]

\[e^p/e^q = e^{p-q} \]

Выражение показательной функции через экспоненту:

\[q^x=e^{xln a}\]

Где можно решить уравнение с экспонентой онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Производная e в степени x и показательной функции

Основные формулы

Производная экспоненты равна самой экспоненте (производная e в степени x равна e в степени x):
(1)   ( e ^x )′ = e ^x.

Производная показательной функции с основанием степени a равна самой функции, умноженной на натуральный логарифм от a:
(2)   .

Экспонента – это показательная функция, у которой основание степени равно числу e, которое является следующим пределом:
.
Здесь может быть как натуральным, так и действительным числом. Далее мы выводим формулу (1) производной экспоненты.

Вывод формулы производной экспоненты

Рассмотрим экспоненту, e в степени x:
y = e ^x.
Эта функция определена для всех . Найдем ее производную по переменной x. По определению, производная является следующим пределом:
(3)   .

Преобразуем это выражение, чтобы свести его к известным математическим свойствам и правилам. Для этого нам понадобятся следующие факты:
А) Свойство экспоненты:
(4)   ;
Б) Свойство логарифма:
(5)   ;
В) Непрерывность логарифма и свойство пределов для непрерывной функции:
(6)   .
Здесь – некоторая функция, у которой существует предел и этот предел положителен.
Г) Значение второго замечательного предела:
(7)   .

Применяем эти факты к нашему пределу (3). Используем свойство (4):
;
.

Сделаем подстановку   . Тогда   ; .
В силу непрерывности экспоненты,
.
Поэтому при , . В результате получаем:
.

Сделаем подстановку . Тогда . При , . И мы имеем:
.

Применим свойство логарифма (5):
. Тогда
.

Применим свойство (6). Поскольку существует положительный предел и логарифм непрерывен, то:
.
Здесь мы также воспользовались вторым замечательным пределом (7). Тогда
.

Тем самым мы получили формулу (1) производной экспоненты.

Вывод формулы производной показательной функции

Теперь выведем формулу (2) производной показательной функции с основанием степени a. Мы считаем, что и . Тогда показательная функция
(8)  
Определена для всех .

Преобразуем формулу (8). Для этого воспользуемся свойствами показательной функции и логарифма.
;
.
Итак, мы преобразовали формулу (8) к следующему виду:
.

Находим производную. Выносим постоянную за знак производной:
.
Применяем формулу производной сложной функции:
.
Здесь .

Тем самым, мы нашли производную показательной функции с произвольным основанием степени:
.

Другие способы вывода производной экспоненты

Пусть нам известна формула производной натурального логарифма:
(9)   .
Тогда мы можем вывести формулу производной экспоненты, учитывая, что экспонента является обратной функцией к натуральному логарифму.

Перепишем формулу (9) в следующем виде:
,
где .
Переменные можно обозначать любыми буквами. Поменяем местами x и y:
(10)   ,
где .

Теперь рассмотрим экспоненту (e в степени x):
(11)   .
Применим формулу производной обратной функции:
(12)   .
Обратной функцией к экспоненте является натуральный логарифм. Подставим значение производной натурального логарифма (10):
.
И, наконец, выразим y через x по формуле (11):
.
Формула доказана.

Теперь докажем формулу производной экспоненты, применяя формулу производной сложной функции. Поскольку функции и являются обратными друг к другу, то
.
Дифференцируем это уравнение по переменной x:
(13)   .
Производная от икса равна единице:
.
Применим формулу производной сложной функции:
.
Здесь . Подставим в (13):
.
Отсюда
.

Пример

Найти производные от e в степени 2x, e в степени 3x и e в степени nx. То есть найти производные функций
y = e ^2x,   y = e ^3x   и   y = e ^nx.

Решение

Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции   y = e ^nx. Затем подставим n = 2 и n = 3. И из общей формулы найдем выражения для производных от e ^2x, e ^3x и e ^nx.

Итак, имеем исходную функцию
.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1)   Функции , зависящей от переменной : ;
2)   Функции , зависящей от переменной : .
Тогда исходная функция составлена из функций и :
.

Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции.
.
Здесь мы подставили .

Итак, мы нашли:
.
Подставляем n = 2 и n = 3.

Ответ

;   ;   .

См. также
Все примеры вычисления производных с решениями > > >

Производные высших порядков от e в степени x

Теперь найдем производные высших порядков. Сначала рассмотрим экспоненту:
(14)   .
Мы нашли ее производную первого порядка:
(1)   .

Мы видим, что производная от функции (14) равна самой функции (14). Дифференцируя (1), получаем производные второго и третьего порядка:
;
.

Отсюда видно, что производная n-го порядка также равна исходной функции:
.

Производные высших порядков показательной функции

Теперь рассмотрим показательную функцию с основанием степени a:
.
Мы нашли ее производную первого порядка:
(15)   .

Дифференцируя (15), получаем производные второго и третьего порядка:
;
.

Мы видим, что каждое дифференцирование приводит к умножению исходной функции на . Поэтому производная n-го порядка имеет следующий вид:
.

Автор: Олег Одинцов.     Опубликовано: 27-03-2017

1cov-edu.ru

Натуральный логарифм, функция ln x

Приведены основные свойства натурального логарифма, график, область определения, множество значений, основные формулы, производная, интеграл, разложение в степенной ряд и представление функции ln x посредством комплексных чисел.

Определение

Натуральный логарифм

– это функция   y = ln x, обратная к экспоненте, x = e ^y, и являющаяся логарифмом по основанию числа е:   ln x = log_e x.

Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x)′ = 1/x.

Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045…;
.

График натурального логарифма ln x

График функции y = ln x.

График натурального логарифма (функции y = ln x) получается из графика экспоненты зеркальным отражением относительно прямой y = x.

Натуральный логарифм определен при положительных значениях переменной x. Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x^a с положительным показателем степени a растет быстрее логарифма.

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.

Область определения	0 < x + ∞
Область значений	– ∞ < y < + ∞
Монотонность	монотонно возрастает
Нули, y = 0	x = 1
Точки пересечения с осью ординат, x = 0	нет
	+ ∞
	– ∞

Значения ln x

ln 1 = 0

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе «Логарифм».

Обратная функция

Обратной для натурального логарифма является экспонента.

Если    ,   то   

Если    ,   то    .

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x:
.
Производная n-го порядка:
.
Вывод формул > > >

Интеграл

Интеграл вычисляется интегрированием по частям:
.
Итак,

Выражения через комплексные числа

Рассмотрим функцию комплексной переменной z:
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n.

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов.     Опубликовано: 05-04-2014   Изменено: 20-03-2017

1cov-edu.ru

Простейшие показательные уравнения

5 февраля 2012

Если взять обычную степень и «засунуть» в показатель переменную x , получим показательное уравнение. Таких уравнений великое множество, и для них есть собственные методы решения.

Сегодня мы познакомимся с простейшими конструкциями. Они так и называются — простейшие показательные уравнения (кэп?). Все остальные, как бы сложно они ни выглядели, в итоге сводятся к простейшим. Но это уже материал следующих уроков.

Простейшее показательное уравнение — это уравнение вида:

a ^x = b , где a > 0, a ≠ 1

Такое уравнение не имеет корней при b ≤ 0, а при b > 0 имеет единственный корень: x = log _a b . Более сложные показательные уравнения решаются по следующей схеме:

1. Перевести все степени к одинаковому основанию. Желательно, чтобы оно было целым и минимальным. Например, вместо 4 ^x лучше писать 2^{2 x} , а вместо 0,01 ^x — вообще 10^{−2 x} . Почему — узнаете из примеров;
2. В уравнениях, где есть умножение или деление, надо выполнить эти действия. Напомню: при умножении степеней с одинаковым основанием показатели складываются, при делении — вычитаются;
3. Если все сделано правильно, получим уравнение вида a ^{f ( x )} = a ^{g ( x )}, где a — просто число. Его можно отбросить, поскольку показательная функция монотонна. Получим уравнение f ( x ) = g ( x ), которое легко решается.

Помните, что корни — тоже степени, но с дробным основанием:

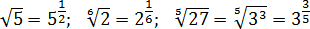
Задача. Решите уравнение:

Итак, приведем все степени к основанию 2:

4 ^x = (2²) ^x = 2^{2 x} ; 1 = 2⁰; 256 = 2⁸

Теперь перепишем исходное уравнение и выполним деление:

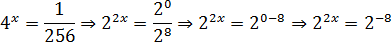
Получили простейшее показательное уравнение. Отбрасываем основание — получаем:

2 x = −8 ⇒ x = −4

Задача. Решите уравнение:

Снова приводим все степени к наименьшему целому основанию:

9^{2 x} = (3²)^{2 x} = 3^{4 x} ; 1 = 3⁰; 27 = 3³

Обратите внимание: число 27 не является целой степенью девятки. Именно поэтому надо приводить все степени к основанию 3, а не 9. Возвращаемся к исходному уравнению:

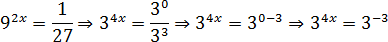
Осталось избавиться от основания степени:

4 x = −3 ⇒ x = −3/4 = −0,75

Задача. Решите уравнение:

В уравнении присутствуют сразу 4 множителя, которые надо перевести в степени с одинаковым основанием:

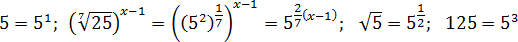
Учитывая эти факты, перепишем исходное уравнение:

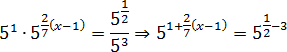
Избавимся от основания — и после приведения дробей к общему знаменателю получим классическую пропорцию:

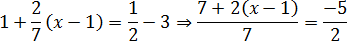
Дальше все стандартно: произведение крайних элементов пропорции равно произведению средних. Имеем:

14 + 4 x − 4 = −35 ⇒ 4 x = −45 ⇒ x = −45 : 4 = −11,25

Ниже даны 12 тренировочных задач. Если что-то не получается — ничего страшного, потому что есть второй вариант этого теста (см. «Простейшие показательные уравнения — 2 вариант»). Попробуйте решить его.

Смотрите также:

1. Тест: простейшие показательные уравнения (2 вариант)
2. Показательные уравнения с логарифмами
3. Тест на тему «Значащая часть числа»
4. Сводный тест по задачам B12 (1 вариант)
5. Задача 18: метод симметричных корней
6. Задача B4: Скачать файл на разной скорости

www.berdov.com

Экспоненциальная функция — Exponential function

Естественная экспоненциальная функция у = е ^х 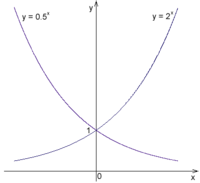Показательные функции с основаниями 2 и 1/2

В математике , экспоненциальная функция является функцией вида

е(Икс)знак равноaбИкс,{\ Displaystyle F (X) = аб ^ {х},}

где Ь является положительным действительным числом, и в котором аргумент х имеет место в качестве показателя. Для действительных чисел с и д, функция формы также является экспоненциальной функция, так как она может быть переписана в виде е(Икс)знак равноaбсИкс+d{\ Displaystyle F (X) = аб ^ {сх + d}}

aбсИкс+dзнак равно(aбd)(бс)Икс,{\ Displaystyle аб ^ {сх + d} = \ влево (аb ^ {d} \ справа) \ влево (Ь {с} \ справа) ^ {х}.}

Как функции действительного переменного, экспоненциальные функции однозначно характеризуется тем фактом , что скорость роста такой функции (то есть, его производное ) является прямо пропорционально к значению функции. Константа пропорциональности этих отношений является натуральный логарифм базового б :

ddИксбИксзнак равнобИксжурнале⁡б,{\ Displaystyle {\ гидроразрыва {d} {дх}} В ^ {х} = {Ь ^ х} \ лог _ {е} Ь.}

При б = 1 реальный экспоненциальная функция является постоянной , а производная равна нулю , так как для положительных а и б > 1 действительные экспоненциальные функции монотонно возрастает (как изображено для Ь = е и Ь = 2 ), поскольку производная больше нуль для всех аргументов, и б <1 они монотонно убывают (как изображены на Ь = 1 / 2 ), поскольку производная меньше нуля для всех аргументов. журнале⁡бзнак равно0,{\ Displaystyle \ лог _ {е} Ь = 0}

Константа е = 2,71828 … является уникальной базой для которой константа пропорциональности равна 1, так что производная этой функции является самим собой:

ddИксеИксзнак равноеИксжурнале⁡езнак равноеИкс,{\ Displaystyle {\ гидроразрыва {d} {дх}} е ^ {х} = е ^ {х} \ лог _ {е} е = е ^ {х}.}

Так как изменение базы экспоненциальной функции только приводит к появлению дополнительного постоянного множителя, вычислительно удобно свести изучение показательной функции в математическом анализе к изучению этой конкретной функции, обычно называют «естественной экспоненциальной функцией», или просто «экспоненциальная функция» и обозначается

Икс↦еИкс{\ Displaystyle х \ mapsto е ^ {х}} или же Икс↦ехр⁡(Икс),{\ Displaystyle х \ mapsto \ ехр (х).}

Хотя оба обозначения являются общими, бывшим обозначение обычно используется для простых показателей, в то время как последние, как правило, используются, когда показатель является сложным выражением.

Экспоненциальная функция удовлетворяет фундаментальному мультипликативный идентичности

еИкс+Yзнак равноеИксеY,{\ Displaystyle е ^ {х + у} = е ^ {х} е ^ {у}} для всех Икс,Y∈р,{\ Displaystyle х, у \ в \ mathbb {R}.}

Это тождество распространяется комплекснозначными показатели. Можно показать , что каждое непрерывное, ненулевое решением функционального уравнения является экспоненциальной функцией, с Фундаментальной мультипликативной идентичностью, наряду с определением числа е как е ¹ , показывает , что для положительных целых чисел п и относится экспоненциальная функция к элементарное понятие потенцирования. е(Икс+Y)знак равное(Икс)е(Y){\ Displaystyle Р (х + у) = F (X) F (Y)}е:р→р, Икс↦бИкс,{\ Displaystyle F: \ mathbb {R}, \ в \ mathbb {R}, \ х \ mapsto Ь {х},}б>0.{\ Displaystyle Ь> 0.}еNзнак равное×⋯×е⏟N термины{\ Displaystyle е ^ {п} = \ underbrace {е \ время \ cdots \ раз е} _ {п {\ текст {условия}}}}

Аргумент экспоненциальной функции может быть любым реальным или комплексным числом или даже совершенно другой вид математического объекта (например, матрица).

Его повсеместное явление в чистой и прикладной математике привело математик У. Рудин к полагает , что экспоненциальная функция является «наиболее важной функцией в математике». В прикладных настройках, экспоненциальные функции модели отношения , в которых постоянное изменение в независимой переменной дает тот же пропорциональное изменение (то есть процентное увеличение или уменьшение) в зависимой переменной. Это происходит широко в области естественных и общественных наук; Таким образом, экспоненциальная функция также появляется в различных контекстах в рамках физики , химии , машиностроения , математической биологии и экономики .

График , из является восходящим, и увеличивает быстрее , так как х возрастает. График , всегда лежит выше х Оу , но может быть сколь угодно близко к нему для отрицательных х ; таким образом, х Оу представляет собой горизонтальную асимптоту . Наклон от касательной к графике в каждой точке равен его у -координаты в этой точке, как следует из ее производной функции ( смотрите выше ). Его обратная функция является натуральный логарифм , обозначенная или из — за этого, некоторые старые тексты относятся к экспоненциальной функции , как антилогарифм . Yзнак равноеИкс{\ Displaystyle у = е ^ {х}}журнал,{\ Displaystyle \ лог} пер,{\ Displaystyle \ пер}журнале;{\ Displaystyle \ лог _ {е};}

Формальное определение

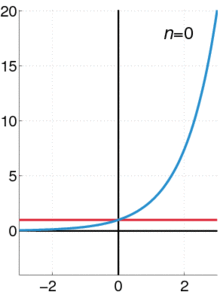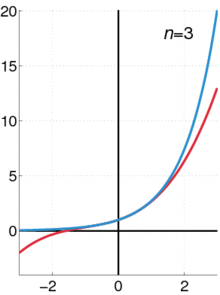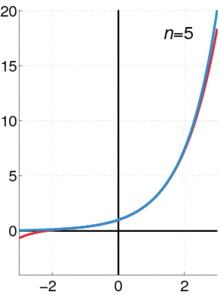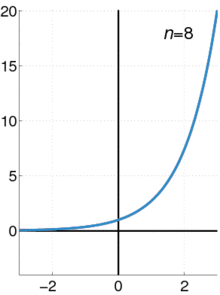Экспоненциальная функция (синим цветом), а сумма первого п + 1 с точки зрения его степенной ряд (в красном цвете).

Реальная экспоненциальная функция может быть охарактеризована различными эквивалентными способами. Чаще всего, она определяется по следующей степенной ряд : ехр:р→р{\ Displaystyle \ ехр: \ mathbb {R}, \ в \ mathbb {R}}

ехр⁡(Икс)знак равноΣКзнак равно0∞ИксКК!знак равно1+Икс+Икс22+Икс36+Икс424+⋯{\ Displaystyle \ ехр (х): = \ сумма _ {к = 0} ^ {\ infty} {\ гидроразрыва {х ^ {к}} {k}} = 1 + х + {\ гидроразрыва {х ^ {2 }} {2}} + {\ гидроразрыва {х ^ {3}} {6}} + {\ гидроразрыва {х ^ {4}} {24}} + \ cdots}

Так как радиус сходимости этого степенного ряда является бесконечным, этим определением является, по сути, применимо ко всем комплексным числам (см ниже для расширения на комплексную плоскость). Константа е , то может быть определена какZ∈С{\ Displaystyle г \ в \ mathbb {C}}ехр⁡(Икс){\ Displaystyle \ ехр (х)}езнак равноехр⁡(1)знак равноΣКзнак равно0∞(1/К!),{\ TextStyle е = \ ехр (1) = \ сумма _ {к = 0} ^ {\ infty} (1 / к!).}

Термин-на-перспектива дифференциация этого степенного ряда показывает , что для всех действительных х , что приводит к другой общей характеристике из , как единственное решения дифференциального уравнения(d/dИкс)(ехр⁡Икс)знак равноехр⁡Икс{\ Displaystyle (д / дх) (\ ехр х) = \ ехр х}ехр⁡(Икс){\ Displaystyle \ ехр (х)}

Y'(Икс)знак равноY(Икс),{\ Displaystyle у ‘(х) = у (х),}

удовлетворяющее начальному условию Y(0)знак равно1.{\ Displaystyle у (0) = 1.}

Основываясь на этой характеристике, то цепное правило показывает , что ее обратная функция, то натуральный логарифм , удовлетворяет для или Это соотношение приводит к менее общее определение реальной экспоненциальной функции в качестве решения для уравнения (d/dY)(журнале⁡Y)знак равно1/Y{\ Displaystyle (д / д) (\ _ {войти е} у) = 1 / у}Y>0,{\ Displaystyle у> 0}журнале⁡Yзнак равно∫1Y1TdT,{\ TextStyle \ лог _ {е} у = \ int _ {1} ^ {у} {\ гидроразрыва {1} {т}} \, дт.}ехр⁡(Икс){\ Displaystyle \ ехр (х)}Y{\ Displaystyle у}

Иксзнак равно∫1Y1TdT,{\ Displaystyle х = \ int _ {1} ^ {у} {\ гидроразрыва {1} {т}} \, дт.}

По пути биномиальной теоремы и определения степенного ряда, экспоненциальная функция также может быть определена как следующий лимит:

еИксзнак равноИтN→∞(1+ИксN)N,{\ Displaystyle е ^ {х} = \ Нт _ {п \ к \ infty} \ влево (1 + {\ гидроразрыва {х} {п}} \ справа) ^ {п}.}

обзор

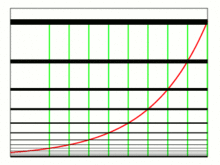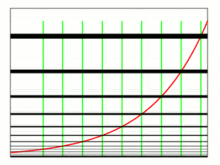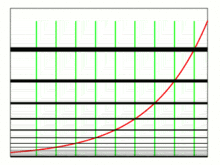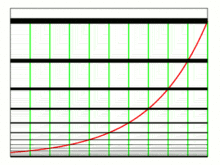Красная кривая является экспоненциальной функцией. Черные горизонтальные линии показывают, где она пересекает зеленые вертикальные линии.

Экспоненциальная функция возникает всякий раз , когда величина возрастает или убывает со скоростью , пропорциональной его текущим значением. Одна такая ситуация постоянно усугубляется интерес , и на самом деле это было такое наблюдение , что привело Якоба Бернулли в 1683 году к числу

ИтN→∞(1+1N)N{\ Displaystyle \ Нт _ {п \ к \ infty} \ влево (1 + {\ гидроразрыва {1} {п}} \ справа) ^ {п}}

В настоящее время известно , как е . Позже, в 1697 году, Иоганн Бернулли изучал исчисление экспоненциальной функции.

Если основная сумма 1 получает проценты по годовой ставке х усугубляется ежемесячно, то проценты , полученных каждый месяц х / 12 раз текущего значения, так что каждый месяц суммарного значения умножаются на (1 + х / 12 ) , и значение в конце года составляет (1 + х / 12 ) ¹² . Если вместо того, чтобы интерес усугубляется ежедневно, это становится (1 + х / 365 ) ³⁶⁵ . Позволить количество временных интервалов в год растут без связанных приводит к пределу определения показательной функции,

ехр⁡(Икс)знак равноИтN→∞(1+ИксN)N{\ Displaystyle \ ехр (х) = \ Пт _ {п \ к \ infty} \ влево (1 + {\ гидроразрыва {х} {п}} \ справа) ^ {п}}

впервые дано Леонард Эйлер . Это одна из ряда характеристик показательной функции ; другие включают серию или дифференциальные уравнения .

Из любого из этих определений , можно показать , что экспоненциальная функция подчиняется основной возведения в степень идентичности,

ехр⁡(Икс+Y)знак равноехр⁡(Икс)⋅ехр⁡(Y){\ Displaystyle \ ехр (х + у) = \ ехр (х) \ CDOT \ ехр (у)}

что оправдывает обозначение е ^х .

Производная (скорость изменения) экспоненциальной функции сама является экспоненциальной функцией. В более общем смысле , функция со скоростью изменения , пропорциональной к самой функции (а не равна ей) выражается в терминах экспоненциальной функции. Это свойство функции приводит к экспоненциальному росту или экспоненциальному распаду .

Показательная функция продолжается до целой функции на комплексной плоскости . Формула Эйлера относится его значение в чисто мнимых аргументах тригонометрических функций . Экспоненциальная функция также имеет аналогов , для которых аргумент является матрицей , или даже элемент банаховой алгебры или алгебры Ли .

Производные и дифференциальные уравнения

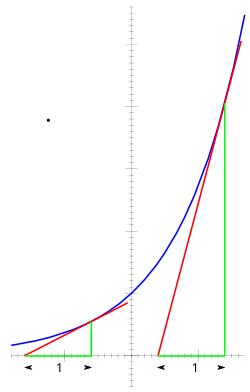Производная показательной функции равна значению функции. Из любой точки Р на кривой (синий), пусть касательную линию (красный), а вертикальная линия (зеленый) с высотой ч быть нарисованы, образуя прямоугольный треугольник с базовой Ь на х Оу. Так как наклон красной касательной линии (производной) при Р равен отношению высоты треугольника к основанию треугольника (рост в течение пробега), а производная равна значению функции, ч должна быть равна отношение ч к б . Поэтому базовые б всегда должны быть 1.

Значение экспоненциальной функции в области математики и науки проистекает главным образом из его определения в качестве уникальной функцией , которая равна ее производной и равен 1 , когда х = 0 . То есть,

ddИксеИксзнак равноеИкса такжее0знак равно1.{\ Displaystyle {\ гидроразрыва {d} {дх}} е ^ {х} = е ^ {х} \ четырехъядерных {\ текст {и}} \ четырехъядерных е ^ {0} = 1.}

Функции вида с ^х для постоянная C являются единственными функциями, которые равны их производного (по теореме Пикара-Линделёф ). Другие способы сказать то же самое , включают в себя:

Если скорость роста или гниения к переменной, пропорционально его размеру, как это бывает в неограниченном росте населения (см Мальтуса катастрофы ), постоянно усугубляются интерес , или радиоактивный распад -Тогда переменный может быть записана в виде постоянная раз экспоненциальной функции времени , Явный для любого действительных постоянных к , функции F : R → R удовлетворяет ф ‘= КФ тогда и только тогда , когда F ( х ) = с ^км для некоторой константы с .

Кроме того, для любой дифференцируемой функции F ( х ) , мы находим, по правилу цепи :

ddИксее(Икс)знак равное'(Икс)ее(Икс),{\ Displaystyle {\ гидроразрыва {d} {дх}} е ^ {F (X)} = Р ‘(х) е ^ {Р (х)}.}

Непрерывные дроби для е ^х

Непрерывная дробь для х ^х может быть получена с помощью тождества Эйлера :

еИксзнак равно1+Икс1-ИксИкс+2-2ИксИкс+3-3ИксИкс+4-⋱{\ Displaystyle е ^ {х} = 1 + {\ cfrac {х} {1 — {\ cfrac {х} {х + 2 — {\ cfrac {2x} {х + 3 — {\ cfrac {3x} {х + 4- \ ddots}}}}}}}}}

Ниже обобщаются цепная дробь для е ^г сходится быстрее:

еZзнак равно1+2Z2-Z+Z26+Z210+Z214+⋱{\ Displaystyle е ^ {г} = 1 + {\ cfrac {2z} {2z + {\ cfrac {г ^ {2}} {6 + {\ cfrac {г ^ {2}} {{10 + \ cfrac {г ^ {2}} {14+ \ ddots}}}}}}}}}

или, применяя подстановку г = х / у :

еИксYзнак равно1+2Икс2Y-Икс+Икс26Y+Икс210Y+Икс214Y+⋱{\ Displaystyle е ^ {\ гидроразрыва {х} {у}} = 1 + {\ cfrac {2x} {2y-х + {\ cfrac {х ^ {2}} {6y + {\ cfrac {х ^ {2}} {10у + {\ cfrac {х ^ {2}} {14Y + \ ddots}}}}}}}}}

с особым случаем для г = 2 :

е2знак равно1+40+226+2210+2214+⋱знак равно7+25+17+19+111+⋱{\ Displaystyle е ^ {2} = 1 + {\ cfrac {4} {0 + {\ cfrac {2 ^ {2}} {6 + {\ cfrac {2 ^ {2}} {10 + {\ cfrac { 2 ^ {2}} {14+ \ ddots \,}}}}}}}} = 7 + {\ cfrac {2} {{5 + \ cfrac {1} {7 + {\ cfrac {1} {9 + {\ cfrac {1} {11+ \ ddots \,}}}}}}}}}

Эта формула также сходится, хотя и более медленно, для г > 2 . Например:

е3знак равно1+6-1+326+3210+3214+⋱знак равно13+547+914+918+922+⋱{\ Displaystyle е ^ {3} = 1 + {\ cfrac {6} {- 1 + {\ cfrac {3 ^ {2}} {6 + {\ cfrac {3 ^ {2}} {10 + {\ cfrac {3 ^ {2}} {14+ \ ddots \,}}}}}}}} = {13 + \ cfrac {54} {7 + {\ cfrac {9} {14 + {\ cfrac {9} { 18 + {\ cfrac {9} {22+ \ ddots \,}}}}}}}}}

Комплексная плоскость

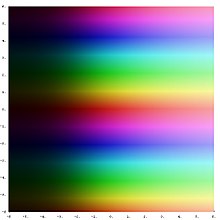Показательная функция на комплексной плоскости. Переход от темного до светлого цвета показывает , что величина экспоненциальной функции увеличивается вправо. Периодические горизонтальные полосы показывают , что экспоненциальная функция является периодической в мнимой части его аргумента.

Как и в реальном случае, экспоненциальная функция может быть определена на комплексной плоскости в нескольких эквивалентных формах. Наиболее общее определение комплексной экспоненциальной функции параллельно определение степенного ряда для реальных аргументов, где действительные переменным заменяются сложным:

ехр⁡(Z)знак равноΣКзнак равно0∞ZКК!{\ Displaystyle \ ехр (г): = \ сумма _ {к = 0} ^ {\ infty} {\ гидроразрыва {г ^ {к}} {k}}}

Term-накрест умножение двух копий этих степенных рядов в Кошах смысла, разрешенных теоремами Мертенса , показывает , что определяющее мультипликативное свойство показательной функции продолжает выполняться для всех комплексных аргументов:

ехр⁡(вес+Z)знак равноехр⁡(вес)ехр⁡(Z){\ Displaystyle \ ехр (ш + Z) = \ ехр (ш) \ ехр (г)} для всех вес,Z∈С{\ Displaystyle ш, г \ в \ mathbb {C}}

Определение комплексной экспоненциальной функции , в свою очередь , приводит к соответствующим определениям , проходящим в тригонометрических функции сложных аргументов.

В частности, когда ( реальный), определение серии дает разложение Zзнак равнояT{\ Displaystyle г = это}T{\ Displaystyle т}

ехр⁡(яT)знак равно(1-T22!+T44!-T66!+⋯)+я(T-T33!+T55

ru.qwertyu.wiki

А) Разложение экспоненты

Для всех имеет место равенство

Для доказательства равенства (2) убеждаемся, что

при любом фиксированном и любых величинах. Далее применяем предложение предыдущего параграфа. По другому докажем равенство (2):как функция , так и сумма ряда в (2) — решения дифференциального уравнения с начальным условием y(0)=1. Из теоремы единственности решения дифференциального уравнения следует, что в этом случае функции совпадают.

2. Б) Разложение гармоник

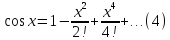
Равенства (3) и (4) можно доказать так же как и для экспоненты, доказав, что остаток в разложении по формуле Маклорена стремится к нулю при . По другому, можно рассуждать так: рассмотрим дифференциальное уравнение с начальными условиями y(0)=0, y'(0)=1 для функции sin x и y(0)=1, y'(0)=0 для функции cos x. Тогда ряды (3) и (4) также как и функции — решения этого диф. уравнения с указанными начальными условиями. По теореме единственности решения диф. уравнения с заданными начальными условиями, получаем совпадение гармоник с рядами (3) и (4). Можно поступить и иначе: подставить в разложение (2) вместо чисто мнимое число, а далее приравнять действительные и мнимые части — получим в точности (3) и (4).

Заметим, что во всех трех равенствах (2),(3),(4) радиус сходимости ряда, стоящего справа равен бесконечности, т.е. разложения имеют место на всей числовой оси.

13. ???Приближенные вычисления, вычисления определенных интегралов и решения дифференциальных уравнений с помощью рядов.

Вычислим интеграл :

Решим дифференциальное уравнение c начальным условием 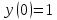. Полагаяи подставляя этот ряд в дифференциальное уравнение, а затем почленно интегрируя, а затем приравнивая коэффициенты при одинаковых степенях, получим

Так как , то последовательно находим коэффициенты,и т.д.. Получаем. Полученный ряд имеет бесконечный радиус сходимости. Это оправдывает операцию почленного дифференцирования при любом.

1. Общие понятия (определение дифференциального уравнения, решения, порядка, нормальной формы записи). Дифференциальные уравнения 1-го порядка, задача Коши, теорема существования и единственности.

Дифференциа́льное уравне́ние — уравнение, связывающее значение производной функции с самой функцией, значениями независимой переменной, числами (параметрами).

В этом разделе мы будем решать уравнения, неизвестным в которых ответом является функция. В разделе «Неопределенный интеграл» мы фактически занимались решением уравнения

Требовалось найти такую функцию-первообразную , производная которой тождественно равна. Решений у уравнения (1) бесконечно много, и все они отличаются друг от друга на константу. Эту множественность решений можно обозревать и с другой точки зрения. Фиксируем значение первообразной в определенной точке:

Считаем начальными условиями. Тогда для непрерывной функции, заданной на интервалеи начальных условий

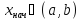c условием существует и единственно решениеуравнения (1), удовлетворяющее соотношению (2). Более того, ответ задается формулой

Сформулирована теорема существования и единственности для дифференциального уравнения самого простого вида. Рассмотрим теперь уравнение вида

Его полное название – обыкновенное дифференциальное уравнение первого порядка в нормальной форме. Обыкновенное, так как неизвестная функция зависит лишь от одной переменной, в отличии, например, от уравнения Лапласа

Первого порядка – так как старшая производная, входящая в уравнение (4) имеет первый порядок. Нормальная форма записи дифференциального уравнения означает, что старшая производная выражена через младшие производные, а также саму неизвестную функцию, а также переменную. Таким образом,

есть дифференциальное уравнение второго порядка в нормальной форме, а

есть общий вид дифференциального уравнения n-го порядка в нормальной форме. Решение уравнений вида (4) составляет основную задачу данной темы. При этом функция называется (частным) решением уравнения (4) или (6), если при подстановки вместо

в это уравнение получаем тождество.

Задача решения дифференциального уравнения с заданными начальными условиями называется задачей Коши. Начальные условия для уравнения (6) задаются рядом чисел и выглядят так

Теорема существования и единственности. Если в дифференциальном уравнении первого порядка(4) функция вместе со своей частной производнойнепрерывны в области, содержащейкак свою внутреннюю точку, то найдется интервал

для которого, существует и единственно решениезадачи Коши.

Общая теорема для уравнения n-го порядка (6) гласит, что если функция вместе со всеми своими частными производными по второй, третьей и т.д. поn-ой переменной непрерывны в пространственной области , содержащей точку, то локальное решение задачи Коши существует и единственно.

2. Дифференциальные уравнения 1-го порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка.

studfile.net

Экспонента — это… Что такое Экспонента?

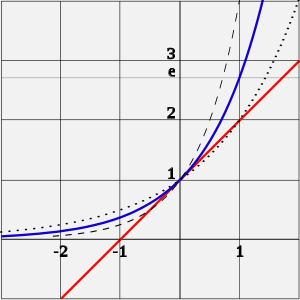
Экспонента — показательная функция , где e — основание натуральных логарифмов ().

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:

или через предел:

Здесь x — любое комплексное число.

Свойства

• , в частности
• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
• Экспонента является выпуклой функцией.
• Обратная функция к ней — натуральный логарифм .
• Фурье-образ экспоненты не существует
• однако преобразование Лапласа существует
• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
• Основное функциональное свойство экспоненты, как и всякой показательной функции:

  .

  • Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид , где c — некоторая константа.

Комплексная экспонента

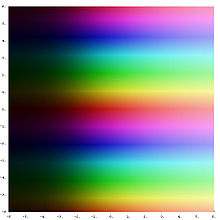График экспоненты в комплексной плоскости.
Легенда

Комплексная экспонента — математическая функция, задаваемая соотношением , где есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты вещественного переменного :

Определим формальное выражение

.

Определенное таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции , то есть показать, что разлагается в некоторый сходящийся к данной функции ряд. Покажем это:

Сходимость данного ряда легко доказывается:

.

Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция всюду определена и аналитична.

Свойства

Вариации и обобщения

Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

Определённый таким образом ряд сходится для любого оператора с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием имеет своим решением

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм. Обозначается :

См. также

Литература

• Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.
• Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.

dic.academic.ru