Вычисление длины (модуля) вектора в MS EXCEL. Примеры и методы

Найдем длину вектора по его координатам (в прямоугольной системе координат), по координатам точек начала и конца вектора и по теореме косинусов (задано 2 вектора и угол между ними).

Вектор – это направленный отрезок прямой. Длина этого отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора.

1. Вычисление длины вектора по его координатам

Если даны координаты вектора в плоской (двухмерной) прямоугольной системе координат, т.е. известны a_x и a_y, то длину вектора можно найти по формуле

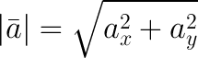
В случае вектора в пространстве добавляется третья координата

В MS EXCEL выражение =КОРЕНЬ(СУММКВ(B8:B9)) позволяет вычислить модуль вектора (предполагается, что координаторы вектора введены в ячейки B8:B9, см. файл примера).

Функция СУММКВ() возвращает сумму квадратов аргументов, т.е. в данном случае эквивалентна формуле =B8*B8+B9*B9.

В файле примера также вычислена длина вектора в пространстве.

Альтернативной формулой является выражение =КОРЕНЬ(СУММПРОИЗВ(B8:B9;B8:B9)).

2. Нахождение длины вектора через координаты точек

Если вектор задан через координаты точек его начала и конца, то формула будет другой =КОРЕНЬ(СУММКВРАЗН(C28:C29;B28:B29))

В формуле предполагается, что координаты точек начала и конца введены в диапазоны C28:C29 и B28:B29 соответственно.

Функция СУММКВРАЗН() возвращает сумму квадратов разностей соответствующих значений в двух массивах.

По сути, в формуле сначала вычисляются координаты вектора (разности соответствующих координат точек), затем вычисляется сумма их квадратов.

3. Нахождение длины вектора по теореме косинусов

Если требуется найти длину вектора по теореме косинусов, то обычно заданы 2 вектора (их модули и угол между ними).

Найдем длину вектора с используя формулу =КОРЕНЬ(СУММКВ(B43:C43)-2*B43*C43*COS(B45))

В ячейках B43:B43 содержатся длины векторов а и b, а в ячейке В45 — угол между ними в радианах (в долях числа ПИ()).

Если угол задан в градусах, то формула будет немного отличаться =КОРЕНЬ(B43*B43+C43*C43-2*B43*C43*COS(B46*ПИ()/180))

Примечание: для наглядности в ячейке со значением угла в градусах можно применить пользовательский формат, см. например, статью Отображение широты и долготы в MS EXCEL

4. Нахождение длины вектора через координаты точек треугольника

Пусть заданы 3 точки треугольника, образованного векторами.

Найдем длину вектора ВС через координаты соответствующих точек (аналогично 2-й задаче, рассмотренной выше) по формуле =КОРЕНЬ(СУММКВРАЗН(C54:C55;D54:D55)).

Зная координаты точек можно найти все длины сторон (длины векторов) и углы треугольника (по теореме косинусов).

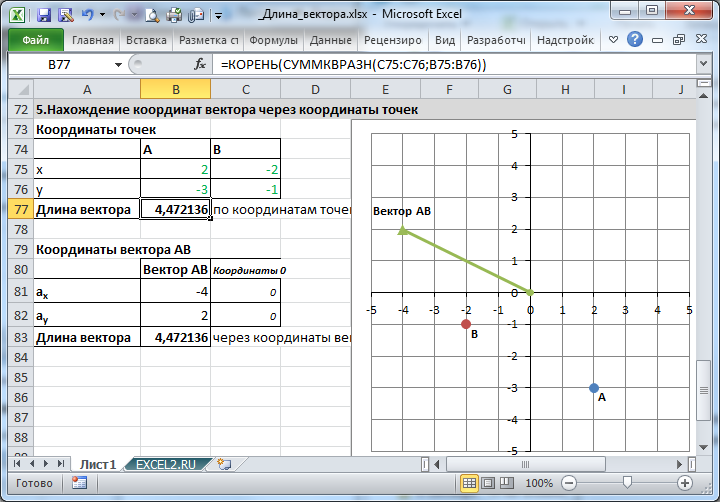
5. Нахождение координат вектора через координаты точек

Сделаем в MS EXCEL удобную форму для вычисления координат вектора и его длины через координаты точек. Также отобразим как сами точки, так и сам вектор.

excel2.ru

Координаты векторов. Операции с векторами.. Видеоурок. Геометрия 9 Класс

Можно встретить удачные и неудачные жилые массивы: в первых ветра практически нет, независимо от погоды, а во вторых, наоборот, есть почти всегда. Это зависит от того, были ли учтены при проектировании направление и сила ветра, который преимущественно дует в данном районе. Эту информацию нужно использовать при строительстве не только жилых районов, но и аэродромов, дорог и т. д.

Чтобы ее получить, на основании многолетних наблюдений, наносят направления ветра на так называемую розу ветров (см. рис. 1). Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки

 (см. рис. 2).

Рис. 1. Роза ветров

Рис. 2. Чем чаще дует ветер в данном направлении, тем дальше соответствующая точка от точки

Рассмотрим декартову систему координат с центром в точке

 на плоскости. Соединяя точку  с точкой розы ветров вдоль выбранного направления  получаем вектор, который называется радиус-вектором (см. рис. 3) (чем длиннее радиус-вектор, тем чаще ветер в данной местности дует вдоль его направления).

Рис. 3. Радиус-вектор

Название «радиус-вектор» понятно – как и радиус окружности, начало любого радиус-вектора зафиксировано в одной точке, центре (начале координат) (см. рис. 4).

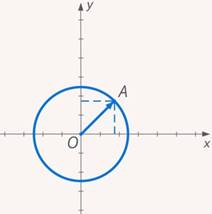
Рис. 4. Начало любого радиус-вектора зафиксировано в начале координат

Как описать этот вектор алгебраически? Любой точке на плоскости будет соответствовать ровно один радиус-вектор (см. рис. 5) (говорят, что точка  и радиус-вектор  однозначно задают друг друга).

Рис. 5. Любой точке на плоскости соответствует ровно один радиус-вектор

Сама же точка однозначно задается своими координатами. Т. е. координаты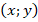

 точки  задают и саму точку, и радиус-вектор  (см. рис. 6).

Рис. 6. Координаты 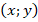 точки  задают и саму точку, и радиус-вектор

Но тогда почему бы координаты точки

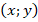 не принять и за координаты радиус-вектора ? Именно так мы и поступим. Будем называть координатами радиус-вектора координаты  его конца :

Мы говорили, что векторы равны (см. рис. 7), если у них равны длины и они сонаправлены:

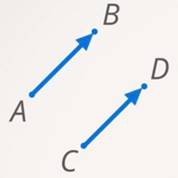
Рис. 7. Равные векторы 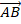 и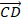

Понятно, что у равных векторов должны быть равны и координаты:

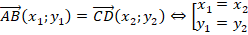
Рассмотрим произвольный вектор  (см. рис. 8).

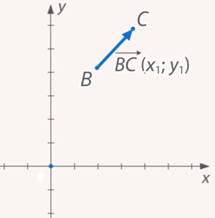
Рис. 8. Произвольный вектор

Построим вектор  так, чтобы:

Получаем параллелограмм  (см. рис. 9) (по признаку – две противоположные стороны равны и параллельны).

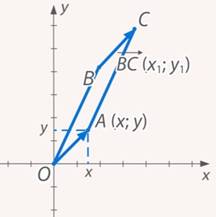
Рис. 9. Параллелограмм

Векторы 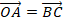 (по построению), значит, координаты вектора  равны координатам радиус-вектора  и, соответственно, равны координатам точки :

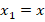
Как видим, любому вектору на плоскости можно поставить в соответствие упорядоченную пару чисел – его координаты.

Понятно, что координаты вектора должны однозначно определяться координатами его конца и начала (т. к. начало и конец задают сам вектор).Попробуем определить, как именно.

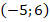Пусть точки  и  из нашего предыдущего примера имеют координаты, соответственно,  и 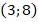. Вычислим координаты точки , такой что радиус-вектор 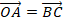 (см. рис. 10).

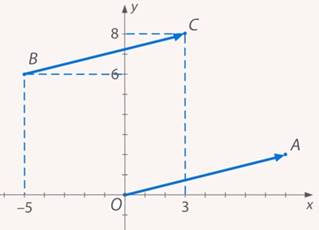
Рис. 10. Радиус-вектор , где ,

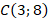
Чтобы из точки  попасть в точку , нужно передвинуться на 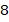 единиц вправо и на  вверх (см. рис. 11).

Рис. 11. Путь из точки  в точку

Такое же перемещение из начала координат приведет нас в точку 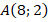 (см. рис. 12).

Рис. 12. Путь из точки 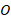 в точку

Значит, координаты радиус-вектора . Тогда и координаты равного ему вектора .

Уберем вспомогательный радиус-вектор  и попробуем определить координаты вектора  без его помощи. Чтобы переместиться их точки  в точку , нам нужно переместиться на 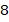 единиц вправо и на  вверх – это и будут координаты вектора  (см. рис. 13).

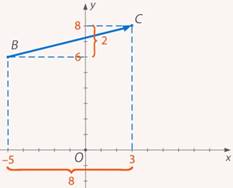
Рис. 13. Чтобы переместиться их точки  в точку , нужно переместиться на 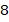 единиц вправо и на  вверх

---

 

Связанные и свободные векторы

Чтобы определить координаты радиус-вектора , нам было достаточно двух чисел – координат точки . Чтобы определить координаты произвольного вектора  – уже четыре числа: координаты точек  и . Есть ли в этом противоречие?

Конечно, нет. В определении радиус-вектора уже «спрятаны» две дополнительные координаты – его начало всегда совпадает с точкой , координаты которой мы знаем –

interneturok.ru

Как найти длину вектора

Понятие длины вектора

Для того, чтобы разобраться с понятием длины вектора, прежде всего надо разобрать само понятие вектора. Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.

Определение 1

Отрезком будем называть часть прямой, которая имеет две границы в виде точек.

Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.

Определение 2

Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.

Обозначение: Двумя буквами: $\overline{AB}$ – (где $A$ его начало, а $B$ – его конец).

Одной маленькой буквой: $\overline{a}$ (рис. 1).

Введем теперь, непосредственно, понятие длин вектора.

Определение 3

Длиной вектора $\overline{a}$ будем называть длину отрезка $a$.

Обозначение: $|\overline{a}|$

Понятие длины вектора связано, к примеру, с таким понятием, как равенство двух векторов.

Определение 4

Два вектора будем называть равными, если они удовлетворяют двух условиям: 1. Они сонаправлены; 1. Их длины равны (рис. 2).

Для того, чтобы определять векторы вводят систему координат и определяют координаты для вектора во введенной системе. Как мы знаем, любой вектор можно разложить в виде $\overline{c}=m\overline{i}+n\overline{j}$, где $m$ и $n$ – действительные числа, а $\overline{i}$ и $\overline{j}$ — единичные векторы на оси $Ox$ и $Oy$, соответственно.

Определение 5

Коэффициенты разложения вектора $\overline{c}=m\overline{i}+n\overline{j}$ будем называть координатами этого вектора во введенной системе координат. Математически:

$\overline{c}={m,n}$

Как найти длину вектора?

Для того, чтобы вывести формулу для вычисления длины произвольного вектора по данным его координатам рассмотрим следующую задачу:

Пример 1

Дано: вектор $\overline{α}$, имеющий координаты ${x,y}$. Найти: длину этого вектора.

Решение.

Введем на плоскости декартову систему координат $xOy$. От начал введенной системы координат отложим $\overline{OA}=\overline{a}$. Построим проекции $OA_1$ и $OA_2$ построенного вектора на оси $Ox$ и $Oy$, соответственно (рис. 3).

Построенный нами вектор $\overline{OA}$ будет радиус вектором для точки $A$, следовательно, она будет иметь координаты ${x,y}$, значит

$[OA_1 ]=x$, $[ OA_2]=y$

Теперь мы легко можем найти искомую длину с помощью теоремы Пифагора, получим

$|\overline{α}|^2=[OA_1]^2+[OA_2]^2$

$|\overline{α}|^2=x^2+y^2$

$|\overline{α}|=\sqrt{x^2+y^2}$

Ответ: $\sqrt{x^2+y^2}$.

Вывод: Чтобы найти длину вектора, у которого задан его координаты, необходимо найти корень из квадрата суммы этих координат.

Пример задач

Пример 2

Найдите расстояние между точками $X$ и $Y$, которые имеют следующие координаты: $(-1,5)$ и $(7,3)$, соответственно.

Решение.

Любые две точки можно легко связать с понятием вектора. Рассмотрим, к примеру, вектор $\overline{XY}$. Как мы уже знаем, координаты такого вектора можно найти, вычтя из координат конечной точки ($Y$) соответствующие координаты начальной точки ($X$). Получим, что

$\overline{XY}=(7+1,3-5)=(8,-2)$

Теперь, найдя длину этого вектора по формуле, выведенной выше, мы и получим искомую длину. Получим:

$d=\sqrt{8^2+(-2)^2}=\sqrt{64+4}=\sqrt{68}=2\sqrt{17}$

Ответ: $2\sqrt{17}$.

Замечание 1

Из этой задачи можно вывести формулу для вычисления такого расстояния. Пусть две точки имеют координаты ${(x’,y’)}$ и ${(x»,y»)}$. Тогда длину между такими точками можно найти по следующей формуле:

$d=\sqrt{(x’-x»)^2+(y’-y»)^2}$

Пример 3

Пусть нам дан треугольник своими координатами вершин $(5,-9)$, $(12,-2)$ и $(4,0)$. Найдем его периметр.

Решение.

Найдем для начала длины всех его сторон по формуле из замечания к задаче 2.

Первая сторона равняется:

$\sqrt{(5-12)^2+(-9+2)^2}=\sqrt{(-7)^2+(-7)^2}=\sqrt{98}=7\sqrt{2}$

Вторая сторона равняется:

$\sqrt{(5-4)^2+(-9-0)^2}=\sqrt{1^2+(-9)^2}=\sqrt{82}$

Третья сторона равняется:

$\sqrt{(12-4)^2+(-2-0)^2}=\sqrt{8^2+(-2)^2 }=\sqrt{68}=2\sqrt{17}$

Складывая, получим

Ответ: $7\sqrt{2}+\sqrt{82}+2\sqrt{17}$

spravochnick.ru

Определение координат вектора заданного координатами его начальной и конечной точки.

Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.

Формулы определения координат вектора заданного координатами его начальной и конечной точки

Формула определения координат вектора для плоских задач

В случае плоской задачи вектор AB заданный координатами точек A(A_x ; A_y) и B(B_x ; B_y) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y}

Формула определения координат вектора для пространственных задач

В случае пространственной задачи вектор AB заданный координатами точек A(A_x ; A_y ; A_z) и B(B_x ; B_y ; B_z) можно найти воспользовавшись следующей формулой

AB = {B_x — A_x ; B_y — A_y ; B_z — A_z}

Формула определения координат вектора для n -мерного пространства

В случае n-мерного пространства вектор AB заданный координатами точек A(A₁ ; A₂ ; … ; A_n) и B(B₁ ; B₂ ; … ; B_n) можно найти воспользовавшись следующей формулой

AB = {B₁ — A₁ ; B₂ — A₂ ; … ; B_n — A_n}

Примеры задач связанных с определением координат вектора по двум точкам

Примеры для плоских задач

Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).

Решение: AB = {3 — 1; 1 — 4} = {2; -3}.

Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3

Ответ: B(8; -3).

Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5

Ответ: A(-2; -5).

Примеры для пространственных задач

Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).

Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.

Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).

Решение:

AB_x = B_x — A_x   =>   B_x = AB_x + A_x   =>   B_x = 5 + 3 = 8
AB_y = B_y — A_y   =>   B_y = AB_y + A_y   =>   B_y = 1 + (-4) = -3
AB_z = B_z — A_z   =>   B_z = AB_z + A_z   =>   B_z = 2 + 3 = 5

Ответ: B(8; -3; 5).

Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).

Решение:

AB_x = B_x — A_x   =>   A_x = B_x — AB_x   =>   A_x = 3 — 5 = -2
AB_y = B_y — A_y   =>   A_y = B_y — AB_y   =>   A_y = -4 — 1 = -5
AB_z = B_z — A_z   =>   A_z = B_z — AB_z   =>   A_z = 1 — 4 = -3

Ответ: A(-2; -5; -3).

Примеры для n -мерного пространства

Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).

Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.

Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).

Решение:

AB₁ = B₁ — A₁   =>   B₁ = AB₁ + A₁   =>   B₁ = 5 + 3 = 8
AB₂ = B₂ — A₂   =>   B₂ = AB₂ + A₂   =>   B₂ = 1 + (-4) = -3
AB₃ = B₃ — A₃   =>   B₃ = AB₃ + A₃   =>   B₃ = 2 + 3 = 5
AB₄ = B₄ — A₄   =>   B₄ = AB₄ + A₄   =>   B₄ = 1 + 2 = 3

Ответ: B(8; -3; 5; 3).

Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).

Решение:

AB₁ = B₁ — A₁   =>   A₁ = B₁ — AB₁   =>   A₁ = 3 — 5 = -2
AB₂ = B₂ — A₂   =>   A₂ = B₂ — AB₂   =>   A₂ = -4 — 1 = -5
AB₃ = B₃ — A₃   =>   A₃ = B₃ — AB₃   =>   A₃ = 1 — 4 = -3
AB₄ = B₄ — A₄   =>   A₄ = B₄ — AB₄   =>   A₄ = 8 — 5 = 3

Ответ: A(-2; -5; -3; 3).

ru.onlinemschool.com