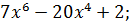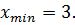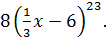Конспект урока по алгебре «, тема » Наибольшее и наименьшее значения функции». (10 класс)
Конспект урока по алгебре и началам анализа в 10 классе
Учитель математики МБОУ «Сизябская СОШ» Семяшкина Елизавета Михайловна
Тема урока: «Наибольшее и наименьшее значения функции».
Цель:
— повторение изученного материала главы IV «Применение производной к исследованию функции»
— обобщение умений и навыков учащихся применения производной функции в решении заданий.
Задачи:
— совершенствовать навыки и умения учащихся применения производной функции в нахождении промежутков возрастания и убывания функции, определения критических точек функции, а также нахождения наибольшего и наименьшего значения функции;
— развивать у учащихся навыки самостоятельного выполнения заданий и решения примеров, а также навыки взаимооценивания работы учащихся класса и осмысления собственного участия в процессе учебной деятельности на уроке;
— воспитывать у учащихся сознательное отношение к данному виду работы.
Ожидаемые результаты
учащиеся должны:
знать: алгоритмы нахождения промежутков возрастания и убывания функции, критических точек функции и наибольшего и наименьшего значения функции;
уметь: решать задания на нахождение промежутков возрастания и убывания функции, критических точек функции и наибольшего и наименьшего значения функции;
понимать: основные сходства и различия в приемах нахождения промежутков возрастания и убывания функции, критических точек функции и наибольшего и наименьшего значения функции.
Тип урока: Урок закрепления знаний, умений и навыков..
Методы: Устный опрос, беседа, работа в паре и в группе, практическое решение заданий по карточкам, тестовых заданий.
Ресурсы: учебник, карточки, тестовые задания, листы взаимооценивания и самооценивания.
Ход урока
Организационный момент
Проверка подготовленности учащихся к уроку.
Приветствие учителя и учащихся.
Фиксация отсутствующих учащихся.
Постановка цели и задач урока
Сегодня на уроке мы с вами повторим ранее изученный материал главы IV «Применение производной к исследованию функции», а также будем совершенствовать навыки и умения использования производной функции в нахождении промежутков возрастания и убывания функции, определения критических точек, а также нахождения наибольшего и наименьшего значения функции.
Актуализация опорных знаний
Для того чтобы вспомнить основные алгоритмы, которые нужны для выполнения данных заданий, я вам предлагаю выполнить следующее задание, суть которого состоит в том, что необходимо будет правильно составить порядок действий в нахождении промежутков возрастания и убывания, критических точек и наибольшего и наименьшего значения функции.
Признаки возрастания и убывания функции
Критические точки функции
Наибольшее и наименьшее значения функции
Алгоритм:
Найти производную функции;
Решить неравенство
 или
или  ;
;Используя утверждение теоремы, найти промежутки возрастания и убывания функции.
Алгоритм:
Найти производную функции;
Решить уравнение
 , найти критические точки;
, найти критические точки;С помощью метода интервалов определить знаки производной в окрестностях критических точек;
Используя достаточное условие существования экстремума, найти точки максимума и минимума.
Алгоритм:
Найти производную функции;
Решить уравнение
 и найти критические точки;
и найти критические точки;Выяснить, принадлежат ли полученные критические точки данному отрезку;
Найти значения функции на концах отрезка и в критических точках, принадлежащих отрезку;
Сравнивая полученные значения функции, определить наибольшее и наименьшее значения функции.
Проверка задания.
Практическое выполнение заданий
Для совершенствования навыков и умений решения заданий на нахождение промежутков возрастания и убывания функции, определения критических точек, а также нахождения наибольшего и наименьшего значения функции, учащимся предоставляется следующее задание: решение примеров по карточкам (каждый учащийся выбирает себе карточку с заданием, которую он должен решить). Один-два учащихся могут записать решения примеров на доске.
Карточка №1
Найдите промежутки возрастания и убывания функции

Решение
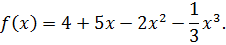
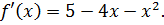
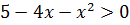
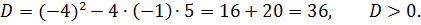
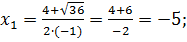
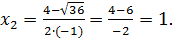
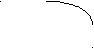




 – + – x
– + – x
-5 1
Ответ: 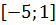 — возрастает,
— возрастает,
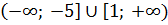 — убывает.
— убывает.
Карточка №2
Найдите критические точки функции

Решение
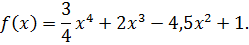
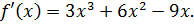
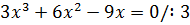
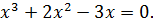
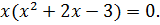
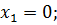
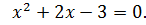
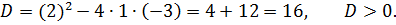
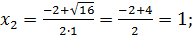
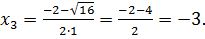
Ответ: 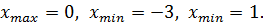
Карточка №3
Найдите наибольшее и наименьшее значения функции

Решение
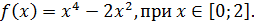
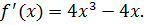
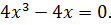
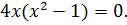
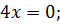
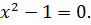
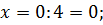
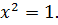
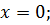
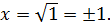
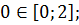
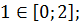
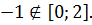
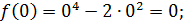
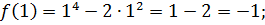
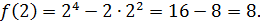
Ответ: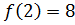 – наибольшее,
– наибольшее,
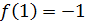 — наименьшее.
— наименьшее.
Карточка №4
Найдите промежутки возрастания и убывания функции

Ответ: 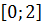 — убывает,
— убывает,
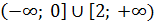 – возрастает.
– возрастает.
Карточка №5
Найдите критические точки функции

Ответ: 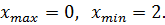
После выполнения задания учащиеся меняются тетрадями и проводят взаимопроверку с последующим выставлением отметок в лист взаимооценивания.
Затем учащимся предоставляется следующее задание – выполнение тестовой
работы. Всего в задании пять примеров, за каждый правильный пример, учащаяся получает один балл. Далее, после выполнения задания, учитель совместно с учащимися проводит взаимопроверку заданий. Затем, каждая учащаяся ставит отметку в лист взаимооценивания.
Тестовое задание
Найдите промежутки убывания функции

 B)
B)  C)
C)  D)
D) 
Найдите производную функции

 B)
B) 
C) 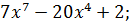 D)
D) 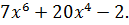
Найдите точки минимума функции

 B)
B)  C)
C)  D)
D) 
Вычислите наименьшее значение функции
 на отрезке
на отрезке 
0; B) 1; C) 2; D) 3.
Найдите производную функции

 B)
B)  C)
C)  D)
D) 
Рефлексия
Каждый учащиеся заполняет лист самооценивания, где проводит рефлексию над своей учебной деятельностью и уровнем понимания и усвоения учебного материала.
После того, как каждый учащийся заполнил лист самооценивания, можно заслушать некоторые из них.
Подведение итогов урока
Обсуждение с учащимися достижения цели и задач урока.
Аргументированное комментирование оценок за урок. Каждая ученица подсчитывает количество баллов, и учитель выставляет соответствующую отметку.
Разъяснение домашнего задания, стр.150-152.
Раздаточный материал
Найдите промежутки убывания функции

 B)
B)  C)
C)  D)
D) 
Найдите производную функции

 B)
B) 
C) 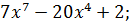 D)
D) 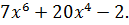
Найдите точки минимума функции

 B)
B)  C)
C)  D)
D) 
Вычислите наименьшее значение функции
 на отрезке
на отрезке 
0; B) 1; C) 2; D) 3.
Найдите производную функции

 B)
B)  C)
C)  D)
D) 
Лист взаимооценивания ученицы 10 класса ____________________________.
(максимальное количество баллов от 1 до 5)
Актуализация опорных знаний (работа в группе)
Выполнение заданий по карточкам (самост. работа)
Выполнение тестовых заданий
Общее количество баллов
Отметка
Лист самооценивания ученицы 10 класса __________________________________
Критерии
Хорошо
Недостаточно хорошо
Плохо
Знала алгоритм нахождения промежутков возрастания и убывания функции
Знала алгоритм нахождения критических точек функции
Знала алгоритм нахождения наибольшего и наименьшего значения функции
Понимаю алгоритм нахождения промежутков возрастания и убывания функции
Понимаю алгоритм нахождения критических точек функции
Понимаю алгоритм нахождения наибольшего и наименьшего значения функции
Понимаю основные сходства и различия между основными алгоритмами нахождения промежутков возрастания и убывания функции, критических точек функции и наибольшего и наименьшего значения функции
Умею применять алгоритм нахождения промежутков возрастания и убывания функции в решении заданий
Умею применять алгоритм нахождения критических точек функции при решении заданий
Умею применять алгоритм нахождения наибольшего и наименьшего значения функции при решении заданий
Ш К А Л А
О Ц Е Н И В А Н И Я
14-15 баллов – «5»
11-13 баллов – «4»
8-10 баллов – «3»
менее 8 баллов – «2»
Признаки возрастания и убывания функции
Критические точки функции
Наибольшее и наименьшее значения функции
Алгоритм:
___ Найти производную функции
___ Используя утверждение теоремы, найти промежутки возрастания и убывания функции.
___ Решить неравенство 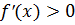 или
или 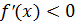
Алгоритм:
___ Решить уравнение 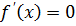 , найти критические точки
, найти критические точки
___ Найти производную функции
___ Используя достаточное условие существования экстремума, найти точки максимума и минимума
___ С помощью метода интервалов определить знаки производной в окрестностях критических точек
Алгоритм:
___ Решить уравнение 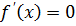 и найти критические точки
и найти критические точки
___ Найти значения функции на концах отрезка и в критических точках, принадлежащих отрезку
___ Выяснить, принадлежат ли полученные критические точки данному отрезку
___ Сравнивая полученные значения функции, определить наибольшее и наименьшее значения функции.
___ Найти производную функции
infourok.ru
Урок по теме «Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке». 10-й класс
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
В разработке представлен урок по §46.п.1. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке по учебнику А. Г.Мордковича, П.В.Семенова “Алгебра и начала анализа. Профильный уровень.10 класс”.
Урок проводится с целью изучения и первичного закрепления материала по теме “ Наибольшее и наименьшее значения функции на промежутке”, как одной из основных тем по исследованию функций. Это первый урок из четырёх по теме “Применение производной для нахождения наибольших и наименьших значений величин” и рассчитан на 1 час учебного времени. По ходу урока акцент делается на изучение и отработку как общих методов решения задач (по известному алгоритму), так и перевод задачи на другой язык (использование свойств функций).
Тип урока: урок изучения нового материала с использованием ИКТ.
Учебно-методическое обеспечение: учебник, задачник “Алгебра и начала анализа. Профильный уровень. 10 класс” А.Г.Мордкович, П.В. Семенов.
Оборудование и материалы для урока: компьютерный класс, проектор, интерактивная доска, презентация для сопровождения урока, карточки-бланки для ответов учащихся, карточки-инструкторы для проведения работы.
Цель: познакомить учащихся с приемами нахождения наибольшего и наименьшего значения функции на промежутке.
Задачи.
Образовательная — повторить необходимые и достаточные условия существования точек экстремума, понятия: стационарная и критическая точка; вывести алгоритм нахождения наименьшего и наибольшего значений функции, формировать умения решать задачи на отыскание наибольших и наименьших значений функции.
Развивающая – развивать познавательный интерес обучающихся, умение исследовать, выделять главное, сравнивать, анализировать, делать выводы.
Воспитательная – воспитывать умения работать в сотрудничестве в парах и группе, оценивать работу товарища.
Знания, умения, навыки и качества, которые актуализируют/приобретут/ закрепят/ др. ученики в ходе урока:
— овладение практическими умениями и навыками по теме “Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке”
— умение устанавливать причинно-следственные связи, выделять главное, обобщать, систематизировать;
— формирование навыков самостоятельной работы с учебным материалом;
— формирование навыков самоконтроля.
Структура урока.
Оргмомент.
Ход урока
1. Оргмомент.
Организация групп (до урока). Приветствие. Эпиграф к уроку (слайд 1).
2. Актуализация знаний.
Устная работа (слайды 2-4). Повторение материала, изученного на предыдущих уроках. Фронтальная работа. Учитель обращает внимание обучающихся на существенное различие понятий максимума (минимума) функций и наибольшего (наименьшего) значений.
3. Мотивация.
Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач на нахождение наилучших, оптимальных решений при наименьших затратах труда, так называемые задачи на оптимизацию.
С некоторыми из таких задач мы познакомимся на следующих уроках. Чтоб успешно решать такие задачи необходимо уметь находить наибольшее и наименьшее значения заданных функций на заданном промежутке.
Постановка обучающимися темы и целей урока (слайд 6-7).
4. Изучение нового материала. Первичное осмысление.
Ребятам предлагается три графика функции для самостоятельного определения точек наибольшего и наименьшего значений. Проанализировать расположение данных точек на графике и сделать вывод (слайд 8). Работа выполняется по группам. Если возникают затруднения, то можно воспользоваться карточкой-инструкцией. (Приложение 1)
Затем спикер одной из групп высказывает мнение своей группы, а остальные сравнивают его со своим мнением, дополняют или уточняют, возможно, опровергают. В итоге обучающиеся делают вывод (слайд 9).
Постановка проблемы.
Учитель задает вопрос: “Как, не изображая графика функции, определить наибольшее и наименьшее значение функции на отрезке?”
Задание 1. Найти наибольшее и наименьшее значение функции у = х3 — 3х2 — 45х + 1 на [-4; 6] без построения графика. (Слайд 10). Ребята предлагают решение. Учитель корректирует работу, задавая наводящие вопросы. Решение оформляется на доске в интерактивном режиме учителем.
Ответ: у наим = у (5) = -174; у наиб = у(-3) = 82.
Задание 2. (Слайд 11) Выполнить задание, рассуждая аналогично. Задание на репродуктивном уровне выполняется самостоятельно.
Ответ: у наим = у (-1) = -13; у наиб = у(1) = 3
Задание 3. Проанализировать решения предыдущих примеров и сформулировать алгоритм нахождения наименьшего и наибольшего значений функции на отрезке. Обучающиеся вновь по группам обсуждают данный вопрос, затем, обменявшись мнениями с другими группами, приходят к общему выводу.
Решение проблемы.
Ребята формулируют алгоритм. Проверяется алгоритм по учебнику стр.371 (слайд 12). (Ситуация успеха).
Учитель дополняет. Если речь идет о нахождении наибольшего или наименьшего значений функции, непрерывной на незамкнутом промежутке, то удобно использовать следующую теорему (слайд 13). Данная теорема в курсе 10 класса не доказывается. Ребята записывают теорему в тетрадь.
5. Закрепление “добытых” знаний.
При подготовке к уроку учитель делает закладку необходимой для занятия Web-страницы. Интернет-сайт “ЕГЭ по математике: подготовка к тестированию” http://www.uztest.ru. включает “Тренажер”, позволяющий проходить on-line тест по теме “Наибольшее, наименьшее значение функции” на конструктивном уровне. Ребятам предлагается выполнить тест из 5 заданий. Верные ответы заносятся в таблицу (Приложение 1). Осуществляя дифференцированный подход к обучающимся, предлагаются дополнительные примеры из учебника № 46.20(а), №46.21(а).
6. Итог. Рефлексия деятельности на уроке. Домашнее задание.
Учитель беседует с ребятами, говоря о новых знаниях полученных на уроке, о достигнутых целях, интересуется их ощущениями от происходящего и предлагает заполнить карточки рефлексии. (Приложение 1)
Домашнее задание. §46.п.1. Каждый ученик получает индивидуальное разноуровневое задание на сайте http://www.uztest.ru. Для входа на личную страницу учитель сообщает логин и пароль для каждого ученика. Оценки выставляются в электронный журнал.
Учитель благодарит обучающихся за хорошую работу на уроке (слайд 15).
Литература:
1. А.Г. Мордкович, П.В. Семенов, учебник “Алгебра и начала анализа. Профильный уровень. 10 класс” - М: Мнемозина, 2006.
2. А.Г. Мордкович, П.В. Семенов, задачник “Алгебра и начала анализа. Профильный уровень. 10 класс” - М: Мнемозина, 2006.
urok.1sept.ru
Презентация к уроку по алгебре (10 класс) по теме: Наибольшее и наименьшее значение функции
Этапы
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее или наибольшее
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3
-3
x = 3
[0; 4]
x = –3
[0; 4]
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
3
х
1
0
х
В 11
—
5
4
3) y(0) = 0
Алгоритм решения задач
Этапы
1. Найти f /(x)
2. Найти критические точки, взять те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее и наибольшее
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
1) y / = 3×2 – 27
2) y / = 3×2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
3
-3
y(3) = 33– 27 3 = –54
3
х
1
0
х
В 11
—
5
4
3)
Другой способ решения
+
+
–
x
y\
y
-3
3
0
4
min
Наименьшее значение функция будет принимать в точке минимума.Можно сэкономить на вычислениях значений функции в концах отрезка.
Этот способ будет удобно вспомнить, когда вычисления значений функции в концах отрезка будет сложным.
наибольшее значение
наибольшее значение
наименьшеезначение
наименьшеезначение
a
b
a
b
Предположим, что функция f не имеет на отрезке [а; b] критических точек. Тогда она возрастает (рис. 1) или убывает (рис. 2) на этом отрезке.Значит, наибольшее и наименьшее значения функции f на отрезке [а; b] — это значения в концах а и b.
функция возрастает
функция убывает
наибольшее значение
наименьшеезначение
a
b
a
b
Предположим, что функция f имеет на отрезке [а; b] одну точку экстремума.Если это точка минимума, то в этой точке функция будет принимать наименьшее значение. Если это точка максимума, то в этой точке функция будет принимать наибольшее значение.
СЛОЖНАЯ ФУНКЦИЯ – функция, представленная как композиция нескольких функций. Сложная функция – функция от функции. Сложная функция представлена в виде цепочки простых функций. – промежуточный аргумент, – независимая переменная.
Производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента.
)
(
)
(
)
(
x
v
x
v
u
x
v
u
/
/
/
Ч
=
[
]
(
)
(
)
)
(
)
(
x
v
u
(
)
x
v
x
Чтобы найти производную сложной функции, нужно:Определить, какая функция является внешней и найти по таблице производных соответствующую производную.2. Определить промежуточный аргумент.
Функция промежуточного аргумента – квадратичная функция
Функция квадратного корня
Показательная функция
Функция промежуточного аргумента – квадратичная функция
Логарифмическая функция
Функция промежуточного аргумента – тригонометрическая функция sinx
Степенная функция
Функция промежуточного аргумента – квадратичная функция
Проверим, принадлежит ли х=ln3 промежутку [1; 2]
Найдите наименьшее значение функции y = e2x – 6ex + 3 на отрезке [1; 2]
1.
Найдем критические точки, которые принадлежат заданному отрезку.
Значения функции в концах отрезка.
1) y(1) = e2 – 6e + 3;
y(2) = e4– 6e2+ 3
2) y / =
[1; 2]
Найдем значение функции в критической точке.
2ex(ex – 3) = 0
ex – 3 = 0
x = ln3
(e2x)/ =
e2x
(ex)/ = ex
(2x)/
= e2x
2
= 2e2x
(kx)/ = k
0
№
(
)
)
(
v
v
u
v
u
/
/
/
Ч
=
]
[
– 6ex
+ 0
2e2x
1) производнаядля внешней функции:
(ex)/ = ex
= 2ex(ex – 3)
(С)/ = 0
+
–
x
y\
y
ln3
min
Наименьшее значение функция будет принимать в точке минимума.Можно сэкономить на вычислениях значений функции в концах отрезка.
>0
Найдите наибольшее значение функции
2.
(
)
(
)
(
)
(
)
(
)
x
g
x
g
f
x
g
f
/
/
/
Ч
=
5 – 4х – х2 0
D(y):
і
x = – 2
D(y)
Найдем критические точки, которые принадлежат D(у).
Вычислим производную, используя формулу для вычисления производной сложной функции.
х
(
)
х
2
1
/
=
–
+
x
y\
y
-2
max
Наибольшее значение функция примет в точке максимума.
3
х
1
0
х
В 14
3
При решении некоторых заданий на вычисление наибольшего и наименьшего значений функции можно найти ответ и без вычисления производной.
)
(
g(x)
f
Сложная функция представлена в виде цепочки простых функций. Где g(x) – промежуточный аргумент, квадратичная функция
g(x) = ax2 +bx + c
Если внешняя функция является монотонно возрастающей на всей области определения, значит, наибольшее значение она будет иметь, когда функция промежуточного аргумента, т.е. квадратичная функция будет иметь наибольшее значение.
А наименьшее значение она будет иметь, когда функция промежуточного аргумента, т.е. квадратичная функция будет иметь наименьшее значение.
Рассмотрим примеры.
Найдите наибольшее значение функции
2.
5 – 4х – х2 0
D(y):
і
2 способ
Решим задание без вычисления производной.
Функция квадратного корня монотонно возрастает на всей области определения, значит, наибольшее значение она будет иметь, когда функция промежуточного аргумента, т.е. квадратичная функция – х2 – 4х + 5 будет иметь наибольшее значение. Старший коэффициент квадратного трехчлена равен – 1(-1)
-4
х
2*
0
—
=
= -2
a
b
х
2
0
—
=
Итак, наибольшее значение функция квадратного корня примет, когда промежуточная квадратичная функция примет наибольшее значение, т.е. в точке х = – 2. Вычислим его:
3
х
1
0
х
В 14
3
D(y)
Найдите наименьшее значение функции
4.
(
)
(
)
(
)
(
)
(
)
x
g
x
g
f
x
g
f
/
/
/
Ч
=
x = — 1
D(y)
Найдем критические точки, которые принадлежат D(у).
Вычислим производную, используя формулу для вычисления производной сложной функции.
+
–
x
y\
y
-1
min
Наименьшее значение функция примет в точке минимума.
3
х
1
0
х
В 14
1
6
D(y):
R
x
О
(
)
a
a
a
х
х
ln
/
=
>0
>0
Найдите наименьшее значение функции
4.
D(y):
R
x
О
Решим задание без вычисления производной.
Показательная функция с основанием 2>1 монотонно возрастает на всей области определения. Значит, наименьшее значение она будет иметь, когда функция промежуточного аргумента, т.е. квадратичная функция х2 + 2х + 5 будет иметь наименьшее значение. Старший коэффициент квадратного трехчлена равен +1> 0, значит, ветви параболы направлены вверх. И наименьшее значение квадратичная функция будет иметь в вершине.
1
2
х
2*
0
—
=
a
b
х
2
0
—
=
Итак, наименьшее значение показательная функция примет, когда промежуточная квадратичная функция примет наименьшее значение, т.е. в точке х = – 1. Вычислим его:
D(y)
= – 1
3
х
1
0
х
В 14
1
6
2 способ
Найдите наибольшее значение функции
6.
4 – 2х – х2 0
D(y):
>
Решим задание без вычисления производной.
Логарифмическая функция с основанием 5 является монотонно возрастающей на всей области определения. Значит, наибольшее значение она будет иметь, когда функция промежуточного аргумента, т.е. квадратичная функция 4 – 2х – х2 будет иметь наибольшее значение. Старший коэффициент квадратного трехчлена равен –1(-1)
-2
х
2
0
—
=
= -1
1
3
х
1
0
х
В 14
4
a
b
х
2
0
—
=
« Самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что, прежде чем строить ячейку из воска, он уже построил ее в своей голове. » К. Маркс
Задача :Какими должны быть размеры участка прямоугольной формы площадью , чтобы на его ограждение было израсходовано наименьшее количество материала ?
Составим математическую модель задачи :из всех прямоугольников площадью 1600 кв. м найти прямоугольник наименьшего периметра
1. Р – периметр прямоугольника
2. х ( м ) – длина прямоугольника
х
x = 40 – точка минимума, значит функция р ( х ) в этой точке принимает наименьшее значение. Следовательно и периметр прямоугольника будет наименьшим.
0
40
х
+
—
Длина участка – 40 ( м )
Ширина участка – 40 м
Длина прямоугольника – 40 ( м )
Ширина прямоугольника –
Ответ: длина участка 40 м, ширина участка – 40 м.
Задача :Выращенную на участке клубнику ученики отправляют в детский сад в коробках, имеющих форму прямоугольного параллелепипеда с квадратным основанием, периметр боковой грани которого 72 см. Какими должны быть размеры коробки, чтобы ее вместимость была наибольшей ?
Математическая модель :Из всех прямоугольных параллелепипедов с квадратным основанием, периметр боковой грани которого 72 см, найти параллелепипед наибольшего объема.
Выращенную на участке клубнику ученики отправляют в детский сад в коробках, имеющих форму прямоугольного параллелепипеда с квадратным основанием, периметр боковой грани которого 72 см. Какими должны быть размеры коробки, чтобы ее вместимость была наибольшей ?
Р = 72 см
Из всех прямоугольных параллелепипедов с квадратным основанием, периметр боковой грани которого 72 см, найти параллелепипед наибольшего объема.
Р = 72 см
х
36 – х
х
1. V – объем прямоугольного параллелепипеда
2. х ( см ) – длина прямоугольного параллелепипеда , х ( см ) – ширина прямоугольного параллелепипеда36 – х ( см ) – высота прямоугольного параллелепипеда
x = 24 – точка максимума, значит функция v ( х ) в этой точке принимает наибольшее значение. Следовательно и объем прямоугольного параллелепипеда при х = 24 будет наибольшим.
0
36
х
+
—
24
Длина прямоугольного параллелепипеда – 24 ( см )
Ширина прямоугольного параллелепипеда – 24 ( см )
Высота прямоугольного параллелепипеда – 36 – 24 = 12 ( см )
Ответ : чтобы вместимость коробки была наибольшей, ее размеры должны быть 24 см, 24 см, 12 см
nsportal.ru
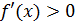 или
или 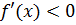 ;
;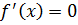 , найти критические точки;
, найти критические точки;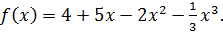
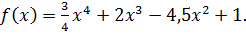
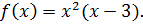
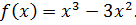
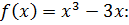
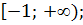 B)
B) 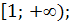 C)
C) 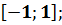 D)
D) 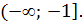
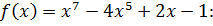
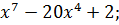 B)
B) 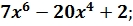
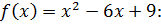
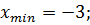 B)
B) 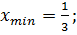 C)
C) 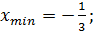 D)
D) 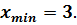
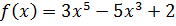 на отрезке
на отрезке 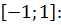
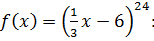
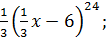 B)
B) 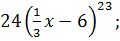 C)
C) 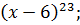 D)
D) 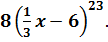
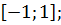 D)
D)