Открытый урок по теме «Наибольшее и наименьшее значение функции на отрезке» 10 класс
Открытый урок по теме «Наибольшее и наименьшее значение функции на отрезке»
10 класс.
(Использование проблемного обучения)
Разработала учитель математики
МОУ «Розгребельская средняя общеобразовательная школа» Большесолдатского района
Апанасенко Т.В.
Цели урока: Составить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке, используя создание проблемной ситуации на уроке. Провести первичное закрепление и первичный контроль усвоения алгоритма. Развивать логическое мышление, вычислительные навыки.
I.
Организационный момент.
Здравствуйте, садитесь. Сегодня на
уроке мы будем применять рейтинговую
оценку знаний. У вас на столе лежит лист
с таблицей, сразу подпишите свою фамилию
и имя. Вы будите сами оценивать свою
работу на каждом этапе урока по
пятибалльной системе и выставлять
набранные баллы в таблицу.
Откройте свои тетради, запишите тему урока: «Отыскание наибольшего и наименьшего значений непрерывной функции на отрезке.
II Актуализация опорных знаний
. Для изучения новой темы нам необходимо повторить пройденный материал. Сделаете вы это, выполнив устно следующие задания. В тетрадь запишите только ответы к каждому пункту. (3мин.)
По графику функции у=f(x) найдите:
1.Область определения функции.
[-3;6]
2. Абсциссы точек, в которых f`(x)=0
0;3,5
3. Абсциссы точек, в которых f`(x) не существует.
-1
4. Наибольшее значение функции. (Унаиб.).
Унаиб=3
5. Наименьшее значение функции (Унаим.).
Унаим.=-2
(Задание находится на слайде, отображается проектором на экран. Ответы к заданиям появляются по щелчку).
Учащиеся
проверяют свои работы и выставляют
набранные баллы в рейтинговую таблицу,
каждое правильно выполненное задание
соответствует одному баллу.
Вопросы учителя:
Скажите, пожалуйста, как называются точки 0 и 3.5 в п.2 (ответ стационарные)
Дайте полное определение стационарных точек (внутренние точки области определения, в которых производная равна 0).
Как называется точка -1 в п.3 (критическая).
Дайте полное определение критических точек (внутренние точки области определения функции, в которых функция непрерывна, в которых производная не существует.
III. Постановка цели.
Вы видите, что когда функция задана графически наибольшее и наименьшее значения её на ограниченной области определения отыскать не сложно, но как быть если функция задана аналитически? (постановка проблемной ситуации)
Требуется
найти наибольшее и наименьшее значения
функции у=x
Поэтому
наша задача отыскать алгоритм нахождения
наибольшего и наименьшего значений
непрерывной функции на указанном
отрезке. Для этого проанализируем по
графикам непрерывных функций, в каких
точках функция может достигать своего
наибольшего и наименьших значений на
отрезке.
Для этого проанализируем по
графикам непрерывных функций, в каких
точках функция может достигать своего
наибольшего и наименьших значений на
отрезке.
Унаиб= f(b),b –конец отрезка
Унаим=f(x1 ), x1 – стационарная точка, т.е. f`(x1)=0.
Унаиб= f(а), а – конец отрезка
Унаим=f(b), b – конец отрезка.
Унаиб f(x1), х 1 -стационарная точка, т.е. f`(x1)=0
Унаим=f(x2 ), x2 — критическая точка, т.е. f`(x2 ) не существует.
Подвожу учащихся к выводу, что наибольшего и наименьшего значений функция непрерывная на указанном отрезке может достигать в стационарных, критических точках входящих в этот отрезок, а так же на концах отрезка. Но мы уже умеем находить стационарные и критические точки функции заданной аналитически. Что же нужно для этого найти? (производную).
Далее
найдем стационарные и критические
точки, приравняв производную к 0 и сравнив
области определения производной и
функции. Но нужны ли нам все такие точки?
(только те которые попадают внутрь
указанного отрезка)
Но нужны ли нам все такие точки?
(только те которые попадают внутрь
указанного отрезка)
Алгоритм отыскания наименьшего и наибольшего значений непрерывной функции у=f(x) на отрезке [a;b]
1. Найти производную f`(x)
2. Найти стационарные и критические точки функции, лежащие внутри отрезка [a;b]
3. Вычислить значения функции у=f(x) в точках, отобранных на втором шаге, и в точках a и b выбрать среди этих значений наименьшее ( это будет Унаим.) и наибольшее (это будет Унаиб.).
IV. Фронтальная работа с классом. (Образец применения алгоритма) Теперь вы можете решить задачу, записанную на доске. (у доски работает один человек, постоянно опираясь на составленный алгоритм).
V. Индивидуальная работа учащихся. Работа с карточкой тренажером по вариантам. (Приложение)
Проверка
по слайду, выставление набранных баллов
в рейтинговую шкалу.
I Вариант.
Карточка №1
Решение:
Д(у)=R
1.у´= 4х-8 (1балл)
Д(у´)=R
2. Критических точек нет
Стационарные: х=2; (2балла)
3. у(2)=-2; У(-1)=16; у(4)=6 (2балла)
Ответ
Унаиб=16
Унаим=-2
II Вариант
Карточка №1
Решение:
Д(у)=R
1.у´= 2х+4 (1балл)Д(у´)=R
2. Критических точек нет
Стационарные: х=-2; (2балла)
3. у(-2)=-7; У(-3)=-6; у(2)=9 (2 балла)
Ответ
Унаиб=9
Унаим=-7
VI. Дифференцированная работа. Кто не испытывает трудностей самостоятельно выполняют №936а. (Один учащийся работает за закрытой доской). у=2sin x [ — ;П] Остальные работают коллективно с учащимся у доски. №935а у=x2-8x+19 на отрезке
[-1;5].
Учащиеся, работающие самостоятельно
проверяют правильность выполнения
заданий у себя и у учащегося, работающего
за закрытой доской. Выставляют оценки
в рейтинговую шкалу.
VII. Самостоятельная работа дифференцированного характера. Учащиеся выбирают в зависимости от степени сложности задания. Выполняют их. И осуществляют самопроверку по готовым решениям.
№939(а)
Карточка №2
Решение:
Д(у)=R
1.у´= 48 (1балл)
Д(у´)=R
2. Критических точек нет
Стационарные: х=0; (1балл)
3. у(0)=0; У(-1)=12; у(2)=192 (1балл)
Ответ
Унаиб=192
Унаим=0
№936(в)
Карточка №2
Решение:
Д(у)=R
1.у´= -6sin x (1балл)
Д(у´)=R
2. Критических точек нет
Стационарные: не входят внутрь отрезка; (2балла)
3. у(- )=0; У(0)=6;
(2 балла)
Ответ
Унаиб=6
Унаим=0
VIII Итог урока. (Рефлексия).
Скажите, что мы учились сегодня делать.
Посчитайте, пожалуйста, набранные вами
баллы за урок и поднимите руку, чей
рейтинг соответствует оценке «5»
(поднимают), чей «4» (поднимают), чей «3». Если кому–то не удалось сегодня набрать
высокие баллы, не огорчайтесь, вы сможете
отработать эту тему на следующих уроках.
Поднимите руку, кто набрал больше 25
баллов. (1человек) Я поздравляю вас,
сегодня вы лидер, у вас самый высокий
рейтинг. Идет выставление оценок.
Записываем домашнее задание, если вы
не испытывали сегодня трудностей, вам
все понятно, вы выбираете второй уровень:
№934б, в;№936г;№938а. Остальные №934а, в;№935г.
Если кому–то не удалось сегодня набрать
высокие баллы, не огорчайтесь, вы сможете
отработать эту тему на следующих уроках.
Поднимите руку, кто набрал больше 25
баллов. (1человек) Я поздравляю вас,
сегодня вы лидер, у вас самый высокий
рейтинг. Идет выставление оценок.
Записываем домашнее задание, если вы
не испытывали сегодня трудностей, вам
все понятно, вы выбираете второй уровень:
№934б, в;№936г;№938а. Остальные №934а, в;№935г.
Приложение
I Вариант.
Карточка №1
Задание:
Найдите Унаиб. И У наим. Функции у=2-8x+6 на отрезке[-1;4]
Решение
Д(у)=______________________________________________________________
1.у´=___________________________________________________________________2. Д(у´)=_________________________________________________________
Сделай вывод о наличии критических точек______________________________________________________________
Найди стационарные точки, решив уравнение у´=0
Отбери точки, принадлежащие отрезку [-1;4] ______________________________________________________________________________________________________________________________________________
3. Найди у(-1)
__________________________________________________________
Найди у(-1)
__________________________________________________________
У(4)_______________________________________________________________
И в отобранных точках на втором шаге__________________________________________________________________________________________________________________________________________
_______________________________________________________________________
Отбери среди найденных значений наибольшее и наименьшее.
Ответ
Унаиб=________________________________________________________________
Унаим.=___________________________________________________________
II Вариант.
Карточка №2Задание:
Найдите Унаиб. И У наим. Функции У=+4x-3 на отрезке
[-3;2]
Решение
Д(у)=_________________________________________________________________________
1. у´=___________________________________________________________________2.
Д(у´)=_________________________________________________________
у´=___________________________________________________________________2.
Д(у´)=_________________________________________________________
Сделай вывод о наличии критических точек__________________________________________________________________
Найди стационарные точки, решив уравнение у´=0
Отбери точки, принадлежащие отрезку [-3;2] ______________________________________________________________________________________________________________________________________________
3. Найди у(-3) _____________________________________________________________
У(2)___________________________________________________________________
И в отобранных точках на втором шаге__________________________________________________________________________________________________________________________________
Отбери среди найденных значений наибольшее и наименьшее.
Ответ
Унаиб=____________________________________________________________
Унаим. =____________________________________________________________
=____________________________________________________________
Урок по теме «Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке». 10-й класс
В разработке представлен урок по §46.п.1. Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке по учебнику А. Г.Мордковича, П.В.Семенова “Алгебра и начала анализа. Профильный уровень.10 класс”.
Урок проводится с целью изучения и первичного
закрепления материала по теме “ Наибольшее и
наименьшее значения функции на промежутке”, как
одной из основных тем по исследованию функций.
Это первый урок из четырёх по теме “Применение
производной для нахождения наибольших и
наименьших значений величин” и рассчитан на 1
час учебного времени. По ходу урока акцент
делается на изучение и отработку как общих
методов решения задач (по известному алгоритму),
так и перевод задачи на другой язык
(использование свойств функций).
Тип урока: урок изучения нового материала с использованием ИКТ.
Учебно-методическое обеспечение: учебник, задачник “Алгебра и начала анализа. Профильный уровень. 10 класс” А.Г.Мордкович, П.В. Семенов.
Оборудование и материалы для урока: компьютерный класс, проектор, интерактивная доска, презентация для сопровождения урока, карточки-бланки для ответов учащихся, карточки-инструкторы для проведения работы.
Цель: познакомить учащихся с приемами нахождения наибольшего и наименьшего значения функции на промежутке.
Задачи.
Образовательная — повторить необходимые и
достаточные условия существования точек
экстремума, понятия: стационарная и критическая
точка; вывести алгоритм нахождения наименьшего и
наибольшего значений функции, формировать
умения решать задачи на отыскание наибольших и
наименьших значений функции.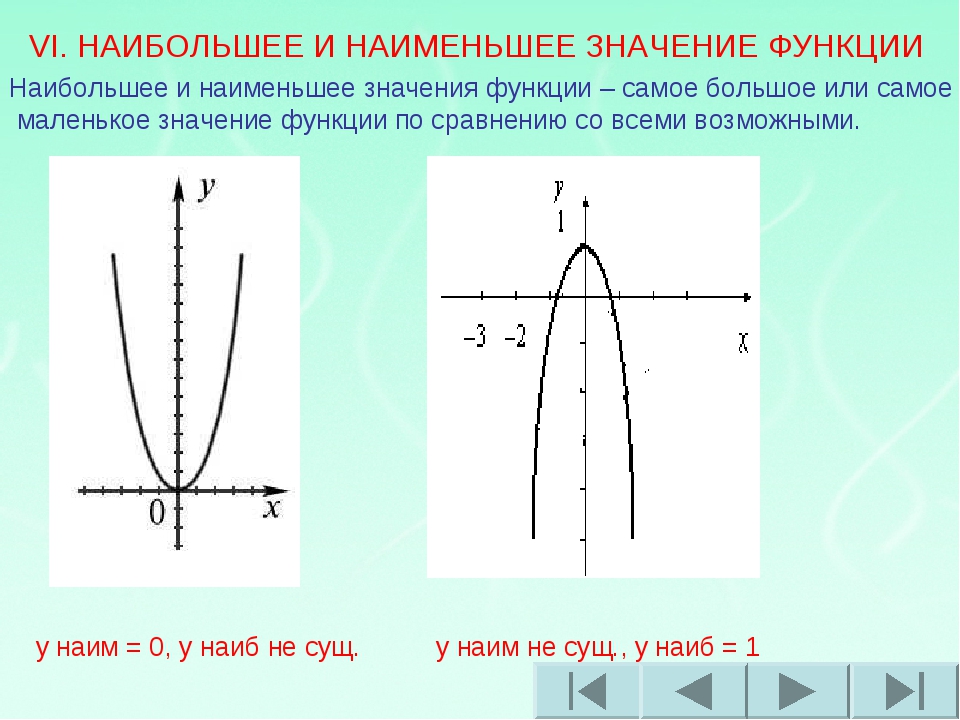
Развивающая – развивать познавательный интерес обучающихся, умение исследовать, выделять главное, сравнивать, анализировать, делать выводы.
Воспитательная – воспитывать умения работать в сотрудничестве в парах и группе, оценивать работу товарища.
Знания, умения, навыки и качества, которые актуализируют/приобретут/ закрепят/ др. ученики в ходе урока:
— овладение практическими умениями и навыками по теме “Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке”
— умение устанавливать причинно-следственные связи, выделять главное, обобщать, систематизировать;
— формирование навыков самостоятельной работы с учебным материалом;
— формирование навыков самоконтроля.
Структура урока.
Оргмомент.

Ход урока
1. Оргмомент.
Организация групп (до урока). Приветствие. Эпиграф к уроку (слайд 1).
2. Актуализация знаний.
Устная работа (слайды 2-4). Повторение материала, изученного на предыдущих уроках. Фронтальная работа. Учитель обращает внимание обучающихся на существенное различие понятий максимума (минимума) функций и наибольшего (наименьшего) значений.
3. Мотивация.
Нахождение наибольшего и наименьшего значений функции широко применяется при решении многих практических задач на нахождение наилучших, оптимальных решений при наименьших затратах труда, так называемые задачи на оптимизацию.
С некоторыми из таких задач мы познакомимся на
следующих уроках.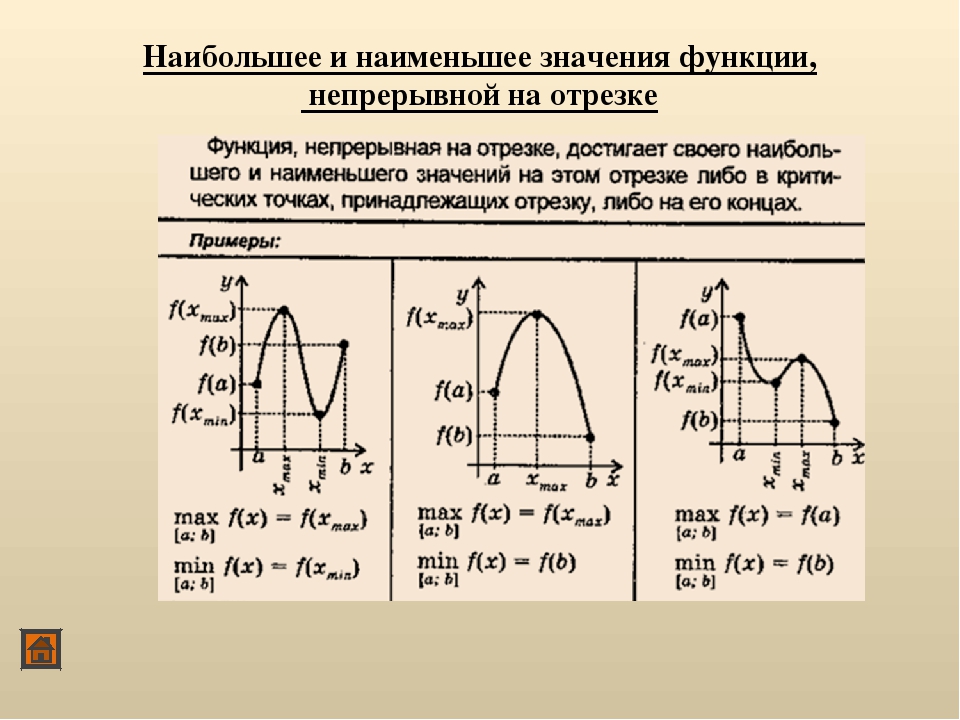 Чтоб успешно решать такие
задачи необходимо уметь находить наибольшее и
наименьшее значения заданных функций на
заданном промежутке.
Чтоб успешно решать такие
задачи необходимо уметь находить наибольшее и
наименьшее значения заданных функций на
заданном промежутке.
Постановка обучающимися темы и целей урока (слайд 6-7).
4. Изучение нового материала. Первичное осмысление.
Ребятам предлагается три графика функции для самостоятельного определения точек наибольшего и наименьшего значений. Проанализировать расположение данных точек на графике и сделать вывод (слайд 8). Работа выполняется по группам. Если возникают затруднения, то можно воспользоваться карточкой-инструкцией. (Приложение 1)
Затем спикер одной из групп высказывает мнение своей группы, а остальные сравнивают его со своим мнением, дополняют или уточняют, возможно, опровергают. В итоге обучающиеся делают вывод (слайд 9).
Постановка проблемы.
Учитель задает вопрос: “Как, не изображая графика функции, определить наибольшее и наименьшее значение функции на отрезке?”
Задание 1. Найти наибольшее и наименьшее
значение функции у = х3 — 3х2 — 45х + 1 на [-4;
6] без построения графика. (Слайд 10). Ребята
предлагают решение. Учитель корректирует работу,
задавая наводящие вопросы. Решение оформляется
на доске в интерактивном режиме учителем.
Найти наибольшее и наименьшее
значение функции у = х3 — 3х2 — 45х + 1 на [-4;
6] без построения графика. (Слайд 10). Ребята
предлагают решение. Учитель корректирует работу,
задавая наводящие вопросы. Решение оформляется
на доске в интерактивном режиме учителем.
Ответ: у наим = у (5) = -174; у наиб = у(-3) = 82.
Задание 2. (Слайд 11) Выполнить задание, рассуждая аналогично. Задание на репродуктивном уровне выполняется самостоятельно.
Ответ: у наим = у (-1) = -13; у наиб = у(1) = 3
Задание 3. Проанализировать решения предыдущих примеров и сформулировать алгоритм нахождения наименьшего и наибольшего значений функции на отрезке. Обучающиеся вновь по группам обсуждают данный вопрос, затем, обменявшись мнениями с другими группами, приходят к общему выводу.
Решение проблемы.
Ребята формулируют алгоритм. Проверяется алгоритм по учебнику стр.371 (слайд 12). (Ситуация успеха).
Учитель дополняет. Если речь идет о нахождении наибольшего или наименьшего значений функции, непрерывной на незамкнутом промежутке, то удобно использовать следующую теорему (слайд 13). Данная теорема в курсе 10 класса не доказывается. Ребята записывают теорему в тетрадь.
5. Закрепление “добытых” знаний.
При подготовке к уроку учитель делает закладку
необходимой для занятия Web-страницы.
Интернет-сайт “ЕГЭ по математике: подготовка к
тестированию” http://www.uztest.ru. включает “Тренажер”,
позволяющий проходить on-line тест по теме
“Наибольшее, наименьшее значение функции” на
конструктивном уровне. Ребятам предлагается
выполнить тест из 5 заданий. Верные ответы
заносятся в таблицу (Приложение 1). Осуществляя
дифференцированный подход к обучающимся,
предлагаются дополнительные примеры из учебника
№ 46. 20(а), №46.21(а).
20(а), №46.21(а).
6. Итог. Рефлексия деятельности на уроке. Домашнее задание.
Учитель беседует с ребятами, говоря о новых знаниях полученных на уроке, о достигнутых целях, интересуется их ощущениями от происходящего и предлагает заполнить карточки рефлексии. (Приложение 1)
Домашнее задание. §46.п.1. Каждый ученик получает индивидуальное разноуровневое задание на сайте http://www.uztest.ru. Для входа на личную страницу учитель сообщает логин и пароль для каждого ученика. Оценки выставляются в электронный журнал.
Учитель благодарит обучающихся за хорошую работу на уроке (слайд 15).
Литература:
1. А.Г. Мордкович, П.В. Семенов, учебник “Алгебра и начала анализа. Профильный уровень. 10 класс” - М: Мнемозина, 2006.
2. А.Г. Мордкович, П.В. Семенов, задачник “Алгебра
и начала анализа. Профильный уровень. 10 класс” -
М: Мнемозина, 2006.
10 класс” -
М: Мнемозина, 2006.
Найти наибольшее значение функции на промежутке
Найти наибольшее значение функции на промежутке — YouTube: Женщина просит разрешения отлучиться на два часа с работы. Начальник отдела говорит:— Но вы же знаете, какие могут быть неприятности. Идите сразу к директору.
У директора.
— Я должен знать, куда вы идете.
— Но я не могу этого сказать.
— Тогда — никаких отлучек!
— Я иду к любовнику, моему репетитору по математике и физике,- краснеет женщина.
— Хорошо. Только никаких магазинов — сразу в постель!
Найдем наибольшее значение этой непрерывной функции на замкнутом промежутке
Дополнительные упражнения. Найти наименьшее и наибольшее значение функции на замкнутом отрезке.
Как найти наибольшее значение функции на интервале
Наибольшее и наименьшее значение функции на интервале (на отрезке) находят по такой же процедуре, только с учетом того, что, возможно, не все критические точки будут лежать внутри указанного интервала.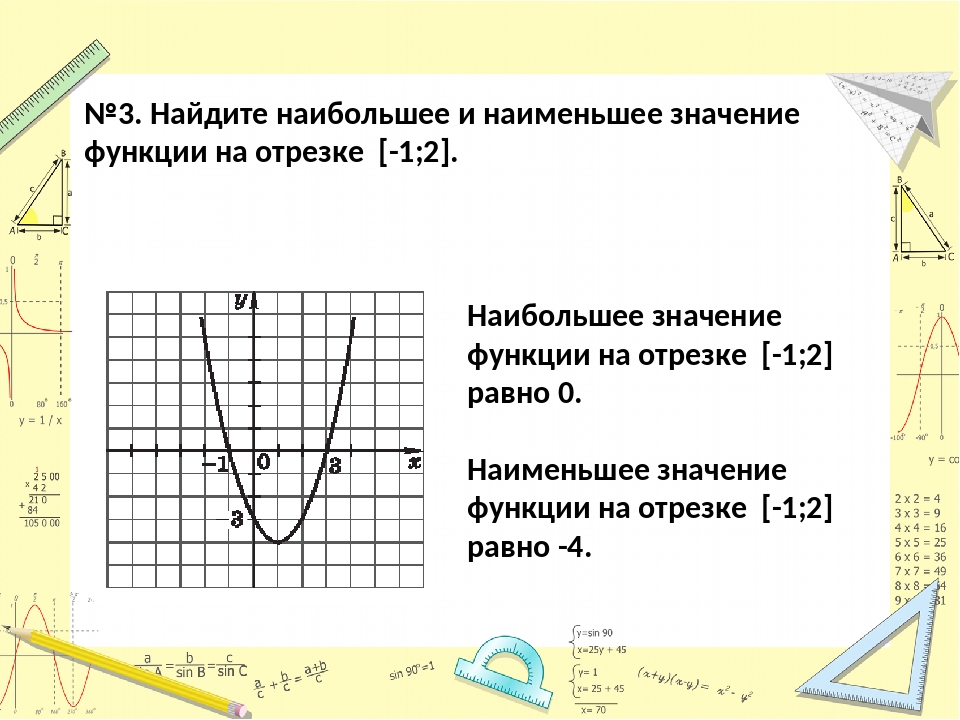
Найти наибольшее значение функции на промежутке — смотрите как пожаловаться на ЕГЭ.
Пример ОГЭ ГИА. Найдите наибольшее значение функции:
your #tutor info решаем-задачи-b14-из-егэ
Как найти наибольшее значение функции на промежутке по графику.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке
10 класс. Решение задач на нахождение наибольшего и наименьшего значения функции на отрезке. Применение производной функции для нахождения точек максимума и минимума. Почему точи экстремума — это не всегда те точки, в которых достигается наибольшее или наименьшее значение?
Примеры решения реальных задач.
Ответы: производная положительна при каких условиях? и как это понять, если можно на конкретных примерах #question
Если на некотором промежутке производная функции положительна, то функция возрастает на этом промежутке, если отрицательна, то убывает.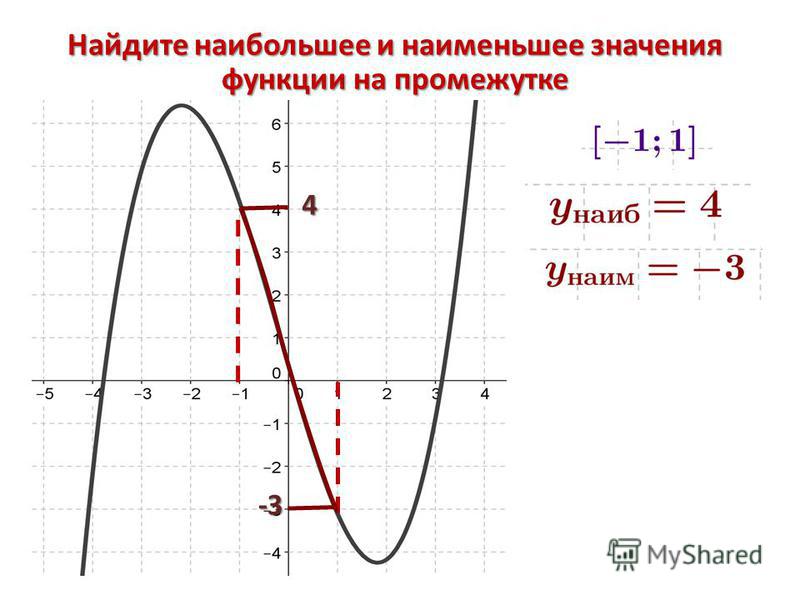 Примеры.
Примеры.
Если функция возрастает, то её производная больше.
Квадратичные задачи «Макс/Мин»
Квадратичный Задачи Word «Макс./Мин.» (стр. 3 из 3)
Секции: Снаряд движение, Общие текстовые задачи, Макс/мин проблемы
Когда вы доберетесь до исчисления, вы снова увидите некоторые из этих упражнений на макс/минимум.В этот момент они хочу, чтобы вы различали, чтобы найти максимумы и минимумы; с этой точки зрения, вы найдете вершину, так как вершина будет максимальной или минимальной связанных графических парабола. Но они одно и то же упражнение, и тогда вы получите те же ответы, что и сейчас.
- У вас есть 500 -ноги
рулон ограждения и большое поле. Вы хотите построить прямоугольную
детская площадка.
 Каковы размеры самого большого такого двора? Что
это самая большая площадь?
Каковы размеры самого большого такого двора? Что
это самая большая площадь?
Информация о длине ограждения дает мне периметр. Если длина замкнутого пространства L а ширина w , тогда периметр равен 2 L + 2 ш = 500, так л = 250 w . От решая уравнение периметра для одной из переменных, я могу заменить в формулу площади и получить уравнение только с одной переменной:
Чтобы найти максимум, я нужно найти вершину ( h , к ).
В моем уравнении площади я подключите значения «ширины» и получите значения «площади». Итак, ч -значение в вершине — максимизирующая ширина, а k -значение будет максимальная площадь:
Проблема не спрашивала
мне «какое значение переменной w ?»,
но «какие размеры?» у меня с = 125. Тогда длина л = 250 w = 250 125 = 125.
Тогда длина л = 250 w = 250 125 = 125.
Самая большая площадь
будет иметь размеры 125′ по 125′ ,
на общую площадь 15
625 кв.
ноги.
Обратите внимание, что самый большой прямоугольный площадь была квадратной. Это всегда верно: для данного периметра наибольшая прямоугольная площадь будет площадью квадрата.Однако учителя начинают заметить, что студенты поняли это, поэтому они дают больше сложные задачи площадь-периметр.
- У вас есть 1200 -фут
рулон ограждения и большое поле. Вы хотите сделать два загона
разделить прямоугольный корпус пополам. Каковы размеры
самый большой такой корпус?
Это не совсем так
независимо от того, какую сторону я обозначу как «длину», а какую
Я обозначаю как «ширину», если я обозначаю четко и
работать последовательно. |
|
С маркировкой Ive выбрано, ограждение дает мне «периметр» 2 L + 3 w = 1200. Решив одну из переменных, я получаю:
Тогда площадь: авторское право Элизабет Стапель 2004-2011 Все права защищены
Чтобы максимизировать эту площадь, Я должен найти вершину.Поскольку все, что мне нужно, это размеры (не площадь), все, что мне нужно от вершины ( h , k ) значение ч , так как это даст мне максимальную ширину.
Тогда длина будет л = 1,5(200) + 600 = 300 + 600 = 300.
Загон должен
быть 300′ по 200′, с разделителем
, идущим параллельно 200 длиной в фут
боковая сторона.
Обратите внимание, что с разделителем бегая по середине загона, вы не получите квадрат, как будто максимальная форма. Если они добавят соображения стоимости (например, размещение красивее, но дороже ограждение со стороны загона улица), вы также получите странные результаты. Предупреждение: не просто предполагайте что максимальная прямоугольная форма всегда будет квадратом.
Во многих квадратичных макс./мин. проблемы, вам будет предоставлена формула, которую нужно использовать.Не пытайтесь понять откуда они это взяли. Просто найдите вершину. Затем интерпретируйте переменные выяснить, какой номер из вершины вам нужен, где и с чем единицы.
- Ваш завод производит
вещицы с запахом лимона. Вы знаете, что каждая единица тем дешевле, чем больше
вы производите. Но вы также знаете, что затраты в конечном итоге возрастут, если вы
сделать слишком много виджетов из-за затрат на хранение излишков.
 Парень из бухгалтерии говорит, что ваши затраты на производство x тысяч единиц в день можно вычислить по формуле C = 0,04 х 2 8,504 х + 25302 . Находить
ежедневный уровень производства, который сведет к минимуму ваши затраты.
Парень из бухгалтерии говорит, что ваши затраты на производство x тысяч единиц в день можно вычислить по формуле C = 0,04 х 2 8,504 х + 25302 . Находить
ежедневный уровень производства, который сведет к минимуму ваши затраты.
Как нетрудно догадаться, это будет намного проще использовать вершину формула, чтобы найти минимизирующее значение для этого квадратичного уравнения, чем было бы для завершения квадрат.Поэтому я буду использовать формулу вершины:
Так как входы в
формула, которую они мне дали, — это уровни производства («тысячи единиц»),
Я нашел нужный мне номер. Другое число для вершины будет
быть фактическими затратами на изготовление такого количества виджетов, а проблема
этого не просит. Однако мне нужно помнить, что x исчисляется тысячами единиц, поэтому мой лучший уровень производства — не 106. 3
единиц, но (106,3)(1 000)
= 106 300 ед.
3
единиц, но (106,3)(1 000)
= 106 300 ед.
Иногда тебя бьют с проблемой, которая кажется гораздо более сложной, особенно когда у вас есть придумать формулу самостоятельно.
- Вы занимаетесь прокатом каноэ бизнес на небольшой реке в Огайо. В настоящее время вы берете $12 на каноэ и в среднем 36 аренды в день.В отраслевом журнале говорится, что на каждые пятьдесят центов увеличения в арендной плате средний бизнес может рассчитывать на потерю двух арендных платежей. день. Используйте эту информацию, чтобы попытаться максимизировать свой доход. Что вы должны зарядить?
Допустим, я понятия не имею
как поставить эту проблему. Вместо того, чтобы сразу перейти к уравнению,
Мне нужно ввести некоторые реальные цифры, посмотреть, что я сделаю, когда узнаю, что
значения, а затем следуйте шаблону, чтобы получить мою формулу. Здесь
мои рассуждения, аккуратно изложенные в таблице:
Здесь
мои рассуждения, аккуратно изложенные в таблице:
цена походы | цена за аренду | номер | всего доход / выручка |
нет | 12 долларов.00 | 36 | $12. |
1 цена поход | $12.00 + 1(0,50) | 36 1(2) | 12 долларов.5034 = 425,00 долларов США |
2 цена походы | $12.00 + 2(0,50) | 36 2(2) | 13 долларов.0032 = 416,00 долларов США |
3 цена походы | $12. | 36 3(2) | 13 долларов.5030 = 405,00 долларов США |
х повышение цен | $12.00 + х (0,50) | 36 х (2) | (12+ 0.5 х )(36 2 х ) |
Тогда моя формула для моего выручка р после х повышение цен на пятьдесят центов составляет:
Максимальный доход составит
происходят в вершине этой квадратичной параболы, и вершина
в
(3,
441):
То есть мой доход будет
быть максимальным (при условии, что журнальная статья верна), если I ниже моя текущая цена 12$
в три раза по пятьдесят центов, или на 1 доллар. 50.
50.
Всякий раз, когда вы не уверены вашей формулы, попробуйте сделать то, что я сделал выше: напишите, что бы вы сделать, если бы вы знали, что это за числа, и посмотреть, сможете ли вы превратить это в формула. Но убедитесь, что вы записываете все полностью, как я, чтобы вы могли видеть узор. Предупреждение: не упрощайте слишком много в своей голове, или вы можете пропустить, какой должна быть ваша формула.
<< Предыдущий Топ | 1 | 2 | 3 | Возвращение к индексу
Процитировать эту статью как: | Стапель, Элизабет.«Квадратичные задачи на максимальное и минимальное количество слов». Пурпурная математика .
Доступно по номеру |
Функция Excel RANK и другие способы расчета ранга
В учебном пособии объясняются особенности функций ранжирования Excel и показано, как выполнять ранжирование в Excel на основе нескольких критериев, ранжировать данные по группам, вычислять ранг в процентилях и многое другое.
Когда вам нужно определить относительное положение числа в списке чисел, проще всего отсортировать числа в порядке возрастания или убывания. Если по какой-либо причине сортировка невозможна, формула ранжирования в Excel является идеальным инструментом для выполнения этой работы.
Функция Excel РАНГ
Функция РАНГ в Excel возвращает порядок (или ранг) числового значения по сравнению с другими значениями в том же списке. Другими словами, он сообщает вам, какое значение является самым высоким, вторым по величине и т. д.
В отсортированном списке ранг определенного числа будет его позицией. Функция РАНГ в Excel может определять ранг, начиная с наибольшего значения (как при сортировке по убыванию) или с наименьшего значения (как при сортировке по возрастанию).
Функция РАНГ в Excel может определять ранг, начиная с наибольшего значения (как при сортировке по убыванию) или с наименьшего значения (как при сортировке по возрастанию).
Синтаксис функции Excel РАНГ следующий:
РАНГ(номер,ссылка,[порядок])
Где:
Число (обязательно) — значение, ранг которого вы хотите найти.
Ref (обязательно) — список числовых значений для ранжирования.Он может быть представлен в виде массива чисел или ссылки на список чисел.
Заказ (необязательно) — номер, указывающий, как ранжировать значения:
- Если 0 или опущено, значения ранжируются в порядке убывания, т. е. от наибольшего к наименьшему.
- Если 1 или любое другое ненулевое значение, значения ранжируются в порядке возрастания, т. е. от наименьшего к наибольшему.
Функция Excel RANK.EQ
РАНГ.EQ — это улучшенная версия функции РАНГ, представленная в Excel 2010. Он имеет тот же синтаксис, что и RANK, и работает по той же логике: если несколько значений ранжируются одинаково, всем таким значениям присваивается наивысший ранг. (EQ означает «равный»).
Он имеет тот же синтаксис, что и RANK, и работает по той же логике: если несколько значений ранжируются одинаково, всем таким значениям присваивается наивысший ранг. (EQ означает «равный»).
РАНГ.EQ(число,ссылка,[порядок])
В Excel 2007 и более ранних версиях всегда следует использовать функцию РАНГ. В Excel 2010, Excel 2013 и Excel 2016 вы можете использовать либо RANK, либо RANK.EQ. Однако было бы разумно использовать RANK.EQ, потому что RANK может быть прекращен в любой момент.
Функция Excel РАНГ.СРЕДНЯЯ
РАНГ.AVG — это еще одна функция для определения ранга в Excel, которая доступна только в Excel 2010, Excel 2013, Excel 2016 и более поздних версиях.
Имеет тот же синтаксис, что и две другие функции:
РАНГ.СРЕДНИЙ(номер,ссылка,[порядок])
Разница в том, что если несколько чисел имеют одинаковый ранг, возвращается средний ранг (AVG означает «средний»).
4 вещи, которые вы должны знать о RANK в Excel
- Любая формула ранга в Excel работает только для числовых значений: положительных и отрицательных чисел, нулей, значений даты и времени.
 Нечисловые значения в аргументе ref игнорируются.
Нечисловые значения в аргументе ref игнорируются. - Все функции RANK возвращают один и тот же ранг для повторяющихся значений и пропускают последующее ранжирование, как показано в примере ниже.
- В Excel 2010 и более поздних версиях функция РАНГ была заменена функциями РАНГ.EQ и РАНГ.СРЕДН. В целях обратной совместимости РАНГ по-прежнему работает во всех версиях Excel, но в будущем он может быть недоступен.
- Если номер не найден в пределах ref , любая функция Excel Rank вернет ошибку #N/A.
Базовая формула ранжирования Excel (от высшего к низшему)
Чтобы лучше понять ранжирование данных в Excel, посмотрите на этот снимок экрана:
Все три формулы ранжируют числа в столбце B в порядке убывания (аргумент порядка опущен):
Во всех версиях Excel 2003–2016:
=РАНГ($B2,$B$2:$B$7)
В Excel 2010–2016:
=РАНГ. EQ($B2,$B$2:$B$7)
EQ($B2,$B$2:$B$7)
=РАНГ.СРЕДНЕЕ ($B2,$B$2:$B$7)
Разница заключается в том, как эти формулы обрабатывают повторяющиеся значения. Как видите, одна и та же оценка появляется дважды, в ячейках B5 и B6, что влияет на последующее ранжирование:
.- Формулы RANK и RANK.EQ присваивают обеим повторяющимся оценкам ранг 2. Следующая наивысшая оценка (Даниэла) занимает 4-е место. Ранг 3 никому не дается.
- Формула РАНГ.СРЕДНИЙ присваивает разный ранг каждому дубликату за кулисами (2 и 3 в этом примере) и возвращает среднее значение этих рангов (2.5). Опять же, 3 ранг никому не присваивается.
Как использовать РАНГ в Excel — примеры формул
Путь к совершенству, как говорят, вымощен практикой. Итак, чтобы лучше узнать, как использовать функцию РАНГ в Excel отдельно или в сочетании с другими функциями, давайте разработаем решения для нескольких задач из реальной жизни.
Как ранжировать в Excel от самого низкого до самого высокого
Как показано в приведенном выше примере, для ранжирования чисел от высшего к низшему используется одна из формул Excel Rank с аргументом порядка , равным 0 или опущенным (по умолчанию).
Чтобы ранжировать число по сравнению с другими числами, отсортированными в порядке возрастания , поместите 1 или любое другое ненулевое значение в необязательный третий аргумент.
Например, чтобы ранжировать время бега студентов на 100 м, вы можете использовать одну из следующих формул:
=РАНГ(B2,$B$2:$B$7,1)
=РАНГ.EQ(B2,$B$2:$B$7,1)
Обратите внимание, что мы блокируем диапазон в аргументе ref , используя абсолютные ссылки на ячейки, поэтому он не изменится, когда мы скопируем формулу вниз по столбцу.
В результате наименьшее значение (самое быстрое время) получает 1-е место, а самое большое значение (самое медленное время) получает самый низкий ранг 6. Равные времена (B2 и B7) получают одинаковый ранг.
Как однозначно ранжировать данные в Excel
Как указывалось ранее, все функции Excel Rank возвращают один и тот же рейтинг для элементов равной ценности. Если вы этого не хотите, используйте одну из следующих формул для решения ситуаций тай-брейка и присвойте уникальный ранг каждому номеру.
Если вы этого не хотите, используйте одну из следующих формул для решения ситуаций тай-брейка и присвойте уникальный ранг каждому номеру.
Уникальный рейтинг от высшего к низшему
Чтобы ранжировать результаты наших учеников по математике в порядке убывания, используйте следующую формулу:
=РАНГ.EQ(B2,$B$2:$B$7)+СЧЁТЕСЛИ($B$2:B2,B2)-1
Уникальный рейтинг от низшего к высшему
Чтобы ранжировать результаты забега на 100 м в порядке возрастания без дубликатов, используйте следующую формулу:
=РАНГ.EQ(B2,$B$2:$B$7,1) + СЧЁТЕСЛИ($B$2:B2,B2)-1
Как работают эти формулы
Как вы, возможно, заметили, единственное различие между двумя формулами заключается в аргументе порядка РАНГ.Функция эквалайзера: опущена для ранжирования значений по убыванию, 1 — для ранжирования по возрастанию.
В обеих формулах функция СЧЁТЕСЛИ с умным использованием относительных и абсолютных ссылок на ячейки делает своё дело. Короче говоря, вы используете СЧЁТЕСЛИ, чтобы узнать, сколько вхождений ранжируемого числа есть в вышеуказанных ячейках, включая ячейку числа. В самой верхней строке, где вы вводите формулу, диапазон состоит из одной ячейки ($B$2:B2). Но поскольку вы блокируете только первую ссылку ($B$2), последняя относительная ссылка (B2) изменяется в зависимости от строки, в которую копируется формула.Таким образом, для строки 7 диапазон расширяется до $B$2:B7, а значение в ячейке B7 сравнивается с каждой из указанных выше ячеек.
Короче говоря, вы используете СЧЁТЕСЛИ, чтобы узнать, сколько вхождений ранжируемого числа есть в вышеуказанных ячейках, включая ячейку числа. В самой верхней строке, где вы вводите формулу, диапазон состоит из одной ячейки ($B$2:B2). Но поскольку вы блокируете только первую ссылку ($B$2), последняя относительная ссылка (B2) изменяется в зависимости от строки, в которую копируется формула.Таким образом, для строки 7 диапазон расширяется до $B$2:B7, а значение в ячейке B7 сравнивается с каждой из указанных выше ячеек.
Следовательно, для всех первых вхождений функция СЧЁТЕСЛИ возвращает 1; и вы вычитаете 1 в конце формулы, чтобы восстановить исходный ранг.
Для 2-го вхождения функция СЧЁТЕСЛИ возвращает 2. Вычитая 1, вы увеличиваете ранг на 1 пункт, тем самым предотвращая дублирование. Если окажется, что одно и то же значение встречается 3 раза, COUNTIF()-1 добавит 2 к их ранжированию и так далее.
Альтернативное решение для разрыва связей Excel RANK
Еще один способ уникально ранжировать числа в Excel — сложить две функции СЧЁТЕСЛИ:
- Первая функция определяет, сколько значений больше или меньше ранжируемого числа, в зависимости от того, ранжируете ли вы по убыванию или по возрастанию, соответственно.

- Вторая функция (с «расширяемым диапазоном» $B$2:B2, как в приведенном выше примере) получает количество значений, равное числу.
Например, для уникального ранжирования чисел от высшего к низшему можно использовать следующую формулу:
=СЧЁТЕСЛИ($B$2:$B$7,">"&$B2)+СЧЁТЕСЛИ($B$2:B2,B2)
Как показано на снимке экрана ниже, тай-брейк успешно разрешен, и каждому ученику присваивается уникальный ранг:
Ранжирование в Excel на основе нескольких критериев
В предыдущем примере продемонстрированы два рабочих решения для ситуации с тай-брейком Excel RANK.Однако может показаться несправедливым, что одинаковые числа ранжируются по-разному исключительно в зависимости от их положения в списке. Чтобы улучшить свой рейтинг, вы можете добавить еще один критерий, который будет учитываться в случае ничьей.
В нашем образце данных давайте добавим общее количество баллов в столбец C и рассчитаем рейтинг следующим образом:
- Первое место с Результатом по математике (основной критерий)
- Если есть ничья, разбить ее с помощью Общий балл (вторичные критерии)
Для этого мы будем использовать обычный RANK/RANK. Формула EQ для определения ранга и функция СЧЁТЕСЛИМН для определения ничьей:
Формула EQ для определения ранга и функция СЧЁТЕСЛИМН для определения ничьей:
=РАНГ.EQ($B2,$B$2:$B$7)+СЧЁТЕСЧЕТЫ($B$2:$B$7,$B2,$C$2:$C$7,">"&$C2)
По сравнению с приведенным выше примером эта формула ранжирования более объективна: Тимоти занимает 2 и места, потому что его общий балл выше, чем у Юлии:
Как работает эта формула
Часть формулы РАНГ очевидна, и функция СЧЁТЕСЛИМН делает следующее:
- Первая пара из критериев_диапазон / критериев ($B$2:$B$7,$B2) подсчитывает вхождения ранжируемого значения.Обратите внимание, что мы фиксируем диапазон с помощью абсолютных ссылок, но не блокируем строку критерия ($B2), чтобы формула проверяла значение в каждой строке отдельно.
- Вторая пара критериев_диапазон / критериев ($C$2:$C$7,»>»&$C2) определяет, на сколько общих баллов больше, чем общий балл ранжируемого значения.
Поскольку СЧЁТЕСЛИМН работает с логикой И, т. е. подсчитывает только те ячейки, которые соответствуют всем указанным условиям, для Тимати возвращается 0, поскольку ни один другой учащийся с таким же баллом по математике не имеет более высокого общего балла.Следовательно, ранг Тимоти, возвращенный RANK.EQ, не изменился. Для Юлии функция СЧЁТЕСЛИМН возвращает 1, потому что у одного учащегося с таким же баллом по математике сумма выше, поэтому её ранг увеличивается на 1. Если ещё один учащийся имеет такой же балл по математике и общий балл ниже, чем у Тимати и Юлии , его/ее ранг будет увеличен на 2 и так далее.
е. подсчитывает только те ячейки, которые соответствуют всем указанным условиям, для Тимати возвращается 0, поскольку ни один другой учащийся с таким же баллом по математике не имеет более высокого общего балла.Следовательно, ранг Тимоти, возвращенный RANK.EQ, не изменился. Для Юлии функция СЧЁТЕСЛИМН возвращает 1, потому что у одного учащегося с таким же баллом по математике сумма выше, поэтому её ранг увеличивается на 1. Если ещё один учащийся имеет такой же балл по математике и общий балл ниже, чем у Тимати и Юлии , его/ее ранг будет увеличен на 2 и так далее.
Альтернативные решения для ранжирования чисел с несколькими критериями
Вместо функции РАНГ или РАНГ.РВ вы можете использовать СЧЁТЕСЛИ для проверки основных критериев, а СЧЁТЕСЛИМН или СУММПРОИЗВ для разрешения тай-брейка:
=СЧЁТЕСЛИ($B$2:$B$7,">"&$B2)+СЧЁТЕСЧЁТЕ($B$2:$B$7,$B2,$C$2:$C$7,">"&$C2)+ 1
=СЧЁТЕСЛИ($B$2:$B$7,">"&B2)+СУММПРОИЗВ(--($C$2:$C$7=C2),--($B$2:$B$7>B2))+ 1
Результат этих формул точно такой же, как показано выше.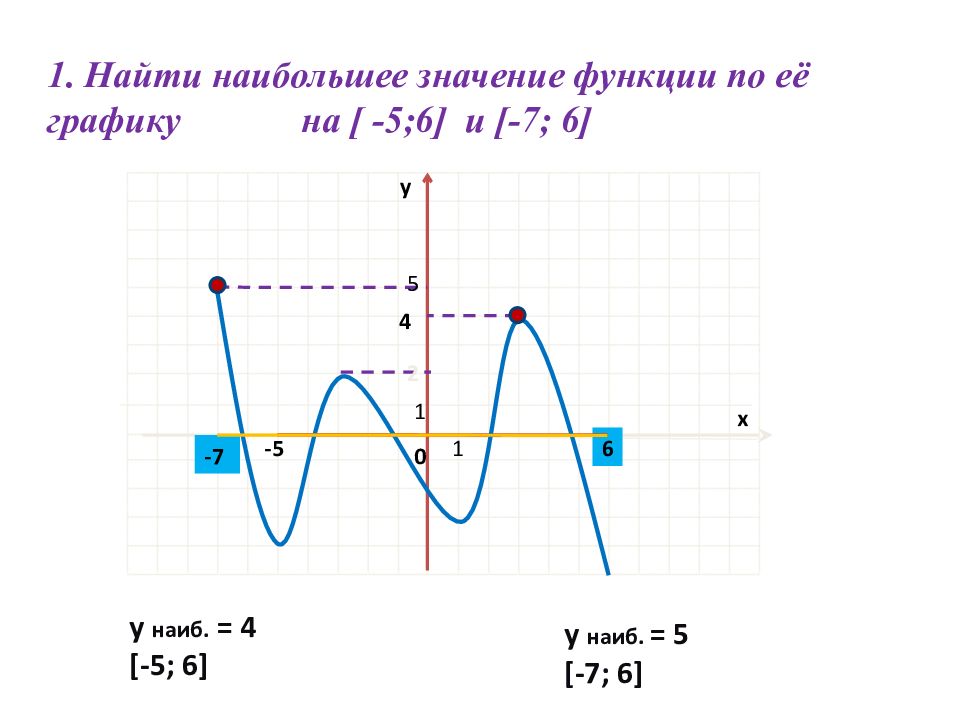
Как рассчитать процентильный ранг в Excel
В статистике процентиль (или процентиль ) — это значение, ниже которого падает определенный процент значений в заданном наборе данных. Например, если 70 % учащихся имеют такой же или более низкий балл за тест, ваш процентильный ранг равен 70.
Чтобы получить процентильный ранг в Excel, используйте функцию RANK или RANK.EQ с ненулевым аргументом порядка для ранжирования чисел от наименьшего к наибольшему, а затем разделите ранг на количество чисел.Итак, общая формула Excel Percentile Rank выглядит следующим образом:
RANK.EQ( topmost_cell , диапазон ,1)/COUNT( диапазон )
Для расчета процентного ранга наших студентов формула принимает следующий вид:
=РАНГ.EQ(B2,$B$2:$B$7,1)/СЧЁТ($B$2:$B$7)
Чтобы результаты отображались правильно, обязательно установите Процентный формат для ячеек формулы:
Как ранжировать числа в несмежных ячейках
В ситуациях, когда вам нужно ранжировать несмежные ячейки, укажите эти ячейки непосредственно в аргументе ref вашей формулы ранжирования Excel в форме объединения ссылок, заблокировав ссылки знаком $. Например:
Например:
=РАНГ(B2,($B$2,$B$4,$B$6))
Чтобы предотвратить ошибки в неранжированных ячейках, оберните РАНГ в функцию ЕСЛИОШИБКА, например:
=ЕСЛИОШИБКА(РАНГ(B2,($B$2,$B$4,$B$6)), "")
Обратите внимание, что повторяющемуся числу также присваивается ранг, хотя ячейка B5 не включена в формулу:
Если вам нужно ранжировать несколько несмежных ячеек, приведенная выше формула может стать слишком длинной. В этом случае более элегантным решением будет определение именованного диапазона и ссылка на это имя в формуле:
. =ЕСЛИОШИБКА(РАНГ(B2,диапазон), "")
Как ранжировать в Excel по группам
При работе с записями, организованными в какую-либо структуру данных, данные могут принадлежать к разным группам, и может потребоваться ранжировать числа в каждой группе отдельно.Функция Excel RANK не может решить эту проблему, поэтому мы собираемся использовать более сложную формулу СУММПРОИЗВ:
.
Ранжирование по группам в порядке по убыванию :
=СУММПРОИЗВ((A2=$A$2:$A$7)*(C2<$C$2:$C$7))+1
Ранг по группам в по возрастанию порядок:
=СУММПРОИЗВ((A2=$A$2:$A$7)*(C2>$C$2:$C$7))+1
Где:
- A2:A7 — группы, назначенные номерам.
- C2:C7 — числа для ранжирования.
В этом примере мы используем первую формулу для ранжирования чисел в каждой группе от большего к меньшему:
Как работает эта формула
По сути, формула оценивает 2 условия:
- Сначала вы проверяете группу (A2=$A$2:$A$7). Эта часть возвращает массив значений TRUE и FALSE в зависимости от того, принадлежит ли элемент диапазона к той же группе, что и A2.
- Во-вторых, вы проверяете счет. Чтобы ранжировать значения от наибольшего к наименьшему ( в порядке убывания ), используйте условие (C2<$C$2:$C$11), которое возвращает TRUE для ячеек, больших или равных C2, и FALSE в противном случае.

Поскольку в терминах Microsoft Excel ИСТИНА = 1 и ЛОЖЬ = 0, умножение двух массивов дает массив из 1 и 0, где 1 возвращается только для строк, в которых выполняются оба условия.
Затем СУММПРОИЗВ складывает элементы массива 1 и 0, таким образом, возвращая 0 для наибольшего числа в каждой группе. И вы добавляете 1 к результату, чтобы начать ранжирование с 1.
Формула ранжирования чисел в группах от наименьшего к наибольшему ( по возрастанию по порядку ) работает по той же логике.Разница в том, что СУММПРОИЗВ возвращает 0 для наименьшего числа в определенной группе, поскольку ни одно число в этой группе не удовлетворяет условию 2 и (C2>$C$2:$C$7). Опять же, вы заменяете нулевой ранг 1-м рангом, добавляя 1 к результату формулы.
Вместо СУММПРОИЗВ можно использовать функцию СУММ для сложения элементов массива. Но для этого потребуется использовать формулу массива, заполняемую с помощью Ctrl + Shift + Enter. Например:
Например:
=СУММ((A2=$A$2:$A$7)*(C2<$C$2:$C$7))+1
Как ранжировать положительные и отрицательные числа отдельно
Если ваш список чисел содержит как положительные, так и отрицательные значения, функция Excel RANK мгновенно ранжирует их все.Но что, если вы хотите, чтобы положительные и отрицательные числа ранжировались отдельно?
С числами в ячейках от A2 до A10 используйте одну из следующих формул, чтобы получить индивидуальное ранжирование для положительных и отрицательных значений:
Ранг положительных чисел по убыванию:
=ЕСЛИ($A2>0,СЧЁТЕСЛИ($A$2:$A$10,">"&A2)+1,"")
Ранг положительных чисел по возрастанию:
=ЕСЛИ($A2>0,СЧЁТЕСЛИ($A$2:$A$10,">0")-СЧЁТЕСЛИ($A$2:$A$10,">"&$A2),"")
Ранг отрицательных чисел по убыванию:
=ЕСЛИ($A2<0,СЧЁТЕСЛИ($A$2:$A$10,"<0")-СЧЁТЕСЛИ($A$2:$A$10,"<"&$A2),"")
Ранг отрицательных чисел по возрастанию:
=ЕСЛИ($A2<0,СЧЁТЕСЛИ($A$2:$A$10,"<"&$A2)+1,"")
Результаты будут выглядеть примерно так:
Как работают эти формулы
Для начала разберем формулу, которая ранжирует положительные числа в порядке по убыванию :
- При логическом тесте функции ЕСЛИ вы проверяете, больше ли число нуля.

- Если число больше 0, функция СЧЁТЕСЛИ возвращает количество значений, превышающих ранжируемое число.
В этом примере A2 содержит второе по величине положительное число, для которого СЧЁТЕСЛИ возвращает 1, что означает, что есть только одно число больше его. Чтобы начать ранжирование с 1, а не с 0, мы добавляем 1 к результату формулы, поэтому она возвращает ранг 2 для A2.
- Если число больше 0, формула возвращает пустую строку ("").
Формула ранжирования положительных чисел в порядке по возрастанию работает несколько иначе:
Если число больше 0, первый СЧЁТЕСЛИ получает общее количество положительных чисел в наборе данных, а второй СЧЁТЕСЛИ определяет, сколько значений больше этого числа.Затем вы вычитаете последнее из первого и получаете желаемый ранг. В этом примере есть 5 положительных значений, 1 из которых больше, чем A2. Итак, вы вычитаете 1 из 5, таким образом получая ранг 4 для A2.
Формулы ранжирования отрицательных чисел основаны на аналогичной логике.
. Например, чтобы ранжировать положительные числа и нули от наибольшего к наименьшему, используйте следующую формулу: =ЕСЛИ($A2>=0,СЧЁТЕСЛИ($A$2:$ 10 австралийских долларов, ">"&A2)+1,"")
Как ранжировать данные в Excel, игнорируя нулевые значения
Как вы уже знаете, формула РАНГ в Excel обрабатывает все числа: положительные, отрицательные и нули.Но в некоторых случаях мы просто хотим ранжировать ячейки с данными, игнорируя 0 значений. В сети можно найти несколько возможных решений этой задачи, но формула Excel RANK IF, мне кажется, самая универсальная:
Номера рангов по убыванию без учета нуля:
=ЕСЛИ($B2=0,"",ЕСЛИ($B2>0,РАНГ($B2,$B$2:$B$10), РАНГ($B2,$B$2:$B$10)-СЧЁТЕСЛИ( $B$2:$B$10,0)))
Номера рангов по возрастанию без учета нуля:
=ЕСЛИ($B2=0,"",ЕСЛИ($B2>0,РАНГ($B2,$B$2:$B$10,1) - СЧЁТЕСЛИ($B$2:$B$10,0), РАНГ ($B2,$B$2:$B$10,1)))
Где B2:B10 — диапазон ранжируемых чисел.
Лучшее в этой формуле то, что она прекрасно работает как для положительных, так и для отрицательных чисел, оставляя нулевые значения вне ранжирования:
Как работает эта формула
На первый взгляд, формула может показаться сложной. При ближайшем рассмотрении логика очень проста.
Вот как формула Excel RANK IF ранжирует числа от наибольшего к наименьшему, игнорируя нули:
- Первый IF проверяет, равно ли число 0, и если да, то возвращает пустую строку:
ЕСЛИ($B2=0,"", …)
- Если число не равно нулю, вторым IF проверяется, больше ли оно 0, и если больше, то обычный RANK/РАНГ.Функция эквалайзера вычисляет его ранг:
ЕСЛИ($B2>0,РАНГ($B2,$B$2:$B$10),…)
- Если число меньше 0, вы корректируете ранжирование по нулевому счету. В этом примере 4 положительных числа и 2 нуля. Таким образом, для наибольшего отрицательного числа в ячейке B10 формула Excel RANK вернет 7. Но мы пропускаем нули, и поэтому нам нужно скорректировать ранг на 2 балла.
 Для этого вычтем из ранга количество нулей:
Для этого вычтем из ранга количество нулей:РАНГ($B2,$B$2:$B$10)-СЧЁТЕСЛИ($B$2:$B$10,0))
Да, это так просто! Формула для ранжирования чисел от наименьшего к наибольшему, игнорируя нули, работает аналогичным образом, и это может быть хорошим упражнением для мозга, чтобы вывести ее логику 🙂
Как вычислить ранг в Excel по абсолютному значению
При работе со списком положительных и отрицательных значений может возникнуть необходимость ранжировать числа по их абсолютным значениям без учета знака.
Задачу можно решить с помощью одной из следующих формул, в основе которых лежит функция ABS, возвращающая абсолютное значение числа:
Рейтинг ABS по убыванию:
=СУММПРОИЗВ((ABS(A2)<=ABS(A$2:A$7)) * (A$2:A$7<>"")) - СУММПРОИЗВ((ABS(A2)=ABS($A$2:$ A$7)) * (A$2:A$7<>""))+1
Рейтинг ABS по возрастанию:
=СУММПРОИЗВ((ABS(A2)>=ABS(A$2:A$7)) * (A$2:A$7<>"")) - СУММПРОИЗВ((ABS(A2)=ABS($A$2:$ A$7)) * (A$2:A$7<>""))+1
В результате отрицательные числа ранжируются так, как если бы они были положительными числами:
Как получить N наибольших или наименьших значений
Если вы хотите получить фактическое число N наибольших или наименьших значений, а не их ранжирование, используйте функцию НАИБОЛЬШИЙ или МАЛЕНЬКИЙ соответственно.
Например, мы можем получить 3 лучших результата наших студентов с помощью этой формулы:
=БОЛЬШОЙ($B$2:$B$7, $D3)
Где B2:B7 — список баллов, а D3 — желаемый ранг.
Кроме того, вы можете получить имена учащихся, используя формулу ИНДЕКС ПОИСКПОЗ (при условии, что в первой тройке нет повторяющихся результатов):
=ИНДЕКС($A$2:$A$7,ПОИСКПОЗ(E3,$B$2:$B$7,0))
Точно так же вы можете использовать функцию МАЛЕНЬКИЙ, чтобы получить 3 нижних значения:
=МАЛЕНЬКИЙ($B$2:$B$7, $D3)
Вот как вы делаете ранжирование в Excel.Чтобы лучше понять и, возможно, перепроектировать формулы, обсуждаемые в этом руководстве, вы можете загрузить нашу рабочую книгу Sample Rank Excel.
Благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Исчисление I - Оптимизация
Показать мобильное уведомление Показать все примечания Скрыть все примечания Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. у вас наверное на мобильнике). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. у вас наверное на мобильнике). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-8: Оптимизация
В этом разделе мы рассмотрим проблемы оптимизации.В задачах оптимизации мы ищем наибольшее значение или наименьшее значение, которое может принимать функция. Мы видели, как решить одну из задач оптимизации в разделе «Абсолютные экстремумы», где мы нашли наибольшее и наименьшее значение, которое функция может принимать на интервале.
В этом разделе мы рассмотрим другой тип задач оптимизации. Здесь мы будем искать наибольшее или наименьшее значение функции с некоторым ограничением. Ограничением будет некоторое условие (которое обычно может быть описано каким-либо уравнением), которое должно быть абсолютно, безусловно, истинным, независимо от того, какое у нас решение.Иногда ограничение не может быть легко описано уравнением, но в этих задачах с ним будет легко справиться, как мы увидим.
Ограничением будет некоторое условие (которое обычно может быть описано каким-либо уравнением), которое должно быть абсолютно, безусловно, истинным, независимо от того, какое у нас решение.Иногда ограничение не может быть легко описано уравнением, но в этих задачах с ним будет легко справиться, как мы увидим.
Этот раздел, как правило, является одним из самых сложных для студентов, изучающих курс исчисления. Одна из основных причин этого заключается в том, что незначительное изменение формулировки может полностью изменить проблему. Существует также проблема определения количества, которое мы будем оптимизировать, и количества, которое является ограничением, и записи уравнений для каждого из них.
Первым шагом во всех этих задачах должно быть очень внимательное прочтение задачи. После того, как вы это сделаете, следующим шагом будет определение количества, которое необходимо оптимизировать, и ограничения.
При определении ограничения помните, что ограничение — это величина, которая должна быть истинной независимо от решения. Почти в каждой из задач, которые мы здесь рассмотрим, одна величина будет четко указана как имеющая фиксированное значение, и поэтому она должна быть ограничением.После того, как вы это определили, количество, которое нужно оптимизировать, должно быть довольно просто получить. Однако их легко спутать, если вы просто пробежитесь по задаче, поэтому сначала внимательно прочитайте задачу!
Почти в каждой из задач, которые мы здесь рассмотрим, одна величина будет четко указана как имеющая фиксированное значение, и поэтому она должна быть ограничением.После того, как вы это определили, количество, которое нужно оптимизировать, должно быть довольно просто получить. Однако их легко спутать, если вы просто пробежитесь по задаче, поэтому сначала внимательно прочитайте задачу!
Давайте начнем этот раздел с простой задачи, чтобы проиллюстрировать виды проблем, с которыми мы будем иметь дело здесь.
Пример 1 Нам нужно обнести прямоугольное поле забором. У нас есть 500 футов материала для ограждения, а здание находится на одной стороне поля, поэтому ограждение не понадобится.Определите размеры поля, которое будет охватывать наибольшую площадь. Показать решение Во всех этих задачах у нас будет две функции. Первая — это функция, которую мы на самом деле пытаемся оптимизировать, а вторая будет ограничением. Набросок ситуации часто помогает нам прийти к этим уравнениям, поэтому давайте сделаем это.
В этой задаче мы хотим максимизировать площадь поля, и мы знаем, что для этого потребуется 500 футов ограждающего материала.Таким образом, площадь будет функцией, которую мы пытаемся оптимизировать, а количество ограждений — ограничением. Два уравнения для них:
\[\begin{align*}{\mbox{Максимизация:}} & A = xy\\ {\mbox{Ограничение:}} & 500 = x + 2y\end{align*}\]Итак, мы знаем, как найти наибольшее или наименьшее значение функции, если она имеет только одну переменную. Функция площади (как и ограничение) содержит две переменные, поэтому то, что мы знаем о поиске абсолютных экстремумов, не работает.Однако, если мы решим ограничение для одной из двух переменных, мы можем подставить это в область, и тогда у нас будет функция одной переменной.
Итак, давайте решим ограничение для \(x\). Обратите внимание, что мы могли бы так же легко решить для \(y\), но это привело бы к дробям, и поэтому в этом случае решение для \(x\), вероятно, будет лучшим.
Подстановка этого значения в функцию площади дает функцию \(y\).2}\]
Теперь мы хотим найти наибольшее значение, которое оно будет иметь на интервале \(\left[ {0,250} \right]\). Пределы в этом интервале соответствуют взятию \(y = 0\) ( т.е. без сторон забора) и \(y = 250\) ( т.е. только две стороны и без ширины, также если есть две стороны каждый должен быть 250 футов, чтобы использовать все 500 футов).
Обратите внимание, что конечные точки интервала не будут иметь никакого смысла с физической точки зрения, если мы на самом деле хотим заключить некоторую область, потому что обе они дадут нулевую площадь.Однако они дают нам набор ограничений на \(y\), и поэтому теорема об экстремальном значении говорит нам, что у нас будет максимальное значение площади где-то между двумя конечными точками. Наличие этих пределов также будет означать, что мы можем использовать процесс, который обсуждался в разделе «Нахождение абсолютных экстремумов». 2}\).Таким образом, согласно методу из раздела Абсолютные экстремумы, это должна быть максимально возможная площадь, поскольку площадь в любой конечной точке равна нулю.
2}\).Таким образом, согласно методу из раздела Абсолютные экстремумы, это должна быть максимально возможная площадь, поскольку площадь в любой конечной точке равна нулю.
Наконец, давайте не забудем получить значение \(x\), и тогда у нас будут размеры, поскольку это то, о чем просило условие задачи. Мы можем получить \(x\), подставив наш \(y\) в ограничение.
\[x = 500 - 2\влево ({125} \вправо) = 250\]Размеры поля, которое даст наибольшую площадь, при условии, что мы использовали ровно 500 футов ограждающего материала, составляют 250 х 125.
Не забудьте прочитать задачу и дать ответ, который просили. Для решения этих типов проблем может потребоваться значительное количество времени/усилий, и иногда несложно забыть, о чем на самом деле шла речь.
В предыдущей задаче мы использовали метод из раздела «Поиск абсолютных экстремумов», чтобы найти максимальное значение функции, которую мы хотели оптимизировать. Однако, как мы увидим в следующих примерах, не всегда будет легко найти конечные точки.Кроме того, даже если мы сможем найти конечные точки, мы увидим, что иногда иметь дело с конечными точками тоже может быть непросто. Кроме того, этот метод требует, чтобы оптимизируемая функция была непрерывной на рассматриваемом интервале, включая конечные точки, а это не всегда так.
Однако, как мы увидим в следующих примерах, не всегда будет легко найти конечные точки.Кроме того, даже если мы сможем найти конечные точки, мы увидим, что иногда иметь дело с конечными точками тоже может быть непросто. Кроме того, этот метод требует, чтобы оптимизируемая функция была непрерывной на рассматриваемом интервале, включая конечные точки, а это не всегда так.
Итак, прежде чем перейти к другим примерам, давайте уделим немного времени обсуждению некоторых методов определения того, действительно ли наше решение является абсолютным минимальным/максимальным значением, которое мы ищем.В некоторых примерах все они будут работать, в то время как в других один или несколько не будут такими уж полезными. Однако нам всегда нужно будет использовать какой-то метод, чтобы убедиться, что наш ответ действительно является оптимальным значением, которое мы ищем.
Метод 1 : Используйте метод, использованный в разделе Поиск абсолютных экстремумов.
Это метод, использованный в первом примере выше. Напомним, что для использования этого метода интервал возможных значений независимой переменной в оптимизируемой нами функции, назовем ее \(I\), должен иметь конечные точки.Кроме того, оптимизируемая функция (после того, как она сводится к одной переменной) должна быть непрерывной на \(I\), включая конечные точки. Если эти условия выполняются, то мы знаем, что оптимальное значение, либо максимальное, либо минимальное в зависимости от задачи, будет иметь место либо в конечных точках диапазона, либо в критической точке, которая находится внутри диапазона возможных решений.
Однако есть две основные проблемы, которые часто препятствуют использованию этого метода. Во-первых, не каждая проблема на самом деле будет иметь ряд возможных решений с конечными конечными точками на обоих концах.Мы увидим по крайней мере один пример этого, когда будем работать с оставшимися примерами. Кроме того, многие из функций, которые мы будем оптимизировать, не будут непрерывными, как только мы сократим их до одной переменной, и это не позволит нам использовать этот метод.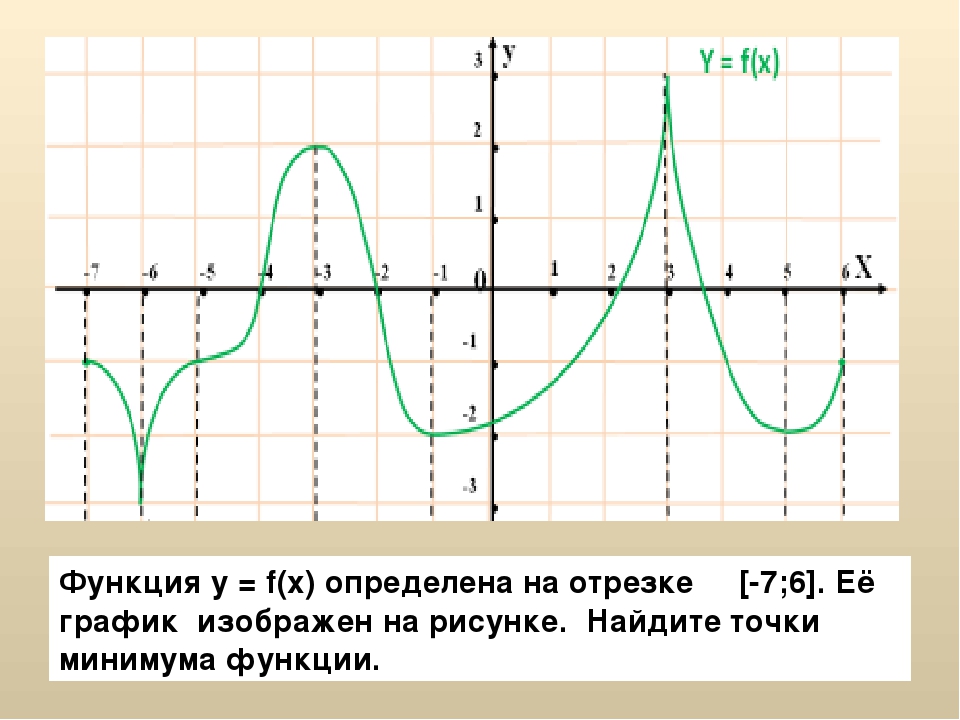
Метод 2 : Используйте вариант теста первой производной.
В этом методе нам также понадобится интервал возможных значений независимой переменной в оптимизируемой функции \(I\).Однако в этом случае, в отличие от предыдущего метода, конечные точки не обязательно должны быть конечными. Кроме того, нам нужно будет потребовать, чтобы функция была непрерывной внутри интервала \(I\), и нам потребуется, чтобы функция была непрерывной только в конечных точках, если конечная точка конечна и функция действительно существует в конечной точке . Мы увидим несколько проблем, когда оптимизируемая функция фактически не существует в одной из конечных точек. Это не помешает использовать этот метод.
Предположим, что \(x = c\) является критической точкой функции, которую мы пытаемся оптимизировать, \(f\left( x \right)\). Мы уже знаем из теста первой производной, что если \(f'\left( x \right) > 0\) сразу слева от \(x = c\) (, т. е. , функция возрастает сразу слева) и если \(f'\left( x \right) < 0\) непосредственно справа от \(x = c\) ( т.е. функция убывает сразу справа), то \(x = c\) будет относительным максимумом для \(f\left( x \right)\).
е. , функция возрастает сразу слева) и если \(f'\left( x \right) < 0\) непосредственно справа от \(x = c\) ( т.е. функция убывает сразу справа), то \(x = c\) будет относительным максимумом для \(f\left( x \right)\).
Это не означает, что абсолютный максимум \(f\left( x \right)\) будет находиться в точке \(x = c\). Однако предположим, что мы знали немного больше информации. Предположим, что на самом деле мы знаем, что \(f'\left( x \right) > 0\) для всех \(x\) в \(I\) таких, что \(x < c\). Точно так же предположим, что мы знали, что \(f'\left( x \right) < 0\) для всех \(x\) в \(I\), таких что \(x > c\). В этом случае мы знаем, что слева от \(x = c\), если мы, конечно, остаемся в \(I\), функция всегда возрастает, а справа от \(x = c\), снова оставаясь в \(I\) мы всегда убываем.В этом случае мы можем сказать, что абсолютный максимум \(f\left( x \right)\) в \(I\) произойдет в точке \(x = c\).
Аналогично, если мы знаем, что слева от \(x = c\) функция всегда убывает, а справа от \(x = c\) функция всегда возрастает, то абсолютный минимум \(f\left ( x \right)\) в \(I\) будет происходить в \(x = c\).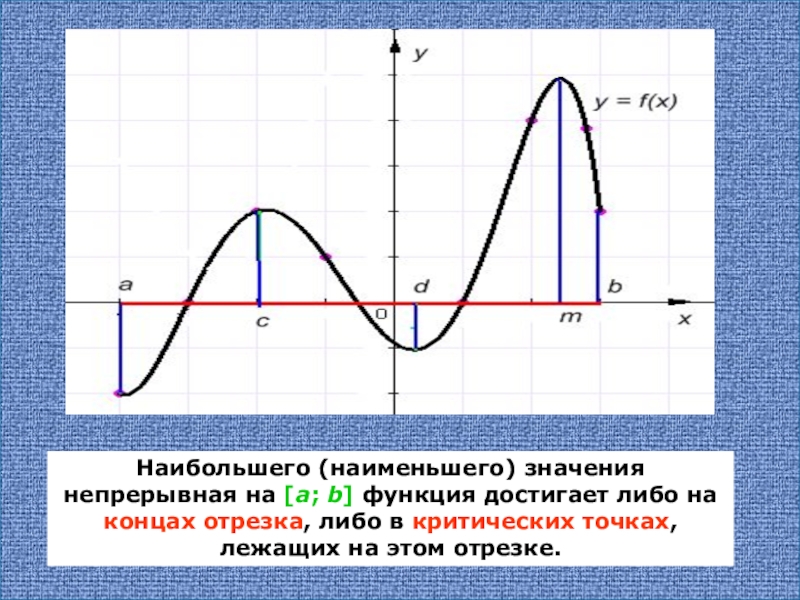
Прежде чем мы дадим краткое описание этого метода, давайте немного обсудим требование непрерывности. Нигде в приведенном выше обсуждении, по-видимому, не вступало в действие требование непрерывности.Мы требуем, чтобы оптимизируемая функция была непрерывной в \(I\), чтобы предотвратить следующую ситуацию.
В этом случае относительный максимум функции явно приходится на \(x = c\). Кроме того, функция всегда убывает вправо и всегда возрастает влево. Однако из-за разрыва в точке \(x = d\) мы можем ясно видеть, что \(f\left( d \right) > f\left( c \right)\), и поэтому абсолютный максимум функции равен не встречаются в \(x = c\).Если бы не было разрыва в точке \(x = d\), этого бы не произошло, и абсолютный максимум имел бы место в точке \(x = c).
Вот краткое описание этого метода.
Первый производный тест для абсолютных экстремумов
Пусть \(I\) будет интервалом всех возможных значений \(x\) в \(f\left( x \right)\), функции, которую мы хотим оптимизировать, и далее предположим, что \(f\left ( x \right)\) непрерывен на \(I\) , за исключением, возможно, концов. Наконец, предположим, что \(x = c\) является критической точкой \(f\left( x \right)\) и что \(c\) находится в интервале \(I\). Если мы ограничим \(x\) значениями из \(I\) (, т.е. , мы рассматриваем только возможные оптимальные значения функции), то
Наконец, предположим, что \(x = c\) является критической точкой \(f\left( x \right)\) и что \(c\) находится в интервале \(I\). Если мы ограничим \(x\) значениями из \(I\) (, т.е. , мы рассматриваем только возможные оптимальные значения функции), то
- Если \(f'\left( x \right) > 0\) для всех \(x < c\) и если \(f'\left( x \right) < 0\) для всех \(x > c\) тогда \(f\left( c \right)\) будет абсолютным максимальным значением \(f\left( x \right)\) на интервале \(I\).
- Если \(f'\left( x \right) < 0\) для всех \(x < c\) и если \(f'\left( x \right) > 0\) для всех \(x > c \) тогда \(f\left( c \right)\) будет абсолютным минимумом значения \(f\left( x \right)\) на интервале \(I\).
Метод 3 : Используйте вторую производную.
На самом деле есть два способа использования второй производной, чтобы помочь нам определить оптимальное значение функции, и оба в той или иной степени используют тест второй производной.
Первый способ использования второй производной на самом деле не помогает нам определить оптимальное значение. Что он делает, так это позволяет нам потенциально исключать значения, и знание этого может несколько упростить нашу работу, и поэтому это неплохо.
Предположим, что мы ищем абсолютный максимум функции и после нахождения критических точек обнаруживаем, что у нас есть несколько критических точек. Давайте также предположим, что мы прогоняем все их через тест второй производной и определяем, что некоторые из них на самом деле являются относительными минимумами функции. Поскольку мы ищем абсолютный максимум, мы знаем, что максимум (любого рода) не может встречаться при относительных минимумах, и поэтому мы сразу знаем, что можем исключить эти точки из дальнейшего рассмотрения.Мы могли бы сделать аналогичную проверку, если бы искали абсолютный минимум. Выполнение этого может показаться не таким уж замечательным, но иногда это может привести к приятному сокращению объема работы, которую нам нужно выполнить на более поздних этапах.
Второй способ использования второй производной для определения оптимального значения функции фактически очень похож на второй способ, описанный выше. Фактически, у нас будут те же требования к этому методу, что и к этому методу. Нам нужен интервал возможных значений независимой переменной в функции, которую мы оптимизируем, назовем его \(I\), как и раньше, и конечные точки могут быть или не быть конечными.Нам также нужно потребовать, чтобы функция \(f\left( x \right)\) была непрерывной везде в \(I\), за исключением, возможно, конечных точек, как указано выше.
Теперь предположим, что \(x = c\) является критической точкой и что \(f''\left(c \right) > 0\). Второй критерий производной говорит нам, что \(x = c\) должен быть относительным минимумом функции. Предположим, однако, что мы также знаем, что \(f''\left(x \right) > 0\) для всех \(x\) в \(I\). В этом случае мы знали бы, что функция вогнута во всех \(I\), а это, в свою очередь, означало бы, что абсолютный минимум \(f\left( x \right)\) в \(I\) будет на самом деле должны быть в \(x = c\).
Аналогично, если \(x = c\) является критической точкой и \(f''\left(x \right) < 0\) для всех \(x\) в \(I\), то мы будем знать, что функция была вогнутой вниз в \(I\) и что абсолютный максимум \(f\left( x \right)\) в \(I\) должен быть в точке \(x = c\).
Вот краткое описание этого метода.
Тест второй производной для абсолютных экстремумов
Пусть \(I\) будет интервалом всех возможных значений \(x\) в \(f\left( x \right)\), функции, которую мы хотим оптимизировать, и предположим, что \(f\left( x \right)\) непрерывен на \(I\) , за исключением, возможно, концов.Наконец, предположим, что \(x = c\) является критической точкой \(f\left( x \right)\) и что \(c\) находится в интервале \(I\). Тогда
- Если \(f''\left( x \right) > 0\) для всех \(x\) в \(I\), то \(f\left( c \right)\) будет абсолютным минимумом значение \(f\left( x \right)\) на интервале \(I\).
- Если \(f''\left( x \right) < 0\) для всех \(x\) в \(I\), то \(f\left( c \right)\) будет абсолютным максимальным значением из \(f\left( x \right)\) на интервале \(I\).

При работе с примерами в следующих двух разделах мы будем использовать каждый из этих методов по мере необходимости в примерах. В некоторых случаях метод, который мы используем, будет единственным методом, который мы можем использовать, в других это будет самый простой метод, а в других это будет просто метод, который мы выбрали для этого примера. Важно понимать, что мы не сможем использовать каждый из методов для каждого примера. В некоторых примерах один метод будет проще всего использовать или может быть единственным, который можно использовать, однако каждый из описанных выше методов будет использоваться по крайней мере пару раз во всех примерах.
Также важно знать, что некоторые проблемы не позволяют использовать любой из рассмотренных выше методов точно так, как описано выше. Нам может понадобиться изменить один из них или использовать их комбинацию, чтобы полностью решить проблему. В следующем разделе есть пример, в котором ни один из вышеперечисленных методов не работает легко, хотя мы также представляем альтернативный метод решения, в котором мы можем использовать по крайней мере один из методов, обсуждавшихся выше.
Далее, подавляющее большинство примеров, рассмотренных в следующем разделе, будут иметь только одну критическую точку.В задачах с более чем одной критической точкой часто бывает трудно понять, какие критические точки дают оптимальное значение. В следующих двух разделах есть несколько примеров с более чем одной критической точкой, включая один в следующем разделе, упомянутом выше, в котором ни один из методов, обсуждаемых выше, не работает. В этом примере вы можете увидеть некоторые идеи, которые вам могут понадобиться, чтобы найти оптимальное значение.
Наконец, во всех приведенных выше методах мы ссылались на интервал \(I\).Это было сделано для того, чтобы немного облегчить обсуждение. Однако во всех примерах следующих двух разделов мы никогда не будем явно говорить «это интервал \(I\)». Только помните, что интервал \(I\) — это просто наибольший интервал возможных значений независимой переменной в оптимизируемой нами функции.
Хорошо, давайте поработаем еще над несколькими примерами.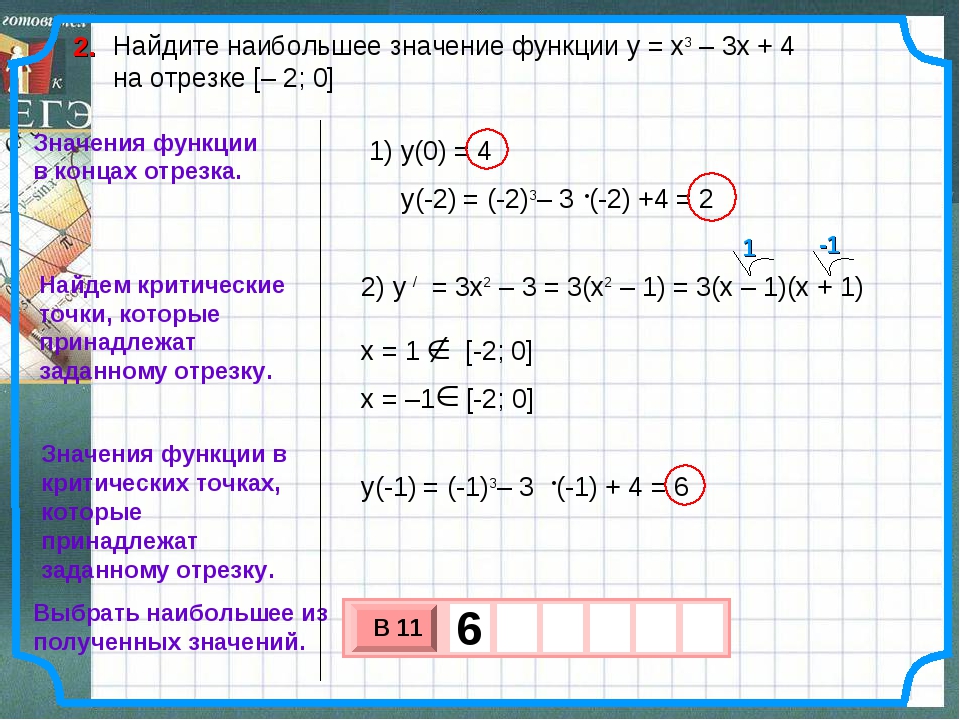
Во-первых, краткий рисунок (наверное, не в масштабе…).
Мы хотим минимизировать стоимость материалов при условии, что объем должен быть 50 футов 3 . Также обратите внимание, что стоимость каждой стороны равна произведению площади этой стороны на соответствующую стоимость.{- 3}}\]
Теперь нам нужны критические точки для функции стоимости. Во-первых, обратите внимание, что \(w = 0\) не является критической точкой. Ясно, что производная не существует в \(w = 0\), но тогда и функция не существует, и помните, что значения \(w\) будут критическими точками только в том случае, если функция также существует в этой точке. Обратите внимание, что есть и физическая причина избегать \(w = 0\). Мы строим коробку, и было бы бессмысленно иметь нулевую ширину коробки.
Ясно, что производная не существует в \(w = 0\), но тогда и функция не существует, и помните, что значения \(w\) будут критическими точками только в том случае, если функция также существует в этой точке. Обратите внимание, что есть и физическая причина избегать \(w = 0\). Мы строим коробку, и было бы бессмысленно иметь нулевую ширину коробки.
Таким образом, похоже, что единственная критическая точка будет заключаться в определении того, где числитель равен нулю.3} - 800 = 0\hspace{0,25 дюйма} \Стрелка вправо \hspace{0,25 дюйма}\,\,w = \sqrt[3]{{\frac{{800}}{{120}}}} = \sqrt [3] {{\ гидроразрыва {{20}} {3}}} = 1,8821 \]
Итак, у нас есть единственная критическая точка, и теперь мы должны убедиться, что это действительно то значение, которое даст абсолютный минимум затрат.
В этом случае мы не можем использовать метод 1, описанный выше. Во-первых, функция не является непрерывной в одной из конечных точек \(w = 0\) нашего интервала возможных значений т. е.е. \(ш > 0\). Во-вторых, не существует теоретического верхнего предела ширины, которая дает ящик объемом 50 футов 3 . Если \(w\) очень велико, нам просто нужно сделать \(h\) очень маленьким.
е.е. \(ш > 0\). Во-вторых, не существует теоретического верхнего предела ширины, которая дает ящик объемом 50 футов 3 . Если \(w\) очень велико, нам просто нужно сделать \(h\) очень маленьким.
Здесь подойдет второй метод из перечисленных выше, но он потребует некоторых вычислений, несложных вычислений, но, тем не менее, больше работы.
Однако третий способ здесь сработает быстро и просто. Во-первых, мы знаем, что какое бы значение \(w\) мы ни получили, оно должно быть положительным, и мы можем видеть вторую производную выше, чем при условии \(w > 0\), у нас будет \(C''\left( w \right) > 0\) и поэтому в интервале возможных оптимальных значений функция стоимости всегда будет вогнутой вверх и поэтому \(w = 1.2}}} = 4,7050\конец{выравнивание*}\]
Также, несмотря на то, что это не запрашивалось, минимальная стоимость составляет: \(C\left( {1,8821} \right) = \$ 637,60\).
Пример 3 Мы хотим построить коробку с квадратным основанием, и у нас есть только 10 м 2 материала для строительства коробки. Предполагая, что весь материал используется в процессе строительства, определите максимальный объем, который может иметь коробка.
Показать решение
Предполагая, что весь материал используется в процессе строительства, определите максимальный объем, который может иметь коробка.
Показать решениеЭтот пример во многом противоположен предыдущему.В этом случае мы хотим оптимизировать объем, и на этот раз ограничением является количество используемого материала. Здесь у нас нет стоимости, но если подумать, стоимость — это не что иное, как количество использованного материала, умноженное на стоимость, поэтому количество материала и стоимость в значительной степени связаны друг с другом. Если вы можете сделать одно, вы можете сделать и другое. Обратите также внимание на то, что количество используемого материала — это просто площадь поверхности коробки.
Как всегда, начнем с быстрого наброска коробки.2}} \right)\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}V''\left( w \right) = - 3w\]
Обратите также внимание на то, что при условии \(w > 0\), которое с физической точки зрения, как мы знаем, должно быть истинным для ширины ящика, тогда функция объема будет вогнутой вниз, и поэтому, если мы получим единственную критическую точку, то мы знаем, что это должно быть значение, дающее абсолютный максимум.
Установка первой производной равной нулю и решение дает нам две критические точки,
\[w = \pm \,\sqrt {\frac{5}{3}} = \pm \,1.2910\]В этом случае мы можем исключить отрицательную критическую точку, поскольку мы имеем дело с длиной ящика и знаем, что она должна быть положительной. Однако не приобретайте привычку просто исключать любую отрицательную критическую точку. Есть проблемы, где отрицательные критические точки являются вполне допустимыми возможными решениями.
Теперь, как отмечалось выше, мы получили единственную критическую точку, 1,2910, и поэтому это должно быть значение, которое дает максимальный объем, а поскольку максимальный объем - это все, что было запрошено в постановке задачи, ответ тогда: \[V \влево({1.3}\].
Обратите внимание, что здесь мы могли бы также отметить, что если \(0 < w < 1,2910\), то \(V'\left( w \right) > 0\) (используя контрольную точку, мы имеем \(V'\left( 1 \right) = 1 > 0\)) и аналогично, если \(w > 1,2910\), то \(V'\left( w \right) < 0\) (используя контрольную точку, мы имеем \(V'\left ( 2 \right) = - {\ frac {7} {2}} < 0 \}} и поэтому, если мы находимся слева от критической точки, объем всегда увеличивается, а если мы находимся справа от критической точки объем всегда уменьшается, и поэтому с помощью метода 2 выше мы также можем видеть, что единственная критическая точка должна давать абсолютный максимум объема. 2}}}{{2\влево( {1,2910} \вправо)}} = 1,2910\]
2}}}{{2\влево( {1,2910} \вправо)}} = 1,2910\]
Итак, похоже, что в данном случае у нас действительно идеальный куб.
В последних двух примерах мы видели, что многие из этих оптимизационных задач можно решать, так сказать, в обоих направлениях. В обоих примерах у нас есть по существу два одинаковых уравнения: объем и площадь поверхности. Однако в примере 2 объем был ограничением, а стоимость (которая напрямую связана с площадью поверхности) была функцией, которую мы пытались оптимизировать.С другой стороны, в примере 3 мы пытались оптимизировать объем, а площадь поверхности была ограничением.
Важно не зацикливаться на одном способе решения этих проблем, чтобы мы не могли делать это и в противоположном направлении, если это необходимо. Это одна из наиболее частых ошибок, которую допускают студенты при решении подобных задач. Они видят одну проблему, а затем пытаются привести все остальные проблемы, которые кажутся одинаковыми, в соответствие с этим единственным решением, даже если проблему нужно решать по-другому. Относитесь к этим проблемам непредвзято и убедитесь, что вы понимаете, что оптимизируется и каково ограничение, прежде чем переходить к решению.
Относитесь к этим проблемам непредвзято и убедитесь, что вы понимаете, что оптимизируется и каково ограничение, прежде чем переходить к решению.
Кроме того, как видно из последнего примера, мы использовали два разных метода проверки того, что получили оптимальное значение. Не слишком зацикливайтесь на одном методе проверки, иначе вы забудете о других методах.
Давайте поработаем над другим примером, на этот раз без прямоугольника или коробки.
Пример 4 Производителю необходимо изготовить цилиндрическую банку, вмещающую 1,5 литра жидкости. Определить размеры банки, которые сведут к минимуму количество материала, используемого при ее изготовлении. Показать решение Прежде чем начать решение, давайте сначала обратимся к тому факту, что мы используем литры для объема. Поскольку нам нужны измерения длины для радиуса и высоты, нам также понадобится объем с точки зрения измерения длины. Мы можем легко сделать это, используя тот факт, что 1 литр = 1000 см 3 , и поэтому мы можем преобразовать 1. 5 литров на 1500 см 3 . Это, в свою очередь, даст радиус и высоту в сантиметрах.
5 литров на 1500 см 3 . Это, в свою очередь, даст радиус и высоту в сантиметрах.
В этой задаче ограничением является объем, и мы хотим минимизировать количество используемого материала. Это означает, что мы хотим свести к минимуму площадь поверхности банки, и нам нужно включить как стенки банки, так и верхнюю и нижнюю «крышки». Вот быстрый набросок, чтобы мы начали.
Нам понадобится площадь поверхности этой банки, и это будет площадь поверхности стенок банки (которая на самом деле представляет собой просто цилиндр), а также площадь верхней и нижней крышек (которые являются просто дисками, а не Забудь, что их два).
Обратите внимание, что если вы представляете цилиндр высотой \(h\) и радиусом \(r\) просто набором дисков/кругов радиуса \(r\), уложенных друг на друга, уравнения для площади поверхности и громкость довольно легко запомнить. Объем - это просто площадь каждого из дисков, умноженная на высоту. 2}\) к общей площади поверхности.2}}}\]
2}\) к общей площади поверхности.2}}}\]
Отсюда видно, что у нас есть одна критическая точка: \(r = \sqrt[3]{\frac{750}{\pi}} = 6,2035\)(где производная равна нулю). Обратите внимание, что \(r = 0\) не является критической точкой, потому что там не существует функции площади, что имеет смысл и с физической точки зрения, учитывая, что мы знаем, что \(r\) должно быть положительным, чтобы на самом деле иметь банка.
Итак, у нас есть только одна критическая точка, и обратите внимание, что 6.2035 — это единственное значение, для которого производная будет равна нулю, и, следовательно, единственное место (конечно, при \(r > 0\)), где производная может изменить знак. Нетрудно с помощью контрольных точек проверить, что если \(0 < r < 6,2035\), то \(A'\left( r \right) < 0\), и аналогично, если \(r > 6,2035\), то \( А'\влево( г \вправо) > 0\). Приведенный выше вариант теста первой производной говорит нам, что абсолютное минимальное значение площади (для \(r > 0\)) должно иметь место при
\[г = 6. 2}}} = 12,4070\]
2}}} = 12,4070\]
Следовательно, если производитель изготовит банку с радиусом 6,2035 см и высотой 12,4070 см, на изготовление банки будет использовано наименьшее количество материала.
В качестве интересной побочной задачи и расширения приведенного выше примера вы можете показать, что для заданного объема \(L\) будет использоваться минимальный материал, если \(h = 2r\) независимо от объема банки .
В примерах к этому моменту мы довольно подробно обсуждали решение.По оставшимся задачам мы не будем вдаваться в подробности и предоставим вам заполнить недостающие детали.
Пример 5. У нас есть кусок картона размером 14 на 10 дюймов, и мы собираемся вырезать углы, как показано ниже, и загнуть стороны, чтобы сформировать коробку, также показанную ниже. Определите высоту ящика, которая даст максимальный объем. Показать решение Пусть высота ящика равна \(h\). Таким образом, ширина/длина вырезаемых углов также равна \(h\), поэтому вертикальная сторона будет иметь «новую» высоту \(10 - 2h\), а горизонтальная сторона будет иметь «новую» ширину. из \(14 - 2ч\). Вот эскиз со всей этой информацией,
Таким образом, ширина/длина вырезаемых углов также равна \(h\), поэтому вертикальная сторона будет иметь «новую» высоту \(10 - 2h\), а горизонтальная сторона будет иметь «новую» ширину. из \(14 - 2ч\). Вот эскиз со всей этой информацией,
В этом примере мы впервые столкнулись с проблемой, когда ограничение на самом деле не имеет уравнения. Ограничение — это просто размер куска картона, и оно уже учтено на рисунке выше.2}\]
Установка первой производной равной нулю и решение дает следующие две критические точки,
\[h = \frac{{12 \pm \sqrt {39} }}{3} = 1,9183,\,\,\,\,6,0817\] Теперь у нас явная проблема. У нас есть две критические точки, и нам нужно определить, какая из них является нужным нам значением. Тот факт, что у нас есть две критические точки, означает, что здесь нельзя использовать ни тест первой производной, ни тест второй производной, поскольку они оба требуют одной критической точки. Однако это не настоящая проблема. Вернитесь к рисунку в начале решения и обратите внимание, что мы можем довольно легко найти ограничения на \(h\). Наименьшее \(h\) может быть равно \(h = 0\), хотя это не имеет особого смысла, поскольку в этом случае мы не получим коробку. Кроме того, со стороны 10 дюймов мы можем видеть, что наибольшее \(h\) может быть равно \(h = 5\), хотя опять же, это не имеет большого физического смысла.
Однако это не настоящая проблема. Вернитесь к рисунку в начале решения и обратите внимание, что мы можем довольно легко найти ограничения на \(h\). Наименьшее \(h\) может быть равно \(h = 0\), хотя это не имеет особого смысла, поскольку в этом случае мы не получим коробку. Кроме того, со стороны 10 дюймов мы можем видеть, что наибольшее \(h\) может быть равно \(h = 5\), хотя опять же, это не имеет большого физического смысла.
Итак, зная, что чем бы ни было \(h\), оно должно находиться в диапазоне \(0 \le h \le 5\), мы можем видеть, что вторая критическая точка находится вне этого диапазона, и поэтому единственная критическая точка, которая нам нужна беспокоиться о 1.9183.
Наконец, поскольку объем определен и непрерывен на \(0 \le h \le 5\), все, что нам нужно сделать, это подключить критические точки и конечные точки к объему, чтобы определить, какая из них дает наибольший объем. Вот эти оценки функций.
\[V\влево( 0 \вправо) = 0\hspace{0,25 дюйма}\hspace{0,25 дюйма}V\влево({1,9183} \right) = 120,1644\hspace{0,25 дюйма}\hspace{0,25 дюйма}V\ влево( 5 \вправо) = 0\] Итак, если мы возьмем \(h = 1. 9183\) получаем максимальную громкость.
9183\) получаем максимальную громкость.
Эта проблема немного отличается от предыдущих проблем. И ограничение, и функция, которую мы собираемся оптимизировать, являются областями.Ограничение состоит в том, что общая площадь плаката должна быть 200 в 2 , в то время как мы хотим оптимизировать область печати (, т.е. площадь плаката с удаленными полями).
Определим высоту плаката как \(h\), а ширину плаката как \(w\). Вот новый набросок плаката, и мы видим, что после того, как мы приняли во внимание поля, ширина области печати равна \(w - 2\), а высота области печати равна \(h - 3.5\).
Вот уравнения, с которыми мы будем работать.
Решение ограничения для \(h\) и подстановка в уравнение для области печати дает,
\[A\влево(ш \вправо) = \влево({ш - 2} \вправо)\влево({\ гидроразрыва {{200}}{ш} - 3.3}}}\]Из первой производной получаем следующие две критические точки (\(w = 0\) не является критической точкой, потому что там не существует функции площади).
\[w = \ pm \, \ sqrt {\ frac {400} {3,5}} = \ pm \, 10,6904 \]Однако, поскольку мы имеем дело с размерами листа бумаги, мы знаем, что должно быть \(w > 0\), поэтому только 10,6904 будет иметь смысл.
Также обратите внимание, что при \(w > 0\) вторая производная всегда будет отрицательной, поэтому в диапазоне возможных оптимальных значений ширины функция площади всегда вогнута вниз, и поэтому мы знаем, что максимальная площадь печати будет равна \(ш = 10. 6904\,\,{\mbox{дюймы}}\).
6904\,\,{\mbox{дюймы}}\).
Тогда высота бумаги, дающая максимальную площадь печати, равна
. \[h = \frac{{200}}{{10,6904}} = 18,7084\,\,{\mbox{дюймы}}\]К этому моменту мы проработали довольно много примеров, и нам еще предстоит проработать еще немало. Однако этот раздел стал довольно длинным, поэтому давайте продолжим наши примеры в следующем разделе. Это делается в основном потому, что эти заметки также представлены в Интернете, и это поможет несколько снизить время загрузки страниц.
Среднее, медиана и мода
Мы используем статистику , такую как среднее, медиана и мода, чтобы получить информацию о совокупности из нашего выборочного набора наблюдаемых значений.Среднее
среднее (или среднее) набора значений данных представляет собой сумму всех
значения данных, разделенные на количество значений данных. То есть:
То есть:
Пример 1
Оценки семи учащихся на тесте по математике с максимально возможным
20 баллов приведены ниже:
15
13 18
16 14
17 12
Найдите среднее значение этого набора значений данных.
Решение:
Итак, средний балл равен 15.
Символически мы можем представить решение следующим образом:
Значит, средний балл 15.
Медиана Медиана набора значений данных — это среднее значение данных. устанавливается, когда он расположен в порядке возрастания.То есть из от наименьшего значения к наибольшему значению.
Пример 2
Оценки девяти учащихся за тест по географии, который имел максимальное
возможная оценка 50 приведена ниже:
47
35 37
32 38
39 36
34 35
Найдите медиану этого набора значений данных.
Решение:
Расположите значения данных в порядке от наименьшего значения к наибольшему значение:
32 34 35 35 36 37 38 39 47
Пятое значение данных, 36, является средним значением в этом расположении.
Примечание:
В целом:
Если количество значений в наборе данных четное, то медиана равна среднее из двух средних значений.
Пример 3
Найдите медиану следующего набора данных:
12
18 16
21 10
13 17 19
Решение:
Расположите значения данных в порядке от наименьшего значения к наибольшему
значение:
10
12 13
16 17
18 19 21
Число значений в наборе данных равно 8, что является четным. Так что
медиана — это среднее из двух средних значений.
Так что
медиана — это среднее из двух средних значений.
Альтернативный способ:
В наборе данных 8 значений.
Четвертая и пятая оценки, 16 и 17, находятся посередине. Это, нет единого среднего значения.
Примечание:
- Половина значений в наборе данных лежат ниже медианы и половина лежат выше медианы.
- Медиана — это наиболее часто цитируемая цифра, используемая для измерять цены на недвижимость. Использование медианы позволяет избежать проблемы средняя цена недвижимости, на которую влияет несколько дорогих объектов, не являются репрезентативными для общего рынка недвижимости.
Режим Режим набора значений данных — это значение(я), которое встречается чаще всего.
 довольно часто.
довольно часто.Режим имеет приложения в печати. Например, важно печатать больше самых популярных книг; потому что печать разных книг в одинаковое количество вызвало бы нехватку некоторых книг и избыток другие.
Кроме того, этот режим имеет применение в производстве. Например, это важно производить больше самой популярной обуви; так как Производство разной обуви в равных количествах приведет к нехватке некоторые туфли и переизбыток других.
Пример 4
Найдите режим следующего набора данных:
48 44 48 45 42 49 48
Решение:
Режим 48, так как встречается чаще всего.
Примечание:
- Набор значений данных может иметь более одного
режим.

- Если есть два значения данных, которые встречаются чаще всего, мы скажем, что набор значений данных равен бимодальным .
- Если нет значения данных или значений данных, которые встречаются чаще всего часто мы говорим, что набор значений данных не имеет моды.
Анализ данных
Среднее значение, медиана и мода набора данных вместе известны как меры. центральной тенденции , поскольку эти три показателя сосредоточены на том, где находятся данные. центрированные или сгруппированные.Чтобы проанализировать данные, используя среднее значение, медиану и моду, мы необходимо использовать наиболее подходящую меру центральной тенденции. Следующее точек следует запомнить:
- Среднее полезно для предсказания будущих результатов, когда нет
крайние значения в наборе данных.
 Однако влияние экстремальных значений на
среднее значение может быть важным, и его следует учитывать. Например. Влияние
крах фондового рынка по средней доходности инвестиций.
Однако влияние экстремальных значений на
среднее значение может быть важным, и его следует учитывать. Например. Влияние
крах фондового рынка по средней доходности инвестиций. - Медиана может быть более полезной, чем среднее, когда есть экстремальные значения. значения в наборе данных, так как на него не влияют экстремальные значения.
- Режим полезен, когда наиболее распространенный элемент, характеристика или значение требуется набор данных.
Основные термины
статистика, среднее, среднее, медиана, мода, меры центральной тенденции
Как найти диапазон - Алгебра 1
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Функция МАКС - формула, примеры, как использовать МАКС в Excel
Что такое функция МАКС?
Функция MAX относится к категории Excel Статистические функцииФункцииСписок наиболее важных функций Excel для финансовых аналитиков. Эта шпаргалка охватывает сотни функций, которые важно знать аналитику Excel. MAX вернет наибольшее значение в заданном списке аргументов. Из заданного набора числовых значений он вернет наибольшее значение. В отличие от функции МАКС, функция МАКС подсчитывает числа, но игнорирует пустые ячейки, текст, логические значения ИСТИНА и ЛОЖЬ и текстовые значения.
Эта шпаргалка охватывает сотни функций, которые важно знать аналитику Excel. MAX вернет наибольшее значение в заданном списке аргументов. Из заданного набора числовых значений он вернет наибольшее значение. В отличие от функции МАКС, функция МАКС подсчитывает числа, но игнорирует пустые ячейки, текст, логические значения ИСТИНА и ЛОЖЬ и текстовые значения.
В финансовом анализе MAX может быть полезен для расчета наивысшего балла, самого быстрого времени, наибольшей суммы расходов или доходов и т. д.
Формула
= Max (№1, [Number2], ...)
Number1 и Number1 - это аргументы, используемые для функции, где требуется №1, и последующие значения являются по желанию.
В MS Excel 2007 и более поздних версиях мы можем предоставить до 255 числовых аргументов функции MAX. Однако в Excel 2003 и более ранних версиях он может принимать только до 30 числовых аргументов.
Аргументы могут быть предоставлены как константы или как ссылки на ячейки или диапазоны.Если аргумент предоставляется функции как ссылка на ячейку или массив ячеек, функция МАКС будет игнорировать пустые ячейки, а также текстовые или логические значения, содержащиеся в предоставленном диапазоне ячеек. Однако логические значения и текстовые представления чисел, переданные непосредственно в функцию, будут включены в вычисление.
Как использовать функцию MAX в Excel?
В качестве функции рабочего листа функцию MAX можно ввести как часть формулы в ячейку рабочего листа.Чтобы понять использование функции, давайте рассмотрим пример:
Пример
Давайте рассчитаем самые высокие оценки по следу следуции:
Используемая формула была:
Функция MAX проигнорировала пустое значение и в результате вернула 100.
Как показано выше, MAX игнорирует пустые значения. В этом примере, если мы предоставим логическое значение, функция проигнорирует его и выдаст тот же результат, как показано ниже:
В этом примере, если мы предоставим логическое значение, функция проигнорирует его и выдаст тот же результат, как показано ниже:
Несколько вещей, которые следует помнить о функции MAX 5
- #ЗНАЧ! ошибка — возникает, если какие-либо значения, переданные непосредственно функции MAX, не являются числовыми.
- Если аргументы не содержат чисел, MAX возвращает 0.
- Основное различие между MAX и MAXA заключается в том, что MAXA оценивает значения TRUE и FALSE как 1 и 0 соответственно. Следовательно, если мы хотим включить логические значения, нам нужно использовать функцию MAXA.
Щелкните здесь, чтобы загрузить образец файла Excel. Потратив время на изучение и освоение этих функций, вы значительно ускорите свое финансовое моделирование.Чтобы узнать больше, ознакомьтесь со следующими дополнительными ресурсами CFI:
- Функции Excel для финансовExcel для финансовВ этом руководстве по Excel для финансов представлены 10 лучших формул и функций, которые вы должны знать, чтобы стать отличным финансовым аналитиком в Excel.

- Расширенный курс по формулам Excel
- Расширенные формулы Excel, которые необходимо знатьРасширенные формулы Excel, которые необходимо знатьЭти расширенные формулы Excel очень важны, чтобы их знать, и они выведут ваши навыки финансового анализа на новый уровень. Загрузите нашу бесплатную электронную книгу Excel!
- Ярлыки Excel для ПК и MacExcel Ярлыки ПК MacExcel Ярлыки — список наиболее важных и распространенных ярлыков MS Excel для пользователей ПК и Mac, финансовых и бухгалтерских профессий.Сочетания клавиш ускоряют ваши навыки моделирования и экономят время. Изучите редактирование, форматирование, навигацию, ленту, специальную вставку, работу с данными, редактирование формул и ячеек и другие сочетания клавиш
Range In Math | Определение, как найти и примеры
Что такое диапазон?
В математике диапазон — это статистическое измерение дисперсии, или насколько данный набор данных растянут от наименьшего к наибольшему. В наборе данных диапазон представляет собой разницу между наибольшим и наименьшим значением.
В наборе данных диапазон представляет собой разницу между наибольшим и наименьшим значением.
Range — один из четырех простых инструментов статистики:
- Среднее – Среднее арифметическое набора чисел – это его среднее (сумма чисел, деленная на количество чисел)
- Медиана — Статистическая медиана — это среднее число в упорядоченном наборе чисел
- Режим — режим является наиболее часто встречающимся числом в наборе данных
- Диапазон — диапазон набора данных представляет собой математическую разницу между наибольшим и наименьшим значением
Первые три статистических инструмента измеряют центральную тенденцию или то, насколько похожи числа.
Только диапазон является мерой дисперсии, подчеркивая, насколько различаются числа, и существует простая формула для расчета диапазона.
Диапазон Формула
Диапазон = наибольшее значение – наименьшее значение
Как найти диапазон
Чтобы найти диапазон в наборе чисел, вы должны собрать данные, упорядочить данные от меньшего к большему, а затем вычесть наименьшее значение из наибольшего. Вы можете найти диапазон положительных чисел и отрицательных чисел.
Вы можете найти диапазон положительных чисел и отрицательных чисел.
Шаги для расчета диапазона:
- Соберите свои данные, чтобы знать все числа, которые нужно изучить.
- Упорядочить набор данных в порядке от меньшего к большему.
- Напишите предложение вычитания, чтобы вычесть наименьшее значение из наибольшего (или наибольшего) значения.
Например, если вы читаете биографию и записываете, сколько страниц вы читаете каждый день, вы можете взять диапазон:
- Понедельник – 12 страниц
- Вторник – 9 страниц
- Среда – 11 страниц
- Четверг – 3 страницы
- Пятница – 8 страниц
Чтобы найти диапазон, расположите количество страниц в порядке от наименьшего к наибольшему:
3, 8, 9, 11, 12
Вычесть наименьшее значение из наибольшего:
Р = 12 - 3 = 9
Диапазон этого набора данных – 9 страниц.
Давайте вычислим диапазон следующего набора действительных чисел. Ниже приведены пять игр с самым низким результатом в истории НБА с указанием команд и общего количества игровых очков:
Ниже приведены пять игр с самым низким результатом в истории НБА с указанием команд и общего количества игровых очков:
- Вашингтон Кэпитолис (49) против Питтсбург Айронмен (40) – 89 очков
- Форт Уэйн Пистонс (19) против Миннеаполис Лейкерс (18) – 37 очков
- Вашингтон Кэпитолс (50) против Детройт Фэлконс (33) – 83 очка
- Бостон Селтикс (46) vs.Питтсбург Айронмен (44) – 90 очков
- Бостон Селтикс (47) против Вашингтон Кэпитолс (38) – 85 очков
Выполните три шага, чтобы найти диапазон этих пяти игр:
- Соберите точки данных, чтобы знать все числа, которые необходимо изучить:
- Упорядочить набор данных в порядке от наименьшего к наибольшему числу
- Вычесть наименьшее значение из наибольшего:
89 баллов, 37 баллов, 83 балла, 90 баллов, 85 баллов
89, 37, 83, 90, 85
37, 83, 85, 89, 90
Диапазон = 90 - 37 = 53
Диапазон = 53 точки
Диапазон пяти самых результативных игр в истории НБА составляет 53 очка.
Давайте попробуем это с некоторыми более сложными числами, такими как население страны.
Население Китая составляет 1 420 062 022 человека. Население Мексики составляет 132 328 035 человек. Население Индии составляет 1 368 737 513 человек. Население Соединенных Штатов составляет 329 093 110 человек.
Каков диапазон этого набора данных?
1) Собрать данные:
- 1 420 062 022
- 132 328 035
- 1 368 737 513
- 329 093 110
2) Расположите набор данных в порядке от меньшего к большему:
- 132 328 035
- 329 093 110
- 1 368 737 513
- 1 420 062 022
3) Вычесть наименьшее значение из наибольшего (наибольшего) значения:
- Диапазон = 1 420 062 022 - 132 328 038
- Диапазон = 1 287 733 987 человек
Как найти диапазон между двумя числами
Диапазон обычно используется для поиска разброса значений в наборе данных, состоящем из нескольких значений. Однако вам не нужны все остальные числа, чтобы найти диапазон между двумя числами.
Однако вам не нужны все остальные числа, чтобы найти диапазон между двумя числами.
Поиск диапазона между двумя числами аналогичен поиску диапазона набора данных.
Вот вам набор цифр:
{6,4,10,8}
Чтобы найти диапазон, вы берете наибольшее значение, 10, минус наименьшее значение, 4. Диапазон равен 6.
А что, если в вашем наборе есть только два числа 10 и 4:
{10,4}
Диапазон между этими двумя числами одинаков, 10 - 4 = 6
Диапазон по-прежнему 6.
Поиск диапазона набора данных аналогичен поиску диапазона между двумя числами.
Примеры диапазонов
Ниже приведено несколько примеров задач, которые необходимо решить на диапазон.
1) В НБА есть игроки с огромными ногами. Вот размеры обуви некоторых известных игроков НБА:
.- Пол Джордж, Размер 12
- Рассел Уэстбрук, Размер 15
- Яо Мин, Размер 18
- Тадж Гибсон, размер 13
Каков диапазон размеров обуви этих четырех игроков НБА?
2) Шкала твердости Мооса для минералов включает следующие образцы:
- Алмаз, 10
- Флюорит, 4
- Тальк, 1
- Кварц, 7
- Апатит, 5
Каков диапазон пяти перечисленных минералов?
3) Чистокровная лошадь весит примерно 1100 фунтов. Шетландский пони весит около 200 фунтов. Лошадь Клайдсдейл весит около 2000 фунтов. Каков диапазон веса этих трех пород лошадей?
Шетландский пони весит около 200 фунтов. Лошадь Клайдсдейл весит около 2000 фунтов. Каков диапазон веса этих трех пород лошадей?
4) Марко получил оценки за контрольную по математике 67%, 101% (он получил дополнительный балл – всегда пытайтесь получить дополнительный балл!), 93%, 81% и 96%. Каков диапазон оценок Марко за контрольную по математике?
Согласно статистике, большинство людей сразу переходит к ответам, не посчитав сначала. Не будьте статистикой! Сначала решай проблемы!
Вот ответы:
- Размеры обуви игроков НБА имеют диапазон 6, разница между Полом Джорджем и Яо Мином.
- Шкала твердости Мооса имеет диапазон 9, показанный здесь как разница между алмазом и тальком.
- Диапазон веса трех пород лошадей составляет 1800 фунтов.
- У Марко диапазон оценок за контрольную по математике составляет 34 процентных пункта.
Использование диапазона в реальной жизни
Диапазон используется в реальной жизни для выполнения математических расчетов. Диапазон можно использовать для расчета количества прошедшего времени, например, при расчете вашего возраста.
Диапазон можно использовать для расчета количества прошедшего времени, например, при расчете вашего возраста.
Текущий год 2020, а вы родились в 2005.Сколько тебе лет? Или сколько времени прошло?
2020 - 2005 = 15
Прошло 15 лет, значит, если ваш день рождения 2020 уже прошел, то вам 15 лет.
Диапазонтакже используется в реальной жизни, чтобы выяснить разброс результатов тестов старшеклассников, определить диапазон цен за услугу и многое другое.
.
 Каковы размеры самого большого такого двора? Что
это самая большая площадь?
Каковы размеры самого большого такого двора? Что
это самая большая площадь? 
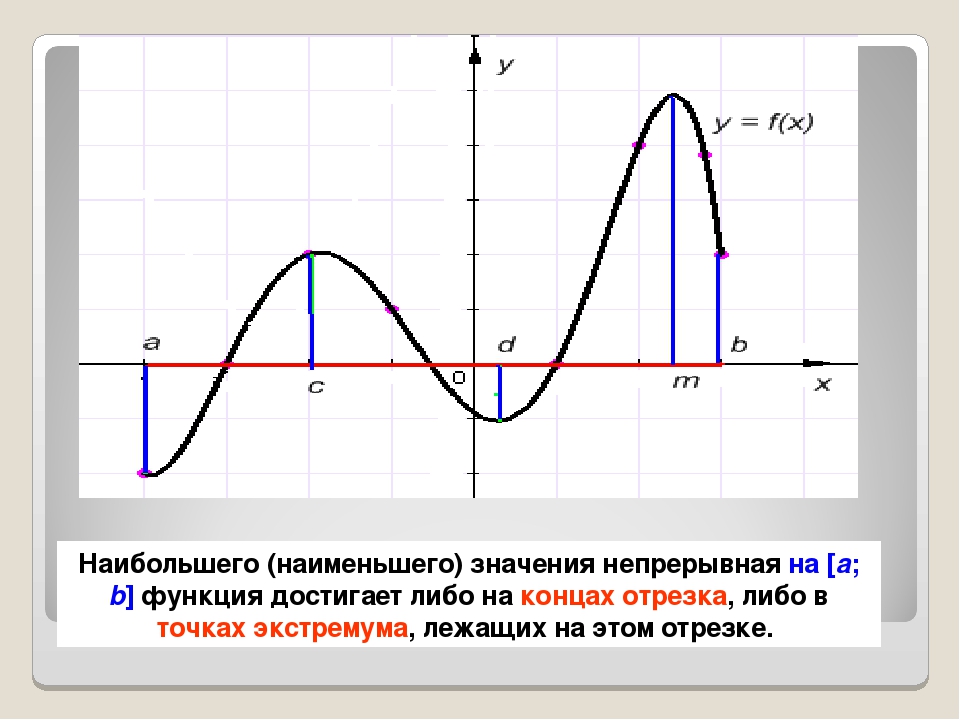 Парень из бухгалтерии говорит, что ваши затраты на производство x тысяч единиц в день можно вычислить по формуле C = 0,04 х 2 8,504 х + 25302 . Находить
ежедневный уровень производства, который сведет к минимуму ваши затраты.
Парень из бухгалтерии говорит, что ваши затраты на производство x тысяч единиц в день можно вычислить по формуле C = 0,04 х 2 8,504 х + 25302 . Находить
ежедневный уровень производства, который сведет к минимуму ваши затраты.  0036
= 432,00
0036
= 432,00 00
+ 3(0,50)
00
+ 3(0,50) purplemath.com/modules/quadprob3.htm .
Доступ [Дата] [Месяц] 2016
purplemath.com/modules/quadprob3.htm .
Доступ [Дата] [Месяц] 2016  Нечисловые значения в аргументе ref игнорируются.
Нечисловые значения в аргументе ref игнорируются.


 Для этого вычтем из ранга количество нулей:
Для этого вычтем из ранга количество нулей:

 Однако влияние экстремальных значений на
среднее значение может быть важным, и его следует учитывать. Например. Влияние
крах фондового рынка по средней доходности инвестиций.
Однако влияние экстремальных значений на
среднее значение может быть важным, и его следует учитывать. Например. Влияние
крах фондового рынка по средней доходности инвестиций.