Тема 10. Стереометрия — Материалы для подготовки к вступительным экзаменам в СГГА
Если AB||A’B’ и BC||B’C’, то плоскости ABC и A’B’C’ параллельны.
Прямая BC, лежащая в плоскости ABC, перпендикулярна наклонной DB, тогда и только тогда, когда она перпендикулярна ее проекции на плоскость AB.
Площадь поверхности: S=2Sосн+Sбок, где Sбок – площадь боковой поверхности, равная сумме площадей всех граней.
Прямая призма – призма, боковое ребро которой перпендикулярно основанию.
Объем: V=Sосн∙l .
Площадь боковой поверхности: Sбок=P∙l, где P – периметр основания.
Правильная призма – прямая призма, основание которой – правильный многоугольник.
1) В основании прямой призмы лежит прямоугольный треугольник с катетами, равными 5 и 12. Высота призмы равна 8. Найдите полную поверхность призмы.
2) В прямой треугольной призме основания равны 36, 29 и 25, а полная поверхность призмы 1620.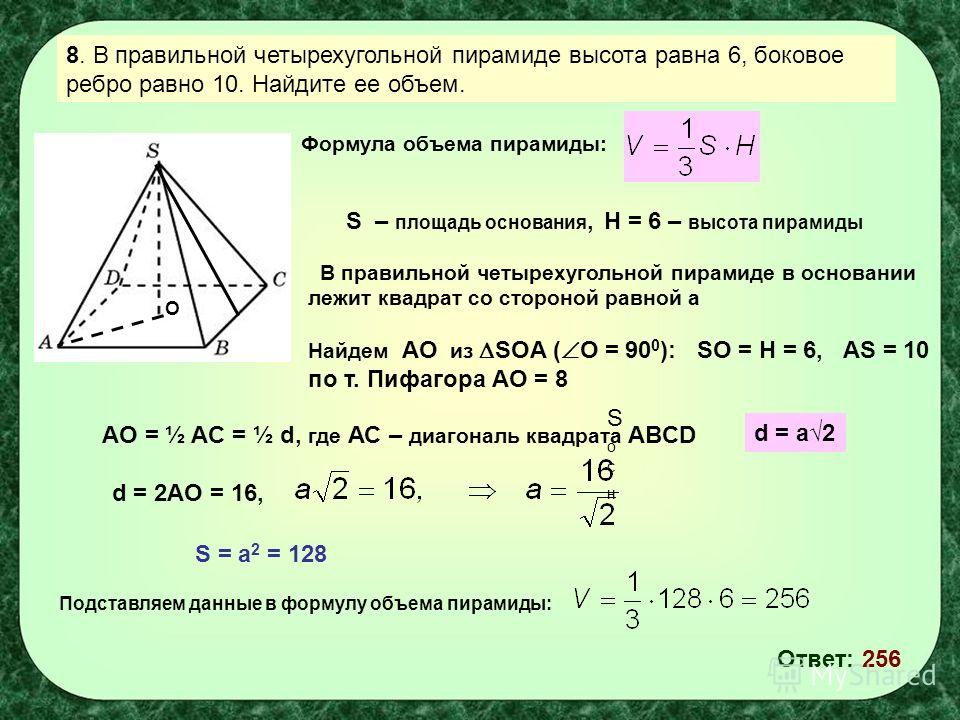 Найдите высоту призмы.
Найдите высоту призмы.
4) Стороны основания прямой треугольной призмы равны 10, 17 и 21, а ее боковое ребро равно меньшей из высот основания. Найдите объем призмы.
5) Объем правильной треугольный призмы равен . Найдите высоту призмы, если радиус описанной около основания окружности равен 2. 6) Высота правильной треугольной призмы равна 8, а площадь основания . Найдите диагональ боковой грани призмы. 7) Все ребра прямой треугольной призмы равны. Найдите площадь основания призмы, если площадь ее полной поверхности равна . 8) Высота правильной четырёхугольной призмы равна , а диагональ призмы наклонена к плоскости основания под углом 300. Найти сторону основания призмы. 9) Основание прямой призмы – прямоугольный треугольник с катетами 6м и 8м, а диагональ большей по площади боковой грани равна м. Найдите объём призмы. 10) Найдите площадь поверхности куба, диагональ которого равна . 11) Площадь диагонального сечения куба равна . Найдите ребро куба.
Найдите объём призмы. 10) Найдите площадь поверхности куба, диагональ которого равна . 11) Площадь диагонального сечения куба равна . Найдите ребро куба.12) Сумма длин всех ребер куба равна 48. Чему равна площадь всех его граней?
13) Если ребро куба уменьшить на 10%, на сколько процентов уменьшится его объем?
14) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Расстояние от плоскости сечения до вершины нижнего основания, не лежащей в плоскости сечения, равно 5см. Площадь сечения равна 10см2. Найти объём параллелепипеда.
15) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Объём меньшего из двух многогранников, на которые параллелепипед делится плоскостью сечения, равен 40см3. Найдите объём параллелепипеда.
16) Стороны основания прямоугольного параллелепипеда 6м и 8м, а угол между диагональю параллелепипеда и плоскостью основания 300. Найдите диагональ параллелепипеда.
Найдите диагональ параллелепипеда.
17) Стороны основания прямоугольного параллелепипеда равны 4м и 3м, а угол между диагональю параллелепипеда и плоскостью основания 450. Найдите длину диагонали параллелепипеда.
18) Сторона основания правильной треугольной призмы ABCDA1B1C1D1 равна 12, а боковое ребро . Найдите градусную меру угла между плоскостями A1BC и ABC. 19) ABCDA1B1C1D1 – призма, в основании которой лежит квадрат, боковые ребра которой наклонены к плоскости основания под углом 300. Диагональ AD1 перпендикулярна плоскости основания. Площадь боковой поверхности призмы равна . Найдите объем призмы. 20) В основании прямой призмы ABCDA1B1C1D1 лежит квадрат. Боковое ребро равно . Найдите длину стороны основания, если угол между плоскостью AB1C и плоскостью основания призмы равен 300.
21) Ребра треугольной пирамиды длины 4, 5 и 9 взаимно перпендикулярны. Чему равен объем пирамиды?
22) Пирамида имеет 28 ребер. Сколько у нее граней?
23) Высота правильной треугольной пирамиды равна 15, а высота ее основания 12. Найдите длину бокового ребра.
24) Высота правильной треугольной пирамиды в два раза меньше стороны основания. Найдите угол между боковой гранью пирамиды и плоскостью основания.
25) Сторона основания правильной треугольной пирамиды равна 10 см. Боковые грани наклонены к плоскости основания под углом 450. Найдите высоту пирамиды.
26) Боковое ребро правильной треугольной пирамиды равно 10, а периметр основания 36. Найдите высоту пирамиды.
27) В правильной четырёхугольной пирамиде высота равна 3см, а площадь боковой поверхности 80см2. Найти объём пирамиды.
28) Боковые грани правильной четырёхугольной пирамиды наклонены к плоскости основания под углом 600. Площадь основания равна 14м2. Найти площадь боковой поверхности пирамиды.
Найти площадь боковой поверхности пирамиды.
29) В правильной четырёхугольной пирамиде боковое ребро образует с плоскостью основания угол 600. Сторона основания пирамиды равна 6см. Найдите объём пирамиды.
30) В правильной четырёхугольной пирамиде апофема образует с плоскостью основания угол 600. Высота пирамиды равна 8см. Найдите площадь поверхности пирамиды.
31) В правильной треугольной пирамиде высота равна , а величина двугранного угла при основании 600. Найдите сторону основания пирамиды.32) В правильной треугольной пирамиде высота равна 4, а апофема равна 5. Найдите сторону основания пирамиды.
33) Высота треугольной пирамиды SABC равна 8, а площадь треугольника ABC 12. Точки A1, B1, C1 делят ребра SA, SB и SC в отношении 1 : 1. Найдите объем усеченной пирамиды ABCA1B1C1.
34) В основании пирамиды SABC лежит прямоугольный треугольник ABC с катетами AC=4 и BC=3. Все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, тангенс которого равен 4/5. Найдите объем пирамиды.
Все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, тангенс которого равен 4/5. Найдите объем пирамиды.
35) Найдите площадь боковой поверхности цилиндра, если площадь его осевого сечения равна 12.
36) Площадь основания цилиндра равна 4, а площадь его боковой поверхности равна . Найдите высоту цилиндра. 37) Высота и радиус основания цилиндра равны, соответственно, 9 и 6. Концы отрезка AB длины лежат на окружностях верхнего и нижнего оснований. Найдите расстояние от оси цилиндра до отрезка AB.38) Радиус основания конуса равен 6, а образующая составляет с плоскостью основания угол, равный 300. Найдите расстояние от центра основания до образующей.
39) Образующая конуса равна диаметру его основания. Найдите площадь боковой поверхности конуса, если его высота равна .40) Площадь осевого сечения конуса равна 8, а радиус основания 2. Найдите площадь боковой поверхности конуса.
41) Осевое сечение конуса – правильный треугольник со стороной .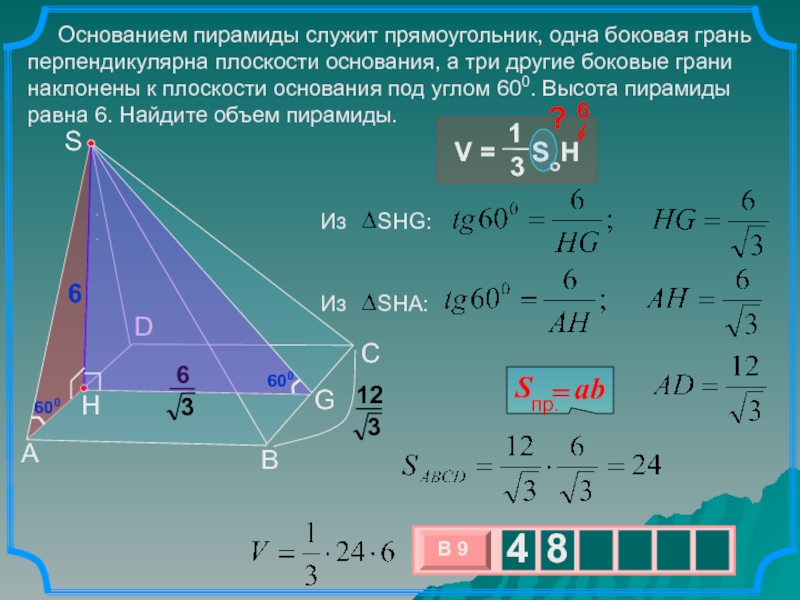 Найдите полную поверхность конуса.
Найдите полную поверхность конуса.42) Из точки M вне шара проведена касательная AM к его поверхности. Кратчайшее расстояние от этой точки до поверхности шара равно 6, а до центра шара 15. Найдите длину AM.
43) Если радиус сферы увеличить на 50%, на сколько процентов увеличится площадь ее поверхности?
44) Радиус шара равен . Через конец радиуса под углом 600 к нему проведена плоскость. Найти площадь сечения шара плоскостью.45) Стороны треугольника, равные 10, 10 и 12 касаются поверхности шара Найдите радиус шара, если расстояние от центра шара до плоскости треугольника равно 4.
46) Как относятся объемы куба и описанного около него шара?
47) В шар объема вписан конус, таким образом, что основанием конуса является осевое сечение шара. Найдите площадь осевого сечения конуса.Вычисление площади боковой поверхности пирамиды. Площадь боковой поверхности правильной четырехугольной пирамиды: формулы и примеры задач
– это многогранная фигура, в основании которой лежит многоугольник, а остальные грани представлены треугольниками с общей вершиной.
Если в основании лежит квадрат, то пирамиду называется четырехугольной , если треугольник – то треугольной . Высота пирамиды проводится из ее вершины перпендикулярно основанию. Также для расчета площади используется апофема – высота боковой грани, опущенная из ее вершины.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей ее боковых граней, которые равны между собой. Однако этот способ расчета применяется очень редко. В основном площадь пирамиды рассчитывается через периметр основания и апофему:
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана пирамида с основанием ABCDE
и вершиной F
. AB
=BC
=CD
=DE
=EA
=3 см. Апофема a
= 5 см. Найти площадь боковой поверхности пирамиды.
Теперь можно найти боковую площадь пирамиды:
Площадь правильной треугольной пирамиды
Правильная треугольная пирамида состоит из основания, в котором лежит правильный треугольник и трех боковых граней, которые равны по площади.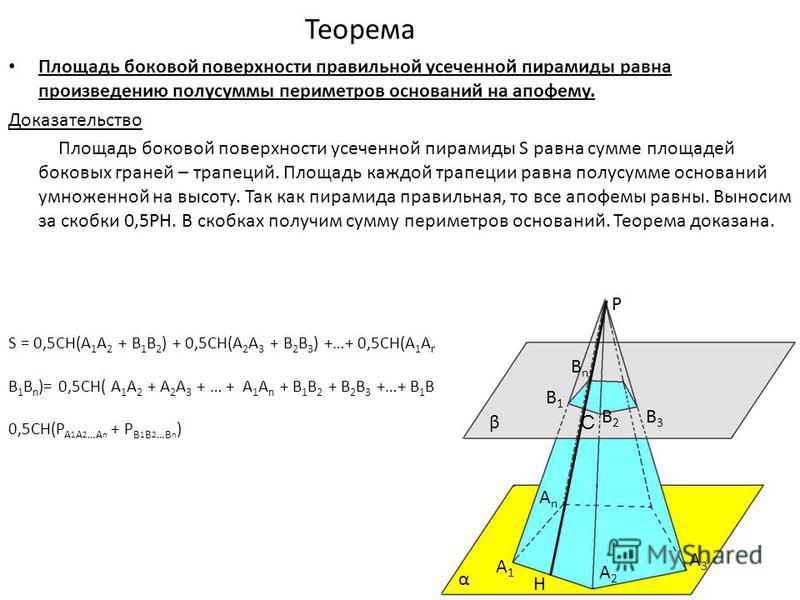
Формула площади боковой поверхности правильной треугольной пирамиды может быть рассчитана разными способами. Можно применить обычную формулу расчета через периметр и апофему, а можно найти площадь одной грани и умножить ее на три. Так как грань пирамиды – это треугольник, то применим формулу площади треугольника. Для нее потребуется апофема и длина основания. Рассмотрим пример расчета площади боковой поверхности правильной треугольной пирамиды.
Дана пирамида с апофемой a
= 4 см и гранью основания b
= 2 см. Найдите площадь боковой поверхности пирамиды.
Подставляем значения в формулу:
Так как в правильной пирамиде все боковые стороны одинаковы, то площадь боковой поверхности пирамиды будет равна сумме площадей трех граней. Соответственно:
Площадь усеченной пирамиды
Усеченной пирамидой называется многогранник, который образовывается пирамидой и ее сечением, параллельным основанию.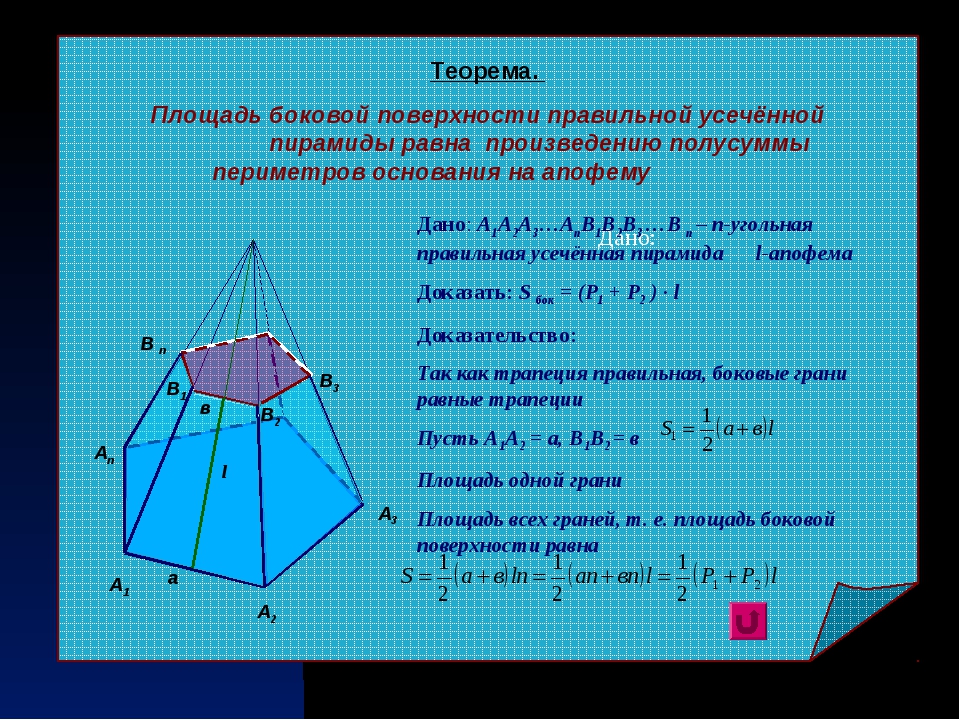
Формула площади боковой поверхности усеченной пирамиды очень проста. Площадь равняется произведению половины суммы периметров оснований на апофему:
Пирамида — одна из разновидностей многогранника, образованного из многоугольников и треугольников, которые лежат в основании и являются его гранями.
Причем на вершине пирамиды (т.е. в одной точке) все грани объединяются.
Для того чтобы вычислить площадь пирамиды, стоит определить, что ее боковая поверхность состоит из нескольких треугольников. А их площади мы сможем легко найти, применяя
различные формулы. В зависимости от того, какие данные треугольников нам известны, мы ищем их площадь.
Перечислим некоторые формулы, с помощью которых можно найти площадь треугольников:
- S = (a*h)/2 . В данном случае нам известна высота треугольника h , которая опущена на сторону a .
- S = a*b*sinβ . Здесь стороны треугольника a , b , а угол между ними — β .

- S = (r*(a + b + c))/2 . Здесь стороны треугольника a, b, c . Радиус окружности, которая вписана в треугольник — r .
- S = (a*b*c)/4*R . Радиус, описанной окружности вокруг треугольника — R .
- S = (a*b)/2 = r² + 2*r*R . Данную формулу нужно применять только в том случае, когда треугольник является прямоугольным.
- S = (a²*√3)/4 . Эту формулу применяем к равностороннему треугольнику.
Лишь после того, как рассчитаем площади всех треугольников, которые являются гранями нашей пирамиды, можно вычислить площадь ее боковой поверхности. Для этого будем использовать выше перечисленные формулы.
Для того чтобы вычислить площадь боковой поверхности пирамиды, никаких сложностей не возникает: нужно узнать сумму площадей всех треугольников. Выразим это формулой:
Sп = ΣSi
Здесь Si является площадью первого треугольника, а S п —
площадь боковой поверхности пирамиды.
Рассмотрим на примере. Дана правильная пирамида, ее боковые грани образованы несколькими равносторонними треугольниками,
Галилео Галилей.
а квадрат является основанием пирамиды. Причем ребро пирамиды имеет длину 17 см. Найдем площадь боковой поверхности данной пирамиды.
Рассуждаем так: нам известно, что гранями пирамиды являются треугольники, они равносторонние. Также нам известно, какова длина ребра у данной пирамиды. Отсюда выходит, что все треугольники имеют равные боковые стороны, их длина 17 см.
Для вычисления площади каждого из данных треугольников, можно использовать такую формулу:
S = (17²*√3)/4 = (289*1.732)/4 = 125.137 см²
Так, как мы знаем, что квадрат лежит в основании пирамиды, то выходит, что мы имеем четыре равносторонних треугольника. А это значит, что площадь боковой поверхности пирамиды легко рассчитать по следующей формуле: 125. 137 см² * 4 = 500.548 см²
137 см² * 4 = 500.548 см²
Наш ответ следующий: 500.548 см² — такова площадь боковой поверхности данной пирамиды.
– это фигура, в основании которой лежит произвольный многоугольник, а боковые грани представлены треугольниками. Их вершины лежат в одной точке и соответствуют вершине пирамиды.
Пирамида может быть разнообразной – треугольной, четырехугольной, шестиугольной и т.д. Ее название можно определить в зависимости от количества углов, прилегающих к основанию.
Правильной пирамидой называется пирамида, в которой равны стороны основания, углы, и ребра. Также в такой пирамиде будет равна площадь боковых граней.
Формула площади боковой поверхности пирамиды представляет собой сумму площадей всех ее граней:
То есть, чтобы рассчитать площадь боковой поверхности произвольной пирамиды, необходимо найти площадь каждого отдельного треугольника и сложить их между собой. Если пирамида усеченная, то ее грани представлены трапециями. Для правильной пирамиды существует другая формула.
Рассмотрим пример расчета площади боковой поверхности пирамиды.
Пусть дана правильная четырехугольная пирамида. Сторона основания b = 6 см, а апофема a = 8 см. Найдите площадь боковой поверхности.
В основании правильной четырехугольной пирамиды лежит квадрат. Для начала найдем его периметр:
Теперь можем просчитать площадь боковой поверхности нашей пирамиды:
Для того чтобы найти полную площадь многогранника, потребуется найти площадь его основания. Формула площади основания пирамиды может отличаться, в зависимости от того, какой многоугольник лежит в основании. Для этого используются формулы площади треугольника, площади параллелограмма и т.д.
Рассмотри пример расчета площади основания пирамиды, заданной нашими условиями. Так как пирамида правильная, в ее основании лежит квадрат.
где a – сторона квадрата.
 У нас она равна 6 см. Значит площадь основания пирамиды:
У нас она равна 6 см. Значит площадь основания пирамиды:Теперь остается только найти полную площадь многогранника. Формула площади пирамиды состоит из суммы площади ее основания и боковой поверхности.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Перед изучением вопросов о данной геометрической фигуре и её свойствах, следует разобраться в некоторых терминах. Когда человек слышит о пирамиде, ему представляются большущие постройки в Египте. Так выглядят самые простые из них. Но они бывают разных видов и форм, а значит и формула вычисления для геометрических фигур будет разной.
Когда человек слышит о пирамиде, ему представляются большущие постройки в Египте. Так выглядят самые простые из них. Но они бывают разных видов и форм, а значит и формула вычисления для геометрических фигур будет разной.
Виды фигуры
Пирамида – геометрическая фигура , обозначающая и представляющая собой несколько граней. По сути – это тот же многогранник, в основании которого лежит многоугольник, а по бокам расположены треугольники, соединяющиеся в одной точке – вершине. Фигура бывает двух основных видов:
- правильная;
- усечённая.
В первом случае, в основании лежит правильный многоугольник. Тут все боковые поверхности равны между собой и сама фигура порадует глаз перфекциониста.
Во втором случае, оснований два — большое в самом низу и малое между вершиной, повторяющее форму основного. Иными словами – усечённая пирамида представляет собой многогранник с сечением, образованным параллельно основанию.
Термины и обозначения
Основные термины:
- Правильный (равносторонний) треугольник – фигура с тремя одинаковыми углами и равными сторонами.
 В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.
В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой. - Вершина – самая верхняя точка, где сходятся грани. Высота вершины образуется прямой линией, исходящей от вершины к основанию пирамиды.
- Грань – одна из плоскостей многоугольника. Она может быть в виде треугольника в случае с треугольной пирамидой либо в виде трапеции для усечённой пирамиды.
- Сечение – плоская фигура, образующаяся в результате рассечения. Не стоит путать с разрезом, так как разрез показывает и то, что находится за сечением.
- Апофема – отрезок, проведённый из вершины пирамиды к её основанию. Он также является высотой той грани, где находится вторая точка высоты. Данное определение справедливо лишь по отношению к правильному многограннику.
 К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.
К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.
Формулы площади
Находить площадь боковой поверхности пирамиды любого типа можно несколькими способами. Если фигура не симметричная и представляет собой многоугольник с разными сторонами, то в данном случае легче вычислить общую площадь поверхности через совокупность всех поверхностей. Иными словами – надо посчитать площадь каждой грани и сложить их вместе.
В зависимости от того, какие параметры известны, могут потребоваться формулы вычисления квадрата, трапеции, произвольного четырёхугольника и т.д. Сами формулы в разных случаях тоже будут иметь отличия.
В случае с правильной фигурой находить площадь намного проще. Достаточно знать всего несколько ключевых параметров. В большинстве случаев требуются вычисления именно для таких фигур. Поэтому далее будут приведены соответствующие формулы.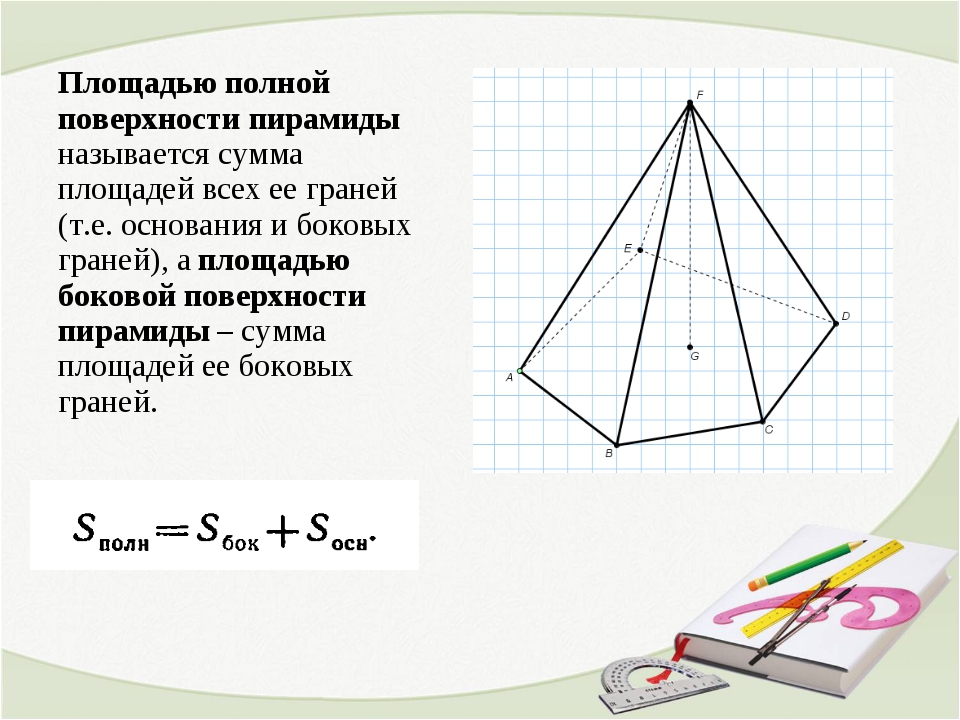 В противном случае пришлось бы расписать всё на несколько страниц, что только запутает и собьёт с толку.
В противном случае пришлось бы расписать всё на несколько страниц, что только запутает и собьёт с толку.
Основная формула для вычисления площади боковой поверхности правильной пирамиды будет иметь следующий вид:
S=½ Pa (P – периметр основания, а – апофема)
Рассмотрим один из примеров. Многогранник имеет основание с отрезками A1, А2, А3, А4, А5, и все они равны 10 см. Апофема пусть будет равна 5 см. Для начала надо найти периметр. Так как все пять граней основания одинаковые, можно находить так: Р=5*10=50 см. Далее применяем основную формулу: S =½*50*5=125 см в квадрате.
Площадь боковой поверхности правильной треугольной пирамиды вычислить легче всего. Формула имеет следующий вид:
S =½* ab *3, где а – апофема, b – грань основания. Множитель тройки здесь означает количество граней основания, а первая часть – площадь боковой поверхности. Рассмотрим пример. Дана фигура с апофемой 5 см и гранью основания 8 см. Вычисляем: S =1/2*5*8*3=60 см в квадрате.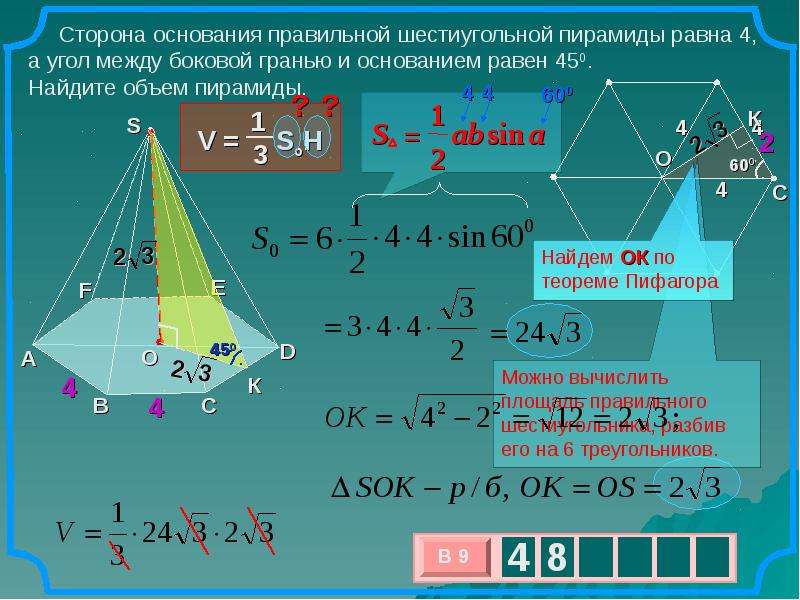
Площадь боковой поверхности усечённой пирамиды вычислять немного сложнее. Формула выглядит так: S =1/2*(p _01+ p _02)*a , где р_01 и р_02 являются периметрами оснований, а – апофема. Рассмотрим пример. Допустим, для четырёхугольной фигуры даны размеры сторон оснований 3 и 6 см, апофема равна 4 см.
Тут для начала следует найти периметры оснований: р_01 =3*4=12 см; р_02=6*4=24 см. Осталось подставить значения в основную формулу и получим: S =1/2*(12+24)*4=0,5*36*4=72 см в квадрате.
Таким образом, можно найти площадь боковой поверхности правильной пирамиды любой сложности. Следует быть внимательным и не путать эти вычисления с полной площадью всего многогранника. А если это всё же понадобится сделать – достаточно вычислить площадь самого большого основания многогранника и прибавить её к площади боковой поверхности многогранника.
Видео
Закрепить информацию о том, как найти площадь боковой поверхности разных пирамид, вам поможет это видео.
Площадь поверхности пирамиды
Площадь поверхности пирамиды. В этой статье мы рассмотрим с вами задачи с правильными пирамидами. Напомню, что правильная пирамида – это пирамида, основанием которой является правильный многоугольник, вершина пирамиды проецируется в центр этого многоугольника.
Боковая грань такой пирамиды это равнобедренный треугольник. Высота этого треугольника, проведенная из вершины правильной пирамиды, называется апофемой, SF – апофема:
В представленном ниже типе задач требуется найти площадь поверхности всей пирамиды или площадь её боковой поверхности. На блоге уже рассмотрено несколько задач с правильными пирамидами, где ставился вопрос о нахождении элементов (высоты, ребра основания, бокового ребра), можете посмотреть.
В типовых заданиях, как правило, рассматриваются правильные треугольные, четырёхугольные и шестиугольные пирамиды. Задач с правильными пятиугольными и семиугольными пирамидами пока не встречал.
Кстати, на проекте youclever неплохой визуальный гид по пирамиде: с красивыми картинками, основными формулами и свойствами.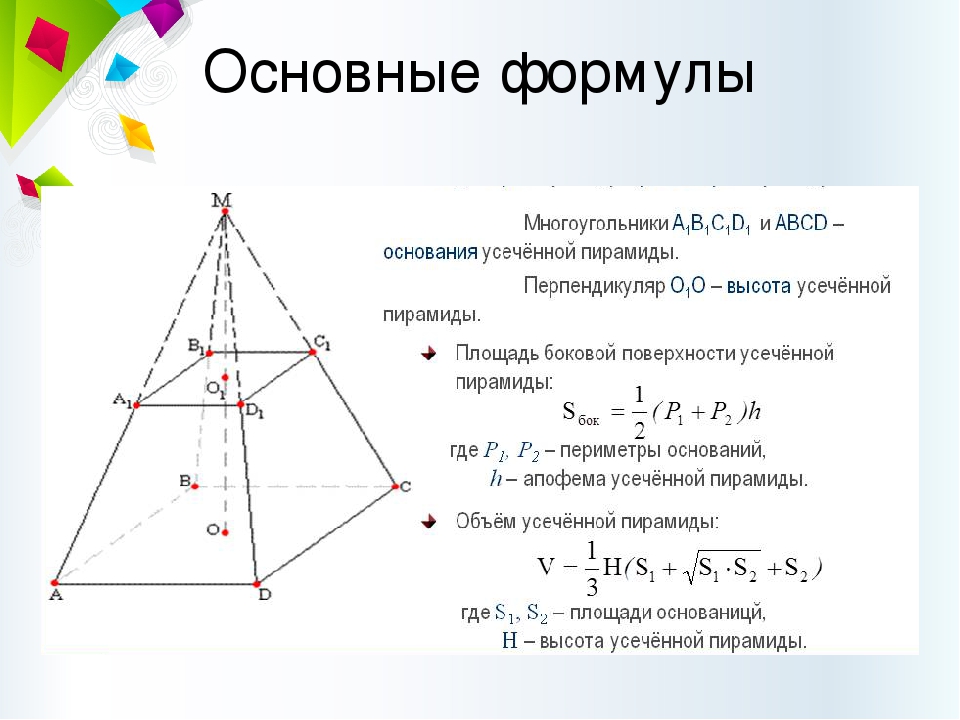 Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Подходит тем, кто лучше воспринимает информацию визуально. Там весь учебник по геометрии такой — мало задач, но много понятных рисунков.
Формула площади всей поверхности проста — требуется найти сумму площади основания пирамиды и площади её боковой поверхности:
Рассмотрим задачи:
Стороны основания правильной четырехугольной пирамиды равны 72, боковые ребра равны 164. Найдите площадь поверхности этой пирамиды.
Площадь поверхности пирамиды равна сумме площадей боковой поверхности и основания:
*Боковая поверхность состоит из четырёх равных по площади треугольников. Основание пирамиды это квадрат.
Площадь боковой стороны пирамиды можем вычислить воспользовавшись формулой Герона:
Таким образом, площадь поверхности пирамиды равна:
Ответ: 28224
Стороны основания правильной шестиугольной пирамиды равны 22, боковые ребра равны 61. Найдите площадь боковой поверхности этой пирамиды.
Основанием правильной шестиугольной пирамиды является правильный шестиугольник.
Площадь боковой поверхности данной пирамиды состоит из шести площадей равных треугольников с сторонами 61,61 и 22:
Найдём площадь треугольника, воспользуемся формулой Герона:
Таким образом, площадь боковой поверхности равна:
Ответ: 3240
*В представленных выше задачах площадь боковой грани можно было найти используя другую формулу треугольника, но для этого нужно вычислить апофему.
27155. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Для того, чтобы найти площадь поверхности пирамиды нам необходимо знать площадь основания и площадь боковой поверхности:
Площадь основания равна 36, так как это квадрат со стороной 6.
Боковая поверхность состоит из четырёх граней, которые являются равными треугольниками. Для того, чтобы найти площадь такого треугольника требуется знать его основание и высоту (апофему):
*Площадь треугольника равна половине произведения основания и высоты проведённой к этому основанию.
Основание известно, оно равно шести. Найдём высоту. Рассмотрим прямоугольный треугольник (он выделен жёлтым):
Один катет равен 4, так как это высота пирамиды, другой равен 3, так как он равен половине ребра основания. Можем найти гипотенузу, по теореме Пифагора:
Значит площадь боковой поверхности пирамиды равна:
Таким образом, площадь поверхности всей пирамиды равна:
Ответ: 96
27069. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.
Посмотреть решение
27070. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
Посмотреть решение
Существуют ещё формулы площади боковой поверхности правильной пирамиды. В правильной пирамиде основание является ортогональной проекцией боковой поверхности, поэтому:
где φ — двугранный угол при основании
Отсюда площадь полной поверхности правильной пирамиды может быть найдена по формуле:
Еще одна формула боковой поверхности правильной пирамиды:
P — периметр основания, l — апофема пирамиды
*Эта формула основывается на формуле площади треугольника.
Если хотите узнать подробнее как эти формулы выводятся, не пропустите, следите за публикацией статей. На этом всё. Успеха Вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Площадь поверхности пирамиды | Мозган калькулятор онлайн
На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте площадь основания и апофему.
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. Пирамида является частным случаем конуса. Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.
Боковая поверхность через периметр и апофемуАпофема – опущенный перпендикуляр из вершины на ребро основания.
Формула площади боковой поверхности правильной пирамиды через периметр и апофему:
p — периметр основания пирамиды; l — апофема пирамиды. 2)»/> a — сторона основания.
2)»/> a — сторона основания.Объём правильной пирамиды
Нахождение высоты пирамиды
Как найти высоту пирамиды? Очень просто! Для нахождения высоты любой треугольной пирамиды можно воспользоваться формулой объема: V = (1/3)Sh, где S — это площадь основания, V — объем пирамиды, h — ее высота. Из этой формулы вывести формулу высоты: для нахождения высоты треугольной пирамиды, нужно умножить объем пирамиды на 3, а потом поделить получившееся значение на площадь основания, это будет: h = (3V)/S. Поскольку основание треугольной пирамиды — это треугольник, можно воспользоваться формулой подсчета площади треугольника. Если нам известны: площадь треугольника S и его сторона z, то по формуле площади S=(1/2)γh: h = (2S)/γ, где h — это высота пирамиды, γ — это ребро треугольника; угол между сторонами треугольника и сами две стороны, то по такой формуле: S = (1/2)γφsinQ, где γ, φ — это стороны треугольника, находим площадь треугольника. Значение синуса угла Q нужно посмотреть в таблице синусов, которая есть в Интернете. Далее подставляем значение площади в формулу высоты: h = (2S)/γ. Если в задании требуется вычислить высоту треугольной пирамиды, то объем пирамиды уже известен.
Далее подставляем значение площади в формулу высоты: h = (2S)/γ. Если в задании требуется вычислить высоту треугольной пирамиды, то объем пирамиды уже известен.
Формулы объема треугольной пирамиды
Определить объем совершенно любой пирамиды с произвольным n-угольником в основании можно с помощью следующего выражения:
V = 1/3 × So × h
Здесь символ So обозначает площадь основания, h — это высота фигуры, проведенная к отмеченному основанию из вершины пирамиды.
Поскольку площадь произвольного треугольника равна половине произведения длины его стороны a на апофему ha, опущенную на эту сторону, то формула объема треугольной пирамиды может быть записана в следующем виде:
V = 1/6 × a × ha × h
Для треугольной пирамиды общего типа определение высоты является непростой задачей. Для ее решения проще всего воспользоваться формулой расстояния между точкой (вершиной) и плоскостью (треугольным основанием), представленной уравнением общего вида.
Для правильной пирамиды формула объема имеет конкретный вид. Площадь основания (равностороннего треугольника) для нее равна:
Площадь основания (равностороннего треугольника) для нее равна:
So = √3/4 × a2
Подставляем ее в общее выражение для V, получаем:
V = √3/12 × a2 × h
Частным случаем является ситуация, когда у тетраэдра все стороны оказываются одинаковыми равносторонними треугольниками. В этом случае определить его объем можно, только исходя из знания параметра его ребра a. Соответствующее выражение имеет вид:
V = √2/12 × a3
Теория
Это интересно: Как оформлять реферат в школе по ГОСТу + образец титульного листа 2019
Для решения задач понадобится знать теоремы равнобедренного треугольника:
Равнобедренный треугольник
Основные свойства
1В правильную пирамиду можно вписать и описать сферу, так как при пересечении диагоналей, основание делится на равные части. Сферу нельзя вписать в любую фигуру.
2Площадь боковой поверхности – половина произведения периметра основания на апофему. Апофема есть на каждой грани, а не только на одной.
Пирамида
Четырехугольная пирамида
В основании – многоугольник; остальные грани – треугольники, соединяющиеся в общей вершине.
Четырехугольная пирамида
Треугольная пирамида
В качестве основания можно рассматривать любую грань. Вся фигура состоит из треугольников.
Треугольная пирамида
Необходимые знания для нахождения высоты
1Нужно понимать, что из себя представляют треугольники: свойства, формулы, определение. Большинство задач решается через треугольники (боковые грани).
2Понимать, что такое сечение и как оно влияет на геометрическую фигуру.
3Что такое правильные многоугольники: виды, свойства, формулы.
Когда теория закреплена, можно переходить к формулам.
Формулы для нахождения высоты
Формулы
Запомните, что маленькая буква h – это апофема, а большая H – высота.
В некоторых задачах, высоту можно найти через объем:
Объем пирамиды
Нахождение высоты в правильной пирамиде
Нахождение высоты в правильной пирамиде
Ниже будут представлены текстовые решения часто встречающихся задач.
Треугольная пирамида
Треугольная пирамида
Задача 1
В правильной треугольной пирамиде DBAC с вершиной D биссектрисы треугольника BAC пересекаются в точке N. Площадь треугольника BAC равна 4; объем пирамиды равен 12. Найдите длину отрезка DN.
DN – высота, следовательно, объем фигуры можно выразить по формуле:
DN = 3V/S основания = 3*12/4 = 9
Ответ: 9
Задача 2
DBAC – медианы основания BAC. Они пересекаются в точке N. Площадь ΔBAC равна 18, V = 20; найдите высоту.
Пользуясь формулой объема, получается:
DN = 3V/S ΔBAC = 3*36/18 = 108/18 = 6
Ответ: 6
Четырехугольная пирамида
Четырехугольная пирамида
Задача 1
Найдите высоту пирамиды, если ML = 10, а DC = 12. В основании квадрат.
ML – это апофема, сторона нам известна, следовательно, можно применить формулу для нахождения OL:
OL = ½*12 = 6
Известно, что MOL – прямоугольный угол. Применим теорему Пифагора:
MO ² = √ML ² — √OL ² = √100- √36 = √64
MO = 8
Задача 2
Известно, что диагональ AC = 20, ML = 10, а сторона DC = 12; найдите MO правильной четырехугольной пирамиды.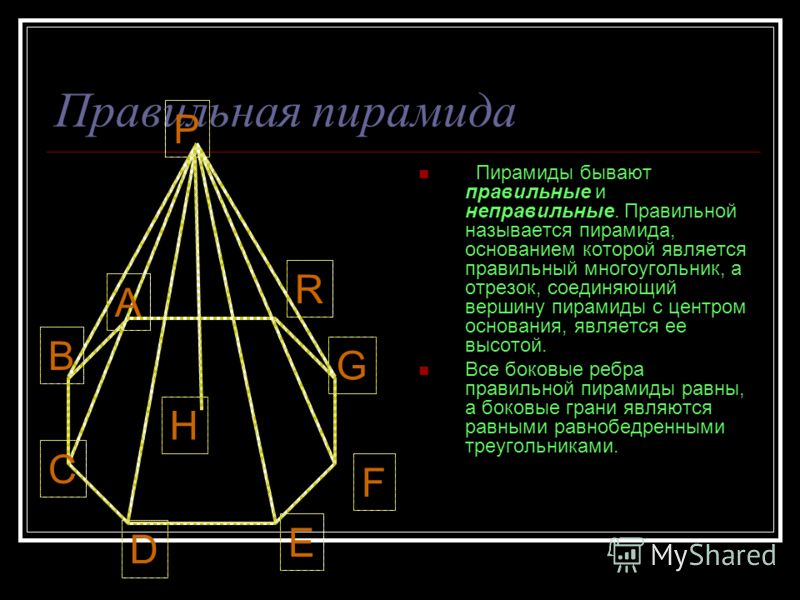
Найдем OL
В основании фигуры – квадрат, стороны и углы которого равны. Значит, половина диагонали = 10. Рассмотрим треугольник LOC, он – прямоугольный. Из исходных данный ясно, что LC = 6 (в равнобедренном треугольнике, высота, проведенная из вершины, делит основание на 2 равные части – это свойство р/б треугольника).
Пользуясь теоремой Пифагора, находим OL:
OL² = √OC² — √LC² = √100 – √36 = √64 = 8
Задача 3
Ищем MO
Пользуясь той же теоремой, находим высоту:
MO² = √ML² – √OL² = 100 – 64 = 36
Ответ: 36
Задача 4
Известно, что в основании ABCD, AB=CD=BC=AD. Треугольник DMC имеет площадь 36см, DC = 4, OL = 6. Определите тип фигуры и найдите высоту.
Исходя из информации про основание, мы сделали вывод, что перед нами правильная пирамида – стороны основания равны. Следовательно, перед нами четырехугольная правильная пирамида.
Из первого вывода следует, что боковые грани – равнобедренные треугольники, а высота и медиана этих треугольников – апофема.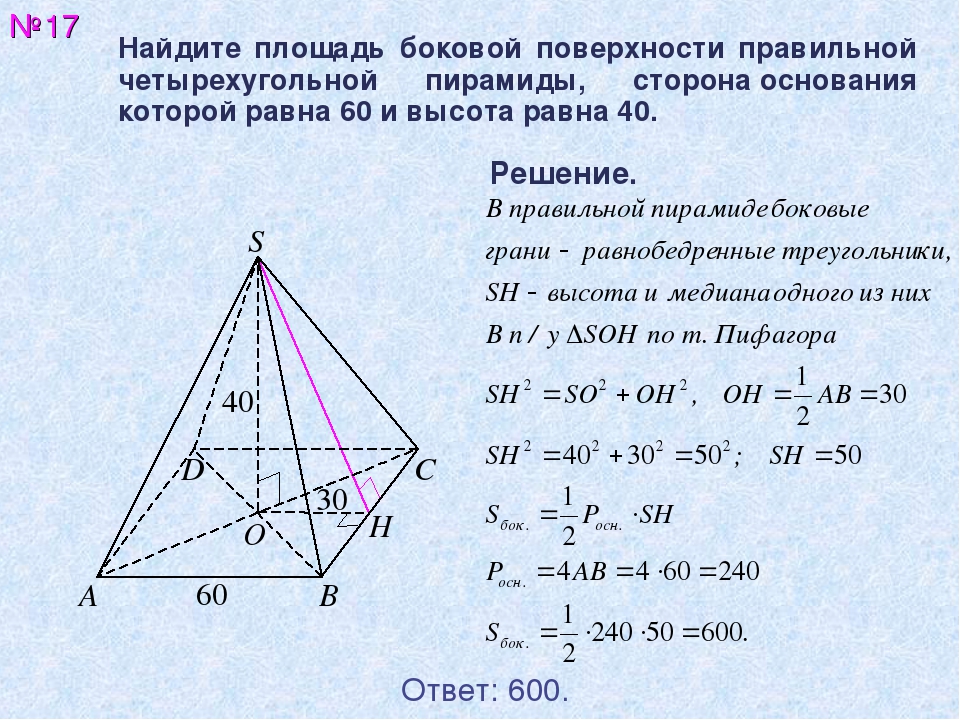 Пользуясь формулами, найдем высоту.
Пользуясь формулами, найдем высоту.
Площадь равнобедренного треугольника
36 = ½ * 4 *h
36 = 2h
H = 18
Теперь у нас есть апофема, а OL нам было уже давно. MOL – прямоугольный треугольник, 2 стороны которого, мы уже знаем. Следовательно, мы можем посчитать высоту.
MO = ML – OL = 18 – 6 = 12
Ответ: 12
Правильная усеченная пирамида
Если провести сечение, параллельное основанию пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Это сечение для усеченной пирамиды является одним из её оснований.
Высота боковой грани (которая является равнобокой трапецией), называется — апофема правильной усеченной пирамиды.
Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная.
- Расстояние между основаниями усеченной пирамиды называется высотой усеченной пирамиды
- Все грани правильной усеченной пирамиды являются равнобокими (равнобедренными) трапециями
Примечания
См. также: частные случаи (формулы) для правильной пирамиды:
также: частные случаи (формулы) для правильной пирамиды:
Для правильной треугольной пирамиды
Как воспользоваться приведенными здесь теоретическими материалами для решения своей задачи:
- Ознакомьтесь со справочными материалами
- Выясните, по условию задачи, о какой именно правильной пирамиде идет речь
- После этого в дереве знаний справа, найдите подходящий урок с данной фигурой (см. решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там
- Если Вы просмотрели весь раздел, но аналогичной задачи не нашлось, напишите о своей проблеме на форуме «раздел для школьников» в соответствующей теме. Обязательно ознакомьтесь предварительно с правилами форума.
Содержание главы:
Апофема правильной пирамиды
Объем правильной усеченной пирамиды
Правильная пирамида с четырехугольником в основании
Правильная пирамида с четырехугольником в основании
Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании
Правильная пирамида с четырехугольником в основании (часть 3)
Нахождение углов пирамиды
Нахождение величины наклона боковых граней правильной прамиды
Нахождение расстояний в правильной четырехугольной пирамиде
Пирамида и вписанный конусОписание курса Апофема правильной пирамиды
Призма, формула вычисления объёма призмы
Призма – это многогранник, основаниями которого являются равные многоугольники, а боковыми гранями – параллелограммы.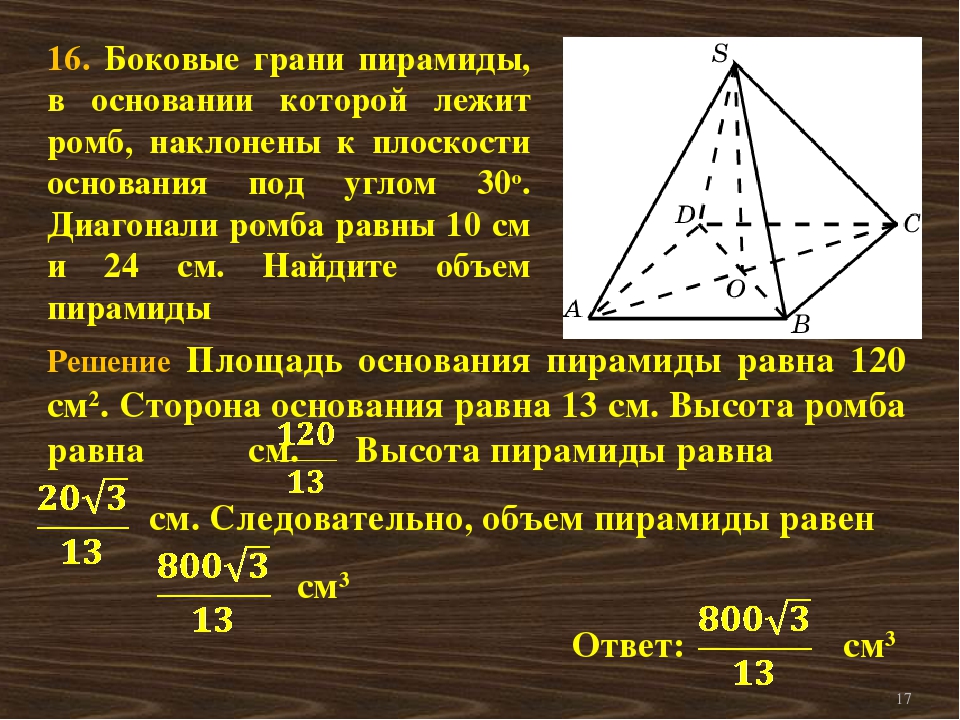
На рисунке 2 изображена наклонная призма. Многогранники и в основаниях лежат в параллельных плоскостях, равны и расположены так, что боковые рёбра () между собой параллельны.
Рис. 2. Наклонная призма
Формула для вычисления объёма призмы:
, где S – площадь основания ( или ), h – высота между основаниями, которая получается при опускании перпендикуляра из любой точки основания на плоскость, в которой лежит другое основание этой призмы ().
Если мы рассмотрим пирамиду , то её объём будет равен:
, где V – объём призмы
Часто задаваемые вопросы
1Как понять, что пирамида правильная, если в условии это не указано?
Часто в задании не указывают какой тип фигуры, чтобы человек сам догадался и применил нужные формулы. Понять какой тип фигуры легко – начните решение задачи с рассмотрения основания и заучивания свойств фигуры.
Зная определения и свойства, определить тип фигуры очень легко.
2Могут ли быть указаны в задании лишние данные?
Чтобы решать задачи, человек должен включать логику, а не подставлять исходные числа в знакомые формулы. С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
С этим расчетом, в некоторых задачах умышленно добавляют лишние данные, которые могут даже не использоваться при решении. Чаще такое встречается в задачах на ЕГЭ.
3Обязательно ли оформлять высоту большой буквой H? Нужно ли выделять апофему?
Для удобства, человек может не выделять отдельно высоту, а сразу писать, например, BE (если B – вершина, а E – основание). То же с апофемой
Важно, чтобы сам человек осознавал, что это за линия и как ее использовать в решении
4Как можно быстро изучить стереометрию?
Ключ к пониманию стереометрии – умение визуализировать объекты в пространстве. Если в дополнение к этому умению, знать формулы, свойства и теорию – задачи будут решаться быстро и безошибочно.
4Как искать высоту, если известен объем?
Если выразить высоту через формулу объема, то получится следующее:
H = (3*V)/ S;
Пример: объем пирамиды равен 70 куб. см., а площадь боковых граней – 30см²
H = 3*70/30 = 7см
Усеченная пирамида
Если верхнюю часть, содержащую вершину, отсечь у правильной треугольной пирамиды, то получится усеченная фигура. В отличие от исходной она будет состоять из двух равносторонних треугольных оснований и трех равнобедренных трапеций.
В отличие от исходной она будет состоять из двух равносторонних треугольных оснований и трех равнобедренных трапеций.
Ниже на фото показано, как выглядит правильная усеченная пирамида треугольная, изготовленная из бумаги.
Для определения объема треугольной пирамиды усеченной необходимо знать три ее линейных характеристики: каждую из сторон оснований и высоту фигуры, равную расстоянию между верхним и нижним основаниями. Соответствующая формула для объема записывается так:
V = √3/12 × h × (A2 + a2 + A × a)
Здесь h — высота фигуры, A и a — длины сторон большого (нижнего) и малого (верхнего) равносторонних треугольников соответственно.
Что это — треугольная пирамида?
Каждый слышал о древних египетских пирамидах, тем не менее они являются четырехугольными правильными, а не треугольными. Объясним, как получить треугольную пирамиду.
Возьмем произвольный треугольник и соединим все его вершины с некоторой одной точкой, расположенной вне плоскости этого треугольника.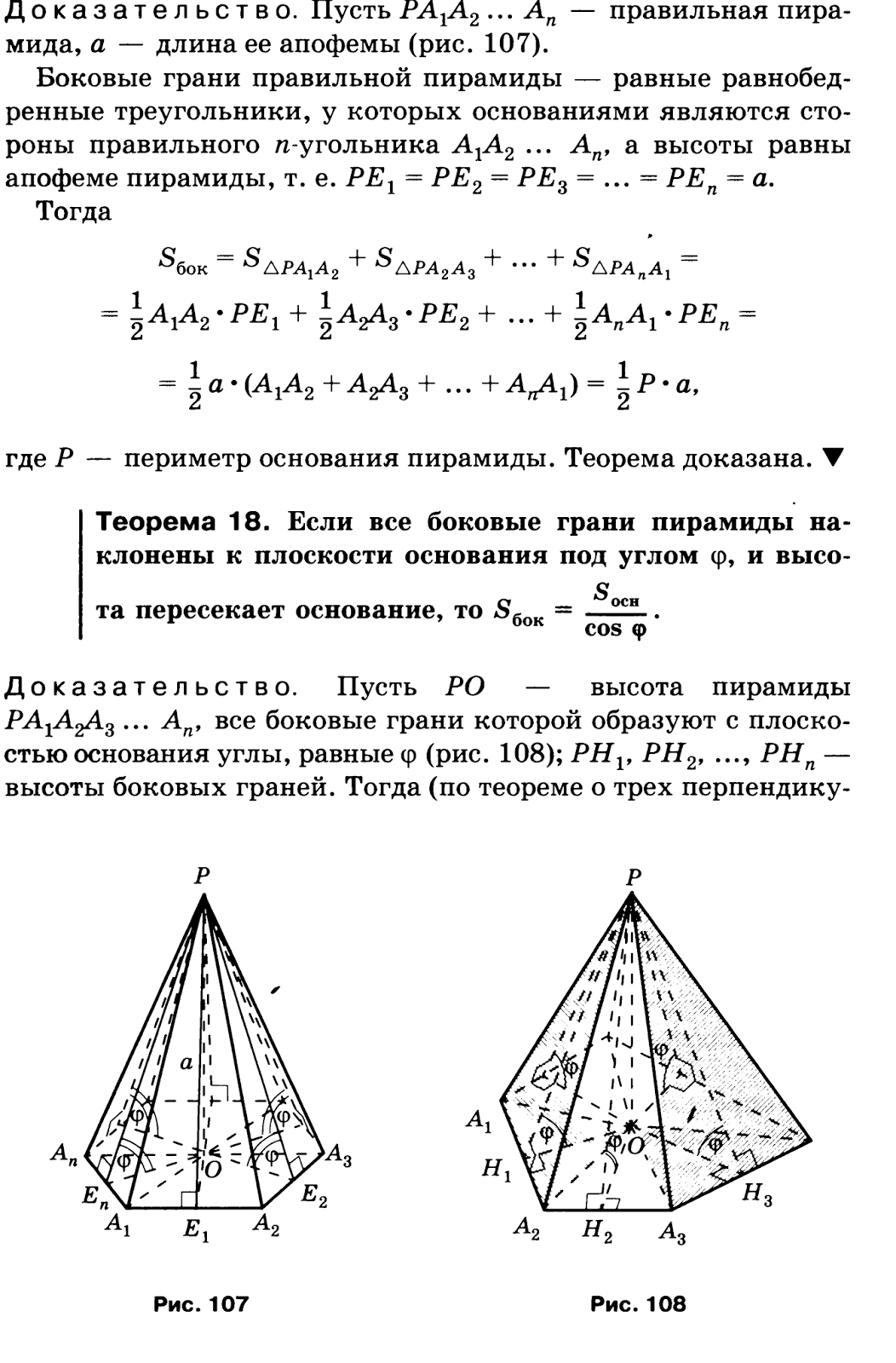 Образованная фигура будет называться треугольной пирамидой. Она показана на рисунке ниже.
Образованная фигура будет называться треугольной пирамидой. Она показана на рисунке ниже.
Вам будет интересно:Как мыться в русской печи: описание обычая, исторические факты
Как видно, рассматриваемая фигура образована четырьмя треугольниками, которые в общем случае являются разными. Каждый треугольник — это стороны пирамиды или ее грань. Эту пирамиду часто называют тетраэдром, то есть четырехгранной объемной фигурой.
Помимо сторон, пирамида также обладает ребрами (их у нее 6) и вершинами (их 4).
Типичные ошибки на ЕГЭ
Незнание темы Когда человек не знает, где находится апофема и что для нее есть определенные формулы, задачу может и можно решить, но тогда необходимо выполнить в 2 раза большей действий.То же обстоит с теорией – если человек не знает свойства многоугольников, то и решить задание он не сможет. Для того, чтобы понимать геометрию, не нужно обладать особенными способностями. Даже при отсутствии способностей к математике, зная теорию, вы будете понимать геометрию.
Отсутствие проверки Хотите потерять балл на ЕГЭ? – не перепроверяйте решения. Часто, задания решаются хаотично и на листе бумаге разные решения намешаны в кучу. Когда приходит время написать ответ, человек по невнимательности либо забывает выполнить последнее действие, либо вписывает не тот ответ.Решайте задачи по действиям, проставляйте пункты и делайте проверку ответа, каким бы он ни был.
Задачи под копирку Решая сотни аналогичных задач, человек настолько привыкает, что теряет бдительность, игнорируя многие исходные данные. Придя на экзамен, в задании может быть вопрос с подвохом и человек ошибается в теме, которую он знал идеально. Помните, к каждой задаче нужен индивидуальный подход, как бы хорошо вы в ней не разбирались.
Запись Структурируйте решения, прописывая каждое действие и каждый полученный вывод. Это необходимо для того, чтобы не запутаться. Решая задания хаотично, можно легко записать неправильное число, не тот ответ, подставить не те числа, и задача уже решена неверно. Обидно получать низкий балл из-за невнимательности.
Обидно получать низкий балл из-за невнимательности.
Подсчеты в уме На экзамене все нервничают и переживают, а потому зарабатывают баллы ниже, чем планировалось изначально. Когда человек нервничает, уровень концентрации и внимания резко снижается
Он может упустить что-то важное, не поставить запятую или запутаться в ходе размышлений.Считая примеры в столбик, вы обезопасите себя от глупых ошибок.
Незнание структуры экзамена Очень обидные ошибки допускают люди, пересдающие ЕГЭ через несколько лет, либо обучающиеся в экстернате. Как правило, они плохо знакомы с процедурой заполнения бланков и внесения ответов.Заполнение бланков для части А и С – различно
Внимательно посмотрите, как необходимо их заполнять, так как неправильное внесение ответа (например, запятая и число в одной клетке) будет приравниваться к ошибке и ответ будет не засчитан.Также, если вы самостоятельно готовитесь к экзамену, учитесь рассчитывать время на каждое задание.
Поспешные решения В случае, если ответ был записан с ошибкой, его можно внести в графе ниже, заменив неправильный ответ на правильный. Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Однако, клетки для внесения результатов ограничены в количестве, а заданий в общей сложности 19!Несколько раз перепроверьте ответы, прежде чем внести их в бланк ответов.
Незнание степеней числа В теореме Пифагора будут использованы не только маленькие числа (до 10). В профильной математике, могут быть крупные числа, которые тяжело посчитать в столбик.Также, степени числа могут понадобиться для других заданий. Выучите значение чисел в квадрате и кубе от 1 до 20. Помните, что на профильном экзамене, пользовать методической таблицей нельзя!
Усеченная правильная пирамида
Усеченная правильная пирамида
Любая усеченная пирамида является многогранником, образованным пирамидой и её сечением, параллельным основанию.
Теорема о боковой поверхности правильной усеченной пирамиды
Площадь боковой поверхности правильной усечённой пирамиды равна произведению полу суммы периметров на апофему.
Площадь одной боковой грани усеченной пирамиды есть площадь трапеции (рис. 5)
5)
Рис. 5
А площадь всей боковой поверхности
Выводы:
Мы рассмотрели правильную пирамиду и стандартные задачи на нее, включая двугранные углы. А также усеченную правильную пирамиду.
Список литературы
- И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
- Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
- Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.
Домашнее задание
- Какое наименьшее число ребер может иметь пирамида?
- Сколько ребер у n-угольной усеченной пирамиды?
- На Рис.
 4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC.
4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC. - В правильной четырехугольной пирамиде SABCD (точка O – центр основания, S – вершина) боковое ребро SB=13, а диагональ основания AC =24. Найдите длину отрезка SO.
- В правильной треугольной пирамиде SABC точка L – середина ребра AC, S – вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Я Класс (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Интернет-портал Slideshare.net (Источник).
Полезные советы
- Если в задаче указан объем – ищите высоту через него.
- Делите равнобедренные треугольники на прямоугольные – так быстрее и проще решить задачу.
- Учите квадратные корни чисел – так, вы будете быстрее справляться с теоремой Пифагора.
- Не кидайтесь сразу к решению – изучите исходные данные и сделайте правильные выводы.

- Если в заданиях получаются слишком крупные числа (от 1000), то перепроверьте решение – вероятно, вы допустили ошибку. В заданиях в учебнике и на экзамене практически не используются крупные числа.
6.5 Общий Балл
Найти высоту в пирамиде
Достоверность информации
8.5
Актуальность информации
7.5
Раскрытие темы
8.5
Доступность применения
7
Удобство
8
Плюсы
Благодаря доступной информации можно легко научиться решать задачи по геометрии
Минусы
Необходимы знания математики
|
Элементы правильной пирамиды
- Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
- Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
- Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)
- Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
- Диагональное сечение пирамиды — это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
- Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды (ABCD)
Если в основании правильной пирамиды лежит треугольник, четырехугольник и т. д. то она называется правильной треугольной, четырехугольной и т.д.
д. то она называется правильной треугольной, четырехугольной и т.д.
Треугольная пирамида есть четырехгранник — тетраэдр.
Подведение итогов урока
На данном уроке мы повторили формулы расчёта объёмов призмы и пирамиды. Решили задачи с использованием этих формул.
Список литературы
- Геометрия: учеб. для 10–11 кл. для общеобразовательных учреждений: базовый и профильный уровни /Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: «Просвещение», 2008.
- Задачи по геометрии. Пособие для учащихся 7–11 кл. общеобразовательных учреждений /Б. Г. Зив, В. М. Мейлер. – М.: «Просвещение», 2003–2008.
- Геометрия. Задачи и упражнения на готовых чертежах. 10–11 кл. /Е. М. Рабинович – Харьков: «Гимназия», 2003, М.: «Илекса», 2003.
- Геометрия. 10 кл. Самостоятельные и контрольные работы. /А. И. Ершова, В. В. Голобородько – М.: «Илекса», 2008.
- Математика. ЕГЭ – 2011. Тематические тренировочные задания./В. В. Кочагин, М. Н. Кочагина – М.
 : «Эксмо», 2011.
: «Эксмо», 2011. - Математика. ЕГЭ – 2009 /Ф. Ф. Лысенко. – Ростов-на-Дону: «Легион», 2008.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Clck.ru (Источник).
- Clck.ru (Источник).
- Clck.ru (Источник).
Домашнее задание
- От треугольной призмы, объем которой равен 129, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.
- Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 12. Найдите объем пирамиды.
- В прямом параллелепипеде диагонали и взаимно перпендикулярны и равны 6 см и 8 см, АВ = 3 см. Найдите объем параллелепипеда.
Площадь боковой поверхности правильной пирамиды
Просмотр содержимого документа
«Площадь боковой поверхности правильной пирамиды»
Робота с теоремой: «Площадь боковой поверхности правильной пирамиды»
Логико-математический анализ
٧ xє M (мно-во пирамид): А(х- является правильной пирамидой) = D(x)-площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Знания для актуализации:
правильная пирамида
апофема
боковая поверхность
площадь треугольника.
периметр основания
Цели в блоках достижений:
предметных результатов:
развитие пространственного представления об окружающем мире
получить вывод формулы площади боковой поверхности правильной пирамиды.
личностных результатов:
самопознание (выявление субъектного опыта)
формирование умения видеть в окружающих объектах математические объекты
развитие пространственного мышления
метапредметных результатов:
смысловое чтение
формирование логического УУД анализ
умение осознанно использовать речевые средства в соответствии с задачей коммуникации (ответы на вопросы, отчет о проделанном опыте, выводы)
умение оценивать правильность выполнения задания (самопроверка, взаимопроверка)
умение применить и преобразовать модели для решение учебных и поставленных задач
ХОД УРОКА
Диктант Слайд 1-3
Выпишите номер правильной пирамиды:
Выпишите апофему данной пирамиды:
Выпишите из чего состоит боковая поверхность пирамиды SABС.

Найдите площадь грани ASB, если АВ=6, SF=2
Найдите периметр основания правильной пирамиды SABС.
А сейчас проверьте себя Слайд 4.
Поднимите руку у кого нет ошибок? А кто совершил только одну ошибку?
Давайте обсудим каждое задание в отдельности, и какие ошибки вы могли совершить!
А сейчас представим, что мы с вами строительная фирма и к нам обратилось посольство Франции, для того чтобы мы застеклили пирамиду Лувра, причем она является правильной пирамидой:
Что нам необходимо знать для этого? (площадь боковой поверхности пирамиды).
А из чего состоит боковая поверхность правильной пирамиды? (Из равных треугольников)
Тогда чему будет равна площадь боковой поверхности пирамиды? (Сумме четырех равных площадей треугольников)
S= 4 ∙1/2∙а∙h
А чем является 4а для нашей пирамиды? (Периметр основания)
А что такое h для нашей пирамиды? (Апофема)
S=1/2∙P∙h
А это верно для всех правильных пирамид или нет?
Постарайтесь сформулировать теорему о боковой поверхности правильной пирамиды?
Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему. (Если пирамида правильная, то площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему)
(Если пирамида правильная, то площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему)
Что нам с вами было дано?(Правильная пирамида)
А что надо доказать? (Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему).
Доказательство Слайд 5.
Что мы доказали? А если нам дана пирамида, то площадь ее боковой поверхности равна половине произведения периметра основания на апофему?
Задача: В правильной четырех угольной пирамиде сторона основания равна 5, а площадь боковой поверхности равна 20. Найдите апофему данной пирамиды.
Записываем, что дано, что надо найти, и делаем чертеж.
А затем приступаем к решению задачи № 244 на стр 72. Первым трем правильно решившим оценка в журнал.
Подводим итоги урока.
Д/з №245
Видео с вопросом: Определение периметра основания пирамиды с учетом ее объема и высоты
Стенограмма видеозаписи
Учитывая, что квадратная пирамида имеет объемом 372 кубических сантиметра и высотой 31 сантиметр определяют периметр его основания.
Нам не выдали схему здесь, но иногда может быть полезно сделать набросок. Во-первых, нам говорят, что это квадратная пирамида, поэтому мы будем знать, что длина и ширина будут точно такими же. измерение на базе.Нам дан объем пирамида составляет 372 кубических сантиметра, а высота перпендикуляра равна 31 сантиметры. Напомним, что объем пирамида равна одной трети площади основания, умноженной на перпендикуляр высота. Мы можем использовать тот факт, что мы учитывая объем пирамиды и ее высоту по перпендикуляру, чтобы найти площадь база. Это позволит нам тогда рассчитать периметр основания.
Можно подставить в значения тогда. Объем 372, высота 31, чтобы получить 372, равно одной трети площади основания, умноженной на 31. Умножая обе стороны на три, мы have 1116 равно площади основания, умноженной на 31. Затем мы делим обе стороны на 31, чтобы дайте нам площадь основания 36 квадратных сантиметров. Итак, как нам перейти от знания площадь основания этой пирамиды до ее периметра? Что ж, помните, что база — это квадратный.Итак, если мы определим длину одного сторона как 𝑙, тогда все остальные стороны будут иметь длину 𝑙. Площадь квадрата будет рассчитывается как 𝑙 в квадрате. В этом случае 𝑙 в квадрате должно иметь дает нам 36. Чтобы вычислить 𝑙, мы возьмем квадратный корень из обеих сторон, а квадратный корень из 36 равен шести. И, конечно же, единицы длины будет в сантиметрах.
Чтобы найти периметр, это расстояние по внешнему краю.Мы могли бы добавить шесть, шесть и шесть а шесть или более просто сложить шесть умножить на четыре, что даст нам значение 24. И поскольку периметр по-прежнему длина, то у нас будут сантиметры. Итак, мы обнаружили, что периметр основания этой пирамиды составляет 24 сантиметра, и мы сделали это, используя объем Сначала рассчитываем площадь основания.
Площадь поверхности пирамиды — объяснение и примеры
Прежде чем мы начнем, давайте рассмотрим, что такое пирамида.В геометрии пирамида — это трехмерное твердое тело, основание которого — любой многоугольник, а боковые грани — треугольники.
В пирамиде боковые грани (которые представляют собой треугольники) встречаются в общей точке, известной как вершина. Название пирамиды происходит от названия многоугольника, образующего ее основу. Например, квадратная пирамида, прямоугольная пирамида, треугольная пирамида, пятиугольная пирамида и т. Д.
Площадь поверхности пирамиды — это сумма площадей боковых граней.
В этой статье будет обсуждаться , как найти общую площадь поверхности и площадь боковой поверхности пирамиды .
Как найти площадь поверхности пирамиды?
Чтобы найти площадь поверхности пирамиды, вам нужно получить площадь основания, а затем добавить площадь боковых сторон, которая равна одной грани, умноженной на количество сторон.
Формула поверхности пирамиды
Общая формула для площади поверхности любой пирамиды (правильной или неправильной) задается как:
Площадь поверхности = площадь основания + боковая площадь
Площадь поверхности = B + LSA
Где TSA = общая площадь поверхности
B = площадь основания
LSA = площадь боковой поверхности.
Для правильной пирамиды формула имеет следующий вид:
Общая площадь поверхности правильной пирамиды = B + 1/2 ps
, где p = периметр основания и s = наклонная высота.
Примечание. Никогда не путайте наклонную высоту (ы) и высоту (h) пирамиды. Перпендикулярное расстояние от вершины до основания пирамиды называется высотой (h), а расстояние по диагонали от вершины пирамиды до края основания называется наклонной высотой (ями).
Площадь поверхности квадратной пирамиды
Для квадратной пирамиды общая площадь поверхности = b (b + 2s)
Где b = длина основания и s = наклонная высота
Площадь поверхности треугольной пирамиды
Площадь поверхности треугольной пирамиды = ½ b (a + 3s)
Где a = апофема длина пирамиды
b = длина основания
s = наклонная высота
Площадь пятиугольной пирамиды
Общая площадь правильной пятиугольной пирамиды равна;
Площадь поверхности пятиугольной пирамиды = 5⁄2 b (a + s)
Где a = апофема длина основания
и b = длина стороны основания, s = наклонная высота пирамиды
Площадь поверхности шестиугольной пирамиды
Гексагональная пирамида — это пирамида с шестиугольником в основании.
Общая площадь поверхности шестиугольной пирамиды = 3b (a + s)
Площадь боковой поверхности пирамиды
Как указано ранее, площадь боковой поверхности пирамиды — это площадь боковых граней пирамиды. Поскольку все боковые грани пирамиды представляют собой треугольники, площадь боковой поверхности пирамиды равна половине произведения периметра основания пирамиды и высоты наклона.
Площадь боковой поверхности (LSA = 1/2 ps)
Где p = периметр основания и s = наклонная высота.
Давайте разберемся с площадью поверхности формулы пирамиды, решив несколько примеров задач.
Пример 1
Какова площадь поверхности квадратной пирамиды, длина основания которой составляет 4 см, а высота наклона — 5 см?
Решение
Дано:
Базовая длина, b = 4 см
Наклонная высота, s = 5 см
По формуле
Общая площадь квадратной пирамиды = b (b + 2s)
TSA = 4 (4 + 2 x 5)
= 4 (4 + 10)
= 4 x 14
= 56 см 2
Пример 2
Какова площадь поверхности квадратная пирамида с перпендикулярной высотой 8 м и длиной основания 12 м?
Решение
Дано;
Высота по перпендикуляру, h = 8 м
Длина основания, b = 12
Чтобы получить наклонную высоту s, применим теорему Пифагора.
с = √ [8 2 + (12/2) 2 ]
с = √ [8 2 + 6 2 ]
с = √ (64 + 36)
с = √100
= 10
Следовательно, наклонная высота пирамиды составляет 10 м
Теперь вычислите площадь поверхности пирамиды.
SA = b (b + 2s)
= 12 (12 + 2 x 10)
= 12 (12 + 20)
= 12 x 32
= 384 м 2 .
Пример 3
Вычислите площадь поверхности пирамиды, наклонная высота которой составляет 10 футов, а ее основание представляет собой равносторонний треугольник с длиной стороны 8 футов.
Решение
Дано:
Базовая длина = 8 футов
Наклонная высота = 10 футов
Примените теорему Пифагора, чтобы получить длину апофемы пирамиды.
a = √ [8 2 — (8/2) 2 ]
= √ (64 — 16)
= √48
a = 6,93 фута
Таким образом, длина апофемы пирамиды составляет 6,93 фута
Но площадь поверхности треугольной пирамиды = ½ b (a + 3s)
TSA = ½ x 8 (6.93 + 3 x 10)
= 4 (6,93 + 30)
= 4 x 36,93
= 147,72 футов 2
Пример 4
Найдите площадь поверхности пятиугольной пирамиды, длина апофемы которой составляет 8 м, длина основания 6 м, высота уклона 20 м.
Решение
Дано;
Длина апофемы, a = 8 м
Длина основания, b = 6 м
Наклонная высота, s = 20 м
Площадь поверхности пятиугольной пирамиды = 5⁄2 b (a + s)
TSA = 5 / 2 x 6 (8 + 20)
= 15 x 28
= 420 м 2 .
Пример 5
Рассчитайте общую площадь поверхности и площадь боковой поверхности шестиугольной пирамиды с апофемой 20 м, длиной основания 18 м и наклонной высотой 35 м.
Решение
Дано;
апофема, a = 20 м
Длина основания, b = 18 м
Наклонная высота, s = 35 м
Площадь поверхности шестиугольной пирамиды = 3b (a + s)
= 3 x 18 ( 20 + 35)
= 54 x 55
= 2970 м 2 .
Площадь боковой поверхности пирамиды = 1/2 пс
Периметр, p = 6 x 18
= 108 м
LSA = ½ x 108 x 35
= 1890 м 2
Предыдущий урок | Главная страница | Следующий урокКалькулятор объема пирамиды
Определите объем любого пирамидального твердого тела с помощью нашего калькулятора объема пирамиды. Выберите один из двух вариантов: рассчитать объем пирамиды с обычным основанием, поэтому вам нужно указать только сторону, форму и высоту, или непосредственно ввести площадь основания и высоту пирамиды.Калькулятор не имеет проблем с определением объема тетраэдра или объема квадратной пирамиды. Если вы все еще не знаете, как пользоваться инструментом и как рассчитать объем пирамиды — продолжайте читать!
Формула объема пирамиды
Пирамида — это многогранник, образованный соединением многоугольного основания и вершины. Основная формула для объема пирамиды такая же, как для конуса:
-
объем = (1/3) * base_area * height, гдеheight— высота от основания до вершины.
Эта формула работает для любого типа базового многоугольника, а также для наклонных и прямых пирамид. Все, что вам нужно знать, это эти два значения — базовая площадь и высота. Однако есть и другие полезные формулы, если вы не знаете базовую площадь. Для любой пирамиды с правильным основанием можно использовать уравнение:
-
объем = (n / 12) * высота * длина стороны² * кроватка (π / n), гдеn— количество сторон основания правильного многоугольника
Как рассчитать объем пирамиды? Пример расчета объема квадратной пирамиды
Мы знаем формулу, а что дальше? Как использовать этот калькулятор объема пирамиды? Лучший способ продемонстрировать, как это работает, — самая известная пирамида в мире — пирамида Хеопса:
.- Выберите базовую форму .Для пирамиды Хеопса, также называемой пирамидой Хуфу, это квадрат. Конечно, это не идеальный квадрат, но можно предположить, что это так — разница в длине ребер меньше 1.
- Введите высоту пирамиды . Высота пирамиды Хуфу равна 146 м (вы можете изменить единицы измерения на метры, просто нажав на единицу измерения. Также вы можете ознакомиться с нашим конвертером объема).
- Определите длину стороны . Длина ребра пирамиды Хеопса в среднем 230.36 мес.
- Примерный объем квадратной пирамиды равен 2 582 532 м³.
Названия томов пирамид
Пирамида с n-сторонним основанием имеет:
- n + 1 грань (n-треугольник + 1 n-угольник)
- 2n ребра
- n + 1 вершина
Название пирамиды происходит от формы основания:
| Грани | Кромки | Вершины | Форма основания | Название пирамиды | ||||
|---|---|---|---|---|---|---|---|---|
| 4 | 6 | 4 | треугольник | 9040 8 треугольник | треугольник треугольниктреугольник | треугольник5 | квадрат | квадратная пирамида |
| 6 | 10 | 6 | пятиугольник | пятиугольная пирамида | ||||
| 7 | 12 | шестигранник | 9040 814 | 8 | семиугольник | семиугольная пирамида | ||
| 9 | 16 | 9 | восьмиугольник | восьмиугольная пирамида |
| Введите длину апофемы = | |||
| Введите длину стороны = | |||
| Введите высоту наклона = | |||
| Введите высоту = | 040 | ||
| Площадь поверхности пирамиды = | |||
| Объем пирамиды = |
Площадь основания: [½as]
Площадь поверхности пирамиды: [½as + (3/2) sl]
Объем пирамиды: [(1/6) abh]
Правильная квадратная пирамида
| Введите длину стороны = | ||||||
| Введите высоту наклона = | ||||||
| Введите высоту = | ||||||
| Площадь основания = | Площадь пирамиды = | |||||
| Объем пирамиды = |
Площадь основания: [с²]
Площадь поверхности пирамиды: [с² + 2sl]
Объем пирамиды: [(1/3) b²h]
Правильная пятиугольная пирамида
| Введите длину апофемы = | |
| Введите длину стороны = | |
| Введите высоту наклона = | |
| Введите высоту | |
| Площадь поверхности пирамиды = | |
| Объем пирамиды = |
Площадь основания: [(5/2) as]
Площадь поверхности пирамиды: [(5/2) as + (5/2) sl]
Объем пирамиды: [(5 / 6) abh]
Правильная шестиугольная пирамида
| Введите длину апофемы = | |
| Введите длину стороны = | |
| Введите высоту наклона = | |
| Введите высоту | |
| Площадь поверхности пирамиды = | |
| Объем пирамиды = |
Площадь основания: [(6/2) as]
Площадь поверхности пирамиды: [3as + 3sl]
Объем пирамиды: [abh]
h = высота s = наклонная высота a = длина стороны V = объем B = Площадь базы T = Площадь пирамиды
Пирамиды имеют трехмерную (3-D) форму, основание которой представляет собой многоугольник, а каждый угол многоугольника прикреплен к единственной вершине, которая придает пирамидам отличительную форму.Вершина и каждое основание образуют треугольник.
Тип пирамиды
1. Треугольная пирамида2. Квадратная пирамида
3. Пятиугольная пирамида
4. Шестиугольная пирамида
5. Правая пирамида
6. Наклонная пирамида
7. Правильная пирамида
8. Неправильная пирамида
| Типы пирамид | База | Форма |
| Треугольная пирамида | Треугольник | |
| Квадратная пирамида | Квадрат | |
| Пятиугольная пирамида | Пентагон | |
| Шестиугольная пирамида | Шестиугольный | |
| Пирамида правая | Пирамидаимеет вершину над центром основания |
Треугольная пирамида: определение, формула и примеры — видео и стенограмма урока
Формула объема для треугольной пирамиды
Объем объекта — это сколько места внутри объекта, поэтому объем треугольной пирамиды — это сколько места внутри пирамиды.Объем треугольной пирамиды можно определить по формуле: V = 1/3 A H , где A = площадь основания треугольника, а H = высота пирамиды или расстояние от основание пирамиды до вершины.
Например, если бы у нас была треугольная пирамида высотой 12 единиц, а площадь основания составляла 24 квадратных единицы, то объем пирамиды был бы V = (1/3) (24) (12) = 96 куб.
Формула площади поверхности для треугольной пирамиды
Площадь поверхности объекта — это общая площадь поверхности объекта.Таким образом, площадь поверхности треугольной пирамиды — это площадь всех ее граней и основания вместе взятых. Когда у нас есть правильная треугольная пирамида, все грани пирамиды имеют одинаковую площадь. Следовательно, площадь поверхности правильной треугольной пирамиды можно найти, добавив площадь основания в 3 раза больше площади одной из граней. То есть SA = A + 3 a , где A — это площадь основания пирамиды, а a — это площадь одной из граней пирамиды.
Чтобы найти площадь треугольника, мы используем формулу A = 1/2 bh , где b — основание треугольника, а h — высота треугольника.
Следовательно, наша формула площади поверхности принимает вид SA = A + 3 (1/2 bh ) = A + 3/2 bh , где b — основание одной из пирамид. Faces, которая также является длиной одной из сторон основания пирамиды, а h — высота одной из граней пирамиды.
Например, если у нас есть правильная треугольная пирамида с гранями, имеющими высоту = 10 единиц и основание = 6 единиц, а площадь основания пирамиды составляет 16 квадратных единиц, то площадь поверхности пирамиды равна SA = 16 + (3/2) (6) (10) = 106 квадратных единиц. Это говорит нам о том, что если вы сложите все площади граней пирамиды и основания пирамиды, вы получите 106 квадратных единиц.
Когда у нас есть неправильная пирамида, мы просто вычисляем площади каждой из граней пирамиды и основания пирамиды по отдельности, а затем складываем их все.То есть SA = Площадь основания + Площадь грани 1 + Площадь грани 2 + Площадь грани 3.
Примеры
Рассмотрим треугольник Рубика. Треугольник Рубика — это правильная треугольная пирамида. От основания пирамиды до вершины 3 дюйма. Площадь основания треугольника Рубика составляет 6,5 квадратных дюймов. Высота одной из граней составляет 3,5 дюйма, а основание одной из граней — 4 дюйма. Зная эту информацию, мы можем найти объем и площадь треугольника Рубика.
Объем = 1/3 AH = (1/3) (6.5) (3) = 6.5 кубических единиц
Площадь поверхности = A + (3/2) bh = 6.5 + (3/2 ) (4) (3.5) = 27,5 квадратных единиц
Рассмотрим еще один пример. Найдите объем и площадь следующей правильной треугольной пирамиды.
Сначала мы найдем объем, поэтому нам нужна площадь основания пирамиды и высота пирамиды. Мы видим, что A = 8.7 квадратных сантиметров и H = 9 см. Поэтому мы подставляем эти значения в нашу формулу объема, чтобы получить V = (1/3) (8,7) (9) = 26,1, поэтому наш объем составляет 26,1 кубических сантиметра.
Теперь мы находим нашу площадь поверхности. Это правильная треугольная пирамида, поэтому нам нужны основание и высота одной из наших граней и площадь основания пирамиды. Из рисунка мы видим, что A = 8,7 квадратных сантиметра, b = 10 см, а h = 7 см. Мы подставляем эти значения в нашу формулу, чтобы получить SA = 8.7 + (3/2) (10) (7) = 113,7. Следовательно, площадь нашей пирамиды составляет 113,7 квадратных сантиметра.
Краткое содержание урока
Треугольные пирамиды — это пирамиды с треугольным основанием. Стороны треугольной пирамиды называются гранями , а точка, где все грани встречаются, называется вершиной . У нас есть формулы для вычисления объема и площади поверхности треугольной пирамиды.
Чтобы найти объем, мы используем формулу V = (1/3) A H , где A = площадь основания пирамиды и H = высота пирамиды.Чтобы найти площадь правильной треугольной пирамиды, воспользуемся формулой SA = A + (3/2) b h , где A = площадь основания пирамиды, b = основание одной из граней, а h = высота одной из граней.
Ключевые термины
Пирамида — трехмерная форма, имеющая многоугольник в качестве основания и треугольники в качестве сторон, все они встречаются в общей точке
Грани — треугольные стороны пирамиды
Основание — нижний многоугольник пирамиды
Вершина — точка пересечения всех треугольных граней на пирамиде
Треугольная пирамида — пирамида с треугольником в основании
Правильная треугольная пирамида — пирамида, имеющая основание с равными по длине сторонами
Неправильная треугольная пирамида — пирамида с основанием с разной длиной сторон
Объем — сколько места внутри объекта
Площадь поверхности — общая площадь поверхности объекта
Результаты обучения
После этого урока вы должны уметь:
- 9 0335 Сопоставьте следующие термины с соответствующими частями пирамиды: грань, основание, вершина
- Как отличить правильную треугольную пирамиду от неправильной
- Объясните, как найти объем и площадь любой треугольной пирамиды
Обзор площади поверхности пирамид
Не в ущерб призмам и цилиндрам.Они великолепны. Но мы не едим мороженое из призм, путешествуя по египетским цилиндрам Гизы. Мы говорим о том, что пирамиды и конусы ничем не заменим, так что мы могли бы немного узнать о них.
Пирамида — это правильная пирамида , если основание представляет собой правильный многоугольник с вершиной, перпендикулярной центру основания. Пирамида нерегулярна, если у нее нет ежедневного испражнения.
Высота всей пирамиды называется высотой , но боковые грани имеют свою собственную высоту, называемую наклонной высотой .Давайте возьмем правильную шестиугольную пирамиду и посмотрим на ее сетку (которая удивительно похожа на Звезду Давида. L’chaim!).
Боковая площадь — это площадь всех треугольников вместе взятых. Площадь треугольника равна половине основания, умноженной на высоту. В этом случае основание — это сторона шестиугольника s , а высота треугольника — это наклонная высота l . Так как у нас шесть таких треугольников, поперечная площадь определяется следующим уравнением:
Или, упрощенно, это равно:
Поскольку мы знаем, что периметр шестиугольника равен 6 s , мы можем заменить стороны с периметром шестигранника P .
Мазел тов! Мы нашли формулу боковой площади любой пирамиды.
Все, что нам не хватает, чтобы найти площадь поверхности, это основание пирамиды, B . Помните, что в отличие от цилиндров и призм, пирамиды имеют только и одно основание . Если мы знаем площадь основания, мы можем узнать площадь поверхности всей пирамиды.
Пример задачи
На День отца вы решаете построить своему папе скворечник. Вы знаете, как сильно он любит птиц, и вы бы предпочли сделать это, чем в миллионный раз стать его кедом для гольфа.(Серьезно, сколько раз он может называть вас «чемпионом» за один день?) Вы решаете, что крыша скворечника будет квадратной пирамидой, потому что она самая простая. Наклон крыши составляет 10 дюймов, а каждая сторона квадрата — 8 дюймов. Сколько дерева в квадратных дюймах вам понадобится, чтобы сделать крышу?
Что ж, мы можем начать с нашей формулы боковой площади.
Периметр квадратного основания равен 8 + 8 + 8 + 8 = 32 дюйма. Высота наклона крыши составляет 10 дюймов.
Осторожно с ножовкой. Вы же не хотите закончить тем, что учитель столярной мастерской с отсутствующим мизинцем.
Мы можем использовать гораздо больше, чем эти формулы, чтобы вычислить площадь поверхности. Помните теорему Пифагора? Помните тригонометрию? Эти математические призраки никогда не покинут вас. Если мы будем относиться к ним правильно, они будут больше похожи на Каспера, чем на Экзорциста.
Пример задачи
Какова площадь поверхности этой пятиугольной пирамиды?
Зная высоту и наклонную высоту, мы можем получить достаточно информации для расчета всего, что нам нужно.Если мы посмотрим на эти два значения как на прямоугольный треугольник, высота будет катетом, а наклонная высота — гипотенузой. Решение для оставшейся ноги (и, надеюсь, это не протез) даст нам расстояние от центра основания до одной из сторон.
a 2 + b 2 = c 2
a 2 + 12 2 = 13 2
2
a 2 = 25
a = 5
Быстрое касание: расстояние от центра любого правильного многоугольника до середины одного из его ребер называется апофемой , что мы только что нашли. .
Хорошо, по касательной. Теперь увеличьте масштаб основания нашей пирамиды. Отрезок перпендикулярной линии от центра в сторону составляет 5 дюймов (это апофема). Поскольку пятиугольник правильный, мы также можем найти углы в прямоугольном треугольнике. 360 ° вокруг центра равномерно разделены на 5, что дает нам 72 ° на равнобедренный треугольник. Мы разделяем эти треугольники пополам, так что каждый угол равен 36 °. Вот что мы знаем о стиле Pictionary.
Эй, кстати говоря о выходе по касательной…
Мы можем решить для s и найти длину каждой стороны пятиугольника.
s = 10tan (36 °) ≈ 7,27 дюйма
Обязательно поблагодарите тригонометрию в своей речи о вручении Нобелевской премии.
Теперь мы можем сделать две вещи:
- Найти площадь пятиугольного основания
- Найти периметр, который поможет нам найти боковую площадь
Площадь первая, поэтому мы начнем с нее.
Если вы вообразите разрезание пятиугольника на 5 одинаковых треугольников (не стесняйтесь вообразить разрезание его еще немного, если вы действительно злитесь), мы можем найти площадь каждого треугольника и умножить ее на 5.Основание треугольника — длина стороны и высота 5.
На полпути. Если бы это была романтическая комедия, мы были бы в той точке, где два главных героя уже полюбили друг друга, но еще не знали об этом, и только что произошел случайный конфликт, который их разлучил. Это оставляет достаточно времени для прозрения их любви, безумной погони друг за другом в последнюю минуту и обязательного обмена слюной в конце.
Основание — пятиугольник («пятиугольник» означает пять), поэтому периметр в пять раз больше длины стороны.Мы знаем, что сторона составляет около 7,27 дюйма, что означает, что периметр составляет около 36,35 дюйма. Высокая пента!
Теперь о той части, где два главных героя осознают свою бессмертную любовь и соревнуются в поисках друг друга. Боковая площадь пирамиды определяется формулой:
Мы знаем, что наклонная высота l равна 13, поскольку она была нам предоставлена, и мы только что вычислили P .
L = ½ (36,35 × 13) ≈ 236,2 дюйма 2
Два влюбленных воссоединились и наконец признались в своей любви.Остается только тот слюнявый поцелуй, который длится веками.
SA = L + B
SA = 236,2 дюйма 2 + 90,8 дюйма 2 = 327 дюймов 2
Конец. Бросьте кредиты под какую-нибудь приятную песню Майкла Болтона.
цоколи, боковые и в сборе? Как найти периметр основания в правой пирамиде
Пирамида, в основании которой лежит правый шестиугольник, а стороны образованы прямоугольными треугольниками, называется шестиугольником .
Этот многогранник отличается множеством свойств:
- Все стороны и углы основания равны между собой;
- Все ребра и двугранные угольные пирамиды также равны друг другу;
- Треугольники, образующие стороны, одинаковые, соответственно, имеют одинаковую площадь, сторону и высоту.
Для расчета площади правильной шестиугольной пирамиды применяется стандартная формула площади боковой поверхности шестиугольной пирамиды:
где P — периметр основания, A — длина апофема пирамиды.В большинстве случаев можно рассчитать боковую площадь по этой формуле, но иногда можно использовать другой метод. Поскольку боковые грани пирамид образованы равными треугольниками, можно найти площадь одного треугольника, а затем умножить ее на количество боковых сторон. В гексагональной пирамиде их 6. Но этот метод можно применить и при расчете. Подходим пример расчета площади боковой поверхности шестиугольной пирамиды.
Пусть дана правильная шестиугольная пирамида, в которой апофем равен а = 7 см, сторона основания В = 3 см.Вычислите площадь боковой поверхности многогранника.
Для начала найдем периметр основания. Поскольку пирамида правильная — в ее основании правильный шестиугольник. Это означает, что все его стороны равны, а периметр рассчитывается по формуле:
Подставляем данные в формулу:
Теперь мы легко можем найти площадь боковой поверхности, подставив значение в основную формулу:
Также немаловажным моментом является поиск площади основания.Формула основания шестиугольной пирамиды основана на свойствах правильного шестиугольника:
Рассмотрим пример расчета площади основания шестиугольной пирамиды, взяв за основу условие из прошлого примера. Конечно, мы знаем, что сторона основания В = 3 см. Подставьте данные в формулу:
Формула шестиугольной пирамиды представляет собой сумму площади основания и бокового поворота:
Рассмотрим пример вычисления площади гексагональной пирамиды.
Пусть дана пирамида, в основании которой правильный шестиугольник со стороной B = 4 см. Апофем данного многогранника равен а = 6 см. Найдите общую площадь.
Мы знаем, что общая площадь состоит из площадей основания и бокового свеса. Поэтому начать их искать. Рассчитаем периметр:
Теперь находим площадь боковой поверхности:
Далее вычисляем площадь основания, в которой лежит правый шестиугольник:
Теперь мы можем сложить полученные результаты:
Определение. Сторона — это треугольник, у которого один угол лежит в вершине пирамиды, а противоположная ему сторона совпадает со стороной основания (многоугольником).
Определение. Боковые кромки — Это общие стороны боковых граней. У пирамиды столько ребер, сколько углов имеет многоугольник.
Определение. Высота пирамиды — Это перпендикуляр, опущенный сверху к основанию пирамиды.
Определение. Апофема — это перпендикуляр боковой грани пирамиды, опускающийся от вершины пирамиды к стороне основания.
Определение. Диагональное сечение — это поперечное сечение пирамиды с плоскостью, проходящей через вершину пирамиды и диагональ основания.
Определение. Правая пирамида — Это пирамида, в которой основанием является правый многоугольник, а высота попадает в центр основания.
Объем и площадь поверхности пирамиды
Формула. Объем пирамиды По площади основания и по высоте:
Свойства пирамиды
Если все боковые ребра равны, то можно описать основание пирамиды, причем центр основания совпадает с центром круга.Также перпендикуляр, опущенный сверху, проходит через центр основания (круг).
Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.
Боковые ребра равны, если они образуют с плоскостью основания равные углы или если можно описать круг вокруг основания пирамиды.
Если боковые грани наклонены к плоскости основания на один угол, то в основании пирамиды можно вписать круг, а вершина пирамиды рассчитана на ее центр.
Если боковые грани наклонены к базовой плоскости на один угол, то апофемы боковых граней равны.
Свойства правой пирамиды
1. Вершина пирамиды равноудалена от всех углов основания.
2. Все боковые ребра равны.
3. Все боковые грани наклонены под одинаковые углы к основанию.
4. Апофимы всех боковых граней равны.
5. Площади всех боковых граней равны.
6.Все грани имеют одинаковые двугранные (плоские) углы.
7. Вокруг пирамиды можно описать сферу. Центр описываемой сферы — это точка пересечения перпендикуляров, которые проходят через середину ребер.
8. В пирамиде вы можете войти в сферу. Центр вписанной сферы будет точкой пересечения биссектрисы, исходящей из угла между краем и основанием.
9. Если центр вписанной сферы совпадает с центром описанной сферы, то сумма плоских углов вверху равна π или наоборот, один угол равен π / n, где N — количество углов. у основания пирамиды.
Соединение пирамиды со сферой
Вокруг пирамиды можно описать сферу, если в основании пирамиды лежит многогранник, вокруг которого можно описать круг (необходимое и достаточное условие). Центр сферы — это точка пересечения плоскостей, проходящих перпендикулярно через середину боковых ребер пирамид.
Кругом любую треугольную или правильную пирамиду всегда можно описать сферой.
В пирамиду можно войти в сферу, если плоскости бис-секторов внутренних карликовых углов пирамид пересекаются в одной точке (необходимое и достаточное условие).Эта точка будет центром сферы.
Пирамидальное соединение с конусом
Конус называется вписанным в пирамиду, если их вершины совпадают, а основание конуса вписано в основание пирамиды.
Конус можно ввести в пирамиду, если апофемы пирамид равны друг другу.
Конус называется описываемой пирамидой, если их вершины совпадают, а основание конуса описывается вокруг основания пирамиды.
Конус можно описать вокруг пирамиды, если все боковые ребра пирамиды равны друг другу.
Пирамидальное соединение с цилиндром
Пирамида называется вписанной в цилиндр, если вершина пирамиды лежит на одном основании цилиндра, а основание пирамиды вписано в другое основание цилиндра.
Цилиндр можно описать вокруг пирамиды, если вокруг основания пирамиды можно описать круг.
Определение. Усеченная пирамида (пирамидальная призма) — Это многогранник, который находится между основанием пирамиды и плоскостью сечений, параллельной основанию. Таким образом, пирамида имеет большое основание и аналогичное основание меньшего размера. Боковые грани — трапеции. Определение. Треугольная пирамида (квадруп) — Это пирамида, в которой три грани и основание представляют собой произвольные треугольники.Четыре ребра с четырьмя гранями, четырьмя вершинами и шестью ребрами, где любые два ребра не имеют общих вершин, но не соприкасаются.
Каждая вершина состоит из трех граней и ребер, образующих три угла .
Отрезок, соединяющий вершину тетраэдра с центром противоположной грани, называется средним тетраэдром (GM).
Bimedian Его называют сегментом, соединяющим середину противоположных ребер, которые не соприкасаются (KL).
Все бимедианы и медианы тетраэдра пересекаются в одной точке (точках). При этом бимедианы делятся пополам, а медианы относительно 3: 1, начиная с вершины.
Определение. Наклонная пирамида — Это пирамида, в которой одно из ребер образует дурацкий угол (β) с основанием. Определение. Прямоугольная пирамида — Это пирамида, у которой одна из боковых граней перпендикулярна основанию.Определение. Акредитованная пирамида — Это пирамида, в которой апофем составляет более половины длины стороны основания основания.
Определение. Глупая пирамида — Это пирамида, в которой апофем меньше половины длины стороны основания.
Определение. Правый тетраэдр — Тетраэдр, у которого все четыре грани — равносторонние треугольники. Это один из пяти правильных многоугольников. В правом тетраэдре все условные углы (между краями) и треугольные углы (вверху) равны.
Определение. Прямоугольный тетраэдр Тетраэдром называется прямой угол между тремя ребрами вверху (ребра перпендикулярны). Три грани образуют прямоугольный треугольный угол А грани являются прямоугольными треугольниками и основанием произвольного треугольника.Апофема любого лица равна половине той стороны основания, на которую падает апофем.
Определение. Промывной тетраэдр Тетраэдром называют боковые грани, равные друг другу, а основание — прямоугольный треугольник. Такой тетраэдр обслуживает изолированные треугольники.
Определение. Ортоцентрический тетраэдр Тетраэдром называют все высоты (перпендикулярные), которые опущены сверху до противоположной грани, пересекаются в одной точке.
Определение. Звездная пирамида Многогранник называется основанием — звезда.
Определение. Бипирамида — многогранник, состоящий из двух разных пирамид (можно также разрезать пирамиды), имеющих общее основание, а вершины лежат по разные стороны от плоскости основания.При подготовке к экзамену по математике студенты должны систематизировать знания по алгебре и геометрии. Я хочу объединить всю известную информацию, например, как рассчитать площадь пирамиды.Причем начиная с основания и боковых граней на площадь всей поверхности. Если с боковыми гранями ситуация понятна, так как они треугольники, то основание всегда разное.
Как быть при нахождении площади основания пирамиды?
Это может быть абсолютно любая фигура: от произвольного треугольника до n-квадрата. И эта основа, помимо разницы в количестве углов, может быть правильным рисунком или неправильным. В интересующих школьников заданиях в основе находятся только задания с нужными фигурами.Поэтому речь пойдет только о них.
Треугольник прямоугольный
То есть равносторонний. Тот, в котором все партии равны и обозначается буквой «А». В этом случае площадь основания пирамиды рассчитывается по формуле:
S = (A 2 * √3) / 4.
Квадрат
Формула расчета ее площади: самый простой, здесь «А» — снова сторона:
Произвольно правильный n-квадрат
Сторона многоугольника имеет такое же обозначение.В качестве количества углов используется латинская буква n.
S = (N * A 2) / (4 * TG (180º / N)).
Как это сделать при расчете стороны боковой и полной поверхности?
Поскольку у основания правильная фигура, все грани пирамид равны. Более того, каждый из них представляет собой равноправный треугольник, поскольку боковые ребра равны. Тогда для того, чтобы рассчитать площадь стороны пирамиды, потребуется формула, состоящая из количества таких же одностворчатых.Количество компонентов определяется количеством баз.
Площадь равновесного треугольника рассчитывается по формуле, в которой половина произведения основания умножается на высоту. Эта высота в пирамиде называется апофей. Ее обозначение — «А». Общая формула площади боковой поверхности выглядит так:
S = ½ P * A, где p — периметр основания пирамиды.
Бывают ситуации, когда стороны основания не известны, но заданы боковые кромки (c) и плоский угол в его вершине (α).Затем следует использовать такую формулу для расчета боковой площади пирамиды:
S = N / 2 * B 2 SIN α .
Номер задачи 1.
Условие. Найдите общую площадь пирамиды, если она лежит со стороной 4 см в основании, а апофем равен √3 см.
Решение. Начать нужно с расчета периметра фундамента. Так как это правильный треугольник, то p = 3 * 4 = 12 см.Поскольку апофем известен, можно сразу рассчитать площадь всей боковой поверхности: ½ * 12 * √3 = 6√3 см 2.
Для треугольника в основании такое значение площадь получится: (4 2 * √3) / 4 = 4√3 см 2.
Для определения всей площади необходимо будет сложить два из полученных значений: 6√3 + 4√3 \ u003d 10√3 см 2.
Ответ. 10√3 см 2.
Задача №2.
Условие . Есть правильная четырехугольная пирамида.Длина базовой стороны 7 мм, боковой кромки 16 мм. Необходимо знать площадь его поверхности.
Решение. Поскольку многогранник четырехугольный и правильный, то в его основании квадрат. Узнав площадь основания и боковых граней, можно будет посчитать площадь пирамиды. Формула для квадрата приведена выше. А боковые грани известны для всех сторон треугольника. Следовательно, можно использовать формулу Герона для расчета их площадей.
Первые вычисления просты и приводят к такому числу: 49 мм 2. Для второго значения потребуется вычислить полметр: (7 + 16 * 2): 2 = 19,5 мм. Теперь можно вычислить площадь равностороннего треугольника: √ (19,5 * (19,5-7) * (19,5-16) 2) = √2985,9375 = 54,644 мм 2. Таких треугольников всего четыре, так что при вычислении итогового числа надо будет его умножить на 4.
Получается: 49 + 4 * 54 644 = 267 576 мм 2.
Ответ . Требуемое значение — 267,576 мм 2.
Номер задачи 3.
Условие . Справа одна четырехугольная пирамида. Необходимо вычислить площадь. Он знает сторону квадрата — 6 см и высоту — 4 см.
Решение. Самый простой способ использовать формулу с работой периметра и апонемии. Первое значение простое. Второй вариант посложнее.
Придется вспомнить теорему Пифагора и считать, что она образована высотой пирамиды и апофея, которая является гипотенузой.Второй катат равен половине стороны квадрата, так как высота многогранника приходится на его середину.
Искомый апофем (гипотенус прямоугольного треугольника) равен √ (3 2 + 4 2) = 5 (см).
Теперь можно рассчитать искомое значение: ½ * (4 * 6) * 5 + 6 2 = 96 (см 2).
Ответ. 96 см 2.
Номер задания 4.
Состояние. Правая сторона его основания — 22 мм, боковые ребра — 61 мм. Какова площадь боковой поверхности этого многогранника?
Решение. Аргументы в нем те же, что и в задаче № 2. Только была дана пирамида с квадратом в основании, а теперь это шестиугольник.
Первым делом рассчитывается площадь основания по приведенной выше формуле: (6 * 22 2) / (4 * TG (180º / 6)) = 726 / (TG30º) = 726√3 см 2.
Теперь необходимо найти половину версии треугольника равновесия, которая является боковой гранью. (22 + 61 * 2): 2 = 72 см. Осталось по формуле Герона посчитать площадь каждого такого треугольника, а затем умножить ее на шесть и сложить с тем, что случилось с основанием.
Расчеты по формуле Герона: √ (72 * (72-22) * (72-61) 2) = √435600 = 660 см 2. Расчеты, которые дадут площадь боковой поверхности: 660 * 6 = 3960 см 2. Осталось сложить, чтобы узнать всю поверхность: 5217,47≈5217 см 2.
Ответ. Основания 726√3 см 2, боковая поверхность — 3960 см 2, вся площадь 5217 см 2.
Треугольная пирамида Называется многогранником, в основании которого лежит прямоугольный треугольник.
В такой пирамиде край основания и края сторон сторон равны друг другу. Соответственно, сторона боковых граней располагается из суммы площадей трех одинаковых треугольников. Найдите площадь боковой поверхности правой пирамиды по формуле. И вы можете произвести расчет в несколько раз быстрее. Для этого применим формулу площади боковой поверхности треугольной пирамиды:
где P — периметр основания, в котором все стороны равны b, A — апофем, опущенный сверху на это основание.Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Дать правильную пирамиду. Сторона лежащего в основании треугольника B = 4 см. Пирамида Апперам равна = 7 см. Найдите площадь боковой поверхности пирамиды.
Так как по условиям задания мы знаем длину всех необходимых элементов, то найдем периметр. Помним, что в прямоугольном треугольнике все стороны равны, а значит, периметр рассчитывается по формуле:
Подставим данные и найдем значение:
Теперь, зная периметр, можем посчитать сторону площадь поверхности:
Чтобы применить Формулу квадрата треугольной пирамиды для вычисления полного значения, необходимо найти площадь основания многогранника.Для этого используется формула:
Формула основания треугольной пирамиды может быть другой. Допускается применять любой расчет параметров для данной фигуры, но чаще всего это не требуется. Рассмотрим пример расчета площади основания треугольной пирамиды.
Задача: В правой пирамиде сторона нижележащего треугольника равна = 6 см. Рассчитайте базовую площадь.
Для расчета нам понадобится только длина стороны прямоугольного треугольника, расположенного в основании пирамиды.Подставьте данные в формулу:
Довольно часто требуется найти полную площадь многогранника. Для этого потребуется сложить боковую поверхность и основание.
Рассмотрим пример расчета площади треугольной пирамиды.
Задача: Дать правильную треугольную пирамиду. Сторона основания равна В = 4 см, апофем а = 6 см. Найдите всю площадь пирамиды.
Для начала находим площадь боковой поверхности по уже известной формуле.Вычисляем периметр:
Подставляем данные в формулу:
Теперь находим площадь фундамента:
Зная площадь основания и боковой поверхности, находим полную площадь пирамиды:
При вычислении площади правой пирамиды стоит не забывать, что в основании лежит прямоугольный треугольник и многие элементы этого многогранника равны между собой.

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.
В этом случае все углы имеют 60 градусов. Фигура является простейшей из правильных многогранников. Если эта фигура лежит в основании, то такой многогранник будет называться правильной треугольной. Если в основании лежит квадрат, пирамида будет называться правильной четырёхугольной пирамидой.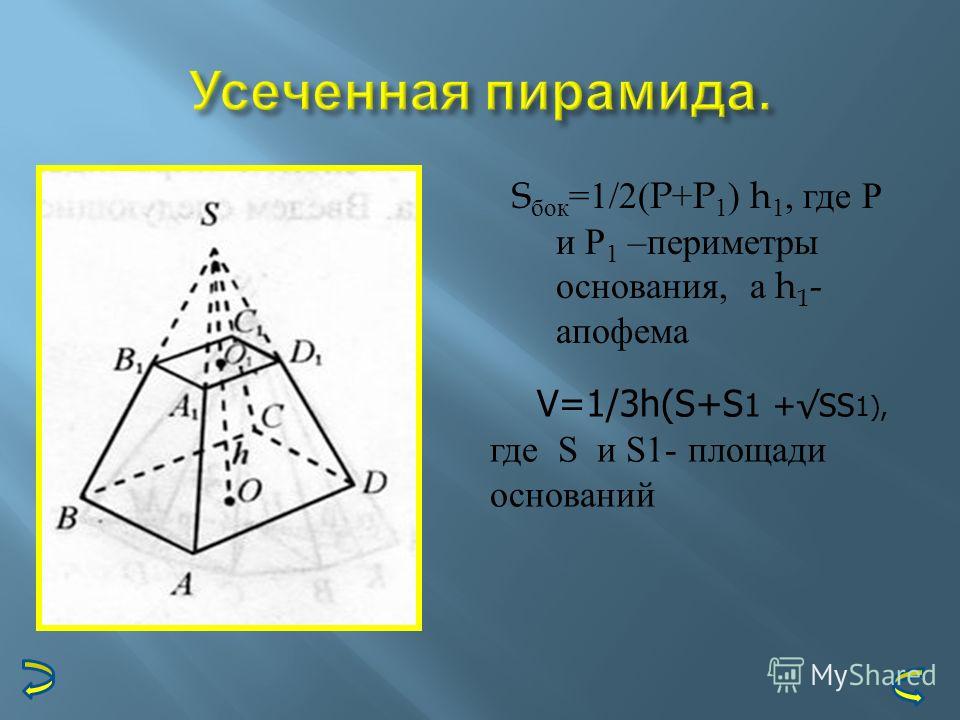 К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой.
К примеру – если это не усечённая пирамида, то грань будет представлять собой треугольник. В данном случае высота этого треугольника и станет апофемой. 4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC.
4 мы провели перпендикуляр СР к ребру SC и соединили точку В и Р. Докажите, что ВР⊥SC.
 : «Эксмо», 2011.
: «Эксмо», 2011.