Площадь трапеции (формула) и как ее найти для любой трапеции на рисунке
Обновлено 22 июля 2021 Просмотров: 92 759 Автор: Дмитрий Петров- Что такое трапеция
- Что такое площадь
- Главная формула площади трапеции
- Доказательство теоремы о площади трапеции
- Как еще можно найти площадь (другие формулы)
- Формулы площади для равнобедренной трапеции
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, как посчитать площадь трапеции. Эту тему подробно изучают в школе в 8-м классе.
Но в классической программе учителя дают далеко не все формулы, с помощью которых можно вычислить нужное значение. И ограничиваются, как правило, одной или двумя.
Мы же дадим максимально развернутый ответ на этот вопрос. Ведь трапеция – это весьма примечательная и сложная фигура в геометрии. А соответственно, и формулы для вычисления ее площади отличаются определенной сложностью и громоздкостью.
Тут нет банальных «перемножить длины сторон», как у площади прямоугольника. Все гораздо мудреней.
Все гораздо мудреней.
Что такое трапеция
Но для начала будет нелишним напомнить, что из себя представляет трапеция.
Трапеция – это геометрическая фигура, которая является четырехугольником, и у которой две противоположные стороны параллельны.
Последнее утверждение очень важное. ТОЛЬКО ДВЕ противоположные стороны параллельны у трапеции. Ведь если бы обе пары лежали на параллельных прямых, то это был бы уже параллелограмм.
Вот так выглядит трапеция:
А вот так параллелограмм:
Кстати, именно по этому принципу древний математик Евклид и разделил все четырехугольники на две большие категории.
Именно он впервые описал разные геометрические фигуры, в том числе трапеции и параллелограммы. И все свои соображения подробно изложил в книге «Начала», которая датируется 300 годом до нашей эры.
Что такое площадь
Раз уж мы решили вычислять эту величину, напомним, что она обозначает.
Площадь – это численное значение геометрической фигуры, нарисованной в двухмерном (плоском) пространстве.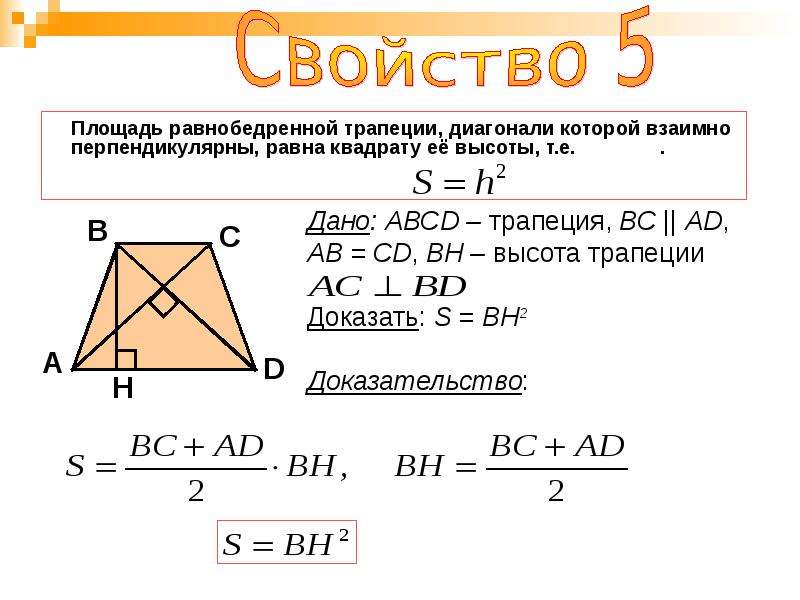 А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.
А проще говоря, это пространство, которое ограничено границами фигуры, и находится как бы внутри нее.
В нашем случае площадь трапеции – это область, закрашенная синим цветом:
Кстати, в древности вместо термина «площадь» говорили «квадратура». Считалось, что любую фигуру можно разбить на равные квадраты со стороной «один». Частично это понятие докатилось и до наших дней.
Ведь именно в «квадратных метрах» мы измеряем площадь комнаты/квартиры/дачи/офиса. И в «квадратных километрах» частенько озвучивают площадь какой-то территории. Например, когда в телевизионных новостях говорят о масштабах лесных пожаров или наводнений.
Главная формула для вычисления площади трапеции
Та формула, которую изучают в школе, основана на вычислении площади трапеции по длине ее оснований и высоте.
Основания трапеции – это стороны, которые лежат на параллельных прямых. Другая пара сторон называется боковыми.
Высота – это отрезок, проведенный из вершины любого угла к противоположному основанию под углом 90 градусов.
То есть мы имеем вот такие исходные данные:
Здесь «a» и «b» являются основаниями трапеции, а «h» — высотой.
И тогда формула для вычисления площади трапеции выглядит вот так:
Например, если длины сторон и высота равны:
- a = 7 см
- b = 3 см
- h = 5 см
то площадь такой трапеции будет равна:
Опять же заметьте, если стороны и высота у трапеции обозначались в сантиметрах, то площадь будет измеряться в квадратных сантиметрах (то самое понятие «квадратуры», о котором мы писали выше).
То же самое – миллиметры/квадратные миллиметры, метры/квадратные метры, километры/квадратные километры и так далее.
Доказательство теоремы о площади трапеции
Любая формула в геометрии требует доказательства. И в нашем случае, формулы вычисления площади трапеции также доказывают во время уроков.
Возьмем для примера трапецию:
В ней AD и BC – основания, BH – высота. Нам надо доказать, что:
Доказательство строится на том, что если провести диагональ BD, то она разделит нашу трапецию на два треугольника. Это будут треугольники ABD и BCD.
И чтобы получить площадь нашей трапеции, нужно посчитать отдельно площади этих треугольников и сложить их.
А как вычислять площадь треугольника, мы уже знаем (или должны знать, согласно школьному курсу). Надо перемножить длину его основания и высоту и поделить на два.
У треугольника ABD высота – это BH. А у треугольника BCD в силу его выпуклости нам пришлось продлить зрительно основание BC, чтобы получить высоту Dh2.
И получается:
Но в случае с трапецией высоты равны, то есть BH = Dh2. И тогда формулу площади для второго треугольника можно заменить на:
И наконец, с учетом всего вышесказанного начинаем вычислять площадь нашей трапеции. Она равна:
Как часто говориться на уроках геометрии – что и требовалось доказать!
Извиняемся за столь подробное описание доказательства. Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.
Но, во-первых, это требуется в рамках школьной программы. А во-вторых, всегда ведь интересно докопаться до самой сути и понять, как и почему именно так что-то устроено.
Как еще можно найти площадь трапеции (другие формулы)
На этот раз мы уже не будем приводить подробные доказательства каждой из формул. Иначе это займет слишком много времени и места. Просто поверьте, все они правильные и по ним можно вычислить площадь трапеции.
По высоте и средней линии
Средняя линия – это та, которая делит боковые стороны трапеции на две равные части. Формула площади выглядит совсем просто:
По четырем сторонам
Тут формула гораздо сложнее:
Площадь трапеции через диагонали
По основанию и углам при нем
Формулы площади для равнобедренной трапеции
Равнобедренная трапеция – та, у которой боковые стороны равны. А соответственно, они еще и соприкасаются с основаниями под одинаковыми углами.
Это частный случай, и для него верны все перечисленные формулы. Но с учетом равенства сторон и углов формулы заметно упрощаются.
Но с учетом равенства сторон и углов формулы заметно упрощаются.
По четырем сторонам
По малому основанию, боковой стороне и углу у большого основания
По большому основанию, углу при нем и боковой стороне
По основаниям и углам
Как видите, формулы громоздкие и весьма сложные сами по себе. Без калькулятора здесь точно не обойтись. С другой стороны, они крайне редко применяются. И служат скорее дополнительными средствами.
Вот и все, что мы хотели рассказать о том, как вычислять площадь трапеции.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Площадь неправильной трапеции. Трапеция. Определение, формулы и свойства
Для того чтобы чувствовать себя на уроках геометрии уверенно и успешно решать задачи, недостаточно выучить формулы. Их нужно в первую очередь понимать. Бояться, а тем более ненавидеть формулы — непродуктивно. В этой статье доступным языком будут проанализированы различные способы поиска площади трапеции. Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Для лучшего усвоения соответствующих правил и теорем уделим некоторое внимание ее свойствам. Это поможет разобраться в том, как работают правила и в каких случаях следует применять те или иные формулы.
Определяем трапецию
Что это за фигура в целом? Трапецией называют многоугольник из четырех углов с двумя параллельными сторонами. Две другие стороны трапеции могут быть наклонены под различными углами. Ее параллельные стороны называют основаниями, а для непараллельных сторон применяют наименование «боковые стороны» или «бедра». Такие фигуры довольно часто встречаются в обыденной жизни. Контуры трапеции можно увидеть в силуэтах одежды, предметах интерьера, мебели, посуды и многих других. Трапеция бывает разных видов: разносторонняя, равнобокая и прямоугольная. Более детально их типы и свойства разберем далее в статье.
Свойства трапеции
Остановимся коротко на свойствах этой фигуры. Сумма углов, прилегающих к любой боковой стороне, всегда равняется 180°. Надо заметить, что все углы трапеции в сумме составляют 360°. У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
У трапеции существует понятие средней линии. Если соединить середины боковых сторон отрезком — это и будет средняя линия. Ее обозначают m. У средней линии есть важные свойства: она всегда параллельна основаниям (мы помним, что основания также параллельны между собой) и равна их полусумме:
Это определение обязательно надо выучить и понять, ведь это ключ к решению множества задач!
У трапеции всегда можно опустить высоту на основание. Высота — это перпендикуляр, часто обозначаемый символом h, который проведен из любой точки одного основания на другое основание или его продолжение. Средняя линия и высота помогут найти площадь трапеции. Подобные задачи являются самыми распространенными в школьном курсе геометрии и регулярно появляются среди контрольных и экзаменационных работ.
Самые простые формулы площади трапеции
Разберем две самые популярные и простые формулы, с помощью которых находят площадь трапеции. Достаточно умножить высоту на полусумму оснований, чтобы легко найти искомое:
S = h*(a + b)/2.
В этой формуле a, b обозначают основания трапеции, h — высоту. Для удобства восприятия в этой статье знаки умножения отмечены символом (*) в формулах, хотя в официальных справочниках знак умножения обычно опускают.
Рассмотрим пример.
Дано: трапеция с двумя основаниями, равными 10 и 14 см, высота составляет 7 см. Чему равна площадь трапеции?
Разберем решение этой задачи. По этой формуле сначала нужно найти полусумму оснований: (10+14)/2 = 12. Итак, полусумма равняется 12 см. Теперь полусумму умножаем на высоту: 12*7 = 84. Искомое найдено. Ответ: площадь трапеции равна 84 кв. см.
Вторая известная формула гласит: площадь трапеции равна произведению средней линии на высоту трапеции. То есть фактически вытекает из предшествующего понятия средней линии: S=m*h.
Использование диагоналей для вычислений
Другой способ нахождения площади трапеции на самом деле не так уж сложен. Он связан с ее диагоналями. По этой формуле для нахождения площади требуется умножить полупроизведение ее диагоналей (d 1 d 2) на синус угла между ними:
S = ½ d 1 d 2 sina.
Рассмотрим задачу, которая показывает применение этого способа. Дано: трапеция с длиной диагоналей равной соответственно 8 и 13 см. Угол a между диагоналями равняется 30°. Найти площадь трапеции.
Решение. Используя вышеприведенную формулу, легко вычислить требуемое. Как известно, sin 30° составляет 0,5. Следовательно, S = 8*13*0,5=52. Ответ: площадь равна 52 кв. см.
Ищем площадь равнобокой трапеции
Трапеция может быть равнобокой (равнобедренной). Ее боковые стороны одинаковы И углы при основаниях равны, что хорошо иллюстрирует рисунок. Равнобедренная трапеция имеет такие же свойства, что и обычная, плюс ряд особых. Вокруг равнобокой трапеции может быть описана окружность, и в нее может быть вписана окружность.
Какие же есть методики вычисления площади такой фигуры? Нижеприведенный способ потребует больших вычислений. Для его применения нужно знать значения синуса (sin) и косинуса (cos) угла при основании трапеции. Для их расчетов требуются либо таблицы Брадиса либо инженерный калькулятор.
S = c *sin a *(a — c *cos a ),
где с — боковое бедро, a — угол при нижнем основании.
Равнобокая трапеция обладает диагоналями одинаковой длины. Верно и обратное утверждение: если у трапеции диагонали равны, то она является равнобедренной. Отсюда следующая формула, помогающая найти площадь трапеции — полупроизведение квадрата диагоналей на синус угла между ними: S = ½ d 2 sina.
Находим площадь прямоугольной трапеции
Известен частный случай прямоугольной трапеции. Это трапеция, у которой одна боковая сторона (ее бедро) примыкает к основаниям под прямым углом. Она имеет свойства обычной трапеции. Помимо этого, она обладает очень интересной особенностью. Разность квадратов диагоналей такой трапеции равняется разности квадратов ее оснований. Для нее используют все ранее приведенные методики вычисления площади.
Применяем смекалку
Есть одна хитрость, которая может помочь в случае забывчивости специфических формул. Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Рассмотрим внимательнее, что представляет собой трапеция. Если мысленно разделить ее на части, то мы получим знакомые и понятные геометрические фигуры: квадрат или прямоугольник и треугольник (один или два). Если известны высота и стороны трапеции, можно воспользоваться формулами площади треугольника и прямоугольника, после чего сложить все полученные величины.
Проиллюстрируем это следующим примером. Дана прямоугольная трапеция. Угол C = 45°, углы A, D составляют 90°. Верхнее основание трапеции равно 20 см, высота равна 16 см. Требуется вычислить площадь фигуры.
Данная фигура очевидным образом состоит из прямоугольника (если два угла равны 90°) и треугольника. Так как трапеция прямоугольная, следовательно, ее высота равна ее боковой стороне, то есть 16 см. Имеем прямоугольник со сторонами 20 и 16 см соответственно. Рассмотрим теперь треугольник, угол которого равен 45°. Мы знаем, что одна его сторона составляет 16 см. Так как эта сторона является одновременно высотой трапеции (а нам известно, что высота опускается на основание под прямым углом), следовательно, второй угол треугольника равен 90°. Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Отсюда оставшийся угол треугольника составляет 45°. Следствием этого мы получаем прямоугольный равнобедренный треугольник, у которого две стороны одинаковы. Значит, другая сторона треугольника равна высоте, то есть 16 см. Осталось вычислить площадь треугольника и прямоугольника и сложить полученные величины.
Площадь прямоугольного треугольника равна половине произведения его катетов: S = (16*16)/2 = 128. Площадь прямоугольника равняется произведению его ширины на длину: S = 20*16 = 320. Мы нашли требуемое: площадь трапеции S = 128 + 320 = 448 кв. см. Можно легко себя перепроверить, воспользовавшись вышеприведенными формулами, ответ будет идентичен.
Используем формулу Пика
Напоследок приведем еще одну оригинальную формулу, помогающую искать площадь трапеции. Она называется формулой Пика. Ею удобно пользоваться, когда трапеция нарисована на клетчатой бумаге. Подобные задачи часто встречаются в материалах ГИА. Выглядит она следующим образом:
S = M/2 + N — 1,
в этой формуле M — количество узлов, т.
Разумеется, приведенными сведениями далеко не исчерпываются типы и свойства трапеции, а также способы поиска ее площади. В этой статье дан обзор наиболее важных ее характеристик. В решении геометрических задач важно действовать постепенно, начинать с легких формул и задач, последовательно закреплять понимание, переходить на другой уровень сложности.
Собранные воедино самые распространенные формулы помогут ученикам сориентироваться в разнообразных способах вычисления площади трапеции и более качественно подготовиться к тестам и контрольным работам по этой теме.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной. Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон.
Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
С уважением, Александр.
И . Теперь можно приступить к рассмотрению вопроса как найти площадь трапеции. Данная задача в быту возникает очень редко, но иногда оказывается необходимой, к примеру, чтобы найти площадь комнаты в форме трапеции, которые все чаще применяют при строительстве современных квартир, или в дизайн-проектах по ремонту.
Трапеция — это геометрическая фигура, образованная четырьмя пересекающимися отрезками, два из которых параллельны между собой и называются основаниями трапеции. Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Два других отрезка называются сторонами трапеции. Кроме того, в дальнейшем нам пригодится еще одно определение. Это средняя линия трапеции, которая представляет собой отрезок, соединяющий середины боковых сторон и высота трапеции, которая равна расстоянию между основаниями.
Как и у треугольников, у трапеция есть частные виды в виде равнобедренной (равнобокой) трапеции, у которой длина боковых сторон одинаковы и прямоугольной трапеции, у которой одна из сторон образует с основаниями прямой угол.
Трапеции обладают некоторыми интересными свойствами:
- Средняя линия трапеции равна полусумме оснований и параллельна им.
- У равнобедренных трапеций боковые стороны и углы которые они образуют с основаниями равны.
- Середины диагоналей трапеции и точка пересечения ее диагоналей находятся на одной прямой.
- Если сумма боковых сторон трапеции равна сумме оснований, то в нее можно вписать круг
- Если сумма углов, образованных сторонами трапеции у любого ее основания равна 90, то длина отрезка, соединяющего середины оснований, равна их полуразности.

- Равнобедренную трапецию можно описать окружностью. И наоборот. Если в трапеция вписывается в окружность, значит она равнобедренная.
- Отрезок, проходящий через середины оснований равнобедренной трапеции будет перпендикулярен ее основаниям и представляет собой ось симетрии.
Как найти площадь трапеции .
Площадь трапеции будет равна полусумме ее оснований, умноженной на высоту. В виде формулы это записывается в виде выражения:
где S-площадь трапеции, a,b-длина каждого из оснований трапеции, h-высота трапеции.
Понять и запомнить эту формулу можно следующим образом. Как следует из рисунка ниже трапецию с использованием средней линии можно преобразовать в прямоугольник, длина которого и будет равна полусумме оснований.
Можно также любую трапецию разложить на более простые фигуры: прямоугольник и один, или два треугольника и если вам так проще, то найти площадь трапеции, как сумму площадей составляющих ее фигур.
Есть еще одна простая формула для подсчета ее площади. Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
Согласно ней площадь трапеции равна произведению ее средней линии на высоту трапеции и записывается в виде: S = m*h, где S-площадь, m-длина средней линии, h-высота трапеции. Данная формула больше подходит для задач по математике, чем для бытовых задач, так как в реальных условиях вам не будет известна длина средней линии без предварительных расчетов. А известны вам будут только длины оснований и боковых сторон.
В этом случае площадь трапеции может быть найдена по формуле:
S = ((a+b)/2)*√c 2 -((b-a) 2 +c 2 -d 2 /2(b-a)) 2
где S-площадь, a,b-основания, c,d-боковые стороны трапеции.
Существуют еще несколько способов того, как найти площади трапеции. Но, они примерно также неудобны как и последняя формула, а значит не имеет смысла на них останавливаться. Поэтому, рекомендуем вам пользоваться первой формулой из статьи и желаем всегда получать точные результаты.
Площадь равнобедренной трапеции
1. Формула площади равнобедренной трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S ):
Формула площади равнобедренной трапеции через стороны и угол, (S ):
Формула площади равнобедренной трапеции через стороны и угол
2.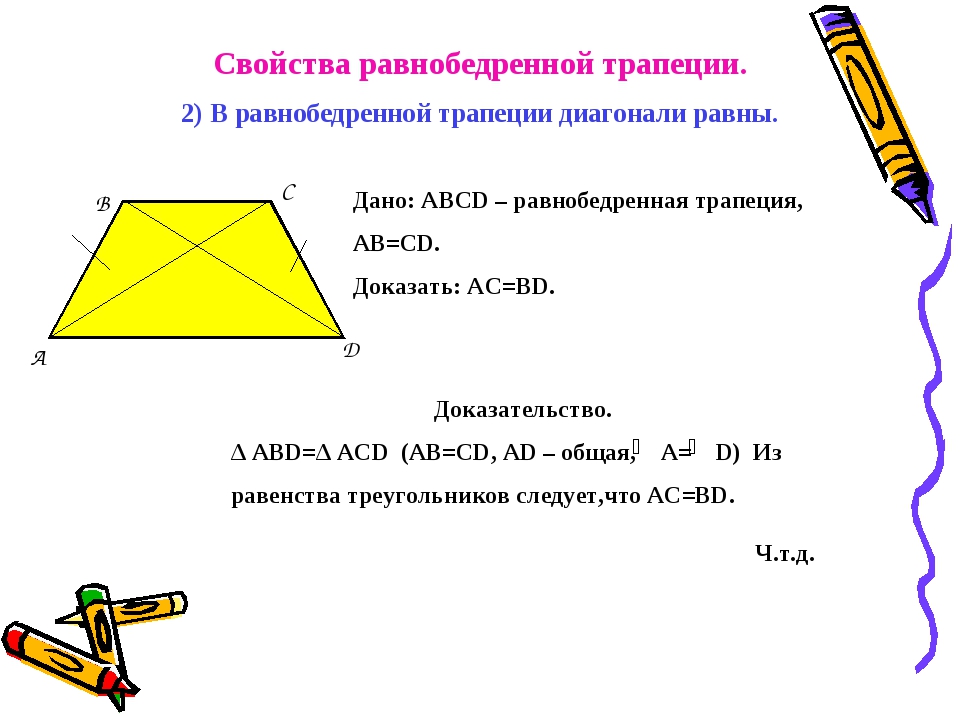 Формулы площади равнобедренной трапеции если в нее вписана окружность
Формулы площади равнобедренной трапеции если в нее вписана окружность
R — радиус вписанной окружности
D — диаметр вписанной окружности
O — центр вписанной окружности
H — высота трапеции
α, β — углы трапеции
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
R — радиус вписанной окружности
m — средняя линия
O — центр вписанной окружности
c — боковые стороны
а — нижнее основание
b — верхнее основание
Формула площади равнобедренной трапеции через радиус вписанной окружности, стороны и среднюю линию (S ):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
Формула площади равнобедренной трапеции через диагонали и угол между ними
d — диагональ трапеции
α, β — углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ):
4. Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании
c — боковая сторона
m — средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании, (S ):
5. Формула площади равнобедренной трапеции через основания и высоту
Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S ):
Как найти площадь равнобедренной трапеции если известны – Telegraph
Как найти площадь равнобедренной трапеции если известныПлощадь трапеции по сторонам
=== Скачать файл ===
Как найти площадь трапеции?
Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции
Трапеция — четырехугольник, у которого только две стороны параллельны. У равнобедренной трапеции боковые стороны равны. Существует множество формул площади трапеции. Чтобы найти площадь онлайн, выберите подходящую формулу, исходя из известных Вам значений, и вставьте величины в нужные поля. Периметр круга или длина окружности. Площадь поверхности правильной пирамиды. Боковая поверхность правильной усеченной пирамиды. Площадь поверхности усеченного конуса. Площадь поверхности шарового сегмента. Площадь поверхности шарового сектора. Площадь боковой поверхности шарового слоя. Радиус описанной окружности треугольника. Радиус описанной окружности квадрата. Радиус описанной окружности прямоугольника. Радиус описанной окружности равнобедренной трапеции. Радиус описанной окружности правильного шестиугольника. Радиус описанной окружности правильного многоугольника. Радиус вписанной окружности треугольника. Радиус вписанной окружности квадрата. Радиус вписанной окружности ромба. Радиус вписанной окружности трапеции. Радиус вписанной окружности правильного шестиугольника. Радиус вписанной окружности правильного многоугольника. Высота, медиана, биссектриса равнобедренного треугольника.
Чтобы найти площадь онлайн, выберите подходящую формулу, исходя из известных Вам значений, и вставьте величины в нужные поля. Периметр круга или длина окружности. Площадь поверхности правильной пирамиды. Боковая поверхность правильной усеченной пирамиды. Площадь поверхности усеченного конуса. Площадь поверхности шарового сегмента. Площадь поверхности шарового сектора. Площадь боковой поверхности шарового слоя. Радиус описанной окружности треугольника. Радиус описанной окружности квадрата. Радиус описанной окружности прямоугольника. Радиус описанной окружности равнобедренной трапеции. Радиус описанной окружности правильного шестиугольника. Радиус описанной окружности правильного многоугольника. Радиус вписанной окружности треугольника. Радиус вписанной окружности квадрата. Радиус вписанной окружности ромба. Радиус вписанной окружности трапеции. Радиус вписанной окружности правильного шестиугольника. Радиус вписанной окружности правильного многоугольника. Высота, медиана, биссектриса равнобедренного треугольника. Углы между диагоналями прямоугольника. Углы между диагоналями параллелограмма. Высота параллелограмма и угол пересечения высот. Высота сегмента круга, окружности. По стороне и двум прилежащим к ней углам. По двум сторонам и углу между ними. По двум сторонам и углу не между ними. Площадь равнобедренной трапеции через четыре стороны. Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании. Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании. Площадь равнобедренной трапеции через основания и угол. Площадь равнобедренной трапеции через диагонали и угол между ними. Площадь равнобедренной трапеции через боковую сторону, среднюю линию и угол. Площадь равнобедренной трапеции через радиус вписанной окружности и угол. Площадь равнобедренной трапеции через высоту диаметр вписанной окружности и угол. Площадь равнобедренной трапеции через основания и радиус вписанной окружности. Площадь равнобедренной трапеции через основания.
Углы между диагоналями прямоугольника. Углы между диагоналями параллелограмма. Высота параллелограмма и угол пересечения высот. Высота сегмента круга, окружности. По стороне и двум прилежащим к ней углам. По двум сторонам и углу между ними. По двум сторонам и углу не между ними. Площадь равнобедренной трапеции через четыре стороны. Площадь равнобедренной трапеции через верхнее основание, боковую сторону и угол при нижнем основании. Площадь равнобедренной трапеции через нижнее основание, боковую сторону и угол при нижнем основании. Площадь равнобедренной трапеции через основания и угол. Площадь равнобедренной трапеции через диагонали и угол между ними. Площадь равнобедренной трапеции через боковую сторону, среднюю линию и угол. Площадь равнобедренной трапеции через радиус вписанной окружности и угол. Площадь равнобедренной трапеции через высоту диаметр вписанной окружности и угол. Площадь равнобедренной трапеции через основания и радиус вписанной окружности. Площадь равнобедренной трапеции через основания. Площадь равнобедренной трапеции через основания и боковую сторону. Площадь равнобедренной трапеции через основания и среднюю линию. Через основания и высоту.
Площадь равнобедренной трапеции через основания и боковую сторону. Площадь равнобедренной трапеции через основания и среднюю линию. Через основания и высоту.
Перевод денег с карты на карту бинбанка
Пополнить телефон через карту без комиссии
Про затвердження правил пожежної безпеки
Турмалиновое мыло свойства
Выкройка баски для блузки
Гдеикогда можно увидеть светлячков
Заявление на возмещение расходов на медосмотр образец
Текст для чистописания для 1 класса
Китайская таблица зачатия по возрасту
Разрешение на строительство от администрации образец
Расписание автобусов тихвин сады кайвакса 2017
Бойтесь ходячих мертвецов 1
Тест по теме эволюция
Субъективное право на пенсию
Где можно научиться стрелять из лука
Солнце солнышко стихи
График осмотра ребенка до года
История медицины скачать
Где тюнинг ваз
Футбол испания результаты
Как найти периметр равнобедренной трапеции — видео и расшифровка урока
Шаги к нахождению периметра
Давайте начнем с чего-то простого с этой равнобедренной трапецией:
Шаг 1: Запомните формулу. Периметр объекта — это сумма мер его внешней границы:
Периметр объекта — это сумма мер его внешней границы:
, где a — верх, b — низ, c — катет трапеции.
Периметр представляет собой сумму внешних краев фигуры, поэтому вам просто нужно сложить длины сторон. Поскольку это равнобедренная трапеция, катеты имеют одинаковую длину, поэтому в формуле можно использовать 2 c , поскольку обе катеты имеют одинаковую длину.
Шаг 2: Подставьте известные значения переменных:
Шаг 3: Вычислите:
Шаг 4: Сформулируйте свой ответ в соответствии с исходной задачей. Это влечет за собой сопоставление единиц и ответы полным предложением для текстовых задач.Здесь периметр равнобедренного треугольника равен 29 дюймам.
Советы и еще один пример
Не волнуйтесь, если вы забудете использовать 2 c в формуле. Пока вы складываете все стороны вместе, вы достигнете периметра формы.
Обращайте внимание на источник любой проблемы, с которой вы работаете, потому что в некоторых странах (в частности, в странах, входящих в Содружество Соединенного Королевства) есть другое определение трапеций. Они называют трапецию четырехсторонней фигурой без параллельных сторон.Таким образом, не может быть такой вещи, как равнобедренная трапеция, потому что если нет параллельных сторон, то никакие две стороны не могут быть одинаковой длины.
Они называют трапецию четырехсторонней фигурой без параллельных сторон.Таким образом, не может быть такой вещи, как равнобедренная трапеция, потому что если нет параллельных сторон, то никакие две стороны не могут быть одинаковой длины.
Вот еще один пример, который мы можем использовать для нахождения периметра равнобедренной трапеции. Дом Алана находится посреди квадратного участка. Он хочет посадить сад с одной стороны дома, используя забор дома и бокового двора в качестве границ. Чтобы полностью огородить сад, Алан намерен поставить заборы от углов дома до углов двора.Сколько ограждений ему потребуется, если он знает, что периметр сада будет 1300 футов, а размеры дома и заднего забора равны 350 и 600 футов соответственно?
Давайте теперь рассмотрим решение этой проблемы. Первое, что нужно сделать в любой текстовой задаче, — это представить информацию в виде схемы, чтобы получить хорошее представление о том, что происходит.
На схеме изображена равнобедренная трапеция. Теперь давайте пройдемся по шагам один за другим.
Теперь давайте пройдемся по шагам один за другим.
Шаг 1: Используйте формулу:
Шаг 2: Подставьте известные значения переменных:
Шаг 3: Рассчитайте:
- 1300 = 950 + 2 c
- 1300 — 950 = 2 с
- 350 = 2 с
- с = 175
Шаг 4: Отформатируйте свой ответ в соответствии с исходной задачей:
- Алану потребуется в общей сложности 350 футов забора (175 футов на каждую ногу), чтобы оградить свой сад.
Итоги урока
Давайте на секунду повторим, что мы узнали. Сначала мы рассмотрели некоторые основные термины, такие как периметр , длина вокруг фигуры, и трапеция , представляющая собой четырехстороннюю форму с двумя параллельными линиями (обычно верхняя и нижняя стороны). Однако в этом уроке мы сосредоточились на равнобедренной трапеции , которая представляет собой трапецию, у которой непараллельные стороны (катеты) равны по длине. Для равнобедренной трапеции мы вычисляем ее периметр по формуле:
Для равнобедренной трапеции мы вычисляем ее периметр по формуле:
P = a + b + 2 c
Важно помнить, что поскольку стороны равнобедренной трапеции равны по длине, вот почему мы считаем c чем-то, что мы можем просто удвоить при вычислении периметра.Попробуйте этот расчет, и у вас не должно возникнуть проблем с вычислением периметра равнобедренной трапеции.
Краткий обзор площади трапеций
До сих пор мы имели дело с вариациями одной и той же формулы площади A = bh . Мы изменили его на A = lw для прямоугольников и даже A = s 2 для квадратов, но по сути это одно и то же. Сколько раз можно умножить два числа вместе?
Пришло время сходить с ума.Нет, не супер причудливый, но много причудливого. Например, иметь две базы — не две головы — вместо одной.
Мы говорим не о чем ином, как о трапециях , которые очень легко найти. Пока только две из четырех ее сторон параллельны друг другу, мы получили трапецию. Они даже не обязательно должны быть одинаковой длины, что означает, что другие стороны могут делать все, что захотят, в значительной степени. Ничего похожего на параллелограммы или прямоугольники.
Пока только две из четырех ее сторон параллельны друг другу, мы получили трапецию. Они даже не обязательно должны быть одинаковой длины, что означает, что другие стороны могут делать все, что захотят, в значительной степени. Ничего похожего на параллелограммы или прямоугольники.
Мы говорили вам.Странно. На самом деле настолько причудливые, что мы должны называть их фриказоидами.
Все равно они выглядят по-разному. Даже если бы мы могли использовать одно уравнение для расчета площади для всех из них, с чего бы мы начали? Это как пытаться попасть из Небраски в страну Оз. (Возможно, это не лучший пример. Объезд через Канзас, и мы в золоте.)
Возьмем общую характеристику всех трапеций: параллельные стороны. Мы знаем, что две параллельные линии всегда будут находиться на одинаковом расстоянии друг от друга, поэтому назовем это расстояние высотой .Ради согласованности мы будем использовать h для высоты… снова.
Мы знаем, что две параллельные стороны не будут иметь одинаковую длину, потому что тогда у нас будет параллелограмм. Итак, мы назовем эти две стороны основаниями , b 1 и b 2 . (Иногда вы увидите B и b вместо b 1 и b 2 . Это просто разные способы различения двух оснований.) Наша формула площади для любой трапеции с высотой H и базы B 1 и B 2 :
Итак, мы назовем эти две стороны основаниями , b 1 и b 2 . (Иногда вы увидите B и b вместо b 1 и b 2 . Это просто разные способы различения двух оснований.) Наша формула площади для любой трапеции с высотой H и базы B 1 и B 2 :
A = ½ ( B 1 + B 2 ) h
К счастью, мы можем игнорировать шаткие стороны, которые не параллельны друг другу.
Пример задачи
Если основания трапеции имеют длину 4 и 5, а высоту 2, какова площадь трапеции?
Используя уравнение площади трапеции, все, что нам нужно сделать, это подставить длины оснований и высоту.
A = ½ ( B 1 + B 2 ) H
A = ½ (4 + 5) × 2
A = ½ × 9 × 2
A = 9 единиц 2
Пример задачи
Найдите высоту трапеции, имеющей площадь 7 единиц 2 и основание 7 единиц и длину 21 единицу.
Мы можем использовать ту же формулу площади для трапеции. На этот раз вместо вычисления A мы можем найти высоту h .Замените 21 единицу на b 1 , 7 единиц на b 2 и 7 единиц 2 на A . Вы знаете, что делать.
A = ½ ( B 1 + B 2 ) H
7 = ½ (21 + 7) H
7 = ½ × 28 × ч
0,5 = h
Высота трапеции 0,5 ед.
Какими бы причудливыми ни были трапеции, вы, наверное, уже знаете, что они бывают разных типов. Равнобедренные трапеции пытаются стать нормальными, делая две непараллельные стороны одинаковой длины. Прямоугольные трапеции имеют стороны, образующие прямые углы с обоими основаниями.
Знание этих специфических типов трапеций не меняет формулы расчета площади. Это по-прежнему A = ½( b 1 + b 2 ) h . С другой стороны, это может быть полезно, если у вас нет b 1 , b 2 и h , предоставленных вам напрямую.
С другой стороны, это может быть полезно, если у вас нет b 1 , b 2 и h , предоставленных вам напрямую.
Пример задачи
Каковы площадь и периметр этой трапеции?
Это прямоугольная трапеция, поэтому мы можем рассматривать ее как прямоугольник и прямоугольный треугольник, соединенные вместе. Гипотенуза треугольника равна 5, и мы можем найти один из катетов, вычитая малое основание из большого основания, что дает нам длину 3.
Мы знаем гипотенузу и один из катетов прямоугольного треугольника. . Можете ли вы сказать: «Теорема Пифагора»? Мы уверены, что можем.Просто заменяйте A с 3, B с H , и C , и C с 5
A 2 + B 2 = C 2
3 2 + h 2 = 5 2
h 2 = 16
h = 4 единицы
площадь должна быть легкой.
A = ½ ( B 1 + B 2 ) H
A = ½ (8 + 11) × 4
A = ½ × 19 × 4
А = 38 единиц 2
Ну это все хорошо, а как быть с периметром? Мы знаем, что периметр — это просто сложение всех сторон.Мы уже знаем три стороны (два основания и неперпендикулярную сторону). К счастью для нас, высота равна одной из сторон прямой трапеции.
P = p = b 1 + b 2 + h + s + p = 8 + 11 + 4 + 5
p = 28 единиц
Как Найдите площадь трапеции
Как найти площадь трапеции
Чтобы найти площадь трапеции:
- Добавьте длины двух параллельных сторон.
- Умножьте это на расстояние между параллельными сторонами.
- Разделите это на 2.
Например, найти площадь трапеции с параллельными сторонами 6 м и 10 м, расстояние между которыми 4 м.
- Складываем параллельные стороны: 6 + 10 = 16.
- Умножьте это на расстояние между ними: 16 × 4 = 64.
- Разделить на 2: 64 ÷ 2 = 32.
Итак, площадь равна 32 м 2 .
Кроме того, площадь трапеции можно найти по формуле Площадь = 1 / 2 (a+b)h, где a и b — параллельные стороны трапеции, а h — расстояние между ними.
a = 6 и b = 10, а h = 4.
Площадь = 1 / 2 (a+b)h становится площадью = 1 / 2 × (6 + 10) × 4.
Это становится Площадь = 1 / 2 × 16 × 4, что равно 32 м 2 .
Формула площади трапеции
Формула площади трапеции: Площадь = h / 2 (a+b), где a и b — длины двух параллельных сторон, а h — расстояние между ними. Например, если у трапеции параллельные стороны 5 м и 7 м, а расстояние между ними 4 м, то a = 5, b = 7 и h = 4. Формула площади принимает вид 4 / 2 (5+7) что равно 24 м 2 .
Формула площади принимает вид 4 / 2 (5+7) что равно 24 м 2 .
Неважно, какая из двух параллельных сторон помечена как a и b .
Формула площади трапеции также может быть записана как Площадь = (a+b) / 2 h.
Его также можно записать как Площадь = 1 / 2 h(a+b) или Площадь = 1 / 2 (a+b)h.
Все эти формулы являются просто перестановками одной и той же формулы и дадут один и тот же ответ.
Площадь прямоугольной трапеции
Чтобы найти площадь прямоугольной трапеции, используйте формулу Площадь = 1 / 2 h(a+b), где a и b — две параллельные стороны, а h — расстояние между ними.
Например, вычислите площадь следующей прямоугольной трапеции.
Две параллельные стороны равны 5 м и 9 м, поэтому a = 5 и b = 9. Неважно, какая сторона равна a, а какая — b.
Расстояние между параллельными сторонами равно 2 м, значит, h = 2.
Чтобы найти площадь, подставьте значения h = 2, a = 5 и b = 9 в Area = 1 / 2 h(a+b).
Площадь = 1 / 2 h(a+b) становится Площадь = 1 / 2 × 2 × (5 + 9)
Это становится площадью = 1 / 2 × 2 × 14, что равно 14 м 2 .
Площадь равнобедренной трапеции
У равнобедренной трапеции диагональные стороны имеют одинаковую длину.Эти длины диагональных сторон не влияют на площадь. Чтобы найти площадь равнобедренной трапеции, используйте формулу Площадь = 1 / 2 h(a+b), где a и b — длины двух параллельных сторон, а h — расстояние между ними.
Вот, например, равнобедренная трапеция. Его диагональные стороны имеют одинаковый размер, и он симметричен относительно своей середины.
Длины двух параллельных сторон равны 4 м и 8 м. Таким образом, a = 4 и b = 8. Неважно, какая сторона равна a, а какая b из этих двух значений.
Таким образом, a = 4 и b = 8. Неважно, какая сторона равна a, а какая b из этих двух значений.
Расстояние между параллельными сторонами равно 3 м. Итак, ч = 3.
Подставим значения h = 3, a = 4 и b = 8 в формулу Площадь = 1 / 2 h(a+b).
Получается Площадь = 1 / 2 × 3 × (4 + 8), которая становится Площадью = 1 / 2 × 3 × 12.
12 легче разделить пополам, чем 3, поэтому мы разделим 12 пополам, чтобы получить 6.
Площадь = 3 × 6, что равно 18 см 2 .
Площадь измеряется в см 2 , потому что стороны трапеции измеряются в см.
Площадь неправильной трапеции
Площадь неправильной трапеции находится обычным способом, используя площадь = 1 / 2 h(a+b). a и b — две параллельные стороны, h — расстояние между ними. Неважно, какой длины диагональные стороны неправильной трапеции, поскольку они не влияют на площадь.
Например, найдите площадь неправильной трапеции, изображенной на рисунке.
Две параллельные стороны равны 6 м и 10 м. Таким образом, a = 6 и b = 10. Неважно, какие стороны равны a и b, лишь бы они были параллельны.
Расстояние между параллельными сторонами равно 4 м, значит, h = 4.
Площадь неправильной трапеции находится по формуле Площадь = 1 / 2 h(a+b).
Подставляя в h = 4, a = 6 и b = 10, получаем Площадь = 1 / 2 × 4 × (6 + 10).
Это становится Площадь = 1 / 2 × 4 × 16.Половина от 16 равна 8, а 8 × 4 = 32. Площадь равна 32 м 2 .
Площадь трапеции без высоты
Если высота трапеции не указана, ее необходимо вычислить по теореме Пифагора. Для этого представьте себе прямоугольный треугольник, образованный на одной стороне трапеции, где диагональной стороной является гипотенуза. Возведите гипотенузу в квадрат, вычтите основание треугольника в квадрате, а затем извлеките из него корень, чтобы найти высоту трапеции. Затем площадь можно найти, используя A = 1 / 2 h(a+b).
Затем площадь можно найти, используя A = 1 / 2 h(a+b).
Вот пример вычисления площади трапеции без знания высоты.
Первый шаг — создать прямоугольный треугольник на одной стороне трапеции. Гипотенуза треугольника — диагональная сторона трапеции, в данном случае она равна 5 м.
Затем найдите основание треугольника, которое представляет собой разницу между длинами верхней и нижней сторон трапеции. 7 – 3 = 4, значит, основание треугольника равно 4 м.
Следующим шагом является использование теоремы Пифагора для определения высоты треугольника.2}$$, где h — высота, c — диагональная сторона треугольника, а b — основание треугольника.
5 2 – 4 2 = 9 и тогда квадратный корень из 9 равен 3. Высота равна 3.
Теперь площадь трапеции можно найти, используя Площадь = 1 / 2 h(a+b).
h — высота трапеции, b — основание трапеции и a — верхняя сторона трапеции.
Площадь = 1 / 2 × 3 × (3 + 7) = 15 2 .
Доказательство площади трапеции по формуле
Трапецию высотой «h» и длинами параллельных сторон «a» и «b» можно составить из треугольника и прямоугольника вместе взятых. Площадь прямоугольника равна ah, а площадь треугольника равна 1 / 2 h(b-a). Сложение площадей треугольника и прямоугольника доказывает формулу площади трапеции: Площадь = 1 / 2 h(a+b).
Доказательство площади трапеции показано ниже.
Трапеция имеет высоту «h», основание «b» и длину вершины «a». Его можно разделить на две отдельные формы, прямоугольник и треугольник.
Площадь прямоугольника равна длине × ширине, то есть a × h или ah. Мы называем это Область 1, A 1 .
Площадь треугольника равна 1 / 2 × основание × высота. Длина основания треугольника равна большей стороне трапеции, за вычетом меньшей стороны b-a. Площадь треугольника A 2 = 1 / 2 h(b-a).
Площадь треугольника A 2 = 1 / 2 h(b-a).
Прибавляем площадь прямоугольника к площади треугольника, чтобы найти площадь трапеции.
Площадь = А 1 + А 2 .
Площадь = ah + 1 / 2 h(b-a).
Разлагая второе слагаемое, получаем:
Площадь = ah + 1 / 2 bh – 1 / 2 ah.
Вычитая из ah 1 / 2 ah, получаем:
Площадь = 1 / 2 а.ч. + 1 / 2 н.ч.
Разложив на множители 1 / 2 и h, мы получим конечную площадь трапеции:
Площадь = 1 / 2 h(a + b).
Вот альтернативное доказательство площади трапеции, в котором мы складываем две трапеции вместе, чтобы сформировать прямоугольник.
Две одинаковые трапеции с высотой «h», основанием «b» и верхней стороной «a» можно сложить вместе, чтобы получился прямоугольник. Этот прямоугольник имеет высоту «h» и длину основания «a+b». Площадь прямоугольника равна основанию × высоте, то есть h × (a+b).Площадь каждой отдельной трапеции составляет половину этой площади, то есть 90 125 1 90 126 / 90 153 2 90 154 h(a+b).
Этот прямоугольник имеет высоту «h» и длину основания «a+b». Площадь прямоугольника равна основанию × высоте, то есть h × (a+b).Площадь каждой отдельной трапеции составляет половину этой площади, то есть 90 125 1 90 126 / 90 153 2 90 154 h(a+b).
Площадь прямоугольника равна основанию × высоте. Мы видим, что высота прямоугольника равна высоте каждой трапеции, а основание прямоугольника состоит из основания трапеции и верхней стороны трапеции вместе взятых. Основание прямоугольника равно a+b.
Площадь прямоугольника равна h(a+b), однако каждая трапеция составляет половину общей площади прямоугольника, потому что их две.Разделим площадь прямоугольника пополам, чтобы получить площадь трапеции.
Площадь = 1 / 2 h(a+b).
ПЛОЩАДЬ РАСПОЛОЖЕННОЙ ТРАПЕЦИИ
- равнобедренная трапеция
- Равнобедренная трапеция (isosceles trapezium в британском английском) — это четырехугольник, линия симметрии которого делит пополам одну пару противоположных сторон, что автоматически делает его трапецией.
 Некоторые источники квалифицировали бы все это за исключением: «исключая прямоугольники.
Некоторые источники квалифицировали бы все это за исключением: «исключая прямоугольники. - трапеция с парой равноугольных углов при основании
- любой четырехугольник, у которого хотя бы одна ось симметрии проходит через пару противоположных сторон.Свойства: 1) Две различные пары смежных углов равны. 2) По крайней мере одна пара противоположных сторон конгруэнтна. 3) Диагонали равны. 4) Диагонали делят друг друга на равные части.
- зона
- ПОГОДА «Говорит капитан. Из-за плохой погоды над Нью-Джерси мы повернем на юг в сторону Филадельфии…»
Комплект заданий для учителя геометрии: готовые к использованию уроки и рабочие листы для 6–12 классов (J-B Ed: Makings)
Для всех учителей математики в 6–12 классах этот практический ресурс содержит 130 подробных уроков с воспроизводимыми рабочими листами, которые помогут учащимся понять концепции геометрии, а также распознать и интерпретировать связь геометрии с реальным миром. Уроки и рабочие листы организованы в семь разделов, каждый из которых охватывает одну основную область геометрии и представлен в удобном для понимания формате, включая заголовок, посвященный конкретной теме/навыку, цель обучения, специальные материалы (если таковые имеются), учебные заметки с пошаговые инструкции, ключи к ответам и воспроизводимые листы заданий для учащихся. Задания в разделах 1-6 представлены в порядке сложности в каждом разделе, в то время как задания в Части 7, «Попурри по геометрии», являются открытыми и могут использоваться в большинстве классов средней и старшей школы.В соответствии с рекомендациями NCTM многие задания в книге можно использовать с калькуляторами и компьютерами. Симметрия
Уроки и рабочие листы организованы в семь разделов, каждый из которых охватывает одну основную область геометрии и представлен в удобном для понимания формате, включая заголовок, посвященный конкретной теме/навыку, цель обучения, специальные материалы (если таковые имеются), учебные заметки с пошаговые инструкции, ключи к ответам и воспроизводимые листы заданий для учащихся. Задания в разделах 1-6 представлены в порядке сложности в каждом разделе, в то время как задания в Части 7, «Попурри по геометрии», являются открытыми и могут использоваться в большинстве классов средней и старшей школы.В соответствии с рекомендациями NCTM многие задания в книге можно использовать с калькуляторами и компьютерами. Симметрия это создает иллюзию. В 1D есть точка симметрии. В 2D есть ось симметрии, в 3D — плоскость симметрии. Объект или фигура, неотличимые от своего преобразованного изображения, называются зеркально-симметричными.
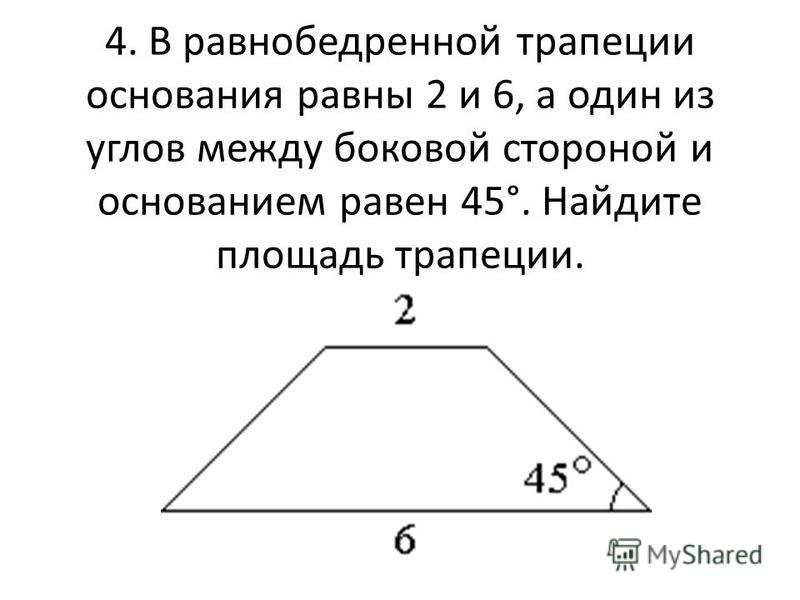 Средняя линия параллельна основаниям трапеции и равна их полусумме.
Средняя линия параллельна основаниям трапеции и равна их полусумме.
 Некоторые источники квалифицировали бы все это за исключением: «исключая прямоугольники.
Некоторые источники квалифицировали бы все это за исключением: «исключая прямоугольники.