Высота и угол «α» равнобедренного треугольника
Высота равнобедренного треугольника, которая лежит под прямым углом к основанию, создает внутри еще два одинаковых прямоугольных треугольника, являясь катетом в каждом из них. Второй катет такого треугольника представляет собой половину основания, так как эта высота является одновременно медианой и биссектрисой, а гипотенузой будет боковая сторона равнобедренного треугольника. Соответственно, зная высоту и угол α при основании, через прямоугольный треугольник можно узнать стороны равнобедренного треугольника. (рис.88.2) a=h/sinα b=2h/tanα
Поскольку сумма всех углов в треугольнике равна 180 градусам, следовательно, угол при вершине будет равен разности 180 градусов и двух углов при основании. β=180°-2α
Периметр равнобедренного треугольника через высоту и угол α равен сумме двух отношений высоты к синусу угла и двух отношений высоты к тангенсу. Площадь, в свою очередь, преобразовывается в квадрат высоты, деленный на тангенс.
Чтобы вычислить среднюю линию, необходимо разделить на два ту сторону треугольника, которая ей параллельна. Поскольку ни одна из сторон не известна, то средняя линия, параллельная основанию, равна высоте, деленной на тангенс угла α, а средняя линия, параллельная боковой стороне равна высоте, деленной на два синуса угла α. (рис.88.5) M_b=b/2=h/tanα M_a=a/2=h/(2 sinα )
Чтобы вычислить радиус вписанной в равнобедренный треугольник окружности, нужно подставить вместо сторон a и b в формулу отношения высоты и тангенса или синуса соответственно, а затем упростить выражение (рис.88.6) r=b/2 √((a-2b)/(a+2b))=h/tanα √((h/sinα -2 2h/tanα )/(h/sinα +2 2h/tanα ))=h/tanα √((1-4 cosα)/(1+4 cosα ))
Радиус окружности, описанной вокруг равнобедренного треугольника также зависит от обеих сторон – основания и боковой стороны, поэтому его формула видоизменяется аналогично радиусу вписанной окружности.
Высота равнобедренного треугольника
Примечание. Это часть урока с задачами по геометрии (раздел равнобедренный треугольник). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Задача
В равнобедренном треугольнике ABC боковые стороны AB, и AC равны 13а. Тангенс угла B равен 3/4. Найдите высоту AK, проведенную к основанию BC этого равнобедренного треугольника.
Поскольку мы знаем тангенс угла B, то стороны прямоугольного треугольника AKB соотносятся как
AK/KB = tg B = 3/4
Обозначим коэффициент пропорциональности этих сторон как х.
Тогда по теореме Пифагора для данного треугольника будет справедливо выражение:
(3x)2 + (4x)2 = (13a)2
9x2 + 16x2
= 169a2
25x2
= 169a2
x2
= 169/25a2
x = 13/5a
Откуда
AK = 3x = 13/5a*3= 7,8a
Ответ: 7,8a и
10,4a
Как найти площадь треугольника — Лайфхакер
Как найти площадь любого треугольника
Посчитать площадь треугольника можно разными способами.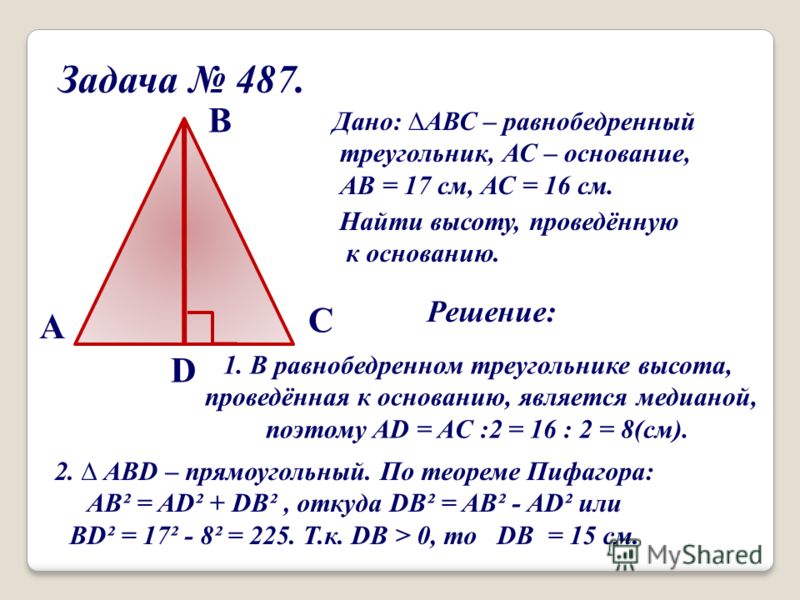 Выбирайте формулу в зависимости от известных вам величин.
Выбирайте формулу в зависимости от известных вам величин.
Зная сторону и высоту
- Умножьте сторону треугольника на высоту, проведённую к этой стороне.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — сторона треугольника.
- h — высота треугольника. Это перпендикуляр, опущенный на сторону или её продолжение из противоположной вершины.
Зная две стороны и угол между ними
- Посчитайте произведение двух известных сторон треугольника.
- Найдите синус угла между выбранными сторонами.
- Перемножьте полученные числа.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a и b — стороны треугольника.
- α — угол между сторонами a и b.
Сейчас читают 🔥
Зная три стороны (формула Герона)
- Посчитайте разности полупериметра треугольника и каждой из его сторон.

- Найдите произведение полученных чисел.
- Умножьте результат на полупериметр.
- Найдите корень из полученного числа.
- S — искомая площадь треугольника.
- a, b, c — стороны треугольника.
- p — полупериметр (равен половине от суммы всех сторон треугольника).
Зная три стороны и радиус описанной окружности
- Найдите произведение всех сторон треугольника.
- Поделите результат на четыре радиуса окружности, описанной вокруг прямоугольника.
- S — искомая площадь треугольника.
- R — радиус описанной окружности.
- a, b, c — стороны треугольника.
Зная радиус вписанной окружности и полупериметр
Умножьте радиус окружности, вписанной в треугольник, на полупериметр.
- S — искомая площадь треугольника.
- r — радиус вписанной окружности.
- p — полупериметр треугольника (равен половине от суммы всех сторон).
Как найти площадь прямоугольного треугольника
- Посчитайте произведение катетов треугольника.

- Поделите результат на два.
- S — искомая площадь треугольника.
- a, b — катеты треугольника, то есть стороны, которые пересекаются под прямым углом.
Как найти площадь равнобедренного треугольника
- Умножьте основание на высоту треугольника.
- Поделите результат на два.
- S — искомая площадь треугольника.
- a — основание треугольника. Это та сторона, которая не равняется двум другим. Напомним, в равнобедренном треугольнике две из трёх сторон имеют одинаковую длину.
- h — высота треугольника. Это перпендикуляр, опущенный на основание из противоположной вершины.
Как найти площадь равностороннего треугольника
- Умножьте квадрат стороны треугольника на корень из трёх.
- Поделите результат на четыре.
- S — искомая площадь треугольника.
- a — сторона треугольника. Напомним, в равностороннем треугольнике все стороны имеют одинаковую длину.

Читайте также 🧠👨🏻🎓✍🏻
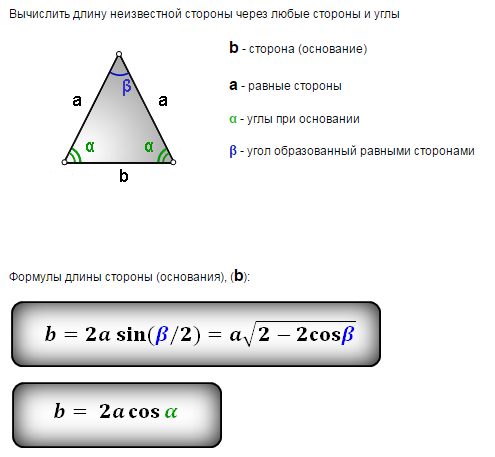
Формула основания равнобедренного треугольника через стороны. Как найти площадь фигуры, если один угол прямой? Обозначения величин, принятые в рассматриваемых формулах
Буквенные обозначения сторон и углов на приведенном рисунке соответствуют обозначениям, которые указаны в формулах. Таким образом, это поможет Вам сопоставить их с элементами равнобедренного треугольника. Из условия задачи определите, какие элементы известны, найдите на чертеже их обозначения и подберите подходящую формулу.
Формула площади равнобедренного треугольника
Далее приведены формулы нахождения площади равнобедренного треугольника : через стороны, боковую сторону и угол между ними, через боковую сторону, основание и угол при вершине, через сторону основания и угол при основании и т.д. Просто найдите наиболее подходящую на рисунке слева. Для самых любопытных в тексте справа поясняется, почему формула явяляется правильной и как именно с ее помощью находится площадь.
- можно найти, зная его сторону и основание . Данное выражение было получено путем упрощения более общей, универсальной формулы. Если за основу взять формулу Герона, а затем принять во внимание, что две стороны треугольника равны меду собой, то выражение упрощается до формулы, представленной на картинке.
Пример использования такой формулы приведен на примере решения задачи ниже. - Вторая формула позволяет найти его площадь через боковые стороны и угол между ними — это половина квадрата боковой стороны, умноженная на синус угла между боковыми сторонами
Если мысленно опустить высоту на боковую сторону равнобедренного треугольника, заметим, что ее длина будет равна a * sin β. Поскольку длина боковой стороны нам известна, высота, опущенная на нее теперь известна, половина их произведения и будет равна площади данного равнобедренного треугольника (Пояснение: полное произведение дает площадь прямоугольника, что очевидно. Высота делит этот прямоугольник на два малых прямоугольника, при этом стороны треугольника являются их диагоналями, которые делят их ровно пополам. Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5
Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 - Третья формула показывает нахождение площади через боковую сторону, основание и угол при вершине .
Строго говоря, зная один из углов равнобедренного треугольника, можно найти и остальные, поэтому применение данной или предыдущей формулы — вопрос вкуса (кстати, поэтому можно запомнить только одну из них).
У третьей формулы также есть еще одна интересная особенность — произведение a sin α - Площадь равнобедренного треугольника можно также найти через сторону основания и угол при основании (углы при основании равны) как квадрат основания, деленный на четыре тангенса половины угла, образованного его боковыми сторонами. Если присмотреться внимательнее, то станет очевидно, что половина основания (b/2) умноженная на tg(β/2) даст нам высоту треугольника.
 Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2)). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2)). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна. - Разумеется, площадь равнобедренного треугольника можно найти, опустив высоту из вершины на основание, в результате чего получится два прямоугольных треугольника. Далее — все очевидно. Половина произведения высоты на основание и есть искомая площадь. Пример использования данной формуле см. в задаче ниже (2-й способ решения)
- Эта формула получается, если попытаться найти площадь равнобедренного треугольника с помощью теоремы Пифагора . Для этого выразим высоту из предыдущей формулы, которая одновременно, является катетом прямоугольного треугольника, образованного боковой стороной, половиной его основания и высотой, через теорему Пифагора. Боковая сторона является гипотенузой, поэтому из квадрата боковой стороны (а) вычтем квадрат второго катета.
 Поскольку он равен половине основания (b/2) то его квадрат будет равен b 2 /4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Поскольку он равен половине основания (b/2) то его квадрат будет равен b 2 /4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Обозначения , которые были применены в формулах на рисунке:
a — длина одной из двух равных сторон треугольника
b — длина основания
α — величина одного из двух равных углов при основании
β — величина угла между равными сторонами треугольника и противолежащего его основанию
h — длина высоты, опущенная из вершины равнобедренного треугольника на основание
Важно .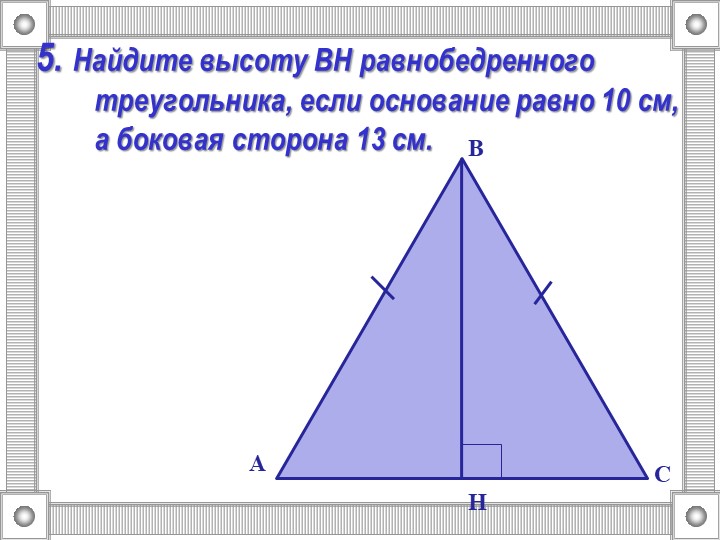 Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b !
Обратите внимание на обозначения переменных! Не перепутайте α и β, а также a и b !
Примечание . Это часть урока с задачами по геометрии (раздел площадь равнобедренного треугольника). Здесь размещены задачи, которые вызывают трудности при решении. Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение .
Задача
Боковая сторона равнобедренного треугольника равна 13 см, а основание равно 10 см. Найдите площадь равнобедренного треугольника.Решение .
1-й способ . Применим формулу Герона. Поскольку треугольник равнобедренный, то она примет более простой вид (см. формулу 1 в списке формул выше):
где а — длина боковых сторон, а b — длина основания.
Подставив значения длин сторон треугольника из условия задачи, получим:
S = 1/2 * 10 * √ ((13 + 5)(13 — 5)) = 5 √ (18 * 8) = 60 см 2
2-й способ
. Применим теорему Пифагора
Применим теорему Пифагора
Предположим, что мы не помним формулу, использованную в первом способе решения. Поэтому опустим из вершины B на основание AC высоту BK.
Поскольку высота равнобедренного треугольника делит его основание пополам, то длина половины основания будет равна
AK = AC / 2 = 10 / 2 = 5 см.
Высота с половиной основания и стороной равнобедренного треугольника образует прямоугольный треугольник ABK. В этом треугольнике нам известна гипотенуза AB и катет AK. Выразим длину второго катета через теорему Пифагора.
Математика — это удивительная наука. Однако такая мысль приходит только тогда, когда ее понимаешь. Чтобы этого достичь, нужно решать задачи и примеры, чертить схемы и рисунки, доказывать теоремы.
Путь к пониманию геометрии лежит через решение задач. Отличным примером могут служить задания, в которых нужно найти площадь равнобедренного треугольника.
Что такое равнобедренный треугольник, и в чем его отличие от других?
Чтобы не пугаться терминов «высота», «площадь», «основания», «равнобедренного треугольника» и прочих, потребуется начать с теоретических основ.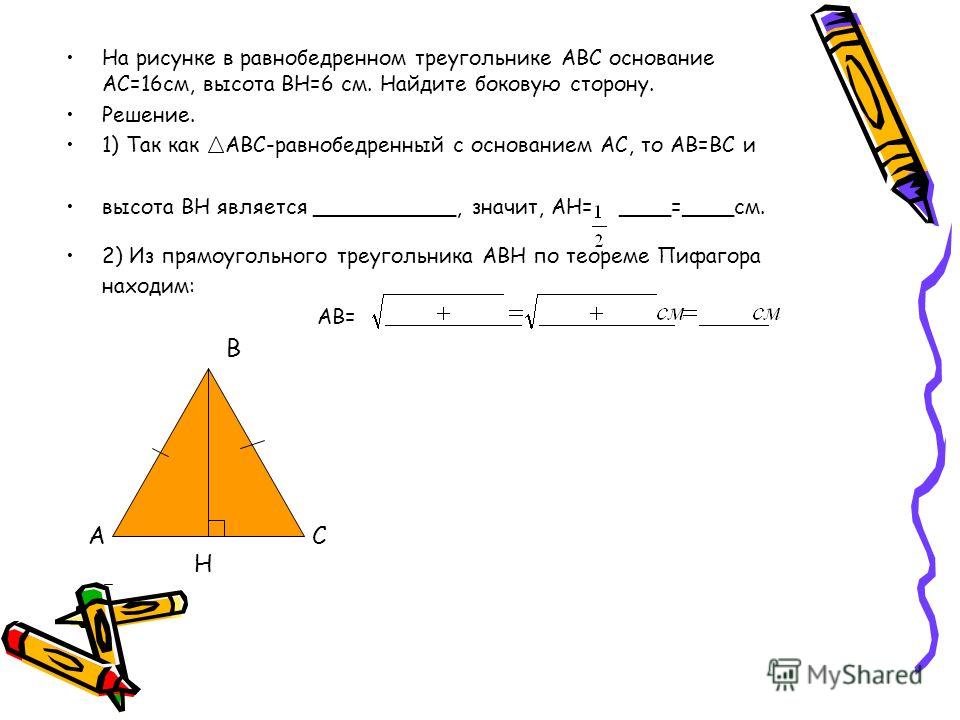
Сначала о треугольнике. Это плоская фигура, которая образована из трех точек — вершин, в свою очередь, соединенных отрезками. Если два из них оказываются равны друг другу, то треугольник становится равнобедренным. Эти стороны получили название боковых, а оставшаяся стала основанием.
Существует частный случай равнобедренного треугольника — равносторонний, когда и третья сторона равна двум боковым.
Свойства фигуры
Они оказываются верными помощниками в решении задач, которые требуют найти площадь равнобедренного треугольника. Поэтому знать и помнить о них необходимо.
- Первое из них: углы равнобедренного треугольника, одна сторона которых — основание, всегда равны друг другу.
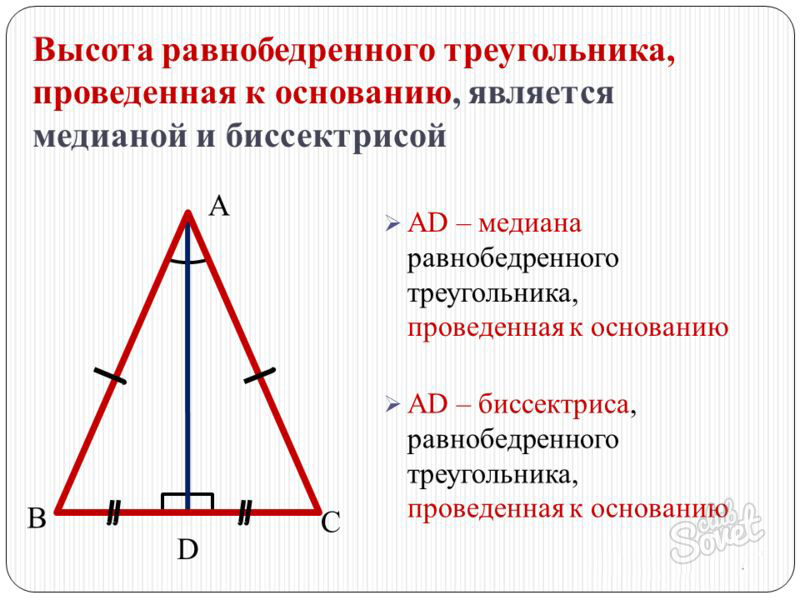
- Важным является и свойство о дополнительных построениях. Проведенные к непарной стороне высота, медиана и биссектриса совпадают.
- Эти же отрезки, проведенные из углов при основании треугольника, попарно равны. Это тоже часто облегчает поиск решения.
- Два равных угла в нем всегда имеют значение меньше чем 90º.

- И последнее: вписанная и описанная окружности строятся так, что их центры лежат на высоте к основанию треугольника, а значит медиане и биссектрисе.
Как в задаче распознать равнобедренный треугольник?
Если при решении задания встает вопрос о том, как найти площадь равнобедренного треугольника, то сначала нужно понять, что он относится к этой группе. А в этом помогут определенные признаки.
- Равны два угла или две стороны треугольника.
- Биссектриса является еще и медианой.
- Высота треугольника оказывается медианой или биссектрисой.
- Равны две высоты, медианы или биссектрисы фигуры.
Обозначения величин, принятые в рассматриваемых формулах
Для упрощения того, как находить площадь равнобедренного треугольника по формулам, введена замена его элементов на буквы.
Внимание! Важно не путать «а» с «А» и «в» с «В». Это разные величины.
Формулы, которыми можно воспользоваться в разных задачах
Известны длины сторон, и требуется найти площадь равнобедренного треугольника.
В этом случае нужно возвести в квадрат оба значения. То число, которое получилось от изменения боковой стороны, умножить на 4 и вычесть из него второе. Из полученной разности извлечь квадратный корень. Длину основания разделить на 4. Два числа перемножить. Если записать эти действия буквами, то получится такая формула:
Пусть она будет записана под №1.
Найти по значениям сторон площадь равнобедренного треугольника. Формула, которая кому-то может показаться проще, чем первая.
Первым действием нужно найти половину основания. Потом найти сумму и разность этого числа с боковой стороной. Два последних значения перемножить и извлечь квадратный корень. Последним действием умножить все на половину основания. Буквенное равенство будет выглядеть так:
Это формула №2.
Способ найти площадь равнобедренного треугольника, если известны основание и высота к нему.
Одна из самых коротких формул. В ней нужно перемножить обе данные величины и разделить их на 2. Вот как она будет записана:
Вот как она будет записана:
Номер этой формулы — 3.
В задании известны стороны треугольника и значение угла, лежащего между основанием и боковой стороной.
Здесь, для того чтобы узнать, чему будет равна площадь равнобедренного треугольника, формула будет состоять из нескольких множителей. Первый из них — это значение синуса угла. Второй равен произведению боковой стороны на основание. Третий — дробь ½. Общая математическая запись:
Порядковый номер формулы — 4.
В задаче даны: боковая сторона равнобедренного треугольника и угол, лежащий между его боковыми сторонами.
Как и в предыдущем случае, площадь находится по трем множителям. Первый равен значению синуса угла, указанного в условии. Второй — это квадрат стороны. И последний также равен половине единицы. В итоге формула запишется так:
Ее номер — 5.
Формула, которая позволяет найти площадь равнобедренного треугольника, если известны его основание и угол, лежащий напротив него.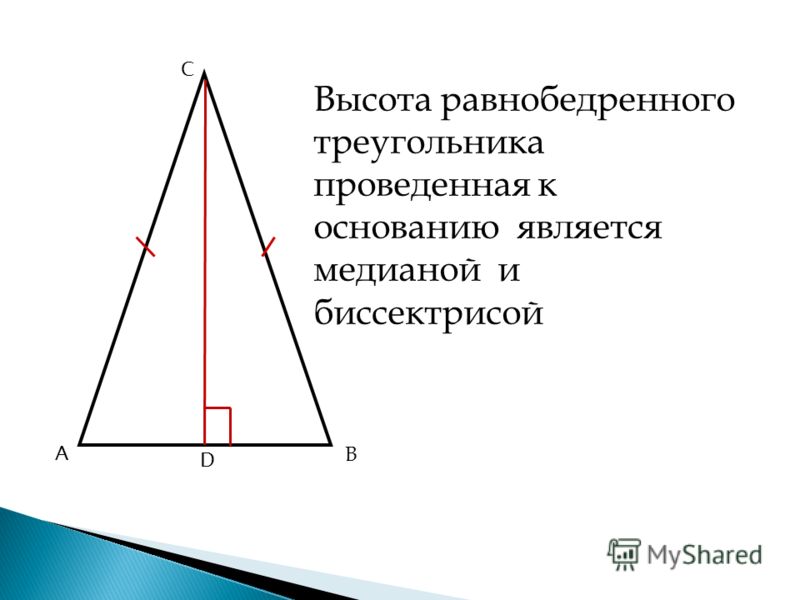
Сначала нужно вычислить тангенс половины известного угла. Полученное число умножить на 4. Возвести в квадрат длину боковой стороны, которое потом разделить на предыдущее значение. Таким образом, получится такая формула:
Номер последней формулы — 6.
Примеры задач
Первая задача: известно, что основание равнобедренного треугольника равно 10 см, а его высота — 5 см. Нужно определить его площадь.
Для ее решения логично выбрать формулу под номером 3. В ней все известно. Подставить числа и сосчитать. Получится, что площадь равна 10 * 5 / 2. То есть 25 см 2 .
Вторая задача: в равнобедренном треугольнике даны боковая сторона и основание, которые равны соответственно 5 и 8 см. Найти его площадь.
Первый способ. По формуле №1. При возведении в квадрат основания получается число 64, а учетверенный квадрат боковой стороны — 100. После вычитания из второго первого получится 36. Из него прекрасно извлекается корень, который равен 6. Основание, поделенное на 4, равно 2. Итоговое значение определится как произведение 2 и 6, то есть 12. Это ответ: искомая площадь равна 12 см 2 .
Итоговое значение определится как произведение 2 и 6, то есть 12. Это ответ: искомая площадь равна 12 см 2 .
Второй способ. По формуле №2. Половина основания равна 4. Сумма боковой стороны и найденного числа дает 9, их же разность — 1. После умножения получается 9. Извлечение квадратного корня дает 3. И последнее действие, умножение 3 на 4, что дает те же 12 см 2 .
Решая задачи по геометрии и определяя, как найти площадь равнобедренного треугольника, можно получить неоценимый опыт. Чем больше различных вариантов заданий выполнено, тем проще найти ответ в новой ситуации. Поэтому регулярное и самостоятельное выполнение всех заданий — это путь к успешному усвоению материала.
Выясните, как найти площадь параллелограмма. Квадраты и прямоугольники являются параллелограммами, как и любая другая четырехсторонняя фигура, у которой противоположные стороны параллельны. Площадь параллелограмма вычисляется по формуле: S = bh , где «b» – основание (нижняя сторона параллелограмма), «h» – высота (расстояние от верхней до нижней стороны; высота всегда пересекает основание под углом 90°).
- В квадратах и прямоугольниках высота равна боковой стороне, так как боковые стороны пересекают верхнюю и нижнюю стороны под прямым углом.
Сравните треугольники и параллелограммы. Между этими фигурами существует простая связь. Если любой параллелограмм разрезать по диагонали, получатся два равных треугольника. Аналогично, если сложить два равных треугольника, получится параллелограмм. Поэтому площадь любого треугольника вычисляется по формуле: S = ½bh , что составляет половину площади параллелограмма.
Найдите основание равнобедренного треугольника. Теперь вы знаете формулу для вычисления площади треугольника; осталось выяснить, что такое «основание» и «высота». Основание (обозначается как «b») – это сторона, которая не равна двум другим (равным) сторонам.
Опустите перпендикуляр на основание. Сделайте это из вершины треугольника, которая противоположна основанию. Помните, что перпендикуляр пересекает основание под прямым углом. Такой перпендикуляр является высотой треугольника (обозначается как «h»). Как только вы найдете значение «h», вы сможете вычислить площадь треугольника.
Такой перпендикуляр является высотой треугольника (обозначается как «h»). Как только вы найдете значение «h», вы сможете вычислить площадь треугольника.
- В равнобедренном треугольнике высота пересекает основание точно посередине.
Посмотрите на половину равнобедренного треугольника. Обратите внимание, что высота разделила равнобедренный треугольник на два равных прямоугольных треугольника. Посмотрите на один из них и найдите его стороны:
- Короткая сторона равна половине основания: b 2 {\displaystyle {\frac {b}{2}}} .
- Вторая сторона – это высота «h».
- Гипотенуза прямоугольного треугольника является боковой стороной равнобедренного треугольника; обозначим ее как «s».
Воспользуйтесь теоремой Пифагора . Если известны две стороны прямоугольного треугольника, его третью сторону можно вычислить по теореме Пифагора: (сторона 1) 2 + (сторона 2) 2 = (гипотенуза) 2 . В нашем примере теорема Пифагора запишется так: . {2})}
{2})}
h = (25 − 9) {\displaystyle h={\sqrt {(}}25-9)}
h = (16) {\displaystyle h={\sqrt {(}}16)}
h = 4 {\displaystyle h=4} см.
Подставьте значения основания и высоты в формулу для вычисления площади треугольника. Формула: S = ½bh; подставьте в нее значения «b» и «h» и вычислите площадь. В ответе не забудьте написать квадратные единицы измерения.
- В нашем примере основание равно 6 см, а высота равна 4 см.
- S = ½bh
S = ½(6 см)(4 см)
S = 12 см 2 .
Рассмотрим более сложный пример. В большинстве случаев вам будет дана более трудная задача, чем рассмотренная в нашем примере. Чтобы вычислить высоту, нужно извлечь квадратный корень, который, как правило, не извлекается нацело. В этом случае запишите значение высоты в виде упрощенного квадратного корня . Вот новый пример:
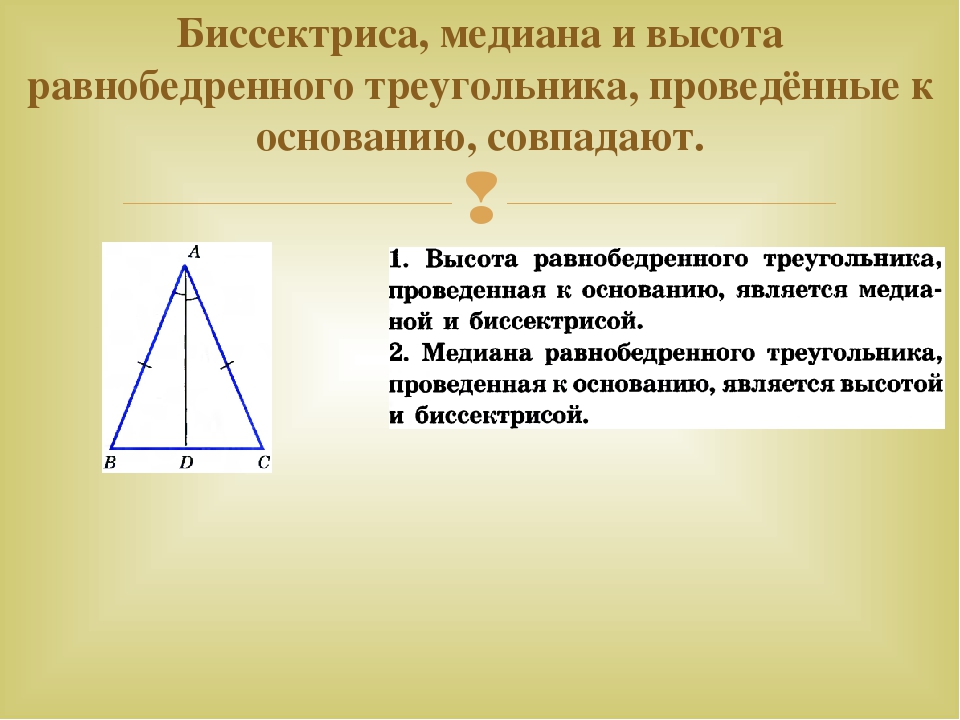
- Вычислите площадь равнобедренного треугольника, стороны которого равны 8 см, 8 см, 4 см.
- В качестве основания «b» выберите сторону, которая равна 4 см.
 {2}}}}
{2}}}}
= 64 − 4 {\displaystyle ={\sqrt {64-4}}}
= 60 {\displaystyle ={\sqrt {60}}} - Упростите квадратный корень с помощью множителей: h = 60 = 4 ∗ 15 = 4 15 = 2 15 . {\displaystyle h={\sqrt {60}}={\sqrt {4*15}}={\sqrt {4}}{\sqrt {15}}=2{\sqrt {15}}.}
- S = 1 2 b h {\displaystyle ={\frac {1}{2}}bh}
= 1 2 (4) (2 15) {\displaystyle ={\frac {1}{2}}(4)(2{\sqrt {15}})}
= 4 15 {\displaystyle =4{\sqrt {15}}} - Ответ можно записать с корнем или извлечь корень на калькуляторе и записать ответ в виде десятичной дроби (S ≈ 15,49 см 2).
Встаёт не только перед школьниками или студентами, но и в реальной, практической жизни. Например, во время строительства возникает необходимость отделки фасадной части, находящейся под крышей. Как вычислить количество нужного материала?
Часто с подобными задачами сталкиваются мастера, которые работают с тканью или кожей. Ведь многие детали, которые предстоит выкроить мастеру, имеют как раз форму равнобедренного треугольника.
Итак, существует несколько способов, помогающих найти площадь равнобедренного треугольника. Первый — вычисление её по основанию и высоте.
Для решения нам необходимо построить для наглядности треугольник MNP с основанием MN и высотой PO. Теперь кое-что достроим в чертеже: из точки P провести линию, параллельную основанию, а из точки M — линию, параллельную высоте. Точку пересечения назовём Q. Чтобы узнать, как найти площадь равнобедренного треугольника, нужно рассмотреть полученный четырёхугольник MOPQ, в котором боковая сторона данного нам треугольника MP является уже его диагональю.
Докажем сначала, что это прямоугольник. Так как мы строили его сами, то знаем, что стороны MO и OQ параллельны. И стороны QM и OP тоже параллельны. Угол POM прямой, значит и угол OPQ тоже прямой. Следовательно, получившийся чётырёхугольник является прямоугольником. Найти его площадь не составит труда, она равна произведению PO на OM. OM — это половина основания данного треугольника MPN. Отсюда вытекает, что площадь построенного нами прямоугольника равна полупроизведению высоты прямоугольного треугольника на его основание.
Отсюда вытекает, что площадь построенного нами прямоугольника равна полупроизведению высоты прямоугольного треугольника на его основание.
Вторым этапом поставленной перед нами задачи, как определить площадь треугольника, является доказательство того факта, что полученный нами прямоугольник по площади соответствует данному равнобедренному треугольнику, то есть, что площадь треугольника также равна полупроизведению основания и высоты.
Сравним для начала треугольник PON и PMQ. Они оба прямоугольны, так как прямой угол в одном из них образован высотой, а прямой угол в другом является углом прямоугольника. Гипотенузы в них являются сторонами равнобедренного треугольника, следовательно, также равны. Катеты PO и QM также равны как параллельные стороны прямоугольника. Значит, и площадь треугольника PON , и треугольника PMQ равны между собой.
Площадь прямоугольника QPOM равна площадям треугольников PQM и MOP в сумме. Заменив надстроенный треугольник QPM треугольником PON, получаем в сумме данный нам для вывода теоремы треугольник. Теперь мы знаем, как найти площадь равнобедренного треугольника по основанию и высоте — вычислить их полупроизведение.
Теперь мы знаем, как найти площадь равнобедренного треугольника по основанию и высоте — вычислить их полупроизведение.
Но можно узнать, как найти площадь равнобедренного треугольника по основанию и боковой стороне. Здесь также существует два варианта: теорема Герона и Пифагора. Рассмотрим решение с применением теоремы Пифагора. Для примера возьмём тот же PMN с высотой PO.
В прямоугольном треугольнике POM MP — гипотенуза. Её квадрат равен сумме квадратов PO и OM. А так как OM — половина основания, которое нам известно, то мы легко может найти OM и возвести число в квадрат. Произведя вычитание из квадрата гипотенузы полученное число, узнаем, чему равен квадрат другого катета, который в равнобедренном треугольнике является высотой. Найдя из разности и узнав высоту прямоугольного треугольника, можно дать ответ на поставленное перед нами задание.
Нужно просто перемножить высоту на основание и полученный результат разделить напополам. Почему именно так следует поступать, мы объяснили в первом варианте доказательства.
Бывает, что нужно произвести вычисления по боковой стороне и углу. Тогда находим высоту и основание, используя формулу с синусами и косинусами, и, опять же, перемножаем их и делим результат пополам.
Как найти стороны равнобедренного треугольника зная периметр. Периметр и площадь треугольника. Что мы узнали
Периметр – это сумма всех сторон фигуры. Эта характеристика, наравне с площадью, одинаково востребована для всех фигур. Формула периметра равнобедренного треугольника логично вытекает из его свойств, но формула не столь сложна, как получение и закрепление практических навыков.
Формула вычисления периметра
Боковые стороны равнобедренного треугольника равны между собой. Это проистекает из определения и хорошо видно даже из названия фигуры. Именно из этого свойства и проистекает формула периметра:
P=2a+b, где b-это основание треугольника, a-значение боковой стороны.
Рис. 1. Равнобедренный треугольник
Из формулы видно, что для нахождения периметра достаточно знать величину основания и одной из боковых сторон. 2}=\sqrt{9+16}=\sqrt{25}=5$$
2}=\sqrt{9+16}=\sqrt{25}=5$$
Найдем периметр: P=AC+AB*2=6+5*2=16
Задача 2
- В равнобедренном треугольнике высота, проведенная к основанию, равна 10, а острый угол при основании 30 градусам. нужно найти периметр треугольника.
Рис. 3. Рисунок к задаче 2
Эта задача осложнена отсутствием сведений о сторонах треугольника, но, зная значение высоты и угла, в прямоугольном треугольнике ABH можно найти катет AH, а после решение пойдет по тому же сценарию, что и в задаче 1.
Найдем AH через значение синуса:
$$sin (ABH)={BH\over AB}={1\over2}$$ — синус 30 градусов является табличным значением.
Выразим нужную сторону:
$$AB={{BH\over {1\over 2}}} =BH*2=10*2=20$$
Через котангенс найдем значение AH:
$$ctg(BAH)={AH\over BH}={1\over\sqrt{3}}$$
$$AH={BH\over\sqrt{3}}=10*\sqrt{3}=17,32$$ — получившееся значение округлим до сотых.
Найдем основание:
AC=AH*2=17,32*2=34,64
Теперь, когда все требуемые значения найдены, определим периметр:
P=AC+2*AB=34,64+2*20=74,64
Задача 3
- В равнобедренном треугольнике ABC известна площадь, которая равна $$16\over\sqrt{3}$$ и острый угол при основании в 30 градусов.
 Найти периметр треугольника.
Найти периметр треугольника.
Значения в условии часто приводятся в виде произведения корня на число. Это делается, чтобы максимально оградить последующее решение от погрешностей. Округлять результат лучше в конце вычислений
При такой постановке задачи может показаться, что решений нет, ведь сложно выразить одну из сторон или высоту из имеющихся данных. Попробуем решить по-другому.
Обозначим высоту и половину основания латинскими буквами: BH=h и AH=a
Тогда основание будет равно: AC=AH+HC=AH*2=2a
Площадь: $$S={1\over 2}*AC*BH={1\over 2}*2a*h=ah$$
С другой стороны, значение h можно выразить из треугольника ABH через тангенс острого угла. Почему именно тангенс? Потому что в треугольнике ABH мы уже обозначили два катета a и h. Нужно выразить одно через другое. Два катета вместе связывают тангенс и котангенс. Традиционно к котангенсу и косинусу обращаются, только если не подходит тангенс или синус. Это не правило, можно решать так, как удобно, просто так принято. 2}=4,62$$
2}=4,62$$
Подставим значения в формулу периметра:
P=AB*2+AH*2=4,62*2+4*2=17,24
Что мы узнали?
Мы разобрались подробно во всех тонкостях нахождения периметра равнобедренного треугольника. Решили три задачи разного уровня сложности, показав на примере, как решаются типовые задачи на решение равнобедренного треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.4 . Всего получено оценок: 83.
Предварительные сведения
Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Определение 1
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Определение 2
Точки в рамках определения 1 будем называть вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.
В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.
Определение 4
Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.
Определение 5
Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.
Определение 6
Треугольник будем называть равносторонним, если все его стороны равняются друг другу.
Все виды этих треугольников Вы можете видеть на рисунке 2.
Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Пример 1
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.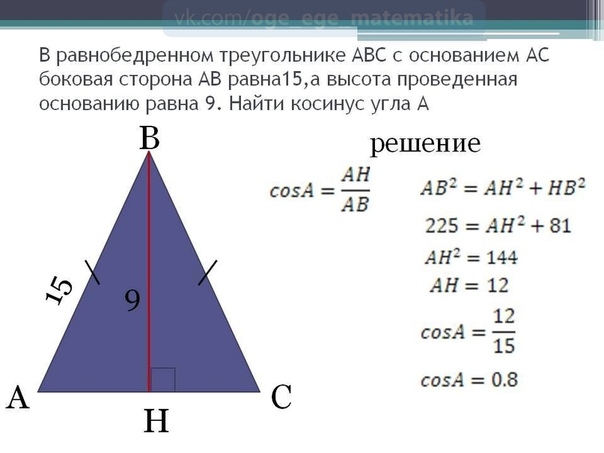
$P=34+12+11=57$ см
Ответ: $57$ см.
Пример 2
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α=10$ По правилу вычисления периметра разностороннего треугольника, получим
$P=10+8+6=24$ см
Ответ: $24$ см.
Как найти периметр равнобедренного треугольника?
Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+β=2α+β$
Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.
Пример 3
Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.
По рассмотренному выше примеру, видим, что
$P=2\cdot 12+11=35$ см
Ответ: $35$ см.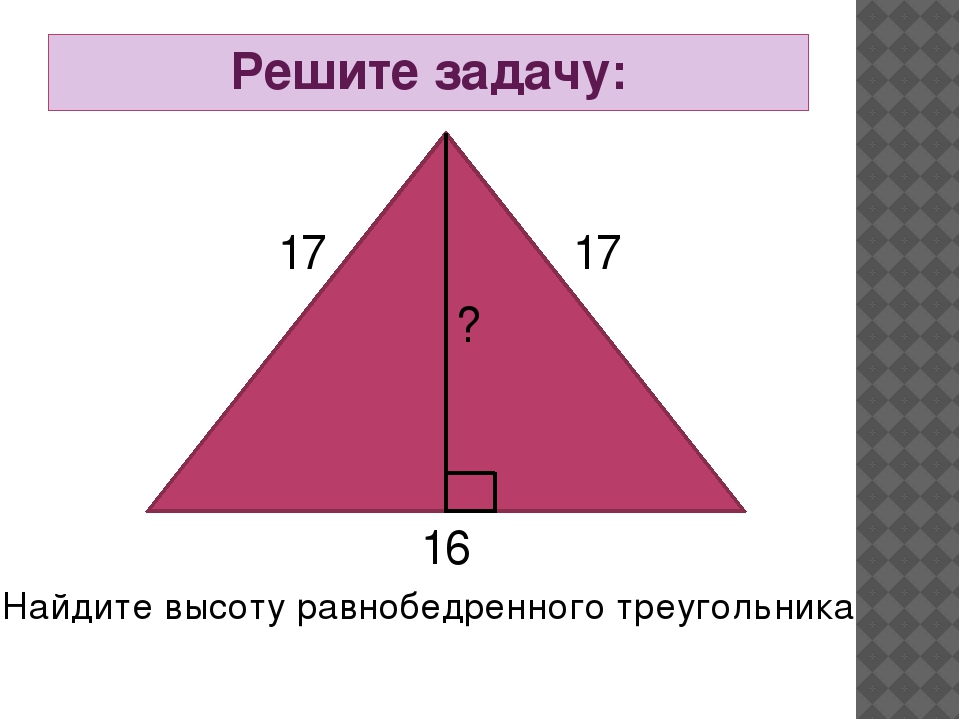
Пример 4
Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.
Рассмотрим рисунок по условию задачи:
Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.
По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда
По правилу вычисления периметра равнобедренного треугольника, получим
$P=2\cdot 10+12=32$ см
Ответ: $32$ см.
Как найти периметр равностороннего треугольника?
Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+α=3α$
Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.
Пример 5
Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.
По рассмотренному выше примеру, видим, что
$P=3\cdot 12=36$ см
Предварительные сведения
Периметр любой плоской геометрической фигур на плоскости определяется как сумма длин всех его сторон. Исключением из этого не является и треугольник. Сначала приведем понятие треугольника, а также виды треугольников в зависимости от сторон.
Определение 1
Треугольником будем называть геометрическую фигуру, которая составлена из трех точек, соединенных между собой отрезками (рис. 1).
Определение 2
Точки в рамках определения 1 будем называть вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 будем называть сторонами треугольника.
Очевидно, что любой треугольник будет иметь 3 вершины, а также три стороны.
В зависимости от отношении сторон друг к другу, треугольники делятся на разносторонние, равнобедренные и равносторонние.
Определение 4
Треугольник будем называть разносторонним, если ни одна из его сторон не равняется никакой другой.
Определение 5
Треугольник будем называть равнобедренным, если две его стороны равны друг другу, но не равняются третьей стороне.
Определение 6
Треугольник будем называть равносторонним, если все его стороны равняются друг другу.
Все виды этих треугольников Вы можете видеть на рисунке 2.
Как найти периметр разностороннего треугольника?
Пусть нам дан разносторонний треугольник, у которого длины сторон будут равняться $α$, $β$ и $γ$.
Вывод: Для нахождения периметра разностороннего треугольника надо все длин его сторон сложить между собой.
Пример 1
Найти периметр разностороннего треугольника равняются $34$ см, $12$ см и $11$ см.
$P=34+12+11=57$ см
Ответ: $57$ см.
Пример 2
Найти периметр прямоугольного треугольника, у которого катеты равняются $6$ и $8$ см.
Сначала найдем длину гипотенуз этого треугольника по теореме Пифагора. Обозначим ее через $α$, тогда
$α=10$ По правилу вычисления периметра разностороннего треугольника, получим
$P=10+8+6=24$ см
Ответ: $24$ см.
Как найти периметр равнобедренного треугольника?
Пусть нам дан равнобедренный треугольник, у которого длины боковых сторон будут равняться $α$, а длина основания равняется $β$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+β=2α+β$
Вывод: Для нахождения периметра равнобедренного треугольника надо удвоенную длину его сторон сложить с длиной его основания.
Пример 3
Найти периметр равнобедренного треугольника, если его боковые стороны равняются $12$ см, а основание $11$ см.
По рассмотренному выше примеру, видим, что
$P=2\cdot 12+11=35$ см
Ответ: $35$ см.
Пример 4
Найти периметр равнобедренного треугольника, если его высота, проведенная на основание, равняется $8$ см, а основание $12$ см.
Рассмотрим рисунок по условию задачи:
Так как треугольник равнобедренный, то $BD$ также является и медианой, следовательно, $AD=6$ см.
По теореме Пифагора, из треугольника $ADB$, найдем боковую сторону. Обозначим ее через $α$, тогда
Обозначим ее через $α$, тогда
По правилу вычисления периметра равнобедренного треугольника, получим
$P=2\cdot 10+12=32$ см
Ответ: $32$ см.
Как найти периметр равностороннего треугольника?
Пусть нам дан равносторонний треугольник, у которого длины всех сторон будут равняться $α$.
По определению периметра плоской геометрической фигуры, получим, что
$P=α+α+α=3α$
Вывод: Для нахождения периметра равностороннего треугольника надо длину стороны треугольника умножить на $3$.
Пример 5
Найти периметр равностороннего треугольника, если его сторона равняется $12$ см.
По рассмотренному выше примеру, видим, что
$P=3\cdot 12=36$ см
Любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:
P = a + b + c
где P — это периметр треугольника, a , b и c — его стороны.
Можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:
P = 2a + b
где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.
Можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:
P = 3a
где P — это периметр равностороннего треугольника, a — любая из его сторон.
Площадь
Для измерения площади треугольника можно сравнить его с параллелограммом . Рассмотрим треугольник ABC :
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2 . Общая формула для нахождения площади треугольников будет выглядеть так:
где S — это площадь треугольника, a — его основание, h a — высота, опущенная на основание a .
Для каких вычислений понадобится высота равнобедренного треугольника
Треугольник – одна из основных фигур в геометрии. Принято выделять треугольники прямые (один угол у которых равен 900), остро- и тупоугольные (величина углов меньше или больше 900 соответственно), равносторонние и равнобедренные. При вычислениях различного рода используют основные геометрические понятия и величины (синус, медиана, радиус, перпендикуляр и т.п.)
Темой для нашего исследования станет высота равнобедренного треугольника. Углубляться в терминологию и определения мы не станем, лишь коротко обозначим основные понятия, которые будут необходимы для понимания сути.
Итак, равнобедренным треугольником принято считать треугольник, в котором величина двух сторон выражена одним тем же числом (равенство сторон). Равнобедренный треугольник может быть и остроугольным, и тупоугольным, и прямым. Также он может быть и равносторонним (все стороны фигуры равны по величине). Нередко можно услышать: все равносторонние треугольники равнобедренные, но не все равнобедренные – равносторонние.
Высотой любого треугольника считается перпендикуляр, опущенный из угла на противоположную сторону фигуры. В качестве медианы выступает отрезок, проведенный из угла фигуры на центр противолежащей стороны.
Чем примечательна высота равнобедренного треугольника?
- Если высота, опущенная на одну из сторон, является медианой и биссектрисой, то данный треугольник будет считаться равнобедренным, и наоборот: треугольник является равнобедренным, если высота, опущенная на одну из сторон, является одновременно биссектрисой и медианой. Эту высоту называют основной.
- Высоты, опущенные на боковые (равные) стороны равнобедренного треугольника, тождественны и образуют две подобные фигуры.
- Если известна высота равнобедренного треугольника (как, впрочем, и любого другого) и сторона, на которую эта высота была опущена, можно узнать площадь данного многоугольника. S=1/2* (c*hc)
Как используется высота равнобедренного треугольника в вычислениях? Свойства ее, проведенной к его основанию, делают справедливыми следующие утверждения:
- Основная высота, являясь одновременно медианой, делит основание на два равных отрезка.
 Это позволяет нам узнать величину основания, площадь треугольника, образованного высотой, и т.д.
Это позволяет нам узнать величину основания, площадь треугольника, образованного высотой, и т.д. - Являясь перпендикуляром, высота равнобедренного треугольника может считаться стороной (катетом) нового прямоугольного треугольника. Зная величину каждой из сторон, опираясь на теорему Пифагора (всем известное соотношение значений квадратов катетов и гипотенузы), можно вычислить числовое значение высоты.
Чему равна высота треугольника? В целом равнобедренный треугольник, высота которого нам необходима, не перестает быть таковым по своей сути. Поэтому для него не теряют своей актуальности все формулы, используемые для этих фигур, как таковых. Можно вычислить длину высоты, зная величину углов и стороны, величину сторон, площадь и сторону, а также ряд других параметров. Высота треугольника равна определенному соотношению этих величин. Приводить сами формулы не имеет смысла, найти их просто. Кроме этого, обладая минимумом информации, можно найти нужные значения и уже после этого приступать к вычислению высоты.
Равнобедренный треугольник. Вычисление длин, углов. Синус угла
Задача 1. В треугольнике Найдите
Решение: + показать
Задача 2. В треугольнике Найдите
Решение: + показать
Задача 3. В треугольнике Найдите
Решение: + показать
Задача 8. В треугольнике Найдите высоту .
Решение: + показать Треугольник По теореме Пифагора: Ответ:
Задача 9. В равнобедренном треугольнике с основанием боковая сторона равна Найдите длину высоты
Решение: + показать
Задача 10. В равнобедренном треугольнике с основанием боковая сторона равна Найдите
Решение: + показать
Задача 11. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна Найдите площадь этого треугольника.
Решение: + показать Ответ:
Задача 12. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Найдите боковую сторону треугольника, если его площадь равна
Решение: + показать
Задача 13. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна Найдите площадь этого треугольника.
Решение: + показать Ответ:
Задача 18. В треугольнике высота равна Найдите угол Ответ дайте в градусах.
Решение: + показать В прямоугольном треугольнике значит Ответ:
Задача 19. В треугольнике угол равен Найдите угол Ответ дайте в градусах.
Решение: + показать В равнобедренном треугольнике Поэтому Ответ:
Задача 20. Один угол равнобедренного треугольника на больше другого. Найдите меньший угол. Ответ дайте в градусах.
Найдите меньший угол. Ответ дайте в градусах.
Решение: + показать Пусть тогда Тогда Ответ:
Задача 21. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен Боковая сторона треугольника равна Найдите длину основания этого треугольника.
Решение: + показать Пусть Тогда в прямоугольном треугольнике Стало быть, По теореме Пифагора Откуда Ответ:
Задача 22. В треугольнике Внешний угол при вершине равен Найдите угол Ответ дайте в градусах.
Решение: + показать
Вы можете пройти тест по теме «Равнобедренный треугольник. Вычисление углов и длин».
Как найти площадь равнобедренного треугольника?
В этом уроке мы покажем простой способ решения следующей задачи: как найти площадь равнобедренного треугольника.
Применим на практике ряд уже доказанных свойств в следующей геометрической задаче:
Задача
В равнобедренном треугольнике ΔABC с длиной катета 10 высота до основания равна две трети основания. Найдите площадь треугольника.
Стратегия
Чтобы решить эту проблему, мы будем работать в обратном направлении от того, что нам нужно сделать.
Нам нужно найти площадь треугольника, который, как мы знаем, определяется формулой (основание умножить на высоту)/2.
Проблема в том, что мы не знаем ни длины основания, ни высоты. Но нам дана связь между ними, которая является подсказкой о том, что нам нужно делать. Обозначим длину основания ВС за х.
Тогда мы знаем, что высота AD равна 2x/3, как указано в задаче.
Таким образом, ответ, который мы ищем, равен (основание умножить на высоту)/2, или х умножить на 2х/3, разделить на два.
Но как найти х? В задаче нам дали две дополнительные вещи, которые мы еще не использовали: длину катета (10) и тот факт, что это равнобедренный треугольник. Нам, вероятно, нужно использовать эти две вещи, чтобы решить проблему.
Нам, вероятно, нужно использовать эти две вещи, чтобы решить проблему.
Рассмотрим свойства равнобедренных треугольников. Сразу следует вспомнить, что, как мы показали, в равнобедренном треугольнике высота основания делит основание пополам, поэтому CD=DB=x/2.
Наконец, AD — это высота, что означает, что угол ∠ADC — прямой, и у нас есть прямоугольный треугольник ΔADC, гипотенузу которого мы знаем (10) и можем использовать для нахождения катетов по теореме Пифагора c 2 =a 2 +b 2,
где c= 10 ,a = x/2 и b=2x/3 . И мы закончили, остальное просто алгебраическое решение для x.
Доказательство
(1) ΔADC — прямоугольный треугольник //дан, так как AD — высота до основания 3) AC = 10 // Дано
(4) CB = x
(5) CD = X / 2 // Высота до базы в изоляре Triangle Bisects Base
(6) AD = 2x / 3 // Дано
(7) 10 2 = (x/2) 2 + (2x/3) 2 //Подставить в (2)
(8) 100 = x 2 /4+4x 2 /9 // Упростите
(9) 100 * 36 = 9x 2 + 16x 2 // Умножьте обе стороны на 36
(10) 100 * 36 = 25x 2 // Соберите похожие термины
(11) 4*36 = x 2 // разделить на 25
(12) √144 = x = // извлечь квадратный корень из обеих сторон x
(390) CB
(14) AD = 2x/3 = 2*12/3 = 8
(15) Площадь = 12 * 8 / 2 = 48
Вот как легко найти площадь равнобедренного треугольника!
Как найти высоту равностороннего треугольника
Овладейте семью столпами успеха в школе
Улучшите свои оценки и снизьте стресс
Давайте рассмотрим еще несколько примеров нахождения высоты равностороннего треугольника.
Найдите высоту равностороннего треугольника со стороной 8 см.
8/2 = 4 4√3 = 6,928 см.
Когда вы используете десятичные дроби и когда вы используете ответ с квадратным корнем. Ответ с квадратным корнем является точным ответом. На стандартизированных тестах, таких как SAT, они ожидают точного ответа. Десятичный ответ является оценкой.
Найдите высоту равностороннего треугольника со стороной 12 единиц.
12/2 = 6, тогда 6√3 единиц = 10.392 единицы
Сторона равностороннего треугольника равна 16 единицам. Чему равна высота этого равностороннего треугольника.
16/2=8√3 единиц или 13,856 единиц
Высота равностороннего треугольника равна 10 единицам. Какова длина стороны?
h = √3 / 2 * a = a = √3 / 2 * a = a = a = √3 / 2 * a = a = a = a = a = a = √3 / 2 * a
a = 6 / √3 / 2
a = 4√3
0 Common Core Standard 6.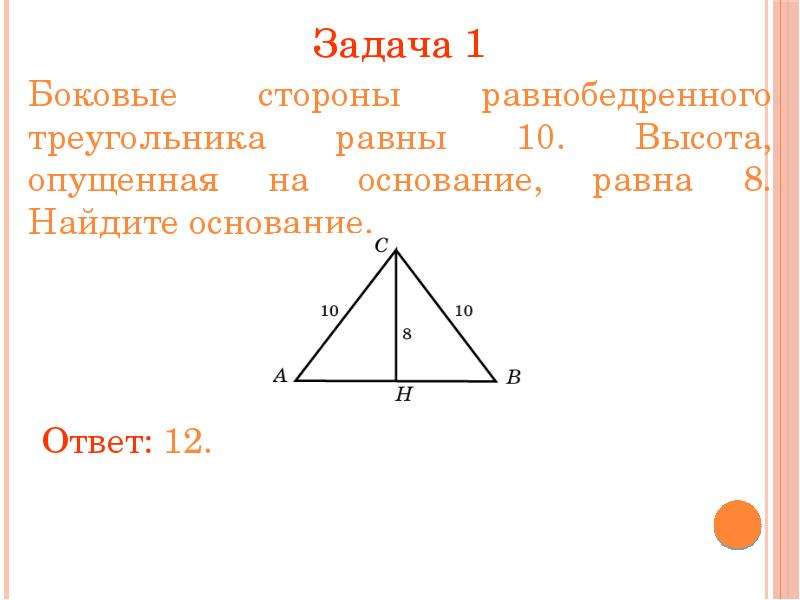 g.1
g.1
|


 Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5
Таким образом, площадь равнобедренного треугольника и будет равна половине произведения боковой стороны на высоту). См. также Формулу 5 Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2)). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна.
Поскольку высота в равнобедренном треугольнике является, одновременно, биссектрисой и медианой, то tg(β/2) — это отношение половины основания (b/2) к высоте — tg(β/2) = (b/2)/h. Откуда h = b / (2 tg(β/2)). В итоге формула снова будет сведена к более простой Формуле 5, которая вполне очевидна. Поскольку он равен половине основания (b/2) то его квадрат будет равен b 2 /4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно».
Поскольку он равен половине основания (b/2) то его квадрат будет равен b 2 /4. Извлечение корня из данного выражения и даст нам высоту. Что и видно в Формуле 6. Если числитель и знаменатель умножить на два, а потом двойку числителя внести под знак корня, получим второй вариант той же самой формулы, который написан через знак «равно». 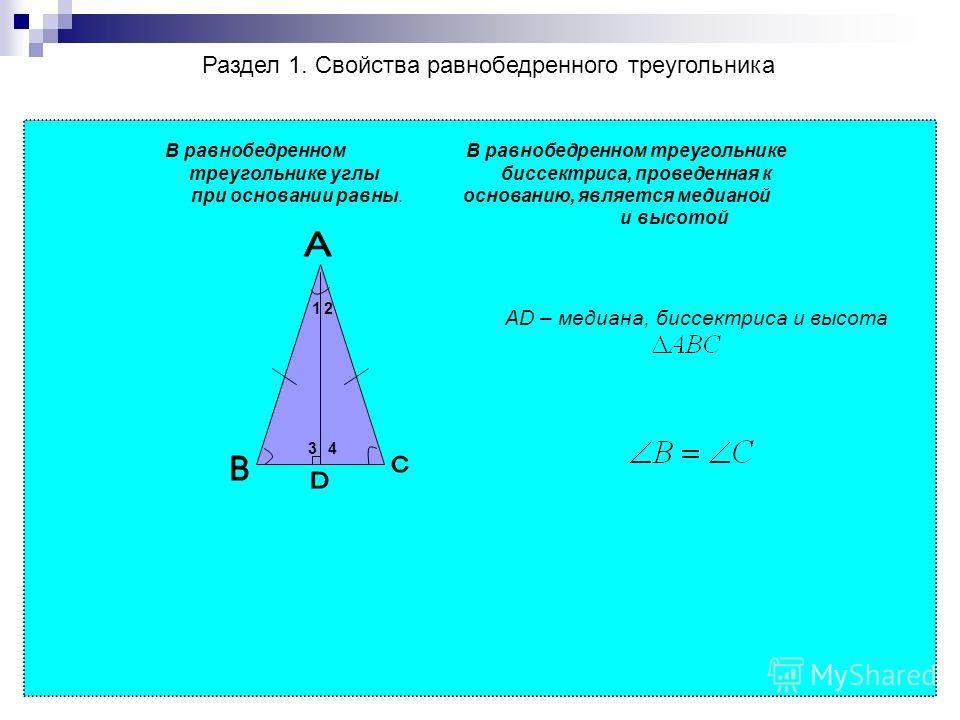
 {2}}}}
{2}}}} 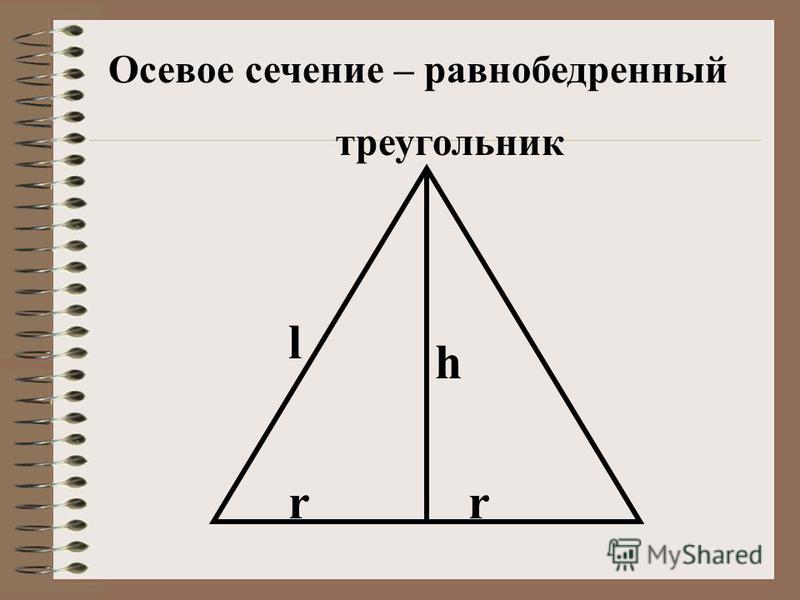 Найти периметр треугольника.
Найти периметр треугольника.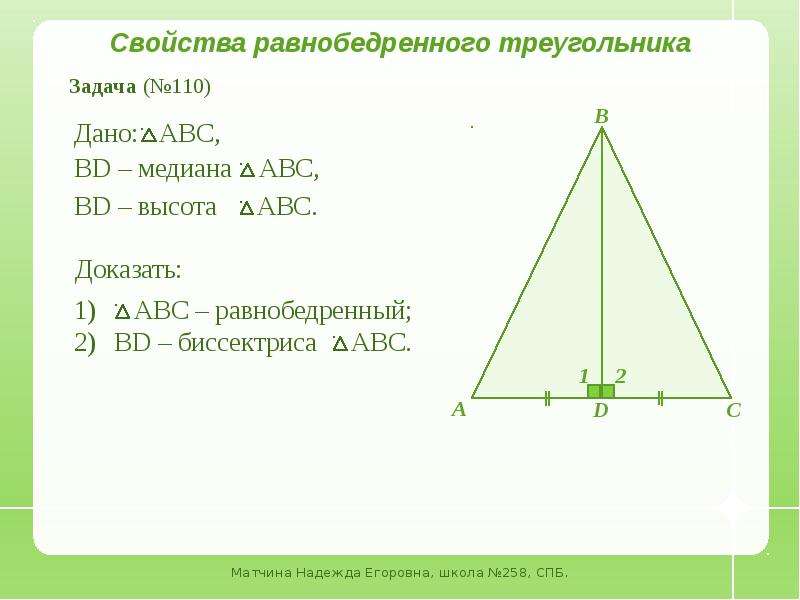 Это позволяет нам узнать величину основания, площадь треугольника, образованного высотой, и т.д.
Это позволяет нам узнать величину основания, площадь треугольника, образованного высотой, и т.д.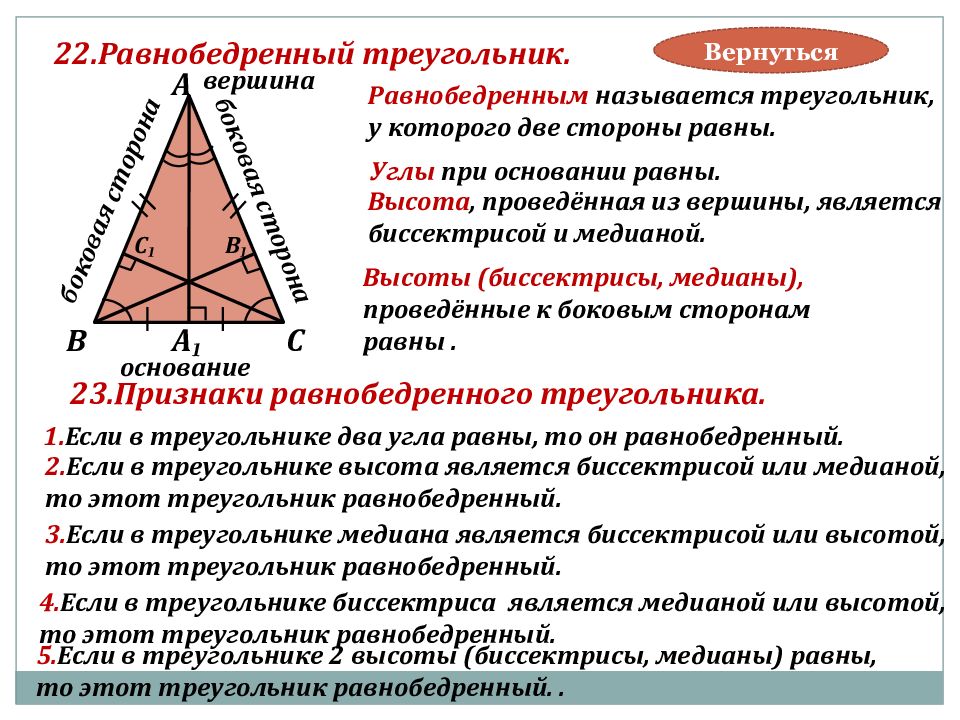 Используйте формулу высоты: ( сторона/2 * √3 ) для расчета высоты.
Используйте формулу высоты: ( сторона/2 * √3 ) для расчета высоты.  Равносторонний треугольник обладает следующими свойствами.
Равносторонний треугольник обладает следующими свойствами. 


 Это также знания, которые часто требуются в жизни. Например, при строительстве дома с высокой крышей нужно рассчитать толщину бревен и их количество. Это легко, если вы знаете, как найти высоту в равнобедренном треугольнике. Архитектурные сооружения строятся на знании свойств геометрических фигур. Формы зданий часто визуально напоминают их. Египетские пирамиды, пакеты с молоком, художественная вышивка, северная роспись и даже пирожки – все это окружающие человека треугольники.Как сказал Платон, весь мир основан на треугольниках.
Это также знания, которые часто требуются в жизни. Например, при строительстве дома с высокой крышей нужно рассчитать толщину бревен и их количество. Это легко, если вы знаете, как найти высоту в равнобедренном треугольнике. Архитектурные сооружения строятся на знании свойств геометрических фигур. Формы зданий часто визуально напоминают их. Египетские пирамиды, пакеты с молоком, художественная вышивка, северная роспись и даже пирожки – все это окружающие человека треугольники.Как сказал Платон, весь мир основан на треугольниках.
 И, следовательно, все соответствующие углы равны. И, конечно же, вечеринки, но к этому моменту мы вернемся позже.
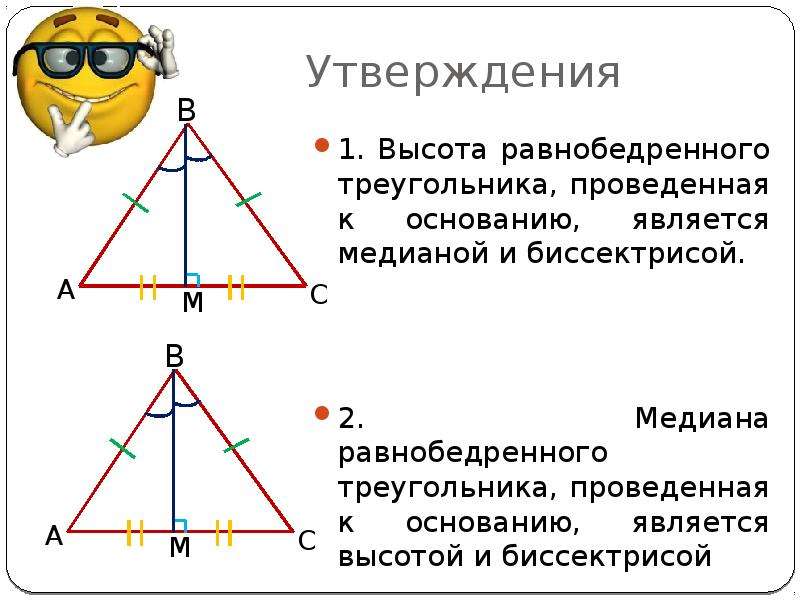
И, следовательно, все соответствующие углы равны. И, конечно же, вечеринки, но к этому моменту мы вернемся позже. Используя тот же транспортир, проверьте углы, образованные теперь по высоте. Они равны. Это означает, что высота также является биссектрисой. Вооружившись линейкой, измерьте длины, на которые разбивается высота основания. Они равны. Следовательно, высота в равнобедренном треугольнике делит основание пополам и является медианой.
Используя тот же транспортир, проверьте углы, образованные теперь по высоте. Они равны. Это означает, что высота также является биссектрисой. Вооружившись линейкой, измерьте длины, на которые разбивается высота основания. Они равны. Следовательно, высота в равнобедренном треугольнике делит основание пополам и является медианой.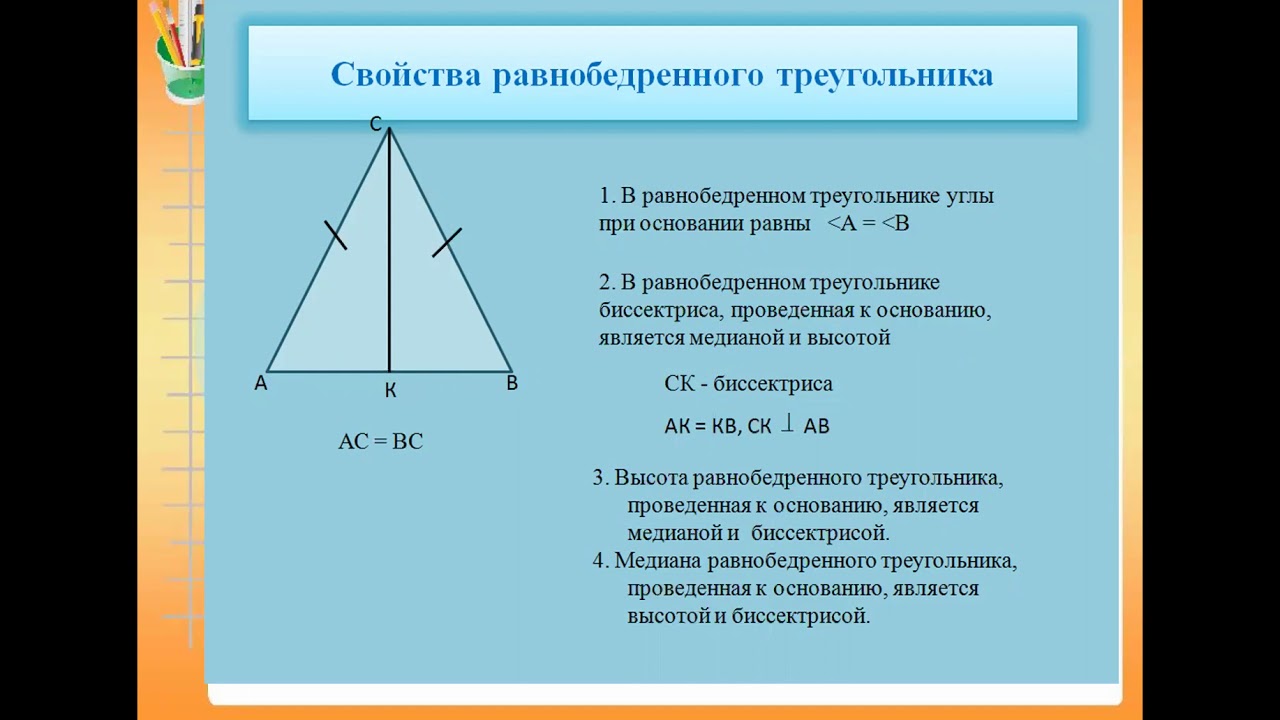 Таким образом, VD — это высота в равнобедренном треугольнике, проведенном к основанию. КЭД
Таким образом, VD — это высота в равнобедренном треугольнике, проведенном к основанию. КЭД VD — высота этого треугольника, она имеет обозначение h.
VD — высота этого треугольника, она имеет обозначение h.


 Итак, до конца этого урока ваша первая задача — определить, какая сторона является базовой, особенно когда вы доберетесь до более сложных сторон.
Итак, до конца этого урока ваша первая задача — определить, какая сторона является базовой, особенно когда вы доберетесь до более сложных сторон.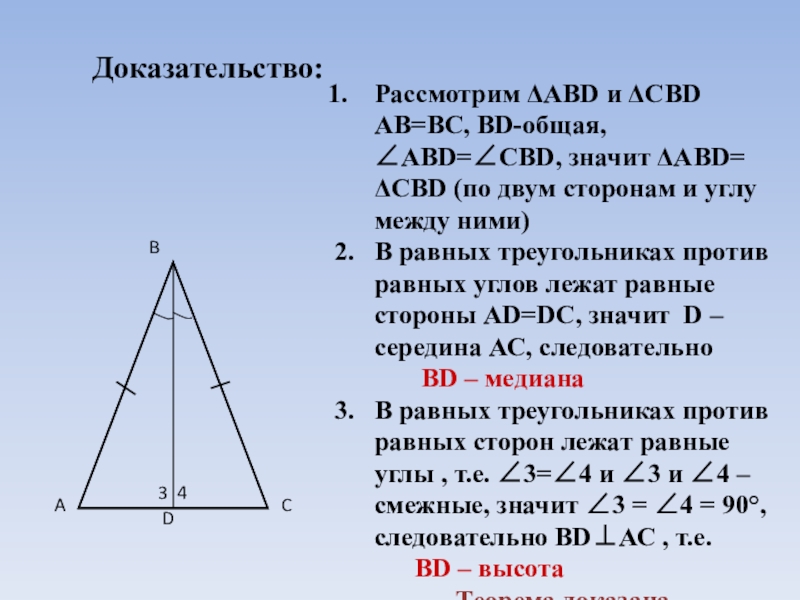 8 квадратных футов и его основание 24 дюйма, какова высота?
8 квадратных футов и его основание 24 дюйма, какова высота?
 6 = \frac 1 2 \cdot 2 \cdot \red{ \text{h } } $
6 = \frac 1 2 \cdot 2 \cdot \red{ \text{h } } $ 8 квадратных единиц, найдите его высоту.
8 квадратных единиц, найдите его высоту. 8 = \frac 1 2 \cdot \text{12 } \cdot \red{ \text{h } }
$
8 = \frac 1 2 \cdot \text{12 } \cdot \red{ \text{h } }
$ 9
$
9
$ В каждом треугольнике есть 3 пары основание/высота, но по рисунку видно, что основание — это сторона длины 11.Помните, что основание и высота перпендикулярны.
В каждом треугольнике есть 3 пары основание/высота, но по рисунку видно, что основание — это сторона длины 11.Помните, что основание и высота перпендикулярны.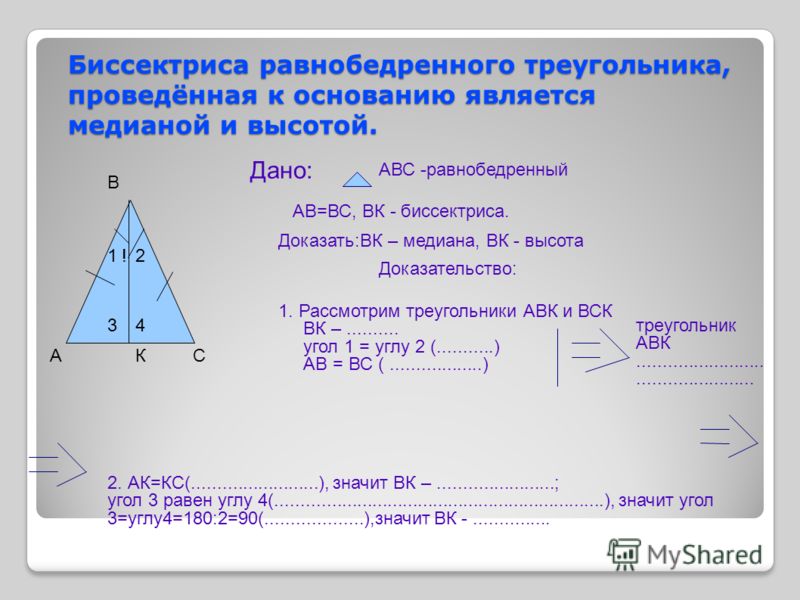 5 = 5,5 \красный час
\\
\ гидроразрыва {73,5} {5,5} = ч
\\
ч = 13,4
$
5 = 5,5 \красный час
\\
\ гидроразрыва {73,5} {5,5} = ч
\\
ч = 13,4
$
 9 = \frac 1 2 \cdot 21 \cdot \red{ \text{h } } $
9 = \frac 1 2 \cdot 21 \cdot \red{ \text{h } } $ 6 квадратных единиц, какова мера его высоты? Кроме того, имеет ли значение, какую сторону вы выберете в качестве своей базы?
6 квадратных единиц, какова мера его высоты? Кроме того, имеет ли значение, какую сторону вы выберете в качестве своей базы? Помните, что основание и высота перпендикулярны.
Помните, что основание и высота перпендикулярны.
 Вычислите размеры основания и стороны треугольника.
Вычислите размеры основания и стороны треугольника. Вычислите периметр и площадь треугольника, зная, что его высота равна 20 см.
Вычислите периметр и площадь треугольника, зная, что его высота равна 20 см. Вычислите амплитуды трех внутренних углов треугольника.
Вычислите амплитуды трех внутренних углов треугольника. Вычислите меру основания равнобедренного треугольника, подобного показанному выше, с равными сторонами длиной 15 см.
Вычислите меру основания равнобедренного треугольника, подобного показанному выше, с равными сторонами длиной 15 см. Вычисляет длину гипотенузы.
Вычисляет длину гипотенузы. Вычислите периметр.
Вычислите периметр. Рассчитайте протяженность двух катетов и периметр.
Рассчитайте протяженность двух катетов и периметр.
 Вычислите периметр и площадь.
Вычислите периметр и площадь.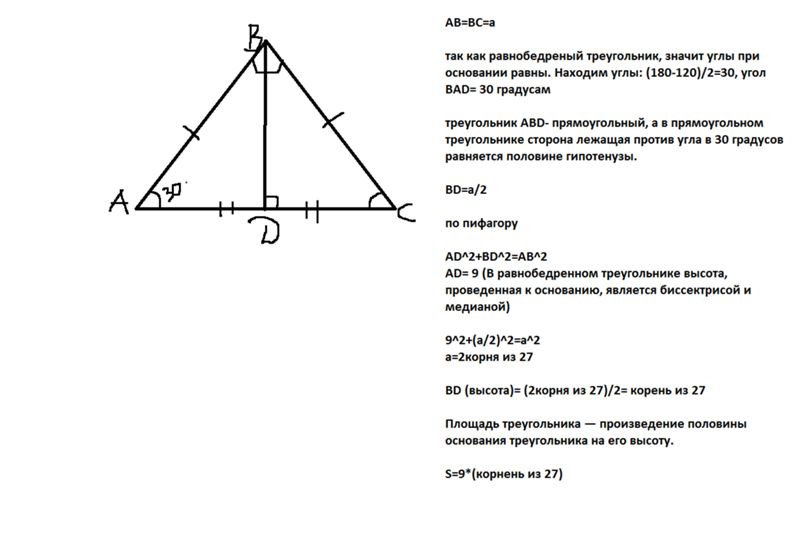 Вычислите периметр треугольника.
Вычислите периметр треугольника. 
 Зная, что проекция катета меньше на гипотенузу 1,8 см, вычислить периметр данного треугольника.
Зная, что проекция катета меньше на гипотенузу 1,8 см, вычислить периметр данного треугольника.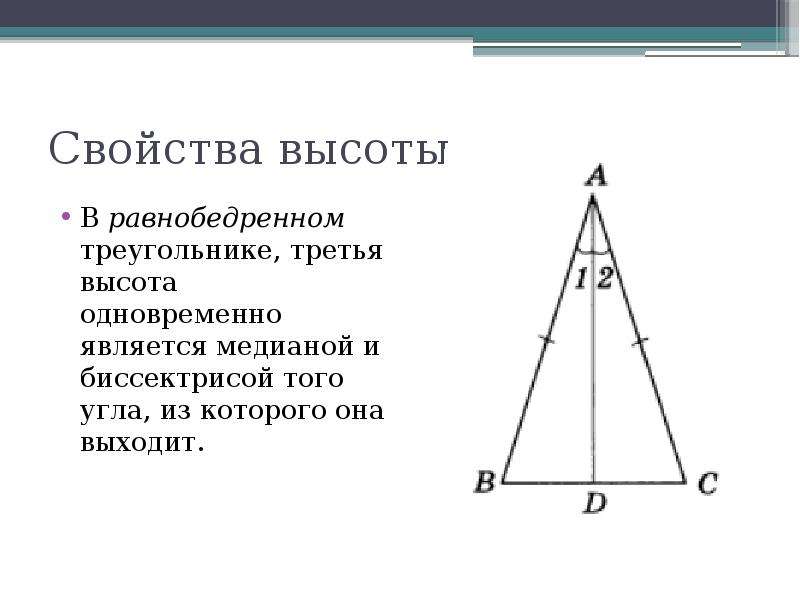 Вычислите периметр, зная, что две короткие стороны составляют одну из 3/4 другой.
Вычислите периметр, зная, что две короткие стороны составляют одну из 3/4 другой. Найдите амплитуду каждого внешнего угла.
Найдите амплитуду каждого внешнего угла.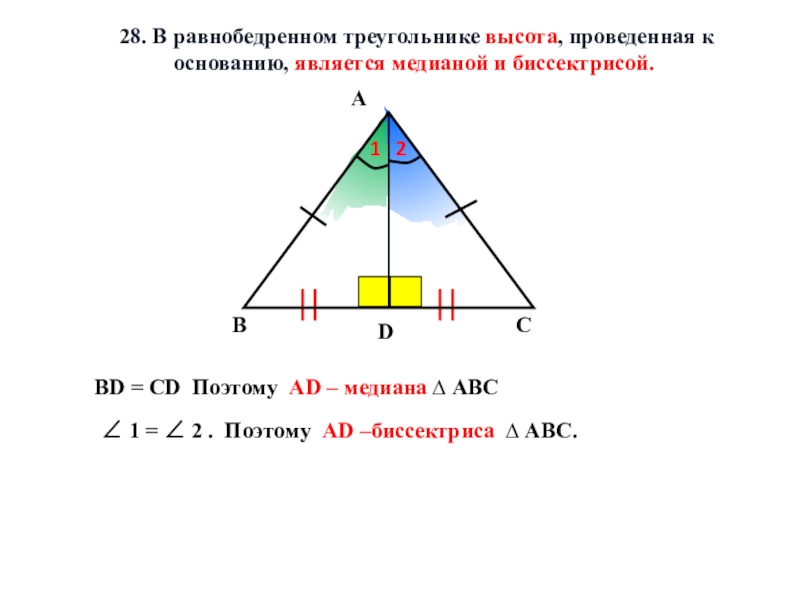 Вычислите площадь, зная, что основание равно 5/3 высоты.
Вычислите площадь, зная, что основание равно 5/3 высоты.

 Вычислите площадь круга, вписанного в треугольник.
Вычислите площадь круга, вписанного в треугольник.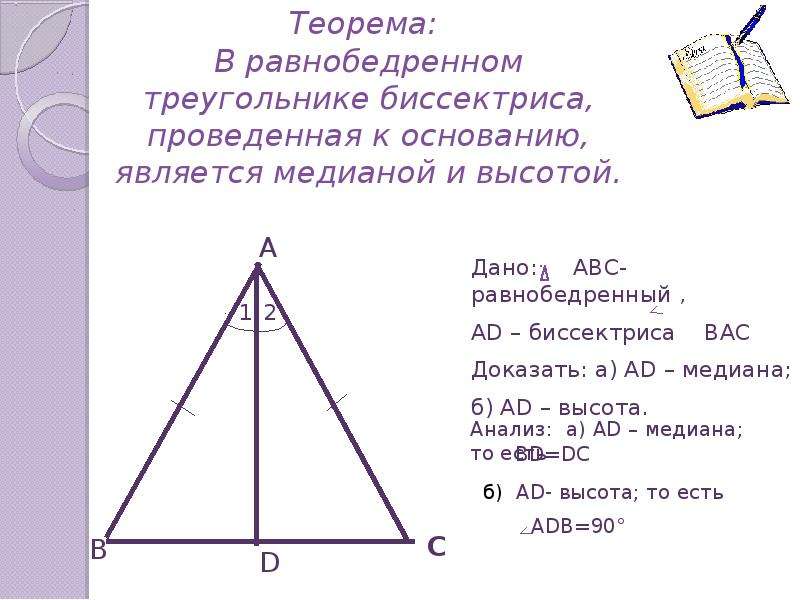 Вычислите периметр и длину радиуса окружности, вписанной в треугольник.
Вычислите периметр и длину радиуса окружности, вписанной в треугольник.  Проведите из точки P вне окружности касательные PA и PB и соединив точку O с точками касания A и B, вы получите четырехугольник APBO. Зная, что периметр четырехугольника равен 100 см, вычислите размеры его сторон.
Проведите из точки P вне окружности касательные PA и PB и соединив точку O с точками касания A и B, вы получите четырехугольник APBO. Зная, что периметр четырехугольника равен 100 см, вычислите размеры его сторон.  Вычисляет измерение длины периметра треугольника ОВА и площади треугольника.
Вычисляет измерение длины периметра треугольника ОВА и площади треугольника.  Вычислите периметр треугольника.
Вычислите периметр треугольника. Найдите площадь квадрата, периметр которого равен 4/3 периметра треугольника.
Найдите площадь квадрата, периметр которого равен 4/3 периметра треугольника.

 Зная, что размер прямоугольника равен 48 см, вычислите длину диагонали и периметр прямоугольника.
Зная, что размер прямоугольника равен 48 см, вычислите длину диагонали и периметр прямоугольника.
 Определяет периметр алмаза.
Определяет периметр алмаза.
 Вычислите длину окружности, радиус которой на 3/4 больше катета.
Вычислите длину окружности, радиус которой на 3/4 больше катета. Найдите периметр треугольника АВС.
Найдите периметр треугольника АВС. Вычислите периметр обоих треугольников.
Вычислите периметр обоих треугольников.
 Вычислите периметр и площадь равностороннего треугольника, длина стороны которого равна основанию данного равнобедренного треугольника.
Вычислите периметр и площадь равностороннего треугольника, длина стороны которого равна основанию данного равнобедренного треугольника.
 Вычислите длину окружности и площадь круга.
Вычислите длину окружности и площадь круга. Треугольник, у которого две стороны (катеты) равны, а углы при основании равны, называется равнобедренным треугольником. Название «равнобедренный треугольник» происходит от греческих слов iso , что означает «такой же» и Skelos , что означает ноги.
Треугольник, у которого две стороны (катеты) равны, а углы при основании равны, называется равнобедренным треугольником. Название «равнобедренный треугольник» происходит от греческих слов iso , что означает «такой же» и Skelos , что означает ноги. °\).
°\). 2}}}{4}} \)
2}}}{4}} \)