10 Основные типы дифференциальных уравнений первого порядка » СтудИзба
Лекция 10. Основные типы дифференциальных уравнений первого порядка.
Уравнения с разделяющимися переменными.
Уравнение с разделяющимися переменными имеет вид
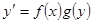 .
.
В этом уравнении переменные «можно разделить», т.е. функции от x и dx собрать в правую часть, а функции от y и dy – в левую часть. Затем интегрируем полученное соотношение и получаем соотношение вида 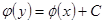 .
.
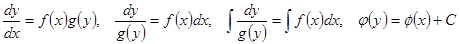 .
.
Пример. 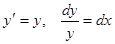 . Заметим, что
. Заметим, что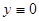 — решение, это так называемое тривиальное решение. Только, проанализировав, является ли
— решение, это так называемое тривиальное решение. Только, проанализировав, является ли 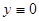 решением или нет, мы имеем право, разделив обе части на
решением или нет, мы имеем право, разделив обе части на 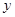 , двигаться дальше. Иначе тривиальное решение будет потеряно.
, двигаться дальше. Иначе тривиальное решение будет потеряно.
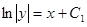 .
.
Здесь нельзя потерять модуль, иначе потеряем решения при  .
.
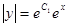 .
.
Обозначим 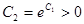 и раскроем модуль:
и раскроем модуль:
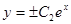 .
.
Заменим  и разрешим С быть равной нулю, т.к. тривиальное решение есть. Окончательно,
и разрешим С быть равной нулю, т.к. тривиальное решение есть. Окончательно,
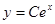 , где С – произвольная действительная постоянная.
, где С – произвольная действительная постоянная.
Обычно все эти «подводные камни» опускают (достаточно сказать о них один раз) и сразу выписывают решение уравнения 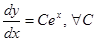 .
.
Пример. Найти кривую, проходящую через точку  , если угловой коэффициент касательной к кривой в три раза больше углового коэффициента радиус-вектора в точке касания.
, если угловой коэффициент касательной к кривой в три раза больше углового коэффициента радиус-вектора в точке касания.
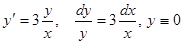 — решение,
— решение, 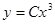 . Подставляя начальные условия, получим
. Подставляя начальные условия, получим 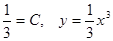 .
.
Пример. Формула Циолковского.
Ракета вместе с топливом, массой 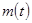 , движется прямолинейно, без учета гравитации. Скорость истечения топлива
, движется прямолинейно, без учета гравитации. Скорость истечения топлива 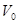 , в начальный момент времени
, в начальный момент времени 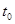 ракета неподвижна и имеет вместе с топливом массу M. Вывести формулы для скорости ракеты
ракета неподвижна и имеет вместе с топливом массу M. Вывести формулы для скорости ракеты 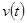 .
.
Выделим элемент массы dm. По закону сохранения количества движения
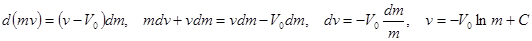 Подставляя
Подставляя 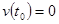 , получим
, получим 
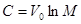 . Отсюда
. Отсюда
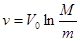 — формула Циолковского.
— формула Циолковского.
Однородное уравнение.
Правая часть однородного уравнения зависит от отношения 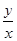 :
:
 .
.
Это позволяет заменить отношение новой переменной  или
или 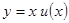 .
.
 .
.
Получено уравнение с разделяющимися переменными. Если 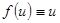 , то исходное уравнение уже является уравнением с разделяющимися переменными.
, то исходное уравнение уже является уравнением с разделяющимися переменными.
Пример.  .
. 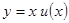 ,
, 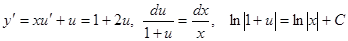 ,
, 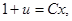
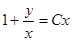
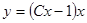
Обобщенно-однородное уравнение.
Обобщенно-однородное уравнение имеет вид
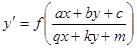 .
.
Возможны два случая
1) 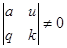
 Рекомендуется замена
Рекомендуется замена  ,
,

 , получили однородное уравнение.
, получили однородное уравнение.
2)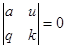
Здесь вводят новую функцию 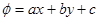 старой переменной x.
старой переменной x.
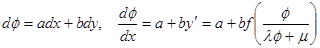 , где
, где 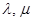 определяются из пропорциональности строк определителя. Получено уравнение с разделяющимися переменными.
определяются из пропорциональности строк определителя. Получено уравнение с разделяющимися переменными.
Пример. 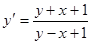 , случай1).
, случай1).
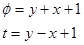 ,
, 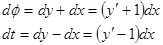 ,
, 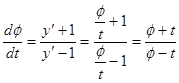
Получили однородное уравнение.
Пример. 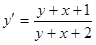 , случай 2).
, случай 2).
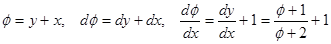 .
.
Получили уравнение с разделяющимися переменными.
Линейное уравнение.
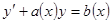
Существует два метода решения линейного уравнения: метод вариации произвольной постоянной и метод подстановки.
Метод вариации произвольной постоянной будет встречаться нам часто: при решении неоднородных линейных уравнений высшего порядка, при решении неоднородных систем линейных уравнений. Его надо знать твердо.
При решении методом вариации произвольной постоянной сначала решают однородное уравнение (с нулевой правой частью)

Это – уравнение с разделяющимися переменными.
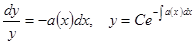 .
.
Затем варьируют произвольную постоянную, полагая 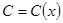 .
.
 .
.
Подставляем в неоднородное уравнение:
 .
.
При вариации произвольной постоянной здесь обязательно должны сократиться два члена, в этом идея метода.
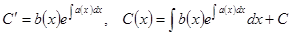 , где С – произвольная постоянная.
, где С – произвольная постоянная.
 .
.
Видно, что общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения. Это справедливо не только для линейных уравнений первого порядка, но и для линейных уравнений высших порядков, и для линейных систем. Там подобное утверждение называется теоремой о структуре общего решения неоднородного уравнения или системы.
Замечание. Решая уравнение методом вариации, обязательно приводите его к виду 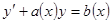 (если при
(если при  стоит коэффициент, то делить на него обязательно), иначе метод вариации даст ошибку.
стоит коэффициент, то делить на него обязательно), иначе метод вариации даст ошибку.
При решении методом подстановки полагают
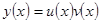 . Мы видели выше, что решение действительно является произведением двух функций от x. Этот факт здесь и используется.
. Мы видели выше, что решение действительно является произведением двух функций от x. Этот факт здесь и используется.
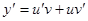 . Подставляем в уравнение:
. Подставляем в уравнение:
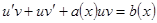 .
.
Теперь решают либо уравнение  , определяя отсюда
, определяя отсюда
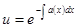 , либо уравнение
, либо уравнение 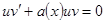 , определяя отсюда
, определяя отсюда
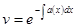 . Здесь при интегрировании не надо добавлять константу, она появится позже, при отыскании второй функции. В первом случае, остается найти v из
. Здесь при интегрировании не надо добавлять константу, она появится позже, при отыскании второй функции. В первом случае, остается найти v из  .
.
Теперь 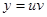 =
= , как и выше.
, как и выше.
Во втором случае остается найти u из  ,
, 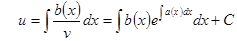 .
.
Теперь 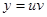 =
= , как и выше.
, как и выше.
Пример. 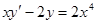 .
.
Решение методом вариации. Приводим уравнение, деля на коэффициент при  :
:
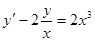 .
.
Решаем однородное уравнение 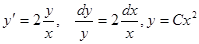 .
.
Варьируем произвольную постоянную  .
.
Подставляем в неоднородное уравнение 
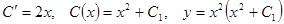 .
.
Решение методом подстановки.
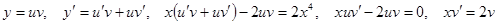
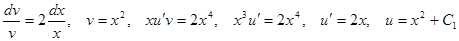
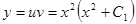 .
.
Уравнение Бернулли.
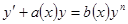
Если n = 1, то это – уравнение с разделяющимися переменными, если n = 0, то это – линейное уравнение.
Заметим, что при n > 0 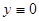 — решение уравнения.
— решение уравнения.
Решать уравнение Бернулли можно тремя способами
1) сведение к линейному уравнению заменой 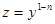
Разделим обе части уравнения на 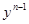 ,
,

Получили линейное уравнение относительно 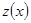
 .
.
Этот метод применяется редко, так как уравнение Бернулли можно решать теми же методами, что и линейное уравнение, не приводя его предварительно к линейному.
2) Решение методом вариации произвольной постоянной.
Решение проводится аналогично линейному уравнению.
Решим сначала однородное уравнение, полагая правую часть уравнения нулевой.
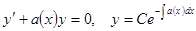 .
.
Затем ищем решение уравнения в виде 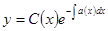 , варьируя произвольную постоянную
, варьируя произвольную постоянную 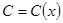 ,
,
вычисляем  и подставляем в исходное уравнение .
и подставляем в исходное уравнение .
 .
.
Вновь, как и в линейном уравнении, два слагаемых сокращаются, получаем уравнение с разделяющимися переменными.

Определяя отсюда функцию 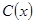 , подставляем ее в
, подставляем ее в 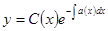 .
.
3)Решение методом подстановки.
Полагаем 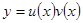 , подставляем
, подставляем 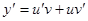 в исходное уравнение
в исходное уравнение
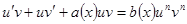 .
.
Точно так же, как при решении линейного уравнения, решаем, например, уравнение 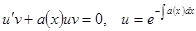 . Подставляем полученную функцию, решаем «оставшееся» уравнение с разделяющимися переменными
. Подставляем полученную функцию, решаем «оставшееся» уравнение с разделяющимися переменными 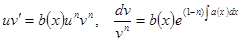 .
.
Заметим, что оно получилось точно таким же, как в методе вариации. Поэтому вторая функция в методе подстановки и есть та самая варьируемая постоянная. Затем записываем решение 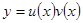 .
.
Видим, что метод вариации и метод подстановки, фактически, один и тот же метод. Просто в методе подстановки с самого начала используется то, что решение представляется в виде произведения двух функций независимой переменной.
Пример. 
Решим это уравнение Бернулли методом вариации произвольной постоянной.
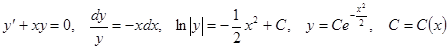 ,
,
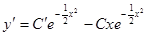 ,
, 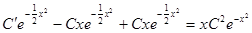
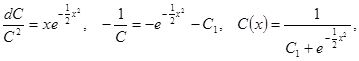
Уравнение в полных дифференциалах.
Любое дифференциальное уравнение первого порядка, разрешенное относительно старшей производной, можно записать в виде
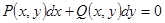 .
.
Если выполнено соотношение 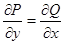 , то уравнение называется уравнением в полных дифференциалах.
, то уравнение называется уравнением в полных дифференциалах.
Причину такого названия понять легко. Пусть 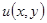 — функция двух переменных, дифференцируемая и имеющая непрерывные вторые частные производные по своим переменным. Тогда
— функция двух переменных, дифференцируемая и имеющая непрерывные вторые частные производные по своим переменным. Тогда 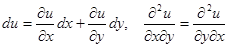 .
.
Если обозначить 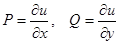 , то исходное уравнение можно записать в виде полного дифференциала
, то исходное уравнение можно записать в виде полного дифференциала
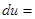
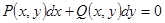 , а соотношение
, а соотношение 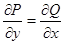 как раз и означает равенство смешанных производных
как раз и означает равенство смешанных производных  .
.
Поэтому решить уравнение в полных дифференциалах – означает найти функцию 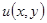 (она называется потенциалом). Так как
(она называется потенциалом). Так как 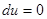 на решениях дифференциального уравнения, то потенциал будет первым интегралом исходного дифференциального уравнения:
на решениях дифференциального уравнения, то потенциал будет первым интегралом исходного дифференциального уравнения:

Для решения уравнения в полных дифференциалах можно использовать два способа.
1) 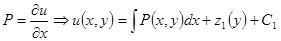 ,
,
 +
+ .
.
Здесь интегрирование ведется «частным образом»: только по переменной x, считая y константой или только по y, считая x константой.
Сравнивая оба выражения для 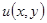 , находим функции
, находим функции 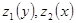 и константы.
и константы.
Если какой-либо из интегралов, например, 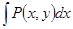 не берется или его вычислить сложно, то можно найти
не берется или его вычислить сложно, то можно найти  +
+ .
.
Затем, дифференцируя 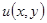 частным образом по x, надо сравнить
частным образом по x, надо сравнить  с
с 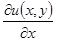 и определить функции
и определить функции 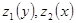 и константы.
и константы.
2) Потенциал можно определять по формуле (она будет выведена из независимости криволинейного интеграла от пути интегрирования позже, в 3 семестре)
.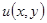
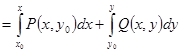 .
.
Пример. 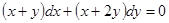 .
.
Решим уравнение первым способом.
Так как 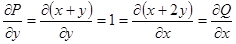 , то это – уравнение в полных дифференциалах.
, то это – уравнение в полных дифференциалах.
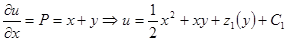 ,
,
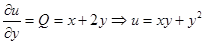
 .
.
Сравнивая оба равенства, видим, что 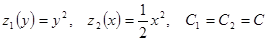 , поэтому
, поэтому 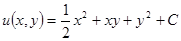 . Соотношение
. Соотношение  — это первый интеграл заданного дифференциального уравнения.
— это первый интеграл заданного дифференциального уравнения.
Решим уравнение вторым способом.
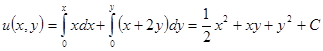 . Здесь принято
. Здесь принято 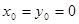 .
.
Интегрирующий множитель.
Можно поставить вопрос, нельзя ли любое дифференциальное уравнение первого порядка свести к уравнению в полных дифференциалах?
Оказывается, что существует такой интегрирующий множитель 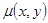 , умножая на который обе части любого дифференциального уравнения, удовлетворяющего условиям теоремы Коши, можно привести это уравнение к уравнению в полных дифференциалах.
, умножая на который обе части любого дифференциального уравнения, удовлетворяющего условиям теоремы Коши, можно привести это уравнение к уравнению в полных дифференциалах.
Однако неясно, как в общем случае найти этот интегрирующий множитель. Ясно только, что он должен удовлетворять уравнению
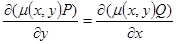 .
.
Оказывается, если 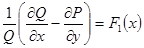 (является функций только одной переменной x), то
(является функций только одной переменной x), то 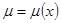 . Если
. Если 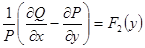 (является функций только одной переменной y), то
(является функций только одной переменной y), то 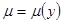 .
.
Пример. 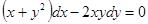 .
.
Покажите, что здесь выполняется первое условие и 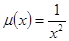 .
.
Найдите потенциал, покажите, что он равен 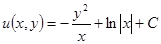 .
.
Как определять тип дифференциального уравнения первого порядка — КиберПедия
Ø Прежде всего, нужно знать типы всех уравнений и признаки каждого из них на память.
Ø Затем усвоить алгоритм распознавания типа дифференциального уравнения, который состоит из проверки признаков типов дифференциальных уравнений.
Ниже приводится сводная таблица типов дифференциальных уравнений первого порядка и их признаков.
Как только данное уравнение совпадает по признакам (или общему виду) с одним из типов, его следует решать, воспользовавшись соответствующим этому типу методом.
Чтобы определить дифференциального уравнения, его лучше записать либо в виде
, либо − как проще.
Дифференциальные уравнения второго порядка
Дифференциальное уравнение второго порядка имеет вид
(2.1)
или
. (2.2)
Общим решением уравнения (2.1) называется функция
(2.3)
Эта функция зависит от переменной x и двух произвольных постоянных , обращает данное уравнение в верное равенство.
Общее решение уравнения (2.1), заданное в неявном виде
, (2.4)
называется общим интегралом.
Частное решение
, (2.5)
где − фиксированные числа, получаются из общего решения (2.3) при фиксированных значениях .
Задача Коши. Найти решение дифференциального уравнения (2.1), удовлетворяющее условиям: .
Константы определяются из системы уравнений:
(2.6)
Дифференциальные уравнения второго порядка, допускающие
Понижение порядка
Рассмотрим три частных случая, когда решение уравнения (2.2) с помощью замены переменной сводится к решению уравнения первого порядка. Такие преобразования уравнения (2.2) называются понижением порядка.
Уравнения вида
Уравнение не содержит
.Уравнение интегрируется подстановкой , которая дает возможность свести его к уравнению с разделяющимися переменными .
Уравнения вида
Уравнение не содержитy.
Положим, как и в предыдущем случае, , тогда , и уравнение преобразуется в уравнение первого порядка относительно .
Уравнения вида
Уравнение не содержитx.
Вводим новую функцию , полагая . Тогда
.
Подставляя в уравнение выражения , получаем уравнение первого порядка относительно z как функции : .
Ниже приводится сводная таблица трех типов дифференциальных уравнений второго порядка, допускающих понижение порядка, и их признаков.
Обыкновенное дифференциальное уравнение — Википедия
Обыкновенное дифференциальное уравне́ние (ОДУ) — дифференциальное уравнение для функции от одной переменной. (Этим оно отличается от уравнения в частных производных, где неизвестная — функция нескольких переменных.) Таким образом, ОДУ — уравнения вида
- F(x,y,y′,y″,…,y(n))=0,(1){\displaystyle F(x,y,y’,y»,…,y^{(n)})=0,\qquad (1)}
где y(x){\displaystyle y(x)} — неизвестная функция (возможно, вектор-функция, тогда F{\displaystyle F}, как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной x{\displaystyle x}, штрих означает дифференцирование по x{\displaystyle x}. Число n{\displaystyle n} (порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).
Независимая переменная x{\displaystyle x} часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой t{\displaystyle t}. Переменная y{\displaystyle y} — некоторая величина (или совокупность величин, если y{\displaystyle y} является вектор-функцией), изменяющаяся со временем. Например, y{\displaystyle y} может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, то есть изменение её координат с течением времени. Независимая переменная x{\displaystyle x} обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная x{\displaystyle x} комплексная (так называемые уравнения с комплексным временем).
Наиболее часто встречаются дифференциальные уравнения вида
- y(n)=f(x,y,y′,y″,…,y(n−1)),(2){\displaystyle y^{(n)}=f(x,y,y’,y»,…,y^{(n-1)}),\qquad (2)}
в которых старшая производная y(n){\displaystyle y^{(n)}} выражается в виде функции от переменных x,{\displaystyle x,} y{\displaystyle y} и производных y(i){\displaystyle y^{(i)}} порядков меньше n.{\displaystyle n.} Такие дифференциальные уравнения называются нормальными или разрешёнными относительно производной.
В противоположность уравнениям вида (2), дифференциальные уравнения вида (1) называются уравнениями, не разрешёнными относительно производной или неявными дифференциальными уравнениями.
Классическим решением дифференциального уравнения (2) называется n{\displaystyle n} раз дифференцируемая функция y(x){\displaystyle y(x)}, удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие
- y(x0)=y0, y′(x0)=y0(1),y″(x0)=y0(2),…,y(n−1)(x0)=y0(n−1),(3){\displaystyle y(x_{0})=y_{0},\ y'(x_{0})=y_{0}^{(1)},y»(x_{0})=y_{0}^{(2)},\,\ldots ,\,y^{(n-1)}(x_{0})=y_{0}^{(n-1)},\qquad (3)}
где x0{\displaystyle x_{0}} — некоторое фиксированное значение независимой переменной (фиксированный момент времени), а y0{\displaystyle y_{0}} и y0(i){\displaystyle y_{0}^{(i)}} — соответственно, фиксированные значения функции y{\displaystyle y} и всех её производных до порядка n−1{\displaystyle n-1} включительно. Дифференциальное уравнение (2) вместе с начальным условием (3) называется начальной задачей или задачей Коши:
- {y(n)=f(x,y,y′,y″,…,y(n−1)),y(x0)=y0, y′(x0)=y0(1),y″(x0)=y0(2),…,y(n−1)(x0)=y0(n−1).{\displaystyle \left\{{\begin{array}{lcl}y^{(n)}=f(x,y,y’,y»,…,y^{(n-1)}),\\{}\\y(x_{0})=y_{0},\ y'(x_{0})=y_{0}^{(1)},y»(x_{0})=y_{0}^{(2)},\,\ldots ,\,y^{(n-1)}(x_{0})=y_{0}^{(n-1)}.\end{array}}\right.}
Теорема Пикара утверждает, что при достаточно общих ограничениях на функцию f{\displaystyle f}, стоящую в правой части уравнения (2), задача Коши для этого уравнения имеет единственное решение, определённое на некотором интервале оси времени x{\displaystyle x}, содержащем начальное значение x0{\displaystyle x_{0}} (этот интервал, вообще говоря, может не совпадать со всей осью).
Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач для ОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.
Дифференциальные уравнения встречались уже в работах И. Ньютона и Г. Лейбница; термин «дифференциальные уравнения» принадлежит Лейбницу. Ньютон при создании исчисления «флюксий» и «флюент» ставил две задачи: по данному соотношению между флюентами определить соотношение между флюксиями; по данному уравнению, содержащему флюксии, найти соотношение между флюентами. С современной точки зрения, первая из этих задач (вычисление по функциям их производных) относится к дифференциальному исчислению, а вторая составляет содержание теории обыкновенных дифференциальных уравнений. Задачу нахождения неопределённого интеграла F(x) функции f(x) Ньютон рассматривал просто как частный случай его второй задачи. Такой подход был для Ньютона как создателя основ математического естествознания вполне оправданным: в очень большом числе случаев законы природы, управляющие теми или иными процессами, выражаются в форме дифференциальных уравнений, а расчёт течения этих процессов сводится к решению дифференциального уравнения.[1]
Основное открытие Ньютона, то, которое он счёл нужным засекретить и опубликовал лишь в виде анаграммы, состоит в следующем: «Data aequatione quotcunque fluentes quantitae involvente fluxiones invenire et vice versa». В переводе на современный математический язык это означает: «Полезно решать дифференциальные уравнения». В настоящее время теория дифференциальных уравнений представляет собой трудно обозримый конгломерат большого количества разнообразных идей и методов, в высшей степени полезный для всевозможных приложений и постоянно стимулирующий теоретические исследования во всех отделах математики.[2][3]
- Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения. Например, в соответствии со вторым законом Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид mx¨=F(x,t){\displaystyle m{\ddot {x}}=F(x,t)}. Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки.
- Дифференциальное уравнение y′=y{\displaystyle y’=y}, вместе с начальным условием y(0)=1{\displaystyle y(0)=1}, задаёт экспоненту: y(x)=ex{\displaystyle y(x)=e^{x}}. Если x{\displaystyle x} обозначает время, то эта функция описывает, например, рост популяции в условиях неограниченности ресурсов, а также и многое другое.
- Решением дифференциального уравнения y′=f(x){\displaystyle y’=f(x)}, правая часть которого не зависит от неизвестной функции, является неопределённый интеграл
- y(x)=∫f(x)dx+C,{\displaystyle y(x)=\int \!f(x)\,dx+C,}
где C{\displaystyle C} — произвольная константа.
Дифференциальные уравнения первого порядка[править | править код]
Уравнения с разделяющимися переменными[править | править код]
Дифференциальное уравнение y˙=f(x,y){\displaystyle {\dot {y}}=f(x,y)} называется уравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде y′=f1(x)f2(y){\displaystyle y’=f_{1}(x)f_{2}(y)}. Тогда, в случае f2(y)≠0{\displaystyle f_{2}(y)\neq 0}, общим решением уравнения является ∫dyf2(y)=∫f1(x)dx{\displaystyle \int \!{\frac {dy}{f_{2}(y)}}=\int \!f_{1}(x)\,dx}.
Примеры физических задач, приводящих к уравнениям с разделяющимися переменными[править | править код]
Охлаждение тела[править | править код]
Пусть T{\displaystyle T} — температура тела, T0{\displaystyle T_{0}} — температура окружающей среды (T>T0{\displaystyle T>T_{0}}). Пусть Q{\displaystyle Q} — количество теплоты, c{\displaystyle c} — удельная теплоёмкость. Тогда количество теплоты, передаваемое окружающей среде до выравнивания температур, выражается формулой Q=mc(T−T0){\displaystyle Q=mc(T-T_{0})}, или, в дифференциальной форме, dQ=mcdT{\displaystyle dQ=mc\,dT}. С другой стороны, скорость отдачи тепла можно выразить в виде dQ=−k(T−T0)dt{\displaystyle dQ=-k(T-T_{0})\,dt}, где k{\displaystyle k} — некий коэффициент пропорциональности. Исключая из этих двух уравнений dQ{\displaystyle dQ}, получаем уравнение с разделяющимися переменными:
- mcdT=−k(T−T0)dt{\displaystyle mc\,dT=-k(T-T_{0})\,dt}.
Общим решением этого уравнения является семейство функций T=T0+Ce−ktmc{\displaystyle T=T_{0}+Ce^{-{\frac {kt}{mc}}}}.
Однородные уравнения[править | править код]
Дифференциальное уравнение y˙=f(x,y){\displaystyle {\dot {y}}=f(x,y)} называется однородным, если f(x,y){\displaystyle f(x,y)} — однородная функция нулевой степени. Функция f(x,y){\displaystyle f(x,y)} называется однородной степени k{\displaystyle k}, если для любого λ>0{\displaystyle \lambda >0} выполняется равенство f(λx,λy)=λkf(x,y){\displaystyle f(\lambda x,\lambda y)=\lambda ^{k}f(x,y)}.
Замена y(x)=xz(x){\displaystyle y(x)=xz(x)} приводит при x>0{\displaystyle x>0} однородное уравнение к уравнению с разделяющимися переменными:
- f(x,xz)=x0f(1,z)=f(1,z){\displaystyle f(x,xz)=x^{0}f(1,z)=f(1,z)}
- y˙=xz˙+z{\displaystyle {\dot {y}}=x{\dot {z}}+z}
Подставив в исходное уравнение, получаем:
- z˙=1x(f(1,z)−z){\displaystyle {\dot {z}}={\frac {1}{x}}(f(1,z)-z)},
что является уравнением с разделяющимися переменными.
Квазиоднородные уравнения[править | править код]
Дифференциальное уравнение y˙=f(x,y){\displaystyle {\dot {y}}=f(x,y)} называется квазиоднородным, если для любого λ>0{\displaystyle \lambda >0} выполняется соотношение f(λαx,λβy)=λβ−αf(x,y){\displaystyle f\left(\lambda ^{\alpha }x,\lambda ^{\beta }y\right)=\lambda ^{\beta -\alpha }f(x,y)}.
Данное уравнение решается заменой y=zβα{\displaystyle y=z^{\frac {\beta }{\alpha }}}:
- z˙=αβ(z−1α)β−αf(x,zβα){\displaystyle {\dot {z}}={\frac {\alpha }{\beta }}\left(z^{-{\frac {1}{\alpha }}}\right)^{\beta -\alpha }f\left(x,z^{\frac {\beta }{\alpha }}\right)}
В силу квазиоднородности, положив λ=z−1α{\displaystyle \lambda =z^{-{\frac {1}{\alpha }}}}, получаем:
- (z−1α)β−αf(x,zβα)=f(xz,1){\displaystyle \left(z^{-{\frac {1}{\alpha }}}\right)^{\beta -\alpha }f\left(x,z^{\frac {\beta }{\alpha }}\right)=f\left({\frac {x}{z}},1\right)}
- z˙=αβf(xz,1){\displaystyle {\dot {z}}={\frac {\alpha }{\beta }}f\left({\frac {x}{z}},1\right)},
что, очевидно, является однородным уравнением.
Линейные уравнения[править | править код]
Дифференциальное уравнение y′+a(x)y=b(x){\displaystyle y’+a(x)y=b(x)} называется линейным и может быть решено тремя методами: методом интегрирующего множителя, методом вариации постоянной или методом Бернулли.
Метод интегрирующего множителя[править | править код]
Пусть задана функция μ(x){\displaystyle \mu (x)} — интегрирующий множитель, в виде:
- μ(x)=e∫a(x)dx{\displaystyle \mu (x)=e^{\int \!a(x)\,dx}}
Умножим обе части исходного уравнения на μ(x){\displaystyle \mu (x)}, получим:
- y˙e∫a(x)dx+ya(x)e∫a(x)dx=b(x)μ(x){\displaystyle {\dot {y}}e^{\int \!a(x)\,dx}+ya(x)e^{\int \!a(x)\,dx}=b(x)\mu (x)}
Легко заметить, что левая часть является производной функции μ(x)y(x){\displaystyle \mu (x)y(x)} по x{\displaystyle x}. Поэтому уравнение можно переписать:
- (μ(x)y(x))′=b(x)μ(x){\displaystyle (\mu (x)y(x))’=b(x)\mu (x)}
Проинтегрируем:
- y(x)μ(x)=∫b(x)μ(x)dx+C{\displaystyle y(x)\mu (x)=\int \!b(x)\mu (x)\,dx+C}
Таким образом, решение линейного уравнения будет:
- y(x)=e−∫a(x)dx(∫b(x)μ(x)dx+C){\displaystyle y(x)=e^{-\int \!a(x)\,dx}\left(\int \!b(x)\mu (x)\,dx+C\right)}
Метод вариации постоянной (метод Лагранжа)[править | править код]
Рассмотрим однородное уравнение y˙+a(x)y=0{\displaystyle {\dot {y}}+a(x)y=0}. Очевидно, это уравнение с разделяющимися переменными, его решение:
- y(x)=ce−∫a(x)dx{\displaystyle y(x)=ce^{-\int \!a(x)\,dx}}
Решения исходного уравнения будем искать в виде:
- y(x)=c(x)e−∫a(x)dx{\displaystyle y(x)=c(x)e^{-\int \!a(x)\,dx}}
Подставив полученное решение в исходное уравнение:
- c˙=b(x)e∫a(x)dx{\displaystyle {\dot {c}}=b(x)e^{\int \!a(x)\,dx}},
получаем:
- c(x)=c1+∫b(x)e∫a(x)dxdx{\displaystyle c(x)=c_{1}+\int \!b(x)e^{\int \!a(x)\,dx}\,dx},
где c1{\displaystyle c_{1}} — произвольная константа.
Таким образом, решение исходного уравнения можно получить путём подстановки c(x){\displaystyle c(x)} в решение однородного уравнения:
- y(x)=e−∫
Линейное дифференциальное уравнение — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июля 2018; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 июля 2018; проверки требует 1 правка.В математике линейное дифференциальное уравнение имеет вид
- Ly=f{\displaystyle Ly=f}
где дифференциальный оператор L линеен, y — неизвестная функция y=y(t){\displaystyle y=y(t)}, а правая часть f=f(t){\displaystyle f=f(t)} — функция от той же переменной, что и y.
Линейный оператор L можно рассматривать в форме
- Ln(y)≡dnydtn+A1(t)dn−1ydtn−1+⋯+An−1(t)dydt+An(t)y{\displaystyle L_{n}(y)\equiv {\frac {d^{n}y}{dt^{n}}}+A_{1}(t){\frac {d^{n-1}y}{dt^{n-1}}}+\cdots +A_{n-1}(t){\frac {dy}{dt}}+A_{n}(t)y}
При этом, если f(t)≡0{\displaystyle f(t)\equiv 0}, то такое уравнение называется линейным однородным уравнением, иначе — линейным неоднородным уравнением.
Уравнения с переменными коэффициентами[править | править код]
Линейное дифференциальное уравнение порядка n с переменными коэффициентами имеет общий вид
- pn(x)y(n)(x)+pn−1(x)y(n−1)(x)+⋯+p0(x)y(x)=r(x){\displaystyle p_{n}(x)y^{(n)}(x)+p_{n-1}(x)y^{(n-1)}(x)+\cdots +p_{0}(x)y(x)=r(x)}
Пример[править | править код]
Уравнение Коши — Эйлера, используемое в инженерии, является простым примером линейного дифференциального уравнения с переменными коэффициентами
- xny(n)(x)+an−1xn−1y(n−1)(x)+⋯+a0y(x)=0{\displaystyle x^{n}y^{(n)}(x)+a_{n-1}x^{n-1}y^{(n-1)}(x)+\cdots +a_{0}y(x)=0}
Пример
Решение уравнения
- y′(x)+3(y)=2{\displaystyle y’\left(x\right)+3\left(y\right)=2}
с начальными условиями
- y(0)=2{\displaystyle y\left(0\right)=2}
Имеем решение в общем виде
- y=e−3x(∫2e3xdx+κ){\displaystyle y=e^{-3x}\left(\int 2e^{3x}\,dx+\kappa \right)}
Решение неопределённого интеграла
- y=e−3x(2/3e3x+κ){\displaystyle y=e^{-3x}\left(2/3e^{3x}+\kappa \right)}
Можно упростить до
- y=2/3+κe−3x{\displaystyle y=2/3+\kappa e^{-3x}}
где κ={\displaystyle \kappa =} 4/3, после подстановки начальных условий в решение.
Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид
- y′(x)+f(x)y(x)=g(x){\displaystyle y'(x)+f(x)y(x)=g(x)}
Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель
- e∫f(x)dx{\displaystyle e^{\int f(x)\,dx}}
получим
- y′(x)e∫f(x)dx+f(x)y(x)e∫f(x)dx=g(x)e∫f(x)dx,{\displaystyle y'(x)e^{\int f(x)\,dx}+f(x)y(x)e^{\int f(x)\,dx}=g(x)e^{\int f(x)\,dx},}
используем правило дифференцирования произведения
- (y(x)e∫f(x)dx)′=g(x)e∫f(x)dx{\displaystyle \left(y(x)e^{\int f(x)\,dx}\right)’=g(x)e^{\int f(x)\,dx}}
что, после интегрирования обеих частей, дает нам
- y(x)e∫f(x)dx=∫g(x)e∫f(x)dxdx+C ,{\displaystyle y(x)e^{\int f(x)\,dx}=\int g(x)e^{\int f(x)\,dx}\,dx+C~,}
- y(x)=∫g(x)e∫f(x)dxdx+Ce∫f(x)dx .{\displaystyle y(x)={\dfrac {\int g(x)e^{\int f(x)\,dx}\,dx+C}{e^{\int f(x)\,dx}}}~.}
Таким образом, решение линейного дифференциального уравнения первого порядка
- y′(x)+f(x)y(x)=g(x),{\displaystyle y'(x)+f(x)y(x)=g(x),}
(в частности, с постоянными коэффициентами) имеет вид
- y(x)=e−∫f(x)dx(∫g(x)e∫f(x)dxdx+C){\displaystyle y(x)=e^{-{\int {f(x)\,dx}}}\left(\int g(x)e^{\int {f(x)\,dx}}\,dx+C\right)}
где C{\displaystyle C} является константой интегрирования.
Пример[править | править код]
Возьмём дифференциальное уравнение первого порядка с постоянными коэффициентами:
- dydx+by=1.{\displaystyle {\frac {dy}{dx}}+by=1.}
Это уравнение имеет особое значение для систем первого порядка, таким как RC-схемы и масс-демпфер[неизвестный термин] системы.
В этом случае p(x) = b, r(x) = 1.
Следовательно, решение будет:
- y(x)=e−bx(ebx/b+C)=1/b+Ce−bx.{\displaystyle y(x)=e^{-bx}\left(e^{bx}/b+C\right)=1/b+Ce^{-bx}.}